中考数学几何专项——相似模型(相似三角形)

合集下载

2025届中考数学复习专项(相似三角形-手拉手旋转型综合应用)练习(附答案)

2025届中考数学复习专项（相似三角形-手拉手旋转型综合应用）练习1．如图（1）以O点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出ΔOB1C1；（2）点B的对应点B1的坐标是，点C的对应点C1的坐标是．2．如图，在△ABC和△ADE中，∠BAD＝∠CAE，∠ABC＝∠ADE．（1）求证：△ABC∽△ADE；（2）判断△ABD与△ACE是否相似？并证明．3．如图1，在Rt△ABC中，∠B＝90°，AB＝4，BC＝2，点D、E分别是边BC，AC的中点，连接DE．（1）求：的值；（2）将△CDE绕点C逆时针方向旋转一定的角度，的大小有无变化？请仅就图2的情形给出证明．4．如图，在△ABC与△DEC中，已知∠ACB＝∠DCE＝90°，AC＝6，BC＝3，CD＝5，CE＝2.5，连接AD，BE．（1）求证：△ACD∽△BCE；（2）若∠BCE＝45°，求△ACD的面积．5．问题背景：如图（1），已知△ABC∽△ADE，求证：△ABD∽△ACE；尝试应用：如图（2），在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE ＝30°，AC与DE相交于点F．点D在BC边上，，求的值．6．如图，在△ABC与△ADE中，∠ACB＝∠AED＝90°，∠ABC＝∠ADE，连接BD、CE，求证：（1）△ABC∽△ADE（2）若AC：BC＝3：4，求BD：CE为多少7．【问题背景】如图1，在Rt△ABC和Rt△ADE中，AB＝AC，AD＝AE，由已知可以得到：①△ ≌△ ；②△ ∽△ ．【尝试应用】如图2，在△ABC和△ADE中，∠ACB＝∠AED＝90°，∠ABC＝∠ADE ＝30°，求证：△ACE∽△ABD．【问题解决】如图3，在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE ＝30°，AC与DE相交于点F，点D在BC上，，求的值．8．如图，点B在线段CD上，在CD的同一侧作两个等腰直角△ABC和△BDE，且∠ACB ＝∠BED＝90°，AD与CE，BE分别交于点P，M，连接PB．（1）若AD＝k•CE，则k的值是；（2）求证：△BMP∽△DME；（3）若BC＝，P A＝3，求PM的长．9．如图1，在Rt△ABC中，AC＝BC＝5，等腰直角△BDE的顶点D，E分别在边BC，AB 上，且BD＝，将△BDE绕点B按顺时针方向旋转，记旋转角为α（0°≤α＜360°）．（1）问题发现当α＝0°时，的值为，直线AE，CD相交形成的较小角的度数为；（2）拓展探究试判断：在旋转过程中，（1）中的两个结论有无变化？请仅就图2的情况给出证明：（3）问题解决当△BDE旋转至A，D，E三点在同一条直线上时，请直接写出△ACD的面积．。

相似三角形重要模型-手拉手模型(学生版)-初中数学

相似三角形重要模型-手拉手模型相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

手拉手模型相似是手拉手模型当中相对于手拉手全等模型较难的一种模型，在实际的应用和解题当中出现时，对于同学们来说，都比较困难。

而深入理解模型内涵，灵活运用相关结论可以显著提高解题效率，本专题重点讲解相似三角形的“手拉手”模型(旋转模型)。

手拉手相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等；②分子和分子组成一个三角形、分母和分母组成一个三角形；③第②步成立，直接从证这两个三角形相似，逆向证明到线段乘积相等；④第②步不成立，则选择替换掉线段比例式中的个别线段，之后再重复第③步。

模型1.“手拉手”模型(旋转模型)【模型解读与图示】“手拉手”旋转型定义：如果将一个三角形绕着它的项点旋转并放大或缩小(这个顶点不变)，我们称这样的图形变换为旋转相似变换，这个顶点称为旋转相似中心，所得的三角形称为原三角形的旋转相似三角形。

1)手拉手相似模型(任意三角形)条件:如图，∠BAC =∠DAE =α，AD AB =AE AC=k ；结论：△ADE ∽△ABC ，△ABD ∽△ACE ；EC BD =k .2)手拉手相似模型(直角三角形)条件:如图，∠AOB =∠COD =90°，OC OA =OD OB =k (即△COD ∽△AOB )；结论：△AOC ∽△BOD ；BD AC =k ，AC ⊥BD ，S ABCD =12AB ×CD .3)手拉手相似模型(等边三角形与等腰直角三角形)条件:M 为等边三角形ABC 和DEF 的中点；结论：△BME ∽△CMF ；BE CF=3.条件:△ABC 和ADE 是等腰直角三角形；结论：△ABD ∽△ACE .1(2023秋·福建泉州·九年级校考期末)问题背景：(1)如图①，已知△ABC ∽△ADE ，求证：△ABD ∽△ACE ；尝试应用：(2)如图②，在△ABC 和△ADE 中，∠BAC =∠DAE =90°，∠ABC =∠ADE =60°，AC 与DE相交于点F ，点D 在BC 边上，DF CF=233，求AD BD 的值；拓展创新：(3)如图③，D 是△ABC 内一点，∠BAD =∠CBD =30°，∠BDC =90°，AB =4，AC =23，求AD 的长．2(2023秋·江苏无锡·九年级校考阶段练习)【模型呈现：材料阅读】如图，点B ，C ，E 在同一直线上，点A ，D 在直线CE 的同侧，△ABC 和△CDE 均为等边三角形，AE ，BD 交于点F ，对于上述问题，存在结论(不用证明)：(1)△BCD ≌△ACE (2)△ACE 可以看作是由△BCD 绕点C 旋转而成；⋯【模型改编：问题解决】点A ，D 在直线CE 的同侧，AB =AC ，ED =EC ，∠BAC =∠DEC =50°，直线AE ，BD 交于F ，如图1：点B 在直线CE 上，①求证：△BCD ∽△ACE ； ②求∠AFB 的度数．如图2：将△ABC 绕点C 顺时针旋转一定角度．③补全图形，则∠AFB 的度数为；④若将“∠BAC =∠DEC =50°”改为“∠BAC =∠DEC =m °”，则∠AFB 的度数为．(直接写结论)【模型拓广：问题延伸】如图3：在矩形ABCD和矩形DEFG中，AB=2，AD=ED=23，DG=6，连接AG，BF，求BFAG的值．图1 图2 图33(2023春·湖北黄冈·九年级专题练习)【问题呈现】△CAB和△CDE都是直角三角形，∠ACB=∠DCE=90°,CB=mCA,CE=mCD，连接AD，BE，探究AD，BE的位置关系．(1)如图1，当m=1时，直接写出AD，BE的位置关系：；(2)如图2，当m≠1时，(1)中的结论是否成立？若成立，给出证明；若不成立，说明理由．【拓展应用】(3)当m=3,AB=47,DE=4时，将△CDE绕点C旋转，使A,D,E三点恰好在同一直线上，求BE的长．4(2023秋·福建泉州·九年级校考阶段练习)如图，已知△ABC中，AB=AC，∠BAC=α．点D是△ABC 所在平面内不与点A、C重合的任意一点，连接CD，将线段CD绕点D顺时针旋转α得到线段DE，连接AD、BE．(1)如图1，当α=60°时，求证：BE=AD．(2)当α=120°时，请判断线段BE与AD之间的数量关系是，并仅就图2的情形说明理由．(3)当α=90°时，且BE⊥AB时，若AB=8，BE=2，点E在BC上方，求CD的长．5(2023·黑龙江齐齐哈尔·统考中考真题)综合与实践数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．(1)发现问题：如图1，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=30°，连接BE，CF，延长BE交CF于点D．则BE与CF的数量关系：，∠BDC=°；(2)类比探究：如图2，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；(3)拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC=∠EAF=90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系：；(4)实践应用：正方形ABCD中，AB=2，若平面内存在点P满足∠BPD=90°，PD=1，则S△ABP=．6(2023·山东济南·九年级统考期中)问题背景：一次小组合作探究课上，小明将一个正方形ABCD和等腰Rt△CEF按如图1所示的位置摆放(点B、C、E在同一条直线上)，其中∠ECF=90°．小组同学进行了如下探究，请你帮助解答：初步探究(1)如图2，将等腰Rt△CEF绕点C按顺时针方向旋转，连接BF，DE．请直接写出BF与DE的关系；(2)如图3，将(1)中的正方形ABCD和等腰Rt△CEF分别改成菱形ABCD和等腰△CEF，其中CE=CF，∠BCD=∠FCE，其他条件不变，求证：BF=DE；深入探究：(3)如图4，将(1)中的正方形ABCD和等腰Rt△CEF分别改成矩形ABCD和Rt△CEF，其中∠ECF=90°且CECF =CDBC=34，其它条件不变．①探索线段BF与DE的关系，说明理由；②连接DF，BE若CE=6，AB=12，直接写出DF2+BE2=．7(2023春·广东·九年级专题练习)已知在△ABC中，O为BC边的中点，连接AO，将△AOC绕点O顺时针方向旋转(旋转角为钝角)，得到△EOF，连接AE，CF．(1)如图1，当∠BAC=90°且AB=AC时，则AE与CF满足的数量关系是；(2)如图2，当∠BAC=90°且AB≠AC时，(1)中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；(3)如图3，延长AO到点D，使OD=OA，连接DE，当AO=CF=5，BC=6时，求DE的长．课后专项训练1(2023秋·北京顺义·九年级校考期中)如图，△ABC和△ADE都是等腰直角三角形，∠ABC=∠ADE=90°．连接BD，CE．则BDCE的值为()A.12B.22C.2D.22(2023春·浙江金华·九年级校考期中)如图，在Rt△ABC中，∠ABC=90°，以AB，AC为边分别向外作正方形ABFG和正方形ACDE，CG交AB于点M，BD交AC于点N．若GMCM=12，则CGBD=()A.12B.34C.255D.130133(2023春·浙江丽水·九年级专题练习)如图，在△ABC 中，过点C 作CD ⊥AB ，垂足为点D ，过点D 分别作DE ⊥AC ，DF ⊥BC ，垂足分别为E ，F ．连接EF 交线段CD 于点O ，若CO =22，CD =32，则EO ⋅FO 的值为( )．A.63B.4C.56D.64(2022·广西梧州·统考一模)如图，在△ABC 中，∠C =45°，将△ABC 绕着点B 逆时针方向旋转，使点C 的对应点C ′落在CA 的延长线上，得到△A ′BC ′，连接AA ′，交BC ′于点O ．下列结论：①∠AC ′A ′=90°；②AA ′=BC ′；③∠A ′BC ′=∠A ′AC ′；④△A ′OC ′∽△BOA ．其中正确结论的个数是()A.1B.2C.3D.45(2023·广东深圳·校联考模拟预测)如图，已知▱ABCD ，AB =3，AD =8，将▱ABCD 绕点A 顺时针旋转得到▱AEFG ，且点G 落在对角线AC 上，延长AB 交EF 于点H ，则FH 的长为．6(2022·安徽·模拟预测)如图，将边长为3的菱形ABCD绕点A逆时针旋转到菱形AB C D 的位置，使点B 落在BC上，B C 与CD交于点E．若BB =1，则CE的长为．7(2021·湖南益阳·统考中考真题)如图，Rt△ABC中，∠BAC=90°,tan∠ABC=32，将△ABC绕A点顺时针方向旋转角α(0°<α<90°)得到△AB C ，连接BB ，CC ，则△CAC 与△BAB 的面积之比等于．8(2023秋·山东济南·九年级校考阶段练习)如图，已知∠ACB=∠DCE=90°，∠ABC=∠CED=∠CAE=30°．(1)求证：△ACD∽△BCE；(2)若AC=3，AE=8，求AD．9(2023·安徽滁州·九年级校考阶段练习)如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，CD与BE、AE分别交于点P、M．求证：(1)△BAE∽△CAD；(2)MP⋅MD=MA⋅ME．10(2023秋·湖北孝感·九年级校联考阶段练习)问题背景：如图1，在△ABC中，∠ACB=90°，AC= BC，AD是BC边上的中线，E是AD上一点，将△CAE绕点C逆时针旋转90°得到△CBF，AD的延长线交BF于点P．问题探究：(1)当点P在线段BF上时，证明EP+FP=2BP．①先将问题特殊化，如图2，当CE⊥AD时，证明：EP+FP=2BP；②再探究一般情形，如图1，当CE不垂直AD时，证明：EP+FP=2BP；拓展探究：(2)如图3，若AD的延长线交BF的延长线于点P时，直接写出一个等式，表示EP，FP，BP之间的数量关系．11(2022·河南·九年级专题练习)规定：有一角重合，且角的两边叠合在一起的两个相似四边形叫做“嵌套四边形”，如图，四边形ABCD和AMPN就是嵌套四边形．(1)问题联想：如图①，嵌套四边形ABCD，AMPN都是正方形，现把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N'，连接BM'，DN'交于点O，则BM'与DN'的数量关系为，位置关系为；(2)类比探究：如图②，将(1)中的正方形换成菱形，∠BAD=∠MAN=60，其他条件不变，则(1)中的结论还成立吗?若成立，请说明理由；若不成立，请给出正确的结论，并说明理由；(3)拓展延伸：如图3，将(1)中的嵌套四边形ABCD和AMPN换成是长和宽之比为2:1的矩形，旋转角换成α(90°<α<180°)，其他条件不变，请直接写出BM'与DN'的数量关系和位置关系．12(2023·山东青岛·模拟预测)某校一数学兴趣小组在一次合作探究活动中，将两块大小不同的等腰直角三角形ABC和等腰直角三角形CDE，按如图1的方式摆放，∠ACB=∠ECD=90°，随后保持△ABC不动，将△CDE绕点C按逆时针方向旋转α(0°<α<90°)，连接AE，BD，延长BD交AE于点F，连接CF．该数学兴趣小组进行如下探究，请你帮忙解答：(1)【初步探究】如图2，当ED ∥BC 时，则α=；(2)【初步探究】如图3，当点E ，F 重合时，请直接写出AF ，BF ，CF 之间的数量关系：；(3)【深入探究】如图4，当点E ，F 不重合时，(2)中的结论是否仍然成立？若成立，请给出推理过程；若不成立，请说明理由．(4)【拓展延伸】如图5，在△ABC 与△CDE 中，∠ACB =∠DCE =90°，若BC =mAC ，CD =mCE (m 为常数)．保持△ABC 不动，将△CDE 绕点C 按逆时针方向旋转α(0°<α<90°)，连接AE ，BD ，延长BD 交AE 于点F ，连接CF ，如图6．试探究AF ，BF ，CF 之间的数量关系，并说明理由．13(2023秋·湖北恩施·九年级校考阶段练习)问题提出如图1，在△ABC 中，AB =BC ，点D 是边BC 上一点，△ADE 是等腰三角形，AD =DE ，∠ADE =∠B =α0<α≤90° ，DE 交AC 于点F ，探究∠DCE 与α的数量关系.问题探究 (1)先将问题特殊化，如图2，当α=90°时，直接写出∠DCE 的大小；(2)再探究一般情形，如图1，求∠DCE 与α的数量关系.问题拓展将图1特殊化，如图3，当α=60°时，若CD BD =12，求CF AF的值.14(2023春·河南·九年级专题练习)由两个顶角相等且有公共顶角顶点的特殊多边形组成的图形，如果把它们的底角顶点连接起来，则在相对位置变化的过程中，始终存在一对全等三角形，我们把这种模型称为“手拉手模型”．(1)【问题发现】如图1所示，两个等腰直角三角形△ABC 和△ADE 中，AB =AC ，AE =AD ，∠BAC =∠DAE =90°，连接BD 、CE ，两线交于点P ，BD 和CE 的数量关系是；BD 和CE 的位置关系是；(2)【类比探究】如图2所示，点P 是线段AB 上的动点，分别以AP 、BP 为边在AB 的同侧作正方形APCD 与正方形PBEF ，连接DE 分别交线段BC 、PC 于点M 、N ．①求∠DMC 的度数；②连接AC 交DE 于点H ，直接写出DH BC 的值；(3)【拓展延伸】如图3所示，已知点C 为线段AE 上一点，AE =6，△ABC 和△CDE 为AE 同侧的两个等边三角形，连接BE 交CD 于N ，连接AD 交BC 于M ，连接MN ，直接写出线段MN 的最大值．15(2023秋·江苏泰州·九年级校考阶段练习)类比探究【问题背景】已知D 、E 分别是△ABC 的AB 边和AC 边上的点，且DE ∥BC ，则△ABC ∽△ADE 把△ADE 绕着A 逆时针方向旋转，连接BD 和CE ．①如图2，找出图中的另外一组相似三角形②若AB =4，AC =3，BD =2，则CE =．【迁移应用】在Rt △ACB 中，∠BAC =90°，∠C =60°，D 、E 、M 分别是AB 、AC 、BC 中点，连接DE 和CM ．①如图3，写出CE 和BD 的数量关系；②如图4，把Rt △ADE 绕着点A 逆时针方向旋转，当D 落在AM 上时，连接CD 和CE ，取CD 中点N ，连接MN ，若CE =23，求MN 的长．【创新应用】如图5：AB =AC =AE =25，BC =4，△ADE 是直角三角形，∠DAE =90°，tan ∠ADE =2，将△ADE绕着点A旋转，连接BE，F是BE上一点，且BFBE=25，连接CF，请直接写出CF的取值范围．16(2023秋·山东济南·九年级校考阶段练习)(1)如图1，正方形ABCD和正方形DEFG(其中AB> DE)，连接CE，AG交于点H，请直接写出线段AG与CE的数量关系是，位置关系是．(2)如图2，矩形ABCD和矩形DEFG，3AD=2DG，3AB=2DE，DC=DG，将矩形DEFG绕点D逆时针旋转α(0°<α<360°)，连接AG，CE交于点H，(1)中线段关系还成立吗？若成立，请写出理由；若不成立，请写出线段AG，CE的数量关系和位置关系，并说明理由．17(2023秋·重庆沙坪坝·九年级校考阶段练习)如图，△ABC中，∠BAC=90°，AB=AC=8，△AEF 中，∠EAF=90°，AE=AF，连接BE．(1)如图1，当AE平分∠BAC时，EF与AB交于点D，若AE=32，求tan∠DBE的值；(2)如图2，当AE⊥BE时，连接CF，与AE交于点H．猜想AH与BE之间的数量关系，并证明你的猜想；(3)如图3，AN⊥BC于点N，取BE的中点M，连接AM、CM、MN．将△AEF绕点A旋转．若AE= 22，在旋转过程中，当线段CM最大时，请直接写出△AMN的面积．18(2022秋·广东深圳·九年级校联考期中)【模型发现】如图1，△ABC∽△ADE，求证：△ABD∽△ACE．【深入探究】如图2，等边△ABC中，AB=3，D是AC上的动点，连接BD，将BD绕着点D逆时针旋转60°得到DE，连接CE，当点D从A运动到C时，求点E的运动路径长．【应用拓展】如图3，等腰Rt△ABC中，∠BAC=90°，AD⊥BC于D，E是AD上的一点，连接BE，将BE绕着点E逆时针旋转90°得到EF，EF交BC于点G，连接CF，若EG=12FG，则ABCF的值为．。

初三数学相似三角形典型例题(附含答案解析)

2初三数学相似三角形（一）相似三角形是初中几何的一个重点，同时也是一个难点，本节复习的目标是：1. 理解线段的比、成比例线段的概念，会根据比例线段的有关概念和性质求线段的长或两线段的比，了解黄金分割。

2. 会用平行线分线段成比例定理进行有关的计算、证明，会分线段成已知比。

3. 能熟练应用相似三角形的判定和性质解答有关的计算与证明题。

4.能熟练运用相似三角形的有关概念解决实际问题本节的重点内容是相似三角形的判定定理和性质定理以及平行线分线段成比例定理。

本节的难点内容是利用判定定理证明两个三角形相似以及相似三角形性质的应用。

相似三角形是平面几何的主要内容之一，在中考试题中时常与四边形、圆的知识相结合构成高分值的综合题，题型常以填空、选择、简答或综合出现，分值一般在 10%左右，有时也单独成题，形成创新与探索型试题；有利于培养学生的综合素质。

（二）重要知识点介绍： 1.比例线段的有关概念：在比例式 ab c (a ： bc ：d )中， a 、 d 叫外项，db 、c 叫内项， a 、c 叫前项， b 、d 叫后项， d 叫第四比例项，如果 b=c ，那么 b 叫做 a 、 d 的比例中项。

把线段 AB 分成两条线段 AC 和 BC ，使 AC=AB BC ，叫做把线段 AB 黄金分割， C 叫做线段 AB 的黄金分割点。

2. 比例性质：①基本性质： ac b d②合比性质：acb dad bca b c d bd③等比性质：a c⋯b dm (b d ⋯ nn ≠ 0) a c ⋯ m ab d ⋯ nb3.平行线分线段成比例定理：①定理：三条平行线截两条直线，所得的对应线段成比例，如图：l 1∥ l 2∥ l 3 。

AB 则BCDE ， ABEF AC DE ， BCDF AC EF ，⋯DF②推论：平行于三角形一边的直线截其他两边（或两边的延长线）所得的对应线段成比例。

③定理：如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边。

初三数学相似三角形典例及练习(含答案)

初三数学相似三角形（一）相似三角形是初中几何的一个重点，同时也是一个难点，本节复习的目标是：1。

理解线段的比、成比例线段的概念，会根据比例线段的有关概念和性质求线段的长或两线段的比，了解黄金分割.2. 会用平行线分线段成比例定理进行有关的计算、证明，会分线段成已知比。

3. 能熟练应用相似三角形的判定和性质解答有关的计算与证明题。

4. 能熟练运用相似三角形的有关概念解决实际问题本节的重点内容是相似三角形的判定定理和性质定理以及平行线分线段成比例定理。

本节的难点内容是利用判定定理证明两个三角形相似以及相似三角形性质的应用。

相似三角形是平面几何的主要内容之一,在中考试题中时常与四边形、圆的知识相结合构成高分值的综合题,题型常以填空、选择、简答或综合出现，分值一般在10%左右，有时也单独成题,形成创新与探索型试题；有利于培养学生的综合素质。

（二）重要知识点介绍： 1。

比例线段的有关概念：在比例式：：中，、叫外项，、叫内项，、叫前项，a b cda b c d a d b c a c ==() b 、d 叫后项，d 叫第四比例项，如果b=c ，那么b 叫做a 、d 的比例中项。

把线段AB 分成两条线段AC 和BC,使AC 2=AB ·BC ，叫做把线段AB 黄金分割，C 叫做线段AB 的黄金分割点。

2. 比例性质: ①基本性质：a b cdad bc =⇔= ②合比性质：±±a b c d a b b c d d=⇒= ③等比性质：……≠……a b c d m n b d n a c m b d n a b===+++⇒++++++=()03。

平行线分线段成比例定理：①定理：三条平行线截两条直线，所得的对应线段成比例，如图：l 1∥l 2∥l 3。

则，，，…AB BC DE EF AB AC DE DF BC AC EFDF===②推论：平行于三角形一边的直线截其他两边(或两边的延长线）所得的对应线段成比例。

中考数学相似三角形重要模型一线三等角模型

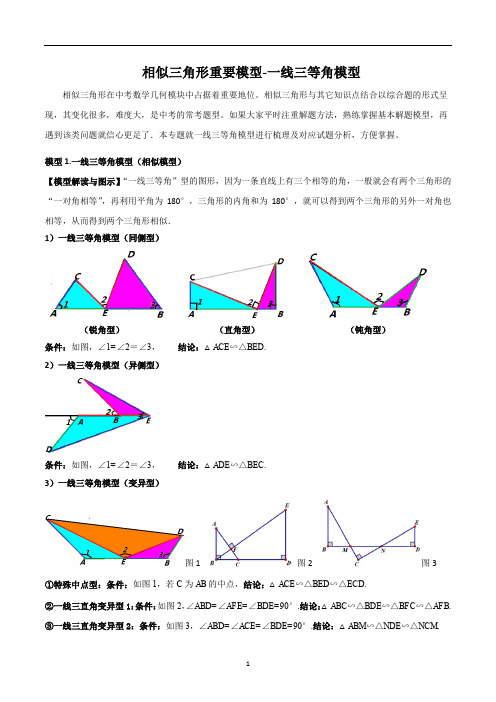
相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。

相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。

如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了．本专题就一线三等角模型进行梳理及对应试题分析，方便掌握。

模型1.一线三等角模型（相似模型）【模型解读与图示】“一线三等角”型的图形，因为一条直线上有三个相等的角，一般就会有两个三角形的“一对角相等”，再利用平角为180°，三角形的内角和为180°，就可以得到两个三角形的另外一对角也相等，从而得到两个三角形相似．1）一线三等角模型（同侧型）（锐角型）（直角型）（钝角型）条件：如图，∠1=∠2＝∠3，结论：△ACE∽△BED.2）一线三等角模型（异侧型）条件：如图，∠1=∠2＝∠3，结论：△ADE∽△BEC.3）一线三等角模型（变异型）图1 图2 图3①特殊中点型：条件：如图1，若C为AB的中点，结论：△ACE∽△BED∽△ECD.②一线三直角变异型1：条件：如图2，∠ABD=∠AFE=∠BDE=90°.结论：△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2：条件：如图3，∠ABD=∠ACE=∠BDE=90°.结论：△ABM∽△NDE∽△NCM.例1．（2023·山东东营·统考中考真题）如图，A B C为等边三角形，点D，E分别在边B C，A B上，60A D E∠=︒，若4B D D C=， 2.4D E=，则A D的长为（）A．1.8B．2.4C．3D．3.2例2．（2023·湖南·统考中考真题）如图，,C A ADE D A D⊥⊥，点B是线段A D上的一点，且C B B E⊥．已知8,6,4A B A C D E===．(1)证明：A B C D E B∽△△．(2)求线段B D的长．例3．（2022·河南新乡·九年级期中）某学习小组在探究三角形相似时，发现了下面这种典型的基本图形．（1）如图1，在ABC中，∠BAC＝90°，A BA C＝k，直线l经过点A，BD⊥直线I，CE上直线l，垂足分别为D、E．求证：B DA E＝k．（2）组员小刘想，如果三个角都不是直角，那么结论是否仍然成立呢？如图2，将（1）中的条件做以下修改：在ABC中，A BA C＝k，D、A、E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问（1）中的结论还成立吗？若成立，请你给出证明；若不成立，请说明理由．（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，在ABC中，沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG，A BA E ＝A CA G＝12，AH是BC边上的高，延长HA交EG于点I．①求证：I是EG的中点．②直接写出线段BC与AI之间的数量关系：．例4．（2022·四川·一模）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形：（1）如图1，已知：在△ABC 中，A B A C=，D 、A 、E 三点都在直线m 上，并且有B D AA E CB AC α∠=∠=∠=．试猜想DE 、BD 、CE 有怎样的数量关系，请证明你的结论；（2）老师鼓励学习小组继续探索相似的情形．于是，学习小组又研究以下问题：如图2，△ABC 中，(060)B C αα∠=∠=<<︒．将一把三角尺中30°角顶点P 放在BC 边上，当P 在BC 边上移动时，三角尺中30°角的一条边始终过点A ，另一条边交AC 边于点Q ，P 、Q 不与三角形顶点重合．设C P Qβ∠=．当β在许可范围内变化时，α取何值总有△ABP ∽△PCQ ？当α在许可范围内变化时，β取何值总有△ABP ∽△QCP ？（3）试探索有无可能使△ABP 、△QPC 、△ABC 两两相似？若可能，写出所有α、β的值（不写过程）；若不可能，请说明理由．例5．（2022·山西晋中·一模）阅读材料：我们知道：一条直线经过等腰直角三角形的直角顶点，过另外两个顶点分别向该直线作垂线，即可得三垂直模型”如图①，在A B C中，90A C B ∠=︒，A C B C=，分别过A 、B 向经过点C 直线作垂线，垂足分别为D 、E ，我们很容易发现结论：A D C C E B△≌△．（1）探究问题：如果A CB C≠，其他条件不变，如图②，可得到结论；A D CC E B△∽△．请你说明理由．（2）学以致用：如图③，在平面直角坐标系中，直线12y x=与直线C D 交于点()2,1M ，且两直线夹角为α，且3ta n 2α=，请你求出直线C D 的解析式．（3）拓展应用：如图④，在矩形A B C D 中，3A B=，5B C=，点E为B C 边上—个动点，连接A E ，将线段A E 绕点E 顺时针旋转90︒，点A 落在点P 处，当点P 在矩形A B C D外部时，连接P C ，P D ．若D P C △为直角三角形时，请你探究并直接写出B E 的长．Rt ABD中，上一动点，连接折叠得H E F，延长②B E M H E M≅；③当M2B，则正确的有（九年级校考阶段练习）已知A B C是等边三角形，E F和B D F∠，将B C E沿B则A F=P C D△；九年级校考阶段练习）如图，在A B C中，12．（2022·山东济宁·二模）情境观察:将含45°角的三角板的直角顶点R放在直线l上，分别过两锐角的顶点M，N作l的垂线，垂足分别为P，Q，（1）如图1.观察图1可知：与NQ相等的线段是______________，与N R Q∠相等的角是_____(2)问题探究直角A B C中，90B∠=︒，在AB边上任取一点D，连接CD，分别以AC，DC为边作正方形ACEF 和正方形CDGH，如图2，过E，H分别作BC所在直线的垂线，垂足分别为K，L.试探究EK与HL之间的数量关系，并证明你的结论.(3)拓展延伸：直角A B C中，90B∠=︒，在AB边上任取一点D，连接CD，分别以AC，DC为边作矩形ACEF和矩形CDGH，连接EH交BC所在的直线于点T，如图3.如果A C kC E=，试探究TE与TH=，C D kC H之间的数量关系，并证明你的结论.将．A B P沿着这样的点P，使得点问题解决（3）15．（2023春·四川广安·九年级校考阶段练习）如图1和图2，在平面直角坐标系中，点C的坐标为（0，4），A是x轴上的一个动点，M是线段AC的中点．把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB．过B作x轴的垂线、过点C作y轴的垂线，两直线交于点D，直线DB交x轴于点E．设A点的横坐标为m．（1）求证：△AOC∽△BEA；（2）若m=3，则点B的坐标为；若m=﹣3，则点B的坐标为；（3）若m＞0，△BCD的面积为S，则m为何值时，S=6？（4）是否存在m，使得以B、C、D为顶点的三角形与△AOC相似？若存在，求此时m的值；若不存在，请说明理由．16．（2020·四川雅安·中考真题）如图，已知边长为10的正方形A B C D E、不重，是B C边上一动点（与B C 合），连结A E G，是B C延长线上的点，过点E作A E的垂线交D C G∠的角平分线于点F，若F G B G⊥．（1）求证：A B E E G FE C=，求C E F△△；（2）若2∽△的△的面积；（3）请直接写出E C为何值时，C E F面积最大．的何位置时有B E H B A E∽？B C。

最全相似模型专题(中考数学必考)

几何模型09——相似模型三角形相似是每一年中考必考的知识点，相似模型主要包括：“A”型和“X”型相似，母子模型相似（共边共角型），一线三等角，双垂直模型和旋转相似，中考命题者经常把这些模型放在圆，四边形，或函数图象当中，特别要留意母子模型相似的一种特殊情况：射影定理中的知二求四和一线三垂直（k型相似），下面对这些类型做如下总结：一、“A”型和“X”型相似例1.如图，在△ABC中，点D是AC上的点，且AD＝2CD，过D作DE∥BC交AB于E，过D作DF∥AB交BC于F．（1）若BC＝15，求线段DE的长．（2）若△ADE的面积为16，求△CDF的面积．变式1.如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB．（1）求证：△BDE∽△EFC．（2）设，①若BC＝12，求线段BE的长；②若△EFC的面积是20，求△ABC的面积．变式2.如图，Rt△ABC中，∠C＝90°，AB＝14，AC＝7，D是BC上一点，BD＝8，DE⊥AB，垂足为E，求线段DE的长．变式3.如图，AB为半圆O的直径，C为BA延长线上一点，CD切半圆O于点D，连接OD．作BE⊥CD于点E，交半圆O于点F．已知CE＝12，BE＝9．（1）求证：△COD∽△CBE．（2）求半圆O的半径r的长．变式4.如图，AG是∠HAF的平分线，点E在AF上，以AE为直径的⊙O交AG于点D，过点D作AH的垂线，垂足为点C，交AF于点B．（1）求证：直线BC是⊙O的切线；（2）若AC＝2CD，设⊙O的半径为r，求BD的长度．变式5.如图，在矩形ABCD中，AB＝6，BC＝8，沿直线MN对折，使A、C重合，直线MN 交AC于O．（1）求证：△COM∽△CBA；（2）求线段OM的长度．变式6.如图，已知AB为⊙O的直径，F为⊙O上一点，AC平分∠BAF且交⊙O于点C，过点C作CD⊥AF于点D，延长AB、DC交于点E，连接BC、CF．（1）求证：CD是⊙O的切线；（2）若AD＝6，DE＝8，求BE的长；变式7.如图，在△ABC中，∠C＝90°，点O在CB上，⊙O经过点C，且与AB相切于点D，与CB的另一个交点为E．（1）求证：DE∥OA；（2）若AB＝10，tan∠DEO＝2，求⊙O的半径．例2.如图，在Rt△ABC中，∠A＝90°，AC＝9，BC＝15．（1）求BC边上的高AD的长度；（2）正方形的一边FG在BC上，另两个顶点E、H分别在边AB、AC上，求正方形EFGH 的边长．（相似比等于高之比）例3.如图，⊙O的半径为5，点P在⊙O外，PB交⊙O于A、B两点，PC交⊙O于D、C 两点．求证：PA•PB＝PD•PC（割线定理）；变式1.如图，在△ABC中，AB＝AC，以AC为直径的⊙O交AB于点D，交BC于点E．（1）求证：BE＝CE；（2）若BD＝2，BE＝3，求AC的长．变式2.如图，以△ABC 的边BC 为直径的⊙O 分别交AB ，AC 于点D ，E ，且点E 是的中点，连接DE ．（1）求证：△ABC 是等腰三角形．（2）若BC ＝10，CE ＝6，求线段AD 的长．变式3.如图，在△ABC 中，AB ＝AC ，以AB 为直径的半圆O 分别交BC ，AC 于点D ，E ，连结EB ，OD ，DE ．（1）求证：OD ⊥EB ．（2）若DE ＝，AB ＝10，求AE 的长．例4.如图，在△ABC 中，D ，E 分别是边AC ，AB 的中点，BD 与CE 交于点O ，连接DE ．求证：2OE CO OD BO ==变式1.如图，AB 、CD 相交于点O ，连接AC 、BD ，点E 、F 分别为AC 、BD 的中点，连接OE 、OF ，若∠A ＝∠D ，OA ＝OF ＝6，OD ＝9，求OE 的长．变式2.如图，已知圆O，弦AB、CD相交于点M．（1）求证：AM•MB＝CM•MD；（相交弦定理）（2）若M为CD中点，且圆O的半径为3，OM＝2，求AM•MB的值．变式3.如图，在⊙O中，弦AB、CD相交于点P，且PD＜PC．（1）求证：△P AD∽△PCB；（2）若P A＝3，PB＝8，CD＝10，求PD．例5.如图，过△ABC的边AC的中点D作直线交AB于E，交BC的延长线于F．求证：＝；（梅捏劳斯定理特殊情况）变式1.如图，已知△ABC的边AB上有一点D，边BC的延长线上有一点E，且AD＝CE．DE 交AC于点F，试证明：AB•DF＝BC•EF．变式2.如图，△ABC中，D为BC的中点，过D的直线交AC于E，交AB的延长线于F．求证：＝．变式3.如图，△ABC中，D是BC边的中点，过点D的直线交AB于点E，交AC的延长线于点F，且BE＝CF．求证：AE＝AF．二、共边共角型相似例1.如图，在△ABC中，D为BC边上的一点，且∠CAD＝∠B．（1）求证：；（2）若AC＝2，BC＝4，设△ADC面积为S1，△ABD面积为S2，求证：S2＝3S1．变式1.如图，在△ABC中，D为边AB上一点，∠ACD＝∠B，若AC＝6，BC＝5，CD＝4，求AD，AB的长．变式2.如图，已知正方形ABCD中，BE平分∠DBC且交CD边于点E，将△BCE绕点C顺时针旋转到△DCF的位置，并延长BE交DF于点G．（1）求证：△BDG∽△DEG；（2）若EG•BG＝4，求BE的长．变式3.如图，在Rt△ABC中，∠C＝90°，以AB上一点O为圆心，OA的长为半径作⊙O，交AC、AB分别于D，E两点，连接BD，且∠A＝∠CBD．若CD＝1，BC＝2，求AD 的长度．例2.如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E．（1）求证：AG＝CG．（2）求证：AG2＝GE•GF．变式1.如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于点E，交BA的延长线于点F．（1）求证：PC2＝PE•PF；（2）若菱形边长为8，PE＝2，EF＝6，求FB的长．例3.如图，CD是⊙O的切线，点C在直径AB的延长线上．（切割线模型）（1）求证：∠CAD＝∠BDC；（2）若BD＝AD，AC＝3，求CD的长．变式1.如图，O为线段PB上一点，以O为圆心，OB长为半径的⊙O交PB于点A，点C 在⊙O上，连接PC，满足PC2＝P A•PB．若AB＝3P A，求的值．例4.如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D．（1）（射影定理）求证：AC2＝AD•AB；BC2＝BD•BA；CD2＝AD•BD；（2）若AD＝2，DB＝8，求AC，BC，CD的长；（知二求四）（3）若AC＝6，DB＝9，求AD，CD，BC的长；（知二求四）（4）求证：AC•BC＝AB•CD．（等面积法）变式1.如图，AB是⊙O的直径，点C是圆上一点，连接AC和BC，过点C作CD⊥AB于点D．若CD＝4，BD＝3，求⊙O的半径长．（直径所对的圆周角为直角）变式2.如图，在Rt△ABC中，∠BAC＝90°，∠BAD＝∠C，点D在BC边上，以AD为直径的⊙O交AB于点E，交AC于点F．已知：AB＝6，AC＝8，求AF的长．变式3.在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O交AB于点D，点E是边BC的中点，连结DE．（1）求证：DE是⊙O的切线；（2）若AD＝4，BD＝9，求⊙O的半径．例4.如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点恰好为BC的中点D，过点D作⊙O的切线交AC于点E．（1）求证：DE⊥AC；（2）若AB＝3DE，求tan∠ACB的值．（射影定理知二求四）（3）若AB＝5CE，求tan∠ACB的值．（射影定理知二求四）变式1.如图，四边形ABCD内接于⊙O，对角线AC为⊙O的直径，过点C作AC的垂线交AD的延长线于点E，点F为CE的中点，连接DB，DC，DF．（1）求证：DF是⊙O的切线；（2）若AC＝2DE，求tan∠ABD的值．三、双垂直例1.如图，在矩形ABCD中，点E在边BC上，AF⊥DE，垂足为F，AD＝4，CE＝2，DE ＝2，求DF的长．变式1.如图，点P是正方形ABCD边AD上一点，Q是边BC延长线上一点，若AB＝12，P A＝5，PQ⊥BP．求CQ的长．变式2.如图，△ABC中，BD、CE分别是AC、AB边上的高，若AE＝5，AD＝6，CD＝2．求EB的长．变式3.如图，在Rt△ABC中，∠ABC＝90°，E是边AC上一点，且BE＝BC，过点A作BE的垂线，交BE的延长线于点D，求证：△ADE∽△ABC．四、一线三等角例1.已知：如图，△ABC中，∠BAC＝90°，AB＝AC＝1，点D是BC边上的一个动点（不与B，C点重合），∠ADE＝45°．（1）求证：△ABD∽△DCE；（2）设BD＝x，AE＝y，求y关于x的函数关系式；例2.如图，E是正方形ABCD的边AB上的点，过点E作EF⊥DE交BC于点F．（1）求证：△ADE∽△BEF；（2）若AB＝6，AE＝2，求线段CF的长．变式1.如图，将一个直角的顶点P放在矩形ABCD的对角线BD上滑动，并使其一条直角边始终经过点A，另一条直角边与边BC相交于点E．且AD＝8，DC＝6，则＝．五、旋转相似例1.如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF＝∠GAC．（1）求证：△ADE∽△ABC；（2）若AD＝3，AB＝5，求的值．变式1.如图，△ABC和△CEF中，AB＝BC，CF＝EF，∠CBA＝∠CFE＝90°，E在△ABC 内，∠CAE+∠CBE＝90°，连接BF．（1）求证：△CAE∽△CBF；（2）若BE＝1，AE＝2，求EF的长．。

中考相似模型知识点总结

中考相似模型知识点总结一、相似概念相似是指两个图形，在形状上虽然不同，但其形状结构、比例尺寸、角度大小等方面存在一定的对应关系，因而可以通过某种变换，将一个图形变为另一个图形。

相似图形具有诸如角对应相等、对应边成比例等性质。

相似是几何中的重要概念，不仅在理论研究中有重要应用，而且在实际生活和各类工程设计中也有广泛应用。

二、相似三角形的判定1. AAA判定若两个三角形的对应角相对应相等，则这两个三角形是相似的。

2. AA相似判定若两个三角形中各对应角都相等，则这两个三角形是相似的。

3. SAS相似判定若两个三角形中有一对对应的角相等，而他们的对应的两边成比例，则这两个三角形是相似的。

4. SSS相似判定若两个三角形的对应边成比例，则这两个三角形是相似的。

三、相似三角形的性质1. 相似三角形的对应角相等在两个相似三角形ABC和A′B′C′中，对应角A和A′、对应角B和B′、对应角C和C′是相等的。

2. 相似三角形的对应边成比例在两个相似三角形ABC和A′B′C′中，AB/AC=A′B′/A′C′、BC/AC=B′C′/A′C′、AB/BC=A′B′/B′C′。

3. 相似三角形的高成比例在两个相似三角形ABC和A′B′C′中，AA′/BB′=CC′/A′C′。

4. 相似三角形的面积成比例在两个相似三角形ABC和A′B′C′中，S(ABC)/S(A′B′C′)=AB²/A′B′²。

四、相似折线的性质1. 相似折线的顶角相等在相似折线中，对应顶点的角相等。

2. 相似折线的对应边成比例在相似折线中，对应边的长度成比例。

五、相似几何图形的相似比相似图形的对应边的成比例值叫做相似比。

相似比在数学中有重要的应用，通过相似比我们可以计算图形的缩放比例、面积比例等。

六、相似变换相似变换是指一个原图形经过某种变换，变为另一个图形。

相似变换包括平移、旋转、放缩等，通过这些变换我们可以得到相似图形。

七、相似图形的应用1. 在建筑设计中在建筑设计中，通过相似图形的知识可以实现建筑设计的比例缩放，确保建筑的各个部分比例协调，美观大方。

三角形全等、相似及综合应用模型(6大模型+解题技巧)—2024年中考数学(全国通用)(解析版)

三角形全等、相似及综合应用模型题型解读｜模型构建｜通关试练三角形基础知识部分多以选择或者填空题形式，考察其三边关系、内角和/外角和定理、“三线”基本性质等。

特殊三角形的性质与判定也是考查重点，年年都会考查，最为经典的“手拉手”模型就是以等腰三角形为特征总结的，且等腰三角形单独出题的可能性还是比较大。

直角三角形的出题类型可以是选择填空题这类小题，也可以是各类解答题，以及融合在综合压轴题中，作为问题的几何背景进行拓展延伸。

模型01 与三角形有关的线段应用高（AD）中线（AD）角平分线（AD）中位线（DE）模型02 与三角形有关的角的应用（1）三角形的内角：（1）三角形内角的概念：三角形内角是三角形三边的夹角．每个三角形都有三个内角，且每个内角均大于0°且小于180°．（2）三角形内角和定理：三角形内角和是180°．（3）三角形内角和定理的证明证明方法，不唯一，但其思路都是设法将三角形的三个内角移到一起，组合成一个平角．在转化中借助平行线．（4）三角形内角和定理的应用主要用在求三角形中角的度数．①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．（2）三角形的外角：（1）三角形外角的定义：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．三角形共有六个外角，其中有公共顶点的两个相等，因此共有三对．（2）三角形的外角性质：①三角形的外角和为360°．②三角形的一个外角等于和它不相邻的两个内角的和．③三角形的一个外角大于和它不相邻的任何一个内角．（3）若研究的角比较多，要设法利用三角形的外角性质②将它们转化到一个三角形中去．（4）探究角度之间的不等关系，多用外角的性质③，先从最大角开始，观察它是哪个三角形的外角．模型03 三角形全等的判定及应用（1）全等三角形的定义：全等的图形必须满足：（1）形状相同；（2）大小相等能够完全重合的两个三角形叫做全等三角形。

2023年中考数学常见几何模型之相似模型中的母子型与A(X)字型

专题06 相似模型-母子型（共角共边模型）和A （X ）字型相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到相似三角形的问题就信心更足了．本专题重点讲解相似三角形的六大基本模型．模型1.“母子”模型(共边角模型)【模型解读与图示】“母子”模型的图形（通常有一个公共顶点和另外一个不是公共的顶点，由于小三角形寓于大三角形中，恰似子依母怀），也是有一个“公共角”，再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似．“双垂线”型是其特例。

“ 母子”模型（斜射影）双垂直（射影定理） “母子型”的变形斜射影结论：△ABD ∽△ACB ，AB 2＝AD ·AC .双垂直结论：①△ABD ∽△ACB ，AB 2＝AD ·AC ；②△ADC ∽△ACB ，AC 2＝AD ·AB ；③△CDB ∽△ACB ，CB 2＝BD ·BA .1．（2022·贵州贵阳·中考真题）如图，在ABC V 中，D 是AB 边上的点，B ACD ∠=∠，:1:2AC AB =，则ADC V 与ACB △的周长比是（）A ．B ．1:2C ．1:3D ．1:4 【答案】B【分析】先证明△ACD ∽△ABC ，即有12AC AD CD AB AC BC ===，则可得12AC AD CD AB AC BC ++=++，问题得解．【详解】∵∠B =∠ACD ，∠A =∠A ，∴△ACD ∽△ABC ，∴AC AD CD AB AC BC ==， ∵12AC AB =，∴12AC AD CD AB AC BC ===， ∴12AC AD CD AC AD CD AB AC BC AB AC BC ++====++， ∴△ADC 与△ACB 的周长比1:2，故选：B ．【点睛】本题主要考查了相似三角形的判定与性质，证明△ACD ∽△ABC 是解答本题的关键．2．（2022·陕西汉中·九年级期末）如图，CD 是等腰直角ABC V 斜边AB 的中线，以点D 为顶点的EDF ∠绕点D 旋转，角的两边分别与AC 、BC 的延长线相交，交点分别为点E 、F ，DF 与AE 交于点M ，DE 与BC 交于点N ，且45EDF ∠=︒．(1)如图1，若CE CF =，求证：DE DF =；(2)如图2，若CE CF ≠，求证：2CD CE CF =⋅；(3)如图2，过D 作DG BC ⊥于点G ，若2CD =，CF DN 的长．∵DG⊥BC，∠ACB=90°，∠∴∠DGN=∠ECN=90°，∠当CD=2，CF=2时，由CD在Rt△DCG中，CG DG=3．（2022·浙江绍兴·九年级期末）如果两个相似三角形的对应边存在2倍关系，则称这两个相似三角形互为母子三角形．（1）如果DEF V 与ABC V 互为母子三角形，则DE AB 的值可能为（） A ．2 B ．12 C ．2或12（2）已知：如图1，ABC V 中，AD 是BAC ∠的角平分线，2,AB AD ADE B =∠=∠．求证：ABD △与ADE V 互为母子三角形．（3）如图2，ABC V 中，AD 是中线，过射线CA 上点E 作//EG BC ，交射线DA 于点G ，连结BE ，射线BE 与射线DA 交于点F ，若AGE V 与ADC V 互为母子三角形．求AG GF 的值．V互为母子三角形，∴QV与ADCAGE4．（2022.浙江中考模拟）如图，在V ABC中，∠ACB＝90°，CD⊥AB．（1）图1中共有对相似三角形，写出来分别为（不需证明）：（2）已知AB＝5，AC＝4，请你求出CD的长：（3）在（2）的情况下，如果以AB为x轴，CD为y轴，点D为坐标原点O，建立直角坐标系（如图2），若点P从C点出发，以每秒1个单位的速度沿线段CB运动，点Q出B点出发，以每秒1个单位的速度沿线段BA运动，其中一点最先到达线段的端点时，两点即刻同时停止运动；设运动时间为t秒是否存在点P，使以点B、P、Q为顶点的三角形与△ABC相似？若存在，请求出点P的坐标；若不存在，请说明理由．【答案】（1）3，V ABC∽V ACD，V ABC∽V CBD，V ACD∽V CBD；（2）125；（3）存在，(2740，32)，(98，910)【分析】（1）根据两角对应相等的两三角形相似即可得到3对相似三角形，分别为：△ABC∽△ACD，△ABC∽△CBD，△ACD∽△CBD．（2）先在△ABC中由勾股定理求出BC的长，再根据△ABC的面积不变得到12AB•CD＝12AC•BC，即可求出CD的长．（3）由于∠B公共，所以以点B、P、Q为顶点的三角形与△ABC相似时，分两种情况进行讨论：①△PQB∽△ACB；②△QPB∽△ACB．【详解】解：（1）图1中共有3对相似三角形，分别为：△ABC∽△ACD，△ABC∽△CBD，△ACD∽△CBD．证明：∵CD⊥AB，∴∠ADC=∠ACB=90°，又∵∠A=∠A，∴△ADC∽△ACB同理可证：△ABC∽△CBD，△ACD∽△CBD．故答案为：3；△ABC∽△ACD，△ABC∽△CBD，△ACD∽△CBD．（2）如图2中，在△ABC中，∵∠ACB＝90°，AB＝5，AC＝4，∴BC3．∵△ABC的面积＝12AB•CD＝12AC•BC，∴CD＝AC BCAB⋅＝125．（3）存在点P，使以点B、P、Q为顶点的三角形与△ABC相似，理由如下：在△BOC中，∵∠COB＝90°，BC＝3，OC＝125，∴OB＝95．分两种情况：①当∠BQP＝90°时，如图2①，此时△PQB∽△ACB，∴BP AB ＝BQ BC ，∴353t t −=，解得t ＝98，即98BQ CP ==，∴915388BP BC CP =−=−=．在△BPQ中，由勾股定理，得32PQ ===，∴点P 的坐标为273(,)402； ②当∠BPQ ＝90°时，如图2②，此时△QPB ∽△ACB ，∴BP BQ BC AB =，∴335t t −=，解得t ＝158，即15159,3888BQ cP BP BC CP ===−=−=，过点P 作PE ⊥x 轴于点E ．∵△QPB ∽△ACB ，∴PE BQ CO AB ⋅=，即1581255PE =，∴PE ＝910．在△BPE中，2740BE ==， ∴92795408OE OB BE =−=−=，∴点P 的坐标为99(,)810，综上可得，点P 的坐标为(2740，32)；(98，910)．【点睛】本题属于相似形综合题，考查了相似三角形的判定与性质，勾股定理等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建方程解决问题，属于中考常考题型．模型2. “A ”字模型【模型解读与图示】“A ”字模型图形（通常只有一个公共顶点）的两个三角形有一个“公共角”（是对应角），再有一个角相等或夹这个公共角的两边对应成比例，就可以判定这两个三角形相似．1．（2022·湖南怀化·中考真题）如图，△ABC 中，点D 、E 分别是AB 、AC 的中点，若S △ADE ＝2，则S △ABC ＝_____．【答案】8【分析】根据三角形中位线定理求得DE ∥BC ，12DE BC =，从而求得△ADE ∽△ABC ，然后利用相似三角形的性质求解．【详解】解：∵D 、E 分别是AB 、AC 的中点，则DE 为中位线，所以DE ∥BC ，12DE BC =所以△ADE ∽△ABC ∴21()4ADE ABC S DE S BC ==V V ∵S △ADE =2，∴S △ABC =8故答案为：8．【点睛】本题考查中位线及平行线性质，本题难度较低，主要考查学生对三角形中位线及平行线性质等知识点的掌握．2．（2022·浙江杭州·中考真题）如图，在V ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，连接DE ，EF ，已知四边形BFED 是平行四边形，DE 1BC 4=．(1)若8AB =，求线段AD 的长．(2)若ADE V 的面积为1，求平行四边形BFED 的面积．【答案】(1)2(2)6【分析】（1）利用平行四边形对边平行证明ADE ABC △△∽，得到DE AD BC AB=即可求出；（2）利用平行条件证明ADE EFC ∽V V ，分别求出ADE EFC V V 与、ADE ABC V V 与的相似比，通过相似三角形的面积比等于相似比的平方分别求出EFC S、ABC S V ，最后通过BFED ABC EFC ADE S S S S =−−Y V V V 求出． (1)∵四边形BFED 是平行四边形，∴∥DE BC ，∴ADE ABC △△∽，∴DE AD BC AB =， ∵DE 1BC 4=，∴AD 1AB 4=，∴118244AD AB ==⨯=； (2)∵四边形BFED 是平行四边形，∴∥DE BC ，EF AB ∥，DE =BF ，∴,AED ECF EAD CEF ∠=∠∠=∠，∴ADE EFC ∽V V ∴2ADE EFC S DE S FC ⎛⎫= ⎪⎝⎭V V ， ∵DE 1BC 4=，DE =BF ，∴43FC BC DE DE DE DE =−=−=， ∴133DE DE FC DE ==，∴221139ADE EFC S DE S FC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭V V ， ∵ADE ABC △△∽，DE 1BC 4=，∴2211416ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭V V ， ∵1ADE S =△，∴9,16EFC ABC S S ==V V ，∴16916BFED ABC EFC ADE S S S S =−−=−−=Y V V V ．【点睛】本题考查了相似三角形，熟练掌握相似三角形的面积比等于相似比的平方、灵活运用平行条件证明三角形相似并求出相似比是解题关键．3．（2022·浙江宁波·中考真题）(1)如图1，在ABC V 中，D ，E ，F 分别为,,AB AC BC 上的点，,,DE BC BF CF AF =∥交DE 于点G ，求证：DG EG =．(2)如图2，在（1）的条件下，连接,CD CG ．若,6,3⊥==CG DE CD AE ，求DE BC的值． (3)如图3，在ABCD Y 中，45,︒∠=ADC AC 与BD 交于点O ，E 为AO 上一点，EG BD ∥交AD 于点G ，⊥EF EG 交BC 于点F ．若40,︒∠=EGF FG 平分,10∠=EFC FG ，求BF 的长．【答案】(1)证明见详解(2)13(3)5+【分析】（1）利用∥DE BC ，证明,ADG ABF AEG ACF △△△△::，利用相似比即可证明此问；（2）由（1）得DG EG =，CG DE ⊥，得出DCE V 是等腰三角形，利用三角形相似即可求出 DE BC的值；（3）遵循第（1）、（2）小问的思路，延长GE 交AB 于点M ，连接FM ，作MN BC ⊥，垂足为N ．构造出等腰三角形、含30°、45°角的特殊直角三角形，求出BN 、FN 的值，即可得出BF 的长．(1)解：∵DE BC ∥，∴,ADG ABF AEG ACF △△△△::， ∴,==DG AG EG AG BF AF CF AF ，∴DG EG BF CF=． ∵BF CF =，∴DG EG =．(2)解：由（1）得DG EG =，∵CG DE ⊥，∴6CE CD ==．∵3AE =，∴9AC AE CE =+=．∵DE BC ∥，∴ADE ABC V :V ． ∴13DE AE BC AC ==． (3)解：如图，延长GE 交AB 于点M ，连接FM ，作MN BC ⊥，垂足为N ．在ABCD Y 中，,45=∠=∠=︒BO DO ABC ADC ．∵EG BD ∥，∴由（1）得=ME GE ，∵⊥EF EG ，∴10==FM FG ，∴∠=∠EFM EFG ．∵40∠︒=EGF ，∴40EMF ∠=︒，∴50EFG ∠=︒．∵FG 平分EFC ∠，∴50∠=∠=︒EFG CFG ，∴18030∠=︒−∠−∠−∠=︒BFM EFM EFG CFG ．∴．在Rt FMN V 中，sin 305,cos30=︒==︒=MN FM FN FM∵45,∠=︒⊥MBN MN BN ，∴5==BN MN ，∴5=+=+BF BN FN【点睛】本题考查了相似三角形的性质及判定、等腰三角形的性质及判定、解特殊的直角三角形等知识，遵循构第（1）、（2）小问的思路，构造出等腰三角形和特殊的直角三角形是解决本题的关键．4．（2022·辽宁·中考真题）如图，在ABC V 中，4AB AC BC ===，D ，E ，F 分别为,,AC AB BC 的中点，连接,DE DF ．(1)如图1，求证：2DF DE =；(2)如图2，将EDF ∠绕点D 顺时针旋转一定角度，得到PDQ ∠，当射线DP 交AB 于点G ，射线DQ 交BC 于点N 时，连接FE 并延长交射线DP 于点M ，判断FN 与EM 的数量关系，并说明理由；(3)如图3，在（2）的条件下，当DP AB ⊥时，求DN 的长．【答案】(1)见解析(2)FN EM =，理由见解析(3)103 【分析】（1）连接AF ，可得AF BC ⊥，根据直角三角形斜边上的中线等于斜边的一半可得12DF AC ==122DE BC ==，即可得证；（2）证明DNF DME V V ∽，根据（1）的结论即可得FN ；（3）连接AF ，过点C 作CH AB ⊥于H ，证明AGD AHC V V ∽，可得12GD HC ==，勾股定理求得,GE AG ，根据3tan 4AG ADG GD ∠==，EMG ADG ∠=∠，可得3tan 4EG EMG MG ∠==，进而求得MG ，根据MD MG GD =+求得MD ，根据（2）的结论2DN DM =，即可求解． (1)证明：如图，连接AF ，Q 4AB AC BC ===，D ，E ，F 分别为,,AC AB BC 的中点，122DE BC ∴==，AF BC ⊥，∴12DF AC ==∴2DF DE =，(2)FN =，理由如下，连接AF ，如图，Q 4AB AC BC ===，D ，E ，F 分别为,,AC AB BC 的中点，1,2EF AC CD EF DC ∴==∥，∴四边形CDEF 是平行四边形，DEF C ∴∠=∠， Q 12DF AC DC ==，DFC C ∴∠=∠，DEF DFC ∴∠=∠， 180180DEF DFC ∴︒−∠=︒−∠，∴DEM DFN ∠=∠，Q 将EDF ∠绕点D 顺时针旋转一定角度，得到PDQ ∠，∴EDF ∠=PDQ ∠，FDN NDE EDM NDE ∠+∠=∠+∠Q ，FDN EDM ∴∠=∠，DNF DME ∴V V ∽，NF DF EM DE ∴==，∴FN =， (3)如图，连接AF ，过点C 作CH AB ⊥于H ，Rt AFC △中，122FC BC ==,∴4AF ==， 1122ABC S BC AF AB CH =⋅=⋅V Q，BC AF HC AB ⋅∴== Q DP AB ⊥，AGD AHC ∴V V ∽，12GD AD HC AC ∴==，12GD HC ∴== Rt GED V中，5GE ===， Rt AGD V中，5AG ==，35tan 44AG ADG GD ∴∠===，EF AD ∥Q ，EMG ADG ∴∠=∠，3tan 4EG EMG MG ∴∠==，4433515MG GE ∴==⨯=，1553MD MG GD ∴=+=+=，Q DNF DME V V ∽，DN DF DM DE ∴==，103DN ∴==．【点睛】本题考查了勾股定理，直角三角形斜边上的中线等于斜边的一半，中位线的性质定理，相似三角形的性质与判定，求角的正确，掌握相似三角形的性质与判定是解题的关键．模型3. “X ”字模型（“8”模型）【模型解读与图示】“X ”字模型图形的两个三角形有“对顶角”，再有一个角相等或夹对顶角的两边对应成比例就可以判定这两个三角形相似．1．（2022·河北·中考真题）如图是钉板示意图，每相邻4个钉点是边长为1个单位长的小正方形顶点，钉点A ，B 的连线与钉点C ，D 的连线交于点E ，则（1）AB 与CD 是否垂直？______（填“是”或“否”）；（2）AE ＝______．【答案】是【分析】（1）证明△ACG ≌△CFD ，推出∠CAG =∠FCD ，证明∠CEA =90°，即可得到结论；（2）利用勾股定理求得AB 的长，证明△AEC ∽△BED ，利用相似三角形的性质列式计算即可求解．【详解】解：（1）如图：AC =CF =2，CG =DF =1，∠ACG =∠CFD =90°，∴△ACG ≌△CFD ， ∴∠CAG =∠FCD ，∵∠ACE +∠FCD =90°，∴∠ACE +∠CAG =90°，∴∠CEA =90°，∴AB 与CD 是垂直的，故答案为：是；（2）AB =AC ∥BD ，∴△AEC ∽△BED ，∴AC AE BD BE =，即23AE BE =，∴25AE BE =，∴AE =25BE【点睛】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，解答本题的关键是明确题意，找出所求问题需要的条件．2．（2022·四川内江·中考真题）如图，在矩形ABCD 中，AB ＝6，BC ＝4，点M 、N 分别在AB 、AD 上，且MN ⊥MC ，点E 为CD 的中点，连接BE 交MC 于点F ．(1)当F 为BE 的中点时，求证：AM ＝CE ；(2)若EF BF＝2，求AN ND 的值；(3)若MN ∥BE ，求AN ND 的值．【答案】(1)见解析(2)2737(3)27 【分析】(1)根据矩形的性质，证明△BMF ≌ △ECF ，得BM ＝CE ，再利用点E 为CD 的中点，即可证明结论； (2)利用△BMF ∽△ECF ，得12BM B EF CE F ==，从而求出BM 的长，再利用△ANM ∽△BMC ，得AN AM BM BC= ，求出AN 的长，可得答案； (3)首先利用同角的余角相等得 ∠CBF ＝ ∠CMB ，则tan ∠CBF ＝tan ∠CMB ，得CE BC BC BM= ，可得BM 的长，由（2）同理可得答案． (1)证明：∵F 为BE 的中点，∴BF ＝EF ，∵四边形ABCD 是矩形，∴AB ∥CD ，AB ＝CD ∴∠BMF ＝∠ECF ，∵∠BFM ＝∠EFC ，∴△BMF ≌△ECF （AAS ），∴BM ＝CE ， ∵点E 为CD 的中点，∴CE ＝12CD ，∵AB ＝CD ，∴12BM CE AB ==， ∴AM BM =，∴AM ＝CE ；(2)∵∠BMF ＝∠ECF ，∠BFM ＝∠EFC ，∴△BMF ∽△ECF ，∴12BM B EF CE F ==， ∵CE ＝3，∴BM ＝32，∴AM ＝92，∵CM ⊥MN ，∴∠CMN ＝90°，∴∠AMN +∠BMC ＝90°，∵∠AMN +∠ANM ＝90°，∴∠ANM ＝∠BMC ，∵∠A ＝∠MBC ，∴△ANM ∽△BMC ，∴AN AM BM BC =，∴92342AN =，∴7162AN =， ∴DN ＝AD ﹣AN ＝4﹣2716＝3716，∴272716373716AN DN ==； (3)∵MN ∥BE ，∴∠BFC ＝∠CMN ，∴∠FBC +∠BCM ＝90°，∵∠BCM +∠BMC ＝90°，∴∠CBF ＝∠CMB ，∴tan ∠CBF ＝tan ∠CMB ， ∴CE BC BC BM =，∴344BM =，∴163BM =，∴162633AM AB BM =−=−=，由（2）同理得，AN AM BM BC=，∴231643AN =，解得：AN ＝89， ∴DN ＝AD ﹣AN ＝4﹣89＝289，∴8292879AN ND ==．【点睛】本题是相似形综合题，主要考查了矩形的性质，全等三角形的判定与性质，相似三角形的判定与性质，三角函数等知识，求出BM 的长是解决（2）和（3）的关键． 3．（2022·广西贵港·中考真题）已知：点C ，D 均在直线l 的上方，AC 与BD 都是直线l 的垂线段，且BD 在AC 的右侧，2BD AC =，AD 与BC 相交于点O ．(1)如图1，若连接CD ，则BCD △的形状为______，AO AD的值为______； (2)若将BD 沿直线l 平移，并以AD 为一边在直线l 的上方作等边ADE V ．①如图2，当AE 与AC 重合时，连接OE ，若32AC =，求OE 的长； ②如图3，当60ACB ∠=︒时，连接EC 并延长交直线l 于点F ，连接OF ．求证：OF AB ⊥．【答案】(1)等腰三角形，13(2)①OE =②见解析【分析】（1）过点C 作CH ⊥BD 于H ，可得四边形ABHC 是矩形，即可求得AC =BH ，进而可判断△BCD 的形状，AC 、BD 都垂直于l ，可得△AOC ∽△BOD ，根据三角形相似的性质即可求解．（2）①过点E 作EF AD ⊥于点H ，AC ，BD 均是直线l 的垂线段，可得//AC BD ，根据等边三角形的性质可得30BAD ∠=︒，再利用勾股定理即可求解．②连接CD ，根据//AC BD ，得60CBD ACB ∠=∠=︒，即BCD △是等边三角形，把ABD △旋转得90ECD ABD ∠=∠=︒，根据30°角所对的直角边等于斜边的一般得到13AF AO AB AD ==，则可得AOF ADB △∽△，根据三角形相似的性质即可求证结论． (1)解：过点C 作CH ⊥BD 于H ，如图所示：∵AC ⊥l ，DB ⊥l ，CH ⊥BD ，∴∠CAB =∠ABD =∠CHB =90°，∴四边形ABHC 是矩形，∴AC =BH ，又∵BD =2AC ，∴AC=BH=DH ，且CH ⊥BD ，∴BCD △的形状为等腰三角形，∵AC 、BD 都垂直于l ，∴△AOC ∽△BOD ，122AO AC AC DO DB AC ∴===，即2DO AO =， 133AO AO AD AO DO A AO O ∴===+，故答案为：等腰三角形，13． (2)①过点E 作EF AD ⊥于点H ，如图所示：∵AC ，BD 均是直线l 的垂线段，∴//AC BD ，∵ADE V 是等边三角形，且AE 与AC 重合，∴∠EAD =60°，∴60ADB EAD ∠=∠=︒，∴30BAD ∠=︒，∴在Rt ADB V 中，2AD BD =，AB ，又∵2BD AC =，32AC =，∴6,AD AB ==132AH DH AD ===，又Rt ADB V ，∴EH ==又由（1）知13AO AD ，∴123AO AD ==，则1OH =，∴在Rt EOH △中，由勾股定理得：OE =②连接CD ，如图3所示：∵//AC BD ，∴60CBD ACB ∠=∠=︒，∵BCD △是等腰三角形，∴BCD △是等边三角形，又∵ADE V 是等边三角形， ∴ABD △绕点D 顺时针旋转60︒后与ECD V 重合，∴90ECD ABD ∠=∠=︒，又∵60BCD ACB ∠=∠=︒，∴30ACF FCB FBC ∠=∠=∠=︒，∴2FC FB AF ==，∴13AF AO AB AD ==，又OAF DAB ∠=∠，∴AOF ADB △∽△， ∴90AFO ABD ∠=∠=︒，∴OF AB ⊥．【点睛】本题考查了矩形的判定及性质、三角形相似的判定及性质、等边三角形的判定及性质、勾股定理的应用，熟练掌握三角形相似的判定及性质和勾股定理的应用，巧妙借助辅助线是解题的关键．4．（2022·江苏镇江·九年级期末）梅涅劳斯（Menelaus ）是古希腊数学家，他首先证明了梅涅劳斯定理，定理的内容是：如图（1），如果一条直线与△ABC 的三边AB ，BC ，CA 或它们的延长线交于F 、D 、E 三点，那么一定有••1AF BD CE FB DC EA=．下面是利用相似三角形的有关知识证明该定理的部分过程：证明：如图（2），过点A 作AG BC ∥，交DF 的延长线于点G ，则有AF AG FB BD =，CE CD EA AG =，∴1AF BD CE AG BD CD FB DC EA BD DC AG••=••=．请用上述定理的证明方法解决以下问题：(1)如图（3），△ABC 三边CB ，AB ，AC 的延长线分别交直线l 于X ，Y ，Z 三点，证明：1BX CZ AY XC ZA YB⋅⋅=． (2)如图（4），等边△ABC 的边长为2，点D 为BC 的中点，点F 在AB 上，且2BF AF =，CF 与AD 交于点E ，则AE 的长为________．(3)如图（5），△ABC 的面积为2，F 为AB 中点，延长BC 至D ，使CD BC =，连接FD 交AC 于E ，则四边形BCEF 的面积为________．课后专项训练：1．（2022•江苏中考模拟）对于两个相似三角形，如果沿周界按对应点顺序环绕的方向相同，那么称这两个三角形互为顺相似；如果沿周界按对应点顺序环绕的方向相反，那么称这两个三角形互为逆相似．例如，如图（1），△CDE∽△CAB，且沿周界CDEC与CABC环绕的方向（同为逆时针方向）相同，因此△CDE和△CAB互为顺相似；如图（2），△CDE∽△CBA，且沿周界CDEC与CBAC环绕的方向相反，因此△CDE和△CBA互为逆相似．（1）根据以上材料填空：①如图（3），AB∥CD，则△AOB∽△COD，它们互为相似（填“顺”或“逆”，下同）；②如图（4），Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，则△ABC∽，它们互为相似；③如图（5），若∠DAB＝∠EBC＝90°，并且BD⊥CE于点F，则△ABD∽，它们互为相似；（2）如图（6），若△AOB∽△COD，指出图中另外的一对相似三角形并说明理由，同时指出它们互为顺相似还是互为逆相似；（3）如图（7），在Rt△ABC中，∠C＝90°，AC＝20，BC＝15，点P在△ABC的斜边上，且AP＝16，过点P画直线截△ABC，使截得的一个三角形与△ABC相似，则满足的截线共有条．【答案】（1）①逆；②△ACD或△CBD，逆；③△BCE，顺；（答案不唯一）；（2）△AOC∽△BOD，理由见解析；△AOC和△BOD互为顺相似；（3）3．【分析】（1）①根据新定义直接判断，即可得出结论；②先判断出∠ADC=∠BDC=90°=∠ACB，进而分两种情况，判断出两三角形相似，最后根据新定义判断，即可得出结论；③先判断出∠ABD=∠C，进而得出△ABD∽△BCE，最后用新定义判断，即可得出结论；（2）先由△AOB∽△COD，判断出AO OBCO OD=，∠AOB=∠COD，进而得出∠AOC=∠BOD，即可得出结论；（3）先求出BP=9，分三种情况，过点P作AB，AC，BC的垂线，利用相似三角形得出比例式，建立方程求解，即可得出结论．【详解】（1）①∵AB∥CD，∴△AOB∽△COD，∴△AOB和△COD互为逆相似，故答案为：逆；②∵CD⊥AB，∴∠ADC＝∠BDC＝90°＝∠ACB，Ⅰ、∵∠A＝∠A，∴△ABC∽△ACD，∴△ABC和△ACD互为逆相似；Ⅱ、∠B＝∠B，∴△ABC∽△CBD，∴△ABC和△CBD互为逆相似；故答案为：△ACD或△CBD，逆；③∵BD⊥CE，∴∠BFC＝90°，∴∠CBD+∠C＝90°，∵∠EBC＝90°，∴∠CBD+∠ABD＝90°，∴∠ABD＝∠C，∴△ABD∽△BCE，∴△ABD和△BCE互为顺相似；故答案为：△BCE，顺；（2）△AOC∽△BOD，△AOC和△BOD互为顺相似；理由：∵△AOB∽△COD，∴AOCO＝OBOD，∠AOB＝∠COD，∴∠AOB﹣∠BOC＝∠COD﹣∠BOC，∴∠AOC＝∠BOD，∵AOCO＝OBOD，∴OAOB＝OCOD，∴△AOC∽△BOD，∴△AOC和△BOD互为顺相似；（3）在Rt△ABC中，AC＝20，BC＝15，根据勾股定理得，AB ＝25，∵AP＝16，∴BP＝AB﹣AP＝9，如图1，①过点P 作PG ⊥BC 于G ，∴∠BGP ＝90°＝∠ACB ，∵∠B ＝∠B ，∴△ABC ∽△PBG ，∴AB BC BP BG =，∴25159BG =， ∴BG ＝15925⨯＝275＜BC ，∴点G 在线段BC （不包括端点）上， ②过点P 作PG ''⊥AC 于G ''，∴∠AG ''P ＝∠ACB ，∵∠A ＝∠A ，∴△ABC ∽△APG ''，∴AB AC AP AG =''，∴252016AG =''， ∴AG ''＝201625⨯＝645＜AC ，∴点G ''在线段AC （不包括端点）上， ③过点P 作PG '⊥AB ，交直线BC 与G '，交直线AC 于H ，∵∠APG '＝∠APH ＝90°＝∠ACB ，∵∠A ＝∠A ，∴△ABC ∽△G 'BP ，∴AB BC BG BP ='，∴25159BG ='，∴BG '＝25915⨯＝15＝BC ， ∴点G '和点H 都和点C 重合（注：为了说明问题，有意将点G '和点H 没画在点C 处），故答案为：3．【点睛】此题是相似形综合题，主要考查了相似三角形的判定和性质，新定义的理解和应用，理解新定义、熟练掌握相似三角形的判定和性质是解本题的关键．2．（2022·吉林·中考真题）下面是王倩同学的作业及自主探究笔记，请认真阅读并补充完整．【作业】如图①，直线12l l ∥，ABC V 与DBC △的面积相等吗？为什么？解：相等．理由如下：设1l 与2l 之间的距离为h ，则12ABC S BC h =⋅，12DBC S BC h =⋅△．∴ABC DBC S S =V V ．【探究】(1)如图②，当点D 在1l ，2l 之间时，设点A ，D 到直线2l 的距离分别为h ，h '，则ABC DBC S h S h ='△△．证明：∵ABC S V(2)如图③，当点D 在1l ，2l 之间时，连接AD 并延长交2l 于点M ，则ABC DBC S AM S DM=△△．证明：过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，则90AEM DFM ∠=∠=︒，∴AE ∥ ．∴AEM △∽ ． ∴AE AM DF DM=．由【探究】（1）可知ABC DBC S S =△△ ，∴ABC DBC S AM S DM =△△． (3)如图④，当点D 在2l 下方时，连接AD 交2l 于点E ．若点A ，E ，D 所对应的刻度值分别为5，1.5，0，ABC DBCS S △△的值为．【答案】(1)证明见解析(2)证明见解析(3)73【分析】（1）根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅V V ，由此即可得证；（2）过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，先根据平行线的判定可得AE DF P，再根据相似三角形的判定可证AEM DFM ~V V ，根据相似三角形的性质可得AE AM DF DM=，然后结合【探究】（1）的结论即可得证；（3）过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥于点N ，先根据相似三角形的判定证出AME DNE ~，再根据相似三角形的性质可得73AM AE DN DE ==，然后根据三角形的面积公式可得12ABC S BC AM =⋅V ，12DBC S BC DN =⋅V ，由此即可得出答案． (1)证明：12ABC S BC h =⋅V Q ，12DBC BC h S '=⋅V ，ABC DBC S h S h ∴='V V ． (2)证明：过点A 作AE BM ⊥，垂足为E ，过点D 作DF BM ⊥，垂足为F ，则90AEM DFM ∠=∠=︒，AE DF ∴∥．AEM DFM ~∴V V ．AE AM DF DM ∴=．由【探究】（1）可知ABC DBC SAE S DF=，ABC DBC S AM S DM ∴=． (3)解：过点A 作AM BC ⊥于点M ，过点D 作DN BC ⊥于点N ，则90AMEDNE ∠=∠=︒，AM DN ∴，AME DNE ∴~，AM AE DN DE∴=， Q 点,,A E D 所对应的刻度值分别为5，1.5，0，5 1.5 3.5AE ∴=−=， 1.5DE =， 3.571.53AM DN ∴==，又12ABC S BC AM =⋅V Q ，12DBC S BC DN =⋅V ， 73ABC DBC SAM S DN =∴=，故答案为：73．【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点，熟练掌握相似三角形的判定与性质是解题关键．3．（2022·上海·九年级专题练习）如图，在Rt ABC ∆中，90ACB ∠=︒，60BAC ∠=︒，6AC =，AD 平分BAC ∠，交边BC 于点D ，过点D 作CA 的平行线，交边AB 于点E ．（1）求线段DE 的长；（2）取线段AD 的中点M ，联结BM ，交线段DE 于点F ，延长线段BM 交边AC 于点G ，求EF DF的值．【答案】（1）4；（2）23【分析】（1）分别求出CD ，BC ，BD ，证明BDE BCA V V ∽，根据相似性质即可求解；（2）先证明DF AG =，再证明BEF BAG △∽△，根据相似三角形性质求解即可．【详解】解：（1）∵AD 平分BAC ∠，60BAC ∠=︒，∴30DAC ∠=︒．在Rt ACD ∆中，90ACD ∠=︒，30DAC ∠=︒，6AC =，∴CD =在Rt ACB ∆中，90ACB ∠=︒，60BAC ∠=︒，6AC =，∴BC =∴BD BC CD =−=//DE CA ，∴BDE BCA V V ∽∴23DE BD CA BC ==．∴4DE =．（2）∵点M 是线段AD 的中点，∴DM AM =．∵//DE CA ，∴DFM AGM △∽△∴DF DM AG AM =．∴DF AG =． ∵//DE CA ，∴BEF BAG △∽△∴23EF BE BD AG BA BC ===∴23EF DF =．【点睛】本题考查了含30°角的直角三角形性质，相似的判定与性质，解题的关键是能根据题意确定相似三角形，并根据相似性质解题．4．（2022·上海市奉贤区古华中学九年级期中）已知：如图，四边形ABCD 是平行四边形，在边AB 的延长线上截取BE ＝AB ，点F 在AE 的延长线上，CE 和DF 交于点M ，BC 和DF 交于点N ，联结BD ．（1）求证：△BND ∽△CNM ；（2）如果AD 2＝AB •AF ，求证：CM •AB ＝DM •CN ．【分析】（1）利用平行四边形的性质得AB =CD ，AB ∥CD ，再证明四边形BECD 为平行四边形得到BD ∥CE ，根据相似三角形的判定方法，由CM ∥DB 可判断△BND ∽△CNM ；（2）先利用AD 2=AB •AF 可证明△ADB ∽△AFD ，则∠1=∠F ，再根据平行线的性质得∠F =∠4，∠2=∠3，所以∠3=∠4，加上∠NMC =∠CMD ，于是可判断△MNC ∽△MCD ，所以MC ：MD =CN ：CD ，然后利用CD =AB 和比例的性质即可得到结论．【详解】证明：（1）∵四边形ABCD 是平行四边形，∴AB =CD ，AB ∥CD ，而BE =AB ， ∴BE =CD ，而BE∥CD，∴四边形BECD为平行四边形，∴BD∥CE，∵CM∥DB，∴△BND∽△CNM；（2）∵AD2=AB•AF，∴AD：AB=AF：AD，而∠DAB=∠F AD，∴△ADB∽△AFD，∴∠1=∠F，∵CD∥AF，BD∥CE，∴∠F=∠4，∠2=∠3，∴∠3=∠4，而∠NMC=∠CMD，∴△MNC∽△MCD，∴MC：MD=CN：CD，∴MC•CD=MD•CN，而CD=AB，∴CM•AB=DM•CN．【点睛】本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．5．（2022•安庆模拟）在四边形ABCD中，对角线AC、BD相交于点O．（1）如图①，若四边形ABCD为矩形，过点O作OE⊥BC，求证：OE＝CD．（2）如图②，若AB∥CD，过点O作EF∥AB分别交BC、AD于点E、F．求证：＝2．（3）如图③，若OC平分∠AOB，D、E分别为OA、OB上的点，DE交OC于点M，作MN ∥OB交OA于一点N，若OD＝8，OE＝6，直接写出线段MN长度．【分析】（1）由OE⊥BC，DC⊥BC，可知EO∥CD，且OB＝OD，可得结论；（2）由△DFO∽△DAB，得，同理，，，利用等式的性质将比例式相加，从而得出结论；（3）作DF∥OB交OC于点F，连接EF，可知△ODF是等腰三角形，得DO＝DF＝8，由△DMF∽△EMO，可得EM＝，由△DMN∽△DOE，得，从而得出答案．【解答】（1）证明：∵四边形ABCD是矩形，∴O是AC中点，AB⊥BC，∵OE⊥BC，∴OE∥AB，∴E是BC中点，∴OE＝；（2）证明：∵EF∥AB，∴△DFO∽△DAB，∴，同理，，，∴＝，∴，即；（3）解：作DF∥OB交OC于点F，连接EF，∵OC平分∠AOB，∴∠AOC＝∠BOC，∵DF∥OB，∴∠DFO＝∠BOC＝∠AOC，∴△ODF是等腰三角形，∴DO＝DF＝8，∵DF∥OE，∴△DMF∽△EMO，∴，∴EM＝，∴，∵MN∥OE，∴△DMN∽△DOE，∴，∴，∴MN＝．【点评】本题是相似形综合题，主要考查了矩形的性质，相似三角形的判定与性质，等腰三角形的性质，对比例式进行恒等变形是解题的关键．6．（2022•重庆中考模拟）问题提出：如图1，D、E分别在△ABC的边AB、AC上，连接DE，已知线段AD＝a，DB＝b，AE＝c，EC＝d，则S△ADE，S△ABC和a，b，c，d之间会有怎样的数量关系呢？问题解决：探究一：（1）看到这个问题后，我们可以考虑先从特例入手，找出其中的规律．如图2，若DE ∥BC ，则∠ADE ＝∠B ，且∠A ＝∠A ，所以△ADE ∽△ABC ，可得比例式：a c a b c d =++而根据相似三角形面积之比等于相似比的平方．可得()22ADE ABC S a S a b =+V V ．根据上述这两个式子，可以推出：()()()22ADE ABC S a a a a c ac S a b a b a b c d a b c d a b ==⋅=⋅=+++++++V V ．（2）如图3，若∠ADE ＝∠C ，上述结论还成立吗？若成立，请写出证明过程；着不成立，请说明理由．探究二：回到最初的问题，若图1中没有相似的条件，是否仍存在结论：()()ADE ABC S ac S a b c d =++V V 方法回顾：两个三角形面积之比，不仅可以在相似的条件下求得，当两个三角形的底成高具有一定的关系时，也可以解决．如图4，D 在△ABC的边上，做AH ⊥BC 于H ，可得：1212ABDADC BD AH S BD S DC DC AH ⋅==⋅V V ．借用这个结论，请你解决最初的问题．延伸探究：（1）如图5，D 、E 分别在△ABC 的边AB 、AC 反向延长线上，连接DE ，已知线段AD ＝a ，AB ＝b ，AE ＝c ，AC ＝d ，则ADE ABCS S =V V ．（2）如图6，E 在△ABC 的边AC 上，D 在AB 反向延长线上，连接DE ，已知线段AD ＝a ，AB ＝b ，AE ＝c ，AC ＝d ，ADE ABCS S =V V ．结论应用：如图7，在平行四边形ABCD 中，G 是BC 边上的中点，延长GA 到E ，连接DE 交BA 的延长线于F ，若AB ＝5，AG ＝4，AE ＝2，▱ABCD 的面积为30，则△AEF 的面积是．【答案】探究一：（2）见解析；延伸探究：（1）ac bd ;（2）ac bd ；结论应用： 32【分析】问题解决：探究一（2）：参照（1）中证明方法解答即可；探究二，过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ，然后按照探究一中方法证明即可；延伸探究：（1）过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ，然后按照探究一中方法证明即可；（2）过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ，然后按照探究一中方法证明即可；结论应用：取AD 的中点M ，连接GM 并延长交DE 于点N ，连接DG ，可得15ADG S =V ,根据题意，进而得出152ADE S =V ,根据AM =DM ,MN AF ∥,可得FN =DN ，根据AE =2，AG =4，GN AF ∥，可得FN =2EF ，进而可得ED =5EF ，即可得出1352AEF ADE S S ==V V ．【详解】解：问题解决：探究一：（2）成立，理由如下：∵∠ADE ＝∠C ，∠A ＝∠A ，∴ADE ACB V V ∽,∴a c c d a b =++， ∴()22()()ADE ABC S b a S c a c ac c d a b c d a d =+=++++=V V g ；探究二：过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ，∵,DM AC BN AC ⊥⊥，∴//DM BN ,∴AD DM a AB BN a b==+,121()()2ADEABC AE DM S AE DM c a ac S AC BN c d a b a b c d AC BN ⨯==⨯=⨯=++++⨯V V ；延伸探究：（1）过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ，∵,DM AC BN AC ⊥⊥，∴//DM BN ,∴AD DM a AB BN b==,1212ADEABC AE DM S AE DM c a ac S AC BN d b bd AC BN ⨯==⨯=⨯=⨯V V ；（2）过D 、B 点分别作,DM AC BN AC ⊥⊥,垂足分别为M 、N ，∵,DM AC BN AC ⊥⊥，∴//DM BN ,∴AD DM a AB BN b==,1212ADEABC AE DM S AE DM c a ac S AC BN d b bd AC BN ⨯==⨯=⨯=⨯V V ; 结论应用：取AD 的中点M ，连接GM 并延长交DE 于点N ，连接DG ，∴AM =DM ，1152ADG ABCD S S ==V 平行四边形，∵AE =2，AG =4，∴11522ADE ADG S S ==V V , ∵AM =DM ,MN AF P ,∴FN =DN ，∵AE =2，AG =4，GN AF ∥,∴12EF AE FN AG ==,即：FN =2EF ,∴ED =5EF ，∴1352AEF ADE S S ==V V ．【点睛】本题考查了相似三角形的判定与性质，平行线分线段成比例等知识点，熟练运用相似三角形的性质是解题的关键．7．（2022·贵州铜仁·中考真题）如图，在四边形ABCD 中，对角线AC 与BD 相交于点O ，记COD △的面积为1S ，AOB V 的面积为2S ．（1）问题解决：如图①，若AB //CD ，求证：12⋅=⋅S OC OD S OA OB（2）探索推广：如图②，若AB 与CD 不平行，（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由．（3）拓展应用：如图③，在OA 上取一点E ，使OE OC =，过点E 作EF CD ∥交OD 于点F ，点H 为AB 的中点，OH 交EF 于点G ，且2=OG GH ，若56=OE OA ，求12S S 值．【答案】（1）见解析；（2）（1）中的结论成立，理由见解析：（3）2554【分析】（1）如图所示，过点D 作AE ⊥AC 于E ，过点B 作BF ⊥AC 于F ，求出sin sin DE OD DOE BF OB BOF =⋅=⋅∠，∠，然后根据三角形面积公式求解即可；（2）同（1）求解即可；（3）如图所示，过点A 作AM EF ∥交OB 于M ，取BM 中点N ，连接HN ，先证明△OEF ≌△OCD ，得到OD =OF ，证明△OEF ∽△OAM ，得到5==6OF OE OM OA ，设55OE OC m OF OD n ====，，则66OA m OM n ==，，证明△OGF ∽△OHN ，推出31522n ON OF ==，32n BN MN ON OM ==−=，则9OB ON BN n =+=，由（2）结论求解即可．【详解】解：（1）如图所示，过点D 作AE ⊥AC 于E ，过点B 作BF ⊥AC 于F ， ∴sin sin DE OD DOE BF OB BOF =⋅=⋅∠，∠，∴111===sin 22OCD S S OC DE OC OD DOE ⋅⋅⋅△∠， 211==sin 22AOB S S OA BF OA OB BOF ⋅=⋅⋅△∠， ∵∠DOE =∠BOF ，∴sin sin DOE BOF ∠=∠； ∴121sin 2==1sin 2OC OD DOE S OC OD S OA OBOA OB BOF ⋅⋅⋅⋅⋅⋅∠∠；（2）（1）中的结论成立，理由如下：如图所示，过点D 作AE ⊥AC 于E ，过点B 作BF ⊥AC 于F ，∴sin sin DE OD DOE BF OB BOF =⋅=⋅∠，∠， ∴111===sin 22OCD S S OC DE OC OD DOE ⋅⋅⋅△∠， 211==sin 22AOB S S OA BF OA OB BOF ⋅=⋅⋅△∠， ∵∠DOE =∠BOF ，∴sin sin DOE BOF ∠=∠； ∴121sin 2==1sin 2OC OD DOE S OC OD S OA OBOA OB BOF ⋅⋅⋅⋅⋅⋅∠∠；（3）如图所示，过点A 作AM EF ∥交OB 于M ，取BM 中点N ，连接HN ，∵EF CD ∥，∴∠ODC =∠OFE ，∠OCD =∠OEF ，又∵OE =OC ，∴△OEF ≌△OCD （AAS ），∴OD =OF ，∵EF AM ∥，∴△OEF ∽△OAM ，∴5==6OF OE OM OA ，设55OE OC m OF OD n ====，，则66OA m OM n ==，，∵H 是AB 的中点，N 是BM 的中点，∴HN 是△ABM 的中位线，∴HN AM EF ∥∥，∴△OGF ∽△OHN ，∴OG OF OH ON=，。

相似三角形重要模型之(双)A字型与(双)8字型(解析版)-2024年中考数学常见几何模型

相似三角形重要模型之(双)A字型与(双)8字型相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

本专题重点讲解相似三角形的(双)A字模型和(双)8(X)字模型．A字型和8(X)字型的应用难点在于过分割点(将线段分割的点)作平行线构造模型，有的是直接作平行线，有的是间接作平行线(倍长中线就可以理解为一种间接作平行线)，这一点在模考中无论小题还是大题都是屡见不鲜的。

模型1. “A”字模型【模型解读与图示】“A”字模型图形(通常只有一个公共顶点)的两个三角形有一个“公共角”(是对应角)，再有一个角相等或夹这个公共角的两边对应成比例，就可以判定这两个三角形相似．图1 图2 图31)“A”字模型条件：如图1，DE∥BC；结论：△ADE∽△ABC⇔ADAB =AEAC=DEBC.2)反“A”字模型条件：如图2，∠AE D=∠B；结论：△ADE∽△ACB⇔ADAC =AEAB=DEBC.3)同向双“A”字模型条件：如图3，EF∥BC；结论：△AEF∽△ABC，△AEG∽△ABD，△AGF∽△ADC⇔EGBD=FGCD=AGAD1(2023·湖北十堰·统考中考真题)如图，在菱形ABCD中，点E，F，G，H分别是AB，BC，CD，AD上的点，且BE=BF=CG=AH，若菱形的面积等于24，BD=8，则EF+GH=．【答案】6【分析】连接AC，交BD于点O，由题意易得AC=6，AC⊥BD，AO=3，BO=4，则有AB=AD=5，然后可得EF∥AC∥GH，设BE=BF=CG=AH=a，则有DH=5-a，进而根据相似三角形的性质可进行求解．【详解】解：连接AC，交BD于点O，如图所示：∵四边形ABCD 是菱形，BD =8，∴AB =BC =AD =CD ，AC ⊥BD ，AO =OC =12AC ，BO =OD =12BD =4，∵S 菱形ABCD =12AC ⋅BD =24，∴AC =6，∴AO =3，∴AB =AO 2+BO 2=5=AD ，∵BE =BF =CG =AH ，∴AE =CF =DH =DG ，∴BE AE=BF CF ，∴EF ∥AC ，同理可得GH ∥AC ，设BE =BF =CG =AH =a ，则有DH =5-a ，∵EF ∥AC ，∴△BEF ∽△BAC ，∴BE BA =EF AC ，即a 5=EF 6，∴EF =65a ，同理可得DH DA =GH CA，即5-a 5=GH 6，∴GH =6-65a ，∴EF +GH =6；故答案为6．【点睛】本题主要考查相似三角形的性质与判定及菱形的性质，熟练掌握菱形的性质及相似三角形的性质与判定是解题的关键．2(2023·安徽·九年级期末)如图，在三角形△ABC 中，点D 、E 分别在边AB 、AC 上，AD =3，BD =1，AE =2，EC =4．(1)求证：∠ADE =∠C ；(2)若∠BAC 的平分线交DE 于点F ，交BC 于点G ，求AF FG．【答案】(1)见解析(2)AF FG =1【分析】(1)证明AE AB =24=12，AD AC =36=12，可得AE AB =AD AC，结合∠DAE =∠CAB ，从而可得结论；(2)由(1)可得△DAE ∽△CAB ，可得∠ADE =∠C ，证明∠DAF =∠CAG ，可得△ADF ∽△ACG ，再利用相似三角形的性质可得答案．【详解】(1)解：∵AD =3，BD =1，AE =2，EC =4，∴AB =AD +BD =4，AC =AE +CE =6．∴AE AB =24=12，AD AC =36=12，∴AE AB =AD AC，又∵∠DAE =∠CAB ，∴△DAE ∽△CAB ，∴∠ADE =∠C ．(2)由(1)可得△DAE ∽△CAB ，∴∠ADE =∠C ，又∵AG 平分∠BAC ，∴∠DAF =∠CAG ，∴△ADF ∽△ACG ，∴AF AG =AD AC=12，∴AF FG =1．【点睛】本题考查的是角平分线的定义，相似三角形的判定与性质，相似三角形的判定方法是解本题关键．3(2022·山东东营·中考真题)如图，在△ABC 中，点F 、G 在BC 上，点E 、H 分别在AB 、AC 上，四边形EFGH 是矩形，EH =2EF ,AD 是△ABC 的高．BC =8,AD =6，那么EH 的长为．【答案】245##4.8【分析】通过四边形EFGH 为矩形推出EH ∥BC ，因此△AEH 与△ABC 两个三角形相似，将AM 视为△AEH 的高，可得出AM AD=EH BC ，再将数据代入即可得出答案．【详解】∵四边形EFGH 是矩形，∴EH ∥BC ，∴△AEF ∽△ABC ，∵AM 和AD 分别是△AEH 和△ABC 的高，∴AM AD =EH BC ,DM =EF ，∴AM =AD -DM =AD -EF =6-EF ，∵EH =2EF ，代入可得：6-EF 6=2EF 8，解得EF =125，∴EH =2×125=245，故答案为：245．【点睛】本题考查了相似三角形的判定和性质及矩形的性质，灵活运用相似三角形的性质是本题的关键．4(2022·浙江宁波·中考真题)(1)如图1，在△ABC 中，D ，E ，F 分别为AB ,AC ,BC 上的点，DE ∥BC ,BF =CF ,AF 交DE 于点G ，求证：DG =EG ．(2)如图2，在(1)的条件下，连接CD ,CG ．若CG ⊥DE ,CD =6,AE =3，求DE BC的值．(3)如图3，在▱ABCD 中，∠ADC =45°,AC 与BD 交于点O ，E 为AO 上一点，EG ∥BD 交AD 于点G ，EF ⊥EG 交BC 于点F ．若∠EGF =40°,FG 平分∠EFC ,FG =10，求BF 的长．【答案】(1)证明见详解(2)13(3)5+53【分析】(1)利用DE ∥BC ，证明△ADG ∼△ABF ,△AEG ∼△ACF ，利用相似比即可证明此问；(2)由(1)得DG =EG ，CG ⊥DE ，得出△DCE 是等腰三角形，利用三角形相似即可求出DE BC的值；(3)遵循第(1)、(2)小问的思路，延长GE 交AB 于点M ，连接FM ，作MN ⊥BC ，垂足为N ．构造出等腰三角形、含30°、45°角的特殊直角三角形，求出BN 、FN 的值，即可得出BF 的长．(1)解：∵DE ∥BC ，∴△ADG ∼△ABF ,△AEG ∼△ACF ，∴DG BF =AG AF ,EG CF =AG AF，∴DG BF =EG CF ．∵BF =CF ，∴DG =EG ．(2)解：由(1)得DG =EG ，∵CG ⊥DE ，∴CE =CD =6．∵AE =3，∴AC =AE +CE =9．∵DE ∥BC ，∴△ADE ∼△ABC ．∴DE BC =AE AC=13．(3)解：如图，延长GE 交AB 于点M ，连接FM ，作MN ⊥BC ，垂足为N ．在▱ABCD 中，BO =DO ,∠ABC =∠ADC =45°．∵EG ∥BD ，∴由(1)得ME =GE ，∵EF ⊥EG ，∴FM =FG =10，∴∠EFM =∠EFG ．∵∠EGF =40°，∴∠EMF =40°，∴∠EFG =50°．∵FG 平分∠EFC ，∴∠EFG =∠CFG =50°，∴∠BFM =180°-∠EFM -∠EFG -∠CFG =30°．∴．在Rt △FMN 中，MN =FM sin30°=5,FN =FM cos30°=53．∵∠MBN =45°,MN ⊥BN ，∴BN =MN =5，∴BF =BN +FN =5+53．【点睛】本题考查了相似三角形的性质及判定、等腰三角形的性质及判定、解特殊的直角三角形等知识，遵循构第(1)、(2)小问的思路，构造出等腰三角形和特殊的直角三角形是解决本题的关键．5(2023•安庆一模)如图，在△ABC 中，点D 、E 、F 分别在边BC 、AB 、CA 上，且DE ∥CA ，DF ∥AB ．(1)若点D 是边BC 的中点，且BE =CF ，求证：DE =DF ；(2)若AD ⊥BC 于D ，且BD =CD ，求证：四边形AEDF 是菱形；(3)若AE =AF =1，求1AB +1AC的值．【分析】(1)根据中点和平行两个条件可得中点，从而可得DE 是△ABC 的中位线，进而可得DE =FC ，同理可得DF =BE ，即可解答；(2)根据已知易证四边形AEDF 是平行四边形，再利用等腰三角形的三线合一性质可得∠BAD =∠CAD ，然后利用平行线的性质可得∠EDA =∠CAD ，从而可得∠BAD =∠EDA ，进而可得EA =ED ，即可解答；(3)根据A 字模型相似三角形可知△BED ∽△BAC ，△CDF ∽△CBA ，从而可得DE AC=BD BC ，DF AB =CD BC ，然后把两个式子相加进行计算，即可解答．【解答】(1)证明：∵点D 是边BC 的中点，DE ∥CA ，∴点E 是AB 的中点，∴DE 是△ABC 的中位线，∴DE =12AC ，∵点D 是边BC 的中点，DF ∥AB ，∴点F 是AC 的中点，∴FC =12AC ，∴DE =FC ，同理可得：DF =BE ，∵BE =FC ，∴DE =DF ；(2)证明：∵DE ∥CA ，DF ∥AB ，∴四边形AEDF 是平行四边形，∵AD ⊥BC ，BD =CD ，∴AD 是BC 的垂直平分线，∴AB =AC ，∴∠BAD =∠CAD ，∵DE ∥AC ，∴∠EDA =∠CAD ，∴∠BAD =∠EDA ，∴EA =ED ，∴四边形AEDF 是菱形；(3)∵DE ∥CA ，∴∠EDB =∠C ，∵∠B =∠B ，∴△BED ∽△BAC ，∴DE AC =BD BC ，∵DF ∥AB ，∴∠B =∠FDC ，∵∠C =∠C ，∴△CDF ∽△CBA ，∴DF AB =CD BC ，∴DE AC +DF AB=BD BC +CD BC =BD +CD BC =1，∵四边形AEDF 是平行四边形，∴DE =AF ，DF =AE ，∵AE =AF =1，∴DE =DF =1，∴1AB +1AC =1，∴1AB +1AC的值为1．【点评】本题考查了相似三角形的判定与性质，全等三角形的判定与性质，线段垂直平分线的性质，分式的化简求值，菱形的判定与性质，熟练掌握菱形的判定与性质，以及A 字模型相似三角形的关键．模型2.“X ”字模型(“8”模型)【模型解读与图示】“8”字模型图形的两个三角形有“对顶角”，再有一个角相等或夹对顶角的两边对应成比例就可以判定这两个三角形相似．图1图2图3图41)“8”字模型条件：如图1，AB ∥CD ；结论：△AOB ∽△COD ⇔AB CD =OA OC =OB OD.2)反“8”字模型条件：如图2，∠A =∠D ；结论：△AOB ∽△DOC ⇔AB CD =OA OD =OB OC .3)平行双“8”字模型条件：如图3，AB ∥CD ；结论：AE DF =BE CF =AB CD4)斜双“8”字模型条件：如图4，∠1=∠2；结论：△AOD ∽△BOC ，△AOB ∽△DOC ⇔∠3=∠4.1(2022·辽宁·中考真题)如图，在正方形ABCD 中，E 为AD 的中点，连接BE 交AC 于点F ．若AB =6，则△AEF 的面积为．【答案】3【分析】由正方形的性质可知AE =12AD =12AB =12BC =3，AD ⎳BC ，则有△AEF ∽△CBF ，然后可得EF BF =AE BC=12，进而问题可求解．【详解】解：∵四边形ABCD 是正方形，AB =6，∴AD =BC =AB =6，AD ⎳BC ，∴△AEF ∽△CBF ，∴EF BF =AE BC，∵E 为AD 的中点，∴AE =12AD =12AB =12BC =3，∴EF BF =AE BC=12，S △ABE =12AE ⋅AB =9，∴EF BE =13，∴S △AEF =13S △ABE =3；故答案为3．【点睛】本题主要考查正方形的性质及相似三角形的性质与判定，熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键．2(2023·黑龙江·哈尔滨九年级阶段练习)如图，AB ∥CD ,AE ∥FD ，AE ，FD 分别交BC 于点G ，H ，则下列结论中错误的是()A.DH FH =CH BHB.GE DF =CG CBC.AF CE =HG CGD.FH AG =BF FA【答案】D【分析】根据平行线分线段成比例和相似三角形的性质与判定，进行逐一判断即可．【详解】解：∵AB ∥CD ∴DH FH =CH BH ，∴A 选项正确，不符合题目要求；∵AE ∥DF ，∴∠CGE =∠CHD ，∠CEG =∠D ，∴△CEG ∽△CDH ，∴GE DH =CG CH ，∴EG CG =DH CH ，∵AB ∥CD ，∴CH CB =DH DF ，∴DH CH =DF CB ，∴GE CG =DF CB ，∴GE DF =CG CB，∴B 选项正确，不符合题目要求；∵AB ∥CD ，AE ∥DF ，∴四边形AEDF 是平行四边形，∴AF =DE ，∵AE ∥DF ∴DE CE =GH GC ，∴AF CE =HG CG ；∴C 选项正确，不符合题目要求；∵AE ∥DF ，∴△BFH ∽△BAG ，∴FH AG =BF AB ，∵AB >FA ，∴FHAG ≠BF FA∴D 选项不正确，符合题目要求．故选D ．【点睛】本题考查了平行线分线段成比例定理，相似三角形的性质和判定的应用，能根据定理得出比例式是解此题的关键．3(2021·上海·中考真题)如图，在梯形ABCD中，AD⎳BC,∠ABC=90°,AD=CD,O是对角线AC的中点，联结BO并延长交边CD或边AD于E．(1)当点E在边CD上时，①求证：△DAC∽△OBC；②若BE⊥CD，求ADBC的值；(2)若DE=2,OE=3，求CD的长．【答案】(1)①见解析；②23；(2)1+19或3+19【分析】(1)①根据已知条件、平行线性质以及直角三角形斜边上的中线等于斜边的一半可推导，∠DAC=∠DCA=∠OBC=∠OCB，由此可得△DAC∽△OBC；②若BE⊥CD，那么在Rt△BCE中，由∠2=∠3=∠4．可得∠2=∠3=∠4=30°，作DH⊥BC于H．设AD=CD=2m，那么BH=AD=2m．根据30°所对直角边是斜边的一半可知CH=m，由此可得ADBC的值．(2)①当点E在AD上时，可得四边形ABCE是矩形，设AD=CD=x，在Rt△ACE和Rt△DCE中，根据CE2=CE2，列方程62-(x-2)2=x2-22求解即可．②当点E在CD上时，设AD=CD=x，由△DAC∽△OBC，得DCOC=ACBC，所以xm=2OCBC，所以OCBC=x2m；由△EOC∽△ECB得EOEC=ECEB=OCCB，所以3x-2=x-2m+3=OCCB，解出x的值即可．【详解】(1)①由AD=CD，得∠1=∠2．由AD⎳BC，得∠1=∠3．因为BO是Rt△ABC斜边上的中线，所以OB=OC．所以∠3=∠4．所以∠1=∠2=∠3=∠4．所以△DAC∽△OBC．②若BE⊥CD，那么在Rt△BCE中，由∠2=∠3=∠4．可得∠2=∠3=∠4=30°．作DH⊥BC于H．设AD=CD=2m，那么BH=AD=2m．在Rt△DCH中，∠DCH=60°,DC=2m，所以CH=m．所以BC=BH+CH=3m．所以ADBC=2m3m=23．(2)①如图5，当点E在AD上时，由AD⎳BC,O是AC的中点，可得OB=OE，所以四边形ABCE是平行四边形．又因为∠ABC=90°，所以四边形ABCE是矩形，设AD =CD =x ，已知DE =2，所以AE =x -2．已知OE =3，所以AC =6．在Rt △ACE 和Rt △DCE 中，根据CE 2=CE 2，列方程62-(x -2)2=x 2-22．解得x =1+19，或x =1-19(舍去负值)．②如图6，当点E 在CD 上时，设AD =CD =x ，已知DE =2，所以CE =x -2．设OB =OC =m ，已知OE =3，那么EB =m +3．一方面，由△DAC ∽△OBC ，得DC OC =AC BC ，所以x m =2OC BC ，所以OC BC=x 2m ，另一方面，由∠2=∠4，∠BEC 是公共角，得△EOC ∽△ECB ．所以EO EC =EC EB =OC CB ，所以3x -2=x -2m +3=OC CB．等量代换，得3x -2=x -2m +3=x 2m ．由3x -2=x 2m ，得m =x 2-2x 6．将m =x 2-2x 6代入3x -2=x -2m +3，整理，得x 2-6x -10=0．解得x =3+19，或x =3-19(舍去负值)．【点睛】本题主要考查相似三角形的判定与性质，斜边上的中线，勾股定理等，能够运用相似三角形边的关系列方程是解题的关键．4(2022·贵州铜仁·中考真题)如图，在四边形ABCD 中，对角线AC 与BD 相交于点O ，记△COD 的面积为S 1，△AOB 的面积为S 2．(1)问题解决：如图①，若AB ⎳CD ，求证：S 1S 2=OC ⋅OD OA ⋅OB(2)探索推广：如图②，若AB 与CD 不平行，(1)中的结论是否成立？若成立，请证明；若不成立，请说明理由．(3)拓展应用：如图③，在OA 上取一点E ，使OE =OC ，过点E 作EF ∥CD 交OD 于点F ，点H 为AB的中点，OH 交EF 于点G ，且OG =2GH ，若OE OA=56，求S 1S 2值．【答案】(1)见解析；(2)(1)中的结论成立，理由见解析：(3)2554【分析】(1)如图所示，过点D 作AE ⊥AC 于E ，过点B 作BF ⊥AC 于F ，求出DE =OD ⋅sin ∠DOE ，BF=OB ⋅sin ∠BOF ，然后根据三角形面积公式求解即可；(2)同(1)求解即可；(3)如图所示，过点A 作AM ∥EF 交OB 于M ，取BM 中点N ，连接HN ，先证明△OEF ≌△OCD ，得到OD=OF ，证明△OEF ∽△OAM ，得到OF OM =OE OA =56，设OE =OC =5m ，OF =OD =5n ，则OA =6m ，OM =6n ，证明△OGF ∽△OHN ，推出ON =32OF =15n 2，BN =MN =ON -OM =3n 2，则OB =ON +BN =9n ，由(2)结论求解即可．【详解】解：(1)如图所示，过点D 作AE ⊥AC 于E ，过点B 作BF ⊥AC 于F ，∴DE =OD ⋅sin ∠DOE ，BF =OB ⋅sin ∠BOF ，∴S △OCD =S 1=12OC ⋅DE =12OC ⋅OD ⋅sin ∠DOE ，S △AOB =S 2=12OA ⋅BF =12OA ⋅OB ⋅sin ∠BOF ，∵∠DOE =∠BOF ，∴sin ∠DOE =sin ∠BOF ；∴S 1S 2=12OC ⋅OD ⋅sin ∠DOE 12OA ⋅OB ⋅sin ∠BOF =OC ⋅OD OA ⋅OB ；(2)(1)中的结论成立，理由如下：如图所示，过点D 作AE ⊥AC 于E ，过点B 作BF ⊥AC 于F ，∴DE =OD ⋅sin ∠DOE ，BF =OB ⋅sin ∠BOF ，∴S △OCD =S 1=12OC ⋅DE =12OC ⋅OD ⋅sin ∠DOE ，S △AOB =S 2=12OA ⋅BF =12OA ⋅OB ⋅sin ∠BOF ，∵∠DOE =∠BOF ，∴sin ∠DOE =sin ∠BOF ；∴S 1S 2=12OC ⋅OD ⋅sin ∠DOE 12OA ⋅OB ⋅sin ∠BOF =OC ⋅OD OA ⋅OB ；(3)如图所示，过点A 作AM ∥EF 交OB 于M ，取BM 中点N ，连接HN ，∵EF ∥CD ，∴∠ODC =∠OFE ，∠OCD =∠OEF ，又∵OE =OC ，∴△OEF ≌△OCD (AAS )，∴OD =OF ，∵EF ∥AM ，∴△OEF ∽△OAM ，∴OF OM =OE OA=56，设OE =OC =5m ，OF =OD =5n ，则OA =6m ，OM =6n ，∵H 是AB 的中点，N 是BM 的中点，∴HN 是△ABM 的中位线，∴HN ∥AM ∥EF ，∴△OGF ∽△OHN ，∴OG OH =OF ON ，∵OG =2GH ，∴OG =23OH ，∴OG OH =OF ON =23，∴ON =32OF =15n 2，BN =MN =ON -OM =3n 2，∴OB =ON +BN =9n ，由(2)可知S 1S 2=OC ⋅OD OA ⋅OB=5m ⋅5n 6m ⋅9n =2554．【点睛】本题主要考查了解直角三角形，相似三角形的性质与判定，全等三角形的性质与判定，三角形中位线定理，正确作出辅助线是解题的关键．模型3. “AX”字模型(“A8”模型)【模型解读与图示】图1图2图3 1)一“A”一“8”模型条件：如图1，DE∥BC；结论：△ADE∽△ABC，△DEF∽△CBF⇔ADAB=AEAC=DEBC=DFFC=FEBF2)两“A”一“8”模型条件：如图2，DE∥AF∥BC；结论：1BC +1DE=1AF.3)四“A”一“8”模型条件：如图3，DE∥AF∥BC,1BC+1DE=1AF=1AG；结论：AF=AG1(2022·山东东营·中考真题)如图，点D为△ABC边AB上任一点，DE∥BC交AC于点E，连接BE、CD 相交于点F，则下列等式中不成立的是()A.ADDB =AEECB.DEBC=DFFCC.DEBC=AEECD.EFBF=AEAC【答案】C【分析】根据平行线分线段成比例定理即可判断A，根据相似三角形的性质即可判断B、C、D．【详解】解：∵DE∥BC，∴AD BD =AEEC，△DEF∽△CBF，△ADE∽△ABC，故A不符合题意；∴DE CB =DFCF=EFBF，DECB=AEAC，故B不符合题意，C符合题意；∴EF BF =AEAC，故D不符合题意；故选C．【点睛】本题主要考查了相似三角形的性质与判定，平行线分线段成比例定理，熟知相似三角形的性质与判定，平行线分线段成比例定理是解题的关键．2(2021·江苏南京·中考真题)如图，AC与BD交于点O，OA=OD,∠ABO=∠DCO，E为BC延长线上一点，过点E作EF⎳CD，交BD的延长线于点F．(1)求证△AOB≌△DOC；(2)若AB=2,BC=3,CE=1，求EF的长．【答案】(1)证明见解析；(2)EF=8 3【分析】(1)直接利用“AAS”判定两三角形全等即可；(2)先分别求出BE和DC的长，再利用相似三角形的判定与性质进行计算即可．【详解】解：(1)∵OA=OD,∠ABO=∠DCO，又∵∠AOB=∠DOC，∴△AOB≌△DOC AAS；(2)∵△AOB≌△DOC AAS，AB=2,BC=3,CE=1∴AB=DC=2，BE=BC+CE=3+1=4，∵EF⎳CD，∴△BEF∽△BCD，∴EFCD =BE BC，∴EF2=43，∴EF=83，∴EF的长为83．【点睛】本题考查了全等三角形的判定与性质、平行线分线段成比例的推论、相似三角形的判定与性质等，解决本题的关键是牢记相关概念与公式，能结合图形建立线段之间的关联等，本题较基础，考查了学生的几何语言表达和对基础知识的掌握与应用等．3(2022·重庆九年级期中)如图，AD与BC相交于点E，点F在BD上，且AB∥EF∥CD，求证：1AB +1CD=1EF.证明：∵AB∥EF，∴△DEF∽△DAB，∴EFAB=DFDB.又∵EF∥CD，∴△BEF∽△BCD.∴EFCD=BFBD.∴EF AB +EFCD=DFDB+BFBD=BDBD=1.∴1AB+1CD=1EF.4(2022•安庆模拟)在四边形ABCD中，对角线AC、BD相交于点O．(1)如图①，若四边形ABCD为矩形，过点O作OE⊥BC，求证：OE=12CD．(2)如图②，若AB∥CD，过点O作EF∥AB分别交BC、AD于点E、F．求证：EFAB =EFCD=2．(3)如图③，若OC平分∠AOB，D、E分别为OA、OB上的点，DE交OC于点M，作MN∥OB交OA于一点N，若OD=8，OE=6，直接写出线段MN长度．【分析】(1)由OE⊥BC，DC⊥BC，可知EO∥CD，且OB=OD，可得结论；(2)由△DFO∽△DAB，得FOAB =DODB，同理OFCD=AOAC，OEAB=COCA，EOCD=BOBD，利用等式的性质将比例式相加，从而得出结论；(3)作DF∥OB交OC于点F，连接EF，可知△ODF是等腰三角形，得DO=DF=8，由△DMF∽△EMO，可得EM=34DM，由△DMN∽△DOE，得MNOE=DMDE=47，从而得出答案．【解答】(1)证明：∵四边形ABCD是矩形，∴O是AC中点，AB⊥BC，∵OE⊥BC，∴OE∥AB，∴E是BC中点，∴OE=12CD；(2)证明：∵EF∥AB，∴△DFO∽△DAB，∴FOAB =DO DB，同理OFCD=AOAC，OEAB=COCA，EOCD=BOBD，∴FOAB+OFCD+OEAB+EOCD=DODB+AOAC+COCA+BOBD，∴FO+OEAB +EO+OFCD=AO+COAC+BO+DOBD，即，EFAB+EFCD=2；(3)解：作DF∥OB交OC于点F，连接EF，∵OC平分∠AOB，∴∠AOC=∠BOC，∵DF∥OB，∴∠DFO=∠BOC=∠AOC，∴△ODF是等腰三角形，∴DO=DF=8，∵DF∥OE，∴△DMF∽△EMO，∴EM DM =EODF=EODO=68=34，∴EM=34DM，∴DMDE=DMDM+ME=DMDM+34DM=47，∵MN∥OE，∴△DMN∽△DOE，∴MNOE =DMDE=47，∴MN6=47，∴MN=247．【点评】本题是相似形综合题，主要考查了矩形的性质，相似三角形的判定与性质，等腰三角形的性质，对比例式进行恒等变形是解题的关键．课后专项训练1(2021·山东淄博·中考真题)如图，AB,CD相交于点E，且AC⎳EF⎳DB，点C,F,B在同一条直线上．已知AC=P,EF=r,DB=q，则p,q,r之间满足的数量关系式是()A.1r +1q=1pB.1p+1r=2qC.1p+1q=1rD.1q+1r=2p【答案】C【分析】由题意易得△BEF∽△BAC，△CEF∽△CDB，则有EFAC=BFBC，EFBD=CFBC，然后可得EFAC+EFBD=1，进而问题可求解．【详解】解：∵AC⎳EF⎳DB，∴△BEF∽△BAC，△CEF∽△CDB，∴EF AC =BFBC，EFBD=CFBC，∴EFAC+EFBD=BFBC+CFBC=1，∵AC=P,EF=r,DB=q，∴rp +rq=1，即1p+1q=1r；故选C．【点睛】本题主要考查相似三角形的性质与判定，熟练掌握相似三角形的性质与判定是解题的关键．2(2023秋·山西阳泉·九年级统考期末)如图，在四边形ABCD中，AB=AC，对角线AC与BD相交于点E，DE=3BE，AC⊥AD，∠ACB=75°，AE=33，则对角线AC与BD的长分别是()A.AC=43，BD=123B.AC=9，BD=419C.AC=6，BD=83D.AC=8，BD=419【答案】D【分析】过点B作BO∥AD交AC于点O，证明△AED∽△OEB，可求得OE=3，AO=43，根据勾股定理求出BO的长，进而可求出AC的长，再根据勾股定理求出BE的长，进而求出BD的长．【详解】过点B作BO∥AD交AC于点O，如图所示：∵AC ⊥AD ，BO ∥AD ，∴∠DAC =∠BOA =90°．∵∠AED =∠OEB ，∴△AED ∽△OEB ，∴BE DE =EO AE =BODA．∵DE =3BE ，∴EO AE =BO DA=13．∵AE =33，∴OE =3，∴AO =43．∵AB =AC ，∠ACB =75°，∵∠ABC =∠ACB =75°，∴∠BAC =30°，∴AB =2BO ．在Rt △AOB 中，BO 2+AO 2=AB 2，即43 2+BO 2=2BO 2，解得：BO =4，∴AB =AC =8．∵OE =3，BO =4，∴BE =BO 2+OE 2=19，∴DE =3BE =319，∴BD =BE +DE =419．故选D ．【点睛】本题考查了相似三角形的判定与性质，等腰三角形的性质，含30度角的直角三角形的性质，勾股定理以及平行线的性质，解题的关键是利用勾股定理求出BE 的长度．3(2023·福建福州·校考二模)在数学综合实践课上，某学习小组计划制作一个款式如图所示的风筝．在骨架设计中，两条侧翼的长度设计AB =AC =50cm ，风筝顶角∠BAC 的度数为110°，在AB ，AC 上取D ，E 两处，使得AD =AE ，并作一条骨架AF ⊥DE ．在制作风筝面时，需覆盖整个骨架，根据以上数据，B ，C 两点间的距离大约是( )(参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43)A.41cmB.57cmC.82cmD.143cm【答案】C【分析】设AF 与DE 交于点G ，连接BC ，交AF 于点H ，根据已知易证△ADE ∽△ABC ，然后利用相似三角形的性质可得∠ADE =∠ABC ，从而可得DE ∥BC ，进而可得BC ⊥AF ，再利用等腰三角形的三线合一性质可得BC =2BH ，∠BAH =12∠BAC =55°，最后在Rt △BAH 中，利用锐角三角函数的定义求出BH 的长，即可解答．【详解】解：设AF 与DE 交于点G ，连接BC ，交AF 于点H ，∵AD =AE ，AB =AC ，∴AD AB =AEAC，∵∠DAE =∠BAC ，∴△ADE ∽△ABC ，∴∠ADE =∠ABC ，∴DE ∥BC ，∵AF ⊥DE ，∴BC ⊥AF ，∵AB =AC ，AF ⊥BC ，∴BC =2BH ，∠BAH =12∠BAC =55°，在Rt △BAH 中，AB =50cm ，∴BH =AB ⋅sin55°≈50×0.82=41cm ，∴BC =2BH =82cm ，∴B ，C 两点间的距离大约是82cm ，故选：C ．【点睛】本题考查了解直角三角形的应用，相似三角形的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．4(2022·湖北十堰·中考真题)如图，某零件的外径为10cm ，用一个交叉卡钳(两条尺长AC 和BD 相等)可测量零件的内孔直径AB ．如果OA ：OC =OB ：OD =3，且量得CD =3cm ，则零件的厚度x 为()A.0.3cmB.0.5cmC.0.7cmD.1cm【答案】B【分析】求出△AOB 和△COD 相似，利用相似三角形对应边成比例列式计算求出AB ，再根据外径的长度解答．【详解】解：∵OA ：OC =OB ：OD =3，∠AOB =∠COD ，∴△AOB ∽△COD ，∴AB ：CD =3，∴AB ：3=3，∴AB =9(cm )，∵外径为10cm ，∴19+2x =10，∴x =0.5(cm )．故选：B ．【点睛】本题考查相似三角形的应用，解题的关键是利用相似三角形的性质求出AB 的长．5(2022·湖南怀化·中考真题)如图，△ABC 中，点D 、E 分别是AB 、AC 的中点，若S △ADE =2，则S △ABC =．【答案】8【分析】根据三角形中位线定理求得DE ∥BC ，DE BC=12，从而求得△ADE ∽△ABC ，然后利用相似三角形的性质求解．【详解】解：∵D 、E 分别是AB 、AC 的中点，则DE 为中位线，所以DE ∥BC ，DE BC =12所以△ADE ∽△ABC ∴S △ADE S △ABC =DE BC2=14∵S △ADE =2，∴S △ABC =8故答案为：8．【点睛】本题考查中位线及平行线性质，本题难度较低，主要考查学生对三角形中位线及平行线性质等知识点的掌握．6(2023·广东梅州·九年级统考期末)如图，在△ABC 中，点F 、G 在BC 上，点E 、H 分别在AB 、AC 上，四边形EFGH 是矩形，EH =2EF ，AD 是△ABC 的高，BC =15，AD =5，那么EH 的长为．【答案】6【分析】通过四边形EFGH 为矩形推出EH ∥BC ，因此△AEH 与△ABC 两个三角形相似，将AM 视为△AEH 的高，可得出AM AD=EHBC ，再将数据代入即可得出答案．【详解】解：设AD 与EH 交于点M ．∵四边形EFGH 是矩形，∴EH ∥BC ，∴△AEH ∽△ABC ，∵AM 和AD 分别是△AEH 和△ABC 的高，∴AM AD=EHBC ,DM =EF ，∴AM =AD -DM =AD -EF =5-EF ，∵EH =2EF ，代入可得：5-EF 5=2EF15，解得EF =3，∴EH =2×3=6，故答案为：6．【点睛】本题考查了相似三角形的判定和性质及矩形的性质，灵活运用相似三角形的性质是本题的关键．7(2023·广东深圳·校考三模)如图，在Rt △ABC 中，∠ACB =90°，AC =BC =6，D 是AB 上一点，点E 在BC 上，连接CD ，AE 交于点F ，若∠CFE =45°，BD =2AD ，则CE =．【答案】2【分析】过D 作DH 垂直AC 于H 点，过D 作DG ∥AE 交BC 于G 点，先利用解直角三角形求出CD 的长，其次利用△CDG ∽△CBD ，求出CG 的长，得出BG 的长，最后利用△BDG ∽△BAE ，求出BE 的长，最后得出答案．【详解】解：如图：过D 作DH 垂直AC 于H 点，过D 作DG ∥AE 交BC 于G 点，∵在Rt △ABC 中，AC =BC =6，∴AB =AC 2+BC 2=62，又∵BD =2AD ，∴AD =22，∴在等腰直角三角形AHD 中，AH =DH =2，∴CH =6-2=4，在Rt △CHD 中，CD =CH 2+DH 2=25，∵DG ∥AE ，∴∠CFE =∠CDG =45°，∠B =45°，∴∠CDG =∠B ，又∵∠DCG =∠BCD ，∴△CDG ∽△CBD ，∴CD CB =CGCD ，∴CD 2=CG ⋅CB ，即20=6CG ，∴CG =103，∴BG =BC -CG =6-103=83，又∵DG ∥AE ，∴△BDG ∽△BAE ，又∵BD =2AD ，∴BD BA=BG BE =23，又BG =83，∴BE =BG ×32=4，∴CE =6-4=2，故答案为：2．【点睛】本题考查勾股定理，等腰直角三角形性质及相似三角形的判定与性质综合，解题关键在于正确做出辅助线，利用相似三角形的性质得出对应边成比例求出答案．8(2022·四川宜宾·中考真题)如图，△ABC 中，点E 、F 分别在边AB 、AC 上，∠1=∠2．若BC =4，AF =2，CF =3，则EF =．【答案】85【分析】易证△AEF ∽△ABC ，得EF BC =AF AC 即EF BC =AFAF +CF即可求解．【详解】解：∵∠1=∠2，∠A =∠A ，∴△AEF ∽△ABC ，∴EF BC =AF AC ，即EF BC =AF AF +CF∵BC =4，AF =2，CF =3，∴EF 4=22+3，∴EF =85，故答案为：85．【点睛】本题考查相似三角形的判定与性质，熟练掌握相似三角形的判定与性质定理是解题的关键．9(2022·辽宁阜新·中考真题)如图，在矩形ABCD中，E是AD边上一点，且AE=2DE，BD与CE相交于点F，若△DEF的面积是3，则△BCF的面积是．【答案】27【分析】根据矩形ABCD的性质，很容易证明△DEF∽△BCF，相似三角形之比等于对应边比的平方，即可求出△BCF的面积．【详解】解：∵四边形ABCD是矩形，∴AD=BC，AD∥BC∴∠EDF=∠CBF，∵∠EFD=∠CFB，∠EDF=∠CBF∴△DEF∽△BCF，∵AE=2DE，AD=BC，∴DE：BC=1：3，∴S△DEF：S△BCF=DE2：BC2，即3：S△BCF=1：9，∴S△BCF=27．故答案为：27．【点睛】本题考查了相似三角形的判定与性质，矩形的性质，综合性比较强，学生要灵活应用．掌握相似三角形的面积比是相似比的平方是解题的关键．10(2022·湖北荆门·中考真题)如图，点G为△ABC的重心，D，E，F分别为BC，CA，AB的中点，具有性质：AG：GD=BG：GE=CG：GF=2：1．已知△AFG的面积为3，则△ABC的面积为．【答案】18【分析】根据线段比及三角形中线的性质求解即可．【详解】解：∵CG：GF=2：1，△AFG的面积为3，∴△ACG的面积为6，∴△ACF的面积为3+6=9，∵点F为AB的中点，∴△ACF的面积=△BCF的面积，∴△ABC的面积为9+9=18，故答案为：18．【点睛】题目主要考查线段比及线段中点的性质，熟练掌握线段中点的性质是解题关键．11(2023·福建·统考中考真题)阅读下列材料，回答问题任务：测量一个扁平状的小水池的最大宽度，该水池东西走向的最大宽度AB远大于南北走向的最大宽度，如图1．工具：一把皮尺(测量长度略小于AB)和一台测角仪，如图2．皮尺的功能是直接测量任意可到达的两点间的距离(这两点间的距离不大于皮尺的测量长度)；测角仪的功能是测量角的大小，即在任一点O处，对其视线可及的P，Q两点，可测得∠POQ的大小，如图3．小明利用皮尺测量，求出了小水池的最大宽度AB ，其测量及求解过程如下：测量过程：(ⅰ)在小水池外选点C ，如图4，测得AC =am ，BC =bm ；(ⅱ)分别在AC ，BC ，上测得CM =a 3m ，CN =b3m ；测得MN =cm ．求解过程：由测量知，AC =a ，BC =b ，CM =a 3，CN =b3，∴CM CA=CN CB =13，又∵①，∴△CMN ∽△CAB ，∴MN AB=13．又∵MN =c ，∴AB =②m ．故小水池的最大宽度为m ．(1)补全小明求解过程中①②所缺的内容；(2)小明求得AB 用到的几何知识是；(3)小明仅利用皮尺，通过5次测量，求得AB ．请你同时利用皮尺和测角仪，通过测量长度、角度等几何量，并利用解直角三角形的知识求小水池的最大宽度AB ，写出你的测量及求解过程．要求：测量得到的长度用字母a ，b ，c ⋯表示，角度用α，β，γ⋯表示；测量次数不超过4次(测量的几何量能求出AB ，且测量的次数最少，才能得满分)．【答案】(1)①∠C =∠C ；②3c (2)相似三角形的判定与性质(3)最大宽度为a cos α+a sin αtan βm ，见解析【分析】(1)根据相似三角形的判定和性质求解即可；(2)根据相似三角形的判定和性质进行回答即可；(3)测量过程：在小水池外选点C ，用测角仪在点B 处测得∠ABC =α，在点A 处测得∠BAC =β；用皮尺测得BC =am ；求解过程：过点C 作CD ⊥AB ，垂足为D ，根据锐角三角函数的定义推得BD =a cos α，CD =a sin α，AD =a sin αtan β，根据AB =BD +AD ，即可求得．【详解】(1)∵AC =a ，BC =b ，CM =a 3，CN =b 3，∴CM CA =CN CB =13，又∵∠C =∠C ，∴△CMN ∽△CAB ，∴MN AB=13．又∵MN =c ，∴AB =3c m ．故小水池的最大宽度为3cm ．(2)根据相似三角形的判定和性质求得AB =3MN =3c ，故答案为：相似三角形的判定与性质．(3)测量过程：(ⅰ)在小水池外选点C ，如图，用测角仪在点B 处测得∠ABC =α，在点A 处测得∠BAC =β；(ⅱ)用皮尺测得BC =am ．求解过程：由测量知，在△ABC 中，∠ABC =α，∠BAC =β，BC =a ．过点C 作CD ⊥AB ，垂足为D ．在Rt △CBD 中，cos ∠CBD =BDBC，即cos α=BD a ，所以BD =a cos α．同理，CD =a sin α．在Rt △ACD 中，tan ∠CAD =CDAD，即tan β=a sin αAD，所以AD =a sin αtan β．所以AB =BD +AD =a cos α+a sin αtan βm ．故小水池的最大宽度为a cos α+a sin αtan βm ．【点睛】本题考查了相似三角形的判定与性质，解直角三角形的实际应用，根据题意画出几何图形，建立数学模型是解题的关键．12(2023秋·山西运城·九年级统考期末)综合与实践问题情境：如图1，在Rt △ABC 中，∠C =90°，AC =3，BC =4，点D 是AC 上一点，将△BCD 沿直线BD 折叠，点C 落在AB 上的点E ，连接DE ．独立思考(1)如图1，求tan ∠DBC 的值；问题拓展如图2，点F 是图1中AB 上一动点，连接CF ，交BD 于点G ．(2)当点F 是AB 的中点时，求证：DG BG=49；(3)当点G 是BD 的中点时，请你直接写出AFBF 的值．【答案】(1)13；(2)见解析；(3)94【分析】(1)由折叠性质可知DE =CD ，利用等面积求出CD 长即可；(2)添加辅助线构造全等三角形和相似三角形，利用性质即可证明；(3)作平行线构造全等三角形和相似三角形，利用性质即可求解．【详解】解：(1)方法一：在Rt △ABC 中，∠C =90°，AB =AC 2+BC 2=32+42=5，由折叠可知：DC =DE ，∵S △ABC =S △ABD +S △BCD ，∴12BC ·AC =12BC ·CD +12AB ·DE ，∴12×3×4=12×4CD +12×5DE ，∴CD =43，在Rt △BCD 中，∠C =90°，tan ∠DBC =CD BC=434=13，方法二：在Rt △ABC 中，∠C =90°，AB =AC 2+BC 2=32+42=5，由折叠可知：DC =DE ，BC =BE ，∠C =∠DEB =90°，∴AE =AB -BE =5-4=1，∵∠C =∠DEA =90°，∠A =∠A ，∴△ABC ∽△ADE ，∴AE AC=DE BC ，∴13=DE 4，∴DE =43，∴CD =DE =43，在Rt △BCD 中，∠C =90°，∴tan ∠DBC =CD BC=434=13，方法三：在Rt △ABC 中，∠C =90°，AB =AC 2+BC 2=32+42=5，由折叠可知：DC =DE ，BC =BE ．∠C =∠DEB =90°，∴AE =AB -BE =5-4=1，在Rt △ABC 中，∠C =90°，tan A =BC AC ，在Rt △ADE 中，∠AED =90°，tan A =DEAE，∴BC AC =DE AE，∴43=DE 1∴DE =43，∴CD =DE =43，在Rt △BCD 中，∠C =90°，∴tan ∠DBC =CD BC =434=13，(2)方法一：延长CF 到点M ，使FM =FC ，连接BM ，∵FA =FB ，∠BFM =∠AFC ，∴△BFM ≌△AFC SAS ．∴AC =BM ，∠M =∠ACF ，∴BM ∥AC ，∴∠MBG =∠CDG ，∴△MBG ∽△CDG ，∴DG BG =CD BM ，∴DG BG=433=49，方法二：过点B 作BM ∥AC 交CF 的延长线于点M ，∴∠MBF =∠A ，∠M =∠ACF ，∠MBG =∠CDG ，又∵FA =FB ，∴△BFM ≌△AFC AAS ，∴AC =BM ，∠M =∠ACF ，∴△MBG ∽△CDG ，∴DG BG =CD BM ，∴DG BG=433=49．方法三：作GM ⊥BC 于点M ，∴∠GMB =∠DCB =90°，∴GM ∥DC ∴DG BG =CD BM ∵∠ACB =90°，FA =FB ．∴FB =FC ，∴∠FBC =∠FCB ，在Rt △ABC 中，∠ACB =90°，tan ∠ABC =AC BC =34，∴tan ∠GCM =tan ∠ABC =34设GM =a ，在Rt △GMC 中，∠GMC =90°，tan ∠GCM =GM CM =34．∴CM =43a ，在Rt △GMB 中，∠GMB =90°，tan ∠GBM =GM BM =13．∴BM =3a ．∴DG BG=43a 3a =49(3)如图，过B 作BN ∥AC ，交CF 延长线于点N ，∴∠BNG =∠DCG ，△BNF ∽△ACF ，∵G 为BD 中点，∴BG =GD ，∵∠BGN =∠DGC ，∴△BGN ≌△DGC AAS ，∴BN =CD =43，。

中考数学专题训练：相似三角形模型的运用(附参考答案)

中考数学专题训练：相似三角形模型的运用（附参考答案）1．如图，在△ECD中，∠C＝90°，AB⊥EC于点B，AB＝1.2，EB＝1.6，BC＝12.4，则CD的长是( )A．14 B．12.4C．10.5 D．9.32．如图，把△ABC绕点A旋转得到△ADE，当点D刚好落在边BC上时，连接CE，设AC，DE相交于点F，则图中相似三角形的对数是( )A．3对B．4对 C．5对D．6对3．如图，在矩形纸片ABCD中，AB＝4，AD＝3，折叠纸片使边AD与对角线BD 重合，折痕为DG，记与点A重合的点为A′，则△A′BG的面积与该矩形的面积比为( )A．112B．19C．18D．164．如图，正方形ABCD与正方形BEFG有公共顶点B，连接EC，GA，交于点O，GA与BC交于点P，连接OD，OB，则下列结论一定正确的是( )①EC⊥AG；②△OBP∽△CAP；③BO平分∠CBG；④∠AOD＝45°.A．①③ B.①②③C．②③ D.①②④5．如图，BD，CE为△ABC的高，且BD与CE交于点O．(1)求证：△AEC∽△ADB;(2)若∠A＝40°，求∠BOC的度数．的值．6．)如图，AG∥BD，AF∶FB＝1∶2，BC∶CD＝2∶1，求GEED7．如图，在正方形ABCD中，点E为对角线AC，BD的交点，AF平分∠DAC交BD 于点G，交DC于点F.(1)求证：△AEG∽△ADF；(2)判断△DGF的形状并说明理由；(3)若AG＝1，求GF的长．8．如图，等边三角形ABC的边长为3，点P为边BC上的一点，点D为边AC上的一点，连接AP，PD，∠APD＝60°.(1)求证：①△ABP∽△PCD；②AP2＝AD·AC.(2)若PC＝2，求CD和AP的长．9．如图，点P是正方形ABCD边AB上一点(点P不与点A，B重合)，连接PD，将线段PD绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F，连接BE，DF.(1)求∠PBE的度数；的值．(2)若△PFD∽△BFP，求APAB10．如图，四边形ABCD和四边形AEFG都是正方形，C，F，G三点在同一条直线上，连接AF并延长交边CD于点M.(1)求证：△MFC∽△MCA；(2)求证：△ACF∽△ABE；(3)若DM＝1，CM＝2，求正方形AEFG的边长．参考答案1．C 2．B 3．C 4．D5．(1)证明略(2)∠BOC＝140°6．GEED ＝327．(1)证明略(2)△DGF是等腰三角形，理由略(3)GF＝√2－1 8．(1)①证明略②证明略(2)CD＝23AP＝√79．(1)∠PBE＝135°(2)APAB 的值为1210．(1)证明略(2)证明略(3)正方形AEFG的边长为3√55。

初三相似三角形的基本模型

初三相似三角形的基本模型相似三角形在数学中，相似三角形是指具有相同形状但大小不同的三角形。

在相似三角形的证明中，常见的基本模型是AA、辅助线构造成比例线段和面积法。

AA模型AA模型指的是两个三角形的两个角分别相等，那么这两个三角形就是相似的。

例如，如果三角形DEF的两个角分别等于三角形ABC的两个角，那么我们就可以得出这两个三角形相似的结论。

辅助线构造成比例线段在相似三角形的证明中，常见的辅助线的作法是做平行线构造成比例线段或相似三角形，同时再结合等量代换得到要证明的结论。

常见的等量代换包括等线代换、等比代换、等积代换等。

例如，对于图中的问题，我们可以通过做平行线CE∥AD 来得到证明。

这种方法利用了“A”型图的基本模型。

面积法面积法主要是将面积的比，和线段的比进行相互转化来解决问题。

常用的面积法基本模型包括“山字”型。

“田字”型和“燕尾”型等。

在题型方面，与三角形有关的相似问题是常见的。

例如，对于图中的问题，我们需要证明角ADE等于角B，可以通过使用AA模型来得出结论。

在三角形ABC中，已知AB=3，AC=4，BC=5，以BC为边在A点的异侧作△ABD，使△ABD为等腰直角三角形，求线段CD的长．解：首先，我们需要构造双垂直辅助线，如图所示：由于△ABD为等腰直角三角形，所以AD=BD=AB=3，又由于BC=5，所以BD=5-3=2，根据勾股定理可得CD=√(BC²-BD²)=√(5²-2²)=√21．因此，线段CD的长为√21．例2：在△ABC中，AC=BC，∠ACB=90°，点M是AC上的一点，点N是BC上的一点，沿着直线MN折叠，使得点C恰好落在边AB上的P点．求证：MC：NC=AP：PB．证明：方法一：连接PC，过点P作PD⊥AC于D，则PD//BC。

根据折叠可知XXX⊥CP。

由∠2+∠PCN=90°，∠PCN+∠XXX°可得∠2=∠CNM。

相似三角形中的常见五种基本模型(原卷版)-2023年中考数学重难点解题大招复习讲义-几何模型篇

模型探究相似三角形考查范围广，综合性强，其模型种类多，其中有关一线三垂直模型在前面的专题已经很详细的讲解，这里就不在重复.模型一、A字型相似模型A字型（平行）反A字型（不平行）模型二、8字型与反8字型相似模型模型三、AX型相似模型（A字型及X字型两者相结合）模型四、共边角相似模型（子母型）模型五、手拉手相似模型考点一、A 字相似模型【例1】．如图，在△ABC 中，∠A ＝78°，AB ＝4，AC ＝6，将△ABC 沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A ．B ．C ．D ．➢变式训练【变式1-1】．如图，在△ABC 中，DE ∥BC ，AH ⊥BC 于点H ，与DE 交于点G ．若，则＝．例题精讲【变式1-2】.如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM 并延长，交BC的延长线于D，则＝__________.【变式1-3】．如图，在△ABC中，点D在边AB上，AD＝9，BD＝7．AC＝12．△ABC的角平分线AE交CD于点F．（1）求证：△ACD∽△ABC；（2）若AF＝8，求AE的长度．考点二、8字与反8字相似模型【例2】．如图，AG∥BD，AF：FB＝1：2，BC：CD＝2：1，求的值➢变式训练【变式2-1】．如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（）A．B．C．D．【变式2-2】．如图，在平行四边形ABCD中，E为边AD的中点，连接AC，BE交于点F．若△AEF的面积为2，则△ABC的面积为（）A．8B．10C．12D．14【变式2-3】.如图，锐角三角形ABC中，∠A＝60°，BE⊥AC于E，CD⊥AB于D，则DE：BC＝．考点三、AX型相似模型（A字型及X字型两者相结合）【例3】.如图，在△ABC中，点D和E分别是边AB和AC的中点，连接DE，DC与BE交于点O，若△DOE的面积为1，则△ABC的面积为（）A．6B．9C．12D．13.5➢变式训练【变式3-1】.如图，DE是△ABC的中位线，F为DE中点，连接AF并延长交BC于点G，若S△EFG＝1，则S△ABC＝．【变式3-2】．如图：AD∥EG∥BC，EG交DB于点F，已知AD＝6，BC＝8，AE＝6，EF ＝2．（1）求EB的长；（2）求FG的长．【变式3-3】.如图，已知AB∥CD，AC与BD相交于点E，点F在线段BC上，，．（1）求证：AB∥EF；（2）求S△ABE：S△EBC：S△ECD．模型四、子母型相似模型【例4】.如图，点C，D在线段AB上，△PCD是等边三角形，且∠APB＝120°，求证：（1）△ACP∽△PDB，（2）CD2＝AC•BD．➢变式训练【变式4-1】.如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）A．∠ABP＝∠C B．∠APB＝∠ABC C．D．【变式4-2】.如图，在△ABC中，点D在AC边上，连接BD，若∠ABC+∠BDC＝180°，AD＝2，CD＝4，则AB的长为（）A．3B．4C．D．2【变式4-3】．如图，边长为4的正方形，内切圆记为圆O，P为圆O上一动点，则P A+PB 的最小值为．模型五、手拉手相似模型【例5】.如图，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD：BE的值为．➢变式训练【变式5-1】.如图，在△ABC与△ADE中，∠BAC＝∠DAE，∠ABC＝∠ADE．求证：（1）△BAC∽△DAE；（2）△BAD∽△CAE．【变式5-2】.如图，点D是△ABC内一点，且∠BDC＝90°，AB＝2，AC＝，∠BAD＝∠CBD＝30°，AD＝．【变式5-3】．如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB（k为常数），则BD的长为．（用含k的式子表示）实战演练1．如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）A．＝B．C．D．2．如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝3，则△ABC与△DCA的面积比为（）A．2：3B．2：5C．4：9D．：3．如图，菱形ABCD中，E点在BC上，F点在CD上，G点、H点在AD上，且AE∥HC ∥GF．若AH＝8，HG＝5，GD＝4，则下列选项中的线段，何者长度最长？（）A．CF B．FD C．BE D．EC4．如图，在△ABC中，BC＝6，E，F分别是AB，AC的中点，动点P在射线EF上，BP 交CE于点D，∠CBP的平分线交CE于点Q，当CQ＝CE时，EP+BP的值为（）A．6B．9C．12D．185．如图，在四边形ABCD中，AD∥BC，∠ABC＝90°，AB＝2，AD＝2，将△ABC绕点C顺时针方向旋转后得△A′B′C，当A′B′恰好经过点D时，△B′CD为等腰三角形，若BB′＝2，则AA′等于（）A．B．2C．D．6．如图，已知，△ABC中边AB上一点P，且∠ACP＝∠B，AC＝4，AP＝2，则BP＝．7．如图，在▱ABCD中，AC、BD相交于点O，点E是OA的中点，联结BE并延长交AD 于点F，如果△AEF的面积是4，那么△BCE的面积是．8．如图，在△ABC中，点G为ABC的重心，过点G作DE∥AC分别交边AB、BC于点D、E，过点D作DF∥BC交AC于点F，如果DF＝4，那么BE的长为．9．如图，已知Rt△ABC中，两条直角边AB＝3，BC＝4，将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE，并且点A落在DE边上，则sin∠ABE＝．10．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝6，AD平分∠BAC，交边BC于点D，过点D作CA的平行线，交边AB于点E．（1）求线段DE的长；（2）取线段AD的中点M，联结BM，交线段DE于点F，延长线段BM交边AC于点G，求的值．11．如图，在菱形ABCD中，∠ADE、∠CDF分别交BC、AB于点E、F，DF交对角线AC 于点M，且∠ADE＝∠CDF．（1）求证：CE＝AF；（2）连接ME，若＝，AF＝2，求ME的长．12．[问题背景]（1）如图①，已知△ABC∽△ADE，求证：△ABD∽△ACE．[尝试应用]（2）如图②，在△ABC和△ADE中，∠BAC＝∠DAE＝90°∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，①填空：＝；②求的值．13．如图，在正方形ABCD中，AB＝4，E、F分别是BC、CD上的点，且∠EAF＝45°，AE、AF分别交BD于点M、N，连接EN、EF．（1）求证：△ABN∽△MBE；（2）求证：BM2+ND2＝MN2；（3）①求△CEF的周长；②若点G、F分别是EF、CD的中点，连接NG，则NG的长为．14．问题背景如图（1），已知△ABC∽△ADE，求证：△ABD∽△ACE；尝试应用如图（2），在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝30°，AC与DE相交于点F，点D在BC边上，＝，求的值；拓展创新如图（3），D是△ABC内一点，∠BAD＝∠CBD＝30°，∠BDC＝90°，AB ＝4，AC＝2，直接写出AD的长．15．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG、线段DE的数量关系BG＝DE及所在直线的位置关系BG⊥DE；②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断；（2）将原题中正方形改为矩形（如图4﹣6），且AB＝a，BC＝b，CE＝ka，CG＝kb（a ≠b，k＞0），则线段BG、线段DE的数量关系＝及所在直线的位置关系BG ⊥DE；（3）在第（2）题图5中，连接DG、BE，且a＝4，b＝3，k＝，直接写出BE2+DG2的值为．。

2024年中考数学复习(全国版)重难点09 相似三角形8种模型(解析版)

∴△ 퐶퐴 ∽△ 퐶 ，
∴ ∠퐶퐴 = ∠퐶 ，
∵ ∠퐶퐴 = ∠퐶퐵 ，
∴ ∠퐶 퐵 = ∠퐶퐵 ，
∴ 퐵퐶 = 퐶，
∴ 퐶 = 퐶퐵， ∴ ∠퐵 퐶 = ∠퐵퐴 ，
∴ 퐶//퐴 ，
∴
푃퐶 퐶
=
푃 퐴
=
2� �
=
2，
∴ 푃퐶 = 2퐶 = 4 2，
∵ ∠푃퐶퐵 = ∠푃퐴 ，∠퐶푃퐵 = ∠퐴푃 ，
．
【答案】2 【分析】过 D 作垂直퐴퐶于 H 点，过 D 作 ∥퐴 交 BC 于 G 点，先利用解直角三角形求出퐶 的长，其次利用△ 퐶 ∽△ 퐶퐵 ，求出퐶 的长，得出퐵 的长，最后利用△ 퐵 ∽△ 퐵퐴 ，求出퐵 的长，最后得出答案．【详解】解：如图：过 D 作垂直퐴퐶于 H 点，过 D 作 ∥퐴 交퐵퐶于 G 点，
∴퐴
= 퐴�，即
퐴 �+
�
=
� 퐴
∴2
2+
�
=
� 2
解得 � = 5 − 1 或 � =− 5 − 1 < 0（不符题意，舍去）
则퐵 = � = 5 − 1
故答案为：2， 5 − 1．【点睛】本题考查了矩形的性质、折叠的性质、三角形全等的判定定理与性质、相似三角形的判定与性质等知识点，根据矩形与折叠的性质，正确找出两个相似三角形是解题关键． 3．（2020·山东济宁·中考真题）如图,在四边形 ABCD 中，以 AB 为直径的半圆 O 经过点 C,D．AC 与 BD 相
BC=DC，证明
OC∥AD，利用平行线分线段成比例定理得到퐶푃퐶
=
푃 퐴
=
2，则푃퐶
=
2퐶
= 4 2，然后证

2024中考备考重难点重难点相似三角形模型及其综合题综合训练(11大题型+满分技巧+限时分层检测)

重难点02 相似三角形模型及其综合题综合训练中考数学中《相似三角形模型及其综合题综合训练》部分主要考向分为五类：一、K型相似二、8字图相似三、A字图相似四、母子型相似五、手拉手相似相似三角形的综合题中各种相似模型的掌握是解决对应压轴题的便捷方法，所以本专题是专门针对相似三角形模型压轴题的，对提高类型的学生可以自主训练。

考向一：K型相似1．（2023•锡山区校级四模）如图，矩形ABCD中，AB＝10，BC＝8．点P在AD上运动（点P不与点A、D重合）将△ABP沿直线翻折，使得点A落在矩形内的点M处（包括矩形边界），则AP的取值范围是，连接DM并延长交矩形ABCD的AB边于点G，当∠ABM＝2∠ADG时，AP的长是．2．（2023•福田区模拟）综合与探究在矩形ABCD的CD边上取一点E，将△BCE沿BE翻折，使点C恰好落在AD边上的点F处．（1）如图①，若BC＝2BA，求∠CBE的度数；（2）如图②，当AB＝5，且AF•FD＝10时，求EF的长；（3）如图③，延长EF，与∠ABF的角平分线交于点M，BM交AD于点N，当NF＝AN+FD时，请直接写出的值．3．（2023•桐柏县一模）【初步探究】（1）把矩形纸片ABCD如图①折叠，当点B的对应点B'在MN的中点时，填空：△EB'M△B'AN （“≌”或“∽”）．【类比探究】（2）如图②，当点B的对应点B'为MN上的任意一点时，请判断（1）中结论是否成立？如果成立，请写出证明过程；如果不成立，请说明理由．【问题解决】（3）在矩形ABCD中，AB＝4，BC＝6，点E为BC中点，点P为线段AB上一个动点，连接EP，将△BPE沿PE折叠得到△B'PE，连接DE，DB'，当△EB'D为直角三角形时，BP的长为．考向二：8字图相似1．（2023•海州区校级二模）“关联”是解决数学问题的重要思维方式．角平分线的有关联想就有很多……【问题提出】（1）如图①，PC是△P AB的角平分线，求证：．小明思路：关联“平行线、等腰三角形”，过点B作BD∥P A，交PC的延长线于点D，利用“三角形相似”．小红思路：关联“角平分线上的点到角的两边的距离相等”，过点C分别作CD⊥P A交P A于点D，作CE⊥PB交PB于点E，利用“等面积法”．请根据小明或小红的思路，选择一种并完成证明．【理解应用】（2）如图②，在Rt△ABC中，∠BAC＝90°，D是边BC上一点．连接AD，将△ACD沿AD所在直线折叠，使点C恰好落在边AB上的E点处，落AC＝1，AB＝2，则DE的长为．【深度思考】（3）如图③，△ABC中，AB＝6，AC＝4，AD为∠BAC的角平分线．AD的垂直平分线EF交BC延长线于点F，连接AF，当BD＝3时，AF的长为．【拓展升华】（4）如图④，PC是△P AB的角平分线，若AC＝3，BC＝1，则△P AB的面积最大值是．2．（2023•衢州二模）如图1，在正方形ABCD中，点E在线段BC上，连接AE，将△ABE沿着AE折叠得到△AFE，延长EF交CD于点G．（1）求证：DG＝FG；（2）如图2，当点E是BC中点时，求tan∠CGE的值；（3）如图3，当时，连接CF并延长交AB于点H，求的值．考向三：A字图相似1．（2023•宿城区一模）如图，在矩形ABCD中，AB＝5，AD＝3，先将△ABC沿AC翻折到△AB′C处，再将△AB'C沿翻折到△AB'C'处，延长CD交AC′于点M，则DM的长为．2．（2023•沙坪坝区校级模拟）如图，△ABC中，D在AB上，E在BC上，∠AED＝∠ABC，F在AE上，EF＝DE．（1）如图1，若CE＝BD，求证：BE＝CF；（2）如图2，若CE＝AD，G在DE上，∠EFG＝∠EFC，求证：CF＝2GF；（3）如图3，若CE＝AD，EF＝2，∠ABC＝30°，当△CEF周长最小时，请直接写出△BCF的面积．3．（2023•中山区模拟）如图，在平面直角坐标系中，直线y＝﹣x+4与x轴，y轴分别交于点A、B，点P为射线AO上的一个动点，过点P作PQ⊥AB于点Q，将沿PQ翻折得到R．设△PQR与△AOB重合部分的面积为S，点P的坐标为（m，0）．（1）求AR的长．（用含m的代数式表示）（2）求S关于m的函数解析式，并直接写出自变量m的取值范围．考向四：母子型相似1．（2023•樊城区模拟）【基础巩固】（1）如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC2＝AD•AB．【尝试应用】（2）如图2，在▱ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE＝∠A．若BF ＝6，AD＝9，求CE的长．【拓展提高】（3）如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC＝2EF，连接DE、DF分别交AC于M，N，∠EDF＝∠BAD，DF＝AE，若MN＝18，求EF的值．2．（2023•润州区二模）如图1，在△ABC中，点D在边AB上，点P在边AC上，若满足∠BPD＝∠BAC，则称点P是点D的“和谐点”．（1）如图2，∠BDP+∠BPC＝180°．①求证：点P是点D的“和谐点”；②在边AC上还存在某一点Q（不与点P重合），使得点Q也是点D的“和谐点”，请在图2中仅用圆规作图，找出点Q的位置，并写出证明过程．（保留作图痕迹）（2）如图3，以点A为原点，AB为x轴正方向建立平面直角坐标系，已知点B（6，0），C（2，4），点P在线段AC上，且点P是点D的“和谐点”．①若AD＝1，求出点P的坐标；②若满足条件的点P恰有2个，直接写出AD长的取值范围是．考向五：手拉手相似1．（2023•宝安区校级三模）【问题背景】已知D、E分别是△ABC的AB边和AC边上的点，且DE∥BC，则△ABC∽△ADE，把△ADE绕着A逆时针方向旋转，连接BD和CE．①如图2，找出图中的另外一组相似三角形；②若AB＝4，AC＝3，BD＝2，则CE＝；【迁移应用】在Rt△ACB中，∠BAC＝90°，∠C＝60°，D、E，M分别是AB、AC、BC中点，连接DE和CM．①如图3，写出CE和BD的数量关系；②如图4，把Rt△ADE绕着点A逆时针方向旋转，当D落在AM上时，连接CD和CE，取CD中点N，连接MN，若，求MN的长．【创新应用】如图5：，BC＝4，△ADE是直角三角形，∠DAE＝90°，tan∠ADE＝2，将△ADE绕着点A旋转，连接BE，F是BE上一点，，连接CF，请直接写出CF的取值范围．2．（2023•东港市二模）（1）问题发现：如图1，已知正方形ABCD，点E为对角线AC上一动点，将BE绕点B顺时针旋转90°到BF处，得到△BEF，连接CF．填空：①＝；②∠ACF的度数为；（2）类比探究：如图2，在矩形ABCD和Rt△BEF中，∠EBF＝90°，∠ACB＝∠EFB＝60°，连接CF，请分别求出的值及∠ACF的度数；（3）拓展延伸：如图3，在（2）的条件下，将点E改为直线AC上一动点，其余条件不变，取线段EF 的中点M，连接BM，CM，若，则当△CBM是直角三角形时，请直接写出线段CF的长．3．（2023•晋中模拟）综合与实践问题情境：（1）如图1，在△ABC和△ADE中，AB＝AC，AD＝AE．如图2，将△ABC绕顶点A按逆时针方向旋转15°得到△AB'C'，连接B′D，C′E，求证：B′D＝C′E．深入研究：（2）①如图3，在正方形ABCD和正方形CEFG中，已知点B，C，E在同一直线上，连接DE，AF，交于点P，求AF：DE的值；②如图4，若将正方形CEFG绕点C按顺时针方向旋转一定角度，AF：DE的值变化吗？请说明理由．拓展应用：（3）如图5，若把正方形ABCD和正方形CEFG分别换成矩形ABCD和矩形CEFG，且AD：AB＝CG：CE＝k，请直接写出此时AF：DE的值．（建议用时：150分钟）1．（2023•菏泽）（1）如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G．求证：△ADE∽△DCF．【问题解决】（2）如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE＝DF，延长BC到点H，使CH＝DE，连接DH．求证：∠ADF＝∠H．【类比迁移】（3）如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE＝DF＝11，DE＝8，∠AED＝60°，求CF的长．2．（2023•济南）在矩形ABCD中，AB＝2，AD＝2，点E在边BC上，将射线AE绕点A逆时针旋转90°，交CD延长线于点G，以线段AE，AG为邻边作矩形AEFG．（1）如图1，连接BD，求∠BDC的度数和的值；（2）如图2，当点F在射线BD上时，求线段BE的长；（3）如图3，当EA＝EC时，在平面内有一动点P，满足PE＝EF，连接P A，PC，求P A+PC的最小值．3．（2023•武汉）问题提出如图（1），E是菱形ABCD边BC上一点，△AEF是等腰三角形，AE＝EF，∠AEF＝∠ABC＝α（α≥90°），AF交CD于点G，探究∠GCF与α的数量关系．问题探究（1）先将问题特殊化，如图（2），当α＝90°时，直接写出∠GCF的大小；（2）再探究一般情形，如图（1），求∠GCF与α的数量关系．问题拓展将图（1）特殊化，如图（3），当α＝120°时，若，求的值．4．（2023•内蒙古）已知正方形ABCD，E是对角线AC上一点．（1）如图1，连接BE，DE．求证：△ABE≌△ADE；（2）如图2，F是DE延长线上一点，DF交AB于点G，BF⊥BE．判断△FBG的形状并说明理由；（3）在第（2）题的条件下，BE＝BF＝2．求的值．5．（2023•湖州）【特例感知】（1）如图1，在正方形ABCD中，点P在边AB的延长线上，连结PD，过点D作DM⊥PD，交BC的延长线于点M．求证：△DAP≌△DCM．【变式求异】（2）如图2，在Rt△ABC中，∠ABC＝90°，点D在边AB上，过点D作DQ⊥AB，交AC于点Q，点P在边AB的延长线上，连结PQ，过点Q作QM⊥PQ，交射线BC于点M．已知BC＝8，AC＝10，AD ＝2DB，求的值．【拓展应用】（3）如图3，在Rt△ABC中，∠BAC＝90°，点P在边AB的延长线上，点Q在边AC上（不与点A，C重合），连结PQ，以Q为顶点作∠PQM＝∠PBC，∠PQM的边QM交射线BC于点M．若AC＝mAB，CQ＝nAC（m，n是常数），求的值（用含m，n的代数式表示）．6．（2023•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝α，点D是射线BC上的动点（不与点B，C重合），连接AD，过点D在AD左侧作DE⊥AD，使AD＝kDE，连接AE，点F，G分别是AE，BD的中点，连接DF，FG，BE．（1）如图1，点D在线段BC上，且点D不是BC的中点，当α＝90°，k＝1时，AB与BE的位置关系是，＝．（2）如图2，点D在线段BC上，当α＝60°，k＝时，求证：BC+CD＝2FG．（3）当α＝60°，k＝时，直线CE与直线AB交于点N，若BC＝6，CD＝5，请直接写出线段CN的长．7．（2023•益阳）如图，在Rt△ABC中，∠ACB＝90°，AC＞BC，点D在边AC上，将线段DA绕点D按顺时针方向旋转90°得到DA′，线段DA′交AB于点E，作A′F⊥AB于点F，与线段AC交于点G，连接FC，GB．（1）求证：△ADE≌△A′DG；（2）求证：AF•GB＝AG•FC；（3）若AC＝8，tan A＝，当A′G平分四边形DCBE的面积时，求AD的长．8．（2023•福建）如图1，在△ABC中，∠BAC＝90°，AB＝AC，D是AB边上不与A，B重合的一个定点．AO ⊥BC于点O，交CD于点E．DF是由线段DC绕点D顺时针旋转90°得到的，FD，CA的延长线相交于点M．（1）求证：△ADE∽△FMC；（2）求∠ABF的度数；（3）若N是AF的中点，如图2，求证：ND＝NO．9．（2022•湖北）问题背景：一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论．如图1，已知AD是△ABC的角平分线，可证＝．小慧的证明思路是：如图2，过点C作CE∥AB，交AD的延长线于点E，构造相似三角形来证明＝．尝试证明：（1）请参照小慧提供的思路，利用图2证明：＝；应用拓展：（2）如图3，在Rt△ABC中，∠BAC＝90°，D是边BC上一点．连接AD，将△ACD沿AD所在直线折叠，点C恰好落在边AB上的E点处．①若AC＝1，AB＝2，求DE的长；②若BC＝m，∠AED＝α，求DE的长（用含m，α的式子表示）．10．（2022•宁波）【基础巩固】（1）如图1，在△ABC中，D，E，F分别为AB，AC，BC上的点，DE∥BC，BF＝CF，AF交DE于点G，求证：DG＝EG．【尝试应用】（2）如图2，在（1）的条件下，连结CD，CG．若CG⊥DE，CD＝6，AE＝3，求的值．【拓展提高】（3）如图3，在▱ABCD中，∠ADC＝45°，AC与BD交于点O，E为AO上一点，EG∥BD交AD于点G，EF⊥EG交BC于点F．若∠EGF＝40°，FG平分∠EFC，FG＝10，求BF的长．11．（2023•广州）如图，AC是菱形ABCD的对角线．（1）尺规作图：将△ABC绕点A逆时针旋转得到△ADE，点B旋转后的对应点为D（保留作图痕迹，不写作法）；（2）在（1）所作的图中，连接BD，CE．①求证：△ABD～△ACE；②若tan∠BAC＝，求cos∠DCE的值．。

中考数学几何专项——相似模型(相似三角形)

相似模型【相似模型一：A 字型】特征模型结论DE ∥BCCBCBBC D E ADA E DA AD:AB=AE:AC=DE:BC 顺着比∠B=∠AEDCB CBDA EDAAD:AC=AE:AB=DE:BC 反着比AD×AB=AE×AC 顺着乘∠B =∠ACDCBED AAD:AC=AC:AB=CD:BC AC²=AD×AB当∠ BAC=90°AD B CB①△ABD ∽△CBA AB ²=BD×BC ②△ACD ∽△BCAAC²=CD×BC③△ADB ∽△CDA AD²=BD×CD特征模型结论AC ∥BDAD B CO DB A CC A OD BAD B CODBACCAO D B① △BD0∽△ACO ② DO:0C=BO:0A=BD:AC 交叉比③ △AOD 与△C0B 不相似∠B=∠C（也叫蝴蝶型相似）A D BC ODBACCAD B CODBACC① △AOC ∽△DOB② AO:OD=0C:0B=AC:BDAO×OB=OC×0D 顺着比，交叉乘 ③ △BOC∽△DOA特征模型结论成比例线段共端点① △ABC ∽△ADE② △ABD∽△ACE特征模型结论AB ∥EF ∥CDFEBCD AF EDCBA图2① 有两对A 字型相似△BEF ∽△BCD △DEF∽△DAB ② 有一对X 型相似△AEB ∽△DEC ③111AB CD EF+=特征模型结论ECD BAA BDC EEDCBA90度，45度； 120度，60度60°45°图2图1旋转N M 60°120°E D CB A 45°ED C B A ①△ABN ∽△MAN ∽△MCA ②△ABD ∽△CAE ∽△CBA【相似模型六：三角形内接矩形模型】特征模型结论矩形EFGH 或正方形EFGH 内接与三角形H G FED C BA【相似模型七：十字模型】特征模型结论正方形①若AF=BE,则AF ⊥BE ②若AF ⊥BE ，则AF=BE,长方形PEAB CD矩形ABCD 中，CE ⊥BD ，则△CDE ∽△BCD ，CE CDBD BC平行四边形△GME ∽△HNF△MED ≌△BFA三角形MED CAB在△ABC 中，AB ＝AC ，AB ⊥AC ，①D 为中点，②AE ⊥BD ，③BE ：EC＝2：1，④∠ADB ＝∠CDE ，⑤∠AEB ＝∠CED ，⑥∠BMC ＝135°，⑦2BMMC =，这七个结论中，“知二得五”【A 型，X 型，三平行模型】1.如图，在△ABC 中，EF ∥DC ，∠AFE =∠B ，AE =6，ED =3，AF =8，则AC =_________，CDBC=_________．F E DCBABCDE FA2．如图，AB ∥CD ，线段BC ，AD 相交于点F ，点E 是线段AF 上一点且满足∠BEF =∠C ，其中AF =6，DF =3，CF =2，则AE =_________．3.如图，在Rt △ABD 中，过点D 作CD ⊥BD ，垂足为D ，连接BC 交AD 于点E ，过点E 作EF ⊥BD 于点F ，若AB =15，CD =10，则BF :FD =_____________．FEBCAN MEDCBA4.如图，在□ABCD 中，E 为BC 的中点，连接AE ，AC ，分别交BD 于M ，N ，则BM :DN =_____________．5.如图所示，AB ∥CD ，AD ，BC 相交于点E ，过E 作EF ∥AB 交BD 于点F ．则下列结论：①△EFD ∽△ABD ；②EF BF CD BD =；③1EF EF FD BF AB CD BD BD +=+=；④111AB CD EF+=．其中正确的有___________． F EDCBA图26.在△ABC 中，AB=9，AC=6，点M 在边AB 上，且AM=3，点N 在AC 边上.当AN= 时，△AMN 与原三角形相似.7.如图，在△ABC 中，∠C=90°，AC=8，BC=6，D 是边AB 的中点，现有一点P 位于边AC 上，使得△ADP 与△ABC 相似，则线段AP 的长为 .8.如图，已知O 是坐标原点，点A.B 分别在y x 、轴上，OA=1，OB=2，若点D 在x 轴下方，且使得△AOB 与△OAD 相似，则这样的点D 有个.9.如图，在Rt △ACB 中，∠C=90°，AC=16cm ，BC=8cm ，动点P 从点C 出发，沿CA 方向运动；动点Q 同时从点B 出发，沿BC 方向运动,如果点P 的运动速度均为4cm/s ，Q 点的运动速度均为2cm/s ，那么运动几秒时，△ABC 与△PCQ 相似.10.将△ABC的纸片按如图所示的方式折叠，使点B落地边AC上，记为点B＇，折叠痕为EF，已知AB=AC=8，BC=10,若以点B＇.F.C为顶点的三角形与△ABC相似，那么BF的长度是.11.如图,在中,,,是角平分线.求证:(1)(2)12.如图，四边形中，平分，，，为的中点．（1）求证：；（2）与有怎样的位置关系？试说明理由；（3）若，，求的值．13.如图，在中，为上一点，，，，于，连接．（1）求证：；（2）找出图中一对相似三角形，并证明．14.如图，在中，，分别是，上的点，，的平分线交于点，交于点．（1）试写出图中所有的相似三角形，并说明理由（2）若，求的值．15.如图，在平行四边形ABCD中，对角线AC、BD交于点O．M为AD中点，连接CM交BD于点N，且ON=1．（1）求BD的长；（2）若△DCN的面积为2，求四边形ABNM的面积．16.如图,在中,于点,于点,连接,求证: ..17.如图,在△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,若EG=3,则AC=________.图1 图218..如图,平行于BC的直线DE把△ABC分成的两部分面积相等.则ADAB= _________.19.如图所示，AD=DF=FB, DE∥FG∥BC,则S1:S2:S3=__________.20.如图，在矩形ABCD中，对角线AC，BD相交于点O，OE⊥BC于点E，连接DE交OC于点F，作FG⊥BC于点G，则线段BG与GC的数量关系是___.21. 如图，已知点C 为线段AB 的中点，CD ⊥AB 且CD=AB=4，连接AD ，BE ⊥AB ，AE 是∠DAB 的平分线，与DC 相交于点F ，EH ⊥DC 于点G ，交AD 于点H ，则HG 的长为 .22.如图1，在△ABC 中，点D 、E 、Q 分别在边AB 、AC 、BC 上，且DE ∥BC ，AQ 交DE 于点P ．（1）求证：；（2）如图，在△ABC 中，∠BAC =90°，正方形DEFG 的四个顶点在△ABC 的边上，连接AG 、AF ，分别交DE 于M 、N 两点．如图2，若AB =AC =1，直接写出MN 的长；如图3，求证MN 2=DM【母子型】1、已知：如图，△ABC 中，∠ACB=90°，CD ⊥AB 于D ，S △ABC=20，AB=10。

相似专题四相似三角形的四大模型初中数学

【证明】∵∠ACD＝∠BCA，∠DAC＝∠B， ∴△ACD∽△BCA，∴CADD＝AACB. ∵CD＝CE，∴∠CDE＝∠CED，∴∠ADB＝∠CEA. ∵∠DAC＝∠B，∴△ADB∽△CEA， ∴AACB＝BADE，∴CADD＝BADE，∴CD·BD＝AD·AE.
模型展示
结论
条件：∠C＝∠ABD＝∠E＝90°. 结论：△ABC∽△BDE.
条件：∠C＝∠AGD＝∠F＝90°. 结论：△ABC∽△EDF.
3 【2023·济南市中区期末】如图，在矩形ABCD中，点 E是BC的中点，EF⊥AE交CD于点F.
(1)求证：△ABE∽△ECF. 【证明】∵四边形ABCD是矩形， ∴∠B＝∠C＝90°，∴∠＝90°， ∴∠AEB＋∠CEF＝90°，∴∠BAE＝∠CEF， ∴△ABE∽△ECF.
模型2 8字型【模型解读】两个三角形若有“一对对顶角＋一对等角”，则出现“8”字型相似．没有说明对应角的关系时，需分 ∠B＝∠C或∠B＝∠D两种情况讨论．
模型展示
结论
条件：AB∥CD．结论：△AOB∽△DOC．
条件：∠A＝∠C或∠B＝∠D．结论：△AOB∽△COD．
2 【2023·济南期末】如图，AD，BC相交于点P，连接 AC，BD，且∠1＝∠2，AC＝3，CP＝2，DP＝1，求 BD的长．
第九章图形的相似
专题(四) 相似三角形的四大模型
模型1 A字型【模型解读】两个三角形若有“一个公共角＋一对等角”，则出现“A”字型相似，没有说明对应角的关系时，需分 ∠AED＝∠B或∠AED＝∠C两种情况讨论．
模型展示
结论
条件：DE∥BC．结论：△AED∽△ACB．
模型展示
结论条件：∠AED＝∠B 或AADC＝AAEB. 结论：△ AED∽△ABC．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

求AD 、BD 的长.DP PEBQ QC图2A DMN EC GB图1Q PA DBEC 图3GNMF EDCBA2. 如图，△ABC 是直角三角形，∠ACB =90°，CD ⊥AB 于点D ，点E 是AC 的中点，ED 的延长线与CB 的延长线交于点F ．求证：FC FB FD ⋅=2．AB FED3.如图所示，在△ABC 中，∠ACB=90°，AM 是BC 边的中线，CN ⊥AM 于N 点，连接BN ，求证：BM 2=MN ·AM 。

4.已知：如图，在四边形ABCD 中，∠ABC=∠ADC=90º，DF ⊥AC 于E ，且与AB 的延长线相交于F ，与BC 相交于G 。

求证：AD 2=AB ·AF5.已知ABC ∆中，︒=∠90ACB ，AB CD ⊥，垂足为D ，DE 、DF 分别是BDC ADC ∆∆和的高，这时CAB DEF ∆∆和是否相似？A EF B D AB MC NFEGDCAB6.已知：如图，AD 是△ABC 的高，BE ⊥AB ，AE 交BC 于点F ，AB ·AC=AD ·AE 。

求证：△BEF ∽△ACF7.已知，如图，CE 是直角三角形斜边AB 上的高，在EC 的延长线上任取一点P ，连结AP BG AP ⊥,，垂足为G ，交CE 于D ，求证：DE PE CE ⋅=2.8.如图，在四边形ABCD 中，︒=∠=∠90D B ，由点D 作AC 的垂线交AB 于E ，交AC 于F 。

求证：AE AB AD ⋅=2。

9.已知ABC ∆中，CD ACB ,90︒=∠是高，若b AC a BC ==,，q AD h CD ==,，p BD =，且4,3==b a ，则=c ，=p ，=q ，=h .10.若直角三角形斜边上的高将斜边分成的两条线段的长分别为cm 2和cm 8，则两条直角边的长分别为，斜边上的高为 .11.如图，ABC Rt ∆，AB CD ACB ⊥︒=∠,90于D ，,6cm BD =cm AD 4=，则=BC .FBCAEDBCDF12.如图，在△ABC 中，∠ACB=90°，AC ＞BC ，CD ⊥AB ，DE ⊥AC ，EF ⊥AB ，CD=4，AC=54，则EF:AF=（） A ．1:2 B ．5:2 C ．5:5 D ．52:513.如图所示，在Rt △ABC 中，∠C=90°，CD ⊥AB ，垂足为点D ，若AD ：BD=9：4则AC ：BC 的值为（）A ．9：4B ．3：2C ．4：9D ．2：314.如图所示，CD 是Rt △ABC 斜边AB 边上的高，23=AC AB ，则=BCCD（） A ．2:5 B ．2:3 C ．3:2 D ．3:215.如图所示，△ABC 中，∠ACB=90°，AC=10cm ，AB 上的高CD=6cm ，DE ⊥BC 于E ，求DE 的长。

16.如图，在ABC ∆中，BC AH BAC ⊥︒=∠,90于H ，以AC 和AB 为边在ABC Rt ∆形外作等边三角形ABD ∆和ACE ∆，求证：BDH ∆∽AEH ∆.17.如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB 于点D ，BD =2，AD =8，则CD =_________，AC =_________，BC =________．CE AFDBD C18.如图，在矩形ABCD 中，对角线AC ，BD 相交于点O ，E 为AD 的中点，连接BE 交AC 于点F ，连接FD ．若∠BFA =90°，给出以下三对三角形：①△BEA 与△ACD ；②△FED 与△DEB ；③△CFD 与△ABO ．其中相似的有_____________（填写序号）．19.如图，在△ABC 中，∠ACB =90°，CE ⊥AB 于点E ，D 在AB 的延长线上，且∠DCB =∠A ，BD :CD =1:2，45AE ，则△BCD 的面积是（）A ．13B 5C ．23D 25DB E C20.如图，在矩形ABCD 中，对角线AC ，BD 相交于点O ，E 为AD 的中点，连接BE 交AC 于点F ，连接FD ，若∠BFA =90°，给出以下三对三角形：①△BEA 与△ACD ；②△FED 与△DEB ；③△CFD 与△ABO ．其中相似的有_____________．ABCDEFOAB CD EF21.如图，在Rt △ABC 中，∠ACB =90°，∠B =30°，BC =3．点D 是BC 边上一动点（不与点B ，C 重合），过点D 作DE ⊥BC 交AB 边于点E ，将∠B 沿直线DE 翻折，点B 落在射线BC 上的点F 处，当△AEF 为直角三角形时，BD 的长为________．OFE DCBA22.如图，在△ABC 中，AB =AC ，AD ⊥BC ，DE ⊥AC ，M 为DE 的中点，AM 与BE 相交于点N ，AD 与BE 相交于点F ．求证：（1）DE ADCE CD=；（2）△BCE ∽△ADM ；（3）猜想AM 与BE 的位置关系，并说明理由．ABCDE MN F23.如图，CD 是Rt △ABC 斜边AB 上的高，E 为BC 的中点，ED 的延长线交CA 的延长线于点F ．求证：AC CF BC DF ⋅=⋅．FCA DB24.如图，在Rt △ABC 中，CD 是斜边AB 上的高，点M 在CD 上，DH ⊥BM 且与AC 的延长线交于点E ．求证：（1）△AED ∽△CBM ；（2）AE CM AC CD ⋅=⋅．HM EBDAC FE DC BA25.如图，在正方形ABCD 中，△BPC 是等边三角形，BP 、CP 的延长线分别交AD 于点E 、F ，连接BD 、DP ，BD 与CF 相交于点H ，给出下列结论：①BE=2AE ；②△DFP ∽△BPH ；③△PFD ∽△PDB ；④DP 2=PH•PC 其中正确的是（）A ．①②③④B ．②③C ．①②④D ．①③④ 26.如图，在△ABC 中，AB=AC=，BC=4，点E 为BC 边上一动点，连接AE ，作∠AEF=∠B ，EF 与△ABC 的外角∠ACD 的平分线交于点，当EF ⊥AC 时，EF 的长为（）27.如图，Rt △ABC 中，CD ⊥AB ，垂足为D ，DE ⊥AC ，垂足为E ，求证：22AC AEBC CE =.【三角形内接矩形模型】1.如图，在△ABC 中，CD ⊥AB 于点D ，正方形EFGH 的四个顶点都在△ABC 的边上．求证：111AB CD EF+=．H G FED C BA【半角模型】1.如图，在同一平面内，将两个全等的等腰直角三角形ABC 和AFG 摆放在一起，A 为公共顶点，∠BAC =∠AGF =90°，它们的斜边长为2．若△ABC 固定不动，△AFG 绕点A 旋转，AF ，AG 与边BC 的交点分别为D ，E （点D 不与点B 重合，点E 不与点C 重合）． ①请写出图中所有的相似三角形_____________________； ②若BD 12，则CE =________.GFED C BA2.如图1，将两个全等的等腰直角三角形如图摆放（顶点A 重合），所有的点都在同一平面内．请找出图1中的相似三角形（不包括全等）；（2）如图2，已知A 是等边△PQR 的边RQ 延长线上的点，B 是QR 延长线上的点．若∠APB =120°，请找出图2中的相似三角形．图221R QBAP3.如图，在中，,为延长线上一点，为延长线上一点，且满足.求证：.4.如图，在△ABC 中，∠ACB =90°，AC =BC ，点E ，F 在AB 上，∠ECF =45°．（1）求证：△ACF ∽△BEC ；（2）设△ABC 的面积为S ，求证：AF ·BE =2S ．45°F ECB A5.如图，点C ，D 在线段AB 上，△PCD 是等边三角形，且∠APB =120°，CD =3，设AC =x ，BD =y ，求y 与x 之间的函数关系式．PD C A图1GFEDCBA【旋转模型】1.如图，D 是Rt △ABC 的斜边AB 上一点，点E 在AC 上，连接DE ，CD ，且∠ADE =∠BCD ，CF ⊥CD 交DE 的延长线于点F ，连接AF ．求证：AF ⊥AB ．BD ECFA2.问题背景：某学习小组正在研究如下问题：如图1所示，四边形ABCD 与四边形CEFG 均为正方形，且点E 、G 分别在边BC 上、CD 上，连接DE 、BG ，点M 是BG 中点,连接CM ，试猜测CM 与DE 的数量关系与位置关系，学习小组经过分析，得到结论：CM 与DE 的数量关系为CM =12DE ,位置关系为CM DE .解决问题：小华从旋转的角度提出一个问题：如图2，将正方形CEFG 绕点C 顺时针旋转一定角度，其他条件不变.此时，“问题背景”中的两个结论还成立吗？如果成立，请加以证明；如果不成立，请说明理由.MGF EDCBAMGFEDCBA类比探究：这时，小颖提出了一个问题：如图3所示，四边形ABCD 与四边形CEFG 均为菱形，且ÐABC =ÐECG ,其他条件不变.此时，CM 与DE 有怎样的数量关系？直接写出结论.拓展延伸这时，小刚提出了一个更加一般化的问题：如图4所示，,且AB BC =ab，其他条件不变，此时，CM 与DE 又有怎样的数量关系？直接写出结论.MGFED CBAMGF ED CBA3.如图1，在Rt△ABC 中，∠B=90°，BC=2AB=8，点D ，E 分别是边BC ，AC 的中点，连接DE. 将△EDC 绕点C 按顺时针方向旋转，记旋转角为α. （1）问题发现 ① 当︒=0α时，_____________=BD AE ；② 当︒=180α时，.__________=BDAE（2）拓展探究试判断：当0°≤α＜360°时，DBAE的大小有无变化？请仅就图2的情况给出证明. （3）问题解决当△EDC 旋转至A 、D 、E 三点共线时，直接写出线段BD 的长.4.请你认真阅读下面的小探究系列,完成所提出的问题.(1)如图1,将角尺放在正方形ABCD 上,使角尺的直角顶点E 与正方形ABCD 的顶点D 重合,角尺的一边交CB 于点F,另一边交BA 的延长线于点G.求证:EF=EG;图1 图2 图3(2)如图2,移动角尺,使角尺的顶点E 始终在正方形ABCD 的对角线BD 上,其余条件不变,请你思考后直接回答EF 和EG 的数量关系:EF________EG(用“=”或“≠”填空);(3)运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图3,将(2)中的“正方形ABCD”改成“矩ECD A（图1）E DBAC （图2）（备用图）CBA形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,AD=3,求EFEG的值.5.在四边形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F. (1)如图1,若四边形ABCD是正方形,判断AF与BE的数量关系;明明发现,AF与BE分别在△AOF和△BOE中,可以通过证明△AOF和△BOE全等,得到AF与BE的数量关系;请回答:AF与BE的数量关系是________.(2)如图2,若四边形ABCD是菱形,∠ABC=120°,请参考明明思考问题的方法,求AFBE的值.6.将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°.在Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过点C,且BC=2.(11分)(1)求证:△ADC∽△APD;(2)求△APD的面积;(3)如图②,将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE'F',DE'交AC于点M,DF'交BC于点N,试判断PMCN 的值是否会随着α的变化而变化.如果不变,请求出PMCN的值;反之,请说明理由.7.如图，点E是四边形ABCD的对角线BD上一点，且∠BAC=∠BDC=∠DAE．（1）求证：BE·AD=CD·AE；（2）根据图形特点，猜想BCDE可能等于哪两条线段的比（只需写出图形中已有线段的一组比即可），并证明你的结论．ABCDE8.如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，垂足为D ．E ，F 分别是AC ，BC 边上一点，且CE =13AC ，BF =13BC ．求∠EDF 的度数．EFC DBA9.数学课上，魏老师出示图1和下面框中条件：如图1，两个等腰直角三角板ABC 和DEF 有一条边在同一条直线l 上，∠ABC =∠DEF =90°，AB =1，DE =2．将直线EB 绕点E 逆时针旋转45°，交直线AD 于点M ．将图1中的三角板ABC 沿直线l 向右平移，设C ，E 两点间的距离为x ．图2MDAl图1DMAB F（1）①当点C 与点F 重合时，如图2所示，可得AMDM的值为___________； ②在平移过程中，AMDM的值为___________（用含x 的代数式表示）．（2）将图2中的三角板ABC 绕点C 逆时针旋转，原题中的其他条件保持不变．当点A 落在线段DF 上时，如图3所示，请计算AMDM的值．（3）将图1中的三角板ABC 绕点C 逆时针旋转m 度，090m <≤，原题中的其他条件保持不变，如图4所示，请计算AMDM的值（用含x 的代数式表示）．10.如图，在矩形ABCD 中，点M 是AD 的中点，AD =42，CD =22，直角∠PME 绕点M 进行旋转，其两边分别和BC ，CD 交于点P 和点E ，连接PE 交MC 于点Q ．（1）判断线段MP ，ME 的数量关系，并进行证明；（2）当动点P ，E 分别在线段BC 和CD 上运动时，设PC =x ，MQ =y ，求y 与x 之间的函数关系式．M QPBCA ED11.已知，矩形ABCD 中，8,6==BC AB ,对角线BD AC ,相交于点O ，以O 为顶点作︒=∠90MON ，图4BA MD图3DM AB且F E BC AB ON OM ,,,交于点分别与射线。