格林公式及其应用共35页
合集下载
738-第三节 格林公式及其应用-PPT精选文档

解 用格林公式。 记右半圆域为 D。 A Q P ( )dxdy 原式 x y D D
OA
OA
L
D
3dxdy
D
3 2 1 . 3| D | 0 sinydy cos 2
2
5/23
OA : x 0
D
例2. 求 (2x y4 )dx (3x5y6 )dy , L:
L
(0 ,0 ) 、 (3 ,0 ) 、 (3 ,2 )为 顶 点 的 三 角 形 , 的 顺 边 时针方向。 D。 解 用格林公式。 记 相 应 三 角 域 为
原式
D
Q P ( ) dxdy x y D
L
3) 在 D 上, Pdx Qdy 与路径无 ;
AB
4) 在 D 上, Pdx Qdy 是某个函数的全 ( x, y) ( Qdy 是一个原函 . 数 即 有原函数 (x ,y ) Pdx
0 0
8/23
说明: 积分与路径无关时, 曲线积分可记为
P d xQ d y P dxQ dy AB A
21/23
r
x
Q P d x d y P d x Q d y 格林公式 x y D L
用格林公式易证: xOy 面上有界闭区 D 的面
| D| xdy D ydx
D
1 xdy ydx . 2 D
x a cos 所围面积 : ( 0 2 π) 例如, 椭圆 L y b sin 1 A x d y y d x 2L 2 π 1 2 2 πab ( ab cos ab sin ) d 0 2
格林公式及其应用

L1 L2 L2
Pdx Qdy Pdx Qdy
L2
Pdx Qdy Pdx Qdy 0,
L1 L1 ( L2 ) L2
Pdx Qdy 0
此时L1 ( L2 )为有向闭曲线,故结论成立, 反之也成立.
3、定理2
设区域G是一个单连通域,函数P( x, y )、Q( x, y ) 在G内具有一阶连续偏导数,则曲线积分 Pdx Qdy
Q y2 x2 P 2 2 2 x ( x y ) y 则
L
xdy ydx x y
2 2
0
(2) 原点在D内时
选取适当小的r 0, 作位于D内的圆周l x2 y2 r 2 记L与l所围的闭区域为D1;
即D1为复连通区域,
l的方向取逆时针方向 有 , xdy ydx x y
P 因 连续,故第一式左边 y 2 ( x ) P ( x, y ) P b dy dx y dxdy a 1 ( x ) y D a Px, 2 ( x) Px,1 ( x)dx
b
第一式右边 Pdx Pdx Pdx
第三节
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径 无关的条件 三、二元函数的全微分求积
一、 格林公式
平面单连通区域: 设D为平面区域,如果D内任一闭曲线所围的部
分都属于D,则称D为平面单连通区域,否则称为复连
通区域.
通俗的说,平面单连通区域是不含有“洞”的区
域.
例如 圆形区域: x, y ) x 2 y 2 1} {(
Pdx Qdy
ABPA
Q P x y dxdy Pdx Qdy D3 BCNB
Pdx Qdy Pdx Qdy
L2
Pdx Qdy Pdx Qdy 0,
L1 L1 ( L2 ) L2
Pdx Qdy 0
此时L1 ( L2 )为有向闭曲线,故结论成立, 反之也成立.
3、定理2
设区域G是一个单连通域,函数P( x, y )、Q( x, y ) 在G内具有一阶连续偏导数,则曲线积分 Pdx Qdy
Q y2 x2 P 2 2 2 x ( x y ) y 则
L
xdy ydx x y
2 2
0
(2) 原点在D内时
选取适当小的r 0, 作位于D内的圆周l x2 y2 r 2 记L与l所围的闭区域为D1;
即D1为复连通区域,
l的方向取逆时针方向 有 , xdy ydx x y
P 因 连续,故第一式左边 y 2 ( x ) P ( x, y ) P b dy dx y dxdy a 1 ( x ) y D a Px, 2 ( x) Px,1 ( x)dx
b
第一式右边 Pdx Pdx Pdx
第三节
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径 无关的条件 三、二元函数的全微分求积
一、 格林公式
平面单连通区域: 设D为平面区域,如果D内任一闭曲线所围的部
分都属于D,则称D为平面单连通区域,否则称为复连
通区域.
通俗的说,平面单连通区域是不含有“洞”的区
域.
例如 圆形区域: x, y ) x 2 y 2 1} {(
Pdx Qdy
ABPA
Q P x y dxdy Pdx Qdy D3 BCNB
113格林公式及其应用共35页文档

D的边界上对坐标的曲线积分的关系,是牛顿-莱布尼茨 公式的推广. (2)格林公式的应用
1)在计算上,可以实现二重积分与曲线积分的
相互转化;
2)在应用上,通过它可以求出曲线积分与路径
无关的条件.(下面的内容)
(3)格林公式成立的条件:
L封闭且取正向
P、Q在D上一阶偏导数连续
9
D ( Q x P y)d x d yL P d x Q d y
3.格林公式的应用
(1) 计算二重积分
例1 计 算 e y 2 d x d y 其 中 D 是 以 O ( 0 ,0 ) ,A ( 1 , 1 ) ,
B ( 1 , 1 ) 为 顶 D 点 的 三 角 形 闭 区 域 . y B
A
解 取 P0,Qxey2, 则
D
利用格林公式 , 有
x e y 2d y
D
1
1
me1m.
4
D的反向边界
14
应用格林公式计算曲线积分添加辅助曲线应注意
(1)一般辅助线取平行坐标轴的直线或折线;
(2)辅助曲线的方向为它能使得封闭曲线构成 正方向.
y
y
4dxdy
0
4
x2
dx
D
8 64 .
3
A O :y 0 ,x :4 0 .
13
例4 计 算 ( 2 x y e x 2 ) d x ( e x 2 m x ) d y 其 中 L 为 由 点 L
O ( 0 ,0 ) 沿 曲 线 y 2 x x 2 到 点 B ( 1 ,1 ) . y
两式相加得: Q P
D ( x y)d x d yL P d x Q d y
7
2) 若D不满足以上条件, 则可通过加辅助线将其分割
高等数学-格林公式及其应用.ppt

l D1
O D2
x
1
2π
d
1 2π
π
20
2
l :4x2 y2 2
法二
l
ydx xdy 4x2 y2
l
ydx
2
xdy
1
2
ydx xd y
l
格林公式
D2是由l 所围区域
4x2 y2 2
所以 I 0 π
π.
1
2
1
2
(1
D2
(2)
π
2
1)dxdy
2
π
25
10.3 格林公式及其应用
Pdx Qdy
L
(L1, L2, L3对D来说为正方向)
8
10.3 格林公式及其应用
(3) 对复连通区域证明:
对若复区连域通不区止域由D一, 格条林闭公曲式线
的右所曲端围线应成积 包.添分 括加,沿且直区边线域界段D的的A方全B向,部CE对边.区界 G D
域则DD来的说边都界是曲正线向由. AB, L2 , BA,
2π 0
格林公式
sin d(
2
(Q P )dxdy D1 x y 0
cos ) cos d(
2
2
0 sin
)
24
10.3 格林公式及其应用
l
ydx xdy 4x2 y2
2π
sin
d(
2
cos
)
2
cos
d(
sin
)
0
2
2 0
π
2
2
sin
2
2
2
2
cos2
d
y L: x2 y2 4
4.1格林公式及其应用

1 U 0 ln r
(r 0),
2
通常称它为二维拉普拉斯方程的基本解。
现在我们介绍三维拉普拉斯方程
u xx u yy u zz 0
的球对称解。 作球坐标变换
x r sin cos ,
r
x2 y2 z2 ,
z x y z
2 2 2
y r sin sin , z r cos ,
其中
n
表示外法向导数。
u(v n)dS
8
(
P Q R )d x y z
( P cos(n, x) Q cos(n, y) R cos(n, z))dS, (3)
设函数 u u( x, y, z) 和 v v( x, y, z )以及它们的所有 一阶偏导数在 上是连续的, 且在 内具有 连续的所有二阶偏导数。 在公式(3)中, 令P u 则得格林第一公式:
(6)
(7)
(8)
1 u(M 0 ) 4
因为函数 v 在点 M 0 处变为无穷大, 故对区域 不能直接应用格林第二公式(6). 但是,如果在 区域 内挖去一个以 M 0 为心,充分小正数 为 半径的球 K M , 则在剩下的区域 K M 中函数 v 就是连续可微的了(如图4.1)。
(6)
(7)
(8)
1 u(M 0 ) 4
1 u ( M ) rMM n 0
0
1 u ( M ) dS. rMM n 0
证
在区域 K M 上对上述的调和函数 u 和
1 v 应用公式(6)得 r
(4’)
在式(4’)中,交换函数 u , v 的位置,得
(r 0),
2
通常称它为二维拉普拉斯方程的基本解。
现在我们介绍三维拉普拉斯方程
u xx u yy u zz 0
的球对称解。 作球坐标变换
x r sin cos ,
r
x2 y2 z2 ,
z x y z
2 2 2
y r sin sin , z r cos ,
其中
n
表示外法向导数。
u(v n)dS
8
(
P Q R )d x y z
( P cos(n, x) Q cos(n, y) R cos(n, z))dS, (3)
设函数 u u( x, y, z) 和 v v( x, y, z )以及它们的所有 一阶偏导数在 上是连续的, 且在 内具有 连续的所有二阶偏导数。 在公式(3)中, 令P u 则得格林第一公式:
(6)
(7)
(8)
1 u(M 0 ) 4
因为函数 v 在点 M 0 处变为无穷大, 故对区域 不能直接应用格林第二公式(6). 但是,如果在 区域 内挖去一个以 M 0 为心,充分小正数 为 半径的球 K M , 则在剩下的区域 K M 中函数 v 就是连续可微的了(如图4.1)。
(6)
(7)
(8)
1 u(M 0 ) 4
1 u ( M ) rMM n 0
0
1 u ( M ) dS. rMM n 0
证
在区域 K M 上对上述的调和函数 u 和
1 v 应用公式(6)得 r
(4’)
在式(4’)中,交换函数 u , v 的位置,得
高等数学Green公式的应用
D
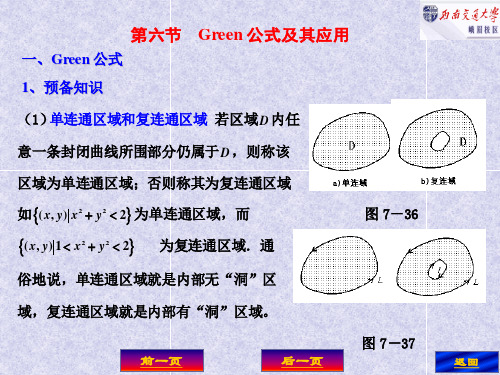
∂Q ∂P )dxdy − ∂x ∂y
的边界正向曲线. 其中 L 为 D 的边界正向曲线.
前一页 后一页
返回
为简单区域, 证明 设 D 为简单区域,即垂直 x 轴(或 y 轴)的 的边界至多只有两个交点, 直线与 D 的边界至多只有两个交点,则 D 可用不 等式表示为: 等式表示为:ϕ1 ( x ) ≤ y ≤ ϕ 2 ( x ) (a ≤ x ≤ b) 或
ψ 1 ( y ) ≤ x ≤ ψ 2 ( y ) ( c ≤ y ≤ d ) 如图 7- 38 ,由二重积分 38,
的计算有
图 7-38
b ϕ 2 ( x ) ∂P b ∂P dxdy = ∫ dx ∫ dy = = ∫ { P[ x , ϕ 2 ( x )] − P[ x , ϕ1 ( x )]} dx ∫∫ ∂y a ϕ1 ( x ) ∂y a D
第 六节
一、Gree n 公式 1、预备知识
Green 公式及其应用
(1 ) 单连通区域和复连通区域 若区域 D 内任 意一条封闭曲线所围部分仍属于 D ,则称该 区域为单连通区域;否则称其为复连通区域 区域为单连通区域; 为单连通区域, 如 {( x , y ) x 2 + y 2 < 2} 为单连通区域,而 图 7-36
2 、Green 公式 定理( 公式) 为光滑(或分段光滑) 定理(Green 公式) 设 D 为光滑(或分段光滑)闭曲线 L 所围平面的闭 : 区域, 上具有连续的一阶偏导, 区域,函数 P ( x , y ) , Q( x , y ) 在 D 上具有连续的一阶偏导,则
∫
L
Pdx + Qdy = ∫∫ (
注 (1 )
∂Q ∂P 上必须连续, , 在 D 上必须连续,这 ∂x ∂y
∂Q ∂P )dxdy − ∂x ∂y
的边界正向曲线. 其中 L 为 D 的边界正向曲线.
前一页 后一页
返回
为简单区域, 证明 设 D 为简单区域,即垂直 x 轴(或 y 轴)的 的边界至多只有两个交点, 直线与 D 的边界至多只有两个交点,则 D 可用不 等式表示为: 等式表示为:ϕ1 ( x ) ≤ y ≤ ϕ 2 ( x ) (a ≤ x ≤ b) 或
ψ 1 ( y ) ≤ x ≤ ψ 2 ( y ) ( c ≤ y ≤ d ) 如图 7- 38 ,由二重积分 38,
的计算有
图 7-38
b ϕ 2 ( x ) ∂P b ∂P dxdy = ∫ dx ∫ dy = = ∫ { P[ x , ϕ 2 ( x )] − P[ x , ϕ1 ( x )]} dx ∫∫ ∂y a ϕ1 ( x ) ∂y a D
第 六节
一、Gree n 公式 1、预备知识
Green 公式及其应用
(1 ) 单连通区域和复连通区域 若区域 D 内任 意一条封闭曲线所围部分仍属于 D ,则称该 区域为单连通区域;否则称其为复连通区域 区域为单连通区域; 为单连通区域, 如 {( x , y ) x 2 + y 2 < 2} 为单连通区域,而 图 7-36
2 、Green 公式 定理( 公式) 为光滑(或分段光滑) 定理(Green 公式) 设 D 为光滑(或分段光滑)闭曲线 L 所围平面的闭 : 区域, 上具有连续的一阶偏导, 区域,函数 P ( x , y ) , Q( x , y ) 在 D 上具有连续的一阶偏导,则
∫
L
Pdx + Qdy = ∫∫ (
注 (1 )
∂Q ∂P 上必须连续, , 在 D 上必须连续,这 ∂x ∂y
《格林公式及其应用》PPT课件

n (cos,cos).
v nds L
(P cos Q cos)ds
L
由格林公式
Pdy Qdx =========
(P Q )d .
L
D y x
(格林公式的另一种形式)
称函数
为平面向量场 v (P(x, y),Q(x, y))
的散度.物理意义:稳定流体通过某一闭曲线的流量,等
于其散度在该闭曲线所的区域上的二重积分之值.
(x y)dx (x y)dy
( L )
x2 y2
0dxdy 0.
D1
首页
上页
返回
下页
结束
铃
这里(L ) 表示多连通区域 D1的正向边界曲线 .这时L按 逆时针方向,而按顺时针方向.因而
(x y)dx (x y)dy
( L )
x2 y2
(x y)dx (x y)dy (x y)dx (x y)dy,
(x y)dx (x y)dy
L
x2 y2
1 r2
2 [r2 (cost sin t)(sin t) r2 (cost sin t)(cost)]dt
0
2
0 1dt 2.
例 4 设函数u(x,y)在有界闭区域D上有连续的二阶
偏导数,L 为D 的边界且逐段光滑.证明:
u
L
u n
ds
y
x
(x2 y)dx (x y2 sin3 y)dy, AO
oA
(x2 y)dx (x y2 sin3 y)dy
AO
0 x2dx 8 .
2
3
首页
上页
返回
下页
结束
铃
当曲线积分 (x2 y)dx (x y2 sin3 y)dy 与路径无 AB
格林公式及其应用-课件

OB
y
(1 )
o
y x2
x y2
B(1,1)
x
A(1,0)
进一步猜测:沿任意分 段光滑的曲线 LOB:
2xydx x2dy ?
LOB
(1 )
问题1
一、Green公式
是否所有二型线积分都 有这样的性质: 积分值只与曲线 L的起点和终点有关
而与曲线 L所走过的路径无关? ( 否 )
B(1,1)
I 1 2 y2 y 2 ydy 1 y4dy o
0
0
x
A(1,0)
5 1 y4dy 1 0
1. 引例
一、Green公式
引 求I 2xydx x2dy,其中L分别为:1) y2 x;2) y x2;
例
L
1 3)OAB上由O(0,0) B(1,1)一段有向曲线 (如图)。
L
LOAAB 来自12x 0dx
112 dy 1
0
0
1. 引例
一、Green公式
引 求I 2xydx x2dy,其中L分别为:1) y2 x;2) y x2;
例
L
1 3)OAB上由O(0,0) B(1,1)一段有向曲线 (如图)。
猜一猜:
2xydx x2dy ?
ydx
其中,L是D的正向边界曲线。
G.F .:P 0,Q x
证:xdy
L
Py 0,Qx 1
(1 0)d D
D
同理: ydx d D ydx
L
D
L
例1
4. Green公式举例
求椭圆
x2 a2
y
(1 )
o
y x2
x y2
B(1,1)
x
A(1,0)
进一步猜测:沿任意分 段光滑的曲线 LOB:
2xydx x2dy ?
LOB
(1 )
问题1
一、Green公式
是否所有二型线积分都 有这样的性质: 积分值只与曲线 L的起点和终点有关
而与曲线 L所走过的路径无关? ( 否 )
B(1,1)
I 1 2 y2 y 2 ydy 1 y4dy o
0
0
x
A(1,0)
5 1 y4dy 1 0
1. 引例
一、Green公式
引 求I 2xydx x2dy,其中L分别为:1) y2 x;2) y x2;
例
L
1 3)OAB上由O(0,0) B(1,1)一段有向曲线 (如图)。
L
LOAAB 来自12x 0dx
112 dy 1
0
0
1. 引例
一、Green公式
引 求I 2xydx x2dy,其中L分别为:1) y2 x;2) y x2;
例
L
1 3)OAB上由O(0,0) B(1,1)一段有向曲线 (如图)。
猜一猜:
2xydx x2dy ?
ydx
其中,L是D的正向边界曲线。
G.F .:P 0,Q x
证:xdy
L
Py 0,Qx 1
(1 0)d D
D
同理: ydx d D ydx
L
D
L
例1
4. Green公式举例
求椭圆
x2 a2
《格林公式及其应用》课件

特殊型格林公式
特殊形式的格林公式适用于计算具有特殊形 状的曲线或曲面上的积分,如圆形、椭圆形 等。
格林公式的应用
1 线积分的计算
通过格林公式,我们可以计算曲线上的积分,从而得到与曲线相关的物理量,如流量、 环流等。
2 面积的计算
利用格林公式,我们可以计算平面上的闭合曲线所围成的面积,为测量和计算提供了方 便。
3 体积的计算
基于格林公式,我们可以计算由曲线围成的立体图形的体积,为求解三维图形的体积提 供了便利。
格林公式的计算方法
1
极坐标系下的计算方法
当曲线在极坐标系下表达时,我们可以利用极坐标的性质,简化格林公式的计算 过程。
2
直角坐标系下的计算方法
当曲线在直角坐标系下表达时,我们可以借助直角坐标系的符号和定义,求解格 林公式中的各个参数。
格林公式及其应用
本课件介绍格林公式的形式、应用场景及计算方法,以及灵活应用格林公式 的技巧。让我们一起探索格林公式的奥秘!
什么是格林公式
格林公式是一个在向量分析中常用的定理,它将二重积分与线积分、面积积分联系起来。了解它的基本 原理对于理解多变量微积分至关重要。
格林公式的形式
一般型格林公式
一般形式的格林公式在计算线积分与面积积 分时特别有用,它将曲线的内部区域与曲线 的边界联系起来。
例题分析
给定一个曲线和一个区域,我们将应用格林公式来计算相关的积分和物理 量,以解决问题。
总结
格林公式的优势与不足
格林公式在解决某些问题中非常有用,但在特定场景下可能有其局限性,我们需理解其应用ቤተ መጻሕፍቲ ባይዱ范围和限制。
如何灵活应用格林公式
学习了格林公式的基本原理和计算方法后,我们可以尝试将其巧妙应用于实际问题中,创造 性地解决难题。
§2 格林公式及其应用

1 =0,从而 因为 是 基 本 解 , 所 以 ∆ M0 r rM 0 M M0M 由叠加原理, (见引 ∆R( M 0 ) = 0 。由叠加原理, ∆V ( M 0 ) = F ( M 0 ) 。 见引 (
1
力场势函数) 。 力场势函数)
1 F ( M ) 可理解为电荷体密度或质量密度。 称为体位势: 可理解为电荷体密度或质量密度。 − ∆ V ( M 0 ) 称为体位势: 4π
(2.11)
证 明: 将调和函数基本积分公式应用到Γa 上有:
1 ∂ 1 1 ∂u u( M 0 ) = − ∫∫ u r − r dS = 0 4π Γa ∂n r r ∂n
上页 下页 返回
1 1 1 ∂ 1 在Γa 上 = , r = − 2 ,所以 r a ∂n r a 1 ∂u 1 ∂u r r ∫∫ r ∂n dS = a ∫∫ ∂n dS = 0 Γa Γa
1 1 1 ∂u ∂ 1 1 ∂u − ∫∫∫ ∆udΩ = ∫∫ u r − r dS + 2 ∫∫ udS − ∫∫ r dS r ∂n r r ∂ n ε Γε ∂n ε Γε Ω\ Kε Γ
ε ε ε
上页 下页 返回
1 ∂u 1 ∂u dS , 即 u∗ 和 udS , r = 记u = 2 ∫∫ r 2 ∫∫ 4πε Γε ∂n 4πε Γε ∂n
当 u 是Ω 内的调和函数, M 0 ≠ Ω ,则由格林第二公式 有:
∂ 1 u( M ) r ∫∫ ∂n rM 0 M Γ
1 ∂u( M ) − r dS = 0 r ∂n M0M
当 u 是 Ω 内的调和函数,M 0 ∈ ∂Ω = Γ ,类似基本积分公 内的调和函数, 式的推导, 式的推导,记 Γε′ = Γε I Ω , Γ ′ = Γ \ K ε ,则有
1
力场势函数) 。 力场势函数)
1 F ( M ) 可理解为电荷体密度或质量密度。 称为体位势: 可理解为电荷体密度或质量密度。 − ∆ V ( M 0 ) 称为体位势: 4π
(2.11)
证 明: 将调和函数基本积分公式应用到Γa 上有:
1 ∂ 1 1 ∂u u( M 0 ) = − ∫∫ u r − r dS = 0 4π Γa ∂n r r ∂n
上页 下页 返回
1 1 1 ∂ 1 在Γa 上 = , r = − 2 ,所以 r a ∂n r a 1 ∂u 1 ∂u r r ∫∫ r ∂n dS = a ∫∫ ∂n dS = 0 Γa Γa
1 1 1 ∂u ∂ 1 1 ∂u − ∫∫∫ ∆udΩ = ∫∫ u r − r dS + 2 ∫∫ udS − ∫∫ r dS r ∂n r r ∂ n ε Γε ∂n ε Γε Ω\ Kε Γ
ε ε ε
上页 下页 返回
1 ∂u 1 ∂u dS , 即 u∗ 和 udS , r = 记u = 2 ∫∫ r 2 ∫∫ 4πε Γε ∂n 4πε Γε ∂n
当 u 是Ω 内的调和函数, M 0 ≠ Ω ,则由格林第二公式 有:
∂ 1 u( M ) r ∫∫ ∂n rM 0 M Γ
1 ∂u( M ) − r dS = 0 r ∂n M0M
当 u 是 Ω 内的调和函数,M 0 ∈ ∂Ω = Γ ,类似基本积分公 内的调和函数, 式的推导, 式的推导,记 Γε′ = Γε I Ω , Γ ′ = Γ \ K ε ,则有
格林公式及其应用(整理).ppt

用二重积分计算: P(x, y) 2xy x2 ,Q(x, y) x y2 , 故
D
(
Q x
P y
)dxdy
D
(1
2
x)dxdy
y 1
x
1
2x
dx
0
x2 (1 2 y)dy
[y
0
] dx x2
0.0
29
x x x 1
(
1
2x
2
4)dx
0
2111 1 3 2 3 5 30
所以格林公式:
2
)dy]
L1 L2
0.0
28
x x x y y y y 1
[(2
3
2) (x
4)2x]dx
0
[(2
3
4
)2y (
2
2
)]dy
0
1
x x x y y y 1
(2
52
3
2)dx
0
(2
5
4
4
2
2
)dy
0
1
(1 1 1) ( 1 4 2) 1 3 2 3 3 3 3 30
D
(
Q x
P y
)dxdy
L
Pdx
Qdy
正确。
2. 利用曲线积分,求下面曲线所围成的图形面积: 圆 :
x2 y2 2ax
解:
y a 圆 : (x a)2
2
2
的参数方程为:
x a a cos, y a sin,0 2 ,
0.0
30
A
1 2
L
xdy
ydx
1
2
复变函数课件第三节 格林公式及其应用

∂Q ∂P ∫∫ ( ∂x − ∂y )dxdy = ∫L Pdx + Qdy D 的取正向的边界曲线, 其中 L是 D的取正向的边界曲线,
公式(1)叫做格林公式. 公式(1)叫做格林公式. (1)叫做格林公式
20122012-2-20 第十一章曲线积分和曲面积分
(1)
1
y
D
o
x
20122012-2-20
则以下四个条件等价: 则以下四个条件等价: (1)沿 D 中任意光滑闭曲线 L ,有 ∫ L Pdx + Qdy = 0 ; (1)沿 (2)对 (2)对 D 中任一分段光滑曲线 L ,曲线积分
∫
L
Pdx + Qdy 与路径无关,只与起点和终点有关. 与路径无关,只与起点和终点有关.
ห้องสมุดไป่ตู้记为
20122012-2-20
2013115第十一章曲线积分和曲面积分设闭区域d由分段光滑的曲线l上具有一阶连续偏导数则有qdypdxdxdy的取正向的边界曲线公式1叫做格林公式
格林公式
定理1 定理1 设闭区域 D由分段光滑的曲线 L围
成,函数 P( x, y)及Q( x, y)在 D 上具有一阶连 续偏导数, 续偏导数, 则有
第十一章曲线积分和曲面积分
2
格林公式的实质: 格林公式的实质:
沟通了沿闭曲线的积分与
二重积分之间的联系. 二重积分之间的联系
便于记忆形式: 便于记忆形式
∂ ∂ ∫∫ ∂x ∂ydxdy = ∫L Pdx + Qdy. D P Q
20122012-2-20
第十一章曲线积分和曲面积分
3
平面上曲线积分与路径无关的条件 是一个单连 单连域 定理 2 设 D 是一个单连域,函数 P ( x , y ) 及 Q ( x , y ) 在区域 D 内具有一阶连续偏导数. 内具有一阶连续偏导数.
格林公式

【例 6】 计算抛物线( x + y )2 = ax ( a > 0) 与 x 轴所 围成的面积.
【解】 ONA 为直线 y = 0 .
M
A(a ,0)
N
曲线 AMO 由函数 y = ax − x , x ∈ [0, a ]表示,
1 ∴ A = ∫ xdy − ydx 2 L 1 1 = ∫ONA xdy − ydx + ∫AMO xdy − ydx 2 2 1 a 1 0 = ∫AMO xdy − ydx = ∫a x ( − 1)dx − ( ax − x )dx 2 2 ax 2
∂Q y2 − x2 ∂P = 2 2 2 = ∂x ( x + y ) ∂y
当(0,0) ∉ D时,
设L所围区域为D,
由格林公式知
xd y − yd x ∫L x2 + y2 = 0
y o
L x
机动
目录
上页
下页
返回
结束
当(0,0) ∈ D 时,由于P,Q在 (0,0)点无定义,不满足格林公式条件
L
[证毕]
机动 目录 上页 下页 返回 结束
【应用格林公式时应注意】
1.积分曲线L必须是封闭曲线,取D的正向边界. 2. P , Q 在区域 D及其边界上具有一阶连 续偏导数 . 3.D可为单连通域,也可为复连通域; 当D为复连通域时,L包括D的所有正向边界. (三条缺一不可)
机动
目录
上页
下页
返回
机动 目录 上页 下页 返回 结束
【证明】 (1) 线, 则
(2)
设 L1 , L2 为D 内任意两条由A 到B 的有向分段光滑曲
∫L
=∫
1
格林(Green)公式及其应用

格林(green)公式及其应用
• 格林公式简介 • 格林公式的基本性质 • 格林公式的应用 • 格林公式的扩展 • 格林公式的实际例子 • 总结与展望
01
格林公式简介
格林公式的定义
格林公式是一个数学定理,用于描述二维平面上的向量场和路径之间的关系。它 指出,在一个封闭的区域内,沿任意路径的积分等于该区域内散度的体积分。
在实变函数中的应用
证明定理
格林公式在证明实变函数中的一些定 理中发挥了重要作用,如黎曼定理和 克雷洛夫定理等。
求解积分方程
利用格林公式,可以将积分方程转化 为边界积分方程,从而简化求解过程。
04
格林公式的扩展
高维格林公式
总结词
高维格林公式是格林公式在高维空间中 的推广,它描述了高维空间中向量场和 标量场之间的关系。
THANKS
感谢观看
格林公式的变种
总结词
格林公式的变种是原始格林公式的不同形式 或应用,它们在特定情况下可能更加方便或 有效。
详细描述
随着数学和物理学的发展,人们发现了许多 格林公式的变种。这些变种可能在某些特定 情况下更加适用,例如在处理非线性问题或 复杂边界条件时。了解这些变种有助于我们
更好地理解和应用格林公式。
03
格林公式在数学分析中占有重要的地位,是微积分学中的基本定理之一。它为 解决许多复杂的积分问题提供了一种有效的方法,使得许多难以计算的问题变 得简单明了。
对未来研究的展望
随着数学和其他学科的发展,格 林公式在各个领域的应用越来越 广泛。未来,我们可以进一步探 索格林公式的各种应用,如数值 计算、物理模拟、图像处理等。
解决偏微分方程的实例
总结词
格林公式还可以用于解决偏微分方程的问题,通过将 偏微分方程转化为等价的积分方程,可以简化求解过 程。
• 格林公式简介 • 格林公式的基本性质 • 格林公式的应用 • 格林公式的扩展 • 格林公式的实际例子 • 总结与展望
01
格林公式简介
格林公式的定义
格林公式是一个数学定理,用于描述二维平面上的向量场和路径之间的关系。它 指出,在一个封闭的区域内,沿任意路径的积分等于该区域内散度的体积分。
在实变函数中的应用
证明定理
格林公式在证明实变函数中的一些定 理中发挥了重要作用,如黎曼定理和 克雷洛夫定理等。
求解积分方程
利用格林公式,可以将积分方程转化 为边界积分方程,从而简化求解过程。
04
格林公式的扩展
高维格林公式
总结词
高维格林公式是格林公式在高维空间中 的推广,它描述了高维空间中向量场和 标量场之间的关系。
THANKS
感谢观看
格林公式的变种
总结词
格林公式的变种是原始格林公式的不同形式 或应用,它们在特定情况下可能更加方便或 有效。
详细描述
随着数学和物理学的发展,人们发现了许多 格林公式的变种。这些变种可能在某些特定 情况下更加适用,例如在处理非线性问题或 复杂边界条件时。了解这些变种有助于我们
更好地理解和应用格林公式。
03
格林公式在数学分析中占有重要的地位,是微积分学中的基本定理之一。它为 解决许多复杂的积分问题提供了一种有效的方法,使得许多难以计算的问题变 得简单明了。
对未来研究的展望
随着数学和其他学科的发展,格 林公式在各个领域的应用越来越 广泛。未来,我们可以进一步探 索格林公式的各种应用,如数值 计算、物理模拟、图像处理等。
解决偏微分方程的实例
总结词
格林公式还可以用于解决偏微分方程的问题,通过将 偏微分方程转化为等价的积分方程,可以简化求解过 程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
格林公式及其应用
11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
பைடு நூலகம்
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
35
