第七章时序逻辑电路
数字电路部分二-时序逻辑电路-王翰卓
第七章 时序逻辑电路7.1 常见触发器的功能验证7.1.1SR触发器74LS279为两个SR触发器的集成芯片。
1S1和1S2为一个触发器的两个接口。
连接电路如图,可验证SR触发器的功能。
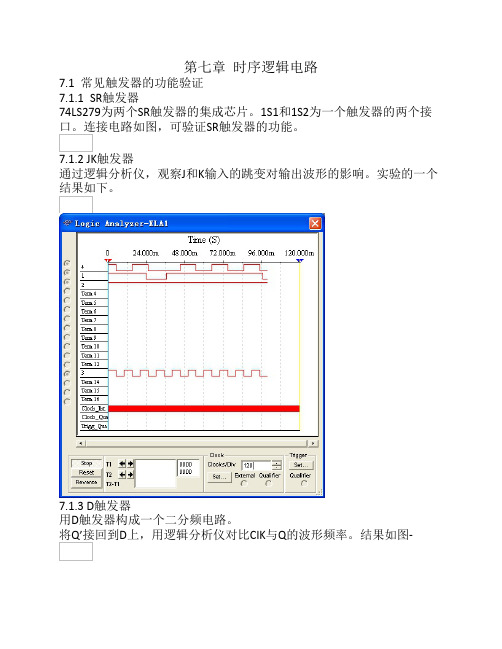
7.1.2 JK触发器通过逻辑分析仪,观察J和K输入的跳变对输出波形的影响。
实验的一个结果如下。
7.1.3 D触发器用D触发器构成一个二分频电路。
将Q’接回到D上,用逻辑分析仪对比ClK与Q的波形频率。
结果如图-7.2 常用时序逻辑电路及其相关设计7.2.1 寄存器应用双向移位寄存器74LS194改串行输入改为并行输出。
SL、SR为串行的数据输入端,S1S0=00时保持,S1S0=11时置数,S1S0=10时左移串行输入,由高位移向低位,S1S0=01时右移串行输入,由低位移向高位。
例如下面用左移方式,将SL产生的四个数据并行输出。
Word Generator设置为Burst模式。
7.2.2 计数器7.2.2.1 用74LS160设计一个六进制的计数器。
应用异步置零的方法,当QDQCQBQA=0110时,使异步置零端CLR’=0。
为保证置零的有效性,加入了改进电路-SR触发器,使输出为6的CLOCK下降沿到来后的整个低电平期间触发器输出恒为低电平。
采用同步置数法,将四个输入ABCD接为低电平,QDQCQBQA=0101时LOAD’=0。
7.2.2.2 验证74LS290的功能74LS290为2-5-10进制计数器。
R01=R02=1,S01=S02=0时,输出为0,R01=R02=0,S01=S02=1时输出为9。
S和R都置为0时正常计数。
INA接入clock后,实现二进制计数;INB接入clock后,实现五进制计数;INB接到QA,INA接clock时,实现十进制计数。
如下电路通过开关的切换可以实现不同的计数和置数功能。
7.3 时序逻辑电路的设计7.3.1 同步时序逻辑电路的设计7.3.1.1 同步时序逻辑电路的状态化简设计一个串行输入的数据检测器,连续输入3个或3个以上1时输出为1,其他情况下输出为0。
时序逻辑电路分类

时序逻辑电路分类介绍时序逻辑电路是一种用于处理时序信号的电路,它由逻辑门和存储元件组成。
时序逻辑电路按照其功能和结构的不同,可以分为多种类型。
本文将对时序逻辑电路的分类进行全面、详细、完整和深入的探讨。
一、根据功能分类1. 同步时序逻辑电路同步时序逻辑电路是指其数据在同一个时钟上升沿或下降沿进行传递和存储的电路。
这类电路广泛应用于计算机中的寄存器、时钟驱动器和状态机等。
同步时序逻辑电路具有可靠性高、稳定性强的特点。
2. 异步时序逻辑电路异步时序逻辑电路是指其数据不依赖时钟信号而进行传递和存储的电路。
这种电路在通信系统中常用于数据传输和处理,如异步串行通信接口(UART)。
异步时序逻辑电路具有处理速度快和实时性强的特点。
二、根据结构分类1. 寄存器寄存器是一种时序逻辑电路,用于存储和传递数据。
寄存器通常采用D触发器作为存储元件,可以实现数据的暂存和移位操作。
寄存器广泛应用于计算机的数据存储和寄存器阵列逻辑器件(RALU)等。
2. 计数器计数器是一种时序逻辑电路,用于生成特定的计数序列。
计数器可以按照时钟信号对计数进行增加或减少,并可以在达到指定计数值时触发其他操作。
计数器被广泛应用于时钟发生器、频率分频器和时序控制等电路中。
3. 时序控制器时序控制器是一种时序逻辑电路,用于控制其他电路的时序和操作。
时序控制器根据输入的控制信号和当前的状态,通过逻辑运算和状态转移进行运算和控制。
时序控制器被广泛应用于计算机的指令译码和状态机的设计中。
三、根据存储方式分类1. 同步存储器同步存储器是一种时序逻辑电路,用于存储和读取数据。
同步存储器是在时钟信号作用下进行数据存取的,并且数据的读取和写入操作都在时钟的上升沿或下降沿进行。
同步存储器主要包括静态随机存储器(SRAM)和动态随机存储器(DRAM)等。
2. 异步存储器异步存储器是一种时序逻辑电路,用于存储和读取数据。
与同步存储器不同的是,异步存储器的读取和写入操作不依赖时钟信号,而是由数据访问信号和存储器内部的同步电路进行控制。
时序电路逻辑功能描述方式

时序电路逻辑功能描述方式时序电路是一种电子电路,其逻辑功能在不同时间点上发生变化。
在时序电路中,电路的输出不仅依赖于当前的输入信号,还依赖于过去的输入信号和电路的内部状态。
时序电路通常由触发器(Flip-Flop)和组合逻辑门组成。
触发器是一种存储元件,可以存储一个二进制位的状态。
组合逻辑门通过将触发器的输出连接起来,并根据输入信号的条件决定是否改变触发器的状态。
通过这种方式,时序电路可以实现复杂的逻辑功能。
为了描述时序电路的逻辑功能,我们可以使用状态图、状态表和状态方程等方式。
状态图(State Diagram)是时序电路的一种图形表示方法。
它通过节点和有向边来表示电路的不同状态和状态之间的转换关系。
每个节点表示一个电路的状态,每条边表示一种条件下的状态转换。
状态图可以直观地描述时序电路的逻辑功能。
状态表(State Table)是时序电路的一种表格表示方法。
它列出了电路的每个状态和每个状态下的输出。
状态表通常包括当前状态、下一个状态和输出信号等列。
状态表可以清晰地描述电路的逻辑功能,并方便进行状态迁移和输出信号的计算。
状态方程(State Equation)是时序电路的一种数学描述方法。
它通过逻辑代数或布尔代数的形式表示电路的当前状态、输入信号和输出信号之间的关系。
状态方程可以使用逻辑门的真值表或卡诺图来推导得到。
在描述时序电路的逻辑功能时,我们通常需要确定以下几个方面的内容:1.电路的输入信号:输入信号是时序电路的触发条件,决定触发器状态的改变。
输入信号可以是外部输入,如开关和按钮,也可以是其他逻辑电路的输出。
2.电路的内部状态:内部状态是触发器的状态,它存储了电路的前一时刻的信息。
内部状态可以是一个或多个触发器的组合。
3.电路的输出信号:输出信号是根据当前输入信号和内部状态计算得到的结果。
输出信号可以是一个或多个逻辑电平。
4.电路的逻辑功能:逻辑功能是指输入信号和输出信号之间的关系,在不同的状态和条件下,输出信号如何发生改变。
最新数字电路教案-阎石-第七章-时序逻辑电路

第7章 时序逻辑电路7.1 概述时序电路在任何时刻的稳定输出,不仅与该时刻的输入信号有关,而且还与电路原来的状态有关。
图7.1.1 时序逻辑电路的结构框图2、时序电路的分类 (1) 根据时钟分类同步时序电路中,各个触发器的时钟脉冲相同,即电路中有一个统一的时钟脉冲,每来一个时钟脉冲,电路的状态只改变一次。
异步时序电路中,各个触发器的时钟脉冲不同,即电路中没有统一的时钟脉冲来控制电路状态的变化,电路状态改变时,电路中要更新状态的触发器的翻转有先有后,是异步进行的。
(2)根据输出分类米利型时序电路的输出不仅与现态有关,而且还决定于电路当前的输入。
穆尔型时序电路的其输出仅决定于电路的现态,与电路当前的输入无关;或者根本就不存在独立设置的输出,而以电路的状态直接作为输出。
7.2 时序逻辑电路的分析方法时序电路的分析步骤:电路图 时钟方程、输出方程、驱动方程 状态方程 计算 状态表(状态图、时序图) 判断电路逻辑功能 分析电路能否自启动。
7.2.1 同步时序电路的分析方法 分析举例:[例7.2.1]7.2.2 异步时序电路的分析方法 分析举例:[例7.2.3] 7.3 计数器概念:在数字电路中,能够记忆输入脉冲CP 个数的电路称为计数器。
计数器累计输入脉冲的最大数目称为计数器的“模”,用M 表示。
计数器的“模”实际上为电路的有效状态。
计数器的应用:计数、定时、分频及进行数字运算等。
计数器的分类:(1)按计数器中触发器翻转是否同步分:异步计数器、同步计数器。
(2)按计数进制分:二进制计数器、十进制计数器、N 进制计数器。
(3)按计数增减分:加法计数器、减法计数器、加/减法计数器。
7.3.1 异步计数器X X Y 1Y m输入输出一、异步二进制计数器1、异步二进制加法计数器分析图7.3.1 由JK触发器组成的4位异步二进制加法计数器。
分析方法:由逻辑图到波形图(所有JK触发器均构成为T/触发器的形式,且后一级触发器的时钟脉冲是前一级触发器的输出Q),再由波形图到状态表,进而分析出其逻辑功能。
第七章 时序逻辑电路

Q1上升沿时刻有效 Q0上升沿时刻有效 CP上升沿时刻有效
FF0
3
计算、列状态表
Q0
CP
1D C1
Q0
FF1 1D C1
Q1
FF2 1D C1
Q2
Q1
Q2
现
态
次
态
注 时钟条件 CP0 CP1 CP2 CP0 CP0 CP1 CP0 CP0 CP1 CP2 CP0 CP0 CP1 CP0
n 1 Q2 Q2n Q1 Q2n Q1n Q0n n 1 n Q Q Q0 0 0 0 1 1 n 1 n 0 0 1 Q Q CP 0 0
n 1
K1 Q0n K0 Q
n 2
2
求状态方程
n n J Q K Q n 1 n n 1 2 1 2 n n Q JQ KQ J Q K Q 1 0 1 0 n n J 0 Q2 K Q 0 2 将各触发器的驱动方程代入,即得电路的状态方程:
0 0 0 0 1 1 0 0
3
n 1 n Q2 Q1 n 1 n Q Q 1 0 n 1 n Q Q 2 0
时序逻辑电路的输出,与电路的原状态 -回复

时序逻辑电路的输出,与电路的原状态-回复时序逻辑电路的输出与电路的原状态息息相关,它们之间的关系是通过时钟信号来实现的。
时序逻辑电路是一种具有状态的电路,它会根据输入信号和当前的状态产生不同的输出信号。
其输出与电路的原状态有着密切的联系,下面我将一步一步回答这个问题,详细阐述时序逻辑电路的输出与电路的原状态之间的关系。
首先,让我们来了解一下时序逻辑电路的基本原理。
时序逻辑电路由触发器(flip-flop)和组合逻辑电路(combinational logic)两部分组成。
触发器用于存储电路的状态,而组合逻辑电路则用于实现输入信号对于状态的转换。
时序逻辑电路的最重要的特点就是其输出不仅与当前的输入信号有关,还与之前的输入信号和状态有关。
时序逻辑电路的输出由两个主要因素决定:输入信号和电路的当前状态。
输入信号就是电路的外部输入,它们会触发电路的状态变化。
电路的当前状态则由之前的输入信号和状态经过逻辑运算得到。
我们可以利用触发器来存储电路的状态,通常使用D触发器和JK触发器。
这些触发器有时也被称为时序存储器,因为它们能够存储电路的状态,并且在时钟信号到来时根据输入信号和当前状态产生输出。
时序逻辑电路的输出在时钟信号的控制下发生变化。
时钟信号是一个周期性的信号,它的高电平和低电平分别代表了一个时钟周期的开始和结束。
在每个时钟周期的上升沿或下降沿,电路会根据当前的状态和输入信号产生新的输出。
时钟信号的频率决定了电路的工作速度,它通常以赫兹(Hz)为单位表示。
时序逻辑电路的输出也可以被称为时钟输出,它在时钟周期的每个时间点都会有一个确定的值。
时序逻辑电路的输出是通过组合逻辑电路计算得到的。
组合逻辑电路是由逻辑门和逻辑门之间的连线组成的,它们根据输入信号和电路的当前状态计算出输出信号。
逻辑门实现了逻辑运算,例如与门、或门、非门等,它们能够实现逻辑与、逻辑或、逻辑非等运算。
组合逻辑电路的输出会被反馈到触发器中,以更新电路的状态。
时序逻辑电路

输出 F
0 0 0 0 0 1 0 1
/0
100
/0 /0
011
正常情况下,触发器状态在000~101循环, 但若由于干扰使电路的状态为110或111, 也可以在1、2个时钟后回到以上的主循环。
这称为电路具有自启动能力
例2.2
分析图示时序逻辑电路
解:状态表的另一种形式:
CP
0 1
Q3 Q2 Q1
0 0 0 0 0 1 0 1 1 0 1 0 0 1 0 1 0 1
0 0 0
0
可见,每来一个CP脉冲触发器作加1计算,每6个脉冲一个循环,所以这是一个6进 制加法计数器。
例2.2
分析图示时序逻辑电路
解:状态表的另一种 形式:
CP
0 1
Q3 Q2 Q1
0 0 0 0 0 1 0 1 1 0 1 0 0 1 0 1 0 1
F
0 0 0 0 0 1
画时序图:
CP Q1 Q2 Q3
J1 X J 2 XQ 1 K 1 XQ 2 K2 X
Q
n 1
JQ
n
KQn
得到各触发器的次态方程:
Q Q
n 1 1 n 1 2
X Q 1 XQ 2 Q 1 X Q 2 Q 1 XQ 2
例2.4
ቤተ መጻሕፍቲ ባይዱ
分析图示时序逻辑电路
Q Q
输入
X 0 0 0 0 1 1 1
时序逻辑电路
1 2 3 4 5 6 时序逻辑电路的基本概念 时序逻辑电路的分析 同步时序电路的设计 计数器 寄存器 算法状态机
时序逻辑电路
数字电路分为 1. 组合电路: 2. 时序电路:
电路在某一给定时刻的输出 还取决于前一时刻电路的状态
时序逻辑电路

3 . 异步减 法计 数器
(1)3位递减计数器的状态
(2)电路组成
二 、 十进制计数器
十进制递减计数器的状态
1.电路组成
异步十进制加法计数器
2.工作原理
(1)计数器输入0~9个计数脉冲时,工作过程与4位二进制异步加法计数器完 全相同,第9个计数脉冲后,Q3Q2Q1Q0状态为1001。 (2)第10个计数脉冲到来后,此时计数器状态恢复为0000,跳过了1010~1111 的6个状态,从而实现842lBCD码十进制递增计数的功能。
④ 最 高 位 触 发 器 FF 3 是 在 Q 0 、 Q 1 、 Q 2 同 时 为 1 时 触 发 翻 转 , 即 FF 0 ~ FF 2 原均为 1 ,作加 l 计数时,产生进位使 FF 3 翻转为 l 。
(2)电路组成
4位二进制同步加法计数器逻辑图
工
程
应
用
计数不正常的故障检测 第一步,先查工作电源是否正常;第二步,检查触 发器的复位端是否被长置成复位状态;第三步,用示波器观测计数脉冲是否加到 了触发器的CP端;第四步,替换触发器,以确定集成电路是否损坏。
第二节 计数器
在数字系统中,能统计输入脉冲个数的电路称为计数器。
一 、二进 制计 数器 1 . 异步二 进制 加法计 数器
每输入一个脉冲,就进行一次加 1 运算的计数器称为加法 计数器,也称为递增计数器。 4 个 JK 触发器构成的异步加 法计数器如下图所示。
图中 FF 0 为最低位触发器,其控制端 C l 接收输入脉冲,输 出信号 Q 0 作为触发器 FF 1 的 CP , Q 1 作为触发器 FF 2 的 CP , Q 2 作为 FF 3 的 CP 。各触发器的 J 、 K 端均悬空,相当于 J = K =1 ,处于计数状态。各触发器接收负跳变脉冲信号时 状态就翻转,它的时序图见下图。
第7章 常用时序逻辑功能器件

5
第七章 常用时序逻辑功能器件
*** 中规模集成计数器
学习应注意以下几点: (1)编码 自然二进制/8421十进制 (2)模数 5进制、10进制、16进制 (3)加、减、可逆 (4)清0、置数端 同步还是异步
6
第七章 常用时序逻辑功能器件
74x161(74LS161 ,74HCT161): 4位二进制同步加法计数器 74x160: 8421十进制加法计数器(实验五) 74x290:异步二—五—十进制计数器 74x390:异步二—十进制计数器 主要任务: 读功能表掌握计数器使用方法 学会使用集成计数器构成任意进制计数器的方法
RCO ET Q D Q C Q B Q A
10
第七章 常用时序逻辑功能器件
74x161计数状态
1
CR D D D D 1 CET 0 1 2 3 TC 1 CEP 74x161 CP > Q Q Q Q PE 0 1 2 3
1
M=16
11
第七章 常用时序逻辑功能器件
1)异步清零。CR=0 时, 计数器输出直 接清零 Q3Q2Q1Q0 = 0000.无需CP 2)同步并行预置制数。
31
第七章 常用时序逻辑功能器件
基本寄存器 按照功能
Q0
FF0
Q1
FF1
移位寄存器 并行
串行
按照存、取 数据方式
D0
D1
应用: 存储代码、串/并行转换、数值计算、缓冲区
32
第七章 常用时序逻辑功能器件
一、 集成中规模双向移位寄存器74x194 P284 DSR:右移串行输入端 Q0 Q1 Q2 Q3 CP S1 S0 DSL:左移串行输入端 VCC DI3,2,1,0 :并行输入端 Q3~ Q0:数据输出端 74x194 CP:时钟脉冲输入端 D GND 上升沿触发 CR DSRDI0DI1 DI2 DI3 SL CR CR :清零端, =0时清零
数字电路 第七章 时序逻辑电路

/0 001
/0
010 /0
101
100 /1 /0
011
结论:该电路是一个同步五进制( ⑥ 结论:该电路是一个同步五进制(模5)的加 法计数器,能够自动启动, 为进位端. 法计数器,能够自动启动,C为进位端.
§7.3 计数器
7.3.1 计数器的功能和分类
1. 计数器的作用
记忆输入脉冲的个数;用于定时,分频, 记忆输入脉冲的个数;用于定时,分频,产 生节拍脉冲及进行数字运算等等. 生节拍脉冲及进行数字运算等等.
1 0 1 0 1 0 1 0
3. 还可以用波形图显示状态转换表. 还可以用波形图显示状态转换表.
CP Q0 Q1 Q2
思考题: 思考题:试设计一个四位二进制同步加法计数 器电路,并检验其正确性. 器电路,并检验其正确性.
7.3.4 任意进制计数器的分析
例:
Q2 J2 Q2 K2 Q1 J1 Q1 K1 Q0 J0 Q0 K0
第七章 时序逻辑电路
§7.1 概述 §7.2 时序逻辑电路的分析方法 §7.3 计数器 §7.4 寄存器和移位寄存器 §7.5 计数器的应用举例
§7.1Байду номын сангаас概述
在数字电路中, 在数字电路中,凡是任一时刻的稳定 输出不仅决定于该时刻的输入,而且还和 输出不仅决定于该时刻的输入,而且还和 电路原来的状态有关者 电路原来的状态有关者,都叫做时序逻辑 电路,简称时序电路 时序电路. 电路,简称时序电路. 时序电路的特点:具有记忆功能. 时序电路的特点:具有记忆功能.
下面将重点 讨论蓝颜色 电路—移位 电路 移位 寄存器的工 寄存器的工 作原理. 作原理. D0 = 0 D1 = Q0 D2 = Q1 D3 = Q2
有限状态机

7.2 MEALY型状态机
output clk input 组合电路 reset 当前状态
0/0000
S0
寄 存 器
1/1001
S1
1/1001
0/0000
0/1100
1/1111
S3
1/1111
S2
0/1100
entity demo is port (clk, inl, reset: in std_logic; outl : out std_ logic) end demo; architecture moore of demo is type state_type is ( so, sl, s2, s3 ); signal state: state_ type; begin demo_ process: process ( clk, reset ) begin if reset = '1' then state <= so; elsif clk'event and clk = '1' then case state is when s0 => if inl= '1' then state <= sl; end if; when s1 => if inl = '0' then state <= s2; end if; when s2 => if inl = '1' then state <= s3; end if;
输 出 译 码 器 输出
输入
状态 译码 器 反馈
状态 寄存 器
状态
状态机的结构示意图
2. 状态机的优点.
•结构模式相对简单,设计方案相对固定
时序电路概念总结

3、 MSI 移位寄存器 74x194 双向移位寄存器 (1) 注意左移和右移的定义
(2) 注意输入位置:LIN 是从最右边输入(左移寄存器的输入)。RIN 是从最左边输入。 4、 环形计数器 (1) 不具有健壮性,无法自动校正 (2) 自校正环形计数器:P531——BCD 加一个或非(非与) 6、 约翰逊计数器
(4) 画出状态转移图 区分 MOORE 机与 MEALY 机
注意!!!:每一根箭头都标有一个转移表达式: 转移表达式必须是互斥的! 转移表达式最好是完备的!
5、 状态机的设计! Lec13、 14——两个班都讲了密码锁和雷鸟车的例子。罗老师班还讲 了猜谜游戏。 设计过程: 1) 问题翻译:构造状态输出表 2) 选择时序器件 3) 状态\输出表中的状态数目最小化 4) 状态编码 5) 构造激励表 6) 写出激励方程 7) 电路实现 (1) 状态翻译 注意一定要设定初始状态 (2) 状态最小化 LEC14 相同状态的判断:(a)输出必须完全相同。 (b)对外状态转移必须完全相同 (二者之间的状态转移可以不同,因为如果是相同状态了,两状态之间的转移 应该互不关心) Nelson 的梯形表的画法! (3) 状态编码 状态编码方式有相当多。编码的时候以下几点是需要考虑的: 复位电路简单:一般设置为 000; 激励方程简单:——最好能找到相邻状态 输出方程简单 几种编码方式的分析: (a) 自然数编码: 容易复位,可以用最小的 BIT(最少的 D 触发器) (b) One-hot 编码: 复位没有 00 状态,非法状态太多,需要保护,从而减慢了速 度。 但是可以省略译码电路。 (c) GRAY 码:每次改变最小 bit 位。(关键是如何找到相邻状态) (d) 相邻项编码相邻原则:两个班都强调了 输入确定时,下一状态的相同的当前状态放在一起。 输出相同的状态放在一起。 对于同一现态,下一装态相邻的放在一起。
数字逻辑设计第七章(2)D锁存器

RD DOUT[3:0]
Xi Yi Ci
X Y
S
CI CO
锁存器的应用
Si Ci+1
串行输入、串行输出 注意:时钟同步
QD Q C CLK
Xi Yi
时钟控制
再谈串行输入 加法器的实现
Ci
暂存
XY CI CO
S
Si
Ci+1
9
触发器
只在时钟信号的边沿改变其输出状态
正边沿 上升沿
负边沿 下降沿
CLK
Q
15
D锁存器 ——电平有效 D触发器 —— 边沿有效
触发器的应用
利用触发器作为移位寄存器(图1)
思考:能否将触发 器改为锁存器(图2) D
F/F
F/F
D Q Q1 D Q Q
CLK Q
CLK Q
D CLK
Q1 Q
16
CLK D
CLK
(图1)
latch
latch
Q1
DQ
DQ Q
CQ
CQ
(图1)
D触发器的定时参数
QQn+*1==SS++RR’’··QQ
Q —— 当前状态(原态、现态)
Q* —— 下一状态(新态、次态)
S·R = 0(约束条件)
31
J K C
C J K Qm Q
32
SQ
SQ
C 主 Qm C 从
RQ
RQ
逻辑符号 Q
JQ QL C
KQ
1 箝位
功能表
C=1期间,
JK Q
0 1
J的变化只引起 Qm改变一次
CLK=1时, 主锁存器不工作,Qm 保持不变 从锁存器工作,将 Qm 传送到输出端
第七章 几种常用的时序逻辑电路试题及答案

第七章 几种常用的时序逻辑电路一、填空题1.(9-1易)与组合逻辑电路不同,时序逻辑电路的特点是:任何时刻的输出信号不仅与____________有关,还与____________有关,是______(a.有记忆性b.无记忆性)逻辑电路。
2.(9-1易)触发器是数字电路中______(a.有记忆b.非记忆)的基本逻辑单元。
3.(9-1易)在外加输入信号作用下,触发器可从一种稳定状态转换为另一种稳定状态,信号终止,稳态_________(a.不能保持下去 b. 仍能保持下去)。
4.(9-1中)JK 触发器是________(a.CP 为1有效b.CP 边沿有效)。
5.(9-1易)1n n n Q J Q K Q +=+是_______触发器的特性方程。
6.(9-1中)1n n Q S RQ +=+是________触发器的特性方程,其约束条件为___________。
7.(9-1易)1n n n Q T Q T Q +=+是_____触发器的特征方程。
8. (9-1中)在T 触发器中,若使T=____,则每输入一个CP ,触发器状态就翻转一次,这种具有翻转功能的触发器称为'T 触发器,它的特征方程是________________。
9.(9-1难)我们可以用JK 触发器转换成其他逻辑功能触发器,令 __________________,即转换成T 触发器;令_______________, 即转换为'T 触发器;令________________,即转换成D 触发器。
10.(9-1难)我们可以用D 触发器转换成其他逻辑功能触发器,令 __________________,即转换成T 触发器;令_______________, 即转换为'T 触发器。
11.(9-2易)寄存器存放数据的方式有____________和___________;取出数据的方式有____________和___________。
数电课件时序电路

通过测试和验证手段,发现时序电路中存在的故障和问题。
故障定位
确定故障发生的位置和原因,以便进行针对性的修复。
故障排除
根据故障定位结果,采取适当的措施排除故障,恢复时序电路的正常工作。
预防性维护
通过定期检查和维护,预防时序电路出现故障,提高系统的可靠性和稳定性。
THANKS
感谢观看
06
时序电路的测试与验证
测试方法
静态测试
通过输入一组已知的测试向量,观察输出结果是否符合预期,以检测 时序电路的功能性。
动态测试
模拟实际工作时序电路的行为,通过输入激励信号,观察输出响应是 否符合预期。
边界测试
针对电路的输入和输出边界进行测试,以确保电路在极限条件下的正 常工作。
仿真测试
利用仿真软件对时序电路进行模拟测试,以验证电路的功能和性能。
使用HDL对时序电路进行详细设计描述, 包括逻辑功能、输入输出接口和时序约
束等。
逻辑综合与优化
将HDL代码转换为具体的门级电路, 并进行优化,以满足性能、面积和功
耗等要求。
逻辑仿真与验证
利用HDL仿真工具对时序电路进行仿 真测试,验证设计的正确性和可靠性。
可编程逻辑器件开发
使用HDL在可编程逻辑器件(如 FPGA)上进行时序电路的开发和实 现。
详细描述
状态图是一种图形化表示时序电路状态转换的工具,通过状态图可以清晰地看出时序电 路的状态转换过程和状态转换条件。在状态图中,每个节点表示一个状态,箭头表示状 态转换的方向和条件。通过分析状态图,可以得出时序电路的次态方程和输出方程,进
而理解时序电路的工作原理。
状态转换表分析法
总结词
通过状态转换表可以系统地列出时序电路的所有可能的状态转换情况,是分析时序电路的另一种重要方法。
第七章触发器及时序电路

第七章触发器及时序电路第一节RS触发器一、填空题1触发器具有_______ 个稳定状态,在输入信号消失后,它能保持 __________ 不变。
2、“与非”门构成的基本RS触发器,输入端是 ____________ 和_____________ ;输出端是 _____________ 和_____________________ ,将 _____________ 称为触发器的0状态,称为触发器的1状态。
3、“与非”门构成的基本RS触发器R D =1,S D =0时,其输出状态为 ____ 。
4、触发器电路中,R D端、S D端可以根据需要预先将触发器____________ 或_______ ,而不受的同步控制。
5、同步RS 触发器状态的_________ 与___________ 同步。
二、判断题(正确的在括号中打“,错误的打“X” ))1、触发器只需具备两个稳态功能,不必具有记忆功能。
2、基本RS触发器要受时钟的控制。
3、Q n+1表示触发器原来所处的状态,即现态。
4、当CP处于下降沿时,触发器的状态一定发生翻转。
二、绘图题1、设“与非”门组成的基本RS触发器的输入信号波形如图所示,试在输入波形下方画出Q和Q端的信号波形。
R ----- ----------------------QQ2、已知同步RS触发器的S、R、CP脉冲波形如图所示。
试在它们下方画出Q端的信号波形(设触发器的初始状态为0)R -------------- ---------Q第二节JK触发器一、填空题1、在时钟脉冲的控制下,JK触发器根据输入信号J、K的不同情况,具有______、、和功能。
2、在时钟脉冲下,JK触发器输入端J = 0、K = 0时,触发器状态为_________ ; J= 0、K = 1时,触发器状态为 ________ ; J= 1、K = 0时,触发器状态为_______ ;J= 1、K = 1时,触发器状态随CP脉冲的到来而。
数字电路教案-阎石-第七章-时序逻辑电路

第7章 时序逻辑电路7.1 概述时序电路在任何时刻的稳定输出,不仅与该时刻的输入信号有关,而且还与电路原来的状态有关。
图7.1.1 时序逻辑电路的结构框图2、时序电路的分类 (1) 根据时钟分类同步时序电路中,各个触发器的时钟脉冲相同,即电路中有一个统一的时钟脉冲,每来一个时钟脉冲,电路的状态只改变一次。
异步时序电路中,各个触发器的时钟脉冲不同,即电路中没有统一的时钟脉冲来控制电路状态的变化,电路状态改变时,电路中要更新状态的触发器的翻转有先有后,是异步进行的。
(2)根据输出分类米利型时序电路的输出不仅与现态有关,而且还决定于电路当前的输入。
穆尔型时序电路的其输出仅决定于电路的现态,与电路当前的输入无关;或者根本就不存在独立设置的输出,而以电路的状态直接作为输出。
7.2 时序逻辑电路的分析方法时序电路的分析步骤:电路图 时钟方程、输出方程、驱动方程 状态方程 计算 状态表(状态图、时序图) 判断电路逻辑功能 分析电路能否自启动。
7.2.1 同步时序电路的分析方法 分析举例:[例7.2.1]7.2.2 异步时序电路的分析方法 分析举例:[例7.2.3] 7.3 计数器概念:在数字电路中,能够记忆输入脉冲CP 个数的电路称为计数器。
计数器累计输入脉冲的最大数目称为计数器的“模”,用M 表示。
计数器的“模”实际上为电路的有效状态。
计数器的应用:计数、定时、分频及进行数字运算等。
计数器的分类:(1)按计数器中触发器翻转是否同步分:异步计数器、同步计数器。
(2)按计数进制分:二进制计数器、十进制计数器、N 进制计数器。
(3)按计数增减分:加法计数器、减法计数器、加/减法计数器。
7.3.1 异步计数器X X Y 1Y m输入输出一、异步二进制计数器1、异步二进制加法计数器分析图7.3.1 由JK触发器组成的4位异步二进制加法计数器。
分析方法:由逻辑图到波形图(所有JK触发器均构成为T/触发器的形式,且后一级触发器的时钟脉冲是前一级触发器的输出Q),再由波形图到状态表,进而分析出其逻辑功能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章时序逻辑电路
一、概述
1、时序逻辑电路的特点
逻辑功能特点:任何时刻的输出不仅取决于该时刻的输入信号,而且与电路原有的状态有关。
电路结构特点:由存储电路和组合逻辑电路组成。
2、时序逻辑电路的类型
同步时序逻辑电路:所有触发器的时钟端连在一起,所有触发器在同一个时钟脉冲CP控制下同步工作。
异步时序逻辑电路:时钟脉冲CP只触发部分触发器,其余触发器由电路内部信号触发。
因此,触发器不在同一时钟作用下同步工作。
米利型电路:输出不仅取决于存储电路的状态,还和电路的输入信号有关。
摩尔型电路:输出仅仅取决于存储电路的状态。
3、时序逻辑电路的各种方程和图表
时钟方程
驱动方程:各触发器输入信号的逻辑表达式。
输出方程:时序电路的输出逻辑表达式。
状态方程:将驱动方程代入相应触发器的特性方程中所得到的方程
状态转换真值表:简称状态转换表,是反映电路状态转换的规律与条件的表格。
填写方法:将电路现态的各种取值代入状态方程和输出方程进行计算,求出相应的次态和输出,从而列出状态转换表。
如现态起始值已给定,则从给定值开始计算;如没有给定,则可设定一个现态起始值依次进行计算。
状态转换图:用圆圈及其内的标注表示电路的所有稳态,用箭头表示状态转换的方向,箭头旁的标注表示状态转换的条件,从而得到的状态转换示意图。
时序图:在时钟脉冲CP作用下,各触发器状态变化的波形图。
二、时序逻辑电路的分析方法
1、同步时序逻辑电路的分析方法
a、根据给定的电路,写出它的输出方程和驱动方程,并求状态方程;
b、列状态转换真值表;
c、分析逻辑功能;
d、画状态转换图和时序图。
2、异步时序逻辑电路的分析方法
异步与同步时序电路的根本区别在于前者不受同一时钟控制,而后者受同一时钟控制。
因此,分析异步时序电路时需写出时钟方程,并特别注意各触发器的时钟条件何时满足。
三、计数器
1、计数器的作用与分类
计数器(Counter)用于计算输入脉冲个数,还常用于分频、定时等,其分类如下:
按时钟控制方式不同分:同步计数器和异步计数器。
(同步计数器比异步计数器的速度快得多。
)
按计数增减分:加法计数器、减法计数器、加/减计数器
按计数进制分:二进制计数器、十进制计数器、N进制计数器
2、计数器的计数规律举例
下面分别是二进制加法计数器和二进制减法计数器的计数规律:
下面是8421码十进制计数器和任意进制(五进制)计数器计数规律:
计数的最大数目称为计数器的“模”,用M表示,模也称为计数长度或计数容量。
n个触发器有n2种输出,最多可实现模n2计数器,五进制计数器也称模5计数器;十进制计数器则为模10计数器;3位二进制计数器为模8计数器。
3、同步计数器
(1)、3位二进制同步加法计数器
下图为同步3位二进制同步加法计数器的电路图:
串行进位:触发器负载均匀并行进位:低位触发器负载重电路分析:
a、逻辑电路图只由T触发器构成,且T触发器的特性方程为:n
n
n Q
T
Q
T
Q+
=
+1。
b、由图可知,各触发器的驱动方程为:n
j
i
j
i
Q
T∏-
=
=
1
,即:
n
n
n Q
Q
T
Q
T
T
1
2
1
;
;1=
=
=
c、将各触发器的驱动方程带入相应触发器的特性方程,得到各触发器的状态方程为:
n
n
n
n
n
n
n
n
n
n
n
n
n
n
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
Q
2
2
2
1
1
2
1
1
1
1
1
+
=
+
=
=
+
+
+
d、电路的输出方程为:n
n
n Q
Q
Q
C
1
2
=
根据上述,可列出电路的状态转换表:
(2)、3位二进制同步减法计数器
下图为同步3位二进制同步减法计数器的电路图:
电路分析:
与二进制加法计数器相比,各触发器的驱动方程变为:n j i j i Q T ∏-==1
0 ,
其状态转换表如下:
(3)、二进制可逆同步计数器
二进制可逆同步计数器是加法计数器和减法计数器的合并,并通过控制电路选择加、减计数功能。
如上图,当0/=D U 时,实现加计数器功能;当1/=D U ,实现减计数器功能。
(4)、十进制加法同步计数器
(5)、十进制减法同步计数器
4、异步计数器
5、集成计数器
6、任意进制计数器的构成
目前常见的集成计数器有十进制、4位二进制、12位二进制等。
若现在有M 进制计数器,需构成N 进制计数器,此时有N M >和N M <两种情况。
(1)、N M >的情况
在M 进制计数器的计数过程中,只要跳过
)N M -(个状态,就可以获得N 进制计数器。
集成计数器一般都有置零输入端和置数输入端,可以利用这两个输入端来跳过
)N M -(个状态实现N 进制计数器,分别称为反馈复位法和反馈置数法。
当输入第 N 个计数脉冲时,利用置 0 功能对计数器进行置 0 操作,强迫计数器进入计数循环,从而实现 N 进制计数。
这种计数器的起始状态值必须是零。
当输入第 N 个计数脉冲时,利用置数功能对计数器进行置数操作,强迫计数器进入计数循环,从而实现 N 进制计数。
这种计数器的起始状态值就是置入的数,可以是零,也可以非零,因此应用更灵活。
