量子力学的矩阵形式与表象变换
合集下载
量子力学 第7章-2(第20讲)
H
p' p"
p2 2m
p
'
p "
V
i
p
'
p
'
p
"
2． 力学量的表象变换
力学量 Fˆ 在表象A中的表示矩阵：
Fmn
m
(
x)Fˆ
n
(
x)d
x
在表象B中的表示矩阵：
F (x)Fˆ (x)d x
F Fmn
F F
Sm
m
(
x)
Fˆ
n
(
x)d
x Sn
mn
Sm FmnSn
问题？
坐标算符、动量算符、动能算符、任意力 学量算符在坐标表象、动量表象、 Q表象 （任一力学量表象）中分别如何表示？
力学量算符从一个表象如何变换到另一个 表象？
幺正变换有何主要性质和特点?
力学量算符在坐标表象与动量表象中的表示
坐标表象
xˆ x
Pˆx i
x
Tˆ
2
2m
2 x2
动量表象
xˆ i p x
a1(t)
(q, t)
an
(t
)
任一态矢 (x, t) an (t)un (x)
n 1
(r, t)
an (t)
un*
(r)
(r ,
t
)
d
3
r
(q, t)是粒子状态波函数 (r , t) 在Q 表象中的表示，
称为Q 表象波函数
量子力学表象与几何空间坐标系的比较
量子力学表象
Ai Aei
矢量:
A1
A
A2
量子力学的表象变换与矩阵形式
基矢变换的一个重要应用是求解量子力学中的本征值 问题。通过选择合适的基矢，可以将一个复杂的二次 型哈密顿量变为简单的形式，从而方便求解。
坐标表象与动量表象
01
坐标表象和动量表象是量子力学中最常用的两种表象。在 坐标表象中，波函数是坐标的函数，而在动量表象中，波 函数是动量的函数。
02 03
在坐标表象中，哈密顿量是一个关于坐标的二次型，而在 动量表象中，哈密顿量是一个关于动量的二次型。因此， 这两种表象适用于不同类型的问题。在求解一些与位置和 动量有关的物理问题时，选择合适的表象可以大大简化计 算过程。
表象变换
基矢变换
基矢变换的基本思想是通过线性组合的方式，将一组 旧的基矢变换为新的基矢。在量子力学中，这种变换 通常是通过一个可逆矩阵来实现的。
基矢变换是指在不同表象之间进行转换时，基矢的选 择会发生改变。在量子力学中，一个量子态由一个波 函数来描述，而波函数在不同的表象下会有不同的形 式。基矢变换就是用来描子计算
01
量子纠缠是量子力学中的一种现象，指两个或多个量子系统之 间存在一种特殊的关联，使得它们的状态无法单独描述。
02
量子纠缠在量子计算中具有重要作用，是量子并行性和量子算
法复杂性的基础。
利用量子纠缠，可以实现更高效的量子算法和量子通信协议。
03
量子通信与量子密码学
量子通信利用量子力学原理实现 信息的传输和保护，具有无条件
描述了密度矩阵的演化，其矩阵形式为密度矩阵与时间导数的乘积。
矩阵形式的测量与观测
量子测量
通过测量操作，将量子态投影到测量 算子的本征态上，其结果以概率的形 式给出。
观测结果
观测结果以概率分布的形式给出，反 映了量子态的测量结果与测量算子的 本征值的关联。
量子力学的矩阵形式和表象变换
§4.5 量子力学的矩阵形式和表象变换态和力学量算符的不同表示形式称为表象。
态有时称为态矢量。
力学量算符对态的作用实际上是对矢量量进行变换，因此可与代数中线性变换进行类比。
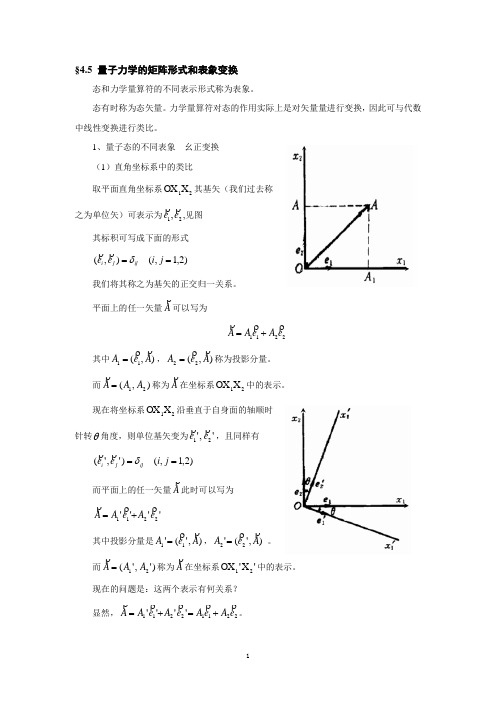
1、量子态的不同表象 幺正变换（1）直角坐标系中的类比取平面直角坐标系21X OX 其基矢（我们过去称之为单位矢）可表示为21,e e,见图其标积可写成下面的形式)2,1,(),(==j i e e ijj i δ我们将其称之为基矢的正交归一关系。
平面上的任一矢量A可以写为2211e A e A A +=其中),(11A e A =，),(22A e A=称为投影分量。
而),(21A A A = 称为A在坐标系21XOX 中的表示。
现在将坐标系21X OX 沿垂直于自身面的轴顺时针转θ角度，则单位基矢变为','21e e，且同样有)2,1,()','(==j i e e ijj i δ而平面上的任一矢量A此时可以写为 ''''2211e A e A A +=其中投影分量是),'('11A e A=，),'('22A e A =。
而)','(21A A A = 称为A在坐标系'X 'OX21中的表示。
现在的问题是：这两个表示有何关系？显然，22112211''''e A e A e A e A A+=+=。
用'1e 、'2e分别与上式中的后一等式点积（即作标积），有),'(),'('2121111e e A e e A A+= ),'(),'('2221212e e A e e A A+=表成矩阵的形式为⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛212212211121),'(),'(),'(),'(''A A e e e e e e e e A A由于'1e、1e及'2e、2e的夹角为θ，显然有⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛21212212211121cos sin sin cos ),'(),'(),'(),'(''A A A A e e e e e e e e A A θθθθ或记为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛2121)(''A A R A A θ 其中⎪⎪⎭⎫⎝⎛-=θθθθθcos sin sin cos )(R 是把A在两坐标中的表示⎪⎪⎭⎫⎝⎛''21A A 和⎪⎪⎭⎫⎝⎛21A A 联系起来的变换矩阵。
量子力学的矩阵形式与表象变换
A A 1 2 ＝ U － 1 A A 1 2 ＝ R （ ） A A 1 2 ， R （ ）U － ＝ 1
练习，求证U是么正矩阵。
么正变换小结
基矢变换： (e 1 ,e 2 ) (e 1 ,e 2 )U ()
基矢变换：Ψ´＝ΨS-1，＜－ Ψ a = Ψ ´ a´ = Ψ ´ Sa
Δ 有关矩阵知识 (参考周世勋书P250－255）
1．对角矩阵 Anm=amδnm. 2. 转置矩阵 (A ~)nmAmn
3．厄米共轭矩阵 (或称共轭矩阵) (A )nm (A ~ ) nm A m 运算规则：(AB) BA (A) A
A 1 A A2
A 3
A1 A A2
A3
以二维坐标系间变换为例。
设新坐标系 (e1,e2)相对原坐标系 (e1,e2) 顺时针 转过θ角。则
e1 c1e1c2e2,
e2 d1e1d2e2,
r (r )(r r )
动量表象
i
p x
px,
, i p
p
Fˆ(ip, p)
r (p )(12)3/2e ip r
p (r )(12)3/2e ip r
p (p )(p p )
(列矩阵的本征矢正交定义: XiXj 0 .)
C. 厄米矩阵的本征矢的正交归一完备。XiXj ij
（若简并情况下k个本征矢不正交,可以通过线性 组合,变为正交的k个本征矢）.
Δ.本征矢的归一化: XiXi 1
1
Δ.未归一的归一化系数C:
C
X
i
X
i
Δ.任意列矩阵X可用厄米矩阵的本征矢展开
练习，求证U是么正矩阵。
么正变换小结
基矢变换： (e 1 ,e 2 ) (e 1 ,e 2 )U ()
基矢变换：Ψ´＝ΨS-1，＜－ Ψ a = Ψ ´ a´ = Ψ ´ Sa
Δ 有关矩阵知识 (参考周世勋书P250－255）
1．对角矩阵 Anm=amδnm. 2. 转置矩阵 (A ~)nmAmn
3．厄米共轭矩阵 (或称共轭矩阵) (A )nm (A ~ ) nm A m 运算规则：(AB) BA (A) A
A 1 A A2
A 3
A1 A A2
A3
以二维坐标系间变换为例。
设新坐标系 (e1,e2)相对原坐标系 (e1,e2) 顺时针 转过θ角。则
e1 c1e1c2e2,
e2 d1e1d2e2,
r (r )(r r )
动量表象
i
p x
px,
, i p
p
Fˆ(ip, p)
r (p )(12)3/2e ip r
p (r )(12)3/2e ip r
p (p )(p p )
(列矩阵的本征矢正交定义: XiXj 0 .)
C. 厄米矩阵的本征矢的正交归一完备。XiXj ij
（若简并情况下k个本征矢不正交,可以通过线性 组合,变为正交的k个本征矢）.
Δ.本征矢的归一化: XiXi 1
1
Δ.未归一的归一化系数C:
C
X
i
X
i
Δ.任意列矩阵X可用厄米矩阵的本征矢展开
第7章 量子力学的矩阵形式与表象变换
这组数(a1,a2, … an, …)就是态ψ在Q表象中 的表示。可用列矩阵表示。设ψ是归一化的， 那么就有
* * d a a u m n mun d 2 mn
a an mn a an 1
* m * n mn n
9
由此可见，|an|2是ψ所描述的态中测量力学量Q所
ˆ 的共同本征态un(n代表 的任何一个力学量完全集 Q
一组完备的量子数，并先考虑分立谱情况)可以用
来构成此态空间的一组正交归一完备基矢，称为Q
表象。基矢满足正交归一性
(u m , u n ) mn
8
按态叠加原理，体系的任何一个态ψ可以用它们 展开
an u n
n
其中an (u n , )
为λ。可见，幺正变换不改变算符的本征值。
ˆ 自身的表象， 如果F' 是对角矩阵，即B表象是 F ˆ 本征值的问题归结为寻找一个幺正变换把算符 F
ˆ 的本征值。于是求算符 那么F' 的对角元素就是 F ˆ 自身的表象，使 F ˆ 的矩阵 从原来的表象变换到 F 表示对角化。解定态薛定谔方程求定态能级的问
ˆ 在A表象中的本征值方程为Fa=λa。λ为本 设F
征值，a为本征矢。通过幺正变换将F和a从A表 象变换到B表象，则有
F ' SFS ; b Sa
1
在B表象中有
F ' b (SFS1 )Sa
SFa Sa b
即 F'b b
19
ˆ 在B表象中的本征值仍 这个本征值方程说明算符 F
am ' u m ' an u n
第八章 量子力学的矩阵形式与表象变换 2 量子力学教学课件
xnn
当 m n 时，非对角元为:
xmn
2 a a 2 nx x sin dx a 0 a 2
2 a mx nx (sin ) x(sin )dx a 0 a a
x dx
1 a (m n) (m n) x cos x cos 0 a a a
j j , S j j j j k k
ˆ Lkj k , L j
L
ˆ , L
, k S k
ˆ S L S ( SLS ) S k S 得 L , L j k j k kj j kj kj
Qm为Q在自身空间中的的本征值
Qnm u ( x)Qum (x)dx u ( x)Qmu m (x)dx
n n
m u ( x)u m (x)dx Qm nm
n
结论：算符在自身的表象中是一个对角矩阵
15
例：一维谐振子的坐标x,动量p和Hamilton量H在能量表象中 的矩阵表示。 谐振子的能量本征函数记为ψn (n=0, 1, 2, ……)
第16页
第17页
例: 求一维无限深势阱中粒子的坐标算符 ˆ 在能量表象中的矩阵表示。 H 解：
ˆ 及哈密顿算符 x
一 维无限深势阱能量的本征函数基矢为:
n
2 n x sin a a
2 2 2
n 能级 En 2 2 a
n=1,2,3,…..
18
坐标算符x
当m=n时,对角元为:
即变换矩阵S是么正矩阵， 所以变换也称为么正变换。
10
§ 2.力学量（算符）的矩阵表示
第4章 量子力学的矩阵形式与表象变换
第4章 量子力学的矩阵形式与表象变换§1 量子态的不同表象态的表象 量子力学中态和力学量的具体表示方式研究表象的意义 根据不同问题选择不同表象，还可以进行表象变换。
一、坐标表象波函数ψ(x ,t ) 1、ψ(x ,t )2、dx t x 2),(ψ——表示体系处在ψ(x ,t )所描述的态中，在x →x +d x 范围内找到粒子的几率，也就是说，当体系处在ψ(x ,t )所描述的态中，测量坐标x 这个力学量所得值在x →x +d x 这个范围内的几率。
3、2(,)1x t dx ψ=⎰4、动量为x p '的自由粒子的本征函数 xp ip e x ''=2/1)2(1)(πψ5、x 在坐标表象中对应于本征值x '的本征函数)(x x '-δ， 即，)()(x x x x x x '-'='-δδ 二、动量表象波函数 动量本征函数：pxip e x2/1)2(1)(πψ=组成完备系，任一状态ψ可按其展开(,)(,)()p x t c p t x dp ψψ=⎰ (1) 展开系数*(,)()(,)pc p t x x t dx ψψ=⎰ (2) ψ(x ,t )与c (p ,t )互为Fourier （付里叶）变换，一一对应关系，所不同的是变量不同。
认为c (p ,t )和ψ(x ,t )描述同一个状态。
ψ(x ,t )是这个状态在坐标表象中的波函数，c (p ,t )是同一个状态在动量表象中的波函数。
1、),(t p c ——状态波函数2、dp t p c 2),(表示体系处在c (p ,t )所描述的态中测量动量这个力学量p 所得结果为p →p +d p 范围内的几率。
3、1),(2=⎰dp t p c命题：假设ψ(x ,t )是归一化波函数，则c (p ,t )也是归一。
(在第一章中已经证明) 4、x p '的本征函数（具有确定动量x p '的自由粒子的态）若ψ(x ,t )描写的态是具有确定动量 p'的自由粒子态，即：1/21()(2)ip xp x eψπ''=则相应动量表象中的波函数：*(,)()(,)pc p t x x t dx ψψ=⎰()p i E te p p δ'-'=-所以，在动量表象中，具有确定动量p' 的粒子的波函数是以动量p 为变量的δ函数。
13-量子力学的矩阵形式
k
a1 S11 S12 . a1
a Sa a2 S21 S22 . a2
. . .
15
一、表象及其变换(5)
任一量子态在F表象中的表示a
a1 a2
可以通过矩
1
!!
2
( r)l e 2r2 / 2 F (nr , l 3 / 2, 2r 2 )
2
d
0
sin d
0
a
0
* nr
l
m
(r
,
,
)
nr
lm
(
r
,
,
)
r
2
dr
nrnr ll mm
N 2nr l, m l, l 1,, l 1, l
系：a Sa，幺正矩阵S (Sk ), Sk ( , k )
17
表象及其变换的理解
量子力学中态和力学量的具体表示方式称为表象。波函数的 表示方式在量子力学中并不是唯一的，波函数也可以选用其 他变量的函数。量子力学中表象的选取决定于所讨论的问题。 表象选取得适当可以使问题的讨论大为简化。 对于表象和表象变换，通俗的理解，即坐标和坐标变换，表 象就是经典物理中的坐标，就如直角坐标系和极坐标系。
nxnynz (x, y, z) nx (x)ny ( y)nz (z), nx , ny , nz 0,1, 2,
H H x H y H z , H nxnynz (x, y, z) Enxnynz (x, y, z) 其解为(H x , H y , H z )的共同本征态，设此本征态为： nxnynz (x, y, z) nx (x)ny ( y)nz (z), nx , ny , nz 0,1, 2, 则H nxnynz (x, y, z) (H x H y H z )nx (x)ny ( y)nz (z) (Ex Ey Ez )nx (x)ny ( y)nz (z) Enxnynz (x, y, z)
a1 S11 S12 . a1
a Sa a2 S21 S22 . a2
. . .
15
一、表象及其变换(5)
任一量子态在F表象中的表示a
a1 a2
可以通过矩
1
!!
2
( r)l e 2r2 / 2 F (nr , l 3 / 2, 2r 2 )
2
d
0
sin d
0
a
0
* nr
l
m
(r
,
,
)
nr
lm
(
r
,
,
)
r
2
dr
nrnr ll mm
N 2nr l, m l, l 1,, l 1, l
系：a Sa，幺正矩阵S (Sk ), Sk ( , k )
17
表象及其变换的理解
量子力学中态和力学量的具体表示方式称为表象。波函数的 表示方式在量子力学中并不是唯一的，波函数也可以选用其 他变量的函数。量子力学中表象的选取决定于所讨论的问题。 表象选取得适当可以使问题的讨论大为简化。 对于表象和表象变换，通俗的理解，即坐标和坐标变换，表 象就是经典物理中的坐标，就如直角坐标系和极坐标系。
nxnynz (x, y, z) nx (x)ny ( y)nz (z), nx , ny , nz 0,1, 2,
H H x H y H z , H nxnynz (x, y, z) Enxnynz (x, y, z) 其解为(H x , H y , H z )的共同本征态，设此本征态为： nxnynz (x, y, z) nx (x)ny ( y)nz (z), nx , ny , nz 0,1, 2, 则H nxnynz (x, y, z) (H x H y H z )nx (x)ny ( y)nz (z) (Ex Ey Ez )nx (x)ny ( y)nz (z) Enxnynz (x, y, z)
量子力学讲义第七章讲义
(8)
是|>在F表象中的基矢|j>方向的投影。式(8)即的本征方程在F表象中的表
述形式。
(6) A2=0，但A=0不一定成立
5、对角矩阵 6、单位矩阵
除对角元外其余为零 即
单位矩阵与任何矩阵A的乘积仍为A：IA=A，并且与任何矩阵都是可
对易的：IA=AI
7、转置矩阵：把矩阵A的行和列互相调换，所得出的新矩阵称为A的转
置矩阵。
m列n行n列m行 共轭矩阵： m列n行n列m行转成共轭复数
8、厄密矩阵：
矢量。选取一个特定力学量F表象，相当于选取特定的坐标系。该坐标
系是以力学量F的本征函数系为基矢，态矢量在各基矢上的分量则为展
开系数，在F表象中态矢量可用这组分量来表示。
F表象的基矢有无限多个，所以态矢量所在的空间是一个无限维的 抽象的函数空间，称为Hilbert空间。
§7.2 力学量(算符)的矩阵表示
它就是与本征值相应的本征态在F表象中的表示。 给定算符如何求本征值与本征函数 ——（1）先求用矩阵表示的本征 方程；（2）代入久期方程求得本征值的解；（3）本征值代入本征方程 求本征函数。
4、 举例： 例1、已知体系的哈密顿算符Ĥ与某一力学量算符在能量表象中的矩阵 形式为：
， 其中和b为实常数，问
(1)、H和B是否是厄密矩阵； (2)、H和B是否对易； (3)、求算符的本征值及相应的本征函数； (4)、算符的本征函数是否也是Ĥ的本征函数。
态矢与的标积记为，
而记为
若，则称与正交；若，则称为归一化态矢。 设力学量完全集F的本征态（离散）记为|k>，它们的正交归一性表
示为
连续谱的本征态的正交“归一性”，则表成函数形式。 例如动量本征态，，坐标本征态，等。
第七章量子力学的矩阵形式与表象变换汇总
A11B12 A12 B22 A21B12 A22 B22
A11 B13 A21 B13
A12 B23 A22 B23
(1) AB BA 称A、B矩阵相互不对易 AB BA 称A、B矩阵相互对易
（2） ABC (AB)C A(BC)
(3) (A B)C AB BC
(4) AB AC ，但B=C不一定成立
E10t
10 00
1 2
R Y e
i
E21t
21 11
1
2
e
i
E10t
100
1 2
e
i
E21t
211
中心力场能量表象为：
a100
1
e
i
E10t
2
a200 0
E
a210 a211
a211
1 2
0
e
i
E21t
0
Hilbert（希耳伯特）空间：态矢量所在的无限维空间
A A 则称A矩阵为厄密矩阵
A 0i
i 0
Байду номын сангаас
A
0* (i)*
i* 0*
0 i
i 0
A
( AB) B A ( ABCD) D C B A
表象理论
•根据量子力学的基本原理，微观粒子的量子态用波函数描述， 力学量用线性厄密算符描述。前面所使用的波函数及力学量 算符均以坐标为变量而写出其具体表达形式的。是否有其它 描述方法？（即以其它力学量的本征值谱为变量）
历史回顾： 量子力学的建立---矩阵力学和波动力学的提出
1925年7月初，海森伯终于完成了题为“从量子理论重新 解释运动学和力学关系”的论文。建立了矩阵力学。
量子力学的矩阵形式和表象变换考试题PPT课件
A1 A2
(e'1 e1 ) (e'2 e1 )
(e'1 e2 ) (e'2e2 )
A1 A2
x2
x’2
A’2
cos sin
sin cos
A1 A2
A1 A2
R(
)
A1 A2
（5） （6）
A2
e2 θ e’2
O
e1
θ
e’1 A’1
A A1
x1 x’1
R（θ）称为变换矩阵元，是两个坐标系基矢之间的标积。当R确定后，任何两个 坐标系之间的关系也就确定了。
0
x e 1 xdx
1
(
1)!(
N0)
2 3
xe( px )xdx
23 1 ( px )2
第10页/共98页
c( px )
23 1 ( px )2
动量的几率分布为
wp
c( px ) 2
23
(
1 px )4
动量的平均值为
p *(x) pˆ (x)
pˆ (x) i
43
n
下标n表示能级，上式两边同乘以u*m(x), 并积分
（16）
am (t) um (x) (x,t)dx,
（17）
粒子态完全由an完全集确定，即能量表象。
第12页/共98页
(x,t) 2 dx
an
(t
)a
* m
(t
)
um*(x)un (x)dx
m,n
an (t)a*m(t)mn a*n (t)an (t)
4. 2算符的矩阵表示
设算符F有如下关系 ：
Fˆ(x,t) (x,t)
4.6 量子力学的矩阵形式和表象变换
an给(t出) 2在
态(中r,测t)量粒子的力学量Q 取 值的几q率n。
69
13
以上讨论与三维矢量空间一矢量的表示很类似。
三维矢量空间
e1,
e2
,
e3
A A1e1 A2e2 A3e3
A1 A A2
A3
Hilbert空间：满足态迭加原理的状态全体构成一个复线性空间，称
为Hilbert空间，体系的状态波函数 是Hilbert空间中的一个矢量，称为
并引入记号： Fnm
un*
(
x)Fˆ
(
x,
i
x
)um
(
x)dx
69
26
可将（2）式写成：bn (t) Fnmam (t)
排成矩阵形式：
m
b1(t) F11 F12
b2
(t
)
F21
F1m
a1(t)
a2
(t
)
bn (t) Fn1 Fn2
Fnm
am (t)
69
a
1
e
i
pa
2 p2a2 / 2
22
能量表象：本征函数 n x
2 sin n x
aa
展开系数：
anE
1
x
* n
(
x)dx
1,n
即在自身表象中取δ形式。
∴ 基态在能量表象中的表示：
1
0
an
0
.
. .
1x an E n x a1E1x
n
69
23
2、算符的矩阵表示
力学量算符在不同表象中的表示
阵力学（海森堡Heisenberg）
量子力学 07量子力学的矩阵形式与表象变换
p p' ψ (x)=p' p' ψ (x)
p (p'-p)=p' (p'-p) δ δ
这类似于一个矢量可以在不同坐标系描写一样。矢量 A在直角 坐标系由三分量Ax ，Ay ，Az 描述；在球坐标系用三分量Ar ， A ， A 描述。 Ax ， Ay ， Az 和 Ar, ， A, ， A 形式不同，但描 写同一矢量A。
共轭矩阵
a 1 ( t ) *
a2 (t ) *
an (t ) *
归一化可写为
a1 ( t ) *
a2 ( t ) *
an (t ) *
a1 ( t ) a2 (t ) an (t )
n
n
( x , t )
归一化则变为： an * ( t )an ( t ) aq * ( t )aq ( t )dq 1
n
|an(t)|2 是在 Ψ(x,t) 态中 测量力学量 Q 所得结果 为 Qn 的几率；
a (t ) n aq (t )
|aq(t)|2dq 是在Ψ(x,t) 态中 测量力学量 Q 所得结果在 q → q + dq之间的几率。
坐标表象 动量本 1 1 i(p' x-E't)/h Ψp' (x,t)=[ π ]2 e 2 h 征函数
1 不含时 ψp' [ 1 ]2 i(p' x)/h (x)= 动量本 π 2 h e 征函数
动量表象 C(p,t)= (p'-p)exp[ iE't/ h] δ -
C(p)=δ (p'-p)
第八章 量子力学的矩阵形式与表象变换 2
它就是与本征值Lj′相应的本征态在F表象中的表示。若L′有重根，则 出现简并，本征函数解不能唯一确定，在量子力学中常找与L对易的另 外力学量，求其共同本征态，来消除简并，从而把解确定下来。
第8章 矩阵形式与表象变换@ Quantum Mechanics
Fang Jun
26
（2）薛定谔方程
ˆ i H t
H12 H 22
a1 a2
Fang Jun
第2页
第八章 量子力学的矩阵形式与表象变换
教学内容
§1 量子态的不同表象，幺正变换 §2 力学量（算符）的矩阵表示 §3 量子力学的矩阵形式 §4 Dirac 符号
第8章
矩阵形式与表象变换@ Quantum Mechanics
Fang Jun
第3页
§1 量子态的不同表象，幺正变换
F表象中(基矢Ψk )，力学量L表示成矩阵(Lkj )
ˆ Lkj k , L j
F’表象中(基矢Ψ’α )，L表示成矩阵(L’αβ ) L 利用 k k , k S k
j j , S j j j j k k
A1
x’1
是把在两个坐标系的表示联系起来的变换矩阵。
第8章 矩阵形式与表象变换@ Quantum Mechanics
Fang Jun
第5页
RT(θ)是R(θ)的转置矩阵。易看出，变换矩阵R有如下的性质
又因R＊=R ，所以 R＋=RT＊=RT，因而
即R是么正矩阵，因此，一个矢量在两个坐标系中的表示通 过一个么正变换相联系。
n
2 n x sin a a
2 2 2
第8章 矩阵形式与表象变换@ Quantum Mechanics
Fang Jun
26
（2）薛定谔方程
ˆ i H t
H12 H 22
a1 a2
Fang Jun
第2页
第八章 量子力学的矩阵形式与表象变换
教学内容
§1 量子态的不同表象，幺正变换 §2 力学量（算符）的矩阵表示 §3 量子力学的矩阵形式 §4 Dirac 符号
第8章
矩阵形式与表象变换@ Quantum Mechanics
Fang Jun
第3页
§1 量子态的不同表象，幺正变换
F表象中(基矢Ψk )，力学量L表示成矩阵(Lkj )
ˆ Lkj k , L j
F’表象中(基矢Ψ’α )，L表示成矩阵(L’αβ ) L 利用 k k , k S k
j j , S j j j j k k
A1
x’1
是把在两个坐标系的表示联系起来的变换矩阵。
第8章 矩阵形式与表象变换@ Quantum Mechanics
Fang Jun
第5页
RT(θ)是R(θ)的转置矩阵。易看出，变换矩阵R有如下的性质
又因R＊=R ，所以 R＋=RT＊=RT，因而
即R是么正矩阵，因此，一个矢量在两个坐标系中的表示通 过一个么正变换相联系。
n
2 n x sin a a
2 2 2
第七章 量子力学的矩阵形式与表象变换
x表象的基函数是坐标算符的本征函数
ˆδ ( x − x′) = x′δ ( x − x′) x
二、 p表象 1. 状态 ϕ ( p, t )
ϕ ( p, t ) ：几率密度
2
∂ ˆ ˆ (x ˆ = iℏ , p ) ˆ, p ˆ) = ? F (x 2. 力学量 F ∂p
n ∂ ∂ n n ℏ ˆ = i? i. x ˆ x = ( i ℏ ) 同理 ∂p ∂p n n n ˆ ˆ ii. p = p p = p
−∞ +∞
或ψ p′ ( x)
ψ ( x, t ) = ∫ ϕ ( p′, t )ψ p′ ( x) dp′
−∞ ∞
ˆ δ ( p − p′) = p′δ ( p − p′) p
ˆ ψ p′ ( x ) = p ′ψ p′ ( x) p
p表象的基函数是动量算符的本征函数
例1：在p表象计算一维谐振子的定态能量和 波函数。
� � � � � � � � ∫ψ (r ′, t )δ (r − r ′)dr ′ 或 ∫ ϕ ( p′,t )δ ( p − p′)dp′
3. 波函数是态矢在基上的投影或分量。
五、力学量完全集 1.力学量变量 力学量的测值可作为波函数的变量 2. 力学量变量的个数等于自由度数 3. 作为波函数变量的力学量必须相互对易
n
* cn = (ϕ n , ϕ (0)) = ∫ ϕ n ( p )ϕ ( p,0) dp −∞ ∞
∂ ˆ v. 平均值 F = ∫ ϕ ( p, t ) F ( x ˆ = iℏ , p)ϕ ( p, t )dp −∞ ∂p
+∞ *
4. 基函数
{δ ( p − p′) | p′ ∈ R}
第七章量子力学的矩阵形式与表象变换
a
2
(1)
mn
1 1 4amn mn 1 (1) 1 2 2 2 2 2 2 ( m n ) ( m n ) ( m n )
ˆ 哈密顿算符 H
对角元：
n En 2a 2
2 2
2
§7.3 量子力学公式的矩阵表示
一、Schrö dinger方程
n
F表象的基矢有无限多个，所以态矢量所在的空间是一个
无限维的抽象的函数空间，称为Hilbert空间。
§7.2 力学量(算符)的矩阵表示
力学量算符的具体形式应该与波函数的具体形式相对应， 以保证对波函数的作用有意义。 F表象中的算符表示（分立谱的情况） ：
ˆ 运算后变成另一个态： 设量子态经过算符 L
L12 L22 Ln 2
L1m L2 m Lnm
左边的一列矩阵和右边的一列矩阵分别是波函数和波函数
在F表象中的矩阵表示，而矩阵 L jk 即算符
中的表示。
用 LF 表示这个矩阵
ˆ L
在F表象
则有：
F LF F
b1 L11 b2 L21 bn Ln1
LL
其对角矩阵元为实数
Lnm L
* mn
证明:
Lnm L m dx ( L n ) * m dx
* n
[ L n dx] L
* m *
* mn
例: 求一维无限深势阱中粒子的坐标算符 ˆ 在能量表象中的矩阵表示。 H
ˆ x
及哈密顿算符
L12 L22 Ln 2
L1m L2 m Lnm
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§2 力学量算符的矩阵形式 §3 量子力学公式的矩阵形式 §4 Dirac符号
§1 量子态在不同表象下的矩阵表示与幺正变换
（一）例子
同同 表一 象个 下状 的态 表在 示不
Ψ(r,t) (p,t)
以坐标为自变量—坐标表象中 的波函数表示
以动量为自变量—动量表象中 的波函数表示
表象=“坐标系”
问题：量子态在其他力学量表象下的表示？ 表象之间的联系或变换关系？
k
左乘' 再取标积
a' ( ' ,k )ak
k
令
Sk ( ' ,k )
两个表象的基矢的 标积，反映基矢之
间的关系
反映表象之间的变换关系？
则 a' Skak
k
写成矩阵形式
a '1 S11 S12
a
'2
S21
S22
Sk ( ' ,k )
a1
a2
F'表象中 的表示
新的基矢组：
( ' , ' ) —F ' 表象或Q'表象
任意态矢量
a' ' ;
在F' 表象下的矩阵表示
a ' ( ' , )
a ' ( ' , )
a'1
a
'2
F'表象下的 具体表示
（四）表象之间的变换—幺正变换
F表象： akk ; F'表象： a' '
k
a' ' akk
(t) ak (t)k
k
i
k
ak ( t
t
)k
k
ak (t)Hˆ k
左乘j 再取标积
i
k
ak (t t
)
(
j
,
k
)
k
ak (t)(j , Hˆ k )
(j ,k ) ij 基矢的正交归一性
( j , Hˆ k ) H jk 能量算符在F表象中的矩阵元
i
aj (t) t
k
H jkak (t )
(k , ) ( x x ') dx ( x ') ( x)
常用的表象：坐标表象，动量表象，能量表象。
（三）量子态在不同表象中的矩阵表示
在F表象(或Q表象)中，任意量子态的具体表示
可以写成一个列矩阵：
ak (k , )
a1
a2
考虑另一力学量完全集F' ( 或者另一力学量算符
Q' )，其正交、归一完备的共同本征态 { ' }构成
k
k
ak ( j , Lˆk ) ak ( j ,k )
*第七章 量子力学的矩阵形式与表象变换
本章要求
1. 了解量子态在不同表象下的矩阵表示以 及表象之间的幺正变换（幺正矩阵）。
2.了解力学量算符的矩阵表示；了解量子 力学公式(如薛定谔方程、本征方程、平均 值等)的矩阵形式；
3.了解Dirac符号
*第七章 量子力学的矩阵形式与表象变换
教学内容
§1 量子态在不同表象下的矩阵表示与 幺正变换
（二）希尔伯特（Hilbert）空间
一个微观体系所有可能的量子态的态函数张成 一个抽象的函数空间，称为希耳伯特空间，每一个 量子态（不涉及表象）看成希耳伯特空间的一个 “矢量”，称为态矢量。
如同三维实空间需要建立一组正交、归一的基
矢{eˆ1 , eˆ2 , eˆ3 }，即建立坐标系，空间中的任何矢量
k
k
bj ak ( j , Lˆk )
k
令
Ljk ( j , Lˆk )
则有
bj Ljkak
k
写成矩阵形式：
bj Ljkak
k
b1 L11 L12
b2
L21
L22
a1
a2
相应的矩阵元
算符Lˆ 在F表象中
的矩阵表示
Ljk ( j , Lˆk )
特别地，在算符L的自身表象中
(k ,j ) kj
因为体系的任何量子态（对应Hilbert空间的一个
抽象矢量）可以按 {k } 展开
akk ; ak (k , )
k
这组数（a1, a2 , …）就是量子态在F表象下的表示。
k是F表象的基矢。
可见，态函数张成的Hilbert空间的维数可以是有
限的，也可无限的，甚至不可数的（基矢k为连
表象间的 变换矩阵S
F表象中 的表示
变换矩阵S是幺正矩阵
SS SS I S S 1
相应的表象变换称为幺正变换。
幺正变换的特点：变换后不改变矢量的长度(模)。 因此态矢量（波函数）在表象变换下不改变模的 大小，即相应的概率不变。
§2 力学量算符的矩阵表示
力学量算符 Lˆ 作用于量子态后变成另一态
或表示为
a1 t H11 H12
i
a2
t
H
21
H 22
a1
a2
此为薛定谔方程在F表象中的矩阵形式
（二）本征值方程的矩阵形式
力学量算符 Lˆ 的本征值方程
Lˆ （本征值 ）
在F 表象中，本征函数
akk
k
ak Lˆk akk
k
k
左乘j 再取标积
ak ( j , Lˆk ) ak ( j ,k )
续谱时），同时由于态函数是复数，Hilbert空 间又是一个复空间。
Q表象
任何一个厄米算符Q的本征函数系{k }具有正交、
归一、完备性，也可以用来构成Hilbert空间的基矢 从而建立所谓的Q表象。
例如，用坐标算符x的本征函数系 ( x x ')（本征值
谱x'连续）构成Hilbert空间的基矢，就是坐标表象。 Hilbert空间的任意态矢量在坐标表象下的表示：
A才能按这组基矢展开（即矢量有了具体表示）：
A A1eˆ1 A2eˆ2 A3eˆ3
那么，如何建立Hilbert空间的基矢组（表象）以便 任何态矢量都能按此展开（态矢量的具体表示）？
体系的任何一组对易力学量完全集F有完备的
共同的本征函数组{k }（其本征值谱可离散或连
续），可以用来构成该态空间的一组正交、归一 完备的基矢（称为F表象）。
Lˆ (不涉及表象)
因此，在Hilbert空间力学量算符相当于一个线性映射。
一旦在Hilbert空间建立具体的表象，力学量算符 （线性映射）就有了具体的数学表示：
F 表象 基矢{k}
bkk
akk
k
k
bkk ak Lˆk
k
k
bkk ak Lˆk
k
k
左乘j 再取标积
bk (j ,k ) ak (j , Lˆk )
Ljk ( j , Lˆk ) (j , Lkk ) Lkபைடு நூலகம்jk （*）
（基矢k是算符L的本征态，对应本征值Lk）
因此，算符在其自身表象中是一个对角矩阵，即
L11 0
0
L22
且由(*)式，对角元就是其本征值。
§3 量子力学公式的矩阵表示
（一）薛定谔方程的矩阵形式
i Hˆ
t
在F 表象中
§1 量子态在不同表象下的矩阵表示与幺正变换
（一）例子
同同 表一 象个 下状 的态 表在 示不
Ψ(r,t) (p,t)
以坐标为自变量—坐标表象中 的波函数表示
以动量为自变量—动量表象中 的波函数表示
表象=“坐标系”
问题：量子态在其他力学量表象下的表示？ 表象之间的联系或变换关系？
k
左乘' 再取标积
a' ( ' ,k )ak
k
令
Sk ( ' ,k )
两个表象的基矢的 标积，反映基矢之
间的关系
反映表象之间的变换关系？
则 a' Skak
k
写成矩阵形式
a '1 S11 S12
a
'2
S21
S22
Sk ( ' ,k )
a1
a2
F'表象中 的表示
新的基矢组：
( ' , ' ) —F ' 表象或Q'表象
任意态矢量
a' ' ;
在F' 表象下的矩阵表示
a ' ( ' , )
a ' ( ' , )
a'1
a
'2
F'表象下的 具体表示
（四）表象之间的变换—幺正变换
F表象： akk ; F'表象： a' '
k
a' ' akk
(t) ak (t)k
k
i
k
ak ( t
t
)k
k
ak (t)Hˆ k
左乘j 再取标积
i
k
ak (t t
)
(
j
,
k
)
k
ak (t)(j , Hˆ k )
(j ,k ) ij 基矢的正交归一性
( j , Hˆ k ) H jk 能量算符在F表象中的矩阵元
i
aj (t) t
k
H jkak (t )
(k , ) ( x x ') dx ( x ') ( x)
常用的表象：坐标表象，动量表象，能量表象。
（三）量子态在不同表象中的矩阵表示
在F表象(或Q表象)中，任意量子态的具体表示
可以写成一个列矩阵：
ak (k , )
a1
a2
考虑另一力学量完全集F' ( 或者另一力学量算符
Q' )，其正交、归一完备的共同本征态 { ' }构成
k
k
ak ( j , Lˆk ) ak ( j ,k )
*第七章 量子力学的矩阵形式与表象变换
本章要求
1. 了解量子态在不同表象下的矩阵表示以 及表象之间的幺正变换（幺正矩阵）。
2.了解力学量算符的矩阵表示；了解量子 力学公式(如薛定谔方程、本征方程、平均 值等)的矩阵形式；
3.了解Dirac符号
*第七章 量子力学的矩阵形式与表象变换
教学内容
§1 量子态在不同表象下的矩阵表示与 幺正变换
（二）希尔伯特（Hilbert）空间
一个微观体系所有可能的量子态的态函数张成 一个抽象的函数空间，称为希耳伯特空间，每一个 量子态（不涉及表象）看成希耳伯特空间的一个 “矢量”，称为态矢量。
如同三维实空间需要建立一组正交、归一的基
矢{eˆ1 , eˆ2 , eˆ3 }，即建立坐标系，空间中的任何矢量
k
k
bj ak ( j , Lˆk )
k
令
Ljk ( j , Lˆk )
则有
bj Ljkak
k
写成矩阵形式：
bj Ljkak
k
b1 L11 L12
b2
L21
L22
a1
a2
相应的矩阵元
算符Lˆ 在F表象中
的矩阵表示
Ljk ( j , Lˆk )
特别地，在算符L的自身表象中
(k ,j ) kj
因为体系的任何量子态（对应Hilbert空间的一个
抽象矢量）可以按 {k } 展开
akk ; ak (k , )
k
这组数（a1, a2 , …）就是量子态在F表象下的表示。
k是F表象的基矢。
可见，态函数张成的Hilbert空间的维数可以是有
限的，也可无限的，甚至不可数的（基矢k为连
表象间的 变换矩阵S
F表象中 的表示
变换矩阵S是幺正矩阵
SS SS I S S 1
相应的表象变换称为幺正变换。
幺正变换的特点：变换后不改变矢量的长度(模)。 因此态矢量（波函数）在表象变换下不改变模的 大小，即相应的概率不变。
§2 力学量算符的矩阵表示
力学量算符 Lˆ 作用于量子态后变成另一态
或表示为
a1 t H11 H12
i
a2
t
H
21
H 22
a1
a2
此为薛定谔方程在F表象中的矩阵形式
（二）本征值方程的矩阵形式
力学量算符 Lˆ 的本征值方程
Lˆ （本征值 ）
在F 表象中，本征函数
akk
k
ak Lˆk akk
k
k
左乘j 再取标积
ak ( j , Lˆk ) ak ( j ,k )
续谱时），同时由于态函数是复数，Hilbert空 间又是一个复空间。
Q表象
任何一个厄米算符Q的本征函数系{k }具有正交、
归一、完备性，也可以用来构成Hilbert空间的基矢 从而建立所谓的Q表象。
例如，用坐标算符x的本征函数系 ( x x ')（本征值
谱x'连续）构成Hilbert空间的基矢，就是坐标表象。 Hilbert空间的任意态矢量在坐标表象下的表示：
A才能按这组基矢展开（即矢量有了具体表示）：
A A1eˆ1 A2eˆ2 A3eˆ3
那么，如何建立Hilbert空间的基矢组（表象）以便 任何态矢量都能按此展开（态矢量的具体表示）？
体系的任何一组对易力学量完全集F有完备的
共同的本征函数组{k }（其本征值谱可离散或连
续），可以用来构成该态空间的一组正交、归一 完备的基矢（称为F表象）。
Lˆ (不涉及表象)
因此，在Hilbert空间力学量算符相当于一个线性映射。
一旦在Hilbert空间建立具体的表象，力学量算符 （线性映射）就有了具体的数学表示：
F 表象 基矢{k}
bkk
akk
k
k
bkk ak Lˆk
k
k
bkk ak Lˆk
k
k
左乘j 再取标积
bk (j ,k ) ak (j , Lˆk )
Ljk ( j , Lˆk ) (j , Lkk ) Lkபைடு நூலகம்jk （*）
（基矢k是算符L的本征态，对应本征值Lk）
因此，算符在其自身表象中是一个对角矩阵，即
L11 0
0
L22
且由(*)式，对角元就是其本征值。
§3 量子力学公式的矩阵表示
（一）薛定谔方程的矩阵形式
i Hˆ
t
在F 表象中