一次函数的图像与性质 (1)PPT课件
合集下载
一次函数图像课件(共14张PPT)

(增的大图2)而象当从_减_k左_<小_到_0,时右这下,__时y_降随_函_x数.的
做一做
画出函数y=-2x+2的图象,结合图象回答 下列问题:
(2)当x取何值时,y=0? 解:((2)因3)为当yx=取0 何所值以时-,2yx>+20=?0 ,x=1
(3)因为 y>0 所以 -2x+2 > 0 ,x < 1
(1)当k>0时,y随x的增大而增大, 这时函数的图象从左到右上升;
y x 2
y x 2
(增的大图2)而象当从_减_k左_小<_到_0,时右下这,__时y降_随_函_x数.的
y减少
x增大
概括
一次函数y=kx+b有下列性质: (1) 当k>0时,y随x的增大而增大,这时函 数的图象从左到右上升;
一次函数的性质(1)
说一说:
1、一次函数的一般式。 y=kx+b(k,b为常数,k≠0)
2、一次函数的图象是什么?
一条直线。
1.掌握一次函数y=kx+b(k≠0)的性质。 2.能根据k与b的值说出函数的有关性质。
y 2 x 1 3
x 0 3 2
y10
y 3x 2 y 2 x 1 3
y增大 x增大
解:方法一 把两点的坐标代入函数关系式
当 x=2 时, m= 4
3
1
当 x= -3 时, n= 2
所以 m > n。
方法二因为
1
K= 6
>0,所以函数y随x增大而增大。
从而直接得到 m > n。
小结
经过本节课的学习,你有哪些收获?
(2) 当k<0时,Байду номын сангаас随x的增大而减___小__,这时函 数的图象从左到右下__降___.
一次函数图像与性质ppt课件

图
象时,只要描出函数图象中的两个点就可画出此
函 数的图象.
b ,0 k
(2)一般地,一次函数y=kx+b(k,b是常数,k≠0)
都过(0,b) (与y轴交点坐标)和(
)(与x轴交点
总结
一次函数的图象是一条直线,我们称它为直线 y=kx+b;它必过(0,b)和( b , 0 )两点.
k
例1 画出函数y=-6x与y=-6x+5的图象.
从 k、b的值看一次函数的图像 (1)当k>0,b>0时,图象过一、二、三象限; (2)当k>0,b<0时,图象过一、三、四象限; (3)当k<0,b>0时,图象过一、二、四象限; (4)当k<0,b<0时,图象过二、三、四象限.
例2 已知直线y=(1-3k)x+2k-1. (1)k为何值时,直线与y轴交点的纵坐标是-2?
一次函数的图象是一条直线,这条直线与坐标轴 有交点,正比例函数只有一个交点,一般的一次函数 有两个交点. 注意:一次函数图象的画法与我们前边学过的函数图 象的画法一样,其步骤为列表、描点、连线.通过实际 操作,我们可得出:
(1)一次函数 y=kx+b(k,b是常数,k≠0)的图象是
一
条直线.由两点确定一条直线可知,在画一次函数
要点精析: (1)在实际问题中,当自变量x的取值受限制时,一次函 数 y=kx+b的图象就不一定是一条直线了,有时是线段、 射线或直线上的部分点. (2)k决定直线的倾斜角度: k>0⇔直线y=kx+b在x轴上方的部分与x轴正方向的夹 角为锐角; k<0⇔直线y=kx+b在x轴上方的部分与x轴正方向的夹 角为钝角; k1=k2⇔直线y1=k1x+b1∥直线y2=k2x+b2(b1≠b2). (3)k>0⇔y随x的增大而增大;k<0⇔y随x的增大而减小 .
一次函数的图象及性质精选教学PPT课件

我开始虚伪,听着谎言却装做一无所知;我学会窥探,四处打听如蛇之祟行,而十分看轻自己; 我的故事越编越好,好莱坞金牌编剧也没这般丰富多采,只为让他多留一分钟。
最后,我打他一巴掌。干脆痛快,出手的瞬间,像那位绝望的母亲,远远掷出她的高跟鞋。掷中没有?并不重要。 有多爱,就有多不舍;有多温柔,就有多暴烈,爱得唇边有血,眼中有泪,胸口有纠缠的爱与恨,爱到如连体婴般骨肉相连。割爱,就一定不可能如拈去一片花叶般轻松微笑。 明知留不住,收不下,却不能自控我颠倒狂乱的脚步。那一遭,我是夜深街上,追逐汽车的女子。而我无声的哭泣,他没有听见。快乐是人类社会众望所归的最高境界。所谓君子之交谈如水。一个把名缰利锁看得太重的人。注定是不快乐的。快乐就是看淡尘世的物欲、烦恼,不慕荣利。假如你喜欢武侠小说,你没有必要愧对红楼梦; 假如你喜欢的人突然销声匿迹,你没有必要寻死觅活地断言他一定洒脱地离去;假如你的朋友不幸,你没有必要怨天尤人;假如你认为张曼玉艳美绝俗,你没有必要眼馋肚饱虐待老婆;假如你已经身心交病,那就去教堂忏悔,没有必要仇视别人的平庸;坦然面对心融神会,快乐就在你心里。我怜悯一个有点荣誉的人,就旁若无人而因此失 去快乐的人。能把名利得失置之度外,而凡事都能以诚相待的人一生将是快乐的。我们应从平谈的生活中去提炼体会,如:赤城待人的那种快乐。低待遇下一如既往工作的快乐,助人为乐一介不取的快乐,一片至诚去感化恶人的快乐,热心被人误解依然如故的快乐,信实可靠的服务态度为目的的快乐,尽责任吃苦耐劳的快乐,因为这些 “快乐”能保持住人内心的快乐,使人的容貌永远那么牵挂,一句亲切的问候。甚至一个关切的眼神,快乐无处不有,唯有胸襟开阔的人,才能体会到。形单影只的人仍然可以享受着闲情逸致的快乐。乐山乐水各不相同。爱静的人可以看书、听音乐、上网、写作、画画、搜集各种收藏品。爱动的人则不妨练习舞蹈、慢跑、爬山、游泳。看 电影、上健身房。做编织、陶艺。练瑜枷、潜心发明、闭门创作,摄影、观鸟,我们仍然兴复不浅,乐不可支。人生苦短,岁月如流,乐天知命,为什么不乐乐陶陶的。为什么要疾首蹙额,为眼前一时的顿挫心胆俱碎?为什么要对那些你看不惯的人和事心烦率乱?岂不知我们都是尘世间相映成趣的战友。人世一切冤天屈地,无妄之灾,荣 华富贵,香娇玉嫩……都将随身亡命殒。而人生长着百年,短则数十寒暑,又有何值得耀武扬威的,不过是烟云过眼矣?人生如月,月满则亏,凡事岂能尽人意,但求于心无愧。无愧我心,则恩同再造,那些得失又算不了甚么。世界上没有完美无缺得事物。奉劝多愁善感的朋友。饮醇自醉,快乐起来吧!芸芸众生,绿水青山,名胜古迹,
最后,我打他一巴掌。干脆痛快,出手的瞬间,像那位绝望的母亲,远远掷出她的高跟鞋。掷中没有?并不重要。 有多爱,就有多不舍;有多温柔,就有多暴烈,爱得唇边有血,眼中有泪,胸口有纠缠的爱与恨,爱到如连体婴般骨肉相连。割爱,就一定不可能如拈去一片花叶般轻松微笑。 明知留不住,收不下,却不能自控我颠倒狂乱的脚步。那一遭,我是夜深街上,追逐汽车的女子。而我无声的哭泣,他没有听见。快乐是人类社会众望所归的最高境界。所谓君子之交谈如水。一个把名缰利锁看得太重的人。注定是不快乐的。快乐就是看淡尘世的物欲、烦恼,不慕荣利。假如你喜欢武侠小说,你没有必要愧对红楼梦; 假如你喜欢的人突然销声匿迹,你没有必要寻死觅活地断言他一定洒脱地离去;假如你的朋友不幸,你没有必要怨天尤人;假如你认为张曼玉艳美绝俗,你没有必要眼馋肚饱虐待老婆;假如你已经身心交病,那就去教堂忏悔,没有必要仇视别人的平庸;坦然面对心融神会,快乐就在你心里。我怜悯一个有点荣誉的人,就旁若无人而因此失 去快乐的人。能把名利得失置之度外,而凡事都能以诚相待的人一生将是快乐的。我们应从平谈的生活中去提炼体会,如:赤城待人的那种快乐。低待遇下一如既往工作的快乐,助人为乐一介不取的快乐,一片至诚去感化恶人的快乐,热心被人误解依然如故的快乐,信实可靠的服务态度为目的的快乐,尽责任吃苦耐劳的快乐,因为这些 “快乐”能保持住人内心的快乐,使人的容貌永远那么牵挂,一句亲切的问候。甚至一个关切的眼神,快乐无处不有,唯有胸襟开阔的人,才能体会到。形单影只的人仍然可以享受着闲情逸致的快乐。乐山乐水各不相同。爱静的人可以看书、听音乐、上网、写作、画画、搜集各种收藏品。爱动的人则不妨练习舞蹈、慢跑、爬山、游泳。看 电影、上健身房。做编织、陶艺。练瑜枷、潜心发明、闭门创作,摄影、观鸟,我们仍然兴复不浅,乐不可支。人生苦短,岁月如流,乐天知命,为什么不乐乐陶陶的。为什么要疾首蹙额,为眼前一时的顿挫心胆俱碎?为什么要对那些你看不惯的人和事心烦率乱?岂不知我们都是尘世间相映成趣的战友。人世一切冤天屈地,无妄之灾,荣 华富贵,香娇玉嫩……都将随身亡命殒。而人生长着百年,短则数十寒暑,又有何值得耀武扬威的,不过是烟云过眼矣?人生如月,月满则亏,凡事岂能尽人意,但求于心无愧。无愧我心,则恩同再造,那些得失又算不了甚么。世界上没有完美无缺得事物。奉劝多愁善感的朋友。饮醇自醉,快乐起来吧!芸芸众生,绿水青山,名胜古迹,
一次函数的图像与性质ppt1 人教版

)
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限 2(2009宁夏)5.一次函数y=3x-2的图象不经过( )
B
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3(2009年株洲市)一次函数y=2x+1的图象不经过( )
A.第一象限 B.第二象限C.第三象限D.第四象限
b>0 b<0
向上平移|b|个单位长度 向下平移|b|个单位长度
课堂检测:
1、把直线y=x+1向下平移3个单位长度,得到直线( ) A、y=x+4 B、y=x-3 C、y=x-2 D、y=x+3
2、函数y=(m-1)x&当m
时,y随x的增大而减小;
3、已知直线y=kx+b的图象如图所示,则( ) A、k<0,b<0 B、 k>0,b<0 C、k<0,b>0 D、 k>0,b>0
课后作业
1、在一次函数y=-3x+6的图象中 :
(1)可看作由一次函数y=-3x的图象向 平移 个单位长度得到;
(2)随着x的增大,y将
(填“增大”或“减小”);
(3)它的图象从左到右
(填“上升”或“下降”);
(4)图象经过第
象限;
(5)图象与x轴的交点是
;与y轴的交点是
;
(6)当x=
时,y=2,当x=1时,y=
下 平移 2 单 上 平移 3 单
课堂练习
4、对于函数y=5x+6,y的值随x的值减小 而__减__少__。
5、函数y=2x-1经过 一、三、四象限
6、函数y=2x - 4与y轴的交点为( 0,-4 ),与 x轴交于( 2,0 ) 7.已知点(-4,y1),(2,y2)都在直线 y= 2x+1上,则y1与
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限 2(2009宁夏)5.一次函数y=3x-2的图象不经过( )
B
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3(2009年株洲市)一次函数y=2x+1的图象不经过( )
A.第一象限 B.第二象限C.第三象限D.第四象限
b>0 b<0
向上平移|b|个单位长度 向下平移|b|个单位长度
课堂检测:
1、把直线y=x+1向下平移3个单位长度,得到直线( ) A、y=x+4 B、y=x-3 C、y=x-2 D、y=x+3
2、函数y=(m-1)x&当m
时,y随x的增大而减小;
3、已知直线y=kx+b的图象如图所示,则( ) A、k<0,b<0 B、 k>0,b<0 C、k<0,b>0 D、 k>0,b>0
课后作业
1、在一次函数y=-3x+6的图象中 :
(1)可看作由一次函数y=-3x的图象向 平移 个单位长度得到;
(2)随着x的增大,y将
(填“增大”或“减小”);
(3)它的图象从左到右
(填“上升”或“下降”);
(4)图象经过第
象限;
(5)图象与x轴的交点是
;与y轴的交点是
;
(6)当x=
时,y=2,当x=1时,y=
下 平移 2 单 上 平移 3 单
课堂练习
4、对于函数y=5x+6,y的值随x的值减小 而__减__少__。
5、函数y=2x-1经过 一、三、四象限
6、函数y=2x - 4与y轴的交点为( 0,-4 ),与 x轴交于( 2,0 ) 7.已知点(-4,y1),(2,y2)都在直线 y= 2x+1上,则y1与
一次函数课件ppt

奇偶性
一次函数既不是奇函数也不是偶函数 ,因为它们的图像不关于原点或 y 轴 对称。
02 一次函数的表达式与系数
一次函数的表达式
01
一次函数的一般表达式为 $y = ax + b$,其中 $a$ 和 $b$ 是常 数,且 $a neq 0$。
02
当 $a > 0$ 时,函数为增函数; 当 $a < 0$ 时,函数为减函数。
已知函数与$x$轴和$y$轴的截距,使用截 距式$y = frac{x}{a} + frac{b}{a}$求函数解 析式。
一次函数的解题技巧
数形结合
利用函数图像直观理解 函数性质,如增减性、
最值等。
整体代入
在求解过程中,将表达 式整体代入,简化计算
。
分类讨论
根据不同情况分类讨论 ,得出不同情况下的函
斜率与图像
斜率决定了图像的倾斜程 度,当 a > 0 时,图像向 右倾斜;当 a < 0 时,图 像向左倾斜。
一次函数的性质
单调性
无界性
一次函数的单调性由斜率决定,当 a > 0 时,函数单调递增;当 a < 0 时 ,函数单调递减。
一次函数的值域是全体实数,即对于 任意实数 x,y = ax + b 总有一个对 应的值。
一次函数的系数
一次函数的斜率为 $a$,表示函数图 像的倾斜程度。
当 $a > 0$ 时,函数图像从左下到右 上倾斜;当 $a < 0$ 时,函数图像从 左上到右下倾斜。
一次函数的应用
一次函数在数学、物理、工程等领域都有广泛应用。
在实际生活中,一次函数可以用来描述一些简单的问题,如速度与时间的关系、 价格与数量的关系等。
八年级数学《一次函数的图像与性质》优秀课件

设点〔-1,m)和点〔1,n)是直线y=(k 2-1)x+b(0<k<1)上的两 个点,那么m,n的大小关系__________
4、一次函数y=(2m-1)x+2的值, 都是随着x值的增大而减小.求m 得取值范围。
2m-1<0
7、以下图形中,表示一次函数 y=mx+n与正比例函数y=mnx(m,n是
1、列表
y=2x+2 6
·
· 5 y=2x
4
x … -3 -2 -1 0 1 2 3 … y=2x … -6 -4 -2 0 2 4 6 …
·· 3
2
y=2x+2 … -4 -2 0 2 4 6
·o1
x
8 …-4 -3 -2 -1
1 23 4 5
-6+2 -4+2 -2+2 0+2 2+2 4+2 6+2
一次函数y=(k-2)x+k不经过第三象限,那么k的取值范围是 _____________
一次函数y=(1-2m)x+m-1,假设y随x的增大而减小,并且不 经过第一象限,那么m的取值范围是_____________
一次函数y=2x-6的图像与x轴的交点坐标为___________
点〔-4,y1〕,〔2,y2〕都在直线y=2x+2上,那么y1__y2( 填<,>或=〕
一次函数y=(1-2m)x+m的图像交y轴于正半轴,并经过点 A(x1,y1),B(x2,y2),当x1<x2时,y1<y2
求m的取值范围?
如图,一次函数y=(m-3)x-m+1的图像分别与x轴,y轴的
负半轴交于A、B两点,求m的取值的范围?
4、一次函数y=(2m-1)x+2的值, 都是随着x值的增大而减小.求m 得取值范围。
2m-1<0
7、以下图形中,表示一次函数 y=mx+n与正比例函数y=mnx(m,n是
1、列表
y=2x+2 6
·
· 5 y=2x
4
x … -3 -2 -1 0 1 2 3 … y=2x … -6 -4 -2 0 2 4 6 …
·· 3
2
y=2x+2 … -4 -2 0 2 4 6
·o1
x
8 …-4 -3 -2 -1
1 23 4 5
-6+2 -4+2 -2+2 0+2 2+2 4+2 6+2
一次函数y=(k-2)x+k不经过第三象限,那么k的取值范围是 _____________
一次函数y=(1-2m)x+m-1,假设y随x的增大而减小,并且不 经过第一象限,那么m的取值范围是_____________
一次函数y=2x-6的图像与x轴的交点坐标为___________
点〔-4,y1〕,〔2,y2〕都在直线y=2x+2上,那么y1__y2( 填<,>或=〕
一次函数y=(1-2m)x+m的图像交y轴于正半轴,并经过点 A(x1,y1),B(x2,y2),当x1<x2时,y1<y2
求m的取值范围?
如图,一次函数y=(m-3)x-m+1的图像分别与x轴,y轴的
负半轴交于A、B两点,求m的取值的范围?
第8课 一次函数的图象与性质(1)

19. 一等腰三角形的周长为20 cm,底边长为y cm,腰长 为x cm. (1)求出底边长y(cm)与腰长x(cm)的函数关系式. (2)求出自变量x的取值范围.
解:(1)y=20-2x (2)∵x-x<y<2x ∴x-x<20-2x<2x ∴5<x<10 ∴自变量x的取值范围为5<x<10
谢谢!
2. (例1)在同一直角坐标系中画出y=2x,y=2x+1和
y=2x-1的图象
解: x
-2 -1 0 1 2
y=2x -4 -2 0 2 4
y=2x+1 -3 -1 1 3 5
y=2x-1 -5 -3 -1 1 3
发现: y=2x 的图象向___上____平移___1___个单位得到 y=2x+1 的 图象,向___下____平移_______个单位得到 y=2x-1 的图象.
(1)y=12x+3 和 y=12x-5:__平__行____ (2)y=-5x+2 和 y=4x+1:__相__交____
11. (1)直线y=8x-4和y=8x+3的位置关系是__平__行____.
(2)若直线y=-4x+5和y=kx+7平行,则k=___-__4___.
三、过关检测
第1关 12.(1)一次函数y=- 1 x+5中,y随x的增大而___减__小___;
PPT课程 第8课 一次函数的图象与性质(1) 主讲老师:
一、知识储备
1. (1)正比例函数y=2x的图象从左到右__上__升____,即 y随x的增大而__增__大____. (2)正比例y=-2x的图象从左到右__下__降____,即y 随x的增大而___减__小___.
二、新课学习
提出问题:正比例函数y=kx的图象是一条经过____原____ 点的直线,且k决定直线的升降,那一般的一次函数y=kx +b中的b有什么作用呢?一次函数y=kx+b的图象与正比 例函数y=kx的图象有什么关系呢?
一次函数ppt课件免费

线性关系判断方法
01
观察法
通过观察散点图或数据表,判断两个变量之间是否存在线性关系。
02 03
计算法
通过计算相关系数r的值,判断两个变量之间的线性关系强度。当|r|接 近于1时,表示两个变量之间存在较强的线性关系;当|r|接近于0时,表 示两个变量之间不存在线性关系。
残差分析法
通过绘制残差图或计算残差平方和,判断回归模型是否符合线性关系。 如果残差图呈现随机分布且残差平方和较小,则表明回归模型符合线性 关系。
实际应用问题建模与求解
01
02
03
列方程
根据实际问题中的条件, 列出反映问题中数量关系 的方程。
解方程
运用一次函数的运算技巧, 求解所列出的方程。
检验与作答
将求得的解代入原方程进 行检验,确认解的合理性, 并根据实际问题要求进行 作答。
03
一次函数图像变换规律
平移变换规律
一次函数 y = kx + b (k ≠ 0) 的图像是一条直线, 01 当 b 值发生变化时,图像会沿着 y 轴上下平移。
当 b > 0 时,图像向上平移 b 个单位;当 b < 0 02 时,图像向下平移 |b| 个单位。
平移后的直线斜率不变,仍为 k。 03
伸缩变换规律
01 当 k > 1 时,图像的斜率增大,函数值增长的速 度变快,图像相对于原直线更陡峭。
02 当 0 < k < 1 时,图像的斜率减小,函数值增长 的速度变慢,图像相对于原直线更平缓。
学习数学不仅仅是为了应付考试,更重要的是培养解决实际问题的能力。通过学习和应用一 次函数,可以强化数学与实际生活的联系,提高数学应用意识。
拓展数学思维
一次函数的性质和图像(一)课件

在物理中,许多现象可以用一次函数来描述,如速度与时间的关系、电阻与电流 的关系等。通过这些实例,可以深入理解一次函数在实际问题中的应用。
经济问题中的应用
在经济学中,许多经济指标之间的关系可以用一次函数来描述,如价格与需求的 关系、成本与产量的关系等。通过这些实例,可以了解一次函数在经济分析中的 应用。
像会向右平移。
03
一次函数的应用
一次函数在实际生活中的应用
一次函数在经济学中的应用
一次函数可以用来描述经济现象之间的关系,例如成本与产量的 关系、价格与需求量的关系等。
一次函数在物理学中的应用
在物理学中,一次函数可以用来描述线性关系,例如速度与时间的 关系、力与位移的关系等。
一次函数在工程领域的应用
02
一次函数的图像
一次函数图像的绘制
步骤二
在坐标系上选择一个点,例如 原点$(0,0)$。
步骤四
在坐标系上标出该点,即 $(0,1)$。
步骤一
确定函数表达式。例如,$y = 2x + 1$。
步骤三
使用一次函数的表达式,计算 出该点沿x轴和y轴的坐标值。 例如,$y = 2(0) + 1 = 1$。
一次函数的图像是一条直线,其斜率 为$a$,截距为$b$。
一次函数的图像可以通过平移得到, 向上平移$k$个单位得到$y = ax + b + k$,向下平移$k$个单位得到$y = ax + b - k$。
一次函数的单调性由斜率$a$决定, 当$a > 0$时,函数为增函数;当$a < 0$时,函数为减函数。
一次函数在概率统计问题中的应用
03
在概率统计问题中,一次函数可以用来描述概率分布、平均数
经济问题中的应用
在经济学中,许多经济指标之间的关系可以用一次函数来描述,如价格与需求的 关系、成本与产量的关系等。通过这些实例,可以了解一次函数在经济分析中的 应用。
像会向右平移。
03
一次函数的应用
一次函数在实际生活中的应用
一次函数在经济学中的应用
一次函数可以用来描述经济现象之间的关系,例如成本与产量的 关系、价格与需求量的关系等。
一次函数在物理学中的应用
在物理学中,一次函数可以用来描述线性关系,例如速度与时间的 关系、力与位移的关系等。
一次函数在工程领域的应用
02
一次函数的图像
一次函数图像的绘制
步骤二
在坐标系上选择一个点,例如 原点$(0,0)$。
步骤四
在坐标系上标出该点,即 $(0,1)$。
步骤一
确定函数表达式。例如,$y = 2x + 1$。
步骤三
使用一次函数的表达式,计算 出该点沿x轴和y轴的坐标值。 例如,$y = 2(0) + 1 = 1$。
一次函数的图像是一条直线,其斜率 为$a$,截距为$b$。
一次函数的图像可以通过平移得到, 向上平移$k$个单位得到$y = ax + b + k$,向下平移$k$个单位得到$y = ax + b - k$。
一次函数的单调性由斜率$a$决定, 当$a > 0$时,函数为增函数;当$a < 0$时,函数为减函数。
一次函数在概率统计问题中的应用
03
在概率统计问题中,一次函数可以用来描述概率分布、平均数
《一次函数的图像和性质》一次函数PPT优秀课件

2020/8/19
例2:在同一坐标系作出下列函数的图象
(1)y = 2x+1 (2)y = -2x+1
根据图象回答,当自变量x逐渐增大时,函数
y的值怎样变化?
y
解: x 0 -1/2
4
y =2x+1 1 0
3
y =2x+1
x
0 1/2
2
y=-2x+1 1 0
1 (0,1)
(-1/2,0)
(1/2,0)
(1)函数值y 随x的增大而增大;
m 1 2
(2)函数图象与y
轴的负半轴相交;
m
1且m
1 2
(3)函数的图象过第二、三、四象限; 1 m 1
2
(4)函数的图象过原点。 m 1
2020/8/19
会画一次函数的图象 一次函数的图象与性质,常 数k,b的意义和作用. 数形结合的思想与方法,从 特殊到一般的思想与方法. 进一步体验研究函数的一般 思路与方法.
x
-4 -3 -2 -1 o 1 2 3 4 -1
2020/8/19
-2 y= -2x+1
一次函数通常选取(0,b), (-b/k,0)两点连线
• 一次函数 y = kx + b ( k ≠ 0 ) 有以 下性质:
• (1)当 k > 0 时,y 随 x 的增大 而 增大 。
• (2)当 k < 0 时,y 随 x 的增大 而 减小 。
2020/8/19
o
y=kx+b
y=kx
y
特性:
▲k1=k2=k3 b1≠b2≠b3三 线平行
2020/8/19
x
o y = k1x+b1 y = k2x+b2
例2:在同一坐标系作出下列函数的图象
(1)y = 2x+1 (2)y = -2x+1
根据图象回答,当自变量x逐渐增大时,函数
y的值怎样变化?
y
解: x 0 -1/2
4
y =2x+1 1 0
3
y =2x+1
x
0 1/2
2
y=-2x+1 1 0
1 (0,1)
(-1/2,0)
(1/2,0)
(1)函数值y 随x的增大而增大;
m 1 2
(2)函数图象与y
轴的负半轴相交;
m
1且m
1 2
(3)函数的图象过第二、三、四象限; 1 m 1
2
(4)函数的图象过原点。 m 1
2020/8/19
会画一次函数的图象 一次函数的图象与性质,常 数k,b的意义和作用. 数形结合的思想与方法,从 特殊到一般的思想与方法. 进一步体验研究函数的一般 思路与方法.
x
-4 -3 -2 -1 o 1 2 3 4 -1
2020/8/19
-2 y= -2x+1
一次函数通常选取(0,b), (-b/k,0)两点连线
• 一次函数 y = kx + b ( k ≠ 0 ) 有以 下性质:
• (1)当 k > 0 时,y 随 x 的增大 而 增大 。
• (2)当 k < 0 时,y 随 x 的增大 而 减小 。
2020/8/19
o
y=kx+b
y=kx
y
特性:
▲k1=k2=k3 b1≠b2≠b3三 线平行
2020/8/19
x
o y = k1x+b1 y = k2x+b2
一次函数的图象(一)课件

坐标轴的交点称为函 数的解
示例
如f(x) = 2x + 3是一个一次函 数,它表示一个斜率为2、截 距为3的直线。
一次函数的斜率和截距
斜率
斜率代表函数图像的倾斜程度,可以通过计算任意 两个点之间的纵坐标差与横坐标差的比值来求得。
截距
截距是函数图像与纵坐标轴的交点,表示在横坐标 值为0时,函数的值。
一次函数的解析式
一次函数的解析式是指它的数学表达式,通常是形如y = ax + b的形式。
一次函数的实际应用
一次函数在实际生活中有许多应用,例如:
1 物体在匀速直线运动中的位置与时间关系
2 销售额与广告投入之间的关系
3 水平距离与时间的关系
一次函数的求解题型
一次函数的求解题型多种多样,包括:
1 求解函数的零点
一次函数的图像的斜率与截距关系
斜率 正数 负数 正数 负数 零
截距 正数 正数 负数 负数 正数或负数
一次函数的图像的导数与斜率关系
一次函数的导数就是它的次函数的图像的性质
一次函数的图像呈现直线特征,具有以下性质:
1 单调性
一次函数在整个定义域上都是单调递增或单调递减的。
2 求解函数的定义域和 3 求解函数在某个区间
值域
上的最值
一次函数的应用题型
一次函数的应用题型可以与实际生活中的问题相联系,例如:
1 汽车加速度问题
2 水桶注满水的时间问题
3 走远近路所需时间问题
一次函数的错解分析
一次函数的错解指的是对一次函数的定义、特点或解法等方面存在误解。
一次函数的题型解法技巧
下或左右平移。
对直线上的每个横坐标x进行缩放,可以
改变斜率以实现上下或左右伸缩。
示例
如f(x) = 2x + 3是一个一次函 数,它表示一个斜率为2、截 距为3的直线。
一次函数的斜率和截距
斜率
斜率代表函数图像的倾斜程度,可以通过计算任意 两个点之间的纵坐标差与横坐标差的比值来求得。
截距
截距是函数图像与纵坐标轴的交点,表示在横坐标 值为0时,函数的值。
一次函数的解析式
一次函数的解析式是指它的数学表达式,通常是形如y = ax + b的形式。
一次函数的实际应用
一次函数在实际生活中有许多应用,例如:
1 物体在匀速直线运动中的位置与时间关系
2 销售额与广告投入之间的关系
3 水平距离与时间的关系
一次函数的求解题型
一次函数的求解题型多种多样,包括:
1 求解函数的零点
一次函数的图像的斜率与截距关系
斜率 正数 负数 正数 负数 零
截距 正数 正数 负数 负数 正数或负数
一次函数的图像的导数与斜率关系
一次函数的导数就是它的次函数的图像的性质
一次函数的图像呈现直线特征,具有以下性质:
1 单调性
一次函数在整个定义域上都是单调递增或单调递减的。
2 求解函数的定义域和 3 求解函数在某个区间
值域
上的最值
一次函数的应用题型
一次函数的应用题型可以与实际生活中的问题相联系,例如:
1 汽车加速度问题
2 水桶注满水的时间问题
3 走远近路所需时间问题
一次函数的错解分析
一次函数的错解指的是对一次函数的定义、特点或解法等方面存在误解。
一次函数的题型解法技巧
下或左右平移。
对直线上的每个横坐标x进行缩放,可以
改变斜率以实现上下或左右伸缩。
一次函数的图象和性质(第1课时)PPT课件
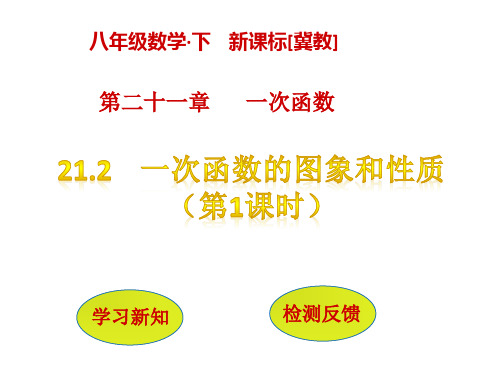
7.若一次函数y=kx+4的图像经过点(1,2).
(1)求k的值;
(2)在所给直角坐标系中画出此函数的图像;
(3)根据图像回答:当x
时,y>0.
解析:(1)把点(1,2)代入函数解析式,利用方程来求得k的值;(2)由 两点确定一条直线进行作图;(3)根据图像解答即可.
解:(1)依题意,得2=k+4,解得k=-2,即k的值是-2.
A.x<-2
B.x>-2
C.x<2
D.x>2
解析:由图像可得一次函数的图像与x轴的 交点为(-2,0),当y<0时,x<-2.故选A.
6.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若
该水库的蓄水量v(万米3)与降雨的时间t(天)的关系如图所示,
则下列说法正确的是
( B)
A.降雨后,蓄水量每天减少5万米3
达成共识. 1.图像为一条直线. 2.由画图过程,知一次函数y=2x-1的图像是由所有满足关系式y=2x-1 的点(x,y)连线而得到的.因此,凡满足关系式y=2x-1的x,y的值所对应 的点都在一次函数y=2x-1的图像上.
因为一次函数的图像是一条直线,所以也把一次函数y=kx+b 的图像称为直线y=kx+b.
为(0,2),与x轴的交点为
2 3
,0
.故选C.
4.函数
yk x
的图像经过点(1,-1),则函数y=kx-2的图像是
图中的
(A)
解析:∵
y
k x
的图像经过点(1,-1),∴k=xy=-1,∴函数解析式
为y=-x-2,所以函数图像经过(-2,0)和(0,-2).故选A.
一次函数的图像和性质PPT演示课件

•31
1.下列函数中,是正比例函数的是
A.y=-8x
B.y=-x8
C.y=5x2+6
D.y=-0.5x-1
2.一次函数 y=x-2 的图象不经过 ( B )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
( A)
•32
3.已知正比例函数 y=kx(k≠0)的图象经过点(1,-2),则正比例
函数的解析式为
考点聚焦
考点1 一次函数与正比例函数的概念
•1
考点2 一次函数的图象和性质 (2)正比例函数与一次函数的性质
第一、三 象限
第二、四 象限
•2
第一、二、 三象限
第一、三、 四象限
第一、二、 四象限
第二、三、 四象限
•3
考点3 两条直线的位置关系
k1≠k2 k1=k2,b1≠b2
•4
考点4 两直线的交点坐标及一次函数的图象与坐标 轴围成的三角形的面积
•21
变式题
5.已知直线 y=kx+b 经过点(k,3)和(1,k),则 k
的值为( B )
A. 3
B.± 3
C. 2
D.± 2
•22
变式题
▪ 6、在平面直角坐标系中,点O为原点,直线y
=kx+b交x轴于点A(-2,0),交y轴于点
B.若△AOB的面积为8,则k的值为( D ) ▪ A.1 B.2 C.-2或4 D.4或-4
图10-2 •26
变式题
▪ 1(1)根据图象信息可求得关于x的不等式 ▪ kx+b>0的解集为____________ ▪ (2)根据图象信息可求得关于x的不等式 ▪ kx+b≥0的解集为____________ ▪ (3)根据图象信息可求得关于x的不等式 ▪ kx+b≤0的解集为____________
1.下列函数中,是正比例函数的是
A.y=-8x
B.y=-x8
C.y=5x2+6
D.y=-0.5x-1
2.一次函数 y=x-2 的图象不经过 ( B )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
( A)
•32
3.已知正比例函数 y=kx(k≠0)的图象经过点(1,-2),则正比例
函数的解析式为
考点聚焦
考点1 一次函数与正比例函数的概念
•1
考点2 一次函数的图象和性质 (2)正比例函数与一次函数的性质
第一、三 象限
第二、四 象限
•2
第一、二、 三象限
第一、三、 四象限
第一、二、 四象限
第二、三、 四象限
•3
考点3 两条直线的位置关系
k1≠k2 k1=k2,b1≠b2
•4
考点4 两直线的交点坐标及一次函数的图象与坐标 轴围成的三角形的面积
•21
变式题
5.已知直线 y=kx+b 经过点(k,3)和(1,k),则 k
的值为( B )
A. 3
B.± 3
C. 2
D.± 2
•22
变式题
▪ 6、在平面直角坐标系中,点O为原点,直线y
=kx+b交x轴于点A(-2,0),交y轴于点
B.若△AOB的面积为8,则k的值为( D ) ▪ A.1 B.2 C.-2或4 D.4或-4
图10-2 •26
变式题
▪ 1(1)根据图象信息可求得关于x的不等式 ▪ kx+b>0的解集为____________ ▪ (2)根据图象信息可求得关于x的不等式 ▪ kx+b≥0的解集为____________ ▪ (3)根据图象信息可求得关于x的不等式 ▪ kx+b≤0的解集为____________
初中数学课件《一次函数的图像与性质》

?
?
新知探究一: 一次函数y=kx+b的图象与直线y=kx的关系
画一次函数 y =2x-3 的图象. 列表 描点 连线
x … -2 -1 0 1 2 …
y=2x-3 … -7 -5 -3 -1 1 … y
y=2x … -4 -2 0 2 4 … 2
1.观察:函数y=2x-3的图象
它可以看作由直线 y=2x向下 平
新知探究二: 一次函数y=kx+b的性质
一次函数y=kx+b有下列性质: 1.当k>0时,y随x的增大而__增_大__ 这时函数
的图象从左到右__上_升__
(2) 当k<0时,y随x的增大而_减__小__,这
时函数的图象从左到右_下__降__.
新知探究二: 一次函数y=kx+b的性质
当k>0时,y随x的增大而增大
例:在同一坐标系中画出函数 y=2x-1 与 y=-0.5x+1的图象.
x y=2x-1
x
y= -0.5x+1
y 6
5
4
3
2
1
- - - - - - o1 2 3 4 5 6x 6 5 4 3 2 1-
1 2 3 4 5-6
例:用两点法在同一坐标系中画出函数y=2x-1 与y=-0.5x+1的图象.
数学思想:类比、数形结合、从特殊到一般。
归纳
对于一次函数y=kx+b(k,b为常数,k≠0) (1)判断k值符号的方法
①增减性法:当y随x的增大而增大时k > 0;反之k < 0 ②直线升降法:当直线从左到右上升时,k > 0; 反之k < 0 ③经过象限法:直线经过一、三象限时k > 0;
?
新知探究一: 一次函数y=kx+b的图象与直线y=kx的关系
画一次函数 y =2x-3 的图象. 列表 描点 连线
x … -2 -1 0 1 2 …
y=2x-3 … -7 -5 -3 -1 1 … y
y=2x … -4 -2 0 2 4 … 2
1.观察:函数y=2x-3的图象
它可以看作由直线 y=2x向下 平
新知探究二: 一次函数y=kx+b的性质
一次函数y=kx+b有下列性质: 1.当k>0时,y随x的增大而__增_大__ 这时函数
的图象从左到右__上_升__
(2) 当k<0时,y随x的增大而_减__小__,这
时函数的图象从左到右_下__降__.
新知探究二: 一次函数y=kx+b的性质
当k>0时,y随x的增大而增大
例:在同一坐标系中画出函数 y=2x-1 与 y=-0.5x+1的图象.
x y=2x-1
x
y= -0.5x+1
y 6
5
4
3
2
1
- - - - - - o1 2 3 4 5 6x 6 5 4 3 2 1-
1 2 3 4 5-6
例:用两点法在同一坐标系中画出函数y=2x-1 与y=-0.5x+1的图象.
数学思想:类比、数形结合、从特殊到一般。
归纳
对于一次函数y=kx+b(k,b为常数,k≠0) (1)判断k值符号的方法
①增减性法:当y随x的增大而增大时k > 0;反之k < 0 ②直线升降法:当直线从左到右上升时,k > 0; 反之k < 0 ③经过象限法:直线经过一、三象限时k > 0;
一次函数的性质和图像(一)课件

斜率和函数单调性
1 斜率为正
表示函数是递增的,随 x 的增加,y 也增加。
2 斜率为
3 斜率为0
表示直线是水平的,函数与 y 轴平行。
一次函数的图像特点
直线
一次函数的图像是直线,与 x 轴和 y 轴相交。
斜率
斜率决定了直线的倾斜程度,越大越陡峭。
截距
截距表示直线与 y 轴的交点,反映了函数值在 x = 0 时的取值。
一次函数的定义域和值域
1 定义域
一次函数的定义域为全体实数。
2 值域
值域取决于斜率,如果斜率为正,则值 域为负无穷至正无穷;如果斜率为负, 则值域为正无穷至负无穷。
一次函数与直线的关系
相同点
不同点
• 一次函数是直线的一种特殊情况。 • 都满足直线上两点确定一条直线的性质。
一次函数的性质和图像 (一) PPT课件
本次课程将讲解一次函数的定义、解析式形式以及图像的特点。我们将深入 探讨斜率、截距和函数的性质,以及在实际生活和经济学中的应用。
一次函数的定义
一次函数是指不含有次数大于等于2的项的代数式,形式为y = mx + b(其中 m 和 b 都是实数,且 m ≠ 0)。
• 一次函数具有函数性质,每个 x 对应 唯一的 y 值。
• 直线可以是一次函数,也可以是其他 类型的函数。
一次函数的应用和实际联系
一次函数的应用广泛,可以用于建模经济学中的供求关系、利润函数等。它 们也用于描述线性运动、金融领域等实际问题。
示例和总结
1
示例
一次函数的性质可以帮助我们解决实际问题,如利润最大化的方程。
2
总结
一次函数是数学中的基础概念,它们的图像和性质在现实世界中有广泛的应用。
11.5《一次函数的图像与性质》课件ppt(共26张PPT)(青岛版七年级下)

创设问题 导入新课
磁悬浮列车自上海 浦东 机场出发,运行 1000米 后,便以 110米∕秒的 速度匀 速行驶。如果从 运行 1000米后开始计 时, 你能写出该列车离 开 浦东机场站的距离s (单位:米)与时间t (单位:秒)之间的函 数 关系式吗?
S=1000+110t
上节提到的函数y=x-1, y=2x-1,y=-3x-1以及本节中
k>0
k>0 k<0 k<0
b的符号
b>0 b<0 b>0 b<0
对一次函数y=x+4,x依次取-3,-2,-1,0,1,2,3 逐渐增大的过程中,y的值是否也在增大? 对y=-x+4呢?
x … -3 -2 -1 0 1 2 3 …
y=x+ … 1 2 3 4 5 6 7 … y增
4
7 6 543 2 1
(必做题) 65页A组4、 5题
(选做题) 66页B组1、 2题
28380万千瓦时的电量.
写出下列函数关系式是否为一次函
交流
数?是否为正比例函数?如果是正比例函 数,指出比例系数k的值.
(1)圆的周长C与它的半径r之间的关系;Fra bibliotekC=2πr
C是r的一次函数,也是 正比例函数,k=2π
(2)正方形周长y与边长x之间的函数关系:
y=4x
y是x的一次函数,也是 正比例函数,k=4
画一次函数y=kx+b(k ≠ 0)的图 象有什么简单方法吗?
过(0,b)、(-k/b,0) 两点画直线.
例2.你会画出函数y=2x-1与 y=x+1
的图象吗?
y=2x-1
x
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
画出一次函数
y
2 x 1 3
函数y=3x-2的图
的图象象是否也有这种现
象
X03
y13 观察分析:
y 2 x 1 3
自变量x由_小__到_大__ 函数y的值从_小__到_大__
结 y随x的增大而增大,
y 3x 2
论
这时函数的图象从左到右上升;
观察分析:
y 2 x 1和
3
y 2象限?
k>0,y随x的增大而增大;过一,三象限 k<0,y随x增大而减小 ;过二,四象限。
(4)直线的倾斜程度 ?
|k|越大,越接近y轴;|k|越小,越接近x轴
一线正作次通比函常例你函数又函所数y称数画图=为yk=出象x直kx+的一线(b图般yk(≠=象步kk0≠x)是骤+0是什)b是经(的么什过k图形≠么原象0状?点)是?(一0列条,表直0描)线连点的,线一这条条直直线.
经过几点可以 确定一条直线?
画图象时,只要取两个 点即可
一般情况下,画一次函数
的图象取与x轴、y轴的交
点比较简便 画正比例的图象只要过原
点(0,0)和(1,k)最 y 3x 2
为简便.
y 3x
y 1 x2 2
y1x 2
一次函数y=kx+b(k≠0) 图象的画法 (两点)
例1 在同一平面直角坐标系中画出下列 每组函数的图象:
y x 2 的图象
3
自变量x由_小__到_大__ 函数y的值从_大__到_小__
结 y随x的增大而减小, 论
这时函数的图象从左到右下降;
y x 2
概括
一次函数y=kx+b有下列性质:
(1) 当k>0时,y随x的增大而_增__大__ ,这时 函数的图象从左到右_上__升__ ; (2) 当k<0时,y随x的增大而_减__小__,这时 函数的图象从左到右下___降__.
y 3x 2 y 3x
K不同 b相同 直线(图象)相交
y 1 x2 2
y1x 2
y 1 x2 2
y1x 2
K相同 b不同 直线(图象)平行
y 3x 2
y 3x
画出一次函数
y
2 x 1 3
的图当一象个点在直线上从
X03
左向右移动时,它的 位置怎样变化
y13
观察分析:
自变量x由_小__到_大__ 函数y的值从_小__到_大__
(3)
(4)
2.下列哪个图像是一次函数y=-3x+5 和y=2x-4的大致图像( B )
(A)
(B)
(C)
(D)
历史使人聪明,诗歌使人机智,数学使人精细。
3.如果一次函数y=kx-3k+6的图象经 过原点,那么k的值为__K__=__2___。
4.写出m的3个值,使相应的一次函数 y = (2m-1)x+2的值都是随x的增大而减小.
y
y 5 x5
4
6
4
2
-6 -4 -2 o -2
-4
y 2x2 3
24 6
x
一.复习:
1.作函数图像的步骤是什么?
(1)列表 (2)描点 (3)连线
2.一次函数图像的特点是什么?
是一条直线,所以我们在作一次图像 的时候只需要确定两个点,再过这两 个点作直线就可以了。
二.尝试探索
1.在同一坐标系中作出正比例函数 y=0.5x y= –2x , y=-x的图象
24
6
-2
-4
x
平行
(3)直线y=2x+6与y=-x+6的位置关系如何?
y=-x+6 y
6 4 2
y=2x+6
-6 -4 -2 o -2
-4
24 6
x
相交
六.探索发现
(1) 在同一坐标系中作出下列函数的图象
1
y
y (1) x
3
3
2
1
(2)
-3 -2 -1 o
12 3
x
1
-1
y (3) x 1
K>o
b>0
b<0
b=0
K<0
b>0
b<0
一,三 一,二,三 一,三,四 当k>0时,y的值随x的增大而增大
二,四 一,二,四 二,三,四 当k<0时,y的值随x的增大而减小
七.练一练
1.下列一次函数中,y的值随x的增大 而减小的有_(_2_) __(_4_) _。
(1) y=10x-9
(2) y=-0.3x+2
可以写无数个,只要满足2m-1<0就可以了。 例如:m=0.m=-1,m=-2
八.小结:
本节课的主要内容有:
1.正比例函数的特点是什么? 2.一次函数及其图像的性质有哪些?
3.函数图像的位置关系有几种? 4.关于函数y=kx+b图像的大致 位置跟k,b的关系。
写在最后
成功的基础在于好的学习习惯
五.想一想
1)x从0开始逐渐增 大时,y=2x+6和y=5x 哪一个的值先达到20? 这说明了什么?
y
y=5x
20
y=2x+6
15
10
5
-15 -10 -5 o -5
5 10 15 x
你看出来了吗?
-10
(2)直线y=-x与y=-x+6的位置关系如何?
y=-x
y
y=-x+6
6
4
2
-6 -4 -2 o
1 y 2x与
y 2x 3
2 y 2x 1与
y 1 x 1 2
比对较于下直列线一y=对k一1x次+函b1数与的直图线象y有=k什2x么+共b同2 点, 有当 当什kk么11=≠不kk同22, 点b, b1?≠1=bb22时时,,两两直直线线平相行交;于点(0,b) ;
直线(图象)平行 K相同 b不同
-2
3
思考:k,b的值跟图像有什么关系?
(2)在同一坐标系中作出下列函数的图象
(1)
-
(2)
(3)
y
3
2
1
-3 -2 -1 o -1
y
1 3
x
1
12 3
x
思考
-2
y
1 3
x
1
做了这三个图像你发现了
K,b跟图像的关系吗?
结论
(3)
b=0
通过作以上一次函数的图像我们发现y=kx+b 中,k,b的取值跟图像的关系如下:
在同一平面直角坐标系中画出下列函数的图象
1 y 1 x
2
y 1 x2 2
2 y 1 x 2
2
y1x 2
3 y 3x
4 y 3x 2
y 3x 2 y 3x
一次函数y=kx+b (k≠0)的图象是一条直线,这条直 线通常又称为直线y=kx+b(k≠0)
正比例函数y=kx(k≠0)是经过原点(0,0)的一条直线.
y=x ,y=3x和
y
y=-2x 6
y=-x
4
2
-6 -4 -2 o -2
-4
y=3x y=x
y=0.5x
24 6
x
y
y=-2x 6
y=-x
4
2
-6 -4 -2 o -2
-4
y=3x (1)上面的函数都是什么函数?
y=x
正比例函数
(2)正比例函数y=kx的
y=0.5x 图象有什么特点?
24 6
x 正比例函数y=kx的图象是经 过(0,0),(1,K)的一条直线
