《计算方法习题集》
计算方法习题集及实验指导书

《计算方法习题集及实验指导书》计算机科学与技术系檀明2008-02-10课程性质及目的要求(一)课程性质自计算机问世以来,科学计算一直是计算机应用的一个重要领域,数值计算方法是解决各种复杂的科学计算问题的理论与技术的基础。
《计算方法》课程讨论用于科学计算中的一些最基本、最常用的算法,不但具有数学的抽象性与严密的科学性的特点,而且具有应用的高度技术性的特点。
它对于培养从事计算机应用的科技人才有着重要的作用,是计算机应用专业(本科段)的一门重要的技术基础课程。
(二)目的要求通过本课程的学习和上机实验,了解用计算机解决科学计算问题的方法特点,掌握计算方法中的一些基本概念、基本公式和相应的算法流程,提高根据算法描述设计高级语言程序并进行验证的技能。
在学习过程中,应注重理解和应用,在搞清基本原理和基本概念的基础上,通过习题、编程和上机等环节,巩固和加深已学的内容,掌握重要的算法及其应用。
注重理论与算法的学习和应用相结合,强调编程及上机计算的技能培养,是本课程不同于一般数学课程的重要特点。
(三)学习方法指导1.循序渐进逐章学习本课程从第二章开始,每章都讨论一个大类的算法。
虽然各算法是相对独立的,但是也存在相互XXX与前后继承的关系。
前面的概念和算法学好了,后面的内容也就容易学,越学越感到容易。
前面的内容没有学好,后面就会感到难学,甚至会出现越来越感到困难、失去学习信心的情况。
2.稳扎稳打融会贯通学习要扎实、要讲求实效。
每一个重要的概念和公式,都会搞清楚,做到融会贯通。
只有这样,才能取得学习的学习效果。
3.多学练勤做习题教材及本习题集中的每一章都附有适量的习题,可以帮助考生巩固和加深理解所学的知识,提高解题能力。
因此,在学习过程中,应当适合习题进行思考,应当尽可能多做习题,遇到某些不会做的题,应三思之后再请老师给予提示。
4.抓住特点前后XXX 本课程只讲了五大类算法。
每类算法都是针对一类特定的计算问题,都有其自身的特点。
计算方法习题集及解答(总结版)

左边 ( )- 右边 证明:当 m=0 时
∑∞
= T0 h
T=
∆ i
h
2i
=
i=1
设 时等式成立,即 ( )- m=k
Tk h
∑∞
T=
∆ h (k ) 2k +2i i
i =1
当 时 m=k+1
∑ ∑ Tk+(1 h)-T=
4k
+1Tk
(
h 2
)
−
Tk
(h)
4k +1 −1
−T=
4k +1[T
+
∞ i =1
0
1
2
3
4
5
6
7
8
1.5 1.44444 1.47929 1.456976 1.47108 1.46209 1.46779 1.4416 1.46647
9 1.4650
10
11
1.46593 1.4653
x* ≈ 1.466
迭代公式(2):
k
0
xk
1.5
12 1.46572
13 1.46548
14 1.46563
xk +1
=
ln(4 − xk ln 2
)
k
0
1
2
3
4
5
6
7
8
9
10
2
xk 1.5 1.322 1.421 1.367 1.397 1.380 1.390 1.384 1.387 1.386 1.386
x* ≈ 1.386
2. 方程 x3 − x2 −1 = 0 在 x = 1.5附近有根,把方程写成三种不同的等价形式:
计算方法习题集及答案(总结版)

雅克比法:
3 10 12 5
3 (k ) 2 (k ) x1( k +1) = − 5 x2 − 5 x3 −
,x
( k +1) 2
(k ) 1 (k ) =1 4 x1 − 2 x 3 + 5
18 i
,x
( k +1) 3 −4
(k ) 3 =−1 + 10 x (2 k ) + 5 x1
取初始向量 x
(2) x (3) x
3
= 1+ x2 =
,对应迭代公式 x 对应迭代公式 x
0
k +1
= 3 1 + x k2 ;
2
1 , x −1
k
+1 =
1 xk − 1
。
0
判断以上三种迭代公式在 x 解: (1) ϕ ( x) = 1 + x1
2
= 1 .5
的收敛性,选一种收敛公式求出 x
2 x3
−
2 3
= 1 .5
5
习题 3
1.
设有方程组
5 x1 + 2 x 2 + x3 = −12 − x1 + 4 x 2 + 2 x3 = 20 2 x − 3x + 10 x = 3 2 3 1
( k +1) (k )
∞
(1)
考察用 Jacobi 法,Gauss-Seidal 法解此方程组的收敛性; −x (2) 用 Jacobi 法及 Gauss-Seidal 法解方程组,要求当 x
1.
x
k +1 k k
'
<1
公式收敛
《大学计算机基础》习题集

《大学计算机基础》习题集第1章习题一单选题1.第一台电子数字计算机ENIAC诞生在()。
(A)英国(B)美国(C)德国(D)中国2.世界上第二代计算机采用的主要逻辑部件是()。
(A)电子管(B)继电器(C)晶体管(D)集成电路3.世界上第一台计算机采用的主要逻辑部件是()。
(A)电子管(B)集成电路(C)晶体管(D)大规模和超大规模集成电路4.计算机的发展经历了()个时代。
(A)2 (B)3 (C)4 (D)55.大规模、超大规模集成电路计算机在计算机发展史中属于第()代。
(A)2 (B)3 (C)4 (D)56.计算机当前已应用于各行业、各领域,而计算机最早的设计是针对()。
(A)数据处理(B)科学计算(C)辅助设计(D)过程控制7.当前气象预报已广泛采用数值预报方法,这种预报方法会涉及计算机应用中的()。
(A)科学计算和数据处理(B)科学计算与辅助设计(C)科学计算和过程控制(D)数据处理和辅助设计8.计算机内部采用的数制是()。
(A)十进制(B)二进制(C)八进制(D)十六进制9.下列每组数依次为二进制、八进制和十六进制数值,合法的一组是()。
(A)11,58,19 (B)20,34,10 (C)12,23,AB (D)10,77,3C 10.在下列4个数中,()是最小的一个数。
(A)(54)10(B)(65)8 (C)(3B)16(D)(110000)211.下列数中,数值最小的一个是()。
(A)八进制数52 (B)十进制数44(C)十六进制数2B (D)二进制数10100112.下列数据中,有可能是八进制数的是()。
(A)488 (B)317 (C)597 (D)18913.下列两个二进制数进行算术加运算,100001+1111= ()。
(A)111110 (B)111000 (C)110000 (D)11110114.下列算数运算,结果不正确的是()。
(A)0+0=0 (B)1+0=1 (C)0+1=0 (D)1-1=015.假设计算机字长为一个字节,+68的原码是()。
《结构力学习题集》(上)第四章超静定结构计算——力法
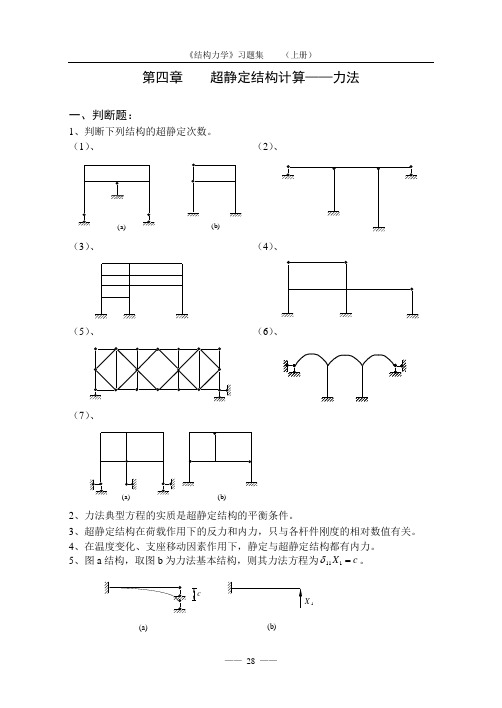
第四章 超静定结构计算——力法一、判断题:1、判断下列结构的超静定次数。
(1)、 (2)、(a )(b)(3)、 (4)、(5)、 (6)、(7)、(a)(b)2、力法典型方程的实质是超静定结构的平衡条件。
3、超静定结构在荷载作用下的反力和内力,只与各杆件刚度的相对数值有关。
4、在温度变化、支座移动因素作用下,静定与超静定结构都有内力。
5、图a 结构,取图b 为力法基本结构,则其力法方程为δ111X c =。
(a)(b)X 16、图a 结构,取图b 为力法基本结构,h 为截面高度,α为线膨胀系数,典型方程中∆12122t a t t l h =--()/()。
t 21t l Ah(a)(b)X 17、图a 所示结构,取图b 为力法基本体系,其力法方程为。
(a)(b)1二、计算题:8、用力法作图示结构的M 图。
3mm9、用力法作图示排架的M 图。
已知 A = 0.2m 2,I = 0.05m 4,弹性模量为E 0。
qa a11、用力法计算并作图示结构的M 图。
ql /212、用力法计算并作图示结构的M 图。
q3 m4 m13、用力法计算图示结构并作出M 图。
E I 常数。
(采用右图基本结构。
)l 2/3l /3/3l/314、用力法计算图示结构并作M 图。
EI =常数。
3m 3m2m2m 2m2m16、用力法计算图示结构并作M 图。
EI =常数。
l lql l17、用力法计算并作图示结构M 图。
E I =常数。
18、用力法计算图示结构并作弯矩图。
161kNmmmm19、已知EI = 常数,用力法计算并作图示对称结构的M 图。
ql lqa a21、用力法作图示结构的 M 图 。
EI = 常数。
2ql22、用力法作M 图。
各杆EI 相同,杆长均为 l 。
23、用力法计算图示结构并作M 图。
EI = 常数。
4m2kN24mmm24、用力法计算并作出图示结构的M 图。
E = 常数。
20kN3m 4m 3m26、用力法计算图示结构并作M 图。
《工程量计算》习题集(1)

平整场地工程量计算举例
例:计算下图平整场地的工程量。
解
平整场地工程量 S=(5.64×2+15.0)×9.24+5.64×2.12×2=266.74㎡
土石方工程量计算举例
【例】根据下图有关数据,计算室内回填土工程量。已知:室 内外地坪高差0.30m,C15混凝土地面垫层80厚,l:2水泥砂 浆面层25厚。
《定额与预算》(1)
工程量计算
习题集
成都市工业职业技术学校 土木系 授课教师 刘嘉
第三章 建筑面积计算
建筑面积计算举例(1)
例:计算下图单层建筑的建筑面积
解
建筑面积:S= 45.24×15.24= 689.46 (㎡)
建筑面积计算举例(2)
例:计算下图的建筑面积(墙厚均为240mm。)
建筑面积计算举例(3)
建筑面积计算举例(17)
例1:计算下图所示建筑物各种阳台的建筑面积
解
阳台的建筑面积(凹阳台面积+挑阳台面积) S=1/2×(3.3-0.24) ×1.5 + 1/2(3.6+0.24)×1.2= 4.60(㎡)
建筑面积计算举例(17)
例2:计算下图所示建筑物各种阳台的建筑面积。
解
挑阳台=1/2(3.3×1)=1.65(㎡) 凹阳台=1/2(2.7×1.2)=1.62(㎡) 半凸半凹阳台=1/2(2.52×1.2+3×1)=3.01(㎡)
建筑面积计算举例(9)
例:计算下图剧院的建筑面积。
解 剧院建筑面积=(100+0.24)×(50+0.24)
=5036.06(㎡) 舞台灯光控制室建筑面积
=1/2× 3.14×1.242 ×4
=9.66(㎡) 总建筑面积=5036.06+9.66=5045.72(㎡)
《水文水利计算》习题集

《水文水利计算》习题第一章 年径流量分析与计算1、某水库垻址处共有21年年平均流量Q i 的资料,已计算出∑==2113/2898i is m Q,()80012211⋅=-∑=i iK(1)求年径流量均值Q ,离势系数C v ,均方差σ ?(2)设C s = 2C v 时,P-III 型曲线与经验点配合良好,试按表2-1-1求设计保证率为90%时的设计年径流量?表2-1-1 P —III 型曲线离均系数Φ值表(P=90%)解:(1)∑===2128981iQ n Q 138m 3/s ()20012180112⋅=-⋅=--=∑n kC iv s m C Q v /6272001383⋅=⋅⨯==σ(2)C s = 2C v = 0.40,查表1-5-3 Φ值表,得Φ = -1.23,则 ()()[]s m C Q Q v p /10423.1200113813=-⨯⋅+⨯=Φ+=2、某水库多年平均流量Q =15m 3/s ,C v = 0.25 ,C s = 2.0 C v ,年径流理论频率曲线为P —III 型。
(1)按表2-2-1求该水库设计频率为90%的年径流量? (2)按表2-2-2径流年分配典型,求设计年径流的年分配?表2-2-1 P —III 型频率曲线模比系数Kp 值表(C s = 2.0 C v )表2-2-2 枯水代表年年分配典型解:(1)C s = 2.0 C v ,C v = 0.25,P = 90%时查表1-5-6 Kp 值表,得K 90%=0.70,则s m K Q Q P /510700153%90⋅=⋅⨯==(2)由Q 90%乘以12,得全年累积平均流量∑Q 90% ,再乘各月的分配百分比(见表1-5-7),即得各月的的月平均流量。
计算结果列于答案表2-5-1中。
表2-5-1 设计年径流年分配表(m 3/s )3、某水库有24年实测径流资料,经频率计算已求得频率曲线为P —III 型,统计参数为:多年平均径流深 R = 711.0 mm ,C v = 0.30, C s = 2C v ,试结合表2-3-1推求该水库十年一遇丰水年的年径流深?表2-3-1 P —III 型曲线离均系数Φ值表解:C s = 2C v = 2×0.30 = 0.60, 查表1-5-9得Φ10%=1.329,则R P =R (1+ C v ΦP )=711×(1+ 0.30× 1.329)=994.5 mm4、某水文站多年平均流量Q=266 m3/s ,C v = 0.20,C s = 0.40,试结合表2-4-1在P—III型频率曲线上推求设计频率P = 90% 的年平均流量?表2-4-1 P—III型频率曲线模比系数Kp值表(C s = 2.0 C v)解:由已知的C v = 0.20,C s=2C v = 0.40,查表1-5-10得K P=90% = 0.75 ,则Q P = K P Q= 0.75×266 =199.5 m3/s5、某水文站多年平均流量Q=328 m3/s ,C v = 0.25,C s = 0.60,试结合表2-5-1在P—III型频率曲线上推求设计频率P = 95% 的年平均流量?表2-5-1 P—III型频率曲线离均系数Φp值表解:由C s= 0.60查表1-5-11得ΦP=95% = -1.45 ,则Q P =Q(1+ C vΦP)=328×[1+ 0.25×(-1.45)]= 209.1 m3/s 6、设本站只有1998年一年的实测径流资料,其年平均流量Q=128 m3/s 。
20140506 计算机数值方法习题集(学生)

(A) (B) (C) (D)
已知 ,则 为(D)
(A) 0(B) 1(C)2(D)4
已知 且 , ; , 用拉格朗日线性插值求 的近似值,并估计截断误差。
解:
即
余项估计 ,其中
9.已知 ,求 及 的值。(8分)
A、牛顿(Newton)法B、迭代法C、消去法D、二分法
下面程序实现的公式是(D)
for(k=1;k<=n;k++)
for(j=1;j<=n;j++)
{
if(j==k) continue;
a[k][j]=a0[k][j]/a0[k][k];
}
A. B.
C. D.
1.试用c程序实现下面公式。
定义a[k][j]为本次计算所得数组a的结果;a0[k][j]为上一次计算所得数组a的结果。
for(k=1;k<=n;k++)
for(j=1;j<=n;j++)
{
if(j==k) continue;
a[k][j]=a0[k][j]/a0[k][k];
}
要使 的近似值的相对误差不超过0.1%,应取几位有效数字。
第
若f(x)再[a,b]上连续,且f(a)f(b)<0,则方程f(x)=0在[a,b]内至少有一个根。
二分法只能用于求实函数的实根
求解方程 ,若 可以表成 ,则用简单迭代法求根,那么 满足 ,近似根序列 一定收敛。
2.用迭代法求方程 的正根,下面有三种迭代格式:
xi
yi
xi2
xi3
xi4
水文水利计算习题集

项目一:年径流的分析与计算一、填空题1.年径流是指。
2.影响年径流量的因素有和。
3.对同一条河流而言,一般年径流流量系列均值从上游到下游是,变差系数值从上游到下游是。
4.流域的大小对年径流的影响主要通过流域的而影响年径流的变化。
5.为了保证设计年径流计算成果的精度和合理性,必须审查年径流资料的、、。
6.代表性是指。
7.参证变量的选择必须考虑应满足的条件是。
8.偏态系数反映的是。
9.某一年的年径流量与多年平均的年径流量之比称为。
二、问答题1.年径流分析计算的任务是什么?2.三个水文统计参数的含义及其对频率曲线的影响(画图表示)。
3.推求设计年径流量的年内分配时,应遵循什么原则选择代表年?4.简述具有长期实测资料情况下,用设计代表年法推求年内分配的方法步骤?5.缺乏实测资料时,怎样推求设计年径流量?6.日历年度、水文年度、水利年度的涵义各是什么?三、计算题1.某水库坝址集水面积为212500kmF=,流域多年平均年降雨量为mmH1100=,坝址处多年平均流量为smQ/1003=。
要求计算多年平均径流量W、径流深R、蒸发量E、径流模数M、径流系数α。
2.已知某河流某断面的多年平均流量为100m3/s C V=0.20,C S=0.40。
(1)计算十年一遇设计枯水年的年径流量。
(2)计算百年一遇设计丰水年的年径流量。
3.某以发电为主的工程,已求得设计断面处年径流量的统计参数为s m Q /0.503 ,Cv=0.35,C s =2C v 。
要求计算:①设计枯水年(P=90%)和设计平水年(P=50%)的设计年径流量;②根据表1中所列资料选用设计枯水代表年,推求设计年径流量的年内分配;③根据设计平水年年内分配百分比(见表2),推求设计平水年年径流量的年内分配。
34.已知某站历年(1990~2001)径流资料,见表3。
试用图解适线法推求该站设计频率P=10%、50%和90%的年径流量。
3项目二:由流量资料推求设计洪水一、填空题1.洪水的三要素是指、、。
计算方法习题集及答案第四版

解:
y次迭代公式
k
0
1
2
3
3.5
3.64
3.63
3.63
6. 试证用牛顿法求方程在[1,3]内的根是线性收敛的。 解:
令
y次迭代公式 故
从而 ,时, 故, 故牛顿迭代公式是线性收敛的 7. 应用牛顿法于方程, 导出求立方根的迭代公式,并讨论其收敛
性。
解:
相应的牛顿迭代公式为 迭代函数,, 则,
习题1.1
1. 什么叫数值方法?数值方法的基本思想及其优劣的评价标准如 何?
数值方法是利用计算机求解数学问题近似解的方法 2. 试证明 及
证明: (1)令
即 又 即 ⑵ 设,不妨设, 令 即对任意非零,有 下面证明存在向量,使得, 设,取向量。其中。 显然且任意分量为, 故有即证。 3. 古代数学家祖冲之曾以作为圆周率的近似值,问此近似值具有
解: (1)迭代公式,公式收敛
k
0
1
2
3
0
(2),, 局部收敛 k0 1 2 3
0.25
0.25098 0.25098
456789
1.5 1.322 1.421 1.367 1.397 1.380 1.390 1.384 1.387 1.386
2. 方程在附近有根,把方程写成三种不同的等价形式:
(1),对应迭代公式;
9
10
11
12
13
14
15
16
1.4650 1.46593 1.4653 1.46572 1.46548 1.46563 1.465534 1.465595
迭代公式(2):
k
0
1
2
3
计算方法课后习题集规范标准答案

习 题 一3.已知函数y =4, 6.25,9x x x ===处的函数值,试通过一个二次插值函解:0120124, 6.25,9;2, 2.5,3y x x x y y y =======由题意 (1) 采用Lagrange插值多项式220()()j j j y L x l x y ==≈=∑27020112012010*********()|()()()()()()()()()()()()(7 6.25)(79)(74)(79)(74)(7 6.25)2 2.532.255 2.25 2.75 2.7552.6484848x y L x x x x x x x x x x x x x y y y x x x x x x x x x x x x ==≈------=++------------=⨯+⨯+⨯⨯-⨯⨯= 其误差为(3)25(3)25(3)2[4,9]2()(7)(74)(7 6.25)(79)3!3()83max |()|40.0117281|(7)|(4.5)(0.01172)0.008796f R f x x f x R ξ--=---==<∴<=又则(2)采用Newton插值多项式2()y N x =≈ 根据题意作差商表:224(7)2(74)()(74)(7 6.25) 2.64848489495N =+⨯-+-⨯-⨯-≈4. 设()()0,1,...,k f x x k n ==,试列出()f x 关于互异节点()0,1,...,i x i n =的Lagrange 插值多项式。
注意到:若1n +个节点()0,1,...,i x i n =互异,则对任意次数n ≤的多项式()f x ,它关于节点()0,1,...,i x i n =满足条件(),0,1,...,i i P x y i n ==的插值多项式()P x 就是它本身。
可见,当k n ≤时幂函数()(0,1,...,)kf x x k n ==关于1n +个节点()0,1,...,i x i n =的插值多项式就是它本身,故依Lagrange 公式有()00(),0,1,...,nn n k kk i j j j j j i j ii jx x x l x x x k n x x ===≠-=≡=-∑∑∏特别地,当0k =时,有()0001nn n ij j j i j ii jx x l x x x ===≠-=≡-∑∑∏而当1k =时有()000nnn ij j j j j i j ii jx x x l x x x x x ===≠⎛⎫- ⎪=≡ ⎪- ⎪⎝⎭∑∑∏ 5.依据下列函数表分别建立次数不超过3的Lagrange 插值多项式和Newton 插值多项式,并验证插值多项式的唯一性。
简便计算教案和习题集

一、使用加法结合律实行简算(a+b)+c=a+(b+c) 或a+b+c+d=(a+c)+(b+d)例1、5.76+13.67+4.24+6.33=(5.76+4.24)+(13.67+6.33)=10+10=20例2、37.24+23.79-17.24=37.24-17.24+23.79=20+23.79=43.79二、使用乘法结合律实行简算:这种题型往往含特殊数字之间相乘(a×b)×c=a×(b×c)特殊数字之间相乘:25×4=100 125×8=1000 25×8=200 125×4=500例3、4×3.78×0.25=4×0.25×3.78=1×3.78=3.78例4、125×246×0.8=125×0.8×246=100×246=246002.5×0.125×8×4等,如果遇到除法同样适用,或将除法变为乘法来计算。
如:8.3×67÷8.3÷6.7等。
三、利用乘法分配律实行简算:(a+b)×c=a×c+b×c(a-b)×c=a×c-b×c做这种题,一定不要急着去算,先要分析各数字之间的特殊关系。
也就是先要仔细观察,找到做题的窍门。
例5、(2.5+12.5)×40=2.5×40+12.5×40=100+500=600例6、3.68×4.79+6.32×4.79=(3.68+6.32)×4.79=10×4.79=47.9例7. 26.86×25.66-16.86×25.66=(26.86-16.86) ×25.66=10×25.66=256.6例8、 5.7×99+5.7= 5.7×(99+1)=5.7×100=570使用乘法分配律实行简算,遇到除以一个数,先化为乘以一个数的倒数,再分配。
数值计算基础习题集

《数值计算基础》习题集第1章引论1、已知,求近似值的有效数字位数、绝对误差限和相对误差限。
2、下列各数均为四舍五入得到,指出它们各具有几位有效数字及绝对误差限和相对误差限: (1) 6000 (2)7000.00 (3)2.00023、将下列各数舍入成三位有效数字,并确定近似值的绝对误差和相对误差。
(1) 2.1514 (2) -392.85 (3) 0.0039224、已知各近似值的相对误差,试确定其绝对误差: (1) 13267 (2) 0.2965、已知各近似值及其绝对误差,试确定各数的有效位数。
(1) 0.3941 (2)293.481 (3) 0.003816、已知各近似值及其相对误差,试确定各数的有效位数。
(1) 1.8921 (2) 22.351 (3) 48361 注:相对误差与有效数字的关系请使用以下定理定理:设x 是准确值,x*是近似值)(10....0*21Z k x x x x k n ∈⨯±=,其中n x x x ,...,,21都是0~9十个数字之一,且01≠x 。
(1)若x*有n 位有效数字,则其相对误差限为111021+-⨯n x 。
(2)若x*的相对误差限为1110)1(21+-⨯+n x ,则x*有n 位有效数字。
参考答案1、有效数字位数4位,,2、(1)4位,, (2)6位,, (3)5位,,3、(1)2.15,, (2)-393,, (3)0.00392,,4、(1)(2)5、(1)2位(2)3位(3)2位6、(1)3位(2)1位(3)2位第2章解线性方程组的直接法1、用高斯顺序消元法解线性方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡141421123412321x x x 2、用高斯列主元消去法解线性方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--11124112345111321x x x 3、用Doolittle 三角分解法求解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----5481332222224321x x x4、求矩阵的Crout 三角分解⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----13322222245、求矩阵的Cholesky 三角分解⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--22484548416参考答案 1、 2、 3、4、⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----1112121192212413322222245、⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--33221433221422484548416第3章插值法与最小二乘法Newton 插值法求其插值多项式,并给出余项。
高三化学物质量的计算习题集

高三化学物质量的计算习题集
1. 硝酸铝是一种常见的无机化合物,化学式为Al(NO3)3。
如果我们有15克的硝
酸铝,求其含有多少摩尔的硝酸铝?
2. 有一个包含30克的钠离子(Na+)溶液,求该溶液中含有多少克的钠?
3. 乙醇是一种广泛应用的有机溶剂,化学式为C2H5OH。
如果我们有0.5摩尔的乙醇,求其含有多少克的乙醇?
4. 氨气(NH3)是一种常见的气体,用于制造化学品和肥料。
如果我们有8克的氨气,求其含有多少摩尔的氨气?
5. 环己烷(C6H12)是一种常见的有机化合物,化学式为C6H12。
如果我们有2摩尔
的环己烷,求其含有多少克的环己烷?
6. 一种含有40克氯离子(Cl-)的溶液,求该溶液中含有多少克的氯?
7. 水合铜(II)硫酸铜(CuSO4·5H2O)是一种常见的无机盐,用于实验室和工业中。
如
果我们有10克的水合铜(II)硫酸铜,求该化合物中含有多少摩尔的铜离子(Cu2+)?
8. 乙酸是一种常见的有机酸,化学式为CH3COOH。
如果我们有1摩尔的乙酸,
求其含有多少克的乙酸?
以上习题涉及了化学物质量的计算,从给定的物质量和化学式中求出物质的摩尔
数或质量。
这些问题对于高三化学学习的巩固和提高理解能力非常有帮助。
通过解决
这些习题,学生可以更好地理解化学计算的基本原理和应用方法。
《整式的乘法--幂的运算》习题集-有详细答案哦

word格式-可编辑-感谢下载支持平面图形的认识试卷副标题1.(﹣2)0的相反数等于()A. 1 B.﹣1 C. 2 D.﹣22.计算(﹣x2)•x3的结果是()A. x3B.﹣x5C. x6D.﹣x63.下列各数(﹣2)0,﹣(﹣2),(﹣2)2,(﹣2)3中,负数的个数为()A. 1个B. 2个C. 3个D. 4个4.若(2x+1)0=1则()A.x≥﹣B.x≠﹣C.x≤﹣D.x≠5.计算:﹣1﹣(﹣1)0的结果正确是()A. 0 B. 1 C. 2 D.﹣26.计算:(﹣1)2010﹣()﹣1的结果是()A. 1 B.﹣1 C. 0 D. 27.下列算式,计算正确的有①10﹣3=0.0001;②(0.0001)0=1;③3a﹣2=;④(﹣x)3÷(﹣x)5=﹣x﹣2.A. 1个B. 2个C. 3个D. 4个8.下列四个算式中正确的算式有()①(a4)4=a4+4=a8;②[(b2)2]2=b2×2×2=b8;③[(﹣x)3]2=(﹣x)6=x6;④(﹣y2)3=y6.A. 0个B. 1个C. 2个D. 3个9.把2﹣333、3﹣222、5﹣111这三个数按从大到小的顺序排列,正确的是()A. 2﹣333>3﹣222>5﹣111 B. 5﹣111>3﹣222>2﹣333C. 3﹣222>2﹣333>5﹣111 D. 5﹣111>2﹣333>3﹣22210.若有意义,则x的取值范围是()A.x≠2011 B.x≠2011且x≠2012C.x≠2011且x≠2012且x≠0D.x≠2011且x≠011.纳米是非常小的长度单位,已知1纳米=10﹣6毫米,某种病毒的直径为100纳米,若将这种病毒排成1毫米长,则病毒的个数是()A. 102个B. 104个C. 106个D. 108个12.若3x+2=36,则= .13.计算:(a3)2+a5的结果是.14.若a m=2,a n=3,则a2m+n= .15.多项式﹣5(ab)2+ab+1是次项式.16.已知(a﹣3)a+2=1,则整数a= .17.= ;4101×0.2599= .18.若x+x﹣1=3,则x2+x﹣2的值是.19.如果a m=p,a n=q(m,n是正整数)那么a3m= . a2n= ,a3m+2n= .20.若a x=2,a y=3,则a2x+y= .21.已知a m=9,a n=8,a k=4,则a m﹣2k+n= .22.计算2﹣2的结果是.23.人们以分贝为单位来表示声音的强弱.通常说话的声音是50分贝,它表示声音的强度是105;摩托车发出的声音是110分贝,它表示声音的强度是1011.摩托车的声音强度是说话声音强度的倍.24.计算:a3•a6= .25.有一道计算题:(﹣a4)2,李老师发现全班有以下四种解法,①(﹣a4)2=(﹣a4)(﹣a4)=a4•a4=a8;②(﹣a4)2=﹣a4×2=﹣a8;③(﹣a4)2=(﹣a)4×2=(﹣a)8=a8;④(﹣a4)2=(﹣1×a4)2=(﹣1)2•(a4)2=a8;你认为其中完全正确的是(填序号).26.n为正整数,且x2n=3,则(3x3n)2的值为:.27.计算:(﹣)0= .28.计算:a n﹣5(a n+1b3m﹣2)2+(a n﹣1b m﹣2)3(﹣b3m+2)29.已知a m=3,a n=21,求a m+n的值.30.阅读下列材料:一般地,n个相同的因数a相乘记为a n,记为a n.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若a n=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为log a b(即log a b=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).(1)计算以下各对数的值:log24= ,log216= ,log264= .(2)观察(1)中三数4、16、64之间满足怎样的关系式,log24、log216、log264之间又满足怎样的关系式;(3)由(2)的结果,你能归纳出一个一般性的结论吗?log a M+log a N= ;(a>0且a≠1,M>0,N>0)(4)根据幂的运算法则:a n•a m=a n+m以及对数的含义证明上述结论.word格式-可编辑-感谢下载支持参考答案1.B【解析】试题分析:先根据0指数幂的运算法则求出(﹣2)0的值,再由相反数的定义进行解答即可.解:∵(﹣2)0=1,1的相反数是﹣1,∴(﹣2)0的相反数是﹣1.故选B.考点:零指数幂;相反数.点评:本题考查的是0指数幂及相反数的定义,解答此题的关键熟知任何非0数的0次幂等于1.2.B【解析】试题分析:根据同底数幂相乘,底数不变,指数相加,计算后直接选取答案.解:(﹣x2)•x3=﹣x2+3=﹣x5.故选B.考点:同底数幂的乘法.点评:本题主要考查同底数幂的乘法运算法则:底数不变,指数相加.熟练掌握运算法则是解题的关键.3.A【解析】试题分析:分别计算后,再找出负数的个数.解:∵(﹣2)0=1,﹣(﹣2)=2,(﹣2)2=4,(﹣2)3=﹣8,∴负数的个数有1个.故选A.考点:零指数幂;有理数的乘方.点评:本题主要考查有理数的运算,涉及到0指数幂,有理数的乘方等知识点.4.B【解析】试题分析:根据任何非0实数的0次幂的意义分析.解:若(2x+1)0=1,则2x+1≠0,∴x≠﹣.故选B.考点:零指数幂.点评:本题较简单,只要熟知任何非0实数的0次幂等于1即可.5.D【解析】试题分析:先计算出(﹣1)0的值,再根据有理数的减法进行运算即可.解:原式=﹣1﹣1=﹣2.故选D.考点:零指数幂.点评:本题考查的是0指数幂,即任何非0数的0次幂等于1.6.B【解析】试题分析:根据负整数指数为正整数指数的倒数计算.解:(﹣1)2010﹣()﹣1=1﹣2=﹣1.故选B.考点:负整数指数幂.点评:本题主要考查了负整数指数幂的运算.注意:﹣1的偶次幂是1,奇次幂还是﹣1.7.A【解析】试题分析:本题根据零指数幂、负整数指数幂、同底数指数幂的除法等知识点进行判断.解:10﹣3=0.001,故①错误;任何不等于0的0次幂等于1,所以②(0.0001)0=1,正确;3a﹣2=3×,所以③错误;(﹣x)3÷(﹣x)5=x﹣2,④错误.故选A.考点:负整数指数幂;同底数幂的除法;零指数幂.点评:熟练掌握负整数指数幂、零指数幂的计算以及同底数指数幂的除法法则.8.C【解析】试题分析:根据幂的乘方,底数不变指数相乘的性质计算即可.(a m)n=a mn.解:①应为(a4)4=a4×4=a16,故不对;②[(b2)2]2=b2×2×2=b8,正确;③[(﹣x)3]2=(﹣x)6=x6,正确;④应为(﹣y2)3=﹣y6,故不对.所以②③两项正确.故选C.考点:幂的乘方与积的乘方.点评:本题考查了幂的乘方的运算法则.应注意运算过程中的符号.9.D【解析】试题分析:先根据幂的乘方化成指数都是111的幂,再根据底数的大小判断即可.解:∵2﹣333=(2﹣3)111=()111,3﹣222=(3﹣2)111=()111,5﹣111=(5﹣1)111=()111,又∵>>,∴5﹣111>2﹣333>3﹣222.故选D.考点:幂的乘方与积的乘方;负整数指数幂.点评:本题考查了负整数指数幂,幂的乘方等知识点,注意:a mn=(a n)m,当p≠0时,p﹣n=.10.C【解析】试题分析:将原式化为不含负整数指数幂的形式,再根据分式有意义的条件和0指数幂的意义解答.word格式-可编辑-感谢下载支持解:原式可化为:(x﹣2011)0+()2,根据分式有意义的条件和0指数幂的意义可知:x≠2011,x≠0,根据原式可知,x﹣2012≠0,x≠2012.故选C.考点:负整数指数幂;零指数幂.点评:本题考查了负整数指数幂、零指数幂的意义,要知道,任何非0数的0次幂等于1.11.B【解析】试题分析:根据1毫米=直径×病毒个数,列式求解即可.解:100×10﹣6=10﹣4;=104个.故选B.考点:同底数幂的除法;同底数幂的乘法.点评:此题考查同底数幂的乘除运算法则,易出现审理不清或法则用错的问题而误选.解答此题的关键是注意单位的换算.12.2【解析】试题分析:根据同底数幂的乘法的性质等式左边可以转化为3x×32=36,即可求得3x的值,然后把3x的值代入所求代数式求解即可.解:原等式可转化为:3x×32=36,解得3x=4,把3x=4代入得,原式=2.故答案为:2.考点:同底数幂的乘法.点评:本题考查了同底数幂的乘法的性质,熟练掌握性质是解题的关键,注意运用整体思想解题可以简化运算.13.a6+a5【解析】试题分析:根据幂的乘方,底数不变指数相乘计算即可.解:(a3)2+a5=a3×2+a5=a6+a5.考点:幂的乘方与积的乘方.点评:本题考查了幂的乘方的性质,熟练掌握运算性质是解题的关键,要注意不是同类项的不能合并.14.12【解析】试题分析:根据同底数幂的乘法与幂的乘方的性质,即可得a2m+n=a2m•a n=(a m)2•a n,又由a m=2,a n=3,即可求得答案.解:∵a m=2,a n=3,∴a2m+n=a2m•a n=(a m)2•a n=22×3=12.故答案为:12.考点:幂的乘方与积的乘方;同底数幂的乘法.点评:此题考查了同底数幂的乘法与幂的乘方的性质.此题难度适中,注意掌握积的乘方法则:(ab)n=a n b n(n是正整数)与同底数幂的乘法法则:a m•a n=a m+n(m,n是正整数),注意公式的逆用.15.四三【解析】试题分析:根据多项式的次数与项数的定义作答.解:∵(ab)2=a2b2,∴多项式﹣5(ab)2+ab+1是四次三项式.考点:幂的乘方与积的乘方;多项式.点评:本题主要考查了多项式的次数与项数的定义.几个单项式的和叫做多项式,其中每个单项式叫做多项式的项,一个多项式含有几项就叫几项式;多项式中次数最高的项的次数叫做多项式的次数.本题运用积的乘方的运算性质将(ab)2写成a2b2,是解题的关键.16.﹣2、2、4【解析】试题分析:由于(a﹣3)a+2=1,底数和指数都不确定,所以本题应分三种情况进行讨论.①若a﹣3≠±1时,根据零指数幂的定义,a+2=0,进而可以求出a的值;②若a﹣3=1时,1的任何次幂都等于1;③若a﹣3=﹣1时,﹣1的偶次幂等于1.解:①∵若a﹣3≠±1时,(a﹣3)a+2=1,∴a+2=0,∴a=﹣2.②若a﹣3=1时,1的任何次幂都等于1,∴a=4;③若a﹣3=﹣1时,﹣1的偶次幂等于1,∴a=2;故应填﹣2、2、4.考点:零指数幂.点评:本题主要考查了一些特殊数据的幂的性质,解题的关键是根据所给代数式的特点,分析a的值.17.16【解析】试题分析:根据数的乘方,零指数幂、积的乘方运算法则计算.解:=+1=;4101×0.2599=42×499×0.2599=16×(4×0.25)99=16×1=16.考点:零指数幂;有理数的乘方.点评:本题主要考查非0数的零指数幂是1,积的乘方运算的逆运算,熟练掌握运算性质是解决本题的关键.18.7【解析】试题分析:此题可对x+x﹣1=3两边同时平方求得x2+x﹣2的值.解:由于x+x﹣1=3,则(x+x﹣1)2=32,x2+x﹣2+2=9,即x2+x﹣2=7.word格式-可编辑-感谢下载支持故答案为7.考点:负整数指数幂.点评:本题主要考查整体法求值,涉及到负整数指数幂的知识点.19.p3;q2;p3q2.【解析】试题分析:利用幂的乘方和同底数幂的乘法法则计算即可.解:a3m=(a m)3=p3,a2n=(a n)2=q2,a3m+2n=a3m•a2n=p3q2.故填p3;q2;p3q2.考点:幂的乘方与积的乘方;同底数幂的乘法.点评:本题主要考查了幂的有关运算.幂的乘方,底数不变指数相乘;同底数幂的乘法,底数不变指数相加;熟练掌握性质是解题的关键.20.12【解析】试题分析:根据幂的乘方和同底数幂的乘法法则计算即可.解:∵a x=2,a y=3,∴a2x+y=a2x•a y,=(a x)2•a y,=4×3,=12.考点:幂的乘方与积的乘方;同底数幂的乘法.点评:本题主要考查了幂的有关运算.幂的乘方法则:底数不变指数相乘.同底数幂的乘法法则:底数不变指数相加.21.4.5【解析】试题分析:根据幂的乘方,同底数幂的除法,同底数幂的乘法的逆运算整理成已知条件的形式,然后代入数据求解即可.解:∵a m=9,a n=8,a k=4,∴a m﹣2k+n=a m÷a2k•a n,=a m÷(a k)2•a n,=9÷16×8,=4.5.考点:同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方.点评:本题主要考查幂的乘方,同底数幂的乘法,同底数幂的除法性质的逆运用,熟练掌握运算性质并灵活运用是解题的关键.22.【解析】试题分析:根据负整数指数幂的运算法则进行计算即可.解:原式==.故答案为.考点:负整数指数幂.点评:幂的负整数指数运算,先把底数化成其倒数,然后将负整数指数幂当成正的进行计算.23.106【解析】试题分析:用摩托车的声音强度除以说话声音强度,再利用同底数幂相除,底数不变指数相减计算.解:1011÷105=1011﹣5=106.答:摩托车的声音强度是说话声音强度的106倍.考点:同底数幂的除法.点评:本题主要考查同底数幂的除法的运算性质,熟练掌握运算性质是解题的关键.24.a9【解析】试题分析:根据同底数幂的乘法法则,同底数幂相乘,底数不变,指数相加,即a m•a n=a m+n 计算即可.解:a3•a6=a3+6=a9.考点:同底数幂的乘法.点评:主要考查同底数幂的乘法的性质,熟练掌握性质是解题的关键.25.①④【解析】试题分析:根据乘方的意义和幂的乘方的性质,利用排除法求解.解:①、乘方意义(﹣a4)2=(﹣a4)(﹣a4)=a4•a4=a8,正确;②、幂的乘方(﹣a4)2=a4×2=a8,错误;③、(﹣a4)2=(﹣a)4×2=(﹣a)8=a8,计算过程中(﹣a4)2应该等于a4×2,这里的负号不是底数a的,所以本答案错误.④、积的乘方(﹣a4)2=(﹣1×a4)2=(﹣1)2•(a4)2=a8,正确.故应填①④.考点:同底数幂的乘法;幂的乘方与积的乘方.点评:本题考查了同底数幂的乘法,幂的乘方的性质,熟练掌握各运算性质是解题的关键.26.243【解析】试题分析:根据积的乘方先求出结果,再根据幂的乘方得出9(x2n)3,代入求出即可.解:∵x2n=3,∴(3x3n)2=9x6n=9(x2n)3=9×33=9×27=243,故答案为:243.考点:幂的乘方与积的乘方.点评:本题考查了幂的乘方和积的乘方,有理数的混合运算的应用,注意:x mn=(x m)n,用了整体代入思想.27.1【解析】试题分析:根据非0数的0指数幂为1来解答.word格式-可编辑-感谢下载支持解:(﹣)0=1.考点:零指数幂.点评:解答此题要熟知,任何非0数的0次幂等于1.28.0【解析】试题分析:先利用积的乘方,去掉括号,再利用同底数幂的乘法计算,最后合并同类项即可.解:原式=a n﹣5(a2n+2b6m﹣4)+a3n﹣3b3m﹣6(﹣b3m+2),=a3n﹣3b6m﹣4+a3n﹣3(﹣b6m﹣4),=a3n﹣3b6m﹣4﹣a3n﹣3b6m﹣4,=0.考点:幂的乘方与积的乘方;同底数幂的乘法.点评:本题考查了合并同类项,同底数幂的乘法,幂的乘方,积的乘方,理清指数的变化是解题的关键.29.63【解析】试题分析:根据同底数的幂的乘法,把a m+n变成a m×a n,代入求出即可.解:∵a m=3,a n=21,∴a m+n=a m×a n=3×21=63.考点:同底数幂的乘法.点评:本题考查了同底数的幂的乘法的应用,关键是把a m+n变成a m×a n,题目比较好,但是一道比较容易出错的题目.30.(1)2 4 6(2)log24+log216=log264(3)log a(MN)(4)首先可设log a M=b1,log a N=b2,再根据幂的运算法则:a n•a m=a n+m以及对数的含义证明结论.【解析】试题分析:首先认真阅读题目,准确理解对数的定义,把握好对数与指数的关系.(1)根据对数的定义求解;(2)认真观察,不难找到规律:4×16=64,log24+log216=log264;(3)有特殊到一般,得出结论:log a M+log a N=log a(MN);(4)首先可设log a M=b1,log a N=b2,再根据幂的运算法则:a n•a m=a n+m以及对数的含义证明结论.解:(1)log24=2,log216=4,log264=6;(2)4×16=64,log24+log216=log264;(3)log a M+log a N=log a(MN);(4)证明:设log a M=b1,log a N=b2,则=M,=N,∴MN=,∴b1+b2=log a(MN)即log a M+log a N=log a(MN).考点:幂的乘方与积的乘方.点评:本题是开放性的题目,难度较大.借考查对数,实际考查学生对指数的理解、掌握的程度;要求学生不但能灵活、准确的应用其运算法则,还要会类比、归纳,推测出对数应有的性质.。
计算方法习题集

计算方法习题集(一)考核知识点误差的**型别;绝对误差和绝对误差限,相对误差和相对误差限,有效数字;绝对误差的传播。
(二)複习要求1.知道产生误差的主要**。
2.了解绝对误差和绝对误差限、相对误差和相对误差限和有效数字等概念以及它们之间的关係。
3.知道四则运算中的误差传播公式。
一、重点内容一个物理量的真实值和我们算出的值往往不相等,其差称为误差。
引起误差的原因是多方面的,主要有:模型误差,观测误差,截断误差,舍入误差。
在计算方法中主要讨论的是截断误差和舍入误差。
误差:设精确值x*的近似值为x,差e=x-x*称为近似值x的误差(绝对误差)。
误差限近似值x的误差限是误差e的一个上界,即|e|=|x-x*|≤ε。
相对误差er是误差e与精确值x*的比值,。
常用计算。
相对误差限是相对误差的最大限度,,常用计算相对误差限。
有效数字如果近似值x的误差限ε是它某一个数位的半个单位,我们就说x 準确到该位。
从这一位起到前面第一个非0数字为止的所有数字称为x的有效数字。
二、难点内容(1)设精确值x*的近似值x,x=±…an×10m,a1,a2,…,an是0~9之中的自然数,且a1≠0,|x-x*|≤ε=×10m-l,1≤l≤n。
则x有l位有效数字。
(2)设近似值x=±…an×10m有n位有效数字,则其相对误差限(3)设近似值x=±…an×10m的相对误差限不大于则它至少有n位有效数字。
(4)要求精确到10-3,取该数的近似值应保留4位小数。
三、例题例1设x*==…近似值x==×101,即m=1,它的误差是0.XX…,有,即n=3,故x=有3为有效数字。
x=3.14準确到小数点后第2位。
近似值x=,它的误差是…,有,即m=1,n=5,x=有5位有效数字。
近似值x=,它的误差是…,有即m=1,n=4,x=有4位有效数字。
这就是说某数有s位数,若末位数字是四捨五入得到的,那幺该数有s位有效数字;若末位数字不是四捨五入得到的,那幺该数有s位或s-1位有效数字。
最优化计算方法课后习题集答案解析

解:取 , 时,DFP法的第一步与最速下降法相同
, ,
,
以下作第二次迭代
,
其中,
,
所以
令 , 利用 ,求得
所以 ,
以下作第三次迭代
,
,
所以
令 , 利用 ,求得
所以 , 因为 ,于是停止
即为最优解。
习题四
包括题目: P95页 3;4;8;9(1);12选做;13选做
3题解如下
3.考虑问题 ,其中
X1,x2,x3≥0 (3)
求出点(1,1,0)处的一个下降可行方向.
解:首先检查在点(1,1,0)处哪些约束为有效约束。检查易知(1),X3≥0为有效约束。设所求可行方向d=(d1,d2,d3)T。根据可行方向d的定义,应存在a>0,使对∀t∈(0,a)能有
X+td=(1+td1,1+td2,0+td3)T
(1)
s.t.
(2)
s.t.
(1)解:非线性规划的K-T条件如下:
(1)
(2)
(3)
再加上约束条件 (4)
为求出满足(1)~(4)式的解,分情况考虑:
①若(4)式等号不成立,即 ,那么由(2)式得 ,将 代入(1)式解得 , ,所得值不满足 的条件,故舍去。
②若(4)式等号成立,由(1)式可以解得 , ,代入(4)式有:
JBi
1
2
3
4
5
6
7
8
9
di0
1
1
0
-5/6
-1/6
1
10/6
4
0
0
38/6
2
0
1
-9/6
《工程量计算》习题集(1)

3600 120
3600
120
H
3600
3600
解:
当H=3.0m时 S =(3.6×6+7.2+0.24) ×(5.4×2+2.4+0.24) ×5=1951.49(㎡)
分析:多层建筑物,当层高在2.20m及其以上者,应计算全面积
当H=2.0m时
S =(3.6×6+7.2+0.24)×(5.4×2+2.4+0.24)×4 +1/2(3.6×6+7.2+0.24)×(5.4×2+0.24)=1756.39(㎡)
平整场地工程量计算举例
例:计算下图平整场地的工程量。
解
平整场地工程量 S=(5.64×2+15.0)×9.24+5.64×2.12×2=266.74㎡
土石方工程量计算举例
【例】根据下图有关数据,计算室内回填土工程量。已知:室 内外地坪高差0.30m,C15混凝土地面垫层80厚,l:2水泥砂 浆面层25厚。
建筑面积计算举例(9)
例:计算下图剧院的建筑面积。
解 剧院建筑面积=(100+0.24)×(50+0.24)
=5036.06(㎡) 舞台灯光控制室建筑面积
=1/2× 3.14×1.242 ×4
=9.66(㎡) 总建筑面积=5036.06+9.66=5045.72(㎡)
建筑面积计算举例(10)
例:计算下图所示建筑物门斗的建筑面积。
现浇混凝土板工程量计算案例
【例】根据下图所示,计算现浇混凝土工程量 (1)、框架柱KZ1 (2)、框架梁KL-1,KL-2, KL-3
(3)、有梁板
现浇混凝土板工程量计算案例
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绪论(一)考核知识点误差的来源类型;绝对误差和绝对误差限,相对误差和相对误差限,有效数字;绝对误差的传播。
(二)复习要求1.知道产生误差的主要来源。
2.了解绝对误差和绝对误差限、相对误差和相对误差限和有效数字等概念以及它们之间的关系。
3.知道四则运算中的误差传播公式。
一、重点内容一个物理量的真实值和我们算出的值往往不相等,其差称为误差。
引起误差的原因是多方面的,主要有:模型误差,观测误差,截断误差,舍入误差。
在计算方法中主要讨论的是截断误差和舍入误差。
误差:设精确值x*的近似值为x,差e=x-x*称为近似值x的误差(绝对误差)。
误差限近似值x的误差限e是误差e的一个上界,即|e|=|x-x*|≤ε。
相对误差e r是误差e与精确值x*的比值,。
常用计算。
相对误差限是相对误差的最大限度,,常用计算相对误差限。
有效数字如果近似值x的误差限ε是它某一个数位的半个单位,我们就说x准确到该位。
从这一位起到前面第一个非0数字为止的所有数字称为x的有效数字。
二、难点内容(1)设精确值x*的近似值x,x=±0.a1a2…a n×10m,a1,a2,…,a n是0~9之中的自然数,且a1≠0,|x -x*|≤ε=0.5×10m-l,1≤l≤n。
则x有l位有效数字。
(2)设近似值x=±0.a1a2…a n×10m有n位有效数字,则其相对误差限(3)设近似值x=±0.a1a2…a n×10m的相对误差限不大于则它至少有n位有效数字。
(4)要求精确到10-3,取该数的近似值应保留4位小数。
三、例题例1设x*=p=3.1415926…近似值x=3.14=0.314×101,即m=1,它的误差是0.0015926…,有,即n=3,故x=3.14有3为有效数字。
x=3.14准确到小数点后第2位。
近似值x=3.1416,它的误差是0.0000074…,有即m=1,n=5,,x=3.1416有5位有效数字。
近似值x=3.1415,它的误差是0.0000926…,有即m=1,n=4,x=3.1415有4位有效数字。
这就是说某数有s位数,若末位数字是四舍五入得到的,那么该数有s位有效数字;若末位数字不是四舍五入得到的,那么该数有s位或s-1位有效数字。
例2指出下列各数具有几位有效数字,及其绝对误差限和相对误差限:2.0004 -0.00200 9000 9000.00解因为x1=2.0004=0.20004×101,它的误差限0.00005=0.5×101―5,即m=1,n=5,故x=2.0004有5位有效数字.相对误差限x2=-0.00200,误差限0.000005,因为m=-2,n=3,x2=-0.00200有3位有效数字。
相对误差限e r=0.00005/0.00200=0.25%。
x3=9000,绝对误差限为0.5,因为m=4,n=4,x3=9000有4位有效数字,相对误差限e r=0.5/9000=0.0056%x4=9000.00,绝对误差限0.005,因为m=4,n=6,x4=9000.00有6位有效数字,相对误差限为e r=0.005/9000.00=0.000056%由x3与x4可以看到小数点之后的0,不是可有可无的,它是有实际意义的。
例3ln2=0.69314718…,精确到10-3的近似值是多少?解精确到10-3=0.001,即绝对误差限是e=0.05,故至少要保留小数点后三位才可以。
Ln2»0.693。
例4如何去设计一个好的算法?答:一个好的算法必须满足:1、计算步骤简化以减少运算次数及误差积累;2、避免两个相同号数数值相近的数相减;3、计算若干同号数时的和,按绝对值增大的顺序相加;4、避免乘除法中数值绝对值过大或过小;5、防止大数吃掉小数;6、选用数值稳定性好的算法。
四、练习题1.设某数x*,它的保留三位有效数字的近似值的绝对误差是___________________________。
2.设某数x*,它的精确到10-4的近似值应取小数点后____位。
3.()的3位有效数字是0.236×102。
(A)235.54×10-1(B)235.418(C)2354.82×10-2(D)0.0023549×1034.设a*=2.718181828…,取a=2.718,则有(),称a有四位有效数字。
(A)(B)(C)(D)5.设某数x*,对其进行四舍五入的近似值是(),则它有3位有效数字,绝对误差限是。
(A)0.315 (B)0.03150 (C)0.0315 (D)0.003156.以下近似值中,保留四位有效数字,相对误差限为。
(A)0.01234 (B)–12.34 (C)–2.20 (D)0.2200五、练习题答案该数有效数字第四位的一半。
2.四 3.(A) 4.(B) 5.(C) 6.(D)方程求根(一) 考核知识点二分法;迭代法――牛顿法;弦截法。
(二)复习要求1.知道有根区间概念,方程f (x )=0在区间(a ,b )有根的充分条件。
2.掌握方程求根的二分法;二分法及二分次数公式,迭代法及其收敛性。
3.熟练掌握牛顿法,掌握初始值的选择条件。
4.掌握弦截法。
一、重点内容1.二分法:设方程f (x )=0在区间[a ,b ]内有根,用二分有根区间的方法,得到有根区间序列:x *≈x n =(a 0=a ,b 0=b ),n =0,1,2,…有误差估计式:½x *-x n ½≤,n =0,1,2,…,二分区间次数:2.牛顿法:用切线与x 轴的交点,逼近曲线f (x )与x 轴的交点。
迭代公式为(n =1,2,…),选初始值x 0满足f (x 0)f ²(x 0)>0,迭代解数列一定收敛。
3.弦截法:用两点连线与x 轴交点逼近曲线f (x )与x 轴的交点。
迭代公式为(n =1,2,…)二、难点内容:(1)、迭代法概念:若方程f (x )=0表成x =j(x ),于是有迭代格式:x n =j(x n -1)(n =1,2,…),,x *≈x n ,存在0<l <1,|¢j(x )|£l,在区间[a ,b ]内任一点为初始值进行迭代,迭代数列收敛。
(2)定理一:设)(x φ在区间【a,b 】上具有一阶连续的导数,且满足如下两个条件:①当],[b a x ∈时,],[)(b a x ∈φ;②存在正常数L<1,使得对任意],[b a x ∈有L x ≤')(φ。
则① 方程f(x)=0在区间【a,b 】上有唯一根;② 对任意],[0b a x ∈,迭代格式x =j(x )收敛,且*lim x x n n =∞→;(3)定理二:设方程f(x)=0在区间【a,b 】内有根x *,且当],[b a x ∈时,1)(≥'x φ,则对任意初始值],[0b a x ∈,且*≠x x 0,迭代格式x =j(x )发散。
(4)定理三(局部收敛):设方程x =j(x )有根x *,且在x *的某个邻域δ≤-=*x x x S 内j(x )存在一阶连续的导数,则①当1)(*<'x ϕ时,迭代公式)(1n n x x φ=+局部收敛;②当1)(*>'x ϕ时,迭代公式)(1n n x x φ=+发散。
(5)迭代序列收敛阶的概念若存在0<l <1,|¢j(x)|£l,在区间[a,b]内任一点为初始值进行迭代,迭代数列收敛。
设迭代序列{}n x 收敛于*x ,如果存在实数1≥p 与正常数c ,使得c xx x x pn n n =--**+∞→1lim,则称序列{}n x 是p 阶收敛于*x 。
特别地,当1=p 时,称序列{}n x 为线性(一次)收敛;{}n x 为线性收敛时,必须要求1<c 。
当2=p 时,称序列{}n x 为平方(二次)收敛;当21<<p 时,称序列{}n x 为超线性收敛;收敛阶p 越大,则序列{}n x 与*x 的误差缩减越快,也就是序列{}n x 收敛越快。
(6)定理四:若j(x )在x *附近的某个邻域内有)1(≥p p 阶连续导数,且0)(,0)(,,0)(,)(**)1(***≠=='=-x x x x x p p ϕϕϕϕ ,且对一个任意靠近x *的初始值,迭代公式)(1n n x x φ=+是p 阶收敛的。
三、例题例1证明方程1-x -sin x =0在区间[0,1]内有一个根,使用二分法求误差不超过0.5×10-4的根要迭代多少次?证明令f (x )=1-x -sin x , ∵f (0)=1>0,f (1)=-sin1<0 ∴f (x )=1-x -sin x =0在[0,1]有根。
又f ¹(x )=-1-c os x <0(x Î[0.1]),故f (x )=0在区间[0,1]内有唯一实根。
给定误差限e =0.5×10-4,有2877.1312ln 10ln 45.0ln 12ln ln )ln(=-+-=---≥εa b n ,只要取n =14。
例2用迭代法求方程x 5-4x -2=0的最小正根,计算过程保留4位小数。
[分析]容易判断[1,2]是方程的有根区间。
若建立迭代格式))2,1((145)(,42)(,42455∈>='-=-=x x x x x x x ϕϕ即,此时迭代发散。
建立迭代格式))2,1((542454)(,24)(,244455∈<+='+=+=x x x x x x x )(ϕϕ,此时迭代收敛。
解建立迭代格式,552+4=2+4=x x x x )(,ϕ,1=21∈54<2+454='04x x x x 取初始值)),,(()(ϕ,1.4316245501≈=+=x x , 1 1.505724.7245512≈=+=x x ,51.5160204.8245523≈=+=x x ,2 1.518066.8245534≈=+=x x , 1.51850728.8245545≈=+=x x 。
取≈*x 1.5185。
例3试建立计算3a 的牛顿迭代格式,并求3791411.的近似值,要求迭代误差不超过10-6。
[分析]首先建立迭代格式.确定取几位小数,求到两个近似解之差的绝对值不超过10-6。
解令0=-==33a x x f a x )(,,求x 的值.牛顿迭代格式为 ),...,,()()(10=3+32=3--='-=2231+k x ax x a x x x f x f x x kk k k k k k k k 。
