最新2.1.1-合情推理-课件教学讲义PPT
合集下载
课件2:2.1.1合情推理

(2)b2k-1=___2_____(用k表示).
8.已知在数列{an}中,a1=0,an+1=an+(2n-1),写出它的前4项, 并归纳出该数列的通项公式.
答案:a1=0,a2=1,a3=4,a4=9,…,an=(n-1)2
9.在平面内有 n(n∈N*,n ≥ 3)条直线,其中任意两条
不平行,任意三条不过同一点,若这 n 条直线把平面分成 f(n) 个 平 面 区 域 , 则 f (5) 的 值 是 _________ , f (n) 的 表 达 式 是
内切球的半径是高的 .
4._归__纳__类__比___和__类__比__推__理__都是根据已有的事实,经过____联__想____、 ____观__察____、___分__析_____、___比__较_____,再进行__归__纳__推__理__,然后提出猜想 的推理,把它们统称为合情推理.
自测自评
1.根据下图中所示的5个图形及相应点的个数的变化规律,试猜想 第n个图中有__n_2_-__n_+__1__个点.
2.类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四
体的下列性质,你认为比较恰当的是( D )
①各棱长相等,同一顶点上的任意两条棱的夹角都相等;
②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;
那么:
(1)在圆内画5条线段,它们彼此最多分割成多少条线段?将圆最多分 割成多少部分?
(2)猜想:圆内两两相交的n(n≥2)条线段,彼此最多分割成多少条线 段?将圆最多分割成多少部分?
解析:设圆内两两相交的 n 条线段彼此最多分割成的线段为 f(n)条,将圆最多分割为 g(n)部分.
(1)f(1)=1=12,g(1)=2=12+21+2; f(2)=4=22,g(2)=4=22+22+2; f(3)=9=32,g(3)=7=32+23+2; f(4)=16=42,g(4)=11=42+24+2; 所以 n=5 时,f(5)=25,g(5)=52+25+2=16.
8.已知在数列{an}中,a1=0,an+1=an+(2n-1),写出它的前4项, 并归纳出该数列的通项公式.
答案:a1=0,a2=1,a3=4,a4=9,…,an=(n-1)2
9.在平面内有 n(n∈N*,n ≥ 3)条直线,其中任意两条
不平行,任意三条不过同一点,若这 n 条直线把平面分成 f(n) 个 平 面 区 域 , 则 f (5) 的 值 是 _________ , f (n) 的 表 达 式 是
内切球的半径是高的 .
4._归__纳__类__比___和__类__比__推__理__都是根据已有的事实,经过____联__想____、 ____观__察____、___分__析_____、___比__较_____,再进行__归__纳__推__理__,然后提出猜想 的推理,把它们统称为合情推理.
自测自评
1.根据下图中所示的5个图形及相应点的个数的变化规律,试猜想 第n个图中有__n_2_-__n_+__1__个点.
2.类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四
体的下列性质,你认为比较恰当的是( D )
①各棱长相等,同一顶点上的任意两条棱的夹角都相等;
②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;
那么:
(1)在圆内画5条线段,它们彼此最多分割成多少条线段?将圆最多分 割成多少部分?
(2)猜想:圆内两两相交的n(n≥2)条线段,彼此最多分割成多少条线 段?将圆最多分割成多少部分?
解析:设圆内两两相交的 n 条线段彼此最多分割成的线段为 f(n)条,将圆最多分割为 g(n)部分.
(1)f(1)=1=12,g(1)=2=12+21+2; f(2)=4=22,g(2)=4=22+22+2; f(3)=9=32,g(3)=7=32+23+2; f(4)=16=42,g(4)=11=42+24+2; 所以 n=5 时,f(5)=25,g(5)=52+25+2=16.
课件6:2.1.1 合情推理
(2)分成两列数,奇数位的数:32,16,( ),4,2.偶数位的 数:31,26,( ),16,11,所以括号中的数依次是 8,21.
2.观察下列式子:1+212<32,1+212+312<54,1+212+312+412 <78,…,由此可以归纳出的一般结论是__________.
【答案】1+212+312+…+n12+n+112<2n2+n 1(n∈N*) 【解析】不等式的左边是i12的前 n+1 项和,右边的分母是 2n, 分子是 2n+1,故一般性的结论是 1+212+312+…+n12+n+112 <2n2+n 1(n∈N*).
2.1.1 合情推理
新知导学
1.归纳推理 由某类事物的_部__分___对__象__具有某些特征,推出该类事物的 __全__部__对__象__都具有这些特征的推理,或者由_个__别__事__实___概括出 _一__般__结__论___的推理,称为归纳推理(简称归纳).简言之,归纳 推理是由___部__分___到__整__体___、由__个__别___到__一__般___的推理. 2.金导电、银导电、铜导电、铁导电,金、银、铜、铁 都是金属,因此可猜想所有金属都导电,这种推理形式为 __归__纳__推__理__.
新知导学
3.类比推理 由 两 类 对 象 具 有 _某__些__类__似__特__征___ 和 其 中 一 类 对 象 的 __某__些__已__知__特__征__,推出另一类对象也具有_这__些__特__征___的推理称 为类比推理(简称类比).简言之,类比推理是由__特__殊__到__特__殊__ 的推理.
5.归纳推理是由部分到_整__体___,由具体到_抽__象___,由特 殊到_一__般___,从个别事实中概括出_一__般__结__论___的思维模式. 类比推理是在__两__类__不__同__的事物之间进行对比,找出若干相同 或相似之处之后,推测在其他方面也可能存在__相__同__或__相__似___
2.观察下列式子:1+212<32,1+212+312<54,1+212+312+412 <78,…,由此可以归纳出的一般结论是__________.
【答案】1+212+312+…+n12+n+112<2n2+n 1(n∈N*) 【解析】不等式的左边是i12的前 n+1 项和,右边的分母是 2n, 分子是 2n+1,故一般性的结论是 1+212+312+…+n12+n+112 <2n2+n 1(n∈N*).
2.1.1 合情推理
新知导学
1.归纳推理 由某类事物的_部__分___对__象__具有某些特征,推出该类事物的 __全__部__对__象__都具有这些特征的推理,或者由_个__别__事__实___概括出 _一__般__结__论___的推理,称为归纳推理(简称归纳).简言之,归纳 推理是由___部__分___到__整__体___、由__个__别___到__一__般___的推理. 2.金导电、银导电、铜导电、铁导电,金、银、铜、铁 都是金属,因此可猜想所有金属都导电,这种推理形式为 __归__纳__推__理__.
新知导学
3.类比推理 由 两 类 对 象 具 有 _某__些__类__似__特__征___ 和 其 中 一 类 对 象 的 __某__些__已__知__特__征__,推出另一类对象也具有_这__些__特__征___的推理称 为类比推理(简称类比).简言之,类比推理是由__特__殊__到__特__殊__ 的推理.
5.归纳推理是由部分到_整__体___,由具体到_抽__象___,由特 殊到_一__般___,从个别事实中概括出_一__般__结__论___的思维模式. 类比推理是在__两__类__不__同__的事物之间进行对比,找出若干相同 或相似之处之后,推测在其他方面也可能存在__相__同__或__相__似___
人教版选修2-2《2.1.1合情推理》课件(共23张PPT)
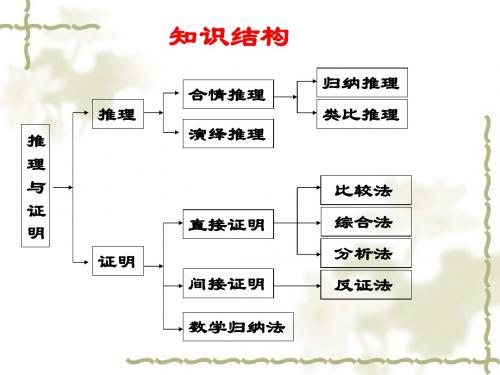
三棱锥
4
4
6
四棱锥
5
5
8
三棱柱
5
6
9
五棱锥
6
6
10
立方体
6
8
12
正八面体
8
6
12
五棱柱
截角正方体
尖顶塔
猜想 F+V-E=2 欧拉公式
多面体 面数(F) 顶点数(V) 棱数(E)
三棱锥
4
4
6
四棱锥
5
5
8
三棱柱
5
6
9
五棱锥
6
6
10
立方体
6
8
12
正八面体86Fra bibliotek12五棱柱
7
10
15
截角正方体 7
10
15
尖顶塔
7.利用等差数列性质类比等比数列性质
歌德巴赫猜想的提出过程:
3+7=10,3+17=20,13+17=30,
改写为:10=3+7,20=3+17,30=13+17.
6=3+3, 8=3+5,
10=5+5, 12=5+7, 14=7+7, 16=5+11,
18 =7+11, …,
1000=29+971, 1002=139+863,
…
这种由某类事物的部分对象具有某些特征, 推出该类事物的全部对象都具有这些特征 的推理,或者由个别事实概栝出一般结论 的推理,称为归纳推理.(简称;归纳)
解;设an表示移动n块金属片时的移动次数. 当n=1时,a1=1 当n=2时,a2= 3
2
1
3
解;设an表示移动n块金属片时的移动次数. 当n=1时,a1=1
2.1.1合情推理

9
9
A.28
B.32
3
9
C.11
D.48
第28页
答案 B
第29页
2.如图为一串白黑相间排列的珠子,按这种规律排列,那 么第2 016颗珠子应是什么颜色( )
A.白色 C.白色可能性大
B.黑色 D.黑色可能性大
第30页
答案 A
第31页
3.古希腊人常用小石子在沙摊上摆成各种形状来研究数.比如:
他们研究过上图(1)中的 1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,
第24页
思考题3
观察下列式子:1+212<32,1+212+312<53,1+
1 22
+312+412<74,…,则可归纳出:________.
第25页
【答案】 (1)1+212+312+412+…+n12<2n-n 1
第26页
课后巩固
第27页
1.数列12,35,151,270,…中的第五项为( )
第5页
第6页
第7页
第8页
第9页
第10页
题型一 归纳推理在数列中的应用 例1 (1)已知数列{an},满足a1=1,an+1=2an+1(n=1, 2,3,…). ①求a2,a3,a4,a5; ②归纳猜想通项公式an.
第11页
【解析】 ①当n=1时,知a1=1, 由an+1=2an+1,得a2=3, a3=7,a4=15,a5=31. ②由a1=1=21-1,a2=3=22-1, a3=7=23-1,a4=15=24-1,a5=31=25-1. 可归纳猜想出an=2n-1(n∈N*).
第14页
思考题1
(1)若将本例中的an+1=2an+1改为an+1=
2[1].1.1合情推理okppt课件
![2[1].1.1合情推理okppt课件](https://img.taocdn.com/s3/m/6e614f7ec8d376eeaeaa31d2.png)
1.如图,在平行四边形 ABCD 中,有
AC 2 BD2 2 AB2 AD2
那么,在平行六面体 ABCD A1B1C1D1 中,有
AC12 BD12 CA12 DB12 4( AB2 AD2 AA12 )
D1
C1
D A
C B
A1 D
A
B1
C
33
B
类比推理
由特殊到特殊的推理
类比推理 注意
R ________________ .
3V S1 S2 S3 S4 B
O
O D
C
46
练习
(直击高考:09浙江文第16题)
设等差数列an的前n项和为Sn ,则S4,S8 S4,
S12 S8,S16 S12成等差数列.类比以上结论:
设等比数列bn的前n项积为Tn ,
则T4,____,
_____,
6
佛教《百喻经》中有这样一则故事。 从前有一 位富翁想吃芒果,打发他的仆人到果园去买,并告诉 他:"要甜的,好吃的,你才买."仆人拿好钱就去了.到了 果园,园主说:"我这里树上的芒果个个都是甜的,你尝 一个看."仆人说:"我尝一个怎能知道全体呢 我应当个 个都尝过,尝一个买一个,这样最可靠."仆人于是自己 动手摘芒果,摘一个尝一口,甜的就都买回去.带回家去, 富翁见了,觉得非常恶心,一齐都扔了.
(2)用一类对象的已知特征去猜测另一类对象的特征, 从而得出一个猜想; (3)检验这个猜想.
观察、比较 联想、类推
猜想新结论
2、类比推理的一般模式:
A类事物具有性质a,b,c,d,
B类事物具有性质a’,b’,c’,
(a,b,c与a’,b’,c’相似或相同)
AC 2 BD2 2 AB2 AD2
那么,在平行六面体 ABCD A1B1C1D1 中,有
AC12 BD12 CA12 DB12 4( AB2 AD2 AA12 )
D1
C1
D A
C B
A1 D
A
B1
C
33
B
类比推理
由特殊到特殊的推理
类比推理 注意
R ________________ .
3V S1 S2 S3 S4 B
O
O D
C
46
练习
(直击高考:09浙江文第16题)
设等差数列an的前n项和为Sn ,则S4,S8 S4,
S12 S8,S16 S12成等差数列.类比以上结论:
设等比数列bn的前n项积为Tn ,
则T4,____,
_____,
6
佛教《百喻经》中有这样一则故事。 从前有一 位富翁想吃芒果,打发他的仆人到果园去买,并告诉 他:"要甜的,好吃的,你才买."仆人拿好钱就去了.到了 果园,园主说:"我这里树上的芒果个个都是甜的,你尝 一个看."仆人说:"我尝一个怎能知道全体呢 我应当个 个都尝过,尝一个买一个,这样最可靠."仆人于是自己 动手摘芒果,摘一个尝一口,甜的就都买回去.带回家去, 富翁见了,觉得非常恶心,一齐都扔了.
(2)用一类对象的已知特征去猜测另一类对象的特征, 从而得出一个猜想; (3)检验这个猜想.
观察、比较 联想、类推
猜想新结论
2、类比推理的一般模式:
A类事物具有性质a,b,c,d,
B类事物具有性质a’,b’,c’,
(a,b,c与a’,b’,c’相似或相同)
新课标高中数学A版必修2-2 2.1.1合情推理 优质课件 .ppt

类 比n 1维 球 的 情 形,从 中 获
得 启 发 和 联 想.
这 种 由 两 类 对 象 具 有 某些 类
似 特 征 和 其 中 一 类 对 象的 某
些 已 知 特 征,推 出 另 一 类 对 象
也 具 有 这 些 特 征 的 推 理称 为
类比推理 简称类比.简言之,
类 比 推 理 是 由 特 殊 到 特殊 的
用符号13表示,共移动了1次.
29
3把上面两个金属片从2号针移到3号针.
30
31
32
33
ห้องสมุดไป่ตู้
34
18
解 1两个实数经过加法运算或乘法运算后,所
得的结果仍然是一个实数.
19
3从逆运算角度考虑,二者都有逆运算,加法的逆
运算是减法,乘法的逆运算是除法,这就使得方程
ax 0
ax 1a 0
都有唯一解
x a
x 1 a
20
21
22
23
24
25
26
27
28
解 当n 1时,只需把金属片从一号针移到3号针,
1
2
3
4
5
2.1.1 合情推理
6
7
8
9
10
11
12
13
14
15
表 21
圆的概念和性质
球的类似概念和性质
圆的周长
圆的面积
圆心与弦非直径中
点的连线垂直于弦.
与圆心距离相等的两弦相等;
与圆心距离不等的两弦不等,
距圆心较近的弦较长.
以点x0,y0 为圆心,r为半
径的圆的方程为x x0 2
y y0 2 r2.
得 启 发 和 联 想.
这 种 由 两 类 对 象 具 有 某些 类
似 特 征 和 其 中 一 类 对 象的 某
些 已 知 特 征,推 出 另 一 类 对 象
也 具 有 这 些 特 征 的 推 理称 为
类比推理 简称类比.简言之,
类 比 推 理 是 由 特 殊 到 特殊 的
用符号13表示,共移动了1次.
29
3把上面两个金属片从2号针移到3号针.
30
31
32
33
ห้องสมุดไป่ตู้
34
18
解 1两个实数经过加法运算或乘法运算后,所
得的结果仍然是一个实数.
19
3从逆运算角度考虑,二者都有逆运算,加法的逆
运算是减法,乘法的逆运算是除法,这就使得方程
ax 0
ax 1a 0
都有唯一解
x a
x 1 a
20
21
22
23
24
25
26
27
28
解 当n 1时,只需把金属片从一号针移到3号针,
1
2
3
4
5
2.1.1 合情推理
6
7
8
9
10
11
12
13
14
15
表 21
圆的概念和性质
球的类似概念和性质
圆的周长
圆的面积
圆心与弦非直径中
点的连线垂直于弦.
与圆心距离相等的两弦相等;
与圆心距离不等的两弦不等,
距圆心较近的弦较长.
以点x0,y0 为圆心,r为半
径的圆的方程为x x0 2
y y0 2 r2.
数学:2.1.1《合情推理与演绎推理-合情推理》PPT课件

第八页,编辑于星期日:十二点 一分。
哥德巴赫猜想(Goldbach Conjecture)
在陈景润之前,关於偶数可表示为 s个质数的乘积 与t个质数的乘积之和( 简称“s + t ”问题)之进展情况如下: 1920年,挪威的布朗(Brun)证明了 “9 + 9 ”。 1924年,德国的拉特马赫(Rademacher)证明了“7 + 7 ”。 1932年,英国的埃斯特曼(Estermann)证明了 “6 + 6 ”。 1937年,意大利的蕾西(Ricei)先後证明了“5 + 7 ”, “4 + 9 ”, “3 + 15 ”和“2 + 366 ”。 1938年,苏联的布赫 夕太勃(Byxwrao)证明了“5 + 5 ”。 1940年,苏联的布赫 夕太勃(Byxwrao)证明了 “4 + 4 ”。 1948年,匈牙利的瑞尼(Renyi)证明了“1 + c ”,其中c是一很大的自然 数。 1956年,中国的王元证明了 “3 + 4 ”。 1957年,中国的王元先後证明了 “3 + 3 ”和 “2 + 3 ”。 1962年,中国的潘承洞和苏联的巴尔巴恩(BapoaH)证明了 “1 + 5 ”, 中 国的王元证明了“1 + 4 ”。 1965年,苏联的布赫 夕太勃(Byxwrao)和小维诺格拉多夫(BHHopappB),及 意大利的朋比利(Bombieri)证明了“1 + 3 ”。 1966年,中国的陈景润证明了 “1 + 2 ”。 最终会由谁攻克 “1 + 1 ”这个难题呢?现在还没法预测。
即:偶数=奇质数+奇质数
第五页,编辑于星期日:十二点 一分。
哥德巴赫猜想(Goldbach Conjecture)
哥德巴赫猜想(Goldbach Conjecture)
在陈景润之前,关於偶数可表示为 s个质数的乘积 与t个质数的乘积之和( 简称“s + t ”问题)之进展情况如下: 1920年,挪威的布朗(Brun)证明了 “9 + 9 ”。 1924年,德国的拉特马赫(Rademacher)证明了“7 + 7 ”。 1932年,英国的埃斯特曼(Estermann)证明了 “6 + 6 ”。 1937年,意大利的蕾西(Ricei)先後证明了“5 + 7 ”, “4 + 9 ”, “3 + 15 ”和“2 + 366 ”。 1938年,苏联的布赫 夕太勃(Byxwrao)证明了“5 + 5 ”。 1940年,苏联的布赫 夕太勃(Byxwrao)证明了 “4 + 4 ”。 1948年,匈牙利的瑞尼(Renyi)证明了“1 + c ”,其中c是一很大的自然 数。 1956年,中国的王元证明了 “3 + 4 ”。 1957年,中国的王元先後证明了 “3 + 3 ”和 “2 + 3 ”。 1962年,中国的潘承洞和苏联的巴尔巴恩(BapoaH)证明了 “1 + 5 ”, 中 国的王元证明了“1 + 4 ”。 1965年,苏联的布赫 夕太勃(Byxwrao)和小维诺格拉多夫(BHHopappB),及 意大利的朋比利(Bombieri)证明了“1 + 3 ”。 1966年,中国的陈景润证明了 “1 + 2 ”。 最终会由谁攻克 “1 + 1 ”这个难题呢?现在还没法预测。
即:偶数=奇质数+奇质数
第五页,编辑于星期日:十二点 一分。
哥德巴赫猜想(Goldbach Conjecture)
《2.1.1 合情推理》PPT课件(安徽省市级优课)

答:C60分子中有90条棱.
应用归纳推理可以 发现新事实,获得新结论!
“世界末日”的传说.
在印度北部的一个佛教的圣庙里,桌上的黄铜板上,放 着三根宝石针,据说印度教的主神梵天在创造世界时,在 其中的一根针上,自上而下由小到大放了六十四片金 片.每天二十四小时内,都有僧侣值班,按照以下的规律, 不停地把这些金片在三根宝石针上移来移去:每次只准移 动一片,且不论在那根针上“,较小的金片只能放在较大的 金片上.当所有六十四片金片都从梵天创造世界时所放的 那根针上移到另一根针上时,世界的末日就要到临.
(1)对有限的资料进行观察、分析、归纳 整理;
(2)剔除不带有规律性的结论,即猜想; (3)检验猜想。
归纳推理所得的结论仅是一种猜想,未必可靠,还 需证明 例如,法国数学家费马观察到
221 1 5, 222 1 17, 223 1 257, 224 1 65537
都是质数,于是他用归纳推理提出猜想:任何形如
可以根据已知的递推公式,算出数列的前几项, 然后归纳猜想它的通项公式。
an
1 n
.
在例1和例2中,我们通过归纳得到了两个 猜想。虽然它们是否正确还有待严格的证明, 但猜想可以为我们的研究提供一种方向。
应用示例:
例3、 1996年的诺贝尔化学奖授予 对发现C60有重大贡献的三位科学 家.C60是有60 个C原子组成的分子, 它结构为简单多面体形状.这个多面 体有60个顶点,各面的形状只有五边 形或六边形两种.其中五边形和六边 形的面各有12个和20个.
由此猜想,n为任何正整数时 f(n)=n2+n+41都是质数
n=40呢?
归纳推理
由某类事物的部分对象具有某些特征,推出该类事物 的全部对象都具有这些特征,或者由个别事实概括出一般 性的结论,这样的推理称为归纳推理(简称归纳).
应用归纳推理可以 发现新事实,获得新结论!
“世界末日”的传说.
在印度北部的一个佛教的圣庙里,桌上的黄铜板上,放 着三根宝石针,据说印度教的主神梵天在创造世界时,在 其中的一根针上,自上而下由小到大放了六十四片金 片.每天二十四小时内,都有僧侣值班,按照以下的规律, 不停地把这些金片在三根宝石针上移来移去:每次只准移 动一片,且不论在那根针上“,较小的金片只能放在较大的 金片上.当所有六十四片金片都从梵天创造世界时所放的 那根针上移到另一根针上时,世界的末日就要到临.
(1)对有限的资料进行观察、分析、归纳 整理;
(2)剔除不带有规律性的结论,即猜想; (3)检验猜想。
归纳推理所得的结论仅是一种猜想,未必可靠,还 需证明 例如,法国数学家费马观察到
221 1 5, 222 1 17, 223 1 257, 224 1 65537
都是质数,于是他用归纳推理提出猜想:任何形如
可以根据已知的递推公式,算出数列的前几项, 然后归纳猜想它的通项公式。
an
1 n
.
在例1和例2中,我们通过归纳得到了两个 猜想。虽然它们是否正确还有待严格的证明, 但猜想可以为我们的研究提供一种方向。
应用示例:
例3、 1996年的诺贝尔化学奖授予 对发现C60有重大贡献的三位科学 家.C60是有60 个C原子组成的分子, 它结构为简单多面体形状.这个多面 体有60个顶点,各面的形状只有五边 形或六边形两种.其中五边形和六边 形的面各有12个和20个.
由此猜想,n为任何正整数时 f(n)=n2+n+41都是质数
n=40呢?
归纳推理
由某类事物的部分对象具有某些特征,推出该类事物 的全部对象都具有这些特征,或者由个别事实概括出一般 性的结论,这样的推理称为归纳推理(简称归纳).
课件5:2.1.1 合情推理

(2)归纳推理的步骤 ①归纳对有限资料进行观察、分析,发现某些相同性质.一 般地,如果归纳的个别情况越多越具有代表性,那么推广的 一般性命题就越可能为真. ②猜想:在以上基础上提出带有规律性的结论. ③检验:检验猜想.
2.类比推理 (1)类比推理的一般步骤 ①找出两类事物之间的相似性或一致性. ②用一类事物的性质去推测另一类事物的性质,得出一 个明确的命题. (2)类比推理的特点 ①类比是从人们已经掌握了的事物的属性,推测正在研 究中的事物的属性,以旧认识为基础,类比出新结果.
2.1 合情推理与演绎推理 2.1.1 合情推理
●三维目标 1.知识与技能 了解合情推理的含义,认识归纳推理的基本方法与步 骤,能利用归纳进行简单的推理应用.
2.过程与方法
通过学生的积极参与,经历归纳推理概念的获得过程,了 解归纳推理的含义.让学生通过欣赏一些伟大猜想产生的 过程,体会如何利用归纳去猜测和发现一些新的结论,培 养学生归纳推理的思维方式.
本节内容结束 更多精彩内容请登录:
,得 3
f(0)+f(1)=30+1
3+31+1
3
= 33,
f(-2)+f(3)=3-2+1
3+33+1
= 3
3 3.
归纳猜想一般性结论为
f(-x)+f(x+1)=
3 3
证明如下:
f(
-
x)
+
f(x
+
1)
=
1 3-x+
3
+
1 3x+1+
3
=
3x 1+ 3·3x
+
1 3x+1+
= 3
3+3·33xx+1+3x+1+1
算上具有相似性.等差与等比类比是和与积、倍与乘方、商与开
2.1.1合情推理课件

解:猜想:sin2θ+cos2(θ+30°)+sin θcos(θ+30°)=34. 证明:∵sin2θ+cos2(θ+30°)+sin θcos(θ+30°)
=sin2θ+ 23cos θ-12sin θ2+sin θ 23cos θ-12sin θ
=sin2θ+
3 2 cos
θ-12sin
θ
3 2 cos
含义 __分__析__、__比__较__、_联__想___,再进行__归__纳__、__类__比__,然后 提出_猜__想___的推理,我们把它们统称为合情推理
过程
从具体问题出发
→
观察、分析 比较、联想
→
归纳、类比
→ 提出猜想
题点知识巩固
知识点一 归纳推理 1.(2019·湖南邵东月考)设 f0(x)=cos x,f1(x)=f0′(x),f2(x)
2.1.1 合情推理
基础知识梳理
1.归纳推理和类比推理
归纳推理
类比推理
由某类事物的部__分__对__象__具有 由两类对象具有某些_类__似___
某些特征,推出该类事物的
定义
__全__部__对__象__都具有这些特征 的推理,或者由_个__别__事___实__
特征和其中一类对象的某些 __已__知__特__征__,推出另一类对
θ+12sin
θ Βιβλιοθήκη =sin2θ+34cos2θ-14sin2θ=34.
∴等式成立.
在△AHD 中,∠DAH=90°,AO⊥DH, 有 AH2=OH·DH. S2△ABC=12BC·AH2=14BC2·AH2, S△BCO·S△BCD=12BC·OH·12BC·DH=14BC2·OH·DH, ∴S2△ABC=S△BCO·S△BCD,A 正确.
课件4:2.1.1 合情推理

点评:以上归纳推出一般性结论的方法称作不完 全归纳法,由不完全归纳法推出的结论不一定正 确,必须通过证明才能最后得出正确的结论.
命题方向:归纳推理在几何问题中的应用
例2:数一数图中的凸多面体的面数F、顶点数V和棱 数E,然后用归纳推理得出它们之间的关系.
【解析】仔细观察,通过几何图形的构造特征,找出 三者之间的关系. 解:各多面体的面数F、顶点数V、棱数E如下表所示.
所以a33=a6×5+3=a3=3,故选A. 【答案】A
2.由170>58,191>180,1235>291,…若 a>b>0,m>0,则ba+ +mm
与ba之间的大小关系为
()
A.相等 B.前者大 C.后者大 D.不确定
【解析】∵170=58++22>58,191=180++11>180, 1235=291++44>291,…都成立, ∴猜想:若 a>b>0,m>0,则ab++mm>ba,下面证明 ∵ba++mm-ba=ab+aam(a-+amb)-bm=ma((aa+-mb))>0, ∴ba++mm>ba,故应选 B.
多面体 三棱锥 四棱锥 三棱柱 五棱锥 正方体 正八面体 五棱柱 截角正方体 尖顶塔
面数(F) 4 5 5 6 6 8 7 7 9
顶点数(V) 4 5 6 6 8 6 10 10 9
棱数(E) 6 8 9 10 12 12 15 15 16
观察其数字特征:
4+4-6=2;
5+5-8=2;
5+6-9=2; 6+6-10=2;
个别事实 概括出 一般结论 的推理,称为归纳推理 (简称归纳).简言之,归纳推理是由 部分 到 整体、由 个别 到一般 的推理.归纳推理包括 不完全归纳法 和 完全归纳法.
2.1.1合情推理课件人教新课标

自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
归纳推理
定义
特征
由某类事物的_部__分__对__象__具有某些特征, 归纳推理是由
推出该类事物的__全__部__对__象__都具有这些 _部__分__到__整__体___、
特征的推理,或者由_个__别__事__实___概括出 由_个__别__到__一__般___
方法二:5件首饰的珠宝颗数依次为:1,1+5,1+5+9,1+5 +9+13,1+5+9+13+17,则第6件首饰上的珠宝颗数为1+5 +9+13+17+21=66,即每件首饰上的珠宝数是以1为首项, 4为公差的等差数列的前n项和,故第n件首饰的珠宝颗数为1+ 5+9+…+(4n-3)=2n2-n.
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
2.类比推理的特点及适用前提 (1)类比推理的特点 ①类比是由已经解决的问题和已经获得的知识出发,估计 正在研究的事物的属性,提出新问题,作出新发现. ②类比的结果是猜测性的,不一定可靠,但它有发现功 能.
数学 选修2-2
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
高效测评 知能提升
合情推理
1.合情推理的含义 归纳推理和类比推理都是根据已有的事实,经过_视__察___、 _分__析____、_比__较___、___联__想_,再进行__归__纳___、_类__比___,然后提 出__猜__想___的推理,我们把它们统称为合情推理. 2.合情推理的过程
数学 选修2-2
第二章 推理与证明
自主学习 新知突破
合作探究 课堂互动
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-方程 --.-------------------------------------------------------
-
--------.
利用圆的性质类比得出求的性质
圆的概念和性质
圆的周长 S = 2πR
圆的面积 S =πR2
圆心与弦(非直径)中点的连线 垂直于弦
球的概念和性质
球的表面积 S = 4πR2
-F共16个计数符号,这些符号与十进制
的数的对应关系如下表;
十六进位 0 1 2 3 4 5 6 7
十进位
012345 6 7
十六进位 8 9 A B C D E F
十进位
8 9 10 11 12 13 14 15
例如用16进位制表示E+D=1B,则 A×B=( A )
A.6E B.72 C.5F D.0B
2.1.1-合情推理-课件
哥德巴赫猜想(Goldbach Conjecture)
目前最佳的结果是中国数学家陈景润於1966年 证明的,称为陈氏定理(Chen‘s Theorem) ? “任何充份大的偶数都是一个质数与一个自然 数之和,而後者仅仅是两个质数的乘积。” 通常都简称这个结果为大偶数可表示为 “1 + 2 ”的形式。
2
1
3
费马猜想
221 1 5, 222 1 17, 223 1 257, 224 1 65537, 都是质数
猜想:22n 1是质数.
半个世纪之后,欧拉发现:
225 1 4294967297 641 6700417
不是质数,从而推翻了费马的猜想
练习:计算机中常用的十六进位制是逢1
6进1的计算制,采用数字0-9和字母A
球的体积 V = 4πR3
3
球心与不过球心的截面(圆面) 的圆点的连线垂直于截面
与圆心距离相等的两弦相等 与球心距离相等的两截面面积相等
与圆心距离不相等的两弦不相 与球心距离不相等的两截面面积
等,距圆心较近的弦较长
不相等,距球心较近的面积较大
以点(x0,y0)为圆心, r为半径 的圆的方程为(x-x0)2+(yy0)2 = r2
归纳推理的一般步骤:
⑴ 对有限的资料进行观察、分析、归纳 整理;
⑵ 提出带有规律性的结论,即猜想; ⑶ 检验猜想。
例1:已知数列{an}的第1项a1=1且a n +1
=
an 1 + an
(n=1,2,3 …),试归纳出这个数列的通项公式
.
答案:an=1/n
1.工匠鲁班类比带齿的草叶和蝗虫的牙齿,发 明了锯 2.仿照鱼类的外型和它们在水中沉浮的原理, 发明了潜水艇.
B c2=a2+b2
a
c
s1 o s2 s3
Cb
A
ห้องสมุดไป่ตู้
B
C
猜想: S2△ABC =S2△AOB+S2△AOC+S2△BOC
我们把前面所进行的推理过程概括为:
从具体问题出发 → 观察、分析、比较、联想
→归纳、类比→ 提出猜想
可见,归纳推理和类比推理都是根据已有的事实, 经过观察、分析、比较、联想,再进行归纳、类 比,然后 提出猜想的推理,我们把它们统称为 合情推理.
3.科学家对火星进行研究,发现火星与地球有许 多类似的特征; 1)火星也绕太阳运行、饶轴自转的行星; 2)有大气层,在一年中也有季节变更; 3)火星上大部分时间的温度适合地球上某些已 知生物的生存,等等.
科学家猜想;火星上也可能有生命存在.
4)利用平面向量的本定理类比得到空间向量的 基本定理.
这种由两类对象具有某些类似特征和其中 一类对象的某些已知特征,推出在另一类 对象也具有这些特征的推理, 称为类比推 理.(简称;类比) 类比推理的几个特点;
1.类比是从人们已经掌握了的事物的属性,推测正 在研究的事物的属性,是以旧有的认识为基础,类比 出新的结果. 2.类比是从一种事物的特殊属性推测另一种事物的 特殊属性.
3.类比的结果是猜测性的不一定可靠,单它却有发 现的功能.
例2:类比平面内直角三角形的勾股定理 ,试给出空间中四面体性质的猜想.
A
河内塔(Tower of Hanoi)
例3.传说在古老的印度有一座神庙,神庙中有三根针和套 在一根针上的64个圆环.古印度的天神指示他的僧侣们按下列规 则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡 ”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面. 如果有一天,僧侣们将这64个圆环全部移到另一根针上, 那么世界末日就来临了. 请你试着推测:把 64 个圆环从1号针移到3号针,最少需要 移动多少次?把n个圆环从1号针移到3号针最少需要移动多少次 ?
2
1
3
设 an为把 n 个圆环从1号针移到3号针的最少次数,则
n =1时,a1 =1 第1个圆环从1到
3.
2
1
3
设 an为把 n 个圆环从1号针移到3号针的最少次数,则
n =1时,a1 =1 第1个圆环从1到3. n =2时,a2=3 前1个圆环从1到2;
第2个圆环从1到3; 第1个圆环从2到3.
练习2:(2001年上海)已知两个圆①x2+y2=1: 与②x2+(y-3)2=1,则由①式减去②式可得上述 两圆的对称轴方程.将上述命题在曲线仍然 为圆的情况下加以推广,即要求得到一个更 一般的命题,而已知命题应成为所推广命题 的一个特例,推广的命题为设圆---的---方--程---为--①----------(-x----a-)2+(y-b)2=r2与②(x-c)2+(y-d)2=r2(a≠c或 --b-≠---d--)-,--则--由---①---式--减---去--②---式---可--得---上--述---两---圆--的---对---称--轴--
以点(x0,y0,z0)为球心, r为半 径的球的方程为(x-x0)2+(yy0)2+(z-z0)2 = r2
子宫腺肌病
子宫腺肌病(adenomyosis,ADM)是指 异位内膜浸润正常的子宫肌层,周围平 滑肌细胞增生包裹异位的内膜上皮和基
2
1
3
设 an为把n 个圆环从1号针移到3号针的最少次数,则
n=1时, a1 =1 第1个圆环从1到3. n=2时, a2=3 前1个圆环从1到2;
猜想:a64=264-1
第2个圆环从1到3;
n=3时,a3=7
前1个圆环从2到3. 前2个圆环从1到2;
猜想:an=2n-1
n=4时,a4=15
第3个圆环从1到3; 前2个圆环从2到3.
-
--------.
利用圆的性质类比得出求的性质
圆的概念和性质
圆的周长 S = 2πR
圆的面积 S =πR2
圆心与弦(非直径)中点的连线 垂直于弦
球的概念和性质
球的表面积 S = 4πR2
-F共16个计数符号,这些符号与十进制
的数的对应关系如下表;
十六进位 0 1 2 3 4 5 6 7
十进位
012345 6 7
十六进位 8 9 A B C D E F
十进位
8 9 10 11 12 13 14 15
例如用16进位制表示E+D=1B,则 A×B=( A )
A.6E B.72 C.5F D.0B
2.1.1-合情推理-课件
哥德巴赫猜想(Goldbach Conjecture)
目前最佳的结果是中国数学家陈景润於1966年 证明的,称为陈氏定理(Chen‘s Theorem) ? “任何充份大的偶数都是一个质数与一个自然 数之和,而後者仅仅是两个质数的乘积。” 通常都简称这个结果为大偶数可表示为 “1 + 2 ”的形式。
2
1
3
费马猜想
221 1 5, 222 1 17, 223 1 257, 224 1 65537, 都是质数
猜想:22n 1是质数.
半个世纪之后,欧拉发现:
225 1 4294967297 641 6700417
不是质数,从而推翻了费马的猜想
练习:计算机中常用的十六进位制是逢1
6进1的计算制,采用数字0-9和字母A
球的体积 V = 4πR3
3
球心与不过球心的截面(圆面) 的圆点的连线垂直于截面
与圆心距离相等的两弦相等 与球心距离相等的两截面面积相等
与圆心距离不相等的两弦不相 与球心距离不相等的两截面面积
等,距圆心较近的弦较长
不相等,距球心较近的面积较大
以点(x0,y0)为圆心, r为半径 的圆的方程为(x-x0)2+(yy0)2 = r2
归纳推理的一般步骤:
⑴ 对有限的资料进行观察、分析、归纳 整理;
⑵ 提出带有规律性的结论,即猜想; ⑶ 检验猜想。
例1:已知数列{an}的第1项a1=1且a n +1
=
an 1 + an
(n=1,2,3 …),试归纳出这个数列的通项公式
.
答案:an=1/n
1.工匠鲁班类比带齿的草叶和蝗虫的牙齿,发 明了锯 2.仿照鱼类的外型和它们在水中沉浮的原理, 发明了潜水艇.
B c2=a2+b2
a
c
s1 o s2 s3
Cb
A
ห้องสมุดไป่ตู้
B
C
猜想: S2△ABC =S2△AOB+S2△AOC+S2△BOC
我们把前面所进行的推理过程概括为:
从具体问题出发 → 观察、分析、比较、联想
→归纳、类比→ 提出猜想
可见,归纳推理和类比推理都是根据已有的事实, 经过观察、分析、比较、联想,再进行归纳、类 比,然后 提出猜想的推理,我们把它们统称为 合情推理.
3.科学家对火星进行研究,发现火星与地球有许 多类似的特征; 1)火星也绕太阳运行、饶轴自转的行星; 2)有大气层,在一年中也有季节变更; 3)火星上大部分时间的温度适合地球上某些已 知生物的生存,等等.
科学家猜想;火星上也可能有生命存在.
4)利用平面向量的本定理类比得到空间向量的 基本定理.
这种由两类对象具有某些类似特征和其中 一类对象的某些已知特征,推出在另一类 对象也具有这些特征的推理, 称为类比推 理.(简称;类比) 类比推理的几个特点;
1.类比是从人们已经掌握了的事物的属性,推测正 在研究的事物的属性,是以旧有的认识为基础,类比 出新的结果. 2.类比是从一种事物的特殊属性推测另一种事物的 特殊属性.
3.类比的结果是猜测性的不一定可靠,单它却有发 现的功能.
例2:类比平面内直角三角形的勾股定理 ,试给出空间中四面体性质的猜想.
A
河内塔(Tower of Hanoi)
例3.传说在古老的印度有一座神庙,神庙中有三根针和套 在一根针上的64个圆环.古印度的天神指示他的僧侣们按下列规 则,把圆环从一根针上全部移到另一根针上,第三根针起“过渡 ”的作用.
1.每次只能移动1个圆环;
2.较大的圆环不能放在较小的圆环上面. 如果有一天,僧侣们将这64个圆环全部移到另一根针上, 那么世界末日就来临了. 请你试着推测:把 64 个圆环从1号针移到3号针,最少需要 移动多少次?把n个圆环从1号针移到3号针最少需要移动多少次 ?
2
1
3
设 an为把 n 个圆环从1号针移到3号针的最少次数,则
n =1时,a1 =1 第1个圆环从1到
3.
2
1
3
设 an为把 n 个圆环从1号针移到3号针的最少次数,则
n =1时,a1 =1 第1个圆环从1到3. n =2时,a2=3 前1个圆环从1到2;
第2个圆环从1到3; 第1个圆环从2到3.
练习2:(2001年上海)已知两个圆①x2+y2=1: 与②x2+(y-3)2=1,则由①式减去②式可得上述 两圆的对称轴方程.将上述命题在曲线仍然 为圆的情况下加以推广,即要求得到一个更 一般的命题,而已知命题应成为所推广命题 的一个特例,推广的命题为设圆---的---方--程---为--①----------(-x----a-)2+(y-b)2=r2与②(x-c)2+(y-d)2=r2(a≠c或 --b-≠---d--)-,--则--由---①---式--减---去--②---式---可--得---上--述---两---圆--的---对---称--轴--
以点(x0,y0,z0)为球心, r为半 径的球的方程为(x-x0)2+(yy0)2+(z-z0)2 = r2
子宫腺肌病
子宫腺肌病(adenomyosis,ADM)是指 异位内膜浸润正常的子宫肌层,周围平 滑肌细胞增生包裹异位的内膜上皮和基
2
1
3
设 an为把n 个圆环从1号针移到3号针的最少次数,则
n=1时, a1 =1 第1个圆环从1到3. n=2时, a2=3 前1个圆环从1到2;
猜想:a64=264-1
第2个圆环从1到3;
n=3时,a3=7
前1个圆环从2到3. 前2个圆环从1到2;
猜想:an=2n-1
n=4时,a4=15
第3个圆环从1到3; 前2个圆环从2到3.
