二分图匹配详解(C++版)
图论:二分图多重匹配

图论:⼆分图多重匹配使⽤最⼤流和费⽤流解决⼆分图的多重匹配之前编辑的忘存了好⽓啊。
本来打算学完⼆分图的乱七⼋糟的匹配之后再去接触⽹络流的,提前撞到了之前我们说的⼆分图最⼤匹配和⼆分图最⼤权匹配有⼀个特点,那就是没个点只能与⼀条边相匹配如果规定⼀个点要与L条边相匹配,这样的问题就是⼆分图的多重匹配问题然后根据边是否带权重,⼜可以分为⼆分图最⼤多重匹配和⼆分图最⼤权多重匹配(⼆分图多重最佳完美匹配)⾸先给出⼆分图多重最⼤匹配的做法:在原图上建⽴源点S和汇点T,S向每个X⽅点连⼀条容量为该X⽅点L值的边,每个Y⽅点向T连⼀条容量为该Y⽅点L值的边原来⼆分图中各边在新的⽹络中仍存在,容量为1(若该边可以使⽤多次则容量⼤于1),求该⽹络的最⼤流,就是该⼆分图多重最⼤匹配的值然后给出⼆分图多重最优匹配(⼆分图多重最⼤权匹配)的做法:在原图上建⽴源点S和汇点T,S向每个X⽅点连⼀条容量为该X⽅点L值、费⽤为0的边,每个Y⽅点向T连⼀条容量为该Y⽅点L值、费⽤为0的边原来⼆分图中各边在新的⽹络中仍存在,容量为1(若该边可以使⽤多次则容量⼤于1),费⽤为该边的权值。
求该⽹络的最⼤费⽤最⼤流,就是该⼆分图多重最优匹配的值这道题⾥⾯,⼀共有X⽅点这么多的电影,每个电影需要拍摄多少天就是对应的X⽅点L值,然后每⼀天是⼀个Y⽅点,由于每⼀天只能拍摄⼀部电影,所有Y⽅点的L值均为1下⾯介绍⼀下实现:int n,sum,cnt,ans;int g[maxn],cur[maxn];int str[25][10];struct Edge{int u,v,next,cap,flow;}e[maxm];这⾥⾯的cur数组是g数组的临时数组str⽤来保存每⼀个电影可以在哪⼀天拍摄Edge是⽹络流图⾥⾯的边void addedge(int u,int v,int c){e[++cnt].u=u;e[cnt].v=v;e[cnt].cap=c;e[cnt].flow=0;e[cnt].next=g[u];g[u]=cnt;e[++cnt].u=v;e[cnt].v=u;e[cnt].cap=0;e[cnt].flow=0;e[cnt].next=g[v];g[v]=cnt;}建图的时候,注意怎么赋值的接下来根据题意建图:for(int i=1;i<=n;i++){for(int j=1;j<=7;j++)scanf("%d",&str[i][j]);scanf("%d%d",&d,&w);sum+=d;addedge(0,i,d); //容量为需要多少天for(int j=1;j<=7;j++)for(int k=0;k<w;k++)if(str[i][j]) addedge(i,20+k*7+j,1);}for(int i=21;i<=370;i++) addedge(i,371,1);ans=maxflow(0,371);0为源点,371为汇点sum最后进⾏⼀个统计,和源点出发的最⼤流量进⾏⽐较,如果相等,说明电影排的开然后是求最⼤流的⼀个板⼦int maxflow(int st,int ed){int flowsum=0;while(bfs(st,ed)){memcpy(cur,g,sizeof(g));flowsum+=dfs(st,ed,INF);//cout<<"#"<<flowsum<<" ";}return flowsum;}具体的DFS和BFS这⾥不作为重点,以后再说下⾯给出完整的实现:1 #include<cstdio>2 #include<cstring>3 #include<algorithm>4using namespace std;5const int INF=1000000000;6const int maxn=1005;7const int maxm=20005;8int n,sum,cnt,ans;9int g[maxn],cur[maxn];10int str[25][10];11struct Edge{int u,v,next,cap,flow;}e[maxm];12void addedge(int u,int v,int c)13 {14 e[++cnt].u=u;e[cnt].v=v;e[cnt].cap=c;15 e[cnt].flow=0;e[cnt].next=g[u];g[u]=cnt;1617 e[++cnt].u=v;e[cnt].v=u;e[cnt].cap=0;18 e[cnt].flow=0;e[cnt].next=g[v];g[v]=cnt;19 }20int q[maxn],vis[maxn],d[maxn];21bool bfs(int st,int ed)22 {23 memset(q,0,sizeof(q));24 memset(vis,0,sizeof(vis));25 memset(d,-1,sizeof(d));26 vis[st]=1;d[st]=0;27int h=0,t=1;28 q[t]=st;29while(h!=t)30 {31 h=h%maxn+1;32int u=q[h];33for(int tmp=g[u];tmp;tmp=e[tmp].next)34 {35if(!vis[e[tmp].v]&&e[tmp].cap>e[tmp].flow)36 {37 vis[e[tmp].v]=1;38 d[e[tmp].v]=d[u]+1;39if(e[tmp].v==ed) return true;40 t=t%maxn+1;41 q[t]=e[tmp].v;42 }43 }44 }45return false;46 }47int getpair(int x)48 {49if(x%2==0)50return x-1;51else return x+1;52 }53int dfs(int x,int ed,int a)54 {55if(x==ed||a==0) return a;56int flow=0,f;57for(int tmp=cur[x];tmp;tmp=e[tmp].next)58 {59if(d[e[tmp].v]==d[x]+1&&(f=dfs(e[tmp].v,ed,min(a,e[tmp].cap-e[tmp].flow)))>0)60 {61 e[tmp].flow+=f;62 e[getpair(tmp)].flow-=f;63 a-=f;64 flow+=f;65if(a==0) break;66 }67 }68return flow;69 }70int maxflow(int st,int ed)71 {72int flowsum=0;73while(bfs(st,ed))74 {75 memcpy(cur,g,sizeof(g));76 flowsum+=dfs(st,ed,INF);77//cout<<"#"<<flowsum<<" ";78 }79return flowsum;8081 }82void init()83 {84 sum=cnt=0;85 memset(g,0,sizeof(g));86 }87int main()88 {89int T,d,w;90 scanf("%d",&T);91while(T--)92 {93 init();94 scanf("%d",&n);95for(int i=1;i<=n;i++)96 {97for(int j=1;j<=7;j++)98 scanf("%d",&str[i][j]);99 scanf("%d%d",&d,&w);100 sum+=d;101 addedge(0,i,d); //容量为需要多少天102for(int j=1;j<=7;j++)103for(int k=0;k<w;k++)104if(str[i][j]) addedge(i,20+k*7+j,1);105 }106for(int i=21;i<=370;i++) addedge(i,371,1);107 ans=maxflow(0,371);108if(ans==sum) printf("Yes\n");109else printf("No\n");110 }111return0;112 }据说这是典型的最⼤流题⽬,然⽽为了强⾏安利⼀波⼆分图的多重匹配,就不说成那个了。
二分图匹配(匈牙利算法)

设G=(V,{R})是一个无向图。
如顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属两个不同的子集。
则称图G为二分图。
v给定一个二分图G,在G的一个子图M中,M的边集{E}中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
v选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)v如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配。
最大匹配在实际中有广泛的用处,求最大匹配的一种显而易见的算法是:先找出全部匹配,然后保留匹配数最多的。
但是这个算法的复杂度为边数的指数级函数。
因此,需要寻求一种更加高效的算法。
匈牙利算法是求解最大匹配的有效算法,该算法用到了增广路的定义(也称增广轨或交错轨):若P是图G中一条连通两个未匹配顶点的路径,并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M 的一条增广路径。
由增广路径的定义可以推出下述三个结论:v 1. P的路径长度必定为奇数,第一条边和最后一条边都不属于M。
v 2. P经过取反操作(即非M中的边变为M中的边,原来M中的边去掉)可以得到一个更大的匹配M’。
v 3. M为G的最大匹配当且仅当不存在相对于M的增广路径。
从而可以得到求解最大匹配的匈牙利算法:v(1)置M为空v(2)找出一条增广路径P,通过取反操作获得更大的匹配M’代替Mv(3)重复(2)操作直到找不出增广路径为止根据该算法,我选用dfs (深度优先搜索)实现。
程序清单如下:int match[i] //存储集合m中的节点i在集合n中的匹配节点,初值为-1。
int n,m,match[100]; //二分图的两个集合分别含有n和m个元素。
bool visit[100],map[100][100]; //map存储邻接矩阵。
bool dfs(int k){int t;for(int i = 0; i < m; i++)if(map[k][i] && !visit[i]){visit[i] = true;t = match[i];match[i] = k; //路径取反操作。
二分图匹配

二分图匹配一、二分图的概念二分图又称作二部图,是图论中的一种特殊模型。
设G=(V,{R})是一个无向图。
如顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属两个不同的子集。
则称图G为二分图。
二、最大匹配给定一个二分图G,在G的一个子图M中,M的边集{E}中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配。
三、匈牙利算法求最大匹配的一种显而易见的算法是:先找出全部匹配,然后保留匹配数最多的。
但是这个算法的复杂度为边数的指数级函数。
因此,需要寻求一种更加高效的算法。
1、增广路的定义(也称增广轨或交错轨):若P是图G中一条连通两个未匹配顶点的路径,并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
由增广路的定义可以推出下述三个结论:●P的路径长度必定为奇数,第一条边和最后一条边都不属于M。
●P经过取反操作可以得到一个更大的匹配M’。
●M为G的最大匹配当且仅当不存在相对于M的增广路径。
2、用增广路求最大匹配(称作匈牙利算法,匈牙利数学家Edmonds于1965年提出)。
算法轮廓:(1)置M为空(2)找出一条增广路径P,通过取反操作获得更大的匹配M’代替M(3)重复(2)操作直到找不出增广路径为止程序清单:Function find(k:integer):integer;var st,sf,i,j,t:integer;queue,father:array[1..100] of integer;beginqueue[1] := k; st := 1; sf := 1;fillchar(father,sizeof(father),0);repeatfor i:=1 to n doif (father[i]=0)and(a[queue[st],i]=1) thenbeginif match2[i]<>0 thenbegininc(sf);queue[sf] := match2[i];father[i] := queue[st];end elsebeginj := queue[st];while true dobegint := match1[j];match1[j] := i;match2[i] := j;if t = 0 then break;i := t; j := father[t];end;find := 1;exit;end;end;inc(st);until st>sf;find := 0;end;在主程序中调用下面的程序即可得出最大匹配数。
匈牙利匹配算法的原理

匈牙利匹配算法的原理匈牙利匹配算法(也被称为二分图匹配算法或者Kuhn-Munkres算法)是用于解决二分图最大匹配问题的经典算法。
该算法由匈牙利数学家Dénes Kőnig于1931年提出,并由James Munkres在1957年进行改进。
该算法的时间复杂度为O(V^3),其中V是图的顶点数。
匹配问题定义:给定一个二分图G=(X,Y,E),X和Y分别代表两个不相交的顶点集合,E表示连接X和Y的边集合。
图中的匹配是指一个边的集合M,其中任意两条边没有公共的顶点。
匹配的相关概念:1.可增广路径:在一个匹配中找到一条没有被占用的边,通过这条边可以将匹配中的边个数增加一个,即将不在匹配中的边添加进去。
2. 增广路径:一个可增广路径是一个交替序列P=v0e1v1e2v2...ekvk,其中v0属于X且不在匹配中,v1v2...vk属于Y且在匹配中,e1e2...ek在原图中的边。
3.增广轨:一个交替序列形如V0E1V1E2...EkVk,其中V0属于X且不在匹配中,V1V2...Vk属于Y且在匹配中,E1E2...Ek在原图中的边。
增广轨是一条路径的特例,它是一条从X到Y的交替序列。
1.初始时,所有的边都不在匹配中。
2.在X中选择一个点v0,如果v0已经在匹配中,则找到与v0相连的在Y中的顶点v1、如果v1不在匹配中,则(v0,v1)是可增广路径的第一条边。
3. 如果v1在匹配中,则找到与v1相连的在X中的顶点v2,判断v2是否在匹配中。
依此类推,直到找到一个不在匹配中的点vn。
4.此时,如果n是奇数,则(n-1)条边在匹配中,这意味着我们找到了一条增广路径。
如果n是偶数,则(n-1)条边在匹配中,需要进行进一步的处理。
5.如果n是偶数,则将匹配中的边和非匹配中的边进行颠倒,得到一个新的匹配。
6.对于颠倒后的匹配,我们再次从第2步开始,继续寻找增广路径。
7.重复步骤2到步骤6,直到找不到可增广路径为止,此时我们得到了最大匹配。
最大二分图匹配(匈牙利算法)

最大二分图匹配(匈牙利算法)二分图指的是这样一种图:其所有的顶点分成两个集合M和N,其中M或N中任意两个在同一集合中的点都不相连。
二分图匹配是指求出一组边,其中的顶点分别在两个集合中,并且任意两条边都没有相同的顶点,这组边叫做二分图的匹配,而所能得到的最大的边的个数,叫做最大匹配。
计算二分图的算法有网络流算法和匈牙利算法(目前就知道这两种),其中匈牙利算法是比较巧妙的,具体过程如下(转自组合数学):令g=(x,*,y)是一个二分图,其中x={x1,x2...},y={y1,y2,....}.令m为g中的任意匹配。
1。
将x的所有不与m的边关联的顶点表上¥,并称所有的顶点为未扫描的。
转到2。
2。
如果在上一步没有新的标记加到x的顶点上,则停,否则,转33。
当存在x被标记但未被扫描的顶点时,选择一个被标记但未被扫描的x的顶点,比如xi,用(xi)标记y 的所有顶点,这些顶点被不属于m且尚未标记的边连到xi。
现在顶点xi 是被扫描的。
如果不存在被标记但未被扫描的顶点,转4。
4。
如果在步骤3没有新的标记被标记到y的顶点上,则停,否则转5。
5。
当存在y被标记但未被扫描的顶点时。
选择y的一个被标记但未被扫描的顶点,比如yj,用(yj)标记x的顶点,这些顶点被属于m且尚未标记的边连到yj。
现在,顶点yj是被扫描的。
如果不存在被标记但未被扫描的顶点则转道2。
由于每一个顶点最多被标记一次且由于每一个顶点最多被扫描一次,本匹配算法在有限步内终止。
代码实现:bfs过程:#include<stdio.h>#include<string.h>main(){bool map[100][300];inti,i1,i2,num,num1,que[300],cou,stu,match1[100],match2[300],pqu e,p1,now,prev[300],n;scanf("%d",&n);for(i=0;i<n;i++){scanf("%d%d",&cou,&stu);memset(map,0,sizeof(map));for(i1=0;i1<cou;i1++){scanf("%d",&num);for(i2=0;i2<num;i2++){scanf("%d",&num1);map[i1][num1-1]=true;}}num=0;memset(match1,int(-1),sizeof(match1)); memset(match2,int(-1),sizeof(match2)); for(i1=0;i1<cou;i1++){p1=0;pque=0;for(i2=0;i2<stu;i2++){if(map[i1][i2]){prev[i2]=-1;que[pque++]=i2;}elseprev[i2]=-2;}while(p1<pque){now=que[p1];if(match2[now]==-1)break;p1++;for(i2=0;i2<stu;i2++){if(prev[i2]==-2&&map[match2[now]][i2]){prev[i2]=now;que[pque++]=i2;}}}if(p1==pque)continue;while(prev[now]>=0){match1[match2[prev[now]]]=now; match2[now]=match2[prev[now]]; now=prev[now];}match2[now]=i1;match1[i1]=now;num++;}if(num==cou)printf("YES\n");elseprintf("NO\n");}}dfs实现过程:#include<stdio.h>#include<string.h>#define MAX 100bool map[MAX][MAX],searched[MAX]; int prev[MAX],m,n;bool dfs(int data){int i,temp;for(i=0;i<m;i++){if(map[data][i]&&!searched[i]){searched[i]=true;temp=prev[i];prev[i]=data;if(temp==-1||dfs(temp))return true;prev[i]=temp;}}return false;}main(){int num,i,k,temp1,temp2,job;while(scanf("%d",&n)!=EOF&&n!=0) {scanf("%d%d",&m,&k);memset(map,0,sizeof(map));memset(prev,int(-1),sizeof(prev)); memset(searched,0,sizeof(searched));for(i=0;i<k;i++){scanf("%d%d%d",&job,&temp1,&temp2); if(temp1!=0&&temp2!=0)map[temp1][temp2]=true;}num=0;for(i=0;i<n;i++){memset(searched,0,sizeof(searched)); dfs(i);}for(i=0;i<m;i++){if(prev[i]!=-1)num++;}printf("%d\n",num);}}。
二分图的完备匹配

这个算法的要点是把初始匹配通过可增广轨逐次增 广,以至得到最大匹配。然后根据有无未盖点来判 定这个最大匹配是否为完备匹配。 例如求图7—8(d)中的最大匹配, 设初始匹配M={(X2Y2,X3Y3,X5Y5} 以未盖点X1为根,生成交错树,结果得到可增广 轨X1Y2X2Y1(见)。
X1
X2
X3
X4
X5
Y1
Y2
Y3
Y4
Y5
X1
X2
X3
X4
X5
Y1
Y2
Y3
Y4
Y5
求二分图最佳匹配的算法——匈牙利算法 变量说明; S——外点集合,初始时为交错树的根; T——内点集合,初始时为空; N(S)——与S中的顶点相邻的顶点集合。显然,若N(S)= T,表明与任一外点相连的端点都在内点集合里,找不出一 条不属于交错树的边,图G无完备匹配; M——匹配边集合; E(P)——可增广轨P上的边。 · MOE(P)——进行对称差运算的结果,为可增广轨P上的 匹配边与非匹配边对换,P轨外的匹配边不变,使得M改进 成一个多包含一条边的匹配。
问是否能从g中得出一个不含未盖点的匹配这种将g的每一个顶点盖住的匹配称为二分图的完备匹可能存在完备匹配的图是否仅限于二分图呢
二分图的完备匹配
某公司有工作人员X1,X2,…,Xm,他们去做 工作Y1,Y2,…,Yn,每人适合做其中的一项或几 项工作,问能否每人都分配一项合适的工作。 这个问题的数学模型是:构造一个二分图G, 顶点划分为两个部分: 一个是工作人员集合X={Xl,X2,…,Xm}, 一个是工作集合Y={Y1,Y2,…,Yn}, 当且仅当Xi适合干工作Yi时,Xi与Yi之间连一条边。 问是否能从G中得出一个不含未盖点的匹配,这种 将G的每一个顶点盖住的匹配称为二分图的完备匹 配。
二分图的讲解

例 3个图的匹配数 依次为3, 3, 4.
4
匹配 (续)
设M为G中一个匹配 vi与vj被M匹配: (vi,vj)M v为M饱和点: M中有边与v关联 v为M非饱和点: M中没有边与v关联 M为完美匹配: G的每个顶点都是M饱和点
例 关于M1, a,b,e,d是饱和点 f,c是非饱和点
M1不是完美匹配
(1)
(2)
(3)
6
Hall定理
定理(Hall定理) 设二分图G=<V1,V2,E>中,|V1||V2|. G中存 在从V1到V2的完备匹配当且仅当V1中任意k 个顶点至少与V2 中的k个顶点相邻(k=1,2,…,|V1|). 由Hall定理不难证明, 上一页图(2)没有完备匹配.
定理 设二部图G=<V1,V2,E>中, 如果存在t1, 使得V1中每个 顶点至少关联 t 条边, 而V2中每个顶点至多关联t条边,则G 中存在V1到V2的完备匹配.
注意: n 阶零图为二分图.
2
二分图的判别法
定理 非平凡无向图G=<V,E>是二分图当且仅当G中 无奇数长度的回路
例 下述各图都是二分图
3
匹配
设G=<V,E>, 匹配(边独立集): 任2条边均不相邻的边子集 极大匹配: 添加任一条边后都不再是匹配的匹配 最大匹配: 边数最多的匹配
匹配数: 最大匹配中的边数, 记为1
M2是完美匹配
M1
M2
5
二分图中的匹配
定义 设G=<V1,V2,E>为二部图, |V1||V2|, M是G中最 大匹配, 若V1中顶点全是M饱和点, 则称M为G中V1 到V2的完全匹配. 当|V1|=|V2|时, 完备匹配变成完美 匹配.
二分图最大匹配及常用建图方法

算法———艺术二分图匹配剖析很多人说,算法是一种艺术。
但是对于初学者的我,对算法认识不是很深刻,但偶尔也能感受到他强大的魅力与活力。
这让我追求算法的脚步不能停止。
下面我通过分析匈牙利算法以及常用建图方式,与大家一起欣赏算法的美。
匈牙利算法匈牙利算法是用来解决最大二分图匹配问题的,所谓二分图即“一组点集可以分为两部分,且每部分内各点互不相连,两部分的点之间可以有边”。
所谓最大二分图匹配即”对于二分图的所有边,寻找一个子集,这个子集满足两个条件,1:任意两条边都不依赖于同一个点。
2:让这个子集里的边在满足条件一的情况下尽量多。
首先可以想到的是,我们可以通过搜索,找出所有的这样的满足上面条件的边集,然后从所有的边集中选出边数最多的那个集合,但是我们可以感觉到这个算法的时间复杂度是边数的指数级函数,因此我们有必要寻找更加高效的方法。
目前比较有效的方法有匈牙利算法和通过添加汇点和源点的网络流算法,对于点的个数都在200 到300 之间的数据,我们是采取匈牙利算法的,因为匈牙利算法实现起来要比网络流简单些。
下面具体说说匈牙利算法:介绍匈牙利之前,先说说“增广轨”。
定义:若P是图G中一条连通两个未匹配顶点的路径,并且属最大匹配边集M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广轨定义总是抽象的下面通过图来理解它。
图中的线段(2->3, 3->1, 1->4)便是上面所说的p路径,我们假定边(1,3)是以匹配的边,(2,3)(1,4)是未匹配的边,则边(4,1)边(1,3)和边(3,2)在路径p上交替的出现啦,那么p就是相对于M的一条增广轨,这样我们就可以用边1,4 和边2,3来替换边1,3 那么以匹配的边集数量就可以加1,。
匈牙利算法就是同过不断的寻找增广轨实现的。
很明显如果二分图的两部分点分别为n 和m,那么最大匹配的数目应该小于等于MIN(n,m); 因此我们可以枚举任第一部分(的二部分也可以)里的每一个点,我们从每个点出发寻找增广轨,最后吧第一部分的点找完以后,就找到了最大匹配的数目,当然我们也可以通过记录找出这些边。
二分图最大权最小权完美匹配模板KM
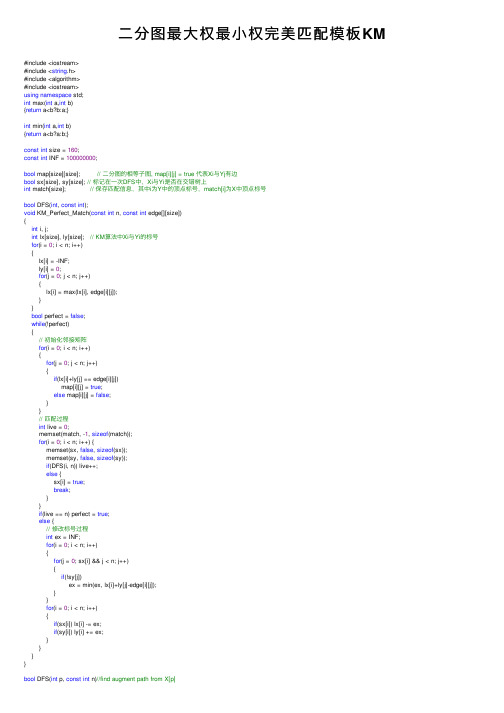
⼆分图最⼤权最⼩权完美匹配模板KM #include <iostream>#include <string.h>#include <algorithm>#include <iostream>using namespace std;int max(int a,int b){return a<b?b:a;}int min(int a,int b){return a<b?a:b;}const int size = 160;const int INF = 100000000;bool map[size][size]; // ⼆分图的相等⼦图, map[i][j] = true 代表Xi与Yj有边bool sx[size], sy[size]; // 标记在⼀次DFS中,Xi与Yi是否在交错树上int match[size]; // 保存匹配信息,其中i为Y中的顶点标号,match[i]为X中顶点标号bool DFS(int, const int);void KM_Perfect_Match(const int n, const int edge[][size]){int i, j;int lx[size], ly[size]; // KM算法中Xi与Yi的标号for(i = 0; i < n; i++){lx[i] = -INF;ly[i] = 0;for(j = 0; j < n; j++){lx[i] = max(lx[i], edge[i][j]);}}bool perfect = false;while(!perfect){// 初始化邻接矩阵for(i = 0; i < n; i++){for(j = 0; j < n; j++){if(lx[i]+ly[j] == edge[i][j])map[i][j] = true;else map[i][j] = false;}}// 匹配过程int live = 0;memset(match, -1, sizeof(match));for(i = 0; i < n; i++) {memset(sx, false, sizeof(sx));memset(sy, false, sizeof(sy));if(DFS(i, n)) live++;else {sx[i] = true;break;}}if(live == n) perfect = true;else {// 修改标号过程int ex = INF;for(i = 0; i < n; i++){for(j = 0; sx[i] && j < n; j++){if(!sy[j])ex = min(ex, lx[i]+ly[j]-edge[i][j]);}}for(i = 0; i < n; i++){if(sx[i]) lx[i] -= ex;if(sy[i]) ly[i] += ex;}}}}bool DFS(int p, const int n)//find augment path from X[p]{int i;for(i = 0; i < n; i++){if(!sy[i] && map[p][i]){sy[i] = true;int t = match[i];match[i] = p;if(t == -1 || DFS(t, n)){return true;}match[i] = t;if(t != -1) sx[t] = true;}}return false;}int main(){int n, edge[size][size]; // edge[i][j]为连接Xi与Yj的边的权值int i;int m;/**************************************************** record edge[i][j] as edge value between vertex i in X and vertex j in Y* save n as vertexs need to be match (used in KM_Perfect_Match(n, edge);) ***************************************************/int s,d,pow;while(scanf("%d%d",&n,&m)!=EOF){if(n==0 && m==0) break;memset(edge,0,sizeof(edge));/*最⼩权: 去掉memset(edge,0,sizeof(edge));改为如下:for(i=0;i<n;i++)for(int j=0;j<n;j++)edge[i][j]=-INF;*/memset(sx,0,sizeof(sx));memset(sy,0,sizeof(sy));memset(match,0,sizeof(0));while(m--){scanf("%d%d%d",&s,&d,&pow);s--;d--;/*最⼩权:edge[s][d]=pow; 改为edge[s][d]= - pow;*/edge[s][d]=pow;}KM_Perfect_Match(n, edge);int cost = 0;for(i=0;i<n;i++){cost += edge[match[i]][i];}/*最⼩权:output 改为 -cost*/cout<<cost<<endl;}// cost 为最⼤匹配的总和, match[]中保存匹配信息return0;}View Code感觉这个模板也不错,⽐较符合审美。
[hdu1533]二分图最大权匹配最小费用最大流
![[hdu1533]二分图最大权匹配最小费用最大流](https://img.taocdn.com/s3/m/306f8633bdd126fff705cc1755270722192e59a0.png)
[hdu1533]⼆分图最⼤权匹配最⼩费⽤最⼤流题意:给⼀个n*m的地图,'m'表⽰⼈,'H'表⽰房⼦,求所有⼈都回到房⼦所⾛的距离之和的最⼩值(距离为曼哈顿距离)。
思路:⽐较明显的⼆分图最⼤权匹配模型,将每个⼈向房⼦连⼀条边,边权为曼哈顿距离的相反数(由于是求最⼩,所以先取反后求最⼤,最后再取反回来即可),然后⽤KM算法跑⼀遍然后取反就是答案。
还可以⽤最⼩费⽤最⼤流做,⽅法是:从源点向每个⼈连⼀条边,容量为1,费⽤为0,从每个房⼦向汇点连⼀条边,容量为1,费⽤为0,从每个⼈向每个房⼦连⼀条边,容量为1,费⽤为曼哈顿距离的值,建好图后跑⼀遍最⼩费⽤最⼤流就是答案。
附上代码:(1)KM算法,40ms左右(2)最⼩费⽤最⼤流,400+ms(1)1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84/* ******************************************************************************** */#include <iostream> //#include <cstdio> //#include <cmath> //#include <cstdlib> //#include <cstring> //#include <vector> //#include <ctime> //#include <deque> //#include <queue> //#include <algorithm> //#include <map> //#include <cmath> //using namespace////#define pb push_back //#define mp make_pair //#define X first //#define Y second //#define all(a) (a).begin(), (a).end() //#define fillchar(a, x) memset(a, x, sizeof(a)) ////void int int for int scanf"%d"//void void int scanf"%d"template typename//void int void int int int//while scanf"%d"void template typename// void const template typename typename// void const const", "template typename//void int while", "////typedef int int//typedef long long//typedef long long////template typename bool const return false true// template typename bool const return false true// template typename//void const for int// template typename//void const for int////const double acos/////* -------------------------------------------------------------------------------- */structconst static intconst static intintintintintvoid int int intbool inttruefor intiftrueifreturn trueelse if//j属于B,且不在交错路径中return falseint int intthis thisintmemset sizeofmemset sizeofmemset sizeofforforforforwhile84858687888990919293949596979899 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135(2)12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849whilememset sizeofmemset sizeofif break//从i点出发找到交错路径则跳出循环for//取最⼩的slack[j]iffor//集合A中位于交错路径上的-diffor//集合B中位于交错路径上的+difelse//注意修改不在交错路径上的slack[j]intforif (~match[j])return//点从0开始编号intreturn abs absint#ifndef ONLINE_JUDGEfreopen"in.txt""r"#endif // ONLINE_JUDGEintwhilefor intcharscanf"%s"for intif'H'if'm'for intfor intreturn/* ******************************************************************************** *//* ******************************************************************************** */#include <iostream> //#include <cstdio> //#include <cmath> //#include <cstdlib> //#include <cstring> //#include <vector> //#include <ctime> //#include <deque> //#include <queue> //#include <algorithm> //#include <map> //#include <cmath> //using namespace////#define pb push_back //#define mp make_pair //#define X first //#define Y second //#define all(a) (a).begin(), (a).end() //#define fillchar(a, x) memset(a, x, sizeof(a)) ////void int int for int scanf"%d"//void void int scanf"%d"template typename//void int void int int int//while scanf"%d"void template typename// void const template typename typename// void const const", "template typename//void int while", "////typedef int int//typedef long long//typedef long long////template typename bool const return false true// template typename bool const return false true// template typename//void const for int// template typename//void const for int////const double acos/////* -------------------------------------------------------------------------------- */structconst static intconst static intstruct49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145structintint int int intintintintvoid intthisfor intvoid int int int intintbool int int int intfor intmemset sizeofintwhileintfor intififif return falseintwhilereturn trueint int intintwhilereturnintreturn abs absint#ifndef ONLINE_JUDGEfreopen"in.txt""r"#endif // ONLINE_JUDGEintwhilefor intcharscanf"%s"for intif'H'if'm'for intfor intfor intfor intreturn/* ******************************************************************************** */。
Kuhn-Munkres算法(二分图最大权匹配)===

二分图如果是没有权值的,求最大匹配。
则是用匈牙利算法求最大匹配。
如果带了权值,求最大或者最小权匹配,则必须用KM算法。
其实最大和最小权匹配都是一样的问题。
只要会求最大匹配,如果要求最小权匹配,则将权值取相反数,再把结果取相反数,那么最小权匹配就求出来了。
KM算法及其难理解。
看了几天还无头绪。
先拿上一直采用的KM算法模板,按照吉林大学的模板写的。
试试了好多次感觉都没有出错。
/******************************************************二分图最佳匹配(kuhn munkras 算法 O(m*m*n)).邻接矩阵形式。
返回最佳匹配值,传入二分图大小m,n邻接矩阵 mat ,表示权,match1,match2返回一个最佳匹配,为匹配顶点的match值为-1,一定注意m<=n,否则循环无法终止,最小权匹配可将全职取相反数。
初始化: for(i=0;i<MAXN;i++)for(j=0;j<MAXN;j++) mat[i][j]=-inf;对于存在的边:mat[i][j]=val;//注意不能负值********************************************************/#include<string.h>#define MAXN 310#define inf 1000000000#define _clr(x) memset(x,-1,sizeof(int)*MAXN)int KM(int m,int n,int mat[][MAXN],int *match1,int *match2){int s[MAXN],t[MAXN],l1[MAXN],l2[MAXN];int p,q,i,j,k,ret=0;for(i=0;i<m;i++){l1[i]=-inf;for(j=0;j<n;j++)l1[i]=mat[i][j]>l1[i]?mat[i][j]:l1[i];if(l1[i]==-inf) return -1;}for(i=0;i<n;i++)l2[i]=0;_clr(match1);_clr(match2);for(i=0;i<m;i++){_clr(t);p=0;q=0;for(s[0]=i;p<=q&&match1[i]<0;p++){for(k=s[p],j=0;j<n&&match1[i]<0;j++){if(l1[k]+l2[j]==mat[k][j]&&t[j]<0){s[++q]=match2[j];t[j]=k;if(s[q]<0){for(p=j;p>=0;j=p){match2[j]=k=t[j];p=match1[k];match1[k]=j;}}}}}if(match1[i]<0){i--;p=inf;for(k=0;k<=q;k++){for(j=0;j<n;j++){if(t[j]<0&&l1[s[k]]+l2[j]-mat[s[k]][j]<p) p=l1[s[k]]+l2[j]-mat[s[k]][j];}}for(j=0;j<n;j++)l2[j]+=t[j]<0?0:p;for(k=0;k<=q;k++)l1[s[k]]-=p;}}for(i=0;i<m;i++)ret+=mat[i][match1[i]];return ret;}下面是从网上的博客摘抄的一些零散的总结。
组合_chapt13_16二部图匹配

35 M classicism programming 0 M baroque skiing 43 M baroque chess 30 F baroque soccer
二分图(p224-225)
定义: 称三元组G=(X,,Y)是二分图, 其中X = {x1, x2, …, xm}是左顶点集合, Y = {y1, y2, …, yn}是右顶点集合, { {x,y} | xX, yY }是无向边集合 x1 x2 x3 y1 y2 X = {x1, x2, x3, x4} Y = {y1, y2, y3} = { {x1,y1}, {x1,y3}, {x2,y1}, {x3,y2}, {x3,y3}, {x4,y3} } 对比图的定义
x1 x2 y1 y2
y5
Guardian of Decency(补充)
一保守教师想带学生郊游, 却怕他们途中谈恋爱, 他认为满足下面条件之一的两人谈恋爱几率很小: (1) 身高差>40 (2) 性别相同 (3) 爱好不同类型的音乐 (4) 爱好同类型的运动 输入是学生的数据, 求最多能带多少学生. 例:
二分图最佳匹配,求最大权匹配或最小权匹配

⼆分图最佳匹配,求最⼤权匹配或最⼩权匹配Beloved Sons题意:国王有N个⼉⼦,现在每个⼉⼦结婚都能够获得⼀定的喜悦值,王⼦编号为1-N,有N个⼥孩的编号同样为1-N,每个王⼦⼼中都有⼼仪的⼥孩,现在问如果安排,能够使得题中给定的式⼦和最⼤。
分析:其实题⽬中那个开根号是个烟雾弹,只要关⼼喜悦值的平⽅即可。
那么对王⼦和⼥孩之间构边,边权为喜悦值的平⽅,对于每⼀个王⼦虚拟出⼀个⼥孩边权为0,这样是为了所有的王⼦都能够有⼥孩可以配对,以便算法能够正确的执⾏。
求⼆分图最佳匹配,要求权值最⼤,lmatch返回⼀个最佳匹配。
1 #include<cstdio>2 #include<cstring>3#define mt(a,b) memset(a,b,sizeof(a))4const int inf=0x3f3f3f3f;5class Kuhn_Munkras { ///⼆分图最佳匹配O(ln*ln*rn)邻接阵6 typedef int typec;///边权的类型7static const int MV=1024;///点的个数8int ln,rn,s[MV],t[MV],ll[MV],rr[MV],p,q,i,j,k;9 typec mat[MV][MV];10public:11int lmatch[MV],rmatch[MV];12void init(int tln,int trn) { ///传⼊ln左部点数,rn右部点数,要求ln<=rn,下标0开始13 ln=tln;14 rn=trn;15for(i=0; i<ln; i++)16for(j=0; j<rn; j++)17 mat[i][j]=-inf;18 }19void add(int u,int v,typec w) {///最⼩权匹配可将权值取相反数20 mat[u][v]=w;21 }22 typec solve() {///返回最佳匹配值,-1表⽰⽆法匹配23 typec ret=0;24for (i=0; i<ln; i++) {25for (ll[i]=-inf,j=0; j<rn; j++)26 ll[i]=mat[i][j]>ll[i]?mat[i][j]:ll[i];27if( ll[i] == -inf ) return -1;// ⽆法匹配!28 }29for (i=0; i<rn; rr[i++]=0);30 mt(lmatch,-1);31 mt(rmatch,-1);32for (i=0; i<ln; i++) {33 mt(t,-1);34for (s[p=q=0]=i; p<=q&&lmatch[i]<0; p++)35for (k=s[p],j=0; j<rn&&lmatch[i]<0; j++)36if (ll[k]+rr[j]==mat[k][j]&&t[j]<0) {37 s[++q]=rmatch[j],t[j]=k;38if (s[q]<0)39for (p=j; p>=0; j=p)40 rmatch[j]=k=t[j],p=lmatch[k],lmatch[k]=j;41 }42if (lmatch[i]<0) {43for (i--,p=inf,k=0; k<=q; k++)44for (j=0; j<rn; j++)45if(t[j]<0&&ll[s[k]]+rr[j]-mat[s[k]][j]<p)46 p=ll[s[k]]+rr[j]-mat[s[k]][j];47for (j=0; j<rn; rr[j]+=t[j]<0?0:p,j++);48for (k=0; k<=q; ll[s[k++]]-=p);49 }50 }51for (i=0; i<ln; i++) {52if( lmatch[i] < 0 ) return -1;53if( mat[i][lmatch[i]] <= -inf ) return -1;54 ret+=mat[i][lmatch[i]];55 }56return ret;57 }58 } gx;59int a[512];60int main() {61int t,n,m;62while(~scanf("%d",&t)) {63while(t--) {64 scanf("%d",&n);65for(int i=0; i<n; i++) {66 scanf("%d",&a[i]);67 a[i]*=a[i];68 }69 gx.init(n,n<<1);70for(int i=0,j; i<n; i++) { 71 scanf("%d",&m);72while(m--) {73 scanf("%d",&j);74 gx.add(i,j-1,a[i]);75 }76 gx.add(i,i+n,0);77 }78int flag=gx.solve();79for(int i=0; i<n; i++) {80int ans=0;81if(gx.lmatch[i]<n) {82 ans=gx.lmatch[i]+1;83 }84 printf("%d ",ans);85 }86 puts("");87 }88 }89return0;90 }View Codeend。
离散数学--第7章 图论-5(匹配)

MM’
其中回路包含相同数目的M边和M’边。由|M’|>|M|, 必 存在M’边开始, M‘边终止的M交互道路,即M-可增广 道路,矛盾!
返回 结束
7.5 .2 最大匹配的基本定理
例] 从匹配M={(v6,v7)}开始,求下图的最大匹 配
11
(a)
(b)
系统地检查不饱和点出发有无可增 广道路,如,v1出发有可增广道路 v1,v7v6,v8(可画以v1为根的交互树), 由此得到匹配(a), v2出发没有,v3出 发存在v3v4,可得更大匹配(b), 其他 点出发不存在可增广道路,故(b)是 最大匹配。
交错路为一条 M可增广路。
例
v1 v6 v2 v3 v4
匹配, M {v1v6 , v2v5 }是一个对集;但不是
最大对集,有路 P:v3v2v5v4,通过 匹配, ( M E ( P)) ( E ( P) M )得比M 更大的对集。 匹配,P称为M 可扩路。 增广路
返回 结束
v5
7.5 .2 最大匹配的基本定理
为图G的最大匹配。
[匹配数] G中最大匹配中的边数称为匹配数,记作
(G)。设G的所有匹配为M1、M2、… 、Mk,记
' (G) max | M i |
i 1,...,k
返回 结束
7.5 .1 匹配的基本概念
e2 e6 e1
5
最大匹配: {e1,e5 ,e6} e7
e4 e3 匹配数:3
返回 结束
7.5 .2 最大匹配的基本定理
[M交错路] 设G和M如上所述,G的一条M交错路 指G中一条路,其中的边在M和 EM 中交错出现 。
路是由属于M的匹配边和不属于M的非匹配边交替出现组成
二分图最大匹配:匈牙利算法的python实现

⼆分图最⼤匹配:匈⽛利算法的python实现⼆分图匹配是很常见的算法问题,⼀般⽤匈⽛利算法解决⼆分图最⼤匹配问题,但是⽬前⽹上绝⼤多数都是C/C++实现版本,没有python版本,于是就⽤python实现了⼀下深度优先的匈⽛利算法,本⽂使⽤的是递归的⽅式以便于理解,然⽽迭代的⽅式会更好,各位可以⾃⾏实现。
1、⼆分图、最⼤匹配什么是⼆分图:⼆分图⼜称作⼆部图,是图论中的⼀种特殊模型。
设G=(V,E)是⼀个⽆向图,如果顶点V可分割为两个互不相交的⼦集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为⼀个⼆分图。
什么是匹配:把上图想象成3位⼯⼈和4种⼯作,连线代表⼯⼈愿意从事某项⼯作,但最终1个⼯⼈只能做⼀种⼯作,最终的配对结果连线就是⼀个匹配。
匹配可以是空。
什么是最⼤匹配:在愿意从事的基础上,能够最多配成⼏对。
现在要⽤匈⽛利算法找出最多能发展⼏对。
[color=green][size=medium]匈⽛利算法是解决寻找⼆分图最⼤匹配的。
更多⼆分图最⼤匹配的图解可以参考 /5576502/1297344以下是代码,为了图省事使⽤了类,实际上并不需要这样M=[]class DFS_hungary():def__init__(self, nx, ny, edge, cx, cy, visited):self.nx, self.ny=nx, nyself.edge = edgeself.cx, self.cy=cx,cyself.visited=visiteddef max_match(self):res=0for i in self.nx:if self.cx[i]==-1:for key in self.ny: # 将visited置0表⽰未访问过self.visited[key]=0res+=self.path(i)return resdef path(self, u):for v in self.ny:if self.edge[u][v] and (not self.visited[v]):self.visited[v]=1if self.cy[v]==-1:self.cx[u] = vself.cy[v] = uM.append((u,v))return 1else:M.remove((self.cy[v], v))if self.path(self.cy[v]):self.cx[u] = vself.cy[v] = uM.append((u, v))return 1return 0ok,接着测试⼀下:if__name__ == '__main__':nx, ny = ['A', 'B', 'C', 'D'], ['E', 'F', 'G', 'H']edge = {'A':{'E': 1, 'F': 0, 'G': 1, 'H':0}, 'B':{'E': 0, 'F': 1, 'G': 0, 'H':1}, 'C':{'E': 1, 'F': 0, 'G': 0, 'H':1}, 'D':{'E': 0, 'F': 0, 'G': 1, 'H':0}} # 1 表⽰可以匹配, 0 表⽰不能匹配cx, cy = {'A':-1,'B':-1,'C':-1,'D':-1}, {'E':-1,'F':-1,'G':-1,'H':-1}visited = {'E': 0, 'F': 0, 'G': 0,'H':0}print DFS_hungary(nx, ny, edge, cx, cy, visited).max_match()结果为4,是正确的。
主要定理二分图的最大匹配算法二分图的带权重的最大匹配

2021/2/13
山东大学 软件学院
22
时间复杂度分析
令|S| = m,|T| = n,假设 m n。 找一条增广路(或判断不能找到)标号算法最多进行 O(mn)
次检查(因为最多有这么多条边)。 初始匹配最多被增广 m 次。 所以,总的计算量为 O(m2n)。
2021/2/13
山东大学 软件学院
2021/2/13
山东大学 软件学院
17
例子
1
6
2
72
3
82
4
9
5
10
找到一条增广路(2, 8)。更新M。
2021/2/13
山东大学 软件学院
18
例子
1
63
2
7
3
83
4
93
5
10 3
找到一条增广路(3, 10)。更新M。
2021/2/13
山东大学 软件学院
19
例子
2021/2/13
1 2 10 3 4 5
2021/2/13
山东大学 软件学院
4
例子
2021/2/13
山东大学 软件学院
5
定理
定理:记G’上的最大流为f*,流值为|f*|。G上的最大匹配 为M*。则|f*| = |M*|。 证明:首先证|f*| |M*|。 给定最大匹配M*,令G’上M*中的边的流值为1,s到M*匹 配的V一侧点的各条边上流值为1,M*匹配的U一侧点到t的 各条边上流值为1,则构造了一个流值为|M*|的流f。 因此,显然有|f*| |M*|。 再证|f*| |M*|。 设f*为G’上的最大流。 由整流定理,G’上每条边上的流值为整数。由于每条边的 容量均为1,因此G’上每条边的流值不是0就是1。
二分图的最优匹配(KM算法)

(4) 用修改后的顶标 l 得 Gl 及其上面的一个完备匹配如图 7.13。图中粗实线给出了一个最佳匹配,其 最大权是 2+4+1+4+3=14。
我们看出:al>0;修改后的顶标仍是可行顶标;Gl 中仍含 Gl 中的匹配 M;Gl 中至少会出现不属于 M 的 一条边,所以会造成 M 的逐渐增广。
得到可行顶标后求最大匹配:
1) 我们寻找一个 d 值,使得 d= min{ (x,y)| Lx(x)+ Ly(y)- W(x,y), x∈ S, y∉ T },因些,这时 d= min{ Lx(1)+Ly(1)-W(1,1), Lx(1)+Ly(2)-W(1,2), Lx(2)+Ly(1)-W(2,1), Lx(2)+Ly(2)-W(2,2) }= min{ 3+0- 1, 3+0-2, 4+0-3, 4+0-2 }= min{ 2, 1, 1, 2 }= 1。 寻找最小的 d 是为了保证修改后仍满足性质对于边 <x,y> 有 Lx(x)+ Ly(y)>= W(x,y)。 2) 然后对于顶点 x 1. 如果 x∈ S 则 Lx(x)= Lx(x)- d。 2. 如果 x∈ T 则 Ly(x)= Ly(x)+ d。 3. 其它情况保持不变。 如此修改后,我们发现对于边<x,y>,顶标 Lx(x)+ Ly(y) 的值为 1. Lx(x)- d+ Ly(y)+ d, x∈ S, y∈ T。 2. Lx(x)+ Ly(y), x∉ S, y∉ T。 3. Lx(x)- d+ Ly(y), x∈ S, y∉ T。 4. Lx(x)+ Ly(y)+ d, x∉ S, y∈ T。 易知,修改后对于任何边仍满足 Lx(x)+ Ly(y)>= W(x,y),并且第三种情况顶标值减少了 d,如此定会使等价子图扩大。 就上例而言: 修改后 Lx(1)= 2, Lx(2)= 3, Lx(3)= 5, Ly(1)= 0, Ly(1)= 0, Ly(2)= 0, Ly(3)= 1。 这时 Lx(2)+Ly(1)=3+0=3= W(2,1),在等价子图中增加了一条边,等价子图变为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
输入描述Input Description
第一行输入两个数n和m。
以下n行每行若干个数,这些数都是不超过m的正整数。其中第i行的数表示社团i的全部成员。每行用一个0结束。
输出描述Output Description
输出最多的能够成为代表的人数。
对每组测试数据输出一行
仅有一个整数s
表示最多有多少个小杉能成功脱逃
Sample Input
1 1 Output
1
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
int r,a,t;
inline int cal(int x,int y){return (x-1)*m+y;}
bool find(int x){
for(int i=1;i<=sum;i++)
if(map[x][i]&&!vis[i]){
vis[i]=1;
if(!res[i]||find(res[i]))return res[i]=x,1;
{
cp[i]=k;
return 1;
}
}
}
return 0;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>x;
while(x!=0)
{
a[i][x]=1;
cin>>x;
}
}
for(int i=1;i<=m;i++)
{
memset(old,0,sizeof(old));
}
return 0;
}
int main(){
scanf("%d%d%d",&n,&m,&k);sum=n*m;
for(int i=1;i<=n;i++)
二分图匹配
1、Way Selection(Vijos P1212)
描述Description
小杉家族r个人正在一片空地上散步,突然,外星人来了……
留给小杉家族脱逃的时间只有t秒,每个小杉都有一个跑的速度v
总共有a个传送点,小杉们必须在t秒内到达传送点才能脱逃
另外一个小杉进入一个传送点以后,该传送点就会消失
4 4
6
1 1
1 4
2 2
4 1
4 2
4 4
样例输出Sample Output
4
#include<cstdio>
#include<cstring>
int n,m,k,x,y,sum,ans;
int xx[4]={1,0,-1,0},yy[4]={0,1,0,-1},res[10010];
bool f[110][110],map[10010][10010],vis[10010];
样例输入Sample Input
4 4
1 2 0
1 2 0
1 2 0
1 2 3 4 0
样例输出Sample Output
3
数据范围及提示Data Size & Hint
各个测试点1s
数据范围
n,m<=200
#include<iostream>
#include<cstdio>
#include<cstring>
输入文件的第一行是两个整数N,M (1<=N,M<=100),第二行为一个整数K( K<=50),接下来的K行,每行两个整数X,Y表示K个水塘的行列位置。(1<=X<=N,1<=Y<=M)。
输出描述Output Description
输出所覆盖的最大面积块(1×2面积算一块)。
样例输入Sample Input
return 0;
}
bool find(int v)
{
for(int i=1;i<=a;i++)
if(mp[v][i]&&!y[i])
{
y[i]=1;
if(!lk[i]||find(lk[i]))
{
lk[i]=v;
return 1;
}
}
return 0;
}
int main()
{
double xx,yy,v;
using namespace std;
int n,m,x=1;
int a[210][210],old[210],cp[210];
bool find(int k)
{
for(int i=1;i<=n;i++)
{
if(a[i][k]==1&&old[i]==0)
{
old[i]=1;
if(cp[i]==0||find(cp[i]))
double px[1001],py[1001];
int lk[1001],y[1001],mp[1001][1001];
int ans=0;
bool pd(double x,double y,double v,int k)
{
if(v*t>=sqrt((x-px[k])*(x-px[k])+(y-py[k])*(y-py[k])))return 1;
cin>>r>>a>>t;
for(int i=1;i<=a;i++)
cin>>px[i]>>py[i];
for(int i=1;i<=r;i++)
{
cin>>xx>>yy>>v;
for(int j=1;j<=a;j++)
{
if(pd(xx,yy,v,j))mp[i][j]=1;
}
}
for(int i=1;i<=r;i++)
{
memset(y,0,sizeof(y));
if(find(i))ans++;
}
cout<<ans;
return 0;
}
2、寻找代表元(codevs2776)
题目描述Description
广州二中苏元实验学校一共有n个社团,分别用1到n编号。广州二中苏元实验学校一共有m个人,分别用1到m编号。每个人可以参加一个或多个社团,也可以不参加任何社团。
if(find(i)==1)x++;
}
cout<<x<<endl;
return 0;
}
3、覆盖
题目描述Description
有一个N×M的单位方格中,其中有些方格是水塘,其他方格是陆地。如果要用1×2的矩阵区覆盖(覆盖过程不容许有任何部分重叠)这个陆地,那么最多可以覆盖多少陆地面积。
输入描述Input Description
现在请你安排一种方案,使脱逃的小杉尽可能的多
输入格式Input Format
每组测试数据的
第一行有三个整数r和a和t(0<a,r,t<=1000)
第二行有a对实数,第i对数表示第i个传送点的坐标,这些坐标绝对值均不超过1e6
接下来r行,每行有三个实数x,y,v,表示第i个小杉的坐标和奔跑的速度
输出格式Output Format
