质点系的动能定理
理论力学经典课件-第六章 质点系动能定理

θ
ω AB
y
G1
R
δ W = G1δ yC
(b)
A vA ω A
G2
Cv1 dT dT δ W 由dT = δ W,有 ,将式(b)代入,有 (b) = dt dt l d( cosθ ) 3 G2 1 G1 2 G1 l 2 l 2 vA aA + [ l + ]ω ABα AB = G1 = G1 sin θω AB 2 g 12 g g 4 dt 2
T T0 = ∑W
(包括内,外力功)
6-2-1 动能定理的三种形式 6-2-2 动能定理的应用
第六章 质点系动能定理
6-2-1 动能定理的三种形式 1 .微分式
dT = δW
所有力的元功之和
2 .积分式 外主动功 T2 T1 = W1 2 约束功 内 功 对于理想约束,约束力功为零(如光滑铰,光滑面…)
b
图(b)示瞬时,C为BC杆瞬心
θ0
mg mg
(a)
θ0
C
vC = 0 ,ωC = 0
由 T T0 = ∑W 而 T0 = 0,
A
r
m1
(a)
A
B
C
ω AB
(b)
1 1 2 2 T = mb ω AB × 2 2 3
6-2 质点系动能定理
6-2-2 动能定理的应用 代入式(a)得
1 2 2 mb ω AB = Fb sin θ 0 + mgb sin θ 0 3
k
l 2
l 2
(a)
对!弹簧静力与重力在转动时仍平衡,其功之和 为零,可同时不考虑.又如图(b)
k
1 2 V = kδ 2
6-2 质点系动能定理
质点系的动能定理⒈质点系动能定理的微分形式

§14-4
一.势力场
机械能守恒定律
1.力场
若质点在某空间内的任何位置都受到一个大小和方向完全 由所在位置确定的力的作用,则此空间称为力场。 2.势力场
在力场中, 如果作用于质点的场力作功只决定于质点的始
末位置,与运动路径无关,这种力场称为势力场(保守力场) 。 重力场、万有引力场、弹性力场都是势力场。
即
dT Wi
— 微分形式的质点系动能定理
质点系动能的微分,等于作用于质点系上所有力的元功 之和。 ⒉ 质点系动能定理的积分形式 将上式沿路径 M1M 2 积分,可得
T2 T1 W — 积分形式的质点系动能定理
质点系在某一段路程中始末位置动能的改变量等于作用于
质点系上所有的力在相应路程中所作功的和。
③ 运动分析计算动能;
④ 根据动能定理求解:
1 1 1 2 2 2 T2 2m 0.9 mv 2 3 2 5 2 0.9 v T2 mv 6
T1 0
代入到 T2 T1 W ( F ) 得
5 2 mv 0 1.35mg 6 v 3.98m/s
§ 14-1
力的功
力的功是力沿路程累积效应的度量。 一.常力的功
W FS cos F S
时,负功。 时,正功; 时,功为零; 力的功是代数量。
单位:焦耳(J);
2
1J 1N1m
2
2
二.变力的功 ⒈ 力的元功
W F cosds
F ds F dr
P
W
dt
F dr 作用力的功率: P F v F v dt dt
力矩的功率:
W
d n P Mz M z M z dt dt 30
大学物理第二章动能定理
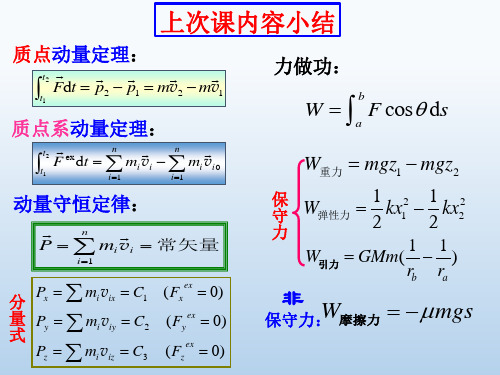
例题3. 如图,一轻绳跨过一定滑轮,两边分别拴有质量
为m及M的物体,M离地面的高度为h: (1)若滑轮质量及
摩擦力不计,m与桌面的摩擦也不计,开始时两物体均静
止,求M落到地面时的速度(m始终在桌面上); (2)若m与
桌面的静摩擦系数和滑动摩擦系数均为,结果又如何?
解:
m
(1)不计摩擦,系统(m,M,地球)机械能守恒:
v
m
0 M f c
f
s
s
Wf Wf 0
N
v c
N
WN WN 0
质点系动能定理:
质点系的动能的增量等于作用于质点系的一切外力与
内力做功之和.
W ex
W in
n i1
1 2
mi vi2
n i1
1 2
mi vi20
2.2.1 质点系动量定理
作用于质点系的合外力的冲量等于质点系动量的增量.
t2
系统内所有质点对同一参考点角动量的矢量和称为
质点系的角动量.
L Li ri pi ri mivi
i
i
i
dL dt
d dt
Li
i
Mi外
i
Mi内
i
0
M外
M 外
dL dt
积分得:
t2 t1
M外dt
L2
L1
注意:只有外力矩对质点系的角动量变化有贡献,
内力矩对质点系的角动量变化没有贡献.
W
F dr
l
F dr
acb
F dr
bda
0
a
c
F dr F dr F dr
acb
adb
bda
d
质点系的动能定理

2.弹性力的功 设弹簧原长为l0,在弹性极限内,弹簧的刚度系数为k(使弹簧 发生单位变形所需的力,单位:N/m),变形后长为r,沿矢径
的单位矢量为
er r / r 则 F k(r l0 )er
M2
d
1 2
mivi
2
δ Wi
d
1 2mivi
2
δWi
即
dT δWi
此即质点系动能定理的微分形式。
将上式沿路径 M1M 2 积分,可得
T2 T1 (Wi )12
此即质点系动能定理的积分形式。即质点系在某段运动过程 中动能的增量,等于作用于质点系的全部力在这段过程中所 作功的和。
3.理想约束及内力作功 理想约束:约束力作功为零的约束。
1.光滑固定面 δW N dr 0 (N dr ) 2.固定铰支座、活动铰支座和向心轴承、固定端
3.刚体沿固定面作纯滚动 4.光滑铰链(中间铰)
δW N dr N 'dr N dr N dr 0
5.不可伸长的绳索、刚性二力杆(不计质量) 绳拉紧时,内部拉力的元功之和恒等于零。
下面考察质点系内力的功 δW F drA F ' drB
解:取系统为研究对象。T1 0
T2
1 2
Q g
v2
1 2
J
2
OA
1 2
J C B2
1 2
Q g
v2
1 2
P 2g
R2
2 A
1 2
3 2
P g
R2B2
v2 (8Q 7P) 16g
(v RA 2RB )
质点和质点系的动能定理

W f1 dr12 f2 dr21
4 – 3 质点和质点系的动能定理
例如: A板相对B板滑动
A板对B板旳摩擦力为 f
B板对A板旳摩擦力为 f
求:当B板从一端移到另 一端时,摩擦力所作功 .
解:
b
f B A
a
v f
摩擦力是一对力,据对力作功旳一般体现式,应有:
A f (a b)
a b 是相对位移量
4 – 3 质点和质点系的动能定理
二 . 成对力旳功
dA f1 dr1 f2 dr2
B1
dr1
f1
B2
f2 r
dr2
21
A1
A2
f2 d (r2 r1) f2 dr21
f1 d (r1 r2 ) f1 dr12
一对内力(internal force)
做旳功与参照系选择无关 , 只决定于两质点旳相互作用力 及其相对位移.
例:炸弹爆炸过程,内力和为零,但内力所做 旳功转化为弹片旳动能。
4 – 3 质点和质点系的动能定理
例:摩擦力做功 从地面看摩擦力对物体作功
W f s
在物体参照系(也是惯性系),物
体没有移动,
v
摩擦力对物体作功 W ? W 0
摩擦力是一对力,成对摩擦力作旳功: f
W物,地 f S
一对摩擦力所做旳功与参照系旳选择无关 = 运动中放出热能
4.3.4 , 4.3.7.
2
dA F dr 称为元功, 描述了力旳空间累积效应。
物理上,称
Ek
1 mv2 P2
2
2m
为质点旳动能.
于是有:
dEk
d(1 2
mv2 )
F
dr
质点系动能定理

动能
一、质点的动能 设质点的质量为m,速度为 v 二、质点系的动能
由速度合成定理:
vi vO viO 2 2 2 vi vi vi (vO viO ) (vO viO ) vO 2 v v v O iO iO
1 n 2 T mi vi 2 i 1
1 2 T mv 2
vO mi viO vO mvCO 若令点O'与质心C重合, 则 1 2 1 2 T mv C mi viC 得: 2 2
1 1 1 2 2 T mi vi mi vO mi vi2 m v O i O viO 2 2 2 1 1 2 2 mv O mi viO vO mi viO 2 2
vB
I AB
C
B
vC
1 2 1 2 mvC J C 2 2 1 l 2 1 ml 2 2 1 2 2 m( ) ml 2 2 2 12 6
1 2 1 2 2 1 2 2 mvB m( ) ml 2 2 2 4
2 2 A 1 A A
vC mvCC 0
柯尼希定理:
质点系的动能等于随同其质心平动的动能 与相对其质心运动的动能之和。
Байду номын сангаас
三、刚体的动能 1.平移刚体的动能:
1 1 1 T mi vi2 mi v 2 mv 2 2 2 2 2.定轴转动刚体的动能:
1 1 1 2 T mi vi2 (mi i ) 2 J z 2 2 2 2
功质点动能定理
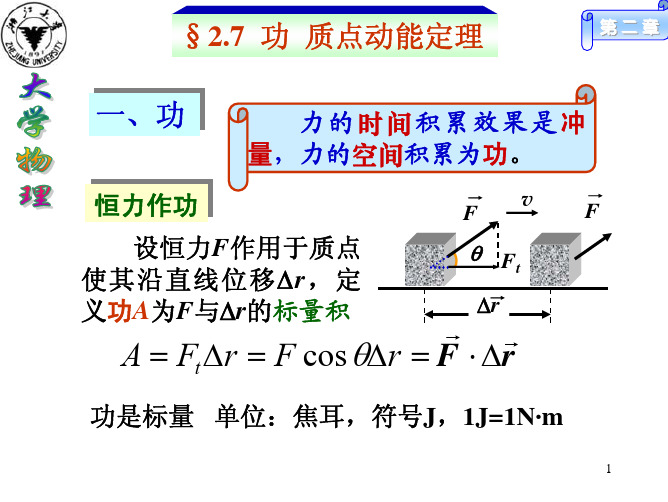
变力作功 变力作功 质点沿曲线从a移到b过程中力F作的功 取微元过程,力近似恒力
第 第二 二章 章
G F
G G G dA = F ⋅ dr = F cos θ dr = F cos θ dl = Ft dl
总功 a
元功
θ
dl
Ft G rb
G dr
b
G (b ) (b ) G A = ∫( a ) F ⋅ dr = ∫( a ) F cos θ d l
4
质点动能定理 设质点m受合力F作用,沿 曲线由a移到b,微元过程作功 G G dA = F ⋅ dr = Ft dl
G F
dl θ G dr
G r G ra
Ft
第 第二 二章 章
b
G rb
dv a 切向力 Ft = mat = m dt o dv (b ) v d A = 功 d A = m d l = mv d v ∫( a ) ∫v0 mv d v dt v0和v为质点在a点和b点时的速率
14
2.重力势能 重力势能是引力势能的特例 Mm +C 利用引力势能 E p = −G r Mm 地球表面为势能零点 C =G R r = R时,Ep= 0,得 在离地面h高处,r = R+h,重力势能为
mM mM mM +G =G E p = −G h ( R + h) R R+h R GM Ep ≈ m 2 h h<<R时,R+h ≈ R R M Epp= =mgh mgh 由 g =G 2 E R
o F12 F21
G G F12 = − F21
相对位矢 G G G G G G G G G G dA = F12 ⋅ dr1 + F21 ⋅ dr2 = F21 ⋅ (dr2 − dr1 ) = F21 ⋅ d (r2 − r1 ) 在m1上建立参照系
大学物理2-5质点系动能定理 机械能守恒定律

初态 末态
Ek1 0 Ek 2 0
x
E p1
1 2
kx12
Ep2
1 2
kx22
x0 x
F
x2
O
x1
根据能量守恒定律,应有
1 2
kx12
1 2
kx2 2
因恰好提起m2时,k(x2-x0)=m2g,而kx1=F, kx0=m1g
代入解得
F m1 m2 g
这就是说F(m1+m2)g时,下板就能被拉起 。
d
rr1
b1 a1
r f12
d rr1
1 2
m1v12b
1 2
m1v12a
对m2运用质点动能定理:
b2 a2
r F2
d
rr2
b2 a2
r f21
d
rr2
1 2
m2v22b
1 2
m2v22a
F1
F2
m1
f1 2
f21
m2
作为系统考虑时,得到:
b1 a1
或 E EK EP 常量
或 EKb EKa EPa EPb
四、能量守恒定律
一个孤立系统经历任何变化时,该系统的所有能量 的总和是不变的,能量只能从一种形式变化为另外一 种形式,或从系统内一个物体传给另一个物体。这就 是普遍的能量守恒定律.
例题2-15 起重机用钢丝绳吊运一质量为m 的物体, 以速度v0作匀速下降,如图所示。当起重机突然刹车 时,物体因惯性进行下降,问使钢丝绳会有多少微小 的伸长?(设钢丝绳的劲度系数为k,钢丝绳的重力忽 略不计)。这样突然刹车后,钢丝绳所受的最大拉力 将有多大?
第十二章 第三节 动能定理

例(P263例12-4) 绞车,已知力偶M、重物质量m;主动轴I和从 动轴II的转动惯量J1和J2,传动比i12=w1/w2;鼓轮半径R。。绞 车初始时静止,试求当重物上升距离h时的速度v及加速度a。 M 解 (1)整个质点系 I (2)运动分析 Ek1=0
1 1 m 2 2 2 Ek 2 J1w1 J 2w2 v 2 2 2 w1 iw 2 iv / R w2 v / R
将作用力分成外力和内力 注意:内力作功的和一般不等于零。
A rA
O FA BA rB FB
ቤተ መጻሕፍቲ ባይዱ
B
FA的元功FA · A; dr FB的元功FB · B。 dr 元功之和 d'W = FA · A + FB · B dr dr = FA · A - FA · B dr dr = FA · A-rB) d(r = FA · d(BA) = - FA d(BA)
第三节 动能定理
一、质点的动能定理 M1
M
a
F
M2
质点动能定理的微分形式:质点动能的微分,等于作用在质 点上的力的元功。
ma=F mat=Ft mdv/dt=Ft (mdv/dt) ds=Ftds mvdv=Ftds d(mv2/2) = d'W dEk = d'W
dEk = M Ftds
v2 v1
当质点系内质点间的距离发生变化时,内力功的总和一般不等 于零。 可变质点系: BA可变化,内力功之和不等于零 刚 体: BA不可变(刚体上任意两点的距离保持不变) 内力功之和等于零
内力作功举例: (1)汽车发动机的气缸内气体压力 (膨胀气体对活塞、气缸的作用力) ——内力功使汽车的动能增加 (2)机器中轴与轴承间的摩擦力,它们作负功,总和为负。 (3)人体活动 三、理想约束 理想约束:约束反力作功等于零的约束。 光滑接触面、光滑铰支座、固定端、一端固定的绳索、光滑铰 链、二力杆、不可伸长的细绳等 滑动摩擦力:摩擦力作负功,不是理想约束,但可将摩擦力作 为主动力,仍能应用动能定理 纯滚动:接触点为瞬心,滑动摩擦力作用点位移为零,滑动摩 擦力不作功。 ——纯滚动的接触点是理想约束。 在理想约束条件下应用动能定理求解速度、加速度非常方便。
大学物理之质点系的动能定理.ppt
注意
内力可以改变质点系的动能
第三章 动量守恒定律和能量守恒定律
3 – 5 保守力与非保守力 势能
物理学教程 (第二版)
二 质点系的功能原理
质点系动能定理 W ex W in Ek Ek0
W in Wiin Wcin Wnicn
i
非保守 力的功
Wcin ( Epi Epi0 ) Ep Ep0
物理学教程 (第二版)
的相互碰作撞用两. 物体互F相ex接触 时F 间in 极短而互p作i 用C力 较大
i
完全弹性碰撞 两物体碰撞之后, 它们的动能之
和不变 .
Ek Ek1 Ek2 C
非弹性碰撞 由于非保守力的作用 ,两物体碰撞
后,使机械能转换为热能、声能,化学能等其他形式
的能量 .
完全非弹性碰撞 两物体碰撞后,以同一速度运动 .
向相同. 若碰撞是完全弹性的, 求碰撞后的速度 v1和v2.
解 取速度方向为正向,由动
量守恒定律得
m1v10 m2v20 m1v1 m2v2
m1(v10 v1) m2 (v2 v20 )
由机械能守恒定律得
1 2
m1v120
1 2
m2 v220
1 2
m1v12
1 2
m2 v22
碰前
m1
v10
质点系的动量定理:系统所受合外力的冲量等
于系统动量的t增2 F量e
。
xdt
t1
n i 1
mi vi
n mi vi0
i 1
第三章 动量守恒定律和能量守恒定律
3 – 5 保守力与非保守力 势能
物理学教程 (第二版)
二. 质点系动量守恒定律
质点系所受合外力为零,系统总动量守恒。即
动能定理

v
2 B
vB vA vBA
m1 A
vA
θ l ωAB
vBA lAB vBA x lABcos vBA y lAB sin
B vBA
m2
vA
T= 1 2
(m1
m2
)v
2 A
m2lv A ABcos
m2l
2
2 AB
12
y
y´
思考题 已知滑块A的质量
O
m1 A
附加一力偶
图a):
s WFT FT s FT r r
图b):
s WFT -FT s FT r r 0
27
基本概念—功
圆轮向前滑滚,摩擦力参与做功,此种情况下动能定理与动量 定理、动量矩定理可互换。
圆轮受力如图 Fs mgf vC r
根据 T T0 W
1 2
J C 2
23
4). 圆轮沿支承面滚动时,摩擦力(约束力)的功。
vO O
Cv F
(1)圆轮连滚带滑运动时,动摩擦力F 所作元 功为
WF F drCv f FN vCvdt
(2)圆轮纯滚动时,这时出现静摩擦力F 。
FN
因为Cv 为速度瞬心,其速度为零。所以作用
在Cv点的静摩擦力F 所作元功为
W12
M2 M1
δW
M2 M1
F·dr
17
二、 几种常见力的功
1 重力的功
重力在曲线路程 A1A2 上的功为
W
z2 Gdz
z1
G( z1 z2 ) Gh
对于质点系
W12 mg(zC1 zC2 )
质点系的动能定理
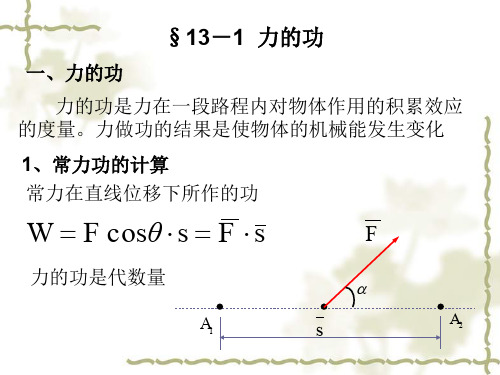
T1 0
T21Biblioteka 2(m1R12 )12
1 2
m2 2 2
1 2
势力场:场力作功只决定于力作用点的始末位置,而与 路径无关的力场。如:重力场、万有引力场、弹性力场
保守力:势力场内对应的场力。如:重力、万有引力、 弹性力等
二、势能
势能:势力场中,质点从位置 M 0 运动到位置 M1,有
势力所作功称为位置
M
相对位置
1
M 0的势能。
V
M1 F dr
Wi
We i
Wi i
对于刚体:
Wi i
0
对于可变形体:
Wi i
0
§13-3 功率、功率方程
一、功率
功率:单位时间内力所做的功,即
P w
dt
P
w
dt
F dr dt
F v
F v
对于作用于刚体上的力(力偶)功率:
P w
dt
M z d
dt
§13-1 力的功
一、力的功
力的功是力在一段路程内对物体作用的积累效应 的度量。力做功的结果是使物体的机械能发生变化
1、常力功的计算 常力在直线位移下所作的功
W F cosθ s F s
F
力的功是代数量
A1
s
A2
2、变力功的计算
(1)自然表达式 则力在微段路径上 所作元功为:
z
F
B:在某瞬时,在速度瞬心不明显时候,也可将平面 运功刚体的运动视为绕质心的定轴转动和随质心的平动 两部分运动的合成。
功能原理 机械能 质点系的动能定理功能原理

质点末动能 之和
N个质点初动能 之和
能点作 定系用 理的于 动质 能点 增系 量的 。力 这所 也作 叫的 做功 质, 点等 系于 的该 动质
质点系的动能定理
外力对质点所做 的功
质点系内一切内力所作 的功
质点系的动能的增量等于作用于质点系的一切外力做的 功与一切内力作的功之和。
质点系的功能原理
质点系内各保 守力做功之和
3-6 功能原理 机械能守恒定律质系的动能定理 质点系的功能原理
弹簧和物体(质点)构成系统.。 动 能 功 能
质点系的动能定理
W1=Ek1-Ek10; W2=Ek2-Ek20; W3=Ek3-Ek30; …………
作用力F所做 的功w
Eki Eki0 系统内 n个质 点
N个质点上的 力所作的功之 和
质点系内各非保 守力做功之和
势能增量
质点系的功能原理
初机械能
末机械能
质点系的机械能的增量等于外力与非保守力内力作 功之和,这就是质点系的功能原理
质点和质点系的动能定理

由动能定理,有
M
m2 g
sin
r
m2 g
cos
r
1 4
m1
2m2
r 22
得
2 M m2gr(sin f cos )
r
m1 2m2
将上式两边对时间t求导,并注意d/dt=ω,得鼓轮的角加速度为
2[M m2gr(sin f cos )]
r 2 (m1 2m2 )
目录
动能定理\质点和质点系的动能定理 【例8.6】 物块A质量为m1,挂在不可伸长的绳索上,绳索跨过定
T1=0
设物块下滑s=2m时的速度为v,其动能为
T2
1 2
mv2
51v2
在物块由静止到下滑2m 的过程中,
作用于物块上的重力的功为
W1 mg sin s 1000 N
2 2 m 1414 J 2
摩擦力的功为
W2 mg cos f s 1000 N
2 0.1 2 m -141.4 J 2
目录
动能定理\质点和质点系的动能定理
【解】 取鼓轮和重物组成的
质点系为研究对象,其上作用的 外力有:重物的重力m2g,斜面 的法向反力FN,摩擦力Ff,鼓轮 上的力矩M,以及鼓轮的重力和 轴承处的约束反力(图中未画 出)。
开始时,系统处于静止,其动能为
T1=0
设当鼓轮转过角时的角速度为,则重物的速度为 v=r
目录
动能定理\质点和质点系的动能定理 【例8.5】 一不变的力矩M作用在铰车的鼓轮上,轮的半径为r,
质量为m1。缠绕在鼓轮上的绳子系一质量为m2的重物,使其沿倾角
为的斜面上升(如图)。已知重物与斜面间的动摩擦因数为f,绳
子质量不计,鼓轮可视为均质圆柱。在开始时,此系统处于静止。
第13章质点系动能定理

1k 2
(12
22
)
初变形 1 未变形2
转动刚体上作用力的功
WM
2
mz (F )d
mz(F) C
W mz (F )(2 1)
1
力偶的功 WM M(2 1)
摩檫力的功 •两物有相对滑动, 摩擦力 作负功
vO O
P Fs
纯滚动时, 作用在速度瞬心P点 的摩擦力F 所作元功为
1
T ( 2i
mi )vC2
i
1 2
mi
vi2r
Te
Tr
质点系的动能(绝对运动动能),等于系统跟 随质心平移的动能(牵连运动动能)与相对于质 心平移系运动的动能(相对运动动能)之和。
结论与讨论
正确计算刚体 平面运动时的动能
x
vA xA
OA
x
B
均质杆AB长度为l、质量为m , A端与小圆滚轮铰接,小圆滚轮
dt
dt
力(偶)矩的功率: P W M d M
质点系动能定理 dt
dt
质点: m dv F m dv v F v
d( 1 mv 2 ) 2
P
dt
质点系:d(
1
2 dt
mv
2
)
dt
P
dT dt
dt
P — 功率方程
dT Pdt dT W -微分形式
W
O
Ax
为求物块A下降至 任意位置(x)时的加速 度,可以采用哪一个
动力学定理?
W x
结论与讨论
关于动能定理 与
3.3质点系的动能定理

3.3.2 一对内力的功 系统内任意二质点1 系统内任意二质点1、2
r int r int 位移d 一对内力 F21 F12 位移dr1
z
dr1
1 •
• • •
dr2
O x
Fint Fint dr2 12
*例3.3-2滑块A置于光滑的水平面上,物体B 3.3- 滑块A置于光滑的水平面上,物体B 放在滑块A 假设滑块A足够长. 放在滑块A上,假设滑块A足够长.现用外力 F拉动A由静止开始运动,则B在A上滑动,A、 拉动A由静止开始运动, 上滑动, 间的滑动摩擦因数为µ. B间的滑动摩擦因数为 .若B在A上向后相对 滑动的距离为. 的质量分别为m 滑动的距离为.设A、B的质量分别为 A、 mB.求在此过程中A、B间的一对摩擦力所做 求在此过程中A 的功之和为多少? 的功之和为多少
S-l l F
解:以地面为参考系 设A滑动的距离为S
B A f
3.2 3.3质点系的动能定理和机械能守恒 质点系的动能定理和机械能守恒 质点系的动能定理和机械能守恒
r r A1 = f ⋅ S = fS cos π = − fS
S-l B A
l F
B滑块对地 移动S-l 摩擦力f´做功
f r r (f '= −f) r r r A2 = f ′ ⋅ ( S − l ) = f ( S − l ) cos 0 = f ( S − l )
21 •
2
r1 r2
一对内力的功
r int r r int r r int r r F21 ⋅ d r2 + F12 ⋅ d r1 = F21 ⋅ d(r2 − r1 )
§4.2质点和质点系动能定理

dA F dr
F
s1
Ft ds mat ds O dr dset dv t s0 m ds mvt dvt dt 1 d ( mv t 2 ) d ( 1 mv 2 ) 2 2 1 E k mv 2 称为质点的动能 2
dA Nm drmM 0
Nm
drmM
m M
fr
在无相对位移或相对位移与一对力垂直的情况 下,一对力的功必为零。
三、质点系动能定理
质点系:n个质点组成
第i个质点
Ai外 Ai内 Eki Eki 0
所有质点
i 1
Ai外 Ai内 Eki Eki
3、分析动能改变
5、求解方程
例2
已知: m、M, μ1、μ2, v 解:(一)质点系动能定理 质点系:卡车、木箱 由质点系动能定理,得:
v
L
f2
求: l 、L
f1
l
m
f1'
2 2(m M ) gL 1mgl 0 1 ( M m ) v 2
再以木箱m为质点,应用质点动能定理:
解得:
Mv2 L 2 g[ 2(m M ) 1m]
l
v2 2 1 g
L
2 1mg( L l ) 0 1 mv 2
(二)质点动能定理
以木箱m为质点,应用质点动能定理:
1mg( L l ) 0 mv
1 2 2
f1
v
L f2
l
m
对卡车M应用质点动能定理:
f1'
2 1mgL 2(m M ) gL 0 1 Mv 2
65质点系的动能定理和机械能守恒定律

§6.5质点系的动能定理和机械能守恒定律一、质点系的动能1. 质点系动能的定义.质点系的总动能T 定义为质点系内每个质点动能之和, 即21121i i ni n i i v m T T ∑∑==== 2. 柯尼希定理.212t 2121i i n i c c v m v m T T T ′+=′+=∑= 式中c T 为位于质心的假想质点的动能, T ′为质点系在质心系中的动能.证明: 由i c i r r r ′+= 可知i c i v v v ′+= , 所以)()(2121121i c i c i n i i i ni v v v v m v m T ′+⋅′+==∑∑== 211212121i i n i i n i c i c i n i v m v v m v m ′+′⋅+=∑∑∑=== 由于0=′⋅=′⋅=′⋅∑∑c t c i i c i c i v m v v m v v v m , 则 212t 2121i i n i c v m v m T ′+=∑= 例题7 质量为m 、 半径为R 的匀质圆盘, 在Oxy 平面沿x 轴做无滑滚动, 盘心速度为0v , 如图所示, 求圆盘动能.解 盘心即为圆盘质心, 建立质心系y x C ′′如图. 则222121ωI mv T c += 220220212121Rv mR mv ⋅⋅+= 2043mv =二、质点系在惯性系中的动能定理和机械能守恒定律1. 质点系的动能定理.质点系的动能定理表述为: 在惯性系中, 质点系动能的微分等于质点系所受所有外力和内力的元功之和, 即∑∑==+=+=ni i i n i e ii e W W W W T 1)(1)()()(δδδδd i n i i i i ni e i r F r F d d 1)(1)(⋅+⋅=∑∑== 证明: 质点系内第i 个质点的动能定理为i i i i e i i r F r F T d d d )()(⋅+⋅=对n 个质点求和, 则)()(1)(1)(δδd d d i e i n i i i i n i e i W W r F r F T +=⋅+⋅=∑∑== 质点系动能的微分与内力元功有关.由于刚体内力做功之和为零, 即0δ)(=i W , 所以刚体动能的微分与内力元功无关.2. 内势能.从严格意义上讲动能与势能的转化, 要用一对保守力做功之和来度量.由于一对内力所做元功之和, 已归结为其中一个力在其受力质点相对另一质点的相对位移中所做元功, 即ij ij ij ij j ji i ij r F r F r F r F d d d d ±=⋅=⋅+⋅因此, 一对内力为保守力, 自然可以使用在§3-5中给出的等价定义中的任意一种来定义. 比如实际中涉及的内力均)(ij ij ij r F F =,若)(d d d )(ij i ij j ji i ij r V r F r F −=⋅+⋅ 则这一对内力为保守内力.为与质点力学中讨论的外势能)(e V区分, 一对内保守力的势能记为)(i V , 称为内势能.物理本质——内势能.外势能是对势能的一种理解方式, 是简化功能关系的一种方法.外势能的概念又必须存在, 否则完整的质点动力学就不能建立.3. 质点系的机械能定理和机械能守恒定律.对于第i 个质点所受保守外力)(e ic F , 可引入外势能)(e i V)()(d d e i i e ic V r F −=⋅则质点系总外势能∑==n i e ie V V 1)()( 对于第i 个质点与第j 个质点间的一对保守内力, 可引入内势能)(i ij V)(d d )(ij i ij ij ij r V r F −=⋅则质点系总内势能∑≠==n j i j i i ij i V V ,1,)()(21并把第i 个质点所受非保守外力所做元功记为)(nc δe i W ,把第i 个质点与第j 个质点间的一对非保守内力所做元功记为)(nc δi ij W ,则由质点系的动能定理,可导出∑∑≠==+=++n j i j i i ij ni e i i e W W V V T ,1,)(nc 1)(nc )()(δ21δ)(d 定义质点系总势能)()(i e V V V +=, 总机械能)()(i e V V T V T E ++=+=, 则上式称为质点系的机械能定理.作为其推论, 质点系的机械能守恒定律表述为:若在某一过程中, 质点系所受非保守外力均恒不做功, n i W e i ,,2,1,0δ)(nc ⋅⋅⋅=≡; 每一对内非保守力做功之和均恒为零, n j i W i ij ,,2,1,,0)(nc ⋅⋅⋅=≡δ且j i ≠,则在该过程中质点系的总机械能守恒,=++=+=)()(i e V V T V T E 常量质点系机械能守恒说明, 在运动过程中质点系的动能与势能可以相互转化, 但没有机械运动与其他形式的运动之间的能量转化.三、质点系在质心系中的动能定理质点系在质心系中的动能定理为i n i i i i n i e i i i ni r F r F v m T ′⋅+′⋅=′=′∑∑∑=== d d 21d d 1)(1)(21 亦与惯性系中的动能定理形式相同, 与内力元功有关.证明: 在作为非惯性系的质心系中讨论质点系运动时, 需考虑惯性力, 且视惯性力为外力. 由于各质点所受惯性力在质心系内做功之和0)(d d =′⋅−=′⋅−∑∑i i c i c i r m a r a m , 所以惯性力不在方程中出现, 定理形式与惯性系内定理形式相同.四、小结牛顿力学基本理论框架.一般情况下, 质点系力学的三个定理只能对质点系的运动进行整体描述, 而不能确定其中每个质点的运动细节.内力. 质心和质心系.从整体上研究质点系运动的基本思想是把其整体运动分解为以质心为代表的“平动”和相对质心系的运动.在质点系力学中三个基本定理有相对的独立性, 因此如何选取适当的定理去解决问题, 往往是成败的关键.例题8 绞车安装在水平梁上, 梁的两端搁在支座A 和B 上, 质量为1m 的重物向下做加速运动, 并通过不可伸长的轻绳带动滑轮转动. 滑轮质量为2m , 半径为R , 可视为匀质圆盘. 梁及支架总质量为3m , 其质心C 在AB 的垂直平分线上. 滑轮轴承光滑, l AB 2=, d AD =, 如图所示, 设初时各物体均为静止、 绳与滑轮间滑动.试求: (1) 重物1m 的加速度; (2)A 处支座对梁的作用力.解 先分析各物体运动情况……在重物下落过程中梁固定不动.(1)以重物、 绳和滑轮构成系统, 受外力g m W 11=, g m W 22=, NO F (NO F 沿竖直方向). 建立坐标系Oxyz 如图, 由对z 轴的角动量定理g Rm Rx R m x Rm t 1221)21(d d =+ 所以21122m m g m x +=(2) 以重物、 绳、 滑轮及梁构成了系统, 受外力g m W 11=, g m W 22=, g m W 33=, NA F , NB F , 建立BZ 轴与z 轴同向, 由对BZ 轴的角动量定理+−R x R m x m d l t 22121)2(d dNA lF g lm g m R d l g m d l 2)2()2(321−+−−+−=利用)2(2211m m g m x +=, 可求得 g lm g Rm g m m d l lF NA 3221))(2{(21+−+−= ]})2(2[)2(21211R m m d l m m g m +−+− 讨论:(1) 可以根据动能定理求x. 以)(21m m ++绳为系统, 由于在运动中只有保守力g m W 11=做功, 所以系统机械能守恒, 以o 为重力势能零点, 则0112221)(212121gx m gx m Rx R m x m −=−⋅+ 0x 为重物初始位置.(2) 当我们用角动量定理求x时, 系统选取要适当.(3) 用动量定理无法求出x. (4) 求出x后,用动量定理NO F g m g m x m −+=211 求出NO F , 再以3m 为系统求出NA F .选取系统、 定理和参考点(轴)的原则是: 尽量减少在方程中出现的未知量个数……(1) 选用动量和角动量定理时, 内力不在方程中出现;(2) 选用角动量定理时, 对参考点(轴)力矩为零的外力不在方程中出现;(3) 应用动能定理时, 不做功的外力及内力均不在方程中出现.优先选用守恒定律解决问题.例题9 一水平匀质细管长为L , 质量为0m , 能绕过管一端并与其固连的竖直轴转动. 轴质量可忽略, 轴承处光滑. 管内放有一质量为m 的小球, 如图所示. 初始时, 管的角速度为0ω, 小球位于管的中点, 小球相对管的速度为零. 设小球与管壁间无摩擦, 试求小球出口时的速率.解 以小球、 管和轴构成系统, 建立柱坐标系如图所示, 极轴沿管的初始位置. 系统受外力g m W 01=, g m W =2, NA F 和NB F 对z 轴力矩均为零,所以系统对z 轴角动量守恒. 设小球出口时管的角速度为ω , 小球速度为v , 则02020220)2(3131ωωωωL m L m mL L m +=+ 所以000)3(434ωωm m m m ++=由于系统所受所有外力、 内力均不做功, 所以系统机械能守恒2020202220)2(213121213121ωωωL m L m mv L m +⋅=+⋅ 故202000366928)3(4mm m m m m L v +++=ω请读者思考: 若小球与管壁间有摩擦, 对小球出口速度v 及径向速度r v有何影响?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力的功
W F S FS cos
力的功是代数量。
时,正功; 时,功为零; 时,负功。 2
2
2
单位:焦耳(J):1J = 1N 1m 二.变力的功 元功: δW F d r 变力 F 在曲线路程 M1M 2中作功为
M2
W
M1
F d r
在直角坐标系中,知
F Fx i Fy j Fz k
dr dx i dy j dz k
变力 F 在曲线路程 M1M 2中作功为
W
M2 M1
F d r F dx F dy F dz
x y z M1
M2
三.合力的功
W
解:我们取物体M为研究
对象,作用于M上的力有
重力 mg ,斜面法向反力 FN ,摩 擦 力 F′ 以及 弹簧 力F,各力所作的功为
WG mg s sin30o
(10 9.8) 0.5 0.5 24.5J o W F s f mg cos30 s WF 0 F
d rC MC d δW FR
则刚体质心C由C1移到C2,同时刚体又由角 1转到角 2时, 力系所作的功为
C2
W12
C1
F d r M
R C
1
2
C
d
注意:以上结论也适用于作一般运动的刚体,基点也可以是 刚体上任意一点(不一定取在质心)。
[例1] 质量为m = 10 kg的物体,放在倾角为 = 30º的斜面上, 用刚度系数为 k = 100 N/m 的弹簧系住,如图示。斜面与物体 间的动摩擦系数为f = 0.2,试求物体由弹簧原长位置 M0 沿斜面 运动到 M1 时,作用于物体上的各力在路程 s = 0.5 m 上的功及 合力的功。
柯尼希定理
三.刚体的动能
1.平动刚体
2.定轴转动刚体 3.平面运动刚体
1 1 1 2 2 2 T mi vi ( mi )vC M vC 2 2 2 1 1 1 T mi vi 2 ( mi ri 2 ) 2 J z 2 2 2 2
记刚体平面运动某瞬时的速度瞬心为P,质心为C,则
3.定轴转动刚体上作用力的功
设刚体绕 z 轴转动,在其上M点作用有力F,则
δW F d r F Rd cos Ft Rd M z d
其中Ft 为力F 在作用点M处的轨迹切线上的投影。
于是力F 在刚体从角 1转到角 2过程中作的功为
W12
2
M d
z
1
作用于转动刚体上力的功等于力矩的功。
如果刚体上作用的是力偶,则力偶所 作的功仍可用上式计算,其中Mz为力偶 对z 轴的矩。 若Mz = 常量, 则 W12 M z (2 1 )
4.平面运动刚体上力系的功 平面运动刚体上力系的功,等于力系向质心简化所得的 力(主矢)与力偶(主矩)作功之和。 首先可以证明,刚体上力系的全部力所作的元功之和为
M2
M1 M2
R dr (F F
1 r
M2 n
M1
F d r F d r F d r
M1
W1 W2 Wn
即在任一路程上,合力的功等于各分力功的代数和。
故质点系重力的功,等于质点系的重量与其在始末位置 重心的高度差的乘积,而与各质点的运动路径无关。
2.弹性力的功 设弹簧原长为l0,在弹性极限内,弹簧的刚度系数为k(使弹簧
发生单位变形所需的力,单位:N/m),变形后长为r,沿矢径
的单位矢量为
er r / r 则 F k (r l0 )er
W12
M2 M1
F d r k ( r l )e
0 M1
M2
r
dr
r 1 1 er d r d r d(r r ) d(r 2 ) d r r 2r 2r r2 r2 k k 2 W12 k (r l0 )d r d(r l0 ) [(r1 l0 ) 2 (r2 l0 ) 2 ] 2 2 r1 r1 k 2 2 则 W ( 令:1 r1 l0 , 2 r2 l0 12 1 2 ) 2 故弹性力的功只与弹簧在初始和终了位置的变形有关,而与 力作用点的路径无关。
质点和质点系的动能
物体的动能是由于物体运动而具有的能量,是机械运动
T 1 m v2 2
动能是一个瞬时的、与速度方向无关的正标量,具有与功
相同的量纲,单位也是焦耳(J)。 1 二.质点系的动能 T mi vi 2 2 对任一质点系,若记 vi′为第 i 个质点相对质心的速度,则
可证明有
1 1 2 T MvC mi vi '2 2 2
1 1 2 T J P ( J C M d 2 ) 2 2 2 1 1 1 1 2 2 2 2 J C M (d ) J C M vC 2 2 2 2 即作平面运动刚体的动能,等于随质心平动的动能与绕质心
转动的动能之和。
N
0.2 (10 9.8 0.866) 0.5 8.5J k 2 100 2 WF (1 2 ) (0 0.52 ) 12.5 J 2 2 合力的功为 W Wi 24.5 0 8.5 12.5 3.5J
§13-2
强弱的又一种度量。 一.质点的动能
四.几种常见力的功 1.重力的功 取 z 轴铅垂向上,则:
Fx 0, Fy 0, Fz mg
W12 ( mg )dz mg ( z1 z2 )
z1 z2
对于质点系,重力作功为
W12 Wi12 mi g ( zi1 zi 2 ) Mg ( zC1 zC 2 )
