次函数中的特殊三角形存在性问题
二次函数特殊三角形存在性问题(等腰三角形、直角三角形)

特殊图形存在性问题一、等腰三角形1、情景:平面内有点A、B,要找到点P使得△ABP为等腰三角形。
2、思想:分类讨论(1)A为顶点:AB=AP(以A为圆心、AB长为半径画圆)(2)B为顶点:AB=BP(以B为圆心、AB长为半径画圆)(3)P为顶点:PA=PB(AB中垂线)【注】:1.利用两圆一线,找到符合要求的点,如P在抛物线对称轴上,在x轴上等;然后将问题转化为,求线段等长。
2.求线段等长:两点间距离(最笨的方法);向坐标轴做垂线,构造一线三等角例1.如图,抛物线y=−x2+2x+3y=−x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为______.练习1.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B 两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,−3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式;(2)在直线BC找一点Q,使得△QOC为等腰三角形,写出Q点坐标.练习2、已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.练习3.如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣x+1与y轴交于点D.(1)求抛物线的解析式;(2)证明:△DBO∽△EBC;(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.练习4.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c(a≠0)与x轴交A(−1,0),B(−3,0)两点,与y轴交于点C(0,−3),其顶点为D.(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x−h)2+k的形式;(2)动点M从点D出发,沿抛物线对称轴方向向上以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?练习5.如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n (m<n)分别是方程x2﹣2x﹣3=0的两根.(1)求抛物线的解析式;(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E 两点(点D在y轴右侧),连接OD、BD.①当△OPC为等腰三角形时,求点P的坐标;②求△BOD 面积的最大值,并写出此时点D的坐标.25.(10分)如图,在平面直角坐标系中,抛物线y=x2+bx+c经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).(Ⅰ)求抛物线的解析式及它的对称轴;(Ⅱ)点P(0,n)在线段OB上,点Q在线段BC上,若OP=2BQ,且P A=QA.求n 的值;(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.19-红桥一模25.(10分)如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.(17河北一模)25(10分)如图,己知抛物线y=x2+bx+c图象经过点A(﹣1,0),B(0,﹣3),抛物线与x轴的另一个交点为C.(1)求这个抛物线的解析式:(2)若抛物线的对称轴上有一动点D,且△BCD为等腰三角形(CB≠CD),试求点D的坐标;二、直角三角形1.情景:平面内有点A、B,要找到点P使得△ABP为直角三角形2.思想:分类讨论(1)A为顶点:∠A(过A做垂线)(2)B为顶点:∠B(过B做垂线)(3)P为顶点:∠C(AB为直径的圆)【注】1.等腰直角三角形,只需在两直线上上下找与AB等长以及过O做AB垂线与圆交点即可例1.如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过矩形OABC的顶点A,B与x 轴交于点E,F且B,E两点的坐标分别为B(2,32)E(−1,0)(1)求二次函数的解析式;(2)在抛物线上是否存在点Q,使△QBF为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.练习1.如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=13(1)求抛物线的对称轴和PP的坐标.(2)在抛物线的对称轴上是否存在这样的点D,使△ABD为直角三角形?如果存在,求点D 的坐标;如果不存在,请说明理由.例2.如图,抛物线y=−x2+bx+c与x轴相交于AB两点,与y 轴相交与点C,且点B与点CC 的坐标分别为(3,0),C(0,3),点M是抛物线的顶点.(1)求二次函数的关系式(2)在MB上是否存在点P,过点P作PD⊥x轴于点D,OD=m,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由练习2.如图,在平面直角坐标系中,直线y=−13x+2交x轴点P,交y轴于点A.抛物线y=x2+bx+c的图象过点E(−1,0),并与直线相交于A、B两点.(1)求抛物线的解析式(关系式);(2)过点A作AC⊥AB交x轴于点C,求点C的坐标;(3)除点C外,在坐标轴上是否存在点M,使得△MAB是直角三角形?若存在,请求出点M 的坐标;若不存在,请说明理由.练习3.如图,抛物线y=x2+bx+c与直线y=x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.(1)求抛物线的解析式;(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.(18东丽-一模)25.如图,在平面直角坐标系中,点A、B的坐标分别为(1,1)、(1,2),过点A、B分别作y轴的垂线,垂足为D、C,得到正方形ABCD,抛物线y=x2+bx+c经过A、C两点,点P为第一象限内抛物线上一点(不与点A重合),过点P分别作x轴y轴的垂线,垂足为E、F,设点P的横坐标为m,矩形PFOE与正方形ABCD重叠部分图形的周长为l.(1)直接写出抛物线所对应的函数表达式.(2)当矩形PFOE的面积被抛物线的对称轴平分时,求m的值.(3)当m<2时,求L与m之间的函数关系式.(4)设线段BD与矩形PFOE的边交于点Q,当△FDQ为等腰直角三角形时,直接写出m的取值范围.三、平行四边形存在性问题类型一:1.情景:一直平面内三点A、B、C,求一点P使四边形ABCP为平行四边形2.思想:分类讨论(1)以AC为对角线:ABCP1(2)以AB为对角线:ACBP3(3)以BC为对角线:ACP2B【注】找到P点后,用平行四边形的判定定理,求等长线段,或利用等角度、平行线求坐标即可。
一次函数中(特殊三角形)的存在性问题优秀教学设计

辅助策略:借助几何画板,使学生直观形象地观察、操作。
2、教法
演示法:通过几何画板演示两圆一中垂线和外K全等,使学生直观、形象的感知因动点的移动,在何时会出现等腰三角形和等腰直角三角形,思考在没有几何画板的时候,我们自己该如何作图,快速确定动点的位置。
《一次函数中特殊三角形的存在性问题》教学设计
【教学目标】
1、知识与技能
(1)使学生体会定点与动点之间的关系,做到以静制动。
(2)通过数形结合,利用几何法和代数法求一次函数中特殊三角形的存在性问题。
2、过程与方法
(1)借助几何画板探究一次函数中特殊三角形的存在性问题,使学生初步形成正确、科学的分析解决问题的方法。
①设点:设点P(0,m)A(3,0),B(0,4)
②表示三条边:
③列方程:
三、小组讨论
已知A(2,0),B(0,4),在第一象限内是否存在一点P,使得△PAB是等腰直角三角形,若存在请求出点P的坐标;若不存在,请说明理由。
讨论目标:①这样的动点P可能有多少个?如何分类?
②你能不能画出等腰直角三角形?
等腰三角形可以是两条边相等或者两个角相等,在我们所学的知识中,是边好表示,还是角好表示呢?
探究一:用几何法确定动点的位置——两圆一中垂线
例1、已知,A(3,0),B(0,4),在y轴上是否存在一点P,使得△PAB是等腰三角形,若存在,请求出点P的坐标,若不存在,请说明理由
探究二:用代数法确定动点的位置——设点法
实验法:让学生自己动手、在探究过程中,自己发现动点的规律
中考数学专题复习《特殊三角形存在性问题+将军饮马问题》

特殊三角形存在性问题+将军饮马问题1.如图1,已知长方形OABC的顶点O在坐标原点,A、C分别在x、y轴的正半轴上,顶点B(8,6),直线y= -x+b经过点A交BC于D、交y轴于点M,点P是AD的中点,直线OP交AB于点E.(1)求点D的坐标及直线OP的解析式;(2)点N是直线AD上的一动点(不与A重合),设点N的横坐标为a,请写出△AEN的面积S和a之间的函数关系式,并请求出a为何值时S=12;(3)在x轴上有一点T(t,0)(5<t<8),过点T作x轴的垂线,分别交直线OE、AD于点F、G,在线段AE上是否存在一点Q,使得△FGQ为等腰直角三角形,若存在,请写出点Q的坐标及相应的t的值;若不存在,请说明理由.2.如图,在平面直角坐标系中,直线y=-2x+4交坐标轴于A、B两点,过x轴负半轴上一点C作直线CD交y轴正半轴于点D,且△AOB≌△DOC.(1)OC= ,OD= ;(2)点M(-1,a)是线段CD上一点,作ON⊥OM交AB于点N,连接MN,则点N的坐标为 ;(3)若E(1,b)为直线AB上的点,P为y轴上的点,请问:直线CD上是否存在点Q,使得△EPQ是以E为直角顶点的等腰直角三角形,若存在,请求出此时Q点的坐标;若不存在,请说明理由.3.如图,已知:在矩形ABCD中,AB=3cm,BC=4cm,点P从点B出发,沿BC方向匀速运动,速度为2cm/s;与点P同时,点Q从D点出发,沿DA方向匀速运动,速度为1cm/s;过点Q作QE∥AC,交DC于点E,设运动时间为t(s),(0<t<2),解答下列问题:(1)在运动过程中,是否存在某一时刻t,使PQ平分∠APC?若存在,求出t的值;若不存在,请说明理由;(2)设五边形APCEQ的面积为y,求y与t的函数关系式;(3)是否存在某一时刻t,使△PQE是直角三角形?若存在,求出t的值;若不存在,请说明理由.4.如图,已知直线l1经过点(5,6),交x轴于点A(-3,0),直线l2:y=3x交直线l1于点B.(1)求直线l1的函数表达式和点B的坐标;(2)求△AOB的面积;(3)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标;若不存在,请说明理由.5.如图,直线l1经过A(6,0)、B(0,8)两点,点C从B出发沿线段BO以每秒1个单位长度的速度向点O运动,点D从A出发沿线段AB以每秒2个单位长度的速度向点B运动,设运动时间为t秒(t>0),(1)求直线l1的表达式;(2)当t= 时,BC=BD;(3)将直线l1沿x轴向右平移3个单位长度后,与x轴,y轴分别交于E、F两点,求四边形BAEF的面积;(4)在第一象限内,是否存在点P,使A、B、P三点构成等腰直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.6.如图,在平面直角坐标系中,直线AB:y=-54x+74与x轴交于点C,且点A(-1,m),B(n,-2).(1)求点C的坐标;(2)求原点O到直线AB的距离;(3)在x轴上是否存在一点P,使得△ACP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.7.如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D.(1)若点D的横坐标为1,求四边形AOCD的面积;(2)若点D的横坐标为1,在x轴上是否存在点P,使得以点P,C,D为顶点的三角形是直角三角形?若存在求出点P的坐标;若不存在,请说明理由.8.如图,在平面直角坐标系中,点O为坐标原点,等腰直角三角形OAB的斜边OB在x轴上,∠OAB=90°,点A(3,3).(1)求点B的坐标;(2)点P从点O出发沿x轴以每秒2个单位的速度向x轴正方向运动,设点P运动时间为t秒,求t为何值时,OP=2PB;(3)在(2)的条件下,当OP=2PB时,在第一象限内是否存在点Q,使△BPQ为等腰直角三角形?若存在,请直接写出点Q的坐标;(写出四个即可)若不存在,请说明理由.9.如图,在平面直角坐标系中A(a,0),B(0,b),满足a2-4a+4+|b-4|=0.(1)求A,B两点的坐标;(2)∠OBA的平分线BC与∠OAB的外角平分线AM交于点C,求点∠C的度数;(3)在平面内是否存在点P,使△ABP为等腰直角三角形.若存在,请写出点P的个数,并直接写出其中两个点的坐标;若不存在,请说明理由.10.问题探究(1)如图1,在四边形ABCD中,∠B=∠C=90°,点E是边BC上一点,AB=EC,BE=CD,连接AE,DE,判断△AED的形状,并说明理由.(2)如图2,在△ABC中,∠C=90°,点D为边CA的延长线上一点,且AD=2BC,过点A作AE⊥AB且AE=AB,连接DE,求证:DE=AE.(3)如图3,在平面直角坐标系xOy中,已知点A(3,2),连接OA,在x轴上方是否存在一点B,使得△OAB是等腰直角三角形,若存在,请直接写出点B的坐标;若不存在,请说明理由.11.如图,在△ABC中,∠B=90°,AB=11cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒2cm的速度沿BC向点C匀速运动,到达点C后返回点B,当有一点停止运动时,另一点也停止运动,设运动时间为t秒.(1)当t=1时,直接写出P,Q两点间的距离.(2)是否存在t,使得△BPQ是等腰三角形,若存在,请求出t的值;若不存在,请说明理由.(3)是否存在t,使得△BPQ的面积等于10cm2,若存在,请求出t的值:若不存在,请说明理由.12.如图,在平面直角坐标中,把长方形OABC沿对角线OB所在的直线折叠,点A落在点D处,OD与BC交于点E.已知OA=6,OC=3.(1)求出过点A,E的直线的函数表达式.(2)在x轴上是否存在点F,使△OBF为等腰三角形?若存在,直接写出点F的坐标;若不存在,请说明理由.13.如图,等腰直角△ABC中,BC=AC,∠ACB=90°,现将该三角形放置在平面直角坐标系中,点B坐标为(0,3),点C坐标为(9,0).过点A作AD⊥x轴,垂足为D.(1)求OD的长及点A的坐标;(2)取AB中点E,连接OE、DE,请你判定OE与DE的关系,并证明你的结论;(3)连接OA,已知OA=15,试探究在x轴上是否存在点Q,使△OAQ是以OA为腰的等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.14.如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B,CD⊥x轴于点D.(1)求点B和点C的坐标;(2)求直线l2的函数表达式;(3)在x轴上是否存在点P,使得以B、C、P为顶点的三角形是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.15.在平面直角坐标系xOy中,直线l过(1,3)和(3,1)两点,且与x轴,y轴分别交于A、B两点.(1)求直线l对应的函数解析式;(2)求△AOB的面积;(3)在x轴上是否存在一点C,使△ABC为等腰三角形,若存在,直接写出点C坐标;若不存在,请说明理由.16.古罗马时代,亚历山大有一个著名的学者叫海伦,一天罗马的一位将军专程跑去问海伦这样一个问题:每天从军营A出发,先到河边给马喝水,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?海伦思考后便给出了答案,也就是现在著名的“将军饮马”问题.其实“将军饮马”实质要解决的问题是:要在直线l上找一点P使得PA+PB的值最小.(1)如图1,点A到直线l的距离AO1=2,点B到直线l的距离BO2=3,O1O2=4,要解决该最小值问题,如图2,作点A关于直线l的对称点A',连结A'B交直线l于点P,此时P即为所求点,则PA+PB的最小值为 ;(2)如图3,在等腰Rt△ABC中,AC=BC=8,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是 ;(3)如图4,正方形ABCD的边长是6,点E是AD边上一动点,连接BE,过点A作AF⊥BE于点F,点P是AD边上另一动点,则PC+PF的最小值为 .17.【情景回顾】在进行13.4《最短路径问题》的学习时,同学们从一句唐诗“白日登山望烽火,黄昏饮马傍交河”(唐•李颀《古从军行》出发,一起研究了蕴含在其中的数学问题--“将军饮马”问题.同学们先研究了最特殊的情况,再利用所学的轴对称知识,将复杂问题转化为简单问题,找到了问题的答案,并进行了证明.下列图形分别说明了以上研究过程.证明过程如下:如图4,在直线l上另取任一点C',连结AC',BC',B'C',∵点B,B'关于直线l对称,点C,C'在l上,∴CB= ,C'B= ,∴AC+CB=AC+CB'= .在△AC'B'中,∵AB'<AC'+C'B',∴AC+CB<AC'+C'B',即AC+CB最小.【问题解决】(1)请将证明过程补充完整.(直接填在横线上)(2)课堂小结时,小明所在的小组同学提出,如图1,A,B是直线/同旁的两个定点.在直线l上是否存在一点P,使PB-PA的值最大呢?请你类比“将军饮马”问题的探究过程,先说明如何确定点P的位置,再证明你的结论是正确的.(3)如图,平面直角坐标系中,M(2,2),N(4,-1),MN=13,P是坐标轴上的点,则|PM-PN|的最大值为 ,此时P点坐标为 .(直接写答案)18.龙岗区八年级某班级在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:(1)格点应用:如图2,边长为1的正方形网格内有两点A、B,直线l与A、B的位置如图所示,点P是直线l上一动点,则PA+PB的最小值为 ;(2)几何应用:如图3,△ABC中,∠C=90°,AC=4,BC=6,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为 ;(3)代数应用:代数式x2+4+6-x2+36(0≤x≤6)的最小值为 .19.古罗马时代,亚历山大有一个著名的学者叫海伦,一天罗马的一位将军专程跑去问海伦这样一个问题:每天从军营A出发,先到河边给马喝水,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?海伦思考后便给出了答案,也就是现在著名的“将军饮马”问题.其实“将军饮马”实质要解决的问题是:要在直线l上找一点P使得PA+PB的值最小.(1)如图1,点A到直线l的距离AO1=1,点B到直线l的距离BO2=3,O1O2=3,要解决该最小值问题,如图2,作点A关于直线l的对称点A′,连结A′B交直线l于点P,此时P即为所求点,则PA+PB的最小值为 ;(2)如图3,在等腰Rt△ABC中,AC=BC=4,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是 ;(3)如图4,在正△ABC中,AB=4,P、M、N分别是BC、CA、AB上的动点,①PM+MN的最小值为 ;②求PM+MN+NP的最小值.(4)如图5,正方形ABCD的边长为4,E、F分别是边AB和BC上的动点且始终满足AE=BF,连结DE、DF,求DE+DF的最小值.20.【源模:模型建立】白日登山望峰火,黄昏饮马傍交河.--《古从军行》唐李欣诗中隐含着一个有趣的数学问题,我们称之为“将军饮马”问题.关键是利用轴对称变换,把直线同侧两点的折线问题转化为直线两侧的线段问题,从而解决距离和最短的一类问题.“将军饮马”问题的数学模型如图4所示:【新模1:模型应用】如图1,正方形ABCD的边长为3,点E在边AB上,且BE=1,F为对角线AC上一动点,欲使△BFE周长最小.(1)在图中确定点F的位置(要有必要的画图痕迹,不用写画法);(2)△BFE周长的最小值为 .【新模2:模型变式】(3)如图2,在矩形ABCD中,AB=5,AD=4,在矩形ABCD内部有一动点P,满足S△PAB=14S,矩形ABCD 则点P到A,B两点的距离和PA+PB的最小值为 .【超模:模型拓广】(4)如图3,∠ABD=∠BDE=90°,AB=2,BD=DE=3.请构造合理的数学模型,并借助模型求x2+4+3-x2+9(x>0)的最小值.21.古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营A,B.他总是先去A营,再到河边饮马,之后,再巡查B营.他时常想,怎么走,才能使他每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图2,作B关于直线l的对称点B′,连结AB′与直线l交于点C,点C就是所求的位置.证明:如图3,在直线l上另取任一点C′,连结AC′,BC′,B′C′,∵直线l是点B,B′的对称轴,点C,C′在l上,∴CB= ,C′B= ,∴AC+CB=AC+CB′= .在△AC′B′,∵AB′<AC′+C′B′,∴AC+CB<AC′+C′B′即AC+CB最小.本问题实际上是利用轴对称变换的思想,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A,C,B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.拓展应用:如图4,等腰直角△ABC中,∠ACB=90°,BD平分∠ABC交AC于D,点P是BD上一个动点,点M是BC上一个动点,请在图5中画出PC+PM的值最小时P的位置.(可用三角尺)22.李明酷爱数学,勤于思考,善于反思.在学习八年级下册数学知识之后,他发现“二次根式、勾股定理、一次函数、平行四边形”都和“将军饮马”问题有关联,并且为解决“饮马位置”“最短路径长”等问题,提供了具体的数学方法.于是他撰写了一篇数学作文.请你认真阅读思考,帮助李明完成相关问题.“将军饮马”问题的探究与拓展八年级三班李明“白日登山望烽火,黄昏饮马傍交河”(唐•李颀《古从军行》),这句诗让我想到了有趣的“将军饮马”问题:将军从A地出发到河边l饮马,然后再到B地军营视察,怎样走路径最短?【数学模型】如图1,A,B是直线l同旁的两个定点.在直线l上确定一点P,使PA+PB的值最小.【问题解决】作点A关于直线l的对称点A',连接A'B交l于点P,则点P即为所求.此时,PA+PB的值最小,且PA+PB=A'P+PB=A'B.【模型应用】问题1.如图2,经测量得A,B两点到河边l的距离分别为AC=300米,BD=900米,且CD=900米.请计算出“将军饮马”问题中的最短路径长.问题2.如图3,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是 .问题3.如图4,在平面直角坐标系中,点A(-2,4),点B(4,2).(1)请在x轴上确定一点P,使PA+PB的值最小,并求出点P的坐标;(2)请直接写出PA+PB的最小值.【模型迁移】问题4.如图5,菱形ABCD中,对角线AC,BD相交于点O,AC=12,BD=16.点P和点E分别为BD,CD上的动点,求PE+PC的最小值.23.【模型介绍】古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营A,B.他总是先去A营,再到河边饮马,之后,再巡查B营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点B关于直线l的对称点B′,连接AB′与直线l交于点P,连接PB,则AP+BP的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线l上另取任一点P′,连接AP′,BP′,B′P′,∵直线l是点B,B′的对称轴,点P,P′在l上,∴PB= ,P′B= ,∴AP+PB=AP+PB′= .在△AP′B′中,∵AB′<AP′+P′B′,∴AP+PB<AP+P′B′,即AP+BP最小.【归纳总结】在解决上述问题的过程中,我们利用轴对称变换,把点A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点P为AB′与l的交点,即A,P,B′三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.【模型应用】(1)如图④,正方形ABCD的边长为4,E为AB的中点,F是AC上一动点.求EF+FB的最小值.解析:解决这个问题,可借助上面的模型,由正方形对称性可知,点B与D关于直线AC对称,连接DE交AC于点F,则EF+FB的最小值就是线段ED的长度,则EF+FB的最小值是 .(2)如图⑤,圆柱形玻璃杯,高为14cm,底面周长为16cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短路程为 cm.(3)如图⑥,在边长为2的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移,得到△A′B′D′,分别连接A′C,A′D,B′C,则A′C+B′C的最小值为 .24.早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图2,作B关于直线l的对称点B′,连接AB′与直线l交于点C,点C就是所求的位置.证明:如图3,在直线l上另取任一点C′,连接AC′,BC′,B′C′,∵直线l是点B,B′的对称轴,点C,C′在l上,∴CB=CB′,C′B=C′B′,∴AC+CB=AC+ = .在△AC′B′中,∵AB′<AC′+C′B′∴AC+CB<AC′+C′B′即AC+CB最小.本问题实际上是利用轴对称变换的思想,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A、C、B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.【简单应用】(1)如图4,在等边△ABC中,AB=6,AD⊥BC,E是AC的中点,M是AD上的一点,求EM+MC的最小值借助上面的模型,由等边三角形的轴对称性可知,B与C关于直线AD对称,连接BM,EM+MC的最小值就是线段 的长度,则EM+MC的最小值是 ;(2)如图5,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M、N当△AMN周长最小时,∠AMN+∠ANM= °.【拓展应用】如图6,是一个港湾,港湾两岸有A、B两个码头,∠AOB=30°,OA=1千米,OB=2千米,现有一艘货船从码头A出发,根据计划,货船应先停靠OB岸C处装货,再停靠OA岸D处装货,最后到达码头B.怎样安排两岸的装货地点,使货船行驶的水路最短?请画出最短路线并求出最短路程.25.某班级在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:如图1,作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:(1)几何应用:如图2,△ABC中,∠C=90°,AC=BC=2,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为 ;(2)代数应用:求代数式x2+1+3-x2+9(0≤x≤3)的最小值;(3)几何拓展:如图3,△ABC中,AC=2,∠A=30°,若在AB、AC上各取一点M、N使CM+MN的值最小,最小值是 .参考答案1.解:(1)∵四边形OABC 为长方形,点B 的坐标为(8,6),∴点A 的坐标为(8,0),BC ∥x 轴.∵直线y =-x +b 经过点A ,∴0=-8+b ,∴b =8,∴直线AD 的解析式为y =-x +8.当y =6时,有-x +8=6,解得:x =2,∴点D 的坐标为(2,6).∵点P 是AD 的中点,∴点P 的坐标为(2+82,6+02),即(5,3),设直线OP 的解析式为y =kx ,∴3=5k ,解得k =35,∴直线OP 的解析式为y =35x ;(2)当x =8时,y =35x =245,∴点E 的坐标为(8,245),设点N 的坐标为(a ,-a +8),∴S =12×245×|8-a |=125|8-a |,当a <8时,S =125|8-a |=-125a +965,当a >8时,S =125|8-a |=125a -965,∴S =-125a +965(a <8)125a -965(a >8),当S =12时,125|8-a |=12,解得:a =3或a =13;(3)∵点T 的坐标为(t ,0)(5<t <8),∴点F 的坐标为(t ,35t ),点G 的坐标为(t ,-t +8).分三种情况考虑:①当∠FGQ =90°时,如图1所示.∵△FGQ 为等腰直角三角形,∴FG =GQ ,即35t -(-t +8)=8-t ,解得:t =8013,此时点Q 的坐标为(8,2413);②当∠GFQ =90°时,如图2所示.∵△FGQ 为等腰直角三角形,∴FG =FQ ,即35t -(-t +8)=8-t ,解得:t =8013,此时点Q 的坐标为(8,4813);③当∠FQG =90°时,过点Q 作QS ⊥FG 于点S ,如图3所示.∵△FGQ 为等腰直角三角形,∴FG =2QS ,即35t -(-t +8)=2(8-t ),解得:t =203,此时点F 的坐标为(203,4),点G 的坐标为(203,43),此时点Q 的坐标为(8,4+432),即(8,83).综上所述:在线段AE 上存在一点Q ,使得△FGQ 为等腰直角三角形,当t =8013时点Q 的坐标为(8,2413)或(8,4813),当t =203时点Q 的坐标为(8,83).2.解:(1)把x =0代入y =-2x +4得:y =4,∴点B (0,4),∴OB =4,把y =0代入y =-2x +4得:x =2,∴点A (2,0),∴OA =2,∵△AOB ≌△DOC ,∴OC =OB =4,OD =OA =2,故答案为:4,2;(2)设直线CD 对应的函数表达式为:y =kx +b ,∵OC =4,OD =2,∴C (-4,0),D (0,2),把C (-4,0),D (0,2)代入y =kx +b 得-4k +b =0b =2,解得k =12b =2,∴直线CD 对应的函数表达式为y =12x +2,∴M (-1,32),∵△AOB ≌△DOC ,∴∠OBA =∠OCD ,OB =OC ,又∵ON ⊥OM ,即∠MOD +∠BON =90°,∵∠COD =90°,即∠COM +∠MOD =90°,∴∠BON =∠COM ,∴△OBN ≌△OCM (ASA ),∴OM =ON ,分别过点M 、N 作ME ⊥x 轴于点E ,NF ⊥y 轴于点F ,∴∠OFN =∠OEM ,∵∠BON =∠COM ,OM =ON ,∴△OFN ≌△OEM (AAS ),∴OF =OE =1,FN =EM =32,∴点N 的坐标为(32,1),故答案为:(32,1);(3)直线CD 上存在点Q ,使△EPQ 得是以E 为直角顶点的等腰三角形.∵E (1,b )为直线AB 上的点,∴b =-2×1+4=2,∴E (1,2),①当点P 在点B 下方时,如图,连接DE ,过点Q 作QM ⊥DE ,交DE 的延长线于M 点,∵D (0,2),∴DE ⊥y 轴,DE =1,点M 的纵坐标为2,∠M =∠EDP =90°,∵△EPQ 是以E 为直角顶点的等腰直角三角形,∴EP =EQ ,∠PEQ =90°,∴∠QEM +∠PED =90°=∠QEM +∠EQM ,∴∠DEP =∠EQM ,∴△DEP ≌△MQE (AAS ),∴MQ =DE =1,∴Q 点的纵坐标为3,把y =3代入y =12x +2中得:x =2,∴点Q (2,3);②当点P 在点B 上方时,如图,过E 点作EM ∥y 轴,过点Q 作QM ⊥EM 于M 点,过P 点作PN ⊥EM 交ME 的延长线于N 点.则∠M =∠N =90°,∴N 点的橫坐标为1,则PN =1,∵△EPQ 是以E 为直角顶点的等腰三角形,∴EP =EQ ,∠PEQ =90°,∴∠QEM +∠PEN =90°=∠PEN +∠NPE ,∴∠MEQ =∠NPE ,∴△EQM ≌△PEN (AAS ),∴M 点的纵坐标为1,∴Q 点的纵坐标为1,把y =1代入y =12x +2中得:x =-2,∴Q (-2,1);综上所述,直线CD 上存在点Q ,使得△EPQ 是以E 为直角顶点的等腰直角三角形,Q 点的坐标为(2,3)或(-2,1).3.解:(1)如图1,当PQ 平分∠APC ,有∠APQ =∠CPQ ,∵矩形ABCD 中,AB =3cm ,BC =4cm ,∴AD ∥BC ,AD =BC =4cm ,AB =CD =3cm ,∠B =90°,∴∠CPQ =∠AQP ,∴∠APQ =∠AQP =∠CPQ ,∴AP =AQ ,∴AP 2=AQ 2,由题意知:BP =2t cm ,DQ =t cm ,∴AQ =AD -DQ =(4-t )cm ,∵∠B =90°,∴AP 2=AB 2+BP 2=32+(2t )2,∴32+(2t )2=(4-t )2,解得:t 1=-4+423,t 2=-4-423,∵0<t <2,∴t =-4+423,∴当t =-4+423秒时,PQ 平分∠APC ;(2)如图2,当P 、Q 运动时间为ts 时,BP =2t cm ,DQ =t cm ,∵QE ∥AC ,∴△DQE ∽△DAC ,∴DQDA =DE DC,∴t 4=DE 3,∴DE =34t cm ,∴S △ABP =12AB •BP =12×3×2t =3t (cm 2),S △QDE =12t ×34t =38t 2(cm 2),∵S 矩形ABCD =AB •BC =3×4=12(cm 2),∴y =S 五边形APCEQ =S 矩形ABCD -S △ABP -S △QDE =12-3t -38t 2(0<t <2),∴y 与t 的函数关系式为:y =-38t 2-3t +12(0<t <2);(3)①当∠QEP =90°,如图3,∵∠QED +∠EQD =90°,∠QED +∠EQD =90°,∴∠CEP =∠DQE ,∵∠QDE =∠ECP =90°,∴△QDE ∽△ECP ,当运动时间为ts 时,∵QD =t cm ,由(2)可知,DE =34t cm ,∴EC =DC -DE =(3-34t )cm ,∵BP =2t cm ,∴CP =(4-2t )cm ,∴QDEC =DE CP ,∴t 3-34t =34t4-2t,解得:t =2823或t =0(舍去),∴t =2823;②当∠PQE =90°时,如图4,过点P 作线段PI ⊥AD 于点I ,∵∠EQD +∠PQI =90°,∠QED +∠EQD =90°,∴∠PQI =∠QED ,∵∠QDE =∠PIQ =90°,∴△QDE ∽△PIQ ,当运动时间为ts 时,∵QD =t cm ,由(2)可知,DE =34t cm ,∵BP =AI =2t cm ,∴QI =AD -QD -AI =4-t -2t =(4-3t )cm ,∵PI =AB =3cm ,∴PI QD =IQDE ,∴3t =4-3t34t ,解得:t =712或t =0(舍去),∴t =712;③当∠QPE =90°,不满足题意,综上所述,t 的值为2823或712时,△PQE 是直角三角形.4.(1)解:设直线l 1的函数表达式为y =kx +b (k ≠0).∵图象经过点(5,6),A (-3,0),∴5k +b =6-3k +b =0 ,解得k =34b =94 ,∴直线l 1的函数表达式为y =34x +94.联立y =34x +94y =3x,解得:x =1y =3 ,∴点B 的坐标为(1,3);(2)解:∵A (-3,0),B (1,3),∴S △AOB =12×3×3=92;(3)解:∵点C 在x 轴上,∴∠BAC ≠90°,∴当△ABC 是直角三角形时,需分∠ACB =90°和∠ABC =90°两种情况.①当∠ACB =90°时,点C 在图中C 1的位置:∵点A 和点C 1均在x 轴上,∴BC 1⊥x 轴.∵B (1,3),∴C 1(1,0);②当∠ABC =90°时,点C 在图中C 2的位置:设C 2(m ,0),(m >0)∵A (-3,0),B (1,3),C 1(1,0),∴AC 1=4,BC 1=3,C 1C 2=m -1,AC 2=m +3,∴AB =AC 12+BC 21=42+32=5.在Rt △ABC 2中,AC 22-AB 2=BC 12,在Rt △BC 1C 2中,BC 12+C 1C 22=BC 22,∴AC 22-AB 2=BC 12+C 1C 22,即(m +3)2-52=32+(m -1)2,解得m =134,∴C 2134,0 .综上可知,在x 轴上存在点C ,使得△ABC 是直角三角形,点C 的坐标为(1,0)或134,0.5.解:(1)设直线l 1的表达式为y =kx +b ,将A (6,0)、B (0,8)代入得:6k +b =0b =8 ,解得:k =-43b =8,∴直线l 1的表达式为y =43x +8;(2)由点A 、B 的坐标知,OA =6,OB =8,则AB =10,t 秒时,BC =t ,BD =BA -AD =10-2t ,当BC =BD 时,则t =10-2t ,解得:t =103;故答案为:103.(3)由平移可得:直线EF 的关系式为:y =43x -3 +8=-43x +12,当x =0时,y =12,F (0,12),当y =0时,x =9,E (9,0),四边形BAEF 的面积=S △EFO -S △ABO ,即S 四边形BAEF =12×9×12-12×6×8=30,答:四边形BAEF 的面积是30.(4)存在.当∠ABP =90°,AB =BP 时,如图所示:过点P 作PM ⊥y 轴于点M ,可证△AOB ≌△BMP (AAS ),∴AO =BM =6,BO =MP =8,∴OM =14,∴P (8,14).当∠BAP =90°,AB =AP 时,如图所示:过点P 作PM ⊥x 轴于点M ,可证△AOB ≌△PMA (AAS ),∴AO =PM =6,BO =AM =8,∴OM =14,∴P (14,6).当∠APB =90°,BP =AP 时,如图所示:过点P 作PM ⊥x 轴于点M ,PN ⊥y 轴于点N ,可证△AMP ≌△BNP (AAS ),∴AM =BM ,PM =PN ,∴6+AM =8-BN ,∴AM ==BN =1,∴OM =7=PN =PM ,∴P (7,7),∴P (8,14).综上,点P (8,14)或(14,6)或(7,7).6.解:(1)令y =54x +74=0,解得:x =75,∴点C 的坐标为75,0 ;(2)由(1)知OC =75;代入点A (-1,m ),B (n ,-2)两点可得:m =54+74,-2=-54n +74,解得:m =3,n =3,∴A (-1,3),B (3,-2),∴S △AOC =12×75×3=2110,AC =75+1 2+32=3415,设原点O 到直线AB 的距离为d ,∴S △AOC =12×3415d =2110,解得:d =741=74141;(3)存在,理由如下:设点P 的坐标为(x ,0),∵∠ACP 为锐角,∴△ACP 是直角三角形,而分两种情况分析:①若∠APC =90°,此时点P 的坐标为(-1,0);②若∠PAC =90°,AC 2+AP 2=CP 2,故75+1 2+32+x +1 2+32=75-x 2,解得:x =-194,此时点P 的坐标为(-6,0);综上所述,存在满足条件的点P 的坐标为(-1,0)或-194,0.7.解:(1)把D 坐标(1,n )代入y =x +1中得:n =2,即D (1,2),把B (0,-1)与D (1,2)代入y =kx +b 中得:b =-1k +b =2 ,解得:k =3b =-1 ,∴直线BD 解析式为y =3x -1,对于直线y =x +1,令y =0,得到x =-1,即E (-1,0);令x =0,得到y =1,对于直线y =3x -1,令y =0,得到x =13,即C (13,0),则S 四边形AOCD =S △DEC -S △AEO =12×43×2-12×1×1=56;(2)存在.如图,当∠DPC =90°时,P (1,0).当∠CDP ′=90°时,△DPC ∽△P ′PD ,∴PD 2=CP •PP ′,∴22=23×PP ′,∴PP ′=6,∴OP =OP +PP ′=1+6=7,∴P ′(7,0).综上所述,满足条件的点P 的坐标为(1,0)或(7,0).8.解:(1)如图1中,过点A 作AH ⊥OB 于点H ,∵A(3,3),∴AH=OH=3,∵OA=AB,AH⊥OB,∴HB=OH=3,∴OB=6,∴B(6,0);(2)当点P在线段OB上时,2t=2(6-2t),∴t=2.当点P在线段OB的延长线上时,2t=2(2t-6),∴t=6.综上所述,满足条件的t的值为2或6.(3)存在.如图2中,当P(4,0)时,满足条件的点Q的坐标为(5,1)或(6,2)或(4,2).如图3中,当P(12,0)时,点Q的坐标为(9,3)或(12,6)或(6,6).综上所述,满足条件的点Q的坐标为(5,1)或(6,2)或(4,2)或(9,3)或(12,6)或(6,6).9.解:(1)∵a2-4a+4+|b-4|=0,∴(a-2)2+|b-4|=0,∵(a-2)2≥0,|b-4|≥0,∴a=2,b=4,∴A(2,0),B(0,4);(2)∵BC平分∠OBA,AM平分∠BAD,∴∠CBA=12∠OBA,∠BAM=12∠BAD,∵∠C+∠CBA=∠BAM,∠AOB=∠BAD-∠OBA,∴∠C=∠BAM-∠CBA=12∠BAD-12∠OBA=12∠AOB=12×90°=45°;(3)存在,满足条件的点共有6个,如图所示,P 1(6,2),P 2(-2,-2),P 3(4,6),P 4(-4,2),P 5(3,3),P 6(-1,1).10.(1)解:结论:△AED 是等腰直角三角形.理由:在△ABE 和△ECD 中,AB =EC∠B =∠C BE =CD,∴△ABE ≌△ECD (SAS ),∴AE =DE ,∠BAE =∠CED ,∵∠BAE +∠AED =90°,∴∠CED +∠AEB =90°,∴∠AED =90°,∴△AED 是等腰直角三角形;(2)证明:过点E 作EF ⊥AD 于F ,由(1)可知△EFA ≌△ACB ,∴AF =BC ,∵AD =2BC ,∴AD =2AF ,∴AF =DF ,又∵EF ⊥AD ,∴DE =AE ;(3)解:存在.分三种情况,①若点O 为直角顶点,如图3,∵A (3,2),∴OF =3,AF =2,过点A 作AF ⊥x 轴于F ,过点B 作BE ⊥x 轴于E ,由(1)知△BEO ≌△OFA ,∴BE =OF =3,OE =AF =2,∴B (-2,3);②若点A 为直角顶点,如图4,过点A 作AF ⊥x 轴于F ,过点B 作BE ⊥AF ,交FA 的延长线于E ,由(1)知△BEA ≌△AFO ,∴BE =OF =2,AE =PF =5,∴B (1,5);③若点B 为直角顶点,如图5,过点B 作BE ⊥y 轴于E ,过点A 作AF ⊥BE ,交EB 的延长线于F ,由(1)知△BEO ≌△AFB ,∴BE =AF ,OE =BF ,设BE =AF =a ,则OE =2+a,∴a +2+a =3,∴a =12,∴OE =a +2=12+2=52,∴B (12,52);综上所述,存在点B ,使得△OAB 是等腰直角三角形,点B 的坐标为(-2,3)或(1,5)或B (12,52).11.解:(1)当t =1时,由题意可知:AP =1cm ,BQ =2cm ,∵AB =11cm ,∴PB =10cm ,∵∠B =90°,∴PQ =PB 2+BQ 2=102+22=226cm ;(2)∵∠B =90°,∴△BPQ 是等腰三角形时,只有BP =BQ ,由题意可知:BP =(11-t )cm ,∵Q 从点B 出发以每秒2cm 的速度沿BC 向点C 匀速运动,到达点C 后返回点B ,当有一点停止运动时,另一点也停止运动,∴当0≤t ≤4时,BQ =2t cm ;当4<t ≤8时,BQ =(16-2t )cm ;当8<t ≤11时,BQ =(2t -16)cm ;∵BP =BQ ,∴11-t =2t ,解得:t =113>4,故不符合题意;11-t =16-2t ,解得:t =5,符合题意;11-t =2t -16,解得:t =9,符合题意;综上所述:t =5或t =9;(3)假设存在t 使得△BPQ 的面积等于10cm 2,由(2)可知:BP =(11-t )cm ,当0≤t ≤4时,BQ =2t cm ;当4<t ≤8时,BQ =(16-2t )cm ;当8<t ≤11时,BQ =(2t -16)cm ;∴当0≤t ≤4时,12×11-t ×2t =10;解得:t =1或t =10(舍去);当4<t ≤8时,12×11-t ×16-2t =10;,解得:t =6或t =13(舍去);当8<t ≤11时,12×11-t ×2t -16 =10,因为Δ<0,故无解,综上所述,当t =1或t =6时△BPQ 的面积等于10cm 2.12.解:(1)∵四边形OABC 是矩形,∴OA ∥BC ,∴∠CBO =∠AOB ,根据翻折的性质可知:∠EOB =∠AOB ,∴∠EOB =∠EBO ,∴EO =EB ,设EO=EB=x,在Rt△ECO中,EO2=OC2+CE2,∴x2=32+(6-x)2,解得x=15 4,∴CE=BC-EB=6-154=94,∴E(94,3),设直线AE的解析式为y=kx+b,∴6k+b=094k+b=3 ,解得k=-45b=245,∴直线AE的函数解析式为y=-45x+245;(2)如图,OB=32+62=35.设F(n,0).①当OB=OF时,F(35,3)或(-35,0);②当OB=BF时,∴OB2=BF2,∴45=9+(6-n)2,解得n=12或0(舍去),∴F(12,0),③当OF=BF时,∴OF2=BF2,∴n2=9+(6-n)2,解得n=15 4,∴F(154,0),综上所述,在x轴上是存在点F,使△OBF为等腰三角形,点F的坐标为(35,3)或(-35,0)或(12,0)或(154,0).13.(1)解:∵点B坐标为(0,3),点C坐标为(9,0),∴OB=3,OC=9,∵∠ACB=90°,∴∠BCO+∠ACD=90°,且∠BCO+∠OBC=90°,∴∠ACD=∠OBC,且AC=BC,∠BOC=∠ADC=90°,∴△BOC≌△CDA(AAS),∴CD=OB=3,∴OD=OC+CD=12,AO=OC=9,∴点A的坐标(12,9);(2)OE =DE 且OE ⊥DE ;证明:过E 作EF ⊥y 轴于F ,并交AD 于G ,则FG =OD =12且FG ⊥AD ,∵B (0,3),A (12,9),E 为AB 中点,∴E (6,6),∴EF =EG =6,OF =DG =6,又∵∠EFO =∠EGD =90°,∴△EFO ≌△EGD ,且△EFO 和△EGD 都为等腰直角三角形,∴OE =DE ,∠FEO =∠GED =45°,∴∠OED =180°-∠FEO -∠GED =90°,∴OE ⊥DE ;(3)解:①当以点A 为顶角顶点时,且OA 是腰,∵AD ⊥x 轴,∴点Q 1,O 关于直线AD 对称,即:Q 1(24,0);②当以点A 为底角顶点时,且OA 是腰,形成锐角三角形时,则OQ 2=OA =15,∴Q 2(15,0);③当以点A 为底角顶点时,且OA 是腰,形成钝角三角形时,则OQ 3=OA =15,∴Q 3(-15,0),综上所述:Q 的坐标为:(24,0)或(15,0)或(-15,0).14.解:(1)在y =x +3中,令y =0,得x =-3,∴B (-3,0).将C (1,m )代入y =x +3得m =4,∴C (1,4);(2)设直线l 2的函数表达式为y =kx +b (k ≠0),将C (1,4),A (3,0)代入得,k +b =43k +b =0 ,解得k =-2b =6 ,∴直线l 2的函数表达式为y =-2x +6;(3)∵C (1,4),CD ⊥x 轴于点D ,∴D (1,0).又∵B (-3,0),∴CD =4,BD =4,BC =CD 2+BD 2=42.①当点B 为等腰△BCP 的顶点,即BC =BP 时,∵BC =42,B -3,0 ,∴此时点P 的坐标为-3-42,0 或42-3,0 ;②当点P 为等腰△BCP 的顶点,即PB =PC 时,。
2022年中考数学复习之二次函数压轴题40个问题

中考复习之二次函数压轴40个问题主要题型:1.二次函数之面积问题2.二次函数之特殊三角形的存在性问题3.二次函数之特殊四边形的存在性问题4.二次函数之线段最值问题5.二次函数之角度问题题目:如图,抛物线与x轴交于A、B两点,与y轴交于点C,OB=OC=3,OA=1,顶点为D第1问.如图,抛物线与x轴交于A、B两点,与y轴交于点C,OB=OC=3,OA=1,顶点为D.求二次函数的解析式;解:设:设二次函数解为y=a(x+1)(x-3)将(0,3)代入得a=-1,故二次函数解析式为y=-x2+2x +3第2问.如图,抛物线与x轴交于A、B两点,与y轴交于点C,OB=OC=3,OA=1.顶点为D1.判断∆BCD的形状;解:D(1,4),B(3,0),C(0,3),方法一:BC=32,CD=2,BD=25,BC2+CD2=BD2,故∆BCD是直角三角形;方法二:KCD =1,KBC=-1,KCD∙KBC=-1,故CD⊥CB,所以∆BCD是直角三角形;yxBCAODyxBCAODyxBCAODyxBCAOD第3问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1.顶点为D, 2. 四边形ABDC 的面积解:BC:y =-x +3,铅垂法:E(1,2)DE=2,S BCD ∆=21∙2∙3=3 S ABDC 四=21∙4∙3+3=9第4问:如图,抛物线与x 轴交于A 、B 两点,与y 交于点C,OB=OC=3,OA=1,顶点为D, 1. P 为直线BC 上方抛物线上一点,求∆PBC 面积最大值及P 点坐标;解:方法一:设P(m,-m+2m+3)S PBC ∆=21∙3∙[-m 2+2m+3-(m+3)] =23(-m 2+3m),当m=23时,S 有最大值,此时P(23,415)S m ax =827 方法二:平移BC 至抛物线相切时,面积可取最大值设切线为y =-x +n,与抛物线y =-x 2+2x+3联立得x2-3x +n -3=0,∆=0,n=23,y =415,故P(23,415)S m ax =827y xBCAODy xBCAODEy xBCAOD第5问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D5点M 为BC 上方抛物线上一点,过点M 作y 轴的平行线交BC 于点N,求MN 的最大值;解:设点M(m,-m 2+2m+3),BC:y =-x +3,则点N(m,-m+3)MN=-m 2+2m+3-(-m+3)=-m 2+3m 当m=23时,MN m ax =49第6问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OC=3,OA=1,顶点为D, 6. 在对称轴上找一点P,使∆ACP 的周长最小,并求出最小值解:点A 、B 关于对称轴对称,连接BP,则BP=AP,PA+PC=PB+PC,当点B 、P 、C 三点共线时,可取最小值,此时P(1,2),∆ACP 周长的最小值为10+32第7问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1,顶点为D 1. 在y 轴上找一点E,使∆BDE 为直角三角形,求出E 点坐标, 方法一:y xBCAOPDy xBCAODy xNBCAODMy xBCAOD P1.DE ⊥BE 时,设E(0,m)易知∆DEF~∆EBO,OE DF =BO EF ,即m 1=34m-,m=3或1,故E 1(0,1)、E 2(0,3)2. DE ⊥DB 时,设E(0,m)易知∆DEN~∆BDM,BM DN =DM EN ,即m 1=34m -,m=27故E ;(0,27)3. DB ⊥BE 时,设E(0,m),易知∆DBF~∆BEG,BG DF =EG BF ,即m -2=34,m=-23,故E 4(0,-23)第8问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1. 在y 轴上找一点F,使∆BDF 为等腰三角形,求出F 点坐标;2. BD=DF,设F(0,m),22)4()01(m -+-=25,m=4+9 或4-19,F 1(0,4+19);F 2(0,4-19)yxFBCAODExyN MBCAODExy GFEBCAODxy BCAODF2.BD=BF,设F(0,m),22)0()03(m -+-=25,m=±11,F 1(0,11),F 2(0,-11)3.DF=BF,设F(0,m),22)0()03(m -+-=22)4()01(m -+-,m=1,F 4(0,1)第9问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1,顶点为D 1. 求抛物线上一点N,使S ABN ∆=S ABC ∆;解:设N 点的坐标(m,n),则∆ABC 与∆ABN 底相同,故n=±3,-m 2+2m+3=3或者-m 2+2m+3=3得m 1=0,m 2=2,m 3=1-7,m 4=1+7,N(0,3),(2,3),(1-7,-3),(1+7,-3)第10问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于点C,OB=OC=3,OA=1,顶点为D, 1. 在抛物线上找一点Q,使S BDQ ∆=S AOC ∆解:设Q(m,-m 2+2m+3),S AOC ∆=23,BD :y =-2x +6,铅垂高QS=|-m 2+2m+3-(-2m+6)| S BDQ ∆=|-m 2+2m+3-(-2m+6)|∙21∙1=23得m=0或4Q(0,3),(4,-5),xBCAODFBCAOD FBCAODFBCAODN第11问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.在抛物线上找一点E,使BE 平分∆ABC 的面积; 解:BE 平分∆ABC 的面积,故BE 经过AC 的中点,AC 中点(-21,23),BE:y =-73x +79; 与抛物线联立得-x 2+2x +3=-73+79x =-74或722,E(-74;4919)或(722;491849)第12问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA =1,顶点为D 1.在对称轴上找一点M,使|MB -MC|取最大值,并求出最大值;解:点B 关于对称轴对称的点A,连接MA,则MB=MA,MA -MC<AC, 当点A 、C 、M 共线时,|MB -MA|m ax =AC=10, AC:y =3x x +3,M(1,6)第13问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.M 、N 为对称轴上的两点(M 在N 点上方),且MN=1,求四边形ACNM 周长的最小值; 解:A 关于对称轴对称的点B,连接BN,则BN=AN,将点向下平移1个单位得C’、N,则C’N=CM, 故CM+BN=C’N+BN,当C’、N 、B 共线时,取最小值(CM+BN)m in =13,故ACNM 周长得最小值为1+10+13BCAODQABCODEABCODM第14问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.E 在抛物线对称轴上,在抛物线上找一点F,使得点四边形ACFE 为平行四边形; 解:设E(1,m)F(n,-n 2+2n+3),A(-1,0),C(0,3),A 平行至点C 与E 平移至点F, n=1+1=2,m+3=-n 2+2n+3,m=0,故E(1,0)F(2,3)第15问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.M 为y 轴上一点,在坐标平面内找一点N,使A 、C 、M 、N 为顶点的四边形为菱形; 解:当 ACM 为等腰三角形时,问题转化为等腰三角形问题 1.ACNM 为菱形时,M(0,3),N(1,0),2.AMCN 为菱形时,M(0,34),N(-1,35),3.ACMN 为菱形时,M(0,3+10),N(-1,10)ABCODMNABCODM NC'ABCODEFABCODMN ABCONDM4.ACMN 为菱形时,M(0,3-10),N(-1,-10)第16问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.E 为x 轴上一点,以BE 为边的正方形BEFG ; 另一点G 在抛物线上,求点F 坐标;设E(m,0)则EF=|-m 2+2m+3|由EF=EB 得3-m=|-m 2+2m+3|,m=0或m=-2故F(0,3)或F(-2,-5)第17问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.P 是抛物线上任意一点,过点P 作PE ⊥y 轴于点E,交直线BC 于点G ;过点G 作GF ⊥x 轴,连接EF,求EF 的最小值;连接OG,则OG=EF,当OG ⊥BC 时,OG 最小,即EF 最小,故EF m in =233x C,OB=OC=3,OA=1,顶点为D1.M 在抛物线上CB 上方一点过点M 作y 轴的平行线,交BC 于点E,则ME 的最大值是多少? 解:设M(m,-m 2+2m+3),BC :y =-x +3,E(m,3-m),ME=-m 2+2m+3-(3-m)=-m 2+3m,当m=23ABCONDMABCNODMGCABO EFF CABOE GFEGCABOPFEGCABOP时,ME m ax =49第19问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.求一点P,使∠POC=∠PCO ; 解:点P 在OC 得垂直平分线上,-x2+2x +3=23,x =1±210P 1(1-210,23)P 2(1+210,23)第20问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D1.E(2,-2),M 为x 轴上一点,且∠EMO=∠CMO ; 1.M 在右侧时,易知∆CMO~∆EMG,设M(m,0)则有2-m m =23,m=6 2.M 在左侧时,同理易知∆CMO~∆EMG ,m m --2=23,m=6(舍) 第21问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.P 是直线y =x 上的动点,当直接y =x 平分∠APB 时,求点P 的坐标; 如图,∆PAO ≅∆PEO,此时OE=OA=1,故E(0,-1),EB :y =31x -1,与y =x 得x =-23,P(-23,-23) ECABOMPPCABOCABOEMG第22问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.点P 在抛物线上,且∠ABP=∠CBD,求P 坐标;解:C(0,3)D(1,4)B(3,0)tan ∠CBD=31,故tan ∠PBO=31,OE=1或者OF=1,PB :y =-31x +1或y 且=31x -1,联立可得P 1(-32,911)P 2(-23,-23)第23问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D1.在抛物线上找一点P,使∠ACP=450;方法1:∠OCB=∠ACP=450,得∠ACO=∠ECB,故tan ∠ECB=31,作EH ⊥BC,设BH=m,则EH=m;CH=3m,故4m=32,m=423,E(23,0)故CE:y =-2x +3,联立得P(4,-5) 方法2:由12345模型得tan ∠ECO=21得E(23,0)第24问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.P 在抛物线上,∠DBP=450; 由tan ∠CBD=31,∠CBD+∠CBP=450,而∠PBO+∠CBP=450,故tan ∠PBO=31,BP:y =-31x +1,P(-32,911) ECABOPPEFCABODPPHECABOPDP第25问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.点P 在抛物线上,∠PCB=150,求点P 的坐标;解:由∠BCO=450得∠PCO=30或∠PCO=600,故PC:y =-3x +3或y =-33x +3联立得P(2+3,-23)P(2+33,3328-)第26问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D1.直线y =31x -1与y 轴交于点E,求∠EBC -∠CBD ; 由tan ∠DBC=tan ∠EBO=31,故∠EBC -∠CBD=450第27问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 1.过点P(3,0)作直线与抛物线交于F 、G 、FM 、GN 分别垂直于x 轴,求PM,PN ;设F(1x ,1y )G(2x ,2y ),直线y =k (x +3)与抛物线y =-2x +2x +3联立得2x +(k -2)x +3k -3=0;1x +2x =2-k ,1x •2x =3k -3,PM •PN=(1x +3)(2x +3)=1x •2x +3(1x +2x )+9=12CABOPDPPF CABODPEECABODENMGFCABOPD第28问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为DP 是第一象限抛物线上,PE ⊥AB,求BEAE的值,若PE 2=AE •BE,求P 点坐标 设P(m,-m 2+2m+3),AE=m+1,BE=3-m,BE AE =mm -+31,(m+1)(3-m)=(-m 2+2m+3)2得m=1+3,P(1+3,1)第29问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D M 为直线y =33x 3上的点,N(0,-1),求23BM+MN 的最小值, 过点B 作I ⊥x 轴,MH ⊥I,∠MBH=600,MH=23BM,23BM+MN=MH+MN,当N 、M 、H 共线且垂直于I 时取最值(23BM+MN)min=3第30问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D M 为直线y =33x 3上的点,求21BM+OM 的最小值 过点B 作I:y =3x -33,MH ⊥I,∠MBH=300,MH=21BH,21BH+OM=MH+OM,当Q 、M 、H共线且垂直于I 时取最值(21BM+MN )min=233xy EBCAOPxy BCA O MN H第31问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D M 为直线y =33x 3上的点,求22BM+OM 的最小值 过点B 作I,I 与直线MN 夹角450,MH ⊥I,∠MBH=450,MH=22BM,22BM+OM=MH+OM,当Q 、M 、H 共线且垂直于I 时取最值两着色三角形相似,得cos150=426,(21BM +MN)min=423-63第32问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D在AB 上是否存在点M,使CM+21BM 取最小值. 过点B 作I,I 与x 轴夹角为300,MH=21BM,21BM+CM=MH+CM,当C 、M 、H 共线且垂直于I 时取最值(21BM+CM)min=2333+第33问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为Dxy BCAMO Hxy BCAMOHxy BCAO M EHM 是抛物线上一点,作MH ⊥x 轴,交BC 于点E,当ME:EH=3:2时,求M 点的横坐标, 设M(m,-m 2+2m+3),则E(m,3-m),ME=-m 2+2m+3-(3-m),EH=3-m,ME:EH=3:2 即有-m 2+2m+3-(3-m)=23(3-m) m=23第34问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于顶点为D P 是抛物线上一点,且∠PAB=2CBD,求P 点坐标. tan ∠CBD=31,tan ∠PAB=tan2∠CBD=43(12345模型) 设P(m,-m 2+2m+3)(1)tan ∠PAB=1322+++-m m m =43,m=49,P(49,1639)(2)tan ∠PAB=1322+--m m m =43,m=415,P(415,1657)第35问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为DF(1,415)直线y =417,(1)证明:M 上任意一点到直线y =417距离等于到F 点的距离, M(m,-m 2+2m+3),MH=417-(-m 2+2m+3)=m 2-2m+45MF=222)41532()1(-++-+-m m m =m 2-2m+45,故MH=MF xyEBCAOMHxy BCAODPP第36问:如图,抛物线与x 轴交于、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为DF(1,415)直线y =417,(2)证明:N(2,-1)M 为抛物线上一点,求NM+MF 的最小值 由(1)可知MF=MH,故NM+MF=MN+MH,(NM+MF)min=421第37问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D ∠BAC 的角平分线交y 轴于点M,绕点M 作直线I,与x 轴交于点E,与A 交于点F,求证:AE 1+AF 1为定值 过点M 、F 、C 作x 轴的平行线,交AC 于点G,交AM 于点H 、I ,易知:∆AEM~∆HFM,∆AFH~∆ACI,AO GM =AC CG ,CI GM =AC AG ,相加得AO GM +CI GM =AC CG +ACAG=1 即有AO 1+AC 1=GM 1,同理可得AE 1+AF 1=GM1=1+1010第38问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D P 为第四象限抛物线上一点,且tan ∠APC=21,求出点P 的坐标; 过点C 作CE ⊥AC,取一点E 使CE=2AC,过点C 作MN||x 轴,作A M ⊥MN 、EN ⊥MN,易知∆ACM~∆CEN,CN=6,EN=2,E(6,1),P 为以AE 为直径的圆与抛物线的交点AE 的中点F,F(25,21) xy BCOFMHxy BCNOFMHA过点易知AE HF AFACGM AO =CG AC ,GM CI =AGAC,GM AO +GM CI =CG AC +AGAC =1即有1AO +1AC =1GM,同1AE +1AF =1GM =11010xy H G FEMBCOIPF=225,设P(m,-m 2+2m+3),PF 2=(m -25)2+(-m 2+2m+325)2=225m=255,y =2531--,P(255,2531--)第39问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 直线y =x -3与抛物线交于点P,在x 轴正半轴上找一点E,使tan(∠PBO+∠PEO)=25 在x 轴上找一点F,使tan ∠HPF=25,∠HPF=450+∠BPH=∠PBO+∠PEO=450+∠PEO, 故∠BPF=∠PEO,故∆BEP~∆BPF,BP BE =BF BP ,即253-m =21525,m -3=320,m=329故E(329,0)第40问:如图,抛物线与x 轴交于A 、B 两点,与y 轴交于C,OB=OC=3,OA=1,顶点为D 对称轴与BC 交于点E,在直线BC 上找一点P,使∆ABP 与∆DEB 相似,∠BED=1350=∠ABP,故P 在CB 的延长线上,DE=2,BE=22,AB=3,1.当∆EDB~∆BAP,AB DE =BP EB ,即42=BP22,BP=42,P(7,-4) 2.∆EDB~∆BPA 时,BP=22,P(5,-2)AxyN MPFEBCOAH PE FAxyIHEBCODP 1P 2。
2020中考数学专题17—存在性问题之特殊三角形

2020中考专题17——存在性问题之特殊三角形姓名____________ . 【方法解读】特殊二和形存化件问题L婪足指寻找符介条件的点使之构成等腰二角形、江用三角形、全第一;角形等特殊二用形.解决此类问题的美犍在于恰当地分类4M避免M籽.【例题分析】例L如图,直线产3x-3交x轴例点A,交y轴J点B,过A, B两点的他物线交x例J另一点C(3, 0).(1)求点A,B的坐标.(2)求旭物线对应的函数表认式.(3)在附物线的对称轴上是否存在点Q,使△ABQ皓笔腰三角形?若存在,求出符合条件的点Q的坐标: 若不存在.请说明毋山.例2.如凰tl知直线.kx 6与抛物线y』x'b乂,c相交十A, 3两点,口点A(l,⑷为抛物段的顶点, 点B 在x轴上.⑴求旭利线对应的函数及辽揖⑵任⑴中:次函数的第.拿限的图象上是否存在•点P,便△FOB与APOC全等?若存在,求出点P 的%标:若不存在,请说明理由.(3)若点Q是y轴上…点,HAABQ为直角三角形,求点Q的坐标.D.【巩固训练】1.(2019•止宾〉已刈抛物纹y = x'-l,j轴文于点A.。
宜纹/=代内为任总实数)出文于S , C两点.则下列结论不正确的是()A.存在实数使得448C为等腰三角形民存在实数A ,使得&46C的内角中仃两角分别为3伊和60)C.任意实数A,伐得部为血角三角形D.存在实数4,使得M8c为等边三处形2. M图.在平行四边形ABCD中,AB 7 cm, BC 4 c0 NA-30' .点P从点A出发沿着AB边向燃B运劭, 速度为I cm/.连结印,若以运动时间为则当〔二 w时,AADP为等小」角形.3.(2019 •泰安)已知次函数】七公十)的图象。
反比例函数y =巴的图象大丁点T,与x他交丁x 点用 5.U).若 08 二4 8, H.S^=y .(1)求反比例函数与一次函数的表达式,<2)苦点P为x粕上一点,是等股三角形.求点「的坐乐.1. (2D18・ F州)如图,池物线y = a/+bx-4经过,4(-3.0).£(5.-4)两点, I j•地文于点C ,性接力&•4C. RC.(1)求抛物线的表达式,(2)求证,.48平分NO6(3)抛物线的对称轴卜.是否存在点M,使得M8W是以48为宜用边的汽角H角形,若存在,求山点M的坐标:苍不存在,请说刚理由.5.(2019•的卅)如图I.在平面直用坐标系中•点。
二次函数与几何综合-特殊三角形存在问题(解析版)

专项12 二次函数与几何综合-特殊三角形存在问题等腰三角形的存在性问题【方法1 几何法】“两圆一线”(1)以点A 为圆心,AB 为半径作圆,与x 轴的交点即为满足条件的点C ,有AB=AC ;(2)以点B 为圆心,AB 为半径作圆,与x 轴的交点即为满足条件的点C ,有BA=BC ;(3)作AB 的垂直平分线,与x 轴的交点即为满足条件的点C ,有CA=CB .注意:若有重合的情况,则需排除.以点 C 1 为例,具体求点坐标:过点A 作AH ⊥x 轴交x 轴于点H ,则AH=1, 又32121131311==-=∴=HC AC ,()03211,坐标为故点-C 类似可求点 C 2 、C 3、C 4 .关于点 C 5 考虑另一种方法.【方法2 代数法】点-线-方程表示点:设点C 5坐标为(m ,0),又A (1,1)、B (4,3),表示线段:11-m 225+=)(AC 94-m 225+=)(BC 联立方程:914-m 1-m 22+=+)()(,623m =解得:,),坐标为(故点06232C直角三角形的存在性【方法1 几何法】“两线一圆”(1)若∠A 为直角,过点 A 作 AB 的垂线,与 x 轴的交点即为所求点 C ;(2)若∠B 为直角,过点 B 作 AB 的垂线,与 x 轴的交点即为所求点 C ;(3)若∠C 为直角,以 AB 为直径作圆,与 x 轴的交点即为所求点 C .(直径所对的圆周角为直角)如何求得点坐标?以C 2为例:构造三垂直.),坐标为(故代入得:坐标得、由易证0213232222C C C BN AM B A N MBBN AM BN AMB ===∆≈∆()),坐标为(,,坐标为故或故又即代入得:,设,坐标得、由易证求法相同,如下:、040231a ,4a ,3ab ,3ab 1N a,31,4333333343C C C C C C C C C C b bM BN AM B A NBM N AMNB AM ==+=======∆≈∆【方法2 代数法】点-线-方程23m 20352235110,m 135-m 1-m 35-m 11-m 22222122111=+=+=+=+==,解得:)代入得方程(,,,)表示线段:();,()、,(),又坐标为()表示点:设(:不妨来求下)()()()(BC C C C A AB B A【考点1 等腰角形的存在性】【典例1】(2020•泰安)如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A (﹣4,0)、B(2,0),交y轴于点C(0,6),在y轴上有一点E(0,﹣2),连接AE.(1)求二次函数的表达式;(2)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标,若不存在,请说明理由.【答案】(1)y=,(2)m=时,△ADE的面积取得最大值为(3)点P坐标为:(﹣1,1),(﹣1,),(﹣1,﹣2)【解答】解:(1)∵二次函数y=ax2+bx+c经过点A(﹣4,0)、B(2,0),C(0,6),∴,解得,所以二次函数的解析式为:y=,(2)y=的对称轴为x=﹣1,设P(﹣1,n),又E(0,﹣2),A(﹣4,0),可求P A2=9+n2,PE2=1+(n+2)2,AE2=16+4=20,当P A2=PE2时,9+n2=1+(n+2)2,解得,n=1,此时P(﹣1,1);当P A2=AE2时,9+n2=20,解得,n=,此时点P坐标为(﹣1,);当PE2=AE2时,1+(n+2)2=20,解得,n=﹣2,此时点P坐标为:(﹣1,﹣2).综上所述,P点的坐标为:(﹣1,1),(﹣1,),(﹣1,﹣2).【变式1-2】(2020•贵港)如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).(1)求这个二次函数的表达式;(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与线段BC 交于点M,连接PC.当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.【答案】(1)y=x2﹣2x﹣3 (2)①n=时,PM最大=②P(3﹣,2﹣4)或(2,﹣3).【解答】解:(1)将A,B,C代入函数解析式,得,解得,这个二次函数的表达式y=x2﹣2x﹣3;(2)解法一:当PM=PC时,(﹣n2+3n)2=n2+(n2﹣2n﹣3+3)2,解得n1=n2=0(不符合题意,舍),n3=2,n2﹣2n﹣3=﹣3,P(2,﹣3).当PM=MC时,(﹣n2+3n)2=n2+(n﹣3+3)2,解得n1=0(不符合题意,舍),n2=3﹣,n3=3+(不符合题意,舍),n2﹣2n﹣3=2﹣4,P(3﹣,2﹣4).综上所述:P(3﹣,2﹣4)或(2,﹣3).解法二:当PM=PC时,∵BC:y=x﹣3∴∠ABC=45°∵PH⊥AB∴∠BMH=∠CMP=45°∴PM=PC时,△CPM为等腰直角三角形,CP∥x轴设P(n,n2﹣2n﹣3),则CP=nMP=﹣n2+3n∴n=﹣n2+3n解得n=0(舍去)或n=2,∴P(2,﹣3)当PM=CM时,设P(n,n2﹣2n﹣3),则=﹣n2+3n=﹣n2+3n∵n>0∴n=﹣n2+3n解得n=3﹣∴P(3﹣,2﹣4)综上所述:P(3﹣,2﹣4)或(2,﹣3)【变式1-2】(2022•澄海区模拟)如图,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,点A的坐标为(﹣1,0),点C坐标为(0,3),对称轴为x=1.点M为线段OB上的一个动点(不与两端点重合),过点M作PM⊥x轴,交抛物线于点P,交BC 于点Q.(1)求抛物线及直线BC的表达式;(2)试探究点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线对称轴为x=1,点B与A(﹣1,0)关于直线x=1对称,∴B(3,0),设y=a(x﹣3)(x+1),把C(0,3)代入得:﹣3a=3,解得:a=﹣1,∴y=﹣(x﹣3)(x+1)=﹣x2+2x+3,设直线BC的解析式为y=kx+d,则,解得:,∴直线BC的解析式为y=﹣x+3,故抛物线解析式为y=﹣x2+2x+3,直线BC的解析式为y=﹣x+3;(2)存在,设Q(m,﹣m+3)(0<m<3),∵A(﹣1,0),C(0,3),∴AC2=OA2+OC2=12+32=10,AQ2=(m+1)2+(﹣m+3)2=2m2﹣4m+10,CQ2=m2+m2=2m2,∵以A,C,Q为顶点的三角形是等腰三角形,∴AC=AQ或AC=CQ或AQ=CQ,当AC=AQ时,10=2m2﹣4m+10,解得:m=0(舍去)或m=2,∴Q(2,1);当AC=CQ时,10=2m2,解得:m=﹣(舍去)或m=,∴Q(,3﹣);当AQ=CQ时,2m2﹣4m+10=2m2,解得:m=,∴Q(,);综上所述,点Q的坐标为(2,1)或(,3﹣)或(,).【考点2 直角三角形的存在性】【典例2】(2021秋•建华区期末)抛物线y=x2+bx+c经过A、B(1,0)、C(0,﹣3)三点.点D为抛物线的顶点,连接AD、AC、BC、DC.(1)求抛物线的解析式;(2)在y轴上是否存在一点E,使△ADE为直角三角形?若存在,请你直接写出点E的坐标;若不存在,请说明理由.【解答】解(1)∵抛物线y=x2+bx+c经过B(1,0)、C(0,﹣3),∴,解得,∴抛物线的解析式为:y=x2+2x﹣3.(4)在y轴上存在点E,使△ADE为直角三角形,理由如下:∵抛物线的解析式为y=x2+2x﹣3=(x+1)2﹣4,∴D(﹣1,﹣4),设E点坐标为(0,m),∴AE2=m2+9,DE2=m2+8m+17,AD2=20,当∠EAD=90°时,有AE2+AD2=DE2,∴m2+9+20=m2+8m+17,解得m=,∴此时点E的坐标为(0,);当∠ADE=90°时,DE2+AD2=AE2,m2+8m+17+20=m2+9,解得m=﹣,∴此时点E的坐标为(0,﹣);当∠AED=90°时,AE2+DE2=AD2,m2+9+m2+8m+17=20,解得m=﹣1或m=﹣3,∴此时点E的坐标为(0,﹣1)或(0,﹣3).综上所述,符合题意的点E的坐标为(0,)或(0,﹣)或(0,﹣1)或(0,﹣3).【变式2-1】(2022•灞桥区校级模拟)如图,抛物线与x轴交于点A(1,0),B(3,0),与y轴交于点C(0,3).(1)求二次函数的表达式及顶点坐标;(2)连接BC,在抛物线的对称轴上是否存在一点E,使△BCE是直角三角形?若存在,请直接写出点E的坐标;若不存在,请说明理由.【解答】解:(1)设抛物线的解析式为y=a(x﹣1)(x﹣3),将点C(0,3)代入y=a(x﹣1)(x﹣3),∴3a=3,∴a=1,∴y=(x﹣1)(x﹣3)=x2﹣4x+3,∵y=x2﹣4x+3=(x﹣2)2﹣1,∴顶点为(2,﹣1);(2)存在一点E,使△BCE是直角三角形,理由如下:∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的对称轴为直线x=2,设E(2,t),∵△BCE是直角三角形,∴BE⊥CE,∵B(3,0),C(0,3),∴BC=3,BE=,CE=,①当BC为斜边时,∴18=()2+()2,解得t=,∴E点坐标为(2,)或(2,);②当BE为斜边时,∴18+()2=()2,解得t=5,∴E点坐标为(2,5);③当CE为斜边时,∴18+()2=()2,解得t=﹣1,∴E点坐标为(2,﹣1);综上所述:E点坐标为(2,)或(2,)或(2,5)或(2,﹣1).【变式2-2】(2022•碑林区校级四模)如图,在平面直角坐标系中,抛物线C1:y=ax2+bx+c 交x轴于点A(﹣5,0),B(﹣1,0),交y轴于点C(0,5).(1)求抛物线C1的表达式和顶点D的坐标.(2)将抛物线C1关于y轴对称的抛物线记作C2,点E为抛物线C2上一点若△DOE是以DO为直角边的直角三角形,求点E的坐标.【解答】解:(1)将点A(﹣5,0),B(﹣1,0),C(0,5)代入y=ax2+bx+c,∴,解得,∴y=x2+6x+5,∵y=x2+6x+5=(x+3)2﹣4,∴顶点D(﹣3,﹣4);(2)设抛物线C2上任意一点(x,y),则(x,y)关于y轴对称的点为(﹣x,y),∵点(﹣x,y)在抛物线C1上,∴抛物线记作C2的解析式为y=x2﹣6x+5,设E(t,t2﹣6t+5),过点D作DG⊥x轴交于点G,过点E作EH⊥x轴交于点H,∵∠DOE=90°,∴∠GOD+∠HOE=90°,∵∠GOD+∠GDO=90°,∴∠HOE=∠GDO,∴△GDO∽△HOE,∴=,∵DG=4,GO=3,HE=﹣t2+6t﹣5,OH=t,∴=,∴t=4或t=,∴E(4,﹣3)或E(,﹣).【变式2-3】(2022•武功县模拟)如图,经过点A(2,6)的直线y=x+m与y轴交于点B,以点A为顶点的抛物线经过点B,抛物线的对称轴为直线l.(1)求点B的坐标和抛物线的函数表达式;(2)在l右侧的抛物线上是否存在点P,使得以P、A、B为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.【解答】解:(1)∵直线y=x+m经过点A(2,6),∴2+m=6,解得m=4,即y=x+4.令x=0,得y=4,即点B的坐标为(0,4).∵点A(2,6)为抛物线的顶点,∴可设抛物线的函数表达式为y=a(x﹣2)2+6(a≠0),将点B(0,4)代入,得4=4a+6,解得,∴抛物线的函数表达式为.∴点B的坐标为(0,4),抛物线的函数表达式为y=﹣x2+2x+4;(2)∵点A(2,6)为抛物线的顶点,∴抛物线的对称轴l:x=2.①当AB为该等腰三角形的底边时:如图,点P在P2的位置.过点A作AC⊥y轴于点C,过点P2作P2D⊥AC交CA的延长线于点D,作P2E⊥y轴于点E,连接P2A,P2B,则P2A=P2B,∠D=∠P2EB=90°.∵A(2,6),B(0,4),AC⊥BC,∴AC=BC=2,∴△ABC是等腰直角三角形,∴∠CAB=∠CBA.∵P2A=P2B,∴∠P2AB=∠P2BA,∴180°﹣∠CAB﹣∠P2AB=180°﹣∠CBA﹣∠P2BA,即∠P2AD=∠P2BE.在△P2AD和△P2BE中,∠D=∠P2EB,∠P2AD=∠P2BE,P2A=P2B,∴△P2AD≌△P2BE(AAS),∴P2D=P2E.设,则P2E=m,,∴,解得(舍去)或,∴;②当AB为该等腰三角形的腰时,作点B关于l的对称点P1,由抛物线的对称性可知,AB=AP1.∵B(0,4),抛物线的对称轴为直线x=2,∴P1(4,4).综上可知,在l右侧的抛物线上存在点P,使得以P、A、B为顶点的三角形是等腰三角形,点P的坐标为(4,4)或.【考点3 等腰直角三角形的存在性】【典例3】(2022•黔东南州一模)抛物线y=ax2+bx﹣经过点(1,﹣1),现将一块等腰直角三角板ABC(∠ACB=90°)按照如图的方式放在第二象限,斜靠在两坐标轴上,且点A、C坐标分别为(0,2)、(﹣1,0).B点在抛物线y=ax2+bx﹣图象上.(1)求点B的坐标:(2)求抛物的解析式;(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求出点P的坐标:若不存在,请说明理由.【解答】解:(1)过点B作BD⊥x轴,垂足为D.∵∠BCD+∠ACO=90°,∠ACO+∠CAO=90°,∴∠BCD=∠CAO,又∵∠BDC=∠COA=90°,CB=AC,∴△BCD≌△CAO(AAS),∴BD=OC=1,CD=OA=2,∴点B的坐标为(﹣3,1);(2)抛物线y=ax2+bx﹣经过点(1,﹣1),点B(﹣3,1),则,解得,所以抛物线的解析式为y=x2+x﹣;(3)假设存在点P,使得△ACP仍然是以AC为直角边的等腰直角三角形:①若以点C为直角顶点;则延长BC至点P1,使得P1C=BC,得到等腰直角三角形△ACP1,过点P1作P1M⊥x轴,∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,∴△MP1C≌△DBC(AAS),∴CM=CD=2,P1M=BD=1,∵OC=1,∴OM=1,∴P1(1,﹣1);②若以点A为直角顶点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形△ACP2,过点P2作P2N⊥y轴,同理可证△AP2N≌△CAO,∴NP2=OA=2,AN=OC=1,∴点P2(2,1),③以A为直角顶点的等腰Rt△ACP的顶点P有两种情况.即过点A作直线L⊥AC,在直线L上截取AP=AC时,点P可能在y轴右侧,即现在解答情况②的点P2;点P也可能在y轴左侧,即还有第③种情况的点P3.因此,然后过P3作P3G⊥y轴于G,同理:△AGP3≌△CAO,∴GP3=OA=2,AG=OC=1,∴P3为(﹣2,3);经检验,点P1(1,﹣1)与在抛物线y=x2+x﹣上,点P2(2,1)点P3(﹣2,3)都不在抛物线y=x2+x﹣上.综上,存在,点P的坐标为(1,﹣1).【变式1-1】(2022•兴宁区校级模拟)如图,已知二次函数y=ax2+bx+c的图象经过点C(2,﹣3),且与x轴交于原点及点B(8,0),点A为抛物线的顶点.(1)求二次函数的表达式;(2)在抛物线的对称轴上是否存在点M,使△ABM是等腰三角形?如果存在,请求出点M的坐标.如果不存在,请说明理由;【解答】解:(1)由题意,解得:,∴二次函数的表达式为y=x2﹣2x;(2)过点A作直线AF⊥x轴于点F,由(1)得y=(x﹣4)2﹣4,∴抛物线的顶点A(4,﹣4),①AM=BM,∵B(8,0),∴BF=4,∵∠AFB=90°,AF=BF=4,∴△ABF是等腰直角三角形,∴M在点F处,△ABM是等腰直角三角形,此时M为(4,0),②AB=AM,由①得△ABF是等腰直角三角形,BF=4,∴AB===4,∴M为(4,﹣4﹣4)或(4,﹣4+4),③AB=BM,∵AB=BM,BF⊥AM,∴MF=AF,∴M为(4,4),综上所述,M为(4,0),(4,﹣4﹣4)或(4,﹣4+4)或(4,4);【变式3-2】(2022•禅城区二模)如图,抛物线经过原点O,对称轴为直线x=2且与x轴交于点D,直线l:y=﹣2x﹣1与y轴交于点A,与抛物线有且只有一个公共点B,并且点B在第四象限,直线l与直线x=2交于点C.(1)连接AD,求证:AD⊥AC.(2)求抛物线的函数关系式.(3)在直线l上有一点动点P,抛物线上有一动点Q,当△PBQ是以PQ为斜边的等腰直角三角形时,直接写出此时点P的坐标.【解答】解:(1)如图1,过点C作CE⊥y轴于点E,则∠AEC=∠DOA=90°,∵直线y=﹣2x﹣1与y轴交于点A,与直线x=2交于点C,∴A(0,﹣1),C(2,﹣5),∴E(0,﹣5),∴OA=1,OD=2,CE=2,AE=4,∴=,==,∴=,∵∠AEC=∠DOA,∴△AEC∽△DOA,∴∠CAE=∠ADO,∵∠ADO+∠DAO=90°,∴∠CAE+∠DAO=90°,∴∠DAC=180°﹣(∠CAE+∠DAO)=180°﹣90°=90°,∴AD⊥AC.(2)设抛物线的函数关系式为y=ax2+bx,∵对称轴为直线x=2,∴=2,∴b=﹣4a,∴y=ax2﹣4ax,由ax2﹣4ax=﹣2x﹣1,整理得ax2+(2﹣4a)x+1=0,∵直线y=﹣2x﹣1与抛物线有且只有一个公共点B,∴Δ=(2﹣4a)2﹣4a=0,解得:a1=,a2=1,当a=时,抛物线解析式为y=x2﹣x,联立得x2﹣x=﹣2x﹣1,解得:x1=x2=﹣2,∴B(﹣2,3)与点B在第四象限矛盾,故a=不符合题意,舍去,当a=1时,y=x2﹣4x,联立得x2﹣4x=﹣2x﹣1,解得:x1=x2=1,∴B(1,﹣3),点B在第四象限符合题意,∴a=1,∴该抛物线的函数关系式为y=x2﹣4x.(3)如图2,过点B作BQ⊥AB交抛物线于点Q,作GH∥x轴交y轴于点G,过点Q 作QH⊥GH,则∠AGB=∠BHQ=∠ABQ=90°,∴∠ABG+∠QBH=∠ABG+∠BAG=90°,∴∠QBH=∠BAG,∴△ABG∽△BQH,∴=,设Q(t,t2﹣4t),∵A(0,﹣1),B(1,﹣3),∴AG=2,BG=1,BH=t﹣1,QH=t2﹣4t+3,∴=,解得:t=1(舍去)或t=,∴BH=﹣1=,QH=()2﹣4×+3=,过点B作EF∥y轴,过点P1作P1E⊥EF,过点P2作P2F⊥EF,∵△PBQ是以PQ为斜边的等腰直角三角形,∴P1B=BQ=P2B,∵∠P1BE+∠EBQ=∠EBQ+∠QBH=90°,∴∠P1BE=∠QBH,∵∠BEP1=∠BHQ=90°,∴△BEP1≌△BHQ(AAS),∴EP1=QH=,BE=BH=,∴P1(﹣,﹣),同理可得:P2(,﹣),综上,点P的坐标为P1(﹣,﹣),P2(,﹣).1.(2022•榆阳区一模)如图,已知抛物线y=mx2+4x+n与x轴交于A、B两点,与y轴交于点C.直线y=x﹣3经过B,C两点.(1)求抛物线的函数表达式;(2)抛物线的顶点为M,在该抛物线的对称轴l上是否存在点P,使得以C,M,P为顶点的三角形是等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.【解答】解:(1)y=x﹣3中,令x=0,则y=﹣3,∴C(0,﹣3),令y=0,则x=3,∴B(3,0),将C(0,﹣3),B(3,0)代入y=mx2+4x+n中,∴,解得,∴y=﹣x2+4x﹣3;(2)存在点P,使得以C,M,P为顶点的三角形是等腰三角形,理由如下:∵y=﹣x2+4x﹣3=﹣(x﹣2)2+1,∴M(2,1),对称轴为直线x=2,设P(2,t),∴MP=|t﹣1|,MC=2,CP=,①当MP=MC时,|t﹣1|=2,∴t=2+1或t=﹣2+1,∴P(2,2+1)或(2,﹣2+1);②当MP=CP时,|t﹣1|=,解得t=﹣,∴P(2,﹣);③当MC=CP时,2=,解得t=1(舍)或t=﹣7,∴P(2,7);综上所述:P点坐标为(2,2+1)或(2,﹣2+1)或(2,﹣)或(2,7).2.(2022•岚山区一模)已知抛物线y=ax2+bx+8与x轴交于A(﹣3,0),B(8,0)两点,交y轴于点C,点P是抛物线上一个动点,且点P的横坐标为m.(1)求抛物线的解析式;(2)如图2,将直线BC沿y轴向下平移5个单位,交x轴于点M,交y轴于点N.过点P作x轴的垂线,交直线MN于点D,是否存在一点P,使△BMD是等腰三角形?若存在,请直接写出符合条件的m的值;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+bx+8与x轴交于A(﹣3,0),B(8,0)两点,∴,解得,,∴抛物线的解析式为y=﹣x2+x+8;(3)易证线BC的解析式为y=﹣x+8,向下平移5个单位得到y=﹣x+3,当y=0时,x=3,∴M(3,0),当x=0时,y=3,∴N(0,3),由题意得PD⊥MB,∵MB=8﹣3=5,D(m,﹣m+3),∴MD2=(m﹣3)2+(﹣m+3)2,BD2=(8﹣m)2+(﹣m+3)2,若△BMD是等腰三角形,可分三种情况:①当MB=MD时,∴(m﹣3)2+(﹣m+3)2=25,解得m1=3+,m2=3﹣,②当MB=BD时,∴(8﹣m)2+(﹣m+3)2=25,解得,m1=3(舍去),m2=8(舍去),③当MD+BD时,∴(8﹣m)2+(﹣m+3)2=(m﹣3)2+(﹣m+3)2,解得,m=5.5.综上所述,m的值为3+或3﹣或5.5时,△BMD是等腰三角形.3.(2022•兴宁区校级模拟)如图,抛物线y=﹣x2+bx+c过点A、B,抛物线的对称轴交x 轴于点D,直线y=﹣x+3与x轴交于点B,与y轴交于点C,且.(1)求抛物线的解析式;(2)在x轴上是否存在点P,使得△PDC为等腰三角形?若存在,请求出点P的坐标,若不存在,请说明理由.【解答】解:(1)对于直线y=﹣x+3,令y=0,即﹣x+3=0,解得:x=3,令x=0,得y=3,∴B(3,0),C(0,3),∵A为x轴负半轴上一点,且OA=OB,∴A(﹣1,0).将点A、B的坐标分别代入y=﹣x2+bx+c中,得,解得,∴抛物线的解析式为y=﹣x2+2x+3;(3)存在.如图2,∵点P在x轴上,∴设P(m,0).∵C(0,3),D(1,0),∴由勾股定理,得:CD2=OC2+OD2=32+12=10,PD2=(m﹣1)2,CP2=OP2+OC2=m2+32=m2+9,分为三种情况讨论:①当CD=PD时,CD2=PD2,即10=(m﹣1)2,解得m1=1+,m2=1﹣,此时点P的坐标为(1+,0)或(1﹣,0);②当CD=CP时,CD2=CP2,即10=m2+9,解得m1=﹣1,m2=1(不符合题意,舍去),此时点P的坐标为(﹣1,0);③当PC=PD时,PC2=PD2,即m2+9=(m﹣1)2,解得m=﹣4,此时点P的坐标为(﹣4,0).综上所述,在x轴上存在点P,使得△PDC为等腰三角形,满足条件的点P的坐标为(1+,0)或(1﹣,0)或(﹣1,0)或(﹣4,0).4.(2022•鞍山模拟)抛物线与坐标轴交于A(﹣1,0)、B(4,0)、C(0,4),连接AC、BC.(1)求抛物线的解析式;(3)如图2,点E是抛物线上第一象限内对称轴右侧的一点,连接EC,点D是抛物线的对称轴上的一点,连接ED、CD,当△CED是以点E为顶点的等腰直角三角形时,直接写出点E的横坐标.【解答】解:(1)设抛物线的解析式为y=ax2+bx+c,∵抛物线y=ax2+bx+c过A(﹣1,0),B(4,0),C(0,4)三点,∴.解得:.∴抛物线对应的二次函数的解析式为y=﹣x2+3x+4;(2)设G(x,﹣x2+3x+4),∵S△BHG=S△ABG﹣S△ABH,S△AHC=S△ABC﹣S△ABH,△BHG与△AHC的面积差为1,∵A(﹣1,0)、B(4,0),∴AB=5,(3)∵y=﹣x2+3x+4,∴抛物线对称轴为x=﹣=,,点E分别作EM⊥y轴于M,作EN⊥EM,过点D作DN⊥EN,垂足为N,∴∠CME=∠DNE=90°,∠MEN=90°,∵△CED是以点E为顶点的等腰直角三角形,∴∠CED=90°,∴∠CEM+∠MED=∠DEN+∠MED=90°,CE=DE,∴∠CEM=∠DEN,∴△EMC≌△END(AAS),∴CM=DN,设E(m,﹣m2+3m+4)(m>),∴4﹣(﹣m2+3m+4)=m﹣,∴m=或(不合题意,舍去),∴点E的横坐标为.5.(2022•渭滨区模拟)如图,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.M为线段OB上的一个动点,过点M作PM⊥x轴,交抛物线于点P,交BC于点Q.(1)求抛物线的表达式;(2)试探究点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.【解答】解:(1)将A(﹣3,0),B(4,0)代入y=ax2+bx+4,∴,解得,∴抛物线的表达式为:;(2)存在点Q,使得以A,C,Q为顶点的三角形是等腰三角形,理由如下:令x=0,则y=4,∴点C(0,4),∵A(﹣3,0)、C(0,4),∴AC=5,设直线BC的解析式为y=kx+b,∴,解得,∴y=﹣x+4,设点M(m,0),则点Q(m,﹣m+4),①当AC=CQ时,过点Q作QE⊥y轴于点E,连接AQ,∵CQ2=CE2+EQ2,即m2+[4﹣(﹣m+4)]2=25,解得:舍去负值),∴点;②当AC=AQ时,则AQ=AC=5,在Rt△AMQ中,由勾股定理得:[m﹣(﹣3)]2+(﹣m+4)2=25,解得:m=1或m=0(舍去0),∴点Q(1,3);③当CQ=AQ时,则2m2=[m﹣(﹣3)]2+(﹣m+4)2,解得:舍去);综上所述,点Q的坐标为(1,3)或.31。
2023年中考数学一轮复习课件 二次函数综合题特殊三角形存在性问题

直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(2)存在.理由如下:
设点P(1,p),
∵A(-1,0),C(0,3),
∴AC2=12+32=10,
AP2=(1+1)2+p2=CAP=90°,
例题图①
则AC2+AP2=CP2,
∴10+4+p2=p2-6p+10,
解得p=- 2 ,
3
∴此时点P的坐标为(1,-
2
);
3
②若∠ACP=90°,则AC2+CP2=AP2,
∴10+p2-6p+10=4+p2,
解得p= 8 , ∴此时点3P的坐标为(1,8 );
3
③若∠APC=90°,则AP2+CP2=AC2,
例题图①
即4+p2+p2-6p+10=10,
随堂练习
1. 如图,已知抛物线y=ax2+bx+4(a≠0)与x轴交于点A(1,0)和B,与y
轴交于点C,对称轴为直线x= 5 .
2
(1)求抛物线的解析式;
a b 4 0
解:(1)根据题意,得
b 2a
5 2
,
解得
a b
1 ,
5
∴抛物线的解析式为y=x2-5x+4;
第1题图
(2)如图①,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y 轴的平行线交抛物线于点Q,连接OQ.当线段PQ长度最大时,判断四边 形OCPQ的形状并说明理由; (2)四边形OCPQ是平行四边形,理由如下: 令x=0,则y=4, 令y=0,即x2-5x+4=0, 解得x1=1,x2=4.∴B(4,0),C(0,4), ∴直线BC的解析式为y=-x+4.
第1题解图
当△BEF是等腰三角形时,分三种情况讨论:
成都市中考数学复习难题突破专题四特殊三角形存在性问题

难题突破专题四特殊三角形存在性问题特殊三角形存在性问题主要是指寻找符合条件的点使之构成等腰三角形、直角三角形、全等三角形等特殊三角形.解决此类问题的关键在于恰当地分类讨论,避免漏解.类型1等腰三角形存在性问题1如图Z4-1,直线y=3x+3交x轴于点A,交y轴于点B,过A,B两点的抛物线交x轴于另一点C(3,0).(1)求点A,B的坐标.(2)求抛物线对应的函数表达式.图Z4-1(3)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的点Q的坐标;若不存在,请说明理由.例题分层分析(1)如何求一次函数图象与坐标轴的交点坐标?(2)如何求抛物线对应的函数表达式?根据题意,设抛物线对应的函数表达式时,应该用哪种形式?(3)①根据抛物线对应的函数表达式求出对称轴为直线________,所以可设点Q的坐标为________;②△ABQ是等腰三角形可分为________种情况,分别是____________________;③根据勾股定理分别列出方程即可求出点Q的坐标.解题方法点析对于等腰三角形的分类应分三种情况.可以设一个未知数,然后用这个未知数分别表示出三角形的三边,再根据两边相等,得到三个方程,即三种情况.特别注意求出的值需检验能否构成三角形.类型2直角三角形、全等三角形存在性问题图Z4-22如图Z4-2,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.(1)求抛物线对应的函数表达式.(2)在(1)中二次函数的第二象限的图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由.(3)若点Q是y轴上一点,△且ABQ为直角三角形,求点Q的坐标.例题分层分析(1)已知点A的坐标可确定直线AB对应的函数表达式,进一步能求出点B的坐标.点A是抛物线的顶点,那么可以将抛物线对应的函数表达式设为________式,再代入________的坐标,依据________法可解.(2)△ABQ为直角三角形,直角顶点没确定,故分别以________为直角顶点,进行分类讨论,找出相关的相似三角形,依据对应线段成比例进行求解或者利用勾股定理列方程求解.解题方法点析本题为综合题,考查了平面直角坐标系中,利用待定系数法求抛物线对应的函数表达式,利用方程、分类讨论和数形结合等思想解题.专题训练1.如图Z4-3,点O(0,0),A(2,2),若存在点P,使△APO为等腰直角三角形,则点P的个数为________.图Z4-32.[2019·湖州]如图Z4-4,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数 1 91y=和y=在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交y=的图象于点C,连结AC.若△ABC x x x是等腰三角形,则k的值是________.图Z4-43.如图Z4-5所示,在平面直角坐标系中,已知点A(2,2),点B(2,-3).试问坐标轴上是否存在一点P,使得△ABP为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.图Z4-54.[2019·张家界]如图Z4-6,已知抛物线C的顶点坐标为A(-1,4),与y轴的交点为D(0,3).1(1)求C的解析式;1(2)若直线l:y=x+m与C仅有唯一的交点,求m的值;11(3)若将抛物线C关于y轴对称的抛物线记作C,平行于x轴的直线记作l:y=n.试结合图象回答:122当n为何值时,l与C和C共有:①两个交点;②三个交点;③四个交点;212(4)若将C与x轴正半轴的交点记作B,试在x轴上求点P,使得△PAB为等腰三角形.2图Z4-65.[2019·攀枝花] 如图Z4-7,抛物线y=x2+bx+c与x轴交于A,B两点,B点坐标为(3,0),与 y 轴交于点C(0,3).(1)求抛物线的解析式.(2)点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE +EF的最大值.(3)点D为抛物线对称轴上一点.①当△BCD是以BC为直角边的直角三角形时,求点D的坐标;②若△BCD是锐角三角形,求点D的纵坐标的取值范围.图Z4-76.如图Z4-8,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).(1)求该抛物线对应的函数表达式.(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连结CQ,△当CQE的面积最大时,求点Q的坐标.(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.图Z4-8参考答案类型1等腰三角形存在性问题例 1 【例题分层分析】(1)令一次函数表达式中的 x 或 y 为 0,即可求出图象与 y 轴或 x 轴的交点坐标.(2)求抛物线对应的函数表达式一般有三种方法:一般式法、顶点式法和交点式法.本题利用一般式 法或交点式法都比较简单.(3)①x =1 (1,a)②三 AQ =BQ ,AB =BQ ,AQ =AB解:(1)∵直线 y =3x +3,∴当 x =0 时,y =3,当 y =0 时,x =-1,∴点 A 的坐标为(-1,0),点 B 的坐标为(0,3).0=a -b +c ,a =-1,(2)设抛物线对应的函数表达式为 y =ax 2+bx +c ,由题意,得3=c ,解得b =2,∴抛物线对应的函数表达式为 y =-x 2+2x +3.(3)∵抛物线对应的函数表达式为 y =-x 2+2x +3,配方,得 y =-(x -1)2+4,∴抛物线的对称轴为直线 x =1,设 Q(1,a).①当 AQ =BQ 时,如图①,设抛物线的对称轴交 x 轴于点 D ,过点 B 作 BF ⊥DQ 于点 F.由勾股定理,得BQ = BF 2+QF 2= (1-0)2+(3-a )2,AQ = AD 2+QD 2= 22+a 2,得 (1-0)2+(3-a )2= 22+a 2,解得 a =1,∴点 Q 的坐标为(1,1).②当 AB =BQ 时,如图②,由勾股定理,得 (1-0)2+(a -3)2= 10,解得 a =0 或 6,当点 Q 的坐标为(1,6)时,其在直线 AB 上,A ,B ,Q 三点共线,舍去,∴点 Q 的坐标是(1,0).0=9a +3b +c , c =3.③当AQ=AB时,如图③,由勾股定理,得22+a2=10,解得a=±6,此时点Q的坐标是(1,6)或(1,-6).综上所述,存在符合条件的点Q,点Q的坐标为(1,1)或(1,0)或(1,6)或(1,-6).类型2直角三角形、全等三角形存在性问题例2【例题分层分析】(1)顶点点B待定系数(2)点A,B,Q解:(1)把(1,-4)代入y=kx-6,得k=2,∴直线AB对应的函数表达式为y=2x-6.令y=0,解得x=3,∴点B的坐标是(3,0).∵点A为抛物线的顶点,∴设抛物线对应的函数表达式为y=a(x-1)2-4,把(3,0)代入,得4a-4=0,解得a=1,∴抛物线对应的函数表达式为y=(x-1)2-4=x2-2x-3.(2)存在.∵OB=OC=3,OP=OP,∴当∠POB=∠POC时,△POB≌△POC,此时OP平分第二象限,即直线PO对应的函数表达式为y=-x.设P(m,-m),则-m=m2-2m-3,解得m=1-131+13m=>0,舍去1 2,1-1313-1∴点P的坐标为,2 2.(3)如图,①当∠Q AB=90°时,△DAQ∽△DOB,11∴AD DQ5DQ =,即=,OD DB65 7∴DQ=,∴OQ=,2 27即点Q的坐标为0,-2113 5 111;②当∠Q BA =90°时,△BOQ ∽△DOB ,22∴ OB OQ 3 OQ= ,即 = , OD OB 6 33 3 ∴OQ = ,即点 Q 的坐标为0,22;③当∠AQ B =90°时,过点 A 作 A E ⊥y 轴于点 E , 3则△BOQ ∽△Q EA ,33 OB OQ 3 OQ ∴ = ,即 = , Q E AE 4-OQ 13 3∴OQ2 3 -4OQ +3=0,∴OQ =1 或 3, 3 3即点 Q 的坐标为(0,-1)或(0,-3). 3综上,点 Q 的坐标为0,- 或0,2 2 专题训练1.6或(0,-1)或(0,-3).2.3 7 15 或7 5 [解析] 考查反比例函数中系数 k 的几何意义及等腰三角形的性质. 用 B ,A 两点的坐标来表示 C 点坐标,得到 BC 的长度,然后分三种情况讨论 k 值.9 1 1 9 1 9 1 8 设 B(a , ),A(b , ),∴C(a , ),ka = ,kb = ,∴a 2= ,b 2= .又∵BD⊥x 轴,∴BC = .a b a a b k k a①当 AB =BC 时,AB = (a -b )2+(ka -kb )2,8 3 1 8∴ 1+k 2(a -b)= ,∴ 1+k 2( - )= ,a 3k∴k =3 7 7.②当 AC =BC 时,AC =1 1(b -a )2+( - )2,b ak 2 3 1 64k 15∴(1+ )( - )2= ,∴k = .9 9 5k 2 3 715③当 AB =AC 时,∴1+ =1+k 2,∴k =0(舍去).综上所述,k = 或. 9 753.解:①若∠BAP =90°,易得 P (0,2).1②若∠ABP =90°,易得 P (0,-3).22 2 2 2337 3 k kk k③若∠BPA=90°,如图,以AB为直径画⊙O′与x轴、y轴分别交于点P,P,P,P,AB与x轴交3456于点 C ,过点 O ′作 O ′D⊥y 轴于 D 点.5 在 △R t DO ′P 中易知 O ′D =2,O ′P = ,则 P D = 225 3-4= ,4 2 3 1OP =P D -OD = - =1,则 P (0,1).易知 P D =P D ,则 P (0,-2).连结 O ′P ,O ′P ,5 5 5 56 6 3 4易求出 P (2- 6,0),P (2+ 6,0).34综上所述,存在点 P ,使得△ABP 为直角三角形,坐标为 P (0,2),P (0,-3),P (2- 6,0),123P (2+ 6,0),P (0,1),P (0,-2).4564.解:(1)∵抛物线 C 的顶点坐标为 A(-1,4),1∴设 C 的解析式为 y =a(x +1)2+4,1把 D(0,3)代入得 3=a(0+1)2+4,解得 a =-1,∴C 的解析式为 y =-(x +1)2+4=-x 2-2x +3.1y =-x 2-2x +3,(2)由方程组y =x +m ,得 x 2+3x +m -3=0,Δ=32-4×1×(m -3)=-4m +21=0,∴m =21 4.(3)抛物线 C 的顶点坐标为(1,4),l 与 C 和 C 共有:①两个交点,这时 l 过抛物线的顶点,∴n =4;22122②三个交点,这时 l 过两条抛物线的交点 D ,∴n =3;③四个交点,这时 l 在抛物线的顶点与点 D 之间或 22在点 D 的下方,∴3<n<4 或 n<3.(4)根据抛物线的对称性可知,C 的解析式为 y =-(x -1)2+4=-x 2+2x +3,与 x 轴正半轴的交点 B2的坐标为(3,0),又 A(-1,4),∴AB = 42+42=4 2.①若 AP =AB ,则 PO =4+1=5,这时点 P 的坐标为(-5,0);②若 BA =BP ,若点 P 在点 B 的左侧,则 OP =BP -BO =4 2-3,这时点 P 的坐标为(3-4 2,0), 若点 P 在点 B 的右侧,则 OP =BP +BO =4 2+3,这时点 P 的坐标为(3+4 2,0);③若 PA =PB ,这时点 P 是线段 AB 的垂直平分线与 x 轴的交点,显然 PA =PB =4,∴P(-1,0). 综上所述,点 P 的坐标为(-5,0)或(3-4 2,0)或(3+4 2,0)或(-1,0).32+3b +c =0,b =-4,5.解:(1)由题意得 解得c =3,c =3,∴抛物线的解析式为 y =x 2-4x +3.(2)由题易知 OC =OB =3,∴∠OCB =45°.5 5 5 2 2同理可知∠OFE=45°,∴△CEF为等腰直角三角形.以BC为对称轴将△FCE对称得到△F′CE,作PH⊥CF′于H点,如图①,则PE+EF=PF′=2PH.又PH=y-y=3-y,C P P∴当y最小时,PE+EF取得最大值,P∵抛物线的顶点坐标为(2,-1),∴当y=-1时,(PE+EF)=2×(3+1)=4 2.P max(3)①由(1)知抛物线的对称轴为直线x=2,设D(2,n),如图②.当△BCD是以BC为直角边的直角三角形且D在C的上方D位置时,由勾股定理得CD2+BC2=BD2,即1(2-0)2+(n-3)2+(32)2=(3-2)2+(0-n)2,解得n=5;当△BCD是以BC为直角边的直角三角形且D在C的下方D位置时,由勾股定理得BD2+BC2=CD2,即2(2-3)2+(n-0)2+(32)2=(2-0)2+(n-3)2,解得n=-1.综上所述,当△BCD是以BC为直角边的直角三角形时,D为(2,5)或(2,-1).3 31②如图③,以BC的中点T(,)为圆心,BC为半径作⊙T,与抛物线的对称轴x=2交于D和D,2 2234由直径所对的圆周角是直角得∠CD B=∠CD B=90°,341 32设D(2,m)为⊙T上一点,由DT=BC=,2 23 332得(-2)2+(-m)2=()2,2 223 17解得m=±,2 23 17 3 17∴D (2, + ),D (2, - ),2 2 2 2又由①得 D 为(2,5),D (2,-1),12∴若△BCD 是锐角三角形,则 D 点在线段 D D 或 D D 上(不与端点重合),则点 D 的纵坐标的取值范围1 32 43 17 3 17是-1<y < - 或 + <y <5.2 2 2 20=8a +c , a =- ,6.解:(1)由题意,得 解得4=c ,1∴所求抛物线对应的函数表达式为 y =- x 2+x +4.2(2)如图①,设点 Q 的坐标为(m ,0),过点 E 作 EG ⊥x 轴于点 G.1由- x 2+x +4=0,得 x =-2,x =4, 2∴点 B 的坐标为(-2,0),∴AB =6,BQ =m +2.∵QE ∥AC ,∴△BQE ∽△BAC ,∴EG BQ EG m +2 = ,即 = , CO BA 4 6 2m +4 ∴EG = ,31 1∴ =S -S = BQ·CO - BQ· △S CQE △CBQ △EBQ1 EG = (m +2) 22m +4 1 2 8 14- =- m 2+ m + =- (m -1)3 3 3 3 32 +3. ∵-2≤m≤4,∴当 m =1 时,S 有最大值 3,此时点 Q 的坐标为(1,0).△CQE(3)存在.在△ODF 中,①若 DO =DF ,∵A(4,0),D(2,0),∴AD =OD =DF =2.又在 Rt △AOC 中,OA =OC =4,∴∠OAC =45°,∴∠DFA =∠OAC =45°,3 4 D D1 2c =4,1 2 2 2∴∠ADF=90°,此时点F的坐标为(2,2). 1由-x2+x+4=2,得x=1+5,x=1-5,212∴点P的坐标为(1+5,2)或(1-5,2).②若FO=FD,如图②,过点F作FM⊥x轴于点M,1由等腰三角形的性质得OM=OD=1,2∴AM=3,∴在等腰直角三角形AMF中,MF=AM=3,∴F(1,3).1由-x2+x+4=3,2得x=1+3,x=1-3,12∴点P的坐标为(1+3,3)或(1-3,3).③若OD=OF,∵OA=OC=4,且∠AOC=90°,∴AC=42,∴点O到AC的距离为22,而OF=OD=2,与OF≥22相矛盾,∴AC上不存在点F,使得OF=OD=2,∴不存在这样的直线l,使得△ODF是等腰三角形.综上所述,存在这样的直线l,使得△ODF是等腰三角形,所求点P的坐标为(1+5,2)或(1-5, 2)或(1+3,3)或(1-3,3).2019-2020学年数学中考模拟试卷一、选择题1.下列各式中,不相等的是()A.23和-23 B.32和32 C.2和23 D.32和322.在平面直角坐标系中,点A的坐标是(1,3),将点A绕原点O顺时针旋转90°得到点A′,则点A′的坐标是()A.(﹣3,1) C.(﹣1,3)B.(3,﹣1) D.(1,﹣3)3.某市连续10天的最低气温统计如下(单位:℃):4,5,4,7,7,8,7,6,5,7,该市这10天的最低气温的中位数是()A.6℃B.6.5℃C.7℃D.7.5℃4.已知关于的一元二次方程A. B. C.有两个不相等的实数根,则的取值范围为()D.5.今年父亲的年龄是儿子年龄的3倍,5年前父亲的年龄是儿子年龄的4倍.设今年儿子的年龄为x岁,则下列式子正确的是()A.4x-5=3(x-5) C.3x+5=4(x+5)6.估计A.0到1之间B.4x+5=3(x+5)D.3x-5=4(x-5)的值在()B.1到2之间C.2到3之间D.3到4之间7.如图,四边形A BCD中,AC平∠DAB,∠ADC=∠ACB=90°,E为AB的中点,若A D=4,AB=6,则的值为()AC AFA.2B.74C.32D.628.计算2x 12x3x 13x 1的结果为( )A.1B.-1C.3x 3D.3x 13x 19.如图,O的直径AB 8,CBD 30,则CD的长为().3A.2B.23C.4D.4310.正比例函数y=kx(k≠0)的图象上一点A到x轴的距离与到y轴的距离之比为2 :3,且y随x的增大而减小,则k的值是()A.23B.32C.32D.2311.如图,将一副三角尺叠放在一起,使直角的顶点重合于点O,DC与O B交于点E,若AB∥OC,则CEB的度数为()A.95B.100C.105D.11012.把边长相等的正六边形A BCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG=()A.141°B.144°C.147°D.150°二、填空题13.折纸飞机是我们儿时快乐的回忆,现有一张长为290mm,宽为200mm的白纸,如图所示,以下面几个步骤折出纸飞机:(说明:第一步:白纸沿着EF折叠,AB边的对应边A′B′与边CD平行,将它们的距离记为x;第二步:将EM,MF分别沿着MH,MG折叠,使EM与MF重合,从而获得边HG与A′B′的距离也为x),则PD=______mm.14.如图,在Rt△ABC中,∠ACB=90°,BC =3,AC=4,点D为边AB上一点.将△BCD沿直线CD翻折,点B落在点E处,联结AE.如果AE //CD,那么BE =________.15.如图,菱形O ABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=图象经过点C,与AB交与点D,则△COD的面积的值等于_____;412,反比例函数y=﹣的3x16.如图,传送带AB和地面BC所成斜坡的坡度为1:3,如果它把物体从地面送到离地面2米高的地方,那么物体所经过的路程是______米.(结果保留根号)17.计算:3282=_____.18.﹣6的绝对值的结果为_____.三、解答题19.某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线A BD表示该产品每千克生产成本y (单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y(单位:元)与产12量x(单位:kg)之间的函数关系.(1)请解释图中点D的横坐标、纵坐标的实际意义.(2)求线段AB所表示的y与x之间的函数表达式.1(3)当0≤x≤90时,销售该产品获得的利润与产量的关系式是;当90≤x≤130时,销售该产品获得的利润与产量的关系式是;总之,当产量为kg时,获得的利润最大,最大利润是.20.民俗村的开发和建设带动了旅游业的发展,某市有A、B、C、D、E五个民俗旅游村及“其它”景点,该市旅游部门绘制了2018年“五•一”长假期间民俗村旅游情况统计图如下:根据以上信息解答:(1)2018年“五•一”期间,该市五个旅游村及“其它”景点共接待游客万人,扇形统计图中D 民俗村所对应的圆心角的度数是,并补全条形统计图;(2)根裾近几年到该市旅游人数增长趋势,预计2019年“五•一”节将有70万游客选择该市旅游,请估计有多少万人会选择去E民俗村旅游?(3)甲、乙两个旅行团在A、C、D三个民俗村中,同时选择去同一个民俗村的概率是多少?请用画树状图或列表法加以说明.21.如图,已知一次函数y=k x+b的图象与x轴、y轴分别交于A.B两点,与反比例函数y=112象分别交于C.D两点,点D(2,﹣3),OA=2.k2x的图(1)求一次函数y=k x+b与反比例函数y=112k2x的解析式;(2)直接写出k x+b﹣1k2x≥0时自变量x的取值范围.22.如图是小明同学的一款琴谱架,他由谱板、立杆和三角支架组成(立杆垂直于地面,三角支架的三条1腿长相等),谱板的长为47.5cm,宽为30cm,在谱板长的中间,宽的下端处可调节谱板的倾斜度.如图3是这款琴谱架的一种截面图.已知立杆AB=80cm,三角支架CD=30cm,CD与地面夹角∠CDE为35°,BC的长度为9cm.根据小明的身高,当谱板与水平面的夹角∠FAH调整为65°时,视谱效果最好,求此时谱板的上边沿到地面的距离FM的长.(结果精确到1cm.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin65°≈0.91,cos65°≈0.42,tan65°≈2.15)2x 80 23.解不等式组,并把它们的解集在数轴上表示出来:x 2).24.在平面直角坐标系中,如图1,抛物线y=ax2+bx+c的对称轴为x 32,与x轴的交点A(﹣1,0)与y轴交于点C(0,﹣2).(1)求抛物线的解析式;(2)如图2.点P是直线BC下方抛物线上的一点,过点P作BC的平行线交抛物线于点Q(点Q在点P右侧),连结BQ,当△PCQ的面积为△BCQ面积的一半时,求P点的坐标;(3)现将该抛物线沿射线AC的方向进行平移,平移后的抛物线与直线AC的交点为A'、C'(点C'在点 A'的下方),与x轴的交点为B',当△AB'C'与△AA'B'相似时,求出点A′的横坐标.25.为弘扬泰山文化,某校举办了“泰山诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):组别第1组第2组第3组第4组第5组请根据以上信息,解答下列问题:分数90<x≤10080<x≤9070<x≤8060<x≤7050<x≤60人数8a10b33(…x 4(1)求出a,b的值;(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;(3)若该校共有1800名学生,那么成绩高于80分的共有多少人?【参考答案】***一、选择题题号123456789101112答案D B B C D B B A C D二、填空题13.2601602C B14.245(或4.8)15.16.21017.218.6三、解答题19.(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)y=﹣0.2x+60(0≤x≤90);(3)w=﹣0.4(x﹣75)2+2250;w=﹣0.6(x﹣65)2+2535,75,2250.【解析】【分析】(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可;(3)利用总利润=单位利润×产量列出有关x的二次函数,求得最值即可.【详解】解:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)设线段 AB 所表示的 y 与 x 之间的函数关系式为 y =k x+b ,111∵y =k x+b 的图象过点(0,60)与(90,42),11b 60 ∴90kb4211,k 0.2∴解得: ,b 601∴这个一次函数的表达式为;y =﹣0.2x+60(0≤x ≤90); (3)设 y 与 x 之间的函数关系式为 y =k x+b ,222∵经过点(0,120)与(130,42),b 120∴130kb4222,k 0.6解得: ,b 1202∴这个一次函数的表达式为 y =﹣0.6x+120(0≤x ≤130),2设产量为 xkg 时,获得的利润为 W 元,当 0≤x≤90 时,W =x[(﹣0.6x+120)﹣(﹣0.2x+60)]=﹣0.4(x ﹣75)2+2250, ∴当 x =75 时,W 的值最大,最大值为 2250;当 90≤x ≤130 时,W =x[(﹣0.6x+120)﹣42]=﹣0.6(x ﹣65)2+2535,由﹣0.6<0 知,当 x >65 时,W 随 x 的增大而减小,∴90≤x ≤130 时,W ≤2160, ∴当 x =90 时,W =﹣0.6(90﹣65)2+2535=2160,因此当该产品产量为 75kg 时,获得的利润最大,最大值为 2250.故答案为:w =﹣0.4(x ﹣75)2+2250;w =﹣0.6(x ﹣65)2+2535,75,2250. 【点睛】本题考查了二次函数的应用,解题的关键是从实际问题中抽象出二次函数模型,难度不大.20.(1)50,64.8°;(2)8.4 万人;(3)13【解析】【分析】(1)根据 A 景点的人数以及百分比进行计算即可得到该市景点共接待游客数,用 360°乘以 D 对应的百 分比可得其圆心角度数,总人数乘以 B 对应百分比求得其人数即可补全条形图;(2)根据样本估计总体的思想解决问题即可;(3)根据甲、乙两个旅行团在 A 、C 、D 三个景点中各选择一个景点,画出树状图,根据概率公式进行计 算,即可得到同时选择去同一景点的概率.【详解】(1)该市五个旅游村及“其它”景点共接待游客 15÷30%=50(万人), 扇形统计图中 D 民俗村所对应的圆心角的度数是 18%×360°=64.8°, B 景点接待游客数为:50×24%=12(万人),补全条形统计图如下:11 22故答案为:50,64.8°;(2)估计选择去E民俗村旅游的人数约为70×(3)画树状图可得:650=8.4(万人);∵共有9种可能出现的结果,这些结果出现的可能性相等,其中同时选择去同一个景点的结果有3种,∴同时选择去同一个民俗村的概率是13.【点睛】本题考查的是条形统计图、扇形统计图、用样本估计总体以及概率的计算的综合应用,读懂统计图、从中获取正确的信息是解题的关键.当有两个元素时,可用树形图列举,也可以列表列举.解题时注意:概率=所求情况数与总情况数之比.21.(1)y 336x ;y422x;(2)x≤﹣4或0<x≤2.【解析】【分析】(1)把点D的坐标代入反比例函数,利用待定系数法即可求得反比例函数的解析式,作DE⊥x轴于E,根据题意求得A的坐标,然后利用待定系数法求得一次函数的解析式;(2)根据图象即可求得k x+b﹣1【详解】k2x≥0时,,自变量x的取值范围.解:(1)∵点D(2,﹣3)在反比例函数y=2∴k=2×(﹣3)=﹣6,2k2x的图象上,∴y=﹣26x;如图,作DE⊥x轴于E∵OA=2∴A(﹣2,0),∵A(﹣2,0),D(2,﹣3)在y=k x+b的图象上,112k b 0 2kb 31,解得 3 3 k , b 1 4 2, 3 3y x ;4 2(2)由图可得,当 k x+b ﹣ 1k2 x≥0 时,x ≤﹣4 或 0<x ≤2.【点睛】本题考查了反比例函数和一次函数的交点问题,待定系数法求一次函数和反比例函数的解析式,方程组的 解等知识,解题的关键是灵活应用所学知识解决问题.22.谱板的上边沿到地面的距离 FM 的长为 106cm . 【解析】 【分析】延长 AB 交 DE 于 N ,过 B 作 BG ⊥FM 于 G ,则 AH =BG ,HG =AB =80,MG =BN ,解直角三角形即可得到结论. 【详解】延长 AB 交 DE 于 N ,过 B 作 BG ⊥FM 于 G , 则 AH =BG ,HG =AB =80,MG =BN ,在 Rt △AFH 中,AF =30× 2 3=20,∠FAH =65°,∴FH =AF •sin65°=20×0.91≈18.2,在 Rt △CDN 中,CD =30,∠CDE =35°, ∴CN =CD •sin35°=30×0.57≈17.1, ∴GM =BN =17.1﹣9=8.1,∴FM =FH+HG+GM =18.2+80+8.1≈106cm ,答:谱板的上边沿到地面的距离 FM 的长为 106cm .【点睛】本题考查了解直角三角形的应用,作辅助线构造直角三角形以及正确应用锐角三角函数关系是解题的关 键.23.1≤x <4,见解析.【解析】1【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,然后把不等式的解集表示在数轴上即可.【详解】2x 80①解:3(x 2)…x 4②解不等式①得:x<4,解不等式②得:x≥1,所以不等式组的解集是:1≤x<4,表示在数轴上如下:【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.24.(1)y 13x2x 2223214;(2)点P(1,﹣3);(3)点A′的横坐标为.4【解析】【分析】(1)由对称性可知B(4,0),设抛物线解析式为y=a(x+1)(x﹣4),由待定系数法可求得抛物线的解析式;(2)由平行线间距离处处相等可知,当△PCQ的面积为△BCQ面积的一半时,可求相关线段的长,再求得 BC 的解析式,将其与抛物线解析式联立可解;(3)由平移的相关知识,结合图形分析,得出方程组,从而得解.【详解】解:(1)由对称性可知B(4,0)设抛物线解析式为y=a(x+1)(x﹣4)1将(0,﹣2)代入得a=213∴y=x2﹣x﹣2.22(2)由平行线间距离处处相等可知,当△PCQ的面积为△BCQ面积的一半时,PQ=∵C(0,﹣2),B(4,0)∴BC=25∴PQ=512 BC∴PQ2=x xQ P 2yQyP2=51∵直线 BC 的解析式为 y = x ﹣2,PQ ∥BC2 1∴设直线 PQ 的解析式为 y = x+b2则 y = P1 1 x +b ,y =y = x +b2 2联立y y1x b 21 3x 2 x 2 22得x 2﹣4x ﹣4﹣2b =0 则 x +x =4PQ∵PQ2 =x xQP2yQyP 2=5∴54x x2=5,x ﹣x =2QP∴点 P (1,﹣3)(3)由点 A (﹣1,0),C (0,﹣2)得直线 AC 的解析式为 y =﹣2x ﹣2设点 A'坐标为(a ,﹣2a ﹣2),由平移的性质,可知 AC =A'C'= 5 平移距离为 AA'= 5 (a+1)∴AC' 5 (a+2)当△AB'C'与△AA'B'相似时,只有当△AB'C'∽△AA'B'∴AB'2=AA'×AC'=5(a+1)(a+2)过点 B'作 AA'的平行线,交原抛物线于点 D ,连接 AD ,由平移知四边形 ADB'A'为平行四边形,点 D 的纵坐标为 2a+2 设点 D 的横坐标为 m ,则点 B'坐标为(m+a+1,0)∴AB'2=(m+a+2)2=5(a+1)(a+2),①将点 D (m ,2a+2)代入 y = 1 3m 2 ﹣ ﹣2=2a+2,② 22P QQQP13x2﹣x﹣2得22联立①②,解得:a = ,4m 2﹣9m+15=0,∴m =9+ 21 9- 21 22m 3m 8 6m 23 3 21 44 4 4∴点 A ′的横坐标为 .4【点睛】此题考查二次函数综合题,抛物线与一次函数的交点问题,利用待定系数法求解析式是解题关键25.(1)a =12,b =7;(2)27°;(3)900 人【解析】 【分析】(1)根据第三组人数和所占比例求出抽取学生人数,再根据抽取学生人数和比例分别求出第 2 组和第 4 组人数;(2)求出第五组人数所占比例,可得 “第 5 组”所在扇形圆心角的度数;(3)先求出成绩高于 80 分人数所占比例,根据全校人员可得成绩高于 80 分的人数. 【详解】解:(1)抽取学生人数 10÷25%=40(人), 第 2 组人数 40×30%=12(人),第 4 组人数 40﹣8﹣12﹣10﹣3=7(人), ∴a =12,b =7;(2)360°× 3 40=27°,∴“第 5 组”所在扇形圆心角的度数为 27°;(3)1800× 8 +12 40=900(人),∴成绩高于 80 分的共有 900 人.【点睛】本题考查了统计图和样本估计总体,熟练掌握条形统计图与扇形统计图是解题的关键.m 2 3m 8 ,或 m =(舍)2∴a ═= 3 21+42019-2020学年数学中考模拟试卷一、选择题1.下列命题中真命题是()A.若a2=b2,则a=b B.4的平方根是±2C.两个锐角之和一定是钝角D.相等的两个角是对顶角2.如果解关于x的分式方程m2xx22x1时出现增根,那么m的值为A.-2B.2C.4D.-4 3.下列说法正确的是()A.打开电视,它正在播天气预报是不可能事件B.要考察一个班级中学生的视力情况适合用抽样调查C.在抽样调查过程中,样本容量越大,对总体的估计就越准确D.甲、乙两人射中环数的方差分别为S22甲,S 2 1乙,说明甲的射击成绩比乙稳定4.在平面直角坐标系中,点P(3,-5)关于原点对称的点的坐标是()A.(3,5)B.(3,-5)C.(-3,-5)D.(-3,5)3x 725.不等式组2x 9 1整数解的个数是()A.4B.5C.6D.76.已知a 3,b 2,而且b和a的方向相反,那么下列结论中正确的是()A.3a 2b B.2a 3b C.3a 2b D.2a 3b7.某射击运动员练习射击,5次成绩分别是:8、9、7、8、x(单位:环).下列说法中正确的是( A.若这5次成绩的中位数为8,则x=8B.若这5次成绩的众数是8,则x=8C.若这5次成绩的方差为8,则x=8D.若这5次成绩的平均成绩是8,则x=88.如图,数轴上有A,B,C,D四点,则所表示的数与5﹣11最接近的是())A.点AB.点BC.点CD.点D9.某赛季甲、乙两名篮球运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是()A.甲运动员得分的平均数小于乙运动员得分的平均数B.甲运动员得分的中位数小于乙运动员得分的中位数C.甲运动员得分的最小值大于乙运动员得分的最小值D.甲运动员得分的方差大于乙运动员得分的方差10.如图,矩形ABCD的边AB在x轴上,反比例函数y kx(k 0)的图象过D点和边BC的中点E,连接DE,若△CDE的面积是1,则k的值是()A.3B.4C.25D.611.如图一,在等腰△ABC中,AB=AC,点P、Q从点B同时出发,点P以3cm/s的速度沿BC方向运动到点C停止,点Q以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则y与x之间的函数关系图象如图二所示,则BC长为()A.4cm B.8cm C.83D.4312.如图,在平行四边形ABCD中,E是DC上的点,DE:EC=4:3,连接AE交BD于点F,△则DEF与△BAF的面积之比为()A.4:3B.16:49C.4:7D.9:49二、填空题13.二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式是________.14.如图,正方形ABCD中,点E,F分别在线段BC,C D上运动,且满足EAF 450,AE,AF分别与BD相交于点M,N,下列说法中:①BE DF EF;②点A到线段EF的距离一定等于正方形的边长;③若tan BAE 11,则tan DAF23;④若BE 2,DF 3,则S 15AEF.其中结论正确的是___________;(将正确的序号填写在横线上)15.若关于的方程x mx 12的解是非负数,则的取值范围是__________.16.如图,在矩形ABCD中,过点B作对角线AC的垂线,交AD于点E,若AB=2,BC=4,则AE=_____.17.如图,某人从点A出发,前进5m后向右转60°,再前进5m后又向右转60°,这样一直走下去,当他第一次回到出发点A时,共走了_____m.18.如图,已知AB∥CD,OE平分∠AOD,OF⊥OE,∠CDO=50°,则∠DOF=_____度.三、解答题19.如图,甲楼AB高20米,乙楼CD高10米,两栋楼之间的水平距离BD=30m,为了测量某电视塔EF 的高度,小明在甲楼楼顶A处观测电视塔塔顶E,测得仰角为37°,小明在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求该电视塔的高度EF.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,2 1.4)x m20.如图,点P是AB所对弦AB上一动点,点Q是AB与弦AB所围成的图形的内部的一定点,作射线PQ交AB于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y cm,B,1C两点间的距离为y cm.(当点P与点A重合时,x的值为0).2小平根据学习函数的经验,分别对函数y,y随自变量x的变化而变化的规律进行了探究.12下面是小平的探究过程,请补充完整:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;x/cm x/cm 1y/cm 205.372.6814.063.5722.834.903m5.5443.865.7254.835.7965.825.82经测量m的值是(保留一位小数).(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y),(x,y),并画出12函数y,y的图象;12(3)结合函数图象,解决问题:当△BCP为等腰三角形时,AP的长度约为cm.21.如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.(1)在图中以AB为边画△R t BAC,点C在小正方形的顶点上,使∠BAC=90°,tan∠ACB=23;(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的顶点上,连接CD、 BD,使△BDC是锐角等腰三角形,直接写出∠DBC的正切值.。
一次函数视角下的特殊三角形存在性问题解题策略探究

一次函数视角下的特殊三角形存在性问题解题策略探究【摘要】一次函数视角下的特殊三角形存在问题的探究,借助几何画板画图操作活动,正确分析问题、转化化归,模型意识反思,对数形结合思想、方程思想、分类讨论思想的感悟,利用几何法和代数法求解问题。
【关键词】运算意识;几何作图;模型意识;一次函数;特殊三角形一次函数视角下的特殊三角形存在性问题是在变化的过程中,研究背景图形,根据条件探索某种状态是否存在,把函数信息坐标或表达式转化为几何信息。
分析不变特征,确定分类标准,探寻特殊状态运动的结果,画出符合题意的图形求解。
知识储备:用待定系数法求解一次函数的解析式,联立方程组求解两个一次函数图象的交点,求解三个顶点为定点的三角形的面积,用铅锤法求解有顶点是动点的三角形的面积。
解题困惑:对一次函数视角下的特殊三角形存在性问题,如直角三角形、等腰三角形、等腰直角三角形、全等三角形等的存在性问题,学生解题过程存在一些困难,无法画图,进行正确的分类讨论,易出现漏解、错解。
策略探究:假设特殊三角形存在→推理论证→得出相应结论。
类型:两定一动及一定两动,思路:代数法→算理意识,几何法→构图识图,函数法→待定系数法。
一、直角三角形的构造→直角顶点的分类讨论方法策略:分别对三角形三个顶点为直角顶点的情況进行分类讨论,需要同时利用全等、勾股定理等相关知识计算,从而求出对应的点坐标。
【数学活动1】一次函数图象与坐标轴交于点A、B,在坐标轴上找一点C,使得△ABC为直角三角形,求符合条件的C点坐标。
思路探析:找点→两条垂线一个圆,求点→解析式法、距离公式与勾股定理、斜率法(圆上的点),增(舍)点→斜率不存在或等于零,需结合图形检查是否遗漏。
画图探寻:满足条件的坐标轴上的 C 点共有 3 个,如图所示:两垂线→→①若∠BAC=90°,则AB⊥AC,所以以A为垂足作线段AB的垂线,交x轴于C1,则△C1AB是以AB为直角边的直角三角形。
第二讲二次函数中有关三角形存在性问题
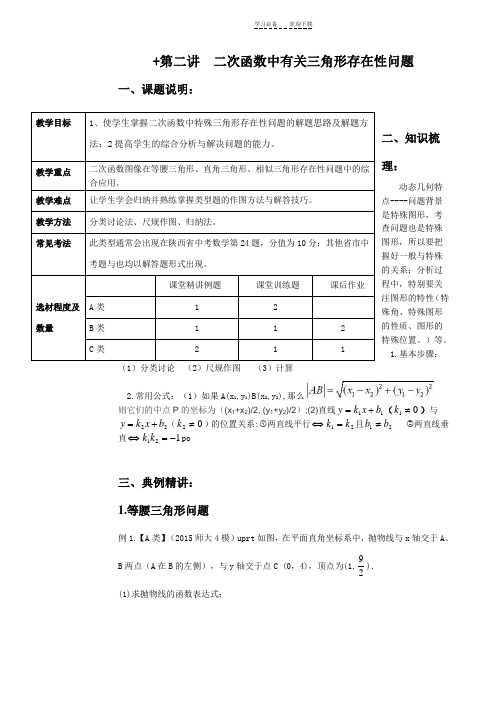
+第二讲 二次函数中有关三角形存在性问题一、课题说明:二、知识梳理:动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)等。
1.基本步骤:(1)分类讨论 (2)尺规作图 (3)计算 2.常用公式:(1)如果A(x 1,y 1)B(x 2,y 2),那么则它们的中点P 的坐标为((x 1+x 2)/2, (y 1+y 2)/2);(2)直线11b x k y +=(01≠k )与22b x k y +=(02≠k )的位置关系:①两直线平行⇔21k k =且21b b ≠ ②两直线垂直⇔121-=k k po三、典例精讲: 1.等腰三角形问题例1.【A 类】(2015师大4模)uprt 如图,在平面直角坐标系中,抛物线与x 轴交于A 、B 两点(A 在B 的左侧),与y 轴交于点C (0,4),顶点为(1,29). (1)求抛物线的函数表达式;教学目标1、使学生掌握二次函数中特殊三角形存在性问题的解题思路及解题方法;2提高学生的综合分析与解决问题的能力。
教学重点 二次函数图像在等腰三角形、直角三角形、相似三角形存在性问题中的综合应用。
教学难点 让学生学会归纳并熟练掌握类型题的作图方法与解答技巧。
教学方法 分类讨论法、尺规作图、归纳法。
常见考法此类型通常会出现在陕西省中考数学第24题,分值为10分;其他省市中考题与也均以解答题形式出现。
选材程度及数量课堂精讲例题课堂训练题课后作业A 类 1 2B 类 1 1 2C 类211(2)设抛物线的对称轴与x 轴交于点D ,试在对称轴上找出点P ,使△CDP 为等腰三角形,请直接写出满足条件的所有点P 的坐标;【教法参考】(1).分类讨论:分类标准:讨论顶角的位置或者底边的位置例如:本题第二问:在抛物线上找一点p ,使得P D C 、、三点构成等腰三角形,则可分成以下几种情况:(1)当C ∠为顶角时,CP CD = (2)当D ∠为顶角时,DP DC = (3)当P ∠为顶角时,PD PC =(2).尺规作图:两圆一线(①当C ∠为顶角时,以C 为圆心CD 为半径画圆,与对称轴交点即为所求点P ,②当D ∠为顶角时,以D 为圆心DC 为半径画圆,与对称轴交点即为所求点P ,③当P ∠为顶角时,线段DC 的垂直平分线与对称轴交点即为所求点P 。
一次函数与等腰三角形存在性问题

每日一题 079一次函数与等腰三角形武穴市百汇学校徐国纲解题技巧如果△ABC是等腰三角形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.已知腰长画等腰三角形用圆规画圆,已知底边画等腰三角形用刻度尺画垂直平分线.如图,已知线段AB作等腰三角形,则符合要求的点都在以A、B为圆心,AB长为半径的圆和AB的垂直平分线上,这就是传说中的“两圆一线”.解等腰三角形的存在性问题,有几何法和代数法,把几何法和代数法相结合,可以使得解题又好又快.几何法一般分三步:分类、画图、计算.代数法一般也分三步:表示三边长,分类列方程,解方程并检验.例题解析例❶ 如图1-1,在平面直角坐标系xOy中,已知点D的坐标为(3, 4),点P是x轴正半轴上的一个动点,如果△DOP是等腰三角形,求点P的坐标.图1-1【解析】分三种情况讨论等腰三角形△DOP:①DO=DP,②OD=OP,③PO=PD.①当DO=DP时,以D为圆心、DO为半径画圆,与x轴的正半轴交于点P,此时点D 在OP的垂直平分线上,所以点P的坐标为(6, 0)(如图1-2).②当OD=OP=5时,以O为圆心、OD为半径画圆,与x轴的正半轴交于点P(5, 0) (如图1-3).③当PO=PD时,画OD的垂直平分线与x轴的正半轴交于点P,设垂足为E(如图1-4).可求325:48PEl y x=-+,∴25(,0)6P.图1-2 图1-3 图1-4上面是几何法的解题过程,我们可以看到,画图可以帮助我们快速找到目标P ,其中①和②画好图就知道答案了,只需要对③进行计算.代数法先设点P 的坐标为(x , 0),其中x >0,然后表达△DOP 的三边长(的平方). DO 2=52,OP 2=x 2,PD 2=(x -3)2+42.①当DO =DP 时,52=(x -3)2+42.解得x =6,或x =0.当x =0时既不符合点P 在x 轴的正半轴上,也不存在△DOP .②当OD =OP 时,52=x 2.解得x =±5.当x =-5时等腰三角形DOP 是存在的,但是点P 此时不在x 轴的正半轴上(如图1-5).③当PO =PD 时,x 2=(x -3)2+42.这是一个一元一次方程,有唯一解,它的几何意义是两条直线(x 轴和OD 的垂直平分线)有且只有一个交点.代数法不需要画三种情况的示意图,但是计算量比较大,而且要进行检验.图1-5例❷ 如图2-1,直线3y x =+与y 、x 轴相交于点A 、C ,动点P 以1个单位/秒的速度从点A 出发,沿AC 向点C 移动,同时动点Q 以1个单位/秒的速度从点C 出发,沿CO 向点O 移动,当P 、Q 两点中其中一点到达终点时则停止运动.在P 、Q 两点移动的过程中,当△PCQ 为等腰三角形时,求t 的值.图2-1【解析】在P 、Q 两点移动的过程中,△PCQ 的6个元素(3个角和3条边)中,唯一不变的就是∠PCQ 的大小,夹∠PCQ 的两条边CQ =t ,CP =6-t .因此△PQC 符合“边角边”的解题条件,我们只需要在∠PCQ 的边上取点P 或Q 画圆.图2-2 图2-3 图2-4①如图2-2,当CP =CQ 时,t =6-t ,解得3t =(秒).②如图2-3,当QP =QC 时,过点Q 作QM ⊥AC 于M ,则CM 1622t PC -==. 在Rt △QMC 中,∵30PCQ =︒∠,∴2CQ =,62tt -=,解得3t =-(秒). ③如图2-4,当PQ =PC 时,过点P 作PN ⊥BC 于N ,则1122CN CQ t ==. 在Rt △PNC 中,∵30PCQ =︒∠,∴2CP =,62tt -=,解得9t =-秒).例❸ 如图3-1,已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P(0, m)是线段OC 上一动点(C 点除外),直线PM 交AB 的延长线于点D .当△APD 是等腰三角形时,求m 的值.图3-1【解析】点P(0, m)在运动的过程中,△APD 的三个角都在变化,因此不符合几何法“边角边”的解题条件,我们用代数法来解.因为PC//DB ,M 是BC 的中点,所以BD =CP =2-m .所以D(2, 4-m).于是我们可以表达出△APD 的三边长(的平方):22(4)AD m =-,224AP m =+,2222(42)PD m =+-.①当AP =AD 时,22(4)4m m -=+.解得32m =(如图3-2). ②当P A =PD 时,22242(42)m m +=+-. 解得43m =(如图3-3)或4m =(不合题意,舍去). ③当DA =DP 时,222(4)2(42)m m -=+-.解得23m=(如图3-4)或2m=(不合题意,舍去).综上所述,当△APD为等腰三角形时,m的值为32,43或23.图3-2 图3-3 图3-4其实①、②两种情况,可以用几何说理的方法,计算更简单:①如图3-2,当AP=AD时,AM垂直平分PD,那么△PCM∽△MBA.所以12PC MBCM BA==.因此12PC=,32m=.②如图3-3,当P A=PD时,P在AD的垂直平分线上.所以DA=2PO.因此42m m-=.解得43m=.小结:1、等腰三角形的存在性问题,又可以细分为两个定点一个动点,或一个定点一个定角,或只有一个定点,甚至三个点都是动点等几种类型;2、当条件中有定线段时,可以利用“两圆一线”来画图,再计算;在有定角时,可以借助特殊三角形三边比的特征或相似来建立方程;对于既无定线又无定角的问题,可以用代数法来解,即先表达三边,再分类列方程求解,要注意根据题目条件进行检验.对于不同类型的等腰三角形,我们可以灵活选用几何法或代数法,有时候将两种方法结合起来使用,可以使得解题又快又好;3、在进行有关等腰三角形的计算时,常用到勾股定理、三线合一、特殊角的三角函数、相似、一元二次方程等知识;在这个过程中,贯穿了分类讨论、数形结合、方程等数学思想方法.。
《二次函数专题提优》:特殊三角形存在性问题

《二次函数专题提优》:特殊三角形存在性问题(一)、直角三角形存在性问题:1、在平面直角坐标系x O y 中,抛物线y =ax 2+bx +2过点A (-2,0),B (2,2),与y 轴交于点C . (1)、求抛物线y =ax 2+bx +2的函数表达式;(2)、若点D 在抛物线y =ax 2+bx +2的对称轴上,求△ACD 的周长的最小值;(3)、在抛物线y =ax 2+bx +2的对称轴上是否存在点P ,使△ACP 是直角三角形?若存在直接写出点P 的坐标,若不存在,请说明理由.2、如图,在矩形OABC 中,点O 为原点,点A 的坐标为(0,8),点C 的坐标为(6,0).抛物线y =﹣94x 2+bx +c 经过点A 、C ,与AB 交于点D . (1)、求抛物线的函数解析式;(2)、点P 为线段BC 上一个动点(不与点C 重合),点Q 为线段AC 上一个动点,AQ =CP ,连接PQ ,设CP =m ,△CPQ 的面积为S .①、求S 关于m 的函数表达式; ②、当S 最大时,在抛物线y =﹣94x 2+bx +c 的对称轴l 上,若存在点F ,使△DFQ 为直角三角形, 请直接写出所有符合条件的点F 的坐标;若不存在,请说明理由.3、如图所示,直线y=x+2与抛物线y=ax 2+bx+6(a ≠0)相交于A (21,25)和B (4,m ),点P 是线段AB 上异于A 、B 的动点,过点P 作PC ⊥x 轴于点D ,交抛物线于点C . (1)、求抛物线的解析式;(2)、是否存在这样的P 点,使线段PC 的长有最大值?若存在,求出这个最大值;若不存在,请说明理由; (3)、求△PAC 为直角三角形时点P 的坐标.4、如图,已知一条直线过点(0,4),且与抛物线2x 41y 交于A ,B 两点,其中点A 的横坐标是﹣2. (1)、求这条直线的函数关系式及点B 的坐标;(2)、在x 轴上是否存在点C ,使得△ABC 是直角三角形?若存在,求出点C 的坐标,若不存在,请说明理由; (3)、过线段AB 上一点P ,作PM ∥x 轴,交抛物线于点M ,点M 在第一象限,点N (0,1),当点M 的横坐标为何值时,MN +3MP 的长度最大?最大值是多少?(二)、等腰三角形存在性问题:5、如图所示,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.(1)、求抛物线的解析式;(2)、已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;(3)、将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.6、如图所示,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A、B、C三点的抛物线上.(1)、求抛物线的函数表达式;(2)、在直线AC上方的抛物线上,是否存在点P,使得△PAC的面积最大?若存在,求出P点坐标及△PAC面积的最大值;若不存在,请说明理由.(3)、在x轴上是否存在点Q,使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.7、如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A、B、C三点的抛物线上.(1)、求抛物线的函数表达式;(2)、在直线AC上方的抛物线上,是否存在点P,使得△PAC的面积最大?若存在,求出P点坐标及△PAC面积的最大值;若不存在,请说明理由.(3)、在x轴上是否存在点Q,使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.8、已知抛物线y=ax²+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.(1)、求抛物线的函数关系式;(2)、设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)、在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.9、如图1,抛物线与4x 31x 31-y 2++=与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C , 连接AC 、BC ,点D 是线段AB 上一点,且AD =CA ,连接CD .(1)、如图2,点P 是直线BC 上方抛物线上的一动点,在线段BC 上有一动点Q ,连接PC 、PD 、PQ ,当△PCD 面积最大时,求PQ +1010CQ 的最小值; (2)、将过点D 的直线绕点D 旋转,设旋转中的直线l 分别与直线AC 、直线CO 交于点M 、N ,当△CMN 为等腰三角形时,直接写出CM 的长.10、如图,在平面直角坐标系中,抛物线y =√33x 2-2√33x -√3与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,对称轴与x 轴交于点D ,点E (4,n )在抛物线上. (1)求直线AE 的解析式;(2)点P 为直线CE 下方抛物线上的一点,连接PC ,PE .当△PCE 的面积最大时,连接CD ,CB ,点K 是线段CB 的中点,点M 是CP 上的一点,点N 是CD 上的一点,求KM+MN+NK 的最小值; (3)点G 是线段CE 的中点,将抛物线y =√33x 2-2√33x -√3沿x 轴正方向平移得到新抛物线y ′,y ′经过点D ,y ′的顶点为点F .在新抛物线y ′的对称轴上,是否存在一点Q ,使得△FGQ 为等腰三角形?若存在,直接写出点Q 的坐标;若不存在,请说明理由.10、如图,已知二次函数y=ax2﹣6ax﹣16a(a<0)的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.(1)、①线段BC的长为;②点A的坐标为(用a的代数式表示).(2)、设M是抛物线的对称轴上的一点,以点A、C、M为顶点的三角形能否成为以AC为斜边且有一个锐角是30°的直角三角形?若能,求出a的值;若不能,请说明理由.(3)、若a=﹣,点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有2个?(三)、等腰直角三角形的存在性问题:11、如图,抛物线bxaxy+=2经过A(4,0),B(1,3)两点,点B. C关于抛物线的对称轴l对称,过点B作直线BH⊥x轴,交x轴于点H.(1)、求抛物线的解析式;(2)、若点M在直线BH上运动,点N在x轴上运动,是否存在这样的点M、N,使得以点M为直角顶点的△CNM是等腰直角三角形?若存在,请求出点M、N的坐标;若不存在,请说明理由。
二次函数中的特殊三角形存在性问题课件

(5)若点H在抛物线的对称轴上,是否存在点H 使得△BCH是直角三角形?若存在,求出点H的 坐标;若不存在,请说明理由;
(6)设点P是第一象限内抛物线上的动点,点Q 是线段BC上一点,是否存在点P使△PCQ是等腰 直角三角形?若存在,求出点Q的坐标;若不存 在,请说明理由.
方法总结: 1、 2、
ቤተ መጻሕፍቲ ባይዱ
(2)连接AC,CF,判断△CAF的形状,并说明 理由;
(3)连接AC,在x轴上是否存在点G使得△ACG 是以AC为底边的等腰三角形?若存在,求出点G 的坐标;若不存在,请说明理由;;
(4)若点p在抛物线上,点Q在抛物线的对称轴 上,是否存在点p使得△PDQ是等边三角形?若 存在,求出点P的坐标;若不存在,请说明理由;
三、课堂小结
二次函数中有关 特殊三角形 存在性问题
1. 复习二次函数相关知识点; 1. 复习特殊三角形的性质。
例. 如图,在平面直角坐标系xOy中,抛物线与x 轴交于点A(-1,0),B(3,0),与y轴交于点 C,直线BC的解析式为y=kx+3,抛物线的顶点为 D,对称轴与直线BC交于点E,与x轴交于点F. (1)求抛物线解析式;
专题一:二次函数中等腰三角形存在性问题

专题:二次函数中等腰三角形存在性问题类型一、等腰三角形存在性问题以(,)A A A x y 、(,)B B B x y 为三角形的边,在x 轴上找一点P 使得△PAB 为等腰三角形(二定一动)一.找法:画圆和作垂直平分线①以A 为圆心,线段AB 为半径画圆,与x 轴交点即为1P 、2P 点;(AB=AP )②以B 为圆心,线段AB 为半径画圆,与x 轴交点即为3P 、4P 点;(AB=BP )③作线段AB 的垂直平分线,与x 轴交点即为5P 点;(AP=BP )二、算法:利用两点距离公式进行计算 公式:22()()A B A B AB x x y y =-+- ,设(,)p p P x y ,分三种情况:①AB=AP 时 2222()()()()A B A B A P A P x x y y x x y y -+-=-+-可得1P 、2P ,(特殊情况可能是一个点,例如2P 与B 重合)②AB=BP 时2222()()()()A B A B B P B P x x y y x x y y -+-=-+-可得3P 、4P ,(特殊情况可能是一个点,例如3P 与A 重合)③AP=BP 时2222()()()()A P A P B P B P x x y y x x y y -+-=-+-可得5P 、例题1、如图,已知二次函数2y x bx c =++的图像与x 轴交于点A 、B 两点,其中A 点坐标为(-3,0),与y 轴交于点C ,点D (-2,-3)在抛物线上.(1)求抛物线的表达式;(2)抛物线的对称轴上是否存在动点Q ,使得△BCQ 为等腰三角形?若存在,求出点Q 的坐标;若不存在,说明理由.1、(2021·云南九年级一模)如图所示,抛物线()240y ax bx a =++≠经过点()1,0A -,点()4,0B ,与y 轴交于点C ,连接AC ,BC .点M 是线段OB 上不与点O 、B 重合的点,过点M 作DM x ⊥轴,交抛物线于点D ,交BC 于点E .(1)求抛物线的表达式;(2)过点D 作DF BC ⊥,垂足为点F .设M 点的坐标为(),0M m ,请用含m 的代数式表示线段DF 的长,并求出当m 为何值时DF 有最大值,最大值是多少?(3)试探究是否存在这样的点E ,使得以A ,C ,E 为顶点的三角形是等腰三角形.若存在,请求出此时点E 的坐标;若不存在,请说明理由.2、(八中2020级初三第三次月考)如图在平面直角坐标系中,已知抛物线2(0)y ax bx c a =++≠交x 轴于A (-4,0),B (1,0),交y 轴于C (0,3)(1)求此抛物线解析式;(2)如图1,点P 为直线AC 上方抛物线上一点,过点P 作PQ ⊥x 轴于点Q ,再过点Q 作QR//AC 交y 轴于点R ,求PQ+QR 的最大值及此时点P 的坐标;(3)如图2,点E 在抛物线上,横坐标为-3,连接AE ,将线段AE 沿直线AC 平移,得到线段''A E ,连接'CE ,当△''A E C 为等腰三角形时,只写写出点'A 的坐标。
专题59 二次函数背景下的等腰三角形、直角三角形存在性问题(解析版)-中考数学解题大招复习讲义

模型介绍一、如图,点A 坐标为(1,1),点B 坐标为(4,3),在x 轴上取点C 使得△ABC 是等腰三角形.【几何法】“两圆一线”得坐标(1)以点A 为圆心,AB 为半径作圆,与x 轴的交点即为满足条件的点C ,有AB =AC ;(2)以点B 为圆心,AB 为半径作圆,与x 轴的交点即为满足条件的点C ,有BA =BC ;(3)作AB 的垂直平分线,与x 轴的交点即为满足条件的点C ,有CA =CB .【注意】若有三点共线的情况,则需排除.作图并不难,问题是还需要把各个点坐标算出来,可通过勾股或者三角函数来求.34C C 、同理可求,下求5C .显然垂直平分线这个条件并不太适合这个题目,如果A 、B 均往下移一个单位,当点A 坐标为(1,0),点B 坐标为(4,2)时,可构造直角三角形勾股解:而对于本题的5C ,或许代数法更好用一些.【代数法】表示线段构相等(1)表示点:设点5C 坐标为(m ,0),又A 点坐标(1,1)、B 点坐标(4,3),(2)表示线段:5AC =,5BC =(3)分类讨论:根据55AC BC =,可得:(4)求解得答案:解得:236m =,故5C 坐标为23,06⎛⎫ ⎪⎝⎭.小结几何法:(1)“两圆一线”作出点;(2)利用勾股、相似、三角函数等求线段长,由线段长得点坐标.代数法:(1)表示出三个点坐标A 、B 、C ;(2)由点坐标表示出三条线段:AB 、AC 、BC ;(3)根据题意要求取①AB =AC 、②AB =BC 、③AC =BC ;(4)列出方程求解.问题总结:(1)两定一动:动点可在直线上、抛物线上;(2)一定两动:两动点必有关联,可表示线段长度列方程求解;(3)三动点:分析可能存在的特殊边、角,以此为突破口.二、【问题描述】如图,在平面直角坐标系中,点A 坐标为(1,1),点B 坐标为(5,3),在x 轴上找一点C 使得△ABC 是直角三角形,求点C 坐标.【几何法】两线一圆得坐标(1)若∠A 为直角,过点A 作AB 的垂线,与x 轴的交点即为所求点C ;(2)若∠B 为直角,过点B 作AB 的垂线,与x 轴的交点即为所求点C ;(3)若∠C 为直角,以AB 为直径作圆,与x 轴的交点即为所求点C .(直径所对的圆周角为直角)重点还是如何求得点坐标,12C C 、求法相同,以2C 为例:【构造三垂直】34C C 、求法相同,以3C 为例:构造三垂直步骤:第一步:过直角顶点作一条水平或竖直的直线;第二步:过另外两端点向该直线作垂线,即可得三垂直相似.例题精讲考点一:二次函数中的直角三角形存在性问题【例1】.如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且A (﹣1,0),对称轴为直线x=2.(1)求该抛物线的表达式;(2)直线l过点A与抛物线交于点P,当∠PAB=45°时,求点P的坐标;(3)在抛物线的对称轴上是否存在一点Q,使得△BCQ是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)设y=(x﹣2)2+k,把A(﹣1,0)代入得:(﹣1﹣2)2+k=0,解得:k=﹣9,∴y=(x﹣2)2﹣9=x2﹣4x﹣5,答:抛物线的解析式为y=x2﹣4x﹣5;(2)过点P作PM⊥x轴于点M,如图:设P(m,m2﹣4m﹣5),则PM=|m2﹣4m﹣5|,∵A(﹣1,0),∴AM=m+1∵∠PAB=45°∴AM=PM,∴|m2﹣4m﹣5|=m+1,即m2﹣4m﹣5=m+1或m2﹣4m﹣5=﹣(m+1),当m2﹣4m﹣5=m+1时,解得:m1=6,m2=﹣1(不合题意,舍去),当m2﹣4m﹣5=﹣(m+1),解得m3=4,m4=﹣1(不合题意,舍去),∴P的坐标是(6,7)或P(4,﹣5);(3)在抛物线的对称轴上存在一点Q,使得△BCQ是直角三角形,理由如下:在y=x2﹣4x﹣5中,令x=0得y=﹣5,令y=0得x=﹣1或x=5,∴B(5,0),C(0,﹣5),由抛物线y=x2﹣4x﹣5的对称轴为直线x=2,设Q(2,t),∴BC2=50,BQ2=9+t2,CQ2=4+(t+5)2,当BC为斜边时,BQ2+CQ2=BC2,∴9+t2+4+(t+5)2=50,解得t=﹣6或t=1,∴此时Q坐标为(2,﹣6)或(2,1);当BQ为斜边时,BC2+CQ2=BQ2,∴50+4+(t+5)2=9+t2,解得t=﹣7,∴此时Q坐标为(2,﹣7);当CQ为斜边时,BC2+BQ2=CQ2,∴50+9+t2=4+(t+5)2,解得t=3,∴此时Q坐标为(2,3);综上所述,Q的坐标为(2,3)或(2,﹣7)或(2,1)或(2,﹣6).变式训练【变1-1】.如图,在平面直角坐标系中,抛物线y=ax2+bx+4经过点A(4,0),B(﹣1,0),交y轴于点C.(1)求抛物线的解析式;(2)点D是直线AC上一动点,过点D作DE垂直于y轴于点E,过点D作DF⊥x轴,垂足为F,连接EF,当线段EF的长度最短时,求出点D的坐标;(3)在AC上方的抛物线上是否存在点P,使得△ACP是直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.解:(1)∵抛物线y=ax2+bx+4经过点A(4,0),B(﹣1,0),∴,解得:,∴抛物线的解析式为:y=﹣x2+3x+4;(2)连接OD,由题意知,四边形OFDE是矩形,则OD=EF,据垂线段最短,可知:当OD⊥AC时,OD最短,即EF最短.由(1)知,在Rt△AOC中,OC=OA=4,∴AC=4.又∵D为AC的中点.∴DF∥OC,∴DF=OC=2,∴点D的坐标为(2,2);(3)假设存在,设点P的坐标为(m,﹣m2+3m+4).∵点A的坐标为(4,0),点C的坐标为(0,4),∴AP2=(m﹣4)2+(﹣m2+3m+4﹣0)2=m4﹣6m3+2m2+16m+32,CP2=(m﹣0)2+(﹣m2+3m+4﹣4)2=m4﹣6m3+10m2,AC2=(0﹣4)2+(4﹣0)2=32.分两种情况考虑,①当∠ACP=90°时,AP2=CP2+AC2,即m4﹣6m3+2m2+16m+32=m4﹣6m3+10m2+32,整理得:m2﹣2m=0,解得:m1=0(舍去),m2=2,∴点P的坐标为(2,6);②当∠APC=90°时,CP2+AP2=AC2,即m4﹣6m3+10m2+m4﹣6m3+2m2+16m+32=32,整理得:m(m3﹣6m2+6m+8)=0,∴m(m﹣4)(m2﹣2m﹣2)=0,解得:m1=0(舍去),m2=4(舍去),(舍去),,∴点P的坐标为(1+,3+).综上所述,假设成立,即存在点P(2,6)或(1+,3+),使得△ACP是直角三角形.考点二:二次函数中的等腰三角形存在性问题【例2】.如图,抛物线y=﹣x2+5x+n经过点A(1,0),与y轴交于点B.(1)求抛物线的解析式;(2)求抛物线的对称轴和顶点坐标.(3)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.解:(1)由题意得,﹣1+5+n=0,解得,n=﹣4,∴抛物线的解析式为y=﹣x2+5x﹣4;(2)y=﹣x2+5x﹣4=﹣(x﹣)2+,抛物线对称轴为:x=,顶点坐标为(,);(3)∵点A的坐标为(1,0),点B的坐标为(0,﹣4),∴OA=1,OB=4,在Rt△OAB中,AB==,①当PB=BA时,PB=,∴OP=PB﹣OB=﹣4,此时点P的坐标为(0,﹣4),②当PA=AB时,OP=OB=4此时点P的坐标为(0,4).变式训练【变2-1】.如图.已知二次函数y=﹣x2+bx+3的图象与x轴的一个交点为A(4,0),与y 轴交于点B.(1)求此二次函数关系式和点B的坐标;(2)在x轴的正半轴上是否存在点P.使得△PAB是以AB为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)把点A(4,0)代入二次函数有:0=﹣16+4b+3得:b=所以二次函数的关系式为:y=﹣x2+x+3.当x=0时,y=3∴点B的坐标为(0,3).(2)如图:作AB的垂直平分线交x轴于点P,连接BP,则:BP=AP设BP=AP=x,则OP=4﹣x,在直角△OBP中,BP2=OB2+OP2即:x2=32+(4﹣x)2解得:x=∴OP=4﹣=所以点P的坐标为:(,0)综上可得点P的坐标为(,0).【变2-2】.如图,抛物线y=ax2+4+c经过A(﹣3,﹣4),B(0,﹣1)两点,点P是y 轴左侧且位于x轴下方抛物线上一动点,设其横坐标为m.(1)直接写出抛物线的解析式;(2)将线段AB绕点B顺时针旋转90°得线段BD(点D是点A的对应点),求点D的坐标,并判断点D是否在抛物线上;(3)过点P作PM⊥x轴交直线BD于点M,试探究是否存在点P,使△PBM是等腰三角形?若存在,求出点m的值;若不存在,说明理由.解:(1)把点A(﹣3,﹣4),B(0,﹣1)代入解析式y=ax2+4x+c,得,解得,∴y=x2+4x﹣1;(2)如图,作AC⊥y轴于点C,作DH⊥y轴于点H,∵∠CAB+∠ABC=90°,∠HBD+∠ABC=90°,∴∠CAB=∠HBD,在△ABC和△DBH中,,∴△ABC≌△BDH(AAS),∴HB=AC=3,DH=BC=3,∴OH=2,∴D(﹣3,2),把D(﹣3,2)代入y=x2+4x﹣1中,得(﹣3)2+4×(﹣3)﹣1=﹣4≠2,∴点D不在抛物线上;(3)存在点P,∵D(﹣3,2),B(0,﹣1),∴直线BD的解析式为y=﹣x﹣1,设P(m,m2+4m﹣1),则M(m,﹣m﹣1),由(2)知:∠BMP=45°,当△PBM是等腰三角形,且45°为底角时,有∠MBP=90°或∠MPB=90°,若∠MBP=90°,则P与A重合,即m=﹣3,若∠MPB=90°,则PB∥x轴,即P的纵坐标为﹣1,∴m2+4m﹣1=﹣1,解得m=0(舍)或m=﹣4,∴m=﹣4,若45°为顶角,即MP=MB,∵MP=﹣m﹣1﹣m2﹣4m+1=﹣m2﹣5m,MB=﹣=﹣,∴﹣m2﹣5m=﹣m,解得m=0(舍)或m=﹣5+,∴m的值为﹣3,﹣4,﹣5.1.如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣3,0),B (1,0)两点,与y轴交于点C(0,3),连接AC,点P为第二象限抛物线上的动点.(1)求a、b、c的值;(2)连接PA、PC、AC,求△PAC面积的最大值;(3)在抛物线的对称轴上是否存在一点Q,使得△QAC为直角三角形,若存在,请求出所有符合条件的点Q的坐标;若不存在,请说明理由.解:(1)∵抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点∴,解得:∴a=﹣1,b=﹣2,c=3;(2)如图1,过点P作PE∥y轴,交AC于E,∵A(﹣3,0),C(0,3),∴直线AC的解析式为y=x+3,由(1)知,抛物线的解析式为y=﹣x2﹣2x+3,设点P(m,﹣m2﹣2m+3),则E(m,m+3),=PE•(x C﹣x A)=×[﹣m2﹣2m+3﹣(m+3)]×(0+3)=﹣(m2﹣3m)∴S△ACP=﹣(m+)2+,=;∴当m=﹣时,S△P AC最大(3)存在,点Q的坐标为:(﹣1,﹣2)或(﹣1,4)或(﹣1,)或(﹣1,).如图2,∵A(﹣3,0),C(0,3),∴OA=OC=3,∴AC2=OA2+OC2=32+32=18,∵y=﹣x2﹣2x+3=﹣(x+1)2+4∴抛物线对称轴为x=﹣1,设点Q(﹣1,n),则AQ2=[﹣1﹣(﹣3)]2+n2=n2+4,CQ2=[0﹣(﹣1)]2+(n﹣3)2=n2﹣6n+10,∵△QAC为直角三角形,∴∠CAQ=90°或∠ACQ=90°或∠AQC=90°,①当∠CAQ=90°时,根据勾股定理,得:AQ2+AC2=CQ2,∴n2+4+18=n2﹣6n+10,解得:n=﹣2,∴Q1(﹣1,﹣2);②当∠ACQ=90°时,根据勾股定理,得:CQ2+AC2=AQ2,∴n2﹣6n+10+18=n2+4,解得:n=4,∴Q2(﹣1,4);③当∠AQC =90°时,根据勾股定理,得:CQ 2+AQ 2=AC 2,∴n 2﹣6n +10+n 2+4=18,解得:n 1=,n 2=,∴Q 3(﹣1,),Q 4(﹣1,);综上所述,点Q 的坐标为:(﹣1,﹣2)或(﹣1,4)或(﹣1,)或(﹣1,).2.已知抛物线y =﹣x 2﹣x 的图象如图所示:(1)将该抛物线向上平移2个单位,分别交x 轴于A 、B 两点,交y 轴于点C ,则平移后的解析式为y =﹣x 2﹣x +2.(2)判断△ABC 的形状,并说明理由.(3)在抛物线对称轴上是否存在一点P ,使得以A 、C 、P 为顶点的三角形是等腰三角形?若存在,求出点P 的坐标;若不存在,说明理由.解:(1)将该抛物线向上平移2个单位,得y=﹣x2﹣x+2,故答案为:y=﹣x2﹣x+2;(2)当y=0时,﹣x2﹣x+2=0,解得x1=﹣4,x2=1,即B(﹣4,0),A(1,0).当x=0时,y=2,即C(0,2).AB=1﹣(﹣4)=5,AB2=25,AC2=(1﹣0)2+(0﹣2)2=5,BC2=(﹣4﹣0)2+(0﹣2)2=20,∵AC2+BC2=AB2,∴△ABC是直角三角形;(3)y=﹣x2﹣x+2的对称轴是直线x=﹣,设P(﹣,n),AP2=(1+)2+n2=+n2,CP2=+(2﹣n)2,AC2=12+22=5当AP=AC时,AP2=AC2,+n2=5,方程无解;当AP=CP时,AP2=CP2,+n2=+(2﹣n)2,解得n=0,即P1(﹣,0),当AC=CP时AC2=CP2,+(2﹣n)2=5,解得n1=2+,n2=2﹣,P2(﹣,2+),P3(﹣,2﹣).综上所述:使得以A、C、P为顶点的三角形是等腰三角形,点P的坐标(﹣,0),(﹣,2+),(﹣,2﹣).3.如图,抛物线y=﹣x2+x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D,抛物线的对称轴与x轴交于点E,连接AC,BD.(1)求点A,B,C,D的坐标;(2)点F为抛物线对称轴上的动点,且△BEF与△AOC相似,请直接写出符合条件的点F的坐标;(3)点P为抛物线上的动点,是否存在这样的点P,使△BDP是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.解:(1)对于y=﹣x2+x+3,令y=﹣x2+x+3=0,解得x=6或﹣2,令x=0,则y =3,故点A、B、C的坐标分别为(﹣2,0)、(6,0)、(0,3),则函数的对称轴为直线x=(6﹣2)=2,当x=2时,y=﹣x2+x+3=4D(2,4);(2)tan∠CAO=,当△BEF与△AOC相似时,则,即,解得:EF=6或,故点F的坐标为:(2,6)或(2,﹣6)或或;(3)存在,理由:△BDP是直角三角形只要可能是∠DBP和∠BDP为直角,①当∠DBP为直角时,过点B作y轴的平行线,交过点P与x轴的平行线于点H,交过点D与x轴的平行线于点G,∵DG=BG=4,则△BDG为等腰三角形,∠DBG=45°,则∠PBH=45°,即△PBH为等腰直角三角形,则设PH=BH=m,则点P(6﹣m,﹣m),将点P的坐标代入抛物线表达式得:﹣m=﹣(6﹣m)2+(6﹣m)+3,解得:m=0(舍去)或12,故点P的坐标为(﹣6,﹣12);②当∠BDP为直角时,∵AD=BD=3,AB=64,则△ABD为等腰直角三角形,即∠ADB=90°,即点P于点A重合,故点P(﹣2,0);综上,点P的坐标为(﹣2,0)或(﹣6,﹣12).4.如图,已知抛物线y=﹣x2+bx+c与x轴交于A,B两点,与y轴交于点C,其中A(﹣1,0),C(0,3).(1)求该抛物线的函数表达式;(2)抛物线与直线y=﹣x﹣1交于A、E两点,P是x轴上点B左侧一动点,当以P、B、C为顶点的三角形与△ABE相似时,求点P的坐标;(3)若F是直线BC上一动点,在抛物线上是否存在动点M,使△MBF为等腰直角三角形,若存在,请直接写出点M的坐标;否则说明理由.解:(1)把A(﹣1,0),C(0,3)代入y=﹣x2+bx+c,得:,解得:,∴抛物线的函数表达式为y=﹣x2+2x+3;(2)联立直线AE和抛物线的函数关系式成方程组,得:,解得:,,∴点E的坐标为(4,﹣5),∴AE==5,在y=﹣x2+2x+3中,令y=0,得:﹣x2+2x+3=0,解得:x1=3,x2=﹣1,∴点B的坐标为(3,0),∵C(0,3),∴OB=OC=3,∵∠BOC=90°,∴∠CBO=45°,BC=3,∵直线AE的函数表达式为y=﹣x﹣1,∴∠BAE=45°=∠CBO.设点P的坐标为(m,0),则PB=3﹣m,∵以P、B、C为顶点的三角形与△ABE相似,∴=或=,∴=或=,解得:m=或m=﹣,∴点P的坐标为(,0)或(﹣,0);(3)∵∠CBO=45°,∴存在两种情况(如图2).①取点M1与点A重合,过点M1作M1F1∥y轴,交直线BC于点F1,∵∠CBM1=45°,∠BM1F1=90°,∴此时△BM1F1为等腰直角三角形,∴点M1的坐标为(﹣1,0);②取点C′(0,﹣3),连接BC′,延长BC′交抛物线于点M2,过点M2作M2F2∥y 轴,交直线BC于点F2,∵点C、C′关于x轴对称,∠OBC=45°,∴∠CBC′=90°,BC=BC′,∴△CBC′为等腰直角三角形,∵M2F2∥y轴,∴△M2BF2为等腰直角三角形.∵点B(3,0),点C′(0,﹣3),∴直线BC′的函数关系式为y=﹣3,联立直线BC′和抛物线的函数关系式成方程组,得:,解得:,,∴点M2的坐标为(﹣2,﹣5),综上所述:点M的坐标为(﹣1,0)或(﹣2,﹣5).5.如图,抛物线y=ax2+bx﹣3(a≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的点P坐标;若不存在,请说明理由.解:(1)∵抛物线y=ax2+bx﹣3,∴c=﹣3,∴C(0,﹣3),∴OC=3,∵BO=OC=3AO,∴BO=3,AO=1,∴B(3,0),A(﹣1,0),∵该抛物线与x轴交于A、B两点,∴,∴,∴抛物线解析式为y=x2﹣2x﹣3,(2)存在,理由:设P(1,m),∵B(3,0),C(0,﹣3),∴BC=3,PB=,PC=,∵△PBC是等腰三角形,①当PB=PC时,∴=,∴m=﹣1,∴P(1,﹣1),②当PB=BC时,∴3=,∴m=±,∴P(1,)或P(1,﹣),③当PC=BC时,∴3=,∴m=﹣3±,∴P(1,﹣3+)或P(1,﹣3﹣),∴符合条件的P点坐标为P(1,﹣1)或P(1,)或P(1,﹣)或P(1,﹣3+)或P(1,﹣3﹣).6y=ax2+bx+c(a≠0)的图象交x轴于点A、B,交y轴于点C,其顶点为D,已知AB=4,∠ABC=45°,OA:OB=1:3.(1)求二次函数的表达式及其顶点D的坐标;(2)点M是线段BC上方抛物线上的一个动点,点N是线段BC上一点,当△MBC的面积最大时,求:①点M的坐标,说明理由;②MN+BN的最小值;(3)在二次函数的图象上是否存在点P,使得以点P、A、C为顶点的三角形为直角三角形?若存在,求出点P坐标;若不存在,请说明理由.解:(1)∵∠ABC =45°,∴OB =OC ,∵OA :OB =1:3,AB =4,∴OA =1,OB =3,∴OC =3,∴A (﹣1,0),B (3,0),C (0,3),将A 、B 、C 代入y =ax 2+bx +c 中,∴,解得,∴y =﹣x 2+2x +3,∵y =﹣x 2+2x +3=﹣(x ﹣1)2+4,∴D (1,4);(2)①设BC 的解析式为y =kx +b ,∴,解得,∴y =﹣x +3,过点M 作MG ∥y 轴交BC 于点G ,设M (t ,﹣t 2+2t +3),则G (t ,﹣t +3),∴PG =﹣t 2+2t +3+t ﹣3=﹣t 2+3t ,∴S △MBC =×3×(﹣t 2+3t )=﹣(t ﹣)2+,∵0<t<3,有最大值,∴当t=时,S△MBC此时M(,);②过点M作MH⊥x轴交于H,交BC于N,∵∠OBC=45°,∴NH=BN,∴MN+BN=MN+NH≥MH,∵M(,),∴MH=,∴MN+BN的最小值为,故答案为:;(3)存在点P,使得以点P、A、C为顶点的三角形为直角三角形,理由如下:设P(m,﹣m2+2m+3),如图2,当∠ACP=90°时,过点C作EF∥x轴,过点A作AE⊥EF交于E,过点P作PF⊥EF交于F,∴∠ECA+∠FCP=90°,∵∠ACE+∠EAC=90°,∴∠FCP=∠EAC,∴△ACE∽△CPF,∴=,∴=,解得m=0(舍)或m=,∴P(,);如图3,当∠CAP=90°时,过点A作MN⊥x轴,过点C作CM⊥MN交于M,过点P 作PN⊥MN交于N,∵∠MAC+∠NAP=90°,∠MAC+∠MCA=90°,∴∠NAP=∠MCA,∴△ACM∽△PAN,∴=,∴=,解得m=﹣1(舍)或m=,∴P(,﹣);综上所述:P点坐标为(,)或(,﹣).7.如图,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.M为线段OB上的一个动点,过点M作PM⊥x轴,交抛物线于点P,交BC于点Q.(1)求抛物线的表达式;(2)试探究点M在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.解:(1)将A(﹣3,0),B(4,0)代入y=ax2+bx+4,∴,解得,∴抛物线的表达式为:;(2)存在点Q,使得以A,C,Q为顶点的三角形是等腰三角形,理由如下:令x=0,则y=4,∴点C(0,4),∵A(﹣3,0)、C(0,4),∴AC=5,设直线BC的解析式为y=kx+b,∴,解得,∴y=﹣x+4,设点M(m,0),则点Q(m,﹣m+4),①当AC=CQ时,过点Q作QE⊥y轴于点E,连接AQ,∵CQ2=CE2+EQ2,即m2+[4﹣(﹣m+4)]2=25,解得:舍去负值),∴点;②当AC=AQ时,则AQ=AC=5,在Rt△AMQ中,由勾股定理得:[m﹣(﹣3)]2+(﹣m+4)2=25,解得:m=1或m=0(舍去0),∴点Q(1,3);③当CQ=AQ时,则2m2=[m﹣(﹣3)]2+(﹣m+4)2,解得:舍去);综上所述,点Q的坐标为(1,3)或.8.如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,且与y轴相交于点C,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当点P到点A、点C的距离之和最短时,求点P的坐标;(3)点M也是直线l上的动点,且△MAC为直角三角形,请直接写出所有符合条件的点M的坐标.解:∵抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点,∴,∴,∴抛物线的解析式为y=x2﹣2x﹣3,(2)如图1,∵点A,B关于直线l对称,∴连接BC交直线l于点P,由(1)知,抛物线的解析式为y=x2﹣2x﹣3,∴直线l:x=1,C(0,﹣3),∵B(3,0),∴直线BC的解析式为y=x﹣3,当x=1时,y=﹣2,∴P(1,﹣2),(3)设点M(1,m),∵A(﹣1,0),C(0,﹣3),∴AC2=10,AM2=m2+4,CM2=(m+3)2+1=m2+6m+10,∵△MAC为直角三角形,∴当∠ACM=90°时,∴AC2+CM2=AM2,∴10+m2+6m+10=m2+4,∴m=﹣,∴M(1,﹣)当∠CAM=90°时,∴AC2+AM2=CM2,∴10+m2+4=m2+6m+10,∴m=,∴M(1,)当∠AMC=90°时,AM2+CM2=AC2,∴m2+4+m2+6m+10=10,∴m=﹣1或m=﹣2,∴M(1,﹣1)或(1,﹣2),即:满足条件的点M的坐标为(1,﹣)或(1,)或(1,﹣1)或(1,﹣2).9.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.(1)求抛物线及直线AC的函数表达式;(2)在抛物线对称轴上是否存在一点M,使以A,N,M为顶点的三角形是直角三角形?若存在,请求出M点的坐标.若不存在,请说明理由.解:(1)由抛物线y=﹣x2+bx+c过点A(﹣1,0)及C(2,3)得,解得,故抛物线的函数表达式为y=﹣x2+2x+3.设直线AC的函数表达式为y=kx+n,将A(﹣1,0)、C(2,3)分别代入y=kx+n中可得解得,故直线AC的函数表达式为y=x+1.(2)存在,理由:由抛物线的表达式知,其对称轴为x=1,设点M(1,m),∵A(﹣1,0),M(1,m),N(0,3),∴AM2=(1+1)2+m2=4+m2,同理AN2=10,MN2=1+(m﹣3)2.当AM是斜边时,则4+m2=10+1+(m﹣3)2,解得;当AN是斜边时,4+m2+1+(m﹣3)2=10,解得:m=1或2;当MN是斜边时,4+m2+10=1+(m﹣3)2,解得:.故点M的坐标为或(1,1)或(1,2)或.10.抛物线y=ax2+bx+c的图象与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C (0,﹣3),顶点为D.(1)求此抛物线的解析式.(2)求此抛物线顶点D的坐标和对称轴.(3)探究对称轴上是否存在一点P,使得以P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.解:(1)∵抛物线y=ax2+bx+c的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴,解得,即此抛物线的解析式是y=x2﹣2x﹣3;(2)∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴此抛物线顶点D的坐标是(,﹣4),对称轴是直线x=1;(3)存在点P,使得以点P、D、A为顶点的三角形是等腰三角形,设点P的坐标为(1,y),当PA=PD时,则=,解得y=﹣,当DA=DP时,则=,解得y=﹣4±2,当AD=AP时,则=,解得,y=±4(舍去﹣4),由上可得,以点P、D、A为顶点的三角形是等腰三角形时,点P的坐标为(1,﹣)或(1,﹣4﹣2)或(1,﹣4+2)或(1,4).11.如图,已知抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B(3,0)两点(点A在点B 的左侧),与y轴交于点C.(1)求抛物线的解析式;(2)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请求出点M的坐标.(3)如图1,P为直线BC上方的抛物线上一点,PD∥y轴交BC于D点,过点D作DE ⊥AC于E点.设m=PD+DE,求m的最大值及此时P点坐标.解:(1)把A(﹣1,0),B(3,0)两点代入解析式y=ax2+bx+3,得,解得,∴抛物线的解析式为y=﹣x2+2x+3.(2)如图,当∠MCB=90°时,延长MC交x轴于点G,∵A(﹣1,0),B(3,0),C(0,3),∴OB=OC=3,AB=3﹣(﹣1)=4∴∠OBC=∠OCB=45°,∵∠MCB=90°,∴∠GCB=90°,∠GCO=45°,∴∠GCO=∠CGO=45°,∴OG=OC=3,∴G(﹣3,0),设直线GC的解析式为y=kx+3,∴0=﹣3k+3,解得k=1,∴直线GC的解析式为y=x+3,∴x=1时,y=x+3=4,此时M(1,4);如图,当∠MBC=90°时,延长BM交y轴于点H,∵A(﹣1,0),B(3,0),C(0,3),∴OB=OC=3,∴∠OBC=∠OCB=45°,∵∠MBC=90°,∴∠HBO=45°,∴∠HBO=∠BHO=45°,∴OH=OB=3,∴H(0,﹣3),设直线BH的解析式为y=px﹣3,∴0=3p﹣3,解得p=1,∴直线BH的解析式为y=x﹣3,∴x=1时,y=x﹣3=﹣2,此时M(1,﹣2);当∠CMB=90°时,设M(1,a),∵B(3,0),C(0,3),∴OB=OC=3,∴BC2=32+32=18,MC2=1+(a﹣3)2,BM2=4+a2,∵∠CMB=90°,∴BC2=MC2+BM2,∴18=1+(a﹣3)2+4+a2,整理,得a2﹣3a﹣2=0,解得,此时或;综上所述,点M(1,4)或点M(1,﹣2)或点或点.(3)如图,设PD与x轴的交点为F,点P(n,﹣n2+2n+3),∵B(3,0),C(0,3),设直线BC的解析式为y=qx+3,∴0=3q+3,解得q=﹣1,∴直线BC的解析式为y=﹣x+3,∴D(n,﹣n+3),∴PD=﹣n2+2n+3﹣(﹣n+3)=﹣n2+3n;∵A(﹣1,0),C(0,3),∴,∴,连接AD,∴,=S△ABC﹣S△ADB,AB=3﹣(﹣1)=4∵S△ADC∴,∴,∴∵抛物线开口向下,∴m有最大值,且当时,取得最大值,且为,此时,故点.12.如图,抛物线y=﹣x2+bx+c与x轴交于点A和B(5,0),与y轴交于点C(0,5).(1)求抛物线的解析式;(2)抛物线的对称轴与x轴交于点M,与BC交于点F,点D是对称轴上一点,当点D 关于直线BC的对称点E在抛物线上时,求点E的坐标;(3)点P在抛物线的对称轴上,点Q在直线BC上方的抛物线上,是否存在以O,P,Q为顶点的三角形是等腰直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)∵点B(5,0),C(0,5)在抛物线y=﹣x2+bx+c上,∴,解得,,∴抛物线的解析式为y=﹣x2+4x+5;(2)设点M关于直线BC的对称点为点M′,连接MM′,BM′,则直线FM′为抛物线对称轴关于直线BC的对称直线,∵点E是点D关于直线BC的对称点,点E落在抛物线上,∴直线FM′与抛物线的交点E1,E2为D1,D2落在抛物线上的对称点,∵对称轴与x轴交于点M,与BC交于点F,∴,∴点M的坐标为(2,0),∵点C的坐标为(0,5),点B的坐标为(5,0),∴OB=OC,∴△OBC是等腰直角三角形,∴∠OBC=45°,∴△MBF是等腰直角三角形,∴MB=MF,∴点F的坐标为F(2,3),∵点M关于直线BC的对称点为点M′,∴BM′=BM,∠MBM′=90°,∴△MBM′是等腰直角三角形,∴BM′=BM=3,∴点M′的坐标为(5,3),∴FM′∥x轴,∴﹣x2+4x+5=3,解得,x1=,x2=,∴E1(,3),E2(,3),∴点E的坐标为(,3)或(,3);(3)存在,Q1(,),Q2(,),Q3(,2).设Q(m,﹣m2+4m+5),P(2,p),①当OP=PQ,∠OPQ=90°时,作PL⊥y轴于L,过Q作QK⊥x轴,交PL于K,∴∠LPO=90°﹣∠LOP=90°﹣KPQ,∠PLO=∠QKP=90°,∴∠LOP=∠KPQ,∵OP=PQ,∴△LOP≌△KPQ(AAS),∴LO=PK,LP=QK,∴,解得m1=,m2=(舍去),当m1=时,﹣m2+4m+5=,∴Q(,);②当QO=PQ,∠PQO=90°时,作PL⊥y轴于L,过Q作QK⊥x轴于T,交PL于K,同理可得△PKQ≌△QTO(AAS),∴QT=PK,TO=QK,∴,解得m1=,m2=(舍去),当m1=时,﹣m2+4m+5=,∴Q(,);③当QO=OP,∠POQ=90°时,作PL⊥y轴于L,过Q作QK⊥x轴于T,交PL于K,同理可得△OLP≌△QSO(AAS),∴SQ=OL,SO=LP,∴,解得m1=2+,m2=2﹣(舍去),当m1=2+时,﹣m2+4m+5=2,∴Q(,2);综上,Q1(,),Q2(,),Q3(,2).13.已知如图1,在以O为原点的平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,﹣),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1.(1)求抛物线对应的二次函数的解析式;(2)若D(﹣4,m)为抛物线y=x2+bx+c上一定点,点D到直线l的距离记为d,当d=DO时,求t的值.(3)如图2,若E(﹣4,m)为上述抛物线上一点,在抛物线上是否存在点F,使得△BEF是直角三角形,若存在求出点F的坐标,若不存在说明理由.解:(1)∵C(0,﹣1),∴y=x2+bx﹣1,又∵AO=2OC,∴点A坐标为(﹣2,0),代入得:1﹣2b﹣1=0,解得:b=0,∴解析式为:y=x2﹣1;(2)∵D(﹣4,m)为抛物线y=x2﹣1上一定点,∴m=×16﹣1=3,∴D(﹣4,3),∴OD==5,∴d=5,∴t=﹣(5﹣3)=﹣2;(3)点E(﹣4,m)在抛物线y=x2﹣1的上,∴m=3,∴E(﹣4,3),∵B(2,0),∴直线BE为y=﹣x+1,①如图1,当B点为直角顶点时,则BF⊥BE,∴直线BF的斜率为2,设直线BF的解析式为y=2x+n,把B(2,0)代入得2×2+n=0,∴n=﹣4,∴直线BF的解析式为y=2x﹣4,解得或,∴F(6,8);②当F点为直角顶点时,设BE的平行线y=﹣x+b与抛物线有且只有一个交点P,∴﹣x+b=x2﹣1,整理得x2+2x﹣4b﹣4=0,∴△=4+4(4b+4)=0,解得b=﹣,∴平行线为y=﹣﹣,∴x2+2x+1=0,解得x=﹣1,∴y=﹣,∴平行线与抛物线的交点P为(﹣1,﹣),∵B(2,0),E(﹣4,3),∴BE==3,∴BE的中点Q为(﹣1,),∴QP=+=<=BE,∴此种情况不存在,③当E点为直角顶点时,如图2,设点F(n,n2﹣1),而点E(﹣4,3),B(2,0),过点E作y轴的平行线交x轴于点N,交过点F与x轴的平行线于点M,则∠EBN=∠MEF,则tan∠EBN=tan∠MEF,即,∴,解得:n=﹣4(舍去)或12,故点F的坐标为(12,35);故在抛物线上存在点F,使得△BEF是直角三角形,点F的坐标为(6,8)或(12,35).14.如图①,抛物线y=ax2+bx+c与x轴相交于O、A两点,直线y=﹣x+3与y轴交于B 点,与该抛物线交于A,D两点,已知点D横坐标为﹣1.(1)求这条抛物线的解析式;(2)如图①,在线段OA上有一动点H(不与O、A重合),过H作x轴的垂线分别交AB于P点,交抛物线于Q点,若x轴把△POQ分成两部分的面积之比为1:2,请求出H点的坐标;(3)如图②,在抛物线上是否存在点C,使△ABC为直角三角形?若存在,求出点C 的坐标;若不存在,请说明理由.(1)解:y=﹣x+3,当x=0时,y=3,∴B(0,3),把x=﹣1代入y=﹣x+3得:y=4,∴D(﹣1,4),当y=0时,0=﹣x+3,∴x=3,∴A(3,0),∵抛物线过A(3,0),O(0,0),把D(﹣1,4)代入y=ax2+bx+c=a(x﹣0)(x﹣3)得:4=a(﹣1﹣0)(﹣1﹣3),∴a=1,∴y=(x﹣0)(x﹣3),即抛物线的解析式是y=x2﹣3x.(2)解:设H(x,0),则P(x,﹣x+3),Q(x,x2﹣3x),∴PH=﹣x+3,QH=3x﹣x2,∵x轴把△POQ分成两部分的面积之比为1:2,∴=或=2,即=或=2,解得:x1=2,x2=3(舍去),x3=3(舍去),x4=,∴H点的坐标是(2,0)或(,0).(3)解:分为三种情况:①若∠BAC=90°,设C(x,x2﹣3x),∵△AOB是等腰直角三角形,∴∠BAO=45°,∴∠OAC=45°,∴tan∠OAC=1,∴=1,解得:x1=1,x2=3(舍去),∴C(1,﹣2);②若∠ABC=90°时,∵∠OBA=45°,∴∠OBC=45°,设直线BC交于x轴于E,其解析式是y=kx+3,∴OE=OB=3,∴E(﹣3,0),代入得:0=﹣3k+3,∴k=1,∴y=x+3,解方程组得:,,∴C(2+,5+)或(2﹣,5﹣);③若∠ACB=90°时,设C(n,k),AC2+BC2=AB2,即(n﹣3)2+k2+n2+(k﹣3)2=18,n2﹣3n+k2﹣3k=0,∵k=n2﹣3n,代入求出k1=0,k2=2,∴n2﹣3n=0,n2﹣3n=2,解得:n1=0,n2=3(舍去),n3=,n4=,∴C(0,0)或(,2)或(,2),综合上述:存在,点C的坐标是(1,﹣2)或(2+,5+)或(2﹣,5﹣)或(0,0)或(,2)或(,2).15.如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D.(1)求此函数的关系式;(2))在AC下方的抛物线上有一点N,过点N作直线l∥y轴,交AC与点M,当点N 坐标为多少时,线段MN的长度最大?最大是多少?(3)在对称轴上有一点K,在抛物线上有一点L,若使A,B,K,L为顶点形成平行四边形,求出K,L点的坐标.(4)在y轴上是否存在一点E,使△ADE为直角三角形,若存在,直接写出点E的坐标;若不存在,说明理由.解:(1)∵抛物线y=x2+bx+c经过点A(﹣3,0),C(0,﹣3),∴将其分别代入抛物线解析式,得,解得.故此抛物线的函数表达式为:y=x2+2x﹣3;(2)设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,﹣3)代入,得,解得,∴直线AC的解析式为y=﹣x﹣3,设N的坐标为(n,n2+2n﹣3),则M(n,﹣n﹣3),∴MN=﹣n﹣3﹣(n2+2n﹣3)=﹣n2﹣3n=﹣(n+)2+,把n=﹣代入抛物线得,N的坐标为(﹣,﹣),当N的坐标为(﹣,﹣),MN有最大值;(3)①当以AB为对角线时,根据平行四边形对角线互相平分,∴KL必过(﹣1,0),∴L必在抛物线上的顶点D处,∵y=x2+2x﹣3=(x+1)2﹣4,∴L(﹣1,﹣4),K(﹣1,4)②当以AB为边时,AB=KL=4,∵K在对称轴上x=﹣1,∴L的横坐标为3或﹣5,代入抛物线得L(﹣5,12)或L(3,12),此时K都为(﹣1,12),综上,K(﹣1,4),L(﹣1,﹣4)或K(﹣1,12),L(﹣5,12)或K(﹣1,12),L (3,12);(4)存在,∵A(﹣3,0),D(﹣1,﹣4),∴AD2=(﹣3+1)2+(0+4)2=20,设E(0,m),则AE2=(﹣3﹣0)2+(0﹣m)2=9+m2,DE2=(﹣1﹣0)2+(﹣4﹣m)2=17+m2+8m,①AE为斜边,由AE2=AD2+DE2得:9+m2=20+17+m2+8m,解得:m=,②DE为斜边,由DE2=AD2+AE2得:9+m2+20=17+m2+8m,解得:m=,③AD为斜边,由AD2=ED2+AE2得:20=17+m2+8m+9+m2,解得:m=﹣1或﹣3,∴点E的坐标为(0,)或(0,)或(0,﹣1)或(0,﹣3).16.如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C(1)求抛物线的解析式;(2)设抛物线的对称轴与x轴交于点M,请问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;(3)在抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.解:(1)∵抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),∴,解得:.∴所求抛物线解析式为:y=﹣x2﹣2x+3;(2)存在,如图1,∵抛物线解析式为:y=﹣x2﹣2x+3,∴其对称轴为,∴设P点坐标为(﹣1,a),∴C(0,3),M(﹣1,0),PM2=a2,CM2=(﹣1)2+32,CP2=(﹣1)2+(3﹣a)2,分类讨论:(1)当PC=PM时,(﹣1)2+(3﹣a)2=a2,解得,∴P点坐标为:P1(﹣1,);(2)当MC=MP时,(﹣1)2+32=a2,解得,∴P点坐标为:或;(3)当CM=CP时,(﹣1)2+32=(﹣1)2+(3﹣a)2,解得a=6,a=0(舍),∴P点坐标为:P4(﹣1,6).综上所述存在符合条件的点P,其坐标为或或P(﹣1,6)或.(3)存在,Q(﹣1,2),理由如下:如图2,点C(0,3)关于对称轴x=﹣1的对称点C′的坐标是(﹣2,3),连接AC′,直线AC′与对称轴的交点即为点Q.设直线AC′函数关系式为:y=kx+t(k≠0).将点A(1,0),C′(﹣2,3)代入,得,解得,所以,直线AC′函数关系式为:y=﹣x+1.将x=﹣1代入,得y=2,即Q(﹣1,2).17.如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B在y轴上,点C(3,1),二次函数y=x2+bx﹣的图象经过点C.(1)求二次函数的解析式,并把解析式化成y=a(x﹣h)2+k的形式;(2)把△ABC沿x轴正方向平移,当点B落在抛物线上时,求△ABC扫过区域的面积;(3)在抛物线上是否存在异于点C的点P,使△ABP是以AB为直角边的等腰直角三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.解:(1)∵点C(3,1)在二次函数的图象上,∴x2+bx﹣=1,解得:b=﹣,∴二次函数的解析式为y=x2﹣x﹣y=x2﹣x﹣=(x2﹣x+﹣)﹣=(x﹣)2﹣(2)作CK⊥x轴,垂足为K.∵△ABC为等腰直角三角形,∴AB=AC.又∵∠BAC=90°,∴∠BAO+∠CAK=90°.又∵∠CAK+∠ACK=90°,∴∠BAO=∠ACK.在△BAO和△ACK中,∠BOA=∠AKC,∠BAO=∠ACK,AB=AC,∴△BAO≌△ACK.∴OA=CK=1,OB=AK=2.∴A(1,0),B(0,2).∴当点B平移到点D时,D(m,2),则2=m2﹣m﹣,解得m=﹣3(舍去)或m =.∴AB==.+S△DEH=×2+××=9.5∴△ABC扫过区域的面积=S四边形ABDE(3)当∠ABP=90°时,过点P作PG⊥y轴,垂足为G.∵△APB为等腰直角三角形,∴PB=AB,∠PBA=90°.∴∠PBG+∠BAO=90°.又∵∠PBG+∠BPG=90°,∴∠BAO=∠BPG.在△BPG和△ABO中,∠BOA=∠PGB,∠BAO=∠BPG,AB=PB,∴△BPG≌△ABO.∴PG=OB=2,AO=BG=1,∴P(﹣2,1).当x=﹣2时,y≠1,∴点P(﹣2,1)不在抛物线上.当∠PAB=90°,过点P作PF⊥x轴,垂足为F.同理可知:△PAF≌△ABO,∴FP=OA=1,AF=OB=2,∴P(﹣1,﹣1).当x=﹣1时,y=﹣1,∴点P(﹣1,﹣1)在抛物线上.18.如图,已知抛物线y=ax2+bx+4(a≠0)与x轴交于点A(1,0)和B,与y轴交于点C,对称轴为直线x=.(1)求抛物线的解析式;(2)如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ,当线段PQ长度最大时,判断四边形OCPQ的形状并说明理由;(3)点N坐标为(0,2),点M在抛物线上,且∠NBM=45°,直接写出点M坐标;(4)如图2,在(2)的条件下,D是OC的中点,过点Q的直线与抛物线交于点E,且∠DQE=2∠ODQ.在y轴上是否存在点F,使得△BEF为等腰三角形?若存在,求点F 的坐标;若不存在,请说明理由.解:(1)将点A(1,0)代入y=ax2+bx+4,得a+b+4=0,∵对称轴为直线x=,∴﹣=,∴b=﹣5a,∴a﹣5a+4=0,∴a=1,∴b=﹣5,∴y=x2﹣5x+4;(2)令x=0,则y=4,∴C(0,4),令y=0,则x2﹣5x+4=0,∴x=4或x=1,∴A(1,0),B(4,0),设直线BC的解析式为y=kx+d,∴,∴,∴y=﹣x+4,设P(t,﹣t+4),则Q(t,t2﹣5t+4),∴PQ=﹣t+4﹣(t2﹣5t+4)=﹣t2+4t=﹣(t﹣2)2+4,∴当t=2时,PQ的长度最大,∴P(2,2),Q(2,﹣2),∴PQ=4,OQ=2,∵CO=4,∴四边形OCPQ是平行四边形;(3)∵OB=OC=4,∴∠CBO=45°,∵∠NBM=45°,∴∠OBM=∠CBN,过点N作NF⊥BC于点F,∵N(0,2),C(0,4),∴CN=2,∴NF=CF=,∵B(4,0),∴OB=4,∴NB=2,∴BF=3,∴tan∠CBN=,∴tan∠OBG===,∴OG=,∴G(0,﹣),设直线OM的解析式为y=kx+b,∴,∴,∴y=x﹣,联立方程组,解得x=4(舍)或x=,∴M(,﹣);过B点作BK⊥BG交y轴于点K,此时∠NBK=45°,∴∠OKB=∠OBG,∵tan∠OBG====,∴OK=12,∴K(0,12),设直线KB的解析式为y=k1x+b1,∴,∴,∴y=﹣3x+12,联立方程组,解得x=4(舍)或x=﹣2,∴M(﹣2,18);综上所述:M点坐标为(﹣2,18)或(,﹣);(4)存在点F,使得△BEF为等腰三角形,理由如下:过点Q作x轴的垂线,过点Q作QN⊥y轴交于点N,过点E作y轴的垂线ME,∵QM∥y轴,∴∠ODQ=∠MQD,∵∠DQE=2∠ODQ,∴∠MQE=∠ODQ,∵C(0,4),D是OC的中点,∴D(0,2),∵Q(2,﹣2),∴tan∠ODQ==,。
中考复习函数专题28 二次函数中的三角形问题(老师版)

专题28 二次函数中的三角形问题知识对接考点一、二次函数中的三角形问题考点分析:二次函数与三角形的综合解答题一般涉及到这样几个方面:1.三角形面积最值问题2.特殊三角形的存在问题包括等腰等边和直角三角形。
这类题目一般出现在压轴题最后两道上,对知识的综合运用要求比较高。
考点二、解决此类题目的基本步骤与思路1.抓住目标三角形,根据动点设点坐标2.根据所设未知数去表示三角形的底和高,一般常用割补法去求解三角形的面积从而得出面积的关系式3. 根据二次函数性质求出最大值.4.特殊三角形问题首先要画出三角形的大概形状,分类讨论的去研究。
例如等腰三角形要弄清楚以哪两条边为要,直角三角形需要搞清楚哪个角作为直角都需要我们去分类讨论。
要点补充:1.简单的直角三角形可以直接利用底乘高进行面积的表示2.复杂的利用“补”的方法构造矩形或者大三角形,整体减去部分的思想3.利用“割”的方法时,一般选用横割或者竖割,也就是做坐标轴的垂线。
4.利用点坐标表示线段长度时注意要用大的减去小的。
5.围绕不同的直角进行分类讨论,注意检验答案是否符合要求。
6.在勾股定理计算复杂的情况下,灵活的构造K字形相似去处理。
要点补充:专项训练一、单选题1.如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为()A .B .C .D .【答案】A 【分析】设三角形运动速度为1,分0≤t≤2时,2<t≤2时,2<时,时五种情况,可知等腰直角三角形与正方形的不重叠部分面积变化过程是变小--不变--变大,分别求出函数关系式,即可得出答案. 【详解】∵等腰直角三角形的直角边长为1, ∵当s =12×1×1+2×2﹣212t ⨯=92﹣12t 2;s =22-12+2×12t)2=t 2﹣112;t≤2时,s =2122-×1×1=72;当2<时,s =22-2×12(t -2)2=t 2﹣4t+152;当2+2<s =22+12-2×12t+2)2=92t+2)2,∵等腰直角三角形与正方形的不重叠部分面积变化过程是变小--不变--变大,且变小、变大时的图象为抛物线,不变时的图象为直线, ∵A 符合要求, 故选:A . 【点睛】考查了动点问题的函数图象,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论,熟练掌握二次函数的图象是解题关键.2.定义:若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.如图,直线l :13y x b =+经过点10,4M ⎛⎫⎪⎝⎭一组抛物线的顶点()111B y ,,()222,B y ,()333,B y ,…(),n n B n y (n 为正整数),依次是直线l 上的点,这组抛物线与x 轴正半轴的交点依次是:()11,0A x ,()22,0A x ,()33,0A x ,…()11,0n n A x ++(n 为正整数).若()101x d d =<<,当d 为( )时,这组抛物线中存在美丽抛物线A .512或712B .512或1112C .712或1112D .712【答案】B 【分析】由抛物线的对称性可知,所有构成的直角三角形必是以抛物线顶点为直角顶点的等腰三角形,所以此等腰三角形斜边上的高等于斜边的一半,又0<d <1,所以等腰直角三角形斜边的长小于2,所以等腰直角三角形斜边的高一定小于1,即抛物线的顶点纵坐标必定小于1,据此对上一步结论分析可得满足美丽抛物线对应的顶点,再确定抛物线与x 轴的交点值与对称轴的距离,从而可求得d 的值 【详解】解: 直线l :13y x b =+经过点M (0,14)则b=14,∵直线l :1134y x =+由抛物线的对称性知:抛物线的顶点与x 轴的两个交点构成的直角三角形必为等腰直角三角形; ∵该等腰三角形的高等于斜边的一半 ∵0<d <1∵该等腰直角三角形的斜边长小于2,斜边上的高小于1(即抛物线的顶点纵坐标小于1)∵当x=1时,11173412y =+=<1;当x=2时,221113412y =+= <1; 当x=3时,315144y =+=>1; ∵美丽抛物线的顶点只有12,B B ∵若1B 为顶点,由17(1,)12B ,则7511212d =-= , ∵若2B 为顶点,由211(2,)12B ,则11111(2)11212d ⎡⎤=---=⎢⎥⎣⎦综上所述,d 的值为512或1112时,存在美丽抛物线. 故选B . 【点睛】此题主要考查抛物线与x 轴的交点,抛物线的对称性.3.如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是A.16B.15C.14D.13【答案】C【详解】根据在OB上的两个交点之间的距离为3,然后作出最左边开口向下的抛物线,再向右平移1个单位,向上平移1个单位得到开口向下的抛物线的条数,同理可得开口向上的抛物线的条数,然后相加即可得解:如图,开口向下,经过点(0,0),(1,3),(3,3)的抛物线的解析式为y=﹣x2+4x,然后向右平移1个单位,向上平移1个单位一次得到一条抛物线,可平移6次,∵一共有7条抛物线.同理可得开口向上的抛物线也有7条.∵满足上述条件且对称轴平行于y轴的抛物线条数是:7+7=14.故选C.4.如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果∵ABC是该抛物线的内接格点三角形,A,B,C的横坐标x A,x B,x C满足x A<x C<x B,那么符合上述条件的抛物线条数是()。
一次函数视角下的特殊三角形存在性问题解题策略探究

LiberalArtsGuidance2024年第14期(总第518期)文理导航No.14,2024Serial No.518次函数视角下的特殊三角形存在性问题解题策略探究【摘要】一次函数视角下的特殊三角形存在问题的探究,借助几何画板画图操作活动,正确分析问题、转化化归,模型意识反思,对数形结合思想、方程思想、分类讨论思想的感悟,利用几何法和代数法求解问题。
【关键词】运算意识;几何作图;模型意识;一次函数;特殊三角形一次函数视角下的特殊三角形存在性问题是在变化的过程中,研究背景图形,根据条件探索某种状态是否存在,把函数信息坐标或表达式转化为几何信息。
分析不变特征,确定分类标准,探寻特殊状态运动的结果,画出符合题意的图形求解。
知识储备:用待定系数法求解一次函数的解析式,联立方程组求解两个一次函数图象的交点,求解三个顶点为定点的三角形的面积,用铅锤法求解有顶点是动点的三角形的面积。
解题困惑:对一次函数视角下的特殊三角形存在性问题,如直角三角形、等腰三角形、等腰直角三角形、全等三角形等的存在性问题,学生解题过程存在一些困难,无法画图,进行正确的分类讨论,易出现漏解、错解。
策略探究:假设特殊三角形存在→推理论证→得出相应结论。
类型:两定一动及一定两动,思路:代数法→算理意识,几何法→构图识图,函数法→待定系数法。
一、直角三角形的构造→直角顶点的分类讨论方法策略:分别对三角形三个顶点为直角顶点的情况进行分类讨论,需要同时利用全等、勾股定理等相关知识计算,从而求出对应的点坐标。
【数学活动1】一次函数图象与坐标轴交于点A 、B ,在坐标轴上找一点C ,使得△ABC 为直角三角形,求符合条件的C 点坐标。
思路探析:找点→两条垂线一个圆,求点→解析式法、距离公式与勾股定理、斜率法(圆上的点),增(舍)点→斜率不存在或等于零,需结合图形检查是否遗漏。
画图探寻:满足条件的坐标轴上的C 点共有3个,如图所示:两垂线→→①若∠BAC =90°,则AB ⊥AC ,所以以A 为垂足作线段AB 的垂线,交x 轴于C 1,则△C 1AB 是以AB 为直角边的直角三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数中的特殊三角形存在性问题
例1 :如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).(1)求抛物线的解析式;(2)求△ABC的面积;(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
例2:如图,已知一次函数y=+2的图象与x轴交于点A,与二次函数y=ax2+bx+c的图象交于y轴上的一点B,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2.:(1)求二次函数y=ax2+bx+c的解析式;(2)设一次函数y=+2的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标.
例3:如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).:(1)求直线BD和抛物线的解析式.(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
1、如图,已知抛物线22
4233
y x x =-++的图象与x 轴交于A ,B 两点,与y 轴交于点C ,抛物线的对称轴与x 轴交于点D . 点M 从O 点出发,以每秒1个单位长度的速度向B 运动,过M 作x 轴的垂线,交抛物线于点P ,交BC 于Q .(1)求点B 和点C 的坐标;(2)设当点M 运动了x (秒)时,四边形OBPC 的面积为S ,求S 与x 的函数关系式,并指出自变量x 的取值范围.(3)在线段BC 上是否存在点Q ,使得△DBQ 成为以.BQ ..为一腰...的等腰三角形?若存在,求出点Q 的坐标,若不存在,说明理由.
2、二次函数21
8
y x =的图象如图所示,过y 轴上一点(0M ,2)的直线与抛物线交于A ,B 两点,过点A ,B 分别作y 轴的垂线,垂足分别为C ,D .⑴ 当点A 的横坐标为2-时,求点B 的坐标;⑵ 在⑴的情况下,分别过点A ,B 作AE x ⊥轴于E ,BF x ⊥轴于F ,在EF 上是否存在点P ,使APB ∠为直角.若存在,求点P 的坐标;若不存在,请说明理由;⑶ 当点A 在抛物线上运动时(点A 与点O 不重合),求AC BD ⋅的值.
y
x O M
D
C B
A。
