线段树
线段树及其应用场景

线段树及其应用场景一、引言线段树(Segment Tree)是一种基于树状数组(Binary Indexed Tree)的数据结构,用于高效地处理区间查询问题。
它在许多算法和数据结构问题中都有广泛应用,如区间最值查询、区间修改和区间统计等。
二、线段树的定义和构建线段树是一种二叉树结构,每个节点代表一个区间。
叶子节点表示原始数据的单个元素,而非叶子节点则表示区间的合并结果。
线段树的构建过程可以通过递归或迭代的方式完成。
3、线段树的应用场景3.1 区间最值查询线段树的一个常见应用是区间最值查询。
给定一个数组,我们希望能够快速找到指定区间内的最大或最小值。
线段树能够在O(log n)的时间复杂度内完成单次查询,并且支持O(log n)的时间复杂度的区间修改操作。
3.2 区间修改线段树还可以用于区间修改问题。
例如,给定一个数组,我们需要对指定区间内的元素进行加法或乘法操作。
线段树可以在O(log n)的时间复杂度内完成单次修改,并且支持O(log n)的时间复杂度的区间查询操作。
3.3 区间统计线段树还可以用于区间统计问题。
例如,给定一个数组,我们需要统计指定区间内满足某种条件的元素个数。
线段树可以在O(log n)的时间复杂度内完成单次统计,并且支持O(log n)的时间复杂度的区间修改操作。
4、线段树的实现和优化4.1 线段树的存储结构线段树可以使用数组或链表来实现。
数组实现简单高效,但需要额外的空间;链表实现节省空间,但查询和修改操作的时间复杂度会增加。
4.2 线段树的查询和修改算法线段树的查询和修改算法可以通过递归或迭代的方式来实现。
递归实现简洁直观,但可能会导致函数调用过多;迭代实现效率较高,但代码复杂度较高。
4.3 线段树的优化技巧线段树的性能可以通过一些优化技巧来提升。
例如,使用延迟标记(Lazy T ag)来延迟区间修改操作的执行,减少递归或迭代次数;使用预处理技巧来提前计算一些中间结果,减少查询或修改的时间复杂度。
线段树中的操作方法

线段树中的操作方法
线段树是一种二叉树结构,用于高效地处理区间查询问题。
线段树常用于解决范围最值查询、区间修改等问题。
线段树的操作方法主要包括以下几点:
1. 构建线段树:线段树的构建方法一般是采用递归的方式,将待处理区间一分为二,构建左右子树,然后将左右子树的值合并到根节点。
2. 查询区间最值:对于一个区间查询问题,可以从根节点开始递归地向下查询。
如果当前节点表示的区间与待查询区间完全不重叠,则返回一个无效值。
如果当前节点表示的区间完全包含待查询区间,则返回当前节点的值。
如果当前节点表示的区间与待查询区间相交但不完全包含,则将查询问题分为左右两个子问题,然后将子问题的结果进行合并。
3. 区间修改:对于一个区间修改问题,可以从根节点开始递归地向下修改。
如果当前节点表示的区间与待修改区间完全不重叠,则不需要修改。
如果当前节点表示的区间完全包含待修改区间,则直接将当前节点的值修改为新值。
如果当前节点表示的区间与待修改区间相交但不完全包含,则将修改问题分为左右两个子问题,然后将子问题的结果进行合并。
4. 更新节点:在线段树中,如果某个节点的值发生了变化,则需要更新该节点
以及其父节点的值。
可以从叶节点开始递归地向上更新。
线段树的操作方法可以根据具体问题的需求进行扩展和优化。
以上是线段树的基本操作方法,具体实现时需要根据具体问题进行适当的调整和改进。
线段树 区间最大值 模板

线段树区间最大值模板一、引言线段树是一种在区间求最大值的算法,常常用于处理一些涉及区间最大值的问题。
下面我们将介绍线段树的基本概念,并给出使用线段树解决区间最大值问题的模板。
二、线段树的基本概念线段树是一种将线段划分为若干个小区间,并使用树状结构来表示这些区间的划分方式。
在每个节点处,我们可以记录该节点覆盖的区间最大值,这样就可以方便地通过遍历树状结构来求出某个区间的最大值。
三、区间最大值问题的模板模板一:问题描述给定一个区间[a,b],请使用线段树来求出该区间的最大值。
模板二:代码实现假设线段树的节点类型为Node,其中Node包含一个整数值val和两个指向子节点的指针left和right。
以下是使用Python实现的线段树代码:```pythonclassNode:def__init__(self,val=None,left=None,right=None):self.val=valself.left=leftself.right=rightdefbuild_segment_tree(arr,start,end):ifstart>end:returnNonemid=(start+end)//2root=Node(arr[mid])root.left=build_segment_tree(arr,start,mid-1)root.right=build_segment_tree(arr,mid+1,end)returnrootdefquery(root,start,end):ifrootisNone:returnNoneifstart<=root.val<=end:returnroot.valreturnmax(query(root.left,start,end),query(root.right,start,end)) ```使用方法:首先构建线段树,然后通过查询节点来获取区间[a,b]的最大值。
线段树

对于线段树中的每个结点, 其表示一个区间,我们可以记录和这个区间相关 的一些信息(如最大值、最小值、和等) ,但要满足可二分性,即能直接由其子
结点的相关信息得到。 对于询问区间信息和修改区间信息的操作,线段树一般在能 O(log n) 的时间 内完成,而且常数相对较小(和后面的伸展树比较) ,算是一种高效实用的数据 结构。 (2)线段树的基本操作——查询区间信息 使用线段树的目的就是能高效地查找和修改区间信息, 下面先介绍第一个操 作——查询操作。 对于当前要查询的区间 a, b ,我们从线段树的根结点开始,如果当前结点 表示的区间被查询区间完全包含,那么更新结果,否则分别考察左右子结点,如 果查询区间与某个子结点有交集(也可能两个都有) ,那么就递归考察这个子结 点。代码框架如下1:
对于任意一个区间,会被划分成很多在线段树上存在的区间,可以证明,划 分出来的区间在线段树的每层最多有两个,又因为线段树的深度为 O(log n) ,因 此查询操作的时间复杂度为 O(log n) 。
(3)线段树的基本操作——修改区间信息 相对于查询区间信息,修改区间信息显得稍微复杂一些。
1
本文中的代码均使用 C++语言描述
(4)线段树特点总结 利用线段树, 我们可以高效地询问和修改一个数列中某个区间的信息,并且 代码也不算特别复杂。 但是线段树也是有一定的局限性的, 其中最明显的就是数列中数的个数必须 固定,即不能添加或删除数列中的数。对于这个问题,下面介绍的伸展树就可以 完美的解决。
(7,10]
(0,1] (1,2] (2,3] (3,5] (5,6]
(6,7] (7,8]
(8,10]
(3,4]
线段树

线段树目录定义基本结构实现代码树状数组编辑本段定义区间在[1,5]内的线段树线段树又称区间树,是一种对动态集合进行维护的二叉搜索树,该集合中的每个元素 x 都包含一个区间 Interval [ x ]。
线段树支持下列操作:Insert(t,x):将包含区间 int 的元素 x 插入到树中;Delete(t,x):从线段树 t 中删除元素 x;Search(t,i):返回一个指向树 t 中元素 x 的指针。
编辑本段基本结构线段树是建立在线段的基础上,每个结点都代表了一条线段[a , b]。
长度为1的线段称为元线段。
非元线段都有两个子结点,左结点代表的线段为[a , (a + b ) / 2],右结点代表的线段为[( a + b ) / 2 , b]。
右图就是一棵长度范围为[1 , 5]的线段树。
长度范围为[1 , L] 的一棵线段树的深度为log ( L - 1 ) + 1。
这个显然,而且存储一棵线段树的空间复杂度为O(L)。
线段树支持最基本的操作为插入和删除一条线段。
下面以插入为例,详细叙述,删除类似。
将一条线段[a , b] 插入到代表线段[l , r]的结点p中,如果p不是元线段,那么令mid=(l+r)/2。
如果b<mid,那么将线段[a , b] 也插入到p的左儿子结点中,如果a>mid,那么将线段[a , b] 也插入到p的右儿子结点中。
插入(删除)操作的时间复杂度为O (Log N)。
上面的都是些基本的线段树结构,但只有这些并不能做什么,就好比一个程序有输入没输出,根本没有任何用处。
最简单的应用就是记录线段有否被覆盖,并随时查询当前被覆盖线段的总长度。
那么此时可以在结点结构中加入一个变量int count;代表当前结点代表的子树中被覆盖的线段长度和。
这样就要在插入(删除)当中维护这个count值,于是当前的覆盖总值就是根节点的count值了。
另外也可以将count换成bool cover;支持查找一个结点或线段是否被覆盖。
线段树(区间和)

线段树(区间和) 给定⼀组数据(n个数据),进⾏m次操作,想要求某⼀段区间和,或者区间上同时加上或减去⼀个数。
对于这种问题,采⽤最朴素的算法思想,求区间和的时间复杂度为O(mn),删改操作为O(mn^2),若使⽤前缀和预处理,可以将求区间和的复杂度降低⾄O(m),⽤差分预处理,也可以将删改的复杂度降⾄O(m)。
但是如果m次操作中既有求区间和删改,那么时间复杂度将⾼得⽆法接受,于是我们可以使⽤线段树这种神奇的算法,两种操作的时间复杂度都可以降低⾄O(mlogn)。
线段树,顾名思义,每⼀个树的节点存储的信息为⼀个区间,对于本题,其对应的便是⼀个区间所有元素之和。
树的根节点,存储的是1到n所有数据之和,其左节点存储1到n/2所有数据和,右节点存储n/2+1到n所有数据之和,之后以此类推。
想要得到某⼀段数据和,只要从根节点开始搜索,只要O(logn)即可找到,删改操作也是同理。
线段树算法分为三步。
⼀.建树void build(ll s,ll t,ll p){if(s==t){d[p]=a[s];return;}ll m=s+((t-s)>>1);build(s,m,2*p);build(m+1,t,2*p+1);d[p]=d[2*p]+d[2*p+1];} ⼆.更新操作(懒惰标记)void add(ll l,ll r,ll c,ll s,ll t,ll p){if(l<=s&&r>=t){d[p]+=(t-s+1)*c;lazy[p]+=c;return;}ll m=s+((t-s)>>1);if(lazy[p]){d[p*2]+=lazy[p]*(m-s+1);d[p*2+1]+=lazy[p]*(t-m);lazy[p*2]+=lazy[p];lazy[p*2+1]+=lazy[p];lazy[p]=0;}if(l<=m)add(l,r,c,s,m,p*2);if(r>m)add(l,r,c,m+1,t,p*2+1);d[p]=d[p*2]+d[p*2+1];} 三.求区间和ll getsum(ll l,ll r,ll s,ll t,ll p){if(l<=s&&t<=r)return d[p];ll m=s+((t-s)>>1);if(lazy[p]){d[p*2]+=lazy[p]*(m-s+1);d[p*2+1]+=lazy[p]*(t-m);lazy[p*2]+=lazy[p];lazy[p*2+1]+=lazy[p];lazy[p]=0;}ll sum=0;if(l<=m)sum+=getsum(l,r,s,m,p*2);if(r>m)sum+=getsum(l,r,m+1,t,p*2+1);return sum;} 完整代码#include<bits/stdc++.h>using namespace std;typedef long long ll;const int maxn=300005;ll a[maxn];ll d[maxn];void build(ll s,ll t,ll p){if(s==t){d[p]=a[s];return;}ll m=s+((t-s)>>1);build(s,m,2*p);build(m+1,t,2*p+1);d[p]=d[2*p]+d[2*p+1];}ll lazy[maxn];void add(ll l,ll r,ll c,ll s,ll t,ll p){if(l<=s&&r>=t){d[p]+=(t-s+1)*c;lazy[p]+=c;return;}ll m=s+((t-s)>>1);if(lazy[p]){d[p*2]+=lazy[p]*(m-s+1);d[p*2+1]+=lazy[p]*(t-m);lazy[p*2]+=lazy[p];lazy[p*2+1]+=lazy[p];lazy[p]=0;}if(l<=m)add(l,r,c,s,m,p*2);if(r>m)add(l,r,c,m+1,t,p*2+1);d[p]=d[p*2]+d[p*2+1];}ll getsum(ll l,ll r,ll s,ll t,ll p){if(l<=s&&t<=r)return d[p];ll m=s+((t-s)>>1);if(lazy[p]){d[p*2]+=lazy[p]*(m-s+1);d[p*2+1]+=lazy[p]*(t-m);lazy[p*2]+=lazy[p];lazy[p*2+1]+=lazy[p];lazy[p]=0;}ll sum=0;if(l<=m)sum+=getsum(l,r,s,m,p*2);if(r>m)sum+=getsum(l,r,m+1,t,p*2+1); return sum;}int main(){ll n,m;scanf("%lld %lld",&n,&m);for(ll i=1;i<=n;i++)scanf("%lld",&a[i]); build(1,n,1);while(m--){int opt;scanf("%d",&opt);ll x,y;if(opt==1){ll k;scanf("%lld %lld %lld",&x,&y,&k); add(x,y,k,1,n,1);}else{scanf("%lld %lld",&x,&y);printf("%lld\n",getsum(x,y,1,n,1)); }}return0;}。
线段树ppt课件

•
else Count := 0; 连接处颜色相同并且
非底色,则总数减1
统计算法
最左边的颜色
• end • else if r – l > 1 then
最右边的颜色
• begin
最左颜色=最右颜色=本身
•
result := Count(p * 2, l,非(底l +色则r)统d计iv数加2,1 lc, tl) +
•
else if a >= m then Insert(p * 2 + 1, m, r, a, b, c)
•
else begin
•
Insert(p * 2, l, m, a, m, c);
•
Insert(p * 2 + 1, m, r, m, b, c);
•
end;
•
end;
• end;
• end;
示例
• 初始情况 0 0 0 0 0
• [1,2]
10000
• [3,5]
10110
• [4,6]
10111
• [5,6]
10111
4个1
缺点
• 此方法的时间复杂度决定于下标范围的平 方。
• 当下标范围很大时([0,10000]),此方法 效率太低。
离散化的做法
• 基本思想:先把所有端点坐标从小到大排 序,将坐标值与其序号一一对应。这样便 可以将原先的坐标值转化为序号后,对其 应用前一种算法,再将最后结果转化回来 得解。
Wall
分析
• 这道题目是一个经典的模型。在这里,我 们略去某些处理的步骤,直接分析重点问 题,可以把题目抽象地描述如下:x轴上有 若干条线段,求线段覆盖的总长度。
线段树 区间最大值 模板

线段树区间最大值模板线段树是一种二叉树的数据结构,它被广泛应用于解决与区间相关的问题。
其中,区间最大值是线段树的一个常见应用。
在本文中,我将详细介绍线段树的概念和实现,并提供一个用于解决区间最大值问题的模板。
1. 线段树的概念线段树是一种将区间划分为多个子区间并以二叉树形式表示的数据结构。
每个节点代表一个区间,并保存该区间的一些属性,例如区间的最大值、最小值、总和等。
通过将区间逐层划分为子区间,线段树可以高效地处理区间操作。
2. 线段树的实现线段树的实现可以使用数组或链表。
在这里,我将使用数组来实现线段树。
2.1 初始化线段树首先,我们需要定义一个数组来表示线段树。
对于给定的区间,我们可以使用递归的方式将其划分为左右子区间,直到区间的长度为1。
然后,我们将每个区间的最大值保存在线段树的相应节点中。
2.2 更新线段树当某个区间的值发生改变时,我们需要更新线段树中相应的节点。
首先,我们找到包含要更新的值的叶子节点,并更新该节点的值。
然后,我们通过递归地向上更新父节点的值,直到根节点。
2.3 查询线段树查询线段树的最大值需要考虑两种情况。
如果查询的区间与当前节点的区间完全重叠,那么我们可以直接返回该节点保存的最大值。
否则,我们需要继续向下递归查询左右子节点,并返回两者中的最大值。
3. 线段树区间最大值的模板下面是一个用于解决区间最大值问题的线段树模板:```#include <iostream>#include <vector>#include <climits>using namespace std;// 定义线段树节点的数据结构struct SegmentTreeNode {int start;int end;int max_value;SegmentTreeNode* left;SegmentTreeNode* right;SegmentTreeNode(int s, int e) : start(s), end(e), max_value(INT_MIN),left(nullptr), right(nullptr) {}};// 构建线段树SegmentTreeNode* buildSegmentTree(vector<int>& nums, int start, int end) { if (start > end) return nullptr;SegmentTreeNode* root = new SegmentTreeNode(start, end);if (start == end) {root->max_value = nums[start];} else {int mid = start + (end - start) / 2;root->left = buildSegmentTree(nums, start, mid);root->right = buildSegmentTree(nums, mid + 1, end);root->max_value = max(root->left->max_value, root->right->max_value); }return root;}// 更新线段树中的值void updateSegmentTree(SegmentTreeNode* root, int index, int value) {if (!root) return;if (root->start == root->end) {root->max_value = value;} else {int mid = root->start + (root->end - root->start) / 2;if (index <= mid) {updateSegmentTree(root->left, index, value);} else {updateSegmentTree(root->right, index, value);}root->max_value = max(root->left->max_value, root->right->max_value);}}// 查询线段树中的最大值int querySegmentTree(SegmentTreeNode* root, int start, int end) {if (!root) return INT_MIN;if (root->start == start && root->end == end) {return root->max_value;} else {int mid = root->start + (root->end - root->start) / 2;if (end <= mid) {return querySegmentTree(root->left, start, end);} else if (start > mid) {return querySegmentTree(root->right, start, end);} else {return max(querySegmentTree(root->left, start, mid), querySegmentTree(root->right, mid + 1, end));}}}int main() {vector<int> nums = {1, 3, 5, 7, 9, 11};int n = nums.size();SegmentTreeNode* root = buildSegmentTree(nums, 0, n - 1);updateSegmentTree(root, 2, 10);int max_value = querySegmentTree(root, 1, 4);cout << "Max value in range [1, 4]: " << max_value << endl;return 0;}```这是一个完整的线段树模板,可以根据具体的问题进行修改和扩展。
线段树的概念与应用

线段树的概念与应用线段树(Segment Tree)是一种用于解决区间查询问题的数据结构。
它可以高效地支持以下两种操作:区间修改和区间查询。
线段树的应用非常广泛,在离线查询、区间统计、区间更新等问题中有着重要的作用。
一、概念线段树是一颗二叉树,其中每个节点代表了一个区间。
根节点表示整个待查询区间,而叶子节点表示的是单个元素。
每个内部节点包含了其子节点所代表区间的并集。
二、构建线段树线段树的构建过程是自底向上的。
将待查询数组划分成一颗满二叉树,并将每个区间的和存储在相应的节点中。
对于叶子节点,直接存储对应元素的值。
而非叶子节点的值可以通过其子节点的值计算得到。
三、线段树的查询对于区间查询操作,可以通过递归方式实现。
从根节点开始,判断查询区间和当前节点所代表的区间是否有交集。
若没有交集,则返回当前节点的默认值。
若查询区间包含当前节点所代表的区间,则返回当前节点存储的值。
否则,将查询区间分割成左右两部分继续递归查询。
四、线段树的更新对于区间更新操作,也可以通过递归方式实现。
与查询操作类似,首先判断查询区间和当前节点所代表的区间的关系。
若没有交集,则无需更新。
若查询区间包含当前节点所代表的区间,则直接更新当前节点的值。
否则,将更新操作分割成左右两部分继续递归更新。
五、应用案例:区间最值查询一个常见的线段树应用是求解某个区间的最值。
以查询区间最小值为例,可以通过线段树来高效地解决。
首先构建线段树,然后进行区间查询时,分为以下几种情况处理:若当前节点所代表的区间完全包含于查询区间,则直接返回该节点的值;若当前节点所代表的区间与查询区间没有交集,则返回默认值;否则,将查询区间分割成左右两部分继续递归查询,最后返回两个子区间查询结果的较小值。
六、总结线段树是一种非常有用的数据结构,能够高效地解决区间查询问题。
通过合理的构建和操作,线段树可以应用于多种场景,如区间最值查询、离线查询等。
熟练掌握线段树的概念和应用方法,对解决问题具有重要意义。
线段树求解区间最大公约数

线段树求解区间最大公约数好了,今天我们聊聊线段树和区间最大公约数(GCD)。
听起来有点学术对吧?别担心,别一听这名字就往头上顶,来,咱们慢慢聊,肯定能让你觉得其实这玩意儿挺简单。
先说说,区间最大公约数是什么?大白话就是,给你一段数,问你这段数里面,能整除所有数的最大的那个数到底是多少。
比方说,给你一段数,求这三者的最大公约数。
你说,12能整除24,能整除36,24和36互相之间也能整除,那最大公约数就是12。
是不是挺简单的?但是要是给你一大堆数,这个问题可就复杂了。
假如这段数的长度是10万,你可不可能一个个去算?太浪费时间了,对吧?这时候线段树就登场了。
线段树啊,听起来很酷,其实它就是一个用来处理区间问题的二叉树。
就像是一个能高效处理大量数据的“小帮手”,一旦有了它,我们就可以瞬间把问题解决,别看它名字生疏,其实好用得很!你可以把线段树想象成一个超级有条理的仓库。
仓库里面分了好多格子,每个格子里都有一段数据。
你想要查哪一段的最大公约数,就可以直接找过去,根本不用一项一项地查看。
这就像你去超市,想找番茄酱,直接去酱料区,而不是一瓶一瓶地在每个货架上找。
是不是立马让你感到轻松多了?不过,问题来了,如何在这么复杂的结构中找到每一段数据的最大公约数呢?其实很简单,线段树的每个节点代表的是一个区间,而每个节点存储的是它所管辖区间的最大公约数。
比如,节点代表的是的最大公约数,线段树就会把你指向包含这个区间的最小几个节点,快速把答案给你。
所以,我们通过查询,能很快知道某一段区间的最大公约数。
简直是秒杀所有传统方法。
你可能会想,既然查起来这么方便,那更新数据是不是也很麻烦?其实也不难!线段树的更新也是基于树的结构进行的。
比如说,某个数发生了变化,更新操作就会沿着树的路径向上走,更新每一个与这个数相关的节点。
这种操作类似你换灯泡:换一个,然后每次走回去检查一遍,确保没问题。
就这么简单,效率超高。
想象一下,我们的线段树就像一位经验丰富的工匠,手里拿着工具箱,每当遇到问题时,总能快速拆解,不拖泥带水。
线段树入门(一)

线段树入门OI中经常能碰见统计类型的题目。
要求出某些时刻、某种情况下,状态是怎样的。
这类问题往往比较简单明了,也能十分容易地写出模拟程序。
但较大的数据规模使得模拟往往不能满足要求。
一、线段树的结构:线段树是一棵二叉树,其结点是一条“线段”——[a,b],它的左儿子和右儿子分别是这条线段的左半段和右半段,即[a, (a+b)/2]和[(a+b)/2,b]。
线段树的叶子结点是长度为1的单位线段[a,a+1]。
下图就是一棵根为[1,10]的线段树:【1,10】/ \【1,5】【5,10】 / \/ \【1,3】【3,5】【5,7】【7,10】/ \ / \ /\ / \【1,2】【2,3】【3,4】【4,5】【5,6】【6,7】【7,8】【8,10】 / \【8,9】【9,10】易证一棵以[a,b]为根的线段树结点数是2*(b-a)-1。
由于线段树是一棵平衡二叉树,因此一棵以[a,b]为根的线段树的深度为log2(2*(b-a))。
一般采用静态完全二叉树来表示线段树。
(但有时有一些缺点)struct segtree{int a,b,left,right;};其中分别表示线段的左端点和右端点,Left,Right 表示左儿子和右儿子的编号。
因此我们可以用一个一维数组来表示一棵线段树:segtree tree[MaxN];根据实际需要,我们可以增加其它的域,例如cover域来计算该线段被覆盖的次数,或是其它一些形式的域。
二、建立线段树:void build(int step, int s, int t){a[step].a = s;a[step].b = t;a[step].cn = 0;if (t-s>1){int mid=(s+t)/2;build(step*2, s, mid);build(step*2+1, mid, t);}}建立以step为根结点,范围从s到t的线段树。
这里应用了完全二叉树的特点:step 的左孩子结点编号为2*step,右孩子结点编号为2*step+1。
统计的力量-线段树

清华大学 张昆玮
21
2019年10月17日
清华大学 张昆玮
*堆式存储是关键
指针退休了? 后面再讲……
22
2019年10月17日
*N 的左儿子是 2N *N 的右儿子是 2N + 1 *N 的父亲是 N >> 1 *…… *不就是个堆存储么?不用讲了吧?
清华大学 张昆玮
*一些简单的问题
清华大学 张昆玮
*线段树?
3
2019年10月17日
*POJ上的某题,时限很紧…… *大家都用树状数组,但是有人只会用线段树呢? *而且我可以轻易改出一道不能用树状数组的题 *在线段树一次次TLE后,有一个ID发帖抱怨 *“下次写一个汇编版非递归线段树,再超时?” *可是大家都知道,超时的代码已经2k了。
*因为查询是连续的?
清华大学 张昆玮
12
2019年10月17日
*为什么用线段树?
功利点说,没啥用的东西咱不学……
清华大学 张昆玮
13
2019年10月17日
*且慢
区区区间和,用的着线段树?
*直接把原数组处理成前缀和 *For i=2 to n do
* A[i] += A[i-1]
*Ans(a,b) = A[a] - A[b-1]
*Warning
32
2019年10月17日
*如果需要查询 0 就整个向后平移一下 *所有下标加一!
*如果需要在[0,1024)中查询1023结尾的区间? *慢!你的数据规模不是 1000 么? *…… *如果真的要到1023,直接把总区间变成[0,2048) *就是这么狠!
*不要紧张
清华大学 张昆玮
线段树 维护标记 经典题

线段树维护标记经典题
线段树是一种用于解决区间查询问题的数据结构,它可以高效地处理区间操作,例如区间最大值、区间和、区间更新等。
线段树通常用于解决动态区间查询问题,比如区间修改、区间查询等。
在线段树中,维护标记是一种常见的技巧,它可以帮助我们在区间内进行延迟更新,从而减少不必要的操作。
维护标记通常用于延迟更新操作,当我们需要对区间内的元素进行更新时,我们可以先将更新操作记录在节点上,而不立即更新区间内的所有元素,这样可以减少不必要的更新操作,提高效率。
经典题目中常涉及使用线段树维护标记的问题包括区间修改、区间查询等。
例如,区间修改问题可以是给定一个数组,进行一系列区间修改操作,然后查询某个位置的元素值;区间查询问题可以是给定一个数组,进行一系列区间查询操作,然后求解区间内的最大值、最小值、和等。
在解决经典题目时,我们需要注意线段树的构建、更新、查询等操作,以及维护标记的技巧,这样才能高效地解决问题。
同时,我们也需要注意处理边界情况和特殊情况,保证算法的正确性和鲁
棒性。
总之,线段树是一种非常有用的数据结构,通过合理地维护标记,我们可以解决许多经典的区间查询问题。
在解决这些问题时,
我们需要充分理解线段树的原理和操作,灵活运用维护标记的技巧,才能更好地解决问题。
可持久化线段树总结(可持久化线段树,线段树)

可持久化线段树总结(可持久化线段树,线段树)最近正在学习⼀种数据结构——可持久化线段树。
看了⽹上的许多博客,弄了⼏道模板题,思路有点乱了,所以还是来总结整理下吧。
可持久化线段树⾸先要了解此数据结构的基础——线段树。
百度⼀下,你就知道!推荐⼀下,对线段树的基本操作讲得挺详细的。
为了更好地理清思路,我在这⾥先放个模板题吧。
题⽬描述你需要维护这样的⼀个长度为\(N\)的数组,⽀持如下⼏种操作1. 在某个历史版本上修改某⼀个位置上的值2. 访问某个历史版本上的某⼀位置的值此外,每进⾏⼀次操作(对于操作2,即为⽣成⼀个完全⼀样的版本,不作任何改动),就会⽣成⼀个新的版本。
版本编号即为当前操作的编号(从1开始编号,版本0表⽰初始状态数组)输⼊输出格式输⼊格式:输⼊的第⼀⾏包含两个正整数\(N,M\)分别表⽰数组的长度和操作的个数。
第⼆⾏包含 N N个整数,依次为初始状态下数组各位的值(依次为\(a_i, 1 \leq i \leq N\))。
接下来\(M\)⾏每⾏包含3或4个整数,代表两种操作之⼀(\(i\)为基于的历史版本号):对于操作1,格式为\(v_i \ 1 \ {loc}_i \ {value}_i v\),即为在版本\(v_i\)的基础上,将\(a_{{loc}_i}\)修改为\({value}_i\)对于操作2,格式为\(v_i \ 2 \ {loc}_i\),即访问版本\(v_i\)中的\(a_{{loc}_i}\)的值输出格式:输出包含若⼲⾏,依次为每个操作2的结果。
输⼊输出样例输⼊样例#1:5 1059 46 14 87 410 2 10 1 1 140 1 1 570 1 1 884 2 40 2 50 2 44 2 12 2 21 1 5 91输出样例#1:598741878846说明数据规模:对于30%的数据:\(1 \leq N, M \leq {10}^3\)对于50%的数据:\(1 \leq N, M \leq {10}^4\)对于70%的数据:\(1 \leq N, M \leq {10}^5\)对于100%的数据:\(1 \leq N, M \leq {10}^6, 1 \leq {loc}_i \leq N, 0 \leq v_i < i, -{10}^9 \leq a_i, {value}_i \leq {10}^9\)经测试,正常常数的可持久化数组可以通过,请各位放⼼数据略微凶残,请注意常数不要过⼤另,此题I/O量较⼤,如果实在TLE请注意I/O优化询问⽣成的版本是指你访问的那个版本的复制样例说明:⼀共11个版本,编号从0-10,依次为:0 : 59 46 14 87 411 : 59 46 14 87 412 : 14 46 14 87 413 : 57 46 14 87 414 : 88 46 14 87 415 : 88 46 14 87 416 : 59 46 14 87 417 : 59 46 14 87 418 : 88 46 14 87 419 : 14 46 14 87 4110 : 59 46 14 87 91思路分析很裸的可持久化线段树板⼦题。
历史版本和线段树

历史版本和线段树
历史版本和线段树是计算机科学中的两个重要概念。
历史版本,顾名思义,是指数据结构在不同时间点上的不同状态。
在软件开发中,我们经常需要对数据进行修改和更新,但有时候我们也需要回溯到前面的某个状态。
历史版本技术就是为了解决这个问题而提出的。
它可以记录数据结构在不同时间点上的状态,并且可以在需要时恢复到特定的历史状态。
这在很多应用中都非常有用,比如版本控制系统和数据库管理系统。
线段树是一种用于解决区间查询的数据结构。
它可以高效地计算一个区间内的某种属性或者进行某种操作,比如求和、最大值、最小值等。
线段树通过将区间逐步细分成更小的子区间,并且计算每个子区间的属性来构建一个树状结构,从而实现高效的查询和修改。
线段树广泛应用于各种领域,比如计算几何、图像处理、离散数学等。
历史版本和线段树都是计算机科学中非常有用的技术。
历史版本可以帮助我们记录和恢复数据结构的历史状态,而线段树可以高效地解决区间查询问题。
它们在各种应用中都发挥着重要作用,并且得到了广泛的研究和应用。
菜鸟都能理解的线段树入门经典
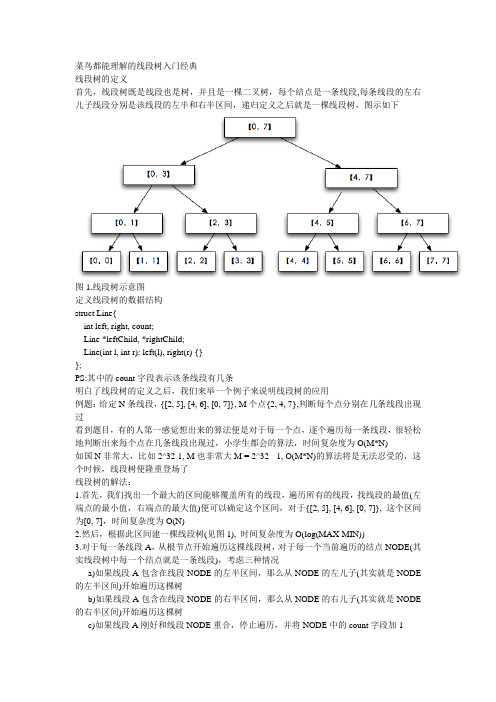
菜鸟都能理解的线段树入门经典线段树的定义首先,线段树既是线段也是树,并且是一棵二叉树,每个结点是一条线段,每条线段的左右儿子线段分别是该线段的左半和右半区间,递归定义之后就是一棵线段树,图示如下图1.线段树示意图定义线段树的数据结构struct Line{int left, right, count;Line *leftChild, *rightChild;Line(int l, int r): left(l), right(r) {}};PS:其中的count字段表示该条线段有几条明白了线段树的定义之后,我们来举一个例子来说明线段树的应用例题:给定N条线段,{[2, 5], [4, 6], [0, 7]}, M个点{2, 4, 7},判断每个点分别在几条线段出现过看到题目,有的人第一感觉想出来的算法便是对于每一个点,逐个遍历每一条线段,很轻松地判断出来每个点在几条线段出现过,小学生都会的算法,时间复杂度为O(M*N)如国N非常大,比如2^32-1, M也非常大M = 2^32 - 1, O(M*N)的算法将是无法忍受的,这个时候,线段树便隆重登场了线段树的解法:1.首先,我们找出一个最大的区间能够覆盖所有的线段,遍历所有的线段,找线段的最值(左端点的最小值,右端点的最大值)便可以确定这个区间,对于{[2, 5], [4, 6], [0, 7]}, 这个区间为[0, 7],时间复杂度为O(N)2.然后,根据此区间建一棵线段树(见图1), 时间复杂度为O(log(MAX-MIN))3.对于每一条线段A,从根节点开始遍历这棵线段树,对于每一个当前遍历的结点NODE(其实线段树中每一个结点就是一条线段),考虑三种情况a)如果线段A包含在线段NODE的左半区间,那么从NODE的左儿子(其实就是NODE 的左半区间)开始遍历这棵树b)如果线段A包含在线段NODE的右半区间,那么从NODE的右儿子(其实就是NODE 的右半区间)开始遍历这棵树c)如果线段A刚好和线段NODE重合,停止遍历,并将NODE中的count字段加1d)除了以上的情况,就将线段A的左半部分在NODE的左儿子处遍历,将A的右半部分在NODE的右儿子处遍历补充说明:对于以上的步骤,所做的工作其实就是不断地分割每一条线段,使得分割后的每一条小线段刚好能够落在线段树上,举个例子,比如要分割[2, 5],首先将[2, 5]和[0, 7]比较,符合情况d, 将A分成[2, 3]与[4, 5]I)对于[2, 3]从[0, 7]的左半区间[0, 3]开始遍历将[2, 3]与[0, 3]比较,满足情况b,那么从[0, 3]的右半区间[2, 3]开始遍历,发现刚好重合,便将结点[2, 3]count字段加1II)对于[4, 5]从[0, 7]的右半区间[4, 7]开始遍历将[4, 5]与[4, 7]比较,满足情况b,从[4, 7]的左半区间[4, 5]开始遍历,发现刚好重合,便将结点[4, 5]count字段加1于是对于[2, 5]分割之后线段树的情况为图2图2.分割[2,5]之后线段树的情况显然,我们看到,上述的遍历操作起始就是将[2, 5]按照线段树中的线段来分割,分割后的[2, 3]与[4, 5]其实是与[2, 5]完全等效的最后,我们将剩下的两条线段按照同样的步骤进行分割之后,线段树的情况如下图3这一步的时间复杂度为O(N*log(MAX-MIN))4.最后,对于每一个值我们就可以开始遍历这一颗线段树,加上对于结点的count字段便是在线段中出现的次数比如对于4,首先遍历[0, 7],次数= 0+1=1;4在右半区间,遍历[4, 7],次数= 1+0=0;4在[4, 7]左半区间, 次数= 1+2=3;4在[4, 5]左半区间,次数= 3+0 = 4,遍历结束,次数= 3说明4在三条线段中出现过,同理可求其他的值,这一步的时间复杂度为O(M*log(MAX-MIN))最后,总的时间复杂度为O(N)+O(log(MAX-MIN))+O(N*log(MAX-MIN))+(M*log(MAX-MIN)) = O((M+N)*log(MAX-MIN))由于log(MAX-MIX)<=64所以最后的时间复杂度为O(M+N)最后,放出源码[cpp] view plaincopy#include <iostream>using namespace std;struct Line{int left, right, count;Line *leftChild, *rightChild;Line(int l, int r): left(l), right(r) {}};//建立一棵空线段树void createTree(Line *root) {int left = root->left;int right = root->right;if (left < right) {int mid = (left + right) / 2;Line *lc = new Line(left, mid);Line *rc = new Line(mid + 1, right);root->leftChild = lc;root->rightChild = rc;createTree(lc);createTree(rc);}}//将线段[l, r]分割void insertLine(Line *root, int l, int r) {cout << l << " " << r << endl;cout << root->left << " " << root->right << endl << endl;if (l == root->left && r == root->right) {root->count += 1;} else if (l <= r) {int rmid = (root->left + root->right) / 2;if (r <= rmid) {insertLine(root->leftChild, l, r);} else if (l >= rmid + 1) {insertLine(root->rightChild, l, r);} else {int mid = (l + r) / 2;insertLine(root->leftChild, l, mid);insertLine(root->rightChild, mid + 1, r);}}}//树的中序遍历(测试用)void inOrder(Line* root) {if (root != NULL) {inOrder(root->leftChild);printf("[%d, %d], %d\n", root->left, root->right, root->count);inOrder(root->rightChild);}}//获取值n在线段上出现的次数int getCount(Line* root, int n) {int c = 0;if (root->left <= n&&n <= root->right)c += root->count;if (root->left == root->right)return c;int mid = (root->left + root->right) / 2;if (n <= mid)c += getCount(root->leftChild, n);elsec += getCount(root->rightChild, n);return c;}int main() {int l[3] = {2, 4, 0};int r[3] = {5, 6, 7};int MIN = l[0];int MAX = r[0];for (int i = 1; i < 3; ++i) {if (MIN > l[i]) MIN = l[i];if (MAX < r[i]) MAX = r[i];}Line *root = new Line(MIN, MAX);createTree(root);for (int i = 0; i < 3; ++i) {insertLine(root, l[i], r[i]);}inOrder(root);int N;while (cin >> N) {cout << getCount(root, N) << endl; }return 0;}。
线段树入门

小结
ቤተ መጻሕፍቲ ባይዱ
其实线段树就是用某个值来代替(概括) 一段区间的值,来避免求解时用到大量的 基础元素。
框架:建树
procedure maketree(k,q,p:longint); //建树,k表示区间[q,p] 的代号 begin if q=p then begin 赋初值 exit; end; maketree(k*2,q,(q+p) div 2); //分割 访问左儿子 代号为 k*2 maketree(k*2+1,(q+p) div 2+1,p); //分割 访问右儿子 代号 为k*2+1 递归回来后由两儿子决定父亲的值 end;
线段树的定义
线段[1, 9]的线段树
[1,9] [1,4] [1,2] 1 2 [3,4] 3 4 [5,9] [5,6] 5 6 [7,9] 7 [8,9] 8 9
1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 8 9
框架:修改基础元素
procedure change(k,q,p,a,s:longint); 修改第a位置的值变为s,[q,p]为当前 查找到的区间 var m:longint; begin if (q>a) or (p<a) then //如果a不在[q,p]中,就退出 exit; if (a=q) and (q=p) then //如果查找到了a,就更新 begin 更新相关量 exit; end; m:=(q+p) div 2; insert(k*2,q,m,a,s); //分割,查找左儿子 insert(k*2+1,m+1,p,a,s); //分割,查找右儿子 用儿子的相关量更新父亲 end;
线段树详解(C++版)

build(((l+r)/2)+1,r);
t[h].data=min(t[t[h].ls].data,t[t[h].rs].data);
}
else
{
t[h].data=a[l];f[l]=h;
}
}
int find(int h,int p,int q)
{
int v;
if((t[h].l==p)&&(t[h].r==q)) return(t[h].data);
Input
输入中第一行有两个数m,n表示有m(m< =100000)笔账,n表示有n个问题,n< =100000。
接下来每行为3个数字,第一个p为数字1或数字2,第二个数为x,第三个数为y
当p=1则查询x,y区间
当p=2则改变第x个数为y
Output
输出文件中为每个问题的答案。具体查看样例。
Sample Input
if(t[x].data!=min(t[t[x].ls].data,t[t[x].rs].data))
struct ss
{
int l,r,ls,rs,f,data;
}t[400001];
void build(int l,int r)
{
int h;
num++;
h=num;
t[h].l=l;
t[h].r=r;
if(l!=r)
{
t[h].ls=num+1;
t[num+1].f=h;
l,(l+r)/2);
1、忠诚(TYVJ 1038)
Description
老管家是一个聪明能干的人。他为财主工作了整整10年,财主为了让自已账目更加清楚。要求管家每天记k次账,由于管家聪明能干,因而管家总是让财主十分满意。但是由于一些人的挑拨,财主还是对管家产生了怀疑。于是他决定用一种特别的方法来判断管家的忠诚,他把每次的账目按1,2,3…编号,然后不定时的问管家问题,问题是这样的:在a到b号账中最少的一笔是多少?为了让管家没时间作假他总是一次问多个问题。
线段树_刘汝佳(有版权)

SUM的计算
• 右图表示影响 SUM(7, 9)的所 有区间
– 影响全部: [1,9], [5,9], [7,9] – 影响部分: 7, [8,9], 8, 9
[1,2] 1 2 [1,9] [1,4] [3,4] 3 4 [5,9] [5,6] 5 6 [7,9] 7 [8,9] 8 9
完整的算法
– 得到讨论区间(可能要先离散化) – 设计区间附加信息和维护/统计算法
• 线段树自身没有任何数据, 不像BST一样有 一个序关系 • 警告 想清楚 警告: 想清楚附加信息的准确含义 不能有 准确含义, 准确含义 半点含糊! • 建议 先设计便于解题 建议: 便于解题的附加信息,如果难 便于解题 以维护就加以修改
[3,4]
5 3 3 5 5 1 1
[4,5]
5 3 3 5
1 2 2 3 3 4 4 5
1 2 2 3 3 4 4 5
1 2 2 3 3 4 4
1 2 2 3 3 4 4 5
矩形树
• 每个矩形分成四份
– 空间复杂度:XY – 时间复杂度:X+Y
(x2,y2) (1,1)
(4,3)
Son1
Son2
– ADD: 给i对应结点的所有直系祖先s值增加k – SUM: 做区间分解, 把对应结点的s值相加
动态统计问题II
• 包含n个元素的数组A
– ADD(i, j, k): 给A[i], A[i+1], … A[j]均增加k – QUERY(i): 求A[i]
• 先看看是否可以沿用刚才的附加信息
– QUERY(i)就是读取i对应的结点上的s值 – ADD呢? 极端情况下, 如果是修改整个区间, 则 所有结点都需要修改!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
递推法
• MODIFY操作仍然只需要修改从根到叶子的一条 路径上所有m值, 但关键是: 如何修改? • 回忆: 动态统计问题I中, 区间[I, j]中任何一个元素 增加了k, 则区间综合增加k. 但最小值呢? 只根据 原来的m(p)自身无法计算出新的m(p) • 方法: 递推. 设p的儿子为l和r, 则 m(p)=min{m(l), m(r)} • 前提: 计算m(p)时m(l)和m(r)已经算出. • 保证: 自底向上递推
• 增加区间时进行分解, 设置计数器c(p), 表示 分解后指令Add(x, y)的条数
覆盖长度可以维护么?
• 考虑根结点. 如果c(root)>0, 则整个区间都 被覆盖, 返回L, 但如果c(root)=0呢? 需要根 据左右儿子递推 • 是否可以定义l(p), 表示结点p对应的区间内 被覆盖到的总长度呢? 不可以!
• 包含n个元素的数组A
– MODIFY(i, j): 设A[i] = j – MIN(p, q): 求min{A[p], A[p+1],…,A[q]}
• 和动态统计问题I很类似, 因此考虑设计附加 信息: m(p)表示结点p所代表区间内所有元 素的最小值, 那么MIN仍可以通过区间分解 做. 但MODIFY呢?
• 实现: 一个归并排序可以同时构造线段树和 每个节点内的排序数组. 空间:O(nlogn)
分析
• 有修改的情形: 每个结点不能用有序表了, 而需要是一棵平衡树 • 每次Modify需要修改O(logn)棵平衡树, 总时 间为O(log2n)
例题3. 动态连通块
• 给出n*n棋盘,有黑有白.每次改变其中一个格 子颜色,输出黑白连通块的个数 • 左图,翻转(3,2)和(2,3)后分别得到中图和右图, 应依次输出”4,3”、”5,2”
– 如果[I, j]不对应任何结点怎么办? 区间分解! – 这样的信息实质上是把所有ADD指令合并到了 一起. 可以吗? 可以的, 因为ADD具有叠加性
• QUERY: 把所有直系祖先的a值相加, 就是 A[i]的增加量
继续讨论
• 附加信息a(p)到底是什么?
– 首先要在同一条指令中被增加 – 但在同一条指令中被增加的结点却不能都被修 改, 否则ADD(1, n)仍然要修改所有结点 – 正确的理解是: 先把指令ADD分解为不超过 2log2L条指令, 每条指令的区间[i, j]都在树中有 单一的结点与之对应, 然后每条原子ADD操作 只修改该结点本身的计数器
SUM的计算
• 右图表示影响 SUM(7, 9)的所 有区间
– 影响全部: [1,9], [5,9], [7,9] – 影响部分: 7, [8,9], 8, 9
[1,2] 1 2 [1,9] [1,4] [3,4] 3 4 [5,9] [5,6] 5 6 [7,9] 7 [8,9] 8 9
完整的算法
– 把[i,j]进行区间分解 – 二分W, 每次统计这些区间内一共有多少个数 比W大,用logW次统计可求出第k大元素
• 如何统计原子区间内比W大的元素总个数?
分析
• 统计原子区间内一共有多少个数比W大
– 区间内的数已排序,用二分每个区间求比W大 的数logn – 累加所有2logn个区间比W大的数,共log2n – 总时间: logW*log2n
例题1. 火星地图
• 2051年,科学家们探索出了火星上 n(n<=10000)个不同的矩形(坐标为不超过 109的正整数)区域并绘制了这些局部的地 图,如图所示。波罗的海太空研究所希望 绘制出火星的完整地图。 • 科学家们首先需要知道这些矩形共占了多 大的面积,你能帮助他们写一个程序计算 出结果吗?
[1,2] 1 2 [1,4] [3,4] 3 4 [1,9] [5,9] [5,6] 5 6 [7,9] 7 [8,9] 8 9
和应用相关的几个小问题
• 线段长度为偶数: 左小右大还是左大右小 • 一样大 • 原始线段长度不是2的幂: 允许不平均分割还是补 齐到2的幂? • (允许不平均分割) • 叶子是单个元素i还是单位线段[i, i+1]? • (是单个元素) • 静态 or 动态?(静态) • 建立: 自顶向下递归分割还是自底向上合并? • 分割合并都可以
• 元素(x,y)的最终值完全取决于在C’中(x,y)的 右下方的元素和的奇偶性
分析
• 水平离散化 • 从左到右扫描, 利用”区间并的长度” • 时间复杂度: O(nlogn)
例题2. 动态区间k大数
• 维护一个数组A[1…n] • 实现两个操作
– Modify(i,j), 设A[i] = j – Query(i,j,k), 返回A[i..j]第k大元素
分析
• 首先考虑没有修改的情形 • 预处理:建立线段树,每个线段保存该区 间内元素排序好的序列 • 查询Query(i,j,k)
线段树及其应用
刘汝佳
目录
• • • • 线段树的定义 动态统计问题I 动态统计问题II 动态统计问题III
线段树的定义
• 线段[1, 9]的线段树和[2, 8]的分解
1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 8 9
• 由于ADD操作和问题II一样, 这里沿用它的 ADD实现, 那SUM怎么办?
SUM的实现
• 前面曾经提到, 区间统计的一般做法是把查 询区间进行分解, 一一统计然后加起来 • 在本题中,需要计算每个原子区间的数之 和. 它们的和是多少呢? 这取决于有多少 ADD操作影响到它 • 回忆: 任何两个树中区间要么相互包含要么 没有公共部分. 因此影响一个原子区间的 ADD操作都是它的直接祖先和后代
• 附加信息: s(p)表示结点p所代表区间内所有 元素之和 • 维护算法
– ADD: 给i对应结点的所有直系祖先s值增加k – SUM: 做区间分解, 把对应结点的s值相加
问题2. 动态统计问题II
• 包含n个元素的数组A
– ADD(i, j, k): 给A[i], A[i+1], … A[j]均增加k – QUERY(i): 求A[i]
问题5. 区间并的长度
• 实现一个区间集合
– Add(x, y): 增加区间[x, y] (1<=x<y<=n) – Delete(x, y): 删除区间[x, y] – Total: 区间并的长度(即被至少一个区间覆盖到 的总长度) – 约定: 删除的区间[x, y]一定是以前插入过 – (保证存在)
问题3. 动态统计问题III
• 包含n个元素的数组A
– ADD(i, j, k): 给A[i], A[i+1], … A[j]均增加k – SUM(p, q): 求A[p]+A[p+1]+…+A[q]
• 显然动态统计问题I和II都是它的特殊情况
– 问题I中, ADD操作的i=j – 问题II中, SUM操作的p=q
• 先看看是否可以沿用刚才的附加信息
– QUERY(i)就是读取i对应的结点上的s值 – ADD呢? 极端情况下, 如果是修改整个区间, 则 所有结点都需要修改!
• 需要新的附加信息
新的附加信息
• Lazy思想: 记录有哪些指令, 而不真正执行 它们. 等到需要计算的时候再说 • 假设结点p对应的区间是[i, j], a(p)表示所有 形如ADD(i, j, k)的所有k之和
基本算法
• 找点: 根据定义,从根一直走到叶子logL • 区间分解: 兵分两路 [1,9]
– 每层最多两个区间 – 总时间4log2L
[1,4] [1,2] 1 2 [3,4] 3 4 [5,9] [5,6] 5 6 [7,9] 7 [8,9] 8 9
线段树的关键
• 用线段树解题的关键
– 得到讨论区间(可能要先离散化) – 设计区间附加信息和维护/统计算法
分析
• 对行集合建立线段树,区间[i,j]保存内部的 黑白连通块个数以及第i行和第j行每个格子 所属于的连通块编号 • 由[i,mid]和[mid+1,j]可以合并成为[i,j],时间 为O(n)(对交界线进行合并操作,修改内 部连通块个数) • 根据指令(x,y)所在行修改叶子区间,并往上 递推。最多修改logn个区间,因此每次操作 时间复杂度为O(nlogn)
• 至此, 算法轮廓已经出来
– 再附加一个sa(p), 表示以p为根的子树所有结点 的a值之和 – ADD: 区间分解后除了修改各原子区间的a值外, 还要沿途修改sa值 – SUM: 在区间分解的同时统计经过的a值, 然后 把原子区间的sa值累加进来
• 两个操作均为O(logn)
问题4. 动态区间最小值
• 线段树自身没有任何数据, 不像BST一样有 一个序关系 • 警告: 想清楚附加信息的准确含义, 不能有 半点含糊! • 建议: 先设计便于解题的附加信息,如果难 以维护就加以修改
问题1. 动态统计问题I
• 包含n个元素的数组A
– ADD(i, k): 设A[i] = A[i] + k – SUM(p, q): 求A[p]+A[p+1]+…+A[q]
例题4. 01矩阵
• 给n*n的01矩阵,支持
– C(x0,y0,x1,y1):改变矩形(每个元素取反) – Q(x,y):查询(x,y)的值
分析
• 构造辅助01矩阵C’,初始为0 • 矩形分解: C(x0,y0,x1,y1)
– C’(x0,y0) – C’(x0,y1) – C’(x1,y0) – C’(x1,y1) – 改变此4点的值(取反)
– 初始为空时进行Add(1, n), 则树中所有结点对 应的l(p)都应被修改! – 怎么办? 修改l(p)的定义
