岩土弹塑性物理力学参数
常用地岩土和岩石物理力学全参数

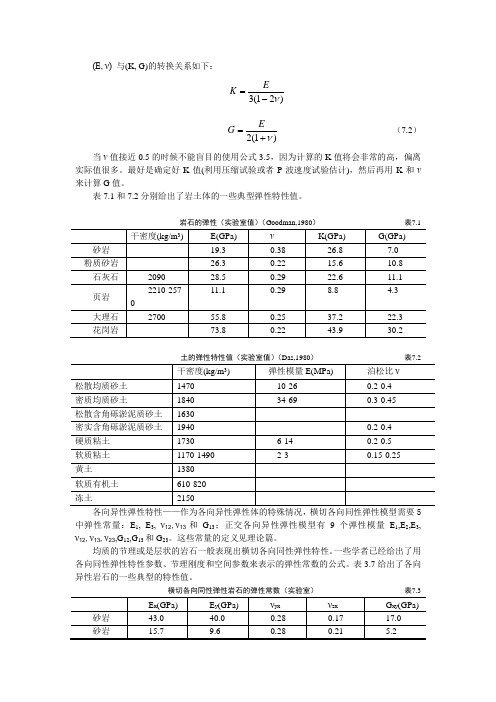
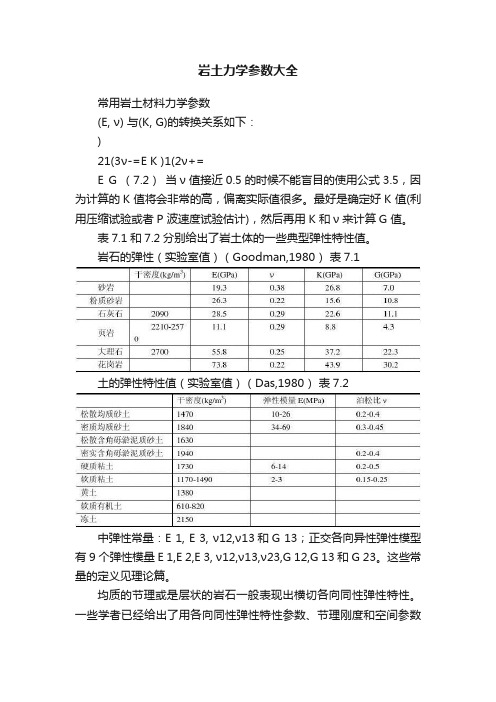
(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
常用岩土材料参数和岩石物理力学性质一览表
(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
岩土力学参数大全
常用岩土材料力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.37.3 固有的强度特性在FLAC 3D 中,描述材料破坏的基本准则是摩尔-库仑准则,这一准则把剪切破坏面看作直线破坏面:s 13N f φσσ=-+ (7.7)其中 )sin 1/()sin 1(N φφφ-+=1σ——最大主应力 (压缩应力为负);3σ——最小主应力φ——摩擦角c ——粘聚力当0f s <时进入剪切屈服。
这里的两个强度常数φ和c 是由实验室的三轴实验获得的。
当主应力变为拉力时,摩尔-库仑准则就将失去其物理意义。
简单情况下,当表面的在拉应力区域发展到3σ等于单轴抗拉强度的点时,tσ ,这个次主应力不会达到拉伸强度—例如;t 3t f σσ-= (7.8)当0f t >时进入拉伸屈服。
岩石和混凝土的抗拉强度通常有由西实验获得。
岩土体物理力学参数

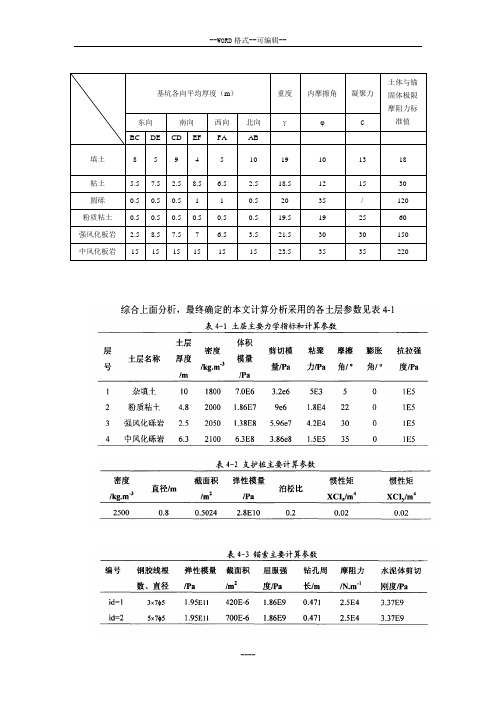
岩土体物理力学参数在边坡稳定性定量分析中,岩土体的物理力学参数往往直接控制着稳定系数和支护工程量。
常规的获取参数的方法主要有试验法、经验法、工程地质类比法、反演分析法等。
此外,当边坡稳定受成组结构面和岩桥共同控制时,仍常采用结构面连通率,即采用结构面和岩桥强度进行加权平均来求取潜在滑移面的综合抗剪强度。
以下对两种参数获取方法进行简单介绍。
1.试验法试验法一般可分为室内试验和现场试验两类。
现场试验试件尺寸一般较大,多为(50~70)cm×(50~70)cm,它能保持岩土体的原始状态,并能反映结构面二、三级起伏差对强度的影响,但加工困难,周期长,试验费用相对较高。
室内试验试件一般较小,多为扰动样,存在尺寸效应问题,但取样简单,可以开展各种不同工况下的试验,如三轴直剪试验、饱和固结快剪试验、饱和固结排水剪试验、慢剪试验等。
室内试验由于试验周期短,费用相对较低,可以大量开展。
目前,随着取样技术的发展,已具备取原状样的条件,且可在刚性伺服机上开展试验,能有效地确定有效正应力,控制剪切速度,试验成果较为真实可靠。
2.经验估算法可根据一些经验公式,如利用Hoek-Brown强度准则确定岩体的综合抗剪强度。
一般是在工程前期和缺乏试验的地区应用,该方法存在的问题是岩石强度权重偏大,应用在坚硬和极坚硬岩石中时,确定的抗剪强度常常偏高。
8.5.2 选择原则对于一些不重要或者工程前期缺乏试验资料的边坡,可通过经验法和工程地质类比法,初步确定岩土体的物理力学参数,以此估算边坡的稳定性和支护工程量。
对于一些已经失稳或正在变形的边坡,采用反演分析法来获取岩土体的物理力学参数是一种最有效的办法,但由于此时的抗剪强度已不是常规物理意义上的抗剪强度,而是岩土体抗剪强度参数、边界条件、地下水条件等因素的综合反映,因此,在应用时应严格注意条件的相似性。
同时,应考虑在工程有效期内工作条件的可能变化趋势对强度参数的影响,并适当进行调整。
岩土力学参数大全
岩土力学参数大全常用岩土材料力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=E K )1(2ν+=E G (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980)表7.1土的弹性特性值(实验室值)(Das,1980)表7.2中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室)表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,? tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK n t ∝? (7.3)对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f 'K n m k C +=νν (7.4)其中3/4G K 1m +=ν f 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒)f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102?)减少,利用上面得表达式看看其产生的误差。
常用的岩土和岩石物理力学参数
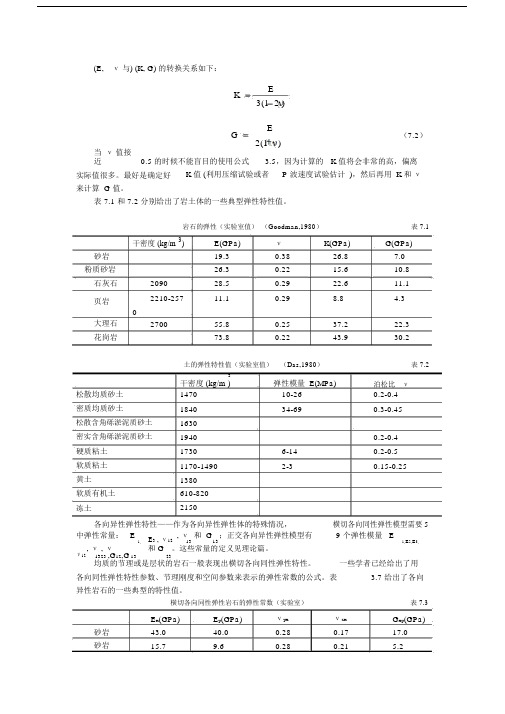
(E, ν与) (K, G) 的转换关系如下:KE3(1 2 )GE(7.2)2(1 )当 ν值接近0.5 的时候不能盲目的使用公式 3.5,因为计算的 K 值将会非常的高,偏离实际值很多。
最好是确定好K 值 (利用压缩试验或者P 波速度试验估计 ),然后再用 K 和 ν来计算 G 值。
表 7.1 和 7.2 分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值) (Goodman,1980) 表 7.1干密度 (kg/m 3)E(GPa) ν K(GPa)G(GPa)砂岩 19.3 0.38 26.8 7.0 粉质砂岩26.30.22 15.6 10.8石灰石 2090 28.5 0.29 22.6 11.1页岩 2210-25711.10.298.84.3大理石 270055.8 0.25 37.2 22.3花岗岩73.80.2243.930.2土的弹性特性值(实验室值) (Das,1980)表 7.2松散均质砂土 密质均质砂土松散含角砾淤泥质砂土 密实含角砾淤泥质砂土硬质粘土 软质粘土 黄土软质有机土冻土3弹性模量 E(MPa)泊松比 ν 干密度 (kg/m ) 1470 10-260.2-0.41840 34-690.3-0.45163019400.2-0.41730 6-14 0.2-0.5 1170-1490 2-30.15-0.251380610-820 2150各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5 中弹性常量: E E 3 , ν12 , ν 和 G 13 ;正交各向异性弹性模型有9 个弹性模量 E1, 131,E 2,E 3,ν12 , ν , ν 和 G 23。
这些常量的定义见理论篇。
1323 ,G 12,G 13均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
岩土力学重要参数取值大全
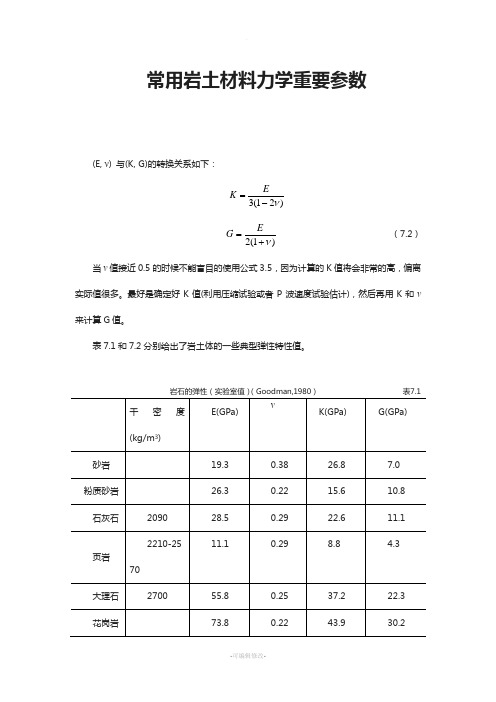
常用岩土材料力学重要参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E1, E3,ν12,ν13和G13;正交各向异性弹性模型有9个弹性模量E1,E2,E3,ν12,ν13,ν23,G12,G13和G23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f k K nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
常用的岩土和岩石物理力学参数

(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3砂岩 15.7 9.6 0.28 0.21 5.2 石灰石 39.8 36.0 0.18 0.25 14.5 页岩 66.8 49.5 0.17 0.21 25.3 大理石 68.6 50.2 0.06 0.22 26.6 花岗岩10.75.20.200.411.2流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D中用到的流动时间步长, tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
岩土主要物理力学指标参考值

岩土主要物理力学指标参考值
1、稳定性指标参考值:
1.1压缩模量:水泥改良的砂、砾状粘结土的压缩模量一般在100-
500kPa,粉状粘结土的压缩模量在200-1000kPa,蠕变模量在101-500kPa。
1.2抗拉强度:水泥改良的砂、砾状粘结土的抗拉强度一般在0.1-
2.0kPa,粉状粘结土的抗拉强度在0.2-4.0kPa,蠕变强度在0.3-5.0kPa。
1.3抗剪强度:水泥改良的砂、砾状粘结土的抗剪强度一般在0.1-
2.5kPa,粉状粘结土的抗剪强度一般在0.2-7.0kPa,蠕变强度一般在
0.4-7.5kPa。
1.4抗冲击强度:水泥改良的砂、砾状粘结土的抗冲击强度一般在
0.1-2.5kPa,粉状粘结土的抗冲击强度一般在0.2-7.0kPa,蠕变强度一
般在0.3-8.0kPa。
2、抗损伤指标参考值:
2.1抗湿胀系数:水泥改良的砂、砾状粘结土的抗湿胀系数一般在
0.1-2.5,粉状粘结土的抗湿胀系数一般在0.2-5.0,蠕变系数一般在
0.3-6.0。
2.2抗冻结强度:水泥改良的砂、砾状粘结土的抗冻结强度一般在
0.1-2.5MPa,粉状粘结土的抗冻结强度一般在0.2-7.0MPa,蠕变强度一
般在0.4-7.5MPa。
2.3抗集水能力:水泥改良的砂、砾状粘结土的抗集水能力一般在
0.2-1.5kPa,粉状粘结土的抗集水能力一般在0.4-3.0kPa。
岩土主要物理力学指标参考值
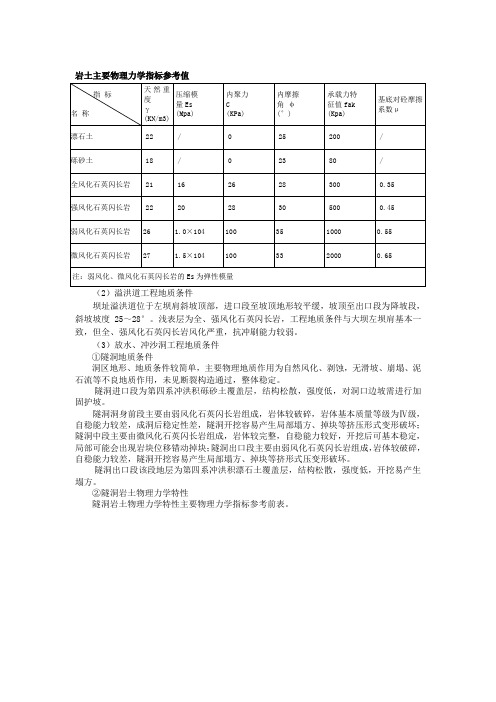
岩土主要物理力学指标参考值(2)溢洪道工程地质条件坝址溢洪道位于左坝肩斜坡顶部,进口段至坡顶地形较平缓,坡顶至出口段为降坡段,斜坡坡度25~28°。
浅表层为全、强风化石英闪长岩,工程地质条件与大坝左坝肩基本一致,但全、强风化石英闪长岩风化严重,抗冲刷能力较弱。
(3)放水、冲沙洞工程地质条件①隧洞地质条件洞区地形、地质条件较简单,主要物理地质作用为自然风化、剥蚀,无滑坡、崩塌、泥石流等不良地质作用,未见断裂构造通过,整体稳定。
隧洞进口段为第四系冲洪积砾砂土覆盖层,结构松散,强度低,对洞口边坡需进行加固护坡。
隧洞洞身前段主要由弱风化石英闪长岩组成,岩体较破碎,岩体基本质量等级为Ⅳ级,自稳能力较差,成洞后稳定性差,隧洞开挖容易产生局部塌方、掉块等挤压形式变形破坏;隧洞中段主要由微风化石英闪长岩组成,岩体较完整,自稳能力较好,开挖后可基本稳定,局部可能会出现岩块位移错动掉块;隧洞出口段主要由弱风化石英闪长岩组成,岩体较破碎,自稳能力较差,隧洞开挖容易产生局部塌方、掉块等挤形式压变形破坏。
隧洞出口段该段地层为第四系冲洪积漂石土覆盖层,结构松散,强度低,开挖易产生塌方。
②隧洞岩土物理力学特性隧洞岩土物理力学特性主要物理力学指标参考前表。
工程岩体分级标准(上)2010-04-15 | 作者:| 来源:中国地质环境信息网| 【大中小】【打印】【关闭】1 总则1.0.1 为建立统一的评价工程岩体稳定性的分级方法;为岩石工程建设的勘察、设计、施工和编制定额提供必要的基本依据,制定本标准。
1.0.2 本标准适用于各类型岩石工程的岩体分级。
1.0.3 工程岩体分级,应采用定性与定量相结合的方法,并分两步进行,先确定岩体基本质量,再结合具体工程的特点确定岩体级别。
1.0.4 工程岩体分级所必需的地质调查和岩石试验,除应符合本标准外,尚应符合有关现行国家标准的规定。
2 术语、符号2.l 术语2.1.1 岩石工程rock engineering以岩体为工程建筑物地甚或环境,并对岩体进行开挖或加固的工程,包括地下工程和地面工程。
关于常用的岩土和岩石物理力学参数
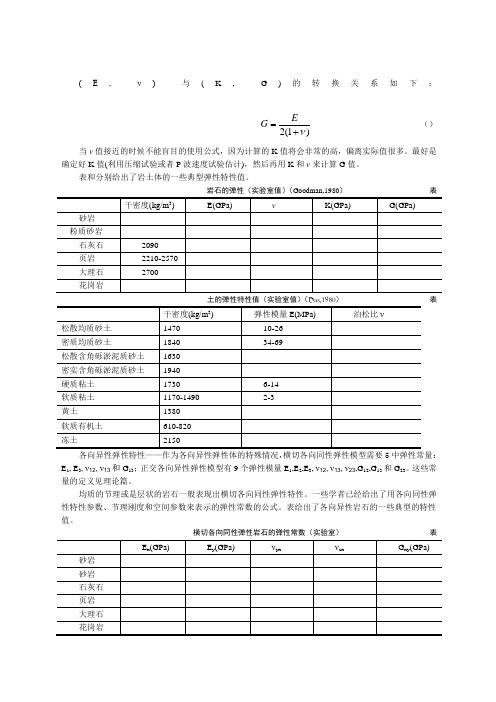
(E , ν) 与(K , G )的转换关系如下:)1(2ν+=EG ()当ν值接近的时候不能盲目的使用公式,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表和分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表土的弹性特性值(实验室值)(Das,1980) 表各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,? tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f k K nt ∝∆ () 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K n m k C +=νν ()其中其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
常用的岩土和岩石物理力学参数
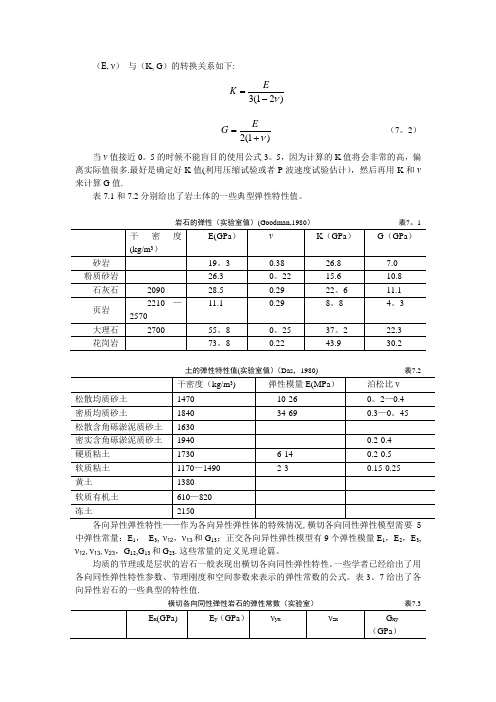
(E, ν) 与(K, G )的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7。
2)当ν值接近0。
5的时候不能盲目的使用公式3。
5,因为计算的K 值将会非常的高,偏离实际值很多.最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值.表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7。
1土的弹性特性值(实验室值)(Das ,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23.这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3。
7给出了各向异性岩石的一些典型的特性值.横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性—-用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa.其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减.这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7。
3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K n m k C +=νν (7。
岩土力学重要参数取值大全
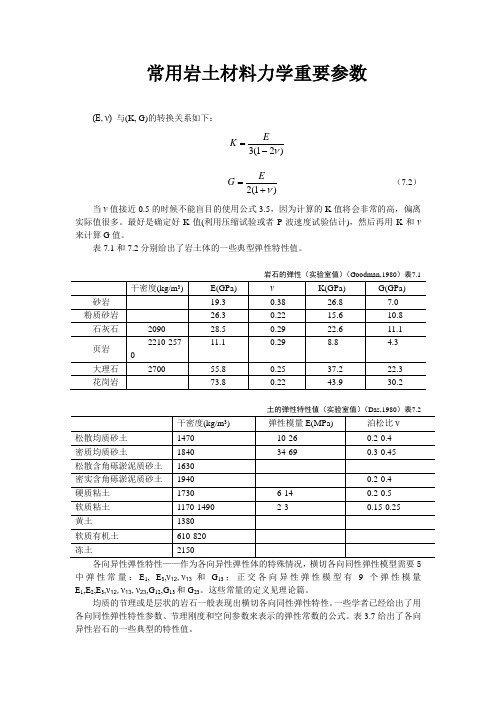
常用岩土材料力学重要参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=E K )1(2ν+=E G (7.2) 当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980)表7.1土的弹性特性值(实验室值)(Das,1980)表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3,ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3,ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室)表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK n t ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f 'K n m k C +=νν(7.4)其中3/4G K 1m +=ν f 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数 k ——渗透系数,单位和速度单位一样(如米/秒)f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
常用岩土材料参数和岩石物理力学性质一览表
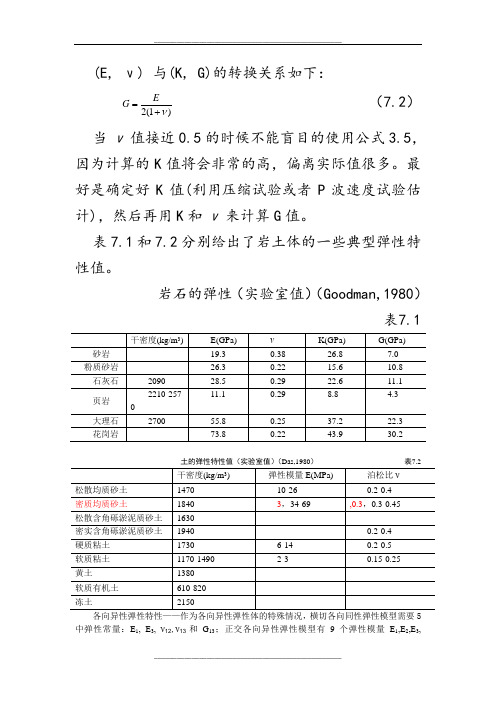
(E, ν) 与(K, G)的转换关系如下:)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980)表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3,ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
岩土的物理力学性质指标

岩土的物理力学性质指标岩土的物理力学性质指标是边坡的稳定性计算的基本参数和重要依据。
应根据工程地质划分的扇形区及各区的边坡变形破坏特点,选取与之有关的试样进行力学试验,测定岩石及软弱夹层物理力学性质指标。
岩石及软弱夹层的物理性质指标详见表1至表7。
表2 部分岩石的孔隙率与吸水率岩石名称孔隙率n (%)吸水率^(%)变化范围平均值H-R UJ-J U-J 花冈石流纹斑岩闪长岩正长岩安山岩玄武岩辉绿岩霏细岩凝灰岩火山角砾岩安山凝灰集块岩砾岩砂岩砂岩(第三纪)砂岩(白垩纪)砂岩(侏罗纪)砂岩(三迭纪)砂岩新鲜的风化的石英砂岩0.04 〜2.801.10 〜3.400.25 〜3.00—0.29 〜1.131.10 〜4.301.00 〜2.200.29 〜5.101.59 〜2.230.90 〜7.540.40 〜4.102.00 〜5.101.04 〜9.305.00 〜20.002.20〜42.007.20〜37.704.20〜24.600.60 〜27.70—0.952.001.252.540.702.301.702.201.803.202.103.205.0413.0015.3017.1013.2019.3021.112.260.10 〜1.700.14 〜1.650.18 〜1.000.48—0.20 〜1.000.30 〜0.800.20 〜1.000.18 〜0.350.34 〜2.120.14 〜4.000.40 〜1.000.14 〜4.101.00 〜9.00—————石英砂岩新鲜的风化的页岩砂质页岩泥质页岩煤质页岩泥灰岩石灰石石灰岩(第三纪)石灰岩(中生代)石灰岩(古生代)白垩石膏硬石膏片麻岩大理岩白云岩石英岩石英片岩角闪石片岩云母片岩绿泥石片岩千枚岩——0.70 〜7.000.80 〜4.15——1.00 〜52.000.53 〜27.00—1.20 〜26.500.80 〜27.005.00 〜58.000.10 〜4.000.63 〜6.260.30 〜2.400.10 〜6.000.30 〜25.000.00 〜8.701.53 〜2.80—1.714.91——1.35I.0318.0012.0020.00II.6512.0026.401.701.651.351.007.702.402.002.960.792.103.60——2.30 〜6.00———1.00—5.000.20 〜6.40——————0.14 〜0.30——0.02 〜0.280.10〜0.300.110.08 〜0.420.55〜1.12表3 不同成因粘土的有关物理力学性质指标(一)表4 不同成因粘土的有关物理力学性质指标(二)表5 几种土的渗透系数表表6 土的平均物理、力学性质指标(一)表7 土的平均物理、力学性质指标(二)注:1.平均比重取:砂为2.65;轻亚粘土为2.70;亚粘土为2.71 ;粘土2.74。
常用的岩土和岩石物理力学参数

(E, ν) 与(K, G )的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7。
2)当ν值接近0。
5的时候不能盲目的使用公式3。
5,因为计算的K 值将会非常的高,偏离实际值很多.最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值.表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7。
1土的弹性特性值(实验室值)(Das ,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23.这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3。
7给出了各向异性岩石的一些典型的特性值.横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性—-用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa.其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减.这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7。
3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K n m k C +=νν (7。
岩土弹塑性力学

J216
(xy)2(yz)2(zx)26(x2yy2zz2x)
16 (xy)2(yz)2(zx)2 12SijSij
〔八面体
J3SxSySz2xyyzzxSxy2zSyz2xSzx2yS1S2S3剪〔应与力剪倍应数〕
力方向有关〕
在岩土塑性理论中,常用I1、J2、J3表示一点的 应力状态
27
q 应力张量分解及其不变量
Ø 理论、试验及工程实践相结合,通过试验确定屈服条 件及其参数,以提供客观与符合实际的力学参数
Ø 建立复杂加荷条件下、各向异性情况下、动力加荷 以及非饱和土情况下的各类实用模型
Ø 引入损伤力学、不连续介质力学、智能算法等新理 论,宏细观结合,开创土的新一代结构性本构模型
Ø 岩土材料的稳定性、应变软化、损伤、应变局部化
采用真三轴仪,通过改 变 1、 3的比值,在 改变 2试验直至破坏, 可得到不同的 与r 值,即能给出偏 平面上的破坏曲线
三轴压缩
三轴拉伸
偏平面上的应力路径
38
q 应变张量的分解
=
+
立方体变形
纯体积变形
纯畸变变形
x ij 1 2 yx
1 2 xy
y
1 2
1 2
x z m y z 0
F(ij) 0 或 F(ij) 0 均质各向同性,不考虑应力主轴旋转时
F (1 ,2 ,3 ) F 1 ( I 1 , J 2 , J 3 ) F 2 ( p , q , ) 0
47
q 基本概念
传统塑性力学中与I1无关
F ( 1 ,2 ,3 ) F 1 ( J 2 , J 3 ) F 2 ( q ,) F 3 ( J 2 ,) 0
Ø 不同加荷方式的应力路径
新编[物理]岩土主要物理力学指标参考值
![新编[物理]岩土主要物理力学指标参考值](https://img.taocdn.com/s3/m/896dcb66fe4733687e21aa9e.png)
岩土主要物理力学指标参考值(2)溢洪道工程地质条件坝址溢洪道位于左坝肩斜坡顶部,进口段至坡顶地形较平缓,坡顶至出口段为降坡段,斜坡坡度25~28°。
浅表层为全、强风化石英闪长岩,工程地质条件与大坝左坝肩基本一致,但全、强风化石英闪长岩风化严重,抗冲刷能力较弱。
(3)放水、冲沙洞工程地质条件①隧洞地质条件洞区地形、地质条件较简单,主要物理地质作用为自然风化、剥蚀,无滑坡、崩塌、泥石流等不良地质作用,未见断裂构造通过,整体稳定。
隧洞进口段为第四系冲洪积砾砂土覆盖层,结构松散,强度低,对洞口边坡需进行加固护坡。
隧洞洞身前段主要由弱风化石英闪长岩组成,岩体较破碎,岩体基本质量等级为Ⅳ级,自稳能力较差,成洞后稳定性差,隧洞开挖容易产生局部塌方、掉块等挤压形式变形破坏;隧洞中段主要由微风化石英闪长岩组成,岩体较完整,自稳能力较好,开挖后可基本稳定,局部可能会出现岩块位移错动掉块;隧洞出口段主要由弱风化石英闪长岩组成,岩体较破碎,自稳能力较差,隧洞开挖容易产生局部塌方、掉块等挤形式压变形破坏。
隧洞出口段该段地层为第四系冲洪积漂石土覆盖层,结构松散,强度低,开挖易产生塌方。
②隧洞岩土物理力学特性隧洞岩土物理力学特性主要物理力学指标参考前表。
工程岩体分级标准(上)2010-04-15 | 作者:| 来源:中国地质环境信息网| 【大中小】【打印】【关闭】1 总则1.0.1 为建立统一的评价工程岩体稳定性的分级方法;为岩石工程建设的勘察、设计、施工和编制定额提供必要的基本依据,制定本标准。
1.0.2 本标准适用于各类型岩石工程的岩体分级。
1.0.3 工程岩体分级,应采用定性与定量相结合的方法,并分两步进行,先确定岩体基本质量,再结合具体工程的特点确定岩体级别。
1.0.4 工程岩体分级所必需的地质调查和岩石试验,除应符合本标准外,尚应符合有关现行国家标准的规定。
2 术语、符号2.l 术语2.1.1 岩石工程rock engineering以岩体为工程建筑物地甚或环境,并对岩体进行开挖或加固的工程,包括地下工程和地面工程。
岩土物理力学性质指标

1、塑性指数plasticity index塑性指数是液限和塑限之差称为塑性指数,用不带百分号的小数表示,符号为IP。
概述塑性是表征细粒土物理性能一个重要特征,一般用塑性指数来表示;液限与塑限的差值称为塑性指数IP,即IP=WL-WP。
过去的研究表明,细粒土的许多力学特性和变形参数均与塑性指数有密切的关系。
特征塑性指数可塑性是粘性土区别于砂土的重要特征。
可塑性的大小用土处在塑性状态的含水量变化范围来衡量,粘性土由一种状态过渡到另一种状态的分界含水量叫作界限含水量,也称为阿太堡界限,有缩限含水量、塑限含水量、液(流)限含水量、粘限含水量、浮限含水量五种,在建筑工程中常用前三种含水量。
固态与半固态间的界限含水量称为缩限含水量,简称缩限,用ω表示。
半固态与可塑状态间的含水量称为塑限含水量,简称塑限,用ωp表示。
可塑状态与流动状态间的含水量称为液(流)限含水量,简称液限,用ωl表示。
含水量用百分数表示。
天然含水量大于液限时土体处于流动状态;天然含水量小于缩限时,土体处于固态;天然含水量大于缩限小于塑限时,土体处于半固态;天然含水量大于塑限小于液限时,土体处于可塑状态。
塑性指数习惯上用不带%的数值表示。
塑性指数是粘土的最基本、最重要的物理指标之一,它综合地反映了粘土的物质组成,广泛应用于土的分类和评价。
因素由于塑性指数在一定程度上综合反映了影响粘性土特征的各种重要因素。
塑性指数愈大,表明土的颗粒愈细,比表面积愈大,土的粘粒或亲水矿物(如蒙脱石)含量愈高,土处在可塑状态的含水量变化范围就愈大。
也就是说塑性指数能综合地反映土的矿物成分和颗粒大小的影响。
因此,在工程上常按塑性指数对黏性土进行分类。
粉土为塑性指数小于等于10且粒径大于0.075的颗粒含量不超过总质量50%的土;黏性土为塑性指数大于10且粒径大于0.075的颗粒含量不超过总质量50%的土,其中:Ip>17 黏土Ip>10 粉质黏土Ip<10或Ip=10 粉土对黏性土来说,有一个指标叫液性指数,是判断土的软硬状态,表示天然含水率与界限含水率相对关系的指标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
