最新空间与图形复习题及答案
新人教版六年级下册数学总复习专题五――空间与图形的试题及答案个人整理

创新与拓展: 通过解决开放 性问题,激发 学生的创新思 维和拓展学生 的解题思路。
实际应用举例
建筑设计:利用空间与图形知识进行建筑设计和规划,确保建筑物的安全 性和美观性。
机械制造:在制造和设计机械零件时,需要运用空间与图形的知识来确保 零件的精确度和稳定性。
航天科技:在航天领域中,空间与图形的知识是必不可少的,如卫星轨道 的设计、航天器的定位等。
01
添加章节标题
空间与图形试题回
02
顾
回顾各类题型
填空题:考察学 生对空间与图形 基本概念和性质 的掌握情况。
选择题:测试学 生对空间与图形 相关问题的判断 和推理能力。
计算题:要求学 生运用几何知识 进行计算和证明, 考察学生的计算 能力和对几何图 形的理解。
作图题:要求学 生根据题意绘制 图形,考察学生 的空间想象能力 和作图技能。
答案解析的要点:强调了解题的关键点和易错点,帮助学生避免常见错误,提高解题的准确性 和效率。
答案解析的深度:对每个答案进行了深入的剖析和解释,不仅提供了正确的答案,还解释了为 什么这样做,以及如何理解和应用相关知识。
答案解析的全面性:涵盖了新人教版六年级下册数学总复习专题五――空间与图形的所有试题, 确保学生能够全面掌握相关知识和技能。
答案:192
题目:一个正方体的棱长是4厘米,它的表面积是多 少平方厘米. 答案:96
答案:96
YOUR LOGO
T:在地理信息系统中,空间与图形知识用于地图制作、地理 数据的分析和可视化等。
综合题解析练习
题目:一个长方体的体积是45立方分米,它的底 面积是9平方分米,它的高是多少分米? 答案:5 答案:5
题目:一个正方体的棱长总和是48厘米,它的表面积 是多少平方厘米. 答案:96
四年级数学空间与图形试题答案及解析

四年级数学空间与图形试题答案及解析1.边长是4米的正方形,它的周长和面积相等。
( )【答案】×【解析】解:周长和面积的单位不同,不能比较大小。
2.画一条线段,将下面的梯形分割成一个平行四边形和一个三角形.【答案】【解析】经过梯形的上底的顶点,画出梯形的一条腰的平行线,即可把梯形分成一个三角形和一个平行四边形;据此即可画图;据此解答.解:如图:【点评】此题考查了梯形、三角形、平行四边形的特征及性质,应灵活运用.3.直线端点,射线有个端点,线段有个端点.【答案】无,一,两【解析】根据直线、线段、射线的定义解答即可.解:直线无端点,射线有一个端点,线段有两个端点;故答案为:无,一,两.【点评】本题考查直线、线段、射线的知识,属于基础题,注意基本概念的掌握.4. 1周角= 平角= 直角.【答案】2,4.【解析】根据周角、平角、直角的定义可知,1周角=360°,1平角=180°,1直角=90°.根据度数关系,找倍数关系.解:因为1周角=360°,1平角=180°,1直角=90°,所以1周角=2平角=4直角.故答案为:2,4.【点评】本题主要考查周角和平角.直角的定义,是需要熟记的内容.5.每天下午的时候,钟面上时针和分针基本上在一条直线上.①3时整②3时30分③3时50分.【答案】③【解析】首先判断出钟表上一共有12个大格,每个大格是30°,然后判断出每个时刻时针和分针之间相差的大格数,求出时针与分针所成的角各是多少度,即可推得每天下午几时几分的时候,钟面上时针和分针基本上在一条直线上.解:每天下午3时整的时候,时针指向数字3,分针指向数字12,钟面上时针和分针所成的角是90°;每天下午3时30分的时候,时针和分针之间相差2.5个大格,钟面上时针和分针所成的角是:30°×2.5=75°每天下午3时50分的时候,时针和分针之间相差6个大格,钟面上时针和分针所成的角是:30°×6=185°所以每天下午3时50分的时候,钟面上时针和分针基本上在一条直线上.故选:③.【点评】解答此题的关键是分别求出每个时刻下时针与分针所成的角各是多少度.6.如果直线a与直线b平行,那么a是平行线.(判断对错)【答案】×【解析】根据平行的含义:在同一个平面内的不相交的两条直线,叫做平行线;由此可知:只能说一条直线是另一条直线的平行线;据此解答即可.解:由平行的含义可知:如果直线a与直线b平行,那么a是平行线,说法错误;因为a是b的平行线;故答案为:×.【点评】明确平行的含义是解答此题的关键.7.先判断下列图形哪些是轴对称图形,再画出下面轴对称图形的对称轴,能画几条就画几条【答案】【解析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可.解:【点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.8.小猴要给一块地围上篱笆,你认为()的围法更牢固些.A. B. C.【答案】B【解析】紧扣三角形具有稳定性的性质,即可选择正确答案.解:A和C中,围成的图形为四边形,而四边形有容易变形的特点,B中,围成的图形为三角形,三角形具有稳定性,所以B的围法更牢固些.故选:B.【点评】此题考查了三角形的稳定性.9.在同一平面内,( ) 的两条直线叫做平行线.两条直线相交,如果其中一个角是90°,那么这两条直线叫做( )【答案】不相交,相互垂直。
四年级数学空间与图形试题答案及解析

四年级数学空间与图形试题答案及解析1.请用作垂线和平行线的方法:①画一个长3厘米,宽2厘米的长方形.②画一个长4厘米,高2厘米的平行四边形.【答案】①.②.【解析】①长方形特征:长方形的对边相等,四个角都是直角.首先用三角板画一条3厘米的线段,三角板不动,再用另一三角板的一直角边靠着这块三角板,另一条边上下滑动,过3厘米线段的两个端点分别画两条2厘米的垂线段,再连接这两条线段的另外两点,即可画出一个长3厘米,宽2厘米的长方形.②首先作一条2厘米的线段,再分别过这条线段的两个端点作一组平行线,并分别在这组平行线上截取4厘米长的线段;然后连接这两条线段的另外两点,即可画出一个长4厘米,高2厘米的平行四边形.解:根据分析,可得①.②.【点评】此题主要考查了画指定长、宽的长方形的方法,以及画指定底、高的平行四边形,要熟练掌握.2.一个平角减去一个钝角的差一定是一个锐角.(判断对错)【答案】√【解析】依据角的定义及分类即可判断.解:因为平角是180°,钝角大于90°,平角减钝角,差小于90°,即为锐角.故答案为:√.【点评】此题主要考查角的概念及分类,弄清各类角的度数即可判断.3.一条直线长6厘米,它的一半是3厘米..(判断对错)【答案】×【解析】根据题意知道,一条直线长6厘米是错误,因为直线是无限长的,没有具体长度,而说成有长度.据此判断.解:一条直线长6厘米,它的一半是3厘米,是错误的,因为直线是无限的.故答案为:×【点评】考查了认识直线的性质,要注意是直线,不是线段.4.以一点为端点,可以作出()A.一条射线 B.两条射线 C.无数条射线【答案】C【解析】根据射线的特点:有一个端点,无限长;可以得出由一点可以引出无数条射线,由此解答即可.解:以一点为端点,可以作出无数条射线;故选:C.【点评】此题考查了射线的特点.5.把你学过的角按从小到大的顺序排列..【答案】锐角<直角<钝角<平角<周角【解析】根据角的含义:大于0°、小于90°的角叫做锐角;等于90°的角,叫做直角;大于90°、小于180°的角叫做钝角;平角等于180°;周角等于360°;根据题意进行排列即可.解:由分析可得:锐角<直角<钝角<平角<周角;故答案为:锐角<直角<钝角<平角<周角.【点评】此题应根据各种角的定义进行分析、解答.6.经过两点可以画条直线,梯形有条高.【答案】一条,无数【解析】(1)根据直线的性质:两点确定一条直线;解答即可;(2)梯形的上、下底平行,梯形的高是两平行边之间的距离,有无数条.解:根据直线的性质,经过两点可以画一条直线,梯形有无数条高;故答案为:一条,无数.【点评】本题主要考查了直线的性质和梯形的特征.7.钟面2:00时,时针和分针形成的角是度,它是角,时整,时针和分针形成的是直角,5:00时,时针和分针形成的角是度,它是角.【答案】60、锐、3或9、150、钝.【解析】(1)因为钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°;当面上2时整,时针与分针之间有2个大格是60°,是锐角;据此解答即可;(2)钟表上共有12个大空格,每个空格是30°,90°的角需要分针与时针之间有3个空格,在3点或9点的时间恰好成90°;(3)钟面上被分成了12个大格,每格是360°÷12=30°,在5点时,分针指向12,时针指向5,分针与时针相差5格,它们之间的夹角是30°×5=150°,进而根据钝角的含义“大于90度小于180度的角是钝角”解答即可.解:钟面2:00时,时针和分针形成的角是 60度,它是锐角,3或9时整,时针和分针形成的是直角,5:00时,时针和分针形成的角是 150度,它是钝角;故答案为:60、锐、3或9、150、钝.【点评】解答此题应结合题意,根据角的概念和分类进行解答.在学习角的时候,渗透了钟表的认识,及两者的共性,时针和分针在旋转过程中组成的两个特殊角.一个两针互相垂直,一个两针成一直线.8.从直线外一点到直线的所有线段中,垂线段最短..(判断对错)【答案】√【解析】根据从直线外一点向直线所作的所有线段中,垂线段最短解答即可.解:因为从P点向已知直线所作的垂线段PC最短,所以原题说法正确.故答案为:√.【点评】此题主要考查垂线段的性质的灵活运用.9.平角是180度,它等于两个()A.锐角 B.直角 C.周角【答案】B【解析】根据直角、平角的含义解答:等于90°的角是直角;等于180°的角是平角;因为180÷90=2,所以一个平角等于两个直角;据此解答.解:180°÷90°=2(个),即一个平角等于两个直角;故选:B.【点评】此题应根据直角、平角的含义进行解答.10.一个三角形剪成两个小三角形,则每个小三角形的内角和是90°..(判断对错)【答案】×【解析】根据三角形的内角和是180度,把一个三角形分成两个小三角形,不管分成几个,只要是三角形,它的内角和就是180°;据此判断即可.解:根据三角形的内角和是180度,所以把一个三角形分成两个三角形,每个小三角形的内角和是90°,说法错误;故答案为:×.【点评】解答此题应明确:不管把一个三角形分成几个小三角形,只要是三角形,它的内角和就是180°.11.有四根分别为5厘米、6厘米、7厘米、11厘米的小棒,从中任意选三根小棒围成一个三角形,有()种不同的围法.A.4B.3C.2D.1【答案】B【解析】根据三角形边的特征,在三角形中任意两边之和大于第三边,由此解答.解:根据三角形的特性:任意两边之和大于第三边;可以组成的三角形有:①5厘米,6厘米,7厘米;②6厘米,7厘米,11厘米;③5厘米,7厘米,11厘米;所以一共可以拼成3个三角形;故选:B.【点评】此题考查了三角形的特性中的三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.12.画出下面三角形底边上的高.【答案】【解析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高(直角三角形一条直角边上的高就是另条直角边).解:画出下面三角形底边上的高:【点评】本题是考查作三角形的高.注意作高用虚线,并标出垂足.13.一个三角形∠A=30°,∠B=28°,求∠C的大小,并判断它是什么三角形.【答案】∠C是122度,它是一个钝角三角形.【解析】依据三角形的内角和是180°,已知∠A和∠B的度数,用180°减去∠A和∠B的度数即可得到∠C的度数,再根据最大角进行判断三角形的类型即可.解:∠C=180°﹣∠A﹣∠B=180°﹣30°﹣28°=150°﹣28°=122°因为∠C是钝角,所以这个三角形是钝角三角形.答:∠C是122度,它是一个钝角三角形.【点评】解答此题应明确三角形的内角和是180°,求出最大的角的度数,然后根据三角形的分类判定类型.14.仔细观察下面的物体,画出你从不同角度看到的形状.从正面看.从侧面看.从上面看.【答案】,,.【解析】这个立方体图形由两部分组成,左边2个相同的小正方体,右边3个同样的小正方体.从正面能看到5个正方形,左部分一行2个,右部分能看到3个正方形,分两行,下行3个,上行1个;从侧面只能看到一列2个正方形;从上面能看到4个正方形,左部分一行2个,右部分一行2个.解:仔细观察下面的物体,从不同角度看到的形状:从正面看从侧面看从上面看.故答案为:,,.【点评】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形.15.钝角三角形的内角和大于锐角三角形的内角和..(判断对错)【答案】×【解析】根据任何三角形内角和都是180°即可解决.解:因为任何三角形内角和都是180°,所以原题说法是错误的.故答案为:×.【点评】此题考查了三角形的内角和是180°.16.在同一平面内,( ) 的两条直线叫做平行线.两条直线相交,如果其中一个角是90°,那么这两条直线叫做( )【答案】不相交,相互垂直。
【苏教版】六年级数学《空间与图形》总复习指导及练习题

六年级数学《空间与图形》总复习指导及练习题一、整理复习图形特征这部分知识是按形状特征及一般图形与特殊图形的关系整理的,按“线—角—形”的线索进行。
1、直线、射线和线段。
【知识串联】小学数学里,把直的、有两个端点的线称为线段,线段向一端无限延长得到射线,向两端无限延长得到直线。
这些既是线段、射线、直线的概念,也是它们的关系。
同一平面内两条直线的位置关系有互相平行或相交,垂直是特殊的相交。
【试试身手】⑴把线段的一端无限延长,就得到一条();把它的两端无限延长,就得到一条()。
⑵()有两个端点,()有一个端点,()没有端点。
⑶()叫做平行线。
⑷从直线外的一点到这条直线的所有线段中()最短。
⑸如右图,过直线外的A点画已知直线的垂线和平行线。
⑹如图,小明和小华两家要各修一条小路与公路连通,要使这两条小路最短,应该怎样修,请你在图中画出来。
2、角。
【知识串联】从一点向不同方向画两条射线,组成的图形是角。
把一条射线绕它的端点旋转,能形成大大小小的角。
角从小到大地变化依次是锐角、直角、钝角、平角与周角。
直角的度数是90°,平角的度数是180°,周角的度数是360°。
【试试身手】⑴ 1平角=()直角, 1周角=()平角=()直角。
⑵钟面上分针1小时走过的角度是()度,时针1小时走过的角度是()度。
⑶ 3点时,钟面上的时针与分针间的夹角(较小角)是()度;9点30分时,钟面上的时针与分针间的夹角(较小角)是()度。
⑷用一幅三角板分别画出1350和150的角。
3、三角形、四边形和圆。
【知识串联】小学阶段学过的平面图形可以分成由线段围成的和由曲线围成的两类,由线段围成的图形按边的数量分成三角形、四边形,由曲线围成的图形是圆。
任意一个三角形中,两边之和大于第三边,内角和是180°,最多有一个直角(或钝角)。
三角形按角分为锐角三角形、直角三角形和钝角三角形,等腰三角形是特殊的三角形,等边三角形是特殊的等腰三角形。
三年级下册知识复习精选题—03《空间与图形》(解析版)人教版

人教版数学三升四暑期衔接—提优复习精选汇编题专训温故知新篇03《空间与图形》一.选择题1.(2020春•盐城期中)小新上学先向东,再向北,那么小新家在学校的()面.A.西南B.东北C.东南【解答】解:小新上学先向东,再向北,那么小新家在学校的西南面.故选:A.2.(2019春•荥阳市期末)三一班的黑板在教室的东面,讲课时老师面对着学生,老师的左面是()A.西B.南C.北【解答】解:三一班的黑板在教室的东面,讲课时老师面对着学生,老师的左面是南面.故选:B.3.(2019春•巨野县期中)明明在亮亮的东南方向,那么亮亮在明明的()方向.A.西南B.东北C.西北【解答】解:明明在亮亮的东南方向,那么亮亮在明明的西北方向.故选:C.4.(2019秋•肥城市期末)正方形的边长扩大到原来的2倍,则它的面积()A.扩大到原来的2倍B.扩大到原来的3倍C.扩大到原来的4倍【解答】解:设原来的边长为a原正方形的面积:S=a2扩大后正方形的面积:S=2a×2a=4a24a2÷a2=4答:面积扩大到原来的4倍.故选:C.5.(2019秋•成华区期末)将一个长24cm,宽18cm的长方形纸剪成若干个面积相等的正方形,要求没有剩余且正方形的面积最大,每个正方形的面积是多少平方厘米?()A.6 B.24 C.36【解答】解:24=2×2×2×318=2×3×3所以24和18的最大公因数是:2×3=66×6=36(平方厘米)答:每个正方形的面积是36平方厘米.故选:C.6.(2019秋•望城区期末)小红家、小明家和学校在一条直线上,小红家离学校300米,小明家离学校500米,小红家和小明家相距()米.A.200 B.800 C.200或800【解答】解:小红和小明家都在学校的同一方时,两家的距离:500﹣300=200(米);小红和小明家都在学校的两边时,两家的距离:500+300=800(米).故选:C.7.(2017•云阳县)三(2)班教室的黑板在教室的西面,那么老师讲课时面向()面.A.东B.南C.西D.北【解答】解:方向是两两相对的,北与南相对,西与东相对,东北与西南相对,西北与东南相对.三(2)班教室的黑板在教室的西面,那么老师讲课时面向东面.故选:A.8.(2011春•德州校级期末)如图:在一幅七巧板中涂色部分的面积是15平方厘米,那么大正方形的面积是()平方厘米.A.90 B.105 C.120 D.1【解答】解:小正方形的面积占整个正方形面积的;15=120(平方厘米);答:大正方形的面积是120平方厘米.故选:C.9.(2006秋•张家港市期末)在一张长18厘米,宽12厘米的长方形纸片上剪一个最大的正方形,剪去的纸片面积是()平方厘米.A.216 B.144 C.72【解答】解:12×(18﹣12),=12×6,=72(平方厘米);答:剪去的纸片的面积是72平方厘米,故选:C.二.填空题10.(2020春•盐城期中)明明坐在美术教室里上课,前面是北,后面是南,左面是西,右面是东.【解答】解:明明坐在美术教室里上课,前面是北,后面是南,左面是西,右面是东.故答案为:南;西;东.11.(2020春•盐城期中)下面是小红家附近的交通示意图.(1)超市在公园的东面,图书馆在小红家的东北面,学校在小红家的东南面.(2)从小红家去学校,可以先向东走到公园,再向南走到学校.【解答】解:(1)超市在公园的东面,图书馆在小红家的东北面,学校在小红家的东南面.(2)从小红家去学校,可以先向东走到公园,再向南走到学校.故答案为:东,图书馆,东南;东,南.12.(2020春•洪泽区校级期中)(1)体育场在公园的东面,图书馆在体育场的东南面.(2)学校的东面是图书馆,超市的北面是体育场.【解答】解:根据分析可知:(1)体育场在公园的东面,图书馆在体育场的东南面.(2)学校的东面是图书馆,超市的北面是体育场.故答案为:东,东南;图书馆,体育场.13.(2020春•连云区校级期中)一个长方形长10米,宽6米,如果长减少4米或者宽增加4米,这个长方形就变成了正方形,这两个正方形相差64平方米.【解答】解:10﹣6=4(米)这个长方形的长减少4米,或宽增加4米,都可以得到一个正方形,10×(6+4)﹣(10﹣4)×6=10×10﹣6×6=100﹣36=64(平方米)答:这两个正方形的面积相差64平方米.故答案为:4、4、64.14.(2020春•新田县期中)一块长方形绿地长50米,宽25米,8块这样的绿地面积约是1公顷.【解答】解:50×25=1250(平方米)1公顷=10000平方米10000÷1250=8(块)答:8块这样的绿地面积约是1公顷.故答案为:8.15.如果你的前面是西北方,那么你的右面是C方,左面是A方.A.西南B.东南C.东北.【解答】解:如果你的前面是西北方,那么你的右面是东北方,左面是西南方.故选:C,A.16.填一填.当你面向西北方向的时候,后面是东南,左面是西南,右面是东北.当你面向西南方向时,你的后面是东北,左面是东南,右面是西北.【解答】解:当你面向西北方向的时候,后面是东南,左面是西南,右面是东北.当你面向西南方向时,你的后面是东北,左面是东南,右面是西北.故答案为:东南,西南,东北,东北,东南,西北.17.(2019春•成都月考)把一根长度是40厘米的铁丝围成一个长方形或者一个正方形,长与宽都是整厘米数,那么围成的图形中,面积最大的图形与面积最小的图形,它们面积相差81平方厘米.【解答】解:长+宽=40÷2=20(厘米)因长=宽=10最接近,此正方形的面积应最大,10×10=100(平方厘米),19、1相差最大,此长方形的面积应最小,19×1=19(平方厘米),它们面积相差100﹣19=81(平方厘米).故答案为:81.三.判断题18.(2019秋•蓝山县期末)小丽家在学校的东南面,学校在小丽家的西北面.√(判断对错)【解答】解:小丽家在学校的东南面,学校在小丽家的西北面,说法正确;故答案为:√.19.(2019春•巨野县期中)乐乐面向西南站立,她背朝东北面.√(判断对错)【解答】解:乐乐面向西南站立,她背朝东北面.原说法正确.故答案为:√.20.(2019秋•澄海区校级期末)边长100米的正方形面积是1公顷√(判断对错)【解答】解:100×100=10000(平方米),10000平方米=1公顷,故答案为:√.21.(2019春•无棣县期末)边长是4米的正方形,面积是16米.×(判断对错)【解答】解:4×4=16(平方米)答:正方形的面积是16平方米.所以边长是4米的正方形,面积是16米的说法是错误的.故答案为:×.22.哈三中在继红小学的西南面,继红小学在哈三中的东北面.√.(判断对错)【解答】解:哈三中在继红小学的西南面,继红小学在哈三中的东北面.所以原题的说法正确.故答案为:√.23.将一根长是16cm的铁丝,围成一个正方形,这个正方形的面积是16cm2.√.(判断对错)【解答】解:16÷4=4(厘米)4×4=16(平方厘米)这个正方形的面积是16cm2,原题说法正确.故答案为:√.四.应用题24.(1)四名同学的家分别在学校的什么方向?(2)从笑笑家经过学校到圆圆家要走多少米?合多少千米?(3)笑笑去乐乐家比圆圆去乐乐家至少要多走多少米?【解答】解:(1)圆圆家在西北方向,乐乐家在东北方向,淘淘家在东南方向,笑笑家在西南方向.(2)520+480=1000(米)1000米=1千米.答:从笑笑家经过学校到圆圆家要走1000米,合1千米.(3)630+240﹣750=870﹣750=120(米)答:笑笑去乐乐家比圆圆去乐乐家至少要多走120米.25.(2020春•盐城期中)新庄小学原来有一块长方形草坪,长20米.修建校园时,把草坪的长减少4米,这样草坪的面积就减少了60平方米.现在草坪的面积是多少平方米?(先在图上画一画,再解答)【解答】解:如图所示:(20﹣4)×(60÷4)=16×15=240(平方厘米)答:现在草坪的面积是240平方米.26.(2020春•黄冈期中)一个长方形的周长是56cm,它的长和宽是两个质数,这个长方形的面积可能是多少平方厘米?【解答】解:56÷2=28(厘米)可以分为:①长23厘米,宽5厘米面积:23×5=115(平方厘米)②长17厘米,宽11厘米面积:17×11=187(平方厘米)答:这个长方形的面积可能是115平方厘米或187平方厘米.27.(2018秋•诸暨市校级期末)一个长方形的面积是495平方米,宽是15米.当长不变,将宽延长,使其变成一个正方形,面积增加了多少平方米?【解答】解:495÷15=33(米)33×33﹣495=1089﹣495=594(平方米)答:面积增加了594平方米.五.操作题28.(2018秋•齐河县期末)(1)马丽家在张玲家的北面.李芳家文化中心的西面.丁丁家在李芳家的南面.(2)晓明家在文化中心的东南面.东东家在文化中心的西北面.【解答】解:(1)马丽家在张玲家的北面.李芳家文化中心的西面.丁丁家在李芳家的南面.(2)晓明家在文化中心的东南面.东东家在文化中心的西北面.29.(2019•娄底模拟)看图回答①在学校东面40米是邮局,用箭头连一连邮局所在的位置.②在学校西面20米是少年宫,用箭头连一连少年宫所在位置.【解答】解:①在学校东面40米是邮局,用箭头连一连邮局所在的位置.②在学校西面20米是少年宫,用箭头连一连少年宫所在位置.30.(2018春•新罗区期末)填一填.走进动物园大门,正北面是假山石和小鹿家,假山石的东面是小马家,西面是小羊家,西北面是“小狗家”.根据以上的描述请你把动物们的家的序号标在适当的位置上.①小鹿家②小马家③小羊家④小狗家【解答】解:六.解答题31.(2020春•洪泽区校级期中)按要求画图形并填一填.(1)在☆的东南面画△.(2)在☆的西南面画□(3)在☆的东北面画〇.(4)在☆的西北面,☆在的东南面.【解答】解:如图所示:故答案为:西北,东南.32.(2020春•洪泽区校级期中)你能帮小朋友找到各自的家吗?在每幛房子下面的括号里写上小朋友的名字.(1)玲玲家在学校的东南面,萍萍家在学校的南面,红红家在学校的西南面;(2)萍萍家的东北面是冬冬家,萍萍家的西北面是婷婷家.【解答】解:在每幛房子下面的括号里写上小朋友的名字.(1)玲玲家在学校的东南面,萍萍家在学校的南面,红红家在学校的西南面;(2)萍萍家的东北面是冬冬家,萍萍家的西北面是婷婷家.33.(2019秋•红安县期末)下面这块长方形菜地的宽增加到36米,长不变,扩大后的面积是多少?【解答】解:378÷9=42(米)42×36=1512(平方米)答:扩大后的菜地面积是1512平方米.34.(2019春•单县期末)陈俊家的厨房地面长3米,宽2米,用面积是4平方分米的正方形地砖铺厨房地面,需要多少块?【解答】解:3×2=6(平方米)6平方米=600平方分米600÷4=150(块)答:需要150块.35.(2019秋•潍坊期末)一个长方形的长和宽均为质数,并且周长为36厘米.这个长方形的面积最大可以是多少平方厘米?【解答】解:36÷2=18(厘米)18=11+7=13+513×5=65(平方厘米)11×7=77(平方厘米)77>65也就是长是11厘米,宽是7厘米面积最大答:这个长方形的面积最大是77平方厘米.36.(2018秋•成都期末)如图:一个长方形面积864平方厘米,长比宽多12厘米,求长方形的长和宽.【解答】解:12×12=144(平方厘米)144+864×4=144+3456=3600(平方厘米)3600=60×60,所以大正方形的边长是60厘米,(60+12)÷2=72÷2=36(厘米)36﹣12=24(厘米)答:长方形的长是36厘米,宽是24厘米.。
2024年北师大版六年级下册数学暑假必刷专题:空间与图形(含答案)

2024年北师大版六年级下册数学暑假必刷专题:空间与图形一、单选题1.把一个棱长是6分米的实心正方体木块削成一个最大的圆柱,削去部分的体积是( )立方分米。
A.46.44B.100.48C.102.96D.169.562.一个立体图形,从上面看到的形状是,从正面看到的形状是,搭这个立体图形至少需要( )个小正方体。
A.5B.6C.7D.83.如图,小明从地铁站到学校,要向( )方向走。
A.西偏南30°B.北偏东30°C.东偏北30°D.西偏北30°4.一个圆柱与圆锥的体积相等,圆柱的半径与圆锥的半径相等,圆柱的高与圆锥的高的比是( )A.3:1B.1:3C.9:1D.1:95.如图,下面( )圆锥的体积与左边圆柱的体积相等。
A.A B.B C.C D.相等6.一个三角形的一条边为2cm,另一条边为4cm,那么这个三角形第三条边a的取值范围是( )A.2<a<4B.4<a<6C.2<a<6D.2<a<8二、填空题7.一个高10厘米的圆柱体,沿底面直径切拼成一个近似的长方体,表面积增加了200平方厘米。
原来圆柱体的体积是 立方厘米。
8.一个长方体、一个圆柱体和一个圆锥体,它们的底面积和体积分别相等,如果长方体的高是12厘米,那么圆柱体的高是 厘米,圆锥体的高是 厘米。
9.如图所示,把底面直径10厘米,侧面积62.8平方厘米的圆柱切成若干等份,拼成一个近似的长方体。
这个长方体的底面积是 平方厘米,体积是 立方厘米。
10.用5个大小相等的小正方体搭成下面三个立体图形,从 面看这三个立体图形所看到的形状是完全一样的。
11.把一个棱长是a厘米的正方体锯成两个相同的长方体,表面积增加了 cm2。
12.下图中圆和长方形面积相等,圆的半径等于长方形的宽.阴影部分面积是60cm2,圆的面积是 cm2。
13.一个长方体和一个正方体的棱长总和相等,已知长方体的长、宽、高分别是3dm、2dm、4dm,那么正方体的体积是 dm3。
三年级数学空间与图形试题答案及解析

三年级数学空间与图形试题答案及解析一、填空题1. 一个长方形的长是10厘米,宽是5厘米,它的周长是______厘米。
答案:30厘米解析:长方形的周长计算公式是(长+宽)×2。
将长和宽的数值代入公式,得到(10+5)×2=30厘米。
2. 一个正方形的边长是8厘米,它的面积是______平方厘米。
答案:64平方厘米解析:正方形的面积计算公式是边长×边长。
将边长的数值代入公式,得到8×8=64平方厘米。
3. 一个圆的半径是5厘米,它的直径是______厘米。
答案:10厘米解析:圆的直径等于半径的两倍,所以直径为5×2=10厘米。
二、选择题4. 下列图形中,周长最长的是()A. 长方形B. 正方形C. 圆形答案:C解析:在相同边长的情况下,圆的周长最长,因为圆的周长公式是2πr,而长方形和正方形的周长分别是(长+宽)×2和4×边长。
5. 下列图形中,面积最大的是()A. 长方形B. 正方形C. 圆形答案:C解析:在相同边长或半径的情况下,圆的面积最大,因为圆的面积公式是πr²,而长方形和正方形的面积分别是长×宽和边长×边长。
三、解答题6. 一个长方形的长是12厘米,宽是6厘米,求它的面积和周长。
答案:面积是72平方厘米,周长是36厘米。
解析:(1)面积计算:长方形的面积公式是长×宽,所以面积为12×6=72平方厘米。
(2)周长计算:长方形的周长公式是(长+宽)×2,所以周长为(12+6)×2=36厘米。
7. 一个正方形的边长是10厘米,求它的面积和周长。
答案:面积是100平方厘米,周长是40厘米。
解析:(1)面积计算:正方形的面积公式是边长×宽,由于正方形的边长相等,所以面积为10×10=100平方厘米。
(2)周长计算:正方形的周长公式是4×边长,所以周长为4×10=40厘米。
五年级数学空间与图形试题答案及解析

五年级数学空间与图形试题答案及解析1.求组合图形的体积(单位:分米)【答案】99立方分米【解析】根据正方体的体积公式:v=a3,长方体的体积公式:v=abh,把数据分别代入公式求出它们的体积之和即可.解:3×3×3+8×3×3=27+72=99(立方分米)答:这个组合图形的体积是99立方分米.【点评】解答求组合图形的体积,关键是观察分析图形是由哪几部分组成的,再利用相应的体积公式解答即可.2.下列物体中,形状不是长方体的是()A.火柴盒 B.红砖 C.茶杯【答案】C【解析】根据长方体的特征:6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等,12条棱分为互相平行的3组,每组4条棱的相等相等,有8个顶点.据此解答即可.解:火柴盒、红砖具备了长方体的特征,而茶杯不具备长方体的特征,所以茶杯不是长方体.故选:C.【点评】此题考查的目的是掌握长方体的特征.3.将,则与2号面相对的面是第()号面.A.6B.5C.4D.3【答案】C【解析】如图,属于正方体展开图的“1﹣3﹣2”型,折成正方体后,1号面与5号面相对,2号面与4号面相对,3号面与6号面相对.解:如图,根据正方体展开图的特征,1号面与5号面相对,2号面与4号面相对,3号面与6号面相对.故选我:C.【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住,能快速解答此类题.4.一个水池能蓄水430立方米,我们就说,这个水池的()是430立方米.A.表面积B.重量C.体积D.容积【答案】D【解析】一个容器所能容纳物体的体积,叫做这个容器的容积,由此即可选择.解:根据容积的定义可得:一个水池能蓄水430立方米,我们就说,这个水池的容积是430立方米,故选:D.【点评】此题考查了容积的定义.5.如图三角形的面积是平方厘米;如果把两个这样的三角形拼成一个平行四边形,且要使这个平行四边形的周长最长,这样的平行四边形周长是厘米.(单位:厘米)【答案】0.5a2;2(a+b).【解析】三角形是一个直角三角形,它的两个直角边相互垂直,所以它的底是a厘米,高是a厘米,由此求出面积.要使拼成的平行四边形周长最长就把最短的边a厘米的重合在一起就可以.解:a×a÷2=0.5a2(平方厘米)平行四边形周长是2(a+b)厘米答:三角形的面积是0.5a2平方厘米;这样的平行四边形周长是2(a+b)厘米.故答案为:0.5a2;2(a+b).【点评】本题关键是拼出图形,理解把最短的边拼在一起周长最大.6.等边三角形一定是()三角形.A.锐角 B.直角 C.钝角【答案】A【解析】等边三角形的三个角都相等,都是60°,由此根据三角形按角分类的方法即可进行选择.解:等边三角形的三个角都是60°,都是锐角,所以等边三角形是锐角三角形.故选:A.【点评】抓住等边三角形的三个角都相等的性质和锐角三角形的定义即可解决问题.7.一个长方体和一个正方体的棱长总和相等,已知长方体的长是6厘米,宽是5厘米,高是4厘米,那么正方体的棱长是厘米.【答案】5.【解析】首先根据长方体的棱长总和=(长+宽+高)×4,求出长方体的棱长总和,再用棱长总和除以12求出正方体的棱长,解答即可.解:(6+5+4)×4÷12=15×4÷12=60÷12=5(分米)答:正方体的棱长是5厘米.故答案为:5.【点评】此题主要考查长方体、正方体的棱长总和公式的灵活运用.8.正方体和长方体的体积都可以用底面积乘以高来进行计算..(判断对错)【答案】√【解析】根据长方体和正方体的体积公式,长方体的长×宽=长方体的底面积;正方体的棱长×棱长=正方体的底面积;由此解答.解:长方体的体积=底面积×高,正方体的体积=底面积×高;因此正方体和长方体的体积都可以用底面积乘以高来进行计算,这种说法是正确的.故答案为:正确.【点评】此题主要考查长方体和正方体的统一的体积计算公式,v=sh.9.一个棱长是4分米的正方体,棱长总和是()分米.A.16B.24C.32D.48【答案】D【解析】一个正方体有12条棱,棱长总和为12条棱的长度和.解:4×12=48(分米).故选:D.【点评】此题考查计算正方体的棱长总和的方法,即用棱长乘12即可.10.如果两个圆的面积大小相等,那么这两个圆的周长()。
2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练【含答案】

2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练一、基本技能练1.下列说法中,正确的是()A.棱柱的侧面可以是三角形B.若棱柱有两个侧面是矩形,则该棱柱的其他侧面也是矩形C.正方体的所有棱长都相等D.棱柱的所有棱长都相等2.如图所示的等腰梯形是一个几何图形的斜二测直观图,其底角为45°,上底和腰均为1,下底为2+1,则此直观图对应的平面图形的面积为()A.1+2B.2+2C.2+22D.4+223.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为()A.4B.43D.3C.234.已知在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2,则将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为() A.(5+2)π B.(4+2)πC.(5+22)πD.(3+2)π5.如图,位于西安大慈恩寺的大雁塔,是唐代玄奘法师为保存经卷、佛像而主持修建的,是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥,其侧棱与底面所成的角为45°,则该正四棱锥的一个侧面与底面的面积之比为()A.3∶2B.2∶2C.3∶3D.3∶46.过圆锥的轴作截面,如果截面为正三角形,则称该圆锥为等边圆锥.已知在一等边圆锥中,过顶点P 的截面与底面交于CD ,若∠COD =90°(O 为底面圆心),且S △PCD =72,则这个等边圆锥的表面积为()A.2π+2πB.3πC.2π+3πD.π+3π7.如图,四边形ABCD 是边长为2的正方形,ED ⊥平面ABCD ,FC ⊥平面ABCD ,ED =2FC =2,则四面体ABEF 的体积为()A.13B.23C.1D.438.黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值为5-12,约为0.618.这个比例被公认为是最能引起美感的比例,因此被称为黄金比.在几何世界中有很多黄金图形,在三角形中,如果相邻两边之比等于黄金比,且它们夹角的余弦值为黄金比值,那么这个三角形一定是直角三角形,且这个三角形称为黄金分割直角三角形.在正四棱锥中,以黄金分割直角三角形的长直角边作为正四棱锥的高,黄金分割直角三角形的短直角边的边长作为底面正方形的边心距(正多边形的边心距是正多边形的外接圆圆心到正多边形某一边的距离),斜边作为正四棱锥的斜高,这样得到的正四棱锥称为黄金分割正四棱锥.在黄金分割正四棱锥中,以该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为()A.5-12B.5+12C.1D.149.如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F,G分别是棱A′B′,B′C′,CD的中点,则由点E,F,G确定的平面截正方体所得的截面多边形的面积等于________.10.已知圆锥的顶点为S,底面圆周上的两点A,B满足△SAB为等边三角形,且面积为43,又知圆锥轴截面的面积为8,则圆锥的侧面积为________.11.如图,已知正三棱柱ABC-A1B1C1的各棱长均为2,点D在棱AA1上,则三棱锥D-BB1C1的体积为________.12.已知三棱锥S-ABC中,∠SAB=∠ABC=π2,SB=4,SC=213,AB=2,BC =6,则三棱锥S-ABC的体积为________.二、创新拓展练13.(多选)攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为撮尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为θ,这个角接近30°.若取θ=30°,侧棱长为21米,则()A.正四棱锥的底面边长为6米B.正四棱锥的底面边长为3米C.正四棱锥的侧面积为243平方米D.正四棱锥的侧面积为123平方米14.(多选)如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=12,则下列结论中错误的是()A.AC⊥AFB.EF∥平面ABCDC.三棱锥A-BEF的体积为定值D.△AEF的面积与△BEF的面积相等15.(多选)《九章算术》是《算经十书》中最重要的一部,其中将有三条棱互相平行且有一个面为梯形的五面体称为“羡除”,则()A.“羡除”有且仅有两个面为三角形B.“羡除”一定不是台体C.不存在有两个面为平行四边形的“羡除”D.“羡除”至多有两个面为梯形16.(多选)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB.记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则()A.V3=2V2B.V3=V1C.V3=V1+V2D.2V3=3V1参考答案与解析一、基本技能练1.答案C解析棱柱的侧面都是平行四边形,选项A错误;其他侧面可能是平行四边形,选项B错误;棱柱的侧棱与底面边长并不一定相等,选项D错误;易知选项C正确.2.答案B解析∵平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,∴平面图形为直角梯形,且直角腰长为2,上底边长为1,下底边长为2+1,∴平面图形的面积S=1+1+22×2=2+ 2.故选B.3.答案B解析易知该几何体是由上、下两个全等的正四棱锥组成的,其中正四棱锥底面边长为2,棱锥的高为1,所以该多面体的体积V =2×13×(2)2×1=43.4.答案A解析因为在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2,所以将梯形ABCD 绕AD 所在的直线旋转一周得到的几何体是一个底面半径为1,高为2的圆柱挖去一个底面半径为1,高为1的圆锥后剩余的部分,如图所示.所以该几何体的表面积S =π×12+2π×1×2+π×1×12+12=(5+2)π.5.答案D解析设塔顶是正四棱锥P -ABCD (如图),PO 是正四棱锥的高.设正四棱锥底面边长为a ,则底面面积S 1=a 2,因为AO =22a ,∠PAO =45°,所以PA =2×22a =a ,所以△PAB 是正三角形,其面积为S 2=34a 2,所以S 2∶S 1=34a 2∶a 2=3∶4.6.答案B解析如图,连接PO ,设圆锥的母线长为2a ,则圆锥的底面圆的半径为a ,高为PO =3a .由已知得CD =2a ,PC =PD =2a ,则S △PCD =12×2a ×(3a )2+22a 2=72,从而可得a =1,圆锥的表面积为πa ×2a +πa 2=3πa 2=3π.7.答案B解析∵ED ⊥平面ABCD 且AD ⊂平面ABCD ,∴ED ⊥AD .∵在正方形ABCD 中,AD ⊥DC ,又DC ∩ED =D ,DC ,ED ⊂平面CDEF ,∴AD ⊥平面CDEF .易知FC =ED2=1,V A -BEF =V ABCDEF -V F -ABCD -V A -DEF .∵V E -ABCD =13·ED ·S 正方形ABCD =13×2×2×2=83,V B -EFC =13·BC ·S △EFC =13×2×2×1×12=23,∴V ABCDEF =V E -ABCD +V B -EFC =83+23=103.又V F -ABCD =13·FC ·S 正方形ABCD =13×1×2×2=43,V A -DEF =13·AD ·S △DEF =13×2×2×2×12=43,∴V A -BEF =V ABCDEF -V F -ABCD -V A -DEF =103-43-43=23.故选B.8.答案D解析如图,在黄金分割正四棱锥P -ABCD 中,O 是正方形ABCD 的中心,PE 是正四棱锥的斜高,设OE =a ,则CD =2a ,∴Rt△POE为黄金分割直角三角形,则OEPE=5-12,∴PE=5+12,则PO=PE2-OE2=1+52a,∴以该正四棱锥的高为边长的正方形的面积S=PO2=1+52a2,又正四棱锥的四个侧面是全等的,∴S侧=4S△PCD=4×12×CD×PE=2(1+5)a2,∴该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为1 4 .9.答案332解析分别取AD,CC′和AA′的中点为P,M,N,可得出过E,F,G三点的平面截正方体所得截面为正六边形EFMGPN,则正六边形的边长MG=CG2+CM2=222+2221,故截面多边形的面积S=6×34×12=332.10.答案82π解析设圆锥的母线长为l,由△SAB为等边三角形,且面积为43,所以12l 2sin π3=43,解得l =4;又设圆锥底面半径为r ,高为h ,则由轴截面的面积为8,得rh =8;又r 2+h 2=l 2=16,解得r =h =22,所以圆锥的侧面积S =πrl =π·22·4=82π.11.答案233解析如图,取BC 的中点O ,连接AO .∵正三棱柱ABC -A 1B 1C 1的各棱长均为2,∴AC =2,OC =1,则AO = 3.∵AA 1∥平面BCC 1B 1,∴点D 到平面BCC 1B 1的距离为3.又S △BB 1C 1=12×2×2=2,∴V D -BB 1C 1=13×2×3=233.12.答案43解析∵∠ABC =π2,AB =2,BC =6,∴AC =AB 2+BC 2=22+62=210.∵∠SAB =π2,AB =2,SB =4,∴AS =SB 2-AB 2=42-22=2 3.由SC =213,得AC 2+AS 2=SC 2,∴AC ⊥AS .又∵SA ⊥AB ,AC ∩AB =A ,AC ,AB ⊂平面ABC ,∴AS ⊥平面ABC .∴AS 为三棱锥S -ABC 的高,∴V 三棱锥S -ABC =13×12×2×6×23=4 3.二、创新拓展练13.答案AC解析如图,在正四棱锥S -ABCD 中,O 为正方形ABCD 的中心,H 为AB 的中点,则∠SHO 为侧面SAB 与底面ABCD 所成的锐二面角,且SH ⊥AB ,∠SHO =30°,设底面边长为2a ,所以OH =AH =a ,OS =33a ,SH =233.在Rt △SAH 中,a 2=21,解得a =3,所以正四棱锥的底面边长为6米,侧面积为S =12×6×23×4=243(平方米).14.答案AD解析由题意及图形知,当点F 与点B 1重合时,∠CAF =60°,故A 错误;由正方体ABCD -A 1B 1C 1D 1的两个底面平行,EF ⊂平面A 1B 1C 1D 1,知EF ∥平面ABCD ,故B 正确;由几何体的性质及图形知,三角形BEF 的面积是定值,点A 到平面DD 1B 1B 的距离是定值,故可得三棱锥A -BEF 的体积为定值,故C 正确;由图形可以看出,B 到直线EF 的距离与A 到直线EF 的距离不相等,故△AEF 的面积与△BEF 的面积不相等,故D 错误.故选AD.15.答案ABC解析由题意知AE ∥BF ∥CD ,四边形ACDE 为梯形,如图所示.选项A ,由题意知“羡除”有且仅有两个面为三角形,故A 正确;选项B ,因为AE ∥BF ∥CD ,所以“羡除”一定不是台体,故B 正确;选项C ,假设四边形ABFE 和四边形BCDF 为平行四边形,则AE ∥BF ∥CD ,且AE =BF =CD ,即四边形ACDE 为平行四边形,与已知四边形ACDE 为梯形矛盾,故不存在,故C 正确;选项D ,若AE ≠BF ≠CD ,则“羡除”有三个面为梯形,故D 错误.故选ABC.16.答案CD 解析如图,连接BD 交AC 于O ,连接OE ,OF .设AB =ED =2FB =2,则AB =BC =CD =AD =2,FB =1.因为ED ⊥平面ABCD ,FB ∥ED ,所以FB ⊥平面ABCD ,所以V 1=V E -ACD =13S △ACD ·ED =13×12AD ·CD ·ED =13×12×2×2×2=43,V 2=V F -ABC =13S △ABC ·FB =13×12AB ·BC ·FB =13×12×2×2×1=23.因为ED ⊥平面ABCD ,AC ⊂平面ABCD ,所以ED ⊥AC ,又AC ⊥BD ,且ED ∩BD =D ,ED ,BD ⊂平面BDEF ,所以AC ⊥平面BDEF .因为OE ,OF ⊂平面BDEF ,所以AC ⊥OE ,AC ⊥OF .易知AC=BD=2AB=22,OB=OD=12BD=2,OF=OB2+FB2=3,OE=OD2+ED2=6,EF=BD2+(ED-FB)2=(22)2+(2-1)2=3,所以EF2=OE2+OF2,所以OF⊥OE.又OE∩AC=O,OE,AC⊂平面ACE,所以OF⊥平面ACE,所以V3=V F-ACE=13S△ACE·OF=13×12AC·OE·OF=13×12×22×6×3=2,所以V3≠2V2,V1≠V3,V3=V1+V2,2V3=3V1,所以选项A,B不正确,选项C,D正确.故选CD.。
小升初数学专项复习训练一空间与图形空间与图形专项训练1含解析

空间与图形一、选择题1.一个长方体的长、宽、高都扩大2倍,它的体积扩大()倍。
A、2B、6C、8【答案】C【解析】长方体的体积=长×宽×高,长、宽和高都扩大2倍,则体积就扩大了2×2×2=8倍,根据此选择即可。
2.正方体的棱长扩大2倍,它的表面积就()。
A.扩大2倍B.扩大4倍C.扩大6倍【答案】B【解析】根据正方体的表面积计算公式,棱长扩大2倍,则表面积扩大:2×2=4倍,根据此选择即可。
3.用两个棱长是1分米的正方体小木块拼成一个长方体,拼成的长方体的表面积是()。
A.增加了B.减少了C.没有变【答案】B【解析】把小正方体拼成一个长方体后,减少了2个小正方形的面积,因此拼成的长方体的表面积比原来减少了。
4.做一个长方体抽屉,需要()块长方形木板。
A.4 B.5 C.6【答案】B【解析】长方体抽屉没有上面一个面,因此一共有5个面,需要5块长方形木板,根据此选择即可。
5.用一根长()铁丝正好可以做一个长6厘米、宽5厘米、高3厘米的长方体框架。
A.28厘米 B.126平方厘米 C.56厘米 D.90立方厘米【答案】C。
【解析】长方体有4条长,4条宽和4条高,求出棱长之和,即可求出需要多少铁丝,即:(6+5+3)×4=56厘米,根据此选择即可。
6.我们在画长方体时一般只画出三个面,这是因为长方体()。
A.只有三个面 B.只能看到三个面 C.最多只能看到三个面【答案】C【解析】把长方体放在桌面上,最多可以看到3个面。
根据此选择。
7.将一个正方体钢坯锻造成长方体,正方体和长方体()。
A.体积相等,表面积不相等B.体积和表面积都不相等.C.表面积相等,体积不相等.【答案】A【解析】将一个正方体钢坯锻造成长方体,形状改变,体积不变。
8.一个正方体的棱长之和是12a厘米,它的棱长是()厘米。
A.6aB.aC.2aD.12a【答案】B【解析】棱长之和÷12=棱长9.一个正方体的棱长是8分米,它的棱长总和是()分米。
初中数学空间几何复习 题集附答案

初中数学空间几何复习题集附答案一、选择题1. 平行四边形的对角线A. 互相垂直且长度相等B. 互相垂直但长度不相等C. 互相平行但长度不相等D. 互相平行且长度相等答案:A2. 圆柱的底面是一个正方形,它的椎面是一个等腰三角形,该几何体的名称是:A. 圆锥B. 圆柱C. 正方体D. 平行四边形答案:A3. 以下哪个是二面角?A. 直角B. 同位角D. 平行角答案:B4. 一个立方体的所有棱长都为3 cm,它的体积是多少立方厘米?A. 81B. 27C. 9D. 54答案:B5. 已知平行四边形ABCD,如果BD = 10 cm,AC = 8 cm,那么BD 与AC的比值是多少?A. 1:2B. 2:3C. 4:5D. 5:8答案:A二、填空题1. 正方形的对角线长度等于边长的__________倍。
2. 一个直角三角形的两条直角边长分别为3 cm和4 cm,斜边的长度是__________。
答案:5 cm3. 正方体的棱长为3 cm,它的体积为__________立方厘米。
答案:274. 以下哪个角不是平面几何角?答案:二面角5. 一个长方体的表面积为60 cm²,如果它的长、宽、高分别为2 cm、3 cm和h cm,那么h的值为__________。
答案:10三、计算题1. 一座对边长度都为5 cm的正方形,它的对角线的长度是多少厘米?解答:由勾股定理可知,对角线的长度等于边长乘以√2。
所以,对角线的长度为5 cm × √2 ≈ 7.07 cm。
2. 一个正方体的体积为125 cm³,它的边长是多少厘米?解答:正方体的体积等于边长的立方。
设正方体的边长为x cm,则x³ = 125。
解得x = 5 cm。
所以,正方体的边长为5 cm。
3. 一个长方体的长、宽、高分别为4 cm、6 cm和3 cm,求它的表面积。
解答:长方体的表面积等于各个面的面积之和。
设长方体的长、宽、高分别为a、b、c,则表面积为2(ab + bc + ac)。
通用版数学六年级下册总复习专题:空间与图形1 含答案 17页
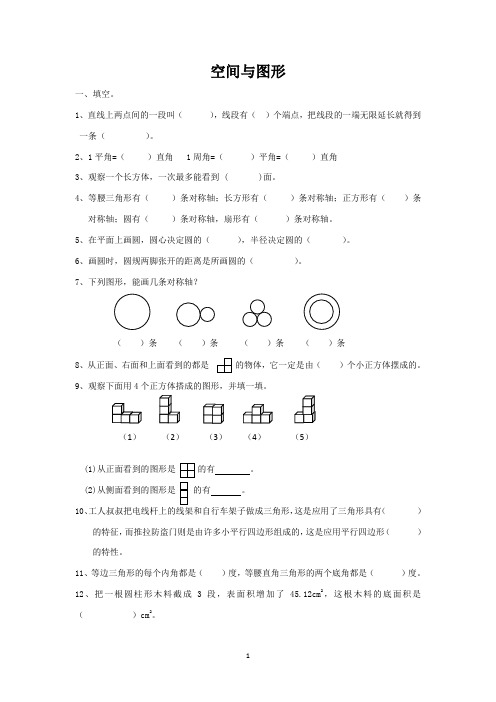
空间与图形一、填空。
1、直线上两点间的一段叫( ),线段有( )个端点,把线段的一端无限延长就得到一条( )。
2、1平角=( )直角 1周角=( )平角=( )直角3、观察一个长方体,一次最多能看到 ( )面。
4、等腰三角形有( )条对称轴;长方形有( )条对称轴;正方形有( )条对称轴;圆有( )条对称轴,扇形有( )条对称轴。
5、在平面上画圆,圆心决定圆的( ),半径决定圆的( )。
6、画圆时,圆规两脚张开的距离是所画圆的( )。
7、下列图形,能画几条对称轴?8、从正面、右面和上面看到的都是的物体,它一定是由()个小正方体摆成的。
9、观察下面用4个正方体搭成的图形,并填一填。
(1)从正面看到的图形是的有 。
(2)从侧面看到的图形是的有 。
10、工人叔叔把电线杆上的线架和自行车架子做成三角形,这是应用了三角形具有( )的特征,而推拉防盗门则是由许多小平行四边形组成的,这是应用平行四边形( )的特性。
11、等边三角形的每个内角都是( )度,等腰直角三角形的两个底角都是( )度。
12、把一根圆柱形木料截成3段,表面积增加了45.12cm 2,这根木料的底面积是( )cm 2。
13、一个圆锥体的底面半径是6cm ,高是1dm ,体积是( )cm 3。
14、把一个圆柱体钢坯削成一个最大的圆锥体,要削去 1.8 cm 3,未削前圆柱的体积是( )cm 3。
15、一个圆柱体的侧面展开后,正好得到一个边长25.12 cm 的正方形,圆柱体的高是( )cm ,底面半径是( )cm 。
16、等底等高的圆柱和圆锥,体积的和是72 dm 3,圆柱的体积是( ),圆锥的体积是( )。
17、三角形三个角度数的比是2:4:3,最大的角是( )。
18、一个三角形底是3dm ,高是4dm ,它的面积是( )。
19、一个平行四边形的底长18cm ,高是底的12,它的面积是( )。
20、一个直径4cm 的半圆形,它的周长是( ),它的面积是( )。
初中数学七年级下册专题复习——空间与图形(附答案 )

专题三 空间与图形 数学 七年级下册(湘教版)时间:90分钟 满分:100分题 号一二三总 分得 分一㊁选择题(每小题3分,共30分)1.ø1和ø2是直线A B 和C D 被直线EF所截得到的同位角,那么ø1和ø2的大小关系是( )A.ø1=ø2B .ø1>ø2C .ø1<ø2 D.无法确定2.下列图形不能通过基本图形平移得到的是( )(第3题)3.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )A.垂线段最短B .经过一点有无数条直线C .经过两点,有且仅有一条直线D.两点之间,线段最短4.下列说法中,正确的是()A.过点P 画线段A B 的垂线B .P 是直线A B 外一点,Q 是直线A B 上一点,连接P Q ,使P Q ʅA B C .在平面内,过一点有且只有一条直线垂直于已知直线D.两直线平行,同旁内角相等5.(博才中学模拟)有下列语句:①同一平面内的三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条直线所截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行.其中正确的是()A.①②B .②③C .①③ D.以上皆错6.如图,在әA B C 中,øC =90ʎ,A C =BC =5,现将әA B C 沿C B 方向平移到әD F E 的位置,若平移距离为2,则图中阴影部分的面积为( )A.9B .4.5C .8 D.无法确定7.下列说法正确的是( )A.平移不改变图形的形状和大小,而旋转改变图形的形状和大小B .平移和旋转的共同点是改变图形的位置C .图形可以向某方向平移一定距离,也可以向某方向旋转一定距离D.由平移得到的图形也一定可由旋转得到8.下列图形一定是轴对称图形的是( )A.直角三角形B .平行四边形C .直角梯形 D.正方形9.(2019铜陵)一副直角三角板按如图所示的方式摆放,其中点C 在FD 的延长线上,且A BʊF C ,则øC B D 的度数为( )A.15ʎB .20ʎC .25ʎ D.30ʎ(第9题) (第10题)10.(2019邵阳)如图,已知两直线l 1与l 2被第三条直线l 3所截,下列等式一定成立的是( )A.ø1=ø2B .ø2=ø3C .ø2+ø4=180ʎ D.ø1+ø4=180ʎ二㊁填空题(每小题3分,共24分)11.如图,图形①经过变化成图形②,图形②经过变化成图形经过变化成图形12.如图,әA B C 中,B C =5c m ,将әA B C 沿B C 方向平移至әA 'B 'C ',A 'B '恰好经过A C 的中点O ,则әA B C 平移的距离为c m .(第12题) (第13题)13.如图,请写出能判断C E ʊA B 的一个条件,这个条件是:①;②;③.14.同一平面内的三条直线a ,b ,c ,若a ʅb ,b ʅc ,则a c ;若a ʊb ,b ʊc ,则a c ;若a ʊb ,bʅc ,则a c .15.如图,一块梯形玻璃的下半部分打碎了,若øA =125ʎ,øD =107ʎ,则打碎部分的两个角的度数分别为 .(第15题)(第16题)16.如图,直角三角形A O B 绕直角顶点O 顺时针旋转后与әC O D 重合,若øA O D =129ʎ,则旋转角度是.17.如图,C 岛在A 岛的北偏东50ʎ方向,C 岛在B 岛的北偏西40ʎ方向,则从C 岛看A ㊁B 两岛的视角øA C B 等于.(第17题)(第18题)18.如图,已知直线a ʊb ,A C ʅb ,A B =4,A C =7,则әA B D 的面积是. 三㊁解答题(共46分)19.(8分)如图,已知ø1+ø2=180ʎ,ø3=øB ,求证:øD E C +øC =180ʎ. ㊃73㊃20.(8分)如图,将әA B C 沿射线A B 的方向平移2个单位长度到әD E F的位置,点A ,B ,C 的对应点分别点D ,E ,F .(1)直接写出图中与A D 相等的线段;(2)若A B =3,则A E = ;(3)若øA B C =75ʎ,求øC F E 的度数.21.(10分)如图,长方形的长为8c m ,宽为4c m ,求图中阴影部分的面积.22.(10分)已知A B ʊC D ,分别探讨下面四个图形中øA P C 与øP A B ,øP C D 的关系,请你从所得到的关系中任选一个加以证明.23.(10分)如图,在正方形网格中,每个小正方形的边长均为1,әA B C 的顶点A ,B ,C 均在格点上,将әA B C 向右平移5格,得到әA 1B 1C 1;再将әA 1B 1C 1绕着点B 1按顺时针方向旋转90ʎ,得到әA 2B 1C 2.请在网格中画出әA 1B 1C 1和әA 2B 1C 2(不要求写画法),并求出四边形A C 1B 1B 的面积.㊃83㊃。
五年级数学空间与图形练习题及答案

五年级数学空间与图形练习题及答案1. 判断题:(1) 一个四边形有且只有两对对边平行。
( )(2) 直角三角形的两条直角边相等。
( )(3) 一个五边形有五条对角线。
( )(4) 两个形状相同的图形面积一定相等。
( )答案:(1) 错误 (2) 正确 (3) 错误 (4) 正确2. 单选题:(1) 下面哪个选项不是正方形的性质?A. 四条边相等B. 四个内角都是直角C. 对角线平分D. 有两对对边平行答案:D(2) 下面哪个图形是五边形?A.B.C.D.答案:C(3) 下面哪个选项不是长方体的性质?A. 有六个面B. 所有面都是正方形C. 所有的边都相等D. 有12条边答案:B(4) 若正方形的边长为6cm,则其面积是多少平方厘米?A. 12平方厘米B. 18平方厘米C. 24平方厘米D. 36平方厘米答案:D3. 计算题:(1) 一个正方形的边长为5cm,求其周长和面积。
解答:周长 = 4 ×边长 = 4 × 5 = 20cm面积 = 边长 ×边长 = 5 × 5 = 25平方厘米(2) 一个长方体的长、宽、高分别为2cm、3cm和4cm,求其体积。
解答:体积 = 长 ×宽 ×高 = 2 × 3 × 4 = 24立方厘米(3) 若一个平行四边形的底边长为8cm,高为5cm,求其面积。
解答:面积 = 底边长 ×高 = 8 × 5 = 40平方厘米(4) 若一个三角形的底边长为6cm,高为4cm,求其面积。
解答:面积 = 底边长 ×高 ÷ 2 = 6 × 4 ÷ 2 = 12平方厘米4. 应用题:(1) 一块长方形的纸板长15cm,宽8cm。
若将其剪去一块正方形,使剩余面积为120平方厘米,求剪去的正方形的边长。
解答:设剪去的正方形的边长为x,则剩余面积 = 长 ×宽 - 正方形面积120 = 15 × 8 - x²120 = 120 - x²x² = 0x = 0答案:剪去的正方形的边长为0,即无需剪去。
空间与图形 精选带答案

空间与图形一、选择题1.平面上三个点可以确定的直线条数是( )A. 1B. 2C. 3D. 1或32.上午8点整时表的时针与分针的夹角是()A. 60°B. 80°C. 120°D. 150°3.下列说法中正确的个数有()①一个30°角的余角有无数个;②一个30°角的邻补角只有两个;③在射线AE上,从A点起顺次截取线段AB、BC,使AB=4cm,BC=2cm,则AC=6cm;④在射线AE上,从A点起截取线段AB、BC,使AB=4cm,BC=2cm,则AC=6cm;⑤103.3°+176°42′=280°A. 1B. 2C. 3D. 44.如图,在△ABC中,∠CAB=70°.在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′`∥AB,则∠BAB′等于()A. 30°B. 35°C. 40°D.50°5.如图,AB∥CD∥EF,且CG∥AF,图中与∠BAF相等的角(包括∠BAF)的个数为()A. 5B. 6C. 7D.86.用12根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余和折断,则能摆出的不同形状的三角形的个数是()A. 1B. 2C. 3D.47.如图,过边长为1的等边△ABC的边AB上的一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC边于D,则DE的长为()(A)1/3 (B)1/2 (C)2/3 (D)不能确定8.如图,⊙O的半径为1,AB 是⊙O 的一条弦,且AB=根号3,则弦AB所对圆周角的度数为()A. 30°B. 60°C. 30°或150°D.60°或120°9.下列说法正确的有(1)如图(a),可以利用刻度尺和三角板测量圆形工件的直径;(2)如图(b),可以利用直角曲尺检查工件是否为半圆形;(3)如图(c),两次使用丁字尺(CD所在直线垂直平分线段AB)可以找到圆形工件的圆心;(4)如图(d),测倾器零刻度线和铅垂线的夹角度数,等于从P点看A点时仰角的度数.A. 1 个B. 2 个C. 3 个D. 4个10.一个正方体的表面展开图如图所示,每个面内都标注了字母,如果从正方体的右面看是面D,则正方体的上面是。
初三空间图形试题及答案

初三空间图形试题及答案一、选择题(每题3分,共30分)1. 下列选项中,属于平面图形的是()。
A. 圆柱体B. 圆锥体C. 正方体D. 圆2. 在空间几何中,如果一个点到一个平面的距离是固定的,那么这个点在空间中的轨迹是()。
A. 直线B. 曲线C. 圆D. 抛物线3. 一个正方体的体积是27立方厘米,那么它的对角线长度是()。
A. 3厘米B. 6厘米C. 9厘米D. 无法确定4. 一个长方体的长、宽、高分别是2cm、3cm、4cm,那么它的表面积是()。
A. 52平方厘米B. 40平方厘米C. 60平方厘米D. 48平方厘米5. 一个球体的直径是10厘米,那么它的体积是()。
A. 523.6立方厘米B. 314立方厘米C. 785立方厘米D. 无法确定6. 一个圆锥的底面半径是3厘米,高是4厘米,那么它的体积是()。
A. 37.68立方厘米B. 12立方厘米C. 36立方厘米D. 45立方厘米7. 一个圆柱体的底面半径是2厘米,高是5厘米,那么它的体积是()。
A. 62.8立方厘米B. 50立方厘米C. 100立方厘米D. 78.5立方厘米8. 一个三棱锥的底面边长是2厘米,高是3厘米,那么它的体积是()。
A. 3立方厘米B. 6立方厘米C. 2立方厘米D. 4立方厘米9. 在空间几何中,如果两个平面互相垂直,那么它们之间的夹角是()。
A. 0度B. 90度C. 180度D. 无法确定10. 一个正四面体的棱长是a,那么它的体积是()。
A. a³/6B. a³/4C. a³/3D. a³/2二、填空题(每题3分,共30分)1. 一个长方体的长、宽、高分别是5cm、4cm、3cm,那么它的体积是______立方厘米。
2. 一个球体的半径是5厘米,那么它的表面积是______平方厘米。
3. 如果一个圆锥的体积是45立方厘米,底面半径是3厘米,那么它的高是______厘米。
小学数学空间与图形专题(试题+答案)

小学数学空间与图形专题(试题+答案) 图形与几何试题一、填空题(19分)1.从直线外一点到这条直线可以画无数条线段,其中最短的是与这条直线垂直的线段。
2.半圆的直径是10厘米,它的周长是π×10厘米。
3、圆柱的体积比与它等底等高的圆锥的体积大π:3.4.一个三角形中,最小的角是46°,按角分类,这个三角形是锐角三角形。
5.用百分数表示以下阴影部分是整个图形面积的百分之几。
6.把一个底面直径2分米的圆柱体截去一个高1分米的圆柱体,原来的圆柱体表面积减少π平方分米。
7.“∠ABC=60°”和“∠DEF=120°”的周长之比是2:1,面积之比是1:4.8.画一个周长25.12厘米的圆,圆规两脚间的距离是12.56厘米,画成的圆的面积是100π平方厘米。
9.一个梯形,上底长a厘米,下底长b厘米,高h厘米。
它的面积是(a+b)h/2平方厘米。
如果a=b,那么这个图形就是一个菱形。
10.在一块边长是20厘米的正方形木板上锯下一个最大的圆,这个圆的面积是100π平方厘米,剩下的边料是(400-100π)平方厘米。
11.5个棱长为30厘米的正方体木箱堆放在墙角(如下图),露在外面的表面积是1500平方厘米。
12、如图所示,把底面周长18.84厘米、高1分米的圆柱切成若干等分,拼成一个近似的长方体。
这个长方体的右侧面积是π平方厘米。
二、判断题(7分)1.小于18°的角是锐角。
(错)2.用一副三角板可以拼成105°的角。
(对)3.只要有一个角是直角的平行四边形,就是长方形或正方形。
(错)4.如果圆柱的底面周长和高相等,则它的侧面展开一定是个长方形。
(错)5.把一个长方形拉成一个平行四边形后,保持不变的是面积。
(对)6.一个正方形的边长与一个圆的直径相等,那么这个正方形的周长一定大于圆的周长。
(错)7.长6厘米的正方体,表面积和体积相等。
(错)三、选择题(每题1.5分共18分)1.有2cm,3cm,4cm,6cm长的小棒各1根,选其中的3根小棒围成三角形,最多可以围成4个。
二年级下册知识复习精选题 ——02《空间与图形》(解析版)北师大版

北师大版数学二升三暑期衔接—提优复习精选汇编题专训温故知新篇02《空间与图形》一、单选题1.(2020二下·西安期末)9千米比9000厘米()A. 长得多B. 短得多C. 长一些【答案】A【解析】【解答】9千米=900000厘米,900000厘米>9000厘米,9千米比9000厘米长得多。
故答案为:A。
【分析】根据1千米=1000米,1米=100厘米,1千米=100000厘米,将单位化统一,再比较大小。
2.(2020二下·偃师期中)乐乐家在学校的东南面,那么学校在乐乐家的()面。
A. 西南B. 东北C. 西北【答案】C【解析】【解答】解:乐乐家在学校的东南面,那么学校在乐乐家的西北面。
故答案为:C。
【分析】一个地点在另一个地点的某个方向上,那么另一个地点就在这个地点的相对的方向上。
3.时针和分针形成的较小的角是直角时,时间可能是()。
A. 6时B. 12时C. 9时【答案】C【解析】【解答】时针和分针形成的较小的角是直角时,时间可能是3时或9时。
故答案为:C。
【分析】3时,时针指向3,分针指向12,9时,时针指向9,分针指向12。
这两个时间分针与时针的夹角都有3大格,夹角是直角。
4.(2019二下·龙岗期末)下边图形中有()个直角。
A. 3B. 5C. 6【答案】C【解析】【解答】下边图形中有6个直角。
故答案为:C.【分析】此题主要考查了直角的特征,直角=90°,借助三角板上的直角判断。
5.下列图形中,都是直角的图形是()A. B. C. D.【答案】B二、判断题6.(2020二下·期末)三角形有3个角,将一张三角形纸剪掉一个角后,还剩2个角。
()【答案】错误【解析】【解答】解:将一张三角形纸剪掉一个角后,还剩4个角。
故答案为:错误。
【分析】如图所示:,将三角形剪掉一个角就变成四边形,四边形有四个角。
7.同学们面向南站在操场做早操,贝贝的右手边是丽丽,丽丽在贝贝的西面。
初三空间图形试题及答案

初三空间图形试题及答案
在几何学中,空间图形的理解和应用是非常重要的。
以下是一份针对
初三学生的关于空间图形的试题及答案,旨在考察学生对空间几何概
念的掌握程度。
试题:
1. 已知一个长方体的长、宽、高分别为a、b、c,求该长方体的体积。
2. 一个正四面体的棱长为d,求其表面积。
3. 一个圆锥的底面半径为r,高为h,求其体积。
4. 一个圆柱的底面半径为R,高为H,求其侧面积。
5. 一个球的半径为s,求其表面积。
答案:
1. 长方体的体积可以通过其长、宽、高的乘积来计算。
因此,体积
V=abc。
2. 正四面体的表面积由四个等边三角形组成。
每个等边三角形的面积
为\(\frac{\sqrt{3}}{4}d^2\),所以总表面积
S=4×\(\frac{\sqrt{3}}{4}d^2\)=\(\sqrt{3}d^2\)。
3. 圆锥的体积可以通过公式\(\frac{1}{3}\pi r^2h\)来计算,其中r 是底面半径,h是高。
4. 圆柱的侧面积可以通过底面周长乘以高来计算。
底面周长为2πR,所以侧面积A=2πR×H。
5. 球的表面积可以通过公式4πs^2来计算,其中s是球的半径。
通过这些题目,学生可以更好地理解和掌握空间图形的体积和表面积的计算方法,同时也能够提高他们解决实际问题的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间与图形复习题及答案
填空(27﹪)
1、将一个大正方体切成大小相同的8个小正方体,每个小正方体的表面积是18
平方厘米,原正方体的表面积是()平方厘米.
2、把一个底面直径2分米的圆柱体截去一个高1分米的圆柱体,原来的圆柱体表面积减少()平方分米.
3、一个圆柱体的底面积是45平方厘米,高是20厘米,体积是()立方厘米,
与它等底等体积的圆锥体的高是()厘米.
判断(27﹪)
4、不相交的两条直线是平行线.()
5、圆柱体积比它等底等高圆锥体积多2\3 .()
6、圆柱的底面半径扩大3倍,它的侧面积扩大9倍.()
选择(16﹪)
7、比较右图中二个三角形的周长和面积,结果是()
A、面积相等,周长相等
B、面积相等周长不相等
C、面积不相等周长相等 d面积不相等周长不相等
8、圆柱、正方体和长方体的底面周长相等,高也相等,则()的体积最大.
A、圆柱
B、正方体
C、长方体
解决问题(30﹪)
9、在长4分米,宽3分米的长方形纸剪成一个最大的半圆,这个半圆的周长和面积各是多少?
10、一种易拉罐高12厘米,底面直径6厘米,生产一个易拉罐需多少平方厘米的铝合金材料?如果把24罐装一盒,你准备怎样包装,需要用多少平方分米的硬纸板?(请写出你的包装方案)
评分标准:
填空题每空9分答案:①72 ②6.28 ③900 60
判断题每题9分④×⑤×⑥×
选择题每题8分⑦ B ⑧A
解决问题每题15分⑨ 3.14 ×4×1/2﹢4﹦10.28分米
3.14×(4/2)(4/2)×1/2=6.28平方分米
⑩ 3.14 ×(6/2)×(6/2)×2﹢3.14×6×12=282.6(平方厘米)
(36×12﹢12×24﹢36×24)×2﹦3168平方厘米=31.68平方分米
(答案不唯一)。
