高中数学全套知识点思维导图椭圆
高中数学知识体系结构16 椭圆

高中数学知识体系结构----椭圆一、椭圆 1. 椭圆的定义:平面内与两个定点12F F ,的距离之和等于常数(大于12||F F )的点的轨迹(或集合)叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距. 2. 椭圆的标准方程:(1)焦点在x 轴上的椭圆标准方程是:22221(0)x ya b a b+=>>,焦点是1(0)F c -,,2(0)F c ,,且222c a b =-.(2)焦点在y 轴上的椭圆标准方程是:22221(0)y xa b a b+=>>,焦点是1(0)F c -,,2(0)F c ,,且222c a b =-. 3. 椭圆的几何性质x a ≤y b ≤,x b y a ≤≤4. 求椭圆标准方程的技巧(1) 与椭圆()222210x y a b a b +=>>有相同离心率的椭圆方程可设为()2211220x y t t a b+=>或()2222220y x t t a b +=>. (2) 已知椭圆上两个点的坐标,可设椭圆方程为()221,0,0mx ny m n n m +=≠>>(3) 已知椭圆的焦点和椭圆上一点的坐标,则用椭圆定义求出2a .注:求椭圆方程一定要先确定是横版还是竖版. 5. 椭圆常用的二级结论(1) 椭圆第二定义:到定点()1,0F c (或()2,0F c -)与定直线2a x c =(或2ax c=-)之比为定值()1ce e a=<的点的轨迹是椭圆. (2) 通径:过椭圆的焦点且与椭圆的长轴垂直的直线与椭圆相交于,A B 两点,则22bAB a=. (3) 焦半径范围:椭圆的焦点为F ,椭圆上有一点P ,则PF 的范围是[],a c a c -+.(4) 焦点三角形面积:已知椭圆()222210x y a b a b+=>>的左右焦点为12,F F ,椭圆上有一点P ,则12212tan2PF F F PF S b ∠=. (5) 中点弦(点差法):(a )已知椭圆()222210x y a b a b+=>>,直线l 与椭圆交于,A B 两点,点M 为线段AB 的中点,则有22AB OMb k k a⋅=-.(b )已知椭圆()2222:10y x C a b a b+=>>,直线l 与椭圆交于,A B 两点,点M 为线段AB 的中点,则有22AB OM a k k b⋅=-.(6) 中点弦(点差法)结论推广:已知()222210x y a b a b+=>>,直线l 过原点且与椭圆交于,A B 两点,点P 为椭圆上一点,且不与,A B 重合,则22PA PB bk k a⋅=-.(7) 椭圆的参数方程:已知椭圆的方程为()222210x y a b a b+=>>,则椭圆上一点P 的坐标可设为()cos ,sin a b θθ.(8) 椭圆上点的切线方程:过椭圆()222210x y a b a b+=>>上的一点()00,P x y 作椭圆的切线,则切线方程为00221x x y ya b+=. (9) 椭圆外一点的切点弦方程:过椭圆()222210x y a b a b +=>>外一点()00,P x y 作椭圆的切线,PA PB ,则切点弦AB 的方程为00221x x y ya b+=.。
高中数学知识框架思维导图(整理版)

基本初等函数 指数函数、对数函数、幂函数、三角函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用 分段探究,整体考察 复合函数的单调性:同增异减 赋值法、典型的函数模型 零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换:������ = ������(������) → ������ = ������(������ ± ������),������ = ������(������) → ������ = ������(������) ± ������,������, ������ > 0 函数图象 及其变换 对称变换:������ = ������(������) → ������ = −������(������),������ = ������(������) → ������ = ������(−������),������ = ������(������) → ������ = −������(−������) 翻折变换:������ = ������(������) → ������ = |������(������)|,������ = ������(������) → ������ = ������(|������|) 伸缩变换:������ = ������(������) → ������ = ������������(������),������ = ������(������) → ������ = ������(������������)
������
第二部分
角的概念
三角函数与平面向量
弧长公式������ = ������������、扇形面积公式������ = ������������
2 1 π 2
高中椭圆知识点归纳

高中椭圆知识点归纳椭圆是高中数学中一个重要的曲线类型,在解析几何中占据着重要的地位。
下面我们来对高中椭圆的知识点进行一个全面的归纳。
一、椭圆的定义平面内与两个定点$F_1$、$F_2$的距离之和等于常数(大于$|F_1F_2|$)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。
用数学语言表述为:$|PF_1| +|PF_2| = 2a$($2a >|F_1F_2| = 2c$)其中,$P$为椭圆上的动点,$F_1$、$F_2$为焦点,$a$为长半轴长,$c$为半焦距。
二、椭圆的标准方程1、焦点在$x$轴上的椭圆标准方程:$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$($a > b > 0$)其中,$a$为长半轴长,$b$为短半轴长,$c =\sqrt{a^2 b^2}$。
2、焦点在$y$轴上的椭圆标准方程:$\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1$($a > b > 0$)同样,$a$为长半轴长,$b$为短半轴长,$c =\sqrt{a^2 b^2}$。
三、椭圆的性质1、范围对于焦点在$x$轴上的椭圆,$a \leq x \leq a$,$b \leq y \leq b$;对于焦点在$y$轴上的椭圆,$b \leq x \leq b$,$a \leq y \leq a$。
2、对称性椭圆关于$x$轴、$y$轴和原点对称。
3、顶点焦点在$x$轴上的椭圆顶点坐标为$(\pm a, 0)$,$(0, \pm b)$;焦点在$y$轴上的椭圆顶点坐标为$(0, \pm a)$,$(\pm b, 0)$。
4、离心率椭圆的离心率$e =\frac{c}{a}$($0 < e < 1$),它反映了椭圆的扁平程度。
$e$越接近$0$,椭圆越接近圆;$e$越接近$1$,椭圆越扁。
5、焦半径焦点在$x$轴上,若点$P(x_0, y_0)$在椭圆上,则$|PF_1| = a +ex_0$,$|PF_2| = a ex_0$;焦点在$y$轴上时,焦半径公式类似。
理数思维导图

十十五、平面面向量量
不不等式的基本概念
具有大大小小和方方向的量量叫做向量量
空间向量量
七、不不等式
同向不不等式与异向不不等式 同解不不等式与不不等式的同解变形
共线向量要不不等式 几几个著名不不等式 不不等式的解法
整式不不等式分式不不等式;指数不不等式;对数不不等式;含绝对值不不等式
平面面
集合的性质
两条平行行行线在同一一平面面内的射影图形是一一条直线或两条平行行行线或两点 异面面直线判定定理理:过平面面外一一点与平面面内一一点的直线和平面面内不不经过该点的直线是 异面面直线.(不不在任何一一个平面面内的两条直线) 平行行行公理理:平行行行于同一一条直线的两条直线互相平行行行 等⻆角定理理:若果一一个⻆角的两边和另一一个⻆角的两边分别平行行行并且方方向相同,那么这两个⻆角相等 相交、平行行行、在平面面内. 空间直线与平面面位置
直线与平面面平行行行、直线与平面面垂直
八八、立立体几几何
一一、集合与常 用用逻辑语言言
“或”、“且”、“非非”这些词叫做逻辑联结词;不不含有逻辑 联结词的命题是简单命题;由简单命题和逻辑联结 词“或”、“且”、“非非”构成的命题是复合命题。
平面面平行行行判定定理理:如果一一个平面面内有两条相交直线都平行行行于另一一个平面面,那么这两个平面面平行行行.(“线面面平行行行,面面面面平行行行”) 从n个不不同的元素中任取m(m≤n)个元素,按照一一 定顺序排成一一列列,叫做从n个不不同元素中取出m个 元素的一一个排列列. 如果,两个排列列相同,不不仅这两个排列列的元素必须完全相同,而而 且排列列的顺序也必须完全相同. 定义 相同排列列. 排列列数. 排列列公式 含有可重元素的排列列问题. 排列列 对排列列定义的理理解. ①棱柱的各个侧面面都是平行行行四边形,所有的侧棱都相等;直棱柱 的各个侧面面都是矩形;正棱柱的各个侧面面都是全等的矩形. ②棱柱的两个底面面与平行行行于底面面的截面面是对应边互相平行行行的全等多边形. ③过棱柱不不相邻的两条侧棱的截面面都是平行行行四边形. 棱柱具有的性质 平行行行六面面体 两个平面面平行行行的性质定理理:如果两个平面面平行行行同时和第三个平面面相交,那么它们交线平行行行.(“面面面面平行行行,线线平行行行”) 一一、两个平面面所成二二面面⻆角是直二二面面⻆角,则两个平面面垂直 二二、如果一一个平面面与一一条直线垂直,那么经过这条直线的平面面垂直于这个平面面.(“线面面垂直,面面面面垂直”) 1. 乘法原理理、加法原理理. 2. 可以有重复元素的排列列. 两个平面面垂直,那么在一一个平面面内垂直于它们交线的直线垂直于另一一个平面面。 两个原理理 两个平面面垂直的判定 两个平面面垂直性质定理理 直棱柱侧面面积 斜棱柱侧面面积
椭圆的全部知识点高考

椭圆的全部知识点高考椭圆是高中数学中的一个重要的几何概念,也是高考中常会涉及的一个知识点。
它具有许多特殊的性质和应用,掌握椭圆的基本知识对于高考数学的学习和应试至关重要。
本文将从定义、性质、方程和参数等多个方面来论述椭圆的全部知识点。
一、定义椭圆是平面上到两个定点F1和F2距离之和与给定正常数2a的和等于一定正常数2c的点P的轨迹。
其中F1和F2称为焦点,而定常数2c称为椭圆的离心率,而定常数2a称为椭圆的长轴。
离心率e和椭圆长轴的关系是e=c/a。
二、性质1. 椭圆是对称图形,对称中心为原点O。
2. 椭圆的长轴是x轴,短轴是y轴。
3. 焦点到椭圆上任意一点的距离之和等于椭圆的长轴距离。
4. 椭圆的离心率介于0到1之间。
5. 椭圆的离心率越小,椭圆形状越接近于圆形;离心率越大,椭圆形状越扁平。
6. 椭圆的上下焦点连线与椭圆上任意一点的连线相交于右旋点。
7. 椭圆的切线和法线在焦点处垂直。
三、方程椭圆的一般方程为x^2/a^2 + y^2/b^2 = 1。
其中a和b分别为椭圆的长半轴和短半轴。
当椭圆的中心位置不在原点时,方程会出现平移项。
四、参数在椭圆的参数方程中,椭圆上的每个点都可以由参数θ来表示。
椭圆的参数方程为:x = a cosθy = b sinθ其中θ的取值范围是[0, 2π]。
五、其他知识点1. 椭圆的离心率与焦距的关系:e = √(a^2 - b^2)/a2. 椭圆的射线方程:y = mx ± √(a^2m^2 + b^2)椭圆作为高考数学的一个重要的知识点,需要掌握其定义、性质、方程和参数等多个方面的知识。
理解和应用这些知识将有助于解决与椭圆相关的问题,提高解题的能力。
因此,我们在备考高考数学的过程中应该注重对椭圆及其相关知识的学习和理解。
总之,椭圆的全部知识点在高考数学中占有一定的比重,掌握这些知识点是解题的基础。
通过理论的学习和大量的练习,我们可以更好地理解椭圆的特性和运用,提高我们的解题能力。
椭圆高中知识点总结

椭圆高中知识点总结一、椭圆的定义椭圆是平面上到两定点F1和F2的距离之和等于常数2a的所有点P的轨迹。
这两个定点叫做椭圆的焦点,常数2a叫做椭圆的长轴。
将F1F2的中点O为原点,x轴为椭圆的长轴线,y轴为椭圆的短轴线,椭圆的方程可以写成(x/a)² + (y/b)² = 1,其中a为椭圆的长半轴,b为椭圆的短半轴。
二、椭圆的性质1. 对称性:椭圆具有关于x轴和y轴的对称性。
椭圆关于x轴、y轴对称的焦点、焦斜率等均相等。
椭圆中心的对称轴上都有一个点。
2. 焦点性质:椭圆的焦点到椭圆上任意一点的距离之和等于椭圆的长轴长。
3. 四边形定理:对于椭圆上的任意一点P, 则焦点连线与椭圆的法线与椭圆的法线,这三线共点。
4. 儆功:椭圆焦点与椭圆上任意点构成的两个与正切线互为正交。
5. 现行性质:s忧圆上的点处的切线与椭圆的法线垂直。
三、椭圆的方程椭圆的标准方程是(x/a)² + (y/b)² = 1,其中a为椭圆的长半轴,b为椭圆的短半轴。
椭圆的方程也可以用直角坐标系表示,通常我们会通过平移、旋转等操作将椭圆方程转化成标准方程。
四、椭圆的图形特征在平面直角坐标系中,椭圆的图像是一个闭合曲线,呈现出椭圆形的形状。
椭圆的长轴和短轴决定了椭圆的大小和形状,而椭圆的焦距和离心率则决定了椭圆的位置和离心程度。
椭圆和圆的关系:椭圆是圆的一种特殊形式,当椭圆的长轴和短轴长度相等时,即a=b时,椭圆就变成了圆。
因此,圆可以看作是具有无穷大长轴的椭圆。
六、椭圆的相关运用椭圆作为一种特殊的几何曲线,在实际生活和科学技术中有着广泛的应用。
在建筑设计中,一些建筑物的拱形结构就采用了椭圆的形状;在椭圆周长和面积的计算中,椭圆的数学性质也得到了广泛的应用;在天文学中,行星的轨道也可以被理想化为椭圆形。
综上所述,椭圆是数学中的重要内容,具有丰富的性质和特征。
通过对椭圆相关知识点的总结和了解,我们可以更好地理解和应用椭圆的性质,在数学学习的过程中取得更好的效果。
高二椭圆知识点思维导图

高二椭圆知识点思维导图椭圆是高二数学中的一个重要知识点,它在几何形状、实践问题以及数学应用中具有广泛的应用。
本文将通过思维导图的形式,对高二椭圆的关键知识点进行概括、总结和归纳,帮助学生更好地理解和掌握这一内容。
椭圆的定义(Ellipse Definition)- 椭圆是平面上到两个定点(焦点)F₁和F₂的距离之和等于常数2a的点P的轨迹。
椭圆的性质(Properties of Ellipse)1. 离心率(Eccentricity)- 离心率定义为离心距c与轴长2a之比,即e = c/a。
- 离心率e描述了椭圆的扁平程度,e<1时表示椭圆,e=1时表示半径为a的圆,e>1时表示双曲线。
2. 焦点与准线- 焦点是与椭圆定义中的两个定点F₁和F₂相关联的点。
- 准线是椭圆定义中与焦点F₁、F₂的连线垂直且通过椭圆中心的直线。
3. 主轴与短轴- 主轴是通过椭圆中心且与准线垂直的线段,长度为2a。
- 短轴是通过椭圆中心且与主轴垂直的线段,长度为2b。
4. 焦半径与定位点- 焦半径是从焦点到椭圆上任意一点P的距离。
- 定位点是椭圆上离焦点F₁和F₂等距离的两点,分别记作A₁和A₂。
椭圆的方程(Equation of Ellipse)- 椭圆的标准方程为(x - h)²/a² + (y - k)²/b² = 1,其中(h, k)为椭圆中心坐标。
- 椭圆的参数方程为x = h + a * cosθ,y = k + b * sinθ,其中θ为参数。
椭圆的求解(Solving Ellipse)1. 椭圆的离心率与长轴、短轴的关系- 离心率e与长轴2a和短轴2b的关系为e² = 1 - (b²/a²)。
2. 椭圆的焦点坐标- 焦点的坐标为F₁(-c, 0)和F₂(c, 0),其中c² = a² - b²。
椭圆(知识点讲解)高考数学一轮复习(新教材新高考)(解析版)
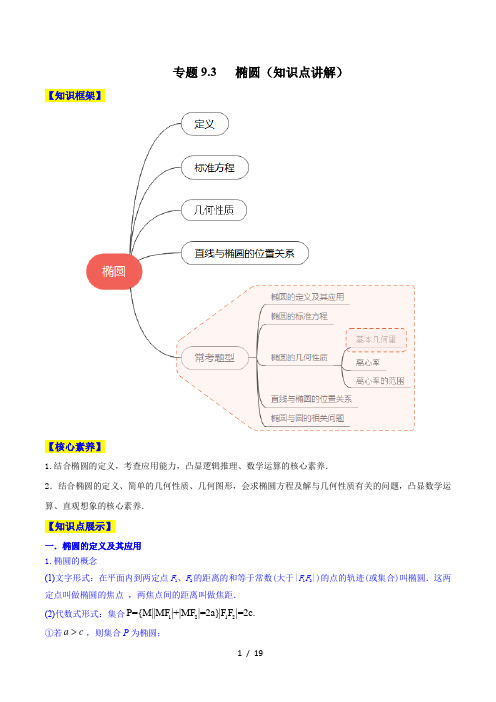
专题9.3 椭圆(知识点讲解)【知识框架】【核心素养】1.结合椭圆的定义,考查应用能力,凸显逻辑推理、数学运算的核心素养.2.结合椭圆的定义、简单的几何性质、几何图形,会求椭圆方程及解与几何性质有关的问题,凸显数学运算、直观想象的核心素养.【知识点展示】一.椭圆的定义及其应用1.椭圆的概念(1)文字形式:在平面内到两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹(或集合)叫椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距.(2)代数式形式:集合①若,则集合P为椭圆;1212P={M||MF|+|MF|=2a|FF|=2c.}a c>②若,则集合P 为线段; ③若,则集合P 为空集.2.椭圆的标准方程:焦点在轴时,;焦点在轴时,二.椭圆的标准方程 1. 椭圆的标准方程:(1)焦点在轴,;(2)焦点在轴,.2.满足条件:三.椭圆的几何性质椭圆的标准方程及其几何性质条件图形标准方程范围对称性曲线关于轴、原点对称 曲线关于轴、原点对称 顶点 长轴顶点 ,短轴顶点长轴顶点 ,轴顶点焦点a c =a c <x 2222=1(a>b>0)x y ab +y 2222=1(a>b>0)y x a b+x 2222+=1(a>b>0)x y a by 2222y +=1(a>b>0)x a b22222000a c a b c a b c >,=+,>,>,>22222000a c a b c a b c >,=+,>,>,>2222+=1(a>b>0)x y a b 2222y +=1(a>b>0)x a bx a y b ≤≤,x b y a ≤≤,,x y ,x y (),0a ±()0,b ±()0,a ±(),0b ±(),0c ±()0,c ±焦距离心率,其中通径过焦点垂直于长轴的弦叫通径,其长为四.直线与椭圆的位置关系 1.直线与椭圆位置关系的判断(1)代数法:把椭圆方程与直线方程联立消去y ,整理得到关于x 的方程Ax 2+Bx +C =0.记该一元二次方程根的判别式为Δ,①若Δ>0,则直线与椭圆相交;②若Δ=0,则直线与椭圆相切;③若Δ<0,则直线与椭圆相离.(2)几何法:在同一直角坐标系中画出椭圆和直线,利用图象和性质可判断直线与椭圆的位置关系. 2.直线与椭圆的相交长问题:(1)弦长公式:设直线与椭圆有两个公共点则弦长公式为或 (2)弦中点问题,适用“点差法”. (3)椭圆中点弦的斜率公式若M (x 0,y 0)是椭圆的弦AB (AB 不平行y 轴)的中点,则有k AB ·k OM =22b a-,即k AB =2020b x a y -.【常考题型剖析】题型一:椭圆的定义及其应用例1.(2021·全国高考真题)已知1F ,2F 是椭圆C :22194x y+=的两个焦点,点M 在C 上,则12MF MF ⋅的最大值为( ) A .13 B .12C .9D .6【答案】C 【分析】本题通过利用椭圆定义得到1226MF MF a +==,借助基本不等式212122MF MF MF MF ⎛+⎫⋅≤ ⎪⎝⎭即可得到答222122()F F c c a b -==() 0,1ce a∈=c =22a b -22b a1122()()M x y N x y ,,,,MN =221212(1)[()4]k x x x x ++-MN 2121221(1)[(y )4]y y y k++-2222+=1(a>b>0)x y a b案. 【详解】由题,229,4a b ==,则1226MF MF a +==,所以2121292MF MF MF MF ⎛+⎫⋅≤= ⎪⎝⎭(当且仅当123MF MF ==时,等号成立). 故选:C .例2. (2021·全国)已知椭圆22:143x y C +=的右焦点为F ,P 为椭圆C 上一动点,定点(2,4)A ,则||||PA PF -的最小值为( ) A .1 B .-1 C 17 D .17-【答案】A 【分析】设椭圆的左焦点为F ',得到||4PF PF '=-,得出||||||4PA PF PA PF '-=+-,结合图象,得到当且仅当P ,A ,F '三点共线时,||PA PF '+取得最小值,即可求解.【详解】设椭圆的左焦点为F ',则||4PF PF '+=,可得||4PF PF '=-, 所以||||||4PA PF PA PF '-=+-,如图所示,当且仅当P ,A ,F '三点共线(点P 在线段AF '上)时, 此时||PA PF '+取得最小值,又由椭圆22:143x y C +=,可得(1,0)F '-且(2,4)A ,所以2(21)165AF '=++=,所以||||PA PF -的最小值为1. 故选:A .例3.(2023·全国·高三专题练习)已知P 是椭圆221259x y +=上的点,1F 、2F 分别是椭圆的左、右焦点,若1212PF PF PF PF ⋅=⋅12,则12F PF △的面积为( )A .33B .3C 3D .9【答案】A【分析】由已知可得12F PF ∠,然后利用余弦定理和椭圆定义列方程组可解. 【详解】因为121212121212cos 1cos 2PF PF F PF PF PF F PF PF PF PF PF ⋅∠⋅==∠=⋅⋅,120F PF π∠≤≤所以123F PF π∠=,又224c a b =-=记12,PF m PF n ==,则222464210m n mn c m n a ⎧+-==⋅⋅⋅⎨+==⋅⋅⋅⎩①②,②2-①整理得:12mn =,所以12113sin 12332322F PF S mn π==⨯⨯= 故选:A【规律方法】1.应用椭圆的定义,可以得到结论:(1)椭圆上任意一点P (x ,y )(y ≠0)与两焦点F 1(-c,0),F 2(c,0)构成的△PF 1F 2称为焦点三角形,其周长为2(a +c ).(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a 是斜边,a 2=b 2+c 2.2.对焦点三角形的处理方法,通常是运用.3.椭圆定义的应用技巧(1)椭圆定义的应用主要有:求椭圆的标准方程,求焦点三角形的周长、面积及弦长、最值和离心率等. (2)通常定义和余弦定理结合使用,求解关于焦点三角形的周长和面积问题. 题型二:椭圆的标准方程例4.(2022·全国·高考真题(文))已知椭圆2222:1(0)x y C a b a b+=>>的离心率为13,12,A A 分别为C 的左、右顶点,B 为C 的上顶点.若121BA BA ⋅=-,则C 的方程为( )A .2211816x y +=B .22198x yC .22132x y +=D .2212x y +=【答案】B【分析】根据离心率及12=1⋅-BA BA ,解得关于22,a b 的等量关系式,即可得解.【详解】解:因为离心率22113c b e a a ==-=,解得2289b a =,2289=b a ,12,A A 分别为C 的左右顶点,则()()12,0,,0A a A a -,B 为上顶点,所以(0,)B b .所以12(,),(,)=--=-BA a b BA a b ,因为121BA BA ⋅=-所以221-+=-a b ,将2289=b a 代入,解得229,8a b ==,故椭圆的方程为22198x y .12F PF △⎧⎪⎨⎪⎩定义式的平方余弦定理面积公式2212222121212(2a)212S θθ∆⎧⎪=⎪=-⋅⎨⎪⎪=⋅⎩⇔(|PF|+|PF|)(2c)|PF|+|PF||PF||PF|cos |PF||PF|sin故选:B.例5.(2019·全国高考真题(文))已知椭圆C 的焦点为121,01,0F F -(),(),过F 2的直线与C 交于A ,B两点.若222AF F B =││││,1AB BF =││││,则C 的方程为( )A.2212x y += B.22132x y +=C.22143x y +=D.22154x y += 【答案】B 【解析】法一:如图,由已知可设2F B n =,则212,3AF n BF AB n ===,由椭圆的定义有121224,22a BF BF n AF a AF n =+=∴=-=.在1AF B △中,由余弦定理推论得22214991cos 2233n n n F AB n n +-∠==⋅⋅.在12AF F △中,由余弦定理得2214422243n n n n +-⋅⋅⋅=,解得3n =. 22224233312,a n a b a c ∴==∴=∴=-=-=∴所求椭圆方程为22132x y +=,故选B .法二:由已知可设2F B n =,则212,3AF n BF AB n ===,由椭圆的定义有121224,22a BF BF n AF a AF n =+=∴=-=.在12AF F △和12BF F △中,由余弦定理得2221222144222cos 4,422cos 9n n AF F n n n BF F n⎧+-⋅⋅⋅∠=⎨+-⋅⋅⋅∠=⎩,又2121,AF F BF F ∠∠互补,2121cos cos 0AF F BF F ∴∠+∠=,两式消去2121cos cos AF F BF F ∠∠,,得223611n n +=,解得32n =.22224233,312,a n a b a c ∴==∴=∴=-=-=∴所求椭圆方程为22132x y +=,故选B . 例6.【多选题】(2023·全国·高三专题练习)点1F ,2F 为椭圆C 的两个焦点,若椭圆C 上存在点P ,使得1290F PF ∠=︒,则椭圆C 方程可以是( )A .221259x y +=B .2212516x y +=C .221189x y +=D .221169x y +=【答案】AC【分析】设椭圆上顶点为B ,由题满足1290F BF ∠≥︒,即2221212BF BF F F +≤,可得222a b ≥,即可得出答案.【详解】设椭圆方程为22221x y a b+=()0a b >>,设椭圆上顶点为B ,椭圆C 上存在点P ,使得1290F PF ∠=︒, 则需1290F BF ∠≥︒, 2221212BF BF F F ∴+≤,即2224a a c +≤,222c a b =-,222424a a b -≤, 则222a b ≥,所以选项AC 满足. 故选:AC. 【总结提升】1.用待定系数法求椭圆标准方程的一般步骤是: (1)作判断:根据条件判断焦点的位置.(2)设方程:焦点不确定时,要注意分类讨论,或设方程为 . (3)找关系:根据已知条件,建立关于的方程组. (4)求解,得方程.2.(1)方程与有相同的离心率.(2)与椭圆共焦点的椭圆系方程为,恰当运用椭圆系方程,可使运算简便. 题型三:椭圆的几何性质例7.(2022·全国·高考真题(理))椭圆2222:1(0)x y C a b a b+=>>的左顶点为A ,点P ,Q 均在C 上,且关于y 轴对称.若直线,AP AQ 的斜率之积为14,则C 的离心率为( )A 3B 2C .12D .13【答案】A【分析】设()11,P x y ,则()11,Q x y -,根据斜率公式结合题意可得2122114y x a =-+,再根据2211221x y a b+=,将1y 用1x 表示,整理,再结合离心率公式即可得解.221mx ny +=(0)0m n m n ≠>,>且a b c m n 、、或、2222y +=1x a b 2222y +=(>0)x a bλλ2222+=1(a>b>0)x y a b 22222+=1(a>b>0,0)x y b k a k b k+>++【详解】解:(),0A a -, 设()11,P x y ,则()11,Q x y -, 则1111,AP AQ y y k k x a x a==+-+, 故21112211114AP AQy y y k k x a x a x a ⋅=⋅==+-+-+, 又2211221x y a b +=,则()2221212b a x y a-=, 所以()2221222114b a x a x a -=-+,即2214b a =, 所以椭圆C 的离心率22312c b e a a ==-=. 故选:A .例8.(2023·全国·高三专题练习)画法几何的创始人——法国数学家加斯帕尔·蒙日发现:与椭圆相切的两条垂直切线的交点的轨迹是以椭圆中心为圆心的圆.我们通常把这个圆称为该椭圆的蒙日圆.已知椭圆C :()222210x y a b a b +=>>的蒙日圆方程为2222x y a b +=+,1F ,2F 分别为椭圆C 的左、右焦点.5M 为蒙日圆上一个动点,过点M 作椭圆C 的两条切线,与蒙日圆分别交于P ,Q 两点,若MPQ 面积的最大值为36,则椭圆C 的长轴长为( ) A .25B .45C .3D .43【答案】B【分析】利用椭圆的离心率可得5a c =,分析可知PQ 为圆2223x y b +=的一条直径,利用勾股定理得出222236MP MQ PQ c +==,再利用基本不等式即可求即解【详解】因为椭圆C 的离心率55c e a ==,所以5a c =. 因为222a b c =+,所以2b c =,所以椭圆C 的蒙日圆的半径为223a b c +=. 因为MP MQ ⊥,所以PQ 为蒙日圆的直径, 所以6PQ c =,所以222236MP MQ PQ c +==. 因为222182MP MQMP MQ c +⋅≤=,当32MP MQ c ==时,等号成立, 所以MPQ 面积的最大值为:2192MP MQ c ⋅=.由MPQ 面积的最大值为36,得2936c =,得2c =,进而有24b c ==,25a =, 故椭圆C 的长轴长为45. 故选:B例9.(2018·全国·高考真题(文))已知椭圆C :2221(0)4x y a a +=>的一个焦点为(20),,则C 的离心率为( ) A .13B .12C 2D 22【答案】C【详解】分析:首先根据题中所给的条件椭圆的一个焦点为()20,,从而求得2c =,再根据题中所给的方程中系数,可以得到24b =,利用椭圆中对应,,a b c 的关系,求得22a =,最后利用椭圆离心率的公式求得结果.详解:根据题意,可知2c =,因为24b =, 所以2228a b c =+=,即22a =, 所以椭圆C 的离心率为22222e ==,故选C. 例10.(2022·四川成都·高三期末(理))已知椭圆()2222:10x y C a b a b +=>>的左,右焦点分别为1F ,2F ,以坐标原点O 为圆心,线段12F F 为直径的圆与椭圆C 在第一象限相交于点A .若122AF AF ≤,则椭圆C 的离心率的取值范围为______. 【答案】25,23⎛⎤⎥ ⎝⎦【分析】根据题意可得1290F AF ∠=,且c b >,再根据焦点三角形中的关系表达出离心率,结合函数的单调性求解即可【详解】由题意,因为线段12F F 为直径的圆与椭圆C 在第一象限相交于点A . 故半径1OF b >,即 c b >,且1290F AF ∠=.又离心率()22212121212121212222AFAF AF AF AF AF F F c c a a AF AF AF AF AF AF +-⋅+====+++()12212122122112AF AF AF AF AFAF AF AF ⋅=-=-+++,因为122AF AF ≤,结合题意有1212AF AF <≤, 设12AF t AF =,则2112c a t t=-++,易得对勾函数12y t t =++在(]1,2上单调递增, 故2112y t t=-++在(]1,2上单调递增, 故2221111111222212t t -<-≤-++++++,即2523c a <≤故答案为:25,23⎛⎤⎥ ⎝⎦【总结提升】1.关于椭圆几何性质的考查,主要有四类问题,一是考查椭圆中的基本量a ,b ,c ;二是考查椭圆的离心率;三是考查离心率发最值或范围;四是其它综合应用.2.学习中,要注意椭圆几何性质的挖掘:(1)椭圆中有两条对称轴,“六点”(两个焦点、四个顶点),要注意它们之间的位置关系(如焦点在长轴上等)以及相互间的距离(如焦点到相应顶点的距离为a -c ),过焦点垂直于长轴的通径长为等.(2)设椭圆上任意一点P (x ,y ),则当x =0时,|OP |有最小值b ,这时,P 在短轴端点处;当x =a 时,|OP |有最大值a ,这时P 在长轴端点处.(3)椭圆上任意一点P (x ,y )(y ≠0)与两焦点F 1(-c,0),F 2(c,0)构成的△PF 1F 2称为焦点三角形,其周长为2(a +c ).(4)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a 是斜边,a 2=b 2+c 2. 3.重视向量在解析几何中的应用,注意合理运用中点、对称、弦长、垂直等几何特征.4.求解有关离心率的问题时,一般并不是直接求出c 和a 的值,而是根据题目给出的椭圆的几何特征,建2222e?b b c a =2222+=1(a>b>0)x y a b立关于参数c 、a 、b 的方程或不等式,通过解方程或不等式求得离心率的值或范围.较多时候利用.题型四:直线与椭圆的位置关系例11.(2022·全国·高三专题练习)椭圆2214x y +=,则该椭圆所有斜率为12的弦的中点的轨迹方程为_________________. 【答案】2xy =-()22-<<x 【分析】设斜率为12的直线方程为12y x b =+,与椭圆的交点为()()1122,,,A x y B x y ,利用点差法可得答案. 【详解】设斜率为12的直线方程为12y x b =+,与椭圆的交点为()()1122,,,A x y B x y , 设中点坐标为(),x y ,则211221121,,222y y x xy y x y x x -++=-==-, 所以221122221414⎧+=⎪⎪⎨⎪+=⎪⎩x y x y ,两式相减可得()()()()12221214+=-+-x x x x y y y y ,()()22121124-+-=+x x y y y y x x ,即2xy =-,由于在椭圆内部,由221412⎧+=⎪⎪⎨⎪=+⎪⎩x y y x b得22102++-=x bx b ,所以()22210∆=--=b b 时,即2b =±直线与椭圆相切,此时由22102±+=x x 解得2x =或2x =-,所以22x -<<, 所求得轨迹方程为2xy =-()22-<<x . 故答案为:2xy =-()22-<<x . 例12.(2022·北京八中高三阶段练习)已知P 为椭圆2222:1(0)x y E a b a b +=>>上任意一点,12,F F 为左、右焦点,M 为1PF 中点.如图所示:若1122OM PF +=,离心率3e = 22 ,1c b e e a a=-=(1)求椭圆E 的标准方程; (2)已知直线l 经过11,2且斜率为12与椭圆交于,A B 两点,求弦长AB 的值.【答案】(1)2214x y +=(2)5【分析】(1)由题意可得21||||2OM PF =结合1122OM PF +=求得a ,继而求得b ,即可得椭圆方程; (2)写出直线l 的方程,联立椭圆方程,可求得交点坐标,从而求得弦长. (1)由题意知,M 为1PF 中点,O 为12F F 的中点,故21||||2OM PF =, 又 1122OM PF +=,故121()22PF PF +=,即124PF PF +=,所以24,2a a == , 又因为32e =,故3c =,所以2221b a c =-= , 故椭圆E 的标准方程为2214x y += ;(2)由直线l 经过11,2⎛⎫- ⎪⎝⎭且斜率为12可知直线方程为11(1)22y x =+-,即112y x =+,联立2214x y +=,消去y 可得220x x += ,解得120,2x x ==- ,则,A B 两点不妨取为(0,1),(2,0)-, 故22215AB =+=.例13.(2022·天津·高考真题)椭圆()222210x y a b a b+=>>的右焦点为F 、右顶点为A ,上顶点为B ,且满足3BF AB=(1)求椭圆的离心率e ;(2)直线l 与椭圆有唯一公共点M ,与y 轴相交于N (N 异于M ).记O 为坐标原点,若=OM ON ,且OMN 3 【答案】(1)63e =(2)22162x y +=【分析】(1)根据已知条件可得出关于a 、b 的等量关系,由此可求得该椭圆的离心率的值;(2)由(1)可知椭圆的方程为2223x y a +=,设直线l 的方程为y kx m =+,将直线l 的方程与椭圆方程联立,由0∆=可得出()222313m a k =+,求出点M 的坐标,利用三角形的面积公式以及已知条件可求得2a 的值,即可得出椭圆的方程.(1)解:()2222222222234332BF b c aa b a a b AB b a b a+===⇒=+⇒=++,离心率为22263c a b e a a -===. (2)解:由(1)可知椭圆的方程为2223x y a +=,易知直线l 的斜率存在,设直线l 的方程为y kx m =+,联立2223y kx mx y a=+⎧⎨+=⎩得()()222213630k x kmx m a +++-=,由()()()222222223641330313k m k m a m a k ∆=-+-=⇒=+,①2331M kmx k =-+,213M Mm y kx m k =+=+,由=OM ON 可得()()222229131m k m k+=+,②由3OMN S =可得2313213km m k⋅=+,③联立①②③可得213k =,24m =,26a =,故椭圆的标准方程为22162x y +=. 【规律方法】一.涉及直线与椭圆的基本题型有: 1.位置关系的判断2.弦长、弦中点问题.弦及弦中点问题的解决方法(1)根与系数的关系:直线与椭圆方程联立,消元,利用根与系数的关系表示中点; (2)点差法:利用弦两端点适合椭圆方程,作差构造中点、斜率. 3.轨迹问题4.定值、最值及参数范围问题5.存在性问题二.常用思想方法和技巧有:1.设而不求;2.坐标法;3.根与系数关系.三. 若直线与椭圆有两个公共点可结合韦达定理,代入弦长公式或 题型五:椭圆与圆的相关问题例14. (2019·天津·高考真题(文)) 设椭圆22221(0)x y a b a b+=>>的左焦点为F ,左顶点为A ,上顶点为B .3|2||OA OB =(O 为原点). (Ⅰ)求椭圆的离心率;(Ⅱ)设经过点F 且斜率为34的直线l 与椭圆在x 轴上方的交点为P ,圆C 同时与x 轴和直线l 相切,圆心C在直线4x =上,且OC AP ∥,求椭圆的方程.【答案】(I )12;(II )2211612x y +=.【分析】(I )根据题意得到32a b =,结合椭圆中,,a b c 的关系,得到2223()2a a c =+,化简得出12c a =,从而求得其离心率;(II )结合(I )的结论,设出椭圆的方程2222143x y c c +=,写出直线的方程,两个方程联立,求得交点的坐标,利用直线与圆相切的条件,列出等量关系式,求得2c =,从而得到椭圆的方程. 【详解】(I )解:设椭圆的半焦距为c ,由已知有32a b =, 又由222a b c =+,消去b 得2223()2a a c =+,解得12c a =,所以,椭圆的离心率为12.(II )解:由(I )知,2,3a c b c ==,故椭圆方程为2222143x y c c +=,由题意,(,0)F c -,则直线l 的方程为3()4y x c =+,点P 的坐标满足22221433()4x y c c y x c ⎧+=⎪⎪⎨⎪=+⎪⎩,消去y 并化简,得到2276130x cx c +-=,解得1213,7cx c x ==-, 代入到l 的方程,解得1239,214y c y c ==-,因为点P 在x 轴的上方,所以3(,)2P c c ,1122()()M x y N x y ,,,,MN =221212(1)[()4]k x x x x ++-MN 2121221(1)[(y )4]y y y k++-由圆心在直线4x =上,可设(4,)C t ,因为OC AP ∥,且由(I )知(2,0)A c -,故3242ct c c =+,解得2t =, 因为圆C 与x 轴相切,所以圆的半径为2,又由圆C 与l 相切,得23(4)24231()4c +-=+,解得2c =, 所以椭圆的方程为:2211612x y +=.【点睛】本小题主要考查椭圆的标准方程和几何性质、直线方程、圆等基础知识,考查用代数方法研究圆锥曲线的性质,考查运算求解能力,以及用方程思想、数形结合思想解决问题的能力.例15.(陕西高考真题)已知椭圆()的半焦距为,原点到经过两点,的直线的距离为. (Ⅰ)求椭圆的离心率;(Ⅱ)如图,是圆的一条直径,若椭圆经过,两点,求椭圆的方程.【答案】;(Ⅱ).【解析】(Ⅰ)过点的直线方程为, 则原点到直线的距离, 由,得,解得离心率. :E 22221x y a b+=0a b >>c O (),0c ()0,b 12c E AB :M ()()225212x y ++-=E A B E 3221123x y +=()(),0,0,c b 0bx cy bc +-=O 22bcd ab c ==+12d c =2222a b a c ==-32c e a ==(Ⅱ)由(1)知,椭圆的方程为. 依题意,圆心是线段的中点,且. 易知,不与轴垂直.设其直线方程为,代入(1)得.设,则,.由,得,解得. 从而.于是.由.故椭圆的方程为.例16.(2021·山东·高三开学考试)在平面直角坐标系xOy 中,已知点1(6,0)F -,2(6,0)F ,动点M 满足1243MF MF +=M 的轨迹为曲线C .(1)求C 的方程;(2)圆224x y +=的切线与C 相交于A ,B 两点,P 为切点,求||||PA PB ⋅的值.【答案】(1)221126x y +=(2)||||4PA PB ⋅=【分析】(1)结合椭圆的定义求得,,a b c ,由此求得C 的方程.(2)当直线AB 斜率不存在时,求得,PA PB ,从而求得PA PB ⋅;当直线AB 斜率存在时,设出直线AB 的方程,根据直线和圆的位置关系列方程,联立直线的方程和椭圆的方程,化简写出根与系数关系,求得0OA OB ⋅=,由此判断出90AOB ∠=︒,结合相似三角形求得PA PB ⋅.E 22244x y b +=()2,1M -AB 10AB =AB x ()21y k x =++()()()22221482142140k x k k x k b +++++-=()()1122,,,A x y B x y ()12282114k k x x k++=-+()22122421414k b x x k+-=-+124x x +=-()2821=414k k k +--+12k =21282x x b =-()()222121212151410222AB x x x x x b ⎛⎫=+-=+-=- ⎪⎝⎭10AB ()210210b -=23b =E 221123x y +=(1)为12124326MF MF F F +=>=,所以点M 的轨迹曲线C 是以1F ,2F 为焦点的椭圆.设其方程为22221(0)x y a b a b+=>>,则243a =,226a b -=,解得23a =,6b =,所以曲线C 的方程为221126x y +=.(2)当直线AB 的斜率不存在时,(2,0)P ±,此时||||2PA PB ==,则||||4PA PB ⋅=. 当直线AB 的斜率存在时,设直线AB 的方程为y kx m =+, 由直线AB 与圆224x y +=相切可得2||21m k =+,化简得()2241m k =+.联立22,1,126y kx m x y =+⎧⎪⎨+=⎪⎩得()2222142120k x kmx m +++-=,0∆>.设()11,A x y ,()22,B x y ,则122421km x x k -+=+,212221221m x x k -=+,所以1212OA OB x x y y ⋅=+()()2212121k x x km x x m =++++()()2222222121242121km k mm k k +-=-+++()222312121m k k -+=+()()222121121021k k k +-+==+,所以90AOB ∠=︒,所以AOB 为直角三角形.由OP AB ⊥,可得AOP OBP ∽△△, 所以||||||||PA OP OP PB =,所以2||||||4PA PB OP ⋅==. 综上,||||4PA PB ⋅=. 【总结提升】从高考命题看,与椭圆、圆相结合问题,一般涉及到圆的方程(圆心、半径)、直线与圆的位置关系(相切、相交)、点到直线的距离、直线方程等.。
高中数学知识框架思维导图(整理版)
柯西不等式
第四部分
位置关系
截距
解析几何
斜率公式、倾斜角的变化与斜率的变化: = tan , =
倾斜角和斜率
重合
A1B2-A2B1=0,C1B2-C2B1=0
平行
A1B2-A2B1=0,C1B2-C2B1≠0
相交
A1B2-A2B1≠0
垂直
直线的方程
z 的几何意义:
过可行域内一点(, )
向直线 = , = 作
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
对称性
y=Asin(x+)+b
化简、求值、
证明(恒等变形)
)
值域
图象
对称轴(正切函数除外)经过函数图象
的最高(或低)点且垂直 x 轴的直线,
对称中心是正余弦函数图象的零点,正
切函数的对称中心为( ,0)(k∈Z).
最值
2
①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1
2+1 −1
高中数学思维导图大全

国
`截式: y =妇干 b
',两点式:� V-VI-=-X-— X1 芍( :¢:X动 五) y?-P1 芬寸
!截距式: :+责= l (吐 0,b#o)
注意(1)截距百 :,可负,也可
1彝为o. (2)方程
各种形式的变化 和适用范围
宜 线
一般式:Ax+By+ C = O(AB-:f:. o)
的
两直线 行
序性
组合的分类
^集 卜巳渠合的表示一 口
列举法,特征性质描述法、Veen图法 性质
(2)A云小(3)则A�B则A.::B或4=, 凡 (4)若A�B, B竺C,则AGC; (5)含有11. '个元素的集合有2“ 个子无宇 有2片-i 个真丁采:
(6)E心;的区别�E表示元素与集合关系
已表示集合与集合关系; (7)屿{叶区别· 一 般地,a表示元压 {叶表示只有 一 个元素tr的菜合:
咖
(
5 l, 万
L1 5 ` 为方向向泣}
la•司 lal• 2直线与平面的夹角6cosO=
恒|
(a 为直线方向向址,行为平面法向盘}
I· 杭I 面角0:cos_0·=� 匠.开介 1 枫
飞,h,.为两平面 向优).
倾斜角与斜卒
倾斜伽「包18OO)和斜率K气na的变化
!点斜式:,V - y0 =沁-X。)
,p) +b
描点法(五点作阻法— ) I 斗几何作图法
对称轴.(正切函数 除外)经过函数图 象的蚊扁氓t低)
点且垂直x轴的直线
对称中心是正余弦函
_佟]象的零点,正切 函数的对称中心为 (一 .k.2it ,.0) (kGZ)
碑象可由正千玄曲线经过平移、伸缩得到,但耍注意先平移后伸缩与先伸缩后平移不同:
第2章2.3~2.4 椭圆与双曲线的参数方程

2.3 椭圆的参数方程2.4 双曲线的参数方程1.椭圆的参数方程(1)椭圆x 2a 2+y 2b 2=1的参数方程为⎩⎨⎧x =a cos φ,y =b sin φ(φ为参数),参数的几何意义是以a为半径所作圆上一点和椭圆中心的连线与x 轴正半轴的夹角. (2)中心在C (x 0,y 0)的椭圆的参数方程是⎩⎨⎧x =x 0+a cos φ,y =y 0+b sin φ(φ为参数).2.双曲线的参数方程中心在原点,焦点在x 轴上的双曲线x 2a 2-y 2b 2=1的参数方程为⎩⎪⎨⎪⎧x =a cos φ,y =b tan φ(φ为参数),规定φ的取值范围为φ∈[0,2π)且φ≠π2,φ≠32π. 【思维导图】【知能要点】 1.椭圆的参数方程. 2.双曲线的参数方程.题型一 椭圆的参数方程1.和圆的参数方程⎩⎨⎧x =r cos θ,y =r sin θ中的参数θ是半径OM 的旋转角不同,椭圆参数方程⎩⎨⎧x =a cos φ,y =b sin φ中的参数φ是椭圆上点M 的离心角.2.椭圆(x -m )2a 2+(y -n )2b 2=1 (a >b >0)的参数方程为⎩⎨⎧x =m +a cos φ,y =n +b sin φ(φ为参数).【例1】 已知A 、B 分别是椭圆x 236+y 29=1的右顶点和上顶点,动点C 在该椭圆上运动,求△ABC 的重心G 的轨迹的普通方程.解 由动点C 在该椭圆上运动,故据此可设点C 的坐标为(6cos θ,3sin θ),点G 的坐标为(x ,y ),则由题意可知点A (6,0),B (0,3). 由重心坐标公式可知⎩⎪⎨⎪⎧x =6+0+6cos θ3=2+2cos θ,y =0+3+3sin θ3=1+sin θ. 由此消去θ得到(x -2)24+(y -1)2=1即为所求.【反思感悟】 本题的解法体现了椭圆的参数方程对于解决相关问题的优越性.运用参数方程显得很简单,运算更简便.1.设F 1、F 2分别为椭圆C :x 2a 2+y 2b 2=1 (a >b >0)的左、右焦点.(1)若椭圆C 上的点A ⎝ ⎛⎭⎪⎫1,32到F 1、F 2距离之和等于4,写出椭圆C 的方程和焦点坐标;(2)设P 是(1)中椭圆上的动点,求线段F 1P 的中点的轨迹方程. 解 (1)由椭圆上点A 到F 1、F 2的距离之和是4, 得2a =4,即a =2. 又点A ⎝ ⎛⎭⎪⎫1,32在椭圆上,因此14+⎝ ⎛⎭⎪⎫322b 2=1,得b 2=3, 于是c 2=a 2-b 2=1,所以椭圆C 的方程为x 24+y 23=1, 焦点坐标为F 1(-1,0),F 2(1,0).(2)设椭圆C 上的动点P 的坐标为(2cos θ,3sin θ), 线段F 1P 的中点坐标为(x ,y ), 则x =2cos θ-12,y =3sin θ+02, 所以x +12=cos θ,2y3=sin θ.消去θ,得⎝ ⎛⎭⎪⎫x +122+4y23=1,这就是线段F 1P 的中点的轨迹方程.题型二 双曲线的参数方程与椭圆类似,双曲线的参数方程⎩⎪⎨⎪⎧x =a cos φ,y =b tan φ (φ为参数)中φ的几何意义也是双曲线上一点M 的离心角.【例2】 直线AB 过双曲线x 2a 2-y 2b 2=1的中心O ,与双曲线交于A ,B 两点,P 是双曲线上的任意一点.求证:直线P A ,PB 的斜率的乘积为定值. 证明 如图所示,设P ⎝ ⎛⎭⎪⎫a cos α,b tan α,A ⎝ ⎛⎭⎪⎫a cos θ,b tan θ.∵AB 过原点O ,∴A ,B 的坐标关于原点对称, 于是有B ⎝ ⎛⎭⎪⎫-a cos θ,-b tan θ,从而:k P A ·k PB =b (tan α-tan θ)a ⎝ ⎛⎭⎪⎫1cos α-1cos θ·b (tan α+tan θ)a ⎝ ⎛⎭⎪⎫1cos α+1cos θ =b 2(tan 2 α-tan 2 θ)a 2⎝ ⎛⎭⎪⎫1cos 2 α-1cos 2 θ=b 2a 2为定值.【反思感悟】 本例的求解充分利用了双曲线的参数方程.一般地,当与二次曲线上的动点有关时,可将动点用参数形式表示,从而将x ,y 都表示为某角θ的函数,运用三角知识求解,可大大减少运算量,收到事半功倍的效果.2.如图所示,设M 为双曲线x 2a 2-y 2b 2=1(a ,b >0)上任意一点,O 为原点,过点M 作双曲线两渐近线的平行线,分别与两渐近线交于A ,B 两点.探求平行四边形MAOB 的面积,由此可以发现什么结论?解 双曲线的渐近线方程为y =±ba x . 不妨设M 为双曲线右支上一点,其坐标为 ⎝ ⎛⎭⎪⎫a cos φ,b tan φ,则直线MA 的方程为 y -b tan φ=-b a ⎝ ⎛⎭⎪⎫x -a cos φ.①将y =ba x 代入①,解得点A 的横坐标为 x A =a 2⎝ ⎛⎭⎪⎫1cos φ-tan φ.同理可得,点B 的横坐标为x B =a 2⎝ ⎛⎭⎪⎫1cos φ-tan φ.设∠AOx =a ,则tan α=ba .所以,▱MAOB 的面积为S ▱MAOB =|OA |·|OB |sin 2α =x A cos α·x B cos α·sin 2α=a 2⎝ ⎛⎭⎪⎫1cos 2φ-tan 2φ4cos 2α·sin 2α =a 22·tan α=a 22·b a =ab 2.由此可见,平行四边形MAOB 的面积恒为定值,与点M 在双曲线上的位置无关.题型三 参数方程的应用若曲线的参数方程⎩⎨⎧x =2pt 2,y =2pt(t 为参数),由于y x =1t ,因此t 的几何意义是曲线上的点(除顶点外)与曲线的顶点连线的斜率的倒数.【例3】 设飞机以匀速v =150 m/s 做水平飞行,若在飞行高度h =588 m 处投弹(假设炸弹的初速度等于飞机的速度). (1)求炸弹离开飞机后的轨迹方程;(2)试问飞机在离目标多远(水平距离)处投弹才能命中目标.分析 这是物理学中的平抛运动,选择合理的参变量将炸弹(看作质点)的水平方向和竖直方向的运动表示出来.解 (1)如图所示,A 为投弹点,坐标为(0,588),B 为目标,坐标为(x 0,0).记炸弹飞行的时间为t ,在A 点t =0.设M (x ,y )为飞行曲线上的任一点,它对应时刻t ,炸弹初速度v 0=150 m/s ,用物理学知识,分别计算水平、竖直方向的路程,得 ⎩⎪⎨⎪⎧x =v 0t ,y =588-12gt 2 (g =9.8 m/s 2),即⎩⎨⎧x =150t ,y =588-4.9t 2, 这是炸弹飞行曲线的参数方程.(2)炸弹飞行到地面目标B 处的时间t 0满足方程y =0, 即588-4.9t 2=0,解得t 0=230.由此得x 0=150×230=30030≈1 643 (m).即飞机在离目标约1 643 m(水平距离)处投弹才能击中目标.【反思感悟】 准确把握题意,分析物理学中运动过程,选择适当的坐标系及变量,将物理问题转化为数学问题.利用抛物线的参数方程解决.3.青海省玉树县发生7.1级地震,灾区人民的安危牵动着全国人民的心,一批批救援物资源源不断地运往灾区.现在一架救援飞机在离灾区地面593 m 高处以150 m/s 的速度作水平飞行.为使投放救援物资准确落于灾区某指定的地点(不记空气阻力),飞行员应如何确定投放时机呢?解 如图所示,物资投出机舱后,设在时刻t 的水平位移为x ,垂直距离为y ,则⎩⎪⎨⎪⎧x =150t ,y =593-12gt 2(g =9.8 m/s 2). 令y =0,得t ≈11 s ,代入x =150 t ,得x ≈1 650 m.所以,飞行员在离救援点的水平距离约1 650米时开始投放物资,可使其准确落在指定位置.1.已知实数x ,y 满足x 225+y 216=1,求目标函数z =x -2y 的最大值与最小值. 解 椭圆x 225+y 216=1的参数方程为⎩⎨⎧x =5cos φ,y =4sin φ(φ为参数).代入目标函数得z =5cos φ-8sin φ=52+82cos(φ+φ0)=89cos(φ+φ0)(tan φ0=85).所以目标函数z min =-89,z max =89.2.点P 在椭圆x 216+y 29=1上,求点P 到直线3x -4y =24的最大距离和最小距离. 解 设P (4cos θ,3sin θ), 则d =|12cos θ-12sin θ-24|5.即d =⎪⎪⎪⎪⎪⎪122cos ⎝ ⎛⎭⎪⎫θ+π4-245,当cos ⎝ ⎛⎭⎪⎫θ+π4=-1时,d max =125(2+2);当cos ⎝ ⎛⎭⎪⎫θ+π4=1时,d min =125(2-2).3.已知弹道曲线的参数方程为⎩⎪⎨⎪⎧x =20t cos π6,y =20t sin π6-12gt 2(g =9.8 m/s 2)(1)求炮弹从发射到落地所需的时间; (2)求炮弹在运动中达到的最大高度. 解 (1)令y =20t sin π6-12gt 2=0, 即4.9t 2-10t =0. 解得t =0或t ≈2.所以炮弹从发射到落地所需时间约为2秒.(2)由y =10t -4.9t 2,得y =-4.9⎝ ⎛⎭⎪⎫t 2-10049t =-4.9⎝ ⎛⎭⎪⎫t -50492+25049.所以当t =5049时,y max =25049≈5.1.所以炮弹在运动中达到的最大高度为5.1米.4.已知双曲线方程为x 2-y 2=1,M 为双曲线上任意一点,M 点到两条渐近线的距离分别为d 1和d 2,求证:d 1与d 2的乘积是常数.证明 设d 1为M 点到渐近线y =x 的距离,d 2为M 点到渐近线y =-x 的距离, 因为M 点在双曲线x 2-y 2=1上,则可设M 点坐标为⎝ ⎛⎭⎪⎫1cos α,tan α.d 1=⎪⎪⎪⎪⎪⎪1cos α-tan α2,d 2=⎪⎪⎪⎪⎪⎪1cos α+tan α2,d 1·d 2=⎪⎪⎪⎪⎪⎪1cos 2α-tan 2α2=12,故d 1与d 2的乘积是常数.[P 36思考交流] 参照求圆的参数方程 ⎩⎪⎨⎪⎧x =(1-k 2)r1+k 2,y =2kr 1+k 2(k 为参数)的方法,给出椭圆另一种形式的参数方程(如图).答 设椭圆的方程为x 2a 2+y 2b 2=1其中a >b >0,则点A 的坐标为(-a ,0),设AP 的斜率为k .直线AP 的方程为y =k (x +a )由⎩⎨⎧y =k (x +a ),x 2a 2+y 2b 2=1,可得直线AP 与椭圆的交点的横坐标,x 1=-a ,x 2=ab 2-a 3k 2b 2+a 2k2. 直线AP 与椭圆交点的纵坐标为y 1=0,y 2=2ab 2k b 2+a 2k2即点P 的坐标为⎝ ⎛⎭⎪⎪⎫ab 2-a 3k 2b 2+a 2k 2,2ab 2k b 2+a 2k 2. ∵点P 是椭圆任意的不同于A 的点,∴⎩⎪⎨⎪⎧x =ab 2-a 3k 2b 2+a 2k2,y =2ab 2kb 2+a 2k2(k 为参数),上面参数方程即为椭圆的另一种形式的参数方程.其中参数k 表示直线AP 的斜率.也由此可以看出,由于参数的选取不同,参数方程也不同. [P 37思考交流]1.双曲线的参数方程⎩⎪⎨⎪⎧x =a cos φ,y =b tan φ中,参数的几何意义是什么?答 参数的几何意义是以原点为圆心,a 为半径的圆的半径的旋转角. 2.试求双曲线y 2a 2-x 2b 2=1(a >0,b >0)的参数方程.答 如图:分别以a ,b 为半径,原点为圆心作同心圆. 设OA =a ,OB =b ,A 为圆上任一点.∠AOx =φ(参数),B 为圆与y 轴的交点,过B 作平行于x 轴的直线交OA 的延长线于B 1点,在Rt △OBB 1中,∠BB 1O =φ,BB 1=btan φ. 过A 的切线交y 轴于A 1点,A 1P ⊥y 轴,A 1P ⊥B 1P . 设点P 的坐标为(x ,y ),在Rt △OAA 1中,∠OA 1A =φ,OA =a ,OA 1=asin φ. x =BB 1=b tan φ,y =OA 1=asin φ.∴⎩⎪⎨⎪⎧x =b tan φ,y =a sin φ(其中φ为参数),∴y 2a 2-x 2b 2=1(a >0,b >0)的参数方程为⎩⎪⎨⎪⎧x =btan φ,y =a sin φ(φ为参数).3.试求抛物线y 2=2px (p >0)的参数方程.(1)以抛物线上一点(x ,y )与其顶点连线斜率的倒数t 为参数. (2)以抛物线上任意一点(x ,y )的纵坐标y 0为参数. 答 (1)抛物线y 2=2px ,p 为焦点到准线的距离. 抛物线上任意一点M (x ,y ),∠MOx =α,则yx =tan α代入y 2=2px 中y ·tan α=2p .∴y =2p tan α.x =y 22p =12p ·(2p )2tan 2 α=2p tan 2α.设t =1tan α,则⎩⎪⎨⎪⎧x =2pt 2,y =2pt .其中t 为参数.几何意义是抛物线上任意一点与抛物线顶点的连线的斜率的倒数.故⎩⎪⎨⎪⎧x =2pt 2,y =2pt 即为所求.(2)⎩⎨⎧x =y 22p ,y =y 0(y 0为参数).几何意义是抛物线上任意点的纵坐标.【规律方法总结】1.椭圆和双曲线的参数方程中,参数φ的几何意义都是曲线上点M 的离心角;抛物线参数方程中参数t 的几何意义是抛物线上的点(除顶点外)和顶点连线斜率的倒数.2.利用圆锥曲线的参数方程,可以方便求解一些需要曲线上点的两个坐标独立表示的问题,如求最大值、最小值问题、轨迹问题等.3.圆锥曲线的参数方程可以有不同的形式,求曲线的参数方程可根据具体问题选取角度、长度、斜率、时间等作为参数.一、选择题1.下列参数方程(t 为参数)与普通方程x 2-y =0表示同一曲线的方程是( ) A.⎩⎨⎧x =|t |,y =tB.⎩⎨⎧x =cos t ,y =cos 2t C.⎩⎨⎧x =tan t ,y =1+cos 2t 1-cos 2tD.⎩⎨⎧x =tan t ,y =1-cos 2t 1+cos 2t解析 注意参数范围,可利用排除去.普通方程x 2-y =0中的x ∈R ,y ≥0.A 中x =|t |≥0,B 中x =cos t ∈[-1,1],故排除A 和B.而C 中y =2cos 2t 2sin 2t =cos 2t =1tan 2t =1x 2,即x 2y =1,故排除C. 答案 D2.下列在曲线⎩⎨⎧x =sin 2θ,y =cos θ+sin θ(θ为参数)上的点是( )A.⎝ ⎛⎭⎪⎫12,-2 B.⎝ ⎛⎭⎪⎫-34,12 C.(2,3)D.(1,3)解析 转化为普通方程:y 2=1+x (|y |≤2),把选项A 、B 、C 、D 代入验证得,选B. 答案 B3.若点P (3,m )在以点F 为焦点的抛物线⎩⎨⎧x =4t 2,y =4t(t 为参数)上,则|PF |等于( )A.2B.3C.4D.5解析 抛物线为y 2=4x ,准线为x =-1,|PF |为P (3,m )到准线x =-1的距离,即为4.答案 C4.已知椭圆的参数方程⎩⎨⎧x =2cos t +1,y =4sin t(t 为参数),点M 在椭圆上,对应参数t =π3,点O 为原点,则直线OM 的倾斜角α为( )A.π3B.π6C.2π3D.5π6解析 M 点的坐标为(2,23),∴k =3,tan α=3,α=π3.答案 A二、填空题5.曲线⎩⎨⎧x =3t -2,y =t 2-1与x 轴交点的坐标是______________. 解析 将曲线的参数方程化为普通方程:(x +2)2=9(y +1),令y =0,得x =1或x =-5.答案 (1,0),(-5,0)6.双曲线⎩⎪⎨⎪⎧x =3+3tan φ,y =1cos φ(φ为参数)的渐近线方程是________. 解析 将参数方程化为普通方程是y 2-(x -3)29=1, a =1,b =3,渐近线的斜率k =±13,双曲线的中心为(3,0),∴渐近线方程为y=±13(x -3).答案 y =±13(x -3)7.二次曲线⎩⎨⎧x =5cos θ,y =3sin θ(θ是参数)的左焦点的坐标是________. 解析 题中二次曲线的普通方程为x 225+y 29=1左焦点为(-4,0).答案 (-4,0)8.过双曲线x 2-y 2=4的右焦点F 作倾斜角为105°的直线,交双曲线于P ,Q 两点,则|FP |·|FQ |的值为________.解析 因双曲线的标准方程为x 24-y 24=1,∴a =b =2.∴c =a 2+b 2=4+4=2 2.故右焦点为F (22,0).∴可设过F (22,0),倾斜角为105°的直线的参数方程为⎩⎪⎨⎪⎧x =22+t cos 105°,y =t sin 105°(t 为参数).代入双曲线方程x 2-y 2=4,整理得32t 2+(23-2)t -4=0, ∴|FP |·|FQ |=|t 1t 2|=⎪⎪⎪⎪⎪⎪-432=833. 答案 833三、解答题9.已知圆O 1:x 2+(y -2)2=1上一点P 与双曲线x 2-y 2=1上一点Q ,求P ,Q 两点距离的最小值.解 圆心O 1坐标为(0,2),Q 点坐标为⎝ ⎛⎭⎪⎫1cos φ,tan φ, |QO 1|2=1cos 2φ+(tan φ-2)2=1cos 2φ+tan 2φ-4tan φ+4=2tan 2φ-4tan φ+5.设t =tan φ,|QO 1|2=2t 2-4t +5=2(t -1)2+3≥3,∴|QO 1|min =3,∴PQ 两点间的距离的最小值为3-1.10.已知曲线C :x 24+y 29=1,直线l :⎩⎨⎧x =2+t ,y =2-2t (t 为参数). (1)写出曲线C 的参数方程,直线l 的普通方程;(2)过曲线C 上任意一点P 作与l 夹角为30°的直线,交l 于点A ,求|P A |的最大值与最小值.解 (1)曲线C 的参数方程为⎩⎨⎧x =2cos θ,y =3sin θ(θ为参数).直线l 的普通方程为2x +y -6=0.(2)曲线C 上任意一点P (2cos θ,3sin θ)到l 的距离为d =55|4cos θ+3sin θ-6|,则|P A |=d sin 30°=255|5sin(θ+α)-6|,其中α为锐角,且tan α=43.当sin(θ+α)=-1时,|P A |取得最大值, 最大值为2255.当sin(θ+α)=1时,|P A |取得最小值, 最小值为255.11.已知椭圆x 24+y 2=1上任一点M (除短轴端点外)与短轴两端点B 1,B 2的连线分别交x 轴于P ,Q 两点,求证:|OP |·|OQ |为定值.证明 设M (2cos φ,sin φ),φ为参数,B 1(0,-1),B 2(0,1).则MB 1的方程:y +1=sin φ+12cos φ·x ,令y =0,则x =2cos φsin φ+1,即|OP |=|2cos φ1+sin φ|. MB 2的方程:y -1=sin φ-12cos φx ,∴|OQ |=⎪⎪⎪⎪⎪⎪2cos φ1-sin φ. ∴|OP |·|OQ |=⎪⎪⎪⎪⎪⎪2cos φ1+sin φ×⎪⎪⎪⎪⎪⎪2cos φ1-sin φ=4. 即|OP |·|OQ |=4为定值.12.已知抛物线y 2=2px (p >0),过动点M (a ,0)且斜率为1的直线l 与该抛物线交于不同的两点A ,B ,|AB |≤2p .(1)求a 的取值范围;(2)若线段AB 的垂直平分线交x 轴于点N ,求△NAB 面积的最大值.解 设直线l 的方程为y =x -a 代入y 2=2px 中,得:x 2-2(a +p )x +a 2=0.(1)设A ,B 两点的坐标为(x 1,y 1)、(x 2,y 2),则x 1+x 2=2(a +p ),x 1x 2=a 2.∴|AB |=1+12(x 1+x 2)2-4x 1x 2=24(a +p )2-4a 2=28ap +4p 2≤2p ,∴2(8ap +4p 2)≤4p 2,解得a ≤-p 4. (2)A ,B 的中点坐标为⎝ ⎛⎭⎪⎫x 1+x 22,y 1+y 22,即为(a +p ,p ),斜率为-1,垂直平分线方程为y -p =-(x -a -p )=-x +a +p .y =0时,x =a +2p ,∴点N 的坐标为(a +2p ,0),∴点N (a +2p ,0)到直线AB 的距离为|2p |2=2p , 则S △NAB =12·2p ·28ap +4p 2=p 8ap +4p 2=2p ·p 2+2ap =2p 2pa +p 2,当a 最大时,S △NAB 取最大值,故a =-p 4时,S 取最大值为2p 2.。
人教版高中数学知识框架思维导图(04)-按章节整理(含目录高清版)

几何意义
归纳
合情推理
猜想
类比
推理
演绎推理
推理与证明
三段论
大前提、小前提、结论
综合法
由因导果
分析法
执果索因
直接证明
证明
间接证明
1.验证 = 0 (初始值)命题成立;
2.若 = ( ≥ 0 )时命题成立,证明 = + 1时命题也成立.
数学归纳法
两个原理
反设、归谬、结论
反证法
分类加法计算原理和分步乘法计算原理
1.f (a+x)=f (b-x),对称轴为 =
对称性
2.f (a+x)+f (b-x)=c,对称中心为(
2
+
2
, )
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
最值
一次、二次函数、反比例函数、双勾函数
基本初等函数
指数函数、对数函数、幂函数、三角函数
分段函数
利用对称性求函数
对称变换: = () → = −(), = () → = (−), = () → = −(−)
函数图象
及其变换
翻折变换: = () → = |()|, = () → = (||)
伸缩变换: = () → = (), = () → = ()
②减法:( + i)-( + i)=(-c)+(b-d)i;
③乘法:( + i)·( + i)=(c-bd)+(d+bc)i;
运算
④除法:
+i
+i
=
(+i)(−i)
(+i)(−i)
高中数学椭圆思维导图脑图
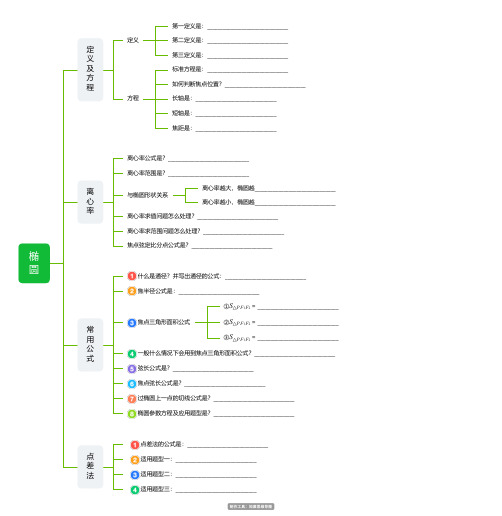
椭圆定义及方程定义第一定义是:_______________________________第二定义是:_______________________________第三定义是:_______________________________方程标准方程是:_______________________________如何判断焦点位置?_______________________________长轴是:_______________________________短轴是:_______________________________焦距是:_______________________________离心率离心率公式是?_______________________________离心率范围是?_______________________________与椭圆形状关系离心率越大,椭圆越_______________________________离心率越小,椭圆越_______________________________离心率求值问题怎么处理?_______________________________离心率求范围问题怎么处理?_______________________________焦点弦定比分点公式是?_______________________________常用公式什么是通径?并写出通径的公式:_______________________________焦半径公式是:_______________________________焦点三角形面积公式①= _______________________________S△P F F12②= _______________________________S△P F F12③= _______________________________S△P F F12一般什么情况下会用到焦点三角形面积公式?_______________________________弦长公式是?_______________________________焦点弦长公式是?_______________________________过椭圆上一点的切线公式是?_______________________________椭圆参数方程及应用题型是?_______________________________点差法点差法的公式是:_______________________________适用题型一:_______________________________适用题型二:_______________________________适用题型三:_______________________________。
高中数学知识框架思维导图(整理版)

点斜式:y-y0=k(x-x0)
注意:截距可正、
可负,也可为 0.
2 −1
注意各种形式的转化和运用范围.
x y
截距式: + =1
a b
两直线的交点
距离
一般式:Ax+By+C=0
两点间的距离公式|1 2 | = √(1 − 2 )2 + (1 − 2 )2 .
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1ቤተ መጻሕፍቲ ባይዱ
2+1 −1
− (+2)2 )
= (−1) (
1
2−1
+
错位相加法: = ( + )−1 → = ( + ) −
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
与 的关系
1 ,
= 1,
= {
− −1 , ≥ 2.
构造等差数列
an+1 p an
= · +1 转为③
qn q qn-1
⑤an + 1=pan+qn
椭圆的知识点总结框架

椭圆的知识点总结框架1. 椭圆的定义和基本特征- 椭圆的定义:椭圆是平面上到两个定点F1和F2的距离之和等于常数2a的点的集合构成的曲线。
这个常数2a称为椭圆的主轴。
- 椭圆的基本特征:椭圆具有对称性,主轴的长度为2a,两个定点F1和F2到椭圆的距离之和为2a,辅轴的长度为2b,焦距为c,焦距与半焦距的关系是c^2=a^2-b^2。
2. 椭圆的标准方程和参数方程- 椭圆的标准方程:椭圆的标准方程是(x-h)^2/a^2 + (y-k)^2/b^2 = 1,其中(h,k)为椭圆的中心坐标。
- 椭圆的参数方程:椭圆的参数方程为x = h + a*cos(t),y = k + b*sin(t),其中t为参数。
3. 椭圆的离心率和焦点- 椭圆的离心率:椭圆的离心率定义为e=c/a,离心率越小,椭圆越扁,离心率等于0时,代表圆形。
- 椭圆的焦点:椭圆的焦点是定点F1和F2,用来确定椭圆的形状和大小。
4. 椭圆的性质- 椭圆的面积和周长:椭圆的面积S=πab,周长L=4aE(e),其中E(e)为第二类椭圆积分。
- 椭圆的直径和焦距:椭圆的直径等于主轴的长度,焦距等于c=√(a^2-b^2)。
- 椭圆的切线方程:椭圆的切线方程是y-y1 = (dy/dx)(x-x1),其中(x1,y1)为椭圆上的点。
5. 椭圆的应用- 椭圆的几何应用:椭圆在几何中有许多应用,例如椭圆的光学性质,抛物面的形成,椭圆的天文应用等。
- 椭圆的工程应用:椭圆在工程中也有许多应用,例如椭圆的建筑设计,椭圆的机械设计,椭圆的无线通信等。
总结:椭圆是一种重要的曲线,在数学、几何和工程中有着广泛的应用。
通过了解椭圆的定义和特征,我们可以更好地理解椭圆的性质和应用,为我们的学习和工作带来更多的启发和想象。
希望本文能够对大家对椭圆有更深入的了解和认识。
(完整版)椭圆的经典知识总结,推荐文档

8.如何求解与焦点三角形△PF1F2(P 为椭圆上的点)有关的计算问题? 思路分析:与焦点三角形△PF1F2 有关的计算问题时,常考虑到用椭圆的定义及余弦定理(或勾股
定理)、三角形面积公式 S PF1F2
1 2
PF1
PF2
sin F1PF2 相结合的方法进行计算解题。
将有关线段 PF1 、PF2 、F1F2 ,有关角 F1PF2
x a2 ; ⑤离心率: e c ,椭圆 0 e 1, e 越小,椭圆越圆; e 越大,椭圆越扁。⑥通
c
a
2b2
径
a
2.点与椭圆的位置关系:(1)点 P(x0 , y0 ) 在椭圆外
x02 a2
y02 b2
1;(2)点 P(x0 , y0 ) 在椭圆
上
x02 a2
y02 b2
=1;(3)点 P(x0 , y0 ) 在椭圆内
借助右图理解记忆:显然: a, b, c 恰构成一个直角三角形的三条边,其中 a 是斜边,b、c 为两条直
角边。 3.如何由椭圆标准方程判断焦点位置
椭圆的焦点总在长轴上,因此已知标准方程,判断焦点位置的方法是:看 x 2 , y 2 的分母的大小,
哪个分母大,焦点就在哪个坐标轴上。
wedzxiucisddytfyedtwetehcbxzfsdhgwetyeqwhbxbgsdhksdapoweeuhdhchbjcbcghgcsteuydshgbcxygsddusauasuisaydassddfddggs
知识点三:椭圆的简单几何性质 椭圆: x 2 y 2 1 (a b 0) 的简单几何性质
a2 b2
(1)对称性:对于椭圆标准方程 x2 y2 1 (a b 0) :
高中椭圆的知识点归纳

高中椭圆的知识点归纳在高中数学中,椭圆是一个重要的图形和知识点,它在解析几何中有着广泛的应用。
下面我们来详细归纳一下椭圆的相关知识点。
一、椭圆的定义平面内与两个定点$F_1$,$F_2$的距离之和等于常数(大于$|F_1F_2|$)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。
用数学表达式表示为:$|PF_1| +|PF_2| = 2a$($2a > 2c$,其中$2c =|F_1F_2|$)二、椭圆的标准方程1、焦点在$x$轴上的椭圆标准方程:$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$($a > b > 0$),其中$a$为椭圆的长半轴长,$b$为椭圆的短半轴长,$c =\sqrt{a^2 b^2}$为半焦距。
2、焦点在$y$轴上的椭圆标准方程:$\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1$($a > b > 0$)三、椭圆的性质1、范围对于焦点在$x$轴上的椭圆:$a \leq x \leq a$,$b \leq y \leq b$;对于焦点在$y$轴上的椭圆:$b \leq x \leq b$,$a \leq y \leq a$。
2、对称性椭圆关于$x$轴、$y$轴和原点对称。
3、顶点焦点在$x$轴上的椭圆顶点坐标为$(\pm a, 0)$,$(0, \pm b)$;焦点在$y$轴上的椭圆顶点坐标为$(0, \pm a)$,$(\pm b, 0)$。
4、离心率椭圆的离心率$e =\frac{c}{a}$($0 < e < 1$),它反映了椭圆的扁平程度。
$e$越接近于$0$,椭圆越接近于圆;$e$越接近于$1$,椭圆越扁。
5、准线方程焦点在$x$轴上的椭圆准线方程为$x =\pm \frac{a^2}{c}$;焦点在$y$轴上的椭圆准线方程为$y =\pm \frac{a^2}{c}$。
四、椭圆中的重要结论1、焦半径公式对于焦点在$x$轴上的椭圆,设点$P(x_0, y_0)$为椭圆上一点,则$|PF_1| = a + ex_0$,$|PF_2| = a ex_0$;对于焦点在$y$轴上的椭圆,设点$P(x_0, y_0)$为椭圆上一点,则$|PF_1| = a + ey_0$,$|PF_2| = a ey_0$。
