磁学及其常见物理量的单位换算表

磁场单位：高斯单位制与国际单位制的转换关系

磁场单位：高斯单位制与国际单位制的转换关系若是以B SI表示际单位制磁感应强度的单位，其他量类推，那么磁场强度、磁感应强度、磁化强度在高斯单位制与国际单位制的转换关系为：以下推出高斯单位制下磁化强度：以下是这2种单位制的介绍：一、力学量纲和单位力学物理定律在国际单位制(记作SI)和高斯单位制(又称为厘米克秒制，记CGS)中具有相同的形式，并且它们都以长度、时间和质量作为基本量纲，所以所有的力学量都具有相同的量纲。

表1 力学量纲和单位二、静电制量纲和单位高斯制在电磁学中具两套单位制，一套以库仑定律为基础，称为静电制，记作CGSE，另一套以安培定律为基础，称为静磁制，记作CGSM。

静电学中最基本的定律是库仑定律,其国际制的形式是：F = Q1 * Q2 / 4 / Pi / r ^ 2 (1)这里，e0是真空中的介电常数，其数值为8.8541878*10^-12 C^2/Nm^2。

而静磁制则是：F = Q1 * Q2 / r ^ 2 (2)在国际制中，电流是基本量纲。

而由公式(2)可以看出，静电制不需要新的基本量纲。

为此静电制电量的量纲就是：L^(3/2)*T^(-1)*M^(1/2)，它具有一个新的单位：esu(C)，称为静电单位电量(或称静电库仑)，其值为1dyn^(1/2)cm。

不同单位制中的单位可以互相转换，这里给出从esu转换成库仑(C)的方法：(1) 设1C = x esu；(2) 根据公式(1)，当r = 1m，q1 = q2 = 1C时，F = 8.9875518*10^9 N；(3) 把r = 1m = 10^2cm，q1 = q2 = x esu，F = 8.9875518*10^9 N =8.9875518*10^14 dyn代入公式(2)，得：x = 2.99792458*10^9，(4) 得出结论1C = 2.99792458*10^9 esu(C)[1] (3)1esu(C) = 3.33564096*10^-10C (3\')公式(3)和(3\')是国际制单位和高斯制单位相互转换的基本公式。

磁场单位：高斯单位制与国际单位制的转换关系

磁场单位：高斯单位制与国际单位制的转换关系若是以B SI表示际单位制磁感应强度的单位，其他量类推，那么磁场强度、磁感应强度、磁化强度在高斯单位制与国际单位制的转换关系为：以下推出高斯单位制下磁化强度：以下是这2种单位制的介绍：一、力学量纲和单位力学物理定律在国际单位制(记作SI)和高斯单位制(又称为厘米克秒制，记CGS)中具有相同的形式，并且它们都以长度、时间和质量作为基本量纲，所以所有的力学量都具有相同的量纲。

表1 力学量纲和单位二、静电制量纲和单位高斯制在电磁学中具两套单位制，一套以库仑定律为基础，称为静电制，记作CGSE，另一套以安培定律为基础，称为静磁制，记作CGSM。

静电学中最基本的定律是库仑定律,其国际制的形式是：F = Q1 * Q2 / 4 / Pi / r ^ 2 (1)这里，e0是真空中的介电常数，其数值为8.8541878*10^-12 C^2/Nm^2。

而静磁制则是：F = Q1 * Q2 / r ^ 2 (2)在国际制中，电流是基本量纲。

而由公式(2)可以看出，静电制不需要新的基本量纲。

为此静电制电量的量纲就是：L^(3/2)*T^(-1)*M^(1/2)，它具有一个新的单位：esu(C)，称为静电单位电量(或称静电库仑)，其值为1dyn^(1/2)cm。

不同单位制中的单位可以互相转换，这里给出从esu转换成库仑(C)的方法：(1) 设1C = x esu；(2) 根据公式(1)，当r = 1m，q1 = q2 = 1C时，F = 8.9875518*10^9 N；(3) 把r = 1m = 10^2cm，q1 = q2 = x esu，F = 8.9875518*10^9 N =8.9875518*10^14 dyn代入公式(2)，得：x = 2.99792458*10^9，(4) 得出结论1C = 2.99792458*10^9 esu(C)[1] (3)1esu(C) = 3.33564096*10^-10C (3\')公式(3)和(3\')是国际制单位和高斯制单位相互转换的基本公式。

磁场单位：高斯单位制与国际单位制的转换关系

磁场单位：高斯单位制与国际单位制的转换关系磁场单位:高斯单位制与国际单位制的转换关系若是以B表示际单位制磁感应强度的单位，其他量类推，那么磁场强度、磁感应强度、磁SI化强度在高斯单位制与国际单位制的转换关系为:以下推出高斯单位制下磁化强度:以下是这2种单位制的介绍:一、力学量纲和单位力学物理定律在国际单位制(记作SI)和高斯单位制(又称为厘米克秒制，记CGS)中具有相同的形式，并且它们都以长度、时间和质量作为基本量纲，所以所有的力学量都具有相同的量纲。

表1 力学量纲和单位物理量量纲国际制单位高斯制单位换算关系长度 L m(米) cm(厘米) 1 m = 100 cm 时间 T s(秒) s(秒) 频率 T^(-1) Hz(赫兹) Hz(赫兹) 质量 M kg(千克) g(克) 1 kg = 1000 g 力 L*T^(-2)*M N(牛顿) dyn(达因) 1 N = 10^5 dyn 能量L^2*T^(-2)*M J(焦耳) erg(耳格) 1 J = 10^7 erg 功率 L^2*T^(-3)*M W(瓦特) erg/s 1 W = 10^7 erg/s二、静电制量纲和单位高斯制在电磁学中具两套单位制，一套以库仑定律为基础，称为静电制，记作CGSE，另一套以安培定律为基础，称为静磁制，记作CGSM。

静电学中最基本的定律是库仑定律,其国际制的形式是:F = Q1 * Q2 / 4 / Pi / r ^ 2 (1)这里，e0是真空中的介电常数，其数值为8.8541878*10^-12 C^2/Nm^2。

而静磁制则是:F = Q1 * Q2 / r ^ 2 (2) 在国际制中，电流是基本量纲。

而由公式(2)可以看出，静电制不需要新的基本量纲。

为此静电制电量的量纲就是:L^(3/2)*T^(-1)*M^(1/2)，它具有一个新的单位:esu(C)，称为静电单位电量(或称静电库仑)，其值为1dyn^(1/2)cm。

磁学常用名词解释

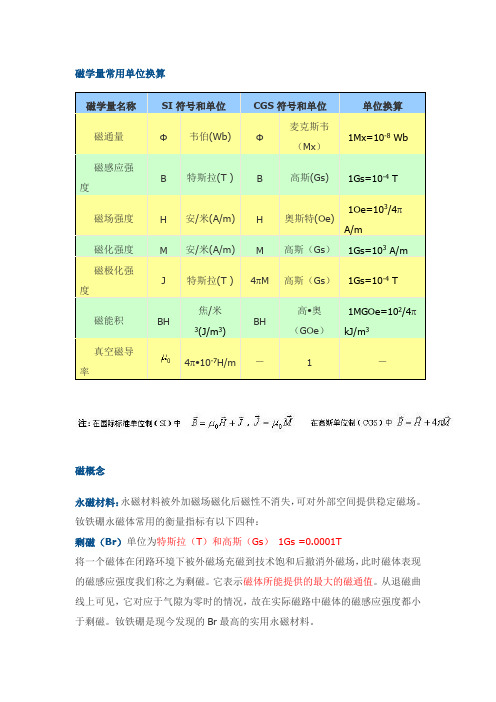
磁学量常用单位换算磁概念永磁材料：永磁材料被外加磁场磁化后磁性不消失，可对外部空间提供稳定磁场。

钕铁硼永磁体常用的衡量指标有以下四种：剩磁（Br）单位为特斯拉（T）和高斯（Gs）1Gs =0.0001T将一个磁体在闭路环境下被外磁场充磁到技术饱和后撤消外磁场，此时磁体表现的磁感应强度我们称之为剩磁。

它表示磁体所能提供的最大的磁通值。

从退磁曲线上可见，它对应于气隙为零时的情况，故在实际磁路中磁体的磁感应强度都小于剩磁。

钕铁硼是现今发现的Br最高的实用永磁材料。

磁感矫顽力（Hcb）单位是安/米（A/m）和奥斯特（Oe）或1 Oe≈79.6A/m处于技术饱和磁化后的磁体在被反向充磁时，使磁感应强度降为零所需反向磁场强度的值称之为磁感矫顽力（Hcb）。

但此时磁体的磁化强度并不为零，只是所加的反向磁场与磁体的磁化强度作用相互抵消。

（对外磁感应强度表现为零）此时若撤消外磁场，磁体仍具有一定的磁性能。

钕铁硼的矫顽力一般是11000Oe 以上。

内禀矫顽力（Hcj）单位是安/米（A/m）和奥斯特（Oe）1 Oe≈79.6A/m使磁体的磁化强度降为零所需施加的反向磁场强度，我们称之为内禀矫顽力。

内禀矫顽力是衡量磁体抗退磁能力的一个物理量，如果外加的磁场等于磁体的内禀矫顽力，磁体的磁性将会基本消除。

钕铁硼的Hcj会随着温度的升高而降低所以需要工作在高温环境下时应该选择高Hcj的牌号。

磁能积(BH)单位为焦/米3（J/m3）或高•奥（GOe） 1 MGOe≈7. 96k J/m3退磁曲线上任何一点的B和H的乘积既BH我们称为磁能积,而B×H的最大值称之为最大磁能积(BH)max。

磁能积是恒量磁体所储存能量大小的重要参数之一，(BH)max越大说明磁体蕴含的磁能量越大。

设计磁路时要尽可能使磁体的工作点处在最大磁能积所对应的B和H附近。

各向同性磁体：任何方向磁性能都相同的磁体。

各向异性磁体：不同方向上磁性能会有不同；且存在一个方向，在该方向取向时所得磁性能最高的磁体。

SI与CGSM换算关系

1 CGSM(χm) 4
-3 -3 2 9 8 4
7 1 ×10 CGSM(μ) 4
1 安培·米=10CGSM(qm) 1 安培/米 2=10 CGSM(ρm) 1 安培/米=10 CGSM(δm) 1 安培=4π×10制的磁学量单位换算关系表物理量磁感应强度 B 磁通量φm 自感系数 L 磁矩 Pm 磁化强度 J 磁场强度 H 磁化率χm 导磁系数（磁导率）磁量 qm 磁荷体密度ρm 磁荷面密度δm 磁位（磁标位）ψm CGSM 制单位名称高斯、伽马（γ）高斯·厘米 CGSM(L) CGSM(Pm) CGSM(J) 奥斯特（Oe） CGSM(χm) CGSM(μ) CGSM(qm) CGSM(ρm) CGSM(δm) SI 制单位名称特斯拉（T）、纳特（nT）特斯拉·米（T·m2）亨利（H） ·米安培·米（A·m2）安培/米（A/m）安培/米（A/m） SI(χm) 亨利/米（H/m）安培·米（A·m）安培/米 2（A/m2）安培/米（A/m）安培（A） 1nT=10-5Oe 换算关系 1 特斯拉=10 高斯、1 纳特=1 伽马 1 特斯拉·米=10 高斯·厘米 1 亨利=10 CGSM(L) 1 安培·米（A·m2）=10 CGSM(Pm) 1 安培/米=10 CGSM(J) 1 安培/米=4π×10 奥斯特 1SI(χm)= 1 亨利/米=

磁学单位换算

12
=

r t
2
（附录 1－4）
式中 t 为时间，因此 r/t 具有速度的量纲，由麦克斯韦（James Clerk Maxwell）方程式可知
为电磁波在真空中的传播速度 c0。利用真空介电常数ε0、真空磁导率µ0 和真空电磁波速度
c0，通过引入 k1、k2、k3 和υ等系数，将三个比例因子改写为：
所谓单位制，就是按照（人为选择）给定的规则来确定一组彼此相关的量的计量单位。物理量是通过描述自然规律的方程式或者根据需要人为定义新量的方程式而相互联系的。为了制定单位制和引入量纲的概念，通常把某些量作为相互独立的量，即把它们当作基本量，而其它量则根据这些基本量来定义，或者用方程式来表示，这些量称为导出量。理论上，任何量都不比其它量更基本，各种量都是等价的。用多少或者用哪些量作为基本量，只是一个选择的问题，从而形成了很多种单位制。例如，在国际单位制（SI 单位制）中，选定长度、质量、时间、电流、热力学温度、物质的量和发光强度等 7 个物理量作为基本量，并分别以 L、M、T、I、Θ、N、J 来表示其量纲。所有的量（包括基本量和导出量）形式上都可以表示为：κLαMβTγIδΘεNζ Jη，其中，κ为量的数字因数，α、β、γ、δ、ε、 ζ和 η称为量纲指数，所有量纲指数都等于零的量，通常称为无量纲量。
中获得更多的相关知识。在此仅从实用的角度，也为了便于理解和记忆单位换算关系，对
电磁学单位制进行适当的展开讨论，并给出一些例子。
在绝对单位制中，建立电磁学单位制所依据的是三个基本量方程，分别为，将力学量
与电学量相联系的电荷受力库仑定律、将力学量与磁学量相联系的磁极受力库仑定律
（Charles-Augustin de Coulomb，1785 年）和将电学量与磁学量相联系的电流磁场毕奥－萨

磁场单位：高斯单位制与国际单位制的转换关系

磁场单位：高斯单位制与国际单位制的转换关系磁场单位:高斯单位制与国际单位制的转换关系若是以B表示际单位制磁感应强度的单位，其他量类推，那么磁场强度、磁感应强度、磁SI化强度在高斯单位制与国际单位制的转换关系为:以下推出高斯单位制下磁化强度:以下是这2种单位制的介绍:一、力学量纲和单位力学物理定律在国际单位制(记作SI)和高斯单位制(又称为厘米克秒制，记CGS)中具有相同的形式，并且它们都以长度、时间和质量作为基本量纲，所以所有的力学量都具有相同的量纲。

表1 力学量纲和单位物理量量纲国际制单位高斯制单位换算关系长度 L m(米) cm(厘米) 1 m = 100 cm 时间 T s(秒) s(秒) 频率 T^(-1) Hz(赫兹) Hz(赫兹) 质量 M kg(千克) g(克) 1 kg = 1000 g 力 L*T^(-2)*M N(牛顿) dyn(达因) 1 N = 10^5 dyn 能量L^2*T^(-2)*M J(焦耳) erg(耳格) 1 J = 10^7 erg 功率 L^2*T^(-3)*M W(瓦特) erg/s 1 W = 10^7 erg/s二、静电制量纲和单位高斯制在电磁学中具两套单位制，一套以库仑定律为基础，称为静电制，记作CGSE，另一套以安培定律为基础，称为静磁制，记作CGSM。

静电学中最基本的定律是库仑定律,其国际制的形式是:F = Q1 * Q2 / 4 / Pi / r ^ 2 (1)这里，e0是真空中的介电常数，其数值为8.8541878*10^-12 C^2/Nm^2。

而静磁制则是:F = Q1 * Q2 / r ^ 2 (2) 在国际制中，电流是基本量纲。

而由公式(2)可以看出，静电制不需要新的基本量纲。

为此静电制电量的量纲就是:L^(3/2)*T^(-1)*M^(1/2)，它具有一个新的单位:esu(C)，称为静电单位电量(或称静电库仑)，其值为1dyn^(1/2)cm。

磁学量常用单位换算

使磁体的磁化强度降为零所需施加的反向磁场强度，我们称之为内禀矫顽力。内禀矫顽力是衡量磁体抗退磁能力的一个物理量，如果外加的磁场等于磁体的内禀矫顽力，磁体的磁性将会基本消除。钕铁硼的Hcj会随着温度的升高而降低所以需要工作在高温环境下时应该选择高Hcj的牌号。
磁能积(BH)单位为焦/米3（J/m3）或高•奥（GOe）1 MGOe≈7. 96k J/m3
各向异性磁体：不同方向上磁性能会有不同；且存在一个方向，在该方向取向时所得磁性能最高的磁体。烧结钕铁硼永磁体是各向异性磁体。
取向方向：各向异性的磁体能获得最佳磁性能的方向称为磁体的取向方向。也称作“取向轴”，“易磁化轴”。
磁场强度：指空间某处磁场的大小，用H表示，它的单位是安/米（A/m）。
磁化强度：指材料内部单位体积的磁矩矢量和，用M表示，单位是安/米（A/m）。
磁学量常用单位换算
磁学量名称
SI符号和单位
CGS符号和单位
单位换算
磁通量
Φ
韦伯(Wb)
Φ
麦克斯韦（Mx）
1Mx=10-8 Wb
磁感应强度
B
特斯拉(T )
B
高斯(Gs)
1Gs=10-4 T
磁场强度
H
安/米(A/m)
H
奥斯特(Oe)
1Oe=103/4p A/m
磁化强度
M
安/米(A/m)
M
高斯（Gs）
1Gs=103 A/m
磁极化强度
J
特斯拉(T )
4ห้องสมุดไป่ตู้M
高斯（Gs）
1Gs=10-4 T
磁能积
BH
焦/米3(J/m3)
BH
高•奥（GOe）
1MGOe=102/4p kJ/m3

磁学单位转换

很多文献上是用4pi*Ms来表征磁化强度，严格来说，这个不能称为饱和磁感应强度，之所以有很多人这样来表示，是因为关注对于告饱和磁化强度的材料来说，B更重要一些，而这些材料多为软磁材料，能在很小的场下饱和，所以H可以忽略，而且4pi*Ms给出的是更本征的一个参数，而且是Bs的量纲，更容易和工业参数Bs联系起来，但严格来说，他们俩是不对等的，这是我个人的理解，不一定准确。

第二个问题是一样的，emu/cc是高斯单位下磁化强度的单位，4pi*Ms的单位是Gs，再初以10000，则就变成MKSA单位制下的特斯拉了。

B=H+4*Pi*M，一般情况下，可以使用B=4*Pi*M来计算，再除以10000，则就变成MKSA单位制下的特斯拉。

M的单位是emu/(cm^3)，从单位为emu/g的物理量转换成emu/(cm^3)，要乘以密度g/(cm^3).即：emu/(cm^3)={ emu/g}*{ g/(cm^3)} 1奥斯特OE＝1000/4π安/米A/M
1楞次＝1安/米
磁学量常用单位换算。

磁学量常用单位换算

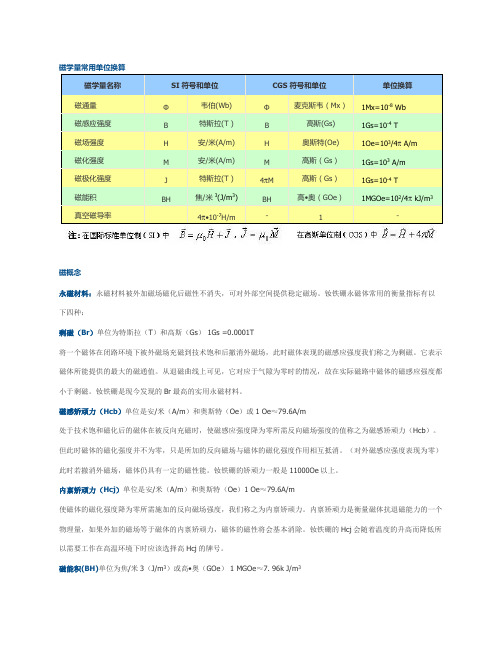
磁概念永磁材料：永磁材料被外加磁场磁化后磁性不消失，可对外部空间提供稳定磁场。

钕铁硼永磁体常用的衡量指标有以下四种：剩磁（Br）单位为特斯拉（T）和高斯（Gs） 1Gs =0.0001T将一个磁体在闭路环境下被外磁场充磁到技术饱和后撤消外磁场，此时磁体表现的磁感应强度我们称之为剩磁。

它表示磁体所能提供的最大的磁通值。

从退磁曲线上可见，它对应于气隙为零时的情况，故在实际磁路中磁体的磁感应强度都小于剩磁。

钕铁硼是现今发现的Br最高的实用永磁材料。

磁感矫顽力（Hcb）单位是安/米（A/m）和奥斯特（Oe）或1 Oe≈79.6A/m处于技术饱和磁化后的磁体在被反向充磁时，使磁感应强度降为零所需反向磁场强度的值称之为磁感矫顽力（Hcb）。

但此时磁体的磁化强度并不为零，只是所加的反向磁场与磁体的磁化强度作用相互抵消。

（对外磁感应强度表现为零）此时若撤消外磁场，磁体仍具有一定的磁性能。

钕铁硼的矫顽力一般是11000Oe以上。

内禀矫顽力（Hcj）单位是安/米（A/m）和奥斯特（Oe）1 Oe≈79.6A/m使磁体的磁化强度降为零所需施加的反向磁场强度，我们称之为内禀矫顽力。

内禀矫顽力是衡量磁体抗退磁能力的一个物理量，如果外加的磁场等于磁体的内禀矫顽力，磁体的磁性将会基本消除。

钕铁硼的Hcj会随着温度的升高而降低所以需要工作在高温环境下时应该选择高Hcj的牌号。

磁能积(BH)单位为焦/米3（J/m3）或高•奥（GOe） 1 MGOe≈7. 96k J/m3退磁曲线上任何一点的B和H的乘积既BH我们称为磁能积,而B×H的最大值称之为最大磁能积(BH)max。

磁能积是恒量磁体所储存能量大小的重要参数之一，(BH)max越大说明磁体蕴含的磁能量越大。

设计磁路时要尽可能使磁体的工作点处在最大磁能积所对应的B和H附近。

各向同性磁体：任何方向磁性能都相同的磁体。

各向异性磁体：不同方向上磁性能会有不同；且存在一个方向，在该方向取向时所得磁性能最高的磁体。

高斯单位制与国际单位制的转换关系

磁场单位磁场单位：：高斯单位制与国际单位制的转换关系磁场中有三个基本的物理量H(磁场),M(磁化强度),B(磁感应强度)，在国际单位制中(SI)单位为：A/m ，A/m ，T ；在高斯单位制（CGS ）中是：Oe ，3/emu cm(或Gs )，Gs ，也可以都用emu 作为单位。

下文中加上下标加与区别，如emu (H) ,emu (M) ,emu (B)。

这些量数值上的换算关系是:※4H M π=+,它们差一个系数4π高斯单位制中几个基本量的单位是：时间s ，长度cm ，质量g ，电流()esu I(高斯制中，电流使用静电单位制量度CGSE)，换算关系是91310()A esu I =×另外，磁矩与磁化强度的单位换算式（磁场单位采用静磁单位制量度CGSM）是：2-3-232331()=10A1()=(I)S=10A*1cm =10A m()1()===10A/m V1cmm 10A m emu emu emu emu •••∑磁矩磁化强度电流磁矩注：以上出现了两种电流单位，在高斯制下，电流使用CGSE 单位制量度；但在推导磁学量时，使用静磁单位制。

以下具体介绍国际单位制、静电单位制量度、静磁单位制量度。

一、力学量纲和单位力学量纲和单位力学物理定律在国际单位制(记作SI)和高斯单位制(又称为厘米克秒制，记CGS)中具有相同的形式，并且它们都以长度、时间和质量作为基本量纲，所以所有的力学量都具有相同的量纲。

表1 力学量纲和单位二、静电制量纲和单位高斯制在电磁学中具两套两套两套单位制，一套以库仑定律为基础，称为静电制，记作CGSE CGSE，另一套以安培定律为基础，称为静磁制，记作CGSM CGSM。

静电学中最基本的定律是库仑定律,其国际制的形式是：122014q q F r πε=(1)这里，0ε是真空介电常数，数值为12228.8541878*10/C Nm −。

而静磁制则是：122q q F r =(2) 在国际制中，电流是基本量纲。

磁导率单位换算

磁导率单位换算介绍磁导率是表征材料对于磁场的响应程度的物理量，它描述了材料在给定的磁场中的磁化能力。

磁导率的单位换算是在磁学研究中常用的操作，本文将深入探讨磁导率单位换算的相关知识。

磁导率的定义磁导率（μ）定义为材料中磁感应强度（B）与磁场强度（H）之比，即μ = B/H。

磁导率的单位由国际单位制（SI）规定，为亚伏每米（A/m）。

磁导率单位换算在磁导率的单位换算中，常用的单位包括亚伏每米（A/m）、毫亨每米（mH/m）、高斯每安培（G/A）等。

下面将详细介绍它们之间的换算关系。

1. 亚伏每米（A/m）亚伏每米是国际单位制中磁导率的基本单位，表示每米长度内磁感应强度与磁场强度之比。

其他单位都可以通过亚伏每米与其他物理量之间的换算关系来换算。

2. 毫亨每米（mH/m）毫亨每米是一个常用的磁导率单位，通常用于描述铁磁材料。

它与亚伏每米之间的换算关系为1 mH/m = 4π × 10^-3 A/m。

换句话说，如果要将亚伏每米转换为毫亨每米，需要将亚伏每米乘以4π × 10^-3。

3. 高斯每安培（G/A）高斯是用于表示磁感应强度的单位，安培是用于表示电流强度的单位。

高斯每安培表示单位电流在单位长度上产生的磁感应强度。

磁感应强度与磁导率之间的换算关系为1 G/A = 10^-3 T = 4π × 10^-3 A/m。

换句话说，如果要将亚伏每米转换为高斯每安培，需要将亚伏每米乘以4π × 10^-3。

磁导率的应用磁导率在物理学和工程学中有广泛的应用。

以下介绍几个磁导率的应用领域。

1. 电磁感应根据法拉第电磁感应定律，变化的磁场可以引起感应电动势。

磁导率的概念可以帮助我们理解电磁感应现象，并为电动势的计算提供依据。

2. 电感电感是指导体中产生感应电动势的能力，与导体的磁导率密切相关。

通过了解磁导率的概念，我们可以更好地理解电感对电流变化的影响。

3. 材料磁性磁导率可以用来描述材料对磁场的响应程度，不同材料的磁导率不同。

主要磁学量及相关物理量的单位及换算_20110426

主要磁学量及相关物理量的单位及换算1000emu＝1A*m2其中，Gs m A 310/1-=。

其中，333/10/1cm g m kg -=，ρσ⋅=M 。

H and B:由于磁场是电流或者说运动电荷引起的,而磁介质（除超导体以外不存在磁绝缘的概念，故一切物质均为磁介质）在磁场中发生的磁化对源磁场也有影响（场的迭加原理）。

因此，磁场的强弱可以有两种表示方法： B ：在充满均匀磁介质的情况下，若包括介质因磁化而产生的磁场在内时，用磁感应强度B 表示；（物质内部的磁场强度）H ：单独由电流或者运动电荷所引起的磁场（不包括介质磁化而产生的磁场时）。

（在磁场中每一点都具有大小和方向，因此可以用向量H 表示该点磁场的大小，方向与磁力线方向一致）磁通：垂直于某一面积所通过的磁力线的条数，用ф表示，单位韦伯（Wb ）。

磁通密度：单位面积上的磁通量，用B 表示，单位是特斯拉（T ）或高斯（Gs ）。

假设分子磁矩B s m μρπρπππmJ m J V J M S S S s 4444===假设1mol)(55824)(55824)/(10582.54)(582.5410273.91002.6)()/(4444623224233Gs Mm Gs Mm m A M m m A g cm g M m m A g M m cm g M m N m J M ss s s sB s A S s ρππρπρπρπρρμπρππ=⋅=⨯⋅=⋅⋅⋅⋅=⋅⨯⋅⨯⋅===-其中，22410273.9m A B ⋅⨯=-μ，Gs m A 310/1-=。

磁学单位转换表 Magnetic Units Conversion Table

A. TABLE OF CONVERSIONSUNITS FOR MAGNETIC PROPERTIESConversionQuantity Symbol Gaussian & cgs emu a factor, C b SI & rationalized mks c Magnetic flux density,B gauss (G) d10-4tesla (T), Wb/m2magnetic inductionMagnetic fluxφmaxwell (Mx), G∗cm210-8weber (Wb), volt second (V∗s) Magnetic potential difference,U, F gilbert (Gb)10/4πampere (A)magnetomotive forceMagnetic field strength,H oersted (Oe),e Gb/cm103/4πA/m fmagnetizing force(Volume) magnetization g M emu/cm3 h103A/m(Volume) magnetization4πΜG103/4πA/mMagnetic polarizationintensity of magnetization J, I emu/cm34π ××10-4T, Wb/m2 i1A∗m2/kg(Mass) magnetizationσ , M emu/g4π×10-7Wb∗m/kgMagnetic moment m emu, erg/G10-3A∗m2, joule per tesla(J/T) Magnetic dipole moment j emu, erg/G4π×10-10Wb∗m i(Volume) susceptibilityχ, κdimensionless, emu/cm34πdimensionless(4π)2×10-7henry per meter (H/m), Wb/(A∗m)4π×10-3m3/kg(Mass) susceptibilityχρ , κρcm3/g, emu/g(4π)2×10-10H∗m2/kg4π×10-6m3/mol(Molar) susceptibilityχmol,κmol cm3/mol, emu/mol(4π)2×10-13H∗m2/molPermeabilityµdimensionless4π×10-7H/m, Wb/(A∗m)Relative permeability jµr not defined dimensionless(Volume) energy density,W erg/cm310-1J/m3energy product kDemagnetization factor D, N dimensionless l/4πdimensionlessa. Gaussian units and cgs emu are the same for magnetic properties. The defining relation is B =H+4πΜ.b. Multiply a number in Gaussian units by C to convert it to SI (e.g., 1 G × 10-4 T/G = 10-4 T).c. SI (Système International d'Unités) has been adopted by the National Bureau of Standards. Where two conversion factors aregiven, the upper one is recognized under, or consistent with, SI and is based on the definition B=µ0(H+M), whereµ0=4π×10-7 H/m. The lower one is not recognized under SI and is based on the definition B = µ0H +J, where the symbolI is often used in place of J.d. 1 gauss= 105 gamma (γ).e. Both oersted and gauss are expressed as cm-1/2∗g-1/2∗s-1 in terms of base units.f. A/m was often expressed as "ampere-turn per meter" when used for magnetic field strength.g. Magnetic moment per unit volume.h. The designation "emu" is not a unit.i. Recognized under SI, even though based on the definition B = µ0H +J. See footnote c.j.µr = µ /µ0 = 1 +χ, all in SI. µr is equal to Gaussian µ.k. B∗H and µ0M∗H have SI units J/m3; M∗H and B∗H/4πhave Gaussian units erg/cm3.R. B. Goldfarb and F. R. Fickett, U.S. Department of Commerce, National Bureau of Standards, Boulder, Colorado 80303, March 1985 NBS Special Publication 696 For sale by the Superintendent of Documents, U.S. Government Printing Office, Washington, DC 20402。