电力系统交流采样算法

交流采样常用计算公式

交流采样常用计算公式
电压有效值计算公式：
离散化有效电压计算公式：
（以一个周期内有限个采样电压数字量来代替一个周期内连续变化的电压函数值）
式中：ΔTm为相邻两次采样的时间间隔；um为第m-1个时间间隔的电压采样瞬时值；N为1个周期的采样点数。

相等间隔采样有效电压计算公式：
相等间隔采样有效电流计算公式：
　计算一相有功功率的离散化公式为：
同理，三相有功功率为：
交流采样基本原理
电工原理中连续周期交变电压、电流有效值及平均功率的计算公式为：
式中：u（t）、i（t）———电压、电流的瞬时值；
T———交流电周期。

而微机所能处理的是离散化的数字信号，因此需要对以上公式进行离散化处理，采用均方根算法时，其相对应的离散化公式为：
式中：N———每周期均匀采样点数；
uk———第k点电压采样值；
ik———第k点电流的采样值。

交流采样技术及其DSP实现方法

交流采样技术及其DSP实现方法摘要：本文提出了对电力系统参数进行交流采样的设计思想，结合实例介绍以TMS320C240DSP与高速14位A/D转换器AD7863构成的数据采集系统，给出了采样算法、硬件电路及软件流程等。

关键词：交流采样 DSP 锁相环1．引言目前，交流电参量的采样测量方法主要有两种：直流采样法和交流采样法。

直流采样法是采样经过整流后的直流量，对采样值只需作一次比例变换即可得到被测量的数值，软件设计简单，计算方便。

但直流采样法存在一些问题：测量精度直接受整流电路的精度和稳定性的影响；整流电路参数调整困难且受波形因素影响较大；此外，用直流采样法测量工频电压、电流是通过测量平均值来求出有效值的，当电路中谐波含量不同时，平均值与有效值之间的关系也将发生变化，给计算结果带来了误差。

因此，要获得高精度、高稳定性的测量结果，必须采用交流采样技术。

交流采样技术是按一定规律对被测信号的瞬时值进行采样，再按一定算法进行数值处理，从而获得被测量的测量方法。

该方法的理论基础是采样定理，即要求采样频率为被测信号频谱中最高频率的2倍以上，这就要求硬件处理电路能提供高的采样速度和数据处理速度。

目前，高速单片机、DSP及高速A/D转换器的大量涌现，为交流采样技术提供了强有力的硬件支持。

交流采样法包括同步采样法、准同步采样法、非同步采样法等几种，本文介绍的是同步采样法。

同步采样法就是整周期等间隔均匀采样，要求被测信号周期T与采样时间间隔Δt及一周内采样点数N之间满足关系式T=N·Δt，即：采样频率为被测信号频率的N倍。

根据提供采样信号方式不同，同步采样法又分为软件同步采样法和硬件同步采样法两种。

硬件同步采样法是由专门的硬件电路产生同步于被测信号的采样脉冲。

它能克服软件同步采样法存在截断误差等缺点，测量精度高。

利用锁相频率跟踪原理实现同步等间隔采样的电路如图1所示。

图1 倍频锁相同步电路在相位比较器PD、低通滤波器LP、压控振荡器VCO构成的锁相环内加入N 分频器，输入f i为被测信号的频率，作为锁相环的基准频率，输出f0 为采样频率。

交流采样常用计公式

交流采样常用计公式
————————————————————————————————作者：————————————————————————————————日期：
交流采样常用计算公式
电压有效值计算公式：
离散化有效电压计算公式：
（以一个周期内有限个采样电压数字量来代替一个周期内连续变化的电压函数值）
式中：ΔTm为相邻两次采样的时间间隔；um为第m-1个时间间隔的电压采样瞬时值；N为1个周期的采样点数。

相等间隔采样有效电压计算公式：
相等间隔采样有效电流计算公式：
计算一相有功功率的离散化公式为：
同理，三相有功功率为：
交流采样基本原理
电工原理中连续周期交变电压、电流有效值及平均功率的计算公式为：
式中：u（t）、i（t）———电压、电流的瞬时值；
T———交流电周期。

而微机所能处理的是离散化的数字信号，因此需要对以上公式进行离散化处理，采用均方根算法时，其相对应的离散化公式为：
式中：N———每周期均匀采样点数；
uk———第k点电压采样值；
ik———第k点电流的采样值。

CH6 交流采样常用算法的分析

号经过离散采样和模/ 数变换成可用计算机处理的数字量后，计算
机将对这些数字量(采样值)进行分析、计算。得到所需的电流、电压的有效值和相位以及有功功率、无功功率等参量，或者算出它们
的序分量，或者输电线路和元件的视在阻抗，或者某次谐波的大小
和相位等；并根据这些参数的计算结果以及定值，通过比较判断决定装置的动作行为。而完成上述分析计算和比较判断以实现各种预
S 2 I sin( t ) dt 2 I sin tdt
0 0
N 1 2 k 1
T 2
T 2
2 2

I
1 i S 2 0

iK
1 iN 2 2
I S

T S
2 2
半周积分算法
图解Biblioteka 6.4.4 突变量电流算法
叠加原理：故障后系统可以分解成正常负荷网络和故障附加网络的叠加 im (t ) iL (t ) ik (t )
ik (t ) im (t ) iL (t )
iL (t ) iL (t T ) iL (t ) t时刻的负荷电流 iL (t T ) 比t时刻提前一个周期的负荷电流 T 工频信号的周期 ik (t )=im (t ) iL (t T )
突变量电流算法
在非故障阶段，测量电流就是负荷电流
iL (t T ) im (t T )
突变量电流算法
故障分量电流的表达式
ik (t ) im (t ) im (t T )
突变量电流算法
离散形式
ik ik ik N
三要点 1. 正常运行时无故障分量 2. 故障后一周内，得到得到故障分量的离散采样值 3. 一周之后，故障分量消失——由于采用的计算式导致消失频率变化时，一般采用下式，其抗频率变化能力增强

煤矿井下交流电量信号的采样及算法

·测试与控制·修稿日期：2012－11－25作者简介：唐会成（1980-），男，工程师。

主要从事煤矿井下电气产品的设计和开发工作。

0引言为了实现对煤矿井下供电电网各种故障有效保护，需要对各种电量信号进行数据采集。

电量的数据采集是实现电网保护的重要环节，尤其如何准确、快速地采集系统中的各个电量，一直是令人关注的。

对于模拟量采集，根据采样信号的不同，可分为直流采样﹑交流采样及压频变换法。

基于电量采集的实践和理论，对各种电量的采集主要有两种途径：①利用各类模拟仪表，直接或者间接地获取电量；②根据采样定理，对连续时间信号做等间隔抽样，并进行数字化处理，来获取电量，然后用一定算法，对采集到的交流电量进行数据分析。

算法就是将连续变化的电流、电压输入信号经过离散采样和模数变化转换成可以用计算机处理的数字量，再算出电流、电压的有效值。

1采样方式的比较[1～3]国内、外监控系统以前一般都用传统的模拟量经变送器输入的直流采样方法来获取遥测数据，即将各种交流电量，通过降压、整流、滤波、非线性校准等各种电子电路变为相应大小的直流电量，然后对直流量进行采样和A/D 转换。

这种方法软件设计简单，计算方便，只需对采样值做一次比例变换，即可得到被测的数值，且便于滤波，因此在进行电量采集的初期得到了广泛的应用。

但直流采样存在以下问题，限制了它的广泛应用：（1）实时性差。

直流采样不能及时反应被测量的突变，具有较大的滞后时间常数。

被测信号送入变送器后，要经过互感器转换成交流低压信号，再经硬件整流滤波，转换成与被测信号成比例的直流电压信号输出，整个过程花费时间较长，在快速性要求较高的保护系统中不易使用。

另外，变送器的造价高、功耗大，从经济效益上考虑也不适合于推广使用。

（2）精度低。

测量精度直接受变送器的精度和稳定性影响，无法实现实时信号采集，因而在电力系统中的应用受到限制。

压频变换法通过专用硬件变换电路，把电压信号转换成与输入电压大小成比例的频率信号。

电网监控与调度自动化第二章交流数据采集与处理

电子式电压互感器分压原理电压互感器 (采用电容分压、电阻分压或阻容分压原理)
分压原理电压互感器
对数据采集装置的输入阻抗的要求很高，尤其是母线电压互感器，应该先把二次电压转换为数字量，然后通过网络进行数据传送。
电子式电压互感器
光学电压互感器(OVT) 透明的光学介质(也称压电晶体)在没有外加电场作用时是各向同性的。在外加电场作用下，晶体将变为各向异性的双轴晶体，从而导致其折射率发生变化，通过晶体的偏振光将产生双折射，使一束偏振光变为两束相位不同(因两束光的传播速度不同)的偏振光。电场对透明晶体影响的电光效应被称为Pockels效应。
模拟量输出
现场电力设备
放大驱动
D/A转换器
锁存器
输出接口
微型计算机
D/A转换器基本原理
-UR R 2R S1 1 2R S2 R 2R S3 R 2R S4
+ A
2R Rf UD
UD D
Rf UR R
, D S1 2 S2 2 S3 2 S4 2
第二章交流数据采集与处理

概述互感器直流采样交流采样与合并单元电力系统数据预处理标度变换
实现对电网的监视和控制表征电网实时运行状态的遥测量值和遥信状态采集与传送对这些信息进行适当的加工处理，形成控制电
网安全、稳定和经济运行的遥控、遥调命令。直流采样整流、二进制转换交流采样一周期多次采样、转换、计算电能数据采集脉冲与计数
全光纤电流互感器的原理
法拉第磁光效应原理
光学电流互感器（OCT）
光学电流互感器（OCT）
v Hdl

3第三章交流采样技术

第三章交流采样及其算法第一节交流采样原理所谓交流采样技术，就是通过对电力互感器二次回路中的交流电压信号和交流电流信号直接采样，获得一组采样值，通过对其模／数变换，将其变换为数字量，再对这组数字量进行计算，从而获得电压、电流、功率、电能、频率等电气量值。

在发电厂、变电站中，使用交流采样技术，可取消变送器测量环节，也有利于测量精度的提高，交流采样技术已在变电站自动化系统中广泛使用。

一、交流采样对一个信号采样就是测取该信号的瞬时值，它可由一个采样器来完成，如图3－1所示。

（a ）f(t)0 t1(t) 0 tf*(t) 0 f h (t) 0（b ）图3－1 信号的采样与保持 (a)采样器保持；（b ）信号波形采样器按定时或不定时的方式将开关瞬间接通，使输入采样器的连续信号f (t )转变为离散信号f *(t )输出，设采样开关按周期T s 瞬间接通，则采样得到的离散信号为：f *(t )= ⎩⎨⎧≠=nTst nTs t nTs f 当当0)( （3—1）式中 n ──正整数。

在交流采样技术中，只用一个单独的采样器是无法工作的，因为采样所得信号要经过/A D 变换成数字量，而/A D 变换需要一定的时间才能完成，并要求变换过程中被变换量保持不变。

所以采样器必须有一个保持器配合工作，如图3－1所示。

在两次采样的间隔时间内，保持器输出信号()h f t 保持不变。

对于需要同时采样的多个交流信号，应配备各自的采样保持器。

二、采样定理采样将一段时间的连续信号变为离散的信号，改变了信号的外在形式，这通常是为了使之易于处理或借助于更好的工具对其进行处理。

因此，信号经过采样后不应改变原有的本质特性，或者说，根据采样得到的()*f t ，可以复现()f t 的所有本质信息。

从直观上看，采样周期越短，即采样频率越高，()h f t 越接近()f t 。

香农定理阐明了信号不失真采样的基本原理，即：为了对连续信号()f t 进行不失真的采样，采样频率ωs 应不低于()f t 所包含最高频率max ω的两倍。

电力系统数据采样的方法

采样直接计算ｕ、，后计算Ｐ、ＣＳ口ＷｈＩ然Ｑ、Ｏ、、Ｗｖｒ，ａｈ因为电流和电压在Ａ／Ｄ转换中消耗了精
度。在当前电力系统发展中，Ｔ装置（讯远ＲＵ通动装置）本为交流采样。基
交流采样的应用范围非常广泛，据应用场根合不同，其算法也有很多种，照其模型函数，按大
（ｔ＋１０）叫＋２。］
＝
值。
议 “＝Ｕｓｎｃｔｉｏ
要ｕ３＝ｕ
贝：１Ｕｓｎｃ）０“ ＝ｉ（ｏｔ＋
同理：
“ ＝Ｕｓ（ｏ＋＋９。２ｉｃｎｔ０）
；ｉｓｃ＋）Ｏ＋＝ｉ（ｔ＋ｕＣＳｎｏ２
ＧＥｉｇ～ｌｎＭｎａ
Ａｂｔａｔｓｒｃ：Ａｌｎｔｒｐｉｅｅｏｏｇｗｉｈａｄｄｖｌｐｍｅｆｐｗｅｎｓｒｎｔｏｏｒｉｄｕｔｙ，ｐｗｅｙｔｍｅａｄｓｈｉｈｅｅｕｒｎｎｔｏａａａ — ｏｒｓｓｅｄｍｎｇｒｒｑｉｅｍｎｄｔｃ
（ｆ）ｕ叫＋：＝２Ｕ
Ｐ吉［６） “（－＋＝ｚ（６＋ｋ屯）ｆ一
“ ｉ一ｉ）（］Ｑ：
其中：
“ ｉｉ）＋ｚｉｉ）＋“ ｉ（一６ｆ一（（一ｉ）
： —
所：＝／● 以ｕ√２２｛
中图分类号：ＴＭ９３文献标识码：Ａ文章编号：０６１８２０）一００ —０１０ —８９（０７增０１３

电力系统常用交流采样算法2013

电力系统常用交流采样方法比较1 正弦函数模型算法1.1 最大值算法假定正弦量为纯交流量，通过采集最大值即可得到有效值。

设u=Um sin(ωt+ψu)则式中Um——同步采样得到的电压最大值。

同样1.2 单点算法这种算法适用于对称三相正弦电路，在某一时刻同时对三相线电流和线电压采集1点，就可计算出各线电压和线电流有效值、各相有功及无功功率。

其中同理其中1.3 半周期积分法设则把积分离散化，有其中N为半周期中采样点数。

同理1.4 2点采样对正弦电压、电流，相差90°采2组值。

设u=Umsinωt则u1=Umsin(ωt+ψ)u 2=Umsin(ωt+ψ+90°)∴ u21+u22=U2msin2(ωt+ψ)+U2mcos2(ωt+ψ)=U2m=2U2又i=Imsin(ωt-φ)同理下边再讨论P、Q采集：2 非正弦周期函数算法2.1 均方根法sinωt设u=Um离散化得到为第k次采样值。

其中N为每周期等间隔采样次数，uk由采样定理知，这种算法可计及次谐波。

同理由离散化2.2 全周波付里叶算法设u(t)为周期函数，并且满足狄里赫利条件，则U(t)可展开为级数。

离散化有其中N 为采样点数，u k 为第k 次采样值。

基波电压幅值n 次谐波幅值：Un =√Uan 2+Ubn 2初相角：Ø=arctg(Ubn/Uan)基波功率计算，由u a1i a1+u b1i b1=U m cosψI m cos(ψ-φ)+2.3 递推付里叶算法参考全周波付氏算法，可得到递推计算各次谐波实部、虚部的表达式递推开始时取 u (k-N)=0，当k ＞N 时再计及u (k-N)，这种方法的计算数据仍是最近 1 个周波的。

基波电压以及有功功率和无功功率分别表示为3 几种采样算法的应用前面介绍的几种算法各有其特点，在应用时主要根据对准确或实时性的不同要求来选择。

如果采集三相对称正弦信号，单点算法不失为理想算法，对采样时刻没有要求，既准确又快捷，并且可以同时得到电压、电流、有功、无功等信号，但这种算法对采样信号要求较高，硬件较为复杂。

电力系统交流采样算法

一、实验名称：电力系统交流采样算法二、实验目的通过课程实验，使学生进一步掌握电力系统自动测控装置的原理。

理解微机是如何采集电力系统各物理量，运用自己学过的知识，设计编程实现电力系统常用的交流采样算法。

要求自己准备实验数据、自己设计、自己编程，最后自行调试。

最终以图形和数值形式实现自己的设计。

培养学生初步的设计编程能力。

在实验中应能做到以下几点：1、进一步掌握直流采样、交流采样原理；2、通过产生实验数据、绘图等环节，培养学生使用电力系统相关科学计算软件的能力；3、通过对电力系统交流采样算法的设计、编程、调试，使理论与实际相结合，增加感性认识；4、培养初步利用计算机进行科学研究的能力。

三、实验内容1、利用软件产生理想的工频波形（数据）以及包含3、5、7次谐波的电流、电压信号；2、编程实现基于正弦函数模型的交流采样算法，计算工频电流、电压的有效值，线路阻抗；3、编程实现傅式算法，计算工频电流、电压有效值，各次谐波的有效值、相位角；4、编程实现解微分方程算法，计算线路的正序电阻、电感；5、比较不同交流采样算法的精度；四、实验要求1、原始数据，计算数据以数值、图形两种方式表达；2、分析设计中出现的问题，实验中出现的故障，原因何在？你是如何认识和解决的？3、你对本实验的体会，看法，建议？4、实验现场考试；五、程序清单x=0:pi/6:2*pi;yu1=380*sin(x);yu2=380/3*sin(3*x);yu3=380/5*sin(5*x);yu4=380/7*sin(7*x);yu5=380*sin(x)+380/3*sin(3*x)+380/5*sin(5*x)+380/7*sin(7*x);subplot(2,4,1);plot(x,yu1);xlabel('x');ylabel('yu1');title('基波电压');subplot(2,4,2);plot(x,yu2);xlabel('x');ylabel('yu2');title('三次谐波电压');subplot(2,4,3);plot(x,yu3);xlabel('x');ylabel('yu3');title('五次谐波电压');subplot(2,4,4);plot(x,yu4);xlabel('x');ylabel('yu4');title('七次谐波电压');subplot(2,4,5);plot(x,yu5);xlabel('x');ylabel('yu5');title('总电压');'基波电压'A=[];A=yu1;'傅氏算法';a11=[(A(1,3)-A(1,9))+0.5*(A(1,1)+A(1,5)-A(1,7)-A(1,11))+sqrt(3)/2*(A(1,2)+A(1,4)-A(1,8)-A(1,10))]/6; '6a1=(i3-i9)+1/2*(i1+i5-i7-i11)+sqrt(3)/2*(i2+i4-i8-i10)';b11=[sqrt(3)/2*(A(1,1)-A(1,5)-A(1,7)-A(1,11))+0.5*(A(1,2)-A(1,4)-A(1,8)+A(1,10)+A(1,12))-A(1,6)]/6; '6b1=sqrt(3)/2*(i1-i5-i7+i11)+1/2*(i0+i2-i4-i8+i10+i12)-i6';'基波电压有效值'U110=sqrt([(a11*a11+b11*b11)/2])'相角'FU1=atan(b11/a11)'两点乘积算法'U11=sqrt([(A(1,3)*A(1,3)+A(1,6)*A(1,6))/2])'精度比较:';Max=A(1,1);for i=1:12I=A(1,i);if I>MaxMax=I;endend'傅氏算法'FJU1=[(U110*sqrt(2))/Max]*100'两点乘积算法'LJU1=[(U11*sqrt(2))/Max]*100'基波电流'yi1=10*sin(x);subplot(2,4,6);plot(x,yi1);xlabel('x');ylabel('yi1');title('基波电流');A=yi1;'傅氏算法';a11=[(A(1,3)-A(1,9))+0.5*(A(1,1)+A(1,5)-A(1,7)-A(1,11))+sqrt(3)/2*(A(1,2)+A(1,4)-A(1,8)-A(1,10))]/6; b11=[sqrt(3)/2*(A(1,1)-A(1,5)-A(1,7)-A(1,11))+0.5*(A(1,2)-A(1,4)-A(1,8)+A(1,10)+A(1,12))-A(1,6)]/6; '基波电流有效值'I110=sqrt([(a11*a11+b11*b11)/2])'相角'FI1=atan(b11/a11)'两点乘积算法'I11=sqrt([(A(1,3)*A(1,3)+A(1,6)*A(1,6))/2])'傅氏算法求线性电阻'R110=U110/I110'两点乘积算法求线性电阻'R11=U11/I11'精度比较:';Max=A(1,1);for i=1:12I=A(1,i);if I>MaxMax=I;endendMax;'傅氏算法'FJI1=[(I110*sqrt(2))/Max]*100'两点乘积算法';LJI1=[(I11*sqrt(2))/Max]*100'复合电压'B=[];B=yu5;'傅氏算法';a51=[(B(1,3)-B(1,9))+0.5*(B(1,1)+B(1,5)-B(1,7)-B(1,11))+sqrt(3)/2*(B(1,2)+B(1,4)-B(1,8)-B(1,10))]/6; b51=[sqrt(3)/2*(B(1,1)-B(1,5)-B(1,7)-B(1,11))+0.5*(B(1,2)-B(1,4)-B(1,8)+B(1,10)+B(1,12))-B(1,6)]/6; '复合电压有效值'U510=sqrt([(a51*a51+b51*b51)/2])'相角'FU5=atan(b51/a51)'两点乘积算法'U51=sqrt([(B(1,3)*B(1,3)+B(1,6)*B(1,6))/2])'精度比较:';Max=B(1,1);for i=1:12I=B(1,i);if I>MaxMax=I;endend'傅氏算法'FJU5=[(U510*sqrt(2))/B(1,3)]*100'两点乘积算法'LJU5=[(U51*sqrt(2))/B(1,3)]*100'复合电流'yi5=12*sin(x)+4*sin(3*x)+2.4*sin(5*x)+1.8*sin(7*x);subplot(2,4,7);plot(x,yi5);xlabel('x');ylabel('yi5');title('总电流');B=yi5;'傅氏算法';a51=[(B(1,3)-B(1,9))+0.5*(B(1,1)+B(1,5)-B(1,7)-B(1,11))+sqrt(3)/2*(B(1,2)+B(1,4)-B(1,8)-B(1,10))]/6; b51=[sqrt(3)/2*(B(1,1)-B(1,5)-B(1,7)-B(1,11))+0.5*(B(1,2)-B(1,4)-B(1,8)+B(1,10)+B(1,12))-B(1,6)]/6; '复合电流有效值'I510=sqrt([(a51*a51+b51*b51)/2])'相角'FI5=atan(b51/a51)'两点乘积算法'I51=sqrt([(B(1,3)*B(1,3)+B(1,6)*B(1,6))/2])'精度比较:';Max=B(1,1);for i=1:12I=B(1,i);if I>MaxMax=I;endend'傅氏算法'FJI5=[(I510*sqrt(2))/B(1,3)]*100'两点乘积算法'LJI5=[(I51*sqrt(2))/B(1,3)]*100'傅氏算法求线性电阻'R510=U510/I510'两点乘积算法求线性电阻'R51=U51/I51附图：数据对比傅氏算法两点乘积算法相角基波电压有效值239.3401 268.7006 -0.2361基波电压精度89.0732 100.0000基波电流有效值 6.2984 7.0711 -0.2361基波电流精度89.0732 100.0000线性电阻38 38.0000总电压有效值238.3786 319.0206 -0.2187总电压精度108.6481 145.4031总电流有效值7.5250 10.0886 -0.2170总电流精度107.7921 144.5143总线性电阻31.6782 31.6219在实验中遇到的问题1、Matlab如何改变图形颜色? plot(x,yu1,'b');2、Matlab中为什么只能在小数点后显示四位? 用format命令来改变命令窗口数字的显示格式和精度，但不会影响matlab的计算精度，matlab的矩阵运算默认都是双精度浮点型运算。

电力系统常用交流采样方法对比评价

电力系统常用交流采样方法对比评价摘要：伴随着科学技术的不断发展和进步，要对电量进行计量就要利用数据采集机制，是实现自动化管理的根本，其中，交流采样能提升实时性和相位准确性，且整体采样处理工序的成本投资少，更加便于后期维护，具有一定的推广价值。

本文简要分析了电力系统内交流采样的过程，并对不同采样方法和对比展开了讨论，仅供参考。

关键词：电力系统；交流采样；方法；对比一、交流采样概述在电力系统不断发展的时代背景下，电力网容量在不断增加，相应的应用结构复杂程度也在加深，这就需要相关部门借助实时监控体系对自动化进行集中调度和处理，确保能准确且快速地完成采集系统中模拟电量的处理和收集。

需要注意的是，若是依据不同的采样信号进行分类，主要分为直流采样以及交流采样，前者就是将交流电压以及电流信号直接转变为0到5V的直流电压，然后借助相应的处理机制对电流数量予以采集分析，因为处理机制的算法较为简单，所以更加利于开展滤波工作。

但是，因为直流采样维护难度较大且不能完成实时信号采集，因此在电力系统中的应用受限。

后者则主要是将交流电量转变为±5V交流电压或者是0到5V交流电压，整体相位失真程度较小，维护便利，但是算法较为简单，在计算技术不断发展的情况下，其技术便捷化程度也有所提高，将逐步取代传统的直流采样[1]。

二、电力系统常用交流采样方法（一）正弦函数模型算法正弦函数模型算法中主要包括2点采样算法、半周期积分法、最大值算法以及单点算法，不同的算法的原理也有所差异。

1.半周期积分算法主要是基于正弦量在任意半个周期内绝对值进行的算法处理，因为绝对值本身是一个常数，因此，要结合数据窗长度和算法自身的滤波能力对相关数据进行处理，偶次高频分量正负半个周期内的相关积分也会形成抵消量，且奇次波不能完全抵消，但是相应的影响会随之降低。

具体算法如下：假设，能得出相应的关系式，若是将公式中的内容进行离散化处理，则能得出，在公式中可知N就是整个采样计算体系中的采样点数，将其进行对比分析后能得出。

交流采样测量装置在电力系统中的应用

交流采样测量装置在电力系统中的应用摘要：交流采样测量装置是现阶段电网测量中的重要测量仪器，具有精准度高、稳定效果好等优点，现从交流采样测量装置的工作原理出发，对测量装置的校准情况进行了简单分析，讨论了交流采样测量装置在电力系统中的应用情况，旨在进一步提高电网电能管理效果，提高电力企业经济效益。

关键词：交流采样测量装置；电力系统；校验一、交流采样测量装置的基本原理交流采样法是按一定规律对被测交流信号的瞬时值进行采样,再用一定的数学算法求得被测量,用软件功能代替硬件的计算功能。

它是用一条阶梯曲线代替一条光滑被测正弦信号,其原理误差主要有项①用时间上离散的数据近似代替时间上连续的数据所产生的误差,这主要是由每个正弦信号周期中的采样点数决定的,实际上它取决于A/D转换器转换速度和CPU的处理时间②将连续的电压和电流进行量化而产生的量子化误差,这主要取决于A/D刀转换器的位数。

交流采样法包括同步采样法、准同步采样法、非同步采样法等几种。

这种采样原理也各有缺点,同步采样法需要保证采样的时间区间正好等于被测信号周期的整数倍。

同步采样法的实现方法有种一是硬件同步采样法二是软件同步采样法。

但在实际采样测量中,采样周期不能与被测信号周期实现严格同步,此时测量结果就将产生同步误差。

这时,可通过适当增加采样数据量和增加迭代次数来提高测量准确度,这种方式就是准同步采样法。

也可以使用固定的采样间隔,通过软件判断处理调整采样值,使采样周期与信号周期或信号周期的整数倍的差值小于一个采样间隔的测量方法,这就是非同步采样法。

二、概述随着综合自动化的发展,交流采样测量装置的使用已越来越普及,它已代替电测量变送器作为电网电测量参数有功功率、无功功率、电压、电流、相位、频率、功率因素测量的在线测量仪器。

由于交流采样装置作为综合自动化系统的一个测量模块,是综合自动化的测量单元,是原电测量变送器和远动终端（RTU）的合成装置,它是一个计量检测仪器,具有较高的测量精度,目前安装于电力系统的变电站和电厂的交流采样装置的测量准确度等级已达到0.2级。

基于单片机的电力监控系统交流采样技术的实现.doc

基于单片机的电力监控系统交流采样技术的实现随着电力系统的快速开展，电网容量的扩大使其结构更加复杂，实时监控、调芳的自动化显得尤为重要；而在电力调度自动化系统中，电力参数的测量是最根本的功能。

如何快速、准确地采集各种电力参数显得尤为重要。

在实现自动化的过程中，最关键的环节是数据采集。

根据采集信号的不同，可分直流采样和交流采样两种。

直流采样，顾名思义，采样对象为直流信号。

它是把交流电压、电流信号经过各种变送器转化为0～5V的直流电压，再由各种装置和仪表采集。

此方法软件设计简单，对采样值只需作一次比例变换即可得到被测量的数值。

但直流采样仍有很大的局限性：无法实现实时信号的采集；变送器的精度和稳定性对测量精度有很大影响；设备复杂，维护难等。

交流采样是将二次测得的电压、电流经高精度的CT、PT变成计算机可测量的交流小信号，然后再送入计算机进行处理。

由于这种方法能够对被测量的瞬时值进行采样，因而实时性好，相位失真小。

它用软件代替硬件的功能又使硬件的投资大大减小。

随着微机技术的不断开展，交流采样必将以其优异的性能价格比，逐步取代传统的直流采样方法。

本系统采用8031单片机实现电力参数的交流采样。

通过LED显示器显示频率、电压、电流的实时值，在过压30%、欠压30%时进行声光报警，并能定时打印电压、电流及频率值。

实践证明，采用交流采样方法进行数据采集，通过算法运算后获得的电压、电流、有功功率、功率因数等电力参数有着较好的精确度和稳定性。

一、交流采样原理假设将电压有效值公式离散化，以一个周期内有限个采样电压数字量来代替一个周期内连续变化的电压函数值，那么式中：ΔTm为相邻两次采样的时间间隔；um为第m-1个时间间隔的电压采样瞬时值；N为1个周期的采样点数。

假设相邻两采样的时间间隔相等，即ΔTm为常数ΔT，考虑到N=(T/ΔT) 1，那么有式（1）就是根据一个周期各采样瞬时值及每周期采样点数计算电压信号有效值的公式。

交直流电压电流采样电路分析和计算

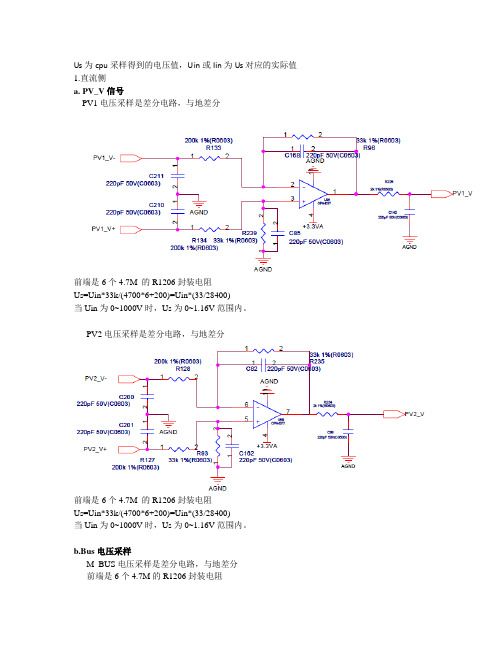
Us为cpu采样得到的电压值，Uin或Iin为Us对应的实际值1.直流侧a.PV_V信号PV1电压采样是差分电路，与地差分前端是6个4.7M 的R1206封装电阻Us=Uin*33k/(4700*6+200)=Uin*(33/28400)当Uin为0~1000V时，Us为0~1.16V范围内。

PV2电压采样是差分电路，与地差分前端是6个4.7M 的R1206封装电阻Us=Uin*33k/(4700*6+200)=Uin*(33/28400)当Uin为0~1000V时，Us为0~1.16V范围内。

b.Bus电压采样M_BUS电压采样是差分电路，与地差分前端是6个4.7M的R1206封装电阻Us=Uin*33k/(4700*6+200)=Uin*(33/28400)当Uin为0~800V时，Us为0~0.93V范围内。

M_BUS_MID电压采样是差分电路，与地差分前端是4个4.7M的R1206封装电阻Us=Uin*100k/(4700*4+200)=Uin*(1/190)当Uin为0~400V时，Us为0~2.1V范围内。

c.PV电流采样BOOST1_CT采样是差分电路，与地差分4646-X661是1:2000，Vi=2.5±( I_inv /12 )*0.625,经过差分后，把信号放大5倍，Vi=（100k/20k）*I_linv/20,即是I_inv/4 所以Vs在0~2.8V范围内。

当最大电流设为11A时，放大输出最大值为2.8VBOOST2_CT采样是差分电路，与地差分4646-X661是1:2000，Vi=2.5±( I_inv /12 )*0.625,经过差分后，把信号放大5倍，Vi=（100k/20k）*I_linv/20,即是I_inv/4 所以Vs在0~2.8V范围内。

当最大电流设为11A时，放大输出最大值为2.8Vd.PV_ISO检测PV_ISO电路采用差分电路前端采用4个4.7M R1206封装的电阻经过差分之后输出电压Vs=Viso*100k/(4700*4+300k)=Viso*(1/191)2.交流侧a.交流电压采样(电网侧)R相采用差分电路电网侧有4个R1206封装的4.7M电阻。

电力系统自动监控技术交流数据采集与处理PPT课件

Voltage will be 0 to 100V and current may as high as 25 times of the rated current, that is 125A or 25A.
.
13
The voltage and current are still too big for the AAF, S/H, MUX, ADC and other electronic circuit.
.
9
Typical hardware structure
❖ The following Figure shows the general hardware outline of a numeric protection relay.
❖ It consists of: Galvanic Isolation Transformer Anti-Alias Filter S/H Amplifier Multiplexer ADC Micro-Processor Timer
.
28
原理电路
.
29
工作过程
❖ Sample mode:
S/H is high and AS is closed.
Vout=Vin
❖ Hold mode:
S/H is low and AS is opened.
Vout=VC= Vin (just before AS
open)
.
30
波形
.
31
基本要求:
多路切换开关
❖ Function :
In general case, relays need multichannel inputs
(3phase voltage, 3phase current, zero sequence current etc.)

什么是交流采样？

什么是交流采样？定义：交流采样技术是按一定规律对被测信号的瞬时值进行采样，再按一定算法进行数值处理，从而获得被测量的测量方法。

一、交流采样简介交流采样是相对直流采样而言，它是指对电流和电压采集时，输入至A/D转换器的是与电力系统的一次电流和一次电压同频率、大小成比例的电信号。

由于电力系统、发电厂或变电站等一次电流和电压都是大电流或高电压信号，不能直接送至A/D转换器，所以必须将高电压大电流的强电信号，经过电压传感器或电流传感器，变换成A/D 转换器所能接受的电信号。

二、交流采样一般算法交流采样技术的的理论基础是采样定理，即要求采样频率为被测信号频谱中最高频率的2倍以上。

按一定的规律对被测量的瞬时值进行采样，然后按一定的算法可求出被测量，国内外已提出许多交流采样的算法。

下面介绍交流采样的一般算法：交流电压有效值公式为：离散化，以一个周期内有限个采样电压数字量代替一个周期内的连续变化的电压函数值，则式中：△Tm——相邻两次采样的时间间隔；Um——第n-1个时间间隔的电压采样瞬时值；N——一个周期内的采样点数。

同理，采样电流有效值计算公式在交流采样方式中，对于有功功率、无功功率和功率因数，是通过采样所得到的u、i计算出来的。

计算一相有功功率的离散化公式为：式中：im、um---同一时刻的电流、电压采样值。

功率因数可由下式求得：三、交流采样特点1. 实时性好。

它能避免直流采样中整流、滤波环节的时间常数大的影响。

2. 能反映原来电流、电压的实际波形，便于对所测量的结果进行波形分析。

因此在需要谐波分析或故障录波的场合，必须采用交流采样。

3. 有功功率和无功功率是通过采样得到的u、i计算出来的，因此可以省去有功功率和无功功率变送器，可以节约投资并缩小测量设备的体积。

4. 对A/D转换器的转换速率和采样保持器要求较高。

为了保证测量的精度，一个周期内，必须保证有足够的采样点数，因此要求A/D 转换器要有足够的转换速度。

电力系统交流采样算法

交流采样常用计算公式

交流采样技术及其DSP实现方法

交流采样常用计公式

CH6 交流采样常用算法的分析

煤矿井下交流电量信号的采样及算法

电网监控与调度自动化第二章交流数据采集与处理

3第三章 交流采样技术

电力系统数据采样的方法

电力系统常用交流采样算法2013

电力系统交流采样算法

电力系统常用交流采样方法对比评价

交流采样测量装置在电力系统中的应用

基于单片机的电力监控系统交流采样技术的实现.doc

交直流电压电流采样电路分析和计算

电力系统自动监控技术交流数据采集与处理PPT课件

什么是交流采样？

3第三章交流采样技术