GAC试题 20-26期
GAC第三期培训试题

第三期珠宝鉴定师试题(A卷)-----元实珠宝学院整理一、是非题(你认为是正确的在题后面的括号中写〝是〞,你认为是错误的在题后面的括号中写〝否〞。
)1、宝石一般取材于矿物,玉石主要取材于岩石。
2、同一种属宝石的主要化学成分是固定不变的。
3、宝石的折射率越高,光泽也越强。
4、因蓝宝石晶体多为歪晶,所以蓝宝石晶体对应晶面之间的夹角是变化的。
5、宝石的光轴与晶轴都是一致的。
6、〔111〕是单形符号,代表八面体。
7、在上下偏光镜平行时宝石的光率体椭圆切面与偏光镜斜交不会产生干涉色。
8、宝石都是结晶物质。
9、同一种宝石的晶体形态是相同的。
10、海蓝宝石与祖母绿都是绿柱石的亚种。
11、二轴晶光率体只有垂直光轴面方向的光率体切面是圆的。
12、钻石颜色定级时,如果所测钻石在颜色介于两个样品之间,则应定为色级较低的一档13、钻石在不同方向上的压入硬度是相同的。
14、珊瑚主要由方解石组成的。
15、光波在宝石中传播速度比在空气中快。
二、选择题(每题一分,共25分。
把你所选择的答案:1或2或3填写在题后的括号内)1、金绿宝石属于:(1)、三方晶系(2)、单斜晶系(3)、斜方晶系2、红宝石内常可以看到:(1)、解理(2)、裂开(3)、晶面3、宝石光泽由强到弱的顺序为:(1)、玻璃光泽、半金属光泽、金属光泽(2)、金刚光泽、半金属光泽、玻璃光泽(3)、半金属光泽、金刚光泽、玻璃光泽4、坦桑石常呈现出(1)、单色性(2)、二色性(3)、三色性5、对称面的交线必然为:(1)、对称轴(2)、晶棱(3)、对称面6、宝石有无二色性取决于:(1)、化学成分(2)、晶体结构(3)、生成环境7、翡翠俗称的〝翠性〞是指:(1)、解理闪光(2)、解理面反光(3)、裂开面反光8、静水力学法测定宝石的密度要求密度精确为小数点后第二位,则称重精度必须:()(1)、0.01g (2)、0.001g (3)、0.0001g9、在紫外光下,天然绿色蓝宝石表现为:(1)、强的荧光(2)、弱的荧光(3)、无荧光10、珍珠的珠光产生的原理是由于:(1)、内部电子跃迁(2)、光的散射(3)、光的干涉11、目前我国对辐照处理黄玉的携带放射性残留,参照日用工业品的辐射防护规定,放射性允许标准为:(1)、70贝克(2)、30贝克(3)、50γ12、钻石的天然黄色是由于钻石中含有微量的元素:(1)、硼(2)、氮(3)、钴13、我国目前钻石的主要产地有:(1)、山东、湖南、辽宁(2)、辽宁、江苏、河南(3)、湖南、山东、贵州14、肉眼鉴别石英玻璃球与水晶球,常采用的方法是:(1)、掂量估计相对密度(2)、透视球下面的字有重影(3)、看哪个球反光好15、鉴别天然与辐射改色的蓝色钻石,可用:(1)、热导仪(2)、电导仪(3)、折射仪16、宝石显微镜的垂直照明法是一种观察宝石_____的照明方式。
2021重庆中考复习数学第26题专题训练五(含答案解析)(1) (1)

2021重庆中考复习数学第26题专题训练五1、如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.2、[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△,可推证△CEF是三角形,从而求得∠DCE=.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.3、(2019秋•锦江区校级期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.4、(2019•镇平县三模)如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为;∠EFC的度数为;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.5、(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.6、【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.7、(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.8、【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.9、(2018•大东区一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.10、模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于时,线段BC的长取得最大值,且最大值为(用含b,c的式子表示)(直接填空).模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.12、已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.13、已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.14、如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)16、在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.17、在△ABC中,∠BAC=60°,点D、E分别在边AC、AB上,AD=AE,连接CE、BD相交于点F,且∠BEC=∠ADF,连接AF.(1)如图1,连接ED,求证:∠ABD=∠CED;(2)如图2,求证:EF+FD=AF;(3)如图3,取BC的中点G,连接AG交BD于点H,若∠GAC=3∠ABD,BH=7,求△ABH的面积.18、点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠F AE=∠F AD,FE=FD.(1)如图1,若∠AEF=∠ADF,求证:AE=AD;(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.2020重庆中考复习数学第26题专题训练五参考答案1、(2019秋•天桥区期末)如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G,(1)求证:CF=BG;(2)延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=3,BG=6,求AC的长.证明:(1)如图1,∵∠ACB=90°,AC=BC,∴∠A=45°,∵CG平分∠ACB,∴∠ACG=∠BCG=45°,∴∠A=∠BCG,在△BCG和△CAF中,∵,∴△BCG≌△CAF(ASA),∴CF=BG;(2)如图2,∵PC∥AG,∴∠PCA=∠CAG,∵AC=BC,∠ACG=∠BCG,CG=CG,∴△ACG≌△BCG,∴∠CAG=∠CBE,∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,∠PGC=∠GCB+∠CBE=∠CBE+45°,∴∠PCG=∠PGC,∴PC=PG,∵PB=BG+PG,BG=CF,∴PB=CF+CP;(3)解法一:如图3,过E作EM⊥AG,交AG于M,∵S△AEG=AG•EM=3,由(2)得:△ACG≌△BCG,∴BG=AG=6,∴×6×EM=3,EM=,设∠FCH=x°,则∠GAC=2x°,∴∠ACF=∠EBC=∠GAC=2x°,∵∠ACH=45°,∴2x+x=45,x=15,∴∠ACF=∠GAC=30°,在Rt△AEM中,AE=2EM=2,AM==3,∴M是AG的中点,∴AE=EG=2,∴BE=BG+EG=6+2,在Rt△ECB中,∠EBC=30°,∴CE=BE=3+,∴AC=AE+EC=2+3+=3+3.解法二:同理得:∠CAG=30°,AG=BG=6,如图4,过G作GM⊥AC于M,在Rt△AGM中,GM=3,AM===3,∵∠ACG=45°,∠MGC=90°,∴GM=CM=3,∴AC=AM+CM=3+3.2、(2019秋•淮安期末)[问题背景]如图1所示,在△ABC中,AB=BC,∠ABC=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.[问题初探]如果点D在线段BC上运动,通过观察、交流,小明形成了以下的解题思路:过点E作EF⊥BC 交直线BC于F,如图2所示,通过证明△DEF≌△ADB,可推证△CEF是等腰直角三角形,从而求得∠DCE=135°.[继续探究]如果点D在线段CB的延长线上运动,如图3所示,求出∠DCE的度数.[拓展延伸]连接BE,当点D在直线BC上运动时,若AB=,请直接写出BE的最小值.解:[问题初探]如图2,过点E作EF⊥BC交直线BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=135°,故答案为:ADB,等腰直角,135;[继续探究]如图3,过点E作EF⊥BC于F,∴∠DFE=90°=∠ABD,∴∠EDF+∠DEF=90°,由旋转知,AD=DE,∠ADE=90°,∴∠ADB+∠EDF=90°,∴∠ADB=∠DEF,∴△ABD≌△DFE(AAS),∴BD=EF,DF=AB,∵AB=BC,∴BC=DF,∴BD=CF,∴EF=CF,∴△CEG是等腰直角三角形,∴∠ECF=45°,∴∠DCE=45°;[拓展延伸]如图4,在△ABC中,∠ABC=90°,AB=BC=,∴∠ACB=45°当点D在射线BC上时,由[问题初探]知,∠BCM=135°,∴∠ACM=∠BCM﹣∠ACB=90°,当点D在线段CB的延长线上时,由[继续探究]知,∠BCE=45°,∴∠ACN=∠ACB+∠BCM=90°,∴点E是过点C垂直于AC的直线上的点,∴当BE⊥MN时,BE最小,∵∠BCE=45°,∴∠CBE=45°=∠BCE,∴BE=CE,∴BE最小=BC=,即:BE的最小值为.3、(2019秋•锦江区校级期末)在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线.(1)如图1,求证:AD=2DC.(2)如图2,作∠CBD的角平分线交线段CD于点M,若CM=1,求△DBM的面积;(3)如图3,过点D作DE⊥AB于点E,点N是线段AC上一点(不与C、D重合),以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,试探究线段ND,DG与AD之间的数量关系,并说明理由.证明:(1)如图1,过点D作DE⊥AB,∵BD是△ABC的角平分线,DE⊥AB,∠ACB=90°,∴DC=DE,∵∠A=30°,DE⊥AB,∴AD=2DE,∴AD=2DC;(2)如图2,过点M作ME∥BD,∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,∴∠ABD=∠DBC=30°,∵BM平分∠CBD,∴∠CBM=15°=∠DBM,∵ME∥BD,∴∠MEC=∠CBD=30°,∠EMB=∠DBM=∠MBE,∴ME=BE,∵∠MEC=30°,∠C=90°∴CE=MC=,ME=2MC=2=BE,∴BC=+2,∵∠CBD=30°,∠C=90°,∴BC=CD,∴CD=1+,∴DM=,∴△DBM的面积=××(+2)=1+;(3)若点N在CD上时,AD=DG+DN,理由如下:如图3所示:延长ED使得DW=DN,连接NW,∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,∴∠ADE=∠BDE=60°,AD=BD,∵DN=DW,且∠WDN=60°∴△WDN是等边三角形,∴NW=DN,∠W=∠WND=∠BNG=∠BDN=60°,∴∠WNG=∠BND,在△WGN和△DBN中,∴△WGN≌△DBN(SAS),∴BD=WG=DG+DN,∴AD=DG+DN.(3)若点N在AD上时,AD=DG﹣DN,理由如下:如图4,延长BD至H,使得DH=DN,连接HN,由(1)得DA=DB,∠A=30°.∵DE⊥AB于点E.∴∠2=∠3=60°.∴∠4=∠5=60°.∴△NDH是等边三角形.∴NH=ND,∠H=∠6=60°.∴∠H=∠2.∵∠BNG=60°,∴∠BNG+∠7=∠6+∠7.即∠DNG=∠HNB.在△DNG和△HNB中,∴△DNG≌△HNB(ASA).∴DG=HB.∵HB=HD+DB=ND+AD,∴DG=ND+AD.∴AD=DG﹣ND.4、(2019•镇平县三模)如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.(1)发现问题:线段EF,CF之间的数量关系为EF=CF;∠EFC的度数为120°;(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.解:(1)如图1中,∵DE⊥AB,∴∠BED=90°,∵∠BCD=90°,BF=DF,∴FE=FB=FD=CF,∴∠FBE=∠FEB,∠FBC=∠FCB,∴∠EFC=∠EFD+∠CFD=∠FBE+∠FEB+∠FBC+∠FCB=2(∠FBE+∠FBC)=2∠ABC=120°,故答案为:EF=CF,120°.(2)结论成立.理由:如图2中,取AB的中点M,AD的中点N,连接MC,MF,ED,EN,FN.∵BM=MA,BF=FD,∴MF∥AD,MF=AD,∵AN=ND,∴MF=AN,MF∥AN,∴四边形MFNA是平行四边形,∴NF=AM,∠FMA=∠ANF,在Rt△ADE中,∵AN=ND,∠AED=90°,∴EN=AD=AN=ND,同理CM=AB=AM=MB,在△AEN和△ACM中,∠AEN=∠EAN,∠MCA=∠MAC,∵∠MAC=∠EAN,∴∠AMC=∠ANE,又∵∠FMA=∠ANF,∴∠ENF=∠FMC,在△MFC和△NEF中,,∴△MFC≌△NEF(SAS),∴FE=FC,∠NFE=∠MCF,∵NF∥AB,∴∠NFD=∠ABD,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,△BMC是等边三角形,∠MCB=60°∴∠EFC=∠EFN+∠NFD+∠DFC=∠MCF+∠ABD+∠FBC+∠FCB=∠ABC+∠MCB=60°+60°=120°.(3)如图3中,作EH⊥AB于H.在Rt△ABC中,∵∠BAC=30°,BC=3,∴AB=2BC=6,在Rt△AED中,∠DAE=30°,AD=2,∴DE=AD=1,在Rt△DEH中,∵∠EDH=60°,DE=1,∴EH=ED•sin60°=,DH=ED•cos60°=,在Rt△EHG中,EG==.5、(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.解:(1)BC=2BD,理由:如图2,连接CD,由旋转可得,CP=DP,∠CPD=60°,∴△CDP是等边三角形,∴∠CDP=60°=∠PCD,又∵P是AB的中点,AB=AC,∠A=60°,∴等边三角形ABC中,∠PCB=30°,CP⊥AB,∴∠BCD=30°,即BC平分∠PCD,∴BC垂直平分PD,∴∠BDC=∠BPC=90°,∴Rt△BCD中,BC=2BD.(2)如图3,取BC中点F,连接PF,∵∠A=90°,AB=AC,∴△ABC是等腰直角三角形,∵P是AB的中点,F是BC的中点,∴PF是△ABC的中位线,∴PF∥AC,∴∠PFB=∠ACB=45°,∠BPF=∠A=90°,∴△BPF是等腰直角三角形,∴BF=BP,BP=PF,∵∠DPC=∠BPF=90°,∴∠BPD=∠FPC,又∵PD=PC,∴△BDP≌△FCP,∴BD=CF,∵BC=BF+FC,∴BC=BD+BP.6、(2019春•碑林区校级月考)【发现问题】如图1,已知△ABC,以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE.请你以A 为直角顶点、AC为腰,向△ABC外作等腰直角△ACD(不写作法,保留作图痕迹).连接BD、CE.那么BD与CE的数量关系是BD=CE.【拓展探究】如图2,已知△ABC,以AB、AC为边向外作正方形AEFB和正方形ACGD,连接BD、CE,试判断BD与CE之间的数量关系,并说明理由.【解决问题】如图3,有一个四边形场地ABCD,∠ADC=60°,BC=15,AB=8,AD=CD,求BD的最大值.【发现问题】解:延长CA到M,作∠MAC的平分线AN,在AN上截取AD=AC,连接CD,即可得到等腰直角△ACD;连接BD、CE,如图1所示:∵△ABE与△ACD都是等腰直角三角形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE,【拓展探究】解:BD=CE;理由如下:∵四边形AEFB与四边形ACGD都是正方形,∴AB=AE,AD=AC,∠BAE=∠CAD=90°,∴∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;【解决问题】解:以AB为边向外作等边三角形ABE,连接CE,如图3所示:则∠BAE=60°,BE=AB=AE=8,∵AD=CD,∠ADC=60°,∴△ACD是等边三角形,∴∠CAD=60°,AC=AD,∴∠CAD+∠BAC=∠BAE+∠BAC,即∠BAD=∠EAC,在△BAD和△EAC中,,∴△BAD≌△EAC(SAS),∴BD=CE;当C、B、E三点共线时,CE最大=BC+BE=15+8=23,∴BD的最大值为23.7、(2018春•铁西区期中)(1)如图1,点C为线段AB外一个动点,已知AB=a,AC=b.当点C位于BA的延长线上时,线段BC取得最大值,则最大值为a+b(用含a,b的式子表示);(2)如图2,点C为线段AB外一个动点,若AB=10,AC=3,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接AE,DB.①求证:AE=DB;②请直接写出线段AE的最大值;(3)如图3,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,请直接写出线段AN的最大值.(1)解:∵点C为线段AB外一动点,且AC=b,AB=a,∴当点C位于BA的延长线上时,线段BC的长取得最大值,且最大值为AC+AB=a+b,(2)①证明:如图2中,∵△ACD与△BCE是等边三角形,∴CD=AC,CB=CE,∠ACD=∠BCE=60°,∴∠DCB=∠ACE,在△CAD与△EAB中,,∴△CAD≌△EAB(SAS),∴AE=BD.②∵线段AE长的最大值=线段BD的最大值,由(1)知,当线段BD的长取得最大值时,点D在BA的延长线上,∴最大值为AD+AB=3+10=13;(3)如图3中,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP,则△APM是等腰直角三角形,∴MA=MP=2,BP=AN,∴P A=2,∵AB=6,∴线段AN长的最大值=线段BP长的最大值,∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=6+2.8、(2019秋•武冈市期中)【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是∠BAE+∠F AD=∠EAF;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF=BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.解:(1)∠BAE+∠F AD=∠EAF.理由:如图1,延长FD到点G,使DG=BE,连接AG,根据SAS可判定△ABE≌△ADG,进而得出∠BAE=∠DAG,AE=AG,再根据SSS可判定△AEF≌△AGF,可得出∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF.故答案为:∠BAE+∠F AD=∠EAF;(2)仍成立,理由:如图2,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,∴∠B=∠ADG,又∵AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF;(3)∠EAF=180°﹣∠DAB.证明:如图3,在DC延长线上取一点G,使得DG=BE,连接AG,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADC=∠ABE,又∵AB=AD,∴△ADG≌△ABE(SAS),∴AG=AE,∠DAG=∠BAE,∵EF=BE+FD=DG+FD=GF,AF=AF,∴△AEF≌△AGF(SSS),∴∠F AE=∠F AG,∵∠F AE+∠F AG+∠GAE=360°,∴2∠F AE+(∠GAB+∠BAE)=360°,∴2∠F AE+(∠GAB+∠DAG)=360°,即2∠F AE+∠DAB=360°,∴∠EAF=180°﹣∠DAB.9、(2018•大东区一模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P逆时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P在BC延长线上时,若∠BPO=45°,AC=,请直接写出BQ的长.解:(1)CP=BQ,理由:如图1,连接OQ,由旋转知,PQ=OP,∠OPQ=60°⊅∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(2)CP=BQ,理由:如图2,连接OQ,由旋转知,PQ=OP,∠OPQ=60°∴△POQ是等边三角形,∴OP=OQ,∠POQ=60°,在Rt△ABC中,O是AB中点,∴OC=OA=OB,∴∠BOC=2∠A=60°=∠POQ,∴∠COP=∠BOQ,在△COP和△BOQ中,,∴△COP≌△BOQ(SAS),∴CP=BQ,(3)如图3,在Rt△ABC中,∠A=30°,AC=,∴BC=AC•tan∠A=,过点O作OH⊥BC,∴∠OHB=90°=∠BCA,∴OH∥AB,∵O是AB中点,∴CH=BC=,OH=AC=,∵∠BPQ=45°,∠OHP=90°,∴∠BPQ=∠PQH,∴PH=OH=,∴CP=PH﹣CH=﹣=,连接BQ,同(1)的方法得,BQ=CP=.10、(2018秋•东海县期末)模型发现:同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.特别的,当点C位于线段BA的延长线上时,线段BC的长取得最大值,且最大值为b+c(用含b,c的式子表示)(直接填空)模型应用:点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD 和等边三角形BCE,连接BD,AE.(1)求证:BD=AE.(2)线段AE长的最大值为5.模型拓展:如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB =8.若AC⊥AB,AC=3,试求OC长的最大值.解:当点C位于线段BA的延长线上时,线段BC的长取得最大值,最大值为b+c,故答案为:线段BA的延长线上;b+c;模型应用:(1)证明:∵△ACD、△BCE都是等边三角形,∴CD=CA=AD,CB=CE,∠ACD=60°,∠BCE=60°,∴∠DCB=∠ACE,在△DCB和△ACE中,,∴△DCB≌△ACE(SAS)∴BD=AE;(2)当点D位于线段BA的延长线上时,线段BD的长取得最大值,最大值为AB+AD=AB+AC=3+2=5,∵AE=BD,∴线段AE长的最大值为5,模型拓展:取AB的中点G,连接OG、CG,在Rt△AOB中,G为AB的中点,∴OG=AB=4,在Rt△CAG中,CG===5,当点O、G、C在同一条直线上时,OC最大,最大值为4+5=9.11、已知:△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D在BC的延长线上,连AD,过B作BE⊥AD于E,交AC于点F.求证:AD=BF;(2)如图2,点D在线段BC上,连AD,过A作AE⊥AD,且AE=AD,连BE交AC于F,连DE,问BD与CF有何数量关系,并加以证明;(3)如图3,点D在CB延长线上,AE=AD且AE⊥AD,连接BE、AC的延长线交BE于点M,若AC =3MC,请直接写出的值.(1)证明:如图1中,∵BE⊥AD于E,∴∠AEF=∠BCF=90°,∵∠AFE=∠CFB,∴∠DAC=∠CBF,∵BC=CA,∴△BCF≌△ACD,∴BF=AD.(2)结论:BD=2CF.理由:如图2中,作EH⊥AC于H.∵∠AHE=∠ACD=∠DAE=90°,∴∠DAC+∠ADC=90°,∠DAC+∠EAH=90°,∴∠DAC=∠AEH,∵AD=AE,∴△ACD≌△EHA,∴CD=AH,EH=AC=BC,∵CB=CA,∴BD=CH,∵∠EHF=∠BCF=90°,∠EFH=∠BFC,EH=BC,∴△EHF≌△BCF,∴FH=CF,∴BD=CH=2CF.(3)如图3中,同法可证BD=2CM.∵AC=3CM,设CM=a,则AC=CB=3a,BD=2a,∴==.12、(2019秋•松北区期末)已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°,∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:∠1=∠2;②如图2,若BF=2AF,连接CF,求证:BF⊥CF;(2)如图3,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,求的值.(1)①证明:如图1中,∵AB=AC,∠ABC=60°∴△ABC是等边三角形,∴∠BAC=60°,∵AD⊥BN,∴∠ADB=90°,∵∠MBN=30°,∠BFD=60°=∠1+∠BAF=∠2+∠BAF,∴∠1=∠2②证明:如图2中,在Rt△BFD中,∵∠FBD=30°,∴BF=2DF,∵BF=2AF,∴BF=AD,∵∠BAE=∠FBC,AB=BC,∴△BFC≌△ADB,∴∠BFC=∠ADB=90°,∴BF⊥CF(2)在BF上截取BK=AF,连接AK.∵∠BFE=∠2+∠BAF,∠CFE=∠4+∠1,∴∠CFB=∠2+∠4+∠BAC,∵∠BFE=∠BAC=2∠EFC,∴∠1+∠4=∠2+∠4∴∠1=∠2,∵AB=AC,∴△ABK≌CAF,∴∠3=∠4,S△ABK=S△AFC,∵∠1+∠3=∠2+∠3=∠CFE=∠AKB,∠BAC=2∠CEF,∴∠KAF=∠1+∠3=∠AKF,∴AF=FK=BK,∴S△ABK=S△AFK,∴=2.13、(2017春•合肥期末)已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG;①若AG平分∠CAD,求证:AH=AC;②如图3,当G落在△ABC外时,若将△EFG沿EF边翻折,点G刚好落在AB边上点P,直接写出AG与EF的数量关系.(1)解:如图1中,在AB上取一点M,使得BM=ME,连接ME.在Rt△ABE中,∵OB=OE,∴BE=2OA=2,∵MB=ME,∴∠MBE=∠MEB=15°,∴∠AME=∠MBE+∠MEB=30°,设AE=x,则ME=BM=2x,AM=x,∵AB2+AE2=BE2,∴(2x+x)2+x2=22,∴x=(负根已经舍弃),∴AB=AC=(2+)•,∴BC=AB=+1.方法二:作EH⊥BC于H,求出BH,CH即可解决问题.(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.∵BE⊥AP,∴∠AHB=90°,∴∠ABH+∠BAH=90°,∵∠BAH+∠P AC=90°,∴∠ABE=∠P AC,在△ABE和△CAP中,,∴△ABE≌△CAP,∴AE=CP=CF,∠AEB=∠P,在△DCF和△DCP中,,∴△DCF≌△DCP,∴∠DFC=∠P,∴∠GFE=∠GEF,∴GE=GF,∵GM⊥EF,∴FM=ME,∵AE=CF,∴AF=CE,∴AM=CM,在△GAH和△GAM中,,∴△AGH≌△AGM,∴AH=AM=CM=AC(3)解:结论:AG=EF.理由:如图3中,作CM⊥AC交AD的延长线于M,连接PG交AC于点O.由(2)可知△ACM≌△BAE,△CDF≌△CDM,∴∠AEB=∠M=∠GEF,∠M=∠CFD=∠GFE,AE=CM=CF,∴∠GEF=∠GFE,∴GE=GF,∵△EFP是由△EFG翻折得到,∴EG=EP=GF=PF,∴四边形EGFP是菱形,∴PG⊥AC,OE=OF,∵AE=CF,∴AO=OC,∵AB∥OP,∴BP=PC,∵PF∥BE,∴EF=CF=AE,∵PB=PC,AO=OC,∴PO=OG=AB,∴AB=PG,AB∥PG,∴四边形ABPG是平行四边形,∴AG∥BC,∴∠GAO=∠ACB=45°,设EO=OF=a,则OA=OG=3a,AG=3a,∴==,∴AG=EF14、(2017春•南岗区校级月考)如图所示,Rt△ABC中,∠ACB=90°,E为AC中点,作ED⊥AC交AB于D,连接CD;(1)如图1,求证:AB=2CD;(2)如图2,作CF⊥AB交AB于F,点G为CF上一点,点H为DE延长线上一点,分别连接AH、GH,若∠AHG=2∠B,求证:AH=GH;(3)如图3,在(2)的条件下,连接DG,且有DE=BF,∠EDG=90°,若AC=6,求AH的长度.解:(1)∵E为AC中点,作ED⊥AC交AB于D,∴AD=CD,∵∠ACB=90°,∴BC∥DE,∴AD=BD,∴CD=BD,∴AB=2CD;(2)如图2,连接CH,∵点E是AC的中点,∴AE=CE,∵DE⊥AC,∴CH=AH,∴∠ACH=∠CAH,∵∠ACB=90°,∴∠B+∠BAC=90°,∵CF⊥AB,∴∠BAC+∠ACF=90°,∴∠ACF=∠B,∴∠HCG=∠ACH+∠ACF=∠CAH+∠B,∠AHG=2∠B∴在四边形AHGF中,∠AFG+∠FGH+∠AHG+∠F AH=360°,∴∠FGH=360°﹣(∠AFG+∠AHG+∠F AH)=360°﹣(90°+2∠B+∠CAH+∠BAC)=360°﹣(90°+2∠B+∠CAH+90°﹣∠B)=360°﹣(180°+∠B+∠CAH)=180°﹣(∠B+∠CAH),∵∠CGH=180°﹣∠FGH=∠B+∠CAH=∠HCG,∴CH=GH,∵CH=AH,∴AH=GH;(3)如图3,由(1)知,DE∥BC,∴∠B=∠ADE,在△BFC和△DEA中,,∴△BFC≌△DEA,∴BC=AD,∵AD=BD=CD,∴BC=BD=CD,∴△BCD是等边三角形,∴∠B=60°,在Rt△ABC中,AC=6,∴BC=2,AB=4,∵CF⊥BD,∴DF=,CF=3,∵∠BAC=30°,∴∠ADE=60°,∵∠EDG=90°,∠FDG=30°,在Rt△DFG中,DF=,∴FG=1,DG=2,∴CG=CF﹣FG=2过点H作HN⊥CF,由(2)知,CH=GH,∴NG=CG=1,∴FN=NG+FG=2,过点H作HM⊥AB,∴∠FMH=∠NFM=∠HNF=90°,∴四边形NFMH是矩形,∴HM=FN=2,在Rt△DMH中,∠ADE=60°,HM=2,∴DH=,在Rt△HDG中,根据勾股定理得,HG==.15、【问题情境】一节数学课后,老师布置了一道课后练习题:如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.(1)阅读理解,完成解答本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写这道练习题的证明过程;(2)特殊位置,证明结论若CE平分∠ACD,其余条件不变,求证:AE=BF;(3)知识迁移,探究发现如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)(1)证明:∵AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵CD⊥AB,∴∠CDB=90°,∴∠DCB=45°,∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2,∴∠ECF=∠EFC,∴CE=EF,∵CD⊥AB,FG⊥AB,∴∠CDE=∠EGF=90°,在△CDE和△EGF中,,∴△CDE≌△EGF(AAS);(2)证明:由(1)得:CE=EF,∠A=∠B,∵CE平分∠ACD,∴∠ACE=∠1,∵∠1=∠2,∴∠ACE=∠2,在△ACE和△BEF中,,∴△ACE≌△BEF(AAS),∴AE=BF;(3)AE=BF,作EH⊥BC与H,如图3所示:设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x,根据勾股定理得:BC=AC=2x,∵∠ABC=45°,EH⊥BC,∴BH=x,∴CH=BC﹣BH=x,∵EC=EF,∴FH=CH=x,∴BF=x﹣x=x,∴=,∴AE=.16、(2019秋•丹东期末)在正方形ABCD和等腰直角△BGF中,∠BGF=90°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,延长GP交DC于点E.求证:PG=PC;(2)如图2,当点F在AB的延长线上时,(1)中的结论是否成立?请证明你的结论;(3)如图3,若四边形ABCD为菱形,且∠ABC=60°,△BGF为等边三角形,点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,请直接写出你的结论,并画出论证过程中需要添加的辅助线.证明:(1)∵∠DCB=∠FGB=∠FGC=90°,∴CD∥GF,∴∠EDP=∠GFP,且DP=PF,∠DPE=∠FPG,∴△DPE≌△FPG(ASA)∴PE=PG,DE=GF,∵BC=CD,∴EC=GC,且∠DCG=90°,PE=PG,∴CP=PG;(2)延长GP到E,使PE=PG,连接DE,CE,CG,∵DP=PF,∠DPE=∠FPG,PE=PG,∴△DPE≌△FPG(SAS)∴PE=PG,DE=GF,∠EDP=∠GFP,∵GF=GB,∴DE=BG,∵DC∥BF,。
2013上海市第二十六届初中物理竞赛(大同杯)复赛试题及答案

上海市第二十六届初中物理竞赛(大同中学杯)复赛试题(2013年)说明:1.本试卷共有五大题,答题时间为120分钟,试题满分为150分2.答案及解答过程均写在答卷纸上。
其中第一、第二大题只要写出答案,不写解答过程;第三至第五大题按题型要求写出完整的解答过程。
解答过程中可以使用计算器。
3.本试卷中常数g ×103焦/千克·℃,冰的比热容32.110⨯焦/千克·℃×103千克/米3,冰的熔化热为3.33×105焦/千克。
一、选择题(以下每题只有一个选项符合题意,每小题4分,共32分)1.儿童要多参加户外运动,这是因为太阳光中的某种频率的电磁波可以促成维生素D 的活化,从而促进骨骼对钙的吸收,这种电磁波是 ( )A. 红外线B. 紫外线C. X 射线D. 绿色光2.冬天雨雪过后,停在户外的汽车的前窗玻璃上常会结有一层冰。
要想除去这些冰,下列做法中不可采用的是 ( )3.“达人秀”中用冬瓜、土豆做成吹奏乐器,用它们吹奏出来的声音可能具有的相同特征是 ( )A. 音色 音调B. 音色 响度C. 音调 响度D. 音色 音调 响度“特斯拉线圈”的表演,表演者通过变压器与电磁振荡制造出人工闪电。
在表演时,表演者与“特斯拉线圈”之间会放出美妙的电火花,对此,你认为对人体不会造成危害的原因是 ( )A. “特斯拉线圈”产生的电火花电压很低,电流很小B. 表演者穿的防护服是绝缘的,电流并没有流经防护服C. 人体的电阻很小,“特斯拉线圈”产生的电流经人体导入地面D. 表演者穿的防护服里有很多金属丝,电流都眼防护服流过5.小轩很喜欢爸爸新买的数码照相机,在旅途中拍下了火车内桌面上塑料杯瞬间的不同状态,如下图的甲乙丙,则下列关于火车运动状态的判断可能正确的是 ( )A.甲图中火车在加速运动,乙图中火车突然向左加速,丙图中火车突然向左减速B.甲图中火车在匀速运动,乙图中火车突然向右加速,丙图中火车突然向左加速C.甲图中火车在减速运动,乙图中火车突然向左减速,丙图中火车突然向右加速D.甲图中火车在匀速运动,乙图中火车突然向左加速,丙图中火车突然向右减速6.如图所示,一根轻杆长为2,:3A B L R A B m m ==两端固定、两球,,放置在半径为R 的光滑半球形碗中,在图示位置平衡,A 球与球心连线和竖直方向的夹角为θ,碗固定在长木板上,长木板可绕O 点转动,现对长木板的另一端施加外力F ,使其逆时针缓慢转动,在A 、B 两球均未脱离碗的过程中,A 球与球心连线和竖直方向的夹角θ的变化情况是 ( )7.如图电路,a b c、、分别表示电流表或电压表,电表都是理想的,则下列各组电表示数中可能实现的是( )A.a的示数为1安培,b的示数为2伏特,cB.a的示数为2伏特,b的示数为1安培,cC.a的示数为0.5安培, b的示数为1安培,c的示数为2伏特D.a的示数为2伏特,b的示数为0.5安培, c的示数为1安培8.因为地震,造成了很多堰塞湖,假设有一块立方体石块堵住了水的去路,设水的密度为ρ,石块的质量为m,石块的左右侧面为正方形,边长为a,宽度为b,石块与地面足够粗糙,不会滑动,水若能推倒石块,则石块的宽度b应该满足的条件是( )A.49abmρ< B.42abmρ< C.43abmρ< D.44abmρ<二、填空题(每小题6分,共30分)“客运效率”来反映交通工具的某项效能,即客运效率=人数×路程/消耗能量。
珠宝鉴定师GAC第九期培训试题

珠宝鉴定师GAC第九期培训试题珠宝鉴定师宝石协会GAC第九期考试试题——由元实珠宝学院整理一、是非题(你认为叙述是正确的.请在题后括号内填写“Y”,否则填“N”;每题0.5分,共15分)1.白珊瑚是钙质珊瑚,而红珊瑚是角质珊瑚。
N2.蓝晶石不同方向具有明显不同的硬度表明该宝石没有均一性。
N3.类质同象是一些矿物成为宝石的重要因素之一。
Y4.砂金效应是宝石对光的干涉造成的。
N5.月光石的“蜈蚣状”包裹体和橄榄石的“睡莲叶状”包裹体都与应力有关。
N6.铂金片是焰熔法合成宝石的重要鉴定特征。
N7.一轴晶负光性宝石的主折射率Ne小于No。
Y8.刚玉解理不发育却常出现裂理。
Y9.黑曜岩是一种酸性玻璃质结构的火山岩。
Y10.目前世界上琥珀的主要来源地是波罗的海南岸的几个国家。
N11.绿松石和孔雀石产于热液矿床中。
N12.按“国标”,拼合宝石和再造宝石都属于人工宝石。
Y13.大部分合成钻石属于Ib型。
常常为高色级的白色。
N14.宝石的热处理主要用于改善宝石颜色,也可用于提高宝石的透明度。
Y15.Il型热导仪背面的直角三角形金属板是可有可无的装饰部件。
N16.钻石表面具有亲油性和疏水性。
Y17.天然晶面一般应留在成品钻石底瓣的底边附近。
Y18.阴极发光可用来区分天然钻石和合成钻石。
Y19.金绿宝石和祖母绿都是含铍的硅酸盐矿物。
N20.变石的变色效应与其中杂质元素镍有关。
N21.目前合成水晶主要采用提拉法。
N22.高型锆石含较多的U、Th,常常发生蜕晶质化。
Y23.碧玺的颜色十分丰富,甚至一个单晶上就可见两种以上的颜色。
Y24.长石很普通,成为宝石者都是因为具有砂金、月光等特殊光学效应。
N25.榍石的鉴定特征是明显的火彩、显著的三色性和明显的双影。
N26.油青种翡翠的主要组成矿物是绿辉石,天龙生翡翠的主要组成矿物是钠铬辉石。
Y27.软玉中青玉和糖玉的颜色都属于原生色。
Y28.水晶和欧泊的化学成分相同。
2020年中学生百科知识竞赛题库及答案(共200题)

2020年中学生百科知识竞赛题库及答案(共200题)2020年中学生百科知识竞赛题库及答案(共200题)1、最晚被发现的天然元素,后来被命名什么?(A)A.铼B.铀C.锂2、何时美国XXX和XXX制造出世界上第一台工业机器人,机器人的历史才真正开始?(C)A.1946年B.1950年C.1959年3、1990年在工业机器人国际标准大会上把机器人分为几类?(B)A.三类B.四类C.五类4、地球表面的70%是被水覆盖着的,其中有多少是海水?(B)A.90.6%。
B.96.5%。
C.97.3%5、地球上淡水资源其中一半以上是冰,江河湖泊等可直接利用的水资源,仅占整个水量的多少?(A)A.0.003%左右B.0.002%左右C.0.001%左右6、最基本的光污染是什么?(B)A.激光污染B.眩光污染C.聚光污染7、到1996年底,我国已经树立了几何个自然保护区?(B)A.700.B.799.C.8508、根据自然保护区的保护对象、性质、功能与发展趋势,科学家把我国的自然保护区分为几种类型?(A)A.5种B.6种C.4种9、英国研制成功的“主动声音控制”技术的基本原理是以声制声与德国的“反噪声器”的基本原理相似吗?(A)A.相似B.不相似10、1974年第一个“世界环境日”的主题是什么?A)A.只要一个地球B.列国人民结合起来,发明愈加美好的世界C.可持续发展11、100g含水99%的食盐溶液酿成含水98%的食盐溶液,可采用的措施是(B )A.再加入1g的食盐B.蒸发掉50%的水C.再加入100g1%的食盐水12、卧床的病人,可用50%的酒精擦拭受压的部分,以促进血液轮回,防止生褥疮。
用市售的酒精(95%的)100g 配制50%的酒精时,加水量应为(B )A.45g。
B.90g。
C.95g13、不能称为“绿色商品”的是(A)A.汽油B.无水硫酸铜C.无氟冰箱D.无磷洗涤剂14、减排中,对主要污染物实施总量控制减排的两项污染物是(C)A.一氧化碳和二氧化碳B.可吸入颗粒和甲烷C.化学需氧量和二氧化碳15、汽车尾气中至少含有150至200种有害物资,主要有( A )等。
珠宝鉴定师GAC第二十六期考试试题

中国宝玉石协会宝石鉴定师资格考试第二十六期理论试卷——元实珠宝学院整理一、是非题(你认为叙述是正确的,请在题后括号内填写“Y”,否则填“N”;每题0.5分。
共15分)1.金刚石不能在不足1大气压的低压下人工合成。
2.辐照改色的蓝色钻石无导电性。
3.浓硫酸具强腐蚀性,不能用于清洗钻石。
4.具有压电性的宝石都无对称中心。
5.从内部结构看,平行连生的晶体等同于单晶体。
6.替代前后电荷平衡是类质同象发生的重要条件之一。
7.电气石富含Li和Mn时呈玫瑰色或浅黄色。
8.蓝宝石的铍扩散处理需要比普通热处理更高的温度。
9.水晶具有“牛眼”干涉图是由于它有旋光性。
10.芬兰产的“光谱石”是一种七彩蛋白石。
11.红珊瑚属于国家一级保护动物,禁止交易。
12.单形组成聚形后,对称程度降低。
13.宝石的双折射率越大,多色性越强。
14.韧性强的宝石,其摩氏硬度也很大。
1 5.木变石与硅化本的成分相同,外观特征也一样。
16.粉红色碧玺切磨时,台面最好平行于柱面。
17.海蓝宝石在二碘甲烷中悬浮。
18.磷灰石在折射仪上会表现出假均质体现象。
19.金绿宝石和塔菲石都是含铍的氧化物矿物。
20.变石猫眼主要产于俄罗斯。
21.缅甸产一种达碧兹红宝石。
22.天然欧泊与合成欧泊在色斑结构上明显不同。
23.黑珍珠低温漂白可形成巧克力色珍珠。
24.波状生长纹是水热法合成祖母绿的鉴定特征之一。
25.天龙生翡翠的主要组成矿物是钠铬辉石。
26.软玉的典型结构为纤维交织(毛毡状)结构。
27.我国山东蓝宝石矿和吉林橄榄石矿都属于岩浆型矿床。
28.贵翠、佘太翠、京白玉都是我国产的石英岩玉。
29.市场上的“红纹石”实际上是主要由菱锰矿组成的玉石。
30.我国现行国标规定,足金首饰因使用需要,其配件含金量不得低于990‰。
二、选择题(一)单项选择题(三选一:每选对一题得1分,选错无分;共15分)1.六方柱和菱面体的聚形可见于:(a)绿柱石(b)石英(c)方柱石2.以下经改善的宝石不需要注明“处理”的是:(a)热处理监宝石(b)镀膜翡翠(c)浸蜡绿松石3.天河石属于:(a)正长石(b)微斜长石(c)斜长石4.橄榄石是铁橄榄石与镁橄榄石的固溶体,宝石级橄榄石的成分:(a)不含镁(b)含少量铁(c)含少量镁5.合成紫品一般要经过:(a)水热法+加热处理 (b)焰熔法+辐照处理 (c)水热法+辐照处理6.一粒具猫眼效应的天然黄绿色宝石戒面,折射率为1.74,它可能是:(a)透辉石猫眼(b)金绿猫眼(c)矽线石猫眼7.绝大多数合成金刚石为:(a)IIb型(b)Ia型(c)Ib型8.染色红宝石可能具有下列的哪种特征?(a)特征的吸收光谱(b)气泡(c)发育的裂隙9.阴极发光仪所用辐照源发射出的是:(a)电子束(b)X射线(c)λ射线10.俗称蓝纹石的玉石中主要组成矿物是:(a)方钠石(b)蓝纹石(c)青金石11.绿松石属于:(a)硅酸盐(b)硫酸盐(c)磷酸盐12.提拉法合成变石的特征包裹体为:(a)弯曲生长纹(b)气液两相包裹体(c)愈合裂隙中三相同生包裹体13.祖母绿的化学式为:(a)BeAl2O4(b)Be3Al2SiO4(c)Be3A12Si6O1814.用于模仿宝石的玻璃,其折射率范围一般是:(a)1.33-1.80 (b)1.40-1.70 (c)1.54-1.7815.标准圆钻型钻石,如果亭深太大,可能出现:(a)黑底效应(b)鱼眼效应(c)领结效应(二)多项选择题(可有几项答案是对的,每题每选对一项答案得1分,每选错一项超过正确答案数的答案时则要倒扣1分。
gac
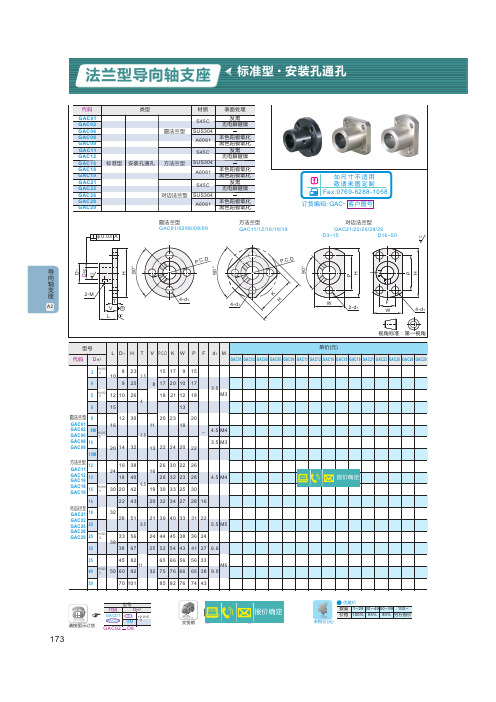
方法兰型 GAC11/12/16/18/19
对边法兰型
GAC21/22/26/28/29
D3~15
D16~50
6.3
D1 DH7
1.6
H 90° 90° 90° P H P H
P.C.D
P.C.D
0.8
导向轴支座
2-M
T
A2
V
L
A
4-d1
K
H 4-d1
W 2-d1
F
W
4-d1
视角标准:第一视角
型号 代码 DH7
单价(元) L D1 H T V P.C.D K W P F d1 M
GAC01 GAC02 GAC06 GAC08 GAC09 GAC11 GAC12 GAC16 GAC18 GAC19 GAC21 GAC22 GAC26 GAC28 GAC29
+0.010308104
9
+0.012
5 0 12 10
3.5 M3
10M
方法兰型 12
16 38
26 30 22 26
GAC11
24
16
GAC12 13
18 40
28 32 23 28
GAC16
GAC18 15 GAC19
+0.018
0 30 20
6.5 42 19 30 33 25
30
4.5 M4
16
对边法兰型 GAC21 18 GAC22 GAC26 20 GAC28 GAC29 25
优惠价 数量 1~29 30~49 50~99 100~ 价格 100% 95% 90% 另行报价
法兰型导向轴支座 标准型·安装孔通孔
不同氧浓度微环境中脑胶质瘤细胞生物学行为变化观察

不同氧浓度微环境中脑胶质瘤细胞生物学行为变化观察冯鹏程,曹奕强,汤荡,宋海,龙江,王永刚昆明医科大学第一附属医院神经外一科,昆明650000摘要:目的 观察高氧、低氧、极低氧微环境中胶质瘤细胞生物学行为变化,并探讨其可能的机制。
方法 取人胶质瘤U251细胞进行体外培养,将细胞分为极低氧组、低氧组、常氧组、高氧组,分别置于5%极低氧条件(37 ℃,5% CO 2,5% O 2)、10.5%低氧条件(37 ℃,5% CO 2,10.5% O 2)、21%常氧条件(37 ℃,5% CO 2,21% O 2)、42%高氧条件(37 ℃,5% CO 2,42% O 2)中培养96 h 。
采用CCK -8检测各组细胞在0、24、48、72、96 h 时的增殖情况,流式细胞术检测细胞凋亡情况,Transwell 实验检测细胞侵袭能力,实时定量qPCR 法检测细胞HIF -1α mRNA 表达,DCFH -DA 荧光探针染色法检测细胞ROS 水平。
结果 与常氧组比较,极低氧组、低氧组、高氧组在24、48、72、96 h 的增殖能力均降低;低氧组在48、72、96 h 的增殖能力高于极低氧组和高氧组(P <0.05或<0.01)。
与常氧组比较,极低氧组、低氧组、高氧组细胞凋亡率升高、细胞侵袭数量减少;与低氧组比较,极低氧组和高氧组细胞凋亡率升高、细胞侵袭数量减少(P 均<0.05)。
与常氧组比较,较极低氧组、低氧组、高氧组细胞HIF -1α mRNA 表达水平升高(P 均<0.01);与低氧组比较,极低氧组HIF -1α mRNA 表达水平升高、高氧组表达水平降低(P <0.05或<0.01)。
与常氧组比较,低氧组、极低氧组、高氧组中细胞ROS 水平均升高(P 均<0.01);与低氧组比较,极低氧组和高氧组细胞ROS 水平升高,且极低氧组高于高氧组(P 均<0.01)。
珠宝鉴定师GAC第二十五期考试试题

中国宝玉石协会宝石鉴定师资格考试第二十五期理论试卷——元实珠宝学院整理一、是非题(你认为叙述是正确的,请在题后括号内填写“Y”,否则填“N”;每题0.5分。
共15分)1.玻璃地翡翠由硬玉质成分的玻璃(非晶)态物质组成。
2.托帕石的晶格常数β>90°。
3.钻石的三角薄片双晶属于接触双晶。
4.锆石外形可表现为八面体和四方柱组成的聚形。
5.单斜晶系晶体的Y轴与其光率体的一个主轴重合。
6.无色钻石表现的“火彩”来自于光的色散。
7.等轴晶系宝石各方向的导热性应相同。
8.裂隙充填钻石常具有“闪光效应”。
9.改色的蓝色钻石与IIb型天然蓝色钻石可通过导电性区别。
10.合成钻石与天然钻石的阴极发光常显示完全不同的颜色和生长条纹图象。
11.热导仪只能用于区分钻石与仿钻石。
12.无色的刚玉宝石经铍(Be)扩散处理呈蓝色。
13.折射仪所测的折射率是宝石平行于折射仪工作台面的光率体切面的折射率。
14.拉曼光谱属于分子振动谱。
15.金属铂片包体是合成祖母绿的典型包体之一。
16.金绿宝石为一轴晶,光性可正可负。
17.钙铬榴石多呈翠绿色至深绿色,也称翠榴石。
18.我国宝石级橄榄石产于玄武岩中的橄榄岩包体。
19.拉长石的密度和折射率通常比水晶高。
20.单晶刻面榍石戒面可见明显的双影现象。
21.目前市场上常见的“红绿二色宝”是一种红宝石黝帘石岩。
22.青金石与方钠石颜色相似,但前者密度和折射率都比后者偏低。
23.孔雀石主要形成于内生地质作用。
24.硅化木是一种树木化石,以明显的木质纹理结构与其他玉石相区别。
25.东陵石都具有砂金效应。
26.葡萄石是一种氧化物矿物。
27.角质珊瑚与钙质珊瑚密度相同。
28.玳瑁具可切性和热塑性,热针试有辛辣焦味。
29.珍珠中含有多种对其色彩形成有重要作用的金属元素。
30.苏达(soude)祖母绿是一种拼合石。
二、选择题(一) 单项选择题(三选一:每选对一题得1分。
选错无分:共15分)1.冷坩埚法可用于合成:A.红宝石B.钻石C.立方氧化锆2.确定宝石包体成分的有效大型仪器是:A.阴极发光仪B.红外光谱仪C.拉曼光谱仪3.下列不属于天然玻璃的是:A.玻陨石B.燧石玻璃C.火山玻璃4.下列玉石中韧性最高的是:A.软玉B.翡翠C.玛瑙5.猫眼石的化学式为:A.BeAl2O4B.MgAl2O4C.Be3A12[Si6O18]6.水晶中的三组定向排列的针状包体属于:A.原生包裹体B.同生包裹体C.后生包裹体7.交叉滤色镜可用来检验宝石有无:A.蓝色荧光B.红色荧光C.紫外荧光8.无损鉴定蔷薇辉石和菱锰矿玉石雕件时,不应测试:A.折射率值B.酸溶性C.相对密度9.山东蓝宝石产于:A.伟晶岩中B.玄武岩中C.大理岩中10.一具猫眼效应的褐黄色宝石,折射率为1.63(点测),小刀可划动,该宝石是:A.电气石猫眼B.磷灰石猫眼C.透闪石猫眼11.区分海蓝宝石和蓝色托帕石可使用:A.偏光镜B.22色镜C.二碘甲烷重液12.下列为一轴晶正光性的宝石是:A.蓝宝石B.锆石C.碧玺13.焰熔法合成蓝色尖晶石的折射率通常为:A.1.718 B.大于1.81 C.1.72814.红色翡翠致色的机理是:A.磁铁矿致色B.赤铁矿致色C.氧化锰致色15.目前一般认为IIa型褐色钻石的颜色是由于:A.塑性变形B.含B元素C.含N元素(二) 多项选择题(可有几项答案是对的,每题每选对一项答案得1分,每选错一项超过正确答案数的答案时则要倒扣1分。
2024-年全国中学生生物学联赛试题及答案

2024年全国中学生生物学联赛试题注意事项:1.所有试题使用2B铅笔在机读卡上作答;2.试题按学科分类,单选和多选题混排。
未加注明的题目均为单选题,每题1分;多选题均已注明,每题2分,多选题答案完全正确才可得分;3.试卷12页,106题,共计169分,答题时间120分钟。
一.生物化学、分子生物学、细胞生物学、微生物学(共31题,44分)1. 下列不属于真核生物基因组DNA特点的是:A. 大部分为非编码序列;B. 含有大量重复序列,例如高度重复的卫星DNA;C. 功能相关的基因串联在一起,转录产生一条mRNA链;D. 基因组的完整复制依赖于逆转录。
2. 下列实验方法中能直接鉴定蛋白质磷酸化位点的有:A. 蛋白质免疫印迹法;B. 酶联免疫吸附;C. 酵母双杂交系统;D. 质谱分析。
3.关于豆科植物与根瘤菌的共生关系,下列叙述正确的是(多选):A. 根瘤菌为豆科植物提供含氮化合物;B. 根瘤菌固定的氮元素不会释放到土壤中;C. 豆科植物为根瘤菌提供生长所需氨基酸;D. 豆科植物分泌特殊物质, 诱导根瘤菌靠近并感染其根部。
4.三羧酸循环由8步反应组成,其中不可逆的反应是(多选):A. 柠檬酸经顺乌头酸转变为异柠檬酸;B. 异柠檬酸氧化脱羧转变为α-酮戊二酸;C. α-酮戊二酸氧化脱羧生成琥珀酰辅酶A;D. 琥珀酰辅酶A经底物水平磷酸化形成琥珀酸。
5.与胆固醇合成密切相关的HMG-COA还原酶(H酶)位于内质网膜。
研究者在培养细胞CHO中表达了跨膜结构域融合了GFP的H酶,即H-GFP。
经不同浓度的胆固醇和二氢羊毛甾醇(DHL)处理后,用免疫印迹法检测H酶的表达。
如图所示的实验结果不支持的结论有(多选):A. H酶在DHL缺乏的条件下比较稳定;B. DHL能够直接与H酶跨膜结构域结合;C. DHL对维持胆固醇稳态发挥调控作用;D. DHL导致H酶的翻译过程受阻。
6. 溶菌酶是一个碱性蛋白质,其相对分子质量约为14 kDa,用以下方法从蛋清中得到溶菌酶,纯度最高的方法是:A. 硫酸铵沉淀,然后有机溶剂沉淀;B. 硫酸铵沉淀,然后离子交换层析;C. 等电点沉淀,然后离子交换层析;D. 有机溶剂沉淀,然后凝胶过滤层析。
成都市双流区2023-2024学年八年级数学上期期末试题及答案(pdf版)

2023—2024学年度上期期末学生学业质量监测·八年级数学试题(样题)·第1页共6页成都市双流区2023~2024学年度上期期末学生学业质量监测八年级数学试题(样题)注意事项:1.全卷分A 卷和B 卷,A 卷满分100分,B 卷满分50分;考试时间120分钟.2.考生使用答题卡作答.3.在作答前,考生务必将自己的姓名、准考证号涂写在答题卡上.考试结束,监考人员将试卷和答题卡一并收回.4.答题必须使用0.5毫米黑色墨水签字笔书写,字体工整、笔迹清楚.5.请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效.6.保持答题卡面清洁,不得折叠、污染、破损等.A卷(共100分)一、选择题(每小题4分,共32分)每小题均有四个选项,其中只有一项符合题目要求.2.如图,a ∥b ,∠1=50°,则∠2的度数是()(A )40°(B )50°(C )110°(D )130°3.在平面直角坐标系中,已知点A (-3,5),则点A 关于x 轴的对称点的坐标是()(A )(3,5)(B )(-3,-5)(C )(3,-5)(D )(5,-3)4.下列各组中的三条线段,能构成直角三角形的是()(A )3,4,5(B )4,5,6(C )2,3,2(D )8,15,165.某射击队准备挑选运动员参加射击比赛,下表是其中一名运动员10次射击的成绩(单位:环),则该名运动员射击成绩的平均数是()成绩88.5910频数3241(A )8.9(B )8.7(C )8.3(D )8.2ab122023—2024学年度上期期末学生学业质量监测·八年级数学试题(样题)·第2页共6页6.如图是小颖画的一张脸的示意图,如果用(3,3)表示右眼,用(2,1)表示嘴,那么左眼的位置可以表示成()(A )(1,2)(B )(-1,3)(C )(-1,-1)(D )(1,3)7.如图,D 是△ABC 的边BC 上一点,若∠DAC =∠B ,∠ADC =97.5°,则∠BAC 的度数为()(A )73.5°(B )83.5°(C )97.5°(D )107.5°8.关于一次函数y =-7x +9,下列说法不正确的是()(A )图象经过第一、三、四象限(B )图象与y 轴交于点(0,9)(C )函数值y 随自变量x 的增大而减小(D )当x >97时,y <0二、填空题(本大题共5个小题,每小题4分,共20分)9.比较大小:3-1212(填“﹥”、“=”或“﹤”).10.如图,在△ABC 中,DE ∥BC ,∠A =50°,∠C =70°,则∠ADE 的度数是.11x =-2y =3是二元一次方程ax +4y =8的一个解,则a 的值为.12.如图,要围一个长方形ABCD 的菜园,菜园的一边利用足够长的墙,用35米长的篱笆围成另外三边.为了方便进出,在BC 边上留了一个2米宽的小门.设AB 边的长为x 米,BC 边的长为y 米,则y 与x 之间的关系式是.13.如图,数轴上点A ,B 分别对应2,4,过点B 作PQ ⊥AB ,以点B 为圆心,AB 长为半径画弧,交PQ 于点C ;以原点O 为圆心,OC 长为半径画弧,交数轴于点M ,则BM的长为.ABCDAB CD墙A B C D E O 246CPQM AB三、解答题(本大题共5个小题,共48分)14.(本小题满分12分,每题6分)(1)计算:(3+1)(3-1)+327+8-|1-22|;(2x-y=-4x-5y=-23.15.(本小题满分8分)如图,已知△ABC的两个顶点的坐标分别为B(-4,4)和C(-3,-1),A,B,C三点在格点上.(1)请补全原有的直角坐标系;(2)画出△ABC关于y轴对称的△A1B1C1,其中点A,B,C的对应点分别为A1,B1,C1,写出点A1的坐标;16.(本小题满分8分)双流区某校八年级学生开展踢毽子比赛活动,甲、乙两班分别派5名学生参加,下表根据上表,回答下列问题:(1)填空:甲班5名学生的比赛得分的众数是分,乙班5名学生的比赛得分的中位数是分;(2)分别计算甲班、乙班参赛学生比赛得分的方差,并判断哪一个班选手的比赛得分较为整齐.2023—2024学年度上期期末学生学业质量监测·八年级数学试题(样题)·第3页共6页2023—2024学年度上期期末学生学业质量监测·八年级数学试题(样题)·第4页共6页17.(本小题满分10分)为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息:自来水销售价格污水处理价格每户每月用水量单价:元/吨单价:元/吨17吨及以下1.80.90超17吨但不超过30吨的部分2.80.90超过30吨的部分6.00.90(说明:①每户生产的污水量等于该户自来水用量;②水费=自来水费用+污水处理费)设每户家庭月用水量为x 度时,应交水费y 元.(1)分别求出当17<x ≤30和x >30时,y 与x 之间的函数关系式;(2)如果小明家12月份上交水费156.1元,则小明家这个月用水多少吨?18.(本小题满分10分)如图,在△ABC 中,∠ACB =90°,AC =8,BC =6,D 为AB 中点,点E ,F 分别在直线BC ,AC 上,DF ⊥DE ,连接EF .(1)当点E 与点B 重合时,求EF 的长;(2)当点F 不与点A 重合时,求证:AF 2+BE 2=EF 2;(3)若EC =1,求线段CF 的长.ACBD E FACBD备用图2023—2024学年度上期期末学生学业质量监测·八年级数学试题(样题)·第5页共6页B卷(共50分)一、填空题(每小题4分,共20分)19.计算:(-2)2=.20.如图,直线m ∥n ,以直线m 上的点A 为圆心,适当长为半径画弧,分别交直线m ,n 于点B ,C ,连接AB ,BC .若∠1=32°,则∠ABC =°.21.若关于x ,yx +y =5m-2y =3m 的解也是二元一次方程2x +3y =6的一个解,则m 的值为.22.如图,在Rt △ABC 中,∠ACB =90°,以AC ,BC 为边分别作正方形ACDE 和正方形BCGF ,若图中阴影部分的面积为20,S △ABC =4,则BD 的长为.23.如图,在△ABC 中,AB =AC =10,BC =12,以BC 所在直线为x 轴,过点A 作BC 的垂线为y 轴建立直角坐标系,D ,E 分别为线段AO 和线段AC 上一动点,且AD =CE .当BD +BE 的值最小时,点E 的坐标为.二、解答题(本大题共3个小题,共30分)24.(本小题满分8分)为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.通过市场调研发现:购进1千克甲种水果和2千克乙种水果共需17元;购进3千克甲种水果和1千克乙种水果共需21元.(1)求甲、乙两种水果的进价分别是多少?(2)已知甲、乙两种水果的售价分别为7元/千克和9元/千克.若水果店购进这两种水果共300千克,其中甲种水果的重量不低于120千克.则水果店应如何进货才能获得最大利润,最大利润是多少?mnA CB 1ABCDEFG A BC ODE xy2023—2024学年度上期期末学生学业质量监测·八年级数学试题(样题)·第6页共6页25.(本小题满分10分)如图1,在Rt △ABC 中,∠ACB =90°,AC =BC ,点D 为△ABC 内部一点,AD =AC ,连接DC ,将DC 绕点D 逆时针旋转90°得到DE ,连接CE 交AD 于点F ,连接AE ,BD .(1)求证:△ADE ≌△BCD ;(2)如图2,当点E 落在AB 上时,求∠DBE 的度数;(3)如图3,若F 为AD 的中点,BD =2,求AD 的长.26.(本小题满分12分)如图,直线y =kx +b 经过点B (0,25),与直线y =34x 交于点C (m ,9),与x 轴交于点A ,点D 为直线AB 上一动点,过D 点作x 轴的垂线交直线OC 于点E .(1)求点A 的坐标;(2)当DE =12OB 时,求△CDE 的面积;(3)连接OD ,当△OAD 沿着OD 折叠,使得点A 的对应点A 1落在直线OC 上,求此时点D 的坐标.xy BD C AOE C A图1BDEFCA图2B EDF CA图3BEF D2023-2024学年度上期期末学生学业质量监测·八年级数学试题答案·第1页共6页成都市双流区2023~2024学年度上期期末学生学业质量监测八年级数学参考答案A卷(共100分)一、选择题题号12345678答案C DBABDCA二、填空题9.﹤;10.60;11.2;12.y =-2x +37;13.25-4.三、解答题14.(1)解:原式=2+3+22-22+1……4分=6……6分(2)解:2x -y =-44x -5y =-23①×2-②,得3y =15∴y =5……2分把y =5带入①得:x =12……4分∴方程组的解为x =12y =5……6分(注:用代入消元法解得结果根据解答情况酌情给分)15.解:(1)原有直角坐标系如图所示:……3分(2)如图,△A 1B 1C 1即为所求,点A 1的坐标为(1,5).……8分……①……②2023-2024学年度上期期末学生学业质量监测·八年级数学试题答案·第2页共6页16.解:(1)88,90……2分(2)甲班5名学生比赛得分的平均数为:87+93+88+88+945=90乙班5名学生比赛得分的平均数为:90+96+87+91+865=90∴s 2甲=15[(87-90)2+(93-90)2+(88-90)2+(88-90)2+(94-90)2]=8.4…4分s 2乙=15[(90-90)2+(96-90)2+(87-90)2+(91-90)2+(86-90)2]=12.4…6分∴s 2甲﹤s 2乙∴甲班选手的比赛得分较为整齐.……8分17.解:(1)当17<x ≤30时,y =(1.8+0.9)×17+(2.8+0.9)×(x -17)=3.7x -17……3分当x >30时,y =(1.8+0.9)×17+(2.8+0.9)×(30-17)+(6+0.9)×(x -30)=6.9x -113……6分(2)根据题意知,30吨的水费为:17×2.7+13×3.7=94∵156.1>94,∴小明家12月份用水超过了30吨,即x >30,……8分由题知y =156.1,即6.9x -113=156.1,解得x =39∴小明家这个月用水39吨.……10分18.解:(1)当点E 与点B 重合时∵D 为AB 中点,DF ⊥DE ,∴DE 垂直平分AB ,∴AF =EF 设AF =EF =x ,在Rt △CEF 中,由勾股定理得,CF 2+EC 2=EF 2∴(8-x )2+62=x 2,解得x =254∴EF =254……3分(2)作AG ⊥AC ,交ED 的延长线于G ,连接FG ∵点D 为AB 的中点,∴AD =BD ∵AG ⊥AC ,∴∠GAC =∠ACB =90°∴AG ∥BC ,∴∠AGD =∠BED 又∵∠ADG =∠BDE∴△AGD ≌△BED ,∴BE =AG ,DG =DE2023-2024学年度上期期末学生学业质量监测·八年级数学试题答案·第3页共6页∵DF ⊥DE ,∴DF 是GE 的垂直平分线,∴GF =EF ∵∠GAF =90°,∴AG 2+AF 2=FG 2∴BE 2+AF 2=EF 2……6分(3)当点E 在线段BC 上时,作BH ∥AC ,交FD 的延长线于H ,连接EH 由(2)同理可得,△ADF ≌△BDH ,∴BH =AF ,DH =DF ∴DE 是HF 的垂直平分线,∴EF =HE ∴CF 2+EC 2=AF 2+BE 2设CF =m ,则AF =8-m ,∴m 2+12=(8-m )2+52,解得m =112∴CF =112……8分当点E 在BC 延长线上时,如图,作BG ∥AC ,交FD 的延长线于G ,连接EF ,EG ,同理可得CF 2+EC 2=AF 2+BE 2,设CF =m ,则AF =8-m ,∴m 2+12=(8-m )2+72,解得m =7∴CF =7综上:线段CF 的长为112或7.……10分B卷(共50分)一、填空题19.2;20.74;21.3;22.6;23.(1813,8013).二、解答题24.解:(x 元,甲种水果的进价为y 元,根据题意得:+2y =17x +y =21x =5y =6答:甲种水果的进价为5元/千克,则乙种水果的进价为6元/千克.……3分(2)设购进甲种水果m 千克,则乙种水果(300-m )千克,利润为w 元,由题意得:w =(7-5)m +(9-6)(300-m )=-m +900(m ≥120)……5分∵-1<0,则w 随m 的增大而减小∴当m =120时,w 最大,最大值为-120+900=780,则300-m =180……7分答:购进甲种水果120千克,乙种水果180千克才能获得最大利润,最大利润为180元.……8分2023-2024学年度上期期末学生学业质量监测·八年级数学试题答案·第4页共6页25.解:(1)证明:∵AD =AC ,∴∠ACD =∠ADC∵∠ACB =∠CDE =90°,∴∠ADE =∠BCD ∵AC =BC ,∴AD =BC ∵DE =DC ,∴△ADE ≌△BCD……3分(2)过点C 作CH ⊥AB 于点H ,连接DH ,过点D 作DP ⊥DH ,交CH 于点P 则∠DCP =∠DEH ,∠CDP =∠EDH ∵DC =DE ,∴△DCP ≌△DEH ∴DP =DH ,∴∠DHC =45°=∠DHB ∵AC =BC ,∴CH =BH ∵DH =DH ,∴△DCH ≌△DBH ∴CD =BD ,∴BD =DE∵△ADE ≌△BCD ,∴AE =BD ,∴AE =DE ∵∠ACD =∠ADC ,∴∠CAD =180°-2∠CAD ∵∠BCD =90°-∠ACD ,∴∠CAD =2∠BCD设∠BCD =α,则∠CAD =2α,∠DAE =∠CBD =∠BCD =α∵∠CAB =45°,∴2α+α=45°,∴α=15°∴∠DBE =30°……7分(3)过点A 作AG ∥DE ,交CE 于点G 则∠FAG =∠FDE ,∠FGA =∠FED =45°∵AF =DF ,∴△AFG ≌△DFE ∴AG =DE ,EF =FG ∵CD =DE ,∴AG =CD∵∠ACD =∠ADC ,∴∠CAD =180°-2∠CAD ∵∠BCD =90°-∠ACD ,∴∠CAD =2∠BCD ∵∠BCD =∠ADE =∠FAG ,∴∠CAD =2∠FAG ∴∠CAG =∠FAG =∠BCD∵AC =BC ,∴△CAG ≌△BCD ,∴CG =BD ,∠ACG =∠CBD ∵△ADE ≌△BCD ,∴AE =BD =2∴∠EAG =∠FAG +∠DAE =∠CAG +∠ACG =45°∴∠EAG =∠EGA ,∠AEG =90°,∴EG =AE =2,∴EF =1∴AF =22+12=5,∴AD =25……10分C ABE DFH P CABEF DG2023-2024学年度上期期末学生学业质量监测·八年级数学试题答案·第5页共6页26.解:(1)∵直线y =34x 过点C (m ,9)∴9=34m ,解得m =12,∴点C 的坐标为(12,9)∵直线y =kx +b 经过点C (12,9),点B (0,25)12k +b =9b =25=-43=25∴直线AB 的表达式为y =-43x +25当y =0时,即-43x +25=0,解得x =754∴点A 的坐标为(754,0)……3分(2)∵B (0,25),∴OB =25设D 点横坐标为m ,则点D 坐标为(m ,-43m +25)∵DE 平行于y 轴,∴点E 坐标为(m ,34m )∴DE =|-43m +25-34m |=|-2512m +25|∵DE =12OB =252,∴|-2512m +25|=252,解得m =6或m =18当m =6时,△CDE 的面积为12×252×(12-6)=752当m =18,△CDE 的面积为12×252×(18-12)=752综上所述:△CDE 的面积为752……7分(3)过点C 作CG ⊥OA 于点G∵点C 的坐标为(12,9)∴OG =12,CG =9,OA =754∴AG =754-12=274∴OC 2=OG 2+CG 2=225,AC 2=AG 2+CG 2=202516又OC 2+AC 2=562516,OA 2=562516∴OC 2+AC 2=OA 2,∴∠OCA =90°,即OC ⊥AB当△OAD 沿着OD 折叠,且点A 落在射线CO 上的A 1时,设DA 1交x 轴于点H 根据折叠的性质,OA =OA 1,∠DAO =∠DA 1O又∠COA =∠HOA 1,∴△COA ≌△HOA12023-2024学年度上期期末学生学业质量监测·八年级数学试题答案·第6页共6页∴∠A 1HO =∠ACO =90°,HO =CO =225=15,∴DA 1∥y 轴当x =-15时,y =-43×(-15)+25=45∴点D 的坐标为(-15,45)……10分当△OAD 沿着OD 折叠,且点A 落在射线OC 上的A 2时如图,延长A 2D 交x 轴于点I根据折叠的性质,OA =OA 2,∠DAO =∠DA 2O又∠COA =∠IOA 2,∴△COA ≌△IOA 2∴∠A 2IO =∠ACO =90°,IO =CO =15∴DA 2∥y 轴当x =15时,y =-43×15+25=5∴点D 的坐标为(15,5)综上所述:点D 的坐标为(15,5)或(-15,45).……12分。
2023-2024学年四川省成都市天府七中八年级(上)期中数学试卷(含解析)

2023-2024学年四川省成都市天府七中八年级(上)期中数学试卷一.选择题(本大题共8小题,每小题4分,共32分)1.(4分)的算术平方根是( )A.4B.2C.±4D.±22.(4分)若m<n,则下列不等式不成立的是( )A.1+m<2+n B.1﹣m<1﹣n C.2m<2n D.<3.(4分)下列方程组,属于二元一次方程组的是( )A.B.C.D.4.(4分)△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC 为直角三角形的是( )A.∠A=∠B+∠C B.∠A:∠B:∠C=1:1:2C.b2=a2+c2D.a:b:c=1:1:25.(4分)在平面直角坐标系中,若点P(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )A.B.C.D.6.(4分)下列说法正确的有( )个.①任何实数都可以开立方;②0的相反数、倒数、平方都是0;③数轴上的点和有理数一一对应;④有限小数和无限循环小数都是有理数;⑤无理数都是无限小数.A.1B.2C.3D.47.(4分)图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长(图乙中的实线)是( )A.52B.48C.72D.768.(4分)如图,地面上有一个长方体盒子,一只蚂蚁在这个长方体盒子的顶点A处,盒子的顶点C′处有一小块糖粒,蚂蚁要沿着这个盒子的表面A处爬到C′处吃这块糖粒,已知盒子的长和宽为均为20cm,高为30cm,则蚂蚁爬行的最短距离为( )cm.A.10B.50C.10D.70二.填空题(本大题共5小题,每小题4分,共20分)9.(4分)在平面直角坐标系中,点(m,﹣2)与点(3,n)关于x轴对称,则m+n = .10.(4分)不等式2x﹣3≥5x﹣10的所有正整数解的和为 .11.(4分)已知关于x,y的二元一次方程组,则x+y= .12.(4分)如图所示的数轴上,点B与点C关于点A对称,A、B两点对应的实数是和﹣1,则点C所对应的实数是 .13.(4分)如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,点C到AB边的距离为 .三.解答题(本大题共5个小题,共48分)14.(10分)计算:(1);(2).15.(10分)解方程组或不等式组:(1)解方程组:;(2)解不等式组:.16.(8分)如图1,这是由8个同样大小的正方体组成的魔方,其体积为64.(1)求出这个魔方的棱长;(2)图1中阴影部分是一个正方形ABCD,求出阴影部分的边长及其面积;(3)如图2,把正方形ABCD放到数轴上,使点A与﹣1重合,那么点B表示的数为a,请计算(a﹣1)(a+1)﹣|2﹣a|的值.17.(10分)如图,一根直立的旗杆高8m,因刮大风旗杆从点C处折断,顶部B着地且离旗杆底部A的距离为4m.(1)求旗杆距地面多高处折断(AC);(2)工人在修复的过程中,发现在折断点C的下方1m的点D处,有一条明显裂痕,将旗杆修复后,若下次大风将旗杆从点D处吹断,则距离旗杆底部周围多大范围内有被砸伤的风险?18.(10分)如图,已知在Rt△ABC中,∠ACB=90°,AC=8,BC=16,D是AC上的一点,CD=3,点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动,设点P 的运动时间为t.连接AP.(1)当t=3秒时,求△BPA的面积;(2)若AP平分∠CAB,求t的值;(3)过点D作DE⊥AP于点E.在点P的运动过程中,当t为何值时,能使DE=CD?一.填空题(本大题共5个小题,每小题4分,共20分)19.(4分)化简﹣()2的结果是 .20.(4分)对于有理数a、b,我们定义新运算a⊗b=ax+by,等号右边是正常运算,其中x,y是常数,若1⊗2=1,(﹣3)⊗3=6,则2⊗(﹣5)的值是 .21.(4分)如果一个数表中某一列各数之和为负数,那么改变该列中所有数的符号,称之为一次“操作”,下表是由8个整数组成的数表,若经过一次“操作”后,使可使新的数表每行的各数之和与每列的各数之和均为非负数,则整数a的值为 .a a2﹣1﹣a﹣a22﹣a1﹣a2a﹣2a222.(4分)如图,在△AOB中,∠AOB=90°,AO=2,AB=2,将△AOB绕顶点O 逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,线段B′E 的长为 .23.(4分)如图,线段AB的长度为5,点P,M为线段AB外一动点,且PA=4,PM=PB,∠BPM=90°,线段AM长的最大值为 .二.解答题(本大题共3小题,共30分)24.(8分)已知a=,b=.求:(1)a2b﹣ab2的值;(2)a3﹣5a2﹣6a﹣b+2015的值.25.(10分)问题情境:在学习了《勾股定理》和《实数》后,某班同学们以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动,同学们想到借助曾经阅读的数学资料进行探究:材料1.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式(其中a,b,c为三角形的三边长,,S为三角形的面积).材料2.我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S=,其中三角形边长分别为a,b,c,三角形的面积为S.(1)利用材料1解决下面的问题:当,b=3,时,求这个三角形的面积?(2)利用材料2解决下面的问题:已知△ABC三条边的长度分别是,,,记△ABC的周长为C△ABC.①当x=2时,请直接写出△ABC中最长边的长度;②若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.26.(12分)如图1,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB 边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G.(1)求证:△ACF≌△CBG;(2)如图2,延长CG交AB于H,连接AG交CF于点M,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)在(2)问的条件下,当∠FCH=2∠GAC时,若BG=4,求AM的长.2023-2024学年四川省成都市天府七中八年级(上)期中数学试卷参考答案与试题解析一.选择题(本大题共8小题,每小题4分,共32分)1.【解答】解:∵=4,4的算术平方根为2,∴的算术平方根是2,故选:B.2.【解答】解:A.∵m<n,∴1+m<1+n<2+n,故本选项不符合题意;B.∵m<n,∴﹣m>﹣n,∴1﹣m>1﹣n,故本选项符合题意;C.∵m<n,∴2m<2n,故本选项不符合题意;D.∵m<n,∴<,故本选项不符合题意;故选:B.3.【解答】解:方程组中,属于二元一次方程组的是,故选:A.4.【解答】解:∵∠A+∠B+∠C=180°,∠A=∠B+∠C,∴∠A=90°,故选项A中的三角形是直角三角形,不符合题意;∵∠A+∠B+∠C=180°,∠A:∠B:∠C=1:1:2,∴∠C=90°,故选项B中的三角形是直角三角形,不符合题意;∵b2=a2+c2,∴△ABC是直角三角形,故选项C不符合题意;∵a:b:c=1:1:2,1+1=2,∴线段a、b、c不能构成三角形,故选项D符合题意;故选:D.5.【解答】解:∵点P(1﹣2x,x﹣1)在第二象限,∴,解不等式①得:,解不等式②得:x>1,∴不等式组的解集为:x>1,则x的取值范围在数轴上表示为:,故选:B.6.【解答】解:①任何实数都可以开立方,正确;②0的相反数、平方都是0,0没有倒数,错误;③数轴上的点和实数一一对应,错误;④有限小数和无限循环小数都是有理数,正确;⑤无理数都是无限小数,正确;正确的有:①④⑤,共3个,故选:C.7.【解答】解:依题意,设“数学风车”中的四个直角三角形的斜边长为x,则x2=122+52=169,所以x=13,所以“数学风车”的周长是:(13+6)×4=76.故选:D.8.【解答】解:分两种情况:(其它情况与之重复)①当蚂蚁从前面和右面爬过去时,如图1,连接AC′,在Rt△ACC′中,AC=20+20=40(cm),CC′=30(cm),根据勾股定理得:AC′===50(cm),②当蚂蚁从前面和上面爬过去时,如图2,连接AC′,在Rt△ABC′中,BC′=BB′+B′C′=30+20=50(cm),AB=20(cm),根据勾股定理得:AC′===10(cm)>50(cm);蚂蚁爬行的最短距离为50cm.故选:B.二.填空题(本大题共5小题,每小题4分,共20分)9.【解答】解:∵点(m,﹣2)与点(3,n)关于x轴对称,∴m=3,n=2,∴m+n=3+2=5.故答案为:5.10.【解答】解:2x﹣3≥5x﹣10,2x﹣5x≥﹣10+3,﹣3x≥﹣7,x≤,∴该不等式的所有正整数解为:1,2,∴等式2x﹣3≥5x﹣10的所有正整数解的和为3,故答案为:3.11.【解答】解:,①+②得:4x+4y=4,则x+y=1.故答案为:1.12.【解答】解:设点C所对应的实数是x.则有x﹣=﹣(﹣1),解得x=2+1.故答案为:2+1.13.【解答】解:∵S△ABC=3×3﹣×1×2﹣×2×3﹣×1×3=,AB==,∴点C到AB边的距离==.故答案为:.三.解答题(本大题共5个小题,共48分)14.【解答】解:(1)原式=﹣3××2×=﹣×5=﹣;(2)原式=﹣2﹣(﹣1)﹣2×1=﹣2﹣+1﹣2=﹣3﹣.15.【解答】解:(1)方程组整理得,②×2﹣①得5x=12,解得x=,把x=代入②得﹣y=8,解得y=,∴原方程的解为;(2),解不等式①得x≥﹣2;解不等式②得x<3.5;∴原不等式组的解集为﹣2≤x<3.5.16.【解答】解:(1)这个魔方的棱长为:=4;(2)每个小正方体的棱长为:4÷2=2;阴影部分的边长为:CD==2,阴影部分的面积为:CD2=(2)2=8;(3)根据图可知a=2﹣1,(a﹣1)(a+1)﹣|2﹣a|=(2﹣1﹣1)×(2﹣1+1)﹣|2﹣(2﹣1)|=(2﹣2)×2﹣|3﹣2|=8﹣4﹣3+2=5﹣2.17.【解答】(1)解:由题意,知AC+BC=8m.因为∠A=90°,设AC长为x m,则BC长(8﹣x)m,则42+x2=(8﹣x)2,解得x=3.故旗杆距地面3m处折断;(2)如图.因为点D距地面AD=3﹣1=2(m),所以B'D=8﹣2=6(m),所以,所以距离旗杆底部周围m的范围内有被砸伤的风险.18.【解答】解:(1)根据题意得BP=2t,∵t=3,AC=8,∴BP=2×3=6,∴S△BPA=BP•AC=×6×8=24,答:△BPA的面积为24;(2)当线段AP恰好平分∠CAB时,作PM⊥AB于M,如图1,∵线段AP平分∠CAB,∠ACB=90°,PM⊥AB,∴PC=PM,AC=AM=8,∵AB==8,∴BM=AB﹣AM=8﹣8,在Rt△BPM中,PB2=PM2+BM2,即(16﹣PC)2=PC2+(8﹣8)2,解得,PC=4﹣4,∴BP=2t=16﹣(4﹣4),解得:t=10﹣2;(3)①点P在线段BC上时,过点D作DE⊥AP于E,如图2所示:则∠AED=∠PED=90°,∴∠PED=∠ACB=90°,∴PD平分∠APC,∴∠EPD=∠CPD,又∵PD=PD,∴△PDE≌△PDC(AAS),∴ED=CD=3,PE=PC=16﹣2t,∴AD=AC﹣CD=8﹣3=5,∴AE=4,∴AP=AE+PE=4+16﹣2t=20﹣2t,在Rt△APC中,由勾股定理得:82+(16﹣2t)2=(20﹣2t)2,解得:t=5;②点P在线段BC的延长线上时,过点D作DE⊥AP于E,如图3所示:同①得:△PDE≌△PDC(AAS),∴ED=CD=3,PE=PC=2t﹣16,∴AD=AC﹣CD=8﹣3=5,∴AE=4,∴AP=AE+PE=4+2t﹣16=2t﹣12,在Rt△APC中,由勾股定理得:82+(2t﹣16)2=(2t﹣12)2,解得:t=11;综上所述,在点P的运动过程中,当t的值为5或11时,能使DE=CD.一.填空题(本大题共5个小题,每小题4分,共20分)19.【解答】解:∵一定有意义,∴x﹣2≥0,解得:x≥2,∴原式=x﹣1﹣(x﹣2)=1.故答案为:1.20.【解答】解:∵1⊗2=1,∴x+2y=1,∵(﹣3)⊗3=6,∴﹣3x+3y=6,∴x﹣y=﹣2,∴,①﹣②得:3y=3,解得:y=1,把y=1代入①中可得:x+2=1,解得:x=﹣1,∴原方程组的解为:,2⊗(﹣5)=2x+(﹣5)y=2x﹣5y=﹣2﹣5=﹣7,故答案为:﹣7.21.【解答】解:∵每一列所有数之和分别为2,0,﹣2,0,每一行所有数之和分别为﹣1,1,则:如果操作第三列,a a2﹣1a﹣a22﹣a1﹣a22﹣a a2第一行之和为2a﹣1,第二行之和为5﹣2a,,解得:≤a≤,又∵a为整数,∴a=1或a=2.故答案为:1或2.22.【解答】解:作OH⊥A′B′于H,如图,在△AOB中,∠AOB=90°,AO=2,AB=2,∴△AOB是直角三角形,在Rt△AOB中,依据勾股定理得:BO===6,∵△AOB绕顶点O逆时针旋转到△A′OB′,∴∠A′OB′=∠AOB=90°,A′B′=2,OA′=OA=2,OB′=OB=6,∵OH•A′B′=OA′•OB′,∴OH==,∵点E为BO的中点,∴OE=3,在Rt△OHE中,HE==,在Rt△OHA′中,HA′==,∴B′E=A′B′﹣HE﹣HA′=2﹣﹣=﹣.故答案为:﹣.23.【解答】解:如图,由题意知,PM=PB,∠BPM=90°,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN是等腰直角三角形,∴PN=PA=4,BN=AM,∵AB=5,∴线段AM长的最大值=线段BN长的最大值,∴当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN,∵△APN是等腰直角三角形,∴AN=AP=4,∴线段AM长的最大值为4+5,故答案为:4+5.二.解答题(本大题共3小题,共30分)24.【解答】解:(1)∵a==3+2,b==3﹣2,∴a2b﹣ab2=ab(a﹣b)=(3+2)(3﹣2)(3+2﹣3+2)=1×4=4.(2)a3﹣5a2﹣6a﹣b+2015=a(a2﹣5a﹣6)﹣b+2015=(3+2)(9+8+12﹣15﹣10﹣6)﹣(3﹣2)+2015=(3+2)(2﹣4)﹣(3﹣2)+2015=6﹣12+8﹣8﹣3+2+2015=2008.25.【解答】解:(1)当,b=3,时,==,∴p﹣a=﹣=,p﹣b=﹣3=,p﹣c=﹣2=,∴p(p﹣a)(p﹣b)(p﹣c)=×××=×=18×2=36,∴==6,∴三角形的面积为6;(2)①当x=2时,=,=3,=4﹣()2=4﹣2=2,故△ABC中最长边的长度为3;②∵x+1≥0,4﹣x≥0,∴﹣1≤x≤4.∵4﹣()2=4﹣(4﹣x)=x,三角形的边为正值,∴x>0,∴0<x≤4.∴=5﹣x,4﹣()2=4﹣(4﹣x)=x,∴C△ABC=++=+5﹣x+x=+5,∵C△ABC=+5(﹣1≤x≤4),且x为整数,当x=4时,三边为,1,4,∵+1<4,∴不合题意舍去,当x=3时,三边为2,2,3,∴C△ABC=2+2+3=7,∴S△ABC====.∴△ABC的面积为.26.【解答】(1)证明:∵∠ACB=90°,AC=BC,∴∠A=∠CBA=45°,∵CG平分∠ACB,∴∠ACG=∠BCG=45°,∴∠A=∠BCG,在△BCG和△CAF中,,∴△BCG≌△CAF(ASA),(2)证明:∵PC∥AG,∴∠PCA=∠CAG,∵AC=BC,∠ACG=∠BCG,CG=CG,在△ACG和△BCG中,,∴△ACG≌△BCG(SAS),∴∠CAG=∠CBE,∵∠PCG=∠PCA+∠ACG=∠CAG+45°=∠CBE+45°,∠PGC=∠GCB+∠CBE=∠CBE+45°,∴∠PCG=∠PGC,∴PC=PG,∵PB=BG+PG,BG=CF,∴PB=CF+CP;(3)过点G作GM⊥AC,垂足为M,设∠FCH=2x°,则∠GAC=x°,∴∠ACF=∠EBC=∠GAC=x°,∵∠ACH=45°,∴2x+x=45,解得x=15,∴∠FCH=15°,∴∠ACF=∠GAC=30°,由(2)得:△ACG≌△BCG,∴BG=AG=4,在Rt△AGM中,GM=AG=2,AM=2.。
珠宝鉴定师宝协GAC30期考题

b. 暗域照明 b. 石榴子石 b. VS1 b. 更粗,呈空管状 b. 观察吸收光谱 b. 电导性 b. Be3Al2[Si6O18] b. 无特征吸收光谱 b. 不变红 b. 天然和合成钻石
c. 点光照明 c. 水晶 c. VVS2 c. 更短,呈短柱状 c. 观察二色性 c. 热电性 c. BeAl2O4 c. 可见“管风琴状”吸收光谱 c. 可变红,也可不变红 c. 天然和辐照处理钻石
2. 下列宝石在偏光镜下常出现异常消光的是: 3. 一颗钻石10倍放大镜下见冠部主刻面处有一针点状包裹体,其净度级别为: 4. 斯里兰卡红宝石与缅甸红宝石相比,其金红石包裹体: 5. 一枚透明红色刻面宝石戒指,可能是铁铝榴石,进一步检测确定可:
9. 染色处理的翡翠在查尔斯滤色镜下:
11. 红柱石、蓝晶石、矽线石为同质多像变体,故三者: b. 化学成分相同,晶体结构不同
b. 需有三组折射率与红宝石不同的针状包体; e. 针状包体为黑色电气石
d. 针状包体多为金红石;
三、 填空题(每空 1 分,共 50 分)
1. 水在宝石矿物中存在形式有: 、 。 、 和 、 三类。 、蓝铜矿、 。 和 。 、 、 和沸石水、层间水。 、 、 和 。 2. 软玉按颜色可分为:白玉、青白玉、 3. 红宝石和水晶的摩氏硬度分别为 和 4. 中国四大名石(图章石)的产地是 5. 天然珠宝玉石分为: 、
、玄武玻璃和 元素致色,其双折射率为
包裹体是合成水晶中的特征包裹体。 法、区域熔炼法和助熔剂法。
18. 合成变石的常用方法有
19. 铁钛扩散处理的蓝宝石在散射光下观察,亭部颜色呈 20. 堇青石为强三色性宝石, 其三色性表现为 有时也称为 。
3
6. 除灰岩、白云岩和大理岩外,碳酸盐类玉石常见的有 星光、 星光可见于同一球体上。 8. 评价珍珠质量的主要因素是 10. 著名的希望(Hope)钻石属 11. 泰国红宝石 、 型,因含 、 等。
冀教版九年级数学上册《第二十六章解直角三角形》单元检测卷-附答案

冀教版九年级数学上册《第二十六章解直角三角形》单元检测卷-附答案一、选择题(每题3分,共36分)1.cos 45°的值为()A.12B.1 C.22D.22.△ABC中,∠A,∠B,∠C的对边分别为a,b,c.已知a=6,b=8,c=10,则cos∠A的值为()A.35B.34C.45D.433.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC 的值为()A.35B.34C.105D.14.如图,在矩形ABCD中,AB=6,BC=8,分别以点A和C为圆心,以大于12AC的长为半径作弧,两弧相交于点M和N,作直线MN分别交AD,BC于点E,F,则AE的长为()A.74B.94C.154D.2545.如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=44 cm,则高AD约为()(参考数据:sin 27°≈0.45,cos 27°≈0.89,tan 27°≈0.51)A.9.90 cm B.11.22 cm C.19.58 cm D.22.44 cm6.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.已知AB=4,BC=5,则cos∠EFC的值为()A.34B.43C.35D.457.如图,在矩形ABCD中,AB=60 cm,∠AOD=90°,设∠DAO=α,若AO=100 cm,则点O到BC的距离OE是()A.(60+100sin α) cmB.(60+100cos α) cmC.(60+100tan α) cmD.以上选项都不对8.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10 m,坝高12 m,斜坡AB的坡度i=1∶1.5,则坝底AD的长度为()A.26 m B.28 m C.30 m D.46 m9.如图,已知在四边形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为()A.863B.4 3 C.823D.4210.如图①是一个小区入口的双翼闸机,它的双翼展开时,双翼边缘的端点A与B之间的距离为8 cm(如图②),边缘AC=BD=60 cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为()A.(603+8)cmB.(602+8)cmC.64 cmD.68 cm11.如图,菱形ABCD的周长为20 cm,DE⊥AB,垂足为E,sin A=35,则下列结论中正确的有()①DE=3 cm;②BE=1 cm;③菱形的面积为15 cm2;④BD=210 cm.A.1个B.2个C.3个D.4个12.[2022·荆州]如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C 在OB 上,OC BC =12,连接AC ,过点O 作OP ∥AB 交AC 的延长线于P .若P (1,1),则tan ∠OAP 的值是( ) A .33B .22C .13D .3二、填空题(每题3分,共12分)13.[2024·石家庄第九中学期中]sin 30°+2cos 45°=________.14.如图,在△ABC 中,∠ACB =90°,点O 是AB 的中点,CO =6.5,BC =5,则tan B 的值为________.15.如图,在△ABC 中,sin B =13,tan C =22,AB =3,则AC 的长为________,△ABC 的面积为________.16.[2023·衢州]下面是勾股定理的一种证明方法:图①所示纸片中,∠ACB =90°(AC <BC ),四边形ACDE ,CBFG 是正方形.过点C ,B 将纸片CBFG 分别沿与AB 平行、垂直两个方向剪裁成四部分,并与正方形ACDE ,△ABC 拼成图②.(1)若cos ∠ABC =34,△ABC 的面积为16,则纸片Ⅲ的面积为________; (2)若PQ BQ =1915,则BKAK =________.三、解答题(第17~22题每题10分,第23题12分,共72分) 17.计算:(1)tan 30°cos 60°+tan 45°cos 30°; (2)[2023·盐城]⎝ ⎛⎭⎪⎫12-1+4cos 60°-(5-π)0.18.在△ABC中,∠C=90°.(1)已知c=23,∠A=30°,求∠B,a,b;(2)已知a=56,∠A=45°,求∠B,b,c.19.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.(1)若∠A=60°,求BC的长;(2)若sin A=45,求AD的长.20.图①是某款篮球架,图②是其示意图,立柱OA垂直地面OB,支架CD与OA交于点A,支架CG⊥CD交OA于点G,支架DE平行地面OB,篮筺EF与支架DE在同一直线上,OA=2.5 m,AD=0.8 m,∠AGC=32°.(1)求∠GAC的度数.(2)某运动员准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3 m处,那么他能挂上篮网吗?请通过计算说明理由.(参考数据:sin 32°≈0.53,cos32°≈0.85,tan 32°≈0.62)21.如图,湖边A,B两点由两段笔直的观景栈道AC和CB相连.为了计算A,B两点之间的距离,经测量得:∠BAC=37°,∠ABC=58°,AC=80 m,求A,B两点之间的距离.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.60)22.如图是由6个形状、大小完全相同的小矩形组成的,小矩形的顶点称为格点.已知小矩形较短的边长为1,△ABC的顶点都在格点上.(1)用无刻度的直尺作图:找出格点D,连接CD,使∠ACD=90°;(2)在(1)的条件下,连接AD,求tan ∠BAD的值.23.【初建模型】(1)如图①,△ABC和△ADE都是等腰三角形,AD=AE,AB=AC,∠BAC=∠DAE,连接BD,CE.求证:BD=CE.分析:要证明BD=CE,我们可以通过________(只填序号)的方法证明△ADB和△AEC全等即可.①SSS②ASA③AAS④SAS【类比探究】(2)如图②,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,连接BD,CE.请你写出BD与CE的数量关系,并说明理由.【拓展提升】(3)如图③,在图②的基础上,延长BD,交AC于点F,交CE的延长线于点G,求sin G的值.参考答案一、1.C2.C3.B4.D 【点拨】设MN与AC的交点为O∵四边形ABCD为矩形∴∠ADC=90°,DC=AB=6,AD=BC=8.∴AC=AD2+DC2=82+62=10.∴cos∠CAD=ADAC=810=45.又由作图知MN为AC的垂直平分线∴∠MOA=90°,AO=12AC=5.∴在Rt△AOE中,cos∠EAO=AO AE.∵cos∠CAD=cos∠EAO,∴5AE =45.∴AE =254. 5.B6.D 【点拨】根据题意可得AB =4,AF =AD =BC =5,∠AFE =∠D =∠B =90° ∴∠BAF +∠AFB =∠EFC +∠AFB . ∴∠BAF =∠EFC .∴cos ∠EFC =cos ∠BAF =AB AF =45. 故选D . 7.A8.D 【点拨】过点B 作AD 的垂线,垂足为E .∵坝高12 m ,斜坡AB 的坡度i =1∶1.5 ∴AE =1.5BE =18 m.∴易得AD =2AE +BC =2×18+10=46(m) .9.A 【点拨】如图,分别作AE ⊥BC 于点E ,DF ⊥BC ,交BC 的延长线于点F ,则有sin B=sin 45°=AE AB =22,易知DF =AE ,∴DF =22AB =4 2.∵∠DCF =180°-∠BCD =60°,∴sin ∠DCF =sin 60°=DF DC =32.∴CD =DF 32=4232=863,故选A .10.D 【点拨】过点A 作AE ⊥PC 于点E ,过点B 作BF ⊥QD 于点F ,如图.∵AC =60 cm ,∠PCA =30°,∴AE =12AC =30 cm. 同理可得BF =30 cm∴通过闸机的物体的最大宽度为30+8+30=68(cm).故选D .11.C 【点拨】∵菱形ABCD 的周长为20 cm ∴菱形的边长AB =AD =20÷4=5(cm). ∵DE ⊥AB ,sin A =35,∴DE =5×35=3(cm) 故①正确;∵AE =AD 2-DE 2=52-32=4(cm) ∴BE =AB -AE =5-4=1(cm),故②正确; 菱形的面积=AB ·DE =5×3=15(cm 2) 故③正确;在Rt △BDE 中,BD =DE 2+BE 2=32+12=10(cm),故④错误. 综上所述,正确的有①②③,共3个. 12.C 【点拨】∵点P 坐标为(1,1) ∴OP 与x 轴正方向的夹角为45°. 又∵OP ∥AB ,∴∠BAO =45°. 又∵∠AOB =90°,∴OA =OB .设OC =x ,则BC =2OC =2x ,∴OA =OB =3x ∴tan ∠OAP =OC OA =x 3x =13.二、13.32 【点拨】原式=12+2×22=12+1=32.14.12515. 3 3 22 【点拨】如图,过点A 作AD ⊥BC .在Rt △ABD 中,sin B =13,AB =3 ∴AD =AB ·sin B =1.∴BD =AB 2-AD 2=32-12=2 2. 在Rt △ACD 中,tan C =22,∴AD DC =22. 又∵AD =1,∴CD = 2.∴BC =BD +CD =3 2. ∴S △ABC =12BC ·AD =322.16.(1)9 (2)259 【点拨】(1)设剪裁线的交点为T ,过C 作CM ⊥AB 于M ,如图.∵CT ∥AB ,∴∠ABC =∠BCT .∵cos ∠ABC =34,∴cos ∠BCT =34,即CT BC =34.∴CT =34BC . ∵∠ACM =90°-∠BCM =∠ABC ∴cos ∠ACM =cos ∠ABC =34,即CM AC =34.∴CM =34AC .∴CT ·CM =34BC ·34AC =916BC ·AC .∵△ABC 的面积为16,∴12BC ·AC =16. ∴BC ·AC =32.∴CT ·CM =18.易知BT =CM∴纸片Ⅲ的面积为12CT ·BT =12CT ·CM =9.(2)如图,设CT 的延长线交BF 于点W ,BT 的延长线交GF 于点N . ∵PQ BQ =1915,∴NT BT =1915.设NT =19t ,则BT =15t ,∴BN =34t .∵∠FBN =90°-∠CBN =∠BCW ,BF =BC ,∠BFN =∠CBW =90°∴△BFN ≌△CBW (ASA).∴CW =BN =34t . ∵∠BCT =∠WBT ,∠BTC =∠WTB =90° ∴△BCT ∽△WBT . ∴BT WT =CTBT .∴CT ·WT =BT 2. ∴CT ·(34t -CT )=(15t )2 解得CT =9t 或CT =25t .当CT =9t 时,WT =25t ,这情况不符合题意,舍去; 当CT =25t 时,WT =9t∵BK =CT ,AK =WT ,∴BK AK =259.三、17.【解】(1)原式=33×12+1×32=36+32=233.(2)原式=2+4×12-1=3.18.【解】(1)∵∠C =90°,∠A =30°,∴∠B =60°.∵sin A =a c ,sin B =bc ∴a =c ·sin A =23×12=3 b =c ·sin B =23×32=3.(2)∵∠C =90°,∠A =45°,∴∠B =45°. ∴b =a =5 6.∴c =a 2+b 2=10 3. 19.【解】(1)在Rt △ABE 中∵∠A =60°,∠ABE =90°,AB =6,tan A =BE AB ∴∠E =30°,BE =AB ·tan A =6×tan 60°=6 3. 在Rt △CDE 中∵CD =4,sin E =CDCE ,∠E =30°∴CE =CD sin E =412=8.∴BC =BE -CE =63-8.(2)∵在Rt △ABE 中,sin A =45=BEAE∴可设BE=4x(x>0),则AE=5x.由勾股定理可得AB=3x又∵AB=6,∴3x=6,解得x=2.∴BE=8,AE=10.∴tan E=ABBE=68=CDDE=4DE.∴DE=163.∴AD=AE-DE=10-163=143.20.【解】(1)∵CG⊥CD,∴∠ACG=90°.又∵∠AGC=32°,∴∠GAC=90°-32°=58°.(2)该运动员能挂上篮网,理由如下:如图,延长OA,ED交于点M∵OA⊥OB,DE∥OB,∴∠DMA=90°.又∵∠DAM=∠GAC=58°,∴∠ADM=32°.在Rt△ADM中AM=AD·sin 32°≈0.8×0.53=0.424(m)∴OM=OA+AM≈2.5+0.424=2.924(m)<3 m.∴该运动员能挂上篮网.21.【解】如图,过点C作CD⊥AB,垂足为点D在Rt△ACD中∵∠DAC=37°,AC=80 m,sin∠DAC=CDAC,cos∠DAC=ADAC∴CD=AC·sin37°≈80×0.60=48(m)AD=AC·cos37°≈80×0.80=64(m).在Rt△BCD中∵∠CBD=58°,CD≈48 m,tan∠CBD=CD BD∴BD=CDtan58°≈481.60=30(m).∴AB=AD+BD≈64+30=94(m).答:A,B两点之间的距离约为94 m.22.【解】(1)如图所示,点D即为所求.(2)如图,连接BD.∵∠BED=90°,BE=DE=1∴∠EBD=∠EDB=45°,BD=BE2+DE2=12+12= 2.易知BF=AF=2,∠BF A=90°,∴∠ABF=∠BAF=45°,AB=BF2+AF2=22+22=2 2.∴∠ABD=∠ABF+∠EBD=45°+45°=90°.∴tan ∠BAD=BDAB=22 2=12.23.【解】(1)④【点拨】∵∠BAC=∠DAE ∴∠BAD=∠CAE.又∵AD=AE,AB=AC∴△ADB≌△AEC(SAS).(2)2BD=CE,理由如下:∵△ABC和△ADE都是等腰直角三角形∴ADAE=ABAC=12,∠DAE=∠BAC=45°.∴∠DAE-∠DAC=∠BAC-∠DAC 即∠BAD=∠CAE.∴△BAD∽△CAE.∴BDCE=ABAC=12.∴2BD=CE.(3)由(2)可知:△CAE∽△BAD∴∠ACE=∠ABD.又∵∠AFB=∠CFG,∴△BAF∽△CGF.∴∠G=∠BAC.∴sin G=sin∠BAC=2 2.。
江西省抚州市广昌二中2024-2025学年七年级(上)竞赛生物试卷(解析版)

2024-2025学年江西省抚州市广昌二中七年级(上)竞赛生物试卷一、单项选择题(每题2.5分)1.古人云:“橘生淮南则为橘,橘生淮北则为枳.”就是说,淮南的橘子移种到淮北就不甜蜜了.想一想,产生这一差异的主要因素是()A.土壤B.空气C.温度D.阳光2.属于生物基本特征的是()A.生物都能快速运动B.生物都是由细胞构成的C.生物都能进行光合作用 D.生物都能生长和繁殖3.生物能够生长发育和繁殖后代的基础是()A.遗传B.变异C.应激性D.新陈代谢4.下列现象中,属于与温度变更相适应的现象是()A.蛾类夜间活动B.仙人掌的叶变成刺C.候鸟的迁徙D.山顶的旗形树5.下列不属于生态系统的是()A.一片农田 B.一块草地C.生物圈D.一条河中的全部的鱼6.像骆驼刺这样根系发达的植物分布在什么环境里()A.干旱地B.潮湿地区 C.寒冷地区 D.暖和地区7.含羞草的叶子被碰后会合拢,这说明生物具有()A.生长现象 B.应激性C.繁殖D.呼吸8.下列不属于生物对环境的影响的是()A.蚯蚓改良土壤B.森林净化空气C.沙漠变绿洲D.山顶上和山脚下植物的形态差别很大9.一棵榕树的树叶、根的细胞遗传物质含量()A.一样多B.不一样多 C.叶比根多 D.根比叶多10.在显微镜下视察写在纸片上的“b”字母时,物像是()A.b B.d C.p D.q11.炎炎夏日,我们通常吃西瓜解渴.切开西瓜时,会发觉有很多红色的汁液流出.这些汁液主要来自于西瓜果肉细胞的()A.细胞壁B.细胞核C.液泡D.叶绿体12.植物细胞和动物细胞都有的结构是()①细胞壁②细胞膜③细胞质④线粒体⑤液泡⑥细胞核⑦叶绿体.A.①②③④ B.②③④⑥ C.④⑤⑥⑦ D.①③⑤⑦13.植物细胞分裂过程的正确依次是()①细胞质平分为二,各含一个细胞核②在细胞中心形成新的细胞膜和细胞壁③细胞核平分成两个.A.②①③B.①②③C.①③②D.③①②14.制作人口腔上皮细胞临时装片时,滴加0.9%的生理盐水的目的是()A.利于染色 B.利于盖盖玻片C.杀灭细菌 D.维持细胞形态15.把簇新水草放在养鱼缸里的主要目的是供应()A.食物B.氧气C.能量D.二氧化碳16.某同学运用显微镜时,在低倍镜视野中看到的图象在左上方,他想将物像移到视野正中,则应将玻片()A.向左上移动B.向右上移动C.向左下移动D.向右下移动17.克隆羊多莉长得特别像()A.供细胞核的母羊 B.供无核卵的母羊C.代孕的母羊D.A,B,C三种羊的一部分18.在华北,小麦播种比棉花早,有些种子在播种前要浸种,要常常中耕松土,这些现象反映种子萌发所须要的条件分别是()A.温度、水分、空气B.温度、空气、水分C.空气、水分、温度D.水分、温度、空气19.在稻田中,影响水稻生活的非生物因素有()①阳光②杂草③水分④土壤⑤田鼠⑥空气⑦蝗虫⑧稻螟A.①②⑤⑥ B.③④⑦⑧ C.①③④⑥ D.②⑤⑦⑧20.下列哪一生态系统被誉为“地球之肾”()A.湿地生态系统B.草原生态系统C.森林生态系统D.湖泊生态系统21.小红同学在用显微镜视察洋葱鳞片表皮细胞,显微镜的目镜有5╳和10╳两种,物镜有10╳和40╳两种,下列组合中视察到细胞数目最少的是()A.目镜5╳,物镜10╳B.目镜10╳,物镜10╳C.目镜5╳,物镜40╳D.目镜10╳,物镜40╳22.在光线较暗的教室用显微镜,对光时,应选择()A.小光圈B.大光圈C.大光圈凹面镜D.小光圈凸面镜23.某生物体细胞中含有12对染色体,在细胞分裂后形成的子细胞中,染色体的数目是()A.12条B.24对C.12对D.6对24.俗话说“种瓜得瓜,种豆得豆”,这主要是与细胞中何种结构有关()A.细胞核B.细胞质C.细胞膜D.细胞壁25.下列各项中,属于非生物的是()A.引起疾病的细菌 B.休眠的青蛙C.会弹琴的机器人 D.生长在橘子皮上的青霉26.在探究“光对鼠妇生活的影响”这一试验过程中,试验变量是()A.温度B.湿度C.光 D.四周的环境27.下列结构属于器官的是()A.表皮B.血液C.心脏D.骨骼肌28.依据生物的用途进行分类,玉米属于()A.家畜B.作物C.宠物D.家禽29.生活在沙漠地区的仙人掌叶呈针状,主要是哪种生态因素的影响造成的()A.阳光B.水 C.土壤D.温度30.消费者和生产者的关系是()A.相互利用 B.吃与被吃 C.互惠互利 D.相互竞争31.在细胞分裂时,变更最明显的是()A.细胞核B.染色体C.叶绿体D.线粒体32.下列试验法探讨的一般步骤的排列依次中,正确的是()①设计试验方案②收集与问题相关的信息③得出结论④作出假设⑤分析试验现象⑥发觉并提出问题⑦实施试验并记录.A.⑥②④①⑦⑤③ B.①②⑤④③⑦⑥ C.①⑦②④③⑤⑥D.①②④⑤⑦⑥③33.能利用太阳光的能量,为动植物供应有机物和能量的结构是()A.线粒体B.细胞核C.液泡D.叶绿体34.植树造林可以削减风沙,这说明()A.环境改造生物B.环境制约生物C.生物适应环境D.生物影响环境35.下列生物现象中,哪一项是动物对环境的适应()A.河边垂柳的枝条,垂向河面B.仙人掌适应干旱而叶变成刺C.蚯蚓的活动使土壤变得疏松而肥沃D.秋天大雁由北飞向南方越冬36.在做“光对鼠妇生活的影响”试验时,用10只鼠妇做试验,并算出全班同学平均值的目的是()A.有利于视察B.简单确定变量C.削减误差 D.使鼠妇能自由运动37.草原中存在着“牧草→兔→狐→狼”的食物链,假如牧草受到DDT的污染,则下列生物中DDT含量最多的是()A.牧草B.兔 C.狐 D.狼38.北极狐的耳朵比非洲狐的小,与此有关的环境因素是()A.阳光不足 B.温度较低 C.水分较少 D.食物缺乏39.用显微镜视察洋葱表皮细胞时,由低倍镜换成高倍镜时发觉()A.视野变大,细胞数目增多B.视野变大,细胞数目削减C.视野变小,细胞数目增多D.视野变小,细胞数目削减40.影响生物生活的因素中,属于生物因素的是()A.水是鱼的生活环境B.大雁南飞C.错过季节播种,水稻减产D.田间杂草多,作物产量低2024-2025学年江西省抚州市广昌二中七年级(上)竞赛生物试卷参考答案与试题解析一、单项选择题(每题2.5分)1.古人云:“橘生淮南则为橘,橘生淮北则为枳.”就是说,淮南的橘子移种到淮北就不甜蜜了.想一想,产生这一差异的主要因素是()A.土壤B.空气C.温度D.阳光【考点】环境对生物的影响.【分析】此题考查的学问点是非生物因素对生物的影响.解答时可以从环境特点和生物的关系方面来切入.【解答】解:环境中影响生物生活的各种因素叫环境因素,分为非生物因素和生物因素.非生物因素包括:光、温度、水、空气、土壤等.生物因素是指环境中影响某种生物个体生活的其他所生物.非生物因素温度对植物的分布有着重要影响.橘在南方生长得得很好,在北方生长不好.主要是南方、北方温度不同造成的,橘是热带水果相宜生长在高温的南方,北方温度低不相宜橘子的生长,故淮南的橘子移种到淮北,就结不出甜蜜多汁的果实.主要是温度不同造成的.故选:C.【点评】解答此类题目的关键是运用所学学问对某些自然现象做出科学的说明.2.属于生物基本特征的是()A.生物都能快速运动B.生物都是由细胞构成的C.生物都能进行光合作用 D.生物都能生长和繁殖【考点】生物的特征.【分析】此题考查的学问点是生物的特征,解答时结合题意从生物的特征方面来切入.【解答】解:生物的特征是:①生物的生活须要养分,②生物能进行呼吸,③生物能排出身体内产生的废物,④生物能对外界刺激作出反应,⑤生物能生长和繁殖,⑥生物都有遗传和变异的特性,⑦除病毒以外,生物都是由细胞构成的.A、动物一般能运动,植物不能.A错误;B、除病毒以外,生物都是由细胞构成的.病毒也属于生物,B错误;C、制造有机物不是全部生物的特征,是绿色植物所特有的.C错误;D、生物都能生长和繁殖,属于生物基本特征,D正确.故选:D【点评】解答此类题目的关键是理解生物的特征.3.生物能够生长发育和繁殖后代的基础是()A.遗传B.变异C.应激性D.新陈代谢【考点】能量来自细胞中有机物的氧化分解.【分析】人体与外界环境之间的物质和能量的交换,以与人体内物质和能量的转变过程叫做新陈代谢.【解答】解:新陈代谢是人和生物维持生命活动的基本条件,是生命的基本特征,在新陈代谢的基础上,人和生物才能表现诞生长、发育、生殖、遗传和变异等其他的基本特征.因此生物能够生长发育和繁殖后代的基础是新陈代谢.故选:D【点评】此题考查了新陈代谢的概念和意义,新陈代谢是一切生命活动的基础.4.下列现象中,属于与温度变更相适应的现象是()A.蛾类夜间活动B.仙人掌的叶变成刺C.候鸟的迁徙D.山顶的旗形树【考点】环境对生物的影响.【分析】本题考查的是非生物因素对生物的影响,非生物因素有阳光、温度、空气和水分等.【解答】解:A、蛾类夜间活动,白天不出来与阳光有关,故不符合题意.B、仙人掌的叶演化成刺与沙漠地区缺少水有关,故不符合题意.C、候鸟在秋天飞往南方越冬,到了春每天气转暖,又飞回来,与温度有关,故符合题意.D、山顶的树由于在山顶,风比较大,使得树长成旗形,所以山顶的旗形树和风有关,故不符合题意.故选:C【点评】非生物因素对生物的影响可结合着详细的实例驾驭.5.下列不属于生态系统的是()A.一片农田 B.一块草地C.生物圈D.一条河中的全部的鱼【考点】生态系统的概念.【分析】在肯定区域内生物和它所生活的环境就形成一个生态系统.它包括生物部分和非生物部分.只有生物不叫生态系统,只有环境也不叫生态系统.据此可以解答本题.【解答】解:ABC属于生态系统,D、只有生物成分,没有非生物成分,不符合生态系统的概念.故选:D【点评】只要娴熟驾驭了生态系统的概念,细致分析选项中的内容是否符合生态系统的概念,即可正确答题.6.像骆驼刺这样根系发达的植物分布在什么环境里()A.干旱地B.潮湿地区 C.寒冷地区 D.暖和地区【考点】生物对环境的适应.【分析】生物必需适应环境才能生存,否则就会被自然界淘汰.【解答】解:生物必需适应环境才能生存,如沙漠上的植物必需耐旱才能生存.荒漠中生活的骆驼刺,根比地上部分长很多,可以吸取到荒漠深处的水分,适应干旱缺水的沙漠环境,故选A.【点评】解答此类题目的关键是理解生物的形态结构特点与环境是相适应的.7.含羞草的叶子被碰后会合拢,这说明生物具有()A.生长现象 B.应激性C.繁殖D.呼吸【考点】生物的特征.【分析】生物具有一下特征:1、生物的生活须要养分.2、生物能够进行呼吸.3、生物能排出体内产生的废物.4、生物能够对外界刺激作出反应.5、生物能够生长和繁殖.6、除病毒外,生物都是由细胞构成的.【解答】解:含羞草的叶子被碰后会合拢,表明生物能够对外界刺激作出反应.属于应激性.如植物的叶具有向光性,根的向地性、向水性、向肥性.故选:B.【点评】解答此类题目的关键是理解生物的特征.8.下列不属于生物对环境的影响的是()A.蚯蚓改良土壤B.森林净化空气C.沙漠变绿洲D.山顶上和山脚下植物的形态差别很大【考点】生物对环境的影响.【分析】此题考查的学问点是生物影响环境.解答时可以从生物影响环境的表现方面来切入.【解答】解:生物必需适应环境才能生存,如沙漠上的植物必需耐旱才能生存.生物也能影响环境如蚯蚓改良土壤,千里之堤毁于蚁穴,植物的蒸腾作用可以增加空气湿度等.蚯蚓改良土壤是生物蚯蚓对环境土壤的影响;森林净化空气,是生物森林对环境空气的影响;沙漠变绿洲是绿色植物对环境沙漠的影响;山顶上和山脚下植物的形态差别很大,是山顶上和山脚下的温度不同造成的,是环境对生物(植物)的影响.故选:D.【点评】解答此类题目的关键是运用所学学问对某些自然现象做出科学的说明.9.一棵榕树的树叶、根的细胞遗传物质含量()A.一样多B.不一样多 C.叶比根多 D.根比叶多【考点】染色体、DNA和基因的关系.【分析】此题考查基因、DNA、染色体、细胞核之间的关系和植物体的结构层次.【解答】解:基因是染色体上具有限制生物性状的DNA 片段. DNA 是主要的遗传物质,呈双螺旋结构.染色体是细胞核内能被碱性染料染成深色的物质,由DNA和蛋白质组成.一条染色体上包含一个DNA分子.一棵榕树的生长发育是从一个受精卵起先的.受精卵经过细胞分裂、分化,形成组织、器官、榕树的个体.正常状况下,同种生物的体细胞内的染色体的形态和数目都是肯定的.故选:A【点评】同一物种染色体的数目是稳定不变的,若缺少或增多,则形成的后代个体是异样的.10.在显微镜下视察写在纸片上的“b”字母时,物像是()A.b B.d C.p D.q【考点】显微镜的基本构造和运用方法.【分析】解答本题的关键是理解显微镜的成像特点是显微镜成倒立的像.要理解“倒立”不是相反,是旋转180度后得到的像,是上下左右都相反.【解答】解:显微镜成倒立的像,是旋转180度后得到的像.A、b旋转180度后得到的像是q,故该选项不符合题意;B、d旋转180度后得到的像是p,故该选项不符合题意;C、p旋转180度后得到的像是d,故该选项不符合题意;D、q旋转180度后得到的像是b,故该选项符合题意.故选:D.【点评】本题主要考查了显微镜成倒立的像.学生简单误选B或C.11.炎炎夏日,我们通常吃西瓜解渴.切开西瓜时,会发觉有很多红色的汁液流出.这些汁液主要来自于西瓜果肉细胞的()A.细胞壁B.细胞核C.液泡D.叶绿体【考点】细胞中的物质.【分析】此题重点考察的关于植物细胞结构与功能方面的学问,思索解答.【解答】解:A、细胞壁具有爱护和支持作用.不符合题意.B、细胞核内含遗传物质,对生物的遗传具有重要的意义,不符合题意.C、液泡中含有细胞液,有各种味道的物质以与养分物质,如各种蔬果汁中含各种有味道的物质以与丰富的养分物质,如西瓜汁,就是来自于细胞中液泡的细胞液,符合题意.D、叶绿体是光合作用的场所,是细胞中的能量转换器,不符合题意.故选:C【点评】本题考查的是基础性的学问点,只要基础扎实,驾驭了细胞的结构以与功能,即可答题.12.植物细胞和动物细胞都有的结构是()①细胞壁②细胞膜③细胞质④线粒体⑤液泡⑥细胞核⑦叶绿体.A.①②③④ B.②③④⑥ C.④⑤⑥⑦ D.①③⑤⑦【考点】动、植物细胞结构的相同点和不同点.【分析】此题考查植物细胞与动物细胞的结构.解题关键是指出植物细胞与动物细胞的相同点和不同点.【解答】解:植物细胞与动物细胞的相同点:都有细胞膜、细胞质、细胞核、线粒体;植物细胞与动物细胞的不同点:植物细胞具有细胞壁、叶绿体和液泡,动物细胞不具有细胞壁、液泡、叶绿体.故选:B【点评】植物细胞与动物细胞的联系:都有细胞膜、细胞质、细胞核、线粒体;区分:植物细胞具有细胞壁、叶绿体和液泡,而动物细胞不具有细胞壁、液泡、叶绿体.13.植物细胞分裂过程的正确依次是()①细胞质平分为二,各含一个细胞核②在细胞中心形成新的细胞膜和细胞壁③细胞核平分成两个.A.②①③B.①②③C.①③②D.③①②【考点】细胞分裂的基本过程.【分析】细胞分裂就是一个细胞分成两个细胞.在细胞分裂过程中,染色体分成形态和数目相同的两份,分别进入两个新细胞中.【解答】解:植物细胞分裂的过程是:分裂时细胞核先由一个分成两个,随后,细胞质分成两份,每份各含有一个细胞核,最终,在原来的细胞的中心,形成新的细胞膜和细胞壁,这样,一个细胞就分裂成为两个细胞.如图所示:故选:D【点评】细胞的分裂并不是由外向内,而是由内向外分裂的,应记住.14.制作人口腔上皮细胞临时装片时,滴加0.9%的生理盐水的目的是()A.利于染色 B.利于盖盖玻片C.杀灭细菌 D.维持细胞形态【考点】制作临时装片视察人的口腔上皮细胞.【分析】本题考查制作临时装片视察人的口腔上皮细胞.制作人口腔上皮细胞临时装片时,滴加0.9%的生理盐水的作用.【解答】解:人体口腔上皮细胞生活的液体环境无机盐的浓度是0.9%.此环境下细胞可保持正常的形态结构,低于该浓度时口腔上皮细胞会吸水膨胀,高于该浓度又会失水变瘪.所以制作人口腔上皮细胞临时装片时,滴加0.9%的生理盐水的目的是维持细胞形态.综上所述A、B、C选项错误,只有D选项正确.故选:D【点评】此题综合考查了制作临时装片视察人的口腔上皮细胞.考查学生运用所学学问解决实际问题的实力.属中档题.15.把簇新水草放在养鱼缸里的主要目的是供应()A.食物B.氧气C.能量D.二氧化碳【考点】光合作用的意义.【分析】绿色植物能进行光合作用,在叶绿体里利用光能把二氧化碳和水合成有机物,释放氧气,同时把光能转变成化学能储存在合成的有机物中的过程.分析答题.【解答】解:绿色水草放在金鱼缸里可以进行光合作用,由分析可知光合作用能够产生氧气,因此能增加鱼缸中氧气的含量,为金鱼供应足够的氧气以促进其长时间的存活.故B是正确的.故选B【点评】真正理解光合作用的相关学问,在完成本题的同时,还要留意把学到的学问应用于我们实际的生活中.16.某同学运用显微镜时,在低倍镜视野中看到的图象在左上方,他想将物像移到视野正中,则应将玻片()A.向左上移动B.向右上移动C.向左下移动D.向右下移动【考点】运用显微镜和制作临时装片.【分析】显微镜下看到的物像是上下左右均颠倒的物像,标本移动的方向正好与物像移动的方向相反.【解答】解:我们在显微镜下看到的物像是上下左右均颠倒的物像,所以我们移动玻片标本时,标本移动的方向正好与物像移动的方向相反.通过分析题目中某物像在显微镜视野的左上方,要使该物像移至视野正中心,物像应向右上方移动,而物像移动的方向与玻片标本移动的方向相反,所以玻片标本应向左上方移动,才能使物像移至视野正中心.故选A.【点评】显微镜中看到的物像是实物的倒像,所以物像移动的方向与玻片标本移动的方向相反,这点肯定记清晰.17.克隆羊多莉长得特别像()A.供细胞核的母羊 B.供无核卵的母羊C.代孕的母羊D.A,B,C三种羊的一部分【考点】细胞核在生物遗传中的重要功能.【分析】细胞核是遗传信息库,是细胞代谢和遗传的限制中心.据此解答.【解答】解:由分析可知,细胞核是遗传信息库,是细胞代谢和遗传的限制中心.对生物的遗传具有重要意义.因此在克隆的过程中,谁供应了细胞核,克隆出来的生物就像谁.因此小羊多莉长的像供细胞核的母羊.故选:A【点评】关键点:遗传物质位于细胞核中.18.在华北,小麦播种比棉花早,有些种子在播种前要浸种,要常常中耕松土,这些现象反映种子萌发所须要的条件分别是()A.温度、水分、空气B.温度、空气、水分C.空气、水分、温度D.水分、温度、空气【考点】探究种子萌发的条件.【分析】种子萌发必需同时满意外界条件和自身条件,外界条件为肯定的水分、相宜的温度和足够的空气;自身条件是有完整而有活力的胚与胚发育所需的养分物质;以与种子不在休眠期.【解答】解:在华北,小麦播种比棉花早,有些种子在播种前要浸种,要常常中耕松土,这些现象反映种子萌发所须要的条件分别是温度、水分、空气.故选:A【点评】解答此类题目的关键是理解驾驭种子萌发的条件.19.在稻田中,影响水稻生活的非生物因素有()①阳光②杂草③水分④土壤⑤田鼠⑥空气⑦蝗虫⑧稻螟A.①②⑤⑥ B.③④⑦⑧ C.①③④⑥ D.②⑤⑦⑧【考点】环境对生物的影响.【分析】环境中影响生物生活的各种因素叫环境因素,分为非生物因素和生物因素.非生物因素包括:光、温度、水、空气、土壤等.生物因素是指环境中影响某种生物个体生活的其他所生物,包括同种和不同种的生物个体.【解答】解:非生物因素包括:光、温度、水、空气、土壤等;水稻进行光合作用须要阳光、水、空气(二氧化碳),阳光、水、空气、土壤等属于非生物因素.而杂草、田鼠、蝗虫、稻螟与水稻之间属于生物因素关系.故选:C①阳光,属于影响水稻生活的非生物因素,①正确;②杂草,属于影响水稻生活的生物因素,②错误;③水分,属于影响水稻生活的非生物因素,③正确;④土壤,属于影响水稻生活的非生物因素,④正确;⑤田鼠,属于影响水稻生活的生物因素,⑤错误;⑥空气,属于影响水稻生活的非生物因素,⑥正确;⑦蝗虫,属于影响水稻生活的生物因素,⑦错误;⑧稻螟,属于影响水稻生活的生物因素,⑧错误;故选:C.【点评】解答此类题目的关键是运用所学学问对某些自然现象做出科学的说明.20.下列哪一生态系统被誉为“地球之肾”()A.湿地生态系统B.草原生态系统C.森林生态系统D.湖泊生态系统【考点】生态系统中的类型.【分析】本题应从各个生态系统的特点与在自然界的作用方面来解答.地球的肾主要是指湿地,包括多种类型,珊瑚礁、滩涂、红树林、湖泊、河流、河口、沼泽、水库、池塘、水稻田等都属于湿地.湿地在抵挡洪水调整径流、限制污染、调整气候、美化环境等方面起到重要作用,它既是陆地上的自然蓄水库,又是众多野生动植物资源,特殊是珍稀水禽的繁殖和越冬地,它可以给人类供应水和食物.湿地与人类休戚相关,是人类拥有的珍贵资源,因此湿地被称为“生命的摇篮”、“地球之肾”和“鸟类的乐园”.湿地的过滤作用是指湿地独特的吸附、降解和解除水中污染物、悬浮物和养分物的功能,使潜在的污染物转化为资源的过程.如香蒲以与藻类在生长过程中从污水中吸取养分物质的作用,从而使污水净化.生物作用是湿地环境净化功能的主要方式.沼泽湿地象自然的过滤器,它有助于减缓水流的速度,当含有毒物和杂质(农药、生活污水和工业排放物)的流水经过湿地时,流速减慢有利于毒物和杂质的沉淀和解除.一些湿地植物如芦苇、水葫芦等还能有效地吸取水中的有毒物质,净化水质.沼泽湿地能够分解、净化环境,起到“排毒”、“解毒”的功能,因此被人们喻为“地球之肾”.【解答】解:A、湿地生态系统湿地广泛分布于世界各地,是地球上生物多样性丰富和生产力较高的生态系统.湿地是地球上具有多种功能的生态系统,可以沉淀、解除、吸取和降解有毒物质,因而被誉为“地球之肾”.故该选项符合题意.B、草原生态系统分布在干旱地区,这里年降雨量很少.与森林生态系统相比,草原生态系统的动植物种类要少得多,群落的结构也不如前者困难.因此没有抵挡洪水、调整径流、“排毒”、“解毒”的功能,故该选项不符合题意.C、森林生态系统主要分布在潮湿和半潮湿地区,动植物种类繁多.是地球环境中最具有生物多样性的地区.森林在涵养水源,保持水土方面起着重要作用,有绿色水库之称.因此没有抵挡洪水、调整径流、“排毒”、“解毒”的功能,故该选项不符合题意.D、湖泊生态系统是指湖泊中的水生生物和其生存的环境构成的,湖泊界限明显;面积较小;水温分层现象明显;水量变更大;演替、发育缓慢,因此抵挡洪水、调整径流、“排毒”、“解毒”的作用有限,故该选项不符合题意.故选:A.【点评】本难题主要考查了生态系统的类型,解答的难点是对“地球之肾”的理解.。
临床医学基础综合试题题库

临床医学基础综合试题题库一.单选题(共135题,每题1分)1. 结核分枝杆菌感染时被激活的Th1细胞主要分泌哪种细胞因子激活招募巨噬细胞A. IL-4B. IL-10C. TNFD. IFN-γE. 以上都是正确答案:D。
考生答案:D。
2. 患者,男,21岁.缓起腹痛, 逐渐加剧并转移至右下腹疼痛3小时.检查呈右下腹压痛和反跳痛体征.首先考虑的诊断是A. 胃穿孔B. 急性肠炎C. 急性阑尾炎D. 腹膜炎E. 急性胆囊炎正确答案:C。
考生答案:C。
3. 属于前庭小脑的是A. 小脑前叶B. 小脑后叶C. 小脑蚓部D. 小脑半球E. 绒球小结叶正确答案:E。
考生答案:A。
4. 男,30岁,消化性溃疡反复发作4年,经抑制胃酸分泌、抗幽门螺杆菌等内科治疗无效,行手术治疗。
术中见胃皱襞显著增厚,组织病理学检查发现明显的壁细胞增生。
导致上述病理改变最可能的内源性物质是A. 乙酰胆碱B. 促胃液素C. 组胺D. 促胰液素E. 生长抑素正确答案:B。
考生答案:B。
5. 缺乏细胞壁结构的原核细胞型微生物是:A. 螺旋体B. 放线菌C. 支原体D. 噬菌体E. 酵母菌正确答案:C。
考生答案:C。
6. 6个月-2岁婴幼儿“秋季腹泻”的最主要病原体A. 肠道腺病毒B. 肠产毒性大肠埃希氏菌C. 志贺菌D. 肠出血性大肠埃希氏菌E. 轮状病毒正确答案:E。
考生答案:E。
7. 9个月男孩,反复抽搐4次,智力差,表情呆滞。
皮肤白嫩,头发黄色,尿有霉臭味。
为明确诊断,应选择的检查是( )A. 脑电图B. 腕部摄片C. 染色体检查D. 血T3、T4、TSHE. 尿三氯化铁试验正确答案:E。
考生答案:E。
8. 关于化学性突触传递的特征,以下描述错误的是A. 总和B. 后放C. 双向性传递D. 兴奋节律的改变E. 对内环境变化敏感正确答案:C。
考生答案:C。
9. 某女性糖尿病患者自叙不洁性生活后外阴搔痒和白带增多三天,取少许阴道分泌物镜检可见阴道毛滴虫活动和假菌丝,但未见革兰氏阴性双球菌,应首选哪种药物治疗()A. 甲硝唑B. 咪康唑C. 氟康唑D. 头孢三嗪(菌必治)E. 制霉菌素正确答案:E。
考向26元素元素周期表(重点难点)-2022年中考化学一轮复习考点微专题

考向26 元素、元素周期表例1.(2021·湖南怀化·中考真题)我们在商场的货架上经常会看到标有“补钙”“补铁”等字样的食品和保健品。
这里的“钙”“铁”指的是()A.原子B.物质C.元素D.分子【答案】C【解析】这里的“钙”“铁”不是以分子、原子、单质的形式存在的,而是强调存在的元素,与具体形态无关。
故选C。
例2.(2021·江西·中考真题)下列属于非金属元素的是()A.铝B.铁C.钙D.氧【答案】D【解析】A、铝含有“钅”字旁,属于金属元素;B、铁含有“钅”字旁,属于金属元素;C、钙含有“钅”字旁,属于金属元素D、氧含有“气”字旁,属于非金属元素。
故选D。
例3.(2021·广东·中考真题)2021年3月,三星堆遗址出士了黄金面具残片,结合如图,下列说法正确的是()A.金的元素符号是AU B.金原子的质子数是79C.金原子的核外电子数是118 D.金的相对原子质量是197.0g【答案】B【解析】A、金的元素符号是Au,A错误。
B、元素周期表小方格左上方数字表示原子序数,原子序数=质子数,故金原子的质子数是79,B正确。
C、在原子中,核外电子数=质子数,金原子的核外电子数是79,C错误。
D、相对原子质量单位“1”不是“g”,D错误。
故选B。
例4.(2021·湖北随州·中考真题)“宏观一微观一符号”是学习化学的重要内容和方法。
甲图表示镓在元素周期表中的部分信息和核外电子排布情况,乙图A、B、C表示部分原子核外电子排布情况,据图所得信息描述正确的是A.镓的相对原子质量为69.72g B.镓是一种金属元素C.图C表示的是一种阳离子D.氯化镓的化学式为GaCl2【答案】B【解析】A、根据元素周期表一格的信息可知,元素名称下方的数字表示相对原子质量,镓的相对原子质量为69.72,相对原子质量单位是“1”,不是“g”,A错误;B、镓带“钅”字旁,属于金属元素,B正确;C、图C中核电荷数为17,小于核外电子数2+8+8=18,属于阴离子,C错误;D、镓最外层电子数是3,容易失去3个电子,形成带3个单位正电荷的阳离子,在化合物中化合价为+3价,氯元素化合价为1价,氯化镓的化学式为GaCl3,D错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国宝玉石协会宝石鉴定师资格考试第二十期理论试卷(此卷不宣读、不解释)考区:准考证号:一、是非题(你认为叙述是正确的.请在题后括号内填写“Y”,否则填“N”;每题0.5分,共15分)l.石榴石单晶宝石不同方向上的摩氏硬度基本相同。
2.蓝宝石的各种力学性质都是各向同性的。
3.非均质宝石一定是晶体。
4.因祖母绿晶体多是歪晶,故其晶体对应晶面之间的夹角是变化的。
4高次对称轴,它一定四方晶系。
5.某宝石晶体只有一个Li6.等轴晶系晶体可以没有对称中心。
7.六方柱单形可在三方晶系的宝石晶体上出现。
8.一束自然光通过一非均质单晶宝石后可以变成偏振光。
9.二轴晶光率体垂直光轴面的切面都是圆的。
10.具二色性的宝石从任何方向都能见到二色性。
11.用二色镜看不到多色性的宝石一定是均质体宝石。
12.按“国标”规定,所有染色宝玉石均须在鉴定报告中注明“处理”。
13.翡翠中的红色和黄色是原生色。
14.和田玉的主要组成矿物是透闪石。
15.湖北省郧阳地区是我国著名的绿松石产地。
16.马贝珍珠(半边珍珠或贝附珍珠)是天然珍珠。
17.白光只有穿过均质体时才能产生色散。
18.变色效应是指从不同角度观察宝石,宝石呈现不同颜色的现象。
19.墨西哥的火欧泊也可以有变彩效应。
20.解理是沿双晶结合面裂开的面网。
21.含金74.5%的黄金饰品可以标记为18K。
22.月光石在紫外光及X射线照射下均发荧光。
23.格令的“格令钻”的重量约0.25g。
24.市场上常见的、含大量“太阳光芒”的琥珀是合成琥珀。
25.无色托帕石可经人工处理成蓝色托帕石。
26.红柱石三色性清晰,甚至肉眼都能查觉。
27.磷灰右的多条吸收谱线是稀土元素谱。
28.合成尖晶石的折射率值经常是1.717。
29.“国标”规定,养殖珍珠属于天然珍珠。
30.查罗右(紫硅碱钙石)是一种产于俄罗斯的紫色玉石。
二、选择题(一) 单项选择题(三选一;每选对一题得1分,选错无分;共15分)1.晶体的基本性质不包括:a.稳定性b.自限性c.耐久性2.属于非晶质的SiO宝石是:2a.欧泊b.蓝玉髓c.东陵石3.菱铁矿:a.与冷稀盐酸快速反应b.与热盐酸反应c.与热盐酸也不反应4.田黄是的一个品种。
a.巴林石b.青田石c.寿山石5.目前,矿山分选金刚石不利用其:a.发光性b.导热性c.高密度6.钻石出现“鱼眼”现象是因为:a.亭深太大b.亭深太小c.台面过小7.以长石为主要组成矿物的宝石品种不包括:a.独山玉b.月光石c.芙蓉石8.天然水晶罕见的颜色是:a.紫色b.黄色c.蓝色9.翠榴石的典型包裹体呈:a.马尾丝状b.睡莲叶状c.蜈蚣状10.象牙中的主要无机成分是:a.硅酸盐b.磷酸盐c.碳酸盐11.钙质型珊瑚的颜色主要有:a.红色b.黑色c.金黄色12.某艳绿色的透明宝石,折射率1.73以上,相对密度3.8左右,它可能是:a.翡翠b.祖母绿c.石榴石13.亚历山大石与猫眼石:a.都是金绿宝石b.分别是金绿宝石和辉石猫眼c.分别是具变色效应和猫眼效应的蓝宝石14.市场上称为“紫袍玉带玉”的玉石是:a.闪石玉b.蛇纹石玉c.轻微变质的两色粉砂质泥岩15.蓝晶石在(100)面上:a.沿c轴方向硬度大于垂直c轴方向b.沿c轴方向硬度小于垂直C轴方向c.平行和垂直c轴两个方向硬度无差别(二)多项选择题(可有几项答案是对的,每题每选对一项答案得1分,每选错一项超过正确答案数的答案时则要倒扣1分。
例如:某一题只有两项答案是对的,可以选两项、不论对错均不倒扣分,超过两项则要倒扣分。
共20分)1.目前我国实行的珠宝玉石标准(GBTl6552-GBTl6554)属于:a.珠宝玉石行业标准; b.国家珠宝玉石标准; c.推荐标准;d.强制标准;e.最低标准2.偏光镜的应用:a.可以测定宝石的轴性:b.不能测定有色宝石的多色性;c.正交偏光下转动宝石360°,宝石全消光(全黑),该宝石一定是单折射的;d.正交偏光下转动宝石360°,宝石全消光(全黑),该宝石不一定是单折射的:e.正交偏光下均质体宝石也可以看到异常消光3.钻石最常见的品形有:a.五角十二面体;b.八面体;c.菱形十二面体;d.三角三八面体;e.四角三八面体4.金刚石的硬度:a.不同单形晶面的维氏硬度都相同;b.不同单形晶面的维氏硬度都不同;c.八面体晶面硬度最大;d.立方体晶面硬度最大;e.各品面的摩氏硬度均为105.祖母绿和海蓝宝石:a.不是类质同象;b.属于同一种硅酸盐矿物c.内部结构(晶体结构)不同:d.无多色性: e.颜色都是他色6.蓝宝石和海蓝宝石:a.属于同一种矿物;b.属于不同的矿物种; c.都是硅酸盐矿物;d.分别属于三方和六方晶系; e.光学性质相同,而力学性质有所区别7.闪石类玉石中的碧玉:a.主要产于加拿大、俄罗斯、中国的和田:b.主要组成矿物是透闪石;c.主要产于加拿大、俄罗斯、中国的玛纳斯;d.硬度为6.5~7;e.常含黑色斑点8.方解石和文石:a.都是结晶体,成分为CaMg[CO3]2b.是同质多象矿物c.都是碳酸盐矿物,加稀盐酸会很慢的放出少量CO2;d.是类质同象矿物e.是珊瑚的主要组成矿物三、填空题(每空1分,共50分)1.晶体是具有的固体。
2.斜方晶系无高次对称轴,六方品系个高次对称轴,等轴晶系个L3。
3.晶体的宏观对称要素有:、、和等。
4.摩氏硬度计硬度为5和6的标准矿物是和。
5.传统上,翡翠的绿色常用、、、四个字来评价。
6.目前玉的命名方法主要有:、、-------------------------------等。
7.翡翠中的辉石族矿物按矿物种有、和等。
8.辽宁省岫岩县所产的玉的品种按矿物组成分为:和。
9.翡翠最好的地子是地。
10.青金岩是由青金石、和等组成。
11.用高温高压法处理钻石,可将IIa型褐色钻石处理成高色级的色钻石。
12.刚玉的化学成分是,尖品石的化学成分是。
13.常见的长石类宝石品种有、日光石、拉长石、蓝绿色的。
14.助熔剂法合成祖母绿的原料有BeO、A12O3、Cr2O3及,助熔剂为等。
15.合成碳化硅(α-碳硅石,莫依桑石)属晶系、明显可见,这是与钻石最重要的区别。
16.欧泊二层石是用无色胶将薄层复合在一个基底上制成。
17.琥珀燃烧时有,塑料燃烧时有。
18.绿松石的蓝色是铜离子致色的,橄榄石的绿色是铁离子致色的,优质蓝宝石的蓝色是离子致色的。
19.正交偏光下石英常出现干涉图。
20.金绿宝石的特征吸收线在 nm、Ia型钻石的特征吸收线在 nm。
21.常见的宝石镶嵌方法镶、镶、镶、密钉镶等。
22.要区分一包小颗粒无色宝石是钻石还是莫依桑石(碳化硅)最快的方法是利用,钻石,碳化硅。
中国宝玉石协会宝石鉴定师资格考试第二十二期理论试卷(此卷不宣读、不解释)考区:准考证号:一、是非题(你认为叙述是正确的,请在题后括号内填写“Y”。
否则填“N”;每题0.5分,共15分)1.相对于理想晶体,实际晶体都是不同程度的歪晶。
2.L2P是单斜晶系的对称型之一。
3.珍珠的颜色是其体色、伴色和晕彩的综合表现。
4.斜方晶系宝石的光率体主轴和结晶轴之间或者平行(重合)或者垂直。
5.树脂光泽、蜡状光泽、丝绢光泽等特殊光泽在光泽分级上都属于玻璃光泽。
6.玻璃的颜色、密度、折射率变化范围很大,常被用来仿制各种天然宝石。
;7.珊瑚的主要化学成分都是无机质CaCO38,“松花”是翡翠绿色在皮壳上的表现,它是赌石者最关注的翡翠表象之一。
9.目前,电子探针可以用来分析宝石中的水含量;10.八面体形态的钻坯取标准圆钻型琢型,其原料损耗率低。
11.准确的钻石颜色分级要使用比色石进行。
12.标记Pd900的贵金属首饰表示其铂含量是千分之九百。
13.宝石级电气石主要属于镁电气石和锂电气石系列。
14.河北张家口和吉林蛟河是我国宝石级橄榄石的重要产地。
15.合成欧泊常见与天然欧泊类似的“蜥蜴皮”状色斑结构。
16.龟裂纹是B货翡翠的重要表面特征,藉此可与A货翡翠相区分。
l 7.超基性岩蛇纹石化形成的蛇纹石玉颜色通常较深,且带黑色斑点(块)。
18.顾名思义,木变石是石化的树木化石。
19.因含铬云母、蓝线石、锂云母等不同的致色矿物,东陵石有不同的颜色。
20.琥珀的英文名称是Agate。
21.Maxixe型绿柱石经辐照处理后可以变为蓝色。
22.添加钴的合成蓝色尖晶石在查尔斯滤色镜下呈红色。
23.坦桑石是一种具有三色性的绿帘石。
24.刚玉类宝石可以借助热导仪做辅助鉴别。
25.软玉中糖玉与翡翠中红(黄)翡的颜色都是氧化作用导致的次生色。
26.蓝纹石是四川产出的一种蓝色玉石,其蓝色来自主要组成矿物方钠石。
27。
金绿宝石的猫眼效应是白光干涉作用的结果。
28.用点测法可以获得宝石的双折射率。
29.加热是宝石优化最常用的方法,它可以|改善宝石的颜色和透明度。
30.美国C3公司推出的鉴别无色—浅黄系列钻石与合成碳硅石的“Tester Model 590”检测仪利用了两种材料对长波紫外光透过性的差异。
二、选择题(一) 单项选择题(三选一:每选对。
题得1分.选错无分:共15分)1.橄榄石中的特征包裹体是:a.蜈蚣状包裹体b.睡莲叶包裹体c.锆石晕2.用分光镜观察宝石的吸收光谱时应用的光源是:a.黄色光b.荧光c.400-700nm连续光谱3.钻石的三角薄片双晶的识别标志是可见:a.青鱼骨刺纹b.三角座c.须状腰4.绿色钻石的颜色成因源于:a.N原子代替C原子b.含有微量B c.天然辐射作用5.下列不属于氧化物的宝石为:a.尖晶石b.金绿宝石c.碧玺6.通常将斯里兰卡的Gueda刚玉(半透明—乳白色刚玉)改成蓝宝石的方法是:a.加热b.染色c.充填7.我国山东蓝宝石主要产于下列哪种岩石中a.碱性玄武岩b.伟晶岩c.区域变质岩8.一轴晶正光性的宝石是:a.紫晶b.方柱石c.堇青石9.水热法合成祖母绿中常可见:a.钉状包裹体b.弧形生长纹c.气泡10.10×放大镜下,一裸钻台面中央可见一白色针点状包裹体,该钻石净度应定为:a.VS1b.VVS1c.VVS211.一粒具有猫眼效应的褐黄色宝石,折射率为1.63(点测),具有580nm 的双线吸收,该宝石是:a. 扎电气石猫眼b.磷灰石猫眼c.金绿猫眼12.市场上B+C货翡翠指的是经过下列哪种方法处理的?a. 乱酸浸+充填b.染色 c. 酸浸+充填+染色13.与贝壳紧紧粘连在一起的珍珠称为:a. 附壳珠b.游离珠c.聚合珠14.和田玉由白玉经青白玉至青玉,其FeO含量:a. 逐渐增高b.逐渐降低c.无变化15.翡翠的水头长指的是:a.透明度好b.透明度不好c.不透明(二) 多项选择题(可有几项答寨是对的,每题每选对一项答案得1分,每选错一项超过正确答案数的答案时则要倒扣1分。
