计量经济学(李子奈第4版)数据表(全)
李子奈《计量经济学》(第4版)笔记和课后习题(含考研真题)详解

李子奈《计量经济学》(第4版)笔记和课后习题(含考研真题)详解李子奈《计量经济学》(第4版)笔记和课后习题详解第1章绪论一、计量经济学1计量经济学计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。
2计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。
根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。
表1-1 模型分类(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。
②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。
③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。
3计量经济学的内容体系(1)根据所应用的数理统计方法划分广义计量经济学根据所应用的数理统计方法包括回归分析方法、投入产出分析方法、时间序列分析方法等;狭义计量经济学所应用的数理统计方法主要是回归分析方法。
需要注意的是,通常所述的计量经济学指的是狭义计量经济学。
(2)根据内容深度划分初级计量经济学的主要研究内容是计量经济学的数理统计学基础知识和经典的线性单方程计量经济学模型理论与方法;中级计量经济学的主要研究内容是用矩阵描述的经典的线性单方程计量经济学模型理论与方法、经典的线性联立方程计量经济学模型理论与方法,以及传统的应用模型;高级计量经济学的主要研究内容是非经典的、现代的计量经济学模型理论、方法与应用。
(3)根据研究目标和研究重点划分理论计量经济学的主要研究目标是计量经济学的理论与方法的介绍与研究;应用计量经济学的主要研究目标是计量经济学模型的建立与应用。
理论计量经济学的研究重点是理论与方法的数学证明与推导;应用计量经济学的研究重点是建立和应用计量模型处理实际问题。
完整版李子奈计量经济学版第四版课件

Wassily Leontief USA
The Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel 1980 or the crtheeataiopnpolicf aetcioonnotomtehtericanmaolydseislsoafnd
第一章 绪论
§1.1 计量经济学 §1.2 经典计量经济学模型的建模步骤 §1.3 计量经济学模型的应用 §1.4 本书内容安排说明
关于绪论
○绪论是课程的纲。 ○学好绪论,可以说学好了课程的一半。参观一个城
市,先站在最高处俯瞰,然后走街串巷;了解一 座建筑,先看模型,后走进每一个房间。各起一 半作用。 ○绪论课的目的:了解课程的性质和在课程体系中的 地位;了解课程完整的内容体系和将要讲授的内 容;了解课程的重点和难点;了解课程的学习方 法;介绍课程中不讲的但是必须了解的课程内容。 ○不必全懂,只需似懂非懂。
? 广义计量经济学和狭义计量经济学
–广义计量经济学,是利用经济理论、数学以及统计 学定量研究经济现象的经济计量方法的统称,包括 回归分析方法、投入产出分析方法、时间序列分析 方法等。
–狭义计量经济学,即通常所说的计量经济学,以揭 示经济现象中的因果关系为目的,在数学上主要应 用回归分析方法。
–本课程中的计量经济学模型,就是狭义计量经济学 意义上的经济数学模型。
Ragnar Frisch Norway
Jan Tinbergen the etherlands
The Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel 1973 moretthheoddeavnedlofoprmitesnat popf ltihcaetiionnputot-oimutppourttant
计量经济学试验完整版--李子奈

计量经济学试验——李子奈目录实验一一元线性回归 (5)一实验目的 (5)二实验要求 (5)三实验原理 (5)四预备知识 (5)五实验内容 (5)六实验步骤 (5)1.建立工作文件并录入数据 (5)2.数据的描述性统计和图形统计: (7)3.设定模型,用最小二乘法估计参数: (8)4.模型检验: (8)5.应用:回归预测: (9)实验二可化为线性的非线性回归模型估计、受约束回归检验及参数稳定性检验 (12)一实验目的: (12)二实验要求 (12)三实验原理 (12)四预备知识 (12)五实验内容 (12)六实验步骤 (13)实验三多元线性回归 (15)一实验目的 (15)三实验原理 (15)四预备知识 (15)五实验内容 (15)六实验步骤 (15)6.1 建立工作文件并录入全部数据 (15)6.2 建立二元线性回归模型 (16)6.3 结果的分析与检验 (16)6.4 参数的置信区间 (17)6.5 回归预测 (17)6.6 置信区间的预测 (19)实验四异方差性 (21)一实验目的 (21)二实验要求 (21)三实验原理 (21)四预备知识 (21)五实验内容 (21)六实验步骤 (21)6.1 建立对象: (21)6.2 用普通最小二乘法建立线性模型 (22)6.3 检验模型的异方差性 (22)6.4 异方差性的修正 (25)实验五自相关性 (29)一实验目地 (29)二实验要求 (29)三实验原理 (29)四预备知识 (29)五实验内容 (29)六实验步骤 (29)6.1 建立Workfile和对象 (30)6.2 参数估计、检验模型的自相关性 (30)6.3 使用广义最小二乘法估计模型 (34)6.4 采用差分形式作为新数据,估计模型并检验相关性 (36)实验六多元线性回归和多重共线性 (38)一实验目的 (38)二实验要求 (38)三实验原理 (38)四预备知识 (38)五实验内容 (38)六实验步骤 (38)6.1 建立工作文件并录入数据 (38)6.2 用OLS估计模型 (38)6.3 多重共线性模型的识别 (39)6.4 多重共线性模型的修正 (40)实验七分布滞后模型与自回归模型及格兰杰因果关系检验 (43)一实验目的 (43)二实验要求 (43)三实验原理 (43)四预备知识 (43)五实验内容 (43)六实验步骤 (43)6.1 建立工作文件并录入数据 (43)6.2 使用4期滞后2次多项式估计模型 (44)6.3 格兰杰因果关系检验 (46)实验八联立方程计量经济学模型 (50)一实验目的 (50)二实验要求 (50)三实验原理 (50)四预备知识 (50)五实验内容 (50)六实验步骤 (51)6.1 分析联立方程模型。
计量经济学(李子奈第4版)大数据表(全)
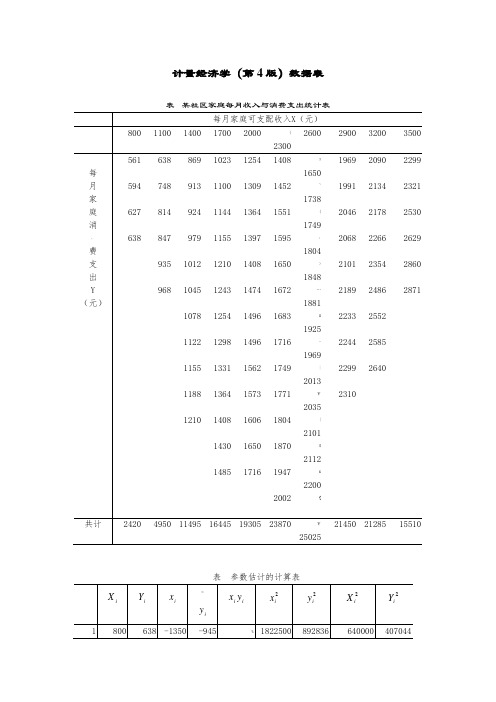
计量经济学(第4版)数据表表某社区家庭每月收入与消费支出统计表表中国各地区居民家庭人均全年可支配收入与人均全年消费性支出(元)资料来源:《中国统计年鉴》(2014)。
第2章练习12中国某年各地区税收Y和国内生产总值GDP的统计资料单位:亿元{表 2013年中国各地区城镇居民人均收入与人均消费性支出(元)表 2010年中国制造业各行业的总产出及要素投入资料来源:根据《中国统计年鉴》(2011年)整理。
表 2013年中国居民人均收入与人均生活消费支出数据(元)资料来源:《中国统计年鉴》(2014)。
表 2012年中国农村居民对蛋类食物的消费及相关食物的价格指数蛋类$消费量Q (千克)各类食品的消费价格指数(上年=100)居民消费价格指数P0(上年=100)人均消费支出X(元)蛋类P肉禽类P1水产类P2粮食P01油脂P02蔬菜P03北京(天津`河北;山西(内蒙古…辽宁'吉林…黑龙江^上海| 江苏"浙江安徽*福建:江西【山东'河南?湖北·湖南-广东、广西:海南【重庆|四川)贵州@云南|西藏|陕西*甘肃?青海@ 宁夏(新疆资料来源:《中国统计年鉴》(2013)。
第3章练习17中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y,资表中国粮食生产与相关投入资料表中国2001年各地区农村居民家庭人均纯收入与消费支出(单位:元)注:从事农业经营的纯收入由从事第一产业的经营总收入与从事第一产业的经营支出之差计算,其他来源的纯收入由总纯收入减去从事农业经营的纯收入后得到。
资料来源:《中国农村住户调查年鉴(2002)》、《中国统计年鉴(2002)》。
;AR · AZCA ~COCT !DE FL GAIA &ID IL IN $ KSKY 《LAMA {MD ME MIMN ;MO MS MT / NCND 】NENH ,NJ NM资源来源:根据Introduction to Econometrics (2 edition) 整理。
(2024年)完整版李子奈计量经济学版第四版课件

• 三阶段最小二乘法(3SLS):三阶段最小二乘法是对二阶段最小二乘法的改进。 该方法在第二阶段估计时,不仅考虑了残差作为解释变量,还考虑了其他所有 内生变量的估计值作为解释变量。这样可以进一步提高参数估计量的效率。
在社会科学领域,这些方法可用于分析人口 统计数据、经济指标等,揭示社会经济现象 背后的复杂关系。
2024/3/26
30
THANKS
感谢观看
2024/3/26
31
多重共线性的检验
相关系数矩阵法、方差膨胀因子 法、条件指数法等。
14
04
时间序列计量经济学模型
Chapter
2024/3/26
15
时间序列基本概念与性质
01
02
03
时间序列定义
按时间顺序排列的一组数 据,反映现象随时间变化 的发展过程。
2024/3/26
时间序列构成要素
现象所属的时间(年、季、 月、日等)和反映现象在 各个时间上的统计指标数 值。
28
半参数回归分析方法
部分线性模型
模型中既包含参数部分也包含非参数部分,参数部分用于描述主要 影响因素,非参数部分用于捕捉其他未知影响因素。
单指标模型
通过投影寻踪方法将高维数据降维到一维,然后利用非参数方法进 行回归分析。
变系数模型
模型系数随着某个或多个变量的变化而变化,可以灵活捕捉变量间的 动态关系。
不可识别的情况 当联立方程模型中的某个方程不能被任何其他方程所替代 时,该方程就是不可识别的。此时,无法对该方程的参数 进行一致估计。
计量经济学实验操作指导完整版李子奈

计量经济学试验(完整版)——李子奈目录实验一一元线性回归 (5)一实验目的 (5)二实验要求 (5)三实验原理 (5)四预备知识 (5)五实验内容 (5)六实验步骤 (5)1.建立工作文件并录入数据 (5)2.数据的描述性统计和图形统计: (7)3.设定模型,用最小二乘法估计参数: (8)4.模型检验: (8)5.应用:回归预测: (9)实验二可化为线性的非线性回归模型估计、受约束回归检验及参数稳定性检验 (12)一实验目的: (12)二实验要求 (12)三实验原理 (12)四预备知识 (12)五实验内容 (12)六实验步骤 (13)实验三多元线性回归 (15)一实验目的 (15)三实验原理 (15)四预备知识 (15)五实验内容 (15)六实验步骤 (15)6.1 建立工作文件并录入全部数据 (15)6.2 建立二元线性回归模型 (16)6.3 结果的分析与检验 (16)6.4 参数的置信区间 (17)6.5 回归预测 (17)6.6 置信区间的预测 (19)实验四异方差性 (21)一实验目的 (21)二实验要求 (21)三实验原理 (21)四预备知识 (21)五实验内容 (21)六实验步骤 (21)6.1 建立对象: (21)6.2 用普通最小二乘法建立线性模型 (22)6.3 检验模型的异方差性 (22)6.4 异方差性的修正 (25)实验五自相关性 (29)一实验目地 (29)二实验要求 (29)三实验原理 (29)四预备知识 (29)五实验内容 (29)六实验步骤 (29)6.1 建立Workfile和对象 (30)6.2 参数估计、检验模型的自相关性 (30)6.3 使用广义最小二乘法估计模型 (34)6.4 采用差分形式作为新数据,估计模型并检验相关性 (36)实验六多元线性回归和多重共线性 (38)一实验目的 (38)二实验要求 (38)三实验原理 (38)四预备知识 (38)五实验内容 (38)六实验步骤 (38)6.1 建立工作文件并录入数据 (38)6.2 用OLS估计模型 (38)6.3 多重共线性模型的识别 (39)6.4 多重共线性模型的修正 (40)实验七分布滞后模型与自回归模型及格兰杰因果关系检验 (43)一实验目的 (43)二实验要求 (43)三实验原理 (43)四预备知识 (43)五实验内容 (43)六实验步骤 (43)6.1 建立工作文件并录入数据 (43)6.2 使用4期滞后2次多项式估计模型 (44)6.3 格兰杰因果关系检验 (46)实验八联立方程计量经济学模型 (50)一实验目的 (50)二实验要求 (50)三实验原理 (50)四预备知识 (50)五实验内容 (50)六实验步骤 (51)6.1 分析联立方程模型。
李子奈计量经济学课件完整版

回归诊断与异常值处理
回归诊断
回归诊断是对回归模型进行检验和评估的过程,包括残差分析、模型假设检验等,以判断模 型是否满足假设条件、是否存在异常值等。
异常值处理
在回归分析中,异常值可能对模型估计和预测产生较大影响。常用的异常值处理方法包括删 除异常值、使用稳健回归方法等。
实际应用
回归诊断和异常值处理是回归分析中不可或缺的步骤,有助于提高模型的准确性和可靠性。 例如,在经济学研究中,通过对回归模型进行诊断和异常值处理,可以得到更准确的经济预 测和政策建议。
模型检验
拟合优度检验、显著性检验、 异方差性检验等。
预测与决策
利用回归模型进行预测和决策 分析。
假设检验与置信区间
假设检验基本原理
原假设、备择假设、检验统计量、显著性水 平等。
假设检验与置信区间的关系
联系与区别。
置信区间构建
点估计、区间估计、置信水平等。
常用的假设检验方法
t检验、F检验、卡方检验等。
季节性调整方法
包括基于移动平均的季节性调整、基于回归的季节性调整以及基于 时间序列分解的季节性调整等。
ARIMA模型构建及预测应用
01
ARIMA模型基本概念
ARIMA是自回归移动平均模型的简称,是一种用于时间序列预测的统
计模型。
02
ARIMA模型构建步骤
包括模型识别、参数估计、模型检验和预测等步骤。
04
非线性回归模型及转换技巧
常见非线性回归模型介绍
指数回归模型
用于描述因变量与自变量之间的 指数关系,如人口增长、放射性
衰变等现象。
对数回归模型
适用于因变量变化范围较大,且 自变量与因变量的对数之间存在 线性关系的情况。
(2024年)计量经济学教案李子奈版ppt课件

2024/3/26
7
线性回归模型基本概念
01
02
03
线性回归模型定义
描述因变量与一个或多个 自变量之间线性关系的数 学模型。
2024/3/26
回归方程
表示因变量与自变量之间 关系的数学表达式,形如 Y=β0+β1X1+β2X2+…+ βkXk。
估计的回归方程
根据样本数据计算得到的 回归方程,用于预测因变 量的值。
单位根检验法
通过检验时间序列是否存在单位 根来判断其平稳性,常用方法包 括ADF检验和PP检验。
2024/3/26
19
时间序列预测方法
移动平均法
通过对时间序列数据进行移动平均处理,消除其随机波动,从而揭示其长期趋势。
指数平滑法
通过对时间序列数据进行加权平均处理,给予近期数据更大的权重,使得预测结果更加 准确。
02
GLM扩展了线性回归模型,以包括非正态分布的响应变量和非
线性的链接函数。
在GLM中,响应变量的期望值是预测变量的线性组合通过链接
03
函数进行变换。
14
Logistic回归模型
01
Logistic回归是一种用于二元分 类问题的广义线性模型。
02
在Logistic回归中,响应变量是 二元的(0或1),而预测变量可
2024/3/26
5
计量经济学发展历史与现状
发展历史
计量经济学的发展大致可分为三个阶段,即初创时期 、经典时期和现代时期。初创时期主要代表人物有弗 里希、丁伯根等,他们为计量经济学的产生和发展做 出了重要贡献。经典时期主要代表人物有克莱因、戈 德菲尔德等,他们进一步完善了计量经济学的理论和 方法体系。现代时期则是在计算机技术广泛应用的基 础上,计量经济学的研究领域和方法得到了极大的拓 展和深化。
李子奈计量经济学课件

从20世纪初的初创期,到20世纪中期 的快速发展期,再到20世纪后期的成 熟期和21世纪的创新期,计量经济学 经历了不断发展和完善的过程。
计量经济学研究对象与方法
研究对象
主要研究经济现象中的数量关系 ,包括经济变量之间的关系、经 济系统的运行规律等。
研究方法
主要包括理论建模、数据收集与 处理、模型估计与检验、预测与 政策分析等步骤。
面板数据模型检验与诊断
模型检验
在估计出模型参数后,需要进行模型的统计检验,包括拟 合优度检验、方程的显著性检验、变量的显著性检验等。
诊断方法
如果模型检验不通过,需要采用一些诊断方法来识别问题 所在,如异方差性检验、自相关性检验、多重共线性检验 等。
模型修正
根据诊断结果,可以对模型进行修正,如添加或删除解释 变量、改变模型形式等,以提高模型的拟合效果和预测精 度。
计量经济学前沿领域探讨
空间计量经济学发展动态
空间权重矩阵的构建 与应用
空间权重矩阵是空间计量经济学中的 核心工具,用于描述不同地理单元之 间的空间关系。近年来,空间权重矩 阵的构建方法和应用领域不断拓展, 如基于地理距离、经济距离、社会网 络等多种方式构建空间权重矩阵,应 用于区域经济、环境经济、城市规划 等领域。
面板数据模型设定与估计
面板数据模型类型
根据对截距项和解释变量系数的不同限制,面板数据模型可以分 为混合回归模型、固定效应模型和随机效应模型。
模型设定检验
通过F检验、LM检验和Hausman检验等方法来确定应该使用哪种 类型的面板数据模型。
参数估计方法
对于不同类型的面板数据模型,可以采用普通最小二乘法、广义最 小二乘法、极大似然估计等方法进行参数估计。
计量经济学(李子奈第4版)数据表(全)
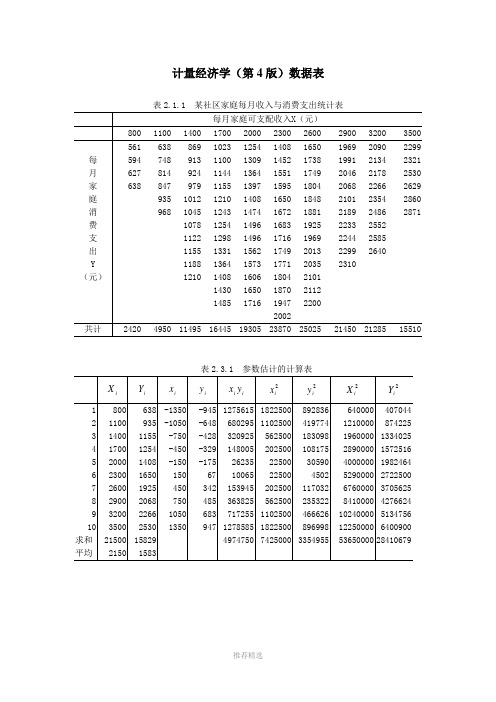
计量经济学(第4版)数据表表2.1.1 某社区家庭每月收入与消费支出统计表表2.3.1 参数估计的计算表表2.6.1 中国各地区居民家庭人均全年可支配收入与人均全年消费性支出(元)资料来源:《中国统计年鉴》(2014)。
第2章练习12中国某年各地区税收Y和国内生产总值GDP的统计资料单位:亿元表3.2.1 2013年中国各地区城镇居民人均收入与人均消费性支出(元)资料来源:根据《中国统计年鉴》(2014)整理。
表3.5.1 2010年中国制造业各行业的总产出及要素投入资料来源:根据《中国统计年鉴》(2011年)整理。
表3.6.1 2013年中国居民人均收入与人均生活消费支出数据(元)表3.7.1 2012年中国农村居民对蛋类食物的消费及相关食物的价格指数蛋类消费量Q (千克)各类食品的消费价格指数(上年=100)居民消费价格指数P0(上年=100)人均消费支出X(元)蛋类P肉禽类P1水产类P2粮食P01油脂P02蔬菜P03北京11.0596.9106.7104.8102.6104.5112.0103.311878.92天津12.84101.7105.7106.7102.4103.7119.6102.78336.55河北10.4296.4101.1104.8102.9106.3114.9102.55364.14山西7.8296.2101.4107.4103.0105.2114.2102.65566.19内蒙古 6.4598.1105.3107.7105.7105.3112.3102.56381.97辽宁8.4896.2102.6107.3103.6105.0117.5102.55998.39吉林7.9094.6103.7108.5104.2105.7110.5102.46186.17黑龙江 6.3398.3105.4104.8104.6102.6115.3102.95718.05上海8.9298.2105.1105.8102.9103.8111.1102.811971.50江苏 6.9697.0102.5108.4102.3104.2109.0102.69138.18浙江 5.5697.6100.9108.8103.7103.7115.2102.310652.73安徽7.2394.398.7110.8104.2105.8113.3102.45555.99福建 5.3296.8102.0107.8103.0105.4116.5102.47401.92江西 4.2296.998.9112.6103.8104.2118.2103.05129.47山东12.3295.9101.6108.8102.5107.5111.2102.06775.95河南9.0694.499.4108.9104.1105.0113.2102.45032.14湖北 5.0298.6101.7111.1105.3105.2113.2103.05726.73湖南 4.92100.198.5110.9105.3102.5110.8101.65870.12广东 3.3998.2104.4107.3105.0106.0114.9102.97458.56广西 2.2297.3103.0104.9103.8108.2116.7103.34933.58海南 2.43102.7103.8102.2104.1106.2115.6103.24776.30重庆 5.18100.699.1106.7107.7106.0112.3102.65018.64四川 4.8797.799.9111.5104.9105.2118.1102.05366.71贵州 2.3595.7101.3107.6104.5104.4109.0102.83901.71云南 2.82100.1103.1104.9103.5102.9117.8102.34561.33西藏0.56102.4108.9102.8103.0105.5114.6103.42967.56陕西 3.9197.6101.5110.4103.3105.9111.7103.15114.68甘肃 3.9397.4104.2105.2102.3104.5108.5103.14146.24青海 1.5899.2107.6109.6102.8105.6112.8103.15338.91宁夏 3.4097.7104.8107.2101.0103.0108.7101.75351.36新疆 3.62102.1105.9105.2107.3105.3117.6104.75301.25资料来源:《中国统计年鉴》(2013)。
李子奈计量经济学-2024鲜版

假设检验方法
面板数据的假设检验主要包括模型的设定检验、参数的显著性检验和模型的稳定性检验等。常用的假设检验方法 有F检验、LR检验、Hausman检验、Sargan检验等。这些检验方法可以帮助我们判断模型的适用性、变量的重 要性和模型的稳定性。
2024/3/28
22
06 计量经济学在金融领域的 应用
市场有效性检验 利用计量经济学模型和方法,检验金融市场的有效性,即 市场价格是否充分反映了所有可用信息,为市场监管和投 资决策提供依据。
25
计量经济学在风险管理中的应用
风险评估与测量
利用计量经济学方法,如VaR、CVaR等,对金融风险进行评估和测量,帮助金融机构和投资 者了解自身面临的风险水平。
风险对冲与分散
组合预测方法
将确定性预测方法和随机性预测方法相结合,形成组合预测模型,以提 高预测精度和稳定性。
18
05 面板数据分析
2024/3/28
19
面板数据的基本概念
面板数据的定义
面板数据(Panel Data)也称时 间序列截面数据(Time Series Cross-Sectional Data)或混合 数据(Pool Data),是指同时 包含时间序列和截面信息的数据
李子奈计量经济学
2024/3/28
1
目
录
2024/3/28
• 计量经济学概述 • 线性回归模型 • 非线性回归模型 • 时间序列分析 • 面板数据分析 • 计量经济学在金融领域的应用
2 contents
01 计量经济学概述
2024/3/28
3
计量经济学的定义与特点
定义
计量经济学是以经济理论和统计数据为基础,运用数学、统计学和计算机技术, 建立经济模型来分析经济变量之间的关系和预测经济现象的一门学科。
计量经济学实验四--李子奈
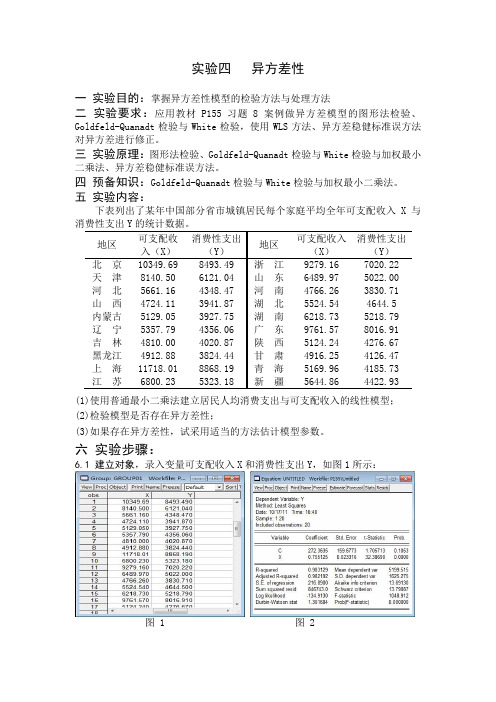
实验四异方差性一实验目的:掌握异方差性模型的检验方法与处理方法二实验要求:应用教材P155习题8案例做异方差模型的图形法检验、Goldfeld-Quanadt检验与White检验,使用WLS方法、异方差稳健标准误方法对异方差进行修正。
三实验原理:图形法检验、Goldfeld-Quanadt检验与White检验与加权最小二乘法、异方差稳健标准误方法。
四预备知识:Goldfeld-Quanadt检验与White检验与加权最小二乘法。
五实验内容:下表列出了某年中国部分省市城镇居民每个家庭平均全年可支配收入X与消费性支出Y的统计数据。
地区可支配收入(X)消费性支出(Y)地区可支配收入(X)消费性支出(Y)北京10349.69 8493.49 浙江9279.16 7020.22 天津8140.50 6121.04 山东6489.97 5022.00 河北5661.16 4348.47 河南4766.26 3830.71 山西4724.11 3941.87 湖北5524.54 4644.5 内蒙古5129.05 3927.75 湖南6218.73 5218.79 辽宁5357.79 4356.06 广东9761.57 8016.91 吉林4810.00 4020.87 陕西5124.24 4276.67 黑龙江4912.88 3824.44 甘肃4916.25 4126.47 上海11718.01 8868.19 青海5169.96 4185.73 江苏6800.23 5323.18 新疆5644.86 4422.93(1)使用普通最小二乘法建立居民人均消费支出与可支配收入的线性模型;(2)检验模型是否存在异方差性;(3)如果存在异方差性,试采用适当的方法估计模型参数。
六实验步骤:6.1 建立对象,录入变量可支配收入X和消费性支出Y,如图1所示:图 1 图 26.2 用普通最小二乘法建立线性模型设定一元线性回归模型为:01Y X ββμ∧=++ 点击主界面菜单Quick\Estimate Equation ,在弹出的对话框中输入Y 、C 、X ,点击确定即可得到回归结果,如图2所示。
计量经济学试验完整版--李子奈

计量经济学试验完整版--李子奈计量经济学试验??李子奈目录实验一一元线性回归5一实验目的 5二实验要求 5三实验原理 5四预备知识 5五实验内容 5六实验步骤 51.建立工作文件并录入数据 52.数据的描述性统计和图形统计: 73.设定模型,用最小二乘法估计参数: 84.模型检验: 85.应用:回归预测: 9实验二可化为线性的非线性回归模型估计、受约束回归检验及参数稳定性检验12一实验目的: 12二实验要求12三实验原理12四预备知识12五实验内容12六实验步骤13实验三多元线性回归14一实验目的14三实验原理15四预备知识15五实验内容15六实验步骤156.1 建立工作文件并录入全部数据 15 6.2 建立二元线性回归模型156.3 结果的分析与检验166.4 参数的置信区间166.5 回归预测176.6 置信区间的预测18实验四异方差性20一实验目的20二实验要求20三实验原理20四预备知识20五实验内容20六实验步骤206.1 建立对象: 206.2 用普通最小二乘法建立线性模型216.3 检验模型的异方差性216.4 异方差性的修正24实验五自相关性28一实验目地28二实验要求28三实验原理28四预备知识28五实验内容28六实验步骤286.1 建立Workfile和对象 296.2 参数估计、检验模型的自相关性296.3 使用广义最小二乘法估计模型 336.4 采用差分形式作为新数据,估计模型并检验相关性35 实验六多元线性回归和多重共线性37一实验目的37二实验要求37三实验原理37四预备知识37五实验内容37六实验步骤376.1 建立工作文件并录入数据386.2 用OLS估计模型386.3 多重共线性模型的识别386.4 多重共线性模型的修正39实验七分布滞后模型与自回归模型及格兰杰因果关系检验 41 一实验目的41二实验要求41三实验原理41四预备知识41五实验内容41六实验步骤426.1 建立工作文件并录入数据426.2 使用4期滞后2次多项式估计模型426.3 格兰杰因果关系检验45实验八联立方程计量经济学模型49一实验目的49二实验要求49三实验原理49四预备知识49五实验内容49六实验步骤506.1 分析联立方程模型。
计量经济学四五章 李子奈

ii i i i i i i X X X X X X e εαααααα++++++=215224213221102~第四章异方差1.异方差的概念和类型概念:对于模型 如果出现 即对于不同的样本点,随机误差项的方差不再是常数,而互不相同,则认为出现了异方差性。
异方差一般可归结为三种类型:(1)单调递增型: σi 2随X 的增大而增大(2)单调递减型: σi 2随X 的增大而减小(3)复杂型: σi 2与X 的变化呈复杂形式2.几种异方差的检验方法(描述原理即可)(1)图示检验法①用X-Y 的散点图进行判断:看是否存在明显的散点扩大、缩小或复杂型趋势(即不在一个固定的带型域中)②用X-的散点图进行判断:看是否形成一斜率为零的直线(2)帕克(Park)检验与戈里瑟(Gleiser)检验选择关于变量X 的不同的函数形式,对方程进行估计并进行显著性检验,如果存在某一种函数形式,使得方程显著成立,则说明原模型存在异方差性。
(3)G-Q 检验先将样本一分为二,对子样①和子样②分别作回归,然后利用两个子样的残差平方和之比构造统计量进行异方差检验。
由于该统计量服从F 分布,因此假如存在递增的异方差,则F 远大于1;反之就会等于1(同方差)、或小于1(递减方差)。
(4)怀特(White )检验怀特检验不需要排序,且适合任何形式的异方差。
以二元为例 先进行OLS 回归,得到 然后做辅助回归 可以证明,在同方差假设下,从该辅助回归所得到的可决系数R2与样本容量n 的乘积,渐进地服从自由度为辅助回归方程中解释变量个数的卡方分布:(R2为辅助回归的可决系数,h 为辅助回归法人解释变量的个数)如果存在异方差性,则表明确与解释变量的某种组合有显著的相关性,这时往往显示出有较高的可决系数并且某一参数的t 检验值较大。
3.异方差的后果(1)参数估计量非有效OLS 估计量仍然具有无偏性,但不具有有效性。
因为在有效性证明中利用了而且,在大样本情况下,尽管参数估计量具有一致性,但仍然不具有渐近有效性。
李子奈计量经济学课件

1
e
1 2
2
(Yi
ˆ0
ˆ1
X
i
)
2
(2
)
n 2
n
将该或然函数极大化,即可求得到模型 参数的极大或然估计量。
由于或然函数的极大化与或然函数的对数的极 大化是等价的,所以,取对数或然函数如下:
L* ln(L)
n ln(
2
)
1
2
2
(Yi
ˆ 0
ˆ1 X i
)2
解得模型的参数估计量为:
ˆ
0
ˆ1
P lim( ˆ1 ) P lim( 1
ki i ) P lim( 1 ) P lim(
xii )
x
2 i
P lim( 1 P lim(
xii / n)
xi2 / n)
1
Cov( X , )
Q
1
0 Q
1
五、参数估计量的概率分布及随机干扰 项方差的估计
1、参数估计量ˆ0 和ˆ1 的概率分布
-159 23910 22500 25408
28 4140 22500
762
402 180720 202500 161283
511 382950 562500 260712
1018 1068480 1102500 1035510
963 1299510 1822500 926599
5769300 7425000 4590020
ˆ0 的样本方差:
S2 ˆ0
ˆ 2
X
2 i
n
x
2 i
ˆ0 的样本标准差:
S ˆ0 ˆ
X
2 i
n
xi2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计量经济学(第4版)数据表表2.1.1 某社区家庭每月收入与消费支出统计表每月家庭可支配收入X (元)800 1100 1400 1700 2000 2300 2600 2900 3200 3500 每 月 家 庭 消 费 支 出 Y (元)561 638 869 1023 1254 1408 1650 1969 2090 2299 594 748 913 1100 1309 1452 1738 1991 2134 2321 627 814 924 1144 1364 1551 1749 2046 2178 2530 638 847 979 1155 1397 1595 1804 2068 2266 2629 935 1012 1210 1408 1650 1848 2101 2354 2860 968 1045 1243 1474 1672 1881 2189 2486 28711078 1254 1496 1683 1925 2233 2552 1122 1298 1496 1716 1969 2244 2585 1155 1331 1562 1749 2013 2299 2640 1188 1364 1573 1771 2035 2310 1210 1408 1606 1804 2101 1430 1650 1870 2112 1485 1716 1947 22002002 共计 2420 4950 1149516445 19305 23870 25025 21450 2128515510表2.3.1 参数估计的计算表i Xi Y i xi yi i y x 2i x 2i y2i X 2i Y1 800 638 -1350 -945 892836 640000 4070442 1100 935 -1050 -648 680295 419774 8742253 1400 1155 -750 -428 320925 562500 1830984 1700 1254 -450 -329 148005 202500 108175 5 2000 1408 -150 -175 26235 22500 305906 2300 1650 150 67 10065 22500 4502 7 2600 1925 450 342 153945 202500 1170328 2900 2068 750 485 363825 562500235322 9 3200 2266 1050 683 717255466626 10 350025301350947896998求和 21500 15829平均2150 1583表2.6.1 中国各地区居民家庭人均全年可支配收入与人均全年消费性支出(元)地区可支配收入X 消费支出Y地区可支配收入X消费支出Y北京40830.0 29175.6 湖北16472.5 11760.8天津26359.2 20418.7 湖南16004.9 11945.9河北15189.6 10872.2 广东23420.7 17421.0山西15119.7 10118.3 广西14082.3 9596.5内蒙古18692.9 14877.7 海南15733.3 11192.9辽宁20817.8 14950.2 重庆16568.7 12600.2吉林15998.1 12054.3 四川14231.0 11054.7黑龙江15903.4 12037.2 贵州11083.1 8288.0上海42173.6 30399.9 云南12577.9 8823.8江苏24775.5 17925.8 西藏9746.8 6310.6浙江29775.0 20610.1 陕西14371.5 11217.3安徽15154.3 10544.1 甘肃10954.4 8943.4福建21217.9 16176.6 青海12947.8 11576.5江西15099.7 10052.8 宁夏14565.8 11292.0山东19008.3 11896.8 新疆13669.6 11391.8河南14203.7 10002.5资料来源:《中国统计年鉴》(2014)。
第2章练习12中国某年各地区税收Y和国内生产总值GDP的统计资料单位:亿元地区Y GDP 地区Y GDP北京1435.7 9353.3 湖北434.0 9230.7 天津438.4 5050.4 湖南410.7 9200.0 河北618.3 13709.5 广东2415.5 31084.4 山西430.5 5733.4 广西282.7 5955.7 内蒙古347.9 6091.1 海南88.0 1223.3 辽宁815.7 11023.5 重庆294.5 4122.5 吉林237.4 5284.7 四川629.0 10505.3 黑龙江335.0 7065.0 贵州211.9 2741.9 上海1975.5 12188.9 云南378.6 4741.3 江苏1894.8 25741.2 西藏11.7 342.2 浙江1535.4 18780.4 陕西355.5 5465.8 安徽401.9 7364.2 甘肃142.1 2702.4 福建594.0 9249.1 青海43.3 783.6 江西281.9 5500.3 宁夏58.8 889.2 山东1308.4 25965.9 新疆220.6 3523.2 河南625.0 15012.5表3.2.1 2013年中国各地区城镇居民人均收入与人均消费性支出(元)地区现金消费支出Y 工资性收入X1其他收入X2地区现金消费支出Y工资性收入X1其他收入X2北京26274.930273.015000.8湖北15749.515571.89608.7天津21711.923231.912423.7湖南15887.113951.410691.6河北13640.614588.49554.4广东24133.325286.511217.5山西13166.216216.47797.2广西15417.615647.89381.0内蒙古19249.118377.98600.1海南15593.015773.09146.8辽宁18029.715882.012022.9重庆17813.916654.710195.7吉林15932.314388.39155.9四川16343.514976.08917.9黑龙江14161.712525.88623.4贵州13702.913627.67785.5上海28155.033235.415643.9云南15156.115140.79557.6江苏20371.521890.013241.0西藏12231.919604.02956.7浙江23257.224453.016788.0陕西16679.716441.07667.8安徽16285.215535.39470.8甘肃14020.713329.76819.3福建20092.721443.411939.3青海13539.514015.68115.4江西13850.514767.58181.9宁夏15321.115363.98402.8山东17112.221562.19066.0新疆15206.215585.36802.6河南14822.014704.28982.3资料来源:根据《中国统计年鉴》(2014)整理。
表3.5.1 2010年中国制造业各行业的总产出及要素投入编号行业Y(亿元)K(亿元)L(万人)K1(亿元)K2(亿元)1 煤炭开采和洗选业22109.3 21785.1 527.2 9186.86 12598.272 石油和天然气开采业9917.8 12904.0 106.1 9381.72 3522.313 黑色金属矿采选业5999.3 4182.5 67.0 1630.93 2551.534 有色金属矿采选业3799.4 2317.5 55.4 1109.92 1207.545 非金属矿采选业3093.5 1424.4 56.5 675.55 748.836 其他采矿业31.3 14.2 0.5 7.64 6.587 农副食品加工业34928.1 14373.1 369.0 5493.82 8879.328 食品制造业11350.6 6113.6 175.9 2515.71 3597.879 饮料制造业9152.6 6527.0 130.0 2540.24 3986.79 10烟草制品业5842.5 4569.6 21.1 859.08 3710.47 11纺织业28507.9 16253.0 647.3 6276.68 9976.28 12纺织服装、鞋、帽制造业12331.2 6044.7 447.0 1791.52 4253.18 13皮革、毛皮、羽毛(绒)及其制品业7897.5 3410.6 276.4 963.81 2446.80 14木材加工及木、竹、藤、棕、草制品业7393.2 3037.7 142.3 1404.12 1633.60 15家具制造业4414.8 2261.3 111.7 741.82 1519.47 16造纸及纸制品业10434.1 7949.1 157.9 3797.64 4151.47 17印刷业和记录媒介的复制3562.9 2801.6 85.1 1146.82 1654.82 18文教体育用品制造业3135.4 1602.1 128.1 517.56 1084.54 19石油加工、炼焦及核燃料加工业29238.8 13360.6 92.2 6561.08 6799.50 20化学原料及化学制品制造业47920.0 31948.6 474.1 14679.02 17269.53 21医药制造业11741.3 9017.0 173.2 3023.11 5993.89 22化学纤维制造业4954.0 3526.1 43.9 1361.12 2164.94 23橡胶制品业5906.7 3595.5 102.9 1503.38 2092.10 24塑料制品业13872.2 8033.2 283.3 2808.75 5224.49 25非金属矿物制品业32057.3 21490.5 544.6 10382.38 11108.09 26黑色金属冶炼及压延加工业51833.6 37101.9 345.6 17309.25 19792.66 27有色金属冶炼及压延加工业28119.0 16992.7 191.6 6768.77 10223.92 28金属制品业20134.6 11477.4 344.6 3701.16 7776.22 29通用设备制造业35132.7 24005.6 539.4 7200.64 16804.98 30专用设备制造业21561.8 16879.4 334.2 4426.12 12453.31 31交通运输设备制造业55452.6 40224.8 573.7 10364.94 29859.82 32电气机械及器材制造业43344.4 27454.8 604.3 6467.85 20986.90 33通信设备、计算机及其他电子设备制造业54970.7 34005.4 772.8 10437.66 23567.72 34仪器仪表及文化、办公用机械制造业6399.1 4565.8 124.9 1140.44 3425.38 35工艺品及其他制造业5662.7 2904.5 140.4 819.12 2085.35 36废弃资源和废旧材料回收加工业2306.1 829.8 13.9 206.13 623.67 37电力、热力的生产和供应业40550.8 58989.3 275.6 47901.41 11087.90 38燃气生产和供应业2393.4 2263.8 19.0 1255.33 1008.42 39水的生产和供应业1137.1 4207.7 45.9 2858.79 1348.86 资料来源:根据《中国统计年鉴》(2011年)整理。
