第5章552均方误差准则MSE和LMS算法
mse准则

mse准则mse准则是均方误差(Mean Squared Error)的简称,是一种常用的评估指标,用于衡量预测值与真实值之间的差异程度。
mse准则广泛应用于各个领域,比如机器学习、统计学、经济学等。
本文将从不同角度介绍mse准则的定义、应用领域和计算方法。
一、mse准则的定义mse准则是通过计算预测值与真实值之间的差异平方的均值来评估模型的预测能力。
一般而言,mse准则越小,意味着模型的预测能力越好。
mse准则的计算公式如下所示:MSE = Σ(yi - ŷi)² / n其中,yi代表真实值,ŷi代表预测值,n代表样本数量。
mse准则的取值范围为0到正无穷,当mse准则等于0时,表示预测值完全与真实值一致。
mse准则广泛应用于各个领域,以下是一些常见的应用领域:1. 机器学习:mse准则常用于评估机器学习算法的预测准确性。
在回归问题中,可以使用mse准则来评估模型对连续型变量的预测能力。
通过比较不同模型的mse准则,可以选择最优模型。
2. 统计学:mse准则也是统计学中常用的评估指标之一。
在线性回归分析中,可以使用mse准则来评估模型对自变量和因变量之间关系的拟合程度。
3. 经济学:mse准则在经济学中也有广泛的应用。
例如,在经济预测中,可以使用mse准则来评估模型对未来经济指标的预测精度。
三、mse准则的计算方法mse准则的计算方法相对简单,可以通过以下步骤进行计算:1. 确定样本数量n。
2. 收集真实值和预测值的数据。
3. 计算每个样本的预测值与真实值之间的差异。
4. 将差异的平方累加起来。
5. 将累加值除以样本数量n,得到mse准则的值。
需要注意的是,mse准则只能用于评估预测值与真实值之间的差异程度,对于模型的其他表现指标,需要使用其他准则进行评估。
mse准则是一种常用的评估指标,用于衡量预测值与真实值之间的差异程度。
mse准则的定义清晰明确,应用领域广泛,计算方法简单易行。
第5章(5.5,5.5.1)线性均衡器

5.5线性均衡{kI }k η{}ˆkI Tx+ch+MF+WF()nLn n zf z F -=∑=0eP 00 Lk n k n kn k n k n kn kf I f I f I ηη-=-≠=+=++∑∑v ISI1. 对最佳离散系统的要求:a) 消除由{}n f 引起的ISI ——取k v 的(L +1)个样值(ISI 覆盖范围)按一定最佳准则处理——即FIR 滤波器。
b) 有自适应能力——抽头可变FIR ,在一定最佳准则下的自适应算法。
c) 输出噪声及残余ISI 影响最小化——由调整j c 的最佳准则确定。
2. 最佳离散系统的结构:抽头系数可变的FIR 滤波器(自适应均衡器)。
3. 调整抽头系数{}j c 的最佳准则:a) 理想:最小错误概率准则,但}{~j e c P 函数关系是复杂的非线性函数关系。
b) 实际采用的最佳准则: i. 峰值失真准则(PD 准则,Peak Distortion )——只考虑ISI 。
ii.均方误差准则(MSE 准则,Mean Square Error )——同时考虑ISI 及噪声影响最小化5.5.1 峰值失真准则和迫零算法(10-2-1节,11-1-1节)一、峰值失真和峰值失真准则峰值失真——最大可能的ISI ,以D 表示。
(Peak Distortion ) 峰值失真准则——使D 最小。
考虑两种情况下,如何设计{}j c 及性能分析:a) 无限抽头的均衡器 b) 有限抽头的均衡器二、无限抽头系数的ZF 均衡器 (ZF -Zero Forcing )ZF 均衡器——根据峰值失真准则建立起来的均衡器。
1. 传输系统的模型2. 峰值失真及峰值失真准则{}001 (1) (10-2-4)~n n jn j n n n j n n n j D q q q cf q D c ∞∞∞∞-=-∞=-∞=-∞=-∞≠≠≠===∴∑∑∑∑令归一化的函数若{}j c 有无限多个抽头,则根据PD 准则,可选择适当{}j c 值使得满足D =0。
均方误差mse计算公式

均方误差mse计算公式均方误差(Mean Squared Error,MSE)是一种常用的衡量预测模型准确度的指标。
在机器学习和统计学中,我们经常需要根据已有的数据集构建模型,并使用该模型对未知数据进行预测。
为了评估模型的预测能力,我们需要一个可靠的指标来度量预测值与真实值之间的差距。
MSE的计算公式如下:MSE = (1/n) * Σ(yi - ŷi)²其中,n表示样本数量,yi表示真实值,ŷi表示预测值。
MSE的计算方法十分直观。
对于每个样本,我们先计算预测值与真实值之间的差距,然后对这些差距的平方求和,最后除以样本数量n,得到均方误差。
MSE的优点在于它对预测误差的量级进行了平方处理,使得较大的误差对结果的影响更为显著。
这种平方处理还能够避免正负误差相互抵消的情况,确保误差的正负对最终结果有明确的影响。
此外,MSE计算简单,易于理解和解释,因此被广泛应用于各种领域的预测模型评估中。
然而,MSE也存在一些缺点。
首先,MSE对异常值(outliers)非常敏感。
由于误差被平方处理,任何一个较大的误差都会对MSE产生较大的影响,从而导致模型评估的偏差。
其次,MSE对预测误差的量级没有进行归一化处理,因此在比较不同数据集、不同模型的预测能力时,需要谨慎使用。
为了解决MSE对异常值敏感的问题,研究人员提出了一些改进的方法,如均方根误差(Root Mean Squared Error,RMSE)和平均绝对误差(Mean Absolute Error,MAE)。
RMSE在计算MSE的基础上,再开方,使得计算结果具有与原始数据相同的量纲。
MAE 则是对预测误差进行绝对值处理,消除了平方带来的影响,使得评估结果更加稳健。
在实际应用中,根据具体的任务需求和数据特点,我们可以选择合适的误差度量指标。
如果数据集中存在较多的异常值,可以考虑使用RMSE或MAE进行评估;如果异常值较少,MSE依然是一个简单有效的选择。
第5章552均方误差准则MSE和LMS算法

第5章552均方误差准则MSE和LMS算法第5章主题:均方误差准则(MSE)和最小均方算法(LMS)在信号处理和机器学习中,常常需要优化一些模型的性能,使其能够更好地适应数据。
均方误差准则(Mean Square Error, MSE)和最小均方算法(Least Mean Squares, LMS)是两种常用的优化方法。
均方误差准则(MSE)是一种衡量模型性能的方法,它通过计算预测值与实际值之间的差异来评估模型的准确性。
MSE的计算公式如下:MSE = (1/n) * Σ(y - yhat)²其中,n表示数据点的数量,y表示实际值,yhat表示预测值。
MSE 越小,表示模型的拟合效果越好。
最小均方算法(LMS)是一种基于梯度下降的优化算法,用于寻找使MSE最小化的模型参数。
LMS的基本思想是通过迭代的方式逐步调整模型参数,使MSE逐渐减小。
具体而言,LMS算法根据梯度信息来更新模型参数的值。
LMS算法的更新公式如下:w_new = w_old + η * (y - yhat) * x其中,w_new表示更新后的参数值,w_old表示之前的参数值,η是学习率(learning rate),用于控制每次更新的步幅,y表示实际值,yhat表示预测值,x表示输入数据。
LMS算法的步骤如下:1.初始化参数w和学习率η的值。
2. 对于每个数据点,计算预测值yhat。
3.计算MSE,并检查是否达到了停止条件。
4.如果未达到停止条件,根据LMS算法的更新公式,更新参数w的值。
5.重复步骤2-4,直到满足停止条件。
LMS算法的优点是简单易于实现,但其性能可能受到初始参数和学习率的选择影响。
学习率过大可能导致算法不稳定,学习率过小可能导致算法收敛速度慢。
总结起来,MSE和LMS算法是两种常用的优化方法,用于评估模型的准确性和调整模型参数的值。
它们在信号处理和机器学习领域应用广泛,可以用于回归问题和分类问题的优化。
均方误差的计算公式

均方误差的计算公式均方误差(Mean Square Error,简称MSE)是机器学习中常用的一种评估模型预测精度的指标。
它的计算公式如下:MSE = (1/n) * Σ(yi - ŷi)^2其中,n代表样本数量,yi代表真实值,ŷi代表模型预测值,Σ表示求和运算。
均方误差可以衡量模型预测值与真实值之间的差距,并将差距的平方值求和后取平均。
因此,均方误差越小,表示模型的预测值与真实值越接近,模型的预测精度越高。
均方误差的计算公式中,首先对每个样本的预测值与真实值之间的差距进行平方运算,然后对所有样本的差距平方值进行求和,最后再除以样本数量n,即可得到均方误差。
为了更好地理解均方误差的计算过程,下面举一个简单的例子。
假设有一个回归问题,需要预测某个城市的房价。
我们收集了10个样本,每个样本包含了房屋的面积和实际售价。
我们使用一个线性回归模型对房价进行预测,并计算均方误差。
我们使用模型对这10个样本的房价进行预测,得到了10个预测值。
然后,对于每个样本,我们计算预测值与真实值之间的差距,并将差距的平方值作为该样本的误差。
接着,将所有样本的误差平方值进行求和,并除以样本数量10,即可得到均方误差。
通过计算,我们得到了均方误差为1000。
这个值代表了模型的预测精度,即模型预测的房价与实际房价之间的平均差距的平方值。
均方误差作为一种常见的评估指标,具有以下特点:1. 均方误差始终为非负值,当预测值与真实值完全一致时,均方误差为0,表示模型的预测精度达到最高;2. 均方误差对预测值与真实值之间的差距较大的样本更加敏感,因为差距较大的样本的平方值较大;3. 均方误差的单位与预测值的单位平方相同,例如,如果预测房价的单位是万元,那么均方误差的单位就是万元的平方。
除了均方误差之外,还有其他评估指标可以用来衡量模型的预测精度,例如平均绝对误差(Mean Absolute Error,简称MAE)、均方根误差(Root Mean Square Error,简称RMSE)等。
mse均方误差范围

mse均方误差范围均方误差(Mean Squared Error,简称MSE)是衡量预测模型准确性的一种常见指标。
它计算了预测值与真实值之间的差异,通过平方误差的平均值来衡量模型的性能。
本文将介绍MSE的计算方法以及其应用的范围。
一、MSE的计算方法MSE的计算方法相对简单,可以通过以下公式来求得:MSE = Σ(yi - ŷi)² / n其中,yi代表实际值,ŷi代表预测值,n代表样本数量。
这个公式的核心思想是,将每个样本的预测误差平方后求和,再除以样本数量,得到了平均误差的平方。
通过MSE,我们可以评估预测模型的准确程度,MSE越小,模型的拟合程度越好。
二、MSE的应用范围MSE广泛应用于各个领域的预测模型评估中。
以下是一些常见的应用范围:1. 金融领域:MSE可用于评估股票市场的预测模型。
通过计算预测值与实际值之间的差异平方的平均,可以判断模型的准确性,为投资者提供决策依据。
2. 经济学领域:MSE可用于衡量宏观经济模型的预测精度。
通过比较预测值和实际值之间的误差平方的平均,可以评估模型的准确性,并为政策制定者提供参考。
3. 数据科学领域:MSE常用于回归模型的性能评估。
在机器学习和统计建模中,我们经常需要对不同模型进行比较,选择最优模型来进行预测任务。
通过计算MSE,可以快速评估模型的预测能力。
4. 工程领域:MSE可用于评估各类工程预测模型的准确性。
比如建筑工程中的项目成本预测、交通工程中的交通流量预测等。
通过MSE 的计算,可以指导相关决策,提高工程预测的准确性。
5. 自然科学领域:MSE也常用于物理学、地质学、生态学等领域的预测模型评估。
通过计算实际观测值和预测值之间的差异,可以评估模型在复杂自然系统中的表现。
总之,MSE作为一种常见的预测模型评估指标,被广泛应用于各个领域。
通过计算MSE,我们可以了解预测模型的准确程度,并为决策提供依据。
无论是金融、经济、工程还是科学领域,MSE都能帮助我们评估模型的性能,指导相关工作的进行。
第5章(552)均方误差准则(MSE)和LMS算法

第5章(552)均⽅误差准则(MSE)和LMS算法5.5.2均⽅误差准则(MSE )和LMS 算法引⾔:均⽅误差准则同时考虑ISI 及噪声的影响,使其最⼩化。
本节讨论问题: 1. 均⽅误差准则;2. ⽆限长LMS 均衡器(C (z ),J min );3. 有限长LMS 均衡器(C opt ,J min );4. LMS 算法;5. 均衡器的操作;6. 递推LMS 算法收敛特性的分析。
⼀. 均⽅误差准则信息符号的估计值:?k j k jj I c ∞-=-∞=∑v (⽆限长均衡器情况)其中,接收数据样本为:k n k n k n f I η-=+∑v ,k η为⽩噪声。
估计误差:?ISI k k k kI I εε=-,包括及噪声定义:估计值2?[]k kI J E ε=的均⽅误差为均衡器的性能指数。
}{k ηε均⽅误差准则:使均⽅误差性能指数J 最⼩(min J ),此准则同时考虑使ISI 及噪声影响最⼩。
获得min J 的途径:调整{}j c ,当min J J =时,opt C C =(最佳抽头系数)寻找opt C 的⽅法:1)根据正交性原理(线性均⽅估计):*[]0k k l E l ε-=,所有v 。
(注:与ZF 准则不同的是,这⾥的输⼊是经过两个输⼊滤波器的数据样本k v ,这就包含了噪声)。
即*?[]0kkl E l ε-=,所有I 。
2)求函数极值⽅法:令0=→=??opt kJC C 2013年5⽉3⽇星期五上午讲于此处,已经是第⼗次矣。
这两种⽅法是等价的,证明如下。
l i m Kkjkj j kjK j j KI c c∞--→∞=-∞=-==∑∑v vlim T k K →∞=V c假如均衡器为有限长,则T k kI =V c 其中11Tk k K k K kk K k K v v v v v ++--+-??=??V ,以及 1 1TKK K K c c c c c --+-??=??c 。
均方误差(mse)计算公式

均方误差(mse)计算公式
均方误差(MSE)是衡量预测值与真实值之间差异程度的一种统计指标。
其计算公式如下:
MSE = Σ (预测值真实值)^2 / n.
其中,Σ表示求和,预测值和真实值分别表示预测模型给出的值和实际观测到的值,n表示样本数量。
MSE的计算步骤包括首先计算每个样本的预测值与真实值之差的平方,然后将所有样本的平方差值相加,并最后除以样本数量得到均方误差。
MSE常用于衡量回归模型的预测精度,数值越小表示模型的预测能力越准确。
然而,MSE也存在一些局限性,例如对异常值(outliers)敏感,因此在实际应用中,有时候会结合其他指标一起评估模型的性能。
除了上述计算公式,还可以从数学角度和实际应用角度来解释MSE的含义和计算方法。
从数学角度来看,MSE是预测误差的平方的平均值,它可以帮助我们量化预测值与真实值之间的偏差程度。
从实际应用角度来看,MSE可以帮助我们评估模型的预测准确度,从
而指导我们对模型进行调整和改进。
总之,MSE作为一种常用的性能评估指标,在统计学和机器学习领域有着广泛的应用。
希望以上回答能够满足你的要求。
第5章552均方误差准则MSE和LMS算法

第5章552均方误差准则MSE和LMS算法第5章介绍了两个与均方误差准则相关的概念和算法,分别是均方误差(Mean Square Error, MSE)和最小均方(Least Mean Squares, LMS)算法。
首先,我们来介绍均方误差准则。
均方误差是一种常用的衡量预测或估计结果与真实结果之间差异的指标。
在机器学习和模式识别中,我们常常需要根据一些输入数据来预测或估计一些输出结果。
而均方误差就能够帮助我们评估这些预测或估计结果的准确性。
均方误差的计算方法非常简单。
我们首先计算预测结果与真实结果之间的差值,然后将其平方,最后计算这些平方差的平均值。
表达式如下所示:MSE=(1/n)*Σ(y-y')^2其中,MSE表示均方误差,n表示样本数量,y表示真实结果,y'表示预测或估计结果。
接下来,我们来介绍最小均方(Least Mean Squares, LMS)算法。
LMS算法是一种常用的自适应滤波算法,用于根据输入数据来估计一些未知系统的参数,从而实现对输入数据的滤波处理。
LMS算法的核心思想是用当前的估计结果与真实结果之间的误差来调整估计参数,不断更新估计结果,从而逐步逼近真实结果。
具体来说,LMS算法中的参数更新公式如下所示:w(k+1)=w(k)+α*e(k)*x(k)其中,w表示待估计的参数,k表示当前的时间步,α表示学习率,e表示当前的估计误差,x表示当前的输入数据。
根据LMS算法的参数更新公式,我们可以发现,LMS算法每次都会根据当前的估计误差来调整估计参数。
如果当前的估计误差较大,那么LMS 算法就会加大参数的调整量,使得估计结果更快地接近真实结果;反之,如果当前的估计误差较小,那么LMS算法就会减小参数的调整量,从而防止估计结果频繁地跳动。
总结来说,第5章主要介绍了均方误差准则MSE和最小均方(LMS)算法。
均方误差是衡量预测或估计结果与真实结果之间差异的指标,而LMS算法则是一种自适应滤波算法,通过不断调整估计参数来逼近真实结果。
mse 均方误差

mse 均方误差《均方误差(MeanSquaredError,MSE)》均方误差(Mean Squared Error,MSE)是统计学和机器学习领域中极为常用的一种损失函数。
它衡量的是预测值(或称估计值)与实际值(或称真实值)之间的误差的平均值的平方,表达式如下: MSE=1 n∑i=1n(xix^i)2其中,xi是实际值,x^i预测值,n样本个数。
MSE在统计学和机器学习中被广泛应用,既可以用于评估观测值拟合参数值的好坏,也可以用于评估线性回归模型或者其他机器学习模型的拟合效果。
它可以通过比较不同模型对数据拟合程度,来决定模型的最佳参数值,从而提高模型的预测准确性。
有许多算法,如最小二乘法(Least Squares)和类似的算法,它们的基本目的就是要找到使得MSE最小的参数。
MSE作为衡量模型预测准确度的一个指标,有着其他评价指标所没有的优点,例如:(1)MSE对异常值具有良好的鲁棒性;(2)MSE不受随机变量的分布形式的影响;(3)MSE不受变量缩放的影响,也就是说,如果变量x被x = ax 替代,而真实值y和估计值y不变,则MSE也不变;(4)MSE具有量纲平衡的特点,使得多个变量的模型拟合时不会受到其中一个变量的影响。
但MSE也同时存在局限性,例如:(1)MSE不是很适合衡量后验概率分布的性能,而后验概率分布是模型预测准确性的重要指标;(2)当训练样本规模 n大时,MSE可能会出现过度优化现象,也就是由于噪声数据太多,导致估计出来的模型预测准确度反而不如测试数据。
MSE的计算过程一般可以分为两个步骤,即先确定损失函数及损失函数的参数,然后计算平均损失函数的值的平方。
在实际应用中,我们可以通过反向传播算法(Back Propagation)和梯度下降法(Gradient Descent)来优化MSE达到最小值,从而提升模型的准确性。
总之,均方误差MSE是一个统计学和机器学习中非常重要的量化指标,可以用来评价模型的预测精度。
(整理)第5章552均方误差准则MSE和LMS算法

5.5.2均方误差准则(MSE )和LMS 算法引言:均方误差准则同时考虑ISI 及噪声的影响,使其最小化。
本节讨论问题: 1. 均方误差准则;2. 无限长LMS 均衡器(C (z ),J min );3. 有限长LMS 均衡器(C opt ,J min );4. LMS 算法;5. 均衡器的操作;6. 递推LMS 算法收敛特性的分析。
一. 均方误差准则信息符号的估计值:ˆk j k jj I c ∞-=-∞=∑v (无限长均衡器情况)其中, 接收数据样本为:k n k n k n f I η-=+∑v ,k η为白噪声。
估计误差:ˆISI k k k kI I εε=-,包括及噪声 }{k ηε定义:估计值2ˆ[]k kI J E ε=的均方误差为均衡器的性能指数。
均方误差准则:使均方误差性能指数J 最小(min J ),此准则同时考虑使ISI 及噪声影响最小。
获得min J 的途径:调整{}j c ,当min J J =时,opt C C =(最佳抽头系数)寻找opt C 的方法:1)根据正交性原理(线性均方估计):*[]0k k l E l ε-=,所有v 。
(注:与ZF 准则不同的是,这里的输入是经过两个输入滤波器的数据样本k v ,这就包含了噪声)。
即*ˆ[]0kkl E l ε-=,所有I 。
2)求函数极值方法:令?0=→=∂∂opt kJC C 2013年5月3日星期五上午讲于此处,已经是第十次矣。
这两种方法是等价的,证明如下。
证明:求导置零方法与正交性原理等价。
ˆl i m Kkjkj j kjK j j KI c c∞--→∞=-∞=-==∑∑v vlim T k K →∞=V c假如均衡器为有限长,则ˆT k kI =V c 其中11Tk k K k K kk K k K v v v v v ++--+-⎡⎤=⎣⎦V ,以及11TKK K K c c c c c --+-⎡⎤=⎣⎦c 。
最小均方算法原理

最小均方算法原理最小均方算法(Least Mean Square Algorithm,简称LMS算法)是一种常用的自适应滤波算法,用于逼近线性时变系统。
它基于随机梯度下降(Stochastic Gradient Descent)的思想,通过对滤波器的系数进行迭代更新,逐步调整滤波器的输出,以减小期望输出与实际输出之间的均方误差(Mean Square Error, MSE)。
LMS算法的原理可以通过以下步骤概括:1. 初始化:开始时,先对滤波器的系数进行初始化,常见的方法是使用随机数生成一个初始系数矩阵。
2. 输入数据和期望输出:给定输入信号向量x(n)和期望输出d(n),其中n表示时间步。
3. 估计输出:将输入信号向量x(n)通过滤波器的系数矩阵w(n)做卷积运算得到滤波器的估计输出y(n)。
4. 计算误差:将期望输出d(n)与估计输出y(n)相减,得到误差信号e(n)。
5. 更新系数:根据误差信号e(n)和输入信号向量x(n),对滤波器的系数矩阵w(n)进行更新。
更新的公式可以用以下形式表示:w(n+1) = w(n) + 2*μ*x(n)*e(n)其中,μ表示步长参数,用来调整每次更新的幅度。
步长参数的选择需要根据具体问题进行合理调整。
较小的步长可能导致收敛速度较慢,而较大的步长可能导致系统不稳定。
6. 重复上述步骤:重复步骤3-5,直到滤波器的系数收敛或达到预设的停止条件。
LMS算法的收敛性和稳定性与系数的选择有关。
如果步长参数选择合理,并且输入信号的相关性较低,LMS算法通常能够收敛到一个稳定的滤波器解。
然而,在一些情况下,由于相关性较高或者输入信号的统计特性发生变化,LMS算法可能会收敛到一个次优的解。
LMS算法的应用十分广泛,特别是在自适应滤波、信号处理、通信系统等领域。
由于其简单性和实时性,LMS算法在很多实时自适应滤波问题中被广泛采用,如降噪、回声消除等。
在通过训练数据来学习系统行为或估计未知参数的问题中,LMS算法也是一种常用的解决方法。
NLMS,LMS算法介绍参考

CO N T E N T改进的LMS算法——NLMS算法LMS算法原理两种算法性能分析总结LMS(最小均方误差)算法是基于梯度的算法,应用准则是均方误差函数(MSE )最小化原则,它在迭代运算中不断地调整滤波器权系数,直到MSE 达到最小值为止。
设计自适应滤波器的最常用的结构就是横向滤波器结构,输出信号y n 为:y n =w T n ∗x n = i=0N−1w i n x(n −i)N 为滤波器阶数,w T n 为权系数的转置。
FIR 自适应滤波器输出的形式可以看做是x n 与w n 两个矩阵的卷积,误差信号为参考输入信号与实际输出信号的差值e n =d n −y n =d n −w T n ∗x(n)1LMS算法的基本思想是利用e n与x(n)的某种关系,来不断更新自适应滤波器的权系数,从而使均方误差达到最小值,达到最优滤波效果。
均方误差J n为:J n=E e2n=E[d2n−2d n w T n∗x n+w T n∗x n2]通过对J n求导来得到使取得最小值的滤波器权系数,得到使代价函数最小的滤波器系数值:w=R−1∗P其中P=E d n∗x n为输入信号和参考信号的互相关矩阵R=E[x n∗x T n]为输入信号的自相关矩阵将均方误差E e2n对各w i矢量求导,获得均方误差梯度∇n为:∇n=ðE[e2(n)]ðw i⋮ðE[e2(n)]ðw n1设w n +1表示n +1时刻的滤波器系数权矢量,根据最陡下降法,滤波器权系数递归迭代公式表示为:w n +1=w n +μx n ∗e(n)其中μ为自适应步长,用来控制滤波器算法收敛性和稳定性。
对于LMS 算法为了保证收敛,μ的取值范围为:0<μ<2λmax输入信号为加了高斯噪声后的随机信号,取μ=1,α=0.001,μ= 0.2得到两种算法的误差曲线如下图所示:下降曲线的斜率反应了算法的收敛速度,稳定后的误差反映了算法的精度。
均方误差的计算公式

均方误差的计算公式
均方误差是一个常用的统计学指标,用于衡量数据预测模型的准确性。
均方误差是指实际观测值和预测值之间差异的平方和的平均值。
通俗地讲,均方误差就是预测误差的平方和除以样本数量。
均方误差的计算公式为:
MSE = (1/n) * Σ(yi - ŷi)²
其中,MSE表示均方误差,n表示样本数量,yi表示实际观测值,ŷi 表示预测值,Σ表示求和。
均方误差通常用于比较不同预测模型的表现。
预测模型的均方误差越小,说明模型的预测能力越好。
均方误差越大,则说明模型存在较大的预测误差。
在实际应用中,均方误差常常用于评估机器学习模型的表现。
例如,在一个房价预测模型中,我们可以用均方误差来评估模型的准确性。
我们可以将训练数据分为训练集和测试集,使用训练集训练模型,然后将测试集输入模型,计算出测试集的均方误差,以此来评估模型的预测能力。
在时间序列预测中,均方误差也是一个常用的指标。
例如,在股票价格预测中,我们可以使用均方误差来评估预测模型的表现。
我们可以使用历史数据来训练模型,然后使用模型来预测未来的股票价
格,最后通过计算均方误差来评估模型的准确性。
需要注意的是,均方误差只是评估模型表现的一种指标,它并不能代表模型的全部性能。
在实际应用中,我们还需要考虑其他因素,例如模型的复杂度、训练时间、泛化能力等等。
均方误差是一个常用的统计学指标,用于衡量数据预测模型的准确性。
在实际应用中,我们可以使用均方误差来评估机器学习模型、时间序列预测模型等模型的表现。
LMSAPANLMSFRLS算法分析

LMSAPANLMSFRLS算法分析
LMS算法是最常用的自适应滤波算法之一,它是基于最小均方差(MSE)原则的一种加权最小二乘算法。
它的基本思想是以期望和观察误差之间的均方差作为一个指标,试图最小化误差,从而获得一个最优滤波器设计。
LMS算法可以快速而高效地调整滤波器系数,以最大化信号的抑制噪声的能力,是一种逐步增加信号的方法。
APA算法是另一种常用的自适应滤波器算法。
它基于最大似然准则,试图估计出使得观测值合理和自相关系数最大的滤波器。
APA算法不仅考虑了噪声的强度,而且考虑了噪声的自相关性,从而更有效地抑制噪声。
在大多数情况下,APA算法比LMS算法更有效,更稳定,滤波器系数的更新也更平滑。
NLMS算法是一种非线性自适应滤波算法,其基本思想是受到距离准
则的启发,以希尔伯特误差函数作为最小化准则,从而来寻求最优的滤波器设计。
NLMS算法的主要优势在于它的精确度高,收敛速度快,在噪声
多的情况下也有良好的表现。
它也比其他算法更容易实现,因为它只需要计算一个最小二乘系数来计算中间变量,而不需要逆矩阵的计算。
FRLS算法是一种近似最小二乘的自适应滤波算法,它基于利用逆维
费雪滤波器的思想,可以有效地处理一些求逆复杂的情况。
均方误差mse和样本中心矩

均方误差mse和样本中心矩一、什么是均方误差(MSE)均方误差(MSE)是评估回归算法性能的常用指标之一。
它是预测值与真实值之间差异的平方和除以样本数量的平均值,即:MSE = 1/n * Σ(yi - ŷi)²其中,n为样本数量,yi为真实值,ŷi为预测值。
MSE越小,说明模型的预测结果越接近真实值,模型拟合效果越好。
二、如何计算MSE1. 计算每个样本的预测误差:yi - ŷi2. 将每个预测误差取平方:(yi - ŷi)²3. 对所有平方误差求和:Σ(yi - ŷi)²4. 将总和除以样本数量n:1/n * Σ(yi - ŷi)²三、MSE的优缺点1. 优点:(1)易于计算;(2)对于异常值不敏感;(3)可以量化模型预测结果与真实结果之间的差异。
2. 缺点:(1)MSE只考虑了误差的大小,并没有考虑误差的正负;(2)当存在多个离群点时,会导致MSE偏大;(3)当数据分布不均匀时,MSE也会失去一定的意义。
四、什么是样本中心矩样本中心矩是描述数据集分布情况的统计量之一。
它是数据集中各个数据离其均值的距离的幂次方和除以样本数量的幂次方,即:μk = 1/n * Σ(xi - x̄)k其中,n为样本数量,xi为第i个数据点,x̄为样本均值,k为幂次方。
五、如何计算样本中心矩1. 计算每个数据点与均值之间的差异:xi - x̄2. 将每个差异取幂:(xi - x̄)k3. 对所有幂求和:Σ(xi - x̄)k4. 将总和除以样本数量n:1/n * Σ(xi - x̄)k六、常用的样本中心矩1. k=1时,μ1即为样本均值;2. k=2时,μ2即为方差;3. k=3时,μ3即为偏度(衡量分布偏斜程度);4. k=4时,μ4即为峰度(衡量分布峰态程度)。
七、结语MSE和样本中心矩都是评估数据集特征和模型性能的常用指标。
MSE 可以衡量模型预测结果与真实结果之间的差异,而样本中心矩可以描述数据集分布情况。
第5章(56)判决反馈均衡(DFE)
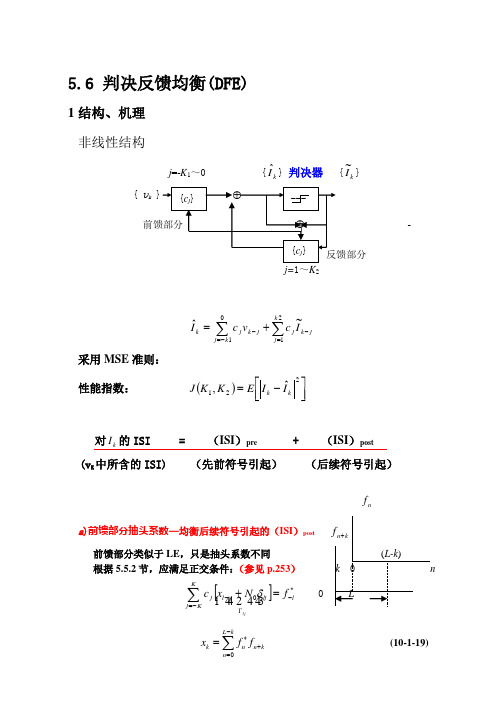
5.6 判决反馈均衡(DFE)1结构、机理非线性结构j =-K 1~0 {k I ˆ} 判决器 {kI ~} { v k-j=1~K 2∑∑-==--+=0121~ˆk j k j j k j jk jkI c vc I采用MSE 准则:性能指数: ()⎥⎦⎤⎢⎣⎡-=221ˆ,k k I I E K K J对k I 的ISI = (ISI )pre + (ISI )post(v K 中所含的ISI) (先前符号引起) (后续符号引起)n fa )前馈部分抽头系数—均衡后续符号引起的(ISI )post 前馈部分类似于LE ,只是抽头系数不同 根据5.5.2节,应满足正交条件:(参见p.253)[]∑-=--=+KKj llj jl jf N x c lj*Γ04434421δ 0L kk n n kn x ff-*+==∑ (10-1-19){}{}{}0:0~:~:~,,n k K k jkn n kn f n L x k L Lc j K K K L K L x ff-*+===-=-≥=→=∑取(均衡范围与信道覆盖范围一致)对DFE 的前馈抽头系数:1- Kj Kj K =-=→∑∑则*0Kj l j lj l j KCx N f δ--=-⎡⎤+=⎣⎦∑()()00K l j Kj n n l j lj j K n C f f N δ--*+-=-=⎡⎤=+⎢⎥⎣⎦∑∑即 ∑∑-=-+-=-+-==⎥⎦⎤⎢⎣⎡+01*00*10,K j l j l m lj j l m m j ~K j l ,f N f f C δ43421ΛΛ01*0*=-=-=∑∑+jm mlm mff所以, ∑∑-=--=-+=⎥⎦⎤⎢⎣⎡+0*00*1K j l l m lj j l m m j ,f N f f C δ即*1j lj l j K C f ψ-=-=∑0,1,,1--=ΛK l (10-3-3)其中,*00, llj m m l j lj m f f N ψδ-+-==+∑ 1,,,1,0l j K =--L(10-3-4)b)反馈部分抽头系数——消除(ISI )pre 。
mse均方误差计算公式 csdn

MSE(Mean Squared Error)均方误差是衡量预测值与真实值之间差异的一个重要指标,在机器学习和统计学中得到广泛应用。
它可以帮助我们评估模型的准确性和稳定性,是许多模型评价指标和优化算法的基础。
本文将介绍 MSE 的计算公式及其在实际应用中的意义和作用。
1. MSE 的定义MSE 是在统计学和机器学习领域中常用的一个指标,用于衡量模型预测值与真实值之间的差异程度。
它是通过计算预测值与真实值之间差异的平方和的均值来得到的,具体的计算公式如下:MSE = Σ (预测值 - 真实值)^2 / n其中,Σ表示对所有样本进行求和,n表示样本数量。
MSE 的数值越小,表示模型的预测能力越准确。
2. MSE 的意义在机器学习中,我们通常会使用模型对数据进行预测,然后通过与真实值进行比较来评估模型的准确性。
MSE 就是用来衡量预测值与真实值之间的差异的指标之一。
当我们得到了一个模型的预测结果后,可以使用 MSE 来评价这个模型的预测性能,从而选择出最优的模型。
MSE 还可以用来比较不同模型之间的预测能力,帮助我们选择最适合当前数据集的模型。
3. MSE 的应用MSE 在实际应用中有着广泛的作用,尤其是在回归分析和预测模型中。
在股票市场预测中,我们可以使用 MSE 来评估不同的预测模型对股价的预测能力;在天气预测中,可以使用 MSE 来评估不同的气象模型对未来气温或降水量的预测准确性。
另外,在工程领域中,MSE 也常常被用来衡量模型预测结果与实际观测结果之间的偏差,帮助工程师们改进设计和优化方案。
4. MSE 的局限性虽然 MSE 是一个重要的模型评价指标,但它也有一些局限性。
MSE对异常值(outliers)比较敏感,这意味着当数据集中存在异常值时,MSE 可能会受到影响,从而影响模型的评价结果。
MSE 也没有考虑到预测值与真实值之间的准确性问题,有时候可能并不能完全反映模型的预测能力。
5. 结语MSE 作为衡量模型预测准确性的重要指标,在机器学习和统计学领域中发挥着重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.5.2均方误差准则(MSE )和LMS 算法引言:均方误差准则同时考虑ISI 及噪声的影响,使其最小化。
本节讨论问题: 1. 均方误差准则;2. 无限长LMS 均衡器(C (z ),J min );3. 有限长LMS 均衡器(C opt ,J min );4. LMS 算法;5. 均衡器的操作;6. 递推LMS 算法收敛特性的分析。
一. 均方误差准则其中, 接收数据样本为:k n k n k nf I η-=+∑v ,k η为白噪声。
估计误差:ˆISI k k k kI I εε=-,包括及噪声 定义:估计值2ˆ[]k kI J E ε=的均方误差为均衡器的性能指数。
均方误差准则:使均方误差性能指数J 最小(min J ),此准则同时考虑使ISI 及噪声影响最小。
获得min J 的途径:调整{}j c ,当min J J =时,opt C C =(最佳抽头系数)寻找opt C 的方法:1)根据正交性原理(线性均方估计):*[]0k k l E l ε-=,所有v 。
(注:与ZF 准则不同的是,这里的输入是经过两个输入滤波器的数据样本k v ,这就包含了噪声)。
即*ˆ[]0k k lE l ε-=,所有I 。
2)求函数极值方法:令?0=→=∂∂opt kJC C 2013年5月3日星期五上午讲于此处,已经是第十次矣。
这两种方法是等价的,证明如下。
证明:求导置零方法与正交性原理等价。
ˆlimKkj k jj k jK j j KI c c ∞--→∞=-∞=-==∑∑vvlim T k K →∞=V c假如均衡器为有限长,则ˆT k kI =V c 其中11Tk k K k K kk K k K v v v v v ++--+-⎡⎤=⎣⎦V ,以及11TKK K K c c c c c --+-⎡⎤=⎣⎦c 。
()2ˆˆ[][()()]k k k k kJ E E I I I I ε**==--c *[()]T k k k E I ε=-V c故{}k k J E ε*∂=-∂V c另一种方法:()22*ˆˆ[][()()] {()()}[][][][]k k k k k k i k i k j k j ijk i k k i j k k j i j k i k j ijijJ E E I I I I E I c I c E I c E I c E I c c E ε*****--****----==--=--=--+∑∑∑∑∑∑c v v v v v v2*[][][][]k i k k i j k k j i j k i k j ijijE I c E I c E I c c E ****----=--+∑∑∑∑v v v v可见,()J c 是{}j c 的平方函数(二次型)。
求导置零可得:*0k k l j k l k j jl J E I c E c **---∂⎡⎤⎡⎤=-+=⎣⎦⎣⎦∂∑v v v 即,***0, k j k j k l j l J E I c l c --⎧⎫⎡⎤∂⎪⎪=--=-∞<<∞⎨⎬⎢⎥∂⎪⎪⎣⎦⎩⎭∑v v ()()**00k k i k k i E E εε--∴==,或v v ,i -∞<<∞{}k k J E ε*∂=-∂V c11Tk k Kk K kk K k K v v v v v ++--+-⎡⎤=⎣⎦V结论:求导方法与正交性原理是等价的,满足正交条件,就可以获得最小MSE 。
二、无限长LMS 均衡器(()min J z C ,性能)1. 求()z C :从正交原理出发,()*0k k l E ε-=v(10-2-27)即*[()]0k j k jk l j E I c ∞--=-∞-=∑vv即()()*jk -jk -l k k l j c E E I ∞-=-∞=∑*vv v (*) 正交条件注: k l -v 是收数据样本,其中的噪声已经白化。
在(*)式左边可以得到:{}********0 k j k l n k j n k j m k l m k l n m n m k j n k l m k j k l n m n m k j n k l m ljnmE E f I f I E f f I I f f E I I N ηηηηδ*------------------⎧⎫⎡⎤⎡⎤⎡⎤=++⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎩⎭⎧⎫=+⎨⎬⎩⎭=+∑∑∑∑∑∑v v式中利用了[]0k n k n k k nf I E ηη-=+=∑,v 。
注:j k jk j k kj j k ,)(δδδδδ==-==-都是Kroenecker 冲激或离散冲激的不同写法。
因此我们有:***,00[]k j k l n m n m l j lj m m l j lj nmmE f f N f f N δδδ--+-+-=+=+∑∑∑v v*00Ln n l j lj n f f N δ+-==+∑0 0,l j lj x N l j L else δ-⎧+-≤⎪=⎨⎪⎩ (A)注:()()(1/)X z F z F z **=,()1F z **-代表了()F z 序列的共轭颠倒序列。
或者说()1F z **-代表了()F z 的MF(零时延)。
()()(1/)X z F z F z **=()101L L f f z f z --=+++11110()L L L L L z f f z f z f z **-*-+*--⎡⎤++++⎣⎦000LLLLL ijLi j iL jiL j i j i j zfzfzzff z -*-*----======∑∑∑∑00LLLi j iL j i j zff z *---===∑∑00L Ln i i n i n f f z *-===∑∑L Ll n ln l L n ff z *-+=-==∑∑(注:令l i n =-)故*0Ll n n l n x f f +==∑,其支撑为:L l L -≤≤或者说,可以得到*****0LL kk n nlk l l l k n n kn n k lln n x f ff f f f f ff f ----+++===*====∑∑∑∑也可以写为j l j l L n jl n n Ln jl n n x fff f---=-+=-+==∑∑)(0**(*)式右边:,*******, 1(){[]}{}{}k k l n k k l k n k l n k l n k k l n k k l nnc c E I E I f I f E I I E I δηη---------==+=+∑∑v式中,,,10k k l n l n n l n lδδ---=-⎧==⎨≠-⎩,当,当由此可得{}** , 0l k k lf L l E I --⎧-≤≤=⎨⎩v (B)将(A )、(B )两式代入(*)式:*0[]jl jlj l j c xN f δ∞--=-∞+=∑上式就是: *0l l l l c x N c f -⊗+=取Z 变换: ()()110[()]()C z F z F z N F z **-**-+= (10-2-31)则MMSE 均衡器 ()110()()()F z C z F z F z N **-**-=+ (10-2-32) 等效MMSE 均衡器: ()()10011()()C z F z F z N X z N **-'==++ (10-2-33)kI ^()z C '2. 求min J (最小均方误差) (1) 时域2*****ˆ[][()][][]k k k k k k k j k jjJ E E I I E I E c εεεε-==-=-∑v 利用正交原理第二项为零,所以2**min ˆ[()][][()]k k k k k j k jjJ E I I I E I E I c -=-=-∑v *[]j k j k j j jjc c E I c c f --=-=-∑∑v (利用(B)式)令信息符号的平均功率为1,则2[]1k c E I ==min 011jj l ll j J cf c f ∞-==-∞=-=-⊗∑{k I ⎭⎬⎫k I ^()z C ()z F ∞Tx ,Ch,MF,WF{}()0min 01b J f c b f cb z b z B b j jj jn j jn nn n n -=∴===↔--∞-∞=-∞-∞=∑∑∑(2)频域通过z 变换及令,T j e z ω=将min J 式的{}关系变换成n f J ~min()()关系ωωH e X J T j ⋅~min全传输系统响应:{}()()()0N z X z X z B b n +=↔ (10-2-35)以z 反变换(留数法)求:()112n-n cb B z z dz j π=⎰()()()1001122ccX z b B z z dz dz j j z X z N ππ-∴==+⎡⎤⎣⎦⎰⎰(10-2-36)j T z e Tωπω=≤令,且,()()()()()0012 2j T Tj T j T j TTj TTj TTX e b e e jT d j X eNX e Td Xe Nωπωωπωωππωωπωπ---=⋅⋅+=+⎰⎰ (10-2-37)代入 min 01J b =-,得 ()0min2T j TTN T J d X eNππωωπ-=+⎰将()j T X e ω以信道折叠谱表示。
因为()()()k t kTx x kT h t h t *===⊗-()()h t h t *⊗-的傅里叶变换为2()H ω,故212()FTk k n n x t kT H T T πδω∞∞=-∞=-∞⎛⎫-←−→+ ⎪⎝⎭∑∑又22()()()j ft j fkT k k k k k k k FT x t kT x t kT e dt x e DTFT x ππδδ∞∞∞∞--=-∞=-∞=-∞-∞⎧⎫-=-==⎨⎬⎩⎭∑∑∑⎰所以()212 j Tn n X e H T T T ωππωω∞=-∞⎛⎫=+≤ ⎪⎝⎭∑, (10-2-18) 所以min2for ISI 0212T Tn T TN J d n H N T T ππωππω-∞=-∞===⎛⎫++ ⎪⎝⎭⎰∑ (10-2-38)所以,当ISI=0时, 0min min 0011N J J N =<<+, (10-2-39)因k k k I I ˆ-=ε,故ˆk k k I I ε=+,22ˆ[||]||k k k E I E I ε=-,利用正交原理*ˆ[]0k k lE ε-=I ,易证:222ˆ||||||k k k E I E I E ε=+,即2min ˆ[]1k E I J =-。
