第六章 弹体的空气动力特征计算
空气动力系数及导数精品文档
• 6.6弹身零攻角下的阻力系数
• 6.7升力面零攻角零舵偏角下的阻力系数
• 6.8诱导阻力系数
2019/10/15
2
6.1升力系数
计算导弹的空气动力系数时,常用的坐标系有两个:弹 体坐标系与速度坐标系。
在速度坐标系中的升力系数 与弹体坐标系中的轴 向力系数 和法向力系数 之间有如下关系式:
在攻角和舵偏角不大时,可近似表示为:
损失了一部分法向力;另一面由于弹身的有效径展比增大,又
增大了干扰法向力。
2019/10/15
19
6.2升力系数导数
• 6.2.1升力系数对攻角的导数
6.2.1.3弹身与升力面的气动干扰 2.弹身附面层的影响
可引入一个修正系数
2019/10/15
20
6.2升力系数导数
• 6.2.1升力系数对攻角的导数
6空气动力系数及导数
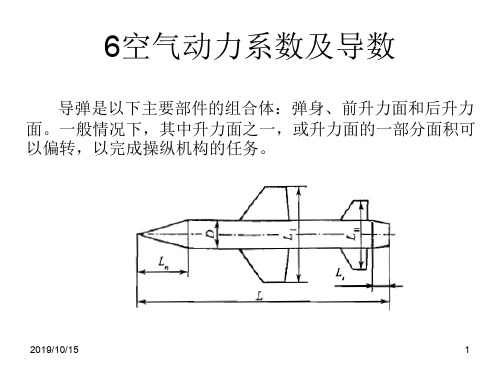
导弹是以下主要部件的组合体:弹身、前升力面和后升力 面。一般情况下,其中升力面之一,或升力面的一部分面积可 以偏转,以完成操纵机构的任务。
2019/10/15
1
6空气动力系数及导数
• 6.1升力系数
• 6.2升力系数导数
• 6.3大攻角下的升力系数
• 6.4侧向力系数
• 6.5阻力系数
干扰系数
操纵机构相对效率
前升力面在后升力面处产生的下洗角对舵偏角的导数
2019/10/15
28
6.2升力系数导数
• 6.2.2升力系数对舵偏角的导数
6.2.2.1弹身与操纵面的气动干扰
设弹身攻角为零,而外露翼相对于弹身轴线转动 角, 称为 情况。计算与实验都表明,在这种情况下计及弹身 干扰的外露翼的法向力近似等于单独翼的法向力。
空气动力矩系数及导数

2014-7-2
30
7.4导弹绕z轴旋转时的俯仰力矩
实验表明,阻尼力矩值与角速度 成正比,可表示为
由于 式中
有 导弹的俯仰阻尼导数。
这个导数的值主要与导弹的几何参数、质心位置和马赫数 有关,始终为负数。
2014-7-2 31
7.4导弹绕z轴旋转时的俯仰力矩
• 导弹稳定飞行时的纵向平衡
导弹稳定运动时,运动学参数(飞行速度、攻角、侧滑 角、滚转角以及角速度 等)不随时间变化。 在稳定飞行时,导弹的转动角速度 不变,即 角加速度等于零。由此可见,在稳定飞行时,相对于通过质 心的ox,oy,oz轴的力矩平衡,即导弹处于平衡状态。
7空气动力矩系数及导数
• • • • • •
2014-7-2
7.1俯仰力矩系数 7.2导弹对攻角和舵偏角的焦点 7.3导弹绕z轴转动时的俯仰力矩 7.4偏航力矩系数 7.5滚转力矩系数 7.6舵面的铰链力矩
1
7.1俯仰力矩系数
• 7.1.1一般公式
在研究作用在导弹上的力矩时,将采用弹体坐系oxyz。坐 标原点取在质心;ox轴沿弹身轴线,指向前方;oy轴垂直于 ox轴,指向上方;oz轴垂直于ox轴和oy轴,指向右方。 俯仰力矩也称为纵向力矩,由空气动力和喷气反作用力产 生。研究空气动力矩采用无量纲的系数比较方便,对于俯仰力 矩有。
一般情况下,这个关系式具有复杂的非线性特征,但当自 变量的值很小时,非线性很弱,上式可写成以下的线性函数的 形式:
2014-7-2
其中,
为俯仰力矩对各个自变量的偏导数。
3
7.1俯仰力矩系数
• 7.1.1一般公式
严格讲,俯仰力矩还与其他一些参数有关,例如:侧滑角、 副翼偏角、导弹绕ox轴的滚转角速度等。但是在一般情况下, 这些影响不显著,可以忽略。 无量纲的力矩系数是无量纲参数的函数。由于 量纲为1/s,所以需要把它们无量纲化,得到 的
空气动力计算课件

在不可压缩、无粘性流体的稳定流动中,流体的压力、速度和位置 之间遵循伯努利定理。
牛顿第二定律
流体的加速度与作用力成正比,与流体的质量成反比,即F=ma。
03
空气动力学的应用
航空航天
1 2 3
飞机设计
飞机设计过程中需要考虑空气动力学原理,如机 翼设计和尾翼布局,以实现升力、阻力和稳定性 等性能要求。
可压缩性
流体的密度随着压力和温 度的变化而变化,称为可 压缩性。
流体静力学
01
流体平衡
在无外力作用的情况下,流体内 部各部分之间不会发生相对运动 ,称为流体平衡。
02
03
压力
浮力
流体对容器壁施加的压力,称为 压力。
由于流体静压力的存在,物体在 流体中受到向上的力,称为浮力 。
流体动力学
流体运动
流体在力的作用下发生的运动,称为流体运动。
实验测量方法的优势
实验测量方法能够提供直接、真实的实验数据,有助于验证理论分析和 数值模拟的结果,同时也有助于发现新现象和开发新技术。
03
实验测量方法的局限
实验测量方法受限于实验设备和条件,难以模拟复杂的流场和力场,同
时实验结果可能受到环境因素的影响。
理论分析方法
理论分析方法概述
理论分析方法是基于物理原理和数学推导来分析空气动力 现象。这种方法能够提供深入的理论解释和预测,有助于 指导实验和数值模拟。
学习目标
培养解决实际问题的能力 ,提高科研素养
学会使用专业软件进行空 气动力计算和分析
掌握空气动力学基本概念 、原理和方法
01
03 02
02
空气动力学基础
流体性质
01
02
气动力计算公式

气动力计算公式
气动力是指空气对物体的作用力,其大小与物体的形状、速度、密度等因素有关。
常见的气动力计算公式有:
1. 空气阻力公式:Fd=ρv^2CdA。
其中,Fd表示空气阻力,ρ表示空气密度,v表示物体速度,Cd表示阻力系数,A表示物体在垂直于运动方向上的投影面积。
2. 升力公式:Fp=ρv^2ClA。
其中,Fp表示升力,Cl表示升力系数,其他符号同上。
此外,对于飞行器(如飞机),通常取一个原点位于飞行器重心的气流坐标系,将空气动力分解为三个方向上的分量。
设坐标系的x轴平行于气流方向且正向与气流方向相反,y轴在飞行器对称面内与x轴垂直且正向指向飞行器上方,z轴垂直于xy平面,指向右翼。
则合力在x、y、z三个轴上的分量分别称为阻力、举力和侧向力。
若空气动力作用点与飞行器重心不重合,则飞行器还受到一个合力矩的作用,它在x、y、z三个轴上的分量分别称为滚转力矩、偏航力矩和俯仰力矩。
以上信息仅供参考,建议查阅空气动力学书籍或者咨询专业人士以获取更准确的信息。
100毫米加农炮杀伤爆破弹空气动力特性分析和弹道计算详解

综合课程设计(B2)任务书一、设计题目:100毫米加农炮杀伤爆破弹空气动力特性分析和弹道计算二、已知条件:1 结构尺寸(见附图)2 弹丸直径 D =100 mm3 弹丸初速 v 0 =900m/s4 弹丸射角 045θ=︒5 弹丸质量 m =15.6 kg6 弹丸转动惯量比 222.03540.21529.46y x J J kgm kgm ==7 火炮缠度 η=32(d)8 引信为海时-1 引信,其外露长度为129 mm ,质量0.641kg,旋入弹体深度为29mm ,小端直径为8mm ;9 质心位置(距弹底) X =172mm10弹体材料 D60三、设计要求: 1 用AUTOCAD 绘制弹体零件图和半备弹丸图 2 对弹丸结构进行空气动力特性分析 3 利用所学方法进行弹丸空气动力参数计算 4 根据弹丸空气动力参数进行弹道计算 5 进行弹道飞行稳定性计算 6 总结分析计算结果7 撰写课程设计说明书学生签名:日 期:2010-6-29课程设计(论文)评语及成绩评定前言本次的综合课程设计是在学习了《弹丸空气动力学》与《弹道学》的基础上进行的,主要对弹丸结构进行空气动力特性分析,计算弹丸空气动力参数及弹道计算并对弹丸的飞行稳定性进行校核。
任何武器弹药的设计,总是在一定的战术技术要求下进行的。
一般对武器弹药的战术技术要求,主要有威力、射程、精度和机动性等。
而这些战术要求之间又是相互依存相互矛盾的。
一个先进武器的设计过程,也是一个发现矛盾、分析矛盾和解决矛盾的过程。
弹丸在空气中飞行,周围空气与弹丸在相互作用下产生力和力矩,所受的空气动力和力矩取决于弹丸表面的受力情况,实际上就是压强和切向应力沿弹体表面的分布。
寻求改善作用弹丸上的空气动力,提高飞行稳定性。
空气动力学导源于流体力学,流体力学是物理学的一个分支,它研究的是流体中的作用力和流体的运动规律。
弹丸空气动力学是在空气动力学的基础上发展起来的,是研究空气与在空气中飞行的弹丸之间相互作用的科学,可归纳为:研究弹丸飞行时,周围空气的相对运动规律;空气与弹丸相互作用的力和力矩组;寻求改善作用弹丸上的空气动力,提高飞行稳定性的一门科学。
空气动力学的力量计算公式

空气动力学的力量计算公式空气动力学是研究物体在空气中受到的力和运动的学科。
在空气动力学中,力的计算是至关重要的,因为它可以帮助我们理解物体在空气中的运动规律。
在本文中,我们将讨论空气动力学的力量计算公式,以及这些公式的应用。
空气动力学的力量计算公式可以分为两类,气动力和阻力。
气动力是指物体在空气中受到的推力或拉力,而阻力则是物体在空气中受到的阻碍运动的力。
下面我们将分别介绍这两种力的计算公式。
首先是气动力的计算公式。
气动力的大小取决于物体的形状、速度和空气的密度。
一般来说,气动力可以通过以下公式进行计算:F = 0.5 ρ v^2 A Cd。
其中,F表示气动力的大小,ρ表示空气的密度,v表示物体的速度,A表示物体的横截面积,Cd表示物体的阻力系数。
这个公式告诉我们,气动力与空气密度、速度的平方和物体的横截面积成正比,与物体的阻力系数成反比。
这个公式在飞行器设计和空气动力学研究中有着广泛的应用。
接下来是阻力的计算公式。
阻力的大小取决于物体的形状、速度和空气的密度。
一般来说,阻力可以通过以下公式进行计算:D = 0.5 ρ v^2 A Cd。
其中,D表示阻力的大小,ρ表示空气的密度,v表示物体的速度,A表示物体的横截面积,Cd表示物体的阻力系数。
这个公式与气动力的计算公式非常相似,只是它们的物理意义不同。
阻力的大小与空气密度、速度的平方和物体的横截面积成正比,与物体的阻力系数成反比。
以上是空气动力学的力量计算公式,它们可以帮助我们理解物体在空气中受到的力和运动规律。
这些公式在飞行器设计、汽车设计和建筑结构设计等领域都有着重要的应用。
通过对这些公式的研究和应用,我们可以更好地理解物体在空气中的运动规律,从而设计出更加高效和安全的产品。
除了以上介绍的气动力和阻力的计算公式,空气动力学还涉及到其他一些力的计算公式,比如升力的计算公式和升阻比的计算公式。
这些公式在飞行器设计和空气动力学研究中也有着重要的应用。
弹体的空气动力特征计算

弹体形状的影响
弹头形状
弹头的形状对空气阻力、升力、稳定 性等特性有显著影响。尖头弹头通常 具有较低的阻力系数,而钝头弹头则 具有较高的阻力系数。
弹翼形状
弹翼的形状和大小对升力和阻力有重 要影响。合理的弹翼设计可以减小阻 力,提高射程和精度。
弹体速度的影响
亚音速与超音速
在亚音速时,空气阻力是主要影响因 素;而在超音速时,波阻成为主要因 素。超音速弹体的阻力系数随速度增 加而减小。
弹体的空气动力特征 计算
目 录
• 引言 • 弹体空气动力学基础 • 弹体空气动力特征参数计算 • 弹体空气动力特征参数的影响因素 • 弹体空气动力特征参数的实验验证 • 结论与展望
01
引言
研究背景和意义
军事应用
弹体的空气动力特性在军事领域具有重要意义,如导弹、炮弹等武器的精确制导需要依 赖于对弹体空气动力特性的准确计算。
弹体俯仰力矩系数计算
俯仰力矩系数定义
01
表示弹体在空气中运动时受到的俯仰力矩与作用在弹体上的力
矩之比。
俯仰力矩系数计算公式
02
根据空气动力学原理,俯仰力矩系数可以通过测量弹体的速度
和俯仰力矩来计算。
俯仰力矩系数影响因素
03
俯仰力矩系数受到弹体形状、迎角、空气密度等因素的影响。
04
弹体空气动力特征参数 的影响因素
研究不足与展望
目前对弹体空气动力特性的研究主要 集中在理想状态下的数值模拟和实验 测试,实际应用中需要考虑更多复杂 因素的影响。
未来可以结合先进的数值方法和实验 技术,深入研究弹体空气动力特性与 飞行性能之间的关系,为弹体设计提 供更为精准的理论依据。
针对不同形状、不同飞行速度的弹体, 需要开展更为细致的空气动力特性研 究,以揭示其内在规律。
空气动力系数及导数49页

03.09.2019
5
6.1升力系数
对上式除以 ,对 取导数,得到在
点有
03.09.2019
前、后升力区域的气流阻滞系数 飞行器部件的相对面积
6
6.1升力系数
为单独弹身的法向力,不涉及升力面对它的影响 为前升力面的法向力导数,一部分由外露面(两片翼 组合在一起)产生,一部分由外露翼面影响区内的弹 身产生。合成后表示为单独翼面的法向力导数与干扰 系数的乘积
其中
和
03.09.2019
应按马赫数
计算
7
6.1升力系数
与等号右边第二项类似,唯一区别是后升力面的攻角 应考虑由前升力面对后升力面产生的平均下洗角,因 而
在小攻角下,关系式
近似为线性,这时有
而导数 可表示为
03.09.2019 式中所有量 应按马赫数
计算 8
6.1升力系数
因此,为了寻求飞行器升力(或法向力)系数对攻角的导 数,必须确定以下的量:
• 6.6弹身零攻角下的阻力系数
• 6.7升力面零攻角零舵偏角下的阻力系数
• 6.8诱导阻力系数
03.09.2019
2
6.1升力系数
计算导弹的空气动力系数时,常用的坐标系有两个:弹 体坐标系与速度坐标系。
在速度坐标系中的升力系数 与弹体坐标系中的轴 向力系数 和法向力系数 之间有如下关系式:
在攻角和舵偏角不大时,可近似表示为:
其中干扰系数
03.09.2019
16
6.2升力系数导数
• 6.2.1升力系数对攻角的导数
6.2.1.3弹身与升力面的气动干扰
根据细长体理论,干扰系数
安装升力面的弹身区段的直径
通过弹身的升力面的翼展
空气动力系数及导数-PPT精品文档49页
04.10.2019
30
6.2升力系数导数
• 6.2.2升力系数对舵偏角的导数
6.2.2.2操纵机构的相对效率
1. 旋转翼(全动舵)
为了保证飞行器在宽广马赫数范围内具有良好的操纵 性,可把整个翼作为舵面来使用,而不作为稳定面。这时 舵旋转轴一般与弹轴线垂直,但在某些情况下,它可有后 掠角,这时舵偏角在与旋转轴垂直的平面内计量。
的关系只在这些角的量
值小时保持线性特性。随着角度增大的程度,
都与线性显著偏离。
非线性程度与马赫数和飞行器的几何形状有关。当弹
身相对直径增大和升力面展弦比减少时,非线性更加显著,
而这恰恰是现代无人驾驶飞行器具有的特征。此外,当飞
行速度增大到超声速
时,非线性也增大。
所有这些将导致,从攻角和舵偏角数值达到10度开始, 升力的计算必须考虑非线性分量。
摩擦阻力是作用在弹身所有表面的粘性摩擦力的合力; 压差阻力是作用在头部和尾部以及底部分离的压力与远 前方来流压力之差的合力。
全弹身的摩擦阻力系数
弹头部压差阻力系数
弹尾部压差阻力系数
04.10.2019
弹底部压差阻力系数
39
6.6弹身零攻角下的阻力系数
• 6.6.1摩擦阻力系数 1. 一般公式
04.10.2019
04.10.2019
35
6.3大攻角下的升力系数
6.3.1 弹身的升力系数
6.3.2 前升力面的升力系数
04.10.2019
36
6.4侧向力系数
侧向力 是总空气动力在速度坐标系 轴上的投影。 除侧向力外,还常研究横向力Z,它是总空气动力在弹体坐标 系oz 轴上的投影。侧向力系数与横向力系数的关系是
课程设计30mm杀伤爆破弹的空气动力特性分析和弹道计算

摘要本次课程设计主要是对130mm杀伤爆破弹的空气动力特性分析和弹道的计算。
是以《弹道学》为基础的课程设计。
是在学习课程之后对我们的知识的加深理解和检验。
空气动力学是航天航空重要的基础学科之一,是飞行器设计的先行官,是航天航空领域的重要专业之一。
它在学术研究内容是流体力学的一个分支,但是在航天航空的作用流体力学本身。
著名的空气动力学家吴镇远在他的1981年的学术论文说到,19世纪末开始预测作用在运动物体上的空气作用力和力矩将成为空气动力学的研究主题。
弹丸空气动力学与外弹道学的关系极为密切,外弹道学是讨论弹丸在空中飞行运动规律及其相关问题的科学。
外弹道学研究对象中所谓“弹丸在空中的运动”是指弹丸质心运动——旋转和摆动;所谓“相关问题”是指弹丸在空中运动时所形成的空气动力、弹丸飞行稳定性理论和外弹道学的重要应用。
主要任务:“130mm杀爆弹空气动力特性分析和弹道计算” 就是应用《外弹道学》相关的弹道表的相关知识,结合弹丸结构参数分析空气动力特性、计算迎角为零时的空气动力,以及空气中的弹道计算和飞行稳定性计算。
关键词:弹丸结构;空气动力;弹道计算目录前言 01 绘制弹体零件图和半备弹丸图 (1)2 弹丸结构空气动力特性分析 (2)旋成体的几何参数及外形 (2)作用于弹丸的空气动力和力矩 (3)作用于弹丸的空气动力及空气动力的分析 (3)作用于弹丸的空气动力矩及其分析 (4)3 弹丸空气动力参数计算 (5)摩擦阻力系数的计算 (5)雷诺数的计算 (5)3.1.2 S f/S的计算 (5)计算马赫数(Ma) (5)旋转弹丸的摩阻系数的计算 (6)涡阻系数的计算 (6)涡阻系数的计算 (6)波阻系数的计算 (7)弹头部波阻系数的计算 (7)弹尾部波阻系数的计算 (7)波阻系数的计算 (7)阻力系数的计算 (8)各阻力所占百分数的计算 (8)弹形系数及弹道系数的计算 (8)计算弹形系数 (8)计算弹道系数 (8)4弹道诸元的计算 (9)5飞行稳定性的计算 (11)陀螺稳定性的计算 (11)翻转力矩特征数Kmzo的计算 (12)阻质心矩的计算 (12)追随稳定性的计算 (13)对H(ys)的计算 (13)5.2.2 vs的计算 (13)Kmz(Ms)的计算 (15)6计算结果分析 (16)弹丸空气动力参数计算结果分析 (16)摩阻系数分析 (16)涡阻系数分析 (16)波阻系数分析 (16)弹道计算结果分析 (17)弹形系数分析 (17)弹道系数分析 (17)空气弹道分析 (17)弹丸飞行稳定性计算结果分析 (17)7总结 (19)参考文献 (20)附图一:弹体半剖 (21)附图二:三维弹体图 (21)前言弹道学是研究各种弹丸或其他发射体从发射开始到终点的运动规律及伴随发生的有关现象的学科。
第六章 弹体的空气动力特征计算

6.2 底部阻力
3. 热传导对Cxd的影响 当弹体向附面层传热的强度加大,伴随有底部阻 力的减小。在同一情况下,假若弹体由外部气流加热, 则Cxd增大。 二、弹体底部阻力的工程计算 1.估算底阻的近似公式 对于底部压强的极限情况即静压强为零的时侯,此 时压强系数为 pd p 2
C pd max 1 2 V 2 1 2 kM p 2
当ReL <Re*时,即LB<xt。说明整个弹体是层流附面层。 弹体摩阻系数CxfB为
CxfB S f 1.328 Sf 1 2 1/ 3 (2Cxfp ) M 0 M (1 0.03M ) 2 Sm Sm Re L
6.1 摩擦阻力
当ReL >Re* 时,即LB >xt 。说明整个弹体是混合附面层。 弹体摩阻系数CxfB 为
式中Cxn为头部波阻系数,Cxt为尾部波阻系数;Cxd为底部 阻力系数;Cxf为弹体摩阻系数。
6.3 迎角为零时弹体空气动力特征计算
图6-10为具有锥形头部的弹体总阻力系数以及其各 分量随M∞数的变化情况。 (一)弹头部波阻系数的计算 1、圆锥形头部 圆锥表面压强系数可 用下列经验公式计算
空气动力计算

)0.5
对曲线形收缩尾部,尾部波阻系数查图6-3的曲线。收缩比 用下式计算
Db Db / Dc
上一页 下一页 返回
第三节 弹体气动特性计算
三、底部阻力系数Cx1b
底部阻力是由于底部压强不等于环境大气压强而形成的。底部阻 力大小不但与弹体底部形状和飞行马赫数有关,而且还与弹底是否有 火箭喷流有关。
四、弹体摩擦阻力系数CxfB
计算弹体摩擦阻力系数是以平板在不可压缩流体中摩擦阻力系数 为基础的。考虑到弹体表面不是平板,引入形状修正系数ηλ,由于 空气是可压缩的,引入压缩性修正系数ηM;再加上空气阻力计算是以 弹体最大横截面积(SM或Sc)为参考面积,可以得到
CxfB
1 2
(2Cxfp
)M
0M
S
f
Cx ln
0.3(1 2M )
n2
M
2
1
上一页 下一页 返回
第三节 弹体气动特性计算
二、尾部波阻系数Cx1t 尾部波阻是在弹体存在收缩(或扩张)尾部,M>1时形成激波
而产生的。对截锥形收缩尾部的波阻系数,在估算中可用下式 计算
Cx ln
Байду номын сангаас
[(0.0016
0.002
M
2
)
(
01.7
)
](1
S
b
xvpf
式中 xcpn、xcpt、xcpf-头部、尾部和黏性附加法向力压力 中心到弹顶的距离。
上一页 下一页 返回
第三节 弹体气动特性计算
6.3.5 弹体俯仰力矩系数
在外弹道计算中需要的力矩系数通常是对质心而言的,若弹体质 心位置距弹顶距离为XG,则法向力所提供的俯仰力矩系数为
作用在弹上力

C
y
:升力系数对攻角的导数。
C
z
:侧向力系数对侧滑角的导数。
空气动力作用于压心,通常压心不与 质心重合,有力矩产生。
求力矩公式见 P46,式2-37
此式是气动力力矩相对于体坐标系的 求解式。
2.2.3 重力
重力= 地心引力+地球自转产生离心力
离心加速度: g vae(eR 0)
引力由引力势函数对距离求微分得到.
设:
(4)
:所有质量点到O1 点距离的矢量和。
把(4)代入(3)整理后 变质量弹(箭)运动方程有:
(各项含义见书P38)
(5)
2. 变质量弹(箭)相对惯性坐标系绕质心 动力学方程
角动量守恒定律:刚体相对惯性坐标系中 的固定参考点转动的角动量(动量矩) 的变化率等于外力矩之和。
即: dH M
dt
,, :产生俯仰、偏航、滚动控制
的发动机综合摆角。 控制力矩见式2-46。
2.2.5 晃动力、力矩
是由于液体燃料在储箱内晃动产生的, 火箭飞行时储箱晃动使液体震荡造成 .
2.2.6 发动机惯性力、力矩
执行机构摆动发动机喷管 ,而发动机 具有质量和转动惯量,即产生惯性力和 力矩。
见P52 图2-22
§ 2.3 弹(箭)运动方程
弹(箭)运动方程组通常包括:
1) 质心运动的动力学方程-----弹(箭)质 心的加速度与作用在质心上的力的相互 关系式。
2) 绕质心运动的动力学方程---弹(箭)绕 质心的角加速度与作用的力矩之间的相 互关系。
3) 运动学方程--A. 质心运动学方程: 速度和位移关系。
dt
dm dt
< 0 ,系统质量减小 ,推力 ,速度增加
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.2 底部阻力
1.Re数、附面层特性对Cxd的影响 对不同形状的弹丸,Re数对底部压强系数的影响有 不同的结果。如以层流绕流而言,1号模型在研究的Re 数范围内底压系数大约变化了60%,而2、3、4号模 型约变化一倍左右,如图(a)所示。对于比较短粗的 模型其压强系数的变化范围没有细长模型那样大,并 且是在小Re数时达最小值,然后逐渐增大。在紊流附 面层中Re数对Cxd的影响不太大,见图(b)。
6.3 迎角为零时弹体空气动力特征计算
2、尖拱形头部 尖拱形头部的波阻计算公式为
196n2 16 0.002 1.7 Cxn 0.0016 ( 0 ) 1 2 2 M 14( M 18) n
当头部为圆锥,其锥面压强系数按虚线所示。当来流 M∞数>1时,圆锥形头部产生圆锥激波,气流经激波产 生突跃压缩,然后在锥型流区继续进行等熵压缩。这样, 在圆锥面上得到的压强系数Cp 为正值并为常数,它所产 生的阻力系数称头部波阻。图中实线为曲母线头部表面 压强系数的变化情况。 在圆锥形头部和圆柱部的结合部,气流向外折转产生 膨胀波,压强下降,使圆柱部表面压强系数Cp突降为负 值,然后逐步回升呈曲线形分布。在迎角为零的情况下, 作用在圆柱部上的压强与轴线垂直,不产生阻力。
CxfB
Sf 1 (2Cxfp ) 2 Sm
其中, 为形状修正系数。 1 显然 ,它取决于弹体 的关 B B 和 的长径比 。 系曲线见图6-1。
6.1 摩擦阻力
当气流M增大时,空气的可压缩性对附面层内的流动 产生一定的影响。在层流附面层内,外层气流速度较高。 通过粘性力对内层气流作用。致使内层空气微团温度升 高,而且沿物面法线的速度分布规律也有显著变化。如 图6-2所示。随着M∞增大,附面层厚度也显著增大。在 高速下,附面层内速度分布的改变使法向速度梯度减小。 从而使摩擦应力以及摩擦应力减小。对于层流平板 Cxf Re 与 M∞的关系如图6-3。在M∞=0时, 随 M∞ Cxf Re 1.33 Re 增大, C下降。 xf
(Cxfp ) M 0
三、临界雷诺数Re* 1、平板 从层流转捩为紊流的临界雷诺数Re*为 V xt Re* 5 105 2、弹体 临界雷诺数Re*取决于弹体表面粗糙度,弹体表面压强 梯度、以及表面温度、气流紊流度等。一般情况下取
6.1 摩擦阻力
当ReL <Re*时,即LB<xt。说明整个弹体是层流附面层。 弹体摩阻系数CxfB为CxfB的增长会引起底 阻系数Cxd的减小。这一现象的物理本质是, CxfB增大时, 在弹体底截面处的附面层要变厚。变厚的附面层就好象 隔板一样,阻碍着外部高速气流的引射作用,因而在弹 体后面的稀薄度就减小了,底阻系数也就变小了。 (二)超音速下弹体的底部阻力 超音速下底阻形成的原因要比亚音速时复杂。它不 仅与外部气流的引射作用有关,而且与尾激波有关。超 音速时,影响底部阻力的主要因素有:Re数、附面层 特性、尾部外形、底部的热状态、有无喷流、马赫数、 迎角及飞行高度等。下面介绍一些对底阻有重要影响的 实验曲线。
6.2 底部阻力
2.尾部外形对Cxd的影响 由图可见有尾部的弹体会使底部压强系数增加很快, 尤其是紊流附面层情况。但随β t增大,尾锥表面的稀薄 度也在增大。这样就存在对应尾部最小阻力的最佳角。 图6-7表明紊流附面层和层流附面层的最佳角在7~lO 度之间,并且紊流附面层的Cxd在最佳区域的变化很缓 慢。
6.1 摩擦阻力
一、摩擦阻力 弹体表面摩擦阻力的计算,严格说必须考虑雷诺数、 附面层特性、弹体的几何形状、表面状况、马赫数、以 及气流与弹体表面间的热交换,但实际情况要同时考虑 这些因素的影响是不可能的。而且由于对轴对称物体的 附面层理论研究还不充分,所以目前求摩擦阻力系数时, 基本上还是利用平面物体,特别是利用平板的研究结果。 把弹体展成一“相等平板”来处理。所谓“相当平板” 是这样一块平板,它的单面面积等于弹体实际受摩擦表 面积Sf ,其长度等于弹长LB,转捩点的位置xt与原弹体 转捩点的位置相同。
当附面层全部是紊流时,弹体摩阻系数CxfB 为
CxfB Sf 0.032 2 0.467 (1 0.2M ) 0.145 Re L Sm
对于高速的弹丸(尤其是旋转弹丸)的摩阻通常把附面层 全部视为紊流状态。
6.2 底部阻力
一、弹体底部形成负压的物理原因 (一)亚音速下弹体的底部阻力 亚音速气流绕流弹丸时,弹体表面附面层在尾端分离, 使尾部气流分为两部分,外部流速较高的气流对于底部几 乎是滞止的气体起着掺混和引射的作用,并把这些气体引 射开,因为没有来自其它方面补充的空气流量,底部的气 流变得稀薄起来,并在底部空间形成一个低压区。 实验指出:底部负压在很大程度上取决于弹体长度、 相对底截面积和附面层状态,因而在计算底部压强与底 部阻力时可以与摩擦阻力联系起来。为此引入相对于底 截面积Sd的摩阻系数Cxfd,则 Sf C xfd C xfp Sd 其中Cxfp是相对于侧表面积的平板摩阻系数。
2 kM
6.2 底部阻力
对于空气k=1.4
C pd max
图8-8中曲线表明:实际情况下的底部压强系数和极限值 有很大差别,并且只是后者的一部分。即 Cpd kd Cpd max 式中kd 为修正系数。 在实验数据的基础上 有以下关系式 Kd=0.6 k1(2-k1)
1.43 2 M
6.3 迎角为零时弹体空气动力特征计算
头部波阻Xn 为
X n ( p p )Sm
0.002 1.7 Cxn C p 0.0016 ( ) 0 2 M
当圆锥半顶角β0≤50°时,按此公式计算,误差不大于5%, 适用于M∞ ≤7-8。 图6-11为不同长 径比圆锥形头部波阻 系数随M的变化曲线。
式中Cxn为头部波阻系数,Cxt为尾部波阻系数;Cxd为底部 阻力系数;Cxf为弹体摩阻系数。
6.3 迎角为零时弹体空气动力特征计算
图6-10为具有锥形头部的弹体总阻力系数以及其各 分量随M∞数的变化情况。 (一)弹头部波阻系数的计算 1、圆锥形头部 圆锥表面压强系数可 用下列经验公式计算
0.002 1.7 C p 0.0016 ( ) 0 2 M 其中β 0为头部半顶角,以度计。
2 Dm 其中 S m 是弹体最大截面积。 4
两者应相等,得 CxfB Cxfp
Sf 1 (2Cxfp ) Sm 2 Sm
Sf
6.1 摩擦阻力
上式是近似的,由此算得的结果比实际要小一些。因为 弹体与平板上的情况有所不同。弹体前部存在负的压强 梯度,它使附面层变薄了。在较薄的附面层中空气速度 沿法向由零变为V∞,梯度 必然要大些,因此摩擦应力 比平板要大一些。为此,对弹体的摩阻系数计算作一形 状修正。
CxfB S f 1.328 Sf 1 2 1/ 3 (2Cxfp ) M 0 M (1 0.03M ) 2 Sm Sm Re L
6.1 摩擦阻力
当ReL >Re* 时,即LB >xt 。说明整个弹体是混合附面层。 弹体摩阻系数CxfB 为
0.032 0.032 1.328 2 0.467 2 0.467 2 1/ 3 Sl CxfB (1 0.2 M ) (1 0.2 M ) (1 0.03 M ) 0.145 0.145 0.5 Re Re Re L * * Sf Sf Sm
6.2 底部阻力
亚音速弹体底部的压强系数的近似表达式为 0.029 C pd C xfd 再用CxfB来表示相当于弹体最大横截面积的摩阻系数, 即 Sf C xfB C xfp Sm 则有
C xfd C xfB
底阻系数可以写为
Sm Sd
3
C xd
0.029 Dd C xfB Dm
当迎角为零时,由于对称关系,弹体只受到轴向力 (即阻力),法向力和俯仰力矩均等于零。阻力的一般表 达式可写为 1 X 0 Cx 0 V2 S m 2 其中Cx0为迎角为零时阻力系数。 一、超音速绕流情况下弹体阻力的组成 图6-9所示的是典型的超音速绕流弹体的画图。
6.3 迎角为零时弹体空气动力特征计算
6.1 摩擦阻力
实验指出,在层流时,压缩性的修正量是不大的。 当M∞不大于1.5时,甚至可以不予修正。在较大M∞数 时,层流附面层压缩性影响的修正可按下式进行 [Cxfp ] 2 1/ 3 Ml (1 0.03M ) [Cxfp ]M 0
]M 0 其中 [Cxfp是层流附面层未计及压缩性影响的平板摩阻系 数。 附面层为紊流状态时,压缩性影响远较层流状态严重。 紊流附面层时压缩性影响的修正公式可按下式进行 [Cxfp ] 2 1/ 2 Mt (1 0.12M ) [Cxfp ]M 0 其中[Cxfp ]是紊流附面层未计及压缩性影响的平板摩阻系 M 0 数。
6.1 摩擦阻力
上式中的系数值0.12适用于雷诺数 Re 。随着 Re∞数增 106 大,此系数值有所增长,特别是当Re∞的数量级为108 时,取0.18能给出更好的近似结果。 有时也采用
2 0.467 Mt (1 0.2M )
在考虑了形状修正和压缩性修正后,弹体摩阻系数CxfB 可 Sf 改写为 1 CxfB (2Cxfp ) M 0 M 2 Sm 其中ηM 可用经验公式求得。
6.1 摩擦阻力
二、关于平板摩擦系数Cxfp 1.在低速及附面层全部为层流时,摩阻系数 Cxfp为 1.328 V L (Cxfp )M 0 Re L B ReL 2.在低速及附面层全部为紊流时,摩阻系数 Cxfp按 ReL的 大小分别为
5 105 Re L 107 107 Re L 108 2 108 Re L 1010 (Cxfp ) M 0 (Cxfp ) M 0 0.0742 Re L 0.2 0.455 (log Re L )2.58 0.032 Re L 0.145
