小升初计数重点考查内容————计数方法综合(1)——标数法、递推法
小升初计数高频考点汇总与方法总结

五、常见方法 1.标数法——加法原理 2.递推法——枚举归纳 3.对应法 4.整体法 5.排除法
六、概率与统计 1.古典概型 2.概率可乘性
【例1】(★★) 四个人分别穿着红、黄、绿、蓝四种颜色的球衣练习传球,每人都 可以把球传给另外三个人中的任意一个。先由红衣人发球,并作为 第1次传球,经过4次传球后球仍然回到红衣人手中。请问:整个传 球过程共有多少种不同的可能?
五、常见方法 1.标数法——加法原理 2.递推法——枚举归纳 3.对应法 4.整体法 5.排除法
六、概率与统计 1.古典概型 2.概率可乘性
重点例题:例1,例3,例4,例6 3
1
【例2】(★★★)
小悦买了10块相同的巧克力,每天最少吃一块,直到吃完, 共有多少种吃法?
【例3】(★★★★)
用1至9这9个数字组成一个没有重复数字的九位数,满足以下要 求:每一位上的数字要么大于它前面的所有数字,要么小于它前 面的所有数字。请问:这样的九位数共有多少个?
【例4】(★★★)
正方形内部共有2016个点(结合正方形4个顶点,共2020个点,其 中任意三点,不在同一条直线上)任意两点间可剪一刀,将正方 形剪成以2020个点为顶点的三角形,最多可剪成多少个三角形?
小升初计数高频考点汇总与方法总结
加油站
一、枚举归纳
分类枚举——有序,规律 树形枚举——对应,对称
二、加法原理
分类用加:结合容斥,合理分类 分步用乘:特殊位置,优先考虑
三、排列组合 1.排列,组合意义,计算方法 2.三种经典方法:捆绑法,插空法,挡板法 3.先选后排思想
四、容斥原理 1.容斥计算公式——单层要加,双层要减 2.韦恩图及意义——各区域具体含义
【例5】(★★★★)
小升初计数重点考查内容计数方法综合标数法递推法

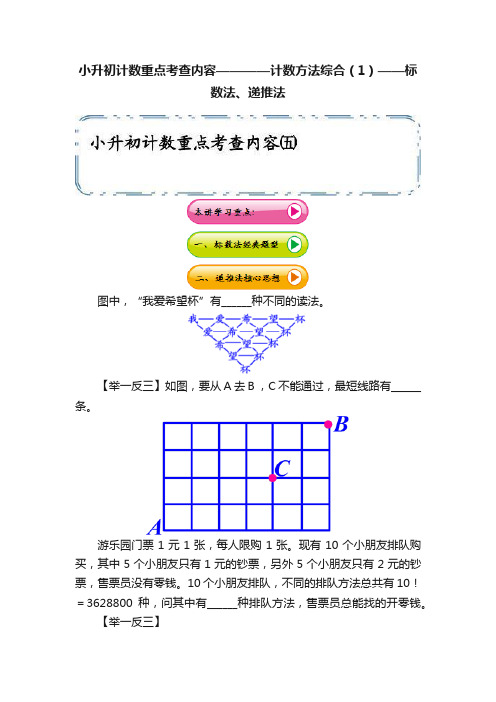
图中,“我爱希望杯”有______种不同的读法。
【举一反三】如图,要从A 去B ,C 不能通过,最短线路有______条。
游乐园门票1元1张,每人限购1张。
现有10个小朋友排队购买,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有零钱。
10个小朋友排队,不同的排队方法总共有10!=3628800种,问其中有______种排队方法,售票员总能找的开零钱。
【举一反三】在一次选举中甲、乙两人参加竞选,甲得5张选票,乙也得5张选票,问在对这10张选票逐一唱票的过程中,乙的得票始终未能领先的点票记录共有______种可能。
小升初计数重点考查内容㈤计数方法综合⑴——标数法、递推法(★★)(★★★★★)一个楼梯共有10级阶梯,规定每步可以逐一级台阶或两级台阶,走完这10级台阶,一共有______种不同走法。
对一个自然数进行如下操作:如果是偶数则除以2,如果是奇数则加1,如此进行下去直到得数为1停止。
问经过9次操作变为1的数有______个。
在平面上画8个圆,最多可以把平面分成_______部分。
在线测试题温馨提示:请在线作答,以便及时反馈孩子的薄弱环节。
1.如下图所示,要从A 点沿线段走到B ,要求每一步都是向右、向上或者斜上方。
问有多少种不同的走法?B A FA A .18B .20C .22D .24(★★★) (★★★) (★★★☆)2.有15个相同的棋子,一个人分若干次取,每次可取1个,2个,3个或4个,但要求每次取之后留下的棋子数不是3或4的倍数,有种不同的方法取完这堆棋子。
A.11 B.22 C.33 D.183.上一段12级楼梯,规定每一步只能上一级或两级楼梯,要登上第12级楼梯,不同的走法共有多少种?A.233 B.230 C.243 D.2534.给你一架天平和两个砝码,这两个砝码分别重20克和50克,如果再添四个砝码,则这六个砝码可以称的重量种类最多是多少种。
(天平的左右两盘均可放砝码)A.268 B.256 C.364 D.2805.平面上的5个圆和3条直线最多能把平面分成多少部分?A.55 B.57 C.32 D.48。
小升初数学计数知识点

计数模块枚举法一内容概述:教学一对一:1. 冬冬在一张纸上画了一些图形,如图4-1所示,每个图形都是由若干条线段连接组成的。
请你数一数,纸上一共有多少条线段?(最外面的大长方形是纸的边框,不算在内)2. 要沿着如图2-4所示的道路从A点走到B点,并且每段路最多只能经过一次,一共有多少种不同的走法?3. 小明决定去香山、颐和园、圆明园这三个景点旅游,要走遍这三个景点,他一共有多少种不同的游览顺序?4. 小王准备从青岛、三亚、桂林、杭州这4个地方中选2个去旅游,小王有多少种不同的选择方式?如果小王想去其中的3个地方,又有多少种选择方式?5. 小烧饼每个5角钱,大烧饼每个2元钱,冬冬一共有6元钱,如果把这些钱全部用来买烧饼,一共有多少种不同的买法?6. 在一次知识抢答比赛中,小悦和冬冬两个人一共答对了10道题,并且每人都有答对的题目。
如果每道题1分,那么小悦和冬冬分别可能得多少分?请把所有的可能填写到下面的表格里:7. 两个海盗分20枚金币。
请问:(1)如果每个海盗最少分5枚金币,一共有多少种不同的分法?(2)如果每个海盗最多分到16枚金币,一共有多少种不同的分法?8. 有15个玻璃球,要把它们分成两堆,一共有几种不同的分法?这两堆球的个数可能相差几个?装10盒。
张奶奶一共有几种不同的装法?10. 小悦、冬冬、阿奇三个人一共有7本课外书,每个人至少有一本。
小悦、冬冬、阿奇分别有几本课外书?请写出全部可能的情况。
11. 如图4-3,小悦画了一个小房子,如果每画一笔都不能拐弯,那么她最少画了几笔?12. 小悦把8块绿豆糕摆成如图4-4所示的图形,让冬冬挑两块挨在一起的绿豆糕。
请问:冬冬一共有多少种不同的挑法?13. 小悦、冬冬、阿奇三个人去看电影,他们买了三张座位相邻的票。
他们三人的座位顺序一共有多少种不同的安排方法?14. 小李摆摊卖货,小木偶每个卖1元,大木偶每个卖2元。
他今天一共卖出了5个木偶。
小李今天一共可能卖了多少钱?15. (1)老师给小悦14个相同的练习本。
小升初计数题知识点总结

小升初计数题知识点总结一、计数的基本概念计数是数学中重要的基本概念之一。
所谓计数就是指把同类事物按照一定的顺序进行标记。
在小升初的数学学习中,计数是一个非常基础的概念,许多其他数学知识都是建立在计数的基础上的。
1.1 计数的概念计数是数学中一个非常基本的概念。
在日常生活中,我们经常要进行计数,比如数小朋友的人数、家里有多少个苹果等等。
计数的目的是为了对一组事物进行量化,使得我们能够更方便地理解和操作这组事物。
1.2 计数的表示方式在实际的计数中,我们通常会使用阿拉伯数字来表示数量,比如1、2、3、4……。
除了阿拉伯数字外,计数还可以用汉字、英文单词等不同的方式来表示。
1.3 整数和小数的计数在计数中,整数和小数都有其特定的用途。
整数通常用于表示事物的个数,比如有5本书、10个苹果等。
而小数通常用于表示事物的部分,比如0.5升水、1.5公斤大米等。
1.4 计数中的连续性在实际的计数中,有时需要对一段范围内的事物进行计数。
这时我们需要掌握计数的连续性,即能够按照一定的规律对事物进行连续计数。
1.5 计数中的分类在进行计数时,通常会遇到需要对事物进行分类的情况。
这时我们需要掌握对事物进行分类计数的方法,比如使用表格、图表等形式进行分类统计。
二、计数问题的解决方法在小升初的数学学习中,我们不仅需要了解计数的基本概念,还需要掌握如何解决各种不同形式的计数问题。
下面介绍几种常见的计数问题解决方法。
2.1 顺序计数顺序计数是最基本的计数方式,通常用于对一组事物进行依次编号。
解决顺序计数问题时,我们需要注意事物的顺序,确保每个事物都被正确地编号。
2.2 分类计数在实际的计数中,我们经常需要对一组事物进行分类计数。
解决分类计数问题时,我们需要对事物进行合适的分类,然后分别对不同的类别进行计数。
2.3 集合计数集合计数是对一组事物进行整体计数的方法。
解决集合计数问题时,我们需要对整个集合进行综合计数,确保每个事物都被正确地统计。
小学数学计数之递推法.教师版

7-6-4. 计数之递推法教学目标前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法,比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等,这里再集中学习一下计数中其他常见的方法,主要有归纳法、整体法、对应法、递推法.对这些计数方法与技巧要做到灵活运用.对于某些难以发现其一般情形的计数问题,可以找出其相邻数之间的递归关系,有了这一递归关系就可以利用前面的数求出后面未知的数,这种方法称为递推法.【例1】每对小兔子在出生后一个月就长成大兔子,而每对大兔子每个月能生出一对小兔子来.如果一个人在一月份买了一对小兔子,那么十二月份的时候他共有多少对兔子?【考点】计数之递推法【难度】 3 星【题型】解答【解析】第一个月,有1对小兔子;第二个月,长成大兔子,所以还是 1 对;第三个月,大兔子生下一对小兔子,所以共有 2 对;第四个月,刚生下的小兔子长成大兔子,而原来的大兔子又生下一对小兔子,共有3 对;第五个月,两对大兔子生下 2 对小兔子,共有 5 对;⋯⋯这个特点的说明每月的大兔子数为上月的兔子数,每月的小兔子数为上月的大兔子数,即上上月的兔子数,所以每月的兔子数为上月的兔子数答案】144与上上月的兔子数相加.依次类推可以列出下表:经过月数:---1---2---3---4---5---6---7---8---9---10---11---12 兔子对数:---1---1---2---3---5---8--13--21--34--55--89 —144,所以十二月份的时候总共有144 对兔子.例 2 】树木生长的过程中,新生的枝条往往需要一段“休息”时间供自身生长,而后才能萌发新枝.一棵树苗在一年后长出一条新枝,第二年新枝“休息”,老枝依旧萌发新枝;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则依次“休息”.这在生物学上称为“鲁德维格定律”.那么十年后这棵树上有多少条树枝?考点】计数之递推法【难度】 3 星【题型】解答解析】一株树木各个年份的枝桠数,构成斐波那契数列:1,2,3,5,8,13,21,34,55,89,⋯⋯所以十年后树上有89 条树枝.答案】89例3】一楼梯共10 级,规定每步只能跨上一级或两级,要登上第10 级,共有多少种不同走法?考点】计数之递推法【难度】 4 星【题型】解答3 级4 级 10 级 3 种5 种 ?解析】 登 1 级 1 种方法 2级2种我们观察每级的种数,发现这么一个规律:从第三个数开始,每个数是前面两个数的和;依此规律 我们就可以知道了第 10 级的种数是 89.其实这也是加法的运用:假如我们把这个人开始登楼梯的位 置看做 A 0,那么登了 1 级的位置是在 A 1,2 级在 A 2... A 10 级就在 A 10.到 A 3 的前一步有两个位置;分 别是 A 2 和 A 1 .在这里要强调一点,那么 A 2 到 A 3 既然是一步到了,那么 A 2 、A 3 之间就是一种选 择了; 同理 A 1 到 A 3 也是一种选择了. 同时我们假设到 n 级的选择数就是 An .那么从 A 0 到 A 3 就 可以分成两类了:第一类: A0 A1 --------------------------------------------- A3 ,那么就可以分成两步.有 A1×1 种,也就是 A1 种;(A1 A3 是一种选择 )第二类:A0 A2 A3, 同样道理 有 A2 .类类相加原理: A3 = A1 + A2,依次类推 An = An-1 + An-2.89 一楼梯共 10 级,规定每步只能跨上一级或三级,要登上第 10 级,共有多少种不同走法? 计数之递推法 【难度】 4 星 【题型】解答登 1 级 2 级 3 级 4 级 5 级 10 级1 种方法 1 种2 种3 种4 种 ............. ?我们观察每级的种数,发现这么一个规律:从第三个数开始,每个数是前面相隔的两个数的和;依 此规律我们就可以知道了第 10 级的种数是 28. 28 1×2 的小长方形 ( 横的竖的都行 ) 覆盖 2×10 的方格网,共有多少种不同的盖法. 计数之递推法 【难度】 4 星 【题型】解答如果用 1 2的长方形盖 2 n 的长方形, 设种数为 a n ,则 a 1 1,a 2 2,对于 n 3,左边可能竖放 1 个 1 2的,也可能横放 2 个1 2的,前者有 a n-1种,后者有 a n-2种,所以 a n a n-1 a n-2 ,所以根据递推, 覆盖 2 10的长方形一共有 89 种. 89用 1 3 的小长方形覆盖 3 8 的方格网,共有多少种不同的盖法? 计数之递推法 【难度】 5 星 【题型】解答如果用 1 3的长方形盖 3 n 的长方形,设种数为 a n ,则 a 1 1,a 2 1,a 3 2,对于 n 4 ,左边可能竖 放 1 个1 3的,也可能横放 3 个1 3的,前者有 a n-1种,后者有 a n-3种,所以 a n a n-1 a n-3 ,依照这 条递推公式列表:13 13 有一堆火柴共 12 根,如果规定每次取 1~3 根,那么取完这堆火柴共有多少种不同取法? 计数之递推法【难度】 4 星 【题型】解答取 1 根火柴有 1 种方法,取 2 根火柴有 2 种方法,取 3 根火柴有 4 种取法,以后取任意根火柴的种 数等于取到前三根火柴所有情况之和,以此类推,参照上题列表如下:取完这堆火柴一共有 927 种方法. 答案】 927答案】 巩固】解析】 答案】例 4 】 考答案】例答案】例 6 】 考巩固】 一堆苹果共有 8个,如果规定每次取 1~3 个,那么取完这堆苹果共有多少种不同取法? 考点】计数之递推法 【难度】 4 星 【题型】解答解析】 取 1个苹果有 1种方法,取 2个苹果有 2 种方法,取 3 个苹果有 4 种取法,以后取任意个苹果的种数等于取到前三个苹果所有情况之和,以此类推,参照上题列表如下:1个 2个 3个 4个 5个 6个 7个 8个 1 2 4713244481取完这堆苹果一共有 81 种方法.答案】 81例 7 】 有 10 枚棋子,每次拿出 2 枚或 3 枚,要想将 10 枚棋子全部拿完,共有多少种不同的拿法? 考点】计数之递推法 【难度】 4 星 【题型】解答 解析】本题可以采用递推法,也可以进行分类讨论,当然也可以直接进行枚举.(法 1)递推法.假设有 n 枚棋子,每次拿出 2枚或 3枚,将 n 枚棋子全部拿完的拿法总数为 a n种. 则a 2 1, a 3 1 , a 4 1 .由于每次拿出 2 枚或 3 枚,所以 a n a n 3 a n 2 (n 5).所以,a 5 a 2 a 3 2; a 6 a 3 a 4 2; a 7 a 4 a 5 3; a 8 a 5 a 64; a 9 a 6 a 7 5; a 10 a 7 a 8 7 .即当有 10枚棋子时,共有 7 种不同的拿法. ( 法 2)分类讨论.由于棋子总数为 10枚,是个偶数,而每次拿 2枚或 3枚,所以其中拿 3 枚的次数也应该是偶数.由 于拿 3 枚的次数不超过 3 次,所以只能为 0 次或 2 次. 若为 0 次,则相当于 2 枚拿了 5次,此时有 1 种拿法;若为 2 次,则 2 枚也拿了 2 次,共拿了 4 次,所以此时有 C 42 6 种拿法. 根据加法原理,共有 1 67 种不同的拿法.答案】 7行,共有多少种回家的方法? 解析】 蜜蜂 “每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行 ”这意味着它只能从小号码的蜂房爬近相邻大号码的蜂房.明确了行走路径的方向,就可以运用标数法进行计算.如右图所示,小蜜蜂从 出发到 B 处共有 89 种不同的回家方法. 答案】 89 巩固】小蜜蜂通过蜂巢房间,规定只能由小号房间进入大号房间问小蜜蜂由 方法?考点】计数之递推法 【难度】 4 星 【题型】解答 解析】斐波那契数列第八项. 21 种.例 8】 如下图,一只蜜蜂从 A 处出发,回到家里 B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆考点】计数之递推法 【难度】 4 星 【题型】A 房间到达B 房间有多少种 例 9 】 如下图,一只蜜蜂从 A 处出发,回到家里 B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?解析】按照蜜蜂只能从小号码的蜂房爬近相邻大号码的蜂房的原则,运用标号法进行计算.如右图所示,小蜜蜂从 A 出发到 B 处共有296 种不同的回家方法.答案】296例10】对一个自然数作如下操作:如果是偶数则除以2,如果是奇数则加1,如此进行直到得数为1操作停止.问经过9 次操作变为1的数有多少个?考点】计数之递推法【难度】4星【题型】解答解析】可以先尝试一下,倒推得出下面的图:1264其中经 1 次操作变为 1 的 1 个,即2,经 2 次操作变为1的 1 个,即4,经 3 次操作变为1的 2 个,是一奇一偶,以后发现,每个偶数可以变成两个数,分别是一奇一偶,每个奇数变为一个偶数,于是,经1、2、⋯次操作变为 1 的数的个数依次为:1,1,2,3,5,8,⋯这一串数中有个特点:自第三个开始,每一个等于前两个的和,即即经过9 次操作变为 1 的数有34 个.为什么上面的规律是正确的呢?道理也很简单. 设经过n次操作变为1的数的个数为a n,则a1 1,a2 1,a3 2,⋯从上面的图看出,a n 1比a n大.一方面,每个经过n次操作变为 1 的数,乘以2,就得出一个偶数,经过n 1次操作变为1;反过来,每个经过n 1次操作变为 1 的偶数,除以2,就得出一个经过n次操作变为 1 的数. 所以经过n次操作变为 1 的数与经过n 1次操作变为 1 的偶数恰好一样多.前者的个数是a n ,因此后者也是a n个. 另一方面,每个经过n次操作变为1的偶数,减去1,就得出一个奇数,它经过n 1次操作变为1,反过来.每个经过n 1次操作变为 1 的奇数,加上1,就得出一个偶数,它经过n次操作变为 1. 所以经过n次操作变为1的偶数经过n 1次操作变为 1 的奇数恰好一样多. 而由上面所说,前者的个数就是a n 1 ,因此后者也是a n 1 .经过n 1 次操作变为 1 的数,分为偶数、奇数两类,所以a n 1 a n a n 1,即上面所说的规律的确成立.答案】34例11】有20个石子,一个人分若干次取,每次可以取 1 个,2个或 3 个,但是每次取完之后不能留下质数个,有多少种方法取完石子?(石子之间不作区分,只考虑石子个数)考点】计数之递推法【难度】 5 星【题型】解答解析】如果没有剩下的不能使质数这个条件,那么递推方法与前面学过的递推法相似,只不过每次都是前面 3 个数相加.现在剩下的不能是质数个,可以看作是质数个的取法总数都是0,然后再进行递推.答案】25巩固】有20个相同的棋子,一个人分若干次取,每次可取1个,2个,3个或4个,但要求每次取之后留下的棋子数不是 3 或 4 的倍数,有种不同的方法取完这堆棋子.考点】计数之递推法【难度】 5 星【题型】填空解析】把20、0和20以内不是3或4的倍数的数写成一串,用递推法把所有的方法数写出来:答案】54例12】 4 个人进行篮球训练,互相传球接球,要求每个人接球后马上传给别人,开始由甲发球,并作为第一次传球,第五次传球后,球又回到甲手中,问有多少种传球方法?考点】计数之递推法【难度】 5 星【题型】解答解析】设第n次传球后,球又回到甲手中的传球方法有a n 种.可以想象前n 1次传球,如果每一次传球都任选其他三人中的一人进行传球,即每次传球都有3种可能,由乘法原理,共有31 43 434⋯2 434 34n31 (种) (n 1) 个 3 传球方法.这些传球方法并不是都符合要求的,它们可以分为两类,一类是第n 1次恰好传到甲手中,这有a n 1种传法,它们不符合要求,因为这样第n 次无法再把球传给甲;另一类是第n 1次传球,球不在甲手中,第n次持球人再将球传给甲,有a n种传法.根据加法原理,有a n 1 a n3 3 ⋯3 3n 1.1n41 4 4n42 4 4 4 43( n 1)个 3由于甲是发球者,一次传球后球又回到甲手中的传球方法是不存在的,所以a1 0 .利用递推关系可以得到:a2 3 0 3 ,a3 3 3 3 6 ,a4 3 3 3 6 21 ,a5 3 3 3 3 21 60 .这说明经过 5 次传球后,球仍回到甲手中的传球方法有60种.本题也可以列表求解.由于第n 次传球后,球不在甲手中的传球方法,第n 1次传球后球就可能回到甲手中,所以只需求从表中可以看出经过五次传球后,球仍回到甲手中的传球方法共有60 种.答案】60巩固】五个人互相传球,由甲开始发球,并作为第一次传球,经过 4 次传球后,球仍回到甲手中.问:共有多少种传球方式?考点】计数之递推法【难度】 5 星【题型】解答解析】递推法.设第n 次传球后球传到甲的手中的方法有a n种.由于每次传球有 4 种选择,传n 次有4n 次可能.其中有的球在甲的手中,有的球不在甲的手中,球在甲的手中的有a n 种,球不在甲的手中的,正八边形的任一顶点跳到其相邻两个顶点中任意一个,落到顶点 点 A 出发恰好跳 10次后落到 E 的方法总数为 种. 考点】计数之递推法 【难度】 5 星 【题型】填空 关键词】清华附中 解析】可以使用递推法.回到 A跳到 B 或 H跳到 C 或 G跳到 D 或 F 停在 E1步12步 213步314步 6425步1046步 201487步34148步 6848289步11648其中, 第一列的每一 个数都等于它的上一行的第二列的数的2 倍,第二列的每 一个数都等于它的上 一行的第一列和第三列的两个数的和,第三列的每一个数都等于它的上一行的第二列和第四列的两 个数的和,第四列的每一个数都等于它的上一行的第三列的数,第五列的每一个数都等于都等于它 的上一行的第四列的数的 2 倍.这一规律很容易根据青蛙的跳动规则分析得来.所以,青蛙第 10 步跳到 E 有 48 2 96种方法. 答案】 96 A 点开始跳动,它每次可以随意跳到相邻两个顶点中的一个上,6 次之内 (含 6 次)跳到 D 点有种不同跳法.考点】计数之递推法 【难度】 5 星 【题型】填空解析】采用递推的方法. 列表如下:跳到 A 跳到 B 跳到 C 停在 D 跳到 E1步11 2步 21 13步31 2 4步 53 25步83 5 6步 138 5其中, 根据规则, 每次可以随意跳到相邻两个顶点中的一个上, 一旦跳到 D 点上就停止跳动.所以, 每一步跳到 A 的跳法数等于上一步跳到 B 和 E 的跳法数之和,每一步跳到 B 的跳法数等于上一步跳 到 A 和C 的跳法数之和,每一步跳到 C 的跳法数等于上一步跳到 B 的跳法数,每一步跳到 E 的跳法 数等于上一步跳到 A 的跳法数,每一步跳到 D 的跳法数等于上一步跳到 C 或跳到 E 的跳法数. 观察可知,上面的递推结果与前面的枚举也相吻合,所以青蛙在 6 次之内 (含 6 次)跳到 D 点共有 1 1 2 3 5 12种不同的跳法.答案】 12例 14】 有 6 个木箱,编号为 1,2,3,⋯⋯,6,每个箱子有一把钥匙, 6 把钥匙各不相同,每个箱子放进一把钥匙锁好.先挖开 1,2 号箱子,可以取出钥匙去开箱子上的锁,如果最终能把 6 把锁都打 开,则说这是一种放钥匙的 “好 ”的方法,那么 “好”的方法共有 种.考点】计数之递推法 【难度】 5 星 【题型】填空下一次传球都可以将球传到甲的手中,故有 由于 a 1 0,所以 a 2 41 a 1 4, a 3 42 到甲手中的传球方法有 52 种.答案】 52a n 1种.所以 a n a n 1 4n . a 2 12 , a 4 43 a 3 52 .即经过 4次传球后,球仍回例 13 】 设 A 、 E 为正八边形 ABCDEFGH 的相对顶点,顶点 A 处有一只青蛙,除顶点 E 外青蛙可以从E 时青蛙就停止跳动,则青蛙从顶 巩固】在正五边形 ABCDE 上,一只青蛙从 一旦跳到 D 点上就停止跳动.青蛙在 CD关键词】迎春杯,中年级组,决赛解析】(法1)分类讨论.如果1,2号箱中恰好放的就是1,2号箱的钥匙,显然不是“好”的方法,所以“好” 的方法有两种情况:⑴1,2号箱的钥匙恰有1把在1,2号箱中,另一箱装的是3~6箱的钥匙.⑵1,2 号箱的钥匙都不在1,2号箱中.对于⑴,从1,2号箱的钥匙中选 1 把,从3~6 号箱的钥匙中选1把,共有 2 4 8(种)选法,每一种选法放入1,2 号箱各有 2 种放法,共有8 2 16(种)放法.不妨设1,3号箱的钥匙放入了1,2号箱,此时 3 号箱不能装2号箱的钥匙,有3种选法,依次类推,可知此时不同的放法有 3 2 1 6(种).所以,第⑴种情况有“好”的方法16 6 96(种).对于⑵,从3~6 号箱的钥匙中选 2 把放入1,2 号箱,有 4 3 12(种)放法.不妨设3, 4 号箱的钥匙放入了1, 2 号箱.此时1, 2 号箱的钥匙不可能都放在3,4 号箱中,也就是说3,4 号箱中至少有 1 把5, 6 号箱的钥匙.如果3,4号箱中有2把5,6 号箱的钥匙,也就是说3,4号箱中放的恰好是5,6号箱的钥匙,那么1, 2 号箱的钥匙放在5, 6 号箱中,有 2 2 4 种放法;如果3,4 号箱中有1把5,6号箱的钥匙,比如3,4号箱中放的是5,1号箱的钥匙,则只能是 5 号箱放 6 号箱的钥匙, 6 号箱放 2 号箱的钥匙,有 2 1 2 种放法;同理,3,4号箱放5,2 号箱或6,1号箱或6,2号箱的钥匙,也各有 2 种放法.所以,第⑵种情况有“好”的放法12 4 2 2 2 2 144(种).所以“好”的方法共有96 144 240(种).(法2)递推法.设第1,2,3,⋯,6号箱子中所放的钥匙号码依次为k1,k2,k3,⋯,k6.当箱子数为n(n 2 )时,好的放法的总数为a n.当n 2时,显然a2 2( k1 1,k2 2或k1 2,k2 1).当n 3时,显然k3 3,否则第3个箱子打不开,从而k1 3或k2 3,如果k1 3,则把 1 号箱子和 3 号箱子看作一个整体,这样还是锁着1, 2 两号钥匙,撬开1,2 两号箱子,那么方法有a2种;当k2 3也是如此.于是n 2时的每一种情况对应k1 3或k2 3时的一种情况,这样就有a3 2a2 4 .当n 4时,也一定有k n n ,否则第n 个箱子打不开,从而k1、k2、⋯⋯、k n 1中有一个为n ,不论其中哪一个是n ,由于必须要把该箱子打开才能打开n 号箱子,所以可以将锁着这把钥匙的箱子与第n号箱子看作1个箱子,于是还是锁着k1、k2、⋯⋯、k n 1这n 1 把钥匙,需要撬开1,2两号箱子,所以每种情况都有a n 1种.所以a n n 1 a n 1.所以,a6 5a5 5 4a4 L 5 4 3 2a2 2 5! 240 ,即好的方法总数为240 种.答案】240巩固】有10 个木箱,编号为1,2,3,⋯⋯,10,每个箱子有一把钥匙,10 把钥匙各不相同,每个箱子放进一把钥匙锁好.先挖开1,2 号箱子,可以取出钥匙去开箱子上的锁,如果最终能把10 把锁都打开,则说这是一种放钥匙的“好”的方法,那么“好”的方法共有种.考点】计数之递推法【难度】 5 星【题型】填空解析】递推法.设第1,2,3,⋯,6 号箱子中所放的钥匙号码依次为k1 ,k2 ,k3 ,⋯,k6 .当箱子数为n(n 2)时,好的放法的总数为a n.当n 2时,显然a2 2( k1 1,k2 2或k1 2,k2 1).当n 3时,显然k3 3,否则第3个箱子打不开,从而k1 3或k2 3,如果k1 3,则把 1 号箱子和 3 号箱子看作一个整体,这样还是锁着1, 2 两号钥匙,撬开1,2 两号箱子,那么方法有a2种;当k2 3也是如此.于是n 2时的每一种情况对应k1 3或k2 3时的一种情况,这样就有a 32a24 .当n 4时,也一定有k n n,否则第n个箱子打不开,从而k1、k2、⋯⋯、k n 1中有一个为n,不论其中哪一个是n ,由于必须要把该箱子打开才能打开n 号箱子,所以可以将锁着这把钥匙的箱子与第n号箱子看作1个箱子,于是还是锁着k1、k2、⋯⋯、k n 1这n 1 把钥匙,需要撬开1,2 两号箱子,所以每种情况都有a n 1种.所以a n n 1 a n 1.所以,a10 9a9 9 8a8 L 9 8 7 6 5 4 3 2a2 2 9!=725760 ,即好的方法总数为725760 种.答案】725760。
小升初计数高频考点汇总与方法总结

【例3】(★★★★)
用1至9这9个数字组成一个没有重复数字的九位数,满足以下要 求:每一位上的数字要么大于它前面的所有数字,要么小于它前 面的所有数字。请问:这样的九位数共有多少个?
【例4】(★★★)
正方形内部共有2016个点(结合正方形4个顶点,共2020个点,其 中任意三点,不在同一条直线上)任意两点间可剪一刀,将正方 形剪成以2020个点为顶点的三角形,最多可剪成多少个三角形?
【本讲总结】
一、枚举归纳
分类枚举——有序,规律 树形枚举——对应,对称
二、加乘原理
分类用加:结合容斥,合理分类 分步用乘:特殊位置,优先考虑
三、排列组合 1.排列,组合意义,计算方法 2.三种经典方法:捆绑法,插空法,挡板法 3.先选后排思想
四、容斥原理 1.容斥计算公式——单层要加,双层要减 2.韦恩图及意义——各区域具体含义
小升初计数高频考点汇总与方法总结
加油站
一、枚举归纳
分类枚举——有序,规律 树形枚举——对应,对称
二、加法原理
分类用加:结合容斥,合理分类 分步用乘:特殊位置,优先考虑
三、排列组合 1.排列,组合意义,计算方法 2.三种经典方法:捆绑法,插空法,挡板法 3.先选后排思想
四、容斥原理 1.容斥计算公式——单层要加,双层要减 2.韦恩图及意义——各区域具体含义
五、常见方法 1.标数法——加法原理 2.递推法——枚举归纳 3.对应法 4.整体法 5.排除法
六、概率与统计 1.古典概型 2.概率可乘性
重点例题:例1,例3,例4,例6 3
五、常见方法 1.标数法——加法原理 2.递推法——枚举归纳 3.对应法 4.整体法 5.排除法
小升初数学计数加法原理知识点总结

小升初数学计数加法原理知识点总结临近考试时,请你放下背上的包袱,用平和积极的心态,坦然的迎接考试,迎接梦想的飞翔。
下面是为大家收集的小升初数学计数加法原理知识点,供大家参考。
1、小明要登上10级台阶,他每一步只能登1级或2级台阶,他登上10级台阶共有多少种不同的登法?
分析与解:登上第1级台阶只有1种登法。
登上第2级台阶可由第1级台阶上去,或者从平地跨2级上去,故有2种登法。
登上第3级台阶可从第1级台阶跨2级上去,或者从第2级台阶上去,所以登上第3级台阶的方法数是登上第1级台阶的方法数与登上第2级台阶的方法数之和,共有
1+2=3(种)……一般地,登上第n级台阶,或者从第(n—1)级台阶跨一级上去,或者从第(n—2)级台阶跨两级上去。
根据加法原理,如果登上第(n—1)级和第(n—2)级分别有a种和b种方法,那么登上第n级有(a+b)种方法。
因此只要知道登上第1级和第2级台阶各有几种方法,就可以依次推算出登上以后各级的方法数。
由登上第1级有1种方法,登上第2级有2种方法,可得出下面一串数:
1,2,3,5,8,13,21,34,55,89。
其中从第三个数起,每个数都是它前面两个数之和。
登上第10级台阶的方法数对应这串数的第10个,即89。
也可以在图上直接写出计算得出的登上各级台阶的方法数(见以下
图)。
以上是查字典数学网为大家准备的小升初数学计数加法原理知识点,希望对大家有所帮助。
小升初计数高频考点汇总与方法总结

加油站
一、枚举归纳
分类枚举——有序,规律 树形枚举——对应,对称
二、加法原理
分类用加:结合容斥,合理分类 分步用乘:特殊位置,优先考虑
三、排列组合 1.排列,组合意义,计算方法 2.三种经典方法:捆绑法,插空法,挡板法 3.先选后排思想
四、容斥原理 1.容斥计算公式——单层要加,双层要减 2.韦恩图及意义——各区域具体含义
【本讲总结】
一、枚举归纳
分类枚举——有序,规律 树形枚举——对应,对称
二、加乘原理
分类用加:结合容斥,合理分类 分步用乘:特殊位置,优先考虑
三、排列组合 1.排列,组合意义,计算方法 2.三种经典方法:捆绑法,插空法,挡板法 3.先选后排思想
四、容斥原理 1.容斥计算公式——单层要加,双层要减 2.韦加法原理 2.递推法——枚举归纳 3.对应法 4.整体法 5.排除法
六、概率与统计 1.古典概型 2.概率可乘性
重点例题:例1,例3,例4,例6 3
五、常见方法 1.标数法——加法原理 2.递推法——枚举归纳 3.对应法 4.整体法 5.排除法
六、概率与统计 1.古典概型 2.概率可乘性
【例1】(★★) 四个人分别穿着红、黄、绿、蓝四种颜色的球衣练习传球,每人都 可以把球传给另外三个人中的任意一个。先由红衣人发球,并作为 第1次传球,经过4次传球后球仍然回到红衣人手中。请问:整个传 球过程共有多少种不同的可能?
【例5】(★★★★)
5人被分到4个不同的岗位服务,每个岗位至少有一名志愿者。 求甲乙两人不在同一个岗位服务的安排数。
2
【例6】(★★★)
小红的箱子中有4副手套,完全相同,但左、右手不能互 换,有一副是姑姑送的,两副是奶奶送的,还有一副是 自己买的,她从中任拿一副,恰好是姑姑送的那副的概 率是多少?
西安小升初考点

小学升初中重点考查内容一、计算专题(一)抵消思想--裂项(二)抵消思想--约分(三)数学基本功--四则混合运算(四)初中基本功--解方程(五)定义新运算(六)计算技巧综合--重要公式、常用结论、经典方法等等。
如循环小数与分数互化、等比数列求和、平方和公式等等例1. 计算15%)]203132(5232[922⨯⨯--÷ (分数、小数四则混合运算)分析:此类题中包含了分数、小数和百分数。
计算时应先统一化成分数,再按照运算顺序计算。
解:原式=15)5131********(920⨯⨯+-÷ =15)5131(920⨯⨯÷ =1515920⨯⨯ =500例2. 655161544141433121⨯+⨯+⨯(运用四则运算定律和性质速算和巧算) 分析:观察发现3121拆分为31+34后再用乘法分配律,可简便运算,以此类推。
解:原式=(20+34)43⨯+(40+45)54⨯+65)5660(⨯+ =15+1+32+1+50+1=100例3.x5.6%18:203= (解方程) 分析:这道题符号右边的分数线变为比号,即x x :5.65.6=就成了一个比例方程,解比例方程,需用到比的性质,内相积=外向积。
解:x5.6%18:203= (先变“—”为“:”) x5.6%18:203=6.5⨯18%=203:xx =32010018213⨯⨯ x =539 二、计数专题 (一)尝试性探索思维--枚举法(二)计数两大原理--加乘原理(三)排列组合--盘点排列组合常见的三个考点(四)容斥原理--总结容斥原理中常考的几种题型(五)计数方法综合(1)--标数法、递推法等(六)计数方法综合(2)--对应法、整体法等(七)概率与统计--两个知识点:古典概型与概率可乘性例1. 六个人分成3组,每组2人,有几种分法?分析:很多人认为,应该是p (6,3)或者c (6,3),很明显不对,这6人必须都得分出去。
小升初计数重点考查内容————计数方法综合(1)——标数法、递推法
小升初计数重点考查内容————计数方法综合(1)——标数法、递推法图中,“我爱希望杯”有______种不同的读法。
【举一反三】如图,要从A 去B ,C 不能通过,最短线路有______条。
游乐园门票1元1张,每人限购1张。
现有10个小朋友排队购买,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有零钱。
10个小朋友排队,不同的排队方法总共有10!=3628800种,问其中有______种排队方法,售票员总能找的开零钱。
【举一反三】在一次选举中甲、乙两人参加竞选,甲得5张选票,乙也得5张选票,问在对这10张选票逐一唱票的过程中,乙的得票始终未能领先的点票记录共有______种可能。
(★★)(★★★★★)一个楼梯共有10级阶梯,规定每步可以逐一级台阶或两级台阶,走完这10级台阶,一共有______种不同走法。
对一个自然数进行如下操作:如果是偶数则除以2,如果是奇数则加1,如此进行下去直到得数为1停止。
问经过9次操作变为1的数有______个。
在平面上画8个圆,最多可以把平面分成_______部分。
在线测试题温馨提示:请在线作答,以便及时反馈孩子的薄弱环节。
1.如下图所示,要从A 点沿线段走到B ,要求每一步都是向右、向上或者斜上方。
问有多少种不同的走法?B AA A .18B .20C .22D .24(★★★)(★★★)(★★★☆)2.有15个相同的棋子,一个人分若干次取,每次可取1个,2个,3个或4个,但要求每次取之后留下的棋子数不是3或4的倍数,有种不同的方法取完这堆棋子。
A.11B.22C.33D.183.上一段12级楼梯,规定每一步只能上一级或两级楼梯,要登上第12级楼梯,不同的走法共有多少种?A.233B.230C.243D.2534.给你一架天平和两个砝码,这两个砝码分别重20克和50克,如果再添四个砝码,则这六个砝码可以称的重量种类最多是多少种。
(天平的左右两盘均可放砝码)A.268B.256C.364D.2805.平面上的5个圆和3条直线最多能把平面分成多少部分?A.55B.57C.32D.48。
小升初计数高频考点汇总与方法总结

【例5】(★★★★)
5人被分到4个不同的岗位服务,每个岗位至少有一名志愿者。 求甲乙两人不在同一个岗位服务的安排数。
2
【例6】(★★★)
小红的箱子中有4副手套,完全相同,但左、右手不能互 换,有一副是姑姑送的,两副是奶奶送的,还有一副是 自己买的,她从中任拿一副,恰好是姑姑送的那副的概 率是多少?
【本讲总结】
一、枚举归纳
分类枚举——有序,规律 树形枚举——对应,对称
二、加乘原理
分类用加:结合容斥,合理分类 分步用乘:特殊位置,优先考虑
三、排列组合 1.排列,组合意义,计算方法 2.三种经典方法:捆绑法,插空法,挡板法 3.先选后排思想
四、容斥原理 1.容斥计算公式——单层要加,双层要减 2.韦恩图及意义——各区域具体含义
五、常见方法 1.标数法——加法原理 2.递推法——枚举归纳 3.对应法 4.整体法 5.排除法
六、概率与统计 1.古典概型 2.概率可乘性
重点例题:例1,例3,例4,例6 3
小升初计数高频考点汇总与方法总结
加油站
一、枚举归纳
分类枚举——有序,规律 树形枚举——对应,对称
二、加法原理
分类用加:结合容斥,合理分类 分步用乘:特殊位置,优先考虑
三、排列组合 1.排列,组合意义,计算方法 2.三种经典方法:捆绑法,插空法,挡板法 3.先选后排思想
四、容斥原理 1.容斥计算公式——单层要加,双层要减 2.韦恩图及意义——各区域具体含义
1
【例2】(★★★)
小悦买了10块相同的巧克力,每天最少吃一块,直到吃完, 共有多少种吃法?
【例3】(★★★数,满足以下要 求:每一位上的数字要么大于它前面的所有数字,要么小于它前 面的所有数字。请问:这样的九位数共有多少个?
小升初计数高频考点汇总与方法总结

【例5】(★★★★)
5人被分到4个不同的岗位服务,每个岗位至少有一名志愿者。 求甲乙两人不在同一个岗位服务的安排数。
2
【例6】(★★★)
小红的箱子中有4副手套,完全相同,但左、右手不能互 换,有一副是姑姑送的,两副是奶奶送的,还有一副是 自己买的,她从中任拿一副,恰好是姑姑送的那副的概 率是多少?
小举——有序,规律 树形枚举——对应,对称
二、加法原理
分类用加:结合容斥,合理分类 分步用乘:特殊位置,优先考虑
三、排列组合 1.排列,组合意义,计算方法 2.三种经典方法:捆绑法,插空法,挡板法 3.先选后排思想
四、容斥原理 1.容斥计算公式——单层要加,双层要减 2.韦恩图及意义——各区域具体含义
1
【例2】(★★★)
小悦买了10块相同的巧克力,每天最少吃一块,直到吃完, 共有多少种吃法?
【例3】(★★★★)
用1至9这9个数字组成一个没有重复数字的九位数,满足以下要 求:每一位上的数字要么大于它前面的所有数字,要么小于它前 面的所有数字。请问:这样的九位数共有多少个?
【例4】(★★★)
正方形内部共有2016个点(结合正方形4个顶点,共2020个点,其 中任意三点,不在同一条直线上)任意两点间可剪一刀,将正方 形剪成以2020个点为顶点的三角形,最多可剪成多少个三角形?
五、常见方法 1.标数法——加法原理 2.递推法——枚举归纳 3.对应法 4.整体法 5.排除法
六、概率与统计 1.古典概型 2.概率可乘性
重点例题:例1,例3,例4,例6 3
五、常见方法 1.标数法——加法原理 2.递推法——枚举归纳 3.对应法 4.整体法 5.排除法
六、概率与统计 1.古典概型 2.概率可乘性
小升初数学拔高之计数方法之标数法、递推法

---------------------------------------------------------------最新资料推荐------------------------------------------------------ 小升初数学拔高之计数方法之标数法、递推法1 、标数法、递推法2 、标数法的应用。
3 、递推法的应用。
本讲主线一轮复习计数方法之标数法、递推法 1 、标数法,寻找最短路径的条数.2、基本步骤:⑴ 确定大方向;⑵ 在起始点标、基本步骤:⑴ 确定大方向;⑵ 在起始点标1;⑶ 某点数字=它前面两个点的方法数之和;⑷ 终点数字即为最短路径条数。
;⑶ 某点数字=它前面两个点的方法数之和;⑷ 终点数字即为最短路径条数。
2、应用:⑴ 最短路径;⑵ 拼单词;⑶ 买票问题、应用:⑴ 最短路径;⑵ 拼单词;⑶ 买票问题.知识要点屋( ★)如图,从A 到B 的最短路线有_____条。
【课前小练习】条。
【课前小练习】1、、AB2、、G点学校家点学校家如图,小明从家去往学校,途中G点有积水不能通过。
从家去学校的最短路线有点有积水不能通过。
从家去学校的最短路线有_____ 条。
【例1】】( ★) 如图,为一幅街道图,从A 出发经过十字路口B,但不经过,但不经过C 走到D 的不同的最短路线有多少条?例题1 / 4精讲1【拓展】( ★★) 如图,从A 到B 沿网格线不经过线段CD 和EF的最短路径的条数是多少条?的最短路径的条数是多少条?AC DEFB【例2】】( ★★☆) 如图所示,科学家爱因斯坦的英文名拼写为Einstein ,按图中箭头所示方向有______种不同的方法拼出英文单词种不同的方法拼出英文单词Einstein。
【例3】】( ★★★★) 游乐园门票5 元1 张,每人限购1 张. 现有10个小朋友排队购买,其中个小朋友排队购买,其中5 个小朋友只有5 元的钞票,另外5个小朋友只有个小朋友只有10 元的钞票,售票员没有零钱。
小升初奥数计数问题之递推方法的解题技巧

小升初奥数计数问题之递推方法的解题技巧数学给予人们的不仅是知识,更重要的是能力,这种能力包括观察实验、收集信息、归纳类比、直觉判断、逻辑推理、建立模型和精确计算。
这些能力和培养,将使人终身受益。
以下是无忧考网整理的相关资料,希望对您有所帮助。
【篇一】递推方法的概述在不少计数问题中,要很快求出结果是比较困难的,有时可先从简单情况入手,然后从某一种特殊情况逐渐推出与以后比较复杂情况之间的关系,找出规律逐步解决问题,这样的方法叫递推方法。
例 1、线段 AB 上共有 10 个点(包括两个端点),那么这条线段上一共有多少条不同的线段 ?分析与解答:从简单情况研究起:AB 上共有 2 个点,有线段: 1 条AB 上共有 3 个点,有线段: 1+2=3(条)AB 上共有 4 个点,有线段: 1+2+3=6(条)AB 上共有 5 个点,有线段: 1+2+3+4=10(条)AB 上共有 10 个点,有线段: 1+2+3+4+ ⋯+9=45(条)一般地, AB 上共有 n 个点,有线段:1+2+3+4+ ⋯+(n-1)=n ×(n-1) ÷2即:线段数 =点数×(点数-1) ÷2例 2 、2000 个学生排成一行,依次从左到右编上 1 ~2000 号,然后从左到右按一、二报数,报一的离开队伍,剩下的人继续按一、二报数,报一的离开队伍,⋯⋯按这个规律此下去,直至当队伍只剩下一人为止。
问:这时一共报了多少次 ?最后留下的这个人原来的号码是多少 ?分析与解答:难的不会想简单的,数大的不会想数小的。
我们先从这2000 名同学中选出 20 人代替 2000 人进行分析,试着找出规律,然后再用这个规律来解题。
这 20 人第一次报数后共留下 10 人,因为 20 ÷2=10 ,这10 人开始时的编号依次是: 2、4、6、8、10、12、14、16、18 、20,都是 2 的倍数。
计数之递推法

7-6-4计数之递推法教学目标前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法,比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等,这里再集中学习一下计数中其他常见的方法,主要有归纳法、整体法、对应法、递推法.对这些计数方法与技巧要做到灵活运用.例题精讲对于某些难以发现其一般情形的计数问题,可以找出其相邻数之间的递归关系,有了这一递归关系就可以利用前面的数求出后面未知的数,这种方法称为递推法.【例1】每对小兔子在出生后一个月就长成大兔子,而每对大兔子每个月能生出一对小兔子来.如果一个人在一月份买了一对小兔子,那么十二月份的时候他共有多少对兔子?【例2】树木生长的过程中,新生的枝条往往需要一段“休息”时间供自身生长,而后才能萌发新枝.一棵树苗在一年后长出一条新枝,第二年新枝“休息”,老枝依旧萌发新枝;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则依次“休息”.这在生物学上称为“鲁德维格定律”.那么十年后这棵树上有多少条树枝?【例3】一楼梯共10级,规定每步只能跨上一级或两级,要登上第10级,共有多少种不同走法?【巩固】一楼梯共10级,规定每步只能跨上一级或三级,要登上第10级,共有多少种不同走法?【例4】1×2的小长方形(横的竖的都行)覆盖2×10的方格网,共有多少种不同的盖法.【例5】用13⨯的方格网,共有多少种不同的盖法?⨯的小长方形覆盖38【例6】有一堆火柴共12根,如果规定每次取1~3根,那么取完这堆火柴共有多少种不同取法?【巩固】一堆苹果共有8个,如果规定每次取1~3个,那么取完这堆苹果共有多少种不同取法?【例7】有10枚棋子,每次拿出2枚或3枚,要想将10枚棋子全部拿完,共有多少种不同的拿法?【例8】如下图,一只蜜蜂从A处出发,回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?AB【巩固】小蜜蜂通过蜂巢房间,规定只能由小号房间进入大号房间问小蜜蜂由A房间到达B房间有多少种方法?【例9】如下图,一只蜜蜂从A处出发,回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?【例10】对一个自然数作如下操作:如果是偶数则除以2,如果是奇数则加1,如此进行直到得数为1操作停止.问经过9次操作变为1的数有多少个?【例11】有20个石子,一个人分若干次取,每次可以取1个,2个或3个,但是每次取完之后不能留下质数个,有多少种方法取完石子?(石子之间不作区分,只考虑石子个数)【巩固】有20个相同的棋子,一个人分若干次取,每次可取1个,2个,3个或4个,但要求每次取之后留下的棋子数不是3或4的倍数,有种不同的方法取完这堆棋子.【例12】4个人进行篮球训练,互相传球接球,要求每个人接球后马上传给别人,开始由甲发球,并作为第一次传球,第五次传球后,球又回到甲手中,问有多少种传球方法?【巩固】五个人互相传球,由甲开始发球,并作为第一次传球,经过4次传球后,球仍回到甲手中.问:共有多少种传球方式?【例13】设A、E为正八边形ABCDEFGH的相对顶点,顶点A处有一只青蛙,除顶点E外青蛙可以从正八边形的任一顶点跳到其相邻两个顶点中任意一个,落到顶点E时青蛙就停止跳动,则青蛙从顶点A出发恰好跳10次后落到E的方法总数为种.【巩固】在正五边形ABCDE上,一只青蛙从A点开始跳动,它每次可以随意跳到相邻两个顶点中的一个上,一旦跳到D点上就停止跳动.青蛙在6次之内(含6次)跳到D点有种不同跳法.【例14】有6个木箱,编号为1,2,3,……,6,每个箱子有一把钥匙,6把钥匙各不相同,每个箱子放进一把钥匙锁好.先挖开1,2号箱子,可以取出钥匙去开箱子上的锁,如果最终能把6把锁都打开,则说这是一种放钥匙的“好”的方法,那么“好”的方法共有种.【巩固】有10个木箱,编号为1,2,3,……,10,每个箱子有一把钥匙,10把钥匙各不相同,每个箱子放进一把钥匙锁好.先挖开1,2号箱子,可以取出钥匙去开箱子上的锁,如果最终能把10把锁都打开,则说这是一种放钥匙的“好”的方法,那么“好”的方法共有种.。
小升初数学六年级重点-计数

一、本讲任务熟练掌握树形图、标数法、韦恩图、分类枚举及乘法原理的应用。
【举一反三】(★★★)一个六位数由1、2、3、4、5组成,而且任意相邻两个数位的数字之差都是1,这样的六位数有多少个?(★★)有些四位数的各位数字均取自1,2,3,4,5(可重复选取),并且任意相邻两位数字(大减小)的差都是1。
则这样的四位数共有_______个。
计数例1【举一反三】(★★★)体育课上,60名学生面向老师站成一行,按老师口令,从左到右报数:1,2,3,…,60,然后,老师让所报的数是4的倍数的同学向后转,接着又让所报的数是5的倍数的同学向后转,最后让所报的数是6的倍数的同学向后转,现在面向老师的学生有________人。
(★★★)50名同学面向老师站成一行,老师先让大家从左至右按1,2,3…,49,50依次报数;先让报数是5的倍数的同学向后转,再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转,这时面向老师的同学还有______名。
(★★★)在下图的街道示意图中,C 处因施工不能通行,从A 到B 的最短路线有多少种?例2例3例4(★★★☆)有______个这样的三位数abc,满足abc与cba除以7的余数相同。
(a,b,c可以相同)【举一反三】(★★★☆)在图中1×5的格子中填入1,2,3,4,5,6,7,8中的5个数,要求,填入的数各不相同并且填在黑格里的数比它旁边的两个数都大。
共有种不同的填法。
例5(★★★☆)用数字0,1,2,3,4,5一共可以组成______个没有重复数字且能被5整除的四位数。
【举一反三】(★★★★)某信号兵用红、黄、蓝三面旗子从上到下挂在竖直的旗杆上表示信号,每次可以挂一面、二面或三面,并且不同的顺序表示不同的信号,一共可以表示( )种信号。
(★★★★)学学和思思一起洗5个互不相同的碗,思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放入碗柜摞成一摞,思思一边洗,学学一边拿,那么学学摞好的碗一共有 种不同的摞法。
五年级奥数.计数综合.计数方法与技巧(ABC级).教师版

(1) 归纳法:从条件值较小的数开始,找出其中规律,或找出其中的递推数量关系,归纳出一般情况下的数量关系.(2) 整体法:解决计数问题时,有时要“化整为零”,使问题变得简单;有时反而要从整体上来考虑,从全局、从整体来研究问题,反而有利于发现其中的数量关系.(3) 对应法:将难以计数的数量与某种可计量的事物联系起来,只要能建立一一对应的关系,那么这两种事物在数量上是相同的.事实上插入法和插板法都是对应法的一种表现形式.(4) 递推法:对于某些难以发现其一般情形的计数问题,可以找出其相邻数之间的递归关系,有了这一递归关系就可以利用前面的数求出后面未知的数,这种方法称为递推法.【例 1】 一条直线分一个平面为两部分.两条直线最多分这个平面为四部分.问5条直线最多分这个平面为多少部分?【考点】计数之归纳法【难度】3星【题型】解答【解析】 方法一:我们可以在纸上试着画出1条直线,2条直线,3条直线,……时的情形,于是得到下表:由上表已知5条直线最多可将这个平面分成16个部分,并且不难知晓,当有n 条直线时,最多可将平面分成2+2+3+4+…+n =()12n n ++1个部分.方法二:如果已有k 条直线,再增加一条直线,这条直线与前k 条直线的交点至多k 个,因而至多被分成k +1段,每一段将原有的部分分成两个部分,所以至多增加k +1个部分.于是3条直线至多将平面分为4+3=7个部分,4条直线至多将平面分为7+4=11个部分,5条直线至多将平面分例题精讲知识结构计数方法与技巧为11+5=16个部分.一般的有k条直线最多将平面分成:1+1+2+…+k=()12k k++1个部分,所以五条直线可以分平面为16个部分.【答案】16【巩固】平面上5条直线最多能把圆的内部分成几部分?平面上100条直线最多能把圆的内部分成几部分?【考点】计数之归纳法【难度】4星【题型】解答【解析】假设用a k表示k条直线最多能把圆的内部分成的部分数,这里k=0,1,2,……a0=1a1=a0+1=2a2=a1+2=4a3=a2+3=7a4=a3+4=11……故5条直线可以把圆分成16部分,100条直线可以把圆分成5051部分【答案】5051部分【例 2】平面上10个两两相交的圆最多能将平面分割成多少个区域?【考点】计数之归纳法【难度】4星【题型】解答【解析】先考虑最简单的情形.为了叙述方便,设平面上k个圆最多能将平面分割成ka个部分.从图中可以看出,12a =,24221a ==+⨯,38422a ==+⨯,414823a ==+⨯,…… 可以发现k a 满足下列关系式:()121k k a a k -=+-.实际上,当平面上的(1k -)个圆把平面分成1k a -个区域时,如果再在平面上出现第k 个圆,为了保证划分平面的区域尽可能多,新添的第k 个圆不能通过平面上前()1k -个圆之间的交点.这样,第k 个圆与前面()1k -个圆共产生2(1)k ⨯-个交点,如下图:这2(1)k ⨯-个交点把第k 个圆分成了2(1)k ⨯-段圆弧,而这2(1)k ⨯-段圆弧中的每一段都将所在的区域一分为二,所以也就是整个平面的区域数增加了2(1)k ⨯-个部分.所以,()121k k a a k -=+-.那么,10987292829272829a a a a =+⨯=+⨯+⨯=+⨯+⨯+⨯=12122...272829a =+⨯+⨯++⨯+⨯+⨯()2212...78992=+⨯+++++=.故10个圆最多能将平面分成92部分.【答案】92【巩固】 10个三角形最多将平面分成几个部分?【考点】计数之归纳法【难度】4星【题型】解答【解析】 设n 个三角形最多将平面分成n a 个部分.1n =时,12a =;1413121110987654321876521344312212n =时,第二个三角形的每一条边与第一个三角形最多有2个交点,三条边与第一个三角形最多有236⨯=(个)交点.这6个交点将第二个三角形的周边分成了6段,这6段中的每一段都将原来的每一个部分分成2个部分,从而平面也增加了6个部分,即2223a =+⨯.3n =时,第三个三角形与前面两个三角形最多有4312⨯=(个)交点,从而平面也增加了12个部分,即:322343a =+⨯+⨯. ……一般地,第n 个三角形与前面()1n -个三角形最多有()213n -⨯个交点,从而平面也增加()213n -⨯个部分,故()()222343213224213332n a n n n n ⎡⎤=+⨯+⨯++-⨯=++++-⨯=-+⎣⎦;特别地,当10n =时,2103103102272a =⨯+⨯+=,即10个三角形最多把平面分成272个部分.【答案】272【例 3】 一个长方形把平面分成两部分,那么3个长方形最多把平面分成多少部分?【考点】计数之归纳法【难度】4星【题型】解答【解析】 一个长方形把平面分成两部分.第二个长方形的每一条边至多把第一个长方形的内部分成2部分,这样第一个长方形的内部至多被第二个长方形分成五部分.同理,第二个长方形的内部至少被第一个长方形分成五部分.这两个长方形有公共部分(如下图,标有数字9的部分).还有一个区域位于两个长方形外面,所以两个长方形至多把平面分成10部分.第三个长方形的每一条边至多与前两个长方形中的每一个的两条边相交,故第一条边被隔成五条小线段,其中间的三条小线段中的每一条线段都把前两个长方形内部的某一部分一分为二,所以至多增加3×4=12个部分.而第三个长方形的4个顶点都在前两个长方形的外面,至多能增加4个部分.所以三个长方形最多能将平面分成10+12+4=26.【小结】n 个图形最多可把平面分成部分数:直线:()112n n ⨯++;圆:()21n n +⨯-; 三角形:()231n n +⨯⨯- ; 长方形:()241n n +⨯⨯-.【答案】26【巩固】 在平面上画5个圆和1条直线,最多可把平面分成多少部分?【考点】计数之归纳法【难度】5星【题型】解答【解析】 先考虑圆.1个圆将平面分成2个部分.这时增加1个圆,这个圆与原有的1个圆最多有两个交点,成为2条弧,每条弧将平面的一部分一分为二,增加了2个部分,所以2个圆最多将平面分成4个部分.当有3个圆时,第3个圆与原有的2个产生4个交点而增加4个部分,所以3个圆最多将平面分成8个部分.同样的道理,5个圆最多将平面分成22个部分.再考虑直线.直线与每个圆最多有2个交点,这样与5个圆最多有10个交点.它们将直线分成11条线段或射线,而每条线段又将平面的一部分一分为二,2条射线增加了一部分,因此5个圆和1条直线最多可将平面分成32个部分.【答案】32【例4】一个正方形的内部有1996个点,以正方形的4个顶点和内部的1996个点为顶点,将它剪成一些三角形.问:一共可以剪成多少个三角形?如果沿上述这些点中某两点之间所连的线段剪开算作一刀,那么共需剪多少刀?【考点】计数之整体法【难度】4星【题型】解答【解析】方法一:归纳法,如下图,采用归纳法,列出1个点、2个点、3个点…时可剪出的三角形个数,需剪的刀数.不难看出,当正方形内部有n个点时,可以剪成2n+2个三角形,需剪3n+l刀,现在内部有1996个点,所以可以剪成2×1996+2=3994个三角形,需剪3×1996+1=5989刀.方法二:整体法.我们知道内部一个点贡献360度角,原正方形的四个顶点共贡献了360度角,所以当内部有n个点时,共有360n+360度角,而每个三角形的内角和为180度角,所以可剪成(360n+360)÷180=2n+2个三角形.2n+2个三角形共有3×(2n+2)=6n+6条边,但是其中有4条是原有的正方形的边,所以正方形内部的三角形边有6n+6—4=6n+2条边,又知道每条边被2个三角形共用,即每2条边是重合的,所以只用剪(6n+2)÷2=3n+1刀.本题中n=1996,所以可剪成3994个三角形,需剪5989刀.【答案】可剪成3994个三角形,需剪5989刀【巩固】在三角形ABC内有100个点,以三角形的顶点和这100点为顶点,可把三角形剖分成多少个小三角形?【考点】计数之整体法【难度】4星【题型】解答【解析】整体法.100个点每个点周围有360度,三角形本身内角和为180度,所以可以分成()⨯+÷=个小三角形.360100180180201【答案】201个小三角形【例 5】在8×8的黑白相间染色的国际象棋棋盘中,以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个?【考点】计数之图形中的对应关系【难度】3星【题型】解答【解析】首先可以知道题中所讲的13⨯长方形中间的那个小主格为黑色,这是因为两个白格不相邻,所以不能在中间.显然,位于棋盘角上的黑色方格不可能被包含在这样的长方形中.下面分两种情况来分析:第一种情况,一个位于棋盘内部的黑色方格对应着两个这样的13⨯长方形(一横一竖);第二种情况,位于边上的黑色方格只能对应一个13⨯长方形.由于在棋盘上的32个黑色方格中,位于棋盘内部的18个,位于边上的有12个,位于角上的有2个,所以共有1821248⨯+=个这样的长方形.本题也可以这样来考虑:事实上,每一行都有6个13⨯长方形,所以棋盘上横、竖共有13⨯⨯=个.由于棋盘上的染色具有对称性,因此包含两个白色小方格与一⨯长方形68296个黑色小方格的长方形正好与包含两个黑色小方格与一个白色小方格的长方形具有一一对应关系,这说明它们各占一半,因此所求的长方形个数为96248÷=个.【答案】48【巩固】用一张如图所示的纸片盖住66⨯方格表中的四个小方格,共有多少种不同的放置方法?【考点】计数之图形中的对应关系【难度】3星【题型】解答【解析】【解析】如图,将纸片中的一个特殊方格染为黑色,下面考虑此格在66⨯方格表中的位置.易见它不能位于四个角上;若黑格位于方格表中间如图浅色阴影所示的44⨯正方形内的某格时,纸片有4种不同的放法,共计44464⨯⨯=种;若黑格位于方格表边上如图深色阴影所示的方格中时,纸片的位置随之确定,即只有1种放法,此类放法有4416⨯=种.所以,纸片共有641680+=种不同的放置方法.【答案】80种【例 6】有多少个四位数,满足个位上的数字比千位数字大,千位数字比百位大,百位数字比十位数字大?【考点】计数之数字问题中的对应关系【难度】4星【题型】解答【解析】由于四位数的四个数位上的数的大小关系已经非常明确,而对于从0~9中任意选取的4个数字,它们的大小关系也是明确的,那么由这4个数字只能组成1个符合条件的四位数(题目中要求千位比百位大,所以千位不能为0,本身已符合四位数的首位不能为0的要求,所以进行选择时可以把0包含在内),也就是说满足条件的四位数的个数与从0~9中选取4个数字的选法是一一对应的关系,那么满足条件的四位数有41010987210 4321C⨯⨯⨯==⨯⨯⨯个.【答案】210个【巩固】三位数中,百位数比十位数大,十位数比个位数大的数有多少个?【考点】计数之数字问题中的对应关系【难度】4星【题型】解答【解析】相当于在10个数字中选出3个数字,然后按从大到小排列.共有10×9×8÷(3×2×1)=120种.实际上,前铺中每一种划法都对应着一个数.【答案】120种【例 7】学学和思思一起洗5个互不相同的碗(顺序固定),思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放入碗柜摞成一摞,思思一边洗,学学一边拿,那么学学摞好的碗一共有种不同的摞法.【考点】计数之对应与阶梯型标数法【难度】5星【题型】解答【关键词】2008年,第一届,学而思杯,5年级,第7题【解析】方法一:如下所示,共有42种不同的摞法:----,34521----,53421----,----,3542154321----,45321----,24531----,52431----,----,2543154231----,45231----,54312----,----,23451----,23541----,2534152341----,54132----,34512----,----,3541245312----,53412----,51342----,14532----,----,5143245132----,15432----,45123----,----,54123----,13452----,1354215342----,12543----,----,51243----,14523----,5142315423----,15234----,12534----,----,1235415243----,12453----,12345----。
小学奥数计数之递推法(完整版)

小学奥数计数之递推法7-6-4.计数之递推法教学目标前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法,比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等,这里再集中学习一下计数中其他常见的方法,主要有归纳法、整体法、对应法、递推法.对这些计数方法与技巧要做到灵活运用.例题精讲对于某些难以发现其一般情形的计数问题,可以找出其相邻数之间的递归关系,有了这一递归关系就可以利用前面的数求出后面未知的数,这种方法称为递推法.【例 1】每对小兔子在出生后一个月就长成大兔子,而每对大兔子每个月能生出一对小兔子来.如果一个人在一月份买了一对小兔子,那么十二月份的时候他共有多少对兔子?【考点】计数之递推法【难度】3星【题型】解答【解析】第一个月,有1对小兔子;第二个月,长成大兔子,所以还是1对;第三个月,大兔子生下一对小兔子,所以共有2对;第四个月,刚生下的小兔子长成大兔子,而原来的大兔子又生下一对小兔子,共有3对;第五个月,两对大兔子生下2对小兔子,共有5对;……这个特点的说明每月的大兔子数为上月的兔子数,每月的小兔子数为上月的大兔子数,即上上月的兔子数,所以每月的兔子数为上月的兔子数与上上月的兔子数相加.依次类推可以列出下表:经过月数:---1---2---3---4---5---6---7---8---9---10---11---12兔子对数:---1---1---2---3---5---8--13--21--34--55--89—144,所以十二月份的时候总共有144对兔子.【答案】144【例 2】树木生长的过程中,新生的枝条往往需要一段“休息”时间供自身生长,而后才能萌发新枝.一棵树苗在一年后长出一条新枝,第二年新枝“休息”,老枝依旧萌发新枝;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则依次“休息”.这在生物学上称为“鲁德维格定律”.那么十年后这棵树上有多少条树枝?【考点】计数之递推法【难度】3星【题型】解答【解析】一株树木各个年份的枝桠数,构成斐波那契数列:1,2,3,5,8,13,21,34,55,89,……所以十年后树上有89条树枝.【答案】89【例 3】一楼梯共10级,规定每步只能跨上一级或两级,要登上第10级,共有多少种不同走法?【考点】计数之递推法【难度】4星【题型】解答【解析】 登 1级 2级 3级 4级 ...... 10级1种方法 2种 3种 5种 ...... ?我们观察每级的种数,发现这么一个规律:从第三个数开始,每个数是前面两个数的和;依此规律我们就可以知道了第10级的种数是89.其实这也是加法的运用:假如我们把这个人开始登楼梯的位置看做A 0,那么登了1级的位置是在A 1,2级在A 2... A 10级就在A 10.到A 3的前一步有两个位置;分别是A 2 和A 1 .在这里要强调一点,那么A 2 到A 3 既然是一步到了,那么A 2 、A 3之间就是一种选择了;同理A 1 到A 3 也是一种选择了.同时我们假设到n 级的选择数就是An .那么从A 0 到A 3 就可以分成两类了:第一类:A 0 ---- A 1 ------ A 3 ,那么就可以分成两步.有A 1×1种,也就是A 1 种;(A 1 ------ A 3 是一种选择)第二类:A 0 ---- A 2 ------ A 3, 同样道理 有A 2 .类类相加原理:A 3 = A 1 +A 2,依次类推An = An -1 + An -2.【答案】89【巩固】一楼梯共10级,规定每步只能跨上一级或三级,要登上第10级,共有多少种不同走法?【考点】计数之递推法 【难度】4星 【题型】解答【解析】 登 1级 2级 3级 4级 5级 ...... 10级1种方法 1种 2种 3种 4种...... ?我们观察每级的种数,发现这么一个规律:从第三个数开始,每个数是前面相隔的两个数的和;依此规律我们就可以知道了第10级的种数是28.【答案】28【例 4】 1×2的小长方形(横的竖的都行)覆盖2×10的方格网,共有多少种不同的盖法.【考点】计数之递推法 【难度】4星 【题型】解答【解析】 如果用12⨯的长方形盖2n ⨯的长方形,设种数为n a ,则11a =,22a =,对于3n ≥,左边可能竖放1个12⨯的,也可能横放2个12⨯的,前者有-1n a 种,后者有-2n a 种,所以-1-2n n n a a a =+,所以根据递推,覆盖210⨯的长方形一共有89种.【答案】89【例 5】 用13⨯的小长方形覆盖38⨯的方格网,共有多少种不同的盖法?【考点】计数之递推法 【难度】5星 【题型】解答【解析】 如果用13⨯的长方形盖3n ⨯的长方形,设种数为n a ,则11a =,21a = ,32a = ,对于4n ≥,左边可能竖放1个13⨯的,也可能横放3个13⨯的,前者有-1n a 种,后者有-3n a 种,所以-1-3n n n a a a =+,依照这条递推公式列表:31⨯ 32⨯ 33⨯ 34⨯ 35⨯ 36⨯ 37⨯ 38⨯1 1234 6 9 13所以用13⨯的小长方形形覆盖38⨯的方格网,共有13种不同的盖法.【答案】13【例 6】 有一堆火柴共12根,如果规定每次取1~3根,那么取完这堆火柴共有多少种不同取法?【考点】计数之递推法 【难度】4星 【题型】解答【解析】 取1根火柴有1种方法,取2根火柴有2种方法,取3根火柴有4种取法,以后取任意根火柴的种数等于取到前三根火柴所有情况之和,以此类推,参照上题列表如下: 1根 2根 3根 4根 5根 6根 7根 8根 9根 10根 11根 12根1 2 4 7 13 24 44 81 149 274 504 927取完这堆火柴一共有927种方法.【答案】927【巩固】 一堆苹果共有8个,如果规定每次取1~3个,那么取完这堆苹果共有多少种不同取法?【考点】计数之递推法 【难度】4星 【题型】解答【解析】 取1个苹果有1种方法,取2个苹果有2种方法,取3个苹果有4种取法,以后取任意个苹果的种数等于取到前三个苹果所有情况之和,以此类推,参照上题列表如下:1个 2个 3个 4个 5个 6个 7个 8个1 2 4 7 13 24 44 81取完这堆苹果一共有81种方法.【答案】81【例 7】 有10枚棋子,每次拿出2枚或3枚,要想将10枚棋子全部拿完,共有多少种不同的拿法?【考点】计数之递推法 【难度】4星 【题型】解答【解析】 本题可以采用递推法,也可以进行分类讨论,当然也可以直接进行枚举.(法1)递推法.假设有n 枚棋子,每次拿出2枚或3枚,将n 枚棋子全部拿完的拿法总数为n a 种.则21a =,31a =,41a =.由于每次拿出2枚或3枚,所以32n n n a a a --=+(5n ≥).所以,5232a a a =+=;6342a a a =+=;7453a a a =+=;8564a a a =+=;9675a a a =+=;10787a a a =+=.即当有10枚棋子时,共有7种不同的拿法.(法2)分类讨论.由于棋子总数为10枚,是个偶数,而每次拿2枚或3枚,所以其中拿3枚的次数也应该是偶数.由于拿3枚的次数不超过3次,所以只能为0次或2次.若为0次,则相当于2枚拿了5次,此时有1种拿法;若为2次,则2枚也拿了2次,共拿了4次,所以此时有246C =种拿法.根据加法原理,共有167+=种不同的拿法.【答案】7【例 8】 如下图,一只蜜蜂从A 处出发,回到家里B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?【考点】计数之递推法 【难度】4星 【题型】解答【解析】 蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬近相邻大号码的蜂房.明确了行走路径的方向,就可以运用标数法进行计算.如右图所示,小蜜蜂从A 出发到B 处共有89种不同的回家方法.【答案】89【巩固】小蜜蜂通过蜂巢房间,规定只能由小号房间进入大号房间问小蜜蜂由A 房间到达B房间有多少种方法?【考点】计数之递推法 【难度】4星 【题型】解答【解析】 斐波那契数列第八项.21种.【答案】21【例 9】 如下图,一只蜜蜂从A 处出发,回到家里B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法? 【考点】计数之递推法 【难度】4星 【题型】解答 【解析】 按照蜜蜂只能从小号码的蜂房爬近相邻大号码的蜂房的原则,运用标号法进行计算.如右图所示,小蜜蜂从A 出发到B 处共有296种不同的回家方法.【答案】296【例 10】 对一个自然数作如下操作:如果是偶数则除以2,如果是奇数则加1,如此进行直到得数为1操作停止.问经过9次操作变为1的数有多少个?【考点】计数之递推法 【难度】4星 【题型】解答【解析】 可以先尝试一下,倒推得出下面的图:BA AB 135794682123581321345589186427531BA其中经1次操作变为1的1个,即2,经2次操作变为1的1个,即4,经3次操作变为1的2个,是一奇一偶,以后发现,每个偶数可以变成两个数,分别是一奇一偶,每个奇数变为一个偶数,于是,经1、2、…次操作变为1的数的个数依次为:1,1,2,3,5,8,…这一串数中有个特点:自第三个开始,每一个等于前两个的和,即即经过9次操作变为1的数有34个.为什么上面的规律是正确的呢?道理也很简单. 设经过n 次操作变为1的数的个数为n a ,则1a =1,2a =1,3a =2,… 从上面的图看出,1n a +比n a 大.一方面,每个经过n 次操作变为1的数,乘以2,就得出一个偶数,经过1n +次操作变为1;反过来,每个经过1n +次操作变为1的偶数,除以2,就得出一个经过n 次操作变为1的数. 所以经过n 次操作变为1的数与经过1n +次操作变为1的偶数恰好一样多.前者的个数是n a ,因此后者也是n a 个.另一方面,每个经过n 次操作变为1的偶数,减去1,就得出一个奇数,它经过1n +次操作变为1,反过来.每个经过1n +次操作变为1的奇数,加上1,就得出一个偶数,它经过n 次操作变为1. 所以经过n 次操作变为1的偶数经过1n +次操作变为1的奇数恰好一样多.而由上面所说,前者的个数就是1n a -,因此后者也是1n a -.经过n +1次操作变为1的数,分为偶数、奇数两类,所以11n n n a a a +-=+,即上面所说的规律的确成立.【答案】34【例 11】 有20个石子,一个人分若干次取,每次可以取1个,2个或3个,但是每次取完之后不能留下质数个,有多少种方法取完石子?(石子之间不作区分,只考虑石子个数)【考点】计数之递推法 【难度】5星 【题型】解答【解析】 如果没有剩下的不能使质数这个条件,那么递推方法与前面学过的递推法相似,只不过每次都是前面3个数相加.现在剩下的不能是质数个,可以看作是质数个的取法总数都是0,然后再进行递推.【答案】25【巩固】有20个相同的棋子,一个人分若干次取,每次可取1个,2个,3个或4个,但要2410131112514302831643215167683421求每次取之后留下的棋子数不是3或4的倍数,有 种不同的方法取完这堆棋子.【考点】计数之递推法 【难度】5星 【题型】填空【解析】 把20、0和20以内不是3或4的倍数的数写成一串,用递推法把所有的方法数写出来:【答案】54【例 12】 4个人进行篮球训练,互相传球接球,要求每个人接球后马上传给别人,开始由甲发球,并作为第一次传球,第五次传球后,球又回到甲手中,问有多少种传球方法?【考点】计数之递推法 【难度】5星 【题型】解答【解析】 设第n 次传球后,球又回到甲手中的传球方法有n a 种.可以想象前1n -次传球,如果每一次传球都任选其他三人中的一人进行传球,即每次传球都有3种可能,由乘法原理,共有11333333n n --⨯⨯⨯=()个…(种)传球方法.这些传球方法并不是都符合要求的,它们可以分为两类,一类是第1n -次恰好传到甲手中,这有1n a -种传法,它们不符合要求,因为这样第n 次无法再把球传给甲;另一类是第1n -次传球,球不在甲手中,第n 次持球人再将球传给甲,有n a 种传法.根据加法原理,有11133333n n n n a a ---+=⨯⨯⨯=(个…).由于甲是发球者,一次传球后球又回到甲手中的传球方法是不存在的,所以10a =. 利用递推关系可以得到:2303a =-=,33336a =⨯-=,4333621a =⨯⨯-=,533332160a =⨯⨯⨯-=.这说明经过5次传球后,球仍回到甲手中的传球方法有60种.本题也可以列表求解.由于第n 次传球后,球不在甲手中的传球方法,第1n +次传球后球就可能回到甲手中,所以只需求出第四次传球后,球不在甲手中的传法共有多少种.从表中可以看出经过五次传球后,球仍回到甲手中的传球方法共有60种.【答案】60【巩固】五个人互相传球,由甲开始发球,并作为第一次传球,经过4次传球后,球仍回到甲手中.问:共有多少种传球方式?【考点】计数之递推法 【难度】5星 【题型】解答【解析】 递推法.设第n 次传球后球传到甲的手中的方法有n a 种.由于每次传球有4种选择,传n 次有4n 次可能.其中有的球在甲的手中,有的球不在甲的手中,球在甲的手中的有n a 种,球不在甲的手中的,下一次传球都可以将球传到甲的手中,故有1n a +种.所以14n n n a a ++=.由于10a =,所以12144a a =-=,232412a a =-=,343452a a =-=.即经过4次传球后,球仍回到甲手中的传球方法有52种.【答案】52【例 13】 设A 、E 为正八边形ABCDEFGH 的相对顶点,顶点A 处有一只青蛙,除顶点E外青蛙可以从正八边形的任一顶点跳到其相邻两个顶点中任意一个,落到顶点E 时青蛙就停止跳动,则青蛙从顶点A 出发恰好跳10次后落到E 的方法总数为 种.【考点】计数之递推法 【难度】5星 【题型】填空【关键词】清华附中【解析】 可以使用递推法.回到A 跳到B 或H 跳到C 或G 跳到D 或F 停在E1步 12步 2 13步 3 14步 6 4 25步 10 46步 20 14 87步 34 148步 68 48 289步 116 48其中,第一列的每一个数都等于它的上一行的第二列的数的2倍,第二列的每一个数都等于它的上一行的第一列和第三列的两个数的和,第三列的每一个数都等于它的上一行的第二列和第四列的两个数的和,第四列的每一个数都等于它的上一行的第三列的数,第五列的每一个数都等于都等于它的上一行的第四列的数的2倍.这一规律很容易根据青蛙的跳动规则分析得来.所以,青蛙第10步跳到E 有48296⨯=种方法.【答案】96【巩固】在正五边形ABCDE 上,一只青蛙从A 点开始跳动,它每次可以随意跳到相邻两个顶点中的一个上,一旦跳到D 点上就停止跳动.青蛙在6次之内(含6次)跳到D 点有 种不同跳法.【考点】计数之递推法 【难度】5星 【题型】填空【解析】 采用递推的方法.列表如下:跳到A 跳到B 跳到C 停在D 跳到E1步 1 12步 2 1 13步 3 1 24步 5 3 25步 8 3 56步 13 8 5其中,根据规则,每次可以随意跳到相邻两个顶点中的一个上,一旦跳到D 点上就停止跳动.所以,每一步跳到A 的跳法数等于上一步跳到B 和E 的跳法数之和,每一步跳到B 的跳法数等于上一步跳到A 和C 的跳法数之和,每一步跳到C 的跳法数等于上一步跳到B 的跳法数,每一步跳到E 的跳法数等于上一步跳到A 的跳法数,AB C DE每一步跳到D 的跳法数等于上一步跳到C 或跳到E 的跳法数.观察可知,上面的递推结果与前面的枚举也相吻合,所以青蛙在6次之内(含6次)跳到D 点共有1123512++++=种不同的跳法.【答案】12【例 14】 有6个木箱,编号为1,2,3,……,6,每个箱子有一把钥匙,6把钥匙各不相同,每个箱子放进一把钥匙锁好.先挖开1,2号箱子,可以取出钥匙去开箱子上的锁,如果最终能把6把锁都打开,则说这是一种放钥匙的“好”的方法,那么“好”的方法共有 种.【考点】计数之递推法 【难度】5星 【题型】填空【关键词】迎春杯,中年级组,决赛【解析】 (法1)分类讨论.如果1,2号箱中恰好放的就是1,2号箱的钥匙,显然不是“好”的方法,所以“好”的方法有两种情况:⑴1,2号箱的钥匙恰有1把在1,2号箱中,另一箱装的是3~6箱的钥匙.⑴1,2号箱的钥匙都不在1,2号箱中.对于⑴,从1,2号箱的钥匙中选1把,从3~6号箱的钥匙中选1把,共有248⨯=(种)选法,每一种选法放入1,2号箱各有2种放法,共有8216⨯=(种)放法.不妨设1,3号箱的钥匙放入了1,2号箱,此时3号箱不能装2号箱的钥匙,有3种选法,依次类推,可知此时不同的放法有3216⨯⨯=(种).所以,第⑴种情况有“好”的方法16696⨯=(种).对于⑴,从3~6号箱的钥匙中选2把放入1,2号箱,有4312⨯=(种)放法.不妨设3,4号箱的钥匙放入了1,2号箱.此时1,2号箱的钥匙不可能都放在3,4号箱中,也就是说3,4号箱中至少有1把5,6号箱的钥匙.如果3,4号箱中有2把5,6号箱的钥匙,也就是说3,4号箱中放的恰好是5,6号箱的钥匙,那么1,2号箱的钥匙放在5,6号箱中,有224⨯=种放法;如果3,4号箱中有1把5,6号箱的钥匙,比如3,4号箱中放的是5,1号箱的钥匙,则只能是5号箱放6号箱的钥匙,6号箱放2号箱的钥匙,有212⨯=种放法; 同理,3,4号箱放5,2号箱或6,1号箱或6,2号箱的钥匙,也各有2种放法. 所以,第⑴种情况有“好”的放法()1242222144⨯++++=(种).所以“好”的方法共有96144240+=(种).(法2)递推法.设第1,2,3,…,6号箱子中所放的钥匙号码依次为1k ,2k ,3k ,…,6k .当箱子数为n (2n ≥)时,好的放法的总数为n a .当2n =时,显然22a =(11k =,22k =或12k =,21k =).当3n =时,显然33k ≠,否则第3个箱子打不开,从而13k =或23k =,如果13k =,则把1号箱子和3号箱子看作一个整体,这样还是锁着1,2两号钥匙,撬开1,2两号箱子,那么方法有2a 种;当23k =也是如此.于是2n =时的每一种情况对应13k =或23k =时的一种情况,这样就有3224a a ==.当4n ≥时,也一定有n k n ≠,否则第n 个箱子打不开,从而1k 、2k 、……、1n k -中有一个为n ,不论其中哪一个是n ,由于必须要把该箱子打开才能打开n 号箱子,所以可以将锁着这把钥匙的箱子与第n 号箱子看作1个箱子,于是还是锁着1k 、2k 、……、1n k -这()1n -把钥匙,需要撬开1,2两号箱子,所以每种情况都有1n a -种.所以()11n n a n a -=-.所以,6542554543225!240a a a a ==⨯==⨯⨯⨯=⨯=,即好的方法总数为240种.【答案】240【巩固】有10个木箱,编号为1,2,3,……,10,每个箱子有一把钥匙,10把钥匙各不相同,每个箱子放进一把钥匙锁好.先挖开1,2号箱子,可以取出钥匙去开箱子上的锁,如果最终能把10把锁都打开,则说这是一种放钥匙的“好”的方法,那么“好”的方法共有 种.【考点】计数之递推法 【难度】5星 【题型】填空【解析】 递推法.设第1,2,3,…,6号箱子中所放的钥匙号码依次为1k ,2k ,3k ,…,6k .当箱子数为n (2n ≥)时,好的放法的总数为n a .当2n =时,显然22a =(11k =,22k =或12k =,21k =).当3n =时,显然33k ≠,否则第3个箱子打不开,从而13k =或23k =,如果13k =,则把1号箱子和3号箱子看作一个整体,这样还是锁着1,2两号钥匙,撬开1,2两号箱子,那么方法有2a 种;当23k =也是如此.于是2n =时的每一种情况对应13k =或23k =时的一种情况,这样就有3224a a ==.当4n ≥时,也一定有n k n ≠,否则第n 个箱子打不开,从而1k 、2k 、……、1n k -中有一个为n ,不论其中哪一个是n ,由于必须要把该箱子打开才能打开n 号箱子,所以可以将锁着这把钥匙的箱子与第n 号箱子看作1个箱子,于是还是锁着1k 、2k 、……、1n k -这()1n -把钥匙,需要撬开1,2两号箱子,所以每种情况都有1n a -种.所以()11n n a n a -=-.所以,109829989876543229!=725760a a a a ==⨯==⨯⨯⨯⨯⨯⨯⨯=⨯,即好的方法总数为725760种.【答案】725760。
小升初奥数计数方法

模块一、归纳法从条件值较小的数开始,找出其中规律,或找出其中的递推数量关系,归纳出一般情况下的数量关系.【例1】一条直线分一个平面为两部分.两条直线最多分这个平面为四部分.问5条直线最多分这个平面为多少部分?(6级)【巩固】平面上5条直线最多能把圆的内部分成几部分?平面上100条直线最多能把圆的内部分成几部分?(6级)【例 2】平面上10个两两相交的圆最多能将平面分割成多少个区域?(8级)【例 3】10个三角形最多将平面分成几个部分?(8级)【例4】一个长方形把平面分成两部分,那么3个长方形最多把平面分成多少部分?(8级)【例5】在平面上画5个圆和1条直线,最多可把平面分成多少部分?(10级)【例 6】在一个西瓜上切6刀,最多能将瓜皮切成多少片?(8级)【例 7】在一大块面包上切6刀最多能将面包切成多少块.(注:面包是一个立体几何图形,切面可以是任何方向)(10级)模块二、整体法解决计数问题时,有时要“化整为零”,使问题变得简单;有时反而要从整体上来考虑,从全局、从整体来研究问题,反而有利于发现其中的数量关系.【例8】一个正方形的内部有1996个点,以正方形的4个顶点和内部的1996个点为顶点,将它剪成一些三角形.问:一共可以剪成多少个三角形?如果沿上述这些点中某两点之间所连的线段剪开算作一刀,那么共需剪多少刀?(8级)【巩固】在三角形ABC内有100个点,以三角形的顶点和这100点为顶点,可把三角形剖分成多少个小三角形?(8级)【例 9】在一个六边形纸片内有60个点,以这60个点和六变形的6个顶点为顶点的三角形,最多能剪出_______个.(8级)模块三、对应法将难以计数的数量与某种可计量的事物联系起来,只要能建立一一对应的关系,那么这两种事物在数量上是相同的.事实上插入法和插板法都是对应法的一种表现形式.一、图形中的对应关系形(如图),一共有多少种不同的方法?(6【例10】在8×8的方格棋盘中,取出一个由三个小方格组成的“L”级)【例11】在8×8的黑白相间染色的国际象棋棋盘中,以网格线为边的、恰包含两个白色小方格与一个黑色小方格的长方形共有多少个?(6级)【巩固】用一张如图所示的纸片盖住66方格表中的四个小方格,共有多少种不同的放置方法?(6级)【例12】图中可数出的三角形的个数为.(8级)【例 13】如图所示,在直线AB上有7个点,直线CD上有9个点.以AB上的点为一个端点、CD上的点为另一个端点的所有线段中,任意3条线段都不相交于同一个点,求所有这些线段在AB与CD之间的交点数.(8级)ABC D二、数字问题中的对应关系【例 14】有多少个四位数,满足个位上的数字比千位数字大,千位数字比百位大,百位数字比十位数字大?(8级)【巩固】三位数中,百位数比十位数大,十位数比个位数大的数有多少个?(8级)【例 15】数3可以用4种方法表示为一个或几个正整数的和,如3,12,21,111.问:1999表示为一个或几个正整数的和的方法有多少种?(8级)【例 16】(2008年国际小学数学竞赛)请问至少出现一个数码3,并且是3的倍数的五位数共有多少个?(8级)三、对应与阶梯型标数法【例 17】游乐园的门票1元1张,每人限购1张.现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱.问有多少种排队方法,使售票员总能找得开零钱?(10级)【例 18】(2008年第一届“学而思杯”五年级试题)学学和思思一起洗5个互不相同的碗(顺序固定),思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放入碗柜摞成一摞,思思一边洗,学学一边拿,那么学学摞好的碗一共有种不同的摞法.(10级)【例 19】(第七届走美试题)一个正在行进的8人队列,每人身高各不相同,按从低到高的次序排列,现在他们要变成并列的2列纵队,每列仍然是按从低到高的次序排列,同时要求并排的每两人中左边的人比右边的人要矮,那么,2列纵队有种不同排法.(10级)【巩固】将1~12这12个数填入到2行6列的方格表中,使得每行右边比左边的大,每一列上面比下面的大,共有多少种填法?(10级)四、不完全对应关系【例 20】圆周上有12个点,其中一个点涂红,还有一个点涂了蓝色,其余10个点没有涂色,以这些点为顶点的凸多边形中,其顶点包含了红点及蓝点的多边形称为双色多边形;只包含红点(蓝点)的多边形称为红色(蓝色)多边形.不包含红点及蓝点的称无色多边形.试问,以这12个点为顶点的所有凸多边形(边数可以从三角形到12边形)中,双色多边形的个数与无色多边形的个数,哪一种较多?多多少个?(8级)【例 21】有一类各位数字各不相同的五位数M,它的千位数字比左右两个数字大,十位数字也比左右两位数字大.另有一类各位数字各不相同的五位数W,它的千位数字比左右两个数字小,十位数字也比左右两位数字小.请问符合要求的数M与W,哪一类的个数多?多多少?(10级)【例 22】用1元,2元,5元,10元四种面值的纸币若干张(不一定要求每种都有),组成99元有P种方法,组成101元有Q种方法,则Q P.(10级)模块四、递推法对于某些难以发现其一般情形的计数问题,可以找出其相邻数之间的递归关系,有了这一递归关系就可以利用前面的数求出后面未知的数,这种方法称为递推法.【例1】每对小兔子在出生后一个月就长成大兔子,而每对大兔子每个月能生出一对小兔子来.如果一个人在一月份买了一对小兔子,那么十二月份的时候他共有多少对兔子?(6级)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图中,“我爱希望杯”有______种不同的读法。
【举一反三】如图,要从A 去B ,C 不能通过,最短线路有______条。
游乐园门票1元1张,每人限购1张。
现有10个小朋友排队购买,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有零钱。
10个小朋友排队,不同的排队方法总共有10!=3628800种,问其中有______种排队方法,售票员总能找的开零钱。
【举一反三】
在一次选举中甲、乙两人参加竞选,甲得5张选票,乙也得5张选票,问在对这10张选票逐一唱票的过程中,乙的得票始终未能领先的点票记录共有______种可能。
(★★)
(★★★★★)
一个楼梯共有10级阶梯,规定每步可以逐一级台阶或两级台阶,走完这10级台阶,一共有______种不同走法。
对一个自然数进行如下操作:如果是偶数则除以2,如果是奇数则加1,如此进行下去直到得数为1停止。
问经过9次操作变为1的数有______个。
在平面上画8个圆,最多可以把平面分成_______
部分。
在线测试题
温馨提示:请在线作答,以便及时反馈孩子的薄弱环节。
1.如下图所示,要从A 点沿线段走到B ,要求每一步都是向右、向上或者斜上方。
问有多少种不同的走法?
B A
A A .18
B .20
C .22
D .24
(★★★)
(★★★)
(★★★☆)
2.有15个相同的棋子,一个人分若干次取,每次可取1个,2个,3个或4个,但要求每次取之后留下的棋子数不是3或4的倍数,有种不同的方法取完这堆棋子。
A.11B.22C.33D.18
3.上一段12级楼梯,规定每一步只能上一级或两级楼梯,要登上第12级楼梯,不同的走法共有多少种?
A.233B.230C.243D.253
4.给你一架天平和两个砝码,这两个砝码分别重20克和50克,如果再添四个砝码,则这六个砝码可以称的重量种类最多是多少种。
(天平的左右两盘均可放砝码)
A.268B.256C.364D.280
5.平面上的5个圆和3条直线最多能把平面分成多少部分?
A.55B.57C.32D.48。
