各种SAR成像算法总结
SAR数字成像算法

SAR Digital Imaging Algorithms 主要汇报内容:一、SAR 的工作原理二、主要成像算法简介汇报人:张彦飞(博士生)导师:关键(教授)2005年5月14日一、SAR 的工作原理1 感性认识正侧视条带(stripmap) SAR 的空间几何关系(正视图)正侧视条带SAR 的空间几何关系(后视图)SAR 的天线位置与点目标的几何关系SAR的天线为什么要侧视工作?技术上可以提高距离向在地面上的分辨率;战术上可以在远距离上实施对战场的侦察。
SAR天线侧视的作用从不同角度对SAR的工作原理的理解(1)从阵列天线上看实孔径ULA阵列天线一个小孔径的天线在直线上移动形成的合成阵列天线可以等效于上面的实孔径ULA 阵列天线 但是两者还有以下的重要区别: SAR 与实孔径阵列雷达的区别:实孔径雷达 目标在远区场(夫琅和费区); R p >2D 2/λ 平面波 单程相移 SAR 目标在近区场(菲涅尔区); R p <2L 2S /λ 球面波 双程相移0/,s D L R θλθ==, 例如:X 波段,波长 3cm ,D=2m ,R 0=20公里,得到:合成孔径长度L S=300米,2D 2/λ=267米,2L 2S /λ=6000公里。
见下图实孔径阵列天线 合成阵天线 (2) 从匹配滤波上看频域上:匹配滤波器-------相位校正网络--------移相(延时)和相加SAR 的聚焦过程与匹配虑波作用的类比匹配虑波作用:对信号进行 :相位校正(同相)和同相相加(3) 从相关接收看 :时域处理,与频域上的匹配滤波等价。
匹配滤波器的输出就是输入信号的自相关函数。
(4) 从脉冲压缩上看:对线调频信号,‘压缩’滤波器就是‘匹配’滤波器。
(5) 从多普勒效应上看。
对时间(距离)的分辨可以转化为对频率的分辨(因为:SAR 回波的平方相位的线性调频特性使时间(距离)和频率二者有线性关系。
)SAR 的近似简化物理模型:雷达在一个位置发射并在同一位置接收,然后跳到下个位置发射和接收。
(完整版)各种SAR成像算法总结,推荐文档

sr
(t)
Wa
t
R(t) c
st
t
2R(t) c
(1.20)
n
Wa
t
R(t) c
p
t
nPRT
2R(t) c
其中, 为目标的后向散射特性,Wa (A) 为方位向的天线方向性函数, c 为 光速。
sr (t) 经正交解调后的复信号 s(t) 可以表示为:
s(t)
n
Wa
t
R(t) c
s0
t
1.2 SAR 回波信号模型
1.1 节分析了 SAR 成像的基本原理,本节推导 SAR 回波信号的数学模型,
给出 SAR 信号处理的理论基础。
chirp 信号是 SAR 系统中最常用的发射信号形式。假设雷达发射的 chirp 脉
冲串 st (t) 为:
n
st (t) p(t nPRT ) n
(1.19)
1.1 SAR 成像原理
本节以基本的正侧视条带工作模式为例,对 SAR 的成像原理进行分析和讨
论。
正侧视条带 SAR 的空间几何关系如下图所示。图中,αoβ 平面为地平面,
oγ 垂直于 αoβ 平面。SAR 运动平台位于 S 点,其在地面的投影为 G 点。SAR
运动平台的运动方向 Sx 平行于 oβ,速度大小为 va 。SAR 天线波束中心与地面 的交点为 C,CG 与运动方向 Sx 垂直;S 与 C 的距离为 Rs , B1SB2 称为天线波 束的方位向宽度,大小为 a 。P 为测绘带内的某一点,一般情况下取斜距平面 CSP 进行分析,称 SAR 运动的方向 Sx 为方位向(或方位维),称天线波束指向
量 fd (t) 为:
fd
sar成像算法核心是傅里叶变换

sar成像算法核心是傅里叶变换【原创版】目录1.SAR 成像算法的核心2.傅里叶变换的概念和作用3.傅里叶变换在 SAR 成像算法中的应用4.傅里叶变换的优势和局限性5.未来发展趋势正文一、SAR 成像算法的核心SAR(Synthetic Aperture Radar)成像算法是一种利用合成孔径雷达技术进行成像的方法。
其核心是傅里叶变换,通过将原始数据进行傅里叶变换,提取出目标物体的频谱信息,再经过逆傅里叶变换,将频谱信息转换回图像域,从而实现对目标物体的成像。
二、傅里叶变换的概念和作用傅里叶变换是一种在信号处理、图像处理等领域具有重要应用的数学方法。
其基本思想是将一个信号(或图像)分解为一系列不同频率的正弦波(或余弦波)的叠加。
傅里叶变换可以将非周期信号转换为周期信号,也可以将周期信号转换为非周期信号。
在 SAR 成像算法中,傅里叶变换的作用是将原始数据转换为频谱数据,从而提取出目标物体的频率信息。
三、傅里叶变换在 SAR 成像算法中的应用在 SAR 成像算法中,傅里叶变换被用于提取目标物体的频谱信息。
通过对原始数据进行傅里叶变换,可以得到目标物体的频谱图,从而提取出目标物体的频率信息。
再通过逆傅里叶变换,将频谱信息转换回图像域,从而实现对目标物体的成像。
四、傅里叶变换的优势和局限性傅里叶变换在 SAR 成像算法中的优势在于,它可以将非周期信号转换为周期信号,从而方便地进行频谱分析。
同时,傅里叶变换可以提取出目标物体的频率信息,从而实现对目标物体的成像。
然而,傅里叶变换也存在一些局限性。
首先,傅里叶变换只能处理有限长度的信号,对于无限长度的信号,需要进行截断处理。
其次,傅里叶变换对噪声敏感,噪声的存在可能会影响频谱分析的结果。
五、未来发展趋势随着 SAR 技术的不断发展,对成像算法的要求也越来越高。
未来,SAR 成像算法将朝着更高的分辨率、更准确的成像结果和更强的抗干扰能力方向发展。
sar 常用成像算法

sar 常用成像算法SAR(Synthetic Aperture Radar)是合成孔径雷达的缩写,是一种利用雷达技术进行成像的方法。
常用成像算法是指在SAR成像过程中常用的数据处理方法,用于从原始雷达数据中提取目标信息并生成可视化图像。
本文将介绍几种常用的SAR成像算法。
一、Range-Doppler算法Range-Doppler算法是最基础、最常用的SAR成像算法之一。
它通过两个主要步骤来实现成像:距离向(Range)压缩和多普勒向(Doppler)压缩。
首先,进行距离向压缩,将接收到的信号与发射的信号进行相关运算,得到目标在距离上的分布信息。
然后,进行多普勒向压缩,根据目标的运动情况对信号进行频率调整,得到目标在速度上的分布信息。
最后,将两个方向上的信息进行合成,得到最终的成像结果。
二、Chirp Scaling算法Chirp Scaling算法是一种用于高分辨率SAR成像的算法。
它通过对原始SAR数据进行频率调整,实现对目标的高精度成像。
具体而言,该算法通过对接收到的信号进行线性调频,使得距离上的分布信息与目标的距离成线性关系。
然后,对调频后的信号进行快速傅里叶变换,得到目标在频谱上的分布信息。
最后,对频谱信息进行逆变换,得到目标在距离上的高分辨率成像结果。
三、Omega-K算法Omega-K算法是一种用于高分辨率SAR成像的频域算法。
它通过对SAR数据进行快速傅里叶变换,将时域数据转换为频域数据,然后根据目标的运动情况对频域数据进行调整,实现高分辨率成像。
具体而言,该算法通过对频域数据进行插值,使得目标的速度信息与频率成线性关系。
然后,对插值后的数据进行逆傅里叶变换,得到目标在距离上的高分辨率成像结果。
四、Polar Format算法Polar Format算法是一种用于SAR成像的快速算法。
它通过将SAR数据从直角坐标系转换为极坐标系,实现对目标的快速成像。
具体而言,该算法首先将原始SAR数据进行极坐标变换,得到距离和方位两个维度上的数据。
sar影像地理编码算法

sar影像地理编码算法【实用版】目录1.SAR 影像概述2.地理编码算法的定义和作用3.SAR 影像地理编码算法的分类4.常见 SAR 影像地理编码算法的原理和应用5.SAR 影像地理编码算法的发展趋势正文一、SAR 影像概述SAR(Synthetic Aperture Radar)影像,即合成孔径雷达影像,是一种利用雷达技术获取地表信息的遥感技术。
与传统的光学遥感影像相比,SAR 影像具有全天候、全天时、高精度、高分辨率等优点,被广泛应用于地质勘探、环境监测、城市规划等领域。
二、地理编码算法的定义和作用地理编码算法是指将 SAR 影像中的像素信息转换为实际地理坐标系的过程,其主要目的是实现 SAR 影像与现实地理空间的准确匹配。
通过地理编码,可以方便地对 SAR 影像进行空间分析和定位,为后续的遥感应用提供基础数据支持。
三、SAR 影像地理编码算法的分类根据地理编码算法的原理和方法,SAR 影像地理编码算法主要分为以下几类:1.基于地面控制点的地理编码算法2.基于区域生长法的地理编码算法3.基于多普勒雷达原理的地理编码算法4.基于极化信息的地理编码算法5.基于 SAR 影像自身特征的地理编码算法四、常见 SAR 影像地理编码算法的原理和应用(1)基于地面控制点的地理编码算法该算法通过在 SAR 影像上选取一定数量的地面控制点(如道路、建筑物、水体等明显地物),利用地面控制点的已知地理坐标,求解影像中像素到地理坐标的映射关系。
该算法适用于地面控制点较为丰富的区域,但计算量较大,且容易受到地面控制点质量的影响。
(2)基于区域生长法的地理编码算法该算法以 SAR 影像中某个像素为种子,根据其周边像素的强度、纹理等信息,逐步向外扩展,形成一个区域。
通过对比该区域与实际地理区域的相似性,确定该像素的地理坐标。
该算法适用于复杂地形和地貌区域,但计算量较大,对初始种子像素的选择较为敏感。
(3)基于多普勒雷达原理的地理编码算法该算法利用多普勒雷达原理,通过测量 SAR 影像中地物回波的频率变化,计算地物的三维坐标信息。
SAR成像算法docx
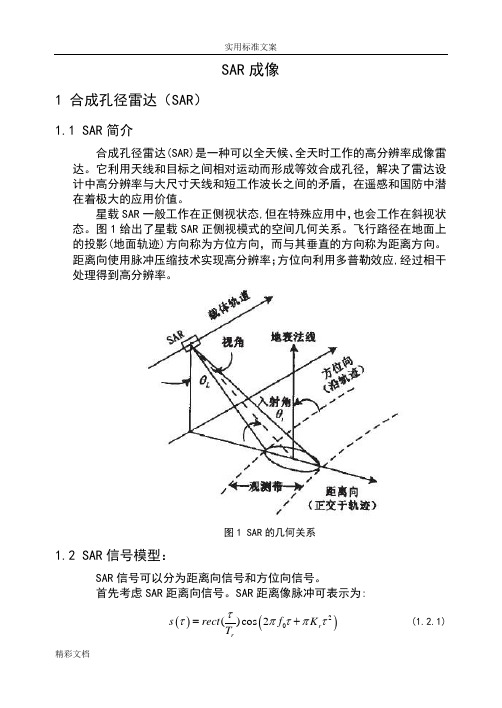
SAR 成像1 合成孔径雷达(SAR )1.1 SAR 简介合成孔径雷达(SAR)是一种可以全天候、全天时工作的高分辨率成像雷达。
它利用天线和目标之间相对运动而形成等效合成孔径,解决了雷达设计中高分辨率与大尺寸天线和短工作波长之间的矛盾,在遥感和国防中潜在着极大的应用价值。
星载SAR 一般工作在正侧视状态,但在特殊应用中,也会工作在斜视状态。
图1给出了星载SAR 正侧视模式的空间几何关系。
飞行路径在地面上的投影(地面轨迹)方向称为方位方向,而与其垂直的方向称为距离方向。
距离向使用脉冲压缩技术实现高分辨率;方位向利用多普勒效应,经过相干处理得到高分辨率。
图1 SAR 的几何关系1.2 SAR 信号模型:SAR 信号可以分为距离向信号和方位向信号。
首先考虑SAR 距离向信号。
SAR 距离像脉冲可表示为:()()20()cos 2r rs rect f K T ττπτπτ=+ (1.2.1)其中,r T 为脉冲持续时间,r K 为距离向昧冲的调频率,0f 为中心频率, τ以脉神中心为参考原点。
任一照射时刻的反射能量脉冲波形和照射区域内地面反射系数r g 的卷积,如下所示:()()()r r s g s τττ=⊗ (1.2.2) 考察距雷达0R 处的一个目标点,其后向散射系数0σ的幅度为A ,则式(1.2.2)中的()02r g A R c δτ=-,其中c 为光速,02R c 为该点的信号延时。
所以可知,该点目标的接收信号为:()()()()200002()cos 222r r rR cs Arect f R c K R c T ττπτπτφ-=-+-+(1.2.3)其中,φ表示地表散射过程可能引起的首达信号相位改变。
现在考虑方位向信号。
由于大多数SAR 天线在方位面内没有加权,其单程方向图可以近似为一个sin c 函数:()0.886sin a bw P c θθβ⎛⎫≈⎪⎝⎭(1.2.4) 其中θ为斜距平面内测得的与视线的夹角,bw β方位向波束宽度0.886a L θλ,a L 为方位向天线长度。
SAR成像算法及其应用研究

SAR成像算法及其应用研究合成孔径雷达(SAR)通过合成大孔径天线或雷达模拟大孔径天线等技术获得极高的分辨率和距离测量精度,成为遥感、军事、海洋、气象、地球物理和石油勘探等领域不可或缺的高精度雷达。
SAR的成像算法是SAR成像的核心,它直接影响SAR成像系统的分辨率和图像质量。
本文将对SAR成像算法进行探究,并简单介绍其应用研究。
一、SAR成像算法SAR成像算法包括多普勒校正、相位解调、像元赋权等一系列的信息处理过程。
其中,多普勒校正的目的是对地物进行正确的距离测量;相位解调则是生成复合数据,提取目标的信息;像元赋权则决定了目标在合成孔径雷达观测中的光滑性质。
SAR成像算法可以分为傅里叶变换和波束形成两类。
傅里叶变换方法主要用于解决点目标的成像问题,如快速傅里叶变换(FFT)算法、极化编码算法等;波束形成方法则主要用于解决区域目标的成像问题,如扫描成像算法、斜视SAR成像算法等。
1. 快速傅里叶变换(FFT)算法快速傅里叶变换算法是目前SAR成像中最为常用的算法之一。
该算法主要用于处理单个点目标,其基本思想是对雷达信号进行傅里叶变换,将时域数据转换为频域数据,并利用频域信号的峰值位置计算目标的距离。
然后再反变换回时域,从而得到目标图像。
FFT算法具有高效、简单、精度高等优点,在实际应用中得到了广泛的应用。
2. 极化编码算法极化编码算法是一种非常适合处理点状目标的快速SAR成像算法。
在该算法中,先将多次停波的SAR信号进行脉冲压缩,对合成孔径的平面分别进行FFT,然后进行极化编码,以提高信号噪声比。
最后进行逆傅里叶变换,得到点目标的图像。
实际应用中,极化编码算法可以用于飞机、卫星、地球观测卫星等的SAR成像。
3. 扫描成像算法扫描成像算法是一种非常适合处理区域目标的SAR成像算法。
扫描成像算法主要通过扫描合成孔径雷达的波束,将二维信息变为一维信息,然后进行数据处理和图像重建。
扫描成像算法可以分为空时扫描和频移扫描两种形式。
曲线运动sar成像算法研究

曲线运动sar成像算法研究曲线运动SAR成像是近几年新型的一种成像技术。
它是将目标物体轨迹在空间中曲线转化成距离时间变化模式表示,并借助SAR 技术获得物体图像信息。
由于曲线运动SAR成像具有阵列排列紧凑、成像效率高、探测范围可调等特点,在无人机目标跟踪、地面目标识别等应用领域具有重要的战略意义和重要的应用价值。
一、曲线运动SAR成像原理曲线运动SAR成像是把物体运动轨迹转化为时间序列的距离变化模式,然后借助SAR技术,对时间序列的距离变化模式进行采样,获得物体图像信息。
曲线运动SAR成像由以下四个步骤组成: 1.迹参数估计:轨迹参数估计主要是用来确定物体运动轨迹及其有关参数,如最大运动速度、运动方向等。
2. matlab模拟时间序列:在估计出物体运动轨迹的参数后,利用Matlab的曲线拟合算法拟合曲线,确定物体在不同时间的位置,得到物体在空间中的时间序列,从而得出物体的距离时间变化模式。
3. SAR信号采样:根据物体的距离时间变化模式,对其采样,获得信号采样序列,从而得到物体的位置信息。
4.像恢复:将采样得到的信号序列进行预处理,然后使用图像恢复技术,将目标图像恢复出来。
二、曲线运动SAR成像算法曲线运动SAR成像算法的核心是将物体的运动轨迹转化为时间序列的距离变化模式,并借助SAR技术获得物体图像信息。
具体算法步骤如下:1.择运动轨迹模型:首先选择最适合物体行走轨迹的模型,包括线性运动模型、圆弧运动模型和组合运动模型等;2. 估计轨迹参数:利用模型估计物体的运动轨迹的参数,如最大运动速度、运动方向等;3. matlab模拟时间序列:利用Matlab的曲线拟合算法,确定物体在不同时间的位置,获得物体的时间序列,从而得出距离时间变化模式;4. SAR信号采样:根据物体的距离时间变化模式,对其采样,获得信号采样序列,并由此确定物体的位置;5.像恢复:将采样得到的信号序列进行预处理,然后使用图像恢复技术,将目标图像恢复出来。
弹载SAR多种工作模式的成像算法研究

弹载SAR多种工作模式的成像算法研究弹载SAR多种工作模式的成像算法研究一、引言合成孔径雷达(Synthetic Aperture Radar,SAR)是一种获取地面目标信息的重要无源遥感技术,具有天气无关性、全天候能力、高分辨率等优点,在军事、航天、气象、资源和环境等领域得到广泛应用。
随着科技的不断发展,弹载SAR成为了一种新的应用方式,其具有携带灵活、部署迅速、任务响应快的特点,对于执行突击、侦查和监视任务具有明显优势。
弹载SAR系统中的成像算法是实现优质成像的核心技术,研究多种工作模式的成像算法对于提高弹载SAR的性能具有重要意义。
二、弹载SAR多种工作模式弹载SAR系统可根据不同的任务需求,通过调整参数和配置,实现多种工作模式。
常见的工作模式包括宽带成像模式、高分辨率成像模式、低频成像模式和多视角成像模式等。
1. 宽带成像模式宽带成像模式是弹载SAR系统中的基本工作模式。
它采用宽带脉冲信号,通过接收天线接收反射回波信号,并进行距离向合成孔径成像处理,得到高分辨率的成像结果。
该模式适用于对地面目标进行普遍探测和情报收集。
2. 高分辨率成像模式高分辨率成像模式是弹载SAR系统的一种特殊工作模式。
在该模式下,系统通过改变脉冲信号的参数,增加工作频率和带宽,进一步提高距离向和方位向分辨率,实现更精细的目标成像。
该模式常用于对小型目标或需要高精度位置和形状信息的目标进行定位和跟踪。
3. 低频成像模式低频成像模式是弹载SAR系统的一种特殊工作模式,主要应用于穿透探测任务。
在此模式下,系统采用较低的工作频率和带宽,通过改变脉冲信号的参数,减小信号在目标穿透介质中的衰减,从而实现对地下目标的成像。
该模式在地质勘探、隧道检测等领域具有广阔应用前景。
4. 多视角成像模式多视角成像模式是弹载SAR系统的一种特殊工作模式,通过引入多个接收天线,实现对目标在不同角度的成像观测。
通过比较不同视角的成像结果,可以获得更全面、立体的目标信息。
聚束sar pfa成像算法原理

一、概述SAR (Synthetic Aperture Radar) 是一种应用于遥感和监测的重要技术,其通过合成孔径雷达成像技术,可以在任何天气条件下获取地面的高分辨率雷达图像。
而sar pfa (Synthetic Aperture Radar Processing and Automatic Target Recognition) 成像算法则是一种用于处理和识别sar图像中目标的重要算法。
本文将介绍sar pfa成像算法的原理及其工作流程。
二、SAR成像的基本原理1. SAR雷达的发射和接收SAR雷达通过发射一束窄带宽的雷达波并接收其回波来获取地面图像。
在这个过程中,雷达评台会在地面上的不同位置进行移动,以获取不同位置的雷达回波。
2. SAR成像的合成孔径原理合成孔径雷达利用雷达评台的运动形成一条合成孔径,通过对地面目标的多个回波信号进行叠加,从而达到提高分辨率的效果。
3. SAR图像的生成通过对不同位置的雷达回波信号进行时域或频域的处理,可以生成高分辨率的sar图像,这为后续的目标识别和分类提供了基础数据。
三、SAR PFA成像算法原理1. SAR PFA的处理流程SAR PFA成像算法主要包括三个处理步骤,即预处理、目标检测和目标识别。
在预处理过程中,需要进行滤波、去斑点、配准等操作;在目标检测阶段,利用一定的检测算法对图像中的目标进行初步识别;在目标识别阶段,对检测出的目标进行特征提取和分类识别。
2. SAR PFA的算法原理SAR PFA成像算法采用了多种信号处理、图像处理和模式识别技术,其中包括波门、超分辨、极化分解、统计特征提取等,来实现对sar图像中目标的快速、准确识别。
四、SAR PFA成像算法的应用SAR PFA成像算法在军事、环境监测、资源勘探、灾害监测等领域都有着重要的应用。
在军事领域,SAR PFA成像算法可用于目标识别和情报获取;在环境监测中,可用于地质勘探和环境监测;在资源勘探中,可用于矿产勘探和土地利用调查;在灾害监测中,可用于地震、洪涝和火灾等自然灾害的监测和评估。
SAR成像及成像算法

SAR成像及成像算法
SAR(Synthetic Aperture Radar),即合成孔径雷达,是一种具有视距的雷达成像技术,它利用通过雷达发射的电磁波的返回信号来构建成像,是今天最受欢迎的遥感成像技术之一、它是由空间技术应用罗列公司(STARS)于1970年首次研制完成的。
由于它的无损探测、低成本、通用性强、快速更新和相当高的精度等优点,使SAR成像广泛应用于地表特性探测、航空和海洋地理资源监测、地表热分辨观测、大气和气候研究等多种领域,并取得了突出的成果。
SAR成像的本质是利用雷达发射的电磁波探测地表物质的反射状态,从而构建三维图像。
SAR成像算法主要分成基线分析、多普勒解析和像元投影三个过程。
首先,基线分析是处理多普勒解析的基本步骤,它识别SAR图像的物理位置,将地表物质的反射信号与它们在同一物理位置的多普勒频率作对比,从而计算出相应的基线;其次,多普勒解析处理SAR图像所涉及的空间结构,它可以利用反射信号的多普勒频率,将不同波段中的多普勒信号重建成三维定量数据;最后,像元投影过程会将三维数据转换成二维图像,以实现SAR成像。
当前。
各种SAR成像算法总结

各种SAR成像算法总结
(一)介绍
SAR (Synthetic Aperture Radar)成像技术是一种用来收集远距离目
标的远程遥感技术,它的优势在于具有良好的晴雨不分时,可以在夜间拍
摄和多光谱等条件下多视角拍摄等特点。
由于具有良好的分辨率、应用范
围广泛,SAR成像技术已经广泛应用于测绘、航空遥感、军事监视等领域。
SAR的成像算法是SAR成像技术的基础,它是指在给定的原始SAR数
据集上使用算法,以提取出有用的信息,生成可视为图像或图像的相关信息。
它可以根据用户需求将原始数据处理成有意义的图像,以及根据特定
的目的来分析和提取有用的信息。
SAR成像算法的种类多样,根据应用范
围和特点不同,可以分为集合成像法、多普勒成像法、干涉成像法和多普
勒微波成像法等。
(二)集合成像法
集合成像法是最常用的SAR成像算法之一,它是利用多次重复的SAR
数据,通过集中成像算法,将收集的多次SAR数据组合在一起,形成良好
的成像分辨率,从而获得较高的空间分辨率图像。
它具有易于操作、实时
性高等优势,且能够提取出反射系数、目标的形状、尺寸、傅立叶变换等
信息,为活动目标的跟踪和识别提供了便利。
双基SAR成像算法

03
数据处理系统对接收到的信号 进行处理,得到目标的高分辨 率图像。
双基SAR系统分类
根据发射站的数目,双基SAR可以分为两站SAR 和多站SAR。
多站SAR则有多个发射站和多个接收站,可以提 供更高的成像分辨率和更广的覆盖范围。
两站SAR是最简单的双基SAR,只有一个发射站 和一个接收站。
根据工作方式,双基SAR可以分为同步SAR和异 步SAR。同步SAR要求各接收站与发射站同步接 收信号,而异步SAR则不要求严格的时间同步。
实例
例如,可以采用基于小波变换的成像算法提 高图像质量和分辨率;采用基于压缩感知的 成像算法降低采样率和数据处理量;采用基 于深度学习的目标检测算法提高目标检测的
准确性和鲁棒性。
05
双基SAR系统实现与验证
系统硬件组成与工作模式
发射和接收天线
双基SAR系统需要使用两个 不同的天线,一个用于发射 射频信号,另一个用于接收 反射信号。发射天线通常采 用线性或圆形天线阵列,而 接收天线则采用高灵敏度的 接收器。
06
双基SAR应用与发展趋势
双基SAR在战场侦察与监视中的应用
战场侦察
双基SAR算法可以用于生成高分辨率的战场环境图像,帮助指 挥官了解敌方阵地和武器部署情况。
目标识别
双基SAR算法可以结合其他传感器数据,对目标进行分类和识 别,提高打击精度。
动态监视
双基SAR可以实时获取地面动态变化信息,如车辆移动、人员 聚集等,为决策提供支持。
双基SAR在灾害监测与救援中的应用
01
02
03
灾害预警
灾后评估
救援导航
双基SAR可以快速获取灾区图像 ,帮助有关部门及时发现灾情并 做出响应。
机载聚束模式合成孔径雷达的成像算法

机载聚束模式合成孔径雷达的成像算法机载聚束模式合成孔径雷达(SAR)是一种通过雷达波束的聚焦操作,在平台上获取到的一系列散射信号并进行处理后,得到高分辨率地物目标图像的技术。
SAR成像算法主要包括数据预处理、聚焦操作、图像重建和图像增强等步骤。
第一步是数据预处理,主要包括去噪、速度补偿、多普勒频率校正等。
去噪操作是为了消除由信号传播和原始数据采集等过程引入的噪声,提高成像质量。
速度补偿是为了校正因平台运动引起的多普勒频移问题,以保证聚焦操作的准确性。
多普勒频率校正是为了校正被测目标的运动造成的频率变化,以实现距离向的重建。
第二步是聚焦操作,主要是通过将回波信号与发射信号进行相乘,得到一个平台上各个散射目标的相干照片。
该操作类似于光学成像中的光束焦聚,对雷达回波信号进行远场近似,使得目标间的距离得到重建。
第三步是图像重建,主要通过将得到的相干照片进行二维傅里叶变换(FFT)和滤波操作,从而得到一个被测目标的二维散射场图像。
FFT可以将时域中的信号转换到频域中,通过频域上的滤波操作,去除干扰信号和杂散信号,提高目标的对比度和分辨率。
最后一步是图像增强,主要包括去斑点、边缘增强、动态范围调整等。
去斑点操作是为了除去由于信号传播过程中出现的突发斑点状干扰,提高图像的清晰性。
边缘增强操作是为了加强目标物与周围背景间的边界特征,使图像更容易观察和分析。
动态范围调整是为了调整图像亮度和对比度,使目标物体的细节更加清晰可见。
除了以上步骤外,SAR成像算法还需要考虑系统误差校正、多目标分离、散斑噪声抑制等问题。
系统误差校正是通过对辐射源和接收系统间的误差进行准确建模和校正,以提高成像的精度和准确度。
多目标分离是为了从得到的散射场图像中提取出多个目标,并对其进行分析和识别。
散斑噪声抑制是为了降低由传播过程和成像过程中引入的散斑噪声,提高图像质量。
总之,机载聚束模式合成孔径雷达的成像算法是一个复杂而精细的过程,需要通过数据预处理、聚焦操作、图像重建和图像增强等步骤,以及系统误差校正、多目标分离、散斑噪声抑制等技术手段,来实现高分辨率地物目标图像的获取。
sar成像算法时域 频域 波数域

SAR成像算法是合成孔径雷达(Synthetic Aperture Radar)技术的重要组成部分。
该算法主要是通过对雷达信号进行处理和分析,从而得到目标区域的高分辨率成像结果。
在SAR成像算法中,常常涉及到时域、频域和波数域等不同的数据处理方法。
本文将针对这三个主题展开详细的介绍和分析。
一、时域处理时域处理是SAR成像算法中最基本的数据处理方法之一。
时域处理主要是对雷达接收到的信号进行时域分析,包括距离-时间图像(Range-Time Image)的形成、脉冲压缩(Pulse Compression)等。
时域处理的关键是对信号的时延进行精确测量和定位,从而实现对目标的定位和成像。
在时域处理中,常用的算法包括FFt变换、匹配滤波等,这些算法可以提高雷达系统的距离分辨率和速度分辨率,从而实现对目标的高精度成像。
二、频域处理频域处理是SAR成像算法中另一个重要的数据处理方法。
频域处理主要是通过对雷达信号进行频谱分析,从而得到目标的频谱特征和频率分布信息。
频域处理可以通过傅里叶变换等算法将时域信号转换为频域信号,从而实现对信号的频率分辨率和频谱分布的分析。
在频域处理中,常用的算法包括FFT变换、滤波器设计等,这些算法可以对雷达信号进行频谱分析和滤波处理,从而提高SAR系统的信噪比和成像质量。
三、波数域处理波数域处理是SAR成像算法中较为复杂和高级的数据处理方法。
波数域处理主要是通过对雷达信号进行波数域分析,从而得到目标的波数分布和散射特征。
波数域处理可以通过波数变换、波数域滤波等算法实现对雷达信号的波数分布和散射特征的提取。
在波数域处理中,常用的算法包括快速波数变换算法、极化分析算法等,这些算法可以对雷达信号进行全波数域分析和波数域成像,从而实现对目标的高分辨率成像和三维重构。
时域、频域和波数域是SAR成像算法中常用的数据处理方法,它们各自具有特定的优点和适用范围,通过合理的组合和应用,可以实现对目标的高分辨率成像和高精度测量。
SAR总结——精选推荐

SAR总结1.星载InSAR技术简介 星载合成孔径雷达⼲涉测量(InSAR)是⼀种⽤于⼤地测量和遥感的雷达技术。
InSAR使⽤两个或多个SAR图像,利⽤返回卫星的波的相位差来计算⽬标地区的地形、地貌以及表⾯的微⼩变化,该技术可以潜在地测量n天到n年跨度的毫⽶级变形。
与可见光或红外光不同,雷达波可以穿透⼤多数云、雾和烟对地表物体进⾏观测,并在⿊暗中也同样有效。
因此,借助InSAR,即使在恶劣的天⽓和夜间,也可以监测地表的变形。
此外,InSAR的全天候、全天时、⾼分辨率、⾼精度、范围⼴等优点,不仅对可见光、近红外被动遥感技术具有很好的补充作⽤,⽽且在提取数字⾼程模型、制图、监测地表形变等⽅⾯具有⼴阔的前景。
常⽤的星载SAR及InSAR卫星系统参数SAR 、InSAR、D-InSAR的区别: SAR 合成孔径雷达技术是⼲涉雷达和差分⼲涉雷达技术的基础,⽽⼲涉雷达和差分⼲涉雷达技术则是合成孔径雷达技术的应⽤延伸和扩展。
InSAR ⼲涉雷达测量技术(INSAR)是以同⼀地区的两张SAR图像为基本处理数据,通过求取两幅SAR图像的相位差,获取⼲涉图像,然后经相位解缠,从⼲涉条纹中获取地形⾼程数据的空间对地观测新技术。
D-InSAR 差分⼲涉雷达测量技术(D-INSAR)是指利⽤同⼀地区的两幅⼲涉图像,其中⼀幅是通过形变事件前的两幅SAR获取的⼲涉图像,另⼀幅是通过形变事件前后两幅SAR图像获取的⼲涉图像,然后通过两幅⼲涉图差分处理(除去地球曲⾯、地形起伏影响)来获取地表微量形变的测量技术。
2.InSAR技术相关原理 将在不同时间从同⼀区域的相位位置获取两个雷达图像进⾏⽐较,可以测量地⾯朝向或远离卫星的任何运动,并将这些变形运动表达为雷达⼲涉图,从⼲涉图⾥得出两幅雷达图像在相隔的时间间隔内地形表⾯移动多少。
微波被反射后,卫星接收⽬标反射的回波,可以得到同⼀⽬标区域成像的SAR复图像对,若复图相对之间存在相⼲条件,则SAR复图像对共轭相乘可以得到⼲涉图。
sar影像地理编码算法

sar影像地理编码算法摘要:1.SAR影像地理编码算法简介2.SAR影像地理编码算法原理3.SAR影像地理编码算法应用4.算法优缺点分析5.未来发展趋势与展望正文:一、SAR影像地理编码算法简介SAR(Synthetic Aperture Radar,合成孔径雷达)影像地理编码算法是一种将SAR影像与地理坐标系(经纬度)相互转换的算法。
通过这种算法,我们可以将SAR影像中的像素点映射到地球表面的地理坐标系上,从而实现对SAR影像的地理空间分析。
在我国,SAR遥感技术已广泛应用于地质勘探、环境保护、城市规划等领域。
二、SAR影像地理编码算法原理SAR影像地理编码算法的核心是将SAR影像的像素坐标(行、列)转换为地理坐标(经度、纬度)。
这个过程主要包括以下几个步骤:1.传感器校正:由于SAR传感器的成像原理,原始SAR影像存在几何畸变。
通过传感器校正,可以消除这种畸变,得到均匀尺度的像素。
2.地理校正:根据SAR影像的成像几何模型,将像素坐标转换为地球坐标系下的地理坐标。
这一步通常包括去除地球自转影响、投影转换、尺度变换等操作。
3.地理编码:将经过地理校正的像素坐标与地理坐标系下的参考数据(如DEM、行政边界等)进行匹配,从而实现SAR影像的地理编码。
三、SAR影像地理编码算法应用SAR影像地理编码算法在多个领域具有广泛应用,如:1.环境监测:通过SAR影像地理编码,可以实现对地表形变、土壤湿度、植被生长状况等环境因子的监测。
2.城市规划:利用SAR影像地理编码结果,可以分析城市空间的扩展、道路网络、土地利用变化等信息。
3.地质勘探:在地震、滑坡等地质灾害预警中,SAR影像地理编码技术具有重要作用。
四、算法优缺点分析优点:1.高分辨率:SAR影像具有较高的空间分辨率,能够捕捉到地表的微小变化。
2.全天时、全天候观测:SAR遥感技术不受天气影响,可实现对地表的持续监测。
3.深穿透能力:SAR雷达波对地表覆盖具有一定的穿透能力,适用于复杂地形地貌区域。
SAR影像滤波算法

3.SAR 图像相干斑滤波算法目前已有大量的雷达相干斑抑制算法,这些算法可分为成像前的多视平滑预处理和成像后的滤波两大类。
而成像后的滤波又包括空域滤波和频域滤波两种。
为了减少相干斑噪声,早期的方法是在SAR 成像处理中,通过降低处理器带宽形成多视图子图像,然后对多视子图像进行非相干叠加来降低相干斑噪声。
这种非相干叠加来降低斑点噪声的方法称为多视处理。
多视处理通过牺牲SAR 图像的空间分辨率为代价来对相干斑进行抑制,已不能满足空间高分辨率的要求。
空域滤波方法是利用图像像素的空间相关性对相干斑进行滤波,一般是利用一个滑动窗口,然后对窗口内的像素进行加权得到窗口中心点的像素值。
频域的方法主要是利用小波变换,比较著名的有小波软阈值方法,基于小波变换和多尺度分析的滤波方法。
以下分别介绍增强Lee 滤波算法, Kuan 滤波算法,Frost 滤波算法,最大后验概率(MAP )滤波算法,边缘保持最优化(Edge Preserving Optimized Speckle ,EPOS )滤波算法等。
3.1 传统滤波方法传统滤波算法包括均值滤波、中值滤波等。
这类算法的特点是直接对图像进行处理,没有考虑任何噪声模型,也没有考虑噪声的统计特性。
这些算法实现起来比较简单,但效果不太理想。
它们计算简单,速度快,均匀区域的斑点噪声去除效果较好。
缺点是细节保持得不好,图像边缘变模糊,点目标损失大,随着处理窗口的增大,图像的整体模糊和分辨率下降更严重。
正是由于这两种传统滤波算法不适合相干斑噪声的乘性特点,实际中较少采用。
3.1.1 均值滤波均值滤波是将平滑窗口内所有像元的灰度值进行平均计算,然后赋给平滑窗口的中心像元,其数学表达式为: (2-17)∑∑===n i n j j i j i DN n R 11,2,1式中,为滤波后中心元素灰度值,为滤波窗口内各个像元的灰度j i R ,j i DN ,值,窗口大小为。
n n ⨯ 3.1.2 中值滤波中值滤波是一种非线性信号处理技术。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1.23)
同时,将时间 分解为快时间分量 和慢时间分量 之和,即:
,
(1.24)
通过变量置换,可以将 转换成二维形式:
(1.25)
其中, 表示对 的卷积, 表示对 的卷积, 表示二维卷积。
因此,雷达系统接收回波信号的过程,可以看作是地面目标的后向散射特性通过一个线性系统的过程。式(1.25)可简化表示为:
当方位向数据积累延迟小于全孔径时间(即方位向为子孔径数据)的情况下,方位向处理必须使用去斜(dechirp)处理及频谱分析的方法。在RD和CS算法的基础之上,采用dechirp处理及频谱分析的方法完成方位向处理的算法分别称为频谱分析(SPECAN)算法和扩展CS(Extended Chirp Scaling ECS)算法。
正侧视条带SAR几何关系示意图
假定P的方位向坐标为 ;在 时刻,SAR运动平台S与P的距离为 。若当 时刻,SAR运动平台位于方位向0点,则当 时刻, 的表达式为:
(1.1)
将式(1.1)在 附近进行2阶Taylor展开,有:
(1.2)
假设雷达发射连续的正弦波,即发射信号 为:
(1.3)
其中, 为发射正弦波的幅度, 为发射信号的载频。
1.1
本节以基本的正侧视条带工作模式为例,对SAR的成像原理进行分析和讨论。
正侧视条带SAR的空间几何关系如下图所示。图中,αoβ平面为地平面,oγ垂直于αoβ平面。SAR运动平台位于S点,其在地面的投影为G点。SAR运动平台的运动方向Sx平行于oβ,速度大小为 。SAR天线波束中心与地面的交点为C,CG与运动方向Sx垂直;S与C的距离为 , 称为天线波束的方位向宽度,大小为 。P为测绘带内的某一点,一般情况下取斜距平面CSP进行分析,称SAR运动的方向Sx为方位向(或方位维),称天线波束指向方向SC为距离向(或距离维)。
1.2
1.1节分析了SAR成像的基本原理,本节推导SAR回波信号的数学模型,给出SAR信号处理的理论基础。
chirp信号是SAR系统中最常用的发射信号形式。假设雷达发射的chirp脉冲串 为:
(1.19)
其中,
为发射信号的包络, 为chirp信号的调频斜率, 为发射信号脉宽, 为发射信号的中心频率, 为脉冲重复周期。则雷达于时刻 ,接收到斜距为 处目标反射的回波信号 为:
发射信号 经点目标P散射后,雷达接收机收到的信号 为:
(1.4)
其中: 为光速, 为复常数, 为回波信号相对于发射信号的时间延迟:
(1.5)
为考虑雷达水平方向增益变化而引入的加权函数。若不考虑雷达天线的加权作用,即令 ,则式(1.4)变为:
(1.6)
根据式(1.6),雷达运动平台相对于点目标的运动将造成回波信号的相位随时间不断变化,从而引起回波瞬时频率的变化,产生多普勒频移。多普勒频移量 为:
各种SAR成像算法总结
1
SAR成像处理的目的是要得到目标区域散射系数的二维分布,它是一个二维相关处理过程,通常可以分成距离向处理和方位向处理两个部分。在处理过程中,各算法的区别在于如何定义雷达与目标的距离模型以及如何解决距离-方位耦合问题,这些问题直接导致了各种算法在成像质量和运算量方面的差异。
一般来说,忽略多普勒频移所引起的距离向相位变化,距离向处理变为一维的移不变过程且相关核已知,即退化为一般的脉冲压缩处理;同时将雷达与目标的距离按2阶Taylor展开并忽略高次项,则方位向处理也是一个一维的移不变过程,并退化为一般的脉冲压缩处理,这就是经典的距离多普勒(Range-DopplerRD)算法的实质。
若考虑多普勒频移对距离向相位的影响,同时精确的建立雷达与目标的距离模型,则不论距离向处理还是方位向处理都变为二维的移变相关过程。线性调频尺度变换(Chirp-ScalingCS)算法即在此基础之上将二维数据变换到频域,利用Chirp Scaling原理及频域的相位校正方法,对二维数据进行距离徙动校正处理、距离向及方位向的聚焦处理,最终完成二维成像处理。
(1.20)
其中, 为目标的后向散射特性, 为方位向的天线方向性函数, 为光速。经正交解调后的复信 可以表示为:(1.21)
其中, 为雷达工作波长。式(1.21)中的两个指数项分别代表方位向的相位调制和距离向发射的相位调制。
考虑到相对于雷达发射脉冲而言, 和 是时间 的慢变化函数,可以作如下近似:
由式(1.12)可见,多普勒历史是一按负斜率变化的chirp信号,其调频斜率 为:
(1.13)
即点目标回波信号的调频斜率与 成正比、与 成反比。
点目标横过波束的最大距离 称为合成孔径长度,其大小与 以及方位向波束宽度 有关;点目标横过波束的时间称为合成孔径时间 。有:
(1.14)
(1.15)
在合成孔径时间里,多普勒频率的变化范围称为多普勒带宽,用 表示。由式(1.14)、(1.15)得到 的表达式为:
(1.16)
考虑到对于方位向天线直径为 的天线,近似有:
(1.17)
因此,SAR的方位向理论分辨率 为:
(1.18)
从上述分析可以看出,由于雷达运动平台作等高匀速直线运动,使得目标的回波信号在方位向上具有线性调频特性,对回波信号进行脉冲压缩处理,可以获得方位向的高分辨率。在理想情况下,SAR方位向分辨率与雷达平台的速度、飞行高度、作用距离、雷达工作波长等参数无关,只与天线尺寸有关,为天线方位向口径尺寸的一半,这是SAR的一大特点和优势。
(1.7)
将式(1.2)内的 代入可得:
(1.8)
其中: 为雷达工作波长,且 , 为雷达波束中心通过P点的时间。
回波信号的瞬时频率 为:
(1.9)
由式(1.9)可知,多普勒频移的存在将使回波信号的瞬时频率在载波频率 附近作线性变化。也就是说,由于雷达运动平台匀速直线前进,回波信号 在方位向将为线性调频(chirp)信号:
(1.10)
其中 为固定相位项,略去后,式(1.10)可简化为:
(1.11)
通常为便于对回波信号进行处理,需要将回波信号经频率变换调至较低频率 ,回波多普勒频率将以 为中心变化。中心频率 称为偏置频率。因此有:
(1.12)
式中 表示回波信号经变频处理将载频降至偏置频率后的瞬时频率变化。通常称它为点目标回波信号的多普勒频率历史,简称多普勒历史。
