流体力学英文版复习

工程流体力学英文原版

工程流体力学英文原版Engineering Fluid Mechanics: An Introduction.Engineering fluid mechanics is a crucial discipline within the field of engineering that deals with the study of fluids and their interactions with solid boundaries. It is a fundamental branch of physics and engineering that finds applications in various fields such as civil, mechanical, aerospace, and chemical engineering. The study of fluid mechanics involves the understanding of fluid properties, fluid statics, fluid dynamics, and fluid control.1. Fluid Properties.Fluids are substances that continuously deform under the application of shear stress. They lack a fixed shape and take the shape of the container in which they are contained. Fluids can be classified as liquids or gases, depending on their state and properties. Liquids have adefinite volume but no fixed shape, while gases expand tofill the available space.Some important fluid properties include density, viscosity, compressibility, and surface tension. Density is the mass per unit volume of a fluid. Viscosity representsthe internal friction of a fluid and affects its flow behavior. Compressibility describes how a fluid responds to changes in pressure, while surface tension arises from the intermolecular forces at the fluid's surface.2. Fluid Statics.Fluid statics deals with the behavior of fluids at rest, or in equilibrium. It involves the study of pressure distribution in fluids, buoyancy, and hydrostatics.Pressure is a force per unit area acting perpendicular tothe surface, and it is a fundamental quantity in fluid mechanics. Buoyancy is the upward force exerted by a fluid on an immersed object, and it is responsible for thefloating of objects on water. Hydrostatics deals with the equilibrium of fluids under the influence of gravity andother external forces.3. Fluid Dynamics.Fluid dynamics is concerned with the motion of fluids and the forces acting on them. It involves the study of fluid flow, fluid mechanics equations, and fluid control. Fluid flow can be laminar or turbulent, depending on the velocity and other fluid properties. Laminar flow is smooth and orderly, while turbulent flow is chaotic and irregular.The fundamental equations of fluid dynamics include the conservation of mass, momentum, and energy. The conservation of mass states that the rate of change of mass within a control volume is equal to the net mass flow rate into the volume. The conservation of momentum relates the forces acting on a fluid element to its acceleration, while the conservation of energy accounts for the conversion of energy forms within a fluid system.4. Fluid Control.Fluid control involves the manipulation and manipulation of fluid flow using pumps, valves, and other devices. Pumps are used to increase the pressure or flow rate of a fluid, while valves are used to control the direction or amount of fluid flow. Other devices such as nozzles, diffusers, and turbines are also employed to modify fluid flow characteristics.In conclusion, engineering fluid mechanics is a crucial discipline that deals with the study of fluids and their interactions with solid boundaries. It involves the understanding of fluid properties, fluid statics, fluid dynamics, and fluid control. This knowledge is essentialfor engineers to design, analyze, and optimize fluid systems in various engineering applications.。

流体力学英文课件第二章

9
Application ?
p0
pA = p0 + ρgh pG = ρgh
绝压表压
h p
Absolute pressure （绝对压力） Gauge pressure（表压力）
Pressure source Connected water tube
Relative pressure（相对压力） Vacuum degree（真空度）
p = p0
ax z =− x g
Equipressure surface（等压面）
ax z = − x +C g
12
Example:
A cup of coffee is 7cm deep at rest. 1. Will it spill out while ax=7m/s2? 3 2. Gage pressure of point A? (ρ =1010 kg m )
dp = ρ( Xdx +Ydy + Zdz)
Pressure increase in the direction of body force.
Equipressure surface（等压面）
Surfaces in fluid with same pressure, vertical to body force everywhere, in gravity field it is a horizontal plane.
∂p dx ∂p dx p− dydz − p + dydz + ρXdxdydz = 0 ∂x 2 ∂x 2
Force on left surface Force on right surface Body force in x direction

流体力学英文版课后习题答案

1.1 What will be the (a) the gauge pressure and (b) the absolute pressure of water at depth 12m below the surface? ρwater = 1000 kg/m 3, and P atmosphere = 101kN/m 2. Solution:Rearranging the equation 1.1-4gh p p a b ρ+=Set the pressure of atmosphere to be zero, then the gauge pressure at depth 12m below the surface iskPa gh p p a b 72.1171281.910000=⨯⨯+=+=ρAbsolute pressure of water at depth 12mkPa Pa gh p p a b 72.2182187201281.91000101000==⨯⨯+=+=ρ1.3 A differential manometer as shown in Fig. is sometimes used to measure small pressure difference. When the reading is zero, the levels in two reservoirs are equal. Assume that fluid B is methane （甲烷）, that liquid C in the reservoirs is kerosene (specific gravity = 0.815), and that liquid A in the U tube is water. The inside diameters of the reservoirs and U tube are 51mm and 6.5mm , respectively. If the reading of the manometer is145mm., what is the pressure difference over the instrument In meters of water, (a) when the change in the level in the reservoirs is neglected, (b) when the change in the levels in the reservoirs is taken into account? What is the percent error in the answer to the part (a)? Solution ：p a =1000kg/m 3 p c =815kg/m 3 p b =0.77kg/m 3 D/d=8 R=0.145mWhen the pressure difference between two reservoirs is increased, the volumetric changes in the reservoirs and U tubesR d x D 2244ππ=(1)soR D d x 2⎪⎭⎫⎝⎛= (2)and hydrostatic equilibrium gives following relationshipg R g x p g R p A c c ρρρ++=+21 (3)sog R g x p p c A c )(21ρρρ-+=- (4)substituting the equation (2) for x into equation (4) givesg R g R D d p p c A c )(221ρρρ-+⎪⎭⎫⎝⎛=- (5)（a ）when the change in the level in the reservoirs is neglected,()Pag R g R g R D d p p c A c A c 26381.98151000145.0)()(221=⨯-=-≈-+⎪⎭⎫⎝⎛=-ρρρρρ（b ）when the change in the levels in the reservoirs is taken into account()Pa g R g R D d gR g R D d p p c A c c A c 8.28181.98151000145.081.9815145.0515.6)()(22221=⨯-+⨯⨯⨯⎪⎭⎫ ⎝⎛=-+⎪⎭⎫⎝⎛=-+⎪⎭⎫⎝⎛=-ρρρρρρerror=％＝7.68.2812638.281-1.4 There are two U-tube manometers fixed on the fluid bed reactor, as shown in the figure. The readings of two U-tube manometers are R 1=400mm ，R 2=50mm, respectively. The indicating liquid is mercury. The top of the manometer is filled with the water to prevent from the mercury vapor diffusing into the air, and the height R 3=50mm. Try to calculate the pressure at point A and B .Solution: There is a gaseous mixture in the U-tube manometer meter. The densities of fluids are denoted by Hg O H g ρρρ,,2, respectively. The pressure at point A is given by hydrostaticequilibriumFigure for problem 1.4g R R g R g R p g H g O H A )(32232+-+=ρρρg ρis small and negligible in comparison with H g ρand ρH2O , equation above can besimplifiedc A p p ≈=232gR gR H g O H ρρ+=1000×9.81×0.05+13600×9.81×0.05=7161N/m²1gR p p p H g A D B ρ+=≈=7161+13600×9.81×0.4=60527N/m1.5 Water discharges from the reservoir through the drainpipe, which the throat diameter is d. The ratio of D to d equals 1.25. The vertical distance h between the tank A and axis of the drainpipe is 2m. What height H from the centerline of the drainpipe to the water level in reservoir is required for drawing the water from the tank A to the throat of the pipe? Assume that fluid flow is a potential flow. The reservoir, tank A and the exit of drainpipe are all open to air.Solution:Bernoulli equation is written between stations 1-1 and 2-2, with station 2-2 being reference plane:2222222111u gz p u gz p ++=++ρρ Where p 1=0, p 2=0, and u 1=0, simplification of the equation22u Hg =1The relationship between the velocity at outlet and velocity u o at throat can be derived by the continuity equation:22⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛D d u u o 22⎪⎭⎫⎝⎛=d D u u o 2Bernoulli equation is written between the throat and the station 2-2 3Combining equation 1,2,and 3 givesSolving for H H=1.39m1.6 A liquid with a constant density ρ kg/m 3 is flowing at an unknown velocity V 1 m/s through a horizontal pipe of cross-sectional area A 1 m 2 at a pressure p 1 N/m 2, and then it passes to a sectionof the pipe in which the area is reduced gradually to A 2 m 2 and the pressure is p 2. Assuming no friction losses, calculate the velocities V 1 and V 2 if the pressure difference (p 1 - p 2) is measured.Solution :In Fig1.6, the flow diagram is shown with pressure taps to measure p 1 and p 2. From the mass-balance continuity equation , for constant ρ where ρ1 = ρ2 = ρ,222200uu p =+ρ()＝＝＝144.281.92100081.910002125.11112442-⨯⨯⨯--⎪⎭⎫ ⎝⎛==ρρgh d D u Hg2112A A V V =For the items in the Bernoulli equation , for a horizontal pipe, z 1=z 2=0Then Bernoulli equation becomes, after substituting 2112A A V V =for V 2, ρρ22121211212020p A A V p V ++=++ Rearranging,2)1(21212121-=-A A V p p ρ ⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫⎝⎛-12221211A Ap p V ρ＝Performing the same derivation but in terms of V 2,⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛--21221212A A p p V ρ＝1.7 A liquid whose coefficient of viscosity is µ flows below the critical veloc ity for laminar flowin a circular pipe of diameter d and with mean velocity V . Show that the pressure loss in a length of pipeL p ∆ is 232d V μ. Oil of viscosity 0.05 Pas flows through a pipe of diameter 0.1m with a average velocity of 0.6m/s.Calculate the loss of pressure in a length of 120m.Solution :The average velocity V for a cross section is found by summing up all the velocities over the cross section and dividing by the cross-sectional area1From velocity profile equation for laminar flow2 substituting equation 2 for u into equation 1 and integrating3rearranging equation 3 gives1.8. In a vertical pipe carrying water, pressure gauges areinserted at points A and B where the pipe diameters are 0.15m and 0.075m respectively. The point B is 2.5m belowA and when the flow rate down the pipe is 0.02 m 3/s, the pressure at B is 14715 N/m 2 greater than that at A. Assuming the losses in the pipe between A and B can beexpressed as gV k 22where V is the velocity at A, find thevalue of k .If the gauges at A and B are replaced by tubes filled with water and connected to a U-tube containing mercury of relative density 13.6, give a sketch showing how the levels in the two limbs of the U-tube differ and calculate the value of this difference in metres. Solution:d A =0.15m; d B =0.075m z A -z B =l =2.5m Q =0.02 m 3/s,p B -p A =14715 N/m 2Figure for problem 1.8⎰⎰==RR rdr uR udA A V 020211ππ⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛--=22014R r R L p p u L μ2032D L pp V L μ-=232dV L p μ=∆Pa d VL p 115201.01206.005.0323222=⨯⨯⨯==∆μs m d QV V d Q AA AA /132.115.0785.002.044222=⨯===ππs m d QV V d Q BB BB /529.4075.0785.002.044222=⨯===ππWhen the fluid flows down, writing mechanical balance equation222222AB B B A A AV kV g z p V g z p +++=++ρρ 213.1253.4100014715213.181.95.2222k++=+⨯ k 638.0260.10715.14638.0525.24++=+=k 0.295making the static equilibriumgR g x g l p g R g x p H g A B ρρρρρ+∆++=+∆+()()mm ggl p p R gH A B 7981.91260081.910005.214715-=⨯⨯⨯-=---=ρρρ1.9．The liquid vertically flows down through the tube from the station a to the station b , then horizontally through the tube from the station c to the station d , as shown in figure. Two segments of the tube, both ab and cd ，have the same length, the diameter and roughness. Find:（1）the expressions ofgp ab ρ∆, h fab , g p cdρ∆ and h fcd , respectively.（2）the relationship between readings R 1and R 2 in the U tube.Solution:(1) From Fanning equationFigure for problem 1.92Vl h fab λ=andsoFluid flows from station a to station b , mechanical energy conservation giveshence2from station c to station d hence3From static equationp a -p b =R 1（ρˊ-ρ）g -l ρg 4 p c -p d =R 2（ρˊ-ρ）g 5 Substituting equation 4 in equation 2 ，thentherefore6Substituting equation 5 in equation 3 ，then7Thus R 1=R 222V d l h fcd λ=fcdfab h h =fab bah p p +=+ρρlg fab b a h p p =+-lg ρfcd d c h pp +=ρρfcd dc h p p =-ρfab h g l g R =+--'lg 1ρρρρ）（gR h fab ρρρ-'=1g R h fcd ρρρ-'=21.10 Water passes through a pipe of diameter d i=0.004 m with the average velocity 0.4 m/s, as shown in Figure.1) What is the pressure drop –∆P when water flows through the pipe length L =2 m, in m H 2O column?2) Find the maximum velocity and point r at whichit occurs.3) Find the point r at which the average velocity equals the local velocity.4）if kerosene flows through this pipe ，how do the variables above change ？（the viscosity and density of Water are 0.001 Pas and 1000 kg/m 3，respectively ；and the viscosity and density of kerosene are 0.003 Pas and 800 kg/m 3，respectively ）solution: 1）1600001.01000004.04.0Re =⨯⨯==μρudfrom Hagen-Poiseuille equation1600004.0001.024.0323222=⨯⨯⨯==∆d uL P μ m g p h 163.081.910001600=⨯=∆=ρ 2）maximum veloc ity occurs at the center of pipe, from equation 1.4-19 max0.5Vu =so u max =0.4×2=0.8m3）when u=V=0.4m/s Eq. 1.4-172max 1⎪⎪⎭⎫ ⎝⎛-=w r r u u5.0004.01max2=⎪⎭⎫⎝⎛-u V r ＝ m r 00284.071.0004.05.0004.0=⨯==4) kerosene:427003.0800004.04.0Re =⨯⨯==μρudPa pp 4800001.0003.01600=='∆='∆μμFigure for problem 1.10m g p h 611.081.98004800=⨯=''∆='ρ1.12 As shown in the figure, the water level in the reservoir keeps constant. A steel drainpipe (with the inside diameter of 100mm) is connected to the bottom of the reservoir. One arm of the U-tube manometer is connected to the drainpipe at the position 15m away from the bottom of the reservoir, and the other is opened to the air, the U tube is filled with mercury and the left-side arm of the U tube above the mercury is filled with water. The distance between the upstream tap and the outlet of the pipeline is 20m.a) When the gate valve is closed, R=600mm, h=1500mm; when the gate valve is opened partly, R=400mm, h=1400mm. The friction coefficient λ is 0.025, and the loss coefficient of the entrance is 0.5. Calculate the flow rate of water when the gate valve is opened partly. (in m³/h)b) When the gate valve is widely open, calculate the static pressure at the tap (in gauge pressure, N/m²). l e /d ≈15 when the gate valve is widely open, and the friction coefficient λ is still 0.025.Solution ：(1) When the gate valve is opened partially, the water discharge isSet up Bernoulli equation between the surface of reservoir 1—1’and the section of pressure point 2—2’，and take the center of section 2—2’ as the referring plane, then∑+++=++21,2222121122—f h p u gZ p u gZ ρρ （a ）In the equation 01=p (the gauge pressure)222/396304.181.910004.081.913600m N gh gR p O H H g =⨯⨯-⨯⨯=-=ρρFigure for problem 1.12021=≈Z uWhen the gate valve is fully closed, the height of water level in the reservoir can be related to h (the distance between the center of pipe and the meniscus of left arm of U tube).gR h Z g H g O H ρρ=+)(12（b ）where h=1.5mR=0.6mSubstitute the known variables into equation b2222_1,113.22)5.01.015025.0(2)(66.65.110006.013600V VV K d l h mZ c f =+⨯=+==-⨯=∑λ Substitute the known variables equation a9.81×6.66=2213.21000396302V V ++the velocity is V =3.13m/s the flow rate of water ish m V d V h /5.8813.312.0436004360032=⨯⨯⨯=⨯=ππ2） the pressure of the point where pressure is measured when the gate valve is wide-open.Write mechanical energy balance equation between the stations 1—1’ and 3-3´，then∑+++=++31,3233121122—f h p V gZ p V gZ ρρ （c ）since m Z 66.61=311300p p u Z =≈= 2223_1,81.4 2]5.0)151.035(025.0[ 2)(V V V K d l l h c e f =++=++=∑λinput the above data into equation c ，9.8122V 81.4266.6+=⨯Vthe velocity is: V =3.51 m/sWrite mechanical energy balance equation between thestations 1—1’and 2——2’, for the same situation of water level∑+++=++21,2222121122—f h p V gZ p V gZ ρρ（d ）since m Z 66.61=2121003.51/0(page pressure Z u u m sp =≈≈=）kg J V K d l hc f /2.26251.3)5.01.015025.0(2)(222_1,=+⨯=+=∑λinput the above data into equation d ，9.81×6.66=2.261000251.322++p the pressure is: 329702=p1.14 Water at 20℃ passes through a steel pipe with an inside diameter of 300mm and 2m long. There is a attached-pipe (Φ60⨯3.5mm) which is parallel with the main pipe. The total length including the equivalent length of all form losses of the attached-pipe is 10m. A rotameter is installed in the branch pipe. When the reading of the rotameter is2.72m 3/h, try to calculate the flow rate in the main pipe and the total flow rate, respectively. The frictional coefficient of the main pipe and the attached-pipe is 0.018 and 0.03, respectively.Solution ： The variables of main pipe are denoted by a subscript1, and branch pipe by subscript 2.The friction loss for parallel pipelines is 2121S S s f f V V V h h+==∑∑The energy loss in the branch pipe is22222222u d l l he f ∑∑+=λ In the equation03.02=λsm u d ml l e /343.0053.04360072.2053.01022222=⨯⨯===+∑πinput the data into equation c kg J hf /333.02343.0053.01003.022=⨯⨯=∑The energy loss in the main pipe is333.022111121===∑∑u d l h hf f λSo s m u /36.22018.023.0333.01=⨯⨯⨯=The water discharge of main pipe ish m V h /60136.23.043600321=⨯⨯⨯=πTotal water discharge ish m V h /7.60372.26013≈+=1.16 A Venturimeter is used for measuring flow of water along a pipe. The diameter of the Venturi throat is two fifths the diameter of the pipe. The inlet and throat are connected by water filled tubes to a mercury U-tube manometer. The velocity of flow along the pipe is found to beR 5.2 m/s, where R is the manometer reading in metres of mercury. Determine the loss of headbetween inlet and throat of the Venturi when R is 0.49m. (Relative density of mercury is 13.6). Solution:Writing mechanical energy balance equation between the inlet 1 and throat o for V enturi meterf o o hg z V p g z V p +++=++22121122ρρ 1 rearranging the equation above, and set (z 2-z 1)=xf o oh xg V V p p ++-=-22121ρ2from continuity equationFigure for problem 1.1611221125.625V V dd V V o o =⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛= 3 substituting equation 3 for V o into equation 2 gives()fff f oh xg R h xg Rh V h xg V V p p ++=++=+=++-=-94.1185.203.1903.19206.3922121211ρ4from the hydrostatic equilibrium for manometerg x g R p p H g o ρρρ+-=-)(1 5substituting equation 5 for pressure difference into equation 4 obtainsf Hgh xg R gx g R ++=+-94.118)(ρρρρ 6rearranging equation 6kg J R R R R gR h Hg f /288.267.494.11861.12394.118)(==-=--=ρρρ1.17.Sulphuric acid of specific gravity 1.3 is flowing through a pipe of 50 mm internal diameter. A thin-lipped orifice, 10mm, is fitted in the pipe and the differential pressure shown by a mercury manometer is 10cm. Assuming that the leads to the manometer are filled with the acid,calculate (a)the weight of acid flowing per second, and (b) the approximate friction loss in pressure caused by the orifice.The coefficient of the orifice may be taken as 0.61, the specific gravity of mercury as 13.6, and the density of water as 1000 kg/m 3Solution: a)2.0501010==D D =⨯-=-=-81.9)130013600(1.0)(21g R p p H g ρρ()sm p p D D C V o /63.231.461.056.1861.0130081.9)130013600(1.022.0161.0214214102=⨯=≈⨯-⨯-=-⎪⎪⎭⎫ ⎝⎛-=ρs kg V D m /268.0130063.201.0442220=⨯⨯⨯==πρπb) approximate pressure drop=⨯-=-=-81.9)130013600(1.0)(21g R p p H g ρρ12066.3Papressure difference due to increase of velocity in passing through the orificePa D D V V V V p p o8.44882)2.01(63.213002242412222212221=-=⎪⎪⎭⎫⎝⎛-=-=-ρρpressure drop caused by friction lossPa p f 5.75778.44883.12066=-=∆2.1 Water is used to test for the performances of pump. The gauge pressure at the discharge connection is 152 kPa and the reading of vacuum gauge at the suction connection of the pump is24.7 kPa as the flow rate is 26m 3/h. The shaft power is 2.45kw while the centrifugal pump operates at the speed of 2900r/min. If the vertical distance between the suction connection and discharge connection is 0.4m, the diameters of both the suction and discharge line are the same. Calculate the mechanical efficiency of pump and list the performance of the pump under this operating condition. Solution:Write the mechanical energy balance equation between the suction connection and discharge connection2_1,2222121122f H gp g u Z H g p g u Z +++=+++ρρwherem Z Z 4.012=-(Pa 1052.1(Pa 1047.22_1,215241≈=⨯=⨯-=f H u u pressure gauge p pressure gauge p ））total heads of pump is m H 41.1881.9100010247.01052.14.055=⨯⨯+⨯+= efficiency of pump isN N e /=ηsince kW g QH N e 3.1360081.9100041.18263600=⨯⨯⨯==ρN=2.45kWThen mechanical efficiency%1.53%10045.23.1=⨯=η The performance of pump isFlow rate ，m³/h 26 Total heads ，m18.41 Shaft power ，kW 2.45 Efficiency ，%53.12.2 Water is transported by a pump from reactor, which has 200 mm Hg vacuum, to the tank, in which the gauge pressure is 0.5 kgf/cm 2, as shown in Fig. The total equivalent length of pipe is 200 m including all local frictional loss. The pipeline is φ57×3.5 mm , the orifice coefficient of C o and orificediameter d o are 0.62 and 25 mm, respectively. Frictionalcoefficient λ is 0.025. Calculate: Developed head H of pump, in m (the reading R of U pressure gauge in orifice meter is 168 mm Hg)Solution: Equation(1.6-9)Mass flow rates kg S V m o o /02.21000025.0414.312.42=⨯⨯⨯==ρ 2) Fluid flow through the pipe from the reactor to tank, the Bernoulli equation is as followsfor V 1=V 2f H z gp p H +∆+-=ρ12 ∆z=10msm Rg D d C V f /12.444.69375.062.01000)100013600(81.9168.025025162.02144000=⨯=-⨯⨯⎪⎭⎫ ⎝⎛-=-⎪⎭⎫⎝⎛-=ρρρ）（Pa p 7570710013.17602001081.95.054=⨯⨯+⨯⨯=∆ ∆p/ρg=7.7mThe relation between the hole velocity and veloc ity of pipeFriction losssoH=7.7+10+5.1=22.8m2.3 . A centrifugal pump is to be used to extract water from a condenser in which the vacuum is 640 mm of mercury, as shown in figure. At the rated discharge, the net positive suction head must be at least 3m above the cavitation vapor pressure of 710mm mercury vacuum. If losses in the suction pipe accounted for a head of 1.5m. What must be the least height of the liquid level in the condenser above the pump inlet? Solution :From an energy balance,WhereP o =760-640=120mmHgP v =760-710=50mmHgUse of the equation will give the minimum height H g as2.4 Sulphuric acid is pumped at 3 kg/s through a 60m length of smooth 25 mm pipe. Calculate the drop in pressure. If the pressure drop falls by one half, what will the new flowrate be ?• Density of acid 1840kg/m 3• V iscosity of acid 25×10-3PasSolution:Velocity of acid in the pipe:sm D d V V /12112.42200=⎪⎭⎫ ⎝⎛⨯=⎪⎭⎫ ⎝⎛=mgu d l f H f 1.581.92105.0200025.02422=⨯⨯==NPSH H gp p H f vog ---=ρmNPSH H gp p H f vo g 55.335.181.9100081.913600)05.012.0-=--⨯⨯⨯-=---=（ρs m d m d mpipe of area tional cross flowrate volumetric u /32.3025.01840785.03785.04sec 222=⨯⨯===-=ρπρReynolds number:6109102532.31840025.0Re 3=⨯⨯⨯==-μρud from Fig.1.22 for a smooth pipe when Re=6109, f=0.0085 pressure drop is calculated from equation 1.4-9kg J u d l f ph f /450232.3025.0600085.042422=⨯==∆=ρkPa p 5.8271840450=⨯=∆or friction factor is calculated from equation1.4-25kgJ u d l u d l f ph f /426232.3025.0606109046.042Re 046.042422.022.02=⨯⨯⨯==∆=--＝ρkPa p 84.7831840426=⨯=∆if the pressure drop falls to 783.84/2=391.92kPa8.18.12.12.038.12.12.022.0012.089.1079`2025.060102518401840046.042046.042Re 046.043919202u u u dl u d l p p =⎪⎭⎫⎝⎛⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯==∆='∆----ρμρρ＝sos m u /27.236.489..1079012.03919208.18.1==⨯=new mass flowrate=0.785d 2u ρ=0.785×0.0252×2.27×1840=2.05kg/s2.4 Sulphuric acid is pumped at 3 kg/s through a 60m length of smooth 25 mm pipe. Calculate the drop in pressure. If the pressure drop falls by one half on assumption that the change of friction factor is negligible, what will the new flowrate be ?Density of acid 1840kg/m 3V iscosity of acid 25×10-3Pa Friction factor 32.0Re 500.00056.0+=f for hydraulically smooth pipeSolution:Write energy balance equation:f h gu z g p H g u z g p +++=+++2222222111ρρ gu d l g p h H f 22λρ=∆== 342=ρπu ds m d u /32.31840025.014.3124322=⨯⨯=⨯=ρπ 611510251840025.032.3Re 3=⨯⨯⨯=-0087.061155.00056.0Re 500.00056.032.032.0=+=+=f92.4681.9232.3025.0600087.04222=⨯⨯==∆==g u d l g p h H f λρΔp=46.92×1840×9.81=847.0kpa2.6 The fluid is pumped through the horizontal pipe from section A to B with the φ38⨯2.5mm diameter and length of 30 meters, shown as figure. The orifice meter of 16.4mm diameter is used to measure the flow rate. Orifice coefficient C o ＝0.63. the permanent loss in pressure is 3.5×104N/m 2, the friction coefficient λ=0.024. find:(1) What is the pressure drop along the pipe AB?(2)What is the ratio of power obliterated in pipe AB to total power supplied to the fluid when the shaft work is 500W , 60%efficiency? (The density of fluid is 870kg/m 3)solution ：∑+++=+++f AA A A AA h u p g z w u p g z 2222ρρρλρ22p u d l h p p f BA ∆+==-∑ 247.0334.162=⎪⎭⎫⎝⎛=A A o()()s m gR C u /5.8870870136006.081.9297.063.02247.01200=-⨯⨯=''--=ρρρ∴u = (16.4/33)2×8.5=2.1m/s∴242/76855105.321.2033.030870024.0m N h p p f B A =⨯+⨯==-∑ρ(2)W u d p Wm 1381.2033.0785.0768554Ne 22=⨯⨯⨯=∆==ρπρ sothe ratio of power obliterated in friction losses in AB to total power supplied to the fluid％％＝461006.0500138⨯⨯AcknowledgementsMy deepest gratitude goes first and foremost to Professor aaa , my supervisor, for her constant encouragement and guidance. She has walked me through all the stages of the writing of this thesis. Without her consistent and illuminating instruction, this thesis could not havereached its present form.Second, I would like to express my heartfelt gratitude to Professor aaa, who led me into the world of translation. I am also greatly indebted to the professors and teachers at the Department of English: Professor dddd, Professor ssss, who have instructed and helped me a lot in the past two years.Last my thanks would go to my beloved family for their loving considerations and great confidence in me all through these years. I also owe my sincere gratitude to my friends and my fellow classmates who gave me their help and time in listening to me and helping me work out my problems during the difficult course of the thesis.My deepest gratitude goes first and foremost to Professor aaa , my supervisor, for her constant encouragement and guidance. She has walked me through all the stages of the writing of this thesis. Without her consistent and illuminating instruction, this thesis could not havereached its present form.Second, I would like to express my heartfelt gratitude to Professor aaa, who led me into the world of translation. I am also greatly indebted to the professors and teachers at the Department of English: Professordddd, Professor ssss, who have instructed and helped me a lot in the past two years.Last my thanks would go to my beloved family for their loving considerations and great confidence in me all through these years. I also owe my sincere gratitude to my friends and my fellow classmates who gave me their help and time in listening to me and helping me work out my problems during the difficult course of the thesis.。

流体力学英文版1

(2) Recovery – For a solid, if the elastic limit is not exceeded, the deformation disappears when the force is removed; – A fluid continues to flow as long as the force is applied and will not recover its original form when the force is removed.
若连续介质不适用，应如何处理呢？ 13
1.3 Dimension and Units 单位与量纲
Dimensions are properties that can be measured, e.g. length, velocity, area, volume, acceleration etc. 可以测量的性质叫量纲。
3
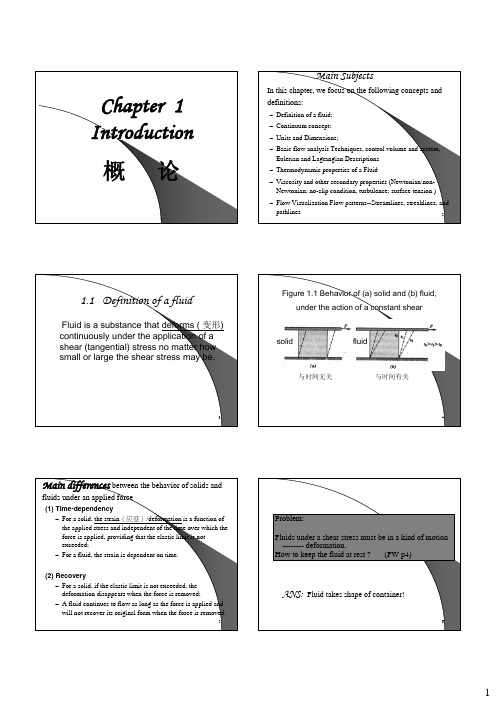
Figure 1.1 Behavior of (a) solid and (b) fluid, under the action of a constant shear
solid
fluid
与时间无关
与时间有关
4
Main differences between the behavior of solids and
It breaks down whenever the mean free path of the molecules （平均分子自由行程,10−7 ）approximately becomes the same magnitude order as the smallest significant characteristic dimension (特征长度) of the problem.

流体力学复习资料及英文专有名词解释

Chapter 1 Fluid statics 流体静力学1. 连续介质假定(Continuum assumption)：The real fluid is considered as no-gap continuousmedia, called the basic assumption of continuity of fluid, or the continuum hypothesis offluid.流体是由连续分布的流体质点(fluid particle)所组成，彼此间无间隙。

它是流体力学中最基本的假定，1755年由欧拉提出。

在连续性假设之下，表征流体状态的宏观物理量在空间和时间上都是连续分布的，都可以作为空间和时间的函数。

2. 流体质点（Fluid particle ）: A fluid elementthat is small enough with enoughmoles to makesure that the macroscopic meandensity has definite valueis defined as a Fluid Particle.宏观上足够小，微观上足够大。

3. 流体的粘性（Viscosity ）: is an internal property of a fluid that offers resistance to sheardeformation. It describes a fluid's internal resistance to flow and may be thought as a measure of fluid friction.流体在运动状态下抵抗剪切变形的性质，称为黏性或粘滞性。

它表示流体的内部流动阻力，也可当做一个流体摩擦力量。

The viscosity of a gas increases with temperature, the viscosity of a liquid decreases with temperature.4. 牛顿内摩擦定律（Newton’s law of viscosity ）：5. The dynamic viscosity （动力黏度）is also called absolute viscosity （绝对黏度）. The kinematicviscosity （运动黏度）is the ratio of dynamic viscosity to density.6. Compressibility （压缩性）：As the temperature is constant, the magnitude ofcompressibility is expressed by coefficient of volume compressibility (体积压缩系数) к , a relative variation rate （相对变化率） of volume per unit pressure.The bulk modulus of elasticity (体积弹性模量) E is the reciprocal of coefficient of volume compressibility к.7. 流体的膨胀性(expansibility; dilatability)：The coefficient of cubical expansion (体积热膨胀系数) αt is the relative variation rate of volume per unit temperature change.8. 表面张力Surfacetension : A property resulting from the attractive forces betweendu dzτμ=μνρ=molecules.σ-----单位长度所受拉力9. 表面力 Surface force ——is the force exerted on the contact surface by the contacted fluidor other body. Its value is proportional to contact area.作用在所研究流体外表面上与表面积大小成正比的力。

流体力学英文版第二章静力学——Hydrostatic

δFs = −
∂pˆi + ∂p ˆj + ∂p kˆ ∂x ∂y ∂z
δxδyδz = −∇pδxδyδz
6 / 32
Basic equation for pressure ﬁeld
Notes
Besides the surface forces, the body force due to the weight of the
δxδz
It is simpliﬁed to
∂p
δFy
=
− δxδyδz ∂y
Similarly, for the x and z directions, the resultant surface forces are
∂p
∂p
δFx
=
− δxδyδz, ∂x
δFz
=
− ∂z
δxδyδz
In the vector form, it can be expressed as
element is
δFv = −ρgδxδyδzkˆ
The whole resultant force acting on the rectangular element of ﬂuid can be expressed as
δF = δFs + δFv = −∇pδxδyδz − ρgδxδyδzkˆ = δma
Figure 4: Face and body forces acting on a rectangular element
5 / 32
Basic equation for pressure ﬁeld
Notes
In the y direction
∂p δy

流体力学基础知识(英文)

1
Fundamentals of Ship Science MSc Course SESS6001 University of Southampton Inviscid Fluid An inviscid fluid or ideal fluid is a simplified conceptual idealisation of a real fluid. An inviscid fluid cannot support shear. Hence in the vicinity of solid boundaries the ‗no-slip‘ boundary condition of a real fluid is not realisable. This implies that continuity of fluid velocity across such boundaries is limited to the normal velocity component as ‗slippage‘ is possible in the tangential directuations of fluid motion (Lagrangian and Eulerian) are only dependent upon pressure gradient and body or gravitational influences and not upon the real fluid shear influences due to fluid viscosity. These alternative forms of motion equations are derived from first principles in a later section. Incompressible Fluid An incompressible fluid is one that neither gains nor losses mass in a selected volume V bounded by the surface S . Schematically we can think of this situation as corresponding to number of particles flowing into V corresponds to number of particles flowing out of V subject to no mass change within V . n ρv . n dS = normal mass flux from the elemental surface dS.

流体力学英文版复习

2013-8-23
5
(3) Relative density and specific gravity The relative density (相对密度) RD of a fluid is the ratio of its density to the density of a given reference material.
AV F h
If the shear stress is =F/A, it can be expressed as
(1.18)
V h
The ratio V/h is the angular velocity of line ab, or it is the rate of angular deformation of the fluid.
2013-8-23
16
Physical meaning
z —— the position potential energy per unit weight of fluid to the base level； p/g —— the pressure potential energy (压强势能) per unit weight of fluid. The energy per unit weight of fluid can be also
2013-8-23
3
(1) Density （密度）
Density is the ratio of the mass of fluid to its volume.
m (kg/m3 ) ρ V
(1.12)
Specific volume (比容) : volume occupied by unit mass.

流体力学专业英语词汇

流体力学专业词汇(V ocabulary of Fluid Mechanics )CHAPTER-1acceleration 加速度average velocity 平均速度Bernoulli 伯努力boundary layer 边界层calculus 微积分coefficient of viscosity 粘性系数compressible(incompressible) (不)可压的conservation of mass(momentum, energy) 质量(动量,能量)守恒continuum 连续介质control-volume 控制体density(mass per unit volume) 密度differential 微分dimension 量刚尺度dynamics 动力学Euler 欧拉eulerian (lagrangian) method of description欧拉(拉格郎日)观点，方法field of flow 流场flow pattern 流型（谱）fluid mechanics 流体力学function 函数inertia 惯性, 惯量integral 积分kinematics 运动学kinetic (potential, internal) energy 动(势,内)能Lagrange 拉格郎日liquid 流体Newtonian fluids 牛顿流体(non)linear (非)线性(non)uniform （非）均匀one-dimensional 一维pathline 迹线perfect-gas law 理想气体定律pressure 压力压强Reynolds 雷诺shear(normal) stress 剪(正)应力solution 解答statics 静力学steady(unsteady) (非)定常strain 应变streamline(tube) 流线(管)thermal conductivity 热传导thermodynamics 热力学variable 变量vector 矢量velocity distribution 速度分布velocity field 速度场velocity gradient 速度梯度viscous(inviscid) (无)粘性的volume rate of flow 体积流量CHAPTER -2absolute (gage,vacuum) pressure 绝对（表，真空）压力area moment of inertia 惯性面积矩atmospheric pressure 大气压力barometer 气压计body force 体力Cartesian [rectangular] coordinates 直角坐标（系）centroid 质心elliptic 椭圆的equilibrium 平衡horizontal 水平的hydrostatic 水静力学，流体静力学hyperbolic 双曲线的mercury 水银moment 矩parabolic 抛物线plane (curved) surface 平（曲）面plate 板pressure center 压力中心pressure distribution(gradient) 压力分布（梯度）reservoir 水库rigid-body 刚体scalar 标量specific weight 比重surface force 表面力vertical 垂直的, 直立的CHAPTER -3Bernoulli equation 伯努力方程Boundaries 边界Conservation of mass 质量Control volume 控制体Energy(hydraulic) grade line 能级线Flux 流率Free body 隔离体Heat transfer 热传到Imaginary 假想Inlet, outlet 进、出口Integrand 被积函数Jet flow 射流Linear(Angular)-momentum relation 线（角）动量关系式Momentum(energy)-flux 动量（能量）流量Net force 合力No slip 无滑移Nozzle 喷嘴Rate of work 功率Reynolds transport theorem 雷诺输运定理Shaft work 轴功Stagnation enthalpy 制止焓Surroundings 外围System 体系Time derivative 时间导数Vector sum 矢量合Venturi tube 文图里管V olume(mass) flow 体积（质量）流量V olume(mass) rate of flow体积（质量）流率CHAPTER -4Soomth 平滑Laminar 层流Transition 转捩Roughness 粗糙度Random fluctuations 随机脉动Reynolds number 雷诺数（Re）Instability 不稳定性Breakdown 崩溃Mean value 平均值Drag 阻力Osborne ReynoldsDye filament 染色丝Internal (external) flow 内(外)流Cartesian 笛卡坐标Infinitesimal 无限小local acceleration 当地加速度dot product 点乘total derivative 全导数convective acceleration 对流加速度substantial(material) derivative 随体(物质)导数operator 算子partial differential equation 偏微分方程Newtonian fluid 牛顿流体Navier-Stokes Equations N-S方程Second-order 二阶Similarity 相似Nondimensionalization 无量纲化Flat-plate boundary layer 平板边界层Thermal conductivity 热传导Heat flow 热流量Fourier’s law 傅立叶定律Couette Flow 库塔流动Channel 槽道Parallel plates 平行平板Pressure gradient 压力梯度No-slip condition 无滑移条件Poiseuille flow 伯肖叶流动Parabola 抛物线Wall shear stress 壁面剪应力Prandtl 普朗特Karman 卡门Momentum-integral relation 动量积分关系Momentum thickness 动量厚度Skin-friction coefficient 壁面摩擦系数Displacement thickness 排移厚度Blasius equation 布拉修斯方程Coordinate transformation 坐标变换Composite dimensionless variable 组合无量纲变量Shape factor 形状因子Velocity profile 速度剖面流体动力学fluid dynamics连续介质力学mechanics of continuous media介质medium流体质点fluid particle无粘性流体nonviscous fluid, inviscid fluid连续介质假设continuous medium hypothesis流体运动学fluid kinematics水静力学hydrostatics液体静力学hydrostatics支配方程governing equation伯努利方程Bernoulli equation伯努利定理Bernonlli theorem毕奥-萨伐尔定律Biot-Savart law欧拉方程Euler equation亥姆霍兹定理Helmholtz theorem开尔文定理Kelvin theorem涡片vortex sheet库塔-茹可夫斯基条件Kutta-Zhoukowski condition 布拉休斯解Blasius solution达朗贝尔佯廖d'Alembert paradox雷诺数Reynolds number施特鲁哈尔数Strouhal number随体导数material derivative不可压缩流体incompressible fluid质量守恒conservation of mass动量守恒conservation of momentum 能量守恒conservation of energy动量方程momentum equation能量方程energy equation控制体积control volume液体静压hydrostatic pressure涡量拟能enstrophy压差differential pressure流[动] flow流线stream line流面stream surface流管stream tube迹线path, path line流场flow field流态flow regime流动参量flow parameter流量flow rate, flow discharge涡旋vortex涡量vorticity涡丝vortex filament涡线vortex line涡面vortex surface涡层vortex layer涡环vortex ring涡对vortex pair涡管vortex tube涡街vortex street卡门涡街Karman vortex street马蹄涡horseshoe vortex对流涡胞convective cell卷筒涡胞roll cell涡eddy涡粘性eddy viscosity环流circulation环量circulation速度环量velocity circulation偶极子doublet, dipole驻点stagnation point总压[力] total pressure总压头total head静压头static head总焓total enthalpy能量输运energy transport速度剖面velocity profile库埃特流Couette flow单相流single phase flow单组份流single-component flow均匀流uniform flow非均匀流nonuniform flow二维流two-dimensional flow三维流three-dimensional flow准定常流quasi-steady flow非定常流unsteady flow, non-steady flow 暂态流transient flow周期流periodic flow振荡流oscillatory flow分层流stratified flow无旋流irrotational flow有旋流rotational flow轴对称流axisymmetric flow不可压缩性incompressibility不可压缩流[动] incompressible flow浮体floating body定倾中心metacenter阻力drag, resistance减阻drag reduction表面力surface force表面张力surface tension毛细[管]作用capillarity来流incoming flow自由流free stream自由流线free stream line外流external flow进口entrance, inlet出口exit, outlet扰动disturbance, perturbation分布distribution传播propagation色散dispersion弥散dispersion附加质量added mass ,associated mass 收缩contraction镜象法image method无量纲参数dimensionless parameter几何相似geometric similarity运动相似kinematic similarity动力相似[性] dynamic similarity平面流plane flow势potential势流potential flow速度势velocity potential复势complex potential复速度complex velocity流函数stream function源source汇sink速度[水]头velocity head拐角流corner flow空泡流cavity flow超空泡supercavity超空泡流supercavity flow空气动力学aerodynamics低速空气动力学low-speed aerodynamics 高速空气动力学high-speed aerodynamics 气动热力学aerothermodynamics亚声速流[动] subsonic flow跨声速流[动] transonic flow超声速流[动] supersonic flow锥形流conical flow楔流wedge flow叶栅流cascade flow非平衡流[动] non-equilibrium flow细长体slender body细长度slenderness钝头体bluff body钝体blunt body翼型airfoil翼弦chord薄翼理论thin-airfoil theory构型configuration后缘trailing edge迎角angle of attack失速stall脱体激波detached shock wave波阻wave drag诱导阻力induced drag诱导速度induced velocity临界雷诺数critical Reynolds number 前缘涡leading edge vortex附着涡bound vortex约束涡confined vortex气动中心aerodynamic center气动力aerodynamic force气动噪声aerodynamic noise气动加热aerodynamic heating离解dissociation地面效应ground effect气体动力学gas dynamics稀疏波rarefaction wave热状态方程thermal equation of state 喷管Nozzle普朗特-迈耶流Prandtl-Meyer flow瑞利流Rayleigh flow可压缩流[动] compressible flow可压缩流体compressible fluid绝热流adiabatic flow非绝热流diabatic flow未扰动流undisturbed flow等熵流isentropic flow匀熵流homoentropic flow兰金-于戈尼奥条件Rankine-Hugoniot condition 状态方程equation of state量热状态方程caloric equation of state完全气体perfect gas拉瓦尔喷管Laval nozzle马赫角Mach angle马赫锥Mach cone马赫线Mach line马赫数Mach number马赫波Mach wave当地马赫数local Mach number冲击波shock wave激波shock wave正激波normal shock wave斜激波oblique shock wave头波bow wave附体激波attached shock wave激波阵面shock front激波层shock layer压缩波compression wave反射reflection折射refraction散射scattering衍射diffraction绕射diffraction出口压力exit pressure超压[强] over pressure反压back pressure爆炸explosion爆轰detonation缓燃deflagration水动力学hydrodynamics液体动力学hydrodynamics泰勒不稳定性Taylor instability盖斯特纳波Gerstner wave斯托克斯波Stokes wave瑞利数Rayleigh number自由面free surface波速wave speed, wave velocity 波高wave height波列wave train波群wave group波能wave energy表面波surface wave表面张力波capillary wave规则波regular wave不规则波irregular wave浅水波shallow water wave深水波deep water wave重力波gravity wave椭圆余弦波cnoidal wave潮波tidal wave涌波surge wave破碎波breaking wave船波ship wave非线性波nonlinear wave孤立子soliton水动[力]噪声hydrodynamic noise 水击water hammer空化cavitation空化数cavitation number空蚀cavitation damage超空化流supercavitating flow水翼hydrofoil水力学hydraulics洪水波flood wave涟漪ripple消能energy dissipation海洋水动力学marine hydrodynamics谢齐公式Chezy formula欧拉数Euler number弗劳德数Froude number水力半径hydraulic radius水力坡度hvdraulic slope高度水头elevating head水头损失head loss水位water level水跃hydraulic jump含水层aquifer排水drainage排放量discharge壅水曲线back water curve压[强水]头pressure head过水断面flow cross-section明槽流open channel flow孔流orifice flow无压流free surface flow有压流pressure flow缓流subcritical flow急流supercritical flow渐变流gradually varied flow急变流rapidly varied flow临界流critical flow异重流density current, gravity flow堰流weir flow掺气流aerated flow含沙流sediment-laden stream降水曲线dropdown curve沉积物sediment, deposit沉[降堆]积sedimentation, deposition沉降速度settling velocity流动稳定性flow stability不稳定性instability奥尔-索末菲方程Orr-Sommerfeld equation涡量方程vorticity equation泊肃叶流Poiseuille flow奥辛流Oseen flow剪切流shear flow粘性流[动] viscous flow层流laminar flow分离流separated flow二次流secondary flow近场流near field flow远场流far field flow滞止流stagnation flow尾流wake [flow]回流back flow反流reverse flow射流jet自由射流free jet管流pipe flow, tube flow内流internal flow拟序结构coherent structure 猝发过程bursting process表观粘度apparent viscosity 运动粘性kinematic viscosity 动力粘性dynamic viscosity 泊poise厘泊centipoise厘沱centistoke剪切层shear layer次层sublayer流动分离flow separation层流分离laminar separation 湍流分离turbulent separation 分离点separation point附着点attachment point再附reattachment再层流化relaminarization起动涡starting vortex驻涡standing vortex涡旋破碎vortex breakdown涡旋脱落vortex shedding压[力]降pressure drop压差阻力pressure drag压力能pressure energy型阻profile drag滑移速度slip velocity无滑移条件non-slip condition壁剪应力skin friction, frictional drag壁剪切速度friction velocity磨擦损失friction loss磨擦因子friction factor耗散dissipation滞后lag相似性解similar solution局域相似local similarity气体润滑gas lubrication液体动力润滑hydrodynamic lubrication浆体slurry泰勒数Taylor number纳维-斯托克斯方程Navier-Stokes equation 牛顿流体Newtonian fluid边界层理论boundary later theory边界层方程boundary layer equation边界层boundary layer附面层boundary layer层流边界层laminar boundary layer湍流边界层turbulent boundary layer温度边界层thermal boundary layer边界层转捩boundary layer transition边界层分离boundary layer separation边界层厚度boundary layer thickness位移厚度displacement thickness动量厚度momentum thickness能量厚度energy thickness焓厚度enthalpy thickness注入injection吸出suction泰勒涡Taylor vortex速度亏损律velocity defect law形状因子shape factor测速法anemometry粘度测定法visco[si] metry流动显示flow visualization油烟显示oil smoke visualization孔板流量计orifice meter频率响应frequency response油膜显示oil film visualization阴影法shadow method纹影法schlieren method烟丝法smoke wire method丝线法tuft method氢泡法nydrogen bubble method相似理论similarity theory相似律similarity law部分相似partial similarity定理pi theorem, Buckingham theorem 静[态]校准static calibration动态校准dynamic calibration风洞wind tunnel激波管shock tube激波管风洞shock tube wind tunnel水洞water tunnel拖曳水池towing tank旋臂水池rotating arm basin扩散段diffuser测压孔pressure tap皮托管pitot tube普雷斯顿管preston tube斯坦顿管Stanton tube文丘里管Venturi tubeU形管U-tube压强计manometer微压计micromanometer多管压强计multiple manometer静压管static [pressure]tube流速计anemometer风速管Pitot- static tube激光多普勒测速计laser Doppler anemometer, laser Doppler velocimeter热线流速计hot-wire anemometer热膜流速计hot- film anemometer流量计flow meter粘度计visco[si] meter涡量计vorticity meter传感器transducer, sensor压强传感器pressure transducer热敏电阻thermistor示踪物tracer时间线time line脉线streak line尺度效应scale effect壁效应wall effect堵塞blockage堵寒效应blockage effect动态响应dynamic response响应频率response frequency底压base pressure菲克定律Fick law巴塞特力Basset force埃克特数Eckert number格拉斯霍夫数Grashof number努塞特数Nusselt number普朗特数prandtl number雷诺比拟Reynolds analogy施密特数schmidt number斯坦顿数Stanton number对流convection自由对流natural convection, free convec-tion强迫对流forced convection热对流heat convection质量传递mass transfer传质系数mass transfer coefficient热量传递heat transfer传热系数heat transfer coefficient对流传热convective heat transfer辐射传热radiative heat transfer动量交换momentum transfer能量传递energy transfer传导conduction热传导conductive heat transfer热交换heat exchange临界热通量critical heat flux浓度concentration扩散diffusion扩散性diffusivity扩散率diffusivity扩散速度diffusion velocity分子扩散molecular diffusion沸腾boiling蒸发evaporation气化gasification凝结condensation成核nucleation计算流体力学computational fluid mechanics多重尺度问题multiple scale problem伯格斯方程Burgers equation对流扩散方程convection diffusion equationKDU方程KDV equation修正微分方程modified differential equation拉克斯等价定理Lax equivalence theorem数值模拟numerical simulation大涡模拟large eddy simulation数值粘性numerical viscosity非线性不稳定性nonlinear instability希尔特稳定性分析Hirt stability analysis相容条件consistency conditionCFL条件Courant- Friedrichs- Lewy condition ,CFL condition狄里克雷边界条件Dirichlet boundary condition熵条件entropy condition远场边界条件far field boundary condition流入边界条件inflow boundary condition无反射边界条件nonreflecting boundary condition 数值边界条件numerical boundary condition流出边界条件outflow boundary condition冯.诺伊曼条件von Neumann condition近似因子分解法approximate factorization method 人工压缩artificial compression人工粘性artificial viscosity边界元法boundary element method配置方法collocation method能量法energy method有限体积法finite volume method流体网格法fluid in cell method, FLIC method通量校正传输法flux-corrected transport method通量矢量分解法flux vector splitting method伽辽金法Galerkin method积分方法integral method标记网格法marker and cell method, MAC method 特征线法method of characteristics直线法method of lines矩量法moment method多重网格法multi- grid method板块法panel method质点网格法particle in cell method, PIC method质点法particle method预估校正法predictor-corrector method投影法projection method准谱法pseudo-spectral method随机选取法random choice method激波捕捉法shock-capturing method激波拟合法shock-fitting method谱方法spectral method稀疏矩阵分解法split coefficient matrix method不定常法time-dependent method时间分步法time splitting method变分法variational method涡方法vortex method隐格式implicit scheme显格式explicit scheme交替方向隐格式alternating direction implicit scheme, ADI scheme 反扩散差分格式anti-diffusion difference scheme紧差分格式compact difference scheme守恒差分格式conservation difference scheme克兰克-尼科尔森格式Crank-Nicolson scheme杜福特-弗兰克尔格式Dufort-Frankel scheme指数格式exponential scheme戈本诺夫格式Godunov scheme高分辨率格式high resolution scheme拉克斯-温德罗夫格式Lax-Wendroff scheme蛙跳格式leap-frog scheme单调差分格式monotone difference scheme保单调差分格式monotonicity preserving difference scheme穆曼-科尔格式Murman-Cole scheme半隐格式semi-implicit scheme斜迎风格式skew-upstream scheme全变差下降格式total variation decreasing scheme TVD scheme 迎风格式upstream scheme , upwind scheme计算区域computational domain物理区域physical domain影响域domain of influence依赖域domain of dependence区域分解domain decomposition维数分解dimensional split物理解physical solution弱解weak solution黎曼解算子Riemann solver守恒型conservation form弱守恒型weak conservation form强守恒型strong conservation form散度型divergence form贴体曲线坐标body- fitted curvilinear coordi-nates[自]适应网格[self-] adaptive mesh适应网格生成adaptive grid generation自动网格生成automatic grid generation数值网格生成numerical grid generation交错网格staggered mesh网格雷诺数cell Reynolds number数植扩散numerical diffusion数值耗散numerical dissipation数值色散numerical dispersion数值通量numerical flux放大因子amplification factor放大矩阵amplification matrix阻尼误差damping error离散涡discrete vortex熵通量entropy flux熵函数entropy function分步法fractional step method广义连续统力学generalized continuum mechanics 简单物质simple material纯力学物质purely mechanical material微分型物质material of differential type积分型物质material of integral type混合物组份constituents of a mixture非协调理论incompatibility theory微极理论micropolar theory决定性原理principle of determinism等存在原理principle of equipresence局部作用原理principle of objectivity客观性原理principle of objectivity电磁连续统理论theory of electromagnetic continuum 内时理论endochronic theory非局部理论nonlocal theory混合物理论theory of mixtures里夫林-矣里克森张量Rivlin-Ericksen tensor声张量acoustic tensor半向同性张量hemitropic tensor各向同性张量isotropic tensor应变张量strain tensor伸缩张量stretch tensor连续旋错continuous dislination连续位错continuous dislocation动量矩平衡angular momentum balance余本构关系complementary constitutive relations共旋导数co-rotational derivative, Jaumann derivative 非完整分量anholonomic component爬升效应climbing effect协调条件compatibility condition错综度complexity当时构形current configuration能量平衡energy balance变形梯度deformation gradient有限弹性finite elasticity熵增entropy production标架无差异性frame indifference弹性势elastic potential熵不等式entropy inequality极分解polar decomposition低弹性hypoelasticity参考构形reference configuration响应泛函response functional动量平衡momentum balance奇异面singular surface贮能函数stored-energy function内部约束internal constraint物理分量physical components本原元primitive element普适变形universal deformation速度梯度velocity gradient测粘流动viscometric flow当地导数local derivative岩石力学rock mechanics原始岩体应力virgin rock stress构造应力tectonic stress三轴压缩试验three-axial compression test三轴拉伸试验three-axial tensile test 三轴试验triaxial test岩层静态应力lithostatic stress吕荣lugeon地压强geostatic pressure水力劈裂hydraulic fracture咬合[作用] interlocking内禀抗剪强度intrinsic shear strength 循环抗剪强度cyclic shear strength 残余抗剪强度residual shear strength 土力学soil mechanics孔隙比void ratio内磨擦角angle of internal friction休止角angle of repose孔隙率porosity围压ambient pressure渗透系数coefficient of permeability [抗]剪切角angle of shear resistance 渗流力seepage force表观粘聚力apparent cohesion粘聚力cohesion稠度consistency固结consolidation主固结primary consolidation次固结secondary consolidation固结仪consolidometer浮升力uplift扩容dilatancy有效应力effective stress絮凝[作用] flocculation主动土压力active earth pressure被动土压力passive earth pressure 土动力学soil dynamics应力解除stress relief次时间效应secondary time effect贯入阻力penetration resistance沙土液化liquefaction of sand泥流mud flow多相流multiphase flow马格努斯效应Magnus effect韦伯数Weber number环状流annular flow泡状流bubble flow层状流stratified flow平衡流equilibrium flow二组份流two-component flow冻结流frozen flow均质流homogeneous flow二相流two-phase flow气-液流gas-liquid flow气-固流gas-solid flow液-气流liquid-gas flow液-固流liquid-solid flow液体-蒸气流liquid-vapor flow浓相dense phase稀相dilute phase连续相continuous phase离散相dispersed phase悬浮suspension气力输运pneumatic transport气泡形成bubble formation体密度bulk density壅塞choking微滴droplet挟带entrainment流型flow pattern流[态]化fluidization界面interface跃动速度saltation velocity非牛顿流体力学non-Newtonian fluid mechanics 非牛顿流体non-Newtonian fluid幂律流体power law fluid拟塑性流体pseudoplastic fluid触稠流体rheopectic fluid触变流体thixotropic fluid粘弹性流体viscoelastic fluid流变测量学rheometry震凝性rheopexy体[积]粘性bulk viscosity魏森贝格效应Weissenberg effect流变仪rheometer稀薄气体动力学rarefied gas dynamics物理化学流体力学physico-chemical hydrodynamics 空气热化学aerothermochemistry绝对压强absolute pressure绝对反应速率absolute reaction rate绝对温度absolute temperature吸收系数absorption coefficient活化分子activated molecule活化能activation energy绝热压缩adiabatic compression绝热膨胀adiabatic expansion绝热火焰温度adiabatic flame temperature电弧风洞arc tunnel原子热atomic heat雾化atomization自燃auto-ignition自动氧化auto-oxidation可用能量available energy缓冲作用buffer action松密度bulk density燃烧率burning rate燃烧速度burning velocity接触面contact surface烧蚀ablation。

流体力学与传热(英文版)chapter1b

the shear stress is proportional to the shear rate du (1.2-3)

dy
(the proportionality constant μ is called the viscosity, unit of μ is kg/(m.s) ) Eq. (1.2-3) is called Newton’s law of viscosity. It is good for Newton’s fluids and laminar flow. Gases and most liquids belong to Newtonian fluids
Chapter 1
1.2 Fluid-flow phenomena
• Ideal fluid
which has zero viscosity. Without friction or resistance when fluid flows through the channel.
• Potential flow
The velocity field
• If the wall is at rest in the reference frame, the velocity of the fluid at the interface is zero, but there’re variations in velocity from point to point in the flowing stream at distances away from the solid . • The velocity field exists in the space occu pied by the fluid.

流体力学英文版课后习题问题详解

1.1 What will be the (a) the gauge pressure and (b) the absolute pressure of waterat depth 12m below the surface? ρwater = 1000 kg/m 3, and P atmosphere = 101kN/m 2.Solution:Rearranging the equation 1.1-4gh p p a b ρ+=Set the pressure of atmosphere to be zero, then the gauge pressure at depth 12m belowthe surface iskPa gh p p a b 72.1171281.910000=⨯⨯+=+=ρAbsolute pressure of water at depth 12mkPa Pa gh p p a b 72.2182187201281.91000101000==⨯⨯+=+=ρ1.3 A differential manometer as shown in Fig. is sometimes used to measure smallpressure difference. When the reading is zero, the levels in two reservoirs are equal.Assume that fluid B is methane （甲烷）, that liquid C in the reservoirs is kerosene(specific gravity = 0.815), and that liquid A in the U tube is water. The insidediameters of the reservoirs and U tube are 51mm and 6.5mm , respectively. If thereading of the manometer is145mm., what is the pressure difference over theinstrument In meters of water, (a) when the change in the level in the reservoirsis neglected, (b) when the change in the levels in the reservoirs is taken intoaccount? What is the percent error in the answer to the part (a)?Solution ：p a =1000kg/m 3 p c =815kg/m 3 p b =0.77kg/m 3 D/d=8 R=0.145mWhen the pressure difference between two reservoirs is increased, the volumetric changes in the reservoirs and U tubesR d x D 2244ππ= (1) so R D d x 2⎪⎭⎫ ⎝⎛= (2) and hydrostaticequilibrium gives followingrelationship g R g x p g R p A c c ρρρ++=+21 (3)sog R g x p p c A c )(21ρρρ-+=- (4)substituting the equation (2) for x into equation (4) givesg R g R D d p p c A c )(221ρρρ-+⎪⎭⎫ ⎝⎛=- (5)（a ）when the change in the level in the reservoirs is neglected,()Pa g R g R g R D d p p c A c A c 26381.98151000145.0)()(221=⨯-=-≈-+⎪⎭⎫ ⎝⎛=-ρρρρρ（b ）when the change in the levels in the reservoirs is taken into account ()Pa g R g R D d g R g R D d p p c A c c A c 8.28181.98151000145.081.9815145.0515.6)()(22221=⨯-+⨯⨯⨯⎪⎭⎫ ⎝⎛=-+⎪⎭⎫ ⎝⎛=-+⎪⎭⎫ ⎝⎛=-ρρρρρρ error=％＝7.68.2812638.281- 1.4 There are two U-tube manometers fixed on the fluid bed reactor, as shown in thefigure. The readings of two U-tube manometers are R 1=400mm ，R 2=50mm, respectively.The indicating liquid is mercury. The top of the manometer is filled with the waterto prevent from the mercury vapor diffusing into the air, and the height R 3=50mm.Try to calculate the pressure at point A and B .Solution: There is a gaseous mixture in the U-tube manometer meter. The densitiesof fluids are denoted by Hg O H g ρρρ,,2, respectively. The pressure at point AFigure for problem 1.4is given by hydrostatic equilibriumg R R g R g R p g Hg O H A )(32232+-+=ρρρg ρis small and negligible in comparison with Hg ρand ρH2O , equation above can be simplifiedc A p p ≈=232gR gR Hg O H ρρ+=1000×9.81×0.05+13600×9.81×0.05=7161N/m ²1gR p p p Hg A D B ρ+=≈=7161+13600×9.81×0.4=60527N/m1.5 Water discharges from the reservoir through the drainpipe, which the throat diameter is d. The ratio of D to d equals 1.25. The vertical distance h between the tank A and axis of the drainpipe is 2m. What height H from the centerline of the drainpipe to the water level in reservoir is required for drawing the water from the tank A to the throat of the pipe? Assume thatfluid flow is a potentialflow. The reservoir, tankA and the exit of drainpipeare all open to air.Solution:Bernoulli equation is written between stations 1-1 and 2-2, with station 2-2 being reference plane:2222222111u gz p u gz p ++=++ρρ Where p 1=0, p 2=0, and u 1=0, simplification of the equation1The relationship between the velocity at outlet and velocity u o at throat can be derived by the continuity equation:22⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛D d u u o 22⎪⎭⎫ ⎝⎛=d D u u o 2 Bernoulli equation is written between the throat and the station 2-2 3Combining equation 1,2,and 3 givesSolving for HH=1.39m1.6 A liquid with a constant density ρ kg/m 3is flowing at an unknown velocity V 1m/s through a horizontal pipe of cross-sectional area A 1 m 2 at a pressure p 1 N/m 2,and then it passes to a section of the pipe in which the area is reduced graduallyto A 2 m 2 and the pressure is p 2. Assuming no friction losses, calculate the velocities V 1 and V 2 if the pressure difference (p 1 - p 2) is measured. Solution :In Fig1.6, the flow diagram is shown with pressure taps to measure p 1 and p 2. From the mass-balance continuity equation , for constant ρ where ρ1 = ρ2 = ρ,222u Hg =222200u u p =+ρ()＝＝＝144.281.92100081.910002125.11112442-⨯⨯⨯--⎪⎭⎫ ⎝⎛==ρρg h d D u Hg2112A A V V = For the items in the Bernoulli equation , for a horizontal pipe,z 1=z 2=0 Then Bernoulli equation becomes, after substituting 2112A A V V = for V 2, ρρ22121211212020p A A V p V ++=++ Rearranging,2)1(21212121-=-A A V p p ρ ⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛-12221211A A p p V ρ＝Performing the same derivation but in terms of V 2,⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--21221212A A p p V ρ＝1.7 A liquid whose coefficient of viscosity is µ flows below the critical velocity for laminar flow in a circular pipe of diameter d and with mean velocity V . Show that the pressure loss in a length of pipe L p ∆ is 232d V μ. Oil of viscosity 0.05 Pas flows through a pipe of diameter 0.1m with a average velocity of 0.6m/s. Calculate the loss of pressure in a length of 120m.Solution : The average velocity V for a cross section is found by summing up all the velocities over the cross section and dividing by the cross-sectional area1From velocity profile equation for laminar flow2 substituting equation 2 for u into equation 1 and integrating3rearranging equation 3 gives1.8. In a vertical pipe carrying water, pressuregauges are inserted at points A and B where the pipediameters are 0.15m and 0.075m respectively. Thepoint B is 2.5m below A and when the flow rate downthe pipe is 0.02 m 3/s, the pressure at B is 14715N/m 2 greater than that at A. Figure for problem 1.8⎰⎰==R R rdr u R udA A V 020211ππ⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛--=22014R r R L p p u L μ2032D L p p V L μ-=232d V L p μ=∆Pa d VL p 115201.01206.005.0323222=⨯⨯⨯==∆μAssuming the losses in the pipe between A and B can be expressed as g V k 22where V is the velocity at A, find the value of k .If the gauges at A and B are replaced by tubes filled with water and connected to a U-tube containing mercury of relative density 13.6, give a sketch showing how the levels in the two limbs of the U-tube differ and calculate the value of this difference in metres.Solution:d A =0.15m; d B =0.075mz A -z B =l =2.5mQ =0.02 m 3/s,p B -p A =14715 N/m 2s m d QV V d Q A A AA /132.115.0785.002.044222=⨯===ππ s m d QV V d Q B B BB /529.4075.0785.002.044222=⨯===ππWhen the fluid flows down, writing mechanical balance equation222222A B B B A A A V k V g z p V g z p +++=++ρρ 213.1253.4100014715213.181.95.2222k ++=+⨯ k 638.0260.10715.14638.0525.24++=+=k 0.295making the static equilibriumgR g x g l p g R g x p Hg A B ρρρρρ+∆++=+∆+()()mm g g l p p R g H A B 7981.91260081.910005.214715-=⨯⨯⨯-=---=ρρρ1.9．The liquid vertically flows down through the tube fromthe station a to the station b , then horizontally throughthe tube from the station c to the station d, as shown inFigure for problem 1.9figure. Two segments of the tube, both ab and cd ，have the same length, the diameter and roughness.Find:（1）the expressions of gp ab ρ∆, h fab , g p cd ρ∆ and h fcd , respectively. （2）the relationship between readings R 1and R 2 in the U tube.Solution:(1) From Fanning equationandsoFluid flows from station a to station b , mechanical energy conservation giveshence2from station c to station dhence3From static equationp a -p b =R 1（ρˊ-ρ）g -l ρg 4p c -p d =R 2（ρˊ-ρ）g 5Substituting equation 4 in equation 2 ，thentherefore6 22V d l h fab λ=22V d l h fcd λ=fcdfab h h =fab b a h p p +=+ρρlg fab b a h p p =+-lg ρfcd d c h p p +=ρρfcd d c h p p =-ρfab h g l g R =+--'lg 1ρρρρ）（g R h fab ρρρ-'=1Substituting equation 5 in equation 3 ，then7ThusR 1=R 21.10 Water passes through a pipe of diameter d i=0.004 m with the average velocity 0.4 m/s, as shown in Figure.1) What is the pressure drop –∆P when water flows through the pipe length L =2 m, in m H 2O column?2) Find the maximum velocity and point r at which it occurs.3) Find the point r at which the averagevelocity equals the local velocity. 4）if kerosene flows through this pipe ，howdo the variables above change ？（the viscosity and density of Water are0.001 Pas and 1000 kg/m 3，respectively ；andthe viscosity and density of kerosene are0.003 Pas and 800 kg/m 3，respectively ）solution:1）1600001.01000004.04.0Re =⨯⨯==μρud from Hagen-Poiseuille equation1600004.0001.024.0323222=⨯⨯⨯==∆d uL P μ m g p h 163.081.910001600=⨯=∆=ρ 2）maximum velocity occurs at the center of pipe, from equation 1.4-19 max 0.5V u =so u max =0.4×2=0.8m3）when u=V=0.4m/s Eq. 1.4-172max 1⎪⎪⎭⎫ ⎝⎛-=w r r u u g R h fcd ρρρ-'=2Figure for problem 1.105.0004.01max2=⎪⎭⎫ ⎝⎛-u V r ＝ m r 00284.071.0004.05.0004.0=⨯== 4) kerosene: 427003.0800004.04.0Re =⨯⨯==μρud Pa p p 4800001.0003.01600=='∆='∆μμ m g p h 611.081.98004800=⨯=''∆='ρ1.12 As shown in the figure, the water level in the reservoir keeps constant. A steel drainpipe (with the inside diameter of 100mm) is connected to the bottom of the reservoir. One arm of the U-tube manometer is connected to the drainpipe at the position 15m away from the bottom of the reservoir, and the other is opened to the air, the U tube is filled with mercury and the left-side arm of the U tube above the mercury is filled with water. The distance between the upstream tap and the outlet of the pipeline is 20m.a) When the gate valve is closed, R=600mm, h=1500mm; when the gate valve is opened partly, R=400mm, h=1400mm. The friction coefficient λ is 0.025, and the loss coefficient of the entrance is 0.5. Calculate the flow rate of water when the gate valve is opened partly. (in m ³/h)b) When the gate valve is widely open, calculate the static pressure at the tap (in gauge pressure, N/m ²). l e /d ≈15 when the gate valve is widely open, and the friction coefficient λ is still 0.025.Solution ：(1) When the gate valve is opened partially, the water discharge isSet up Bernoulli equation between the surface of reservoir 1—1’and the sectionof pressure point 2—2’，and take the center of section 2—2’as the referring plane, then∑+++=++21,2222121122—f h p u gZ p u gZ ρρ （a ）In the equation 01=p (the gauge pressure)222/396304.181.910004.081.913600m N gh gR p O H Hg =⨯⨯-⨯⨯=-=ρρ 0021=≈Z uWhen the gate valve is fully closed, the height of water level in the reservoircan be related to h (the distance between the center of pipe and the meniscus of left arm of U tube).gR h Z g Hg O H ρρ=+)(12（b ）where h=1.5mR=0.6mSubstitute the known variables into equation b2222_1,113.22)5.01.015025.0(2)(66.65.110006.013600V VV K d l h mZ cf =+⨯=+==-⨯=∑λ Substitute the known variables equation a9.81×6.66=2213.21000396302V V ++ the velocity is V =3.13m/sthe flow rate of water isFigure for problem 1.12h m V d V h /5.8813.312.0436004360032=⨯⨯⨯=⨯=ππ2） the pressure of the point where pressure is measured when the gate valve is wide-open.Write mechanical energy balance equation between the stations 1—1’and 3-3´，then∑+++=++31,3233121122—f h p V gZ p V gZ ρρ （c ）since m Z 66.61=311300p p u Z =≈= 2223_1,81.4 2]5.0)151.035(025.0[ 2)(V V V K d l l h c e f =++=++=∑λ input the above data into equation c ，9.8122V 81.4266.6+=⨯V the velocity is: V =3.51 m/sWrite mechanical energy balance equation between thestations 1—1’and 2——2’, for the same situation of water level∑+++=++21,2222121122—f h p V gZ p V gZ ρρ（d ）since m Z 66.61=2121003.51/0(page pressure Z u u m sp =≈≈=）kg J V K d l hc f /2.26251.3)5.01.015025.0(2)(222_1,=+⨯=+=∑λinput the above data into equation d ，9.81×6.66=2.261000251.322++p the pressure is: 329702=p1.14 Water at 20℃ passes through a steel pipe with an inside diameter of 300mm and 2m long. There is a attached-pipe (Φ60⨯3.5mm) which is parallel with the main pipe. The total length including the equivalent length of all form losses of the attached-pipe is 10m. A rotameter is installed in the branch pipe. When the readingof the rotameter is 2.72m 3/h, try to calculate the flow rate in the main pipe and the total flow rate, respectively. The frictional coefficient of the main pipe and the attached-pipe is 0.018 and 0.03, respectively.Solution ： The variables of main pipe are denoted by a subscript1, and branch pipeby subscript 2. The friction loss for parallel pipelines is 2121S S s f f V V V h h+==∑∑The energy loss in the branch pipe is22222222u d l l he f ∑∑+=λ In the equation 03.02=λsm u d ml l e /343.0053.04360072.2053.01022222=⨯⨯===+∑πinput the data into equation c kg J hf /333.02343.0053.01003.022=⨯⨯=∑The energy loss in the main pipe is333.022111121===∑∑u d l h hf f λSo s m u /36.22018.023.0333.01=⨯⨯⨯=The water discharge of main pipe ish m V h /60136.23.043600321=⨯⨯⨯=πTotal water discharge ish m V h /7.60372.26013≈+=1.16 A Venturimeter is used for measuring flow of water along a pipe. The diameter of the Venturi throat is two fifths the diameter of the pipe. The inlet and throat are connected by water filled tubes to a mercury U-tube manometer. The velocity of flow along the pipe is found to be R 5.2 m/s, where R is the manometer reading in metres of mercury. Determine the loss of head between inlet and throat of the Venturi when R is 0.49m. (Relative density of mercury is 13.6). Solution: Writing mechanical energy balance equation between the inlet 1 and throat o for Venturi meterf o o hg z V p g z V p +++=++22121122ρρ 1 rearranging the equation above, and set (z 2-z 1)=xf o oh xg V V p p ++-=-22121ρ2from continuity equation11221125.625V V dd V V o o =⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛= 3 substituting equation 3 for V o into equation 2 gives()fff f oh xg R h xg Rh V h xg V V p p ++=++=+=++-=-94.1185.203.1903.19206.3922121211ρ4from the hydrostatic equilibrium for manometerg x g R p p Hg o ρρρ+-=-)(1 5substituting equation 5 for pressure difference into equation 4 obtainsf Hgh xg R gx g R ++=+-94.118)(ρρρρ 6rearranging equation 6Figure for problem 1.16kg J R R R R gR h Hg f /288.267.494.11861.12394.118)(==-=--=ρρρ1.17.Sulphuric acid of specific gravity 1.3 is flowing through a pipe of 50 mm internal diameter. A thin-lipped orifice, 10mm, is fitted in the pipe and the differential pressure shown by a mercury manometer is 10cm. Assuming that the leads to the manometer are filled with the acid, calculate (a)the weight of acid flowing per second, and (b) the approximate friction loss in pressure caused by the orifice.The coefficient of the orifice may be taken as 0.61, the specific gravity of mercuryas 13.6, and the density of water as 1000 kg/m 3Solution:a)2.0501010==D D =⨯-=-=-81.9)130013600(1.0)(21g R p p Hg ρρs kg V D m /268.0130063.201.0442220=⨯⨯⨯==πρπb) approximate pressure drop=⨯-=-=-81.9)130013600(1.0)(21g R p p Hg ρρ12066.3Papressure difference due to increase of velocity in passing through the orificePa D D V V V V p p o8.44882)2.01(63.213002242412222212221=-=⎪⎪⎭⎫⎝⎛-=-=-ρρpressure drop caused by friction lossPa p f 5.75778.44883.12066=-=∆()s m p p D D C V o /63.231.461.056.1861.0130081.9)130013600(1.022.0161.021*******=⨯=≈⨯-⨯-=-⎪⎪⎭⎫ ⎝⎛-=ρ2.1 Water is used to test for the performances of pump. The gauge pressure at the discharge connection is 152 kPa and the reading of vacuum gauge at the suctionconnection of the pump is 24.7 kPa as the flow rate is 26m 3/h. The shaft power is 2.45kw while the centrifugal pump operates at the speed of 2900r/min. If the vertical distance between the suction connection and discharge connection is 0.4m, the diameters of both the suction and discharge line are the same. Calculate the mechanical efficiency of pump and list the performance of the pump under this operating condition. Solution:Write the mechanical energy balance equation between the suction connection and discharge connection2_1,2222121122f H gp g u Z H g p g u Z +++=+++ρρwherem Z Z 4.012=-(Pa 1052.1(Pa 1047.22_1,215241≈=⨯=⨯-=f H u u pressure gauge p pressure gauge p ））total heads of pump is m H 41.1881.9100010247.01052.14.055=⨯⨯+⨯+= efficiency of pump is N N e /=η since kW g QH N e 3.1360081.9100041.18263600=⨯⨯⨯==ρ N=2.45kWThen mechanical efficiency%1.53%10045.23.1=⨯=η The performance of pump isFlow rate ，m ³/h26Total heads ，m 18.41Shaftpower ，kW 2.45Efficiency，% 53.12.2 Water is transportedby a pump from reactor, which has 200 mm Hg vacuum, to the tank, in which the gaugepressure is 0.5 kgf/cm 2, as shown in Fig. The total equivalent length of pipe is 200 m including all local frictional loss. The pipeline is φ57×3.5 mm , the orifice coefficient of C o and orifice diameter d o are 0.62 and 25 mm, respectively. Frictional coefficient λ is 0.025. Calculate: Developed head H of pump, in m (the reading R of U pressure gauge in orifice meter is 168 mm Hg)Solution:Equation(1.6-9)Mass flow rates kg S V m o o /02.21000025.0414.312.42=⨯⨯⨯==ρ 2) Fluid flow through the pipe from the reactor to tank, the Bernoulli equation is as follows for V 1=V 2f H z gp p H +∆+-=ρ12 ∆z=10mPa p 7570710013.17602001081.95.054=⨯⨯+⨯⨯=∆ ∆p/ρg=7.7mThe relation between the hole velocity and velocity of pipeFriction losssoH=7.7+10+5.1=22.8m2.3 . A centrifugal pump is to be used to extract water from a condenser in which the vacuum is 640 mm of mercury, as shown in figure. At the rated discharge, the net positive suction head must be at least 3m above the cavitation vapor pressure of 710mm mercury vacuum.Ifs m Rg D d C V f /12.444.69375.062.01000)100013600(81.9168.025025162.02144000=⨯=-⨯⨯⎪⎭⎫⎝⎛-=-⎪⎭⎫ ⎝⎛-=ρρρ）（s m D d V V /12112.42200=⎪⎭⎫⎝⎛⨯=⎪⎭⎫ ⎝⎛=m g u d l f H f 1.581.92105.0200025.02422=⨯⨯==losses in the suction pipe accounted for a head of 1.5m. What must be the least height of the liquid level in the condenser above the pump inlet? Solution :From an energy balance,WhereP o =760-640=120mmHg P v =760-710=50mmHgUse of the equation will give the minimum height H g as2.4 Sulphuric acid is pumped at 3 kg/s through a 60m length of smooth 25 mm pipe. Calculate the drop in pressure. If the pressure drop falls by one half, what will the new flowrate be ?• Density of acid 1840kg/m 3• Viscosity of acid 25×10-3PasSolution:Velocity of acid in the pipe:sm d m d mpipe of area tional cross flowrate volumetric u /32.3025.01840785.03785.04sec 222=⨯⨯===-=ρπρReynolds number:6109102532.31840025.0Re 3=⨯⨯⨯==-μρud from Fig.1.22 for a smooth pipe when Re=6109, f=0.0085 pressure drop is calculated from equation 1.4-9kg J u d l f ph f /450232.3025.0600085.042422=⨯==∆=ρkPa p 5.8271840450=⨯=∆or friction factor is calculated from equation1.4-25NPSH H gp p H f vo g ---=ρmNPSH H gp p H f vo g 55.335.181.9100081.913600)05.012.0-=--⨯⨯⨯-=---=（ρkgJ u d l u d l f ph f /426232.3025.0606109046.042Re 046.042422.022.02=⨯⨯⨯==∆=--＝ρkPa p 84.7831840426=⨯=∆if the pressure drop falls to 783.84/2=391.92kPa8.18.12.12.038.12.12.022.0012.089.1079`2025.060102518401840046.042046.042Re 046.043919202u u u dl u d l p p =⎪⎭⎫ ⎝⎛⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯==∆='∆----ρμρρ＝sos m u /27.236.489..1079012.03919208.18.1==⨯=new mass flowrate=0.785d 2u ρ=0.785×0.0252×2.27×1840=2.05kg/s2.4 Sulphuric acid is pumped at 3 kg/s through a 60m length of smooth 25 mm pipe. Calculate the drop in pressure. If the pressure drop falls by one half on assumption that the change of friction factor is negligible, what will the new flowrate be ?Density of acid 1840kg/m 3Viscosity of acid 25×10-3Pa Friction factor 32.0Re500.00056.0+=f for hydraulically smooth pipe Solution:Write energy balance equation:f h gu z g p H g u z g p +++=+++2222222111ρρ gu d l g p h H f 22λρ=∆==342=ρπu ds m d u /32.31840025.014.3124322=⨯⨯=⨯=ρπ 611510251840025.032.3Re 3=⨯⨯⨯=-0087.061155.00056.0Re 500.00056.032.032.0=+=+=f92.4681.9232.3025.0600087.04222=⨯⨯==∆==g u d l g p h H f λρΔp=46.92×1840×9.81=847.0kpa2.6 The fluid is pumped through the horizontal pipe from section A to B with the φ38⨯2.5mm diameter and length of 30 meters, shown as figure. The orifice meter of 16.4mm diameter is used to measure the flow rate. Orifice coefficient C o ＝0.63.the permanent loss in pressure is 3.5×104N/m 2, the friction coefficient λ=0.024. find:(1) What is the pressure drop along the pipe AB?(2)What is the ratio of power obliterated in pipe AB to total power supplied to thefluid when the shaft work is 500W, 60%efficiency? (The density of fluid is 870kg/m 3)solution ：∑+++=+++f AA A A AA h u p g z w u p g z 2222ρρρλρ022p u d l h p p f BA ∆+==-∑247.0334.162=⎪⎭⎫⎝⎛=A A o ()()s m gR C u /5.8870870136006.081.9297.063.02247.01200=-⨯⨯=''--=ρρρ∴u = (16.4/33)2×8.5=2.1m/s∴242/76855105.321.2033.030870024.0m N h p p f B A =⨯+⨯==-∑ρ (2)W u d p Wm 1381.2033.0785.0768554Ne 22=⨯⨯⨯=∆==ρπρ sothe ratio of power obliterated in friction losses in AB to total power supplied to the fluid％％＝461006.0500138⨯⨯。

流体力学（英文版）

流体力学（英文版）Fluid MechanicsCourse Code: 83165000Course Name: Fluid MechanicsCourse Credit: 3Course Duration: The 3rd SemesterTeaching Object: Undergraduate Students in Space Science Pre-course:Advanced Mathematics, General PhysicsCourse Director: Shi Quanqi Lecturer Philosophical Doctor Course Introduction:Fluid Mechanics is a foundation course which is used extensively in the engineering .At the same time, it is also a basic course in learning magnetohydrodynamics (MHD)。

The course includes the concept of the continuum, kinematics, the hydrodynamics Equations, the similarity theory and dimensional analysis, and the dynamics of gas flow. Application examples in fields of power source, dynamics, Aviation, machinery, space science and daily life will be introduced. When the students finish this course, they will be able to understand the basic concept, the general theory and the analytical method in Fluid Mechanics, and will know its application in the Space Sciences, engineering, and our daily life.Course Examination:Students’ Final Scores = Scores of Ordinary Tests * 30% + Scores of the Final Exam * 70%;Scores of ordinary tests vary according to students’ performance in class and homework.;The final exam will be open-book.Appointed Teaching Materials:[1] Ding Zurong，Fluid Mechanics，Beijing：China HigherEducation Press，2005.Bibliography:[1]. Wu Wangyi，Fluid Mechanics，Beijing：Peking University Press，2004.。

流体力学英文版第五章非基本形式-Nondimentional

ContentNotes1.Preface2.Dimensions of variables3.ΠTheorem4.Normalization of equationsProblem:Consider an idealized pendulum consisting of a weightless string ofﬁxed length l and a small sphere of mass m.In this case,the sphere is attached to the lower end of the string and the upper end of the string isﬁxed to a ceiling.Due to gravity,the sphere with initial deviation angle a oscillates around the plumb line at theﬁxed point on the ceiling within a deﬁnite period T.Figure1:An idealizedpendulum.NotesAssumptions:Mass of the string is assumed mass of the small sphere m.Deformation of the string is assumed much smaller than the length,l.Compared to gravity,aerodynamic drag is assumed to be negligible.Clearly,oscillation period T depends on four governing pa-rameters:mass of small sphere,m.length of the string,l.gravitational acceleration,g;initial deviation angleθ,thusT=f(m,l,g,θ)Figure2:An idealizedpendulum.NotesNotesNotesNotesFigure3:Geometrical similarity of two triangle. similarity:a1 L1=a2L2numbers themselves don’t have any physicalrelative”strength”compared to someabout the relations between the sides of thelength of them.Notessimilarity:super super =100p1ρ1U21=NotesNotesDimensionNotesDimensionDimension is used to express the essential nature of a quantity sothat quantities can be grouped.It is important to distinguish dimension from unit:A physical quantity has a particular nature(i.e.,particular di-mension),a unit is a measure used to compare quantities.If two quantities have diﬀerent natures,dimensions of thesequantities diﬀer,cannot be compared proﬁtably,and do notrelate to unit.NotesType of quantitiesNotesDimensional quantities:magnitude depends on the unit se-lected(e.g.,unit of length,unit of time,unit of mass,and unitof force)dimensionless quantities:magnitude usually depends on ratioof two quantities with same dimensions(e.g.,ratio of diﬀerentlengths,ratio of diﬀerent times,and ratio of diﬀerent forces orratio of diﬀerent energies)fundamental quantities:A system of fundamental quantitiesis such that the dimensions of the quantities in this system aremutually independentderived quantities:is such that the dimension of every quan-tity in this system can be expressed by a combination of thedimensions of fundamental quantities in the problem.NotesNotes Requirements apply to a mathematical operation that involve manyphysical quantities in a problem:The operation must consider the dimension of the quantity ex-amined and the relationship between that dimension and di-mensions of fundamental quantities in the problem.The operation must have a uniﬁed measurement unit system.To permit operation related to physical quantities,multiple unitsystems must convert to a single unit system.Notes The dimension of quantity X in a mechanics problem can be ex-pressed by a power law formula in terms of dimensions of funda-mental quantities length,mass,and time:[X]=LαMβTγwhereα,β,andγare real numbers.The dimension of any pure number(e.g.,φ)that is irrelevant to theselection of the unit system can be formulated:φ=L0M0T0=1NotesNotesNotesNotesNotesNotesNotesSix steps are involved in the application ofΠtheorem:List n variables involved in the problem.List the dimensions of each variable according to MLTΘ.Find j.Select j scaling parameters that do not form aπproduct.Add one additional variable to your j repeating variables,andform a power product.Write theﬁnal dimensionless function,and make sure allπterms are dimensionless.NotesNotesNotesNotes Step3:Find j.No variable contains the dimensionΘ,and so j is less than orequal to3(MLT).We inspect the list and see that D,U andρcannot form aπgroup because onlyρcontains mass andonly U contains time.Therefore j does equal3,and n−j=5−3=2=k.Theπtheorem guarantees for this problem thatthere will be exactly two independent dimensionless groups.Step4:Select repeating j variables.The group D,U,ρ,we found in step3will doﬁne.Notes Step5:Combine D,U,ρwith one additional variable,in se-quence,toﬁnd the twoπproducts.First add force toﬁndΠ1.You may select any exponent onthis additional term as you please,to place it in the numeratoror denominator to any power.Since F is the output,or depen-dent,variable,we select it to appear to theﬁrst power in thenumerator:Π1=D a U bρc F:(L)a(LT−1)b(MT−3)c(MLT−2)=M0L0T0Equate exponents:Length:a+b−3c+1=0Mass:c+1=0,a=−2,b=−2,c=−1Time:−b−2=0NotesNotesNotesNotesNotes Step3:Find j.There areﬁve variables(n=5)and three primary dimensions(M,L,T),hence j≤3.But try as we may,we cannotﬁnd anycombination of three variables that does not form aπgroup.This is because{M}and{T}occur only in P and E and only inthe same form,{MT−2}.Thus we have encountered a specialcase of j=2,which is less than the number of dimensions(M,L,T).Step4:Select repeating j variables.We select the group L and E as two variables that cannot formaπgroup.NotesNotes TheΠtheorem method,is often called the repeating variable methodof dimensional analysis.This method is straightforward and system-atically reveals all the desiredπgroups.However,there are draw-backs:Allπgroups contain the same repeating variables and mightlack variety or eﬀectiveness.One must(sometimes laboriously)check that the selected re-peating variables do not form aπgroup among themselves.Ipsen(1960)suggests an entirely diﬀerent procedure,a step-by-stepmethod that obtains all of theπgroups at once,without any count-ing or checking.One simply successively eliminates each dimensionin the desired function by division or multiplication.NotesNotesNotesNotesNotesExercise :The leading-edge aerodynamic moment M LE on a su-personic airfoil is a function of its chord length C ,angle of attack α,and several air parameters:approach velocity V ,density ρ,speed of sound a ,and speciﬁc heat ratio k .There is a very weak eﬀect of air viscosity,which is neglected e Ipsen’s method to rewrite this function in dimensionlessform.NotesNotesNotesNotesNormalization of Navier-Stokes equaitonsRecalling what we did during dimensional analysis,we introduce intrinsic quantities as fundamental UNITS for incompressible viscous ﬂow,such as:ρ,L,UNotesNotesNotesNotesNotes The only eﬀective parameter is Reynolds number,Re.Supposing twoﬂowsshare common Re,the variables”in the intrinsic units”(or dimensionlessquantities)will equal to each other,respectively.We call the twoﬂows aresimilar.Reynolds numberReynolds number is deﬁned as the ratio of inertial forces to viscousforces and consequently quantiﬁes the relative importance of these twotypes of forces for givenﬂow conditions.In addition to determining dynamic similitude between two diﬀerent casesofﬂuidﬂow,it can be used to characterize diﬀerentﬂow regimes within asimilarﬂuid,such as laminar or turbulentﬂow.NotesNotes。

流体力学(英文资料)

Chapter 1 Introduction
1.1 Preliminary Remarks
When you think about it, almost everything
on this planet either is a fluid or moves within or near a fluid.
Ludwig Prandtl (1875-1953)
Boundary layer theory(1904)
To be the single most important tool in modern flow analysis.
The father of modern fluid mechanics
Most engineering problems are concerned with physical dimensions much larger than this limiting volume.
* Small enough in macroscope（宏观）.
微观无穷大
宏观无穷小
So density is essentially a point function and fluid properties can be thought of as varying continually in space .
Body forces act on the entire mass of the element. Gravity , electromagnetic. No cotact Per unit mass(单位质量) g
v vv v R Xi Yj Zk
1.5 Two different points of view in analyzing problems in mechanics

流体力学(英文课件)chap5

分量形式
u x u x u x u x 1 p ux uy uz X t x y z x
4 equations for 4 quantities
u y
ux
u y
uy
u y
uz
u y
1 p y 1 p Z z u z 0 z Y
16
4. Incompressible 2. The Navier-Stokes Equations (3) Ideal Fluid Flow
p xx dx)dydz zx dxdy ( zx zx dz)dxdy x z yx du yx dxdz ( yx dy)dxdz dxdydz x y dt
E
z
F p yy
yz
xz p xx
A G
H
1. index: normal vector on face 2. index: direction of force
xy
D
yx
B
O x 图3-21
zx p zz
y
zy
C
p xx xy xz yx p yy yz p zz zx zy
1 p az Z z
Fluid Mechanics 2010 CN Chapter 4
10
4 - 1 理想流体的运动方程
欧拉运动微分方程
1、采用六面体微元分析法
2、加速度中含当地加速度和迁移加速度
3、x轴方向：
p dx p dx p dydz p dydz X dxdydz dxdydzax x 2 x 2

流体力学英文课件第3章

U1 U2 U3
D2=10 in
3.5 The Linear Momentum Equation (动量方程) （ Newton’s Second Law ）
ds ( i AiV i )out ( i AiV i )in dt i i
1-D in & out steady RTT
x
Example: A fixed control volume of a streamtube in steady flow has a uniform inlet (1,A1,V1 )and a uniform exit (2,A2,V2) . Find the net force on the control volume.
Solution:
F m(V 2 V 1) m 1 A1V 1 2 A2V 2
F x m(V2 x V1x ) m(V 2 V 1 cos )
2
V1
V2
F y m(V2 y V1 y ) mV 1 sin
In the like manner
(d )out ( AVdt )out
s
ds
t
t+dt t t+dt
d s d cv 1 [(d )out (d )in] dt dt dt
d s d cv [( AV )out ( AV )in] dt dt
s
t t+dt
t
t+dt
: any property of fluid (m, mV , H , E )
d dm
:The amount of per unit mass

流体力学专业英语词汇

流体力学专业词汇(V ocabulary of Fluid Mechanics )CHAPTER-1acceleration 加速度average velocity 平均速度Bernoulli 伯努力boundary layer 边界层calculus 微积分coefficient of viscosity 粘性系数compressible(incompressible) (不)可压的conservation of mass(momentum, energy) 质量(动量,能量)守恒continuum 连续介质control-volume 控制体density(mass per unit volume) 密度differential 微分dimension 量刚尺度dynamics 动力学Euler 欧拉eulerian (lagrangian) method of description欧拉(拉格郎日)观点，方法field of flow 流场flow pattern 流型（谱）fluid mechanics 流体力学function 函数inertia 惯性, 惯量integral 积分kinematics 运动学kinetic (potential, internal) energy 动(势,内)能Lagrange 拉格郎日liquid 流体Newtonian fluids 牛顿流体(non)linear (非)线性(non)uniform （非）均匀one-dimensional 一维pathline 迹线perfect-gas law 理想气体定律pressure 压力压强Reynolds 雷诺shear(normal) stress 剪(正)应力solution 解答statics 静力学steady(unsteady) (非)定常strain 应变streamline(tube) 流线(管)thermal conductivity 热传导thermodynamics 热力学variable 变量vector 矢量velocity distribution 速度分布velocity field 速度场velocity gradient 速度梯度viscous(inviscid) (无)粘性的volume rate of flow 体积流量CHAPTER -2absolute (gage,vacuum) pressure 绝对（表，真空）压力area moment of inertia 惯性面积矩atmospheric pressure 大气压力barometer 气压计body force 体力Cartesian [rectangular] coordinates 直角坐标（系）centroid 质心elliptic 椭圆的equilibrium 平衡horizontal 水平的hydrostatic 水静力学，流体静力学hyperbolic 双曲线的mercury 水银moment 矩parabolic 抛物线plane (curved) surface 平（曲）面plate 板pressure center 压力中心pressure distribution(gradient) 压力分布（梯度）reservoir 水库rigid-body 刚体scalar 标量specific weight 比重surface force 表面力vertical 垂直的, 直立的CHAPTER -3Bernoulli equation 伯努力方程Boundaries 边界Conservation of mass 质量Control volume 控制体Energy(hydraulic) grade line 能级线Flux 流率Free body 隔离体Heat transfer 热传到Imaginary 假想Inlet, outlet 进、出口Integrand 被积函数Jet flow 射流Linear(Angular)-momentum relation 线（角）动量关系式Momentum(energy)-flux 动量（能量）流量Net force 合力No slip 无滑移Nozzle 喷嘴Rate of work 功率Reynolds transport theorem 雷诺输运定理Shaft work 轴功Stagnation enthalpy 制止焓Surroundings 外围System 体系Time derivative 时间导数Vector sum 矢量合Venturi tube 文图里管V olume(mass) flow 体积（质量）流量V olume(mass) rate of flow体积（质量）流率CHAPTER -4Soomth 平滑Laminar 层流Transition 转捩Roughness 粗糙度Random fluctuations 随机脉动Reynolds number 雷诺数（Re）Instability 不稳定性Breakdown 崩溃Mean value 平均值Drag 阻力Osborne ReynoldsDye filament 染色丝Internal (external) flow 内(外)流Cartesian 笛卡坐标Infinitesimal 无限小local acceleration 当地加速度dot product 点乘total derivative 全导数convective acceleration 对流加速度substantial(material) derivative 随体(物质)导数operator 算子partial differential equation 偏微分方程Newtonian fluid 牛顿流体Navier-Stokes Equations N-S方程Second-order 二阶Similarity 相似Nondimensionalization 无量纲化Flat-plate boundary layer 平板边界层Thermal conductivity 热传导Heat flow 热流量Fourier’s law 傅立叶定律Couette Flow 库塔流动Channel 槽道Parallel plates 平行平板Pressure gradient 压力梯度No-slip condition 无滑移条件Poiseuille flow 伯肖叶流动Parabola 抛物线Wall shear stress 壁面剪应力Prandtl 普朗特Karman 卡门Momentum-integral relation 动量积分关系Momentum thickness 动量厚度Skin-friction coefficient 壁面摩擦系数Displacement thickness 排移厚度Blasius equation 布拉修斯方程Coordinate transformation 坐标变换Composite dimensionless variable 组合无量纲变量Shape factor 形状因子Velocity profile 速度剖面流体动力学fluid dynamics连续介质力学mechanics of continuous media介质medium流体质点fluid particle无粘性流体nonviscous fluid, inviscid fluid连续介质假设continuous medium hypothesis流体运动学fluid kinematics水静力学hydrostatics液体静力学hydrostatics支配方程governing equation伯努利方程Bernoulli equation伯努利定理Bernonlli theorem毕奥-萨伐尔定律Biot-Savart law欧拉方程Euler equation亥姆霍兹定理Helmholtz theorem开尔文定理Kelvin theorem涡片vortex sheet库塔-茹可夫斯基条件Kutta-Zhoukowski condition 布拉休斯解Blasius solution达朗贝尔佯廖d'Alembert paradox雷诺数Reynolds number施特鲁哈尔数Strouhal number随体导数material derivative不可压缩流体incompressible fluid质量守恒conservation of mass动量守恒conservation of momentum 能量守恒conservation of energy动量方程momentum equation能量方程energy equation控制体积control volume液体静压hydrostatic pressure涡量拟能enstrophy压差differential pressure流[动] flow流线stream line流面stream surface流管stream tube迹线path, path line流场flow field流态flow regime流动参量flow parameter流量flow rate, flow discharge涡旋vortex涡量vorticity涡丝vortex filament涡线vortex line涡面vortex surface涡层vortex layer涡环vortex ring涡对vortex pair涡管vortex tube涡街vortex street卡门涡街Karman vortex street马蹄涡horseshoe vortex对流涡胞convective cell卷筒涡胞roll cell涡eddy涡粘性eddy viscosity环流circulation环量circulation速度环量velocity circulation偶极子doublet, dipole驻点stagnation point总压[力] total pressure总压头total head静压头static head总焓total enthalpy能量输运energy transport速度剖面velocity profile库埃特流Couette flow单相流single phase flow单组份流single-component flow均匀流uniform flow非均匀流nonuniform flow二维流two-dimensional flow三维流three-dimensional flow准定常流quasi-steady flow非定常流unsteady flow, non-steady flow 暂态流transient flow周期流periodic flow振荡流oscillatory flow分层流stratified flow无旋流irrotational flow有旋流rotational flow轴对称流axisymmetric flow不可压缩性incompressibility不可压缩流[动] incompressible flow浮体floating body定倾中心metacenter阻力drag, resistance减阻drag reduction表面力surface force表面张力surface tension毛细[管]作用capillarity来流incoming flow自由流free stream自由流线free stream line外流external flow进口entrance, inlet出口exit, outlet扰动disturbance, perturbation分布distribution传播propagation色散dispersion弥散dispersion附加质量added mass ,associated mass 收缩contraction镜象法image method无量纲参数dimensionless parameter几何相似geometric similarity运动相似kinematic similarity动力相似[性] dynamic similarity平面流plane flow势potential势流potential flow速度势velocity potential复势complex potential复速度complex velocity流函数stream function源source汇sink速度[水]头velocity head拐角流corner flow空泡流cavity flow超空泡supercavity超空泡流supercavity flow空气动力学aerodynamics低速空气动力学low-speed aerodynamics 高速空气动力学high-speed aerodynamics 气动热力学aerothermodynamics亚声速流[动] subsonic flow跨声速流[动] transonic flow超声速流[动] supersonic flow锥形流conical flow楔流wedge flow叶栅流cascade flow非平衡流[动] non-equilibrium flow细长体slender body细长度slenderness钝头体bluff body钝体blunt body翼型airfoil翼弦chord薄翼理论thin-airfoil theory构型configuration后缘trailing edge迎角angle of attack失速stall脱体激波detached shock wave波阻wave drag诱导阻力induced drag诱导速度induced velocity临界雷诺数critical Reynolds number 前缘涡leading edge vortex附着涡bound vortex约束涡confined vortex气动中心aerodynamic center气动力aerodynamic force气动噪声aerodynamic noise气动加热aerodynamic heating离解dissociation地面效应ground effect气体动力学gas dynamics稀疏波rarefaction wave热状态方程thermal equation of state 喷管Nozzle普朗特-迈耶流Prandtl-Meyer flow瑞利流Rayleigh flow可压缩流[动] compressible flow可压缩流体compressible fluid绝热流adiabatic flow非绝热流diabatic flow未扰动流undisturbed flow等熵流isentropic flow匀熵流homoentropic flow兰金-于戈尼奥条件Rankine-Hugoniot condition 状态方程equation of state量热状态方程caloric equation of state完全气体perfect gas拉瓦尔喷管Laval nozzle马赫角Mach angle马赫锥Mach cone马赫线Mach line马赫数Mach number马赫波Mach wave当地马赫数local Mach number冲击波shock wave激波shock wave正激波normal shock wave斜激波oblique shock wave头波bow wave附体激波attached shock wave激波阵面shock front激波层shock layer压缩波compression wave反射reflection折射refraction散射scattering衍射diffraction绕射diffraction出口压力exit pressure超压[强] over pressure反压back pressure爆炸explosion爆轰detonation缓燃deflagration水动力学hydrodynamics液体动力学hydrodynamics泰勒不稳定性Taylor instability盖斯特纳波Gerstner wave斯托克斯波Stokes wave瑞利数Rayleigh number自由面free surface波速wave speed, wave velocity 波高wave height波列wave train波群wave group波能wave energy表面波surface wave表面张力波capillary wave规则波regular wave不规则波irregular wave浅水波shallow water wave深水波deep water wave重力波gravity wave椭圆余弦波cnoidal wave潮波tidal wave涌波surge wave破碎波breaking wave船波ship wave非线性波nonlinear wave孤立子soliton水动[力]噪声hydrodynamic noise 水击water hammer空化cavitation空化数cavitation number空蚀cavitation damage超空化流supercavitating flow水翼hydrofoil水力学hydraulics洪水波flood wave涟漪ripple消能energy dissipation海洋水动力学marine hydrodynamics谢齐公式Chezy formula欧拉数Euler number弗劳德数Froude number水力半径hydraulic radius水力坡度hvdraulic slope高度水头elevating head水头损失head loss水位water level水跃hydraulic jump含水层aquifer排水drainage排放量discharge壅水曲线back water curve压[强水]头pressure head过水断面flow cross-section明槽流open channel flow孔流orifice flow无压流free surface flow有压流pressure flow缓流subcritical flow急流supercritical flow渐变流gradually varied flow急变流rapidly varied flow临界流critical flow异重流density current, gravity flow堰流weir flow掺气流aerated flow含沙流sediment-laden stream降水曲线dropdown curve沉积物sediment, deposit沉[降堆]积sedimentation, deposition沉降速度settling velocity流动稳定性flow stability不稳定性instability奥尔-索末菲方程Orr-Sommerfeld equation涡量方程vorticity equation泊肃叶流Poiseuille flow奥辛流Oseen flow剪切流shear flow粘性流[动] viscous flow层流laminar flow分离流separated flow二次流secondary flow近场流near field flow远场流far field flow滞止流stagnation flow尾流wake [flow]回流back flow反流reverse flow射流jet自由射流free jet管流pipe flow, tube flow内流internal flow拟序结构coherent structure 猝发过程bursting process表观粘度apparent viscosity 运动粘性kinematic viscosity 动力粘性dynamic viscosity 泊poise厘泊centipoise厘沱centistoke剪切层shear layer次层sublayer流动分离flow separation层流分离laminar separation 湍流分离turbulent separation 分离点separation point附着点attachment point再附reattachment再层流化relaminarization起动涡starting vortex驻涡standing vortex涡旋破碎vortex breakdown涡旋脱落vortex shedding压[力]降pressure drop压差阻力pressure drag压力能pressure energy型阻profile drag滑移速度slip velocity无滑移条件non-slip condition壁剪应力skin friction, frictional drag壁剪切速度friction velocity磨擦损失friction loss磨擦因子friction factor耗散dissipation滞后lag相似性解similar solution局域相似local similarity气体润滑gas lubrication液体动力润滑hydrodynamic lubrication浆体slurry泰勒数Taylor number纳维-斯托克斯方程Navier-Stokes equation 牛顿流体Newtonian fluid边界层理论boundary later theory边界层方程boundary layer equation边界层boundary layer附面层boundary layer层流边界层laminar boundary layer湍流边界层turbulent boundary layer温度边界层thermal boundary layer边界层转捩boundary layer transition边界层分离boundary layer separation边界层厚度boundary layer thickness位移厚度displacement thickness动量厚度momentum thickness能量厚度energy thickness焓厚度enthalpy thickness注入injection吸出suction泰勒涡Taylor vortex速度亏损律velocity defect law形状因子shape factor测速法anemometry粘度测定法visco[si] metry流动显示flow visualization油烟显示oil smoke visualization孔板流量计orifice meter频率响应frequency response油膜显示oil film visualization阴影法shadow method纹影法schlieren method烟丝法smoke wire method丝线法tuft method氢泡法nydrogen bubble method相似理论similarity theory相似律similarity law部分相似partial similarity定理pi theorem, Buckingham theorem 静[态]校准static calibration动态校准dynamic calibration风洞wind tunnel激波管shock tube激波管风洞shock tube wind tunnel水洞water tunnel拖曳水池towing tank旋臂水池rotating arm basin扩散段diffuser测压孔pressure tap皮托管pitot tube普雷斯顿管preston tube斯坦顿管Stanton tube文丘里管Venturi tubeU形管U-tube压强计manometer微压计micromanometer多管压强计multiple manometer静压管static [pressure]tube流速计anemometer风速管Pitot- static tube激光多普勒测速计laser Doppler anemometer, laser Doppler velocimeter热线流速计hot-wire anemometer热膜流速计hot- film anemometer流量计flow meter粘度计visco[si] meter涡量计vorticity meter传感器transducer, sensor压强传感器pressure transducer热敏电阻thermistor示踪物tracer时间线time line脉线streak line尺度效应scale effect壁效应wall effect堵塞blockage堵寒效应blockage effect动态响应dynamic response响应频率response frequency底压base pressure菲克定律Fick law巴塞特力Basset force埃克特数Eckert number格拉斯霍夫数Grashof number努塞特数Nusselt number普朗特数prandtl number雷诺比拟Reynolds analogy施密特数schmidt number斯坦顿数Stanton number对流convection自由对流natural convection, free convec-tion强迫对流forced convection热对流heat convection质量传递mass transfer传质系数mass transfer coefficient热量传递heat transfer传热系数heat transfer coefficient对流传热convective heat transfer辐射传热radiative heat transfer动量交换momentum transfer能量传递energy transfer传导conduction热传导conductive heat transfer热交换heat exchange临界热通量critical heat flux浓度concentration扩散diffusion扩散性diffusivity扩散率diffusivity扩散速度diffusion velocity分子扩散molecular diffusion沸腾boiling蒸发evaporation气化gasification凝结condensation成核nucleation计算流体力学computational fluid mechanics多重尺度问题multiple scale problem伯格斯方程Burgers equation对流扩散方程convection diffusion equationKDU方程KDV equation修正微分方程modified differential equation拉克斯等价定理Lax equivalence theorem数值模拟numerical simulation大涡模拟large eddy simulation数值粘性numerical viscosity非线性不稳定性nonlinear instability希尔特稳定性分析Hirt stability analysis相容条件consistency conditionCFL条件Courant- Friedrichs- Lewy condition ,CFL condition狄里克雷边界条件Dirichlet boundary condition熵条件entropy condition远场边界条件far field boundary condition流入边界条件inflow boundary condition无反射边界条件nonreflecting boundary condition 数值边界条件numerical boundary condition流出边界条件outflow boundary condition冯.诺伊曼条件von Neumann condition近似因子分解法approximate factorization method 人工压缩artificial compression人工粘性artificial viscosity边界元法boundary element method配置方法collocation method能量法energy method有限体积法finite volume method流体网格法fluid in cell method, FLIC method通量校正传输法flux-corrected transport method通量矢量分解法flux vector splitting method伽辽金法Galerkin method积分方法integral method标记网格法marker and cell method, MAC method 特征线法method of characteristics直线法method of lines矩量法moment method多重网格法multi- grid method板块法panel method质点网格法particle in cell method, PIC method质点法particle method预估校正法predictor-corrector method投影法projection method准谱法pseudo-spectral method随机选取法random choice method激波捕捉法shock-capturing method激波拟合法shock-fitting method谱方法spectral method稀疏矩阵分解法split coefficient matrix method不定常法time-dependent method时间分步法time splitting method变分法variational method涡方法vortex method隐格式implicit scheme显格式explicit scheme交替方向隐格式alternating direction implicit scheme, ADI scheme 反扩散差分格式anti-diffusion difference scheme紧差分格式compact difference scheme守恒差分格式conservation difference scheme克兰克-尼科尔森格式Crank-Nicolson scheme杜福特-弗兰克尔格式Dufort-Frankel scheme指数格式exponential scheme戈本诺夫格式Godunov scheme高分辨率格式high resolution scheme拉克斯-温德罗夫格式Lax-Wendroff scheme蛙跳格式leap-frog scheme单调差分格式monotone difference scheme保单调差分格式monotonicity preserving difference scheme穆曼-科尔格式Murman-Cole scheme半隐格式semi-implicit scheme斜迎风格式skew-upstream scheme全变差下降格式total variation decreasing scheme TVD scheme 迎风格式upstream scheme , upwind scheme计算区域computational domain物理区域physical domain影响域domain of influence依赖域domain of dependence区域分解domain decomposition维数分解dimensional split物理解physical solution弱解weak solution黎曼解算子Riemann solver守恒型conservation form弱守恒型weak conservation form强守恒型strong conservation form散度型divergence form贴体曲线坐标body- fitted curvilinear coordi-nates[自]适应网格[self-] adaptive mesh适应网格生成adaptive grid generation自动网格生成automatic grid generation数值网格生成numerical grid generation交错网格staggered mesh网格雷诺数cell Reynolds number数植扩散numerical diffusion数值耗散numerical dissipation数值色散numerical dispersion数值通量numerical flux放大因子amplification factor放大矩阵amplification matrix阻尼误差damping error离散涡discrete vortex熵通量entropy flux熵函数entropy function分步法fractional step method广义连续统力学generalized continuum mechanics 简单物质simple material纯力学物质purely mechanical material微分型物质material of differential type积分型物质material of integral type混合物组份constituents of a mixture非协调理论incompatibility theory微极理论micropolar theory决定性原理principle of determinism等存在原理principle of equipresence局部作用原理principle of objectivity客观性原理principle of objectivity电磁连续统理论theory of electromagnetic continuum 内时理论endochronic theory非局部理论nonlocal theory混合物理论theory of mixtures里夫林-矣里克森张量Rivlin-Ericksen tensor声张量acoustic tensor半向同性张量hemitropic tensor各向同性张量isotropic tensor应变张量strain tensor伸缩张量stretch tensor连续旋错continuous dislination连续位错continuous dislocation动量矩平衡angular momentum balance余本构关系complementary constitutive relations共旋导数co-rotational derivative, Jaumann derivative 非完整分量anholonomic component爬升效应climbing effect协调条件compatibility condition错综度complexity当时构形current configuration能量平衡energy balance变形梯度deformation gradient有限弹性finite elasticity熵增entropy production标架无差异性frame indifference弹性势elastic potential熵不等式entropy inequality极分解polar decomposition低弹性hypoelasticity参考构形reference configuration响应泛函response functional动量平衡momentum balance奇异面singular surface贮能函数stored-energy function内部约束internal constraint物理分量physical components本原元primitive element普适变形universal deformation速度梯度velocity gradient测粘流动viscometric flow当地导数local derivative岩石力学rock mechanics原始岩体应力virgin rock stress构造应力tectonic stress三轴压缩试验three-axial compression test三轴拉伸试验three-axial tensile test 三轴试验triaxial test岩层静态应力lithostatic stress吕荣lugeon地压强geostatic pressure水力劈裂hydraulic fracture咬合[作用] interlocking内禀抗剪强度intrinsic shear strength 循环抗剪强度cyclic shear strength 残余抗剪强度residual shear strength 土力学soil mechanics孔隙比void ratio内磨擦角angle of internal friction休止角angle of repose孔隙率porosity围压ambient pressure渗透系数coefficient of permeability [抗]剪切角angle of shear resistance 渗流力seepage force表观粘聚力apparent cohesion粘聚力cohesion稠度consistency固结consolidation主固结primary consolidation次固结secondary consolidation固结仪consolidometer浮升力uplift扩容dilatancy有效应力effective stress絮凝[作用] flocculation主动土压力active earth pressure被动土压力passive earth pressure 土动力学soil dynamics应力解除stress relief次时间效应secondary time effect贯入阻力penetration resistance沙土液化liquefaction of sand泥流mud flow多相流multiphase flow马格努斯效应Magnus effect韦伯数Weber number环状流annular flow泡状流bubble flow层状流stratified flow平衡流equilibrium flow二组份流two-component flow冻结流frozen flow均质流homogeneous flow二相流two-phase flow气-液流gas-liquid flow气-固流gas-solid flow液-气流liquid-gas flow液-固流liquid-solid flow液体-蒸气流liquid-vapor flow浓相dense phase稀相dilute phase连续相continuous phase离散相dispersed phase悬浮suspension气力输运pneumatic transport气泡形成bubble formation体密度bulk density壅塞choking微滴droplet挟带entrainment流型flow pattern流[态]化fluidization界面interface跃动速度saltation velocity非牛顿流体力学non-Newtonian fluid mechanics 非牛顿流体non-Newtonian fluid幂律流体power law fluid拟塑性流体pseudoplastic fluid触稠流体rheopectic fluid触变流体thixotropic fluid粘弹性流体viscoelastic fluid流变测量学rheometry震凝性rheopexy体[积]粘性bulk viscosity魏森贝格效应Weissenberg effect流变仪rheometer稀薄气体动力学rarefied gas dynamics物理化学流体力学physico-chemical hydrodynamics 空气热化学aerothermochemistry绝对压强absolute pressure绝对反应速率absolute reaction rate绝对温度absolute temperature吸收系数absorption coefficient活化分子activated molecule活化能activation energy绝热压缩adiabatic compression绝热膨胀adiabatic expansion绝热火焰温度adiabatic flame temperature电弧风洞arc tunnel原子热atomic heat雾化atomization自燃auto-ignition自动氧化auto-oxidation可用能量available energy缓冲作用buffer action松密度bulk density燃烧率burning rate燃烧速度burning velocity接触面contact surface烧蚀ablation。

流体力学英文版复习

工程流体力学英文原版

流体力学 英文课件第二章

流体力学英文版课后习题答案

流体力学英文版1

流体力学复习资料及英文专有名词解释

流体力学英文版第二章静力学——Hydrostatic

流体力学基础知识(英文)

最新流体力学英文版课后习题答案

流体力学英文版复习

流体力学专业英语词汇

流体力学与传热(英文版)chapter1b

流体力学英文版课后习题问题详解

流体力学（英文版）

流体力学英文版第五章非基本形式-Nondimentional

流体力学(英文资料)

流体力学(英文课件)chap5

流体力学 英文课件第3章

流体力学专业英语词汇

流体力学英文课件第二章

流体力学英文课件第3章