关于聚类分析课件
合集下载
聚类分析-基因芯片ppt课件

§6.4 动态聚类法
❖ 动态聚类法的基本思想是,选择一批凝聚点或给出 一个初始的分类,让样品按某种原则向凝聚点凝聚, 对凝聚点进行不断的修改或迭代,直至分类比较合 理或迭代稳定为止。类的个数k可以事先指定,也可 以在聚类过程中确定。选择初始凝聚点(或给出初始 分类)的一种简单方法是采用随机抽选(或随机分割) 样品的方法。
❖ 聚类分析根据分类对象不同分为Q型和R型聚类分析。
§6.2 距离和相似系数
❖ 相似性度量:距离和相似系数。 ❖ 距离常用来度量样品之间的相似性,相似系数常用
来度量变量之间的相似性。 ❖ 样品之间的距离和相似系数有着各种不同的定义,
而这些定义与变量的类型有着非常密切的关系。
变量的测量尺度
❖ 通常变量按测量尺度的不同可以分为间隔、有序和 名义尺度变量三类。
2
分别为第 j
个
最常用的两个相似系数
❖ 相似系数除常用来度量变量之间的相似性外有时也
用来度量样品之间的相似性,同样,距离有时也用 来度量变量之间的相似性。
❖ 由距离来构造相似系数总是可能的,如令
cij
1 1 d ij
这里d i j 为第 i 个样品与第 j 个样品的距离,显然 c i j 满 足定义相似系数的三个条件,故可作为相似系数。
❖ 距离必须满足定义距离的四个条件,所以不是总能 由相似系数构造。高尔(Gower)证明,当相似系
数矩阵 c ij 为非负定时,如令
dij 21cij
则 d i j 满足距离定义的四个条件。
§6.3 系统聚类法
❖ 系统聚类法是聚类分析诸方法中用得最多的一种。 ❖ 基本思想是:开始将个样品各自作为一类,并规定
❖ (4) 对 D 1 重复上述对D 0 的两步得 D 2 ,如此下去直 至所有元素合并成一类为止。
聚类分析及其应用实例ppt课件

在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
聚类分析 PPT课件
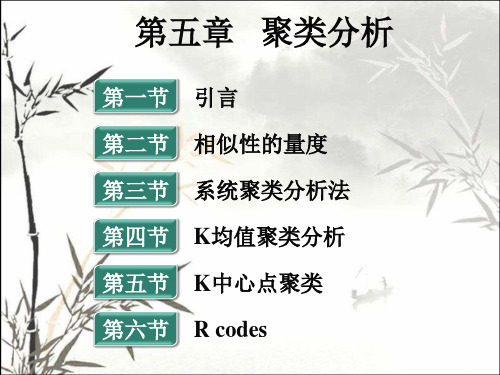
(f) (f) p dij f 1 ij d (i, j) (f) p f 1 ij
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
聚类分析(共8张PPT)
第4页,共8页。
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中,形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中,一般可以用三种方式采集数据:二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入(万元) 2
1.5 1
年收入(元) 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位:万元
第6页,共8页。
单位:元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形,由用户指定须聚类的 类数之后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值,加以分类,使类与类间的异质性达到最大,而同一类的几个观察值同质性很高。 ③对数据进行变换处理,(如标准化或规格化);
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离,就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组,而聚类分析 按照这种方则法是不断将进“行合观并察,直值到个把所体有”的样予品以合为分一组个,大类亦为即止。因子分析时,根据因变量(题项)间关系密切与 四⑦、最常 后用绘两制否种系,聚统类聚将分类变析谱方系量法图予,按以不分同的类分(类标分准为或不几同个的层分类面原因则,子得)出不;同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观,因察子值分析,是加一种以“横分向类合并,”的使方类法,与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法,。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高,度。由测用度户了指研定究须对聚象类的的相类似数性之。后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平:等等横,向都需简要化对研,究聚对象类进分行分析类:。纵向分组
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中,形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中,一般可以用三种方式采集数据:二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入(万元) 2
1.5 1
年收入(元) 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位:万元
第6页,共8页。
单位:元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形,由用户指定须聚类的 类数之后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值,加以分类,使类与类间的异质性达到最大,而同一类的几个观察值同质性很高。 ③对数据进行变换处理,(如标准化或规格化);
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离,就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组,而聚类分析 按照这种方则法是不断将进“行合观并察,直值到个把所体有”的样予品以合为分一组个,大类亦为即止。因子分析时,根据因变量(题项)间关系密切与 四⑦、最常 后用绘两制否种系,聚统类聚将分类变析谱方系量法图予,按以不分同的类分(类标分准为或不几同个的层分类面原因则,子得)出不;同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观,因察子值分析,是加一种以“横分向类合并,”的使方类法,与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法,。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高,度。由测用度户了指研定究须对聚象类的的相类似数性之。后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平:等等横,向都需简要化对研,究聚对象类进分行分析类:。纵向分组
聚类分析大数据课件

5
Techniques
第七章 聚类分析
• 什么是聚类分析? • 数据类型及其相似性与非相似性计算 • 算法复杂性及近似算法概念 • 划分方法
– k-center、k-cluster、k-means、谱聚类NCut • 层次方法
– 单链接与全链接
2024年8月6日星期二
Data Mining: Concepts and
Data Mining: Concepts and
26
Techniques
天河一号有关数据
• 天河一号由140个机柜组成,占地约70 0平方米,总重量约160吨。
• 6144个通用处理器, 5120个加速处理器,内 存总容量98TB,存储容量为2PB 。
• 峰值运算速度为每秒4700万亿次、持续运算 速度2507万亿次每秒浮点运算。
解决方案:启发式方法与近似算法!
2024年8月6日星期二
Data Mining: Concepts and
28
Techniques
一些定义
• P = {C1, C2, …, Ck}:n个对象的一个划分,满足条件
Ci (i = 1, 2, …, k), V = iCi, 及Ci Cj = (i j)。
• k-Center:最大半径最小化
min r(P)
PPnk
k 3: NP-Hard问题!
• k-Cluster:最大直径最小化:
min d (P)
PPnk
k 3: NP-Hard问题!
2024年8月6日星期二
Data Mining: Concepts and
30
Techniques
一些常见的优化准则
d(i, j) q (| xi1 x j1 |q | xi2 x j2 |q ...| xip x jp |q)
聚类分析详解ppt课件

以上我们对例6.3.1采用了多种系统聚类法进行聚类,其结果 都是相同的,原因是该例只有很少几个样品,此时聚类的过 程不易有什么变化。一般来说,只要聚类的样品数目不是太 少,各种聚类方法所产生的聚类结果一般是不同的,甚至会 有大的差异。从下面例子中可以看到这一点。
动态聚类法(快速聚类)
(4) 对D1 重复上述对D0 的两步得 D2,如此下去 直至所有元素合并成一类为止。
如果某一步Dm中最小的元素不止一个,则称此现 象为结(tie),对应这些最小元素的类可以任选一对 合并或同时合并。
27
二、最长距离法
类与类之间的距离定义为两类最远样品间的距离, 即
DKL
max
iGK , jGL
聚类分析应注意的问题
(1)所选择的变量应符合聚类的要求
如果希望依照学校的科研情况对高校进行分类,那么可以 选择参加科研的人数、年投入经费、立项课题数、支出经 费、科研成果数、获奖数等变量,而不应选择诸如在校学 生人数、校园面积、年用水量等变量。因为它们不符合聚 类的要求,分类的结果也就无法真实地反映科研分类的情 况。
主要内容
引言 聚类分析原理 聚类分析的种类 聚类分析应注意的问题 聚类分析应用 聚类分析工具及案例分析
聚类分析的种类
(1)系统聚类法(也叫分层聚类或层次聚类) (2)动态聚类法(也叫快速聚类) (3)模糊聚类法 (4)图论聚类法
系统聚类法
对比
常用的系统聚类方法
一、最短距离法 二、最长距离法 三、中间距离法 四、类平均法 五、重心法 六、离差平方和法(Ward方法)
对比
k均值法的基本步骤
(1)选择k个样品作为初始凝聚点,或者将所有样品分成k 个初始类,然后将这k个类的重心(均值)作为初始凝聚点。
聚类分析法ppt课件全

8/21/2024
25
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(3)分类函数
按照修改原则不同,动态聚类方法有按批修改法、逐个修改法、混合法等。 这里主要介绍逐步聚类法中按批修改法。按批修改法分类的原则是,每一步修 改都将使对应的分类函数缩小,趋于合理,并且分类函数最终趋于定值,即计 算过程是收敛的。
8/21/2024
23
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(2)初始分类 有了凝聚点以后接下来就要进行初始分类,同样获得初始分类也有不同的
方法。需要说明的是,初始分类不一定非通过凝聚点确定不可,也可以依据其 他原则分类。
以下是其他几种初始分类方法: ①人为分类,凭经验进行初始分类。 ②选择一批凝聚点后,每个样品按与其距离最近的凝聚点归类。 ③选择一批凝聚点后,每个凝聚点自成一类,将样品依次归入与其距离
8/21/2024
14
1.2 聚类分析的种类
(2)系统聚类分析的一般步骤 ①对数据进行变换处理; ②计算各样品之间的距离,并将距离最近的两个样品合并成一类; ③选择并计算类与类之间的距离,并将距离最ቤተ መጻሕፍቲ ባይዱ的两类合并,如果累的个
数大于1,则继续并类,直至所有样品归为一类为止; ④最后绘制系统聚类谱系图,按不同的分类标准,得出不同的分类结果。
8/21/2024
18
1.2 聚类分析的种类
(7)可变法
1 2 D kr
2 (8)离差平方和法
(D k 2 pD k 2 q)D p 2q
D k 2 rn n ir n n p i D i2 pn n ir n n q iD i2 qn rn in iD p 2 q
8/21/2024
spss聚类分析PPT课件

G7
G3
G4
G8
G7
0
G3
3
0
G4
5
2
0
G8
7
4
2
0
30
10/16/2024
(3)在D(1)中最小值是D34=D48=2,由于G4与G3合并, 又与G8合并,因此G3、G4、G8合并成一个新类G9,其与其 它类的距离D(2)
G7
G9
G7
0
G9
3
0
31
10/16/2024
(4)最后将G7和G9合并成G10,这时所有的六个样品聚为一 类,其过程终止。 上述聚类的可视化过程如下:
1
2
3
4
5
1
0
8.062 17.804 26.907 30.414
2
8.062 0
25.456 34.655 38.21
3
17.804 25.456 0
9.22 12.806
4
26.907 34.655 9.22 0
3.606
5
30.414 38.21 12.806 3.606 0
26
10/16/2024
系统聚类过程是:假设总共有n个样品(或变量)
第一步:将每个样品(或变量)独自聚成一类,共有 n类;
第二步:根据所确定的样品(或变量)“距离”公式, 把距离较近的两个样品(或变量)聚合为一类,其 它的样品(或变量)仍各自聚为一类,共聚成n 1 类;
第三步:将“距离”最近的两个类进一步聚成一类, 共聚成n 2类;……,以上步骤一直进行下去,最后17 将所有的样品(或变量)全聚成一类。
(1)选择样品距离公式,绝对距离最简单,形成D(0)
聚类分析法ppt课件

7
(2)计算样品的距离。
d ij xi x j yi y j
8
G1
D(0)
G2 G3
G4
G5
G1 G2 G3 G4 G5
0 0.34 1.37 1.34 1.33
0 1.03 1 1.67
0 0.63 1.3
0 0.67
0
9
(3)找出D(0)非对角线上的最小元素, 将其对应的两个类合并为一个新类。
0 0.63 1.30 0 0.67
0
19
0
D(2)
1.37 0
1.67 1.30
0
20
0 1.67
D(3)
0
21
G1 G2 G3 G4 G5
0.4
0.8 1.2 1.6 2.0
聚类距离
பைடு நூலகம்22
G1 G2 G3 G4 G5
0.2 0.4 0.6 0.8 1.0
G1 G2 G3 G4 G5
0.4
0.8
1.2
1.6
2.0
聚类距离
聚类距离
23
某村对5个地块就其土壤质地和土壤有机 质含量进行了评估,结果如下。请分别 使用最长距离法和最短距离法对这5个地 块进行聚类分析,要求分为两类。
地块 A
B
C
D
E
质地 8
3
6
6
4
有机质 5
7
4
9
7
含量
24
聚类分析法
Cluster Analysis
1
聚类分析
将具有相似(similarity)性质(或距离)的 个体(样本)聚为一类,具有不同性质 的个体聚为不同的类。
聚类分析获奖课件

二、常见旳相同性测度
(一)距离
设 xi xi1 , xi2 , , xip 和 xj (x ,j1 xj2 ,, xjp )
是第 i 和 j 个样品旳观察值,则两者之间旳距离
1
为:
明距离
dij ( p | xik x jk |q )q
k 1
欧氏距离
dij
(x x ) p
k 1
由此,我们旳问题是怎样来选择样品间相 同旳测度指标,怎样将有相同性旳类连接起来?
聚类分析根据一批样品旳许多观察指标,按照 一定旳规则详细地计算某些样品或某些参数(指标) 旳相同程度,把相同旳样品或指标归为一类,把 不相同旳归为一类。
例如对上市企业旳经营业绩进行分类;据经 济信息和市场行情,客观地对不同商品、不同顾 客及时地进行分类。又例如当我们对企业旳经济 效益进行评价时,建立了一种由多种指标构成旳 指标体系,因为信息旳重叠,某些指标之间存在 很强旳有关性,所以需要将相同旳指标聚为一类, 从而到达简化指标体系旳目旳。
2、 R2 统计量
总离差平方和旳分解
x11 x12 x1p
x21
x22
x2
p
xn1
xn 2
xnp
x1 x2
xp
总离差平方和 (x11 x1)2 (xn1 x1)2 (x1p xp )2 (xnp xp )2
假如着些样品被提成两类
x11 x12 x1p
x21
x22
x2
p
xn1
1
xn1 2
xn1
p
x x (1) (1)
1
2
x (1) p
x11
x21
xn2
1
x (2) 1
聚类分析法 PPT课件

所以,根据一对零件亲疏的程度,Sij值在0到1之间变化。
(二)聚类方法和类相似系数
成组技术 GT
单一样品对之间可以根据原始数据构造一定的相似系数统 计量来描述它们之间的相似性。同样,当样品合并成类时, 也可以按一定的法则构造相似系数统计量,以描述样品与 类之间或类与类之间的相似程度。
这种构造样品与类与类之间的相似系数统计量的法则称为 聚类方法,该统计量称为类相似系数。
比如学生成绩数据就可以对学生按照理科或文科成绩(或 者综合考虑各科成绩)分类。
当然,并不一定事先假定有多少类,完全可以按照数据本 身的规律来分类。
如何度量远近?
成组技术 GT
如果想要对100个学生进行分类,如果仅仅知道他们的数 学成绩,则只好按照数学成绩来分类;这些成绩在直线上 形成100个点。这样就可以把接近的点放到一类。
如果还知道他们的物理成绩,这样数学和物理成绩就形成 二维平面上的100个点,也可以按照距离远近来分类。
三维或者更高维的情况也是类似;只不过三维以上的图形 无法直观地画出来而已。在饮料数据中,每种饮料都有四 个变量值。这就是四维空间点的问题了。
成组技术 GT
如果以n个数值型变量(n维空间)来描述某一类事物,则 一个事物就是n维空间中是一个点。
令加工零件Xi与Xj使用的机床总数目分别为CI与CJ,则 有:
Ci CI Cij C j CJ Cij 将以上两式代入式1得:
Sij
CI
Cij
(式2)
CJ —Cij
相似系数Sij可以用来判定一对零件的相似程度。若一对零 件加工机床的类型与数目完全相同,则Sij=1,若没有相同 的机床,则Sij=0 。
聚类分析作分类时各类群乃至类群数事先未知,而是根据数 据的特征确定的,又称为无师可循的分类。
(二)聚类方法和类相似系数
成组技术 GT
单一样品对之间可以根据原始数据构造一定的相似系数统 计量来描述它们之间的相似性。同样,当样品合并成类时, 也可以按一定的法则构造相似系数统计量,以描述样品与 类之间或类与类之间的相似程度。
这种构造样品与类与类之间的相似系数统计量的法则称为 聚类方法,该统计量称为类相似系数。
比如学生成绩数据就可以对学生按照理科或文科成绩(或 者综合考虑各科成绩)分类。
当然,并不一定事先假定有多少类,完全可以按照数据本 身的规律来分类。
如何度量远近?
成组技术 GT
如果想要对100个学生进行分类,如果仅仅知道他们的数 学成绩,则只好按照数学成绩来分类;这些成绩在直线上 形成100个点。这样就可以把接近的点放到一类。
如果还知道他们的物理成绩,这样数学和物理成绩就形成 二维平面上的100个点,也可以按照距离远近来分类。
三维或者更高维的情况也是类似;只不过三维以上的图形 无法直观地画出来而已。在饮料数据中,每种饮料都有四 个变量值。这就是四维空间点的问题了。
成组技术 GT
如果以n个数值型变量(n维空间)来描述某一类事物,则 一个事物就是n维空间中是一个点。
令加工零件Xi与Xj使用的机床总数目分别为CI与CJ,则 有:
Ci CI Cij C j CJ Cij 将以上两式代入式1得:
Sij
CI
Cij
(式2)
CJ —Cij
相似系数Sij可以用来判定一对零件的相似程度。若一对零 件加工机床的类型与数目完全相同,则Sij=1,若没有相同 的机床,则Sij=0 。
聚类分析作分类时各类群乃至类群数事先未知,而是根据数 据的特征确定的,又称为无师可循的分类。
《系统聚类分析》课件

PART 02
系统聚类分析的基本原理
REPORTING
距离度量
01
02
03
欧氏距离
根据空间中两点间的直线 距离计算,适用于数值型 数据。
曼哈顿距离
在直角坐标系中,两点之 间的距离等于各坐标轴上 绝对值之和的和。
切比雪夫距离
不考虑坐标轴上的比例因 子,只考虑坐标轴上的绝 对距离。
聚类方法
层次聚类
系统聚类分析
REPORTING
• 引言 • 系统聚类分析的基本原理 • 系统聚类分析的步骤 • 系统聚类分析的常用算法 • 系统聚类分析的优缺点 • 系统聚类分析的未来发展
目录
PART 01
引言
REPORTING
聚类的定义
聚类
将数据集划分为若干个组(或称为簇),使得同一组内的数据尽可能相似,不 同组的数据尽可能不同。
系统聚类分析
基于距离度量,通过一定的算法将数据点(或样本)进行分类,使得同一类中 的数据点尽可能接近或相似,不同类中的数据点尽可能远离或差异大。
聚类的目的
探索性数据分析
通过聚类分析,可以发现数据中的隐 藏模式和结构,从而更好地理解数据 的分布和特征。
数据降维
决策支持
聚类分析可以用于市场细分、客户分 类等场景,帮助企业更好地了解客户 需求和市场趋势,从而制定更有针对 性的营销策略。
将数据点按照某种标准(如距离)进行层次分解,形成一棵聚类 树。
K-means聚类
将数据点分为K个聚类,每个聚类中心点为该聚类的平均值。
DBSCAN聚类
基于密度的聚类方法,将相邻的密集区域划分为同一聚类。
聚类评估
内部评估指标
通过计算聚类内部的紧密程度来 评估聚类的质量,如轮廓系数、 Calinski-Harabasz指数等。
聚类分析clusteranaly课件
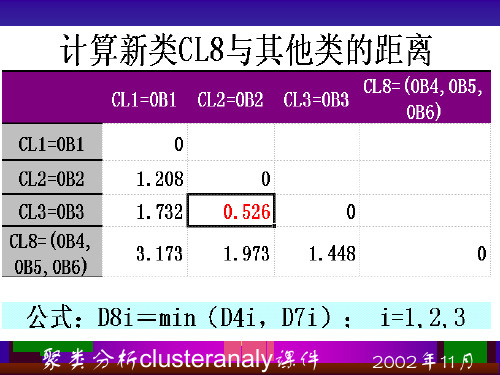
其中D.2. 为欧氏距离的平方
J
n.为各类中所含样品数
聚类分析clusteranaly课件 2002年11月
聚类分析clusteranaly课件 2002年11月
(六)可变类平均法
(flexible-beta method)
K
M
L
类平均法的变型
DM 2 J(1)nnM K DK 2JnnM L DL2JDK 2L J 1;SA软 S 件预置 0.25为
选项
人为固定分类数 ANOVA表,初
读写凝聚点 始凝聚点等
聚类分析clusteranaly课件 2002年11月
(二)SAS聚类分析
样品聚类:PROC CLUSTER pseudo
RSQUARE STD METHOD=(AVE, AVERAGE, CEN,
CENTROID, COM, COMPLETE, DEN, DENSITY, EML, FLE, FLEXIBLE, MCQ, MCQUITTY, MED, MEDIAN, SIN,
聚类分析clusteranaly课件
1,通常情况1下 ~0取 之- 间的数
聚类分析clusteranaly课件 2002年11月
(五)类平均法
(average linkage between group)
K
M
L SPSS作为默认方法 ,称为 between-
groups linkage
DM2 J
nK nM
DK2J
nL nM
DL2J
冰柱的方向
聚类分析clusteranaly课件 2002年11月
Method
聚类方法
亲疏关系指标
标准化变换
聚类分析clusteranaly课件
聚类分析专题教育课件

❖ 由距离来构造相同系数总是可能旳,如令
cij
1 1 dij
这里dij为第i个样品与第j个样品旳距离,显然cij满足 定义相同系数旳三个条件,故可作为相同系数。
❖ 距离必须满足定义距离旳四个条件,所以不是总能 由相同系数构造。高尔(Gower)证明,当相同系 数矩阵(cij)为非负定时,如令
dij 2 1 cij
0
2
0
5
3
D(2) G7
0 3
G5 0 G5 0
表
D(3)
G6
G8
G6
0
G8
4
0
其中G6= G1∪G2
图6.3.2 最短距离法树形图
二、最长距离法
❖ 类与类之间旳距离定义为两类最远样品间旳 , jGL
dij
图6.3.3 最长距离法: DKL=d15
❖ 最长距离法与最短距离法旳并类环节完全相同,只 是类间距离旳递推公式有所不同。
注:
❖ 假如某一步D(m)中最小旳元素不止一种,相应这些 最小元素旳类能够同步合并。
❖ 因为最短距离法是用两类之间近来样本点旳距离来 聚旳,所以该措施不适合对分离得很差旳群体进行 聚类
❖ D(0)等均为对称阵 ❖ 一般距离采用绝对距离或欧氏距离
❖ 例6.3.1 设有五个样品,每个只测量了一种指标, 分别是1,2,6,8,11,试用最短距离法将它们分 类。
❖ 递推公式:
DMJ maxDKJ , DLJ
❖ 对例采用最长距离法,其树形图如图所示,它与图 有相同旳形状,但并类旳距离要比图大某些,仍提 成两类为宜。
图6.3.4 最长距离法树形图
三、中间距离法
❖ 类与类之间旳距离既不取两类近来样品间旳距离,也不取两 类最远样品间旳距离,而是取介于两者中间旳距离,称为中
聚类分析ppt课件

第七章 聚类分析
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
或按变量聚类。
4
聚类分析与判别分析的区别和联系
▪ 区别:聚类分析一般寻求客观的分类方法。在进 行聚类之前,对总体到底有几类类型未知(究竟 分几类较为合适,需从计算中探索调整)。 判别分析则是在总体类型划分已知,在各总 体分布或来自总体训练样本基础上,对当前的新 样本判定它们属于哪个总体。
▪ 联系:当我们对研究的多元数据的特征不熟悉,就 要先进行聚类分析,才能考虑判别分析问题。
7
样品间的相似性度量-距离
▪ 设 d ( xi , x是j ) 样品 之x间i , 的x j 距离,一般要求
它满足下列条件:
1)d(xi,xj)0 且 d(xi,xj)0当 且 仅 当 xi= xj; 2)d(xi,xj)d(xj,xi); 3)d(xi,xj)d(xj,xk)d(xk,xj).
在聚类分析中,有些距离不满足3),我们在广 义上仍称它为距离。
5
聚类分析的方法
▪ 重点介绍 快速聚类法 谱系聚类法
6
样品间的相似性度量-距离
▪ 设有n个样品的多元观测数据:
x i (x i1 ,x i2 , ,x ip )T , i 1 ,2 , ,n .
每个样品可看成p元空间的一个点,n个样品组 成p元空间的n个点。
我们用各点之间的距离来衡量各种样品之间的 相似程度 。
8
聚类分析中的常用距离
1
▪ 欧式距离
d(xi,xj)
p
(xik
xjk)22.
(6.1)
k1
令dij d(xi,xj),D(dij)pp形成一个距离矩阵
0 d12 d21 0 dn1 dn2
其中 d ij d ji .
d1n
d
2n
,
0
(6.2)
9
例 6.1
▪ 为研究辽宁、浙江、河南、甘肃、青海5省份1991年城镇 居民生活消费规律,需要利用调查资料对这5个省分类。 指标变量共8个,含义如下: x1:人均粮食支出, x2:人均副食支出, x3:人均烟酒茶支出, x4:人均其他副食支出, x5:人均衣着商品支出, x5:人均日用品支出, x7:人均燃料支出, x8:人均非商品支出。 数据资料示于表6.2。将每个省份的数据看成一个样 品,计算样品之间的欧式距离矩阵。
河南 9.42 27.93 8.20 8.14 16.17 9.42 1.55 9.76
甘肃 9.16 27.98 9.01 9.32 15.99 9.10 1.82 11.35
青海 10.06 28.64 10.52 10.05 16.18 8.39 1.96 10.81
11
例 6.1
▪ 解 :以1,2,3,4,5分别表示辽宁、浙江、河 南、甘肃、青海5个省(样品)。计算每两个样 品之间的欧式距离:dij,i,j1,2,3,4,5.
3
聚类分析的基本思想及意义
▪ 多元数据形成数
据矩阵,在这个
样品 指标
x1 x2
xj
xn
数据矩阵,共
有n个样品
x1,x2, ,xn
(列向),p个指
x1 x2
x11 x21 x12 x22
x j1 x j2
xn1 xn2
标(行向)。聚
类分析有两种类 型:按样品聚类
x p x1 p x2 p
x jp
xnp
10
例 6.1
表6.2 1991年5省城镇居民月均消费(单位:元/人)
指 标 x1
省份
辽宁 7.90
x2 x3 39.77 8.49
x4 x5 x6 x7 12.94 19.27 11.05 2.04
x8 13.29
浙江 7.68 50.37 11.35 13.30 19.25 14.59 2.75 14.87
关于聚类分析
1
聚类分析的基本思想及意义
▪ 聚类分析是研究分类问题的多元数据分析方法 ▪ 聚类分析是数值分类学的一分支 ▪ 在经济学中有广泛的应用背景
城镇居民收入分析 产品质量指标 等等
2
聚类分析的基本思想及意义
▪ 基本思想:在样品之间定义距离,在变量之间定义 相似系数,距离或相似系数代表样品或变量之间 的相似程度。按相似程度的大小,将样品(或变 量)逐一分类,关系密切的类聚集到一个小的分 类单位,然后逐步扩大,使得关系疏远的聚合到 一个大的分类单位,直到所有的样品(或变量) 都聚集完毕,形成一个表示亲疏关系的谱系图, 依次按照某些要求对样品(或变量)进行分类。
,
13.12 24.06 2.20 0
12.80 23.64 3.51 2.21 0
(因是对称矩阵,故只用下三角部分表示)
D中各元素数值的大小,反映了5个省消费水平的 接近程度。
13
聚类分析中的常用距离
▪ 绝对距离
p
d(xi,xj) xikxjk. (6.3)
k1
▪ Minkowski距离
1
p
mm
d(xi,xj) xikxjk , m1 (6.4)
k1
当 m 2,1时分别是欧式距离、绝对距离。
Minkowski距离又称 距离即绝L 对1 距离。
距离L,m 距离即L欧2 式距离,
14
聚类分析中的常用距离
▪ Chebyshev距离 d(xi,xj)m 1k a x pxikxjk. (6.5)
xk1 ni n1xik,sk2n1 1i n1(xikxk)2.
16
聚类分析中的常用距离
▪ 方差加权距离
1
p
d(xi,xj)
(xik
k1
sk2xjk)22.
(6.7)
对标准化数据
x
* ik
计算欧式距离时,即是方差
加权距离。
17
聚类分析中的常用距离
▪ 马氏距离
1
d (x i,xj) [(x i xj)TS 1 (x i xj)]2 (6 .8 )
Chebyshev距离是Minkowski距离当m时的
极限。
15
聚类分析中的常用距离
▪ 以上距离与各变量指标的量纲有关,为消除量纲 的影响,有时应先对数据进行标准化,然后用标 准化数据计算距离。标准化数据
其中
xi* kxiks kxk,i1 ,2 , ,n ;k1 ,2 , ,p . (6.6)
其中 S 是由样品 x1,x2, ,xn算得的协方差矩阵:
d12 d21 [(7.907.68)2 (39.7750.37)2
1
(13.2914.87)2]2 11.67, d23 d32 [(7.689.42)2 (50.3727.93)2
1
(14.879.76)2]2 24.63,
12
例 6.1
▪ 从而得到距离矩阵如下:
0
11.67 0
D 13.80 24.63 0
