有限元资料讲解
材料力学有限元法知识点总结

材料力学有限元法知识点总结材料力学是一门研究物质内部结构、性质和变形行为的学科,而有限元法则是一种在工程和科学领域中广泛应用的数值计算方法。
有限元法可以将一个复杂的实体划分为无数小的单元,通过对这些小单元进行分析和计算,最终得到整个实体的力学性质和行为。
本文将对材料力学有限元法的一些核心概念和知识点进行总结。
1. 有限元法基础概念有限元法基于将实际连续的物体离散为有限数量的单元,通过计算每个单元的受力、变形等性质,再通过组合这些单元的结果来近似整个物体的行为。
它包含以下几个基础概念:1.1 单元(Element):有限元法中的基本组成单元,可以是一维的线段、二维的三角形或四边形,或三维的四面体、六面体等。
1.2 节点(Node):单元的角点或边上的点,用于定义单元之间的连接关系和边界条件。
1.3 自由度(Degree of Freedom):每个节点与力学性质相关的物理量,如位移、应力等。
根据问题的不同,在每个节点上可能有一个或多个自由度。
1.4 单元刚度矩阵(Element Stiffness Matrix):描述单元内部受力和变形关系的矩阵,在有限元法中通过组合所有单元的刚度矩阵来得到整个系统的刚度矩阵。
1.5 全局刚度矩阵(Global Stiffness Matrix):由所有单元刚度矩阵组合而成的整个系统的刚度矩阵,用于计算节点的位移和应力。
2. 有限元法的数学原理有限元法的数学原理主要基于以下两个方面:2.1 变分原理(Variational Principle):有限元法的数学基础是根据变分原理推导实现的。
它通过对结构的势能进行变分并进行最小化,得到满足结构力学行为和边界条件的位移和应力场。
2.2 加权残差法(Weighted Residuals Method):有限元法通过将变分原理中的势能函数展开为一系列基函数的线性组合,并使用权重函数对残差进行加权求和的方式进行近似。
这样可以将求解连续问题转化为离散问题,进而进行数值计算。
有限元入门ppt课件

有限体积法 (Finite Volume Method)
其基本思路是:将计算区域划分为一系列不重复的控制体积,并使每个网格点周围有一个控制体积;将待解的微分方程对每一个控制体积积分,便得出一组离散方程。其中的未知数是网格点上的因变量的数值。为了求出控制体积的积分,必须假定值在网格点之间的变化规律,即假设值的分段的分布的分布剖面。
1-2 应力的概念
作用于弹性体的外力(或称荷载)可能有两种: 表面力,是分布于物体表面的力,如静水压力,一物体与另一物体之间的接触压力等。单位面积上的表面力通常分解为平行于座标轴的三个成分,用记号 来表示。 体力,是分布于物体体积内的外力,如重力、磁力、惯性力等。单位体积内的体力亦可分解为三个成分,用记号X、Y、Z表示。 弹性体受外力以后,其内部将产生应力。
边界元法 (Boundary Element Method)
边界元法是一种继有限元法之后发展起来的一种新的数值方法,与有限元法不同,边界元法仅在定义域的边界划分单元,用满足控制方程的函数去逼近边界条件。所以边界元与有限元相比具有单元和未知数少、数据准备简单等优点,但边界元法解非线性问题时,遇到同非线性项相对应的区域积分,这种积分奇异点处的强烈的奇异性,使求解遇到困难。边界元法在塑性问题中应用还比较少。
弹性力学 — 区别与联系 — 材料力学 弹性力学与材料力学既有联系又有区别。它们都同属于固体力学领域,但弹性力学研究的对象更普遍,分析的方法更严密,研究的结果更精确,因而应用的范围更广泛。 弹性力学 固有弱点: 由于研究对象的变形状态较复杂,处理的方法又较严谨,因而解算问题时,往往需要冗长的数学运算。但为了简化计算,便于数学处理,它仍然保留了材料力学中关于材料性质的假定:
塑性有限元常用软件
有限元资料讲解

有限元分析计算机辅助工程(CAE)作为一门新兴的学科已经逐渐的走下神坛,成为了各大企业中设计新产品过程中不可缺少的一环。
传统的CAE 技术是指工程设计中的分析计算与分析仿真,具体包括工程数值分析、结构与过程优化设计、强度与寿命评估、运动/动力学仿真,验证未来工程/产品的可用性与可靠性。
如今,随着企业信息化技术的不断发展,CAE 软件与CAD/CAM/CAPP/PDM/ERP 一起,已经成为支持工程行业和制造企业信息化的主导技术,在提高工程/产品的设计质量,降低研究开发成本,缩短开发周期方面都发挥了重要作用。
而CAE 技术出现则是要归功于有限元分析的诞生,在有限元法诞生的早期,几乎所有的CAE 软件都是使用有限元法来进行计算求解。
因此,可以说有限元法的发展也间接反映了CAE 软件在这半个世纪的发展历史。
1 有限元法的诞生每一项新技术的推出都是由于时代的迫切需要,而新技术的出现后也需要经历历史的重重考验。
在上个世纪40 年代,由于航空事业的快速发展,对飞机内部结构设计提出了越来越高的要求,即重量轻、强度高、刚度好,人们不得不进行精确的设计和计算。
正是在这一背景下,有限元分析的方法逐渐的发展起来。
早期的一些成功的实验求解方法与专题论文,完全或部分的内容对有限元技术的产生做出的贡献,首先在应用数学界第一篇有限元论文是1943 年Courant R 发表的《Variational methods for the solution of problems of equilibrium and vibration 》一文,文中描述了他使用三角形区域的多项式函数来求解扭转问题的近似解,由于当时计算机尚未出现,这篇论文并没有引起应有的注意。
1956 年,M.J.Turner (波音公司工程师),R.W.Clough (土木工程教授),H.C.Martin (航空工程教授)及L.J.Topp (波音公司工程师)等四位共同在航空科技期刊上发表一篇采用有限元技术计算飞机机翼的强?的论文,名为《Stiffnessand Deflection Analysis of Complex Structures 》,文中把这种解法称为刚性法(Stiffness),一般认为这是工程学界上有限元法的开端。
有限元基本知识归纳

有限元知识点归纳1.、有限元解的特点、原因?答:有限元解一般偏小,即位移解下限性原因:单元原是连续体的一部分,具有无限多个自由度。
在假定了单元的位移函数后,自由度限制为只有以节点位移表示的有限自由度,即位移函数对单元的变形进行了约束和限制,使单元的刚度较实际连续体加强了,因此,连续体的整体刚度随之增加,离散后的刚度较实际的刚度K为大,因此求得的位移近似解总体上将小于精确解。
2、形函数收敛准则(写出某种单元的形函数,并讨论收敛性)P49(1)在节点i处N i=1,其它节点N i=0;(2)在单元之间,必须使由其定义的未知量连续;(3)应包含完全一次多项式;(4)应满足∑Ni=1以上条件是使单元满足收敛条件所必须得。
可以推证,由满足以上条件的形函数所建单元是完备协调的单元,所以一定是收敛的。
4、等参元的概念、特点、用时注意什么?(王勖成P131)答:等参元—为了将局部坐标中几何形状规则的单元转换成总体(笛卡尔)坐标中的几何形状扭曲的单元,以满足对一般形状求解域进行离散化的需要,必须建立一个坐标变换。
即:为建立上述的变换,最方便的方法是将上式表示成插值函数的形式,即:其中m是用以进行坐标变换的单元节点数,xi,yi,zi是这些结点在总体(笛卡尔)坐标内的坐标值,Ni’称为形状函数,实际上它也是局部坐标表示的插值函数。
称前者为母单元,后者为子单元。
还可以看到坐标变换关系式和函数插值表示式:在形式上是相同的。
如果坐标变换和函数插值采用相同的结点,并且采用相同的插值函数,即m=n,Ni’=Ni,则称这种变换为等参变换。
5、单元离散?P42答:离散化既是将连续体用假想的线或面分割成有限个部分,各部分之间用有限个点相连。
每个部分称为一个单元,连接点称为结点。
对于平面问题,最简单、最常用的离散方式是将其分解成有限个三角形单元,单元之间在三角形顶点上相连。
这种单元称为常应变三角形单元。
常用的单元离散有三节点三角形单元、六节点三角形单元、四节点四边形单元、八节点四边形单元以及等参元。
有限元分析基础 复习资料

1. 什么是等参数单元?(教材)坐标变换和单元内的场函数采用相同数目的节点参数及相同的插值函数,这种变换方法是等参数变换,这种变换方式能满足坐标变换的相容性,采用等参数变换的单元称之为等参数单元。
2. 等参数单元的特点、基本条件、划分单元应注意的问题(教材习题)3.应用等参数单元时为什么要采用高斯积分,高斯积分点的数目如何确定?(教材习题)4.薄板弯曲问题的基本假设是什么?(其他参考书)(1)板弯曲钱垂直于中面的法线,在板弯曲后保持为直线,并垂直于弯曲后的中面。
(2)板面各水平层之间相互挤压(3)薄板受垂直于中面的载荷时可以为中间层各点设有平行于板面的位移.5.位移插值必须满足的三个条件:(教材)(1)位移插值函数应能满足单元的刚体位移(2)位移插值函数应能反映常量应变——常应变准则(3)位移插值函数应能保证单元内及相邻单元间位移的连续性——变形协调准则6.什么是轴对称问题?(其他参考书):轴对称物体的形变及应力分布不一定是轴对称的,只有当约束和载荷都对称于旋转轴时,轴对称物体的变形及应力分布才是轴对称的。
我们把满足上述条件的系统应力分析问题称为轴对称问题。
(教材):如果弹性体的几何形状、约束情况以及所受的外力,都是绕某一轴对称的,则弹性体的应力、应变和位移也就对称于这一轴,这种问题称为轴对称问题。
7.刚度矩阵性质(总刚):(1)对称性,关于正对角线对称(2)稀疏性,矩阵中有大量的零元素(3)带状分布,矩阵中非零元素在主对角线两侧呈带状分布 10.形函数的性质。
(教材) (1)单元内任一点的三个形函数之和恒等于1,即Ni+Nj+Nm=1. (2)在节点i:Ni=1,Nj=0,Nm=0 在节点j:Ni=0,Nj=1,Nm=0 在节点 m:Ni=0,Nj=0,Nm=1 11. 有限元法的特点(其他参考书)(1)概念清楚,容易理解(2)适应性强,应用范围广。
(3)有限元法采用矩阵形式表达,便于编制计算机程序,可以充分利用数字计算机的优势。
第1章有限元基本理论ppt课件

x dx
li
E i
i
E (ui1ui )
x
x
li
1.8 直杆受自重作用的拉伸问题(续)
❖ 外载荷与结点的平衡方程
EA(uiui1 ) li1
EA(ui1ui ) li
q(li1 li ) 2
q(li1li ) 为第i个结点上承受的外载荷
2
1.8 直杆受自重作用的拉伸问题(续)
❖ 假定将直杆分割成3个单元,每个单元长为a=L/3, 则对结点2,3,4列出的平衡方程为:
单元: 一组节点自由度间相互作用的 数值、矩阵描述(称为刚度或系数 矩阵)。单元有线、面或实体以及二 维或三维的单元等种类。
载荷
有限元模型由一些简单形状的单元组成,单 元之间通过节点连接,并承受一定载荷。
1.6 节点和单元 (续)
信息是通过单元之间的公共节点传递的。
. . 2 nodes ...
. . . 1 node
1.1 有限元分析 (FEA)
有限元分析 是利用数学近似的方法对真实物理
系统(几何和载荷工况)进行模拟。它利用简 单而又相互作用的元素,即单元,用有限数量 的未知量去逼近无限未知量的真实系统。
1.2 有限单元法的基本思想
❖ 将连续的结构离散成有限个单元,并在每一单元中 设定有限个节点,将连续体看作只在节点处相连接 的一组单元的集合体。
I
J
O
N
三维实体结构单元
K UX, UY, UZ
P
M L
J
I
J
K J
O N
K J
三维梁单元 UX, UY, UZ, ROTX, ROTY, ROTZ
三维四边形壳单元 UX, UY, UZ, ROTX, ROTY, ROTZ
有限元分析-01资料
2
3
q12 , m12 分别表示单元1的节点2上的节点力、力矩;余类推。
单元刚度方程:
单元1:
p1 p2
1
k11 k 21
k12 k 22
1
12
1
单元2:
p2 p3
2
k 22 k32
k 23 k33
2
2 3
Step 3:单元弹性特征
当建立了与 Q的定量关系后,对于任一Q 就有
对应的 ,则问题就可以求解。
对任一单元e,建立节点位移与截面节点力之间的关 系。
e单元的节点位移 fi ,i , f j , j T ,
单元变形时,节点 i 和 j 处应受到力的作用,有节点
力 pe
qi , mi , q j , mj
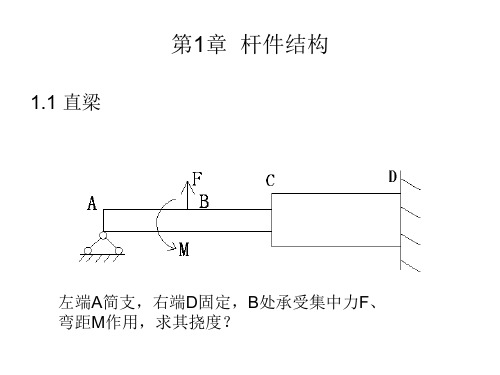
1.1 直梁
第1章 杆件结构
左端A简支,右端D固定,B处承受集中力F、 弯距M作用,求其挠度?
分析步骤: Step 1、离散化
梁的特征?
将结构自然分为三段:AB、BC、CD。每一段内部有 相同的几何尺寸、无外载,可视作一个单位体(单元), 各段内部特性(材料、几何)可与其他单元相互独立。
各段之间的交界截面可看作单元之间的连接节点,两 端支座A、D也可以看作节点。
本步的工作就是要给出k e 的具体表达式。为规范化
编制程序,对梁单元的节点位移、节点力另外编号:
e u1 u2 u3 u4 T
S1
p e s1 s2 s3 s4 T
S2 i
e
则(1.1式)变换为:
s1 a11 a12 a13 a14 u1
ss23 s4
a21 aa3411
i逆时针为正。
记:i 节点的位移为i,
有限元课件ppt

将所有单元的刚度矩阵依照一定的方式组合起来,形成整体的刚度 矩阵。
载荷向量与束缚条件
载荷向量
表示作用在结构上的外力,包括集中力和散布力。
束缚条件
表示结构在某些结点上的位移受到限制,常见的束缚有固定束缚、 弹性束缚等。
载荷向量和束缚条件的引入
在建立整体刚度矩阵后,需要将载荷向量和束缚条件引入到整体刚 度矩阵中,形成完全的线性方程组。
并行计算
采取并行计算技术,提高计算效率。
算法改进
优化算法,提高计算精度和效率。
06 有限元分析软件 介绍
ANSYS
01
功能特点
ANSYS是一款功能强大的有限元分析软件,广泛应用于结构、流体、
电磁等多种工程领域。它提供了丰富的建模工具和求解器,能够处理复
杂的工程问题。
02
优点
ANSYS具有友好的用户界面和强大的前后处理功能,使得建模和网格
有限元法的应用领域
结构分析
有限元法在结构分析中应用最 为广泛,可以用于分析各种类 型的结构,如桥梁、建筑、机
械零件等。
热传导
有限元法可以用于求解温度场 的问题,如热传导、热对流和 热辐射等问题。
流体动力学
有限元法在流体动力学领域也 有广泛应用,可以用于求解流 体流动和流体传热等问题。
其他领域
除了上述领域外,有限元法还 广泛应用于电磁场、声场、化
学反应等领域。
02 有限元的数学基 础
线性代数基础
向量与矩阵
01
介绍向量的基本概念、向量的运算、矩阵的表示和运算规则等
。
线性方程组
02
论述线性方程组的解法,包括高斯消元法、LU分解等。
特征值与特征向量
有限元基本概念ppt课件

i1
i1
其中: Hi( xj )δij H'i(xj )0
'
Hi( xj )0 Hi( xj )δij
1 i j δij 0 i j
眼睛是心灵的窗户,是人体中最宝贵 的感觉 器官, 可很多 孩子对 眼睛的 重要性 不重视 。在每 学期的 视力测 查中情 况都不 容乐观
经推导:
n
n
P 2 n - 1 ( x ) 1 2 W i 'x ix x i W i2 x u ix - x iW i2 x u i '
眼睛是心灵的窗户,是人体中最宝贵 的感觉 器官, 可很多 孩子对 眼睛的 重要性 不重视 。在每 学期的 视力测 查中情 况都不 容乐观
• 有限元方法的分类
依据求解问题的路径不同,有限元方法大致可分为: 位移法:以位移为基本未知量 力法:应力为基本未知量 混合法:部分以位移;部分以应力为基本未知量
• 有限元位移法的基本概念
几何矩阵的一般表达形式:
其中:
ε
B
e
δ
x
0
0
0
y
0
0
B
y
0
x
z
0
N
0
0
1
0 N1 0
0 0 N1
N2 0 0
0 N2 0
0
0
N 2
0
z y
z
0
x
眼睛是心灵的窗户,是人体中最宝贵 的感觉 器官, 可很多 孩子对 眼睛的 重要性 不重视 。在每 学期的 视力测 查中情 况都不 容乐观
ji ji
i,j0,1,2, n
可令:
Ni
x
C x x 0 x x 1 x x i - 1 x x i + 1 x x n
《有限元基本原理》课件

有限元法的历史与发展
01
有限元法的思想起源于20世纪40年代,但直到1960年 才由美国科学家克拉夫(Clough)正式提出“有限元 法”这一术语。
02
随着计算机技术的发展,有限元法得到了广泛应用和推 广,成为工程领域中解决复杂问题的有力工具。
03
近年来,随着计算能力的提升和算法优化,有限元法的 应用范围不断扩大,涉及的领域也更加广泛。
有限元法的基本思想
01
将连续体离散化为有限个单元,每个单元具 有简单的几何形状和物理属性。
03
02
通过在节点处设置位移约束,将各个单元相 互连接,形成一个整体模型。
通过在各个单元上设置方程,建立整个离散 化模型的平衡方程组。
高阶有限元方法
与其他方法的结合
研究高阶有限元方法,以提高计算的精度 和稳定性。
研究有限元方法与其他数值方法的结合, 如有限差分法、有限体积法等,以拓展其 应用范围。
谢谢聆听
04 有限元法的应用实例
静力分析实例
总结词
静力分析是有限元法最常用的领域之一,主要用于分析结构在恒定载荷下的响应。
详细描述
静力分析用于评估结构在恒定载荷下的应力、应变和位移。例如,桥梁、高层建筑和飞机机身等结构 的稳定性分析。通过有限元法,可以模拟复杂结构的整体行为,并预测其在各种载荷条件下的性能。
动力分析实例
总结词
动力分析涉及结构在动态载荷下的响应 ,如地震、风载和冲击载荷等。
VS
详细描述
动力分析用于评估结构在动态载荷作用下 的振动、冲击和响应。例如,地震工程中 建筑物和桥梁的抗震性能分析。通过有限 元法,可以模拟结构的动态行为,预测其 在地震或其他动态载荷下的破坏模式和倒 塌过程。
有限元分析培训教材课件

有限元分析培训教材
注意包含在约束方程中 自由度的反力,不包括 由这个约束方程传递的 力.
4
有限元分析及应用讲义
ANSYS网格划分精度估算
▪ 网格误差估算 ▪ 局部细化 ▪ P方法&举例
有限元分析培训教材
5
有限元分析及应用讲义
ANSYS网格误差估计
ANSYS通用后处理包含网格离散误差估计. 误差估计是依据沿单元内边界的应力或热流的不连续性,是平均 与未平均节点应力间的差值.
有限元分析培训教材
20
有限元分析及应用讲义
映射网格划分
▪ 有两种主要的网格划分方法: 自由划分和映射划分. ▪ 自由划分
– 无单元形状限制. – 网格无固定的模式. – 适用于复杂形状的面和体.
▪ 映射划分
– 面的单元形状限制为四边形,体的单元限制为六面 体 (方块).
– 通常有规则的形式,单元明显成行. – 仅适用于 “规则的” 面和体, 如 矩形和方块.
有限元分析及应用讲义
1.分析的对象的一些基本的行为:
• 重力方向总是竖直向下的 • 离心力总是沿径向向外的 • 没有一种材料能抵抗 1,000,000 psi 的应力 • 轴对称的物体几乎没有为零的 环向应力 • 弯曲载荷造成的应力使一侧受压,另一侧受拉
如果只有一个载荷施加在结构上,检验结果比较容易. 如果有多个载荷,可单独施加一个或几个载荷分别 检验,然后施加所有载荷检验分析结果.
P方法用于线弹性结构分析—实体和壳
体。
P单元由以下5种单元:
▪2-D Quadrilateral (Plane145)
▪2-D Triangle (Plane146)
▪3-D Brick (Solid 147)
有限元基础讲解

有限元基础讲解
有限元分析是一种工程数值分析方法,用于解决复杂结构的力学问题。
它将结构划分为有限数量的小单元,通过对这些小单元进行数值计算,得到整个结构的力学行为。
有限元分析的基本步骤包括:
1. 离散化:将结构划分为有限数量的小单元,如三角形、四边形、六面体等。
每个小单元具有一些自由度,用于描述该单元的位移、应力等信息。
2. 建立单元刚度矩阵:根据单元的几何形状和材料性质,计算每个小单元的刚度矩阵。
刚度矩阵描述了小单元受力和位移之间的关系。
3. 组装全局刚度矩阵:将所有小单元的刚度矩阵组装成整个结构的全局刚度矩阵。
这个过程涉及到将小单元的自由度与整个结构的自由度进行匹配。
4. 施加边界条件:确定结构的边界条件,如固支、受力等。
将这些边界条件转化为对应的约束条件,将其应用于全局刚度矩阵中。
5. 求解方程:将约束条件应用于全局刚度矩阵,得到未知位移的方程。
通过求解这些方程,可以得到结构的位移、应力等信息。
6. 后处理:根据求解结果,进行后处理分析。
可以计算结构的应力、变形、位移等,并进行可视化展示。
有限元分析的优点包括可以处理复杂的几何形状和边界条件,具有较高的计算精度和灵活性。
但也存在一些限制,如需要对结构进行合理的离散化、需要大量的计算资源等。
有限元基本原理与概念

有限元基本原理与概念有限元分析是一种数值计算方法,用于求解连续体力学中的边界值问题。
它是通过将连续体划分为有限数量的离散单元,然后在每个单元内进行力学行为的近似计算来实现的。
有限元基本原理和概念是进行有限元分析的关键。
有限元方法的基本原理包括以下几个方面:1.连续体离散化:连续体被分割为许多有限数量的小单元,例如三角形或四边形,这些小单元被称为有限元。
离散化的目的是将大问题转化为小问题,简化求解过程。
2.描述形函数:在每个有限元内,通过选择适当的形函数来描述位移、应力和应变之间的关系。
它们通常是基于其中一种插值函数,用于近似描述连续体内的位移场。
3.线性方程系统:通过应力和位移之间的平衡关系,可以得到与每个有限元相关的线性方程系统。
该方程系统可以通过组装所有单元的贡献来得到,其中每个单元内的节点位移被认为是未知数。
4.边界条件:为了解决线性方程系统,必须定义适当的边界条件。
这些条件通常包括位移或力的给定值,并且用于将无法由方程系统唯一解决的自由度限制为已知值。
5.求解方程系统:通过解决线性方程系统,可以得到每个节点的位移。
这可以使用各种求解线性方程系统的方法,如直接法(例如高斯消元法)或迭代法(例如共轭梯度法)来实现。
有限元方法的基本概念包括以下几个方面:1.单元:连续体被划分为有限数量的单元,在每个单元内进行近似计算。
常见的单元类型包括一维线元、二维三角形和四边形元,以及三维四面体和六面体元。
2.节点:单元的连接点被称为节点,每个节点在有限元分析中是一个自由度。
节点的数量与单元的选择密切相关,节点的位置和数量会影响结果的精确度。
3.局部坐标系:为了描述单元内的位移和应力,通常引入局部坐标系。
在局部坐标系中,单元的尺寸和形状可以更容易地进行描述和计算。
4.材料特性:有限元分析中需要定义材料的特性参数,例如弹性模量、泊松比、屈服强度等。
这些参数用于描述材料的力学行为和应力-应变关系。
5.后处理:通过有限元分析所得到的结果通常以节点或单元的形式给出,这些结果还需要进行后处理以得到更有意义的结果,如应变、应力分布或变形情况。
通俗易懂的有限元基础原理

通俗易懂的有限元基础原理
有限元分析是一种数值计算方法,用于解决结构力学和其他工程领域的问题。
以下是通俗易懂的有限元基础原理解释:
1. 分割结构:有限元分析中的第一步是将要分析的结构分割成许多小的、简单的部分,称为有限元。
类似于拼图,每个有限元代表结构中的一小部分。
2. 建立本构关系:针对每个有限元,需要建立材料的本构关系,即材料的应力-应变关系。
这是通过材料力学性质的实验测试或理论公式来确定的。
3. 建立单元方程:对于每个有限元,根据其几何形状和材料本构关系建立方程。
这些方程描述了有限元内部的应力和变形之间的关系。
4. 组装全局方程:将所有有限元的方程组装在一起,形成整个结构的全局方程。
这些方程联结了各个有限元之间的边界条件和相互作用。
5. 求解方程:通过数值解法,例如迭代方法或直接求解方法,求解全局方程。
这个过程会得到结构的应力、应变分布以及其他感兴趣的结果。
6. 分析结果:最后,分析人员可以根据求解结果,评估结构的性能,例如应力、变形、位移、振动或热分布等。
这些结果可以帮助工程师优化结构设计、评估结构安全性、指导修复或改进结构性能。
总体来说,有限元分析将大型、复杂的结构问题简化为许多小的、简单的部分,通过数值方法求解其力学行为。
这种方法广泛应用于工程领域,以实现更准确、高效的结构设计和分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元分析计算机辅助工程(CAE)作为一门新兴的学科已经逐渐的走下神坛,成为了各大企业中设计新产品过程中不可缺少的一环。
传统的CAE技术是指工程设计中的分析计算与分析仿真,具体包括工程数值分析、结构与过程优化设计、强度与寿命评估、运动/动力学仿真,验证未来工程/产品的可用性与可靠性。
如今,随着企业信息化技术的不断发展,CAE软件与CAD/CAM/CAPP/PDM/ERP一起,已经成为支持工程行业和制造企业信息化的主导技术,在提高工程/产品的设计质量,降低研究开发成本,缩短开发周期方面都发挥了重要作用。
而CAE技术出现则是要归功于有限元分析的诞生,在有限元法诞生的早期,几乎所有的CAE软件都是使用有限元法来进行计算求解。
因此,可以说有限元法的发展也间接反映了CAE软件在这半个世纪的发展历史。
1 有限元法的诞生每一项新技术的推出都是由于时代的迫切需要,而新技术的出现后也需要经历历史的重重考验。
在上个世纪40年代,由于航空事业的快速发展,对飞机内部结构设计提出了越来越高的要求,即重量轻、强度高、刚度好,人们不得不进行精确的设计和计算。
正是在这一背景下,有限元分析的方法逐渐的发展起来。
早期的一些成功的实验求解方法与专题论文,完全或部分的内容对有限元技术的产生做出的贡献,首先在应用数学界第一篇有限元论文是1943年Courant R发表的《Variational methods for the solution of problems of equilibrium and vibration》一文,文中描述了他使用三角形区域的多项式函数来求解扭转问题的近似解,由于当时计算机尚未出现,这篇论文并没有引起应有的注意。
1956年,M.J.Turner (波音公司工程师),R.W.Clough (土木工程教授),H.C.Martin (航空工程教授)及L.J.Topp (波音公司工程师) 等四位共同在航空科技期刊上发表一篇采用有限元技术计算飞机机翼的强?的论文,名为《Stiffness and Deflection Analysis of Complex Structures》,文中把这种解法称为刚性法(Stiffness),一般认为这是工程学界上有限元法的开端。
1960年,Ray W. Clough教授在美国土木工程学会(ASCE)之计算机会议上,发表另一篇名为《The Finite Element in Plane Stress Analysis》的论文,将应用范围扩展到飞机以外之土木工程上,同时有限元法(Finite Element Method)的名称也第一次被正式提出。
由此之后,有限元法的理论迅速地发展起来,并广泛地应用于各种力学问题和非线性问题,成为分析大型、复杂工程结构的强有力手段。
并且随着计算机的迅速发展,有限元法中人工是难以完成的大量计算工作能够由计算机来实现并快速地完成。
因此,可以说计算机的发展很大程度上促进了有限元法的建立和发展。
2 由理论到程序的转变2.1 FEA技术的探索起源期“有限元法”概念的提出,引出了美国加州大学伯克利分校有限元技术研究小组的最为辉煌的十年历程。
1963年在加州大学Berkeley分校,Edward L.Wilson教授和Ray W. Clough教授为了教授结构静力与动力分析而开发了SMIS(Symbolic Matrix Interpretive System),其目的是为了弥补在传统手工计算方法和结构分析矩阵法之间的隔阂。
1969年,Wilson教授在第一代程序的基础上开发的第二代线性有限元分析程序就是著名的SAP(Structural analysis program),而非线性程序则为NONSAP。
Wilson教授的学生Ashraf Habibullah于1978年创建了Computer and Structures Inc.(CSI),CSI的大部分技术开发人员都是Wilson教授的学生,并且Wilson教授也是CSI的高级技术发展顾问。
而SAP2000则是由CSI在SAP5、SAP80、SAP90的基础上开发研制的通用结构分析与设计软件。
同样是1963年,Richard MacNeal博士和Robert Schwendler先生联手创办了MSC公司,并开发第一个软件程序,名为SADSAM(Structural Analysis by Digital Simulation of Analog Methods)即数字仿真模拟法结构分析。
提到MSC公司,就想到与其有着不解渊源的美国国家太空总署(NASA),当年美国为了能够在与前苏联之间的太空竞赛中取得优胜而成立了NASA。
而为了满足宇航工业对结构分析的迫切需求,NASA于1966年提出了发展世界上第一套泛用型的有限元分析软件Nastran(NASA STRuctural ANalysis Program)的计划,MSC.Software则参与了整个Nastran程序的开发过程。
1969年NASA推出了其第一个NASTRAN版本,称为COSMIC Nastran。
之后MSC继续的改良Nastran程序并在1971年推出MSC.Nastran。
另一个与NASA结缘的是SDRC公司,1967年在NASA的支持下SDRC公司成立,并于1968年发布了世界上第一个动力学测试及模态分析软件包,1971年推出商业用有限元分析软件Supertab(后并入I-DEAS软件中,这也就是为什么I-DEAS作为一款设计软件其有限元分析还如此强大的原因)。
1969年,John Swanson博士建立了自己的公司Swanson Analysis Systems Inc(SASI)。
其实早在1963年John Swanson博士任职于美国宾州匹兹堡西屋公司的太空核子实验室时,就已经为核子反应火箭作应力分析编写了一些计算加载温度和压力的结构应力和变位的程序,此程序当时命名为STASYS (Structural Analysis SYStem)。
在Swanson博士公司成立的次年,结合者早期的STASYS 程序发布了商用软件ANSYS。
1994年Swanson Analysis Systems, Inc.被TA Associates并购,并宣布了新的公司名称改为ANSYS。
2.2 FEA技术的蓬勃发展期进入70年代后,随着有限元理论的趋于成熟,CAE技术也逐渐进入了蓬勃发展的时期,一方面MSC,ANSYS,SDRC三大CAE公司先后组建,并且致力于大型商用CAE软件的研究与开发,另一方面,更多的新的CAE软件迅速出现,为CAE市场的繁荣注入了新鲜血液。
70年代初当时任教于Brown大学的Pedro Marcal创建了MARC公司,并推出了第一个商业非线性有限元程序MARC。
虽然在MARC在1999年被MSC公司收购,但其对有限元软件的发展起到了决定性的推动作用,至今在MSC的分析体系中依然有着MARC程序的身影,更值得一提的是Pedro Marcal早年也是毕业于Berkeley大学。
在早期的商用软件舞台上,还有两位主要人物,他们是David Hibbitt和Klaus J Bathe。
David Hibbitt是Pedro Marcal在Brown的博士生,David Hibbitt与Pedro Marcal 合作到1972年,随后Hibbitt与Bengt Karlsson和Paul Sorenson于1978年共同建立HKS公司,推出了Abaqus软件,使ABAQUS商业软件进入市场。
因为该程序是能够引导研究人员增加用户单元和材料模型的早期有限元程序之一,所以它对软件行业带来了实质性的冲击。
2002年HKS公司改名为ABAQUS,并于2005年被达索公司收购。
另外一位对有限元方法做出重大贡献的是Klaus J. Bathe博士。
Klaus J. Bathe 六十年代末在Berkeley大学Clough和Ed Wilson博士的指导下攻读博士学位,从事结构动力学求解算法和计算系统的研究。
由于Bathe博士在对结构计算以及SAP软件所做的贡献,Bathe博士毕业后被MIT聘请到机械与力学学院任教至今。
1975年在MIT任教的Bathe博士在NONSAP的基础上发表了著名的非线性求解器ADINA (Automatic Dynamic Incremental Nonlinear Analysis),而在1986年ADINA R&D Inc.成立以前,ADINA软件的源代码是公开的,即著名的ADINA81版和ADINA84版本的fortran源程序,后期很多有限元软件都是根据这个源程序所编写的。
1977年Mechanical Dynamics Inc.(MDI)公司成立,致力于发展机械系统仿真软件,其软件ADAMS应用于机械系统运动学、动力学仿真分析。
后被MSC公司收购,成为MSC分析体系中一个重要的组成部分。
在CAE的历史中另一个神奇的程序是显式有限元程序DYNA,DYNA程序由当时在美国Lawrence Livermore国家实验室的John Hallquist编写。
之所以说DYNA神奇,是因为在现在我们熟知的众多软件中,都可以发现DYNA的踪迹,因此LS-DYNA系列也被公认为显式有限元程序的鼻祖。
下面我们来细数一下由DYNA所演变出来的有限元程序:在20世纪80年代,DYNA程序首先被法国ESI公司商业化,命名为PAM-CRASH,现已成为了ESI的明星产品。
除此之外,ESI公司还有多个被人熟知的软件,如铸造软件ProCAST,钣金软件PAM-STAMP,焊接软件SYSWELD,振动噪声软件VA One,空气动力学软件CFD-FASTRAN,多物理场软件CFD-ACE+等等。
1988年,John Hallquist自己创建LSTC(Livermore Software Technology Corporation)公司,发行和扩展DYNA程序商业化版本LS-DYNA。
同样是1988年,MSC在DYNA3D的框架下开发了MSC.Dyna并于1990年发布第一个版本,随后于1993年发布了著名的MSC.Dytran。
另外,ANSYS收购了Century Dynamics公司,把该公司以DYNA程序开发的高速瞬态动力分析软件AUTODYN纳入到ANSYS的分析体系中。
并且在1996年,ANSYS与LSCT公司合作推出了ANSYS/LS-DYNA。
1984 年,ALGOR公司成立于,总部位于宾州的匹兹堡,ALGOR公司在购买SAP5 源程序和vizicad 图象处理软件后,同年推出ALGOR FEAS(Finite Element Analysis System)。
