编译原理 第三章上下文无关文法及分析
第3章 语法分析-编译原理及实践教程(第3版)-黄贤英-清华大学出版社

3.2.1 文法的定义
例1:有如下规则
<句子><主语><谓语> <主语><代词>|<名词> <代词>我 <名词>大学生 <谓语><动词><直接宾语> <动词>是 <直接宾语><代词>|<名词>
(表示由…组成)
• 归约:推导的逆过程。
• 直接归约:直接推导的逆过程
几个概念的形式定义
• 直接推导: 如果αβ是文法 G=(Vn,Vt,P,S)
的产生式,γ和δ是V*中的任意符号,若有符号 串v,w满足: v=γαδ,w=γβδ,则说v直接产生w,(w是v的 直接推导)记作:v=>w 例:S01, 0S0=>0010(直接推导γ=0,δ=0) • 如果存在v=>w0=>w1=>w2...=>Wn=w(n>0),则 称v推导出w(长度为n),记作v+=>w(至少一步) • 若有v=>w或v=w,则记作v*=>w(0步或若干步)
一个非终结符号,β∈V*)
–上例中: G=(Vn,Vt,P,<句子>)
Vn=(<句子>,<主语>,<谓语>,<代词>,<动词>,
<名词>,<直接宾语>)
Vt= (我,是,大学生)
P=
<句子><主语><谓语>
<主语> <代词>|<名词>
03-第3章-语法分析-编译原理-中国科技大学(共13讲)

• 例 ( {id, +, , , (, )}, {expr, op}, expr, P )
expr expr op expr expr expr op +
3.2 语言和文法
• 无二义的文法 stmt matched _stmt | unmatched_stmt matched_stmt if expr then matched_stmt else matched_stmt | other unmatched_stmt if expr then stmt | if expr then matched_stmt else unmatched_stmt
3.2 语言和文法
expr expr + term | term term term factor | factor factor id | (expr)
expr term
term expr factor id term factor id expr + term * factor id id + id id 分析树
3.2 语言和文法
3.2.3 验证文法产生的语言 G : S (S) S | L(G) = 配对的括号串的集合 • 按串长进行归纳:配对括号串可由S推出
–归纳基础: S – 归纳假设:长度小于2n的都可以从S推导出来 – 归纳步骤:考虑长度为2n(n 1)的w = (x) y S (S)S * (x) S * (x) y
编译原理和技术
中国科学技术大学 计算机科学与技术学院 陈意云
编译原理第3章文法和语言

第3章文法和语言第1题文法G=({A,B,S},{a,b,c},P,S)其中P为:S→Ac|aBA→abB→bc写出L(G[S])的全部元素。
答案:L(G[S])={abc}第2题文法G[N]为:N→D|NDD→0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?答案:G[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD....=>NDDDD...D=>D......D或者:允许0开头的非负整数?第3题为只包含数字、加号和减号的表达式,例如9-2+5,3-1,7等构造一个文法。
答案:G[S]:S->S+D|S-D|DD->0|1|2|3|4|5|6|7|8|9第4题已知文法G[Z]:Z→aZb|ab写出L(G[Z])的全部元素。
答案:Z=>aZb=>aaZbb=>aaa..Z...bbb=>aaa..ab...bbbL(G[Z])={anbn|n>=1}第5题写一文法,使其语言是偶正整数的集合。
要求:(1)允许0打头;(2)不允许0打头。
答案:(1)允许0开头的偶正整数集合的文法E→NT|DT→NT|DN→D|1|3|5|7|9D→0|2|4|6|8(2)不允许0开头的偶正整数集合的文法E→NT|DT→FT|GN→D|1|3|5|7|9D→2|4|6|8F→N|0G→D|0第6题已知文法G:<表达式>::=<项>|<表达式>+<项> <项>::=<因子>|<项>*<因子><因子>::=(<表达式>)|i试给出下述表达式的推导及语法树。
(5)i+(i+i)(6)i+i*i答案:(5)<表达式>=><表达式>+<项>=><表达式>+<因子>=><表达式>+(<表达式>)=><表达式>+(<表达式>+<项>)=><表达式>+(<表达式>+<因子>)=><表达式>+(<表达式>+i)=><表达式>+(<项>+i)=><表达式>+(<因子>+i)=><表达式>+(i+i)=><项>+(i+i)=><因子>+(i+i)=>i+(i+i)(6)<表达式>=><表达式>+<项>=><表达式>+<项>*<因子>=><表达式>+<项>*i=><表达式>+<因子>*i=><表达式>+i*i=><项>+i*i=><因子>+i*i=>i+i*i<表达式><表达式>+<项><因子><表达式><表达式>+<项><因子>i<项><因子>i<项><因子>i()<表达式><表达式>+<项><项>*<因子><因子>i<项><因子>ii第7题证明下述文法G[〈表达式〉]是二义的。
编译原理第三章语法分析
3.2 语言和文法
• 文法的优点
–文法给出了精确的,易于理解的语法说明 –自动产生高效的分析器
–可以给语言定义出层次结构
3.2 语言和文法
• 文法的优点
–文法给出了精确的,易于理解的语法说明 –自动产生高效的分析器
–可以给语言定义出层次结构
–以文法为基础的语言实现便于语言的修改
3.2 语言和文法
F id | (E)
3.2 语言和文法
E E+T|T TT* F|F F id | (E)
E T T T * F id F id
E E
T F
+
T F
T * F
id
*
F
id
id id * id * id 和 id + id * id 的分析树
id
3.2 语言和文法
3.2.5 消除二义性 stmt if expr then stmt | if expr then stmt else stmt | other • 句型:if expr then if expr then stmt else stmt
3.2 语言和文法
3.2.5 消除二义性 stmt if expr then stmt | if expr then stmt else stmt | other • 句型:if expr then if expr then stmt else stmt • 两个最左推导: stmt if expr then stmt if expr then if expr then stmt else stmt stmt if expr then stmt else stmt if expr then if expr then stmt else stmt
编译原理语法分析3(1)

3.1.1 上下文无关文法的定义 正规式能定义一些简单的语言,能表示给定结构的固定次数的重复或者没有指定次数的重复 例:a (ba)5, a (ba)* 正规式不能用于描述配对或嵌套的结构 例1:配对括号串的集合 例2:{wcw | w是a和b的串}
3.1 上下文无关文法
3.2 语言和文法
expr expr + term | term term term factor | factor factor id | (expr)
expr
id
term
factor
id
id
term
*
term
factor
factor
*
expr
expr
+
id
factor
term
id
3.2 语言和文法
3.2.9 形式语言鸟瞰 文法 G = (VT , VN, S, P) 0型文法: , , (VN VT)*, | | 1 1型文法:| | | |,但S 可以例外 短语文法
3.2 语言和文法
3.2.9 形式语言鸟瞰 文法 G = (VT , VN, S, P) 0型文法: , , (VN VT)*, | | 1 1型文法:| | | |,但S 可以例外 短语文法、上下文有关文法
1
2
开始
a
0
a
b
b
3.2 语言和文法
3.2.2 分离词法分析器理由 为什么要用正规式定义词法 词法规则非常简单,不必用上下文无关文法 对于词法记号,正规式描述简洁且易于理解 从正规式构造出的词法分析器效率高
3.2 语言和文法
从软件工程角度看,词法分析和语法分析的分离有如下好处 简化设计 编译器的效率会改进 编译器的可移植性加强 便于编译器前端的模块划分
编译原理文法__上下文无关文法及其语法树-二义性
* (6). 文法的二义性和语言的二义性
• 二者是不同的概念 • 例如: 两个等价的文法,一个是二义的,一个是非 二义的,但产生的语言是相同的 G : E→ E+E | E*E | (E) | i G' : E→ T | E+T T→ F | T*F F→ (E) | i 二义文法 非二义文法
(1). 什么是文法的二义性 (2). 二义性的判定 (3). 二义性证明举例 (4). 二义性的消除举例 (5). 先天二义的语言 (6). 文法的二义性和语言的二义性
G:〈语句〉→ if〈条件〉then〈语句〉 | if〈条件〉then〈语句〉else〈语句〉 | 其他语句
语句
if 条 then 语 if 条 then 语 else 语
语句 if 条 then 语 else 语
if 条 then 语
if c1 then if c2 then s1 else s2
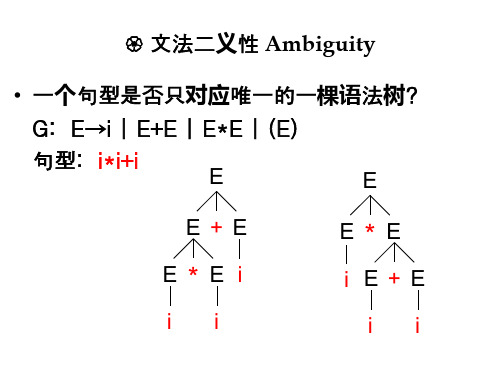
文法二义性 Ambiguity
• 一个句型是否只对应唯一的一棵语法树? G: E→i | E+E | E*E | (E) 句型: i*i+i E E E + E E i E
*E
i i
*E i
i
i E + E
(1). 什么是文法的二义性
• 如果一个文法存在某个句子对应两棵不同的语 法树,则说这个文法是二义的。 • 或者说,若一个文法中存在某个句子,它有两个 不同的最左(最右)推导,则这个文法是二义的。 E E
(4).二义性的消除
定义表达式的无二义文法 G' : E→ T | E+T T→ F | T*F F→ (E) | i
* 定义条件语句的无二义文法
编译原理课程设计之第三章上下文无关文法及分析

14
无关文法及分析
1. 上下文无关文法(即2型文法)的形式定义:
上下文无关文法是一个四元组(VT , VN , P , S):
① ②
终非结终符 结集 符合 集合VTVN(与VT产的不生左相式部交)
产生式 的右部
③ 产生式或文法规则A→α形成的集合P,
其中A∈VN,α∈(VT∪VN)* 4) 开始符号S,其中S∈VN
25
无关文法及分析
3.2 上下文无关文法的形式定义
1. 上下文无关文法(即2型文法)的形式定义 2. chomsky文法的分类 3. 推导和规约的定义 4. 句型和句子的定义 5. 最左和最右推导 6. 文法定义的语言 7. 递归产生式和递归文法 8. 文法和语言
mcy
编译原理课程设计之第三章上下文
mcy
编译原理课程设计之第三章上下文
1
无关文法及分析
第三章 上下文无关文法及分析
本章的目的是为语言的语法 描述寻求形式工具,要求该 工具对程序设计语言给出精 确无二义的语法描述。
mcy
编译原理课程设计之第三章上下文
2
无关文法及分析
第三章 上下文无关文法及分析
✓3.1 语法分析过程 ▪ 3.2 上下文无关文法的形式定义
下面的2型文法描述了包含加法、减法和乘法的简 单整型算术表达式的语法结构。
文法G[exp]:
exp → exp op exp exp →(exp) exp → number
34-3 是符合该 语法结构的简单 整型算术表达式 (句子)吗?
op → + | - | *
mcy
编译原理课程设计之第三章上下文
令G是一个如上所定义的文法,则G=(VT,VN,P,S)
编译原理第三章练习题答案

编译原理第三章练习题答案编译原理第三章练习题答案编译原理是计算机科学中的重要学科,它研究的是如何将高级语言代码转化为机器语言的过程。
在编译原理的学习过程中,练习题是不可或缺的一部分,通过完成练习题可以更好地理解和掌握编译原理的知识。
本文将为大家提供编译原理第三章练习题的答案,希望对大家的学习有所帮助。
1. 什么是语法分析?语法分析是编译器中的一个重要模块,它的主要任务是根据给定的语法规则,对输入的源代码进行分析和解释。
语法分析器会根据语法规则构建一个语法树,用于表示源代码的结构和含义。
常用的语法分析方法有递归下降法、LL(1)分析法和LR分析法等。
2. 什么是LL(1)文法?LL(1)文法是一种特殊的上下文无关文法,它具有以下两个特点:(1) 对于任何一个句子,最左推导和最右推导是唯一的。
(2) 在预测分析过程中,只需要向前看一个输入符号就可以确定所采用的产生式。
LL(1)文法是一种常用的文法形式,它适用于递归下降法和LL(1)分析法。
3. 什么是FIRST集合和FOLLOW集合?FIRST集合是指对于一个文法符号,它能够推导出的终结符号的集合。
FOLLOW 集合是指在一个句型中,某个非终结符号的后继终结符号的集合。
计算FIRST集合和FOLLOW集合可以帮助我们进行语法分析,特别是LL(1)分析。
4. 什么是递归下降语法分析法?递归下降语法分析法是一种基于产生式的自顶向下的语法分析方法。
它的基本思想是从文法的开始符号开始,递归地根据产生式进行分析,直到推导出输入符号串或发现错误。
递归下降语法分析法的实现比较简单,但对于某些文法可能会出现回溯现象,影响分析效率。
5. 什么是LR分析法?LR分析法是一种自底向上的语法分析方法,它的基本思想是从输入符号串开始,逐步构建语法树,直到推导出文法的开始符号。
LR分析法具有较好的分析效率和广泛的适用性,常用的LR分析方法有LR(0)、SLR(1)、LR(1)和LALR(1)等。
编译原理第三章1

《 课前思政教育---疫情期间增强自律性 》
- 19/74页 -
→ * •E E+E | E E | (E) |
i •E
•*
《 课前思政教育---疫情期间增强自律性 》
- 20/74页 -
•5.语言
• 文法G[S]产生的所有句子的集合称为
文
•*
• 法G所定义的语言,记为L(G[S]):
• 由语言定义可知:
E id
id
id
《 课前思政教育---疫情期间增强自律性 》
- 40/74页 -
3.2 语言和文法
• 文法的优点
• 文法给出了精确的,易于理解的语法说明。 • 对于某些文法类,可以为其中的文法自动产生高效的分析器。 • 可以给语言定义出层次结构(如嵌套和配对)。 • 以文法为基础的语言的实现便于语言的修改。
•我们提出一个问题:
•这种推导过程是否唯一?
《 课前思政教育---疫情期间增强自律性 》
- 30/74页 -
• 同一个句型(句子)可以通过不 同的推导序列推导出来,这是因为 在推导过程中与所选择非终结符的 次序有关。
《 课前思政教育---疫情期间增强自律性 》
- 31/74页 -
•例如,设有文法G[N1]
3.2 语言和文法
《 课前思政教育---疫情期间增强自律性 》
- 43/74页 -
3.2 语言和文法
• 从软件工程角度看,词法分析和语法分析的分离有如下好处
ü 简化词法分析器的设计 ü 编译器的效率会改进 ü 编译器的可移植性加强 ü 便于编译器前端的模块划分
《 课前思政教育---疫情期间增强自律性 》
《 课前思政教育---疫情期间增强自律性 》
编译原理-上下无关文法和文法分析

Formal Definition CFL
• • • • A context-free grammar consists of the following: 1) A set T of terminals 2) A set N of nonterminals ( disjoint from T) 3) A set fo productions ,or grammer rles , of the form A a, where A is an element of N and a is an element of (T u N )* • 4) A start symbol S from the set N • A derivation over the grammer G is of the form S=>*w ,where w is belonged to T*.
The Parsing Process
parser Sequence of tokens
Syntax tree
• Usually, the sequence of tokens is not an explicit input parameter, but the parser calls a scanner procedure such as getToken to fetch the next token from the input as it is needed during the parser process.
Context-Free Grammar Rules (cont)
• The rule defines the structure whose name is to the left of the arrow. • The structure is defined to consist of one of the choices on the right-hand side separated by the vertical bars.
编译原理-西安交通大学(冯博琴)第三章上下文无关文法

2、二义性问题
定义:
文法G的某一句子有两棵不同的树,则G为二义的。
二义性对语法分析不便,因此希望:
1)判定二义否 2)无二义性的充分条件 3)如何消除二义性
解决办法:尽量去掉二义性
①如对上例,可以通过阐明运算符的优先性和 结合性来解除文法的二义性
②通过重写一个文法,把结合性和优先规则结 合进文法本身中去 注意到,L(G)=L(G’),G≠G’
AM20.10.1420.10.14
•
2、
。0 5:03:50 05:03:5 005:031 0/14/2 020 5:03:50 AM
每天只看目标,别老想障碍
•
3、
。20.1 0.1405: 03:500 5:03Oct-2014-Oct-20
宁愿辛苦一阵子,不要辛苦一辈子
•
4、
。05:0 3:5005: 03:500 5:03We dnesda y, October 14, 2020
树的内节点:非终结符A标记 若A ->α,则该产生式的一棵子树为 A XYZ
树的叶:非终结符|终结符,对应一个句型
语法树为语法分析提供一些新的途径
在语法树中找出文法中的概念
•内结点A •叶 •子树 •根结点 •任一次全剪 •叶子∈VT时,将叶子顺序排列
VN 文法符号 直接推导 S 句型 句子
例3 E -( id + id )的语法树
得到相同的语法树 •有的语法,对于同一句子、应用不同规则进行推
导得到不同的语法树
例4 根据文法G对句子id + id * id进行推导
①文法G E -> E+E|E*E|( E )| i
②推导1 E => E+E => id+E => id+E*E => id+id*E => id+id*id ③推导2 E => E*E => E+E*E => id+E*E => id+id*E => id+id*id
上下文无关文法的基本概念

上下文无关文法的基本概念上下文无关文法的基本概念定义:上下文无关文法G是一个四元组G = (N,T,P,S),其中N是非终结符的有限集合;T是终结符或单词的有限集合,它与N不相交;P是形如 A →α的产生式的有限集合,其中A∈N,α∈V ﹡,V=T∪NS是N中的区分符号,称为开始符号或句子符号。
V中的符号称为文法符号,包括终结符和非终结符。
特殊情况:A →ε空产生式例如,if语句结构的文法产生式表示:stmt →if expr then stmt else stmtBackus - Naur范式(Backus-Naur form)或BNF文法符号的使用约定:符号是终结符:字母表中比较靠前的小写字母,如a,b,c等。
操作符,如+、-等。
标点符号,如括号、逗号等。
数字0,1, (9)黑体串,如id、if等。
符号的使用约定:下列符号是非终结符:字母表中比较靠前的大写字母,如A、B、C等。
字母S,它常常代表开始符号。
小写斜体名字,如expr、stmt等。
字母表中比较靠后的大写字母,如X、Y、Z等,表示文法符号,也就是说,可以是非终结符也可以是终结符。
符号的使用约定:字母表中比较靠后的小写字母,如u,v,…,z等,表示终结符号的串。
小写希腊字母,如α、β、γ等,表示文法符号的串。
因此,一个通用产生式可以写作A →α,箭头左边(产生式左部)是一个非终结符A,箭头右边是文法符号串(产生式右部)。
符号的使用约定:如果A →α1、A →α2、…、A →αk 是所有以A为左部的产生式(称为A产生式),则可以把它们写成A →α1|α2|…|αk,我们将α1、α2、…、αk称为A的候选式。
除非另有说明,否则第一个产生式左部的符号是开始符号。
例1考虑下面的关于简单算术表达式的文法,非终结符为<表达式>和<运算符>,终结符有ID,+,-,*,/,↑,(,)。
产生式有<表达式> → <表达式> <运算符> <表达式><表达式> → (<表达式>)<表达式> → - <表达式><表达式> →ID<运算符> → +<运算符> → -<运算符> → *<运算符> → /<运算符> →↑正规表达式和上下文无关文法的关系:正规表达式所描述的每一种语言结构都可以用上下文无关文法来描述。
编译原理教程课后习题答案——第三章

第三章语法分析3.1 完成下列选择题:(1) 文法G:S→xSx|y所识别的语言是。
a. xyxb. (xyx)*c. xnyxn(n≥0)d. x*yx*(2) 如果文法G是无二义的,则它的任何句子α。
a. 最左推导和最右推导对应的语法树必定相同b. 最左推导和最右推导对应的语法树可能不同c. 最左推导和最右推导必定相同d. 可能存在两个不同的最左推导,但它们对应的语法树相同(3) 采用自上而下分析,必须。
a. 消除左递 a. 必有ac归b. 消除右递归c. 消除回溯d. 提取公共左因子(4) 设a、b、c是文法的终结符,且满足优先关系ab和bc,则。
b. 必有cac. 必有bad. a~c都不一定成立(5) 在规范归约中,用来刻画可归约串。
a. 直接短语b. 句柄c. 最左素短语d. 素短语(6) 若a为终结符,则A→α·aβ为项目。
a. 归约b. 移进c. 接受d. 待约(7) 若项目集Ik含有A→α· ,则在状态k时,仅当面临的输入符号a∈FOLLOW(A)时,才采取“A→α· ”动作的一定是。
a. LALR文法b. LR(0)文法c. LR(1)文法d. SLR(1)文法(8) 同心集合并有可能产生新的冲突。
a. 归约b. “移进”/“移进”c.“移进”/“归约”d. “归约”/“归约”【解答】(1) c (2) a (3) c (4) d (5) b (6) b (7) d (8) d3.2 令文法G[N]为G[N]: N→D|NDD→0|1|2|3|4|5|6|7|8|9(1) G[N]的语言L(G[N])是什么?(2) 给出句子0127、34和568的最左推导和最右推导。
【解答】(1) G[N]的语言L(G[N])是非负整数。
(2) 最左推导:NNDNDDNDDDDDDD0DDD01DD012D0127NNDDD3D34NNDNDDDDD5DD56D568最右推导:NNDN7ND7N27ND27N127D1270127NNDN4D434NNDN8ND8N68D685683.3 已知文法G[S]为S→aSb|Sb|b,试证明文法G[S]为二义文法。
上下文无关文法的概念

上下文无关文法的概念1. 引言上下文无关文法(Context-Free Grammar,CFG)是形式语言理论中的一种重要概念。
它提供了一种形式化的方法来描述一类形式语言。
CFG在计算机科学、自然语言处理、编译原理等领域有着广泛的应用。
本文将从概念、结构、性质和应用等方面全面介绍上下文无关文法。
2. 上下文无关文法的定义上下文无关文法由四个部分组成:终结符集合、非终结符集合、产生式规则集合和起始符号。
形式上,CFG可以表示为一个四元组G=(V, T, P, S),其中: - V是非终结符集合。
- T是终结符集合。
- P是产生式规则集合,每个产生式规则形如A → α,其中A是非终结符,α是终结符和非终结符的序列。
- S是起始符号,它是一个特殊的非终结符。
3. 上下文无关文法的结构上下文无关文法的产生式规则描述了非终结符之间的替换关系。
例如,A → α表示在推导过程中可以用非终结符A替换成序列α。
产生式规则可以形象地表示为树状结构,其中非终结符是内部节点,终结符是叶子节点。
通过不断地应用产生式规则,可以从起始符号推导出一个语言的句子。
4. 上下文无关文法的性质上下文无关文法的性质对于理解其特点和应用非常重要。
4.1 文法的一致性对于一个给定的上下文无关文法,如果存在至少一种推导方式,可以从起始符号推导出一个句子,那么它是一致的。
4.2 文法的二义性一个上下文无关文法如果存在至少一种句子可以有两个或以上不同的解析树,那么它是二义的。
二义性文法在语言理解和编译的过程中会导致歧义,因此设计文法时需要尽可能避免二义性。
4.3 文法的生成能力上下文无关文法可以生成一类形式语言,包括正则语言和上下文有关语言。
正则语言是最简单的一类形式语言,而上下文有关语言的生成需要更复杂的规则。
4.4 文法的规范形式上下文无关文法可以通过一系列转换规则转化为规范的形式,如Chomsky范式。
规范形式的文法能够更方便地进行分析和转换。
编译原理语法分析—自上而下分析

对文法G的任何符号串=X1X2…Xn构造集 合FIRST()。
1. 置FIRST()=FIRST(X1)\{};
2. 若对任何1ji-1,FIRST(Xj), 则把FIRST(Xi)\{}加至FIRST()中; 特别是,若所有的FIRST(Xj)均含有, 1jn,则把也加至FIRST()中。显 然,若=则FIRST()={}。
T→T*F | F
F→(E) | i
经消去直接左递归后变成:
E→TE E→+TE | T→FT T→*FT | F→(E) | i
(4.2)
例如文法G(S): S→Qc|c Q→Rb|b R→Sa|a
虽没有直接左递归,但S、Q、R都是左递归的
SQcRbcSabc
(4.3)
一个文法消除左递归的条件: 不含以为右部的产生式 不含回路。
即A的任何两个不同候选 i和 j FIRST(i)∩FIRST( j)=
当要求A匹配输入串时,A就能根据它所面临的第
一个输入符号a,准确地指派某一个候选前去执
行任务。这个候选就是那个终结首符集含a的。
提取公共左因子:
假定关于A的规则是 A→ 1 | 2 | …| n | 1 | 2 | … | m (其中,每个 不以开头)
*
特别是,若S A ,则规定
#FOLLOW(A)
构造不带回溯的自上而下分析的文法条件
1. 文法不含左递归,
2. 对于文法中每一个非终结符A的各个产生式 的候选首符集两两不相交。即,若
A→ 1| 2|…| n 则 FIRST( i)∩FIRST( j)= (ij)
3. 对文法中的每个非终结符A,若它存在某个 候选首符集包含,则
1)算符优先分析法:按照算符的优先关系和结 合性质进行语法分析。适合分析表达式。
编译原理第三章语法分析

递归下降程序:
void F() { if(lookahead= =’i’) match(‘i’); else if(lookahead= =’(’) { match(‘(’); E(); if(lookahead= =’)’) match(‘)’); else error(); } else error(); }
输入串
id+id*id;# id+id*id;# id+id*id;# id+id*id;# id+id*id;# +id*id;# +id*id;#
动作
pop(L),push(E;L) pop(E),push(TE’) pop(T),push(FT’) pop(F),push(id) pop(id),next(ip) pop(T’)
形式语言分类
定义:若文法G=(N,T,P,S)的每个产生式α→β中,均有 α∈(N∪T)*N(N∪T)*,且至少含有一个非终结符, β∈(N∪T)*,则称G为0型文法(短语文法)。 ①1型文法(上下文有关文法):G的任何产生式α→β(S→ε 除外)均满足|α|≤| β| (|x|表示x中文法符号的个数); ②2型文法(上下文无关文法):G的任何产生式形如A→β, 其中A∈N,β∈(N∪T)*; ③3型文法(正规文法、线性文法):G的任何产生式形如A→a 或者A→aB(或者A→Ba),其中A,B∈N,a∈T*。
定义:将产生式A→γ的右部代替文法符号序列αAβ 中的A得到αγβ的过程,称为αAβ直接推导 出αγβ,记作:αAβαγβ。
编译原理的语法分析

编译原理的语法分析一、概述编译原理是计算机科学与技术中的重要核心课程,它研究的是将高级语言转化为机器语言的过程。
语法分析是编译器的重要组成部分,它的主要任务是根据给定的文法规则,分析输入的源代码,判断其是否符合语法规范。
二、上下文无关文法在深入了解语法分析前,我们首先需要了解上下文无关文法的概念。
上下文无关文法(Context-Free Grammar,简称CFG)是一个四元组G=(V, Σ, R, S),其中V是非终结符的集合,Σ是终结符的集合,R是产生式规则的集合,S是语法分析的起始符号。
三、自顶向下分析自顶向下分析是一种从语法分析的起始符号开始,逐步扩展推导的方法。
常见的自顶向下分析方法有递归下降分析和LL分析。
1. 递归下降分析递归下降分析是自顶向下分析中最常用的方法之一。
它通过产生式规则的递归调用来实现对源代码的语法分析。
对于每个非终结符,我们可以编写一个对应的递归函数,并按照产生式规则进行展开和匹配。
2. LL分析LL分析是自顶向下分析的一种重要方法。
它的名称来源于产生式规则的左侧扫描(Left-to-right, Leftmost derivation)。
LL分析利用一个预测分析表来进行语法分析,预测分析表的构造基于文法的FIRST和FOLLOW集合。
四、自底向上分析自底向上分析是一种从源代码中的终结符开始,逐步合并生成非终结符的推导过程。
常见的自底向上分析方法有SLR分析、LR分析和LALR分析。
1. SLR分析SLR分析是自底向上分析中的一种重要方法,它利用一个包含项目集的状态机来进行语法分析。
SLR分析器的构造基于LR(0)项目,使用LR(0)项目集家族来构建分析表。
2. LR分析LR分析是自底向上分析的高级方法,它分析的是LR文法,其中L 表示从左向右扫描,R表示右推导。
LR分析器的构造会产生广义项目集族、LR分析表和状态转换图,用于分析输入的源代码。
3. LALR分析LALR分析是对LR分析的改进和优化,LALR分析器的构造与LR 分析类似,但合并了具有相同前缀的状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析的错误处理
错误恢复 报告有意义的错误信息,并继续进行分析(去 找到尽可能多的错误) 错误修复 从提交给它的非正确版本中推断出一个可能正 确的代码版本(这通常在简单情况下才发生的)
3.2 上下文无关文法
作用 上下文无关文法说明程序设计语言的语法结构 除了上下文无关文法涉及到了递归规则之外, 与使用正则表达式说明词法结构很相似
定义 上下文无关文法G= (VT,VN,P,S):
1. VT 是终结符集合 2. VN 是非终结符集合, VN∩VT=φ 3. P 是产生式集合, 或语法规则, 形如A→ α,其中 A∈ VN 且 α ∈ (VN∪VT) * 4. S 是开始符号 , S∈VN
例如
简单的算术表达式的文法G=(VT,VN,P,S) VT={num, +, -, *, /, (, ) }
直接推导 and 直接归约
A-> β是文法 G 的产生式 , 若有v 和w 满 足:v=αAγ,w=αβγ,其中 α,γ ∈ (VN∪VT) * , 则称v 直接推导到 w,或 w直接归约到 v, 记作 v=>w 直接推导就是用产生式的右部替换产生式 的左部(非终结符)的过程 直接归约 就是用产生式的左部非终结符替 换产生式的右部的过程
例如
简单算术表达式的文法可写为: E -> E O E | (E) | num O -> + | - | * | /
文法的Chomsky分类
有四类文法:
1. 2. 3. 4. 无限制文法 (0型) 上下文有关文法 (1型) 上下文无关文法 (2型) 正规文法 (3型)
这四种文法的关系:
无限制 上下文有关 上下文无关 正规
结果的数据 结构
线性结构
3.1 分析过程 3.2 上下文无关文法 3.3 分析树与抽象语法树 3.4 二义性
3.1 分析过程
分析的任务 从由扫描程序产生的记号中确定程序的语 法结构 隐式或显式地构造出表示该结构的分析树 或语法树
分析树/
记号序列
分析程序
语法树
分析的接口
输入: 当分析过程需要下一个记号时,分析程序就调 用扫描程序过程以从输入中获得它 输出: 构造的隐式或显式语法树。语法树的每个节点 包括了编译后面过程所需的特性
类型 无限制文法 ( 0型 ) 上下文有关文法 (1型) 上下文无关文法 (2型) 正规文法 (3型)
产生式 α→β V=VN∪VT α∈V+ , β∈V*
说明 对产生式没有限制
A→, , ∈ V* 将A替换成时,必须 考虑A的上下文, A∈VN , β∈V+ A→β,A∈VN , β∈V* A→aB or A→a, A,B∈VN ,a∈VT 无需考虑A在上下文中 的出现情况 等同于正则表达式
3.2.2 推导 和 归约
推导和归约的作用
上下文无关文法规则确定了为由规则定义的结 构的记号符号符合语法的串集 例如:对应文法 exp->exp op exp | (exp) | number op-> + | - | * (34-3)*42 是合法的串 (34-3*42 不是合法的串 文法规则通过推导或归约确定记号符号的正规 集
分析学习的主要内容
语法结构的描述 : 上下文无关文法 语法分析的方法(代码实现语法规则分析)
自顶向下的语法分析 自底向上的语法分析
词法分析
任务 确定单词的结 构 正则表达式
语法分析 确定程序的语法或结构
描述工具
上下文无关文法
算法表示为DFA源自自顶向下分析 自底向上分析 分析树或语法树,都是 递归的
表示法惯例
按照惯例,我们可以只写出一个文法的产生式 一般来说,第一个产生式的左边是开始符号 使用小写字母表示终结符 使用大写字母或用<…> 括起的表示非终结符 如果 A->α1, A-> α2, …, A-> αn 是所有左边是 A的产生式,我们可以写为 A-> α1 | α2 |… | αn
例如 exp->exp op exp | (exp) | num op-> + | - | * (34-3)*42 的推导是: (1)exp=>exp op exp (exp->exp op exp) (2) =>exp op num (exp->num) (3) =>exp * num (op->*) (4) =>(exp)*num (exp->(exp)) (5) =>(exp op exp)* num (exp->exp op exp) (6) =>(exp op num)*num (exp->num) (7) =>(exp-num)*num (op->-) (8) =>(num-num)*num (exp->num)
例如 整型算术表达式的上下文无关文法是 exp -> exp op exp | (exp) | number op -> + | - | * number的正则表达式 number = digit digit* digit = 0|1|2|3|4|5|6|7|8|9
3.2.1 上下文无关文法的定义
例如 文法 G: S→0S1,S→01 直接推导: 0S1 00S11 00S11 000S111 000S111 00001111 S 0S1
(S→0S1) (S→0S1) (S→01) (S→0S1)
推导和归约
=>的闭包 , α=>*β α=>*β当且仅当有0个或多个 (n>=0)推导序列 α1=>α2=>… =>αn-1=>αn,α=α1且β =αn S=>*w, 其中 w ∈ VT * 且 S是文法G的开始符 号,被称为 S 推导出 w 或 w归约到 S
VN={exp, op}
Exp是开始符号 exp -> exp op exp
exp -> (exp)
exp -> num
产生式是:
op -> +
op -> op -> * op -> /
解释
1. VT 是组成符号串的基本符号。终结符是单词 2. VN 是用来表示符号串集合的结构名 3. 开始符号“S”表示的符号串集合是由语法定 义的语言 4. 产生式定义了一种结构,结构名在箭头的左 边。箭头的右边定义了结构的布局。 5. 产生式的形式 ( A→ α) 被称为Backus-Naur 范式(或 BNF)
