2019年高考圆锥曲线部分大题解析
专题17 圆锥曲线-2019年高考数学考纲解读与题型示例含答案

专题17 圆锥曲线【2019年高考考纲解读】1.以选择题、填空题形式考查圆锥曲线的方程、几何性质(特别是离心率).2.以解答题形式考查直线与圆锥曲线的位置关系(弦长、中点等). 【重点、难点剖析】一、圆锥曲线的定义与标准方程 1.圆锥曲线的定义(1)椭圆:|PF 1|+|PF 2|=2a (2a >|F 1F 2|). (2)双曲线:||PF 1|-|PF 2||=2a (2a <|F 1F 2|).(3)抛物线:|PF |=|PM |,点F 不在直线l 上,PM ⊥l 于点M . 2.求圆锥曲线标准方程“先定型,后计算”所谓“定型”,就是确定曲线焦点所在的坐标轴的位置;所谓“计算”,就是指利用待定系数法求出方程中的a 2,b 2,p 的值. (2)待定系数法.①顶点在原点,对称轴为坐标轴的抛物线,可设为y 2=2ax 或x 2=2ay (a ≠0),避开对焦点在哪个半轴上的分类讨论,此时a 不具有p 的几何意义. ②中心在坐标原点,焦点在坐标轴上,椭圆方程可设为x 2m +y 2n =1(m >0,n >0).双曲线方程可设为x 2m -y 2n=1(mn >0).这样可以避免讨论和烦琐的计算.对于x 2a 2+y 2b 2=1和x 2a 2-y 2b2=1来说,抓住a 、b 、c 间的关系是关键.【变式探究】(2017·北京)若双曲线x 2-y 2m=1的离心率为3,则实数m =________.答案 2解析 由双曲线的标准方程知,a =1,b 2=m ,c =1+m ,故双曲线的离心率e =c a=1+m =3, ∴1+m =3,解得m =2.【变式探究】(2017·全国Ⅲ)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线方程为y =52x ,且与椭圆x 212+y 23=1有公共焦点,则C 的方程为( )A.x 28-y 210=1 B.x 24-y 25=1C.x 25-y 24=1 D.x 24-y 23=1 答案 B 解析 由y =52x ,可得b a =52.① 由椭圆x 212+y 23=1的焦点为(3,0),(-3,0),可得a 2+b 2=9.② 由①②可得a 2=4,b 2=5. 所以C 的方程为x 24-y 25=1.故选B.【变式探究】(1)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右焦点为F 1,F 2,左、右顶点为M ,N ,过F 2的直线l交C 于A ,B 两点(异于M ,N ),△AF 1B 的周长为43,且直线AM 与AN 的斜率之积为-23,则C 的方程为( )A.x 212+y 28=1 B.x 212+y 24=1 C.x 23+y 22=1 D.x 23+y 2=1 答案 C解析 由△AF 1B 的周长为43,可知|AF 1|+|AF 2|+|BF 1|+|BF 2|=4a =43, 解得a =3,则M ()-3,0,N (3,0). 设点A (x 0,y 0)(x 0≠±3), 由直线AM 与AN 的斜率之积为-23,可得y 0x 0+3·y 0x 0-3=-23,即y 20=-23(x 20-3),①又x 203+y 20b 2=1,所以y 20=b 2⎝ ⎛⎭⎪⎫1-x 203,②由①②解得b 2=2.所以C 的方程为x 23+y 22=1.(2)已知以圆C :(x -1)2+y 2=4的圆心为焦点的抛物线C 1与圆C 在第一象限交于A 点,B 点是抛物线C 2:x 2=8y 上任意一点,BM 与直线y =-2垂直,垂足为M ,则|BM |-|AB |的最大值为( ) A .1 B .2 C .-1 D .8 答案 A【感悟提升】(1)准确把握圆锥曲线的定义和标准方程及其简单几何性质,注意当焦点在不同坐标轴上时,椭圆、双曲线、抛物线方程的不同表示形式.(2)求圆锥曲线方程的基本方法就是待定系数法,可结合草图确定.【变式探究】(1)已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,以F 1,F 2为直径的圆与双曲线渐近线的一个交点为()3,4,则双曲线的方程为( ) A.x 216-y 29=1 B.x 23-y 24=1 C.x 24-y 23=1 D.x 29-y 216=1 答案 D解析 ∵点(3,4)在以|F 1F 2|为直径的圆上, ∴c =5,可得a 2+b 2=25.①又∵点(3,4)在双曲线的渐近线y =b ax 上,∴b a =43.② ①②联立,解得a =3且b =4, 可得双曲线的方程为x 29-y 216=1.(2)如图,过抛物线y 2=2px (p >0)的焦点F 的直线l 交抛物线于点A ,B ,交其准线于点C ,若|BC |=2|BF |,且|AF |=3,则此抛物线方程为( )A .y 2=9x B .y 2=6x C .y 2=3x D .y 2=3x 答案 C解析 如图分别过点A ,B 作准线的垂线,分别交准线于点E ,D ,设准线交x 轴于点G .设||BF =a ,则由已知得||BC =2a ,由抛物线定义,得||BD =a ,故∠BCD =30°, 在Rt△ACE 中,∵||AE =|AF |=3,||AC =3+3a ,|AC |=2|AE |, ∴3+3a =6,从而得a =1,||FC =3a =3. ∴p =||FG =12||FC =32,因此抛物线方程为y 2=3x ,故选C. 题型二 圆锥曲线的几何性质例2、 (2018·北京)已知椭圆M :x 2a 2+y 2b 2=1(a >b >0),双曲线N :x 2m 2-y 2n 2=1.若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点,则椭圆M 的离心率为________;双曲线N 的离心率为________. 答案3-1 2解析 方法一 双曲线N 的渐近线方程为y =±nm x ,则n m=tan 60°=3,∴双曲线N 的离心率e 1满足e 21=1+n 2m2=4,∴e 1=2. 由⎩⎪⎨⎪⎧y =3x ,x 2a 2+y 2b2=1,得x 2=a 2b 23a 2+b2.如图,设D 点的横坐标为x ,由正六边形的性质得|ED |=2x =c ,∴4x 2=c 2. ∴4a 2b 23a 2+b2=a 2-b 2,得3a 4-6a 2b 2-b 4=0, ∴3-6b 2a2-⎝ ⎛⎭⎪⎫b 2a 22=0,解得b2a2=23-3.∴椭圆M 的离心率e 2满足e 22=1-b 2a2=4-2 3.∴e 2=3-1.方法二 双曲线N 的渐近线方程为y =±n mx , 则n m=tan 60°= 3.又c 1=m 2+n 2=2m ,∴双曲线N 的离心率为c 1m=2. 如图,连接EC ,由题意知,F ,C 为椭圆M 的两焦点, 设正六边形的边长为1,则|FC |=2c 2=2,即c 2=1. 又E 为椭圆M 上一点,则|EF |+|EC |=2a ,即1+3=2a , ∴a =1+32.∴椭圆M 的离心率为c 2a =21+3=3-1.【变式探究】(2018·全国Ⅰ)设抛物线C :y 2=4x 的焦点为F ,过点(-2,0)且斜率为23的直线与C 交于M ,N两点,则FM →·FN →等于( ) A .5 B .6 C .7 D .8 答案 D【变式探究】(2018·全国Ⅰ)已知双曲线C :x 23-y 2=1,O 为坐标原点,F 为C 的右焦点,过F 的直线与C的两条渐近线的交点分别为M ,N .若△OMN 为直角三角形,则|MN |等于( ) A.32 B .3 C .2 3 D .4 答案 B解析 由已知得双曲线的两条渐近线方程为y =±13 x .设两渐近线的夹角为2α,则有tan α=13=33, 所以α=30°. 所以∠MON =2α=60°.又△OMN 为直角三角形,由于双曲线具有对称性,不妨设MN ⊥ON ,如图所示.在Rt△ONF 中,|OF |=2,则|ON |= 3.则在Rt△OMN 中,|MN |=|ON |·tan 2α=3·tan 60°=3. 故选B.【方法技巧】圆锥曲线几何性质的应用技巧1.求解与椭圆曲线几何性质有关的问题时要结合图形进行分析,即使不画出图形,思考时也要联想到图形.当涉及顶点、焦点、长轴、短轴等椭圆的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.2.解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a ,b ,c 的方程(组)或不等式(组),再根据a ,b ,c 的关系消掉b 得到a ,c 的关系式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.【变式探究】(2017·全国Ⅱ)若双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线被圆(x -2)2+y 2=4所截得的弦长为2,则双曲线C 的离心率为________. 答案 2解析 设双曲线的一条渐近线方程为y =b ax , 圆的圆心为(2,0),半径为2,由弦长为2,得圆心到渐近线的距离为22-12= 3.由点到直线的距离公式,得|2b |a 2+b2=3,解得b 2=3a 2.所以双曲线C 的离心率e =ca =c 2a 2=1+b 2a2=2. 【变式探究】(1)设F 1,F 2分别是椭圆E :x 2a 2+y 2b2=1(a >b >0)的左、右焦点,过点F 1的直线交椭圆E 于A ,B两点,若△AF 1F 2的面积是△BF 1F 2面积的三倍,cos∠AF 2B =35,则椭圆E 的离心率为( )A.12B.23C.32D.22 答案 D解析 设|F 1B |=k ()k >0, 依题意可得|AF 1|=3k ,|AB |=4k , ∴|AF 2|=2a -3k ,|BF 2|=2a -k . ∵cos∠AF 2B =35,在△ABF 2中,由余弦定理可得|AB |2=|AF 2|2+|BF 2|2-2|AF 2||BF 2|cos∠AF 2B , ∴(4k )2=(2a -3k )2+(2a -k )2-65(2a -3k )(2a -k ),化简可得(a +k )(a -3k )=0,而a +k >0,故a -3k =0,a =3k , ∴|AF 2|=|AF 1|=3k ,|BF 2|=5k , ∴|BF 2|2=|AF 2|2+|AB |2,∴AF 1⊥AF 2,∴△AF 1F 2是等腰直角三角形. ∴c =22a ,椭圆的离心率e =c a =22. (2)已知双曲线M :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,||F 1F 2=2c .若双曲线M 的右支上存在点P ,使a sin∠PF 1F 2=3csin∠PF 2F 1,则双曲线M 的离心率的取值范围为( )A.⎝ ⎛⎭⎪⎫1,2+73B.⎝⎛⎦⎥⎤1,2+73C .(1,2) D.(]1,2 答案 A解析 根据正弦定理可知sin∠PF 1F 2sin∠PF 2F 1=|PF 2||PF 1|,所以|PF 2||PF 1|=a 3c ,即|PF 2|=a 3c|PF 1|,||PF 1||-PF 2=2a ,所以⎝ ⎛⎭⎪⎫1-a 3c ||PF 1=2a ,解得||PF 1=6ac 3c -a ,而||PF 1>a +c ,即6ac3c -a>a +c ,整理得3e 2-4e -1<0,解得2-73<e <2+73.又因为离心率e >1,所以1<e <2+73,故选A.【感悟提升】(1)明确圆锥曲线中a ,b ,c ,e 各量之间的关系是求解问题的关键.(2)在求解有关离心率的问题时,一般并不是直接求出c 和a 的值,而是根据题目给出的椭圆或双曲线的几何特点,建立关于参数c ,a ,b 的方程或不等式,通过解方程或不等式求得离心率的值或取值范围.【变式探究】(1)(2018·全国Ⅱ)已知F 1,F 2是椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右焦点,A 是C 的左顶点,点P 在过A 且斜率为36的直线上,△PF 1F 2为等腰三角形,∠F 1F 2P =120°,则C 的离心率为( ) A.23 B.12 C.13 D.14 答案 D解析 如图,作PB ⊥x 轴于点B .由题意可设|F 1F 2|=|PF 2|=2,则c =1, 由∠F 1F 2P =120°, 可得|PB |=3,|BF 2|=1, 故|AB |=a +1+1=a +2, tan∠PAB =|PB ||AB |=3a +2=36,解得a =4,所以e =c a =14.故选D.(2)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的焦距为2c ,直线l 过点⎝ ⎛⎭⎪⎫23a ,0且与双曲线C 的一条渐近线垂直,以双曲线C 的右焦点为圆心,半焦距为半径的圆与直线l 交于M ,N 两点,若|MN |=423c ,则双曲线C 的渐近线方程为( )A .y =±2xB .y =±3xC .y =±2xD .y =±4x答案 B解析 方法一 由题意可设渐近线方程为y =b ax , 则直线l 的斜率k l =-a b,直线l 的方程为y =-a b ⎝ ⎛⎭⎪⎫x -23a ,整理可得ax +by -23a 2=0.焦点(c,0)到直线l 的距离d =⎪⎪⎪⎪⎪⎪ac -23a 2a 2+b 2=⎪⎪⎪⎪⎪⎪ac -23a 2c,则弦长为2c 2-d 2=2c 2-⎝ ⎛⎭⎪⎫ac -23a 22c 2=423c ,整理可得c 4-9a 2c 2+12a 3c -4a 4=0, 即e 4-9e 2+12e -4=0,分解因式得()e -1()e -2()e 2+3e -2=0.又双曲线的离心率e >1,则e =c a=2,所以b a =c 2-a 2a 2= ⎝ ⎛⎭⎪⎫c a 2-1=3, 所以双曲线C 的渐近线方程为y =±3x . 方法二 圆心到直线l 的距离为c 2-⎝⎛⎭⎪⎫223c 2=c3, ∴⎪⎪⎪⎪⎪⎪ac -23a 2c=c3,∴c 2-3ac +2a 2=0, ∴c =2a ,b =3a , ∴渐近线方程为y =±3x . 题型三 直线与圆锥曲线例3、(2018·全国Ⅱ)设抛物线C :y 2=4x 的焦点为F ,过F 且斜率为k (k >0)的直线l 与C 交于A ,B 两点,|AB |=8.(1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为y -2=-(x -3),即y =-x +5.设所求圆的圆心坐标为(x 0,y 0),则⎩⎪⎨⎪⎧ y 0=-x 0+5,(x 0+1)2=(x 0-y 0-1)22+16, 解得⎩⎪⎨⎪⎧ x 0=3,y 0=2或⎩⎪⎨⎪⎧ x 0=11,y 0=-6. 因此所求圆的方程为(x -3)2+(y -2)2=16或(x -11)2+(y +6)2=144. 【变式探究】(2018·天津)设椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,上顶点为B .已知椭圆的离心率为53,点A 的坐标为(b,0),且|FB |·|AB |=6 2.(1)求椭圆的方程;(2)设直线l :y =kx (k >0)与椭圆在第一象限的交点为P ,且l 与直线AB 交于点Q .若|AQ ||PQ |=524sin∠AOQ (O 为原点),求k 的值.解 (1)设椭圆的焦距为2c ,由已知有 c 2a 2=59, 又由a 2=b 2+c 2,可得2a =3b .由已知可得|FB |=a ,|AB |=2b ,由|FB |·|AB |=62,可得ab =6,从而a =3,b =2.所以椭圆的方程为x 29+y 24=1. (2)设点P 的坐标为(x 1,y 1),点Q 的坐标为(x 2,y 2).由已知有y 1>y 2>0,故|PQ |sin∠AOQ =y 1-y 2. 又因为|AQ |=y 2sin∠OAB ,而∠OAB =π4, 所以|AQ |=2y 2.由|AQ ||PQ |=524sin∠AOQ ,可得5y 1=9y 2. 由方程组⎩⎪⎨⎪⎧ y =kx ,x 29+y 24=1,消去x ,可得y 1=6k9k 2+4 . 由题意求得直线AB 的方程为x +y -2=0,由方程组⎩⎪⎨⎪⎧ y =kx ,x +y -2=0,消去x ,可得y 2=2k k +1.由5y 1=9y 2,可得5(k +1)=39k 2+4,两边平方,整理得56k 2-50k +11=0,解得k =12或k =1128. 所以k 的值为12或1128. 【变式探究】[2018·全国卷Ⅰ]设抛物线C :y 2=4x 的焦点为F ,过点(-2,0)且斜率为23的直线与C 交于M ,N 两点,则FM →·FN →=( )A .5B .6C .7D .8【解析】由题意知直线MN 的方程为y =23(x +2), 联立直线与抛物线的方程,得⎩⎪⎨⎪⎧ y =23x +,y 2=4x ,解得⎩⎪⎨⎪⎧ x =1,y =2或⎩⎪⎨⎪⎧ x =4,y =4.不妨设M 为(1,2),N 为(4,4).又∵抛物线焦点为F (1,0),∴FM →=(0,2),FN →=(3,4).∴FM →·FN →=0×3+2×4=8.故选D.【答案】D【方法技巧】解决直线与圆锥曲线位置关系问题的方法1.通法:将直线l 的方程Ax +By +C =0(A ,B 不同时为0)代入双曲线E 的方程F (x ,y )=0,消去y (也可以消去x )得到一个关于变量x (或变量y )的一元二次方程.解此方程或利用根与系数的关系整体代入的思想解题.2.点差法:在涉及直线与圆锥曲线相交弦的中点与斜率问题时,常把直线与圆锥曲线的交点坐标代入圆锥曲线方程,作差后结合已知条件进行转化求解.提醒:利用点差法,对求出的结果要验证其是否满足相交的要求,即Δ>0.【变式探究】(2017·天津)已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F (-c,0),右顶点为A ,点E 的坐标为(0,c ),△EFA 的面积为b 22. (1)求椭圆的离心率;学_科网(2)设点Q 在线段AE 上,|FQ |=3c 2,延长线段FQ 与椭圆交于点P ,点M ,N 在x 轴上,PM ∥QN ,且直线PM 与直线QN 间的距离为c ,四边形PQNM 的面积为3c .①求直线FP 的斜率;②求椭圆的方程.解 (1)设椭圆的离心率为e .由已知可得12(c +a )c =b 22. 又由b 2=a 2-c 2,可得2c 2+ac -a 2=0,即2e 2+e -1=0,解得e =-1或e =12. 又因为0<e <1,所以e =12.所以椭圆的离心率为12. (2)①依题意,设直线FP 的方程为x =my -c (m >0),则直线FP 的斜率为1m. 由(1)知a =2c ,可得直线AE 的方程为x 2c +y c=1, 即x +2y -2c =0,与直线FP 的方程联立,可得x =(2m -2)c m +2,y =3c m +2, 即点Q 的坐标为⎝ ⎛⎭⎪⎫(2m -2)c m +2,3c m +2. 由已知|FQ |=3c 2, 有⎣⎢⎡⎦⎥⎤(2m -2)c m +2+c 2+⎝ ⎛⎭⎪⎫3c m +22=⎝ ⎛⎭⎪⎫3c 22, 整理得3m 2-4m =0,所以m =43(m =0舍去), 即直线FP 的斜率为34. ②由a =2c ,可得b =3c ,故椭圆方程可以表示为x 24c 2+y 23c 2=1. 由①得直线FP 的方程为3x -4y +3c =0,与椭圆方程联立得⎩⎪⎨⎪⎧ 3x -4y +3c =0,x 24c 2+y 23c 2=1,消去y ,整理得7x 2+6cx -13c 2=0,解得x =-13c 7(舍去)或x =c .因此可得点P ⎝ ⎛⎭⎪⎫c ,3c 2,进而可得|FP |= (c +c )2+⎝ ⎛⎭⎪⎫3c 22=5c 2, 所以|PQ |=|FP |-|FQ |=5c 2-3c 2=c . 由已知,线段PQ 的长即为PM 与QN 这两条平行直线间的距离,故直线PM 和QN 都垂直于直线FP . 因为QN ⊥FP , 所以|QN |=|FQ |·tan∠QFN =3c 2×34=9c 8, 所以△FQN 的面积为12|FQ ||QN |=27c 232. 同理△FPM 的面积等于75c 232. 由四边形PQNM 的面积为3c ,得75c 232-27c 232=3c , 整理得c 2=2c .又由c >0,得c =2. 所以椭圆的方程为x 216+y 212=1. 【变式探究】已知椭圆x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1,F 2,过F 1的直线交椭圆于A ,B 两点. (1)若直线AB 与椭圆的长轴垂直,|AB |=12a ,求椭圆的离心率; (2)若直线AB 的斜率为1,|AB |=2a 3a 2+b2,求椭圆的短轴与长轴的比值. 解 (1)由题意可知,直线AB 的方程为x =-c ,∴|AB |=2b 2a =12a , 即a 2=4b 2, 故e =c a =a 2-b 2a 2=1-b 2a 2=32. (2)设F 1(-c,0),则直线AB 的方程为y =x +c , 联立⎩⎪⎨⎪⎧y =x +c ,x 2a 2+y2b2=1,消去y , 得(a 2+b 2)x 2+2a 2cx +a 2c 2-a 2b 2=0, Δ=4a 4c 2-4a 2(a 2+b 2)(c 2-b 2)=8a 2b 4.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-2a 2c a 2+b 2,x 1x 2=a 2(c 2-b 2)a 2+b 2, ∴|AB |=1+1|x 1-x 2| =2·(x 1+x 2)2-4x 1x 2=2·8a 2b 4a 2+b 2 =4ab 2a 2+b 2=2a 3a 2+b 2, ∴a 2=2b 2,∴b 2a 2=12, ∴2b 2a =22,即椭圆的短轴与长轴之比为22. 【感悟提升】解决直线与圆锥曲线问题的通法是联立方程,利用根与系数的关系,设而不求思想,弦长公式等简化计算;涉及中点弦问题时,也可用“点差法”求解.【变式探究】如图,过抛物线M :y =x 2上一点A (点A 不与原点O 重合)作抛物线M 的切线AB 交y 轴于点B ,点C 是抛物线M 上异于点A 的点,设G 为△ABC 的重心(三条中线的交点),直线CG 交y 轴于点D .设点A (x 0,x 20)(x 0≠0).(1)求直线AB 的方程;(2)求|OB ||OD |的值. 解 (1)因为y ′=2x ,所以直线AB 的斜率k =y ′=2x 0.所以直线AB 的方程y -x 20=2x 0(x -x 0),即y =2x 0x -x 20,即直线AB 的方程为2x 0x -y -x 20=0.因为G 为△ABC 的重心,所以y 1=3y 2.由根与系数的关系,得y 1+y 2=4y 2=1-mx 0m 2, y 1y 2=3y 22=x 204m 2. 所以(1-mx 0)216m 4=x 2012m 2, 解得mx 0=-3±23,满足Δ>0. 所以点D 的纵坐标y D =-x 02m =x 206±43, 故|OB ||OD |=|y B ||y D |=43±6.。
2019年高考数学理试题分类汇编:圆锥曲线(含答案)

2019年高考数学理试题分类汇编:圆锥曲线(含答案)2019年高考数学理试题分类汇编——圆锥曲线一、选择题1.(2019年四川高考)设O为坐标原点,P是以F为焦点的抛物线y=2px(p>0)上任意一点,M是线段PF上的点,且PM=2MF,则直线OM的斜率的最大值为2/3.(答案:C)2.(2019年天津高考)已知双曲线x^2/4 - y^2/9 = 1(b>0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A、B、C、D四点,四边形ABCD的面积为2b,则双曲线的方程为x^2/4 - y^2/9 = 1.(答案:D)3.(2019年全国I高考)已知方程x^2/n^2 - y^2/m^2 = 1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是(-1,3)。
(答案:A)4.(2019年全国I高考)以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点。
已知|AB|=42,|DE|=25,则C的焦点到准线的距离为4.(答案:B)5.(2019年全国II高考)圆(x-1)^2 + (y-4)^2 = 13的圆心到直线ax+y-1=0的距离为1,则a=-2/3.(答案:A)6.(2019年全国II高考)已知F1,F2是双曲线E:x^2/4 -y^2/2 = 1的左、右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=1/3,则E的离心率为2/3.(答案:A)7.(2019年全国III高考)已知O为坐标原点,F是椭圆C:x^2/a^2 + y^2/b^2 = 1(a>b>0)的左焦点,A、B分别为C的左、右顶点。
P为C上一点,且PF⊥x轴。
过点A的直线l与线段PF交于点M,与y轴交于点E。
若直线BM经过OE的中点,则C的离心率为1/3.(答案:A)8.(2019年浙江高考)已知椭圆 + y^2/(m^2-1) = 1(m>1)与双曲线- y^2/(n^2-1) = 1(n>0)的焦点重合,e1,e2分别为m,n,则e1+e2=3.(答案:C)解析】Ⅰ)由题意可知,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,根据离心率的定义可得:$\frac{c}{a}=\frac{\sqrt{3}}{2}$,其中$c$为椭圆的焦距之一,即$2c$为椭圆的长轴长度,$a$为椭圆的半长轴长度,$b$为椭圆的半短轴长度,则有:$$\frac{2c}{2a}=\frac{\sqrt{3}}{2}$$ 即:$$\frac{c}{a}=\frac{\sqrt{3}}{4}$$ 又因为焦点$F$在椭圆的一个顶点上,所以该顶点的坐标为$(a,0)$,即$2c=2a$,代入上式可得:$$\frac{b}{a}=\frac{1}{2}$$ 又因为椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,代入$\frac{b}{a}=\frac{1}{2}$可得:$$\frac{x^2}{a^2}+\frac{4y^2}{a^2}=1$$ 即:$$x^2+4y^2=a^2$$ (Ⅱ)(i)设椭圆C的另一个顶点为$V$,则$OV$为椭圆的长轴,$OF$为椭圆的短轴,且$OV=2a$,$OF=\sqrt{3}a$。
2019年数学圆锥曲线分析

2019年高考各地区圆锥曲线汇总(2019,浙江,21)如图,已知点)0,1(F 为抛物线)0(22>=p px y 的焦点,过点F 的直线交抛物线于B A ,两点,点C 在抛物线上,使得△ABC 的重心G 在x 轴上,直线AC 交x 轴于Q ,且Q 在F 的右侧,记△AFG ,△CQG的面积分别为21,S S .(Ⅰ)求p 的值及抛物线的准线方程;(Ⅱ)求21S S 的最小值及此时点G 的坐标.解析:(Ⅰ)由题得12=p ,及2=p 所以抛物线的准线方程为12-=-=p x (Ⅱ)由(Ⅰ)知抛物线的方程为xy 42=设)2,(2t t A ,所以122-=t t k AF ,故121:2+-=y tt x l AF 联立⎪⎩⎪⎨⎧+-==121422y t t x x y 得04)1(222=---y t t y 设),(22y x B ,),(33y x C 所以422-=⋅y t ,即t y 22-=,又B 在抛物线上,所以221t x =所以⎪⎭⎫ ⎝⎛-t tB 2,12因为G 为△ABC 的重心,由坐标重心公式得⎪⎪⎪⎪⎭⎫ ⎝⎛+-++322,313322y t t x t t G 由题得0223=+-y t t ,所以t ty 223-=因为C 在抛物线上,所以231⎪⎭⎫ ⎝⎛-=t t x ,故⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-t t t t C 22,12所以⎪⎪⎭⎫ ⎝⎛+-0,3222224t t t G 因为t t t t t t t k AC 2122222=⎪⎭⎫ ⎝⎛--+-=所以)(22:2t x t t y l AC -=-,令0=y ,得12-=t x 所以()0,12-t Q 由于Q 在F 的右侧,故112>-t ,即22>t |2||13222|212241t tt t S ⋅-+-⋅=t tt t t t S 22322212122422-⋅+---⋅=所以122124242421---=--=t t t t t S S 令)0(22>-=m t m ,22+=m t 所以231324123412342221+=+-≥++-=++-=mm m m m S S 当且仅当3=m 时,不等式取等号所以21S S 的最小值为231+,此时)0,2(Q (2019,全国Ⅰ文,21)已知点B A ,关于坐标原点O 对称,4||=AB ,M 过点B A ,且与直线02=+x 相切.(Ⅰ)若A 在直线上0=+y x ,求M 的半径;(Ⅱ)是否存在定点P ,使得当A 运动时,||||MP MA -为定值?并说明理由.解析:(Ⅰ)设圆M 的半径为r由于圆M 经过B A ,,所以圆心M 经过B A ,的垂直平分线,又A 经过0=+y x ,所以圆心M 经过直线xy =设),(a a M ,由于圆M 与2-=x 相切,所以ra =+|2|因为AB 中点O 与M 共线,所以AOMO ⊥由题可知2=AO ,所以2224a r +=联立⎩⎨⎧+==+2224|2|a r r a ,解得当0=a 时,4=r 当4=a 时,6=r 所以圆M 的半径为4或6(Ⅱ)设),(y x M ,由题得rx =+|2|又AO MO ⊥,所以2224ry x =++所以222)2(4+=++x y x ,化简得xy 42=故M 的轨迹为抛物线所以存在定点)0,1(P ,动点A 在直线1-=x ,使得||||MA MP -为定值,定值为0(2019,全国Ⅰ理,19)已知抛物线x y C 3:2=的焦点为F ,斜率为23的直线l 与C 的交点为B A ,,与x 轴的交点为P .(Ⅰ)若4||||=+BF AF ,求l 的方程;(Ⅱ)若3AP PB = ,求||AB .解析:(Ⅰ)设直线m y x l +=32:,设),(),,(2211y x B y x A 联立⎪⎩⎪⎨⎧=+=x y m y x 3322得0322=--m y y 所以⎩⎨⎧-=*=+(**)3)(22121m y y y y由题得254||||21=+⇒=+x x BF AF 252)(322121=++=+m y y x x 所以127=m ,所以12732:+=y x l (Ⅱ)由(Ⅰ)知m y x l +=32:,令0=y ,得m x =所以)0,(m P 由于3AP PB = ,得),(3),(2211y m x y x m -=--即*)*(*321y y -=由(*)和*)*(*得1,321-==y y 代入(**)得1=m 所以31341249414)(11||212212=+⋅+=-+⋅+=m y y y y k AB (2019,全国Ⅱ文,20)已知21,F F 是椭圆)0(1:2222>>=+b a by a x C 的两个焦点,P 为C 上一点,O 为坐标原点.(Ⅰ)若△2POF 为等边三角形,求C 的离心率;(Ⅱ)如果存在点P ,使得21PF PF ⊥,且△21PF F 的面积等于16,求b 的值和a 的取值范围.解析:(Ⅰ)连接1PF ,由题得△2POF 为等边三角形,所以 9021=∠PF F 因为c PF OF ==22,又因为aPF PF 221=+所以ca PF -=21所以2212221F F PF PF =+,即02222=-+a ac c 所以0222=-+e e ,解得13-=e (Ⅱ)设),(00y x P 由题知(*)162||210=c y因为21PF PF ⊥,所以10000-=-⋅+cx y c x y ,即(**)22020c y x =+又因为P 在椭圆上,所以*)*(*1220220=+by a x 又*)*(*(**),(*),可得4=b ,)()(2222022b c a x b a -=-,所以22bc ≥因为3222222=≥+=b c b a ,所以24≥a ,当且仅当c b =取等号所以),24[+∞∈a (2019,全国Ⅱ理,21)已知点)0,2(-A ,)0,2(B ,动点),(y x M 满足直线AM 与BM 的斜率之积为21-,记M 的轨迹为曲线C .(Ⅰ)求C 的方程,并说明C 是什么曲线;(Ⅱ)过坐标原点的直线交C 于Q P ,两点,点P 在第一象限,x PE ⊥轴,垂足为E 连接QE 并延长交C 于点G .(i )证明:△PQG 是直角三角形;(ii )求△PQG 面积的最大值.解析:(Ⅰ)由题得21-=⋅BM AM k k ,即2122-=-⋅+x y x y 整理得)2|(|12422≠=+x y x 所以C 为椭圆(Ⅱ)(i )设直线kxy l PQ =:联立⎪⎩⎪⎨⎧=+=12422y x kx y 得2212k x +±=设)0,(),,(),,(11111x E kx x Q kx x P --所以2211k x kx k QE ==,则)(2:1x x k y l QE -=联立⎪⎪⎩⎪⎪⎨⎧=+-=124)(2221y x x x k y 得=-+-+42)21(121222x k x x k x k 设),(22y x G 所以2121221k x k x x +=+-,即22122)23(k k x x ++=,则21322k x k y +=所以⎪⎪⎭⎫ ⎝⎛+++2132212,2)23(k x k k k x G 则k x k k x kx k x k k PG 12)23(212211213-=-++-+=所以1-=⋅PQ PG k k ,所以△PQG 为直角三角形(ii )不妨设01>x ,0>k ,所以2112||k x PQ +=22122112212|2)23(|1||k k kx k k x x k PG ++=++-+=所以1)1(2)1(8)2)(21()1(82121221||||21222222121+++=+++=++⋅+⋅==kk k k k k k k k k kx k x PG PQ S PQG △令)2(1≥+=t k k t ,所以t t t t S PQG 1281282+=+=△设t t t f 21)(+=,则212)(tt f -='所以当),2(+∞∈t 时0)(>'t f ,)(t f 单调递增所以29)2()(=≥f t f 所以916298=≤PQG S △所以△PQG 面积的最大值为916(2019,全国Ⅲ,21)已知曲线2:2x y C =,D 为直线21-=y 上的动点,过D 作C 的两条切线,切点分别为B A ,.(Ⅰ)证明:直线AB 过定点;(2019,全国Ⅲ文,21(Ⅱ))(Ⅱ)若以)25,0(E 为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求该圆的方程.(2019,全国Ⅲ理,21(Ⅱ))(Ⅲ)若以)25,0(E 为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积解析:(Ⅰ)设21,(0-x D ,易得直线AB 的方程为210+=x x y 当0=x 时,21=y 所以直线AB 过定点)21,0((Ⅱ)设),(),,(2211y x B y x A 联立⎪⎩⎪⎨⎧+==21202x x y y x 得01202=--x x x 所以0212x x x =+,121-=x x 121)(2021021+=++=+x x x x y y 所以AB 的中点212,(200+x x P 设该圆的半径为r 所以⎪⎪⎩⎪⎪⎨⎧=-++=+r x x r x 2202020)25212(12,解得10±=x ,00=x 当00=x 时,2=r ,所以圆的方程为4)25(22=-+y x当10±=x 时,2=r ,所以圆的方程为225(22=-+y x (Ⅲ)=-+=||1||212x x k AB )1(220x +设E 点到直线AB 的距离为1d ,D 点到直线AB 的距离为2d 所以()21||21d d AB S +=由(Ⅱ)知00=x 或10±=x 当00=x 时21:=y l AB 所以2||=AB ,21=d ,12=d 所以33221=⨯⨯=S 当10±=x 时,21:+±=x y l AB 所以4||=AB ,2221=+d d 所以24=S (2019,北京文,19)已知椭圆1:2222=+by a x C 的右焦点为)0,1(,且经过点()1,0A .(Ⅰ)求椭圆C 的方程;(Ⅱ)设O 为原点,直线)1(:±≠+=t t kx y l 与椭圆C 交于两个不同点Q P ,,直线AP 与x 轴交于点M ,直线AQ 与x 轴交于点N ,若2||||=ON OM ,求证:直线l 经过定点解析:(Ⅰ)由题得1,1==b c ,所以2=a 所以椭圆C 的方程为1222=+y x (Ⅱ)设),(),,(2211y x Q y x P 111x y k AP -=,所以x x y y l AP 1111:-=-令0=y ,则111y x x -=所以)0,1(11y x M -,同理)0,1(22y x N -联立⎪⎩⎪⎨⎧+==+t kx y y x 1222得0224)12(222=-+++t ktx x k 所以⎪⎪⎩⎪⎪⎨⎧+-=+-=+12221242221221k t x x k kt x x 有题得2|1||1|2211=--y x y x 所以212))((22121221=+-++-+t t x x k kt x x k x x 212124)(122212222222222=+-++--++-+-t t k kt k kt k t k k t 整理得0=t 所以kx y l =:,所以l 恒过定点)0,0((2019,北京理,18)已知抛物线py x C 2:2-=,经过点)1,2(-.(Ⅰ)求抛物线C 的方程及其准线方程;(Ⅱ)设O 为原点,过抛物线C 的焦点作直线不为0的直线l 交抛物线C 于N M ,两点,直线1-=y 分别交直线ON OM ,于点A 和B ,求证:以AB 为直径的圆经过y 轴的两个定点.解析:(Ⅰ)因为C 经过)1,2(-所以p 24=,即2=p 所以y x C 4:2-=准线方程为1=y (Ⅱ)设),(),,(2211y x N y x M ,设直线1:-=kx y l MN 联立⎩⎨⎧-=-=yx kx y 412得0442=-+kx x 所以k x x 421-=+,421-=x x 因为11x y k OM =,所以x x y y l OM 11:=令1-=y ,得11y x x -=,故⎪⎪⎭⎫ ⎝⎛--1,11y x A 同理⎪⎪⎭⎫ ⎝⎛--1,22y x B 设y 轴上点),0(t Q ,因为圆经过Q ,所以0QA QB ⋅= 11,1x QA t y ⎛⎫=--- ⎪⎝⎭ ,22,1x QB t y ⎛⎫=--- ⎪⎝⎭所以0)1(22121=++t y y x x ,4)1(2=+t 解得3-=t 或1=t 所以以AB 的圆经过y 轴两个定点)1,0(),3,0(-(2019,江苏,17)如图,在平面直角坐标系xOy 中,椭圆)0(1:2222>>=+b a by a x C 的焦点为)0,1(1-F ,)0,1(2F ,过2F 作x 轴的垂线l ,在x 轴的上方,l 与圆22224)1(:a y x F =+-交于点A ,与椭圆C 交于点D ,连接1AF 并延长交圆2F 于点B ,连接2BF 交椭圆C 于点E ,连接1DF .已知251=DF .(Ⅰ)求椭圆C 的标准方程;(Ⅱ)求点E 的坐标.解析:(Ⅰ)有题得1=c 因为ab DF 22||=,221=F F 所以425424=+a b ,所以a b 322=又因为222c a b -=,所以02322=--a a ,解得2=a ,3=b 所以椭圆C 的标准方程为13422=+y x (Ⅱ)易得)4,1(A ,所以2241==AF k 所以22:1+=x y l AF 联立⎩⎨⎧=+-+=16)1(2222y x x y 得011652=-+x x 所以511-=B A x x ,即511-=B x ,512-=B y 所以⎪⎭⎫ ⎝⎛--512,511B ,则4351115122=+=BF k ,所以)1(43:2-=x y l BF 联立⎪⎪⎩⎪⎪⎨⎧-==+)1(4313422x y y x 得013672=--x x 解得1-=x 或713=x 因为E 是直线2BF 与椭圆的交点,所以1-=x 所以23-=y ,所以E 点坐标为⎪⎭⎫ ⎝⎛--23,1(2019,天津文,19)设椭圆)0(12222>>=+b a by a x 的左焦点为F ,左顶点为A ,上顶点为B .已知||2||3OB OA =(O 为原点).(Ⅰ)求椭圆的离心率;(Ⅱ)设经过点F 且斜率为43的直线l 与椭圆在x 轴上方的交点为P ,圆C 同时与x 轴和直线l 相切,圆心C 在直线4=x 上,且AP OC //,求椭圆的方程.解析:(Ⅰ)由题得b a 23=,即2243ba =又因为222cb a +=,所以224ca =所以椭圆的离心率21=e (Ⅱ)设圆心),4(m C ,圆的半径为r由(Ⅰ)得c a 2=,c b 3=,所以椭圆的方程为1342222=+cy c x 设)(43:c x y l +=联立⎪⎪⎩⎪⎪⎨⎧=++=134)(432222c y c x c x y 得0136722=-+c cx x 解得c x =或c x 713-=当c x =时,c y 23=,满足题意当c x 713-=时,c y 149-=,不符合题意故⎪⎭⎫ ⎝⎛c c P 23,因为AP OC //,所以APOC k k =)0,2()0,(c A a A -⇒-所以cc c m 2234+=,解得2=m 因为圆C 与x 轴相切,所以2=r 所以圆的方程为()()42422=-+-y x又因为圆C 与直线l 相切,所以2534=+c ,解得2=c 所以32,4==b a 所以椭圆的标准方程为1121622=+y x (2019,天津理,18)设椭圆)0(12222>>=+b a by a x 的左焦点为F ,上顶点为B ,已知椭圆的短轴长为4,离心率为55.(Ⅰ)求椭圆的方程;(Ⅱ)设点P 在椭圆上,且异于椭圆的上,下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上,若||||OF ON =(O 为原点),且MN OP ⊥,求直线PB 的斜率.解析:(Ⅰ)由题得55,2==a c b 又因为222c b a +=,可得52=a 所以椭圆的方程为14522=+y x (Ⅱ)由题得)2,0(B ,设),(00y x P 所以002x y k PB -=,所以22:00+-=x x y y l PB 令0=y ,解得0022y x x -=,即⎪⎪⎭⎫ ⎝⎛-0,2200y x M 因为1||=OF ,N 在y 轴负半轴,且||||ON OF =所以)1,0(-N 由于MN OP ⊥,所以0OP MN ⋅= 则(*)2202020y y x -=因为P 在椭圆上,所以(**)1452020=+y x 由(*)和(**)得710,730200-=±=y x 所以5302±=PB k (2019,上海,20)已知椭圆14822=+y x ,21,F F 为其左、右焦点,直线l 过点2F 且交椭圆于B A ,两点.(Ⅰ)AB 垂直于x 轴,求AB ;(Ⅱ)若 901=∠AB F ,且A 在x 轴上方,求B A ,两点坐标;(Ⅲ)直线1AF 交y 轴于点M ,直线1BF 交y 轴于点N ,问:是否存在直线l ,使得MN F AB F S S 11△△=,若存在,求出直线l 的方程,若不存在,请说明理由.解析:(Ⅰ)由于2,22==b a 所以222282||2===a b AB (Ⅱ)设),(),,(2211y x B y x A 由题得120AF AF ⋅= 所以42121=+y x 又因为A 在椭圆上,所以1482121=+y x 联立可得2,011==y x 所以直线AB 的方程为xy -=2联立⎪⎩⎪⎨⎧=+-=148222y x x y 得⎩⎨⎧==20y x 和⎪⎪⎩⎪⎪⎨⎧-==3238y x 所以)2,0(A ,⎪⎭⎫ ⎝⎛-32,38B (Ⅲ)设直线AB 为myx +=2联立⎪⎩⎪⎨⎧=++=148222y x my x 得044)2(22=-++my y m 所以⎪⎪⎩⎪⎪⎨⎧+-=+-=+2424221221m y y m m y y 2111+=x y k AF ,所以)2(2:111++=x x y y l AF 令0=x ,则2211+=x y y 所以⎪⎪⎭⎫ ⎝⎛+22,011x y M ,同理⎪⎪⎭⎫ ⎝⎛+22,022x y N 所以|16)(4|||8|2222|2|2222|212121221221122111+++-=+-+=+-+=y y m y y m y y x y x y x y x y S MN F △因为||1||11||212212y y m y y k AB -+=-+=,点1F 到直线AB 的距离214m d +=所以||2211y y S AB F -=△由题得||2|16)(4|||8212121221y y y y m y y m y y -=+++-1162162442222=++-++-m m m m 所以|8||2|22m m -=+,解得3±=m所以直线AB 的方程为23+±=y x 故存在直线23:+=y x l 使得MN F AB F S S 11△△=。
2019年高考真题理科数学解析分类汇编10圆锥曲线

2019年高考真题理科数学解析分类汇编10 圆锥曲线一、选择题1.【2018高考浙江理8】如图,F 1,F 2分别是双曲线C :22221x y a b-=(a,b >0)的左、右焦点,B 是虚轴的端点,直线F 1B 与C 的两条渐近线分别交于P,Q 两点,线段PQ 的垂直平分线与x 轴交与点M ,若|MF 2|=|F 1F 2|,则C 的离心率是A.3 B。
2【答案】B【解析】由题意知直线B F 1的方程为:b x c b y +=,联立方程组⎪⎪⎩⎪⎪⎨⎧=-+=0,b y a x b x cb y 得点Q ),(ac bc a c ac --,联立方程组⎪⎪⎩⎪⎪⎨⎧=++=0,b y a x b x cb y 得点P ),(ac bc a c ac ++-,所以PQ 的中点坐标为),(222b c b c a ,所以PQ 的垂直平分线方程为:)(222bca xbc b c y --=-,令0=y ,得)1(22b ac x +=,所以c ba c 3)1(22=+,所以2222222a cb a -==,即2223c a =,所以26=e 。
故选B 2.【2018高考新课标理8】等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B两点,AB =C 的实轴长为( )()A ()B()C 4 ()D 8【答案】C【解析】设等轴双曲线方程为)0(22>=-m m y x ,抛物线的准线为4-=x ,由34=AB ,则32=A y ,把坐标)32,4(-代入双曲线方程得4121622=-=-=y x m ,所以双曲线方程为422=-y x ,即14422=-y x ,所以2,42==a a ,所以实轴长42=a ,选C.3.【2018高考新课标理4】设12F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P 为直线32ax =上一点,12PF F ∆是底角为30的等腰三角形,则E 的离心率为( )()A 12 ()B 23 ()C 34 ()D 45【答案】C【解析】因为12PF F ∆是底角为30的等腰三角形,则有PF F F 212=,,因为02130=∠F PF ,所以0260=∠D PF ,0230=∠DPF ,所以21222121F F PF D F ==,即c c c a =⨯=-22123,所以c a 223=,即43=a c ,所以椭圆的离心率为43=e ,选C. 4.【2018高考四川理8】已知抛物线关于x 轴对称,它的顶点在坐标原点O ,并且经过点0(2,)M y 。
2019年高考试题汇编理科数学--圆锥曲线
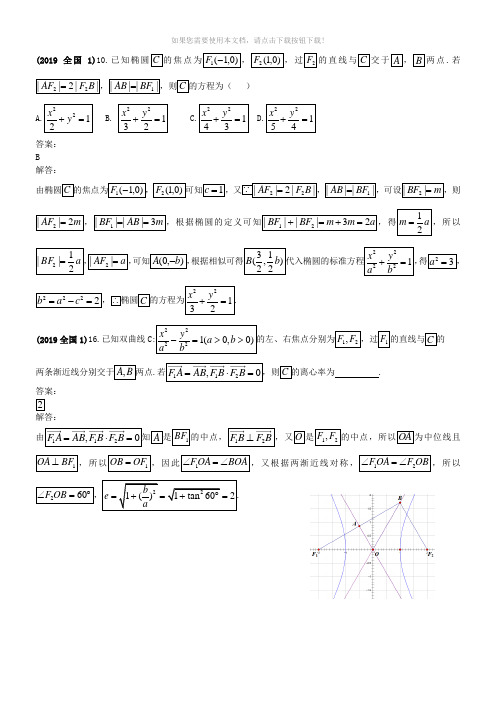
(2019全国1)10.已知椭圆C 的焦点为)0,1(1-F ,)0,1(2F ,过2F 的直线与C 交于A ,B 两点.若||2||22B F AF =,||||1BF AB =,则C 的方程为( )A.1222=+y xB. 12322=+y xC.13422=+y xD.14522=+y x答案: B解答:由椭圆C 的焦点为)0,1(1-F ,)0,1(2F 可知1=c ,又 ||2||22B F AF =,||||1BF AB =,可设m BF =||2,则m AF 2||2=,m AB BF 3||||1==,根据椭圆的定义可知a m m BF BF 23||||21=+=+,得a m 21=,所以a BF 21||2=,a AF =||2,可知),0(b A -,根据相似可得)21,23(b B 代入椭圆的标准方程12222=+by a x ,得32=a ,2222=-=c a b ,∴椭圆C 的方程为12322=+yx . (2019全国1)16.已知双曲线C:22221(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ,过1F 的直线与C 的两条渐近线分别交于,A B 两点.若112,0F A AB F B F B =⋅=,则C 的离心率为 . 答案:2 解答:由112,0F A AB F B F B =⋅=知A 是1BF 的中点,12F B F B ⊥,又O 是12,F F 的中点,所以OA 为中位线且1OA BF ⊥,所以1OB OF =,因此1FOA BOA ∠=∠,又根据两渐近线对称,12FOA F OB ∠=∠,所以260F OB ∠=︒,221()1tan 602b e a=+=+︒=.(2019全国1) 19.(1(2答案:(1(2解答:(1联立直线与抛物线的方程:消去化简整理得,,,满故直方程,即(2)(2019全国2)8. )A.2B.3C.4D.8答案:D解答:(2019全国2)11.)答案:A解答:(2019全国2)21.(1(2. 答案: 见解析 解答:(1)轴的交点).(2),则是直角三角形.②直线,x PQG ∆PQ则,∴(2019全国3)10..若)A:C:答案:A解析:故选A;(2019全国3)15.________.答案:解析:(2019全国3)21..,(1;(2,,.答案:见解析;解答:(1,由已知可得直线. (2)由(1(2019北京)4.a>b>0A. a2=2b2B. 3a2=4b2 C. a=2b D. 3a=4b【答案】B【解析】【分析】.故选B.【点睛】本题考查椭圆的标准方程与几何性质,属于容易题,注重基础知识、基本运算能力的考查.(2019北京)18.已知抛物线C:x2=−2py经过点(2,−1).(Ⅰ)求抛物线C的方程及其准线方程;(Ⅱ)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y=−1分别交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.【答案】(Ⅰ【解析】【分析】(Ⅰ)由题意结合点的坐标可得抛物线方程,进一步可得准线方程;(Ⅱ)联立准线方程和抛物线方程,结合韦达定理可得圆心坐标和圆的半径,从而确定圆的方程,最后令x=0即可证得题中的结论.【详解】(Ⅰ)故抛物线方程(Ⅱ)易知以AB即以AB为直径的圆经过y【点睛】本题主要考查抛物线方程的求解与准线方程的确定,直线与抛物线的位置关系,圆的方程的求解及其应用等知识,意在考查学生的转化能力和计算求解能力.(2019天津)5.线分别交于点A和点B,则双曲线的离心率为A. B. C. 2 D.【解析】【分析】故选D。
2019年高考数学考纲解读与热点难点突破专题18圆锥曲线的综合问题热点难点突破理含解析

圆锥曲线的综合问题1.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率e =33,左、右焦点分别为F 1,F 2,且F 2与抛物线y 2=4的焦点重合.(1)求椭圆的标准方程;(2)若过F 1的直线交椭圆于B ,D 两点,过F 2的直线交椭圆于A ,C 两点,且AC ⊥BD ,求|AC |+|BD |的最小值.解 (1)抛物线y 2=4的焦点坐标为(1,0),所以c =1,又因为e =c a =1a =33,所以a =3, 所以b 2=2,所以椭圆的标准方程为x 23+y 22=1. (2)①当直线BD 的斜率存在且≠0时,直线BD 的方程为y =(+1),代入椭圆方程x 23+y 22=1, 并化简得(32+2)2+62+32-6=0. Δ=364-4(32+2)(32-6)=48(2+1)>0恒成立.设B (1,y 1),D (2,y 2),则1+2=-6k 23k 2+2,12=3k 2-63k 2+2, |BD |=1+k 2·|1-2|=()1+k 2·[]x 1+x 22-4x 1x 2 =43()k 2+13k 2+2. 由题意知AC 的斜率为-1k, 所以|AC |=43⎝ ⎛⎭⎪⎫1k 2+13×1k2+2=43()k 2+12k 2+3.|AC |+|BD |=43()k 2+1⎝ ⎛⎭⎪⎫13k 2+2+12k 2+3 =203()k 2+12()3k 2+2()2k 2+3≥203()k 2+12⎣⎢⎡⎦⎥⎤()3k 2+2+()2k 2+322 =203()k 2+1225k 2+124=1635. 当且仅当32+2=22+3,即=±1时,上式取等号,故|AC |+|BD |的最小值为1635. ②当直线BD 的斜率不存在或等于零时,可得|AC |+|BD |=1033>1635. 综上,|AC |+|BD |的最小值为1635. 5.已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的上顶点为点D ,右焦点为F 2(1,0),延长DF 2交椭圆C 于点E ,且满足|DF 2|=3|F 2E |.(1)求椭圆C 的标准方程;(2)过点F 2作与轴不重合的直线l 和椭圆C 交于A ,B 两点,设椭圆C 的左顶点为点H ,且直线HA ,HB 分别与直线=3交于M ,N 两点,记直线F 2M ,F 2N 的斜率分别为1,2,则1与2之积是否为定值?若是,求出该定值;若不是,请说明理由.解 (1)椭圆C 的上顶点为D (0,b ),右焦点F 2(1,0),点E 的坐标为(,y ).∵|DF 2|=3|F 2E |,可得DF 2→=3F 2E →,又DF 2→=(1,-b ),F 2E →=(-1,y ),∴⎩⎪⎨⎪⎧ x =43,y =-b 3,代入x 2a 2+y 2b2=1,可得⎝ ⎛⎭⎪⎫432a 2+⎝ ⎛⎭⎪⎫-b 32b 2=1,又a 2-b 2=1,解得a 2=2,b 2=1,即椭圆C 的标准方程为x 22+y 2=1.∴y M =y 1()3+2x 1+2.同理可得y N =y 2()3+2x 2+2,∴M ,N 的坐标分别为⎝ ⎛⎭⎪⎪⎫3,y 1()3+2x 1+2,⎝ ⎛⎭⎪⎪⎫3,y 2()3+2x 2+2, ∴12=y M -03-1·y N -03-1=14y M y N =14·y 1()3+2x 1+2·y 2()3+2x 2+2=y 1y 23+224()my 1+1+2()my 2+1+2=y 1y 23+224⎣⎡⎦⎤m 2y 1y 2+()1+2m ()y 1+y 2+()1+22=-11-62m 2+24⎣⎢⎢⎡⎦⎥⎥⎤-m 2m 2+2+-2()1+2m 2m 2+2+3+22=-11-62m 2+24×6+42m 2+2=42-98. ∴1与2之积为定值,且该定值是42-98. 6.已知平面上动点P 到点F ()3,0的距离与到直线=433的距离之比为32,记动点P 的轨迹为曲线E .(1)求曲线E 的方程;(2)设M (m ,n )是曲线E 上的动点,直线l 的方程为m +ny =1.①设直线l 与圆2+y 2=1交于不同两点C ,D ,求|CD |的取值范围;②求与动直线l 恒相切的定椭圆E ′的方程,并探究:若M (m ,n )是曲线Γ:A 2+By 2=1(A ·B ≠0)上的动点,是否存在与直线l :m +ny =1恒相切的定曲线Γ′?若存在,直接写出曲线Γ′的方程;若不存在,说明理由. 解 (1)设P (,y ),由题意,得()x -32+y 2⎪⎪⎪⎪⎪⎪x -433=32. 整理,得x 24+y 2=1, ∴曲线E 的方程为x 24+y 2=1. (2)①圆心到直线l 的距离d =1m 2+n 2, ∵直线与圆有两个不同交点C ,D ,∴|CD |2=4⎝ ⎛⎭⎪⎫1-1m 2+n 2. 又∵m 24+n 2=1(m ≠0),∴|CD |2=4⎝ ⎛⎭⎪⎫1-43m 2+4.∵|m |≤2,∴0<m 2≤4,∴0<1-43m 2+4≤34. ∴|CD |2∈(0,3],|CD |∈(]0,3,即|CD |的取值范围为(]0,3.②当m =0,n =1时,直线l 的方程为y =1;当m =2,n =0时,直线l 的方程为=12. 根据椭圆对称性,猜想E ′的方程为42+y 2=1.下面证明:直线m +ny =1(n ≠0)与42+y 2=1相切, 其中m 24+n 2=1,即m 2+4n 2=4.由⎩⎨⎧ 4x 2+y 2=1,y =1-mx n ,消去y 得(m 2+4n 2)2-2m +1-n 2=0,即42-2m +1-n 2=0,∴Δ=4m 2-16()1-n 2=4()m 2+4n 2-4=0恒成立,从而直线m +ny =1与椭圆E ′:42+y 2=1恒相切. 若点M ()m ,n 是曲线Γ:A 2+By 2=1()A ·B ≠0上的动点,则直线l :m +ny =1与定曲线Γ′:x 2A +y 2B =1()A ·B ≠0恒相切.7. 已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右顶点分别为A 1,A 2,右焦点为F 2(1,0),点B ⎝ ⎛⎭⎪⎫1,32在椭圆C 上.(1)求椭圆C 的方程;(2)若直线l :y =(-4)(≠0)与椭圆C 由左至右依次交于M ,N 两点,已知直线A 1M 与A 2N 相交于点G ,证明:点G 在定直线上,并求出定直线的方程.解析:(1)由F 2(1,0),知c =1,由题意得⎩⎪⎨⎪⎧ a 2=1+b 2,1a 2+94b 2=1,所以a =2,b =3,所以椭圆C 的方程为x 24+y 23=1.(2)因为y =(-4),所以直线l 过定点(4,0),由椭圆的对称性知点G 在直线=0上.当直线l 过椭圆C 的上顶点时,M (0,3),所以直线l 的斜率=-34,由⎩⎪⎨⎪⎧ y =-34x -4x 24+y 23=1,得⎩⎨⎧ x =0,y =3或⎩⎪⎨⎪⎧ x =85,y =335,所以N ⎝ ⎛⎭⎪⎫85,335, 由(1)知A 1(-2,0),A 2(2,0), 所以直线lA 1M 的方程为y =32(+2),直线lA 2N 的方程为y =-332(-2),所以G ⎝ ⎛⎭⎪⎫1,332,所以G 在直线=1上.当直线l 不过椭圆C 的上顶点时,设M (1,y 1),N (2,y 2),由 ⎩⎨⎧ y =k x -4x 24+y 23=1,得(3+42)2-322+642-12=0, 所以Δ=(-322)2-4×(3+42)·(642-12)>0,得-12<<12, 1+2=32k 23+4k 2,1·2=64k 2-123+4k 2, 易得直线lA 1M 的方程为y =y 1x 1+2(+2),直线lA 2N 的方程为y =y 2x 2-2(-2),当=1时,3y 1x 1+2=-y 2x 2-2得212-5(1+2)+8=0,所以264k 2-123+4k 2-5×32k 23+4k 2+83+4k 23+4k 2=0显然成立,所以G 在直线=1上. 8.已知平面直角坐标系内两定点A (-22,0),B (22,0)及动点C (,y ),△ABC 的两边AC ,BC 所在直线的斜率之积为-34.(1)求动点C 的轨迹E 的方程;(2)设P 是y 轴上的一点,若(1)中轨迹E 上存在两点M ,N 使得MP →=2PN →,求以AP 为直径的圆的面积的取值范围.解析:(1)由已知,AC ·BC =-34,即y x +22·y x -22=-34, 所以32+4y 2=24,又三点构成三角形,所以y ≠0, 所以点C 的轨迹E 的方程为x 28+y 26=1(y ≠0). (2)设点P 的坐标为(0,t )当直线MN 的斜率不存在时,可得M ,N 分别是短轴的两端点,得到t =±63. 当直线MN 的斜率存在时,设直线MN 的方程为y =+t (≠0), M (1,y 1),N (2,y 2),则由MP →=2PN →得1=-22. ① 联立得⎩⎨⎧ y =kx +t ,x 28+y 26=1,得(3+42)2+8t +4t 2-24=0,当Δ>0得642t 2-4(3+42)(4t 2-24)>0,整理得t 2<82+6.所以1+2=-8kt 3+4k 2,12=4t 2-243+4k 2, ②。
2019年高考圆锥曲线部分大题解析

2019年高考圆锥曲线部分大题解析1.已知点P在抛物线C:y^2=4x的y轴左侧(不含y轴)一点,且存在不同的两点A、B满足PA、PB的中点均在C上。
1)设AB中点为M,证明:PM垂直于y轴;对于抛物线C:y^2=4x上的动点P(x,y),求△PAB面积的取值范围。
2)若P是半椭圆x^2/4+y^2/16=1上的一点,解析:(1)设P(x,y),A(y1^2/4,y1),B(y2^2/4,y2)。
由于PA、PB的中点均在C上,因此有:PA: y^2-2yy1+4x-y1^2=0PB: y^2-2yy2+4x-y2^2=0解得y1+y2=2y,y1y2=8x-y^2.因此,PM的斜率为(y1-y2)/(y/2-x)=2(y1-y2)/(y-4x),而C的导数为dy/dx=2/y,因此PM与C的切线垂直,即PM垂直于y轴。
2)由(1)可知y1+y2=2y,y1y2=8x-y^2.因此,|PM|=1/2√(y1+y2)^2/4-(y/2-x)^2=y^2/2-3x,|y1-y2|=2√(y1y2)=2√(8x-y^2)。
因此,|PM|·|y1-y2|=1/2(y-4x)^2/3,因此△PAB的面积范围为[6√2,15/√2]。
2.已知斜率为k的直线l与椭圆C: 4x^2/3+y^2/4=1交于A、B两点,线段AB的中点为M(1,m)(m>0)。
1)证明:k<-1/2;2)设F为C的右焦点,P为C上一点且FP+FA+FB=0,证明:FP、FA、FB为等差数列,并求出该数列的公差。
解析:(1)由中点弦公式k=-2m/(4/3)=-(3/2)m,因此k<-1/2.2)由题意知FA+FB=2FM,FP=-2FM,因此P(1,-2m)。
因为点P在椭圆上,代入可得m=3,k=-1/2,即|F P|=2/√5.根据第二定义可知,|FA|=2-2x1/√(16-9x1^2),|FB|=2-2x2/√(16-9x2^2),|FA|+|FB|=4-(x1+x2)/√(16-9x1^2)(16-9x2^2)。
2019年高考数学理真题分项解析:专题09 圆锥曲线

专题九 圆锥曲线1.【2019高考新课标Ⅰ,理10】已知椭圆C 的焦点为121,01,0F F -(),(),过F 2的直线与C 交于A ,B 两点.若222AF F B =││││,1AB BF =││││,则C 的方程为A. 2212x y +=B. 22132x y +=C. 22143x y +=D. 22154x y +=【答案】B 【解析】 【分析】由已知可设2F B n =,则212,3AF n BF AB n ===,得12AF n =,在1AF B △中求得11cos 3F AB ∠=,再在12AF F △中,由余弦定理得32n =,从而可求解. 【详解】法一:如图,由已知可设2F B n =,则212,3AF n BF AB n ===,由椭圆的定义有121224,22a BF BF n AF a AF n =+=∴=-=.在1AF B △中,由余弦定理推论得22214991cos 2233n n n F AB n n +-∠==⋅⋅.在12AF F △中,由余弦定理得2214422243n n n n +-⋅⋅⋅=,解得32n =. 2222423,3,312,a n a b a c ∴==∴=∴=-=-=∴所求椭圆方程为22132x y +=,故选B .法二:由已知可设2F B n =,则212,3AF n BF AB n ===,由椭圆的定义有121224,22a BF BF n AF a AF n =+=∴=-=.在12AF F △和12BF F △中,由余弦定理得2221222144222cos 4,422cos 9n n AF F n n n BF F n⎧+-⋅⋅⋅∠=⎨+-⋅⋅⋅∠=⎩,又2121,AF F BF F ∠∠互补,2121cos cos 0AF F BF F ∴∠+∠=,两式消去2121cos cos AF F BF F ∠∠,,得223611n n +=,解得32n =.2222423,3,312,a n a b a c ∴==∴=∴=-=-=∴所求椭圆方程为22132x y +=,故选B .【点睛】本题考查椭圆标准方程及其简单性质,考查数形结合思想、转化与化归的能力,很好的落实了直观想象、逻辑推理等数学素养.2.【2019高考新课标Ⅱ,理8】若抛物线y 2=2px (p >0)的焦点是椭圆2231x y pp+=的一个焦点,则p =A. 2B. 3C. 4D. 8【答案】D 【解析】 【分析】利用抛物线与椭圆有共同的焦点即可列出关于p 的方程,即可解出p ,或者利用检验排除的方法,如2p =时,抛物线焦点为(1,0),椭圆焦点为(±2,0),排除A ,同样可排除B ,C ,故选D .【详解】因为抛物线22(0)y px p =>的焦点(,0)2p 是椭圆2231x y p p +=的一个焦点,所以23()2p p p -=,解得8p =,故选D .【点睛】本题主要考查抛物线与椭圆的几何性质,渗透逻辑推理、运算能力素养.3.【2019高考新课标Ⅱ,理11】设F 为双曲线C :22221x y a b-=(a >0,b >0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点.若|PQ |=|OF |,则C 的离心率为 A. 2B. 3C. 2D.5【答案】A【分析】准确画图,由图形对称性得出P 点坐标,代入圆的方程得到c 与a 关系,可求双曲线的离心率. 【详解】设PQ 与x 轴交于点A ,由对称性可知PQ x ⊥轴,又||PQ OF c ==Q ,||,2cPA PA ∴=∴为以OF 为直径的圆的半径, A ∴为圆心||2c OA =. ,22c c P ⎛⎫∴ ⎪⎝⎭,又P 点在圆222x y a +=上,22244c c a ∴+=,即22222,22c c a e a=∴==. 2e ∴=,故选A .【点睛】本题为圆锥曲线离心率的求解,难度适中,审题时注意半径还是直径,优先考虑几何法,避免代数法从头至尾,运算繁琐,准确率大大降低,双曲线离心率问题是圆锥曲线中的重点问题,需强化练习,才能在解决此类问题时事半功倍,信手拈来.4.【2019高考新课标Ⅲ,理10】双曲线C :2242x y -=1的右焦点为F ,点P 在C 的一条渐近线上,O 为坐标原点,若=PO PF ,则△PFO 的面积为A.324B.322C. 22D. 32【解析】 【分析】本题考查以双曲线为载体的三角形面积的求法,渗透了直观想象、逻辑推理和数学运算素养.采取公式法,利用数形结合、转化与化归和方程思想解题. 【详解】由222,2,6,a b c a b ===+=.6,2P PO PF x =∴=Q , 又P 在C 的一条渐近线上,不妨设为在22y x =上, 1133262224PFO P S OF y ∴=⋅=⨯⨯=△,故选A . 【点睛】忽视圆锥曲线方程和两点间的距离公式的联系导致求解不畅,采取列方程组的方式解出三角形的高,便可求三角形面积.5.【2019高考北京卷,理4】已知椭圆2222 1x y a b+=(a >b >0)的离心率为12,则A. a 2=2b 2B. 3a 2=4b 2C. a =2bD. 3a =4b【答案】B 【解析】 【分析】由题意利用离心率的定义和,,a b c 的关系可得满足题意的等式. 【详解】椭圆的离心率2221,2c e c a b a ===-,化简得2234a b =, 故选B .【点睛】本题考查椭圆的标准方程与几何性质,属于容易题,注重基础知识、基本运算能力的考查.6.【2019高考北京卷,理8】数学中有许多形状优美、寓意美好的曲线,曲线C :221||x y x y +=+就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C 上任意一点到原点的距离都不超过2; ③曲线C 所围成的“心形”区域的面积小于3. 其中,所有正确结论的序号是 A. ① B. ②C. ①②D. ①②③【答案】C 【解析】 【分析】将所给方程进行等价变形确定x 的范围可得整点坐标和个数,结合均值不等式可得曲线上的点到坐标原点距离的最值和范围,利用图形的对称性和整点的坐标可确定图形面积的范围.【详解】由221x y x y +=+得,221y x y x -=-,2222||3341,10,2443x x x y x ⎛⎫-=-- ⎪⎝⎭厔, 所以x 可为的整数有0,-1,1,从而曲线22:1C x y x y +=+恰好经过(0,1),(0,-1),(1,0),(1,1), (-1,0),(-1,1)六个整点,结论①正确.由221x y x y +=+得,222212x y x y +++…,解得222x y +≤,所以曲线C 上任意一点到原点的距离都不超过2. 结论②正确.如图所示,易知()()()()0,1,1,0,1,1,,0,1A B C D -, 四边形ABCD 的面积13111122ABCD S =⨯⨯+⨯=,很明显“心形”区域的面积大于2ABCD S ,即“心形”区域的面积大于3,说法③错误.故选C.【点睛】本题考查曲线与方程、曲线的几何性质,基本不等式及其应用,属于难题,注重基础知识、基本运算能力及分析问题解决问题的能力考查,渗透“美育思想”.7.【2019高考天津卷,理5】已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 A .2B. 3C. 2D. 5【答案】D 【解析】 【分析】只需把4AB OF =用,,a b c 表示出来,即可根据双曲线离心率的定义求得离心率。
专题21 圆锥曲线综合-2019年高考文数母题题源系列(全国Ⅰ专版)(解析版)

专题21圆锥曲线综合【母题来源一】【2019年高考全国Ⅰ卷文数】已知点A ,B 关于坐标原点O 对称,│AB │=4,⊙M 过点A ,B 且与直线x +2=0相切.(1)若A 在直线x +y =0上,求⊙M 的半径;(2)是否存在定点P ,使得当A 运动时,│MA │−│MP │为定值?并说明理由.【答案】(1)M 的半径=2r 或=6r ;(2)存在,理由见解析.【解析】(1)因为M 过点,A B ,所以圆心M 在AB 的垂直平分线上.由已知A 在直线+=0x y 上,且,A B 关于坐标原点O 对称,所以M 在直线y x =上,故可设(, )M a a .因为M 与直线x +2=0相切,所以M 的半径为|2|r a =+.由已知得||=2AO ,又MO AO ⊥ ,故可得2224(2)a a +=+,解得=0a 或=4a .故M 的半径=2r 或=6r .(2)存在定点(1,0)P ,使得||||MA MP -为定值.理由如下:设(, )M x y ,由已知得M 的半径为=|+2|,||=2r x AO .由于MO AO ⊥,故可得2224(2)x y x ++=+,化简得M 的轨迹方程为24y x =.因为曲线2:4C y x =是以点(1,0)P 为焦点,以直线1x =-为准线的抛物线,所以||=+1MP x .因为||||=||=+2(+1)=1MA MP r MP x x ---,所以存在满足条件的定点P .【名师点睛】本题考查圆的方程的求解问题、圆锥曲线中的定点定值类问题.解决定点定值问题的关键是能够根据圆的性质得到动点所满足的轨迹方程,进而根据抛物线的定义得到定值,验证定值符合所有情况,使得问题得解.【母题来源二】【2018年高考全国Ⅰ文数】设抛物线22C y x =:,点()20A ,,()20B -,,过点A 的直线l 与C 交于M ,N 两点.(1)当l 与x 轴垂直时,求直线BM 的方程;(2)证明:ABM ABN =∠∠.【答案】(1)y =112x +或112y x =--;(2)见解析.【解析】(1)当l 与x 轴垂直时,l 的方程为x =2,可得M 的坐标为(2,2)或(2,–2).所以直线BM 的方程为y =112x +或112y x =--.(2)当l 与x 轴垂直时,AB 为MN 的垂直平分线,所以∠ABM =∠ABN .当l 与x 轴不垂直时,设l 的方程为(2)(0)y k x k =-≠,M (x 1,y 1),N (x 2,y 2),则x 1>0,x 2>0.由2(2)2y k x y x=-⎧⎨=⎩,得ky 2–2y –4k =0,可知y 1+y 2=2k,y 1y 2=–4.直线BM ,BN 的斜率之和为1221121212122()22(2)(2)BM BN y y x y x y y y k k x x x x ++++=+=++++.①将112y x k =+,222y x k =+及y 1+y 2,y 1y 2的表达式代入①式分子,可得121221121224()882()0y y k y y x y x y y y k k++-++++===.所以k BM +k BN =0,可知BM ,BN 的倾斜角互补,所以∠ABM =∠ABN .综上,∠ABM =∠ABN .【名师点睛】本题主要考查抛物线的标准方程与几何性质、直线与抛物线的位置关系,考查考生的化归与转化能力、运算求解能力,考查的数学核心素养是直观想象与数学运算.在设直线的方程时,一定要注意所设方程的适用范围,如用点斜式时,要考虑到直线的斜率不存在的情况,以免解答不严密或漏解.(1)求出直线l 与抛物线的交点,利用两点式写出直线BM 的方程;(2)由(1)知,当直线l 与x 轴垂直时,结论显然成立,当直线l 与x 轴不垂直时,设出斜率k ,联立直线l 与C 的方程,求出M ,N 两点坐标之间的关系,再表示出BM 与BN 的斜率,得其和为0,从而说明BM 与BN 两条直线的斜率互为相反数,进而可知两角相等.【母题来源三】【2017年高考全国Ⅰ卷文数】设A ,B 为曲线C :y =24x 上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.【答案】(1)1;(2)7y x =+.【解析】(1)设A (x 1,y 1),B (x 2,y 2),则12x x ≠,2114x y =,2224x y =,x 1+x 2=4,于是直线AB 的斜率12121214y y x x k x x -+===-.(2)由24x y =,得2x y'=.设M (x 3,y 3),由题设知312x =,解得32x =,于是M (2,1).设直线AB 的方程为y x m =+,故线段AB 的中点为N (2,2+m ),|MN |=|m +1|.将y x m =+代入24x y =得2440x x m --=.当16(1)0m ∆=+>,即1m >-时,1,22x =±从而12|||AB x x -=由题设知||2||AB MN =,即2(1)m =+,解得7m =.所以直线AB 的方程为7y x =+.【名师点睛】本题主要考查直线与圆锥曲线的位置关系,主要利用根与系数的关系:因为直线的方程是一次的,圆锥曲线的方程是二次的,故直线与圆锥曲线的问题常转化为方程组关系问题,最终转化为一元二次方程问题,故用根与系数的关系及判别式是解决圆锥曲线问题的重点方法之一,尤其是弦中点问题,弦长问题,可用根与系数的关系直接解决,但应注意不要忽视判别式的作用.(1)设A (x 1,y 1),B (x 2,y 2),由两点斜率公式求AB 的斜率;(2)联立直线与抛物线方程,消y ,得12|||AB x x -=,解出m 即可.【命题意图】(1)掌握直线方程的几种形式,掌握确定圆的几何要素,掌握圆的标准方程与一般方程,能用直线和圆的方程解决一些简单的问题.(2)了解抛物线的实际背景,了解抛物线在刻画现实世界和解决实际问题中的作用.(3)掌握抛物线的定义、几何图形、标准方程及简单性质.(4)了解圆锥曲线的简单应用.(5)理解数形结合的思想.【命题规律】解析几何的解答题一般难度较大,多为试卷的压轴题之一,常考查直线与圆锥曲线的位置关系及最值范围、定点、定值、存在性问题及证明问题,多涉及最值求法,综合性强.从近三年高考情况来看,多考查直线与圆或抛物线的位置关系,但也要注意对椭圆知识的考查,解题时,充分利用数形结合思想,转化与化归思想.同时注重数学思想在解题中的指导作用,以及注重对运算能力的培养.【方法总结】(一)求直线方程的常用方法有(1)直接法:根据已知条件灵活选用直线方程的形式,写出方程.(2)待定系数法:先根据已知条件设出直线方程,再根据已知条件构造关于待定系数的方程(组)求系数,最后代入求出直线方程.(3)直线在x(y)轴上的截距是直线与x(y)轴交点的横(纵)坐标,所以截距是一个实数,可正、可负,也可为0,而不是距离.(4)求直线方程时,如果没有特别要求,求出的直线方程应化为一般式Ax+By+C=0,且A≥0.(二)求圆的方程(1)求圆的方程必须具备三个独立的条件.从圆的标准方程来看,关键在于求出圆心坐标和半径,从圆的一般方程来讲,能知道圆上的三个点即可求出圆的方程,因此,待定系数法是求圆的方程常用的方法.(2)用几何法求圆的方程,要充分运用圆的几何性质,如“圆心在圆的任一条弦的垂直平分线上”,“半径、弦心距、弦长的一半构成直角三角形”.(三)求椭圆的方程有两种方法:(1)定义法.根据椭圆的定义,确定a2,b2的值,结合焦点位置可写出椭圆方程.(2)待定系数法.这种方法是求椭圆的方程的常用方法,其一般步骤是:第一步,做判断.根据条件判断椭圆的焦点在x轴上,还是在y轴上,还是两个坐标轴都有可能(这时需要分类讨论).第二步,设方程.根据上述判断设方程为22221(0)x y a ba b+=>>或22221(0)y x a ba b+=>>.第三步,找关系.根据已知条件,建立关于,,a b c 的方程组(注意椭圆中固有的等式关系222c a b =-).第四步,得椭圆方程.解方程组,将解代入所设方程,即为所求.【注意】用待定系数法求椭圆的方程时,要“先定型,再定量”,不能确定焦点的位置时,可进行分类讨论或把椭圆的方程设为22100()mx ny m n m n >>+≠=,且.(四)用待定系数法求抛物线标准方程的步骤:若无法确定抛物线的位置,则需分类讨论.特别地,已知抛物线上一点的坐标,一般有两种标准方程.(五)直线与圆锥曲线的弦长问题有三种解法:(1)过圆锥曲线的焦点的弦长问题,利用圆锥曲线的定义可优化解题.(2)将直线的方程与圆锥曲线的方程联立,求出两交点的坐标,再运用两点间距离公式求弦长.(3)它体现了解析几何中的设而不求的思想,其实质是利用两点之间的距离公式以及一元二次方程根与系数的关系.(六)圆锥曲线中的定点、定值问题定点、定值问题多以直线与圆锥曲线为背景,常与函数与方程、向量等知识交汇,形成了过定点、定值等问题的证明.解决此类问题的关键是引进参变量表示所求问题,根据等式的恒成立、数式变换等寻找不受参数影响的量.可以先研究一下特殊情况,找出定点或定值,再视具体情况进行研究.同时,也要掌握巧妙利用特殊值解决相关的定点、定值问题,如将过焦点的弦特殊化,变成垂直于对称轴的弦来研究等.1.【湖南省郴州市2019届高三第二次教学质量监测试卷数学试题】已知抛物线2:2(0)C x py p =>的焦点为F ,过F 的直线交抛物线于A ,B 两点.(1)若以A ,B 为直径的圆的方程为22(2)(3)16x y -+-=,求抛物线C 的标准方程;(2)过A ,B 分别作抛物线的切线1l ,2l ,证明:1l ,2l 的交点在定直线上.【答案】(1)24x y =;(2)见解析.【解析】(1)设AB 中点为M ,A 到准线的距离为1d ,B 到准线的距离为2d ,M 到准线的距离为d ,则2M p d y =+,由抛物线的定义可知,12||,||d AF d BF ==,所以12||8d d AB +==,由梯形中位线可得1242d d d +==,所以42M p y +=,而3M y =,所以342p+=,可得2p =,所以抛物线2:4C x y =.(2)设()11,A x y ,()22,B x y ,由22x py =得22x y p =,则xy p '=.所以直线1l 的方程为()111xy y x x p -=-,直线2l 的方程为()222xy y x x p -=-,联立得122x x x +=,122x x y p =,即1l ,2l 的交点坐标为1212,22xx x xp ⎛⎫+⋅ ⎪⎝⎭,因为AB 过焦点0,2p F ⎛⎫⎪⎝⎭,所以设直线AB 的方程为2py kx -=,将其代入抛物线22x py =中得2220x pkx p --=,所以212x x p =-,所以212222x x p p p p -==-,所以1l ,2l 的交点在定直线 2p y =-上.【名师点睛】本题考查抛物线的定义,以及圆锥曲线中定点定值的求法.题目较综合,对计算量的要求比较高,属于中档题目.(1)由抛物线的定义求出p ,可得抛物线方程.(2)利用导数求出过A 、B 两点的切线方程,并求出其交点.再由直线AB 与抛物线联立得到A 、B 两点的坐标关系.代入交点坐标,可得所求定直线.2.【山东省临沂市2019年普通高考模拟考试(三模)数学试题】已知直线l 过圆()22:21M x y ++=的圆心且平行于x 轴,曲线C 上任一点P 到点(0,1)F 的距离比到l 的距离小1.(1)求曲线C 的方程;(2)过点P (异于原点)作圆M 的两条切线,斜率分别为12,k k ,过点P 作曲线C 的切线,斜率为0k ,若102,,k k k 成等差数列,求点P 的坐标.【答案】(1)24x y =;(2)52⎛⎫ ⎪⎝⎭.【解析】(1)易知直线:2l y =-,∵曲线C 上任一动点P 到点(0,1)F 的距离比到:2l y =-的距离小1,∴点P 到(0,1)F 的距离等于到直线1y =-的距离,∴曲线C 是以F 为焦点,直线1y =-为准线的抛物线,设抛物线方程为22x py =,∵2p =,∴曲线C 的方程为24x y =.(2)由(1)知曲线2:4C x y =,设2000,(40)x P x x ⎛⎫ ⎪≠⎝⎭,则002x k =,曲线C 上过P 点的切线方程为()200042x x y x x -=-,即20024x x y x =-,设过点P 作圆M 的两切线方程为:()20104x y k x x -=-,()20204x y k x x -=-,即:2011004x k x y k x -+-=,2022004x k x y k x -+-=,1=,即()232220001011421024x x x k x k ⎛⎫⎛⎫--+++-= ⎪ ⎪⎝⎭⎝⎭,*同理2k 也适合*式,故1k ,2k 是方程()2322200001421024x x x k x k ⎛⎫⎛⎫--+++-= ⎪ ⎪⎝⎭⎝⎭的两个不相等的根,∴3001220421x x k k x ++=-,∵102,,k k k 成等差数列,∴1202k k k +=,∴300020421x x x x +=-,解得0x =,∴052y =,∴点P的坐标为52⎛⎫ ⎪⎝⎭.【名师点睛】本题主要考查抛物线的轨迹方程以及直线与抛物线的位置关系,属于难题.求轨迹方程的常见方法有:①直接法,设出动点的坐标(),x y ,根据题意列出关于,x y 的等式即可;②定义法,根据题意动点符合已知曲线的定义,直接求出方程;③参数法,把,x y 分别用第三个变量表示,消去参数即可;④逆代法,将()()00x g x y h x ⎧=⎪⎨=⎪⎩代入()00,0f x y =.3.【河北省保定市2019届高三第二次模拟考试数学试题】已知抛物线E :28y x =,直线l :4y kx =-.(1)若直线l 与抛物线E 相切,求直线l 的方程;(2)设(4,0)Q ,0k >,直线l 与抛物线E 交于不同的两点()11,A x y ,()22,B x y ,若存在点C ,使得四边形OACB 为平行四边形(O 为原点),且AC QC ⊥,求2x 的取值范围.【答案】(1)142y x =--;(2)201)x <≤.【解析】(1)由248y kx y x =-⎧⎨=⎩得228(1)160k x k x -++=,由0k ≠及2264(1)640k k ∆=+-=,得12k =-.∴所求的切线方程为142y x =--.(2)由248y kx y x =-⎧⎨=⎩得228(1)160k x k x -++=,2264(1)640,k k ∆=+-> 且0k ≠,12k ∴>-,1228(1),k x x k +∴+=∴12128()8y y k x x k +=+-=,∵四边形OACB 为平行四边形,1212=(,)OC OA OB x x y y ∴+=++ 28(1)8(,)k k k +=,即C 28(1)8(,k k k +,∵AC QC ⊥,0QC AC ∴⋅= ,又222228(1)8(4,(,)(,4)k QC AC OB x y x kx k k +=-===- 2228(1)8[4](4)0k QC AC x kx k k +∴⋅=-+-= ,即2822k x k=++,∵0k >,∴2821)x ≥=+,当且仅当k =取等号,此时,201)x <≤.【名师点睛】本题考查了直线与抛物线的位置关系,根与系数关系的应用,也考查平行四边形的性质、数量积和不等式的运算,属于中档题.(1)由248y kx y x =-⎧⎨=⎩得228(1)160k x k x -++=,由题意得00k ≠⎧⎨∆=⎩,解出k 即可.(2)由四边形OACB 为平行四边形,得1212=(,)OC OA OB x x y y +=++ ,利用根与系数的关系得点C ,又由AC QC ⊥,0QC AC ⋅= ,通过数量积和不等式的运算,求出2x 的范围即可.4.【山东省安丘市、诸城市、五莲县、兰山区2019届高三5月校际联合考试数学试题】已知椭圆()2222:10x y E a b a b +=>>经过点()0,1C,且离心率为2.(1)求椭圆E 的方程;(2)若直线1:3l y kx =-与椭圆E 相交于A ,B 两点,线段AB 的中点为M ,是否存在常数λ,使∠∠AMC ABC =⋅λ恒成立,并说明理由.【答案】(1)2212x y +=;(2)存在.【解析】(1)由题意知1b =,22c a =.又因为222a b c =+,所以解得a =.所以椭圆方程为2212x y +=.(2)存在常数λ,使∠∠AMC ABC =⋅λ恒成立.理由如下:由221312y kx x y ⎧=-⎪⎪⎨⎪+=⎪⎩得()2291812160k x kx +--=,且>0∆.设()11,A x y ,()22,B x y ,则1221221291816918k x x k x x k ⎧+=⎪⎪+⎨⎪=-⎪+⎩,又因为()11,1CA x y =- ,()22,1CB x y =-,()()()()2121212121212444161113339CA CB x x y y x x kx kx k x x k x x ⎛⎫⎛⎫⋅=+--=+--=+-++⎪⎪⎝⎭⎝⎭ ()22216412161091839189k k k k k -=+-⋅+=++,所以CA CB ⊥ .因为线段AB 的中点为M ,所以MC MB =,所以2AMC ABC ∠=∠.所以存在常数2=λ,使∠∠AMC ABC =⋅λ恒成立.【名师点睛】本题主要考查求椭圆的方程以及椭圆的应用,熟记椭圆的标准方程与椭圆的简单性质即可,属于常考题型.(1)根据题意得到1b =,2c a =,求出a =,进而可求出椭圆方程;(2)先由题意判断出结果,再证明,联立直线与椭圆方程,设()11,A x y ,()22,B x y ,根据根与系数的关系,以及向量数量积运算,得到0CA CB ⋅=,进而可得出结果.5.【山西省晋城市2019届高三第三次模拟考试数学试题】已知△ABC 的周长为6,B ,C 关于原点对称,且(1,0)B -,点A 的轨迹为Γ.(1)求Γ的方程;(2)若(2,0)D -,直线l :(1)(0)y k x k =-≠与Γ交于E ,F 两点,若1DE k ,k λ,1DFk 成等差数列,求λ的值.【答案】(1)()221243x y x +=≠±;(2)2.【解析】(1)依题意,(1,0)B -,(1,0)C ,故2BC =,则42AB AC BC +=>=,故点A 的轨迹是以B ,C 为焦点的椭圆(不含左、右两顶点),故Γ的方程为221(2)43x y x +=≠±.(2)依题意,112DE DF k k k ⋅=+λ,故2DE DFk kk k =+λ.联立22(1)34120y k x x y =-⎧⎨+-=⎩,整理得()22223484120k x k x k +-+-=.设11(,)E x y ,22(,)F x y ,则2122834k x x k +=+,212241234k x x k -=+.故()()121222DE DF k x k x k kk k y y +++=+()()()()12122211k x k x k x k x ++=+--1233211x x =++--()()()121232211x x x x +-=+--()()1212123221x x x x x x +-=+-++222222832342412813434k k k k k k ⎛⎫- ⎪+⎝⎭=+--+++()2222238682412834k k k k k --=+--++2242=+==λ,则2=λ.【名师点睛】本题考查椭圆的方程、直线与椭圆的综合性问题,考查运算求解能力、推理论证能力.(1)由椭圆定义得轨迹方程即可;(2)依题意得112DE DF k k k ⋅=+λ,得2DE DF k k k k =+λ,联立22(1)34120y k x x y =-⎧⎨+-=⎩消去y ,整理()()121222DE DF k x k x k kk k y y +++=+结合根与系数关系得λ的值即可.6.【安徽省泗县第一中学2019届高三高考最后一模数学试题】已知椭圆M :22221(0)x y a b a b +=>>的离心率为2,且椭圆上一点P的坐标为2⎫⎪⎪⎝⎭.(1)求椭圆M 的方程;(2)设直线l 与椭圆M 交于A ,B 两点,且以线段AB 为直径的圆过椭圆的右顶点C ,求△ABC 面积的最大值.【答案】(1)2214x y +=;(2)1625.【解析】(1)由已知2c e a ==,又222a b c =+,则2a b =.∴椭圆方程为222214x y b b +=,将)2代入方程得1b =,2a =,故椭圆的方程为2214x y +=.(2)不妨设直线AB 的方程为x ky m =+,联立2214x y x ky m ⎧+=⎪⎨⎪=+⎩消去x 得()2224240k y kmy m +++-=.设11(,)A x y ,22(,)B x y ,则有12224km y y k -+=+,212244m y y k -⋅=+,①又以线段AB 为直径的圆过椭圆的右顶点(2,0)C ,∴0CA CB ⋅=,由11(2,)CA x y =- ,22(2,)CB x y =-得()()1212220x x y y --+=,将11x ky m =+,22x ky m =+代入上式得()()2212121(2)(2)0k y y k m y y m ++-++-=,将①代入上式求得65m =或2m =(舍),则直线l 恒过点6(,0)5D .∴1211||22△ABCS DC y y =-==,设211(0)44t t k =<≤+,则△ABC S =在1(0,4t ∈上单调递增,当14t =时,△ABC S 取得最大值1625.【名师点睛】本小题主要考查椭圆标准方程的求法,考查直线和椭圆相交的弦长公式,考查直线和椭圆的位置关系,考查三角形面积最大值的求法,运算量较大,属于中档题.(1)将P 点坐标代入椭圆方程,结合椭圆的离心率列方程,解方程求得,a b 的值,由此求得椭圆方程.(2)设直线AB 的方程为x ky m =+,联立直线AB 的方程和椭圆的方程,消去x ,得到关于y 的一元二次方程,写出根与系数关系,根据0CA CB ⋅=列方程,解方程求得m 的值.由此判断出直线l 过定点6,05⎛⎫⎪⎝⎭,由121||2△ABC S DC y y =-求得三角形面积的表达式,利用换元法,结合二次函数的单调性,求得三角形面积的最大值.7.【江西省南昌市江西师范大学附属中学2019届高三三模数学试题】已知离心率为2的椭圆()2222:10x y C a b ab +=>>过点22⎫⎪⎪⎭,,A B 分别为椭圆C 的右顶点和上顶点,点P 在椭圆C 上且不与四个顶点重合.(1)求椭圆C 的标准方程;(2)若直线PA 与y 轴交于N ,直线PB 与x 轴交于M ,试探究AM BN ⋅是否为定值?若是,请求出该定值;若不是,请说明理由.【答案】(1)2214x y +=;(2)AM BN ⋅是定值,定值为4.【解析】(1)由题意得:2222222112c aa b a b c ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩,解得:2241a b ⎧=⎨=⎩,∴椭圆C 的标准方程为:2214x y +=.(2) 点P 不与四个顶点重合,∴直线,PA PB 的斜率存在且不为0,设()00,P x y ,且()2,0A ,()0,1B ,∴直线PA 的方程为:()0022y y x x =--,则0020,2y N x ⎛⎫- ⎪-⎝⎭.直线PB 的方程为:0011y y x x -=+,则00,01xM y ⎛⎫- ⎪-⎝⎭.2200000000000000244448211222x y x y x y x y AM BN y x x y x y +++--∴⋅=+⋅+=----+,P 在椭圆上,220044x y ∴+=.0000000000000000844822442222x y x y x y x y AM BN x y x y x y x y +----+∴⋅==⨯=--+--+.4AM BN ∴⋅=,为定值.【名师点睛】本题考查椭圆标准方程的求解、椭圆中的定值问题的求解.解决定值类问题的关键是将所求量利用变量进行表示,通过变量间的关系进行化简、消元,从而整理出所求的定值.(1)根据离心率、点22⎭在椭圆上和222a b c =+建立方程组,解方程求得结果,从而得到椭圆方程;(2)设()00,P x y ,从而可得,PA PB 方程,求得,M N 的坐标,从而可得AM BN ⋅,根据点()00,P x y 在椭圆上得到220044x y +=,代入AM BN ⋅整理可得定值.8.【福建省厦门市厦门外国语学校2019届高三最后一模数学试题】如图,椭圆C :22143x y +=的右焦点为F ,过点F 的直线l 与椭圆C 交于A 、B 两点,直线n :x =4与x 轴相交于点E ,点M 在直线n 上,且满足BM ∥x轴.(1)当直线l 与x 轴垂直时,求直线AM 的方程;(2)证明:直线AM 经过线段EF 的中点.【答案】(1)直线AM 的方程为y =-x +52或y =x -52;(2)见解析.【解析】(1)由c==1,得F (1,0),∵直线l 与x 轴垂直,∴x =1,由221143x x y=⎧⎪⎨+=⎪⎩,解得:113322或x x y y ==⎧⎧⎪⎪⎨⎨==-⎪⎪⎩⎩,当点A 坐标为31,2⎛⎫ ⎪⎝⎭,则点M 坐标为34,2⎛⎫- ⎪⎝⎭,此时直线AM 的斜率为33(22114--=--,∴直线AM 的方程为31(1)2y x -=-⋅-,即y =-x +52;当点A 坐标为31,2⎛⎫-⎪⎝⎭,则点M 坐标为34,2⎛⎫ ⎪⎝⎭,此时直线AM 的斜率为33()22141--=-,∴直线AM 的方程为31(4)2y x -=⋅-,即y =x -52.故直线AM 的方程为y =-x +52或y =x -52.(2)当AB 直线方程为0y =时,直线BM 与x 轴重合,不满足题意;故可设直线l 的方程为x =my +1,由221143x my x y =+⎧⎪⎨+=⎪⎩,得3(my +1)2+4y 2=12,即(3m 2+4)y 2+6my -9=0,设A (x 1,y 1),B (x 2,y 2),由根与系数关系可得,y 1+y 2=2634m m -+,y 1y 2=2934m -+,∵EF 的中点N 502,⎛⎫ ⎪⎝⎭,点M (4,y 2),∴NA =11112533,,,,222x y my y NM y ⎛⎫⎛⎫⎛⎫-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,∵132my ⎛⎫-⎪⎝⎭×y 2-32y 1=my 1y 2-32(y 1+y 2)=2934m m -+-32×2634m m -+=0.∴∥NA NM,故A ,N ,M 三点共线,所以直线AM 经过线段EF 的中点.【名师点睛】本题考查了直线与椭圆的位置关系问题,直线与圆锥曲线问题常见解法是借助根与系数的关系,将多元问题转化为少元(单元)问题,属于中档题.(1)由直线l 与x 轴垂直,可得直线l 的方程,从而求解出点、A B 的坐标,由BM ∥x 轴可得M 点坐标,从而得出直线AM 的方程;(2)要证直线AM 经过线段EF 的中点N ,即证A ,N ,M 三点共线,即证∥NA NM,设出、A B 两点,联立直线与椭圆的方程,借助根与系数关系,从而得证.9.【湖南省株洲市2019届高三第二次教学质量检测(二模)数学试题】已知抛物线()2:20E y px p =>经过点()1,2A ,过A 作两条不同直线12,l l ,其中直线12,l l 关于直线1x =对称.(1)求抛物线E 的方程及准线方程;(2)设直线12,l l 分别交抛物线E 于、B C 两点(均不与A 重合),若以线段BC 为直径的圆与抛物线E 的准线相切,求直线BC 的方程.【答案】(1)24y x =;准线方程为1x =-;(2)10x y +-=.【解析】(1)∵抛物线E 过点()1,2A ,∴24p =,解得2p =,∴抛物线的方程为24y x =,准线方程为1x =-.(2)方法一:不妨设B 在C 的左边,从而可设直线AB 的方程为()12(0)x m y m -=->,即21x my m =-+,由2214x my m y x=-+⎧⎨=⎩消去x 整理得24840y my m -+-=.设(),B B B x y ,则24B y m +=,故42B y m =-,∴2441B x m m =-+,∴点()2441,42B m m m -+-.又由条件得AB 与AC 的倾斜角互补,以m -代替点B 坐标中的m ,可得点()2441,42C m m m ++--.∴BC ==,且BC 中点的横坐标为2412B Cx x m +=+,∵以线段BC 为直径的圆与抛物线E的准线相切,∴2411BC m ++==,解得22m =∴()32B -,()32C +-,∴1BC k =-,∴直线BC的方程为()(23y x -=--+,即10x y +-=.方法二:设()()1122,,,B x y C x y ,因为直线12,l l 关于1x =对称,所以AB 与AC 的倾斜角互补,所以12122212121222224411221144AB AC y y y y k k y y x x y y ----+=+=+=+=--++--,所以124y y +=-,所以1212221212124144BC y y y y k y y x x y y --====--+-.设直线BC 的方程为y x m =-+,由24y x m y x=-+⎧⎨=⎩消去y 整理得()22240x m x m -++=,所以2121224,x x m x x m +=+=,所以12BC x =-=,且BC 中点D 的横坐标为1222x x m +=+.因为以线段BC 为直径的圆与抛物线的准线1x =-相切,所以1212BC x x ++=,即3m +=1m =,所以直线BC 的方程为1y x =-+,即10x y +-=.【名师点睛】由于在解答圆锥曲线问题中需要涉及大量的计算,所以在解题时要注意“设而不求”、“整体代换”等方法的利用,另外还应注意巧设直线的方程,以达到简化运算的目的,考查直线和圆锥曲线的位置关系及计算能力,属于中档题.(1)将点()1,2A 坐标代入曲线方程求出2p =,于是可得曲线方程.(2)方法一:由题意设出直线AB 的方程,与抛物线方程联立消元后,根据根与系数的关系求出点B 的坐标,同理得到点C 的坐标,然后根据以线段BC 为直径的圆与抛物线E 的准线相切可求得点,B C 中的参数,进而可得所求方程.方法二:由题意得AB 与AC 的倾斜角互补,由此可得1BC k =-,于是可设直线BC 的方程为y x m =-+,与曲线方程联立消元后,再根据题意求得参数m ,进而得到直线方程.10.【河南省开封市2019届高三上学期第一次模拟考试数学试题】已知抛物线2:2(0)C y px p =>的焦点F与椭圆22143x y +=的右焦点重合,抛物线C 的动弦AB 过点F ,过点F 且垂直于弦AB 的直线交抛物线的准线于点M .(1)求抛物线的标准方程;(2)求ABMF的最小值.【答案】(1)24y x =;(2)2.【解析】(1)由椭圆方程得,椭圆的右焦点为()1,0,∴抛物线的焦点为()1,0F ,∴2p =,∴抛物线的标准方程为24y x =.(2)①当动弦AB 所在直线的斜率不存在时,易得:24AB p ==,2MF =,2ABMF=.②当动弦AB 所在直线的斜率存在时,易知AB 的斜率不为0.设AB 所在直线方程为()1y k x =-,且()11,A x y ,()22,B x y .联立方程:()241y xy k x ⎧=⎪⎨=-⎪⎩,得()2222220k x k x k -++=,∴()212222k x x k++=,121x x ⋅=,()21610k ∆=+>,∴12AB x =-=()2241k k +=.∵FM 所在的直线方程为()11y x k =--,联立方程()111y x kx ⎧=--⎪⎨⎪=-⎩,得点21,M k ⎛⎫- ⎪⎝⎭,∴MF ==,∴()22412k ABk MF +==,综上所述:ABMF的最小值为2.【名师点睛】圆锥曲线中最值与范围问题的常见求法:(1)几何法:若题目的条件和结论能明显体现几何特征和意义,则考虑利用图形性质来解决;(2)代数法:若题目的条件和结论能体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值.在利用代数法解决最值与范围问题时常从以下几个方面考虑:①利用判别式来构造不等关系,从而确定参数的取值范围;②利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围;③利用基本不等式求出参数的取值范围;④利用函数的值域的求法,确定参数的取值范围.21。
2019高考数学圆锥曲线与方程真题汇总(一题不拉)

(2019•上海20)已知椭圆22184x y +=,1F ,2F 为左、右焦点,直线l 过2F 交椭圆于A ,B 两点.(1)若直线l 垂直于x 轴,求||AB ;(2)当190F AB ∠=︒时,A 在x 轴上方时,求A 、B 的坐标;(3)若直线1AF 交y 轴于M ,直线1BF 交y 轴于N ,是否存在直线l ,使得11F AB F MN S S =V V ,若存在,求出直线l 的方程;若不存在,请说明理由.【解答】解:(1)依题意,2(2,0)F ,当AB x ⊥轴时,则A,(2,B ,得||AB = (2)设1(A x ,1)y ,11290(90)F AB F AF ∠=︒∠=︒Q ,∴2212111111(2,)(2,)40AF AF x y x y x y =+-=-+=u u u r u u u u r g g ,又A 在椭圆上,满足2211184x y +=,即22114(1)8x y =-,∴221144(1)08x x -+-=,解得10x =,即(0,2)A .直线:2AB y x =-+,联立222184y x x y =-+⎧⎪⎨+=⎪⎩,解得8(3B ,2)3-;(3)设1(A x ,1)y ,2(B x ,2)y ,3(0,)M y ,4(0,)N y ,直线:2l x my =+,则11212121||||2||2F AB S F F y y y y =-=-V g ,1134341||||||2F MN S FO y y y y =-=-V g . 联立222184x my x y =+⎧⎪⎨+=⎪⎩,得22(2)440m y my ++-=.则12242m y y m +=-+,12242y y m -=+. 由直线1AF 的方程:11(2)2y y x x =++,得M 纵坐标13122y y x =+;由直线1BF 的方程:22(2)2y y x x =++,得N 的纵坐标24222y y x =+. 若11F AB F MNS S =V V ,即12342||||y y y y -=-,121212341212121222228()||||||||2||2244(4)(4)y y y y y y y y y y x x my my my my --=-=-==-++++++,12|(4)(4)|4my my ∴++=,21212|4()16|4m y y m y y +++=,代入根与系数的关系,得22244|416|422m m m m m --++=++g,解得m =.∴存在直线20x +-=或20x --=满足题意.(2019•上海12)已知2()||(1,0)1f x a x a x =->>-,()f x 与x 轴交点为A ,若对于()f x 图象上任意一点P ,在其图象上总存在另一点(Q P 、Q 异于)A ,满足AP AQ ⊥,且||||AP AQ =,则a = .【解答】解:由题意,可知: 令2()||01f x a x =-=-,解得:21x a=+,∴点A 的坐标为:2(1a +,0).则2,11()2,1AAa x x x f x a x x x ⎧-<⎪⎪-=⎨⎪-+>⎪-⎩….()f x ∴大致图象如下:由题意,很明显P 、Q 两点分别在两个分段曲线上,不妨设点P 在左边曲线上,点Q 在右边曲线上.设直线AP 的斜率为k ,则2:(1)AP l y k x a=--. 联立方程:2(1)21y k x ay ax ⎧=--⎪⎪⎨⎪=-⎪-⎩,整理,得:222[(2)](1)20kx a k x k a a a +-+++--=.2(2)22P A a k a a x x k a k-+∴+=-=+-.21A x a =+Q ,221P A a ax x a k k∴=+--=-. 再将1P ax k=-代入第一个方程,可得: 2P k y a a=--. ∴点P 的坐标为:(1a k -,2)k a a--.||AP ∴==AP AQ ⊥Q ,∴直线AQ 的斜率为1k -,则12:(1)AQ l y x k a=---.同理类似求点P 的坐标的过程,可得: 点Q 的坐标为:2(1,)ak a ak-+.||AQ ∴===||||AP AQ =Q ,及k 的任意性,可知:224a a=,解得:a =(2019•上海9)过曲线24y x =的焦点F 并垂直于x 轴的直线分别与曲线24y x =交于A ,B ,A 在B 上方,M 为抛物线上一点,(2)OM OA OB λλ=+-u u u u r u u u r u u u r,则λ= .【解答】解:过24y x =的焦点F 并垂直于x 轴的直线分别与24y x =交于A ,B ,A 在B 上方,依题意:得到:(1A ,2)(1B ,2)-,设点(,)M x y ,所以:M 为抛物线上一点,(2)OM OA OB λλ=+-u u u u r u u u r u u u r ,则:(x ,)(1y λ=,2)(2)(1λ+-,2)(22λ-=-,4),代入24y x =,得到:3λ=. 故答案为:3(2019•浙江21)如图,已知点(1,0)F 为抛物线22(0)y px p =>的焦点.过点F 的直线交抛物线于A ,B 两点,点C 在抛物线上,使得ABC ∆的重心G 在x 轴上,直线AC 交x 轴于点Q ,且Q 在点F 的右侧.记AFG ∆,CQG ∆的面积分别为1S ,2S . (Ⅰ)求p 的值及抛物线的准线方程; (Ⅱ)求12S S 的最小值及此时点G 的坐标.【解答】解:(Ⅰ)由抛物线的性质可得:12p=,2p ∴=,∴抛物线的准线方程为1x =-; (Ⅱ)设(A A x ,)A y ,(B B x ,)B y ,(C C x ,)C y ,重心(G G x ,)G y ,令2A y t =,0t ≠,则2A x t =,由于直线AB 过F ,故直线AB 的方程为2112t x y t -=+,代入24y x =,得:222(1)40t y y t ---=,24B ty ∴=-,即2B y t =-,21(B t ∴,2)t -,又1()3G A B C x x x x =++,1()3G A B C y y y y =++,重心在x 轴上,∴220C t y t -+=,21(()C t t∴-,12())t t -,422222(3t t G t -+,0),∴直线AC 的方程为222()y t t x t -=-,得2(1Q t -,0),Q Q 在焦点F 的右侧,22t ∴>,∴424222142442222521|||2|||||223221222211|||||1||2|23A C t t t FG y S t t t t t t S t t QG y t t t t-+--====--+-----g g g g,令22m t =-,则0m >,1221322213433424S m S m m m m m m=-=--=++++++g …,∴当3m =时,12S S 取得最小值为31+,此时(2,0)G . (2019•浙江15)已知椭圆22195x y +=的左焦点为F ,点P 在椭圆上且在x 轴的上方.若线段PF 的中点在以原点O 为圆心,||OF 为半径的圆上,则直线PF 的斜率是 .【解答】解:椭圆22195x y +=的3a =,5b =,2c =,23e =,设椭圆的右焦点为F ',连接PF ',线段PF 的中点A 在以原点O 为圆心,2为半径的圆,连接AO ,可得||2||4PF AO '==,设P 的坐标为(,)m n ,可得2343m -=,可得32m =-,15n =,由(2,0)F -,可得直线PF 的斜率为 15215322=-+. 另解:由||2||4PF AO '==,||642PF =-=,||24FF c '==,可得416161cos 2244PFF +-'∠==⨯⨯,115sin 116PFF '∠=-=,可得直线PF 的斜率为sin 15cos PFF PFF '∠='∠.故答案为:15.(2019•浙江2)渐近线方程为0x y ±=的双曲线的离心率是( ) A .22B .1C .2D .2【解答】解:根据渐近线方程为0x y ±=的双曲线,可得a b =,所以2c a = 则该双曲线的离心率为2ce a==,故选:C . (2019•江苏17)如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b +=>>的焦点为1(1,0)F -,2(1,0)F .过2F 作x 轴的垂线l ,在x 轴的上方,1与圆2222:(1)4F x y a -+=交于点A ,与椭圆C 交于点D .连结1AF 并延长交圆2F 于点B ,连结2BF 交椭圆C 于点E ,连结1DF .已知152DF =. (1)求椭圆C 的标准方程;(2)求点E 的坐标.【解答】解:(1)如图,22F A F B =Q ,22F AB F BA ∴∠=∠,22212F A a F D DA F D F D ==+=+Q ,1AD F D ∴=,则11DAF DF A ∠=∠,12DF A F BA ∴∠=∠,则12//F D BF ,1c =Q ,221b a ∴=-,则椭圆方程为222211x y a a +=-,取1x =,得21D a y a -=,则22112a a AD a a a -+=-=. 又152DF =,∴2152a a +=,解得2(0)a a =>.∴椭圆C 的标准方程为22143x y +=;(2)由(1)知,3(1,)2D ,1(1,0)F -,∴2133224BF DF k k ===,则23:(1)4BF y x =-,联立223(1)4143y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩,得22118390x x --=. 解得11x =-或2137x =(舍). ∴132y =-.即点E 的坐标为3(1,)2--.(2019•江苏7)在平面直角坐标系xOy 中,若双曲线2221(0)y x b b-=>经过点(3,4),则该双曲线的渐近线方程是 .【解答】解:Q 双曲线2221(0)y x b b -=>经过点(3,4),∴221631b-=,解得22b =,即b .又1a =,∴该双曲线的渐近线方程是y =.故答案为:y =.(2019•天津文19)设椭圆22221(0)x y a b a b +=>>的左焦点为F ,左顶点为A ,上顶点为B .已|2||(OA OB O =为原点). (Ⅰ)求椭圆的离心率; (Ⅱ)设经过点F 且斜率为34的直线l 与椭圆在x 轴上方的交点为P ,圆C 同时与x 轴和直线l 相切,圆心C 在直线4x =上,且//OC AP .求椭圆的方程.【解答】解:(Ⅰ|2||OA OB =2b =,可得12c e a ==;(Ⅱ)b =,12c a =,即2a c =,b =,可得椭圆方程为2222143x y c c +=,设直线FP 的方程为3()4y x c =+,代入椭圆方程可得2276130x cx c +-=,解得x c =或137cx =-,代入直线PF 方程可得32c y =或914cy =-(舍去),可得3(,)2c P c ,圆心C 在直线4x =上,且//OC AP ,可设(4,)C t ,可得3242ctc c=+,解得2t =,即有(4,2)C ,可得圆的半径为2,由直线FP 和圆C 相切的条件为d r =2=,解得2c =,可得4a =,b =椭圆方程为2211612x y +=.(2019•天津理18)设椭圆22221(0)x y a b a b +=>>的左焦点为F ,上顶点为B .已知椭圆的短轴长为4. (Ⅰ)求椭圆的方程;(Ⅱ)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若||||(ON OF O =为原点),且OP MN ⊥,求直线PB 的斜率.【解答】解:(Ⅰ)由题意可得24b =,即2b =,c e a ==222a b c -=,解得a =,1c =,可得椭圆方程为22154x y +=;(Ⅱ)(0,2)B ,设PB 的方程为2y kx =+,代入椭圆方程224520x y +=,可得22(45)200k x kx ++=,解得22045k x k =-+或0x =,即有220(45kP k -+,22810)45k k -+,2y kx =+,令0y =,可得2(M k-,0),又(0,1)N -,OP MN ⊥,可得281011220k k k-=---g ,解得k =可得PB的斜率为 (2019•天津理5文6)已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b -=>>的两条渐近线分别交于点A 和点B ,且||4||(AB OF O =为原点),则双曲线的离心率为( ) ABC .2D【解答】解:Q 抛物线24y x =的焦点为F ,准线为l .(1,0)F ∴,准线l 的方程为1x =-,l Q 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||(AB OF O =为原点),2||b AB a ∴=,||1OF =,∴24ba=,2b a ∴=,c ∴==,∴双曲线的离心率为ce a=故选:D .(2019•北京文19)已知椭圆2222:1x y C a b +=的右焦点为(1,0),且经过点(0,1)A .(Ⅰ)求椭圆C 的方程;(Ⅱ)设O 为原点,直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P 、Q ,直线AP 与x 轴交于点M ,直线AQ 与x 轴交于点N .若||||2OM ON =g,求证:直线l 经过定点. 【解答】解:(Ⅰ)椭圆2222:1x y C a b +=的右焦点为(1,0),且经过点(0,1)A .可得1b c ==,a =,则椭圆方程为2212x y +=;(Ⅱ)证明:y kx t =+与椭圆方程2222x y +=联立,可得222(12)4220k x ktx t +++-=,设1(P x ,1)y ,2(Q x ,2)y ,△2222164(12)(22)0k t k t =-+->,122412kt x x k+=-+,21222212t x x k -=+,AP的方程为1111y y x x -=+,令0y =,可得111xx y =-,即11(1x M y -,0); AQ 的方程为2211y y x x -=+,令0y =,可得221x y y =-.即22(1xN y -,0). 1212121212(1)(1)1()1()()(2)y y y y y y kx t kx t kx kx t --=+-+=+++-++2222222224(1)(12)()()121212t kt t t t k kt k k k k --=+-++--=+++g g ,||||2OM ON =g ,即为1212||211x xy y =--g ,即有22|1|(1)t t -=-,由1t ≠±,解得0t =,满足△0>,即有直线l 方程为y kx =,恒过原点(0,0).(2019•北京文11)设抛物线24y x =的焦点为F ,准线为l ,则以F 为圆心,且与l 相切的圆的方程为 .【解答】解:如图,抛物线24y x =的焦点为(1,0)F ,Q 所求圆的圆心F ,且与准线1x =-相切,∴圆的半径为2. 则所求圆的方程为22(1)4x y -+=. 故答案为:22(1)4x y -+=.(2019•北京文5)已知双曲线2221(0)x y a a-=>,则(a = )AB .4C .2D .12【解答】解:由双曲线2221(0)x y a a -=>,得21b =,又c e a =,得225c a =,即2222215a b a a a ++==,解得214a =,12a =. 故选:D .(2019•北京理18)已知抛物线2:2C x py =-经过点(2,1)-. (Ⅰ)求抛物线C 的方程及其准线方程;(Ⅱ)设O 为原点,过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ,N ,直线1y =-分别交直线OM ,ON 于点A 和点B .求证:以AB 为直径的圆经过y 轴上的两个定点.【解答】解:(Ⅰ)抛物线2:2C x py =-经过点(2,1)-.可得42p =,即2p =,可得抛物线C 的方程为24x y =-,准线方程为1y =;(Ⅱ)证明:抛物线24x y =-的焦点为(0,1)F -,设直线方程为1y kx =-,联立抛物线方程,可得2440x kx +-=,设1(M x ,1)y ,2(N x ,2)y ,可得124x x k +=-,124x x =-,直线OM 的方程为11y y x x =,即14xy x =-,直线ON 的方程为22y y x x =,即24x y x =-,可得14(A x ,1)-,24(B x ,1)-,可得AB 的中点的横坐标为121142()224k k x x -+==-g ,即有AB 为直径的圆心为(2,1)k -,半径为12||144||222AB x x =-==,可得圆的方程为222(2)(1)4(1)x k y k -++=+,化为224(1)4x kx y -++=,由0x =,可得1y =或3-.则以AB 为直径的圆经过y 轴上的两个定点(0,1),(0,3)-.(2019•北京理8)数学中有许多形状优美、寓意美好的曲线,曲线22:1||C x y x y +=+就是其中之一(如图).给出下列三个结论:①曲线C 恰好经过6个整点(即横、纵坐标均为整数的点); ②曲线C; ③曲线C 所围成的“心形”区域的面积小于3. 其中,所有正确结论的序号是( )A .①B .②C .①②D .①②③【解答】解:将x 换成x -方程不变,所以图形关于y 轴对称,当0x =时,代入得21y =,1y ∴=±,即曲线经过(0,1),(0,1)-;当0x >时,方程变为2210y xy x -+-=,所以△224(1)0x x =--…,解得(0x ∈,所以x 只能取整数1,当1x =时,20y y -=,解得0y =或1y =,即曲线经过(1,0),(1,1),根据对称性可得曲线还经过(1,0)-,(1,1)-,故曲线一共经过6个整点,故①正确.当0x >时,由221x y xy +=+得222212x y x y xy ++-=„,(当x y =时取等),222x y ∴+„,∴,即曲线C 上y ,根据对称性可得:曲线C ②正确.在x 轴上图形面积大于矩形面积122=⨯=,x 轴下方的面积大于等腰直角三角形的面积12112=⨯⨯=,因此曲线C 所围成的“心形”区域的面积大于213+=,故③错误. 故选:C .(2019•北京理4)已知椭圆22221(0)x y a b a b +=>>的离心率为12,则( )A .222a b =B .2234a b =C .2a b =D .34a b =【解答】解:由题意,12c a =,得2214c a =,则22214a b a -=,22244a b a ∴-=,即2234a b =. 故选:B .(2019•新课标Ⅲ文21)已知曲线C :y =x 22,D 为直线y =−12上的动点,过D 作C 的两条切线,切点分别为A ,B . (1)证明:直线AB 过定点.(2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求该圆的方程.【解答】(1)证明:设D (t ,−12),A (x 1,y 1),则x 12=2y 1,由于y ′=x ,∴切线DA 的斜率为x 1,故y 1+12x 1−t=x 1,整理得:2tx 1﹣2y 1+1=0.设B (x 2,y 2),同理可得2tx 2﹣2y 2+1=0. 故直线AB 的方程为2tx ﹣2y +1=0. ∴直线AB 过定点(0,12);(2)解:由(1)得直线AB 的方程y =tx +12. 由{y =tx +12y =x22,可得x 2﹣2tx ﹣1=0. 于是x 1+x 2=2t ,y 1+y 2=t(x 1+x 2)+1=2t 2+1.设M 为线段AB 的中点,则M (t ,t 2+12),由于EM →⊥AB →,而EM →=(t ,t 2−2),AB →与向量(1,t )平行,∴t +(t 2﹣2)t =0,解得t =0或t =±1. 当t =0时,|EM →|=2,所求圆的方程为x 2+(y −52)2=4; 当t =±1时,|EM →|=√2,所求圆的方程为x 2+(y −52)2=2.(2019•新课标Ⅲ理21)已知曲线C :y =x 22,D 为直线y =−12上的动点,过D 作C 的两条切线,切点分别为A ,B . (1)证明:直线AB 过定点;(2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.【解答】解:(1)证明:y =x 22的导数为y ′=x ,设切点A (x 1,y 1),B (x 2,y 2),即有y 1=x 122,y 2=x 222,切线DA 的方程为y ﹣y 1=x 1(x ﹣x 1),即为y =x 1x −x 122,切线DB 的方程为y =x 2x −x 222,联立两切线方程可得x =12(x 1+x 2),可得y =12x 1x 2=−12,即x 1x 2=﹣1,直线AB 的方程为y −x 122=y 1−y 2x 1−x 2(x ﹣x 1),即为y −x 122=12(x 1+x 2)(x ﹣x 1),可化为y =12(x 1+x 2)x +12,可得AB 恒过定点(0,12);(2)法一:设直线AB 的方程为y =kx +12,由(1)可得x 1+x 2=2k ,x 1x 2=﹣1,AB 中点H (k ,k 2+12),由H 为切点可得E 到直线AB 的距离即为|EH |,可得|12−52|√1+k 2=√k 2+(k 2−2)2,解得k =0或k =±1,即有直线AB 的方程为y =12或y =±x +12,由y =12可得|AB |=2,四边形ADBE 的面积为S △ABE +S △ABD =12×2×(1+2)=3; 由y =±x +12,可得|AB |=√1+1•√4+4=4,此时D (±1,−12)到直线AB 的距离为|1+12+12|√2=√2;E (0,52)到直线AB 的距离为|12−52|√2=√2,则四边形ADBE 的面积为S △ABE +S △ABD =12×4×(√2+√2)=4√2; 法二:(2)由(1)得直线AB 的方程为y =tx +12. 由{y =tx +12y =x22,可得x 2﹣2tx ﹣1=0. 于是x 1+x 2=2t ,x 1x 2=﹣1,y 1+y 2=t (x 1+x 2)+1=2t 2+1,|AB |=√1+t 2|x 1−x 2|=√1+t 2×√(x 1+x 2)2−4x 1x 2=2(t 2+1).设d 1,d 2分别为点D ,E 到直线AB 的距离,则d 1=√t 2+1,d 2=2√t +1.因此,四边形ADBE 的面积S =12|AB |(d 1+d 2)=(t 2+3)√t 2+1. 设M 为线段AB 的中点,则M (t ,t 2+12).由于EM →⊥AB →,而EM →=(t ,t 2−2),AB →与向量(1,t )平行,所以t +(t 2﹣2)t =0.解得t =0或t =±1.当t =0时,S =3;当t =±1时,S =4√2. 综上,四边形ADBE 的面积为3或4√2. (2019•新课标Ⅲ理14文15)设F 1,F 2为椭圆C :x 236+y 220=1的两个焦点,M 为C 上一点且在第一象限.若△MF 1F 2为等腰三角形,则M 的坐标为 . 【解答】解:设M (m ,n ),m ,n >0,椭圆C :x 236+y 220=1的a =6,b =2√5,c =4,e =c a =23,由于M 为C 上一点且在第一象限,可得|MF 1|>|MF 2|,△MF 1F 2为等腰三角形,可能|MF 1|=2c 或|MF 2|=2c ,即有6+23m =8,即m =3,n =√15; 6−23m =8,即m =﹣3<0,舍去. 可得M (3,√15). 故答案为:(3,√15).(2019•新课标Ⅲ文理10)双曲线C :x 24−y 22=1的右焦点为F ,点P 在C 的一条渐近线上,O 为坐标原点.若|PO |=|PF |,则△PFO 的面积为( ) A .3√24B .3√22 C .2√2 D .3√2【解答】解:双曲线C :x 24−y 22=1的右焦点为F (√6,0),渐近线方程为:y =±√22x ,不妨P 在第一象限,可得tan ∠POF =√22,P (√62,√32),所以△PFO 的面积为:12×√6×√32=3√24. 故选:A .(2019•新课标Ⅱ文20)已知1F ,2F 是椭圆2222:1(0)x y C a b a b +=>>的两个焦点,P 为C 上的点,O 为坐标原点.(1)若2POF ∆为等边三角形,求C 的离心率;(2)如果存在点P ,使得12PF PF ⊥,且△12F PF 的面积等于16,求b 的值和a 的取值范围. 【解答】解:(1)连接1PF ,由2POF ∆为等边三角形可知在△12F PF 中,1290F PF ∠=︒,2||PF c =,1||PF =,于是122||||1)a PF PF c =+=,故曲线C 的离心率1ce a==. (2)由题意可知,满足条件的点(,)P x y 存在当且仅当:1||2162y c =g ,1y y x c x c=-+-g ,22221x y a b +=,即||16c y =,① 222x y c +=,②22221x y a b +=,③由②③及222a b c =+得422b y c =,又由①知22216y c =,故4b =,由②③得22222()a x c b c=-,所以22c b …,从而2222232a b c b =+=…,故a …4b =,a …点P .所以4b =,a的取值范围为)+∞.(2019•新课标Ⅱ理21)已知点(2,0)A -,(2,0)B ,动点(,)M x y 满足直线AM 与BM 的斜率之积为12-.记M 的轨迹为曲线C .(1)求C 的方程,并说明C 是什么曲线;(2)过坐标原点的直线交C 于P ,Q 两点,点P 在第一象限,PE x ⊥轴,垂足为E ,连结QE 并延长交C 于点G .()i 证明:PQG ∆是直角三角形; ()ii 求PQG ∆面积的最大值.【解答】解:(1)由题意得1222y y x x ⨯=-+-,整理得曲线C 的方程:221(0)42x y y +=≠,∴曲线C 是焦点在x 轴上不含长轴端点的椭圆;(2)()i 设0(P x ,0)y ,则0(Q x -,0)y -,0(E x ,0),(G G x ,)G y ,∴直线QE 的方程为:000()2y y x x x =-,与22142x y +=联立消去y ,得22222220000000(2)280x y x x y x x y x +-+-=,∴2220000220082G x y x x x x y --=+,∴2002200(8)2G y x x x y -=+,∴220000022000(4)()22G G y y x y y x x x x y --=-=+,∴G PG G y y k x x -=-220000220020002200(4)2(8)2y x y y x y x y x x y ---+=--+232300000002320000004282y y x y y x y x x y x x y ----=--- 2200022000(432)2(4)y x y x y x --=--,把220024x y +=代入上式,得2200022000(434)2(442)PG y x x k x y y --+=--+ 20020022y x x y -⨯=00x y =-,0000()1PQ PG y xk k x y ∴⨯=⨯-=-,PQ PG ∴⊥,故PQG ∆为直角三角形; 1()||()2PQG G Q ii S PE x x ∆=⨯- 001()2G y x x =+ 200002200(8)1[]22y x y x x y -=++ 22200000220082122y x y y x x y -++=⨯+ 20002200(4)2y x x x y +=+ 222000002200(2)2y x x y x x y ++=+ 22000022002()2y x x y x y +=+ 220000222200008()(2)(2)y x x y x y x y +=++ 330000442200008()225y x x y x y x y +=++ 0000200008()2()1x y y x x y y x +=++令0000x y t y x =+,则2t …,2881212PQG t S t t t∆==++ 利用“对号”函数1()2f t t t =+在[2,)+∞的单调性可知,19()4(222f t t +==…时取等号),∴816992PQG S ∆=„(此时00x y =,故PQG ∆面积的最大值为169. (2019•新课标Ⅱ理11文12)设F 为双曲线2222:1(0,0)x y C a b a b -=>>的右焦点,O 为坐标原点,以OF 为直径的圆与圆222x y a +=交于P ,Q 两点.若||||PQ OF =,则C 的离心率为()ABC .2D【解答】解:如图,以OF 为直径的圆的方程为220x y cx +-=,又圆O 的方程为222x y a +=,PQ ∴所在直线方程为2a x c=.把2a x c =代入222x y a +=,得2ab PQ c =,再由||||PQ OF =,得2ab c c=,即22244()a c a c -=,22e ∴=,解得e故选:A .(2019•新课标Ⅱ理8文9)若抛物线22(0)y px p =>的焦点是椭圆2213x y p p+=的一个焦点,则(p = )A .2B .3C .4D .8【解答】解:由题意可得:23()2pp p -=,解得8p =.故选:D .(2019•新课标Ⅰ理10文12)已知椭圆C 的焦点为1(1,0)F -,2(1,0)F ,过点2F 的直线与椭圆C 交于A ,B 两点.若22||2||AF F B =,1||||AB BF =,则C 的方程为( )A .2212x y +=B .22132x y +=C .22143x y +=D .22154x y +=【解答】解:22||2||AF BF =Q ,2||3||AB BF ∴=,又1||||AB BF =,12||3||BF BF ∴=,又12||||2BF BF a +=,2||2a BF ∴=,2||AF a ∴=,13||2BF a =,12||||2AF AF a +=Q ,1||AF a ∴=,12||||AF AF ∴=,A ∴在y 轴上.在Rt △2AF O 中,21cos AF O a∠=,在△12BF F 中,由余弦定理可得222134()()22cos 222a a BF F a +-∠=⨯⨯,根据221cos cos 0AF O BF F ∠+∠=,可得214202a a a -+=,解得23a =,a ∴=. 222312b a c =-=-=.所以椭圆C 的方程为:22132x y +=.故选:B .(2019•新课标Ⅰ文10)双曲线2222:1(0,0)x y C a b a b -=>>的一条渐近线的倾斜角为130︒,则C的离心率为( ) A .2sin40︒B .2cos40︒C .1sin50︒D .1cos50︒【解答】解:双曲线2222:1(0,0)x y C a b a b -=>>的渐近线方程为by x a=±,由双曲线的一条渐近线的倾斜角为130︒,得tan130tan50b a -=︒=-︒,则sin50tan50cos50b a ︒=︒=︒,∴2222222222501115050b c a c sin a a a cos cos -︒==-==-︒︒,得22150e cos =︒,1cos50e ∴=︒. 故选:D .(2019•新课标Ⅰ理19)已知抛物线2:3C y x =的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1理)若||||4AF BF +=,求l 的方程; (2理)若3AP PB =u u u r u u u r,求||AB .【解答】解:(1理)设直线l 的方程为3()2y x t =-,将其代入抛物线23y x =得:22999(3)0424x t x t -++=,设1(A x ,1)y ,2(B x ,2)y ,则1293422934t x x t ++==+,①,212x x t =②,由抛物线的定义可得:1243||||2432AF BF x x p t +=++=++=,解得712t =,直线l 的方程为3728y x =-. (2理)若3AP PB =u u u r u u u r ,则123y y =-,∴1233()3()22x t x t -=-⨯-,化简得1234x x t =-+,③由①②③解得1t =,13x =,213x =,||AB ∴=. (2019•新课标Ⅰ文21)已知点A ,B 关于坐标原点O 对称,||4AB =,M e 过点A ,B 且与直线20x +=相切.(1)若A 在直线0x y +=上,求M e 的半径;(2)是否存在定点P ,使得当A 运动时,||||MA MP -为定值?并说明理由.【解答】解:M Q e 过点A ,B 且A 在直线0x y +=上,∴点M 在线段AB 的中垂线0x y -=上,设M e 的方程为:222()()(0)x a y a R R -+-=>,则 圆心(,)M a a 到直线0x y +=的距离d =,又||4AB =,∴在Rt OMB ∆中,2221(||)2d AB R +=,即224R +=① 又M Q e 与2x =-相切,|2|a R ∴+=② 由①②解得02a R =⎧⎨=⎩或46a R =⎧⎨=⎩,M ∴e 的半径为2或6;(2)Q 线段AB 为M e 的一条弦O 是弦AB 的中点,∴圆心M 在线段AB 的中垂线上,设点M的坐标为(,)x y ,则222||||||OM OA MA +=,M Q e 与直线20x +=相切,|||2|MA x ∴=+,22222|2|||||4x OM OA x y ∴+=+=++,24y x ∴=,M ∴的轨迹是以(1,0)F 为焦点1x =-为准线的抛物线,|||||2|||MA MP x MP ∴-=+- |1|||1||||1x MP MF MP =+-+=-+,∴当||||MA MP -为定值时,则点P 与点F 重合,即P的坐标为(1,0),∴存在定点(1,0)P 使得当A 运动时,||||MA MP -为定值.。
2019年高考文数——圆锥曲线(解答)

2019年高考文数——圆锥曲线1.(19全国一文21.(12分))已知点A ,B 关于坐标原点O 对称,│AB │ =4,⊙M 过点A ,B 且与直线x +2=0相切. (1)若A 在直线x +y =0上,求⊙M 的半径;(2)是否存在定点P ,使得当A 运动时,│MA │-│MP │为定值?并说明理由.2.(19全国二文20.(12分))已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的两个焦点,P 为C 上一点,O 为坐标原点.(1)若2POF △为等边三角形,求C 的离心率;(2)如果存在点P ,使得12PF PF ⊥,且12F PF △的面积等于16,求b 的值和a 的取值范围.3.(19全国三文21.(12分))已知曲线C :y =22x ,D 为直线y =12-上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点: (2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求该圆的方程.4.(19北京文(19)(本小题14分))已知椭圆2222:1x y C a b+=的右焦点为(1,0),且经过点(0,1)A .(Ⅰ)求椭圆C 的方程;(Ⅱ)设O 为原点,直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ,Q ,直线AP 与x 轴交于点M ,直线AQ 与x 轴交于点N ,若|OM |·|ON |=2,求证:直线l 经过定点.5.(19天津文(19)(本小题满分14分))设椭圆22221(0)x ya ba b+=>>的左焦点为F,左顶点为A,上顶点为B.已知||2||OA OB=(O为原点). (Ⅰ)求椭圆的离心率;(Ⅱ)设经过点F且斜率为34的直线l与椭圆在x轴上方的交点为P,圆C同时与x轴和直线l相切,圆心C在直线x=4上,且OC AP∥,求椭圆的方程.参考答案:1.解:(1)因为M e 过点,A B ,所以圆心M 在AB 的垂直平分线上.由已知A 在直线+=0x y 上,且,A B 关于坐标原点O 对称,所以M 在直线y x =上,故可设(, )M a a . 因为M e 与直线x +2=0相切,所以M e 的半径为|2|r a =+.由已知得||=2AO ,又MO AO ⊥u u u u r u u u r ,故可得2224(2)a a +=+,解得=0a 或=4a .故M e 的半径=2r 或=6r .(2)存在定点(1,0)P ,使得||||MA MP -为定值. 理由如下:设(, )M x y ,由已知得M e 的半径为=|+2|,||=2r x AO .由于MO AO ⊥u u u u r u u u r ,故可得2224(2)x y x ++=+,化简得M 的轨迹方程为24y x =.因为曲线2:4C y x =是以点(1,0)P 为焦点,以直线1x =-为准线的抛物线,所以||=+1MP x .因为||||=||=+2(+1)=1MA MP r MP x x ---,所以存在满足条件的定点P .2.解:(1)连结1PF ,由2POF △为等边三角形可知在12F PF △中,1290F PF ∠=︒,2PF c =,1PF =,于是1221)a PF PF c =+=,故C 的离心率是1ce a==. (2)由题意可知,满足条件的点(,)P x y 存在.当且仅当1||2162y c ⋅=,1y y x c x c⋅=-+-,22221x y a b +=,即||16c y =,①222x y c +=,②22221x y a b +=,③由②③及222a b c =+得422b y c =,又由①知22216y c=,故4b =.由②③得()22222a x c b c=-,所以22c b ≥,从而2222232,a b c b =+≥=故a ≥.当4b =,a ≥时,存在满足条件的点P .所以4b =,a 的取值范围为)+∞.3.解:(1)设()111,,,2D t A x y ⎛⎫-⎪⎝⎭,则2112x y =.由于y'x =,所以切线DA 的斜率为1x ,故11112y x x t+=-.整理得112 2 +1=0. tx y - 设()22,B x y ,同理可得222 2 +1=0tx y -.故直线AB 的方程为2210tx y -+=.所以直线AB 过定点1(0,)2. (2)由(1)得直线AB 的方程为12y tx =+. 由2122y tx x y ⎧=+⎪⎪⎨⎪=⎪⎩,可得2210x tx --=. 于是()21212122,121x x t y y t x x t +=+=++=+.设M 为线段AB 的中点,则21,2M t t ⎛⎫+⎪⎝⎭. 由于EM AB ⊥u u u u r u u u r ,而()2,2EM t t =-u u u u r ,AB u u u r 与向量(1, )t 平行,所以()220t t t +-=.解得t =0或1t =±.当t =0时,||EM u u u u r =2,所求圆的方程为22542x y ⎛⎫+-= ⎪⎝⎭;当1t =±时,||EM =u u u u r 22522x y ⎛⎫+-= ⎪⎝⎭.4.解:(I )由题意得,b 2=1,c =1.所以a 2=b 2+c 2=2.所以椭圆C 的方程为2212xy +=.(Ⅱ)设P (x 1,y 1),Q (x 2,y 2),则直线AP 的方程为1111y y x x -=+.令y =0,得点M 的横坐标111M x x y =--. 又11y kx t =+,从而11||||1M x OM x kx t ==+-.同理,22||||1x ON kx t =+-. 由22,12y kx t x y =+⎧⎪⎨+=⎪⎩得222(12)4220k x ktx t +++-=. 则122412kt x x k +=-+,21222212t x x k-=+. 所以1212||||||||11x x OM ON kx t kx t ⋅=⋅+-+-()12221212||(1)(1)x x k x x k t x x t =+-++- 22222222212||224(1)()(1)1212t k t ktk k t t k k-+=-⋅+-⋅-+-++12||1tt+=-. 又||||2OM ON ⋅=,所以12||21tt+=-. 解得t =0,所以直线l 经过定点(0,0).5. (Ⅰ)解:设椭圆的半焦距为c2b =,又由222a b c =+,消去b 得222a c ⎫=+⎪⎪⎝⎭,解得12c a =.所以,椭圆的离心率为12. (Ⅱ)解:由(Ⅰ)知,2,a c b ==,故椭圆方程为2222143x y c c +=.由题意,(, 0)F c -,则直线l 的方程为3()4y x c =+ 点P 的坐标满足22221,433(),4x y c c y x c ⎧+=⎪⎪⎨⎪=+⎪⎩消去y 并化简,得到2276130x cx c +-=,解得1213,7cx c x ==-.代入到l 的方程,解得1239,214y c y c ==-.因为点P 在x 轴上方,所以3,2P c c ⎛⎫⎪⎝⎭.由圆心C 在直线4x =上,可设(4, )C t .因为OC AP ∥,且由(Ⅰ)知( 2 , 0)A c -,故3242c t c c=+,解得2t =.因为圆C 与x 轴相切,所以圆的半径长为2,又由圆C 与l 相切,2=,可得=2c .所以,椭圆的方程为2211612x y +=.。
圆锥曲线多变化透视奇异有法眼——一道2019年高考文科数学北京卷“圆锥曲线”问题的思考探究

由韦达定理,得
2 kta2
心
= ~ b2 + a2 k2 ^
a t 1 -a b1 ’ X 2 = b、 a2 k2
题中的条件i c w 卜 i〇yvi= a2,即 a s 2 = o //.〇M . 在 此 ,笔者先证明下面一个结论:(以下线段均为
有向线段)
% + y2 二a:(x 丨 +无2) + 2 z = , 2 2
解 得 t = 0 或 t = fca. 因 为 点 P ,C» 是 双 曲 线 C 上 异 于 顶 点 的 两 个 动
V ,则直线经过定点原点.
点 ,所 以 《=〇.
证 明 当 动 直 线 的 斜 率 不 存 在 时 ,显然
<〇,不符合题意.
所以 动 直 线 P <?的方程 为 7 = & ,过定点原点• 当 点 坐 标 为 4 U ,〇)时 ,N 理可证(1)(2).
在上面的探究中,笔者 得 到 : 性 质 1 在平面直角坐标系x O y 中 ,已 知 楠 圆 C :
\
= l(a > 6 > 0 ) ,点 /!是 椭 圆 C 的顶点,点尸,(?
a0
是 椭 圆 C 上 异 于 点 4 的两个动点.
(1) 若 直 线 的 斜 率 满 足 ^ a为 定
值 ,则 直 线 经 过 +«, 1y = kx + 19
反之 ,得 : 性 质 4 在 平 面 直 角 坐 标 系 * O y 中 ,已知双曲线
7 十 =1’
(b2 - a2k2)x2 - 2kta2x - a212 - a2b2 = 0.
由韦达定理,得
2kta2
a V + a2b2
2019年高考数学 考纲解读与热点难点突破 专题17 圆锥曲线(热点难点突破)理(含解析)

圆锥曲线
1.已知 F1,F2 是双曲线错误!-错误!=1(a>0,b〉0)的左、右焦点,过 F2 作双曲线一条渐 近线的垂线,垂足为点 A,交另一条渐近线于点 B,且错误!=错误!错误!,则该双曲线的离心 率为( ) A。错误! B.错误! C. 错误! D.2 答案 A
2.设椭圆xa22+错误!=1(a>b〉0)的焦点为 F1 ,F2,P 是椭圆上一点,且∠F1PF2=错误!, 若△F1PF2 的外接圆和内切圆的半径分别为 R,r,当 R=4r 时,椭圆的离心率为( ) A。错误! B.错误! C。错误! D。错误! 答案 B 解析 椭圆错误!+错误!=1(a〉b〉0)的焦点为 F1(-c,0),F2(c,0),P 为椭圆上一 点,且∠F1PF2=错误!,|F1F2|=2c,根据正弦定理错误!=错误!=2R, ∴R=错误!c, ∵R=4r,∴r=错误!c, 由余弦定理, 错误!2=|PF1 |2+|PF2|2-2|PF1||PF2|cos∠F1PF2, 由|PF1|+|PF2|=2a,∠F1PF2=错误!,
|PQ|2 所以|MN|=2 2.
综上,错误!=2错误!. 6.已知抛物线 C:y2=2px(p〉0)的焦点为 F,过点 F 的直线 l 与抛物 线 C 交于 A,B 两 点,且直线 l 与圆 x2-px+y2-错误!p2=0 交于 C,D 两点,若|AB|=3|CD|,则直线 l 的斜 率为________. 答案 ±错误! 解析 由题意得 F错误!,由 x2-px+y2-错误!p2=0,配方得错误!2+y2=p2, 所以直线 l 过圆心错误!,可得|CD|=2p, 若直线 l 的斜率不存在,则 l:x=p2,|AB|=2p,|CD|=2p,不符合题意, ∴直线 l 的斜率存在. ∴可设直线 l 的方程为 y=k错误!,A(x1,y1),B(x2,y2), 联立错误! 化为 x2-错误!x+错误!=0, 所以 x1+x2=p+错误!, 所以|AB|=x1+ x2+p=2p+2kp2 , 由|AB|=3|CD|,所以 2p+2kp2 =6p, 可得 k2=错误!,所以 k=±错误!. 7.已知 A,B 是椭圆 C 上关于原点对称的两点,若椭圆 C 上存在点 P,使得直线 PA,PB 斜 率的绝对值之和为 1,则椭圆 C 的离心率的取值范围是________. 答案 错误!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.【2018浙江21】如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线2:4C yx 上存在不同的两点,A B 满足,PA PB 的中点均在C 上。
(1)设AB 中点为M ,证明:PM 垂直于y 轴;(2)若P 是半椭圆221(0)4yxx 上的动点,求PAB 面积的取值范围。
解析:(1)设2200112211(,),(,),(,)44P x y A y y B y y AP 中点满足:2210214()4()22y x y y BP 中点满足:2220224:()4()22y x y y BP 所以12,y y 是方程22024()4()22yx y y即22000280y y y x y 的两个根,所以1202y y y ,故PM 垂直于y 轴。
(2)由(1)可知212012002,8y y y y y x y所以222120013||()384PM y y x y x ,21200||22(4)y y y x 因此,3221200132||||(4)24PABSPM y y yx 因为22001(0)4y xx ,所以22004444[4,5]y x x x 因此,PAB 面积的取值范围是1510[62,]41.距离型问题2.【2018全国3 理20】已知斜率为k 的直线l 与椭圆22:143xyC 交于,A B 两点,线段AB的中点为(1,)(0)M m m(1)证明:12k;(2)设F 为C 的右焦点,P 为C 上一点且0FP FA FB ,证明:,,FP FA FB 为等差数列,并求出该数列的公差。
解析:(1)由中点弦公式22OMb k k a,解得34km又因为点M 在椭圆内,故302m,故12k(2)由题意知2,2FA FB FM FPFM ,故(1,2)P m 因为点P 在椭圆上,代入可得3,14m k ,即3||2FP 根据第二定义可知,1211||2,||222FA x FB x 121||||4()2FA FB x x 联立22212121114371402,42874xyxxx x x x yx即121||||4()32FA FB x x 故满足2||||||FP FA FB ,所以,,FP FA FB 为等差数列设其公差为d ,因为,A B 的位置不确定,则有2121212112||||||||()422d FA FB x x x x x x 代入得3213212,1428dd3.【2018全国3 文20】已知斜率为k 的直线l 与椭圆22:143xyC 交于,A B 两点,线段AB的中点为(1,)(0)M m m(1)证明:12k;(2)设F 为C 的右焦点,P 为C 上一点且0FP FA FB ,证明2||||||FP FA FB 。
解析:(1)设1122(,),(,)A x y B x y ,则222211221,14343x y x y ,因为2121y y kx x 两式相减可得:121243x x y y k 又因为12121,22x x y y m 即12122,2x x y y m 代入上式得34km,又因为点M 在椭圆内,故302m,故12k(2)(1,0)F ,设33(,)P x y ,3311220(1,)(1,)(1,)0FP FA FB x y x y x y 即3123123()1,()2x x x y y y m 因为点P 在椭圆上,代入得34m,所以33(1,),||22P FP 因为22111||(1)22x FA x y ,同理得2||22x FB 故121||||4()32FA FB x x 所以2||||||FP FA FB 注意:文理科题目相同,但是给出的解题思路是不同的。
4.【2018天津理19】设椭圆22221x y ab的左焦点为F ,上顶点为B .已知椭圆的离心率为53,点A 的坐标为(,0)b ,且||||62FB AB (1)求椭圆的方程;(2)设直线:(0)l y kx k 与椭圆在第一象限的交点为P ,且l 与直线AB 交于点Q ,若||52sin ||4AQ AOQ PQ (O 为原点),求k 的值。
解析:(1)由题意知:22222259c ab eaa,解得23ab ,又因为||,||2FB a AB b由||||62FB AB 知6ab ,解得3,2ab故椭圆方程为22194xy(2)设1122(,),(,)P x y P x y ,则122||,||2siny y PQ AQ y AOQ21212||525sin 59||44y AQ AOQ y y PQ y y (得到一个等量关系,然后用k 分别表示出12,y y )联立2221226,2114994y kx y kx k k y y xyyxkk分别代入上式得23018149k k kk,解得12k或1128k5.【2018江苏 18】如图,在平面直角坐标系xoy 中,椭圆C 过点1(3,)2,焦点12(3,0),(3,0)F F ,圆O 的直径为12F F 。
(1)求椭圆C 及圆O 的方程;(2)设直线l 与圆O 相切于第一象限内的点P(i )设直线l 与椭圆C 有且只有一个公共点,求点P 的坐标;(ii )直线l 与椭圆C 交于,A B 两点.若OAB 的面积为267,求直线l 的方程。
解析:(1)设椭圆方程为22221x y a b ,其中3c ,又因为点1(3,)2在椭圆上,故2222223114413a ab bab,所以椭圆C 的方程为2214xy又因为圆O 的直径为12F F ,故圆的方程为223xy(2)(i )本题有两种解法:法一:椭圆和圆有公切线时求点P 的坐标,可先设公切线方程为y kx b然后根据直线分别与圆和椭圆相切求出,k b 的值,再求出点P 的坐标,这个方法很容易想到,但是需要两次计算相切时的条件。
法二:题目中让求点P 的坐标,不如一开始就设出点P 的坐标,利用点P 的坐标表示出切线方程,然后直线与椭圆联立,0即可求出点P 的坐标。
这里我们选用第二种方法:设直线与圆的切点00(,)P x y ,则满足223x y ,故直线l 的方程为:0000()x y y xx y 即003x yxy y 联立2222000223(4)24364014x yx y y x y xx x y xy(1)因为直线l 与椭圆有且只有一个交点,故0,即222222000000(24)4(4)(364)48(2)0x x y y y x 因为点P 位于第一象限,即000,0x y ,故02,1x y 所以点P 的坐标为(2,1)(ii )分析:第二问由于OAB 的高即为圆的半径,故由面积可以得出弦长AB 的值,根据弦长再求出直线方程,最容易想到的就是设出直线方程ykxb ,根据直线与圆相切可得2233bk ,然后直线与椭圆联立,根据韦达定理写出弦长公式,将k 或b 转化成一个,求出即可,但是计算过程很麻烦,下面给出同一个方法的两种不同解法:解析:设直线方程为y kx b ,1122(,),(,)A x y B x y ,根据直线与圆相切得2233bk22222(14)844014y kx b k xkbx bxy2121222844,1414kb bx x x x kk222221212228161642||1()41()14147kb bAB kx x x x kkk将2233bk代入得222222264(33)16(33)16421(14)147k kkkk k注意此处,根据韦达定理得出的两根和与积的形式本来很复杂,如果利用上式还需要进行平方,再将b 转化为k 的形式计算起来相当复杂,因此我们要想办法避开平方,因此不如直接根据直线与椭圆联立的方程解出两根,再利用弦长公式,就可以避开平方的出现,解法也会简单一些。
222221,22841(14)84402(14)kbk bk x kbx bx k 222122244142||4141k b k x x kk2221224242||1||1417k AB k x x kk解得225,18kb所以5,32k b ,直线方程为532y x 5.定值问题6.【2018全国1 理】设椭圆22:12xC y的右焦点为F ,过F 的直线l 与C 交于,A B 两点,点M 的坐标为(2,0)(1)当l 与x 轴垂直时,求直线AM 的方程;(2)设O 为坐标原点,证明:OMA OMB分析:第二问两角度相等如何证明?解析几何中常出现的量无非是距离长度,斜率,面积,周长,如果你想到了证明两个角余弦值相等,那么恭喜你,你想到了长度,但是长度不容易求得,本题目M 点在x 轴上且角度均从O 点出发,,A B 两点一个在x 轴上方一个在下方,因此可以考虑两条直线关于x 轴对称,而对称又反应了斜率互为相反数的关系,因此本题目虽是证明题的形式出现,但本质上是求定值问题,即12k k 解析:(1)由题意知(1,0)F ,当l 与x 轴垂直时,:1l x,此时2(1,)2A ,所以直线AM 的方程为2(2)2yx (2)设直线,AM BM 的斜率分别为12,k k 当直线l 斜率不存在时,此时直线,AM BM 的倾斜角互补,则OMA OMB当直线l 斜率存在时,设1122:(1),(,),(,)l yk x A x y B x y 联立2222221(21)42202(1)xykxk xky k x 22121222422,2121k kx x x x k k 所以1212121212121212(1)(1)[23()4]2222(2)(2)y y k x k x k x x x x k k x x x x x x (注意,此处为什么不需要整理分母部分,因为证明分式为零,只需要证明分子为零即可)所以222212122(22)12[4]21210(2)(2)kkk k k k k x x 所以直线,AM BM 的倾斜角互补,则OMA OMB7.【2018全国1 文20】设抛物线2:2C yx ,点(2,0),(2,0)A B ,过点A 的直线l 与C 交于,M N 两点(1)当l 与x 轴垂直时,求直线BM 的方程;(2)证明:ABM ABN解析:(1)当l 与x 轴垂直时,:2l x,此时(2,2)B ,直线BM 的方程为1(2)2yx(2)具体过程可以参考32题,在上题中是分情况讨论直线斜率不存在与存在的情况,其实无需讨论斜率是否存在,可以直接将直线方程设为2x my 设:2l xmy ,直线,BM BN 的斜率分别为12,k k联立2121222242,42x my ymy y y m y y yx所以12121212121224()022(4)(4)y y my y y y k k x x my my 所以直线,AM BM 的倾斜角互补,则OMAOMB8.【2018全国3 理16】已知点(1,1)M 和抛物线2:4C y x ,过C 的焦点且斜率为k 的直线与抛物线交于,A B 两点,若90ABM,则k =________.解析:用到结论:在抛物线中以焦点弦为直径的圆与准线相切所以1NMy y ,设0(,1)N x ,根据焦点弦斜率公式可得122AB ONABABp k k k k x x x 9.【2018北京理 19】已知抛物线2:2C ypx 经过点(1,2)P ,过点(0,1)Q 的直线l 与抛物线C有两个不同的交点,A B ,且直线PA 交y 轴于M ,直线PB 交y 轴于N .(1)求直线l 的斜率的取值范围;(2)设O 为原点,,QMQO QN QO ,求证:11为定值。
