数学实验一:绘制函数图形的实验-实验一.ppt
泰勒展开.ppt

>>f=sym('exp(-x)'); >>f1=taylor(f,4) >>f2=taylor(f,5) >>f3=taylor(f) >>x=0.1; >>ff=[f f1 f2 f3]; >>yy=eval(ff) >>e=yy([2 3 4])-yy(1) >>ezplot(f1,[-6,5]) >>text(-5,40,'f1') >>hold on
[例4] 求函数
y 2x3 9x2 12x 3
的极值。 >>y1='2*x^3-9*x^2+12*x-3'; >>ezplot(y1,[0,4]) >>[xmin,ymin]=fminbnd(y1,1.5,2.5) >>y2='-2*x^3+9*x^2-12*x+3'; >>[xmax,y]=fminbnd(y2,0.5,1.5)
>>ezplot(y,[-2*pi,4*pi]) >>text(3,0,'cos(x)') >>axis([-2*pi,4*pi,-2,2]) >>hold off f1 =
1-1/2*x^2 f2 =
cos(10)-sin(10)*(x-10)-1/2*cos(10)* (x-10)^2+1/6*sin(10)*(x-10)^3
对默认变量在x0点 展开n项
taylor(f,t,n, x0 )
对指定变量 t 在 x0 点展开n 项
《一次函数》课件

REPORTING
经济问题中的一次函数
总结词:经济模型
详细描述:一次函数在经济领域中常被用作简化经济模型,例如,消费和收入之 间的关系、生产成本和产量之间的关系等。通过一次函数,可以更直观地理解经 济现象和预测未来的经济趋势。
物理问题中的一次函数
总结词:物理定律
详细描述:在物理学中,许多定律和公式都可以用一次函数来表示,例如,重力与距离的关系、电流与电压的关系等。通过 一次函数,可以更准确地描述物理现象和预测实验结果。
2023
《一次函数最新》 ppt课件
REPORTING
2023
目录
• 一次函数简介 • 一次函数的表达式 • 一次函数的应用 • 一次函数的解析方法 • 一次函数的实际案例
2023
PART 01
一次函数简介
REPORTING
一次函数的定义
一次函数是形如y=kx+b的函 数,其中k和b是常数,k≠0。
一次函数在数学问题中的应用
线性规划
利用一次函数解决资源分 配问题,实现资源利用的 最大化。
代数方程求解
通过一次函数表示代数方 程,简化方程求解过程。
几何图形面积计算
利用一次函数计算几何图 形的面积,如三角形、矩 形等。
一次函数与其他数学知识的结合
与二次函数的结合
利用一次函数和二次函数的性质 ,解决更复杂的数学问题。
一次函数是线性函数的一种, 它的图像是一条直线。
一次函数在平面坐标系中表示 为一条直线,该直线经过点 (0,b)和斜率为k。
一次函数的图像
一次函数的图像是一 条直线,其斜率为k ,截距为b。
通过代入不同的x值 ,可以求出对应的y 值,从而得到函数的 图像。
实验一:微积分基础1,2,3

1.5
1
0.5
0
-0.5
-1
-1.5
24
-2
-3
-2
-1
0
1
2
3
y sin(x)
x 3 x 5 x 7 x 9 x 1 1 x 1 3 x 1 5 x 1 7 y x
3 ! 5 ! 7 ! 9 ! 1 1 !1 3 !1 5 !1 7 !
x=-3*pi:0.01:3*pi; y=x-x.^3/6+x.^5/120-x.^7/prod(1:7)
216.2832
6
2 212.5664 1 3
2318.8496 1 9
2 425.1372 2 5 哪个整数最好?
哪个最接近2 2 531.4159 3 1
2637.6991 3 8
2743.9832 4 4
的整数倍?
2 850.2655 5 0
6 13 19 25 31 38 44 50
46
1
表达了什么?
正十六边形
正二十边形
12
空间曲面的绘制
1) vr2h,r0,h0
2) RRR 11 RR 22,R10,R20
3) f(x,y)(x2y2)sinx2 1y2 4) zx2xyy2,(x,y0)
Kongjian_qumian.m
sin x2y2
5) z
,(x,y0)
13
x2 y2
关键点:.^ .* ./
D A 3
x=2*cos(theta);
y=2*sin(theta);
8
E F plot(x,y),axis square
画正n边形
输入下面的语句
n=6; theta=linspace(0,2*pi,n+1)
高等数学:MATLAB实验

MATLAB实验
2.fplot绘图命令 fplot绘图命令专门用于绘制一元函数曲线,格式为:
fplot('fun',[a,b]) 用于绘制区间[a,b]上的函数y=fun的图像.
MATLAB实验 【实验内容】
MATLAB实验
由此可知,函数在点x=3处的二阶导数为6,所以f(3)=3为 极小值;函数在点x= 1处的二阶导数为-6,所以f(1)=7为极大值.
MATLAB实验
例12-10 假设某种商品的需求量q 是单价p(单位:元)的函 数q=12000-80p,商 品的总成本C 是需求量q 的函数 C=25000+50q.每单位商品需要纳税2元,试求使销售 利润达 到最大的商品单价和最大利润额.
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验 实验九 用 MATLAB求解二重积分
【实验目的】 熟悉LAB中的int命令,会用int命令求解简单的二重积分.
MATLAB实验
【实验M步A骤T】 由于二重积分可以化成二次积分来进行计算,因此只要
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
实验七 应用 MATLAB绘制三维曲线图
【实验目的】 (1)熟悉 MATLAB软件的绘图功能; (2)熟悉常见空间曲线的作图方法.
【实验要求】 (1)掌握 MATLAB中绘图命令plot3和 mesh的使用; (2)会用plot3和 mesh函数绘制出某区间的三维曲线,线型
数学实验

数学实验一一、一元函数作图(二维图形)函数的图形不仅揭示了函数的本质特性,有时还是解题的钥匙.例如,观察函数()sin f x x x =的图形可知当0x →时,()sin f x x x =是无穷小;根据函数1()sinf x x=的图形可以判定0x =为函数的振荡间断点等.Matlab 软件为我们提供了众多的功能强大的图形绘制函数.plot 是Matlab 中最常用的画平面曲线的函数,它的主要功能是用于绘制显示函数()y f x =和参数式函数()x x t =,()y y t =的平面曲线.plot 函数的调用格式如下:Plot(x ,y ,′可选项s ′)其中x 是曲线上的横坐标,y 是曲线上的纵坐标,′可选项s ′中通常包含确定曲线颜色、线型、两坐标轴上的比例等等参数.在作图时可根据需要选择可选项,如果在绘图时省略可选项,那么plot 函数将自动选择一组默认值,画出曲线.ezplot 是Matlab 中另外一个画平面曲线的函数,它的主要功能是用于绘制隐函数(,)0F x y =、参数式函数()x x t =,()y y t =和显示函数()y f x =的平面曲polar 的主要功能是用于绘制极坐标函数()ρϕθ=的平面曲线,它的调用格式如下:polar (THETA ,RHO ,′s ′) 其中THETA 是极角(弧度值),RHO 是极径,s 是可选项,s 的内容和用法与前面的plot 函数完全相同.●●例1 作函数sin y x =,cos y x =的图形,并观察它们的周期性.解 先作函数sin y x =在[4,4]-ππ上的图形,用Matlab 作图的程序为 >>x=linspace(-4*pi,4*pi,300); %产生300维向量x >>y=sin(x) ;>>plot(x,y) %二维图形绘图命令运行结果如图1-1.上述语句中,%后面如“%二维图形绘图命令”是说明性语句,无需键入.图1-1 sin y x =的图形如果在同一坐标系下作出sin y x =和cos y x =在[2,2]-ππ上的图形,相应的Matlab 程序为>>x=-2*pi:2*pi/30:2*pi ; %产生向量x >>y1=sin(x) ; y2=cos(x);>>plot(x,y1,x,y2,':') %':'表示绘出的第二条曲线图形是点线 运行结果如图1-2.其中实线是sin y x =的图形,点线是cos y x =的图形.图1-2 sin y x =,cos y x =的图形●●例2 作隐函数2222sin 0x y x y+=+在6-π≤x ≤6π, 5.6-π≤y ≤6.6π上的图形.解 相应的Matlab 程序为>>ezplot('sin(sqrt(x^2+y^2))/sqrt(x^2+y^2) ',[-6*pi,6*pi,-5.6*pi,6.6*pi])运行后画出图形,见图1-3.图1-3 2222sin 0x y x y+=+的图形●●例 3 作函数8100[2sin()0.5cos()]100(0.5)a b θθρθ--=+-π在3,22ππ⎡⎤-⎢⎥⎣⎦上的图形,7a =,30b =.解 相应的Matlab 程序为>>t=-0.5*pi:pi/500:1.5*pi ;r=100*(2-sin(7*t)-1/2*cos(30*t))./(100+(t-1/2*pi).^8);polar(t,r,'p') %'p'表示用五角星符标志图中数据点 运行后画出图形,见图1-4,如果改变参数a ,b ,将会得到很多有趣的图形.图1-4 函数8100[2sin()0.5cos()]100(0.5)a b θθρθ--=+-π的图形二、一元函数极限的计算除数值计算外,像函数极限、积分、微分、公式推导、因式分解等这一类含有x ,y ,z 等符号变量的符号表达式的抽象运算,以及求解代数方程或微分方程的精确解等,在工程和科学研究中占有很大比例.符号表达式是代表数字、函数、算子和变量的Matlab 字符串、字符串数组,不要求变量有预先确定的值.符号方程式是含有符号的表达式.符号计算是使用已知的规则和给定恒等式求解符号方程的过程,它与代数和微积分所学到的求解方法完全一样.Matlab 使用syms 这个函数命令来创建和定义基本的符号对象.其调用格式为:syms Var1 Var2 … Varnlimit(s,n,inf) 返回符号表达式当n 趋于无穷大时表达式s 的极限limit(s,x,a) 返回符号表达式当x 趋于a 时表达式s 的极限limit(s) 返回符号表达式中独立变量趋于0时s 的极限limit(s,x,a, 'left') 返回符号表达式当x 趋于a -时表达式s 的左极限limit(s,x,a, 'right') 返回符号表达式当x 趋于a +时表达式s 的右极限●●例4 判断极限01limcos x x →,01limsin x x→的存在性.解 首先分别作出函数1cos y x=在区间[1,0.01]--,[0.01,1],[1,0.001]--,[0.001,1]等区间上的图形,观察图形在点0x =附近的形状.在区间[1,0.01]--绘图的Matlab 程序为>> x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 运行结果如图1-5.同样,可作出函数1sin y x=在点0x =附近的图形. 根据图形,能否判断极限01limcos x x →,01limsin x x→的存在性?图1-5 函数1cos y x=的图形当然,也可用limit 命令直接求极限,相应的Matlab 程序为 >> clear ;>> syms x ; %说明x 为符号变量 >> limit(cos(1/x),x,0)结果为ans=-1…1,即极限值在-1,1之间,而如果极限存在则必唯一,故极限01limcos x x →不存在.同样,极限01limsin x x→也不存在. ●●例5 用Matlab 求下列函数极限:(1)2211lim 1x x x →+-; (2)sin lim 2x x x x →∞+;(3)10lim(1)tt t +→-;(4)211x x →+-. 解 (1)用limit 命令直接求极限,相应的Matlab 程序为>> syms x ;>> limit((x^2+1)/(x^2-1),x,1) 结果为ans =NaN ,即原式极限不存在.下面作出该函数的图像,考察1x →时()f x 的极限状态,为了便于观察,在区间[3,3]-,上作函数的图像,读者在作图时可以取不同区间绘图.相应的Matlab 程序为>> x=-3:0.01:3; y=(x.^2+1)./(x.^2-1); >> plot(x,y)>> axis([-3,3,-8,8]) %调整图形坐标轴的范围 >> xlabel('X'),ylabel('Y') 运行结果如图1-6.图1-6 函数 2211x x +-的图像由解析式得分母的极限21lim(1)0x x →-=,分子的极限21lim(1)2x x →+=,由无穷大与无穷小的关系知原式的极限为∞,即极限不存在.图1-40的函数图像也说明了这样的数量变化关系.(2) 用limit 命令直接求极限,相应的Matlab 程序为 >> syms x ;>> limit((x+sin(x))/(2*x),x,inf) 结果为ans =1/2,即sin 1lim22x x x x →∞+=.(3) 用limit 命令直接求极限,相应的Matlab 程序为>> syms t ;>> limit((1-t)^(1/t),t,0,'right')结果为ans = exp(-1),即111lim(1)eettt+-→-==.(4)用limit命令直接求极限,相应的Matlab程序为>> syms x;>> limit((cos(2*x)-cos(3*x))/(sqrt(1+x^2)-1),x,0)结果为ans =5,即2lim511x x→=+-.注意:Matlab同其他数学软件一样,进行极限、导数、积分等运算时,都不能给出运算的中间过程,如果仅仅不明就里地求出了运算结果,这样的学习是没有意义的,所以在使用软件计算时,千万不能忽视数学课程的学习.我们一再强调的是:软件应用不应该也不能代替数学课程的学习.三、作图观察函数的连续性●●例6 考察下列函数在0x=点的连续性.若是间断点,说明其类型.2,0()0,02,0x xf x xx⎧<⎪==⎨⎪>⎩解首先作出分段函数在区间[4,4]-上的图形,观察图形在点0x=附近的形状.相应的Matlab程序为>>x1=-4:0.01:0;y1=x1.^2;>>x2=0:0.01:4;y2=2;>>plot(x1,y1,x2,y2)运行结果如图1-7.从函数图像上可以明显看出0x=点是间断点,且在0x=处左右极限存在但不相等,所以0x=点是第一类间断点中的跳跃间断点.图1-7分段函数图数学实验二一、一元函数的导数计算Matlab 系统中为用户提供了一元显函数求导的符号计算函数diff ,可以调用此函数求符号导数,不但使用方便,而且计算准确、迅速,尤其是求结构复杂的高阶导数更显示出其优越性.用diff 可以求一元显函数的各阶导函数和在某点处的各阶导数.用diff 作符号求导函数和一些做表达式简化的函数的调用格式和功能如下所示.●●例1 设()e x f x =,用定义计算(0)f '.解 由导数定义,()f x 在某一点0x 处的导数为:(0)f '=000()()limh f x h f x h→+-,相应的Matlab 程序为>>syms h ;>>limit((exp(0+h)-exp(0))/h,h,0) 结果为ans=1,可知(0)1f '=.●●例2 用Matlab 软件求下列函数的导数: (1)y =;(2)y =;(3)求e sin x y x =的四阶导数(4)y . 解(1) 相应的Matlab 程序为 >> syms x ;>> diff(sqrt(tan(x/3)))结果为ans =1/2/tan(1/3*x)^(1/2)*(1/3+1/3*tan(1/3*x)^2), 即211tan 333x y ⎫'=+⎪⎭. (2) 相应的Matlab 程序为 >> syms t ;>> diff(1/(1+t^(1/2))+1/(1-t^(1/2)))结果为ans =-1/2/(1+t^(1/2))^2/t^(1/2)+1/2/(1-t^(1/2))^2/t^(1/2),即()()221111y -'=++.(3) 相应的Matlab 程序为 >> syms x ;>> diff(exp(x)*sin(x),4)结果为ans =-4*exp(x)*sin(x),即()44e sin x y x =-.下面介绍用Matlab 中的函数diff 间接求参数方程的导数.如果一元函数()y f x =由参数方程()()x x t y y t =⎧⎨=⎩所确定,则y 对x 的导数为d d t x t y y y x x ''==',用Matlab 中的函数diff 间接求参数方程的符号导数的调用格式为yx=diff(f,t)/diff(x,t).●●例3 设一元函数()y y x =由参数方程(sin )(1cos )x a t t y a t =-⎧⎨=-⎩确定,求d d y x .解 相应的Matlab 程序为 >> syms t ;>>xt=diff(a*(t-sin(t)));yt=diff(a*(1-cos(t))); >>yx=yt/xt结果为yx=sin(t)/(1-cos(t)),即d sin d 1cos y tx t=-. 二、一元函数的微分计算下面介绍用Matlab 中的函数diff 间接地计算一元函数的微分.如果一元函数()y f x =可导,则y 对x 的微分为d ()d y f x x '=,故用Matlab 中的函数diff 间接求()y f x =对x 的微分的调用格式为dy=diff(y,x)*dx如果一元函数()y f x =在0x x =处可导,则y 在0x x =处对x 的微分为0d ()d x x y f x x ='=,故用函数diff 间接求()y f x =在0x x =处对x 的微分的步骤如下:步骤1:求yx=diff(y,x)步骤2:将0x x =代入()y x '表达式,求出00()x x y f x =''=,并将值赋给变量y0 步骤3:用程序:>>syms dx dy0=yx0*dx 求出00d ()d x x y f x x ='=.●●例4 求函数的微分: (1)2y =(2)设函数()y y x =由方程225e e 0x y xy --+=确定,求0d x y =.解 (1)相应的Matlab 程序为 >> syms x dx ;>> y=x^2/sqrt(x^2+a^2);>> dy=diff(y,x)*dx ; dy1=simplify(dy) %对求出的导函数进行化简 运行后得函数的微分为dy1 = x*(x^2+2*a^2)*dx/(x^2+a^2)^(3/2) 即所为微分为223222(2)d d ()x x a y x x a +=+.(2)因为当0x =时,0y =.所以求微分0d x y =相应的Matlab 程序为 >> syms x y ;>> F=25*x*y-exp(-2*x)+exp(y);>> Fx=diff(F,x);Fy=diff(F,y);yx=-Fx/Fy ; >> y1=simplify(yx)运行后得化简后的y 对x 的一阶导数如下:y1 =(-25*y-2*exp(-2*x))/(25*x+exp(y)) 再输入代码 >> syms dx ;>> x=0;y=0;dy1=((-25*y-2*exp(-2*x))/(25*x+exp(y)))*dx 运行后得到0x dy =为dy1 =-2*dx ,即所求微分0d 2d x y x ==-.数学实验三在本章中,我们已经介绍了中值定理和导数的应用,下面我们介绍用Matlab 软件做中值定理的验证、泰勒公式的计算、函数性态的研究等方面的实验.一、中值定理的验证●●例 1 作函数()3sin 2f x x =在0≤x ≤π上的图像,并说明罗尔定理的几何意义.解(1)函数作图,相应的Matlab 程序为 >> gtext('y=3*sin(2*x)') >> plot(x,y)>> axis([-0.5 1.2*pi -4 4]) >> gtext('y=3*sin(2*x)')图3-1 (2)运行后生成的图像见图3-1所示.由此图可见,罗尔定理的几何意义是:若函数()y f x =在区间[,]a b 上的曲线弧AB 是一条除端点外处处都有不垂直于x 轴的切线的连续曲线段,且两端点A 、B 等高,则过曲线弧AB 上的最高点11(,())C f ξξ或最低点22(,())D f ξξ处必有水平切线,即()0f ξ'=.●●例2 验证拉格朗日中值定理对函数32452y x x x =-+-在区间[0,2]上的正确性.解 为解题方便,首先求出函数y 的导数,相应的Matlab 程序为>> syms x ;>> y=4*x^3-5*x^2+x-2; >> dy=diff(y)结果为dy =12*x^2-10*x+1,接下来利用该结果来验证拉格朗日中值定理,输入程序>> a=0; b=2; ya=4*a^3-5*a^2+a-2; yb=4*b^3-5*b^2+b-2; %求端点处函数值>> mm= solve('12*x^2-10*x+1-(yb-ya)/(b-a)=0',x) %求解中值点ξ的符号解>>mm=subs(mm,'[a,b,yb,ya]',[0,2,yb,ya]) %代入端点值,求数值解 结果为mm =-0.40411.2374从以上实验结果中可以看到存在一个 1.2374[0,2]ξ=∈,从而验证了拉格朗日中值定理的正确性.二、泰勒公式计算利用Matlab 软件提供的taylor 函数可以迅速进行函数泰勒公式的计算,taylor 函数的调用格式如下:(1)ln(1),7y x m =+=; (2)1,854cos y m x==+.解(1) 输入Matlab 程序 >> syms x>> f=log(1+x); >> r=taylor(f,7)结果为r1 =x-1/2*x^2+1/3*x^3-1/4*x^4+1/5*x^5-1/6*x^6.(2)输入Matlab 程序 >> syms x>> f=1/(5+4*cos(x)); >> r=taylor(f,8)结果为r =1/9+2/81*x^2+5/1458*x^4+49/131220*x^6. ●●例4 求下列函数在指定点的泰勒展开式:(1)4320534, 1.5,5y x x x x x m =-+-+==;(2)20ln ,1,4y x x x m ===.解 (1)输入Matlab 程序 >> syms x>> f=x^4-5*x^3+x^2-3*x+4; >> r=taylor(f,5,1.5)结果为r =325/16-81/4*x-8*(x-3/2)^2+(x-3/2)^3+(x-3/2)^4.(2)输入Matlab 程序 >>syms x>> f=x^2*log(x); >> r=taylor(f,4,1)结果为r =x-1+3/2*(x-1)^2+1/3*(x-1)^3. ●●例5 泰勒级数计算器的使用Matlab 软件提供了一个图形用户界面,用户可以很方便地观察函数()f x 在给定区间上被n 阶泰勒多项式()n T x 逼近的情况.在Matlab 指令窗中运行taylortool 命令,将引出如图3-2所示的图形用户界面.图3-2界面中显示默认函数()cos f x x x =在区间,22ππ⎡⎤-⎢⎥⎣⎦内的图形,同时显示函数f 的前N 项的在0a =附近泰勒多项式函数的图形.界面中函数()f x 的表达式及N ,a 和自变量取值区间的默认值可以键入不同值加以改变,函数f 及对应的泰勒多项式函数图形也会随之改变,用户可动态地观察到不同情况下泰勒多项式的逼近情况.三、研究函数的性态函数()y f x =在区间[,]a b 上的图像可以直观地反映该函数的一些性态,如单调性、凹凸性、极值、拐点、渐近线及其与坐标轴的交点等等,下面我们主要从导数和函数的图像两个方面介绍研究函数的性态的实验.●●例6 求解函数32()6124f x x x x =+++的单调性、凹凸性、极值和拐点. 解 首先求解函数的一、二阶导数,然后画出它们的图像,最后利用图像研究该函数的性态.相应的Matlab 程序如下:>> syms x ;>> f=x^3-6*x^2+12*x+4; >> f1=diff(f,x) >> f2=diff(f1,x)>> f1jie=solve(f1,'x') %求驻点 >> x=-3:0.5:7;>> y=subs(f,'x',x); %代入自变量x 的取值,求()y f x =函数值 >> y1=subs(f1,'x',x); %代入自变量x ,求导函数()y f x '=的值 >> y2=subs(f2,'x',x); %代入自变量x ,求导函数()y f x ''=的值 >> hold on>> plot(x,y); %绘制函数()y f x =的图像 >> plot(x,y1,'-.k') %绘制函数的()y f x '=图像 >> plot(x,y2,'--r'); %绘制函数的()y f x ''=图像 >> grid on %加上网格线,为方便观察函数性态相应输出函数的一阶、二阶导数表达式及驻点如下,三个函数图像如图3-3所示.f1 =3*x^2-12*x+12 f2 =6*x-12 f1jie = 22图3-3由()f x ,()f x ',()f x ''这三个函数的图像可以看到:当x R ∈时,总有()f x '≥0(黑色点划线),所以(,)-∞+∞是()f x 的单调递增区间,又由于()f x '不变号,所以函数没有极值点和极值;又当(,2)x ∈-∞时,()0f x ''<,当(2,)x ∈+∞时,()0f x ''>,所以(,2)-∞是()f x 的凹区间,而(2,)+∞是()f x 的凸区间,又有(2)0f '=,因此(2,12)为函数()f x 的拐点.数学实验四利用Matlab 软件中的函数int 可以对不定积分进行符号计算,其调用格式说明:在初等函数范围内,不定积分有时是不存在的,也就是说,即使()f x 是初等函数,但是不定积分()d f x x ⎰却不一定是初等函数.例如,2ex -,sin xx,e x x ,1log a x 是初等函数,而2e d x x -⎰,sin d x x x⎰,e d x x x ⎰,1d log a x x ⎰却不能用初等函数表示出来.比如,输入程序:>> syms x>> F=int(sin(x)/x) 运行后屏幕显示:F =sinint(x)其中sinint(x)是非初等函数,称作积分正弦函数.在使用int函数求不定积分时,读者要注意这种情况.●●例1 求2sin dx x x⎰.解用符号积分命令int计算此积分,Matlab程序为>> syms x;>> int(x^2*sin(x))结果为ans =-x^2*cos(x)+2*cos(x)+2*x*sin(x)如果用微分命令diff验证积分正确性,Matlab程序为>> diff(-x^2*cos(x)+2*cos(x)+2*x*sin(x))结果为ans =x^2*sin(x)●●例2 求下列函数的一个原函数:(1);(2)sec(sec tan)x x x-;(3)11cos2x+;(4(5)2arctanx x;(6)223310xx x++-解(1)相应的Matlab程序为>> clear all;>> syms x;>> f=x*sqrt(x);>> int(f,x)结果为ans =2/5*x^(5/2);(2)相应的Matlab程序为>> clear all>> syms x;>> f=sec(x)*(sec(x)-tan(x));>> int(f,x)结果为ans =sin(x)/cos(x)-1/cos(x);(3)相应的Matlab程序为>> clear all>> syms x;>> f=1/(1+cos(2*x));>> int(f,x)结果为ans =1/2*tan(x);(4)相应的Matlab程序为>> clear all>> syms x;>> f=log(x+1)/sqrt(x+1); >> int(f,x)结果为ans =2*log(x+1)*(x+1)^(1/2)-4*(x+1)^(1/2);(5)相应的Matlab 程序为 >> clear all >> syms x ;>> f=x^2*atan(x); >> int(f,x)结果为ans =1/3*x^3*atan(x)-1/6*x^2+1/6*log(x^2+1);(6)相应的Matlab 程序为 >> clear all >> syms x ;>> f=(2*x+3)/(x^2+3*x-10); >> int(f,x)结果为ans =log(x^2+3*x-10).●●例3 设曲线通过点(1,2),且其切线的斜率为2329x x +-,求此曲线的方程并绘制其图像.解 设所求的曲线方程为()y f x =,根据题意,2329y x x '=+-,所以2d (329)d y y x x x x '==+-⎰⎰ 相应的Matlab 程序为 >> syms x C ;>> f=3*x^2+2*x-9; >> F=int(f)+C ; >> y=simple(F)结果为y =x^3+x^2-9*x+C.即斜率为2329x x +-的曲线方程为329y x x x C =+-+.又因为曲线通过点(1,2),代入曲线方程,得9C =.于是,所求曲线方程为3299y x x x =+-+.作曲线图,输入程序 >> clear>> x=-5:0.1:5; f=3*x.^2+2*x-9;y=x.^2+x.^3-9*x+9; >> x0=1;y0=2;>> plot(x0,y0,'ro',x,f,'g*',x,y,'b-') >> grid>> legend('点(1,2)','函数f=3x^2+2x-9的曲线','函数f=3x^2+2x-9过点(1,2)的积分曲线')运行结果如图4-1. 函数2329f x x =+-过点(1,2)的积分曲线图4-1数学实验五一、定积分和广义积分的符号计算本节首先介绍用Matlab 软件进行符号计算定积分、变上(下)限积分、无界函数的广义积分、无穷限广义积分.如果函数()f x 在区间[,]a b 上连续,且()F x 是()f x 的一个原函数,则函数()f x 在区间[,]a b 上的定积分为()d ()()ba f x x Fb F a =-⎰.用Matlab 软件进行定积分的符号计int(s,a,b) int(s,x,a,b) 求符号表达式s 的定积分,a ,b 分别为积分的下、上限求符号表达式s 关于变量x 的定积分,a ,b 分别为积分的下、上限(1)求545d (1)(2)(3)t t t t ---⎰;(2)已知21sin ,1()157,12x x f x x x x +≤⎧⎪=⎨+->⎪⎩,求20()d f x x ⎰;(3)计算0(23cos )d x x π+⎰.解 (1)相应的Matlab 程序为>> syms t ;>> f=5/((t-1)*(t-2)*(t-3)); F=int(f,t,4,5) 运行后得到F =25/2*log(2)-15/2*log(3),即54525ln 215ln3d (1)(2)(3)22t t t t =----⎰. (2)相应的Matlab 程序为>> syms x ;>> f1=sin(x)+1;f2=(x^2)/2+5*x-7; >> F=int(f1,x,0,1)+int(f2,x,1,2) 运行后得F =11/3-cos(1),即211()d cos13f x x =-⎰. (3) 由于3cos ,023cos 3cos ,2x x x x x π⎧≤≤⎪⎪=⎨π⎪-<≤π⎪⎩,根据积分的可加性,有202(23cos )d (23cos )d (23cos )d x x x x x x ππππ+=++-⎰⎰⎰相应的Matlab 程序为 >> syms x ;>> f1=3*cos(x)+2; f2=-3*cos(x)+2; >> F=int(f1,x,0,pi/2)+int(f2,x,pi/2,pi) 运行后得F=6+2*pi ,即0(23cos )d 62x x π+=+π⎰. ●●例2 求22sin ()1d x x t t t Φ=+⎰和导数()x 'Φ. 解 先求()x Φ的表达式,相应的Matlab 程序为>> syms x t ;>> F=int(t*(sqrt(1+t^2)),t,sin(x),2)运行后得变下限积分值为F =5/3*5^(1/2)-1/3*(1+sin(x)^2)^(3/2),即322551()(1sin )3x x Φ=-+再求导数()x 'Φ,相应的Matlab 程序为 >> dF=diff(F)运行后得变下限积分函数的导数为dF =-(1+sin(x)^2)^(1/2)*sin(x)*cos(x),即2()1sin sin cos x x x x 'Φ=-+ ●●例3 求02(2323)d lim xx t t tx →+--⎰.解 相应的Matlab 程序为 >> syms x t ;>> F=int(sqrt(2+3*t)-sqrt(2-3*t),t,0,x); >> lF=limit(diff(F)/diff(x^2),x,0) 运行后得极限值为lF =3/4*2^(1/2),即2limxx tx →=⎰. ●●例4 讨论广义积分415d (1,2,3,8)2px x p x +∞=+⎰的敛散性. 解 由定义得 441155d lim d 22ppb b x x x x x x +∞→+∞=++⎰⎰求1,2,3,8p =时,广义积分415d 2px x x +∞+⎰的值,相应的Matlab 程序为 >> syms x ;>> f1=int((5*x)/(x^4+2),x,1,+inf)>>limf1=vpa(f1,5) %求广义积分(符号计算结果)精度为5位数的数值结果>> f2=int((5*x^2)/(x^4+2),x,1,+inf) >>limf2=vpa(f2,5)>> f3=int((5*x^3)/(x^4+2),x,1,+inf) >>limf3=vpa(f3,5)>> f8=int((5*x^8)/(x^4+2),x,1,+inf) >>limf8=vpa(f8,5)运行后得到计算结果及其近似值依次如下:f1= 5/8*pi*2^(1/2)-5/4*atan(1/2*2^(1/2))*2^(1/2) limf1 =1.6888 f2 =5/4*2^(1/4)*pi-5/8*2^(1/4)*log(-2^(3/4)+2^(1/2)+1)+5/8*2^(1/4)*log (2^(3/4)+2^(1/2)+1)-5/4*2^(1/4)*atan(2^(1/4)+1)-5/4*2^(1/4)*atan(2^(1/4)-1)limf2 =3.9735 f3 =Inf limf3 =Inf f8 =Inf limf8 =Inf由输出的结果可知,当p =1,2时,广义积分415d 2px x x +∞+⎰收敛,且415d 1.68882xx x +∞≈+⎰,2415d 3.97352x x x +∞≈+⎰. 当p =3,8,时广义积分415d 2px x x +∞+⎰发散,且3415d 2x x x +∞=∞+⎰,8415d 2x x x +∞=∞+⎰. ●●例5 讨论广义积分21d 1x x +∞-∞+⎰的敛散性. 解 由定义得02220111d d d 111x x x x x x +∞+∞-∞-∞=++++⎰⎰⎰ 求广义积分21d 1x x +∞-∞+⎰的Matlab 程序为 >> syms x ;>> f1=int(1/(x^2+1),x,-inf,0),f2=int(1/(x^2+1),x,0,inf),f=f1+f2 运行后得到计算021d 1x x -∞+⎰,201d 1x x +∞+⎰,21d 1x x +∞-∞+⎰的结果依次如下 f1 =1/2*pi f2 =1/2*pi f =pi由输出的结果可知,021d 12x x -∞π=+⎰,201d 12x x +∞π=+⎰,因此21d 1x x +∞-∞=π+⎰收敛. ●●例6 讨论广义积分211d 23x x x +∞+-⎰的敛散性.解 当3x =-,1x =时,被积函数2123x x +-分母为零,无定义,且211lim23x x x →=∞+-,所以将原广义积分分解为两个积分的和,即2222121111d d d 232323x x x x x x x x x +∞+∞=++-+-+-⎰⎰⎰ 求此广义积分的值的Matlab 程序为>> syms x ; >>f1=int(1/(x^2+2*x-3),x,2,+inf),f2=int(1/(x^2+2*x-3),x,1,2),f=f1+f2运行结果为 f1 =1/4*log(5) f2 =Inff =1/4*log(5)+Inf 即221ln5d 234x x x +∞=+-⎰,收敛;2211d 23x x x =∞+-⎰,发散.故211d 23x x x +∞=∞+-⎰,发散.二、定积分的数值计算对于定积分()d ba f x x ⎰,如果对应的不定积分()d f x x ⎰不易求出,或者根本不能表示为初等函数时,那么就只能用定积分的数值计算方法求定积分的近似值了.例如,2e d x x -⎰,sin d xx x⎰,e d x x x ⎰等,因为它们无法表示成初等函数,计算这种类型的定积分只能用数值方法.求定积分的数值计算方法有很多,在这里,简要介绍Matlab 软件中的几个常用于定积分的数值计算函数quad ,quadl 和trapz.关于数值计算理论和其他计算方法,请读者参阅数值分析等相关书籍.函数quad ,quadl 和trapz 的调用格式和功能如下: 1.函数quad调用格式:quad(fun,a,b,tol)其中fun 为被积函数名,a ,b 为定积分的上下限,tol 为精度,可缺省,其默认值为1.0e-6.2.函数quadl调用格式:quadl(fun,a,b,tol,trace) 其中参数fun ,a ,b ,tol 用法与函数quad 相同,而输入第5个非零参数trace ,是对积分过程通过被积函数上的图像进行跟踪.3.函数trapz调用格式:Z=trapz(X,Y)其中X 表示积分区间的离散化向量,Y 是与X 同维的向量,表示被积函数,Z 是返回定积分的近似值.quad 函数使用的是自适应步长的Simpson 积分法,而quadl 函数使用Lobbato 算法,其精度和速度要比quad 函数高,而trapz 函数用的是梯形积分法,精度低,适用于数值函数和光滑性不好的函数的积分计算. ●●例7 用数值积分的方法计算231d x x -⎰.解 先用trapz(X,Y)来求231d x x -⎰,相应的Matlab 程序为 >> x=-1:0.1:2;y=x.^3; %取积分步长为0.1 >> trapz(x,y) 结果为ans =3.7575现在把步长取到0.01,则有 >> x=-1:0.01:2;y=x.^3; >> trapz(x,y)结果为ans =3.7501通过上面的运算结果可以看到,利用不同的步长进行计算,可以得到不同精度的近似值.如果取步长为0.01,则输出结果为3.7500,与步长取到0.01时的计算值接近.可以利用符号积分命令计算,相应的Matlab 程序为 >> clear all >> syms x ;>> int(x^3,x,-1,2) 结果为ans =15/4下面用quad 和quadl 来计算231d x x -⎰,首先建立名为jifen.m 的m 文件. function y=jifen(x) Y=x>^3;然后在命令窗口输入以下Matlab 程序 >> quad('jifen',-1,2) 结果为ans =3.7500.利用quadl 函数同样可以得到上面结果.●●例8 计算数值积分210sin d 1x x x+⎰,并用符号积分命令求解,观察输出结果.解 利用trapz 函数计算数值积分210sin d 1x x x+⎰,相应的Matlab 程序为>> x=0:0.1:1; y=sin(x.^2)./(1+x); >> trapz(x,y) 结果为ans =0.1811.当步长变为0.01时运算结果为0.1808.利用quad 函数求解,先建立名为jifen1.m 的m 文件,程序为 function y=jifen(x) y=sin(x.^2)./(1+x);在命令窗口进行调用,程序为 >>quad(‘jifen1’,0,1) 结果为ans =0.1808.下面用符号积分命令int 计算,程序为 >> syms x ;>> int(sin(x^2)/(1+x),x,0,1) 输出结果为Warning: Explicit integral could not be found. > In at 58ans =int(sin(x^2)/(1+x),x = 0 .. 1)这是因为被积函数的原函数无法用初等函数表示,int 不能求出210sin d 1x x x+⎰的符号解,但是可以求出其数值解.数学实验六Matlab 软件为我们提供了众多的功能强大的绘制空间图形的函数,它们分别是plot3, mesh ,meshc ,meshz ,meshgrid ,sphere ,cylinder ,hesurfc 等等,下面分别介绍.一、空间曲线的绘制plot3是Matlab 中最常用的画空间曲线的函数,它的主要功能是用于绘制显示函数(,)z f x y =和参数式函数()x x t =,()y y t =,()z z t =的空间曲线,也可以用空间中的一组平行平面上的截线的方式表示曲面. plot3函数的调用格式与plot 十分相似,具体如下:plot3(x ,y ,z , ′可选项s ′) 其中如果x ,y ,z 为同维数的向量时,则绘制以x ,y ,z 元素为横、纵、竖坐标的三维曲线;如果x ,y ,z 为同维矩阵时,则以x ,y ,z 对应元素为横、纵、竖坐标分别绘制曲线,曲线条数等于矩阵的列数.曲线上的′可选项s ′中通常包含确定曲线颜色、线型、两坐标轴上的比例等等的参数.用户在作图时可以根据需要选择可选项,如果不用可选项,那么plot3函数将自动选择一组默认值,画出空间曲线.●●例1 作出以方程0.2e cos 2t x t -π=,0.2e sin 2t y t -π=,z t =,[]0,20t ∈表示的空间曲线.解 相应的Matlab 程序为 >>t=0:0.01:20;>>x=exp(-0.2*t).*cos(0.5*pi*t) ; y= exp(-0.2*t).*sin(0.5*pi*t) ; z=t ;>>plot3(x,y,z);>>text(x(1),y(1),z(1),'start') ; %在(x(1),y(1),z(1)处加标字符串'start'>> n=length(x);text(x(n),y(n),z(n),'end');%在(x(n),y(n),z(n)处加标字符串'end'>> xlabel('X');ylabel('Y'),zlabel('Z') ; %说明坐标轴标记 >> grid on ; % grid on/grid off 为显示/不显示格栅命令 运行结果如图6-1.图6-1●●例2 作出函数22()e b x y x ax -+=在矩形区域1c -≤x ≤2c ,1d -≤y ≤2d 上的图形,其中0.1a b ==,125c c ==,126d d ==. 解 相应的Matlab 程序为 >> [x,y]=meshgrid(-5:0.1:5,-6:0.1:6); %生成自变量矩阵,将坐标(X,Y)网格化>> z=0.1*x.*exp(-0.1*(x.^2+y.^2)); >> plot3(x,y,z)运行后屏幕显示所作的图形如图6-2所示.图6-2二、空间曲面的绘制mesh(x,y,z) meshc(x,y,z) meshz(x,y,z) surf(x,y,z) surfc(x,y,z) surfl(x,y,z) hidden on hidden off 用空间中的两组相关的平行平面上的网状线的方式表示曲面 用mesh 函数的方式表示曲面,并附带有等高线 屏蔽的网格图用空间中网状线并网格中填充色彩的方式表示曲面 用surf 函数的方式表示曲面,并附带有等高线 用surf 函数的方式表示曲面,并附带有阴影 消除掉被遮住部分的网状线 将被遮住部分的网状线显示出来●●例3 画出函数22z x y =+的图形,其中(,)[3,3][3,3]x y ∈-⨯-. 解 相应的Matlab 程序为>> x=-3:0.1:3; % x 的范围为[3,3]- >> y=-3:0.1:3; % y 的范围为[3,3]->> [X,Y]=meshgrid(x,y); %将向量x ,y 指定的区域转化为矩阵X ,Y >>Z=sqrt(X.^2+Y.^2); %产生函数值Z >>mesh(X,Y,Z)运行结果如图6-3.图6-3是网格线图,如果要画完整的曲面图,只需将上述的Matlab 代码mesh(X,Y,Z)改为surf(X,Y,Z),运行结果如图6-4.图6-3 图6-4如果画等高线,还可以单独调用contour ,contour3命令.其中contour 命令画二维等高线,contour3命令画三维等高线.先对上述锥面画二维等高线,相应的Matlab 程序为>> x=-3:0.1:3; y=-3:0.1:3;>> [X,Y]=meshgrid(x,y); Z=sqrt(X.^2+Y.^2);>>contour(X,Y,Z,10) %画10条等高线>>xlabel('X-axis'),ylabel('Y-axis') %坐标轴的标记>> title('Contour of Surface') %加标题>> grid on %画网格线运行结果如图6-5.图6-5对上述锥面画三维等高线,相应的Matlab程序为>> x=-3:0.1:3; y=-3:0.1:3;>> [X,Y]=meshgrid(x,y); Z=sqrt(X.^2+Y.^2);>>contour3 (X,Y,Z,10)>>xlabel('X-axis'),ylabel('Y-axis'), zlabel('Z-axis') >> title('Contour of Surface')>> grid on运行结果如图6-6.图6-6 三、球面和旋转曲面的绘制[X,Y,Z]=sphere( N)[X,Y,Z]=sphere Sphere(N) 生成三个(N+1)×(N+1)阶矩阵,再利用surf(X,Y,Z)可以作出一个单位球面此形式使用默认值20N=只绘制球面图,不返回任何值[X,Y,Z]=cylinder(R ,N)[X,Y,Z]=cylinder (R)或[X,Y,Z]=cylinder 以母线向量R生成单位柱面,母线向量R在单位高度里等分刻度上定义的半径向量,N为旋转圆周上的分格线的条数,再利用surf(X,Y,Z)可作出一个旋转面此形式使用默认值20N=和R=[1,1]>> [a,b,c]=sphere(30);>> surf(a,b,c);>>axis('equal'),axis('square') %将横、纵、竖坐标的刻度控制为相同运行后输出球面如图6-7.四、综合作图我们可以综合使用上面介绍的方法,作平面区域和空间区域的图形,下面将通过一些具体的例题来介绍.●●例5 画出由旋转抛物面228z x y=--,图6-7圆柱面224x y+=和坐标面0z=所围成的空间闭区域及其在xOy面上的投影.解相应的Matlab程序为>> [x,y]=meshgrid(-2:0.01:2);>> z1=8-x.^2-y.^2;>> figure(1)>> meshc(x,y,z1)>> hold on>> x=-2:0.01:2;>> r=2;>> [x,y,z]=cylinder(r,30);>> mesh(x,y,z)>> hold off>> figure(2)>> contour(x,y,z,10)axis('equal'),axis('square')运行后屏幕显示如图6-8、图6-9所示.图6-8图6-9●●例6 画出马鞍面22=-和平面23z x y2=-的交线.z x y解相应的Matlab程序为>>[x,y]=meshgrid(-52:2:52;>> z1=x.^2-2*y.^2;>> z2=2*x-3*y;>> mesh(x,y,z1)>> hold on>> mesh(x,y,z2)>> hold off运行后屏幕显示如图6-10.图6-10数学实验七一、多元函数的偏导数和全微分的符号计算我们不但可以调用diff命令作一元函数的符号求导,而且还可以用它来作多元函数的符号求偏导.用diff可以作多元函数的符号求偏导函数、全微分和一点处的偏导数和全微分,下面以二元函数和三元函数为例说明diff的调用格式和功能,如下表和例题所示.读者可以根据用diff求二元、三元函数的偏导函数和全微分的方法推广到四元和四元以上的函数.●●例1 设二元函数32331z x y xy xy =--+,求z 的一阶偏导数和全微分;求高阶偏导数2z x y ∂∂∂,33z x∂∂,22z y ∂∂;求在0x =,1y =处的一阶偏导数和全微分和高阶偏导数201x y zx y ==∂∂∂,221x y z y ==∂∂.解 (1)计算z 的一阶偏导和全微分,高阶偏导数2z x y ∂∂∂,33zx∂∂,22z y ∂∂,相应的程序为>> syms x y z dx dy dz>> z=x^3*y^2-3*x*y^3-x*y+1;>> zx=diff(z,x), zy=diff(z,y), dz=zx*dx+zy*dy,zxy=diff(zx,y), zxx=diff(zx,x); zxxx=diff(zxx,x), zyy=diff(zy,y),运行后得到z 的一阶偏导函数和全微分,高阶偏导数2z x y ∂∂∂,33zx∂∂,22z y ∂∂分别为zx =3*x^2*y^2-3*y^3-yzy =2*x^3*y-9*x*y^2-xdz =(3*x^2*y^2-3*y^3-y)*dx+(2*x^3*y-9*x*y^2-x)*dy zxy =6*x^2*y-9*y^2-1 zxxx =6*y^2zyy =2*x^3-18*x*y 即求得22333zx y y y x∂=--∂,3229z x y xy x y ∂=--∂,()()22332d 33d 29d z x y y y x x y xy x y =--+--,222691z x y y x y ∂=--∂∂,3236z y x∂=∂,232218z x xy y ∂=-∂. (2)输入计算z 在0x =,1y =处的一阶偏导函数和全微分和高阶偏导数201x y z x y ==∂∂∂,221x y z y ==∂∂的Matlab 程序>> syms dx dy dz >> x=0;y=1;>> zx =3*x^2*y^2-3*y^3-y,zy =2*x^3*y-9*x*y^2-x, dz =(3*x^2*y^2-3*y^3-y)*dx+(2*x^3*y-9*x*y^2-x)*dy, >> zxy =6*x^2*y-9*y^2-1, zyy =2*x^3-18*x*y 运行结果如下zx =-4,zy =0,dz =-4*dx ,zxy =-10,zyy =0即014x y zx ==∂=-∂,10x y z y ==∂=∂,d 4d z x =-,20110x y zx y==∂=-∂∂,22010x y zy==∂=∂.●●例2 求下列方程所确定的函数()y y x =的导数d d y x. (1)cos sin()x y x y =+; (2)ln e e y xx -+=.解 (1)相应的Matlab 程序为 >>syms x y ;>>f=solve(‘x*cos(y)-sin(x+y)=0’,y); >>simplify(diff(f,x))结果为ans=(cos(x)+x*sin(x)-1)/(x^2-2*x*sin(x)+1),即所求导数为2d cos()sin()1d 2sin 1y x x x x x x x +-=-+. (2)令(,)ln e e y xF x y x -=+-,先求x F ',再求y F ',相应的Matlab 程序为 >> syms x y ;>> Fx=diff(log(x)+exp(-y/x)-exp(1),x) 得到x F ': Fx=1/x+y/x^2*exp(-y/x )>> Fy=diff(log(x)+exp(-y/x)-exp(1),y) 得到y F ': Fy=-1/x*exp(-y/x)>>yx=-Fx/Fy 可得所求导数为yx=-(-1/x-y/x^2*exp(-y/x))*x/exp(-y/x),即221e d 1e e d 1eyx y yx x yx y x x y y x x x x x---⎛⎫+ ⎪⎛⎫⎝⎭==+ ⎪⎝⎭. ●●例3 由方程322ex y zx y z ---++=确定函数(,)z z x y =,求z y∂∂和2zy x ∂∂∂.解 相应的Matlab 程序为>> syms x y z>> F=2*x+y+z-exp(-x-3*y-2*z);>> Fy=diff(F,y);Fz=diff(F,z);Zy=-Fy/Fz,Zyx=diff(Zy,x)运行后得到z y∂∂和2zy x ∂∂∂如下Zy =(-1-3*exp(-x-3*y-2*z))/(1+2*exp(-x-3*y-2*z))Zyx=3*exp(-x-3*y-2*z)/(1+2*exp(-x-3*y-2*z))+2*(-1-3*exp(-x-3*y-2*z))/(1+2*exp(-x-3*y-2*z))^2*exp(-x-3*y-2*z)即323213e 12e x y z x y z z y ------∂--=∂+,()2323232232323e 2(13e )e 12e 12e x y z x y z x y z x y z x y z z y x ---------------∂-=+∂∂++.二、多元函数极值的计算●●例4 求函数3322(,)339f x y x y x y x =-++-的极值. 解 相应的Matlab 程序为 >> syms x y>> f=x^3-y^3+3*x^2+3*y^2-9*x ; >> fx=diff(f,x) 输出结果fx =3*x^2+6*x-9>> fy=diff(f,y) 输出结果fy =-3*y^2+6*y>> [x0,y0]=solve(fx,fy) %求驻点 输出结果x0 =1 -3 1 -3 y0 =0 0 2 2>> fxx=diff(fx,x) %求f 对x 的二阶纯偏导数。
《数学实验》实验报告——用MATLAB绘制sin曲线
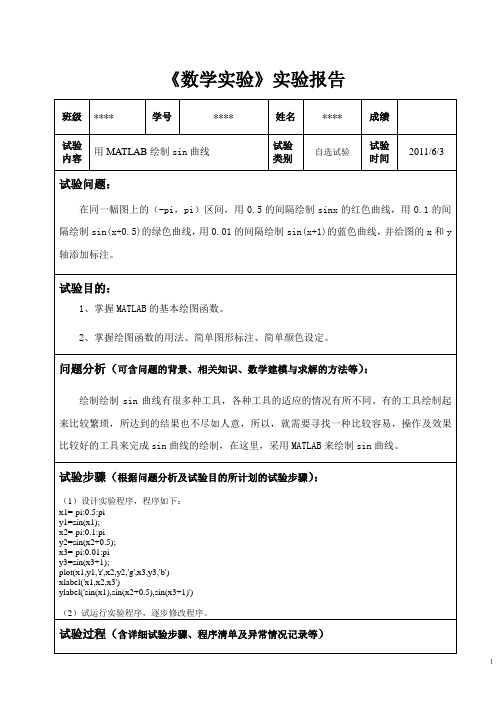
试验步骤(根据问题分析及试验目的所计划的试验步骤):
(1)设计实验程序,程序如下:
(2)试运行实验程序,逐步修改程序。
试验过程(含详细试验步骤、程序清单及异常情况记录等)
(1)将编写的程序在软件中试运行;
(2)逐步修改指令,排除出现的各种异常情况;
(3)运行结果如下:
结果分析:
运行的结果能达到实验的目的和要求,通过在同一幅图上的(-pi,pi)区间,可绘制出用0.5的间隔的sinx的红色曲线,用0.1的间隔的sin(x+0.5)的绿色曲线,用0.01的间隔的sin(x+1)的蓝色曲线,并给图的x和y轴添加标注。
x1=-pi:0.5:pi
y1=sin(x1);
x2=-pi:0.1:pi
y2=sin(x2+0.5);
x3=-pi:0.01:pi
y3=sin(x3+1);
plot(x1,y1,'r',x2,y2,'g',x3,y3,'b')
xlabel('x1,x2,x3')
ylabel('sin(x1),sin(x2+0.5),sin(x3+1)')
有的工具绘制起来比较繁琐所达到的结果也不尽如人意所以就需要寻找一种比较容易操作及效果比较好的工具来完成sin曲线的绘实验报告
班级
****
学号
****
姓名
数学实验报告 (1)

(1)参数方程:z=2^2^/2^2^sin y x y x ++(-8<=x<=8,-8<=y<=8) (2)程序:[X,Y]=meshgrid(-8::8);r=sqrt(x.^2+y.^2)+eps;Z=sin(r)./r;Mesh(x,y,z)Axis square(3)程序的输出结果:3:球面,椭球面,双叶双曲面,单叶双曲面1球面: (4):参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *R z R y R x 0π<=θ<2* 0<=ϕ<π (5)程序:u=[0:pi/60:2*pi];v=[0:pi/60:pi];[U,V]=meshgrid(u,v);R=3;X=R*sin(v).*cos(u);Y=R*sin(v).*sin(u);Z=R*cos(v);Surf(x,y,z);axis equal;(3)程序输出结果:2椭球面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *c z b y a x 0<=θ<2*π 0<=ϕ<=π (2)程序:ezsurf(‘3*sin(u)*cos(v) ,’3*sin(u)*sin(v)’,’1*cos(u)’,[0,pi,0,2*pi]);(3)程序的输出结果:3单叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕtan sin *sec *cos *sec *z a y a x 0<=θ<2*π -π/2<ϕ<π/2 (2)程序:ezsurf(‘3*sec(u)*cos(v),’3*sec(u)*sin(v)’,’5*tan(u)’,[-pi/2,pi/2,0,2*pi]);axis auto(3)输出程序结果:4双叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕsec *sin *tan *cos *tan *c z b y a x 0<=θ<2*π -π<ϕ<3*π/2,ϕ≠π/2(2)程序:ezsurf(‘3*tan(u)*cos(v)’,’3*tan(u)*sin(v)’,’5*sec(u)’,[-pi/2,3*pi/2,0,2*pi]);axis auto(4) (3)输出程序结果:抛物螺线: (1)参数方程:⎪⎩⎪⎨⎧===2^*sin **cos **t c z t t b y t t a x 0<T<+∞ (2)程序:ezplot3(‘2*t*cos(t)’,’2*t*sin(t)’,’t.^2/3’,[0,50]);(3)输出程序结果:(5)马鞍面: (1)参数方程:z=x^2/9-y^2/4 (-25<=x<=25,-25<=y<=25)(2)程序:[X,Y]=meshgrid(-25:1:25);Z=X.^2/9-Y.^2/4;Surf(X,Y,Z)Title(‘马鞍面’)grid off(3)输出程序结果:(6)黎曼函数:(1)程序:n=100;x=[];y=[];k=1;for q=2:nfor p=1:q-1if gcd(q,p)==1 %利用函数gcd(m,n)可求m和n的最大公约数x(k)=p/q;y(k)=1/q;k=k+1;endendendplot(x,y,’.b’); axis([0,1,0,1])(2)程序输出结果:。
(整理)实验一特殊函数与图形37346

第一周特殊函数与图形一、问题背景与实验目的著名的Riemann函数大家都很熟悉了,但是关于它的图像你是否清楚呢?除了最上面那几点,其他都很难画吧?你想不想看看下面那些“挤在一起”的点是怎样分布的呢?还有几何中的马鞍面、单叶双曲面等是怎样由直线生成的,是不是也想目睹一下呢?这些,都离不开绘图.实际上绘图一直是数学中的一种重要手段,借助图形,往往可以化繁为简,使抽象的对象得到明白直观的体现.比如函数的基本性质,一个图形常可以使之一目了然,非常有效.它虽不能代替严格的分析与证明,但在问题的研究过程中,可以帮助研究人员节约相当一部分精力.此外,它还可以使计算、证明、建模等的结果得到更明白易懂的表现,有时,这比科学论证更有说服力.同时,数学的教学与学习过程也离不开绘图.借助直观的图形,常可以使初学者更容易接受新知识.如数学分析中有不少函数,其解析式着实让人望而生畏,即使对其性质作了详尽的分析,还是感到难明就里;但如果能看到它的图形,再配合理论分析,则问题可以迎刃而解.又如在几何的学习中,会遇到大量的曲线与曲面,也离不开图形的配合.传统的手工作图,往往费力耗时,效果也不尽理想.计算机恰恰弥补了这个不足,使你可以方便地指定各种视角、比例、明暗,从各个角度进行观察.本实验通过对函数的图形表示和几个曲面(线)图形的介绍,一方面展示它们的特点,另一方面,也将就Matlab软件的作图功能作一个简单介绍.大家将会看到,Matlab 的作图功能非常强大.二、相关函数(命令)及简介1.平面作图函数:plot,其基本调用形式:plot(x,y,s)以x作为横坐标,y作为纵坐标.s是图形显示属性的设置选项.例如:x=-pi:pi/10:pi;y=sin(x);plot(x,y,'--rh','linewidth',2,'markeredgecolor','b','markerfacecolor','g')图1在使用函数plot时,应当注意到当两个输入量同为向量时,向量x与y必须维数相同,而且必须同是行向量或者同是列向量.绘图时,可以制定标记的颜色和大小,也可以用图形属性制定其他线条特征,这些属性包括:linewidth 指定线条的粗细.markeredgecolor 指定标记的边缘色markerfacecolor 指定标记表面的颜色.markersize 指定标记的大小.若在一个坐标系中画几个函数,则plot的调用格式如下:plot(x1,y1,s1,x2,y2,s2,……)2.空间曲线作图函数:plot3,它与plot相比,只是多了一个维数而已.其调用格式如下:plot3(x,y,z,s).例如:x=0:pi/30:20*pi;y=sin(x);z=cos(x);plot3(x,y,z)得到三维螺旋线:图23.空间曲面作图函数:(1)mesh函数.绘制彩色网格面图形.调用格式:mesh(z),mesh(x,y,z)和mesh(x,y,z,c).其中,mesh(x,y,z,c)画出颜色由c指定的三维网格图.若x、y均为向量,则length(x)=n,length(y)=m,[m,n]=size(z).(2)surf在矩形区域内显示三维带阴影曲面图.调用格式与mesh类似.(3)ezmesh用符号函数作三维曲面网格图.调用格式:ezmesh(x,y,z)其中x = x(s,t), y = y(s,t),z = z(s,t).画图区域默认为:-2*pi < s < 2*pi 且-2*pi < t < 2*pi.或者用格式:ezmesh(x,y,z,[smin,smax,tmin,tmax])(4)ezsurf用符号函数作三维曲面图.调用格式与ezmesh类似.(5)sphere画球体命令.4.meshgrid,调用格式:[x,y]=meshgrid(m,n),这里的m,n为给定的向量,可以定义网格划分区域和划分方法.矩阵x和矩阵y是网格划分后的数据矩阵.5.图像的修饰与其他函数:(1)axis equal 控制各个坐标轴的分度,使其相等;(2)colormap设置绘图颜色.调用格式:colormap([r g b])其中r,g,b都是0-1之间的数.或者用格式:colormap(s)s(3(4)find找出符合条件的元素在数组中的位置.调用格式:y=find(条件)例如:输入:a=[4 5 78 121 4 665 225 4 1];b=find(a>7)输出:b =3 4 6 7三、实验内容数学分析中,特别是积分部分,我们接触了不少有趣的函数,由于其中有的不是一一对应的,用上面的方法无法画出它们的图像,这时就只能用参数了.此外还有些图形只能用参数来画,比如空间曲线,在计算机上不接受“两个曲面的交线”这种表示,所以也只能用参数来实现.用参数方式作图的关键在于找出合适的参数表示,尤其是不能有奇点,最好也不要用到开方.所以要找的参数最好是有几何意义的.当然这也不可一概而论,需要多积累经验.1.利用函数plot在一个坐标系中画以下几个函数图像,要求采用不同颜色、不同线形、不同的符号标记.函数为:sin(),cos(),sin(2),(0,2)===∈.x t y t z t tπ程序如下:t=0:pi/20:2*pi;x=sin(t);y=cos(t);z=sin(2*t);plot(t, x, '--k*', t, y, '-rs', t, z, ':bo')图像如下:图32.绘制类似田螺线的一条三维螺线(方程自己设计).程序如下:t=0:.1:30;x=2*(cos(t)+t.*sin(t));y=2*(sin(t)-t.*cos(t));z=1.5*t;plot3(x,y,-z) %取–z 主要是为了画图看起来更清楚axis equal图像如下:图43.利用函数2222sin x y zx y+ =+程序如下:[a,b]=meshgrid(-8:.5:8); %先生成一个网格c=sqrt(a.^2+b.^2)+eps;z=sin(c)./c;mesh(a,b,z)axis square图像如下:图5思考:这里的 eps 是什么?其作用是什么?4.利用surf 绘制马鞍面图形(函数为:2294x y z =-). 程序如下:[x,y]=meshgrid(-25:1:25,-25:1:25); z=x.^2/9-y.^2/4; surf(x,y,z) title('马鞍面') grid off图像如下:图65.分别用ezmesh 和ezsurf 各绘制一个圆环面,尝试将两个圆环面放在一个图形界面内,观察它们有什么不同之处.提示:圆环面的方程为: 2 ,6 ,)(22222===+-+r R r z R y x ,而圆环面的参数方程为:]2,0[ ],2,0[ ,sin sin )cos (cos )cos (ππ∈∈⎪⎩⎪⎨⎧=+=+=v u u r z v u r R y v u r R x 程序参见附录1. 图像如下:图76.绘制黎曼函数图形,加深对黎曼函数的理解.说明:黎曼函数的定义为1(0,1) 01[01]p p p q x qq q y x x ⎧=∈⎪=⎨⎪=∈⎩,当、为正整数,为既约分数,0,当,及无理点,, 程序参见附录2.图像如下:图8四、自己动手1.做出下图所示的三维图形:图9ezsurf('3*sin(u)*cos(v)','3*sin(u)*sin(v)','3*cos(u)',[0,pi,0,2*pi]);axis equalhold onezsurf('(8+2*cos(u))*cos(v)','(8+2*cos(u))*sin(v)','2*sin(u)',[0,2*pi,0,2*pi]) 2.作出下图所示的墨西哥帽子及其剪裁图形:图10[a,b]=meshgrid(-8:.5:8); c=sqrt(a.^2+b.^2)+eps; z=sin(c)./c; mesh(a,b,z) axis square改变a 、b 的取值范围,可得到裁剪后的图。
matlab--函数图形绘制实验报告1

实验报告课程名称: 数学实验学院名称: 数学与统计学院班级:姓名:学号:2012-2013 学年第学期数学与统计学院制(二)参数方程作图例2: 画出星形线{ 及旋轮线{ 的图形解: 输入以下命令:%星形线作图t=linspace(0,2*pi,5000);x=2*(cos(t)).^3;y=2*(sin(t)).^3;plot(x,y),grid;结果:%旋轮线作图t=linspace(0,4*pi,5000); x=2*(t-sin(t));y=2*(1-cos(t));plot(x,y),axis equal; axis(0,8*pi,0,5);grid;结果:(三)极坐标方程图形例3:画出四叶玫瑰线的图形。
知其极坐标方程: ρ=acos(2 )。
解: 取a=5做图。
在命令窗口输入下命令theta=linspace(0,2*pi);r=2*cos(2*theta);polar(theta,r)结果:(四)空间曲面(线)的绘制例4: 绘制双曲抛物面z= 。
解:将其化为参数方程:{ , 编写m文件运行以下命令r=linspace(-4,4,30);s=r;[u,v]=meshgrid(r,s);x=u;y=v;z=(u.^2-v.^2)./4;surf(x,y,z);bix on;结果:(五)空间曲线在坐标平面上的投影曲面和投影柱面例5: 画出螺旋线{ , 在xOz面上的正投影曲线的图形。
解:化为参数方程{ , 运行下列程序t=linspace(-2*pi,2*pi);x=10*cos(t);z=2*t;h=plot(x,z);grid;xlabel('x');ylabel('z');set(h,'linewidth',2);结果:(一)实验分析:(二)在本次实验中我们初步了解了matlab。
(三)学会了一些简单绘图。
(四)在编制中我们要很明确“点乘的重要性”。
函数的奇偶性 PPT课件

(a, a2)
猜想 : f(-x) __=__ f(x)
设计意图:通过特殊值让学生
认识两个函数的对称性实质:是 自变量互为相反数时,函数值相 等这两种关系。
人民教育出版社B版必修一《2.1.4函数的奇偶性》
四 过程分析
y P/(-x,f(x))
-x O P/(-x,f(-x))
2.概括猜想,揭示内涵
人民教育出版社B版必修一《2.1.4函数的奇偶性》
四 过程分析
3.讨论归纳,形成定义
(1)函数 f(x)与函x 数
图f (x象) 有1 什么共同特征吗?
x
(2)(2)相应的两个函数值对应表是如何体现这些特征的?
函数值的特征探索 你能发现这两个 函数图象有什么 共同特征吗?
设f(-计3)意=-3图=:-f(3这) 一问题f的(-3解)=决-1放/3手=给-f学(3生) ,获
人民教育出版社B版必修一《2.1.4函数的奇偶性》
四 过程分析
3.讨论归纳,形成定义
• 偶函数定义:设函
数 yf的(x)定义域
f(-x)=f(x)
为 ,D如果对定义
域 内D的任意一个
都有x ,xD
且 f(x),f(则x)这个 函数叫做偶函数. 图象关于y轴对称
偶函数
请同学们考察:图象关于原点中心对称的函 数与函数式有怎样的关系?
人民教育出版社B版必修一《2.1.4函数的奇偶性》
四 过程分析
5.讲练结合,巩固新知
练习: 用定义判断下列函数的奇偶性
(1) f(x)=x-
1 x
(2) f(x)= - x2 +1
(3) f(x)= 3√x
(4) f(x)= √x
设计意图:强化练习,巩固所学。通过学生的主体参与,
数学实验课件PPT课件

直观、动态的演示方式有助于学生理解几何概念, 提高学习兴趣。
实例二:数学公式编辑器在课件中的应用
数学公式编辑器介绍
01
一款专门用于编辑和排版数学公式的工具,支持符号计算和公
式排版。
应用实例
02
使用数学公式编辑器制作课件中的数学公式和定理,并进行格
式化排版。
优势分析
03
方便快捷地编辑和排版复杂的数学公式,提高课件的专业性和
行模拟和分析,为理论研究和实际应用提供支持。
03
在实际生产中的应用
在实际生产中,数学实验也具有广泛的应用价值。例如,在工业设计、
金融分析、物流优化等领域中,可以通过数学实验对各种问题进行建模
和优化,提高生产效率和管理水平。
03 数学实验课件内容
课件结构与布局
01
02
03
课件目录
清晰列出课件的章节和主 要内容,方便学习者了解 整体结构。
文字过多
过多的文字容易使课件显得枯燥乏味,应尽量精简文字, 突出重点,使用图表、图片等形式进行辅助说明。
05 数学实验课件实例展示
实例一:几何画板在数学实验中的应用
几何画板介绍
一款专业的几何绘图工具,适用于数学、物理等 学科的教学演示。
应用实例
利用几何画板绘制各种几何图形,如三角形、圆实验课件的展望和期待
技术升级
随着科技的发展,未来数学实验课件将更加注重虚拟现实、增强现 实等技术应用,为学生提供更加沉浸式的学习体验。
个性化学习
未来的课件将更加注重个性化学习,根据学生的学习习惯和需求, 智能推送学习资源和学习路径。
社区化学习
通过建立学习社区,鼓励学生之间的交流与合作,促进知识的共享和 传播,提高学习效果。
《高等数学》(曹治清)课件 高等数学第九章

图9-1
MATLAB集成环境的上层铺放着4个最常用的界面:指令窗 口(CommandWindow)、历史指令(CommandHistory)窗口、工作空 间(Workspace)窗口和当前目录(CurrentDirectory)窗口。此外, 在MATLAB主窗口的左下角还有一个“开始(Start)〞按钮。
最小公倍数
例如,要计算y sin ,可直接在指令窗口输入y=sin(pi/6),得 6
y=0.5000。
如果我们输入:x= linspace (0 , 2*pi , 4);
y= sin(x)
% y被扩展为与x同维数的矩阵
得y=0 0.8660 -0.8660
-
2.点运算 点运算是指在有关算术运算符前面加点。点运算符有“.*〞“./
9.1.3 MATLAB变量与操作
在MATLAB中,变量由字母、数字和下划线组成。第一个字 符必须是字母,并区分大小写。表9-1是MATLAB中常用的系统 预定义变量。
表9-1
预定义变量
ans eps pi
含义
计算结果默认 赋值变量
机器零阈值
圆周率π
预定义变量
含义
i或j inf或lnf NaN或nan
在MATLAB语句后面可以加上注释,用于解释或说明语句的 含义,对语句处理结果不产生任何影响。注释以%开头,后面是 注释的内容。
例
9.1.1
计算
1 4
3
3
2
sin
5
。
解
在MATLAB指令窗口输入命令: x=(1/4-3+2^(1/3)) * sin(pi/5)
%计算表达式的值
按下回车键得输出结果为 x= -
第二讲 用Mathematica画函数图形PPT课件

y2 y2
x x
( 4 ) 画球面 f ( x, y ) 1 x2 y2 的图形。
x2 y2
( 5 ) 画函数 f ( x, y ) e 2 的图形。
( 6 ) 画双曲抛物面 f ( x, y ) x2 y2 的图形。
2
实验2 空间图形的画法
实验目的
✓ 学习空间曲面的画法; ✓ 学习空间曲线的画法;
实验2 空间图形的画法
实验内容
✓ 绘制空间曲面,并给出你的结论。
xy
x2 y
(1) f ( x, y ) x2 y2 ( 2 ) f ( x, y ) x2 y2
(3)
在一条曲线上不连续的函数
f ( x,y )
如: Plot [Exp[1/x], {x, -1, 2}, PlotRange->{-1,5}]
可以同时画多个函数的命令格式
Plot [{ f1[x],f2[x],…}, {x, xmin, xmax}, 可选项] 如: Plot [{Sin[x], Sin[2*x]/2,Sin[3*x]/3},{x, -2Pi, 2Pi}] 如: Plot [Evaluate[Table[x^n,{n,4}]],{x, 0, 1}]
利用Mathematica数学软件使多角度理解函数关系 成为可能。
实验1 函数与图形
实验目的
✓ 学习用Mathematica软件作常见函数的图形; ✓ 通过作图,进一步加深对函数的理解,观察
函数图像绘制实验报告

函数图像绘制实验报告1. 引言函数图像绘制是数学学科中的重要内容,通过绘制函数的图像,可以形象地表示函数的性质和规律,帮助我们更好地理解函数的行为。
本实验旨在通过使用编程语言实现函数图像的绘制,学习和掌握函数图像的绘制方法和技巧。
2. 实验方法本次实验使用Python编程语言,结合Matplotlib库实现函数图像的绘制。
Matplotlib是一种用于创建静态、动态和交互式形式绘图的库,它可以在Python脚本中以相当简单的方式绘制各种各样的图形。
实验流程如下:1. 导入Matplotlib库2. 定义绘图区域,设置坐标轴的范围3. 定义函数,构建函数的数学表达式4. 使用Matplotlib库绘制函数的图像5. 添加图像的标题和标签6. 显示图像3. 实验结果在本实验中,我们选择绘制函数y = sin(x)的图像。
具体代码如下:pythonimport numpy as npimport matplotlib.pyplot as plt定义x范围和步长x = np.arange(0, 2 * np.pi, 0.1)定义函数y = np.sin(x)绘制函数图像plt.plot(x, y)添加标题和标签plt.title('Function Graph: y = sin(x)')plt.xlabel('x')plt.ylabel('y')显示图像plt.show()执行以上代码,我们可以得到函数y = sin(x)的图像,如图1所示。
*图1: 函数图像y = sin(x)*4. 结论与分析通过实验,我们成功地实现了函数图像的绘制。
通过观察图像,我们可以发现函数y = sin(x)的图像是一个周期性的波形,它的振幅在-1到1之间变化。
随着x 从0到2π的增加,函数的周期为2π,图像呈现出周期性重复的特点。
人教版八年级下册19.2一次函数的图像与性质(教案)及说明

-一次函数的性质:斜率k的正负对图像的影响,截距b的几何意义,以及一次函数的单调性。
-实际问题的解决:能够将实际问题转化为一次函数模型,并运用一次函数的性质来解答问题。
举例:讲解斜率k时,通过对比不同k值的函数图像,强调k的正负对直线上升或下降的作用;分析截距b时,结合图像说明b对应直线与y轴的交点。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《一次函数的图像与性质》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过物体匀速运动的情况?”(如骑自行车匀速行驶)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索一次函数的奥秘。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解一次函数的基本概念。一次函数是形如y=kx+b的函数,其中k和b是常数,且k≠0。它是描述线性关系的重要数学模型,广泛应用于自然科学和日常生活中。
2.案例分析:接下来,我们来看一个具体的案例。假设一个物体以匀速运动,我们可以通过一次函数来描述它的位移与时间的关系。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作,如绘制给定斜率和截距的一次函数图像。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
函数的概念ppt课件

。
THANKS
感谢观看
插值法
利用已知的离散数据点,通过数学计算得到更多的数据点,从而绘制出 更精确的函数图像。
03
பைடு நூலகம்计算几何法
利用几何知识,将函数表达式转换为几何图形,从而得到函数的图像。
函数图像的性质
01
02
03
04
连续性
函数图像在定义域内连续不断 ,没有间断点。
单调性
函数在某个区间内单调增加或 单调减少。
奇偶性
函数图像关于原点对称或关于 y轴对称。
周期性
函数图像呈现周期性变化。
函数图像的应用
数学分析
通过函数图像分析函数的性质 和变化规律,解决数学问题。
自然科学
在物理学、化学、生物学等自 然科学领域中,函数图像被广 泛应用于实验数据的分析和解 释。
工程学
在工程学中,函数图像可以用 来描述各种实际问题的变化规 律,如机械运动、电路电流等 。
经济和社会科学
函数的乘法
总结词
函数乘法是指将两个函数的输出值相乘,得到一个新的函数。
详细描述
函数乘法是一种数学运算,其操作是将两个函数的输出值逐一对应相乘。假设有 两个函数f(x)和g(x),函数乘法就是将f(x)和g(x)的输出值相乘,得到一个新的函 数h(x)=f(x)*g(x)。
函数的除法
总结词
函数除法是指将一个函数的输出值除以另一个函数的输出值,得到一个新的函数。
函数的实际应用
生活中的函数
总结词:无处不在
详细描述:函数的概念在日常生活中随处可见,如物品价格与数量的关系、时间 与路程的关系等。这些关系都可以通过函数来描述和预测。
函数图像:绘制函数图像

函数图像:绘制函数图像函数图像是在数学中常见的一种图形表示方式,能够直观地展示出函数的性质和变化规律。
接下来,我们将探讨函数图像的绘制方法以及函数图像在数学中的应用。
一、函数图像的绘制方法函数图像的绘制是通过给定函数的输入值,计算出对应的输出值,并将这些点连线而成的曲线。
具体的绘制方法如下:1. 确定函数的定义域和值域:在绘制函数图像之前,我们首先需要确定函数的定义域(输入值的范围)和值域(输出值的范围),这有助于我们确定绘制图像的范围和比例。
2. 选择合适的坐标系:函数图像的绘制需要借助坐标系来进行,一般我们采用直角坐标系,即x轴和y轴互相垂直。
在确定合适的坐标系后,我们可以将坐标系按照定义域和值域的范围进行调整,以便将函数图像完整地展示出来。
3. 计算关键点的坐标:在绘制函数图像时,我们需要选择一些关键点来确定曲线的形状和走向。
一般而言,我们可以选择定义域中的几个特殊点,如零点、极值点、拐点等,计算它们在坐标系中的具体位置。
4. 连接关键点绘制曲线:在计算完关键点的坐标后,我们可以使用直线或曲线将这些点依次连接起来,形成函数的图像。
在绘制曲线时,需要注意连线的平滑性和曲线的走向,以便更好地展示函数的变化规律。
二、函数图像在数学中的应用函数图像在数学中具有重要的应用价值,可以帮助我们更好地理解和分析各种函数的性质和特点。
以下是函数图像应用的几个方面:1. 函数的可视化分析:函数图像可以直观地展示函数的变化规律,帮助我们分析函数的特点,如增减性、奇偶性、周期性等。
通过观察函数的图像,我们可以更好地理解函数的行为,并在解决实际问题时提供参考。
2. 函数的极值点和拐点:通过绘制函数的图像,我们可以确定函数的极值点和拐点的位置。
极值点是函数在特定区间内取得最大值或最小值的点,而拐点是函数曲线由凹转凸或由凸转凹的点。
这些点的位置可以通过函数图像的特点和走向来确定,有助于我们进一步分析函数的变化规律。
3. 函数的图像变换:函数图像可以通过一系列变换(如平移、伸缩、翻转等)来改变形状和位置。
