基于GARCH模型的股票收益率分析及预测
基于GARCH模型的我国股市风险分析

基于GARCH模型的我国股市风险分析GARCH模型是一种用来分析金融市场风险的统计模型,可以在一定程度上预测金融市场的波动性。
本文将基于GARCH模型对我国股市的风险进行分析。
我们需要收集我国股市的日度收益率数据。
通过计算股票的日度收益率,可以得到一个时间序列,反映了股票价格的波动情况。
然后,我们可以根据这个时间序列构建GARCH模型。
GARCH模型是一种时间序列模型,结合了ARCH模型和GARCH模型的优点。
ARCH模型适用于描述方差随时间变化的非线性特征,而GARCH模型进一步引入了前期的方差信息来预测后期的方差。
这种模型的优点是能够捕捉到金融市场的波动性的不对称性和长尾分布。
在构建GARCH模型之前,需要进行模型的参数估计。
可以使用最大似然估计法来估计模型的参数。
通过拟合历史数据,可以获得GARCH模型的拟合程度,进一步评估模型的有效性。
通过GARCH模型,我们可以获得未来的风险预测。
通过对未来风险的预测,可以制定相应的投资策略。
当预测到市场的风险较高时,可以适当减少投资仓位,降低风险暴露。
当预测到市场的风险较低时,可以增加投资仓位,追求更高的收益。
GARCH模型还可以进行风险价值(Value at Risk,VaR)的计算。
VaR是金融市场风险管理中常用的指标,用于衡量投资组合在给定置信水平下可能面临的最大损失。
通过GARCH模型,可以估计不同置信水平下的VaR,并制定相应的风险管理策略。
需要注意的是,GARCH模型是基于历史数据的统计模型,对未来的预测存在一定的不确定性。
GARCH模型还假设金融市场的波动性是稳定的,但实际情况可能受到各种外部因素的影响,从而导致模型的预测不准确。
基于GARCH模型的股市风险分析可以通过建立一个能反映股价波动情况的时间序列模型,并通过模型的参数估计和拟合程度评估风险模型的有效性。
通过风险预测和VaR计算,可以制定相应的风险管理策略,提高投资组合的收益稳定性。
基于GARCH模型对上证指数收益率的实证分析

基于GARCH模型对上证指数收益率的实证分析基于GARCH模型对上证指数收益率的实证分析【摘要】本文选取上海综合指数在2021年1月4日至2021年12月19日期间共475个上证综合指数每日收盘价数据,并处理成对数收益率,在此根底上对中国股市收益率波动性特征进行了分析。
利用ARCH类模型对上海股票市场的波动性进行了检验,发现中国股市具有明显的ARCH效应,结合ARCH模型和GARCH模型的特点,最终筛选出适合的GARCH模型对沪市收益率序列的波动做拟合。
本文最后针对中国股市的现存问题,借鉴成熟股市的经验,提出了加快开展中国股市的政策建议。
【关键词】上证综合指数ARCH效应ARCH GARCH模型波动性一、引言作为国际金融市场的一局部,我国股票市场的成长历程还不算漫长。
自从1990年成立以来的20多个年头里,经过几次大起大落已经不断完善和开展。
尤其是近几年来,随着市场规模的大幅度增加,沪深证券市场与国民经济的相关程度也逐步增强。
金融环境动乱的加剧促使人们研究股票价格波动的内在规律。
在中国这样一个尚未开展成熟的股票市场中,我们不仅要定性的把握股票价格的走势,更应该定量的研究其内在规律,这样才能使我们在危机来临之际不至于手足无措。
鉴于此,对股市进行合理分析和预测,对于指导投资者合理投资,维护证券交易市场稳定进而促进经济开展有重大意义。
二、中国股市波动特征中国股市的开展很快,从20世纪80年代中后期一些国有企业自行发行企业职工内部股票,到1990年至1991年标准化的上海、深圳证券交易所的成立,中国股市在过去十多年的开展过程中逐渐自我完善和开展壮大,市价总值从1992年的1048.13亿元上升1999年的26471亿元。
股票市场的建立和开展对解决国有企业筹集资金起到了积极的作用,有利地推动了中国经济体制改革的深入开展。
具体来讲,我国股市波动具有以下特征:股市波动大,股价指数走势难以按牛、熊市划分,时常发生暴涨暴跌行情,熊市中常发生暴涨行情,牛市中常发生暴跌行情。
MATLAB中基于GARCH模型对股票指数的拟合与预测

MATLAB中基于GARCH模型对股票指数的拟合与预测股票市场作为金融市场中最具波动性的一部分,在投资者中备受关注。
为了更好地理解和预测股票市场的波动情况,金融学家们开发了各种统计模型来对股票指数进行拟合和预测。
基于GARCH模型的方法因为其能很好地捕捉股票市场波动的特点而备受青睐。
本文将利用MATLAB软件来介绍如何使用GARCH模型对股票指数进行拟合和预测。
GARCH模型,即广义自回归条件异方差模型(Generalized Autoregressive Conditional Heteroskedasticity Model),是由Tim Bollerslev在1986年提出的一种用于描述时间序列波动性的模型。
GARCH模型的提出克服了传统的对等方差假设的限制,使得模型更适应于描述金融市场中存在的波动聚集现象。
GARCH模型能够对股票指数在不同时间点的波动进行建模,并且预测未来一段时间内的波动情况。
我们将使用MATLAB软件来拟合一个GARCH模型,以对股票指数的历史波动进行描述。
假设我们选择了道琼斯工业平均指数(Dow Jones Industrial Average)作为我们的研究对象。
我们需要通过MATLAB中的数据获取功能来获取道琼斯指数的历史数据。
接下来,我们可以利用MATLAB中的统计工具箱(Statistics and Machine Learning Toolbox)来拟合GARCH模型。
我们首先需要导入道琼斯指数的历史数据,并对其进行预处理,包括计算收益率、平方收益率等。
然后,我们可以使用MATLAB中的garch函数来拟合GARCH模型。
在拟合模型时,我们需要提供一个合适的GARCH阶数和条件异方差的分布类型。
在实际中,我们可以通过对不同参数组合的模型进行对比,来选择最合适的模型。
拟合完成后,我们可以得到GARCH模型的参数以及条件异方差的波动度。
这些参数可以帮助我们更好地理解道琼斯指数的波动特点。
基于GARCH模型的股票收益率分析及预测

基于GARCH模型的股票收益率分析及预测耿娟刘怡超【摘要】摘要:GARCH模型是对金融数据波动性进行描述的有效方法,它是最常用、最便捷的异方差序列拟合模型。
资产收益率是金融数据分析常用的指标,比价格序列更易处理且更有研究意义。
本文采用R语言,对2009年1月6日—2019年5月20日沪深300指数的日收盘价进行预处理,将其转化为平稳的收益率序列,检验其ARCH效应,建立GARCH模型以及标准化残差分析,最后对收益率和股票价格进行预测,预测的结果能为投资者进行决策提供一定的参考。
【期刊名称】《河北企业》【年(卷),期】2019(000)010【总页数】2【关键词】股票收益率; GARCH模型; R语言; 股指预测一、引言股票市场是我国市场经济的重要组成部分,对国民经济的发展起到了巨大的推动作用。
因为沪深300指数具有作为表征市场股票价格波动情况的价格揭示功能,是反映市场整体走势的一个重要指标,所以受到了广泛关注。
如果对沪深300指数进行分析,并在一定程度上对其预测,可以为投资者做买卖决策提供重要的参考价值。
国外学者对股票收益率进行预测研究较早。
Black(1977)和Christie(1983)提出了金融时间序列对正向和负向冲击的反应是截然不同的。
PhichhangOu (2010)对三种模型进行了比较,得出了混合模型在预测杠杆效应波动率方面表现更好的结论。
而我国对股票市场收益率的波动分析研究相对较晚,但随着我国金融市场不断发展和完善,对于这方面的研究也逐渐增多。
2006年,孔华强通过建立EGARCH(1,1)-M模型拟合了上证180和深证100指数的波动性。
张豪(2015)利用GARCH(1,1)模型求出个股的年波动率,并结合股票价格的正态性估计出某时段的收益率范围,根据国内股市易受国家政策影响的特点提出投资意见。
李雄英、陈小玲等(2018)将ARMA模型、GARCH模型以及ARMA-GARCH模型进行比较,得出组合模型的预测效果最优。
基于GARCH模型的股价波动预测

基于GARCH模型的股价波动预测基于GARCH模型的股价波动预测一、引言股票市场中的波动性一直是投资者关注的焦点之一。
准确预测股价波动有助于投资者制定合理的投资策略,降低风险并获得收益。
GARCH(Generalized AutoregressiveConditional Heteroscedasticity)模型是一种常用于金融市场波动预测的统计模型,本文将介绍GARCH模型的原理和应用,以及通过该模型进行股价波动预测的方法和步骤。
二、GARCH模型原理GARCH模型通过建模误差项的波动性,捕捉到股票市场的异方差性(Heteroscedasticity)。
GARCH模型基于时间序列分析的基本原理,认为过去的波动对未来波动有重要影响。
该模型通过拟合历史波动性数据,生成一个条件波动性序列,从而预测将来的波动性水平。
GARCH模型由ARCH(Autoregressive Conditional Heteroscedasticity)模型发展而来。
ARCH模型是通过引入滞后误差项的平方,捕捉到异方差性。
然而,ARCH模型只考虑到了平方的影响,而在金融市场中,波动性的影响可能是各种方面的。
GARCH模型在ARCH模型的基础上引入了滞后条件波动性的平方,将过去波动性的信息作为一个冗余变量,从而更好地捕捉到波动性的特征。
三、GARCH模型的应用GARCH模型广泛应用于金融市场,已成为预测股价波动性常用的统计模型。
GARCH模型的应用可以分为两个方面:条件波动性的建模和波动性预测。
1. 条件波动性建模条件波动性建模是GARCH模型的核心内容,通过拟合历史波动性数据,得到一个条件波动性序列。
条件波动性序列可以反映股票市场的波动性水平,投资者可以根据这一信息制定风险管理策略。
条件波动性建模的关键是选择适当的GARCH模型,常用的有GARCH(1,1)、GARCH(1,2)等。
2. 波动性预测GARCH模型的另一个重要应用是波动性预测。
基于GARCH族模型的股市收益率波动性研究

金融研究 山东财政学院学报(双月刊) 2009年第1期(总第99期)基于GARCH 族模型的股市收益率波动性研究安起光 郭喜兵(山东财政学院,山东济南 250014)[摘 要]通过运用GARCH 类模型对我国沪市的日收益进行分阶段分析,得出了对于不同的阶段,利空和利好消息对我国股市的影响是不同的,在熊市,利空消息产生的波动要大于利好消息产生的波动;而在牛市,利好消息产生的波动要大于利空消息产生的波动,而且在不同的阶段,投资者对风险所要求的收益也有较大差异。
[关键词]GARCH 模型;收益率;风险[中图分类号]F830.9 [文献标识码]A [文章编号]1008-2670(2009)01-0047-04[收稿日期]2008-12-24[作者简介]安起光,男,山东莱阳人,山东财政学院金融学院教授、硕士生导师,研究方向:金融工程;郭喜兵,男,山东聊城人,山东财政学院金融学院硕士研究生,研究方向:金融工程。
一、问题的提出近来,金融学家和计量学家对发达国家成熟资本市场的波动性进行了广泛的研究,得出金融时间序列一些共同特点。
首先,股票收益的经验分布显著不同于独立正态分布,表现出明显的尖峰厚尾性;第二,股票价格或指数的运动服从随机游走过程,而且一般是非平稳序列,但是收益序列通常呈现出平稳的特性;第三,收益序列本身几乎不呈现出相关性,而收益的平方序列却表现出比较明显的相关性。
基于以上特点,专家们提出了时变假设,并尝试通过特定的技术来预测金融时间序列的收益波动性。
1982年,Engle 提出了自回归条件异方差模型,即ARC H (Autoregressive Conditional Heteroskedastic)模型。
1986年,Bollerslev 又提出了广义ARC H (GARC H )模型。
国外许多学者也通过大量的实证分析证明了模型对于股票指数研究的适用性,而且也从中不断的对其进行完善与补充,又相继提出了EGARCH 模型、TGARC H 模型等GARC H 模型的延伸模型,我们称之为GARC H 族模型。
基于ARIMA-GARCH模型的股票价格预测研究

基于ARIMA-GARCH模型的股票价格猜测探究一、引言股票市场是金融市场中最重要和最具活力的组成部分之一。
准确猜测股票价格对投资者和股票来往者来说至关重要。
浩繁探究者使用不同的方法和模型来猜测股票价格,其中ARIMA-GARCH模型已被证明在猜测股票价格方面具有很高的准确性和可靠性。
本文将对ARIMA-GARCH模型的股票价格猜测方法进行探究和探讨。
二、ARIMA模型ARIMA模型是指自回归挪动平均模型,它是通过对时间序列数据进行拟合和猜测的一种方法。
ARIMA模型包括差分整合自回归挪动平均模型。
差分是指对时间序列数据进行差分来消除数据的非平稳性,整合是指将差分后的时间序列数据转化为平稳序列,自回归是指使用过去时间点的数据进行拟合和猜测,挪动平均是指使用过去时间点的误差项进行拟合和猜测。
三、GARCH模型GARCH模型是指广义自回归条件异方差模型,它是ARIMA模型的一个扩展,用于建模和猜测时间序列数据的波动率。
GARCH 模型包括ARCH模型和GARCH模型。
ARCH模型用于描述时间序列数据的条件异方差性,GARCH模型在ARCH模型的基础上引入了过去时间点的波动率信息,可以更准确地猜测时间序列数据的波动。
四、ARIMA-GARCH模型ARIMA-GARCH模型是将ARIMA模型和GARCH模型相结合的一种方法,用于猜测股票价格。
ARIMA-GARCH模型可以有效地处理时间序列数据的非平稳性和波动性,并提供准确的股票价格猜测结果。
ARIMA-GARCH模型起首使用ARIMA模型对时间序列数据进行差分和拟合,然后使用GARCH模型对拟合后的序列数据的波动性进行建模和猜测。
最后,将ARIMA模型和GARCH模型的猜测结果结合起来,得到最终的股票价格猜测结果。
五、实证探究为了验证ARIMA-GARCH模型在股票价格猜测中的有效性,我们选择了某股票的历史价格数据作为样本数据,分别使用ARIMA模型、GARCH模型和ARIMA-GARCH模型进行猜测,并比较它们的猜测结果。
基于ARIMA-GARCH模型的股票价格预测研究

基于ARIMA-GARCH模型的股票价格预测研究基于ARIMA-GARCH模型的股票价格预测研究摘要:股票价格的预测是金融市场中的重要研究领域,对投资者和决策者都有重要的意义。
本文通过引入时间序列分析中的ARIMA模型和GARCH模型,构建了ARIMA-GARCH模型用于股票价格预测。
利用该模型对一家上市公司的股票价格进行预测,研究结果表明ARIMA-GARCH模型能够较准确地预测股票价格的变动趋势,有一定的实用价值。
一、引言股票价格的预测是金融市场中重要的研究领域之一,对投资者和决策者都有重要的意义。
股票价格的波动受多种因素的影响,如公司业绩、宏观经济因素、政策变化等。
因此,通过各种模型和方法进行股票价格的预测,能够提供一定的决策依据。
本文旨在研究基于ARIMA-GARCH模型的股票价格预测方法。
二、ARIMA模型ARIMA模型是时间序列分析中常用的模型之一,它基于时间序列的自相关和移动平均来进行预测。
ARIMA模型根据时间序列的平稳性分为AR模型、MA模型和ARMA模型。
AR模型是自相关模型,表示当前的数值与过去一段时间的数值有关;MA模型是移动平均模型,表示当前的数值与过去一段时间的误差项有关;ARMA模型是AR模型和MA模型的组合。
三、GARCH模型GARCH模型是对时间序列的波动进行建模的方法,它能够描述时间序列的条件异方差性。
GARCH模型可以分为GARCH(p,q)模型和EGARCH模型等。
其中,GARCH(p,q)模型建立了波动的自回归关系,用来捕捉时间序列波动的长期影响,而EGARCH模型通过引入对称与非对称杠杆效应,以更好地解释波动。
在本文的研究中,我们选取GARCH(1,1)模型。
四、ARIMA-GARCH模型ARIMA-GARCH模型是将ARIMA模型和GARCH模型相结合,用于预测时间序列的股票价格。
首先,利用ARIMA模型对时间序列数据进行建模,得到其残差项;然后,对ARIMA模型的残差项进行GARCH模型拟合,得到条件异方差项;最后,将AR模型和GARCH模型的结果进行组合,得到ARIMA-GARCH模型预测的股票价格。
基于GARCH模型的沪深300指数收益率波动性分析

基于GARCH模型的沪深300指数收益率波动性分析【基于GARCH模型的沪深300指数收益率波动性分析】一、引言近年来,随着中国资本市场的发展和经济的不断增长,沪深300指数作为中国股市的重要代表,引起了广泛的关注。
股市的波动性分析对于投资者的风险管理和投资决策具有重要的意义。
在这一背景下,本文将运用GARCH模型对沪深300指数的收益率波动性进行深入的分析,并进一步探讨影响指数波动的因素。
二、研究方法本文将采用GARCH模型来分析股市的波动性。
GARCH模型是一种常用的计量经济学方法,能够反映自回归条件异方差特性。
首先,我们需要计算沪深300指数的日收益率。
然后,通过基于过去数据的统计分析,建立GARCH模型,根据历史数据估计模型的参数,从而预测未来股市的波动性。
最后,通过模型拟合和检验,判断模型的有效性。
三、数据分析本文收集了沪深300指数的日收益率数据,并进行了数据预处理,包括收益率平稳性检验、白噪声检验等,以确保数据的可靠性和有效性。
然后,根据历史数据,建立了GARCH模型,拟合数据并进行了参数估计。
最后,通过对模型残差的诊断检验,验证了模型的有效性。
四、实证结果根据GARCH模型的估计结果,我们可以得到如下实证结果:首先,沪深300指数的收益率波动是存在异方差性的。
其次,GARCH模型是有效的,并能够对股市的波动性进行较为准确的预测。
最后,我们还发现股市波动性存在长短期效应,即波动率在不同时间段内呈现出不同的特征。
五、影响因素分析在GARCH模型的基础上,我们进一步分析了影响股市波动性的因素。
通过引入不同的自变量,如市场风险溢价、联动程度、经济增长率等,我们可以利用模型进行多元回归分析,找出具体的影响因素。
结果显示,市场风险溢价和联动程度等因素对股市波动性具有显著的影响。
六、风险管理与投资建议研究股市波动性对于投资者进行风险管理和制定投资策略具有重要的指导意义。
基于GARCH模型的分析结果,我们可以对投资者提出以下建议:首先,要关注股市的波动性,合理评估风险,避免过度乐观或悲观。
基于GARCH模型族上证指数收益率波动的实证分析

基于GARCH模型族上证指数收益率波动的实证分析0 引言目前,我国资本市场正处于发展的初始阶段,国内外大量资金的涌入,活跃了资本市场,同时也大大增加了金融市场风险,其波动幅度和风险大大高于国外成熟的市场,尤其是异常波动和超常波动更是频繁出现。
就股票市场而言,过于频繁的异常波动会影响投资者判断,甚至打击投资者信心,同时也影响国民经济的健康发展,甚至诱发经济危机。
从宏观层面来说,异常波动将加大整个金融体系的系统风险,并使作为资源配置的股价信号产生失真。
从微观层面来说,异常波动将使风险厌恶者规避者居多的投资大众对市场失去信心,进而退出股票市场。
波动率作为度量股市风险的重要工具之一,一直受到学界和业界的广泛重视。
价格波动和投资者的投资行为之间具有某种必然的联系,是投资者投资行为综合作用的结果,投资者总是希望能凭借自己对股市波动性的充分认识来获取超额报酬。
因此,如何去寻找到较能真实刻画和衡量股价波动性特征的研究是学者们和投资者所关注的焦点问题,并已成为如今金融工程学不可分割的一部分。
本文基于GARCH 模型族,对股权分置改革以来我国上海证券市场股票收益率的波动情况进行了分析。
1 数据选取与变量确定本文选取上证指数自 2005 年5 月9 日股权分置改革至2010 年6 月30 日的日收盘指数作为样本来分析上海股市的最新发展变化情况,共1254 个观测值,数据来源于CCER。
选择上证指数是因为上海股票市场不仅开市早,市值高,而且对各种冲击的反应也较为敏感,其价格波动具有一定的代表性;选择日收盘指数在于收盘点位可以基本反映当天信息的一个最终结果。
为了减少舍入误差,在估计时对上证指数spt 进行自然对数处理,得lns 。
股票收益率计算公式为:r =ln(s /s ,式中, s 和s 分别是第t 和t-1 期上证指数日收盘价。
2 实证分析2.1 描述性统计分析对上证指数收益率进行统计分析,结果所示。
由可知,上证指数平均收益率水平较低,仅为0.06%,而标准差为2.03%,意味着波动性大,收益率不稳定,投资风险高;偏度为-0.336<0,说明收益率曲线左偏,左边拖着较正态分布长的尾巴;峰度为5.418>3,说明收益分布曲线尾部较正态分布粗壮;其Jarque-Bera 统计量也远大于5%显著性水平上 χ (2)的临界值(p 值趋近于0),因而其收益率不服从正态分布。
基于时间序列GARCH模型的创业板收益率预测

-111-基于时间序列GARCH 模型的创业板收益率预测□ 西南财经大学 中国金融研究中心 孟前锦 / 文本文运用时间序列Garch 模型,对创业板市场的整体收益率进行建模并预测。
在论证Garch 模型预测可行性的基自2009年创业板成立以来,为中小企业和创新型科技企业提供了新的融资渠道,同时也为投资者提供了新的投资途径。
但是,创业板收益率及其不稳定,波动很大。
因此,给投资者带来了很大的投资风险。
很多学者对创业板的收益率的波动性进行过大量的研究,大多都是采用时间序列建模的方法。
本文借鉴大部分学者的研究方法,采用时间序列GARCH 模型对创业板收益率进行预测。
收益率预测GARCH 模型的建立(1)GARCH 模型GARCH 模型就是广义自回归条件异方差模型,是对ARCH 模型的某些约束条件进行扩展得到的。
GARCH 模型对于时间序列波动率的研究有独特的优势,因此,自诞生以来获得了广泛的运用。
GARCH 是一种运用时间序列过去的变化和过去的方差(即波动性)来预测将来变化的时间序列建模方法。
本文采用最常用的GARCH(1,1)模型进行建模。
该模型的数学表达式如下:22201111t t ttt ttt t r u a a a σεσααβσ--=+==++ 其中,,,由于GARCH 模型要求采用的样本数据量要超过200个,为了保证有足够的数据量,本文采用了从创业板创立以来所有的304个总市值加权周收益率数据,以保证预测效果。
所有的数据均来自RESSET 金融研究数据库。
所有的计算结果均由R 软件实现。
(2(模型的预检验在进行建模之前,我们首先对数据进行分析,检验数据是否具有ARCH 效应。
首先,对样本数据的进行简单的统计分析,相关数据如下表:表1 样本数据统计量由表中数据可以看出样本数据均值为0.004579,方差为0.002785,偏度为-0.522156,峰度为1.069977。
其次,对数据的相关性进行检验,使用R 软件的相关命令,我们得到了序列的ACF 图。
MATLAB中基于GARCH模型对股票指数的拟合与预测

MATLAB中基于GARCH模型对股票指数的拟合与预测引言股票市场是一个充满风险和机遇的地方,投资者们希望能够找到一种能够预测股票价格波动的模型,以便在市场中获取更多的利润。
而GARCH(Generalized Autoregressive Conditional Heteroskedasticity)模型作为股票价格波动预测的重要工具,已经成为了金融领域中的经典模型之一。
本文将使用MATLAB软件对GARCH模型在股票指数上的应用进行探讨,并展示如何使用GARCH模型对股票指数进行拟合与预测。
GARCH模型简介GARCH模型是由Robert F. Engle于1982年提出的,它是对ARCH模型(Autoregressive Conditional Heteroskedasticity)的一个扩展,用于描述时间序列数据中的异方差性。
在金融领域中,股票价格的波动通常表现为异方差性,即波动性会随着时间的变化而变化。
GARCH模型通过考虑过去一段时间内的波动性来预测未来的波动性,从而可以用来进行股票价格的波动预测。
MATLAB中的GARCH模型MATLAB软件提供了丰富的金融工具箱,可以方便地进行金融大数据的处理和分析。
在MATLAB中,使用GARCH模型可以通过Financial Toolbox中的garch函数进行实现。
用户可以通过该函数指定GARCH模型的阶数和参数,并进行模型的参数估计、模型的拟合和预测等操作。
下面我们将通过一个具体的股票指数实例来介绍如何使用MATLAB进行GARCH模型的拟合与预测。
具体实例我们将以上证指数为例来演示如何使用MATLAB对股票指数的波动进行预测。
假设我们已经获取了上证指数的日收益率数据,我们希望使用GARCH模型对其进行建模,并进行未来一段时间的波动性预测。
我们需要导入上证指数的日收益率数据,并对数据进行初步的处理,包括数据的处理和可视化等操作。
接下来,我们可以使用MATLAB的Financial Toolbox中的garch函数来建立GARCH模型,选择适当的模型阶数和参数。
基于GRACH模型对我国股票市场收益率波动性分析-毕业论文

---文档均为word文档,下载后可直接编辑使用亦可打印---摘要在金融学中,收益率的波动性是一个重要概念。
收益率的波动反映了市场不确定性的程度,同时,收益率的波动性也被看成是信息流的一种度量,波动性强一般伴随着较大的市场信息冲击。
由于2008年到2018年这十年期间中国股市经历了两次大起大落,股市的剧烈动荡使我们有必要对其目前的波动性进行研究,发现其问题所在。
因此,本文一沪深300指数作为研究对象,以2008年1月2日到2018年1月2日共2436个日收盘价作为样本,站在经济计量的角度采用CARCH族模型对该样本数据进行分析,从而得出沪深300指数的波动性特征。
首先是引言,简要说明研究的背景及意义,突出研究的必要性;其次是对国内外文献的综述,总结其研究成果,发现其不足,为后文的写作奠定基础;第三部分是模型概述,对ARCH、GARCH、EGARCH这三种模型的特征进行描述和介绍。
第四部分是本文核心,以实证分析为主,建立GARCH(1,1)模型、ARCH模型以及EGARCH(1,1)模型分别对沪深300指数的收益率波动特征进行分析。
研究结果表明:沪深300指数的日收益率呈现出可变与集簇的波动特性,在序列分布上,具有尖峰厚尾的显著特征。
并存在明显的GARCH 效应;根据模型具有GARCH-M效应得出收益存在正溢价,从投资者在股票市场投资的经验可知,大多数偏向于短期的投机性投资。
此外,对沪深300指数的收益率进一步分析可以发现杠杆效应,由此可以推断在股指期货市场中,坏消息产生的影响远大于好消息。
最后根据GARCH族模型检验结果,提出相应的政策建议,以推动中国股市向健康稳定的方向发展。
关键词:收益率、波动性、GARCH族模型、沪深300指数AbstractThe volatility of the rate of return is an important concept in finance. The fluctuation of returns reflects the degree of market uncertainty. Meanwhile, the volatility of returns is also regarded as a measure of information flow. Volatility is usually accompanied by larger market information shocks.During the ten years from 2008 to 2018, China's stock market experienced two ups and downs, and the intense turbulence of the stock market made it necessary for us to study its current volatility and find its problems.Therefore, the CSI 300 index as the object of study, from January 2, 2008 to 2 January 2018, 2436 day closing price as the sample, hope that through the application of GARCH model, describe the Shanghai and Shenzhen 300 index volatility characteristics from the perspective of econometric.This paper mainly studies the volatility of the Shanghai and Shenzhen 300 index returns from five parts. The first is the introduction, a brief description of the research background and significance of the research, highlighting the necessity; secondly it is a survey of the domestic and foreign literatures, summarizes the research results, find its shortcomings, which lays the foundation for later writing; the third part is the model overview, describes and introduces the features of ARCH, GARCH, EGARCH three model. Fourth through theestablishment of ARCH model, GARCH (1,1) model and EGARCH (1,1) model, the volatility of the CSI 300 index returns is empirically analyzed. The results show that the daily yield volatility of the CSI 300 index shows obvious variability and volatility cluster, and the sequence distribution is characterized by peak and thick tail. And there is a significant GARCH effect. There is GARCH-M effect in the model, which shows that there is a positive premium for earnings. Investors in the stock market have strong speculative atmosphere and short term investment preferences are obvious. At the same time, we also found that the CSI 300 index yields obvious leverage effect, which reflects the volatility caused by bad news in China's stock index futures market is greater than that caused by good news. Finally, according to the test results of the GARCH model, the corresponding policy suggestions are put forward to promote the development of Chinese stock market to a healthy and stable direction.Key words:rate of return, volatility, GARCH model, CSI 300 index目录一.引言(一)研究背景纵观我国证券市场的发展历史,自正式成立上证交易所之日起,已有一段发展历程。
基于GARCH族混合模型的沪深300指数波动预测

基于GARCH族混合模型的沪深300指数波动预测GARCH(Generalized Autoregressive Conditional Heteroskedasticity)模型是一种常用的金融时间序列波动预测模型,其主要应用在股票、证券、汇率等金融领域。
GARCH模型的基本思想是对波动进行建模,通过考虑先前波动的影响来预测未来的波动。
GARCH族模型是对GARCH模型的一种扩展,包括EGARCH、TGARCH、GJR-GARCH等多种模型,它们都在GARCH的基础上加入了更多的变量或模型结构,以提高对波动的拟合能力。
本文将基于GARCH族混合模型对沪深300指数的波动进行预测。
首先对沪深300指数的日收益率数据进行收集和处理,然后建立GARCH族混合模型,最后通过模型的拟合和预测来分析沪深300指数的波动情况。
1.数据收集与处理我们需要获取沪深300指数的日收益率数据。
通常可以通过金融数据服务提供商或者证券交易所的官方网站获取相关数据。
在获得数据后,需要进行一定的处理,包括数据清洗、缺失值处理等。
处理完毕后,我们可以得到一段时期内的沪深300指数的日收益率数据,即可进行后续的建模和预测。
2.GARCH族混合模型建立接下来,我们将建立GARCH族混合模型进行波动预测。
GARCH族混合模型是对GARCH模型的扩展,它可以更好地捕捉金融时间序列的波动特征。
这里我们以EGARCH模型为例进行建模,EGARCH是对标准GARCH模型的扩展,它可以捕捉到波动率对于市场冲击的非线性响应。
假设沪深300指数的日收益率数据为rt,EGARCH模型的表达式如下:rt = μt + εtεt = σt * ztμt为条件均值,一般可以设定为0;εt为高斯白噪声序列,σt为条件标准差,zt为标准正态分布随机变量。
EGARCH模型的条件标准差σt的表达式为:log(σt^2) = ω + ∑(αi*|εt-i|/sqrt(2*π)) + ∑(βj*log(σt-j^2))ω为常数项,αi和βj为模型参数。
基于GARCH模型的股价波动预测

基于GARCH模型的股价波动预测摘要:股价波动对于投资者和市场参与者来说是非常重要的。
准确的股价波动预测可以帮助投资者制定更合理的投资策略。
本文利用GARCH模型,探讨了基于历史数据的股价波动预测方法,并通过实证研究验证了该方法的有效性。
1. 引言股票市场是一个充满波动的环境,股票价格会受到多种因素的影响而发生波动,如市场供求关系、经济指标变化、政治因素等。
因此,准确预测股票价格的波动对于投资者来说至关重要。
2. GARCH模型介绍GARCH(Generalized Autoregressive Conditional Heteroskedasticity)模型是一种用于分析和预测时间序列波动的方法。
该模型是由Engle于1982年提出的,通过建立条件异方差结构来捕捉时间序列波动的特征。
GARCH模型的基本形式为:条件异方差模型:σ^2_t = α_0 + α_1ε^2_(t-1) +βσ^2_(t-1),其中,ε_t为白噪声序列,t为时间序列。
3. 数据收集与预处理为了构建GARCH模型,需要收集历史股票价格数据,并进行预处理。
预处理包括检查数据的完整性和准确性,并对异常值或缺失值进行处理。
4. GARCH模型参数估计通过极大似然估计法(Maximum Likelihood Estimation,MLE)对GARCH模型进行参数估计。
该方法基于给定模型下观测到的数据,选择能够使得模型最有可能产生观测数据的参数值。
5. GARCH模型预测利用已估计的参数,可以对未来股票价格的波动进行预测。
预测结果可以帮助投资者决策,并制定相应的投资策略。
6. 实证研究与结果分析本文选择了某上市公司的股票数据作为实证研究对象,实证研究了方法。
结果显示,利用GARCH模型可以较为准确地预测股票价格的波动,为投资者提供了重要参考。
7. 研究不足与展望尽管本文利用GARCH模型对股价波动进行预测取得了较好的效果,但仍存在一定的局限性。
基于GARCH模型的创业板指数收益率分析
肋 # O H } a ☆ O n } i i ●
} t
p el t i a l Co r r e t a S o n 目 i l - j i
I I
AC
P AC 0- 8 l a l P r e b
1— 0 0 3 3・ 003 3 093 6 3 9 3 3 3 2 0 0 3 8 0 03 5 207 7 7 0 3 5 4 3 000 9 000 6 21 4 4 1 , ' 8 5 4 3
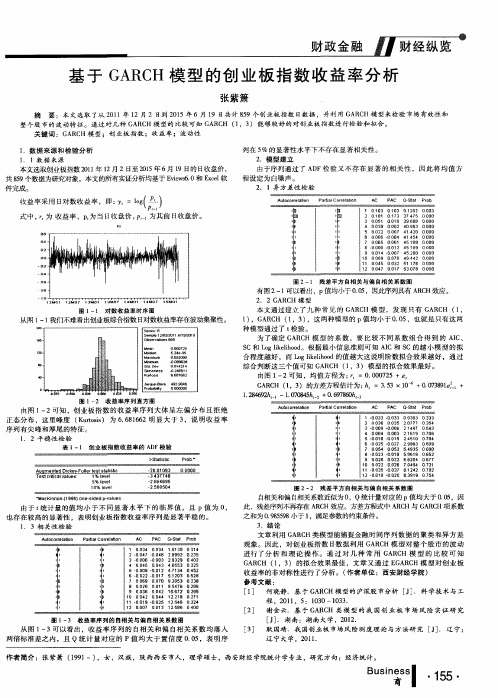
由图 1—2可知 ,创业板指数 的收益 率序列 大体呈左 偏分 布且拒 绝 正态分布 ,这里峰度 ( K u r t o s i s )为 6 . 6 8 1 6 6 2明显大 于 3 ,说 明收益 率 序 列 有 尖 峰 和 厚 尾 的特 征 。
1 . 2平 稳 性 检 验 表 1—1 创 业 板 指 数 收 益 率 的 AD F检 验
7 0 06 8 0 0 6 1 4 51 0 9 0 O O a 8 0 O O O一 0 0' 2 4 51 0 9 0 0 0 0 9 0 0 1 4— 000 7 4 5 2 8 0 0 O O O
l I I
G A R C H( 1 , 3 )的方差方程估计为: h :3 . 5 3 x 1 0 + 0 . 0 7 3 8 9 1  ̄ _ 1+
1 . 2 8 4 6 9 2 h l一 1 . 0 7 0 8 4 5 h 2+n 6 9 7 8 6 0 h 3
一
图 1—2 收 益 率 序 列 直 方 图
基于 G A R C H 模 型 的 创 业 板 指 数 收 益 率 分 析
张紫箫
摘 要 :本文选取 了从 2 0 1 1年 1 2月 2日到 2 0 1 5年 6月 1 9日共计 8 5 9个创业板指数 日数据 ,并利用 G A R C H模 型来检验 市场有效性 和
国有商业银行股票收益率波动的研究——基于GARCH模型

银 行 股 票 相对 整体 的 股 票市 场 更 加 稳定 , 投 资 风 险 较小 。 ( 3 ) 从 偏 度 来看 , 只有 农 业 银行 股 票 表 现 出右 偏 , 其余 _ 二
在 模 型估 计 之前 , 需 要 对 样 本 数 据 的 平 稳 性 进 行 检 验 。使 用 ADF 单 位 根检 验 , 发 现Rt g, Rt n, Rt z , Rt j的t 统
票 收 益率 有 尖峰 厚 尾 性 、 异方 差 性 、 波 动 的持 续 性 和 非 对 称性 。 关键 词 : 商 业银 行 ; G A g C H; 波 动 性
引言 7 月1 5日 到 2 0 1 2 年7 月1 5日的 日收 盘 价 作 为 建 模 数 据 , 四 大 国有 商 业 银 行 作 为 银 行 业 的 代 表 , 反 映 了该 行 业 分 别 用 Pt g, Pt i q, Pt z, Pt j 表 示 。 为 了 考 察 收 益 率 的 变 的 发展 状 况 , 同时也是该 行业发展 的先遣部 队 , 研 究 国有 动 情 况 和 满 足 数 据 平 稳 性 的 要 求 , 定 义 每 H的 收 益 率 商 业 银 行 股 票 的 波 动 性 对 上 市 银 行 、投 资 者 以 及 整 个 国 为 : Rt =i n( P t ) 一 i n ( Pt 一1 ) , 四 家 商 业 银 行 每 日收 益 率 分
F i n a n c i a 【 Vi e w }金 融视 线
国有 商业银行股票收益率波 动的研 究
— —
基G A R C H 模型
林 鹭 福 建 泉 州 华侨 大 学经 济 与金 融 学 院
福 建 泉 州 3 6 2 0 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行 GARCH 模型的拟合遥
渊三冤GARCH 模型的估计
GARCH渊1袁1冤是 GARCH 模型中最常用的一种袁也是最
适用于金融时间序列建模的模型遥这里使用 fGarch 包中提供
的 garchFit 函数来拟合 GARCH 模型遥 模型估计的结果中袁 mu尧omega尧alphal尧betal 所 对 应 的 p 值 分 别 为 0.151尧0.014尧
data: return
Chi-squared = 298.08袁 df = 12袁 p-value < 2.2e-16 由 LM 检验可知袁卡方统计量的值为 298.08袁其对应的 p 值几乎为 0袁 小于 0.05袁 即在 5%的显著性水平下拒绝原假
设袁从而说明收益率序列是存在 ARCH 效应的袁因此可以进
列是平稳序列遥
3.序列正态性检验遥 Jarque Bera Test
data院return
X-squared=1918.3袁df=2袁p-value<2.2e-16
通过 JB 正态性检验可得袁p 值接近 0袁 说明序列不是正
态分布袁且有高峰厚尾的现象遥
4.收益率序列的描述性汇总遥 从沪深 300 指数的收益率
经济纵横
基于 GARCH 模型的股票收益率分析及预测
耿 娟 刘怡超
摘要院GARCH 模型是对金融数据波动性进行描述的有效方法袁它是最常用尧最便捷的异方差序列拟合模型遥 资产收益率是 金融数据分析常用的指标袁比价格序列更易处理且更有研究意义遥 本文采用 R 语言袁对 2009 年 1 月 6 日要2019 年 5 月 20 日沪 深 300 指数的日收盘价进行预处理袁将其转化为平稳的收益率序列袁检验其 ARCH 效应袁建立 GARCH 模型以及标准化残差 分析袁最后对收益率和股票价格进行预测袁预测的结果能为投资者进行决策提供一定的参考遥
1.数据预处理遥 由于金融数据分析中一般研究的是资产 收益率而不是资产的价格袁并且资产收益率比价格序列更容 易处理且更有研究意义遥 因此袁对日收盘价计算对数收益率袁
也就是对2009 年 1 月 6 日要2019 年 5 月 20 日沪深 300 指
数的日收盘价格取对数差分进行分析遥
蓸 蔀 日收益率的表达式为院rt=ln
的统计特征上可以看出袁2009 年 1 月至 2019 年 5 为-0.09袁最大值
为 0.06袁均值和标准差分别为 0.0001930527 和 0.01552898遥
偏度为-0.6539769袁负值说明收益率大幅度下降的概率是比
较高的曰峰度为 7.15袁说明股票时常存在极端的价格变动情
关键词院股票收益率曰GARCH 模型曰R 语言曰股指预测 中图分类号院F832.48 文献标识码院A 作者单位院河北经贸大学数学与统计学学院
一尧引言
股票市场是我国市场经济的重要组成部分袁对国民经济 的发展起到了巨大的推动作用遥 因为沪深 300 指数具有作为 表征市场股票价格波动情况的价格揭示功能袁是反映市场整 体走势的一个重要指标袁所以受到了广泛关注遥 如果对沪深 300 指数进行分析袁并在一定程度上对其预测袁可以为投资 者做买卖决策提供重要的参考价值遥
yt yt-1
袁其中 rt 表示沪深指数
第 t 日的收益率袁yt 表示第 t 日的收盘价遥 计算得到的指数收
益率序列即为本文研究的样本袁共有 2520 个数据遥
2.序列平稳性检验遥 将沪深 300 指数的日收益率序列进
行单位根检验袁检验结果如下院
Augmented Dickey-Fuller Test
国 外 学 者 对 股 票 收 益 率 进 行 预 测 研 究 较 早 遥 Black 渊1977冤和 Christie渊1983冤提出了金融时间序列对正向和负向 冲击的反应是截然不同的遥 PhichhangOu渊2010冤 对三种模型 进行了比较袁得出了混合模型在预测杠杆效应波动率方面表 现更好的结论遥 而我国对股票市场收益率的波动分析研究相 对较晚袁但随着我国金融市场不断发展和完善袁对于这方面 的研究也逐渐增多遥 2006 年袁孔华强通过建立 EGARCH(1袁1) -M 模型拟合了上证 180 和深证 100 指数的波动性遥 张豪 渊2015冤利用 GARCH渊1袁1冤模型求出个股的年波动率袁并结合 股票价格的正态性估计出某时段的收益率范围袁根据国内股 市易受国家政策影响的特点提出投资意见遥 李雄英尧陈小玲 等渊2018冤将 ARMA 模型尧GARCH 模型以及 ARMA-GARCH 模型进行比较袁得出组合模型的预测效果最优遥 黄轩尧张青龙 渊2018冤证明了 ARIMA-GARCH 综合模型对上证指数的短期 预测存在很大优势遥
1.55e-15尧2e-16遥 即所有系数在 0.05 的显著性水平下均异于 0袁
说明沪深 300 指数收益率过去时刻的波动大小对当前波动
二尧实证分析
本文研究对象是沪深 300 指数的日收益率序列遥 从 Wind 数据库中选取了 2009 年 1 月 6 日要2019 年 5 月 20 日 的日收盘价数据袁以这些数据为基础进行数据预处理得到收 益率序列袁利用 R 软件对收益率序列建模袁进行时间序列分 析和预测袁并分析股票的波动情况遥
渊一冤数据预处理与平稳性检验
况遥
渊二冤ARCH 效应检验
建立 GARCH 模型之前要先进行 ARCH 效应检验袁如果
存在 ARCH 效应才可以进行 GARCH 模型的拟合遥 这里用
FinTS 包中的 LM 检验袁其检验的原假设是院不存在 ARCH 效
应遥 得到的结果如下院
圆园19 年第 10 期 61
经济纵横
ARCH LM-test; Null hypothesis: no ARCH effects
data: return
Dickey-Fuller=-13.044袁Lag order=13袁p-value=0.01
alternative hypothesis院stationary
在 ADF 检验中袁p 值=0.01<0.05遥 由此可见袁在 0.05 的显
著性水平下拒绝原假设袁即认为沪深 300 指数的日收益率序
