实验项目一串匹配问题
括号匹配栈实验报告

一、实验目的本次实验旨在通过编写程序实现括号匹配功能,加深对栈数据结构原理的理解和应用。
通过实验,掌握栈的基本操作,如入栈、出栈、判断栈空等,并学会利用栈解决括号匹配问题。
二、实验原理1. 栈是一种后进先出(LIFO)的线性数据结构,它只允许在栈顶进行插入和删除操作。
2. 括号匹配问题是指在一个字符串中,判断左右括号是否成对出现,且对应匹配。
3. 在解决括号匹配问题时,可以使用栈来存储遇到的左括号,并在遇到右括号时进行匹配。
如果栈为空或括号不匹配,则判断为无效括号。
如果栈为空,表示括号匹配正确,否则表示不匹配。
三、实验内容1. 定义栈结构体,包括栈的最大容量、栈顶指针、栈底指针、栈元素数组等。
2. 编写栈的基本操作函数,如初始化、入栈、出栈、判断栈空等。
3. 编写括号匹配函数,利用栈实现括号匹配功能。
4. 编写主函数,接收用户输入的字符串,调用括号匹配函数进行判断,并输出结果。
四、实验步骤1. 定义栈结构体和栈的基本操作函数。
```c#define MAX_SIZE 100typedef struct {char data[MAX_SIZE];int top;} Stack;void InitStack(Stack s) {s->top = -1;}int IsEmpty(Stack s) {return s->top == -1;}void Push(Stack s, char x) {if (s->top == MAX_SIZE - 1) { return;}s->data[++s->top] = x;}char Pop(Stack s) {if (s->top == -1) {return '\0';}return s->data[s->top--];}```2. 编写括号匹配函数。
```cint BracketMatch(char str) {Stack s;InitStack(&s);while (str) {if (str == '(' || str == '[' || str == '{') {Push(&s, str);} else if (str == ')' || str == ']' || str == '}') {if (IsEmpty(&s)) {return 0; // 不匹配}char c = Pop(&s);if ((c == '(' && str != ')') || (c == '[' && str != ']') || (c == '{' && str != '}')) {return 0; // 不匹配}}str++;}return IsEmpty(&s); // 栈为空,匹配成功}```3. 编写主函数。
posnor字母匹配实验

posnor字母匹配实验引言:在计算机科学中,字母匹配实验是一种常见的算法和数据结构问题。
通过对给定的字符串进行分析和比较,我们可以找到其中是否存在与给定模式匹配的子字符串。
本文将以posnor字母匹配实验为标题,探讨该问题的解决方法和应用场景。
一、什么是字母匹配实验?字母匹配实验是一种字符串处理问题,它要求找到给定模式在一个字符串中的所有出现位置。
在该实验中,我们需要通过比较字符串中的字母序列与给定的模式来判断是否匹配。
具体而言,我们需要找到字符串中所有与模式相同的子字符串,并返回它们的起始位置。
二、解决字母匹配实验的方法1. 暴力搜索法最简单和直接的方法是使用暴力搜索法。
该方法通过逐个比较字符串中的字母序列与给定模式来判断是否匹配。
如果匹配成功,则记录该子字符串的起始位置。
然后继续向后移动一个位置,并重复上述过程,直到遍历完整个字符串。
暴力搜索法的时间复杂度为O(n*m),其中n是字符串的长度,m是模式的长度。
2. KMP算法KMP算法是一种高效的字母匹配实验算法。
它通过预处理模式字符串,构建一个部分匹配表(Partial Match Table),来避免不必要的比较操作。
部分匹配表记录了模式字符串中的前缀和后缀的最长公共部分的长度。
利用这个信息,KMP算法能够在匹配过程中跳过一些不可能匹配的位置,从而提高匹配的效率。
KMP算法的时间复杂度为O(n+m),其中n是字符串的长度,m是模式的长度。
三、字母匹配实验的应用场景1. 文本搜索字母匹配实验在文本搜索中有着广泛的应用。
例如,在文本编辑器中,我们可以使用字母匹配实验来查找与给定关键词相匹配的字符串。
这在编程时特别有用,可以帮助我们快速定位和修改代码中的特定字符串。
2. DNA序列分析在生物信息学中,字母匹配实验常用于DNA序列分析。
通过对DNA序列进行字母匹配实验,我们可以找到其中与给定基因序列相匹配的子序列。
这对于研究基因的结构和功能具有重要意义。
算法设计与分析-第3章-蛮力法

哨兵
0123456789 k 10 15 24 6 12 35 40 98 55
查找方向
i
清华大学出版社
算法设计与分析
算法3.2——改进的顺序查找
int SeqSearch2(int r[ ], int n, int k) //数组r[1] ~ r[n]存放查找集合 { r[0]=k; i=n; while (r[i]!=k)
清华大学出版社
算法设计与分析
第3章 蛮力法
3.1 蛮力法的设计思想 3.2 查找问题中的蛮力法 3.3 排序问题中的蛮力法 3.4 组合问题中的蛮力法 3.5 图问题中的蛮力法 3.6 几何问题中的蛮力法 3.7 实验项目——串匹配问题
清华大学出版社
算法设计与分析
3.1 蛮力法的设计思想
蛮力法的设计思想:直接基于问题的描述。 例:计算an
52 37 65 不可行 不可行 不可行 不可行 不可行
清华大学出版社
算法设计与分析
对于一个具有n个元素的集合,其子集 数量是2n,所以,不论生成子集的算法 效率有多高,蛮力法都会导致一个Ω(2n) 的算法。
清华大学出版社
算法设计与分析
3.4.4 任务分配问题
假设有n个任务需要分配给n个人执行, 每个任务只分配给一个人,每个人只分配一 个任务,且第j个任务分配给第i个人的成本 是C[i, j](1≤i , j≤n),任务分配问题要求 找出总成本最小的分配方案。
用蛮力法解决0/1背包问题,需要考虑给定n个 物品集合的所有子集,找出所有可能的子集(总重 量不超过背包容量的子集),计算每个子集的总价 值,然后在他们中找到价值最大的子集。
清华大学出版社
算法设计与分析
10
实验一 匹配网络的设计与仿真
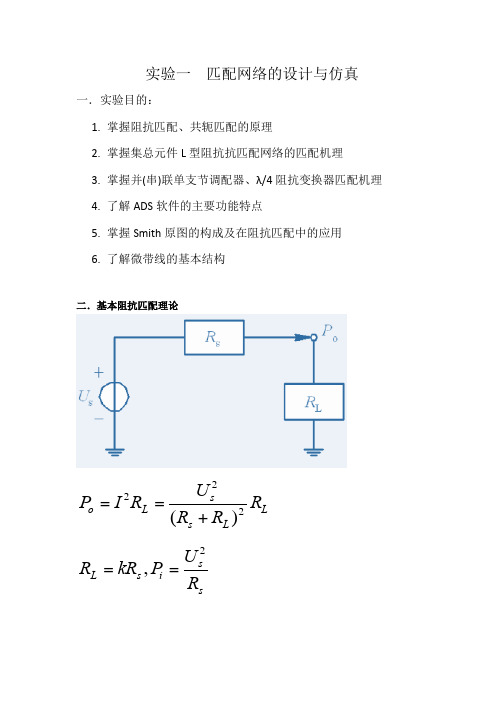
实验一匹配网络的设计与仿真一.实验目的:1. 掌握阻抗匹配、共轭匹配的原理2. 掌握集总元件L 型阻抗抗匹配网络的匹配机理3. 掌握并(串)联单支节调配器、λ/4阻抗变换器匹配机理4. 了解ADS 软件的主要功能特点5. 掌握Smith 原图的构成及在阻抗匹配中的应用6. 了解微带线的基本结构二.基本阻抗匹配理论L L s s L o R R R U R I P 222)(+==s s i s L R U P kR R 2,==信号源的输出功率取决于U s 、R s 和R L 。
在信号源给定的情况下,输出功率取决于负载电阻与信号源内阻之比k 。
当R L =R s 时可获得最大输出功率,此时为阻抗匹配状态。
无论负载电阻大于还是小于信号源内阻,都不可能使负载获得最大功率,且两个电阻值偏差越大,输出功率越小。
1. 共轭匹配:当时,源输出功率最大,称作共轭匹配。
2. 阻抗匹配:λ/4阻抗变换器i o P k k P 2)1(+=*g LZ Z=三、ADS仿真步骤1.打开ADS2.新建一个Workspace,并命名为“学号或姓名”3.新建原理图4.原理图设计界面4.在元件面板列表中选择“Simulating-S Param”,单击和放两个Term和一个S-P控件5.接下来接续设置各个器件的参数6.执行菜单命令【Tools】 【Smith Chart】,弹出“SmartComponent Sync”对话框;选择“Update SmartComponent from Smith Chart Utility”,单击“OK”7.单击“DefineSource/Load Network terminations”按钮8.采用LC分立器件匹配过程如下图所示9.改变L、C 的位置,观察L、C值变化时输入阻抗的变化轨迹单击“Build ADS Circuit”按钮,即可生成相应的电路选中DA_SmithChartMatch控件,单击“”,以查看匹配电路单击“”,返回原理图单击“”图标,进行仿真单击“”,在结果窗口单击,就会出现如下对话框,仿真结果图形输出。
模式匹配KMP算法实验报告

实验四:KMP算法实验报告一、问题描述模式匹配两个串。
二、设计思想这种由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现的改进的模式匹配算法简称为KM P算法。
注意到这是一个改进的算法,所以有必要把原来的模式匹配算法拿出来,其实理解的关键就在这里,一般的匹配算法:int Index(String S,String T,int pos)//参考《数据结构》中的程序{i=pos;j=1;//这里的串的第1个元素下标是1while(i<=S.Length && j<=T.Length){if(S[i]==T[j]){++i;++j;}else{i=i-j+2;j=1;}//**************(1)}if(j>T.Length) return i-T.Length;//匹配成功else return 0;}匹配的过程非常清晰,关键是当‘失配’的时候程序是如何处理的?为什么要回溯,看下面的例子:S:aaaaabababcaaa T:ababcaaaaabababcaaaababc.(.表示前一个已经失配)回溯的结果就是aaaaabababcaaaa.(babc)如果不回溯就是aaaaabababcaaaaba.bc这样就漏了一个可能匹配成功的情况aaaaabababcaaaababc这是由T串本身的性质决定的,是因为T串本身有前后'部分匹配'的性质。
如果T为a bcdef这样的,大没有回溯的必要。
改进的地方也就是这里,我们从T串本身出发,事先就找准了T自身前后部分匹配的位置,那就可以改进算法。
如果不用回溯,那T串下一个位置从哪里开始呢?还是上面那个例子,T为ababc,如果c失配,那就可以往前移到aba最后一个a的位置,像这样:...ababd...ababc->ababc这样i不用回溯,j跳到前2个位置,继续匹配的过程,这就是KMP算法所在。
串匹配算法实验报告

一、实验目的1. 理解串匹配算法的基本原理和实现方法。
2. 掌握KMP算法和朴素算法的原理和实现过程。
3. 通过实验对比分析两种算法的性能,验证算法的效率和适用场景。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.73. 开发工具:PyCharm三、实验内容1. 串匹配算法的原理介绍2. 朴素算法的实现与测试3. KMP算法的实现与测试4. 两种算法的性能对比四、实验步骤1. 串匹配算法的原理介绍串匹配算法是指在一个文本串中查找一个模式串的位置。
常用的串匹配算法有朴素算法和KMP算法。
(1)朴素算法(Brute-Force算法):通过逐个字符比较主串和待匹配串,如果匹配成功,则返回匹配位置;如果匹配失败,则回溯到主串上的一个新位置,并在待匹配串上从头开始比较。
(2)KMP算法:通过构建一个部分匹配表(next数组),记录模式串中每个位置对应的最长相同前缀后缀的长度。
在匹配过程中,当出现不匹配时,通过查阅next数组确定子串指针回退位置,从而避免重复比较。
2. 朴素算法的实现与测试(1)实现朴素算法```pythondef brute_force_search(text, pattern):n = len(text)m = len(pattern)for i in range(n - m + 1):j = 0while j < m:if text[i + j] != pattern[j]:breakj += 1if j == m:return ireturn -1```(2)测试朴素算法```pythontext = "ABABDABACDABABCABAB"pattern = "ABABCABAB"print(brute_force_search(text, pattern)) # 输出:10 ```3. KMP算法的实现与测试(1)实现KMP算法```pythondef kmp_search(text, pattern):def build_next(pattern):next_array = [0] len(pattern)k = 0for i in range(1, len(pattern)):while k > 0 and pattern[k] != pattern[i]: k = next_array[k - 1]if pattern[k] == pattern[i]:k += 1next_array[i] = kreturn next_arrayn = len(text)m = len(pattern)next_array = build_next(pattern)k = 0for i in range(n):while k > 0 and text[i] != pattern[k]:k = next_array[k - 1]if text[i] == pattern[k]:k += 1if k == m:return i - m + 1return -1```(2)测试KMP算法```pythontext = "ABABDABACDABABCABAB"pattern = "ABABCABAB"print(kmp_search(text, pattern)) # 输出:10```4. 两种算法的性能对比为了对比两种算法的性能,我们分别测试了不同的文本串和模式串长度,并记录了运行时间。
CC++下scanf的%匹配以及过滤字符串问题

CC++下scanf的%匹配以及过滤字符串问题最近在写⼀个测试的⼩程序,由于⽤到了sscanf函数对字符串进⾏标准读⼊,⽽sscanf在很多⽅⾯都与scanf⽐较相像,于是对scanf进⾏了⼀番测试,遇到了⼀系列基础性的问题,恶补基础的同时也体现了⾃⼰的薄弱。
话不多说,直接附上问题吧。
问题描述#include<stdio.h>#include<string.h>int main(){while(1){char str[256]={0};int a=0;char b='\0';printf("please input the num:\n");scanf("%[^,],%[^,],%d",str,&b,&a);printf("input is str: %s b: %c a: %d And str length is %u, the first character is %u\n",str,b,a,strlen(str),str[0]);//gets(str);}return 0;}在这段代码⾥,如果我初始输⼊"a,a,0",输出正确。
但输⼊",,0"的话,接下来会⾃动不需要输⼊然后循环着不断的输出,想问⼀下这个是什么原因。
还有⼀个是我将代码改成了如下:#include<stdio.h>#include<string.h>int main(){while(1){char str[256]={0};int a=0;char b='\0';printf("please input the num:\n");scanf("%*[\n\r\t]%[^,],%[^,],%d",str,&b,&a);printf("input is str: %s b: %c a: %d And str length is %u, the first character is %u\n",str,b,a,strlen(str),str[0]);//gets(str);}return 0;}本来⽬的是过滤输⼊的回车,其中%*是过滤满⾜条件的字符,但是如果直接输⼊"a,a,0",也会出现不需要输⼊然后不断地循环输出的现象。
2022年中考物理微专题 串并联电路电流、电压特点的实验中考问题(教师版含解析)匹配最新版教材

专题23 串并联电路电流、电压特点的实验问题知识点1:探究串并联电路电流规律的实验1.串联电路中各处的电流相等。
表达式:I=I1=U2=U32.并联电路的干路总电流等于各支路电流之和。
表达式:I=I1+I2+I33.要把握连接电路以及电路元件使用的注意事项。
4.电路故障分析,电流表的读数,实验数据的处理。
知识点2:探究串并联电路电压规律的实验1.串联电路电压的规律(1)在串联电路中,总电压等于各导体两端电压之和。
(2)表达式:U=U1+U2+U32.并联电路电压的规律(1)并联电路中,各支路两端的电压相等且等于电源电压。
(2)表达式:U=U1=U2=U3知识点3:串并联电路电流、电压特点的应用【例题1】(2020南京模拟)在“探究串联电路的电流特点”的实验中,小虹同学选用两个不同的小灯泡组成了如图甲所示的串联电路,然后用一个电流表分别接在a、b、c三处去测量电流。
(1)她先把电流表接在a处,闭合开关后,发现两灯的亮度不稳定,电流表的指针也来回摆动。
故障的原因可能是。
A.某段导线断开B.某接线柱处接触不良C.某灯泡被短路D.电流表被烧坏(2)她排除故障后,重新闭合开关.电流表的指针指示位置如图乙所示.则所测的电流值为A。
(3)她测量了a、b、c三处的电流,又改变灯泡的规格进行了多次实验,其中-次实验的测量数据如下表,在分析数据时,她发现三处的测量值有差异。
下列分析正确的是。
I a(A)I b(A)I c(A)0.160.150.14A.可能是因为测量误差造成的B.是因为没有对电流表调零造成的C.串联电路中各处的电流本来就不等D.电流从电源正极流向负极的过程中,电流越来越小【答案】(1)B(2)0.22A(3)A【解析】(1)A和D中故障会导致电路中都没有电流,灯也不亮。
C选项故障电流是稳定的,被短路的灯泡不亮,另一个灯泡亮度稳定。
在题干的描述中发现有电流,灯亮度不稳定,有两种情况:一是电源电压不稳定,二是电路中就接触不良的接线柱,故此题只有B选项符合(2)先看量筒量程,再注意分度值即可,难度较易。
串的数据结构实验报告

串的数据结构实验报告串的数据结构实验报告一、引言在计算机科学中,串(String)是一种基本的数据结构,用于存储和操作字符序列。
串的数据结构在实际应用中具有广泛的用途,例如文本处理、搜索引擎、数据库等。
本实验旨在通过实践掌握串的基本操作和应用。
二、实验目的1. 理解串的概念和基本操作;2. 掌握串的存储结构和实现方式;3. 熟悉串的常见应用场景。
三、实验内容1. 串的定义和基本操作在本实验中,我们采用顺序存储结构来表示串。
顺序存储结构通过一个字符数组来存储串的字符序列,并使用一个整型变量来记录串的长度。
基本操作包括:- 初始化串- 求串的长度- 求子串- 串的连接- 串的比较2. 串的模式匹配串的模式匹配是串的一个重要应用场景。
在实验中,我们将实现朴素的模式匹配算法和KMP算法,并比较它们的性能差异。
四、实验步骤1. 串的定义和基本操作首先,我们定义一个结构体来表示串,并实现初始化串、求串的长度、求子串、串的连接和串的比较等基本操作。
2. 串的模式匹配a. 实现朴素的模式匹配算法朴素的模式匹配算法是一种简单但效率较低的算法。
它通过逐个比较主串和模式串的字符来确定是否匹配。
b. 实现KMP算法KMP算法是一种高效的模式匹配算法。
它通过利用已匹配字符的信息,避免不必要的比较,从而提高匹配效率。
3. 性能比较与分析对比朴素的模式匹配算法和KMP算法的性能差异,分析其时间复杂度和空间复杂度,并讨论适用场景。
五、实验结果与讨论1. 串的基本操作经过测试,我们成功实现了初始化串、求串的长度、求子串、串的连接和串的比较等基本操作,并验证了它们的正确性和效率。
2. 串的模式匹配我们对两种模式匹配算法进行了性能测试,并记录了它们的运行时间和内存占用情况。
结果表明,KMP算法相较于朴素算法,在大规模文本匹配任务中具有明显的优势。
六、实验总结通过本实验,我们深入学习了串的数据结构和基本操作,并掌握了串的模式匹配算法。
“串匹配问题“实验报告

实验一串匹配问题1.实验题目:给定一个文本S=“s1,s2,……sn”,在该文本中查找和定位任意给定的字符串T=“t1,t2,……tm”,T称为模式。
2.实验要求:实现BF算法和改进的算法KMP算法,编写实验程序,给出测试数据和测试结果。
并验证两种方法时间效率的差异。
3.实验目的:1)深刻理解蛮力法的设计思想。
2)提高应用蛮力法设计算法的技能。
3)理解这样一个观点,蛮力法经过适当改进,可以改进算法的时间性能。
4.实验源代码:1)BF算法代码如下:// tt.cpp: 主项目文件。
#include"stdafx.h"using namespace System;int bfstring(char s[],int n,char t[],int m){int i,j,k;for(i=1;i<=n-m+1;i++){j=1;k=i;while (s[k]==t[j]) {k++;j++;}if (j>m) return i;}return 0;}int main(array<System::String ^> ^args){char s[5],t[2];int n,m,i;Console::WriteLine(L"前5个为主串,后2个为匹配串");n=5;m=2;for (i=1;i<=n;i++){s[i]=Console::Read();}for (i=1;i<=m;i++){t[i]=Console::Read();}Console::WriteLine("从第"+bfstring(s,n,t,m)+"个位置开始匹配");; Console::Read();}2)KMPl算法代码如下:// y.cpp: 主项目文件。
#include"stdafx.h"using namespace System;int kmpstring(char s[],int n,char t[],int m){int i,j,k,next[5];next[1]=0;next[2]=1;j=2;k=1;while(j<m){if(k==0||t[j]==t[k]){j=j+1;k=k+1;next[j]=k;}else k=next[k];}j=2;for(i=1;i<=n;i++){j=next[j];if (j==0){i++;j++;}while(s[i]==t[j]){i++;j++;}if(j>m) return i-m;i=i-1;}return 0;}int main(array<System::String ^> ^args){char s[10],t[5];int n,m,i;Console::WriteLine(L"前10个为主串,后5个为匹配串");n=10;m=5;for (i=1;i<=n;i++){s[i]=Console::Read();}for (i=1;i<=m;i++){t[i]=Console::Read();}if (kmpstring(s,n,t,m)==0)Console::WriteLine("匹配失败");elseConsole::WriteLine("从第"+kmpstring(s,n,t,m)+"个位置开始匹配成功");Console::Read();}5.实验结果:1)BF算法运行结果:2)KMP算法运行结果;。
实验三实验报告括号匹配的检验

实验三实验报告括号匹配的检验实验题⽬:括号匹配的检验⼀、实验⽬的加深理解栈的定义和特性;掌握栈的存储结构与实现⼆、实验内容:任意输⼊⼀个由若⼲个圆括号、⽅括号和花括号组成字符串,设计⼀个算法判断该串中的括号是否配对。
三、设计与编码1、基本思想基本思想:最内层(最迟出现)的左刮号必须与最内层(最早出现)的同类右刮号配对,它最急切地期待着配对。
配对之后, 期待得以消解。
因此为左刮号设置⼀个栈,置于栈顶的左刮号期待配对的急切程度最⾼。
实例:[ ( [ ] { } ) ]、( [ { } ] )、{ [ ] } )、( { [ ] }、( { [ ] ] )2、编码#include#includeconst int StackSize=100;class SeqStack{public:SeqStack(){top=-1;}~SeqStack(){}void Push(char s);char Pop();void Peidui(char s[StackSize]);private:char data[StackSize];int top;};void SeqStack::Push(char s){if(top==StackSize-1) throw"上溢";top++;data[top]=s;char SeqStack::Pop(){if(top==-1)throw"下溢";else{char a;a=data[top--];return a;}}void SeqStack::Peidui(char *s){int i=0,l=strlen(s);char t;for(i=0;i{if(s[i]=='{'||s[i]=='['||s[i]=='(')Push(s[i]);else{if(top==-1){cout<<"右括号多了,不匹配"<return;}else{t=data[top];if(t=='{'&&s[i]=='}'||t=='['&&s[i]==']'||t=='('&&s[i]==')') {Pop();}elsebreak;}}if(top==-1&&s[i]=='\0')cout <<"配对成功"<elseif(top!=-1&&s[i]=='\0')cout<<"左括号多了,不匹配"<elsecout<<"左右类型不匹配"<}void main(){char str[10];cout<<"请输⼊括号;"<cin>>str;SeqStack S;S.Peidui(str);}四、调试与运⾏1、调试时遇到的主要问题及解决2、运⾏结果(输⼊及输出,可以截取运⾏窗体的界⾯)五、实验⼼得。
括号匹配检测实验报告

括号匹配检测实验报告本实验旨在设计和实现一个括号匹配检测算法,检测给定字符串中的括号是否正确匹配。
实验原理:括号匹配检测是一种常见的算法问题。
其基本原理是利用栈(Stack)数据结构进行括号的匹配。
当遇到左括号时,将其入栈;当遇到右括号时,判断栈顶元素是否与其对应的左括号相匹配,若匹配则将栈顶元素出栈,继续检测下一个字符;若不匹配,则说明括号不正确匹配,返回匹配失败;最后,若栈为空,则说明所有括号都正确匹配,返回匹配成功。
实验步骤:1. 设计栈数据结构及括号匹配检测算法。
2. 实现算法代码。
3. 设计测试用例,包括正确匹配和不正确匹配的字符串。
4. 运行测试用例,检测算法的正确性和效率。
5. 分析实验结果并撰写实验报告。
实验代码:以下是一个用Python语言实现的括号匹配检测算法示例代码:pythonclass Stack:def __init__(self):self.stack = []def is_empty(self):return len(self.stack) == 0def push(self, element):self.stack.append(element)def pop(self):if not self.is_empty():return self.stack.pop()else:return Nonedef peek(self):if not self.is_empty():return self.stack[-1]else:return Nonedef bracket_match(string):stack = Stack() # 创建栈对象brackets = {'(': ')', '[': ']', '{': '}'}for char in string:if char in brackets: # 左括号入栈stack.push(char)elif char in brackets.values(): # 右括号与栈顶元素匹配if stack.is_empty():return Falseif brackets[stack.peek()] == char:stack.pop()else:return Falsereturn stack.is_empty()# 测试用例test_cases = ["()", "{[]}", "[{()}]", "(}", "{[}]"]for test_case in test_cases:if bracket_match(test_case):print(test_case, "匹配成功")else:print(test_case, "匹配失败")实验结果:运行测试用例,可以得到以下结果:- "()" 匹配成功- "{[]}" 匹配成功- "[{()}]" 匹配成功- "(}" 匹配失败- "{[}]" 匹配失败实验讨论:根据实验结果,我们可以看到算法能够正确地检测出括号的匹配情况。
串及其应用的实验报告

串及其应用的实验报告串及其应用的实验报告引言:串是计算机科学中一种基本的数据结构,它由一系列字符组成,可以是字母、数字或其他符号。
在计算机编程中,串常常用于存储和处理文本信息。
本实验旨在通过实践操作,探索串的基本特性和应用。
实验一:串的创建和操作1. 实验目的通过编写程序,学习串的创建和操作方法。
2. 实验步骤(1)使用编程语言创建一个空串。
(2)向串中添加字符,观察串的变化。
(3)使用串的长度函数,计算串的长度。
(4)使用串的比较函数,比较两个串的大小。
(5)使用串的连接函数,将两个串连接起来。
(6)使用串的截取函数,截取指定位置和长度的子串。
3. 实验结果通过实验步骤的操作,我们成功创建了一个空串,并向其中添加了字符。
使用长度函数计算出了串的长度,并使用比较函数比较了两个串的大小。
通过连接函数,我们将两个串连接成了一个新的串。
最后,使用截取函数,我们截取了指定位置和长度的子串。
实验二:串的模式匹配1. 实验目的通过实验操作,了解串的模式匹配算法。
2. 实验步骤(1)使用编程语言实现串的模式匹配算法。
(2)创建一个主串和一个模式串。
(3)使用模式匹配算法,在主串中查找模式串的位置。
3. 实验结果通过实验步骤的操作,我们成功实现了串的模式匹配算法。
创建了一个主串和一个模式串,并使用算法在主串中找到了模式串的位置。
实验三:串的应用——文本编辑器1. 实验目的通过实验操作,熟悉串的应用——文本编辑器。
2. 实验步骤(1)使用编程语言实现一个简单的文本编辑器。
(2)实现文本插入、删除和替换功能。
(3)实现文本搜索和替换功能。
3. 实验结果通过实验步骤的操作,我们成功实现了一个简单的文本编辑器。
可以插入、删除和替换文本,还可以进行文本搜索和替换。
结论:通过本次实验,我们对串及其应用有了更深入的了解。
串作为计算机科学中常用的数据结构,具有广泛的应用领域。
通过实践操作,我们掌握了串的创建和操作方法,并学会了串的模式匹配和文本编辑器的应用。
数据结构实验报告-基于字符串模式匹配算法的病毒感染检测问题

《数据结构》实验报告
abcd abcde abc def
00 输出结果为:
YES
NO 四、分析过程
在主函数中利用键盘输入 human[ ]、virus[ ],即 cin>>human>>virus; ,输入时要注意模 式串 virus 的长度不要超过主串 human 的长度。
调用 BF 子函数,输入的两个实参会送到 BF 算法里进行比较,当比较次数小于各自的长 度 时 , 开 始 匹 配 , 即 while(i<strlen(human)&&j<strlen(virus)) 。 如 果 模 式 串 和 主 串 相 同 human[i]==virus[j]时,i 和 j 都要加 1,否则 i=i-j+1; j=0;。当 j 等于 virus 的长度时,说明匹 配成功,令输出返回值 1;否则返回值为 0。
实验时间 实验地点 指导教师
年月日 电气楼 308
实验项目
实验类别
实 验 目 的 及 要 求
基于字符串模式匹配算法的病毒感染检测问题
基础实验
实验学时
4 学时
实验目的: 1.掌握字符串的顺序存储表示方法 2.掌握字符串模式匹配算法 BF 算法或 KMP 算法的实现
实验要求: 输入多组数据,每组数据占 1 行,输入 0 0 时结束输入;每组数据输
BF 算法的基本思想是:从主串的第 pos 个字符起与模式串的第一个字符比较,若相等, 则继续逐个比较后续字符;否则从主串的下一个字符起再重新和模式串进行比较。直至模式 串中的每一个字符和主串中的一个连续字符序列相同,则称匹配成功,否则不成功。
(1)首先全局定义了两个一定长度的数组用来存储人类和病毒的 DNA,分别是 human[100] 和 virus[100]。分别用 i 和 j 来指示主串 human 和模式串 virus 当前正待比较的字符位置。
括号匹配检测实验报告(3篇)

第1篇实验名称:括号匹配检测实验目的:1. 理解括号匹配的基本原理。
2. 掌握使用栈进行括号匹配检测的方法。
3. 通过编程实现括号匹配检测功能。
实验时间:2023年X月X日实验地点:实验室实验器材:1. 计算机2. 编程软件(如Python、Java等)3. 文档编辑器实验内容:一、实验原理括号匹配检测是计算机科学中的一个基础问题,它涉及到字符串中括号的正确配对。
常见的括号包括圆括号()、方括号[]和花括号{}。
一个有效的括号序列是指,序列中的每个左括号都有一个对应的右括号,并且括号内的内容可以嵌套。
括号匹配检测通常使用栈(Stack)这一数据结构来实现。
栈是一种后进先出(Last In First Out,LIFO)的数据结构,适用于括号匹配检测的原因是括号的匹配顺序与它们出现的顺序相反。
二、实验步骤1. 设计算法:确定使用栈进行括号匹配检测的算法步骤。
2. 编写代码:根据算法步骤,编写实现括号匹配检测功能的代码。
3. 测试代码:使用不同的测试用例对代码进行测试,确保其正确性。
4. 分析结果:对测试结果进行分析,评估代码的性能和正确性。
三、实验代码以下是一个使用Python实现的括号匹配检测的示例代码:```pythondef is_balanced(s):stack = []bracket_map = {')': '(', ']': '[', '}': '{'}for char in s:if char in bracket_map.values():stack.append(char)elif char in bracket_map.keys():if not stack or bracket_map[char] != stack.pop(): return Falsereturn not stack测试用例test_cases = ["((()))", True"([{}])", True"({[}])", False"((())", False"()[]{}", True"([)]", False"(({[]}))", True"" True]for case in test_cases:print(f"Input: {case}, Output: {is_balanced(case)}")```四、实验结果与分析通过上述代码,我们对一系列测试用例进行了括号匹配检测。
模式匹配实验报告

一、实验目的本次实验旨在让学生熟悉并掌握模式匹配的基本概念、算法及其应用。
通过实验,学生能够了解模式匹配算法的原理,掌握几种常见的模式匹配算法(如KMP算法、BF算法等)的实现方法,并能够运用这些算法解决实际问题。
二、实验环境1. 操作系统:Windows 102. 编程语言:C++3. 开发环境:Visual Studio 2019三、实验内容1. 模式匹配基本概念- 模式匹配:在给定的文本中查找一个特定模式的过程。
- 模式:要查找的字符串。
- 文本:包含可能包含模式的字符串。
2. KMP算法- KMP算法(Knuth-Morris-Pratt)是一种高效的字符串匹配算法,其核心思想是避免重复比较已经确定不匹配的字符。
- 实现步骤:1. 构造一个部分匹配表(next数组)。
2. 遍历文本和模式,比较字符,并使用next数组调整模式的位置。
3. BF算法- BF算法(Boyer-Moore)是一种高效的字符串匹配算法,其核心思想是利用坏字符规则和好后缀规则来减少不必要的比较。
- 实现步骤:1. 计算坏字符规则。
2. 计算好后缀规则。
3. 遍历文本和模式,比较字符,并使用坏字符规则和好后缀规则调整模式的位置。
4. 模式匹配算法比较- 比较KMP算法和BF算法的时间复杂度、空间复杂度及适用场景。
四、实验步骤1. 初始化- 定义文本和模式字符串。
- 初始化模式匹配算法的参数。
2. 构造next数组(KMP算法)- 根据模式字符串构造部分匹配表(next数组)。
3. 计算坏字符规则和好后缀规则(BF算法)- 根据模式字符串计算坏字符规则和好后缀规则。
4. 遍历文本和模式- 使用KMP算法或BF算法遍历文本和模式,比较字符,并调整模式的位置。
5. 输出结果- 输出匹配结果,包括匹配的位置和匹配次数。
五、实验结果与分析1. KMP算法- 时间复杂度:O(nm),其中n为文本长度,m为模式长度。
- 空间复杂度:O(m)。
数据结构实验报告-串

实验四串【实验目的】1、掌握串的存储表示及基本操作;2、掌握串的两种模式匹配算法:BF和KMP。
3、了解串的应用。
【实验学时】2学时【实验预习】回答以下问题:1、串和子串的定义串的定义:串是由零个或多个任意字符组成的有限序列。
子串的定义:串中任意连续字符组成的子序列称为该串的子串。
2、串的模式匹配串的模式匹配即子串定位是一种重要的串运算。
设s和t是给定的两个串,从主串s的第start个字符开始查找等于子串t的过程称为模式匹配,如果在S中找到等于t的子串,则称匹配成功,函数返回t在s中首次出现的存储位置(或序号);否则,匹配失败,返回0。
【实验内容和要求】1、按照要求完成程序exp4_1.c,实现串的相关操作。
调试并运行如下测试数据给出运行结果:•求“This is a boy”的串长;•比较”abc3”和“abcde“;表示空格•比较”english”和“student“;•比较”abc”和“abc“;•截取串”white”,起始2,长度2;•截取串”white”,起始1,长度7;•截取串”white”,起始6,长度2;•连接串”asddffgh”和”12344”;#include<stdio.h>#include<string.h>#define MAXSIZE 100#define ERROR 0#define OK 1/*串的定长顺序存储表示*/typedef struct{char data[MAXSIZE];int length;} SqString;int strInit(SqString *s);/*初始化串*/int strCreate(SqString *s); /*生成一个串*/int strLength(SqString *s); /*求串的长度*/int strCompare(SqString *s1,SqString *s2); /*两个串的比较*/int subString(SqString *sub,SqString *s,int pos,int len);/*求子串*/int strConcat(SqString *t,SqString *s1,SqString *s2);/*两个串的连接*//*初始化串*/int strInit(SqString *s){s->length=0;s->data[0]='\0';return OK;}/*strInit*//*生成一个串*/int strCreate(SqString *s){printf("input string :");gets(s->data);s->length=strlen(s->data);return OK;}/*strCreate*//*(1)---求串的长度*/int strLength(SqString *s){return s->length;}/*strLength*//*(2)---两个串的比较,S1>S2返回>0,s1<s2返回<0,s1==s2返回0*/int strCompare(SqString *s1,SqString *s2){int i;for(i=0;i<s1->length&&i<s2->length;i++){if(s1->data[i]>s2->data[i]){return 1;}if(s1->data[i]<s2->data[i]){return -1;}}return 0;}/*strCompare*//*(3)---求子串,sub为返回的子串,pos为子串的起始位置,len为子串的长度*/int subString(SqString *sub,SqString *s,int pos,int len) {int i;if(pos<1||pos>s->length||len<0||len>s->length-pos+1) {return ERROR;}sub->length=0;for(i=0;i<len;i++){sub->data[i]=s->data[i+pos-1];sub->length++;}sub->data[i]='\0';return OK;}/*subString*//*(4)---两个串连接,s2连接在s1后,连接后的结果串放在t中*/int strConcat(SqString *t,SqString *s1,SqString *s2){int i=0,j=0;while(i<s1->length){t->data[i]=s1->data[i];i++;}while(j<s2->length){t->data[i++]=s2->data[j++];}t->data[i]='\0';t->length=s1->length+s2->length;return OK;}/*strConcat*/int main(){int n,k,pos,len;SqString s,t,x;do{printf("\n ---String--- \n");printf(" 1. strLentgh\n");printf(" 2. strCompare\n");printf(" 3. subString\n");printf(" 4. strConcat\n");printf(" 0. EXIT\n");printf("\n ---String---\n");printf("\ninput choice:");scanf("%d",&n);getchar();switch(n){case 1:printf("\n***show strLength***\n");strCreate(&s);printf("strLength is %d\n",strLength(&s));break;case 2:printf("\n***show strCompare***\n");strCreate(&s);strCreate(&t);k=strCompare(&s,&t); /*(5)---调用串比较函数比较s,t*/if(k==0)printf("two string equal!\n");else if(k<0)printf("first string<second string!\n");elseprintf("first string>second string!\n");break;case 3:printf("\n***show subString***\n");strCreate(&s);printf("input substring pos,len:");scanf("%d,%d",&pos,&len);if(subString(&t,&s,pos,len))printf("subString is %s\n",t.data);elseprintf("pos or len ERROR!\n");break;case 4:printf("\n***show subConcat***\n");strCreate(&s);strCreate(&t);if(strConcat(&x,&s,&t)) /*(6)---调用串连接函数连接s&t*/printf("Concat string is %s",x.data);elseprintf("Concat ERROR!\n");break;case 0:exit(0);default:break;}}while(n);return 0;}2、按照要求完成程序exp4_2.c,实现BF&KMP串的模式匹配算法。
近似串匹配问题课程设计

近似串匹配问题课程设计一、课程目标知识目标:1. 理解近似串匹配问题的基本概念和实际意义;2. 掌握常用的近似串匹配算法,如编辑距离、动态规划等;3. 学会分析近似串匹配问题在不同场景下的应用和优化方法。
技能目标:1. 能够运用编程语言实现基本的近似串匹配算法;2. 能够针对具体问题,选择合适的近似串匹配算法并调整参数;3. 能够运用所学知识解决实际生活中的近似串匹配问题。
情感态度价值观目标:1. 培养学生对算法学习的兴趣和热情,增强其自信心;2. 培养学生的团队协作意识和解决问题的能力;3. 培养学生严谨的科学态度和良好的编程习惯。
本课程针对高年级学生,结合学科特点和教学要求,注重理论与实践相结合,培养学生解决实际问题的能力。
通过本课程的学习,学生将能够掌握近似串匹配问题的基本知识和技能,形成良好的编程素养,并在实际应用中发挥所学,为未来的学术研究和职业发展打下坚实基础。
二、教学内容1. 近似串匹配问题引论- 介绍近似串匹配的概念、分类和应用场景;- 分析近似串匹配问题与精确串匹配问题的区别与联系。
2. 常用近似串匹配算法- 编辑距离算法:原理、计算步骤及实现方法;- 动态规划算法:原理、应用场景及优化策略;- 其他近似串匹配算法:如Jaccard相似系数、余弦相似度等。
3. 近似串匹配算法的应用与优化- 分析不同场景下近似串匹配算法的选择与优化;- 实际案例:如基因序列分析、文本查重等;- 高效算法的实现:如索引技术、并行计算等。
4. 编程实践与案例分析- 结合Python等编程语言,实现近似串匹配算法;- 分析实际案例,进行算法优化;- 课堂讨论与展示,分享学习心得和经验。
教学内容依据课程目标进行科学性和系统性组织,确保学生能够循序渐进地掌握知识。
教学大纲明确教学内容安排和进度,与教材章节紧密关联。
通过本章节的学习,学生将全面了解近似串匹配问题的相关知识,为实际应用打下坚实基础。
三、教学方法本章节采用多样化的教学方法,旨在激发学生的学习兴趣,提高主动性和实践能力。
串匹配BM算法、KMP算法、BF算法

实验报告一串匹配问题{printf("success!\n");return 0;}}printf("no found!:%s\n\n",&t);return 0;}KMP算法:#include <stdio.h>#include <string.h>#include <conio.h>main(){char s[100];char t[100];}printf("no found!:%s\n\n",&t); return 0;}BM算法:#include <iostream>using namespace std;#include <stdio.h>#include <string.h>static int time=0;//dist函数int dist(char ch,char *T) {int k=-1,t1;}if(j==-1){cout<<"该串从第&i位开始匹配:"<<i+2<<endl;break;}else{time++;i=i+dist(S[i],T);}}if(i>=s1)cout<<"匹配不成功"<<endl;}void main(){int *next=new int;//给next指针分配空间char *S=new char;//给S指针分配空间char *T=new char;//给T指针分配空间cout<<"请输入串S:";cin>>S;cout<<"请输入串T:";cin>>T;cout<<"BM算法: ";BM(S,T);cout<<"一共执行循环"<<time<<"次"<<endl;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验项目一串匹配问题
1.实验题目
给定一个文本,在该文本中任意查找并定位任意给定字符串。
2.实验目的
(1)深刻理解并掌握蛮力法的设计思想;
(2)提高应用蛮力法设计算法的技能;
(3)理解这样一个观点:用蛮力法设计的算法,一般来说,经过适度的努力后,都可以对算法的第一个版本进行一定程度的改良,改进其时间性能。
3.实验要求
(1)实现BF算法;
(2)实现BF算法的改进算法:KMP算法和BM算法;
(3)对上述三个算法进行时间复杂性分析,并设计实验程序验证分析结果。
4.实验提示
BF算法,KMP算法和BM算法都是串匹配问题中的经典算法,BF算法和KMP算法请参见本章第3.2节。
下面介绍BM算法。
BM算法是Boyer和Moore共同设计的快速匹配算法。
BM算法与KMP算法的主要区别是匹配操作的方向不同。
虽然BM算法仅把匹配操作的字符比较顺序改为从左到右,但匹配发生失败时,模式T右移的计算方法却发生了较大的变化。
5.实验代码
BF算法代码
#include<stdio.h>
#include<string.h>
#define N 50
void main()
{
char a[N],b[N];
printf("请输入待匹配的两个字符串,主串a为:\n");
gets(a);
printf("模式串b为:\n");
gets(b);
int i=1,j=1,s,t;
s=strlen(a);
t=strlen(b);
while(i<s&&j<t){
if(a[i]==b[j]){
i++;
j++;
}
else{
i=i-j+2;
j=1;
}
}
if(j>=t)
printf("从a串的%d个字符开始匹配\n",i-j+1);
else
printf("匹配失败\n");
}
KMP算法代码
#include<stdio.h>
#include<string.h>
#define N 50
void GetNext(char t[],int next[])
{
next[1]=0;
int j=1,k=0,h;
h=strlen(t);
while(j<h)
if((k==0)||(t[j]==t[k]))
{
j++;
k++;
next[j]=k;break;
}
else
k=next[k];
}
void main(){
char s[N],t[N];
int next[N]={0};
printf("请输入主串s:\n");
gets(s);
printf("请输入模式串t:\n");
gets(t);
int i=1,j=1,k=strlen(s)-1,h=strlen(t)-1;
while((i<=k)&&(j<=h))
{
if(s[i]==t[j]){
i++;
j++;
}
else{
GetNext(t,next);
j=next[j];
{if(j==0)
{
i++;
j++;
}
}
}
}
if(j>h)
printf("匹配的起始下表为:%d\n",i-j+1);
else
printf("匹配失败\n");
}
BM算法代码
#include<stdio.h>
#include<string.h>
#define N 50
int GetDist(char t[],char c){
int i,k=0;
int m;
m=strlen(t)-1;
for(i=m;i>0;i--){
if(t[i]==c){
k=i;break;
}
}
if((k!=m)&&(k!=0))
return m-k;
else
return m;
}
int BM(char s[],char t[],int n,int m){
int i,j;
i=m;
while(i<=n){
j=m;
while(j>0&&(s[i]==t[j])){
j=j-1;
i=i-1;
}
if(j==0){
return i+1;
break;
}
else{
i+=GetDist(t,s[i]);
}
}
return 0;
}
void main(){
char s[N],t[N];
int r,n,m;
printf("请输入主串s:\n");
gets(s);
printf("请输入模式串t:\n");
gets(t);
n=strlen(s)-1;
m=strlen(t)-1;
r=BM(s,t,n,m);
if(r!=0)
printf("匹配的起始下标为:%d\n",r);
else
printf("匹配失败");
}
6.实验结果
BF算法实验结果
KMP算法实验结果
BM算法实验结果
时间复杂度分析
算法时间复杂度BF O(n*m)KMP O(n)
BM O(n/3)7.试验心得
、。
