线性代数第二章课后习题

合集下载

第二章-线性代数(第四版)习题答案

y1 2 2 1 2 1 −1 x1 −7 −4 3 2 9 y1
y2 = 3 3 y2
5 3
x2 = 6 3 x3
−7 y2 . y3 −4
即
y1 = −7x1 − 4x2 + 9x3 , y2 = 6x1 + 3x2 − 7x3 , y = 3x + 2x − 4x . 3 1 2 3
由数学归纳法知: Ak =
8 ．设 A = 0
解: 方法一. 首先计算
1 = 0 0 λ λ3 0 λn 猜测: An = 0 0 nλn−1 λn 0
同理得 y2 = 6x1 + 3x2 − 7x3 , y3 = 3x1 + 2x2 − 4x3 .
2 . 已知两个线性变换 x1 = 2y1 + y3 , x2 = −2y1 + 3y2 + 2y3 , x = 4y + y + 5y , 3 1 2 3 y1 = −3z1 + z2 , y 2 = 2 z1 + z3 , y = −z + 3z , 3 2 3
1 0 (6) 0 0
1 3 (1) AB = BA 吗?
5. 设A=
1
2
,B=
1 1
0 2
, 问:
(2) (A + B )2 = A2 + 2AB + B 2 吗? (3) (A + B )(A − B ) = A2 − B 2 吗?
解: (1) 因为
AB = 3 4 4 6 , BA = 1 2 3 8 ,

线性代数第2章习题课

一般地，注：一般地，对于 n 阶方阵 A 有 A = A
.
1 0 0 例6. 设 A = 2 2 0 ，则 (A* )-1 = 3 4 5
A/10
.
第一章
16
知识点6：知识点：矩阵的秩
k 1 1 1 k 1 1 1 k
例7. 设 A =
p.100 习题习题27
第一章
7
分块矩阵的乘法
p.100 习题31 用分块矩阵乘法求下列矩阵的乘积：习题31 用分块矩阵乘法求下列矩阵的乘积：
1 −2 0 0 1 −1 1 1 1 0 = A1 (1) A 0 3 2 0 −1 3
A2 B1 B2 A1 B1 = A B A4 O B4 3 1
A1B2 + A2 B4 A3 B2 + A4 B4
p.100 习题32 习题32
第一章
8
知识点2：知识点：转置与对称矩阵
例1. 设 A, B 均为 n 阶对称阵，则下列矩阵中不对称的是 B . 阶对称阵，
(A ) = A
* * n− 2
( A T )T = A
( A −1 ) −1 = A
三种运算符任意两个任意两个可交换顺序注：AT , A−1, A* 三种运算符任意两个可交换顺序
第一章
A P102 49
2
二、方阵的逆矩阵
1.方阵可逆的判定 1.方阵可逆的判定: 方阵可逆的判定: n 阶方阵 A 可逆 |A|≠0. A 是非奇异矩阵 . AB=I ( 或 BA =I ). A 与 In 相似，相似，即存在可逆阵P 即存在可逆阵、Q，使得，使得PAQ= In. A 可以表示为若干初等矩阵的乘积 . r(A) = n . A 是满秩矩阵 .

《线性代数》第二章矩阵及其运算精选习题及解答

第二章矩阵及其运算2.1 目的要求1．理解矩阵的概念；2．了解单位矩阵, 对角矩阵, 三角矩阵, 对称矩阵以及它们的基本性质； 3．掌握矩阵的线性运算, 乘法, 转置及其运算规则；4．理解逆矩阵的概念; 掌握可逆矩阵的性质; 会用伴随矩阵求矩阵的逆； 5．了解分块矩阵的概念, 了解分块矩阵的运算法则．2.2重要公式和结论1．对于任意方阵A , 总有 E A =A A =AA **，如果0≠A , 即A 为可逆矩阵, 则有 *1A AA1=−或1*A A A −=； 2．数乘以方阵的关系 , TTk k A A =)(111)(−−=A A kk , A A n k k =, A A 11=−；3．矩阵乘法的关系T T T A B (AB)=, , 111A B (AB)−−−=BA AB =；，()22T TA)(A =()2112A )(A−−=，22A A =；4．若A 、均为可逆矩阵, 则; ； B 10B A 0−⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛=−−0AB 011⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛−−−111B 00A B 00A ⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛−−−−−11111B 0CB A A B 0C A ；； ⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛−−−−−11111B CA B 0A BC 0A 5．已知A 为一个n 阶可逆矩阵, 则有)2(≥n 1n *AA −=；6．已知A 为一个阶矩阵，则n A A nk k =，1−=n nk k A A *，()1)1(*−−=n n n kk AA ；7．已知A 为一个n 阶可逆矩阵, 则有)3(≥n A AA 2**)(−=n ．2.3典型例题例2.1计算:(1) (2) .⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛n n b b a a M L 11)(()n n b b a a L M 11⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛解 (1) =;⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛n n b b a a M L 11)(∑==+n k k k n n b a b a b a 111L (2) . ()⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛n n n n n n n n b a b a b a b a b a b a b a b a b a b b a a L M M M L L L M 21222121211111例2.2 设为三阶矩阵, 且已知)(j i a =A a =A , *A 为A 的伴随矩阵又⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=333231232221131211na na na ma ma ma la la la B , 求 *BA 解由于 CA B =⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=333231232221131211333231232221131211000000a a a a a a a a a n m l na na na ma ma ma la la la 其中, ，故⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=n m l 000000C ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛====an am al a 000000C E A C CAA BA **．例2.3 设, , 求的关系, 使⎟⎟⎠⎞⎜⎜⎝⎛=3421A ⎟⎟⎠⎞⎜⎜⎝⎛=y x 21B y x 与A 与是可交换的． B 解要使A , 可交换, 即B BA AB =又⎟⎟⎠⎞⎜⎜⎝⎛++++=⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛=y x y x y x 3464214213421AB ⎟⎟⎠⎞⎜⎜⎝⎛++++=⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛=y y x x y x 3442324342121BA 故的充要条件是，得到 BA AB =⎪⎪⎩⎪⎪⎨⎧+=++=++=++=+yy y x x y x x 343442643221441−=y x .例2.4 设n ×=1)21,0,,0,21(L C , , ,计算C C E A T −=C 2C E B T +=AB ．解: C)C C)(E C (E AB TT +−=C CC 2C C C C 2C E T T T T −−+= )C (CC 2C C C E TTT−+=C C 212C C E T T ××−+=E = 故 E AB =．例2.5 设. , 求⎟⎟⎠⎞⎜⎜⎝⎛=5423A 1−A解由于075423≠==A , 故A 是可逆的，又，故⎟⎟⎠⎞⎜⎜⎝⎛−−=⎟⎟⎠⎞⎜⎜⎝⎛=342522122111*A A A A A ⎟⎟⎠⎞⎜⎜⎝⎛−−==−3425711*1A A A ．例2.6 设阶矩阵n A 的伴随矩阵为*A , 是常数, 试证 k ()*A A 1*−=n k k ．证明把看作一个整体, 根据A k E A AA *=, 有 ()E A A A )()(*k k k =，由于A 是可逆的,则也是可逆的，故)(A k ()*11111*1)()(A A A A A A A A −−−−−==×==n n n k k kk k k k ．证毕例2.7 设, ⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛=2111021100210001A *A 为A 的伴随矩阵, 求． **)(A 解由于 082111021100210001≠==A , 故A 是可逆的, *A 是可逆；根据E A AA *=, 有 E A )(A A ****=，方程左右两边同时左乘以A ，得 E A A )(A AA ****=，即 A A A)(A ***1=，又 1n *A A −=, A 是4阶矩阵，故 10001200()6411201112−⎛⎞⎜⎟⎜⎟===⎜⎟⎜⎟⎜⎟⎝⎠n 22**A AA AA ．例2.8 设A , 是n 阶方阵, 若B AB E −可逆, 试证 BA E −也可逆．证明由于A AB)AB)(E B(E E BA E 1−−−−=−A AB)BAB)(E (B E 1−−−−=A AB)BA)B(E (E E 1−−−−=移项得到E A AB)BA)B(E (E BA)(E 1=−−+−−即E A)AB)B(E BA)(E (E 1=−−−−根据可逆矩阵的定义, BA E −可逆, 并且．证毕A AB)B(E E BA)(E 11−−−+=−例2.9 设, 求．⎟⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎜⎝⎛−=00010000200010L L MM M MLL n n n A 1−nA 解对矩阵分块, , 其中 n A ⎟⎟⎠⎞⎜⎜⎝⎛=0CB 0A n )(n =C ，， ⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−=100020001n L M M M L L B 故1(1n=−C , ⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−=−)1(10002100011n L M M M LLB，根据分块矩阵的逆矩阵公式⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛=−−−−0B C 00C B 0A 1111n⎟⎟⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎜⎜⎝⎛−=0)1(100021000011000n n LM M M M L L L ．例2.10 设阶方阵 , , 求, 使n ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=100001010A ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−=021102341B X B AX =．解由于01100001010≠−==A , 故A 是可逆的; 并且；⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=−1000010101A 方程左右两边同时左乘以1−A 得到⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛==−021341102021102341100001010B A X 1．例2.11 设,求, 使⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=134030201A X X A E AX 2+=+．解对方程移项得 E A X AX 2−=−，根据矩阵乘法分配律得E A E)X (A 2−=−由于 016034020200≠−==−E A , 故E A −可逆．方程左右两边同时左乘以, 得(1−−E A )()()E)(A E A E)(A E A E)(A X 121+−−=−−=−−⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=+=234040202E)(A例2.12 设, 求. 其中E BA)B X(E TT1=−−X , ⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−−−=1000110001100011A ⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛=2000120031204312B 解根据乘法转置公式得 TTT(AB)A B =T T 1T T1A)(B A)]B [B(E BA)B (E −=−=−−−又 011234012300120001)(≠==−TA B , 故可逆，对方程右乘以[，得到． T )(A B −E A)X(B T=−]1)(−−T A B []⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−−−=−=−12100121001200011T A)(B X例2.13 设A 的伴随矩阵, 求, 使． ⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−=8030010100100001*A B 3E BA ABA 11+=−−解根据, 得到 3E BA ABA 11+=−−()3E BA E A 1=−−故皆是可逆的, 并且A E,A −()()()1111A E A A E AB −−−−−=−=33[]1111)A (E E))(A (A −−−−−=−=33又由1n *AA −=, 8*=A , , 故 4=n 2=A ，1*1*11)A E ()A (E )A (E B −−−−⎥⎦⎤⎢⎣⎡−=−=−=22132133 11*1*60300101001000016)2(6)2(213−−−⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−−=−=⎥⎦⎤⎢⎣⎡−=A E A E B . ⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−=1030060600600006例2.14 设阶矩阵n A 的伴随矩阵为*A , 试证(1) 若0=A , 则0*=A ； (2) 1*−=n AA ； (3) 1)1(*)(−−=n n n kk AA ．证明 (1 ) 根据0=A 得到0A =与0A ≠两种情况，① 当0A =时, 则, 显然0A *=0*=A ；② 当0A ≠时, 利用反证法, 不妨反设0*≠A ，则可逆, 即存在*A 1*−A , 又由于E A AA *=,0=A ，得到0)(A 0)(A A A 1*1*=⋅==−−, 这与矛盾.假设0A ≠0*≠A 不成立．故综合①②得到若0=A , 则0*=A .(2 ) 分0=A 和0≠A 两种情况，① 当0=A 时, 由(1)得到0*=A , 显然有1*−=n AA ．② 当0≠A 时, 则A 可逆, 由E A AA *=引入行列式得到n*A A A =, 从而1n *AA −=．(3 ) 根据(2 )中1n *AA −=得到1)1(11*)()()(−−−−===n n n n n n k k k k AA A A ．例2.15 设A , 均为阶方阵, B n 2=A , 3−=B , 求1*B)(A −2．解1*n1*1*1*B A B A B)(A B)(A −−−−⎟⎠⎞⎜⎝⎛===212122，又根据E BB1=−, 得到1=−1B B , 即BB 11=−, 以及1−=n A A *，所以6131)2(212121−=⎟⎠⎞⎜⎝⎛−××⎟⎠⎞⎜⎝⎛=⎟⎠⎞⎜⎝⎛=−−−n n1*n1*B A B)(A例2.16 设5阶矩阵A , 且2=A , 求A A −．解由于2=A , ()()6423225−=×−=−=−=−A A AA A 5．例2.17 设A , 均为3阶矩阵, B 2=A , 21=B , 求()*AB ．解()()122122=⎟⎠⎞⎜⎝⎛====−−1313*****ABA B A B AB ．例2.18 设阶矩阵n A , 有E A m=, 若A 中每个元素用其对应的代数余子式代替, 得到矩阵, 求．ij a ij A B mB 解依题意, 得 , (其中T *)(A B =*A 为A 的伴随矩阵)，由E A m=, 得到1=m A ,即A 是可逆的，故 1ΤΤ1Τ1Τ*)(ΑΑ)(ΑΑ)ΑΑ()(ΑΒ−−−====，又由, 得111A B (AB)−−−=T T T A B (AB)=()()222112)(,)(T T A A A A ==−−，所以 ()()11)()(−−=T m mTA A , 故()()E A A AB===−−11)()(Tm T m mm．例2.19 设⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛−=21232321A , 且E A 6=, 求11A 解由 E A 6=, 得E A12=, 即E AA 11=, 故⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛−=−212323211A A 11. 例2.20 设, )5,4,3,2,1(=A ⎟⎠⎞⎜⎝⎛=51,41,31,21,1B , 又B A X T =, 求n X 解由X XX XnL =B)(A B)B)(A(A T TTL =()()()B BA BA BA A T T T T L =又因为，故 5=T BA ⎟⎠⎞⎜⎝⎛⎟⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎜⎝⎛==−−514131211543215511n n n B A X T ⎟⎟⎟⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎜⎜⎜⎝⎛=−145352555413424534312335242321251413121151n ．例2.21 设, 满足⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=100000001B ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=112012001P PB AP =,求A , 9A ．解．由于01112012001≠−=−=P , 故是可逆的,且，P ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−=−1140120011P 由题意, ， ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−==−1140120011000000011120120011PBPA ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−=116002001又 A PBP P PB PBP PBPA 119119====−−−−L ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−=116002001．例2.22 设, 求⎟⎟⎠⎞⎜⎜⎝⎛=101λA nA ．解由于，⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛==1021101101λλλAA A 2⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛==10311011021λλλA A A 23不妨假设结论,下用归纳法证明. 当⎟⎟⎠⎞⎜⎜⎝⎛=101λn nA 2=k 时,显然成立，不妨设时也成立, 即, 则当1−=n k ⎟⎟⎠⎞⎜⎜⎝⎛−=−10)1(11λn n An k =时⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛−==−10110110)1(1λλλn n A A A 1n n ，故结论成立, 即． ⎟⎟⎠⎞⎜⎜⎝⎛=101λn nA2.4 独立作业2.4.1 基础练习1．设阶矩阵, 且n )(ij a =A ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=n λλO 1D )(j i j i ≠≠λλ则=AD （A ）()ij i a λ ；（B ）()j ij a λ；（C ）()ij i a 1+λ ；（D ）以上都不对． 2．设A 、均为阶矩阵，下列命题正确的是 B n（A ）0B 0A 0AB ==⇒=或；（B ）0B 0A 0AB ≠≠⇔≠且；（C ）00==⇒=B A 0AB 或；（D ）00≠≠⇔≠B A 0AB 且． 3．设阶矩阵满足，则有 n E ABC =（A ）（B ）E ACB =E CBA = （C ）E BAC = （D ）E BCA =4．设，则⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=120001430A =A k（A ）（B ）（C ）311k −311k k 11− （D ） k 115．下列命题正确的是（A ）若A 是阶方阵，且n 0A ≠，则A 可逆；（B ）若A 、是阶可逆方阵，则B n B A +也可逆；（C ）若A 是不可逆方阵，则必有0A =；（D ）若A 是阶方阵，则n A 可逆⇔TA 可逆．6．已知，，则⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−=210413121A ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−=121312410B ()T AB 7．设，，则⎟⎟⎠⎞⎜⎜⎝⎛−=⎟⎟⎠⎞⎜⎜⎝⎛=0111,300121A A ⎟⎟⎠⎞⎜⎜⎝⎛=21A 00A A =−1A8．已知，则 ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=300041003A =−−1)(2E A9．设矩阵满足，其中B 9E 3B A AB 2−=−E 为三阶单位矩阵，⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=400020101A , 则 =B10．已知，满足⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=200012021B A B AB =−，则=A 11．设，，求矩阵，使⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=311201A ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=041012B X B X A =+23成立．12．设，计算⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=141021001A ()()()2181644A A E A E A E +−−−−T ．13．设，,求矩阵⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−−−=1000210032101321B ⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛=1000210002101021C A , 使成立．T T 1C B)A C(2E =−−14．设矩阵，，，⎟⎟⎠⎞⎜⎜⎝⎛=3152P ⎟⎟⎠⎞⎜⎜⎝⎛−=1001B ⎟⎟⎠⎞⎜⎜⎝⎛−−=2153Q PBQ A =，试计算QP 和nA ．15．设（k 为正整数），（1）试证；0A k =1k 1A A E A)(E −−+++=−L （2）求． 1)4(−−E)(A 2.4.2提高练习1．设A 为阶矩阵,且有n A A 2=,则结论正确的是________________ (A)(B) 0A =E A = (C) 若A 不可逆,则0A = (D) 若A 可逆,则E A 2=2．已知，，且⎟⎟⎠⎞⎜⎜⎝⎛=22211211a a a a A ⎟⎟⎠⎞⎜⎜⎝⎛=y a x a 2111B 1,1==B A ，则=+B A (A) 2； (B) 3; (C) 4; (D) 5．3．设，是两个阶方阵，则)(ij a =A )(ij b =B n AB 的第行是 i （A ）的各行的线性组合，组合系数是B A 的第行各元素； i （B ） A 的各行的线性组合，组合系数是的第行各元素； B i （C ）的各列的线性组合，组合系数是B A 的第行各元素； i （D ）的各行的线性组合，组合系数是B A 的第列各元素． i 4．设A 、、C 为可逆矩阵，则B ()=−1T ACB（A ）；（B ）；()1−−−C A B11T 11T A C B −−（C ） ( D ) ()1T 11B CA −−−()11T1A C B−−−．5．设A 为阶矩阵，为其伴随矩阵，则n *A =*A k （A ） A n k （B） nk A （C）1−n n k A（D）nn kA1−6．设三阶矩阵A 的行列式3=A ，则=−−*123A A7．设阶矩阵n A 的行列式5=A ，则()=−1*5A8．已知则⎟⎟⎠⎞⎜⎜⎝⎛−=θθθθcos sin sin cos A =−1A 9．设阶矩阵n A 、、C ，且B E CA BC AB ===，则 =++222C B A10．设A 、是四阶矩阵，且B 2=A ，21=B ，则()=*AB11．设三阶矩阵A 、Β满足关系式,BA 6A BA A 1+=−⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛=710004100031A ，求 B 12．设 B A B A AX AXB 22+−+=，求．其中，X⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−=100110111A ，⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=200020102B 13．设A 、均为阶方阵，若B n AB B A =+，求()1−−E A ．14．设, ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=211021001A *A 为A 的伴随矩阵, 求．1*)(−A第二章参考答案与提示2.4.1 基础练习1．( B ) 提示 AD 表示A 的第i 行与D 的第列j 相乘得到()j ij a λ． 2．（C ）提示 0000==⇒=⇒=⇒=B A B A A 0AB 或B ． 3．（D ）提示 A 、、C 可逆，等式左乘以B 1−A ，右乘以A ． 4．（A ）提示 3311k k k −==A A ．5．（D ）提示由于A 可逆⇔00≠⇔≠T A A ⇔TA 可逆．6．， ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−−=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−=15419102935121312410210413121AB ()⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−−=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−−=1541910293511995103425TAB ． 7．⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−=⎟⎟⎠⎞⎜⎜⎝⎛=−−−110100000310000112111A 00A A．8．，()⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=−1000210012E A ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=−−1000212100121E A ． 9．，，E B A AB 293−=−E A B AB 293−=−)333E E)(A (A E)B (A +−=−由于021*********≠=−−=−E A ，故E)A 3(−是可逆的，．⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=+=7000501043E)(A B 10．A B AB =− ，，B E)A(B =−04100002020≠=−=−E B ，E B −是可逆的,⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛−=⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛−⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=−=−200012102111000021021020********E)B(B A ．11．()⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−−=−=91461121321A B X ．12．()()()21T A A E A E A E +−−−−81644()()()A E A)E (A E A E 1T−−−−=−4444()()A E A E T−−=44()24A E −=324182==．13．左乘以C ，，由于 E B)A C (T=−20110002100321043212≠==−B C ，故是可逆的，(． B C −2()()⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−−−=−=−=−−−1210012100120001222C 1T T1B)C (B)C (B)A 14．，即、互为逆矩阵， ⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛−−=100131522153QP P Q ()()()()BQ QP QP B QP PB PBQ A nn L ==Q PB n =，由于，故．）（－L ,2,1,122===k k kBB E B⎪⎩⎪⎨⎧⎟⎟⎠⎞⎜⎜⎝⎛−−==为奇数为偶数n n 1162011A E A n 15．（1）由于()1k AA E A)(E −+++−L )A A (A )AA (E n 21k +++−+++=−L LE A E n =−=，故，1k 1A A E A)(E −−+++=−L （2）()111A)(E A))(E (E))(A (−−−−−=−−=−4144()1k A A E −+++−=L 41． 2.4.2提高练习 1．（D ）提示：，若0E)A(A A A2=−⇔=A 可逆，则E A =，E A 2=．2．（C ）提示：,⎟⎟⎠⎞⎜⎜⎝⎛++=+y a ax a a 2221121122B A 422221112221121122211211=⎟⎟⎠⎞⎜⎜⎝⎛+=++=+y a x a a a a a y a a x a a B A ． 3．（A ）提示：乘积AB 的第行是i A 的第行与的列的乘积． i B n ,,1L 4．（D ）提示：()()()()()()1−−−−−−−===A C B AC B B AC ACB1T 111T 1T 1T ．5．（C ）提示：1**−==n nn k k k AA A ．6．()()()9313133232333111*1−=×−=−=−=−=−−−−−AA A A A A A ．7．()n n n n211*1*1*5151151)(515−−−−==⎟⎠⎞⎜⎝⎛==A AA A． 8．⎟⎟⎠⎞⎜⎜⎝⎛−==−θθθθcos sin sin cos 1*1A A A ． 9．由于E CA BC AB ===，故，2A A(BC)A ABCA E ===2B B(CA)B BCAB E ===，，2C C(AB)C CABC E ===所以．E CB A 2223=++10．()()11=====−3341*)B A (AB ABABAB AB AB ．11．由于，，右乘以得BA A BA A 1+=−6A E)BA (A 16=−−1−A E E)B (A16=−−又可逆．故A)(E −16−−−=E)(A B1⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛=6100031000216． 12．方程整理得B E)A)(B A(X =−−由于0≠A ，0≠−E B ，故A 、E B −是可逆的，且⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−=−1001102111A ，()⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−=−−1000101011E B 所以11E)B(B A A X −−−=− ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−=200220522100010101200020102100110211故． ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−=300330613X 13．由于AB B A =+B AB A −=⇒()B E A A −=⇒（但是B 不一定可逆，不能同时右乘以1−B）()()B E A E E A −=+−⇒()()E E B E A =−−⇒，故 ()E)(B E A 1−=−−．14．由于0421102101≠==A , 故A 是可逆的, *A 是可逆的；根据E A AA *=, 有 E )(A A **=−1方程左右两边同时左乘以A 得，AE )(A AA **=−1即 A A )(A *11=−，故 ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛==−2110210014111A A )(A *．。

线性代数第二章习题课

3. 设A , B为 n 阶方阵，若E – AB 可逆，则E -BA 可逆。证：∵ (E – AB )A = A – ABA = A( E – BA ) ∴ (E – AB )A = A( E – BA ) 1 又 E – AB 可逆，上式左乘 (E AB) ∴ A = (E - AB)1 A( E – BA) 而 E = E – BA + BA = E – BA + B (E - AB) A( E – BA) 1 = [E +B (E - AB) A](E – BA ) ∴ E – BA 可逆，且
17. (P80-10) 解法1：直接求
A B B (BA E)
-1
1
1
1
B (B A)A
-1 1 1 -1
1
1
1 1
(A B ) [B (B A)A ]
A(A B) B
验证： (A1 B1 )A(A B) 1 B (E B1A)A-1A (A B) 1 B B1 (B A)E(A B) 1 B E
-1
A B = 6E + B
而A - E =
-1
-1
( A - E ) B = 6E
-1
3
4 7
-
1 0 0 0 1 0 0 0 1
2
=
3 6
∵ |A-1 - B| = 36≠0, ∴ ( A -1 - B)可逆，
故 B=6(A
-1
－1
2
－1
-E) = 6
3
6
=6
3
1 1 2 3 1 6
=
2 1
* *
1 *
1 1 A | A |n2 A | A | |A| |A|

线性代数答案第二章(同济)

第二章矩阵及其运算课后习题答案1．已知线性变换：⎪⎩⎪⎨⎧++=++=++=,323,53,22321332123211y y y x y y y x y y y x 求从变量321,,x x x 到变量321,,y y y 的线性变换．解由已知：⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛221321323513122y y y x x x故 ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-3211221323513122x x x y y y ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛----=321423736947y y y ⎪⎩⎪⎨⎧-+=-+=+--=321332123211423736947xx x y x x x y x x x y 2．已知两个线性变换⎪⎩⎪⎨⎧++=++-=+=,54,232,232133212311y y y x y y y x y y x ⎪⎩⎪⎨⎧+-=+=+-=,3,2,3323312211z z y z z y z z y 求从321,,z z z 到321,,x x x 的线性变换．解由已知⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛221321514232102y y y x x x ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛-=321310102013514232102z z z ⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛----=321161109412316z z z所以有 ⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236zz z x z z z x z z z x3．设⎪⎪⎪⎭⎫⎝⎛--=111111111A ,,150421321⎪⎪⎪⎭⎫⎝⎛--=B 求.23B A A AB T 及- 解 A AB 23-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛--=1504213211111111113⎪⎪⎪⎭⎫⎝⎛---1111111112⎪⎪⎪⎭⎫ ⎝⎛-=0926508503⎪⎪⎪⎭⎫ ⎝⎛---1111111112⎪⎪⎪⎭⎫⎝⎛----=22942017222132⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=150421321111111111B A T⎪⎪⎪⎭⎫ ⎝⎛-=0926508504．计算下列乘积：(1)⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-127075321134; (2)()⎪⎪⎪⎭⎫⎝⎛1233,2,1; (3)()2,1312-⎪⎪⎪⎭⎫ ⎝⎛; (4)⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412; (5)⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321332313232212131211321),,(x x x a a a a a a a a a x x x ; (6)⎪⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121. 解 (1)⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-127075321134⎪⎪⎪⎭⎫ ⎝⎛⨯+⨯+⨯⨯+⨯-+⨯⨯+⨯+⨯=102775132)2(71112374⎪⎪⎪⎭⎫⎝⎛=49635(2)()⎪⎪⎪⎭⎫ ⎝⎛123321)10()132231(=⨯+⨯+⨯=(3)()21312-⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛⨯-⨯⨯-⨯⨯-⨯=23)1(321)1(122)1(2⎪⎪⎪⎭⎫⎝⎛---=632142(4)⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎭⎫⎝⎛---=6520876 (5)()⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321332313232212131211321x x x a a a a a a a a a x x x ()333223113323222112313212111x a x a x a x a x a x a x a x a x a ++++++=⎪⎪⎪⎭⎫ ⎝⎛⨯321x x x322331132112233322222111222x x a x x a x x a x a x a x a +++++=(6) ⎪⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎪⎭⎫⎝⎛30003200121013013000120010100121⎪⎪⎪⎪⎭⎫⎝⎛---=90003400421025215．设⎪⎭⎫⎝⎛=3121A , ⎪⎭⎫⎝⎛=2101B ，问： (1)BA AB =吗?(2)2222)(B AB A B A ++=+吗?(3)22))((B A B A B A -=-+吗? 解 (1)⎪⎭⎫⎝⎛=3121A , ⎪⎭⎫ ⎝⎛=2101B . 则⎪⎭⎫ ⎝⎛=6443AB ⎪⎭⎫⎝⎛=8321BA BA AB ≠∴ (2) ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+52225222)(2B A ⎪⎭⎫⎝⎛=2914148但=++222B AB A ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛43011288611483⎪⎭⎫ ⎝⎛=27151610 故2222)(B AB A B A ++≠+ (3) =-+))((B A B A =⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛10205222⎪⎭⎫⎝⎛9060 而 =-22B A =⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛430111483⎪⎭⎫⎝⎛7182 故 22))((B A B A B A -≠-+6．举反列说明下列命题是错误的: （１）若02=A ,则0=A ;（２）若A A =2,则0=A 或E A =; （３）若AY AX =,且0≠A ,则Y X =. 解 (1) 取⎪⎭⎫⎝⎛=0010A , 02=A ,但0≠A (2) 取⎪⎭⎫⎝⎛=0011A , A A =2,但0≠A 且E A ≠ (3) 取⎪⎭⎫⎝⎛=0001A , ⎪⎭⎫⎝⎛-=1111X , ⎪⎭⎫ ⎝⎛=1011Y . AY AX =且0≠A 但Y X ≠. 7．设⎪⎭⎫⎝⎛=101λA ,求k A A A ,,,32 . 解 ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=12011011012λλλA ; ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1301101120123λλλA A A利用数学归纳法证明: ⎪⎭⎫ ⎝⎛=101λk A k当1=k 时,显然成立,假设k 时成立,则1+k 时⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==1)1(01101101λλλk k A A A k k由数学归纳法原理知:⎪⎭⎫ ⎝⎛=101λk A k8．设⎪⎪⎪⎭⎫ ⎝⎛=λλλ001001A ,求kA .解首先观察⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=λλλλλλ0010010010012A ⎪⎪⎪⎭⎫⎝⎛=222002012λλλλλ, ⎪⎪⎪⎭⎫ ⎝⎛=⋅=3232323003033λλλλλλA A A由此推测 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(121)2(≥k用数学归纳法证明:当2=k 时,显然成立.假设k 时成立，则1+k 时，⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⋅=---+λλλλλλλλλ0010010002)1(1211k k k k k k k k k k k k A A A ⎪⎪⎪⎪⎪⎭⎫⎝⎛+++=+-+--+11111100)1(02)1()1(k k k k k k k k k k λλλλλλ 由数学归纳法原理知: ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=---k k k k k k k k k k k A λλλλλλ0002)1(1219．设B A ,为n 阶矩阵，且A 为对称矩阵，证明AB B T 也是对称矩阵. 证明已知：A A T =则 AB B B A B A B B ABB T T T T TT T T===)()(从而 AB B T 也是对称矩阵.10．设B A ,都是n 阶对称矩阵，证明AB 是对称矩阵的充分必要条件是BA AB =. 证明由已知：A A T = B B T =充分性：BA AB =⇒A B AB TT=⇒)(AB AB T=即AB 是对称矩阵. 必要性：AB ABT=)(⇒AB A B T T =⇒AB BA =.11．求下列矩阵的逆矩阵：(1)⎪⎭⎫ ⎝⎛5221； (2)⎪⎭⎫ ⎝⎛-θθθθcos sin sin cos ； (3)⎪⎪⎪⎭⎫⎝⎛---145243121; (4)⎪⎪⎪⎪⎭⎫⎝⎛n a a a 0021)0(21≠a a a n解 (1) ⎪⎭⎫⎝⎛=5221A , 1=A ..1 ),1(2 ),1(2 ,522122111=-⨯=-⨯==A A A A⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=*122522122111A A A A A . *-=A A A 11⎪⎭⎫ ⎝⎛--=1225(2) 01≠=A 故1-A 存在θθθθcos sin sin cos 22122111=-===A A A A从而 ⎪⎭⎫⎝⎛-=-θθθθcos sin sin cos 1A(3) 2=A , 故1-A 存在 024312111==-=A A A 1613322212-==-=A A A 21432332313-==-=A A A故 *-=A A A 11⎪⎪⎪⎪⎭⎫⎝⎛-----=1716213213012(4)⎪⎪⎪⎪⎭⎫⎝⎛=n a a a A 0021. 由对角矩阵的性质知 ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=-n a a a A 1001121112．解下列矩阵方程：(1) ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛12643152X ; (2) ⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛--234311111012112X ; (3) ⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-101311022141X ; (4) ⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛021********0100001100001010X .解(1) ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=-126431521X ⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛--=12642153⎪⎭⎫⎝⎛-=80232 (2) 1111012112234311-⎪⎪⎪⎭⎫⎝⎛--⎪⎭⎫ ⎝⎛-=X ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎭⎫⎝⎛-=03323210123431131⎪⎪⎭⎫ ⎝⎛---=32538122 (3) 11110210132141--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=X ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛-=210110131142121⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=21010366121⎪⎪⎭⎫ ⎝⎛=04111 (4) 11010100001021102341100001010--⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛=X ⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛=010100001021102341100001010⎪⎪⎪⎭⎫⎝⎛---=20143101213．利用逆矩阵解下列线性方程组:(1) ⎪⎩⎪⎨⎧=++=++=++;353,2522,132321321321x x x x x x x x x (2)⎪⎩⎪⎨⎧=-+=--=--.0523,132,2321321321x x x x x x x x x解 (1) 方程组可表示为 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321153522321321x x x故 ⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x从而有 ⎪⎩⎪⎨⎧===001321x x x(2) 方程组可表示为 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛-----012523312111321x x x故 ⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-3050125233121111321x x x 故有 ⎪⎩⎪⎨⎧===305321x x x14．设O A k =(k 为正整数), 证明：121)(--++++=-k A A A E A E . 证明一方面， )()(1A E A E E --=-另一方面，由O A k=有)()()(1122k k k A A A A A A A E E -+--+-+-=-- ))((12A E A A A E k -++++=-故 )()(1A E A E ---))((12A E A A A E k -++++=-两端同时右乘1)(--A E就有121)(--++++=-k A A A E A E15．设方阵A 满足O E A A =--22,证明A 及E A 2+都可逆,并求1-A 及1)2(-+E A .证明由O E A A =--22得E A A 22=-两端同时取行列式: 22=-A A即 2=-E A A ,故 0≠A . 所以A 可逆,而22A E A =+0222≠==+A A E A 故E A 2+也可逆.由O E A A =--22E E A A 2)(=-⇒E A E A A A 112)(--=-⇒)(211E A A -=⇒- 又由O E A A =--22E E A A E A 4)2(3)2(-=+-+⇒ E E A E A 4)3)(2(-=-+⇒11)2(4)3)(2()2(--+-=-++∴E A E A E A E A)3(41)2(1A E E A -=+∴-16．设A 为3阶矩阵，21=A ，求*13)2(A A --。

线代第2章习题答案

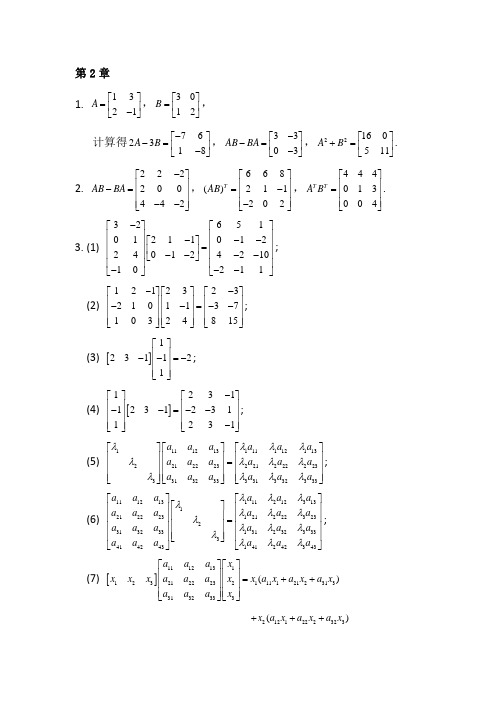
第2章1. 1321A ⎡⎤=⎢⎥-⎣⎦，3012B ⎡⎤=⎢⎥⎣⎦，计算得762318A B -⎡⎤-=⎢⎥-⎣⎦，3303AB BA -⎡⎤-=⎢⎥-⎣⎦，22160511A B ⎡⎤+=⎢⎥⎣⎦. 2. 222200442AB BA -⎡⎤⎢⎥-=⎢⎥⎢⎥--⎣⎦，668()211202T AB ⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦，444013004T T A B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦. 3. (1) 326510121101224012421010211-⎡⎤⎡⎤⎢⎥⎢⎥---⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥----⎣⎦⎢⎥⎢⎥---⎣⎦⎣⎦; (2) 1212323210113710324815--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦; (3) []1231121⎡⎤⎢⎥--=-⎢⎥⎢⎥⎣⎦; (4) []123112312311231-⎡⎤⎡⎤⎢⎥⎢⎥--=--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦; (5) 111121311111211322122232212222233313233331332333a a a a a a a a a a a a a a a a a a λλλλλλλλλλλλ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦; (6) 133131112111212123323212212122223333331321312323433434142141242a a a a a a a a aa a a a a a a a a a a a a aa λλλλλλλλλλλλλλλ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦; (7) []111213112321222321*********3132333()a a a x x x x a a a x x a x a x a x a a a x ⎡⎤⎡⎤⎢⎥⎢⎥=++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦2121222323()x a x a x a x +++3131232333()x a x a x a x +++.4. 解：因为A 与B 可交换，所以AB BA =，又因为A 是对角矩阵，所以可得111112111112121221222221212222121122n n n n n n n n n n n nn n n n nn b b b b b b b b b b b b b b b b b b λλλλλλλλλλλλλλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ ，其中主对角线元素都相等，对于非主对角元，应有()0,i j ij b i j λλ-=≠又因为i j λλ≠，所以只能有0ij b =，当i j ≠时。

《线性代数》第二章参考答案+详解

k ( k 1) 2
k 0
k 2 1 0 k k 1 0 1 0 0 k
k 1 0 0
( k 1) k 1
k 1 0
k 1 ( k 1 ) k 1 k 1
所以(AB)2A22ABB2 (3) (AB)(AB)A2B2 吗? 解: (AB)(AB)A2B2
2 A B 0 0 5 2 0 5 0 2 1 6 9 2 因为 A B 2
2 ( A B)( A B) 2
2 0 1 0
而
3 8 1 0 2 8 A2 B2 4 11 3 4 1 7
故(AB)(AB)A2B2
5 举反列说明下列命题是错误的 (1) 若 A20 则 A0
0 解: 取 A 0 1 则 A20 但 A0 0
(2)
2 1 设 a 1 ,b 2 ,A abT , 3 4
T
求 A100 .
2 解： b a 1 2 4 1 8 . 3
则
A100 (abT )100 a (bT a )( bT a )bT a (bT a )bT 2 99 a (b a ) b 1 8 1 2 4 3 4 8 2 99 8 1 2 4 . 3 6 12
2 2 a11x12 a22 x2 a33 x3 2a12 x1x2 2a13 x1x3 2a23 x2 x3
1 1 1 1 2 3 2 设 A 1 1 1 B 1 2 4 求 3AB2A 及 ATB 1 1 1 0 5 1 1 1 1 1 2 3 1 1 1 解: 3AB 2 A 31 1 1 1 2 4 21 1 1 1 1 1 0 5 1 1 1 1 0 5 8 1 1 1 2 13 22 3 0 5 6 21 1 1 2 17 20 2 9 0 1 1 1 4 29 2 1 1 1 1 2 3 0 5 8 A B 1 1 1 1 2 4 0 5 6 1 1 1 0 5 1 2 9 0

线性代数第二章练习题

第二章矩阵一、选择题 1．设矩阵4203a b a b d c +-æöæö=ç÷ç÷èøèø，则（ C ）（A）3,1,1,3a b c d ==-== （B）1,3,1,3a b c d =-=== （C）3,1,0,3a b c d ==-== （D）1,3,0,3a b c d =-=== 2．设矩阵()1,2A =，1234B æö=ç÷èø，123456C æö=ç÷èø，则下列矩阵运算中有意义的是（B）（A）ACB （B）ABC （C）BAC （D）CBA 3．设A 、B 均为n 阶矩阵，下列命题正确的是 C （A）0B 0A 0AB ==Þ=或（B）0B 0A 0AB ¹¹Û¹且（C）00==Þ=B A 0AB 或（D）00¹¹Û¹B A 0AB 且 4．设A 、B 均为n 阶矩阵，满足22A B =，则必有（ D ）（A）A B = （B）A B =- （C）A B = （D）22A B=5．设A 为n 阶矩阵,且有A A 2=,则结论正确的是________D________ (A) 0A = （B）E A =(C) 若A 不可逆,则0A = (D) 若A 可逆,则E A 2= 6．设B A ,都是n 阶对称矩阵，下列结论不正确的结论是（ A ）（A）AB 为对称矩阵（B）设B A ,可逆，则11--+B A 为对称矩阵（C）B A +为对称矩阵（D）kA 为对称矩阵7．设A 为任意n 阶矩阵，下列矩阵中为反对称矩阵的是（ B ）（A）T A A + （B）T A A - （C）T AA（D）T A A8．设A 为3阶方阵，且2A =，则12A -=（ D ）（A）-4 （B）-1 （C）1 （D）49．设A 为n 阶矩阵，*A 为其伴随矩阵，则=*A k C （A） A n k （B） nk A（C）1-n nkA（D）nn kA1-10．设B A ,都是n 阶可逆矩阵，则÷÷øöççèæ--1002B A T等于（ A ）（A）12)2(--B A n（B）1)2(--B A n （C）B A T2- （D）12--B A11．设n 阶方阵C B A ,,满足关系式E ABC =，其中E 为n 阶单位阵，则必有（ D ）。

高等数学线性代数习题答案第二章

第二章习题2-11. 证明：若lim n →∞x n =a ,则对任何自然数k ，有lim n →∞x n +k =a .证：由lim n n x a →∞=，知0ε∀>，1N ∃，当1n N >时，有n x a ε-<取1N N k =-，有0ε∀>，N ∃，设n N >时（此时1n k N +>）有n k x a ε+-<由数列极限的定义得 lim n k x x a +→∞=.2. 证明：若lim n →∞x n =a ,则lim n →∞∣x n ∣=|a|.考察数列x n =(-1)n ，说明上述结论反之不成立.证：lim 0,,.使当时，有n x n x aN n N x a εε→∞=∴∀>∃>-<而 n n x a x a -≤- 于是0ε∀>，,使当时，有N n N ∃>n n x a x a ε-≤-< 即 n x a ε-<由数列极限的定义得 lim n n x a →∞=考察数列 (1)nn x =-，知lim n n x →∞不存在，而1n x =，lim 1n n x →∞=，所以前面所证结论反之不成立。

3. 证明：lim n →∞x n =0的充要条件是lim n →∞∣x n ∣=0.证：必要性由2题已证，下面证明充分性。

即证若lim 0n n x →∞=，则lim 0n n x →∞=，由lim 0n n x →∞=知，0ε∀>，N ∃，设当n N >时，有0 0n n n x x x εεε-<<-<即即由数列极限的定义可得 lim 0n n x →∞=4. 利用夹逼定理证明：(1) lim n →∞222111(1)(2)n n n ⎛⎫+++ ⎪+⎝⎭ =0； (2) lim n →∞2!n =0. 证：（1）因为222222111112(1)(2)n n n n n n n n n n++≤+++≤≤=+而且 21lim0n n →∞=，2lim 0n n→∞=，所以由夹逼定理，得222111lim 0(1)(2)n n n n →∞⎛⎫+++= ⎪+⎝⎭ . （2）因为22222240!1231n n n n n<=<- ，而且4lim 0n n →∞=，所以，由夹逼定理得2lim 0!nn n →∞= 5. 利用单调有界数列收敛准则证明下列数列的极限存在. (1) x 1＞0,x n +1=13()2n nx x +，n =1,2,…； (2) x 1x n +1,n =1,2,…；(3) 设x n 单调递增，y n 单调递减，且lim n →∞(x n -y n )=0,证明x n 和y n 的极限均存在.证：（1）由10x >及13()2n n nx x x =+知，有0n x >（1,2,n = ）即数列{}n x 有下界。

线性代数第二章习题及解答

··· ··· .. . ···
∗ ∗ . . .
2 a2 n1 + · · · + ann

(1)
(2)
2 2 由 A2 = 0 得到 a2 0 i1 + ai2 + · · · + ain = 0, i = 1, 2, . . . , n 于是 aij = ( ) 1 2 2 cos θ sin θ 8. 设 A = ,B = , C = 2 1 −2 − sin θ cos θ 2 −2 1
证明：|A−1 | =
|A| = ±1
1 |A|
注意到 A−1 的元素为正数所以其行列式必为整数，即
1 |A|
为正数，于是只有
若 |A| = ±1, 由于 A−1 = 整数.
A∗ |A|
注意到 Aij 为整数，于是 A∗ 的元素必为整数，则 A−1 的元素为
1 3 0 0 0
0 2

20 −1 −1 0 , P AP = 0 1 0 求 A 0 0 2 1 2 520 0 0 解：P AP −1 P AP −1 · · · P AP −1 = P A20 P −1 = 0 1 0 20 0 0 220 520 0 0 2 · 520 − 1 1 − 220 2 · 520 − 221 20 20 那么 A20 = P −1 2 · 520 − 221 0 1 0 P = 2 · 5 − 2 2 − 2 0 0 20 −520 + 1 −1 + 220 −520 + 221 19. 设 A, B, A + B 可逆，证明 (A−1 + B −1 )−1 = A(A + B )−1 B

【复旦版线代】线性代数第二章课后习题及详细解答

习题二1. 计算下列矩阵的乘积.（1）[]11321023⎡⎤⎢⎥-⎢⎥-⎢⎥⎢⎥⎣⎦=；（2）500103120213⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦；（3） []32123410⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦；（4）()111213112321222323132333a a a x x x x a a a x a a a x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦；（5） 111213212223313233100011001a a a a a a a a a ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦；（6） 1210131010101210021002300030003⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦⎣⎦. 【解】(1) 32103210;64209630-⎡⎤⎢⎥--⎢⎥⎢⎥-⎢⎥-⎣⎦(2)531⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦; (3) (10);(4) 3322211122233312211213311323322311()()()ij iji j a x a x a x a a x x a a x x a a x x a x x==++++++++=∑∑(5)111212132122222331323233a a a a a a a a a a a a +⎡⎤⎢⎥+⎢⎥⎢⎥+⎣⎦; (6) 1252012400430009⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦. 2. 设111111111⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦A ，121131214⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦B ，求(1)2-AB A ;(2) -AB BA ；(3) 22()()-=-A+B A B A B 吗?【解】(1) 2422;400024⎡⎤⎢⎥-=⎢⎥⎢⎥⎣⎦AB A (2) 440;531311⎡⎤⎢⎥-=--⎢⎥⎢⎥--⎣⎦AB BA (3) 由于AB ≠BA ,故(A +B )(A -B )≠A 2-B 2.3. 举例说明下列命题是错误的.(1) 若2=A O ，则=A O ； (2) 若2=A A ，则=A O 或=A E ； (3) 若AX =AY ，≠A O ，则X =Y . 【解】(1) 以三阶矩阵为例，取2001,000000⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦0A A ,但A ≠0(2) 令110000001-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A ,则A 2=A ,但A ≠0且A ≠E (3) 令11021,=,0111210110⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=≠=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦A Y X 0 则AX =AY ,但X ≠Y .4. 设101A λ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦, 求A 2，A 3，…，A k .【解】2312131,,,.010101kk λλλ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A A A L 5. 100100λλλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A =，求23A ,A 并证明：121(1)2000kk k k kk k k k k k λλλλλλ----⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A =.【解】2322233223213302,03.0000λλλλλλλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A =A = 今归纳假设121(1)2000kk k k kk k k k k k λλλλλλ----⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A =那么11211111(1)1020100000(1)(1)2,0(1)00k k k k k k k k k kk k kk k k k k k k k k λλλλλλλλλλλλλλλ+---+-++=-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦+⎡⎤+⎢⎥⎢⎥=+⎢⎥⎢⎥⎣⎦A A A= 所以，对于一切自然数k ,都有121(1)2.000kk k k kk k k k k k λλλλλλ----⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A =6. 已知AP =PB ，其中100100000210001211⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦B =,P =求A 及5A .【解】因为|P |= -1≠0,故由AP =PB ,得1100200,611-⎡⎤⎢⎥==⎢⎥⎢⎥--⎣⎦A PBP而51551()()100100100100210000210200.211001411611--==⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=--==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦⎣⎦A PBP PB P A7. 设a b c d ba dc cd a b dcb a ⎡⎤⎢⎥--⎢⎥⎢⎥--⎢⎥--⎣⎦A =，求|A |. 解：由已知条件，A 的伴随矩阵为22222222()()a b c d b a dc a b cd a b c d c d a b dcba *⎡⎤⎢⎥--⎢⎥-+++=-+++⎢⎥--⎢⎥--⎣⎦A =A 又因为*A A =A E ，所以有22222()a b c d -+++A =A E ，且0<A ，即 42222222224()()a b c d a b c d -++++++A =A A =A E 于是有22222()a b c d ==-+++A . 8. 已知线性变换112112212321331233232,3,232,2,45;3,x y y y z z x y y y y z z x y y y y z z =+=-+⎧⎧⎪⎪=-++=+⎨⎨⎪⎪=++=-+⎩⎩ 利用矩阵乘法求从123,,z z z 到123,,x x x 的线性变换. 【解】已知112233112233210,232415310,201013421124910116x y x y x y y z y z y z ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦-⎡⎤⎢⎥==-⎢⎥⎢⎥--⎣⎦X AY Y Bz X AY ABz z,从而由123,,z z z 到123,,x x x 的线性变换为11232123312342,1249,1016.x z z z x z z z x z z z =-++⎧⎪=-+⎨⎪=--+⎩ 9. 设A ，B 为n 阶方阵，且A 为对称阵，证明：'B AB 也是对称阵.【证明】因为n 阶方阵A 为对称阵，即A ′=A ,所以 (B ′AB )′=B ′A ′B =B ′AB , 故'B AB 也为对称阵.10. 设A ，B 为n 阶对称方阵，证明：AB 为对称阵的充分必要条件是AB =BA . 【证明】已知A ′=A ,B ′=B ，若AB 是对称阵，即(AB )′=AB .则 AB =(AB )′=B ′A ′=BA , 反之，因AB =BA ,则(AB )′=B ′A ′=BA =AB ,所以，AB 为对称阵.11. A 为n 阶对称矩阵，B 为n 阶反对称矩阵，证明： (1) B 2是对称矩阵.(2) AB -BA 是对称矩阵，AB +BA 是反对称矩阵. 【证明】因A ′=A ,B ′= -B ,故(B 2)′=B ′·B ′= -B ·(-B )=B 2;(AB -BA )′=(AB )′-(BA )′=B ′A ′-A ′B ′= -BA -A ·(-B )=AB -BA ;(AB +BA )′=(AB )′+(BA )′=B ′A ′+A ′B ′= -BA +A ·(-B )= -(AB +BA ).所以B 2是对称矩阵，AB -BA 是对称矩阵，AB+BA 是反对称矩阵. 12. 求与A =1101⎡⎤⎢⎥⎣⎦可交换的全体二阶矩阵. 【解】设与A 可交换的方阵为a b c d ⎡⎤⎢⎥⎣⎦,则由1101⎡⎤⎢⎥⎣⎦a b c d ⎡⎤⎢⎥⎣⎦=a b c d ⎡⎤⎢⎥⎣⎦1101⎡⎤⎢⎥⎣⎦, 得a cb d a a bcd c c d +++⎡⎤⎡⎤=⎢⎥⎢⎥+⎣⎦⎣⎦.由对应元素相等得c =0,d =a ,即与A 可交换的方阵为一切形如0a b a ⎡⎤⎢⎥⎣⎦的方阵，其中a,b 为任意数.13. 求与A =100012012⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦可交换的全体三阶矩阵. 【解】由于A =E +000002013⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦, 而且由111111222222333333000000,002002013013a b c a b c a b c a b c a b c a b c ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦可得11122233333323232302300023222.023333c b c cb c a b c c b c a a b b c c -⎡⎤⎡⎤⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦由此又可得1113232332322333230,230,20,30,2,3,232,233,c b c a a a c b c b b b c c b c c c =-==-===--=-=-所以2311233230,2,3.a a b c c b c b b ======-即与A 可交换的一切方阵为12332300203a b b b b b ⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦其中123,,a b b 为任意数. 14. 求下列矩阵的逆矩阵.(1) 1225⎡⎤⎢⎥⎣⎦； (2) 123012001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦； (3)121342541-⎡⎤⎢⎥-⎢⎥⎢⎥--⎣⎦； (4) 1000120021301214⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦； (5) 5200210000830052⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦； (6) ()1212,,,0nn a a a a a a ⎡⎤⎢⎥⎢⎥≠⎢⎥⎢⎥⎣⎦L O ，未写出的元素都是0（以下均同，不另注）. 【解】(1) 5221-⎡⎤⎢⎥-⎣⎦; (2)121012001-⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦;(3) 12601741632142-⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦; (4) 100011002211102631511824124⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦; (5) 1200250000230058-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦; (6) 12111n a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦O. 15. 利用逆矩阵，解线性方程组12323121,221,2.x x x x x x x ++=⎧⎪+=⎨⎪-=⎩ 【解】因123111102211102x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,而1110022110≠- 故112311101111122.02211130122*********x x x -⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥-⎣⎦⎣⎦16. 证明下列命题：(1) 若A ，B 是同阶可逆矩阵，则（AB ）*=B *A *. (2) 若A 可逆，则A *可逆且（A *）-1=（A -1）*. (3) 若AA ′=E ,则（A *）′=(A *)-1. 【证明】（1）因对任意方阵c ，均有c *c =cc *=|c |E ,而A ,B 均可逆且同阶，故可得|A |·|B |·B *A *=|AB |E (B *A *)=(AB ) *AB (B *A *)=(AB ) *A (BB *)A * =(AB ) *A |B |EA *=|A |·|B |(AB ) *.∵ |A |≠0,|B |≠0, ∴ (AB ) *=B *A *.(2) 由于AA *=|A |E ,故A *=|A |A -1,从而(A -1) *=|A -1|(A -1)-1=|A |-1A . 于是A * (A -1) *=|A |A -1·|A |-1A =E ,所以(A -1) *=(A *)-1. (3) 因AA ′=E ，故A 可逆且A -1=A ′. 由(2)(A *)-1=(A -1) *,得(A *)-1=(A ′) *=(A *)′.17. 已知线性变换11232123312322,35,323,x y y y x y y y x y y y =++⎧⎪=++⎨⎪=++⎩ 求从变量123,,x x x 到变量123,,y y y 的线性变换. 【解】已知112233221,315323x y x y x y ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦X AY且|A |=1≠0,故A 可逆，因而1749,637324---⎡⎤⎢⎥==-⎢⎥⎢⎥-⎣⎦Y A X X所以从变量123,,x x x 到变量123,,y y y 的线性变换为112321233123749,637,324,y x x x y x x x y x x x =--+⎧⎪=+-⎨⎪=+-⎩ 18. 解下列矩阵方程.(1) 12461321-⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦X =； (2)211211************--⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦X ；(3) 142031121101⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦X =； (4) 010100043100001201001010120-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦X .【解】(1) 令A =1213⎡⎤⎢⎥⎣⎦;B =4621-⎡⎤⎢⎥⎣⎦.由于13211--⎡⎤=⎢⎥-⎣⎦A 故原方程的惟一解为13246820.112127----⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦X A B同理(2) X =100010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦; (3) X =11104⎡⎤⎢⎥⎢⎥⎣⎦; (4) X =210.034102-⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦19. 若kA =O (k 为正整数)，证明：121()k ---L E A =E +A+A ++A .【证明】作乘法212121()()k k k k k ----=-----=-=E A E +A+A ++A E +A+A ++A A A A A E A E,L L L 从而E -A 可逆，且121()k ---L E A =E +A+A ++A20.设方阵A 满足A 2－A －2E ＝O ，证明A 及A ＋2E 都可逆，并求A -1及(A +2E )-1.【证】因为A 2-A -2E =0, 故212().2-=⇒-=A A E A E A E由此可知，A 可逆，且11().2-=-A A E同样地2220,64(3)(2)41(3)(2)4--=--=--+=---+=A A E A A E E,A E A E E,A E A E E. 由此知，A +2E 可逆，且1211(2)(3)().44-+=--=-A E A E A E21. 设423110123⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦A =，2AB =A+B ,求B . 【解】由AB =A +2B 得(A -2E )B =A .而22310,1102121==-≠---A E即A -2E 可逆，故11223423(2)110110121123143423386.1531102961641232129--⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦----⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==----⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦B A E A 22. 设1-P AP =Λ. 其中1411--⎡⎤⎢⎥⎣⎦P =，1002-⎡⎤⎢⎥⎣⎦=Λ，求10A . 【解】因1-P 可逆，且1141,113-⎡⎤=⎢⎥--⎣⎦P 故由1Λ-A =P P 得10110101101012121010()()141410331102113314141033110211331365136412421.34134031242--==⎡⎤⎢⎥---⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥--⎢⎥⎣⎦⎡⎤⎢⎥--⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥--⎢⎥⎣⎦⎡⎤-+-+⎡⎤==⎢⎥⎢⎥----⎣⎦⎣⎦A P P P P ΛΛ 23. 设m 次多项式01()m m f x a a x a x =+++L ，记01()mm f a a a =+++L A E A A ,()f A 称为方阵A 的m 次多项式.(1)12λλ⎡⎤⎢⎥⎣⎦A =，证明12kk k λλ⎡⎤⎢⎥⎣⎦A =，12()()()f f f λλ⎡⎤=⎢⎥⎣⎦A ； (2) 设1-A =P BP ，证明1k k -B =PA P ，1()()f f -=B P A P . 【证明】(1)232311232200,00λλλλ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦A A 即k =2和k =3时，结论成立. 今假设120,0kkk λλ⎡⎤=⎢⎥⎣⎦A 那么111111222000,000kk k k k k λλλλλλ+++⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦AA A = 所以，对一切自然数k ，都有120,0kkk λλ⎡⎤=⎢⎥⎣⎦A 而011101220111012212()1100().()mm mm m m m m m f a a a a a a a a a a a a f f λλλλλλλλλλ=⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤+=⎢⎥+⎣⎦⎡⎤=⎢⎥⎣⎦L L L L A E +A++A ++++++ (2) 由(1)与A =P -1BP ,得B =PAP -1.且B k =( PAP -1)k = PA k P -1,又0111011011()()().mm m m mm f a a a a a a a a a f ----=+++=+++=++=B E B B E PAP PA P P E A+A P P A P L L L24. a b c d ⎡⎤⎢⎥⎣⎦A =，证明矩阵满足方程2()0x a d x ad bc -++-=.【证明】将A 代入式子2()x a d x ad bc -++-得222222()()10()()010000.00a d ad bc a b a b a d ad bc c d c d ad bca bc ab bd a ad ab bd ad bc ac cd cb d ac cd ad d -++-⎡⎤⎡⎤⎡⎤=-++-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦-⎡⎤⎡⎤++++⎡⎤=-+⎢⎥⎢⎥⎢⎥-++++⎣⎦⎣⎦⎣⎦⎡⎤==⎢⎥⎣⎦A A E0 故A 满足方程2()0x a d x ad bc -++-=. 25. 设n 阶方阵A 的伴随矩阵为*A ，证明：(1) 若｜A ｜＝０，则｜*A ｜＝０；(2) 1n *-=A A .【证明】（1）若|A |=0，则必有|A *|=0，因若| A *|≠0，则有A *( A *)-1=E ,由此又得 A =AE =AA *( A *)-1=|A |( A *)-1=0,这与| A *|≠0是矛盾的，故当|A | =0，则必有| A *|=0. (2) 由A A *=|A |E ，两边取行列式，得|A || A *|=|A |n ,若|A |≠0，则| A *|=|A |n -1 若|A |=0,由(1)知也有| A *|=|A |n -1.26. 设52003200210045000073004100520062⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A =,B . 求(1) AB ; (2)BA ; (3) 1-A ；(4)｜A ｜k (k 为正整数). 【解】(1)2320001090000461300329⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦AB =; (2) 19800301300003314005222⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦BA =;(3) 11200250000230057--⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦A =; (4)(1)k k =-A . 27. 用矩阵分块的方法，证明下列矩阵可逆，并求其逆矩阵.（1）1200025000003000001000001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦；（2）00310021********-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦; （3）20102020130010*******0001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦.【解】(1) 对A 做如下分块 12⎡⎤=⎢⎥⎣⎦A A A 00其中1230012;,01025001⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦A A12,A A 的逆矩阵分别为1112100523;,01021001--⎡⎤⎢⎥-⎡⎤⎢⎥==⎢⎥-⎢⎥⎣⎦⎢⎥⎣⎦A A 所以A 可逆，且1111252000210001.000030001000001----⎡⎤⎢⎥-⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦A A A同理(2)11112121310088110044.110055230055----⎡⎤-⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦A A A A A (3)1110012211300222.001000001001-⎡⎤--⎢⎥⎢⎥⎢⎥--⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A。

线性代数习题册(第二章矩阵及其运算参考答案)

⇔ αTα = 1
单元 6 逆矩阵、分块矩阵
一、判断题（正确的打√，错误的打×）
1. 可逆矩阵一定是方阵.
（√）
2. 若 A 、 B 为同阶可逆方阵，则 AB 可逆.
（√）
3. 设 A, B 均为可逆矩阵，则 AB 也可逆且 ( AB)−1 = A−1B−1 .
（X）
4. 若 A 可逆，则 AT 也可逆.
分析： |
r1 A|
↔
r2
− | B |，所以
A
+
B
= 0 。
20.
设
A
=
a11 a21
a12 a22
a13 a23
，
B
=
a21 a11
a22 a12
a23 a13
0 1 0
，
P1
=
1
0
0
a31 a32 a33
a31 + a11 a32 + a12 a33 + a13
0 0 1
( A) kA∗
(B) k n−1 A∗
(C ) k n A∗
( D) k −1 A∗
分析：题中对可逆矩阵也要成立，所以不妨设 A 可逆时进行分析。
( ) = (kA)∗ | kA | (= kA)−1 k n | A | ⋅ 1 A−1 = k n−1 | A | A−1 = k n−1 A* k
a31 + a11 a32 + a12 a33 + a13
r1
↔
r2
a21 a11
a31 + a11
a22 a12 a32 + a12
a23
a13

线性代数习题第二章 (附详解)

线性代数习题第二章（附详解）第二章矩阵及其运算【编号】ZSWD2023B0061 1 已知线性变换3213321232113235322y y y x y y y x y y y x 求从变量x 1 x 2 x 3到变量y 1 y 2 y 3的线性变换解：由已知221321323513122y y y x x x故3211221323513122x x x y y y321423736947y y y 321332123211423736947x x x y x x x y x x x y2 已知两个线性变换32133212311542322y y y x y y y x y y x 323312211323z z y z z y z z y求从z 1 z 2 z 3到x 1 x 2 x 3的线性变换解：由已知221321514232102y y y x x x321310102013514232102z z z321161109412316z z z所以有 3213321232111610941236z z z x z z z x z z z x3 设 111111111A150421321B 求3AB 2A 及A TB解：1111111112150421321111111111323A AB2294201722213211111111120926508503092650850150421321111111111B A T4 计算下列乘积(1)127075321134解：127075321134 102775132)2(7111237449635(2)123)321(解：123)321( (1 3 2 2 3 1) (10)(3))21(312解： )21(31223)1(321)1(122)1(2632142(4)20413121013143110412 解：20413121013143110412 6520876(5)321332313232212131211321)(x x x a a a a a a a a a x x x 解：321332313232212131211321)(x x x a a a a a a a a a x x x(a 11x 1 a 12x 2 a 13x 3 a 12x 1 a 22x 2 a 23x 3 a 13x 1 a 23x 2 a 33x 3)321x x x322331132112233322222111222x x a x x a x x a x a x a x a5 设3121A2101B 问(1)AB BA 吗? 解： AB BA 因为6443AB8321BA 所以AB BA(2)(A B)2A 22AB B 2吗? 解： (A B)2A 22AB B 2因为5222B A52225222)(2B A2914148但 43011288611483222B AB A27151610 所以(A B)2A 22AB B 2(3)(A B)(A B) A 2B 2吗?解： (A B)(A B) A 2B 2因为5222B A1020B A906010205222))((B A B A而718243011148322B A 故(A B)(A B) A 2B 26 举反列说明下列命题是错误的 (1)若A 20 则A 0解：取0010A 则A 20 但A 0 (2)若A 2A 则A 0或A E 解：取0011A 则A 2A 但A 0且A E (3)若AX AY 且A 0 则X Y 解：取0001A 1111X1011Y则AX AY 且A 0 但X Y7 设101 A 求A 2A 3A k解：12011011012 A1301101120123 A A A101 k A k8 设001001A 求Ak解：首先观察0010010010012A2220020123232323003033 A A A43423434004064 A A A545345450050105A A AkA k k kk k k k k k k 0002)1(121用数学归纳法证明当k 2时显然成立假设k 时成立，则k 1时，0010010002)1(1211k k k k k k k k k k k k A A A11111100)1(02)1()1(k k k k k k k k k k 由数学归纳法原理知k k k k k k k k k k k A 0002)1(1219 设A B 为n 阶矩阵，且A 为对称矩阵，证明B TAB 也是对称矩阵证明：因为A TA 所以(B TAB)TB T(B TA)TB T A TB B TAB从而B TAB 是对称矩阵10 设A B 都是n 阶对称矩阵，证明AB 是对称矩阵的充分必要条件是AB BA 证明：充分性因为A TA B TB 且AB BA 所以(AB)T(BA)TA TB TAB即AB 是对称矩阵必要性因为A TA B TB 且(AB)TAB 所以AB (AB)TB T A TBA11 求下列矩阵的逆矩阵 (1)5221 解：5221A |A| 1 故A 1存在因为1225*22122111A A A A A故 *||11A A A1225(2)cos sin sin cos 解cos sin sin cos A |A| 1 0 故A 1存在因为cos sin sin cos *22122111A A A A A所以 *||11A A Acos sin sin cos(3)145243121解145243121A |A| 2 0 故A 1存在因为214321613024*332313322212312111A A A AA A A A A A所以 *||11A A A1716213213012(4)n a a a 0021(a 1a 2a n0)解 n a a a A 0021由对角矩阵的性质知n a a a A 1001121112 解下列矩阵方程 (1)12643152X解：126431521X1264215380232(2)234311*********X 解： 1111012112234311X0332321012343113132538122(3)101311022141X解： 11110210132141X2101101311421212101036612104111 (4)021102341010100001100001010X解： 11010100001021102341100001010X01010000102110234110000101020143101213 利用逆矩阵解下列线性方程组(1) 3532522132321321321x x x x x x x x x解：方程组可表示为321153522321321x x x故0013211535223211321x x x从而有 001321x x x(2) 05231322321321321x x x x x x x x x解：方程组可表示为012523312111321x x x故3050125233121111321x x x 故有 305321x x x14 设A kO (k 为正整数) 证明(E A) 1E A A 2A k 1证明：因为A kO 所以E A kE 又因为E A k(E A)(E A A 2A k 1)所以 (E A)(E A A 2A k 1) E由定理2推论知(E A)可逆且 (E A) 1E A A 2A k 1证明一方面有E (E A) 1(E A)另一方面由A kO 有E (E A) (A A 2) A 2A k 1(A k 1A k)(E A A 2 Ak 1)(E A)故 (E A) 1(E A) (E A A 2A k 1)(E A)两端同时右乘(E A) 1就有 (E A) 1(E A) E A A 2A k 115 设方阵A 满足A 2A 2E O 证明A 及A 2E 都可逆并求A 1及(A 2E) 1证明：由A 2A 2E O 得A 2A 2E 即A(A E) 2E或 E E A A)(21 由定理2推论知A 可逆且)(211E A A 由A 2A 2E O 得A 2A 6E 4E 即(A 2E)(A 3E) 4E或 E A E E A)3(41)2( 由定理2推论知(A 2E)可逆且)3(41)2(1A E E A证明由A 2A 2E O 得A 2A 2E 两端同时取行列式得 |A 2A| 2即 |A||A E| 2 故 |A| 0所以A 可逆而A 2E A 2|A 2E| |A 2| |A|20 故A 2E 也可逆由 A 2A 2E O A(A E) 2EA 1A(A E) 2A 1E )(211E A A又由 A 2A 2E O (A 2E)A 3(A 2E) 4E (A 2E)(A 3E) 4 E所以 (A 2E) 1(A 2E)(A 3E) 4(A 2 E) 1)3(41)2(1A E E A16 设A 为3阶矩阵 21||A 求|(2A) 15A*| 解：因为*||11A A A所以 |||521||*5)2(|111 A A A A A |2521|11 A A | 2A 1| ( 2)3|A 1| 8|A| 18 2 1617 设矩阵A 可逆证明其伴随阵A*也可逆且(A*) 1(A 1)*证明：由*||11A A A得A* |A|A 1所以当A 可逆时有|A*| |A|n|A 1| |A|n 10 从而A*也可逆因为A* |A|A 1所以(A*) 1|A| 1A又*)(||)*(||1111A A A A A 所以 (A*) 1|A| 1A |A| 1|A|(A 1)* (A 1)*18 设n 阶矩阵A 的伴随矩阵为A* 证明 (1)若|A| 0 则|A*| 0 (2)|A*| |A|n 1证明：(1)用反证法证明假设|A*| 0 则有A*(A*) 1E 由此得A A A*(A*) 1|A|E(A*) 1O所以A* O 这与|A*| 0矛盾，故当|A| 0时有|A*| 0(2)由于*||11A A A则AA* |A|E 取行列式得到 |A||A*| |A|n若|A| 0 则|A*| |A|n 1若|A| 0 由(1)知|A*| 0 此时命题也成立因此|A*| |A|n 119 设321011330A AB A 2B 求B解：由AB A 2E 可得(A 2E)B A 故321011330121011332)2(11A E A B01132133020 设101020101A 且AB E A 2B 求B解：由AB E A 2B 得(A E)B A 2E即 (A E)B (A E)(A E)因为01001010100|| E A 所以(A E)可逆从而201030102E A B21 设A diag(1 2 1) A*BA 2BA 8E 求B 解：由A*BA 2BA 8E 得 (A* 2E)BA 8E B 8(A* 2E) 1A 18[A(A* 2E)] 18(AA* 2A)18(|A|E 2A) 18( 2E 2A) 14(E A)14[diag(2 1 2)] 1)21 ,1 21(diag 4 2diag(1 2 1)22 已知矩阵A 的伴随阵8030010100100001*A 且ABA 1BA 13E 求B解：由|A*| |A|38 得|A| 2由ABA 1BA 13E 得AB B 3AB 3(A E) 1A 3[A(E A 1)] 1A11*)2(6*)21(3A E A E103006060060000660300101001000016123 设P 1AP 其中1141P2001 求A 11解：由P 1AP 得A P P 1所以A 11A=P 11P 1. |P| 31141*P 1141311P而11111120 012001故31313431200111411111A6846832732273124 设AP P 其中111201111P511求 (A) A 8(5E 6A A 2) 解： ( ) 8(5E 6 2)diag(1 1 58)[diag(5 5 5) diag( 6 6 30) diag(1 1 25)] diag(1 1 58)diag(12 0 0) 12diag(1 0 0) (A) P ( )P 1*)(||1P P P1213032220000000011112011112111111111425 设矩阵A、B 及A B 都可逆证明A 1B 1也可逆并求其逆阵证明：因为A 1(A B)B 1B 1A 1A 1B 1而A 1(A B)B 1是三个可逆矩阵的乘积所以A 1(A B)B 1可逆即A 1B 1可逆(A 1B 1) 1[A 1(A B)B 1] 1B(A B) 1A26 计算30003200121013013000120010100121 解：设10211A30122A 12131B30322B则 2121B O B E A O E A222111B A O B B A A而4225303212131021211B B A90343032301222B A 所以 2121B O B E A O E A 222111B A O B B A A9000340042102521即30003200121013013000120010100121900034004210252127 取1001D C B A 验证|||||||| D C B A D C B A解：4100120021010*********0021010010110100101D C B A 而01111|||||||| D C B A 故|||||||| D C B A D C B A28 设22023443O O A 求|A 8|及A 4解：令 34431A22022A则21A O O A A故 8218 A O O A A8281A O O A 1682818281810|||||||||| A A A A A464444241422025005O O A O O A A29 设n 阶矩阵A 及s 阶矩阵B 都可逆求 (1)1O B A O解：设43211C C C C O B A O 则O B A O 4321C C C Cs n E O O E BC BC AC AC 2143 由此得 s n E BC O BC O AC E AC 2143 121413B C O C O C A C所以O A B O O B A O 111(2)1B C O A解：设43211D D D D B C O A 则s n E O O E BD CD BD CD AD AD D D D D B C O A 4231214321由此得 s n E BD CD O BD CD O AD E AD 423121 14113211B D CA B D O D A D所以11111B CA B O A BC O A30 求下列矩阵的逆阵(1)2500380000120025 解：设1225A2538B 则5221122511A8532253811B于是850032000052002125003800001200251111B A B A(2)4121031200210001 解：设 2101A 4103B2112C 则1111114121031200210001B CA B O A BC O A411212458103161210021210001。

线性代数第二章习题部分答案(

第二章向量组的线性相关性§2-1 §2-2 维向量，线性相关与线性无关（一）一、填空题1. 设3 α1−α +2 α2+α =5 α3+α , 其中α1=(2,5,1,3)T,α2=(10,1,5,10)T, α3=(4,1,−1,1)T, 则α= (1,2,3,4)T .2. 设α1=(1,1,1)T, α2=(2,1,1)T,α3=(0,2,4)T,则线性组合α1−3α2+α3= (−5,0,2)T .3. 设矩阵A= ，设βi为矩阵A的第i个列向量，则2β1+β2−β3= (−2,8,−2)T .二、试确定下列向量组的线性相关性1. α1=(2,1,0)T, α2=(1,2,1)T, α3=(1,1,1)T解：设k1α1+k2α2+k3α3=0,则k1 210 +k2 121 +k3 111 = 000即2k1+k2+k3=0k1+2k2+k3=0k2+k3=0k1+2k2+k3=0−3k2−k3=0k2+k3=0 k1+2k2+k3=0k2+k3=0k3=0 k1=k2=k3=0，线性无关。

2. α1=(1,−1,2)T, α2=(0,0,0)T, α3=(1,4,3)T线性相关三、设有向量组α1=(1,1,0)T, α2=(1,3,−1)T, α3=(5,−3,t)T，问t取何值时该向量组线性相关。

解：设k1α1+k2α2+k3α3=0,则k1 110 +k2 13−1 +k3 5−3t =0即k1+k2+5k3=0k1+3k2−3k3=0−k2+tk3=0k1+k2+5k3=0k2−4k3=0−k2+tk3=0k1+k2+5k3=0k1+3k2−3k3=0(t−4)k3=0所以，t=4, 线性相关; t≠4, 线性无关四、设a1,a2线性无关，a1+b,a2+b线性相关，求向量b用a1,a2线性表示的表示式。

解：因为a1+b,a2+b线性相关，所以存在不全为零的k1，k2，使得k1(a1+b)+k2(a2+b)=0, 即(k1+k2)b=−k1a1−k2a2.又因为a1,a2线性无关，所以k1+k2≠0，于是，b=−k1k1+k2a1−k2k1+k2a2.五、已知向量组α1,α2,⋯,α2n，令β1=α1+α2,β2=α2+α3,⋯,β2n=α2n+α1，求证向量组β1,β2,⋯,β2n线性相关。

经济数学线性代数第二章习题答案

习题二参考答案(Ａ)1.设⎪⎪⎪⎭⎫ ⎝⎛=543212132131A ，⎪⎪⎪⎭⎫ ⎝⎛------=424222242242B ，求(1) B A 32+；(2) 若X 满足X B X A +=-2，求X ．解：(1)⎪⎪⎪⎭⎫ ⎝⎛------+⎪⎪⎪⎭⎫ ⎝⎛=+42422224224254321213213132B A⎪⎪⎪⎭⎫ ⎝⎛----=2221824281828184. (2) 由X B X A +=-2得，B A X -=22，所以B A X 21+=⎪⎪⎪⎭⎫ ⎝⎛-------⎪⎪⎪⎭⎫ ⎝⎛=42422224224221543212132131⎪⎪⎪⎭⎫⎝⎛=351323013012.2.计算解：(1)⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--24317421432231321.(2)⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛--86164233241121123.(3)⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛963642321)321(321.(4)10321)123(=⎪⎪⎪⎭⎫⎝⎛.(5)⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321332313232212131211321)(x x x a a a a a a a a a x x x()⎪⎪⎪⎭⎫⎝⎛++++++=321333223113323222121313212111x x x x a x a x a x a x a x a x a x a x a 322331132112233322222111222x x a x x a x x a x a x a x a +++++=．3.已知两个线性变换⎪⎩⎪⎨⎧+-=-+=-=3213321231123232y y y x y y y x y y x ，⎪⎩⎪⎨⎧+-=+=-=213212211323zz y z z y z z y ，(1)试把这两个线性变换分别写成矩阵形式；(2)用矩阵乘法求连续施行上述变换的结果．解：(1) 写成矩阵形式为⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛321321213121302y y y x x x ,⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛21321311231z z y y y .(2)连续施行上述变换有⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛21213214146155311231213121302z z z z x x x .4.某企业在一月份出口到三个国家的两种货物的数量以及两种货物的积各为多少？解：设矩阵⎪⎪⎭⎫ ⎝⎛=6001300100088012002000A ，⎪⎪⎭⎫ ⎝⎛=2.03.0P ,⎪⎪⎭⎫⎝⎛=05.0012.0W ， ⎪⎪⎭⎫⎝⎛=6.012.0V ，则该企业出口到三个地区的货物总价值为()()384720080060013001000880120020002.03.0=⎪⎪⎭⎫⎝⎛=A P T ；总重量为()()6.1354.7974600130010008801200200005.0012.0=⎪⎪⎭⎫⎝⎛=A W T ；总体积为()()6.46530084060013001000880120020006.012.0=⎪⎪⎭⎫⎝⎛=A V T ．5.计算下列矩阵(其中n 为正整数)．(1) n ⎪⎪⎭⎫ ⎝⎛0011； (2) n⎪⎪⎭⎫⎝⎛101λ； (3)nc b a ⎪⎪⎪⎭⎫⎝⎛000000； (4)n⎪⎪⎪⎪⎪⎭⎫⎝⎛------------1111111111111111．解： 2=n 时，⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛00110011001100112，假设当k n =时，⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛001100110011k成立，则当1+=k n 时，⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛001100110011k ，有归纳法有⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛00110011n． (2) 2=n 时，⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛10211011011012λλλλ，假设当k n =时，⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛101101λλk k 成立，则当1+=k n 时，⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛+10)1(11011011011λλλλk kk ，有归纳法有⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛101101λλn n．(3) 2=n 时，⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛222200000000000000000000000c b a c b a c b a c b a ，假设当k n =时，⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛k k k kc b a c b a 000000000000成立，则当1+=k n 时， ⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛++++1111000000000000000000000000k k k kk c b ac b a c b a c b a ，有归纳法有⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛n n n nc b a c b a 00000000000． (4) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------------=1111111111111111A , 2=n 时，⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------------⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------------=4000040000400004111111111111111111111111111111112AE 22=,3=n 时，A A A A 2232==,于是，当k n 2=（k 为正整数）时，E E A A n k k n 2)2()(22===,当12+=k n （k 为正整数）时，A A E A A A A n k k k n 122122)2(-+====, 因此得⎩⎨⎧=-为奇数）（为偶数）n En EA n n n12(2.6.设0111)(a x a xa x a x f n n nn ++++=-- ，记E a A a A a A a A f n n nn 0111)(++++=-- ，称)(A f 为方阵A 的n 次多项式．现设1)(2+-=x x x f ，⎪⎪⎪⎭⎫ ⎝⎛-=211012113A ，求)(A f ．解: E A A A f +-=2)(⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛-=1000100012110121132110121132⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=100010001211012113527218538⎪⎪⎪⎭⎫ ⎝⎛--=416216426. 7.设矩阵A 、B 是可交换的，试证： (1) 22))((B A B A B A -=-+； (2) 2222)(B AB A B A ++=+．证明:因为矩阵A 、B 是可交换的，所以BA AB =,因此有(1) 22))((B AB BA A B A B A --+=-+22B A -=，(2) 222_)(B AB BA A B A +++=+222B AB A ++=. 8.设A 、B 是同阶矩阵，且)(21E B A +=，证明：A A =2的充分必要条件是E B =2．证明:必要性如果 A A =2，则)(21)](21[2E B E B +=+，由于矩阵B 与E 是可交换的，由上式得)(21)2(412E B E B B +=++ 整理得 E B =2．充分性如果E B =2，则A EB E B B E B A =+=++=+=)(21)2(41)](21[222．9.设矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛------=a bcd b a d c c d a bd c b aA d c b a ,,,(均为实数）， (1)计算TAA ；(2)利用(1)的结果，求A ．解：(1)⎪⎪⎪⎪⎪⎭⎫⎝⎛------⎪⎪⎪⎪⎪⎭⎫⎝⎛------=a b cdb a dc cd a b d c b a a bcd b a d c c d a b d c b aAA T⎪⎪⎪⎪⎪⎭⎫ ⎝⎛++++++++++++=2222222222222222000000000000d c b a d c b a d c b a d c b a(2)由(1)有422222)(d c b a A A A AA T T +++===，所以22222)(d c b a A +++=．10. 证明题：(1)对于任意的n m ⨯矩阵A ，则T AA 和A A T 均为对称矩阵． (2) 对于任意的n 阶矩阵A ，则T A A +为对称矩阵；而-A T A 为反对称矩阵．证明：(1) 因为TTTTTTAA A A AA ==)()(，所以T AA 为对称矩阵；又因为A A A A A A TTTTTT==)()(，所以A A T为对称矩阵．(2) 因为TTTTTTA A A A A A +=+=+)()(，所以TA A +为对称矩阵；又因为)()()(TTTTTTTA A A A A A A A --=-=-=-，所以T A A +为反对称矩阵．11.如果A 、B 是同阶对称阵，则AB 是对称阵的充分必要条件是AB BA =．证明：必要性如果AB 是对称阵，则AB AB T=)(，即AB A B TT =，由已知有 B B A A TT==,，所以BA AB =．充分性如果BA AB =，则AB BA A B AB T T T ===)(，所以AB 是对称阵．12.设n 阶矩阵A 的伴随矩阵为*A ，证明(1) 若 0=A ，则 0=*A ； (2) 1-*=n AA ．证明：(1)假设0≠*A ，则E A A =-**1)(，由此得 O A E A A AA A ===-*-**11)()(，所以 O A =*，这与0≠*A 相矛盾，故0=A 时，有0=*A ．(2) 由E A AA =*得，nA A A =*，若0≠A 时，有1-*=n AA ，若0=A 时，由(1)知0=*A ，等式也成立，故有1-*=n AA ，13.设n 阶矩阵A ,B ,C 满足E ABC =，则下列各式中哪一个必定成立？简述理由．(1)E ACB =，(2)E CBA =，(3)E BAC =，(4)E BCA =.解：由E ABC =可改写为E BC A =)(，即BC 是A 的逆矩阵，所以有E A BC =)(，即(4) 必定成立．类似可得(1)、(2)、(3)未必成立. 14.设A ,B 均为n 阶可逆矩阵，下列各式一定成立的有哪些？简述理由．(1) 1111])[(])[(----=TTA A ；(2) T T T A A ])[(])[(111---=；(3) k k A A )()(11--= (k 为正整数)；(4) 111)(---+=+B A B A ； (5) T T TB A AB )()(])[(111---=； (6) ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛---O B A O O B A O 111．解: (1)由于TTA A =--])[(11,T TA A =--11])[(,所以1111])[(])[(----=T T A A ,即(1)式一定成立．(2) 由于11])[(--=A A T T,T T A A =--])[(11，即(２)式不一定成立．(3) k kk A A A A A AA A )()()(111111------===，(３)式一定成立．(4)设⎪⎪⎭⎫⎝⎛=1001A ，⎪⎪⎭⎫ ⎝⎛--=1001B ，显然A 、B 都可逆，但是 O B A =+不可逆，故(４)式不成立．(5) 由于T T T T T T T B A B A A B AB )()()())()(])[(111111------===，即(５)式一定成立．(6) 由于⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----1111BA O O AB O BA OO B A O 但是11--BA AB 和不一定等于E ，故(6) 式不一定成立15.设A 是n 阶矩阵，满足O A k=k (是正整数),求证：A E -可逆，并且121)(--++++=-k A A A E A E ．证明：因为))((12-++++-k A A A E A Ek A E -= E =，所以A E -可逆，并且121)(--++++=-k A A A E A E ．16.设A 是可逆矩阵，证明：其伴随矩阵*A 也可逆，且*--*=)()(11A A ．证明：因为A 是可逆矩阵，所以0≠A ，由于E A AA =*，有E AA A=*1，因此，伴随矩阵*A 也可逆．由上述证明可知A AA 1)(1=-*，又因为 E A A A 111))((-*--=，所以 A AA A A 1)(1)(111==--*-，故 *--*=)()(11A A ．17.设A 、B 和B A +均是可逆矩阵，试证：11--+B A 也可逆，并求其逆矩阵．解：11111-----+=+AB A A B A)(11--+=AB E A )(111---+=AB BB A11)(--+=B A B A ，由于A 、B 和B A +均是可逆矩阵，它们的乘积也可逆，所以有=+---111)(B A 111])([---+B A B A11111)()()(-----+=A A B B A A B B 1)(-+=．18.设A 为三阶矩阵，*A 是矩阵A 的伴随矩阵，已知21=A ，求 *--A A 2)3(1．解：因为21=A ，所以有A 可逆，且有211==--A A ．而E A AA =*，于是1121--*==A A A A ，因此有*--A A 2)3(11131---=A A 132--=A 1278--=A 2716-=．19.用分块矩阵的乘法计算.(1)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---1102012124221011110200100001；(2)⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--020222202010111101．解：(1) 设⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---B A O E 1011110200100001， ⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---F E D C110201212422，则⎪⎪⎭⎫⎝⎛B A O E ⎪⎪⎭⎫ ⎝⎛F E D C⎪⎪⎭⎫⎝⎛++=BF AD B AC DC而 ⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=+4433101112221102B AC ， BF AD +⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=+35121011241102BF AS ，于是⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---3445332124221102012124221011110200100001． (2)设⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛--321010111101A A A ，()321020222202B B B =⎪⎪⎪⎭⎫⎝⎛--，则()⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛332313322212312111321321B A B A B A B A B A B A B A B A B A B B B A A A ，而()202210111=⎪⎪⎪⎭⎫ ⎝⎛-=B A ，()222010121-=⎪⎪⎪⎭⎫⎝⎛--=B A ，()202210131-=⎪⎪⎪⎭⎫ ⎝⎛--=B A ，()002211112=⎪⎪⎪⎭⎫ ⎝⎛-=B A ，()422011122=⎪⎪⎪⎭⎫ ⎝⎛--=B A ，()402211132-=⎪⎪⎪⎭⎫ ⎝⎛--=B A ，()202201013=⎪⎪⎪⎭⎫ ⎝⎛=B A ，()222001023-=⎪⎪⎪⎭⎫ ⎝⎛-=B A ，()202201033=⎪⎪⎪⎭⎫ ⎝⎛-=B A ，于是⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--222440222020222202010111101． 20.求分块矩阵的逆矩阵．(1) ⎪⎪⎪⎪⎪⎭⎫⎝⎛--4300110000110032； (2)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----2000133412121211．解：(1)记⎪⎪⎭⎫ ⎝⎛=1132A ，⎪⎪⎭⎫ ⎝⎛--=4311B ，则 11132-==A ，14311-=--=B ，所以A 、B 都可逆，且有⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛=--2131113211A ，⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛--=--1314431111B ，于是⎪⎪⎪⎪⎪⎭⎫⎝⎛----=⎪⎪⎪⎪⎪⎭⎫⎝⎛---130014000021003143001100001100321．(2)记⎪⎪⎪⎭⎫ ⎝⎛----=334212211A ，)2(=B ，⎪⎪⎪⎭⎫⎝⎛-=111C ，因为04334212211≠=----=A ，022≠==B ，所以A 、B 均是可逆矩阵，且有 ⎪⎪⎪⎭⎫ ⎝⎛------=-3722524931A，)21(1=-B ，根据例2.17的结论有⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛-----11111B O CB A A B OC A ， -=---11CB A ⎪⎪⎪⎭⎫ ⎝⎛------372252493⎪⎪⎪⎭⎫ ⎝⎛-111⎪⎪⎪⎪⎭⎫ ⎝⎛-=4255)21(，所以=⎪⎪⎭⎫⎝⎛-1B OC A ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-------210004372252525493． 21.设A 为三阶矩阵，2-=A ，把A 按列分块为),,(321A A A A =，其中j A )3,2,1(=j 为A 的第j 列，求(1) 231,2,A A A -； (2) 1213,2,3A A A A -．解： (1) 231231,,2,2,A A A A A A -=- 321,,2A A A =A 2=4-=．(2) 1213,2,3A A A A -123,2,A A A =3212,,A A A = 1232,,A A A =- 2A =-4=．22.设A 为n 阶矩阵，把A 按列分块为),,,(21n A βββ =，j β),,2,1(n j =为A 的第j 列，试用n βββ,,,21 表示A A T ．解：),,,(2121n T N T T T A A ββββββ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=n Tn T n T n n TT T n T T T ββββββββββββββββββ21222121211123.设A 为三阶可逆矩阵，若A 按行分块为⎪⎪⎪⎭⎫⎝⎛=321A A A A ，按列分块为),,(321B B B A =，试判断下列分块矩阵是否可逆．(1) ⎪⎪⎪⎭⎫ ⎝⎛+++133221A A A A A A ； (2) ),,(133221B B B B B B ---．解：(1)利用行列式的性质计算分块矩阵的行列式133232113323211332212)(2A A A A A A A A A A A A A A A A A A A A ++++=++++=+++133212A A A A A ++=33212A A A A +=3212A A A =02≠=A ，从而⎪⎪⎪⎭⎫⎝⎛+++133221A A A A A A 可逆．(2) 0,,,,1332133221=--=---B B B B O B B B B B B ，从而),,(133221B B B B B B ---不可逆．24.设矩阵⎪⎪⎪⎭⎫ ⎝⎛=333231232221131211a a a a a a a a a A ，⎪⎪⎪⎭⎫⎝⎛+++=133312321131131211232221a a a a a a a a a a a a B ， ⎪⎪⎪⎭⎫ ⎝⎛=1000010101P ，⎪⎪⎪⎭⎫⎝⎛=1010100012P ，则下列各式中哪一个必定成立？简述理由．(1)B P AP =21；(2)B P AP =12；(3)B A P P =21；(4)B A P P =12．解：因为A 的第一行加到第三行，再交换的第一行和第二行，从而得得到B ，故用2P 左乘A ，再左乘1P ，即B A P P =21，(3)式必定成立．25.求下列矩阵的等价标准形．(1)⎪⎪⎪⎭⎫ ⎝⎛--021123211； (2)⎪⎪⎪⎭⎫⎝⎛---433221； (3)⎪⎪⎪⎪⎪⎭⎫⎝⎛-34624216311230211111．解：(1)⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛----→⎪⎪⎪⎭⎫ ⎝⎛--210550001210550211021123211⎪⎪⎪⎭⎫ ⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛---→100010001300010001210110001． (2)⎪⎪⎪⎭⎫ ⎝⎛-→⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛---201001201021433221⎪⎪⎪⎭⎫ ⎝⎛→001001． (3)⎪⎪⎪⎪⎪⎭⎫⎝⎛-----→⎪⎪⎪⎪⎪⎭⎫⎝⎛-1022010520105201111134624216311230211111⎪⎪⎪⎪⎪⎭⎫⎝⎛---→⎪⎪⎪⎪⎪⎭⎫⎝⎛-----→0070000000105200000110220105201052000001⎪⎪⎪⎪⎪⎭⎫⎝⎛→00000001000001000001． 26.用初等行变换求下列矩阵的逆矩阵．(1)⎪⎪⎪⎭⎫ ⎝⎛--121322011； (2)⎪⎪⎪⎭⎫⎝⎛300420531； (3)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------111111*********1； (4)⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-000000000000000121nn a a a a ),,2,1(,0n i a i =≠．解：(1)⎪⎪⎪⎭⎫⎝⎛--→⎪⎪⎪⎭⎫ ⎝⎛--101110012340001011100121010322001011 ⎪⎪⎪⎭⎫ ⎝⎛----→⎪⎪⎪⎭⎫ ⎝⎛--→416100101110001011012340101110001011 ⎪⎪⎪⎭⎫ ⎝⎛-----→⎪⎪⎪⎭⎫ ⎝⎛--→416100315010314001416100101110001011，所以1121322011-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛-----=416315314．(2)⎪⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛3100100010420001531100300010420001531⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--→⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛→310010032210010350103131001000210210001531 ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--→31001003221001031231001，所以=⎪⎪⎪⎭⎫ ⎝⎛-1300420531⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--31003221031231． (3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---------→⎪⎪⎪⎪⎪⎭⎫⎝⎛------1001022001012020001122000001111110001111010011110010111100011111⎪⎪⎪⎪⎪⎭⎫⎝⎛--------→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------→1111400000112200010120200001111111002200001122000101202000011111⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-------→⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---------→414141411000414********0414********0414141410001414141411000212121210200212121210020414141430111，所以=⎪⎪⎪⎪⎪⎭⎫⎝⎛-------11111111111111111⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------41414141414141414141414141414141． (4) ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-0100000000010000000000100000000010000121nn a a a a⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛→-01000000000100000000010000100000000121n n a a a a⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛→-----000100000000001000000000100000000011112111n n a a a a，所以=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--1121000000000000000 nn a a a a ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----0000000000000001112111n n a a a a． 27.解下列矩阵方程．(1) ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛3211024311X ； (2) ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛120311*********X ；(3) ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫⎝⎛--101311122131X ； (4) 设⎪⎪⎪⎭⎫ ⎝⎛---=101110011A ，且AX A X =+2，求X ．解：(1)因为14311=，所以矩阵⎪⎪⎭⎫⎝⎛4311可逆，在方程的两边左乘该矩阵的逆矩阵，得⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=-32110243111X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--=3211021314 ⎪⎪⎭⎫ ⎝⎛--=025127．(2) 因为1311211401=，所以矩阵⎪⎪⎪⎭⎫ ⎝⎛311211401可逆，在方程的两边右乘该矩阵的逆矩阵，得1311211*********-⎪⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=X⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫⎝⎛=111211********* ⎪⎪⎭⎫ ⎝⎛--=532100． (3) 设⎪⎪⎭⎫⎝⎛--=2131A ，⎪⎪⎭⎫⎝⎛--=1112B ，则1-=A ，1=B ，故矩阵B A ,都可逆，在方程的两边左乘1-A ，右乘1-B ，得11111210132131--⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=X⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛----=211110131132 ⎪⎪⎭⎫ ⎝⎛----=3345． (4)由AX A X =+2得，A X E A =-)2(，而⎪⎪⎪⎭⎫ ⎝⎛------=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---=-10111001110001000121011100112E A ，且02≠-E A ，所以E A 2-可逆，在A X E A =-)2(两边左乘1)2(--E A 得，A E A X 1)2(--=，又⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------=--212121212121212121)2(1E A ，故⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------=101110011212121212121212121X ⎪⎪⎪⎭⎫ ⎝⎛---=011101110． 28.求下列矩阵的秩．(1)⎪⎪⎪⎭⎫ ⎝⎛---443112112013；(2)⎪⎪⎪⎪⎪⎭⎫⎝⎛---10030116030242201211．解：(1) ⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛---443120131211443112112013 ⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛----→000056401211564056401211，所以该矩阵的秩是２.(2)⎪⎪⎪⎪⎪⎭⎫⎝⎛--→⎪⎪⎪⎪⎪⎭⎫⎝⎛---1003014030000000121110030116030242201211⎪⎪⎪⎪⎪⎭⎫⎝⎛--→00000040001003001211，所以该矩阵的秩是３.29.已知n 阶矩阵A 满足O E A A =--422，证明：E A +为可逆矩阵；并求1)(-+E A ．解：由O E A A =--422得，E E A A =--322，即E E A E A =+-))(3(，所以E A +为可逆矩阵，E A E A 3)(1-=+-．30.已知n 阶矩阵A ,B 满足AB B A =+，(1) 证明：E B -为可逆矩阵；(2) 已知⎪⎪⎪⎭⎫ ⎝⎛-=200012031A ，求矩阵B ．证明：(1)由AB B A =+得， )(E B A B -=，即E E B A E B --=-)(，整理的E E B E A =--))((，因此E B -可逆，且E A E B -=--1)(．解：(2)由(1)得，1)(--=-E A E B ，即1)(--+=E A E B1100002030100010001-⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛= ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=20001310211．(B)1.若A 、B 是n 阶方阵，且AB E +可逆，则BA E +也可逆，且 A AB E B E BA E 11)()(--+-=+．证明：])()[(1A AB E B E BA E -+-+A AB E BAB A AB E B BA E 11)()(--+-+-+=A AB E E AB E B A AB E B BA E 11))(()(--+-+-+-+=E =，所以BA E +也可逆，且A AB E B E BA E 11)()(--+-=+．2. 设B 为可逆矩阵，A 、B 是同阶方阵，且O B AB A =++22，证明：A 和B A +都为可逆矩阵．证明：由O B AB A =++22得，22B AB A -=+，即2)(B B A A -=+，由于B 为可逆矩阵，所以0≠B ，因而有 02≠-=+B B A A ，于是00≠+≠B A A ，所以A 和B A +都为可逆矩阵．3.已知实矩阵33)(⨯=ij a A 满足 (1) ij ij A a =)3,2,1,(=j i ，其中ij A 是ij a 的代数余子式；(2)011≠a ，计算A ．解：由ij ij A a =)3,2,1,(=j i 得， E A AA AA T==*，于是 32A AAA T==，从而0=A 或1=A ，但由于011≠a 得，0213212211131312121111>++=++=a a a A a A a A a A ，因此 1=A ．4.设A 、B 为同阶可逆矩阵，证明：***=A B AB )(．证明：因为A 、B 为同阶可逆矩阵，所以有0≠=B A AB ，即AB 也可逆，而E AB AB AB =*))((，于是AB AB AB 1)()(-*=B A A B 11--=))((11A A B B--=**=A B ． 5.设矩阵B 的伴随矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛-=*8031010100100001B ，且E AB BAB311+=--，求A ．解：由题有E B B B =*，4B B B =*，所以 83==*BB ，即2=B ．又E AB BAB 311+=--从而E ABE B 3)(1=--，B A E B 3)(=-，即 E A B E 3)(1=--于是 E A B B E 3)1(=-*，E A B E 3)21(=-*，E A B E 6)2(=-*，故⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=-=-*1031060100600006)2(61B E A6.已知⎪⎪⎪⎭⎫ ⎝⎛---=111111111A ，且矩阵X 满足X AX A 21+=-*，其中*A 是A 的伴随矩阵，求矩阵X ．解：由E A A A =*，X A X A 21+=-* 有AX E X A 2+=，于是 E X A E A =-)2(，所以 1)2(--=A E A X ．而4111111111=---=A ，于是⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=-22222222211111111124000400042A E A ，所以⎪⎪⎪⎭⎫⎝⎛=-=-10111001141)2(1A E A X ． 7．已知A 、B 都是n 阶矩阵，且满足E B B A 421-=-．其中E 为n 阶单位矩阵．(1) 证明：E A 2-可逆，并求1)2(--E A ；(2) 若⎪⎪⎪⎭⎫ ⎝⎛-=200021021B ，求矩阵A ．证明：(1) 由于E B B A 421-=-，因此A AB B 42-=，于是E E A B AB 8842=+--, 即E E B E A 8)4)(2(=--,从而E A 2-可逆，且有)4(81)2(1E B E A -=--．由(1)得1)4(82--=-E B E A ，即1)4(82--+=E B E A ，而11400040004200021021)4(--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫⎝⎛-=-E B1200021023-⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=21000838104141，所以 ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----+⎪⎪⎪⎭⎫ ⎝⎛=2100083810414181000100012A ⎪⎪⎪⎭⎫ ⎝⎛---=200011020． 8.设n 阶矩阵A 满足A A =2，E 是n 阶单位矩阵，证明：n E A r A r =-+)()(．证明：因为A A =2，因此A A =2，即O E A A =-)(，从而n E A r A r ≤-+)()(，又)()(A E r E A r -=-，所以)()()()(A E r A r E A r A r -+=-+ )(A E A r -+≥n =，故 n E A r A r =-+)()(．9.设*A 是)2(≥n n 阶方阵A 的伴随矩阵，证明：⎪⎩⎪⎨⎧-<-===*1)(01)(1)()(n A r n A r n A r n A r 若若若．证明：(1) 因为n A r =)(，所以A 可逆，于是0≠A ．而E A A A =*，因此*A 也可逆，故n A r =*)(．(2) 因为1)(-=n A r ，所以0=A ，于是0==*E A A A ，从而n A r A r ≤+*)()(，又 1)(-=n A r ，所以 1)(≤*A r ．又1)(-=n A r 知A 中至少有一个1-n 阶子式不为零，所以1)(≥*A r ，从而1)(=*A r ．(3) 因为1)(-<n A r ，所以A 中的任一1-n 阶子式为零，故0=*A ，所以0)(=*A r ．10. 设A 为n 阶非奇异矩阵，α为n 维列向量，b 是常数．记分块矩阵⎪⎪⎭⎫ ⎝⎛-=*A A O EP T α，⎪⎪⎭⎫⎝⎛=b A Q T αα，其中*A 是矩阵A 的伴随矩阵，E 为n 阶单位矩阵． (1)计算并化简PQ ；(2)证明：矩阵Q 可逆的充分必要条件是b A T ≠-αα1．解：(1) 因为E A A A =*，所以⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-=*b A A A O EPQ T T ααα⎪⎪⎭⎫⎝⎛+-+-=**A b A A A A A T T T ααααα⎪⎪⎭⎫⎝⎛+-=-A b A A O A T ααα1 ⎪⎪⎭⎫⎝⎛-=-)(1αααA b A O A T ．证明：(2) 由(1)得 )(1ααα--=A b A OAPQ T ，即 )(12αα--⋅=A b A Q P T，而0≠==-=*A A E AA O E P T α，所以)(1αα--⋅=A b A Q T，由此可知，矩阵0≠Q 的充分必要条件是01≠--ααA b T，即矩阵Q 可逆的充分必要条件是b A T≠-αα1．。

大学线性代数第二章习题答案

第二章矩阵及其运算第一节矩阵 1．解．,251=x 212=x .2.解． ⎪⎩⎪⎨⎧+--=+-=++-=3213321232111610941236zz z x z z z x z z z x 其系数矩阵为⎪⎪⎪⎭⎫ ⎝⎛----161109412316第二节矩阵的运算一填空题：1. ⎪⎪⎭⎫⎝⎛224210 2.3 ， ⎪⎪⎪⎭⎫ ⎝⎛1312123323121 ， 13-k ⎪⎪⎪⎭⎫ ⎝⎛1312123323121（k 为正整数）。

3. ⎪⎪⎪⎭⎫⎝⎛0000000004.⎪⎪⎪⎭⎫ ⎝⎛10100010001 5. 0二选择题：CCCCC B三计算：1．（1）⎪⎪⎪⎭⎫⎝⎛---632142（2）10 （3）322331132112233322222111222x x a x x a x x a x a x a x a +++++（4）⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+++++32155121232272i i i i ii i 2. ()()T T T A I A AA A I A A A T A A I +=+=+=⋅+=⋅+(1)00A A A I A I <⇒-+=+=.3.111101()()2()2000101n T n T n T n A αααααα----⎡⎤⎢⎥===⎢⎥⎢⎥-⎣⎦,则2(2)n n aE A a a -=-. 4.设2222223T T x x xy xz y xy y yz x y z z xz yzy ααααα⎡⎤⎡⎤⎢⎥⎢⎥=⇒=⇒=++=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦5.02()()()A E A B A B E A E A E B A E A E B E +≠--=⇒+-=+⇒-=112A EB B ⇒-⋅=⇒=. 6.()()⎪⎪⎪⎭⎫ ⎝⎛-=+-1154123600022B A B A7．⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-012328317 8．－80第三节逆矩阵一填空题：1.⎪⎪⎪⎭⎫ ⎝⎛100000031212. ⎪⎪⎭⎫ ⎝⎛--24205100010 3. ⎪⎪⎪⎭⎫ ⎝⎛----611859131320001 4. ⎪⎪⎪⎭⎫ ⎝⎛000000213141 5.⎪⎪⎪⎭⎫ ⎝⎛=123B 6. 541-；7.100122()(2)2()0102100B E AB A B A E B E E A E -⎡⎤-⎢⎥=+⇒--=⇒-==⎢⎥⎢⎥⎣⎦8.21()(2)20B A E A E --⎡⎤=--=⎢⎥⎣⎦. 9.由21224()().22A E A EA A E O A E E A E -+++-=⇒-=⇒-=()()kA lE h A E +=10.由111021()102002AB B A A B B E -⎡⎤⎢⎥⎢⎥⎢⎥-=⇒=-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦. 二．选择题：ACBBD三.计算题：1.(1) ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--3131002121001 (2) ⎪⎪⎪⎪⎭⎫ ⎝⎛-----17162132130122. 由BA A BA A +=-61得，B E B A +=-61，所以 E B E A 6)(1=--从而， 11)(6---=E A B ，⎪⎪⎪⎭⎫ ⎝⎛=-7000400031A ，所以⎪⎪⎪⎭⎫⎝⎛=--6321E A3.11010100001693471582100001010--⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=X ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=010100001693471582100001010⎪⎪⎪⎭⎫⎝⎛=963852741. 4. 因为)3,2,1(==i i A i i αα，所以⎪⎪⎪⎭⎫⎝⎛=300020001),,(),,(321321ααααααA ，因此 1321321),,(300020001),,(-⎪⎪⎪⎭⎫⎝⎛=ααααααA .又),,(321ααα⎪⎪⎪⎭⎫ ⎝⎛---=212122221，所以1321),,(-ααα⎪⎪⎪⎭⎫ ⎝⎛---=21212222191，故 =A ⎪⎪⎪⎭⎫ ⎝⎛---212122221⎪⎪⎪⎭⎫ ⎝⎛300020001⎪⎪⎪⎭⎫ ⎝⎛---21212222191⎪⎪⎪⎭⎫ ⎝⎛----=622250207315. 由23**0T T ij ij a A A A AA AA A E A A A =⇒=⇒==⇒=⇒=或1A =.又22211111212131311121301A a A a A a A a a a A =++=++≠⇒=.6. 1100200611AP PB A PBP -⎡⎤⎢⎥=⇒==⎢⎥⎢⎥--⎣⎦.5511A PB P PBP A --===. 7.1*11112(3)2233A A A A A A -----=-=-,所以 1*131228116(3)2()332727A A A A A ----=-=-=-⋅=-.或 *1*1***114(3)222333A A A A A A A A ---=-=⋅-=-,则311**3*446416(3)2()332727A A A A A ---=-=-=-⋅=-.8.E BA E BA A A E B A A B -=-=-=--**11||)(，即E E A B =-)(*，因而⎥⎥⎦⎤⎢⎢⎣⎡----=⎥⎥⎦⎤⎢⎢⎣⎡=-=--1030122211763452221)(11E A B *解 1*n A A-=.9.证 (1)由1124(2)(4)28A B B E A E B E E A E -=-⇒-⋅-=⇒-可逆,且 11(2)(4)8A EB E --=-(2)由(1)得102028(4)110002A E B E -⎛⎫⎪=+-=-- ⎪ ⎪-⎝⎭. 四、证明题：1.证：根据伴随矩阵的性质有E A AA =*又E A A =2，所以2A AA =*，再由于A 可逆，便有A A =*.2.证：假设A 可逆，即1-A 存在，以1-A 左乘0=AB 的两边得0=B ，这与B 是n 阶非零矩阵矛盾；类似的，若B 可逆，即1-B 存在，以1-B 右乘0=AB 的两边得0=A ，这与A 是n 阶非零矩阵矛盾，因此，A 和B 都是不可逆的. 第四节矩阵分块法1. 00011000100000010010010001000010010000100010010010000100011000r ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥→⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,所以100010001001000100100010010001000-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦. 2. ⎪⎪⎪⎪⎪⎭⎫⎝⎛---31313231000000520021. 3.A ；4.若1A -易求得,由*1A A A -=最简便.显然111,A O C C A B OB ---⎡⎤==⎢⎥⎣⎦1**11*A B A OB A OC C C O A B B O A B ---⎡⎤⎡⎤⇒===⎢⎥⎢⎥⎣⎦⎣⎦. 5. (1) 1()T APQ O A b A ααα-⎛⎫=⎪-⎝⎭. (2) 由(1)得0211()P A TT P Q PQ A b A Q b A αααα=≠--⋅==-=-. 6. 23423422288()40A B A B αβγγγαβγγγ+=+=+=+=.7. 11100100112120(2)01221001001B O B O A I A I O O --⎡⎤⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥-==⇒-==-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦⎢⎥⎣⎦. 8. (1)m m mnnnO A A O C B OOB =-从第n+1列开始每一列与前n 列逐列交换(1)mn m n A B =-(1)mn ab =-.自测题一.单项选择题：1.D 2.C 3.C 4．A5. B 二、填空题：1. 912.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-133 3.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---4332211 4.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=-11001200005200211A 5. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----O O 21313725 三.计算题1.由B X A =*得，AB X AA =*，即 AB X A = ，因为2-=A ，所以⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛-=00021152031000221X ⎪⎪⎪⎭⎫⎝⎛----=020111.2、1) B E B A E A AB E B A B A A B AA ⇒=-⇒+=⇒+=-)|(|||)(1*可逆.2) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-=--1111116166666)8(11A EB .3.111()[()]()()T T T T T T T A E C B C E A C C B C E A C B C C E ----=⇒-=⇒-=1()()()T T T A C B CC E A C B E -⇒-=⇒-=110001100[()]12100121T A C B -⎡⎤⎢⎥-⎢⎥⇒=-=⎢⎥-⎢⎥-⎣⎦. 4.-250；415. 由1113()3ABA BA E E A B E ---=+⇒-=.又3*82A A A ==⇒=,则**160000600()36(2)606010306A E B E B E A A -⎛⎫ ⎪⎪-=⇒=-= ⎪⎪ ⎪- ⎪⎝⎭四.证明题1.证由**T T A A AA AA A E =⇒==.假设0T A AA O =⇒=.考虑T AA 的主对角线上的元素,令()T ij AA B b ==,则222121200ii i i in i i in b a a a a a a =+++=⇒==== ,即A 的第i 行的元素全为零,由i 的任意性,得A 的元素全为零,即A O =,矛盾. 2.由23202A E A A E A E A ---=⇒⋅=⇒可逆,且12A EA --=.。

线性代数第二章课后习题

线性代数第二章课后习题习题二（A ）1 请按要求写出下列相应矩阵（1）3E ；（2）35O ?；（3）()3,1,2.=-3Λdiag2 设矩阵221,301A B ?==-+a b c c ，若A B =，请确定a,b,c 的值. 3 设矩阵300012111=,,565042112AB C-==-?，求,,23A B B C A C -++.4 设3023=12531?? ?- ? ?-??A ,求,2,3--+A E E A A E . 5 设矩阵3111110=21,=212031112AB- ? ?-，求矩阵X ，使得()53X B AB X +=+. 6 计算下列乘积：（1）AB 与BA ，其中A =????? ??600040002，B =333231232221131211a a a a a a a a a ；（2）()6543,2,1；（3）1023211231??-??- ? ??-??；（4）()321333231232221131211321,,x x x a a a a a a a a a x x x ；（5）??32142143143243210110100101001000. 7 211312101?? ?= ?-??A ，230101211??=- ? ?-??B ，求23-AB B ,T A B 及()T AB .8 设矩阵110010001?? ?= ? ???A ，求n A ，其中n 为自然数.9 设列矩阵A =()T12,n a a a ，满足T 1,=n A A E 为n 阶单位矩阵，T 2n =-B E AA ，证明（1）矩阵B 是对称矩阵；（2）T=n BB E .证毕10 设矩阵31212,01234031A B ??-==-- ? ??? ???，λ是实数，（1）计算λ-E A 和λ-E B ；（2）计算-E A λ和E B -λ.11 求下列方阵的逆矩阵 (1)4231；（2）cos sin sin cos ?? ?-??θθθθ；（3）111011001；（4）????? ??---145243121；（5）??---6000340042102521. 12 解下列矩阵方程：（1）25323714=X ；（2）211213*********-??-??= ? ??--??X ；(3) 0314********X=-??-??-?； (4) 010********0001201001010120-=- ? ? ? ? ? ?-?X ．13 设矩阵 1111111111111111?? ?--= ?-- ?--??A . (1) 求2A ；(2) 证明矩阵A 可逆，并求1-A ；(3) 求*1()-A .14 已知k=A O （k 为正整数），证明()121---=++++k E A E A A A .15 若矩阵A 满足224--=A A E O ，试证 (1) 矩阵A 可逆，并求1-A ;(2) 矩阵+A E 可逆，并求1()-+A E . 16 利用逆矩阵解下列线性方程组：(1) =++=++=++3531322522321321321x x x x x x x x x ；(2)=-+=--=--05231322321321321x x x x x x x x x ． 17 设矩阵A 和B 满足关系式2=+AB A B ，其中033011312A ??= ? ?-?，求矩阵B . 18 设矩阵A 和X 满足关系式2+=-XA E A X ，其中120340567??= ? ??A ，求矩阵X . 19（研2006数一，数二）设矩阵2112??=-??A ，E 为2阶单位矩阵，矩阵B 满足2=+BA B E ，则=B .20 （研2008数一，数二，数三）设A 为n 阶非零矩阵，E 为n 阶单位矩阵.若3=A O ，则（）（A ）-E A 不可逆，+E A 不可逆；（B ）-E A 不可逆，+E A 可逆；（C ）-E A 可逆，+E A 可逆；（D ）-E A 可逆，+E A 不可逆.21 （研2009数一，数二，数三）设,A B 均为2阶矩阵，,**A B 分别为,A B 的伴随矩阵.若2,3==A B ，则分块矩阵??O A B O 的伴随矩阵为（）（A ）32**?? ???O B A O ；（B ）23**?? ???O B A O ；（C ）32**O A B O ；（D ）23**?? ???O A B O .22 （研2010数二，数三）设,A B 为3阶矩阵，且13,2,2,-==+=A B A B 则1-+=A B .23（研2012数二）设A 为3阶矩阵，3=A ，*A 为A 的伴随矩阵，若交换A 的第1行与第2行得矩阵B ，则*=BA .24（研2013数一，数二，数三）设()ij a =A 是3阶非零矩阵，A 为A 的行列式，ij A 为ij a 的代数余子式，若()0,1,2,3ij ij a A i j +==，则=A .（B ）1（研2002数二）已知,A B 为3阶对称矩阵，且满足124-=-A B B E ，其中E 为3阶单位矩阵.（1）证明：矩阵2-A E 可逆，并求()2--A E ；（2）若矩阵012012002B ??- ?= ? ???，求矩阵A .2 设矩阵X 满足 12*-=+A X A B X ，其中111111111A ??- ?=- ? ?-??，110101B ?? ?= ? ?-??，求矩阵X .3（研2003数二）设3阶矩阵,A B 满足2--=A B A B E ，其中E 为3阶单位矩阵，011002021A ?? ?= ? ?-??，求B .4 设,A B 均为3阶矩阵，E 为3阶单位矩阵.已知2=+AB A B ，202040202??= ? ???B ，求()1--A E .5 设n 阶矩阵A 的伴随矩阵为*A ，证明： (1) 若0=A ，则*0=A ； (2) 1*-=n A A.6 设矩阵111222??=A A A O A ，其中ij A 是j i n n ?矩阵，证明矩阵A 可逆的充分必要条件是11A 及22A 均为可逆矩阵，并求1A -.7 设n 阶矩阵A 及s 阶矩阵B 都可逆，求1O O -??A B .8 求矩阵-000000000000121 n n a a a a 的逆矩阵，其中0≠i a ，n i ,,1 =.9（研2015数二）设矩阵101101a a a ?? ?=- ? ???A 且3=A O .（1）求a 的值；（2）若矩阵X 满足--+22X XA AX AXA =E ，E 为3阶单位阵，求X .10 设n 阶矩阵,,A B C 满足n ===AB BC CA E ，求222++A B C .。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

习题二（A ）
1 请按要求写出下列相应矩阵
（1）3E ；（2）35O ⨯；（3）()3,1,2.=-3Λdiag
2 设矩阵221,301A B ⎛
⎫⎛⎫==
⎪ ⎪
-+⎝⎭⎝⎭a b c c ，若
A B =，请确定a,b,c 的值. 3 设矩阵300012111=,,565042112A B C ⎛⎫⎛⎫⎛⎫
-==
⎪ ⎪ ⎪⎝⎭⎝⎭⎝-⎭
，
求,,23A B B C A C -++.
4 设3023=12
531⎛⎫ ⎪
- ⎪ ⎪-⎝⎭
A ,求,2,3--+A E E A A E . 5 设矩阵3111110=21,=212031112A
B ⎛⎫⎛⎫
- ⎪ ⎪
⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭
，
求矩阵X ，使得()53X B AB X +=+. 6 计算下列乘积：
（1）AB 与BA ，其中A =⎪⎪⎪⎭⎫ ⎝⎛600040002，B =⎪⎪⎪⎭
⎫
⎝⎛3332
31
232221
131211
a a a a a a a a a ；（2）()⎪⎪⎪
⎭
⎫ ⎝⎛6543,2,1；
（3）1023211231⎛⎫-⎛⎫
⎪- ⎪ ⎪⎝
⎭ ⎪-⎝⎭
；
（4）()⎪⎪⎪
⎭
⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321333231232221131211321,,x x x a a a a a a a a a x x x ；
（5）⎪⎪
⎪⎪
⎪
⎭
⎫
⎝⎛⎪⎪
⎪
⎪⎪
⎭⎫
⎝⎛3214214314324321
0110100101001000. 7 211312101⎛⎫ ⎪= ⎪
⎪
-⎝⎭
A ，230101211⎛⎫
⎪
=- ⎪ ⎪-⎝⎭B ，求23-AB B ,T A B 及()T AB .
8 设矩阵110010001⎛⎫ ⎪
= ⎪ ⎪⎝⎭
A ，求n A ，其中n 为自然数.
9 设列矩阵A =()T
12
,n a a a ，满足T 1,=n A A E 为n 阶单位矩阵，T 2n =-B E AA ，
证明（1）矩阵B 是对称矩阵；（2）T
=n BB E .
证毕
10 设矩阵31212,01234031A B ⎛⎫
- ⎪⎛⎫
==-- ⎪ ⎪⎝⎭ ⎪⎝⎭
，λ是实数，
（1）计算λ-E A 和λ-E B ；（2）计算-E A λ和E B -λ.
11 求下列方阵的逆矩阵 (1) ⎪⎪⎭
⎫
⎝⎛4231；（2）cos sin sin cos ⎛⎫ ⎪
-⎝⎭θ
θθθ；（3）⎪⎪⎪⎭
⎫ ⎝⎛111011001；（4）⎪⎪⎪⎭⎫ ⎝⎛---145243121
；（5）⎪⎪
⎪⎪
⎪
⎭
⎫
⎝
⎛---60003400421025
2
1
. 12 解下列矩阵方程：
（1）25323714⎛⎫⎛⎫
=
⎪ ⎪⎝⎭⎝⎭X ；（2）211213*********-⎛⎫-⎛⎫
⎪= ⎪ ⎪⎝
⎭ ⎪--⎝⎭X ；
(3) 0314********X ⎛⎫⎛⎫⎛⎫
=
⎪ ⎪ ⎪⎝-⎭⎝-⎭⎝-⎭
； (4) 010********
00
01201001010120-⎛⎫⎛⎫⎛⎫
⎪ ⎪ ⎪=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝
⎭⎝⎭⎝⎭
X ．
13 设矩阵 1111111111111111⎛⎫ ⎪--
⎪= ⎪-- ⎪--⎝⎭
A . (1) 求2A ；
(2) 证明矩阵A 可逆，并求1-A ；
(3) 求*1
()-A .
14 已知k
=A O （k 为正整数），证明
()
1
21---=++++k E A E A A A .
15 若矩阵A 满足2
24--=A A E O ，试证 (1) 矩阵A 可逆，并求1-A ;
(2) 矩阵+A E 可逆，并求1
()-+A E . 16 利用逆矩阵解下列线性方程组：
(1) ⎪⎩⎪⎨⎧=+
+=++=++3531322
5223
2
1
321
321x x x x x x x x x ；(2) ⎪⎩⎪
⎨⎧=-+=
--
=-
-0
52313223
2
1
32
1
3
21x x x x x x x x x ． 17 设矩阵A 和B 满足关系式2=+AB A B ，其中03
3011
312A ⎛⎫
⎪
= ⎪ ⎪-⎝
⎭，求矩阵B . 18 设矩阵A 和X 满足关系式2
+=-XA E A X ，其中1203
40567⎛⎫
⎪= ⎪ ⎪⎝
⎭
A ，求矩阵X . 19（研2006数一，数二）设矩阵2112⎛⎫
=
⎪-⎝⎭
A ，E 为2阶单位矩阵，矩阵
B 满足
2=+BA B E ，则=
B .
20 （研2008数一，数二，数三）设A 为n 阶非零矩阵，E 为n 阶单位矩阵.若3
=A O ，则（）
（A ）-E A 不可逆，+E A 不可逆；（B ）-E A 不可逆，+E A 可逆；（C ）-E A 可逆，+E A 可逆；（D ）-E A 可逆，+E A 不可逆.
21 （研2009数一，数二，数三）设,A B 均为2阶矩阵，,*
*
A B 分别为,A B 的伴随矩阵.若2,3==A B ，则分块矩阵⎛⎫
⎪⎝⎭
O A B O 的伴随矩阵为（）
（A ）32**⎛⎫ ⎪⎝⎭O B A O ；（B ）23**⎛⎫ ⎪⎝⎭O B A O ；（C ）32**
⎛⎫ ⎪⎝⎭O A B O ；（D ）23**⎛⎫ ⎪⎝⎭
O A B O .
22 （研2010数二，数三）设,A B 为3阶矩阵，且13,2,2,-==+=A B A B 则
1-+=
A B .
23（研2012数二）设A 为3阶矩阵，3=A ，*A 为A 的伴随矩阵，若交换A 的第1行与第2行得矩阵B ，则*=
BA .
24（研2013数一，数二，数三）设()
ij a =A 是3阶非零矩阵，A 为A 的行列式，ij A 为ij a 的代数余子式，若()0,1,2,3ij ij a A i j +==，则=
A .
（B ）
1（研2002数二）已知,A B 为3阶对称矩阵，且满足1
24-=-A B B E ，其中E 为3阶单位矩阵.
（1）证明：矩阵2-A E 可逆，并求
()
1
2--A E ；
（2）若矩阵012012002B ⎛⎫- ⎪
= ⎪ ⎪⎝⎭
，求矩阵A .
2 设矩阵X 满足 1
2*-=+A X A B X ，其中
111111111A ⎛⎫- ⎪=- ⎪ ⎪-⎝⎭，110101B ⎛⎫ ⎪= ⎪ ⎪-⎝⎭
，
求矩阵X .
3（研2003数二）设3阶矩阵,A B 满足2
--=A B A B E ，其中E 为3阶单位矩阵，011002021A ⎛⎫ ⎪
= ⎪ ⎪-⎝⎭
，求B .
4 设,A B 均为3阶矩阵，E 为3阶单位矩阵.已知2=+AB A B ，202040202⎛⎫
⎪
= ⎪ ⎪⎝⎭
B ，
求()1
--A E .
5 设n 阶矩阵A 的伴随矩阵为*
A ，证明： (1) 若0=A ，则*
0=A ； (2) 1
*
-=n A A
.
6 设矩阵11
1222⎛⎫
=
⎪⎝⎭
A A A O A ，其中ij A 是j i n n ⨯矩阵，证明矩阵A 可逆的充分必要条
件是11A 及22A 均为可逆矩阵，并求1A -.
7 设n 阶矩阵A 及s 阶矩阵B 都可逆，求1
O O -⎛⎫
⎪⎝⎭
A B .
8 求矩阵 ⎪⎪⎪⎪⎪
⎪⎭⎫ ⎝⎛-000000000000121 n n a a a a 的逆矩阵，其中0≠i a ，n i ,,1 =.
9（研2015数二）设矩阵101101a a a ⎛⎫ ⎪
=- ⎪ ⎪⎝⎭
A 且3=A O .
（1）求a 的值；
（2）若矩阵X 满足--+22X XA AX AXA =E ，E 为3阶单位阵，求X .
10 设n 阶矩阵,,A B C 满足n ===AB BC CA E ，求222
++A B C .。

线性代数第二章课后习题

第二章-线性代数(第四版)习题答案

线性代数第2章习题课

《线性代数》第二章矩阵及其运算精选习题及解答

线性代数第二章习题课

线性代数答案第二章(同济)

线代第2章习题答案

《线性代数》第二章参考答案+详解

线性代数第二章练习题

高等数学 线性代数 习题答案第二章

线性代数第二章习题及解答

【复旦版线代】线性代数第二章课后习题及详细解答

线性代数习题册(第二章矩阵及其运算参考答案)

线性代数习题 第二章 (附详解)

线性代数第二章习题部分答案(

经济数学线性代数第二章习题答案

大学线性代数第二章习题答案

线性代数第二章课后习题

高等数学线性代数习题答案第二章

线性代数习题第二章 (附详解)