2014年虎跳中学中考数学模拟试题 (15)
广元市虎跳中学2014届九年级上第一次诊断性考试数学试题

虎跳中学2013秋第一次诊断性考试九年级数学试卷(满分120分,考试时间120分钟)一、选择题(每题3分,共30分)1、如果有意义,则的取值范围是()A. B. C. D.2、化简的结果是()A 5B -5C 士5D 253.下列图形中,既是中心对称图形又是轴对称图形的是()A B C D4、一元二次方程的解是()A、 B、 C、 D、5.方程的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法确定是否有实数根6、关于的一元二次方程的一个根为0,则的值是()A. B.C.或-1 D.7.7 7、三角形两边的长分别是4和6,第三边的长是一元二次方程的一个实数根,则该三角形的周长是()A、20B、20或16C、16D、18或218.若,则()A a,b互为相反数B a,b互为倒数CD a=b9、方程(x-5)(x+2)=1的根为()A、 5B、 -2C、 -2或5D、以上均不对10下列语句中不正确的有()①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④半圆是弧.A.1个B.2个C.3个D.4个二、填空题(每小题3分,共15分)11、点P(-2,4)关于坐标原点对称的点的坐标是( )12.一元二次方程x2-8=-2x的.二次项系数是_________,一次项系数是_________,常数项是_______13、关于x的一元二次方程有两个不相等的实数根, 则k的取值范围是_______________________.14、已知方程x2-7x+12=0的两根恰好是Rt△ABC的两条边的长,则Rt△ABC•的第三边长为________ .15、观察下列各式:请你将发现的规律用含自然数n(n≥1)的等式表示出来__________________________三、计算和解方程(每小题5分,共30分)16、计算(1) ① (2)17、解方程(1)(公式法)(2)(3)(4)(配方法)四、解答题(每小题7分,共21分)18、已知当a=+1时先化简再求值。
2014年九年级数学中考模拟复习试卷 及答案
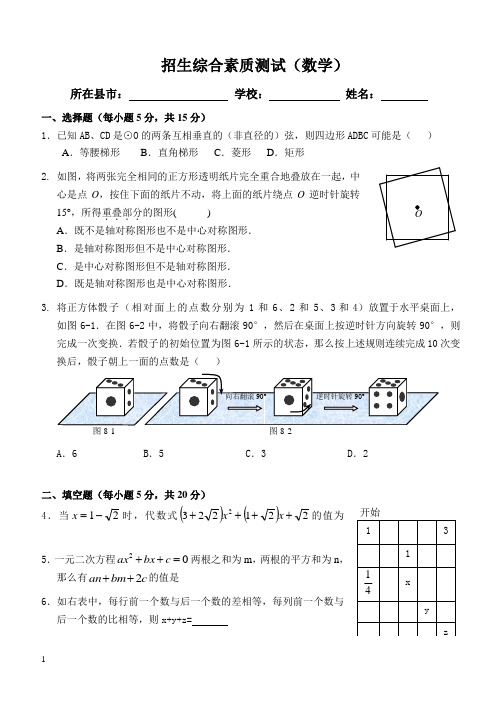
招生综合素质测试(数学)所在县市: 学校: 姓名:一、选择题(每小题5分,共15分)1.已知AB 、CD 是⊙O 的两条互相垂直的(非直径的)弦,则四边形ADBC 可能是( ) A .等腰梯形 B .直角梯形 C .菱形 D .矩形2. 如图,将两张完全相同的正方形透明纸片完全重合地叠放在一起,中心是点O ,按住下面的纸片不动,将上面的纸片绕点O 逆时针旋转15°,所得重叠部分....的图形( ) A .既不是轴对称图形也不是中心对称图形. B .是轴对称图形但不是中心对称图形. C .是中心对称图形但不是轴对称图形. D .既是轴对称图形也是中心对称图形.3. 将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图6-1.在图6-2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图6-1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )A .6B .5C .3D .2二、填空题(每小题5分,共20分)4.当21-=x 时,代数式()()2212232++++x x_________ 5.一元二次方程02=++c bx ax 两根之和为m ,那么有c bm an 2++的值是_________6后一个数的比相等,则x+y+z=AB7.等边三角形等边ABC ∆内接于⊙O ,P 是劣弧 AB ︵上一点(不与A 、B 重合),将PBC ∆绕C 点顺时针旋转60º,得D A C ∆,AB 交PC 于E .则下列结论正确的序号是 . ① P A +PB =PC ; ②CE PC BC ⋅=2;③ 四边形ABCD 有可能成为平行四边形; ④ PCD ∆的面积有最大值. 三、解答题8.(10分)小明有一副三角尺和一个量角器(如图所示).(1; (2)请用这三个图形中的两个..拼成一个轴对称图案,画出草图(须画出四种); (3)小红也有同样的一副三角尺和一个量角器.若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?(请画树状图或列表计算)9.(14分)已知函数222-+=px x y ,当02≤≤-x 时的最小值为M , (1)求M 关于p 的函数解析式;(2)当3-=M 时,求函数222-+=px x y ,当02≤≤-x 时的最大值.10.(16分)如图,在平面直角坐标系中,Rt△ABO的顶点B在x轴上,点A坐标为(0,12),y 沿O→B→A方向进行平移,平移后的抛物线顶点为P.点B坐标为(6,0),抛物线2x(1)求线段AB所在直线的函数表达式;(2)如图1,当点P与点B重合时,抛物线与AB的另一交点为M,求线段BM(即PM)的长;(3)如图2,当点P在AB上时,抛物线与AB的另一交点为N,求以PN为直径的⊙I与y(A,A) (A,B参考答案一、ADB二、 4.2 5. 0 6. 1 7.②③④三、8.解:(1)B,C …………2分(2)如:等…………5分(3或…8分一共有9种结果,每种结果出现的可能性是相同的.而其中能恰好拼成轴对称图形的结果有五种,分别是(A,A) 、(B,B)、(C,C)、(B,C)、(C,B),所以两件文具可以拼成一个轴对称图案的概率是59.…………10分9.解:(1)2)(22222--+=-+=ppxpxxy当02≤≤-x时①当-p<-2,即p>2时,函数最小值M=2-4p …………2分②02≤≤p时,函数最小值M=22--p…………5分③p<0时,函数最小值M=-2 …………7分∴M关于p的函数解析式⎪⎩⎪⎨⎧<-≤≤-->-=,220,22,422pppppy…………9分(2)由M=-3知,⎩⎨⎧-=->3422pp或⎩⎨⎧-=--≤≤3222pp…………12分(A,A) ((C,C)CBA (A∴p=1, ∴y=3)1(2222-+=-+x x x∴当02≤≤-x 时函数最大值为-2. …………14分10. 解:(1)设直线AB 是y =kx +b∵点A 、B 的坐标是(0,12)、(6,0)⎩⎨⎧+==b6k 012b 解得:b =12,k =-2 ∴直线AB 的解析式是y =-2x +12 …………3分 (2)当点F 与点B 重合时,抛物线的顶点是(6,0)∴抛物线的解析式是y =(x -6)2,即y =x 2-12x +36 …………4分 ∵点M 是抛物线与直线AB 的交点由x 2-12x +36=-2x +12解得x 1=4,x 2=6(与点p 重合) 当x 1=4时,y =4∴M 的坐标是(4,4) …………6分作ME ⊥OB 于E ,得MF =4,BE =6-4=2 在Rt △MEB 中,根据勾股定理得BM =522422=+ …………8分 (3)当抛物线沿BA 方向平移时, ∵抛物线的顶点P 在直线AB 上, N 是抛物线与直线AB 的交点∴PN 是由(2)中的线段BM 沿BA 方向平移得到的 根据平移的性质得PN =BM =52 ………10分 已知PN 是⊙I 的直径,I 是PN 的中点当⊙I 与y 轴相切时,IC =PI =5 …………11分过点I 、P 分别作y 轴的垂线,垂足分别是C 、D∴511266sin 22=+=∠==OAB APPD AIIC∴55,55+=+===IP AI AP IC AI∴PD=155)55(5+==+∙AI APIC …………13分∵点P 在直线y =-2x +12,当x =15+时, ∴y =-2521012)15(-=++ …………15分 ∴当⊙I 与y 轴相切时,P 点坐标为(15+,10-25) (也可通过证明△ACI 、△ADP 、△AOB 相似求得) …………16分。
2014年中考数学模拟试卷(五)

2014年中考数学模拟试卷 (五)(满分100分,考试时间120分钟 ) 班级 姓名 考号 等分 一、选择题(本题共10 小题,每小题3分,满分30分)每一个小题都给出代号为A 、B 、C 、D 的四个结论,其中只有一个是正确的,把正确结论的代号写在题后的括号。
每一小题:选对得 4 分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分。
1.-3的绝对值是…………………………………………………………………………【 】 A.3B.-3C.13D. 13- 2. 下列多项式中,能用公式法分解因式的是………………………………………………【 】 A.x 2-xy B. x 2+xy C. x 2-y 2 D. x 2+y 23. 2007年我省为135万名农村中小学生免费提供教科书,减轻了农民的负担,135万用科学计数法可表示为……………………………………………【 】A.0.135×106B.1.35×106C.0.135×107D.1.35×1074.如图,在⊙O 中,∠ABC=50°,则∠AOC 等于………………………………………………【 】 A.50° B.80° C.90° D. 100°5. 分式方程112x x =+的解是………………………………………………………………【 】 A. x=1 B. x=-1 C. x=2 D. x=-26.如图是某几何体的三视图及相关数据,则判断正确的是…………………………………【 】 A. a >c B. b >c C. 4a 2+b 2=c 2 D. a 2+b 2=c 2第4题图OACB第6题图7.函数ky x=的图象经过点(1,-2),则k 的值为……………………………………………【 】 A. 12 B. 12- C. 2 D. -28. 某火车站的显示屏,每隔4分钟显示一次火车班次的信息,显示时间持续1分钟,某人到达该车站时,显示屏上正好显示火车班次信息的概率是……………………………………【 】A.16B.15C.14D. 139. 如图是我国2003~2007年粮食产量及其增长速度的统计图,下列说法不正确...的是…………【 】 A .这5 年中,我国粮食产量先增后减 B .后4年中,我国粮食产量逐年增加 C .这5 年中,我国粮食产量年增长率最大 D .这5 年中,我国粮食产量年增长率最小10.如图,在△ABC 中,AB=AC=5,BC=6,点M 为BC 中点,MN ⊥AC 于点N ,则MN 等于…………………【 】A.65B. 95C. 125D. 165二、填空题(本题共 4 小题,每小题 3分,满分 12分) 11.12.如图,已知a ∥b ,∠1=70°,∠2=40°,则∠3= __________。
2014年初中毕业学业考试模拟考数学试卷(含答案)
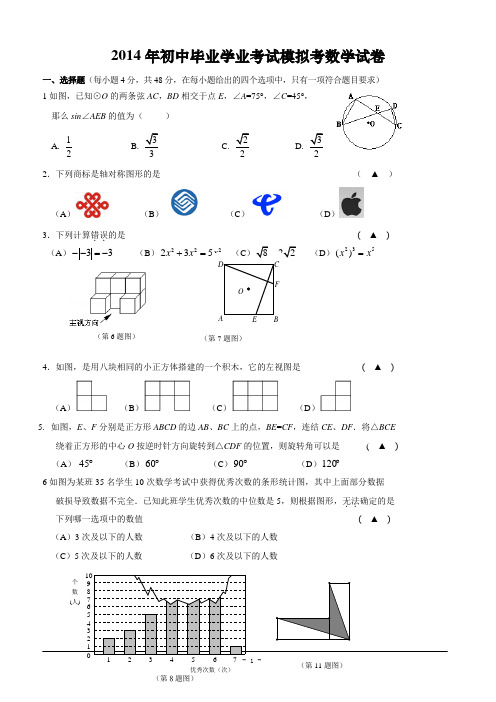
2014年初中毕业学业考试模拟考数学试卷一、选择题(每小题4分,共48分,在每小题给出的四个选项中,只有一项符合题目要求) 1如图,已知⊙O 的两条弦AC ,BD 相交于点E ,∠A =75°,∠C =45°, 那么sin ∠AEB 的值为( ) A.12B.C. 2D. 2.下列商标是轴对称图形的是 ( ▲ )(A ) (B )(C ) (D )3.下列计算错误..的是 ( ▲ ) (A )33--=- (B )2223x x+= (D )235()x x =4.如图,是用八块相同的小正方体搭建的一个积木,它的左视图是 ( ▲ )(A ) (B ) (C ) (D )5. 如图,E 、F 分别是正方形ABCD 的边AB 、BC 上的点,BE =CF ,连结CE 、DF .将△BCE 绕着正方形的中心O 按逆时针方向旋转到△CDF 的位置,则旋转角可以是 ( ▲ )(A ) ︒45 (B )︒60 (C )︒90 (D )︒1206如图为某班35名学生10次数学考试中获得优秀次数的条形统计图,其中上面部分数据 破损导致数据不完全.已知此班学生优秀次数的中位数是5,则根据图形,无法..确定的是 下列哪一选项中的数值 ( ▲ ) (A )3次及以下的人数 (B )4次及以下的人数 (C )5次及以下的人数 (D )6次及以下的人数 (第6题图)7.下面给出了一些关于相似的命题,其中真命题有 ( ▲ ) (1)菱形都相似 (2)等腰直角三角形都相似(3)正方形都相似 (4)矩形都相似 (5)正六边形都相似(A ) 1 个 (B ) 2个 (C ) 3个 (D ) 4个 8在平面直角坐标系中,已知两点A (1,2),B (2,0),把线段AB 平移后得线段CD , 其中A 点对应点是C (3,a ),B 点对应点是D (b ,1),则a -b 的值为 ( ▲ ) (A )1- (B )0 (C )1 (D )29两个完全相同的矩形如图放置,每个矩形的面积为28,图中阴影部分的面积为20,则每个矩形的周长是 ( ▲ ) (A )18 (B )22 (C )26 (D )3210.如图,在△ABC 中,AB =AC ,且∠A =108°,点P 为△ABC 所在平面内一点,且点P 与△ABC 的任意两个顶点构成△PAB 、△PBC 、△PAC 均是等腰三角形,则满足上述条件的所有点P 个数为 ( ▲ )(A )4 (B )6 (C )8 (D )10二、填空题(每小题4分,共24分)13.分解因式:22x x - = ▲ .14.若一个正多边形的一个外角是30,则这个正多边形的边数是 ▲ .15.为了缓解江北区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图).已知立杆AB 的高度是3m ,从侧面D 点测得显示牌顶端C 点和底端B 点的仰角分别是60和45.则路况显示牌的宽度BC 是 ▲ 米.(结果保留根号) 16如图,在△ABC 中,∠C =90°,以AB 上一点O 为圆心,OA 长为半径的圆与BC 相切于点D ,分别交AC 、AB 于点E 、F .若AC =6,AB =10,则⊙O 的半径为______________.17.如图,在正方形网格中,点O 、A 、B 均在格点上,则∠AOB 的正弦值是 ▲ . 18.如图,已知等边ABC △,D 是边BC 的中点,过D 作DE ∥AB 于E , 连结BE 交AD 于D 1;过D 1作D 1E 1∥AB 于E 1,连结BE 1交AD 于D 2;过D 2作D 2E 2∥AB 于E 2,…,如此继续,若记BDE S △为S 1,记11B D E S △为S 2,记22BD E S △为S 3…,若ABC S △面积为Scm 2,则Sn =_________cm 2. (用含n 与S 的代数式表示)三、解答题(本大题有8小题,共78分)(第15题图)(第12题图)(第17题图)19.(本题6分)请先化简:xx x ---2111,再选择一个合适的x 值代入求值.20.(本题8分)如图,已知一次函数与反比例函数的图象交于点 A (-3,-1)和B (a ,3).(1)求反比例函数的解析式和点B 的坐标;(2)连结AO 和BO ,判断△ABO 的形状,请说明理由,并求出它的面积.21.(本题6分)已知:如图,斜坡BQ 坡度为i =1︰2.4(即为QC 与BC 的长度之比),在斜坡BQ 上有一棵香樟树PQ ,柳明在A 处测得树顶点P 的仰角为α,并且测得水平的AB =8米,另外BQ =13米,tanα=0.75.点A 、B 、P 、Q 在同一平面上,PQ ⊥AB 于点C .求香樟树PQ 的高度.22.(本题10分)如图,在△ABC 中,AB =AC ,以AB为直径的O 分别交AC 、BC 于点D 、E ,点F在AC 的延长线上,且12CBF CAB ∠=∠.(1)求证:直线BF 是O 的切线;(2)若AB =5,sin CBF ∠=BC 和BF 的长.(第20题图)(第22题图)C(第21题)23.(本题10分)如图,△ABC 的边长分别为21、23、1,正六边形网格是由24个边长为1的正三角形组成,每个正三角形的顶点称为网格的格点.在下面三个正六边形网格中各画出一个三角形(画出三角形,并用阴影填充),使其同时满足下面三个条件:(1)三个三角形的顶点都在格点上;(2)三个三角形都与△ABC 相似;(3)三个三角形的面积大小都不同.并直接写出三个三角形与△ABC 的相似比.相似比: 相似比: 相似比:24.(本题12分)如图,在矩形ABCD 中,AB =1,BC =3,F 为线段..AD 上一点(不与端点A ,D 重合),过F 的直线交矩形的另一边于点E ,且该直线满足21tan =∠DFE ,设AF 长度为x . (1)记BEF △的面积为S ,求S 与x 的函数关系式;(2)当点E 在线段BC 上时,若矩形ABCD 关于直线EF 的对称图形为矩形A ’B ’C ’D ’,试说明矩形ABCD与矩形A ’B ’C ’D ’理由.CB A25.(本题14分)如图,已知二次函数图象的顶点为P(0,-1),且过点(2,3).点A是抛物线上一点,过点A作y轴的垂线,交抛物线于另一点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD.(1)求此二次函数的解析式;x轴交点记为E,证明:(2)当点A在第一象限....内时,PA与①PED PDA△∽△;②∠APC=90°;(3)若∠APD=45°,当点A在y.轴右侧...时,请直接写出点A的坐标.(第26题图)(备用图)参考答案及评分标准一、选择题(每小题4分,共48分,在每小题给出的四个选项中,只有一项符合题目要求)14分,共78分)注: 1. 阅卷时应按步计分,每步只设整分;2. 如有其它解法,只要正确,都可参照评分标准,各步相应给分.19. (本题6分)2111x x x--- 111(1)x x x =--- 1分 1(1)x x x -=-1x= 4分满足1,0x ≠的值代入都可 6分20.(本题8分):(1)设xky =,将A (﹣3,﹣1)代入,求得k =3, 1分xy 3=2分 将B (a ,3)代入,求得a =1 3分B (1,3) 4分(2)AO =BO =10 5分 等腰三角形 6分 S ABC △=4 8分21.(本题22.(本题10分)相似比:2:1相似比:1:32 相似比:4:1画对1个给2分,2个4分,3个都对得7分,每个相似比正确得1分,共3分。
2014年数学中考模拟测试卷剖析

2014 年数学中考模拟测试卷二一.选择题(共10 小题)1.( 2013?自贡)与﹣ 3 的差为0 的数是()A . 3B.﹣3C.D.2.( 2013?邵阳)如图是某班学生参加兴趣小组的人数占总人数比率的统计图,则参加人数最多的课外兴趣小组是()A .棋类组B.演唱组3.( 2013?漳州)如图,几何体的俯视图是(C.书法组)D.美术组A.B.C.D.4.( 2013?宜昌)以下每组数分别表示三根木棒的长度,将它们首尾连结后,能摆成三角形的一组是()A .1,2,6B. 2,2,4C. 1, 2,3D. 2, 3,45.( 2013?黑龙江)已知对于x 的分式方程=1的解是非正数,则a 的取值范围是()A . a≤﹣ 1B. a≤﹣ 1 且a≠﹣ 2C. a≤1 且 a≠﹣ 2D. a≤16.( 2013?漳州)若反比率函数y=的图象经过点(﹣2, m),则m 的值是()A .B.﹣C.﹣4D. 47.( 2013?徐州)如图, AB 是⊙ O 的直径,弦 CD ⊥ AB ,垂足为 P.若 CD=8 ,OP=3,则⊙ O 的半径为()A .10B . 8C .5D .38.( 2013?贵阳)如图,P 是∠ α的边 OA 上一点,点 P 的坐标为( 12,5),则 tan α等于( )A .B .C .D .9.( 2013?新疆)如图, △ABC 中, DE ∥ BC ,DE=1 ,AD=2 ,DB=3 ,则 BC 的长是( )A .B .C .D .10.( 2013?台湾)如图,将一张直角三角形纸片沿虚线剪成甲、乙、丙三块,此中甲、丙为梯形,乙为三角形.依据图中标示的边长数据,比较甲、乙、丙的面积大小,以下判断何者正确?()A . 甲>乙,乙>丙B . 甲>乙,乙<丙C . 甲<乙,乙>丙D . 甲<乙,乙<丙二.填空题(共 6 小题)11.(2013?昭通)因式分解: 2x 2﹣ 18= _________ .12.( 2013?阳)若一_________.2, 1, 0,2, 1,a 的众数2,数据的均匀数13.( 2013?湘潭)如右,已知:AB ∥CD ,∠ C=25 °,∠ E=30 °,∠A=_________.14.( 2013?黔西南州)已知x=1 是一元二次方程222x +ax+b=0 的一个根,代数式 a +b +2ab的是_________.15.( 2013?州)如,在正方形 ABCD 中, E 是 AB 上一点, BE=2 , AE=3BE ,P 是 AC 上一点,PB+PE 的最小是 _________ .16.( 2013?州)如,△ ABC是斜AB的3的等腰直角三角形,在△ABC内作第1 个内接正方形 A 1B1D1E1( D1、 E1在 AB 上, A 1、B 1分在 AC 、 BC 上),再在△A 1B1C内接同的方法作第 2 个内接正方形 A 2B 2D2E2,⋯这样下去,操作n 次,第 n 个小正方形 A n B n D n E n的是 _________.三.解答(共8 小)217.( 2013?三明)(1)算:( 2) +2sin30°;(2)先化,再求:( a+2)( a 2) +4( a+1) 4a,此中 a=1.18.( 2013?舟山)如图,△ ABC 与△ DCB 中, AC 与 BD 交于点 E,且∠ A= ∠ D,AB=DC .(1)求证:△ ABE ≌ DCE ;(2)当∠ AEB=50 °,求∠ EBC 的度数?19.(2013?枣庄)图 1、图 2 是两张形状、大小完整同样的方格纸,方格纸中的每个小正方形的边长均为 1,点 A 和点 B 在小正方形的极点上.(1)在图 1 中画出△ ABC (点 C 在小正方形的极点上),使△ABC 为直角三角形(画一个即可);(2)在图 2 中画出△ ABD (点 D 在小正方形的极点上),使△ ABD 为等腰三角形(画一个即可).20.( 2013?云南)已知在△ ABC 中, AB=AC=5 , BC=6 , AD 是 BC 边上的中线,四边形ADBE 是平行四边形.(1)求证:四边形 ADBE 是矩形;(2)求矩形 ADBE 的面积.21.( 2013?徐州)一只不透明的袋子中装有白球搅匀后从中随意摸出 1 个球,记下颜色后不放回,或画树状图的方法求两次都摸出白球的概率.2 个和黄球 1 个,这些球除颜色外都同样,搅匀后再从中随意摸出 1 个球,请用列表22.( 2013?营口)如图,点 C 是以 AB 为直径的⊙直,垂足为点 D .(1)求证: AC 均分∠ BAD ;(2)若 CD=1, AC=,求⊙ O的半径长.O 上的一点,AD与过点 C 的切线相互垂23.( 2013?六盘水)为了抓住2013 年凉都消夏文化节的商机,某商场决定购进甲,乙两种纪念品,若购进甲种纪念品 1 件,乙种纪念品 2 件,需要 160 元;购进甲种纪念品 2 件,乙种纪念品 3 件,需要280 元.(1)购进甲乙两种纪念品每件各需要多少元?(2)该商场决定购进甲乙两种纪念品100 件,而且考虑市场需乞降资本周转,用于购置这些纪念品的资本许多于6000 元,同时又不可以超出6430 元,则该商场共有几种进货方案?(3)若销售每件甲种纪念品可赢利30 元,每件乙种纪念品可赢利12 元,在第( 2)问中的各样进货方案中,哪一种方案赢利最大?最大收益是多少元?24.( 2013?太原)综合与研究:如图,抛物线 y=x 2﹣ x ﹣4 与 x 轴交与 A , B 两点(点B 在点 A 的右边),与 y 轴交于点C ,连结 BC ,以 BC 为一边,点 O 为对称中心作菱形 BDEC ,点 P 是 x 轴上的一个动点,设点 P 的坐标为( m , 0),过点 P 作 x 轴的垂线 l 交抛物线于点 Q .( 1)求点 A , B , C 的坐标.( 2)当点 P 在线段 OB 上运动时,直线 l 分别交 BD ,BC 于点 M ,N .尝试究 m 为什么值时, 四边形 CQMD 是平行四边形,此时,请判断四边形 CQBM 的形状,并说明原因.(3)当点 P 在线段 EB 上运动时,能否存在点 Q ,使 △ BDQ 为直角三角形?若存在,请直接写出点 Q 的坐标;若不存在,请说明原因.2014 年 5 月中考模拟试卷参照答案与试题分析一.选择题(共10 小题)1.B2.B3.D4.D5.B6.C7.C8.C9.C10.D解答:解:如图:过点 B 作 BH ⊥GF 于点 H,则 S乙= AB?AC,∵AC∥DE,∴△ ABC ∽△ DBE ,∴,∵BC=7 , CE=3,∴ DE=AC , DB=AB ,∴ AD=BD﹣BA=AB ,∴S丙=( AC+DE)?AD=AB ?AC ,∵A∥ GF, BH ⊥ GF, AC ⊥AB ,∴BH∥AC ,∴四边形BDFH 是矩形,∴ BH=DF , FH=BD=AB ,∴△ GBH ∽△ BCA ,∴,∵GB=2 , BC=7 ,∴GH= AB,BH AC,∴ DF=AC , GF=GH+FH=AB,∴S甲=( BD+GF )?DF=AB ?AC,∴甲<乙,乙<丙.应选 D.评论:本题考察了相像三角形的判断与性质、直角梯形的性质以及直角三角形的性质.本题难度适中,注意掌握数形联合思想的应用.二.填空题(共 6 小题)11.2( x+3 )(x﹣ 3)12.13. 55°14. 115. 10解答:解:如图,连结DE,交 AC∵四边形ABCD 是正方形,于 P,连结BP,则此时PB+PE的值最小.∴B、 D 对于 AC 对称,∴PB=PD,∴PB+PE=PD+PE=DE .∵BE=2 , AE=3BE ,∴ AE=6 , AB=8 ,∴ DE==10 ,故 PB+PE 的最小值是10.故答案为: 10.评论:本题考察了轴对称﹣最短路线问题,正方形的性质,解本题往常是利用两点之间,线段最短的性质得出.16.三.解答题(共8 小题)17.解:(1)原式=4+3﹣2× =4+3﹣1=6;解答:(2)原式 =a 2﹣ 4+4a+4﹣ 4a=a2,当 a=﹣ 1 时,原式 =(2﹣1) =2﹣2 +1=3﹣2 .评论:本题考察了整式的混淆运算﹣化简求值,以及实数的运算,波及的知识有:完整平方公式,平方差公式,单项式乘多项式,去括号法例,以及归并同类项法例,娴熟掌握公式及法例是解本题的重点.18.(1)证明:∵在△ABE和△DCE中解答:∴△ ABE ≌△ DCE ( AAS );(2)解:∵△ ABE ≌△ DCE,∴ BE=EC ,∴∠ EBC= ∠ ECB ,∵∠ EBC+ ∠ ECB= ∠AEB=50 °,∴∠ EBC=25 °.主要考察学生的推理评论:本题考察了三角形外角性质和全等三角形的性质和判断的应用,能力.19.解:( 1)如图1,① 、②,画一个即可;解答:( 2)如图 2,①、② ,画一个即可.评论:本题考察了应用与设计作图,(1)中作直角三角形时依据网格的直角作图即可,比较简单,( 2)中依据网格构造作出与 AB 相等的相等是解题的重点,灵巧性较强.20.解:(1)∵ AB=AC,AD是BC的边上的中线,解答:∴ AD ⊥ BC ,∴∠ ADB=90 °,∵四边形ADBE 是平行四边形.∴平行四边形ADBE 是矩形;(2)∵ AB=AC=5 , BC=6, AD 是 BC 的中线,∴ BD=DC=6 × =3,在直角△ACD 中,AD===4,∴S 矩形ADBE =BD ?AD=3 ×4=12.评论:本题考察了三线合必定理以及矩形的判断,理解三线合必定理是重点.21.解:列表以下:解答:白白黄白﹣﹣﹣(白,白)(黄,白)白(白,白)﹣﹣﹣(黄,白)黄(白,黄)(白,黄)﹣﹣﹣全部等可能的状况数为 6 种,此中两次都是白球的状况数有 2 种,则 P 两次都为白球 == .评论:本题考察了列表法与树状图法,用到的知识点为:概率=所讨状况数与总状况数之比.22.解( 1)证明:连结OC.答:∵ OA=OC ,∴∠ ACO= ∠CAO .∵CD切⊙O于 C,∴ OC⊥CD,又∵ AD ⊥ CD,∴AD ∥CO,∴∠ DAC= ∠ACO ,∴∠ DAC= ∠CAO ,即 AC 均分∠ BAD ;( 2)解法一:如图 2①,过点 O 作 OE⊥ AC 于 E.在 Rt△ADC 中, AD===3,∵OE⊥ AC ,∴ AE= AC=.∵∠ CAO= ∠DAC ,∠ AEO= ∠ ADC=90 °,∴△ AEO ∽△ ADC ,∴,即,∴ AO=,即⊙ O的半径为.解法二:如图2②,连结 BC.在 Rt△ADC 中, AD===3.∵AB 是⊙ O 直径,∴∠ ACB=90 °,∵∠ CAB= ∠DAC ,∠ ACB= ∠ ADC=90 °,∴△ ABC ∽△ ACD ,∴,即,∴ AB=,∴=,即⊙ O 的半径为.评论:本题考察了等腰三角形、平行线的性质,勾股定理,垂径定理,切线的性质,相像三角形的判断与性质.本题难度适中,注意掌握协助线的作法及数形联合思想的应用.23.解:(1)设购进甲乙两种纪念品每件各需要x 元和 y 元,依据题意得:解答:,解得:,答:购进甲乙两种纪念品每件各需要80 元和 40 元;(2)设购进甲种纪念品 a 件,则乙种纪念品( 100﹣ a)件,依据题意得:,解得: 50≤a≤,∵a 只好取整数, a=50, 51,52, 53,54, 55, 56, 57, 58, 59, 60,∴共 11 种进货方案,方案 1:购进甲种纪念品50 件,则购进乙种纪念品50 件;方案 2:购进甲种纪念品51 件,则购进乙种纪念品49 件;方案 3:购进甲种纪念品52 件,则购进乙种纪念品48 件;方案 4:购进甲种纪念品53 件,则购进乙种纪念品47 件;方案 5:购进甲种纪念品54 件,则购进乙种纪念品46 件;方案 6:购进甲种纪念品55 件,则购进乙种纪念品45 件;方案 7:购进甲种纪念品56 件,则购进乙种纪念品44 件;方案 8:购进甲种纪念品57 件,则购进乙种纪念品43 件;方案 9:购进甲种纪念品58 件,则购进乙种纪念品42 件;方案 10:购进甲种纪念品59 件,则购进乙种纪念品41 件;方案 11:购进甲种纪念品60 件,则购进乙种纪念品40 件;( 3)由于甲种纪念品赢利最高,所以甲种纪念品的数目越多总收益越高,所以选择购进甲种纪念品 60 件,购进乙种纪念品 40 件收益最高,总收益 =60×30+40 ×12=2280(元)则购进甲种纪念品 60 件,购进乙种纪念品 40 件时, 可获最大收益, 最大收益是 2280 元.评论:本题考察了一元一次不等式组的应用和二元一次方程组的应用,读懂题意,找到相应的关系,列出式子是解题的重点,注意第二问应求得整数解.24.解答:解:( 1)当 y=0 时, x 2﹣ x ﹣ 4=0 ,解得 x 1=﹣ 2, x 2=8 ,∵点 B 在点 A 的右边, ∴点 A 的坐标为(﹣ 2, 0),点 B 的坐标为( 8,0).当 x=0 时, y= ﹣ 4,∴点 C 的坐标为( 0,﹣ 4).( 2)由菱形的对称性可知,点 D 的坐标为( 0, 4).设直线 BD 的分析式为 y=kx+b ,则,解得 k= ﹣ ,b=4 .∴直线 BD 的分析式为 y= ﹣ x+4 .∵ l ⊥ x 轴,∴点 M 的坐标为( m ,﹣m+4),点 Q 的坐标为( m , m 2﹣ m ﹣4).如图,当 MQ=DC 时,四边形 CQMD 是平行四边形,2化简得: m 2﹣ 4m=0,解得 m 1=0 (不合题意舍去) , m 2=4. ∴当 m=4 时,四边形 CQMD 是平行四边形.此时,四边形 CQBM 是平行四边形.解法一:∵ m=4, ∴点 P 是 OB 的中点.∵ l ⊥ x 轴, ∴ l ∥ y 轴,∴△ BPM ∽△ BOD ,∴= = ,∴ BM=DM ,∵四边形CQMD 是平行四边形,∴DM CQ,∴BM CQ,∴四边形CQBM 是平行四边形.解法二:设直线BC 的分析式为y=k 1x+b 1,则,解得 k1=,b1=﹣4.故直线 BC 的分析式为y=x﹣ 4.又∵ l⊥ x 轴交 BC 于点 N,∴x=4 时, y= ﹣ 2,∴点 N 的坐标为( 4,﹣ 2),由上边可知,点M 的坐标为( 4, 2),点 Q 的坐标为( 4,﹣ 6).∴MN=2 ﹣(﹣ 2) =4, NQ= ﹣ 2﹣(﹣ 6) =4 ,∴MN=QN ,又∵四边形CQMD 是平行四边形,∴DB ∥CQ,∴∠ 3=∠4,∵在△BMN 与△CQN 中,,∴△ BMN ≌△ CQN (ASA )∴BN=CN ,∴四边形CQBM 是平行四边形.( 3)抛物线上存在两个这样的点 Q ,分别是 Q 1(﹣ 2, 0), Q 2( 6,﹣ 4).若 △ BDQ 为直角三角形,可能有三种情况,如答图2 所示:① 以点 Q 为直角极点.此时以 BD 为直径作圆,圆与抛物线的交点,即为所求之Q 点.∵ P 在线段 EB 上运动,∴﹣ 8≤x Q ≤8,而由图形可见,在此范围内,圆与抛物线并没有交点,故此种情况不存在. ② 以点 D 为直角极点.连结 AD ,∵ OA=2 ,OD=4 ,OB=8 , AB=10 ,由勾股定理得: AD=, BD= ,222A 为所求的点∵ AD +BD =AB ,∴△ ABD 为直角三角形,即点 ∴ Q 1(﹣ 2, 0); ③ 以点 B 为直角极点.如图,设 Q 2 点坐标为( x , y ),过点 Q 2 作 Q 2K ⊥ x 轴于点 K ,则BK=8 ﹣ x .易证 △ Q 2KB ∽△ BOD ,Q .Q 2K= ﹣ y , OK=x ,∴,即,整理得: y=2x ﹣ 16.∵点 Q 在抛物线上,∴ y= x 2﹣ x ﹣ 4.∴ x 2﹣ x ﹣ 4=2x ﹣16,解得 x=6 或 x=8,当 x=8 时,点 Q 2 与点 B 重合,故舍去;当 x=6 时, y= ﹣ 4,∴ Q 2(6,﹣ 4).评论:考察了二次函数综合题,波及的知识点有:坐标轴上点的特色,菱形的对称性,待定系数法求直线的分析式,平行四边形的判断和性质,方程思想和分类思想的运用,综合性较强,有必定的难度.。
2014年中考模拟考试试卷

C D
60°
B
(第 20 题)
21. (本题满分 8 分) 今年初我国多地的雾霾天气引发了公众对空气质量的关注. 现随机调查了某城市若干天的 空气质量情况,并将调查的结果绘制成如下的两幅不完整的统计图.
天数 15 12 9 6 3 0 优 良 轻微 轻度中重度 空气 污染 污染 污染 质量 第 3 页 共 10 页 (第 21 题) 轻微 污染 中重度 优 轻度污染 10% 污染 良
请根据图中提供的信息,解答下面的问题: (1)本次调查中,一共调查的天数为 ▲ 天;扇形图中,表示“轻微污染”的扇形的 圆心角为 ▲ 度; (2)将条形图补充完整; (3)估计该城市一年(以 365 天计算)中,空气质量达到良级以上(包括良级)的天数.
22. (本题满分 8 分)列方程(组)解应用题: 从南通到北京,若乘飞机需要 2 h,若乘汽车需要 14 h.这两种交通工具平均每小时二氧 化碳的排放量之和为 136 kg,飞机全程二氧化碳的排放总量比汽车的多 16 kg,分别求飞 机和汽车平均每小时二氧化碳的排放量.
20. (本题满分 8 分) 如皋东方大寿星园, 有一座迄今为止东方唯一巨型寿星雕像. 小李曾经通过测量计算过寿 星雕像的高度,他测量的方法是:如图,从点 B 沿水平线方向走到点 D,测得 BD=28m, 再用高为 1 m 的测角仪 CD,测得雕像顶点 A 的仰角为 60°.请你根据以上数据计算寿 星雕像 AB 的高度(结果保留整数,参考数据 3 ≈1.73, 2 ≈1.41). A
2014 年中考模拟考试试卷
数
学
注 意 事 项
考生在答题前请认真阅读本注意事项: 1.本试卷共 6 页,满分为 150 分,考试时间为 120 分钟.考试结束后,请将本试卷和答题卡 一并交回. 2.答题前,请务必将自己的姓名、考试证号用 0.5 毫米黑色字迹的签字笔填写在试卷及答题 卡指定的位置. 3.答案必须按要求填涂、书写在答题卡上,在试卷、草稿纸上答题一律无效. 一、选择题(本大题共 10 题,每题 3 分,共 30 分.在每小题给出的四个选项中,恰有一项是 符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置 上) ....... 1. 如图,如果数轴上 A,B 两点之间的距离是 8,那么点 B 表示的数是 A.5 B B.-5 · · 0 C .3
2014中考数学试题及答案

2014中考数学试题及答案2014年中考数学试题一、选择题(共10小题,每小题3分,满分30分)1. 下列哪个选项是正确的整数比?A. 2:3B. 1.5:2.5C. 0.6:0.2D. 3.14:2.72. 绝对值不大于5的所有整数之和为:A. 0B. 10C. 15D. 203. 若a、b、c是等差数列,且a+b+c=6,b+c+d=9,则d的值为:A. 1B. 2C. 3D. 44. 一个圆的半径是7厘米,求这个圆的周长(π取3.14):A. 42厘米B. 28厘米C. 18厘米D. 14厘米5. 下列哪个选项是反比例函数的图象?A. 过原点的直线B. 经过第二象限的曲线C. 经过第一、三象限的曲线D. 双曲线6. 一个等腰三角形的底边长为6厘米,腰长为5厘米,这个三角形的面积是多少平方厘米?A. 12B. 14C. 16D. 187. 下列哪个选项是一元二次方程的解?A. x = 2B. x = -2C. x = 1或x = -1D. x = 08. 已知函数f(x) = 2x + 1,求f(3)的值:A. 7B. 6C. 5D. 49. 下列哪个选项是正确的小数与分数之间的转换?A. 0.75 = 3/4B. 0.8 = 4/5C. 0.125 = 1/8D. 0.2 = 1/510. 一个长方体的长、宽、高分别是2厘米、3厘米和4厘米,求这个长方体的体积:A. 24立方厘米B. 21立方厘米C. 16立方厘米D. 12立方厘米二、填空题(共5小题,每小题4分,满分20分)11. 已知一个等差数列的前三项分别是2、5、8,那么第100项是______。
12. 一个圆的直径是10厘米,那么这个圆的面积(π取3.14)是______平方厘米。
13. 一个三角形的三个内角之比为2:3:5,那么这个三角形的最大内角是______度。
14. 已知函数g(x) = x^2 - 3x + 2,求g(4)的值是______。
2014-2015中考数学模拟试题一

2014-2015中考数学模拟试题(时间:120分钟 满分:100分)一、选择题(下列各题的四个选项中,只有一项符合题意,每小题3分,共30分)。
题号 1 2 3 4 5 6 7 8 9 10 答案1. 16的平方根是 ( )A. 4B. 2C.±4 D.±2 2.估算331-的值 ( )A .在2和3之间B .在3和4之间C .在4和5之间D .在5和6之间3.若反比例函数ky x=的图象经过点(3)m m ,,其中0m ≠,则此反比例函数的图象在( ) A .第一、二象限 B .第一、三象限 C .第二、四象限 D .第三、四象限 4.由两块大小不同的正方体搭成如图所示的几何体,它的主视图是( )5.把二次根式1(x-1)1x-中根号外的因式移到根号内,结果是( ) A . 1x -B . 1x --C . 1x --D .1x -6.如图,AB 是⊙O 的直径,点D 在AB 的延长线上,DC 切⊙O 于C ,若25A =∠.则D ∠等于( )A .20 B .30 C .40 D .50 7. 函数134y x x =-+-中自变量x 的取值范围是( ) A .x ≤3 B .x =4 C . x <3且x ≠4 D .x ≤3且x ≠4 8.函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是( ▲ )C BDAOα9.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为60︒ 的菱形,剪口与折痕所成的角α 的度数应为( )A .15︒或30︒B .30︒或45︒C .45︒或60︒D .30︒或60︒10. (引黄冈市 2010年秋期末考试九年级数学模拟试题)正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,正方形BEFG 的边长为4,则DEK △的面积为( )A、10 B、12 C、14 D、16 )11.在如图所示的四边形中,若去掉一个50的角得到一个五边形,则12+=∠∠ 度.12.如图,Rt A BC ''△是由Rt ABC △绕B 点顺时针旋转而得,且点A B C ',,在同一条直线上,在Rt ABC △中,若90C =∠,2BC =,4AB =,则斜边AB 旋转到A B '所扫过的扇形面积为 .13.一元二次方程a 2-4a -7=0的解为 .14.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个小圆.15.如图,直线43y x =与双曲线k y x =(0x >)交于点A .将直线43y x =向右平移92个单位后,与双曲线k y x =(0x >)交于点B ,与x 轴交于点C ,若2AOBC=,则k = .三、解答题(共55分,解答应写出文字说明、证明过程或推演步骤)下列各题需要在答题卷指定位置写出文字说明、证明过程、演算步骤或画出图形. 16.(本题满分5分)CBAC ' A '(12题图)1 250°(11题图)第1个图形 第2个图形第3个图形第4个图形…(第14题图)Oxy AB C(第15题图)D ABRP F C GKE119(2)(1)3-⎛⎫--+-- ⎪⎝⎭+tan 45︒17.(本题满分5分)先化简,再求值:211122x x x -⎛⎫-÷⎪++⎝⎭,其中2x =.18.(本题满分6分)如图,已知ABC ADE Rt △≌Rt △,90ABC ADE ∠=∠=°,BC 与DE 相交于点F ,连接CD ,EB .(1)图中还有几对全等三角形,请你一一列举. (2)求证:.CF EF =19.(本题满分6分)AC EBDF(第18题图)某市要在一块平行四边形ABCD 的空地上建造一个四边形花园,要求花园所占面积是ABCD 面积的一半,并且四边形花园的四个顶点作为出人口,要求分别在ABCD 的四条边上,请你设计两种方案: 方案(1):如图(1)所示,两个出入口E 、F 已确定,请在图(1)上画出符合要求的四边形花园,并简要说明画法; 方案(2):如图(2)所示,一个出入口M 已确定,请在图(2)上画出符合要求的梯形花园,并简要说明画法.20.(本题满分7分)如图,已知ABC △的三个顶点的坐标分别为(23)A -,、(60)B -,、(10)C -,. (1)请直接写出点A 关于y 轴对称的点的坐标;(2)将ABC △绕坐标原点O 逆时针旋转90°.画出图形,直接写出点B 的对应点的坐标; (3)请直接写出:以A B C 、、为顶点的平行四边形的第四个顶点D 的坐标.21.(本题满分8分)如图,Rt ABC △中,90ABC ∠=°,以AB 为直径作O ⊙交AC 边于点D ,E 是边BC 的中点,连接DE .(1)求证:直线DE 是O ⊙的切线;(2)连接OC 交DE 于点F ,若OF CF =,求tan ACO ∠的值.(第20题图)xyCB(第19题图)22.(本题满分8分)如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF =BE .⑴求证:CE =CF ;⑵在图1中,若G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗?为什么? ⑶运用⑴⑵解答中所积累的经验和知识,完成下题: 如图2,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B =90°,AB =BC =12,E 是AB 上一点,且∠DCE =45°,BE =4,求DE 的长.(第22题图)B CA G D FE图1图2B CA DE23.(本题满分10分)已知直线y=3x+43与x轴,y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.(1)试确定直线BC的解析式.(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿CBA向点A运动(不与C、A重合) ,动点P的运动速度是每秒1个单位长度,动点Q 的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S 与t的函数关系式,并写出自变量的取值范围.(3)在(2)的条件下,当△APQ的面积最大时,y轴上有一点M,平面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.A(第23题图)。
2014年虎跳中学中考数学模拟试题 (7)

1201421d b ac233-22-18-2)A B C D 、、()、、(2014年初中学业水平考试模拟数学试卷一、选择题(每小题3分,共24分) 题号 1 2 3 4 5 6 7 8 答案1.-2014的绝对值是( )A 、 -2014B 、±2014C 、2014D 、2.“一方有难,八方支援”,2013年4月20日四川省芦山县遭遇强烈地震灾害,我县某校师生共同为地震灾区捐款135000元用于灾后重建,把135000元用科学记数法表示为( )A 、1.35×10 6B 、13.5×105C 、1.35×105D 13.5×104 3.下列各式化简结果为无理数的是( )4.为了调查某班学生每天使用零花钱的情况,小张随机调查了15名同学,结果如下表:每天使用零花钱(单位:元)0 1 3 4 5 人数13542A 、众数是5元B 、平均数是2.5元C 、极差是4元D 、中位数是3元 5、在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、矩形、圆,在看不见图形的情况下随机摸出1张,这张卡片上的图形既是中心对称图形又是轴对称图形的概率是( )A .16B .13C .12D .236. 如图,直线a 、b 、c 、d ,已知c ⊥a,c ⊥b, 直线b 、c 、d 交于一点,若∠1=500,则∠2等于( ) A 、600 B 、500 C 、400 D 、3007、对于任意实数k ,关于x 的方程x 2-2(k+1)x-k 2+2k-1=0的根的情况为( )A 、有两个不相等的实数根B 、没有实数根C 、有两个相等的实数根D 、无法确定8、如图,直线1:1+=x y l 与直线2121:2+=x y l 相交于点)0,1(-P .直线1l 与y轴交于点A .一动点C 从点A 出发,先沿平行于x 轴的方向运动,到达直线2l 上的点1B 处后,改为垂直于x 轴的方向运动,到达直线1l 上的点1A 处后,再沿平行于x 轴的方向运动,到达直线2l 上的点2B 处后,又改为垂直于x 轴的方向运|a 1|70b -++=001|1-2|-2sin 45( 3.14)32π+-++第11题BCDOA第12题EDCBA第16题G 动,到达直线1l 上的点2A 处后,仍沿平行于x 轴的方向运动,…… 照此规律运动,动点C 依次经过点1B ,1A ,2B ,2A ,3B ,3A ,…,2014B ,2014A ,…则当动点C 到达2014A 处时,运动的总路径的长为( ) A .22014 B .222015- C .122013+ D .122014-二、填空题 (每小题3分,共24分) 9、因式分解:x 3y -xy 3= 。
2014年中考承诺班数学模拟测试题

2014年中考数学模拟测试题第Ⅰ卷 (选择题,共30分)一、选择题(共10小题,每小题3分,共30分) 1.在0,3,-1,-3这四个数中,最大的数是( ) A .0. B .3. C .-1. D .-3.2x 的取值范围是( ) A .x >3. B .x ≥3. C .x <3. D .x ≤3.3.如图,△ ABO 的顶点坐标分别是A (-3,3)、B (3,3)、O (0,0),试将△ABO 放大,使放大后的△EFO 与△ABO 对应边的比为1︰2,则点E 和点F 的坐标分别为( )A .(-6,6),(6,6)B .(6,-6),(6,6)C .(-6,6),(6,-6)D .(6,6),(-6,-6) 4.五箱苹果的质量分别为(单位:千克):18,20,21,22,19.则这五箱苹果质量的平均数和中位数分别为( ).A. 19和20B. 20和19C. 20和20D. 20和21 5.下列计算正确的是 ( )A .a 2·a 3=a 6B .a 3+a 2=a 5C .(a 3)2=a 5D . a 3÷a 2=a6.下列等式正确的是( ). A、(23=- B、3=- C=D2=7.如右图,甲、乙两图是分别由五个棱长为“1”的立方块组成的两个几何体,它们的三视图中完全一致的是( )A.主视图. B .左视图. C .俯视图. D .三视图都一致.8.今年的“六·一”儿童节是个星期五,某校学生会在初一年级进行了学生对学校作息安排的三种期望(全天休息、半天休息、全天上课)的抽样调查,并把调查结果绘成了如图1、2的统计图,已知此次被调查的男、女学生人数相同.根据图中信息,下列判断:①在被调查的学生中,期望全天休息的人数占53%;②本次调查了200名学生;③在被调查的学生中,有30%的女生期望休息半天;④若该校现有初一学生900人,根据调查结果估计期望至少休息半天的学生超过了720人.其中正确的判断有( ) A .4个. B .3个. C .2个. D .1个.9.课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别甲图乙图OCD 被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在( )A .第3天.B .第4天.C .第5天.D .第6天.第9题图 10.如图,半径分别为5的两圆相交于A ﹑B 两点,O 1,,O 2位于AB 的异侧,过点B 任意作直线交两圆于C ﹑D ,AB=8,则△ACD 的最大面积是( ) A.66 B.176 C. 24332 D.88第Ⅱ卷 (非选择题,共90分)二、填空题(共6小题,每小题3分,共18分)11. 因式分解:2a 2-4ab +2b 2=12. 近年来,随着交通网络的不断完善,我市近郊游持续升温.据统计,在今年“五一”期间,某风景区接待游览的人数约为20.3万人,这一数据用科学记数法表示为13. 小明是9人队伍中的一员,他们随机排成一列队伍,从1开始按顺序报数,小明报到奇数的概率是14. 因长期干旱,甲水库水量降到了正常水位的最低值a ,为灌溉需要,由乙水库向甲水库匀速供水,20h 后,甲水库打开一个排灌闸为农田匀速灌溉,又经过20h ,甲水库打开另一个排灌闸同时灌溉,再经过40h 后,乙水库停止供水,甲水库每个排灌闸的灌溉速度相同,图中的折线表示甲书库蓄水量Q (万m 3)与时间t (h )之间的函数关系,则乙水库停止供水后,经过 小时后甲书库蓄水量又降到了正常水位的最低值.15. 如图,在直角坐标系中,点A 在y 轴正半轴上,AC ∥x 轴,点B ,C 的横坐标都是3,且BC=2,点D 在AC 上,且横坐标为1,若反比例函数y =xk(x >0)的图象经过点B ,D ,则k=16. 如图,△ABC 内接于⊙O ,∠B=90°,AB=BC ,D 是⊙O 上与点B 关于圆心O 成中心对称的点,P 是BC 边上一点,连接AD 、DC 、AP .已知AB=8,CP=2,Q 是线段AP 上一动点,连接BQ 并延长交四边形ABCD 的一边于点R ,且满足AP=BR ,则QRBQ= .第14题图 第15题图 第16题图三、解答题(共9小题,共72分)17. 解方程: 5113--=-x xx18. 已知一次函数2+=kx y 的图象经过A (-3, 1), 求不等式2kx +1≥0的解集19. 如图,AB=AE ,∠1=∠2,∠C=∠D .求证:△ABC ≌△AED .20. 在直角坐标系中, △ABC 的顶点坐标是A (-1, 2), B (-3, 1), C (0, -1).将ABC △向右平移2个单位,向下平移3个单位得到△A 1B 1C 1,将 △A 1B 1C 1绕O 点旋转90度得到△A 2B 2C 2. (1)画出三角形△A2B 2C 2. (2)直接写出C 2的坐标. (3)求B 1运动的路径长21.某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E问题:(1)求出样本容量,并补全直方图;(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.22.(本题8分)AB为⊙O的直径,C为弧BD中点,CE⊥AD于E,(1)求证:CE为⊙O的切线(2)在右图中,若sin∠BCF=1/2,求tan∠AEO23. 某书店以每本20元的价格购进一批畅销书《莫言精品集》.销售过程中发现,每月销售量y(本)与销售单价x(元)(1)每月销售量y 与销售单价x 满足我们学习过的三种函数(即一次函数、反比例函数和二次函数)关系中的一种.试求出y 与x 之间的函数关系式,不要求写出自变量x 的取值范围. (2)销售单价在什么范围时,书店不亏损?(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)24. 我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.请你利用重心的概念完成如下问题: (1)如图1,若O 是△ABC 的重心(),连结AO 并延长交BC 于D ,证明:AD AO =32(2)如图2,若O 是△ABC 的重心,若AB =5,点G 从A 出发,在AB 边上以每秒一个单位的速度向B 运动,运动时间为t 秒,连GO ,直线GO 交直线AC 与H 点(G 、H 均不与△ABC 的顶点重合). ①求OHGO(用含有t 的式子表示) ③若G 、H 分别在边AB 、AC 上,S 四边形BCHG ,S △AGH 分别表示四边形BCHG 和△AGH 的面积,直接写出AGHBCHG S S △四边形的最大值.25. 如图1,点A 为抛物线21122c y x x =-的顶点,点B 的坐标为(3,0),直线AB 交抛物线C 1于另一点D 。
2014年中考数学模拟试卷

2014年中考模拟试卷数学卷(南门卷)(满分:150分;考试时间:120分钟)一、精心选一选:本大题共8小题,每小题4分,共32分,每小题给出的四个选项中有且只有一个选项是正确的, 请把正确选项的代号写在题后的括号内,答对的得4分;答错、不答或答案超过一个的一律得0分. 1.下列各数中,最大的数是( ) A .-1B . 0C .1D . 22.如图,在△ABC 中,点D ,E 分别是AB ,AC 的中点,∠A=50°,∠ADE=60°,则下列结论正确的是( )A .∠AED =50°B .∠C =60° C .AD=AED .BC=2DE 3. 下列计算正确的是( )A . 4416x x x ⋅=B . 222()a b a b +=+C .4=± D . ()()23641a a ÷=4. 为了解莆田市今年参加中考的32000名学生的体重情况,抽查了其中1600名学生的体重进行统计分析.下面叙述正确的是( ). A .32000名学生是总体B .1600名学生的体重是总体的一个样本C .每名学生是总体的一个个体D .以上调查是普查5.右图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是( ) A .主视图 B .左视图C .俯视图D . 左视图与俯视图6. 如图,点E 在正方形ABCD 内,满足∠AEB=90°,AE=3,BE=4,则阴影部分的面积是( )A . 19B .15C .12D .67.如图,AB 是半圆的直径,点D 是AC 的中点,∠B=50°,则下列判断不正确的是( )A .∠ACB=90°B .AC=2CDC .∠DAB=65°D .∠DAB+∠DCB=180°8.已知二次函数y=ax 2+bx +c(a≠O)的图象如图所示,则下列结论中正确的是( )A .abc <0B .当-1<x <2时,y 随x 的增大而减小C .b +2a=0D .关于x 的方程ax 2+bx +c=O(a≠0)的根是x=-1二、细心填一填:本大题共8小题,每小题4分,共32分.9.莆田市绶溪公园企溪绿道于2014年1月全线贯通并对外开放,全长约 5100米.5100用科学记数法表示为_______________。
2014年中考数学模拟试题

龙源期刊网 http://www.qikan.com.cn 2014年中考数学模拟试题 作者:杭静 来源:《初中生·考试》2014年第05期
一、选择题(本题共10个小题,每小题3分,共30分.在下列各题的四个选项中,只有一项是符合题意的,请你把认为符合题目要求的选项填在相应的括号内)
1.- 的相反数是( ). A. B.- C.3 D.-3 2.下列计算正确的是( ). A.a2·a3=a6 B.y3÷y3=y C.3m+3n=6mn D.(x3)2=x6 3.下列图形中,既是中心对称图形又是轴对称图形的是( ). A.等边三角形 B.平行四边形 C.梯形 D.矩形 4.2014年5月13日的母亲节快要到了,第一学习小组为了解本地区大约有多少中学生知道自己母亲的生日,随机调查了100个中学生,只有30个学生知道自己母亲的生日.对于这个关于数据收集与处理的问题,下列说法正确的是( ).
A.调查的方式是普查 B.本地区约有30%的中学生知道自己母亲的生日 C.样本是30个中学生 D.本地区约有70个中学生不知道自己母亲的生日 5.将如图1的Rt△ABC绕直角边AC所在直线旋转一周,所得几何体的主视图是( ). 6.一元二次方程x2=-2x的根是( ). A.x=-2 B.x=0 C.x1=0,x2=2 D.x1=0,x2=-2 7.已知三角形的三边分别为2,a-1,4,那么a的取值范围是( ). A.1 8.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是( ). A B C D 龙源期刊网 http://www.qikan.com.cn 9.三角形的边长都是整数,并且唯一的最长边是6,则这样的三角形共有( ). A.5个 B.6个 C.7个 D.8个 10.已知二次函数y=ax2+bx+c的图像如图2所示,对称轴是直线x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac0. 其中正确的是( ).
2014年中考数学 模拟试 卷

2014年中考数学模拟试卷(21)(考试时间120分钟,总分120分)命题人:党延雄一、选择题:本大题共8小题,每小题3分,共24分1.-(-7)的相反数是( )(A)-7 (B)7 (C)7±(D)712.下列计算中,正确的是()(A)145=-(B)aa=2(C)4=(D)236=3.下列运算正确的是( )(A)()()22a b a b a b+--=-(B)()2239a a+=+(C)2242a a a+=(D)()22424a a-=4.在图中的几何体中,它的左视图是()5.不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,蓝球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法,则两次摸到的都是白球的概率为()(A)151(B)91(C)152(D)1816. 以O为圆心的两个同心圆的半径分别为9cm和5 cm,若⊙P与这两个圆都相切,则下列说法中正确的是( ).(A)⊙P的半径一定是2cm (B)⊙P的半径一定是7 cm(C) 符合条件的点P有2个 (D) ⊙P的半径是2 cm或7cm7 . 如图,图中正方形ABCD的边长为4,则图中阴影部分的面积为()(A)16-4∏(B)32-8∏(C)8∏-16 (D)无法确定8.把正方体的八个角切去一个角后,余下的图形有()条棱(A)12或15 (B)12或13(C)13或14 (D)12或13或14或15二、填空题:本大题共10小题,每小题3分,共30分.9.分解因式-4+x4的结果是.10.地球距离月球表面约为384000千米,将这个距离用科学记数法表示为__________米.11.已知:如图.圆锥中,∠OAB=300,母线AB=8,则圆锥的侧面展开图中扇形角为012.如图.在Rt ABC∆中,AC=6cm,BC=8cm,以AB边所在的直线为轴,将ABC∆旋转一周,则所得到的几何体的表面积是2cm(结果保留π).13.当x 时,二次函数y=2x2+12x+m(m为常数)的函数值y随x的增大而减小.14. 如图,△ABC中,D是AC边的二等分点,E是BC边的四等分点,F是BD边的二等分点,若S△ABC=16,则S△DEF =15.如图,△ABC中,∠A=300,∠A沿DE折叠后,A点落在△ABC的内部A’的位置,则∠1 +∠2=16.两圆半径分别是R和r,两圆的圆心距等于5,且R、r是方程x2-5x+4=0的两根,则两圆位置关系是17.前天,孙老师的棉袄被一个铁钉划了一个呈直角三角形的一个口子,经测量三角形两边长分别为1cm和3cm,若用同色圆形布将此洞全部覆盖,那么这个圆布的直径最小值为。
2014年中考模拟考试数学试卷及答案
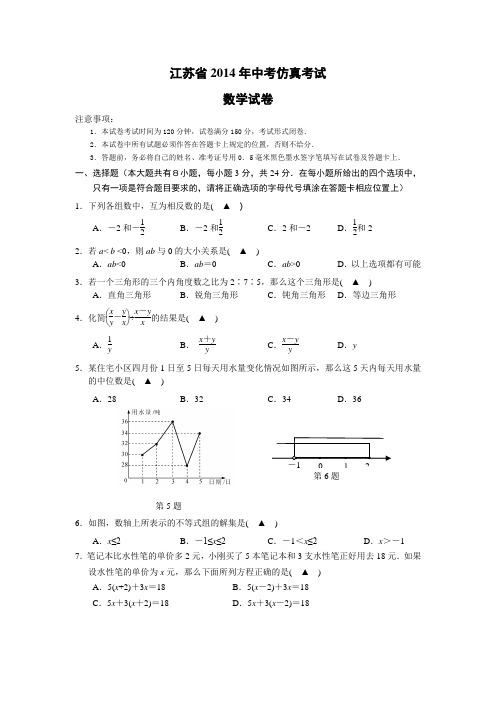
江苏省2014年中考仿真考试数学试卷注意事项:1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上) 1.下列各组数中,互为相反数的是( ▲ )A .-2和-12B .-2和12C .2和-2D .12和22.若a < b <0,则ab 与0的大小关系是( ▲ )A .ab <0B .ab =0C .ab >0D .以上选项都有可能 3.若一个三角形的三个内角度数之比为2∶7∶5,那么这个三角形是( ▲ ) A .直角三角形 B .锐角三角形 C .钝角三角形 D .等边三角形 4.化简⎝⎛⎭⎫x y -y x ÷x -y x 的结果是( ▲ )A .1yB .x +yyC .x -y yD .y5.某住宅小区四月份1日至5日每天用水量变化情况如图所示,那么这5天内每天用水量的中位数是( ▲ )A .28B .32C .34D .366.如图,数轴上所表示的不等式组的解集是( ▲ )A .x ≤2B .-1≤x ≤2C .-1<x ≤2D .x >-17.笔记本比水性笔的单价多2元,小刚买了5本笔记本和3支水性笔正好用去18元.如果设水性笔的单价为x 元,那么下面所列方程正确的是( ▲ ) A .5(x +2)+3x =18 B .5(x -2)+3x =18C .5x +3(x +2)=18D .5x +3(x -2)=18第5题第6题8.已知二次函数y =ax 2+bx +c (a ≠0)的图象如图, 则下列结论中正确的是( ▲ ) A .a >0 B .b >0 C .c <0D .3不是方程ax 2+bx +c =0的一个根二、填空题(本大题共10小题,每小题3分,共30分,将正确答案写在答题卡相应位置上) 9.如图,AB ∥CD ,CP 交AB 于O ,AO =PO ,若∠C =50°,则∠A = ▲ °.10.数轴上点A 、B 的位置如图所示,若点A 关于点O 的对称点为A 1,若点B 关于点O 的对称点为B 1,则线段A 1B 1的长度为 ▲ .11.当x =-7时,代数式(x +5)(x +1)-(x -3)(x +1)的值为 ▲ . 12.已知关于x 的方程x 2+mx -6=0的一个根为2,则m = ▲ . 13.如果分式3x 2-27x -3的值为0,那么x 的值应为 ▲ .14.从标有1到9序号的9张卡片中任意抽取一张,抽到序号是3的倍数的概率是 ▲ . 15.如图,△OPQ 是边长为2的等边三角形,若反比例函数的图象过点P ,则它的解析式是▲ .16.已知分式321x x -+可以写成531x -+,利用上述结论解决:若代数式124--x x 的值为整数,则满足条件的正整数x 的值是 ▲ . 17.已知关于x 的分式方程a +2x +1=1的解是非正数,则a 的取值范围是 ▲ . 18.如图,AB 是圆O 的直径,AC 是圆O 的弦,2AB =,30BAC ∠=︒.在图中画出弦AD ,使AD=1,则CAD ∠的度数为 ▲ .三、解答题(本大题共有10小题,共96分.请在答题卡指定区域内作答,解答时应写出文字说明、推理过程或演算步骤)第15题第10题第9题A第18题第8题19.(本题满分8分)(1)计算:0|12cos45π---︒(); (2)解方程组:⎩⎪⎨⎪⎧x +3y =8,①5x -3y =4.② 20.(本题满分8分)某小区前坪有一块空地,现想建成一块面积大于50平方米,周长小于35米的矩形绿化草地,已知一边长为8米, 设其邻边长为x 米,求x 的整数解.21.(本题满分8分)推理填空:如图 ① 若∠1=∠2,则 ∥ ;( ) 若∠DAB+∠ABC=180,则 ∥ ;( ) ② 当 ∥ 时,∠ C+∠ABC=180 ; ( ) 当 ∥ 时,∠3=∠A . ( )22.(本题满分8分)在△ABC 中,AB =CB ,∠ABC =90°, F 为AB 延长线上一点,点E 在BC 上,且AE =CF . (1)求证:Rt △ABE ≌Rt △CBF ; (2)若∠CAE =25°,求∠ACF 度数.23.(本题满分8分)两枚正四面体骰子的各面上分别标有数字1、2、3、4,现在同时投掷这两枚正四面体骰子,并分别记录着地的面所得的点数为a 、b . (1)请你在下面表格内列举出所有情形(例如“1,2”,表示1,2a b ==); (2)求6a b +=的概率.第20题第22题321DCBA 第21题24.(本题满分10分)如图,在 Rt △ABC 中,∠ACB =90°, D 是AB 边上的一点,以BD 为直径的⊙O 与边 AC 相切于点E , 连接DE 并延长,与BC 的延长线交于点 F . (1)求证: DE =FE ;(2)若 BC =3,AD =2,求 BF 的长.第24题25.(本题满分10分)2012年3月1日,张老师就本班学生对心理健康知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A :不了解,B :一般了解,C :了解较多,D :熟悉).请你根据图中提供的信息解答以下问题: (1)求该班共有多少名学生;(2)在条形统计图中,将表示“一般了解”的部分 补充完整;(3)在扇形统计图中,计算出“了解较多”部分所 对应的圆心角的度数;(4)从该班中任选一人,其对心理健康知识的了解 程度为“了解较多”或者“熟悉”的概率是多少?26.(本题满分10分)如图,△ABC 的顶点坐标分别为A(3,6)、B(1,3) 、C (4,2). (1)直接写出点B 关于x 轴对称的点B 1的坐标是 ;(2)直接写出以A 、B 、C 为顶点的平行四边形ABCD 的第四个顶点D 的坐标是 ; (3)将△ABC 绕C 点顺时针旋转90°,得△A 1B 2C ,在图上画出△A 1B 2C ,并标出顶点.27.(本题满分12分)已知矩形纸片ABCD 中,AB =2,BC =3. 操作:将矩形纸片沿EF 折叠,使点B 落在边CD 上.探究:(1)如图1,若点B 与点D 重合,你认为△EDA 1和△FDC全等吗?如果全等,请了解程度5第25题A 10%B 30%DC给出证明,如果不全等,请说明理由;(2)如图2,若点B 与CD 的中点重合,请你判断△FCB 1、△B 1DG 和△EA 1G 之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比;(3)如图2,请你探索,当点B 落在CD 边上何处,即B 1C 的长度为多少时,△FCB 1与△B 1DG 全等.28.(本题满分14分)已知抛物线y =ax2+bx +c 经过O (0,0),A (4,0),B (3,3)三点,连接AB ,过点B 作BC ∥x 轴交抛物线于点C .动点E 、F 分别从O 、A 两点同时出发,其中点E 沿线段OA 以每秒1个单位长度的速度向A 点运动,点F 沿折线A →B →C 以每秒1个单位长度的速度向C 点运动,动点E 、F 有一个点到达目的点即停止全部运动.设动点运动的时间为t (秒). (1)求抛物线的解析式;(2)记△EFA 的面积为S ,求S 关于t 的函数关系式, 并求S 的最大值;(3)是否存在这样的t 值,使△EFA 是直角三角形? 若存在,求出此时点E 的坐标;若不存在,请说明理由.(B )CD 图1图2B 1第27题。
2014年中考数学模拟考试及参考答案(1-4)

参考答案(一)一、选择题: 1.C 2.A 3.D 4.C 5.C二、填空题:6.2x ≥- 7.7.94×106 8.39.4- 10.6 11.3π 12. 3 13.9,37三、解答题: 14.4 15.x 1=31+-,x 2=31-- 16.化简为:2—x .当22-=x 时,原式=2. 17.P (小菲两次都能摸到白球)=164=4118.(1)小山的高为25米;(2)铁架高约43.3米. 19.(1)80 ,40%;(2)补全条形图(略);(3)380.20.解:(1)∵∠ABC =90°, ∴OB ⊥BC ..∵OB 是⊙O 的半径, ∴CB 为⊙O 的切线..又∵CD 切⊙O 于点D , ∴BC =CD ;.(2)由△ADE ∽△ABD ..∴AD AB =AE AD ..∴21BE +=12,∴BE =3,.∴所求⊙O 的直径长为3. 21.(1)2(21010)(5040)101102100y x x x x =-+-=-++(015x <≤且x 为整数) (2)当2200y =时,21011021002200x x -++=,解得:12110x x ==,.当1x =时,5051x +=,当10x =时,5060x +=.所以,当售价定为每件51或60元时,每个月的利润为2200元. ∴当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2200元).22.①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,∴∠EAB=PAD ,又∵AE=AP ,AB=AD ,∴△APD ≌△AEB ;②∵△APD ≌△AEB ,∴∠APD=∠AEB ,又∵∠AEB=∠AEP+∠BEP ,∠APD=∠AEP+∠PAE , ∴∠BEP=∠PAE=90°,∴EB ⊥ED ;③∵EF=BF= ,AE=1,∴在Rt △ABF 中,AB 2=(AE+EF )2+BF 2=4+ ,∴S 正方形ABCD =4+ (下图)23.(1)解:设所求的抛物线解析式()20y ax bx c a =++≠∵点A B C 、、均在此抛物线上.∴42016404a b c a b c c -+=⎧⎪++=⎨⎪=-⎩ ∴1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴所求的抛物线解析式为2142y x x =--, ∴顶点D 的坐标为912⎛⎫- ⎪⎝⎭, (2)EBC △的形状为等腰三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年初中学业水平考试模拟数学试卷
温馨提示:
1.本试卷满分120分,考试时间120分钟.本试卷共三道大题,25个小题.
一、填空题(本大题共8个小题,请将答案填在答题卡的答案栏内,每小题3分,共24分)1.-2014
-=.
2.永州市2011年财政总收入增长31.7%,完成70.5亿元,请将70.5亿用科学计数法表示为:.
3.布袋里有3个白球和2个红球,从布袋里取一次球,则取出红球的概率是。
4.如图,平行直线AB、CD被直线EF所截,∠1=60°,则∠3的同旁内角为.5.若正比例函数y kx
=的图象经过点(-1,2),则k的值为.
6.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件可以是
(第四题图)(第六题图)
7.观察下列一组数:1,1,2,3,5,8,13,21,34…则紧跟34后面的两个数分别为、。
8.根据指令[s,A](s≥0,0°<A<360°),机器人在平面上能完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离s,现机器人在直角坐标系的坐标原点,且面对x轴正方向.
(1)若给机器人下了一个指令[3,90°],则机器人应移动到点;(2)请你给机器人下一个指令,使其移动到点(6,-6).
二、选择题(本大题共8个小题,每小题只有一个正确选项,请将正确选项填涂到答题卡上.每
小题3分,共24分)
9.在下列图形中,为中心对称图形的是()
A等边三角形;B平行四边形;C正五边形;D等腰三角形。
10.如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是().
主视图 左视图 俯视图 A 4 B 5 C 6 D 8
11.某校八年级一班随机抽取6名同学的一次地生模拟测试成绩如下:90,75,90,86,86,90.数据中的众数和中位数分别是:
A. 90,88
B. 86,90
C. 86,75
D. 90,90
12.在△ABC 中,∠C =90°,sinA =3
5
,则tanB = ( ) A .43 B .34 C .35 D .4
5
13.不等式组⎩⎨
⎧≤-<+5
1
21x x x 的解集是:
A. 5≤x
B. 52≤<-x
C.52≤<x
D. 2<x
14.下列计算正确的是:
A.422a a a =+
B.()a a a a a a +=÷++223
C.1046a a a =⋅ D .()
63
3
a a =
15.二次函数2y ax bx c =++的图象如图所示,则下列关系式不正确的是( )
第15题图 第16题图 A 、a <0 B 、abc >0 C 、c b a ++>0 D 、ac b 42->0 16.反比例函数(0)k
y k x
=
>的部分图如图所示,A 、B 是图象上两点,AC ⊥x 轴于点C ,BD ⊥x 轴于点D ,若△AOC 的面积为S 1,△BOD 的面积为S 2,则S 1和S 2的大小关系为( )
A .S 1>S 2
B .S 1=S 2
C .S 1<S 2
D .无法确定
三、解答题(本大题共9个小题,共72分,解答题要求写出证明步骤或解答过程) 17.(本小题6分)计算:20
+()
(
)(
)
121
213
201-++
--3
1
6⨯
-.
18.(本小题6分)解方程:121
21=-+--x
x x .
19.(本小题6分)先化简,再求值:2
22
11(-)+-xy x y x y x y ÷
-
,其中1,-1x y =.
20.(本小题8分)十八大代表年龄结构比较合理、学历层次较高。
当选代表平均
年龄为52岁。
其中,55岁以上约占35%;45-55岁约占47%; 35-45岁约占8%,35岁以下代表为227人。
现抽取了所有人的年龄进行数据处理,制成扇形统计图和条形统计图(部分)如下:
注:A 代表55岁以上,B 代表55-45岁,C 代表45-35岁,D 代表35岁以下
(1)根据扇形图及提供的信息计算各年龄阶段的代表人数(取整数)并补全条
形图;
(2)计算十八大代表的总人数。
(3)根据统计图提供的信息,谈谈自己的感想.(不超过30字)
21.(本小题8分)如图,在四边形ABCD 中,AE ⊥BD 于点E ,CF ⊥BD 于点F ,AE=CF ,
BF=DE .问四边形ABCD 是否为平行四边形?说明你的理由.
22.(本小题8分)新田绿色、富硒产品在2013年的湖南农产品博览会上喜获金奖。
富硒农产品远销国外.上市时,外商某人按市场价格12元/千克在新田县收购了20000千克富
D
A
C.6
B 47
人数
硒黄豆存放入冷库中.据预测,富硒黄豆的市场价格每天每千克将上涨0.2元,最高的市场价达到20元/千克。
但冷库存放这批富硒黄豆时每天需要支出各种费用合计1400元,同时,平均每天有近50千克的富硒黄豆酶坏不能出售.
(1)若存放x 天后,将这批富硒黄豆一次性出售,设这批富硒黄豆的销售总金额为y 元,
试写出y 与x 之间的函数关系式. (2)将这批富硒黄豆存放多少天后出售可获得最大利润?最大利润是多少?
23.(本小题10分)(1)如图,△ABC 内接于⊙O ,AB 为直径,∠CAE =∠B ,试说明AE 与⊙O 相切于点A .
(2)在(1)中,若AB 为非直径的弦,∠CAE =∠B ,AE 还与⊙O 相切于点A 吗?请说明理由.
24.(本小题10分)直线y=x+m 与双曲线y=
x
m
在第一象限相交点A ,S Rt △AOB 为方程x 2+x-12=0的一根。
. ① 求m 的值 ;
② 设直线与x 轴交于点C ,求点C 的坐标; ③ 求S △ABC . .
25.(本小题10分).
(1)阅读材料:点A 、B 在数轴上分别表示实数a 、b ,A 、B 两点之间的距离记为为AB .
当A 、B 两点中有一点在原点时,不妨设点A 在原点,如图1,AB OB b a b ===-;
当A 、B 两点都不在原点时,
① 如图2,点A 、B 都在原点的右边AB OB OA b a b a a b =-=-=-=-; ② 如图3,点A 、B 都在原点的左边,()AB OB OA b a b a a b =-=-=---=-; ③ 如图4,点A 、B 在原点的两边,()AB OB OA a b a b a b =+=+=+-=-.
(2)回答下列问题:
①数轴上表示1和6的两点之间的距离是_______,数轴上表示-1和-3的两点之间的
距离是_______,数轴上表示1和-3的两点之间的距离是________; ②数轴上表示x 和-1的两点A 和B 之间的距离是_____,如果2AB =,那么x=____; ③当代数式12x x ++-取最小值时,相应的x 的取值范围是____________.。
