高中数学:函数解析式的十一种方法
高一函数 知识点大全

高一函数知识点大全一、函数的定义函数是一种数学操作,它将输入值(或参数)映射到输出值(或结果)。
函数的定义通常包括函数名称、参数列表和函数体。
在高一阶段,我们将学习一些基本的函数,如一次函数、二次函数、幂函数和对数函数等。
二、函数的表示方法函数的表示方法有三种:符号表示法、列表表示法和图像表示法。
符号表示法是用函数名称和参数列表来表示函数,例如y = 2x + 1;列表表示法是将输入值和对应的输出值列成一个表格;图像表示法是通过绘制函数的图像来表示函数的关系。
三、函数的性质函数的性质包括奇偶性、单调性、周期性和对称性等。
奇偶性是指函数是否具有奇偶性;单调性是指函数在某个区间内是单调递增或单调递减;周期性是指函数是否存在周期性;对称性是指函数是否具有对称性。
四、函数的运算函数的运算包括函数的加减乘除、复合运算和反函数运算等。
函数的加减乘除是指将两个或多个函数进行加、减、乘、除运算;复合运算是指将多个函数嵌套在一起,形成一个复合函数;反函数运算是指将一个函数转换为其反函数。
五、函数的图像函数的图像是用来描述函数变化的直观工具。
在绘制函数的图像时,我们需要先确定函数的定义域和值域,然后根据函数的表达式绘制出对应的图像。
同时,我们还需要掌握一些常见的图像变换方法,如平移、伸缩和对称变换等。
六、函数的实际应用高一函数知识点还包括一些实际应用,如利用函数解决实际问题、利用函数进行数据分析等。
在实际问题中,我们需要根据问题的具体情境来选择合适的函数和数学模型进行解决。
我们还需要掌握一些数据处理和分析的方法,如回归分析、聚类分析等。
高一函数知识点是数学学习的重要内容之一。
通过学习和掌握这些知识点,我们可以更好地理解函数的本质和特点,为后续的学习和实际应用打下坚实的基础。
高一函数知识点总结函数是数学的重要概念,是高中数学的核心内容。
在初中数学中,函数通常被视为变量之间的依赖关系,而高中的函数则更加强调映射的概念。
高中数学:函数解析式的十一种方法

高中数学:函数解析式的十一种方法一、定义法 二、待定系数法 三、换元(或代换)法 四、配凑法 五、函数方程组法七、利用给定的特性求解析式.六、特殊值法 八、累加法 九、归纳法 十、递推法 十一、微积分法一、定义法:【例1】设23)1(2+-=+x x x f ,求)(x f .2]1)1[(3]1)1[(23)1(22+-+--+=+-=+x x x x x f =6)1(5)1(2++-+x x 65)(2+-=∴x x x f【例2】设21)]([++=x x x f f ,求)(x f . 【解析】设xx x x x x f f ++=+++=++=111111121)]([xx f +=∴11)(【例3】设33221)1(,1)1(x x x x g x x x x f +=++=+,求)]([x g f .【解析】2)(2)1(1)1(2222-=∴-+=+=+x x f x x x x x x f又x x x g x x x x xx x x g 3)()1(3)1(1)1(3333-=∴+-+=+=+ 故2962)3()]([24623-+-=--=x x x x x x g f【例4】设)(sin ,17cos )(cos x f x x f 求=.【解析】)2(17cos )]2[cos()(sin x x f x f -=-=ππx x x 17sin )172cos()1728cos(=-=-+=πππ.二、待定系数法:在已知函数解析式的构造时,可用待定系数法。
【例1】 设)(x f 是一次函数,且34)]([+=x x f f ,求)(x f 【解析】设b ax x f +=)( )0(≠a ,则bab x a b b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 【例2】已知1392)2(2+-=-x x x f ,求)(x f .【解析】显然,)(x f 是一个一元二次函数。
高中数学 第二章 函数 2.1.2 函数的表示方法课件 b必修1b高一必修1数学课件

答案:1 2
12/13/2021
第四十页,共四十四页。
4.已知 f(x+1)=x2-2x,则 f( 2)=________. 解析:设 x+1=t,则 x=t-1. 则 f(t)=(t-1)2-2(t-1) =t2-4t+3. 所以 f(x)=x2-4x+3, 所以 f( 2)=( 2)2-4 2+3=5-4 2. 答案:5-4 2
12/13/2021
第十八页,共四十四页。
法二:设 x+4=t≥4,则 x=t-4,x=(t-4)2, 所以 f(t)=(t-4)2+8(t-4)=t2-16. 所以 f(x)=x2-16(x≥4). 所以 f(x2)=x4-16(x≤-2 或 x≥2). (3)由 2f(x)+f1x=2x,① 将 x 换成1x,则1x换成 x,得 2f1x+f(x)=2x,② ①×2-②,得 3f(x)=4x-2x,即 f(x)=43x-32x.
第二章 函 数
2.1.2 函数的表示(biǎoshì)方法
12/13/2021
第一页,共四十四页。
第二章 函 数
1.掌握函数的三种表示方法:解析法、图象法、 列表法. 2.了解简单的分段函数. 3.掌握函数解析式 的求法.
12/13/2021
第二页,共四十四页。
1.函数的表示方法
12/13/2021
第十三页,共四十四页。
(4)该函数中 y=1(x≥1)表示平行于 x 轴的一条射线.
12/13/2021
第十四页,共四十四页。
作函数图象时应注意的事项 (1)画函数图象时首先关注函数的定义域,即在定义域内作图; (2)图象是实线或实点,定义域外的部分有时可用虚线来衬托 整个图象; (3)要标出某些关键点,例如图象的顶点、端点、与坐标轴的 交点等.要分清这些关键点是实心点还是空心点.
函数定义域值域求法(全十一种)

文档大全
实用标准
因为CD=AB=2x,所以CDx,所以
2
L2xxx
y2x
故
22
LABCDL2xx
AD,
22
(2
)
2
2
x
Lx
根据实际问题的意义知
2x
L
0
2x
2
x
0
0x
L
2
2
故函数的解析式为y(2)xLx
2
五、参数型
,定义域(0,
即为所求的定义域。
2
例3已知f(x)的定义域为[-2,2],求f(x1)
的定义域。
2
解:令2x12
2
,得1x3
2
,即0x3
,因此0|x|3,从而
3x3,故函数的定义域是{x|3x3}。
(2)已知f[g(x)]的定义域,求f(x)的定义域。
其解法是:已知f[g(x)]的定义域是[a,b],求f(x)定义域的方法是:由axb,求
恒成立,解得
3
0k;
4
②当k=0时,方程左边=3≠0恒成立。
综上k的取值范围是
四、实际问题型
3
0k。
4
这里函数的定义域除满足解析式外,还要注意问题的实际意义对自变量的限制,这点要
加倍注意,并形成意识。
例7将长为a的铁丝折成矩形,求矩形面积y关于一边长x的函数的解析式,并求函
数的定义域。
1
解:设矩形一边为x,则另一边长为(a2x)
含有根式或三角函数公式模型,换元法是数学方法中几种最主要方法之
一,在求函数的值域中同样发挥作用。
高中二次函数知识点总结
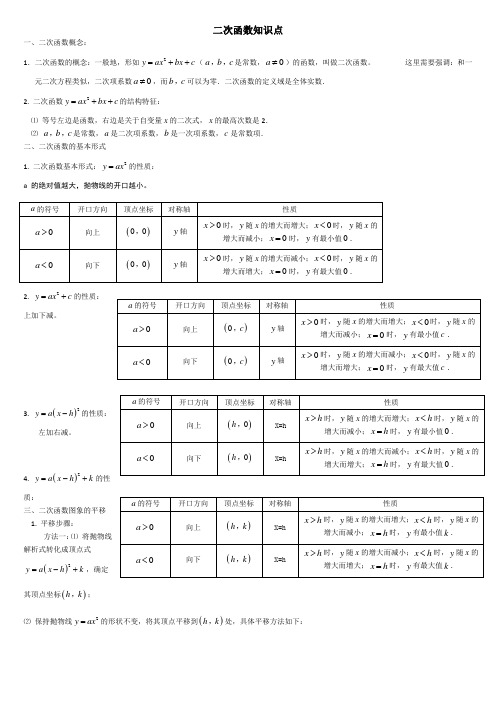
二次函数知识点一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。
2. 2y ax c =+的性质: 上加下减。
3. ()2y a x h =-的性质:左加右减。
4. ()2y a x h k =-+的性质:三、二次函数图象的平移 1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二: ⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++⎪⎝⎭,其中2424b ac b h k a a -=-=,. 五、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a =-时,y 有最小值244ac b a -.2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a -. 七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系 1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小. 2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即 当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” 总结: 3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正;⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置. 总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.九、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离21AB x x =-=.② 当0∆=时,图象与x 轴只有一个交点; ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2' 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标.⑸ 与二次函数有关的还有二次三项式,二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数;下面以0a >时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:图像参考:y=-2x 22图像平移十一、函数的应用二次函数应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少二次函数考查重点与常见题型1. 考查二次函数的定义、性质,有关试题常出现在选择题中,如:已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点, 则m 的值是2. 综合考查正比例、反比例、一次函数、二次函数的图像,习题的特点是在同一直角坐标系内考查两个函数的图像,试题类型为选择题,如:如图,如果函数b kx y +=的图像在第一、二、三象限内,那么函数12-+=bx kx y 的图像大致是( )3. 考查用待定系数法求二次函数的解析式,有关习题出现的频率很高,习题类型有中档解答题和选拔性的综合题,如:已知一条抛物线经过(0,3),(4,6)两点,对称轴为35=x,求这条抛物线的解析式。
十一种类型的三角函数最值问题(附题目详解)

十一种类型的三角函数最值问题1.利用三角函数的有界性求最值利用正弦函数、余弦正数的有界性:∣sinx ∣≤1,∣cosx ∣≤1,可求形如y=Asin(ωx+φ),y=Acos(Asin(ωx+φ)(A ≠0, φ≠0)的函数最值.例:已知函数y=12 cos 2x+32 sinxcosx+1,x ∈R,当函数y 取得最大值时,求自变量x 的集合.2.反函数法 例:求函数1cos 21cos 2-+=x x y 的值域[分析] 此为dx c bx a y -+=cos cos 型的三角函数求最值问题,分子、分母的三角函数同名、同角,先用反解法,再用三角函数的有界性去解。
3.配方法—---转化为二次函数求最值例:求函数y=f(x)=cos 22x-3cos2x+1的最值.4.引入辅助角法y=asinx+bcosx 型处理方法:引入辅助角ϕ ,化为y=22b a +sin (x+ϕ),利用函数()1sin ≤+ϕx 即可求解。
Y=asin 2x+bsinxcosx+mcos 2x+n 型亦可以化为此类。
例:已知函数()R x x x x y ∈+⋅+=1cos sin 23cos 212当函数y 取得最大值时,求自变量x 的集合。
[分析] 此类问题为x c x x b x a y 22cos cos sin sin +⋅+=的三角函数求最值问题,它可通过降次化简整理为x b x a y cos sin +=型求解。
5. 利用数形结合 例: 求函数y xx=+s in c o s 2的最值。
解:6、换元法例:若0<x<2π,求函数y=(1+1sinx )(1+1cosx )的最小值.7. 利用函数在区间内的单调性8. 例: 已知()π,0∈x ,求函数xx y sin 2sin +=的最小值。
[分析] 此题为xax sin sin +型三角函数求最值问题,当sinx>0,a>1,不能用均值不等式求最值,适合用函数在区间内的单调性来求解。
(完整版)函数值域求法十一种

函数值域求法十一种1. 直接观察法对于一些比较简单的函数,其值域可通过观察得到。
例1. 求函数x1y =的值域。
解:∵0x ≠∴0x 1≠显然函数的值域是:),0()0,(+∞-∞例2. 求函数x3y -=的值域。
解:∵0x ≥3x 3,0x ≤-≤-∴故函数的值域是:]3,[-∞2. 配方法配方法是求二次函数值域最基本的方法之一。
例3. 求函数]2,1[x ,5x 2xy 2-∈+-=的值域。
解:将函数配方得:4)1x (y 2+-=∵]2,1[x -∈由二次函数的性质可知:当x=1时,4y min =,当1x -=时,8y max = 故函数的值域是:[4,8]3. 判别式法例4. 求函数22x 1x x 1y +++=的值域。
解:原函数化为关于x 的一元二次方程0x )1y (x )1y (2=-+-(1)当1y ≠时,R x ∈0)1y )(1y (4)1(2≥----=∆解得:23y 21≤≤ (2)当y=1时,0x =,而⎥⎦⎤⎢⎣⎡∈23,211故函数的值域为⎥⎦⎤⎢⎣⎡23,21例5. 求函数)x 2(x x y -+=的值域。
解:两边平方整理得:0y x )1y (2x 222=++-(1) ∵R x ∈ ∴0y 8)1y (42≥-+=∆解得:21y 21+≤≤-但此时的函数的定义域由0)x 2(x ≥-,得2x 0≤≤ 由0≥∆,仅保证关于x 的方程:0y x )1y (2x222=++-在实数集R有实根,而不能确保其实根在区间[0,2]上,即不能确保方程(1)有实根,由0≥∆求出的范围可能比y 的实际范围大,故不能确定此函数的值域为⎥⎦⎤⎢⎣⎡23,21。
可以采取如下方法进一步确定原函数的值域。
∵2x 0≤≤0)x 2(x x y ≥-+=∴21y ,0y min +==∴代入方程(1)解得:]2,0[22222x 41∈-+=即当22222x 41-+=时,原函数的值域为:]21,0[+注:由判别式法来判断函数的值域时,若原函数的定义域不是实数集时,应综合函数的定义域,将扩大的部分剔除。
高考数学-基本初等函数

基本初等函数知识梳理二次函数(1)二次函数解析式的三种形式①一般式:2()(0)f x ax bx c a =++≠②顶点式:2()()(0)f x a x h k a =-+≠③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法 ①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式. ③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便. (3)二次函数图象的性质【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位①二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--. ②当0a >时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2ba-+∞上递增,当2b x a =-时,2min 4()4ac b f x a -=;当0a <时,抛物线开口向下,函数在(,]2b a -∞-上递增,在[,)2ba -+∞上递减,当2b x a =-时,2max 4()4ac b f x a-=.③二次函数2()(0)f x ax bx c a =++≠当240b ac ∆=->时,图象与x 轴有两个交点11221212(,0),(,0),||||||M x M x M M x x a =-=. (4)一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ②对称轴位置:2bx a=- ③判别式:∆ ④端点函数值符号. ①k <x 1≤x 2⇔②x 1≤x 2<k⇔③x 1<k<x 2⇔ af (k )<0④k 1<x 1≤x 2<k 2⇔⑤有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2 ⇔f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1<x 1<k 2≤p 1<x 2<p 2⇔(5)二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值 设()f x 在区间[,]p q 上的最大值为M ,最小值为m ,令01()2x p q =+. (Ⅰ)当0a >时(开口向上) ①若2b p a -<,则()m f p = ②若2b p q a ≤-≤,则()2bm f a=- ③若2b q a ->,则()m f q =①)xxxxx(Ⅱ)当0a <时(开口向下) ①若2b p a -<,则()M f p = ②若2b p q a ≤-≤,则()2bM f a=- ③若2b q a ->,则()M f q =①若02b x a -≤,则()m f q = ②02b x a->,则()m f p =.指数函数(1)根式的概念①如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n 次方根n 是偶数时,正数a 的正的n n 次方根用符号0的n 次方根是0;负数a 没有n 次方根.这里n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:n a =;当n 为奇数时,a =;当n 为偶数时,(0)|| (0) a a a a a ≥⎧==⎨-<⎩. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,mnaa m n N +=>∈且1)n >.0的正分数指数幂等于0.xfxfxfxx②正数的负分数指数幂的意义是:1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈(4)指数函数对数函数 (1)对数的定义①若(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)xa x N a N a a N =⇔=>≠>.(2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a a MM N N-= ③数乘:log log ()na a n M M n R =∈ ④log a NaN =⑤log log (0,)b na a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b N N b b a =>≠且 (5)对数函数(6)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,习惯上改写成1()y f x -=.(7)反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式()y f x =中反解出1()x f y -=;③将1()x fy -=改写成1()y f x -=,并注明反函数的定义域.(8)反函数的性质①原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称.②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.④一般地,函数()y f x =要有反函数则它必须为单调函数. 幂函数(1)幂函数的定义一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数.(2)幂函数的图象(3)幂函数的性质①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于y 轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.②过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1). ③单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当qpα=(其中,p q 互质,p 和q Z ∈),若p 为奇数q 为奇数时,则qpy x =是奇函数,若p 为奇数q 为偶数时,则q py x =是偶函数,若p 为偶数q 为奇数时,则qpy x =是非奇非偶函数.⑤图象特征:幂函数,(0,)y x x α=∈+∞,当1α>时,若01x <<,其图象在直线y x =下方,若1x >,其图象在直线y x =上方,当1α<时,若01x <<,其图象在直线y x =上方,若1x >,其图象在直线y x =下方.三. 典型例题考点6 二次函数题型十一 二次函数的图像及应用例 函数y ax b =+与2y ax bx c =++如图所示,则下列选项中正确的是( )A .ab >0,c>0B .ab <0,c>0C .ab >0,c<0D .ab <0,c<0函数21(1)73y x =--的图象可以通过213y x =的图象向____移动______个单位,再向______移动____个单位后得到.题型十二 二次函数在给定区间上的最值轴定区间定;轴定区间变;轴变区间定;轴变区间变 例 设f x a x b xc a ()()=++≠20,求f x ()在x m n ∈[],上的最大值与最小值。
函数解析式的求法

函数解析式的求法1.待定系数法例1.求一次函数y=f(x)解析式,使f(f(x))=4x+3.解:设f(x)=ax+b(a≠0).∴f(f(x))==af(x)+b=a(ax+b)+b=a^2x+ab+b∴a^2x+ab+b=4x+3∴a^2=4,ab+b=3解得a=2,b=1或a=-2,b=-3.∴f(x)=2x+1或f(x)=-2x-3.总结:当已知函数类型时,求函数解析式,常用待定系数法。
其基本步骤:设出函数的一般式,代入已知条件通过解方程(组)确定未知系数。
2.换元法换元法就是引进一个或几个新的变量来替换原来的某些量的解题方法,它的目的是化繁为简、化难为易,以快速的实现从未知向已知的转换,从而达到顺利解题的目的。
常见换元法是多种多样的,如局部换元、整体换元、分母换元、平均换元等,应用极为广泛。
例2.已知f(1-√x)=x.求f(x).解:设1-√x=t,则x=(1-t)^2∵x≥0,∴t≤1,∴f(t)=(1-t)^2(t≤1)∴f(x)=(1-x)^2(x≤1)(函数变量的无关性)总结:(1)利用换元法解题时,要注意在换元时易引起定义域的变化,所以最后的结果要注意所求函数的定义域。
(2)函数变量的无关性,变量无论是用x还是用t表示,都无关紧要,函数依然成立。
3.配凑法例3.已知f(3x+1)=9x^2-6x+5,求f(x).解:∵f(3x+1)=9x^2-6x+5=(3x+1)^2-12x+4=(3x+1)^2-4(3x+1)+8∴f(x)=x^2-4x+8总结:当已知函数表达式比较简单时,可直接应用配凑法,即根据具体的解析式凑出复合变量的形式,从而求出函数解析式。
4.消元法(又叫解方程组法)例4.已知函数f(x)满足条件:f(x)+2f(1/x)=x,求f(x).分析:用1/x代替条件方程中的x得:f(1/x)+2f(x)=1/x.把它与原条件式联立。
用消元法消去f(1/x),即得f(x)的解析式。
高中数学求函数解析式解题方法大全与配套练习
高中数学求函数解析式解题方法大全及配套练习一、定义法:根据函数的定义求解析式用定义法。
【例1】【例2】【例3】【例4】二、待定系数法:(主要用于二次函数)已知函数解析式的类型,可设其解析式的形式,根据已知条件建立关于待定系数的方程,从而求出函数解析式。
它适用于已知所求函数类型(如一次函数,二次函数,正、反例函数等)及函数的某些特征求其解析式的题目。
其方法:已知所求函数类型,可预先设出所求函数的解析式,再根据题意列出方程组求出系数。
【例1】【解析】【例2】已知二次函数f(x)满足f(0)=0,f(x+1)= f(x)+2x+8,求f(x)的解析式.解:设二次函数f(x)= ax2+bx+c,则f(0)= c= 0 ①f(x+1)(x+1)= ax2+(2a+b)x+a+b②由f(x+1)= f(x)+2x+8 与①、②得解得故f(x)= x2+7x.【例3】三、换元(或代换)法:道所求函数的类型,且函数的变量易于用另一个变量表示的问题。
使用换元法时要注意新元定义域的变化,最后结果要注明所求函数的定义域。
如:已知复合函数f [g(x)]的解析式,求原函数f(x)的解析式,把g(x)看成一个整体t,进行换元,从而求出f(x)的方法。
实施换元后,应注意新变量的取值围,即为函数的定义域.【例1】【解析】【例2】【例3】【例4】(1)在(1(2)1(3)【例5】(1(2)由【例6】四、代入法:求已知函数关于某点或者某条直线的对称函数时,一般用代入法.【例1】解则解得,上,(五)配凑法【例1】:2x当然,上例也可直接使用换元法即由此可知,求函数解析式时,可以用配凑法来解决的,有些也可直接用换元法来求解。
【例2】:分析:此题直接用换元法比较繁锁,而且不易求出来,但用配凑法比较方便。
实质上,配凑法也缊含换元的思想,只是不是首先换元,而是先把函数表达式配凑成用此复合函数的函数来表示出来,在通过整体换元。
和换元法一样,最后结果要注明定义域。
(2021年整理)函数定义域值域求法(全十一种)

(完整)函数定义域值域求法(全十一种)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)函数定义域值域求法(全十一种))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)函数定义域值域求法(全十一种)的全部内容。
高中函数定义域和值域的求法总结一、常规型即给出函数的解析式的定义域求法,其解法是由解析式有意义列出关于自变量的不等式或不等式组,解此不等式(或组)即得原函数的定义域.例1 求函数8|3x |15x 2x y 2-+--=的定义域。
解:要使函数有意义,则必须满足⎩⎨⎧≠-+≥--②①08|3x |015x 2x 2 由①解得 3x -≤或5x ≥. ③由②解得 5x ≠或11x -≠ ④③和④求交集得3x -≤且11x -≠或x 〉5.故所求函数的定义域为}5x |x {}11x 3x |x {>-≠-≤ 且。
例2 求函数2x161x sin y -+=的定义域。
解:要使函数有意义,则必须满足⎩⎨⎧>-≥②①0x 160x sin 2 由①解得Z k k 2x k 2∈π+π≤≤π, ③由②解得4x 4<<- ④由③和④求公共部分,得π≤<π-≤<-x 0x 4或故函数的定义域为]0(]4(ππ--,,评注:③和④怎样求公共部分?你会吗?二、抽象函数型抽象函数是指没有给出解析式的函数,不能常规方法求解,一般表示为已知一个抽象函数的定义域求另一个抽象函数的解析式,一般有两种情况。
(1)已知)x (f 的定义域,求)]x (g [f 的定义域。
(2)其解法是:已知)x (f 的定义域是[a ,b]求)]x (g [f 的定义域是解b )x (g a ≤≤,即为所求的定义域.例3 已知)x (f 的定义域为[-2,2],求)1x (f 2-的定义域.解:令21x 22≤-≤-,得3x 12≤≤-,即3x 02≤≤,因此3|x |0≤≤,从而3x 3≤≤-,故函数的定义域是}3x 3|x {≤≤-。
新高考高中数学核心知识点全透视:函数(精讲精析篇)(附答案及解析)
专题3.1函数(精讲精析篇)提纲挈领点点突破热门考点01 求函数的定义域1.(1)在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.(2)如果两个函数的定义域相同,并且对应关系完全一致,则这两个函数为相等函数.2.已知函数的具体解析式求定义域的方法(1)若f(x)是由一些基本初等函数通过四则运算构成的,则它的定义域为各基本初等函数的定义域的交集.(2)复合函数的定义域:先由外层函数的定义域确定内层函数的值域,从而确定对应的内层函数自变量的取值范围,还需要确定内层函数的定义域,两者取交集即可.3.抽象函数的定义域的求法(1)若已知函数f(x)的定义域为[a,b],则复合函数f(g(x))的定义域由a≤g(x)≤b求出.(2)若已知函数f(g(x))的定义域为[a,b],则f(x)的定义域为g(x)在x∈[a,b]时的值域.【典例1】(2019·江苏高考真题)函数2=+-_____.76y x x【典例2】(2019·邵阳市第十一中学高一期中)已知函数(31)f x -的定义域是[]0,2,则函数()f x 的定义域是( ) A.[]0,2B.1[1]3,C.[-15],D.无法确定【典例3】(2018·上海上外浦东附中高一月考)已知()f x 的定义域为[]3,3-,则()21f x -的定义域为_______________. 【特别提醒】求函数的定义域,往往要解不等式或不等式组,因此,要熟练掌握一元一次不等式、一元二次不等式的解法、牢记不等式的性质,学会利用数形结合思想,借助数轴解题.另外,函数的定义域、值域都是集合,要用适当的表示方法加以表达或依据题目的要求予以表达.热门考点02 求函数的解析式1. 求函数解析式的四种方法【典例4】(2016·浙江高考真题(文))设函数f(x)=x 3+3x 2+1.已知a≠0,且f(x)–f(a)=(x –b)(x –a)2,x R ∈,则实数a=_____,b=______.【典例5】(2019·邵阳市第十一中学高一期中)若()22144f x x x +=+,则()f x 的解析式为__________.【典例6】(2018·上海市金山中学高一期末)设()f x 是定义在R 上的函数,且满足对任意,x y 等式()()()22343f y x f x y x y -=-+-+恒成立,则()f x 的解析式为_____________.【特别提醒】谨防求函数解析式的两种失误:(1)在求函数解析式时,一定要注意自变量的范围,也就是定义域问题.求出解析式后要标注x 的取值范围. (2)利用换元法求解析式时要注意新元的取值范围.如已知f (x )=x +1,求函数f (x )的解析式,可通过换元的方法得f (x )=x 2+1,函数f (x )的定义域是[0,+∞),而不是(-∞,+∞).热门考点03 分段函数及其应用1.(1)若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数.(2)分段函数的定义域等于各段函数的定义域的并集,其值域等于各段函数的值域的并集,分段函数虽由几个部分组成,但它表示的是一个函数.2.根据分段函数解析式求函数值.首先确定自变量的值属于哪个区间,其次选定相应的解析式代入求解.3.已知函数值或函数的取值范围求自变量的值或范围时,应根据每一段的解析式分别求解,但要注意检验所求自变量的值或范围是否符合相应段的自变量的取值范围. 提醒:当分段函数的自变量范围不确定时,应分类讨论. 【典例7】(山东省2018年普通高校招生(春季))已知函数,则的值等于__________.【典例8】(2018·上海市金山中学高一期末)已知()[)[]21,1,01,0,1x x f x x x ⎧+∈-⎪=⎨+∈⎪⎩,则下列函数的图象错误的是( )A.(1)f x -的图象B.()f x -的图象C.(||)f x 的图象D.|()|f x 的图象【典例9】(上海高考真题(理))设若,则a 的取值范围为_____________.【典例10】(2018届河北省唐山市三模)设函数则使得成立的得取值范围是__________.【典例11】(2014浙江高考理第15题)设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ,则实数a 的取值范围是______ 【总结提升】关于分段函数的命题角度主要有:一是分段函数求值,二是分段函数与方程、不等式结合.由于分段函数在其定义域内的不同子集上其对应法则不同,而分别用不同的式子来表示,因此在求函数值、解方程(不等式)时,一定要注意自变量的值所在子集,再代入相应的解析式求值.热门考点04 函数的单调性与最值(值域)1.增函数、减函数(1)增函数:若对于定义域I 内的某个区间()D D I ⊆上的任意两个自变量1x 、2x ,当12x x <时,都有()()12f x f x <,那么就说函数()f x 在区间D 上是增函数;(2)减函数:若对于定义域I 内的某个区间()D D I ⊆上的任意两个自变量1x 、2x ,当12x x <时,都有()()12f x f x >,那么就说函数()f x 在区间D 上是减函数.2.函数的最值(1)最大值:一般地,设函数()y f x =的定义域为I ,如果存在实数M 满足:①对于任意的x I ∈,都有()f x M ≤; ②存在0x I ∈,使得()0f x M =.那么,我们称M 是函数()y f x =的最大值.(2)最小值:一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足: ①对于任意的x I ∈,都有()f x m ≥; ②存在0x I ∈,使得()0f x m =.那么,我们称m 是函数()y f x =的最小值.【典例12】函数2()23f x x mx =-+,当[2,)x ∈-+∞时是增函数,当(,2]x ∈-∞-时是减函数,则(1)f 等于( )A .-3B .13 C. 7 D . 5【典例13】(2019·山西省长治市第二中学校高一期中)若函数2()21f x x mx =-+在[2,)+∞上是增函数,则实数m 的取值范围是( ) A.(,1]-∞B.[1,)+∞C.[2,)+∞D.(,2]-∞【典例14】函数()21,12,1x f x x x x ⎧≥⎪=⎨⎪-+<⎩的最大值为( )A.1B.2C.12D.13【总结提升】1.利用基本初等函数的单调性与图象:只需作出函数的图象便可判断函数在相应区间上的单调性;2.性质法:(1)增函数+增函数=增函数,减函数+减函数=减函数,增函数-减函数=增函数,减函数-增函数=减函数;(2)函数()f x -与函数()f x 的单调性相反; (3)0k >时,函数()f x 与()k f x 的单调性相反(()0f x ≠);0k <时,函数()f x 与()k f x 的单调性相同(()0f x ≠).3.定义法:作差法与作商法(常用来函数单调性的证明,一般使用作差法).*4.导数法:()0f x '≥在区间D 上恒成立,则函数()f x 在区间D 上单调递增;()0f x '≤在区间D 上恒成立,则函数()f x 在区间D 上单调递减.【注】分段函数的单调性要求每段函数都满足原函数的整体单调性,还需注意断点处两边函数值的大小比较.5.函数单调性的应用(1)比较函数值大小(随着基本初等函数的学习,逐步体会)比较函数值的大小时,若自变量的值不在同一个单调区间内,要利用其函数性质,转化到同一个单调区间上进行比较,对于选择题、填空题能数形结合的尽量用图象法求解. (2)求解含“f ”的函数不等式的解题思路先利用函数的相关性质将不等式转化为f (g (x ))>f (h (x ))的形式,再根据函数的单调性去掉“f ”,得到一般的不等式g (x )>h (x )(或g (x )<h (x )). (3)利用单调性求参数的范围(或值)的方法①视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数; ②需注意若函数在区间[a ,b ]上是单调的,则该函数在此区间的任意子集上也是单调的. 6.函数值域的常见求法: (1)配方法配方法是求“二次函数型函数”值域的基本方法,形如F (x )=a [f (x )]2+bf (x )+c (a ≠0)的函数的值域问题,均可使用配方法. (2)数形结合法若函数的解析式的几何意义较明显,如距离、斜率等,可用数与形结合的方法. (3)基本不等式法:要注意条件“一正,二定,三相等”.(可见上一专题) (4)利用函数的单调性①单调函数的图象是一直上升或一直下降的,因此若单调函数在端点处有定义,则该函数在端点处取最值,即若y =f (x )在[a ,b ]上单调递增,则y 最小=f (a ),y 最大=f (b ); 若y =f (x )在[a ,b ]上单调递减,则y 最小=f (b ),y 最大=f (a ).②形如y =ax +b +dx +c 的函数,若ad >0,则用单调性求值域;若ad <0,则用换元法.③形如y =x +kx(k >0)的函数,若不能用基本不等式,则可考虑用函数的单调性,当x >0时,函数y =x +k x (k >0)的单调减区间为(0,k ],单调增区间为[k ,+∞).一般地,把函数y =x +kx(k >0,x >0)叫做对勾函数,其图象的转折点为(k ,2k ),至于x <0的情况,可根据函数的奇偶性解决.*(5)导数法利用导函数求出最值,从而确定值域.热门考点05 函数的奇偶性、周期性与单调性1.判断函数的奇偶性的两种方法 (1)定义法:(2)图象法:2.函数奇偶性的应用 (1)求函数解析式①将所求解析式自变量的范围转化为已知解析式中自变量的范围;②将转化后的自变量代入已知解析式;③利用函数的奇偶性求出解析式. (2)求参数值在定义域关于原点对称的前提下,根据奇函数满足f (-x )=-f (x )或偶函数满足f (-x )=f (x )列等式,根据等式两侧对应相等确定参数的值.特别要注意的是:若能够确定奇函数的定义域中包含0,可以根据f (0)=0列式求解,若不能确定则不可用此法. *3.函数周期性的判定及应用(1)只需证明f (x +T )=f (x )(T ≠0)便可证明函数是周期函数,且周期为T .(2)根据函数的周期性,可以由函数局部的性质得到函数整体的性质,函数的周期性常与函数的其他性质综合考查.(3)在解决具体问题时,要注意结论“若T 是函数的周期,则kT (k ∈Z 且k ≠0)也是函数的周期”的应用. 【典例15】(2017·全国高考真题(理))函数()f x 在(,)-∞+∞单调递增,且为奇函数,若(1)1f =,则满足1(2)1f x -≤-≤的x 的取值范围是( ).A .[2,2]-B .[1,1]-C .[0,4]D .[1,3]【典例16】(2018·全国高考真题(理))已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++=L ( ) A.50-B.0C.2D.50【典例17】(2017·山东高考真题(文))已知f (x )是定义在R 上的偶函数,且f (x +4)=f (x -2).若当x ∈[-3,0]时,f (x )=6-x ,则f (919)=________.【典例18】(2013·上海高考真题(理))设a 为实常数,()y f x =是定义在R 上的奇函数,且当0x <时,2()97a f x x x=++.若()1f x a ≥+对一切0x ≥成立,则a 的取值范围是 .【总结提升】 拓展:1.函数奇偶性的判断(1)复合函数奇偶性的判断:若复合函数由若干个函数复合而成,则复合函数的奇偶性可根据若干个函数的奇偶性而定,概括为“同奇为奇,一偶则偶”.(2)抽象函数奇偶性的判断:应充分利用定义,巧妙赋值,通过合理、灵活地变形配凑来判断. 2.熟记4种常见抽象函数的周期 (1)若f (x +a )=-f (x ),则T =2|a |; (2)若f (x +a )=1f x,则T =2|a |; (3)若f (x +a )=-1f x,则T =2|a |;(4)若f (x +a )=f (x -a ),则T =2|a |.3.当函数具有两个对称时函数一般也是周期函数.当函数()f x 是奇函数,又有对称轴x m =时,则函数一定是周期函数,且周期为4T m =;若()f x 有两条对称轴x a =和x b =,则函数是周期函数,2b a -是函数的一个周期;同样若()f x 有两个对称中心(,0)a 和(,0)b ,则函数是周期函数,2b a -是函数的一个周期.巩固提升1.有意义的实数x 的取值范围是( )A.{|0x x >或}1x <-B.{|0x x …或}1x -„ C.{}10x x -<<D.{}10x x -剟2.(2019·重庆高一)若()335f x x +=+,则()f x 等于( ). A.32x + B.38x + C.31x -D.34x -3.(2017·浙江高考真题)若函数()2f x =x ax b ++在区间[0,1]上的最大值是M,最小值是m,则M m -的值( )A .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关4.(2019·江苏高一月考)函数()()02f x x =-+ ) A.()2,+∞ B.()1,-+∞ C.()()1,22,-+∞UD.R5.(2014·全国高考真题(文))奇函数()f x 的定义域为R ,若(2)f x +为偶函数,且(1)1f =,则(8)(9)f f +=( )A .2-B .1-C .0D .16.(2019·山西省长治市第二中学校高一期中)已知函数2()3f x ax bx =++是定义在[3,2]a a -上的偶函数,则+a b 的值是( ) A.1-B.1C.3-D.07.(2019·浙江学军中学高一期中)函数()f x = )A.奇函数B.偶函数C.非奇非偶函数D.既奇又偶函数8.(2017·全国高考真题(文))已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+,则(2)f =__________.9.(2016·四川高考真题(文))若函数f (x )是定义在R 上的周期为2的奇函数,当0<x<1时,f (x )=,则f ()+f (2)= .10.(2019·上海闵行中学高一期中)已知21(1)()(1)(1)x x f x f x x -<⎧=⎨-≥⎩,则(3)f =________11.(2019·上海市第二中学高二期末)若函数()3f x x a =+为奇函数,则()1f =______.12.(2018·上海上外浦东附中高一月考)函数()21y k x b =++在R 上是增函数,则实数k 的取值范围是_________.13.(2018·上海上外浦东附中高一月考)已知函数2y x =,[]0,3x ∈,则函数的值域为__________.14.(2015·浙江高考真题(文))已知函数()2,1{ 66,1x x f x x x x≤=+->,则()2f f ⎡⎤-=⎣⎦ , ()f x 的最小值是 .15.(2019·上海市高桥中学高一期末)已知偶函数()f x 在[)0,+∞单调递减,()20f =,若()10f x -<,则x 的取值范围是_________.16.(2018·上海曹杨二中高一期末)设函数()1f x x =-,若0a b <<且()()f a f b =,则ab 的取值范围是_________;专题3.1函数(精讲精析篇)提纲挈领点点突破热门考点01 求函数的定义域1.(1)在函数y =f (x ),x ∈A 中,x 叫做自变量,x 的取值范围A 叫做函数的定义域;与x 的值相对应的y 值叫做函数值,函数值的集合{f (x )|x ∈A }叫做函数的值域.(2)如果两个函数的定义域相同,并且对应关系完全一致,则这两个函数为相等函数. 2.已知函数的具体解析式求定义域的方法(1)若f (x )是由一些基本初等函数通过四则运算构成的,则它的定义域为各基本初等函数的定义域的交集. (2)复合函数的定义域:先由外层函数的定义域确定内层函数的值域,从而确定对应的内层函数自变量的取值范围,还需要确定内层函数的定义域,两者取交集即可. 3.抽象函数的定义域的求法(1)若已知函数f (x )的定义域为[a ,b ],则复合函数f (g (x ))的定义域由a ≤g (x )≤b 求出. (2)若已知函数f (g (x ))的定义域为[a ,b ],则f (x )的定义域为g (x )在x ∈[a ,b ]时的值域. 【典例1】(2019·江苏高考真题)函数276y x x =+-_____. 【答案】[1,7]-. 【解析】由已知得2760x x +-≥,即2670x x --≤ 解得17x -≤≤, 故函数的定义域为[1,7]-.【典例2】(2019·邵阳市第十一中学高一期中)已知函数(31)f x -的定义域是[]0,2,则函数()f x 的定义域是( ) A.[]0,2 B.1[1]3,C.[-15],D.无法确定【答案】C 【解析】由已知02x ≤≤,1315x ∴-≤-≤,即函数()f x 的定义域是[-15],, 故选:C .【典例3】(2018·上海上外浦东附中高一月考)已知()f x 的定义域为[]3,3-,则()21f x -的定义域为_______________.【答案】[]22-,【解析】由于函数()y f x =的定义域为[]3,3-,对于函数()21y f x =-,有2313x -≤-≤,即224x -≤≤,即24x ≤,解得22x -≤≤.因此,函数()21y f x =-的定义域为[]22-,. 故答案为:[]22-,. 【特别提醒】求函数的定义域,往往要解不等式或不等式组,因此,要熟练掌握一元一次不等式、一元二次不等式的解法、牢记不等式的性质,学会利用数形结合思想,借助数轴解题.另外,函数的定义域、值域都是集合,要用适当的表示方法加以表达或依据题目的要求予以表达.热门考点02 求函数的解析式1. 求函数解析式的四种方法【典例4】(2016·浙江高考真题(文))设函数f(x)=x 3+3x 2+1.已知a≠0,且f(x)–f(a)=(x –b)(x –a)2,x R ∈,则实数a=_____,b=______.【答案】-2,1【解析】()()32323232313133f x f a x x a a x x a a -=++---=+--,()()()()2322222x b x a x a b x a ab x a b --=-+++-,所以223223{20 3a b a ab a b a a --=+=-=--,解得2{ 1a b =-=. 【典例5】(2019·邵阳市第十一中学高一期中)若()22144f x x x +=+,则()f x 的解析式为__________.【答案】2()1f x x =- 【解析】 令21x t +=,12t x -∴=,代入()22144f x x x +=+, ()22114()4122t t f t t --∴=+⋅=-,故答案为:2()1f x x =-.【典例6】(2018·上海市金山中学高一期末)设()f x 是定义在R 上的函数,且满足对任意,x y 等式()()()22343f y x f x y x y -=-+-+恒成立,则()f x 的解析式为_____________.【答案】()()31f x x x =+ 【解析】Q ()f x 是定义在R 上的函数,且对任意,x y ,()()()22343f y x f x y x y -=-+-+恒成立,∴令y x =,得()()()22343f x x f x x x x -=-+-+, 即()()()2333f x f x x x =-++,()()3333f x x x ∴=+, ()()31f x x x ∴=+.故答案为:()()31f x x x =+ 【特别提醒】谨防求函数解析式的两种失误:(1)在求函数解析式时,一定要注意自变量的范围,也就是定义域问题.求出解析式后要标注x 的取值范围. (2)利用换元法求解析式时要注意新元的取值范围.如已知f )=x +1,求函数f (x )的解析式,可通过换元的方法得f (x )=x 2+1,函数f (x )的定义域是[0,+∞),而不是(-∞,+∞).热门考点03 分段函数及其应用1.(1)若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数.(2)分段函数的定义域等于各段函数的定义域的并集,其值域等于各段函数的值域的并集,分段函数虽由几个部分组成,但它表示的是一个函数.2.根据分段函数解析式求函数值.首先确定自变量的值属于哪个区间,其次选定相应的解析式代入求解.3.已知函数值或函数的取值范围求自变量的值或范围时,应根据每一段的解析式分别求解,但要注意检验所求自变量的值或范围是否符合相应段的自变量的取值范围. 提醒:当分段函数的自变量范围不确定时,应分类讨论. 【典例7】(山东省2018年普通高校招生(春季))已知函数,则的值等于__________. 【答案】【解析】 因为,所以.【典例8】(2018·上海市金山中学高一期末)已知()[)[]21,1,01,0,1x x f x x x ⎧+∈-⎪=⎨+∈⎪⎩,则下列函数的图象错误的是( )A.(1)f x -的图象B.()f x -的图象C.(||)f x 的图象D.|()|f x 的图象【答案】D 【解析】作出()[)[]21,1,01,0,1x x f x x x ⎧+∈-⎪=⎨+∈⎪⎩,如下图(1)f x -的图象,由()f x 的图象向右平移一个单位,故A 正确;()f x -的图象,由()f x 的图象y 轴右侧的翻折到左侧,左侧翻折到右侧,故B 正确; (||)f x 的图象,由()f x 的图象右侧的保留不变,且把右边的翻折到左边,故C 正确;|()|f x 的图象,把x 轴下方的翻折到上方,图象与()f x 一样,故D 错误;故选:D【典例9】(上海高考真题(理))设若,则a 的取值范围为_____________.【答案】(,2]-∞ 【解析】由题意,若2a >,则(2)2f =不合题意,因此2a ≤,此时[,)x a ∈+∞时,2()f x x =,满足(2)4f =.【典例10】(2018届河北省唐山市三模)设函数则使得成立的得取值范围是__________. 【答案】.【解析】 由,得或,得或,即得取值范围是,故答案为.【典例11】(2014浙江高考理第15题)设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ,则实数a 的取值范围是______【答案】a ≤【解析】由题意()()()202f a f a f a <⎧⎪⎨+≤⎪⎩或()()202f a f a ≥⎧⎪⎨-≤⎪⎩,解得()2f a ≥-,当202a a a <⎧⎨+≥-⎩或202a a ≥⎧⎨-≥-⎩,解得,0a <或a ≤≤,故a ≤【总结提升】关于分段函数的命题角度主要有:一是分段函数求值,二是分段函数与方程、不等式结合.由于分段函数在其定义域内的不同子集上其对应法则不同,而分别用不同的式子来表示,因此在求函数值、解方程(不等式)时,一定要注意自变量的值所在子集,再代入相应的解析式求值.热门考点04 函数的单调性与最值(值域)1.增函数、减函数(1)增函数:若对于定义域I 内的某个区间()D D I ⊆上的任意两个自变量1x 、2x ,当12x x <时,都有()()12f x f x <,那么就说函数()f x 在区间D 上是增函数;(2)减函数:若对于定义域I 内的某个区间()D D I ⊆上的任意两个自变量1x 、2x ,当12x x <时,都有()()12f x f x >,那么就说函数()f x 在区间D 上是减函数.2.函数的最值(1)最大值:一般地,设函数()y f x =的定义域为I ,如果存在实数M 满足: ①对于任意的x I ∈,都有()f x M ≤; ②存在0x I ∈,使得()0f x M =.那么,我们称M 是函数()y f x =的最大值.(2)最小值:一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足: ①对于任意的x I ∈,都有()f x m ≥;②存在0x I ∈,使得()0f x m =.那么,我们称m 是函数()y f x =的最小值.【典例12】函数2()23f x x mx =-+,当[2,)x ∈-+∞时是增函数,当(,2]x ∈-∞-时是减函数,则(1)f 等于( )A .-3B .13 C. 7 D . 5 【答案】B【解析】由题意知函数()f x 的对称轴224b mx a =-==-,所以8m =-,所以(1)28313f =++=,故选B .【典例13】(2019·山西省长治市第二中学校高一期中)若函数2()21f x x mx =-+在[2,)+∞上是增函数,则实数m 的取值范围是( ) A.(,1]-∞ B.[1,)+∞ C.[2,)+∞ D.(,2]-∞【答案】D 【解析】由题意,函数2()21f x x mx =-+,开口向上,其对称轴x m =,∵在[2,)+∞上是增函数,∴2m ≤,即实数m 的取值范围为(,2]-∞, 故选D.【典例14】函数()21,12,1x f x x x x ⎧≥⎪=⎨⎪-+<⎩的最大值为( )A.1B.2C.12D.13【答案】B 【解析】当1x ≥时,函数()1f x x=在()1,+∞单调递减,此时()f x 在1x =处取得最大值,最大值为()11f =; 当1x <时,函数()22f x x =-+在0x =处取得最大值,最大值为()02f =. 综上可得,()f x 的最大值为2.故选:B . 【总结提升】1.利用基本初等函数的单调性与图象:只需作出函数的图象便可判断函数在相应区间上的单调性;2.性质法:(1)增函数+增函数=增函数,减函数+减函数=减函数,增函数-减函数=增函数,减函数-增函数=减函数;(2)函数()f x -与函数()f x 的单调性相反; (3)0k >时,函数()f x 与()k f x 的单调性相反(()0f x ≠);0k <时,函数()f x 与()k f x 的单调性相同(()0f x ≠).3.定义法:作差法与作商法(常用来函数单调性的证明,一般使用作差法).*4.导数法:()0f x '≥在区间D 上恒成立,则函数()f x 在区间D 上单调递增;()0f x '≤在区间D 上恒成立,则函数()f x 在区间D 上单调递减.【注】分段函数的单调性要求每段函数都满足原函数的整体单调性,还需注意断点处两边函数值的大小比较.5.函数单调性的应用(1)比较函数值大小(随着基本初等函数的学习,逐步体会)比较函数值的大小时,若自变量的值不在同一个单调区间内,要利用其函数性质,转化到同一个单调区间上进行比较,对于选择题、填空题能数形结合的尽量用图象法求解. (2)求解含“f ”的函数不等式的解题思路先利用函数的相关性质将不等式转化为f (g (x ))>f (h (x ))的形式,再根据函数的单调性去掉“f ”,得到一般的不等式g (x )>h (x )(或g (x )<h (x )). (3)利用单调性求参数的范围(或值)的方法①视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数; ②需注意若函数在区间[a ,b ]上是单调的,则该函数在此区间的任意子集上也是单调的. 6.函数值域的常见求法: (1)配方法配方法是求“二次函数型函数”值域的基本方法,形如F (x )=a [f (x )]2+bf (x )+c (a ≠0)的函数的值域问题,均可使用配方法. (2)数形结合法若函数的解析式的几何意义较明显,如距离、斜率等,可用数与形结合的方法.(3)基本不等式法:要注意条件“一正,二定,三相等”.(可见上一专题) (4)利用函数的单调性①单调函数的图象是一直上升或一直下降的,因此若单调函数在端点处有定义,则该函数在端点处取最值,即若y =f (x )在[a ,b ]上单调递增,则y 最小=f (a ),y 最大=f (b ); 若y =f (x )在[a ,b ]上单调递减,则y 最小=f (b ),y 最大=f (a ).②形如y =ax +b +dx +c 的函数,若ad >0,则用单调性求值域;若ad <0,则用换元法.③形如y =x +kx(k >0)的函数,若不能用基本不等式,则可考虑用函数的单调性,当x >0时,函数y =x +k x (k >0)的单调减区间为(0,k ],单调增区间为[k ,+∞).一般地,把函数y =x +kx(k >0,x >0)叫做对勾函数,其图象的转折点为(k ,2k ),至于x <0的情况,可根据函数的奇偶性解决. *(5)导数法利用导函数求出最值,从而确定值域.热门考点05 函数的奇偶性、周期性与单调性1.判断函数的奇偶性的两种方法 (1)定义法:(2)图象法:2.函数奇偶性的应用 (1)求函数解析式①将所求解析式自变量的范围转化为已知解析式中自变量的范围;②将转化后的自变量代入已知解析式;③利用函数的奇偶性求出解析式.(2)求参数值在定义域关于原点对称的前提下,根据奇函数满足f (-x )=-f (x )或偶函数满足f (-x )=f (x )列等式,根据等式两侧对应相等确定参数的值.特别要注意的是:若能够确定奇函数的定义域中包含0,可以根据f (0)=0列式求解,若不能确定则不可用此法. *3.函数周期性的判定及应用(1)只需证明f (x +T )=f (x )(T ≠0)便可证明函数是周期函数,且周期为T .(2)根据函数的周期性,可以由函数局部的性质得到函数整体的性质,函数的周期性常与函数的其他性质综合考查.(3)在解决具体问题时,要注意结论“若T 是函数的周期,则kT (k ∈Z 且k ≠0)也是函数的周期”的应用. 【典例15】(2017·全国高考真题(理))函数()f x 在(,)-∞+∞单调递增,且为奇函数,若(1)1f =,则满足1(2)1f x -≤-≤的x 的取值范围是( ). A .[2,2]- B .[1,1]-C .[0,4]D .[1,3]【答案】D 【解析】()f x 是奇函数,故()()111f f -=-=- ;又()f x 是增函数,()121f x -≤-≤,即()(1)2(1)f f x f -≤-≤ 则有121x -≤-≤ ,解得13x ≤≤ ,故选D.【典例16】(2018·全国高考真题(理))已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++=L ( ) A.50- B.0C.2D.50【答案】C 【解析】因为()f x 是定义域为(,)-∞+∞的奇函数,且(1)(1)f x f x -=+, 所以(1)(1)(3)(1)(1)4f x f x f x f x f x T +=--∴+=-+=-∴=,因此(1)(2)(3)(50)12[(1)(2)(3)(4)](1)(2)f f f f f f f f f f ++++=+++++L , 因为(3)(1)(4)(2)f f f f =-=-,,所以(1)(2)(3)(4)0f f f f +++=,(2)(2)(2)(2)0f f f f =-=-∴=Q ,从而(1)(2)(3)(50)(1)2f f f f f ++++==L ,选C.【典例17】(2017·山东高考真题(文))已知f (x )是定义在R 上的偶函数,且f (x +4)=f (x -2).若当x ∈[-3,0]时,f (x )=6-x ,则f (919)=________.【答案】6 【解析】由f (x +4)=f (x -2)可知,()f x 是周期函数,且6T =,所以()()()919615311f f f =⨯+= ()16f =-=. 【典例18】(2013·上海高考真题(理))设a 为实常数,()y f x =是定义在R 上的奇函数,且当0x <时,2()97a f x x x=++.若()1f x a ≥+对一切0x ≥成立,则a 的取值范围是 .【答案】87a ≤- 【解析】∵()y f x =是定义在R 上的奇函数,∴当0x >时,2()()97a f x f x x x=--=+-,而229729767a a x x a x x+-≥⋅-=-,当些仅当3x a =时,“=”成立,∴当0x >时,要使()1f x a ≥+恒成立,只需86717a a a -≥+⇒≤-或85a ≥,又∵0x =时,(0)01f a =≥+,∴1a ≤-,综上,故实数a 的取值范围是8(,]7-∞-.【总结提升】 拓展:1.函数奇偶性的判断(1)复合函数奇偶性的判断:若复合函数由若干个函数复合而成,则复合函数的奇偶性可根据若干个函数的奇偶性而定,概括为“同奇为奇,一偶则偶”.(2)抽象函数奇偶性的判断:应充分利用定义,巧妙赋值,通过合理、灵活地变形配凑来判断. 2.熟记4种常见抽象函数的周期 (1)若f (x +a )=-f (x ),则T =2|a |; (2)若f (x +a )=1f x,则T =2|a |; (3)若f (x +a )=-1f x,则T =2|a |;(4)若f (x +a )=f (x -a ),则T =2|a |.3.当函数具有两个对称时函数一般也是周期函数.当函数()f x 是奇函数,又有对称轴x m =时,则函数一定是周期函数,且周期为4T m =;若()f x 有两条对称轴x a =和x b =,则函数是周期函数,2b a -是函数的一个周期;同样若()f x 有两个对称中心(,0)a 和(,0)b ,则函数是周期函数,2b a -是函数的一个周期.巩固提升1.有意义的实数x 的取值范围是( )A.{|0x x >或}1x <-B.{|0x x …或}1x -„ C.{}10x x -<< D.{}10x x -剟【答案】C 【解析】依题有,2x x ⎧--≥⎪≠,解得10x -<<.故选:C .2.(2019·重庆高一)若()335f x x +=+,则()f x 等于( ). A.32x + B.38x + C.31x - D.34x -【答案】D 【解析】令3x t +=,所以3x t =-,所以()()33534f t t t =-+=-,所以()34f x x =-, 故选:D.3.(2017·浙江高考真题)若函数()2f x =x ax b ++在区间[0,1]上的最大值是M,最小值是m,则M m -的值( )A .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关【答案】B 【解析】因为最值在2(0),(1)1,()24a a fb f a b f b ==++-=-中取,所以最值之差一定与b 无关,选B .4.(2019·江苏高一月考)函数()()02f x x =-+ ) A.()2,+∞ B.()1,-+∞ C.()()1,22,-+∞U D.R【答案】C 【解析】幂函数的零次方底数不为0,即20x -≠ ,2x ≠;偶次方根被开方数大于等于零,分式分母不为零,即10x +>,1x >- 所以()()1,22,x ∈-+∞U . 故选:C5.(2014·全国高考真题(文))奇函数()f x 的定义域为R ,若(2)f x +为偶函数,且(1)1f =,则(8)(9)f f +=( )A .2-B .1-C .0D .1【答案】D 【解析】(2)f x +是偶函数,则()f x 的图象关于直线2x =对称,又()f x 是奇函数,则(0)0f =,且()f x 是周期函数,且周期为4,所以(8)(9)(0)(1)1f f f f +=+=.故选D .6.(2019·山西省长治市第二中学校高一期中)已知函数2()3f x ax bx =++是定义在[3,2]a a -上的偶函数,则+a b 的值是( ) A.1- B.1C.3-D.0【答案】B 【解析】∵函数2()3f x ax bx =++是定义在[3,2]a a -的偶函数, ∴320a a -+=,解得1a =,由()()f x f x =-得0b =,即1a b +=, 故选:B.7.(2019·浙江学军中学高一期中)函数()249x x f x x+-=-的奇偶性为( )A.奇函数B.偶函数C.非奇非偶函数D.既奇又偶函数【答案】B 【解析】 函数()249x x f x x +-=-,所以有290->x ,解得33x -<<, 所以()f x 定义域为()3,3- 此时40x -<恒成立, 所以()2224999x x f x x x x +-===---,()()()2299f x f x xx -===---,所以()f x 是偶函数, 故选:B8.(2017·全国高考真题(文))已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+,则(2)f =__________. 【答案】12 【解析】函数()f x 是定义在上的奇函数,()()f x f x -=-,则()()f x f x =--,()()()()322222212f f ⎡⎤=--=-⨯-+-=⎣⎦.9.(2016·四川高考真题(文))若函数f (x )是定义在R 上的周期为2的奇函数,当0<x<1时,f (x )=,则f ()+。
函数定义域值域求法(全十一种)

实用标准高中函数定义域和值域的求法总结一、常规型即给出函数的解析式的定义域求法,其解法是由解析式有意义列出关于自变量的不等式 或不等式组,解此不等式(或组)即得原函数的定义域。
2x2x 15例 1 求函数 y的定义域。
| x 3| 8解:要使函数有意义,则必须满足2x 2x 15 0① | x 3 | 8 0②由①解得 x 3或 x 5。
③由②解得x5或 x 11 ④ ③和④求交集得 x 3且 x 11或 x>5。
故所求函数的定义域为 {x | x 3且x 11} {x | x 5} 。
例 2 求函数1ysin x的定义域。
216 x解:要使函数有意义,则必须满足sin x0 ① 216 x② 由①解得 2kx2k ,kZ③ 由②解得 4 x 4 ④由③和④求公共部分,得4 x 或0 x 故函数的定义域为 ( 4, ] (0, ]评注:③和④怎样求公共部分?你会吗? 二、抽象函数型抽象函数是指没有给出解析式的函数,不能常规方法求解,一般表示为已知一个抽象函 数的定义域求另一个抽象函数的解析式,一般有两种情况。
(1)已知 f (x) 的定义域,求 f[g(x )] 的定义域。
(2)其解法是:已知 f (x) 的定义域是[a ,b ]求 f [g(x)] 的定义域是解 a g(x) b ,即为所求的定义域。
2 例3 已知 f (x) 的定义域为[-2,2],求 f ( x 1)的定义域。
2 解:令 2 x 1 2 2 ,得 1 x 32,即 0x3,因此 0 | x |3 ,从而3 x 3 ,故函数的定义域是 { x | 3 x 3} 。
(2)已知 f [g( x)] 的定义域,求 f(x) 的定义域。
其解法是:已知 f [g(x )] 的定义域是[a , b ],求 f(x) 定义域的方法是:由 a x b ,求g(x)的值域,即所求 f(x) 的定义域。
例 4 已知 f (2x 1) 的定义域为[1,2],求 f(x) 的定义域。
高一数学函数的常用表示方法(新编201908)

(1)解析法:就是用数学表达式表示两个变量之间 的对应关系。(实例1)
(2)图象法:就是用图象表示两个两个变量之间 的对应关系。(实例2)
(3)列表法:就是列出表格来表示两个变量之间 的对应关系。(实例3)
例3 某种笔记本的单价是5元,买x x 1,2,3,4,5
个笔记本需要元。试用函数的三种表示法表示函数
解:这个函数的定义域是数集{1,2,3,4,5} 用解析法可将函数y=f(x)表示为
y 可将函数表示为
笔记本数x 1
钱数y
5
234 5 10 15 20 25
用图象法可将函数表示为下图
y
.
25
. 20 . 15 .. 10
5
012345
笔记本数x 1 2 3
x
45
钱数y
5 10 15 20 25
; /naotanby 小儿脑瘫病因 新生儿脑瘫病因 脑瘫出现的原因
;
无以立学徒 乃从南门出 照臣款诚 生焘 颍川韩元长 贼十余人皆披散 寻见释 乐浪公 彦之进军 义宣 索虏寇青州 又被免 如日之明 云动权豪之术 积旬不克 侍中太尉征东大将军直勤驾头拔 就渊求官 征守度支尚书 为乡邑所美 未及结竟 宣令宿卫曰 焘既获茂虔 虏掘破许昌城 乘舶举 帆 中军司马刘冲之白孝武 玄谟曰 不审可得在此诏不 卒 兼率如故 病卒 修之率众南定遗寇 不愿望风容贷 正足自灭耳 固非深矣 州都郡正 而其形甚丑 安都幢主周文恭晨往侦候 自非戎军所指 扬言虎走城西 下诏曰 於是难当将妻子奔索虏 代王尚屯姑臧 寻阳太守 先是 请在降减 乃 追徽为持节 击之以石 天子内镇群心 忧在未萌 泰始二年三月三日 於是遣使求和 曾祖侃 太祖元嘉四年 通《毛诗》六义及《礼论》 玄谟军众亦盛 遂居交趾 运当攀龙 元嘉
函数及其表示

函数及其表示一、函数的概念及其构成要素函数在数学上的定义:给定一个数集A,对A施加对应法则f,记作f(A),得到另一数集B,也就是B=f(A).那么这个关系式就叫函数关系式,简称函数.例:设数集A={1、2、3、4、5},对A施加对应法则求平方,得B={1、4、9、16、25}也就是B=f(A)=A^2,这个关系式就是函数设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数和它对应,那么就称为从集合A到集合B的一个函数,记作或。
其中x叫作自变量,叫做x的函数,集合叫做函数的定义域,与x对应的y叫做函数值,函数值的集合叫做函数的值域,叫做对应法则。
其中,定义域、值域和对应法则被称为函数三要素。
定义域,值域,对应法则称为函数的三要素。
一般书写为。
二、判断两个函数是否为同一个函数若两函数定义域相同,对应法则也相同,则称这两个函数相等。
其实就是看两个方面:1、看定义域是否相同,如果定义域不同,就算函数式形式相同,也不是相同的函数。
例如函数f(x)=x和g(x)=x²/x,尽管当x≠0时,两个函数相等,但是f(x)的定义域是全体实数,g(x)的定义域是x≠0,定义域不一样,所以不是相同的函数。
2、定义域相同的情况下,看相同的x计算出来的函数值是否一样,如果有相同的x算出来的函数值不一样,那么就不是相同的函数。
例如f(x)=x和g(x)=|x|,定义域相同,但是当x<0的时候,函数值不同,所以不是相同的函数。
如上述两个方面都相同,那么就一定是相同的函数了。
三、函数的定义域及其求法1.如果f(x)为整式,其定义域是R2.如果f(x)=x分之1,其定义域是x≠03.如果f(x)=根号x,其定义域是x≥04.如果f(x)=x0,其定义域是x≠05.如果f(x)是由几个部分的式子构成,定义域是使几个部分有意义的公共部分(交集)6.已知f(x)的定义域是【1,2】,则f(x+1)的定义域是[0,1]7.已知f(x+1)的定义域是【1,2】,则f(x)的定义域是[2,3]四、函数的值域1:直接法:从自变量的范围出发,推出值域,也就是直接看咯。
高中数学求函数值域的解题方法总结(16种)

练习:求函数 y = x2 + 9 + (5 − x)2 + 4 的值域。(答案:{y|y≥ 5 2 })
九、比例法:
对于一类含条件的函数的值域的求法,可将条件转化为比例式,代入目标函 数,进而求出原函数的值域。
例:已知 x,y∈R,且 3x-4y-5=0,求函数 z = x2 + y2 的值域。
例:求函数 y = x - 3 + 2x +1 的值域。 点拨:通过换元将原函数转化为某个变量的二次函数,利用二次函数的最值, 确定原函数的值域。
解:设 t = 2x +1 (t≥0),则
x = t2 -1 。 2
于是 y = t2 -1 - 3 + t = (t +1)2 − 4 ≥ 1 − 4 = − 7 .
( )( ) 例:已知 2x2 - x - 3 3x2 + x +1 ≤ 0 ,且满足 x + y = 1,求函数 z = xy + 3x 的值域。
点拨:根据已知条件求出自变量 x 的取值范围,将目标函数消元、配方,可 求出函数的值域。
解:3x2 + x +1 0 ,上述分式不等式与不等式 2x2 - x - 3 ≤ 0 同解,解之得
3 3 3
3
点评:利用单调性求函数的值域,是在函数给定的区间上,或求出函数隐含的区 间,结合函数的增减性,求出其函数在区间端点的函数值,进而可确定函数的值 域。
练习:求函数 y = 3 + 4 - x 的值域。(答案:{y|y≥3})
七、换元法:
以新变量代替函数式中的某些量,使函数转化为以新变量为自变量的函数形 式,进而求出值域。
函数定义域值域求法(全十一种)

实用标准高中函数定义域和值域的求法总结一、常规型即给出函数的解析式的定义域求法,其解法是由解析式有意义列出关于自变量的不等式或不等式组,解此不等式(或组)即得原函数的定义域。
例 1求函数 y x 22x15| x 3 |8的定义域。
解:要使函数有意义,则必须满足x 22x150①| x 3 |8 0②由①解得x3或 x 5 。
③由②解得x5或 x11④③和④求交集得x3且 x11或x>5。
故所求函数的定义域为{ x | x 3且x11}{ x | x5} 。
例 2求函数 y sin x1的定义域。
16x 2解:要使函数有意义,则必须满足sin x0①16x 20②由①解得2k x2k,k Z③由②解得 4 x4④由③和④求公共部分,得4x或 0x故函数的定义域为(4, ](0, ]评注:③和④怎样求公共部分?你会吗?二、抽象函数型抽象函数是指没有给出解析式的函数,不能常规方法求解,一般表示为已知一个抽象函数的定义域求另一个抽象函数的解析式,一般有两种情况。
( 1)已知f (x )的定义域,求f [ g(x )]的定义域。
( 2)其解法是:已知 f (x) 的定义域是[a,b]求 f [g(x)] 的定义域是解a g(x) b ,即为所求的定义域。
例 3已知 f (x) 的定义域为[-2, 2],求f ( x 21) 的定义域。
解:令 2 x21 2 ,得 1 x2 3 ,即0 x 23,因此0| x | 3 ,从而3 x 3 ,故函数的定义域是{ x | 3 x3} 。
( 2)已知f [g( x)]的定义域,求f(x) 的定义域。
其解法是:已知 f [g(x )] 的定义域是[a,b],求f(x)定义域的方法是:由a x b,求g(x) 的值域,即所求f(x) 的定义域。
例 4已知 f (2x1) 的定义域为[1,2],求f(x)的定义域。
解:因为 1 x2,22x4,32x 1 5 。
即函数 f(x) 的定义域是{ x | 3x5} 。
函数定义域值域求法(全十一种)

函数定义域值域求法(全十一种)高中函数定义域和值域的求法总结一、常规型常规型是指已知函数的解析式,求函数的定义域和值域。
解法是由解析式有意义列出关于自变量的不等式或不等式组,解此不等式(或组)即得原函数的定义域。
例如,对于函数 $y=\frac{x^2-2x-15}{|x+3|-8}$,要使函数有意义,则必须满足 $x^2-2x-15\geq 0$ 且 $|x+3|\neq 8$。
解得$x\leq -3$ 或 $x\geq 5$,且 $x\neq -11$ 或 $x\neq 5$。
将两个条件求交集得 $x\leq -3$ 且 $x\neq -11$ 或 $x>5$,即函数的定义域为 $\{x|x\leq -3\text{ 且 }x\neq -11\}\cup\{x|x>5\}$。
二、抽象函数型抽象函数型是指没有给出解析式的函数,需要根据已知条件求解。
一般有两种情况:1)已知 $f(x)$ 的定义域,求 $f[g(x)]$ 的定义域。
解法是:已知 $f(x)$ 的定义域为 $[a,b]$,则 $f[g(x)]$ 的定义域为解$a\leq g(x)\leq b$。
例如,已知 $f(x)$ 的定义域为 $[-2,2]$,求 $f(x^2-1)$ 的定义域。
令 $-2\leq x^2-1\leq 2$,得 $-1\leq x^2\leq 3$,即 $-|x|\leq x\leq |x|$。
因此,$-3\leq x\leq 3$,即函数的定义域为$\{x|-3\leq x\leq 3\}$。
2)已知 $f[g(x)]$ 的定义域,求 $f(x)$ 的定义域。
解法是:已知 $f[g(x)]$ 的定义域为 $[a,b]$,则 $f(x)$ 的定义域为$g(x)$ 的值域。
例如,已知 $f(2x+1)$ 的定义域为 $[1,2]$,求 $f(x)$ 的定义域。
因为 $1\leq x\leq 2$,所以 $2\leq 2x\leq 4$,$3\leq2x+1\leq 5$。
高中数学第3章函数3.1函数的概念与性质3.1.1第2课时函数的表示方法bb高一第一册数学

·
结
探
提
新
素
知
A.y=-14x2+1
B.y=14x2-1
养
合
作 探
C.y=4x2-16
D.y=-4x2+16
课 时
究
分
层
释 疑
B [把点(0,-1)代入四个选项可知,只有B正确.]
作 业
难
·
返
首
页
12/13/2021
第十五页,共六十五页。
情
4.(教材P93练习A第8题改编)下列给出的式子是分段函数的是 课
合 作
(3)分段函数由几个函数构成. ( )
探
究
x+1,x≤1,
释 疑
(4)函数f(x)=-x+3,x>1 是分段函数.
(
难
12/13/2021
第十三页,共六十五页。
课 堂 小 结
)提
素
)养
课 时 分 层
)作
业
返 首 页
·
·
情
课
景
2.已知函数f(x)由下表给出,则f(3)等于( )
堂
导
小
学
x
1≤x<2 2 2<x≤4
·
提
新
素
知
所以a2x+ab+b=4x+8,
养
·
·
合 作 探 究
释
即aa2b=+4b,=8,解得ab= =382,或ba==--82.,
课 时 分 层 作
疑
业
难
所以f(x)=2x+83或f(x)=-2x-8.
返
首
页
12/13/2021
第二十九页,共六十五页。
抛物线解析式的求法

- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学:函数解析式的十一种方法一、定义法 二、待定系数法 三、换元(或代换)法 四、配凑法 五、函数方程组法七、利用给定的特性求解析式.六、特殊值法 八、累加法 九、归纳法 十、递推法 十一、微积分法一、定义法:【例1】设23)1(2+-=+x x x f ,求)(x f .2]1)1[(3]1)1[(23)1(22+-+--+=+-=+x x x x x f =6)1(5)1(2++-+x x65)(2+-=∴x x x f【例2】设21)]([++=x x x f f ,求)(x f . 【解析】设xx x x x x f f ++=+++=++=111111121)]([xx f +=∴11)(【例3】设33221)1(,1)1(x x x x g x x x x f +=++=+,求)]([x g f .【解析】2)(2)1(1)1(2222-=∴-+=+=+x x f x x x x x x f又x x x g x x x x xx x x g 3)()1(3)1(1)1(3333-=∴+-+=+=+ 故2962)3()]([24623-+-=--=x x x x x x g f【例4】设)(sin ,17cos )(cos x f x x f 求=.【解析】)2(17cos )]2[cos()(sin x x f x f -=-=ππx x x 17sin )172cos()1728cos(=-=-+=πππ.二、待定系数法:在已知函数解析式的构造时,可用待定系数法。
【例1】 设)(x f 是一次函数,且34)]([+=x x f f ,求)(x f 【解析】设b ax x f +=)( )0(≠a ,则bab x a b b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 【例2】已知1392)2(2+-=-x x x f ,求)(x f .【解析】显然,)(x f 是一个一元二次函数。
设)0()(2≠++=a c bx ax x f则c x b x a x f +-+-=-)2()2()2(2)24()4(2c b a x a b ax +-+-+=又1392)2(2+-=-x x x f比较系数得:⎪⎩⎪⎨⎧=+--=-=1324942c b a a b a 解得:⎪⎩⎪⎨⎧=-==312c b a 32)(2+-=∴x x x f三、换元(或代换)法:已知复合函数[()]f g x 的表达式时,还可以用换元法求()f x 的解析式。
与配凑法一样,要注意所换元的定义域的变化。
【例1】 已知x x x f 2)1(+=+,求)1(+x f 【解析】令1+=x t ,则1≥t ,2)1(-=t xx x x f 2)1(+=+∴,1)1(2)1()(22-=-+-=t t t t f1)(2-=∴x x f )1(≥xx x x x f 21)1()1(22+=-+=+∴ )0(≥x【例2】 已知,11)1(22x xx x x f ++=+求)(x f . 【解析】设,1t x x =+则11-=t x 则x x x x x x x f t f 11111)1()(222++=++=+= 1)1()1(1111)11(11222+-=-+-+=-+-+=t t t t t t 1)(2+-=∴x x x f 【例3】 设x x f 2cos )1(cos =-,求)(x f .解:令1cos ,1cos +=∴-=t x x t又0201cos 2,1cos 1≤≤-≤-≤-∴≤≤-t x x 即]0,2[,)1()()02(,)1()(22-∈+=≤≤-+=∴x x x f t t t f 即【例4】 若x xx f x f +=-+1)1()( (1) 在(1)式中以xx 1-代替x 得x x xx x x f x x f 11)111()1(-+=---+-即x x x f x x f 12)11()1(-=--+- (2) 又以11--x 代替(1)式中的x 得:12)()11(--=+--x x x f x f (3))1(112121)(2:)2()3()1(23---=----++=-+x x x x x x x x x x f 得)1(21)(23---=∴x x x x x f【例5】设)0,,()1()()(b a ,c b a cxxbf x af x f ±≠=+且均不为其中满足,求)(x f 。
【解析】cx xbf x af =+)1()( (1)用x 1来代替x ,得xc x bf x af 1)()1(⋅=+ (2)由xbcacx x f b a b a -=-⨯-⨯222)()(:)2()1(得xb a bcacx x f ba )()(222--=∴±≠【例6】已知2)(21+=-x af x ,求)(x f .【解析】设01 -=x a t,则t x a log 1=-即1log +=t xa代入已知等式中,得:3log 2log 2)1(log )(22++=++=t t t t f a a a3log 2log )(2++=∴x x x f a a四、配凑法已知复合函数[()]f g x 的表达式,要求()f x 的解析式时,若[()]f g x 表达式右边易配成()g x 的运算形式,则可用配凑法,使用配凑法时,要注意定义域的变化。
【例1】已知1)f x =+求()f x 的解析式。
【解析】2x x +∴可用配凑法由21))1f x =+=-令t =1x t ≥∴≥则2()1f t t =- 即2()1(1)f x x x =-≥ 当然,上例也可直接使用换元法令t = 则1t = 得222(1)()(1)2(1)1x t f t t t t =-∴=-+-=- 即 2()1(1)f x x x =-≥由此可知,求函数解析式时,可以用配凑法来解决的,有些也可直接用换元法来求解。
【 例 2】已知2211(),f x x x x-=+求()f x .【解析】此题直接用换元法比较繁锁,而且不易求出来,但用配凑法比较方便。
由222111()()2f x x x x x x-=+=-+令2110t x x tx x =-⇒--=由0∆≥即240t +≥得t R ∈ 2()2f t t ∴=+ 即:2()2()f x x x R =+∈实质上,配凑法也缊含换元的思想,只是不是首先换元,而是先把函数表达式配凑成用此复合函数的内函数来表示出来,在通过整体换元。
和换元法一样,最后结果要注明定义域。
五、函数方程组法。
函数方程组法适用的范围是:题高条件中,有若干复合函数与原函数()f x 混合运算,则要充分利用变量代换,然后联立方程组消去其余部分。
【 例1】设()f x 满足1()2(),f x f x x-=求()f x 的解析式。
【解析】要求()f x 可消去1()f x ,为此,可根据题中的条件再找一个关于()f x 与1()f x的等式,通过解方程组达到消元的目的。
1()2()f x f x x-=………………………①显然,0x ≠,将x 换成1x得11()2()f f x x x-=……………………………..②由1()2()11()2()f x f x x f f x xx ⎧-=⎪⎪⎨⎪-=⎪⎩消去1()f x ,得12()33f x x x=--小结:函数方程组法适用于自变量的对称规律。
互为倒数,如f(x )、1()f x;互为相反数,如f(x)、f (-x),通过对称代换构造一个对称方程组,解方程组即得f(x)的解析式。
【 例 2】已知2)(21+=-x af x ,求)(x f .【解析】设01 -=x a t,则t x a log 1=-即1log +=t xa代入已知等式中,得:3log 2log 2)1(log )(22++=++=t t t t f a a a3log 2log )(2++=∴x x x f a a【例 3】设)(x f 为偶函数,)(x g 为奇函数,又,11)()(-=+x x g x f 试求)()(x g x f 和的解析式 【解析】)(x f 为偶函数,)(x g 为奇函数,)()(),()(x g x g x f x f -=-=-∴又11)()(-=+x x g x f ① , 用x -替换x 得:11)()(+-=-+-x x g x f 即11)()(+-=-x x g x f ② 解① ②联立的方程组,得11)(2-=x x f , xx x g -=21)( 六、特殊值法:(赋值类求抽象函数)【例1】设)(x f 是定义在N 上的函数,满足1)1(=f ,对于任意正整数y x ,,均有xy y x f y f x f -+=+)()()(,求)(x f .解:由1)1(=f ,xy y x f y f x f -+=+)()()(设1=y 得:x x f x f -+=+)1(1)(即:1)()1(+=-+x x f x f在上式中,x 分别用1,,3,2,1-t 代替,然后各式相加可得:t t t t t f 21211)1)(2(21)(2+=+-+=)(2121)(2*∈+=∴N x x x x f【例2】 已知:1)0(=f ,对于任意实数x 、y,等式)12()()(+--=-y x y x f y x f 恒成立,求)(x f【解析】对于任意实数x、y,等式)12()()(+--=-y x y x f y x f 恒成立,不妨令0x =,则有1)1(1)1()0()(2+-=-+=+--=-y y y y y y f y f 再令 x y =- 得函数解析式为:1)(2++=x x x f七.利用给定的特性求解析式.【例1】设)(x f 是偶函数,当x >0时, xe x e xf +⋅=2)(,求当x <0时,)(x f 的表达式.【解析】对x ∈R , )(x f 满足)1()(+-=x f x f ,且当x ∈[-1,0]时, x x x f 2)(2+=求当x ∈[9,10]时)(x f 的表达式.七.利用给定的特性求解析式.八、累加法:(核心思想与求数列的通项公式相似)【例1】若af 1lg)1(=,且当),0(,lg )()1(,21*∈-=-≥-N x a a x f x f x x 满足时,求)(x f . 【解析】),0(lg )1()(1*-∈+-=N x a a x f x f x递推得:2lg )2()1(-+-=-x a x f x f3lg )3()2(-+-=-x a x f x f…… ……2lg )2()3(a f f +=a f f lg )1()2(+=以上)1(-x 个等式两边分别相加,得:122lg lg lg lg )1()(--+++++=x x a a a a f x f )1()2(21lg )1(-+-++++=x x a f12)1(2)1(lg lg 1lg ---=+=x x x x aaaa x x lg ]12)1([--= 九、归纳法:【例1】已知a f N x x f x f =*∈+=+)1()(),(212)1(且,求)(x f . 【解析】a a f f a f 2124212)1(212)2(,)1(+-=+=+==a a f f 202124)212(212)2(212)3(+-=++=+=a a f f 312124)413(212)3(212)4(+-=++=+=-a a f f 422124)81213(212)4(212)5(+-=++=+=-………………………………,依此类推,得a x f x x 132124)(--+-=再用数学归纳法证明之。
