金属晶体堆积模型复习及计算
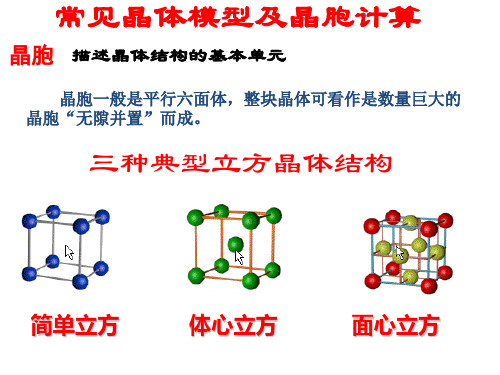
常见晶体模型及晶胞计算
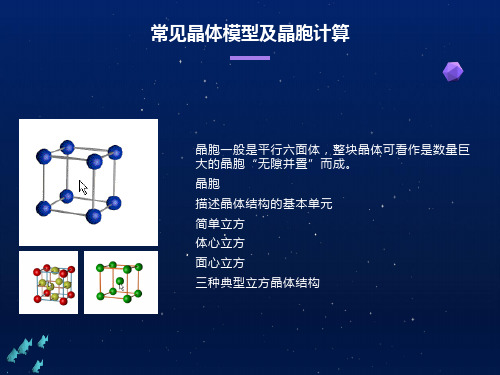
晶胞中微粒个数的计算,求化学式
小结:高考常见题型
1、(2013·江苏,21A(1)) 元素X 位于第四周期,其基态原子的内层轨道全部排满电子,且最外层电子数为2。元素Y基态原子的3p 轨道上有4个电子。
X与Y所形成化合物晶体的晶胞如右图所示。 ①在1个晶胞中,X离子的数目为 。 ②该化合物的化学式为 。
Mg、Zn、Ti 每个晶胞含 个原子 六方最密堆积的配位数 =12 2
④面心立方最密堆积(铜型)
Cu、Ag、Au 面心立方堆积的配位数 =12 每个晶胞含 个原子 4
面心立方最密堆积的空间占有率
=74%
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆积的典型代表
(3)若NaCl晶体的密度为ρg/cm3,则 NaCl晶体中Na+与Na+间的最短距离是多少?
a/2
a/2
=
练习
CsCl的晶体结构
(1)每个Cs+( Cl-)周围等距且紧邻的Cl- (Cs+)有 个, Cs+( Cl-)的配位数为 。
8
8×1/8=1
6
——晶胞为体心立方体
8
(2)每个Cs+ ( Cl-)周围 等距且紧邻的Cs+ ( Cl-)有 个。
1
3
6
4
2
A
5
密置层
配位数为4
配位数为6
返
A
B
A
B
A
返
第三层的另一种排列方式,是将球对准第一层的 2,4,6 位,不同于 AB 两层的位置,这是 C 层。
1
2
3
4
5
6
1
2
3
人教版高中化学选修三课件:第三章 专题课 晶体堆积模型及晶胞相关计算ppt

例5 右图为NaCl晶胞结构,已知FexO晶体晶胞结构为 NaCl型,由于晶体缺陷,x值小于1。测知FexO晶体的
密度为ρ=5.71g/cm3,晶胞边长为4.28×10-10m。
探究1:已知铜晶胞是面心立方晶胞,其晶胞特征如右图所示。 若已知该晶体的密度为a g/cm3,NA代表阿伏加德罗常数,相对原子质量为64 , 请回答:
[来源:学科网]
①晶胞中铜原子的配位数为________ ,一个晶胞中原子的数目为________; ②该晶体的边长为_______________,铜原子半径为________(用字母表示)。 列式并计算Cu空间利用率________________
D.YBa2Cu4O7
题型4、 晶体密度、粒子间距离的计算
例4右图为NaCl晶胞结构示意图。 (1)用X射线衍射法测得晶胞的边长为a cm,求该温度下NaCl晶体的密度。
ρ=m/V=
(2)晶体的密度为ρg/cm3,则晶体中Na +与Na+之间的最短距离是多少?
[练习3]. 已知 NaCl 的摩尔质量为 M g·mol-1, 食盐晶体的密度为ρg·cm-3,若下图中Na+与最邻 近的Cl- 的核间距离为 a cm,那么阿伏加德罗常 数的值可表示为 D
【巩固练习】 1.Al2O3在一定条件下可制得AlN,其晶体结构如图2所示,该 晶体中Al的配位数是_________ .
2.六方氮化硼在高温高压下,可以转化为立方氮化硼,其结构与金刚石相似, 硬度与金刚石相当,晶胞边长为361.5pm,立方氮化硼晶胞中含有______个 氮原子、_______个硼原子,立方氮化硼的密度是____________g·cm-3(只 要求列算式,不必计算出数值,阿伏加德罗常数为NA)
高考化学二轮复习:关于几种常见晶体结构与计算

子晶体的熔沸点都很高
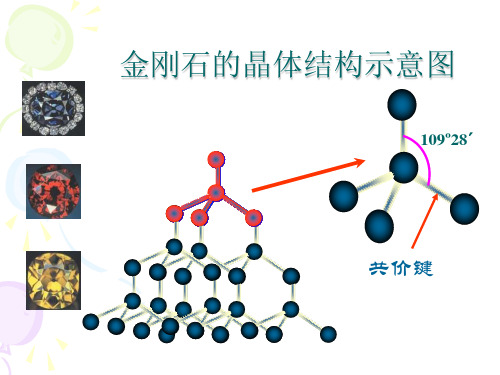
109º28´
共价键
宜城市第一中学化学教研组
宜城市第一中学
金刚石晶胞中含碳原子数:
8× +6× +4= 8
金刚石晶胞的棱边a与碳原子半径r 的关系:
金刚石的空间利用率
金刚石
P0=
= 34.0%
宜城市第一中学化学教研组
宜城市第一中学
练习2:2016. 37.[化学——选修3:物质结构与性质](15分)
•
7.“画竹”是本文的线索,本文记述 文与可 画竹的 情形, 以充满 感情的 笔触回 忆两人 的交往 ,以及 文与可 死后自 己的悲 慨,又 从文与 可的创 作经验 中总结 出艺术 创作的 规律, 熔叙事 、抒情 、议论 于一炉 。
•
8.总之,说明文中使用生动活泼的语 言,不 仅能增 强文章 内容表 达上的 形象性 、可感 性和文 学色彩 ,使读 者获得 不同程 度的美 感体验 ,受到 美的陶 冶,还 有助于 加深读 者对说 明内容 的理解 ,增知 益智。
•
5.在乡土社会里,地缘关系也是如此 。每一 家以自 己的地 位做中 心,周 围划出 一个圈 子,个 圈子是 “街坊 ”。可 是这不 是一个 固定的 团体, 而是一 个范围 。范围 的大小 也要依 着中心 的势力 厚薄而 定。
•
6.在这种富于伸缩性的网络里,随时 随地是 有一个 “己” 作中心 的。这 并不是 个人主 义,而 是自我 主义。 在个人 主义下 ,一方 面是平 等观念 ,指在 同一团 体中各 分子的 地位相 等,个 人不能 侵犯大 家的权 利;一 方面是 宪法观 念,指 团体不 能抹煞 个人, 只能在 个人们 所愿意 交出的 一分权 利上控 制个人 。
3-4:金属晶体的原子堆积模型

有关原子堆积模型的几个重要概念 1、密置:紧密排列2、紧密堆积:微粒间的作用力使微粒尽可能地相互接近,使它们占有最小空间。
3、空间利用率:晶体的空间被微粒占满的体积百分数,用它来表示紧密堆积的程度。
4、配位数:在紧密堆积中,一个原子或离子周围距离最近且相等的原子或离子数目称为配位数。
二维空间的堆积:非密置层与密置层将金属晶体中的原子看成直径相等的球体,并把它们放置在平面内(即二维空间里),则有两种排列方式:按第一个图方式排列,圆球周围剩余空隙大,称为非密置层,配位数为4;而按第二个图方式排列,圆球周围剩余的空隙轻小,称为密置层,配位数为6。
金属晶体可看成金属原子在三维空间中堆积而成。
有如下4种基本模式。
1、简单立方堆积(非密置层) 2、体心立方堆积(非密置层) 3、面心立方最密堆积(密置层) 4、六方最密堆积(密置层)课题:金属晶体的原子堆积模型总第( )期 命题人:①三维空间里非密置层金属原子的堆积方式a.简单立方堆积:金属钋(Po)相邻非密置层原子的原子核在同一直线上堆积,这种堆积方式形成的晶胞是一个立方体,每个晶胞含1个原子,被称为简单立方堆积。
这种堆积方式的空间利用率太低,只有金属钋(Po)采取这种堆积方式。
b.体心立方堆积:钾型(碱金属)非密置层的另一种堆积方式是将上层金属原子填入下层的金属原子形成的凹穴中,并使非密置层的原子稍稍分离,每层均照此堆积。
这种堆积方式的空间利用率显然比简单立方堆积的高多了,许多金属是这种堆积方式,如碱金属,简称为钾型。
体心立方堆积空间占有率=%02.68%10083)34(3423423333=⨯=⨯=⨯πππr r a r②三维空间里密置层金属原子的堆积方式密堆积方式由于充分利用了空间,从而可以使体系的势能尽可能降低,结构稳定。
它的堆积方式整体上可以分为两种分析:密置双层:将两个密置层叠加起来作最密堆积称为密置双层,这只有一种叠合方式叠合过程为:将第二层球的球心投影到第一层中由三个球所围成的三角形空隙的中心上关键是第三层,对第一、二层来说,第三层可以两种最紧密的堆积方式a.六方最密堆积:镁型(Zn、Ti、Mg)六方最密堆积的空间利用率计算在六方堆积中取出六方晶胞,平行六面体的底是四边形,各边长a=2r ,则平行四边行的面积:222360sin a a S ==。
金属晶体金属键堆积方式
修高
3
) 第 三 章
二 化 学 ( 选
第三节
金属晶体
Ti
金属样品 Ti
1、金属共同的物理性质
容易导电、导热、有延展性、有金属光泽等。
金属为什么具有这些共同性质呢? 2、金属的结构
㈠、金属键
(1)定义: 金属离子和自由电子之间的相互作用。 (2)成键微粒: 金属阳离子和自由电子 (3)键的存在: 金属单质和合金中 (4)方向性: 无方向性 (5)键的本质: 电子气理论
【总结】非金属单质是原子晶体还是分子晶体的 判断方法
(1)依据组成晶体的粒子和粒子间的作用判断: 原子晶体的粒子是原子,质点间的作用是共价键; 分子晶体的粒子是分子,质点间的作用是范德华力。
(2)记忆常见的、典型的原子晶体。 (3)依据晶体的熔点判断:原子晶体熔、沸点高, 常在1000℃以上;分子晶体熔、沸点低,常在数百 度以下至很低的温度。 (4)依据导电性判断:分子晶体为非导体,但部 分分子晶体溶于水后能导电;原子晶体多数为非导 体,但晶体硅、晶体锗是半导体。 (5)依据硬度和机械性能判断:原子晶体硬度大, 分子晶体硬度小且较脆。
③ 六方堆积 ——六方晶胞
④面心立方堆积 ——面心立方晶胞
配位数 = 12 空间利用率 = 74.05% 配位数 = 12 空间利用率 = 74.05%
知识拓展-石墨
一种结晶形碳,有天然出产的矿物。铁 黑色至深钢灰色。质软具滑腻感,可沾污手 指成灰黑色。有金属光泽。六方晶系,成叶 片状、鳞片状和致密块状。密度2.25g/cm3, 化学性质不活泼。具有耐腐蚀性,在空气或 氧气中强热可以燃烧生成二氧化碳。石墨可 用作润滑剂,并用于制造坩锅、电极、铅笔 芯等。
4.金属晶体熔点变化规律
常见晶体模型及晶胞计算
(三) 晶体的密度及微粒间距离 的计算
练习
1、(2013·江苏,21A(1)) 元素X 位于第四周期,其基态原子的内层轨道全部 排满电子,且最外层电子数为2。元素Y基态原子的 3p 轨道上有4个电子。
X与Y所形成化合物晶体的晶胞 如右图所示。
①在1个晶胞中,X离子的数目 为4 。
=
58.5 / NA×4 a3
(3)若NaCl晶体的密度为ρg/cm3,则 NaCl晶体中Na+与 Na+间的最短距离是多少?
CsCl的晶体结构——晶胞为体心立方体
(1)每个Cs+( Cl-)周围等距 且紧邻的Cl- (Cs+)有 8 个, Cs+( Cl-)的配位数为 8 。 (2)每个Cs+ ( Cl-)周围 等距且紧邻的Cs+ ( Cl-)有 6 个。 (3)每个晶胞中含 1 个Cs+、含8×1/8=1个Cl-,故每 个晶胞中含有 1 个“CsCl”结构单元; N(Cs+) ︰ N( Cl-) = 1︰1 ,化学为 CsCl 。
(4)能否 把“NaCl”称为分子式?
练习
-的距离为 a cm,该晶体密度为
(1)设NaCl晶胞的边长为acm,则
示晶为胞中Na+和Cl-的最近距离(( 即小)立
方体的边长)为 a/2 cm,则晶胞中 同种离子的最近距离为 a/2 cm。
(2)晶胞的边长为acm,求NaCl晶 体的密度。
ρ
=
M / NA×晶胞所含粒子数 晶胞的体积
思考:NaCl、CsCl同属AB型离子晶体, NaCl晶体中 Na+的配位数与CsCl晶体中Cs+的配位数是否相等?
CaF2的晶体结构
金属晶体模型

铜型 Cu, Ag, Au 74% 12 (ccp)
晶胞
能力训练
1.下列有关金属元素特征的叙述中正确的是 A.金属元素的原子只有还原性,离子只有氧 化性 B.金属元素在化合物中一定显正价 C.金属元素在不同化合物中的化合价均不同 D.金属单质的熔点总是高于分子晶体
3.3.2《金属晶体的原子 堆积模型》
金属晶体的原子堆积模型
一、几个概念 紧密堆积:微粒之间的作用力使微粒间尽
可能的相互接近,使它们占有最小的空间
配位数:在晶体中与每个微粒紧密相邻的 微粒个数
空间利用率:晶体的空间被微粒占满的体积 百分数,用它来表示紧密堆积的程度
二、金属晶体的原子堆积模型
金属晶体中的原子可看成直径相等的小球。将等 径圆球在一平面上排列,有两种排布方式
3.六方堆积
镁、锌、钛等属于六方堆积
第一种: 将第三层球对准第一层的球
A
12
6
3
B
54
A
B
于是每两层形成一个周
A
期,即 AB AB 堆积方式, 形成六方堆积。
上图是此种六方 堆积的前视图
配位数 12 ( 同层 6,上下层各 3 )
六方密堆积-镁型
六方堆积方式的金属晶体: Mg、Zn、Ti
第三层的另一种排列 方式,是将球对准第一层 的 2,4,6 位,不同于 AB 两层的位置,这是 C 层。
体心立方堆积 钾型
配位数:8 空间占有率: 68.02%
思考:密置层的堆积方式有哪些?
第二层 : 对第一层来讲最紧密的堆积方式是将 球对准1,3,5 位。 ( 或对准 2,4,6 位,其情形是一 样的 )
12
金属堆积

,
1
2
两 个 密 置 层 密 置 堆 积
三 个 密 置 层 密 置 堆 积
六方堆积
面心立方 堆积
3.六方堆积(镁型)镁、锌、钛等属于六方堆积
第一种: 将第三层球对准第一层的球 A
1 6 5 4
2
3
B
A B
于是每两层形成一个 周期,即 AB AB 堆积方 式,形成六方堆积。
A
上图是此种六方 堆积的前视图
阅读课文P76《资料卡片》,并填写下表
堆积模型 简单立方 钾型( bcp ) 镁型(hcp) 铜型(ccp) 典型代表 空间利 用率 配位数 晶胞
金属晶体的四中堆积模型对比
能力训练
1.下列有关金属元素特征的叙述中正确的是
A.金属元素的原子只有还原性,离子只有氧 化性 B.金属元素在化合物中一定显正价
A
C B A
1 6
2 3
5
4
C B
配位数 12 ( 同层 6, 上下层各 3 )
A 此种立方紧密堆积的前视图
铜型(面心立方最密堆积)
1 ABC铜型面心立方晶胞的抽取
C
B
B
A C B A
A C
B
晶胞内原子数:4
配位数:12 空间利用率: 74% 典型金属:Cu Ag Au
三、金属晶体的四种堆积模型对比
第二节 金属晶体的原子 堆积模型
金属晶体的原子堆积模型
(1)几个概念 配位数:在晶体中与每个微粒紧密相邻的 微粒个数 空间利用率:晶体的空间被微粒占满的体积 百分数,用它来表示紧密堆积的程度
空间利用率= 球体积 晶胞体积 100%
一、 二维平面堆积方式
非密置层
行列对齐,四球一空 非最紧密排列 配位数:4
金属晶体堆积模型及计算公式31页PPT

35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
Thank you
金属晶体堆积模型及计算公 式
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
2020高考热点---金属晶体四类晶胞空间利用率的计算

3、每个晶胞含 4个原子
4、晶胞边长为a
5、空间利用率=
六方立方晶体
六方最密堆积(镁型) 1、金属---Mg、Zn、Ti 2、六方最密堆积的配位数 12
3、每个晶胞含 2 个原子
4、晶胞边长为a a=2r 5、晶胞高为h h=
V球
2
4
3
r3
(晶胞中有2个球)
6、空间利用率=
V球 V晶胞 100% 74.05%
2、简单立方堆积的配位数 6
3、每个晶胞含 1个原子
4、晶胞边长为a a=2r
5、空间利用率=
体心立方晶体
1、体心立方堆积(钾型) K、Na、Fe 2、体心立方堆积的配位数 8
3、每个晶胞含 2 个原子
4、晶胞边长
5、空间利用率=
面心立方晶体
面心立方堆积
球半径为r
1、金属——铜型 Cu、Ag、Au
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆 积的典型代
表
空间利 用率
配位数
简单立方 Po(钋) 52%
6
体心立方 (钾型)
K、Na、Fe
68%
2
面心立方最
密(铜型) Cu, Ag, Au 74%
12
晶胞
简单立方晶体
简单立方堆积
球半径为r
1、唯一金属——钋
金属晶体堆积模型及计算公式

----体心立方堆积:
5 8 1
6 7 2
4
3
这种堆积晶胞是一个体心立方,每个晶胞含 2 个原子,属于非密置层堆积,配位数 为 8 ,许多金属(如Na、K、Fe等)采取这种 堆积方式。
空间利用率的计算
(2)体心立方:在立方体顶 点的微粒为8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。 微粒数为:8×1/8 + 1 = 2
1200
平行六面体
每个晶胞含 2 个原子
铜型(面心立方紧密堆积)
7 6 5 1 8 9 4 2 3
12
10 11
这种堆积晶胞属于最密置层堆集,配位数 为 12 ,许多金属(如Cu、Ag、Au等)采取这 种堆积方式。
(3)面心立方:在立方体顶点的微粒为8 个晶胞共有,在面心的为2个晶胞共有。 微粒数为: 8×1/8 + 6×1/2 = 4 空间利用率: 4×4лr3/3 (2×1.414r)3
分子间以范德 通过金属键形成的 华力相结合而 晶体 成的晶体
作用力
构成微粒 物 理 性 质 实例 熔沸点
共价键
原子 很高
范德华力
分子 很低
金属键
金属阳离子和自由 电子 差别较大
硬度
导电性
很大
无(硅为半导体) 金刚石、二氧化硅、 晶体硅、碳化硅
很小
无 Ar、S等
差别较大
导体 Au、Fe、Cu、钢 铁等
= 74.05%
堆积方式及性质小结
堆积方式 晶胞类型 空间利 配位数 用率 简单立 方堆积 简单立方 52% 68% 74% 74% 6 8 12 实例
Po Na、K、Fe
体心立方 体心立方 堆积 六方最 密堆积 六方
金属晶体堆积模型复习及计算

质量为183.9,半径为0.137nm。
a
求⑴晶胞的边长;⑵计算金属钨的密度。
晶胞中每个顶角金各有属一钨个的钨晶原子胞,与这已个钨原子为8个晶胞 共原用子,,每 那个 么钨 ,原 这经子 个有 晶学胞1过/中8的属含于哪钨该原种晶子晶胞为,型2 体个心,有一个金属 则ρ=2×183.9/6.02×类10似23×?(0.316×10-7)3
堆积方式及性质小结
堆积方式 晶胞类型 空间利 配位数 用率
实例
简单立 方堆积
简单立方
52%
6
Po
体心立方 密堆积
体心立方
68%
8
Na、K、Fe
六方最 密堆积
六方
74% 12 Cu、Ag、Au
面心立方 面心立方 最密堆积
74%
12
精品课件
Mg、Zn、Ti
精品课件
体 心 立 方 堆 积
配位数:8
精品课件
(1)图中正方形边长 a, (2)铜的原子半径 R
晶胞中每个顶角各有1个铜原子,这个铜原子为8个晶胞 共用,每个铜原子有1/8属于该晶胞,面心有6个金属 原子,有1/6属于该晶胞,1个晶胞中含铜原子4 个,
则ρ= 4×63.54/6.02×1023×(R×10-7)3 =8.936g/cm3
R=
nm
面心(铜型)堆积方式的空间利用率计算
a a
面心
精品课件
课外练习
1、已知金属铜为面心立方晶体,如图所示,
铜的相对原子质量为63.54,密度为
8.936g/cm3,试求
(1)图中正方形边长 a, (2)铜的原子半径 R
r
R
精品课件
R o
a
R
金属晶体的堆积模型

精品课件
金属晶体原子平面排列方式有几种?
探究
2 1A3
4
2
1
3
A
6
4
5
配位数为4 非密置层
精品课件
配位数为6 密置层
非密置层层层堆积情况1: 相邻层原子在同一直线上的堆积
金属晶体的堆积方式──简单立方堆积
精品课件
简单立方堆积
配位数:6 晶胞含金属原子数 1
例: (Po) 精品课件
精品课件
2).立方面心结构 立方面心结构的配位数=12(即每个圆球有12个最
近的邻居,同一层有六个,上一层三个,下一层三 个)。立方密堆积中可以取出一个立方面心的单位 来,每个单位中有四个圆球,球心的位置是000;0 1/2 1/2;1/2 0 1/2;1/2 1/2 0。
等径圆球的最紧密堆积方式,在维持每个球的周围 的情况等同的条件下,就只有上述两种,它们的空 间利用率最高(74.05%)。
精品课件
立方体边长=a';
立方体对角线=
a';
四面体边长=
a';
精品课件
精品课件
设圆半径为R,晶胞棱长为a,晶胞面对角
线长
则
晶胞体
积
立方面心晶胞中含4个圆球,每个球体积
为:
立方最密堆积虽晶胞大小不同,每个晶胞中 含球数不同。但计算得到空间占有率相同。
精品课件
而体心立方堆积(bcp)则空间占有率低一些。 体对角线长为 晶胞体积 体心立方晶胞含2个球
精品课件
2、某些金属晶体(Cu、Ag、Au)的原子按面心 立方的形式紧密堆积,即在晶体结构中可以 划出一块正立方体的结构单元,金属原子处 于正立方体的八个顶点和六个侧面上,试计 算这类金属晶体中原子的空间利用率。
高中化学常见晶体模型及晶胞计算

小结:高考常见题型 (一) 晶胞中微粒个数的计算, 求化学式
(二) 确定配位数
(三) 晶体的密度及微粒间距离 的计算
练习
-的距离为 a cm,该晶体密度为
(1)设NaCl晶胞的边长为acm,则
示晶为胞中Na+和Cl-的最近距离(( 即小)立
方体的边长)为 a/2 cm,则晶胞中 同种离子的最近距离为 a/2 cm。
思考:NaCl、CsCl同属AB型离子晶体, NaCl晶体中 Na+的配位数与CsCl晶体中Cs+的配位数是否相等?
CaF2的晶体结构
(1)每个Ca2+周围等距且 紧邻的F-有 8 个, Ca2+配 位数为 8 。
(2)每个F-周围等距且紧 邻的Ca2+有 4 个, F-配位 数为 4 。
FCa2+
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆积 的典型代表
空间利用率
配位数
简单立方
Po(钋)
52%
6
体心立方 (钾型)
K、Na、Fe
68%
8
六方最密 (镁型)
Mg、Zn、Ti
74%
12
面心立方最密 (铜型)
Cu, Ag, Au
74%
12
晶胞
原子晶体
金刚石
该晶胞实际分摊到的碳原子数为 (4 + 6 ×1/2 + 8 ×1/8) = 8个。
(3)每个晶胞中含 4 个Ca2+、含 8 个F-, Ca2+和 F-的个数比是 1︰2 。
3、金属晶体:
①简单立方堆积 唯一金属——钋 简单立方堆积的配位数 =6
每个晶胞含 1 个原子
球半径为r 正方体边长为a r=a/2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= 74.05% (2×1.414r)实3用文档
(4)六方密堆积(镁型)的空间利用率计算 解:
四点间的夹角均为60°
实用文档
先求S
在镁型堆积中取出六方晶胞,平行六面体的底是
平行四边形,各边长a=2r,则平行四边形的面积:
=19.36g/cm3 1nm=10-9m=10-7cm
复习1pm=10-12m
实用文档
练2:
现有甲、乙、丙、丁四种晶胞,可推知甲
晶晶体体体的中化的与学化的式学粒为式子—E为—F个——或D数——CF—2—比E——为—或;——丁C—1—2—:晶D——1—体———的;;化丙乙学晶 式为—X—Y—2—Z ——。
BA
DC
F
E
Z X
甲
乙
丙
Y
丁
实用文档
练3: 甲
乙
丙
上图甲、乙、丙分别为体心堆积、面心立方堆积、 六方堆积的结构单元,则甲、乙、丙三种结构单元
中,金属原子个数比为————1:—2—:—3——。
乙晶胞中所含金属原子数为8×1/8+6×1/2=4 晶胞中所含金属原子数实用为文档12×1/6+2×1/2+3=6
实用文档
实用文档
C B A
实用文档
实用文档
回顾:配位数 每个小球周围距离最近的小球数
简单立方堆积:
6
体心立方堆积:
8
六方紧密堆积:
12
面心立方紧密堆积: 12
实用文档
三、金属晶体中有关计算
空间利用率的计算
1、空间利用率:指构成晶体的原子、离子 或分子在整个晶体空间中所占有的体积百分比。
1空00间% 利用率 =
实用文档
小结:(2)钾型 (体心立方堆积)
配位数:8
实用文档
(3)面心立方:在立方体顶点的微粒为8个 晶胞共有,在面心的为2个晶胞共有。
微粒数为: 8×1/8 + 6×1/2 = 4
请计算:空间利用率?
实用文档
计算面心立方晶胞中 原子的空间占有率:
2 2
2
面 心
a
a
实用文档
小结:(3)面心立方:
铜型
A
A
C
B
B
A
A
B
C
A
B
实用此文档种立方紧密堆积的前视图A
7 1 9
6
5
8 2
3 4
10
11
12
这种堆积晶胞空间利用率高(74%),属于 最密置层堆集,配位数为 ,许多金属(如 Mg、Zn、Ti等)采取这种堆积方式。
实用文档
回顾镁型的晶胞
1200
平行六面体
实用文档
找铜型的晶胞
实用文档
实用文档
球体积 晶胞体积
实用文档
空间利用率的计算
2、空间利用率的计算步骤: (1)计算晶胞中的微粒数 (2)计算晶胞的体积
实用文档
3、复习:
实用文档
实用文档
三、金属晶体中有关计算
1.晶体中原子空间利用率的计算 (1)计算晶胞中的微粒数
(2)计算晶胞的体积
(一)简单立方:在立方体顶点的 微粒为8个晶胞共享,
许多金属(如Na、K、Fe等)采取这种堆积方式。
( IA,VB,VIB)
实用文档
(3)镁型和铜型
金属晶体的两种最密堆积方式──镁型和铜型
镁型
实用文档
铜型
镁型
12
6
3
54
铜型
12
6
3
54
12
6
3
54
12
6
3
54
实用文档
12
6
3
54
12
6
3
54
配位都是数 12 ( 同层 6, 上下层各 3 )
镁型
面心(铜型)堆积方式的空间利用率计算
a a
面心
实用文档
课外练习
1、已知金属铜为面心立方晶体,如图所示,
铜的相对原子质量为63.54,密度为8.936g/cm3,
试求
(1)图中正方形边长
(2)铜的原子半径 R
a,
r
R
实用文档
R o
a
R
R
r
a
1、已知金属铜为面心立方晶体,如图所 示,铜的相对原子质量为63.54,密度为 8.936g/cm3,试求
1nm=10-9m=10-7cm
复习1pm=10-1实2用m文档
课外练习
2、某些金属晶体(Cu、Ag、Au)的原子按 面心立方的形式紧密堆积,即在晶体结构 中可以划出一块正立方体的结构单元,金 属原子处于正立方体的八个顶点和六个侧 面上,试计算这类金属晶体中原子的空间 利用率。
质量为183.9,半径为0.137nm。
a
求⑴晶胞的边长;⑵计算金属钨的密度。
晶胞中每个顶角金各有属一钨个的钨晶原子胞,与这已个钨原子为8个晶胞 共原用子,,每 那个 么钨 ,原 这经子 个有 晶学胞1过/中8属的含于哪钨该原种晶子晶胞为,型2体个心,有一个金属 则ρ=2×183.9/6.02×类102似3×?(0.316×10-7)3
第三节 金属晶
体
第三课时
教学重点
金属晶体的四种堆积模型及简单计算
实用文档
复习:金属晶体基本构型
(1)简单立方堆积:
非最紧密堆积,空间利用率低(52%)
配位数是 6
个。
只有金属钋(Po)采取这种堆积方式 实用文档
5
6
8
7
1
2
4
பைடு நூலகம்
3
(2)钾型(体心立方堆积) 非密置层堆积
每个晶胞含 2 个原子,空间利用率不高(68%), 配位数为 8 ,
Saasin60 3a2 2
平行六面体的高: 再求S
h 2边长为a的四面体高
2 6 a 2 6 a
3
3
实用文档
V球243 r3 (晶胞2个 中)球 有
V球V晶胞 10% 074.05%
实用文档
练1:金属钨晶胞是一个立方体,在该晶胞
钾型
中每个顶角各有一个钨原子,中心有一个 体心立方晶胞
钨原子,实验测得金属钨原子的相对原子
堆积方式及性质小结
堆积方式 晶胞类型 空间利 配位数 用率
实例
简单立 方堆积
简单立方
52%
6
体心立方 密堆积
体心立方
68%
8
六方最 密堆积
六方
74%
12
面心立方 面心立方 最密堆积
74%
12
实用文档
Po Na、K、Fe Cu、Ag、Au Mg、Zn、Ti
实用文档
体 心 立 方 堆 积
实用文档
配位数:8
(1)图中正方形边长 a, (2)铜的原子半径 R
晶胞中每个顶角各有1个铜原子,这个铜原子为8个晶胞 共用,每个铜原子有1/8属于该晶胞,面心有6个金属 原子,有1/6属于该晶胞,1个晶胞中含铜原子4 个,
则ρ= 4×63.54/6.02×1023×(R×10-7)3 =8.936g/cm3
R=
nm
微粒数为:8×1/8 = 1
4πr3/3 空间利用率:(2r)3
=
52.36%
实用文档
(2)体心立方:在立方体顶 点的微粒为8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。
1个晶胞所含微粒数为:8×1/8 + 1 = 2 请计算:空间利用率?
实用文档
以体心立方晶胞为例,计算晶胞中原 子的空间占有率。
