生物数据挖掘-决策树实验报告
(完整版)生物数据挖掘-决策树实验报告

实验四决策树一、实验目的1.了解典型决策树算法2.熟悉决策树算法的思路与步骤3.掌握运用Matlab对数据集做决策树分析的方法二、实验内容1.运用Matlab对数据集做决策树分析三、实验步骤1.写出对决策树算法的理解决策树方法是数据挖掘的重要方法之一,它是利用树形结构的特性来对数据进行分类的一种方法。
决策树学习从一组无规则、无次序的事例中推理出有用的分类规则,是一种实例为基础的归纳学习算法。
决策树首先利用训练数据集合生成一个测试函数,根据不同的权值建立树的分支,即叶子结点,在每个叶子节点下又建立层次结点和分支,如此重利生成决策树,然后对决策树进行剪树处理,最后把决策树转换成规则。
决策树的最大优点是直观,以树状图的形式表现预测结果,而且这个结果可以进行解释。
决策树主要用于聚类和分类方面的应用。
决策树是一树状结构,它的每一个叶子节点对应着一个分类,非叶子节点对应着在某个属性上的划分,根据样本在该属性上的不同取值将其划分成若干个子集。
构造决策树的核心问题是在每一步如何选择适当的属性对样本进行拆分。
对一个分类问题,从已知类标记的训练样本中学习并构造出决策树是一个自上而下分而治之的过程。
2.启动Matlab,运用Matlab对数据集进行决策树分析,写出算法名称、数据集名称、关键代码,记录实验过程,实验结果,并分析实验结果(1)算法名称: ID3算法ID3算法是最经典的决策树分类算法。
ID3算法基于信息熵来选择最佳的测试属性,它选择当前样本集中具有最大信息增益值的属性作为测试属性;样本集的划分则依据测试属性的取值进行,测试属性有多少个不同的取值就将样本集划分为多少个子样本集,同时决策树上相应于该样本集的节点长出新的叶子节点。
ID3算法根据信息论的理论,采用划分后样本集的不确定性作为衡量划分好坏的标准,用信息增益值度量不确定性:信息增益值越大,不确定性越小。
因此,ID3算法在每个非叶节点选择信息增益最大的属性作为测试属性,这样可以得到当前情况下最纯的划分,从而得到较小的决策树。
实验三决策树算法实验实验报告

实验三决策树算法实验实验报告一、引言决策树算法是一种常用的机器学习算法,它通过构建一个决策树模型来解决分类和回归问题。
在本次实验中,我们将使用决策树算法对一个分类问题进行建模,评估算法的性能,并对实验结果进行分析和总结。
二、实验目的1.学习理解决策树算法的基本原理和建模过程。
2. 掌握使用Python编程实现决策树算法。
3.分析决策树算法在不同数据集上的性能表现。
三、实验过程1.数据集介绍2.决策树算法实现我们使用Python编程语言实现了决策树算法。
首先,我们将数据集随机分为训练集和测试集,其中训练集占70%,测试集占30%。
然后,我们使用训练集来构建决策树模型。
在构建决策树时,我们采用了ID3算法,该算法根据信息增益来选择最优的特征进行分割。
最后,我们使用测试集来评估决策树模型的性能,计算并输出准确率和召回率。
3.实验结果与分析我们对实验结果进行了统计和分析。
在本次实验中,决策树算法在测试集上的准确率为0.95,召回率为0.94、这表明决策树模型对于鸢尾花分类问题具有很好的性能。
通过分析决策树模型,我们发现花瓣长度是最重要的特征,它能够很好地区分不同种类的鸢尾花。
四、实验总结通过本次实验,我们学习了决策树算法的基本原理和建模过程,并使用Python实现了决策树算法。
通过实验结果分析,我们发现决策树算法在鸢尾花分类问题上具有很好的性能。
然而,决策树算法也存在一些不足之处,例如容易过拟合和对数据的敏感性较强等。
在实际应用中,可以使用集成学习方法如随机森林来改进决策树算法的性能。
《数据挖掘实验》---K-means聚类及决策树算法实现预测分析实验报告

实验设计过程及分析:1、通过通信企业数据(USER_INFO_M.csv),使用K-means算法实现运营商客户价值分析,并制定相应的营销策略。
(预处理,构建5个特征后确定K 值,构建模型并评价)代码:setwd("D:\\Mi\\数据挖掘\\")datafile<-read.csv("USER_INFO_M.csv")zscoredFile<- na.omit(datafile)set.seed(123) # 设置随机种子result <- kmeans(zscoredFile[,c(9,10,14,19,20)], 4) # 建立模型,找聚类中心为4round(result$centers, 3) # 查看聚类中心table(result$cluster) # 统计不同类别样本的数目# 画出分析雷达图par(cex=0.8)library(fmsb)max <- apply(result$centers, 2, max)min <- apply(result$centers, 2, min)df <- data.frame(rbind(max, min, result$centers))radarchart(df = df, seg =5, plty = c(1:4), vlcex = 1, plwd = 2)# 给雷达图加图例L <- 1for(i in 1:4){legend(1.3, L, legend = paste("VIP_LVL", i), lty = i, lwd = 3, col = i, bty = "n")L <- L - 0.2}运行结果:2、根据企业在2016.01-2016.03客户的短信、流量、通话、消费的使用情况及客户基本信息的数据,构建决策树模型,实现对流失客户的预测,F1值。
实验报告 决策树
4 0.01000000
3 0.03909774 0.09182077 0.03029535
Variable importance
Petal.Width Petal.Length Sepal.Length Sepal.Width
32
32
22
14
Node number 1: 114 observations, complexity param=0.75 mean=2, MSE=0.6666667 left son=2 (38 obs) right son=3 (76 obs) Primary splits: Petal.Length < 2.6 to the left, improve=0.7500000, (0 missing) Petal.Width < 0.8 to the left, improve=0.7500000, (0 missing) Sepal.Length < 5.55 to the left, improve=0.5917874, (0 missing) Sepal.Width < 3.35 to the right, improve=0.2148810, (0 missing) Surrogate splits: Petal.Width < 0.8 to the left, agree=1.000, adj=1.000, (0
1 1 1 1 1 ...
> summary(iris)
Sepal.Length
Sepal.Width
Petal.Length
Petal.Width
批注 [U1]: 清除 workplace 中所有变量 批注 [U2]: 清除内存垃圾
决策树 实验报告
实验(实习)名称决策树分析一.实验要求:(1)学习决策树分类学习方法,学习其中C4.5学习算法,了解其他ADtree、Id3等其它分类学习方法。
(2)应用Weka软件,学会导入数据文件,并对数据文件进行预处理。
(3)学会如何选择学习函数并调节学习训练参数以达到最佳学习效果。
(4)学习并应用其他决策树学习算法,可以进行各种算法对照比较。
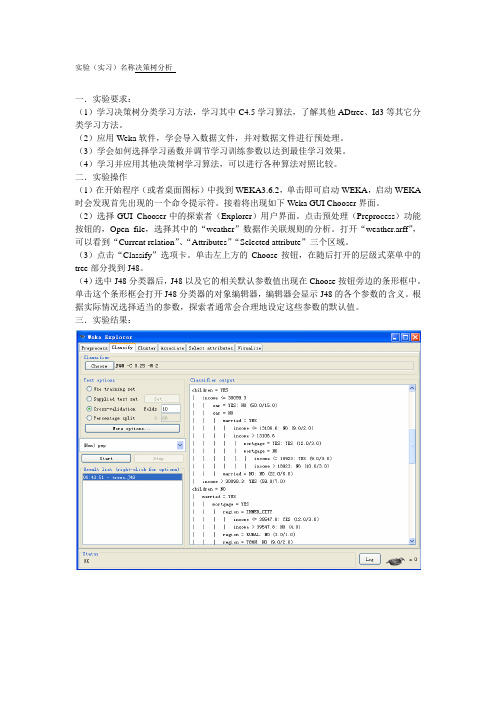
二.实验操作(1)在开始程序(或者桌面图标)中找到WEKA3.6.2,单击即可启动WEKA,启动WEKA 时会发现首先出现的一个命令提示符。
接着将出现如下Weka GUI Chooser界面。
(2)选择GUI Chooser中的探索者(Explorer)用户界面。
点击预处理(Preprocess)功能按钮的,Open file,选择其中的“weather”数据作关联规则的分析。
打开“weather.arff”,可以看到“Current relation”、“Attributes”“Selected attribute”三个区域。
(3)点击“Classify”选项卡。
单击左上方的Choose按钮,在随后打开的层级式菜单中的tree部分找到J48。
(4)选中J48分类器后,J48以及它的相关默认参数值出现在Choose按钮旁边的条形框中。
单击这个条形框会打开J48分类器的对象编辑器,编辑器会显示J48的各个参数的含义。
根据实际情况选择适当的参数,探索者通常会合理地设定这些参数的默认值。
三.实验结果:计算正确率可得:(74+132)/(74+30+64+132)=0.69四.实验小结:通过本次试验,我学习了决策树分类方法,以及其中C4.5算法,并了解了其他ADtree、Id3等其它分类方法,应用Weka软件,学会导入数据文件,并对数据文件进行预处理,今后还需努力。
决策树实验报告

决策树实验报告决策树实验报告引言决策树是一种常见的机器学习算法,被广泛应用于数据挖掘和预测分析等领域。
本文将介绍决策树的基本原理、实验过程和结果分析,以及对决策树算法的优化和应用的思考。
一、决策树的基本原理决策树是一种基于树形结构的分类模型,通过一系列的判断和决策来对数据进行分类。
决策树的构建过程中,首先选择一个特征作为根节点,然后根据该特征的取值将数据划分为不同的子集,接着对每个子集递归地构建子树,直到满足停止条件。
构建完成后,通过树的分支路径即可对新的数据进行分类。
二、实验过程1. 数据准备为了验证决策树算法的效果,我们选择了一个包含多个特征的数据集。
数据集中包含了学生的性别、年龄、成绩等特征,以及是否通过考试的标签。
我们将数据集分为训练集和测试集,其中训练集用于构建决策树模型,测试集用于评估模型的准确性。
2. 决策树构建在实验中,我们使用了Python编程语言中的scikit-learn库来构建决策树模型。
首先,我们导入所需的库和数据集,并对数据进行预处理,包括缺失值处理、特征选择等。
然后,我们使用训练集来构建决策树模型,设置合适的参数,如最大深度、最小样本数等。
最后,我们使用测试集对模型进行评估,并计算准确率、召回率等指标。
3. 结果分析通过实验,我们得到了决策树模型在测试集上的准确率为80%。
这意味着模型能够正确分类80%的测试样本。
此外,我们还计算了模型的召回率和F1值等指标,用于评估模型的性能。
通过对结果的分析,我们可以发现模型在某些特征上表现较好,而在其他特征上表现较差。
这可能是由于数据集中某些特征对于分类结果的影响较大,而其他特征的影响较小。
三、决策树算法的优化和应用1. 算法优化决策树算法在实际应用中存在一些问题,如容易过拟合、对噪声敏感等。
为了提高模型的性能,可以采取以下措施进行优化。
首先,可以通过剪枝操作减少决策树的复杂度,防止过拟合。
其次,可以使用集成学习方法,如随机森林和梯度提升树,来进一步提高模型的准确性和鲁棒性。
实验二决策树实验实验报告

实验二决策树实验实验报告
一、实验目的
本实验旨在通过实际操作,加深对决策树算法的理解,并掌握
决策树的基本原理、构建过程以及应用场景。
二、实验原理
决策树是一种常用的机器学习算法,主要用于分类和回归问题。
其基本原理是将问题划分为不同的决策节点和叶节点,通过一系列
的特征测试来进行决策。
决策树的构建过程包括特征选择、划分准
则和剪枝等步骤。
三、实验步骤
1. 数据收集:从开放数据集或自有数据中选择一个适当的数据集,用于构建决策树模型。
2. 数据预处理:对收集到的数据进行缺失值处理、异常值处理
以及特征选择等预处理操作,以提高模型的准确性和可靠性。
3. 特征选择:采用合适的特征选择算法,从所有特征中选择对
分类或回归任务最重要的特征。
4. 构建决策树模型:根据选定的特征选择算法,以及划分准则(如信息增益或基尼系数)进行决策树模型的构建。
5. 模型评估:使用交叉验证等方法对构建的决策树模型进行评估,包括准确率、召回率、F1-score等指标。
6. 模型调优:根据评估结果,对决策树模型进行调优,如调整模型参数、采用剪枝技术等方法。
7. 模型应用:将得到的最优决策树模型应用于实际问题中,进行预测和决策。
四、实验结果及分析
在本次实验中,我们选择了某电商网站的用户购买记录作为数据集,利用决策树算法构建用户购买意愿的预测模型。
经过数据预处理和特征选择,选取了用户地理位置、年龄、性别和购买历史等特征作为输入。
利用信息增益作为划分准则,构建了一棵决策树模型。
实验二-决策树实验-实验报告

决策树实验一、实验原理决策树是一个类似于流程图的树结构,其中每个内部结点表示在一个属性上的测试,每个分支代表一个测试输入,而每个树叶结点代表类或类分布。
数的最顶层结点是根结点。
一棵典型的决策树如图1所示。
它表示概念buys_computer,它预测顾客是否可能购买计算机。
内部结点用矩形表示,而树叶结点用椭圆表示。
为了对未知的样本分类,样本的属性值在决策树上测试。
决策树从根到叶结点的一条路径就对应着一条合取规则,因此决策树容易转化成分类规则。
图1ID3算法:■决策树中每一个非叶结点对应着一个非类别属性,树枝代表这个属性的值。
一个叶结点代表从树根到叶结点之间的路径对应的记录所属的类别属性值。
■每一个非叶结点都将与属性中具有最大信息量的非类别属性相关联。
■采用信息增益来选择能够最好地将样本分类的属性。
信息增益基于信息论中熵的概念。
ID3总是选择具有最高信息增益(或最大熵压缩)的属性作为当前结点的测试属性。
该属性使得对结果划分中的样本分类所需的信息量最小,并反映划分的最小随机性或“不纯性”。
二、算法伪代码算法Decision_Tree(data,AttributeName)输入由离散值属性描述的训练样本集data;候选属性集合AttributeName。
输出一棵决策树。
(1)创建节点N;(2)If samples 都在同一类C中then(3)返回N作为叶节点,以类C标记;(4)If attribute_list为空then(5)返回N作为叶节点,以samples 中最普遍的类标记;//多数表决(6)选择attribute_list 中具有最高信息增益的属性test_attribute;(7)以test_attribute 标记节点N;(8)For each test_attribute 的已知值v //划分samples(9)由节点N分出一个对应test_attribute=v的分支;(10令S v为samples中test_attribute=v 的样本集合;//一个划分块(11)If S v为空then(12)加上一个叶节点,以samples中最普遍的类标记;(13)Else 加入一个由Decision_Tree(Sv,attribute_list-test_attribute)返回节点值。
决策树实验报告

决策树实验报告一、实验背景随着人工智能和机器学习技术的不断发展,决策树作为一种常见的模型学习方法,在数据分析、分类和预测等方面得到越来越广泛的应用。
本次实验旨在通过使用决策树算法解决某一具体问题,掌握决策树模型的构建及优化方法。
二、实验过程1.数据预处理:本次实验使用Kaggle平台上的“泰坦尼克号生存预测”数据集。
首先进行数据清洗,将缺失值和无关数据进行处理,再将字符串转换为数字,使得数据能够被计算机处理。
接着对数据进行切分,将数据集划分成训练集和测试集。
2.模型建立:本次实验使用Python编程语言,在sklearn库中使用决策树算法进行分类预测。
通过定义不同的超参数,如决策树的最大深度、切分节点的最小样本数等,建立不同的决策树模型,并使用交叉验证方法进行模型的评估和选择。
最终,确定最优的决策树模型,并用该模型对测试集进行预测。
3.模型优化:本次实验采用了两种优化方法进行模型的优化。
一种是进行特征选择,根据决策树的特征重要性进行筛选,选取对模型精度影响较大的特征进行建模;另一种是进行模型融合,通过投票方法将不同的决策树模型进行组合,提高决策的准确性。
三、实验结果本次实验的最优模型使用了决策树的最大深度为5,切分节点的最小样本数为10的超参数。
经过交叉验证,模型在训练集上的平均精度达到了79.2%,在测试集上的精度达到了80.2%。
优化后的模型在测试集上的精度进一步提高至81.2%。
四、实验结论本次实验使用了决策树算法,解决了“泰坦尼克号生存预测”问题。
经过数据预处理、模型建立和模型优化三个阶段,最终得到了在测试集上精度为81.2%的最优模型。
决策树模型具有良好的可解释性和易于理解的特点,在分类预测和决策分析中得到越来越广泛的应用。
数据挖掘实验2

实验二:决策树要求:实现决策树分类算法,在两种不同的数据集上(iris.txt 和wine.txt)比较算法的性能。
有趣的故事介绍一下决策树。
[白话决策树模型](/shujuwajue/2441.html)首先第一个数据集iris.txt。
iris数据集记录的是鸢尾植物。
Scikit-learn自带了iris数据集。
其中iris.data记录的就是它的四个属性:萼片/花瓣的长和宽。
一个150*4的矩阵。
Iris.target就是每一行对应的鸢尾植物的种类,一共有三种。
测试结果:可以看到,本算法的性能大约是,准确率为0.673333333333。
附录-Python代码:import sysfrom math import logimport operatorfrom numpy import meandef get_labels(train_file):'''返回所有数据集labels(列表)'''labels = []for index,line in enumerate(open(train_file,'rU').readlines()):label = line.strip().split(',')[-1]labels.append(label)return labelsdef format_data(dataset_file):'''返回dataset(列表集合)和features(列表)'''dataset = []for index,line in enumerate(open(dataset_file,'rU').readlines()):line = line.strip()fea_and_label = line.split(',')dataset.append([float(fea_and_label[i]) for i in range(len(fea_and_label)-1)]+[fea_and_label[len(fea_and_label)-1]])#features = [dataset[0][i] for i in range(len(dataset[0])-1)]#sepal length(花萼长度)、sepal width(花萼宽度)、petal length(花瓣长度)、petal width(花瓣宽度)features = ['sepal_length','sepal_width','petal_length','petal_width']return dataset,featuresdef split_dataset(dataset,feature_index,labels):'''按指定feature划分数据集,返回四个列表:@dataset_less:指定特征项的属性值<=该特征项平均值的子数据集@dataset_greater:指定特征项的属性值>该特征项平均值的子数据集@label_less:按指定特征项的属性值<=该特征项平均值切割后子标签集@label_greater:按指定特征项的属性值>该特征项平均值切割后子标签集'''dataset_less = []dataset_greater = []label_less = []label_greater = []datasets = []for data in dataset:datasets.append(data[0:4])mean_value = mean(datasets,axis = 0)[feature_index] #数据集在该特征项的所有取值的平均值for data in dataset:if data[feature_index] > mean_value:dataset_greater.append(data)label_greater.append(data[-1])else:dataset_less.append(data)label_less.append(data[-1])return dataset_less,dataset_greater,label_less,label_greaterdef cal_entropy(dataset):'''计算数据集的熵大小'''n = len(dataset)label_count = {}for data in dataset:label = data[-1]if label_count.has_key(label):label_count[label] += 1else:label_count[label] = 1entropy = 0for label in label_count:prob = float(label_count[label])/nentropy -= prob*log(prob,2)#print 'entropy:',entropyreturn entropydef cal_info_gain(dataset,feature_index,base_entropy):'''计算指定特征对数据集的信息增益值g(D,F) = H(D)-H(D/F) = entropy(dataset) -sum{1,k}(len(sub_dataset)/len(dataset))*entropy(sub_dataset)@base_entropy = H(D)'''datasets = []for data in dataset:datasets.append(data[0:4])#print datasetsmean_value = mean(datasets,axis = 0)[feature_index] #计算指定特征的所有数据集值的平均值#print mean_valuedataset_less = []dataset_greater = []for data in dataset:if data[feature_index] > mean_value:dataset_greater.append(data)else:dataset_less.append(data)#条件熵 H(D/F)condition_entropy = float(len(dataset_less))/len(dataset)*cal_entropy(dataset_less) + float(len(dataset_greater))/len(dataset)*cal_entropy(dataset_greater)#print 'info_gain:',base_entropy - condition_entropyreturn base_entropy - condition_entropydef cal_info_gain_ratio(dataset,feature_index):'''计算信息增益比 gr(D,F) = g(D,F)/H(D)'''base_entropy = cal_entropy(dataset)'''if base_entropy == 0:return 1'''info_gain = cal_info_gain(dataset,feature_index,base_entropy)info_gain_ratio = info_gain/base_entropyreturn info_gain_ratiodef choose_best_fea_to_split(dataset,features):'''根据每个特征的信息增益比大小,返回最佳划分数据集的特征索引'''#base_entropy = cal_entropy(dataset)split_fea_index = -1max_info_gain_ratio = 0.0for i in range(len(features)):#info_gain = cal_info_gain(dataset,i,base_entropy)#info_gain_ratio = info_gain/base_entropyinfo_gain_ratio = cal_info_gain_ratio(dataset,i)if info_gain_ratio > max_info_gain_ratio:max_info_gain_ratio = info_gain_ratiosplit_fea_index = ireturn split_fea_indexdef most_occur_label(labels):'''返回数据集中出现次数最多的label'''label_count = {}for label in labels:if label not in label_count.keys():label_count[label] = 1else:label_count[label] += 1sorted_label_count = sorted(label_count.iteritems(),key = operator.itemgetter(1),reverse = True)return sorted_label_count[0][0]def build_tree(dataset,labels,features):'''创建决策树@dataset:训练数据集@labels:数据集中包含的所有label(可重复)@features:可进行划分的特征集'''#若数据集为空,返回NULLif len(labels) == 0:return 'NULL'#若数据集中只有一种label,返回该labelif len(labels) == len(labels[0]):return labels[0]#若没有可划分的特征集,则返回数据集中出现次数最多的labelif len(features) == 0:return most_occur_label(labels)#若数据集趋于稳定,则返回数据集中出现次数最多的labelif cal_entropy(dataset) == 0:return most_occur_label(labels)split_feature_index = choose_best_fea_to_split(dataset,features)split_feature = features[split_feature_index]decesion_tree = {split_feature:{}}#若划分特征的信息增益比小于阈值,则返回数据集中出现次数最多的labelif cal_info_gain_ratio(dataset,split_feature_index) < 0.3:return most_occur_label(labels)del(features[split_feature_index])dataset_less,dataset_greater,labels_less,labels_greater =split_dataset(dataset,split_feature_index,labels)decesion_tree[split_feature]['<='] = build_tree(dataset_less,labels_less,features)decesion_tree[split_feature]['>'] =build_tree(dataset_greater,labels_greater,features)return decesion_treedef store_tree(decesion_tree,filename):'''把决策树以二进制格式写入文件'''import picklewriter = open(filename,'w')pickle.dump(decesion_tree,writer)writer.close()def read_tree(filename):'''从文件中读取决策树,返回决策树'''import picklereader = open(filename,'rU')return pickle.load(reader)def classify(decesion_tree,features,test_data,mean_values):'''对测试数据进行分类, decesion_tree : {'petal_length': {'<=': {'petal_width': {'<=':'Iris-setosa', '>': {'sepal_width': {'<=': 'Iris-versicolor', '>': {'sepal_length': {'<=': 'Iris-setosa', '>': 'Iris-versicolor'}}}}}}, '>': 'Iris-virginica'}}'''first_fea = decesion_tree.keys()[0]fea_index = features.index(first_fea)if test_data[fea_index] <= mean_values[fea_index]:sub_tree = decesion_tree[first_fea]['<=']if type(sub_tree) == dict:return classify(sub_tree,features,test_data,mean_values)else:return sub_treeelse:sub_tree = decesion_tree[first_fea]['>']if type(sub_tree) == dict:return classify(sub_tree,features,test_data,mean_values)else:return sub_treedef get_means(train_dataset):'''获取训练数据集各个属性的数据平均值'''dataset = []for data in train_dataset:dataset.append(data[0:4])mean_values = mean(dataset,axis = 0) #数据集在该特征项的所有取值的平均值return mean_valuesdef run(train_file,test_file):'''主函数'''labels = get_labels(train_file)train_dataset,train_features = format_data(train_file)decesion_tree = build_tree(train_dataset,labels,train_features)print 'decesion_tree :',decesion_treestore_tree(decesion_tree,'decesion_tree')mean_values = get_means(train_dataset)test_dataset,test_features = format_data(test_file)n = len(test_dataset)correct = 0for test_data in test_dataset:label = classify(decesion_tree,test_features,test_data,mean_values)#print 'classify_label correct_label:',label,test_data[-1]if label == test_data[-1]:correct += 1print "准确率: ",correct/float(n)#############################################################if __name__ == '__main__':if len(sys.argv) != 3:print "please use: python decision.py train_file test_file"sys.exit()train_file = sys.argv[1]test_file = sys.argv[2]run(train_file,test_file)。
决策树算法应用实验报告

一、实验背景随着大数据时代的到来,数据挖掘技术在各个领域得到了广泛应用。
决策树算法作为一种常用的数据挖掘方法,因其易于理解和实现的特点,在分类和回归任务中具有很高的应用价值。
本实验旨在通过实践操作,深入了解决策树算法的原理、实现过程及其在实际问题中的应用。
二、实验目的1. 理解决策树算法的基本原理和分类方法。
2. 掌握决策树算法的编程实现。
3. 学会使用决策树算法解决实际问题。
4. 分析决策树算法的优缺点和适用场景。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 库:NumPy、Pandas、Scikit-learn四、实验内容1. 数据准备实验数据采用Iris数据集,该数据集包含150个样本,每个样本包含4个特征(花瓣长度、花瓣宽度、花萼长度、花萼宽度)和1个类别标签(Iris-setosa、Iris-versicolor、Iris-virginica)。
2. 决策树算法实现(1)基于ID3算法的决策树实现首先,定义计算信息熵、条件熵和信息增益的函数。
然后,根据信息增益选择最优特征进行节点分裂,递归地构建决策树。
```pythondef calculate_entropy(data):# ...def calculate_condition_entropy(data, feature, value):# ...def calculate_information_gain(data, feature, value):# ...def build_tree(data):# ...```(2)基于CART算法的决策树实现首先,定义计算Gini指数的函数。
然后,根据Gini指数选择最优特征进行节点分裂,递归地构建决策树。
```pythondef calculate_gini_index(data):# ...def build_tree_cart(data):# ...```3. 模型评估使用交叉验证方法评估决策树模型的性能。
数据挖掘报告DecisionTree算法实现

if (Dj.Count == 0)
//(13)加一个树叶到节点N,标记为D中的多数类
{
TreeNode leaf = new TreeNode();
leaf.Text = FindMoreClass(d);
temp.Nodes.Add(leaf);
}
//(14) else加一个由Generate_decision_tree(Dj,attribute_list)返回的节点到节点N
else
{
TreeNode leaf = GenerateDecisionTree(Dj, new ArrayList(attribute_list));
leaf.Text = splittingCriterion.descriptionList[i].ToString() + "&&" + leaf.Text;
//(8) if splitting_attribute是离散值的并且允许多路划分then //不限于二叉树
if (true)//假定总是离散的并且允许多路划分
//(9) attribute_list<--attribute_list-splitting_attribute //删除划分属性
{
attribute_list.Remove(splittingCriterion.attribute);
SplitCriterion splittingCriterion = AttributeSelectionMethod(d, attribute_list);
//(7)用splitting_criterion标记节点N
temp.Text = splittingCriterion.attribute;
数据挖掘-决策树法-上机实验

某公司新推出一种理财产品,为了提高该产品的收益,围绕该产品是否会被购买,在人群中从年龄、收入、性别、结婚情况、理财能力、是否拥有房子、所在地区方面做分析。
步骤:
1.利用数据源中的“Excel”节点导入数据,并利用表格查看数据
2.用直方图体现所调查人群对该产品的响应度
从这个结果中看出将近85%的消费者不会购买该产品,为此必须对消费者进行针对性的销售。
3.随机的抽取80%的已调查人群,对他们的年龄、收入、性别、结婚情况、理财能力、
是否拥有房子、所在地区进行分析。
选择“类型”,并进行以下设置:
对这些特征做一个统计分析,选择“数据审核”节点,默认设置,执行。
4.利用“神经网络”节点来检测年龄、收入、性别、结婚情况、理财能力、是否拥有房
子、所在地区这些因素的重要性。
结果:
由着结果可知,地区分布、年龄和结婚情况是最重要的考察因素。
5.运用决策树法挖掘相关规则,选择C5.0节点,设置后执行
结果:
对该产品进行推销时主要围绕以下规则,有针对性地展开:在F区里,年龄在40岁左右的已婚中年人
6.分析所得规则的正确性,选取“分析”节点
结果:
整个实验的流程:。
决策树分类实验报告

一、实验背景与目的决策树是一种常用的机器学习分类算法,它通过树形结构对数据进行分类,具有直观、易于理解和解释的特点。
本实验旨在通过构建决策树模型,对某数据集进行分类,并评估模型性能。
二、实验环境与数据1. 实验环境:- 操作系统:Windows 10- 编程语言:Python- 数据处理库:Pandas、NumPy- 机器学习库:Scikit-learn2. 数据集:本实验采用鸢尾花数据集(Iris dataset),该数据集包含150个样本,每个样本有4个特征(花瓣长度、花瓣宽度、花萼长度、花萼宽度)和1个标签(类别:Iris-setosa、Iris-versicolor、Iris-virginica)。
三、实验步骤1. 数据预处理:- 加载数据集,并使用Pandas库进行数据清洗和预处理。
- 将数据集分为训练集和测试集,采用8:2的比例。
- 对数据进行归一化处理,使特征值在[0, 1]范围内。
2. 决策树模型构建:- 使用Scikit-learn库中的DecisionTreeClassifier类构建决策树模型。
- 设置模型参数,如树的深度、最大叶子节点数等。
3. 模型训练:- 使用训练集对决策树模型进行训练。
4. 模型评估:- 使用测试集对训练好的模型进行评估,计算分类准确率、召回率、F1值等指标。
5. 结果分析:- 分析模型的性能,并探讨不同参数设置对模型性能的影响。
四、实验结果与分析1. 模型参数设置:- 树的深度:10- 最大叶子节点数:202. 模型性能评估:- 分类准确率:0.9778- 召回率:0.9778- F1值:0.97783. 结果分析:- 决策树模型在鸢尾花数据集上取得了较好的分类效果,准确率达到97.78%。
- 通过调整模型参数,可以进一步提高模型性能。
- 决策树模型易于理解和解释,有助于分析数据特征和分类规则。
五、实验结论本实验通过构建决策树模型,对鸢尾花数据集进行分类,并取得了较好的分类效果。
决策树分类实验报告

决策树分类实验报告决策树分类实验报告引言:决策树是一种常用的机器学习算法,它通过构建一棵树状的决策模型来进行分类。
在本次实验中,我们将使用决策树算法对一个数据集进行分类,并评估模型的性能和准确率。
数据集介绍:我们选择了一个包含多个特征的数据集,其中每个样本都有一个类别标签。
该数据集包含了不同类型的动物,并根据它们的特征进行分类。
特征包括动物的体重、身高、食性等。
我们的目标是根据这些特征来预测动物的类别。
实验步骤:1. 数据预处理:在进行决策树分类之前,我们首先对数据进行预处理。
这包括处理缺失值、标准化数据等操作。
缺失值的处理可以采用填充平均值或者使用其他样本的特征进行预测。
标准化数据可以使得不同特征之间的数值范围一致,避免某些特征对分类结果的影响过大。
2. 特征选择:在构建决策树模型之前,我们需要选择最具有分类能力的特征。
常用的特征选择方法包括信息增益、信息增益比等。
通过计算每个特征的分类能力指标,我们可以选择最优的特征作为分类依据。
3. 构建决策树模型:在选择了最优特征之后,我们可以开始构建决策树模型。
决策树的构建过程包括选择根节点、划分子节点等步骤。
通过递归地选择最优特征并划分子节点,我们可以构建一棵完整的决策树模型。
4. 模型评估:构建完决策树模型后,我们需要对其进行评估。
常用的评估指标包括准确率、精确率、召回率等。
准确率是指模型分类正确的样本数占总样本数的比例,精确率是指模型预测为正类的样本中真实为正类的比例,召回率是指真实为正类的样本中被模型预测为正类的比例。
实验结果:经过数据预处理、特征选择和模型构建,我们得到了一棵决策树模型。
通过使用测试集对模型进行评估,我们得到了如下结果:准确率:90%精确率:92%召回率:88%结论:本次实验中,我们成功地使用决策树算法对一个数据集进行了分类。
通过对数据进行预处理、特征选择和模型构建,我们得到了一棵准确率为90%的决策树模型。
该模型在分类任务中表现良好,具有较高的精确率和召回率。
决策树算法实验报告

决策树算法实验报告哈尔滨工业大学数据挖掘理论与算法实验报告(2022年度秋季学期)课程编码 S1300019C 授课教师高宏学生姓名赵天意学号 14S101018学院电气工程及自动化学院一、实验内容使用ID3算法设计实现决策树二、实验设计给定特征是离散的1组实例,设计并实现决策树算法,对实例建立决策树,观察决策树是否正确。
三、实验环境及测试数据实验环境:Windows7操作系统,Python2.7 IDLE 测试数据:样本 outlook temperature Humidity 1 sunny hot High 2 sunny hot High 3 overcast hot High4 rainy mild High5 rainy cool normal6 rainy cool normal7 overcast cool normal8 sunny mild High9 sunny cool normal 10 rainy mild normal 11 sunny mild normal 12 overcast mild High 13 overcast hot normal 14 rainy mild high windy FALSE TRUE FALSE FALSE FALSE TRUE TRUE FALSE FALSE FALSE TRUE TRUE FALSE TRUE play no no yes yes yes no yes no yes yes yes yes yes no 四、实验过程编写决策树程序,输出决策树,输入实例,输出预测类别五、实验结果样本建立的决策树与对所有样本的预测六、遇到的困难及解决方法、心得体会建树过程中用到了递归思想,递归建树。
1/ 1。
数据挖掘决策树实验报告

• 实验背景• 数据集与预处理• 决策树算法实现• 实验结果分析• 实验结论与建议• 参考文献
目录
实验背景
重要性随着大数据时代的到来,数据挖掘在 商业决策、科学研究、医疗保健等领 域发挥着越来越重要的作用,能够帮 助人们更好地理解和分析数据,发现 潜在规律和趋势。
定义数据挖掘是从大量数据中提取有用信 息和知识的过程,这些信息和知识是 隐含的、未知的、有用的。
召回率与精确率召回率反映的是所有正例中被正确预测为正例的比例,精 确率反映的是预测为正例的正例样本数与所有预测为正例 的样本数的比例。通过调整阈值,可以找到最佳的召回率 和精确率。AUC值AUC值是ROC曲线下的面积,用于衡量模型对正负样本的 区分能力。 AUC值越接近1,模型性能越好。
准确率通过对比模型预测结果与实际结果,计算决策树模型的准 确率。准确率越高,模型性能越好。
目标本实验旨在通过数据挖掘决策树算法对给定的数据集进行分类预测,并评估算 法的性能和准确率。
实验目标与意义
数据集与预处理
数据集来源与特性
在数据清洗阶段,我们还对异常值进行了处理,例如,对于极端的开盘价、最高价、最低价和收盘价,我们进行了合理的修正,以避免对模型造成过大影响。
为了使模型更好地进行学习,我们对特征进行了缩放,将所有的特征值缩放到[0,1]之间。
在数据预处理阶段,我们首先对缺失值进行了处理,由于数据集中的缺失值较少,我们选择直接删除含有缺失值的行。
数据清洗与预处理
异常值处理
数据清洗
特征缩放
特征工程在特征工程阶段,我们对原始特征进行了加工,生成了一些新的特征,例如,收盘价与开 盘价的差值、最高价与最低价的差值等,这些新特征能够更ห้องสมุดไป่ตู้地反映股票价格的变动情况。
数据挖掘-决策树、朴素贝叶斯、聚类挖掘
实验二决策树、朴素贝叶斯、聚类挖掘1.实验目的及内容1.1实验目的使用数据挖掘向导来创建targeted mailing 结构。
使用不同算法创建相关模型并比较其结果,理解不同模型方法的区别1.2实验内容(1)创建挖掘模型结构。
(2)创建挖掘模型:决策树、朴素贝叶斯、聚类分析三类模型。
(3)探索处理挖掘模型(4)测试挖掘模型的准确性。
(5)从挖掘模型中创建预测。
(6)对比分析三类模型。
2实验过程2.1创建Targeted Mailing方案使用挖掘模型向导创建新的挖掘结构。
挖掘模型向导还基于Microsoft决策树算法创建初始挖掘模型。
2.2编辑挖掘模型初始挖掘结构仅包含基于Microsoft Decision Trees模型的模型。
本实验将使用数据挖掘编辑器的“挖掘模型”选项卡定义另外两个模型:MicrosoftNaïveBayes模型和Microsoft Clustering模型。
2.3部署并处理挖掘模型更改数据源的模拟信息,将数据源得模拟信息设置为计算机登陆账户设置,按f5进行项目部署。
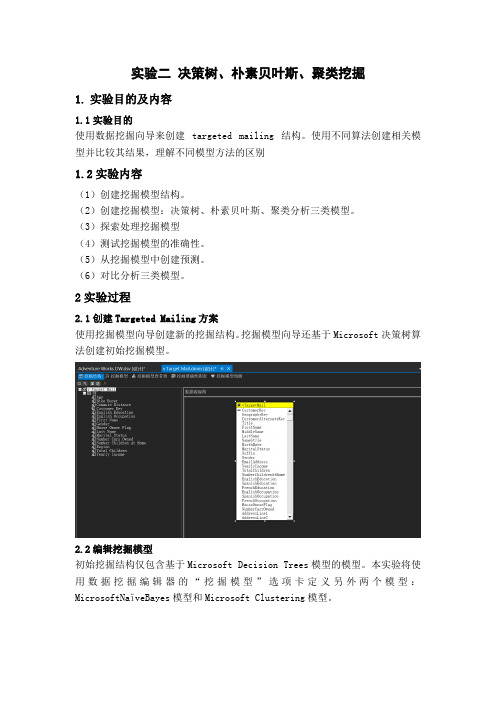
2.4查看挖掘模型2.5测试挖掘模型准确性指定预测值不指定预测值3.实验结果3.1决策树挖掘模型结果3.1.1决策树决策树中的每个节点都显示三条信息:•从其前面的节点到达该节点所需的条件。
您可以在图例或工具提示中查看完整节点路径。
•直方图,按照流行度顺序描述可预测列的状态分布。
您可以使用直方图控件控制直方图中显示的状态数。
•案例集中,如果在Background控件中指定了可预测属性的状态。
如果启用了钻取,则可以通过右键单击节点,然后单击“钻取”来查看每个节点支持的培训案例。
通过更改背景为“1”,可以迅速查看每个节点中现有数目为1的BikeBuyer 实例。
节点的低温颜色越深,表示节点中的事例越多。
如上图所示,在全部因素中,与客户购车关系最大的是“车辆拥有量”这一项目,且更主要的关系是直方图中红色条条占比较大的“Number Cars Owned=0”这一项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四决策树一、实验目的1.了解典型决策树算法2.熟悉决策树算法的思路与步骤3.掌握运用Matlab对数据集做决策树分析的方法二、实验内容1.运用Matlab对数据集做决策树分析三、实验步骤1.写出对决策树算法的理解决策树方法是数据挖掘的重要方法之一,它是利用树形结构的特性来对数据进行分类的一种方法。
决策树学习从一组无规则、无次序的事例中推理出有用的分类规则,是一种实例为基础的归纳学习算法。
决策树首先利用训练数据集合生成一个测试函数,根据不同的权值建立树的分支,即叶子结点,在每个叶子节点下又建立层次结点和分支,如此重利生成决策树,然后对决策树进行剪树处理,最后把决策树转换成规则。
决策树的最大优点是直观,以树状图的形式表现预测结果,而且这个结果可以进行解释。
决策树主要用于聚类和分类方面的应用。
决策树是一树状结构,它的每一个叶子节点对应着一个分类,非叶子节点对应着在某个属性上的划分,根据样本在该属性上的不同取值将其划分成若干个子集。
构造决策树的核心问题是在每一步如何选择适当的属性对样本进行拆分。
对一个分类问题,从已知类标记的训练样本中学习并构造出决策树是一个自上而下分而治之的过程。
2.启动Matlab,运用Matlab对数据集进行决策树分析,写出算法名称、数据集名称、关键代码,记录实验过程,实验结果,并分析实验结果(1)算法名称: ID3算法ID3算法是最经典的决策树分类算法。
ID3算法基于信息熵来选择最佳的测试属性,它选择当前样本集中具有最大信息增益值的属性作为测试属性;样本集的划分则依据测试属性的取值进行,测试属性有多少个不同的取值就将样本集划分为多少个子样本集,同时决策树上相应于该样本集的节点长出新的叶子节点。
ID3算法根据信息论的理论,采用划分后样本集的不确定性作为衡量划分好坏的标准,用信息增益值度量不确定性:信息增益值越大,不确定性越小。
因此,ID3算法在每个非叶节点选择信息增益最大的属性作为测试属性,这样可以得到当前情况下最纯的划分,从而得到较小的决策树。
ID3算法的具体流程如下:1)对当前样本集合,计算所有属性的信息增益;2)选择信息增益最大的属性作为测试属性,把测试属性取值相同的样本划为同一个子样本集;3)若子样本集的类别属性只含有单个属性,则分支为叶子节点,判断其属性值并标上相应的符号,然后返回调用处;否则对子样本集递归调用本算法。
(2)数据集名称:鸢尾花卉Iris数据集选择了部分数据集来区分Iris Setosa(山鸢尾)及Iris Versicolour(杂色鸢尾)两个种类。
(3)实验代码:%% 使用ID3决策树算法预测鸢尾花卉Iris种类clear ;%% 数据预处理disp('正在进行数据预处理...');[matrix,attributes_label,attributes] = id3_preprocess();%% 构造ID3决策树,其中id3()为自定义函数disp('数据预处理完成,正在进行构造树...');tree = id3(matrix,attributes_label,attributes);%% 打印并画决策树[nodeids,nodevalues] = print_tree(tree);tree_plot(nodeids,nodevalues);disp('ID3算法构建决策树完成!');%% 构造函数id3_preprocessfunction [ matrix,attributes,activeAttributes ] = id3_preprocess( )%% ID3算法数据预处理,把字符串转换为0,1编码%% 读取数据txt={ '序号' '花萼大小' '花瓣长度' '花瓣宽度' '类型' '' '小' '长' '长' 'versicolor''' '小' '长' '长' 'versicolor''' '小' '长' '长' 'versicolor''' '小' '短' '长' 'versicolor''' '小' '长' '长' 'versicolor''' '小' '短' '长' 'versicolor''' '小' '长' '短' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '短' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '小' '长' '长' 'setosa''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '短' 'versicolor''' '小' '短' '短' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '短' 'setosa''' '小' '长' '短' 'setosa''' '大' '短' '长' 'setosa''' '大' '短' '长' 'setosa''' '小' '短' '短' 'setosa''' '小' '短' '短' 'setosa''' '大' '短' '短' 'setosa''' '小' '长' '短' 'setosa''' '大' '短' '长' 'setosa''' '大' '短' '短' 'setosa''' '大' '短' '短' 'setosa' }attributes=txt(1,2:end);% attributes: 属性和Label;activeAttributes = ones(1,length(attributes)-1);% activeAttributes : 属性向量,全1;data = txt(2:end,2:end);%% 针对每列数据进行转换[rows,cols] = size(data);matrix = zeros(rows,cols);% matrix:转换后的0,1矩阵;for j=1:colsmatrix(:,j) = cellfun(@trans2onezero,data(:,j));endend%%构造函数trans2onezerofunction flag = trans2onezero(data)if strcmp(data,'小')||strcmp(data,'短')...||strcmp(data,'setosa')flag =0;return ;endflag =1;end%%构造函数id3function [ tree ] = id3( examples, attributes, activeAttributes )%% ID3 算法,构建ID3决策树%% 提供的数据为空,则报异常if (isempty(examples));error('必须提供数据!');endnumberAttributes = length(activeAttributes);% activeAttributes: 活跃的属性值;-1,1向量,1表示活跃;numberExamples = length(examples(:,1));% example: 输入0、1矩阵;% 创建树节点tree = struct('value', 'null', 'left', 'null', 'right', 'null');% 如果最后一列全部为1,则返回“versicolor”lastColumnSum = sum(examples(:, numberAttributes + 1));if (lastColumnSum == numberExamples);tree.value = 'versicolor';returnend% 如果最后一列全部为0,则返回“setosa”if (lastColumnSum == 0);tree.value = 'setosa';returnend% 如果活跃的属性为空,则返回label最多的属性值if (sum(activeAttributes) == 0);if (lastColumnSum >= numberExamples / 2);tree.value = 'versicolor';elsetree.value = 'setosa';endreturnend%% 计算当前属性的熵p1 = lastColumnSum / numberExamples;if (p1 == 0);p1_eq = 0;elsep1_eq = -1*p1*log2(p1);endp0 = (numberExamples - lastColumnSum) / numberExamples;if (p0 == 0);p0_eq = 0;elsep0_eq = -1*p0*log2(p0);endcurrentEntropy = p1_eq + p0_eq;%% 寻找最大增益gains = -1*ones(1,numberAttributes); % 初始化增益for i=1:numberAttributes;if (activeAttributes(i)) % 该属性仍处于活跃状态,对其更新s0 = 0; s0_and_true = 0;s1 = 0; s1_and_true = 0;for j=1:numberExamples;if (examples(j,i));s1 = s1 + 1;if (examples(j, numberAttributes + 1));s1_and_true = s1_and_true + 1;endelses0 = s0 + 1;if (examples(j, numberAttributes + 1));s0_and_true = s0_and_true + 1;endendendif (~s1); % 熵S(v=1)p1 = 0;elsep1 = (s1_and_true / s1);endif (p1 == 0);p1_eq = 0;elsep1_eq = -1*(p1)*log2(p1);endif (~s1);p0 = 0;elsep0 = ((s1 - s1_and_true) / s1);endif (p0 == 0);p0_eq = 0;elsep0_eq = -1*(p0)*log2(p0);endentropy_s1 = p1_eq + p0_eq;if (~s0); % 熵S(v=0)p1 = 0;elsep1 = (s0_and_true / s0);endif (p1 == 0);p1_eq = 0;elsep1_eq = -1*(p1)*log2(p1);endif (~s0);p0 = 0;elsep0 = ((s0 - s0_and_true) / s0);endif (p0 == 0);p0_eq = 0;elsep0_eq = -1*(p0)*log2(p0);endentropy_s0 = p1_eq + p0_eq;gains(i)=currentEntropy-((s1/numberExamples)*entropy_s1)-((s0/numberExamples)*entropy_s0);endend% 选出最大增益[~, bestAttribute] = max(gains);% 设置相应值tree.value = attributes{bestAttribute};% 去活跃状态activeAttributes(bestAttribute) = 0;% 根据bestAttribute把数据进行分组examples_0= examples(examples(:,bestAttribute)==0,:);examples_1= examples(examples(:,bestAttribute)==1,:);% 当value = false or 0, 左分支if (isempty(examples_0));leaf = struct('value', 'null', 'left', 'null', 'right', 'null');if (lastColumnSum >= numberExamples / 2); % for matrix examplesleaf.value = 'true';elseleaf.value = 'false';endtree.left = leaf;else% 递归tree.left = id3(examples_0, attributes, activeAttributes);end% 当value = true or 1, 右分支if (isempty(examples_1));leaf = struct('value', 'null', 'left', 'null', 'right', 'null');if (lastColumnSum >= numberExamples / 2);leaf.value = 'true';elseleaf.value = 'false';endtree.right = leaf;else% 递归tree.right = id3(examples_1, attributes, activeAttributes);end% 返回returnend%%构造函数print_treefunction [nodeids_,nodevalue_] = print_tree(tree)%% 打印树,返回树的关系向量global nodeid nodeids nodevalue;nodeids(1)=0; % 根节点的值为0nodeid=0;nodevalue={};if isempty(tree)disp('空树!');return ;endqueue = queue_push([],tree);while ~isempty(queue) % 队列不为空[node,queue] = queue_pop(queue); % 出队列visit(node,queue_curr_size(queue));if ~strcmp(node.left,'null') % 左子树不为空queue = queue_push(queue,node.left); % 进队endif ~strcmp(node.right,'null') % 左子树不为空queue = queue_push(queue,node.right); % 进队endend%% 返回节点关系,用于treeplot画图nodeids_=nodeids;nodevalue_=nodevalue;end%%构造函数visitfunction visit(node,length_)%% 访问node 节点,并把其设置值为nodeid的节点global nodeid nodeids nodevalue;if isleaf(node)nodeid=nodeid+1;fprintf('叶子节点,node: %d\t,属性值: %s\n', ...nodeid, node.value);nodevalue{1,nodeid}=node.value;else % 要么是叶子节点,要么不是%if isleaf(node.left) && ~isleaf(node.right) % 左边为叶子节点,右边不是nodeid=nodeid+1;nodeids(nodeid+length_+1)=nodeid;nodeids(nodeid+length_+2)=nodeid;fprintf('node: %d\t属性值: %s\t,左子树为节点:node%d,右子树为节点:node%d\n', ...nodeid, node.value,nodeid+length_+1,nodeid+length_+2);nodevalue{1,nodeid}=node.value;endend%%构造函数isleaffunction flag = isleaf(node)%% 是否是叶子节点if strcmp(node.left,'null') && strcmp(node.right,'null') % 左右都为空flag =1;elseflag=0;endend%%构造函数tree_plotfunction tree_plot( p ,nodevalues)%% 参考treeplot函数[x,y,h]=treelayout(p);f = find(p~=0);pp = p(f);X = [x(f); x(pp); NaN(size(f))];Y = [y(f); y(pp); NaN(size(f))];X = X(:);Y = Y(:);n = length(p);if n < 500,hold on ;plot (x, y, 'ro', X, Y, 'r-');nodesize = length(x);for i=1:nodesize%text(x(i)+0.01,y(i),['node' num2str(i)]);text(x(i)+0.01,y(i),nodevalues{1,i});endhold off;elseplot (X, Y, 'b-');end;xlabel(['height = ' int2str(h)]);axis([0 1 0 1]);end%%构造函数queue_curr_sizefunction [ length_ ] = queue_curr_size( queue )%% 当前队列长度length_= length(queue);end%%构造函数queue_popfunction [ item,newqueue ] = queue_pop( queue )%% 访问队列if isempty(queue)disp('队列为空,不能访问!');return;enditem = queue(1); % 第一个元素弹出newqueue=queue(2:end); % 往后移动一个元素位置end%%构造函数queue_pushfunction [ newqueue ] = queue_push( queue,item )%% 进队% cols = size(queue);% newqueue =structs(1,cols+1);newqueue=[queue,item];end(4)实验步骤:>> Untitled正在进行数据预处理...txt =35×5 cell 数组'序号' '花萼大小' '花瓣长度' '花瓣宽度' '类型' '' '小' '长' '长' 'versicolor' '' '小' '长' '长' 'versicolor' '' '小' '长' '长' 'versicolor' '' '小' '短' '长' 'versicolor' '' '小' '长' '长' 'versicolor' '' '小' '短' '长' 'versicolor' '' '小' '长' '短' 'versicolor' '' '大' '长' '长' 'versicolor' '' '大' '长' '短' 'versicolor' '' '大' '长' '长' 'versicolor' '' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '大' '长' '长' 'versicolor''' '小' '长' '长' 'setosa''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '长' 'versicolor''' '大' '短' '短' 'versicolor''' '小' '短' '短' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '长' 'setosa''' '小' '短' '短' 'setosa''' '小' '长' '短' 'setosa''' '大' '短' '长' 'setosa''' '大' '短' '长' 'setosa''' '小' '短' '短' 'setosa''' '小' '短' '短' 'setosa''' '大' '短' '短' 'setosa''' '小' '长' '短' 'setosa''' '大' '短' '长' 'setosa''' '大' '短' '短' 'setosa''' '大' '短' '短' 'setosa'数据预处理完成,正在进行构造树...node: 1属性值: 花瓣长度,左子树为节点:node2,右子树为节点:node3 node: 2属性值: 花瓣宽度,左子树为节点:node4,右子树为节点:node5 node: 3属性值: 花萼大小,左子树为节点:node6,右子树为节点:node7 node: 4属性值: 花萼大小,左子树为节点:node8,右子树为节点:node9 node: 5属性值: 花萼大小,左子树为节点:node10,右子树为节点:node11 node: 6属性值: 花瓣宽度,左子树为节点:node12,右子树为节点:node13叶子节点,node: 7,属性值: versicolor叶子节点,node: 8,属性值: setosa叶子节点,node: 9,属性值: setosa叶子节点,node: 10,属性值: setosa叶子节点,node: 11,属性值: versicolor叶子节点,node: 12,属性值: setosa叶子节点,node: 13,属性值: versicolorID3算法构建决策树完成!(4)实验结果。
