一种开关移位式32位乘法器的设计
VLSI电路系统与设计_32bit移位相加乘法器

《VLSI电路系统与设计》课程设计报告——32bit_32bit移位相加乘法器A 移位相加乘法器原理无符号二进制移位相加乘法器的基本原理是通过逐项移位相加来实现相乘的,从被乘数的最低为开始,若为1,则乘法左移后与上一次的和相加;若为0,左移后以全零相加,直至被乘数的最高位。
以下以4位二进制数为例进行说明:图1 移位相加乘法器原理图如图所示,就可以实现4位二进制数的相乘。
B 电路结构方案根据移位相加乘法器的基本原理,可以将整个电路划分为四个部分:32右移寄存器,32位加法器,乘1模块,64位锁存器。
原理框图如下所示:图2 移位相加乘法器原理框图在上图中,START信号的上跳沿及其高电平有两个功能,即32位寄存器清零和被乘数A[32:0]向移位寄存器SREG32B加载;它的低电平则作为乘法使能信号。
CLK为乘法时钟信号。
当被乘数被加载于32位右移寄存器SREG32B后,随着每一时钟节拍,最低位在前,由低位至高位逐位移出。
当为1时,与门ANDARITH打开,32位乘数B[32:0]在同一节拍进入32位加法器,与上一次锁存在64位锁存器REG16B中的高32位进行相加,其和在下一时钟节拍的上升沿被锁进此锁存器。
而当被乘数的移出位为0时,与门全零输出。
如此往复,直至32个时钟脉冲后,乘法运算过程中止。
此时REG64B的输出值即为最后的乘积。
此乘法器的优点是节省芯片资源,它的核心元件只是一个32位加法器,其运算速度取决于输入的时钟频率。
一、32位加法器模块的设计加法器模块是由8个四位全加器构成的,4位全加器是采用1位全加器构成的。
对于1位全加器,采用门级描述语言,使用了3个异或门和2个与门来实现的。
(1)1位加法器是采用门级描述语言,生成的库文件如图:仿真结果:图1 功能仿真图2 时序仿真(2)32位全加器32位全加器是采用8个4位全加器构成的,其电路原理图如下:图3-32位全加器原理图仿真结果:图4 功能仿真图5 时序仿真由以上的仿真结果可以看出,所设计电路在在功能上能满足要求,在时序上存在一定的时间延迟。
移位乘法器的设计
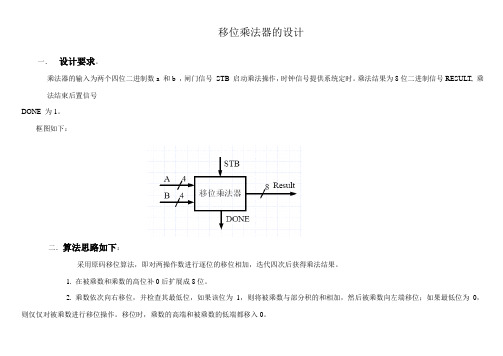
移位乘法器的设计一.设计要求。
乘法器的输入为两个四位二进制数a 和b ,闸门信号STB 启动乘法操作,时钟信号提供系统定时。
乘法结果为8位二进制信号RESULT, 乘法结束后置信号DONE 为1。
框图如下:二.算法思路如下:采用原码移位算法,即对两操作数进行逐位的移位相加,迭代四次后获得乘法结果。
1. 在被乘数和乘数的高位补0后扩展成8位。
2. 乘数依次向右移位,并检查其最低位,如果该位为1,则将被乘数与部分积的和相加,然后被乘数向左端移位;如果最低位为0,则仅仅对被乘数进行移位操作。
移位时,乘数的高端和被乘数的低端都移入0。
3. 当乘数变成全0后,乘法结束。
三. 模块划分和进程设计:把乘法器电路映射为控制器进程CONTROLLER、锁存移位进程SRA和SRB、加法进程ADDER以及锁存结果的进程ACC。
四. 移位乘法器的进程模块图五. 按照书本上的代码仿真后的波形如下:得出的是错误的结果。
经分析,可知道是由于在第三周期是shift 的值出现错误,才导致结果错误。
为此修改源代码。
如下(红色为修改的部分):library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity shift_mul isport (a,b :in std_logic_vector(3 downto 0);stb,clk :in std_logic;done :out std_logic;result :out std_logic_vector(7 downto 0));end shift_mul;architecture behav of shift_mul issignal init,shift,stop,add :std_logic;signal sraa,srbb,accout,addout:std_logic_vector(7 downto 0); begincontroller :processbeginwait until clk'event and clk='1' and stb='1';done<='0';init<='1';shift<='0';add<='0';result<="00000000";wait until clk'event and clk='1';init<='0';wait until clk'event and clk='1';wait until clk'event and clk='1';run_loop: while (stop/='1') loopwait until clk'event and clk='1';if sraa(0)='1' thenwait until clk'event and clk='1';add<='1';wait until clk'event and clk='1';add<='0';shift<='1';wait until clk'event and clk='1';elsewait until clk'event and clk='1';shift<='1';wait until clk'event and clk='1';end if;shift<='0';end loop run_loop;done<='1'; result<=accout;end process controller;sral:processbeginwait until clk'event and clk='1';if init='1'thensraa<="0000"&a;elsif shift='1'thensraa<='0'&sraa(7 downto 1);end if;stop<=not (sraa(3) or sraa(2) or sraa(1) or sraa(0) );end process sral;srar:processbeginwait until clk'event and clk='1';if init='1'thensrbb<="0000"&b;elsif shift='1'thensrbb<=srbb(6 downto 0)&'0';end if;end process srar;adder: process(accout,srbb)variable sum,tmp1,tmp2:std_logic_vector(7 downto 0);variable carry:std_logic;begintmp1:=accout;tmp2:=srbb;carry:='0';for I in 0 to 7 loopsum(I):=tmp1(I) xor tmp2(I) xor carry;carry:=(tmp1(I) and tmp2(I)) or (tmp1(I) and carry) or (tmp2(I) and carry);end loop;addout<=sum;end process adder;acc:processbeginwait until clk'event and clk='1';if init='1' thenaccout<=(others =>'0');elsif add='1' thenaccout<=addout;end if;end process acc;end behav;七。
32位快速乘法器的设计

第27 卷第9 期合肥工业大学学报(自然科学版)V o l. 27 N o. 9 2004 年9 月JOU RNA L O F H EF E I UN IV ER S IT Y O F T ECHNOLO GY Sep. 200432 位快速乘法器的设计詹文法, 汪国林, 杨羽, 张珍(合肥工业大学电气与自动化工程学院, 安徽合肥230009)摘要: 高性能乘法器是现代微处理器中的重要部件, 乘法器完成一次乘法操作的周期基本上决定了微处理器的主频。
传统的乘法器的设计, 在最终的乘积项求和时, 常采用阵列相加或叠代相加的方法, 不适用中小规模的微处理器的设计。
该文提出的32 位乘法器, 采用了Boo th 编码、422 压缩器、W allace 树算法以及超前进位加法器等多种算法和技术, 在节约面积的同时, 获得了高速度的性能。
关键词: 乘法器; Boo th 编码; 超前进位加法器; W allace 树算法中图分类号: T P 342. 21 文献标识码: A文章编号: 100325060 (2004) 0921 099204D es ign of 32-b it m ul t ipl ier w ith good speed performan ceZHAN W en2fa, W A N G Guo 2lin, YA N G Yu, ZHAN G Zhen(Schoo l of E lectri c Engineeri ng and A utom at ion, H efei U niversity of T echno logy, H ef ei 230009, Ch ina)Abstract: A m u lt i p lier w ith good speed perfo rm ance is a very im po rtan t un it in the m odern m icrop ro2 cesso rs becau s e the cycle that a m u lt i p lier com p letes one m u lt i p lica t i o n operat i o n dete r m ines the m ain frequency of the m icrop rocesso r. In summ ing of the last p roduct in the t radit i o nal m u lt i p lier des ign, the array o r iterat i o n summ ing m ethod is u sed, w h ich is no t su itab le to the des ign of sm all o r m iddle scale in t egrat i o n circu i t. A 322b i t m u lt i p lier is p resen t ed in w h ich m any m ethods, such as Boo th algo2 rithm , 422 com p resso rs, W allace t ree algo rithm , and carry2loo kahead adder, are app lied, w h ich re2 su lt s in h igh speed perfo rm ance.Key words: m u lt i p lier; Boo th algo rithm ; carry2loo kahead adder; W allace t ree algo rithm高性能乘法器是现代微处理器中的重要部件, 乘法器完成一次乘法操作的周期基本上决定了微处理器的主频。
定点乘法器设计

防止符号位扩展
• 例: B = 9 = (001001)2,A = 10 = (01010)2, AB = 90 = (01011010)2的执行过程。
防止符号位扩展
• 防止符号扩展的方式解决部分积是负数时可能产生的问题。
• 假定所有的部分积都为负,那么所有符号扩展的“1”的和
是:sig ns(m /2) (1 ( 1 )2n)4i 2n( 1 )(2m1)
= (-2bn-1 + bn-2+bn-3)2n-2 -bn-32n-3 +bn-42n-4+ … +b020
j
B (2b2i1b2i b2i1)22i i0
二阶Booth算法—控制信号编码
b2i+1b2ib2i-1 重编码
000
0
001
1
010
1
011
2
100
-2
101
-1
110
-1
111
-0
乘法计算方法
• 用笔算进行乘法计算的方法为:
0101 1010
0000 0101 0000 0101 00110010
术语
被乘数 乘数
部分积
乘积
乘法运算的关键
• 要提高乘法计算速度,需要:
➢ 加快部分积的形成 ➢ 减少部分积数目
✓ 采用多位扫描、跳过连续的0/1串和对乘数重编码(如 Booth算法)等处理方法
符号与数值分别控制
NEG B1
B2
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
1
1
0
使用乘法器实现各种移位操作
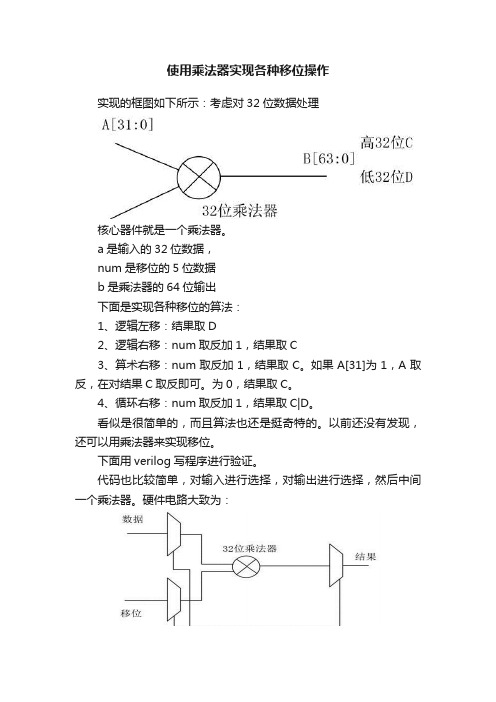
使用乘法器实现各种移位操作实现的框图如下所示:考虑对32位数据处理核心器件就是一个乘法器。
a是输入的32位数据,num是移位的5位数据b是乘法器的64位输出下面是实现各种移位的算法:1、逻辑左移:结果取D2、逻辑右移:num取反加1,结果取C3、算术右移:num取反加1,结果取C。
如果A[31]为1,A取反,在对结果C取反即可。
为0,结果取C。
4、循环右移:num取反加1,结果取C|D。
看似是很简单的,而且算法也还是挺奇特的。
以前还没有发现,还可以用乘法器来实现移位。
下面用verilog写程序进行验证。
代码也比较简单,对输入进行选择,对输出进行选择,然后中间一个乘法器。
硬件电路大致为:有了这个图,写代码就更容易了。
module shitf_according_mul( input [31:0] a, input [4:0] num, input [1:0] shift_mode, output reg[31:0] out ); localparam logic_left_shift = 2'b00; localparam logic_right_shift = 2'b01; localparam cycle_right_shift = 2'b10; localparam airth_right_shift = 2'b11; //data reg [31:0] reg_a; always@(*) begin case(shift_mode) logic_left_shift: reg_a = a; logic_right_shift: reg_a = a; cycle_right_shift: reg_a = a; airth_right_shift: reg_a = a[31] ? ~a:a; endcase end//shift number reg [31:0] reg_num; always@* begin case(shift_mode) logic_left_shift: reg_num = 32'b1(~num>(~num>(~num>纯组合逻辑设计,设计好了,需要写testbench验证吧。
32位浮点乘法器的设计与仿真代码

32位浮点乘法器的设计与仿真代码一、引言随着计算机科学和技术的不断发展,浮点乘法器在科学计算、图像处理、人工智能等领域中扮演着重要的角色。
本文将详细讨论32位浮点乘法器的设计与仿真代码,并深入探讨其原理和实现方法。
二、浮点数表示在开始设计32位浮点乘法器之前,我们首先需要了解浮点数的表示方法。
浮点数由符号位、阶码和尾数组成,其中符号位表示数的正负,阶码确定数的大小范围,尾数表示数的精度。
三、浮点乘法器的原理浮点乘法器的原理基于乘法运算的基本原理,即将两个数的尾数相乘,并将阶码相加得到结果的阶码。
同时需要考虑符号位的处理和对阶的操作。
下面是32位浮点乘法器的基本原理:1.获取输入的两个浮点数A和B,分别提取出符号位、阶码和尾数。
2.将A和B的尾数相乘,得到乘积P。
3.将A和B的阶码相加,得到结果的阶码。
4.对乘积P进行规格化,即将小数点左移或右移,使其满足规定的位数。
5.对结果的阶码进行溢出判断,若溢出则进行相应的处理。
6.将符号位与结果的阶码和尾数合并,得到最终的浮点乘积。
四、浮点乘法器的设计根据浮点乘法器的原理,我们可以开始进行浮点乘法器的设计。
设计的关键是确定乘法器中各个部件的功能和连接方式。
下面是浮点乘法器的设计要点:1.输入模块:负责接收用户输入的两个浮点数,并提取出符号位、阶码和尾数。
2.乘法模块:负责将两个浮点数的尾数相乘,得到乘积P。
3.加法模块:负责将两个浮点数的阶码相加,得到结果的阶码。
4.规格化模块:负责对乘积P进行规格化操作,使其满足规定的位数。
5.溢出判断模块:负责判断结果的阶码是否溢出,并进行相应的处理。
6.输出模块:负责将符号位、阶码和尾数合并,得到最终的浮点乘积。
五、浮点乘法器的仿真代码为了验证浮点乘法器的设计是否正确,我们需要进行仿真测试。
下面是一段简单的浮点乘法器的仿真代码:module floating_point_multiplier(input wire [31:0] a,input wire [31:0] b,output wire [31:0] result);wire [31:0] mantissa;wire [7:0] exponent;wire sign;// 提取符号位assign sign = a[31] ^ b[31];// 提取阶码assign exponent = a[30:23] + b[30:23];// 尾数相乘assign mantissa = a[22:0] * b[22:0];// 规格化assign {result[30:23], result[22:0]} = {exponent, mantissa};// 处理溢出always @(*)beginif (exponent > 255)result = 32'b0; // 结果溢出为0else if (exponent < 0)result = 32'b0; // 结果溢出为0elseresult[31] = sign;endendmodule六、浮点乘法器的应用浮点乘法器在科学计算、图像处理、人工智能等领域中有着广泛的应用。
基于修正Booth算法的实用型移位式二进制乘法器电路

算数运算电路扩展实验(基于修正Booth算法的实用型移位式二进制乘法器电路)1、电路功能设计一个16-bit的移位式乘法器电路,要求:(1)采用修正Booth算法产生部分积;(2)采用右移部分积之和的部分积求和累加方式;(3)结果乘积寄存器为32-bit。
2、电路设计(1)电路设计方案整体框图将电路分为6个子模块进行独立的设计,最后在采用一个顶层模块将之综合起来,6个子模块分别:①部分积产生电路:设被乘数为x,该电路功能是产生0,x,2x,并且x要进行符号位扩展。
②加减法器电路该加减法器为17bit的加减法器,能够由Booth译码产生的控制信号en_add来控制进行加法运算还是减法运算(高电平为加法,低电平为减法),将结果送给乘积寄存器的左半部分。
③Booth译码产生电路通过乘数y右移2位,与之前保留的一位,总共三位构成译码电路的输入,最终将译码结果送给MUX8_3选择器,让其选出正确的部分积(0,x,2x)来参与下次的加法运算,同时Booth译码电路还产生一位控制加法器电路的控制信号en_add。
④MUX数据选择器该MUX选择电路是通过译码电路产生的译码信号来选择下一步所需的部分积(0,x,2x)。
⑤乘数y的右移电路先给y最高位和最低位均补0,然后每个时钟上升沿到来,将之右移2位,在通过内部控制信号,向右移9次。
⑥部分积之和右移电路将加法器产生的输出放在其高16位,同时进行右移2位操作,并进行符号位的扩展。
然后再将移位后的高16位送给加法器的被加数端,进行下一次的部分积求和,再通过内部控制信号,控制其向右移9次,最终得到正确的乘积。
(2)电路设计①部分积的产生电路module Creat_part_pro(input [15:0] x,output reg [16:0] x_0,output reg [16:0] x_1,output reg [16:0] x_2);always@(*)beginif (x[15])beginx_0 = 17'b0;x_1 = {1'b1,x};x_2 = {x<<1};endelsebeginx_0 = 17'b0;x_1 = {1'b0,x};x_2 = {x<<1};endendendmodule电路说明:x:输入的16位被乘数x_0: 输出0x_1:输出x,并进行符号位扩展x_2:输出2x②加减法器module Add(input rst_n,input en_add,//高为加法,低位减法input [16:0] add1,input [16:0] add2,output reg [16:0] part_sum//部分积之和,送往移存器);always @(*)beginif (!rst_n)part_sum = 17'b0;else if(en_add)part_sum = add1 + add2;elsepart_sum = add2 - add1;endendmodule电路说明:add1:被加数add2:加数en_add:加减控制信号(高为加,低为减)part_sum:输出和③数据选择器module Mux_3_1(input [16:0] x_0,//产生的0,X,2Xinput [16:0] x_1,input [16:0] x_2,input [2:0] en_x,//译码产生的控制信号output reg [16:0] addx_i ///送往加法器,与部分积之和相加);always @(*)begincase (en_x)3'b010 : addx_i = x_2;default : addx_i = x_0;endcaseendendmodule电路说明:x_i :分别是电路①产生的0,x,2xenx:选择控制信号,由Booth译码电路产生addx_i:输出送往加法器④Booth译码电路module Booth_encode(input [2:0] y_n,//乘数y的三位需要译码output reg [2:0] en_x,output reg en_add //决定加法器加减,高加低减);always@(*)begincase (y_n)3'b000 : en_x = 3'b000;3'b001 : en_x = 3'b001;3'b010 : en_x = 3'b001;3'b011 : en_x = 3'b010;3'b100 : en_x = 3'b010;3'b101 : en_x = 3'b001;3'b110 : en_x = 3'b001;3'b111 : en_x = 3'b000;default : en_x = 3'b000;endcaseendalways@(*)begincase(y_n)3'b000 : en_add = 1'b1;3'b001 : en_add = 1'b1;3'b010 : en_add = 1'b1;3'b011 : en_add = 1'b1;3'b100 : en_add = 1'b0;3'b101 : en_add = 1'b0;default : en_add = 1'b1;endcaseendendmodule电路说明:y_n:由y产生的三位译码输入en_x:译码电路的输出,送往数据选择器en_add:送往加法器,决定加减⑤乘数y右移电路module Shift_y_right_2bit(input clk,input rst_n,input [15:0] y,output reg [2:0] encode_in);reg [3:0] shift_cnt;wire en_shift;always@(posedge clk or negedge rst_n)beginif (!rst_n)beginshift_cnt <= 4'b0000;endelse if (shift_cnt == 4'b1001)shift_cnt <= 4'b0000;elseshift_cnt <= shift_cnt + 1'b1;endassign en_shift = (shift_cnt == 4'b1001) ? 1'b0 : 1'b1;reg [17:0] y_r;always@(posedge clk or negedge rst_n)beginif (!rst_n)beginy_r <= 18'b0;encode_in <= 3'b000;endelse if(en_shift)beginencode_in <= {y_r[2:0]};y_r <= y_r >> 2;endelsebeginy_r <= {1'b0,y,1'b0};endendendmodule电路说明:clk:系统时钟rst_n:系统复位信号y:乘数encode_in:产生的译码,送往Booth译码器shift_cnt:移位计数器en_shift:允许移位标志⑥求积电路module Creat_product(input clk,input rst_n,input [16:0] part_pro,output reg [32:0] product);reg [3:0] shift_cnt;wire en_shift;always@(posedge clk or negedge rst_n)beginif (!rst_n)beginshift_cnt <= 4'b0000;endelse if (shift_cnt == 4'b1001)beginshift_cnt <= 4'b0000;endelsebeginshift_cnt <= shift_cnt + 1'b1;endendassign en_shift = (shift_cnt == 4'b1001) ? 1'b0 : 1'b1;always@(posedge clk or negedge rst_n)beginif (!rst_n)beginproduct <= 33'b0;product[32:16] <= 17'b0;endelse if(!en_shift)beginproduct <= 33'b0;product[15:0] <= 16'b0;endelsebeginproduct <= {product[32],product[32],product[32:2]}; product[32:16] <= part_pro;endendwire [32:0] product_test;assign product_test = {product[32],product[32],product[32:2]}; endmodule电路说明:clk:系统时钟rst_n:复位信号part_pro:部分积之和,由上述的加法器电路产生product:输出积(此处由于时序问题,并不是正确的乘积)shift_cnt:移位计数器en_shift:允许移位标志product_test:经过仿真,这个才是正确的乘积⑦顶层模块module Booth_16bit_TOP(input clk,input rst_n,input [15:0] x,input [15:0] y,output [32:0] product);wire [16:0] x_0;wire [16:0] x_1;wire [16:0] x_2;Creat_part_pro U_Creat_part_pro //部分积产生模块(.x (x),.x_0 (x_0),.x_1 (x_1),.x_2 (x_2));wire [2:0] encode_in;wire [2:0] en_x;wire en_add;Booth_encode U_Booth_encode //Booth译码电路产生模块(.y_n (encode_in),.en_x (en_x),.en_add (en_add));Shift_y_right_2bit U_Shift_y_right_2bit //右移y产生译码信号(.clk (clk),.rst_n (rst_n),.y (y),.encode_in (encode_in));wire [16:0] addx_i;Mux_3_1 U_Mux_3_1 //选择加x,还是2x(.x_0 (x_0),.x_1 (x_1),.x_2 (x_2),.en_x (en_x),.addx_i (addx_i));wire [16:0] part_sum; ///部分积产生模块Add U_Add(.rst_n (rst_n),.en_add (en_add),.add1 (addx_i),.add2 ({product[32],product[32],product[32:18]}),.part_sum (part_sum));Creat_product U_Creat_product //积的产生(.clk (clk),.rst_n (rst_n),.part_pro (part_sum),.product (product));endmodule电路说明:将之前的六个模块联系起来,形成一个完整的乘法器电路。
位可控加减法器设计32位算术逻辑运算单元

位可控加减法器设计32位算术逻辑运算单元标题:深入探讨位可控加减法器设计中的32位算术逻辑运算单元一、引言在计算机系统中,算术逻辑运算单元(ALU)是至关重要的部件,用于执行数字运算和逻辑运算。
而在ALU中,位可控加减法器设计是其中的重要部分,尤其在32位算术逻辑运算单元中更是不可或缺。
本文将深入探讨位可控加减法器设计在32位算术逻辑运算单元中的重要性,结构特点以及个人观点和理解。
二、位可控加减法器设计的重要性位可控加减法器是ALU中的重要组成部分,它具有对加法和减法操作进行控制的能力,可以根据输入信号来实现不同的运算操作。
在32位算术逻辑运算单元中,位可控加减法器的设计要考虑到对每一位进行并行操作,并且要保证高速、低功耗和稳定性。
位可控加减法器设计在32位算术逻辑运算单元中具有非常重要的意义。
三、位可控加减法器设计的结构特点在32位算术逻辑运算单元中,位可控加减法器的设计需要考虑到以下几个结构特点:1. 并行运算:位可控加减法器需要能够实现对32位数据的并行运算,以提高运算速度。
2. 控制信号:设计需要合理的控制信号输入,来实现不同的运算模式和操作类型。
3. 进位传递:保证进位信号能够正确传递和计算,以确保运算的准确性。
4. 低功耗:设计需要考虑到低功耗的特点,以满足现代计算机系统对能源的需求。
四、个人观点和理解在我看来,位可控加减法器设计在32位算术逻辑运算单元中扮演着十分重要的角色。
它不仅需要具备高速、稳定和精确的运算能力,还需要考虑到功耗和控制信号的合理设计。
只有兼具这些特点,才能更好地满足现代计算机系统对于高效、可靠和低功耗的需求。
五、总结和回顾通过本文对位可控加减法器设计在32位算术逻辑运算单元中的深入探讨,我们可以看到它在计算机系统中的重要性和结构特点。
而个人观点也表明了它需要具备高速、低功耗和稳定性等特点,才能更好地满足现代计算机系统的需求。
在写作过程中,我对位可控加减法器设计在32位算术逻辑运算单元中的重要性和结构特点进行了深入探讨,并分享了个人观点和理解。
32位乘法器

32位乘法器逻辑原理图:
实验原理:乘法可以通过逐渐项相加原理来实现。
从被乘数的最低位开始,若为1则乘数左移后与上一次的和相加;若为0左移后以全零相加,直至被乘数的最高位。
32位移位相加乘法器运算数据时序图:
工作原理:clr信号的上跳沿及其高电平有两个功能,即模块regsht清零和被乘数dina[31.。
0]向移位寄存器shft加载;它的低电平则作为乘法使能信号,clk为乘法时钟信号。
当被乘数加载于32位右移寄存器shft后,随着每一时钟节拍,最低位在前,由低位到高位逐位移出。
当为1时,4位乘法器and32打开,32位乘数din[31..0]在同一节拍进入加法器,与上一次存在regsht的数相加,其和在下一时钟节拍的上升沿被锁进此锁存器。
而当被乘数的移出位为0时,此and32全零输出。
如此反复,直至32个时钟脉冲后,最后乘积完整出现在regsht端口。
位可控加减法器设计32位算术逻辑运算单元

【位可控加减法器设计32位算术逻辑运算单元】1. 引言位可控加减法器是现代计算机中十分重要的组成部分,它可以在逻辑电路中实现对算术运算的功能。
其中,32位算术逻辑运算单元是计算机中非常常见的一个部件,它可以用来进行32位数据的加法、减法和逻辑运算。
本文将就位可控加减法器的设计和32位算术逻辑运算单元进行全面评估,并给出深度和广度兼具的解析。
2. 什么是位可控加减法器位可控加减法器是一种灵活的算术逻辑电路,它可以根据控制信号来选择进行加法运算或减法运算。
这种设计可以大大提高电路的灵活性和适用性,使得算术运算单元可以在不同的情况下实现不同的运算需求。
3. 32位算术逻辑运算单元的设计原理32位算术逻辑运算单元是计算机中进行32位数据运算的核心部件,它通常包括加法器、减法器、逻辑门等组件。
在设计中,需要考虑到加法器和减法器的位宽、进位和溢出等问题,同时还需要考虑逻辑门的多功能性和灵活性。
通过合理的组合和控制,可以实现对32位数据进行高效的算术逻辑运算。
4. 位可控加减法器设计在32位算术逻辑运算单元中的运用位可控加减法器的设计可以很好地应用在32位算术逻辑运算单元中,通过控制信号来选择进行加法或减法运算,从而满足不同情况下对数据的处理需求。
这种设计不仅能简化电路结构和控制逻辑,还能提高算术逻辑运算单元的灵活性和效率,使其更适用于不同的场景和运算需求。
5. 个人观点和理解从我个人的理解来看,位可控加减法器设计在32位算术逻辑运算单元中的应用,可以很好地提高计算机的运算效率和灵活性。
通过合理的设计和控制,可以使得算术逻辑运算单元在不同的情况下具有不同的功能,从而更好地满足计算机对于数据处理的需求。
这种设计也为计算机的设计和优化提供了很好的思路和方法。
6. 总结通过本文的评估和解析,我们对于位可控加减法器的设计以及在32位算术逻辑运算单元中的应用有了更深入的理解。
通过灵活的控制信号,可以实现算术逻辑运算单元在不同情况下对数据进行不同的处理,从而提高了计算机的运算效率和灵活性。
一种开关型乘法器电路的研究

W he l Gy o c p . S n o s a d A cu t r. A: e r so e e s r n taos
图 2是 图 1 示 乘法 器 电路 的几 个 主要 节 点 所 的仿 真 波形 ,图 中可 以看 出节 点 cn 的信 号是 与 ot
一
u
t +) < 争T ( c n
() 3
1 i
£8
u t d) =
j
1 4
f
。
u (1T< 1 n )t+o + c() <n T
由式() 法器 的输 出信号 u t 以看 成是输 3, 乘 d) 可
00 m
㈨
程1 3
●
4u ・ {
U t 一 )2 ) d) u t U ( = + t ( 2 )
图l 是开关型乘法器 的电路结构图. 中 c 其 1 是一个 比较器 ,l S 是一个开关 , 8 E 是一个运算放
将式(代入( , 1 ) 2 可以得到如下表达式: )
一
大器 , 电阻 R 3 R 4 R 5的阻值相等. 1、 1 、 1
E 8的正 向输 入端 , 另外 一端 连接平 衡 电压 V a, bl开
乘法器是对两个模拟信号实现相乘功能的有 源非线性器件 , 这两个模拟信号可以是电压信号或 者电流信号. 在微处理器芯片 中, 乘法器是进行数 字信号处理的核心 , 同时也是微处理器中进行数据
处理 的关键 部件 I】 高频 电子 线 路 中 , 幅调制 、 l. ’在 2 振 同步 检 波 、 混频 、 频 、 频 、 相 等调 制 与解 调 的 倍 鉴 鉴
32位乘法器 c语言

32位乘法器简介在计算机科学中,乘法运算是一个基本且常见的操作。
为了实现快速且准确的乘法运算,计算机中有专门的电路和算法来实现乘法操作。
本文将讨论如何使用C语言编写一个32位乘法器,介绍其原理、实现方法和效果。
原理32位乘法器是指可以将两个32位的二进制数相乘,并得出结果的电路或算法。
乘法运算的基本原理是将两个数的每一位相乘,并将结果相加。
实现方法下面介绍如何使用C语言编写一个32位乘法器。
步骤1:定义变量和输入首先,我们需要定义两个32位的无符号整数作为输入。
可以使用C语言的unsigned int类型来表示这两个数。
unsigned int num1, num2;然后,我们需要从用户输入中获取这两个数的值。
可以使用C语言的scanf函数来实现。
printf("请输入第一个数:");scanf("%u", &num1);printf("请输入第二个数:");scanf("%u", &num2);步骤2:实现乘法运算接下来,我们使用C语言的乘法运算符(*)来计算两个数的相乘结果。
unsigned long long result = (unsigned long long)num1 * num2;由于两个32位的数相乘可能会得到一个64位的结果,我们需要将结果存储在一个64位的变量中。
可以使用unsigned long long类型来表示这个变量。
需要注意的是,在C语言中,两个32位的数相乘得到的结果是一个32位的数,因此我们需要使用强制类型转换将其转换为64位的数。
步骤3:输出结果最后,我们使用printf函数将乘法运算的结果输出。
printf("乘法运算的结果为:%llu\n", result);需要注意的是,在格式字符串中,我们使用%llu来表示64位的无符号整数。
功能测试通过输入不同的数进行测试,验证32位乘法器的正确性和准确性。
32位快速乘法器设计

De i n o g r o m a c 2 b t m u tp i r s g f hi h pe f r n e 3 i l i le s
Hu H a o Z a e l n h oW ni g a Lu o Xi
( .Un v r iy o e t o i inc n c no o y o i a,Ch n d 0 5 1 i e st fEl c r n c Sce e a d Te h l g fCh n e g u 61 0 4; 2 .Do g a g El c rc Co p r to fCh na n f n e t r o a i n o i ,Ch n u 6 00 ) i e gd 1 41
第6O 2年5 0第 21 0月 9 期 卷
摘
要 :本文介绍了一种通过符号位扩展 , 以分别完 成 3 可 2位有 符号/ 无符号 二进 制数 乘法 的高性 能乘 法器设 计 。
该 乘 法 器 采 用 高 基 B oh算 法 , 化 部 分 积 的符 号 扩 展 , 过 采 用 较 之 常 规 W al e 具 有 更 规 则 和 更 简 洁 的 连 接 复 ot 简 通 lc 树 a
Ab t a t Th e i n o i h p ro ma c l p irwh c u p r sb t in d a d u i n d 3 i mu t l a in b n sr c : e d sg f g e f r n e mu t l ih s p o t o h sg e n ns e 2 b t h i e g li i t y a p c o a d tv i n b ti p o o e .P e i e tt e sg i s r a fp r il r d c y u i g t eh g a i o t l o ih . d i es i s rp s d i g r d g s h i n b t p e d o a t o u tb sn h i h r d x B o h a g rt m ap To i r v h p e ft e mu tp ir ,a n v lt e t u t r s a o t d,wh c s p o i e t i p e ig a d mp o e t e s e d o h l l s o e r e s r c u e i d p e i e i h i r vd d wi sm l r wrn n h mo e r g l rs r c u e t a o r e u a tu t r h n c mmo a l c r e Fu t e mo e a n v lla i g c r y a d r i a o t d Th o e n W l e te. a rh r r , o e e d n a r d e s d p e . e wh l d sg s st e t c n lg ff u t g i e i e ,a d i a i a e n t e FP e i n u e h e h o o y o o rs a e p p l s n s v l t d i h GA. Fi al ,i i s c e s u l p l d i n d nl y t s u c s f ly a p i n e t e fe u n y d ma n e u l e . h rq e c - o i q ai r z Ke wo d : li l r h g a i o t l o ih ; n v l a r e d n d e y r s mu tp i  ̄ i h r d x B o h ag r m e t o e c r y la i g a d r
实验5——ALU中的32位移位器设计
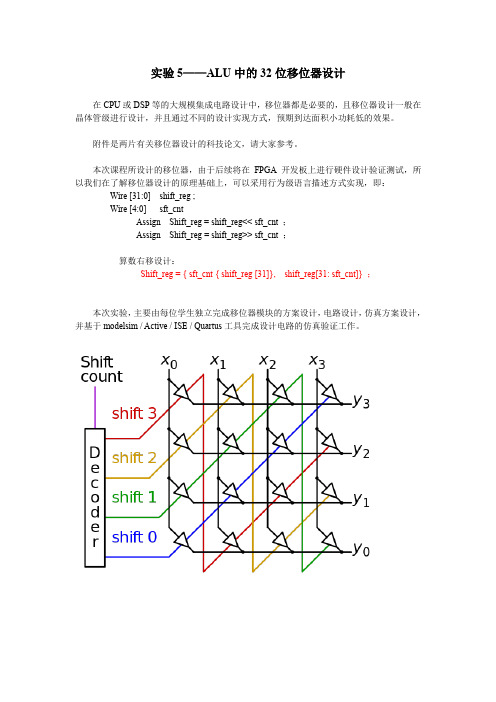
实验5——ALU中的32位移位器设计
在CPU或DSP等的大规模集成电路设计中,移位器都是必要的,且移位器设计一般在晶体管级进行设计,并且通过不同的设计实现方式,预期到达面积小功耗低的效果。
附件是两片有关移位器设计的科技论文,请大家参考。
本次课程所设计的移位器,由于后续将在FPGA开发板上进行硬件设计验证测试,所以我们在了解移位器设计的原理基础上,可以采用行为级语言描述方式实现,即:Wire [31:0] shift_reg ;
Wire [4:0] sft_cnt
Assign Shift_reg = shift_reg<< sft_cnt ;
Assign Shift_reg = shift_reg>> sft_cnt ;
算数右移设计:
Shift_reg = { sft_cnt { shift_reg [31]}, shift_reg[31: sft_cnt]} ;
本次实验,主要由每位学生独立完成移位器模块的方案设计,电路设计,仿真方案设计,并基于modelsim / Active / ISE / Quartus工具完成设计电路的仿真验证工作。
32位乘法器的实现

32位乘法器的实现
32位乘法器的实现
郭桂香;吕文斌
【期刊名称】《高性能计算技术》
【年(卷),期】2006(000)004
【摘要】本文提出了一种高性能32位无符号乘法器的实现,它采用Booth编码为Radix-4的Wallace树算法结构,并以全定制设计方法实现,使用硅生产流片进行功能及性能验证.
【总页数】4页(44-47)
【关键词】乘法器;Booth编码;Wallace树;电路设计;版图设计
【作者】郭桂香;吕文斌
【作者单位】江南计算技术研究所,无锡,214083;江南计算技术研究所,无锡,214083
【正文语种】中文
【中图分类】TP3
【相关文献】
1.32位单精度浮点乘法器的FPGA实现 [J], 胡侨娟; 仲顺安; 陈越洋; 党华
2.一种32位异步乘法器的研究与实现 [J], 李勇; 王蕾; 龚锐; 戴葵; 王志英
3.基于FPGA的32位并行乘法器的设计与实现[J], 蒋勇; 罗玉平; 马晏; 叶新
4.面向低端FPGA的32位硬件乘法器实现 [J], 陈兆梅; 贾立萍
5.32位无符号并行乘法器的设计与实现 [J], 胡小龙; 颜煦阳
以上内容为文献基本信息,获取文献全文请下载。
32_32高速乘法器的设计与实现

对传统的基于全加器组成的压缩单元进行分
析 ,得出其布尔表达式如下 :
S = a1 a2 a3 a4 cin
(3)
Carry = ( a1 a2 a3) ·a4 + ( a1 a2 a3) ·
cin + a4 ·cin
(4)
Cout = a1 ·a2 + a1 ·a3 + a2 ·a3
(5)
对式 (4) 、式 (5) 两个表达式进行等价的逻辑转
首先设 A 为被乘数 , B 为乘数 ,且均为 32 位无 符号数 , P 表示乘积. 则有 A ×B 为
31
16
∑ ∑ P = A ×( bi2 i) = A ×[ ( b2 n - 1 + b2 n -
i =0
n =0
16
∑ 2 b2 n +1) 4 n ] =
A ( b2 n - 1 + b2 n - 2 b2 n +1) 22 n (1)
32 ×32 High2speed Multiplier Design and Implementation
L I J un2qiang1 , L I Dong2sheng1 ,2 , L I Yi2lei1 , ZHOU Zhi2zeng3
一种高性能32位浮点乘法器的ASIC设计

2004年4月第26卷 第4期系统工程与电子技术Systems Engineering and E lectronicsApr.2004V ol 126 N o 14收稿日期:2003-02-24;修回日期:2003-07-10。
作者简介:赵忠武(1977-),男,硕士,主要研究方向为模拟集成电路设计,数字ASIC 设计。
文章编号:1001Ο506X (2004)04Ο0531Ο04一种高性能32位浮点乘法器的ASIC 设计赵忠武,陈 禾,韩月秋(北京理工大学电子工程系,北京100081)摘 要:介绍了一种32位浮点乘法器的ASIC 设计。
通过采用改进Booth 编码的树状4:2列压缩结构,提高了乘法器的速度,降低了系统的功耗,且结构更规则,易于V LSI 实现。
整个设计采用Verilog H D L 语言结构级描述,用TS MC 0.25标准单元库进行逻辑综合。
采用三级流水技术,完成一次32位浮点乘法的时间为28.98ns ,系统的时钟频率可达103.52MH z 。
关键词:浮点乘法器;Booth 编码;树状列压缩中图分类号:T N492 文献标识码:ADesign of high 2perform ance 322bit floating 2point multipliers for ASICZH AO Zhong 2wu ,CHE N He ,H AN Y ue 2qiu(Department o f Electronic Engineering ,Beijing Institute o f Technology ,Beijing 100081,China )Abstract :A design of high 2per formance 322bit floating 2point multipliers for ASIC is presented.By using a structure of 4:2col 2umn com pression trees with the m odified Booth encoding ,the speed of the multipliers is im proved and the power of the system is re 2duced.Furtherm ore ,due to a m ore regular structure ad opted ,it is easy for V LSI realization of the multipliers.The wh ole design is described in Verilog H D L at structurelevel ,and synthesized using the TS MC 0.25standard cell library.W ith the techn ology of three 2stage pipeline ,28.98ns is needed to com plete a 322bit floating 2point multiplication ,and the frequency of the system can reach 103.52MH z.K ey w ords :Floating 2point multiplier ;Booth encoding ;column com pression tree1 引 言随着计算机和DSP 技术的不断发展,人们对速度快、面积小的高性能协处理器的需求也越来越大。
基于Booth算法的32位流水线型乘法器设计

基于Booth算法的32位流水线型乘法器设计
翟召岳;韩志刚
【期刊名称】《微电子学与计算机》
【年(卷),期】2014(31)3
【摘要】为了减少乘法指令在保留站中的等待时间,设计了一款32位流水线型乘法器,该乘法器将应用于作者设计的一款超标量处理器中.该乘法器应用了改进型的booth编码算法,对部分积生成电路进行了优化,并采用了4-2压缩器与3-2压缩器相结合的Wallace树型结构对部分积进行压缩,最后再根据各级的延迟,在电路中插入了流水线寄存器,使其运算速度得到了提高.该乘法器使用GSMC 0.18μm工艺进行综合.经过仿真验证,该乘法器大大减少了在保留站中等待执行的乘法指令的完成时间,使每个时钟周期都有一条新的乘法指令被发送至乘法器进行运算.
【总页数】4页(P146-149)
【关键词】Booth算法;Wallace树;压缩器;流水线
【作者】翟召岳;韩志刚
【作者单位】同济大学电子科学与技术系
【正文语种】中文
【中图分类】TP332.2
【相关文献】
1.基于Booth算法的32×32乘法器IP核设计 [J], 汤晓慧;杨军;吴艳;吴建辉
2.基于改进的BOOTH编码的高速32×32位并行乘法器设计 [J], 刘强;王荣生
3.一种基于改进基4 Booth算法和Wallace树结构的乘法器设计 [J], 吴美琪; 赵宏亮; 刘兴辉; 康大为; 李威
4.一种改进的基4-Booth编码流水线大数乘法器设计 [J], 周怡;李树国
5.基于修正BOOTH编码的32×32位乘法器 [J], 崔晓平
因版权原因,仅展示原文概要,查看原文内容请购买。
32位MIPS微处理器中乘法器的设计和实现

32位MIPS微处理器中乘法器的设计和实现
王谦
【期刊名称】《电子工程师》
【年(卷),期】2004(30)3
【摘要】在Booth算法的基础上 ,结合MIPS 4KC微处理器中的流水线结构和乘法器的工作过程 ,提出了一种改进的Booth乘法器的设计方法 ,并采用全制定方法实现 ,用这种方法实现的乘法器单元具有面积小、单元电路可重复性好、版图设计工作量小、功耗低等特点。
【总页数】3页(P7-9)
【关键词】MIPS;微处理器;乘法器;Booth算法;流水线
【作者】王谦
【作者单位】同济大学超大规模集成电路研发中心
【正文语种】中文
【中图分类】TP332.22
【相关文献】
1.基于FPGA的32位并行乘法器的设计与实现 [J], 蒋勇;罗玉平;马晏;叶新
2.32位无符号并行乘法器的设计与实现 [J], 胡小龙;颜煦阳
3.32位RISC微处理器FPGA验证平台设计与实现 [J], 于海;樊晓桠;张盛兵
4.32位MIPS微处理器的设计与实现 [J], 冀红举;段朝伟;李艳丽
5.32位可重构多功能乘法器的设计与实现 [J], 王卫涛;沈绪榜;单超
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第31卷 第5期2008年10月电子器件Chinese J ournal Of Elect ron DevicesVol.31 No.5Oct.2008A 32bit Multiplier DesignB ased on Switch &ShiftL I U X ue 2yong ,L I X i ao 2j i ang ,M A Chen g 2y an3(T he I nstit ute of Microelect ronics ,CA S ,Hangz hou 310053,Chi na )Abstract :The multiplier is an important and co mplex part in t he AL U design of CPU ,it takes up a relative larger area and longer delay.According to t he different requirement s of system ,we can design out vario us multipliers.This paper makes a compromise between system clock and area ,bringing out a none single clock multiplier design based on switch and shift operation.At last by using SYNOPS YS tools it gives out t he synt hesis report and simulating wave to draw a parallel between t his multiplier and t he one generated f rom S YNOPS YS design_ware.K ey w ords :switch ;multi 2cycle ;shift ;multiplier EEACC :6230一种开关移位式32位乘法器的设计刘学勇,李晓江,马成炎3(杭州中科微电子有限公司,杭州310053)收稿日期:2007212206作者简介:刘学勇(19842),男,现为中国科学院微电子研究所2005级硕士研究生,主要研究方向为数字SOC 设计;李晓江,男,现为中国科学院微电子研究硕士生导师,主要研究方向为数字SOC 设计;马成炎,男,研究员,中国科学院微电子研究所博士生导师,研究方向模拟射频芯片设计,machengyan @ 。
摘 要:乘法器在CPU 的AL U 设计中是很重要,也是较为复杂的一部分,它占据大的面积和较长的延时。
根据系统不同的要求,我们可以设计出不同的乘法器。
本文是在系统时钟要求和面积两方的限制下做了折衷,提出了一种基于开关和移位工作方式的多时钟周期乘法器的设计。
最后用DC 进行综合,并经VCS 仿真得到结果与SYNOPSYS 公司design_ware 里的乘法器进行比较,指出其优缺点。
关键词:开关;移位;多周期;乘法器中图分类号:TN 402 文献标识码:A 文章编号:100529490(2008)0521671203 乘法器的代价很高并且运算很慢,许多计算问题的性能常常是由乘法运算所能执行的速度决定的[3]。
在CPU 的运算功能块AL U 设计中,根据系统不同的要求,我们又可以设计单时钟周期或者多时钟周期的乘法器。
有关单周期和多周期乘法器稍微系统一点的阐述,可以参考文献[7]。
一般说来直接在verilog 代码“×”号会使DC 直接调用design 2ware 里的单时钟乘法器进行综合,此乘法器的面积和延时都比较大。
如果需要降低延时并且减小面积的情况下,我们要对乘法操作时钟数进行牺牲。
为此,针对小面积小延时的情况,作者采用分解成原子操作的方法来实现32带符号位数的乘法,达到减小面积和延时的目的。
其具体思路是把2个32bit 分解成为4个16bit 的数来进行操作。
其分解出来的16×16位的无符号数乘法属于一个原子操作,用一个组合逻辑在一个clock 内完成。
1 原子乘法的实现乘法原子操作是16×16位乘法的一个时钟实现,是整个32位乘法器的关键。
此实现基于开关移位原理。
考虑到图的表示过于复杂,暂用8×8的原子操作来图解原理,以此达到理会16×16的原子操作过程。
先给出A =10111101,B =10110001。
如图1,圆圈里的数字表示乘数B ,如果为1则表示开关打开,选择A ;如为0则不打开选择0。
图1 原子操作原理解析考虑对称性,把B 的8bit 数据首先分为4组,两两相邻为一组,每组2bit ,根据其值来选择是否传递A 。
把每组左边传递出来的数据左移1位(方框L1)加上右边传递出来的数据,形成新的数据,如图形成了A1,S1,0和A 。
再把这四个数据重新分组,此时移位为移2位。
最后得出来的数据只有一组,左边移4位与右边相加就得到乘法原子操作的结果S3。
下面给出每步操作的中间结果,如图2。
图2 原子操作数据运算说明2 32位乘法器的整合有了16×16位乘法原子操作,我们可以由它构造多周期32位乘法器。
两个32位乘数都是被转换成了绝对值的,所以最高位都为0,这样2个32位乘数实质上分解成2个15位数和2个16位的数。
这样也有一个好处就是可以消除一些乘积间有进位的问题。
还是用图来说明问题,取A =F5D8_C3D5,B =7DF8_FA1B 。
先把它们转换成补码即绝对值,分别为0A27_3C2B 和7DF8_FA1B 。
再对这两个补码进行乘数分解,如图3。
这个流程图很明朗,B EHAV IOR 一栏用箭头指出各步骤操作的意义。
在经过4个clock 后已经可以得到一个乘法结果,但其还不是最终结果,还缺图3 32bit 乘法整合实例少符号的判断。
通常的做法是在写代码时分为正数乘正数,负数乘负数等[6]。
这样比较麻烦,本文干脆直接先把两个乘数转换成绝对值后再根据原来两数的最高位符号位来判断乘积结果是否要由补码转成原码。
这只需要用A[31]和B[31]相异出来的结果用来选择乘积和补码就行了。
图中的t rans 以及t rans64都是进行补码转换。
3 进位问题的说明由于两个32位乘数的最高位都为0,所以最终乘积一定是62位的。
分解的乘数中得到的4个子乘积项依次为32位,31位,31位,30位。
要考虑进位问题,我们只需要拿最大的数去相乘,如果最大的数都没有发生进位,则其他数据更不可能有进位问题。
选取最大的数7FFF_FFFF 和它自己7FFF_FFFF 相乘。
以此来考虑进位问题。
下面分时钟来说明子乘积项如何相加。
(1)第1个CL K 后,得到32位乘积FFFE 20001。
(2)第2个CL K 后,得到31位乘积7FFE 28001。
把它与第一个乘积的高16位FFFE 进行相加,得到31位(而不是32位)和7FFF_7FFF 。
所以此31位加法操作没有进位。
(3)第3个CL K 后,得到31位乘积7FFE 28001,然后在加上第2个CL K 后得到的和7FFF 27FFF 得到FFFE_0000,此时两个31位数相加发生了进位但最后结果没有超过32位。
(4)第4个CL K 后,子乘积结果为30位的3FFF 20001,加上上个CL K 得到的和的高16位FFFE 得到30位的3FFF_FFFF ,无加法进位。
这说明,这步操作最多就是产生30位的和。
通过以上4个CL K 的运算,我们可以看到,最2761电 子 器 件第31卷长的是31位加31位得到32位的数据,我们就可以通过资源复用,用一个32位的半加器用来完成上述全部操作,其中位数不够的高位填补0。
这样在最大的数都只采用一个32位加法器和4个时钟周期完成了乘法操作,我们可以推测出其他数据一样满足这样的要求。
4 对比本设计用了4个时钟周期来完成一次带符号32位数据乘法运算,虽然时钟周期多,但换来的是面积的减少。
这在面积要求比较严格而时钟数不太紧的情况下是很有利的。
作者完成乘法器verilog代码[2]并且使用S YNO PS YS工具DC和SM IC0.18μm库综合得到数据如下:面积:35700μm×μm 最大延时:15.18ns而如果调用用S YNOPS YS自身design_ware 的乘法器(单时钟周期)我们得到数据如下:面积:64440μm×μm 最大延时:25.24ns对于design_ware里的乘法器,它本身是采用了Wallace t ree或者基于Boot h编码等途径优化过的[5],所以相对作者自己直接用32位(即一个clock 做完)做原子操作得出的面积和延时来说是比较好的。
所以要想进一步减少延时和面积,只有通过牺牲时钟数来获取。
由数据可见,本设计要求的面积减少了近一半,由于设计中多出了许多不必要的控制,如果是单纯乘法内核的话可以使面积更加少。
再者最大延时缩短了不少,使得系统工作频率得到提高。
如果对16位原子操作进行进一步的优化,比如深入研究使其中一个乘数和积的部分寄存器共用[1],还可以使面积和延时更加小,不过鉴于这是新提出的一种基于开关移位的乘法器,故不做优化保持原样,目的是使读者知道这么一种思路。
用S YNOPS YS的VCS仿真器仿真,得到如下波形,结果正确,注意第一个时钟周期是用来装载数据用,故共5个CLOC K出结果。
图4 仿真波形5 总结本文提出了一种比较新的乘法器设计方法,基于开关和移位,但其本质上是移位相加。
这种设计虽然不是最快的设计,但是也开拓了设计思路。
另外把32位乘法分解这一操作对于减小面积也是种有效的方法。
再者进位的考虑使用了最大数据来衡量其他数据也是可行的。
最后把带符号数相成转换成绝对值后再转换回来也是本文的一个特点。
参考文献:[1] Patterson David A,Hennessy John puter Organization&Design:The Hardware/Software[M].Interface(Second E2 dition).郑纬民,等译.第二版,清华大学出版社,2003,12. [2] Samir Palnit kar.Verilog HDL A Guide to Digital Design andSynt hesis[M].(Second Edition).夏宇闻,胡燕详,刁岚松等译,第二版,电子工业出版社,2004,11.[3] Rabaey J am M,Chandrakasan Anat ha,Digital Integrated Cir2cuit s A Design Perspective(second Edition).周润德等译,第二版,电子工业出版社,2005,7.[4] Hennessy John L,Patterson David A,Computer Architecture:A Quantitative Approach[M].(Third Edition),机械工业出版社,2002.9.[5] 王彬,任艳颖编著.数字IC系统设计[M].西安电子科技大学出版社,2005,9.[6] 朱子玉,李亚民,CPU芯片逻辑设计技术[M].清华大学出版社,2005,1.[7] Ciletti Michael D,Advanced Digital Design wit h t he VerilogHDL[M].张雅绮,李锵等译,电子工业出版社,2005,1.3761第5期刘学勇,李晓江等:一种开关移位式32位乘法器的设计。
