matlab数组,矩阵,绘图指令
matlab常用指令

matlab常用指令MATLAB是一款非常实用的科学计算软件,在使用过程中,一些常用的指令是非常必要的。
在本篇文章中,我们将会介绍MATLAB常用指令,以使你更加熟练掌握MATLAB的使用。
一、基本数学运算+ 加- 减* 乘/ 除^ 幂(指数)sqrt 平方根exp 取指数log 取自然对数log10 取以10为底的对数sin 正弦cos 余弦tan 正切asin 反正弦acos 反余弦atan 反正切abs 绝对值rem 模运算fix 向零取整floor 向负无穷取整ceil 向正无穷取整round 四舍五入mod 取摸余数二、变量与矩阵1、赋值:通过等号将数值赋给变量,如:a=3;b=2.1;c=2+3i;2、数列:建立一个等差数组,例如:d=1:10; %1到10的等差数列e=linspace(0,2*pi,100); %0到2*pi之间的100个等间距点 a=[1 2 3;4 5 6;7 8 9];b=zeros(2,3);c=ones(3,2);d=rand(3,3);e=eye(4);4、矩阵元素操作:通过下标访问矩阵中的元素,例如:a(1,2) %输出a矩阵第一行第二列的元素b(2,3)=7 %将b矩阵第二行第三列的元素赋为75、矩阵运算:矩阵加减乘除,如:a+b %对应元素相加a-b %对应元素相减a*b %矩阵乘法a/b %矩阵除法a' %矩阵转置6、矩阵函数:除了使用基本操作外,还能使用各种矩阵相关函数完成矩阵计算,例如:inv(a) %矩阵求逆det(a) %矩阵求行列式trace(a) %矩阵求迹eig(a) %求特征值rank(a) %矩阵的秩size(a) %返回矩阵的大小max(a) %求矩阵元素最大值min(a) %求矩阵元素最小值sum(a) %求矩阵元素的和prod(a) %求矩阵所有元素的乘积mean(a) %求矩阵元素的平均值三、绘图1、二维绘图:绘制二维函数的曲线、散点图等,例如:x=linspace(-3,3,100); %生成-3到3之间的100个等间距点y=sin(x);plot(x,y); %绘制正弦函数曲线plot(x,y,'r--'); %绘制红色的正弦函数曲线,形状为虚线xlabel('x values');ylabel('y values');title('sine function');grid on;四、数据处理1、数据导入:在MATLAB中,可以通过各种方式将数据导入,如:a=load('filename.txt'); %从文件中载入数据b=xlsread('filename.xls'); %从Excel文件中载入数据五、编程1、条件语句:通过条件语句实现程序的分支结构,例如:if(a<0)disp('a is negative');elseif(a==0)disp('a is zero');elsedisp('a is positive');endfor i=1:10disp(i);end3、函数:在MATLAB中,可以自定义函数,函数调用格式为:function [out1,out2,...]=function_name(in1,in2,...)%函数说明%计算过程end4、脚本:在MATLAB中,脚本是一些命令或函数的集合,可以将脚本保存到文件中执行,例如:%脚本说明a=1;b=2;c=a+b;disp(c);以上便是MATLAB一些常用指令的详细介绍。
matlab基本命令

matlab基本命令
MATLAB是一种广泛使用的数学软件,用于数据分析、图形绘制和科
学计算。
下面是一些MATLAB基本命令,这些命令有助于您快速入门。
1.创建一个向量或矩阵:
a = [1 2 3 4]
b = [3;4;5;2]
2.创建一个特定范围的向量或矩阵:
c = 1:5
d = 2:2:8
e = linspace(0,1,11)
3.访问矩阵中的元素
a(2) //访问a中的第二个元素
b(3,2) // 访问b中的第三行第二列元素
4.矩阵操作
f = a + b
g = a - b
h = a * b
5.数学函数
x = sin(3.1416)
y = sqrt(25)
z = exp(2)
6.图形绘制
x = linspace(0,2*pi,100)
y = sin(x)
plot(x,y)
这些是MATLAB基本命令的一些示例。
学习这些命令是快速掌握MATLAB的关键。
做好练习,加深对这些命令的理解和运用,让您能够轻松地处理各种数据并进行数学计算和可视化。
MATLAB命令大全和矩阵操作大全

MATLAB命令大全和矩阵操作大全 -dengjianqiang2011的专栏 - 博客频道 -MATLAB矩阵操作大全一、矩阵的表示在MATLAB中创建矩阵有以下规则:a、矩阵元素必须在”[ ]”内;b、矩阵的同行元素之间用空格(或”,”)隔开;c、矩阵的行与行之间用”;”(或回车符)隔开;d、矩阵的元素可以是数值、变量、表达式或函数;e、矩阵的尺寸不必预先定义。
二,矩阵的创建:1、直接输入法最简单的建立矩阵的方法是从键盘直接输入矩阵的元素,输入的方法按照上面的规则。
建立向量的时候可以利用冒号表达式,冒号表达式可以产生一个行向量,一般格式是: e1:e2:e3,其中e1为初始值,e2为步长,e3为终止值。
还可以用linspace函数产生行向量,其调用格式为:linspace(a,b,n) ,其中a和b是生成向量的第一个和最后一个元素,n是元素总数。
2、利用MATLAB函数创建矩阵基本矩阵函数如下:(1) ones()函数:产生全为1的矩阵,ones(n):产生n*n维的全1矩阵,ones(m,n):产生m*n维的全1矩阵;(2) zeros()函数:产生全为0的矩阵;(3) rand()函数:产生在(0,1)区间均匀分布的随机阵;(4) eye()函数:产生单位阵;(5) randn()函数:产生均值为0,方差为1的标准正态分布随机矩阵。
3、利用文件建立矩阵当矩阵尺寸较大或为经常使用的数据矩阵,则可以将此矩阵保存为文件,在需要时直接将文件利用load命令调入工作环境中使用即可。
同时可以利用命令reshape 对调入的矩阵进行重排。
reshape(A,m,n),它在矩阵总元素保持不变的前提下,将矩阵A重新排成m*n的二维矩阵。
二、矩阵的简单操作1.获取矩阵元素可以通过下标(行列索引)引用矩阵的元素,如 Matrix(m,n)。
也可以采用矩阵元素的序号来引用矩阵元素。
矩阵元素的序号就是相应元素在内存中的排列顺序。
Matlab数组与绘图操作大全

sort(A)
对A中列向量进行升序排序
sort(A,’descend’) 对A中列向量进行降序排序 sort(A,2)
对A中行向量进行升序排序
sort(A,2,’descend’) 对A中行向量进行降序排序
当只有一个输出参数时,size函数返 sz=size(A) 回的是一个行向量,该行向量的第一 个元素是数组的行数,第二个元素是 数组的列数。 当有两输出参数时,size函数将数组 [r,c]=size(A) 的行数返回到第一个输出变量,将数 组的列数返回到第二个输出变量。
plot(x,y)
(2)若x 是一维数组, y 是二维数组 当 x 的长度与 y 的行数相等,则将 x 与 y 中的各列相对应,绘制多条平面曲线; 否则,若 x 的长度与 y 的列数相等,则将 x 与 y 中的各行相对应,绘制多条平面曲线。
例:利用plot函数的上述功能在同一坐标轴中 同时绘制下列函数的图形:
2、由一维数组创建二维数组
A = [1,3,5] B = [2,4,6] C = [3,5,7]
D = [A;B] E = [A;B;C] F = [A’,B’] G = [A’,B’,C’]
3、由函数创建二维数组
zeros(m,n)
ones(m,n) eye(m,n)
生成一个 m 行 n 列的零矩阵,m=n 时可简写为 zeros(n)
10、与二维数组相关的函数
cmax = max(A) rmax = max(A,[],2)
返回cmax为一个行数组,元素为A中每个列的最大值 返回rmax为一个列数组,元素为A中每个行的最大值
[cmax,index] = max(A)
[rmax,index] = max(A,[],2) max(A,B)
matlab一些基础代码含义

MATLAB(Matrix Laboratory)是一个由MathWorks公司开发的商业数学软件,主要用于算法开发、数据可视化、数据分析以及数值计算。
下面是一些MATLAB基础代码及其含义:
1.x = 1:10;:这将创建一个从1到10的整数数组。
2.y = [1 2 3; 4 5 6; 7 8 9];:这将创建一个3x3的矩阵。
3.z = [1 2 3; 4 5 6; 7 8 9]';:这将创建一个3x3的转置矩阵。
4.plot(x, y);:这将绘制一个线图,其中x是x轴,y是y轴。
5.xlabel('X-axis');:这将为x轴添加标签。
6.ylabel('Y-axis');:这将为y轴添加标签。
7.title('My Plot');:这将为图形添加标题。
8.grid on;:这将打开网格线。
9.x = rand(1,10);:这将创建一个包含10个随机数的数组。
10.y = sin(x);:这将计算每个x值的正弦值。
11.y = y .^ 2;:这将把数组y的每个元素平方。
12.z = max(y);:这将找到数组y中的最大值。
13.z = min(y);:这将找到数组y中的最小值。
14.z = sum(y);:这将计算数组y的总和。
15.z = length(y);:这将返回数组y的长度(即元素数量)。
这只是MATLAB的一些基础代码,实际上MATLAB的功能远不止这些,还包括更复杂的数值计算、信号处理、图像处理等。
最全 Matlab操作 函数指令

一、常用对象操作:除了一般windows窗口的常用功能键外。
1、!dir 可以查看当前工作目录的文件。
!dir& 可以在dos状态下查看。
2、who 可以查看当前工作空间变量名,whos 可以查看变量名细节。
3、功能键:功能键快捷键说明方向左键 Ctrl+B 光标向后移一个字符方向右键 Ctrl+F 光标向前移一个字符Ctrl+方向右键 Ctrl+R 光标向右移一个字符Ctrl+方向左键 Ctrl+L 光标向左移一个字符home Ctrl+A 光标移到行首End Ctrl+E 光标移到行尾Esc Ctrl+U 清除一行Del Ctrl+D 清除光标所在的字符Backspace Ctrl+H 删除光标前一个字符Ctrl+K 删除到行尾Ctrl+C 中断正在执行的命令4、clc可以命令窗口显示的内容,但并不清除工作空间。
二、函数及运算1、运算符:+:加,-:减, *:乘, /:除,\:左除 ^:幂,‘:复数的共轭转置,():制定运算顺序。
2、常用函数表:sin( ) 正弦(变量为弧度)Cot( ) 余切(变量为弧度)sind( ) 正弦(变量为度数)Cotd( ) 余切(变量为度数)asin( ) 反正弦(返回弧度)acot( ) 反余切(返回弧度)Asind( ) 反正弦(返回度数)acotd( ) 反余切(返回度数)cos( ) 余弦(变量为弧度)exp( ) 指数cosd( ) 余弦(变量为度数)log( ) 对数acos( ) 余正弦(返回弧度)log10( ) 以10为底对数acosd( ) 余正弦(返回度数)sqrt( ) 开方tan( ) 正切(变量为弧度)realsqrt( ) 返回非负根tand( ) 正切(变量为度数)abs( ) 取绝对值atan( ) 反正切(返回弧度)angle( ) 返回复数的相位角atand( ) 反正切(返回度数)mod(x,y) 返回x/y的余数sum( ) 向量元素求和3、其余函数可以用help elfun和help specfun命令获得。
matlab基础指令

matlab基础指令Matlab是一种数值计算工具,广泛应用于科学、工程、金融等领域。
Matlab基础指令是Matlab编程的基础,掌握这些基础指令可以帮助开发人员快速建立程序,快速完成各种数值计算,图形绘制等任务。
下面我们将介绍Matlab中的基础指令内容。
1.变量定义和输出Matlab中变量的定义和输出十分简单明了,可以使用“=”来定义变量,使用“disp()”来进行变量输出。
例如:>> a=3;>> b=4;>> disp(a+b);输出结果为:72.矩阵操作在Matlab中,矩阵操作是非常实用的工具,下面我们来介绍矩阵定义、矩阵转置、矩阵相加、矩阵相乘等操作。
矩阵定义:可以使用方括号“[]”来定义一个矩阵,使用逗号“,”分隔元素。
例如:>> A=[1,2,3;4,5,6;7,8,9];矩阵转置:可以使用单引号“’”来对矩阵进行转置操作。
例如:>> B=A’;矩阵相加:可以使用“+”符号来对两个矩阵进行相加操作。
例如:>> C=A+B;矩阵相乘:可以使用“*”符号来对两个矩阵进行相乘操作。
例如:>> D=A*B;3.流程控制语句Matlab中的流程控制语句包括if语句、for循环语句和while循环语句,下面我们来依次介绍这些语句的使用方法。
if语句:if语句用于判断某个条件是否成立,如果条件成立则执行一些操作。
例如:>> A=5;>> if A>2disp(‘A大于2’);endfor循环语句:for循环语句可以用来对一个数据序列进行遍历,并执行某些任务。
例如:>> for i=1:10disp(i);endwhile循环语句:while循环语句会一直执行直到满足某个条件才停止。
例如:>> i=1;>> while i<10disp(i);i=i+1;end4.函数定义与返回值Matlab中可以自己定义函数,函数的定义和调用非常简单。
matlab基本命令

matlab基本命令
1. clear:清除工作空间中的变量
2. clc:清除命令窗口中的所有输出
3. close:关闭图形窗口
4. format:设置命令窗口输出格式
5. save:保存变量到文件
6. load:从文件中加载变量
7. help:查看函数的帮助文档
8. who:列出工作空间中的变量
9. whos:列出工作空间中所有变量的详细信息
10. input:从命令窗口输入变量值
11. disp:显示字符串或变量值
12. fprintf:格式化输出文本
13. plot:绘制二维图形
14. subplot:在同一个图形窗口中绘制多个子图
15. figure:创建一个新的图形窗口
16. axis:设置坐标轴范围和刻度
17. xlabel、ylabel:设置坐标轴标签
18. title:设置图形标题
19. legend:添加图例
20. hold:设置图形是否保持当前状态,以便在之后添加新数据
21. grid:显示坐标轴网格线
22. loglog、semilogx、semilogy:设置坐标轴对数刻度
23. size:返回数组的大小
24. length:返回数组的长度
25. max:返回数组中的最大值
26. min:返回数组中的最小值
27. sum:返回数组中所有元素的和
28. mean:返回数组中所有元素的平均值
29. diff:返回数组元素之间的差分
30. sort:返回数组排序后的结果。
MATLAB操作命令大全

MATLAB操作命令大全1.基本操作:- clear: 清除工作区中的所有变量。
- clc: 清除命令窗口的内容。
- close all: 关闭所有图形窗口。
- help function-name: 显示与函数相关的帮助文档。
- who: 显示当前工作区中的所有变量。
- save file-name: 保存当前工作区中的所有变量到指定的文件。
- load file-name: 从文件中加载变量到当前工作区。
2.变量操作:-=:赋值操作符,将右边的值赋给左边的变量。
-+:加法操作符。
--:减法操作符。
-*:乘法操作符。
-/:除法操作符。
-^:幂运算操作符。
- sqrt(x): 计算 x 的平方根。
- abs(x): 计算 x 的绝对值。
- max(x): 返回 x 中的最大值。
- min(x): 返回 x 中的最小值。
- sum(x): 计算 x 中所有元素的和。
3.数组操作:- zeros(m, n): 创建一个 m 行 n 列的全零数组。
- ones(m, n): 创建一个 m 行 n 列的全一数组。
- eye(n): 创建一个 n 行 n 列的单位矩阵。
- size(x): 返回 x 的维度。
- length(x): 返回 x 的长度。
- reshape(x, m, n): 将 x 重新排列为一个 m 行 n 列矩阵。
- transpose(x): 将 x 的行和列互换。
4.控制流程:- if-else: 条件语句,根据条件执行不同的代码块。
- for loop: 循环语句,执行指定次数的代码块。
- while loop: 循环语句,根据条件反复执行代码块。
- break: 在循环中使用,用来跳出当前循环。
- continue: 在循环中使用,用来跳过当前循环的剩余部分。
5.统计分析:- mean(x): 计算 x 的平均值。
- median(x): 计算 x 的中位数。
- std(x): 计算 x 的标准差。
matlab画图常用命令

matlab画图常用命令clc 清理命令窗口历史内容clear 清除所有内存存储的变量值clf 清除图形whos 显示各变量信息sqrt 开方edit 开编辑窗口linspace(a,b,N) 定义等差数列,a初值,b末值,N步数(即数据个数)logspace(a,b,N) 定义等比数列,初值10^a,末值10^b,N步数(即数据个数)A.*B 矩阵点乘,对应项相乘A./B 矩阵点除A.^B 矩阵点方(指数相同也要用点方)A=[a:n:b] 定义以a为开始,步长为n的等差数列,最后一个数不超过b(n省略代表步长为1)A' 矩阵转置A=[B,C;D] 矩阵拼凑e *10^exp e^format long 后续数据显示小数点后15位format short 后续数据显示小数点后4位format bank 后续数据显示小数点后2位(不适用于复数)format long/short e 后续数据科学技术法显示,并且小数点后15位/4位format long/short eng 后续数据类似科学技术法显示,但指数保持为3的整数倍,并且有效位数(15位+1/4位+1)format + 矩阵中各元素只显示正负,零为空格format rat 以分数形式显示有理数format long/short g Matlab自定最优显示load/save +文件名载入/储存工作区数据rem(a,b) a/b的余数size(A) A矩阵的大小[行数列数]ylim([0,1])help 打开帮助界面help+帮助界面中对应标题查看对应函数的使用nthroot(x,n) x的n次实数根sign(x) x大于零输出1;x等于零输出0;x小于零输出-1log10(x) lg(x)log(x) ln(x)【注:logb(a)=ln(a)/ln(b)】fix(x) 取整round(x) 对x四舍五入floor(x) 对x向负取整ceil(x) 对x向正取整factor(x) 对x因式分解gcd(a,b) 求a,b最大公约数lcm(a,b) 求a,b最小公倍数rats(x) 用分数表示xfactorial(x) x!nchoosek(n,k) 组合数n选kprimes(x) 找出小于x的素数isprime(x) x是素数,返回1sin(),cos(),tan()... 自变量为弧度asin(),acos(),atan()... 结果为弧度max(x),min(x) x适量中的最大、最小值[a,b]=max(A) A为一行时,a为最大值,b为最大值单行位置A为m行n列时,a为m行向量,对应各列最大值,b为m行向量,对应各列最大值在该列位置多个最大值时,位置默认第一个max(A,B) A、B同大,结果为A,B中对应位置最大值的汇总矩阵mean()/median()/mode() 求平均值/中位数/众数(众数选最小值)cumsum/cumprod(A) 求A的累加/累乘结果,生成与A同大小矩阵,(列运算)单矩阵运算sum/prod(A) A矩阵列求和/求积或求行向量和/积sort(A)/sort(A,'descend') 将A升序/降序排列(行向量自身升序/降序,矩阵列升序/降序)sortrows(A,n) 按第n列排列各行,n正升序,n负降序,n省略第一列升序size(x)/[a,b]=size(x) 返回[行数,列数]/给a、b赋值length(A) 矩阵A的最大长度(行数和列数的最大值)std(A) 求A的标准差(行向量自身求解,矩阵列求解)var(A) 求A的方差(行向量自身求解,矩阵列求解)rand/randn(m,n) 生成(0,1)m×n随机数矩阵/生成均值为0,标准差为1的高斯随机数矩阵(正态分布)【通过randn(m,n)*std+mean可得到均值为mean,标准差为std的正态分布随机数矩阵】A+B*i(complex(A,B)) 生成复数或复数矩阵real(A)/imag(A) 求实部/虚部isreal(A) 实数返回1coni(A) 求共轭【或用A'也可,但会发生行列互换】x为复数时abs(x)/angle(x) 求复数的模,与水平方向的夹角realmax/realmin 返回MATLAB能够使用的最大/最小浮点数intmax/intmin 返回MATLAB能够使用的最大/最小整数pi/i/j 圆周率/虚数/虚数clock 当前时间(一般使用fix(clock)增加可读性)date 返回日期,以字符串形式eps 返回MATLAB最小间隔矩阵A(n,:)/(:,m)【A(n,end)/(end,m)】A矩阵的第n行【最后一列】/第m列【最后一行】[A,B]=meshgrid(a,b),A.*B a,b为行向量,运行结果得a*b的m*n 维矩阵【meshgrid(x)等价于meshgrid(x,x)】zeros(m)/(m,n) m*m/m*n全零矩阵ones(m)/(m,n) m*m/m*n全一矩阵diag(A) 取对角元素为列向量diag(x) 若x为行向量或列向量,结果为对角阵其他元素为零diag(A,n/-n) 对角线右上/左下第n斜线上的元素fliplr(A)/flipud(A) A矩阵列/行进行对称翻转magic(m) 创建m*m维魔方矩阵作图xlabel/ylabel('') 添加x/y轴坐标title('') 添加表头grid 使图像出现网格figure(x) 创建或打开figure x窗口,之后作图均在该窗口进行hold on 保持图像窗口中之前的图像,进而在此作图不会清除之前图像(hold off取消)plot(x1,y1,x2,y2) 同时做两个图像plot(x) x为行向量,则以点数1至n为横轴,x为纵轴作图,按顺序依次连线plot(A) A为m*n矩阵,则图像为那条曲线,每条曲线横轴均为1至m,纵轴为相应列对应值plot(x,A) 以x为横轴,A的每一列为纵轴作图(x与A同维)plot(A,B) A与B需同维,对应列分别作为横轴和纵轴作图plot('标识符') 线型:-实线:点-.点画线--虚线点型:.点o圆圈xx形状+加号*星号s方形d菱形v下三角^上三角<左三角>右三角p五角星h六角星颜色:b蓝色g绿色r红色c青色m洋红色y黄色k黑色w白色【注】,多重输出可多重设定axis([a,b,c,d]) 限制图像x轴在[a,b],y轴在[c,d]legend('string1','string2',etc) 按照作图顺序添加图注text(x,y,'string') 在(x,y)处添加文本‘string’gtext('string') 添加文本‘string’,位置由鼠标点击确定【注】(适用于string形式)输入希腊字母需要'\'+希腊字母读法;^ 可出现上标,_ 可出现下标若想输出_或^,可用\+相应符号subplot(m,n,k) 将图形窗口划分成m行n列,所有的绘图操作都在一行一行数的第k个子图中进行【注】clf针对消除一个figure窗口内的内容,而plot等一系列操作针对一个子图中,且hold on/off被限于特定一个子图中,不影响其他子图polar(x,y) 绘制极图semilogx/semilogy(x,y) x轴对数,y轴线性/x轴线性,y轴对数作图loglog(x,y) 双对数坐标作图bar(x)/barh(x) x为矢量时,按x绘制垂直/水平条形图x为矩阵时,按各行分组绘制垂直/水平条形图bar3(x)/bar3h(x) 同上,绘制三维条形图pie(x)/pie3(x) 绘制(三维)饼状图。
Matlab命令大全

cplxpa ir 复数共轭成对排列cs c 余割csch双曲余割cum sum 元素累计和cumt rapz累计梯形积分cy linde r 创建圆柱D d dblq uad 二重数值积分dea l 分配宗量de blank删去串尾部的空格符dec2base十进制转换为X进制dec2bin十进制转换为二进制dec2hex 十进制转换为十六进制deco nv 多项式除、解卷del aunay Dela unay三角剖分del2离散La placi an差分demo Matl ab演示det行列式diag矩阵对角元素提取、创建对角阵diar y Mat lab指令窗文本内容记录d iff 数值差分、符号微分digit s 符号计算中设置符号数值的精度di r 目录列表di sp 显示数组d ispla y 显示对象内容的重载函数dlinm od 离散系统的线性化模型dmper m 矩阵D ulmag e-Men delso hn 分解dos执行DO S 指令并返回结果doub le 把其他类型对象转换为双精度数值drawn ow 更新事件队列强迫Matl ab刷新屏幕ds olve符号计算解微分方程Eee cho M文件被执行指令的显示edi t 启动M文件编辑器eig求特征值和特征向量eig s 求指定的几个特征值en d 控制流FOR等结构体的结尾元素下标eps浮点相对精度er ror 显示出错信息并中断执行err ortra p 错误发生后程序是否继续执行的控制erf 误差函数erfc误差补函数erf cx 刻度误差补函数erf inv 逆误差函数erro rbar带误差限的曲线图etree plot画消去树eval串演算指令ev alin跨空间串演算指令exist检查变量或函数是否已定义exit退出Mat lab环境exp指数函数exp and 符号计算中的展开操作expi nt 指数积分函数expm常用矩阵指数函数expm1 Pad e法求矩阵指数e xpm2Taylo r法求矩阵指数e xpm3特征值分解法求矩阵指数ey e 单位阵ezc ontou r 画等位线的简捷指令ez conto urf 画填色等位线的简捷指令ezg raph3画表面图的通用简捷指令e zmesh画网线图的简捷指令ezm eshc画带等位线的网线图的简捷指令ezpl ot 画二维曲线的简捷指令ezplo t3 画三维曲线的简捷指令ezpol ar 画极坐标图的简捷指令ezsur f 画表面图的简捷指令ez surfc画带等位线的表面图的简捷指令F f fact or 符号计算的因式分解f eathe r 羽毛图fee dback反馈连接fev al 执行由串指定的函数f ft 离散Fouri er变换fft2二维离散Fouri er变换fftn高维离散Fouri er变换ffts hift直流分量对中的谱field names构架域名fig ure 创建图形窗fill3 三维多边形填色图fin d 寻找非零元素下标fin dobj寻找具有指定属性的对象图柄finds tr 寻找短串的起始字符下标find sym 机器确定内存中的符号变量fi nvers e 符号计算中求反函数fi x 向零取整fl ag 红白蓝黑交错色图阵f liplr矩阵的左右翻转flipu d 矩阵的上下翻转flip dim 矩阵沿指定维翻转f loor向负无穷取整fl ops 浮点运算次数flo w Mat lab提供的演示数据fmi n 求单变量非线性函数极小值点(旧版)fmin bnd 求单变量非线性函数极小值点f mins单纯形法求多变量函数极小值点(旧版)fminu nc 拟牛顿法求多变量函数极小值点f minse arch单纯形法求多变量函数极小值点fnde r 对样条函数求导fnin t 利用样条函数求积分fn val 计算样条函数区间内任意一点的值fnpl t 绘制样条函数图形fop en 打开外部文件for构成for环用f ormat设置输出格式f ourie r Fou rier变换f plot返函绘图指令fp rintf设置显示格式f read从文件读二进制数据fsol ve 求多元函数的零点fu ll 把稀疏矩阵转换为非稀疏阵fun m 计算一般矩阵函数fun tool函数计算器图形用户界面fz ero 求单变量非线性函数的零点G g gamm a 函数gamm ainc不完全函数ga mmaln函数的对数gc a 获得当前轴句柄gcbo获得正执行"回调"的对象句柄gcf获得当前图对象句柄gco获得当前对象句柄geom ean 几何平均值get获知对象属性ge tfiel d 获知构架数组的域get frame获取影片的帧画面ginp ut 从图形窗获取数据gl obal定义全局变量gp lot 依图论法则画图gr adien t 近似梯度gr ay 黑白灰度g rid 画分格线gridd ata 规则化数据和曲面拟合gtex t 由鼠标放置注释文字gu ide 启动图形用户界面交互设计工具H hha rmmea n 调和平均值h elp 在线帮助helpw in 交互式在线帮助hel pdesk打开超文本形式用户指南h ex2de c 十六进制转换为十进制h ex2nu m 十六进制转换为浮点数h idden透视和消隐开关hilbHilbe rt矩阵hist频数计算或频数直方图hi stc 端点定位频数直方图histf it 带正态拟合的频数直方图hold当前图上重画的切换开关h orner分解成嵌套形式hot 黑红黄白色图hsv饱和色图I iif-el se-el seif条件分支结构if ft 离散Fouri er反变换iff t2 二维离散Fou rier反变换i fftn高维离散F ourie r反变换ifft shift直流分量对中的谱的反操作ifour ier F ourie r反变换i, j缺省的"虚单元"变量il aplac e Lap lace反变换i mag 复数虚部image显示图象ima gesc显示亮度图象im finfo获取图形文件信息imre ad 从文件读取图象imw rite把im write把图象写成文件ind2s ub 单下标转变为多下标i nf 无穷大in fo Ma thWor ks公司网点地址inlin e 构造内联函数对象inm em 列出内存中的函数名i nput提示用户输入in putna me 输入宗量名int 符号积分int2s tr 把整数数组转换为串数组inte rp1 一维插值inter p2 二维插值i nterp3 三维插值in terpn N维插值int erpft利用FF T插值intro Matl ab自带的入门引导inv求矩阵逆invh ilb H ilber t矩阵的准确逆i permu te 广义反转置isa 检测是否给定类的对象isch ar 若是字符串则为真is equal若两数组相同则为真ise mpty若是空阵则为真i sfini te 若全部元素都有限则为真isfi eld 若是构架域则为真i sglob al 若是全局变量则为真i shand le 若是图形句柄则为真i shold若当前图形处于保留状态则为真isi eee 若计算机执行IEEE规则则为真isin f 若是无穷数据则为真is lette r 若是英文字母则为真is logic al 若是逻辑数组则为真i smemb er 检查是否属于指定集i snan若是非数则为真i snume ric 若是数值数组则为真isobj ect 若是对象则为真is prime若是质数则为真isrea l 若是实数则为真issp ace 若是空格则为真is spars e 若是稀疏矩阵则为真is struc t 若是构架则为真isst udent若是Ma tlab学生版则为真izt rans符号计算Z反变换J j , Kkj acobi an 符号计算中求Jacob ian 矩阵je t 蓝头红尾饱和色jord an 符号计算中获得 Jord an标准型key board键盘获得控制权kronKrone cker乘法规则产生的数组L lla place Lapl ace变换las terr显示最新出错信息lastw arn 显示最新警告信息l easts q 解非线性最小二乘问题(旧版)le gend图形图例ligh ting照明模式line创建线对象li nes 采用plot画线色linm od 获连续系统的线性化模型linm od2 获连续系统的线性化精良模型l inspa ce 线性等分向量ln 矩阵自然对数loa d 从MA T文件读取变量l og 自然对数l og10常用对数log2底为2的对数l oglog双对数刻度图形logm矩阵对数logs pace对数分度向量lo okfor按关键字搜索M文件low er 转换为小写字母lsq nonli n 解非线性最小二乘问题l u LU分解M m mad平均绝对值偏差m agic魔方阵maple &nb, sp;运作 Ma ple格式指令m at2st r 把数值数组转换成输入形态串数组m ateri al 材料反射模式max找向量中最大元素mbuil d 产生E XE文件编译环境的预设置指令mcc创建MEX或EXE文件的编译指令me an 求向量元素的平均值m edian求中位数men uedit启动设计用户菜单的交互式编辑工具m esh 网线图m eshz垂帘网线图mes hgrid产生"格点"矩阵meth ods 获知对指定类定义的所有方法函数mex产生MEX文件编译环境的预设置指令m funli s 能被m fun计算的MAPL E经典函数列表m help引出 Ma ple的在线帮助min 找向量中最小元素m kdir创建目录mkpp逐段多项式数据的明晰化m od 模运算mo re 指令窗中内容的分页显示movi e 放映影片动画movie in 影片帧画面的内存预置mtayl or 符号计算多变量Taylo r级数展开N nndims求数组维数Na N 非数(预定义)变量na rgchk输入宗量数验证nargi n 函数输入宗量数narg out 函数输出宗量数nd grid产生高维格点矩阵newpl ot 准备新的缺省图、轴n extpo w2 取最接近的较大2次幂nnz 矩阵的非零元素总数nonze ros 矩阵的非零元素no rm 矩阵或向量范数nor mcdf正态分布累计概率密度函数n ormes t 估计矩阵2范数norm inv 正态分布逆累计概率密度函数n ormpd f 正态分布概率密度函数n ormrn d 正态随机数发生器not ebook启动Ma tlab和Word的集成环境null零空间num2str 把非整数数组转换为串numd en 获取最小公分母和相应的分子表达式nzma x 指定存放非零元素所需内存Ooo de1 非Stiff微分方程变步长解算器od e15sStiff微分方程变步长解算器od e23t适度Sti ff 微分方程解算器ode23tbStiff微分方程解算器ode45非Sti ff 微分方程变步长解算器odefi le OD E 文件模板od eget获知ODE选项设置参数o depha s2 OD E 输出函数的二维相平面图odeph as3 O DE 输出函数的三维相空间图odep lot O DE 输出函数的时间轨迹图odepr int 在Matla b指令窗显示结果odese t 创建或改写 OD E选项构架参数值ones全1数组opti mset创建或改写优化泛函指令的选项参数值o rient设定图形的排放方式ort h 值空间正交化P ppa ck 收集Matla b内存碎块扩大内存page dlg 调出图形排版对话框patch创建块对象pa th 设置Matla b搜索路径的指令patht ool 搜索路径管理器pa use 暂停pc ode 创建预解译P码文件pcolo r 伪彩图pea ks Ma tlab提供的典型三维曲面permu te 广义转置p i (预定义变量)圆周率p ie 二维饼图p ie3 三维饼图pink粉红色图矩阵pi nv 伪逆plo t 平面线图pl ot3 三维线图plotm atrix矩阵的散点图p lotyy双纵坐标图po issin v 泊松分布逆累计概率分布函数poi ssrnd泊松分布随机数发生器po l2car t 极或柱坐标变为直角坐标polar极坐标图pol y 矩阵的特征多项式、根集对应的多项式poly2str以习惯方式显示多项式pol y2sym双精度多项式系数转变为向量符号多项式poly der 多项式导数poly fit 数据的多项式拟合p olyva l 计算多项式的值poly valm计算矩阵多项式p ow2 2的幂p pval计算分段多项式p retty以习惯方式显示符号表达式print打印图形或SIMU LINK模型pr intsy s 以习惯方式显示有理分式prism光谱色图矩阵p rocre ad 向M APLE输送计算程序pro file函数文件性能评估器prop edit图形对象属性编辑器pwd显示当前工作目录Q qqu ad 低阶法计算数值积分q uad8高阶法计算数值积分(QUADL) qu it 推出Matla b 环境quiv er 二维方向箭头图qui ver3三维方向箭头图R rran d 产生均匀分布随机数ra ndn 产生正态分布随机数randp erm 随机置换向量ran ge 样本极差r ank 矩阵的秩rats有理输出rcon d 矩阵倒条件数估计rea l 复数的实部r eallo g 在实数域内计算自然对数realp ow 在实数域内计算乘方r ealsq rt 在实数域内计算平方根realm ax 最大正浮点数real min 最小正浮点数rec tangl e 画"长方框" rem 求余数r epmat铺放模块数组r eshap e 改变数组维数、大小re sidue部分分式展开r eturn返回ribbo n 把二维曲线画成三维彩带图rmfi eld 删去构架的域roo ts 求多项式的根rose数扇形图rot90 矩阵旋转90度rot ate 指定的原点和方向旋转rota te3d启动三维图形视角的交互设置功能rou nd 向最近整数圆整rre f 简化矩阵为梯形形式rs f2csf实数块对角阵转为复数特征值对角阵r sumsRiema nn和S ssav e 把内存变量保存为文件s catte r 散点图sca tter3三维散点图se c 正割sech双曲正割sem ilogx X轴对数刻度坐标图sem ilogy Y轴对数刻度坐标图ser ies 串联连接set 设置图形对象属性s etfie ld 设置构架数组的域se tstr将ASCI I码转换为字符的旧版指令s ign 根据符号取值函数s ignum符号计算中的符号取值函数sim 运行SIMU LINK模型si mget获取SIM ULINK模型设置的仿真参数simp le 寻找最短形式的符号解simpl ify 符号计算中进行简化操作sim set 对SIMUL INK模型的仿真参数进行设置simu link启动SIM ULINK模块库浏览器si n 正弦sinh双曲正弦siz e 矩阵的大小s lice立体切片图sol ve 求代数方程的符号解s pallo c 为非零元素配置内存sp arse创建稀疏矩阵sp conve rt 把外部数据转换为稀疏矩阵spd iags稀疏对角阵spf un 求非零元素的函数值s ph2ca rt 球坐标变为直角坐标s phere产生球面spi nmap色图彩色的周期变化spli ne 样条插值s pones用1置换非零元素spra ndsym稀疏随机对称阵spran k 结构秩spr ing 紫黄调春色图spr intf把格式数据写成串spy 画稀疏结构图sqr t 平方根sqr tm 方根矩阵s queez e 删去大小为1的"孤维" sscan f 按指定格式读串stai rs 阶梯图st d 标准差ste m 二维杆图st ep 阶跃响应指令str2doubl e 串转换为双精度值str2mat创建多行串数组s tr2nu m 串转换为数s trcat接成长串str cmp 串比较s trjus t 串对齐str match搜索指定串st rncmp串中前若干字符比较str rep 串替换s trtok寻找第一间隔符前的内容s truct创建构架数组s truct2cell把构架转换为元胞数组st rvcat创建多行串数组sub2i nd 多下标转换为单下标s ubexp r 通过子表达式重写符号对象subp lot 创建子图subs符号计算中的符号变量置换s ubspa ce 两子空间夹角sum元素和summe r 绿黄调夏色图super iorto设定优先级su rf 三维着色表面图sur face创建面对象sur fc 带等位线的表面图su rfl 带光照的三维表面图surfn orm 空间表面的法线sv d 奇异值分解s vds 求指定的若干奇异值switc h-cas e-oth erwis e 多分支结构s ym2po ly 符号多项式转变为双精度多项式系数向量sy mmmd对称最小度排序s ymrcm反向Cu thill-McKe e排序syms创建多个符号对象T tta n 正切tanh双曲正切tay lorto ol 进行Taylo r逼近分析的交互界面tex t 文字注释tf创建传递函数对象tic启动计时器tit le 图名toc关闭计时器tr apz 梯形法数值积分tr eelay out 展开树、林tree plot画树图tril下三角阵trim求系统平衡点t rimes h 不规则格点网线图tri surf不规则格点表面图t riu 上三角阵t ry-ca tch 控制流中的T ry-ca tch结构 type显示M文件Uuui conte xtmen u 创建现场菜单uicon trol创建用户控件ui menu创建用户菜单un mkpp逐段多项式数据的反明晰化u nwrap自然态相角up per 转换为大写字母V v var方差v ararg in 变长度输入宗量var argou t 变长度输出宗量vect orize使串表达式或内联函数适于数组运算v er 版本信息的获取vie w 三维图形的视角控制vo ronoi Voro noi多边形vp a 任意精度(符号类)数值W wwa rning显示警告信息w hat 列出当前目录上的文件what snew显示Mat lab中Readm e文件的内容wh ich 确定函数、文件的位置whil e 控制流中的Whi le环结构whi te 全白色图矩阵whit ebg 指定轴的背景色wh o 列出内存中的变量名wh os 列出内存中变量的详细信息win ter 蓝绿调冬色图wor kspac e 启动内存浏览器Xx , Y y ,Z z xlab el X轴名xo r 或非逻辑ye sinpu t 智能输入指令ylabe l Y轴名zer os 全零数组z label Z轴名zoom图形的变焦放大和缩小zt rans符号计算Z变换。
在MATLAB中使用矩阵和数组

在MATLAB中使用矩阵和数组MATLAB(Matrix Laboratory)是一种流行的数值计算软件,广泛用于科学和工程领域。
它具有强大的功能,可以进行各种数学运算和数据分析。
在MATLAB 中,矩阵和数组是基本的数据结构,它们用于存储和处理数据。
一、矩阵和数组的定义和基本操作在MATLAB中,矩阵和数组都可以用来存储和操作多个数据。
矩阵是一个二维的数值数组,而数组可以有多个维度。
在定义矩阵或数组时,我们可以直接输入数据,也可以使用内置的函数来生成。
例如,我们可以用以下方式定义一个矩阵A:A = [1 2 3;4 5 6;7 8 9]这个矩阵A是一个3×3的矩阵,它的元素分别为1到9。
我们可以使用分号来表示矩阵的不同行,并用空格或制表符来分隔不同列。
同样地,在MATLAB中,我们可以使用以下方式定义一个数组B:B = [1, 2, 3, 4]这个数组B是一个包含4个元素的一维数组。
在定义数组时,元素之间通常使用逗号来进行分隔。
一旦定义了矩阵或数组,我们就可以对其进行各种操作。
在MATLAB中,我们可以使用运算符对矩阵和数组进行加、减、乘、除等数学运算。
例如,我们可以使用加法运算符来计算两个矩阵的和:C = A + A这里,C是一个3×3的矩阵,它的元素是矩阵A的对应元素和。
同样地,我们可以使用减法、乘法和除法运算符来进行相应的运算。
此外,MATLAB还提供了许多其他的函数和工具箱,用于矩阵和数组的操作。
例如,我们可以使用sum函数来计算矩阵的和:D = sum(A)这里,D是一个包含3个元素的一维数组,它的元素分别是矩阵A每一列的和。
二、矩阵和数组的索引和切片在MATLAB中,我们可以使用索引和切片操作来访问矩阵和数组中的元素。
索引用来指定元素在矩阵或数组中的位置,而切片则可以选择矩阵或数组的一个子集。
例如,我们可以使用索引获取矩阵A中的某个元素:a = A(2, 3)这里,a的值为6,它是矩阵A的第2行第3列的元素。
Matlab绘图代码以及代码说明文档
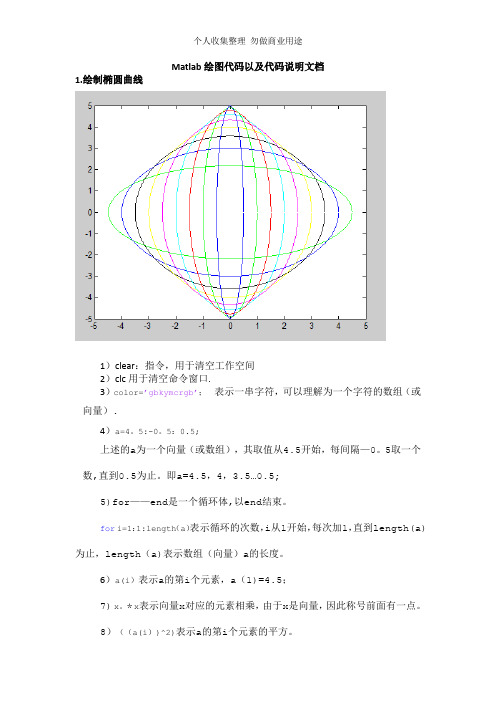
Matlab绘图代码以及代码说明文档1.绘制椭圆曲线1)clear:指令,用于清空工作空间2)clc用于清空命令窗口.3)color=’gbkymcrgb’;表示一串字符,可以理解为一个字符的数组(或向量).4)a=4。
5:-0。
5:0.5;上述的a为一个向量(或数组),其取值从4.5开始,每间隔—0。
5取一个数,直到0.5为止。
即a=4.5,4,3.5…0.5;5)for——end是一个循环体,以end结束。
for i=1:1:length(a)表示循环的次数,i从1开始,每次加1,直到length(a)为止,length(a)表示数组(向量)a的长度。
6)a(i)表示a的第i个元素,a(1)=4.5;7)x。
*x表示向量x对应的元素相乘,由于x是向量,因此称号前面有一点。
8)((a(i))^2)表示a的第i个元素的平方。
9)sqrt(a),是一个函数,对a进行开方.10)color(i)是字符数组color的第i个元素,数组前面有定义。
11)hold on是图像保持,就是绘制下一个椭圆时,上一个已经绘制的仍在图形界面上,不会消失。
2.多图形绘制1)sin(t)表示对t求它的正弦,是一个正弦函数.2)subplot(2,2,1),是一个函数,第一个参数2表示将绘图的窗口分割成两行显示;第二个参数2表示将绘图的界面分为两列显示,因此为两行两列4块显示。
第三个参数1表示在第1块(从左向右,从上向下)绘制图像。
3)plot(t1,y1,'.r’)其中,"。
”表示图像的形状为“点”,r为颜色。
4)axis([0,3。
1427,—1,1])表示固定坐标轴,只显示x轴的0到3.1427的区间;y轴的—1到1的区间.5)plot(t1,y1,'b'),由于b前面没有一点,因此是坐标点之间的连线。
6)title(’子图(3)’)表示该图的标题为“子图(3)”,是一个函数,参量为字符串。
MATLAB命令汇总

MATLAB命令汇总1.基本运算:-`+`:加法运算-`-`:减法运算-`*`:乘法运算-`/`:除法运算-`^`或`**`:幂运算- `sqrt(`: 平方根函数- `exp(`: 指数函数- `log(`: 对数函数2.矩阵和向量:- `zeros(`: 创建全零矩阵- `ones(`: 创建全一矩阵- `eye(`: 创建单位矩阵- `rand(`: 创建随机矩阵- `diag(`: 提取矩阵的对角线元素- `transpose(`或`'`: 转置矩阵- `det(`: 求矩阵的行列式- `inv(`: 求矩阵的逆矩阵- `trace(`: 求矩阵的迹3.数据处理和统计函数:- `mean(`: 求平均值- `median(`: 求中位数- `std(`: 求标准差- `var(`: 求方差- `sort(`: 排序- `histogram(`: 绘制直方图- `corrcoef(`: 计算相关系数矩阵- `cov(`: 计算协方差矩阵- `unique(`: 去掉重复元素4.数据可视化:- `plot(`: 绘制二维折线图- `scatter(`: 绘制散点图- `bar(`: 绘制柱状图- `hist(`: 绘制直方图- `pie(`: 绘制饼图- `imagesc(`: 绘制热图- `contour(`: 绘制等高线图- `surf(`: 绘制三维曲面图5.逻辑和条件语句:- `if`: 条件判断语句- `else`: 条件判断的可选分支- `elseif`: 多个条件判断的中间分支- `while`: 循环语句- `for`: 循环语句- `break`: 跳出循环- `continue`: 跳过本次循环6.文件和数据输入输出:- `load(`: 从文件加载数据- `save(`: 将数据保存到文件- `fopen(`: 打开文件- `fclose(`: 关闭文件- `fprintf(`: 格式化输出到文件- `fscanf(`: 从文件按格式读取数据7.函数和脚本文件:- `function`: 定义函数- `script`: 脚本文件- `input(`: 从命令行输入数据- `disp(`: 显示结果或变量值- `return`: 返回函数结果- `clear(`: 清除变量或内存- `clc(`: 清除命令窗口内容以上是一些常用的MATLAB命令和函数的汇总,这只是冰山一角,MATLAB还提供了许多其他功能和扩展性更强的函数和工具箱,可以根据不同的需求进行更详细的学习和使用。
(整理)matlab绘图指令大全.

绘图指令1 二维曲线图1.1 绘制折线图plot调整坐标范围:axis axis([0,300,0,2])1.2 绘制自定义函数1.3 绘制符号函数1.4 绘制自定义函数1.5 图形修饰设置颜色 y m c r g b w k 设置线型 - : -. --设置标记 . o x + *在指定坐标处,书写文字:1.6 更多类型的二维图e=0.2*rand(size(X));1.7 数值函数的二维图可绘制系统函数,也可绘制自定义函数的图形。
2 三维曲线图2.1 三维曲线plot32.2 三维面填色fill33 曲面图形3.1 网格点坐标的表示3.2 三维网格mesh、meshc、meshz消影开关:hidden on / hidden off利用peaks(50)作为模拟数据矩阵;3.3 着色表面图surf、surfc3.4 二元函数的伪彩色图pcolor3.5 等高线contour3.6 矢量场图quiverZ=X.*exp(-X.^2-Y.^2);3.7 视角控制view视点控制方式及效果:方位角、仰角控制方式及效果:缺省为(-37.5,30)。
3.8 多视区控制subplot3.9 制作、播放动画[x,y,z]=peaks(30); surf(x,y,z)% 制作动画m=moviein(5); % 5帧画面的动画变量for i=1:5view([1 1 i]) % 不断调整视点m(:,i)=getframe; % 将当前画面作为帧保存到序列中end% 播放动画movie(m,2,1); % 每隔1秒播放1帧,循环播放2次3.10 示例:地形图3.11 示例:汶川地形图load dem.txtmesh(dem)4 数据特征的图形展示以pdf结尾的函数,计算概率密度或概率;以cdf结尾的函数,计算累计分布函数。
如:示例:显示t分布与标准正态分布之间的关系。
示例:观察数据的分布特征。
MATLAB绘图的指令

绘图的指令1、plot函数MATLAB中最常用的绘图函数是plot( )。
其基本调用格式为:plot(x, y ),其中x, y均为向量,该函数表示以x向量作为X轴,以y向量作为Y轴。
示例3:绘制从0 ~ 4范围的正弦函数曲线。
t = 0 : pi/20 : 4*pi;y = sin(t);plot(t, y);2、stem函数对于离散序列,MATLAB用stem( )命令实现其绘制。
示例4:绘制从0 ~ 4范围的正弦函数序列。
t = 0 : pi/10 : 4*pi;y = sin(t);stem(t, y);3、subplot函数如果要在一个绘图窗口中显示多个图形,可用subplot函数实现。
其基本调用格式为:subplot(m, n, k) 或subplot(m n k),其中m, n, k取值为1 ~ 9。
该函数表示将绘图窗口划分为m×n个子窗口(子图),并在第k个子窗口中绘图。
示例5:在一个绘图窗口中绘制下列函数的图形。
t = 0 : 0.1 : 2;y1 = 2*exp(-3*t); % (a) 指数函数figure;subplot(221);plot(t,y1);xlabel('(a)');y2 = 2*t.*exp(-3*t); % (b) t乘指数函数subplot(222);plot(t,y2);xlabel('(b)');t1 = -4 : 0.1 : 4;y3 = 1/(2^0.5)*exp(-0.5*t1.^2); % (c) 正态分布函数subplot(223);plot(t1,y3);xlabel('(c)');t2 = -5 : 0.1 : 5;y4 = sinc(t2); % (d) 取样函数subplot(224);plot(t2,y4);xlabel('(d)');ylabel('sinc(t)');axis([-5 5 -0.25 1.1])grid on二维图形的修饰1、坐标轴名称标识函数xlabel、ylabel、title绘制 的nyquist 图和bode 图102.110)(2++=s s s G解MATLAB编程如下:»num=[10];»den=[1,1.2,10];»w=logspace(-2,2,1000); » nyquist(num,den,w)»grid»bode(num,den,w)»grid极小化»fx='10*exp(-x)*cos(x)';»fplot(fx,[2,5])»xmin=fmin(fx,2,5)xmin =2.35619746669214求零点»xzero=fzero(fx,5)xzero =4.71238898038469»xzero=fzero(fx,2)xzero =1.57079632679490曲线拟合»x=0:0.1:1;»y=[-.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];»p=polyfit(x,y,2);»xi=0:0.01:1;»yi=polyval(p,xi);»plot(x,y,xi,yi) 三维图形»x=-4:0.1:4;»y=x;»[x,y]=meshgrid(x,y);»z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...- 1/3*exp(-(x+1).^2 - y.^2);»mesh(x,y,z)二维图形»x=0:0.01:pi*3;»y=sin(x);»plot(x,y)»title('First Figure Example')»xlabel('Time(s)')»ylabel('Value(v)')»grid on»gtext(‘sinx’)»legend(‘sinx’)管理命令和函数help 在线帮助文件doc 装入超文本说明what M、MA T、MEX文件的目录列表 type 列出M文件lookfor 通过help条目搜索关键字which 定位函数和文件Demo 运行演示程序Path 控制MATLAB的搜索路径管理变量和工作空间Who 列出当前变量Whos 列出当前变量(长表) Load 从磁盘文件中恢复变量 Save 保存工作空间变量Clear 从内存中清除变量和函数Pack 整理工作空间内存Size 矩阵的尺寸Length 向量的长度disp 显示矩阵或与文件和*作系统有关的命令cd 改变当前工作目录Dir 目录列表Delete 删除文件Getenv 获取环境变量值! 执行DOS*作系统命令Unix 执行UNIX*作系统命令并返回结果Diary 保存MA TLAB任务控制命令窗口Cedit 设置命令行编辑 Clc 清命令窗口Home 光标置左上角Format 设置输出格式Echo 底稿文件内使用的回显命令more 在命令窗口中控制分页输出启动和退出MA TLABQuit 退出MATLABStartup 引用MA TLAB时所执行的M文件Matlabrc 主启动M文件*作符和特殊字符+ 加—减* 矩阵乘法.* 数组乘法^ 矩阵幂.^ 数组幂\ 左除或反斜杠/ 右除或斜杠./ 数组除Kron Kronecker张量积: 冒号( ) 圆括号[ ] 方括号. 小数点.. 父目录…继续, 逗号; 分号% 注释! 感叹号‘转置或引用= 赋值= = 相等< > 关系*作符& 逻辑与| 逻辑或~ 逻辑非xor 逻辑异或逻辑函数Exist 检查变量或函数是否存在Any 向量的任一元为真,则其值为真All 向量的所有元为真,则其值为真Find 找出非零元素的索引号三角函数Sin 正弦Sinh 双曲正弦Asin 反正弦Asinh 反双曲正弦Cos 余弦Cosh 双曲余弦Acos 反余弦Acosh 反双曲余弦Tan 正切Tanh 双曲正切Atan 反正切Atan2 四象限反正切Atanh 反双曲正切Sec 正割Sech 双曲正割Asech 反双曲正割Csc 余割Csch 双曲余割Acsc 反余割Acsch 反双曲余割Cot 余切Coth 双曲余切Acot 反余切Acoth 反双曲余切指数函数Exp 指数Log 自然对数Log10 常用对数Sqrt 平方根复数函数Abs 绝对值Argle 相角Conj 复共轭Image 复数虚部Real 复数实部特殊变量和常数Ans 当前的答案Eps 相对浮点精度Realmax 最大浮点数Realmin 最小浮点数Pi 圆周率I,j 虚数单位Inf 无穷大Nan 非数值Flops 浮点运算次数Nargin 函数输入变量数Nargout 函数输出变量数基本X—Y图形Plot 线性图形Loglog 对数坐标图形Semilogx半对数坐标图形(X轴为对数坐标) Semilogy 半对数坐标图形(Y轴为对数坐标) Fill 绘制二维多边形填充图特殊X—Y图形Polar 极坐标图Bar 条形图Stem 离散序列图或杆图Stairs 阶梯图Errorbar 误差条图Hist 直方图Rose 角度直方图Compass 区域图Feather 箭头图Fplot 绘图函数Comet 星点图图形注释Title 图形标题Xlabel X轴标记Ylabel Y轴标记Text 文本注释Gtext 用鼠标放置文本Grid 网格线MATLAB不但擅长於矩阵相关的数值运算,也适合用在各种科学目视表示(Scientific visualization)。
MATLAB简介,矩阵及其运算,绘图与数据可视化实验报告总结

MATLAB简介,矩阵及其运算,绘图与数据可视化实验
报告总结
一.实验目的
1.了解MATLAB的基本使用方法。
2.掌握MATLAB数据对象的特点和运算规则。
3.掌握MATLAB中建立矩阵的方法和矩阵的处理方法。
二.实验内容
浏览MATLAB的start菜单,了解所安装的模块和功能。
建立自己的工作目录,使用MATLAB将其设置为当前工作目录。
使用path命令和工作区浏览两种方法。
使用Help帮助功能,查询inv、plot、max、round等函数的用法和功能。
使用help命令和help菜单。
建立一组变量,如x=0:pi/10:2*pi,y=sin(x),在命令窗口显示这些变量;在变量窗口打开这些变量,观察其值并使用绘图菜单绘制y。
分多行输入一个MATLAB命令。
MATLAB中绘图命令介绍

MATLAB中绘图命令介绍本节将介绍MATLAB基本xy平面及xyz空间的各项绘图命令,包含一维曲线及二维曲面的绘制。
plot是绘制一维曲线的基本函数,但在使用此函数之前,我们需先定义曲线上每一点的x 及y座标。
下例可画出一条正弦曲线:close all;x=linspace(0, 2*pi, 100); % 100个点的x坐标y=sin(x); % 对应的y坐标plot(x,y);小整理:MATLAB基本绘图函数plot: x轴与y轴均为线性刻度(Linear scale)loglog: x轴与y轴均为对数刻度(Logarithmic scale)semilogx: x轴为对数刻度,y轴为线性刻度semilogy: x轴为线性刻度,y轴为对数刻度若要画出多条曲线,只需将座标对依次放入plot函数即可:hold on 保持当前图形,以便继续画图到当前坐标窗口hold off 释放当前图形窗口title(’图形名称’)(都放在单引号内)xlabel(’x轴说明’)ylabel(’y轴说明’)text(x,y,’图形说明’)legend(’图例1’,’图例2’,…)plot(x, sin(x), x, cos(x));若要改变颜色,在座标对後面加上相关字串即可:plot(x, sin(x), 'c', x, cos(x), 'g');若要同时改变颜色及图线型态,也是在座标对後面加上相关字串即可:plot(x, sin(x), 'co', x, cos(x), 'g*');小整理:plot绘图函数的叁数字元、颜色元、图线型态,y 黄色 .点k 黑色o 圆w 白色x xb 蓝色++g 绿色* *r 红色- 实线c 亮青色: 点线m锰紫色-. 点虚线-- 虚线plot3 三维曲线作图图形完成后,我们可用axis([xmin,xmax,ymin,ymax])函数来调整图轴的范围: axis([0, 6, -1.2, 1.2]);axis函数的功能丰富,其常用的用法有:axis equal :纵横坐标轴采用等长刻度axis square:产生正方形坐标系(默认为矩形)axis auto:使用默认设置axis off:取消坐标轴axis on :显示坐标轴此外,MATLAB也可对图形加上各种注解与处理:xlabel('Input Value'); % x轴注解ylabel('Function Value'); % y轴注解title('Two Trigonometric Functions'); % 图形标题legend('y = sin(x)','y = cos(x)'); % 图形注解grid on; % 显示格线我们可用subplot来同时画出数个小图形於同一个视窗之中:subplot(2,2,1); plot(x, sin(x));subplot(2,2,2); plot(x, cos(x));subplot(2,2,3); plot(x, sinh(x));subplot(2,2,4); plot(x, cosh(x));MATLAB还有其他各种二维绘图函数,以适合不同的应用,详见下表。
MATLAB操作命令大全

MATLAB操作命令大全1.基本操作- help:查看函数的帮助文档。
- save:将变量保存到文件中。
- load:从文件中加载变量。
- clear:清除当前工作空间中的变量。
- who:列出当前工作空间中的变量。
- whos:显示当前工作空间中变量的详细信息。
- quit:退出MATLAB。
2.变量操作-=:赋值操作,将值赋给变量。
- disp:显示变量的值。
- length:返回数组的长度。
- size:返回数组的大小。
- max:返回数组的最大值。
- min:返回数组的最小值。
- sum:返回数组元素的和。
3.数学操作-+:加法操作,将两个数值相加。
--:减法操作,将两个数值相减。
-*:乘法操作,将两个数值相乘。
-/:除法操作,将两个数值相除。
-^:指数操作,将一个数值提高到指定次幂。
- sqrt:返回一个数值的平方根。
- abs:返回一个数值的绝对值。
4.矩阵操作- eye:创建一个单位矩阵。
- zeros:创建一个全0矩阵。
- ones:创建一个全1矩阵。
- rand:创建一个0到1之间的随机矩阵。
- diag:返回对角线元素。
- inv:返回矩阵的逆矩阵。
- det:返回矩阵的行列式。
5.图形操作- plot:绘制二维线图。
- scatter:绘制散点图。
- bar:绘制柱状图。
- hist:绘制直方图。
- surf:绘制三维曲面图。
- contour:绘制等高线图。
- imagesc:绘制矩阵的颜色图。
6.控制流程操作- if:用于条件判断。
- for:用于循环操作。
- while:用于循环操作。
- switch:用于多条件判断。
- break:跳出循环。
- continue:跳过当前循环,并继续执行下一次循环。
7.文件操作- fopen:打开文件。
- fclose:关闭文件。
- fprintf:将数据写入文件。
- fscanf:从文件中读取数据。
- fseek:设置文件指针的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
eps
浮点数识别精度2^(-52)=2.2204* ,计算机会认为1+0.5*eps与1相等
flops
浮点运算数
NaN或nan
非数,如0/0,∞/∞,0×∞
常用数字显示格式指令
format short
通常保证小数点后4位
format long
小数点后15位
format short e
5位科学计数表示
rot90(A)
将A阵逆时针旋转90度
[x,D]=Eig(A)
A为n阶方阵,A*x=x*D,D的对角元素的特征值,x的列是特征向量
reshape
保持数组总元素个数不变的情况下,改变行数和列数
数组运算函数(都是点运算,matlab只对弧度操作)
Abs(x)
绝对值或复数的幅值
Angle(x)
四象限内取复数相角
Getfield
获取结构数组的数据
Getfield(array,{array_index},field,{field_index})
getfield(PS,{1},'name')
取第1个结构’name’域中的全部数据
getfield(PS,{1},'name',{2})
取第1个结构’name’域中的第2个数据
\uparrow
↑
\leq
≤
\otimes
\prime
,
\circ
。
\neq
≠
\int
∫
\cdot
.
\bullet
·
\pm±\parti来自l\ldots…
\copyright
ⓒ
上下标的控制指令
分类
指令
Arg取值
举例
示例指令
效果
上标
^{arg}
任何合法字符
‘\ite^{_t}sint’
sint
下标
_{arg}
format bank
两个十进制表示
format +
正.负或零分别用“+”.“—”和空格表示
format rat
有理数近似表示
常用标准数组生成函数
diag()
产生对角矩阵(对高维不适用)
eye()
产生单位矩阵(对高维不适用)
magic()
产生魔方数组(对高维不适用)
tril
取矩阵的下三角
Triu
去矩阵的上三角
使用subplot后,如果再想绘制独幅图,应先使用clf清图形窗
Plotyy(x1,y1,x2,y2)
以左右不同纵轴绘制x1-y1,x2-y2两条曲线
Sscanf
按照给定的格式将字符串转换成数字
Sprintf
按照给定的格式将数字转换成字符串
Int2str
整数转换成字符串
Str2num
字符串转换成数字
Num2str
数字转换成字符串
Str2mat
字符串转换成一个文本矩阵
Lower
字符串变为小写
Upper
字符串转换成大写
元胞数组
创建元胞数组
A(1,2):第1行第2列的元胞元素
纵坐标名
Text(x,y,’s’)
在坐标(x,y)处标注文字说明
Gtext(‘s’)
用鼠标在特定处标注文字说明
图形标识用的希腊字母
\alpha
α
\eta
η
\Nu
ν
\upsilon
υ
\Upsilon
Υ
\beta
β
\theta
θ
\xi
ξ
\phi
φ
\Theta
Θ
\Xi
Ξ
\Phi
Φ
\gamma
γ
\pi
π
\delta
由各元胞内容创建
C{1,1}=’Happy birthday!’
C{1,2}=randn(3)
deal
取多个元胞元素内容[X4,X5,X6]=deal(A{[1,2,4]})
结构数组
创建结构数组
直接使用赋值指令创建结构数组
PS(1).name='张三' PS(1).billing=150PS(1).test=[9,75,60;188,44,100]
Round(x)
四舍五入到最接近的整数
Sign(x)
符号函数
[ ]
空数组,对其他非空数组赋值,可使数组变小,但不改变维数
A(:,[2,4])=[ ]
删除A阵的第2,4列
字符串转换函数
Abs double
字符串到ASCII码的转换
Setstr
ASCII码转换成字符串
Fprintf
按照给定的格式把文本写到文件中或显示屏上
若y为向量,以y的分量为纵坐标,元素序号为横坐标用直线一次连接数据点
Plot(x,y)
若y和x为同维向量,以x为横坐标y为纵坐标绘图
若x是向量,y是列数或行数与x长度相等的矩阵,则绘制多条不同色彩的图,x为横坐标
若x和y为同型矩阵,以x,y对应元素为横坐标分别绘制曲线,曲线条数为矩阵列数
Plot(x1,y1,’s1’,x2,y2,’s2’…)
rand()
产生均匀分布的随机数组
randn()
产生正态分布的随机数组
Linspace(a,b,n)
将区间[a,b]做n-1等分,等分成n个数据,公差为
Logspace(a,b,n)
在区间[ , ]上创建一个n个数据的等比数列,公比
random()
生成各种分分布的数组
randsrc()
在指定字符集上生成,产生均匀分布的随机数组
图形标识用的其他特殊字符
\approx
\propto
∝
\exits
\downarrow
↓
\cong
\sim
~
\forall
\leftarrow
←
\div
\times
×
\in
\leftrightarrow
\equiv
≡
\oplus
\infty
∞
\rightarrow
→
\geq
≥
\oslash
\perp
任何合法字符
‘\x~{\chi}_{\alpha}^{2}(3)’
X~ (3)
字体样式设置规则
字体
指令
Arg取值
举例
示例指令
效果
名称
\fontname{arg}
Arial;courier;roman;宋体;隶书……
‘\fontname{courier}Example1’
‘\fontname{隶书}范例2’
Setfield
设置结构数组的数据
New_structure=setfield(array,{array_index},field,{field_index},V)
fieldnames
获取结构数组的所有域
Rmfield
删除域PS=rmfield(PS,'test')
绘图
Plot(y)
若y为实矩阵,则按列绘制每列对应的曲线,曲线数等于矩阵的列数
Axis square
产生正方形坐标系
Axis ij
矩阵式坐标,原点在左上方
Axis xy
普通直角坐标,原点在左下方
Axis([x1,x2,y1,y2])
人工设定坐标范围,x1和x2为横轴初值.终值,y1,y2为纵轴
Set:
设置坐标轴的刻度标识
Set(gca,’xtick’,xs,’ytick’,ys)
δ
\rho
ρ
\Gamma
Γ
\Pi
Π
\Delta
Δ
\psi
ψ
\epsilon
ε
\lambda
λ
\sigma
σ
\Psi
Ψ
\Lambda
Λ
\Sigma
Σ
\omega
ω
\zeta
ζ
\tau
τ
\Omega
Ω
使用示例
‘sin\beta
sinβ
‘\zeta\omega
ξω
‘itA{\in}R^{m\timesn}’
不同对之间没有影响,命令将对每一对x,y绘制曲线
线型控制符
-
细实线(默认)
:
虚点线
-.
点划线
--
虚划线
离散数据点标记字符
.
实心圆点
D
菱形符(diamond)
+
十字符
H
六角星符(hexagram)
*
八线符
O
空心圆圈
^
朝上三角符
P
五角星(pentagram)
<
朝左三角符
S
方块符
>
朝右三角符
x
叉字符
v
朝上三角符
Ceil(x)
对+∞方向取整数
Conj(x)
复数共轭
Fix(x)
对0方向取整数
Floor(x)
对-∞方向取整数
Gcd(x)
整数x和y的最大公约数(greatest common divisor)
Lcm(x)
整数x和y的最小公倍数(lease common multiple)
Rem(x)
X/y的余数(remainder)
A{1,2}:第1行第2列的元胞元素中的内容
直接用{}创建
A={’这是一个元胞数组的元胞’,[1,2;3,4];ones(3,4),{‘Mary’,’Tom’,’Susan’}}
