matlab练习题及答案详解(附程序)
matlab编程考试题及答案

matlab编程考试题及答案1. 题目:编写一个MATLAB函数,计算并返回一个向量中所有元素的和。
答案:```matlabfunction sumResult = vectorSum(vectorInput)sumResult = sum(vectorInput);end```2. 题目:创建一个MATLAB脚本,该脚本可以读取一个文本文件中的数据,并计算其平均值。
答案:```matlab% 假设文件名为data.txt,且数据以空格分隔filename = 'data.txt';data = load(filename);averageValue = mean(data);disp(['平均值为:', num2str(averageValue)]);```3. 题目:编写一个MATLAB函数,该函数接受一个矩阵作为输入,并返回其转置矩阵。
答案:```matlabfunction transposeMatrix = matrixTranspose(inputMatrix) transposeMatrix = inputMatrix';end```4. 题目:创建一个MATLAB脚本,该脚本可以生成一个3x3的魔方矩阵,并显示出来。
答案:```matlabn = 3;magicMatrix = magic(n);disp(magicMatrix);```5. 题目:编写一个MATLAB函数,该函数接受一个字符串作为输入,并返回字符串中每个字符出现的次数。
答案:```matlabfunction charCounts = countCharacters(inputString)charCounts = histcounts(inputString, 'BinMethod','integers');end```6. 题目:创建一个MATLAB脚本,该脚本可以计算并显示一个二次方程ax^2 + bx + c = 0的根。
MATLAB编程练习(含答案很好的)

001双峰曲线图:z=peaks(40);mesh(z);surf(z)002解方程:A=[3,4,-2;6,2,-3;45,5,4];>> B=[14;4;23];>> root=inv(A)*B003傅里叶变换load mtlb ;subplot(2,1,1);plot(mtlb);>> title('原始语音信息');>> y=fft(mtlb);>> subplot(2,1,2);>> yy=abs(y);>> plot(yy);>> title('傅里叶变换')004输入函数:a=input('How many apples\n','s')005输出函数a=[1 2 3 4 ;5 6 7 8;12 23 34 45;34 435 23 34]a =1 2 3 45 6 7 812 23 34 4534 435 23 34disp(a)a =1 2 3 45 6 7 812 23 34 4534 435 23 34b=input('how many people\n' ,'s')how many peopletwo peopleb =two people>> disp(b)two people>>006求一元二次方程的根a=1;b=2;c=3;d=sqrt(b^2-4*a*c);x1=(-b+d)/(2*a)x1 =-1.0000 + 1.4142i>> x2=(-b-d)/(2*a)x2 =-1.0000 - 1.4142i007求矩阵的相乘、转置、存盘、读入数据A=[1 3 5 ;2 4 6;-1 0 -2;-3 0 0];>> B=[-1 3;-2 2;2 1];>> C=A*BC =3 142 20-3 -53 -9>> C=C'C =3 2 -3 314 20 -5 -9>> save mydat C>> clear>> load mydat C008编写数学计算公式:A=2.1;B=-4.5;C=6;D=3.5;E=-5;K=atan(((2*pi*A)+E/(2*pi*B*C))/D) K =1.3121009A=[1 0 -1;2 4 1;-2 0 5];>> B=[0 -1 0;2 1 3;1 1 2];>> H=2*A+BH =2 -1 -26 9 5-3 1 12>> M=A^2-3*BM =3 3 -62 13 -2-15 -3 21>> Y=A*BY =-1 -2 -29 3 145 7 10>> R=B*AR =-2 -4 -1-2 4 14-1 4 10>> E=A.*BE =0 0 04 4 3-2 0 10>> W=A\BW =0.3333 -1.3333 0.66670.2500 1.0000 0.25000.3333 -0.3333 0.6667 >> P=A/BP =-2.0000 3.0000 -5.0000-5.0000 3.0000 -4.00007.0000 -9.0000 16.0000>> Z=A.\BWarning: Divide by zero.Z =0 -Inf 01.0000 0.2500 3.0000-0.5000 Inf 0.4000>> D=A./BWarning: Divide by zero.D =Inf 0 -Inf1.0000 4.0000 0.3333-2.0000 0 2.5000010a=4.96;b=8.11;>> M=exp(a+b)/log10(a+b)M =4.2507e+005011求三角形面积:a=9.6;b=13.7;c=19.4;>> s=(a+b+c)/2;>> area=sqrt(s*(s-a)*(s-b)*(s-c))area =61.1739012逻辑运算A=[-1 0 -6 8;-9 4 0 12.3;0 0 -5.1 -2;0 -23 0 -7]; >> B=A(:,1:2)B =-1 0-9 40 00 -23>> C=A(1:2,:)C =-1.0000 0 -6.0000 8.0000 -9.0000 4.0000 0 12.3000>> D=B'D =-1 -9 0 00 4 0 -23>> A*Bans =1.0000 -184.0000-27.0000 -266.90000 46.0000 207.0000 69.0000>> C<Dans =0 0 1 01 0 0 0>> C&Dans =1 0 0 00 1 0 1>> C|Dans =1 1 1 11 1 0 1>> ~C|~Dans =0 1 1 11 0 1 0013矩阵运算练习:A=[8 9 5;36 -7 11;21 -8 5]A =8 9 536 -7 1121 -8 5>> BB =-1 3 -22 0 3-3 1 9>> RT=A*BRT =-5 29 56-83 119 6-52 68 -21>> QW=A.*BQW =-8 27 -1072 0 33-63 -8 45>> ER=A^3ER =6272 3342 294415714 -856 52608142 -1906 2390 >> BF=A.^3BF =512 729 12546656 -343 13319261 -512 125 >> A/Bans =3.13414.9634 -0.4024-1.2561 12.5244 -3.2317-1.9878 6.4512 -2.0366>> EKV=B\AEKV =10.7195 -1.2683 3.52449.4756 1.5854 3.71954.8537 -1.4878 1.3171>> KDK=[A,B]KDK =8 9 5 -1 3 -236 -7 11 2 0 321 -8 5 -3 1 9 >> ERI=[A;B]ERI =8 9 536 -7 1121 -8 5-1 3 -22 0 3-3 1 9014一般函数的调用:A=[2 34 88 390 848 939];>> S=sum(A)S =2301>> min(A)ans =2>> EE=mean(A)EE =383.5000>> QQ=std(A)QQ =419.3794>> AO=sort(A)AO =2 34 88 390 848 939 >> yr=norm(A)yr =1.3273e+003>> RT=prod(A)RT =1.8583e+012>> gradient(A)ans =32.0000 43.0000 178.0000 380.0000 274.5000 91.0000 >> max(A)ans =939>> median(A)ans =239>> diff(A)ans =32 54 302 458 91>> length(A)ans =6>> sum(A)ans =2301>> cov(A)ans =1.7588e+005>>015矩阵变换:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> tril(A)ans =34 0 08 34 034 55 2>> triu(A)ans =34 44 230 34 230 0 2>> diag(A)ans =34342norm(A)ans =94.5106>> rank(A)ans =3>> det(A)ans =-23462>> trace(A)ans =70>> null(A)ans =Empty matrix: 3-by-0>> eig(A)ans =80.158712.7671-22.9257>> poly(A)ans =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> logm(A)Warning: Principal matrix logarithm is not defined for A with nonpositive real eigenvalues. A non-principal matrixlogarithm is returned.> In funm at 153In logm at 27ans =3.1909 + 0.1314i 1.2707 + 0.1437i 0.5011 - 0.2538i0.4648 + 0.4974i 3.3955 + 0.5438i 0.1504 - 0.9608i0.2935 - 1.2769i 0.8069 - 1.3960i 3.4768 + 2.4663i>> fumn(A)Undefined command/function 'fumn'.>> inv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> cond(A)ans =8.5072>> chol(A)Error using ==> cholMatrix must be positive definite.>> lu(A)ans =34.0000 44.0000 23.00000.2353 23.6471 17.58821.0000 0.4652 -29.1816>> pinv(A)ans =0.0510 -0.0502 -0.0098-0.0326 0.0304 0.02550.0305 0.0159 -0.0343>> svd(A)ans =94.510622.345611.1095>> expm(A)ans =1.0e+034 *2.1897 4.3968 1.93821.31542.6412 1.16431.8782 3.7712 1.6625>> sqrtm(A)ans =5.2379 + 0.2003i 3.4795 + 0.2190i 1.8946 - 0.3869i0.5241 + 0.7581i 5.1429 + 0.8288i 2.0575 - 1.4644i3.0084 - 1.9461i4.7123 - 2.1276i 2.1454 + 3.7589i >>016多项式的计算:A=[34 44 23;8 34 23;34 55 2]A =34 44 238 34 2334 55 2>> P=poly(A)P =1.0e+004 *0.0001 -0.0070 -0.1107 2.3462>> PPA=poly2str(P,'X')PPA =X^3 - 70 X^2 - 1107 X + 23462017多项式的运算:p=[2 6 8 3];w=[32 56 0 2];>> m=conv(p,w)m =64 304 592 548 180 16 6 >> [q,r]=deconv(w,p)q =16r =0 -40 -128 -46>> dp=polyder(w)dp =96 112 0>> [num,den]=polyder(w,p)num =80 512 724 312 -16den =4 24 68 108 100 48 9>> b=polyfit(p,w,4)Warning: Polynomial is not unique; degree >= number of data points. > In polyfit at 74b =-0.6704 9.2037 -32.2593 0 98.1333>> r=roots(p)r =-1.2119 + 1.0652i-1.2119 - 1.0652i-0.5761018求多项式的商和余p=conv([1 0 2],conv([1 4],[1 1]))p =1 5 6 10 8>> q=[1 0 1 1]q =1 0 1 1>> [w,m]=deconv(p,q)w =1 5m =0 0 5 4 3>> cq=w;cr=m;>> disp([cr,poly2str(m,'x')])5 x^2 + 4 x + 3>> disp([cq,poly2str(w,'x')])x + 5019将分式分解a=[1 5 6];b=[1];>> [r,p,k]=residue(b,a)r =-1.00001.0000p =-3.0000-2.0000k =[]020计算多项式:a=[1 2 3;4 5 6;7 8 9];>> p=[3 0 2 3];>> q=[2 3];>> x=2;>> r=roots(p)r =0.3911 + 1.0609i0.3911 - 1.0609i-0.7822>> p1=conv(p,q)p1 =6 9 4 12 9>> p2=poly(a)p2 =1.0000 -15.0000 -18.0000 -0.0000 >> p3=polyder(p)p3 =9 0 2>> p4=polyval(p,x)p4 =31021求除式和余项:[q,r]=deconv(conv([1 0 2],[1 4]),[1 1 1])022字符串的书写格式:s='student's =student>> name='mary';>> s1=[name s]s1 =marystudent>> s3=[name blanks(3);s]s3 =marystudent>>023交换两个数:clearclca=[1 2 3 4 5];b=[6 7 8 9 10];c=a;a=b;b=c;ab24If语句n=input('enter a number,n=');if n<10nend025 if 双分支结构a=input('enter a number ,a=');b=input('enter a number ,b=');if a>bmax=a;elsemax=b;endmax026三个数按照由大到小的顺序排列:A=15;B=24;C=45;if A<BT=A;A=B;B=T;elseif A<CT=A;A=C;C=T;elseif B<CT=B;B=C;C=T;endABC027建立一个收费优惠系统:price=input('please jinput the price : price=') switch fix(price/100)case[0,1]rate =0;case[2,3,4]rate =3/100;case num2cell(5:9)rate=5/100;case num2cell(10:24)rate=8/100;case num2cell(25:49)rate=10/100;otherwiserate=14/100;endprice=price*(1-rate)028:while循环语句i=0;s=0;while i<=1212s=s+i;i=i+1;ends029,用for循环体语句:sum=0;for i=1:1.5:100;sum=sum+i;endsum030循环的嵌套s=0;for i=1:1:6;for j=1:1:8;s=s+i^j;end;end;s031continue 语句的使用:for i=100:120;if rem(i,7)~=0;continue;end;iend032x=input ('输入X的值x=')if x<1y=x^2;elseif x>1&x<2y=x^2-1;elsey=x^2-2*x+1;endy033求阶乘的累加和sum=0;temp=1;for n=1:10;temp=temp*n;sum=sum+temp;endsum034对角线元素之和sum=0;a=[1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16]; for i=1:4;sum=sum+a(i,i);endsum035用拟合点绘图A=[12 15.3 16 18 25];B=[50 80 118 125 150.8];plot(A,B)036绘制正玄曲线:x=0:0.05:4*pi;y=sin(x);plot(x,y)037绘制向量x=[1 2 3 4 5 6;7 8 9 10 11 12;13 14 15 16 17 18] plot(x)x=[0 0.2 0.5 0.7 0.6 0.7 1.2 1.5 1.6 1.9 2.3]plot(x)x=0:0.2:2*piy=sin(x)plot(x,y,'m:p')038在正弦函数上加标注:t=0:0.05:2*pi;plot(t,sin(t))set(gca,'xtick',[0 1.4 3.14 56.28])xlabel('t(deg)')ylabel('magnitude(v)')title('this is a example ()\rightarrow 2\pi')text(3.14,sin(3.14),'\leftarrow this zero for\pi')039添加线条标注x=0:0.2:12;plot(x,sin(x),'-',x,1.5*cos(x),':');legend('First','Second',1)040使用hold on 函数x=0:0.2:12;plot(x,sin(x),'-');hold onplot(x,1.5*cos(x),':');041一界面多幅图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)')subplot(222);plot(x,y2);title('cos(x)')subplot(223);plot(x,y3);title('sin(2x)')subplot(224);plot(x,y4);title('cos(2x)')042染色效果图x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(221);plot(x,y1);title('sin(x)');fill(x,y1,'r') subplot(222);plot(x,y2);title('cos(x)');fill(x,y2,'b') subplot(223);plot(x,y3);title('sin(2x)');fill(x,y3,'k') subplot(224);plot(x,y4);title('cos(2x)');fill(x,y4,'g')043特殊坐标图clcy=[0,0.55,2.5,6.1,8.5,12.1,14.6,17,20,22,22.1] subplot(221);plot(y);title('线性坐标图');subplot(222);semilogx(y);title('x轴对数坐标图');subplot(223);semilogx(y);title('y轴对数坐标图');subplot(224);loglog(y);title('双对数坐标图')t=0:0.01:2*pi;r=2*cos(2*(t-pi/8));polar(t,r)044特殊函数绘图:fplot('cos(tan(pi*x))',[-0.4,1.4])fplot('sin(exp(pi*x))',[-0.4,1.4])045饼形图与条形图:x=[8 20 36 24 12];subplot(221);pie(x,[1 0 0 0 1]);title('饼图');subplot(222);bar(x,'group');title('垂直条形图');subplot(223);bar(x,'stack');title('累加值为纵坐标的垂直条形图'); subplot(224);barh(x,'group');title('水平条形图');046梯形图与正弦函数x=0:0.1:10;y=sin(x);subplot(121);stairs(x);subplot(122);stairs(x,y);047概率图x=randn(1,1000);y=-2:0.1:2;hist(x,y)048向量图:x=[-2+3j,3+4j,1-7j];subplot(121);compass(x);rea=[-2 3 1];imag=[3 4 -7];subplot(122);feather(rea,imag);049绘制三维曲线图:z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)x=-10:0.5:10;y=-8:0.5:8;[x,y]=meshgrid(x,y);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2); subplot(221);mesh(x,y,z);title('普通一维网格曲面');subplot(222);meshc(x,y,z);title('带等高线的三维网格曲面'); subplot(223);meshz(x,y,z);title('带底座的三维网格曲面'); subplot(224);surf(x,y,z);title('充填颜色的三维网格面')050 带网格二维图x=0:pi/10:2*pi;y1=sin(x);y2=cos(x);plot(x,y1,'r+-',x,y2,'k*:')grid onxlabel('Independent Variable x') ylabel('Dependent Variable y1&y2') text(1.5,0.5,'cos(x)')051各种统计图y=[18 5 28 17;24 12 36 14;15 6 30 9]; subplot(221);bar(y)x=[4,6,8];subplot(222);bar3(x,y)subplot(223);bar(x,y,'grouped') subplot(224);bar(x,y,'stack')052曲面图x=-2:0.4:2;y=-1:0.2:1;[x,y]=meshgrid(x,y);z=sqrt(4-x.^2/9-y.^2/4); surf(x,y,z)grid on053创建符号矩阵e=[1 3 5;2 4 6;7 9 11];m=sym(e)符号表达式的计算问题因式分解:syms xf=factor(x^3-1)s=sym('sin(a+b)'); expand(s)syms x tf=x*(x*(x-8)+6)*t; collect(f)syms xf=sin(x)^2+cos(x)^2; simplify(f)syms xs=(4*x^2+8*x+3)/(2*x+1); simplify(s)通分syms x yf=x/y-y/x;[m,n]=numden(f)嵌套重写syms xf=x^4+3*x^3-7*x^2+12; horner(f)054求极限syms x a;limit(exp(-x),x,0,'left')求导数syms xdiff(x^9+x^6)diff(x^9+x^6,4)055求不定积分与定积分syms x ys=(4-3*x^2)^2;int(s)int(x/(x+y),x)int(x^2/(x+2),x,1,3) double(ans)056函数的变换:syms x ty=exp(-x^2);Ft=fourier(y,x,t)fx=ifourier(Ft,t,x)057求解方程syms a b c xs=a*x^2+b*x+c;solve(s)syms x y zs1=2*x^2+y^2-3*z-4;s2=y+z-3;s3=x-2*y-3*z;[x,y,z]=solve(s1,s2,s3)058求微分方程:y=dsolve('Dy-(t^2+y^2)/t^2/2','t')059求级数和syms x ksymsum(k)symsum(k^2-3,0,10)symsum(x^k/k,k,1,inf)060泰勒展开式syms xs=(1-x+x^2)/(1+x+x^2);taylor(s)taylor(s,9)taylor(s,x,12)taylor(s,x,12,5)061练习syms x a;s1=sin(2*x)/sin(5*x);limit(s1,x,0)s2=(1+1/x)^(2*x);limit(s2,x,inf)syms xs=x*cos(x);diff(s)diff(s,2)diff(s,12)syms xs1=x^4/(1+x^2);int(s1)s2=3*x^2-x+1int(s2,0,2)syms x y zs1=5*x+6*y+7*z-16;s2=4*x-5*y+z-7;s3=x+y+2*z-2;[x,y,z]=solve(s1,s2,s3)syms x yy=dsolve('Dy=exp(2*x-y)','x')y=dsolve('Dy=exp(2*x-y)','y(0)=0','x')n=sym('n');s=symsum(1/n^2,n,1,inf)x=sym('x');f=sqrt(1-2*x+x^3)-(1-3*x+x^2)^(1/3);taylor(f,6)062求于矩阵相关的值a=[2 2 -1 1;4 3 -1 2;8 5 -3 4;3 3 -2 2]adet=det(a)atrace=trace(a)anorm=norm(a)acond=cond(a)arank=rank(a)eiga=eig(a)063矩阵计算A=[0.1389 0.6038 0.0153 0.9318;0.2028 0.2772 0.7468 0.4660;0.1987 0.1988 0.4451 0.4186]B=var(A)C=std(A)D=range(A)E=cov(A)F=corrcoef(A)064求根及求代数式的值P=[4 -3 2 5];x=roots(P)x=[3 3.6];F=polyval(P,x)065多项式的和差积商运算:f=[1 2 -4 3 -1]g=[1 0 1]g1=[0 0 1 0 1]f+g1f-g1conv(f,g)[q,r]=deconv(f,g)polyder(f)066各种插值运算:X=0:0.1:pi/2;Y=sin(X);interp1(X,Y,pi/4)interp1(X,Y,pi/4,'nearest')interp1(X,Y,pi/4,'spline')interp1(X,Y,pi/4,'cubic')067曲线的拟合:X=0:0.1:2*pi;Y=cos(X);[p,s]=polyfit(X,Y,4)plot(X,Y,'K*',X,polyval(p,X),'r-')068求函数的最值与0点x=2:0.1:2;[x,y]=fminbnd('x.^3-2*x+1',-1,1) [x,y]=fzero('x.^3-2*x+1',1)069求多项式的表达式、值、及图像y=[1 3 5 7 19]t=poly(y)x=-4:0.5:8yx=polyval(t,x)plot(x,yx)070数据的拟合与绘图x=0:0.1:2*pi;y=sin(x);p=polyfit(x,y,5);y1=polyval(p,x)plot(x,y,'b',x,y1,'r')071求代数式的极限:syms xf=sym('log(1+2*x)/sin(3*x)');b=limit(f,x,0)072求导数与微分syms xf=sym('x/(cos(x))^2');y1=diff(f)y2=int(f,0,1)078划分网格函数[x,y]=meshgrid(-2:0.01:2,-3:0.01:5); t=x.*exp(-x.^2-y.^2);[px,py]=gradient(t,0.05,0.1);td=sqrt(px.^2+py.^2);subplot(221)imagesc(t)subplot(222)imagesc(td)colormap('gray')079求多次多项方程组的解:syms x1 x2 a ;eq1=sym('x1^2+x2=a')eq2=sym('x1-a*x2=0')[x1 x2]=solve(eq1,eq2,x1,x2)v=solve(eq1,eq2)v.x1v.x2an1=x1(1),an2=x1(2)an3=x2(1),an4=x2(2)080求解微分方程:[y]=dsolve('Dy=-y^2+6*y','y(0)=1','x')s=dsolve('Dy=-y^2+6*y','y(0)=1','x')[u]=dsolve('Du=-u^2+6*u','u(0)=1')w=dsolve('Du=-u^2+6*u','z')[u,w]=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z') v=dsolve('Du=-w^2+6*w,Dw=sin(z)','u(0)=1,w(0)=0','z')081各种显现隐含函数绘图:f=sym('x^2+1')subplot(221)ezplot(f,[-2,2])subplot(222)ezplot('y^2-x^6-1',[-2,2],[0,10])x=sym('cos(t)')y=sym('sin(t)')subplot(223)ezplot(x,y)z=sym('t^2')subplot(224)ezplot3(x,y,z,[0,8*pi])082极坐标图:r=sym('4*sin(3*x)')ezpolar(r,[0,6*pi])083多函数在一个坐标系内:x=0:0.1:8;y1=sin(x);subplot(221)plot(x,y1)subplot(222)plot(x,y1,x,y2)w=[2 3;3 1;4 6]subplot(223)plot(w)q=[4 6:3 5:1 2]subplot(224)plot(w,q)084调整刻度图像:x=0:0.1:10;y1=sin(x);y2=exp(x);y3=exp(x).*sin(x);subplot(221)plot(x,y2)subplot(222)loglog(x,y2)subplot(223)plotyy(x,y1,x,y2)085等高线等图形,三维图:t=0:pi/50:10*pi;subplot(2,3,1)plot3(t.*sin(t),t.*cos(t),t.^2) grid on[x,y]=meshgrid([-2:0.1:2])z=x.*exp(-x.^2-y.^2)subplot(2,3,2)plot3(x,y,z)box offsubplot(2,3,3)meshz(x,y,z)subplot(2,3,4)surf(x,y,z)contour(x,y,z)subplot(2,3,6)surf(x,y,z)subplot(2,3,5)contour(x,y,z)box offsubplot(2,3,6)contour3(x,y,z)axis off086统计图Y=[5 2 1;8 7 3;9 8 6;5 5 5;4 3 2]subplot(221)bar(Y)box offsubplot(222)bar3(Y)subplot(223)barh(Y)subplot(224)bar3h(Y)087面积图Y=[5 1 2;8 3 7;9 6 8;5 5 5;4 2 3];subplot(221)area(Y)grid onset(gca,'Layer','top','XTick',1:5)sales=[51.6 82.4 90.8 59.1 47.0];x=90:94;profits=[19.3 34.2 61.4 50.5 29.4];subplot(222)area(x,sales,'facecolor',[0.5 0.9 0.6], 'edgecolor','b','linewidth',2) hold onarea(x,profits,'facecolor',[0.9 0.85 0.7], 'edgecolor','y','linewidth',2) hold offset(gca,'Xtick',[90:94])set(gca,'layer','top')gtext('\leftarrow 销售量') gtext('利润')gtext('费用')xlabel('年','fontsize',14)088函数的插值:x=0:2*pi;y=sin(x);xi=0:0.1:8;yi1=interp1(x,y,xi,'linear')yi2=interp1(x,y,xi,'nearest') yi3=interp1(x,y,xi,'spline')yi4=interp1(x,y,xi,'cublic')p=polyfit(x,y,3)yy=polyval(p,xi)subplot(3,2,1)plot(x,y,'o')subplot(3,2,2)plot(x,y,'o',xi,yy)subplot(3,2,3)plot(x,y,'o',xi,yi1)subplot(3,2,4)plot(x,y,'o',xi,yi2)subplot(3,2,5)plot(x,y,'o',xi,yi3)subplot(3,2,6)plot(x,y,'o',xi,yi4)089二维插值计算:[x,y]=meshgrid(-3:0.5:3);z=peaks(x,y);[xi,yi]=meshgrid(-3:0.1:3); zi=interp2(x,y,z,xi,yi,'spline') plot3(x,y,z)hold onmesh(xi,yi,zi+15)hold offaxis tight090函数表达式;function f=exlin(x)if x<0f=-1;elseif x<1f=x;elseif x<2f=2-x;elsef=0;end091:硬循环语句:n=5;for i=1:nfor j=1:nif i==ja(i,j)=2;elsea(i,j)=0;endendendwhile 循环语句:n=1;while prod(1:n)<99^99;n=n+1endn:092 switch开关语句a=input('a=?')switch acase 1disp('It is raning') case 0disp('It do not know')case -1disp('It is not ranging')otherwisedisp('It is raning ?')end093画曲面函数:x1=linspace(-3,3,30)y1=linspace(-3,13,34)[x,y]=meshgrid(x1,y1);z=x.^4+3*x.^2-2*x+6-2*y.*x.^2+y.^2-2*y; surf(x,y,z)。
Matlab编程与应用习题和一些参考答案

Matlab编程与应用习题和一些参考答案Matlab 上机实验一、二3.求下列联立方程的解⎪⎪⎩⎪⎪⎨⎧=+-+-=-+=++-=--+41025695842475412743w z y x w z x w z y x w z y x >> a=[3 4 -7 -12;5 -7 4 2;1 0 8 -5;-6 5 -2 10];>> b=[4;4;9;4];>> c=a\b4.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=81272956313841A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=793183262345B ,求C1=A*B’;C2=A’*B;C3=A.*B,并求上述所有方阵的逆阵。
>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];>> B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7];>> C1=A*B'>> C2=A'*B>> C3=A.*B>> inv(C1)>> inv(C2)>> inv(C3)5.设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y ,把x=0~2π间分为101点,画出以x 为横坐标,y 为纵坐标的曲线。
>> x=linspace(0,2*pi,101);>> y=cos(x)*(0.5+(1+x.^2)\3*sin(x));>> plot(x,y,'r')6.产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
(mean var )a=randn(8,6)mean(a)var(a)k=mean(a)k1=mean(k)i=ones(8,6)i1=i*k1i2=a-i1i3=i2.*i2g=mean(i3)g2=mean(g)10.利用帮助查找limit 函数的用法,并自己编写,验证几个函数极限的例子。
(完整版)matlab基础练习题(带答案)

Matlab 基础练习题常量、变量、表达式1、 MATLAB 中,下面哪些变量名是合法的?( )(A )_num (B )num_ (C )num- (D )-num 2、 在MA TLAB 中,要给出一个复数z 的模,应该使用( )函数。
(A )mod(z) (B )abs(z) (C )double(z) (D )angle(z) 3、 下面属于MATLAB 的预定义特殊变量的是?( )(A )eps (B )none (C )zero (D )exp4、 判断:在MA TLAB 的内存工作区中,存放一个英文字符 'a' 需要占用1个字节,存放一个中文字符‘啊’需要占用2个字节。
( 错,都是2个字节 )5、 判断:MA TLAB 中,i 和j ( 对 )6、 判断:MA TLAB 中,pi 代表圆周率,它等于3.14。
( 错,后面还有很多位小数 )7、 在MA TLAB 中,若想计算的51)3.0sin(21+=πy 值,那么应该在MA TLAB 的指令窗中输入的MA TLAB 指令是__y1=2*sin(0.3*pi)/(1+sqrt(5))_。
8、 在MA TLAB 中,a = 1,b = i ,则a 占_8__个字节,b 占_16_个字节,c 占________字节。
9、 在MA TLAB 中,inf 的含义是__无穷大__,nan 的含义是__非数(结果不定)___。
数组1、 在MA TLAB 中,X 是一个一维数值数组,现在要把数组X 中的所有元素按原来次序的逆序排列输出,应该使用下面的( )指令。
(A )X[end:1] (B )X[end:-1:1] (C )X (end:-1:1) (D )X(end:1) 2、 在MA TLAB 中,A 是一个字二维数组,要获取A 的行数和列数,应该使用的MATLAB的命令是( )。
(A )class(A) (B )sizeof(A) (C )size(A) (D )isa(A)3、 在MATLAB 中,用指令x=1:9生成数组x 。
matlab程序设计例题及答案

matlab程序设计例题及答案1.编写程序:计算1/3+2/5+3/7+……+10/21法一: s=0;for i=1:10s=s+i/(2*i+1); end ss =法二:sum((1:10)./(3:2:21)) ans =2.编写程序:计算1~100中即能被3整除,又能被7整除的所有数之和。
s=0;for i=1:100if mod(i,3)==0&&mod(i,7)==0 s=s+i; end,end ss =2103.画出y=n!的图,阶乘的函数自己编写,禁用MATLAB 自带的阶乘函数。
x=1:10; for i=1:10try y(i)=y(i-1)*i; catch y(i)=1; end,end plot(x,y)106123456789104.一个数恰好等于它的因子之和,这个数就称为完数。
例如,6的因子为1,2,3,而6=1+2+3,因此6就是一个完数。
编程找出20XX以内的所有完数。
g=;for n=2:20XX s=0;for r=1:n-1if mod(n,r)==0 s=s+r; end endif s==ng=[g n]; end end gg =6 28 4965.编写一个函数,模拟numel函数的功能,函数中调用size函数。
function y=numelnumel(x) m=size(x); y=m(1)*m(2);numelnumel([1 2 3;4 5 6])ans =66. 编写一个函数,模拟length函数的功能,函数中调用size函数。
function y=lengthlength(x) m=size(x);y=max(m(1),m(2));lengthlength([1 2 3;4 5 6])ans =37.求矩阵rand的所有元素和及各行平均值,各列平均值。
s=rand(5);sum=sum(sum(s)) mean2=mean(s,2) mean1=mean(s)sum =mean2 =mean1 =8.编程判断1001,1003,1007,1009,1011为素数,若不是,输出其约数。
matlab练习题及答案

一、填空题1.设有程序A=[2,0,1,0;1,0,1,5;0, 6 ,2, 3];B=[1,2,-1;1,3,1];C=A(1:3,[1,2]);D=size(C)- length(B(2,:));F= C.*B ’将下列命令的运行结果填在横线上D = ; F= .2. A=[2,3,2,1;1,2,2,1; 1,2,3,-2];A1=sum(A>A(2,1));A(2,:)=[],A2=A.^2-4A1= ; A2= ;3.P=[1,2,5,4;2,2,1,3];max(P,[ ],1)= ;mean(P,2)= .二、试编写计算程序画出曲线与曲面图形.22,22,)1((2).);20(cos sin (1).223322≤≤-≤≤-++=≤≤⎪⎩⎪⎨⎧==--y x y x e x z t t y t x y x π%1 %2t=0:0.1: 2*pi; [x,y]=meshgrid(-2:0.1:2);x= sin(t).^3; z=(x.^2+1).* exp(-x.^2- y.^2+)+x .^2.*y; y= cos (t).^3; mesh(x,y,z)plot(x,y)三、(本题满分*分)编写程序解决下列问题:(1)试产生100⨯4阶矩阵使其元素在0—100之间的随机整数,可将此矩阵理解为100名同学的四门课程(课程1, 课程2, 课程3, 课程4)的成绩.(2)计算出每门课程和每位同学的平均成绩;(3)统计出总的优秀人次(90分及以上为优秀);(4)统计出四门课程成绩至少有两门课程不及格的人数.解:(1) a=fix((100-0+1)*rand(100,4));(2) mean(a) mean(a,2)(3)sum(sum(a>=90,2)==4)(4)sum(sum(a<60,2)>=2)四、(本题满分*分)).50,20(]2,0[)2()),(1:(;)1(,sin )1()(11==-=∑=+n n x fun y function kx k x f nk k 分别取内图形用子图画出该函数在程序的第一句为返回该函数并保存试编写函数式文件程序设π(1). function y=fun1(x,n) (2). x=0:0.1:2*pi;y=0; y1= fun1 (x,20);for k=1:n y2= fun1 (x,50);y=y+ ((-1)^(k+1)*sin(k*x))/k; subplot(2,1,1),plot(x,y1)end subplot(2,1,2),plot(x,y2)y五、(本题满分*分)试利用微分方程的数值解法写出下列微分方程的求解步骤和MATLAB 程序.0)0(,2)0(,3='==-'+''x x t x x t x .(t 的变化区间为[0,10]).第一步:先将高阶微分方程转化为一阶微分方程组:选择状态变量x x x x ='=21,,则原方程化为2)0(,0)0(.,32112211==⎩⎨⎧='++-='x x x x t x tx x第二步:建立函数文件function dxdt = fun2(t,x)dxdt = [-3*t*x(1)+ x(2)+t; x(1)];第三步:求解微分方程,命令如下:[t,x]=ode45(@fun2,[0,10],[0;2])⎪⎩⎪⎨⎧=-++=--++03320224:.2122212212221x x x x x x x x x fsolve 组求解下面的非线性方程函数以及符号运算功能用七解一:function y=fc(x)y(1)=4*x(1).^2+x(2).^2+2*x(1).*x(2)-x(2)-2y(2)=2*x(1).^2+x(2).^2+3*x(1).*x(2)-3y=[y(1) y(2)];x0=[1 1];fsolve(@fc,x0)八.已知1000,2141211=++++=n ny ,分别用for 循环和直接用sum 计算y 的值,写出程序.(1)y=1;for i=1:1000;y=y+1/(2*i);endy(2)i=1:1000;y=1+sum(1./(2*i))。
matlab考试题目及答案

matlab考试题目及答案1. 题目:编写一个MATLAB函数,实现计算并返回一个向量中所有元素的平方和。
答案:以下是一个简单的MATLAB函数,用于计算并返回一个向量中所有元素的平方和。
```matlabfunction sumOfSquares = calculateSumOfSquares(vector)sumOfSquares = sum(vector.^2);end```2. 题目:给定一个3x3的矩阵A,使用MATLAB编写代码,求出矩阵A 的转置。
答案:可以通过简单的转置操作来求得矩阵A的转置。
```matlabA = [1 2 3; 4 5 6; 7 8 9];A_transpose = A';```3. 题目:编写一个MATLAB脚本,实现对一个二维数组进行排序,并返回排序后的数组。
答案:以下是一个MATLAB脚本,用于对一个二维数组进行排序,并返回排序后的数组。
```matlabfunction sortedArray = sort2DArray(array)sortedArray = sort(array(:));end```4. 题目:给定一个向量x,使用MATLAB编写代码,计算并返回向量x的元素个数。
答案:可以通过内置函数`numel`来计算向量x的元素个数。
```matlabx = [1, 2, 3, 4, 5];numElements = numel(x);```5. 题目:编写一个MATLAB函数,实现计算并返回两个向量元素的点积。
答案:以下是一个简单的MATLAB函数,用于计算两个向量的点积。
```matlabfunction dotProduct = calculateDotProduct(vector1, vector2)dotProduct = dot(vector1, vector2);end```6. 题目:给定一个矩阵B,使用MATLAB编写代码,求出矩阵B的行列式。
matlab编程考试题及答案

matlab编程考试题及答案1. 编写一个MATLAB函数,该函数接受一个向量作为输入,并返回该向量中所有元素的平方和。
```matlabfunction sumOfSquares = vectorSquareSum(inputVector)sumOfSquares = sum(inputVector .^ 2);end```答案:该函数通过使用点乘运算符(`.^`)来计算向量中每个元素的平方,然后使用`sum`函数计算这些平方值的总和。
2. 给定一个3x3的矩阵A,编写MATLAB代码计算其行列式。
```matlabA = [1 2 3; 4 5 6; 7 8 9];determinantA = det(A);```答案:使用MATLAB内置函数`det`可以直接计算矩阵A的行列式。
3. 编写一个MATLAB脚本,实现对一个给定字符串进行反转。
```matlaboriginalString = 'HelloWorld';reversedString = fliplr(originalString);```答案:使用`fliplr`函数可以将字符串中的字符从左到右翻转,实现字符串的反转。
4. 给定两个向量x和y,编写MATLAB代码计算它们之间的欧几里得距离。
```matlabx = [1 2 3];y = [4 5 6];euclideanDistance = sqrt(sum((x - y) .^ 2));```答案:欧几里得距离可以通过计算两个向量对应元素差的平方和的平方根来得到。
5. 编写一个MATLAB函数,该函数接受两个参数,一个是矩阵,另一个是标量值,返回矩阵中所有元素与该标量值的差的绝对值。
```matlabfunction absDiffMatrix = matrixScalarDifference(matrix, scalar)absDiffMatrix = abs(matrix - scalar);end```答案:该函数通过从矩阵的每个元素中减去标量值,然后使用`abs`函数计算结果的绝对值。
matlab课后习题及答案详解

matlab课后习题及答案详解第1章练习题1.安装matlab时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?在安装matlab时,安装内容由选择组件窗口中个复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即matlab选项)必须安装。
第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可。
2.matlab操作方式桌面存有几个窗口?如何并使某个窗口瓦解桌面沦为单一制窗口?又如何将瓦解过来的窗口再次置放至桌面上?与其他计算机语言相比较,matlab语言注重的特点就是什么?matlab系统由那些部分共同组成?在matlab操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是关闭窗口的close按钮,一个是可以使窗口成为独立窗口的undock按钮,点击undock按钮就可以使该窗口脱离桌面成为独立窗口,在独立窗口的view菜单中选择dock……菜单项就可以将独立的窗口重新防止的桌面上。
matlab具备功能强大、使用方便、输出简便、库函数多样、开放性弱等特点。
matlab系统主要由开发环境、matlab数学函数库、matlab语言、图形功能和应用程序接口五个部分组成。
3.如何设置当前目录和搜寻路径,在当前目录上的文件和在搜寻路径上的文件存有什么区别?命令历史窗口除了可以观测前面键入的命令外,除了什么用途?当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的setpath菜单项来完成。
在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被matlab运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上。
命令历史窗口除了用作查阅以前键入的命令外,还可以轻易执行命令历史窗口中选取的内容、将选取的内容拷贝到剪贴板中、将选取内容轻易拷贝到m文件中。
matlab简单编程21个题目及答案
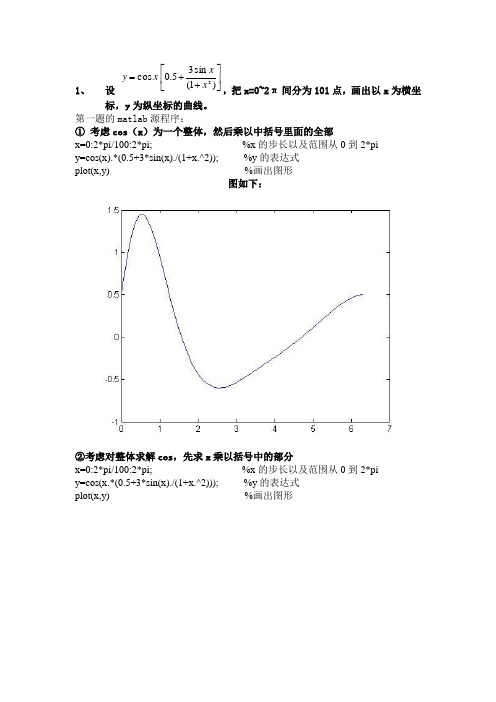
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
matlab试题及答案开卷

matlab试题及答案开卷1. MATLAB基础操作在MATLAB中,如何创建一个名为“myMatrix”的3x3矩阵,其元素从1到9按顺序排列?答案:在MATLAB中,可以使用以下命令创建名为“myMatrix”的3x3矩阵:```matlabmyMatrix = [1 2 3; 4 5 6; 7 8 9];```或者使用内置函数`magic`:```matlabmyMatrix = magic(3);```2. 矩阵运算给定两个矩阵A和B,其中A = [2 3; 4 5],B = [6 7; 8 9],计算A+B的结果。
答案:在MATLAB中,可以使用加号`+`来计算两个矩阵的和:```matlabA = [2 3; 4 5];B = [6 7; 8 9];C = A + B;```计算结果C为:```matlabC = [8 10; 12 14];```3. 向量操作创建一个从0到1的等差数列,步长为0.1。
答案:在MATLAB中,可以使用`linspace`函数或`:`操作符来创建等差数列:```matlabv = 0:0.1:1;```或者使用`linspace`函数:```matlabv = linspace(0, 1, 11);```两种方法都将得到一个包含11个元素的向量,从0开始,到1结束,步长为0.1。
4. 条件语句编写一个MATLAB脚本,判断一个给定的数n是否为素数。
答案:可以通过以下MATLAB脚本来判断一个数n是否为素数:```matlabfunction isPrime = isPrimeNumber(n)if n <= 1isPrime = false;elsefor i = 2:sqrt(n)if mod(n, i) == 0isPrime = false;return;endendisPrime = true;endend```调用此函数时,传入一个数值n,函数将返回一个布尔值,表示n 是否为素数。
matlab考试题库及答案

matlab考试题库及答案1. MATLAB基础题在MATLAB中,如何创建一个名为`myVector`的向量,包含元素1, 2, 3, 4, 5?答案:可以使用以下命令创建向量:```matlabmyVector = [1 2 3 4 5];```或者使用冒号操作符:```matlabmyVector = 1:5;```2. MATLAB数组操作题给定一个3x3的矩阵A,如何计算其转置矩阵?答案:可以使用`transpose`函数或者简单的点转置操作符'来计算矩阵A的转置:```matlabA = [1 2 3; 4 5 6; 7 8 9];A_transpose = transpose(A);```或者```matlabA_transpose = A';```3. MATLAB函数编写题编写一个MATLAB函数,计算并返回两个输入参数的和。
答案:可以创建一个名为`addTwoNumbers`的函数,代码如下:```matlabfunction sum = addTwoNumbers(a, b)sum = a + b;end```调用该函数时,只需传入两个数值参数即可得到它们的和。
4. MATLAB绘图题如何使用MATLAB绘制函数`y = x^2`在区间[0, 10]上的图像?答案:可以使用`plot`函数和`linspace`函数来绘制图像:```matlabx = linspace(0, 10, 100); % 生成100个点的向量y = x.^2; % 计算y值plot(x, y); % 绘制图像xlabel('x'); % x轴标签ylabel('y'); % y轴标签title('y = x^2'); % 图像标题```5. MATLAB循环控制题如何使用for循环计算并打印1到100之间所有偶数的和?答案:可以使用以下代码计算并打印结果:```matlabsumEven = 0;for i = 1:100if mod(i, 2) == 0sumEven = sumEven + i;endenddisp(['Sum of even numbers between 1 and 100 is: ',num2str(sumEven)]);```6. MATLAB条件语句题给定一个变量`x`,如何使用if语句判断其值是否大于10,并打印相应的信息?答案:可以使用以下代码进行判断和打印:```matlabx = 15;if x > 10disp('x is greater than 10');elsedisp('x is not greater than 10');end```7. MATLAB文件操作题如何在MATLAB中读取一个名为`data.txt`的文本文件,并显示其内容?答案:可以使用`fopen`和`fread`函数来读取文件内容,并使用`fclose`函数关闭文件:```matlabfileID = fopen('data.txt', 'r'); % 打开文件data = fread(fileID, '*char')'; % 读取文件内容fclose(fileID); % 关闭文件disp(data); % 显示文件内容```8. MATLAB矩阵运算题给定两个矩阵A和B,如何计算它们的点积?答案:可以使用`dot`函数或者矩阵乘法来计算点积:```matlabA = [1 2; 3 4];B = [5 6; 7 8];dotProduct = dot(A, B);```或者```matlabdotProduct = A * B';```以上为MATLAB考试题库及答案的正文内容。
Matlab考试题库及答案(教师出卷参考专用)

Matlab考试题库及答案(教师出卷参考专用)一、选择题1.以下哪个函数用于在Matlab中创建一个图形窗口?A. figureB. plotC. graphD. window答案:A2.在Matlab中,以下哪个选项可以用来定义一个矩阵?A. A = [1 2 3; 4 5 6]B. A = (1, 2, 3, 4, 5, 6)C. A = {1, 2, 3, 4, 5, 6}D. A = 1 2 3; 4 5 6答案:A3.以下哪个函数用于求解线性方程组Ax=b?A. solveB. linsolveC. solve(A, b)D. linsolve(A, b)答案:D4.在Matlab中,如何计算矩阵A和矩阵B的乘积?A. A BB. A \ BC. A . BD. A .\ B答案:A5.以下哪个函数用于在Matlab中绘制三维散点图?A. scatterB. scatter3C. plot3D. bar3答案:B二、填空题1.在Matlab中,要创建一个名为"myfig"的图形窗口,可以使用______函数。
答案:figure('Name', 'myfig')2.在Matlab中,要计算矩阵A的行列式,可以使用______函数。
答案:det(A)3.在Matlab中,若要计算变量x的平方,可以使用______运算符。
答案:.^24.在Matlab中,若要计算矩阵A的逆矩阵,可以使用______函数。
答案:inv(A)5.在Matlab中,要绘制一个正弦波形,可以使用______函数。
答案:plot(sin(x))三、判断题1.在Matlab中,矩阵的索引从1开始计数。
()答案:正确2.在Matlab中,可以使用逻辑运算符"&&"和"||"。
()答案:错误3.在Matlab中,矩阵乘法满足交换律。
matlab笔试试题及答案

matlab笔试试题及答案MATLAB笔试试题及答案1. MATLAB中,如何创建一个名为`myMatrix`的3x3矩阵,其元素从1到9依次排列?答案:可以使用以下命令创建矩阵:```matlabmyMatrix = [1 2 3; 4 5 6; 7 8 9];```2. 在MATLAB中,如何计算向量`v`的范数?答案:可以使用`norm`函数来计算向量的范数。
例如,如果`v`是一个向量,则:```matlabv = [1, 2, 3];norm_v = norm(v);```3. MATLAB中,如何将一个矩阵`A`转置?答案:可以使用单引号(`'`)来转置矩阵`A`:```matlabA = [1 2 3; 4 5 6; 7 8 9];A_transpose = A';```4. 如果要找到矩阵`B`中的最大元素,应该如何操作?答案:可以使用`max`函数来找到矩阵中的最大元素:```matlabB = [10 20 30; 40 50 60; 70 80 90];max_element = max(B(:));```5. 在MATLAB中,如何实现一个简单的for循环,计算从1到10的和?答案:可以使用以下代码实现:```matlabsum = 0;for i = 1:10sum = sum + i;end```6. MATLAB中,如何创建一个二维数组,其元素为当前索引的乘积?答案:可以使用以下代码创建:```matlabC = zeros(3,3);for i = 1:3for j = 1:3C(i,j) = i * j;endend```7. 如何在MATLAB中使用条件语句?答案:可以使用`if`语句来实现条件判断。
例如:```matlabx = 5;if x > 0disp('x is positive');elsedisp('x is not positive');end```8. 在MATLAB中,如何使用`plot`函数绘制一个正弦波?答案:可以使用以下代码绘制正弦波:```matlabx = 0:0.1:2*pi;y = sin(x);plot(x, y);title('Sine Wave');xlabel('x');ylabel('sin(x)');```9. MATLAB中如何使用`fft`函数计算一个信号的快速傅里叶变换?答案:可以使用以下代码计算信号的FFT:```matlabt = 0:0.001:1;x = cos(2*pi*50*t) + randn(size(t));X = fft(x);f = linspace(0, 1000, length(x));plot(f, abs(X));title('Frequency Domain');xlabel('Frequency (Hz)');ylabel('Amplitude');```10. 如何在MATLAB中使用`subplot`函数创建多个子图?答案:可以使用以下代码创建多个子图:```matlabsubplot(2,1,1); % 第一个子图plot(1:10, (1:10).^2);title('Square of Numbers');subplot(2,1,2); % 第二个子图plot(1:10, (1:10).^3);title('Cube of Numbers');```。
matlab考试题B卷及答案

matlab考试题B卷及答案1. MATLAB基础操作题:请在MATLAB中创建一个名为`myVector`的向量,包含元素1, 2, 3, 4, 5,并计算其元素之和。
答案:首先,创建向量`myVector`可以使用以下代码:```matlabmyVector = [1 2 3 4 5];```然后,计算元素之和可以使用`sum`函数:```matlabsumOfElements = sum(myVector);```最终,`sumOfElements`的值将为15。
2. MATLAB矩阵运算题:给定一个3x3的矩阵A,其元素为A=[1 2 3;4 5 6; 7 8 9],请计算矩阵A的转置。
答案:计算矩阵A的转置可以使用`transpose`函数或者简单的`.'`操作符。
以下是使用`transpose`函数的代码:```matlabA = [1 2 3; 4 5 6; 7 8 9];A_transpose = transpose(A);```或者使用`.'`操作符:```matlabA_transpose = A.';```得到的转置矩阵`A_transpose`将是:```1 4 72 5 83 6 9```3. MATLAB编程题:编写一个MATLAB函数,该函数接受一个整数n作为输入,并返回一个n阶的魔方矩阵。
答案:魔方矩阵是一个方阵,其中每一行、每一列以及两条对角线上的元素之和都相等。
以下是一个生成n阶魔方矩阵的MATLAB函数:```matlabfunction magicMatrix = createMagicSquare(n)if mod(n, 2) == 0error('n must be an odd number.');endmagicMatrix = zeros(n);num = 1;for i = 1:nfor j = 1:nif i == 1j = j;elsej = (j + 2 * (i - 1) - n) % n + 1;endmagicMatrix(i, j) = num;num = num + 1;endendend```调用此函数并传入一个奇数n,例如`createMagicSquare(3)`,将返回一个3阶魔方矩阵。
MatLab练习册5(答案)

MatLab 练习册(5) 参考答案1,求下面的优化问题:min -5x1+4x2+2x36x1-x2+x3<=8x1+2x2+4x3<=103>=x1>=-1;2>=x2>=0;x3>=0;答案: (填写程序语句)c=[-5,4,2,];a=[6 -1 1;1 2 4];b=[8 10];xlb=[-1 0 0];xub=[3 2 inf];x0=[0,0,0];x=lp(c,a,b,xlb,xub,x0);disp(['最优值为:',num2str(c*x)])x =1.3333最优值为:-6.66672,某车间生产A 和B 两种产品.为了生产A 和B,所需的原料分别为2个和3个,而所需要的工时分别为4个和2个单位,现在可以应用的原料为100个单位,工时为120个单位,每生产一台A 和B 分别可获得利润6元和4元,应当安排生产A,B 各多少台,才能获得最大的利润?答案: (填写程序语句)c=[-6,-4];a=[ 2,3;4,2];b=[100,120];xlb=[0,0];xub=[inf,inf];x=lp(c,a,b,xlb,xub,xo)disp(['最优值为: ',num2str(-c*x)])x =20.000020.0000最优值为: 2003,min)12424()(22122211++++=x x x x x e x f xx1+x2=0;1.5+x1x2-x1-x2<=0;-x1x2-10<=10答案: (填写程序语句)function[f,g]=fg(x)f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1); g(1)=x(1)+x(2);g(2)=1.5+x(1)*x(2)-x(1)-x(2);g(3)=-x(1)*x(2)-20;x0=[-1,1];options(13)=1;[x,options]=constr('fg',x0,options)options(8)x =-1.2247 1.2247options(8)ans =1.8951。
(完整版)matlab上机练习题答案

(完整版)matlab 上机练习题答案1.计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积>〉 a=[6 9 3;2 7 5]; 〉〉 b=[2 4 1;4 6 8]; 〉〉 a 。
*b ans =12 36 3 8 42 402。
对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
〉〉 A=[4 9 2;7 6 4;3 5 7]; 〉> B=[37 26 28]’; >〉 X=A\B X = -0.5118 4.0427 1.33183。
⎥⎦⎤⎢⎣⎡-=463521a ,⎥⎦⎤⎢⎣⎡-=263478b ,观察a 与b 之间的六种关系运算的结果 >〉 a=[1 2 3;4 5 6]; 〉> b=[8 –7 4;3 6 2]; >〉 a 〉b ans =0 1 0 1 0 1 〉> a 〉=b ans =0 1 0 1 0 1 >> a 〈b ans =1 0 1 0 1 0 〉> a<=b ans =1 0 1 0 1 0 >〉 a==b ans =0 0 0 0 0 0 〉〉 a~=b ans =1 1 1 1 1 14计算多项式乘法(x 2+2x +2)(x 2+5x +4)>> c=conv ([1 2 2],[1 5 4]) c =1 7 16 18 8 5计算多项式除法(3x 3+13x 2+6x +8)/(x +4) 〉〉 d=deconv ([3 13 6 8],[1 4]) d =3 1 26求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解〉〉 a=[2 4 7 4;9 3 5 6]; 〉> b=[8 5]’; 〉> x=pinv (a )*b x =—0.2151 0.4459 0。
matlab作业练习及答案(有程序和截图)

1. 给出如下方程组:16323313915111081697612534141543s u p w s u p w s u p w s u p w +++=+++=+++=+++=求s ,u ,p ,w 的值,并求出系数行列式。
[答案:s =-0.1258,u =-8.7133,p =11.2875,w =-0.0500。
行列式=7680。
]>> A=[16 32 33 13;5 11 10 8;9 7 6 12;34 14 15 1];>> B=[91 16 5 43]';>> C=A\B2. 求矩阵H1()H X X X X -''=其中1731565419289121110X ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦〔答案:H =〔0.7294,0.9041,0.4477,0.9188〕'〕>> X=[17 31 5;6 5 4;19 28 9;12 11 10]; >> H=X/(X'*X)*X'>> X=[17 31 5;6 5 4;19 28 9;12 11 10]; >> H=X*inv((X'*X))*X'3.用MA TLAB语言实现下面的分段函数,()/,||,h x Dy f x h Dx x Dh x D>⎧⎪==≤⎨⎪-<-⎩。
y=h*(x>D)+h/D*x.x>=-D&x<=D)-h*(x<-D)4.636263 0S=2124822 ii==++++++∑①试不采用循环的形式,用数值方法求出上式的解。
②由于数值方法采用double形式进行计算,难以保证有效数字,试采用符号运算的方法求该式的精确解。
并给出保留16位有效数字的结果。
>> sum(2.^[1:63])>> sum(sym(2).^[1:63])5.编写一个矩阵相加函数mat_add(),使其具体的调用格式为,要求该函数能接受任意多个矩阵进行加法运算。
matlab基础考试题及答案

matlab基础考试题及答案1. MATLAB中,如何创建一个名为"myMatrix"的3x3矩阵,其元素为1到9的连续整数?答案:可以使用以下命令创建矩阵:```matlabmyMatrix = [1 2 3; 4 5 6; 7 8 9];```或者使用`magic`函数:```matlabmyMatrix = magic(3);```2. 在MATLAB中,如何计算一个向量的元素平方?答案:可以使用`.^`运算符来计算向量元素的平方:```matlabv = [1 2 3 4];v_squared = v.^2;```3. MATLAB中,如何将一个向量逆序?答案:可以使用`flip`函数或者`end`索引来逆序一个向量:```matlabv = [1 2 3 4];v_reversed = flip(v);```或者```matlabv_reversed = v(end:-1:1);```4. 在MATLAB中,如何计算矩阵的行列式?答案:可以使用`det`函数来计算矩阵的行列式:```matlabA = [1 2; 3 4];detA = det(A);```5. MATLAB中,如何使用循环结构来计算1到100的自然数之和?答案:可以使用`for`循环来计算总和:```matlabsum = 0;for i = 1:100sum = sum + i;end```或者使用`sum`函数直接计算:```matlabsum = sum(1:100);```6. 在MATLAB中,如何创建一个复数?答案:可以通过指定实部和虚部来创建一个复数:```matlabcomplexNumber = 3 + 4i;```7. MATLAB中,如何绘制一个正弦波?答案:可以使用`plot`函数和`sin`函数来绘制正弦波:```matlabx = linspace(0, 2*pi, 100);y = sin(x);plot(x, y);```8. 如何在MATLAB中计算两个矩阵的点积?答案:可以使用`dot`函数或`*`运算符来计算两个矩阵的点积:```matlabA = [1 2; 3 4];B = [5 6; 7 8];dotProduct = dot(A, B);```或者```matlabdotProduct = A * B;```9. MATLAB中,如何使用条件语句来检查一个数是否为偶数?答案:可以使用`if`语句和模运算符来检查一个数是否为偶数:```matlabnum = 10;if mod(num, 2) == 0disp('The number is even.');elsedisp('The number is odd.');end```10. 在MATLAB中,如何将一个字符串转换为小写?答案:可以使用`lower`函数来将字符串转换为小写:```matlabstr = 'Hello World';lowerStr = lower(str);```结束语:以上是MATLAB基础考试题及答案,希望这些题目能帮助你更好地理解和掌握MATLAB的基础知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab练习题及答案详解一、基础题1、下表为1)2) 把任意两点距离的表中,自己到自己的距离,转变成无穷大clcclearclose alldata=xlsread('ti1.xls');%从excel里导入数据x=data(1,:);%将data里第一行的所有列赋值给xy=data(2,:);%将data里第二行的所有列赋值给xn=length(x);%表x的长度dis=zeros(n,n);%对距离表进行初始化for i=1:nfor j=1:ndis(i,j)=sqrt((x(i)-x(j))^2+(y(i)-y(j))^2);%平面坐标距离公式endenddis(dis==0)=inf;%将距离表中为0的数值,变成无穷大redis=dis;2、按要求步骤,操作下表要求:1) 对每列进行[0,1]区间化'(min())/(max min())=--;x x x x2) 把区间化后的表的右边3列,连接在左边3列下边,构成16行3列的表;3) 把16行3列进行转置,得到3行16列的表。
然后对列进行操作,把3行16列的表变成一列,后转置成一行,得到最终的结果。
clcclearclose allx=load('ti2.txt');%从txt里导入数据big=max(x);small=min(x);%算出每列的最大最小值[m,n]=size(x);%表x的行和列的大小newx1=zeros(m,n);%对newx1进行初始化,大小和初始x一样大for i=1:nnewx1(:,i)=(x(:,i)-small(i))./(big(i)-small(i));endnewx2=zeros(2*m,n/2);%对最新的表进行初始化大小为,行为newx1的2倍,列为一半newx2(1:m,1:n/2)=newx1(1:m,1:n/2);%把左边3列不操作的值,直接赋值给newx2上边newx2(m+1:end,1:n/2)=newx1(1:m,n/2+1:end);%把右边的3列,赋值给newx2下边[p,q]=size(newx2);%表newx2的行和列的大小 newx3=zeros(p*q,1);%对newx3进行初始化 for j=1:qnewx3((j-1)*p+1:j*p,1)=newx2(:,q);%对newx3进行操作 end% newx3=reshape(newx2,[],1); renewx=newx3';%最终的结果3、数值运算1)用matlab 求下列式子极限(a) lim x → (b) 0x →2)用matlab 求下列函数的导数(a)22sin (1)y x =+ (b) arccos()(,)x f x y ye =3)用matlab 求下列式子的定积分(a) 4⎰(b) 312-⎰⎰clc clear %===求极限 %====3.1.a=== syms xy=(x^(1/2)-8)/(x^(1/3)-4);re1a=limit(y,x,64)%====3.1.b===syms xy=((x^2-2*x+4)^(1/2)-2)/x;re1b=limit(y,x,0)%===求导数%====3.2.a===syms xf=(sin(x^2+1))^2;re2a=diff(f,x)%对x求导%====3.2.b===syms x yf=y*exp(acos(x));re2bx=diff(f,x)%对x求偏导re2by=diff(f,y)%对y求偏导%===求定积分===%====3.3.a===syms xre3a=int((x+2)/(2*x+1)^(1/2),x,0,4)%一重积分%====3.3.b===syms x yre3b=int(int(y/(x^2-1),x,-2,-sqrt(2)),y,1,3)%二重积分二、提高题1、画一个正五边形,边长自定。
图1:示例一clcclearclose alla=100;b=a/(2*sin(36/180*pi));x=b*[-cos(18/180*pi) 0 cos(18/180*pi)....sin(36/180*pi) -sin(36/180*pi) -cos(18/180*pi)]; y=b*[sin(18/180*pi) 1 sin(18/180*pi)....-cos(36/180*pi) -cos(36/180*pi) sin(18/180*pi) ]; plot(x,y,'linewidth',2)text(-b/4,0,'正五边形','fontsize',20)text(0,0,'y=','num2str(p(1))')axis([-b-b/5 b+b/5 -b-b/5 b+b/5])axis equalbox off2、模拟小球的斜抛,模拟参数自定,画出速度图像。
图2:示例二clcclearclose allg=9.8;v0=10;theta=pi/4;detat=0.01;x=0;y=0;t=0;X=[];Y=[];V=[];T=[];vy=v0*sin(theta);vx=v0*cos(theta);h=plot(x,y,'r.','markersize',50);while y>=0delete(h)vx=vx-0*detat;vy=vy-g*detat;v=sqrt(vx^2+vy^2);x=x+vx*detat;y=y+vy*detat;t=t+detat;%==图形控制部分subplot(3,1,1)plot(x,y,'.b')h=plot(x,y,'r.','markersize',50); hold ontitle('x-y','fontsize',14)axis([0 11 0 3]);box offsubplot(3,1,2)plot(x,v,'.R','markersize',5)hold ontitle('x-v','fontsize',14)axis([0 11 6 v0+1]);box offsubplot(3,1,3)plot(t,v,'.g','markersize',5)hold ontitle('t-v','fontsize',14)axis([0 1.55 6 v0+1]);box offpause(0.05)X=[X,x];Y=[Y,y];V=[V,v];T=[T,t];endp=polyfit(X,Y,2)3、在1的基础上,加上空气阻力的影响,空气阻力大小与速度的平方成正比,2(比例系数自己定,也可以上网查,建议取0.5),画出速度图像。
f k v图3:示例三clcclearclose allg=9.8;v0=10;theta=pi/4;detat=0.01;x=0;y=0;t=0;X=[];Y=[];V=[];T=[];vy=v0*sin(theta);vx=v0*cos(theta);k=0.5;m=2;h=plot(x,y,'r.','markersize',50); while y>=0delete(h)vx=vx-(k*vx^2)/m*detat;vy=vy-g*detat-(k*vy^2)/m*detat; v=sqrt(vx^2+vy^2);x=x+vx*detat;y=y+vy*detat;t=t+detat;%==图形控制部分subplot(3,1,1)plot(x,y,'.b')h=plot(x,y,'r.','markersize',50); hold ontitle('x-y','fontsize',14)axis([0 11 0 3]);box offsubplot(3,1,2)plot(x,v,'.R','markersize',5) hold ontitle('x-v','fontsize',14)axis([0 11 3 v0+1]);box off subplot(3,1,3)plot(t,v,'.g','markersize',5) hold ontitle('t-v','fontsize',14)axis([0 2.75 3 v0+1]);box off pause(0.1)X=[X,x];Y=[Y,y];V=[V,v];T=[T,t];endp=polyfit(X,Y,2)4、画一个叠的圆环,圆环参数自定。
图4:示例四clear;n=input('圆的层数:');r=5;%圆的半径theta=linspace(0,2*pi);x=r*cos(theta);y=r*sin(theta);figure,title('叠的圆环','fontsize',14) axis equalgrid onhold on;for j=1:nb=(1+sqrt(3)*(j-1))*r;%圆心b for i=1:n+1-ja=(2*(i-1)+j)*r;%圆心aplot(x+a,y+b)endend5、模拟两个小球在水平面上,进行完全弹性碰撞过程,分析两个小球构成系统的机械能随时间的变化,小球参数自定。
(注:考虑摩擦阻力)附加1:分析两个小球构成系统的机械能随时间的曲线中,为什么在碰撞时刻出现拐点?附加2:如果碰撞不是完全弹性碰撞,怎么模拟分析?图5:示例五clcclearclose allm1=2;m2=5;v0=20;detat=0.05;g=9.8; mu=0.1;r=5;a=v0^2/(2*mu*g)*1/2;x1=-a/2;y1=r;x2=0;y2=r;v1=v0;v2=0;k=0;V1=[];V2=[];T=[];t=0;while max(abs(v1),abs(v2))>detat if abs(v1)<detatv1=0;elseif abs(v2)<detatv2=0;endclfaxis equalaxis([-a a -r 4*r ])line([-a a],[0 0])hold onqiu(x1,y1,r,'r')qiu(x2,y2,r,'g')x1=x1+v1*detat;x2=x2+v2*detat;if abs(x1-x2)>2*rv1=v1-sign(v1)*mu*g*detat; if k==1v2=v2-sign(v2)*mu*g*detat; endelsev11=v1;v1=v11*(m1-m2)/(m1+m2);v2=2*v11*m1/(m1+m2);k=1;endpause(0.01)t=t+detat;T=[T,t];V1=[V1,v1];V2=[V2,v2];endE=1/2*m1*V1.^2+1/2*m2*V2.^2;figuresubplot(2,1,1)plot(T,E','linewidth',2)box offgrid ontitle('E-t')subplot(2,1,2)plot(T,V1,T,V2,'linewidth',2)box offgrid ontitle('V1,V2-t')三、挑战题1、模拟圆环的匀减速运动,并画出速度时间(V-T)图像图6:示例六clcclearv=20;%初始速度r=5;g=9.8;mu=0.3;dt=0.1;a=r;b=r;w=v/r;v0=v;t=0;x0=0;t1=t;x0=0;axis equalhold onaxis([0 v.^2/(2*mu*g)+2*r 0 2.5*r]) grid onhold ontheta=0:1/50:2*pi;x=a+r*cos(theta);y=b+r*sin(theta);q=plot(x,y,'.k');p=plot(x(1),y(1),'.k');while v>=0delete(q);delete(p)v=v-mu*g*dt;w=w-(mu*g)/r*dt;theta=theta-w*dt;a=a+v*dt;b=r;t1=t1+dt;v0=[v0,v];t=[t,t1];x=a+r*cos(theta);y=b+r*sin(theta);q=plot(x,y,'.r');p=plot(x(1),y(1),'.k','markersize',15); pause(0.2)title('\rm圆环匀减速滚动','fontsize',15) xlabel('距离\itm')ylabel('高度\itm')endfigureplot(t,v0,'linewidth',2);title('圆环\itV-\itT图像','fontsize',15)xlabel('时间\rmt\it/s')ylabel('速度\rmV\itm/s')grid onhold onbox off2、模拟单摆的运动,并证明单摆的等时性。
