山东交通学院期末考试线性代数课程试卷答案和评分标准(d)卷
(完整版)线性代数期末测试题及其答案.doc

线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题 5 分,共 25 分)1 3 1 1.若0 5 x 0,则__________。
1 2 2x1 x2 x3 02.若齐次线性方程组x1 x2 x3 0 只有零解,则应满足。
x1x2x303.已知矩阵A,B,C (c ij )s n,满足 AC CB ,则 A 与 B 分别是阶矩阵。
4.已知矩阵A为 3 3的矩阵,且| A| 3,则| 2A|。
5.n阶方阵A满足A23A E 0 ,则A1。
二、选择题(每小题 5 分,共 25 分)6.已知二次型 f x12 x22 5x32 2tx1x2 2x1 x3 4x2 x3,当t取何值时,该二次型为正定?()A. 40 B.4 4C. 0 t4 4 1t5t D. t2 5 5 5 51 42 1 2 37.已知矩阵A 0 3 4 , B 0 x 6 ,且 A ~ B ,求x的值()0 4 3 0 0 5A.3B.-2C.5D.-58 .设 A 为 n 阶可逆矩阵,则下述说法不正确的是()A. A0B. A 1 0C.r (A) nD.A 的行向量组线性相关9 .过点( 0, 2, 4)且与两平面x 2z 1和 y 3z 2 的交线平行的直线方程为()1xy 2 z 4A.312xy 2 z 4C.31 2x y2 z 4B.32 2x y2 z 4D.322103 1 .已知矩阵 A, 其特征值为()51A. 12, 2 4 B. C.12,24D.三、解答题(每小题 10 分,共 50 分)1 12,2, 22441 1 00 2 1 3 40 2 1 30 1 1 011.设B, C 0 2 1 且 矩 阵满足关系式0 0 1 1 00 10 0 0 2T X(C B)E,求。
a1 12212. 问 a 取何值时,下列向量组线性相关?111, 2a ,3。
2 1 21 a22x 1 x 2x 3 313.为何值时,线性方程组x 1 x 2x 3 2有唯一解,无解和有无穷多解?当方x 1 x 2x 32程组有无穷多解时求其通解。
线性代数期末考试试卷与评分标准
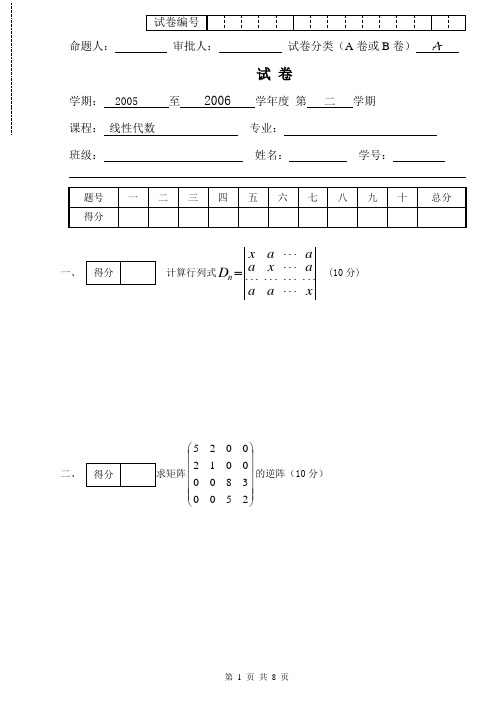
命题人: 审批人: 试卷分类(A 卷或B 卷) A试 卷学期: 2005 至 2006 学年度 第 二 学期 课程: 线性代数 专业:班级:姓名: 学号:一、计算行列式xa a a x a aa xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= (10分)二、⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2500380000120025的逆阵(10分)三、设四元非齐次线性方程组的系数矩阵的秩为3, 已知η1, η2, η3η1=(2, 3, 4, 5)T, η2+η3=(1, 2, 3, 4)T,求该方程组的通解. (12分)四、已知R 3的两个基为a 1=(1, 1, 1)T , a 2=(1, 0, -1)T , a 3=(1, 0, 1)T ;b 1=(1, 2, 1)T , b 2=(2, 3, 4)T , b 3=(3, 4, 3)T .求由基a 1, a 2, a 3到基b 1, b 2, b 3的过渡矩阵P .(12分)设 ⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x 问λ为何值时, 此方程组(1)有唯一解(2)无解(3)有无穷多解? (15分)六、(1)判定向量组 (-1, 3, 1)T, (2, 1, 0)T, (1, 4, 1)T是线性相关还是线性无关;(2)试用施密特法把向量组⎪⎪⎪⎭⎫⎝⎛=931421111) , ,(321a a a正交化(16分)。
七、已知3阶矩阵A 的特征值为3,2,1-, 求A A A 7523+-.(10分)求一个正交变换将二次型322322213214332),,(x x x x x x x x f +++=化成标准形(15分)大学 试 卷 评分标准及参考答案学期: 2005 至 2006 学年度 第 二 学期 课程: 线性代数一、计算行列式xa a a x a aa xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= (10分) 解 将第一行乘(-1)分别加到其余各行, 得ax x a ax x a a x x a aa a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 000 , -------------------------4分 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 0000 )1(-------------------8分 =[x +(n -1)a ](x -a )n -1.-------------------------------------------------10分二、⎪⎪⎪⎪⎪⎭⎫⎝⎛2500380000120025的逆阵(10分) 解 设⎪⎭⎫ ⎝⎛=1225A , ⎪⎭⎫ ⎝⎛=2538B -------------------------------------------2分则⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--5221122511A , ⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛=--8532253811B ----------6分于是 ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛----850032000052002125003800001200251111B A B A -------10分四、设四元非齐次线性方程组的系数矩阵的秩为3, 已知η1, η2, η3η1=(2, 3, 4, 5)T, η2+η3=(1, 2, 3, 4)T,求该方程组的通解. (12分) 解:由于方程组中未知数的个数是4, 系数矩阵的秩为3, 所以对应的齐次线性方程组的基础解系含有一个向量, -----------------------------------------------------------------------4分 且由于η1, η2, η3均为方程组的解, 由非齐次线性方程组解的结构性质得2η1-(η2+η3)=(η1-η2)+(η1-η3)= (3, 4, 5, 6)T为其基础解系向量--------------------------------------------------------------------10分 故此方程组的通解为:x =k (3, 4, 5, 6)T +(2, 3, 4, 5)T , (k ∈R ).---------------------12分五、已知R 3的两个基为a 1=(1, 1, 1)T , a 2=(1, 0, -1)T , a 3=(1, 0, 1)T ;b 1=(1, 2, 1)T , b 2=(2, 3, 4)T , b 3=(3, 4, 3)T .求由基a 1, a 2, a 3到基b 1, b 2, b 3的过渡矩阵P .(12分) 解:设e 1, e 2, e 3是三维单位坐标向量组, 则⎪⎪⎭⎫⎝⎛-=111001111) , ,() , ,(321321e e e a a a ----------------------------------------2分1321321111001111) , ,() , ,(-⎪⎪⎭⎫⎝⎛-=a a a e e e -------------------------------------4分 于是 ⎪⎪⎭⎫⎝⎛=341432321) , ,() , ,(321321e e e b b b -----------------------------------------6分 ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-=-341432321111001111) , ,(1321a a a ---------------------------10分由基a 1, a 2, a 3到基b 1, b 2, b 3的过渡矩阵为⎪⎪⎭⎫⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=-1010104323414323211110011111P .-----------------------12分设 ⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x 问λ为何值时, 此方程组(1)有唯一解(2)无解(3)有无穷多解? (15分) 解⎪⎪⎭⎫ ⎝⎛=21111111λλλλλB ⎪⎭⎫ ⎝⎛+-+----22)1)(1()2)(1(00)1(11011 ~λλλλλλλλλλr . ----------6分 (1)要使方程组有唯一解, 必须R (A )=3. 因此当λ≠1且λ≠-2时方程组有唯一解.-----9分 (2)要使方程组无解, 必须R (A )<R (B ), 故 (1-λ)(2+λ)=0, (1-λ)(λ+1)2≠0.因此λ=-2时, 方程组无解. ----------------------------------------------------------------------------12分 (3)要使方程组有有无穷多个解, 必须R (A )=R (B )<3, 故 (1-λ)(2+λ)=0, (1-λ)(λ+1)2=0.因此当λ=1时, 方程组有无穷多个解.---------------------------------------------------------------15分六、(1)判定向量组 (-1, 3, 1)T, (2, 1, 0)T, (1, 4, 1)T是线性相关还是线性无关;(2)试用施密特法把向量组⎪⎪⎪⎭⎫⎝⎛=931421111) , ,(321a a a 正交化(16分)。
线性代数期末试卷及答案

线性代数期末试卷一、填空题1. 设矩阵A =(−1−12−120011),则||A |A|= 。
2. 设矩阵A 满足A 2+2A −3E =0,则(A +4E)−1= 。
3. 设矩阵A =(0100001000010000),则A 3的秩为 。
4. 设α1,α2,α3是四元非齐次线性方程组Ax =b 的三个解向量,且秩r (A )=3,α1=(1,2,3,4)T ,α2+α3=(0,1,2,3)T 则非齐次线性方程组Ax =b 的通解x = 。
5. 二次型a (x 12+x 22+x 32)+4x 1x 2+4x 1x 3+4x 2x 3经过正交变换后化为6y 12,则a = 。
二、选择题1. 设A,B 均为n ×n 矩阵,则必有( )A.(A +B)2=A 2+2AB +B 2B.A 2−B 2=(A +B)(A −B)C.(AB)2=A 2B 2D.|AB|=|BA|2. 设有向量组α1=(1,−1,2,4),α2=(0,3,1,2),α3=(3,0,7,14),α4=(1,−2,2,0), α5=(2,1,5,1,0),则该向量组的极大线性无关组是( )A.α1,α2,α3B.α1,α2,α4C.α1,α2,α5D.α1,α2,α4,α53. 已知α1,α2,α3是齐次线性方程组Ax =0的一组基础解系,下列结论正确的是( )A.α1−α2,α2−α3,α3−α1也是Ax =0的一组基础解系B.ξ1,ξ2,ξ3与α1,α2,α3等秩,则ξ1,ξ2,ξ3也是Ax =0的一组基础解系C.η1,η2,η3,η4与α1,α2,α3等价,则η1,η2,η3,η4也是Ax =0的一组基础解系D.ξ1,ξ2,ξ3与α1,α2,α3等价,则ξ1,ξ2,ξ3也是Ax =0的一组基础解系4. 设n 阶矩阵A 与B 等价,则必有( )A.当|A |=a (a ≠0)时,|B |=aB.当|A |=a (a ≠0)时,|B |=−aC.当|A|≠0时,|B|=0D.当|A|=0时,|B|=05. 设A为n阶可逆矩阵,λ是A的一个特征值,则A的伴随矩阵A∗的特之一是()A.λ−1|A|B.λ−1|A|nC.λ|A|D.λ|A|n三、求行列式|λ−1000λ−10 00λ−1 432λ+1|四、已知A=(11−101100−1),且A2−AB=E,其中E是三阶单位矩阵,求矩阵B。
线性代数期末考试试卷+答案合集

×××大学线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
3.已知矩阵n s ij c C B A ⨯=)(,,,满足CB AC =,则A 与B 分别是 阶矩阵。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=T A A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,, 21(3 ≤ s ≤ n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关 ② s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③ s ααα,,, 21中任一个向量都不能用其余向量线性表示④ s ααα,,, 21中不含零向量 3. 下列命题中正确的是( )。
山东交通学院线代作业纸及答案

第一章 行列式一、填空1. 按自然数从小到大为标准次序,则排列3421的逆序数为 5 ,32514的逆序数 为 5 .2.四阶行列式中含有因子a a 2311的项44322311a a a a -,42342311a a a a .3.按定义,四阶行列式有!4项,其中有12项带正号,有12项带负号.4.在函数xx x xxx f 21112)(---=中,3x 的系数是2-. 5. =cbac ba222111))()((b c a c a b ---.6.设210132113---=D ,A ij 为元素a ij 的代数余子式)3,2,1,(=j i ,则=-+33231342A A A 37.二、选择1. 四阶行列式a b a b b a b a 4433221100000000的值等于( D ) (A ) b b b b a a a a 43214321- (B ) b b b b a a a a 43214321+(C ) ))((43432121b b a a b b a a -- (D ) ))((41413232b b a a b b a a --2.设1211123111211)(xxxx x f -=,则x 3的系数为 ( C )(A )2 (B )1 (C )1- (D )2- 3.在五阶行列式)det(a ij 中,下列各项中不是)det(a ij 的项为 ( A ) (A )a a a a a 5552214331 (B )a a a a a 5412452331- (C )a a a a a 5145342312 (D )a a a a a 33522514414.行列式1111111111111111--+---+---x x x x 的值为 ( D )(A )0 (B )22)1()1(-+x x (C )2x (D )4x三、计算 1.2605232112131412- 21r r +=====26052321260514120=(因有两行相同)2.ef cfbfde cd bdaeacab--- 123r ar d r f÷=====÷÷ec b e c b e c b adf ---123c bc c c e ÷=====÷÷111111111---abcdef 2131r r r r +=====+abcdef abcdef 4020200111=- 3.dcb a10110011001--- 12r ar +=====d c b a ab 1011011010---+1c =====dc a ab 10111--+32 c dc +=====010111-+-+cd c ad a ab 3r =====cdad ab +-+111ad cd ab +++=)1)(1( 四、证明1.322)(11122b a b b a ab ab a -=+证 1112222b b a a b aba +1323c c c c -=====-1002)(22222b b a b a b b ab b a ----122c c -=====120)(222b b a b b ab b a --- 3)(b a -=2.0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a证=++++++++++++2222222222222222)3()2()1()3()2()1()3()2()1()3()2()1(d d d d c c c c b b b b a a a a 433221c c c c c c -=====--5232125232125232125232122222++++++++++++d d d d c c c c b b b b a a a a4332c c c c -=====-022122212221222122222=++++d d c cb b a a (因有两列相同)3.01111210100000100001a x a x a x a a a a a a xx x n n n n nn ++++=------证: 递推法,按第一列展开,建立递推公式1011)1(021-*---+=++x xa xD D n n n =0022)1(a xD a xD n n n +=-++又 n a D =1,于是=+1n D 0a xD n +011)(a a xD x n ++=+0112a x a D x n ++=-= =01111a x a x a D x n n n++++-- .0111a x a xa x a n n n n ++++=--五、计算1.x a a a x a aa x D n=解x a a a x aa a x D n =121[(1)] n r r r r x n a +++=====÷+-])1([a n x ++xa a ax a11112,,i c ac i n -======])1([a n x ++a x ax --111].)1([)(1a n x a x n -+-=-2.1111)()1()()1(1111n a a a n a a a n a a a D n n n n n n n ------=---+,提示:利用范德蒙德行列式的结果 解 :将行列式上下翻转,即为范德蒙德行列式,若再将行列式左右翻转,由于上下翻转与左右翻转交换次数相等,故行列式于上下翻转再左右翻转其值不变.于是,利用范德蒙德行列式的结果,可得nnnn a n a n a a n a n a D)1()(11111+--+--=+∏+≤<≤-=11).(n i j j i3.nnnnn d c d c b a b a D11112=,其中未写出的元素都是0解: n D 22222n nr r c c ↔=====↔)1(20-n n nn nD d c b a )1(2)(--=n n n n n D c b d a即有递推公式n D 2)1(2)(--=n n n n n D c b d a又111111112c b d a d c b a D -==,利用这些结果递推得n D 2 )(n n n n c b d a -=.)()(11111∏=-=-nk k k k k c b d a c b d a4.nn a a a D +++=11111111121,其中021≠n a a a解 12212332311000010001000100011n n n n na a a c c a a D c c a a a a -----=====---+111213121111121100010000010*******0011()(1)nn ni i nn i ia a a a a a a a a a a a ------===+=+∑∑5.问λ,μ取何值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++02003213.21321x x x x x x x x x μμλ有非零解?解: 方程组的系数行列式必须为01211111μμλ=D 32r r -=====)1(01111--=λμμμλ故只有当0=μ或1=λ时,方程组才可能有非零解.当0=μ,原方程组成为⎪⎩⎪⎨⎧=+=++0031321x x x x x λ 显然1,1,1321-=-==x x x λ是它的一个非零解. 当1=λ,原方程组成为⎪⎩⎪⎨⎧=++=++=++02003213.21321x x x x x x x x x μμ 显然1,0,1321==-=x x x 是它的一个非零解. 因此,当0=μ或1=λ时,方程组有非零解.第一章 练习题1.381141102---解: 利用对角线法则3108)1(2)1()4(1811)1()1(03)4(2⨯⨯-⨯-⨯--⨯-⨯-⨯⨯+-⨯-⨯+⨯-⨯=D4-=2.yxyx x y x y y x y x+++解: 利用对角线法则)(2)()()()(33333y x y x y x yx y x y x yx y y x x D +-=--+-+++++=3.7110251020214214解: 12r r D ↔=====-711002510421420212131410r r r r -=====--711020215042702021---- 42r r ↔=====42702021507110221----3242157r r r r +=====+0459008517007110221= 4.4321532154215431543254321 解: 从最后一行开始,后行减去前行1114111411141114111154321----=D 12,,5i c c i -======0510050105015000143211----=D 51215i i c c =+=====∑050005000505000043213----1875)5(34=-⨯=5. 利用范德蒙德行列式计算四阶行列式cb a db a dc a dc bd c b a d c b a d c b a++++++++33332222解: D 414()r r r a b c d +=====÷+++1111)(33332222dcba d cb a dc b ad c b a +++把行列式的最后一行依次与前面的行交换,共交换三次得333322221111)(d c b a d c b a d c b a d c b a D +++-=))()()()()()((c d b d b c a d a c a b d c b a ------+++-=6.证明na a a 10011121)1(2132∑=-=ni in a a a a a ,其中 021≠n a a a 证: 化行列式为下三角形行列式D112,i inr r a i n -======n a a b * 0002n a a ba 32= 其中,∑=-=ni ia ab 211,于是).1(2132∑=-=n i i n a a a a a D7.=n D )det(a ij ,其中j i a ij -=解: 032131221011210------=n n n n n n D n 11221n n n n r rr r r r ----=====--1111111111111210--------n n12n n c c c c +=====+.2)1()1(112001220132121----=---------n n n n n n n8.求满足下列方程的实数z y x ,,:11000100011=zy x z y x解: 将D 按第一行展开得,,0222=++z y x 解得.0===z y x9. 问λ取何值时,齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(3213.21321x x x x x x x x x λλλ有非零解?解: 方程组的系数行列式必须为0λλλ----=111132421D 13r r ↔=====421132111-----λλλ 21312(1)r r r r λ-=====--2)1(4301210111λλλλλ--+-----2)1(43121λλλλ--+----=21c c +=====2331λλλλλ----)3)(2(---=λλλ 故32,0或=λ,并且当0=λ时,21-=x ,12=x ,13=x ;当2=λ时,21-=x ,32=x ,13=x ;当3=λ时,11-=x ,52=x ,23=x ;均是原方程组的非零解. 因此,当32,0或=λ时,方程组有非零解.第二章 矩阵及其运算 (一)一.填空1.设⎪⎪⎪⎭⎫ ⎝⎛=321a a a A ,()123B b b b = ,则AB =11121212223313233a b a b a b a b a b a b a b a b a b ⎛⎫⎪ ⎪ ⎪⎝⎭;BA = 112233()a b a b a b ++;()T AB =112131122232132333a b a b a b a b a b a b a b a b a b ⎛⎫⎪⎪ ⎪⎝⎭;T T A B =()T BA ;T T B A = ()T AB . 2. 设⎥⎦⎤⎢⎣⎡-=121x A ,⎥⎦⎤⎢⎣⎡=012y B ,若BA AB =,则=x 1 ;=y 2 . 3. 设A 为3阶方阵,且2-=A ,则2A = 4 ;=-T A 2 16 ;*A = 4 .4. 设101A λ⎡⎤=⎢⎥⎣⎦,则kA =101k λ⎡⎤⎢⎥⎣⎦.5. 设101020101A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,而2n ≥为正整数,则12n n A A --= 0 (零矩阵) . 6. 已知3A E =,则1A -=2A .二.选择1. 设n 阶方阵,,A B C 满足关系式ABC E =,其中E 为n 阶单位矩阵,则必有( D ). (A ) ACB E = (B )CBA E = (C) BAC E = (D )BCA E =2. 设A 、B 均为n 阶方阵,满足0AB =,则必有 ( C ) (A ) 0A =或0B = (B )0BA = (C) 0A =或0B = (D )0A B +=3. 设A 、B 都是n 阶方阵,则下列命题中正确的是 ( D ) (A )若0≠A 且0≠B ,则0≠AB . (B )若A 、B 都是对称阵,则AB 是对称阵. (C)若AB 不可逆,则A 、B 都不可逆. (D )若AB 可逆,则A 、B 都可逆.三.计算与证明1. 设111111111A ⎛⎫ ⎪=- ⎪⎪-⎝⎭, 123124051B ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,求32AB A -及T A B . 解:32AB A -1111233111124111051⎛⎫⎛⎫ ⎪⎪=--- ⎪⎪ ⎪⎪-⎝⎭⎝⎭1112111111⎛⎫ ⎪-- ⎪ ⎪-⎝⎭21322217204292-⎛⎫⎪=-- ⎪ ⎪-⎝⎭111123111124111051T A B ⎛⎫⎛⎫ ⎪⎪=--- ⎪⎪ ⎪⎪-⎝⎭⎝⎭058056290⎛⎫⎪=- ⎪ ⎪⎝⎭2. 13121400121134131402⎛⎫⎪-⎛⎫ ⎪ ⎪ ⎪--⎝⎭ ⎪-⎝⎭6782056-⎛⎫= ⎪--⎝⎭3. ()111213112312222321323333a a a x x x x a a a x a a a x ⎛⎫⎛⎫ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭()1111212313121222323131********x a x a x a x a x a x a x a x a x a x x x ⎛⎫⎪=++++++ ⎪⎪⎝⎭222111222333121213132323222a x a x a x a x x a x x a x x =+++++4. 设,A B 为n 阶方阵,且A 为对称阵,证明TB AB 也是对称阵. 证明:已知:TA A =则 ()()TTTTTTTTB AB B B A B A B B AB === 从而 T B AB 也是对称阵.第二章 矩阵及其运算 (二)一.填空1. 设⎥⎦⎤⎢⎣⎡=1211A ,⎥⎦⎤⎢⎣⎡-=1011B ,⎥⎦⎤⎢⎣⎡=B O O A C ,则 =C -1 .2. 设1200n a a A a ⎛⎫⎪⎪= ⎪ ⎪⎝⎭,(120n a a a ≠). 则1A -=1210101n a a a ⎛⎫ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪⎝⎭3. 设A 为三阶可逆矩阵,且1123012001A -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦,则A *=123012001---⎛⎫⎪- ⎪ ⎪⎝⎭4. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=543022001A ,则=-*1)(A 10A ;=*-)(1A 10A .5.设A 为m 阶方阵,B 为n 阶方阵,且a A =,b B =,⎥⎦⎤⎢⎣⎡=O B A O C ,则=C (1)mnab -. 6.设A 为3阶矩阵,且A =12,则1*(2)5A A --=16- . 二.选择题1. 设A 为n 阶可逆矩阵,*A 为A 的伴随矩阵,则必有( A ) (A ) 1-*=n AA (B ) A A =* (C ) nA A =*(D ) 1-*=A A2. 设A 、B 都是n 阶方阵,则下列等式中正确的是 ( D ) (A )BA AB = (B )TTTB A AB =)( (C )111)(---=B A AB (D )BA AB =3. 已知A 为n 阶方阵,且满足关系式0432=++E A A ,则()=+-1E A ( C )(A )1A E -+ (B )12E A +(C ) 12E A -- (D )4A E +三.计算与证明1. 求下列方阵的逆阵(1) 5200210000120011⎛⎫ ⎪⎪⎪- ⎪⎝⎭解:115221A ⎛⎫=⎪⎝⎭,1111225A --⎛⎫= ⎪-⎝⎭,221211A -⎛⎫= ⎪⎝⎭,122121113A -⎛⎫= ⎪-⎝⎭, 112002500120033110033A --⎛⎫⎪- ⎪ ⎪= ⎪⎪⎪-⎪⎝⎭. (2) 121342541-⎛⎫⎪- ⎪ ⎪-⎝⎭解:2A =, 故1A -存在 . 11A A A -*=2101313221671-⎛⎫⎪ ⎪=-- ⎪⎪--⎝⎭. 2. 解下列矩阵方程 (1) 25461321X -⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭解:125461321X --⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭35461221--⎛⎫⎛⎫= ⎪⎪-⎝⎭⎝⎭22308-⎛⎫= ⎪⎝⎭.(2)211113210432111X -⎛⎫-⎛⎫⎪= ⎪ ⎪⎝⎭ ⎪-⎝⎭解:1211113210432111X --⎛⎫-⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪-⎝⎭22182533-⎛⎫ ⎪= ⎪-- ⎪⎝⎭.(3) 010100143100001201001010120X -⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ 解:11010143100100201001001120010X ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪=- ⎪ ⎪⎪ ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭210134102-⎛⎫⎪=- ⎪⎪-⎝⎭(4) 设,AX B X +=其中01011111,20,10153A B -⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦求.X 解:由,AX B X +=得 ()E A X B -=故 1().X E A B -=- 而 21331213311330()10E A -⎛⎫ ⎪-=- ⎪ ⎪-⎝⎭所以 2133213311330113112020.05311X --⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭ 3. 设1P AP -=Λ, 其中1411P --⎛⎫=⎪⎝⎭, 1002-⎛⎫Λ= ⎪⎝⎭, 求11A . 解:1P AP -=Λ故1A P P -=Λ所以11111A P P-=Λ3P = 1411P *⎛⎫= ⎪-⎝⎭ 1141113P -⎛⎫= ⎪-⎝⎭而 11111110100202--⎛⎫⎛⎫Λ== ⎪ ⎪⎝⎭⎝⎭故11111414103311021133A ⎛⎫ ⎪--⎛⎫⎛⎫= ⎪ ⎪⎪- ⎪⎝⎭⎝⎭-- ⎪⎝⎭27312732683684⎛⎫= ⎪--⎝⎭. 4. 设A 为n 阶方阵,并且满足Θ=--E A A 22,证明:A 及E A 2+都可逆,并求1-A 及1)2(-+E A . 解:由已知得:E E A A =-⋅)(21,故A 可逆,且)(211E A A -=- 又E E A E A 4)3)(2(-=-+, 故E A 2+可逆,且)3(41)2(1E A E A --=+-.5. 设0kA =(k 为正整数),证明121()k E A E A A A ---=++++证明: 由 0kA =有 21()()k E A A A E A -++++-2121k k k E A A A A A A A --=++++----E =因此 121()k E A E A A A ---=++++第二章 练习题1.设A 为4阶方阵,1,3A =求134A A *--. 解:111,3A A A A *--==11111343433A A A A A *----∴-=⋅-=-41311(3)81A =-=⋅243.= 2. 已知⎪⎪⎪⎭⎫ ⎝⎛--=130210005A ,求1-A .解: ⎪⎪⎭⎫⎝⎛=2211A O O A A51111-=-A=⎪⎪⎭⎫ ⎝⎛----==*-132********122A A A ⎪⎪⎪⎪⎭⎫ ⎝⎛-71737271 ∴⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛=---717307271000511221111A OO A A 3. 设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=121011322A ,解矩阵方程E AXA =*(其中*A 是矩阵A 的伴随矩阵). 解:计算得1-=A ,并且A 可逆 因为E E A AA -==*,故由已知E AXA =*得A EA A AXA ==*所以A AX =-解得E X -=解:A BA BA A 61=-- A BA E A6)(1=--⎪⎪⎪⎭⎫⎝⎛=-=--123)(611E AB 4. 设三阶矩阵A ,B 满足关系式BA A BA A +=-61,且⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=714131A ,求B .5. 设A 为n 阶方阵,并且满足Θ=-+E A A 2, 证明:A 及E A -都可逆,并求1-A 及1)(--E A .解:由已知得:E E A A =+⋅)(,故A 可逆,且E A A +=-1 又E E A E A -=+-)2)((, 故E A -可逆,且)2()(1E A E A +-=-- .6.设34432022O A O ⎛⎫⎪- ⎪= ⎪ ⎪⎝⎭, 求8A 及4A . 解: 34432022O A O ⎛⎫ ⎪- ⎪= ⎪ ⎪⎝⎭,令13443A ⎛⎫= ⎪-⎝⎭ 22022A ⎛⎫= ⎪⎝⎭ 则12A O A OA ⎛⎫=⎪⎝⎭故8182A O A OA ⎛⎫=⎪⎝⎭8182A O OA ⎛⎫= ⎪⎝⎭8888816121210A A A A A ===444414426450052022O A O A OA O ⎛⎫⎪⎛⎫ ⎪==⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭. 7.设n 阶矩阵A 及s 阶矩阵B 都可逆,求1O A B O -⎛⎫⎪⎝⎭.解 : 将1O A B O -⎛⎫⎪⎝⎭分块为1234C C CC ⎛⎫⎪⎝⎭其中 1C 为s n ⨯矩阵, 2C 为s s ⨯矩阵3C 为n n ⨯矩阵,4C 为n s ⨯矩阵则n n s s O A B O ⨯⨯⎛⎫⎪⎝⎭1234C C C C ⎛⎫ ⎪⎝⎭E ==ns E O O E ⎛⎫⎪⎝⎭由此得到1334411122n s AC E C A AC O C OBC O C O BC E C B --⎧=⇒=⎪=⇒=⎪⎨=⇒=⎪⎪=⇒=⎩(A 、B 均可逆)故 111O A O B B O AO ---⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭.第三章 矩阵的初等变换与线性方程组(一)一、填空1. 设A 为n 阶方阵,若有n 阶初等方阵s P P P ,,21,使 ),(),(21B E E A P P P s = ,则=-1As P P P 21 .2. 设A 是34⨯矩阵,且A 的秩)(A R =2,而⎪⎪⎪⎭⎫⎝⎛-=301020201B ,则=)(AB R 2 .8. 设x 为n 维列向量,1=x x T ,令Txx E H 2-=,证明H 是对称阵,且THH E =. 证明:因为 H xx E xx E xx E H T T T T T T=-=-=-=2)(2)2(,所以H 是对称阵.又 ==2H HHT4)2)(2()2(2+=--=-E xx E xx E xx E T T T T T T xx xx xx 4))((-+=-+=E xx x x x x E T T T 4)(4E xx xx T T =-443. 设四阶方阵A 的秩)(A R =2,则其伴随矩阵*A 的秩为)(*A R = 0 .二.选择1.从矩阵A 中划去一行得到矩阵B ,则A 、B 的秩的关系为( A )(A) 1)()()(-≥≥A R B R A R (B) 1)()()(->≥A R B R A R (C) 1)()()(->>A R B R A R (D) 1)()()(-≥>A R B R A R 2.在秩是r 的矩阵中( C ) (A) 没有等于0的1-r 阶子式 (B) 没有等于0的r 阶子式(C) 等于0的1-r 阶子式和等于0的r 阶子式都可能有 (D) 所有1-r 阶子式等于0三.计算与证明1.把矩阵化为行最简形矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛---8701111121324321 解:⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-000031100313010317001 2.用初等变换求解矩阵方程B AX =,其中⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛---=520321,102123111B A 解:⎪⎪⎪⎭⎫ ⎝⎛--==-13122018971B A X 3.试利用矩阵的初等变换,求方阵⎪⎪⎪⎭⎫⎝⎛=323513123A 的逆阵1-A .解:⎪⎪⎪⎪⎪⎭⎫⎝⎛----=-210212112332671A4.求矩阵⎪⎪⎪⎭⎫ ⎝⎛---=443112112013A 的秩.解:秩为25.设⎪⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ,求k 为何值时可使)(A R 等于:(1) 1 ;(2) 2 ;(3) 3 .解:⎪⎪⎪⎭⎫ ⎝⎛+----)2)(1(300)1(3)1(20321~k k k k k A (1) 当1=k 时,R(A)=1 (2) 当2-=k 时,R(A)=2(3) 当1≠k 且2-≠k 时,R(A)=3第三章 矩阵的初等变换与线性方程组(二)1.求齐次线性方程组⎪⎩⎪⎨⎧=+++=-++=-++02220202432143214321x x x x x x x x x x x x 的解.解:⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-134334C2.求非齐次线性方程组⎪⎪⎩⎪⎪⎨⎧-=+-=-+-=+-=++69413283542432z y x z y x z y x z y x 的解.解:⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-021112C3.设有⎪⎩⎪⎨⎧--=-+--=--+=-+-1)5(4224)5(2122)2(321321321λλλλx x x x x x x x x ,问λ为何值时,此方程组有唯一解、无解或无穷解?并在有无穷解时求其解. 解:)10()1(2λλ--=A(1)1≠λ且10≠λ时,有唯一解;(2)10=λ时,无解;(3)1=λ时,无穷解:⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-00110201221C C第三章 练习题1.求作一个秩是4的方阵,使它的两个行向量是(1,0,1,0,0)和(1,-1,0,0,0)解:⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-00000010000010000011001012.求下列矩阵的秩,并求一个最高阶非零子式:(1)⎪⎪⎪⎭⎫ ⎝⎛---443112112013解:秩为2,01113≠-(2)⎪⎪⎪⎭⎫ ⎝⎛-------815073131213123解:秩为3,087312123≠----3.非齐次线性方程组⎪⎩⎪⎨⎧-=++-=-+=+-22223212321321x x x x x x x x x λλ,当λ取何值时有解?并求出它的通解.解:⎪⎪⎪⎭⎫⎝⎛-+---)1)(2(000)1(2330121~λλλλB (1)当2-=λ时, ⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛022111C(2)当1=λ时, ⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛001111C4.设A 为n m ⨯矩阵,证明:(1)方程m E AX =有解的充分必要条件是m A R =)(; (2)方程n E YA = 有解的充分必要条件是n A R =)(. 解:(1)m E AX =有解),()(E A R A R =⇔(必要性)显然,m A R ≤)(;另一方面,m E A R ≥),(,故m A R =)( (充分性)m E A R A R m ≤≤=),()((2)方程n E YA =有解⇔方程n TT E Y A =有解⇔n A R T =)((由1)⇔n A R =)(5. 设A 为n m ⨯矩阵,证明:若AY AX =,且n A R =)(,则Y X = 证明:Θ=-)(Y X A因为n A R =)(,所以方程Θ=-)(Y X A 只有零解,即Θ=-Y X ,即Y X =6.证明1)(=A R 的充分必要条件是存在非零列向量α及非零行向量T β,使TA βα⋅=. 证明:(充分)1)()(=≤αR A R ,另一方面TA βα⋅=,α和Tβ又都是非零向量,故1)(≥A R ,因此1)(=A R(必要)由于1)(=A R 故⎪⎪⎭⎫ ⎝⎛ΘΘΘ1~A ,所以()TQ P Q P A αβ=⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛ΘΘΘ=0010011 7.已知三阶矩阵0≠B ,且B 的每一个列向量都是以下方程组的解:)(0302022321321321*⎪⎩⎪⎨⎧=-+=+-=-+x x x x x x x x x λ(1) 求λ的值; (2) 证明0=B .解:(1)设⎪⎪⎪⎭⎫⎝⎛---=11312221λA ,由题设0,0=≠AB B ,知0)1(5=--=λA故1=λ(2)由1=λ,知2)(=A R ,由0=AB ,知3)()(≤+B R A R ,故1)(≤B R又已知1)(≥B R ,因此1)(=B R 从而0=B第四章 向量组的线性相关性(一)一、选择1.若向量组γβα,,线性无关,δβα,,线性相关,则 ( C ) (A )α必可由δγβ,,线性表示;(B )β必可由δγα,,线性表示; (C) δ必可由γβα,,线性表示; (D) β必不可由δγα,,线性表示。
《线性代数》期末试卷A答案及评分标准
《线性代数》期末试卷A答案及评分标准A卷2015—2016学年第一学期《线性代数》期末试卷答案(32学时必修)专业班级姓名学号开课系室应用数学系考试日期 2016年1月15日注意事项:1.请用黑色或蓝色笔在试卷正面答题(请勿用铅笔答题),反面及附页可作草稿纸;2.答题时请注意书写清楚,保持卷面清洁;3.本试卷共七道大题,满分100分;试卷本请勿撕开,否则作废;4. 本试卷正文共7页。
说明:试卷中的字母E 表示单位矩阵;*A 表示矩阵A 的伴随矩阵;)(A R 表示矩阵A 的秩;1-A 表示可逆矩阵A 的逆矩阵.一、填空题(请从下面6个题目中任选5个小题,每小题3分;若6个题目都做,按照前面5个题目给分)1.5阶行列式中,项4513523124a a a a a 前面的符号为【负】.2.设1352413120101311--=D ,)4,3,2,1(4=i A i 是D 的第4行元素的代数余子式,则4443424122A A A A +-+ 等于【 0 】.3.设102020103B ??= ? ?-??,A 为34?矩阵,且()2A =R ,则()AB =R 【 2 】. 4.若向量组123(1,1,0),(1,3,1),(5,3,)t ==-=ααα线性相关,则=t 【 1 】.5.设A 是3阶实的对称矩阵,????? ??-=1m m α是线性方程组0=Ax 的解,-=m m 11β是线性方程组0)(=+x E A 的解,则常数=m 【 1 】.6.设A 和B 是3阶方阵,A 的3个特征值分别为0,3,3-,若AB B E =+,则行列式=+-|2|1E B 【 -8 】.二、选择题(共5个小题,每小题3分)1. 设A 为3阶矩阵,且21||=A ,则行列式|2|*-A 等于【 A 】.(A) 2-; (B) 21-; (C) 1-; (D) 2.2. 矩阵110120001??的逆矩阵为【 A 】.(A) 210110001-?? ?- ? ;(B) 210110001?? ? ? ???; (C) 110120001-??- ? ?;110110001??.3.设A 是n 阶非零矩阵,满足2A A =,若A E ≠,则【 A 】.(A) ||0A =; (B) ||1A =; (C) A 可逆; (D) A 满秩.4. 设300300026,110,001342A B==- ? ?--1-=AB C ,则1C -的第3行第1列的元素为【D 】.(A) 4; (B) 8; (C) 0; (D) 1-.5.设323121232221321222222),,(x ax x ax x ax x x x x x x f +++++=,a 是使二次型),,(321x x x f 正定的正整数,则必有【 B 】.(A) 2=a ; (B) 1=a ; (C) 3=a ; (D) 以上选项都不对.三、求解下列各题(共3小题,每小题7分)1. 若,,αβγ线性无关,2,αβ+2k βγ+,3βγ+线性相关,求k . 解:因为2,αβ+2k βγ+与3βγ+线性相关,所以必定存在不全为零的数321,,λλλ,使得0=3+++2+2+321)()()(γβλγβλβαλk----------2分整理得:0=3+++2+2+323211γλλβλλλαλ)()(k 由于,,αβγ线性无关,因此可得由于321,,λλλ不全为零,即上述齐次线性方程组有非零解,因此0=30122001k ,由此得k = 6. ----------7分 2. 设()011201-????? ??=A ,--=03112211a B ,若2)(=+B AB R ,求a .解:由2)(=+B AB R 可知0=+B AB ,由此可得 0=+B E A又 02=12201012=+≠--E A----------2分因此 0=B因此可得 5=-a . ----------7分3. 设矩阵2001000240021603,A a B t -==- ? ? ? ?????,且,A B 相似,求a 与t 的值.解:由,A B 相似可知,A B 的特征值相同,而易知B 的特征值为 -1,t ,3,因此A 的特征值也为 -1,t ,3 利用特征值的性质可得21132(4)3t a t a ++=-++??-=-?----------5分解得12a t ==,. ----------7分四、(共2小题,每小题8分) 1.求向量组的一个最大无关组,并将其余向量用这一最大无关组表示出来. 解:令()123410311301,,,217242140A αααα?? ?--== ?, 把A 进行行变换,化为行最简形,()123410300110~00010000A C ββββ??== ? ?----------6分则421,,βββ是C 的列向量组的一个最大无关组,且421303ββββ++=,故421,,ααα是A 的列向量组的一个最大无关组,且421303αααα++=.----------8分2. 问a 满足什么条件,才能使得21403003A a ??= ? ???共有两个线性无关的特征向量?解:由0=30030412=λλλλ----a E A ,得A 的特征值:3==2=321λλλ,要使A 有两个线性无关的特征向量,则特征值3对应一个线性无关的特征向量,即0=)3(x E A -的解空间的维数为1,则2=)3(E A R -, ----------6分而114300000A E a -?? ?-= ? ???,因此可知0≠a . ----------8分五、问λ为何值时,线性方程组13123123,4226423x x x x x x x x +=??++=+??++=+?λλλ无解,有无穷多解,并在有无穷多解时求出其通解.解:记方程组的增广矩阵为,则101 412261423B ?? ?=+ ? ?+??λλλ,对其进行行变换,化为行阶梯形:101 012320001B λλλ?? ?→--+ ? ?-+??,易知,当1≠λ时,3)(2)(=≠=B R A R ,方程组无解;当1=λ时,2)()(==B R A R ,方程组有无穷多解; ----------6分当1=λ时,101101210000B ??→-- ? ?,与原方程组同解的方程组为1323121x x x x =-+??=-?,由此可得原方程组的通解为()123112110x x k k R x -=+-∈ ? ? ?. ----------12分六、求实二次型32312123222132184444),,(x x x x x x x x x x x x f -+-++=的秩,并求正交变换Py x =,化二次型为标准形.解:记二次型的矩阵为----=442442221A ,122~000,000A -??故二次型f的秩为----------4分由0442442221=-------=-λλλλE A ,可得:0,9321===λλλ,当,91=λ求解0)9(=-x E A 的一个基础解系:??=11-211ξ,单位化:?=3232-311p ,当,032==λλ求解0=Ax 的一个基础解系:=????? ??=102-,01232ξξ,正交化:[][]==?==15452--,012222323322ηηηξηξηξη,单位化:?===3515541552-15452-35,0125132p p , ----------12分令()321p p p P =,则可得正交变换Py x =,二次型的标准形为:232221321009),,(y y y y y y f ++=. ----------14分七、(请从下面2个题目中任选1个,若2个题目都做,按照第1题给分)1. “设A 是n 阶实的反对称矩阵,则对于任何n 维实的列向量α,α和αA 正交,且E A -可逆”.您认为该结论成立吗?请说明理由. 解:该结论成立。
大一线性代数期末考试试卷+答案

大一线性代数期末考试试卷+答案(总6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0100100000010010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=T A A ( )。
① n 2② 12-n③ 12+n④ 42. n 维向量组 s ααα,,, 21(3 ≤ s ≤ n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关 ② s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③ s ααα,,, 21中任一个向量都不能用其余向量线性表示 ④ s ααα,,, 21中不含零向量 3. 下列命题中正确的是( )。
① 任意n 个1+n 维向量线性相关② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ,B 均为n 阶方阵,下面结论正确的是( )。
线性代数期末试题及答案

线性代数
一、填空题(每小题2分,共20分)
1. 如果行列式,则。
2. 设,则。
3. 设=。
4. 设齐次线性方程组的基础解系含有2个解向量,则。
5. A、B均为5阶矩阵,,则。
6. 设, 设,则。
7. 设为阶可逆矩阵,为的伴随矩阵,若是矩阵的一个特征值,则的一个特征值可表示为。
8. 若为正定二次型,则的范围是。
9. 设向量,则与的夹角。
10. 若3阶矩阵的特征值分别为1,2,3,则。
二、单项选择(每小题2分,共10分)
1. 若齐次线性方程组有非零解, 则()
.1 或2.-1或-2.1或-2.-1或2.
2. 已知4阶矩阵的第三列的元素依次为,它们的余子式的值分别为,则()
.5.-5.-3.3
3. 设A、B均为n阶矩阵,满足,则必有()
..
. 或.或
4.设是非齐次线性方程组的两个解向量,则下列向量中仍为该方程组解的是()
A .B.C.D.
5. 若二次型的秩为2,则()
. 1.2. 3. 4
三、计算题( 每题9分,共63分)
1. 计算阶行列式
2. 设均为3阶矩阵,且满足,若矩阵,求矩阵。
3. 已知向量组和;已知可以由线性表示,且与具有相同的秩, 求a ,b 的值。
线性代数期末测试题(卷)与答案解析

线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题5分,共25分)1. 若022150131=---x ,则=c __________。
2.若齐次线性方程组ïîïíì=++=++=++000321321321x x x x x x x x x l l 只有零解,则l 应满足 。
3.已知矩阵n s ij c C B A ´=)(,,,满足CB AC =,则A 与B 分别是 阶矩阵。
4.已知矩阵A 为3´3的矩阵,且3||=A ,则=|2|A 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、选择题 (每小题5分,共25分)6.已知二次型3231212322214225x x x x x tx x x x f +-+++=,当t 取何值时,该二次型为正定?( )A.054<<-tB.5454<<-tC.540<<tD.2154-<<-t7.已知矩阵B A x B A ~,50060321,340430241且÷÷÷øöçççèæ=÷÷÷øöçççèæ-=,求x 的值( )A.3B.-2C.5D.-58.设A 为n 阶可逆矩阵,则下述说法不正确的是( ) A. 0¹A B. 01¹-A C.n A r =)( D.A 的行向量组线性相关9.过点(0,2,4)且与两平面2312=-=+z y z x 和的交线平行的直线方程为( )A.14322-=-=-z y xB.24322-=-=z y xC.14322+=+=-z y x D.24322+=+=z y x10.已知矩阵÷÷øöççèæ-=1513A ,其特征值为() A.4,221==l lB.4,221-=-=l lC.4,221=-=l l D.4,221-==l l三、解答题 (每小题10分,共50分)11.设,1000110001100011÷÷÷÷øöççççèæ---=B ÷÷÷÷÷øöçççççèæ=2000120031204312C 且矩阵C 满足关系式EX B C T=-)(, 求C 。
大学线性代数期末考试题含答案

用心用情 服务社会1广东工业大学考试试卷 ( A )课程名称: 线性代数 试卷满分 100 分考试时间: 2009 年 6 月 9 日 (第 17 周 星期 二 ) 题 号 一 二 三 四 五 六 七 八 九 十 总分 评卷得分评卷签名 复核得分 复核签名一、 填空题 (每小题4分,共20分)1. 已知三阶行列式D 中第一行的元素依次为a 、2 、 1,它们的余子式分别是-2、-5、4,且D =10,则a = 。
2. 5,A A A *=-=设为三阶方阵,若则 。
3. 若n 阶矩阵A 满足O E A A =--422,则 ()1-+E A = 。
4.02030x ky z y z kx y z +-=⎧⎪+=⎨⎪--=⎩如果齐次线性方程组 有非零解,则k= 。
5.设33500012,025A B ⨯⎛⎫ ⎪= ⎪ ⎪⎝⎭的列向量组线性无关,则R(AB)= 。
二、选择题(每小题4分,共16分)1.A 为n m ⨯矩阵,0=AX 仅有零解的充分必要条件是( )(A)A 的列向量组线性无关 (B)A 的列向量组线性相关 (C)A 的行向量组线性无关 (D)A 的行向量组线性相关 2.设A ,B ,C 均为n 阶方阵,E 为n 阶单位矩阵,且E ABC =,则下列等式总成立的有( )(A) E ACB = (B) E CBA = (C) E BAC = (D) E BCA =用心用情 服务社会2 3. 如果1333231232221131211=a a a a a a a a a ,则=---333231312322212113121111324324324a a a a a a a a a a a a ( ) (A)8 (B)-12 (C)24 (D )-244. 下列哪一个不是n 阶方阵为非奇异矩阵的充要条件( )(A) A 的行秩为n (B)A 的每个行向量都是非零向量 (C) n A r =)( (D) 线性方程0=Ax 只有零解三、(10分)四、解矩阵方程 B AX X +=2,其中⎪⎪⎪⎭⎫ ⎝⎛--=101121011A , ⎪⎪⎪⎭⎫ ⎝⎛--=202031B .(12分)五、求非齐次线性方程组的一个解及对应的齐次方程组的基础解系。
山东交通学院期末考试 线性代数 课程试卷答案和评分标准 ( E )卷

…
线 所以当 1且 10 时 方程组有唯一解;
…
… …
要使方程组有无穷多解 必须 R(A) 3,即必须 1 10 0且1 0,
… …
所以当 1或 10 时 方程组有无穷多解
---------------------(4 分)
…
…
…
试卷适用班级 理工科 09 级、专升本 10 级 、路专 09 级等 班级
所以 f 为负定。
--------------(7 分)
…
34 0
…
…
… …
2.设 A 为 3 阶矩阵 A* 为 A 的伴随矩阵,| A |
1
则
A*
1
.
…
2
4
…
…
…
1 0 1 1 2 3
1 2 2
密 … … …
3.设
A
0
10456 Nhomakorabea则
A
4
5
2
0 0 1 7 8 9
7 8 2
…
…
…
1 0 0
… … 封 … …
4.设
A
0
1
0
A* 为 A 的伴随矩阵,则 R A* 3 .
2
6
0
2 0 4
所以 K 可逆 故有 A BK 1 --------------(3 分) 所以向量组1, 2 , , n 能由向量组 1, 2 , , n 线性表示。
-------------------------- (4 分)
因为
5 2
a11 5 0
2
26 0 | A | 80 0 6
2. 设 A, B 均为 n 阶方阵,下面结论正确的是
线性代数期末考试试题及答案c1

线性代数期末考试试题及答案c1一、选择题(每题5分,共20分)1. 设矩阵A为3阶方阵,且满足\( A^2 = A \),则矩阵A的特征值只能是:A. 0B. 1C. 0或1D. 2答案:C2. 如果矩阵B是可逆矩阵,那么\( B^{-1} \)的特征值与B的特征值的关系是:A. 相反数B. 倒数C. 相等D. 互为相反数答案:B3. 向量\( \vec{a} = (1, 2, 3) \)和\( \vec{b} = (4, 5, 6) \)的点积为:A. 14B. 32C. 22D. 40答案:A4. 设\( A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \),则\( A \)的行列式为:A. 2B. -2C. 5D. -5答案:C二、填空题(每题5分,共20分)1. 设矩阵\( A = \begin{pmatrix} 2 & 1 \\ 0 & 3 \end{pmatrix} \),则\( A \)的迹为______。
答案:52. 向量\( \vec{a} = (3, -4) \)和\( \vec{b} = (-1, 2) \)的叉积为向量\( \vec{c} = (x, y) \),则\( x \)的值为______。
答案:103. 设\( A \)为3阶方阵,且\( A \)的秩为2,则\( A \)的零空间的维数为______。
答案:14. 设\( \vec{u} \)和\( \vec{v} \)是两个非零向量,若\( \vec{u} \)和\( \vec{v} \)正交,则\( \vec{u} \cdot \vec{v} \)的值为______。
答案:0三、解答题(共60分)1. (15分)设矩阵\( A = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 1 & 2 & 3 \end{pmatrix} \),求\( A \)的逆矩阵。
大学线性代数期末试卷及答案

大学线性代数期末试题一、填空题(每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
3、n 阶方阵A 满足032=--E A A ,则=-1A。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.已知矩阵n s ij c C B A ⨯=)(,,,满足CB AC =,则A 与B 分别是 阶矩阵。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( ) 三、单项选择题 (每小题仅有一个正确答案。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=TA A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,, 21(3 ≤ s ≤ n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关② s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③ s ααα,,, 21中任一个向量都不能用其余向量线性表示④ s ααα,,, 21中不含零向量3. 下列命题中正确的是( )。
① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ,B 均为n 阶方阵,下面结论正确的是( )。
山东交通学院线代作业纸及答案

a2 b2
证
c2 d2
(a + 1)2 (b + 1)2 (c + 1)2 (d + 1)2
(a + 2)2 (b + 2)2 (c + 2)2 (d + 2)2
(a + 3)2
a2
(b + 3)2
c4 − c3 = =====
b2
(c + 3)2 c3 − c2 c 2
(d + 3)2 c2 − c1 d 2
1 0
===== 0 0
234 0 0 −5 0 − 5 0 = 3× (−5)4 = 1875
0 0 −5 0 0
0 −5 0 0 0
a a2
5. 利用范德蒙德行列式计算四阶行列式
a3 b+c+d
b b2 b3 a+c+d
c c2 c3 a+b+d
d d2 d3 a+b+c
第8页
线性代数标准作业纸答案
(C) x 2
(D) x 4
三、计算
2 1 41
2141
3 −1 2 1 r2 + r1 5 0 6 2
1.
=====
= 0 (因有两行相同)
1 2 32
1232
5 0 62
5062
− ab ac ae r1 ÷ a
− b c e c1 ÷ b
−1 1 1
2. bd − cd de ===== adf b − c e ===== abcdef 1 −1 1
3.
=====
===== −1 c 1
0 −1 c 1
线性代数期末考试精彩试题(卷)+问题详解解析汇报合集

×××大学线性代数期末考试题一、填空题〔将正确答案填在题中横线上.每一小题2分,共10分〕1. 假如022150131=---x ,如此=χ__________. 2.假如齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,如此λ应满足.3.矩阵n s ij c C B A ⨯=)(,,,满足CB AC =,如此A 与B 分别是阶矩阵.4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性. 5.n 阶方阵A 满足032=--E A A ,如此=-1A .二、判断正误〔正确的在括号内填"√〞,错误的在括号内填"×〞.每一小题2分,共10分〕1. 假如行列式D 中每个元素都大于零,如此0〉D .〔 〕2. 零向量一定可以表示成任意一组向量的线性组合.〔 〕3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,如此向量组s a a a ,,, 21线性相关.〔 〕4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,如此A A =-1.〔 〕 5. 假如λ为可逆矩阵A 的特征值,如此1-A 的特征值为λ. < >三、单项选择题 <每一小题仅有一个正确答案,将正确答案题号填入括号内.每一小题2分,共10分>1. 设A 为n 阶矩阵,且2=A ,如此=T A A 〔 〕.①n2②12-n ③12+n ④42. n 维向量组s ααα,,, 21〔3 ≤ s ≤ n 〕线性无关的充要条件是〔 〕. ①s ααα,,, 21中任意两个向量都线性无关 ②s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③s ααα,,, 21中任一个向量都不能用其余向量线性表示 ④s ααα,,, 21中不含零向量3. 如下命题中正确的答案是< >.① 任意n 个1+n 维向量线性相关 ② 任意n 个1+n 维向量线性无关 ③ 任意1+n 个n 维向量线性相关 ④ 任意1+n 个n 维向量线性无关4. 设A ,B 均为n 阶方阵,下面结论正确的答案是< >.① 假如A ,B 均可逆,如此B A +可逆 ② 假如A ,B 均可逆,如此 A B 可逆 ③ 假如B A +可逆,如此 B A -可逆 ④ 假如B A +可逆,如此 A ,B 均可逆5. 假如4321νννν,,,是线性方程组0=X A 的根底解系,如此4321νννν+++是0=X A 的〔〕①解向量② 根底解系③ 通解 ④ A 的行向量四、计算题 < 每一小题9分,共63分>1. 计算行列式x ab c d a x b c d a b x c d abcx d++++.解·2. 设B A AB 2+=,且A ,410011103⎪⎪⎪⎭⎫⎝⎛= 求B .解.A B E A =-)2(⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=--111122112)2(1E A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=-=-322234225)2(1A E A B3. 设,1000110001100011⎪⎪⎪⎪⎭⎫⎝⎛---=B ⎪⎪⎪⎪⎭⎫ ⎝⎛=2000120031204312C 且矩阵X 满足关系式'(),X C B E -=求X . 4. 问a 取何值时,如下向量组线性相关?123112211,,221122a a a ααα⎛⎫⎛⎫-⎛⎫ ⎪ ⎪- ⎪ ⎪ ⎪⎪ ⎪ ⎪=-==- ⎪ ⎪ ⎪⎪ ⎪ ⎪- ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭⎝⎭.5. λ为何值时,线性方程组⎪⎩⎪⎨⎧-=++-=++-=++223321321321x x x x x x x x x λλλλ有唯一解,无解和有无穷多解?当方程组有无穷多解时求其通解.①当1≠λ且2-≠λ时,方程组有唯一解; ②当2-=λ时方程组无解③当1=λ时,有无穷多组解,通解为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=X 10101100221c c 6. 设.77103 ,1301 ,3192 ,01414321⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=αααα 求此向量组的秩和一个极大无关组,并将其余向量用该极大无关组线性表示.7. 设100010021A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,求A 的特征值与对应的特征向量.五、证明题 <7分>假如A 是n 阶方阵,且,I AA =T,1-=A 证明 0=+I A .其中I 为单位矩阵. ×××大学线性代数期末考试题答案一、填空题1. 52. 1≠λ3. n n s s ⨯⨯,4. 相关5. E A 3- 二、判断正误1. ×2. √3. √4. √5. × 三、单项选择题1. ③2. ③3. ③4. ②5. ① 四、计算题 1. 2.A B E A =-)2(⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=--111122112)2(1E A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=-=-322234225)2(1A E A B3. 4.)22()12(812121212121212321-+=------=a a aa aa a a ,,当21-=a 或1=a 时,向量组321a a a ,,线性相关. 5.① 当1≠λ且2-≠λ时,方程组有唯一解; ②当2-=λ时方程组无解③当1=λ时,有无穷多组解,通解为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=X 10101100221c c 6.如此 ()34321=a a a a r ,,,,其中321a a a ,,构成极大无关组,321422a a a a ++-= 7.特征值1321===λλλ,对于λ1=1,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-020*******A E λ,特征向量为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100001l k 五、证明题∴()02=+A I , ∵()0=+A I一、选择题〔此题共4小题,每一小题4分,总分为16分.每一小题给出的四个选项中,只有一项符合题目要求〕1、设A ,B 为n 阶方阵,满足等式0=AB ,如此必有〔 〕<A>0=A 或0=B ; <B>0=+B A ; 〔C 〕0=A 或0=B ; <D>0=+B A . 2、A 和B 均为n 阶矩阵,且222()2A B A AB B +=++,如此必有〔 〕 <A> A E =;<B>B E =; 〔C 〕A B =.<D> AB BA =.3、设A 为n m ⨯矩阵,齐次方程组0=Ax 仅有零解的充要条件是〔 〕 <A>A 的列向量线性无关; <B>A 的列向量线性相关; 〔C 〕 A 的行向量线性无关; <D>A 的行向量线性相关.4、 n 阶矩阵A 为奇异矩阵的充要条件是〔 〕 <A>A 的秩小于n ;<B>0A ≠;<C> A 的特征值都等于零;<D>A 的特征值都不等于零; 二、填空题〔此题共4小题,每题4分,总分为16分〕5、假如4阶矩阵A 的行列式5A =-,A *是A 的伴随矩阵,如此*A =.6、A 为n n ⨯阶矩阵,且220A A E --=,如此1(2)A E -+=.7、方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-+43121232121321x x x a a 无解,如此a =.8、二次型2221231231213(,,)2322f x x x x x tx x x x x =++++是正定的,如此t 的取值X 围是. 三、计算题〔此题共2小题,每题8分,总分为16分〕9、计算行列式1111111111111111x x D y y+-=+-10、计算n 阶行列式四、证明题〔此题共2小题,每一小题8分,总分为16分.写出证明过程〕 11、假如向量组123,,ααα线性相关,向量组234,,ααα线性无关.证明: <1> 1α能有23,αα线性表出; <2>4α不能由123,,ααα线性表出.12、设A 是n 阶矩方阵,E 是n 阶单位矩阵,E A +可逆,且1()()()f A E A E A -=-+. 证明〔1〕 (())()2E f A E A E ++=; 〔2〕 (())f f A A =.五、解答题〔此题共3小题,每一小题12分,总分为32分.解答应写出文字说明或演算步骤〕13、设200032023A ⎛⎫⎪= ⎪ ⎪⎝⎭,求一个正交矩阵P 使得1P AP -为对角矩阵.14、方程组⎪⎩⎪⎨⎧=++=++=++040203221321321xa x x ax x x x x x 与方程组12321-=++a x x x 有公共解. 求a 的值.15、设四元非齐次线性方程组的系数矩阵的秩为3,1η,2η,3η是它的三个解向量,且⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=54321η,⎪⎪⎪⎪⎪⎭⎫⎝⎛=+432132ηη求该方程组的通解.解答和评分标准一、选择题1、C ;2、D ;3、A ;4、A.二、填空题5、-125;6、2π;7、-1;8、53>t . 三、计算题9、解:第一行减第二行,第三行减第四行得:第二列减第一列,第四列减第三列得:00011000011x x D y y-=- 〔4分〕按第一行展开得 按第三列展开得2201x D xyx y y-=-=. 〔4分〕10、解:把各列加到第一列,然后提取第一列的公因子⎪⎭⎫⎝⎛+∑=n i i x 13,再通过行列式的变换化为上三角形行列式2212113313nn n n i i n x x x x D x x x =+⎛⎫=+ ⎪⎝⎭+∑〔4分〕1133n n i i x -=⎛⎫=+ ⎪⎝⎭∑〔4分〕 四、证明题 11、证明:<1>、 因为332,ααα,线性无关,所以32αα,线性无关., 又321ααα,,线性相关,故1α能由32αα,线性表出. <4分> 123()3r ααα=,,,〔2〕、〔反正法〕假如不,如此4α能由321,ααα,线性表出, 不妨设3322114ααααk k k ++=.由〔1〕知,1α能由32αα,线性表出, 不妨设32211αααt t +=.所以3322322114)(αααααk k t t k +++=,这明确432,ααα,线性相关,矛盾. 12、证明〔1〕1(())()[()()]()E f A E A E E A E A E A -++=+-++1()()()()()()2E A E A E A E A E A E A E -=++-++=++-= 〔4分〕〔2〕1(())[()][()]f f A E f A E f A -=-+由〔1〕得:11[()]()2E f A E A -+=+,代入上式得11()()22E A E A A =+--= 〔4分〕 五、解答题 13、解:〔1〕由0E A λ-=得A 的特征值为11λ=,22λ=,35λ=. 〔4分〕〔2〕11λ=的特征向量为1011ξ⎛⎫ ⎪=- ⎪ ⎪⎝⎭,22λ=的特征向量为2100ξ⎛⎫ ⎪= ⎪ ⎪⎝⎭, 35λ=的特征向量为3011ξ⎛⎫ ⎪= ⎪ ⎪⎝⎭. 〔3分〕〔3〕因为特征值不相等,如此123,,ξξξ正交. 〔2分〕〔4〕将123,,ξξξ单位化得1011p ⎛⎫⎪=-⎪⎪⎭,2100p ⎛⎫ ⎪= ⎪ ⎪⎝⎭,3011p ⎛⎫⎪=⎪⎪⎭〔2分〕〔5〕取()123010,,00P p p p ⎛⎫ ⎪ ⎪ == ⎝ 〔6〕1100020005P AP -⎛⎫ ⎪= ⎪ ⎪⎝⎭〔1分〕14、解:该非齐次线性方程组b Ax =对应的齐次方程组为因3)(=A R ,如此齐次线性方程组的根底解系有1个非零解构成,即任何一个非零解都是它的根底解系. 〔5分〕另一方面,记向量)(2321ηηηξ+-=,如此直接计算得0)6,5,4,3(≠=T ξ,ξ就是它的一个根底解系.根据非齐次线性方程组解的结构知,原方程组的通解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=+=543265431k k x ηξ,R k ∈. 〔7分〕15、解:将①与②联立得非齐次线性方程组:假如此非齐次线性方程组有解, 如此①与②有公共解, 且③的解即为所求全部公共解.对③的增广矩阵A 作初等行变换得:→⎪⎪⎪⎪⎪⎭⎫⎝⎛-=112104102101112a a a A ⎪⎪⎪⎪⎪⎭⎫⎝⎛-----11000)1)(2(0001100111a a a a a . 〔4分〕1°当1a =时,有()()23r A r A ==<,方程组③有解, 即①与②有公共解, 其全部公共解即为③的通解,此时⎪⎪⎪⎪⎪⎭⎫⎝⎛→0000000000100101A ,如此方程组③为齐次线性方程组,其根底解系为: ⎪⎪⎪⎭⎫ ⎝⎛-101,所以①与②的全部公共解为⎪⎪⎪⎭⎫ ⎝⎛-101k ,k 为任意常数. 〔4分〕2° 当2a =时,有()()3r A r A ==,方程组③有唯一解, 此时⎪⎪⎪⎪⎪⎭⎫⎝⎛-→0000110010100001A ,故方程组③的解为:011⎛⎫ ⎪ ⎪ ⎪-⎝⎭,即①与②有唯一公共解011x ⎛⎫⎪= ⎪ ⎪-⎝⎭. 〔4分〕线性代数习题和答案第一局部选择题 <共28分>一、单项选择题〔本大题共14小题,每一小题2分,共28分〕在每一小题列出的四个选项中只有一个是符合题目要求的,请将其代码填在题后的括号内.错选或未选均无分. 1.设行列式a a a a 11122122=m,aa a a 13112321=n,如此行列式aa a a a a 111213212223++等于〔 〕A.m+nB. -<m+n>C. n -mD. m -n2.设矩阵A =100020003⎛⎝ ⎫⎭⎪⎪⎪,如此A -1等于〔 〕A. 13000120001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪B. 10001200013⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪ C. 130********⎛⎝ ⎫⎭⎪⎪⎪⎪⎪D. 12000130001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪3.设矩阵A=312101214---⎛⎝⎫⎭⎪⎪⎪,A*是A的伴随矩阵,如此A *中位于〔1,2〕的元素是〔〕A.–6B. 6C. 2D.–24.设A是方阵,如有矩阵关系式AB=AC,如此必有〔〕A.A =0B. B≠C时A=0C.A≠0时B=CD. |A|≠0时B=C5.3×4矩阵A的行向量组线性无关,如此秩〔A T〕等于〔〕A. 1B. 2C. 3D. 46.设两个向量组α1,α2,…,αs和β1,β2,…,βs均线性相关,如此〔〕A.有不全为0的数λ1,λ2,…,λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λsβs=0B.有不全为0的数λ1,λ2,…,λs使λ1〔α1+β1〕+λ2〔α2+β2〕+…+λs〔αs+βs〕=0C.有不全为0的数λ1,λ2,…,λs使λ1〔α1-β1〕+λ2〔α2-β2〕+…+λs〔αs-βs〕=0D.有不全为0的数λ1,λ2,…,λs和不全为0的数μ1,μ2,…,μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=07.设矩阵A的秩为r,如此A中〔〕A.所有r-1阶子式都不为0B.所有r-1阶子式全为0C.至少有一个r阶子式不等于0D.所有r阶子式都不为08.设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,如此如下结论错误的答案是〔〕A.η1+η2是Ax=0的一个解B.12η1+12η2是Ax=b的一个解C.η1-η2是Ax=0的一个解D.2η1-η2是Ax=b的一个解9.设n阶方阵A不可逆,如此必有〔〕A.秩<A><nB.秩<A>=n-1C.A=0D.方程组Ax=0只有零解10.设A是一个n<≥3>阶方阵,如下陈述中正确的答案是〔〕A.如存在数λ和向量α使Aα=λα,如此α是A的属于特征值λ的特征向量B.如存在数λ和非零向量α,使<λE-A>α=0,如此λ是A的特征值C.A的2个不同的特征值可以有同一个特征向量D.如λ1,λ2,λ3是A的3个互不一样的特征值,α1,α2,α3依次是A的属于λ1,λ2,λ3的特征向量,如此α1,α2,α3有可能线性相关11.设λ0是矩阵A的特征方程的3重根,A的属于λ0的线性无关的特征向量的个数为k,如此必有〔〕A. k≤3B. k<3C. k=3D. k>312.设A是正交矩阵,如此如下结论错误的答案是〔〕A.|A|2必为1B.|A|必为1C.A-1=A TD.A的行〔列〕向量组是正交单位向量组13.设A是实对称矩阵,C是实可逆矩阵,B=C T AC.如此〔〕A.A与B相似B. A与B不等价C. A与B有一样的特征值D. A与B合同14.如下矩阵中是正定矩阵的为〔 〕A.2334⎛⎝ ⎫⎭⎪B.3426⎛⎝ ⎫⎭⎪ C.100023035--⎛⎝ ⎫⎭⎪⎪⎪D.111120102⎛⎝ ⎫⎭⎪⎪⎪ 第二局部 非选择题〔共72分〕二、填空题〔本大题共10小题,每一小题2分,共20分〕不写解答过程,将正确的答案写在每一小题的空格内.错填或不填均无分. 15.11135692536=.16.设A =111111--⎛⎝ ⎫⎭⎪,B =112234--⎛⎝ ⎫⎭⎪.如此A +2B =. 17.设A =<a ij >3×3,|A |=2,A ij 表示|A |中元素a ij 的代数余子式〔i,j=1,2,3〕,如此<a 11A 21+a 12A 22+a 13A 23>2+<a 21A 21+a 22A 22+a 23A 23>2+<a 31A 21+a 32A 22+a 33A 23>2=.18.设向量〔2,-3,5〕与向量〔-4,6,a 〕线性相关,如此a=.19.设A 是3×4矩阵,其秩为3,假如η1,η2为非齐次线性方程组Ax=b 的2个不同的解,如此它的通解为.20.设A 是m ×n 矩阵,A 的秩为r<<n>,如此齐次线性方程组Ax=0的一个根底解系中含有解的个数为.21.设向量α、β的长度依次为2和3,如此向量α+β与α-β的内积〔α+β,α-β〕=.22.设3阶矩阵A 的行列式|A |=8,A 有2个特征值-1和4,如此另一特征值为.A =010********---⎛⎝ ⎫⎭⎪⎪⎪,α=212-⎛⎝ ⎫⎭⎪⎪⎪是它的一个特征向量,如此α所对应的特征值为. 24.设实二次型f<x 1,x 2,x 3,x 4,x 5>的秩为4,正惯性指数为3,如此其规X 形为.三、计算题〔本大题共7小题,每一小题6分,共42分〕25.设A =120340121-⎛⎝ ⎫⎭⎪⎪⎪,B =223410--⎛⎝ ⎫⎭⎪.求〔1〕AB T ;〔2〕|4A |. 26.试计算行列式3112513420111533------.27.设矩阵A =423110123-⎛⎝ ⎫⎭⎪⎪⎪,求矩阵B 使其满足矩阵方程AB =A +2B . 28.给定向量组α1=-⎛⎝ ⎫⎭⎪⎪⎪⎪2103,α2=1324-⎛⎝ ⎫⎭⎪⎪⎪⎪,α3=3021-⎛⎝ ⎫⎭⎪⎪⎪⎪,α4=0149-⎛⎝ ⎫⎭⎪⎪⎪⎪. 试判断α4是否为α1,α2,α3的线性组合;假如是,如此求出组合系数.29.设矩阵A =12102242662102333334-----⎛⎝ ⎫⎭⎪⎪⎪⎪. 求:〔1〕秩〔A 〕;〔2〕A 的列向量组的一个最大线性无关组.30.设矩阵A=022234243----⎛⎝ ⎫⎭⎪⎪⎪的全部特征值为1,1和-8.求正交矩阵T 和对角矩阵D ,使T -1AT =D . 31.试用配方法化如下二次型为标准形f<x 1,x 2,x 3>=x x x x x x x x x 12223212132323444+-+--,并写出所用的满秩线性变换.四、证明题〔本大题共2小题,每一小题5分,共10分〕32.设方阵A 满足A 3=0,试证明E -A 可逆,且〔E -A 〕-1=E +A +A 2.33.设η0是非齐次线性方程组Ax=b 的一个特解,ξ1,ξ2是其导出组Ax=0的一个根底解系.试证明 〔1〕η1=η0+ξ1,η2=η0+ξ2均是Ax=b 的解;〔2〕η0,η1,η2线性无关. 答案:一、单项选择题〔本大题共14小题,每一小题2分,共28分〕1二、填空题〔本大题共10空,每空2分,共20分〕15. 616. 337137--⎛⎝ ⎫⎭⎪17. 418. –1019. η1+c<η2-η1>〔或η2+c<η2-η1>〕,c 为任意常数 20. n -r21. –522. –223. 124. z z z z 12223242++-三、计算题〔本大题共7小题,每一小题6分,共42分〕25.解〔1〕AB T=120340*********-⎛⎝ ⎫⎭⎪⎪⎪--⎛⎝ ⎫⎭⎪⎪⎪=861810310⎛⎝ ⎫⎭⎪⎪⎪. 〔2〕|4A |=43|A |=64|A |,而|A |=1203401212-=-. 所以|4A |=64·〔-2〕=-128 26.解 311251342011153351111113100105530------=-----=5111111550----=5116205506255301040---=---=+=. 27.解 AB =A +2B 即〔A -2E 〕B =A ,而 〔A -2E 〕-1=2231101211431531641--⎛⎝ ⎫⎭⎪⎪⎪=-----⎛⎝ ⎫⎭⎪⎪⎪-.所以B=<A-2E>-1A=143153164423110123-----⎛⎝⎫⎭⎪⎪⎪-⎛⎝⎫⎭⎪⎪⎪=3862962129-----⎛⎝⎫⎭⎪⎪⎪.28.解一----⎛⎝⎫⎭⎪⎪⎪⎪−→−-----⎛⎝⎫⎭⎪⎪⎪⎪2130130102243419053213010112013112−→−--⎛⎝⎫⎭⎪⎪⎪⎪−→−⎛⎝⎫⎭⎪⎪⎪⎪1035011200880014141035011200110000−→−⎛⎝⎫⎭⎪⎪⎪⎪1002010100110000,所以α4=2α1+α2+α3,组合系数为〔2,1,1〕.解二考虑α4=x1α1+x2α2+x3α3,即-++=-=-+=+-=⎧⎨⎪⎪⎩⎪⎪230312243491231223123x x xx xx xx x x.方程组有唯一解〔2,1,1〕T,组合系数为〔2,1,1〕.29.解对矩阵A施行初等行变换A−→−-----⎛⎝⎫⎭⎪⎪⎪⎪12102000620328209632−→−-----⎛⎝⎫⎭⎪⎪⎪⎪−→−----⎛⎝⎫⎭⎪⎪⎪⎪12102032830006200021712102032830003100000=B.〔1〕秩〔B〕=3,所以秩〔A〕=秩〔B〕=3.〔2〕由于A与B的列向量组有一样的线性关系,而B是阶梯形,B的第1、2、4列是B的列向量组的一个最大线性无关组,故A的第1、2、4列是A的列向量组的一个最大线性无关组.〔A的第1、2、5列或1、3、4列,或1、3、5列也是〕30.解A的属于特征值λ=1的2个线性无关的特征向量为ξ1=〔2,-1,0〕T, ξ2=〔2,0,1〕T. 经正交标准化,得η1=25555//-⎛⎝⎫⎭⎪⎪⎪,η2=2515451553///⎛⎝⎫⎭⎪⎪⎪.λ=-8的一个特征向量为ξ3=122-⎛⎝⎫⎭⎪⎪⎪,经单位化得η3=132323///.-⎛⎝⎫⎭⎪⎪⎪所求正交矩阵为T=25521515135545152305323////////--⎛⎝⎫⎭⎪⎪⎪. 对角矩阵D=100010008-⎛⎝⎫⎭⎪⎪⎪.〔也可取T=25521515130532355451523////////---⎛⎝⎫⎭⎪⎪⎪.〕31.解 f<x1,x2,x3>=〔x1+2x2-2x3〕2-2x22+4x2x3-7x32=〔x1+2x2-2x3〕2-2〔x2-x3〕2-5x32.设y x x xy x xy x11232233322=+-=-=⎧⎨⎪⎪⎩⎪⎪,即x y yx y yx y112223332=-=+=⎧⎨⎪⎩⎪,因其系数矩阵C=120011001-⎛⎝⎫⎭⎪⎪⎪可逆,故此线性变换满秩.经此变换即得f<x1,x2,x3>的标准形 y12-2y22-5y32.四、证明题〔本大题共2小题,每一小题5分,共10分〕32.证由于〔E-A〕〔E+A+A2〕=E-A3=E,所以E-A可逆,且〔E-A〕-1= E+A+A2.33.证由假设Aη0=b,Aξ1=0,Aξ2=0.〔1〕Aη1=A〔η0+ξ1〕=Aη0+Aξ1=b,同理Aη2= b, 所以η1,η2是Ax=b的2个解.〔2〕考虑l0η0+l1η1+l2η2=0, 即〔l0+l1+l2〕η0+l1ξ1+l2ξ2=0.如此l0+l1+l2=0,否如此η0将是Ax=0的解,矛盾.所以l1ξ1+l2ξ2=0. 又由假设,ξ1,ξ2线性无关,所以l1=0,l2=0,从而l0=0 .所以η0,η1,η2线性无关.。
线性代数期末考试试题及答案

线性代数期末考试试题及答案 A 卷一、填空题:(每空3分, 共 15分)1、在五阶行列式中,项4335521421a a a a a 的符号取 正2、A 为一个四阶方阵,且||=3,A k R ∈,则|k |=A 43k3、设A 为一个三阶方阵,其特征值为1,2,3,则||=A 6 ,则112233++=a a a 64、设=,,T T Tαβγ==(2,1,2)(1,2,2)(2,2,t )线性相关,则t =38二、单项选择题:( 每小题 3 分, 共 15分 )1.设行列式D =333231232221131211a a a a a a a a a =3,D 1=111112132121222331313233737373a a a a a a a a a a a a +++,则D 1的值为( C ) (A) -21(B) –9 (C) 9(D)212、设n 元齐次线性方程组0=AX 的系数矩阵A 的秩为r ,则0=AX 有非零解的充分必要条件是( B )(A )n r =; (B )n r <; (C )n r >; (D )n r ≥3、设,A B 均为n 阶矩阵,则( D )(A) A B A B +=+ (B) AB BA = (C) ()()R AB R BA = (D)AB B A =4、下面的陈述中,正确的选项是( D )(A)向量组中,整体向量线性相关,则部分向量必线性相关 (B)向量组中,部分向量线性无关,则整体向量必线性无关(C)向量组中,整体向量线性无关,则部分向量必线性相关 (D)向量组中,部分向量线性相关,则整体向量必线性相关5、设n n A ⨯是n 阶可逆矩阵,*A 是A 伴随矩阵,则( A ).(A )1-*=n AA ; (B )A A =*;(C )nA A =*; (D )1-*=A A .三、(10分)计算n 阶行列式121212333n n n x x x x x x x x x +++。
(完整版),大一线性代数期末试题及答案,推荐文档

【 】
A. a1 a2 0 b2 b3
B. a1 a2 0 b1 b2
C. a1 a2 a3 b1 b2 b3
9.方程组
2x1 x2 x3 1 x1 2x2 x3 1
3 x1 3x2 2x3 a 1
有解的充分必要的条件是
D. a1 a3 0 b1 b2
【 】
A. a=-3
25. -2 4
0
4 0 1
19. 16 23. 1、2、3
20. 2
三、计算题(每小题 6 分,共 30 分)
0345
345
3 4 1 0
26. D
3 2 2 - 2 …………4 分 96. …………8 分
0 2 2 2
69 2
0 692
27. 解:由于 A2 AB E ,因此 AB A2 E ,又 A 1 0 ,故 A 可逆, ……2 分
101
101 002
a1 (1, 0,1), a2 (1,1, 0), a3 (0,1,1) 为 R3 的一组基,…………4 分
又设
x
x11
x2 2
x3 3
,得线性方程组
x1
x2
x2 x3
2 2
《线性代数》试卷第 6页x1共7x3页 2
解之得向量 x (2, 2, 2) 在该组基下的坐标为 x (1,1,1) 。…………8 分
6 -2 7 2
1 1 1
26.设 A
0
1
1 ,且 A2 AB E ,其中 E 是三阶单位矩阵,求矩阵 B。
0 0 1
27.a
取何值时,方程组 4x1
x1 2x2 7x2 x3
3 10 有解?在有解时求出方程组的通解。
(完整word版)线性代数期末考试试题 答案解析合集

×××大学线性代数期末考试题一、填空题(将正确答案填在题中横线上。
每小题2分,共10分)1. 若022150131=---x ,则=χ__________。
2.若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ只有零解,则λ应满足 。
3.已知矩阵n s ij c C B A ⨯=)(,,,满足CB AC =,则A 与B 分别是 阶矩阵。
4.矩阵⎪⎪⎪⎭⎫⎝⎛=323122211211a a a a a a A 的行向量组线性 。
5.n 阶方阵A 满足032=--E A A ,则=-1A 。
二、判断正误(正确的在括号内填“√”,错误的在括号内填“×”。
每小题2分,共10分)1. 若行列式D 中每个元素都大于零,则0〉D 。
( )2. 零向量一定可以表示成任意一组向量的线性组合。
( )3. 向量组m a a a ,,, 21中,如果1a 与m a 对应的分量成比例,则向量组s a a a ,,, 21线性相关。
( )4. ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010*********0010A ,则A A =-1。
( ) 5. 若λ为可逆矩阵A 的特征值,则1-A 的特征值为λ。
( )三、单项选择题 (每小题仅有一个正确答案,将正确答案题号填入括号内。
每小题2分,共10分)1. 设A 为n 阶矩阵,且2=A ,则=T A A ( )。
① n2② 12-n③ 12+n ④ 42. n 维向量组 s ααα,,, 21(3 ≤ s ≤ n )线性无关的充要条件是( )。
① s ααα,,, 21中任意两个向量都线性无关 ② s ααα,,, 21中存在一个向量不能用其余向量线性表示 ③ s ααα,,, 21中任一个向量都不能用其余向量线性表示④ s ααα,,, 21中不含零向量 3. 下列命题中正确的是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
号学
1.按自然数从小到大为标准次序,排列
、填空题(每小题3分,共15 分)
4 1 3 2的逆序数等于
1 1 1
2.设A 为3阶矩阵,| A| ,则| 2A |
.
2 4 3. 万阵A 可逆的充分必要条件是
(D )
(A ) Ax 0有非零解 (B ) Ax b 无解 (C ) Ax b 有解
(D ) A 0
名姓 级班 等^90
专路、级本升专、^90科工理 级班用适卷试
0 1 0
1 2 3
4 5 6 3.设1 0 0 A
4 5 6 则A 1 2 3
0 0 1
7 8 9
7 8 9
1 0 0
4•设 A 0 0
0 A *为A 的伴随矩阵,贝U R A * 0
0 0 0
3
1 3 5 6 x 的矩阵是 3 5 7
9
5 7 9
1 2 5.二次型 f(x) x T
4
5 7 8 2 0 1.三阶行列式1
4 3 4 单项选择题(每小题3分,
1
1 0 ,则x 等于 x
(A) 1
(B)
2•设A 为n 阶可逆矩阵
*
(A )
A (C ) 1
A *为A 的伴随矩阵,则
*
(B) A
共15分)
(D )
n *
(C ) ( 1) A
(D )
n 1
*
(D ) ( 1) A
定矩阵的是
(A )
(A) A B
(B)
A B
(C)
A * -
B *
(D)
* * AB
5.已知3阶矩阵A 的特征值为
1,2, 3, A *为A 的伴随矩阵,
则|A *
3A 2E
等于
(C )
(A ) 7
(B )
7
(C ) 25
(D )
25
4. 设A, B 均为n 阶正定矩阵, A *和B *分别为A 与B 的伴随矩阵,则在下列矩阵中是正
解将第一行乘
D n
三、(10分)
计算行列式( D n 为n 阶行列式,
x
a a
D n
a
x
a
a a
x
n 2为整数)
1分别加到其余各
行
得
ax 0
再将各列都加到第一列上
得
x (n 1)a a a
0 x a 0 0
0 x a
(5分)
(5分)
号学名姓
级班等级专路、级9本升专、级科工理级
班用适卷试
密
-
-
-
-
-
-
-i ----
---
1
四、(10分)设A 0
1
0 且AB
解由AB
因为|A E |
A2 B 得A E B A2
所以A E可逆从而
E A2B,求B.
(4
分)
(6
分)
(1) 有唯一解
解
(
1
)
(10
分)
取何值时齐次线性方程组
(2)有无穷多个解?
X2
X2
X2
X3
X3
X3
要使方程组有唯一解
(6
分)
(
1
)
(
2
必须R(A) 3.因此当
要使方程组有有无穷多个解必须R(A) 3,故
因此当1或2时方程组有无穷多个解.
2时方程组有唯一解;
(4
分)
知
求该方程组的通
解。
解设该方程组为Ax
为1,从而Ax
又2 3
基础解
系。
又1为Ax
六、(10分)设四元非齐次线性方程组的系数矩阵的秩为3,已
3是它的三个解向量,且
T
3 4 5, 2 3 12 3
b,因为R(A) 3,所以四元齐次线性方程组
0的一个非零解就是它的一个基础解系。
------
2 3 4 T显然是Ax 0的一个非零解,所以1 2
b的一个解,故方程组Ax b的通解为
Ax 0的解集的秩
(4分)
3 4 T是它的一个
(3
分)
(3
分)
山东交通学院期末考试线性代数课程试卷答案和评分标准(B )卷2010 - 2011 学年第一学期第3页共3页号
学
名
姓
级班等级
OD
专路、级本升专、^级o 科工理级班用适卷试
密
-
-
-
-
-
-
-
i
-
-
-
-
-
-
-
七、(10
分)
解令P P
1
P2
因为
征向量依次为
P
3
P 1AP
所以A
设3阶方阵A的特征值为
P1 0 1
diag 2,
2, 2 2, 1,对应的特
,
P2
T
1 , P3 T
0 ,求A.
,a n是一组n维向量,任一n维向量都可
由a「a2,川,a n线性表示证明@,a2,川,a n线性无关。
证明:已知任一n维向量都可由a1,a2^| ,a n线性表示故单位坐标向量组^,e2^| ,e n
九、(10 分)设a1, a2,
2,
1
(4
分)
(3
分)
(3
分)
八
、
解二次型的矩阵为
(10
分)
判定二次型3y29z22xy 4xz的正定性.
因为
所以f为正定
an
(3
分)
|A| 6
(7
分)
能由a「a2,川,a.线性表示于是有
n R e©川,e n R ^忌卅,a. n
即只耳屜卅,a. n所以印忌川,a.线性无关
(8
分)
(2
分)。
