西安交通大学--应用统计学
西安交通大学22春“会计学”《应用统计分析》期末考试高频考点版(带答案)试卷号2

西安交通大学22春“会计学”《应用统计分析》期末考试高频考点版(带答案)一.综合考核(共50题)1.商品的价格在标志分类上属于数量标志。
()A.对B.错参考答案:A2.差异性是统计研究现象总体数量的前提。
()A.正确B.错误参考答案:A3.总体中各标志值之间的差异程度越大,标准差系数就越小。
()A.正确B.错误参考答案:B4.下列现象的相关密切程度最高的是()。
A.某商店的职工人数与商品销售额之间的相关系数为0.87B.流通费用水平与利润率之间的相关关系为-0.94C.商品销售额与利润率之间的相关系数为0.51D.商品销售额与流通费用水平的相关系数为-0.81参考答案:B5.本年与上年相比,若物价上涨10%,则本年的1元只值上年的0.9元。
()B.错误参考答案:B6.加权算术平均数的大小受哪些因素的影响()。
A.受各组频数或频率的影响B.受各组标志值大小的影响C.受各组标志值和权数的共同影响D.只受各组标志值大小的影响E.只受权数大小的影响参考答案:ABC7.只有当相关系数接近于+1时,才能说明两变量之间存在高度相关关系。
()A.正确B.错误参考答案:B8.全面调查是对调查对象总体的所有个体进行调查,下述调查属于全面调查的是()。
A.对某种连续生产的产品质量进行抽查B.某地区对工业企业设备进行普查C.对全国钢铁生产中的重点单位进行调查D.抽选部分地块进行农产量调查参考答案:B9.回归分析中计算的估计标准误就是因变量的标准差。
()A.正确B.错误参考答案:A10.某班4名学生金融考试成绩分别为70分、80分、86分和95分,这4个数字是()。
A.标志B.指标值C.指标D.变量值参考答案:D11.哪几种抽样方式可以通过提高样本的代表性而减小抽样误差?()A.分层抽样B.简单随机抽样C.整群抽样D.等距抽样E.普查参考答案:AD12.每一次抽样的实际误差虽然不可知,但却是唯一的,因而抽样误差不是随机变量。
奥鹏西安交通大学课程考试《统计学》参考资料答案.doc

西安交通大学课程考试复习资料单选题1.已知某地区1995年粮食产量比1985年增长了1倍,比1990年增长了0.5倍,那么1990年粮食产量比1985年增长了( )。
A.0.33倍B.0.5倍C.0.75倍D.2倍答案: A2.在单因素方差分析中,若Q=20,Q2=10,r=4,n=20,则F值为()。
A.2B.6.33C.2.375D.5.33答案: D3.加工零件所使用的毛坯如果过短,加工出来的零件则达不到规定的标准长度μ0,对生产毛坯的模框进行检验,所采用的假设应当为( )。
A.μ=μ0B.μ≥μ0C.μ≤μ0D.μ≠μ0答案: A4.对某地区的全部产业依据产业构成分为第一产业、第二产业和第三产业,这里所使用的计量尺度是( )。
A.定类尺度B.定序尺度C.定距尺度D.定比尺度答案: A5.某地区农民人均收入最高为426元,最低为270元,据此分为六组,形成闭口式等距列,各组的组距为( )。
A.71B.26C.156D.348答案: B6.某地区2000~2009年的每年年末人口数是()A.时间序列数据B.截面数据C.分类数据D.顺序数据答案: A7.问卷调查中,提问项目的设计,应注意()A.一项提问可包含几项内容B.注意敏感性问题提问C.用词要确切、通俗D.时间答案: C8.变量x与y之间负相关,是指()A.x值增大时y值也随之增大B.x值减少时y值也随之减少C.x值增大时y值也随之减少,或者x值减少时y值也随之增大D.y的取值几乎不受x取值的影响答案: C9.描述统计学和推断统计学区分的依据是()A.研究的内容不同B.对总体数据分析研究的方法不同C.研究的范围不同D.研究的领域不同答案: B10.统计分组的核心问题是()A.选择分组方法B.确定组数C.选择分组标志D.确定组中值答案: C11.若甲、乙、丙三人的数学成绩平均为72分,加上丁的数学成绩,平均为78分,则丁的数学成绩为()分。
2015.4—西安交通大学管理学院管理科学系—胡平成功的演示报告

根据问题研究的需要,学习调查/实验的设计和相关 的分析技术;
学习实践报告的撰写和课堂报告幻灯片的准备; 学习小组的实践成果课堂报告,并提交电子版实践报
告; 学习师生之间的提问和相互点评
2. 计算与分析——多方法的结果比较
课程内容简介
以4-5人为小组,学习应用统计学在经济 和工商企业的管理等方面实际问题的资料 收集或调查;运用 SPSS统计分析软件包 或Excel软件为工具;初步掌握应用统计 学解决实际问题的主要环节和方法的综合 应用;完成研究报告写作和课堂报告的全 过程。
2015.4—西安交通大学管理学院管理科学系—胡平
4.20
讲课
实践课的要求和案例分析,第一次小组实践 作业布置。
2
4
10 4.27 报告 第一次小组实践的报告和课堂提问、考核 2
纲
5.4
第一次小组实践结果的分析和点评,第二次 2 4
及
11
讲课 小组实践作业布置。
时
12 5.11 报告 第二次小组实践的报告和课堂提问、考核 2
间
5.18
第二次小组实践结果的分析和点评,第三次 2
2015.4—西安交通大学管理学院管理科学系—胡平
过程考核 考核方式及评分办法
出席 课堂报告 课堂提问 小组报告 课程成绩
10% 30% 30% 30% 100%
三次练习的成绩加权得总成绩
2015.4—西安交通大学管理学院管理科学系—胡平
周日 次期
教学 环节
内
容
课
课 课外 内学 学时 时
程 大
9
西安交通大学博士研究生入学考试科目主要参考书
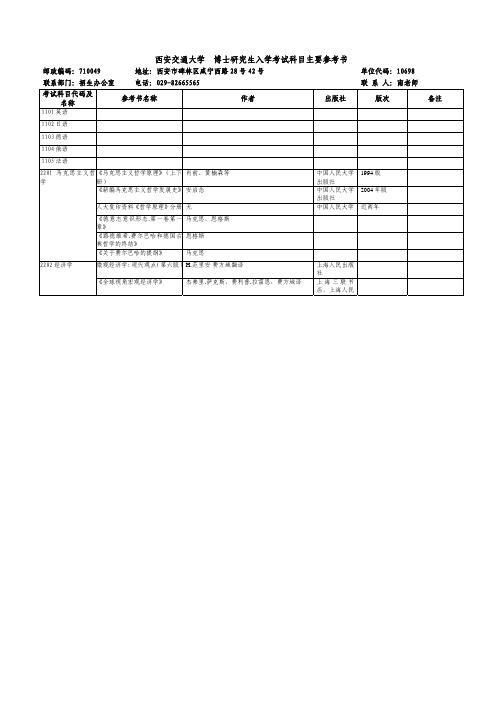
《生物化学》(影印版)
《生物化学》(第三版)
2212 细胞生物学 《医学细胞生物学》
2213 数理统计与随《数理统计》 机过程
方俊鑫,陆栋 贾弘褆 ,冯作化主编 B.D Hames,N.M.Hooper, J.D.Houghton 王镜岩等 胡以平主编 汪荣鑫
上海科技出版 社 人民卫生出版 社 科学技术出版 社 高等教育出版 社 高等教育出版 社 西安交大出版 社
单位代码:10698
联系部门:招生办公室
电话:029-82665565
考试科目代码及 名称
参考书名称
作者
出版社
出版社
联 系 人:南老师
版次
备注
2203 高级微观经济微观经济学:现代观点(第六版)H.范里安 费方域翻译 学
2204 马克思主义经《马克思主义经典著作选读》导 教育部社科司组编
典著作
读
2205 常微分方程 常微分方程
2006 年 1991 年 1989 年 1984 年 1989 年 1984 年 2007 年 8 月 2005 年 1992 年 2006 年 5 月 2000 年
备注
西安交通大学 博士研究生入学考试科目主要参考书
邮政编码:710049
地址:西安市碑林区咸宁西路 28 号 42 号
单位代码:10698
西安交通大学 博士研究生入学考试科目主要参考书
邮政编码:710049
地址:西安市碑林区咸宁西路 28 号 42 号
单位代码:10698
联系部门:招生办公室
电话:029-82665565
考试科目代码及 名称
参考书名称
1101 英语
作者
出版社
联 系 人:南老师 版次
应用数理统计习题答案_西安交大(论文资料)

应用数理统计答案学号:姓名:班级:目录第一章数理统计的基本概念 (2)第二章参数估计 (14)第三章假设检验 (24)第四章方差分析与正交试验设计 (29)第五章回归分析 (32)第六章统计决策与贝叶斯推断 (35)对应书目:《应用数理统计》施雨著西安交通大学出版社第一章 数理统计的基本概念1.1 解:∵2(,)X N μσ∼ ∴ 2(,)n X N σμ∼∴)(0,1)X N μσ−∼分布∴(1)0.95P X P μ−<=<=又∵ 查表可得0.025 1.96u = ∴ 221.96n σ=1.2 解:(1) ∵ (0.0015)X Exp ∼∴ 每个元件至800个小时没有失效的概率为:8000.001501.2(800)1(800)10.0015x P X P X e dxe −−>==−<=−=∫∴ 6个元件都没失效的概率为: 1.267.2()P e e −−==(2) ∵ (0.0015)X Exp ∼∴ 每个元件至3000个小时失效的概率为:30000.001504.5(3000)0.00151x P X e dxe−−<===−∫∴ 6个元件没失效的概率为: 4.56(1)P e −=−1.4 解:ini n x n x ex x x P ni i 122)(ln 2121)2(),.....,(122=−−Π∑==πσμσ1.5证:∵21122)(na a x n x a x ni ni ii+−=−∑∑==∑∑∑===−+−=+−+−=ni i ni i ni i a x n x x naa x n x x x x 1222211)()(222a) 证:)(11111+=+++=∑n ni i n x x n x )(11)(1111n n n n n x x n x x x n n −++=++=++])()1(1 ))((12)[(11)](11[11)(11212111121211212112n n n i n n n i n i n i ni n n n i n i n in x x n n x x x x n x x n x x n x x n x x n S −+++−−+−−+=−+−−+=−+=++=+=+=+=++∑∑∑∑] )(11))1()((12)([112111212n n n n n n n n n x x n x n x x n x x n x x nS n −++−+−+−−++=++++])(11S [1 ])(1[nS 11212n 212n n n n n x x n n n x x n n n −+++=−+++=++ 1.6证明 (1) ∵22112211221()()()2()()()()()nni ii i nni i i i ni i X X X X X X X X X n X X X n X μμμμμ=====−=−+−=−+−−+−=−+−∑∑∑∑∑(2) ∵2221112221221()22ii i nn ni i i i i ni ni XX X X X nX X nX nX X nX =====−=−+=−+=−∑∑∑∑∑1.10 解: (1).∑∑====ni i n i i x E n x n E X E 11)(1)1()(p np n=⋅=1np mp x D n x n D X D ni in i i )1()(1)1()(121−===∑∑==))(1()(122∑=−=n i i x x n E S E)1(1)])1(1())1(([1)])()(())()(([1])()([1])([12222212212212p mp nn p m p mp n n p m p mp n n x E x D n x E x D n x nE x E n x x E n ni i i n i i n i i −−=+−−+−=+−+=−=−=∑∑∑=== 同理,(2). λ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(λnx D n x n D X D ni in i i 1)(1)1()(121===∑∑==λnn x E x D n x E x D n x nE x E n S E ni i i n i i 1)])()(())()(([1])()([1)(2122122−=+−+=−=∑∑==(3). 2)(1)1()(11b a x E n x n E X E ni i n i i +===∑∑==na b x D nx n D X D ni ini i 12)()(1)1()(2121−===∑∑==12)(1)])()(())()(([1])()([1)(22122122a b nn x E x D n x E x D n x nE x E n S E ni i i n i i −⋅−=+−+=−=∑∑==(4). λ===∑∑==ni i n i i x E n x n E X E 11)(1)1()(nx D nx nD X D ni ini i 2121)(1)1()(λ===∑∑==221221221)])()(())()(([1])()([1)(λnn x E x D n x E x D n x nE x E n S E ni i i n i i −=+−+=−=∑∑==(5). μ===∑∑==ni ini i x E nx nE X E 11)(1)1()(nx D nx nD X D ni i ni i 2121)(1)1()(σ===∑∑==221221221)])()(())()(([1])()([1)(σ⋅−=+−+=−=∑∑==nn x E x D n x E x D n x nE x E n S E ni i i n i i1.11 解:由统计量的定义知,1,3,4,5,6,7为统计量,5为顺序统计量 1.17 证:),(~ λαΓX ∵xe x xf λαααλ−−Γ=∴1)()( 令kXY =ke ky k k e ky yf kyky ⋅Γ=⋅Γ=∴−−−−λαααλαααλαλ11)()( )()()(即 ),(~ky Y αΓ1.18 证:),(~ b a X β∵),()1()( 11b a B x xx f b a −−−=∴),(),( ),()1()( 11b a B b k a B b a B x x x X E b a k k +=−=∴∫∞+∞−−−),(),1()( b a B b a B X E +=∴ba a ab a b a b a a a a b a b a a a b b a b a b a +=Γ+Γ++ΓΓ=Γ++Γ+Γ+Γ=ΓΓ+Γ⋅++ΓΓ+Γ=)()()()()()()1()()1()()()()1()()1(),(),2()(2b a B b a B X E +=))(1()1()()()()2()()2(b a b a a a a b b a b a b a ++++=ΓΓ+Γ⋅++ΓΓ+Γ= 22)]([)()( X E X E X D −=∴2))(1())(1()1(b a b a ab ba ab a b a a a +++=+−++++= 1.19 解:∵ (,)X F n m ∼分布2212(1)022()((1))((1)()()()(1)()()n n m n mn m yn m y n mn nP Y y P X X y m myP X y n n n x x dx m mm ++−−+≤=+≤=<−Γ=+ΓΓ∫2222122221122()()()1((1()()11(1)(1)(,)n n m n m n m n m n m f y P Y y y y yy y yy B ++−−−−′=≤Γ=+ΓΓ−−−−=∴ 22(1)(,)n mn n Y X X m mβ=+∼分布1.20 解:∵ ()X t n ∼分布122212()()((2(1n n P Y y P X y P X xdxn ++−≤=≤=≤≤=+112211221212122()()()(1)()1()(1(()()n n n n n f y P Y y y y n y y nn n +++−−+−−′=≤Γ=+Γ=+ΓΓ∴ 2(1,)2nY X F =∼分布1.21 解: (1) ∵ (8,4)X N ∼分布∴ 4(8,)25X N ∼ 分布,即5(8)(0,1)2X N −∼ ∴ 样本均值落在7.88.2∼分钟之间的概率为:5(7.88)5(8)5(8.28)(7.88.2)()2220.383X P X P −−−≤≤=≤≤=(2) 样本均值落在7.58∼分钟之间的概率为:5(7.58)5(8)5(88)(7.58)(2225(8)(0 1.25)20.3944X P X P X P −−−≤≤=≤≤−=≤≤= 若取100个样品,样本均值落在7.58∼分钟之间的概率为:10(7.88)10(8)10(8.28)(7.88.2)(2222*(0.84130.5)0.6826X P X P −−−≤≤=≤≤=−= 单个样品大于11分钟的概率为:110.77340.2266P =−= 25个样品的均值大于9分钟的概率为210.97980.0202P =−= 100个样品的均值大于8.6分钟的概率为310.99870.0013P =−= 所以第一种情况更有可能发生1.23 解:(1) ∵ 2(0,)X N σ∼分布 ∴ 2(0,X N nσ∼分布∴ 22)(1)nXχσ∼∵ 222221()(ni i nXa X an X an σσ===∑∴ 21a n σ=同理 21b m σ=(2) ∵2(0,)X N σ∼分布 ∴222(1)X χσ∼分布由2χ分布是可加性得:2221()ni i X n χσ=∑∼()ninX c X t m ==∑∼ ∴c =(3) 由(2)可知2221()ni i X n χσ=∑∼2221122211(,)nni ii i n mn mi ii n i n X d Xnn dF n m XmXmσσ==++=+=+=∑∑∑∑∼∴ md n=1.25 证明:∵ 211(,)X N μσ∼分布 ∴ 2211((1)i X μχσ−∼∴ 1221111(()n i i X n μχσ=−∑∼同理 2222212(()n i i Y n μχσ=−∑∼ 1122222112211111222221122112()()(,)()()n n i i i i n n i i i i X n n X F n n Y n Y n μσμσμσμσ====−−=−−∑∑∑∑∼ 第二章 参数估计2.1 (1) ∵ ()X Exp λ∼分布∴ ()1E X λ=令 ˆ1X λ= 解得λ的矩估计为: ˆ1X λ= (2) ∵ (,)X U a b ∼分布∴ ()2a bE X +=2()()12b a D X −=令 1ˆˆ2ab A X +==22221ˆˆˆˆ()()1124n i i b a a b A X n =−++==∑ (22211n i i X X S n =−=∑)解得a 和b 的矩估计为:ˆˆaX bX =−=(3) 110()1E X x x dx θθθθ−=∗=+∫令 1ˆˆ1A X θθ==+∴ˆ1XXθ=− (4) 110()(1)!kk x kE X x x e dx k βββ−−=∗=−∫令ˆkX β= ∴ ˆkXβ=(5) 根据密度函数有2221()22()E X a aE X a λλλ=+=++根据矩估计有1222221ˆˆˆ22ˆˆˆa A X a a A S X λλλ+==++==+解得λ和a 的矩估计为:ˆˆaX λ==(6) ∵ (,)X B m p ∼ ∴ ()E X mp =令 1ˆmpA X == 解得p 的矩估计为:ˆXpm= 2.3解:∵ X 服从几何分布,其概率分布为:1()(1)k P X k p p −==−故p 的似然函数为: 1()(1)ni i x nnL p p p =−∑=−对数似然函数为:1ln ()ln ()ln(1)ni i L p n p x n p ==+−−∑令 1ln ()1()01nii L p n x n p p p =∂=−−=∂−∑ ∴ 1ˆpX= 2.4 解:由题知X 应服从离散均匀分布,⎪⎩⎪⎨⎧≤≤==其它01 1)(Nk N k x p2)(NX E =矩估计: 令 7102=∧N1420=∴∧N 极大似然估计:⎪⎩⎪⎨⎧≤≤=其它07101 1)(NN N L ∵要使)(N L 最大,则710=N710=∴∧N 2.5 解:由题中等式知:2196.196.196.1)025.01(025.0)(1S X +=+=∴+=+−Φ=∴=−Φ−∧∧∧−σμθσμμσθσμθ2.6 解:(1) 05.009.214.2=−=R ∵0215.005.04299.05=×==∴∧d Rσ(2)将所有数据分为三组如下所示:1x 2x 3x 4x5x 6x i R1 2.14 2.10 2.15 2.13 2.12 2.13 0.05 2 2.10 2.15 2.12 2.14 2.10 2.13 0.05 32.11 2.14 2.10 2.11 2.15 2.10 0.050197.005.03946.005.0)05.005.005.0(316=×==∴=++=∴∧d R R σ 2.7 解:(1)⎩⎨⎧+<<=其它 01x 1)(θθx f ∵ θθθθθθ≠+==+=++=∴∧21)()(2121)(X E E X E ∴ X =∧θ不是θ的无偏估计,偏差为21=−∧θθ(2) θ=−21(X E ∵ 21−=∴∧X θ是θ的无偏估计(3)22))(()())(()(θθθθ−+=−+=∧∧X E X D E D MSE41121+=n 2.8 证:由例2.24,令2211x a x a +=∧μ,则∧μ 为μ无偏估计应 满足121=+a a因此1μ,2μ,3μ都是μ的无偏估计)()()()(21)()(2513)()(95)9491)(()())(()()(1233212221212∧∧∧∧∧∧=∧<<===+=∴+==∑μμμμμμμD D D X D D X D D X D X D D a a X D X D a D i i i ∵∵2132121X X +=∴∧μ最有效2.9证: )(~λp X ∵ λλ==∴)( )(X D XEX ∵是λ=)(X E 的无偏估计,2*S 是λ=)( X D 的无偏估计)()1()())1((2*2*S E X E S X E αααα−+=−+∴λλααλ=−+=)1(∴2*)1(SX αα−+是λ的无偏估计2.10 解:因为2222((1))()(1)()(1)()1(1)()11(1)1E X S E X E S na E S n n a E S n n n a n nααααλαλαλαλλ∗∗+−=+−=+−−=+−−−=+−=− 所以 2(1)X S αα∗+−是λ的无偏估计量2.15 解:因为ˆθ是θ的有效估计量ˆˆˆ()()()E uE a b aE b a b u θθθ=+=+=+= 221ˆˆˆˆ()()()()D u D a b a D a D θθθ=+=≤ (其中,1ˆθ是θ的任意无偏估计量中的一个)所以 ˆu是u 的有效估计量 2.26 解: 因为总体服从正态分布,所以)01X U N μσ−=∼(,)对于给定的1α−,查标准正态分布表可得2u α,使得2()1P U u αα<=−即:22()1P X p X ααα−<<=−区间的长度2d L α=<,所以 22224u n L ασ>2.28 解:因为总体服从正态分布,所以)01X U N μσ−=∼(,), 222(1)nS V n χσ=−∼由因为U 和V 是相互独立的,所以(1)X T t n =−∼对于给定的1α−,查标t 分布表可得t α,使得 2()1P U t αα<=−,即:22()1P X X ααμα<<+=− 当30n =,35X =,15S =时,第一家航空公司平均晚点时间μ的95%的置信区间为:(29.3032,40.6968)对于给定的1α−,查标t 分布表可得t α,使得 ()1P U t αα>=−, 即:()1P X αμα<+=− 故μ的具有单侧置信上限的单侧置信区间为(,)X α−∞+ 所以经计算可得:第一家航空公司的单侧上限置信区间为(,39.7327)−∞第二种航空公司的单侧上限置信区间为(,36.3103)−∞所以选择第二家航空公司。
西安交通大学《应用统计分析》试题

共5页第1页共5页第2页3、在相关分析中,要求相关的两个变量()A.都是随机变量 B.都不是随机变量C.其中因变量是随机变量 D.其中自变量是随机变量4、抽样估计的优良标准是()A.无偏性B.一致性C.有效性D.代表性E.随机性5、据统计,某行业的平均利润率在6.1-10.8%之间,其置信度为95%,试判断下列说法中正确的有():A.有95%的企业利润率在6.1-10.8%之间;B.若随机抽取该行业许多样本,则其中95%的样本均值,即平均利润在6.1-10.8%之间;C .有95%的把握说,从该行业的平均利润率会落在区间6.1-10.8%内;D .随机抽取该行业的一个企业,有95%的把握说,其利润率在6.1-10.8%之间;6、用P 值进行双侧假设检验时,拒绝原假设的决策准则是()A.P>α;B.P<α;C.P>α/2;D.P<α/2.7、用分布进行拟合优度检验时,要求各组的期望频数()。
2χA.可取任意值; B.大于0; C.不小于10; D.不小于5。
8、在回归分析时,发生严重的多重共线会导致()。
A .对回归方程的F 检验显著,但关于回归系数的t 检验几乎都通不过;B .对回归系数的估计偏误很大,甚至会使回归系数估计值的正负号与预期的相反;C .反映模型拟合程度的判定系数的值变小;D .用回归模型进行预测时,置信区间会变宽。
9、抽样误差是指()。
A、在调查过程中由于观察、测量等差错所引起的误差B、在调查中违反随机原则出现的系统误差C、随机抽样而产生的代表性误差D、人为原因所造成的误差10、某研究人员想要分析学历(高中以下,大专,本科,硕士研究生,博士研究生)与就业状况(失业,临时雇佣,长期雇佣)是否有关联时,适合的统计方法有()。
A .相关分析;B.列联分析;C.方差分析;D.回归分析。
三、计算分析题(共2题,第一题20分,第二题10分,共计30分)1.背景:Metropolitan Research 有限公司是一家消费者市场调查公司,在某一项研究中,Metropolitan 调查了消费者对某一制造商所生产汽车性能的满意程度。
其他系统西安交通大学---统计学所有答案

其他系统西安交通大学---统计学所有答案对变化较大、变动较快的现象应采用经常性调查来取得资料。
()答案是:正确按人口平均的粮食产量是一个平均数。
()答案是:错误算术平均指数是反映平均指标变动程度的相对数。
()答案是:错误在时间数列中,累计增长量等于逐期增长量之和,定基增长速度等于环比增长速度之积。
()答案是:错误3,指数的实质是相对数,它能反映现象的变动和差异程度。
()答案是:正确相对指标的可比性原则是指对比的两个指标柜总体范围、时间范围、指标名称、计算方法等方面都要相同。
()答案是:正确在平均指标变动因素分析中,可变构成指数是专门用以反映总体构成变化影响的指数。
()答案是:正确只有增长速度大于100%才能说明事物的变动是增长的。
答案是:错误未知计算平均数的基本公式中的分子资料时,应采用加权算术平均数方法计算。
()答案是:正确某公司产品产量在一段时期内的平均增长速度是正数正增长,因此其环比增长速度也都是正数答案是:错误移动平均的项数越大,其结果会使序列数据的逐期增长量变得更大。
()答案是:错误要通过移动平均法消除季节变动,则移动平均数N应和季节周期长度一致。
()答案是:正确时间序列的长期趋势如果拟合为抛物线曲线,这说明现象变动的变化率在较长时期中是不断变化的。
()答案是:正确无论是月度数据、季度数据或年度数据都可以清楚地观察出季节变动。
()答案是:错误循环变动与季节变动相同,都属于周期为一年的变动。
()答案是:错误运用季节指数进行预测时的假设前提是预测年份的季节性变化形态基本保持不变()答案是:正确季节比率说明的是各季节相对差异答案是:正确移动平均的平均项数越大,则它对数列的平滑休匀作用越强。
()答案是:正确3,一种回归直线只能作一种推算,不能反过来进行另一种推算。
()答案是:正确相关的两个变量,只能算出一个相关系数。
()答案是:正确,回归分析和相关分析一样所分析的两个变量都一定是随机变量。
()答案是:错误正相关指的就是两个变量之间的变动方向都是上升的。
西交14秋学期《统计学》作业考核试题答案

西交14秋学期《统计学》作业考核试题
一、单选题(共10 道试题,共20 分。
)
V 1. 统计调查对象是(C)。
A. 总体各单位标志值
B. 总体单位
C. 现象总体
D. 统计指标
满分:2 分
2. 对于连续变量的取值通常是采用(B )
A. 计数的方法
B. 计量的方法
C. 汇总的方法
D. 估算的方法
满分:2 分
3. 构成统计总体的那些个体(单位)必须至少在某一方面具有(B )
A. 差异性
B. 同质性
C. 相关性
D. 可加性
满分:2 分
4. 某大学商学院的一位老师依据本院职工2009年6月份收入资料计算出该院全体职工6月份的平均收入,并同其他院系进行比较,该教师运用的是(A)方法
A. 描述统计学
B. 推断统计学
C. 理论统计学
D. 数理统计学
满分:2 分
5. 相关系数的取值范围是(C )。
A. -1<r<1
B. 0≤r≤1
C. -1≤r≤1
D. |r|>1
满分:2 分
6. 某工厂有100名职工,把他们的工资加总除以100,这是对100个(C)求平均数。
A. 变量
B. 标志
C. 变量值
D. 指标
满分:2 分。
西交大考研统计学课后问答整理

行管 盖小静
—
第一章
导论
1. 什么是统计学?怎样理解统计学与统计数据的关系?
1) 统计学是指收集、处理、分析、解释数据并从数据中得出结论的科学。 2) 关系:它是一门关于数据的科学,它提供的是一套关于数据收集、处理、分析、解释并得出
结论的方法,它研究的是来自各个领域的数据。而其中数据收集就是取得统计数据,处理是 将数据用图表等形式展示出来,分析是通过统计方法研究数据、并从数据中取得有用信息以 帮助决策。
第二章
数据收集
1. 简述普查和抽样调查的特点。
它们都是实际中常用的统计调查方式。此外还有统计报表:按照国家有关法律规定,自上而下的提 供基本数据。
1) 抽样调查:从总体中随机抽取一部分单位作为样本进行调查,并根据样本调查结果来推断总 体特征的数据收集方法。它具有四大特点:经济性(人、财、物、时、费较低) 、时效性强、 适应面广、准确性高。
3) 数据分析的方法有描述统计和推断统计。描述统计是指研究数据收集、处理和描述的分支, 推断是指研究如何用样本数据来推断总体特征的分支。
2. 统计数据可以分为哪几类?不同类型的数据各有什么特点?
不同的数据要采用不同的统计方法来处理和分析
1) 按计量尺度分: 分类数据:只能归于某一类别的非数字型数据,由分类尺度计量形成;顺序数据:只能归于某
6. 统计学应用的领域有什么。
统计学可以应用于所有有数据的领域,如政府部门、学术研究领域、日常生活、公司企业的生产 经营管理等。如在工商管理中有:企业发展战略、产品质量管理、市场研究、财务分析、经济预测和
HR 等。统计有助于数据分,数据分析的真正目的是找到规律、获得启发,而不是寻找支持,真正的 分析事先是没有结论的,通过数据的分析才能得出结论。当然,统计也不是万能的。
西安交大统计学题库

1.描述动力学和推断统计学区分的依据是(对总体数据分析研究的方法不同)。
( B)2.统计数据是一个(具体的量)。
(A)3.在抽样推断中,总体参数是一个(未知的量)。
(A)4。
平均数是对(变量值的平均)。
(B)5。
以下哪一条不属于方差分析中假设条件(所以样本的方差都相等)。
(C)6.要对某企业的生产设备的实际生产能力进行调查,则该企业的“生产设备”是(调查对象)。
(A)7.当变量之中有一项为零时,不能计算(几何平均数和调和平均数)。
(D)8.某大学商学院的一位老师依据本院职工2009年6月份收入资料计算出该院全体职工六月份的平均收入,并同其他院系进行比较,该教师运用的是(描述统计学)方法.(A)9.对于连续变量的取值通常是采用(计量的方法)。
(B)10.要了解上海市居民家庭的收支情况,最合适的调查方式是(抽样调查)。
(D)11。
统计调查对象是(现象总体)。
(C)12。
相关系数的取值范围是(—1≤r≤1).(C)13.下列属于时点数列的是(某厂各年生产工人占全部职工的比重)。
(C)14.下面属于品质标志的是(工人性别)。
(B)15。
某工厂有100名职工,把他们的工资加总除以100,这是对100个(变量值)求平均数。
(C)16.当一项科学实验的结果尚未得出时,这种实验将一直进行下去.此时我们可以将由这种实验的次数构成的总体看成(无限总体)。
D17。
某单位职工的平均年龄为35岁,这是对(变量值)的平均。
(B)18。
随机试验所有可能出现得结果,称为(样本空间)。
(B)19.1999年全国从业人员比上年增加629万人,这一指标是(增长量)。
(B)20.下面那个图形不适合描述分类数据(茎叶图)。
(B)21.数据型数据的离散程度测度方法中,受极端变量值影响最大的是(极差).(A)22。
下列指标中,不属于平均数的是(某省人均粮食产量)。
(A)23.加权算术平均数的大小(受各组标志值与各组次数共同影响.)。
(D)24.在变量数列中,当标志值较大的组权数较小时,加权算术平均数(偏向于标志值较小的一方.)。
【满分】西安交通大学18年9月课程考试《应用统计分析》作业考核试题

西安交通大学18年9月课程考试《应用统计分析》作业考核试题-0001 试卷总分:100 得分:0
一、单选题 (共 20 道试题,共 40 分)
1.划分离散变量的组限时,相邻两组的组限()。
A.必须是间断的
B.必须是重叠的
C.既可以是间断的,也可以是重叠的
D.应当是相近的
正确答案:C
2.用指数体系作两因素分析,则同度量因素必须()。
A.是同一时期
B.是不同时期
C.都是基期
D.都是报告期
正确答案:B
3.估计标准误说明回归直线的代表性,因此()。
A.估计标准误数值越大,说明回归直线的代表性越大
B.估计标准误数值越大,说明回归直线的代表性越小
C.估计标准误数值越小,说明回归直线的代表性越小
D.估计标准误数值越小,说明回归直线的实用价值越小
正确答案:B
4.小吴为写毕业论文去收集数据资料,()是次级数据。
A.班组的原始记录
B.车间的台帐
C.统计局网站上的序列
D.调查问卷上的答案
正确答案:C
5.在抽样方法中,最简单和最基本的一种抽样方法是()。
A.分层抽样
B.等距抽样
C.简单随机抽样
D.整群抽样
正确答案:C
6.统计对现象总体数量特征的认识是()。
西安交通大学432统计学历年考研真题(含复试)

目 录第一部分 初试历年真题2015年西安交通大学经济与金融学院432统计学[专业硕士]考研真题(回忆版)2014年西安交通大学经济与金融学院432统计学[专业硕士]考研真题(回忆版)第二部分 复试历年真题2016年西安交通大学经济与金融学院应用统计硕士复试真题(回忆版)2015年西安交通大学经济与金融学院应用统计硕士复试真题(回忆版)2013年西安交通大学经济与金融学院应用统计硕士复试真题(回忆版)2012年西安交通大学经济与金融学院应用统计硕士复试真题(回忆版)第一部分 初试历年真题2015年西安交通大学经济与金融学院432统计学[专业硕士]考研真题(回忆版)西交大的真题不太容易找下午考完跟大家分享下西交15年432统计学题型总分150分题型分三种:一、选择题(15×2=30分)二、简答题(5×10=50分)题目涉及要点如下:1.以总体均值来举例说明双侧检验与单侧检验拒绝域的不同。
答:对总体均值进行单侧和双侧检验的拒绝域分别为:(1)双侧检验①在双侧检验中,原假设和备选假设一般是:,;②拒绝域:双侧检验的拒绝域一般是均匀分布在左右两侧,即|z|>|zα/2|。
(2)单侧检验①在左单侧检验中,原假设和备选假设一般是:,。
其拒绝域为:|z|<|zα|,α为显著性水平。
②在右单侧检验中,原假设和备选假设一般是:,。
其拒绝域为:|z|>|zα|,α为显著性水平。
2.CPI指数编制的相关问题。
说明:由于回忆版真题描述不够准确,这里针对不同侧重点给出两种答案。
答:答案一:(1)CPI的定义CPI是居民消费价格指数的简称,是一个反映居民家庭一般所购买的消费商品和服务价格水平变动情况的宏观经济指标。
它是度量居民消费品和服务项目价格水平随时间变动的相对数,反映居民家庭购买的消费品和服务价格水平的变动情况。
(2)CPI的计算公式CPI=(一组固定商品按当期价格计算的价值/一组固定商品按基期价格计算的价值)×100%。
西安交通大学硕士研究生入学考试科目主要参考书

《工业设计思想基础》
702 数学分析
《数学分析》
陈高翔
贺忠厚 邓晓兰 铁卫 冯宗宪 (美)萨尔瓦多 樊秀峰 张迈曾主编
李彬主编
中国经济出版社 西安交通出版社 西安交大出版社 西安交大出版社
高等教育出版社 清华大学出版社 西安交大出版社 西安交通大学出版 社 新华出版社
2004 年
2007 年 2007 年 2007 年 2011 年 2010 年 2003 年
《东方俄语》(1-2 册) 《大学德语》(修订版)1--3 册
丁树杞 张书良
外语教学与研究出 版社 高等教育出版社
高等教育出版社
上海外语教育出版 社 人民教育出版社与 (日本)光村图书 出版株式会社合作 编写 外语教学与研究出 版社 高等教育出版社
2002 版 2011 版 2011 版 2010 版 2005 版
《固体物理学》 《传热学》
陆栋 陶文铨
上海科学技术出版 2003 年 社
高等教育出版社 1998 年版
814 计算机基础综合
参考范围见我校研究生招生主页
2013 年西安交通大学研究生入学考试
计算机基础综合科目大纲
815 信号与系统(含数字信号《信号与线性系统 》
阎鸿森等
西安交大出版社 1999 年版
434 国际商务专业基础 440 新闻与传播专业基础 819 新闻传播学基础
448 汉语写作与百科知识
《公共财政学》 《财政学》 《税收学》 《国际商务》 《国际经济学》 《国际投资与跨国公司》 《传播学引论》
《传播学引论》
《新闻学概论》
《传播学原理》
《自然科学史十二讲》
《中国文化读本》
701 工业设计思想基础
西南交1112考试批次《应用统计学》复习题及参考答案

应用统计学第1次作业(B) 105%×107%×109%(C) (105%×107%×109%)-1(D)正确答案:C解答参考:5.某地区今年同去年相比,用同样多的人民币可多购买5%的商品,则物价增(减)变化的百分比为(A) –5%(B) –4.76%(C) –33.3%(D) 3.85%正确答案:B解答参考:6.对不同年份的产品成本配合的直线方程为回归系数b=-1.75表示(A) 时间每增加一个单位,产品成本平均增加1.75个单位(B) 时间每增加一个单位,产品成本平均下降1.75个单位(C) 产品成本每变动一个单位,平均需要1.75年时间(D) 时间每减少一个单位,产品成本平均下降1.75个单位正确答案:B解答参考:7.某乡播种早稻5000亩,其中20%使用改良品种,亩产为600公斤,其余亩产为500公斤,则该乡全部早稻亩产为(A) 520公斤(B) 530公斤(C) 540公斤(D) 550公斤正确答案:A解答参考:8.甲乙两个车间工人日加工零件数的均值和标准差如下:哪个车间日加工零件的离散程度较大:(A) 甲车间(B) 乙车间(C) 两个车间相同(D) 无法作比较正确答案:A解答参考:9.根据各年的环比增长速度计算年平均增长速度的方法是(A) 用各年的环比增长速度连乘然后开方(B) 用各年的环比增长速度连加然后除以年数(C) 先计算年平均发展速度然后减“1”(D) 以上三种方法都是错误的正确答案:C解答参考:10.如果相关系数r=0,则表明两个变量之间(A) 相关程度很低(B) 不存在任何相关关系(C) 不存在线性相关关系(D) 存在非线性相关关系正确答案:C解答参考:二、不定项选择题(有不定个选项正确,共7道小题)11.1. 下列数据中属于时点数的有[不选全或者选错,不算完成](A) 流动资金平均余额20万元(B) 储蓄存款余额500万元15.平均差与方差或标准差相比其主要缺点是[不选全或者选错,不算完成](A) 没有充分利用全部数据的信息(B) 易受极端值的影响(C) 数学处理上采用绝对值,不便于计算(D) 在数学性质上不是最优的(E)计算结果不够准确正确答案:C D解答参考:16. 指出下列指数中的拉氏指数[不选全或者选错,不算完成](A)(B)(C)(D)(E)正确答案:C E解答参考:17.若变量x与y之间存在完全线性相关,以下结论中正确的有[不选全或者选错,不算完成](A) 相关系数r=1(B) 相关系数|r|=1(C) 判定系数r =1试比较哪一市场的平均收购价格低,并说明原因. [些出公式,计算过程,结果保留两位小数]参考答案:乙市场的平均价格高于甲市场的主要原因是,乙市场高价格的商品销售量大,由于销售量结构不同导致两市场平均价格不等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
频率% 9.2 13.2 17.1 21.1 19.7 13.2 6.6 100
组中值 28.5 31.5 34.5 37.5 40.5 43.5 46.5 ----
向上累计 向下累计 频数 频数 7 76 17 30 46 61 71 76 ---69 59 46 30 15 5 ----
二、频数分布数列 1、统计分组后,每个组分配的总体单位数称为 频数或次数,频数/总体单位总数=频率。 2、意义 整理了杂乱无章的数据,同时显示出一批数的 分布情况,是数理统计学中随机变量及其概 论分布概念在实际中的应用。
S M e 1 fM e
d Me
40 28 1 0 7 4.8 25
f
2
Me UMe 80
S M e 1 fM e
d Me
40 27 1 0 7 4.8 25
2、百分位数 ——把数据按从小到大的顺序排列后,第P百分 位数是指有P%的值小于或等于它,而有 (100-P)%的值大于或等于它。 ——确定方法。i=(P/100)n就是第P百分位数的 位置。 其中最常用的是四分位数。即把数据分成四个 部分,每个部分包括1/4数值。
2 fM e 2
M e 1
d Me
Me UMe
f S
fM e
M e 1
d Me
80 4 0, LM e 7 0, U M e 8 0, 2 2 S M e 1 2 8, S M e 1 2 7, d Me 1 0, f M e 2 5
f
f
2
M e LM e 70
M0 M0
例、上例中众数组是第3组,
f M 0 25, f M 0 1 21, f M 0 1 19, d M 0 10, LM 0 70, U M 0 80 f M 0 f M 0 1 M 0 LM 0 dM 0 ( f M 0 f M 0 1 ) ( f M 0 f M 0 1 ) 25 21 70 10 74 ( 25 21 ) ( 25 19) f M 0 f M 0 1 M0 UM0 dM 0 ( f M 0 f M 0 1 ) ( f M 0 f M 0 1 ) 80 25 19 10 74 ( 25 21 ) ( 25 19)
二、统计图
组别
20
支付方式
信用卡
现金
10
Fr equency
0 27~30 30~33 33~36 36~39 39~42 42~45 45~48
组别
个人支票
第三章 统计数据的描述分析
第一节 集中趋势分析 集中趋势是数据分布的中心,描述集中趋势的 指标有算术平均数、中位数、众数等。
某单位80个工人生产的零 单位:个 65 78 88 65 58 76 69 66 80 64 77 78 60 65 85 74 73 65 66 79 74 85 59 69 60 87 85 86 64 93 76 62 91 49 74 78 75 79 86 68 87 97 92 82 66 94 75 56 85 77 67 89 78 79 88 83 73 69 84 95 55 79 77 58 80 68 77 87 70 78 79 61 47 69 89 96 66 76 81 99 Min=47 max=99
E( X )
Xf ( X )dX
4、算术平均数的缺陷 10 15 20 25 70
X 28
去掉70后,
X 17.5
二、众数(M0) 1、众数是指一组变量值中出现次数最多的变量 值。 2、众数的确定 ①未分组资料,M0就是出现次数最多的变量值。 上例中,78、79各出现5次,都是M0 数据分布是双峰的。
——剔除了极端值,说明50%数据分布的范围; ——与中位数配合说明数据分布是否对称。若分布对 称,则Q2-Q1=Q3-Q2=(Q3-Q1)/2 若不相等,则是非对称的。
二、极差 1、极差也称为全距,是一组变量中最大值与最 小值的离差,表明变量值变动的范围。用R表 示极差,其计算公式是: R x x 2、缺点:易受极端值的影响。
max min
三、四分位差 1、四分位差用数列中第3/4位次与1/4位次的变量值之 差除以2来表示。
Q Q1 Q 3 2 第75百分位数 第25百分位数 2 2、意义:
k
i fi
f
i
例、某单位80工人一周生产零件数。 1、简单算术平均数
X i 1 n
x
n
i
65 80 ... 61 99 75.49(个) 80
2、加权算术平均数
工人一周 工人数fi 生产零件 数 7 60以下
60-70 70-80 80-90 21 25 19
组中值xi
第二节 数据的整理 一、统计分组 1、统计分组是将统计总体按照一定标志区分成 若干个组成部分的一种统计分析方法。 2、两点注意: ——有时不易确定组与组之间的界限; ——穷尽原则、互斥原则。
钢材抗张 力 27-30 30-33 33-36 36-39 39-42 42-45 45-48 合计
频数 7 10 13 16 15 10 5 76
x f f
i 1 i
k
i i
6000 75 80
E( X )
X P( X )
i i i
3、算术平均数与数学期望 对于离散型随机变量X,设它的概率密度函X )
X P
i
i i
对于连续型随机变量X,设其概率密度函数为f(X), 则的数学期望为
二、标志和指标 1、标志是说明总体单位特征和属性的名称,分 为数量标志和品质标志。 2、指标是说明总体现象数量特征的概念和数值。 中国最大的资料库下载 按其反映数量特点的不同,分为数量指标和质 量指标。
三、统计指标 1、从总体的一个特征到具体数值,中间有很多 步要走。 2、以GDP的核算为例来说明 ①想看一国一年内生产活动的总量,定义GDP是 一国在一定时期内最终产品的总价值。(内 涵) ②最终产品是本期生产本期不再投入生产使用 的产品, 消费、投资、出口产品。(外延)
第二章 统计数据的搜集、整理和 显示
第一节 统计数据的搜集 一、统计调查方式 统计报表制度、普查、抽样调查、典型调查、 重点调查
例2.1、一批钢材,抽样测试其抗张力,随机抽取76个 样本观察值如下:(单位:kg /cm2) 41.0 37.0 33.0 44.2 30.5 27.0 45.0 28.5 40.6 34.8 31.2 33.5 38.5 41.5 43.0 45.5 42.5 39.0 36.2 27.5 38.8 35.5 32.5 29.5 32.6 34.5 37.5 39.5 35.8 29.1 42.8 45.1 42.8 45.8 39.8 37.2 33.8 31.2 31.5 29.5 29.0 35.2 37.8 41.2 43.8 48.0 43.6 41.8 44.5 36.5 36.6 34.8 31.0 32.0 33.5 37.4 40.8 44.7 40.0 41.5 40.2 41.3 38.8 34.1 31.8 34.6 38.3 41.3 44.2 37.1 30.0 35.2 37.5 40.5 38.1 37.3
第一章 绪论
第一节 统计学的学科性质 一、统计学的学科性质 1、争论:“方法论学科” “实质性学科” 2、统计处理数据的过程: 搜集数据——整理数据——分析数据——解释 数据
二、统计学的分类 1、描述统计学和推断统计学 2、理论统计学和应用统计学
第二节 统计学的几个基本概念 一、总体和总体单位 1、总体是由具有某种共同性质的许多个体组成 的整体,构成总体的个体称为总体单位。 2、两层含义: ①统计学研究的是大量现象的数量特征,总体 包含了大量现象; ②统计单位具有某一共同性质,但其他的性质、 特征是不同的,便于在差异中寻找规律。
三、中位数及分位数 1、中位数 ①把一批数按照从小到大的顺序排列,处于数列中点 的变量值就是Me ②确定方法 ——未分组资料:(n+1)/2中位数的位置。 前例Me=77 ———分组资料:根据向上或向下累计频数分布数列, 按照 确定中位数所在的组,然后确定。
f 2
M e LM e
f S
3、分类: 按分组标志的不同,分为: 品质数列 单项数列:一个变量值是一个组 变量数列 组距数列:两个变量值构成的区间是一个组
三、组距分布数列的编制方法 第一步,排序后,极差=max-min 第二步,确定组数、组距。 组数 k=1+3.32lgn(参考) 组距=(max-min)/组数 第三步,组中值。 组中值=(下限+上限)/2
②分组资料: 在等距分组的情况下,频数最多的组是众数组,在该 组内确定众数。
f M 0 f M 0 1 LM 0 dM 0 ( f M 0 f M 0 1) ( f M 0 f M 0 1 ) f M 0 f M 0 1 UM0 dM 0 ( f M 0 f M 0 1) ( f M 0 f M 0 1 )
一、算术平均数(均值) 1、将一批数累加起来,除以数据的个数,即为算术平 均数。 x
n i
X i 1 n
2、分为简单算术平均数和加权算术平均数
X i 1 n
x
n
i
X
x1 f 1 x 2 f 2 x k f k f1 f 2 f k
x
i 1 k i 1
第二节 离中趋势分析 一、离中趋势 1、离中趋势是数据分布的又一特征,它表明变量值的 差异或离散程度。 2、意义:首先,可以衡量算术平均数的代表性。 例:均值都为150的两组数 50,100,150,200,250 100,125,150,175,200 其次,进行产品质量管理和决策。 3、离中趋势测度经常用到的指标有:极差、方差和标 准差、四分位差等,它们也被称为变异指标。
