微光学技术及其应用(最新版)
微纳光学加工及应用
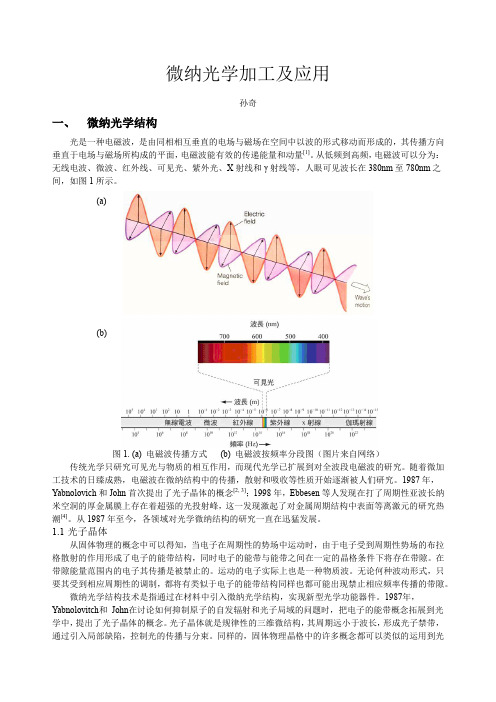
微纳光学加工及应用孙奇一、微纳光学结构光是一种电磁波,是由同相相互垂直的电场与磁场在空间中以波的形式移动而形成的,其传播方向垂直于电场与磁场所构成的平面,电磁波能有效的传递能量和动量[1]。
从低频到高频,电磁波可以分为:无线电波、微波、红外线、可见光、紫外光、X射线和γ射线等,人眼可见波长在380nm至780nm之间,如图1所示。
(a)(b)图1. (a) 电磁波传播方式(b) 电磁波按频率分段图(图片来自网络)传统光学只研究可见光与物质的相互作用,而现代光学已扩展到对全波段电磁波的研究。
随着微加工技术的日臻成熟,电磁波在微纳结构中的传播,散射和吸收等性质开始逐渐被人们研究。
1987年,Yabnolovich和John首次提出了光子晶体的概念[2, 3];1998年,Ebbesen等人发现在打了周期性亚波长纳米空洞的厚金属膜上存在着超强的光投射峰,这一发现激起了对金属周期结构中表面等离激元的研究热潮[4]。
从1987年至今,各领域对光学微纳结构的研究一直在迅猛发展。
1.1光子晶体从固体物理的概念中可以得知,当电子在周期性的势场中运动时,由于电子受到周期性势场的布拉格散射的作用形成了电子的能带结构,同时电子的能带与能带之间在一定的晶格条件下将存在带隙。
在带隙能量范围内的电子其传播是被禁止的。
运动的电子实际上也是一种物质波。
无论何种波动形式,只要其受到相应周期性的调制,都将有类似于电子的能带结构同样也都可能出现禁止相应频率传播的带隙。
微纳光学结构技术是指通过在材料中引入微纳光学结构,实现新型光学功能器件。
1987年,Yabnolovitch和John在讨论如何抑制原子的自发辐射和光子局域的问题时,把电子的能带概念拓展到光学中,提出了光子晶体的概念。
光子晶体就是规律性的三维微结构,其周期远小于波长,形成光子禁带,通过引入局部缺陷,控制光的传播与分束。
同样的,固体物理晶格中的许多概念都可以类似的运用到光子晶体中,诸如倒格矢空间、布里渊区、色散关系、Bloch函数、Van Hove奇点等物理概念。
微纳光学的应用

微纳光学的应用
微纳光学是一种新兴的技术,它利用微米和纳米级别的结构来控制光的传播和交互。
这种技术在许多领域都有广泛的应用,包括光通信、生物医学、纳米电子学和太阳能电池等。
本文将介绍微纳光学的应用。
微纳光学在光通信领域有着广泛的应用。
光通信是一种高速、高带宽的通信方式,它利用光信号传输数据。
微纳光学技术可以用来制造高效的光纤耦合器、光栅和微型光学器件,这些器件可以提高光通信系统的传输效率和可靠性。
微纳光学在生物医学领域也有着重要的应用。
生物医学研究需要对细胞和分子进行高分辨率的成像和检测。
微纳光学技术可以制造出高分辨率的显微镜和光学探针,这些器件可以用来观察细胞和分子的结构和功能,从而帮助科学家研究生物学和医学问题。
微纳光学还可以应用于纳米电子学领域。
纳米电子学是一种新兴的电子学领域,它利用纳米级别的结构来制造电子器件。
微纳光学技术可以用来制造出高效的纳米光电器件,这些器件可以用来控制和检测电子的行为,从而提高电子器件的性能和可靠性。
微纳光学还可以应用于太阳能电池领域。
太阳能电池是一种利用太阳能转换成电能的器件。
微纳光学技术可以用来制造出高效的太阳能电池,这些电池可以利用微米和纳米级别的结构来控制光的传播
和吸收,从而提高太阳能电池的转换效率。
微纳光学技术在许多领域都有着广泛的应用。
随着技术的不断发展,微纳光学将会在更多的领域发挥重要作用,为人类带来更多的福利。
光学显微镜的新技术和应用

光学显微镜的新技术和应用光学显微镜是一种常见的实验室工具,它可以让人们观察到微观世界中棘手的问题和微小的变化。
在科学和医学领域,它发挥着重要作用。
在近年来,光学显微镜的新技术和应用不断涌现,以下是一些相关的主要内容。
一、超分辨率显微镜技术在传统的光学显微镜中,由于光波本身的散射和透过样本的局限性,使得物体的分辨率受到限制。
而超分辨率显微镜则通过巧妙地利用某些特殊效应使得物体的分辨率达到亚纳米级别,大大提高了样本观察的精度。
其中比较重要的一种技术是叫做“STED”技术,这种技术利用特殊的探针和激光,将物体较小区域的光辉限定在更小的尺度之内,然后再通过合适的花样扩展光斑使得样本中的图案被增强和放大。
这种技术丰富了人们对于细胞的结构和功能的理解,对于认知神经学、生物学以及医学的发展都有极大的促进。
二、多光子显微镜技术传统的荧光显微镜需要使用荧光物质或者显微粒子做标记才能实现观测,这些标记物往往在生物样本中的分布和含量会影响样本的生理行为和代谢反应。
而多光子显微镜技术则可以直接通过样本在激光的刺激下自然发射出的光子来实现成像,不需要任何的荧光标记。
这种技术特别适合用在对于比较复杂和难以加标的样本中,例如组织、脑区和胚胎样本中。
这种技术不仅可以非侵入式地观察样本生物学行为,也可以更加深入探讨整个现象的性质和机理。
三、快速成像技术随着大数据时代的到来以及数据处理能力的不断提高,人们对于样本及物体的快速成像需求也随之增加。
而快速成像技术就是在经典的普通光学显微镜中使用高速的探针和电子扫描技术来实现物体非常快速的成像。
这种技术最大的优点就是它可以在高速和快速变化的样本中保持样本斑点清晰且稳定。
它可以应用于关于细胞和组织的生物学研究甚至包括微纳技术领域中的研究。
现在的研究也将发掘表层上的第二层信息,比如物体的纹理和形状信息。
特别是在生物医学领域中,快速成像技术可以帮助医生及时诊断治疗有效性,给减轻疾病带来更快的效果。
光学微纳加工技术在医疗领域中的应用

光学微纳加工技术在医疗领域中的应用随着科技的不断发展,光学微纳加工技术已经在医疗领域中得到了广泛应用。
这种技术基于雷射和光阻剂等物质的特性,能够在微米级和纳米级上实现高精度和高效率的加工。
本文将介绍光学微纳加工技术在医疗领域中的应用,包括医疗器械的制造、组织修复、生物药物研发等方面。
医疗器械的制造光学微纳加工技术可以为医疗器械制造提供高精度加工手段。
比如,在牙科治疗中,患者的牙齿可能需要进行根管治疗,医生需要在牙齿内部进行清理和填充。
传统的治疗方法需要手工进行,而这种方法存在一定的风险。
而光学微纳加工技术可以通过雷射加工实现精确的根管治疗,不仅可以提高治疗质量和效率,还能降低风险和痛苦。
此外,在眼科手术中,光学微纳加工技术也可以发挥作用。
例如,患者需要进行白内障手术,医生需要将白内障晶体取出并替换成人工晶体。
传统的手术方法需要切开眼球,然而这种方法有一定的风险。
而光学微纳加工技术可以通过雷射加工,实现微创手术,提高手术效率和安全性。
组织修复组织修复是医疗领域中一个不断探索和研究的领域。
光学微纳加工技术可以通过雷射加工,实现对组织细胞的精确操作。
在组织修复方面,主要应用于三个方面。
第一方面是细胞培养。
光学微纳加工技术可以通过光阻剂的特性,在光化学反应中控制细胞的定位和生长方向。
这种方法可以实现高通量的细胞培养,大大提高细胞培养的效率和研究的深度。
第二方面是人工组织的制造。
人工组织是可以替代病变或损伤组织的组织,可以为治疗提供有效的手段。
然而,人工组织的制造需要高度的精度和精细的控制。
光学微纳加工技术可以通过光阻剂加工,在微米级和纳米级上实现组织工程的制造,实现精确的控制。
第三方面是细胞移植。
在组织修复中,移植是实现组织修复的关键之一。
光学微纳加工技术可以通过光阻剂的特性,实现对细胞的选取和移植的精确操作。
这种方法可以实现高效的移植和组织修复。
生物药物研发生物药物是近年来医疗领域中的一个重要组成部分,也是医学发展的一个重要方向。
光学微型元件技术的应用

光学微型元件技术的应用光学微型元件技术(Optical Micro-electromechanical Systems, MEMS)是一种结合了微机电系统和光学技术的交叉学科技术,它以微观和纳米级别的元件结构为基础,实现了光学器件的微型化、高集成度和自动化。
近年来,光学微型元件技术已经成为了光学通信、生物医学、光学微处理、环境监测、制造业等领域中不可或缺的核心技术。
在光学通信领域,光学微型元件技术的应用主要包括光电子器件、光学开关、波长多路复用器等。
其中,波长多路复用器是一种用于将多个信号通过同一光纤传输的光学器件。
通过调整光的波长,它可以将多个不同的信号同时传输到同一光纤中,从而大大提高了光纤的传输容量。
光学微型元件技术的广泛应用使得波长多路复用器的精度和带宽更高,同时成本更低,因此在通讯网络中得到了广泛的应用。
光学微型元件技术在生物医学领域也有着广泛的应用。
在分析蛋白质、病毒和其他细胞分子方面,光学微型元件技术可以快速、精准的检测和诊断各种疾病。
通过利用微型探针和精密的光学技术,可以实现细胞分子的单一分子检测,这对于疾病的诊断和治疗提供了重要的帮助。
此外,光学微型元件技术也在外科手术中得到了广泛的应用,它可以通过靶向选择性组织砍伤,在手术操作中减少无关损伤,从而保证手术的成功率和安全性。
光学微型元件技术在光学微处理领域的应用也十分广泛。
在半导体工业中,通过利用显微技术将微型器件制作到晶片上,可以大大提高器件性能。
利用光刻技术和微影技术可以将微处理器芯片的制造工艺大大减少,从而提高制造效率和降低制造成本。
此外,光学微型元件技术还可以用于高精度的物体识别和位置观测,这对于精密制造和智能控制领域有着广泛的应用。
在环境监测领域,光学微型元件技术可以对声、光、电、气体、温度等环境参数进行实时监测和分析。
其中,光学气体传感技术已经成为了环境监测领域中最重要的技术之一。
利用光学微型元件技术,在纳米尺度范围内制作出精密的气体传感器,可以实时检测和分析大气中的二氧化碳和氮氧化合物等污染物,从而保证人类的健康和生态环境的平衡。
现代光学技术的新兴应用

现代光学技术的新兴应用随着科技迅速发展,各个领域都在进行着无止境的创新。
今天,我们要谈论的是现代光学技术的新兴应用,光学技术已经脱离了仅仅在光学领域内使用的局限,它被广泛应用于医学、军事、电子、通信等各个方面。
在接下来的文章中,我们将会讨论这些应用领域及其创新成果。
1. 医疗领域应用医疗领域是光学技术应用最为广泛的一方面。
在现代医学中,我们使用的X光、CT扫描等医疗设备,很大一部分都与光学技术相关。
如今,还有更多新兴的光学技术应用涌现出来。
首先是激光微创手术,它减轻了手术的疼痛和切口大小,缩短了康复期。
同时,激光微创手术也可以进行瘤的消融。
这一技术使得很多人能够在较短时间内完成治疗,让他们能够更快恢复健康。
其次是基于光学的早期癌症诊断技术,它可以在早期就检测出癌症的征兆。
这项新技术能够大大提高癌症治疗的成功率,降低癌症带来的悲痛。
最后是基于光学的视网膜疾病诊断技术。
这项技术使用红外光来扫描视网膜,并精确测量其反射,从而检测出视网膜可能存在的病变。
这一技术也被广泛应用于眼科医疗中,许多患者可以通过这项技术在很短的时间内确诊。
2. 军事领域应用兵器装备从简单的近身白刃战到现代化的信息化战争,光学技术的应用不断的被军方添加。
光学技术已成为现代军事中必不可少的一部分,且在军事领域的应用也是最为深刻的。
激光导航、红外成像和激光测距仪等都是目前军事装备中使用的光学技术产品,而这些装备的进一步升级则对技术的创新成果提出了更高的要求。
其中,激光定位技术更是准确度最高的一种兵器装备,它可以在夜间或恶劣环境下定位。
同时也可以准确锁定目标并发射弹药,有效地打击敌方。
因此,激光定位技术已经被广泛应用于战斗机、无人机和舰船等武器装备上。
3. 电子领域应用光学技术在电子领域的应用也是不容小觑的。
在光纤通信中,激光器用作信号发射源,而激光的强光和窄带宽特性使得该技术的传输速度变得更快,而且信号质量更高。
同时,在 LED 灯的光学设计中,增加植物光合作用和人类睡眠的有效时间。
光学显微技术的新进展与应用场景

光学显微技术的新进展与应用场景光学显微镜是科学研究中常用的仪器,它可以看到细胞、细胞器、细菌、病毒等微生物以及各种材料的组织结构与细节。
而随着科学技术的不断进步,光学显微技术也不断发展。
本文将探讨光学显微技术的新进展,以及它们在生物医学、材料科学等领域的应用场景。
第一节:现代光学显微技术的新进展光学显微技术的发展历程可以追溯到17世纪的荷兰天文学家赫维留发明的单透镜显微镜。
20世纪初,发展出了衍射极限显微镜、共焦显微镜和电子显微镜等先进显微技术。
随着计算机、数字成像技术的发展,现代光学显微技术也在不断创新和进步。
最近,一种叫做“光学开关”的技术被开发出来。
这种技术通过控制光学相位来改变样品的透射和反射,从而实现三维图像的成像。
这种技术可以用来观察细胞、纳米颗粒等微观物体的结构和形态。
“光学超分辨显微镜”是另一种新型光学显微技术,它通过精密控制光束进入样品,实现纳米级别下的分辨率。
这种技术广泛应用于生物医学、材料科学等领域,其高分辨率的成像效果可以帮助科学家解决许多问题。
第二节:光学显微技术在生物医学中的应用光学显微技术在生物医学中有着广泛的应用。
例如,在生物医学领域中,共焦显微技术被广泛应用于细胞、组织和生物材料的成像中。
应用共焦显微技术可以实现非侵入式的、三维高分辨率的成像,能够帮助科学家揭示生物体内部分子和生物过程的详细信息。
除此之外,基于荧光的显微技术也被广泛应用于生物医学中。
例如,在肿瘤治疗领域中,荧光显微技术可以用来追踪肿瘤细胞的行动和研究肿瘤的发展过程。
荧光聚焦显微技术还可以用于观察蛋白质、激素和细胞的互动。
这些都有助于科学家探究生命的奥秘。
第三节:光学显微技术在材料科学中的应用除了在生物医学领域,光学显微技术在材料科学领域也被广泛使用。
例如,在纳米材料的研究领域中,荧光显微技术和原子力显微技术可以用来观察纳米颗粒的成长过程。
这些成像技术允许科学家研究纳米颗粒在极小空间内的物理和化学变化。
光学显微技术的发展与应用前景

光学显微技术的发展与应用前景随着科学技术的不断发展,光学显微技术已经成为了现代科学最为重要的工具之一。
光学显微技术以光学原理为基础,利用电子显微技术、计算机技术等多种技术手段,可以对微观世界进行直接观察和研究,拥有广泛的应用范围。
本文将阐述光学显微技术的发展历程,以及它在各个领域中的应用前景。
一、光学显微技术的发展历程光学显微技术起源于欧洲文艺复兴时期,那时人们利用放大镜来观察微小物体。
17世纪末,荷兰人安东·范·李文霍克创造了第一台现代光学显微镜,这一发明奠定了微生物学和生物学的基础。
19世纪,人们发明了差分显微镜和相衬显微镜,使得显微镜分辨率达到了亚微米级。
20世纪60年代,人们发明了激光和光学存储器,使得显微技术进一步提高了分辨率和成像效果。
二、光学显微技术在生命科学中的应用光学显微技术在生命科学中的应用非常广泛,特别是在细胞生物学和分子生物学领域。
其中,荧光显微技术是应用最为广泛的一种,它可以利用荧光染料标记细胞或分子,在显微镜中进行非侵入性定量分析。
例如,流式细胞术、荧光标记蛋白质定量和活体成像都是利用荧光显微技术来实现的。
三、光学显微技术在物质科学中的应用在物质科学中,光学显微技术可用于材料的表征和分析。
常见的技术包括透射电子显微镜、扫描电子显微镜和原子力显微镜等。
四、光学显微技术的未来发展趋势现代生物医学研究已经进入到了分子生物学的层次,研究对象早已不仅仅是单一细胞,在这种情况下,高分辨率的全息显微镜和非线性显微镜越来越受到青睐。
这两种技术都需要进行复杂的图像处理,利用计算机和人工智能等技术手段,来进一步提高成像清晰度和时间分辨率。
同时,发展中心大型光学显微仪器也是未来的一个方向。
因为成像区域在显微技术中是个限制,长期以来,单个分辨率很高的显微镜很难达到足够大的成像区域。
因此,大型光学显微仪、全景扫描显微镜和超宽场显微镜会继续发展,以满足更多的应用使用。
五、结语光学显微技术的发展已经发展至今,不仅有广泛的应用,同时也涌现出了口感不同的技术手段。
光学显微技术的原理与应用

光学显微技术的原理与应用光学显微技术是一种利用光学原理观察和研究微观结构和微小物体的技术。
它通过利用光的折射、散射、干涉、衍射等现象,利用显微镜放大物体的图像,使我们得以观察到肉眼无法察觉的微细细节。
光学显微技术在生物学、医学、材料科学等领域发挥着重要的作用。
光学显微技术的原理主要基于物体与光的相互作用。
当光通过物体时,会发生折射现象,即光线在物体表面发生偏转。
这一原理被广泛应用于透射显微镜中。
透射显微镜通过物镜和目镜的组合,使光通过待观察的透明物体,并将其图像放大。
此外,衍射现象也是光学显微技术中重要的原理之一。
当光线通过物体表面的细小孔或物体的装置时,光会发生衍射,形成干涉和衍射图样,进一步放大了图像的细节。
光学显微技术广泛应用于生物学和医学领域。
在生物学中,通过显微镜观察细胞和组织的结构,可以帮助科学家了解生命现象和研究疾病的原因。
例如,细菌或病毒的形态和结构可以通过光学显微技术进行观察和分析。
在医学领域,透射显微镜被广泛用于检测和诊断疾病。
通过显微镜观察血液样本中的细胞形态和数量,医生可以判断患者是否患有某种疾病。
除了生物学和医学,光学显微技术在材料科学中也起着重要的作用。
材料科学家使用显微镜观察材料的结构和性质,以改善材料的性能和开发新材料。
透射电子显微镜(TEM)是一种利用电子束代替光束的显微镜,能够对固体材料进行高分辨率观察。
TEM技术在纳米材料研究和纳米器件制造中发挥着重要的作用。
此外,扫描电子显微镜(SEM)也是一种常用的显微镜技术,它可以通过扫描样品表面的电子束来获取高分辨率的图像,对材料的表面形态和成分进行分析。
光学显微技术的发展也带来了许多创新应用。
例如,荧光显微技术结合了荧光探针和显微镜技术,可以用于观察活细胞内特定分子的位置和活动,有助于研究细胞信号传导和分子机制等生物过程。
此外,共聚焦显微镜(Confocal Microscopy)利用激光的焦点聚焦特性,可以获取三维图像,并减少了离焦和背景噪声的影响,成为生物学和医学研究中常用的显微镜技术之一。
光学微纳制造在柔性显示领域的应用有哪些

光学微纳制造在柔性显示领域的应用有哪些在当今科技飞速发展的时代,显示技术不断推陈出新,其中柔性显示以其独特的优势逐渐成为市场的宠儿。
而光学微纳制造技术的出现,为柔性显示领域带来了一系列令人瞩目的应用和突破。
柔性显示,顾名思义,是指具有可弯曲、可折叠甚至可卷曲特性的显示屏幕。
与传统的刚性显示屏幕相比,柔性显示具有更好的便携性、适应性和创新性,能够满足各种不同的应用场景和用户需求。
然而,要实现高质量的柔性显示,离不开先进的制造技术,光学微纳制造就是其中的关键之一。
光学微纳制造技术是一种能够在微观和纳米尺度上对材料进行精确加工和处理的技术手段。
它涵盖了光刻、蚀刻、纳米压印等多种工艺,能够制造出具有高精度、高分辨率和高性能的微纳结构和器件。
在柔性显示中,光学微纳制造技术首先被应用于制造薄膜晶体管(TFT)。
TFT 是控制每个像素显示的关键元件,其性能直接影响显示的质量和响应速度。
通过光学微纳制造技术,可以在柔性基板上制备出高性能的 TFT,实现高分辨率和快速响应的显示效果。
例如,采用纳米光刻技术可以制造出极小尺寸的 TFT 沟道,从而提高器件的集成度和性能。
光学微纳制造技术在柔性显示中的另一个重要应用是制备电极。
在柔性显示中,电极需要具备良好的导电性、柔韧性和透光性。
通过纳米金属线、纳米碳管等材料,并利用微纳制造技术,可以制备出具有高导电性和柔韧性的透明电极。
比如,采用纳米银线网络作为电极材料,通过印刷或涂布等工艺,可以在柔性基板上形成均匀、透明且导电性能优异的电极层。
微纳光学结构也是光学微纳制造在柔性显示领域的一大应用亮点。
通过在显示面板上制造微纳光学结构,如微透镜阵列、光子晶体等,可以实现更好的光学性能。
例如,微透镜阵列可以提高光线的收集效率,增强显示的亮度和均匀性;光子晶体则可以通过调控光的传播和反射,实现彩色显示和提高色彩纯度。
此外,光学微纳制造技术还在柔性显示的封装环节发挥着重要作用。
由于柔性显示器件对水氧的敏感性较高,需要有效的封装来保护器件。
光学微纳制造技术的最新进展与应用前景

光学微纳制造技术的最新进展与应用前景光学微纳制造技术是利用光学原理进行微米级或纳米级加工的一种制造技术。
其优点在于高精度、高效率、非接触式加工等。
这种技术的发展历程很长,应用领域也十分广泛。
近年来,随着人们对微纳制造技术的需求增加,光学微纳技术也得到了更多的研究和应用。
本文将介绍光学微纳制造技术的最新进展与应用前景。
一、光学微纳制造技术的最新进展1. 激光直写技术激光直写技术是一种利用激光束对材料点阵进行加工的技术。
该技术不依赖于掩模,并且加工精度高、加工时间短、加工范围大。
最新的激光直写技术采用的是超短脉冲激光,可以在纳秒甚至飞秒级别内进行加工,使得加工产生的热影响极小。
2. 光刻技术光刻技术是一种利用光学模板的技术,目前已经成为半导体芯片制造的主要工艺之一。
现代光刻机使用的是紫外光,最新的光刻机可以实现低于10纳米的曝光精度。
在半导体芯片制造领域,新一代光刻技术将成为下一代芯片工艺中的核心技术。
3. 光子晶体制造技术光子晶体是具有周期性介电常数的光学纳米结构。
最新的光子晶体制造技术可以实现更高的精度和更大的制造尺寸。
光子晶体在激光、光电子学、生物传感等领域有很多应用。
二、光学微纳制造技术的应用前景1. 半导体芯片半导体芯片是人们日常使用的电子产品的基础。
随着信息技术的迅速发展,对芯片制造工艺的要求越来越高。
光刻技术在芯片制造领域中有着广泛的应用。
2. 激光细加工激光细加工技术可以应用于制造精密仪器、微电子机械系统等领域。
利用激光直写技术,可以在一片硅基板上制造出复杂的微电子元件或微机械系统,例如微型加速度计、微型陀螺仪等。
3. 生物医药生物医药是光学微纳制造技术的另一个重要应用领域。
在生物试剂、诊断药品的研究和开发中,利用准分子激光制备纳米材料已经成为一种新的方法。
在生物医学领域,利用光子晶体技术可以实现灵敏的生物传感器。
结论光学微纳制造技术是一项新兴的高精度加工技术,其发展已经有近30年的历史。
微纳光学技术的原理及其应用

微纳光学技术的原理及其应用随着科技的不断发展,微纳光学技术正在成为一个备受关注的领域。
它通过对光学现象进行研究,开发出适用于微观和纳米尺度的光学器件和技术,具有广泛的应用前景。
本文将从微纳光学技术的原理和应用两个方面来阐述。
一、微纳光学技术的原理微纳光学技术的原理主要涉及到光的微观性质和纳米结构的光学效应两个方面。
光的微观性质包括光的波粒二象性和光的相干性。
波粒二象性指的是光既可以表现出粒子的性质,也可以表现出波的性质。
而光的相干性则是指光波的相位关系对其互相干涉的影响。
这两个性质使得我们可以通过调节光的波长、相位等参数来实现一些微纳尺度下的光学操作。
纳米结构的光学效应,则是指当光与纳米尺度的结构相互作用时,会出现一些非常特殊的光学现象。
例如,金属纳米粒子在光的作用下可以表现出极强的局域表面等离子共振效应,从而可以实现高灵敏度的传感器和光学限域,进而对微观和纳米晶体生长、微生物检测等方面产生了较高的研究兴趣。
二、微纳光学技术的应用微纳光学技术能够实现多种应用,这里着重介绍以下四个方面。
1、生物医疗领域微纳光学技术在生物医疗领域有着广泛的应用。
例如,在细胞成像方面,可以通过选择性地标记细胞结构来实现高分辨率的显微成像,进而探究复杂的细胞过程。
另外,在光治疗方面,微纳光学的方法可以通过寻找、制造和评估生物和药物的亚细胞、分子和基因的间接和直接响应来对主要疾病的治疗进行改进。
光散热和温度分布分析也可以实现带有光学的显微剖面医学断层成像。
2、光子芯片领域微纳光学技术也被广泛应用于光子芯片制造中。
例如,当我们努力将传统电子计算机中的部分元件转换为基于光的计算单元时,微纳光学技术可以为光元件提供支持,从而实现光子相关器件的迅速发展。
3、光电子信息领域微纳光学技术在光电子信息领域也有着广泛应用。
例如,将光和电脑进行耦合,可以实现快速和高效的通讯通道。
此外,研究人员还开始研究基于量子物理的光计算设备,以期获得更快的运算速度和更安全的信息交换方式。
光学微纳加工技术及在微电子中的应用

光学微纳加工技术及在微电子中的应用随着现代科技的不断发展,微纳技术逐渐成为了人们关注的焦点之一。
在微电子工业中,微纳加工技术是电子器件、集成电路、光电子器件等微小尺度设备制造的基础。
而光学微纳加工技术则是一种利用激光或光刻技术进行微纳加工的方法。
其在微电子、光电及生物医学等领域有着广泛的应用。
一、光学微纳加工技术简介光学微纳加工技术是一种基于激光或光刻技术进行微小尺度加工的方法。
目前,激光光学加工技术发展迅速,已成为当今微纳加工领域中的热门技术之一。
在光学微纳加工过程中,激光通过光束聚焦,产生高密度能量,对微小目标进行精确刻蚀。
由于光学加工具有高效、高精度、高质量的特点,在制造微小尺度的元器件、器件模板及微纳结构方面有着广泛的应用。
二、光学微纳加工技术的应用1. 微电子在微电子领域,光学微纳加工技术主要用于制造集成电路、光电器件及传感器等微小尺度的器件。
光学微纳加工技术可以制造出更精度更高、尺寸更小的电子器件,为微电子行业的发展提供了技术保障。
2. 光电子光学微纳加工技术在光电子领域中也有着广泛的应用。
例如,光学微纳加工技术可以用于制造短波长光学器件,包括声光改变器和可变光栅;在光子晶体的制作过程中,可通过光学微纳加工技术得以制作出具有高精度的微纳结构。
3. 生物医学在生物医学领域中,光学微纳加工技术广泛应用于微生物学、细胞学、生命科学的研究中。
例如,可以利用光学微纳加工技术制作出高质量可控制定的微流控芯片,用于有效控制微生物及细胞的运动;制备出高品质的微芯片电极,应用于生命科学中的仿生电极等。
三、光学微纳加工技术的发展趋势目前,光学微纳加工技术才有巨大的发展空间和潜力,可以预见在未来的科技中将会有着广泛的应用。
在未来几年中,光学微纳加工技术将会有下列各方面的发展趋势:1. 提高微纳结构加工精度。
光学微纳加工技术在逐渐提高加工精度的同时,可以在纳米级上进行操作,使其在制作传感器、芯片等领域的应用更加精确。
微光学处理技术

微光学处理技术哎,说起微光学处理技术,这玩意儿可真是个让人又爱又恨的高科技玩意儿。
你可能会问,啥是微光学处理技术?简单来说,就是用激光在超小的尺度上进行加工的技术。
这技术听起来挺高大上的,但别急,让我给你慢慢道来。
记得有一次,我去了一个朋友的实验室,他正在捣鼓这个微光学处理技术。
一进门,就看到满屋子的仪器,各种激光器、显微镜、还有一堆我看不懂的电子设备。
我心想,这玩意儿得花不少钱吧。
我朋友看我一脸好奇,就给我演示了一下。
他拿出一块小小的玻璃片,跟我说:“看,这就是我们要加工的材料。
”我凑近一看,这玻璃片比我指甲盖还小,心想这玩意儿能干啥用啊。
他接着说:“别小看这块玻璃,等会儿你就知道它的厉害了。
”然后他把玻璃片放到一个机器下面,打开激光器,一束细细的激光就打在了玻璃片上。
我看着那激光,心想这玩意儿不会把玻璃烧坏吧。
结果,我朋友告诉我,这激光的温度和强度都是经过精确控制的,不会对玻璃造成损伤。
他一边操作,一边给我解释:“你看,这激光在玻璃上打出来的小孔,精度可以达到微米级别。
”我看着那小孔,确实非常精细,比我用针扎的孔还要小。
过了一会儿,他把加工好的玻璃片拿出来给我看。
我一看,这玻璃片上密密麻麻的全是小孔,排列得整整齐齐。
我问他:“这玩意儿能干啥用啊?”他笑着说:“这你就不懂了吧。
这些小孔可以用来制造光学器件,比如光纤、光栅什么的。
这些器件在通信、医疗、科研等领域都有广泛的应用。
”我听了,这才恍然大悟,原来这小小的玻璃片,竟然有这么大的用途。
不过,我朋友也告诉我,这微光学处理技术虽然厉害,但操作起来也挺麻烦的。
需要精确控制激光的参数,还要小心翼翼地操作,一不小心就容易出错。
我听了,不禁感叹,这技术虽然高大上,但也不是那么容易掌握的。
总的来说,微光学处理技术确实是一门高深的技术,它在很多领域都有重要的应用。
虽然操作起来有些复杂,但只要掌握了技巧,就能发挥出它的巨大潜力。
就像我朋友一样,虽然捣鼓这玩意儿挺费劲的,但看到他做出来的成果,还是挺有成就感的。
光学微纳加工技术的原理与应用

光学微纳加工技术的原理与应用光学微纳加工技术是一种高精度、高效率的微观加工技术。
它利用激光或其他光源对微观或纳米尺度物体进行加工和加工成型,是现代微纳加工技术中重要的一种方法。
本文就详细探讨光学微纳加工技术的原理与应用。
一、光学微纳加工技术的原理1、光场效应光场效应是一种利用强光场作用在物质上的物理现象。
通过调整光场的强度和分布,可以实现对物质的加工和处理。
在微观尺度下,强光场可以通过束缚电子和离子的相互作用来影响物质的形成和变形。
2、激光热效应激光热效应是指当激光照射到材料表面时,被吸收的能量会引起局部温度的升高,从而改变材料的物理性质。
激光热效应可用于制造微观或纳米级别的器件,如光学导纳、微泵、微阀等。
3、电离效应电离是指物质中的一个或多个原子失去一个或多个电子的过程。
当激光照射到物质上时,它可以产生强电场和电磁波。
电离效应可用于制造纳米级别的器件和材料,如纳米晶体和碳纳米管。
二、光学微纳加工技术的应用1、微电子学应用利用光学微纳加工技术,可以制造高精度的微电子元器件,如微波器件、集成电路、传感器等。
它可以提高电子元器件的性能和可靠性,从而促进微电子学的发展。
2、生物医学应用光学微纳加工技术可以制造高精度的生物医学器件,如微型药物输送器、人工器官、药物释放器等。
它可以提高医疗技术的精度和效率,为人类的健康做出贡献。
3、纳米材料制备光学微纳加工技术可以制造纳米材料,如纳米晶体、纳米管、纳米线等。
这些材料具有独特的物理性质和化学性质,可以应用于电子学、催化剂、能源材料等领域。
4、光学元件制造利用光学微纳加工技术,可以制造高精度的光学元件,如微电子学应用中的反射镜、透镜、棱镜等。
这些元件能够提高光学仪器的精度和灵敏度。
5、微机械应用光学微纳加工技术可以制造微机械器件,如微泵、微阀、微机械元器件等。
这些器件可以应用于生物医学、自动化控制系统、机器人等领域。
三、结论光学微纳加工技术的发展为微纳米加工技术和材料科学的发展奠定了坚实的基础。
微纳光学技术在图像传输中的应用

微纳光学技术在图像传输中的应用随着信息技术的飞速发展,图像传输技术越来越受到人们的关注。
在传统的图像传输技术中,由于光的散开和折射等原因,导致图像失真,影响了信号传输的质量。
因此,微纳光学技术应运而生,它通过实现对光场的微纳控制,可以有效克服图像传输中光线偏移、散焦等问题,提升信号传输的质量。
本文将从微纳光学技术的基本原理和应用方面分别进行探讨。
一、微纳光学技术的基本原理微纳光学技术主要针对微型光学器件进行设计和制造,具有精度高、尺寸小、建造周期短等优点。
微纳光学器件主要包括微透镜、光波导、布拉格反射镜、光子晶体等。
其中,微透镜是一种光学器件,具有强大的光聚焦作用,可以将散乱的光聚焦在一个点上,从而提高图像的清晰度。
光波导指的是通过光导纤维或光导薄膜等方式将光线传输到目标位置的器件,可以实现复杂的光学信号处理功能。
布拉格反射镜则是一种用于调制光信号的器件,主要利用光的衍射和反射特性对光信号进行处理。
光子晶体则是一种通过定向光子禁带和光子禁带结构实现光学信号传输的器件。
在微纳光学技术中,光线的操控主要基于几何光学的原理,控制光线的传播路径和方向,从而实现对图像传输的精确调控。
这种技术需要依靠高分辨率显微镜、光学防抖技术、反射振镜和位置控制系统等精密设备来实现。
二、微纳光学技术在图像传输领域中具有广泛的应用。
在医学影像学中,微纳光学技术被广泛应用于癌症检测、细胞成像和神经活动监测等领域。
例如,利用微型透镜阵列可以实现高分辨的体表成像,利用光波导可以实现内窥成像,以及使用二氧化硅微球可以实现细胞膜测量等。
在纳米制造领域中,微纳光学技术也具有重要的应用价值,如在纳米电子、纳米机器人、光子晶体等领域中应用广泛。
此外,在虚拟现实技术、光学信号处理和光学通信等领域中,微纳光学技术也发挥着重要作用。
例如,基于微纳光学的光学通信技术可以实现光纤中的光子晶体波导,可以大大提高光信号的传输速度和精确度。
同时,利用微纳光学技术提供的高分辨率成像能力,也可以实现空间图像合成和复合成像等功能,可以实现高保真度和高清晰度的图像传输。
光学技术在微电子生产制造中的应用

光学技术在微电子生产制造中的应用一、引言光学技术是指通过光学原理和装置实现的各种技术,近年来逐渐在微电子生产制造中得到广泛应用。
本文将从光刻、光学检测和激光加工三个方面说明光学技术在微电子生产制造中的应用。
二、光刻技术的应用光刻技术是一种利用光刻胶和掩膜制作微电子芯片图案的技术。
掩膜上的图案根据需要光刻到硅片上,成为芯片的一部分。
光刻技术的实现需要准确的曝光和对光线的严格控制,光学技术正好满足了这些要求。
光刻胶的曝光是通过紫外线在掩膜上所投射的镭射来实现的,因此掩膜的质量对于光刻的质量至关重要。
另外,曝光过程中需要对光线进行精确控制,包括光线的强度、方向和聚焦效果。
常用的控制光线的元件包括透镜、光栅、反射镜等,这些元件都是由光学原理和技术实现的。
光刻技术的应用广泛,例如制作存储器、集成电路、微机器人等。
三、光学检测技术的应用光学检测技术用来检测电子芯片的质量和电子元器件的可靠性。
它主要基于一个原理:当电子元器件内部发生故障或者质量不好的时候,它会反射或者散射光线,因此利用光线检测可以检测出这些故障或质量问题。
例如,基于近红外反射光谱技术,可以实现对清晰度、分辨率和颜色的快速检测。
利用红外光调制热成像技术,可以对大型电子元器件的故障提供快速准确的定位和分析。
此外,许多光学检测技术在实践中都得到了验证,其性能已经得到广泛认可,是电子行业中核心的技术之一。
四、激光加工技术的应用激光加工技术利用激光器产生的高能量、高强度激光束实现微电子器件的切割、钻孔和加工,广泛应用于半导体、电子器件加工等方面。
利用激光加工技术还可以实现3D打印,具有精度高、生产效率高以及节约原材料等优点。
使用于微电子领域的正确调节和使用激光切割技术,可以显著提高电子元器件的加工效率和稳定性。
五、结论总体而言,光学技术在微电子生产制造中的应用已经得到广泛应用,这不仅是因为光学技术自身的特点和优势所在,同时也是因为它在微电子生产制造领域扮演的重要角色。
光学微操控技术的发展与应用前景

光学微操控技术的发展与应用前景在当今科技飞速发展的时代,光学微操控技术犹如一颗璀璨的明星,在众多领域展现出了令人瞩目的应用潜力。
这一技术利用光的力量来实现对微小物体的精确操控,为科学研究和实际应用带来了前所未有的机遇。
光学微操控技术的发展历程可以追溯到上世纪七十年代。
当时,科学家们首次发现了光压现象,即光具有动量,可以对物体施加力的作用。
这一发现为光学微操控技术的诞生奠定了基础。
随着激光技术的不断进步,高强度、高聚焦性的激光束成为了实现光学微操控的有力工具。
早期的光学微操控技术主要基于光镊原理。
光镊利用高度聚焦的激光束形成的梯度力场来捕获和操控微小粒子,如细胞、细胞器、纳米颗粒等。
通过精确控制激光束的参数,如波长、功率、聚焦位置等,可以实现对微小物体的稳定捕获和移动。
这一技术的出现为生物医学研究带来了革命性的变化。
科学家们可以在不接触和损伤细胞的情况下,对细胞进行精确的操作和研究,例如测量细胞的力学特性、研究细胞内的分子运输等。
除了光镊技术,近年来还出现了一些其他类型的光学微操控技术。
例如,基于光学涡旋的微操控技术。
光学涡旋具有独特的螺旋相位结构,能够产生环形的梯度力场,从而实现对微小物体的旋转和轨道运动操控。
这种技术在微纳加工、粒子分选等领域具有重要的应用前景。
另外,全息光学微操控技术也是当前的研究热点之一。
通过计算机生成的全息图,可以同时产生多个独立可控的光镊,从而实现对多个微小物体的并行操控。
这大大提高了操控的效率和复杂性,为大规模微纳组装等应用提供了可能。
在材料科学领域,光学微操控技术为纳米材料的合成和组装提供了新的途径。
通过精确控制光场,可以实现纳米颗粒的定向排列和自组装,制备出具有特定结构和性能的纳米材料。
例如,利用光镊可以将纳米颗粒组装成复杂的三维结构,用于制造高性能的纳米器件。
在生物医学领域,光学微操控技术的应用更是广泛而深入。
在细胞生物学研究中,它可以用于细胞的分离、分选和融合,有助于揭示细胞的生理和病理过程。
光学技术的进展与应用

光学技术的进展与应用光学技术是指利用光学原理和技术手段进行照明、成像、通讯、检测等各种应用的一种技术。
随着科技的不断发展和人们对于高品质、高效率、高安全性等需求的不断增加,光学技术也得到了越来越广泛的应用和发展。
一、红外光学技术红外光学技术是一种基于红外波段的光学技术,主要应用于热成像、红外显示、夜视和火控系统等领域。
红外探测器是实现红外光学技术的重要基础设施之一。
目前市场上的红外探测器主要包括有热式探测器、半导体探测器和量子点探测器等。
热式探测器主要应用于低分辨率的红外成像系统,半导体探测器则主要用于中高分辨率的红外成像系统。
而量子点探测器由于其具有高灵敏度、高响应速度的特点,因此在近年来得到了广泛的关注。
二、光纤通信技术光纤通信技术是一种基于光学原理的通讯技术。
光纤通讯的主要优势是具有高带宽、低衰减、不易受到电磁干扰等特点,因此被广泛用于电话系统、电视信号传输、互联网和数据中心互联等领域。
在光纤通信技术中,光纤是非常关键的组成部分。
光纤的质量和特性直接关系到光信号的传输质量。
近年来,随着光纤技术和材料的不断更新,新型的光纤如光子晶体光纤、渐进抽芯光纤等不断涌现,使得光纤通信技术得以更加优化和完善。
三、高能激光技术高能激光技术是一种利用强光场作用下的物理和化学过程得到的一种强大工具,被广泛用于材料加工、医疗、节能环保和国防等领域。
在高能激光技术中,灯泵激光器、半导体涵道激光器和光纤激光器等都是激光发生器的重要部件。
除此之外,激光光束的转导和聚焦、激光能量的调控以及对激光器与被切割物的间接冷却等重要技术也在高能激光技术中得到了广泛应用。
四、光学成像技术光学成像技术是一种利用光和光学器件进行成像的技术,主要应用于医学影像、人类视觉研究、空间图像获取等领域。
光学成像技术的核心在于光学镜头和图像传感器。
光学镜头是将物体光线聚焦形成像的装置,而图像传感器则是将光学信号零散的接收到的能量转换成电信号并进行数字信号化处理的装置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13
CODE V中的GRIN Lens
ZEMAX中的GRIN Lens
14
二、折射型微光学元件的设计
1、规则面型微透镜的设计 几何光学成像公式计算、追迹
曲率半径
透镜玻璃牌号
非球面系数
15
2、特殊面型的微光学元件 折射定律、边界条件、能量守恒原则
x
z
微光学 元件
入射光强度分布
像面
像面强度分布
h(x) T1 . | x | p .w2 .[ x .erf (x / w) 1 ex2 /w2 1/ p ], 0 | x | L / 2
2
2A w
p
18
设计仿真结果:
微光学元件浮雕分布
19
高斯→环形的典型应用:
信号探测
副镜
主镜
卡赛格林望远系统示意图
20
利用公式(1)、(2)和(3)计算得到的微光学元件,可以 将任意输入光强分布变换为想要的分布,比如:
– 焦距:f = -1/[n0A1/2sin(A1/2L)] – 聚焦参数:A = 2/a2
– 数值孔径:NA = n0(2)1/2 – 节距:P = 2p/A1/2
• 成像特性:与透镜长度有关:
– 1/4 节距透镜
– 1/2 节距透镜
– 0.23节距透镜
– 0.29 节距透镜
– ……
11
典型应用: 光通信、微型光学系统、医用光学仪器、 光学复印机、传真机、扫描仪
ei(x) comb((x)) *{rect[(x)].L1 eik .rect[k 2p k / L]}
2p
2p k 0
2p / L
L——台阶数
将其代入衍射级的振幅公式中,得到:
Cm
sin(m / L) .{1 m/L L
L1
exp[i(k
k 0
2p mk) /
L]}
衍射效率: CmCm* sin c2 (1/ L)
微光学及其应用
(Microoptics and its applications)
郑国兴 电子信息学院 Tel: 87851024 E-mail: g.x.zheng@
物理光学
应用光学 电磁场理论
微电子学 材料学
化学
应用学科
性质
理论工具 微光学
研究对象
微小光学结构
光学行为
操纵光波实现多种功能
第一步: e dx L/2 x2 / w2
将上述分布代入公式(1),可得:A L/2
T2 T1
(式中L为微光 学元件尺寸)
第二步:利用公式(2)求解与x的关系:
当x>0时,
Q( )d A
x I (x) dx
T1 / 2
0A
T1 p .w .erf (x / w), 0 x L / 2 2 2A
三、衍射光学元件的设计
1、位相的折叠——将位相约束在一定范围以内
(x)
' (x)
采用模除的方法将位 相约束在以内:
mod[(x),]= (x)-n* n= floor[(x)/]
22
衍射元件的复振幅透过率:
t(x) ei.(x)
若=2p,则:
e e .e e i.[ ( x)m.2p ]
i. ( x) i.m.2p
26
G-S算法原理
G-S算法也称迭代傅立叶变换算法,是1972年由英国物理学家 Gerchberg和Saxton首次提出用于设计计算全息片。
RW Gerchberg and WO Saxton, “A practical algorithm for the determination of the phase from image and diffraction plane pictures,” Optik 35, 237–246 (1972).
日本等国的一些高校与研究所
国内:
中科院光电所:微细加工光学技术国家重点实验室
中科院长春光机所
清华大学精密仪器系
浙江大学光电系
华中科技大学光电系等
7
五、微光学研究现状
国外:
已经逐步走向实用化并得到广泛的应用
国内:
军用和民用均得到了较大发展
存在的困难:
1、成本高
2、成品率低
3、深浮雕面型控制困难
4、复制技术不过关
i. ( x)
由此可见,2p整数倍位相的折叠不影响复振幅透过率
最大浮雕深度:h 0 /(n(0 ) 1) (h一般在数微米)
位相最大点:2p 0
.n(0
).h
位相最小点:2p .h 0
23
'(x)
(x)
折叠后的位相'(x)是原位相(x)的周期函数,其周期为调制深度;
因而exp[i'(x)]也是以为周期、(x)的周期函数,将其按傅立叶级数展 开后得到:
台阶数
2
衍射效率 40.5%
4 81.1%
8 95.0%
16 98.7%
32 99.7%
25
3、用于光束整形的衍射光学元件的设计理论
标量衍射理论: 1) G-S算法 2) 直接二元搜索法(DBS) 3) 模拟退火算法(SA) 4) 遗传算法(GA) 5) Y-G算法
矢量衍射理论: 1) 积分法 2) 微分法 3) 模态法 4) 耦合波法
像面强度分布图(激光波长632.8nm)
31
整形举例2:Dammann光栅
Dammann光栅原理:通过对光栅每一个周期内位相分布的特殊设计, 使其各个衍射级数内分配的能量相等 Dammann光栅用途:分束器、光互联、多重成像、图象处理等等
I
白:透光
黑:不透光
普通光栅
-8
-4
0
4
8
I
达曼光栅
白:位相0 黑:位相π
衍射光学元件面 FFT
f=a.exp[i]
修正:令|f'|=a
像平面 F'=|F'|.exp[i]
修正:令|F'|=b
比较:若|F'|2-|b|2<设 定误差值,则 a(x,y).exp[i. (x,y)]即 为衍射光学元件的复 振幅透过率,跳出循 环
f'=|f'|.exp[i]
FFT-1
数据输入 F=b.exp[i]
二、微光学元件的特点
体积小、重量轻、设计自由度大、可集成、 可复制
4
三、微光学元件的分类
折射率调制型:GRIN透镜 (GRIN: gradient-index)
分类
折射型、反射型(几何光学分析)
浮雕调制型:
衍射型(衍 射光学分析)
连续面型
多台阶面型(即: 二元光学元件)
5
n
GRIN透镜
微透镜阵列
误差函数:erf (x)
2 x et2 dt
p0
第三步:利用公式(3)求解微光学元件浮雕分布h(x):
x
h(x) 0 (x)dx
h(x) T1 .x
p .w2 x .[ .erf (x / w)
1 ex2 / w2 1/
p ],0 x L / 2
2
2A w
p
同理可分析 x<0的情况。
平顶分布→环形分布;高斯分布→平顶分布;高斯分 布→环形分布等等
注意:
1、设计的前提是入射光束为准平行光,入射波前为 近似平面,所以实际应用中,如果入射光束发散角较 大,须先进行准直扩束;
2、公式(1) 、(2)和(3)的成立须满足“稳相条件”, 即输入函数变化缓慢,否则计算精度较低;
3、入射光场的相干性对输出强度分布有一定影响, 在图形突变部分会造成强度分布的轻微振荡。 21
y)
B,T2 C,T4
/ /
2 2
| |
x, x,
y y
| |
T3 T5
/ /
2 2
0, 其他
将上述振幅分布置入G-S算法中,循环多次即可得到衍射元件面的位相分布。
28
循环次数:m=1
循环次数:m=2
循环次数:m=3
பைடு நூலகம்
循环次数:m=20
29
位相折叠之前
位相折叠后
衍射元件的位相分布
30
实验结果:
第一个环 第二个环 第三个环
宏光学
聚焦、成像、位相 补偿、光束整形、 分束、滤波、耦合、 互联等等
2
内容
微光学概述 微光学元件的设计原理 微光学元件的加工工艺技术 微光学的应用举例
3
一、微光学(microoptics)的定义 研究微米、纳米级特征尺寸的光学元器件 的设计、制作工艺及利用这类元器件实现 光波的发射、传输、变换及接收的理论和 技术的新学科。
(
x) z
x
,
微光学元件后无Fourier透镜
(x) z
,微光学元件后有Fourier透镜
17
设计举例:将一束具有高斯强度分布的激光变换成环形强度分布
输入场分布:I (x) exp(x2 / w2 )
0,| | T1 / 2
输出场分布:Q( ) 1,T1 / 2 | | T2 / 2
0,| | T2 / 2
如果调制深度不是2p的整数倍(比如实际加工误差引起),则所有的Cm 都不为零,出射光束存在多级衍射光,降低了了衍射效率。
24
2、浮雕结构的二元台阶近似
起因:具有斜度的连续面型用微细加工工艺存在一定困难,而加工 阶梯结构相对较容易。
二元台阶近似下的衍射效率:
设调制深度为2p,则二元器件的复振幅透过率为:
16
x
x
(x)
θ
z
h(x)
