历年全国初中数学联赛试题总汇
历届全国中学生数学竞赛试题

中国数学奥林匹克(CMO)历届试题及解答1986-20052,其余x k 均等于0.则 2(a i + a j ) 4(a i 2(180 2(180第一届中国数学奥林匹克(1986年)天津 南开大学1.已知 a 1, a 2, . . . , a n 为实数, 如果它们中任意两数之和非负,那么对于满足x 1 + x 2 + · · · + x n = 1的任意非负实数 x 1, x 2, . . . , x n , 有不等式a 1x 1 + a 2x 2 + · · · + a n x n成立.请证明上述命题及其逆命题. a 1x 21 + a 2x 22 + · · · + a n x 2n证明:原命题的证明:由0 x i1, x i − x 2i0, x ix 2i (i = 1, 2, . . . , n ).(1)若a i0(i = 1, 2, . . . , n ),则显然有a 1x 1 + a 2x 2 + · · · + a n x na 1x 21 + a 2x 22 + · · · + a n x 2n ;(2)否则至少存在一个a i < 0,由对称性不妨设a 1 < 0. 又因为a 1, a 2, . . . , a n 中任两数之和非负,所 以a i + a 10, a i−a 1 > 0(i = 2, 3, . . . , n ).a 1x 1 + a 2x 2 + · · · + a n x n − a 1x 21 − a 2x 22 − · · · − a n x 2n-37∴= a 1(x 1 − x 21) + a 2(x 2 − x 22) + · · · + a n (x n − x 2n )a 1(x 1 − x 21) + (−a 1)(x 2 − x 22) + · · · + (−a 1)(x n − x 2n ) = (−a 1)(x 21 − x 22 − · · · − x 2n − x 1 + x 2 + · · · + x n ) = (−a 1)(x 21 − x 1 + (1 − x 1) − x 22 − · · · − x 2n ) = (−a 1)((1 − x 1)2 − x 22 − · · · − x 2n ) = (−a 1)((x 2 + · · · + x n )2 − x 22 − · · · − x 2n )-370最后一步是由于x 2, x 3, . . . , x n > 0, (x 2 + · · · + x n )2 = x 22 + · · · + x 2n +2 i<j nx i x jx 22 + · · · + x 2n . 逆命题的证明:对于任意的1 i<jn ,令x i = x j =1 11+ a j ).∴ a i + a j0,即任两数之和非负.证毕.2.在三角形ABC 中,BC 边上的高AD = 12,∠A 的平分线AE = 13,设BC 边上的中线AF = m ,问m 在什 么范围内取值时,∠A 分别为锐角,直角,钝角?解:设O 为 ABC 的外心,不妨设AB > AC ,∠B 为锐角.则OF 垂 直 平 分 线 段BC ,由 外 心 的 性 质,∠C 为 锐 角 时,∠OAB = ∠OBA =1 ◦− 2∠C ) = 90◦ − ∠C .又因为AD ⊥ BC ,∴ ∠CAD = 90◦ − ∠C ,∴ ∠OAB = ∠DAC . 类似地,当∠C 为直角或钝角时也有∠OAB = ∠DAC .由AE 平分∠BAC ,∠BAE = ∠CAE .∴ ∠OAE = ∠DAE .(由于F, D 在E 两侧). ∠A 为锐角时,O, A 在BC 同侧,∠F AE < ∠OAE = ∠DAE ; ∠A 为直角时,O, F 重合,∠F AE = ∠OAE = ∠DAE ; 1 ◦− ∠AOB ) =由正弦定理 sin ∠∠DAE = DE × AD .其中DE =AE 2 − AD 2 = 5,√ √且∠A 为锐角等价于∠A 为直角等价于× ∠A 为钝角等价于 ×< 1;119时,∠A 为锐角;119时,∠A 为直角; 119时,∠A 为钝角.4,即4.∴x k.∴ |z k | = |√ z k ∈Az k ∈Az k ∈A√而4 2 < 6, ∴ |z k |6.√ . 4.√sin F AE FEAF F E = F D − DE = AF 2 − AD 2 − DE = m 2 − 122 − 5 > 0. ∴ m > 13,√√√m 2−122−55m 2−122−55 m 2−122−55×12 m 12 m12 m= 1; > 1.解得当13 < m < 2028 当m = 当m >20282028 3.设z 1, z 2, . . . , z n 为复数,满足|z 1| + |z 2| + · · · + |z n | = 1.求证:上述n 个复数中,必存在若干个复数,它们的和的模不小于 16. 证明:设z k = x k + y k i(x k , y k ∈ R , k = 1, 2 . . . , n ) 将所有的z k 分为两组X,Y.若|x k ||y k |,则将z k 放入X 中;若|y k ||x k |,则将z k 放入Y 中. 其中必有一组中所有复数模长之和不小于 12.不妨设为X. 再将X 中的复数分为两组A,B.若x k0,则将z k 放入A 中;若x k 0,则将z k 放入B 中. 其中必有一组中的所有复数摸长之和不小于 41.不妨设为A. 则 |z k |z k ∈A而对于z k ∈ 1A ,x 2kz k ∈Ay k 2,x 2k + y k 2x 2k + y k 2 1 √2x k . 1 4 21z k ∈A即A 中复数之和的模不小于 16.证毕.x k + iz k ∈Ay k |z k ∈Ax k1 4 2另证:设z k = x k + y k i(x k , y k ∈ R , k = 1, 2 . . . , n ) 则|z k | =x 2k + y k 2|x k | + |y k |.∴ n|x k | + |y k |1.k =1∴ |x k 0x k | + |x k <0x k | + |y k 0y k | + |y k <0y k | 1. 其中必有一项不小于 14,不妨设为第一项,则 |x k 0x k |1 ∴ |x k 0z k | = |x k 0x k + ix k 0y k ||x k 0x k |1 4> 16.证毕.4.已知:四边形P 1P 2P 3P 4的四个顶点位于三角形ABC 的边上. 求证:四个三角形 P 1P 2P 3, P 1P 2P 4,P 1P 3P 4,P 2P 3P 4 中,至少有一个的面积不大于 ABC 的面积的四分之一.证明:有两种情况:(1)四个顶点在两条边上;(2)四个顶点在三条边上.(1)不妨设P 1, P 4在AB 上,P 2, P 3在AC 上,P 1, P 2分别在AP 4, AP 3上. 将B 移至P 4,C 移至P 3,三角形ABC 的BC ,设 AP 1 = 4S4SP 4P 2P 3中有一个不大于 4S面积减小,归为情形(2).(2)不妨设P 1在AB 上,P 2在AC 上,P 3, P 4在BC 上,P 3在P 4C 上. (2.1)若P 1P 2AB AP 2AC= λ,P 1P 2 = λBC .P 1P 2到BC 的距离为(1−λ)h ,h 为三角形ABC 中BC 边上的高的长度. ∴ SP 1P 2P 3= λ(1 − λ)SABC1 ABC .(2.2)若P 1P 2不 平 行 于BC ,不 妨 设P 1到BC 的 距 离 大 于P 2到BC 的 距 离. 过P 2作 平 行 于BC 的 直 线交AB 于E ,交P 1P 4于D .则S P 1P 2P 3, S P 4P 2P 3中有一个不大于S DP 2P 3,也就不大于SEP 2P 3.由(2.1)知SEP 2P 31 ABC .则SP 1P 2P 3, S1ABC .证毕.5.能否把1,1,2,2,. . . ,1986,1986这些数排成一行, 使得两个1之间夹着1个数,两个2之间夹着2个数,. . . , 两 个1986之间夹着1986个数.请证明你的结论.解:不能.假设可以做出这样的排列,将已排好的数按顺序编号为1,2,. . . ,3972.当n 为奇数时,两个n 的编号奇偶性相同;当n 为偶数时,两个n 的编号奇偶性不同. 而1到1986之间有993个 偶数,所以一共有2k + 993个编号为偶数的数.(k ∈ N ∗) 但是1到3972之间有1986个偶数,k = 496.5.矛 盾.所以不能按要求排成这样一行.√6.用任意的方式,给平面上的每一点染上黑色或白色. 求证:一定存在一个边长为1或 3的正三角形,它的 三个顶点是同色的.证明:(1)若平面上存在距离为2的两个点A, B 异色,设O 为它们的中点,不妨设A, O 同色. 考虑以AO 为一 √边的正三角形AOC, AOD ,若C, D 中有一个与A, O 同色,则该三角形满足题意. 否则BCD 为边长 3的 同色正三角形.(2)否则平面上任两个距离为2的点均同色,考虑任意两个距离为1的点,以他们连线为底,2为腰长作等腰 三角形,则任一腰的两顶点同色. 所以三个顶点同色,即任两个距离为1的点同色.所以平面上任意一个边 长为1的正三角形三个顶点同色.证毕.证明:当6|n + 2时,令z = e i 3 = − e + 2 i , z − (− 12 −2 i)2 i)3 3− z − 1 = 0有模为1的复根.6 ,k2 .n 2 .第二届中国数学奥林匹克(1987年)北京 北京大学1.设n 为自然数,求证方程z n +1 − z n − 1 = 0有模为1的复根的充分必要条件是 n + 2可被6整除.∴ z n +1 − z n − 1 = e −i π i π π√1 3 62− 1 = ( 12 − = 1, |z| = 1.√ 3√ 3 − 1 = 0.∴ z n +1n若z n +1 − z n − 1 = 0有模为1的复根e i θ = cos θ + i cos θ.则z n +1 − z n − 1 = (cos(n + 1)θ − cos nθ − 1) + i(sin(n + 1)θ − sin nθ) = 0. ∴ cos(n + 1)θ − cos nθ − 1 = −(2 sin 2n 2+1θ sin θ2 + 1) = 0. sin(n + 1)θ − sin nθ = 2 cos 2n 2+1θ sin θ2 = 0.∴ cos 2n 2+1θ = 0, sin 2n 2+1θ = ±1, sin θ2 = ± 12, 设 θ2 = ϕ. (1)sin ϕ = 12,sin(2n + 1)ϕ = −1. ϕ = 2kπ + π6 或2kπ +5π∈ Z.(2n + 1)ϕ = (2l + 32)π(l ∈ Z). ∴ (2n + 1)(2k + 16) = 2l + 23, 2n 6+1 = 2t + 32, n = 6t + 4(t ∈ Z). 或(2n + 1)(2k + 65) = 2l + 32, 5(2n 6+1) = 2t + 32, 5|4t + 3, t ≡ 3 (mod 5)(t ∈ Z). 设t = 5s + 3,则n = 6s + 4,总有6|n + 2.(2)sin ϕ = − 12,sin(2n + 1)ϕ = 1.显然以−ϕ代ϕ即有(1).所以6|n + 2.证毕.2.把边长为1的正三角形ABC 的各边都n 等分,过各分点平行于其它两边的直线, 将这三角形分成若干个 小三角形,这些小三角形的顶点都称为结点, 并且在每一结点上放置了一个实数.已知: (1)A, B, C 三点上放置的数分别为a, b, c.(2)在每个由有公共边的两个最小三角形组成的菱形之中, 两组相对顶点上放置的数之和相等. 试求:(1)放置最大数的点和放置最小数的点之间的最短距离.(2)所有结点上数的总和S .解:(1)不难证明同一直线上相邻三个结点上放置的数中间一个为两边的等差中项,所以同一直线上的数 按顺序成等差数列. 若两端的数相等,则所有的数都相等.否则两端的数为最大的和最小的. 若a, b, c 相等,显然所有数都相等,最短距离显然为0.若a, b, c 两两不等,最大的数与最小的数必出现在A, B, C 上,最短距离为1.若a, b, c 有两个相等但不与第三个相等,不妨设a = b > c ,最小的数为c ,最大的数出现在线段AB 的任意 结点上. 当n 为偶数时,与C 最近的为AB 中点,最短距离为 √ 3 当n 为奇数时,与C 最近的为AB 中点向两边偏 21n 的点,最短距离为 123+1 (2)将这个三角形绕中心旋转 32π, 43π弧度,得到的两个三角形也满足题意(2). 将这三个三角形对应结 点的数相加形成的三角形也满足(2),三个顶点上的数均为a + b + c .由(1)的分析知所有结点上的数均 为a + b + c . 共 21(n + 1)(n + 2)个结点,∴ S = 13( 12(n + 1)(n + 2))(a + b + c ) = 16(n + 1)(n + 2)(a + b + c ). 3.某次体育比赛,每两名选手都进行一场比赛, 每场比赛一定决出胜负,通过比赛确定优秀选手, 选 手A 被确定为优秀选手的条件是:对任何其它选手B, 或者A 胜B,或者存在选手C,C 胜B,A 胜C. 结果按上证明:可将换成169 +ε(ε > 0).13AB.连结A1C2, A2B1, B2C1交于A0, B0, C0. 正三角形覆盖, 面积之和为( 10)2 + 2 ×点. 即169 +ε(ε > 0)为最优. 169述规则确定的优秀选手只有一名, 求证:这名选手一定胜所有其它选手.证明:假设该优秀选手为A,且存在其他选手胜A.设B为所有胜A的人中胜的场次最多的一个,由B不是优秀选手,必存在选手C使得C胜B, 且不存在选手D使得B胜D,D胜C. 由B胜A,C也胜A,且C胜B胜过的所有人.C至少比B多胜一场,且C胜A,与B的选取矛盾.所以A胜所有人.4.在一个面积为1的正三角形内部,任意放五个点,试证:在此正三角形内, 一定可以作三个正三角形盖住这五个点, 这三个正三角形的各边分别平行于原三角形的边, 并且它们的面积之和不超过0.64.100在面积为1的正三角形ABC中,在AB上取A1, B2,AC上取A2, C1,BC上取B1, C2, 使得AA1 = AA2 =BB1 = BB2 = CC1 = CC2 = 3(1)若AB2C1, BC2A1, CA2B1中有一个至少包含五个点中的三个,另两个点可分别用面积为2ε的13 ε2= 100169+ε.(2)菱形AA1A0A2, BB1B0B2, CC1C0C2中有两个有两个点,另一个中有一个点, 则可用两个边长为136 AB的正三角形和一个面积为ε的正三角形覆盖. 面积之和为2( 136 )2 +ε <100169+ε.(3)菱形AA1A0A2, BB1B0B2, CC1C0C2中有两个有一个点,另一个中有两个点, 不妨设为AA1A0A2,则B1B0C0C2中有一个点,不妨设这个点更靠近B, 则可用一个边长为136 AB的正三角形覆盖AA1A0A2中两个点, 用一个边长为136 AB的正三角形覆盖BB1B0B2, B1B0C0C2中的点. 用一个面积为ε的正三角形覆盖最后一个点, 面积之和为( 136 )2 + ( 138 )2 +ε = 100169+ε.证毕.注:当五个点取为A, B, C, A0, B0C0中点是不难证明不能用三个面积之和为100的正三角形覆盖这五个1005.设A1A2A3A4是一个四面体, S1, S2, S3, S4分别是以A1, A2, A3, A4为球心的球, 它们两两相外切.如果存在一点O, 以这点为球心可作一个半径为r的球与S1, S2, S3, S4都相切, 还可以作一个半径为R的球和四面体的各棱都相切,求证:这个四面体是正四面体.证明:设S i的半径为r i(i = 1, 2, 3, 4),则A i A j = r i + r j(1 i<j 4).设O到A2A3A4的投影为O1,由O到A2A3,A3A4,A4A2的距离相等, 得到O1到A2A3A4的三边距离相等.即O1为A2A3A4的内心,设O到A2A3的投影为B,即O1到A2A3的投影. 而BA3 = 21(A2A3 + A3A4−A2A4) = r3,OB = R. 若半径为r的球与四个球均外切,则A3O = r +r3,(r +r3)2 = r32 +R2, r3 = R2−r22r.若半径为r的球与四个球均内切,则A3O =r−r3,(r−r3)2 = r32+R2, r3 = r2−R22r. 类似可求得r1, r2, r4均为该值,所以该四面体各条棱长相等为正四面体.6.m个互不相同的正偶数与n个互不相同的正奇数的总和为1987, 对于所有这样的m与n,问3m + 4n的最大值是多少?请证明你的结论.解:设m个正偶数为a1 < a2 < · · · < a m,n个正偶数为b1 < b2 < · · · < b n.∴a i 2i, b j 2j − 1.1987 = a1 + a2 + · · · + a m + b1 + b2 + · · · + b n.∴1987 2 + 4 + · · · + 2m + 1 + 3 + · · · + 2n − 1 = m2 + m + n2.s − 8ns + 25n + 3s − 12n − 9 × 1987所以判别式∆ = (3 − 8n ) − 4(25n − 12n − 9 × 1987) = 26(1987 41 − n 2) > 0. 2(8n设f (n ) = 8n + 6 1987 14 − n 2, f (n ) = 8 − 6n (1987 14 − n 2)− 2 ,又n 为奇数. 2(280设s = 3m + 4n ,m = 13(s − 4n ), 13(s − 4n )( 13(s − 4n ) + 1) + n 21987.2 2 s 2 + (3 − 8n )s + 25n 2 − 12n − 9 × 19870. 0.2 2s1− 3+61987 14 − n 2).1不难知道n = 35时,f (n )有最大值280 + 6 762 14. 所以s1+ 6 762 14 − 3),由s ∈ N ∗, s221.又当s = 221, n = 35, m = 27.取2, 4, . . . , 52, 60, 1, 3, . . . , 69为和为1987的35个正奇数与27个正偶数,所 以3m + 4n 的最大值为221.iiii i i r i 2 = 1,由Cauchy不等式取等号的条件知 ∴=a i a n .2第三届中国数学奥林匹克(1988年)上海 复旦大学1.设a 1, a 2, . . . , a n 是给定的不全为零的实数, r 1, r 2, · · · , r n 为实数,如果不等式r 1(x 1 − a 1) + r 2(x 2 − a 2) + · · · + r n (x n − a n )对任何实数x 1, x 2, · · · , x n 成立,求r 1, r 2, · · · , r n 的值. x 21 + x 22 + · · · + x 2n −a 21 + a 22 + · · · + a 2n解:令x i = 0(i = 1, 2, . . . , n ),−(r 1a 1 + r 2a 2 + · · · + r n a n )n n∴ ( r i a i )2 a 2.i =1 i =1 令x i = 2a i (i = 1, 2, . . . , n ),r 1a 1 + r 2a 2 + · · · + r n a n n n∴ ( r i a i )2 a 2.i =1 i =1n n∴ ( r i a i )2 = a 2.i =1 i =1n n n n 由Cauchy 不等式, ( r 2)( a 2) ( r i a i )2, r 2 i =1 i =1 i =1 i =1− a 21 + a 22 + · · · + a 2n .a 21 + a 22 + · · · + a 2n .1.n又令x i = r i (i = 1, 2, . . . , n ),i =1 r i 2 −ni =1r i a ii =1 r i 2 −i =1a 2i .由 i =1r i a i =i =1a 2i =1r i 2i =1r i 2,i =1r i 21. ni =1不难解得r = (i =12n )a 21 + a 22 + · · · + a nr 1a 1r 2 a 2= ··· =r n2.设C 1, C 2为 同 心 圆,C 2的 半 径 是C 1的 半 径 的2倍, 四 边 形A 1A 2A 3A 4内 接 于C 1, 设A 4A 1延 长 线 交 圆C 2于B 1, A 1A 2延长线交C 2于B 2, A 2A 3延长线交圆C 2于B 3, A 3A 4延长线交圆C 2于B 4. 试证:四边形B 1B 2B 3B 4的周长 2(四边形A 1A 2A 3A 4的周长).并确定等号成立的条件. 证明:设圆心为O ,连结OB 1, OB 4, OA 4,设C 1的半径为R ,C 2的半径为2R . 在四边形B 4A 4OB 1中,由Ptolemy 定理,OA 4 × B 1B 4 + OB 1 × A 4B 4 OB 4 × A 4B 1.R × B 1B 4 + 2R × A 4B 4 2R × A 4B 1,即B 1B 42A 4B 1 − 2A 4B 4.同理B 1B 22A 1B 2 − 2A 1B 1,B 2B 3 2A 2B 3 − 2A 2B 2,B 3B 42A 3B 4 − 2A 3B 3.相加得B 1B 2 + B 2B 3 + B 3B 4 + B 4B 1 2(A 1A 2 + A 2A 3 + A 3A 4 + A 4A 1).即四边形B 1B 2B 3B 4的周长 2(四边形A 1A 2A 3A 4的周长).等号成立时OA i B i B i +1共圆,∠A i +1A i O = ∠B i +1B i O = ∠B i B i +1O = ∠A i−1A i O , ∴ A i +1A i = A i−1A i ,(i = 1, 2, 3, 4, A 5 = A 1, A 0 = A 4, B 5 = B 1). ∴ A 1A 2A 3A 4为菱形,又为圆内切四边形,所以A 1A 2A 3A 4为正方形.3.在有限的实数列a 1, a 2, · · · , a n 中, 如果一段数a k , a k +1, · · · , a k +l−1的算术平均值大于1988, 那么我们 把这段数叫做一条“龙”,并把a k 叫做这条龙的“龙头” (如果某一项a n > 1988,那么单独这一项也叫龙). 假设以上的数列中至少存在一条龙, 证明:这数列中全体可以作为龙头的项的算术平均数也必定大a 2 + a 22 + a 23于1988.证明:引理:设a k , a k +1, . . . , a k +m−1均可作为龙头,a k +m 不能作为龙头,或k + m − 1 = n , 则a k , a k +1, . . . , a k +m−1的算术平均值大于1988.引理的证明:对m 用数学归纳法,m = 1时,设以a k 为龙头的一条龙为a k , a k +1, . . . , a k +l−1. 若l = 1,a k > 1988,显然成立.否则l > 1,由a k , a k +1, . . . , a k +l−1算术平均值大于1988,a k +1不是龙头, a k +1, . . . , a k +l−1算术平均值不 大于1988,a k > 1988,结论成立. 设小于m 时结论均成立(m 2),设以a k 为龙头的一条龙为a k , a k +1, . . . , a k +l−1.1lm 时,a k , a k +1, . . . , a k +l−1算术平均值大于1988, 由归纳假设a k +l , . . . , a k +m−1算术平均值大于1988,结论成立.l > m 时,由a k +m 不是龙头,a k +m , a k +m +1, . . . , a k +l−1算术平均值不大于1988, a k , a k +1, . . . , a k +l−1算术 平均值大于1988,结论显然也成立. 综上所述,由数学归纳法,引理成立.设所有的龙头为a i 1, a i 1+1, . . . , a i 1+j 1−1, a i 2, a i 2+1, . . . , a i 2+j 2−1, . . . , a i k , a i k +1, . . . , a i k +j k −1, 其中j 1, j 2, . . . , j k1 且i m +1 > i m + j m (m = 1, 2, . . . , k − 1, k1).由引理:a i m , a i m +1, . . . , a i m +j m −1的算术平均值大于1988(m = 1, 2, . . . , k ). 所以所有龙头的算术平均值 也大于1988.证毕.4.(1)设三个正实数a, b, c 满足(a 2 + b 2 + c 2)2 > 2(a 4 + b 4 + c 4).求证:a, b, c 一定是某个三角形的三条边长. (2)设n 个正实数a 1, a 2, · · · , a n 满足(a 21 + a 22 + · · · + a 2n )2 > (n − 1)(a 41 + a 42 + · · · + a 4n )其中n3. 求证:这些数中任何三个一定是某个三角形的三条边长.证明:(1)若不然,不妨设ca +b ,则2(a 4 + b 4 + c 4) − (a 2 + b 2 + c 2)2 = a 4 + b 4 + c 4 − 2a 2b 2 − 2b 2c 2 − 2c 2a 2= −(a + b + c )(a + b − c )(b + c − a )(c + a − b )矛盾.∴ a, b, c 为某个三角形三边长.(2)n = 3即为(1)中的情况,n > 3时,若存在某三个不是某个三角形三条边长,不妨设为a 1, a 2, a 3.则由均 值不等式(n − 1)(a 41 + a 42 + · · · + a 4n ) < (a 21 + a 22 + · · · + a 2n )2=a 21 + a 22 + a 232 + 1 2+ · · · + a 2n 2(n − 1)a 21 + a 22 + a 2322+a 21 + a 22 + a 2322+ · · · + a 4n1, n 奇数2, n = 2k ·m (m 为奇数)所有小于2k +1的正奇数不全整除n可得 12(a 2 + b 2 + c 2)2 > a 4 + b 4 + c 4,(a 2 + b 2 + c 2)2 > 2(a 4 + b 4 + c 4).但由(1),a 1, a 2, a 3为某个三角形三边长,矛盾.所以这些数中任何三个一定是某个三角形的三条边长. 5.给出三个四面体A i B i C i D i (i = 1, 2, 3), 过点B i , C i , D i 作平面αi , βi , γi (i = 1, 2, 3), 分别与棱A i B i , A i C i , A i D i 垂直(i = 1, 2, 3), 如果九个平面αi , βi , γi (i = 1, 2, 3),相交于一点E , 而三点A 1, A 2, A 3在同一直 线l 上, 求三个四面体的外接球面的交集(形状怎样?位置如何?)解: A i B i ⊥ αi 于B i ,而E 在αi 上,∴ A i B i ⊥ B i E, B i 在以A i E 为直径的球上.同理C i , D i 也在以A i E 为直 径的球上,A i B i C i D i 的外接球即为在以A i E 为直径的球.若E 在l 上,显然这三个球的中心也都在l 上,它们必在E 处两两相切,交集为E .否则E 不在l 上,三个球的球心在同一条直线上( EA 1A 2中位线所在直线),且这三个球都过点E ,交集为 一个圆,直径为EE ,其中E 为E 到l 的垂足.6.如n 是不小于3的自然数,以f (n )表示不是n 的因子的最小自然数, 例如f (12) = 5.如果f (n ) 3,又可作f (f (n )). 类似地,如果,f (f (n ))3,又可作f (f (f (n ))),等等. 如果f (f (· · · f (n ) · · · )) = 2, 共有k 个f ,就把k 叫做n 的“长度”. 如果 l n 表示n 的长度,试对任意自然数n (n 解:设n = 2k · m (m 为奇数). 若k = 0,n 为奇数,f (n ) = 2, l n = 1.若k > 0,考虑所有小于2k +1的正奇数,若它们均为n 的因子,由2k +13),求 l n .并证明你的结论.n 且小于2k +1的偶数t = 2p · q (pk, q 为奇数),由q|n, 2p |n, gcd(q, 2p ) = 1,知t|n ,∴ f (n ) = 2k +1,f (f (n )) = 3, f (f (f (n ))) = 2, l n = 3. 否则取最小的t|n ,t 必为奇数,否则t 必有一个奇因子不整除n . ∴ f (n ) = t, f (f (n )) = 2, l n = 2. 综上所述,l n =3, n = 2k · m (m 为奇数)所有小于2k +1的正奇数均整除n段的长度都等于 m , m 是自然数. 用A j 表示将集合A 逆时针方向在圆周上转动 jmπ 弧度所得的集合 2π L (A )L (B ).设b 1, b 2, . . . , b n 为组成B 的弧段,由已知它们两两不交且每段的长度均为 m ,因此有 i i i L (A ∩ (∪2j =1b −j )) m ,所以∪j =1b iL (A ∩ (∪2j =1b −j )) = L (A ).第四届中国数学奥林匹克(1989年)合肥 中国科技大学1.在半径为1的圆周上,任意给定两个点集A, B , 它们都由有限段互不相交的弧组成, 其中B 的每π(j = 1, 2, ...).求证:存在自然数k ,使得L (A j ∩ B )1这里L (X )表示组成点集X 的互不相交的弧的长度之和.证明:我们把圆周上的点集E 沿顺时针方向在圆周上转动 jm π 弧度所得的集合记为E −j ,于是L (A j ∩ B ) = L (A ∩ B −j ).π2mj =1L (A j ∩ B ) ==2mj =1 2mj =1L (A ∩ B −j )L (A ∩ (∪ni =1b −j ))=2mnL (A ∩ b −j )j =1 i =1=n 2mL (A ∩ b −j )i =1 j =1 n=i =1mi因为L (b i ) = π 2m −j恰好是整个圆周,从而有mi ∴2mj =1L (A j ∩ B ) = nL (A ),至少存在一个k, 1k 2m ,使得L (A j ∩ B )n 2mL (A ) =1L (A )L (B ).2.设x 1, x 2, · · · , x n 都是正数(n2).且 x 1 + x 2 + · · · + x n = 1.求证:ni =1√x i1 − x i√ 1n − 1ni =1√x i .证明:不妨设x 1 x 2 ··· x n ,则√1 1 − x 1√1 1 − x 2···√1 1 − x n由Chebyshev 不等式ni =1√x i 1 − x i1nni =1x ini =1√ 11 − x i= 1nni =1√ 11 − x iB n ,又f 1(z ) = z m ,∴ f n (z ) = z m ∴ f n (z ) = z ⇔ z m = z ,又|z| = 1, ∴ z m 由1989 = 3 × 13 × 17,若k|1989,且k < 1989,k 必 整 除3 × 13 × 17, 32 × 13, 32 × 17中 至 少 一 个.由Cauchy 不等式ni =1√1 − x ini =1√1 1 − x in 2又n√ 1 − x inn(1 − x i ) =n (n − 1)i =1i =1ni =1√ x i1 − x i1 n ni =1√ 11 − x ini =1n √1 − x in n (n − 1)=n n − 1而√1 n − 1ni =1 √ x i√1 n − 1n ni =1x i =n n − 1ni =1√ x i1 − x i√1n − 1ni =1√x i .3.设S 为 复 平 面 上 的 单 位 圆 周 (即 模 为1的 复 数 的 集 合),f 为 从S 到S 的 映 射,对 于 任 意 z ∈ S ,定 义f (1)(z ) = f (z ), f (2)(z ) = f (f (z )), · · · , f (k )(z ) = f (f (k−1)(z )). 如果 c ∈ S ,使得f (1)(c ) = c, f (2)(c ) = c, · · · , f (n−1)(c ) = c, f (n )(c ) = c . 则称 c 为f 的n−周期点.设m 是大于1的自然数, f 定义为f (z ) = z m , 试计算f 的1989-周期点的个数.解:记A n = {z ∈ S|z 是f 的n − 周期点},B n = {z ∈ S|f n (z ) = z}为f n 的 不 动 点 集 合,显 然A n ⊆nn n−1= 1, |B n | = m n − 1.我们证明B n , A n 有如下性质: (1)若k|n ,则B k ⊆ B n ;事实上,令n = kq ,若c ∈ B k , f k (c ) = c ,则f n (c ) = f kq (c ) = f k (f k (· · · f k (c ) · · · )) = c . ∴ c ∈ B n , B k ⊆ B n .q 个(2)B k ∩ B n = B gcd(k,n ), gcd(k, n )为k 与n 的最大公约数. 由(1),B gcd(k,n ) ⊆ B k , B gcd(k,n ) ⊆ B n , ∴ B gcd(k,n ) ⊆ B k ∩ B n .反之,设c ∈ B k ∩ B n ,f k (c ) = c, f n (c ) = c ,不妨设k < n . 则f n−k (c ) = f n−k (f k (c )) = f n (c ) = c ,由辗转相 除法知f gcd(k,n )(c ) = c, ∴ c ∈ B gcd(k,n ), B k ∩ B n ⊆ B gcd(k,n ). ∴ B k ∩ B n = B gcd(k,n ). (3)c ∈ B n \ A n ⇔ ∃k < n, k ∈ N ∗,使k|n 且c ∈ B k .充分性是显然的(由(1)),设c ∈ B n \ A n , f n (c ) = c .且存在l < n ,使得f l (c ) = c ,设k = gcd(l, n ),则f k (c ) = c, c ∈ B k ,且kl < n, k|n .证毕.2∴ B k ⊆ B 663 ∪ B 153 ∪ B 117, ∴ A 1989 = B 1989 \ (k|1989k<1989B k ) = B 1989 \ (B 663 ∪ B 153 ∪ B 117).R .∴由容斥原理f 的1989-周期点个数为|A 1989| = |B 1989| − |B 663| − |B 153| − |B 117| + |B 663 ∩ B 153| + |B 663 ∩ B 117| + |B 117 ∩ B 153|−|B 663 ∩ B 153 ∩ B 117|= |B 1989| − |B 663| − |B 153| − |B 117| + |B 51| + |B 39| + |B 9| − |B 3|= (m 1989 − 1) − (m 663 − 1) − (m 153 − 1) − (m 117 − 1) + (m 51 − 1) + (m 39 − 1)+(m 9 − 1) − (m 3 − 1)= m 1989 − m 663 − m 153 − m 117 + m 51 + m 39 + m 9 − m 34.设点D, E, F 分别在 ABC 的三边BC, CA, AB 上, 且 AEF,BF D,CDE 的内切圆有相等的半径r , 又以r 0和R 分别表示 DEF 和 ABC 的内切圆半径. 求证:r + r 0 = R .证明:设 ABC 周长为l ,面积为S ,内切圆为 I , 在各边的切点为P, Q, R , DEF 周长为l ,面积为S . AEF,BF D,CDE 的面积分别为S 1, S 2, S 3,内切圆分别为 I 1, I 2, I 3,在各边的切点为P i , Q i , R i (i = 1, 2, 3). 由面积公式2S = Rl, 2S = r 0l ,2S 1 = r (AE + EF + F A ), 2S 2 = r (BD + DF + F B ), 2S 3 = r (CD + DE + EC ). 又S = S + S 1 + S 2 + S 3, ∴ Rl = r 0l + r (l + l ),即(R − r )l = (r + r 0)l . 又AQ 1 AQ = AR 1AR= BQ 2BQ= BP 2 BP = CP 3CP= CR 3CR = r Rl − Q 1Q 2 − P 2P 3 − R 1R 3l=r R又Q 1Q 2 + P 2P 3 + R 1R 3 = Q 1F + F Q 2 + P 2D + DP 3 + R 3E + ER 1 = P 1F + R 2F + DR 2 + DQ 3 + EQ 3 + EP 1 = l . l l=1 −r(R − r )R = (r + r 0)(R − r ), R = r + r 0.证毕.5.空间中有1989个点,其中任何三点不共线, 把它们分成点数各不相同的30组, 在任何三个不同的组中 各取一点为顶点作三角形, 求三角形个数的最大值.解:由分组情况有限,三角形个数必存在最大值,设分为30组,各组点数为x 1 < x 2 < · · · < x 30, 三角形个 数为f (x 1, x 2, . . . , x 30) =1 i<j<k 30x i x j x k .f (x ) 4u f (y ) 4v . (f (x )) t .∴ f (x t ) = (f (x )) t .设f (e ) = c, c > 1,则f (x ) = f (e ) ln x = c ln x .另外,当f (x ) = c ln x (c > 1)时,f (x u y v ) = c u ln x +v ln y , f (x ) 4u f (y ) 4v = c 4u ln x + 4v ln y . 4v ln y ) 4v ln y . f (x ) 4u f (y ) 4v . 所以所求函数为f (x ) = c ln x (c > 1).若存在i ∈ {1, 2, . . . , 29}, x i +1 − x i3, 则将(x 1, x 2, . . . , x 30)调整为(x 1, . . . , x i + 1, x i +1 − 1, . . . , x 30).f (x 1, . . . , x i + 1, x i +1 − 1, . . . , x 30) − f (x 1, x 2, . . . , x 30) =[(x i + 1 + x i +1 − 1)−[(x i + x i +1)x j x k + (x i + 1)(x i +1 − 1)1 j<k 30 j,k =i,i +1x j x k + x i x i +1x j ]j =i,i +1x j ]1 j<k 30 j,k =i,i +1j =i,i +1= (x i +1 − x i − 1)j =i,i +1x j > 0f 值增大,类似的,若存在i, j ∈ {1, 2, . . . , 29}, i < j, x i +1−x i2, x j +1−x j2, 将x i 调整为x i +1,x j +1调整为x j +1 − 1,f 值增大.所以当f 取最大值时,x 1, x 2, . . . , x 30中相邻两个的差最多有一个是2,其余均为1. 如果所有的均为1,1989 = x 1 + (x 1 + 1) + · · · + (x 1 + 29) = 30x 1 + 435,x 1不是整数,矛盾. 设x t +1 − x t = 2, 1t29,则1989 = x 1 + x 2 + · · · + x 30 = 30x 1 + (1 + 2 + · · · + t − 1) + (t + 1 + · · · + 30) = 30x 1 + 465 − t . 30x 1 − t = 1524, x 1 = 51, t = 6.此时各组的点的个数分别为51,52,. . . ,56,58,59,. . . ,81.6.设f : (1, +∞) → (1, +∞)满足以下条件: 对于任意实数x, y > 1,及u, v > 0,有试确定所有这样的函数f . f (x u y v ) 1 1解:令x = y, u = v = 2t (t > 0),则f (x t ) 1以x t 代x , 1t 代t ,则f (x ) (f (x t ))t .11 11 1 1 1 1 1由Cauchy 不等式,(u ln x + v ln y )( 4u 1ln x +11.∴1u ln x +v ln y1 4u ln x+1∴ f (x u y v )1 11SB .又 SD x t−1 ·· · ·· x 1 ·x 1是t 个大于1的第五届中国数学奥林匹克(1990年)郑州 《中学生数理化》编辑部1.在凸四边形ABCD 中,AB 与CD 不平行,O 1过A ,B 且与边CD 相切于P ,O 2过C ,D 且与边AB 相切于Q ,O 1与 O 2相交于E ,F .求证:EF 平分线段P Q 的充分必要条件是BC AD .证明:分两部分证明结论.(1)EF 平分P Q 的充要条件为P C · P D = QA · QB . 设EF 与P Q 交于K ,直线P Q 于 O 1, O 2分别交于J, I .P C · P D = P I · P Q, QA · QB = P Q · QJ , KQ · KI = KE · KF = KP · KJ . ∴ KQ · (KP + IP ) = KP · (KQ + QJ ), KQ · IP = KP · QJ . ∴ KP = KQ ⇔ IP = QJ ⇔ P C · P D = QA · QB . (2)BCAD 充要条件为P C · P D = QA · QB .设AB 与DC 交于S .BC AD ⇔SDSC=SA 而SP 2 = SA · SB, SQ 2 = SC · SD .∴ P C · P D = QA · QB ⇔ (SC − SP )(SP − SD ) = (SB − SQ )(SQ − SA )⇔ (SC + SD )SP − SP 2 − SC · SD = (SB + SA )SQ − SQ 2 − SA · SB ⇔ (SC + SD )SP = (SB + SA )SQ⇔ (SC + SD )2 · SA · SB = (SA + SB )2 · SC · SD ⇔SCSD+SD SC +2=SA SB+SB SA+2SC < 1,SA SB< 1, ∴ P C · P D = QA · QB ⇔ SD SC=SASB⇔ BC AD .所以EF 平分线段P Q 的充分必要条件是BC AD .2.设x 是一个自然数,若一串自然数x 0 = 1 < x 1 < x 2 < · · · < x l = x 满足x i−1|x i (i = 1, 2, . . . , l ), 则 称{x 0, x 1, . . . , x l }为x 的一条因子链. l 称为该因子链的长度. L (x )与R (x )分别表示 x 的最长因子链的长 度和最长因子链的条数.对于x = 5k × 31m × 1990n ,k, m, n 都是自然数,试求L (x )与R (x ).解:对 于x = p α1 1p α2 2 · · · p αn n ,(p 1, p 2, . . . , p n 为 互 不 相 同 的 质 数,α1, α2, . . . , αn 为 正 整 数). x 的 因 子链{x 0, x 1, . . . , x l }是最长因子链的充要条件是 xx i−i 1 均为质数(i = 1, 2, . . . , l ).事实上,对于因子链{x 0, x 1, . . . , x l },若存在i, (1il ),使得 xx i−i 1 = q 1q 2,其中q 1, q 2均为大于1的正整数, 则{x 0, x 1, . . . , x i−1, q 1x i−1, x i , . . . , x l }是长度为l + 1的因子链, 所以{x 0, x 1, · · · , x l }不是最长因子 链.反 之,若 xx i−i 1 均 为 质 数(i = 1, 2, . . . , l ), 则x = x l =x lx l−1· ·· ·x 2 x 1· x 1(x 0 = 1)为l 个 质 数 的 积.所以l = α1+α2+· · ·+αn . 而对x 的任意一个因子链{x 0, x 1, . . . , x t },x = x t = x t x 2正整数之积,而x 至多写成l = α1 + α2 + · · · + αn 个大于1的正整数之积,所以t最长因子链.l .所以{x 0, x 1, · · · , x l }是(n !)2(n +k )!m !.2 ) > 22 −2n−1x 2(n ∈ N) x .2( 2k )(22 −2k−1x 2)22( 2k ) xx .x > M .2 )(x 2 )(13a ) . 2 ,(1)与(2)等价,不难验证x2 ,则L (x ) = α1 + α2 + · · · + αn .每个最长因子链对应一个排列x 1, xx 21 , . . . , xx l−l 1 , l = L (x ), 为α1个p 1,α2个p 2,. . . ,αn 个p n 的一个排列. ∴ R (x ) =(α1+α2+···+αn )!α1!α2!···αn !.当x = 5k × 31m × 1990n = 2n × 5n +k × 31m × 1990n 时, L (x ) = 3n + k + m ,R (x ) = (3n +k +m )! 3.设函数f (x )对x 0有定义,且满足条件: (1)对任何x, y0, f (x )f (y )y 2f ( x 2 ) + x 2f ( y 2 ); (2)存在常数M > 0,当0 求证:对任意x 0,f (x )x x 2.1时,|f (x )|M .证明:令x = y ,(f (x ))2 2x 2f ( x 2 ). 令x = 0,(f (0))20,∴ f (0) = 0,满足结论.假设存在x > 0,使得f (x ) > x 2,用归纳法证明f (x nnn = 0时显然成立,设n = k 时成立,f ( 2x k ) > 22k−2k−1 2∴ f (x 2k +1)(f ( 2x k ))2x 2>kx 2= 22 k +1−2(k +1)−1 2即n = k + 1时也成立,所以对任意n ∈ N,f ( 2x n ) > 22 又n → +∞时,2n − 2n − 1 → +∞, 21n → 0. n−2n−1 2∴ ∃m 1,当nm 1时,0 <x 2n< 1,∃m 2,当nm 2时,22n−2n−1 2取m = max {m 1, m 2},0 <x2m< 1, f ( 2x m ) > M ,矛盾.所以对任意x0,f (x )x 2.4.设a 是给定的正整数,A 和B 是两个实数,试确定方程组:x 2 + y 2 + z 2 = (13a )2(1)x 2(Ax 2 + By 2) + y 2(Ay 2 + Bz 2) + z 2(Az 2 + Bx 2) =14(2A + B )(13a )4(2)有整数解的充分必要条件(用A, B 的关系式表示,并予以证明).解:(2) − B 2× (1)2,得(A − B 4 + y 4 + z 4) = 12(A − B 4若A = 若A = B B= 3a, y = 4a, z = 12a 为一组解.2(x 4 + y 4 + z 4) = (13a )4(3)∴ 2|a ,设a = 2a 1,x 4 + y 4 + z 4 = 8(13a 1)4.若x, y, z 不全为偶数,则必为两个奇数一个偶数,x 4 + y 4 + z 4 ≡ 2 (mod 4),矛盾.∴ 2|x, 2|y, 2|z .设x = 2x 1, y = 2y 1, z = 2z 1,则若(x, y, z, a )为(3)的解,(x 1, y 1, z 1, a 1)也为(3)的解. 类似可 依次得到(x , y , z , a )也为(3)的解,等等.但这个过程不能一直进行下去,矛盾.所以方程组有整数解的充分必要条件为A = B2 .5.设X是一个有限集合, 法则f使得X的每一个偶子集E(偶数个元素组成的子集)都对应一个实数f(E),满足条件:(1)存在一个偶子集D,使得f(D) > 1990;(2)对于X的任意两个不相交的偶子集A, B,有f(A ∪B) = f(A) + f(B)− 1990.求证:存在X的子集P, Q,满足(1)P ∩ Q =∅,P ∪Q = X;(2)对P的任何非空偶子集S,有f(S) > 1990;(3)对Q的任何偶子集T ,有f(T ) 1990.证明:考虑X的所有偶子集经法则f得到的实数最大的一个为P ,若不止一个,取元素个数最少的一个.Q = X \ P .则P ∩ Q =∅, P ∪Q = X.令A = B =∅,则f(∅) = 1990.对于∀S ⊆ P, S =∅,f(P ) = f(S) + f(P \ S)− 1990,显然f(P \ S) < f(P ),∴f(S) > 1990.对于∀T ⊆ Q,若T =∅,f(T ) = 1990,否则T =∅,由f(P ∪T ) = f(P )+f(T )−1990 f(P ),f(T ) 1990. ∴P, Q满足条件.证毕.6.凸n边形及n − 3条在n边形内不相交的对角线组成的图形称为一个剖分图.求证:当且仅当3|n时,存在一个剖分图是可以一笔划的图(即可以从一个顶点出发,经过图中各线段恰一次,最后回到出发点).证明:因为n − 3条在形内互不相交的对角线将凸n边形分为n − 2个顶点均是n边形顶点的小区域, 每个区域的内角和不小于π,n边形的内角和为(n − 2)π,所以每个小区域都是三角形.先证必要性.用归纳法容易证明可将每个三角形区域涂成黑白两色之一,使得有公共边的三角形不同色. 假设已按照这样的要求染色,由于剖分图为可以一笔画的圈,所以由每个顶点引出的线段都是偶数条. 从而每个顶点都是奇数个三角形的顶点,因此以原多边形外边界为一边的三角形区域有着相同的颜色, 不妨设为黑色;另一方面,剖分图的每条对角线都是两种不同颜色三角形的公共边, 所以设黑三角形有m1个,白三角形有m2个.则n = 3m1− 3m2,所以3|n.再证充分性,设n = 3m,多边形为A1A2 . . . A3m.连接A1A3i, A3i A3i+2, A3i+2A1(i = 1, 2, . . . , m−1)这3m−3条对角线, 形成m − 1个三角形,可由A1出发,依次走过这些三角形,再走过凸多边形即可一笔画并回到初始点.证毕.2S ABCD ,作平行四边形AEDP ,显然P B, P C 均在AP DCB 内.∴ z k−1 = z (k−1) , (k − 1)(k − 2) = 0, k = 1或2.第六届中国数学奥林匹克(1991年)武汉 华中师范大学1.平面上有一凸四边形ABCD .(1).如果平面上存在一点P ,使得 ABP, BCP, CDP, DAP 面积都相等,问四边形ABCD 应满足什么条件?(2).满足(1)的点P ,平面上最多有几个?证明你的结论. 解:(1)(1.1)P 在ABCD 内部,若A, P, C ,B, P, D 分别三点共线, 显然ABCD 为平行四边形,P 为对角线的交点.若A, P, C 不共线,由于 P AB , P AD 等面积,AP 必经过对角线BD 的中点,同理CP 过BD 的中点,必 有P 为BD 的中点,所以 ABD,BCD 面积相等.即一条对角线平分ABCD 的面积,显然也是充分条件.(1.2)P 在ABCD 之外,不妨设P 与B, C 在AD 异侧,P 必与A, B 在CD 同侧,与C, D 在AB 同侧. 由 P AB,P AD 面积相等,P ABD ,同理P DAC .设AC, BD 相交于E ,AEDP 为平行四边形.S AED = S AP D = S ABP + S CDP + S P BC − S ABCD = 3S AP D − S ABCD . ∴ S AED = 21S ABCD .这个条件也是充分条件,若S AED =1∴ S ABP = S AP D = S CDP = S AED , S P BC = S AP D + S ABCD − S ABP − S CDP = S AED .P 满足要求.所以四边形ABCD 有一条对角线平分面积,或者在对角线分成的四个三角形中有一个为四边形面积的 一半.(2)由(1)知,P 在形内,形外都至多有一个,又由充要条件不同时取到,P 最多有一个. 2.设I = [0, 1],G = {(x, y )|x, y ∈ I}.求G 到I 的所有映射f ,使得对任何x, y, z ∈ I 有 (1)f (f (x, y ), z ) = f (x, f (y, z )); (2)f (x, 1) = x, f (1, y ) = y ;(3)f (zx, zy ) = z k f (x, y ).这里,k 是与x, y, z 无关的正数. 解:由(3),f (x, y ) = f (y · xy , y · 1) = y k f ( xy , 1)(0 < x < y ) f (x, y ) = f (x · 1, x · xy ) = y k f (1, xy )(0 < y < x )再由(2),f (x, y ) = y k−1x (0 < x < y ), f (x, y ) = x k−1y (0 < y < x ) 又x = y 时,f (x, x ) = x k f (1, 1) = x k .在(1)中,取0 < x < y < z < 1,x 充分小时,y k−1x < z, x < z k−1y .f (f (x, y ), z ) = f (y k−1x, z ) = z k−1y k−1x ,f (x, f (y, z )) = f (x, z k−1y ) = x (z k−1y )k−1.2k = 1时,f (x, y ) = min {x, y};k = 2时,f (x, y ) = xy .(x > 0, y > 0)又f (x, 0) = f (x · 1, x · 0) = x k f (0, 1) = 0, f (0, y ) = 0, f (0, 0) = z k f (0, 0), f (0, 0) = 0. ∴ k = 1时,f (x, y ) = min {x, y};k = 2时,f (x, y ) = xy .k = 1, k = 2时,无解.。
历年全国初中数学联赛试题总汇

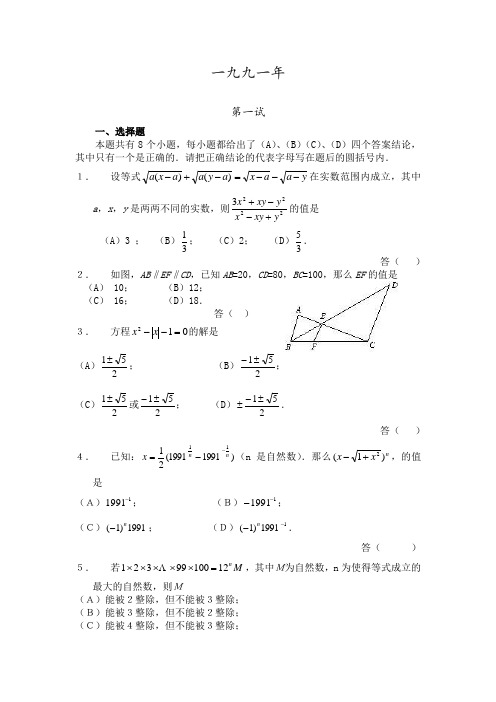
1991年全国初中数学联合竞赛决赛试题第一试一、选择题本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内. 1.设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是两两不同的实数,则22223yxy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )35.答( )2. 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是 (A ) 10; (B )12; (C ) 16; (D )18. 答( ) 3. 方程012=--x x 的解是(A )251±; (B )251±-; (C )251±或251±-; (D )251±-±.答( ) 4.已知:)19911991(2111n nx --=(n 是自然数).那么n x x )1(2+-,的值是(A)11991-; (B)11991--; (C)1991)1(n -; (D)11991)1(--n . 答( ) 5.若M n 1210099321=⨯⨯⨯⨯⨯ ,其中M为自然数,n 为使得等式成立的最大的自然数,则M(A)能被2整除,但不能被3整除; (B)能被3整除,但不能被2整除; (C)能被4整除,但不能被3整除; (D)不能被3整除,也不能被2整除.答( )6. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是 (A)1-;(B)5-;(C)0;(D)1. 答( ) 7.如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ,32=S 和13=S ,那么,正方形OPQR 的边长是(A)2;(B)3;(C)2 ;(D)3. 答( )8.在锐角ΔABC 中,1=AC ,c AB =, 60=∠A ,ΔABC 的外接圆半径R ≤1,则(A)21< c < 2 ; (B)0< c ≤21;答( )(C )c > 2; (D )c = 2. 答( ) 二、填空题1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果ΔBEG 的面积是1,则平行四边形ABCD 的面积是 .2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+a cb 32 .3.设m ,n ,p ,q 为非负数,且对一切x >0,q pn m x x x x )1(1)1(+=-+恒成立,则 =++q p n m 22)2( .4.四边形ABCD 中,∠ ABC 135=,∠BCD 120=,AB 6=,BC 35-=,CD = 6,则AD = .第二试11=S 3S =132=S120135xx + y,x -y,x y,y四个数中的三个又相同的数值,求出所有具有这样性质的数对(x , y).二、ΔABC中,AB<AC<BC,D点在BC上,E点在BA的延长线上,且BD=BE=AC,ΔBDE的外接圆与ΔABC的外接圆交于F点(如图).求证:BF=AF+CF三、将正方形ABCD分割为2n个相等的小方格(n是自然数),把相对的顶点A,C染成红色,把B,D染成蓝色,其他交点任意染成红、蓝两色中的一种颜色.证明:恰有三个顶点同色的小方格的数目必是偶数.1992年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定. 3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7. 答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4. 答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xky 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是(A)21S S > (B)21S S = (C)21S S < (D)不确定答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3. 答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD , ︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , F A=AB .则AE :EB 等于(A)1:2 (B)1:3 (C)2:5 (D)3:10 答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11. 答( ) 二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则xx x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求:M 和N.1993年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ; 2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是 (A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错. 3.设x 是实数,11++-=x x y .下列四个结论: Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值; Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ 4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x 其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是 (A)54321x x x x x >>>>; (B )53124x x x x x >>>>; (C )52413x x x x x >>>>; (D )24135x x x x x >>>>. 5.不等式73)1(12+<-<-x x x 的整数解的个解(A )等于4 (B )小于4 (C )大于5 (D )等于5 6.在ABC ∆中,BC AO O A =∠,,是垂心是钝角, 则)cos(OCB OBC ∠+∠的值是 (A)22-(B)22(C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n ,p ,那么m :n :p 等于(A)cb a 1:1:1; (B)c b a ::(C)C B A cos :cos :cos (D)C B A sin :sin :sin . 答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+ 答( )二.填空题1.当x 变化时,分式15632212++++x x x x 的最小值是___________.2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC 分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________.第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D ,E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8:30—9:30)考生注意:本试共两道大题,满分80分.一、选择题(本题满分48分,每小题6分)本题共有8个小题都给出了A ,B 、C ,D ,四个结论,其中只有一个是正确的,请把你认为正确结论的代表字母写在题后答案中的圆括号内,每小题选对得6分;不选、选错或选出的代表字母超过一个(不论是否写在圆括号内),一律得0分.〔答〕( )2.设a,b,c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA.都不小于0B.都不大于0C.至少有一个小0于D.至少有一个大于0〔答〕( )3.如图1所示,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若BC=2,DA=3,则AB的长A.等于4B.等于5C.等于6D.不能确定〔答〕( )A.1 B.-1 C.22001D.-22001〔答〕( )5.若平行直线EF,MN与相交直线AB,CD相交成如图2所示的图形,则共得同旁内角A.4对B.8对C.12对D.16对〔答〕( )〔答〕( )7.设锐角三角形ABC的三条高AD,BE,CF相交于H。
全国初中数学竞赛试题集锦(附解答)

全国初中数学竞赛试卷一、选择题:(每小题6分,共30分)1、已知a 、b 、c 都是实数,并且c b a >>,那么下列式子中正确的是( ) (A)bc ab >(B)c b b a +>+(C)c b b a ->-(D)cbc a > 2、如果方程()0012>=++p px x 的两根之差是1,那么p 的值为( ) (A)2(B)4(C)3(D)53、在△ABC 中,已知BD 和CE 分别是两边上的中线,并且BD ⊥CE ,BD=4,CE=6,那么△ABC 的面积等于( )(A)12(B)14(C)16(D)18 4、已知0≠abc ,并且p bac a c b c b a =+=+=+,那么直线p px y +=一定通过第( )象限(A)一、二(B)二、三(C)三、四(D)一、四 5、如果不等式组⎩⎨⎧<-≥-0809b x a x 的整数解仅为1,2,3,那么适合这个不等式组的整数a 、b 的有序数对(a 、b )共有( )(A)17个(B)64个(C)72个(D)81个 二、填空题:(每小题6分,共30分)6、在矩形ABCD 中,已知两邻边AD=12,AB=5,P 是AD 边上任意一点,PE ⊥BD ,PF ⊥AC ,E 、F 分别是垂足,那么PE+PF=___________。
7、已知直线32+-=x y 与抛物线2x y =相交于A 、B 两点,O 为坐标原点,那么△OAB 的面积等于___________。
8、已知圆环内直径为a cm ,外直径为b cm ,将50个这样的圆环一个接一个环套地连成一条锁链,那么这条锁链拉直后的长度为___________cm 。
9、已知方程()015132832222=+-+--a a x a a x a (其中a 是非负整数),至少有一个整数根,那么a =___________。
10、B 船在A 船的西偏北450处,两船相距210km ,若A 船向西航行,B 船同时向南航行,且B 船的速度为A 船速度的2倍,那么A 、B 两船的最近距离是___________km 。
全国初中数学联赛试题word版含答案

GFE ABCD全国初中数学联赛试卷1、在高速公路上,从3千米处开始,每隔4千米经过一个限速标志牌;并且从10千米处开始,每隔9千米经过一个速度监控仪. 刚好在19千米处第一次同时经过这两种设施,那么第二次同时经过这两种设施的千米数是( )(A) 36 (B) 37 (C) 55 (D) 902、已知m =1+2,n =1-2,且(7m 2-14m +a ) (3n 2-6n -7)=8,则a 的值等于( )(A) -5 (B) 5 (C) -9 (D) 93、Rt △ABC 的三个顶点A ,B ,C 均在抛物线y =x 2上,并且斜边AB 平行于x 轴. 若斜边上的高为h ,则( )(A) h <1 (B) h =1 (C) 1<h <2 (D) h >24、一个正方形纸片,用剪刀沿一条不过任何顶点的直线将其剪成两部分;拿出其中一部分,再沿一条不过任何顶点的直线将其剪成两部分;又从得到的三部分中拿出其中之一,还是沿一条不过任何顶点的直线将其剪成两部分……如此下去,最后得到了34个六十二边形和一些多边形,则至少要剪的刀数是( )(A) 2004 (B) 2005 (C) 2006 (D) 20075、如图,正方形ABCD 内接于⊙O ,点P 在劣弧AB 上,连结DP ,交AC 于点Q ,若QP =QO ,则QC 的值为( ) (A) 23-1 (B) 23 (C) 3+2 (D) 3+2二、填空题6、已知a ,b ,c 为整数,且a +b =2006,c -a =2005. 若a <b ,则a +b +c 的最大值为___________.7、如图,面积为a b -c 的正方形DEFG 内接于面积为1的正三角形ABC ,其中a ,b ,c 是整数,且b 不能被任何质数的平方整除,则 a -c b的值等于________.8、正五边形广场ABCDE 的周长为2000米. 甲、乙两分分别从A ,C 两点同时出发,沿A →B →C →D →E →A →…方向绕广场行走,甲的速度为50米/分,乙的速度为46米/分,那么出发后经过________分钟,甲、乙两人第一次开始行走在同一条边上.9、已知0<a <1,且满足[a + 1 30]+[a +230]……+[a +29 30]=18 ([x ]表示不超过x 的最大整数),则[10a ]的值等于__________.10、小明家电话号码原为六位数,第一次升位是在首位号码和第二位号码之间加上数字8,成为一个七位数的电话号码;第二次升位是在首位号码前加上数字2,成为一个八位数的电话号码. 小明发现,他家两次升位后的电话号码的八位数恰是原来电话号码的六位数的81倍,则小明家原来的电话号码是_________.三、解答题 11、已知x =b a,a 、b 为互质的正整数,且a ≤8,2-1<x <3-1.(1)试写出一个满足条件x ;(2)求所有满足条件的x .12、设a ,b ,c 为互不相等的实数,且满足关系式:⎪⎩⎪⎨⎧--=++=+54141622222a a bc a a c b 求a 的取值范围.13、如图,点P 为⊙O 外一点,过点P 作⊙O 的两条切线,切点分别为A ,B . 过点A 做PB 的平行线,交⊙O 于点C . 连结PC ,交⊙O 于点E ;连结AE ,延长AE 交PB 于点K . 求证: PE • AC =CE • KB14、有2006个都不等于119的正整数a1,a2,…,a2006排列成一行数,其中任意连续若干项之和都不等于119,求a1+a2+…+a2006的最小值.参考答案(1)解:因为4和9的最小公倍数为36,19+36=55,所以第二次同时经过这两种设施的千米数是在55千米处.故选C.(2)解:由已知可得m2-2m=1,n2-2n=1.又(7m2-14m+a)(3n2-6n-7)=8,AD G所以 (7+a )(3-7)=8,解得a =-9 故选C .(3)解:设点A 的坐标为(a ,a 2),点C 的坐标为(c ,c 2)(|c|<|a|),则点B 的坐标为 (-a ,a 2),由勾股定理,得AC 2=(c -a ) 2+(c 2-a 2) 2,BC 2=(c +a ) 2+(c 2-a 2) 2,AC 2+BC 2=AB 2, 所以 (a 2-c 2) 2=a 2-c 2 .由于a 2>c 2,所以a 2-c 2=1,故斜边AB 上高h =a 2-c 2=1 故选B .(4)解:根据题意,用剪刀沿不过顶点的直线剪成两部分时,每剪开一次,使得各部分的内角和增加360°.于是,剪过k 次后,可得(k +1)个多边形,这些多边形的内角和为(k +1)³360°. 因为这(k +1)个多边形中有34个六十二边形,它们的内角和为34³(62-2)³180°=34³60³180°,其余多边形有(k +1)-34=k -33(个),而这些多边形的内角和不少于(k -33)³180°.所以(k +1)³360°≥34³60³180°+(k -33)³180°,解得k ≥2005.当我们按如下方式剪2005刀时,可以得到符合条件的结论.先从正方形上剪下1个三角形,得到1个三角形和1个五边形;再在五边形上剪下1个三角形,得到2个三角形和1个六边形……如此下去,剪了58刀后,得到58个三角形和1个六十二边形.再取33个三角形,在每个三角形上剪一刀,又可得到33个三角形和33个四边形,对这33个四边形,按上述正方形的剪法,再各剪58刀,便34个六十二边形和33³58个三角形.于是共剪了58+33+33³58=2005(刀). 故选B .(5)解:如图,设⊙O 的半径为r ,QO =m ,则QP =m ,QC =r +m ,QA =r -m . 在⊙O 中,根据相交弦定理,得QA ²QC =QP ²QD 即 (r -m )(r +m )=m ²QD ,所以 QD =r 2-m2m. 连结DO ,由勾股定理,得QD 2=DO 2+QO 2, 即 ( r 2-m 2 m )2=r 2+m 2 ,解得m =33r所以,QC QA =r +m r -m =3+13-1=3+2 故选D .(6)解:由a +b =2006,c -a =2005,得a +b +c =a +4011.因为a +b =2006,a <b ,a 为整数,所以a 的最大值为1002.于是,a +b +c 的最大值为5013.(7)解:设正方形DEFG 的边长为x ,正三角形ABC 的边长为m ,则m 2=43 ,由△ADG∽△ABC,可得xm=32m-x32m,解得x=(23-3)m于是:x2=(23-3)m2=283-48,由题意,a=28,b=3, c=48,,所以a-cb=-203.(8)解:设甲走完x条边时,甲、乙两人第一次开始行走在同一条边上,此时甲走了400x米,乙走了46³400x50=368x米.于是368(x-1)+800-400(x-1)>400,所以,12.5≤x<13.5.故x=13,此时t=400³1350=104.(9)解:因为0<a+130<a+230<……<a+2930<2,所以[a+130],[a+230],…,[a+2930]等于0或1.由题设知,其中有18个等于1,所以[a+130]+[a+230]……+[a+1130]=0,[a+1230]+[a+1330]……+[a+2930]=1,所以 0<a+1130<1 ,1≤a+1230<2.故18≤30a<19,于是6≤10a<193,所以 [10a]=6.(10)解:设原来电话号码的六位数为abcdef,则经过两次升位后电话号码的八位数为2a8bcdef.根据题意,有81³abcdef=2a8bcdef.记x=b³104+c³103+d³102+e³10+f,于是81³a³105+81x=208³105+a³106+x 解得x=1250³(208-71a) .因为0≤x<105,所以0≤1250³(208-71a)<105,故12871<a≤20871.因为a为整数,所以a=2.于是x=1250³(208-71³2)=82500.所以,小明家原来的电话号码为282500.(11)解:(1)x=12满足条件.(2)因为x=ba,a,b为互质的正整数,且a≤8,所以2-1<ba<3-1,即 (2-1)a<b<(3-1)a.当a=1时,(2-1)³1<b<(3-1)³1,这样的正整数b不存在.当a=2时,(2-1)³2<b<(3-1)³2,故b=1,此时x=12.当a=3时,(2-1)³3<b<(3-1)³3,故b=2,此时x=23.当a=4时,(2-1)³4<b<(3-1)³4,与a互质的正整数b不存在.当a=5时,(2-1)³5<b<(3-1)³5,故b=3,此时x=35.当a=6时,(2-1)³6<b<(3-1)³6,与a互质的正整数b不存在.当a=7时,(2-1)³7<b<(3-1)³7,故b=3,4,5此时x=37,47,57.当a=8时,(2-1)³8<b<(3-1)³8,故b=5,此时x=58.所以,满足条件的所有分数为12,23,35,37,47,57,58.(12)解:由①-2³②得 (b-c) 2=24(a+1)>0,所以a>-1.当a>-1时, b2+c2=2a2+16a+14=2(a+1)(a+7)>0 .又当a=b时,由①,②得c2=a2+16a+14 ,③ac=a2-4a-5 ④将④两边平方,结合③得a2 ( a2+16a+14)=(a2-4a-5) 2化简得 24a3+8a2-40a-25=0,故(6a+5)(4a2-2a-5)=0,解得a=-56,或a=1±214.所以,a的取值范围为a>-1且a≠-56,a≠1±214.(13)证明:因为AC∥PB,所以∠KPE=∠ACE.又PA是⊙O的切线,所以∠KAP=∠ACE,故∠KPE=∠KAP,于是△KPE∽△KAP,所以KPKA=KEKP,即KP2=KE²KA .由切割线定理得 KB 2=KE ²KA 所以KP =KB .因为AC ∥PB ,△KPE ∽△ACE ,于是 PE CE =KP AC 故 PE CE =KBAC, 即 PE ²AC =CE ²KB(14)解:设10个学生为S 1,S 2,…,S 10 ,n 个课外小组G 1,G 2,…,G n .首先,每个学生至少参加两个课外小组.否则,若有一个学生只参加一个课外小组,设这个学生为S 1,由于每两个学生至少在某一个小组内出现过,所以其它9个学生都与他在同一组出现,于是这一组就有10个人了,矛盾.若有一学生恰好参加两个课外小组,不妨设S 1恰好参加G 1,G 2,由题设,对于这两组,至少有两个学生,他们没有参加这两组,于是他们与S 1没有同过组,矛盾.所以,每一个学生至少参加三个课外小组.于是n 个课外小组G 1,G 2,…,G n 的人数之和不小于3³10=30.另一方面,每一课外小组的人数不超过5,所以n 个课外小组G 1,G 2,…,G n 的人数不超过5n , 故5n ≥30,所以n ≥6.下面构造一个例子说明n =6是可以的.G 1={S 1,S 2,S 3,S 4,S 5},G 2={S 1,S 2,S 6,S 7,S 8},G 3={S 1,S 3,S 6,S 9,S 10}, G 4={S 2,S 4,S 7,S 9,S 10},G 5={S 3,S 5,S 7,S 8,S 9},G 6={S 4,S 5,S 6,S 8,S 10}.容易验证,这样的6个课外小组满足题设条件.所以,n 的最小值为6.。
1991~2011全国初中数学联赛试题及答案

将这些球的位置按顺序标号为1,2,3,4,…….
由于1号球与7号球中间夹有5个球,1号球与12号球中间夹有10个球,12号球与6号球中间夹有5个球,7号球与13号球中间夹有5个球,13号球与2号球中间夹有10个球,2号球与8号球中间夹有5个球,8号球与14号球中间夹有5个球,14号球与3号球中间夹有10个球,3号球与9号球中间夹有5个球,9号球与15号球中间夹有5个球,15号球与4号球中间夹有10个球,4号球与10号球中间夹有5个球,因此,编号为1,7,12,6, 13,2,8,14,3,9,15,4,10的球颜色相同,编号为5,11的球可以为另外的一种颜色.因此,可以按照要求摆放15个球.
………………………………20分
又因为MD//AC,所以MD和MQ为同一条直线.
又点Q、D均在⊙I上,所以点Q和点D重合,故PD是⊙I的切线.……………………………25分
三.(本题满分25分)已知二次函数 的图象经过两点P ,Q .
(1)如果 都是整数,且 ,求 的值.
(2)设二次函数 的图象与 轴的交点为A、B,与 轴的交点为C.如果关于 的方程 的两个根都是整数,求△ABC的面积.
类似的,可求得 出现的总次数均为 .
因此 =28068.
二、填空题:(本题满分28分,每小题7分)
1.已知实数 满足方程组 则 .
【答】13.
由 得 ,把 代入,可得 .
因此, 是一元二次方程 的两个实数根,易求得这两个实数根分别为3和 ,所以 .
2.二次函数 的图象与 轴正方向交于A,B两点,与 轴正方向交于点C.已知 , ,则 .
如果球的个数多于15个,则一方面,16号球与10号球应同色,另一方面,5号球与16号球中间夹有10个球,所以5号球与16号球同色,从而1到16号球的颜色都相同,进一步可以知道:所有的球的颜色都相同,与要求不符.
全国初中数学联合 竞赛试题及详细解答(含一试二试)

全国初中数学联合竞赛试题第一试一、选择题:(本题满分42分,每小题7分)1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-= ( ) A .1. B .2. C .3. D .4..2.若实数,,a b c 满足等式23||6a b +=,49||6a b c -=,则c 可能取的最大值为 ( ) A .0. B .1. C .2. D .3.3.若b a ,是两个正数,且 ,0111=+-+-ab b a 则 ( )4.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为 ( ) A .-13. B .-9. C .6. D . 0.5.在△ABC 中,已知︒=∠60CAB ,D ,E 分别是边AB ,AC 上的点,且︒=∠60AED ,CE DB ED =+,CDE CDB ∠=∠2,则=∠DCB ( )A .15°.B .20°.C .25°.D .30°.6.对于自然数n ,将其各位数字之和记为n a ,如2009200911a =+++=,201020103a =+++=,则12320092010a a a a a +++++= ( )A .28062.B .28065.C .28067.D .28068.二、填空题:(本题满分28分,每小题7分)1.已知实数,x y 满足方程组3319,1,x y x y ⎧+=⎨+=⎩则22x y += .2.二次函数c bx x y ++=2的图象与x 轴正方向交于A ,B 两点,与y 轴正方向交于点C .已知AC AB 3=,︒=∠30CAO ,则c = .3.在等腰直角△ABC 中,AB =BC =5,P 是△ABC 内一点,且PA 5PC =5,则PB =______.4.将若干个红、黑两种颜色的球摆成一行,要求两种颜色的球都要出现,且任意中间夹有5个或10个球的两个球必为同一种颜色的球.按这种要求摆放,最多可以摆放_______个球.第二试 (A )一.(本题满分20分)设整数,,a b c (a b c ≥≥)为三角形的三边长,满足22213a b c ab ac bc ++---=,___P_A_C_B求符合条件且周长不超过30的三角形的个数.二.(本题满分25分)已知等腰三角形△ABC 中,AB =AC ,∠C 的平分线与AB 边交于点P ,M 为△ABC 的内切圆⊙I 与BC 边的切点,作MD//AC ,交⊙I 于点D.证明:PD 是⊙I 的切线.三.(本题满分25分)已知二次函数2y x bx c =+-的图象经过两点P (1,)a ,Q (2,10)a . (1)如果,,a b c 都是整数,且8c b a <<,求,,a b c 的值.(2)设二次函数2y x bx c =+-的图象与x 轴的交点为A 、B ,与y 轴的交点为 C.如果关于x 的方程20x bx c +-=的两个根都是整数,求△ABC 的面积._ Q_I _ P_ C_ A_M_B第二试 (B )一.(本题满分20分)设整数,,a b c 为三角形的三边长,满足22213a b c ab ac bc ++---=,求符合条件且周长不超过30的三角形的个数(全等的三角形只计算1次).二.(本题满分25分)题目和解答与(A )卷第二题相同. 三.(本题满分25分)题目和解答与(A )卷第三题相同.第二试 (C )一.(本题满分20分)题目和解答与(B )卷第一题相同. 二.(本题满分25分)题目和解答与(A )卷第二题相同.三.(本题满分25分)设p 是大于2的质数,k 为正整数.若函数4)1(2-+++=p k px x y 的图象与x 轴的两个交点的横坐标至少有一个为整数,求k 的值.全国初中数学联合竞赛试题及详解第一试一、选择题:(本题满分42分,每小题7分)1. 若,,a b c 均为整数且满足1010()()1a b a c -+-=,则||||||a b b c c a -+-+-= ( B ) A .1. B .2. C .3. D .4. 解: 由已知可推得011a b b c a c -=⎧⇒-=±⎨-=±⎩ 或110a b b c a c -=±⎧⇒-=±⎨-=⎩,分别代入即得。
全国初中数学联赛数论题目汇编

33. (1998 联赛)1, 2, 3, · · · , 98 共 98 个自然数中, 能够表示成两整数的平方差的个数是
34. (1998 联赛) 每一本书都有一个国际书号:ABCDEF GHIJ , 其中 ABCDEF GHI 由九个数字排列而 成, J 是检查号码. 令 S = 10A + 9B + 8C + 7D + 6E + 5F + 4G + 3H + 2I ,r 是 S 除以 11 所得的 余数, 若 r 不等于 0 或 1, 则规定 J = 11 − r. (若 r = 0, 则规定 J = 0; 若 r = 1, 规定 J 用 x 表示) 现有一本书的书号是 962y 707015, 那么 y = .
20. (1990 联赛)12 , 22 , 32 , · · · , 1234567892 的和的个位数的数字是 21. (1990 联赛)[x] 表示不超过实数 x 的最大整数, 令 {x} = x − [x] 1 (1) 找出一个实数 x, 满足 {x} + { } = 1 x (2) 证明: 满足上述等式的 x, 都不是有理数.
3 29. (1997 联赛) 若正整数 x,y 满足 x2 + y 2 = 1997, 则 x + y 等于 .
30. (1997 联赛) 已知定理:“若三个大于 3 的质数,a, b, c 满足关系式 2a + 5b = c, 则 a + b + c 是整数 n 的倍数”. 试问: 上述定理中的整数 n 的最大可能值是多少? 并证明你的结论. 31. (1998 联赛) 满足 19982 + m2 = 19972 + n2 (0 < m < n < 1998) 的整数对 (m, n), 共有 32. (1998 联赛) 设平方数 y 2 是 11 个相继整数的平方和, 则 y 的最小值是 . . 个.
全国初中数学竞赛试题集锦(附解答)

全国初中数学竞赛试卷一、选择题:(每小题6分,共30分)1、已知a 、b 、c 都是实数,并且c b a >>,那么下列式子中正确的是( ) (A)bc ab >(B)c b b a +>+(C)c b b a ->-(D)cbc a > 2、如果方程()0012>=++p px x 的两根之差是1,那么p 的值为( ) (A)2(B)4(C)3(D)53、在△ABC 中,已知BD 和CE 分别是两边上的中线,并且BD ⊥CE ,BD=4,CE=6,那么△ABC 的面积等于( )(A)12(B)14(C)16(D)18 4、已知0≠abc ,并且p bac a c b c b a =+=+=+,那么直线p px y +=一定通过第( )象限(A)一、二(B)二、三(C)三、四(D)一、四 5、如果不等式组⎩⎨⎧<-≥-0809b x a x 的整数解仅为1,2,3,那么适合这个不等式组的整数a 、b 的有序数对(a 、b )共有( )(A)17个(B)64个(C)72个(D)81个 二、填空题:(每小题6分,共30分)6、在矩形ABCD 中,已知两邻边AD=12,AB=5,P 是AD 边上任意一点,PE ⊥BD ,PF ⊥AC ,E 、F 分别是垂足,那么PE+PF=___________。
7、已知直线32+-=x y 与抛物线2x y =相交于A 、B 两点,O 为坐标原点,那么△OAB 的面积等于___________。
8、已知圆环内直径为a cm ,外直径为b cm ,将50个这样的圆环一个接一个环套地连成一条锁链,那么这条锁链拉直后的长度为___________cm 。
9、已知方程()015132832222=+-+--a a x a a x a (其中a 是非负整数),至少有一个整数根,那么a =___________。
10、B 船在A 船的西偏北450处,两船相距210km ,若A 船向西航行,B 船同时向南航行,且B 船的速度为A 船速度的2倍,那么A 、B 两船的最近距离是___________km 。
全国初中数学竞赛试题(含答案)-20220207144625

全国初中数学竞赛试题(含答案)20220207144625一、选择题(每题5分,共20分)1. 下列哪个数是质数?A. 2B. 3C. 4D. 52. 如果一个三角形的两边长分别为3和4,那么这个三角形的周长可能是多少?A. 7B. 10C. 11D. 123. 下列哪个分数可以化简为最简分数?A. 2/4B. 3/6C. 4/8D. 5/104. 一个正方形的面积是36平方厘米,那么这个正方形的边长是多少厘米?A. 6B. 7C. 8D. 9二、填空题(每题5分,共20分)1. 7的平方根是______。
2. 0.25的小数点向右移动两位后是______。
3. 一个等边三角形的边长是10厘米,那么这个等边三角形的周长是______厘米。
4. 下列哪个数是立方数?A. 2B. 3C. 4D. 5三、解答题(每题10分,共30分)1. 解方程:2x 5 = 11。
2. 计算下列表达式的值:3(2 + 4) 7。
3. 一个长方形的长是8厘米,宽是4厘米,求这个长方形的面积。
四、答案部分一、选择题1. A2. B3. A4. D二、填空题1. ±√72. 253. 304. C三、解答题1. x = 82. 133. 32平方厘米全国初中数学竞赛试题(含答案)20220207144625四、应用题(每题15分,共30分)1. 小明家有一块长方形的地,长是12米,宽是8米。
小明计划将这块地分成两个相同大小的正方形区域。
请问每个正方形的边长是多少米?2. 小红有一笔钱,她将其中的1/3用于购买书,剩下的钱再将其中的1/2用于购买文具。
她剩下的钱是100元。
请问小红最初有多少钱?五、证明题(每题15分,共30分)1. 证明:对于任意实数a和b,如果a < b,那么a² < b²。
2. 证明:等腰三角形的底角相等。
六、答案部分四、应用题1. 每个正方形的边长是6米。
2. 小红最初有300元。
初中数学全国竞赛真题试卷

一、选择题(本大题共20小题,每小题5分,共100分)1. 已知实数a、b满足a+b=1,则a²+b²的最小值为()A. 0B. 1C. 2D. 32. 在△ABC中,∠A=60°,∠B=45°,则∠C的度数为()A. 75°B. 120°C. 135°D. 150°3. 若等差数列{an}的前三项分别为1,-2,3,则该数列的公差为()A. 1B. -1C. 2D. -24. 已知函数f(x)=x²-2x+1,则f(x)的最小值为()A. 0B. 1C. 2D. 35. 若x,y满足x²+y²=1,则x²+y²的最大值为()A. 1B. 2C. 3D. 46. 已知正方体的对角线长为a,则该正方体的体积为()A. a²B. 2a²C. 3a²D. 4a²7. 在等腰三角形ABC中,AB=AC,∠BAC=30°,则底边BC的长度为()A. √3B. 2√3C. 3√3D. 4√38. 已知等比数列{an}的前三项分别为2,6,18,则该数列的公比为()A. 1B. 2C. 3D. 69. 若函数f(x)=ax²+bx+c在x=1时的导数值为2,则a+b+c的值为()A. 2B. 3C. 4D. 510. 在直角坐标系中,点A(2,3),点B(-1,-2),则线段AB的中点坐标为()A. (1,1)B. (1,2)C. (2,1)D. (2,2)11. 已知等差数列{an}的前n项和为Sn,公差为d,首项为a₁,则Sn的表达式为()A. Sn = n(a₁+an)/2B. Sn = n(a₁+an)/2 + d/2C. Sn = n(a₁+an)/2 - d/2D. Sn = n(a₁+an)/2 d12. 在等腰三角形ABC中,AB=AC,∠BAC=30°,则∠B的度数为()A. 30°B. 45°C. 60°D. 90°13. 已知函数f(x)=x³-3x²+4x,则f(x)的零点个数为()A. 1B. 2C. 3D. 414. 若x,y满足x²+y²=4,则x+y的最大值为()A. 2B. 4C. 6D. 815. 在直角坐标系中,点P(3,4),点Q(6,2),则线段PQ的中点坐标为()A. (4,3)B. (5,3)C. (5,4)D. (6,5)16. 已知等比数列{an}的前三项分别为1,-2,4,则该数列的公比为()A. -1B. 2C. -2D. 1/217. 若函数f(x)=ax²+bx+c在x=0时的导数值为0,则a+b+c的值为()A. 0B. 1C. 2D. 318. 在直角坐标系中,点A(1,2),点B(3,4),则线段AB的斜率为()A. 1B. 2C. 3D. 419. 已知等差数列{an}的前n项和为Sn,公差为d,首项为a₁,则Sn²的表达式为()A. S n² = n²(a₁+an)²/4B. Sn² = n²(a₁+an)²/2C. Sn² = n²(a₁+an)²D. Sn² = n(a₁+an)²/220. 在等腰三角形ABC中,AB=AC,∠BAC=60°,则底边BC的长度为()A. √3B. 2√3C. 3√3D. 4√3二、填空题(本大题共5小题,每小题10分,共50分)21. 已知函数f(x)=ax²+bx+c,若f(1)=2,f(2)=5,则a+b+c的值为______。
完整)历年全国初中数学联赛试题总汇

完整)历年全国初中数学联赛试题总汇1991年全国初中数学联合竞赛决赛试题第一试一、选择题1.设等式 $a(x-a)+a(y-a)=x-a-a-y$ 在实数范围内成立,其中 $a$,$x$,$y$ 是两两不同的实数,则 $\dfrac{3x^2+xy-y^2}{2x-xy+y}=$ (A)3;(B)$\dfrac{1}{3}$;(C)2;(D)$\dfrac{15}{33}$。
答案:(B)2.如图,$AB\parallel EF\parallel CD$,已知 $AB=20$,$CD=80$,$BC=100$,那么$EF$ 的值是(A)10;(B)12;(C)16;(D)18.答案:(C)3.方程 $x^2-x-1=0$ 的解是 $\dfrac{-1\pm\sqrt{5}}{2}$;$\dfrac{-1\pm i\sqrt{3}}{2}$ 或 $\dfrac{1\pm i\sqrt{3}}{2}$。
答案:(A)4.已知:$x=(1991-1991n)$($n$ 是自然数)。
那么 $(x-1+x^2)^n$ 的值是(A)$1991^{-1}$;(B)$-1991^{-1}$;(C)$(-1)^n1991$;(D)$(-1)^n1991^{-1}$。
答案:(B)5.若$1\times2\times3\times\cdots\times99\times100=12^nM$,其中$M$ 为自然数,$n$ 为使得等式成立的最大的自然数,则$M$ 能被(A)2 整除,但不能被3整除;(B)能被3整除,但不能被2整除;(C)能被4整除,但不能被3整除;(D)不能被3整除,也不能被2整除。
答案:(D)6.若 $a$,$c$,$d$ 是整数,$b$ 是正整数,且满足$a+b=c$,$b+c=d$,$c+d=a$,那么 $a+b+c+d$ 的最大值是(A)$-1$;(B)$-5$;(C)$0$;(D)$1$。
答案:(B)7.如图,正方形 $OPQR$ 内接于 $\triangle ABC$。
全国初中数学联赛试题及答案详细解析全集

1991年全国初中数学联合竞赛决赛试题第一试一、选择题本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1. 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y是两两不同的实数,则22223y xy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )35. 答( )2. 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是(A ) 10; (B )12;(C ) 16; (D )18.答( )3.方程012=--x x 的解是 (A )251±; (B )251±-; (C )251±或251±-; (D )251±-±. 答( )4. 已知:)19911991(2111n n x --=(n 是自然数).那么n x x )1(2+-,的值是 (A)11991-; (B)11991--;(C)1991)1(n -; (D)11991)1(--n .答( )5. 若M n 1210099321=⨯⨯⨯⨯⨯Λ,其中M为自然数,n 为使得等式成立的最大的自然数,则M(A)能被2整除,但不能被3整除;(B)能被3整除,但不能被2整除;(C)能被4整除,但不能被3整除;(D)不能被3整除,也不能被2整除.答( )6. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么 d c b a +++的最大值是(A)1-;(B)5-;(C)0;(D)1.答( )7. 如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ,32=S 和13=S ,那么,正方形OPQR 的边长是 (A)2;(B)3;(C)2 ;(D)3.答( )8. 在锐角ΔABC 中,1=AC ,c AB =,ο60=∠A ,ΔABC 的外接圆半径R ≤1,则(A)21< c < 2 ; (B)0< c ≤21; 答( )(C )c > 2; (D )c = 2.答( )二、填空题1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果ΔBEG 的面积是1,则平行四边形ABCD 的面积是 .2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+ac b 32 .3.设m ,n ,p ,q 为非负数,且对一切x >0,q pn m xx x x )1(1)1(+=-+恒成立,则 =++q p n m 22)2( .4.四边形ABCD 中,∠ ABC ο135=,∠BCD ο120=,AB 6=,BC 35-=,CD = 6,则AD = .第二试x + y , x - y , x y , yx 四个数中的三个又相同的数值,求出所有具有这样性质的数对(x , y ). 11=S 3S =1 32=S ο120ο135二、ΔABC 中,AB <AC <BC ,D 点在BC 上,E 点在BA 的延长线上,且 BD =BE =AC ,ΔBDE 的外接圆与ΔABC 的外接圆交于F 点(如图).求证:BF =AF +CF三、将正方形ABCD 分割为 2n 个相等的小方格(n 是自然数),把相对的顶点A ,C 染成红色,把B ,D 染成蓝色,其他交点任意染成红、蓝两色中的一种颜色.证明:恰有三个顶点同色的小方格的数目必是偶数.1992年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定. 3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7. 答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4. 答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xky 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是(A)21S S > (B)21S S = (C)21S S < (D)不确定答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3. 答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD , ︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , F A=AB .则AE :EB 等于(A)1:2 (B)1:3 (C)2:5 (D)3:10 答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是答( ) 二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则xx x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90ο的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求:M 和N.1993年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ; 2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是 (A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错. 3.设x 是实数,11++-=x x y .下列四个结论: Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值; Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ 4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x 其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是 (A)54321x x x x x >>>>; (B )53124x x x x x >>>>; (C )52413x x x x x >>>>; (D )24135x x x x x >>>>. 5.不等式73)1(12+<-<-x x x 的整数解的个解(A )等于4 (B )小于4 (C )大于5 (D )等于5 6.在ABC ∆中,BC AO O A =∠,,是垂心是钝角, 则)cos(OCB OBC ∠+∠的值是 (A)22-(B)22(C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n ,p ,那么m :n :p 等于(A)cb a 1:1:1; (B)c b a ::(C)C B A cos :cos :cos (D)C B A sin :sin :sin . 答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+ 答( )二.填空题1.当x 变化时,分式15632212++++x x x x 的最小值是___________.2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC 分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________.第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D ,E ,使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ;(3)求cb,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8:30—9:30)考生注意:本试共两道大题,满分80分.一、选择题(本题满分48分,每小题6分)本题共有8个小题都给出了A,B、C,D,四个结论,其中只有一个是正确的,请把你认为正确结论的代表字母写在题后答案中的圆括号内,每小题选对得6分;不选、选错或选出的代表字母超过一个(不论是否写在圆括号内),一律得0分.〔答〕( )2.设a,b,c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA.都不小于0B.都不大于0C.至少有一个小0于D.至少有一个大于0〔答〕( )3.如图1所示,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若BC=2,DA=3,则AB的长A.等于4B.等于5C.等于6D.不能确定〔答〕( )A.1 B.-1 C.22001D.-22001〔答〕( )5.若平行直线EF,MN与相交直线AB,CD相交成如图2所示的图形,则共得同旁内角A.4对B.8对C.12对D.16对〔答〕( )〔答〕( )7.设锐角三角形ABC的三条高AD,BE,CF相交于H。
初中数学联赛试题及答案

初中数学联赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的自然数?A. 0B. 1C. -1D. 2答案:A2. 一个等腰三角形的两边长分别为3和5,那么它的周长是多少?A. 11B. 13C. 14D. 16答案:B3. 如果一个数的平方等于36,那么这个数是多少?A. 6B. -6C. 6或-6D. 0答案:C4. 计算下列表达式的值:(2x+3)(2x-3)。
A. 4x^2 - 9B. 4x^2 + 9C. 9 - 4x^2D. 9 + 4x^2答案:A5. 一个圆的直径是10厘米,那么它的半径是多少?A. 5厘米B. 10厘米C. 15厘米D. 20厘米答案:A6. 一个数的相反数是-5,那么这个数是多少?A. 5B. -5C. 0D. 10答案:A7. 计算下列分数的和:1/2 + 1/3。
A. 5/6B. 1/6C. 7/6D. 6/7答案:A8. 一个三角形的内角和是多少度?A. 90度B. 180度C. 360度D. 720度答案:B9. 一个数的绝对值是5,那么这个数可能是?A. 5B. -5C. 5或-5D. 0答案:C10. 计算下列表达式的值:(3x-2)^2。
A. 9x^2 - 12x + 4B. 9x^2 + 12x + 4C. 9x^2 - 4x + 4D. 9x^2 + 4x + 4答案:A二、填空题(每题3分,共30分)1. 一个数的立方根是2,那么这个数是______。
答案:82. 如果一个直角三角形的两个直角边长分别是6和8,那么它的斜边长是______。
答案:103. 一个数的倒数是2,那么这个数是______。
答案:1/24. 一个数的平方根是4,那么这个数是______。
答案:165. 一个数的绝对值是3,那么这个数可能是______。
答案:3或-36. 计算下列分数的差:7/8 - 1/4。
答案:5/87. 一个圆的周长是31.4厘米,那么它的半径是______。
近三年初中数学竞赛真题及解答汇总

近三年初中数学竞赛真题及解答汇总在初中数学的学习中,参加数学竞赛是一项极具挑战性和有益的活动。
它不仅能够检验学生对数学知识的掌握程度,还能培养学生的思维能力和创新精神。
以下是近三年初中数学竞赛的部分真题及详细解答,希望能对同学们的学习有所帮助。
一、2021 年真题(1)已知直角三角形的两条直角边分别为 3 和 4,则斜边的长度为()A 5B 7C 5 或 7D 无法确定解答:根据勾股定理,直角三角形的两条直角边的平方和等于斜边的平方。
所以斜边的长度为√(3²+ 4²) =√(9 + 16) =√25 = 5,答案选 A。
(2)若关于 x 的方程 x²+ 2x + k = 0 有两个相等的实数根,则 k 的值为()A 1B -1C 2D -2解答:对于一元二次方程 ax²+ bx + c = 0,当判别式△= b² 4ac = 0 时,方程有两个相等的实数根。
在方程 x²+ 2x + k = 0 中,a =1,b = 2,c = k,所以△= 2² 4×1×k = 4 4k = 0,解得 k = 1,答案选 A。
(3)在平行四边形 ABCD 中,∠A :∠B :∠C :∠D 的值可能是()A 1 : 2 : 3 : 4B 1 : 2 : 2 : 1C 2 : 2 : 1 : 1D 2 : 1 :2 : 1解答:因为平行四边形的两组对角分别相等,所以∠A =∠C,∠B =∠D。
所以∠A :∠B :∠C :∠D 的值应该是 2 : 1 : 2 :1,答案选 D。
二、2022 年真题(1)若 a + b = 5,ab = 6,则 a²+ b²的值为()A 13B 19C 25D 28解答:因为(a + b)²= a²+ 2ab + b²,所以 a²+ b²=(a + b)²2ab = 5² 2×6 = 25 12 = 13,答案选 A。
全国初中数学竞赛历年竞赛试题及参考答案(1)

2 001 年 TI 杯全国初中数学比赛试题一、选择题( 30 分)1. 化简2n 4 2(2n ) ,得()。
2(2n 3 )( A )2n 1 1 (B) 2n 1 (C) 7 (D) 7答案: C8 8 42. 假如 a, b, c 是三个随意整数,那么 a b , b c , c a ()。
2 2 2( A )都不是整数( B)起码有两个整数( C)起码有一个整数( D )都是整数答案: C3. 假如 a, b 是质数,且a2 13a m 0,b 2 13b m 0, 那么b a的值为()。
a b( A )123 (B )125或2 ( C)125( D )123或222 22 22 22答案: B4. 如图,若将正方形分红k 个全等的矩形,此中上、下各横排两个,中间竖排若干个,则k 的值为()( A)6 (B) 8 (C)10 (D)12答案: B5.如图,若(( A)6PA=PB ,∠ APB=2)。
(B)7(C)12∠ACB ,AC(D)16与 PB 交于点D, 且PB=4, PD=3 ,则AD DC 等于答案: B6. 若 a, b 是正数,且知足 12345 (111 a)(111 b) ,则 a和 b 之间的大小关系是()。
( A )a b ( B )a b ( C)a b (D)不可以确立答案: A二、填空题( 30 分)7. 已知: x 3 2, y 3 2 。
那么y x ____________ 。
3 2 3 2 x 2 y 2答案: 9708. 若 x2 xy y 14, y2 xy x 28, 则x y 的值为____________。
答案: 6 或-79. 用长为1, 4, 4, 5 的线段为边作梯形,那么这个梯形的面积等于____________ 。
答案: 6 3或 1010. 销售某种商品,假如单价上升 m %,则售出的数目就将减少m。
为了使该商品的销售总金m 的值应当确立为 ____________ 。
全国初中数学竞赛试题及答案大全

全国初中数学竞赛试题及答案大全试题一:代数基础题目:若\( a \), \( b \), \( c \)为实数,且满足\( a + b + c = 3 \),\( ab + ac + bc = 1 \),求\( a^2 + b^2 + c^2 \)的值。
解答:根据已知条件,我们可以使用配方法来求解。
首先,我们知道\( (a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + ac + bc) \)。
将已知条件代入,得到\( 3^2 = a^2 + b^2 + c^2 + 2 \times 1 \)。
简化后,我们得到\( a^2 + b^2 + c^2 = 9 - 2 = 7 \)。
试题二:几何问题题目:在直角三角形ABC中,∠A=90°,AB=6,AC=8,求斜边BC的长度。
解答:根据勾股定理,直角三角形的斜边BC的平方等于两直角边的平方和,即\( BC^2 = AB^2 + AC^2 \)。
代入已知数值,得到\( BC^2 = 6^2 + 8^2 = 36 + 64 = 100 \)。
因此,\( BC = \sqrt{100} = 10 \)。
试题三:数列问题题目:一个等差数列的首项是2,公差是3,求第10项的值。
解答:等差数列的第n项可以通过公式\( a_n = a_1 + (n - 1)d \)来计算,其中\( a_1 \)是首项,d是公差,n是项数。
将已知条件代入公式,得到\( a_{10} = 2 + (10 - 1) \times 3 = 2 + 9 \times 3 = 29 \)。
试题四:概率问题题目:一个袋子里有5个红球和3个蓝球,随机取出2个球,求取出的两个球颜色相同的概率。
解答:首先计算总的可能情况,即从8个球中取2个球的组合数,用组合公式C(8,2)计算。
然后计算取出两个红球或两个蓝球的情况。
两个红球的情况有C(5,2)种,两个蓝球的情况有C(3,2)种。
历届全国初中数学联赛试题15套.doc
一九九一年第一试一、选择题本题共有8个小题,每小题都给出了(A )、(B )(C )、(D )四个答案结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内. 1.设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立,其中a ,x ,y 是两两不同的实数,则22223yxy x y xy x +--+的值是 (A )3 ; (B )31; (C )2; (D )35.答( ) 2. 如图,AB ‖EF ‖CD ,已知AB =20,CD =80,BC =100,那么EF 的值是(A ) 10; (B )12; (C ) 16; (D )18.答( ) 3. 方程012=--x x 的解是(A )251±; (B )251±-; (C )251±或251±-; (D )251±-±. 答( ) 4.已知:)19911991(2111n nx --=(n 是自然数).那么n x x )1(2+-,的值是(A)11991-; (B)11991--; (C)1991)1(n -; (D)11991)1(--n .答( )5.若M n 1210099321=⨯⨯⨯⨯⨯ ,其中M为自然数,n 为使得等式成立的最大的自然数,则M(A)能被2整除,但不能被3整除; (B)能被3整除,但不能被2整除; (C)能被4整除,但不能被3整除;(D)不能被3整除,也不能被2整除.答( )6. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么d c b a +++的最大值是 (A)1-;(B)5-;(C)0;(D)1.答( )7. 如图,正方形OPQR 内接于ΔABC .已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ,32=S 和13=S ,那么,正方形OPQR 的边长是 (A)2;(B)3;(C)2 ;(D)3.答( )8.在锐角ΔABC 中,1=AC ,c AB =, 60=∠A ,ΔABC 的外接圆半径R ≤1,则 (A)21< c < 2 ; (B)0< c ≤21;答( )(C )c > 2; (D )c = 2.答( )二、填空题1.E是平行四边形ABCD 中BC 边的中点,AE 交对角线BD 于G ,如果ΔBEG 的面积是1,则平行四边形ABCD 的面积是 .2.已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+acb 32.3.设m ,n ,p ,q 为非负数,且对一切x >0,qpn m xx x x )1(1)1(+=-+恒成立,则=++q p n m 22)2( .4.四边形ABCD 中,∠ ABC 135=,∠BCD 120=,AB 6=,BC 35-=,CD = 6,则AD = .11=S3S =132=S120135第二试xx + y,x -y,x y,y四个数中的三个又相同的数值,求出所有具有这样性质的数对(x , y).二、ΔABC中,AB<AC<BC,D点在BC上,E点在BA的延长线上,且BD=BE=AC,ΔBDE的外接圆与ΔABC的外接圆交于F点(如图).求证:BF=AF+CF三、将正方形ABCD分割为2n个相等的小方格(n是自然数),把相对的顶点A,C染成红色,把B,D染成蓝色,其他交点任意染成红、蓝两色中的一种颜色.证明:恰有三个顶点同色的小方格的数目必是偶数.一九九二年第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定. 3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7.答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4.答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xky 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S = (C)21S S < (D)不确定答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3.答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD , ︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , F A=AB .则AE :EB 等于(A)1:2 (B)1:3 (C)2:5 (D)3:10答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11.答( )二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则xx x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点,又AB PE ⊥于E 点,若3,2==AC BC ,则=⋅EB AE .4.若b a ,都是正实数,且0111=+--b a b a ,则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根,当这样的三角形只有一个时,求a 的取值范围.二、如图,在ABC ∆中,D AC AB ,=是底边BC 上一点,E 是线段AD 上一点,且A CED BED ∠=∠=∠2.求证:CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0,1,2,3,5,6这六个不同数字组成,现有四个编码如下:A :320651B :105263C :612305D :316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求:M 和N.一九九三年 第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ; 2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是 (A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错. 3.设x 是实数,11++-=x x y .下列四个结论: Ⅰ.y 没有最小值; Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值; Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ 4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是(A)54321x x x x x >>>>; (B )53124x x x x x >>>>; (C )52413x x x x x >>>>; (D )24135x x x x x >>>>. 5.不等式73)1(12+<-<-x x x 的整数解的个解(A )等于4 (B )小于4 (C )大于5 (D )等于56.在ABC ∆中,BC AO O A =∠,,是垂心是钝角, 则)cos(OCB OBC ∠+∠的值是 (A)22-(B)22 (C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n , p ,那么m :n :p 等于(A)cb a 1:1:1; (B)c b a ::(C)C B A cos :cos :cos (D)C B A sin :sin :sin .答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+答( )二.填空题1.当x 变化时,分式15632212++++x x x x 的最小值是___________.2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC 分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________.第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D ,E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8:30—9:30)考生注意:本试共两道大题,满分80分.一、选择题(本题满分48分,每小题6分)本题共有8个小题都给出了A,B、C,D,四个结论,其中只有一个是正确的,请把你认为正确结论的代表字母写在题后答案中的圆括号内,每小题选对得6分;不选、选错或选出的代表字母超过一个(不论是否写在圆括号内),一律得0分.〔答〕( )2.设a,b,c是不全相等的任意实数,若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,z A.都不小于0B.都不大于0C.至少有一个小0于D.至少有一个大于0〔答〕( )3.如图1所示,半圆O的直径在梯形ABCD的底边AB上,且与其余三边BC,CD,DA相切,若BC=2,DA=3,则AB的长A.等于4B.等于5C.等于6D.不能确定〔答〕( )A.1 B.-1 C.22001D.-22001〔答〕( )5.若平行直线EF,MN与相交直线AB,CD相交成如图2所示的图形,则共得同旁内角A.4对B.8对C.12对D.16对〔答〕( )〔答〕( ) 7.设锐角三角形ABC的三条高AD,BE,CF相交于H。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
