D_output函数说明
ORACLE时间常用函数(字段取年、月、日、季度)

ORACLE时间常⽤函数(字段取年、⽉、⽇、季度)TO_DATE格式Day:dd number 12dy abbreviated friday spelled out fridayddspth spelled out, ordinal twelfthMonth:mm number 03mon abbreviated marmonth spelled out marchYear:yy two digits 98yyyy four digits 199824⼩时格式下时间范围为: 0:00:00 - 23:59:59.... 12⼩时格式下时间范围为: 1:00:00 - 12:59:59 ....Y或YY或YYY 年的最后⼀位,两位或三位Select to_char(sysdate,’YYY’) from dual;002表⽰2002年SYEAR或YEAR SYEAR使公元前的年份前加⼀负号Select to_char(sysdate,’SYEAR’) from dual; -1112表⽰公元前111 2年Q 季度,1~3⽉为第⼀季度 Select to_char(sysdate,’Q’) from dual; 2表⽰第⼆季度①MM ⽉份数 Select to_char(sysdate,’MM’) from dual; 12表⽰12⽉RM ⽉份的罗马表⽰ Select to_char(sysdate,’RM’) from dual; IV表⽰4⽉Month ⽤9个字符长度表⽰的⽉份名 Select to_char(sysdate,’Month’) from dual; May后跟6个空格表⽰5⽉WW 当年第⼏周 Select to_char(sysdate,’WW’) from dual; 24表⽰2002年6⽉13⽇为第24周W 本⽉第⼏周 Select to_char(sysdate,’W’) from dual; 2002年10⽉1⽇为第1周DDD 当年第⼏, 1⽉1⽇为001,2⽉1⽇为032 Select to_char(sysdate,’DDD’) from dual; 363 2002年1 2⽉2 9⽇为第363天DD 当⽉第⼏天 Select to_char(sysdate,’DD’) from dual; 04 10⽉4⽇为第4天D 周内第⼏天 Select to_char(sysdate,’D’) from dual; 5 2002年3⽉14⽇为星期⼀DY 周内第⼏天缩写 Select to_char(sysdate,’DY’) from dual; SUN 2002年3⽉24⽇为星期天HH或HH12 12进制⼩时数 Select to_char(sysdate,’HH’) from dual;02 午夜2点过8分为02 HH24 24⼩时制 Select to_char(sysdate,’HH24’) from dual; 14 下午2点08分为14MI 分钟数(0~59) Select to_char(sysdate,’MI’) from dual; 17下午4点17分SS 秒数(0~59) Select to_char(sysdate,’SS’) from dual; 22 11点3分22秒提⽰注意不要将MM格式⽤于分钟(分钟应该使⽤MI)。
数据结构函数

第七章 函数
6.4 函数的调用
调用形式
函数名(实参表); 说明:
实参与形参个数相等,类型一致,按顺序一一对应 实参表求值顺序,因系统而定(Turbo C 自右向左)
7.2 函数的定义
一般格式
函数返回值类型 缺省int型 无返回值void
合法标识符
现代风格:
函数类型 函数名(形参类型说明表) { 说明部分 语句部分 } 例例 有参函数(现代风格) 有参函数(现代风格) 例 无参函数 例 空函数 int int max(int x, y) max(int x,int y) printstar( ) dummy( ) { {int int z; z; { printf(“********** \n”); } { } z=x>y?x:y; z=x>y?x:y; 或 return(z); return(z); printstar(void ) 函数体为空 } } { printf(“**********\n”); }
函数体
第七章 函数
函数传统风格和例子
传统风格:
函数类型 函数名(形参表) 形参类型说明 { 说明部分 语句部分 }
例 有参函数(传统风格) int max(x,y) int x,y; { int z; z=x>y?x:y; return(z); }
第七章 函数
7.3 函数的返回值
例 无返回值函数 void swap(int x,int y ) 返回语句 { int temp; 形式: return(表达式); temp=x; 或 return 表达式; x=y; y=temp; 或 return; } 功能:使程序控制从被调用函数返回到调用函数中, 同时把返值带给调用函数 说明:
基于rk3568的linux驱动开发——gpio知识点

基于rk3568的linux驱动开发——gpio知识点基于rk3568的Linux驱动开发——GPIO知识点一、引言GPIO(General Purpose Input/Output)通用输入/输出,是现代计算机系统中的一种常用接口,它可以根据需要配置为输入或输出。
通过GPIO 接口,我们可以与各种外设进行通信,如LED灯、按键、传感器等。
在基于Linux系统的嵌入式设备上开发驱动程序时,熟悉GPIO的使用是非常重要的一环。
本文将以RK3568芯片为例,详细介绍GPIO的相关知识点和在Linux驱动开发中的应用。
二、GPIO概述GPIO是系统中的一个基本的硬件资源,它可以通过软件的方式对其进行配置和控制。
在嵌入式设备中,通常将一部分GPIO引脚连接到外部可编程电路,以实现与外部设备的交互。
在Linux中,GPIO是以字符设备的形式存在,对应的设备驱动为"gpiolib"。
三、GPIO的驱动开发流程1. 导入头文件在驱动程序中,首先需要导入与GPIO相关的头文件。
对于基于RK3568芯片的开发,需要导入头文件"gpiolib.h"。
2. 分配GPIO资源在驱动程序中,需要使用到GPIO资源,如GPIO所在的GPIO Bank和GPIO Index等。
在RK3568芯片中,GPIO资源的分配是通过设备树(Device Tree)来进行的。
在设备树文件中,可以定义GPIO Bank和GPIO Index等信息,以及对应的GPIO方向(输入或输出)、电平(高电平或低电平)等属性。
在驱动程序中,可以通过设备树接口(Device Tree API)来获取这些GPIO资源。
3. GPIO的配置与控制在驱动程序中,首先要进行GPIO的初始化与配置。
可以通过函数"gpiod_get()"来打开指定的GPIO,并判断其是否有效。
如果成功打开GPIO,则可以使用函数"gpiod_direction_output()"或"gpiod_direction_input()"来设置GPIO的方向,分别作为输出或输入。
LAPACK函数介绍不完全版

为方便线性代数运算,现将LAPACK中的函数介绍如下:1.函数的命名规则:LAPACK里的每个函数名已经说明了该函数的使用规则。
所有函数都是以XYYZZZ的形式命名,对于某些函数,没有第六个字符,只是XYYZZ的形式。
第一个字母X代表以下的数据类型:S REAL,单精度实数D DOUBLE PRECISION,双精度实数C COMPLEX,单精度复数Z COMPLEX*16 或DOUBLE COMPLEX注:在新版LAPACK中含有使用重复迭代法的函数DSGESV和ZCDESV。
头2个字母表示使用的精度:DS 输入数据是double双精度,算法使用单精度ZC 输入数据是complex*16,算法使用complex单精度复数接下面两个字母YY代表数组的类型。
BD bidiagonal,双对角矩阵DI diagonal,对角矩阵GB general band,一般带状矩阵GE general (i.e., unsymmetric, in some cases rectangular),一般情形(即非对称,在有些情形下为矩形)GG general matrices, generalized problem (i.e., a pair of general matrices),一般矩阵,广义问题(即一对一般矩阵)GT general tridiagonal,一般三对角矩阵HB (complex) Hermitian band,(复数)厄尔米特带状阵HE (complex) Hermitian,(复数)厄尔米特矩阵HG upper Hessenberg matrix, generalized problem (i.e a Hessenberg and a triangular matrix),上海森伯格矩阵,广义问题(即一个海森伯格矩阵和一个三角矩阵)HP (complex) Hermitian, packed storage,(复数)压缩储存的厄尔米特矩阵HS upper Hessenberg,上海森博格矩阵OP (real) orthogonal, packed storage,(实数)压缩储存的正交阵OR (real) orthogonal,(实数)正交阵PB symmetric or Hermitian positive definite band,对称或厄尔米特正定带状矩阵PO symmetric or Hermitian positive definite,对称或厄尔米特正定矩阵PP symmetric or Hermitian positive definite, packed storage,压缩储存的对称或厄尔米特正定矩阵PT symmetric or Hermitian positive definite tridiagonal,对称或厄尔米特正定三对角阵SB (real) symmetric band,(实数)对称带状阵SP symmetric, packed storage,压缩储存的对称阵ST (real) symmetric tridiagonal,(实数)对称三对角阵SY symmetric,对称阵TB triangular band,三角形带状矩阵TG triangular matrices, generalized problem (i.e., a pair of triangular matrices),三角形矩阵,广义问题(即一对三角形阵)TP triangular, packed storage,压缩储存的三角形阵TR triangular (or in some cases quasi-triangular),三角形阵(在某些情形下为类三角形阵)TZ trapezoidal,梯形阵UN (complex) unitary,(复数)酉矩阵UP (complex) unitary, packed storage,(复数)压缩储存的酉矩阵最后三个字母ZZZ代表计算方法。
sEparaTe包的说明文档:最大似然估计和似然比检验函数说明书

Package‘sEparaTe’August18,2023Title Maximum Likelihood Estimation and Likelihood Ratio TestFunctions for Separable Variance-Covariance StructuresVersion0.3.2Maintainer Timothy Schwinghamer<***************************.CA>Description Maximum likelihood estimation of the parametersof matrix and3rd-order tensor normal distributions with unstructuredfactor variance covariance matrices,two procedures,and for unbiasedmodified likelihood ratio testing of simple and double separabilityfor variance-covariance structures,two procedures.References:Dutilleul P.(1999)<doi:10.1080/00949659908811970>,Manceur AM,Dutilleul P.(2013)<doi:10.1016/j.cam.2012.09.017>,and Manceur AM,DutilleulP.(2013)<doi:10.1016/j.spl.2012.10.020>.Depends R(>=4.3.0)License MIT+file LICENSEEncoding UTF-8LazyData trueRoxygenNote7.2.0NeedsCompilation noAuthor Ameur Manceur[aut],Timothy Schwinghamer[aut,cre],Pierre Dutilleul[aut,cph]Repository CRANDate/Publication2023-08-1807:50:02UTCR topics documented:data2d (2)data3d (2)lrt2d_svc (3)lrt3d_svc (5)mle2d_svc (7)12data3d mle3d_svc (8)sEparaTe (10)Index11 data2d Two dimensional data setDescriptionAn i.i.d.random sample of size7from a2x3matrix normal distribution,for a small numerical example of the use of the functions mle2d_svc and lrt2d_svc from the sEparaTe packageUsagedata2dFormatA frame(excluding the headings)with42lines of data and4variables:K an integer ranging from1to7,the size of an i.i.d.random sample from a2x3matrix normal distributionId1an integer ranging from1to2,the number of rows of the matrix normal distributionId2an integer ranging from1to3,the number of columns of the matrix normal distribution value2d the sample data for the observed variabledata3d Three dimensional data setDescriptionAn i.i.d.random sample of size13from a2x3x2tensor normal distribution,for a small numerical example of the use of the functions mle3d_svc and lrt3d_svc from the sEparaTe packageUsagedata3dFormatA frame(excluding the headings)with156lines of data and5variables:K an integer ranging from1to13,the size of an i.i.d.random sample from a2x3x2tensor matrix normal distributionId3an integer ranging from1to2,the number of rows of the3rd-order tensor normal distribution Id4an integer ranging from1to3,the number of columns of the3rd-order tensor normal distribu-tionId5an integer ranging from1to2,the number of edges of the3rd-order tensor normal distribution value3d the sample data for the observed variablelrt2d_svc Unbiased modified likelihood ratio test for simple separability of avariance-covariance matrix.DescriptionA likelihood ratio test(LRT)for simple separability of a variance-covariance matrix,modified tobe unbiased infinite samples.The modification is a penalty-based homothetic transformation of the LRT statistic.The penalty value is optimized for a given mean model,which is left unstruc-tured here.In the required function,the Id1and Id2variables correspond to the row and column subscripts,respectively;“value2d”refers to the observed variable.Usagelrt2d_svc(value2d,Id1,Id2,subject,data_2d,eps,maxiter,startmat,sign.level,n.simul)Argumentsvalue2d from the formula value2d~Id1+Id2Id1from the formula value2d~Id1+Id2Id2from the formula value2d~Id1+Id2subject the replicate,also called the subject or individual,thefirst column in the matrix (2d)datafiledata_2d the name of the matrix dataeps the threshold in the stopping criterion for the iterative mle algorithm(estimation) maxiter the maximum number of iterations for the mle algorithm(estimation)startmat the value of the second factor variance-covariance matrix used for initialization,i.e.,to start the mle algorithm(estimation)and obtain the initial estimate of thefirst factor variance-covariance matrixsign.level the significance level,or rejection rate in the testing of the null hypothesis of simple separability for a variance-covariance structure,when the unbiased mod-ified LRT is used,i.e.,the critical value in the chi-square test is derived bysimulations from the sampling distribution of the LRT statistic n.simul the number of simulations used to build the sampling distribution of the LRT statistic under the null hypothesis,using the same characteristics as the i.i.d.random sample from a matrix normal distributionOutput“Convergence”,TRUE or FALSE“chi.df”,the theoretical number of degrees of freedom of the asymptotic chi-square distribution that would apply to the unmodified LRT statistic for simple separability of a variance-covariance structure“Lambda”,the observed value of the unmodified LRT statistic“critical.value”,the critical value at the specified significance level for the chi-square distribution with“chi.df”degrees of freedom“mbda”will indicate whether or not the null hypothesis of separability was rejected, based on the theoretical LRT statistic“Simulation.critical.value”,the critical value at the specified significance level that is derived from the sampling distribution of the unbiased modified LRT statistic“mbda.simulation”,the decision(acceptance/rejection)regarding the null hypothesis of simple separability,made using the theoretical(biased unmodified)LRT“Penalty”,the optimized penalty value used in the homothetic transformation between the biased unmodified and unbiased modified LRT statistics“U1hat”,the estimated variance-covariance matrix for the rows“Standardized_U1hat”,the standardized estimated variance-covariance matrix for the rows;the standardization is performed by dividing each entry of U1hat by entry(1,1)of U1hat“U2hat”,the estimated variance-covariance matrix for the columns“Standardized_U2hat”,the standardized estimated variance-covariance matrix for the columns;the standardization is performed by multiplying each entry of U2hat by entry(1,1)of U1hat“Shat”,the sample variance-covariance matrix computed from the vectorized data matrices ReferencesManceur AM,Dutilleul P.2013.Unbiased modified likelihood ratio tests for simple and double separability of a variance-covariance structure.Statistics and Probability Letters83:631-636.Examplesoutput<-lrt2d_svc(data2d$value2d,data2d$Id1,data2d$Id2,data2d$K,data_2d=data2d,n.simul=100)outputlrt3d_svc An unbiased modified likelihood ratio test for double separability of avariance-covariance structure.DescriptionA likelihood ratio test(LRT)for double separability of a variance-covariance structure,modified tobe unbiased infinite samples.The modification is a penalty-based homothetic transformation of the LRT statistic.The penalty value is optimized for a given mean model,which is left unstructured here.In the required function,the Id3,Id4and Id5variables correspond to the row,column and edge subscripts,respectively;“value3d”refers to the observed variable.Usagelrt3d_svc(value3d,Id3,Id4,Id5,subject,data_3d,eps,maxiter,startmatU2,startmatU3,sign.level,n.simul)Argumentsvalue3d from the formula value3d~Id3+Id4+Id5Id3from the formula value3d~Id3+Id4+Id5Id4from the formula value3d~Id3+Id4+Id5Id5from the formula value3d~Id3+Id4+Id5subject the replicate,also called individualdata_3d the name of the tensor dataeps the threshold in the stopping criterion for the iterative mle algorithm(estimation) maxiter the maximum number of iterations for the mle algorithm(estimation)startmatU2the value of the second factor variance-covariance matrix used for initialization startmatU3the value of the third factor variance-covariance matrix used for initialization,i.e.,startmatU3together with startmatU2are used to start the mle algorithm(estimation)and obtain the initial estimate of thefirst factor variance-covariancematrix U1sign.level the significance level,or rejection rate in the testing of the null hypothesis of simple separability for a variance-covariance structure,when the unbiased mod-ified LRT is used,i.e.,the critical value in the chi-square test is derived bysimulations from the sampling distribution of the LRT statistic n.simul the number of simulations used to build the sampling distribution of the LRT statistic under the null hypothesis,using the same characteristics as the i.i.d.random sample from a tensor normal distributionOutput“Convergence”,TRUE or FALSE“chi.df”,the theoretical number of degrees of freedom of the asymptotic chi-square distribution that would apply to the unmodified LRT statistic for double separability of a variance-covariance structure“Lambda”,the observed value of the unmodified LRT statistic“critical.value”,the critical value at the specified significance level for the chi-square distribution with“chi.df”degrees of freedom“mbda”,the decision(acceptance/rejection)regarding the null hypothesis of double sep-arability,made using the theoretical(biased unmodified)LRT“Simulation.critical.value”,the critical value at the specified significance level that is derived from the sampling distribution of the unbiased modified LRT statistic“mbda.simulation”,the decision(acceptance/rejection)regarding the null hypothesis of double separability,made using the unbiased modified LRT“Penalty”,the optimized penalty value used in the homothetic transformation between the biased unmodified and unbiased modified LRT statistics“U1hat”,the estimated variance-covariance matrix for the rows“Standardized_U1hat”,the standardized estimated variance-covariance matrix for the rows;the standardization is performed by dividing each entry of U1hat by entry(1,1)of U1hat“U2hat”,the estimated variance-covariance matrix for the columns“Standardized_U2hat”,the standardized estimated variance-covariance matrix for the columns;the standardization is performed by multiplying each entry of U2hat by entry(1,1)of U1hat“U3hat”,the estimated variance-covariance matrix for the edges“Shat”,the sample variance-covariance matrix computed from the vectorized data tensorsReferencesManceur AM,Dutilleul P.2013.Unbiased modified likelihood ratio tests for simple and double separability of a variance-covariance structure.Statistics and Probability Letters83:631-636.Examplesoutput<-lrt3d_svc(data3d$value3d,data3d$Id3,data3d$Id4,data3d$Id5,data3d$K,data_3d=data3d,n.simul=100)outputmle2d_svc Maximum likelihood estimation of the parameters of a matrix normaldistributionDescriptionMaximum likelihood estimation for the parameters of a matrix normal distribution X,which is char-acterized by a simply separable variance-covariance structure.In the general case,which is the case considered here,two unstructured factor variance-covariance matrices determine the covariability of random matrix entries,depending on the row(one factor matrix)and the column(the other factor matrix)where two X-entries are.In the required function,the Id1and Id2variables correspond to the row and column subscripts,respectively;“value2d”indicates the observed variable.Usagemle2d_svc(value2d,Id1,Id2,subject,data_2d,eps,maxiter,startmat)Argumentsvalue2d from the formula value2d~Id1+Id2Id1from the formula value2d~Id1+Id2Id2from the formula value2d~Id1+Id2subject the replicate,also called individualdata_2d the name of the matrix dataeps the threshold in the stopping criterion for the iterative mle algorithmmaxiter the maximum number of iterations for the iterative mle algorithmstartmat the value of the second factor variance-covariance matrix used for initializa-tion,i.e.,to start the algorithm and obtain the initial estimate of thefirst factorvariance-covariance matrixOutput“Convergence”,TRUE or FALSE“Iter”,will indicate the number of iterations needed for the mle algorithm to converge“Xmeanhat”,the estimated mean matrix(i.e.,the sample mean)“First”,the row subscript,or the second column in the datafile“U1hat”,the estimated variance-covariance matrix for the rows“Standardized.U1hat”,the standardized estimated variance-covariance matrix for the rows;the stan-dardization is performed by dividing each entry of U1hat by entry(1,1)of U1hat“Second”,the column subscript,or the third column in the datafile“U2hat”,the estimated variance-covariance matrix for the columns“Standardized.U2hat”,the standardized estimated variance-covariance matrix for the columns;the standardization is performed by multiplying each entry of U2hat by entry(1,1)of U1hat“Shat”,is the sample variance-covariance matrix computed from of the vectorized data matrices ReferencesDutilleul P.1990.Apport en analyse spectrale d’un periodogramme modifie et modelisation des series chronologiques avec repetitions en vue de leur comparaison en frequence.D.Sc.Dissertation, Universite catholique de Louvain,Departement de mathematique.Dutilleul P.1999.The mle algorithm for the matrix normal distribution.Journal of Statistical Computation and Simulation64:105-123.Examplesoutput<-mle2d_svc(data2d$value2d,data2d$Id1,data2d$Id2,data2d$K,data_2d=data2d) outputmle3d_svc Maximum likelihood estimation of the parameters of a3rd-order ten-sor normal distributionDescriptionMaximum likelihood estimation for the parameters of a3rd-order tensor normal distribution X, which is characterized by a doubly separable variance-covariance structure.In the general case, which is the case considered here,three unstructured factor variance-covariance matrices determine the covariability of random tensor entries,depending on the row(one factor matrix),the column (another factor matrix)and the edge(remaining factor matrix)where two X-entries are.In the required function,the Id3,Id4and Id5variables correspond to the row,column and edge subscripts, respectively;“value3d”indicates the observed variable.Usagemle3d_svc(value3d,Id3,Id4,Id5,subject,data_3d,eps,maxiter,startmatU2,startmatU3)Argumentsvalue3d from the formula value3d~Id3+Id4+Id5Id3from the formula value3d~Id3+Id4+Id5Id4from the formula value3d~Id3+Id4+Id5Id5from the formula value3d~Id3+Id4+Id5subject the replicate,also called individualdata_3d the name of the tensor dataeps the threshold in the stopping criterion for the iterative mle algorithmmaxiter the maximum number of iterations for the iterative mle algorithmstartmatU2the value of the second factor variance covariance matrix used for initialization startmatU3the value of the third factor variance covariance matrix used for initialization,i.e.,startmatU3together with startmatU2are used to start the algorithm andobtain the initial estimate of thefirst factor variance covariance matrix U1Output“Convergence”,TRUE or FALSE“Iter”,the number of iterations needed for the mle algorithm to converge“Xmeanhat”,the estimated mean tensor(i.e.,the sample mean)“First”,the row subscript,or the second column in the datafile“U1hat”,the estimated variance-covariance matrix for the rows“Standardized.U1hat”,the standardized estimated variance-covariance matrix for the rows;the stan-dardization is performed by dividing each entry of U1hat by entry(1,1)of U1hat“Second”,the column subscript,or the third column in the datafile“U2hat”,the estimated variance-covariance matrix for the columns“Standardized.U2hat”,the standardized estimated variance-covariance matrix for the columns;the standardization is performed by multiplying each entry of U2hat by entry(1,1)of U1hat“Third”,the edge subscript,or the fourth column in the datafile“U3hat”,the estimated variance-covariance matrix for the edges“Shat”,the sample variance-covariance matrix computed from the vectorized data tensorsReferenceManceur AM,Dutilleul P.2013.Maximum likelihood estimation for the tensor normal distribution: Algorithm,minimum sample size,and empirical bias and dispersion.Journal of Computational and Applied Mathematics239:37-49.10sEparaTeExamplesoutput<-mle3d_svc(data3d$value3d,data3d$Id3,data3d$Id4,data3d$Id5,data3d$K,data_3d=data3d) outputsEparaTe MLE and LRT functions for separable variance-covariance structuresDescriptionA package for maximum likelihood estimation(MLE)of the parameters of matrix and3rd-ordertensor normal distributions with unstructured factor variance-covariance matrices(two procedures),and for unbiased modified likelihood ratio testing(LRT)of simple and double separability forvariance-covariance structures(two procedures).Functionsmle2d_svc,for maximum likelihood estimation of the parameters of a matrix normal distributionmle3d_svc,for maximum likelihood estimation of the parameters of a3rd-order tensor normaldistributionlrt2d_svc,for the unbiased modified likelihood ratio test of simple separability for a variance-covariance structurelrt3d_svc,for the unbiased modified likelihood ratio test of double separability for a variance-covariance structureDatadata2d,a two-dimensional data setdata3d,a three-dimensional data setReferencesDutilleul P.1999.The mle algorithm for the matrix normal distribution.Journal of StatisticalComputation and Simulation64:105-123.Manceur AM,Dutilleul P.2013.Maximum likelihood estimation for the tensor normal distribution:Algorithm,minimum sample size,and empirical bias and dispersion.Journal of Computational andApplied Mathematics239:37-49.Manceur AM,Dutilleul P.2013.Unbiased modified likelihood ratio tests for simple and doubleseparability of a variance covariance structure.Statistics and Probability Letters83:631-636.Index∗datasetsdata2d,2data3d,2data2d,2data3d,2lrt2d_svc,3lrt3d_svc,5mle2d_svc,7mle3d_svc,8sEparaTe,1011。
dproduct函数用法

dproduct函数用法DPRODUCT函数是数据库函数中的一种,主要用于返回数据清单或数据库的指定列中,满足给定条件单元格中的数值乘积。
以下是DPRODUCT函数的具体用法:语法:DPRODUCT(database,field,criteria)。
其中,database 表示构成列表或数据库的单元格区域;field指定函数所使用的数据列;criteria为一组包含给定条件的单元格区域。
参数说明:Database:必需。
构成列表或数据库的单元格区域。
数据库是包含一组相关数据的列表,其中每一列包含一个类型的数据,并且每行都包含一组相关的数据。
第一行应包含列标签,并且每一列中的数据类型应相同。
Field:必需。
指定函数所使用的数据列。
可以是列标签,也可以是代表列在列表中的位置的数字。
例如,如果数据库区域为A1:C10,那么"A"、"B"或"C"可以用作列标签,或者数字1、2或3也可以表示各列(在这种情况下,数字表示从区域的左边界开始的相对列位置)。
Criteria:必需。
包含给定条件的单元格区域。
可以为参数指定任意区域,只要它至少包含一个列标签,并且列标签下方至少有一个用于为列指定条件的单元格。
注意事项:确保database和criteria区域没有重叠,否则函数可能无法正确计算。
如果criteria区域包含多个列,那么函数将返回满足所有给定条件的行的数值乘积。
如果criteria区域为空,则函数将返回指定列中的所有数值的乘积。
如果数据库中没有满足条件的行,则DPRODUCT将返回错误值#NUM!。
以上就是DPRODUCT函数的基本用法和注意事项,希望对你有所帮助。
dput函数

dput函数dput函数是R语言中一个非常常用的函数之一,它的作用是将一个对象转化成一个字符向量。
在数据分析过程中,我们经常需要将一些数据存储下来,方便以后使用。
通常我们会使用R语言中的save函数,将一个R对象序列化成RData文件,这种方式的优点是简单方便,可以保存多个对象,但是它的缺点也很明显,即不能将数据跨越不同的平台,数据也不能被人类可读。
而dput函数则可以很好地解决这些问题,它可以将对象转换成一个字符向量,并且可以被人类直接读取,这样就可以轻松地分享数据或将数据复制粘贴到其他文档或分析环境中。
dput函数的语法格式如下:dput(x, file = "", control = c("all", "quote", "abbreviations", "hex"), …)其中,x表示要转化的对象,file表示要输出的文件名,control用来控制输出的格式。
将对象转化成字符向量我们首先来看一个简单的例子,在R中创建一个向量,然后将它传递给dput函数,观察输出结果。
```Rx <- c(1, 2, 3, 4, 5)dput(x)```输出结果如下所示:输出的结果是一个字符向量,它可以被人类直接读取。
这个例子中,我们将一个向量转化成了一个字符串,这个字符串可以被输出到任何地方,例如写入一个文本文件中,可以保存到版本控制系统中,也可以粘贴到R脚本中。
dput函数不仅可以处理向量,还可以处理各种类型的R对象,例如数据框(data.frame),下面是一个简单的例子。
```Rstructure(list(a = c(1, 2, 3), b = structure(1:3, .Label = c("a","b", "c"), class = "factor")), s = c(NA, -3L), class = "data.frame")```这个输出结果可能有些难以读懂,因为它包含一些额外的信息,例如行名和类别信息。
eboot函数说明

Eboot代码说明一:EBOOT经过NBOOT引导后,一般会跳转到0x30038000开始执行第一条指令。
在我这EBOOT中是先执行目录下2440\Kernel\hal\arm\fw.s。
这个在有些系统能够中是setup.s,总之就是从系统ResetHandle开始执行了。
下面开始分析这段汇编代码,并且讲述它都做了一些什么工作:ldr r0, = INTMSKldr r1, = ~BIT_BAT_FLT ; all interrupt disable, nBATT_FLT =enabledstr r1, [r0]ldr r0, = INTSUBMSKldr r1, = 0x7ff ;all sub interrupt disablestr r1, [r0]ldr r0, = INTMODldr r1, = BIT_BA T_FLT ; set all interrupt as IRQ, BA T_FLT = FIQstr r1, [r0]ldr r1, =MISCCR ; MISCCR's Bit [22:20] -> 100ldr r0, [r1]bic r0, r0, #(7 << 20)bic r0, r0, #(1 << 3)bic r0, r0, #(1 << 13)orr r0, r0, #(4 << 20)str r0, [r1]bl ARMClearUTLBbl ARMFlushICacheldr r0, = (DCACHE_LINES_PER_SET - 1)ldr r1, = (DCACHE_NUM_SETS - 1)ldr r2, = DCACHE_SET_INDEX_BITldr r3, = DCACHE_LINE_SIZEbl ARMFlushDCachenopnopnopldr r0, = GPFCONldr r1, = 0x55aastr r1, [r0]ldr r0, = WTCON ; watch dog disable ldr r1, = 0x0str r1, [r0]//以上代码比较简单,但是很关键,关闭所有中断,刷新cache和快表。
模糊数学MATLAB应用

第6章模糊逻辑6.1 隶属函数6.1.1 高斯隶属函数函数gaussmf格式y=gaussmf(x,[sig c])说明高斯隶属函数的数学表达式为: , 其中为参数, x为自变量, sig为数学表达式中的参数。
例6-1>>x=0:0.1:10;>>y=gaussmf(x,[2 5]);>>plot(x,y)>>xlabel('gaussmf, P=[2 5]')结果为图6-1。
图6-16.1.2 两边型高斯隶属函数函数gauss2mf格式y = gauss2mf(x,[sig1 c1 sig2 c2])说明sig1.c1.sig2.c2为命令1中数学表达式中的两对参数例6-2>>x = (0:0.1:10)';>>y1 = gauss2mf(x, [2 4 1 8]);>>y2 = gauss2mf(x, [2 5 1 7]);>>y3 = gauss2mf(x, [2 6 1 6]);>>y4 = gauss2mf(x, [2 7 1 5]);>>y5 = gauss2mf(x, [2 8 1 4]);>>plot(x, [y1 y2 y3 y4 y5]);>>set(gcf, 'name', 'gauss2mf', 'numbertitle', 'off');结果为图6-2。
6.1.3 建立一般钟型隶属函数函数 gbellmf格式 y = gbellmf(x,params)说明 一般钟型隶属函数依靠函数表达式b 2|ac x |11)c ,b ,a ;x (f -+=这里x 指定变量定义域范围, 参数b 通常为正, 参数c 位于曲线中心, 第二个参数变量params 是一个各项分别为a, b 和c 的向量。
sas输入输出数据的相关语句output、put、remove、replace、file、。。。

sas输⼊输出数据的相关语句output、put、remove、replace、file、。
index: output put replace file infile没⼈任何规定的输出语句,sas系统会输出pdv当前观测到主数据集原先的位置output语句: TIPS: 1:当output没有规定数据集名字时,把当前观测《也就是⼀⾏数据》输出到data步后⾯的所有数据集的末尾<注意是所有数据集>意味着纵向合并,当规定数据集名字时,把pdv当前观测输出到output规定的数据集末尾。
2:在有output语句和run语句同时存在的data步⾥⾯,pdv只会执⾏output的结果到正在被创建的数据集,⽽执⾏run语句的结果是pdv会清空所有的变量为缺失。
3:如果⼀个output语句出现在程序语句中间,⽆论有没有被执⾏,后⾯的语句都将继续被执⾏,但是不会输出结果到正在被创建的输出数据集,⽽是会持续清空pdv中所有变量值(使⽤retain性质的语句除外). 4:sas中有implicit output和explicit output,在每⼀轮data循环后,sas会默认的将pdv中的数据写⼊数据集,这就是implicit output,还有⼀类是⽤户明确写的output语句,也就是explicit output,当明确规定后,隐式的output就不会再执⾏了。
5:output是将数据输⼊数据集,put是将数据输⼊⽂件或⽇志*需求:输出by组的最后⼀⾏观测值并将上⼀⾏的y值输出;data a;input x y@@;cards;11012012002302403503604703804400;run;proc sort data=a;by x;run;data res;set a;by x;retain rt; *如不⽤retain,下⾯的put能输出正确的值,但是运⾏到run后会⾃动清空,这样output的结果集中rt都会为缺失值;if first.x then rt=0;if last.x then output;rt = y;put rt=;run;proc print data=res noobs;*由⼀个输⼊数据⾏输出多条观测;data a;input id x1-x3;cards;101102030102405060;run;data b;set a;x = x1; output;x = x2; output;x = x3; output;output;run;data c1 c2;*根据条件选择输出; set sashelp.class; if _n_ le 7 then output c1; else output c2;run;*输出每个by组的最后⼀条观测和倒数第⼆条的y值;data a;input x y@@;cards;11012012002302403503604703804400;run;proc sort data=a;by x; run;data b;set a;by x;retain rt;if first.x then rt=0;if last.x then output;rt = y;run;/*读⼊第⼀条观测值时,rt被置为0,last.x为0不执⾏,rt=10,执⾏run,retain的rt保留在pdv中,因为output和run同时存在时run不会输出数据,只有output执⾏的时候rt才会被输出,当读⼊第⼆条观测的时候output也不执⾏,但是这时的rt是保留的第⼆条观测值的y,当读⼊第三条观测的时候output执⾏,顺便输出pdv中的rt,这时的rt是倒数第⼆条观测值的rt,还没有进⾏赋值*/remove语句If you specify no argument, the REMOVE statement deletes the current observation from all data sets that are named in the DATA statement.remove和delete和if⼦句都能起到获取部分数据集的效果,但是delete和if都perform only on physical但是remove既可以logical也可以physical,对于不同的引擎。
stdout函数

stdout函数概述在计算机编程中,stdout是一个常用的函数或方法名,是指标准输出(standard output)的缩写。
标准输出是计算机程序向屏幕或终端输出信息的流。
stdout函数就是用来向标准输出打印信息的函数。
为什么需要stdout函数在编程中,我们经常需要打印一些信息来观察程序的执行过程和结果。
stdout函数提供了一种简单而有效的方式来输出这些信息。
通过stdout函数,我们可以将程序运行过程中的关键信息打印出来,方便调试和分析。
stdout函数的基本用法stdout函数一般包含在编程语言的标准库中,可以直接调用。
它通常接受一个参数,即要输出的信息。
下面是一些常见编程语言中使用stdout函数的示例:Pythonprint("Hello, world!")JavaSystem.out.println("Hello, world!");C++#include <iostream>using namespace std;int main() {cout << "Hello, world!" << endl;return 0;}JavaScriptconsole.log("Hello, world!");上述示例中的stdout函数会将字符串”Hello, world!“输出到屏幕或终端。
stdout函数的高级用法除了简单地输出字符串,stdout函数还可以输出变量、格式化的信息和对象等。
下面是一些常用的stdout函数的高级用法:输出变量name = "Alice"print("Hello, " + name + "!")格式化输出age = 30print("I am {} years old.".format(age))输出对象class Person:def __init__(self, name, age): = nameself.age = ageperson = Person("Bob", 25)print("Name: {}, Age: {}".format(, person.age))stdout函数的重定向除了将信息输出到屏幕或终端,stdout函数还可以将信息重定向到文件或其他设备。
codesys所有函数的详细说明.
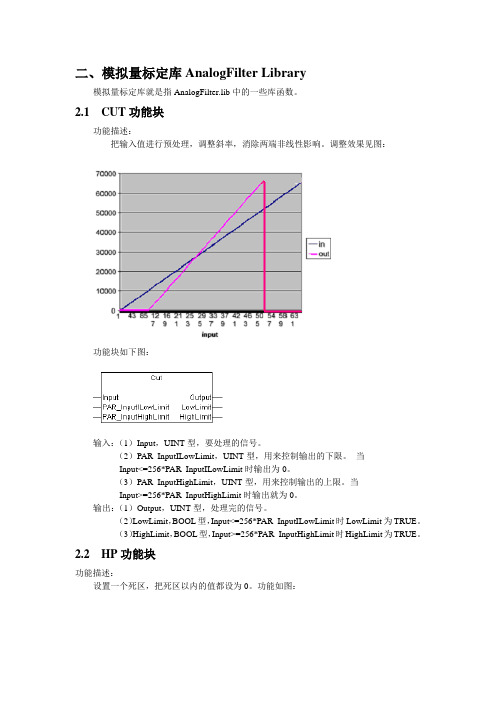
二、模拟量标定库AnalogFilter Library模拟量标定库就是指AnalogFilter.lib中的一些库函数。
2.1 CUT功能块功能描述:把输入值进行预处理,调整斜率,消除两端非线性影响。
调整效果见图:功能块如下图:输入:(1)Input,UINT型,要处理的信号。
(2)PAR_InputILowLimit,UINT型,用来控制输出的下限。
当Input<=256*PAR_InputILowLimit时输出为0。
(3)PAR_InputHighLimit,UINT型,用来控制输出的上限。
当Input>=256*PAR_InputHighLimit时输出就为0。
输出:(1)Output,UINT型,处理完的信号。
(2)LowLimit,BOOL型,Input<=256*PAR_InputILowLimit时LowLimit为TRUE。
(3)HighLimit,BOOL型,Input>=256*PAR_InputHighLimit时HighLimit为TRUE。
2.2 HP功能块功能描述:设置一个死区,把死区以内的值都设为0。
功能如图:功能块如下图:输入:(1)Input,UINT型,输入信号。
. (2)PAR_CutLimit,UINT型,死区控制参数。
当Input<=65535*PAR_CutLimit%时输出为0。
输出:(1)Output,UINT型,处理完的信号。
2.3 JoyFilter功能块功能描述:JoyFilter块是一个双向的模拟量标定块,也就是说它对输入的模拟量进行预处理,把输出范围调整为-32767~32767。
功能块如下图:输入:(1)AnalogInput,UINT型,模拟量的输入信号。
(2)DI_JoystickDirSwitchPOS,BOOL型,正向微动开关。
当PAR_DirSwitchDiagnosticNotUse为FALSE时,此时又手柄向正向移动,那么只有正向微动开关TRUE,OUTPUT才会有输出。
IDL中常用的函数意思

Strtri m:字符串的裁剪Strupc ase:将字符串转成大写Strmid:字符串的提取Strlen:字符串求长度数组章节Intarr:创建一个整型数组Btyarr:创建byte类型数组Bytscl:数组转换成b y te类型Fix:将其他类型的数组转换成整型数组Sort:返回数组排序后的索引Uniq:查找数组中唯一元素的索引Size:返回数组各个维的个数N_elem ents:返回数组元素的个数Make_a rray:创建数组Strspl it:将字符串拆成各个子字符结构体章节{[name],tag1:…,tag2:…,tag3:…}:结构体的创建N_tags:返回结构体中元素的个数Tag_na mes:返回结构体中各个成分的名称指针章节Ptr_ne w:创建新的指针*ptr:指针的引用Ptr_fr ee,ptr:指针的释放循环语句For do beginEndforWhiledo beginEndwhi leIf then beginEndifelse beginendelse或者是If then beginEndifelse if then beginEndifCase ofElse:Endcas eSwitch ofEndswi tch过程与函数(在过程里边调用函数)ProEndReturn,(得有返回值)EndFun(数值):函数调用Pro,,:过程调用输出数据的格式:Format=‘()’B:数值转为二进制O:数值转为八进制Z:数值转为16进制Ascii码文件的读写Openr:以只读方式打开文件Openw:以读写方式打开文件Dialog_pick file:对话框文件选取Dialog_message:弹出对话框提示信息File_b asena me:文件名提取File_d irnam e:文件名提取Query_image:查询信息Free_l un:关闭文件Printf:文件中写入数据Readf:文件中读取数据File_t est:检验文件是否存在File_l ines:检验文件的行数注意:(1)由于read f从文件中读取的数据是字符型的,因此对于re adf中的变量要事先定义(tmp=‘’)。
VB函数说明及使用方法

c、Lock Read:不允许其他进程读该文件。只在没有其他Read存取类型的进程访问该文件时,才允许这种锁定。
d、Lock Write:不允许其他进程写这个文件。只在没有其他Write存取类型的进程访问该文件时,才允许这种锁定
10、Write #文件号,表达式表…:作用同Print
11、Input #文件号,变量表….:读顺序文件,进行与Print相反的操作
12、Line Input #文件号,字符串变量:从顺序文件中读入一行
13、Input$(n,#文件号):从顺序文件读出n个字符的字符串
14、Put #文件号,[记录号],变量:把除对象变量和数组变量外的任何变量(包括号含有单个数组元素的下标变量)的内容写入随机文件。
MsgBox(msg,[type]…)
跳出一个提示窗口
文本操作函数
1、Open文件名[For方式] [Access存取类型] [锁定] AS [#]文件号[Len=记录长度]
功能:为文件的输入输出分配缓冲区,并确定缓冲区所使用的存取方式
说明:
1)方式:指定文件的输入输出方式,可选,默认是Random,可以是以下值
5、FreeFile():取得一个未使用的文件号
6、Loc(文件号):返回指定文件的当前读写位置
7、LOF(文件号):返回文件长度
8、EOF(文件号):用来测试文件是否结束,结束返回true
9、Print #文件号,变量1,变量2,…变量n:按顺序将各变量的值写入顺序文件
如果是print #文件号,则写入空行
a、Output:指定顺序输出方式,将覆盖原有内容
b、Input:指定顺序输入方式
python中output函数的用法

python中output函数的用法Python是一种高级编程语言,它具有简单易学、易读、易维护等特点,因此在数据科学、机器学习、Web开发等领域中被广泛应用。
在Python中,output函数是一个非常重要的函数,它可以用来输出结果或信息。
本文将详细介绍Python中output函数的用法。
一、output函数的基本概念Python中的output函数是一个内置函数,它可以将结果或信息输出到控制台或文件中。
通常情况下,我们使用print语句来输出信息,但是当需要将多个变量或表达式组合成一个字符串时,就需要使用output函数。
二、output函数的语法Python中的output函数有两种形式:1. print(object(s), sep=separator, end=end, file=file, flush=flush)其中:object(s):要输出的对象或表达式,可以是一个或多个。
sep:各个对象之间的分隔符,默认为一个空格。
end:输出结束时要添加到末尾的字符,默认为一个换行符(\n)。
file:要将输出写入的文件对象,默认为sys.stdout(标准输出)。
flush:是否强制刷新缓冲区,默认为False。
2. f.write(string)其中:string:要写入文件的字符串。
f:文件对象,必须以写模式打开('w')。
三、使用print语句输出信息在Python中使用print语句输出信息是最常见的方法。
例如:print("Hello, World!")输出结果为:Hello, World!可以使用多个参数来输出多个信息,例如:name = "Tom"age = 18print("My name is", name, "and I am", age, "years old.")输出结果为:My name is Tom and I am 18 years old.也可以使用sep参数来指定分隔符,例如:print("My name is", name, "and I am", age, "years old.", sep="-") 输出结果为:My name is-Tom-and I am-18-years old.还可以使用end参数来指定结尾字符,例如:print("Hello,", end=" ")print("World!")输出结果为:Hello, World!四、使用output函数将信息写入文件除了将信息输出到控制台外,还可以将信息写入文件。
MATLAB S函数学习
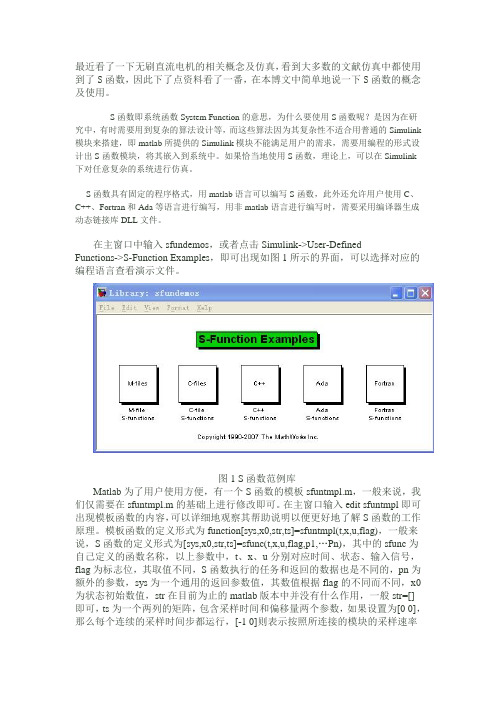
最近看了一下无刷直流电机的相关概念及仿真,看到大多数的文献仿真中都使用到了S函数,因此下了点资料看了一番,在本博文中简单地说一下S函数的概念及使用。
S函数即系统函数System Function的意思,为什么要使用S函数呢?是因为在研究中,有时需要用到复杂的算法设计等,而这些算法因为其复杂性不适合用普通的Simulink模块来搭建,即matlab所提供的Simulink模块不能满足用户的需求,需要用编程的形式设计出S函数模块,将其嵌入到系统中。如果恰当地使用S函数,理论上,可以在Simulink下对任意复杂的系统进行仿真。
sizes.NumOutputs = 3; %输出变量个数
sizes.NumInputs = 2; %输入信号个数
sizes.DirFeedthrough = 1; %输入直接传入输出信号否
sizes.NumSampleTimes = 1; % at least one sample time is neededWO一般来说为1个
sys = simsizes(sizes);
x0=[]; %状态初始化
str=[];
ts=[-1 0]; %采样周期若写成-1表示继承其输入信号
%%%%%%在flag=1的时候进行连续系统状态的更新
function sys=mdlDerivatives(t,x,u)
dequeueoutputbuffer函数

dequeueoutputbuffer函数在许多应用程序中,当一个任务将数据放入输出缓冲区时,另一个任务会负责从缓冲区中取出数据并进行进一步处理,这样可以实现并发和异步处理。
1.检查输出缓冲区是否为空。
如果为空,等待直到缓冲区有新的数据。
2.通过某种数据结构,如队列、链表或缓冲区索引,获取下一个要处理的数据。
3.从输出缓冲区中取出数据。
这可能涉及到内存拷贝操作,例如将数据从缓冲区复制到临时变量中。
4.对取出的数据进行处理。
这可能涉及到计算、读取、写入或者其他业务逻辑操作。
5.如果缓冲区支持删除操作,将已经处理的数据从缓冲区中删除。
6.如果有多个线程或任务在同时访问输出缓冲区,可能需要进行并发控制,以防止竞态条件或数据一致性问题。
7.返回处理后的数据供调用者使用。
这可以是函数的返回值,也可以是通过参数传递给其他函数或对象。
需要注意的是,具体的dequeOutputBuffer函数的实现可能会因应用场景或需求而有所不同。
例如,如果需要按照某种顺序处理数据,可能需要对数据进行排序操作。
又或者,如果需要实现一定的容错能力,可能需要在处理数据时进行错误处理或数据重试机制。
此外,dequeOutputBuffer函数还可能与其他函数或组件进行协作,例如与输入缓冲区、数据处理器、持久化存储等进行交互。
总之,dequeOutputBuffer函数在多线程或异步任务中扮演着重要的角色,它能够高效地处理输出缓冲区中的数据,并将其传递给下一步的处理环节。
正确地实现这个函数可以提高系统的性能和可靠性。
idinput函数的功率谱调节

idinput函数的功率谱调节idinput函数是一种常用的信号输入函数,用于生成具有指定功率谱的信号。
它在信号处理和系统建模领域起着重要的作用。
本文将介绍idinput函数的概念、使用方法以及其在功率谱调节方面的应用。
一、idinput函数概述idinput函数是MATLAB中的一个函数,用于生成具有指定统计特性的输入信号。
它可以生成多种类型的信号,包括随机信号、脉冲信号、步阶信号等。
使用idinput函数可以方便地生成各种类型的输入信号,并且可以根据需要调节信号的功率谱。
二、idinput函数的使用方法使用idinput函数,首先需要确定信号的类型和长度。
可以通过设置输入参数来指定信号类型,如随机信号使用'prbs'参数,脉冲信号使用'pulse'参数,步阶信号使用'stair'参数。
然后可以通过设置其他的参数来调节信号的功率谱,如信号的功率谱形状、功率谱密度等。
例如,要生成长度为N的随机信号,可以使用如下代码:```MATLABu = idinput(N, 'prbs', 'spectrum', [f1 f2], 'amplitude', [A1 A2]);```其中,N为信号的长度,'prbs'为信号的类型,[f1 f2]为信号的频率范围,[A1 A2]为信号的幅度范围。
三、idinput函数在功率谱调节中的应用idinput函数在功率谱调节方面有很多应用。
下面以几个具体的例子来说明:1. 信号的频率响应测试在系统建模和信号处理中,经常需要测试系统对不同频率信号的响应。
可利用idinput函数生成不同频率的信号,通过系统对这些信号的响应得到系统的频率响应。
这对于系统性能分析和滤波器设计等应用非常重要。
2. 信号的噪声特性测试在通信系统、雷达系统等领域中,对信号的噪声特性进行测试是很常见的。
