华北电力大学 电力系统稳态潮流上机计算程序结果
电力系统稳态 潮流计算程序

printf("J0[%d][%d]=%f\t",i,j,J0[i][j]);
J0[4][4]=3.6666;
//**************************************************************************************
J[i][j]=2*fi0[i];
L[i][j]=2*ei0[i];
}
else
{
H[i][j]=-ybi[i][j]*ei0[j]+ybr[i][j]*fi0[j]+Iii0[i];
N[i][j]=ybr[i][j]*ei0[j]+ybi[i][j]*fi0[j]+Iir0[i];
static float yd[4][4]={{0,0.01528,-0.366623,0.0192},{0.01528,0,0,0.01413},
{0.333297,0,0,0},{0.0192,0.01413,0,0}};
float ei0[4]={1,1,1,1.05};
float Max(float a[],int n)
{int i;
float max,b=0;
if(a[0]<0) {b=-a[0];}
max=b;
for(i=1;i<n;i++)
{
b=a[i];
if(a[i]<0){b=-a[i];}
if(max<b)
//*************************************************************************************
电力系统潮流上机计算报告

电力系统潮流上机计算报告
系别:电力工程系
班级:
姓名:
学号:
课号课序号:0110361-2
选课顺序号:22
程序说明
包括:程序设计思想、程序流程图、程序使用说明。
给定题目的手算过程(迭代两次)
包括:原题目、节点导纳矩阵、雅克比矩阵、第一次和第二次迭代结果。
给定题目的程序计算结果
包括:原题目、节点导纳矩阵、雅克比矩阵、程序输入和输出文件(误差0.0001)。
编程特色与创新
包括:程序能够完成的基本功能;程序能够完成的高级功能(如:是否包括平行支路、接地支路、非标准变比变压器支路,是否采用了稀疏矩阵技术,是否增加了人机对话界面,程序的通用性和实用性如何)。
五、总结
包括:手算结果与程序计算结果的分析比较;本次上机体会,如:独立编程体会、跟踪调试技能的掌握情况,C语言中结构体、指针、文件输入输出的掌握情况等。
报告要求:
报告必须手写(最好使用黑色水笔)。
报告统一采用A4打印纸书写(留出页边距: 1.5~2厘米)。
不使用实验报告纸。
封面按上述格式书写。
装订统一在左侧1厘米,三个钉。
上述五部分内容必须齐全,各部分内容可以扩充。
报告书写要求字迹清楚,不得潦草。
报告必须与本人提交程序吻合,否则取消成绩。
报告不得有雷同,否则全部取消成绩。
电力系统潮流计算结果
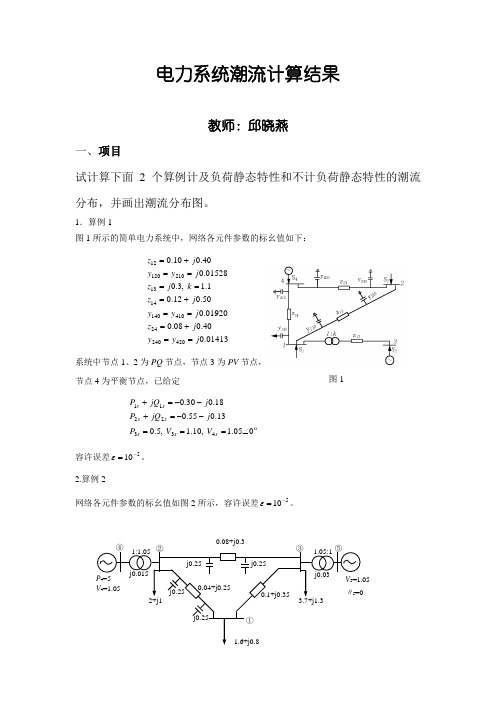
电力系统潮流计算结果教师:邱晓燕一、项目试计算下面2个算例计及负荷静态特性和不计负荷静态特性的潮流分布,并画出潮流分布图。
1.算例1图1所示的简单电力系统中,网络各元件参数的标幺值如下:01413.040.008.001920.050.012.01.1,3.001528.040.010.042024024410140141321012012j y y j z j y y j z k j z j y y j z ==+===+=====+=系统中节点1、2为PQ 节点,节点3为PV 节点,节点4为平衡节点,已给定05.1,10.1,5.013.055.018.030.04332211∠===--=+--=+s s s ss s s V V P j jQP j jQ P容许误差510-=ε。
2.算例2网络各元件参数的标幺值如图2所示,容许误差510-=ε。
图1P 4=5 V 4=1.05j0.0151.05:1 V 5=1.05 θ5=01.6+j0.82+j1④ 1:1.05 ②③① ⑤ j0.033.7+j1.30.08+j0.3j0.25j0.25j0.25 j0.250.04+j0.250.1+j0.35二、仿真结果利用psasp7.0 软件进行仿真,得出以下结果例1:潮流分布图如图1示(1)不计负荷静态特性,将节点4设置为slack节点(平衡节点) 仿真结果如下:(2)计及负荷静态特性,将节点4设置为PV-PQ节点仿真结果如下:例2:潮流分布图如图2所示(1)不计负荷静态特性,将节点5设置为slack节点(平衡节点) 仿真结果如下:(2)计及负荷静态特性,将节点5设置为PV-PQ节点仿真结果如下:。
电力系统潮流计算实验报告

电力系统潮流上机计算实验报告11.手算过程已知:节点1:PQ 节点,节点, s(1)= s(1)= -0.5000-j0.3500 节点2:PV 节点,节点, p(2)=0.4000 v(2)=1.0500 p(2)=0.4000 v(2)=1.0500 节点3:平衡节点,:平衡节点,U(3)=1.0000U(3)=1.0000U(3)=1.0000∠∠0.0000 网络的连接图:0.0500+j0.2000 1 0.0500+j0.2000231)计算节点导纳矩阵由2000.00500.012j Z +=Þ71.418.112j y -=; 2000.00500.013j Z +=Þ71.418.113j y -=;\导纳矩阵中的各元素:42.936.271.418.171.418.1131211j j j y y Y -=-+-=+=;71.418.11212jy Y +-=-=; 71.418.11313j y Y +-=-=; =21Y71.418.11212j y Y +-=-=; 71.418.12122j y Y -==; 002323j y Y +=-=;=31Y 71.418.11313j y Y +-=-=; =32Y 002323j y Y +=-=; 71.418.13133j y Y -==;\形成导纳矩阵B Y :úúúûùêêêëé-++-+-+-+-+--=71.418.10071.418.10071.418.171.418.171.418.171.418.142.936.2j j j j j j j j j Y B 2)计算各PQ PQ、、PV 节点功率的不平衡量,及PV 节点电压的不平衡量:取:000.0000.1)0(1)0(1)0(1j jf e U +=+=000.0000.1)0(2)0(2)0(2j jf e U +=+=节点3是平衡节点,保持000.0000.1333j jf e U +=+=为定值。
华电潮流上机计算实验报告全解

院系:电气与电子工程学院班级:电气1205学号:1121181223学生姓名:王城指导教师:孙英云设计周数:两周成绩:日期:2015年7月7日一、课程设计的目的与要求培养学生的电力系统潮流计算机编程能力,掌握计算机潮流计算的相关知识二、设计正文(详细内容见附录)1.手算2.计算机计算3.思考题三、课程设计总结或结论(详细内容见附录)四、参考文献1.《电力系统计算:电子数字计算机的应用》,西安交通大学等合编。
北京:水利电力出版社;2.《现代电力系统分析》,王锡凡主编,科学出版社;3.《电力系统稳态分析》,陈珩,中国电力出版社,1995年,第三版;附录(设计流程图、程序、表格、数据等)4.机算潮流程序及结果// dierti.cpp : 定义控制台应用程序的入口点。
//#include "stdafx.h"struct Line //线路结构体{int Num,NumI,NumJ; //线路号左节点名右节点名float R,X,B,K; //电阻电抗电纳变比(K等于1为普通支路,不等于1为变压器支路的变比) };struct Bus //节点结构体{int Num ;float Volt,Phase,GenP,GenQ,LoadP,LoadQ;int Type;};#include"stdio.h"#include"string.h"#include"math.h"#include"stdlib.h"#define NBUS 4#define NLINE 4/* Global variables */int nL,nB,nVA,nSH;float X[NBUS];int L;double def[2*NBUS];double mn[50];void Gauss(double a[50][50],double b[50], int n) /*定义高斯法 */{int JS[50];int i,j,k;float d,t,x[50];FILE *fp;int L=1;for(i=0;i<50;i++) JS[i]=0;for(k=0;k<n;k++){d=0.0;for(j=k;j<n;j++)if(fabs(a[k][j])>d){ /*在一行中找到一个最大值赋值d,并用JS[K]记住这个最大值所在的列号*/ d=fabs(a[k][j]);JS[k]=j;}if(fabs(d)<0.000001) /*如果d的数值太小,做为被除数将带来很大的误差 */L=0;else {if(JS[k]!=k)for(i=0;i<n;i++){t=a[i][k];a[i][k]=a[i][JS[k]]; /*进行列交换,让最大值始终在对角元上*/a[i][JS[k]]=t;}}if(L==0)break;for(j=k+1;j<n;j++)a[k][j]=a[k][j]/a[k][k]; /*对角元上的元素消为1*/b[k]=b[k]/a[k][k];for(i=k+1;i<n;i++){for(j=k+1;j<n;j++)a[i][j]=a[i][j]-a[i][k]*a[k][j]; /*使下三角阵的元素为0*/b[i]=b[i]-a[i][k]*b[k];}}if(fabs(a[n-1][n-1])>0.00001){ /*用追赶法,解方程组,求未知数x*/ x[n-1]=b[n-1];for(i=n-2;i>=0;i--){t=0.0;for(j=i+1;j<n;j++)t=t+a[i][j]*x[j];x[i]=(b[i]-t);}}if((fp=fopen("gauss.txt","w"))==NULL) /*将结果写到TXT文件中*/{printf("err");exit(0);}for(i=0;i<n;i++){fprintf(fp,"%lf",x[i]);mn[i]=x[i];fprintf(fp,"\n");}fclose(fp);if(fp!=NULL) fclose(fp);}int _tmain(int argc, _TCHAR* argv[]){FILE *fp;FILE *fpout;int i,j,k,l,h,n,v;int i1,i2,i3,kp,kq;float d1,d2,d3,d4,d5,d6,r,x,g,b,tt,LL,e,ps,qs,shsh,m;struct Line sL[NLINE];struct Bus sB[NBUS];float YG[NBUS+1][NBUS+1],YB[NBUS+1][NBUS+1];double u[50][2];i1=i2=i3=0;d1=d2=d3=d4=d5=d6=ps=qs=0.0;for(i=0;i<NBUS;i++)if((fp=fopen("in.txt","r"))==NULL){ printf("Can not open the file named 'in.txt' \n");exit(0);}fscanf(fp,"%d,%d,%d",&nB,&nL,&nSH);for(i=0;i<nB;i++){sB[i].Num=sB[i].Type=0;sB[i].Volt=1.0;sB[i].Phase=sB[i].GenP=sB[i].GenQ=sB[i].LoadP=sB[i].LoadQ=0.0;fscanf(fp,"%d,%f,%f,%f,%f,%f,%f,%d",&i1,&d1,&d2,&d3,&d4,&d5,&d6,&i2);sB[i].Num=i1;sB[i].Volt=d1;sB[i].Phase=d2;sB[i].GenP=d3;sB[i].GenQ=d4;sB[i].LoadP=d5,sB[i].LoadQ=d6;sB[i].T ype=i2;};for(i=0;i<nL;i++){sL[i].Num=sL[i].NumI=sL[i].NumJ=0;sL[i].R=sL[i].X=sL[i].B=0.0;sL[i].K=1.0;fscanf(fp,"%2d %3d %3d %f %f %f %f",&i1,&i2,&i3,&d1,&d2,&d3,&d4);sL[i].Num=i1;sL[i].NumI=i2;sL[i].NumJ=i3;sL[i].R=d1;sL[i].X=d2;sL[i].B=d3;sL[i].K=d4;}if(fp!=NULL) fclose(fp);/*Make Y Matrix*/for(i=1;i<nB+1;i++)for(j=1;j<nB+1;j++){YG[i][j]=0.0;YB[i][j]=0.0;};for(l=0; l<nL; l++){i=sL[l].NumI;j=sL[l].NumJ;r=sL[l].R;x=sL[l].X;d1=r*r+x*x;g=r/d1;b=-x/d1;m=sL[l].K;if(fabs(sL[l].K-1.0)<0.000001) //普通支路 {YG[i][i]=YG[i][i]+g;YG[j][j]=YG[j][j]+g;YB[i][i]=YB[i][i]+b+sL[l].B;YB[j][j]=YB[j][j]+b+sL[l].B;YG[i][j]=YG[i][j]-g;YG[j][i]=YG[j][i]-g;YB[i][j]=YB[i][j]-b;YB[j][i]=YB[j][i]-b;}else //变压器支路{YG[i][i]=YG[i][i]+g/m+g*(m-1)/m;YG[j][j]=YG[j][j]+g/m+g*(1-m)/m/m;YB[i][i]=YB[i][i]+b/m+b*(m-1)/m;YB[j][j]=YB[j][j]+b/m+b*(1-m)/m/m;YG[i][j]=YG[i][j]-g/m;YG[j][i]=YG[j][i]-g/m;YB[i][j]=YB[i][j]-b/m;YB[j][i]=YB[j][i]-b/m; }}/* Check the Y matrix */if((fp=fopen("GGBB.txt","w"))==NULL){printf("Can not open the file named 'GGBB.txt' \n");exit(0);}fprintf(fp,"---Y Matrix---\n");for(i=1;i<nB+1;i++)for(j=1;j<nB+1;j++)if(fabs(YB[i][j]-0.0)>0.000001) fprintf(fp,"Y(%3d,%-3d)=(%10.5f,%10.5f)\n",i,j,YG[i][j],YB[i][j]);if(fp!=NULL) fclose(fp);/* 节点电压附初值 */for(i=1;i<nB+1;i++){if(sB[i-1].Type==0){u[i][0]=0.0;u[i][1]=1.0;}else if(sB[i-1].Type==1){u[i][1]=sB[i-1].Volt;u[i][0]=0.0;}else if(sB[i-1].Type==2){u[i][1]=sB[i-1].Volt;u[i][0]= sB[i-1].Phase;}}for(v=1;;v++)/* 迭代次数可以无限大 */{/* 节点电压附初值 */printf("迭代第%d次赋予的电压初值为e+jf:\n",v); for(i=1;i<nB+1;i++)printf("%lf,%lf\n",u[i][1],u[i][0]);printf("\n");printf("\n");/* 求偏移量 */double P_P[10];double P_Q[10];double P_UU[10];for(i=1;i<nB+1;i++){if(sB[i-1].Type==2){P_P[i]=0.0;P_Q[i]=0.0;P_UU[i]=1.05;}if(sB[i-1].Type==0){double tempP=0.0;double tempQ=0.0;for(j=1;j<nB+1;j++){tempP+=YG[i][j]*u[j][1]-YB[i][j]*u[j][0];tempQ+=YG[i][j]*u[j][0]+YB[i][j]*u[j][1];}P_P[i]=(sB[i-1].GenP-sB[i-1].LoadP)-tempP*u[i][1]-tempQ*u[i][0]; P_Q[i]=(sB[i-1].GenQ-sB[i-1].LoadQ)-tempP*u[i][0]+tempQ*u[i][1]; P_UU[i]=0.0;}if(sB[i-1].Type==1){double tempP=0.0;double tempQ=0.0;for(j=1;j<nB+1;j++){tempP+=YG[i][j]*u[j][1]-YB[i][j]*u[j][0];tempQ+=YG[i][j]*u[j][0]+YB[i][j]*u[j][1];P_P[i]=(sB[i-1].GenP-sB[i-1].LoadP)-tempP*u[i][1]-tempQ*u[i][0]; }P_UU[i]=sB[i-1].Volt*sB[i-1].Volt-u[i][1]*u[i][1]-u[i][0]*u[i][0]; P_Q[i]=0.0;}}/* 偏移量阵 */double P_PQ[6];int a=0;for(i=1;i<3;i++){P_PQ[a]=P_P[i];a=a+2;}a=1;for(i=1;i<3;i++){P_PQ[a]=P_Q[i];a=a+2;P_PQ[4]=P_P[3];P_PQ[5]=P_UU[3];printf("迭代第%d次的偏移量为:\n",v);for(i=0;i<6;i++){printf("%f",P_PQ[i]);printf("\n");}printf("\n");printf("\n");/* 雅可比矩阵 */double H[6][6],N[6][6],J[6][6],L[6][6],R[6][6],S[6][6],aa[6],bb[6]; for(i=1;i<5;i++){ if(fabs(sB[i-1].Type-2.0)<0.000001)continue;else{for(j=1;j<5;j++)if(i!=j){H[i][j]=-YB[i][j]*u[i][1]+YG[i][j]*u[i][0];N[i][j]=YG[i][j]*u[i][1]+YB[i][j]*u[i][0];J[i][j]=-N[i][j];L[i][j]=H[i][j];R[i][j]=0;S[i][j]=0;}else{aa[i]=bb[i]=0.0;aa[i]+=YG[i][n]*u[n][1]-YB[i][n]*u[n][0];bb[i]+=YG[i][n]*u[n][0]+YB[i][n]*u[n][1];}H[i][i]=-YB[i][i]*u[i][1]+YG[i][i]*u[i][0]+bb[i]; N[i][i]=YG[i][i]*u[i][1]+YB[i][i]*u[i][0]+aa[i]; J[i][i]=-YG[i][i]*u[i][1]-YB[i][i]*u[i][0]+aa[i]; L[i][i]=YG[i][i]*u[i][0]-YB[i][i]*u[i][1]-bb[i]; R[i][i]=2*u[i][0];S[i][i]=2*u[i][1];}}}double ss[50][50];for(i=0;i<6;i++)for(j=0;j<6;j++)ss[i][j]=0.0;for(i=1;i<3;i++)for(j=1;j<4;j++){ss[2*i-2][2*j-2]=H[i][j];ss[2*i-2][2*j-1]=N[i][j];ss[2*i-1][2*j-2]=J[i][j];ss[2*i-1][2*j-1]=L[i][j];}i=3;for(j=1;j<4;j++){ss[2*i-2][2*j-2]=H[i][j];ss[2*i-2][2*j-1]=N[i][j];ss[2*i-1][2*j-2]=R[i][j];ss[2*i-1][2*j-1]=S[i][j];}printf("迭代第%d次的雅可比矩阵为:\n",v);for(i=0;i<6;i++){for(j=0;j<6;j++)printf("%10f",ss[i][j]);printf("\n");}printf("\n");printf("\n");Gauss(ss,P_PQ,6);for(i=1;i<nB;i++){u[i][0]=u[i][0]+mn[2*(i-1)];u[i][1]=u[i][1]+mn[2*i-1];}double max;max=fabs(P_PQ[0]);for(i=0;i<=5;i++)if (max<fabs(P_PQ[i]))max=fabs(P_PQ[i]);if(fabs(max)<0.0001){printf("满足精度要求,迭代终止,迭代次数为%d\n",v); printf("\n");}/* 叠代循环的括号 */printf("最终求得的节点电压值为e+jf:\n");for(i=1;i<nB+1;i++)printf("%lf,%lf\n",u[i][1],u[i][0]);printf("\n");printf("\n");double uu[5],Phase[5];for(i=1;i<nB+1;i++){uu[i]=sqrt(u[i][1]*u[i][1]+u[i][0]*u[i][0]); Phase[i]=atan(u[i][0]/u[i][1]);}for(i=1;i<nB+1;i++)printf("%lf,%lf\n",uu[i],Phase[i]);*计算线路功率和平衡节点 PV节点功率*/double P[5],Q[5];double tempP=0.0;double tempQ=0.0;for(i=1;i<nB+1;i++){for(j=1;j<nB+1;j++){tempP+=YG[i][j]*u[j][1]-YB[i][j]*u[j][0]; tempQ+=YG[i][j]*u[j][0]+YB[i][j]*u[j][1];}P[i]=tempP*u[i][1]+tempQ*u[i][0];Q[i]=tempP*u[i][0]-tempQ*u[i][1];}for(i=1;i<nB+1;i++)printf("节点%d注入功率为%lf,%lf\n",i,P[i],Q[i]);/* 支路功率 */double V[4][2];for(i=1;i<5;i++)for(j=0;j<3;j++)V[i][j]=u[i][j];double sP[5][5],sQ[5][5];double dsq,dsp,dp,sumgen;for(i=1;i<NBUS+1;i++){for(j=1;j<NBUS+1;j++){sP[i][j]=0.0;sQ[i][j]=0.0;}}for(l=0; l<nL; l++){i=sL[l].NumI;j=sL[l].NumJ;r=sL[l].R;x=sL[l].X;d1=r*r+x*x;if(fabs(sL[l].K-1.0)<0.000001){/*Normal lines or transformers*/sP[i][j]=V[i][1]*V[i][1]*g-V[i][1]*V[j][1]*(g*cos(V[i][0]-V[j][0])+b*sin(V[i][0]-V[j][0]));sQ[i][j]=-(V[i][1]*V[i][1]*sL[l].B+V[i][1]*V[i][1]*b+V[i][1]*V[j][1]*(g*sin(V[i][0]-V[j][0])-b*cos(V[i ][0]-V[j][0])));sP[j][i]=V[j][1]*V[j][1]*g-V[i][1]*V[j][1]*(g*cos(V[j][0]-V[i][0])+b*sin(V[j][0]-V[i][0]));sQ[j][i]=-(V[j][1]*V[j][1]*sL[l].B+V[j][1]*V[j][1]*b+V[i][1]*V[j][1]*(g*sin(V[j][0]-V[i][0])-b*cos(V[j ][0]-V[i][0])));}else{/*abnormal transformer ratio*/sP[i][j]=V[i][1]*V[i][1]*g/sL[l].B/sL[l].B-V[i][1]*V[j][1]*(g*cos(V[i][0]-V[j][0])/sL[l].B+b*sin(V[i][ 0]-V[j][0])/sL[l].B);sQ[i][j]=-(V[i][1]*V[i][1]*b/sL[l].B/sL[l].B+V[i][1]*V[j][1]*(g*sin(V[i][0]-V[j][0])/sL[l].B-b*cos(V[i ][0]-V[j][0])/sL[l].B));sP[j][i]=V[j][1]*V[j][1]*g-V[i][1]*V[j][1]*(g*cos(V[j][0]-V[i][0])/sL[l].B+b*sin(V[j][0]-V[i][0])/sL[l ].B);sQ[j][i]=-(V[i][1]*V[i][1]*b+V[i][1]*V[j][1]*(g*sin(V[j][0]-V[i][0])/sL[l].B-b*cos(V[j][0]-V[i][0])/sL [l].B));}}/* 输电效率 */dsp=P[4];sumgen=P[4];for(i=0;i<NBUS;i++){dsp+=sB[i].GenP-sB[i].LoadP;dsq+=sB[i].GenQ-sB[i].LoadQ;sumgen+=sB[i].GenP;}dp=dsp/sumgen*100;/* 输出功率情况 */if((fp=fopen("功率情况.txt","w"))==NULL){printf("Can not open the file named '功率情况.txt' \n");exit(0);}fprintf(fp,"---功率情况---\n");fprintf(fp,"平衡节点功率S=%10.5f+ j%10.5f\n",P[4],Q[4]);for(i=1;i<NBUS+1;i++)for(j=1;j<NBUS+1;j++)if(fabs(sP[i][j]-0.0)>0.000001)fprintf(fp,"S(%3d,%-3d)=(%10.5f,j%10.5f)\n",i,j,sP[i][j],sQ[i][j]); fprintf(fp,"网损为%10.5f+j%10.3f,输电效率为%10.3f\n",dsp,dsq,100-dp);if(fp!=NULL) fclose(fp);return 0;}结果:1.导纳阵Y( 1,1 )=( 1.01534, -8.19201) Y( 1,2 )=( -0.56148, 2.30208) Y( 1,3 )=( 0.00000, 3.66667) Y( 1,4 )=( -0.45386, 1.89107) Y( 2,1 )=( -0.56148, 2.30208) Y( 2,2 )=( 1.04225, -4.67651) Y( 2,4 )=( -0.48077, 2.40385) Y( 3,1 )=( 0.00000, 3.66667) Y( 3,3 )=( 0.00000, -3.33333) Y( 4,1 )=( -0.45386, 1.89107) Y( 4,2 )=( -0.48077, 2.40385) Y( 4,4 )=( 0.93463, -4.26159)2.设定电压初值01.1;01;01)0(3)0(3)0(2)0(2)0(1)0(1j jf e j jf e j jf e +=++=++=+ 3.计算功率和电压偏移;27731.0])()([41)0(11)0(1)0(141)0(11)0(1)0(11)0(11)0(1-=++--=-=∆∑∑==j j j j j j jj s s e B f G ff B eG e P P P P0.05097])()([41)0(11)0(1)0(141)0(11)0(1)0(11)0(11)0(1-=----=-=∆∑∑==jj j j jj jj s s e B f G ef B e G f Q Q Q Q同理可算出52596.0)0(22)0(2-=-=∆P P P s ,0196.0)0(22)0(2=-=∆Q Q Q s 5.0)0(33)0(3=-=∆P P P s ,0.02)0(3232)0(3=-=∆U U U s 4.根据求的第一次迭代时雅可比矩阵各元素的公式计算雅可比矩阵各个元素的具体值:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤-----------⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡20000.200066667.300003334.40052691.406629.130208.256148.00001821.182612.456148.030208.266667.3030208.256148.006298.803803.1066667.356148.030208.299265.032104.85.求高斯计算后的修正量:⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∆∆∆∆∆∆=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∆∆∆∆∆∆-0.0000000.1276520.023566-0.108546-0.006511-0.007919-2)0(3)0(3)0(2)0(2)0(1)0(11)0()0(3)0(3)0(2)0(2)0(1)0(1U P Q P Q P e f e f e f J 6.计算各节点电压的一次近似值:12765.010855.000792.010000.197643.099349.0)0(3)0(3)1(3)0(2)0(2)1(2)0(1)0(1)1(1)0(3)0(3)1(3)0(2)0(2)1(2)0(1)0(1)1(1=∆+=-=∆+=-=∆+==∆+==∆+==∆+=f f f f f f fffe e e e e e e e e返回第三步重新迭代,并校验收敛与否,令410-=ε。
华电潮流上机课程设计报告+程序

院系:电气与电子工程学院班级:学号:学生姓名:指导教师:刘宝柱设计周数:成绩:日期:2012年1月5日一、课程设计的目的与要求培养学生的电力系统潮流计算机编程能力,掌握计算机潮流计算的相关知识二、设计正文(详细内容见附录)1.手算2.计算机计算3.思考题3.1潮流计算的方法有哪些?各有何特点?答:潮流计算的方法主要有高斯-赛德尔迭代法、牛顿-拉夫逊迭代法和P-Q分解法。
它们各自的特点如下:(1)高斯-赛德尔迭代法分为以节点导纳矩阵为基础的高斯-赛德尔迭代法和以以节点阻抗矩阵为基础的高斯-赛德尔迭代法的原理比较简单,要求的数字计算机的内存量也比较小,但收敛性差,当系统规模变大时,迭代次数急剧上升,往往出现迭代不收敛的情况;而阻抗法改善了电力系统潮流计算导纳法德收敛性问题,在当时获得了广泛的应用,但是,阻抗法的主要缺点是占用计算机的内存很大,每次迭代的计算量很大。
当系统不断扩大时,这些缺点就更加突出。
(2)牛顿-拉夫逊法是数学中求解非线性方程式的典型方法,有较好的收敛性。
只要在迭代过程中尽可能保持方程式系数矩阵的稀疏性,就可以大大提高牛顿潮流计算程序的计算效率,牛顿法在收敛性、内存要求、计算速度方面都超过了阻抗法,成为知道目前仍被广泛采用的方法。
(3)P-Q分解法潮流计算派生于以极坐标表示时的牛顿-拉夫逊法,它根据电力系统的特点,抓住主要矛盾,对纯数学的牛顿法进行了改造。
与牛顿法相比,P-Q分解法的修正方程的系数矩阵B’和B”分别是(n-1)和(m-1)的方阵,替代了原有的(n+m-2)阶系数矩阵J;B’、B”在迭代过程中可以保持不变且为对称的系数矩阵,提高了计算速度,降低了对存储容量的要求。
P-Q分解法在计算速度方面有显著地提高,迅速得到了推广。
3.2如果交给你一个任务,请你用已有的潮流计算软件计算北京城市电网的潮流,你应该做哪些工作?(收集哪些数据,如何整理,计算结果如何分析)答:(1)在进行北京城市电网的潮流计算之前需要了解北京城市电网中所有的节点支路的相关数据,并对节点和支路分类。
华北电力大学 电力系统基础 第五章 简单电力系统潮流计算

dU 3ZIZ 3Z ( 3SU22 )
(R jX )( P2 jQ2 ) U2
P2R Q2 X j P2X Q2R U jU
U2
U2
U1 (U2 U)2 U2 arctg U
U2 U
近似计算:
(21.10
j 21.35)
0.0745
j0.0754MVA
S
'
2
(5.62
j3.34) (0.0745
j0.0754)
5.55
j3.26MVA
S
"
1
S'Fra bibliotek2 S1
(5.55
j3.26) (20.15
j13.96)
14.60
j10.70MVA
2 N
1000SN2
QZT
S22
U
2 2
*
U
k
%U
2 N
100SN
PyT
U12
*
P0 1000U
2 N
QyT
U12
*
I0 %SN
100U
2 N
发电厂
PZT
PkU
2 N
S1
2
1000U12 S N2
QZT
U
k
%U
2 N
S1
2
100U
2 2
S
N
PyT
电
电
所
厂
的
的
变
变
压
压
华电潮流上机课程设计报告程序..doc

院系:电气与电子工程学院班级:学号:学生姓名:指导教师:刘宝柱设计周数:成绩:日期:2012年1月5日课程课程设计报告一、课程设计的目的与要求培养学生的电力系统潮流计算机编程能力,掌握计算机潮流计算的相关知识二、设计正文(详细内容见附录)1.手算2.计算机计算3.思考题3.1潮流计算的方法有哪些?各有何特点?答:潮流计算的方法主要有高斯-赛德尔迭代法、牛顿-拉夫逊迭代法和P-Q分解法。
它们各自的特点如下:(1)高斯-赛德尔迭代法分为以节点导纳矩阵为基础的高斯-赛德尔迭代法和以以节点阻抗矩阵为基础的高斯-赛德尔迭代法的原理比较简单,要求的数字计算机的内存量也比较小,但收敛性差,当系统规模变大时,迭代次数急剧上升,往往出现迭代不收敛的情况;而阻抗法改善了电力系统潮流计算导纳法德收敛性问题,在当时获得了广泛的应用,但是,阻抗法的主要缺点是占用计算机的内存很大,每次迭代的计算量很大。
当系统不断扩大时,这些缺点就更加突出。
(2)牛顿-拉夫逊法是数学中求解非线性方程式的典型方法,有较好的收敛性。
只要在迭代过程中尽可能保持方程式系数矩阵的稀疏性,就可以大大提高牛顿潮流计算程序的计算效率,牛顿法在收敛性、内存要求、计算速度方面都超过了阻抗法,成为知道目前仍被广泛采用的方法。
(3)P-Q分解法潮流计算派生于以极坐标表示时的牛顿-拉夫逊法,它根据电力系统的特点,抓住主要矛盾,对纯数学的牛顿法进行了改造。
与牛顿法相比,P-Q分解法的修正方程的系数矩阵B’和B”分别是(n-1)和(m-1)的方阵,替代了原有的(n+m-2)阶系数矩阵J;B’、B”在迭代过程中可以保持不变且为对称的系数矩阵,提高了计算速度,降低了对存储容量的要求。
P-Q分解法在计算速度方面有显著地提高,迅速得到了推广。
3.2如果交给你一个任务,请你用已有的潮流计算软件计算北京城市电网的潮流,你应该做哪些工作?(收集哪些数据,如何整理,计算结果如何分析)答:(1)在进行北京城市电网的潮流计算之前需要了解北京城市电网中所有的节点支路的相关数据,并对节点和支路分类。
华北电力大学电力系统稳态第四章精品PPT课件

Yii yi0 y ij j
节点i: 加单位电压 Ui 1 其余节点j: 全部接地Uj 0
节点 i 注入网络电流 Yii≠0
13
二、节点导纳矩阵
Y 矩阵元素的物理意义 互导纳
if j i
Y ji
Ij Ui
(U j 0, ji)
Yij Yji yij
节点i: 加单位电压 Ui 1
电力网
Y
(0)
Yi1
Yi 2
Yii
Yij
Yin
Y j1
Yj2
Yji
Y jj
Yjn
Yn1 Yn2 Yni Ynj Ynn
20
三、节点导纳矩阵的修改 Y 矩阵的修改
(1)从原网络引出一条支路增加一个节点
Y 增加一行一列(n+1)×(n+1)
电力网
i yik k Ykk yik Yik Yki yik Yii yik Yii Yii (0) Yii
21
三、节点导纳矩阵的修改
Y 矩阵的修改 (2)在原有网络节点i、j之间增加一条支路
Y22 y12 y23 y20 15
二、节点导纳矩阵
节点导纳矩阵中互导纳的确定
1
U1
y12
2
y13 U 3 3 y23
I
+
2
I1
y10 I3
y30
y20
U2
-
Y12
I1
U2
(U1 U3 0)
I1 U2 y12
Y12 y12 16
二、节点导纳矩阵
节点导纳矩阵Y 的特点
1. 直观易得 2. 稀疏矩阵 3. 对称矩阵
18
三、节点导纳矩阵的修改
潮流上机课程设计报告华电

《电力系统潮流上机》课程设计报告院系班级:学号:学生姓名:指导教师:设计周数成绩:日期:年月日一、课程设计的目的与要求培养学生的电力系统潮流计算机编程能力,掌握计算机潮流计算的相关知识二、设计正文(详细内容见附录)1.手算: 要求应用牛顿-拉夫逊法或P-Q 分解法手算求解,要求精度为0.001MW 。
节点1为平衡节点,电压︒∠=00.11U ,节点2为PQ 节点,负荷功率6.08.0~2j S +=,节点3是PV 节点,1.1,4.033==U P ,两条支路分别为04.001.013j Z +=,2.005.012j Z +=,对地支路33.030j y =。
2.计算机计算:编写潮流计算程序,要求如下:2.1据给定的潮流计算任务书整理潮流计算的基础数据:节点的分类,线路模型,等值变压器模型,电压等级的归算,标幺值的计算;2.2基础数据的计算机存储:节点数据,支路数据(包括变压器); 2.3用牛顿-拉夫逊法计算;2.4根据所选潮流计算方法画流程图,划分出功能模块,有数据输入模块,导纳阵形成模块,解线性方程组模块,计算不平衡功率模块,形成雅可比矩阵模块,解修正方程模块,计算线路潮流,网损,PV 节点无功功率和平衡节点功率,数据输出模块; 2.5据上述模块编制程序并上机调试程序,得出潮流计算结果; 2.6源程序及其程序中的符号说明集、程序流图简单系统如下图所示,支路数据如下:41.01.012j z +=,3.013j z =,5.012.014j z +=,40.008.024j z +=01528.01,202,10j y y ==,0192.01,404,10j y y ==,01413.02,404,20j y y ==1.1=k节点数据如下:18.030.01j S --= ,13.055.02j S --= , 5.03=S ,10.13=U ,o U 005.14∠= 32S 1S 4S 4,10y 1,40y 2,10y 1,20y 4,20y 2,40y 12z 24z 14z k)1(13-k k z kz -1131)节点导纳阵#include <stdio.h> #include <math.h> #include <fstream.h> #include "LF.h"//form node conductance matrixintMakeY( intnB, intnL, Line* sL, double** YG, double** YB ) {inti,j,l;double r,x,d1,g,b,t;for(i=0;i<nB;i++)for(j=0;j<nB;j++){ YG[i][j]=0.0;YB[i][j]=0.0;}for(i=0;i<nL;i++){r=sL[i].R;x=sL[i].X;g=r/(r*r+x*x);b=-x/(r*r+x*x);switch(sL[i].Type){case 1://Linebreak;case 2://Transformerg*=1/sL[i].K;b*=1/sL[i].K;break;}YG[sL[i].NumI][sL[i].NumI]+=g;YG[sL[i].NumJ][sL[i].NumJ]+=g;YG[sL[i].NumI][sL[i].NumJ]-=g;YG[sL[i].NumJ][sL[i].NumI]-=g;YB[sL[i].NumI][sL[i].NumI]+=b+sL[i].B;YB[sL[i].NumJ][sL[i].NumJ]+=b+sL[i].B;YB[sL[i].NumI][sL[i].NumJ]-=b;YB[sL[i].NumJ][sL[i].NumI]-=b; }printf("实部:\n");for(i=0;i<nB;i++){for(j=0;j<nB;j++)printf("%lf\t",YG[i][j]);printf("\n");}printf("虚部:\n");for(i=0;i<nB;i++){for(j=0;j<nB;j++)printf("%lf\t",YB[i][j]);printf("\n");}/* Check the Y matrix */ofstreamfout("out.txt");fout<< "--------------Y Matrix--------------------" <<endl;for(i=0;i<nB;i++){for(j=0;j<nB;j++)fout<< YG[i][j] << "+j" << YB[i][j] << "\t";fout<<endl;}fout.close();return 0;}2)计算功率不平衡量#include <stdio.h>#include <math.h>#include <fstream.h>#include "LF.h"//form delta p and delta qintCalDeltaPQ( intnpv, intnpq, Bus* bus, double** YG, double** YB, int* p_Jtobus, double* deltaf ){intk,i,j;for(k=0;k<npv+npq*2;k++){ i=p_Jtobus[k];if(k<npv){ deltaf[k]=bus[i].GenP-bus[i].LoadP;for(j=0;j<npv+npq+1;j++){deltaf[k]-=bus[i].Volt*bus[j].Volt*(YG[i][j]*cos(bus[i].Phase-bus[j].Phase)+YB[i][j ]*sin(bus[i].Phase-bus[j].Phase));}printf("PV节点%d的有功功率是%lf\n",i,deltaf[k]);}if(k<npq+npv&&k>=npv){ deltaf[k]=bus[i].GenP-bus[i].LoadP;for(j=0;j<npv+npq+1;j++){deltaf[k]-=bus[i].Volt*bus[j].Volt*(YG[i][j]*cos(bus[i].Phase-bus[j].Phase)+YB[i][j ]*sin(bus[i].Phase-bus[j].Phase));}printf("PQ节点%d的有功功率是%lf\n",i,deltaf[k]);}if(k<npq*2+npv&&k>=npv+npq){deltaf[k]=bus[i].GenQ-bus[i].LoadQ;for(j=0;j<npv+npq+1;j++){deltaf[k]-=bus[i].Volt*bus[j].Volt*(YG[i][j]*sin(bus[i].Phase-bus[j].Phase)-YB[i][j ]*cos(bus[i].Phase-bus[j].Phase));}printf("PQ节点%d的无功功率是 %lf\n",i,deltaf[k]);}}return 0;}3)雅各比矩阵的计算/*Purpose: for undergraduate courseTask: Load FlowCopyright @ NCEPU, Liu Chongru*/#include <stdio.h>#include <math.h>#include <fstream.h>#include "LF.h"//form Jacobian matrixintFormJacobian( intnpv, intnpq, Bus* bus, double** YG, double** YB, int* p_Jtobus, double** Jac ){ intnp = npv+npq,j,k,i,m;//TODOdouble a[14],q[14];for(k=0;k<npv+npq*2;k++){i=p_Jtobus[k];a[i]=0;q[i]=0;if(k<np)//H N{for(j=0;j<np+1;j++)if(j!=i){a[i]+=bus[j].Volt*(YG[i][j]*sin(bus[i].Phase-bus[j].Phase)-YB[i][j]*cos(bus[i].Phase-bu s[j].Phase));q[i]+=bus[j].Volt*(YG[i][j]*cos(bus[i].Phase-bus[j].Phase)+YB[i][j]*sin(bus[i].Phase-bu s[j].Phase));}for(m=0;m<npv+npq*2;m++){j=p_Jtobus[m];if(j!=i){if(m<np)Jac[k][m]=bus[i].Volt*bus[j].Volt*(YG[i][j]*sin(bus[i].Phase-bus[j].Phase)-YB[i][j]*cos (bus[i].Phase-bus[j].Phase));//Form HelseJac[k][m]=bus[i].Volt*bus[j].Volt*(YG[i][j]*cos(bus[i].Phase-bus[j].Phase)+YB[i][j]*sin (bus[i].Phase-bus[j].Phase));//Form N}else if(j==i){if(m<np)Jac[k][m]=-bus[i].Volt*a[i];//Form HelseJac[k][m]=bus[i].Volt*q[i]+2*bus[i].Volt*bus[i].Volt*YG[i][j];//Form N}}}else{for(j=0;j<np+1;j++)if(j!=i){a[i]+=bus[j].Volt*(YG[i][j]*sin(bus[i].Phase-bus[j].Phase)-YB[i][j]*cos(bus[i].Phase-bu s[j].Phase));q[i]+=bus[j].Volt*(YG[i][j]*cos(bus[i].Phase-bus[j].Phase)+YB[i][j]*sin(bus[i].Phase-bu s[j].Phase));}for(m=0;m<npv+npq*2;m++){j=p_Jtobus[m];if(j!=i){if(m<np)Jac[k][m]=-bus[i].Volt*bus[j].Volt*(YG[i][j]*cos(bus[i].Phase-bus[j].Phase)+YB[i][j]*si n(bus[i].Phase-bus[j].Phase)); //Form JelseJac[k][m]=bus[i].Volt*bus[j].Volt*(YG[i][j]*sin(bus[i].Phase-bus[j].Phase)-YB[i][j] *cos(bus[i].Phase-bus[j].Phase)); //Form L }else if(j==i){ if(m<np)Jac[k][m]=bus[i].Volt*q[i];elseJac[k][m]=bus[i].Volt*a[i]-2*bus[i].Volt*bus[i].Volt*YB[i][j];} }}}for(i=0;i<np+npq;i++){for(int j=0;j<np+npq;j++){printf("%d %d %f ",i,j,Jac[i][j]);}printf("\n");}//Output the matrix to check the Jacobian matrixofstreamfout("out.txt",ios::app);fout<< "--------------Jacobian Matrix--------------------" <<endl;for(i=0; i<np+npq;i++ ){for(j=0; j<np+npq; j++ )fout<<Jac[i][j] << "\t";fout<<endl;}fout.close();return 0;}4)线路损耗//8.calculate the power flowdouble* p_Pij, *p_Qij, *p_Pji, *p_Qji;p_Pij = new double[nL];p_Qij = new double[nL];p_Pji = new double[nL];p_Qji = new double[nL];int x1,x2;for( i=0; i<nL; i++ ){ x1=line[i].NumI;x2=line[i].NumJ;if(line[i].Type==1){p_Pij[i]=bus[x1].Volt*bus[x1].Volt*(-YG[x1][x2])-bus[x1].Volt*bus[x2].Volt*((-YG[x1][x2 ])*cos(bus[x1].Phase-bus[x2].Phase)+(-YB[x1][x2])*sin(bus[x1].Phase-bus[x2].Phase));p_Qij[i]=-bus[x1].Volt*bus[x1].Volt*(line[i].B+(-YB[x1][x2]))-bus[x1].Volt*bus[x2]. Volt*((-YG[x1][x2])*sin(bus[x1].Phase-bus[x2].Phase)-(-YB[x1][x2])*cos(bus[x1].Phase-bu s[x2].Phase));p_Pji[i]=bus[x2].Volt*bus[x2].Volt*(-YG[x2][x1])-bus[x2].Volt*bus[x1].Volt*((-YG[x2][x1 ])*cos(bus[x2].Phase-bus[x1].Phase)+(-YB[x2][x1])*sin(bus[x2].Phase-bus[x1].Phase));p_Qji[i]=-bus[x2].Volt*bus[x2].Volt*(line[i].B+(-YB[x2][x1]))-bus[x2].Volt*bus[x1]. Volt*((-YG[x2][x1])*sin(bus[x2].Phase-bus[x1].Phase)-(-YB[x2][x1])*cos(bus[x2].Phase-bu s[x1].Phase));}else{p_Pij[i]=bus[x1].Volt*bus[x1].Volt*(-YG[x1][x2])/line[i].K-bus[x1].Volt*bus[x2].Vol t*((-YG[x1][x2])*cos(bus[x1].Phase-bus[x2].Phase)+(-YB[x1][x2])*sin(bus[x1].Phase-bus[x 2].Phase));p_Qij[i]=-bus[x1].Volt*bus[x1].Volt*((-YB[x1][x2])/line[i].K+line[i].B)-bus[x1].Volt*bu s[x2].Volt*((-YG[x1][x2])*sin(bus[x1].Phase-bus[x2].Phase)-(-YB[x1][x2])*cos(bus[x1].Ph ase-bus[x2].Phase));p_Pji[i]=bus[x2].Volt*bus[x2].Volt*(-YG[x2][x1]*line[i].K)-bus[x2].Volt*bus[x1].Volt*(( -YG[x2][x1])*cos(bus[x2].Phase-bus[x1].Phase)+(-YB[x2][x1])*sin(bus[x2].Phase-bus[x1].P hase));p_Qji[i]=-bus[x2].Volt*bus[x2].Volt*((-YB[x2][x1])*line[i].K+line[i].B)-bus[x2].Volt*bu s[x1].Volt*((-YG[x2][x1])*sin(bus[x2].Phase-bus[x1].Phase)-(-YB[x2][x1])*cos(bus[x2].Ph ase-bus[x1].Phase));}}//p and q of PH bus and PV busint s=0;double p[9],q[9],Ps[9],Qs[9],PS=0,QS=0;for( i=0; i<nB; i++ ){p[i]=0;q[i]=0;for(int j=0; j<nB; j++ ){p[i]+=(bus[j].Volt*(YG[i][j])*cos(bus[j].Phase)-bus[j].Volt*(YB[i][j])*sin(bus[j].Phas e));q[i]-=(bus[j].Volt*(YG[i][j])*sin(bus[j].Phase)+bus[j].Volt*(YB[i][j])*cos(bus[j].Phase ));}Ps[i]=bus[i].Volt*cos(bus[i].Phase)*p[i]-bus[i].Volt*sin(bus[i].Phase)*q[i]; Qs[i]=bus[i].Volt*cos(bus[i].Phase)*q[i]+bus[i].Volt*sin(bus[i].Phase)*p[i];} for(i=0;i<nB;i++){ PS+=Ps[i];QS+=Qs[i];}printf("PS=%7.7f,QS=%7.7f\n",PS,QS);}//lossdoublePloss=0, Qloss=0;for( i=0; i<nB; i++ ){Ploss+=p_Pij[i]+p_Pji[i];Qloss+=p_Qij[i]+p_Qji[i];}5)程序流图如下6)得到的数据(out.txt )输入原始数据形成节点导纳矩阵设非平衡节点电压初值)0(i e ;)0(i f令迭代次数k=0对PQ 节点计算)()(.k i k i Q P ∆∆对PV 节点计算)(2)(,k i k iU P ∆∆令节点号i=1计算雅客比矩阵各元素)()()()()()(,,,,,k ijk ij k ij k ij k ij k ij S R L J N H 增加节点号i=i+1解修正方程,由)()(.k i k i Q P ∆∆)(2k i U ∆及雅客比矩阵用高斯法求各节点的电压增量)()(,k ik if e∆∆求出max)(max)(,k k f e ∆∆迭代是否收敛ε<∆∆max)(max)(,k k f e 雅客比矩阵是否形成,i>n?计算节点的新电压)()()1(k i k i k i e e e ∆+=+ )()()1(k i k i k i f f f ∆+=+增加迭代次数k=k+1计算平衡节点的功率及线路功率停止启动--------------Y Matrix--------------------0+j-17.3611 0+j0 0+j0 0+j17.3611 0+j0 0+j0 0+j0 0+j0 0+j00+j0 0+j-16 0+j0 0+j0 0+j0 0+j0 0+j16 0+j0 0+j00+j0 0+j0 0+j-17.0648 0+j0 0+j0 0+j0 0+j0 0+j0 0+j17.06480+j17.3611 0+j0 0+j0 3.30738+j-39.3089 -1.36519+j11.6041 -1.94219+j10.5107 0+j0 0+j0 0+j00+j0 0+j0 0+j0 -1.36519+j11.6041 2.55279+j-17.3382 0+j0 -1.1876+j5.97513 0+j0 0+j00+j0 0+j0 0+j0 -1.94219+j10.5107 0+j0 3.2242+j-15.8409 0+j0 0+j0 -1.28201+j5.588240+j0 0+j16 0+j0 0+j0 -1.1876+j5.97513 0+j0 2.80473+j-35.4456 -1.61712+j13.698 0+j00+j0 0+j0 0+j0 0+j0 0+j0 0+j0 -1.61712+j13.698 2.77221+j-23.3032 -1.15509+j9.784270+j0 0+j0 0+j17.0648 0+j0 0+j0 -1.28201+j5.58824 0+j0 -1.15509+j9.78427 2.4371+j-32.1539--------------Jacobian Matrix--------------------16.4 0 0 0 0 -16.4 0 0 0 0 0 0 0 00 17.4915 0 0 0 0 0 -17.4915 0 0 0 0 0 00 0 40.1703 -11.6041 -10.5107 0 0 0 3.30738 -1.36519 -1.94219 0 0 00 0 -11.6041 17.5792 0 -5.97513 0 0 -1.36519 2.55279 0 -1.1876 0 00 0 -10.5107 0 16.0989 0 0 -5.58824 -1.94219 0 3.2242 0 0 -1.28201-16.4 0 0 -5.97513 0 36.0731 -13.698 0 0 -1.1876 0 2.80473 -1.61712 00 0 0 0 0 -13.698 23.4822 -9.78427 0 0 0 -1.61712 2.77221 -1.155090 -17.4915 0 0 -5.58824 0 -9.78427 32.864 0 0 -1.28201 0 -1.15509 2.43710 0 -3.30738 1.36519 1.94219 0 0 0 38.4474 -11.6041 -10.5107 0 0 00 0 1.36519 -2.55279 0 1.1876 0 0 -11.6041 17.0972 0 -5.97513 0 00 0 1.94219 0 -3.2242 0 0 1.28201 -10.5107 0 15.5829 0 0 -5.588240 0 0 1.1876 0 -2.80473 1.61712 0 0 -5.97513 0 34.8181 -13.698 00 0 0 0 0 1.61712 -2.77221 1.15509 0 0 0 -13.698 23.1242 -9.784270 0 0 0 1.28201 0 1.15509 -2.4371 0 0 -5.58824 0 -9.78427 31.4437--------------Jacobian Matrix--------------------16.9269 0 0 0 0 -16.9269 0 0 0 0 0 1.68793 0 00 18.1691 0 0 0 0 0 -18.1691 0 0 0 0 0 0.8836270 0 41.9297 -12.1301 -11.1536 0 0 0 3.54272 -1.0628 -1.76646 0 0 00 0 -12.0455 18.0609 0 -6.01539 0 0 -1.78138 1.30819 0 -2.10262 0 00 0 -11.0484 0 16.8144 0 0 -5.76607 -2.33608 0 2.42598 0 0 -1.97778-16.9269 0 0 -6.36224 0 37.9476 -14.6585 0 0 -0.357534 0 3.05959 -0.930027 00 0 0 0 0 -14.4721 24.8873 -10.4152 0 0 0 -2.509 1.86088 -1.473890 -18.1691 0 0 -6.05157 0 -10.4721 34.6928 0 0 -0.733327 0 -0.9919732.66270 0 -3.52149 1.0628 1.76646 0 0 0 42.0299 -12.1301 -11.1536 0 0 00 0 1.78138 -3.884 0 2.10262 0 0 -12.0455 17.2037 0 -6.01539 0 00 0 2.33608 0 -4.31386 0 0 1.97778 -11.0484 0 16.2993 0 0 -5.766071.68793 0 0 0.357534 0 -2.97549 0.930027 0 0 -6.36224 0 38.3226 -14.6585 00 0 0 0 0 2.509 -3.98289 1.47389 0 0 0 -14.4721 24.2355 -10.41520 0.883627 0 0 0.733327 0 0.991973 -2.60893 0 0 -6.05157 0 -10.4721 34.8585 --------------Jacobian Matrix--------------------16.7457 0 0 0 0 -16.7457 0 0 0 0 0 1.63043 0 00 18.0388 0 0 0 0 0 -18.0388 0 0 0 0 0 0.8501960 0 41.3695 -11.8919 -10.9686 0 0 0 3.48069 -1.02775 -1.73712 0 0 00 0 -11.8057 17.6918 0 -5.8861 0 0 -1.7602 1.28091 0 -2.0217 0 00 0 -10.8651 0 16.5476 0 0 -5.68251 -2.29737 0 2.40655 0 0 -1.91027-16.7457 0 0 -6.21183 0 37.3041 -14.3465 0 0 -0.382862 0 2.95313 -0.937485 00 0 0 0 0 -14.1704 24.4052 -10.2348 0 0 0 -2.42909 1.86079 -1.433530 -18.0388 0 0 -5.94693 0 -10.2872 34.273 0 0 -0.757656 0 -0.9892082.598470 0 -3.48089 1.02775 1.73712 0 0 0 41.3703 -11.8919 -10.9686 0 0 00 0 1.7602 -3.78189 0 2.0217 0 0 -11.8057 16.6941 0 -5.8861 0 00 0 2.29737 0 -4.20764 0 0 1.91027 -10.8651 0 15.9488 0 0 -5.682511.63043 0 0 0.382862 0 -2.95077 0.937485 0 0 -6.21183 0 37.3083 -14.3465 00 0 0 0 0 2.42909 -3.86262 1.43353 0 0 0 -14.1704 23.7059 -10.23480 0.850196 0 0 0.757656 0 0.989208 -2.59706 0 0 -5.94693 0 -10.2872 34.2743 --------------Jacobian Matrix--------------------16.7435 0 0 0 0 -16.7435 0 0 0 0 0 1.63 0 00 18.0374 0 0 0 0 0 -18.0374 0 0 0 0 0 0.850 0 41.3625 -11.8888 -10.9664 0 0 0 3.48016 -1.02713 -1.73662 0 0 00 0 -11.8026 17.6871 0 -5.8845 0 0 -1.76008 1.28053 0 -2.02045 0 00 0 -10.8628 0 16.5444 0 0 -5.68158 -2.29703 0 2.40632 0 0 -1.90929-16.7435 0 0 -6.20987 0 37.296 -14.3426 0 0 -0.383399 0 2.95114 -0.937742 00 0 0 0 0 -14.1667 24.3994 -10.2326 0 0 0 -2.42794 1.86097 -1.433020 -18.0374 0 0 -5.94567 0 -10.285 34.2681 0 0 -0.758139 0 -0.9892032.597340 0 -3.48016 1.02713 1.73662 0 0 0 41.3625 -11.8888 -10.9664 0 0 00 0 1.76008 -3.78053 0 2.02045 0 0 -11.8026 16.6871 0 -5.8845 0 00 0 2.29703 0 -4.20632 0 0 1.90929 -10.8628 0 15.9444 0 0 -5.681581.63 0 0 0.383399 0 -2.95114 0.937742 0 0 -6.20987 0 37.296 -14.3426 00 0 0 0 0 2.42794 -3.86097 1.43302 0 0 0 -14.1667 23.6994 -10.23260 0.85 0 0 0.758139 0 0.989203 -2.59734 0 0 -5.94567 0 -10.285 34.2681--------------iteration---------------iteration = 4--------------voltage magnitude and angle--------------------1.04 0 01.025 0.161967 9.280011.025 0.0814153 4.664761.02579 -0.0386902 -2.216790.995631 -0.0696178 -3.988811.01265 -0.0643572 -3.68741.02577 0.064921 3.71971.01588 0.0126979 0.7275371.03235 0.0343257 1.96672-------------bus P and Q------------------1 0.71641 0.2704592 1.63 0.06653663 0.85 -0.1085974 0 05 -1.25 -0.56 -0.9 -0.37 0 08 -1 -0.359 0 0----------------line flow--------------------NUM------i-------j-----------begin------------end--------------1 4 1 -0.71641+j-0.239232 0.71641+j0.270462 7 2 -1.63+j0.0917816 1.63+j0.06653653 9 3 -0.85+j0.149553 0.85+j-0.1085974 7 8 0.763799+j-0.00797398 -0.759046+j-0.1070415 9 8 0.241834+j0.0311946 -0.240954+j-0.2429586 7 5 0.866201+j-0.0838079 -0.843202+j-0.1131287 9 6 0.608166+j-0.180748 -0.594627+j-0.1345668 5 4 -0.406798+j-0.386872 0.409373+j0.2289319 6 4 -0.305372+j-0.165433 0.307037+j0.0102993--------------------Ploss and Qloss-----------------Ploss = 0.0471901 Qloss = -0.9574833.思考题3.1潮流计算的方法有哪些?各有何特点?答:潮流计算分为手算和机算两大类,其中机算又有高斯-赛德尔迭代法、牛顿-拉夫逊迭代法、P-Q 分解法等算法。
华北电力大学潮流上机课程设计报告

课程设计报告( 2011-- 2012年度第一学期)名称:电力系统潮流上机院系:电气与电子工程学院班级:电管0902学号:1091140202 学生:指导教师:麻秀设计周数:两周成绩:日期:2011年1月6日一、课程设计的目的与要求培养学生的电力系统潮流计算机编程能力,掌握计算机潮流计算的相关知识二、设计正文(详细容见附录)1、手算在此我们同样采取计算机计算这种方便快捷的方法。
具体的方法及结果见附录。
2、计算机计算通过计算机编程,我们可以很方便的求解出相关量,其具体计算方法及计算结果见附录。
3、思考题答案见附录。
三、课程设计总结或结论潮流计算是研究电力系统稳态运行的一种基本运算方法,通过对于潮流的计算,实现对潮流的控制,维护电力系统稳定,防止出现超过约束条件的情况,从而使电力系统免遭崩溃的危险。
最初求解电力系统潮流时大多是用手算,这种计算方法不但耗费时间长,精度差,而且对于大容量的电力系统无法做到很好的控制。
随着电力系统结构日趋复杂,计算量也越来越大,仅靠手算难以求解一些复杂网络的潮流。
计算机作为一种处理数据的工具,其计算速度快,准确率高,存储量大,因此它广泛的应用于大规模复杂化的电力系统网络中。
为了能使计算机能进行潮流计算,就必须编制相应的程序,使其能按照人们在程序中设定的计算流程一步一步的执行,直到计算结果达到要求的精度,得到最终想要的结果。
C语言是一种简单实用的语言,利用它进行程序设计可以大大提高电力系统潮流控制的自动化程度。
本次的潮流上机,就是要求我们利用C语言编程,进行计算机潮流计算。
这既是对我们电力系统潮流计算知识的考验,也是对我们C语言编程能力的考验。
是一次各种知识的交汇综合的运用。
通过这次潮流上机,我对电力系统潮流计算有了更深刻的认识,同时,我的C语言编程能力也得到了提高。
我明白了学习不能仅限于课本,还要做到“学以致用”的道理。
在这次潮流设计中,我遇到了由于多问题,其中既包括由于对潮流知识掌握不牢而导致的问题,也包括由于C语言编程能力有限而导致的问题。
电力系统稳态实验报告

电力系统稳态潮流计算上机实验报告一、问题如下图所示的电力系统网络,分别用牛顿拉夫逊法、PQ解耦法、高斯赛德尔法、保留非线性法计算该电力系统的潮流。
发电机的参数如下,*表示任意值负荷参数如下,如上图所示的电力系统,可以看出,节点1、2、3是PQ节点,节点4是PV节点,而将节点5作为平衡节点。
根据问题所需,采用牛顿拉夫逊法、PQ解耦法、高斯赛德尔法、保留非线性法,通过对每次修正量的收敛判据的判断,得出整个电力系统的潮流,并分析这四种方法的收敛速度等等。
算法分析1.牛顿拉夫逊法节点5为平衡节点,不参加整个的迭代过程,节点1、2、3为PQ节点,节点4为PV 节点,计算修正方程中各量,进而得到修正量,判断修正量是否收敛,如果不收敛,迭代继续,如果收敛,算出PQ节点的电压幅值以及电压相角,得出PV节点的无功量以及电压相角,得出平衡节点的输出功率。
潮流方程的直角坐标形式,()()∑∑∈∈++-=ij j ij j ij i ij j ij j ij i i e B f G f f B e G e P()()∑∑∈∈+--=ij j ij j ij i ij j ij j ij i i e B f G e f B e G f Q直角坐标形式的修正方程式,11112n n n m n m -----∆⎡⎤⎡⎤∆⎡⎤⎢⎥⎢⎥∆=-⎢⎥⎢⎥⎢⎥∆⎣⎦⎢⎥⎢⎥∆⎣⎦⎣⎦PHN e Q M L f UR S修正方程式中的各量值的计算,()()][∑∑∈∈++--=∆ij j ij j ij i ij j ij j ij i is i e B f G f f B e G e p P()()][∑∑∈∈+---=∆ij j ij j ij i ij j ij j ij i is i e B f G e f B e G f Q Q)(2222i i is i f e U U +-=∆Jacobi 矩阵的元素计算,()()()ij i ij i i ijij j ij j ii i ii i jj iB e G f j i Q M G f B e B e G f j i e ∈-⎧≠∂∆⎪==⎨++-=∂⎪⎩∑()()()ij i ij i i ijij j ij j ii i ii i jj iG e B f j i Q L G e B f G e B f j i f ∈+⎧≠∂∆⎪==⎨--++=∂⎪⎩∑)()(202i j i j e e U R ijij i =≠⎩⎨⎧-=∂∆∂=)()(202i j i j f f U S ijij i =≠⎩⎨⎧-=∂∆∂=牛顿拉夫逊法潮流计算的流程图如下,2.PQ 解耦法如同牛顿拉夫逊法,快速解耦法的前提是,输电线路的阻抗要比电阻大得多,并且输电线路两端的电压相角相差不大,此时可利用PQ 快速解耦法,来计算整个电力系统网络的潮流。
潮流计算程序及计算结果

附表1:计算机计算潮流程序:%本程序的功能是用牛顿——拉夫逊法进行潮流计算% B1矩阵:1、支路首端号;2、末端号;3、支路阻抗;4、支路对地电纳% 5、支路的变比;6、支路首端处于K侧为1,1侧为0% B2矩阵:1、该节点发电机功率;2、该节点负荷功率;3、节点电压初始值% 4、PV节点电压V的给定值;5、节点所接的无功补偿设备的容量% 6、节点分类标号clear;n=13;%input('请输入节点数:n=');nl=13;%input('请输入支路数:nl=');isb=1;%input('请输入平衡母线节点号:isb=');pr=0.00001;%input('请输入误差精度:pr=');B1=[];%input('请输入由支路参数形成的矩阵:B1=');B2=[];%input('请输入各节点参数形成的矩阵:B2=');Y=zeros(n);e=zeros(1,n);f=zeros(1,n);V=zeros(1,n);sida=zeros(1,n);S1=zeros(nl); %-------修改部分------------ym=0;SB=100;UB=220;%ym=input('您输入的参数是标么值?(若不是则输入一个不为零的数值)'); if ym~=0%SB=input('请输入功率基准值:SB=');%UB=input('请输入电压基准值:UB=');YB=SB./UB./UB;BB1=B1;BB2=B2;for i=1:nlB1(i,3)=B1(i,3)*YB;B1(i,4)=B1(i,4)./YB;enddisp('B1矩阵B1=');disp(B1)for i=1:nB2(i,1)=B2(i,1)./SB;B2(i,2)=B2(i,2)./SB;B2(i,3)=B2(i,3)./UB;B2(i,4)=B2(i,4)./UB;B2(i,5)=B2(i,5)./SB;enddisp('B2矩阵B2=');disp(B2)end% % %---------------------------------------------------for i=1:nl %支路数if B1(i,6)==0 %左节点处于低压侧p=B1(i,1);q=B1(i,2);elsep=B1(i,2);q=B1(i,1);endY(p,q)=Y(p,q)-1./(B1(i,3)*B1(i,5)); %非对角元Y(q,p)=Y(p,q);Y(q,q)=Y(q,q)+1./(B1(i,3)*B1(i,5)^2)+B1(i,4)./2; %对角元K侧Y(p,p)=Y(p,p)+1./B1(i,3)+B1(i,4)./2; %对角元1侧end%求导纳矩阵disp('导纳矩阵Y=');disp(Y)%----------------------------------------------------------G=real(Y);B=imag(Y); %分解出导纳阵的实部和虚部for i=1:n %给定各节点初始电压的实部和虚部e(i)=real(B2(i,3));f(i)=imag(B2(i,3));V(i)=B2(i,4); %PV节点电压给定模值endfor i=1:n %给定各节点注入功率S(i)=B2(i,1)-B2(i,2); %i节点注入功率SG-SLB(i,i)=B(i,i)+B2(i,5); %i节点无功补偿量end%=========================================================== ========P=real(S);Q=imag(S);ICT1=0;IT2=1;N0=2*n;N=N0+1;a=0;while IT2~=0IT2=0;a=a+1;for i=1:nif i~=isb %非平衡节点C(i)=0;D(i)=0;for j1=1:nC(i)=C(i)+G(i,j1)*e(j1)-B(i,j1)*f(j1);%Σ(Gij*ej-Bij*fj)D(i)=D(i)+G(i,j1)*f(j1)+B(i,j1)*e(j1);%Σ(Gij*fj+Bij*ej)endP1=C(i)*e(i)+f(i)*D(i);%节点功率P计算eiΣ(Gij*ej-Bij*fj)+fiΣ(Gij*fj+Bij*ej)Q1=C(i)*f(i)-e(i)*D(i);%节点功率Q计算fiΣ(Gij*ej-Bij*fj)-eiΣ(Gij*fj+Bij*ej)%求P',Q'V2=e(i)^2+f(i)^2; %电压模平方%========= 以下针对非PV节点来求取功率差及Jacobi矩阵元素=========if B2(i,6)~=3 %非PV节点DP=P(i)-P1; %节点有功功率差DQ=Q(i)-Q1; %节点无功功率差%=============== 以上为除平衡节点外其它节点的功率计算=================%================= 求取Jacobi矩阵===================for j1=1:nif j1~=isb&j1~=i %非平衡节点&非对角元X1=-G(i,j1)*e(i)-B(i,j1)*f(i); % dP/de=-dQ/dfX2=B(i,j1)*e(i)-G(i,j1)*f(i); % dP/df=dQ/deX3=X2; % X2=dp/df X3=dQ/deX4=-X1; % X1=dP/de X4=dQ/dfp=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X4;J(m,q)=X2;elseif j1==i&j1~=isb %非平衡节点&对角元X1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);% dP/deX2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);% dP/dfX3=D(i)+B(i,i)*e(i)-G(i,i)*f(i); % dQ/deX4=-C(i)+G(i,i)*e(i)+B(i,i)*f(i);% dQ/dfp=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;%扩展列△Qm=p+1;J(m,q)=X1;q=q+1;J(p,q)=X4;J(m,N)=DP;%扩展列△PJ(m,q)=X2;endendelse%=============== 下面是针对PV节点来求取Jacobi矩阵的元素===========DP=P(i)-P1; % PV节点有功误差DV=V(i)^2-V2; % PV节点电压误差for j1=1:nif j1~=isb&j1~=i %非平衡节点&非对角元X1=-G(i,j1)*e(i)-B(i,j1)*f(i); % dP/deX2=B(i,j1)*e(i)-G(i,j1)*f(i); % dP/dfX5=0;X6=0;p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2;elseif j1==i&j1~=isb %非平衡节点&对角元X1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);% dP/deX2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);% dP/dfX5=-2*e(i);X6=-2*f(i);p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2;endendendendend%========= 以上为求雅可比矩阵的各个元素===================== for k=3:N0 % N0=2*n (从第三行开始,第一、二行是平衡节点)k1=k+1;N1=N; % N=N0+1 即N=2*n+1扩展列△P、△Qfor k2=k1:N1 % 扩展列△P、△QJ(k,k2)=J(k,k2)./J(k,k); % 非对角元规格化endJ(k,k)=1; % 对角元规格化if k~=3 % 不是第三行%======================================================== ====k4=k-1;for k3=3:k4 % 用k3行从第三行开始到当前行前的k4行消去for k2=k1:N1 % k3行后各行下三角元素J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%消去运算endJ(k3,k)=0;endif k==N0break;end%==========================================for k3=k1:N0for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%消去运算endJ(k3,k)=0;endelsefor k3=k1:N0for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%消去运算endJ(k3,k)=0;endendend%====上面是用线性变换方式将Jacobi矩阵化成单位矩阵=====for k=3:2:N0-1L=(k+1)./2;e(L)=e(L)-J(k,N); %修改节点电压实部k1=k+1;f(L)=f(L)-J(k1,N); %修改节点电压虚部end%------修改节点电压-----------for k=3:N0DET=abs(J(k,N));if DET>=pr %电压偏差量是否满足要求IT2=IT2+1; %不满足要求的节点数加1endendICT2(a)=IT2;ICT1=ICT1+1;end%用高斯消去法解"w=-J*V"disp('迭代次数:');disp(ICT1);disp('没有达到精度要求的个数:');disp(ICT2);for k=1:nV(k)=sqrt(e(k)^2+f(k)^2);sida(k)=atan(f(k)./e(k))*180./pi;E(k)=e(k)+f(k)*j;end%=============== 计算各输出量=========================== disp('各节点的实际电压标幺值E为(节点号从小到大排列):');disp(E);EE=E*UB;disp(EE);disp('-----------------------------------------------------');disp('各节点的电压大小V为(节点号从小到大排列):');disp(V);VV=V*UB;disp(VV);disp('-----------------------------------------------------');disp('各节点的电压相角sida为(节点号从小到大排列):');disp(sida);for p=1:nC(p)=0;for q=1:nC(p)=C(p)+conj(Y(p,q))*conj(E(q));endS(p)=E(p)*C(p);enddisp('各节点的功率S为(节点号从小到大排列):');disp(S);disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~');SS=S*SB;disp(SS);disp('-----------------------------------------------------');disp('各条支路的首端功率Si为(顺序同您输入B1时一致):');for i=1:nlp=B1(i,1);q=B1(i,2);if B1(i,6)==0Si(p,q)=E(p)*(conj(E(p))*conj(B1(i,4)./2)+(conj(E(p)*B1(i,5))-conj(E(q)))*conj(1./( B1(i,3)*B1(i,5))));Siz(i)=Si(p,q);elseSi(p,q)=E(p)*(conj(E(p))*conj(B1(i,4)./2)+(conj(E(p)./B1(i,5))-conj(E(q)))*conj(1./( B1(i,3)*B1(i,5))));Siz(i)=Si(p,q);enddisp(Si(p,q));SSi(p,q)=Si(p,q)*SB;ZF=['S(',num2str(p),',',num2str(q),')=',num2str(SSi(p,q))];disp(ZF);%disp(SSi(p,q));disp('-----------------------------------------------------');enddisp('各条支路的末端功率Sj为(顺序同您输入B1时一致):');for i=1:nlp=B1(i,1);q=B1(i,2);if B1(i,6)==0Sj(q,p)=E(q)*(conj(E(q))*conj(B1(i,4)./2)+(conj(E(q)./B1(i,5))-conj(E(p)))*conj(1./( B1(i,3)*B1(i,5))));Sjy(i)=Sj(q,p);elseSj(q,p)=E(q)*(conj(E(q))*conj(B1(i,4)./2)+(conj(E(q)*B1(i,5))-conj(E(p)))*conj(1./( B1(i,3)*B1(i,5))));Sjy(i)=Sj(q,p);enddisp(Sj(q,p));SSj(q,p)=Sj(q,p)*SB;ZF=['S(',num2str(q),',',num2str(p),')=',num2str(SSj(q,p))];disp(ZF);%disp(SSj(q,p));disp('-----------------------------------------------------');enddisp('各条支路的功率损耗DS为(顺序同您输入B1时一致):');for i=1:nlp=B1(i,1);q=B1(i,2);DS(i)=Si(p,q)+Sj(q,p);disp(DS(i));DDS(i)=DS(i)*SB;ZF=['DS(',num2str(p),',',num2str(q),')=',num2str(DDS(i))];disp(ZF);%disp(DDS(i));disp('-----------------------------------------------------');endfigure(1);subplot(2,2,1);plot(V);xlabel('节点号');ylabel('电压标幺值');grid on;subplot(2,2,2);plot(sida);xlabel('节点号');ylabel('电压角度');grid on;subplot(2,2,3);bar(real(S));ylabel('节点注入有功');grid on;subplot(2,2,4);bar(Siz);ylabel('支路首端无功');grid on;1.冬季最大运行方式潮流计算结果:计算机运行的B1,B2阵如下:B1=[ 1 2 0.0318+0.0454*i 0.282*i 1 01 11 0.0114+0.0374*i 0.2332*i 1 011 3 0.001975+0.0695*i 0 1.025:1.1 11 12 0.0087+0.029*i 0.1788*i 1 012 4 0.0031+0.103*i 0 1:1.05 11 5 0.043+0.142*i 0.22*i 1 05 6 0.0031+0.103*i 0 1:1.05 15 7 0.043+0.142*i 0.22*i 1 01 7 0.051+0.168*i 0.26*i 1 07 8 0.00198+0.0695*i 0 1:1.1 17 13 0.01+0.033*i 0.204*i 1 013 9 0.0025+0.083*i 0 0.9956 11 10 0.00239+0.084*i 0 1.048 1]B2=[0 0 1.1 0 0 10 1.43+0.886*i 1.05 1.05 0 30 0.88+0.545*i 1 0 0 20 0.77+0.4772*i 1 0 0 20 0 1 0 0 20 0.77+0.4772*i 1 0 0 20 0 1 0 0 20 0.88+0.545*i 1 0 0 20.642+0.3817*i 0 1.05 1.05 0 31+0.75*i 0.2+0.1549*i 1.05 1.05 0 30 0 1 0 0 20 0 1 0 0 20 0 1 0 0 2]计算机运行结果如下表:节点号电压值相角值支路标号首端功率末端功率支路功率损耗1 242.0000 0 1-2 148.9391+3.327637i -143-27.45476i 5.93913-24.1271i2 231.0000 -3.0341 1-11 89.1956+37.193i -88.19803-61.4687i 0.997519-24.2757i3 227.4154 -4.4383 11-3 88.19803+61.4687i -88-54.5i 0.19803+6.9687i4 226.3304 -4.9004 1-12 77.8364+36.4186i -77.2404-55.7062i 0.596039-19.2876i5 229.8318 -3.9547 12-4 77.2404+55.7062i -77-47.72i 0.24036+7.9862i6 217.7226 -8.2720 1-5 63.5438+12.2204i -61.8773-32.0321i 1.66656-19.8116i7 234.9326 -3.1047 5-6 77.2597+56.3501i -77-47.72i 0.25974+8.6301i8 226.0991 -6.2429 5-7 15.3825-24.3181i 15.5354+0.274108i 0.152961-24.044i9 231.0000 0.5851 7-8 88.20085+61.55009i -88-54.5i 0.20085+7.0501i10 231.0000 3.4950 1-7 40.806-6.05737i -40.0647-22.0555i 0.741264-28.1128i11 236.1931 -1.3348 7-13 -63.6716-39.7687i 64.0965+17.5832i 0.424934-22.1855i12 237.9346 -0.8892 13-9 -64.0965-17.5832i 64.2+21.0187i 0.10348+3.4355i13 238.1868 -2.2028 1-10 79.8613+4.23546i 80+0.641048i 0.13875+4.8765i 计算机计算结果图形:2.冬季最小运行方式潮流计算结果:计算机运行的B1B2矩阵如下:B1=[ 1 2 0.0318+0.0454*i 0.282*i 1 01 11 0.0114+0.0374*i 0.2332*i 1 011 3 0.001975+0.0695*i 0 1.025:1.1 11 12 0.0087+0.029*i 0.1788*i 1 012 4 0.0031+0.103*i 0 1:1.05 11 5 0.043+0.142*i 0.22*i 1 05 6 0.0031+0.103*i 0 1:1.05 15 7 0.043+0.142*i 0.22*i 1 01 7 0.051+0.168*i 0.26*i 1 07 8 0.00198+0.0695*i 0 1:1.1 17 13 0.01+0.033*i 0.204*i 1 013 9 0.0025+0.083*i 0 0.9956 11 10 0.00239+0.084*i 0 1.048 1]B2=[0 0 1.1 0 0 10 1.43+0.886*i 1.05 1.05 0 30 0.616+0.3817*i 1 0 0 20 0.539+0.3817*i 1 0 0 20 0 1 0 0 20 0.539+0.334*i 1 0 0 20 0 1 0 0 20 0.539+0.334*i 1 0 0 20.642+0.3817*i 0 1.05 1.05 0 31+0.75*i 0.1+0.06197*i 1.05 1.05 0 30 0 1 0 0 20 0 1 0 0 20 0 1 0 0 2]电压调整措施:变电所1、4变压器变比:+2.5% 水电厂变压器变比:-2.5%5 234.2241 -2.0051 (12--4) 54.0234+42.2706i -53.9-38.17i 0.12342+4.1006i6 226.2159 -4.8577 (1--5) 34.1669+4.22856 -33.6427-28.276i 0.524165-24.0474i7 235.1128 -0.4737 (5--6) 54.0179+37.3169i -53.9-33.4i 0.11789+3.9169i8 223.9941 -2.4603 (5--7) -20.3752-9.04094i 20.5371-15.4558i 0.161947-24.4968i9 231.0000 3.4429 (1--7) 11.0013+1.45186i -10.8258-31.4513i 0.175442-29.9995i10 231.0000 3.9321 (7--8) 53.9768+36.0957i -53.9-33.4i 0.076797+2.6957i11 238.4187 -0.9561 (7--13) -63.6881+10.8115i 64.0874-32.7763i 0.39932-21.9648i12 239.1742 -0.6185 (13--9) -64.0874+32.7763i 64.2-29.0386i 0.11258+3.7377i13 234.9468 0.6942 (1--10) -89.8244+5.1673i 90+1.0049i 0.17561+6.1722i 计算机运行结果的图形:3.夏季最大运行方式计算机计算结果:计算机运行B1B2阵如下:B1=[ 1 2 0.0318+0.0454*i 0.282*i 1 01 11 0.0114+0.0374*i 0.2332*i 1 011 3 0.001975+0.0695*i 0 1.025:1.1 11 12 0.0087+0.029*i 0.1788*i 1 012 4 0.0031+0.103*i 0 1:1.05 11 5 0.043+0.142*i 0.22*i 1 05 6 0.0031+0.103*i 0 1:1.05 15 7 0.043+0.142*i 0.22*i 1 01 7 0.051+0.168*i 0.26*i 1 07 8 0.00198+0.0695*i 0 1:1.1 17 13 0.02+0.066*i 0.102*i 1 013 9 0.0025+0.083*i 0 0.9956 11 10 0.00239+0.084*i 0 1.048 1]B2=[0 0 1.1 0 0 10 1.26+0.7814*i 1.05 1.05 0 30 0.776+0.481*i 1 0 0 20 0.543+0.3367*i 1 0 0 20 0 1 0 0 20 0.543+0.3367*i 1 0 0 20 0 1 0 0 20 0.776+0.481*i 1 0 0 21.35+0.6538*i 0.2+0.124*i 1.05 1.05 0 31+0.75*i 0.25+0.1549*i 1.05 1.05 0 30 0 1 0 0 20 0 1 0 0 20 0 1 0 0 2]计算机运行结果如下表:10 231.0000 3.4950 (7,8) 77.7585+53.6634i -77.6-48.1i0.1585+5.5634i11 237.0938 -1.1858 (7,13) -113.4984+9.476406i 114.6926-28.38885i 1.19422-18.9124i12 239.1742 -0.6185 (13,9) -114.6926+28.38885 115-18.18369i0.307384+10.2052i13 233.3912 3.2303 (1,10) -79.8613+4.23546i 80+0.641048i 0.13875+4.8765i 计算机计算结果如图:4.夏季最小运行方式:计算机运行B1B2阵如下:B1=[ 1 2 0.0318+0.0454*i 0.282*i 1 01 11 0.0114+0.0374*i 0.2332*i 1 011 3 0.001975+0.0695*i 0 1.025:1.1 11 12 0.0087+0.029*i 0.1788*i 1 012 4 0.0031+0.103*i 0 1:1.05 11 5 0.043+0.142*i 0.22*i 1 05 6 0.0031+0.103*i 0 1:1.05 15 7 0.043+0.142*i 0.22*i 1 01 7 0.051+0.168*i 0.26*i 1 07 8 0.00198+0.0695*i 0 1:1.1 17 13 0.02+0.066*i 0.102*i 1 013 9 0.0025+0.083*i 0 0.9956 11 10 0.00239+0.084*i 0 1.048 1]B2=[0 0 1.1 0 0 10 1.26+0.7814*i 1.05 1.05 0 30 0.543+0.336*i 1 0 0 20 0.4753+0.2947*i 1 0 0 20 0 1 0 0 20 0.4753+0.2947*i 1 0 0 20 0 1 0 0 20 0.543+0.336*i 1 0 0 21.35+0.6538*i 0.2+0.124*i 1.05 1.05 0 31+0.75*i 0.25+0.1549*i 1.05 1.05 0 30 0 1 0 0 20 0 1 0 0 20 0 1 0 0 2]10 231.0000 3.9321 (7,8) 54.3735+36.2509i -54.3-33.67i 0.073528+2.5809i11 239.0099 -0.8518 (7,13) -113.4428+24.39707i 114.6754-43.79301i 1.23255-19.3959i12 239.8726 -0.5689 (13,9) -114.6754+43.79301i 115-33.01613i 0.324605+10.7769i13 235.9565 4.4510 (1,10) -89.8244+5.1673i 90+1.0049i 0.17561+6.1722i 计算机计算结果如图:5.夏季故障运行状态:调压及无功补偿措施如下:变电所3的变压器变比为-2.5%,无功补偿容量为20Mvar。
第一章华北电力大学 电力系统潮流计算1new

U i
k 1
(1-17) 上式是该算法最基本的迭代计算公式。 其迭代收敛的判据是 maxU k 1 U k
i i i
i 1 n 1 Pi jQi Yi1 U1s ( Yij U i( k 1) Yij U i( k ) i 2,3,, n Yii ( k ) j 2 j i 1 Ui
第三节 潮流计算的几种基本方法
一 高斯-塞德尔法 以导纳矩阵为基础,并应用高斯-塞 德尔迭代的算法是电力系统应用最早的 潮流计算方法。
三.潮流计算的几种基本方法
高斯—塞德尔迭代法原理
已知方程组 (1) 1
( 2)
x1 0 3 0.3333
( x21) 0 2 0.6667 3
第二节 潮流计算问题的数学模型
对这样的线性网络一般采用节点电压 法进行分析。节点电压与节点注入电流 之间的关系为:
或
YU I
U Z I
第二节 潮流计算问题的数学模型
式中:
I1 I I 2 , In . U1 . U U 2 U. n
j 1
Ui
n
或
U i Z ij
j 1
Pj jQ j
i 1,2,, n
Uj
(1-7)
第二节 潮流计算问题的数学模型
上两式是潮流计算问题的基本方程式, 是一个以节点电压为变量的非线性代数 方程组。而采用节点功率作为节点注入 量是造成方程组呈非线性的根本原因。 由于方程组为非线性的,因此必须采用 迭代方法进行数值求解。 根据对方程组的不同处理方式,形成 了不同的潮流算法。
华电潮流上机程序(含网损计算)最终版2015.1.11

// flow.cpp: 主项目文件。
#include"stdafx.h"#include"NEquation.h"#include"math.h"#include"stdio.h"#include"config.h"using namespace System;void test(){NEquation ob1;ob1.SetSize(2);ob1.Data(0,0)=1;ob1.Data(0,1)=2;ob1.Data(1,0)=2;ob1.Data(1,1)=1;ob1.Value(0)=4;ob1.Value(1)=6;ob1.Run();printf("x1=%f\n",ob1.Value(0));printf("x2=%f\n",ob1.Value(1));printf("Test OK!\n");}void GetData() //读取数据{int i;FILE *fp;fp=fopen("E:\\1121180617邵天赐\\data\\data.txt","r");if(fp==NULL){printf("Can not open the file named 'data.txt' \n");return;}for(i=0;i<=Bus_Num-1;i++){fscanf(fp,"%d,%f,%f,%f,%f,%f,%f,%d",&gBus[i].No,&gBus[i].Voltage,&gBus[i].P &gBus[i].GenP,&gBus[i].GenQ,&gBus[i].LoadP,&gBus[i].LoadQ,&gBus[i].Typ }for(i=0;i<=Line_Num-1;i++){fscanf(fp,"%d,%d,%d,%f,%f,%f,%f",&gLine[i].No,&gLine[i].No_I,&gLine[i].No_J &gLine[i].R,&gLine[i].X,&gLine[i].B,&gLine[i].k);}printf("Open the file OK! \n");fclose(fp);}void GetYMatrix()// 由Z阵计算Y阵{int i,j,bus1,bus2;FILE *fp;float r,x,d,g,b,g1,b1,g2,b2,g3,b3;for(i=0;i<=Bus_Num-1;i++){for(j=0;j<=Bus_Num-1;j++){gY_G[i][j]=0;gY_B[i][j]=0;}}for(i=0;i<=Line_Num-1;i++){if(gLine[i].k==0){bus1=gLine[i].No_I-1;bus2=gLine[i].No_J-1;r=gLine[i].R;x=gLine[i].X;d=r*r+x*x;g=r/d;b=-x/d;gY_G[bus1][bus1]=gY_G[bus1][bus1]+g;gY_G[bus2][bus2]=gY_G[bus2][bus2]+g;gY_G[bus1][bus2]=gY_G[bus1][bus2]-g;gY_G[bus2][bus1]=gY_G[bus2][bus1]-g;gY_B[bus1][bus1]=gY_B[bus1][bus1]+b+gLine[i].B;gY_B[bus2][bus2]=gY_B[bus2][bus2]+b+gLine[i].B;gY_B[bus1][bus2]=gY_B[bus1][bus2]-b;gY_B[bus2][bus1]=gY_B[bus2][bus1]-b;}else{bus1=gLine[i].No_I-1;bus2=gLine[i].No_J-1;r=gLine[i].R;x=gLine[i].X;d=r*r+x*x;g=r/d;b=-x/d;g1=g/gLine[i].k;b1=b/gLine[i].k;g2=g*(gLine[i].k-1)/gLine[i].k;b2=b*(gLine[i].k-1)/gLine[i].k;g3=g*(1-gLine[i].k)/(gLine[i].k*gLine[i].k);b3=b*(1-gLine[i].k)/(gLine[i].k*gLine[i].k);gY_G[bus1][bus1]=gY_G[bus1][bus1]+g1+g2;gY_G[bus2][bus2]=gY_G[bus2][bus2]+g1+g3;gY_G[bus1][bus2]=gY_G[bus1][bus2]-g1;gY_G[bus2][bus1]=gY_G[bus2][bus1]-g1;gY_B[bus1][bus1]=gY_B[bus1][bus1]+b1+b2;gY_B[bus2][bus2]=gY_B[bus2][bus2]+b1+b3;gY_B[bus1][bus2]=gY_B[bus1][bus2]-b1;gY_B[bus2][bus1]=gY_B[bus2][bus1]-b1;}}// 输出Y矩阵fp=fopen("E:\\1121180617邵天赐\\data\\ymatrix.txt","w");if(fp==NULL){printf("Can not open the file named 'ymatrix.txt' \n");return ;}fprintf(fp,"----Y Matrix----\n");for(i=0;i<=Bus_Num-1;i++){for(j=0;j<=Bus_Num-1;j++){fprintf(fp,"Y(%d,%d)=(%10.5f,%10.5f)\n",i+1,j+1,gY_G[i] [j],gY_B[i][j]);}}fclose(fp);}void SetInitial(){int i;for(i=0;i<=Bus_Num-1;i++){if(gBus[i].Type==3){gf[i]=gBus[i].Voltage*sin(gBus[i].Phase);ge[i]=gBus[i].Voltage*cos(gBus[i].Phase);}else{gf[i]=0;ge[i]=1;}}}void GetUnbalance(){int i,j,k;k=0;FILE *fp;for(i=0;i<=Bus_Num-1;i++){if(gBus[i].Type==1){gDelta_P[k]=0;gDelta_Q[k]=0;for(j=0;j<=Bus_Num-1;j++){gDelta_P[k]=gDelta_P[k]+ge[i]*(gY_G[i][j]*ge[j]-gY_B[i] [j]*gf[j])+gf[i]*(gY_G[i][j]*gf[j]+gY_B[i][j]*ge[j]);gDelta_Q[k]=gDelta_Q[k]+gf[i]*(gY_G[i][j]*ge[j]-gY_B[i] [j]*gf[j])-ge[i]*(gY_G[i][j]*gf[j]+gY_B[i][j]*ge[j]);}gDelta_P[k]=gBus[i].GenP-gBus[i].LoadP-gDelta_P[k];gDelta_Q[k]=gBus[i].GenQ-gBus[i].LoadQ-gDelta_Q[k];gDelta_PQ[k*2]=gDelta_P[k];gDelta_PQ[k*2+1]=gDelta_Q[k];k++;}else if (gBus[i].Type==2){gDelta_P[k]=0;gDelta_Q[k]=0;for(j=0;j<=Bus_Num-1;j++){gDelta_P[k]=gDelta_P[k]+ge[i]*(gY_G[i][j]*ge[j]-gY_B[i][j]*gf[j])+gf[i]*(gY_G[i][j]*gf[j]+gY_B[i][j]*ge[j]);}gDelta_P[k]=gBus[i].GenP-gBus[i].LoadP-gDelta_P[k];gDelta_Q[k]=gBus[i].Voltage*gBus[i].Voltage-(ge[i]*ge[i]+gf[i]*gf[i]);gDelta_PQ[k*2]=gDelta_P[k];gDelta_PQ[k*2+1]=gDelta_Q[k];k++;}}}void GetJaccobi(){int i,j,k;FILE *fp;float m,n;float H[Bus_Num-1][Bus_Num-1],N[Bus_Num-1][Bus_Num-1];float J[Bus_Num-1][Bus_Num-1],L[Bus_Num-1][Bus_Num-1]; for(i=1;i<=Bus_Num-1;i++){m=0;n=0;for(k=0;k<=Bus_Num-1;k++){m=m+gY_G[i][k]*gf[k]+gY_B[i][k]*ge[k];n=n+gY_G[i][k]*ge[k]-gY_B[i][k]*gf[k];}for(j=1;j<=Bus_Num-1;j++){if(gBus[i].Type==1){if(i!=j){H[i-1][j-1]=gY_B[i][j]*ge[i]-gY_G[i][j]*gf[i];N[i-1][j-1]=-gY_G[i][j]*ge[i]-gY_B[i][j]*gf[i];J[i-1][j-1]=-N[i-1][j-1];L[i-1][j-1]=H[i-1][j-1];}else if(i==j){H[i-1][i-1]=-gY_G[i][j]*gf[i]+gY_B[i][i]*ge[i]-m;N[i-1][i-1]=-gY_G[i][i]*ge[i]-gY_B[i][i]*gf[i]-n;J[i-1][i-1]=gY_G[i][j]*ge[i]+gY_B[i][i]*gf[i]-n;L[i-1][i-1]=-gY_G[i][i]*gf[i]+gY_B[i][j]*ge[i]+m;}}else if(gBus[i].Type==2){if(i!=j){H[i-1][j-1]=gY_B[i][j]*ge[i]-gY_G[i][j]*gf[i];N[i-1][j-1]=-gY_G[i][j]*ge[i]-gY_B[i][j]*gf[i];J[i-1][j-1]=0;L[i-1][j-1]=0;}else if(i==j){H[i-1][i-1]=-gY_G[i][j]*gf[i]+gY_B[i][i]*ge[i]-m;N[i-1][i-1]=-gY_G[i][i]*ge[i]-gY_B[i][i]*gf[i]-n;J[i-1][i-1]=-2*gf[i];L[i-1][i-1]=-2*ge[i];}}}}for(i=1;i<=Bus_Num-1;i++){for(j=1;j<=Bus_Num-1;j++){gJaccobi[2*(i-1)][2*(j-1)]=H[i-1][j-1]; gJaccobi[2*(i-1)][2*j-1]=N[i-1][j-1]; gJaccobi[2*i-1][2*(j-1)]=J[i-1][j-1];gJaccobi[2*i-1][2*j-1]=L[i-1][j-1];}}}void GetRevised(){FILE *fp;int i,j;NEquation ob1;ob1.SetSize(2*(Bus_Num-1));for (i=0;i<=2*(Bus_Num-1)-1;i++){for (j=0;j<=2*(Bus_Num-1)-1;j++)ob1.Data(i,j)=gJaccobi[i][j];ob1.Value(i)=gDelta_PQ[i];}ob1.Run();for(i=0;i<=(Bus_Num-1-1);i++){gDelta_f[i]=ob1.Value(2*i);gDelta_e[i]=ob1.Value(2*i+1);gDelta_fe[2*i]=gDelta_f[i];gDelta_fe[2*i+1]=gDelta_e[i];}}void GetNewValue(){FILE *fp;j=0;for(i=0;i<=Bus_Num-1;i++){if(gBus[i].Type!=3){gDelta_f[j]=gDelta_fe[2*j];gf[i]-=gDelta_f[j];gDelta_e[j]=gDelta_fe[2*j+1];ge[i]-=gDelta_e[j];j++;}}}int main(array<System::String ^> ^args){FILE *fp;int i,j,Count_Num;float maxValue,P_Bus[Bus_Num],Q_Bus[Bus_Num];float P[Bus_Num][Bus_Num],Q[Bus_Num][Bus_Num],PS,QS; float gBus_b[Bus_Num];// test();GetData();GetYMatrix();SetInitial();for(Count_Num=0;Count_Num<=100;Count_Num++){GetUnbalance();// 输出不平衡量fp=fopen("E:\\1121180617邵天赐\\data\\unbalance.txt","w");if(fp==NULL){printf("Can not open the file named 'unbalance.txt' \n");return 0 ;fprintf(fp,"----Unbalance----\n");for(i=0;i<=2*(Bus_Num-1)-1;i++){fprintf(fp,"unbalance(%d)=(%10.5f)\n",i+1,gDelta_PQ[i]); }fclose(fp);GetJaccobi();// 输出雅克比矩阵fp=fopen("E:\\1121180617邵天赐\\data\\Jaccobi.txt","w");if(fp==NULL){printf("Can not open the file named 'Jaccobi.txt' \n");return 0;}fprintf(fp,"----Jaccobi----\n");for(i=0;i<=2*(Bus_Num-1)-1;i++){for(j=0;j<=2*(Bus_Num-1)-1;j++){fprintf(fp,"Jaccobi(%d,%d)=(%10.5f)\n",i+1,j+1,gJaccobi[i][j]); }}fclose(fp);GetRevised();// 输出修正值fp=fopen("E:\\1121180617邵天赐\\data\\revised.txt","w");if(fp==NULL){printf("Can not open the file named 'revised.txt' \n");return 0;}fprintf(fp,"----Revised----\n");for(i=0;i<=2*(Bus_Num-1)-1;i++)fprintf(fp,"Revised(%d)=(%10.5f)\n",i+1,gDelta_fe[i]);}fclose(fp);GetNewValue();//输出新值fp=fopen("E:\\1121180617邵天赐\\data\\newvalue.txt","w");if(fp==NULL){printf("Can not open th file named 'newvalue.txt'\n");return 0;}fprintf(fp,"----Newvalue----\n");for(i=0;i<=Bus_Num-2;i++){fprintf(fp,"f(%d)=%10.5f,e(%d)=%10.5f\n",i+1,gf[i+1],i+1,ge[i+1]);}fclose(fp);//输出每次迭代电压幅值及相角fp=fopen("E:\\1121180617邵天赐\\data\\voltage.txt","a");if(fp==NULL){printf("Can not open th file named 'voltage.txt'\n");return 0;}fprintf(fp,"----第%d次迭代电压幅值及相角情况----\n",Count_Num+1);{for(i=0;i<=Bus_Num-1;i++){fprintf(fp,"节点%d:电压幅值:%10.5f ;相角:%10.5f\n",i+1,sqrt(ge[i]*ge[i]+gf[i]*gf[i]),atan(gf[i]/ge[i]));}fprintf(fp,"\n");fclose(fp);maxValue=fabs(gDelta_fe[0]);for(i=1;i<2*(Bus_Num-1);i++){if(maxValue<fabs(gDelta_fe[i])){maxValue=fabs(gDelta_fe[i]);}}if(maxValue<Precision){break;}}printf("\n");//求节点功率P_Bus,Q_Busfor(i=0;i<Bus_Num;i++){P_Bus[i]=0;Q_Bus[i]=0;}printf("节点注入功率\n");for(i=0;i<Bus_Num;i++){for(j=0;j<Bus_Num;j++){P_Bus[i]=P_Bus[i]+ge[i]*(gY_G[i][j]*ge[j]-gY_B[i][j]*gf[j]) +gf[i]*(gY_G[i][j]*gf[j]+gY_B[i][j]*ge[j]);Q_Bus[i]=Q_Bus[i]+gf[i]*(gY_G[i][j]*ge[j]-gY_B[i][j]*gf[j])-ge[i]*(gY_G[i][j]*gf[j]+gY_B[i][j]*ge[j]);}printf("P(%d)=%10.5f Q(%d)=%10.5f\n",i+1,P_Bus[i],i+1,Q_Bus[i]);}printf("\n节点对地电纳\n");for(i=1;i<=Bus_Num;i++){gBus_b[i-1]=0;for(j=1;j<=Line_Num;j++){if((i==gLine[j].No_I)||(i==gLine[j].No_J)){gBus_b[i-1]=gBus_b[i-1]+gLine[j].B;}elsecontinue;}printf("节点%d:%10.5f\n",i,gBus_b[i-1]);}printf("\n线路功率\n");for(i=0;i<=Bus_Num-1;i++){for(j=0;j<=Bus_Num-1;j++){P[i][j]=ge[i]*(ge[i]-ge[j])*gY_G[i][j]+ge[i]*(gf[j]-gf[i])*gY_B[i][j] +gf[i]*(ge[i]-ge[j])*gY_B[i][j]-gf[i]*(gf[j]-gf[i])*gY_G[i][j];Q[i][j]=-(ge[i]*ge[i]+gf[i]*gf[i])*gBus_b[i]+ge[i]*(ge[i]-ge[j])*gY_B[i][j]+ge[i]*(gf[j]-gf[i])*gY_G[i][j]+gf[i]*(ge[i]-ge[j])*gY_G[i][j] +gf[i]*(gf[j]-gf[i])*gY_B[i][j];printf("P_L[%d %d]=%10.5f Q_L[%d %d]=%10.5f\n",i+1,j+1,-P[i] [j],i+1,j+1,-Q[i][j]);}}printf("\n收敛的迭代次数:%d\n",Count_Num);printf("\n收敛后各节点电压幅值及相角:\n");for(i=0;i<=Bus_Num-1;i++){printf("节点%d:电压幅值:%10.5f ;相角:%10.5f\n",i+1,sqrt(ge[i]*ge[i]+gf[i]*gf[i]),atan(gf[i]/ge[i]));}printf("\n各节点注入功率:\n");for(i=0;i<Bus_Num;i++){if(gBus[i].Type==3){printf("平衡节点(节点%d)功率:P=%10.5fQ=%10.5f\n",i+1,P_Bus[i],Q_Bus[i]);//输出平衡节点功率 }else if(gBus[i].Type==2){printf("PV节点(节点%d)的功率:P=%10.5fQ=%10.5f\n",i+1,P_Bus[i],Q_Bus[i]);}}printf("\n网络线路功率计算的损耗:\n");PS=0;QS=0;for(i=0;i<Bus_Num;i++){for(j=0;j<Bus_Num;j++){if(i!=j){PS=PS+P[i][j];QS=QS+Q[i][j];}else continue;}}printf("损耗有功:%10.5f,损耗无功:%10.5f\n",-PS,-QS); while(true){} return 0; }。
电力系统潮流运算

/*此程序为用牛顿拉夫逊法的直角坐标形式求电力线路的潮流计算程序*//*此程序为一通用程序,按给定的题目输入数据到input文件中,就可求出相关节点的电压相量,支路功率,网络损耗,输电效率平衡节点的功率,pv节点的无功*//*考虑了线路对地导纳支路、平行支路、非标准变比变压器支路、还有无功越限的处理等4种较为复杂的情况*//*本程序通用性很强*/#include <stdio.h>#include<math.h>#include<stdlib.h>void main(){int bus,line,pQ,pv,blzl,transform;/*分别表示节点数,支路数,pQ节点数,pv节点数,对地支路数,变压器数*/int i,j,k,m,n,circle,num,w,r;/*循环变量*/int type[100],node[100],head[100],end[100],branch[100];/*分别表示:节点类型,节点号,支路的首节点,支路的尾节点,支路号*/int t1[100],t2[100];/*中间数组*/float precise;/*计算精度*/float real[100][100],image[100][100],R[100],X[100];/*节点导纳的实部,节点导纳的虚部,支路上的电阻,支路上的电抗*/float p[100],Q[100],p0[100],Q0[100];/*节点的有功功率,节点的无功功率,各节点的给定有功功率初值,各节点的给定无功功率初值*/float e[100],f[100],e0[100],f0[100];/*分别为各节点电压的实部,虚部,给定电压的初始实部和虚部*/float ub[200],ubp[100],ubQ[100],ubu2[100],a[100],b[100];/*分别表示不平衡量,有功不平衡量,无功不平衡量,电压不平衡量,a[]和b[]是中间数组*/floatH[100][100],N[100][100],B[100][100],J[100][100],L[100][100],R1[100][100],S[100][100];/*雅克比矩阵各元素变量*/float a1[100][100],b1[100][100],du[100];/*中间数组和电压修正量*/floatt,s,E[100][100],Ln[100][100],Un[100][100],Bn[100][100],zgjz[100][200],Eu[100][100];/*求逆矩阵的过程中的各数组*/float dumax,ps,Qs,pline[100][100],Qline[100][100],dpline[100][100],dQline[100][100];/*最大电压修正量,平衡节点的有功和无功,支路有功和无功,支路损耗的有功和无功*/ float dpsum,dQsum,efficiency,p1,p2;/*网络总的有功损耗,网络总的无功损耗,输电效率,网络中各节点注入的正的有功的和,网络中各节点注入负的有功的绝对值和*/ float duidi[100],ratio[100],tt1,tt2;/*对地支路的导纳和变压器变比,还有中间变量tt1和tt2*/int x,y,d[100],flag[100];/*flag用来判断平行支路数*/FILE *fp1,*fp2;/*指针变量*/float ee[100],ff[100];/*中间变量*/float Qmax;/*Qmax为无功上限*//*以上为对程序中用到的变量的定义*/fp1=fopen("input.txt","r");/*打开input.txt文件读入数据*/fp2=fopen("output.txt","w");/*打开out.txt文件写入数据*/fprintf(fp2,"\n 华北电力大学\n\n");fprintf(fp2," 电力系统潮流上机班级:电气化0805 姓名:张同学号:200801000528\n");fprintf(fp2,"\n ***************原始数据***************** \n");fprintf(fp2,"============================================================= ======================\n\n");fscanf(fp1,"%d%d%d%d%d%d%f%f",&bus,&line,&pQ,&pv,&blzl,&transform,&precise,&Qmax );fprintf(fp2," 节点数:%d 支路数:%d pQ节点数:%d pv节点数:%d\n 并联对地之路数:%d 变压器数:%d 要求精度:%f \n",bus,line,pQ,pv,blzl,transform,precise);fprintf(fp2,"------------------------------------------------------------------------------------\n");/*下边开始从input.txt文件读入数据*/for(i=1;i<=bus;i++){fscanf(fp1,"%d%d",&node[i],&type[i]);if(type[i]==1)/*type[i]=1,说明第i节点是pQ节点*/fscanf(fp1,"%f%f%f%f",&p0[i],&Q0[i],&e[i],&f[i]);else if(type[i]==2)/*type[i]=1,说明第i节点是pv节点*/fscanf(fp1,"%f%f%f%f%f",&p0[i],&e[i],&f[i],&e0[i],&f0[i]);else if(type[i]==3)/*type[i]=1,说明第i节点是平衡节点*/fscanf(fp1,"%f%f",&e[i],&f[i]);}for(i=1;i<=bus;i++)/*bus表示节点数*/{if(type[i]==1)fprintf(fp2," 节点%d pQ节点%f %f\n",node[i],p0[i],Q0[i]);else if(type[i]==2)fprintf(fp2," 节点%d pv节点%f %f\n",node[i],p0[i],e0[i]);elsefprintf(fp2," 节点%d 平衡节点%f %f\n",node[i],e[i],f[i]);}fprintf(fp2,"------------------------------------------------------------------------------------\n");for(i=1;i<=line;i++){fscanf(fp1,"%d%d%d%f%f%f%d%f",&branch[i],&head[i],&end[i],&R[i],&X[i],&duidi[i],&flag[ i],&ratio[i]);/*读支路信息*/fprintf(fp2," 支路%d %d %d R[%d]=%fX[%d]=%f\n",branch[i],head[i],end[i],branch[i],R[i],branch[i],X[i]); /*打印出给定题目的支路信息*/}/*head里存放支路的首节点,end里存放支路的尾节点*/fprintf(fp2,"============================================================= ======================\n\n");fprintf(fp2,"\n *********************潮流计算开始***************** \n");fclose(fp1);/*关闭文件input.txt文件*//*下边求节点导纳阵开始*//*下面是考虑平行之路时的支路阻抗计算*/for(i=1;i<=line;i++){if(flag[i]==2){R[i]=R[i]/2;X[i]=X[i]/2;duidi[i]=duidi[i]*2;}}/*考虑平行之路的阻抗结束*/for(i=1;i<=bus;i++)for(j=1;j<=bus;j++){real[i][j]=0;/*real是节点导纳的实部*/image[i][j]=0;/*image是节点导纳的虚部*/}for(i=1;i<=line;i++)/*line是总的支路数*/{real[(head[i])][(end[i])]=(-1)*R[i]/(R[i]*R[i]+X[i]*X[i]);image[(head[i])][(end[i])]=X[i]/(R[i]*R[i]+X[i]*X[i]);real[(end[i])][(head[i])]=real[(head[i])][(end[i])];image[(end[i])][(head[i])]=image[(head[i])][(end[i])];for(j=1;j<=bus;j++)if((j==head[i])||(j==end[i])){real[j][j]+=(-1)*real[(head[i])][(end[i])];image[j][j]+=(-1)*image[(head[i])][(end[i])];}}/*下边考虑对地之路*/for(i=1;i<=line;i++){image[head[i]][head[i]]+=duidi[i];image[end[i]][end[i]]+=duidi[i];}/*对地之路考虑结束*//*下边是考虑变压器的非标准变比的程序*/for(i=1;i<=line;i++){tt1=real[(head[i])][(end[i])];tt2=image[(head[i])][(end[i])];real[(head[i])][(end[i])]=real[(head[i])][(end[i])]/fabs(ratio[i]);image[(head[i])][(end[i])]=image[(head[i])][(end[i])]/fabs(ratio[i]);real[(end[i])][(head[i])]=real[(head[i])][(end[i])];image[(end[i])][(head[i])]=image[(head[i])][(end[i])];if(ratio[i]>0){real[head[i]][head[i]]=real[head[i]][head[i]]-tt1*(1-ratio[i])/(ratio[i]*ratio[i])-real[(head[i])][(end[i ])]+tt1;image[head[i]][head[i]]=image[head[i]][head[i]]-tt2*(1-ratio[i])/(ratio[i]*ratio[i])-image[(head[i])] [(end[i])]+tt2;}if(ratio[i]<0){real[end[i]][end[i]]=real[(end[i])][(end[i])]-tt1*(1+ratio[i])/(ratio[i]*ratio[i])-real[(head[i])][(end[i] )]+tt1;image[end[i]][end[i]]=image[(end[i])][(end[i])]-tt2*(1+ratio[i])/(ratio[i]*ratio[i])-image[(head[i])] [(end[i])]+tt2;}}/*考虑变压器的非标准变比的程序结束*/fprintf(fp2,"========================================================= =================================\n\n");fprintf(fp2," 节点导纳阵为:Y=\n");/*打印节点导纳阵*/for(i=1;i<=bus;i++){for(j=1;j<=bus;j++)fprintf(fp2," %f+j%f",real[i][j],image[i][j]);fprintf(fp2,"\n");}/*节点导纳阵已经求出,并已经打印*/fprintf(fp2,"========================================================= ==================================\n\n");for (i=1;i<=bus;i++){ ee[i]=e[i];ff[i]=f[i];}loop : for (i=1;i<=bus;i++){ e[i]=ee[i];f[i]=ff[i];}fprintf(fp2,"=====================================迭代过程==============================================\n\n");fprintf(fp2,"迭代过程中的电压和功率初值为:\n");for(i=1;i<=bus;i++){if(type[i]==1)fprintf(fp2," 节点%d e=%f f=%f p=%f Q=%f\n",node[i],e[i],f[i],p0[i],Q0[i]);else if(type[i]==2)fprintf(fp2," 节点%d e=%f f=%f p=%f\n",node[i],e[i],f[i],p0[i]);}fprintf(fp2,"------------------------------------------------------------------------------------\n");circle=1;/*circle为迭代的次数*//*下边迭代开始*/do{fprintf(fp2,"第%d 次迭代\n",circle);for(i=1;i<=bus;i++){if(type[i]==1){p[i]=0;Q[i]=0;}else if(type[i]==2)p[i]=0;}/*下边是求修正方程的不平衡列向量*/fprintf(fp2,"\n修正方程的不平衡量为:\n");m=1;n=1;for(i=1;i<=bus;i++){if(type[i]==1){for(j=1;j<=bus;j++){p[i]+=(e[i]*(real[i][j]*e[j]-image[i][j]*f[j])+f[i]*(real[i][j]*f[j]+image[i][j]*e[j]));Q[i]+=(f[i]*(real[i][j]*e[j]-image[i][j]*f[j])-e[i]*(real[i][j]*f[j]+image[i][j]*e[j]));}a[m]=p0[i]-p[i];a[(++m)++]=Q0[i]-Q[i];/*a数组存放pQ节点的不平衡量*/ }if(type[i]==2){for(j=1;j<=bus;j++){p[i]+=(e[i]*(real[i][j]*e[j]-image[i][j]*f[j])+f[i]*(real[i][j]*f[j]+image[i][j]*e[j]));}b[n]=p0[i]-p[i];b[(++n)++]=e0[i]*e0[i]+f0[i]*f0[i]-e[i]*e[i]-f[i]*f[i];}/*b数组存放pv节点的不平衡量*/}for(i=1;i<=2*pQ;i++)ub[i]=a[i];/*ub存放的是修正方程的不平衡列向量*/for(i=1;i<=2*pv;i++)ub[i+2*pQ]=b[i];for(i=1;i<=2*bus-2;i++)fprintf(fp2," ub[%d]=%f",i,ub[i]);/*不平衡量已经求出并已经打印*//*下边开始求雅克比矩阵*/fprintf(fp2,"\n------------------------------------------------------------------------------------");fprintf(fp2,"\n雅克比矩阵为:");for(i=1;i<=bus;i++)for(j=1;j<=bus;j++){a1[i][j]=0;b1[i][j]=0;}for(i=1;i<=bus;i++){for(j=1;j<=bus;j++)if(i!=j){a1[i][i]+=(real[i][j]*e[j]-image[i][j]*f[j]);b1[i][i]+=(real[i][j]*f[j]+image[i][j]*e[j]);}a1[i][i]+=(real[i][i]*e[i]-image[i][i]*f[i]);b1[i][i]+=(real[i][i]*f[i]+image[i][i]*e[i]);}for(i=1;i<=bus;i++)for(j=1;j<=bus;j++){if(type[i]==1){H[i][j]=(-1)*image[i][j]*e[i]+real[i][j]*f[i];N[i][j]=real[i][j]*e[i]+image[i][j]*f[i];J[i][j]=(-1)*N[i][j];L[i][j]=H[i][j];}else if(type[i]==2){H[i][j]=(-1)*image[i][j]*e[i]+real[i][j]*f[i];N[i][j]=real[i][j]*e[i]+image[i][j]*f[i];if(i==j){R1[i][j]=2*f[i];S[i][j]=2*e[i];}else if(i!=j){R1[i][j]=0;S[i][j]=0;}}if(i==j){H[i][j]=H[i][j]+b1[i][j];N[i][j]=N[i][j]+a1[i][j];J[i][j]=J[i][j]+a1[i][j];L[i][j]=L[i][j]-b1[i][j];}}num=1;for(i=1;i<=bus;i++){if(type[i]==1){t1[num]=i;num++;}}num=1;{if(type[j]==2){t2[num]=j;num++;}}for(i=1;i<=pQ;i++)d[i]=t1[i];for(i=pQ+1;i<=bus-1;i++)d[i]=t2[i-pQ];for(i=1;i<=2*pQ;i=i+2)for(j=1;j<=2*bus-2;j=j+2){x=d[(i+1)/2];y=d[(j+1)/2];B[i][j]=H[x][y];B[i][j+1]=N[x][y];B[i+1][j]=J[x][y];B[i+1][j+1]=L[x][y];}for(i=2*pQ+1;i<2*bus-1;i=i+2)for(j=1;j<2*bus-1;j=j+2){x=d[(i+1)/2];y=d[(j+1)/2];B[i][j]=H[x][y];B[i][j+1]=N[x][y];B[i+1][j]=R1[x][y];B[i+1][j+1]=S[x][y];}fprintf(fp2,"\n\n");for(i=1;i<2*bus-1;i++){for(j=1;j<2*bus-1;j++)fprintf(fp2," %f",B[i][j]);fprintf(fp2,"\n");}fprintf(fp2,"\n----------------------------------------------------------------------------");/*下面是用LU分解法求雅克比矩阵的逆矩阵的程序*/w=2*bus-2;/*雅克比矩阵的阶数*/for(j=1;j<=w;j++){if(i==j){E[i][j]=1;}elseE[i][j]=0;}/*单位矩阵已经生成*/for(i=1;i<=w;i++)for(j=1;j<=w;j++)zgjz[i][j]=B[i][j];for(i=1;i<=w;i++)for(j=w+1;j<=2*w;j++)zgjz[i][j]=E[i][j-w];for(i=1;i<=2*w;i++)for(j=1;j<=w;j++)Un[1][i]=zgjz[1][i];for(k=2;k<=w;k++)Ln[k][1]=zgjz[k][1]/Un[1][1];for(r=2;r<=w;r++){for(i=r;i<=2*w;i++){t=0;for(k=1;k<=r-1;k++)t+=Ln[r][k]*Un[k][i];Un[r][i]=zgjz[r][i]-t;}for(j=r+1;j<=w;j++){s=0;for(k=1;k<=r-1;k++)s+=Ln[j][k]*Un[k][r];Ln[j][r]=((zgjz[j][r]-s)/Un[r][r]);}}for(i=1;i<=w;i++)for(j=1;j<i;j++)Un[i][j]=0;for(i=1;i<=w;i++)for(j=1;j<=w;j++)Eu[i][j]=Un[i][j+w];for(j=w;j>=1;j--)Bn[w][j]=Eu[w][j]/Un[w][w];for(i=w-1;i>=1;i--)for(j=1;j<=w;j++){t=0;for(k=i+1;k<=w;k++)t+=Un[i][k]*Bn[k][j];for(k=i+1;k<=w;k++)Bn[i][j]=(Eu[i][j]-t)/Un[i][i];/*Bn[i][j]就是原雅克比矩阵的逆矩阵*/ }/*求逆矩阵的程序结束*/for(i=1;i<=w;i++)du[i]=0;for(i=1;i<=w;i++)for(j=1;j<=w;j++)du[i]+=Bn[i][j]*ub[j];fprintf(fp2,"\n修正量为:\n");for(i=1;i<=w;i++)fprintf(fp2," du[%d]=%.6f",i,du[i]);fprintf(fp2,"\n-------------------------------------------------------------------------\n");for(i=1;i<=pQ;i++){f[d[i]]+=du[(2*i-1)];e[d[i]]+=du[(2*i)];fprintf(fp2," f[%d]=%f e[%d]=%f\n",d[i],f[d[i]],d[i],e[d[i]]);}for(i=pQ+1;i<=bus-1;i++){f[d[i]]+=du[2*i-1];e[d[i]]+=du[2*i];fprintf(fp2," f[%d]=%f e[%d]=%f\n",d[i],f[d[i]],d[i],e[d[i]]);}dumax=fabs(du[1]);for(i=2;i<=w;i++){if(fabs(du[i])>dumax)dumax=fabs(du[i]);}circle++;}while(dumax>=0.00010 && circle<=50);fprintf(fp2,"\n-------------------------------------------------------------------------");fprintf(fp2,"\n ***************迭代过程结束*****************\n");fprintf(fp2,"============================================================= ===========================");fprintf(fp2,"\n平衡节点的功率为:\n");ps=0;Qs=0;for(i=1;i<=bus;i++){if(type[i]==3){for(j=1;j<=bus;j++){ps+=(real[i][j]*e[j]-image[i][j]*f[j]);Qs+=((-1)*real[i][j]*f[j]-image[i][j]*e[j]);}ps=ps*e[i];Qs=Qs*e[i];p0[i]=ps;Q0[i]=Qs;fprintf(fp2," S=%f+j%f\n",ps,Qs);}}fprintf(fp2,"pv节点的无功功率为:\n");for(i=1;i<=bus;i++){if(type[i]==2){ Q0[i]=0;for(j=1;j<=bus;j++)Q0[i]+=(f[i]*(real[i][j]*e[j]-image[i][j]*f[j])-e[i]*(real[i][j]*f[j]+image[i][j]*e[j]));fprintf(fp2," Q0[%d]=%f\n",i,Q0[i]);}}/*下边是考虑无功越限情况下的程序*/for(i=1;i<=bus;i++){if(type[i]==2 && Q0[i]>Qmax){ fprintf(fp2,"\n************************无功越限情况下的重新迭代过程*********************\n");pQ++;pv--;Q0[i]=Qmax;/*如果越限,则给pv节点的无功功率赋值为给定的Qmax*/type[i]=1;for(j=1;j<=bus;j++){p[i]=0;Q[i]=0;}goto loop;/*如果pv节点的无功功率超出了给定的Qmax,那么就返回到loop 重新进行迭代过程*/}}/*无功越限程序考虑完毕*//*下边是求线路上的功率的一段程序*/fprintf(fp2,"线路上的功率为:\n");for(i=1;i<=line;i++){real[head[i]][0]=0;real[end[i]][0]=0;image[end[i]][0]=duidi[i];image[head[i]][0]=duidi[i];}for(i=1;i<=line;i++){if(flag[i]==1)/*这是考虑单回线运行时支路的功率和损耗情况*/{pline[head[i]][end[i]]=((real[head[i]][0]+real[head[i]][end[i]])*(e[head[i]]*e[head[i]]+f[head[i]]*f [head[i]])-(e[head[i]]*e[end[i]]+f[head[i]]*f[end[i]])*real[head[i]][end[i]]-(f[head[i]]*e[end[i]]-e[ head[i]]*f[end[i]])*image[head[i]][end[i]])*(-1);Qline[head[i]][end[i]]=((-1)*(image[head[i]][0]+image[head[i]][end[i]])*(e[head[i]]*e[head[i]]+f[ head[i]]*f[head[i]])+(e[head[i]]*e[end[i]]+f[head[i]]*f[end[i]])*image[head[i]][end[i]]+(e[head[i] ]*f[end[i]]-f[head[i]]*e[end[i]])*real[head[i]][end[i]])*(-1);pline[end[i]][head[i]]=((real[end[i]][0]+real[end[i]][head[i]])*(e[end[i]]*e[end[i]]+f[end[i]]*f[end [i]])-(e[head[i]]*e[end[i]]+f[head[i]]*f[end[i]])*real[end[i]][head[i]]-(f[end[i]]*e[head[i]]-e[end[i] ]*f[head[i]])*image[end[i]][head[i]])*(-1);Qline[end[i]][head[i]]=((-1)*(image[end[i]][0]+image[end[i]][head[i]])*(e[end[i]]*e[end[i]]+f[en d[i]]*f[end[i]])+(e[head[i]]*e[end[i]]+f[head[i]]*f[end[i]])*image[end[i]][head[i]]-(f[end[i]]*e[he ad[i]]+e[end[i]]*f[head[i]])*real[end[i]][head[i]])*(-1);dpline[head[i]][end[i]]=pline[head[i]][end[i]]+pline[end[i]][head[i]];dQline[head[i]][end[i]]=Qline[head[i]][end[i]]+Qline[head[i]][end[i]];fprintf(fp2," S[%d][%d]=%f +j %f\n",head[i],end[i],pline[head[i]][end[i]],Qline[head[i]][end[i]]);fprintf(fp2," S[%d][%d]=%f +j %f\n",end[i],head[i],pline[end[i]][head[i]],Qline[end[i]][head[i]]);}else if(flag[i]==2)/*这是考虑双回线运行时支路的功率和损耗情况*/{pline[head[i]][end[i]]=pline[head[i]][end[i]]/2;Qline[head[i]][end[i]]=Qline[head[i]][end[i]]/2;pline[end[i]][head[i]]=pline[end[i]][head[i]]/2;Qline[end[i]][head[i]]=Qline[end[i]][head[i]]/2;dpline[head[i]][end[i]]=dpline[head[i]][end[i]]/2;dQline[head[i]][end[i]]=dQline[head[i]][end[i]]/2;fprintf(fp2," S[%d][%d]=%f +j %f\n",head[i],end[i],pline[head[i]][end[i]],Qline[head[i]][end[i]]);fprintf(fp2," S[%d][%d]=%f +j %f\n",end[i],head[i],pline[end[i]][head[i]],Qline[end[i]][head[i]]);}}fprintf(fp2,"\n-------------------------------------------------------------------------------------------\n");fprintf(fp2,"考虑平行之路和接地之路情况时\n单条线路损耗的功率为:\n");for(i=1;i<=line;i++)fprintf(fp2,"\n 线路%d 上的功率损耗为: %f +j %f",i,dpline[head[i]][end[i]],dQline[head[i]][end[i]]);fprintf(fp2,"\n-------------------------------------------------------------------------------------------\n");/*下边是求网络总损耗的程序*/fprintf(fp2,"网络总损耗为:\n");dpsum=0;dQsum=0;for(i=1;i<=bus;i++)dpsum+=p0[i];for(i=1;i<=bus;i++)dQsum+=Q0[i];fprintf(fp2," ds= %f +j %f\n",dpsum,dQsum);/*网络总损耗完毕*/fprintf(fp2,"-----------------------------------------------------------------------------------------------\n");/*下边是求数点效率的程序*/fprintf(fp2,"输电效率为:\n");p1=0;p2=0;for(i=1;i<=bus;i++){if(type[i]!=3){if (p0[i]>0)p1+=p0[i];elsep2+=(-1)*p0[i];}}p1=p1+ps;efficiency=p2/p1*100;/*输电效率完毕*/fprintf(fp2,"efficiency=%.4f%",efficiency);/*efficiency是输电效率*/fprintf(fp2,"\n============================================================ ===================================\n");fprintf(fp2," **********************潮流计算结束*********************");fclose(fp2);/*关闭output.txt文件*/printf("!!******计算结果存放于out.txt文件中******!!\n");}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
unsigned int i,j,k;
//消元过程
for(i=0;i<Dimension;i++)
{
//规格化过程:(每次消元前,先规格化,以便以下各行消元时,消元系数直接取待消
//列元素的值即可,也便于回代过程,而运算量并不增加)
for( j = i+1; j < Dimension; j++ )
D[y][y].diandao+=lineg;//尾节点自导纳中电导
D[y][x].dianna=D[x][y].dianna;//首节点与尾节点之间导纳与尾节点与首节点之间导纳相等
D[y][x].diandao=D[x][y].diandao;
}
if(gLineData[i].Type==2)//对线路为变压器的类型 对变压器进行π型等值 计算方法与导线型相同
{
if( FactorMatrix[j][i] != 0 ) //如果第j行第i列元素本就是0,则不需本列对应的消元过程
{
for( k = i + 1; k < Dimension; k++ ) //当FactorMatrix[i][k]=0,a[j][k]值不变,可省去运算
{
D[x][y].dianna+=(-1)*lineb/gLineData[i].Conductance;
D[x][y].diandao+=(-1)*lineg/gLineData[i].Conductance;
D[x][x].diandao+=lineg/gLineData[i].Conductance+(1-gLineData[i].Conductance)*lineg/(gLineData[i].Conductance*gLineData[i].Conductance);
{
FactorMatrix[i][j] = FactorMatrix[i][j] / FactorMatrix[i][i];
}
ConstVector[i] = ConstVector[i]/FactorMatrix[i][i];
for( j = i+1; j < Dimension; j++ ) //消去第i列(从i+1行到最后一行)
};
struct daona D[NODE_TOTAL_NUM][NODE_TOTAL_NUM];//定义一个二维数组存放导纳元素并对定义的数组赋0
int j;
for (i=0;i<NODE_TOTAL_NUM;i++)
for (j=0;j<NODE_TOTAL_NUM;j++)
{
D[i][j].dianna=0;
printf("\n节点数据\n");
for(i=0;i<NODE_TOTAL_NUM;i++)
{
fscanf(fp,"%d %d %f %f",&gNodeData[i].Index,
&gNodeData[i].Type,
&gNodeData[i].FirstInput,
float Resistance; //resistance of the line
float Reactance; //reactance of the line
float Conductance; //Line: conductance B/2,transformer:change ratio
lineb=(-1)*gLineData[i].Reactance/tab; //第i条线路电纳
if(gLineData[i].Type==1)//对线路为导线的类型
{
D[x][y].dianna+=(-1)*lineb;//首尾节点之间互导纳中的电纳
&gLineData[i].Reactance,
&gLineData[i].Conductance);
printf("%u %u %u %u %u %f %f %f\n",gLineData[i].Index,
gLineData[i].Type,
{
unsigned int Index; //node index
unsigned int Type; //node type: PQ:1,PV:2,balance point:0
float FirstInput; //PQ or PV:active power,balance point:V
D[x][y].diandao+=(-1)*lineg;//首尾节点之间互导纳中的电导
D[x][x].diandao+=lineg;//首节点自导纳中电导
D[x][x].dianna+=lineb+gLineData[i].Conductance;//首节点自导纳中电纳
D[y][y].dianna+=lineb+gLineData[i].Conductance;//尾节点自导纳中电纳
ConstVector[i-1] = ConstVector[i-1] - FactorMatrix[i-1][j] * ConstVector[j]; //a[i][k]=0时可以不算
}
}
return;
}
int main(int argc, char* argv[])
float SecondInput; //PQ:reactive power,PV:V,balance point:angle
};
struct NodeData gNodeData[NODE_TOTAL_NUM]; // define a global variable of node
unsigned int Status; //line status: on:1,off:0
unsigned int SrcNode; //source node index of this line
unsigned int DestNode;//destination node index of this line
{
printf("Hello World!\n");
//第一阶段 输入节点和线路数据
FILE* fp; //file structure
int i;
fp=fopen(NODE_DATA_FILENAME,"rb"); //open and read the node data输入节点数据
#define NODE_DATA_FILENAME "E:\\loadflow\\node.txt"
#define LINE_TOTAL_NUM 9
struct LineData
{
unsigned int Index; //line index
unsigned int Type; //line type: Line:1,tranformer:2,line connected to ground:3
}
}
//回代过程
for( i = Dimension-1; i > 0; i-- ) //Dimension-2:最后一个变量可直接获得,从n-1个变量求起
{
for(j = Dimension-1; j > i-1 ; j-- )
{
if( FactorMatrix[i-1][j] != 0 )
&gLineData[i].Type,
&gLineData[i].Status,
&gLineData[i].SrcNode,
&gLineData[i].DestNode,
&gLineData[i].Resistance,
};
struct LineData gLineData[LINE_TOTAL_NUM];
#define LINE_DATA_FILENAME "E:\\loadflow\\line.txt"
void SolveEquation(unsigned int Dimension,float FactorMatrix[14][14], float ConstVector[14]) //求解方程的函数 Ax=B
&gNodeData[i].SecondInput);
printf("%d %d %f %f\n",gNodeData[i].Index,
gNodeData[i].Type,
gNodeData[i].FirstInput,
gNodeData[i].SecondInput);
y=gLineData[i].DestNode-1;
tab=pow(gLineData[i].Resistance,2)+pow(gLineData[i].Reactance,2);//第i条线路电阻与电抗平方之和
lineg=gLineData[i].Resistance/tab; //第i条线路电导
gLineData[i].Status,
gLineData[i].SrcNode,
gLineData[i].DestNode,
gLineData[i].Resistance,
gLineData[i].Reactance,
}
