基于matlab的图像去雾算法详细讲解与实现-附matlab实现源代码
基于MATLAB的户外监控图像去雾及清晰化处理方案的研究

基于MATLAB的户外监控图像去雾及清晰化处理方案的研究基于MATLAB的户外监控图像去雾及清晰化处理方案的研究摘要:近年来,随着科技的不断进步与发展,监控设备在社会安全领域中扮演着重要的角色。
然而,由于天气条件或环境因素的影响,户外监控图像中常常存在雾霾及模糊问题,进而降低了监控图像的质量和清晰度。
为此,本文提出了一种基于MATLAB的户外监控图像去雾及清晰化处理方案,旨在提高户外监控图像的质量和清晰度。
1. 引言户外监控系统在保障社会安全方面起着至关重要的作用。
然而,由于气象条件或环境因素的限制,户外监控图像中常常受到雾霾的影响,从而导致图像质量下降、细节模糊等问题。
为了解决这一问题,本文提出了一种基于MATLAB的户外监控图像去雾及清晰化处理方案。
2. 相关技术2.1 雾霾成因与特点雾霾是一种由于大气中的悬浮颗粒物或水滴聚集引起的能见度降低的现象。
其成因主要包括大气污染物、气压变化以及湿度等气象因素。
雾霾导致的图像问题主要表现为色调偏暗、对比度降低以及细节模糊等。
2.2 图像去雾算法图像去雾是一种通过数学模型和算法,将雾霾中的影响因素去除,恢复原本清晰的图像的过程。
常用的图像去雾算法包括大气光估计、逆向模糊以及图像增强等。
2.3 图像清晰化算法图像清晰化算法旨在增强图像的清晰度和细节。
常用的图像清晰化算法包括锐化增强、频率域滤波以及边缘增强等。
3. 方法本文提出了一种综合性的基于MATLAB的户外监控图像去雾及清晰化处理方案。
具体步骤如下:(1) 预处理:对获取到的监控图像进行预处理,包括色彩空间转换、降噪等操作,使得图像更适合后续处理。
(2) 雾霾去除:根据雾霾成因和特点,采用大气光估计和逆向模糊的算法来去除图像中的雾霾,恢复图像的清晰度和对比度。
(3) 图像增强:应用图像增强算法,如锐化增强、频率域滤波和边缘增强等,来增强图像的清晰度和细节。
(4) 结果评估:通过与原始图像进行主观和客观评估,来评估处理结果的质量和性能。
Matlab中的图像去模糊与运动估计技术详解

Matlab中的图像去模糊与运动估计技术详解导言在数字图像处理中,图像模糊是一个常见的问题。
图像模糊可以由多种原因引起,如图像采集设备或相机的不稳定性、图像运动或振动等。
在Matlab中,有许多强大的图像处理工具和函数可以帮助我们解决这些模糊问题。
本文将详细介绍Matlab中的图像去模糊和运动估计技术。
一、图像去模糊技术1.1 点扩散函数(PSF)估计在进行图像去模糊之前,我们首先需要估计点扩散函数(Point Spread Function,PSF)。
PSF描述了从一个点源发出的光在传播过程中如何扩散。
Matlab中有多种方法可以估计PSF。
其中一种常用的方法是利用模糊图像和原始清晰图像之间的关系来估计PSF。
Matlab提供了一些函数,如“deconvblind”和“deconvreg”,可用于此目的。
1.2 盲去卷积在图像模糊恢复中,如果我们没有关于图像模糊的先验知识,就需要使用盲去卷积技术。
盲去卷积是指在不知道点扩散函数的情况下,通过观察被模糊的图像和已知的待恢复的图像之间的差异来进行图像去模糊操作。
Matlab中的“deconvblind”函数可以用于盲去卷积。
1.3 维纳滤波维纳滤波是一种常用的图像去模糊技术,它在图像恢复过程中考虑了模糊和噪声。
维纳滤波通过最小化图像的均方误差来进行优化。
Matlab中的“wiener2”函数可以用于维纳滤波。
1.4 正则约束图像修复正则约束图像修复是一种通过将图像恢复问题转化为最小化一个带有正则项的目标函数来进行图像去模糊操作的技术。
常用的正则项包括全变差(Total Variation)和L1范数。
Matlab中的“deconvreg”函数可以用于正则约束图像修复。
二、运动估计技术2.1 全局运动估计全局运动估计通常用于估计整个图像或图像序列中的全局运动。
这种方法通过找到在两个或多个图像之间最佳匹配的位置来估计运动。
Matlab中的“imregtform”函数可以用于全局运动估计。
图像去雾霭算法及其实现..

图像去雾霭算法及其实现电气工程及其自动化学生姓名杨超程指导教师李国辉摘要雾霭等天气条件下获得的图像,具有图像不清晰,颜色失真等等一些图像退化的现象,直接影响了视觉系统的发挥。
因此,为了有效的改善雾化图像的质量,降低雾霭等天气条件下造成户外系统成像的影响,对雾霭图像进行有效的去雾处理显得十分必要。
本设计提出了三种图像去雾算法,一种是基于光照分离模型的图像去雾算法;一种是基于直方图均衡化的图像去雾算法;还有一种是基于暗原色先验的图像去雾算法。
并在MATLAB的基础上对现实生活的图像进行了去雾处理,最后对不同的方法的处理结果进行了简要的分析。
关键词:图像去雾光照分离直方图均衡化暗原色先验Algorithm and its implementation of image dehazingMajor Electrical engineering and automationStudent Yang Chaocheng Supervisor Li GuohuiAbstract Haze weather conditions so as to obtain the image, the image is not clear, the phenomenon of color distortion and so on some image degradation, directly influence the exertion of the visual system. Therefore, in order to effectively improve the atomization quality of the image, reduce the haze caused by outdoor weather conditions such as imaging system, the influence of the haze image effectively it is necessary to deal with the fog.This design introduced three kinds of algorithms of image to fog, a model is based on the separation of light image to fog algorithm; One is the image to fog algorithm based on histogram equalization; Another is based on the dark grey apriori algorithms of image to fog. And on the basis of MATLAB to the real life to deal with the fog, the image of the processing results of different methods are briefly analyzed.Key words:Image to fog Light separation histogram Dark grey目录摘要 (I)Abstract. (II)目录1绪论图像去雾霭算法及其实现 (1)1.1研究背景及意义 (1)1.2当前图像去雾霭技术发展现状及其趋势 (2)1.3 本文的章节安排 (2)1.4小结 (3)2图像去雾霭基础理论 (4)2.1雾霭的形成机理 (4)2.2图像去雾算法 (4)2.2.1图像增强技术 (5)2.2.2图像复原技术 (5)2.3基于图像增强的去雾霭算法 (5)2.3.1同态滤波 (6)2.3.2光照分离模型 (7)2.3.3小结 (11)2.4基于直方图均衡化的图像去雾算法 (11)2.4.1直方图均衡化去雾原理 (11)2.4.2直方图均衡化模型 (12)2.4.3直方图均衡化的算法步骤 (12)2.4.4小结 (16)2.5基于图像复原的去雾霭方法 (16)2.5.1暗原色先验去雾霭原理 (16)2.5.2暗原色先验模型 (16)2.5.3算法概述 (17)2.5.4小结: (20)3实验结果 (21)4总结与展望 (22)附录1 光照分离代码 (23)附录2 基于直方图均衡化的图像去雾代码 (25)附录3 暗原色先验的去雾代码 (27)参考文献 (29)致谢 (30)图像去雾霭算法及其实现1绪论图像作为人类感知世界的主要视觉基础,是人类获取信息以及表达信息的重要方法。
数字图像去雾算法研究毕业论文

毕业论文(设计) 题目数字图像去雾算法研究学生姓名学号院系计算机与软件学院专业计算机科学与技术指导教师声明本人郑重声明:1、持以“求实、创新”的科学精神从事研究工作。
2、本论文是我个人在导师指导下进行的研究工作和取得的研究成果。
3、本论文中除引文外,所有实验、数据和有关材料均是真实的。
4、本论文中除引文和致谢的内容外,没有抄袭其他人或其他机构已经发表或撰写过的研究成果。
5、其他同志对本研究所做的贡献均已在论文中作了声明并表示了谢意。
作者签名:日期:目录1 引言 (1)2 图像去雾算法 (1)2.1 基于光照分离模型的图像去雾算法 (2)2.1.1 算法概述 (2)2.1.2 同态滤波 (3)2.1.3 模型简介 (3)2.1.4 偏微分方程求解 (4)2.2 基于直方图均衡化的图像去雾算法 (7)2.2.1 算法概述 (7)2.2.2 直方图修正技术的基础 (7)2.2.3 直方图的均衡化 (8)2.2.4 直方图均衡化的算法步骤 (9)2.3 基于暗原色先验的图像去雾算法 (10)2.3.1 算法概述 (10)2.3.2 已有雾成像模型 (10)2.3.2 暗原色先验 (11)2.3.3 暗原色先验去雾算法分析 (11)3 数字图像去雾系统的设计 (12)3.1 开发工具—MATLAB (12)3.2系统设计 (13)3.3 菜单设计 (13)3.4 模块设计 (13)3.5 界面设计 (14)3.5.1 界面设计原则 (14)3.5.2 界面设计步骤 (14)4 数字图像去雾系统的实现 (19)4.1图片打开模块 (19)4.2基于光照分离模型的图像去雾模块 (19)4.2.1 同态滤波及光照分离代码 (19)4.2.2 去雾效果图 (21)4.2.3 结果分析 (21)4.3基于直方图均衡化的图像去雾模块 (22)4.3.1 代码 (22)4.3.2 去雾效果图 (23)4.3.3 结果分析 (23)4.4基于暗原色先验的图像去雾模块 (24)4.4.1代码 (24)4.4.2 去雾效果图 (25)4.4.3 结果分析 (26)4.5图片保存模块 (26)5 系统运行效果 (27)5.1 整体界面运行效果 (27)5.2 文件打开运行效果 (27)5.2 基于光照分离模型图像去雾效果图 (28)5.3直方图均衡化图像去雾效果图 (29)5.4基于暗原色先验的去雾效果图 (30)5.5文件保存界面效果图 (30)6 结论 (31)数字图像去雾算法研究摘要:图像去雾是指运用一定的模型或算法,对已经雾化的图像进行处理,达到还原图像本来特征的过程。
基于MATLAB的图像去雾技术研究

基于MATLAB 的图像去雾技术研究齐卉a ,孙超*b ,苏通b ,马俊智b ,朱勇杰b ,丁建军c (江汉大学a.人工智能学院,b.智能制造学院,c.爆炸与爆破技术研究院,湖北武汉430056)摘要:为了对雾霾天气所采集的退化图像做清晰化处理,在MATLAB 平台下构建开发了一个图像去雾系统。
该系统能通过全局直方图均衡化、局部直方图均衡化、多尺度Retinex 、暗通道先验4种经典去雾算法对雾天降质图像进行不同程度的复原,统计图像质量评价指标对比去雾效果。
实验结果表明,经过不同去雾算法处理的图像的清晰度和对比度都有所提高,实际应用中可根据场景需要选择相应算法。
该系统的实现为图像去雾技术的研究奠定基础,具有良好的可操作性。
关键词:MATLAB ;图像去雾系统;图像质量评价中图分类号:TP391.41文献标志码:A 文章编号:1673-0143(2020)06-0084-07DOI :10.16389/42-1737/n.2020.06.012Study on Image Defogging Technology Based on MATLABQI Hui a ,SUN Chao *b ,SU Tong b ,MA Junzhi b ,ZHU Yongjie b ,DING Jianjun c(a.School of Artificial Intelligence ,b.School of Intelligent Manufacturing ,c.Institute of Explosion Science andBlasting Technology ,Jianghan University ,Wuhan 430056,Hubei ,China )Abstract :In order to restore the degraded images collected by outdoor acquisition devices inhaze weather ,this paper proposes an image defogging system on the MATLAB platform.The system can restore foggy degradation images to different degrees through four classicdefogging algorithms :global histogram equalization ,local histogram equalization ,multi-scale Retinex ,and dark channel prior.The defogging effects are compared by image qualityevaluation indicators.Experimental results show that the sharpness and contrast of theimages processed by different defogging algorithms have been improved ,and thecorresponding algorithm can be selected according to the needs of the scene in practicalapplications.The implement of the system lays a foundation for the research of imagedefogging technology ,and it has good operability.Key words :MATLAB ;image defogging system ;image quality evaluation第48卷第6期2020年12月江汉大学学报(自然科学版)J.Jianghan Univ.(Nat.Sci.Ed.)Vol.48No.6Dec.2020收稿日期:2020-04-08基金项目:国家自然科学基金资助项目(61941502);湖北省自然科学基金资助项目(2019CFB205);湖北省教育厅科学研究计划指导性项目(B2019242);武汉市教育局市属高校产学研项目(CXY201803)作者简介:齐卉(1992—),女,助理实验师,硕士,研究方向:信息获取、分析与处理。
视频图像增强和去雾算法matlab实现

视频图像增强和去雾算法说明摘要 本文档介绍夜间增强和去雾增强算法及其实现。
(1)将图像由RGB空间转换到HSI空间,然后对HSI空间亮度分量(I分量)的灰度直方图进行均衡化处理,然后再转换到RGB空间。
空间。
)利用暗原色先验图像去雾算法对图像进行去雾处理。
(2)利用暗原色先验图像去雾算法对图像进行去雾处理。
1目录一、通过I分量增强夜间图像 (3)1. 算法原理 (3)2. M ATLAB程序 (6) (77)3. 夜间增强效果 .................................................................................................................................二、去雾增强 (9) (99)1. 算法原理 .........................................................................................................................................2. M ATLAB程序 (11) (113)3. 去雾效果 .......................................................................................................................................参考文献 (14)一、通过I分量增强夜间图像1. 算法原理首先将图像由RGB空间转换到HSI空间,然后对HSI空间亮度分量(I分量)的灰度直方空间显示。
图进行均衡化处理,提高图像的亮度,然后转换回RGB空间显示。
(1)图像由RGB空间转换到HSI空间。
RGB向HSI模型的转换是由一个基于笛卡尔直角坐标系的单位立方体向基于圆柱极坐标的双锥体的转换。
图像去雾----暗通道

图像去雾----暗通道暗通道去雾算法原理及实现1. 算法原理。
基本原理来源于何凯明⼤神的CVPR09的论⽂暗通道。
所谓暗通道是⼀个基本假设,这个假设认为,在绝⼤多数的⾮天空的局部区域中,某⼀些像素总会有⾄少⼀个颜⾊通道具有很低的值。
这个其实很容易理解,实际⽣活中造成这个假设的原因有很多,⽐如汽车,建筑物或者城市中的阴影,或者说⾊彩鲜艳的物体或表⾯(⽐如绿⾊的树叶,各种鲜艳的花,或者蓝⾊绿⾊的睡眠),颜⾊较暗的物体或者表⾯,这些景物的暗通道总是变现为⽐较暗的状态。
所以暗通道是什么呢?其实⽐较简单,作者认为暗通道是:暗通道先验理论指出:暗通道实际上是在rgb三个通道中取最⼩值组成灰度图,然后再进⾏⼀个最⼩值滤波得到的。
我们来看⼀下有雾图像和⽆雾图像暗通道的区别:可以发现,有雾的时候会呈现⼀定的灰⾊,⽽⽆雾的时候咋会呈现⼤量的⿊⾊(像素为接近0),作者统计了5000多副图像的特征,基本都符合这样⼀条先验定理。
雾图形成模型计算机视觉中,下⾯这个雾图形成模型是被⼴泛使⽤的:其中I(x)是现有的图像(待去雾),J(x)是要恢复的原⽆雾图像,A是全球⼤⽓光成分,t(x)是透射率,现在的条件就是已知I(x),来求J(x),显然不加任何限制的话是有⽆穷多个解的。
但是现实⽣活中,即使是晴天⽩云,空⽓中也会存在⼀些颗粒,看远⽅的物体还是能够感觉到雾的影响,另外,雾的存在可以让⼈们感觉到景深的存在,所以我们保留⼀部分的雾,上式修正为:其中w是[0-1]之间的⼀个值,⼀般取0.95差不多。
上⾯的推导都是假设全球⼤⽓光是已知的,实际中,我们可以借助暗通道图来从有雾图像中来获取该值:1. 从暗通道图中按照亮度⼤⼩取前0.1%的像素。
2. 在这些位置中,在原始图像中寻找对应具有最⾼亮度点的值,作为A值。
到这⾥,我们就可以进⾏⽆雾图像的恢复了:当投射图t很⼩时,会导致J的值偏⼤,会导致图⽚某些地⽅过爆,所以⼀般可以设置⼀个阈值来限制,我们设置⼀个阈值:⼀般设置较⼩,0.1即可。
烟雾检测Matlab代码

tic;clear all;close all;clc;A = aviinfo('smoke.avi');mov = mmreader('smoke.avi');LEN = A.NumFrames;%得到视频的帧数for i = 1 : LENb = read(mov, i);imwrite(b, strcat('smoke', int2str(i), '.jpg'), 'jpg');endfor x = 1 : LENpic = imread(strcat('smoke', int2str(x), '.jpg'));%读入一张图片pic1 = pic;%pic1中存放的是处理过后的彩色图像pic_hsv = rgb2hsv(pic);s = size(pic1);bw_pic = zeros(s(1), s(2));for i = 1 : s(1)for j = 1 : s(2)if pic_hsv(i, j, 1) > 0.35 && pic_hsv(i, j, 1) < 0.65 && ...pic_hsv(i, j, 2) > 0.06 && pic_hsv(i, j, 2) < 0.3 && ...pic_hsv(i, j, 3) > 0.5 && pic_hsv(i, j, 3) <= 1;pic1(i, j, 1) = 255;pic1(i, j, 2 : 3) = 0;endif pic1(i, j, 1) == 255 && pic1(i, j, 2) == 0bw_pic(i, j) = 1;endendendcov_bw_pic = 1 - bw_pic;fill_pic = imfill(cov_bw_pic, 'holes');fill_pic1 = 1 - fill_pic;B_pic = bwboundaries(fill_pic1);%得到的是一个P×1的单元ss = size(B_pic);%ss的值就是连通分量的数量ss1 = size(B_pic{1, 1});%ss1是一个大小为m×2的矩阵max = ss1(1);for i = 2 : ss(1)%找到最大的连通区域的边界总个数ss2 = size(B_pic{i, 1});if ss2(1)> maxmax = ss2(1);endend%⑤…………………………将小于最大连通区域的连通分量边界赋零for k = 1 : ss(1)%将小于最大连通区域的连通分量边界赋零,%其作用就是将其余小的连通分量与边界隔开Mid = B_pic{k, 1};ss3 = size(Mid);if ss3(1) < maxfor i = 1 : ss3(1)fill_pic1(Mid(i, 1), Mid(i, 2)) = 0;endendend%反转填充cov_fill_pic1 = 1 - fill_pic1;A_fill_pic = imfill(cov_fill_pic1, 'holes');%进行内部填充,再反变换回来,即得到所要求的区域A_fill_pic1 = 1 - A_fill_pic;B_pic1 = bwboundaries(A_fill_pic1);sss = size(B_pic1);%sss的值就是连通分量的数量for k = 1 : sss(1)%该循环作用是找到最大区域的边界,然后在原图像的对应位置上赋红Mid = B_pic1{k};%Mid是一个m×2的矩阵,m就是边界点的数量%ss4(1)表示边界点的数量,Mid(i, 1)和Mid(i, 2)表示边界点的坐标ss4 = size(Mid);if ss4(1) == maxfor i = 1 : ss4(1)pic(Mid(i, 1), Mid(i, 2), 1) = 255;pic(Mid(i, 1), Mid(i, 2), 2 : 3) = 0;endendendimwrite(pic, strcat('lou_smoking', int2str(x), '.jpg'), 'jpg');endaviobj = avifile('lou_smoking.avi');%将处理后的图片连成视频文件aviobj.fps = 25;%初始化视频文件的属性aviobj.Quality = 100;pression = 'None';for i = 1 : LENframe = imread(strcat('lou_smoking', int2str(i), '.jpg'));aviobj = addframe(aviobj, uint8(frame));endaviobj=close(aviobj);%关闭aviobj的对象toc;。
利用Matlab仿真实现图像烟雾识别(k-means聚类图像分割+LBP+PCA+SVM)

利⽤Matlab仿真实现图像烟雾识别(k-means聚类图像分割+LBP+PCA+SVM)⽬录⼀、算法简介1.1 c-means聚类算法1 .2 LBP算法1.3 PCA算法1.4 SVM算法⼆、算法实现2.1 烟雾识别算法流程2.2 c-means算法实现2.3 LBP算法实现2.4 SVM算法实现三、结果分析⼀、算法简介1.1 c-means聚类算法聚类分析是根据在数据中发现的描述对象及其关系的信息,将数据对象进⾏分组。
⽬的是使组内的对象相互之间是相似的(相关的),⽽不同组中的对象是不同的(不相关的)。
组内相似性越⼤,组间差距越⼤,说明聚类效果越好。
也就是说,聚类的⽬标是得到较⾼的类内相似度和较低的类间相似度,使得类间的距离尽可能⼤,类内样本与类中⼼的距离尽可能⼩。
在此,我们选⽤k-means聚类算法。
1 .2 LBP算法LBP(Local Binary Pattern,局部⼆值模式)是⼀种⽤来描述图像局部纹理特征的算⼦;它具有旋转不变性和灰度不变性等显著的优点。
它是⾸先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出,⽤于纹理特征提取,提取的特征是图像的局部的纹理特征。
原始的LBP算⼦定义为在3*3的窗⼝内,以窗⼝中⼼像素为阈值,将相邻的8个像素的灰度值与其进⾏⽐较,若周围像素值⼤于中⼼像素值,则该像素点的位置被标记为1,否则为0。
这样,3*3邻域内的8个点经⽐较可产⽣8位⼆进制数(通常转换为⼗进制数即LBP码,共256种),即得到该窗⼝中⼼像素点的LBP值,并⽤这个值来反映该区域的纹理信息。
1.3 PCA算法PCA(Principal Component Analysis),即主成分分析⽅法,是⼀种使⽤最⼴泛的数据降维算法。
其算法步骤如下:1)数据中⼼化——去均值,根据需要,有的需要归⼀化——Normalized;2)求解协⽅差矩阵;3)利⽤特征值分解/奇异值分解求解特征值以及特征向量;4)将特征值从⼤到⼩排序,保留前k个特征向量5)利⽤特征向量构造投影矩阵;6)利⽤投影矩阵,得出降维的数据。
基于MATLAB的去雾图像质量评价系统

黑龙江工业学院学报JOURNAL OF HEILONGJIANG UNIVERSITY OF TECHNOLOGY第19卷第8期2019年8月Vol. 19 No. 8Aug. 2019文章编号:2096-3874(2019)08 -0036 -04基于MATLAB 的去雾图像质量评价系统韦忠亮,许光宇,张顺香(安徽理工大学,安徽 淮南232001)摘 要:雾霾天气对成像系统产生了很大的影响,在图像处理的发展中,优秀的去雾算法不 断被提出,对算法效果的评价也在不断深化。
针对图像质量评价算法繁多,在去雾效果评价上 针对性偏弱等问题,设计了一种基于MATLAB 可视化编程环境下的去雾图像质量评价系统,结合传统的去雾算法和基于深度学习的图像去雾技术,对选择进行实验测试的图像进行了不同技 术下的去雾处理,并选取了部分图像质量评价的指标,对去雾算法的性能进行了比对。
关键词:图像去雾;图像质量评价;MATLAB中图分类号:TP391 文献标识码:A随着人工智能理论的发展,深度学习对图像 处理、机器视觉领域的推动作用愈加显著,随之而涌现出的各种应用对图像处理的需求不断增加, 对图像质量进行高效、可靠的评价也变得越来越 重要。
工业促进了人类社会的发展,随之而来的负面影响是雾霾天气的增多,对成像系统造成很大 的影响,诸如成像模糊、对比度偏低、细节或部分特征缺失等,造成系统成像质量严重下降,对后期 的图像处理⑴例如人脸识别、图像分割等造成了很大的影响,而在成像后使用去雾算法进行去雾 处理,改善图像质量也一直是图像处理领域研究的前沿问题。
去雾前图像和去雾后图像的质量评价有着极高的研究意义,其决定了去雾算法是否切实可行并且高效,也一直是图像去雾处理后的 关键环节。
本文介绍了几种图像去雾算法,根据常用的 图像质量评价指标,结合原始图像和去雾后的图 像进行图像质量的评价。
去雾算法和图像质量评 价以及最终的GUI 系统的设计和实现都是基于MATLAB ⑵平台完成,该平台对于矩阵运算的能力很强,具有丰富的系统函数库以及可视化的图形用户界面,依据于MATLAB GUI 界面做出的系统 具有很好的鲁棒性。
基于matlab的发动机喷雾图像筛选程序设计

基于matlab的发动机喷雾图像筛选程序设计燃油雾化的好坏对发动机经济性、动力性、排放性等有着重要影响,而在燃油喷雾试验中会得到的大量喷雾图像,其中能满足要求反应雾化真实情况的少之又少。
笔者利用MATLAB编写辅助程序,采用灰度直方图、平均灰度、拉普拉斯算子、graythresh全局阈值、标准偏差等多种算法,结合GUI用户界面来实现喷雾图像自动筛选,避免人工的费时费力以及判别误差。
标签:喷雾实验;图像处理;MATLAB编程;GUI界面Abstract:The quality of fuel atomization has an important impact on engine economy,power performance,emissions and so on. However,a large number of spray images will be obtained in the fuel spray test,and few of them can meet the requirements of the actual conditions of reaction atomization. The author uses MATLAB to write auxiliary program,adopts many algorithms such as grayscale histogram,average gray scale,Laplace Operator,graythresh global threshold,standard deviation and so on,and with GUI user interface,intends to realize automatic screening of spray image,so as to avoid manual time and effort as well as discrimination error.Keywords:spray experiment;image processing;MATLAB programming;GUI interface1 概述發动机燃油雾化的好坏对发动机经济性、动力性、排放性等有着重要影响。
基于MATLAB的图像去雾处理技术

基于MATLAB的图像去雾处理技术基于MATLAB的图像去雾处理技术摘要:图像去雾技术是一项对雾化图像进行恢复处理来提高图像质量的重要技术。
本文基于MATLAB平台,综述了图像去雾处理的基本原理、相关算法和实现方法,并对不同算法进行了对比和性能评估。
结果表明,基于MATLAB的图像去雾技术在提高图像质量、恢复图像细节方面表现出良好的效果,具有较高的应用价值和实际意义。
1. 引言由于天气条件、环境污染等原因,图像中常常出现模糊不清、色彩失真的现象,这时候就需要对图像进行去雾处理,以提高图像的质量和信息的可读性。
图像去雾处理技术已经成为计算机视觉和图像处理领域的重要研究方向之一。
本文基于MATLAB平台,重点介绍基于物理模型和无参考图像去雾算法的原理和实现方法,并进行了详细的对比和性能评估。
2. 图像去雾原理图像去雾原理主要分为两种:物理模型和无参考图像去雾原理。
物理模型方法是基于光线传输模型,通过分析光线在大气中的散射和吸收规律,来恢复图像的细节和信息。
无参考图像去雾方法是不依赖于任何彩色中的参考图像和场景先验知识,仅仅通过分析图像本身的信息来进行去雾操作。
3. 基于物理模型的图像去雾算法基于物理模型的图像去雾算法主要包括大气光估计、雾剔除和图像恢复。
其中,大气光估计通过计算图像中最亮像素的值来估计大气光的强度。
雾剔除是通过将大气光分量从输入图像中减去,以提取出原始图像中的细节和信息。
图像恢复是使用去雾模型来恢复图像的细节和色彩,使得图像更加清晰和真实。
4. 基于无参考图像去雾算法无参考图像去雾方法是通过分析图像的统计特性和纹理信息来进行去雾处理。
其中,常用的算法包括暗通道先验、边缘保持过滤器等。
暗通道先验是基于自然图像中最暗像素通道的特点,通过估计雾浓度和大气光来进行图像去雾操作。
边缘保持过滤器是通过平滑图像中的纹理信息来减小雾的影响,从而提升图像的质量和可读性。
5. 基于MATLAB的图像去雾实现本文采用MATLAB平台进行图像去雾处理的实现,通过调用MATLAB中提供的图像处理工具箱和算法库,可以方便地实现各种图像去雾算法。
基于Matlab的图像去雾系统的设计研究

图 2 去雾系统主界面
在三种算法模式下,除了可以在右上角显示 去雾后的增强图像,还可以在下方显示算法产生 的对应中间结果,包括:暗通道优先处理算法的
针对雾天图像增强处理的研究已经成为计算机视觉和图像处理领域的研究热点吸引了国内外大量研究者提出了大量算法文中三种算法都能在一定程度上完成对带雾图像的清晰化处理但是在处理效果和处理速度上仍然各有差别各有优缺点暗通道优先算法的去雾效果最好但运算时间要远高于其他两种算法
2019 年 第2期
科技开发与应用
学 报(自然科学)
第 40 卷 总第 289 期
基于 Matlab 的图像去雾系统的设计研究
张道华
摘 要:为了实现雾天图像的增强,采用 Matlab 对集成直方图均衡化、Retinex、暗通道优先三种雾天图
像清晰化处理算法的去雾系统进行软件实现,不仅能够对这三种算法的最终结果和中间产物进行输出,还
能够对这三种算法的算法效率和算法结果进行直观数字的对比.实验表明,三种算法各有优缺点,实际应用
中可根据需要选取适当的算法.该系统的设计可为其他去雾算法的研究提供技术参考.
关键词:Matlab;图像增强;去雾系统;三种算法中图分类号:TP311
文献标识码:A
文章编号:1008-7974(2019)02-0001-06
DOI:10.13877/22-1284.2019.04.001
本去雾系统的构建与开发是在 Matlab 2011a 下完成的,因此,运行模块程序需在计算机上安 装 Matlab 2011a 或更高版本.打开 Matlab,在“文 件”(File)菜单栏中选择“打开…”(Open…)在文 件选择对话框中选择“.fig”文件,均可进入相应 界面的编辑窗口.
基于matlab的图像去雾算法详细讲解与实现-附matlab实现源代码

本文主要介绍基于Retinex理论的雾霭天气图像增强及其实现。
并通过编写两个程序来实现图像的去雾功能。
1 Rentinex理论Retinex(视网膜“Retina”和大脑皮层“Cortex”的缩写)理论是一种建立在科学实验和科学分析基础上的基于人类视觉系统(Human Visual System)的图像增强理论。
该算法的基本原理模型最早是由Edwin Land(埃德温•兰德)于1971年提出的一种被称为的色彩的理论,并在颜色恒常性的基础上提出的一种图像增强方法。
Retinex 理论的基本内容是物体的颜色是由物体对长波(红)、中波(绿)和短波(蓝)光线的反射能力决定的,而不是由反射光强度的绝对值决定的;物体的色彩不受光照非均性的影响,具有一致性,即Retinex理论是以色感一致性(颜色恒常性)为基础的。
根据Edwin Land提出的理论,一幅给定的图像S(x,y)分解成两幅不同的图像:反射物体图像R(x,y)和入射光图像L(x,y),其原理示意图如图8.3-1所示。
图-1 Retinex理论示意图对于观察图像S中的每个点(x,y),用公式可以表示为:S(x,y)=R(x,y)×L(x,y) (1.3.1)实际上,Retinex理论就是通过图像S来得到物体的反射性质R,也就是去除了入射光L的性质从而得到物体原本该有的样子。
2 基于Retinex理论的图像增强的基本步骤步骤一: 利用取对数的方法将照射光分量和反射光分量分离,即:S'(x, y)=r(x, y)+l(x, y)=log(R(x, y))+log(L(x, y));步骤二:用高斯模板对原图像做卷积,即相当于对原图像做低通滤波,得到低通滤波后的图像D(x,y),F(x, y)表示高斯滤波函数:D(x, y)=S(x, y) *F(x, y);步骤三:在对数域中,用原图像减去低通滤波后的图像,得到高频增强的图像G (x, y):G(x,y)=S'(x, y)-log(D(x, y));步骤四:对G(x,y)取反对数,得到增强后的图像R(x, y):R(x, y)=exp(G(x, y));步骤五:对R(x,y)做对比度增强,得到最终的结果图像。
【图像增强系列】基于暗原色先验的去雾论文 MATLAB源码及对比效果图

最近,基于单一图像的去雾取得了很大的进展。这些方法的成功往往得益于一个强有力的先验或假 设。Tan[16]观察到无雾图像比有雾图像具有更高的对比度,他通过扩大复原图像的局部对比度来达到去 雾的效果。这样得到的结果在视觉上是很吸引人的,但实际上在光学原理上达到去雾。Fattal[2]通过假 定透射率和表面投影在局部是不相关的,估算景物的反射率,来推断景物光在空气中传播时的透射率。 Fattal 的的做法比较准确,并且能产生很好的去雾结果。然而他的方法在雾浓度较大的时候便显得无能 为力,尤其是当他的假想一旦失效的时候。
根据暗原色先验的规律,无雾自然图像的暗原色项Jdark应该是接近于0的。 Jdark(x) = min c ( min y∈Ω(x) (Jc(y))) = 0. (9)
Ac 总是正的,导致:
min c ( min y∈Ω(x) (Jc(y) Ac )) = 0 (10) 把方程(10)带入方程(8),我们可以简单地估算出透射率t: ˜t(x) = 1 − min c ( min y∈Ω(x) ( Ic(y) Ac )). (11) 事实上,minc(miny∈Ω(x)( Ic(y) Ac )) Ac 是规格化的雾图Ic(y)的暗原色。它直接提供了透射信息。如前所述,暗原色先验对天空区域不成立, 但幸好在带雾的图像中天空的颜色总是同大气光A非常接近,所以在天空区域我们有: min c ( min y∈Ω(x) ( Ic(y) Ac )) → 1, and ˜t(x) → 0, 又因为天空光来自无穷远处,其透射率趋近于 0,所以式子(11)能较好地同时处理包含或者不包含天空的 区域。我们并不需要事先把天空部分单独加以处理。
烟雾动态提取 matlab

烟雾动态提取matlab全文共四篇示例,供读者参考第一篇示例:烟雾动态提取是一个在计算机视觉和图像处理领域常见且重要的任务。
烟雾经常出现在自然或人为灾难中,如火灾、爆炸等,烟雾的存在给图像处理和目标识别带来了很大的困难。
为了更好地理解并处理烟雾图像,烟雾动态提取技术应运而生。
在过去的几年中,烟雾动态提取已经成为了计算机视觉领域的一个研究热点,有很多研究者提出了各种各样的方法来解决这个问题。
基于Matlab的烟雾动态提取技术已经被广泛应用于各种应用中,包括安防监控、自然灾害监测等领域。
在Matlab中,有很多方法可以用来进行烟雾动态提取。
最常用的是基于背景建模和运动检测的方法。
背景建模可以提取出图像中的静态背景信息,而运动检测可以检测出图像中的移动对象,通过两者结合可以提取出烟雾区域。
在Matlab中实现烟雾动态提取的具体步骤如下:1. 读取视频帧:首先要将视频文件导入Matlab中,并且逐帧读取视频帧。
2. 背景建模:利用Matlab中的背景建模算法,如高斯混合模型(GMM)等,提取出视频帧中的静态背景信息。
3. 运动检测:运用Matlab中的光流法(Optical Flow)或运动检测算法,如帧差法等,检测出视频帧中的移动对象。
4. 烟雾提取:将运动对象与背景信息结合,通过一定的规则或算法,提取出视频帧中的烟雾区域。
5. 烟雾跟踪:对烟雾区域进行跟踪,可以利用Kalman滤波等跟踪算法,跟踪烟雾的运动轨迹。
通过以上步骤,就可以实现对烟雾动态信息的提取和跟踪。
在实际应用中,烟雾动态提取技术可以用于火灾监测、烟雾检测、自然灾害监测等领域。
在火灾监测中,可以通过实时监测烟雾信息,以及烟雾的移动轨迹,提前发现并报警火灾的发生。
烟雾动态提取技术在Matlab中的应用具有很大的潜力,可以在各种应用场景中发挥重要作用。
随着科学技术的不断进步和发展,相信烟雾动态提取技术在未来会得到更进一步的完善和应用。
希望本文能为烟雾动态提取技术的研究和应用提供一些参考和帮助。
基于MATLAB的雾天降质图像

毕业论文(设计)基于MATLAB的雾天降质图像的清晰化技术研究学生: 学号:系别: 专业:指导教师: 评阅教师:论文答辩日期2011年5月26日答辩委员会主席摘要随着信息技术的不断发展同时也伴随着人类工业化进程的不断前进,空气污染也越来越严重。
一项调查数据显示,一年雾天气所占的比例在逐年上升,而有雾天气会给人类的生产生活带来极大的不便。
有雾天气时,交通事故发生的概率大大增加。
一方面,数字图像处理已成为一个极其重要的学科和技术领域,在通信、语音、图像、遥感、生物工程等众多领域得到了广泛的应用。
另一方面,随着计算机视觉与图像处理技术的发展,户外视觉系统的研究与应用正在飞速发展。
如地形分类系统、户外监控系统、自动导航系统等的应用数量在急速攀升。
在恶劣天气条件下( 如雾天,雨天等) ,户外景物图像的对比度和颜色都会被改变或退化,图像中蕴含的许多特征都被覆盖或模糊,导致这些视觉系统无常工作。
因此,从大气退化图像中复原和增强景物细节信息具有重要的现实意义。
MATLAB是用于算法开发、数据可视化、数据分析以与数值计算的高级技术计算语言和交互式环境。
MATLAB 应用广泛,其中包括信号处理和通信、图像和视频处理、控制系统、测试和测量,计算金融学与计算生物学等众多应用领域。
在各行业和学术机构中,有一百多万工程师和科学家使用 MATLAB 这一技术计算语言,MATLAB中的GUIDE是专门用于图形用户界面的快速开发环境。
主要针对雾天情况下获取的降质灰度图像进行研究。
通过 MATLAB 对数字图像进行处理,建立衰减模型。
首先运用空间域中的直方图均衡化的领域处理后再经过像素点处理,对像素点处理采用三种方法来实现灰度图像的清晰化处理,即灰度线性变换法,灰度非线性变换法和灰度非线性和线性的综合法。
并对这三种方法得到的结果进行了比较分析。
实验结果表明,在有雾的情况下,第三种方法的去雾处理效果最好。
关键词:数字图像处理,图像去雾,MATLAB,灰度图像清晰化ABSTRACTWiththecontinuous development ofinformation technologyisalsoaccompanied byhumanindustrialization processto continue moving forward,more and more seriousair pollution.A surveydata show thatthe proportionofheavy foginthe yearincreased year by year, andfogwillgivethe production of humanlifecause great inconvenience.Foggyweather,theprobabilityofaccidentisgreatly increased.On the one hand, digital image processinghas becomean extremely importantdisciplinesand technological areas,has been widelyusedincommunications, voice, image, remote sensing,bio-engineeringand many other fields.The other hand,withthedevelopmentofcomputer vision andimage processing technology,theresearch and applicationofoutdoorvision systemsarerapid development.Suchasterrainclassification system,outdoormonitoringsystem, automaticnavigation system,the number of applicationsin the rapidlyrising.Inadverse weather conditions(suchasfog, rain,etc.),outdoorsceneimage contrastand colorwillbe changedor degraded,containsmany of the featuresintheimagearecovered orblurred, resulting inthevisualsystem does not work.Therefore,fromtheatmosphericdegradation ofimagerestorationand enhancement ofthedetailsofthesubjecthas important practicalsignificance.MATLABfor algorithm development,data visualization,data analysis, andnumerical calculation of thehigh-leveltechnical computinglanguage and interactiveenvironment.The GUIDE of MATLAB is a quick development environment.MATLABwide range of applications, includingsignal processingandcommunications, imageandvideo processing,control systems,test and measurement,calculation offinanceandcomputational biologyand many other applications.Invarious industriesand academic institutions,more than one millionengineers and scientistsusing MATLABtechnical computinglanguage.FocusesfogGetdegradedgray-scale image.MATLABfor digital imageprocessing,theattenuationmodel.Thentheprocessingofthefirstuse ofthe spatial domainareasofhistogram equalization.Afterpixelstreatment,thepixelpointscleartreatmentprocessusingth ree methods to achievegray image,thegraylinear transformation,graynon-linear transformationLawand graynon-linear andlinearmethod.A comparative analysisofthe results obtainedbythese three methods.Experimentalresults show that the defogging treatment effectinthecaseoffog,thethird method. Keywords: Digital Image Process, Image to fog , MATLAB, Grayscale imageclarity目录摘要IABSTRACT II1 绪论1.1课题研究的背景11.2课题研究现状与水平11.3课题研究的容与意义22 数字图像处理系统与开发环境的简介2.1数字图像处理系统的简介 (3)2.2MATLAB简介和特点 (4)3 课程演示系统方案设计3.1系统总体结构设计63.2系统设计思路 (6)3.3GUIDE的设计过程 (7)4 课程演示系统具体实现容4.1图像的增强概述 (13)4.2图像增强的基本原理和方法 (14)4.2.1频率域变换处理简介 (15)4.2.2空间域处理简介 (17)4.3雾天降质图像的基本特性分析 (19)4.3.1雾天降质图像的对比度指数衰减特性 (19)4.3.2雾天降质图像的模糊性特性 (20)4.3.3雾天降质图像的时域特性 (20)4.3.4雾天降质图像的频域特性 (21)4.4基于雾天降质图像的清晰化处理的的其他常用算法介绍224.5基于MATLAB降质图像的实验结果254.6基于MATLAB降质图像的处理结果的分析 (36)总结38致39参考文献40独创性声明41学位论文(设计)使用授权书411 绪论1.1 课题研究的背景图像是人类感官系统获得的重要信息来源。
基于卷积去雾代码

基于卷积去雾代码基于卷积去雾代码是用于处理图像去雾问题的一种算法实现方式。
该算法可以通过卷积操作去除图像中的雾霾,提高图像的清晰度和质量。
实现该算法需要使用一些基础的编程知识和图像处理技术。
首先,需要读取原始图像并将其转换为灰度图像。
然后,通过计算图像中每个像素的透射率来估计雾的程度。
最后,使用卷积操作去除雾霾并还原图像。
以下是基于卷积去雾的代码实现:```import cv2import numpy as npdef convolve(image, kernel):# 对图像进行卷积操作return cv2.filter2D(image, -1, kernel)def estimate_transmission(image, kernel_size=15):# 估计图像的透射率gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)gray = gray.astype(np.float32) / 255kernel = np.ones((kernel_size, kernel_size), np.float32) kernel = kernel / (kernel_size * kernel_size)mean = convolve(gray, kernel)mean_sqr = convolve(gray * gray, kernel)variance = mean_sqr - mean * meanstd_deviation = np.sqrt(variance)return np.min(std_deviation)def dehaze(image):# 去除图像的雾霾transmission = estimate_transmission(image)beta = 1 - 0.95 * transmissionkernel_size = int(transmission * 50)kernel_size = kernel_size + 1 if kernel_size % 2 == 0 else kernel_sizekernel = np.ones((kernel_size, kernel_size), np.float32) kernel = kernel / (kernel_size * kernel_size)dark_channel = np.min(image, axis=2)t = 1 - beta * dark_channel / 255t = convolve(t, kernel)t = np.clip(t, 0, 1)result = np.zeros(image.shape, image.dtype)for i in range(3):result[:, :, i] = (image[:, :, i] - 255 * (1 - t)) / t return result# 读取原始图像image = cv2.imread('image.jpg')# 调用去雾函数result = dehaze(image)# 显示去雾后的图像cv2.imshow('Dehazed Image', result)cv2.waitKey(0)```以上是基于卷积去雾的代码实现,可以通过调用该函数实现对图像的去雾处理。
基于MATLAB的户外监控图像去雾及清晰化处理方案的研究
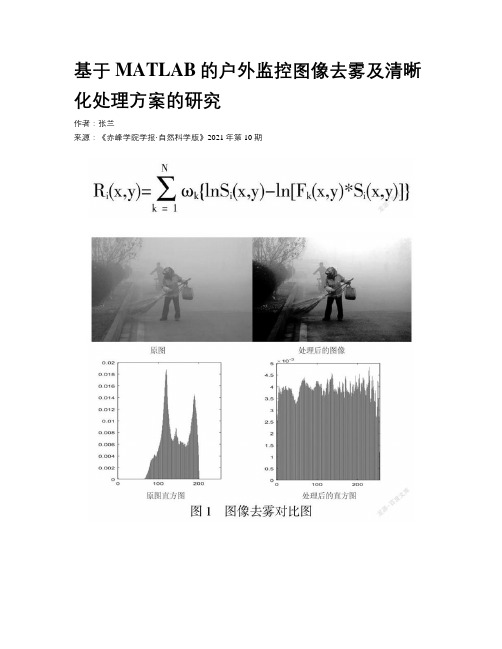
基于MATLAB的户外监控图像去雾及清晰化处理方案的研究作者:***来源:《赤峰学院学报·自然科学版》2021年第10期摘要:隨着视频监控在各行各业的广泛应用,视频图像的清晰化处理也愈加重要。
本文针对雾霾天气下所采集的户外视频图像,构建了一个基于MATLAB的图像去雾及清晰化处理系统,将前期研究的全局直方图均衡化算法、限制对比度自适应直方图均衡算法、多尺度Retinex算法和暗通道先验算法集成到该系统中,进行大量的仿真实验,并构建图像质量评价体系对这四种算法的处理效果进行评价,进一步分析出常用的四种去雾算法所适应的不同场景。
关键词:去雾;图像处理;MATLAB;图像质量评价中图分类号:TP751 文献标识码:A 文章编号:1673-260X(2021)10-0042-05近年来,随着科学技术的迅猛发展,数字多媒体技术也日益提高,监控视频越来越广泛地应用在交通运输、安全防护、军事领域、工农业生产,甚至居家生活等各行各业,并发挥着越来越重要的作用。
但是,户外监控视频对天气条件的要求非常敏感,尤其当下空气污染所造成的雾霾天气严重,使得监控视频所采集的图像严重退化,这就限制了景象的识别,极大地影响了监控视频发挥其效用。
所以,对监控图像以及监控视频的去雾及清晰化处理的研究就显得非常必要。
1 雾霾天气下图像的去雾化研究现状在雾霾天气下,自然光受到大气中颗粒较大的气溶胶悬浮粒子的干扰发生散射,使获取的户外图像的对比度和饱和度明显下降[2,3]。
另外,由于雾霾的存在,使得退化图像中,原来较低的灰度值产生的一定程度的提高,原本较高的灰度值却被削弱,这就大大地降低了视频图像的质量。
现如今,对恶劣天气下视频图像进行清晰化处理的方法可归为两类:基于图像特征的图像增强算法和基于物理模型的图像复原算法。
图像增强算法是从提升对比度、强化细节、改善整体视觉效果等方面对图像进行清晰化处理,这类算法虽然实用性强,但因为它并不是针对图像降质的本质原因进行研究,所以处理后的图像很有可能会造成信息损失或过饱和等现象,清晰化处理效果并不理想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本文主要介绍基于Retinex理论的雾霭天气图像增强及其实现.并通过编写两个程序来实现图像的去雾功能。
1 Rentinex理论Retinex(视网膜“Retina"和大脑皮层“Cortex"的缩写)理论是一种建立在科学实验和科学分析基础上的基于人类视觉系统(Human Visual System)的图像增强理论.该算法的基本原理模型最早是由Edwin Land(埃德温•兰德)于1971年提出的一种被称为的色彩的理论,并在颜色恒常性的基础上提出的一种图像增强方法.Retinex 理论的基本内容是物体的颜色是由物体对长波(红)、中波(绿)和短波(蓝)光线的反射能力决定的,而不是由反射光强度的绝对值决定的;物体的色彩不受光照非均性的影响,具有一致性,即Retinex理论是以色感一致性(颜色恒常性)为基础的.根据Edwin Land提出的理论,一幅给定的图像S(x,y)分解成两幅不同的图像:反射物体图像R(x,y)和入射光图像L(x,y),其原理示意图如图8。
3-1所示.图-1 Retinex理论示意图对于观察图像S中的每个点(x,y),用公式可以表示为:S(x,y)=R(x,y)×L(x,y) (1。
3。
1)实际上,Retinex理论就是通过图像S来得到物体的反射性质R,也就是去除了入射光L的性质从而得到物体原本该有的样子。
2 基于Retinex理论的图像增强的基本步骤步骤一: 利用取对数的方法将照射光分量和反射光分量分离,即:S'(x, y)=r(x, y)+l(x, y)=log(R(x, y))+log(L(x, y));步骤二:用高斯模板对原图像做卷积,即相当于对原图像做低通滤波,得到低通滤波后的图像D(x,y),F(x, y)表示高斯滤波函数:D(x, y)=S(x, y) *F(x, y);步骤三:在对数域中,用原图像减去低通滤波后的图像,得到高频增强的图像G(x, y):G(x,y)=S'(x, y)—log(D(x, y));步骤四:对G(x,y)取反对数,得到增强后的图像R(x, y):R(x, y)=exp(G(x, y));步骤五:对R(x,y)做对比度增强,得到最终的结果图像。
3 多尺度Retinex算法D Jobson等人提出了多尺度Retinex算法,多尺度算法的基本公式是:[][]{}i 1(,)log (,)log (,)(,)Ni n i n n R x y W I x y F x y I x y ==-*∑其中,i R (x,y )是Retinex 的输出,,,i R G B ∈表示3个颜色谱带,(,)F x y 是高斯滤波函数,n W 表示尺度的权重因子,N 表示使用尺度的个数,N =3,表示彩色图像,,,i R G B ∈.N =1,表示灰度图像。
从公式中可以看出:MSR 算法的特点是能产生包含色调再现和动态范围压缩这两个特性的输出图像。
在MSR 算法的增强过程中,图像可能会因为增加了噪声而造成对图像中的局部区域色彩失真,使得物体的真正颜色效果不能很好的显现出来,从而影响了整体视觉效果。
为了弥补这个缺点,一般情况下会应用带色彩恢复因子C 的多尺度算法(MSRCR)来解决。
带色彩恢复因子C的多尺度算法(MSRCR )]是在多个固定尺度的基础上考虑色彩不失真恢复的结果,在多尺度Retinex 算法过程中,我们通过引入一个色彩因子C 来弥补由于图像局部区域对比度增强而导致图像颜色失真的缺陷,通常情况下所引入的色彩恢复因子C 的表达式为(,)(,)(,)i i MSRCR i MSR R x y C x y R x y =1(,)(,)[(,)][](,)i i i Nj j I x y C x y f I x y f I x y ===∑其中,i C 表示第个通道的色彩恢复系数,它的作用是用来调节3个通道颜色的比例,()f •表示的是颜色空间的映射函数。
带色彩恢复的多尺度Retinex 算法(MSRCR )通过色彩恢复因子C 这个系数来调整原始图像中三个颜色通道之间的比例关系,从而通过把相对有点暗的区域的信息凸显出来,以达到消除图像色彩失真的缺陷。
处理后的图像局域对比度提高,而且它的亮度与真实的场景很相似,图像在人们视觉感知下显得极其逼真.因此,MSR 算法具有较好的颜色再现性、亮度恒常性以及动态范围压缩等特性。
4 例程精讲例程1是基于Retinex 理论进行雾霭天气增强的MATLAB 程序,读者可结合程序及注释对基于Retinex 理论进行雾霭天气增强的基本原理进行进一步分析,该程序的运行结果如图—2所示。
例程1:clear;close all;% 读入图像I=imread ('wu.png');% 取输入图像的R 分量R=I(:,:,1);[N1,M1]=size(R);% 对R 分量进行数据转换,并对其取对数R0=double(R );Rlog=log(R0+1);% 对R分量进行二维傅里叶变换Rfft2=fft2(R0);%形成高斯滤波函数sigma=250;F = zeros(N1,M1);for i=1:N1for j=1:M1F(i,j)=exp(-((i—N1/2)^2+(j—M1/2)^2)/(2*sigma*sigma)); endendF = F./(sum(F(:)));% 对高斯滤波函数进行二维傅里叶变换Ffft=fft2(double(F));%对R分量与高斯滤波函数进行卷积运算DR0=Rfft2。
*Ffft;DR=ifft2(DR0);%在对数域中,用原图像减去低通滤波后的图像,得到高频增强的图像DRdouble=double(DR);DRlog=log(DRdouble+1);Rr=Rlog-DRlog;%取反对数,得到增强后的图像分量EXPRr=exp(Rr);% 对增强后的图像进行对比度拉伸增强MIN = min(min(EXPRr));MAX = max(max(EXPRr));EXPRr = (EXPRr-MIN)/(MAX-MIN);EXPRr=adapthisteq(EXPRr);% 取输入图像的G分量G=I(:,:,2);[N1,M1]=size(G);%对G分量进行数据转换,并对其取对数G0=double(G);Glog=log(G0+1);%对G分量进行二维傅里叶变换Gfft2=fft2(G0);%形成高斯滤波函数sigma=250;for i=1:N1for j=1:M1F(i,j)=exp(—((i-N1/2)^2+(j-M1/2)^2)/(2*sigma*sigma));endendF = F。
/(sum(F(:)));%对高斯滤波函数进行二维傅里叶变换Ffft=fft2(double(F));%对G分量与高斯滤波函数进行卷积运算DG0=Gfft2.*Ffft;DG=ifft2(DG0);%在对数域中,用原图像减去低通滤波后的图像,得到高频增强的图像DGdouble=double(DG);DGlog=log(DGdouble+1);Gg=Glog—DGlog;% 取反对数,得到增强后的图像分量EXPGg=exp(Gg);% 对增强后的图像进行对比度拉伸增强MIN = min(min(EXPGg));MAX = max(max(EXPGg));EXPGg = (EXPGg-MIN)/(MAX—MIN);EXPGg=adapthisteq(EXPGg);%取输入图像的B分量B=I(:,:,3);[N1,M1]=size(B);% 对B分量进行数据转换,并对其取对数B0=double(B);Blog=log(B0+1);% 对B分量进行二维傅里叶变换Bfft2=fft2(B0);%形成高斯滤波函数sigma=250;for i=1:N1for j=1:M1F(i,j)=exp(-((i-N1/2)^2+(j-M1/2)^2)/(2*sigma*sigma)); endendF = F./(sum(F(:)));%对高斯滤波函数进行二维傅里叶变换Ffft=fft2(double(F));%对B分量与高斯滤波函数进行卷积运算DB0=Gfft2。
*Ffft;DB=ifft2(DB0);%在对数域中,用原图像减去低通滤波后的图像,得到高频增强的图像DBdouble=double(DB);DBlog=log(DBdouble+1);Bb=Blog—DBlog;EXPBb=exp(Bb);% 对增强后的图像进行对比度拉伸增强MIN = min(min(EXPBb));MAX = max(max(EXPBb));EXPBb = (EXPBb—MIN)/(MAX-MIN);EXPBb=adapthisteq(EXPBb);%对增强后的图像R、G、B分量进行融合I0(:,:,1)=EXPRr;I0(:,:,2)=EXPGg;I0(:,:,3)=EXPBb;%显示运行结果subplot(121),imshow(I);subplot(122),imshow(I0);****************************************************************************************图-2 例程1的运行结果例程2是基于Retinex理论进行雾霭天气增强的MATLAB程序,读者可结合程序及注释对基于Retinex理论进行雾霭天气增强的基本原理进行进一步分析,该程序的运行结果如图—3所示.例程2:****************************************************************************************clear;close all;I=imread(’wu。
png');%分别取输入图像的R、G、B三个分量,并将其转换为双精度型R=I(:,:,1);G=I(:,:,2);B=I(:,:,3);R0=double(R);G0=double(G);B0=double(B);[N1,M1]=size(R);% 对R分量进行对数变换Rlog=log(R0+1);。
