求非线性偏微分方程行波解的几种方法毕业论文答辩PPT
【2024版】微分方程PPT(罗兆富等编)第九章-非线性偏微分方程的Adomian分解法

在求解线性微分方程时, Adomian分解法将方程中的
未知函数u分裂成一个无穷级数
u(x, y) un (x, y) n0
(9.1.01)
而得到其解, 其中级数的通项un(x, y)由递推方式确定.
然而, 将(9.1.01)代入非线性微分方程时, 由于非线性
项的存在, 我们得不到un递推公式.
例如方程
第九章 非线性偏微分方程 的
Adomian分解法
第一节 非线性项的Adomian多项式分解 第二节 用Adomian分解法解非线性偏微分方程
第三节 数学物理中的几个著名偏微分方程 第四节 非线性常微分方程的Adomian分解法
1
机动 目录 上页 下页 返回 结束
第一节 非线性项的Adomian多项式分解
15
机动 目录 上页 下页 返回 结束
将这些求出的un代入(9.1.01)就得到方程(9.2.01)的级 数形式的解.
学者们的研究表明, 如果方程(9.2.01)存在精确解, 则 所得到的级数解将快速收敛到精确解. 但在具体问题中, 如果级数的和函数不容易求出, 则可取适当选取项数从 而得到高精度的数值解.
机动 目录 上页 下页 返回 结束
例3. 计算F(u)=uux的Adomian多项式.
解:
F (u)
uux
1 2
(u
2
)
x
的Adomian多项式已求出,
1 G(u) , 由例1,
2
x
只须对其乘以
1 2
G(u)=u2 的 再关于x求一
阶导数就得到F(u)=uux的Adomian多项式:
A0 u0u0x A1 u1xu0 u1u0x
■
5
非线性波方程求解的新方法!

4 00) ! ( $ - #" ) ( - #. ) 很明显, 这是方程 (20) 的两类周期解: 椭圆正弦波解 和椭圆余弦波解 4 当 * $ 2 时, 因此, 同 6’ 7’ #$ >?’@ #, #$ 6%7@ #, 时可以得到
! !
! [ " (2 - ! * ( )#
"
! *!! (! *! - 2) "
-8 "( . ( 2 ) 2 1 ., ! ! -0 . ( 2 - ) 2 )1 ., "((
! ! ! . ! ! 2 ! 2
(!5) (!8) (!9)
(0 ( - ) ) ! %( # - # ) * )2 - " ) 2 1 ., (!:) ! ! ! ! ! ! ( (2 - 0 )2 ) ! %( # - # . ) * (2 - " ( 2 1 . 4 (!;) 由 (!0) — (!;) 式得到解的两种情况: 2) ( 2 #., ) 2 1 .: ! *!! , (2 / *! ) " ! , %! 1 (2 / *! ) ( #! - #! .) !) ) 2 #., ( 2 1 .: ( . 1 ., (2 1 <
]
$ $ $ ( ’$ [ ( "$ ) "$ ’* ) " )$ !( % ’ $ ) ) ] *) * < &. ) ( "$ ) "$ ($ ’ * ’ . < $ & . & $ ) ’. ) " <[ *) $ $ ( "$ ) "$ ’. ] %12 &. < !((. < % ) # <[ *) $ $ ( "$ ) "$ ’4% &$ )$ # <[ *) "’ * & . < !( % & . ] $ $ ($ ’ * & $ < $ ’ . & . )< !((. < ! % ) &$ ] ’4% )" #%12# $ $ ( "$ ) "$ ($ ’ * ’ $ < ’ $ ’$ ) " <[ *) . ) &. < &$ ) $ $ ($ ’ . & $ < $ ’ $ & . ) ’$ ] %12$# <[ ) " <! !((. < % ) $ $ ($ ’ . ’ $ ) $ & $ & . ) ’4% )$ !( & . ] #%12 # <[ ) " $ %12+# <[ ) $ )$ !( ’ . ] "’ $ & $ $ + $ ( ’$ ’4% )3 !( & $ ] #%12 # <[ ) " $ ) &$ ) $ (!!) %12!# " * )3 !( ’ $ ] 令三角函数各幂次项的系数为零, 得到展开系数的
非线性偏微分方程几种解法的研究

宁波大学硕士学位论文非线性偏微分方程几种解法的研究摘要非线性偏微分方程作为非线性科学的主要内容之一,是被用于描述客观世界随空间、时间变化而产生复杂的物理现象的数学模型。
几十年来,通过相关研究者的努力,对于非线性偏微分方程的求解已经创造了如达布变换法、对称约化法、同伦摄动法等众多方法,本文将针对于其中几种求解方法进行拓展与延伸,使之通过该方法获得更多类型的新解。
其具体包括如下几方面:第一章:对非线性偏微分方程研究背景与相应知识进行介绍。
同时,对本文取得的研究成果进行简略说明。
第二章:对函数展开法进行扩展,首先将解由原来的向正次幂展开对称延拓到负幂次项,然后将展开式中所有的自变量进行完全形式的分离,从而丰富了非线性偏微分方程的精确解。
最后以(G′/G2)-展开法和(F/G)-展开法为例分别求解了(2+1)-维Broer-Kaup-Kupershmidt方程与(2+1)-维分数阶Nizhnik-Novikov-Veselov方程,并给出了它们的特殊孤子的结构激发解。
第三章:使用Hirota双线性导数法先将广义(3+1)-维浅水波方程的Lump型孤子解与呼吸波解进行组合叠加,从而显示出Lump型孤子被扭结孤立波吞噬过程。
然后再将(2+1)-维Sawada-Kotera方程的单孤子解和Lump型孤子解进行组合叠加,从而探究这两种类型解在相互作用过程中表现出来的碰撞、反弹、吸收、分裂等粒子性特征。
此外,Lump型孤子在双条纹孤子的影响下,只在一瞬间出现,然后立即消失,于是Lump型孤子就变成了共振怪波。
通过理论计算和数形结合的方法求得这种新型怪波的运动轨迹、存在时间、面积、体积等等特征量,以便对这种类型怪波有深入的了解。
第四章:通过重正规化方法分别求解了分数阶Klein-Gordon方程在强弱非线性条件下的一级解析近似解。
然后当无需特殊考虑非线性项参数大小的情况下,直接采用线化和校正方法求出方程的一级近似解,并对两种方法所得结果进行比较。
非线性偏微分方程

非线性偏微分方程及其几种解法综述姓名:柏宝红学号:BY目录1、绪论.......................................................................................... 错误!未定义书签。
1.1背景................................................................................... 错误!未定义书签。
1.2 现状.................................................................................. 错误!未定义书签。
2、非线性偏微分方程的几种解法.............................................. 错误!未定义书签。
2.1逆算符法........................................................................... 错误!未定义书签。
2.2 齐次平衡法...................................................................... 错误!未定义书签。
2.3 Jacobi椭圆函数方法 ....................................................... 错误!未定义书签。
2.4 辅助方程方法.................................................................. 错误!未定义书签。
2.5 F-展开法........................................................................... 错误!未定义书签。
非线性方程数值解法详解课件

例如,对于求解非线性方程$f(x)=0$的 应用实例中需要注意选择合适的初始近
根,可以先选择一个初始近似解$x_0$, 似解和设置合适的精度要求,以确保算
然后按照弦截法的迭代过程逐步逼近方
法能够快速收敛到真实解。
程的真实解。
05 共轭梯度法
共轭梯度法的原理
它利用共轭方向的概念,通过迭代过程中不断更新搜 索方向,使得函数值逐渐减小,最终找到方程的解。
牛顿法的实现步骤
确定初始点x0,计算f(x0)和f'(x0),如果f(x0)不等于0,则按照牛顿法的迭代公式 进行迭代,直到满足精度要求。
1. 选取初始点x0;2. 计算函数值f(x0)和导数值f'(x0);3. 如果f(x0)不等于0,则 按照牛顿法的迭代公式x1=x0-f(x0)/f'(x0)进行迭代;4. 重复步骤2和3,直到满 足精度要求。
以求解非线性方程为例,通过选择合 适的迭代法和初值,可以有效地求解 非线性方程的近似解。
03 牛顿法
牛顿法的原理
01
基于函数f(x)的泰勒级数的前两项, 通过迭代的方式逼近方程f(x)=0 的解。
02
牛顿法的基本思想是通过泰勒级 数的近似,将非线性方程f(x)=0 转化为线性方程,然后利用线性 方程的解来逼近非线性方程的解。
当达到预设的迭代次数或满足一定的收敛 条件时,停止迭代,输出结果。
共轭梯度法的收敛性分析
共轭梯度法具有全局收敛性和局部收敛性,即只要初始点 选择得当,算法能够找到方程的解,且在局部范围内具有 快速收敛的特点。
收敛性分析主要涉及算法的迭代矩阵和函数的性质,如连 续性和可微性等。
共轭梯度法的应用实例
牛顿法的收敛性分析
在一定的条件下,牛顿法是收敛的, 且具有二阶收敛速度。
非线性偏微分方程几种解法的研究的开题报告

非线性偏微分方程几种解法的研究的开题报告
题目:非线性偏微分方程几种解法的研究
一、研究背景
非线性偏微分方程是研究物理、工程等领域中的重要问题,如流体力学、天气预报、地震学等。
非线性偏微分方程具有复杂的数学结构和难以求解的特点,因此探索
其解法具有理论和实际意义。
二、研究目的
本文旨在探究几种非线性偏微分方程的解法,包括但不限于分析方法、数值方法、符号计算等,为解决实际问题提供数学工具。
三、研究内容
1. 非线性偏微分方程的数学基础和物理背景简介;
2. 常见的非线性偏微分方程类型及其解法;
3. 非线性偏微分方程的符号计算方法;
4. 非线性偏微分方程的数值解法。
四、研究方法
本文采用文献资料法、数学分析法、符号计算法、数值计算法等多种研究方法,对几种常见的非线性偏微分方程进行分析和求解。
五、研究意义
本文将为非线性偏微分方程的研究提供新的思路和解法,为实际应用提供数学支持,具有一定的理论和实践意义。
六、研究计划
第一阶段:了解非线性偏微分方程的相关知识、理论和方法,对文献进行收集、整理和分析。
第二阶段:研究几种常见的非线性偏微分方程类型,探索不同的解法和应用。
第三阶段:开发相应的计算工具,对数值解法进行实验验证。
第四阶段:撰写论文并进行总结。
七、研究预期成果
1. 对几种常见的非线性偏微分方程类型掌握不同的解法;
2. 对符号计算方法和数值计算方法有更深入的理解;
3. 实现相应的计算工具,提高数值计算的精度和效率;
4. 完成一篇在国内外数学、物理等领域均具有一定影响的学术论文。
【精品完整版】毕业论文:展开法及其非线性演化方程的孤立波解

偏微分方程及其求解实例ppt课件
(hn1-2.*h(k,n)+h(k,n-1))./dr.^2);
end plot(r(3:n)./ra,p(k,3:n).*theta.*2./rb)
h hi1 hi1 r i 2r
2h hi1 2hi hi1
r 2
r 2
i
P
1 rb 4
1
r
h r
2h r 2
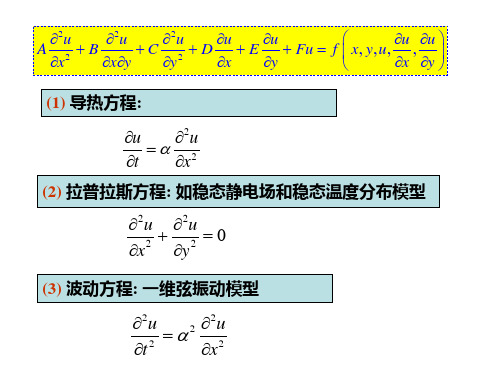
偏微分方程的求解实例2:
2u A x2
2u B
xy
C
2u y 2
D u x
E u y
Fu
f
x,
y,u,
u x
,
u y
(1) 导热方程:
u 2u
t x2 (2) 拉普拉斯方程: 如稳态静电场和稳态温度分布模型
2u 2u 0
x2 y2
(3) 波动方程: 一维弦振动模型
2u 2 2u
t 2
x2
偏微分方程的边界条件
function PDE1Dd_CrankNicolson % 使用Crank-Nicolson有限差分方法求解一维动态传
热模型
c1 = 100; c2 = 0; a = 10; b = 8; alpha = 2; n = 6; m = 8; U = CrankNicolson(@ic,c1,c2,a,b,alpha,n,m)
h t 3 9c
9c
h3 h33
4h r 4
3
h5 4h4
6h3 4h2 r 4
h1
h t
n
V
r i 2r
2h hi1 2hi hi1
r 2
r 2
i
3h r 3
hi2
2hi1 2hi1 2r 3
非线性偏微分方程的几类求解方法的开题报告

非线性偏微分方程的几类求解方法的开题报告非线性偏微分方程是描述自然界中各种现象的重要数学工具之一。
与线性偏微分方程相比,非线性偏微分方程更为复杂和困难,其求解方法也更为多样和复杂。
本文将介绍非线性偏微分方程的几种求解方法,包括常见的解析求解方法和数值方法。
一、常见的解析求解方法1. 可分离变量法可分离变量法是求解非线性偏微分方程的常用方法,其中的求解步骤就是将非线性偏微分方程近似成为可分离变量的形式,然后利用变量分离的方法继续求解。
可分离变量法广泛应用于非线性偏微分方程的解析求解中,尤其是对于形式简单的非线性偏微分方程,它是解析求解的重要方法。
2. 相似变量法相似变量法是求解非线性偏微分方程的重要方法之一,是一种通过变量变换将原问题转化为线性问题的方法。
相似变量法的基本思想是通过一系列的变量变换,将原问题转化为一个常微分方程,然后再利用常微分方程的解法求解。
3. 对称性分析法对称性分析法是比较新的一种求解非线性偏微分方程的方法。
它是一种通过对非线性偏微分方程进行对称性分析,把关于自变量和因变量的函数变换为关于具有更少自变量的函数的方法。
对称性分析法的应用使得求解非线性偏微分方程的难度得到了很大的减轻,但该方法适用于特定条件下的非线性偏微分方程。
二、数值方法除了解析求解方法之外,还有很多数值方法可以用于求解非线性偏微分方程。
下面介绍几种常见的数值方法。
1. 有限差分法有限差分法是数值解偏微分方程的常规方法之一。
有限差分法将偏微分方程中的微分算子用数值微分算子代替,然后将连续微分方程转化为离散的代数方程,最后利用代数方程组求解得到连续的解。
2. 有限元法有限元法是结构分析和流体力学等领域中广泛使用的数值分析方法之一。
有限元法是通过将区域分割成许多小的单元,对每个单元进行解析,然后将它们整合到一起形成一个整个区域的解。
3. 谱方法谱方法也是一种求解非线性偏微分方程的数值方法,其基本思想是利用一组基函数的线性组合对偏微分方程进行离散化,进而求解方程的数值解。
非线性数学物理方程的行波解

非线性偏微分方程行波解1直接积分法行波解形式:0()u x ct φξξξ= =-+代入偏微分方程得常微分方程。
这个过程简记为行波变换。
直接积分法指直接求解这个常微分方程。
例0()()()()0t x xx u uu u c αφξφξφξαφξ''''+-=⇒-+-=积分难计算:1用特殊形式的解试凑:exp()1exp()B a u a ξξ=+ vakhnenko 方程20t x x xx u u u u u +++=;fisher 方程(1)t x x u u u u αβ---= ()exp(())u i kx wt φξ=- Schrodinger 方程20t xx iu u u u αβ++=2椭圆函数在常微分方程求解中的应用。
2混合指数方法适用于多项式方程,非多项式方程需变换。
如sine-Gordon 方程sin xt u u =【1】具体步骤1.行波变换2.进行奇性分析:将p φξ-=代入,平衡方程中最高阶导数项与最高阶非线性项,计算出p 的值。
通常p 为正整数;若n 为有理数12/m m ,可令21m φϕ-=,若n 为负数,可设1φϕ-=。
3.为获得更多的解,引入变换+C φϕ=4.设1,exp()n nn a g g k φξ∞===∑是方程相应线性项部分的指数解(若无则为最低次非线性项构成方程的解),代入方程,得到递推关系。
解出n a 。
得到方程的解。
注:1.n a 的递推关系难解,可以设n a 是n 的多项式。
【2】2.第3步也可以这样假设2020,exp()n n i ii i i ni n n i ii i i n i a g a g g k b g b g φξ=-==-====∑∑∑∑,代入方程令g 前系数为0解出a ,b 。
【3】3齐次平衡法齐次平衡法已推广到寻找非线性发展方程的自Backlund 变换、相似约化、多孤子解等领域。
非线性波方程行波解分岔及其动力学行为的研究的开题报告

非线性波方程行波解分岔及其动力学行为的研究的开题报告摘要:本文旨在研究非线性波方程行波解分岔及其动力学行为。
首先,我们将介绍非线性波方程及其行波解的定义,特别是双曲型方程的行波解。
其次,我们将探讨行波解存在分岔的原因,并讨论分岔现象的数学描述。
然后,我们将考虑分岔前后的行波解的稳定性和动力学行为。
最后,我们将通过数值仿真模拟来验证我们的理论研究成果。
关键词:非线性波方程;行波解;分岔;稳定性;动力学行为1. 研究背景与意义非线性波方程是研究波动现象中的重要数学模型,具有很广泛的应用。
行波解是非线性波方程中的一类非常特殊和重要的解,具有稳定性和可预测性等优良性质。
分岔是一种普遍存在于动力学系统中的现象,其在非线性波方程的行波解中的存在也是非常普遍的。
因此,对于非线性波方程行波解分岔及其动力学行为的研究具有重要的理论和应用价值。
2. 研究方法和思路本文将采用非线性波方程的数学理论和方法,结合动力学系统的基本概念和理论,对非线性波方程中的行波解分岔及其动力学行为进行研究。
在理论分析的基础上,我们将通过数值仿真模拟来验证我们的理论研究成果。
3. 研究内容(1)非线性波方程及其行波解的定义介绍;(2)行波解存在分岔的原因,分岔现象的数学描述;(3)分岔前后的行波解的稳定性和动力学行为;(4)数值仿真模拟及结果分析。
4. 研究进度与计划目前,我们已对非线性波方程的性质和行波解的定义进行了深入的研究,以及分岔现象的分析和数学描述。
接下来,我们将从分岔前后的行波解的稳定性和动力学行为方面展开研究,并对分岔现象进行数值仿真模拟。
最后,我们将完成论文的撰写和修改。
首次积分法下非线性偏微分方程的精确行波解

关 于非 线性 偏 微分 方 程行 波解 的 探讨 在研 究 非
法 [ 、 可 比 椭 圆 函 数 展 开 法[ 力、s ec sn 2 雅 ] t 一 i -oie n
线 性 物理 现 象 中起 着 非 常 重 要 作 用 、 线 性 波 动现 非 象 出现 在各 种科 学 和工 程 领域 , 流体 力 学 、 离 子 如 等 体物 理 、 学 纤 维 、 光 生物 、 体 物理 、 学动 力 学 、 固 化 化 学 物 理 和地球 化 学 等. 线 性波 的 色散 、 散 、 非 耗 扩散 、 反 应 和对 流 现 象 在 非 线 性 波 动 方 程 中是 非 常 重 要 的 , 的精确 行 波解 可 以帮 助人 们发 现 新 的现 象. 新 为 此 , 过 去 的几 十年 里人 们 做 了大 量工 作 , 出 了许 在 提
L U i u 。 ANG J nj I Ka y t D — u - e i
( olg f t e t sa d E o o ti - n n Unv C a g h , n n 4 0 8 , h n ) C l e h mai n c n mer s Hu a i 。 h n s a Hu a 1 0 2 C ia e o Ma c c Ab t a t sr c :Co sd rn h a y m o e s o o l e r p r i ld f e e t l e u to s e itn n p y i s n i e i g t e m n d l fn n i a a ta if r n i q a i n x s i g i h sc n a a d o h r f l s h x s e c fe a tt a e l g wa e s l to so q a i n sp o o e . B t o u i g n t e i d ,t e e it n e o x c r v l n v o u i n f u t swa r p s d e i e o y i r d cn n a wa e v ra l n s n h is n e r l me h d b s d o h i g t e r f c m mu a i e a g b a we v a i b e a d u i g t e fr t i t g a t o a e n t e rn h o y o o t tv l e r , h v b a n d t e e a t t a e l g s l a y wa e s l to s f r t o l e r e o u i n e u to s I a a e o t i e h x c r v li o i r v o u i n o WO n n i a v l t q a i n . t h s n t n o m a y a v n a e v r o h rt a i o a e h i u s ti ie ta d c n i e ta s h wst a h is t - n d a t g s o e t e r d t n l c n q e 。i sd r c n o cs .I l o s o h t efr t n e i t t i g a e h d i n e f c i e m e h d wih g e t p t n il e i d n o rl m t o sa fe tv t o t r a o e ta s wh n fn i g c mp e o ia y wa e s l to s o lx s l r v ou in f t t e n n i e r e u to s h o l a q a in . n Ke r s o l e r d f e e ta q a i n ; r v l n v o u i n ;fr ti t g a e h d y wo d :n n i a i r n i l u t s t a e l g wa e s l t s is n e r lm t o n f e o i o
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学科学学院 2015级1班
答辩人:
导师:
目录
CONTENTS
绪论
研究方法与思路
研究结果与应用
研究总结
绪论
选题背景 研究意义 研究现状
背景
罗素观察到一种奇妙的水波有稳定的速度且波的形状不变,后来 著名的KdV方程解释了这种现象,并说明这是偏微分方程的特殊 解——行波解.这一结果一定程度地推动了流体力学的发展.
研究 现状
研究现状
随着科学技术的发展,前人提出了许多描述非线性现象的偏微分方 程,涉及生物学、物理学以及力学等等领域.例如1895年,数学家 Korteweg研究浅水波运动,提出著名的KdV方程,再到其他科学家 提出的Schrodinger方程、BBM方程等等.
相关研究人员们已经提出了一些方法去寻找非线性偏微分方程的 行波解比如Tanh函数法、反散射变换法、Darboux变换法、辅助 函数法等.但到目前为止,求行波解没有普适的解法.
研究结果与应用
首次积分法的应用 齐次平衡法的应用 雅可比椭圆函数的应用
PHi-four方程的行波解 1
首次积论分文法总的结应用
PHi-four方程的行波解 1
首次积论分文法总的结应用
mKdV方程的行波解 2
首次积论分文法总的结应用
mKdV方程的行波解 2
首次积论分文法总的结应用
mKdV方程的行波解 1
研究思路与方法
预备基 本方法
了解首次积分 法,齐次平衡法, 雅可比椭圆函 数展开法的理 论依据,并分别 提取总结求解 步骤.
应用
应用这些方法 求具有实际应 用背景的非线 性偏微分方程 的行波解.
优缺点 分析
基于前两步分 析这三个方法 的优缺点
研究思路与 方法
对比分 析
从求解过程、 求解结果、方 法的思想以及 方法的失效点 四个维度对这 三种方法进行 对比分析.
最后,我要感谢所有教导我的老师和一齐成长的同学,他们在 我的大学生涯给予了很大的帮助.本论文能够顺利完成,要特 别感谢我的导师张珠洪老师,感谢各位老师的关心和帮助!
谢谢各位老师的观看!
齐次平论衡文法总的结应用
mKdV方程的行波解 1
雅可比椭论圆文函总数结展开法
研ห้องสมุดไป่ตู้总结
各方法的优缺点 对比分析
缺点:该方法的步骤比较繁杂,有两种失效的情况. 优点:可取不同的m寻找同一非线性偏微分方程不同的行波解.
各方法的优缺点
缺点:在于第三步中常微分方程的解法不固定,计算量可能很大. 有一种失效的情况. 优点:该方法具有直观,步骤分明的特点.
选题背景
概念
研究 意义
研究意义
行波解是非线性偏微分方程研究的一个重要部分,它能够很好地描 述和解释自然现象中个体之间的关系,科学家们还能利用它去尝试 理解非线性偏微分方程解的物理意义以及探索其长时间行为.
目前为止,求非线性偏微分方程的行波解没有普适的解法.因此,研究 使用一些已有的方法来求出特定类型的非线性偏微分方程的行波 解是具有重要意义的,也是要研究行波解所不可避免的.
缺点:有一种失效的情况. 优点:求解步骤和过程都比较简洁.该方法实际上还包含了双曲正切函数展开法,
对比分析
求解过程
都具有求解步骤分明 的特点,但一般情况下 雅可比椭圆函数展开 法步骤较少,计算量也
较小.
求解结果
方法思想
首次积分法求出来的一 定是的行波解, 齐次平 衡法求出来可能不是行 波解,雅可比椭圆函数 展开法求出来不仅是行
波解,还是周期解.
齐次平衡法和雅可比 椭圆函数展开法都先 将非线性偏微分方程 的解假设成一个特定 的形式.首次积分法则
没有.
失效点
三种方法都有同一失 效方式,当求出的多项 式的次数为非整数时, 方法失效.除此之外,首 次积分法还可能因为 不能将非线性偏微分 方程化为特定形式的 常微分方程而失效.
THANKS!
