复摆振动的研究
北京大学复摆实验报告

1.28140 1.27314 1.26429 1.25752 1.25029 1.24472 1.23855 1.23435 1.23137 1.23021 1.22986 1.23189 1.23572 1.24205 1.25219 1.26689 1.28497 1.30712 1.33931 1.37785 1.43054 1.49646 1.58282 1.70131 1.866637 2.05579 2.43580
2. 将复摆安装到支架上,利用铅直线调整铁架下部支脚螺钉,使复摆在垂直平面内 摆动,且尽可能使平衡位置在光电门中央;
3. 利用复摆上位置不同的小孔作为刀口悬挂点,记下此点到零刻度线(即质心)的 距离hi,用光电计时器记录此时复摆运动20个周期的时间20Ti,列表记录数据;
4. 数据处理
1) 作T 2h ∼ h2图,用线性拟合法求重力加速度g 2) 用公式求g 3) 作T ∼ h图,求出复摆对于任意悬挂点的等值摆长,从而求出g
g11 = 4π2/k1 = 4π2/4.063 = 9.718m · s−2
(25)
右半部分如Figure 6所示:
斜率k2 = 4.028s2/m, 截距b1 = 0.1420s2m, 相关系数R22 = 0.999996 计算得:
g12 = 4π2/k1 = 4π2/4.028 = 9.802m · s−2
RG = h0
也是图中两条曲线的极小值之间的距离,且h1 + h2 = EF = 2RG. 取一周期为T值 (H点 ) 处 引 一 直 线MN平 行 于 横 轴 , 交 两 条 对 称 曲 线 于A,B,C,D四 点 , 把 这 四 点 分 成A,C和B,D两组,在摆杆上每一组中两点都位于质心G(Figure 3所示)的两旁,并与
复摆振动研究实验报告
复摆振动的研究姓名:黄青中 学号:200902050238摘要:了解用复摆物理模型来测量物体的转动惯量。
通过观测复摆的振动,测定复摆振动的一些参量(重力加速度g ,回转半径r ,转动惯量G I )。
分析复摆的振动,研究振动周期与质心到支点距离的关系。
复摆又称为物理摆,是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系——简谐振动。
通过复摆物理模型的分析,可以用来测量重力加速度、测量物体的转动惯量以及验证平行轴定理等等。
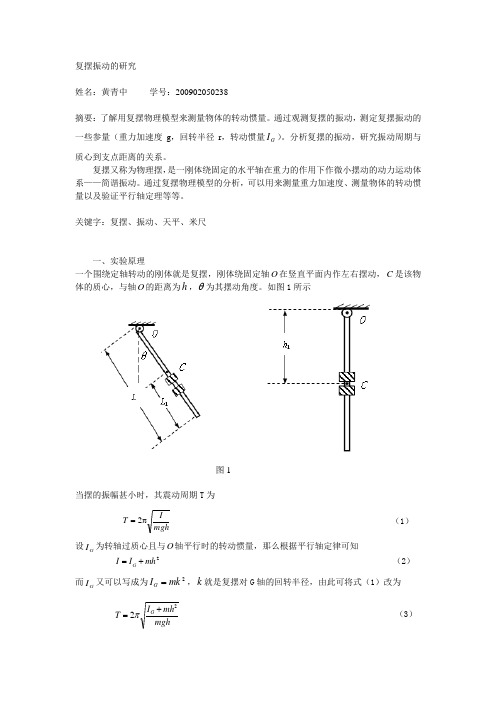
关键字:复摆、振动、天平、米尺一、实验原理一个围绕定轴转动的刚体就是复摆,刚体绕固定轴O 在竖直平面内作左右摆动,C 是该物体的质心,与轴O 的距离为h ,θ为其摆动角度。
如图1所示当摆的振幅甚小时,其震动周期T 为 mghIT π=2 (1) 设G I 为转轴过质心且与O 轴平行时的转动惯量,那么根据平行轴定律可知2mh I I G += (2)而G I 又可以写成为2mk I G =,k 就是复摆对G 轴的回转半径,由此可将式(1)改为mghmh I T G 22+=π (3)图1二、实验步骤与要求1、研究复摆周期与转轴位置的关系1.1确定均匀钢板的质心位置(方便起见,让质心的位置正好在“0”刻度上) 方法:将钢板水平放在支架的刀刃上(如图2),其“0”刻度正好对应刀刃,利用杠杆原理调节钢板两端的微调螺母使其平衡,要求误差在1mm 以内。
1.2将座架放置于实验桌边沿,使上面的三角刀口水平朝外 方法:把复摆摆杆悬挂在三角刀口上,调节座架底下水平螺丝使刀口与孔内径上沿相密合,要求摆杆摆动时没有扭动情况。
1.3测量不同回转轴对应的周期将复摆摆杆的每一小孔依次悬挂在三角刀口上以小摆幅摆动,用周期测定仪测定对每一个孔的振动周期,并记录。
注意:使用周期测定仪时,面板上的周期选择拨到T 30档;在复摆处于平衡位置时,周期测定仪的光电门应对准复摆下端的挡光针,拨动复摆并把周期仪置零,即自动开始测周期至30个周期停止计时,所显示的数字就是30个周期的时间间隔,计时精度为0.01ms 。
物理实验报告复摆

一、实验目的1. 了解复摆的振动规律。
2. 学习使用复摆进行测量,掌握测量摆长、摆角和周期的方法。
3. 通过实验,验证单摆周期公式,加深对单摆理论的理解。
二、实验原理复摆是一种由两个或多个单摆组成的系统,其振动规律与单摆类似。
在理想情况下,复摆的周期仅与摆长和重力加速度有关,与摆角无关。
本实验通过测量复摆的周期,验证单摆周期公式。
单摆周期公式为:\[ T = 2\pi \sqrt{\frac{L}{g}} \]其中,T为周期,L为摆长,g为重力加速度。
三、实验器材1. 复摆装置2. 刻度尺3. 秒表4. 计算器四、实验步骤1. 将复摆装置固定在支架上,确保复摆可以自由摆动。
2. 使用刻度尺测量复摆的摆长,记录数据。
3. 调整复摆的摆角,使其在30°~60°之间。
4. 使用秒表测量复摆摆动n次所需的时间,记录数据。
5. 重复步骤3和4,进行多次测量,取平均值。
6. 根据单摆周期公式,计算理论周期,并与实验周期进行比较。
五、实验数据及处理1. 摆长L = 1.0 m2. 摆角θ = 45°3. n = 104. 实验周期T1 = 1.5 s5. 实验周期T2 = 1.4 s6. 实验周期T3 = 1.6 s7. 平均实验周期T = (T1 + T2 + T3) / 3 = 1.5 s六、实验结果与分析1. 根据单摆周期公式,计算理论周期:\[ T_{理论} = 2\pi \sqrt{\frac{L}{g}} = 2\pi \sqrt{\frac{1.0}{9.8}}\approx 1.97 \text{ s} \]2. 比较实验周期与理论周期:\[ \frac{T_{理论}}{T} = \frac{1.97}{1.5} \approx 1.32 \]3. 分析误差来源:a. 实验误差:由于测量误差、计时误差等因素,导致实验周期与理论周期存在一定偏差。
b. 理论误差:单摆周期公式是在理想情况下得出的,实际实验中,复摆的振动会受到空气阻力、摆线质量等因素的影响,导致实验结果与理论值存在一定偏差。
★复摆的振动周期(小论文示范)

复摆的振动周期1、引言复摆是大学物理中三个简谐振动模型之一,是刚体绕光滑水平轴作小角度摆动。
研究复摆的振动周期可以运用转动定律,也可以运用机械能守恒定律。
本文先介绍与研究复摆振动周期有关的概念和规律,然后用两种方法推导复摆的周期公式,最后讨论复摆周期公式在测量刚体转动惯量中的应用。
2、原理刚体定轴转动定律的表达式为M J α= (1)其中M 为对转轴的力矩,J 为刚体对转轴的转动惯量,α为刚体转动的角加速度。
转动惯量的定义式为2=i i J m r ∑,其中r i 为质点m i 到转轴的距离。
转动角速度为ω的转动刚体的转动动能为 212k E J ω= (2)在重力场中,刚体质心坐标为(C x ,C y )的重力势能为P C E mgy = (3)以摆角θ为变量的简谐振动的表达式为0Θcos()f θωt φ=+ (4)式中Θ和0φ分别为摆幅和初相位,f ω振动圆频率,与振动周期间的关系为 2f πT ω= (5)3、模型如图所示,质量为m 的复摆对转轴O 的转动惯量为J ,质心C 到转轴O 的距离为b 。
当OC 与铅垂线的夹角为θ时,复摆受到的对转轴O 的力矩为sin M mgb θ=-。
根据刚体定轴转动定律M J α=,得sin mgb mgb αθθJ J =-≈-。
将0=Θcos()f θωt φ+代入可得,f mgb ωJ =。
于是求得,复摆振动周期为22f πJ T πωmgb ==。
复摆振动时只有重力作功,因此振动系统的机械能守恒,即21cos 2J ωmgb θC -=。
等式两边对时间t 求导,得sin 0J ωαmgb ωθJ ωαmgb ωθ+≈+=。
将0=Θcos()f θωt φ+代入b可得,f ω=。
同样,求得复摆振动周期为22f πT ω==。
4、讨论对于单摆,b =l ,J =ml 2,周期为2T =。
利用复摆的周期公式可得2T J mgb π=2(),即测量了刚体的质量、质心位置和振动周期,即可计算出刚体的转动惯量。
复摆振动的研究实验报告

复摆振动的研究
实验目的:1、考查复摆振动时振动周期与质心到支点距离的关系; 2、测出重力加速度、回转半径和转动惯量。
实验仪器:
实验原理:一个围绕定轴转动的刚体就是复摆,刚体绕固定轴O 在竖直平面内作左右摆动,C 是该物体的质心,与轴O 的距离为 h ,θ 为其摆动角度。
如图 1 所示
当摆的振幅甚小时,其震动周期 T 为
(1)
设 I G 为转轴过质心且与O 轴平行时的转动惯量,那么根据平行轴定律可知
(2)
而 I G 又可以写成为 I G =mk 2, k 就是复摆对 G 轴的回转半径,由此可将式(1)改为
(3)
实验内容:1、重心G 的位置S G = (h=│S -S G │)
的重心端作为正端,选择复摆上以下刻度位置作为支点位
4、用物理天平测量复摆的质量m. m=
数据处理与分析:(h=│S-S
│)
G
S xx=∑x i2-(∑x i)2/n=
S yy =∑y i 2-(∑y i )2/n = S xy =∑x i y i -∑x i ∑y i /n=
=
∙==-===∑∑yy xx xy i i xx
xy S S S r
n x b n y a
S S b ˆˆˆ
r b n r S b ⋅⎪⎪⎭
⎫ ⎝
⎛--=2
12= b g ⋅=24π =
b s g g U b
=)(=
b
s g g g U g
g U b =)
(=)(=
实验结果与评价:
实验感想:。
复摆振动

1.计算出重力加速度g,并把测量结果与本地区的公认值比较,求实验的相对误差。
实验报告成绩单
学院:___________专业:___________学号:__________姓名:___________
预习(30分)
操作(30分)
数据处理(30分)
其他(10分)
总成绩
指导教师
1.观看仪器介绍并掌握其使用方法及注意事项;
2.仔细阅读课本,初步了解实验并且能够独立回答问题;
3.左侧问题预习前完成,右侧空白处实验后完善与总结。
1.请推导复摆振动周期。(需画出刚体的受力分析图)。
2.实验中取 ,推导用复摆测重力加速度的公式。
3.写出利Leabharlann 复摆测重力加速度的实验步骤。4.在该实验中,如果两砝码置于复摆的摆杆上刻线非对称处的位置固定,对该实验的有怎样的影响?
复摆的振动周期
次数
1
2
3
4
5
平均
——
——
3.原始实验数据不能用铅笔记录,实验数据不能任意涂改,发现错误应重新完成实验。
实验组成员:(1)学号:____________姓名:____________
(2)学号:____________姓名:____________
(3)学号:____________姓名:____________
指导教师签字:____________
实验名称:复摆的振动研究
学生学号:_______________学生姓名:_______________学院专业班级:_______________
上课时间:_______________指导教师:_______________实验报告成绩:_______________
复摆振动的研究1

复摆振动的研究一、实验目的:1、考查复摆振动时振动周期与质心到支点距离的关系;2、测出重力加速度、回转半径和转动惯量。
二、实验仪器:支架、复摆、秒表。
三、实验原理:一个绕定轴转动的刚体就是复摆。
当摆动的振幅甚小时,其振动周期T 为mghI T π2= 如图所示,O 为支点,G 为质心,h 为摆的支点到摆的质心的距离。
2mh I I G += 2mK I G = I 为转动惯量,K 为复摆对G 轴的回转半径,ghh K T 222+=∴π 2222244h g k g h T ππ+=∴ 令h T y 2= 2h x = Bx A y +=∴ 224k g A π= gB 24π= 测出T 和h 值,可得x 、y 值,用最小二乘法求出 Bx A y += 中的A 、B ,由A 、B 求出g 和K 。
四、实验步骤1、测定重心G 的位置。
将复摆水平放在支架的刀刃上,复摆静止不动或左右摆动幅度相同时的支点位置为质心G 点。
(因所给复摆为匀质摆,所以可以用杠杆原理寻找G 点)2、选择不同的支点位置(改变10次支点的位置),测出支点到G 点的距离h ,每个支点测h 三次,求平均值。
3、用秒表测出复摆在不同支点处的振动周期,用振动30次的时间来计算周期,每个支点处测周期三次,求平均值。
4、利用所测得的T 和h 值可得几组成部分(x ,y )值,用最小二乘法求出拟合直线Bx A y +=的A 、B 值,计算A 和B5、由g B 24π=得B g 24π= ,由224k gA π= 得π2Ag k = 6、计算 g 、k 的不确定度及相对误差。
a ArrayOG。
复摆的实验报告.doc

复摆的实验报告.doc摘要:本实验通过利用复摆的摆动周期和摆长与摆角度之间的关系,通过多次实验来研究复摆的动力学规律和特性。
实验结果表明,复摆的摆动周期受到重力加速度和摆长的影响,摆长越长,摆臂相对较长,振幅相对小,周期越长。
同时,复摆的摆角度对振幅和周期都产生了影响,当摆角度较小时,振幅较小,周期较长。
关键词:复摆,摆动周期,摆角度,摆长Abstract:In this experiment, the dynamic laws and characteristics of the compound pendulum are studied by utilizing the relationship between the swinging period and the swinging length and swing angle of the compound pendulum. The experimental results show that the swinging period of the compound pendulum is affected by the gravity acceleration and the swinging length. The longer the swinging length, the longer the swinging arm, the smaller the amplitude, andthe longer the period. At the same time, the swinging angle of the compound pendulum affects the amplitude and period. When the swinging angle is small,the amplitude is small and the period is long.Keywords: compound pendulum, swinging period, swinging angle, swinging length实验方案:所用仪器:复摆、计时器、卡尺、直尺、秤。
实验十三复摆实验实验实验报告

M (h − h′) = mh
化简得
h′ M − m = = 98.8% h m
由于小刀口质量对重心位置改变的影响小于 2%,其对实验结果的测量产生的 影响很小,在精度不高的实验中可以忽略不计。
20T(s) 25.1014 24.9162 24.6173 24.5552 24.3776 24.2379 24.0708 23.9831 23.8758 23.7983 23.7448 23.7388 23.7625 23.8433 23.9861 24.1568 24.3954 24.8841 25.4196 26.0742 26.9978 28.1755 29.8452 31.8723 34.9437 39.5663
h2/cm2
201.07 174.24 148.35 125.44 103.63 84.64 66.91
T2h/cm·s2
20.36 19.30 18.26 17.29 16.40 15.68 14.77
h2/cm2
51.84 38.19 27.04 17.47 10.24
T2h/cm·s2
14.57 13.72 13.26 12.88 12.40
注:记 0 点左侧为负,右侧为正。 复摆质量 M = 412.80g;小刀口质量 m = 5.15g 1、对数据进行最小二乘法处理有:
表 13-2 悬点在 0 点右侧时 h2 与 T2h 数据表
h2/cm2
793.55 739.84 685.39 635.04 584.67 538.24 491.95
̇̇ 则 由于 β = θ ̇̇ + mgh sin θ = 0 Iθ
在摆角很小 ≤ 5� 时, sin θ ≈ θ , (13.3)式化为 (13.3)
复摆振动的研究

实验四 复摆振动的研究复摆又称为物理摆,是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系——简谐振动。
通过复摆物理模型的分析,可以用来测量重力加速度、测量物体的转动惯量以及验证平行轴定理等等。
【实验目的】1.分析复摆的振动,研究振动周期与质心到支点距离的关系。
2.掌握用复摆来测量重力加速度和回转半径的方法。
3.了解用复摆物理模型来测量物体的转动惯量和验证平行轴定理的方法。
【实验仪器】JD-2型复摆实验仪,光电门装置,J-25型周期测定仪,天平,米尺等 【实验原理】刚体绕固定轴O 在竖直平面内作左右摆动,C 是该物体的质心,与轴O 的距离为h ,θ为其摆动角度,如图4-1所示。
若规定右转角为正,此时刚体所受力矩与角位移方向相反,即有h mg M θ-=sin若θ很小时(θ在05以内)近似有θmgh M -= (4-1)又据转动定律,该复摆又有θ I M = (4-2) 其中I 为该物体转动惯量。
由(4-1)和(4-2)可得图4-1 刚体复摆运动20θωθ=- (4-3) 其中20mghIω=。
此方程说明该复摆在小角度下作简谐振动,该复摆周期为 mghIT π=2 (4-4) 设c I 为转轴过质心且与O 轴平行时的转动惯量,那么根据平行轴定律可知2mh I I c += (4-5)代入(4-4)式得:mghmh I T c 22+π= (4-6) 由此可见,周期T 是质心到回转轴距离h 的函数,且当0h →或h →∞时,T →∞。
因此,对下面的情况分别进行讨论:(1)h 在零和无穷大之间必存在一个使复摆对该轴周期为最小的值,此时所对应h 值叫做复摆的回转半径,用R 表示。
由(4-6)式和极小值条件0dTdh=得:minT TR h ===(4-7) 代入公式(4-7)又得最小周期为min 2T = (4-8) (2)在h R =两边必存在无限对回转轴,使得复摆绕每对回转轴的摆动周期相等。
复摆的研究实验报告

在物理学中,复摆常被用作研究力学、振动和波动等现象的 实验模型。在工程学中,复摆可用于测量物体的质量、重心 位置和转动惯量等参数。在天文学中,复摆可用于研究天体 的运动规律和轨道参数。
复摆的分类
总结词
根据不同的分类标准,可以将复摆分为不同的类型。
详细描述
根据形状和尺寸,可以将复摆分为长摆和短摆;根据旋转轴的位置,可以将复 摆分为垂直摆和水平摆;根据运动状态,可以将复摆分为自由摆和受迫摆。
在无外力矩作用的情况下, 刚体的角动量保持不变。
周期公式
复摆的周期与摆长、质量 分布和阻尼等因素有关, 可以通过周期公式进行计算。
实验步骤
数据采集设置
设置数据采集系统的采样频率、 采集参数等,确保能够准确记 录实验数据。
数据处理与分析
对采集到的实验数据进行处理 和分析,提取有用的信息,如 周期、角动量等。
结果意义
探讨了复摆实验在物理学中的意义,为进一步研究提 供了基础。
结果误差分析
误差来源
分析了实验过程中可能产生 的误差来源,如测量误差、 环境干扰等。
误差评估
对误差进行了评估,并计算 了误差范围。
误差控制
提出了控制误差的方法,以 提高实验的准确性和可靠性。
05
结论与展望
研究结论
01
复摆在自由振动时表现出稳定的周期性运动,其振 动频率与摆长、质量和重力加速度有关。
数据分析
通过对实验数据的分析,我们得出了复摆的运动 规律和特性。
数据处理
采用数学方法对实验数据进行处理,绘制了复摆 运动曲线,以便更好地理解其运动特性。
结果对比与讨论
结果对比
将实验结果与理论预测进行对比,验证了理论的正确 性。
复摆振动的研究

复摆振动的研究周云200802050237 08物理(2)班红河学院理学院物理系摘要:复摆振动的研究实验是在理想条件下进行实验的,即不考虑空气阻力的作用,但在实际实验中,是存在空气阻力的。
研究空气阻力对实验结果的影响,将理论结果和实验结果相比较分析空气阻力对实验的影响。
关键词:复摆;空气阻力;阻力系数;振动周期引言:复摆又称为物理摆,是一刚体绕固定的水平轴,在重力的作用下绕不通过质心作微小摆动的动力运动体系,只要满足这一要求便是复摆,复摆是物理学理论和实验都要研究的重要模型。
复摆振动的研究实验是在不计空气阻力的理想情况下,研究复摆的运动规律。
而实际复摆振动时,总要或多或少受到空气的阻尼作用,因此研究空气阻力对复摆振动的影响是十分必要的。
物体所受空气阻力与空气的性质(流速、密度等)、物体的形状、大小及表面状况等因素有关,从理论上计算阻力的大小比较复杂,但根据质点力学的思想在只讨论空气阻尼作用时,一般选用两种假设,一是假设阻力与物体速度成正比;一是假设阻力与速度的平方成正比。
一两种空气阻力假设下的复摆振动周期1、空气阻力与速度一次方成正比如图1所示的复摆,设其质量为M,绕通过某点0的水平轴在竖直平面内摆动.轴0到质心c的距离为L,复摆以角速度ω摆动时OC与铅垂线的夹角为θ。
由于空气阻力的存在,复摆的运动不再是理想的无耗散运动,在运动速度不大的情况下,复摆所受空气阻力与速度成正比即11r f k v k L ω=-=-, (1)其中k 为空气阻力系数,空气阻力对复摆做负功,根据功能原理可得:2102r I M gh f L d ωθ+-=⎰, (2)式中,I 为复摆对回转轴O 的转动惯量,g 为当地的重力加速度,()1cos h L θ=-,当摆角较小时,sin d L d L d θθθθθ=≈。
将(1)式代入(2)式:221102I M gh k L d ωωθ++=⎰又因为d dtθω=,所以对上式两边对时间求导得:22120k L d d M gL dtIdtIθθθ++=, (3)令211k L r I=, 2M gL r I=,则21220d d r r dtdtθθθ++=, (4)令t e αθ=,代入上式得2120r r αα++=, (5)解方程(5)得2α=则()()11121212cos sin22ttr tr tec e c eec c i c c θ⎛ -⎝-⎡⎤=+⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥=++-⎢⎥⎣⎦因为θ是实数,既有1cos2r tceθ-=, (6)式(6)中c 为积分常数,可以看出,复摆振动的角频率为:2ω== (7)此时复摆的振动周期为1T T ==, (8)其中02T π=是不考虑空气阻力时复摆在理想条件下的周期公式。
复摆振动的研究

复摆振动的研究
数据记录参考Байду номын сангаас格
h(m) 10T1(s) 10T2(s)
10T3(s)
10T S
T(S) T2
x
y
复摆振动的研究
数据处理
1.由
y =T h , x =h ,分别计算各χ和y值。
2
2
2.以x为横坐标,y为纵坐标,用坐标纸绘制x—y直线图 3.用作图法求出直线的截距A和斜率B。 4.由公式(6—10)计算重力加速度g和回转半径k。并 计算g的不确定度,最后求出IG及其不确定度。 5.或用最小二乘法处理数据
k 2 +h2 T =2 gh
(6-7)
式中k为回转半径,h为质心到转轴的距离。对式(6-7) 两边平方,并改写成
2 2 4 4 T 2 h= k2+ h2 g g
(6-8)
复摆振动的研究
实验原理
2 2 4 4 2 设 y =T h, x =h ,并令 A= ,则 k , B g g (6-8)式改写成
2.计算g的不确定度
4 g B
2
g u C (g ) u C (B ) B
3.计算IG的不确定度
A I G mk =m B
2
I G uC (I G ) A
2 I G uC (A ) B
2
2 uC (B )
2
不确定度计算(最小二乘法)
1.计算截距A、斜率B的不确定度
A、B的不确定度的B类评定均较小,略去不计。则
u B Sb =
Sy
xi -x
2
u A = S a =S b
2 x i
复摆实验报告

【数据处理及结果】
1) 最小二乘法计算 g 表 2:悬点在 O 点右侧时 h2 与 T2h 数据表
2/7
基础物理实验 复摆实验
h2/cm2 T2h/cm·s2
798.06 44.35
742.56 42.10
689.06 40.06
637.56 37.86
588.06 35.85
540.56 33.95
① 用最小二乘法,作 T2h-h2 图,利用斜率计算 g;
1/7
基础物理实验 复摆实验
②
利用公式4π2 g
=
T12+T22 2(h1+h2)
+
T12−T22 计算 2(h1−h2)
g;
③ 作 T-h 图,从图上求出复摆的等轴单摆长,根据T = 2π√Lg = 2π√h1+gh2计算重力加
速度 g。
+
T12 − T22 2(h1 − h2)
=
975.0cm/s2
② T1 = 1.20753s T2 = 1.20694s h1 = 23.27cm h2 = 13.24cm
4/7
基础物理实验 复摆实验
g2
=
4π2
T12 + T22 2(h1 + h2)
+
T12 − T22 2(h1 − h2)
=
298.25 333.43 371.72 410.47 451.99 495.95 541.49 24.24 25.68 27.23 28.75 30.44 32.20 33.93
h2/cm2 T2h/cm·s2
588.55 638.57 690.11 745.84 801.46 35.94 37.94 40.09 42.22 44.48
复摆实验报告物理

#### 一、实验目的1. 理解复摆的物理特性,掌握其运动规律。
2. 通过实验测量重力加速度,验证牛顿万有引力定律。
3. 掌握作图法研究问题及处理数据的方法。
#### 二、实验原理复摆(物理摆)是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系,其运动可近似看作简谐振动。
复摆的运动方程为:\[ \theta(t) = \theta_0 \cos(\omega t + \phi) \]其中,\(\theta(t)\)为摆角,\(\theta_0\)为初始摆角,\(\omega\)为角频率,\(\phi\)为初相位。
角频率\(\omega\)与摆长\(l\)和重力加速度\(g\)的关系为:\[ \omega = \sqrt{\frac{g}{l}} \]通过测量摆长和周期,可以计算出重力加速度。
#### 三、实验仪器1. 复摆装置(包括摆锤、摆杆、固定轴等)2. 刻度尺3. 秒表4. 计算器#### 四、实验步骤1. 将复摆装置安装在实验台上,调整摆锤的位置,使摆长符合实验要求。
2. 用刻度尺测量摆长\(l\)。
3. 用秒表测量摆动的周期\(T\),重复测量多次,取平均值。
4. 根据公式\(\omega = \sqrt{\frac{g}{l}}\)计算重力加速度\(g\)。
#### 五、实验数据及处理1. 摆长\(l\):1.0 m2. 测量周期\(T\):10.0 s,9.8 s,9.9 s,9.7 s3. 平均周期\(\bar{T}\):9.8 s4. 重力加速度\(g\)计算:\[ g = \frac{4\pi^2 l}{\bar{T}^2} = \frac{4\pi^2 \times 1.0}{(9.8)^2} \approx 9.82 \, \text{m/s}^2 \]#### 六、结果与讨论1. 实验结果显示,复摆的运动符合简谐振动规律,重力加速度的测量结果与理论值较为接近,说明实验设计合理,数据可靠。
复摆实验报告

1.作图如下:
在图中分别取周期为 1.217s,1.204s,1.186s 作与 x 轴平行的直线,和图中交点 的坐标依次为(-24.247,1.217) (-12.538,1.217) (12.421,1.217) (24.334,1.217) (-22.213,1.204) (-13.700,1.204) (13.177, 1.204) (22.678, 1.204) (-17.473,1.186) (17.535,1.186) 由由公式 L=h1 +h1 求出等值单摆长,再由 g= g1=
8.15 26.958 0 1.3497 16.20 23.756 2 1.1878 24.20 24.338 0 1.2169
9.20 26.050 1 1.3025 17.20 23.740 6 1.1870 25.20 24.531 6 1.2266
10.20 25.393 0 1.2697 18.20 23.747 7 1.1874 26.20 24.704 0 1.2352
3研究复摆的振动周期与悬点位置的关系并测定g改变悬点位置从摆杆一端开始知道摆杆另一端测定对应的周期减小测量误差实验时测20个周期的时间合理分布测量点作出th图从图上求出复摆的等值单摆长计算g
复摆实验
实验目的: (1) 研究复摆的物理特性。 (2)用复摆测定重力加速度 (3)用作图法和最小二乘法研究问题及处理数据 仪器用具:复摆(半边长约 30cm,钢铁材质) 光电计时器 米尺及实验所需支 架等。 实验原理:复摆重心距悬点 O 的距离为 h,质量为 m,g 为重力加速度,偏转角 为θ ,则有: M=-mghsin θ,由转动定理 M=Iβ 解得: θ =Acos(ωt + θ0 ) T=2π L=
实验十二复摆(改2010-10-24)

实验二 复摆振动的研究第一篇 实验教材一、实验简介复摆是在重力作用下,能绕通过自身某固定水平轴摆动的刚体。
又称物理摆。
使用复摆可比用单摆更精确的测量重力加速度。
摆振动的现代研究不仅在理论的上,而且在科学研究上和工程技术上都有极其重要的意义。
二、实验要求1. 根据测得数据绘出T -h 图线2. 研究复摆振动周期的变化与复摆重心距离的关系。
3. 测量重力加速度。
三、仪器用具复摆、停表(或光电计时装置)、卷尺、复摆刀架四、实验装置介绍如图(12-1)所示,本实验所用复摆为一均匀钢板(宽约几厘米,长100厘米),它上面从中心向两端对称地开有19个小孔。
测量时分别将复摆通过小圆孔悬挂在固定刀刃上。
五、实验原理 1、复摆的周期如图(12-1)表示一个形状不规则的刚体,挂于过O 点的水平轴(回转轴)上,若刚体离开竖直方向转过θ角度后释放,它在重力力矩的作用下将绕回转轴自由摆动,这就是一个复摆。
摆动过程中,复摆只受重力和转轴的反作用力,而重力矩起着回复力矩的作用。
设质量为m 的刚体绕转轴的转动惯量为I ,让刚体绕固定轴O 在竖直平面内作左右摆动,G 是该物体的质心,质心与轴O 的距离为h ,θ为其摆动角度。
则刚体摆动的回复力矩为:sin M mgh θ=-(负号表示刚体所受力矩与角位移方向相反。
)若θ很小时(θ在5°以内)近似有 θmgh M -= (12-1) 又据转动定律,该复摆又有22d d M I tθ= (12-2)其中I 为该物体转动惯量。
由(1)和(2)可得222d d t θωθ=- (12-3) 其中Imgh=2ω。
此方程说明该复摆在小角度下作简谐振动,该复摆振动周期为 mghIT π=2 (12-4) 式中h 为回转轴到重心G 的距离;I 为刚体对回转轴O 的转动惯量;m 为刚体的质量;g 是当地的重力加速度。
设刚体对过重心G ,并且平行于水平的回转轴O 的转动惯量为I G ,根据平行轴定理得I =I G +mh 2将此公式代入(12-4)式,得mghmh I T G 22+=π(12-5)设a 为复摆对质心轴G 的回转半径,则有2G I ma =。
加配重复摆振动周期变化规律的研究

研究 复摆摆动周 期与 回转轴 到 质心 距离 之 间
的关 系 是 复 摆 实 验 的 一 项 重 要 内 容 . 加 配 重 状 在 态下 , 由于 复 摆 质 心 位 置 的 改 变 , 摆 摆 动 周 期 与 复
式 中 , 为复摆 对 回转 轴 0 的转动惯 量 ; g为 当地 重力 加速度 . 当摆 角较小 时复摆 作 简谐 振动 , 动 振
S TUDY oN THE CHANGI NG RULE BRATI N oF VI o PERI oD oF EI W GHTED CoM PoUND PENDULUM
Z uDe i Wa gYa h i Z a gT a y n Qu Gu n we o bn n n u h n in a g ag i
J d 0+ 2
,
0到 新 质 心 G 的 距 离 ( 图 2 a ) 由式 ( ) 见 ( ). 和
() 4 得
图 1
( + m1 1 m )
mR + mh
,
嘲 ^sn 一 O i
再 一—
一
根据 悬挂 点 ( 所 处 位置 的不 同 , 面分 三种 ) 下
周 期 为
To 一
回转 轴到质 心距 离 之 间 的关 系 将 发 生变 化 , 这 但
种 变 化 不 是 简 单 的 曲 线 平 移 , 重 对 复 摆 摆 动 周 配
√
期大小 的影 响 随 回转 轴 位置 不 同而不 同. 为使 学 生对复 摆实 验有 一 个 更 深刻 的理 解 , 文将 通 过 本 理论分 析和 实验 测 量 , 加配 重 后 复 摆周 期 的变 对
A b ta t By t e r tc la a yss a d e p rm e t lm e u e e t sr c h o e ia n l i n x e i n a as r m n s, t nfu n e o ta hi g he i l e c f a t c n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3卷第1期2001年3月 辽宁师专学报Journal of Liaoning T eachers College V ol.3N o.1Mar.2001
文章编号:1008-5688(2001)01-0029-03
关于复摆实验研究
杨晓强
(锦州师专,锦州 121000)
摘 要:为使学生对教材中复摆(形状规则)实验理解的更加透彻,详细地讨论了复摆实验中
所涉及的T —h 图,并将通过实验绘制的T —d 图与T —h 图加以比较,进而通过复摆实验,使学生掌握一种测定重力加速度的方法.
关键词:复摆;回转半径;等值摆长中图分类号:O 4233 文献标识码:B
复摆是一个具有质量分布的刚体,它绕着一个固定的水平轴自由地转动和振荡.水平轴
刚性地固定在物体上
,而且不通过它的质心.如图1
c 为质心,P 为转轴,当摆角很小时,复摆振动的周期
T =2
πa 2+h 2
g h
(1)
其中:a 为通过重心且垂直摆的方向为轴的回转半径,h 为回转轴到重心c 的距离.如改变回转轴的位置,使h 变化时,摆动周期也将变化,从(1)式可以看出,h →0时,T →∞;h →∞时T →∞.因此,当h 从0变到∞时,T 当有极小
值,极小值的条件是d T
d h =0,即:
d T
d h =2π×12
a 2
+h
2
g h
-12
2g -a 2+h 2
g h 2
=0
(2)
(2)式的解是h =a.即h =a 时周期T 极小,T min =2π
2a
g
.以h 为横轴,T 为纵轴可作T —h 图.对一固定复摆,a 值一定.取点:
h =a , T min =2
π2a
g
h =
a
2 , T =2
π5a 2g
; h =2a , T =2π5a 2g
收稿日期:2000—10—20
作者简介:杨晓强(19542),男,辽宁锦州人,讲师,主要从事物理教学研究,发表论文4篇1
30辽宁师专学报2001年第1期
h=a
3 , T=2π10a
3g
; h=3a , T=2π10a
3g
h=a
4 , T=2π17a
4g
; h=4a , T=2π17a
4g
… …
h=a
n , T=2π
(n2+1)a
n g
; h=na , T=2π
(n2+1)a
n g
由上述各点描绘图线如图2,因P轴是任取的,所以对任意一复摆得出结论:Ⅰ.过重心C 作任一射线,以射线上任意点为回转轴,做得T—h图均相同;Ⅱ.对于以C为圆心,任意长h为半径的圆周上任意点为回转轴,测出周期T是相同的.在图2中看出当h<a时, T增加,h>a时,T也增加.但在h<a时,T增加的幅度比h>a时T增加的幅度大.参考书目中给出的复摆形状是规则的.若取该复摆质心为坐标原点,质心上方h为正,质心下方h为负,可得图3.
复摆实验的最终目的,在于量度周期后利用周期与加速度的关系式计算g值.我们已知
单摆周期T与摆长L之间的关系为T=2πL
g
令该单摆的周期与(1)式复摆周期相等则有
L=a2+h2
h
……(3).(3)式L为复摆的等值摆长.从图2中可看出对应复摆同一周期T的
h值有两个.两者之间应满足a2+h12
h1
=
a2+h22
h2
,即a2=h1h2……(4),将(4)式代入
(3)式有L=h1+h2……(5).这样,我们利用(4)、(5)式,依据T min=2π2a
g
和T=
2πh1+h2
g
即可算出g.
在复摆实验中,学生们实际测量的不是h而是d,即从复摆的一端到各悬挂点的距离,并要求绘制T—d图.为什么不直接绘制T—h图呢?笔者认为理由有:(1)要测出h首先要测出质心位置,给实验增添麻烦.即使是形状规则的复摆,也难免质心不在几何中心处;(2)实验要求测出从复摆一端到各悬挂点的距离d,容易操作,也很方便,误差小.那么T—d图与T—h图有什么关系?对所示的回转半径、等值摆长是否会有影响?答案是两图形状完全一样.具体分析如下:如图4所示.设质
杨晓强关于复摆实验研究31
心位置C,AC=l,∴d=l-h,将h=l-d代入(1)
式,得
T=2πa 2+(l-d)2
g(l-d)
(6)
当: d=l-a , T=2π2a
g
d=l-a
2 , T=2π5a
2g
; d=l-2a , T=2π5a
2g
d=l-a
3 , T=2π10a
3g
; d=l-3a , T=2π10a
3g
d=l-a
4 , T=2π
17a
4g
; d=l-4a , T=2π
17a
4g
… …
d=l-a
n T=2π
(n2+1)a
n g
d=l-na T=2π
(n2+1)a
n g
复摆倒过来时:d=l+a , T=2π2a
g
d=l+a
2
, T=2π5a
2g
; d=l+2a , T=2π5a
2g
d=l+a
3
, T=2π10a
3g
; d=l+3a , T=2π10a
3g
d=l+a
4
, T=2π17a
4g
; d=l+4a , T=2π17a
4g
… …
d=l+a
n
, T=2π
(n2+1)a
n g
; d=l+na , T=2π
(n2+1)a
n g
取上述各点做T—d图,得图5.将图5与图3比较,图线形状没有变化,只是纵坐标向左平移l.
参考文献:
[1]杨述武,等.普通物理实验[M].北京:高等教育出版社,1980.1012104.
(责任编辑 王舜谦)。
