高三第二次模拟试题(最后试题)

合集下载

2024年新高考九省联考高三第二次模拟数学试题及答案

2024年高考第二次模拟考试高三数学（考试时间：120分钟试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设集合(){}{}ln 3,1A x y x Bx x ==−=≤−，则()A B =R （）A ．{}13x x −<≤B ．{}1x x >− C ．{1x x ≤−,或}3x >D ．{}3x x >2.已知复数i z a b =+（a ∈R ，b ∈R 且a b ），且2z 为纯虚数，则zz=（） A ．1B ．1−C ．iD ．i −3.已知向量()2,4a =−，()1,b t = ，若a 与b 共线，则向量a b + 在向量()0,1j = 上的投影向量为（）A ． jB ． j −C ． 2jD ． 2j −4. “1ab >”是“10b a>>”（） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件5.有甲、乙等五人到三家企业去应聘，若每人至多被一家企业录用，每家企业至少录用其中一人且甲、乙两人不能被同一家企业录用，则不同的录用情况种数是（） A ．60 B ．114 C ．278 D ．3366.已知D ：222210x y ax a +−−−=，点()3,0P −，若D 上总存在M ，N 两点使得PMN 为等边三角形，则a 的取值范围是（） A ． ()5,11,3 −−∪−+∞B ． [)5,1,3−∞−∪+∞C ． (][) ,21,−∞−∪+∞D ． [)()2,11,−−−+∞7.已知ABC ∆中，60BAC ∠=°，2AB =，Q 是边BC 上的动点．若PA ⊥平面ABC ，PA =，且PQ与面ABC ，则三棱锥−P ABC 的外接球的表面积为（） A ． 4πB ． 6πC ． 8πD ． 9π8.加斯帕尔-蒙日是1819世纪法国著名的几何学家．如图，他在研究圆锥曲线时发现：椭圆的任意两条互相垂直的切线的交点都在同一个圆上，其圆心是椭圆的中心，这个圆被称为“蒙日圆”．若长方形G 的四边均与椭圆22:164x y M +=相切，则下列说法错误的是（）A ．椭圆MB ．椭圆M 的蒙日圆方程为2210x y +=C ．若G 为正方形，则G 的边长为D ．长方形G 的面积的最大值为18二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得60分．9.已知抛物线2:6C y x =的焦点为F ，过点F 的直线交C 于,M N 两个不同点，则下列结论正确的是（） A ．MN 的最小值是6 B ．若点5,22P，则MF MP +的最小值是4C ．113MF NF+= D ．若18MF NF ⋅=，则直线MN 的斜率为1± 10.已知双曲线()222:102x y E a a−=>的左、右焦点别为1F ，2F ，过点2F 的直线l 与双曲线E 的右支相交于,P Q 两点，则（）A ．若E 的两条渐近线相互垂直，则a =B．若E E 的实轴长为1C ．若1290F PF ∠=°，则124PF PF ⋅=D ．当a 变化时，1F PQ 周长的最小值为11.在棱长为2的正方体1111ABCD A B C D −中，,E F 分别是棱,BC CD 的中点，则（） A ．11B D 与EF 是异面直线B ．存在点P ，使得12A P PF =，且BC //平面1APBC ．1A F 与平面1B EBD ．点1B 到平面1A EF 的距离为45三、填空题：本题共3小题，每小题5分，共15分．12.若二项式nx+的展开式中二项式系数之和为64，则二项展开式中系数最大的项为13.若函数()sin f x ax x =+ 的图像上存在两条互相垂直的切线，则实数a 是__________.14. 若过点()0,1的直线l 自左往右交抛物线214y x =及圆()22114x y +−=于,,,A B C D 四点，则3AB CD +的最小值为________.四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（13分）已知数列{}n a 的前n 项和为n S ，且对于任意的*n ∈N 都有321n n S a =+．（1）求数列{}n a 的通项公式；（2）记数列{}n a 的前n 项中的最大值为n M ，最小值为n m ，令2n nn M m b +=，求数列{}n b 的前20项和20T ．16．（15分）灯带是生活中常见的一种装饰材料，已知某款灯带的安全使用寿命为5年，灯带上照明的灯珠为易损配件，该灯珠的零售价为4元/只，但在购买灯带时可以以零售价五折的价格购买备用灯珠，该灯带销售老板为了给某顾客节省装饰及后期维护的支出，提供了150条这款灯带在安全使用寿命内更换的灯珠数量的数据，数据如图所示.以这150条灯带在安全使用寿命内更换的灯珠数量的频率代替1条灯带更换的灯珠数量发生的概率，若该顾客买1盒此款灯带，每盒有2条灯带，记X 表示这1盒灯带在安全使用寿命内更换的灯珠数量，n 表示该顾客购买1盒灯带的同时购买的备用灯珠数量.（1）求X 的分布列；（2）若满足()0.6P X n ≥≤的n 的最小值为0n ，求0n ；（3）在灯带安全使用寿命期内，以购买替换灯珠所需总费用的期望值为依据，比较01nn =−与0n n =哪种方案更优.17．（15分）如图,在三棱柱111ABC A B C −中,直线1C B ⊥平面ABC,平面11AA C C ⊥平面11BB C C .(1)求证:1AC BB ⊥;(2)若12AC BC BC ===,在棱11A B 上是否存在一点P ,使二面角1P BC C −−?若存在,求111B PA B 的值;若不存在,请说明理由.18．（17分）已知函数()ln =−+f x x x a ．(1)若直线(e 1)yx =−与函数()f x 的图象相切，求实数a 的值； (2)若函数()()g x xf x =有两个极值点1x 和2x ，且12x x <，证明：12121ln()x x x x +>+．（e 为自然对数的底数）．19．（17分）阿波罗尼斯是古希腊著名数学家，他的主要研究成果集中在他的代表作《圆锥曲线》一书中.阿波罗尼斯圆是他的研究成果之一，指的是已知动点M 与两定点Q,P 的距离之比()||0,1,||MQ MP λλλλ=>≠是一个常数，那么动点M 的轨迹就是阿波罗尼斯圆，圆心在直线PQ 上.已知动点M 的轨迹是阿波罗尼斯圆，其方程为224x y +=,定点分别为椭圆2222:1x y C a b+=(0)a b >>的右焦点F 与右顶点A,且椭圆C 的离心率为1.2e = (1)求椭圆C 的标准方程；(2)如图，过右焦点F 斜率为(0)k k >的直线l 与椭圆C 相交于B ,D(点B 在x 轴上方),点S,T 是椭圆C 上异于B,D 的两点，SF 平分,BSD TF ∠平分.BTD ∠（1）求||||BF DF 的取值范围；（2）将点S 、F 、T 看作一个阿波罗尼斯圆上的三点，若△SFT 外接圆的面积为818π,求直线l 的方程.2024年高考第二次模拟考试高三数学全解全析一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．A ．{13x x −<≤B ．{1x x >− C.{1x x ≤−,或}3x >D ．{3x x >【答案】B【分析】先化简集合，再利用集合的交并补运算求解即可，【详解】由题意得{}3A x x =>，{}1B x x =≤−，又{}1B x x =>−R 则(){}1A B x x ∪=>−R ，故选：B.A ．1B ．1−C ．iD ．i −【答案】D【分析】利用复数的概念及四则运算法则运算即可求解.【详解】因为i z a b =+，所以()2222(i)2i z a b a b ab =+=−+，又因为2z 为纯虚数，所以2220a b ab −= ≠，即0a b =≠（舍）或0a b =−≠，所以i z a a =−，所以i z a a =+，所以2i 1i (1i)i i 1i (1i)(1i)z a a a a z −−−====−+++−. 故选：D3.已知向量()2,4a =−，()1,b t = ，若a 与b 共线，则向量a b +在向量()0,1j = 上的投影向量为（）A. jB. j −C. 2jD. 2j −【答案】C 【解析】【分析】根据a 与b 共线，可得240t −−=，求得2t =−，再利用向量a b +在向量()0,1j = 上的投影向量为()a b j jj j+⋅⋅ ，计算即可得解. 【详解】由向量()2,4a =−，()1,b t = ，若a与b共线，则240t −−=，所以2t =−，(1,2)a b +=−，所以向量a b +在向量()0,1j = 上的投影向量为： ()(1,2)(0,1)21a b j j j j j j+⋅−⋅⋅=⋅=，故选：C4. “1ab >”是“10b a>>”（） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件【答案】B 【解析】【分析】根据充分条件和必要条件的定义判断. 【详解】当0a >时，由1ab >，可得10b a>>，当a<0时，由1ab >，得10b a<<；所以“1ab >”不是“10b a>>”的充分条件. 因为01010a b ab a a>>>⇔− > ，所以1ab >，所以“1ab >”是“10b a>>”的必要不充分条件. 故选：B.【点睛】本题考查不等式性质与充分、必要条件的判定，还考查了理解辨析问题的能力，属于基础题. 5.有甲、乙等五人到三家企业去应聘，若每人至多被一家企业录用，每家企业至少录用其中一人且甲、乙两人不能被同一家企业录用，则不同的录用情况种数是（） A.60 B.114 C.278 D.336【答案】D【解析】命题意图本题考查排列与组合的应用.录用3人，有 353360C A = 种情况；录用4 人，有 4232354333162C C A C A −=种情况；录用 5 人，有12323331345333333225)4(C C A C A (C A C A )11A −+−=种情况.所以共有336种.6.已知D ：222210x y ax a +−−−=，点()3,0P −，若D 上总存在M ，N 两点使得PMN 为等边三角形，则a 的取值范围是（） A. ()5,11,3 −−∪−+∞B. [)5,1,3−∞−∪+∞C. (][) ,21,−∞−∪+∞D. [)()2,11,−−−+∞【答案】B 【解析】【分析】D 的圆心坐标为(),0D a ，半径为1ra =+,要使D 上总存在M ，N 两点使得PMN 为等边三角形，则D 上存在一点M ，使得30MPD ∠=°,当PM 与D 相切时，MPD ∠最大，故sin sin 30rMPD PD∠=≥°，由此可求解. 【详解】D 的标准方程为()()2221x a y a −+=+，圆心坐标为(),0D a ，半径为1ra =+.因为,PM PN MD ND ==，所以PMD PND ≅△△.所以30MPD NPD ∠=∠=°.要使D 上总存在M ，N 两点使得PMN 为等边三角形，则D 上存在一点M ，使得30MPD ∠=°,当PM 与D 相切时，MPD ∠最大，此时30MPD ∠≥°，故1sin sin 302r MPDPD ∠=≥°=，即()1132a a +≥+，整理得23250a a +−≥，解得[)5,1,3a∈−∞−∪+∞.故选:B.7.已知ABC 中，60BAC ∠=°，2AB =，Q 是边BC 上的动点．若PA ⊥平面ABC ，PA =，且PQ与面ABC ，则三棱锥−P ABC 的外接球的表面积为（） A. 4π B. 6πC. 8πD. 9π【答案】B 【解析】【分析】根据题意得PQ AQ 的最小值是1，即A 到BC 的距离为1，则∠ACB ＝90°，结合图形找出△ABC 的外接圆圆心与三棱锥−P ABC 外接球的球心，求出外接球的半径，再计算它的表面积．【详解】三棱锥−P ABC 中，PA ⊥平面ABC ，设直线PQ 与平面ABC 所成角为θ，∵sin θ，∴sin PA PQ θ==≤PQ ≥即PQ AQ 的最小值是1，即A 到BC 的距离为1，直角三角形△ABQ 中，AB ＝2，所以∠BAQ =60°,又∠BAC ＝60°，所以,A Q 重合，则∠ACB ＝90°，则△ABC 的外接圆圆心M 为AB 的中点，又PA ⊥平面ABC ，从而外接球的球心O 为PB 的中点，外接球的半径R OB =，∴三棱锥−P ABC 的外接球的表面积224π4π6πS R ==×=．故选：B ．8.加斯帕尔-蒙日是1819世纪法国著名的几何学家．如图，他在研究圆锥曲线时发现：椭圆的任意两条互相【分析】由椭圆标准方程求得,a b 后再求得c ，从而可得离心率，利用特殊的长方形（即边长与椭圆的轴平行）求得蒙日圆方程，从而可得长方形边长的关系，结合基本不等式得面积最大值，并得出长方形为正方形时的边长．【详解】由椭圆方程知a =2b =，则c ，离心率为e =A 正确；当长方形G 的边与椭圆的轴平行时，长方形的边长分别为4，因此蒙，圆方程为2210x y +=，B 正确；设矩形的边长分别为,m n ，因此22402m n mn +=≥，即20mn ≤，当且仅当m n =时取等号，所以长方形G 的面积的最大值是20，此时该长方形G 为正方形，边长为C 正确，D 错误．故选：D ．二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9.已知抛物线2:6C y x =的焦点为F ，过点F 的直线交C 于,M N 两个不同点，则下列结论正确的【分析】A ，根据12||=MN x x p ++结合基本不等式即可判断；B ，由抛物线定义知当,,P M A 三点共线时MF MP +；C ，D ，设直线方程，联立抛物线，应用韦达定理即可求解.【详解】对A ，设112212(,),(,),(,0)M x y N x y x x >，因为这些MN 倾斜角不为0，则设直线MN 的方程为32x ky =+，联立抛物线得2690y ky −−=，则12126,9y y k y y +=⋅=−，所以()()221212121212399363,244k x x k y y k x x k y y y y ∴+=++=+=+++=，则212||=3666MN x x k ++=+≥（当且仅当0k =时等号成立），A 正确；对B ，如图MA ⊥抛物线准线，MF MP MA MP +=+要使其最小，即,,P M A 三点共线时取得最小值，即53||422MF MP MA MP PA +=+==+=，B 正确；对C ，由()121212311||||239||||||||324x x NF MF MF NF MF NF x x x x ++++===+++，C 错误；对D ，1212123339()()()2224MF NF x x x x x x ⋅=+⋅+=+++2293993(63)(63)1842422k k =+++=++=，解得1k =±,D 正确故选：ABD.10.已知双曲线()222:102x y E a a −=>的左、右焦点别为1F ，2F ，过点2F 的直线l 与双曲线E 的右支相交于,P Q 两点，则（） A. 若E的两条渐近线相互垂直，则a =B. 若EE 的实轴长为1C. 若1290F PF ∠=°，则124PF PF ⋅= D. 当a 变化时，1F PQ周长的最小值为【答案】ACD 【解析】【分析】根据双曲线的渐近线、离心率、定义、三角形的周长等知识对选项进行分析，从而确定正确答案.【详解】依题意，b =，A选项，若双曲线的两条渐近线相互垂直，所以1,ba b a===，故A 正确；B 选项，若E的离心率为c e a ==，解得1a =，所以实轴长22a =，故B 错误；C 选项，若1290F PF ∠=°，则122221224PF PF a PF PF c −=+=，整理得222121224448,4PF PF c a b PF PF ⋅=−==⋅=，故C 正确； D 选项，根据双曲线的定义可知，121222PF PF a QF QF a −=−= ，两式相加得11114,4PF QF PQ a PF QF a PQ +−=+=+，所以1F PQ 周长为42a PQ +，当12PQ F F ⊥时，PQ 取得最小值224b a a=，所以8424a PQ a a +≥+≥，当且仅当84a a=，即a = 所以1F PQ周长的最小值为D 正确. 故选：ACD11.在棱长为2的正方体1111ABCD A B C D −中，,E F 分别是棱,BC CD 的中点，则（）【分析】A 选项，建立空间直角坐标系，根据112B D EF = 得到11B D 与EF 平行；B 选项，先求出242,,333P，得到平面1APB 的法向量()1,0,1m =− ，根据数量积为0得到BC m ⊥ ，得到BC //平面1APB ；C 选项，先求出1A F 与平面1B EB 所成角的正弦值，进而求出余弦值；D 选项，求出平面1A EF 的法向量，根据点到平面距离公式求出答案.【详解】A 选项，以A 作坐标原点，1,,AB AD AA 所在直线分别为,,x y z 轴，建立空间直角坐标系，()()()()()()()1112,0,2,0,2,2,2,1,0,1,2,0,0,0,2,2,0,0,2,2,0B D E F A B C ，则()()112,2,0,1,1,0B D EF =−=− ，由于112B D EF =，故11B D 与EF 平行，A 错误； B 选项，设(),,P x y z ，因为12A P PF =，所以()()2,,21,2,x y z x y z −−−−=，即224222x xy y z z =− =− −=−，解得242,,333x y z ===，故242,,333P ，设平面1APB 的法向量为(),,m a b c =，则()()()1242242,,,,0333333,,2,0,2220m AP a b c a b c mAB a b c a c ⋅=⋅=++=⋅=⋅=+= ，令1a =，则0,1b c ==−，则()1,0,1m =−，因为()()0,2,01,0,10BC m ⋅=−= ，故BC m ⊥ ，BC //平面1APB ，故存在点P ，使得12A P PF =，且BC //平面1APB ，B 正确；C 选项，平面1B EB 的法向量为()1,0,0n =，故1A F 与平面1B EB则1A F 与平面1B EBC 正确；D 选项，设平面1A EF 的法向量为()1111,,n x y z =，则()()()()11111111111111,,2,1,2220,,1,1,00n A E x y z x y z n EF x y z x y ⋅⋅−+− ⋅=⋅−=−+= ，令11x =，则1131,2y z ==，故131,1,2n = ，则点1B 到平面1A EFD 错误.故选：BC三、填空题：本题共3小题，每小题5分，共15分．12.若二项式nx+的展开式中二项式系数之和为64，则二项展开式中系数最大的项为【答案】240 【解析】【详解】因为二项式nx+ 的展开式中二项式系数之和为64，所以264n =，得6n =，所以二项式为6x+，则二项式展开式的通项3662166C C 2r r r r r rr T x x −−+=，令第1r +项的系数最大，则11661166C 2C 2C 2C 2r r r r r r r r −−++ ≥ ≥ ，解得111433r ≤≤，因为N r ∈，所以4r =，则二项展开式中系数最大的项为36444256C 2240T x −×==，所以填24013.若函数()sin f x ax x =+ 的图像上存在两条互相垂直的切线，则实数a 是__________.【答案】0 【解析】【详解】注意到，()cos f x a x =+′.若函数()f x 上存在两条切线垂直，则存在1x 、2x R ∈，使得()()()()12121cos cos 1f x f x a x a x ′′=−⇔++=−()21212cos cos cos cos 10a a x x x x ⇔+++⋅+=221212cos cos cos cos 1022x x x x a +−⇔++−=12cos cos 1,0x x a ⇔=−=±=.故答案为014. 若过点()0,1的直线l 自左往右交抛物线214y x =及圆()22114x y +−=于,,,A B C D 四点，则3AB CD +的最小值为________.【答案】2+ 【解析】【分析】根据抛物线的定义求得求出11,22A D AB y CD y =+=+，当l y ⊥轴时，则1D Ay y ==，可求3AB CD +的值；当直线方程为()1x n y =−时，代入抛物线方程，根据韦达定理结合基本不等式求得此时3AB CD +的最小值，即可得结论．【详解】解：如图，其中抛物线214y x =的焦点坐标为()0,1F ，抛物线的准线方程为：1y =−，圆()22114x y +−=的半径12r =又抛物线的定义可得：1,1A D AF y DF y =+=+，又11,22A D AB AF BF y CD DF CF y =−=+=−=+，当l y ⊥轴时，则1A Dy y ==，所以113131622AB CD+=+++=；当l 不垂直于y 轴时，设l 的方程为：()1x n y =−，代入抛物线方程得：()2222240n y n y n −++=，所以2224,1A D A D n y y y y n++=⋅=。

2024届河南省濮阳市高三二模语文试题(解析版)

濮阳市普通高中2023—2024学年高三第二次模拟考试语文全卷满分150分，考试时间150分钟。

注意事项：1.答卷前，考生务必将自己的姓名、班级、考场号、座位号、考生号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，18分）阅读下面的文字，完成下面小题。

在微粒说与波动说的第一次交锋中，以牛顿为首的微粒说战胜了波动说，取得了在物理学界被普遍公认的地位。

近一个世纪过去了，英国米尔沃顿的一个教徒的家庭里诞生了一个男孩，他被取名为托马斯·杨。

经过学习和探究，他最终形成了光具有波动性质的想法，这个认识源于波动中所谓的“干涉”现象，波的干涉现象是各种波所独有的基本特征。

我们都知道，普通的物质是具有累加性的，一滴水加上一滴水一定是两滴水，而不会一起消失。

但是波动就不同了，一列普通的波，有着波的高峰和波的谷底，如果两列振幅相同的波相遇，当它们正好都处在高峰时，那么叠加起来的这个波就会达到两倍的峰值，如果都处在低谷时，叠加的结果就会是两倍深的谷底。

但是，等等，如果正好一列波在它的高峰，另一列波在它的谷底呢？答案是它们会互相抵消。

如果两列波在这样的情况下相遇——物理上叫作“反相”——那么在它们重叠的地方将会波平如镜，既没有高峰，也没有谷底。

这就像一个人把你往左边拉，另一个人用相同的力气把你往右边拉，结果是你会站在原地不动。

托马斯·杨在研究牛顿环的明暗条纹的时候，被这个关于波动的想法给深深打动了。

为什么会形成一明一暗的条纹呢？一个想法渐渐地在杨的脑海里成形：用波来解释不是很简单吗？明亮的地方，那是因为两道光正好是“同相”的，就好像有两个人同时在左边或者右边拉你，它们的波峰和波谷都得到增强，结果造成了两倍光亮的效果；而黑暗的那些条纹，则一定是两道光处于“反相”，它们的波峰、波谷相对时，就好像两个人同时往两边拉你，正好互相抵消了。

江苏省南京市2024届高三年级第二次模拟考试数学试题(解析版)

南京市2024届高三年级第二次模拟考试数学2024.05注意事项：1．本试卷考试时间为120分钟，试卷满分150分，考试形式闭卷．2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分．3．答题前，务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上．一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知向量a ＝(1，2)，b ＝(x ，x ＋3)．若a ∥b ，则x ＝A ．－6B ．－2C ．3D ．62．“0＜r ＜2”是“过点(1，0)有两条直线与圆C ：x 2＋y 2＝r 2(r ＞0)相切”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．为了得到函数y ＝sin(2x ＋π3)的图象，只要把函数y ＝sin2x 图象上所有的点A ．向左平移π6个单位B ．向左平移π3个单位C ．向右平移π6个单位D ．向右平移π3个单位4．我们把各项均为0或1的数列称为0－1数列，0－1数列在计算机科学和信息技术领域有着广泛的应用．把佩尔数列{P n }(P 1＝0，P 2＝1，P n ＋2＝2P n ＋1＋P n ，n ∈N *)中的奇数换成0，偶数换成1，得到0－1数列{a n }．记{a n }的前n 项和为S n ，则S 20＝A ．16B ．12C ．10D ．85．已知P (A )＝35，P (A ―B )＝15P (A |B )＝12，则P (B )＝A ．15B ．25C ．35D ．456．在圆O 1O 2中，圆O 2的半径是圆O 1半径的2倍，且O 2恰为该圆台外接球的球心，则圆台的侧面积与球的表面积之比为A ．3：4B ．1：2C ．3：8D ．3：107．已知椭圆C 的左、右焦点分别为F 1，F 2，下顶点为A ，直线AF 1交C 于另一点B ，△ABF 2的内切圆与BF 2相切于点P ．若BP ＝F 1F 2，则C 的离心率为A ．13B ．12C ．23D ．348．在斜△ABC 中，若sin A ＝cos B ，则3tan B ＋tan C 的最小值为A ．2B ．5C ．6D ．43二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，不选或有选错的得0分．9．已知z1，z2为共轭复数，则A．z12＝z22B．|z1|＝|z2|C．z1＋z2∈R D．z1z2∈R10．已知函数f(x)满足f(x)f(y)＝f(xy)＋|x|＋|y|，则A．f(0)＝1B．f(1)＝－1C．f(x)是偶函数D．f(x)是奇函数11．已知平行六面体ABCD－A1B1C1D1的棱长均为2，∠A1AB＝∠A1AD＝∠BAD＝60°，点P在△A1BD内，则A．A1P∥平面B1CD1B．A1P⊥AC1C．PC1≥6AP D．AP＋PC1≥26三、填空题：本题共3小题，每小题5分，共15分．12．已知集合A＝{1，2，4}，B＝{(x，y)|x∈A，y∈A，x－y∈A}，则集合B的元素个数为▲．13．在平面四边形ABCD中，∠A＝135°，∠B＝∠D＝90°，AB＝2，AD＝2，则四边形ABCD 的面积为▲．14．已知函数f(x)＝x3－ax＋1(a∈R)的两个极值点为x1，x2(x1＜x2)，记A(x1，f(x1))，C(x2，f(x2))．点B，D在f(x)的图象上，满足AB，CD均垂直于y轴．若四边形ABCD为菱形，则a＝▲．四、解答题：本题共5小题，共77分．解答应写出文字说明，证明过程或演算步骤．15．(本小题满分13分)某地5家超市春节期间的广告支出x(万元)与销售额y(万元)的数据如下：超市A B C D E 广告支出x 24568销售额y3040606070(1)从A ，B ，C ，D ，E 这5家超市中随机抽取3家，记销售额不少于60万元的超市个数为X ，求随机变量X 的分布列及期望E (X )；(2)利用最小二乘法求y 关于x 的线性回归方程，并预测广告支出为10万元时的销售额．附：线性回归方程^y ＝^bx ＋^a 中斜率和截距的最小二乘估计公式分别为：^b ＝∑n i ＝1x i y i －n -x -y∑ni ＝1x i 2－n -x 2，^a ＝―y －^b ―x ．16．(本小题满分15分)已知函数f (x )＝x 2－ax ＋ae x，其中a ∈R ．(1)当a ＝0时，求曲线y ＝f (x )在(1，f (1))处的切线方程；(2)当a ＞0时，若f (x )在区间[0，a ]上的最小值为1e，求a 的值．17．(本小题满分15分)在五面体ABCDEF中，CD⊥平面ADE，EF⊥平面ADE．(1)求证：AB∥CD；(2)若AB＝2AD＝2EF＝2，∠ADE＝∠CBF＝90°，点D到平面ABFE的距离为22，求二面角A－BF－C的大小．(第17题图)18．(本小题满分17分)已知抛物线C：y2＝2px(p＞0)与双曲线E：x2a2－y2b2＝1(a＞0，b＞0)有公共的焦点F，且p＝4b．过F的直线l与抛物线C交于A，B两点，与E的两条渐近线交于P，Q两点(均位于y轴右侧)．(1)求E的渐近线方程；(2)若实数λ满足λ(1|OP|＋1|OQ|)＝|1|AF|－1|BF||，求λ的取值范围．19．(本小题满分17分)已知数列{a n}的前n项和为S n．若对每一个n∈N*，有且仅有一个m∈N*，使得S m≤a n＜S m＋1，则称{a n}为“X数列”．记b n＝S m＋1－a n，n∈N*，称数列{b n}为{a n}的“余项数列”．(1)若{a n}的前四项依次为0，1，－1，1，试判断{a n}是否为“X数列”，并说明理由；(2)若S n＝2n，证明{a n}为“X数列”，并求它的“余项数列”的通项公式；(3)已知正项数列{a n}为“X数列”，且{a n}的“余项数列”为等差数列，证明：S n≤(1＋2n－2)a1．。

2024届东北三省高三三校二模联考化学试题(含答案)

哈尔滨师大附中东北师大附中辽宁省实验中学2024年高三第二次联合模拟考试化学试卷性气味气体的产生，设计了由灯座、灯盏、烟管三部分组成的结构。

下列说法错误本试卷共19题，共100分。

考试用时75分钟。

注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

本卷可能用到的相对原子质量：H1Li7C12O16F19Mg24S32K39一、选择题（本题共15小题，每小题3分，共45分。

在每小题给出的四个选项中，只有一个选项符合要求。

）1．东汉错银铜牛灯采用铜、银二种材质制作，常以动物油脂或植物油为燃料，为减少燃烧过程烟尘和刺激的是（）A ．烟管的作用是将燃烧产生的烟气导入铜牛灯座腹腔中B ．古人常用草木灰浸泡液代替牛腹中的水，吸收烟气的效果更佳C ．银、铜的导热性能好，可以使燃料充分燃烧D ．灯具的设计包含了装置、试剂、环保等实验要素 2．下列化学用语或表述错误的是（）A ．乙烯的球棍模型：B ．基态Al 原子最高能级的电子云轮廓图：C ．在()346Ni NH SO 中，阴离子的VSEPR 模型名称：正四面体形D ．次氯酸钠中含有的化学键类型：极性键、离子键 3．下列有关物质的工业制备反应错误的是（）A ．侯氏制碱：23234NaCl H O NH CO NaHCO NH Cl +++↓+B ．工业合成氨：223N 3H 2NH →+← 高温、高压催化剂C ．氯碱工业：2222NaCl 2H O2NaOH H Cl ++↑+↑电解D ．冶炼金属铝：322AlCl 2Al 3Cl +↑电解4．穴醚是一类可以与碱金属离子发生配位的双环或多环多齿配体。

某种穴醚的键线式如图。

2024学年福建省永安市三中高三第二次模拟考试数学试题(详细答案版)

2024学年福建省永安市三中高三第二次模拟考试数学试题（详细答案版）考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题：本题共12小题，每小题5分，共60分。

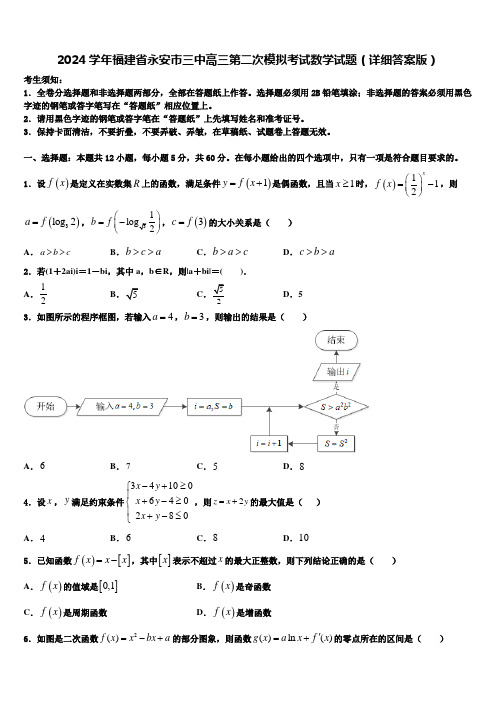
在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设()f x 是定义在实数集R 上的函数，满足条件()1y f x =+是偶函数，且当1x ≥时，()112xf x ⎛⎫=- ⎪⎝⎭，则()3log 2a f =，31log2b f ⎛⎫=- ⎪⎝⎭，()3c f =的大小关系是（） A ．a b c >>B ．b c a >>C ．b a c >>D ．c b a >>2．若(1＋2ai)i ＝1－bi ，其中a ，b ∈R ，则|a ＋bi|＝( )． A ．12B ．5C ．52D ．53．如图所示的程序框图，若输入4a =，3b =，则输出的结果是（）A ．6B ．7C ．5D ．84．设x ，y 满足约束条件34100640280x y x y x y -+≥⎧⎪+-≥⎨⎪+-≤⎩，则2z x y =+的最大值是（）A ．4B ．6C ．8D ．105．已知函数()[]f x x x =-，其中[]x 表示不超过x 的最大正整数，则下列结论正确的是（） A ．()f x 的值域是[]0,1 B ．()f x 是奇函数 C ．()f x 是周期函数D ．()f x 是增函数6．如图是二次函数2()f x x bx a =-+的部分图象，则函数()ln ()g x a x f x '=+的零点所在的区间是（）A ．11,42⎛⎫⎪⎝⎭B ．1,12⎛⎫⎪⎝⎭C ．(1,2)D ．(2,3)7．设a 、b R +∈，数列{}n a 满足12a =，21n n a a a b +=⋅+，n *∈N ，则（）A ．对于任意a ，都存在实数M ，使得n a M <恒成立B ．对于任意b ，都存在实数M ，使得n a M <恒成立C ．对于任意()24,b a ∈-+∞，都存在实数M ，使得n a M <恒成立D ．对于任意()0,24b a ∈-，都存在实数M ，使得n a M <恒成立8．已知y ax b =+与函数()2ln 5f x x =+和2()4g x x =+都相切，则不等式组3020x ay x by -+≥⎧⎨+-≥⎩所确定的平面区域在2222220x y x y ++--=内的面积为（）A ．2πB ．3πC ．6πD ．12π9．已知非零向量a 、b ，若2b a =且23a b b -=，则向量b 在向量a 方向上的投影为（） A ．32b B ．12b C ．32b -D ．12b -10．一个封闭的棱长为2的正方体容器，当水平放置时，如图，水面的高度正好为棱长的一半．若将该正方体绕下底面（底面与水平面平行）的某条棱任意旋转，则容器里水面的最大高度为（）A ．1B 2C 3D ．2211．如图所示，在平面直角坐标系xoy 中，F 是椭圆22221(0)x ya b a b+=>>的右焦点，直线2b y =与椭圆交于B ，C两点，且90BFC ∠=︒，则该椭圆的离心率是（）A ．63B ．34C ．12D ．3212．已知圆截直线所得线段的长度是，则圆与圆的位置关系是（） A ．内切B ．相交C ．外切D ．相离二、填空题：本题共4小题，每小题5分，共20分。

山东省2024届高三下学期5月第二次模拟考试化学含答案

绝密★启用并使用完毕前山东省2024届高三第二次模拟考试化学试题2024.05（答案在最后）本试卷分选择题和非选择题两部分，满分100分，考试用时90分钟注意事项：1．答卷前，先将自己的考生号等信息填写在试卷和答题纸上，并在答题纸规定位置贴条形码。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

3．非选择题的作答：用0.5mm 黑色签字笔直接答在答题卡上对应的答题区域内。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

可能用到的相对原子质量：H 1C 12O 16S 32Ni 59一、选择题：本题共10小题，每小题2分，共20分。

每小题只有一个选项符合题目要求。

1．科技创新是新质生产力的核心要素。

下列说法错误的是（）A ．制造C919飞机的材料——氮化硅陶瓷属于新型无机非金属材料B ．开启航运氢能时代——氢氧燃料电池放电时可将热能转化为电能C ．打造北斗卫星系统——85Rb 与星载铷钟所用87Rb 的物理性质不同D ．突破量子通信技术——作为传输介质的光纤其主要成分为二氧化硅2．已知：42326XeF 12H O 2XeO 4Xe 24HF 3O +++↑+↑，A N 为阿伏加德罗常数的值。

下列说法错误的是（）A ．1mol 4XeF 中心原子的孤电子对数为2A NB ．18g 2H O 中所含质子数为10AN C ．生成1mol 3XeO ，转移电子数为8AN D ．3.36L HF （标准状况）所含的分子数为0.15AN 3．下列含硫化合物的反应中，离子方程式正确的是（）A ．将2SO 通入NaClO 溶液中：223SO H O ClO HCl HSO --+++B ．向硫酸铜溶液中加入NaHS 溶液生成黑色沉淀：22Cu S CuS +-+↓C ．向硫代硫酸钠溶液中加入硫酸：22322Na S O 2H SO S H O 2Na ++++++D ．水垢中的4CaSO 用23Na CO 溶液处理：224334CaSO CO CaCO SO --++ 4．氧氟沙星是一种治疗呼吸道感染的抗菌药物，其结构简式如图，下列关于氧氟沙星的说法正确的是（）A ．属于苯的同系物B ．分子中所有原子可能处于同一平面C ．不能与3NaHCO 溶液反应D ．可发生取代、加成、氧化反应5．继电器在控制电路中应用非常广泛，有一种新型继电器是通过对电池的循环充、放电实现自动离合（如图所示）。

2024届江西省鹰潭市高三下学期第二次模拟考试物理试题(含答案与解析)_1052

鹰潭市2024届高三第二次模拟考试试题物理本试卷满分100分，考试时间75分钟注意事项：1．答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

一、单项选择题：本题共7小题，每小题4分，共28分。

在每小题给出的四个选项中，只有一项符合题目要求。

1. 2023年8月，日本不顾多个国家的反对，公然将含有大量放射性物质的核废水排放到太平洋中，其中有一种放射性物质是碳14，它的半衰期大约为5730年，其衰变方程为141467C N+X →；则下列说法正确的是（）A. 衰变方程中X 为α粒子B. 衰变产生的X 粒子电离本领比γ光子强C. 碳14半衰期很长，所以短期内不会对人类造成影响D. 如果有100个碳14，经过2865年将有25个原子核发生衰变2. 甲、乙两个物体从同一地点同时出发，沿同一直线运动，运动过程中的x t -图像如图所示，下列说法正确的是（）A. 在20~t 时间内，甲、乙两物体的速度大小无相等时刻。

B. 乙物体运动过程中位移大小增加得越来越快C. 甲、乙两物体在相距最远的时刻发生在21~t t 时间内的某时刻D. 甲物体始终沿同一方向运动3. 原地纵跳摸高是常见的体能测试项目。

在某次摸高测试中，一同学从如图A 所示的静止下蹲状态，脚刚离开地面，如图B 所示，身体运动到最高点时位置如图C 所示，三幅图代表同一竖直线上的三个位置，不计空气阻力，关于该同学测试的全过程，下列说法正确的是（）A. 从A 到B 的运动过程中，该同学因为受地面支持力的位移为零，所以支持力冲量为零B. 该同学在C 图位置的机械能等于在A 图位置的机械能C. 从A 到B 运动过程中，地面对脚的支持力始终大于该同学的重力D. 从A 到C 的过程中，地面对脚的支持力冲量与该同学的重力冲量等大反向4. “天问一号”从地球发射后，在如图甲所示的P 点沿地火转移轨道到Q 点，再依次进入如图乙所示的调相轨道和停泊轨道，则天问一号（）A. 发射速度介于7.9km/s 与11.2km/s 之间B. 从P 点转移到Q 点的时间小于6个月C. 在环绕火星的停泊轨道运行的周期比在调相轨道上小D. 在地火转移轨道运动时的速度均大于地球绕太阳的速度5. 真空中的点电荷在其周围产生电场，电场中某点的电势（取无穷远处电势为零）与点电荷的电量成正比，与该点到点电荷的距离成反比，即ϕ=Q k r，在某真空中有一如图所示的正六边形ABCDEF ，O 为中心，A 、C 、E 三个顶点各固定一点电荷，其中A 、C 两点电荷量为q ，E 点电荷量为q -，B E 、O E 分别表示B 、O点场强的大小，B ϕ、O ϕ分别表示B 、O 点的电势，则B E 与O E 的比值及B ϕ与O ϕ的比值，正确的是（）的A. :3:8B O E E =:3:2B O ϕϕ= B. :3:8B O E E = :5:6B O ϕϕ= C. :3:4B O E E = :5:6B O ϕϕ= D. :3:4B O E E = :3:2B O ϕϕ=6. 氢原子光谱按频率展开的谱线如图所示，此四条谱线满足巴耳末公式221112R n λ⎛⎫=- ⎪⎝⎭，n =3、4、5、6，用H δ和H γ光进行如下实验研究，则（）A. 照射同一单缝衍射装置，H γ光中央明条纹宽度更宽B. 以相同的入射角斜射入同一平行玻璃砖，H δ光的侧移量小C. 以相同功率发射的细光束，真空中单位长度上H γ光的平均光子数少D. 相同光强的光分别照射同一光电效应装置，H γ光的饱和光电流小 7. 制作“吸管潜水艇”是深受小朋友喜爱的科学实验，如图所示，将吸管对折后用回形针固定，然后管口竖直向下插入装有水的矿泉水瓶中，使吸管顶部露出水面，最后用盖子封紧矿泉水瓶（如图a 。

四川省成都市第二中学2024届高三下学期第二次高考模拟考试语文试题(含答案)

四川省成都市第二中学2024届高三第二次高考模拟语文试题注意事项:1.请将选择题答案写在答题卷内或者学校提供的机读卡上。

每题选出答案后，学校考生用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动，用橡皮擦干净后，再选涂其他答案。

2.非选择题，必须用黑色字迹的钢笔或签字笔在答题卷上作答，答案必须写在答题卷各题目指定区域内的相应位置上;如需改动，先划掉原来的答案，然后再写上新的答案;不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

一、现代文阅读(35分)(一)现代文阅读I(本题共5小题，18分)材料一我已经讲过，户是基本经济单位。

但一户中并不是全体成员都参加农业劳动；孩子只是有时候到田地里去，女人通常也不参加农业劳动。

农业主要是男人的职业。

男人和女人的这种劳动分工是产丝地区的一个特点。

它说明了蚕丝工业的发展是产生这种特点的主要因素。

在家庭缫丝业兴旺时期，女人忙于缫丝时，男人正忙着准备稻田。

另一方面，从丝业得到的收入可与农业收入比拟。

这也使人们有可能靠小块农地生活下去。

因此农田的大小一直保持在有限的范围内，农业所需的劳动量也相应地有所限制。

为说明村里的劳力和土地是如何恰当安排的，我可引用几个统计数字。

成年男子是实际的或潜在的农业劳动者，年龄在15至55岁之间，总数共450人。

如果将2758.5亩耕地平均分配给劳动者，每人将得6.1亩。

上文我已经说明了工作速度、稻的生长所需时间，以及得出一个人可耕种约7亩地的结论。

从技术上来说，我已经表明了使用铁耙耕作使得大部分劳动成为非常个体性的。

集体工作不比个体劳动增加多少收成，效率也不会提高很多。

目前的技术已决定了这样大小的一片土地需要多少劳动量。

因此，我们也有了每个农业劳动者能种多少亩地的近似数字。

这一事实对土地占有、对农田分散的制度、对分家的频率以及对小型的户都有深远的影响。

目前，丝业的衰落打乱了传统协调的经济活动。

缫丝工业被现代工厂接收后，农田的大小仍然同过去一样。

2024届天津市高三下学期高考英语第二次模拟考试试题(含答案)

2024届天津市高三下学期高考英语第二次模拟考试试题第I 卷(选择题共95分)第一部分：英语知识运用(共两节，满分45分)第一节：单项填空(共15小题，每小题1分，满分15分)从A 、B 、C 、D四个选项中，选出可以填入空白处的最佳选项。

1.—I'm afraid I can't climb to the top of the mountain.I am really exhausted now. —.There is only one third of the journey left.A.GoB.Take B.Take caree onD.All right2.The headmaster blamed the naughty student caught __flowers in the garden.A.toB.pickingking B.pickingC.toC.to pickD.to have picked3.On the exhibition,visitors could not only enjoy looking at the robots,they could also interact with them ,such as playing chess and table tennis.A.appropriatelyB.modestlyC.essentiallyD.literally4.As a physician during the Han Dynasty,Hua Tuo is often with being the first in China to use anesthesia (麻醉)during surgcry.A.presentedB.referredC.creditedD.promoted5.—Did you have a wonderful time in the Palacc Muscum yesterday?—Not really.Some parts of it so l had no chance to see its whole appearance.A.were being rebuiltB.were rebuiltC.had been rebuiltD.have been rebuilt6.On arriving in Athens from Marathon,the messenger whose legs c ollapsed on the spot,told the victory news and entirely exhausted himself.A.Ieft outB.gave outC.held outD.turned out7.—Why are you in such a hurry?—Because the train at 10:00 am,and there is almost no time left.A.leftB.shall leaveC.has lefiD.leaves8.Although written more than a century ago,Mark Twain's novels are still t oday.A.relevantB.likelyC.harmoniousD.sufficient9.It is the way_you apply your body language to your address that greatly determines whether the listeners are engaged and convinced.A.howB.thatC.whichD.where10.—Sorry,Tony.I'm too busy to attend the meeting this Saturday.—Well,you attend it if you truly can't re the time.A.shouldn'tB.needn'tC.can'tD.mustn't11.A variety of applications with filters in allow users to soften wrinkles oradjustthe size and shape of their facial features.A.to buildB.buildingC.builtD.having been built12.The car's has improved a lot since a new engine has been applied to it.A.appearanceB.characterC.performanceD.substance13.With my father's guidance and encouragement,I learned how to ride a bike I knewit.A.whenB.until C,as D.before14.Lily wants to read this science fiction as well,so when you ,please give it to her.A.have finishedB.will finishC.are finishingD.finished15.What is most extraordinary about the complex structures of Maya civilization isthey were built without the use of wheels,metal tools or even animal power. A.why B.how C,where D,when第二节：完形填空(共20小题；每小题1.5分，满分30分)阅读下面短文，掌握其大意，然后从各题所给的四个选项中，选出最佳选项。

湖南省永州市2024届高三上学期二模语文试题含解析

永州市2024年高考第二次模拟考试语文（答案在最后）注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．全卷分值150分；考试时间150分钟。

一、现代文阅读（35分）（一）现代文阅读I（本题共5小题，19分）阅读下面的文字，完成1~5小题。

材料一：传统文化本是在历史上形成并在日常生活中活态传承的文化式样，但长期以来，因受制于“文化遗产”观念，人们对传统文化的认识多停留在“守旧”的层面。

而当前的互联网和各式数字创意技术正使得社会生活诸方面显示出不一样的“生动的传统本色”。

这种作用一方面表现为传统文化的审美化的创新性发展——以其“仪式感”“距离感”和进而带来的“崇高感”，有创意地设计出一种“新中式生活美学”风格；另一方面表现为传统文化所包含的思维、理念、形象、色彩、内涵等的创造性转化——以时代风格推动传统文化“飞入寻常百姓家”，以一种对“灵韵”的消解和戏剧化表达去满足大众的心理、情感需求。

同时，人们在物质需求得到较充分的满足之后，对超越实际功能的价值就会更为注重，由此，审美的日常生活化转变为日常生活的审美化，审美主体和客体的实践边界也就不断被突破。

互联网催生的数字创意体验已日渐成为生活中不可或缺的一部分，传统文化与数字创意的融合也构建了新的审美场域和休闲生活空间。

例如“云游长城”小程序项目，利用“云游戏”技术和超拟真数字模型，对长城文化遗产做了数字化还原和游艺式呈现，对长城及其周边自然环境的影像进行了“镜像”美化，使用户通过手机就能获得实时的交互式体验，感受不同时间“爬长城”带来的身心愉悦，仿佛消解了自己与万里长城的距离感。

传统文化与数字创意的融合可以带来超越日常生活经验但又依托于日常生活的审美愉悦，这既离不开受众关于文化传统的经验积累和传统文化的时空间隔特性（它使美感得以被体会），也顺应着网络数字技术所具有的贴近生活与满足感性需求的能力，审美借此方才升华，“新感性”也油然而生。

2022-2023年高三下学期第二次模拟语文考试试题含参考答案

2022-2023年高三下学期第二次模拟语文考试试题含参考答案第I卷阅读（70分）（一）、论述类文本阅读（一）阅读下面的文字,完成1~3题。

（9分）斯皮尔伯格在拍摄《辛德勒的名单》时说过：“每隔五十年，就是人类合上历史教科书准备遗忘的时候。

”从这个角度讲，《长津湖》的出现正逢其时。

我们观看这部电影，谈论这部电影，经由这部电影所构造的集体感知路径，来回溯那段被尘封的历史，理性沉思，观照现实。

《长津湖》拍出了新主流大片特别是革命历史战争片的新境界。

中国电影有自己的战争片谱系和美学传统，革命英雄主义和革命现实主义的结合诞生过“三战”和《上甘岭》《英雄儿女》《大决战》等一系列优秀作品。

当然，一度也有这样的声音：中国缺乏现代意义上的战争片，没有好莱坞式的“反思战争”的战争电影；中国的战争片只分“敌我”，不站在更高的“人类”的立场上去“反思战争的残酷性与荒诞性”。

从这样的角度来看，《长津湖》肯定不是“好莱坞式”的战争电影，影片的反战是站在正义的立场，站在祖国的立场，站在和平的立场之上，是以爱国主义和家国情怀为基础的。

影片试图传递出“以战止战”的和平愿景，片中令人印象深刻的台词“这场仗，我们这一代人打了，下一代人就不用打了！”，以及毛泽东说的“打得一拳开，免得百拳来”，与伍连长说的“有的枪要开，有的枪可以不开”形成了不同层间的呼应，战争和敌我的辩证关系也具有说服力。

这既是延续了《上甘岭》《英雄儿女》等革命英雄主义、革命乐观主义、现实主义传统，同时也增加了更多的对战争本身的思考，诸如残酷性、荒诞感、生死等。

不被“有敌我，无战争”这种认为国产战争片缺乏所谓现代元素这样的观念带着走，我们拍出了《长津湖》这样的“在有敌我的前提下，有战争”的优秀的中国式战争电影。

值得一提的是，影片对英雄的塑造不是“战狼”式的，而是相对严格地按照英雄叙事的标准模式进行，能激发起观众巨大的共情。

接受使命呼唤：伍千里背着哥哥伍佰里的骨灰回家，可刚到家，就收到了部队的命令出征。

2023届高三第二次模拟考试语文试题及参考答案解析

2023届高三第二次模拟考试语文试题及参考答案解析一、现代文阅读（35分）（一）现代文阅读I（本题共5小题，19分）阅读下面的文字，完成1～5小题。

材料一：《红楼梦》是一部伟大的小说，在叙事上采用了曲折复义的表达方式，明确说小说故事是假语存（贾雨村）、真事隐（甄士隐），在真假、有无、虚实之间，《红楼梦》中有大量的艺术空白点，也就是“不写之写”。

“不写之写”应该主要从美学修辞学上来理解，而不是从索隐或随意联想的角度来理解。

遗憾的是，“不写之写”大多数情况被属于历史学范畴的考证或非文学立场的索隐派所笼罩。

一部艺术作品，所能写到的东西相对于无始无终、波澜壮阔的生活来讲总是有限的。

也就是说，“不写之写”在“写”和“不写”之间有一个辩证关系。

对于作家来说，“写”什么是值得反复思量和推敲的，“写”是主要的，是呈现给广大读者和观众的，是他们能够直接感知和认知的，是直接诉诸读者直觉经验的。

至于“不写”，则属于并不完全由作家掌控的部分，由“写”唤起人们对“不写”感知、认知，这对作家来说不是一个轻而易举的技能，对阅读来说不是轻易能获得的效果。

那么作家和作品中的“不写之写”究竟该怎么理解？作家的“不写之写”，应该是服务于其艺术目的的或者一定的艺术目的的。

作家通过作品写出来的东西，虽然是局部的，但可以意识到它的整体，这才是“不写之写”。

换言之，是有限与无限的统一，是确定性和不确定性的统一，而并不是所有的空白、笔触不到的都叫“不写之写”，不是在阅读过程中随意生发、随意联想到的内容都是“不写之写”。

从《红楼梦》的文本举例，如第三十五回宝玉与薛宝钗丫鬟莺儿的对话。

莺儿笑道：“你还不知道，我们姑娘有几样世上的人没有的好处呢，模样儿还在次。

”宝玉见莺儿娇憨婉转，语笑如痴，早不胜其情了，那更提起宝钗来！便问道：“好处在哪里？好姐姐，细细告诉我听。

”莺儿笑道：“我告诉你，你可不许又告诉她去。

”宝玉笑道：“这个自然的。

”正说着，只听外头说道：“怎么这样静悄悄的！”二人回头看时，不是别人，正是宝钗来了。

湖南省长沙市2024届高三下学期第二次模拟考试数学试题含答案

2024届模拟试卷（二）数学（答案在最后）命题人：注意事项：1.答卷前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.函数()x f =的定义域是A ．[]2,2-B ．()2,2-C ．{}2,2x x x <->或D ．{}2,2-2.已知函数()y f x =的图象是下列四个选项图象之一，且其导函数()y f'x =的图象如图所示，则该函数的图象是A ．B ．C ．D ．3.中心在坐标原点，离心率为53的双曲线的焦点在y 轴上，则该双曲线的渐近线方程为A ．34y x =±B ．43y x =±C ．45y x =±D ．54y x=±4.已知定义在R 上的函数()f x 是奇函数，对任意x ∈R 都有()()11f x f x +=-，当()32f -=-时，则()2023f 等于A ．2B ．2-C ．0D ．4-5.将函数()2sin 24f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移ϕ（0ϕ>）个单位长度，再将图象上每一点的横坐标缩短到原来的12倍（纵坐标不变），所得图象关于直线π4x =对称，则ϕ的最小值为A ．3π4B ．1π2C ．3π8D ．1π86.为调查某地区中学生每天睡眠时间（单位：小时），采用样本量比例分配的分层随机抽样，现抽取初中生800人，其每天睡眠时间均值为9，方差为1，抽取高中生1200人，其每天睡眠时间均值为8，方差为0.5，则估计该地区中学生每天睡眠时间的方差为A ．0.96B ．0.94C ．0.79D ．0.757.在等腰△ABC 中，120BAC ∠=︒，AD 平分∠BAC 且与BC 相交于点D ，则向量BD 在BA上的投影向量为A ．32BAB ．4BAC ．2BAD ．34BA8.如图，点P 在正方体1111ABCD A B C D -的面对角线1BC （包括端点）上运动，则下列结论一定成立的是A ．三棱锥1A A PD -的体积大小与点P 的位置有关B ．1A P 与平面1ACD 相交C ．平面1PDB ⊥平面11A BC D ．1AP D C⊥二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分.9.设a ，b ，c ，d 为实数，且0a b c d >>>>，则下列不等式正确的有A ．2c cd<B ．a c b d -<-C ．ac bd<D ．0c d a b->10.在《增删算法统宗》中有这样一则故事：“三百七十八里关，初行健步不为难；次日脚痛减一半，如此六日过其关.”则下列说法正确的是A ．此人第二天走了九十六里路B ．此人第三天走的路程占全程的18C ．此人第一天走的路程比后五天走的路程多六里D ．此人后三天共走了四十二里路11.三棱锥A -BCD 的侧棱AB 垂直于底面BCD ，BC CD ⊥，2AB BC ==，三棱锥A -BCD 的体积43A BCD V -=，则A ．三棱锥A -BCD 的四个面都是直角三角形B ．2CD =C ．π2CDA ∠=D ．三棱锥A -BCD 外接球的体积三、填空题：本题共3小题，每小题5分，共15分.12.在复数范围内方程210x x ++=的解为.13.已知圆N ：22650x y y +-+=，直线1y =-，圆M 与圆N 外切，且与直线1y =-相切，则点M 的轨迹方程为.14.若m ，*n ∈N ，3m ≥，2n m +≥，则22111222A A A C A A mm m n m n m n ----=++.（请用一个排列数来表示）四、解答题：本题共5小题，共77分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.（本小题满分13分）在△ABC 中，已知22sin cos 212A BC ++=，外接圆半径2R =.（1）求角C 的大小；（2）求△ABC 面积的最大值.16.（本小题满分15分）如图，四棱锥P -ABCD 中，底面ABCD 为平行四边形，60DAB ∠=︒，2AB =，1AD =，PD ⊥底面ABCD ．（1）证明：PA BD ⊥；（2）若PD AD =，求二面角A -PB -C 的余弦值.17.（本小题满分15分）已知椭圆G ：22221x y a b+=（0a b >>）的离心率为63，右焦点为()，斜率为1的直线l 与椭圆G交于A ，B 两点，以AB 为底边作等腰三角形，顶点为()3,2P -.（1）求椭圆G 的方程；（2）求△PAB 的面积.18.（本小题满分17分）某手机App 为了答谢新老用户，设置了开心大转盘抽奖游戏，制定了如下中奖机制：每次抽奖中奖的概率为p ，n 次抽奖仍未中奖则下一次抽奖时一定中奖.每次中奖时有12的概率中积分奖，有12的概率中现金奖.若某一次中奖为积分奖，则下一次抽奖必定中现金奖，抽到现金奖后抽奖结束.（1）若2n =，12p =，试求直到第3次才抽到现金奖的概率；（2）若19n =，0.01p =，X 表示抽到现金奖时的抽取次数.（ⅰ）求X 的分布列（用p 表示即可）；（ⅱ）求X 的数学期望()E X .（180.990.8345≈，结果四舍五入精确到个位数）19.（本小题满分17分）极值的广义定义如下：如果一个函数在一点的一个邻域（包含该点的开区间）内处处都有确定的值，而以该点处的值为最大（小），这函数在该点处的值就是一个极大（小）值.对于函数()y f x =，设自变量x 从0x 变化到0x x +∆，当0x ∆>，()()000limx f x x f x x∆→+∆-∆是一个确定的值，则称函数()y f x =在点0x 处右可导；当0x ∆<，()()000limx f x x f x x∆→+∆-∆是一个确定的值，则称函数()y f x =在点0x 处左可导.当函数()y f x =在点0x 处既右可导也左可导且导数值相等，则称函数()y f x =在点0x 处可导.（1）请举出一个例子，说明该函数在某点处不可导，但是该点是该函数的极值点；（2）已知函数()22132e sin e ax f x x x x x +=--.（ⅰ）求函数()21esin e ax g x x x +=--在0x =处的切线方程；（ⅱ）若0x =为()f x 的极小值点，求a 的取值范围.2024届模拟试卷（二）数学参考答案一、二、选择题题号1234567891011答案DBAACBDCADACDABD2.B【解析】由()y f'x =的图象知，()y f x =为增函数，且在区间()1,0-上增长速度越来越快，而在区间()0,1上增长速度越来越慢.故选B ．3.A【解析】∵53c a =，∴222259a b a +=，∴43b a =.∵双曲线的焦点在y 轴上，∴双曲线的渐近线方程为a y x b =±.∴所求双曲线的渐近线方程为34y x =±.故选A ．4.A【解析】定义在R 上的函数()f x 是奇函数，且对任意x ∈R 都有()()11f x f x +=-，故函数()f x 的图象关于直线1x =对称，∴()()2f x f x =-，故()()()2f x f x f x -=+=-，∴()()()24f x f x f x =-+=+，∴()f x 是周期为4的周期函数.则()()()3(202350533)42f f f f =⨯+==--=.故选A ．6.B【解析】初中生人数800m =，每天睡眠时间的平均数9x =，方差211s =；高中生人数1200n =，每天睡眠时间的平均数8y =，方差220.5s =.总的样本平均数8.4mx n y a m n +==+.总的样本方差()()22221220.94m s x a n s y a s m n⎡⎤⎡⎤+-++-⎢⎥⎢⎥⎣⎦⎣⎦==+.故选B ．7.D【解析】设AB AC x ==，由余弦定理可知22222cos1203BC AB AC AB AC x =+-⋅⋅︒=，∴BC =，30ABC ∠=︒，∵AD 平分∠BAC 且与BC 相交于点D ，△ABC 是等腰三角形，∴D 是BC 中点，2BD x =，由图可知向量BD 在BA 上的投影向量为BE ，3cos304BE BD x =︒= ，34BE BA = ，∴34BE BA =.故选D .8.C 【解析】对于选项A ，11A A PD P AA D V V --=．在正方体中，1BC ∥平面1AA D ，所以点P 到平面1AA D 的距离不变，即三棱锥1P AA D -的高不变，又1AA D ∆的面积不变，因此三棱锥1P AA D -的体积不变，即三棱锥1A A PD -的体积与点P 的位置无关，故A 不成立；对于选项B ，由于11BC AD ∥，1AD ⊂平面1ACD ，1BC ⊂/平面1ACD ，所以1BC ∥平面1ACD ，同理可证1BA ∥平面1ACD ，又11BA BC B = ，所以平面11BA C ∥平面1ACD ，因为1A P ⊂平面11BA C ，所以1A P ∥平面1ACD ，故B 不成立；对于选项C ，因为11A C BD ⊥，111A C BB ⊥，1BD BB B = ，所以11A C ⊥平面1BB D ，则111A C B D ⊥；同理11A B B D ⊥，又1111A C A B A = ，所以1B D ⊥平面11A BC ，又1B D ⊂平面1PDB ，所以平面1PDB ⊥平面11A BC ，故C 成立；对于选项D ，当B 与P 重合时，AP 与1D C 的夹角为π4，故D 不成立.故选C ．9.AD 【解析】因为0a b c d >>>>，所以0a b >>，0c d >>，对于A ，因为0c d >>，由不等式的性质可得2c cd <，故选项A 正确；对于B ，取2a =，1b =，1c =-，2d =-，则3a c -=，3b d -=，所以a c b d -=-，故选项B 错误；对于C ，取2a =，1b =，1c =-，2d =-，则2ac =-，2bd =-，所以ac bd =，故选项C 错误；对于D ，因为0a b >>，0d c <<，则ad bc <，所以c d a b >，故0c da b->，故选项D 正确.故选AD ．10.ACD【解析】设此人第n 天走n a 里路，则数列{}n a 是首项为1a ，公比为12q =的等比数列，因为6378S =，所以166112378112a S ⎛⎫- ⎪⎝⎭==-，解得1192a =，对于A ，由于21192962a =⨯=，所以此人第一天走了九十六里路，所以A 正确；对于B ，由于31192484a =⨯=，4813788>，所以B 不正确；对于C ，由于378192186-=，1921866-=，所以此人第一天走的路程比后五天走的路程多六里，所以C 正确；对于D ，456378192964842a a a ++=---=，所以此人后三天共走了四十二里路，所以D 正确.故选ACD ．11.ABD 【解析】∵AB BC ⊥，BC CD ⊥，构造如图所示的长方体，则AD 为三棱锥A -BCD的外接球的直径.设外接球的半径为R .∵1114223263A BCD V BC CD AB CD -=⨯⨯⨯⨯=⨯⨯⨯=，∴2CD =，∴该长方体为正方体，∴AD =∴R =，∴外接球体积为34π3V R ==.故选ABD ．三、填空题：本题共3小题，每小题5分，共15分.12.12x -=13.212x y=【解析】由题意得，直线l ：1y =-，且圆N ：()2234x y +-=，设点M 到直线l 的距离为r ，则点M 到l ＇：3y =-与点M 到点N 的距离相等，都是2r +，故点M 的轨迹是以N 为焦点，以l ＇为准线的抛物线，故方程为212x y =.14.2A mn -【解析】法一：直接计算，略.法二：实际意义：从n 个元素中选取m 个元素排列到m 个位置上去，对于两个指定的元素a ，b 进行分类，a ，b 都被选出来，有222A A m m n --种排法，a ，b 中有一个被选出来，有11122C A A m m n --种排法，a ，b 都没有被选出来，有2A mn -种排法，所以221112222A A A C A A A mm m mn m n m n n -----=++.法三：特值法试一试，如取3m =，7n =，再猜出排列数.四、解答题：本题共5小题，共77分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.【解析】（1）()cos 2cos cos C A B C =+=-，22cos cos 10C C +-=，1cos 2C =，因为()0,πC ∈，所以π3C =.（2）由外接圆半径2R =和正弦定理知1sin sin 2ABC S ab C A B ∆==，2ππsin sin 3sin 22236ABC S A B A A A A A ∆⎛⎫⎛⎫==-=+=- ⎪ ⎪⎝⎭⎝⎭，当π3A =时，△ABC的面积最大值为16.【解析】（1）因为60DAB ∠=︒，2AB =，1AD =，由余弦定理得BD =，从而222BD AD AB +=，故BD AD ⊥.因为PD ⊥平面ABCD ，BD ⊂平面ABCD ，所以PD BD ⊥．又AD PD D = ，AD ，PD ⊂平面PAD ，所以BD ⊥平面PAD ．因为PA ⊂平面PAD ，所以PA BD ⊥．（2）如图，以D 为坐标原点，射线DA ，DB ，DP 分别为x ，y ，z 的正半轴建立空间直角坐标系D -xyz，则()1,0,0A，()B，()C -，()0,0,1P.()AB =-，()1PB =-，()1,0,0BC =- 设平面PAB 的法向量为(),,n x y z =，则00n AB n PB ⎧⋅=⎪⎨⋅=⎪⎩，即0x z ⎧-+=⎪-=，因此可取n =.设平面PBC 的法向量为m ，则0m PB m BC ⎧⋅=⎪⎨⋅=⎪⎩，可取(0,1,m =-，则cos ,7m n <>==-，经判断，二面角A -PB -C 为钝角，故二面角A -PB -C的余弦值为7-.17.【解析】（1）由已知得c =3c a =，解得a =，又2224b a c =-=，所以椭圆G 的方程为221124x y +=.（2）设直线l 的方程为y x m =+，由221124y x m x y =+⎧⎪⎨+=⎪⎩消去y 得22463120x mx m ++-=，①设A ，B 的坐标分别为()11,x y ，()22,x y （12x x <），AB 中点为()00,E x y ，则120324x x x m +==-，004my x m =+=，因为AB 是等腰△PAB 的底边，所以PE AB ⊥，所以PE 的斜率为241334mk m -==--+，解得2m =，此时方程①为24120x x +=，解得13x =-，20x =，所以11y =-，22y =，所以AB =，又点()3,2P -到直线AB ：20x y -+=的距离2d ==，所以1922PAB S AB d ∆=⋅=.18.【解析】（1）设抽到现金奖时共抽取了3次为事件A ，则事件A 包括第一次未中奖第二次未中奖第三次中了现金奖或第一次未中奖第二次中了积分奖第三次中现金奖，则()1111111222244P A =⨯⨯+⨯⨯=，所以直到第3次才抽到现金奖的概率为14.（2）（ⅰ）X 的可能取值为1，2，3，…，19，20，21.()112P X p ==，()()()()()2121111121222i i i P X i p p p p p p p ---==-⋅+-⋅=--，2i =，3， (19)()()()()18191811120111222P X p p p p ==-⋅+-⋅=-，()()()1919112111122P X p p ==-⋅⨯=-，所以X 的分布列为X 12…i …2021P 12p ()122p p -…()()21212i p p p ---…()18112p -()19112p -其中2i =，3，…，19.（ⅱ）()()()()()()12111112232121192222i E X p p p p p p i p p p -=⨯+⨯-+⨯--++⨯--++⨯ ()()()1719181112120(1)211222p p p p p --+⨯-+⨯-()()()()()()217181911212231411911011222p p p p p p p p ⎡⎤=+-+-+-++-+-+-⎣⎦ ，令()()()21723141191S p p p =+-+-++- ，则()()()()()23181213141191p S p p p p -=-+-+-++- ，作差得()()()17181112191p p pS p p ⎡⎤---⎣⎦=+--，所以()()()()()18182111192221222p p p p p S p p p p ⎡⎤----⎣⎦-=-+---，()()()()()()()181818192111192122110112222p p p E X p p p p p p p ⎡⎤----⎣⎦=+-+---+-+-()1811112192p p p p ⎛⎫=++---≈ ⎪⎝⎭，所以X 的数学期望()E X 约为19.19.【解析】（1）y x =，0x =为该函数的极值点，该函数在0x =处的左导数为1-，右导数为1，所以该函数在0x =处不可导.（2）（ⅰ）切线方程为0y =.（ⅱ）()()22213221e sin e e sin e ax ax f x x x x x x x x ++=--=--，因为当0x ≠时，20x >，故()f x 与()g x 同号，()21e sin e ax g x x x +=--，现考察()g x 的性质，由于()g x 为偶函数，只需分析其在()0,+∞上的性质即可，()212e sin cos ax g'ax x x x x +=--，()0,0g'=，()()222124e 2cos sin ax a a x x x x g''x +=+-+，()2e 20g 'a '=-，则必有()e 2002g''a =-≥，即1e a ≥.①否则，若()e 2002g''a =-<，即1ea <，则必存在一个区间()0,m ，使得()0g''x <，则()g'x 在()0,m 单调递减，又()00g'=，则()g'x 在区间()0,m 内小于0，则()g x 在()0,m 单调递减，又()00g =，故()g x 在区间()0,m 内小于0，故()f x 在区间()0,m 内小于0，则0x =不可能为()f x 的极小值点.②当1ea ≥时，()22111e e sin e e sin e x ax g x x x x x ++=----≥，令()211e esin e x h x x x +=--，()2112e sin cos e x e x h x x x 'x +=--，()2112e 224e 2cos sin e e x h x x x x ''x +⎛⎫=+-+ ⎪⎝⎭，易知2112e 224e e e x y x +⎛⎫=+ ⎪⎝⎭在区间()0,+∞上单调递增，对2cos sin y x x x =-+，2sin sin cos 3sin cos y'x x x x x x x =++=+，则3sin cos y'x x x =+在区间π0,2⎛⎫ ⎪⎝⎭上大于0，故2cos sin y x x x =-+在区间π0,2⎛⎫ ⎪⎝⎭上单调递增.故()2112e 224e 2cos sin e e x h x x x x ''x +⎛⎫=+-+ ⎪⎝⎭在区间π0,2⎛⎫ ⎪⎝⎭上单调递增.又()00h''=，故()0h''x ≥，故()h'x 在区间π0,2⎛⎫ ⎪⎝⎭上单调递增，又()00h'=，故()0h'x ≥，故()h x 在区间π0,2⎛⎫ ⎪⎝⎭上单调递增，又()00h =，故()0h x >，π0,2x ⎛⎫∈ ⎪⎝⎭，则()()21e sin e 0ax x x x g x h +=-->≥，π0,2x ⎛⎫∈ ⎪⎝⎭，故当π0,2x ⎛⎫∈ ⎪⎝⎭时，()0f x >，由偶函数知π,02x ⎛⎫∈-⎪⎝⎭时，()0f x >，故0x =为()f x 的极小值点，所以a 的取值范围为1e a ≥.。

河北省保定市2024届高三下学期二模试题英语含答案

2023—2024学年高三第二次模拟考试高三英语试题（答案在最后）注意事项：1.答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A.£19.15.B.£9.18.C.£9.15.答案是C。

1.What does Tom intend to do?A.Borrow Kate’s bike.B.Help Kate carry her schoolbag.C.Ask Jane how to get to the library.2.What does the woman mean?A.The man can’t use the gym.B.The man hasn’t paid for the hotel room.C.The man shouldn’t live on the first floor.3.What does Bob want?A.Socks.B.Shoes.C.A shirt.4.Where does the conversation probably take place?A.At home.B.In a stadium.C.In an office.5.What does the man plan to do after work today?A.Buy a bag.B.See a dentist.C.Attend a party.第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

江苏南通2024届高三下学期第二次模拟测试化学试题+答案

2023-2024学年高三年级第二学期调研考试（二十一）化学（满分：100分考试时间：75分钟）第I 卷（选择题）一、单选题1．2022年6月末，日本国家警察厅 (NPA) 正式宣布，将开始为富士山可能发生喷发做全面准备。

也就是说，自1707年最后一次喷发后，平静了300多年的富士山，可能真的将正式进入“待机阶段”。

警察厅认为，如果日本富士山喷发，火山灰不仅可能落在富士山附近地区，也有可能落在东京都市圈，也就是还可能影响东京。

下列说法中正确的是A ．硫在自然界中没有以单质存在的情况，大多数的硫元素以矿物的形式存在。

B ．硫化物在地表附近由于受到空气中氧气和水的长期作用，会转化为亚硫酸。

C ．芒硝化学式中有10个水分子，通过风化这一化学变化可以去除其中的水。

D ．火山灰中含硫氧化物，其自身记入PM2.5指标，进入空气一定能形成胶体。

2．国际学术期刊 Nature 《》官网发布 "LK-99不是超导体——科学侦探们如何解开这个谜团"。

LK-99由 424CuO PbO NH H PO 、、制备。

下列说法错误的是 A ．6种元素中，电负性最大的是 O B ．N 的原子结构示意图：C ．Pb 原子位于周期表第六周期第 IVA 族D ．基态 Cu 原子的价层电子轨道表示式：3．下列化学用语正确的是A ．丁烷的结构式：()3232CH CH CHB ．由Na 和Cl 形成NaCl 的过程：C ．羟基的电子式：D ．乙烯的结构简式22CH CH4．绿色化学的原子经济性要求：在生产中所有原子均转化为产物，没有副产物。

以下反应不符合绿色化学原子经济性要求的是A ．氨气被硫酸吸收制备硫酸铵B ．工业制备氯化氢C ．将NO 与2O 按4:3的比例充分混合通入足量水中制备硝酸D ．以铜和浓3HNO 为原料生产硝酸铜5．下列各组离子中，可能能在所处环境中大量共存的是A ．在室温环境下c(OH -)=1×10-11的溶液中：Cr 2+，SO 2-4，NO -3，Na +B ．在4℃的水溶液中：Be 2+，K +，PO 3-4，OH -C ．在漂白液中：OH -，Rb +，SO 2-4，CO 2-3D ．在水玻璃中：H +，SCN -，Cl -，Cs +6．有机增塑剂25X Y WR 和25X Z WR 的质子数均为32，其相对分子质量相差5；X 、W 、R 三种元素同周期，X 原子的最外层电子数为R 电子总数的一半。

南京市 2023届高三年级第二次模拟考试物理试题(后附参考答案)

南京市2023届高三年级第二次模拟考试物理本试卷满分100分、考试时间75分钟一、单项选择题：共10小题，每小题4分，共计40分．每小题只有一个选项符合题意．1、国产新能源汽车安装了“防撞预警安全系统”。

如图所示，其配备的雷达会发射毫米级电磁波（毫米波），并对前车反射的毫米波进行处理。

下列说法正确的是A．毫米波是由于原子核受到激发而产生B．毫米波由空气进入水时传播速度会变小C．毫米波遇到前车时会发生明显衍射现象D．毫米波不能发生偏振现象2、潜艇从海水高密度区域驶入低密度区域，浮力顿减，称之为“掉深”。

如图甲所示，某潜艇在高密度海水区域沿水平方向缓慢航行。

t=0s时，该潜艇“掉深”，随后采取措施成功脱险，在0~30s时间内潜艇竖直方向的v-t图像如图乙所示（设竖直向下为正方向）。

不计水的粘滞阻力，则A．潜艇在“掉深”时的加速度为1m/s2B．t=30s潜艇回到初始高度C．潜艇竖直向下的最大位移为100mD．潜艇在10~30s时间内处于超重状态3、某牧场设计了一款补水提示器，其工作原理如图所示，水量增加时滑片下移，电表均为理想电表。

下列说法正确的是A．若选择电压表，水量增多时电压表示数变大B．若选择电流表，水量增多时电流表示数变小C．若选择电流表，与电压表相比，电路更节能D．若选择电压表，增加R0可提高灵敏度4、运动员用同一足球罚点球，两次射门，足球斜向上踢出，分别水平打在水平横梁上的a 、b 两点，a 为横梁中点，如图所示，不计空气的作用效果。

下列说法正确的是 A ．两次的初速度大小可能相等 B ．击中a 用的时间长C ．击中a 的过程中，重力做功少D ．两过程中动量变化量相等5、理想环形变压器示意图如图甲所示，原线圈两端的电压随时间变化的关系图像如图乙所示，，副线圈接一“12V 22W ”的电灯，恰好正常发光，图中电表均为理想交流电表。

下列说法正确的是A．原、副线圈的磁通量变化率之比为55：3 B ．电流表的读数为0.1AC ．s 时，电压表示数为零D ．若电压表改为非理想电表，电流表示数会变小6、2022年10月31日，搭载梦天实验舱的长征五号B 遥四运载火箭发射取得圆满成功。

湖南省郴州市2024届高三下学期二模语文试题含答案

湖南省郴州市2024届高三联考第二次模拟语文试题（答案在最后）注意事项：1.请将选择题答案写在答题卷内或者学校提供的机读卡上。

每题选出答案后，学校考生用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

2.非选择题，必须用黑色字迹的钢笔或签字笔在答题卷上作答，答案必须写在答题卷各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

一、现代文阅读（35分）（一）现代文阅读I（本题共5小题，18分）阅读下面的文字，完成下面小题。

材料一：疫苗和疫苗接种法的基本理论和方法最早是我国发明的，并在治病实践中得到了广泛运用。

对抗天花病毒的“时苗”，是北宋时期发明的，时称“痘苗”。

明代发明了更为安全的“熟苗”。

在隆庆年之前，明朝暴发了一场大规模的天花瘟疫，致死率竟然高达80%以上。

“嘉靖甲午年春，痘毒流行，病死者什（十）之八九。

”正是这场天花的大流行，促成了熟苗种痘法的推广。

明代医生在大规模接种痘苗的过程中，通过正反方面的实践，不断总结经验，发明了“熟苗”接种法。

《种痘新书》记载：“种痘者八九千人，其莫救者，二三十耳。

”就是说用“熟苗”接种，八九千人中不能救治的仅有二三十人。

显示出这种接种技术对预防天花的安全高效。

18世纪初，预防天花的人痘接种法被引入欧洲。

英国医师爱德华·金纳创造了第一个生物制品——牛痘疫苗。

19世纪巴斯德制作出更加有效的现代疫苗，给人接种达到预防目的。

虽然大规模的现代疫苗制剂是由西方发明普及的，但疫苗和接种疫苗最初理论和基本方法是我们祖先发明的。

中国古代人民在长期与疾病斗争的过程中，观察到有些患过传染病而康复的人，一般不再患同样的疾病，于是他们用物理方法（如捣碎、研磨）处理发病个体的组织脏器制成最原始的疫苗。

早在公元4世纪初，东晋葛洪所著《肘后方》中，就有关于防治狂犬病的记载，其中“治卒猢犬凡所咬毒方”有云：“仍杀所咬犬，取脑敷之，后不复发。

高三第二次模拟试题(最后试题)

2024年新高考九省联考高三第二次模拟数学试题及答案

2024届河南省濮阳市高三二模语文试题(解析版)

江苏省南京市2024届高三年级第二次模拟考试数学试题(解析版)

2024届东北三省高三三校二模联考化学试题(含答案)

2024学年福建省永安市三中高三第二次模拟考试数学试题(详细答案版)

山东省2024届高三下学期5月第二次模拟考试 化学含答案

2024届江西省鹰潭市高三下学期第二次模拟考试物理试题(含答案与解析)_1052

四川省成都市第二中学2024届高三下学期第二次高考模拟考试语文试题(含答案)

2024届天津市高三下学期高考英语第二次模拟考试试题(含答案)

湖南省永州市2024届高三上学期二模语文试题含解析

2022-2023年高三下学期第二次模拟语文考试试题含参考答案

2023届高三第二次模拟考试语文试题及参考答案解析

湖南省长沙市2024届高三下学期第二次模拟考试数学试题含答案

河北省保定市2024届高三下学期二模试题 英语含答案

江苏南通2024届高三下学期第二次模拟测试化学试题+答案

南京市 2023届 高三年级第二次模拟考试 物理试题(后附参考答案)

湖南省郴州市2024届高三下学期二模语文试题含答案

山东省2024届高三下学期5月第二次模拟考试化学含答案

河北省保定市2024届高三下学期二模试题英语含答案

南京市 2023届高三年级第二次模拟考试物理试题(后附参考答案)