04第四章 散列函数与报文鉴别
应用密码学(1-10章全) 精品

• 密码学是信息安全学科建设和信息系统安全工程实践 的基础理论之一。
• 对密码学或密码技术一无所知的人不可能从技术层面 上完全理解信息安全。
4/31
第1章 密码学概述
1.2 密码技术发展简介
根据不同时期密码技术采用的加密和解密实现手段的不同特点 ,密码技术的发展历史大致可以划分为三个时期,即古典密码、 近代密码和现代密码时期。
9/31
第1章 密码学概述
1.3.1密码学的主要任务(续) ③ 鉴别
这是一种与数据来源和身份鉴别有关的安全服务。鉴别服务包括对身 份的鉴别和对数据源的鉴别。对于一次通信,必须确信通信的对端是预期的 实体,这就涉及到身份的鉴别。 对于数据,仍然希望每一个数据单元发送到或来源于预期的实体, 这就是数据源鉴别。数据源鉴别隐含地提供数据完整性服务。密码学可通过 数据加密、数字签名或鉴别协议等技术来提供这种真实性服务。
第1章 密码学概述
本章主要内容
• 信息安全与密码技术 • 密码技术发展简介 • 密码学基本概念 密码学的主要任务 密码系统的概念
对密码系统的攻击
密码系统的安全性 密码体制的分类
对称与非对称密码体制的主要特点
3/31
第1章 密码学概述
1.1
信息安全与密码技术
• 密码技术是一门古老的技术; • 信息安全服务要依赖各种安全机制来实现,而许多安 全机制则需要依赖于密码技术 ; • 密码学贯穿于网络信息安全的整个过程,在解决信息 的机密性保护、可鉴别性、完整性保护和信息抗抵赖 性等方面发挥着极其重要的作用。
应用密码学
清华大学出版社 2008年9月
课程主要内容
报文鉴别与散列函数-精PPT文档42页

报文鉴别与散列函数-精
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事, 只想现 在的事 。现在 有成就 ,以后 才能更 辉煌。
18、敢于向黑暗宣战的人,心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足Байду номын сангаас前,莽撞的 人只能 引为烧 身,只 有真正 勇敢的 人才能 所向披 靡。
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
散列函数与消息认证码

第七讲散列函数与消息认证码马春光machunguang@计算机科学与技术学院哈尔滨工程大学1 /•网络安全威胁:–被动攻击(Passive Attack):敌手通过侦听和截获等手段获取数据;–主动攻击(Active Attack):敌手通过伪造、重放、篡改、乱序等手段改变数据;图1 无线网络中的四种通信安全威胁(a)监听;(b)篡改;(c)伪造;(d)阻断2 /•消息认证(Message Authentication)的目的:–验证消息的完整性,确认数据在传送和存储过程中未受到主动攻击。
•消息认证的方式:–消息加密函数:加密整个消息,以消息的密文文件作为认证,可使用对称密码或公钥密码体制进行加密;–散列函数(Hash):将任意长度的消息变换为定长的消息摘要,并加以认证;–消息认证码(MAC):依赖公开的函数(密钥控制下)对消息处理,生成定长的认证标识,并加以认证;3 /提纲•1 散列函数–1.1 散列函数的定义–1.2 散列函数的通用结构–1.3 MD5•2 消息认证码–2.1 MAC函数–2.2 MAC的安全性–2.3 CBC-MAC•作业4 /提纲•1 散列函数–1.1 散列函数的定义–1.2 散列函数的通用结构–1.3 MD5• 2 消息认证码•作业5 /散列函数的定义•散列函数H 是一个公开的函数,它将任意长度的消息M变换为固定长度的散列码h 。
•h=H (M)–M:变长消息,H(M):定长的散列值•散列函数是一种算法,算法的输出内容称为散列码或者消息摘要。
•消息摘要要唯一地对应原始消息,如果原始消息改变并且再次通过散列函数,它将生成不同的消息摘要,因此散列函数能用来检测消息地完整性,保证消息从建立开始到收到为止没有被改变和破坏。
•运行相同算法的接受者应该收到系统的消息摘要,否则保温是不可信的。
•散列函数又称为:哈希(Hash )函数、数字指纹(Digital fingerprint)、压缩(Compression)函数、数据认证码(DataAuthentication Code)等6 /散列函数的要求•H 能用于任意大小的分组;•H 能产生定长的输出;•对任何给定的x,H(x)要相对易于计算,使得硬件和软件实现成为实际可能;•对任何给定的码h ,寻找x 使得H(x)=h 在计算上是不可行的,即单向性(one-way);•对任意给定的分组x,寻找不等于x 的y,使得H(x)=H(y)在计算上是不可行的,即弱抗冲突性(Weak Collision-free);•寻找对任意的(x, y) 对使得H(x)=H (y) 在计算上是不可行的,即强抗冲突性(Strong Collision-free);7 /提纲•1 散列函数–1.1 散列函数的定义–1.2 散列函数的通用结构–1.3 MD5• 2 消息认证码•作业8 /2.2 Hash函数的通用结构•由Ron Rivest于1990年提出MD4•几乎被所有Hash函数使用•具体做法:–把原始消息M分成一些固定长度的块Y i–最后一块padding 并使其包含消息M长度–设定初始值CV0–压缩函数f, CV i=f(CV i-1, Y i-1)–最后一个CV i为Hash值9 //提纲•1 散列函数–1.1 散列函数的定义–1.2 散列函数的通用结构–1.3 MD5• 2 消息认证码•作业11 /MD5 描述•1989年,Merkle提出Hash function模型•1990年,Ron Rivest提出MD4•1992年, Ron Rivest完成MD5 (RFC 1321) –/rfcs/rfc1321.html•在最近数年之前,MD5是最主要的Hash算法•现行美国标准SHA-1以MD5的前身MD4为基础•MD5(Message Digest)–输入:任意长度的消息–输入分组长度:512 bit–输出:128 bit 消息12 /(4)(3)13 /14/MD5 描述-(1)•消息填充•对消息进行填充,使其比特数与448模512同余,即填充长度为512的整数倍减去64,留出64比特在(2)中使用:•填充方法:填充比特串的最高位为1,其余各位均为0。
04第四章 散列函数与报文鉴别

K EK(M||H(M||S))
D
K
M
H(ห้องสมุดไป่ตู้||S)
H
比较
S
Return
4.3 散列函数
散列函数可以用于报文的完整性鉴别,与加密技 术配合使用可以对报文的起源进行鉴别。此外还 可以用于存储文件的完整性检验。 散列函数将任意长度的报文当作自变量,结果产 生规定长度的报文摘要,可用如下函数形式表示: h = H(M) 其中M为变长报文,H(M)为定长的报文摘要MD。 当确信或已知报文值正确时,报文摘要MD在源 点被加到该报文上。接收端通过计算该报文的 MD来鉴别该报文。由于散列函数是公开的,所 以需要对其进行保护。
FF(a,b,c,d,Mj,s,ti)表示: a=b+((a+F(b,c,d)+Mj+ti)<<<s) GG(a,b,c,d,Mj,s,ti)表示: a=b+((a+G(b,c,d)+Mj+ti)<<<s) HH(a,b,c,d,Mj,s,ti)表示: a=b+((a+H(b,c,d)+Mj+ti)<<<s) II(a,b,c,d,Mj,s,ti)表示: a=b+((a+I(b,c,d)+Mj+ti)<<<s) 这里,Mj表示报文的第j个子分组(从0到15),每一个 循环还使用一个64元素表T[1…64]的四分之一, 用ti表示,ti=4294967296*abs(sin(i))的整数部分,i 的单位是弧度,(4294967296等于2的32次方)。 <<<s表示32位参数循环左移s个比特。
第18讲 消息认证和散列函数

发送方和接收方共享两对密钥k1和k2 发送方: M先被加密再与MAC链接后发送。 接收方:解密后进行比较。
15
避免使用加密方法产生MAC码
生成MAC没有必要对整个报文加密
速度、进出口障碍 不需要能恢复原文 MAC的计算过程只需体现明文的特征唯一 Key是必要的 先计算特征,再把特征加密的思想 把散列函数和Key结合得MAC
12
消息认证码:使用方式之一
特点: MAC函数无需可逆 收发双方使用相同的密钥 只提供消息认证,不能提供机密性
13
消息认证码:使用方式之二
发送方和接收方共享两对密钥k1和k2 发送方:在计算MAC后,对M‖MAC进行整体加密再发送 接收方:解密后进行比较 提供保密性和认证性
14
消息认证码:使用方式三
25
散列函数的使用方式之六
⑥ 将消息与杂凑值链接以后再增加单钥加密运算 功能:提供认证性和保密性.
26
散列函数的使用方式选择
由于加密运算的速度较慢,代价较高, 而且很多加密算法还受到专利保护,在不要 求保密性的情况下,方式②和③将比其他方 式更具优势。
2
27
散列函数应满足的条件
散列函数应满足以下条件: ① 函数的输入可以是任意长。 ② 函数的输出是固定长。 ③ 已知x,求H(x)较为容易,可用硬件或软件实现。 这三个条件是散列函数能用于消息认证的基本要求。
不能够察觉的举例
rc4加密中,对密文部分比特的窜改导致明 文对应部分解密错误 另外,精心伪造的密文可能恰好解密为有 效的明文
结论:加密并不能完全抵抗篡改或假冒
教训:对密文的保护
在加密之前,给明文添加结构特征
消息鉴别和散列函数

网络与信息安全第七讲消息鉴别与散列函数陈钟教授北京大学信息科学技术学院软件研究所--信息安全研究室chen@2008-2009年度北京大学研究生课程2009/03/30 NISC-07 ©CZ@PKU回顾与总结•对称密码算法–运算速度快、密钥短、多种用途(随机数产生、Hash函数)、历史悠久–密钥管理困难(分发、更换)•非对称密码算法–只需保管私钥、可以相当长的时间保持不变、需要的数目较小–运算速度慢、密钥尺寸大、历史短信息安全的需求•保密性(Confidentiality)•完整性(Integrity)–数据完整性,未被未授权篡改或者损坏–系统完整性,系统未被非授权操纵,按既定的功能运行•可用性(Availability)•鉴别(Authenticity)–实体身份的鉴别,适用于用户、进程、系统、信息等•不可否认性(Non-repudiation)–防止源点或终点的抵赖•……讨论议题•消息鉴别(Message Authentication)•散列函数(Hash Functions)定义•消息鉴别(Message Authentication):是一个证实收到的消息来自可信的源点且未被篡改的过程。
•散列函数(Hash Functions):一个散列函数以一个变长的报文作为输入,并产生一个定长的散列码,有时也称报文摘要,作为输出。
•数字签名(Digital Signature)是一种防止源点或终点抵赖的鉴别技术。
通信系统典型攻击1)窃听2)业务流分析3)消息篡改内容修改:消息内容被插入、删除、修改。
顺序修改:插入、删除或重组消息序列。
时间修改:消息延迟或重放。
4)冒充:从一个假冒信息源向网络中插入消息5)抵赖:接受者否认收到消息;发送者否认发送过消息。
两个概念•鉴别(Authentication):真伪性•认证(Certification)资格审查消息鉴别•鉴别的目的•鉴别模型•鉴别函数鉴别的目的•鉴别的主要目的有二:第一,验证信息的发送者是真正的,而不是冒充的,此为信源识别;第二,验证信息的完整性,在传送或存储过程中未被篡改,重放或延迟等。
信息安全与密码学介绍(5)

M
K1 C
||
E
K2
(c)报文鉴别与保密,鉴别与密文连接
9
2. 鉴别函数
• 报文鉴别码——使用范围
1. 有许多应用要求将相同的报文对许多终点进行广播,这样的例子如通知用户 目前网络不通或军用控制中心发出告警信息。仅使用一个终点负责报文的真 实性这一方法既经济又可靠。这样,报文必须以明文加对应报文鉴别码的形 式广播。负责鉴别的系统拥有相应的密钥,并执行鉴别操作。如果鉴别不正 确,其他终点将收到一个一般的告警。 一方有繁重的处理任务,无法负担对所有收到报文进行解密的工作量。仅进 行有选择地鉴别,对报文进行随机检查。 对明文形式的计算机程序进行鉴别是一项吸引人的服务。计算机程序每次执 行时无需进行耗费处理机资源的解密。如果将报文鉴别码附加到该程序上, 通过检查能随时确信该程序的完整性。 对某些应用,也许不关心报文的保密而更看重鉴别报文的真实性。一个例子 是简单网络管理协议第3版(SNMPv3),它将保密函数与鉴别函数分离。对 于这种应用,通常鉴别收到的SNMP报文的真实性对被管系统更为重要,特 别是如果该报文中包含改变被管系统命令时更是如此。在另一方面,它没有 必要取消SNMP通信。 鉴别函数与保密函数的分离能提供结构上的灵活性。例如,可以在应用层完 成鉴别而在更低层(如运输层)来实现保密功能。 用户也许期望在超过接收时间后继续延长保护期限,同时允许处理报文的内 容。使用报文加密,当报文被解密后保护就失效了,因此报文仅能在传输过 程中防止欺诈性的篡改,但在目标系统中却办不到。
由于MAC函数一般是一个多对一的函数,因此对于长度为n比特 的MAC,如果密钥的长度为k比特(k>n),那么如果已知M1和 MAC1,MAC1 = CK1(M1),密码分析者必须对所有可能的密 钥值Ki执行MACi = CKi(M1)。当MACi = MAC1时,则至少找 到一个密钥。注意,总共将产生2k个MAC,但只有2n<2k个 不同的MAC值。因此,许多密钥能产生这个正确的MAC,但 对手却无法确认真正的正确密钥。平均说来,总共2k/2n = 2(k-n) 个密钥将产生一个匹配。因此,对手必须重复这样的攻击:
哈希函数和散列函数

哈希函数和散列函数
哈希函数和散列函数是计算机科学中非常重要的概念。
哈希函数是一种将任意长度的消息映射到固定长度的消息的函数。
散列函数是一种将任意长度的消息映射到固定长度的消息的函数,但它还具有单向性质,即从散列值推导原始消息的难度非常大。
哈希函数可以用于数据的完整性验证、密码学中的消息摘要、散列表等场景。
常见的哈希函数有MD5、SHA-1、SHA-256等。
散列函数则可以用于密码学中的数字签名、加密算法等场景。
常见的散列函数有SHA-1、SHA-2、SHA-3等。
值得注意的是,哈希函数和散列函数虽然都可以将任意长度的消息映射到固定长度的消息,但它们的安全性和用途不同。
对于哈希函数,由于存在哈希碰撞的可能性,因此不能保证将不同的消息映射到不同的哈希值。
而对于散列函数,由于具有单向性质,因此即使知道散列值,也很难推导出原始消息。
在使用哈希函数和散列函数时,需要注意选择合适的算法,根据实际场景进行适当的参数配置,以保证数据的安全。
- 1 -。
第4章 单向散列函数

为了加强算法的安全性,rivest在1990年又开发出md4算法。md4算法同样 需要填补信息以确 保信息的字节长度加上448后能被512整除(信息字节长度 mod 512 = 448)。然后,一个以64位二进制表示的信息的最初长度被添加进来。 信息被处理成512位damg?rd/merkle迭代结构的区块,而且每个区块要 通过三 个不同步骤的处理。den boer和bosselaers以及其他人很快的发现了攻击md4版 本中第一步和第三步的漏洞。dobbertin向大家演示了如何利用一部普通的个人 电 脑在几分钟内找到md4完整版本中的冲突(这个冲突实际上是一种漏洞,它 将导致对不同的内容进行加密却可能得到相同的加密后结果)。毫无疑问, md4就此 被淘汰掉了。
抗逆向特性——给定h(x),计算x十分困难; 抗第二逆向特性——给定h(x),很难找到一个x’,使得 h(x)=h(x’); 冲突特性——很难找到两条消息x和x’,使得h(x)=h(x’)。
在实际中,单向散列函数是建立在压缩函数之上的,
如图4-1所示。
消息分组 1 消息分组 2 … 消息分组 n 填充位
在很多情况下,我们需要鉴别和认证用户。如用户登录计算机 (或自动柜员机等)时,计算机往往需要知道用户是谁,确认是 某个用户而不是其它人在冒充,传统的方法是用户口令来解决这
个问题。用户在登录计算机前输入其口令,由计算机确认口令正 确后,用户才可以登录计算机。用户和计算机均知道口令。用户 每次登录均需输入口令。由于计算机需要知道口令,这就需要把 口令保存在计算机中。这就为入侵计算机偷取口令提供了可能,
为此,我们不直接保存口令本身,而是保存口令的散列值(口令 的某种形式)。当用户输入口令后,计算机先计算口令的散列值 并与保存在计算机中的散列值进行比较,以此来鉴别用户。由于 用来计算散列值的函数具有单向性,即根据散列值不可能逆向恢
公钥密码学数学

公钥密码学数学密码学是一个具有极大实用价值的跨学科领域。
它的子领域公钥密码学则有许多引人注目的应用,例如数字签名。
在作为公钥密码学基础的数学中,具有很强的背景是深入理解这个科目所必需的,而本书恰好是为数学、计算机科学和电器工程专业的学生和研究人员提供这样的背景。
作者通过严谨的写作将公钥密码学的主要概念及技术传播给广大的读者。
贯穿全书,作者利用了涉及这个科目的历史述评以及富有洞察力的观点使得它生动有趣。
本书共有26章,分成7个部分。
还有一个附录。
1.绪论,内容包括公钥密码学、教科书RSA密码系统、公钥密码学形式定义;第1部分背景,含第2-3章:2.基本算法数论;3.散列函数与报文鉴别码。
第2部分代数群,含第4-10章:4.有关代数群的初步陈述;5.簇;6.环面、LUC和XTR;7.曲线和除子类群;8.曲线和除子的有理映射;9.椭圆曲线;10.超椭圆曲线。
第3部分取幂、因式分解和离散对数,含第11-15章:11.代数群的基本算法;12.利用代数群的原始测试和整数因式分解;13.基本离散对数算法;14.借助伪随机行走的因式分解和离散对数;15.子指数时间中的因式分解和离散对数。
第4部分格,含第16-19章:16.格;17.格基归约;18.适用于最近最短向量问题的算法;19.Coppersmith方法及其有关应用。
第5部分与离散对数有关的密码学,含第20-23章:20.DiffieHellman问题及密码学应用;21.DiffieHellman问题;22.基于离散对数的数字签名;23.基于离散对数的公钥密码学。
第6部分与整数因式分解有关的密码学,含第24章:24.RSA和拉宾密码系统。
第7部分椭圆曲线及超椭圆曲线中的高级主题,含第25-26章:25.椭圆曲线的同种影射;26.椭圆曲线的配对。
最后是标题为背景数学的附录A。
本书作者是有关公钥密码学数学领域内具有国际声誉的权威、新西兰奥克兰大学数学系的副教授。
散列函数、消息摘要与数字签名
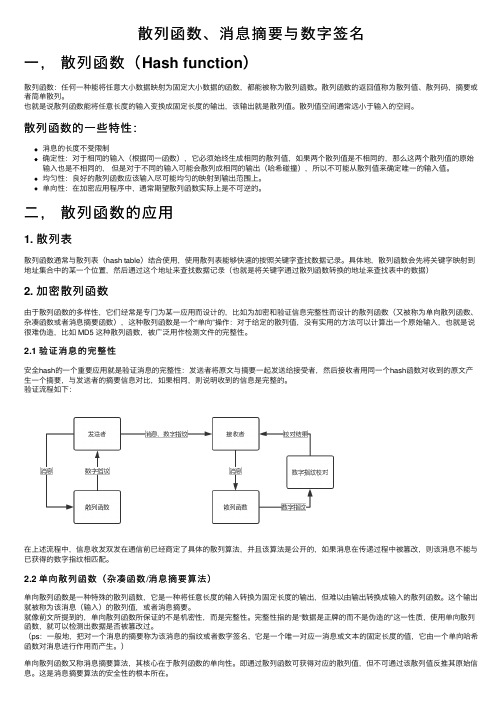
散列函数、消息摘要与数字签名⼀,散列函数(Hash function)散列函数:任何⼀种能将任意⼤⼩数据映射为固定⼤⼩数据的函数,都能被称为散列函数。
散列函数的返回值称为散列值、散列码,摘要或者简单散列。
也就是说散列函数能将任意长度的输⼊变换成固定长度的输出,该输出就是散列值。
散列值空间通常远⼩于输⼊的空间。
散列函数的⼀些特性:消息的长度不受限制确定性:对于相同的输⼊(根据同⼀函数),它必须始终⽣成相同的散列值,如果两个散列值是不相同的,那么这两个散列值的原始输⼊也是不相同的,但是对于不同的输⼊可能会散列成相同的输出(哈希碰撞),所以不可能从散列值来确定唯⼀的输⼊值。
均匀性:良好的散列函数应该输⼊尽可能均匀的映射到输出范围上。
单向性:在加密应⽤程序中,通常期望散列函数实际上是不可逆的。
⼆,散列函数的应⽤1. 散列表散列函数通常与散列表(hash table)结合使⽤,使⽤散列表能够快速的按照关键字查找数据记录。
具体地,散列函数会先将关键字映射到地址集合中的某⼀个位置,然后通过这个地址来查找数据记录(也就是将关键字通过散列函数转换的地址来查找表中的数据)2. 加密散列函数由于散列函数的多样性,它们经常是专门为某⼀应⽤⽽设计的,⽐如为加密和验证信息完整性⽽设计的散列函数(⼜被称为单向散列函数、杂凑函数或者消息摘要函数),这种散列函数是⼀个“单向”操作:对于给定的散列值,没有实⽤的⽅法可以计算出⼀个原始输⼊,也就是说很难伪造,⽐如 MD5 这种散列函数,被⼴泛⽤作检测⽂件的完整性。
2.1 验证消息的完整性安全hash的⼀个重要应⽤就是验证消息的完整性:发送者将原⽂与摘要⼀起发送给接受者,然后接收者⽤同⼀个hash函数对收到的原⽂产⽣⼀个摘要,与发送者的摘要信息对⽐,如果相同,则说明收到的信息是完整的。
验证流程如下:在上述流程中,信息收发双发在通信前已经商定了具体的散列算法,并且该算法是公开的,如果消息在传递过程中被篡改,则该消息不能与已获得的数字指纹相匹配。
数据结构散列查找

数据结构散列查找
散列查找是一种非常快速和高效的查找方法,它可以在 O(1) 的时间复杂度内完成查找操作。
在散列查找中,数据元素被存储在一个散列表中,每个元素都有一个对应的关键字,这个关键字被用来计算出该元素在散列表中的位置。
散列查找的核心是散列函数,它能够将关键字映射到散列表中的一个位置。
散列函数需要满足以下两个条件:
1. 散列函数必须是确定性的,对于相同的输入,必须得到相同
的输出。
2. 散列函数应该尽可能地将不同的关键字映射到不同的位置上,这样可以减少散列表的冲突。
当两个不同的关键字映射到了同一个位置上时,就会发生冲突。
散列查找中有两种方法解决冲突:
1. 开放地址法:在发生冲突时,依次查找散列表的下一个位置,直到找到一个空位置为止。
2. 链地址法:将冲突的元素存储在一个链表中,该链表连接散
列表中对应位置的所有元素。
散列查找的优点是速度非常快,但它也有一些缺点。
首先,散列函数的设计需要考虑到数据的分布情况,否则会导致散列函数不均匀,进而导致冲突增多。
其次,散列查找对内存的使用要求较高,因为需要为散列表预留一定的空间,否则会导致冲突增多。
最后,散列查找的删除操作相对复杂,因为需要保证删除后的散列表仍然是有效的。
总的来说,散列查找是一种非常高效的查找方法,它在多个领域都有广泛的应用,如数据库查询、哈希表等。
在实际应用中,需要根据具体的场景选择合适的散列函数和解决冲突的方法,以保证散列查找的高效性和正确性。
报 文 鉴 别

2.附加长度值
• 用步骤1留出的64位填充报文的原始长度。这时,填充之后的报
文长度恰好是512的整数倍(即512的L倍)。把扩展后的消息 以512位为一组进行分组,可以分为L组,表示为Y0,Y1, Y2,…,YL-1。
产生单向散列的能力。 • (5)散列值有固定的长度,一个短报文的散列与一个非常
长的报文的散列可以产生相同长度的散列值。 • (6)要找到两个不同报文产生相同的散列值在计算上是不
可行的。
1.3 报文摘要MD5
• MD表示报文摘要(message digest),MD5是MD4的改进版, 是由Ron 任意长度的报文进行计算,以512bit的 分组进行处理,产生一个128位长度的报文摘要。
1.4 安全散列算法
• SHA是美国国家标准技术研究院和NSA共同设计的 安全散列算法(secure hash algorithm,SHA), 用于数字签名标准(digital signature standard, DSS)。
• SHA–1产生报文摘要的过程类似MD5。SHA–1的输 入为长度小于264位的报文,输出为160位的报文 摘要,算法的安全性比MD5要高。具体过程如下。
散列函数必须具备如下特征:
• (1)对于不同的报文不能产生相同的散列值,改变原始报 文中的任意一位数值将产生完全不同的散列值。
• (2)对于任意一个报文无法预知它的散列值。 • (3)无法根据散列值倒推报文,因为一条报文的散列值可
能是由无数的报文产生的。 • (4)散列算法是公开的,不需要保密,它的安全性来自它
1.2 散列函数
• 散列函数又称Hash函数、单向函数,它将任意长度的
报文M变换成固定长度的散列值(即报文摘要)h,散
散列函数及其应用

散列函数及其应⽤散列函数 散列,英⽂Hash,也有直接⾳译为“哈希”的,就是把任意长度的输⼊(⼜叫做预映射, pre-image),通过散列算法,变换成固定长度的输出,该输出就是散列值。
这种转换是⼀种压缩映射,也就是,散列值的空间通常远⼩于输⼊的空间,不同的输⼊可能会散列成相同的输出,所以不可能从散列值来确定唯⼀的输⼊值。
简单的说就是⼀种将任意长度的消息压缩到某⼀固定长度的信息摘要的函数。
散列函数的应⽤ 在算法竞赛中,我所接触到的主要有字符串hash⽤于把字符串“索引”为⼀个值,然后对复杂字符串进⾏操作,来加快遍历速度,降低算法复杂度。
把字符串匹配转移到了值匹配。
但是散列函数属于⼀种“概率型算法”,对于模的取值有⼀定概率出现碰撞。
所以在算法竞赛中不常使⽤,或者要多次测验避免碰撞。
在信息安全⽅⾯的应⽤主要体现在以下的3个⽅⾯: 1)⽂件校验 我们⽐较熟悉的校验算法有奇偶校验和CRC校验,这2种校验并没有抗数据篡改的能⼒,它们⼀定程度上能检测并纠正数据传输中的信道误码,但却不能防⽌对数据的恶意破坏。
MD5 Hash算法的"数字指纹"特性,使它成为⽬前应⽤最⼴泛的⼀种⽂件完整性校验和(Checksum)算法,不少Unix系统有提供计算md5 checksum的命令。
2)数字签名 Hash 算法也是现代密码体系中的⼀个重要组成部分。
由于⾮对称算法的运算速度较慢,所以在数字签名协议中,单向散列函数扮演了⼀个重要的⾓⾊。
对 Hash 值,⼜称"数字摘要"进⾏数字签名,在统计上可以认为与对⽂件本⾝进⾏数字签名是等效的。
⽽且这样的协议还有其他的优点。
3)鉴权协议 如下的鉴权协议⼜被称作"挑战--认证模式:在传输信道是可被侦听,但不可被篡改的情况下,这是⼀种简单⽽安全的⽅法。
散列函数的安全性 两个不同的输⼊,经过哈希算法后,得到了同样的哈希值,就叫做哈希碰撞。
散列函数特征范文

散列函数特征范文散列函数(hash function)是一种将输入数据映射为固定长度输出数据的函数。
它将任意长度的输入数据转换为固定长度的二进制值,该二进制值通常称为散列值(hash value)或摘要(digest)。
散列函数的输出值是一段数字签名,通过对比散列值可以判断输入数据是否发生了变化。
散列函数的特征主要包括以下几个方面:1.快速计算:散列函数需要能够在合理的时间内计算出散列值。
尤其在处理大量数据时,散列函数应该具有高效的计算速度。
2.固定输出长度:散列函数所产生的散列值长度应该是固定的,不受输入数据长度的影响。
通常,散列函数的输出长度是一个固定的位数,例如128位、256位等。
3.碰撞几率低:散列函数应该具有很低的碰撞概率。
碰撞是指两个不同的输入数据获得相同的散列值。
好的散列函数应该尽可能地减少碰撞的发生,以提高数据的完整性和安全性。
4.雪崩效应:散列函数具有雪崩效应是指,当输入数据的稍微变化时,散列值应该发生巨大的变化。
这样可以确保散列值对输入数据的细微变化非常敏感,从而提高数据的安全性。
5.扩展性:散列函数应该能够处理各种不同大小和类型的输入数据。
它不仅可以接受文本、数字等常见的数据类型,还可以处理图片、音频、视频等多媒体数据。
6.不可逆性:散列函数是一种单向函数,即很难通过散列值逆推回原始数据。
这种不可逆性可以用于数据的加密存储和验证完整性。
7.随机性:好的散列函数应该具备随机性,即使输入数据的稍微变化也应该产生不可预测的散列值。
这样可以防止攻击者通过分析散列值来推测原始输入数据。
8.均匀性:散列函数应该具有均匀性,即输出的散列值在整个散列空间中均匀分布。
这样可以提高哈希散列算法的效率和性能。
需要注意的是,散列函数虽然具有很多优点,但也存在一些局限性。
首先,由于输出长度是固定的,所以很难避免碰撞。
其次,由于输入数据的多样性,散列函数无法完全避免冲突。
再次,散列函数的计算速度可能会受到输入数据和散列算法本身的影响。
《现代密码学》散列函数与消息鉴别_OK

MD5算法的逻辑程序
1.初始化MD5缓冲区 初始化用于计算消息摘要的128位缓冲区。这 个缓冲区由四个32位寄存器A、B、C、D表示。 寄存器的初始化值为(按低位字节在前的顺序存 放): A: 01 23 45 67 B: 89 ab cd ef C: fe dc ba 98 D: 76 54 32 10
4. 攻击者提供一个对A签名有效的变种。该签名被 附加在这个带有欺诈性报文上发往原来的接收 者。因为这两个报文变种具有相同的散列码, 故它们能产生相同的签名;即使不知道加密密 钥,攻击者也肯定获得成功
15/66
对散列函数的生日攻击
• 假定其输出为m比特,那么寻找一个消息,使其 散列值与给定散列值相同则需要计算2m次;而寻 找两个消息具有相同的散列值仅需要试验2m/2个随 机的消息。
8/66
散列函数的应用
• 数字签名 将散列函数应用于数字签名,一般方法是不 直接对消息m签名,而对m对应的散列码h 进行签名,这样可以提高签名的速度 (|h|<|m|),且不泄露签名所对应的信息,因 此散列函数在数字签名中应用广泛。
9/66
散列函数的一般结构
• 目前使用的大多数散列函数,其结构都是迭代 型的。将输入的消息m分成t个分组 ( m1 ,,m2,…,mt),每组固定长度为b位。如 果最后一个分组的长度不够,需要对其进行填 充。通常的填充方法是保证最后一个分组的最 后64位为m的总长度,然后在中间填充。
26/66
MD5的安全性
• 山东大学的王小云教授在2004年美洲密码年 会上做了攻击MD5等四个算法的报告,并 给出了一个具体的MD5的碰撞的例子。这 清楚表明了MD5不是强抗碰撞的,MD5的 安全性受到了严重的威胁。
第6讲 报文鉴别技术

6.1 概述
5. 鉴别函数的分类
根据鉴别符的生成方式,鉴别函数可以分为以下几类:
基于报文加密方式的鉴别: 以整个报文的密文作为鉴别符。
报文鉴别码(MAC)方式。
散列函数方式: 采用一个公共散列函数,将任意长度的报文
映射为一个定长的散列值,并以散列值作为鉴别符。
6.2 基于报文加密方式的鉴别
对数字签名来说,散列函数h是这样使用的:
消息: x 任意长 消息摘要: Z=h(x) 160bits
签名:y=sigk(Z) 320 bits (签名一个消息摘要)
验证签名:(x,y),其中y= sigk(h(x)) 使用公开的散列函数h, 重构
Z’=h(x) 然后检验Verk(Z,y),来看Z?=Z’
第6讲
报文鉴别技术
1
6.1 概述
1. 报文鉴别(消息认证)的概念
报文鉴别(Message Authentication)
Message:消息、报文。
Authentication: 鉴别、认证。
鉴别:消息的接收者对消息进行的验证。
真实性:消息确实来自于其真正的发送者,而非假冒;
完整性:消息的内容没有被篡改。
这种结构易于识别、不能被复制,同明文相关,并且不依赖于加密。
对称密钥加密方式
解决办法例子:附加报文鉴别结构
附加报文鉴别结构
源点A
对消息明文M首先利用校验函数F 计算出消息的校验码 C=F(M); 校验码 C=F(M)被附加到原始消息明文上,生成新的明文
[M‖C];
利用密钥K对明文 [M‖C]进行加密,得到密文 X=EK [M‖C];
2 .公开密钥加密方式 :提供报文鉴别和签名功能 ,不提供保 密功能。
散列函数在报文鉴别中的应用

散列函数在报文鉴别中的应用
散列函数是一种常见的加密技术,它将任意长度的消息压缩成固定长度的散列值。
在报文鉴别中,散列函数可以用来验证报文的完整性和真实性。
具体地讲,发送方可以先将报文通过散列函数进行处理,得到一个散列值,然后将该散列值附加到报文中一起发送。
接收方在接收到报文后,也将报文进行散列处理,得到一个散列值,并与发送方附加的散列值进行比对,如果两个散列值相同,则说明报文没有被篡改过。
散列函数在报文鉴别中的应用还可以通过添加一个密钥来增强
其安全性。
发送方和接收方都必须共享同一个密钥,才能保证报文的安全性。
总之,散列函数在报文鉴别中的应用可以有效地保护报文的完整性和真实性,以及防止报文被篡改或伪造。
- 1 -。
散列函数与消息认证

认证:认证函数 认证函数
认证系统的工作原理 发送方利用底层的认证函数产生一个用来认证的认证标识; 消息接收方利用上层的认证协议基于认证标识验证真实性。 认证函数的分类 加密函数:用整个消息的密文作为消息认证的认证标识; 加密函数 消息认证码(MAC):指消息被一密钥控制的公开函数作用后产 消息认证码 生的、用作认证符的、固定长度的数值,也称为密码校验和 密码校验和; 密码校验和 散列函数:一个不需要密钥的公开函数,将任意长度的输入消 散列函数 息映射成一个固定长度的输出值,并以此值作为认证标识别。
Page: 17 2010-12-16
HASH函数:生日攻击 生日攻击
攻击过程(Alice发送消息给 发送消息给Bob) 攻击过程 发送消息给 Alice用自己的私钥对消息的HASH值加密,加密结果作为对消息 的签名连同明文消息一起发送给接收者; 敌手对Alice发送的消息m以及一个假冒的消息m‘产生出2|m|/2 个变 形的消息,每个变形的消息本质上的含义与原消息相同; 敌手在产生的两个消息集中找出HASH值相同的一对消息m,m’, 直到成功为止(由上述讨论可知敌手成功的概率大于0.5); 敌手将m’提交给Alice签名,由于m和m’的HASH值相同,所以可 将Alice对m’的签名当成m的签名,将签名m’与一起发给接收者。
Page: 19
2010-12-16
HASH函数:迭代型 迭代型HASH函数 迭代型 函数
迭代型HASH函数的设计思想 函数的设计思想 迭代型 将输入M分为L个分组:Y0, Y1, …, YL-1。每一个分组的长度为b比 特,最后一个分组不足则填充,且最后一个分组还包括整个输 入的长度值; 重复使用一个压缩函数 (两个输入一个输出,算法指定初值 压缩函数f 两个输入一个输出 算法指定初值IV) 压缩函数 两个输入一个输出,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FF(a,b,c,d,Mj,s,ti)表示: a=b+((a+F(b,c,d)+Mj+ti)<<<s) GG(a,b,c,d,Mj,s,ti)表示: a=b+((a+G(b,c,d)+Mj+ti)<<<s) HH(a,b,c,d,Mj,s,ti)表示: a=b+((a+H(b,c,d)+Mj+ti)<<<s) II(a,b,c,d,Mj,s,ti)表示: a=b+((a+I(b,c,d)+Mj+ti)<<<s) 这里,Mj表示报文的第j个子分组(从0到15),每一个 循环还使用一个64元素表T[1…64]的四分之一, 用ti表示,ti=4294967296*abs(sin(i))的整数部分,i 的单位是弧度,(4294967296等于2的32次方)。 <<<s表示32位参数循环左移s个比特。
Return
4.4 MD5 报文摘要算法
MD5报文摘要算法是由Rivest(即RSA中的R)提 出的第5个版本的MD,此算法可对任意长度 的报文进行计算,然后得出128位的MD代码。 其作用是将大容量信息在数字签名前被“压缩” 成一种保密的格式。 MD5算法曾经是使用最普遍的安全散列算法, 但近年来出现了针对该算法的可能攻击手段。 算法描述 算法以任意长度的报文作为输入,产生一个 128位的报文摘要作为输出。输入是按512位分 组进行处理。算法处理流程见图。
4.3.1 对散列函数的要求
使用散列函数的目的是为文件、报文或其它分组数 据产生“指纹”,要用于报文鉴别。散列函数H必 须具有如下性质: – H应该能够用于任何大小的数据块。(实际应用 要求) – H应当生成一个固定长度的输出。 – 对任何给定的报文M,计算H(M)应当是容易的, 不论是用硬件还是用软件实现。 – 对于任何给定的代码m,找出x使得H(x)=m,在 计算上是不可行的。也就是说散列函数的逆运 算H-1(m)=x在计算上是不可行的。这是散列函数 的单向特性。
– 对于任何给定的数据块x,找出y<>x,
使H(y)=H(x),在计算上是不可行的。 该特性保证了不同的报文不易得出相 同的MD码(防止生成替代报文)。弱抗 冲突 – 寻找对任何的(x, y)对使得H(x)=H(y)在 计算上不可行。强抗冲突
4.3.2 简单散列函数
所有散列函数的操作都使用下列一般性原则。 输入(文件或报文)被视作长度为n-bit的分组 序列,输入的处理方式是以迭代的方式每次 处理一个分组,以产生一个l-bit的散列值。(l ≤n) 一个最简单的散列函数是每个分组按比特异 或。 即:Ci = b1i b2i … bmi 其中: Ci =第i比特的散列码,1≤ i ≤ n m =输入中n-bit分组数。
第一轮 : Mj s ti FF(a,b,c,d,M0, 7, 0xd76aa478) FF(d,a,b,c,M1, 12,0xe8c7b756) FF(c,d,a,b,M2, 17,0x242070db) FF(b,c,d,a,M3, 22,0xc1bdceee) FF(a,b,c,d,M4, 7, 0xf57c0faf) FF(d,a,b,c,M5, 12,0x4787c62a) FF(c,d,a,b,M6, 17,0xa8304613) FF(b,c,d,a,M7, 22,0xfd469501) FF(a,b,c,d,M8, 7, 0x698098d8) FF(d,a,b,c,M9, 12,0x8b44f7af) FF(c,d,a,b,M10,17,0xffff5bb1) FF(b,c,d,a,M11,22,0x895cd7be) FF(a,b,c,d,M12,7, 0x6b901122) FF(d,a,b,c,M13,12,0xfd987193) FF(c,d,a,b,M14,17,0xa679438e) FF(b,c,d,a,M15,22,0x49b40821)
Return
4.2 鉴别函数
4.2.1 报文加密
4.2.2 报文鉴别码
4.2.3 散列函数
4.2.1 报文加密
(1) 常规加密 考虑直接使用常规加密方法。通信的双方A和B 共享密钥K,A使用密钥K对发往B的报文M进 行加密。 如果没有其它人知道密钥K,就能提供保密性。 B也能确信收到的报文来自A。因为除B外,A 是惟一拥有密钥K的,并可以构建用K解密的密 文。并且,不知道密钥K的敌方不会知道如何 改变密文来产生明文中期望的变化。所以,如 果M恢复,B知道M中的内容末被任何人改动。 结论:常规加密提供保密性和鉴别。
M E H
K EK(M||H(M||S))
D
K
M
H(M||S)
H
比较
S
Return
4.3 散列函数
散列函数可以用于报文的完整性鉴别,与加密技 术配合使用可以对报文的起源进行鉴别。此外还 可以用于存储文件的完整性检验。 散列函数将任意长度的报文当作自变量,结果产 生规定长度的报文摘要,可用如下函数形式表示: h = H(M) 其中M为变长报文,H(M)为定长的报文摘要MD。 当确信或已知报文值正确时,报文摘要MD在源 点被加到该报文上。接收端通过计算该报文的 MD来鉴别该报文。由于散列函数是公开的,所 以需要对其进行保护。
M
K1
E
K2 EK2(M||Ck1(M))
D
K2
M
C
比较
K1
C
Ck1(M)
(3) 先加密,后生成鉴别码,将MAC与密文连 接传输。(鉴别;加密)
M E
K1 K2
D
C
比较 K1 Ck1 (EK2(M)) K2
M
C
Return
4.2.3 散列函数
散列函数与报文摘要 • 散列函数(hash function)类似报文鉴别码,一 个散列函数以一个变长的报文作为输入,产生 一个定长的散列码H(M)作为输出,H(M)通常 又称为报文摘要MD (Message Digest)。 • 散列码(或MD)是报文所有比特的函数值,并 具有差错检测能力,即报文中任一比特或若干 比特发生改变都将导致(新计算的)散列码的改 变。 MD与MAC的区别:生成函数不同;是否需要 密钥(不需要密钥)
散列函数的使用方式 (1) 使用常规加密方法对附加散列码的报文进 行加密。 (鉴别;加密)
M H E
K EK(M||H(M))
D
K
M
H
比较
H(M)
(2) 使用常规加密方法仅对散列码进行加密。 (鉴别;不加密)
M H
K
M E
H
比较
D
EK(H(M))
K
(3) 使用公开密钥加密方法及发方的私有密钥仅 对散列码进行加密。 (鉴别;不加密)
A
M E EKRa(M) D
B
M
KRa
KUa
具有机密性和鉴别及签名的公开密钥加密: 加密/解密次数太多。仍存在报文合法性问 题。
A
M E
EKRa(M)
KRa KUb KRb KUa EKUb(EKRa(M))
B
D D M
E
解决上述问题的一种方法:强制明文具有 某种结构,这种结构易于识别、不能伪造。 如:计算机网络中采用的FCS(帧校验序列)。
第四章 散列函数与报文鉴别
4.1 鉴别概念 4.2 鉴别函数 4.3 散列函数 ★ 4.4 MD5 报文摘要算法★ 4.5 安全散列算法 SHA ★ 4.6 报文鉴别码 ★
4.1 鉴别概念
报文鉴别(Message Authentication)是防御网络主动攻击 的重要技术。在需要通过网络进行信息交换时,会遇 到以下攻击: ① 泄露:报文内容被透露给没有拥有合法密钥的任何人 或相关过程。 ② 通信量分析:发现通信双方的通信方式。在面向连接 的应用中,连接的频率和连接持续时间。在面向连接 或无连接的环境中,通信双方的报文数量和长度。 ③ 伪装:以假的源点身份将报文插入网络中。包括由敌 方伪造一条报文却声称它来自已授权的某个实体。另 外,还包括由假的报文接收者对收到报文发回假确认, 或者不予接受。
Return
4.2.2 报文鉴别码
原理:发送方使用一个密钥和特定算法对明 文产生一个短小的定长数据分组,即 MAC(报文鉴别码),并将它附加在报文中。 在接收方,使用相同的密钥和算法对明文 计算MAC,如果新的MAC与报文中的MAC 匹配,那么: • 接收者确信报文未被更改过。 • 接收者确信报文来自所期望的发送方。 • 如果报文包含一个序号(如HDLC、X.25和 TCP),那么接收者确信该序号的正确性。
MAC函数:MAC=CK(M),MAC函数类似于 加密过程,一个主要区别是MAC函数无需可 逆。由于鉴别函数的这个特性,使得它比加 密函数更不易破解。 报文鉴别码的基本用法: (1) MAC直接与明文连接后传输(鉴别;不加密)。
M C
K
M
C
K 比较
Ck(M)
(2) MAC与明文连接后一起加密再传输。(鉴 别;加密)
M
H
KR
M
EKR(H(M))
H
比较
E
D
KU
(4) 在(3)的基础上增加保密功能。 (鉴别;加密)
M H E
KR
D
K
M
EKR(H(M))
H
比较
E
K
EK(M|| EKR(H(M)))
D
KU
(5) 使用散列码、公共秘密值的明文方案。 (鉴别;不加密)
SLeabharlann MS HM
H
比较
(6) 使用散列码、公共秘密值的保密方案。 (鉴别;加密) S
报文长度 K mod 264
L×512 K-bit 填充 1-512bit
