用迈克尔逊干涉仪测量斜劈的折射率
《用迈克尔逊干涉仪测量玻璃折射率》

用迈克尔逊干涉仪测量玻璃折射率概述在物理实验中,测量不同介质的折射率是一项基础且常见的实验任务。
而在本次实验中,我们将使用迈克尔逊干涉仪测量玻璃的折射率。
迈克尔逊干涉仪是通过将波源光线分为两束并引入两个不同的光程,使得两束光线再次重合形成干涉条纹的干涉仪。
实验步骤1. 实验仪器本实验需要的仪器包括:•迈克尔逊干涉仪•钠光灯•单色仪•玻璃片•三角架•双目镜2. 原理说明在迈克尔逊干涉仪中,将钠光源通过单色仪使其成为单色光,并引入到二阶干涉切块器中,切块器将单色光分成两束通过两个光路产生不同的光程,光程差大到一定的程度,就发生干涉现象。
引入玻璃片后,会对不同波长的光线产生不同的相位差,从而导致干涉条纹的变化。
通过调整干涉仪中的镜片,可以观察到干涉条纹的变化,从而计算出玻璃的折射率。
3. 实验操作步骤1.在实验室中将迈克尔逊干涉仪放置在三角架上,并将钠光灯放置在光源座上,开启钠光灯,后调整单色仪的角度,使得光线呈现出单色性质,即可看见钠光波长(589.3nm)的光线。
2.调整迈克尔逊干涉仪的各个镜片,使得反射的光线分别照射到两块干涉切块器的入口处,并将反射光线中的一束径线调整向墙上的白色纸板。
3.记录下光程差的初始值。
4.在其中一条路程上插入玻璃片,即可看到干涉条纹的变化,分别在不加玻璃片和加上玻璃片两种情况下测量光程差,计算得到玻璃的折射率。
4. 实验注意事项1.实验过程中要注意保持实验环境的稳定性,避免外界因素干扰实验结果。
2.在调整迈克尔逊干涉仪时,要注意准确调整各个镜片的位置,保证光线的正常传输。
3.测量时,需要多次重复实验以保证结果的精度和可靠性。
结束语通过以上操作步骤,就可以使用迈克尔逊干涉仪来测量玻璃的折射率。
实验过程中,可能会遇到一些问题,但通过不断尝试和调整,一定可以得出准确且可靠的实验结果。
利用迈克尔逊干涉仪测量液体的折射率

第32卷第1期大学物理实验Vol.32No.12019年2月PHYSICALEXPERIMENTOFCOLLEGEFeb.2019收稿日期:2018 ̄10 ̄29基金项目:中国矿业大学教改项目(No.2017YB30)ꎻ中国矿业大学大学生科研创新训练(20180432)∗通讯联系人文章编号:1007 ̄2934(2019)01 ̄0043 ̄03利用迈克尔逊干涉仪测量液体的折射率杜登熔ꎬ李㊀艳∗ꎬ商成林ꎬ党新志ꎬ王洪涛(中国矿业大学ꎬ江苏徐州㊀211116)摘要:在迈克尔逊干涉仪的实验光路中加入可移动的三角形容器ꎬ将待测液体介质装入容器中ꎬ通过移动三角形容器即可改变光束在介质中的光程ꎬ光程差的改变量与三角形容器插入光路中厚度成正相关ꎬ通过计算可以得到折射率的表达式ꎬ用最小二乘法拟合测量数据ꎬ计算斜率ꎬ代入表达式即可求得液体的折射率ꎮ关键词:迈克尔逊干涉仪ꎻ三角形容器ꎻ液体ꎻ折射率中图分类号:O4 ̄34文献标志码:ADOI:10.14139/j.cnki.cn22 ̄1228.2019.01.010㊀㊀折射率是物质的一个重要光学参数ꎬ借助折射率可以了解物质的光学性能㊁浓度㊁纯度和热光系数等[1]ꎬ因此透明介质的折射率测量有重要的研究意义ꎮ测量液体折射率的方法有等倾干涉法[2]ꎬ激光照射法[3]ꎬ衍射光栅法[4]ꎬ玻璃毛细管法[5]ꎬ阿贝折射法[1ꎬ6]等ꎮ迈克尔逊干涉仪是物理实验中的精密光学仪器ꎬ该仪器利用光的等倾干涉可将光程的测量结果精确到与入射光波长同等数量级ꎬ用该仪器测量液体的折射率也是研究的热点之一ꎮ本文利用三角形容器盛放液体ꎬ通过转动鼓轮改变三角形容器的位置ꎬ从而改变光束在介质中的光程ꎬ根据折射率和光程的关系式计算出液体的折射率ꎮ1㊀实验原理实验原理图如图1所示ꎬG1和G2是一对平行的㊁厚度和材质都相同的光学玻璃板ꎬG1背面涂有半透膜ꎬ称为分光板ꎬG2为补偿板ꎬM1和M2是两个平面镜ꎬM1与G1㊁G2夹角为45ʎꎬP为石英片制作的三角形容器ꎬ里面盛放待测液体ꎮ本文采用扩展后的He ̄Ne激光作为光源ꎬ从S发出的光通过G1后被半透膜分成强度相同的互相垂直的两束光(1)和(2)ꎬ透射光(2)经过G2被M1反射再次穿过G2后被半透膜反射到达观察屏ꎮ反射光(1)穿过P后被M2反射再次经过P和G1到达观察屏ꎬ这两束光满足相干条件ꎬ将发生干涉ꎮ图1 实验原理图实验中ꎬ考虑到液体对光线的折射ꎬ经过P的光线会发生偏转ꎬ注入不同的液体时需要对M2进行不同程度的微调以确保经折射后的光可沿原光路返回并与由M1反射回来的光形成干涉条纹ꎮ实验时ꎬ将三角形容器P置于一个由精密丝杆(精度为0.0001mm)控制的可移动载物台上ꎬ通过横向移动P的位置来改变两束光的光程差ꎬ从而推导出折射率表达式ꎮ为了简化计算ꎬ操作中调节P的一条边与G1的反射光线(1)垂直ꎬ如图1所示ꎮ为计算两束光的光程差ꎬ可对光线在P处引起的光程改变进行分析ꎬ如图2所示ꎬα为入射光线所对应的三角形容器顶角ꎬ考虑光线从液体中入射到空气中ꎬ则入射角也为αꎬ设折射角为βꎬ液体折射率为nꎬ根据斯涅耳折射定律[7ꎬ8]ꎬ入射角的正弦与折射角的正弦成正比ꎬ即图2㊀光路分析图sinβ=nsinα(1)设三角形容器横向移动距离为Δdꎬ光线在介质中的距离变化量为Δd1ꎬ在空气中距离的变化量为Δd2ꎬ则光程差为:δ=2(nΔd1-Δd2)(2)根据图2中几何关系可知ꎬΔd1=ΔdtanαꎬΔd2=Δdtanαcos(β-α)]ꎬ结合式(1)ꎬ可得δ=Δdtanα+Δdsinα1-n2sin2α+nΔdsin2αtanα(3)由干涉理论可知ꎬ当δ为波长的λ整数倍时ꎬ出现干涉明纹ꎻ当δ为半波长的奇数倍时ꎬ出现干涉暗纹ꎬ所以当三角形容器横向移动Δd的距离ꎬ相应冒出(或缩入)的条纹为Δkꎬ则有Δdtanα+Δdsinα1-n2sin2α+nΔdsin2αtanα=Δkλ(4)由式(4)可以求出液体折射率表达式为:n=Δkλ2Δdtanα+1-Δkλ2Δdæèçöø÷2(5)式中Δkλ2Δdæèçöø÷2的数量级为10-3ꎬ远小于1ꎬ可以忽略不计ꎬ所以式(5)可以简化为:n=Δkλ2Δdtanα+1(6)2㊀实验数据及处理为了验证本文所提出的实验方案ꎬ我们分别对去离子水㊁无水乙醇和橄榄油的折射率进行了测量ꎬ采用的激光光源波长λ为632.8nmꎬ三角形容器的顶角α为10ʎꎮ在干涉仪的观察屏上调节出清晰的干涉条纹ꎬ如图3所示ꎬ转动微调手轮缓慢改变P的横向位置ꎬ每冒出或缩入50个圆环记录一次读数ꎬ共记录十组数据ꎮ图3㊀干涉圆环按照上述步骤对去离子水的折射率进行测量ꎬ数据如表1所示ꎬ根据式(6)ꎬ若要计算出折射率ꎬ需要计算Δk/Δdꎬ用Excel软件对k和d的测量结果进行线性最小二乘法拟合ꎬ结果如图4所示ꎬ可得Δk/Δd=178.51mm-1ꎬ代入式(6)可得水的折射率为:n=1.3203ꎬn标=1.3330ꎬ计算可得相对百分误差为:0.95%ꎮ表1㊀水的折射率测量数据序号条纹移动数目kP的位置读数d/mm序号条纹移动数目kP的位置读数d/mm10160.315906250158.90203250160.028807300158.621413100159.740208350158.353804150159.472909400158.061625200159.1878210450157.79682图4㊀水的k与d的线性回归直线对无水乙醇的折射率进行测量ꎬ数据如表2所示ꎮ表2㊀无水乙醇的折射率测量数据序号条纹移动数目kP的位置读数d/mm序号条纹移动数目kP的位置读数d/mm10157.059716250155.73405250156.791387300155.480453100156.539568350155.235504150156.272939400154.972125200156.0116210450154.70227用Excel软件对k和d的测量结果进行线性最小二乘法拟合ꎬ结果如图4所示ꎬ可得Δk/Δd=44利用迈克尔逊干涉仪测量液体的折射率191.28mm-1ꎬ代入式(6)可得无水乙醇的折射率为:n=1.3432ꎬn标=1.3611(20ħ)ꎬ计算可得相对百分误差为:1.32%ꎮ图5㊀无水乙醇k与d的线性回归直线表3㊀橄榄油的折射率测量数据序号条纹移动数目kP的位置读数d/mm序号条纹移动数目kP的位置读数d/mm10166.280006250165.28869250166.082057300165.083123100165.883108350164.883804150165.681649400164.681725200165.4834810450164.48328对橄榄油的折射率进行测量ꎬ数据如表3所示ꎮ图6㊀橄榄油k与d的线性回归直线用Excel软件对k和d的测量结果进行线性最小二乘法拟合ꎬ结果如图6所示ꎬ可得Δk/Δd=250.30mm-1ꎬ代入式(6)可得橄榄油的折射率为:n=1.4491ꎬn标=1.4763ꎬ计算可得相对百分误差为:1.84%ꎮ本实验测试结果相对于标准值存在一定的误差ꎬ经分析误差产生的原因主要有三个:(1)三角形容器的一个面与G1的反射光线不严格垂直ꎬ导致光路中的Δd与实际值存在误差ꎻ(2)量角器测量容器的顶角时产生误差ꎻ(3)三角形容器为手工粘接制作ꎬ测量中存在仪器误差ꎮ3㊀结㊀论本文提出了一种测试液体折射率的方法ꎬ将待测液体注入三角形容器ꎬ横向调节容器位置以改变液体在光路中的光程ꎬ进而计算液体折射率ꎬ用该方法测得的液体折射率与标准值相差较小ꎬ操作简单ꎬ对各种透明液体都能进行测量ꎬ也可拓展到测试透明凝胶类介质的折射率ꎮ参考文献:[1]㊀辛督强ꎬ朱民ꎬ解延雷ꎬ等.测量液体折射率的几种方法[J].大学物理ꎬ2007(1):34 ̄37.[2]㊀李素文ꎬ岳巾英ꎬ祝元源ꎬ等.基于等倾干涉原理测液体折射率[J].长春工程学院学报(自然科学版)ꎬ2017ꎬ18(4):118 ̄120.[3]㊀Shyamsingh.Measuringtherefractiveindexofaliquidusingalaser[J].PhysicsEducationꎬ2002(3):152 ̄153.[4]㊀SHYAMS.Diffractionmethodmeasuresrefractiveindicesofliquids[J].PhysicsEducationꎬ2004(3):235.[5]㊀邢曼男ꎬ白然ꎬ普小云.精确测量微量液体折射率的新方法[J].光学精密工程ꎬ2008ꎬ16(7):1196 ̄1202.[6]㊀NemotoS.Measurementoftherefractiveindexofliquidusinglaserbeamdisplacement[J].AppliedOpticsꎬ1992(31):6690 ̄6694.[7]㊀姚启钧.光学教程.高等教育出版社[M].2014.[8]㊀杭乐斌ꎬ李雪梅.迈克尔逊干涉仪测量空气折射率实验中最佳间隔条纹数的探讨[J].大学物理实验ꎬ2017ꎬ30(5):70 ̄73.MeasurementofLiquidRefractiveIndexbyMichelsonInterferometerDUDengrongꎬLIYan∗ꎬSHANGChenglinꎬDANGXinzhiꎬWANGHongtao(ChinaUniversityofMiningandTechnologyꎬJiangsuXuzhou211116)Abstract:AmovabletriangularcontainerwithliquidwasaddedtotheexperimentalopticalpathoftheMichel ̄soninterferometer.Theopticalpathofthebeaminthemediumcanbechangedbymovingthetriangularcon ̄tainerꎬandthechangeofopticalpathwaspositivelycorrelatedwiththethicknessofthetrianglecontainerin ̄sertedintheopticalpath.Theslopeandtherefractiveindexofliquidcanbecalculatedbyfittingthemeasureddatawiththeleastsquaremethod.Keywords:Michelsoninterferometerꎻtriangularcontainerꎻliquidꎻrefractiveindex54利用迈克尔逊干涉仪测量液体的折射率。
迈克尔逊干涉仪测玻璃折射率

用迈克尔逊干涉仪测透明玻璃片折射率总体设计方案思路本实验用迈克尔逊干涉仪,利用等厚干涉图样和已知玻璃片厚度用间接法测出玻璃的折射率。
实验目的1.掌握迈克尔逊干涉仪的工作原理和结构,学会它的调整方法和技巧;2.学会用迈克尔逊干涉仪测透明玻璃片折射率。
实验仪器迈克尔逊干涉仪、NeHe 激光器、汞光灯、白光光源、毛玻璃、扩束镜、千分尺等。
实验原理1. 迈克尔逊干涉仪的光路迈克尔逊干涉仪有多种多样的形式,其基本光路如图1所示。
从光源S发出的一束光,在分束镜A的半反射面M上被分成光强近似相等的反射光束1和透射光束2。
反射光束1射出A后投向反射镜2M,反射回来再穿过A;光束2经过补偿板B投向反射镜1M,反射回来再通过B,在半反射面M上反射。
于是,这两束相干光在空间相遇并产生干涉,通过望远镜或人眼可以观察到干涉条纹。
补偿板B的材料和厚度都和分束镜A相同,并且与分束镜A平行放置,其作用是为了补偿反射光束1因在A中往返两次所多走的光程,使干涉仪对不同波长的光可以同时满足等光程的要求。
2. 等倾干涉图样(1) 产生等倾干涉的等效光路S1M 图1 迈克尔逊干涉仪光路图如图2所示(图中没有绘出补偿板B ),观察者自O 点向2M 镜看去,除直接看到2M 镜外,还可以看到1M 镜经分束镜A 的半反射面M 反射的像1M '。
这样,在观察者看来,两相干光束好象是由同一束光分别经1M '和2M 反射而来的。
因此从光学上来说,迈克尔逊干涉仪所产生的干涉花样与1M '、2M 间的空气层所产生的干涉是一样的,在讨论干涉条纹的形成时,只要考虑1M '、2M 两个面和它们之间的空气层就可以了。
所以说,迈克尔逊干涉仪的干涉情况即干涉图像是由光源以及1M '、2M 和观察屏的相对配置来决定的。
(2) 等倾干涉图样的形成与单色光波长的测量当1M 镜垂直于2M 镜时,1M '与2M 相互平行,相距为d 。
大学物理设计性实验 用迈克尔逊干涉仪测量玻璃折射率

评分:大学物理实验设计性实验实验报告实验题目:用迈克尔逊干涉仪测量玻璃的折射率班级:姓名:学号:指导教师:《用迈克尔逊干涉仪测玻璃片折射率》实验提要实验课题及任务《用迈克尔逊干涉仪测玻璃片厚度》实验课题任务是:根据玻璃的折射率比空气大,当玻璃片加到一个光路中时,必产生一光程差l ∆,这个光程差会造成中央条纹会发生位移的现象,根据这一特定的光学现象和给定的仪器,设计出实验方案,测定玻璃的折射率。
学生根据自己所学的知识,并在图书馆或互联网上查找资料,设计出《用迈克尔逊干涉仪测玻璃片的折射率》的整体方案,内容包括:写出实验原理和理论计算公式,研究测量方法,写出实验内容和步骤,然后根据自己设计的方案,进行实验操作,记录数据,做好数据处理,得出实验结果,按撰写科学论文的要求写出完整的实验报告。
设计要求⑴ 通过查找资料,并到实验室了解所用仪器的实物以及阅读仪器使用说明书,了解仪器的使用方法,找出所要测量的物理量,并推导出计算公式,在此基础上写出该实验的实验原理。
⑵ 选择实验的测量仪器,设计出实验方法和实验步骤,要具有可操作性。
⑶ 测量5组数据,测量玻璃的折射率n 。
⑷ 应该用什么方法处理数据,说明原因。
⑸ 实验结果用标准形式表达,即用不确定度来表征测量结果的可信赖程度。
有关提示若用白光作光源,在一般情况下,不出现干涉条纹。
进一步分析还可看出,在2M 、1'M 两面相交时,交线上0=d ,但是由于1、2两束光在半反射膜面上的反射情况不同,引起不同的附加光程差,故各种波长的光在交线附近可能有不同的光程差。
因此,用白光作光源时,在2M 、1'M ,两面的交线附近的中央条纹可能是白色明条纹,也可能是暗条纹。
在它的两旁还大致对称的有几条彩色的直线条纹,稍远就看不到干涉条纹了。
调出白光干涉条纹,此时1M 镜位置读数为1z 将待测玻璃片插入有1M 镜的臂中,再次调出白光干涉条纹,这时1M 镜位置读数为2z ,评分参考(10分)⑴ 正确写出实验原理和计算公式,2分。
用迈克尔逊干涉仪测定透明介质的折射率

用迈克尔逊干涉仪测定透明介质的折射率物理与电信工程学院物理学二班李智鹏(20082301134) 林晓青 周丹斐 赖燕仪【摘要】:迈克逊尔干涉仪,作为近代精密测量光学仪器之一,被广泛用于科学研究和检测技术等领域。
利用迈克耳逊干涉仪,能以极高的精度测量长度的微小变化及其与此相关的物理量。
本文就通过利用等倾干涉法成功测定了透明玻璃的折射率。
实验证明,这种方法是有效而且方便的,由于迈克尔逊干涉仪的特性,该实验比其他方法测定玻璃的折射率更加简便。
【关键词】:迈克尔逊干涉仪 等倾干涉法 折射率Abstract :Michelson Interferometer is widely used scientific research and testing technology as one of the Precision measuring optical instruments. The main idea of this paper is to measure the Refractive index of Transparent Glass, and to give an interesting asymptotic formula for it. Key words: Michelson Interferometer Refractive index Pour interfering method【正文】: 1、 实验装置1.1实验仪器:迈克逊尔干涉仪、薄玻璃片、螺旋测微器1.2迈克尔孙干涉仪的调整迈克尔孙干涉仪是一种精密、贵重的光学测量仪器,因此必须在熟读讲义,弄清结构,弄懂操作要点后,才能动手调节、使用。
(1)对照讲义,眼看实物弄清本仪器的结构原理和各个旋钮的作用。
(2)水平调节:调节底脚螺丝6(见图5,最好用水准仪放在迈克尔孙干涉仪平台上)。
(3)读数系统调节:① 粗调:将“手柄”转向下面“开”的部位(使微动蜗轮与主轴蜗杆离开),顺时针(或反时针)转动手轮1,使主尺(标尺)刻度指标于30mm 左右(因为M 2镜至G 1的距离大约是32mm 左右,这样便于以后观察等厚干涉条纹用)。
迈克尔逊干涉仪的使用实验报告

迈克尔逊干涉仪的使用实验报告英文回答:Introduction。
The Michelson interferometer is a device that uses interference to measure distances, refractive indices, and other optical properties of materials. It was invented by Albert A. Michelson in 1881, and it has since become one of the most important tools in optics.Principle of Operation。
The Michelson interferometer operates on the principle of interference. When two waves of light with the same wavelength are superimposed, they will interfere with each other, producing a pattern of bright and dark bands. The spacing of these bands is determined by the wavelength of the light and the angle between the two waves.In a Michelson interferometer, light from a single source is split into two beams by a beam splitter. The two beams are then reflected by mirrors and recombined at the beam splitter. The path length of one of the beams is varied by moving one of the mirrors. This causes the interference pattern to shift, and the amount of shift can be used to measure the distance moved by the mirror.Applications。
利用迈克耳逊干涉仪测气体折射率实验报告

利用迈克耳逊干涉仪测气体折射率实验报
告
实验目的:
通过利用迈克耳逊干涉仪测量气体折射率,了解气体对光的折射现象,并掌握实验方法和数据处理技巧。
实验原理:
迈克耳逊干涉仪是一种利用干涉现象来测量光波长和折射率的仪器。
当光波通过气体时,会发生折射现象,导致光程差的变化,从而影响干涉条纹的位置,通过测量干涉条纹的位移,可以计算出气体的折射率。
实验步骤:
1. 将迈克耳逊干涉仪放置在稳定的平台上,调整好光源和反射镜的位置。
2. 将待测气体装入干涉仪的测量室内,确保气体均匀分布。
3. 调整干涉仪,使得观察到清晰的干涉条纹。
4. 记录气体的压强和温度,并测量干涉条纹的位移。
5. 根据实验数据计算气体的折射率。
实验数据处理:
根据实验测得的干涉条纹位移和气体的压强、温度,利用适当
的公式计算出气体的折射率。
同时,需考虑气体的折射率随压强和
温度的变化而变化的影响。
实验结果:
根据实验测得的数据和数据处理,得出了气体的折射率,并与
已知数据进行对比和分析。
实验结论:
通过本次实验,成功利用迈克耳逊干涉仪测量了气体的折射率,并得出了相应的结论。
同时,也发现了一些实验中可能存在的误差
和改进的地方。
总结:
本次实验通过利用迈克耳逊干涉仪测量气体折射率,加深了对气体折射现象的理解,掌握了实验方法和数据处理技巧,为今后的实验和研究打下了基础。
迈克尔逊干涉仪测量液体的折射率及仪器调节方法

第1期1998年1月 光学技术OP T ICA L T ECHNO L OG YN o.1Jan.1998迈克尔逊干涉仪测量液体的折射率及仪器调节方法袁剑辉 周烈生 赵福利 董 雅(中山大学物理系,广州510275)摘 要:本文介绍了用迈克逊干涉仪测量液体折射率的方法,原理简单。
在干涉仪导轨上平放一方形玻璃容器,内装待测液体,动镜铅垂地浸没在液体中。
通过测出动镜在液体内的移动量及其相应的干涉条纹变化数,就能计算液体的折射率,有较高的测量精度。
本文详细分析了干涉仪上分光板的反射光通过空气、玻璃、液体,由反射镜反射后出现的多个反射光点,只有通过对这些反射光点的调节,才能得出干涉条纹并符合计算公式的要求。
关键词:迈克逊干涉仪,液体,折射率,反射光点。
Measurement of Liquid Refractive Index with Michelson Interferometer and Regulation of the InstrumentYuan Jianhui Zhou Lisheng Zhao Fuli Dong Ya(Depart ment of Phy sics,Zho ng sha n U niver sity,Guangzhou510275) Abstract:T he metho d o f measur ing liquid r efr act ive index with M ichelso n int erfer omet er has been intr oduced.On the track o f inter fer ometer w e lay a cuboid co nt ainer filled w ith liquid to be measur ed and t he mov able mirr or w as dipped in lig uid ver tically.By measuring the displacement of t he mov able mir ro r and t he num ber of the fr ing es chang ed,can we calculate the r efractive index of the liquid,It give a compar ativ e high pr ecision.W e have analysed sev eral r eflected bright spots w hich caused by air,liq-uid and g lass.O nly by reg ulating t hose r eflected spots,can w e g ot inter ference fr inges and make the calculatio n satisfied.Keywords:M ichelso n interfer om eter,liquid,r efra ct ive index,r eflected bright spot. 一、引 言迈克尔逊干涉仪是一种较为精密的测量仪器,不少文献都有介绍用它测量气体、固体折射率的方法。
迈克尔逊干涉仪测透明介质的折射率

课例研究飞花四溅的瞬间,孩子的思维已进入心灵深处。
自动生成精彩的课堂,从来都是预设的升华。
1、游戏导入,激发兴趣。
在游戏中明确数的个数,为新课中加数的交换和结合后的组数铺垫,有效地分解了难点。
2、学生是学习的主人,教师引导恰当。
本节课是练习课,先完成一组10以内的数连加,体会运用加法交换律与结合律简算。
然后完成一组1~100的自然数连加,学生先说算法,再计算分享,在分享中思辨,体会省略的部分及结合的组数,有效地突破了重难点。
3、知识链接,开拓学生视野,提高学习数学的兴趣,增强学生学习数学的信心。
4、注重学生解题规范的训练,注重学生说理的过程,培养学生的思维能力。
当然也有不足,导入游戏部分用时太长,导致拓展练习没能全班交流,让学生感受解题方法的多样化。
迈克尔逊干涉仪测透明介质的折射率■曾 吉 (贵州师范大学 物理与电子科学学院 550025)【摘 要】 实验利用光的干涉测量透明介质折射率,在迈克尔逊干涉仪的光路中插入透明介质调出的干涉条纹与未插入时调出的干涉条纹相同,平面反射镜M 1位置的改变量与待测透明介质使光产生的光程差相等,再用光程的定义公式即可求出测透明介质的折射率。
为了结果更加精确,实验采用白光、钠光作为实验光源对其结果进行比较,得出结果符合:波长小折射率大,波长大折射率小。
【关键词】 迈克尔逊干涉仪;透明介质;折射率【中图分类号】 G642.3 【文献标识码】 A 【文章编号】 2095-3089(2018)09-0229-01引言:迈克尔逊干涉仪是光学实验中常用的仪器。
在大学物理光学实验中,测透明介质折射率常用掠入射法。
采用迈克尔逊干涉仪来测量透明介质(玻璃片)的折射率,是一种不常见的测量方法。
在本次实验中,首先用白光作为光源测量透明介质的折射率,白光为光源的干涉实验中,用的是日常台灯发出的光,其主要成分是汞。
再将光源换为钠光来测量透明介质的折射率。
本次实验采用迈克尔逊干涉仪测量透明介质(玻璃片)的折射率是利用不放介质时产生的光程差与放介质时产生的光程差相等,也就是都要调出清晰的干涉圆环。
利用迈克尔逊干涉仪测量折射率的实验方法

利用迈克尔逊干涉仪测量折射率的实验方法迈克尔逊干涉仪是一种常用的实验设备,可以用于测量光的干涉现象。
利用迈克尔逊干涉仪测量折射率的实验方法是一项重要的实验内容,下面将介绍该实验的步骤和操作方法。
实验目的:通过利用迈克尔逊干涉仪测量折射率,掌握干涉实验的基本原理和技巧,加深对光学性质的理解,并验证折射率与光的波长和介质特性的关系。
实验器材:1. 迈克尔逊干涉仪2. 单色光源3. 介质样品4. 光屏5. 准直器6. 透镜7. 平行板8. 三角架等实验辅助设备实验步骤:1. 实验前准备:a. 将迈克尔逊干涉仪放置在光学实验台上,并确认仪器调整好水平。
b. 使用准直器调整光源的方向和强度,使光线垂直照射到迈克尔逊干涉仪上。
2. 调整光程差:a. 在干涉仪的一个光路上放置一个透镜和一个平行板,调整透镜的位置,使得透镜后的光束尽可能平行。
b. 调整平行板的位置和倾斜角度,使得在光束经过透镜后,反射光和透射光的干涉条纹清晰可见。
c. 调整透镜和平行板的位置和角度,使得反射光和透射光的干涉条纹平行且亮暗交替明显。
d. 记录下反射光和透射光的干涉条纹数,用于后续折射率的计算。
3. 测量折射率:a. 将待测样品放置在干涉仪的另一个光路中,调整样品的位置,使得通过样品后的光束尽可能平行。
b. 调整样品的位置和角度,使得反射光和透射光的干涉条纹清晰可见。
c. 调整样品的位置和角度,使得反射光和透射光的干涉条纹平行且亮暗交替明显。
d. 记录下反射光和透射光的干涉条纹数。
e. 根据所测得的干涉条纹数,利用光的波长和上一步中记录的参考干涉条纹数计算出样品的折射率。
4. 数据处理:a. 根据实验中测得的数据,计算出测试样品的折射率。
b. 对于多个样品,可进行比较分析,验证折射率与介质特性之间的关系。
5. 实验注意事项:a. 实验时要保持实验环境的稳定,避免外界震动和干扰。
b. 进行测量时要仔细观察干涉条纹,确保测量的准确性。
c. 实验结束后,要注意将设备归位,并保持实验台的整洁。
用迈克尔逊干涉仪测量气体折射率

实验 用迈克耳孙干涉仪测量气体折射率[引言]大气中随着海拔高度的上升,空气变得稀薄,大气折射率n 随气体压强的降低而减小,使得光线在大气中传播发生弯曲,对航海中天顶角的测定有一定影响。
而天顶角的测定对船舶的定位起着重要作用,因此,了解气体折射率与大气压强之间的关系具有重要的实际意义。
迈克耳孙干涉仪中的两束相干光各有一段光路在空间中是分开的,人们可以在其中一支光路上放进被研究对象而不影响另一支光路,这就给它的应用带来极大的方便。
实际上常用它来测物质的折射率、厚度和气压等一切可以转化为光程变化的物理量。
[实验目的]1.了解迈克耳孙干涉仪的结构、工作原理和使用方法。
2.学习一种测量气体折射率的方法。
[实验器材]氦氖激光器,扩束镜,迈克尔孙干涉仪,气室(带充气装置),数字气压计。
[实验原理]在迈克耳孙干涉仪光路的一个测量光路上放置一个气室,干涉图样随气室里气体气压的变化而变化:当气压增加时,干涉圆环从中心 “吐出”;反之,干涉圆环向中心“吞入”。
通过研究气体压强变化与条纹移动的关系可以得到气体折射率。
当气室内气体压强改变p ∆时,使气体折射率改变n ∆,光程差改变n L ∆2,从而引起干涉条纹移动N 个,则有λN n L =∆2,于是有:LN n 2λ=∆ (1) 其中,L 为气室长度,λ是光的真空波长。
通常,在温度处于15~30C范围时,空气折射率可用下式计算:9,10003671.018793.2)1(-⨯+=-tpn p t (2)式中温度t 的单位为C ,气压p 的单位为Pa 。
在温度一定下,气体折射率p n )1(-与气压p成正比。
因此有:=∆∆=-pnp n 1常数 整理得: p p nn ∆∆+=1将式(1)代入上式得: ppL N n ∆+=21λ (3)式(3)给出了在气压p 时的空气折射率。
[实验内容]1.调节迈克耳孙干涉仪,使其在接收屏上观察到干涉条纹。
2.向气室中充气加压,记录气压值1p 。
高二物理计划利用迈克耳孙干涉仪测量光的折射率

高二物理计划利用迈克耳孙干涉仪测量光的折射率利用迈克耳孙干涉仪测量光的折射率是物理实验中常见的实验方法,旨在通过干涉现象来确定光在不同介质中的折射率。
本文将介绍迈克耳孙干涉仪的原理、实验操作步骤及实验结果分析。
一、迈克耳孙干涉仪原理迈克耳孙干涉仪是一种基于干涉现象测量光的相位差的仪器。
它由一束单色光、两个平行的玻璃片和一片厚度可调的透明物体组成。
当光线从一个介质射向另一个介质时,会发生折射现象,导致相位差。
利用迈克耳孙干涉仪可以通过调整其中一块玻璃片与透明物体之间的距离,观察干涉条纹的变化,从而计算得到光的折射率。
二、实验操作步骤1. 准备实验所需材料:迈克耳孙干涉仪、光源、标定物体(如气泡级液体)、调节装置等。
2. 将迈克耳孙干涉仪放置在稳定的台架上,并调整其水平。
3. 打开光源,将光线通过准直系统射入迈克耳孙干涉仪,保证光线严格平行。
4. 调节仪器,使两个平行的玻璃片与透明物体之间保持恒定的距离。
5. 观察干涉条纹,在每个位置记录干涉条纹的变化情况。
6. 将实验数据整理并计算得到光的折射率。
三、实验结果分析通过实验测量得到的干涉条纹数据,我们可以计算得到光的折射率。
具体计算方法如下:1. 假设光线从空气射入玻璃片,经透明物体后再进入玻璃片。
利用光的反射和折射规律,可以得到光的相位差与透明物体与玻璃片之间的光程差之间的关系式。
2. 将实验中测得的光程差代入上述关系式,可以计算得到相位差的数值。
3. 折射率的计算公式为n=λ/(2d*sinθ),其中λ为光的波长,d为透明物体与玻璃片之间的距离,θ为光线与透明物体的夹角。
4. 代入实验测得的数据,可以计算得到光的折射率。
在实验过程中,需要注意以下几点:1. 确保实验环境稳定,避免外界光线的干扰。
2. 在调整仪器时,要小心操作,防止误伤仪器和自己。
3. 在记录实验数据时,要准确记录每个位置的干涉条纹情况。
总结:利用迈克耳孙干涉仪测量光的折射率是一种常用的物理实验方法。
用迈克尔逊干涉仪测量斜劈的折射率

用迈克尔逊干涉仪测量斜劈的折射率学生姓名:于佳指导教师:卫栋内容提要: 光波干涉现象的长度量纲在纳米数量级,利用干涉方法可以极大地提高测量结果的精确程度。
使用迈克尔逊干涉仪进行如激光波长、小数量级长度、折射率等物理量的测量时,最基本的是对迈克尔逊干涉仪产生的干涉图像的变化进行测量。
但由于其非常高的精确度使得其敏捷度也相当高,同时其抗干扰能力差,这就给仪器的使用和操作提出了很高要求。
本实验对迈克尔逊干涉仪进行了改进,并在改进后的基础上对斜劈的折射率进行了测量。
关键词: 迈克尔逊干涉仪折射率光程干涉光楔Refractive index measurement by using a Michelson interferometer Name:Yu.Jia Supervisor:Wei.DongAbstract:It is in a high level of the precision, because the length of the optical wave is in the level of nm. When we measure the wavelength of the laser, punily length, refractive index by using Michelson interferometer, the variety of the quantitative phase of the interference pattern is the basic of the measurement. But in this way, the precision let the interferometer has a high degree of the delicacy. That will need a strict requisition to the operation and using of it, and it’s hard to avoid disturbance. Our experiment is in order to find a way to improve the interferometer and measure the refractive index by this Michelson interferometer we improved.Keywords:Michelson interferometer, refractive index, optical path, interference, optic wedge1. 简介:关于光的波动性,干涉现象一直是一个热门的话题。
迈克耳逊干涉仪的调整和使用及测空气折射率.

迈克耳逊干涉仪的调整和使用及测空气折射率迈克耳逊干涉仪是1883年迈克耳逊设计制成的用分振幅法产生双光束干涉的仪器,它是一种可以进行精密测量的,有着广泛应用的干涉仪。
迈克耳逊干涉仪的基本结构是许多干涉仪的基础。
目前根据迈克耳逊的基本原理研制的各种精密仪器广泛用于生产和科研领域。
由于创制了精密的光学仪器和利用这些仪器所完成的光谱学和基本度量学研究,迈克耳逊于1907年获诺贝尔物理学奖。
1.实验目的(1) 了解迈克耳逊干涉仪的构造、原理,掌握调节方法。
(2) 学会用迈克耳逊干涉仪测定光波波长。
(3)学习一种测量气体折射率的方法2. 实验仪器迈克耳逊干涉仪,He-Ne 激光器,气室组建,数字气压计。
3. 实验原理迈克耳逊干涉仪的光路图如图6-24所示。
M 1和M 2是经精细磨光的平面反射镜,分别安装在相互垂直的两臂上,M 2是固定的(称为定镜),M 1可通过精密丝杆的带动,在导轨上移动(称为动镜)。
在两臂相交处装有与两臂成45˚角的平行平面玻璃板G 1,G 1后表面镀有一层半透明半反射的薄银膜(A ),这一层薄银膜(A )将入射光分成两束光强近似相等的反射光(1)和透射光(2)。
因此,G 1称为分束板。
另外,G 2为补偿板。
G 2与G 1是两块材料(折射率)和厚度均相同的平行平面的玻璃板,并且G 2和G 1彼此间严格平行。
G 2的作用是使光束(2)在玻璃中的光程与光束(1)在玻璃中的光程相同。
从光源发出的光束,被分束板G 1后表面镀有一层薄银膜(A )分成两束光强近似相等的反射光(1)和透射光(2)。
光束(1)射到M 1上被反射回来,再透过G 1到达观测者E 处(或接收屏);光束(2)透过G 2射到M 2上被反射回来,再透过 G 2后又经A 反射而到达观测者E 处(或接收屏)。
这两条光线是相干光,相遇发生干涉。
因此,在E 处可观测到干涉条纹。
图6-24中的M’2是定镜M 2相对半反半透膜(A )反射而形成的虚像。
用迈克尔逊干涉仪测空气的折射率

用迈克尔逊干涉仪测空气的折射率PB05210153 蒋琪实验原理迈克尔逊干涉仪是一种典型的分振幅干涉仪,本实验要求自己组装迈氏干涉仪,M 1和M 2之间的距离每改变半个波长,其中心就“生出”或“消失”一个圆环。
两平面反射镜之间的距离增大时,中心就“吐出”一个个圆环。
反之,距离减小时中心就“吞进”一个个圆环,同时条纹之间的间隔(即条纹的稀疏)也发生变化。
由公式λn h 21=∆可知,只要读出干涉仪中M 1移动的距离∆h 和数出相应吞进(或吐出)的环数就可求得波长。
本实验中是通过改变气压从而改变光程差,通过数中心吐出圆环的数目来测量光程差。
光程差△d = n ( P +△P )·s 一 n ( P )·s =( N ( P +△P )一N ( P ))·入, 而折射率随压强的变化率P P n P P n P n ∆-∆+=∆∆)()(, 由上面可以推得lP N P n 2λ⋅∆∆=∆∆,记录数据算出⎪⎭⎫ ⎝⎛∆∆P N ,就可以算出n p ∆∆, 由()()p p n p n p n •∆∆+==0就可以推算P 下的空气折射率。
实验仪器光学平台;HeNe 激光;调整架,35x35mm ;平面镜,30x30mm ;磁性基座;分束器50:50;透镜,f=+20mm ;白屏;玻璃容器,手持气压泵,组合夹具,T 形连接,适配器,软管,硅管。
实验内容1.装置建立和调整:注:下文括号中的数字表示的坐标仅适用于开始阶段的粗调。
a)参照图1摆放元件,推荐的光束高度130mm 。
b)使用调整镜M1(1,8)和镜M2(1,4)调整光路时,光线要沿着平台上y=4的直线延伸。
c) 最初不需要放置分束器BS,光线直射M3(9,4), 被M3反射后的光线能够和M2上初始光点重合。
然后放置分束器在(6,4),BS 的镀膜面朝向镜M2,这样一部分的光仍然可无阻碍的到达M3,另外的光射到M4(6,1)。
迈克尔逊干涉测玻璃片折射率

迈克尔逊干涉仪迈克尔逊干涉仪是用分振幅的方法实现干涉的光学仪器,设计十分巧妙。
迈克尔逊发明它后,最初用于著名的以太漂移实验。
后来,他又首次用之于系统研究光谱的精细结构以及将镉(Cd)的谱线的波长与国际米原器进行比较。
迈克尔逊干涉仪在基本结构和设计思想上给科学工作以重要启迪,为后人研制各种干涉仪打下了基础。
迈克尔逊干涉仪在物理学中有十分广泛的应用,如用于研究光源的时间相干性,测量气体、固体的折射率和进行微小长度测量等。
【实验目的】1. 了解迈克尔逊干涉仪的结构、原理和调节方法;2. 了解光的干涉现象及其形成条件;3. 观察等倾干涉条纹,测量氦氖激光器的波长;4. 学习一种测量气体折射率的方法。
【实验仪器】迈克尔逊干涉仪,He-Ne 激光器及电源,扩束镜(凸透镜),挡光片一片,升降台,玻璃板,白光光源【实验原理】一、 一、 一般介绍迈克尔逊干涉仪的原理见图1。
光源S 发出的光束射到分光板1G 上,1G 的后面镀有半透膜,光束在半透膜上反射和透射,被分成光强接近相等、并相互垂直的两束光。
这两束光分别射向两平面镜1M 和2M ,经它们反射后又汇聚于分光板1G ,再射到光屏E 处,从而得到清晰的干涉条纹。
平面镜1M 可在光线1的方向上平行移动。
补偿板2G 的材料和厚度与1G 相同,也平行于1G ,起着补偿光线2的光程的作用。
如果没有2G ,则光线1会三次经过玻璃板,而光线2只能一次经过玻璃板。
2G 的存在使得光线1、2由于经过玻璃板而导致的光程相等,从而使光线1、2的光程差只由其它几何路程决定。
由于本实验采用相干性很好的激光,故补偿板2G 并不重要。
但如果使用的是单色性不好、相干性较差的光,如纳光灯或汞灯,甚至白炽灯,2G 就成为必需了。
这是因为波长不同的光折射率不同,由分光板1G 的厚度所导致的光程就会各不一样。
补偿板2G 能同时满足这些不同波长的光所需的不同光程补偿。
图1 干涉原理图用迈克尔逊干涉仪可以观察各种类型的条纹,见表1。
用迈克尔逊干涉仪测玻璃折射率

用迈克尔逊干涉仪测玻璃折射率实验目的:利用迈克尔逊干涉仪测量玻璃的折射率。
实验仪器:迈克尔逊干涉仪、汞光灯、氦氖激光灯,千分尺,待测玻璃。
实验原理:本实验主要利用白光干涉条纹在光程差e=0的位置时,接收屏出现白色条纹这一现象(或是利用激光在e=0时,接收屏上出现平行等距直条纹),和放置玻璃片后的调出白色条纹时活动镜位置的改变,得出由待测玻璃所引起的光程差的改变量,从而计算得出待测玻璃的折射率n。
1白光干涉条纹(彩色条纹)因为干涉条纹的明暗决定光程差与波长的关系。
用白光源,在e=0处,所有的波长其光程差均为0,故中央条纹为白色。
在中央白条纹两旁,由于不同波长在不同出得到加强,在两旁有十几条对称分布的彩色条纹。
e再大时,因对各种不同波长的光其满足暗纹情况也不同,所产生的干涉花纹,明暗条纹互相重叠,结果显不出条纹来。
用白光可以判断出中央明纹,即在e=0时,白光会出现中央明纹,以此判断e何处为0。
2等厚干涉的变化在观察等倾干涉的基础上,继续增大或减小光程差,使e=0(即在转动微动轮时,使M1镜背离或接近G1镜,并使M1与G1镜的距离逐渐等于M2,G1镜之间的距离),这时可以看到等倾干涉条纹的圆圈由大变小,并变疏,条纹慢慢变直,直至接收屏视图内只能看到1-2个条纹。
然后轻微调节拉簧螺钉1,使M2’与M1间有一个小的角度,这时视场中出现平行的等距条纹,这便是等厚干涉条纹。
若用He-Ne激光器作光源调节迈克尔逊干涉仪,在e=0时,出现等厚干涉,可判断e在何处等于0。
3迈克尔逊干涉仪的干涉原理及对本实验分析(1)迈克尔逊干涉仪原理如图,在图中S为光源,G1为半镀银板(使照在其上的光线既能反射又能折射又能透射,而这两部分的强度又大致相等),又称分光板。
M1,M2为平面反射镜。
光源S发出的光束,射向G1板在半镀银面上分成两束光:光束受半镀银面反射折向M2镜。
由于G1与M1、M2均成45°角,所以两束都垂直射到M1和M2,经反射后按原路返回射向观察者A(或接受屏),相遇发生干涉。
教案-调整和使用迈克尔逊干涉仪以及用迈克尔逊干涉仪测空气折射率
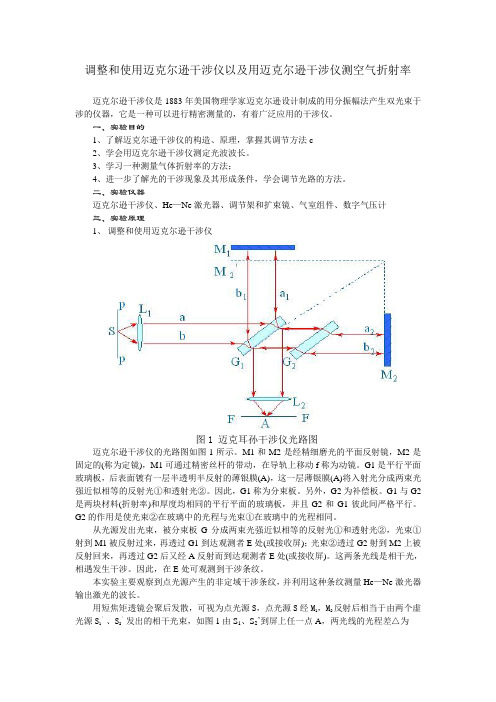
调整和使用迈克尔逊干涉仪以及用迈克尔逊干涉仪测空气折射率迈克尔逊干涉仪是1883年美国物理学家迈克尔逊设计制成的用分振幅法产生双光束于涉的仪器,它是一种可以进行精密测量的,有着广泛应用的干涉仪。
一、实验目的1、了解迈克尔逊干涉仪的构造、原理,掌握其调节方法c2、学会用迈克尔逊干涉仪测定光波波长。
3、学习一种测量气体折射率的方法;4、进一步了解光的干涉现象及其形成条件,学会调节光路的方法。
二、实验仪器迈克尔逊干涉仪、He—Ne激光器、调节架和扩束镜、气室组件、数字气压计三、实验原理1、调整和使用迈克尔逊干涉仪图1 迈克耳孙干涉仪光路图迈克尔逊干涉仪的光路图如图1所示。
M1和M2是经精细磨光的平面反射镜,M2是固定的(称为定镜),M1可通过精密丝杆的带动,在导轨上移动f称为动镜。
G1是平行平面玻璃板,后表面镀有一层半透明半反射的薄银膜(A),这一层薄银膜(A)将入射光分成两束光强近似相等的反射光①和透射光②。
因此,G1称为分束板。
另外,G2为补偿板。
G1与G2是两块材料(折射率)和厚度均相同的平行平面的玻璃板,并且G2和G1彼此间严格平行。
G2的作用是使光束②在玻璃中的光程与光束①在玻璃中的光程相同。
从光源发出光束,被分束板G分成两束光强近似相等的反射光①和透射光②,光束①射到M1被反射过来,再透过G1到达观测者E处(或接收屏);光束②透过G2射到M2上被反射回来,再透过G2后又经A反射而到达观测者E处(或接收屏)。
这两条光线是相干光,相遇发生干涉。
因此,在E处可观测到干涉条纹。
本实验主要观察到点光源产生的非定域干涉条纹,并利用这种条纹测量He—Ne激光器输出激光的波长。
用短焦矩透镜会聚后发散,可视为点光源S,点光源S经M1,M2反射后相当于由两个虚光源S1′、S2′发出的相干光束,如图1由S1、S2’到屏上任一点A,两光线的光程差△为212'1)S A S A ∆=-== 因为L>>d ,2222222222144144[()]]28()Ld d Ld d dR L R L R L L R ++∆≈⨯-⨯≈++++ 由图中三角关系:22cos (1sin )dd Lθθ∆=+ 略去二级无穷小项,可得2cos d θ∆= 明纹:2cos d k θλ∆==暗纹:2cos (21)2d k λθ∆==+当d 变化2Nλ时,(N 整数)即2d N λ∆=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用迈克尔逊干涉仪测量斜劈的折射率学生姓名:于佳指导教师:卫栋内容提要: 光波干涉现象的长度量纲在纳米数量级,利用干涉方法可以极大地提高测量结果的精确程度。
使用迈克尔逊干涉仪进行如激光波长、小数量级长度、折射率等物理量的测量时,最基本的是对迈克尔逊干涉仪产生的干涉图像的变化进行测量。
但由于其非常高的精确度使得其敏捷度也相当高,同时其抗干扰能力差,这就给仪器的使用和操作提出了很高要求。
本实验对迈克尔逊干涉仪进行了改进,并在改进后的基础上对斜劈的折射率进行了测量。
关键词: 迈克尔逊干涉仪折射率光程干涉光楔Refractive index measurement by using a Michelson interferometer Name:Yu.Jia Supervisor:Wei.DongAbstract:It is in a high level of the precision, because the length of the optical wave is in the level of nm. When we measure the wavelength of the laser, punily length, refractive index by using Michelson interferometer, the variety of the quantitative phase of the interference pattern is the basic of the measurement. But in this way, the precision let the interferometer has a high degree of the delicacy. That will need a strict requisition to the operation and using of it, and it’s hard to avoid disturbance. Our experiment is in order to find a way to improve the interferometer and measure the refractive index by this Michelson interferometer we improved.Keywords:Michelson interferometer, refractive index, optical path, interference, optic wedge1. 简介:关于光的波动性,干涉现象一直是一个热门的话题。
当我们讨论干涉问题的时候,引入了光程这一物理量,当两相干光束的光程差是波长的某一倍数的时候,就能决定光束在这一位置是造成的光波的振动加强还是减弱,这一原理可以被想象为两个机械波在空间相遇的情况:当其中一个波的波峰到达某一位置时,另一个波的波谷正好到达,我们可以想象两振动幅度简单的加成以使振动幅度抵消,而相反的情况却能使振动幅度加大,当这样的振动点在空间分布是保持在固定位置的时候,就能形成明显的振动加强区域和振动削弱区域,也就是干涉现象。
而这一振动差别又是由于两个振动源到空间某一位置的距离的不同所导致的(假使振动的波长是一样的),也就是所谓的光程差。
同时光程差也可以被理解为他在这一点处振动相位变化的相位差造成的结果。
虽然这一说法在量子力学中并不是很严格,但是就本实验来说,这种解释方法在我们对光的波动性和干涉现象,以及干涉仪原理的解释是很方便且易于理解的。
迈克尔逊干涉仪作为历史上经典的干涉实验仪器,以其简单的构造,极高的精确度等优点,被人们广泛的用与实验和教学活动中。
但是由于其长度的测量精度都保持在纳米数量级上,这样在得到高精确度的同时也带来了高灵敏度,也正是这个高灵敏度给仪器的操作和实验环境提出了较高的要求,例如至少需要一个抗震的光学平台,需要良好干涉性能的激光器,以及需要沿一个方向移动平面镜以减小螺距差等。
那么怎样在不降低其精确程度的同时,改善迈克尔逊干涉仪,使他能够被应用用于更广泛的环境,以及提升他的可操作性,就是一个值得讨论的问题。
本实验通过对迈克尔逊干涉仪基本构造的简单改进,人为的降低其灵敏度,并以此为突破口来解决迈克尔逊干涉仪的操作性的问题。
最后用改进后仪器测量折射率,并与厂家所给定折射率进行比较,来说明改进后仪器的精确度。
2.迈克尔逊干涉仪:2.1.干涉现象:这里以两同频简谐标量波的合成为例说明光波光强合成与相位差的关系。
即干涉现象的理论分析,把这两列波的震动情况用复振幅表示为:⎪⎩⎪⎨⎧==212211~~ϕϕi i e A U e A U二者合成为:212121~~~ϕϕi i e A e A U U U +=+= 其强度为振幅的模:()ϕϕϕϕϕ∆++=+++==+--cos 2~~2121212121*2121I I I I e e A A A A U U I i i i i 其中21ϕϕϕ-=∆是两光波的相位差。
可见,两光波的光强并不是简单的迭加,而是取决于最后一项中的三角函数因子。
而这个因子的值,又是由两光波的相位差来决定的。
这就是为什么两光波发生干涉的理论原因。
通过简单的分析可以看出:()⎩⎨⎧+=∆=∆干涉减弱。
干涉加强;,12k ,2πϕπϕk 又由相位差和波长的关系:πϕλ2∆=∆L 得到: ()⎪⎩⎪⎨⎧+=∆=∆干涉减弱。
干涉加强;,12k 21,λλL k L 这就是干涉现象光强分布与相位差或光程差的关系,是本实验最基本的原理。
2.2.等厚干涉与等倾干涉:对于这两种分振幅干涉,大家已经很清楚了。
但这里还是要比较一下其异同点,并引入到干涉仪的改进中来。
等厚干涉的情况如图3:当从点光源发出的一束光投射到两种透明介质的分界面上的时候,他被分为两束光,其中一束被反射回来,另一束透射过去,也就是所谓的分振幅。
折射光在介质下表面反射后又从上表面透射出来,回到原来的介质中,与被上表面直接反射的光束汇合,在两光束交叠区域里,每点都有一对相干光线在此相交。
只要光源Q 发出的光束足够宽,相干光束的交叠区域可以从薄膜表面附近一直延伸到无穷远处,此时在广阔的区域里到处都有干涉条纹。
我们通常利用透镜使光束聚焦于一个物平面以便于观察。
这相当于迈克尔逊干涉仪其中一个平面镜相对于另一个有所倾斜的情况。
Qi1A Pi1CB i2h A BCR D PK M N i1i2n1n2图3:等厚干涉原理图 图4:等倾干涉原理图等倾干涉的情况如图4:这样的干涉条纹是薄膜上彼此平行的反射光线产生的,他对应于迈克尔逊干涉仪两平面镜正交的情况。
同样,当光束到达薄膜上表面的时候,被分振幅为反射透射两束光线,其透射光经过下表面反射,从新回到上表面,透射后与反射光平行的出射,并不汇合,这种情况可以被认为是聚焦与无穷远处,可以利用透镜使得干涉条纹聚焦与透镜焦平面上。
现在,我们对这两种干涉的理论进行分析。
对于等倾干涉,如图4,根据无相等光程性,,于是:。
作CD垂直于AR,因为:,。
于是我们得到:其中,分别为介质两边的折射率。
,分别是入射角和折射角。
那么,即:,所以:作薄膜上下表面的垂线KR,再过K点做AR和RC的垂线。
明显:=AM=MD=CN,所以。
又因为,所以:这是等倾干涉的情况,可以看出,当入射角相同的时候,他所产生的光程差是一致的,那么其震动叠加的情况也是一样的。
这样围绕光源,就能形成一个同心圆环型的干涉图样。
而其条纹间隔为:这也就是为什么,条纹边缘处间隔变小的原因。
在这种情况所对应的迈克尔逊干涉仪光路中,可以认为光源是被扩束后的平面光,其入射角为0,且由于其等厚部分是一个平面镜与另一个的像所成的空气薄膜,其n=1。
那么其光程差变为:这就是为什么移动其中一个平面镜就能改变光程的原因。
但正如前面所说,这样的改变必须是微小的,以使图像的改变可以被观测到,这显然给仪器操作带来了不变。
对于等厚干涉的情况分析如下:如图3,很明显的可以看出光程差为,在A 和P点很近的情况下,可以认为:,所以:,又由于:。
所以:。
在这里,公式虽然和上面的 一样。
但是这里的可变量是h,这就是等厚的原理。
同样认为入射为垂直的平面光波。
有:,而当光程差是波长的整数倍的时候,其干涉是加强的。
即干涉图样中的亮条纹。
那么有:,根据倾角与高度差的关系可以得到条纹间隔:。
可见条纹的间距是与入射光波波长,介质折射率和倾角有关的。
当这个四个物理量中已经知道其中三个的时候,就能通过以上公式计算出另一物理量。
我们正是利用了这一性质,来进行迈克尔逊干涉仪的改进。
从等倾干涉的情况来看,要进行物理量的测量,就要对其中一个平面镜沿垂直于光路的方向移动,来改变光程差,以得到周期变化的干涉相位变化。
而从公式中可以看出,当移动的h “很大”的时候,对于λN L =∆来说,其导致的N 是非常多的。
这就是为什么要使用微调齿轮来调节h的原因。
但从等厚来看,同样是空气薄膜,并且光线垂直入射,那么同样,但是。
这里,我们并不调节平面镜的前后移动,而是调节倾角。
由公式可以看出,当倾角变化到很小的范围的时候,x ∆即条纹间隔很大,利于人们观察,同时对公式进行变化,使之成为:λα=∆=∆h x ,并由此看出,当倾角减小到一个很小的程度,并且保持不变的时候,就可以使得条纹的间隔比纳米大很多数量级,同时其纵向变化仍然保持在波长的数量级上。
那么,我们就能得出一种改进方法就是,在x 方向上进行手动调节,来使h 方向被动的变化。
这样,利用很小的倾角使x 方向可以较大范围的变动,并且与此同时能保证h 在纳米的数量级上呈周期的变化。
对于等厚和等倾干涉,他们有着明显的共同点:首先,两者都是分振幅干涉,并且正好对应了迈克尔逊干涉仪的两种情况。
这就使得我们可以通过简单的调节就能在两干涉情况中进行转换,这就为我们改进迈克尔逊干涉仪提供了方便。
其次,两者干涉光源的要求是一样的,就是高相干性点光源或被扩束的扩展平面光源。
这样我们改进后的仪器同样就可以被利用到这样的光源中去。
这两种干涉的不同点恰恰为我们改进仪器指明了方向,很明显,这两种干涉发生在不同的光学薄膜上,一种是平行平面薄膜,另一种是非平行平面薄膜,而对于这种薄膜,当其倾角很小的情况下,就是我们所熟知的光楔了。
其次,在后面的分析中可以看到,等厚干涉其干涉图样的变化是基于其薄膜厚度的,而等倾干涉却是基于入射光的倾角的。
最后,等倾干涉条纹是不等距同心圆环,而等厚干涉条纹是和厚度有关的等间距竖直条纹,有较高的对比度。
那么利用以上不同点就是我们改进迈克尔逊干涉仪的基础。
2.3.迈克尔逊干涉仪基本原理:基于这一原理,研发了很多的干涉仪器,他们被广泛的应用于实验室的测量以及研究。
